最全正余弦定理题型归纳
正余弦定理知识点及题型归纳

正余弦定理是三角学中的重要知识点,用于解决与三角形相关的问题。
下面是对正余弦定理的知识点及题型归纳:一、正弦定理1. 定义:在任意三角形ABC中,设角A、B、C所对应的边分别为a、b、c,那么有sinA/a = sinB/b = sinC/c。
2. 性质:-等式两边同时乘以任意非零常数,等式仍然成立;-等式两边同时除以相同的角,等式仍然成立;-等式两边同时取反函数,等式仍然成立。
3. 应用:-已知三个角的度数,求边长;-已知两个边的长度,求第三个边的长度;-已知一个角和一条边的长度,求另外两个角的度数;-已知一个角和两条边的长度,求第三个角的度数。
二、余弦定理1. 定义:在任意三角形ABC中,设角A、B、C所对应的边分别为a、b、c,那么有cosA = (b ²+ c²- a²) / (2bc)。
2. 性质:-等式两边同时乘以任意非零常数,等式仍然成立;-等式两边同时除以相同的角,等式仍然成立;-等式两边同时取反函数,等式仍然成立。
3. 应用:-已知三个角的度数,求边长;-已知两个边的长度,求第三个边的长度;-已知一个角和一条边的长度,求另外两个角的度数;-已知一个角和两条边的长度,求第三个角的度数。
三、题型归纳1. 已知三个角的度数,求边长:-根据正弦定理或余弦定理,将已知的角度代入公式中,求解边长;-如果已知的是弧度制的角度,需要将其转换为角度制。
2. 已知两个边的长度,求第三个边的长度:-根据正弦定理或余弦定理,将已知的两个边的长度代入公式中,求解第三个边的长度;-如果已知的是弧度制的角度,需要将其转换为角度制。
3. 已知一个角和一条边的长度,求另外两个角的度数:-根据正弦定理或余弦定理,将已知的角度和边的长度代入公式中,求解另外两个角的度数;-如果已知的是弧度制的角度,需要将其转换为角度制。
4. 已知一个角和两条边的长度,求第三个角的度数:-根据正弦定理或余弦定理,将已知的角度和两条边的长度代入公式中,求解第三个角的度数;-如果已知的是弧度制的角度,需要将其转换为角度制。
正余弦定理题型总结(全)汇总

平面向量题型归纳(全)题型一:共线定理应用例一:平面向量→→b a ,共线的充要条件是( )A.→→b a ,方向相 同 B. →→b a ,两向量中至少有一个为零向量 C.存在,R ∈λ→→=a b λ D 存在不全为零的实数0,,2121=+→→b a λλλλ变式一:对于非零向量→→b a ,,“→→→=+0b a ”是“→→b a //”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件变式二:设→→b a ,是两个非零向量( )A.若→→→→=+b a b a _则→→⊥b a B. 若→→⊥b a ,则→→→→=+b a b a _ C. 若→→→→=+ba b a _,则存在实数λ,使得→→=a b λ D 若存在实数λ,使得→→=a b λ,则→→→→=+ba b a _例二:设两个非零向量→→21e e 与,不共线,(1)如果三点共线;求证:D C A e e e e e e ,,,28,23,212121--=+=-= (2)如果三点共线,且D C A e k e e e e e ,,,2,32,212121-=-=+=求实数k 的值。
变式一:设→→21e e 与两个不共线向量,,2,3,2212121e e CD e e CB e k e AB -=+=+=若三点A,B,D 共线,求实数k 的值。
变式二:已知向量→→b a ,,且,27,25,2b a CD b a BC b a AB +=+-=+=则一定共线的三点是( ) A.A,B,D B.A,B,C C.B,C,D D.A,C,D题型二:线段定比分点的向量形式在向量线性表示中的应用例一:设P 是三角形ABC 所在平面内的一点,,2+=则( )A. +=B. +=C. +=D. ++=变式一:已知O 是三角形ABC 所在平面内一点,D 为BC 边的中点,且OC OB OA ++=20,那么( )A. OD A =0B. OD A 20=C. OD A 30=D. OD A =02变式二:在平行四边形ABCD 中a AB =,b AD =,NC AN 3=,M 为BC 的中点,则=MN ( 用b a ,表示)例二:在三角形ABC 中,=,=,若点D 满足2=,则=( )A. ,3132+B. ,3235-C. ,3132-D. ,3231+变式一:(高考题) 在三角形ABC 中,点D 在边AB 上,CD 平分角ACB,a CB =,b CA =21==,则=( )A. ,3231+B. ,3132+C. ,5453+ D. ,5354+变式二:设D,E,F 分别是三角形ABC 的边BC,CA,AB 上的点,且,2=,2=,2=则++,与( )A.反向平行B. 同向平行C.互相垂直D.既不平行也不垂直变式三:在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的中点,若μλ+=,其,,R ∈μλ则μλ+=变式四:在平行四边形ABCD 中,AC 与BD 交于点O,E 是线段OD 的中点,AE 的延长线与CD 交于点F ,若,a AC =,b BD =则=( )A.,2141+ B. ,3132+ C. ,4121+ D. ,3231+题型三:三点共线定理及其应用例一:点P 在AB 上,求证:μλ+=且μλ+=1(,,R ∈μλ)变式:在三角形ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB 、AC 于不同的两点M 和N,若,m =,n =则m+n=例二:在平行四边形ABCD 中,E,F 分别是BC,CD 的中点,DE 与AF 交于点H,设,=,=则= A.,5452- B. ,5452+ C. ,5452+- D. ,5452--变式:在三角形ABC 中,点M 是BC 的中点,点N 是边AC 上一点且AN=2NC,AM 与BN 相交于点P,若,λ=求λ的值。
专题4.5正弦定理和余弦定理的应用(2021年高考数学一轮复习专题)

专题 正弦定理和余弦定理的应用一、题型全归纳题型一 利用正弦、余弦定理解三角形【题型要点】(1)正、余弦定理的选用①利用正弦定理可解决两类三角形问题:一是已知两角和一角的对边,求其他边或角;二是已知两边和一边的对角,求其他边或角;①利用余弦定理可解决两类三角形问题:一是已知两边和它们的夹角,求其他边或角;二是已知三边求角.由于这两种情形下的三角形是唯一确定的,所以其解也是唯一的. (2)三角形解的个数的判断已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.【例1】 (2020·广西五市联考)在①ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =1,b =3,A =30°,B 为锐角,那么A ①B ①C 为( ) A .1①1①3 B .1①2①3 C .1①3①2D .1①4①1【解析】:法一:由正弦定理a sin A =b sin B ,得sin B =b sin A a =32.因为B 为锐角,所以B =60°,则C =90°,故A ①B ①C =1①2①3,选B.法二:由a 2=b 2+c 2-2bc cos A ,得c 2-3c +2=0,解得c =1或c =2.当c =1时,①ABC 为等腰三角形,B =120°,与已知矛盾,当c =2时,a <b <c ,则A <B <C ,排除选项A ,C ,D ,故选B.【例2】(2019·高考全国卷Ⅰ)①ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知a sin A -b sin B =4c sin C ,cos A =-14,则bc =( )A .6B .5C .4D .3【解析】选A.由题意及正弦定理得,b 2-a 2=-4c 2,所以由余弦定理得,cos A =b 2+c 2-a 22bc =-3c 22bc =-14,得bc=6.故选A. 【例3】(2020·济南市学习质量评估)已知①ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且2c +a =2b cos A . ①求角B 的大小;①若a =5,c =3,边AC 的中点为D ,求BD 的长.【解析】 (1)选A.由题意及正弦定理得,b 2-a 2=-4c 2,所以由余弦定理得,cos A =b 2+c 2-a 22bc =-3c 22bc=-14,得bc=6.故选A. (2)①由2c +a =2b cos A 及正弦定理,得2sin C +sin A =2sin B cos A , 又sin C =sin(A +B )=sin A cos B +cos A sin B ,所以2sin A cos B +sin A =0, 因为sin A ≠0,所以cos B =-12,因为0<B <π,所以B =2π3.①由余弦定理得b 2=a 2+c 2-2a ·c cos①ABC =52+32+5×3=49,所以b =7,所以AD =72.因为cos①BAC =b 2+c 2-a 22bc =49+9-252×7×3=1114,所以BD 2=AB 2+AD 2-2·AB ·AD cos①BAC =9+494-2×3×72×1114=194,所以BD =192.题型二 判断三角形的形状【题型要点】判定三角形形状的两种常用途径【易错提醒】“角化边”后要注意用因式分解、配方等方法得出边的相应关系;“边化角”后要注意用三角恒等变换公式、三角形内角和定理及诱导公式推出角的关系.【例1】(2020·蓉城名校第一次联考)设①ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B=a sin A ,则①ABC 的形状为( ) A .直角三角形 B .锐角三角形 C .钝角三角形D .不确定【解析】 (1)法一:因为b cos C +c cos B =b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =2a 22a =a ,所以a sin A =a 即sin A =1,故A =π2,因此①ABC 是直角三角形.法二:因为b cos C +c cos B =a sin A ,所以sin B cos C +sin C cos B =sin 2 A ,即sin(B +C )=sin 2 A ,所以sin A =sin 2 A ,故sin A =1,即A =π2,因此①ABC 是直角三角形.【例2】在①ABC 中,若c -a cos B =(2a -b )cos A ,则①ABC 的形状为 .【解析】因为c -a cos B =(2a -b )cos A ,所以由正弦定理得sin C -sin A cos B =2sin A cos A -sin B cos A , 所以sin(A +B )-sin A cos B =2sin A cos A -sin B cos A ,故cos A (sin B -sin A )=0, 所以cos A =0或sin A =sin B ,A =π2或A =B ,故①ABC 为等腰或直角三角形.题型三 与三角形面积有关的问题命题角度一 计算三角形的面积【题型要点】1.①ABC 的面积公式(1)S ①ABC =12a ·h (h 表示边a 上的高).(2)S ①ABC =12ab sin C =12ac sin B =12bc sin A .(3)S ①ABC =12r (a +b +c )(r 为内切圆半径).2.求三角形面积的方法(1)若三角形中已知一个角(角的大小或该角的正、余弦值),结合题意求解这个角的两边或该角的两边之积,代入公式求面积;(2)若已知三角形的三边,可先求其中一个角的余弦值,再求其正弦值,代入公式求面积,总之,结合图形恰当选择面积公式是解题的关键.【例1】(2019·高考全国卷Ⅰ)①ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若b =6,a =2c ,B =π3,则①ABC的面积为 .【解析】 (1)法一:因为a =2c ,b =6,B =π3,所以由余弦定理b 2=a 2+c 2-2ac cos B ,得62=(2c )2+c 2-2×2c ×c cos π3,得c =23,所以a =43,所以①ABC 的面积S =12ac sin B =12×43×23×sin π3=6 3.法二:因为a =2c ,b =6,B =π3,所以由余弦定理b 2=a 2+c 2-2ac cos B ,得62=(2c )2+c 2-2×2c ×c cos π3,得c =23,所以a =43,所以a 2=b 2+c 2,所以A =π2,所以①ABC 的面积S =12×23×6=6 3.【例2】(2020·福建五校第二次联考)在①ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,已知a 2+b 2-c 2=3ab ,且ac sin B =23sin C ,则①ABC 的面积为 .【解析】因为a 2+b 2-c 2=3ab ,所以由余弦定理得cos C =a 2+b 2-c 22ab =3ab 2ab =32,又0<C <π,所以C =π6.因为ac sin B =23sin C ,所以结合正弦定理可得abc =23c ,所以ab =2 3.故S ①ABC =12ab sin C=12×23sin π6=32. 命题角度二 已知三角形的面积解三角形【题型要点】已知三角形面积求边、角的方法(1)若求角,就寻求这个角的两边的关系,利用面积公式列方程求解; (2)若求边,就寻求与该边(或两边)有关联的角,利用面积公式列方程求解.【提示】正弦定理、余弦定理与三角函数性质的综合应用中,要注意三角函数公式的工具性作用. 【例3】(2020·湖南五市十校共同体联考改编)已知a ,b ,c 分别为①ABC 的内角A ,B ,C 的对边,(3b -a )cos C =c cos A ,c 是a ,b 的等比中项,且①ABC 的面积为32,则ab = ,a +b = . 【解析】 因为(3b -a )cos C =c cos A ,所以利用正弦定理可得3sin B cos C =sin A cos C +sin C cos A =sin(A +C )=sinB .又因为sin B ≠0,所以cos C =13,则C 为锐角,所以sin C =223.由①ABC 的面积为32,可得12ab sin C =32,所以ab =9.由c 是a ,b 的等比中项可得c 2=ab ,由余弦定理可得c 2=a 2+b 2-2ab cos C ,所以(a +b )2=113ab =33,所以a +b =33.【例4】(2020·长沙市统一模拟考试)已知①ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a sin(A +B )=c sin B +C2.(1)求A ;(2)若①ABC 的面积为3,周长为8,求a .【解析】:(1)由题设得a sin C =c cos A 2,由正弦定理得sin A sin C =sin C cos A 2,所以sin A =cos A2,所以2sin A 2cos A 2=cos A 2,所以sin A 2=12,所以A =60°.(2)由题设得12bc sin A =3,从而bc =4.由余弦定理a 2=b 2+c 2-2bc cos A ,得a 2=(b +c )2-12.又a +b +c =8,所以a 2=(8-a )2-12,解得a =134.题型四 三角形面积或周长的最值(范围)问题【题型要点】求有关三角形面积或周长的最值(范围)问题在解决求有关三角形面积或周长的最值(范围)问题时,一般将其转化为一个角的一个三角函数,利用三角函数的有界性求解,或利用余弦定理转化为边的关系,再应用基本不等式求解.【例1】(2020·福州市质量检测)①ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若角A ,B ,C 成等差数列,且b =32. (1)求①ABC 外接圆的直径;(2)求a +c 的取值范围.【解析】:(1)因为角A ,B ,C 成等差数列,所以2B =A +C ,又因为A +B +C =π,所以B =π3.根据正弦定理得,①ABC 的外接圆直径2R =bsin B =32sin π3=1.(2)法一:由B =π3,知A +C =2π3,可得0<A <2π3.由(1)知①ABC 的外接圆直径为1,根据正弦定理得,a sin A =b sin B =c sin C=1, 所以a +c =sin A +sin C =sin A +sin ⎪⎭⎫⎝⎛A -32π=3⎪⎪⎭⎫ ⎝⎛+A A cos 21sin 23=3sin ⎪⎭⎫ ⎝⎛+6πA . 因为0<A <2π3,所以π6<A +π6<5π6.所以12<sin ⎪⎭⎫ ⎝⎛+6πA ≤1,从而32<3sin ⎪⎭⎫ ⎝⎛+6πA ≤3,所以a +c 的取值范围是⎥⎦⎤⎝⎛323, 法二:由(1)知,B =π3,b 2=a 2+c 2-2ac cos B =(a +c )2-3ac ≥(a +c )2-322⎪⎭⎫ ⎝⎛+c a =14(a +c )2(当且仅当a =c 时,取等号),因为b =32,所以(a +c )2≤3,即a +c ≤3,又三角形两边之和大于第三边,所以32<a +c ≤3, 所以a +c 的取值范围是⎥⎦⎤⎝⎛323, 题型五 解三角形与三角函数的综合应用【题型要点】标注条件,合理建模解决三角函数的应用问题,无论是实际应用问题还是三角函数与解三角形相结合的问题,关键是准确找出题中的条件并在三角形中进行准确标注,然后根据条件和所求建立相应的数学模型,转化为可利用正弦定理或余弦定理解决的问题.【例1】 (2020·湖南省五市十校联考)已知向量m =(cos x ,sin x ),n =(cos x ,3cos x ),x ①R ,设函数f (x )=m ·n +12.(1)求函数f (x )的解析式及单调递增区间;(2)设a ,b ,c 分别为①ABC 的内角A ,B ,C 的对边,若f (A )=2,b +c =22,①ABC 的面积为12,求a 的值.【解析】 (1)由题意知,f (x )=cos 2x +3sin x cos x +12=sin ⎪⎭⎫ ⎝⎛+62πx +1.令2x +π6①⎥⎦⎤⎢⎣⎡++ππππk k 22,22-,k ①Z ,解得x ①⎥⎦⎤⎢⎣⎡++ππππk k 6,3-,k ①Z ,所以函数f (x )的单调递增区间为⎥⎦⎤⎢⎣⎡++ππππk k 6,3-,k ①Z .(2)因为f (A )=sin ⎪⎭⎫⎝⎛+62πA +1=2,所以sin ⎪⎭⎫ ⎝⎛+62πA =1. 因为0<A <π,所以π6<2A +π6<13π6,所以2A +π6=π2,即A =π6.由①ABC 的面积S =12bc sin A =12,得bc =2,又b +c =22,所以a 2=b 2+c 2-2bc cos A =(b +c )2-2bc (1+cos A ),解得a =3-1. 【例2】①ABC 中的内角A ,B ,C 的对边分别为a ,b ,c ,已知b =2a -2c cos B . (1)求角C 的大小;(2)求3cos A +sin ⎪⎭⎫⎝⎛+3πB 的最大值,并求出取得最大值时角A ,B 的值. 【解析】:(1)法一:在①ABC 中,由正弦定理可知sin B =2sin A -2sin C cos B ,又A +B +C =π,则sin A =sin(π-(B +C ))=sin(B +C ),于是有sin B =2sin(B +C )-2sin C cos B =2sin B cos C +2cos B sin C -2sin C cos B ,整理得sin B =2sin B cos C ,又sin B ≠0,则cos C =12,因为0<C <π,则C =π3.法二:由题可得b =2a -2c ·a 2+c 2-b 22ac ,整理得a 2+b 2-c 2=ab ,即cos C =12,因为0<C <π,则C =π3.(2)由(1)知C =π3,则B +π3=π-A ,3cos A +sin ⎪⎭⎫⎝⎛+3πB =3cos A +sin(π-A )=3cos A +sin A =2sin ⎪⎭⎫⎝⎛+3πA , 因为A =2π3-B ,所以0<A <2π3,所以π3<A +π3<π,故当A =π6时,2sin ⎪⎭⎫ ⎝⎛+3πA 的最大值为2,此时B =π2.二、高效训练突破 一、选择题1.(2020·广西桂林阳朔三校调研)在①ABC 中,a ①b ①c =3①5①7,那么①ABC 是( ) A .直角三角形 B .钝角三角形 C .锐角三角形D .非钝角三角形【解析】:因为a ①b ①c =3①5①7,所以可设a =3t ,b =5t ,c =7t ,由余弦定理可得cos C =9t 2+25t 2-49t 22×3t ×5t =-12,所以C =120°,①ABC 是钝角三角形,故选B. 2.(2020·河北衡水中学三调)在①ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且b 2+c 2=a 2+bc ,若sin B sin C =sin 2A ,则①ABC 的形状是( ) A .等腰三角形 B .直角三角形 C .等边三角形D .等腰直角三角形【解析】:在①ABC 中,因为b 2+c 2=a 2+bc ,所以cos A =b 2+c 2-a 22bc =bc 2bc =12,因为A ①(0,π),所以A =π3,因为sin B sin C =sin 2A ,所以bc =a 2,代入b 2+c 2=a 2+bc ,得(b -c )2=0,解得b =c ,所以①ABC 的形状是等边三角形,故选C.3.(2020·河南南阳四校联考)在①ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若b =8,c =3,A =60°,则此三角形外接圆的半径R =( ) A.823 B.1433 C.73D .733【解析】:因为b =8,c =3,A =60°,所以a 2=b 2+c 2-2bc cos A =64+9-2×8×3×12=49,所以a =7,所以此三角形外接圆的直径2R =a sin A =732=1433,所以R =733,故选D. 4.(2020·湖南省湘东六校联考)在①ABC 中,A ,B ,C 的对边分别为a ,b ,c ,其中b 2=ac ,且sin C =2sinB ,则其最小内角的余弦值为( )A .-24 B.24 C.528D .34【解析】:由sin C =2sin B 及正弦定理,得c =2b .又b 2=ac ,所以b =2a ,所以c =2a ,所以A 为①ABC 的最小内角.由余弦定理,知cos A =b 2+c 2-a 22bc =(2a )2+(2a )2-a 22·2a ·2a=528,故选C.5.(2020·长春市质量监测(一))在①ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若b =a cos C +12c ,则角A 等于( ) A .60°B .120°C .45°D .135°【解析】:法一:由b =a cos C +12c 及正弦定理,可得sin B =sin A cos C +12sin C ,即sin(A +C )=sin A cos C+12sin C ,即sin A cos C +cos A sin C =sin A cos C +12sin C ,所以cos A sin C =12sin C ,又在①ABC 中,sin C ≠0,所以cos A =12,所以A =60°,故选A.法二:由b =a cos C +12c 及余弦定理,可得b =a ·b 2+a 2-c 22ab +12c ,即2b 2=b 2+a 2-c 2+bc ,整理得b 2+c 2-a 2=bc ,于是cos A =b 2+c 2-a 22bc =12,所以A =60°,故选A.6.(2020·河南三市联考)已知a ,b ,c 分别为①ABC 三个内角A ,B ,C 的对边,sin A ①sin B =1①3,c =2cos C =3,则①ABC 的周长为( ) A .3+3 3 B .23 C .3+2 3D .3+3【解析】:因为sin A ①sin B =1①3,所以b =3a , 由余弦定理得cos C =a 2+b 2-c 22ab =a 2+(3a )2-c 22a ×3a=32,又c =3,所以a =3,b =3,所以①ABC 的周长为3+23,故选C.7.(2020·湖南师大附中4月模拟)若①ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且b =2,c =5,①ABC的面积S =52cos A ,则a =( ) A .1 B.5 C.13D .17【解析】:因为b =2,c =5,S =52cos A =12bc sin A =5sin A ,所以sin A =12cos A . 所以sin 2A +cos 2A =14cos 2A +cos 2A =54cos 2A =1.易得cos A =255.所以a 2=b 2+c 2-2bc cos A =4+5-2×2×5×255=9-8=1,所以a =1.故选A. 8.(2020·开封市定位考试)已知①ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,①ABC 的面积为43,且2b cos A +a =2c ,a +c =8,则其周长为( ) A .10 B .12 C .8+ 3D .8+23【解析】:因为①ABC 的面积为43,所以12ac sin B =4 3.因为2b cos A +a =2c ,所以由正弦定理得2sin B cosA +sin A =2sin C ,又A +B +C =π,所以2sin B cos A +sin A =2sin A cos B +2cos A sin B ,所以sin A =2cos B ·sin A ,因为sin A ≠0,所以cos B =12,因为0<B <π,所以B =π3,所以ac =16,又a +c =8,所以a =c =4,所以①ABC 为正三角形,所以①ABC 的周长为3×4=12.故选B.9.(2020·昆明市诊断测试)在平面四边形ABCD 中,①D =90°,①BAD =120°,AD =1,AC =2,AB =3,则BC =( )A. 5B.6C.7D .22【解析】:如图,在①ACD 中,①D =90°,AD =1,AC =2,所以①CAD =60°.又①BAD =120°,所以①BAC =①BAD -①CAD =60°.在①ABC 中,由余弦定理得BC 2=AB 2+AC 2-2AB ·AC cos①BAC =7,所以BC =7.故选C.10.(2020·广州市调研测试)已知①ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,且sin 2A +sin 2B -sin 2Cc =sin A sin Ba cos B +b cos A ,若a +b =4,则c 的取值范围为( )A .(0,4)B .[2,4)C .[1,4)D .(2,4]【解析】:根据正弦定理可得sin 2A +sin 2B -sin 2C sin C =sin A sin Bsin A cos B +cos A sin B ,即sin 2A +sin 2B -sin 2C sin C =sin A sin Bsin (A +B ),由三角形内角和定理可得sin(A +B )=sin C ,所以sin 2A +sin 2B -sin 2C =sin A sin B ,再根据正弦定理可得a 2+b 2-c 2=ab .因为a +b =4,a +b ≥2ab ,所以ab ≤4,(a +b )2=16,得a 2+b 2=16-2ab ,所以16-2ab -c 2=ab ,所以16-c 2=3ab ,故16-c 2≤12,c 2≥4,c ≥2,故2≤c <4,故选B.二、填空题1.在①ABC 中,角A ,B ,C 满足sin A cos C -sin B cos C =0,则三角形的形状为 . 【解析】:由已知得cos C (sin A -sin B )=0,所以有cos C =0或sin A =sin B ,解得C =90°或A =B . 2.(2020·天津模拟)在①ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知b +c =2a ,3c sin B =4a sin C ,则cos B = .【解析】:在①ABC 中,由正弦定理b sin B =c sin C ,得b sin C =c sin B ,又由3c sin B =4a sin C ,得3b sin C =4a sinC ,即3b =4a .因为b +c =2a ,得到b =43a ,c =23a .由余弦定理可得cos B =a 2+c 2-b 22ac =a 2+49a 2-169a 22·a ·23a=-14.3.(2020·河南期末改编)在①ABC 中,B =π3,AC =3,且cos 2C -cos 2A -sin 2B =-2sin B sin C ,则C = ,BC = .【解析】:由cos 2C -cos 2A -sin 2B =-2sin B sin C ,可得1-sin 2C -(1-sin 2A )-sin 2B =-2sin B sin C ,即sin 2A -sin 2C -sin 2B =-2sin B sin C .结合正弦定理得BC 2-AB 2-AC 2=-2·AC ·AB ,所以cos A =22,A =π4,则C =π-A -B =5π12.由AC sin B =BC sin A,解得BC = 2.4.在①ABC 中,A =π4,b 2sin C =42sin B ,则①ABC 的面积为 .【解析】:因为b 2sin C =42sin B ,所以b 2c =42b ,所以bc =42,S ①ABC =12bc sin A =12×42×22=2.5.(2020·江西赣州五校协作体期中改编)在①ABC 中,A =π3,b =4,a =23,则B = ,①ABC 的面积等于 .【解析】:①ABC 中,由正弦定理得sin B =b sin A a =4×sinπ323=1.又B 为三角形的内角,所以B =π2,所以c =b 2-a 2=42-(23)2=2,所以S ①ABC =12×2×23=2 3.6.在①ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边,且B 为锐角,若sin A sin B =5c 2b ,sin B =74,S ①ABC =574,则b 的值为 .【解析】:由sin A sin B =5c 2b ①a b =5c 2b ①a =52c ,①由S ①ABC =12ac sin B =574且sin B =74得12ac =5,①联立①,①得a =5,且c =2.由sin B =74且B 为锐角知cos B =34, 由余弦定理知b 2=25+4-2×5×2×34=14,b =14.三 解答题1.(2020·兰州模拟)已知在①ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且a sin B +b cos A =0. (1)求角A 的大小;(2)若a =25,b =2,求边c 的长.【解析】:(1)因为a sin B +b cos A =0,所以sin A sin B +sin B cos A =0,即sin B (sin A +cos A )=0,由于B 为三角形的内角,所以sin A +cos A =0,所以2sin ⎪⎭⎫⎝⎛+4πA =0,而A 为三角形的内角,所以A =3π4. (2)在①ABC 中,a 2=c 2+b 2-2cb cos A ,即20=c 2+4-4c ⎪⎪⎭⎫⎝⎛22-,解得c =-42(舍去)或c =2 2. 2.在①ABC 中,角A ,B ,C 的对边分别为a ,b ,c .(1)若a =3c ,b =2,cos B =23,求c 的值;(2)若sin A a =cos B2b ,求cos B 的值.【解析】:(1)因为a =3c ,b =2,cos B =23,由余弦定理cos B =a 2+c 2-b 22ac ,得23=(3c )2+c 2-(2)22×3c ×c ,即c 2=13.所以c =33.(2)因为sin A a =cos B 2b ,由正弦定理a sin A =b sin B ,得cos B 2b =sin Bb ,所以cos B =2sin B .从而cos 2B =(2sin B )2,即cos 2B =4(1-cos 2B ),故cos 2B =45.因为sin B >0,所以cos B =2sin B >0,从而cos B =255.3.(2020·福建五校第二次联考)在①ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,且3a cos C =(2b -3c )cos A . (1)求角A 的大小;(2)若a =2,求①ABC 面积的最大值.【解析】:(1)由正弦定理可得,3sin A cos C =2sin B cos A -3sin C cos A , 从而3sin(A +C )=2sin B cos A ,即3sin B =2sin B cos A .又B 为三角形的内角,所以sin B ≠0,于是cos A =32,又A 为三角形的内角,所以A =π6. (2)由余弦定理a 2=b 2+c 2-2bc cos A ,得4=b 2+c 2-2bc ×32≥2bc -3bc , 所以bc ≤4(2+3),所以S ①ABC =12bc sin A ≤2+3,故①ABC 面积的最大值为2+ 3.4.(2020·广东佛山顺德第二次质检)在①ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,2b sin C cos A +a sin A =2c sin B .(1)证明:①ABC 为等腰三角形;(2)若D 为BC 边上的点,BD =2DC ,且①ADB =2①ACD ,a =3,求b 的值.【解析】:(1)证明:因为2b sin C cos A +a sin A =2c sin B ,所以由正弦定理得2bc cos A +a 2=2cb ,由余弦定理得2bc ·b 2+c 2-a 22bc +a 2=2bc ,化简得b 2+c 2=2bc ,所以(b -c )2=0,即b =c .故①ABC 为等腰三角形.(2)法一:由已知得BD =2,DC =1,因为①ADB =2①ACD =①ACD +①DAC , 所以①ACD =①DAC ,所以AD =CD =1.又因为cos①ADB =-cos①ADC ,所以AD 2+BD 2-AB 22AD ·BD =-AD 2+CD 2-AC 22AD ·CD ,即12+22-c 22×1×2=-12+12-b 22×1×1,得2b 2+c 2=9,由(1)可知b =c ,得b = 3.法二:由已知可得CD =13a =1,由(1)知,AB =AC ,所以①B =①C ,又因为①DAC =①ADB -①C =2①C -①C =①C =①B , 所以①CAB ①①CDA ,所以CB CA =CA CD ,即3b =b1,所以b = 3.5.(2020·重庆市学业质量调研)①ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知①ABC 的面积为32ac cos B ,且sin A =3sin C .(1)求角B 的大小;(2)若c =2,AC 的中点为D ,求BD 的长.【解析】:(1)因为S ①ABC =12ac sin B =32ac cos B ,所以tan B = 3.又0<B <π,所以B =π3.(2)sin A =3sin C ,由正弦定理得,a =3c ,所以a =6.由余弦定理得,b 2=62+22-2×2×6×cos 60°=28,所以b =27. 所以cos A =b 2+c 2-a 22bc =(27)2+22-622×2×27=-714.因为D 是AC 的中点,所以AD =7.所以BD 2=AB 2+AD 2-2AB ·AD cos A =22+(7)2-2×2×7×⎪⎪⎭⎫⎝⎛147-=13.所以BD =13.。
正余弦定理及解三角形整理(有答案)

正余弦定理考点梳理:1.直角三角形中各元素间的关系:如图,在△ABC 中, C = 90°, AB =c , AC = b , BC = a 。
( 1)三边之间的关系: a 2+ b 2= c 2。
(勾股定理) A ( 2)锐角之间的关系: A + B = 90°; c( 3)边角之间的关系: (锐角三角函数定义)bsin A =cos B = a ,cos A = sin B = b , tan A = a。
CBcc b2.2.斜三角形中各元素间的关系:a如图 6-29 ,在△ ABC 中, A 、 B 、 C 为其内角, a 、 b 、c 分别表示 A 、 B 、C 的对边。
( 1)三角形内角和: A +B + C = _____( 2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。
ab c2R 。
( R 为外接圆半径)sin A sin Bsin C3.正弦定理:a= b = c =2R 的常见变形:sin A sin B sin C(1)sinA ∶ sinB ∶ sinC = a ∶ b ∶ c ;(2)a= b c= a + b + csin=sin A + sin = 2R ;A sinBC sinB + sin C(3) a =2R sin_ A , b = 2R sin_ B , c = 2R sin_ C ;A = aB = bC = c(4)sin2R ,sin 2R , sin 2R .1114. 三角形面积公式: S = 2ab sin C = 2bc sin A = 2ca sin B .5.余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
cos A b2c 2 a 2a 22c 22bccos A2bcba2c 2b 2余弦定理的公式:b 2 a 2 c 22accosB 或cos B .c2b2a22ba cosC2accosCb2a2c22ab6. ( 1)两类正弦定理解三角形的问题:1、已知两角和任意一边,求其他的两边及一角.2、已知两边和其中一边的对角,求其他边角. ( 2)两类余弦定理解三角形的问题:1、已知三边求三角 .2、已知两边和他们的夹角, 求第三边和其他两角 .7. 判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式 .8. 解题中利用ABC 中A B C,以及由此推得的一些基本关系式进行三角变换的运算,如: sin( A B) sin C, cos( A B) cosC, tan(A B)tan C,sin A BcosC,cosAB sinC, tanAB cotC. 2222229.解斜三角形的主要依据是:设△ ABC的三边为 a、 b、c,对应的三个角为A、 B、C。
正余弦定理知识点及高考考试题型整理学生理

正、余弦定理一、知识总结 (一)正弦定理1.正弦定理:2,sin sin sin a b cR A B C===其中R 是三角形外接圆半径. 2.变形公式:(1)化边为角:(2)化角为边:(3)(4).3、正弦定理可解决两类问题:(1)两角和任意一边,求其它两边和一角;(解唯一)(2)两边和其中一边对角,求另一边的对角,进而可求其它的边和角. (解可能不唯一)在△ABC 中,已知a 、b 和A 时,解的情况如下:a =b sin A b sin A <a <b a ≥b a >b 1.余弦定理: 2222cos a b c bc A =+-2222cos c a b ab C =+-2222cos b a c ac B =+-2.变形公式:222222222cos ,cos ,cos .222b c a a c b a b c A B C ab ac ab+-+-+-===.注:2a >22c b +⇒A 是钝角;2a =22c b +⇒A 是直角;2a <22c b +⇒A 是锐角;2sin ,2sin ,2sin ;a R A b R B c R C ===sin ,sin ,sin ;222a b cA B C R R R ===::sin :sin :sin a b c A B C =2sin sin sin sin sin sin a b c a b c RA B C A B C ++====++3.余弦定理可以解决的问题:(1)已知三边,求三个角;(解唯一)(2)已知两边和它们的夹角,求第三边和其他两个角;(解唯一):4.由余弦定理判断三角形的形状a2=b2+c2⇔A是直角⇔△ABC是直角三角形,a2>b2+c2⇔A是钝角⇔△ABC是钝角三角形,a2<b2+c⇔A是锐角/△ABC是锐角三角形。
(注意:A是锐角/ △ABC是锐角三角形,必须说明每个角都是锐角)(三) ΔABC的面积公式:(1)1() 2a aS a h h a= 表示边上的高;(2)111sin sin sin() 2224abcS ab C ac B bc A RR====为外接圆半径;(3)1()() 2S r a b c r=++为内切圆半径(四) 实际问题中的常用角1.仰角和俯角在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下文的叫俯角(如图①)2.方位角从指北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②)注:仰角、俯角、方位角的区别是:三者的参照不同。
正余弦定理知识点总结及高考考试题型

正余弦定理知识点总结及高考考试题型一、正余弦定理的概念正余弦定理,又称余正定理、角-边-角定理,是指用三角形中的一个角和与它相对的两边的长度,来表示三角形中的另外两个角与其对应的两边之间的关系的公式。
二、正余弦定理的形式对于一个三角形ABC,设三个边分别为a、b、c,对应的角分别为A、B、C,将角A所对应的边称为边a,角B所对应的边称为边b,角C所对应的边称为边c。
(1)正弦定理:$\frac{a}{\sin A}=\frac{b}{\sinB}=\frac{c}{\sin C}$(2)余弦定理:$a^2=b^2+c^2-2bc\cos A$$b^2=a^2+c^2-2ac\cos B$$c^2=a^2+b^2-2ab\cos C$三、正余弦定理的应用正余弦定理是基本的三角函数之一,它们在高中数学教育中被广泛应用。
通常在三角形的求面积过程中被使用。
考生还需能够将它们应用在其他相关的三角形求解问题中。
例如,可以用正余弦定理解决以下问题:(1)求三角形的面积。
(2)判断三角形是否为等腰三角形,是否为等边三角形。
(3)确定三角形的内角度数。
(4)求解三角形的未知边和角。
四、正余弦定理在高考考试中的出现形式正余弦定理在高考考试中经常作为解决三角形问题的关键公式。
它们常表现为单独的选择题或解答题,也可能是复合型题目的一部分。
(1)选择题样例:已知三角形ABC的边长分别为11、12、13,若$\angle C$ 的角度等于$\frac{\pi}{2}$,则$\sin A+\cos B$ 等于()A. $\frac{24}{13}$B. $\frac{22}{13}$C. $\frac{20}{13}$D. $\frac{18}{13}$(2)解答题样例:已知$\triangle ABC$,且$AB=8, AC=6,BC=10$,则$\triangle ABC$的面积是多少?解:由余弦定理,$\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{100-36-64}{2×10×8}=-\frac{1}{8}$由正弦定理,$2S=\frac{1}{2}bc\sin A=24\sin A=24\sqrt{1-\cos^2 A}=24\sqrt{1-\frac{1}{64}}=\frac{48}{\sqrt{3}}$因此,$\triangle ABC$ 的面积为$\frac{24}{\sqrt{3}}$。
正余弦定理知识点+经典题(有答案)

正余弦定理1.定理内容:(1)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即2sin sin sin a b cR A B C=== (2)余弦定理:三角形中任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的两倍。
即:2222cos a b c bc A =+- 2222cos b a c ac B =+- 2222cos c a b ab C =+-(3)面积定理:111sin sin sin 222ABC S ab C bc A ac B ∆=== 2.利用正余弦定理解三角形: (1)已知一边和两角:(2)已知两边和其中一边的对角: (3)已知两边和它们所夹的角: (4)已知三边:正弦定理1.在△ABC 中,∠A =45°,∠B =60°,a =2,则b 等于( )D .262.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( )A .4 2B .4 3C .4 63.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,A =60°,a =43,b =42,则角B 为( )A .45°或135°B .135°C .45°D .以上答案都不对 4.在△ABC 中,a ∶b ∶c =1∶5∶6,则sin A ∶sin B ∶sin C 等于( )A .1∶5∶6B .6∶5∶1C .6∶1∶5D .不确定 解析:选A.由正弦定理知sin A ∶sin B ∶sin C =a ∶b ∶c =1∶5∶6.5.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,若A =105°,B =45°,b =2,则c =( )A .1 C .26.在△ABC 中,若cos A cos B =ba ,则△ABC 是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰三角形或直角三角形 7.已知△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积为( )或 3 或328.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若c =2,b =6,B =120°,则a 等于( )B .29.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若a =1,c =3,C =π3,则A =________. 10.在△ABC 中,已知a =433,b =4,A =30°,则sin B =________.11.在△ABC 中,已知∠A =30°,∠B =120°,b =12,则a +c =________. 12.在△ABC 中,a =2b cos C ,则△ABC 的形状为________.13.在△ABC 中,A =60°,a =63,b =12,S △ABC =183,则a +b +csin A +sin B +sin C =________,c =________.14.已知△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,a =1,则a -2b +csin A -2sin B +sin C=________.15.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________. 16.在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.17.如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110°,航行半小时后船到达C 点,观测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是多少18.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =23,sin C 2cos C 2=14,sin B sin C =cos 2A2,求A 、B 及b 、c .19.(2009年高考四川卷)在△ABC 中,A 、B 为锐角,角A 、B 、C 所对应的边分别为a 、b 、c ,且cos 2A =35,sin B =1010.(1)求A +B 的值;(2)若a -b =2-1,求a ,b ,c 的值.20.△ABC 中,ab =603,sin B =sin C ,△ABC 的面积为153,求边b 的长.余弦定理1.在△ABC 中,如果BC =6,AB =4,cos B =13,那么AC 等于( )A .6B .2 6C .3 6D .46 2.在△ABC 中,a =2,b =3-1,C =30°,则c 等于( )D .2 3.在△ABC 中,a 2=b 2+c 2+3bc ,则∠A 等于( )A .60°B .45°C .120°D .150°4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则∠B 的值为( )或5π6 或2π35.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( )A .aB .bC .cD .以上均不对6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .由增加的长度决定7.已知锐角三角形ABC 中,|AB →|=4,|AC →|=1,△ABC 的面积为3,则AB →·AC →的值为( )A .2B .-2C .4D .-4 8.在△ABC 中,b =3,c =3,B =30°,则a 为( )B .2 3 或2 3 D .29.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________. 10.△ABC 中,sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10,求最大角的度数.11.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =53,则边c 的值为________. 12.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________.13.在△ABC 中,a =32,cos C =13,S △ABC =43,则b =________.14.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则AB →·BC →的值为________.15.已知△ABC 的三边长分别是a 、b 、c ,且面积S =a 2+b 2-c 24,则角C =________. 16.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________. 17.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-23x +2=0的两根,且2cos(A +B )=1,求AB 的长.18.已知△ABC 的周长为2+1,且sin A +sin B =2sin C .(1)求边AB 的长;(2)若△ABC 的面积为16sin C ,求角C 的度数.19.在△ABC 中,BC =5,AC =3,sin C =2sin A .(1)求AB 的值;(2)求sin(2A -π4)的值.20.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.正弦定理1.在△ABC 中,∠A =45°,∠B =60°,a =2,则b 等于( )D .26解析:选A.应用正弦定理得:a sin A =b sin B ,求得b =a sin Bsin A = 6. 2.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( )A .4 2B .4 3C .4 6解析:选=45°,由正弦定理得b =a sin Bsin A =4 6.3.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,A =60°,a =43,b =42,则角B 为( )A .45°或135°B .135°C .45°D .以上答案都不对解析:选C.由正弦定理a sin A =b sin B 得:sin B =b sin A a =22,又∵a >b ,∴B <60°,∴B =45°. 4.在△ABC 中,a ∶b ∶c =1∶5∶6,则sin A ∶sin B ∶sin C 等于( )A .1∶5∶6B .6∶5∶1C .6∶1∶5D .不确定解析:选A.由正弦定理知sin A ∶sin B ∶sin C =a ∶b ∶c =1∶5∶6.5.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,若A =105°,B =45°,b =2,则c =( )A .1 C .2解析:选=180°-105°-45°=30°,由b sin B =c sin C 得c =2×sin 30°sin45°=1.6.在△ABC 中,若cos A cos B =ba ,则△ABC 是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰三角形或直角三角形解析:选D.∵b a =sin B sin A ,∴cos A cos B =sin Bsin A , sin A cos A =sin B cos B ,∴sin2A =sin2B即2A =2B 或2A +2B =π,即A =B ,或A +B =π2.7.已知△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积为( )或 3 或32解析:选=AC sin B ,求出sin C =32,∵AB >AC ,∴∠C 有两解,即∠C =60°或120°,∴∠A =90°或30°.再由S △ABC =12AB ·AC sin A 可求面积.8.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若c =2,b =6,B =120°,则a 等于( )B .2解析:选D.由正弦定理得6sin120°=2sin C ,∴sin C =12.又∵C 为锐角,则C =30°,∴A =30°, △ABC 为等腰三角形,a =c = 2.9.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若a =1,c =3,C =π3,则A =________.解析:由正弦定理得:a sin A =csin C ,所以sin A =a ·sin C c =12.又∵a <c ,∴A <C =π3,∴A =π6.答案:π610.在△ABC 中,已知a =433,b =4,A =30°,则sin B =________.解析:由正弦定理得a sin A =bsin B⇒sin B =b sin A a =4×12433=32.答案:3211.在△ABC 中,已知∠A =30°,∠B =120°,b =12,则a +c =________.解析:C =180°-120°-30°=30°,∴a =c ,由a sin A =b sin B 得,a =12×sin30°sin120°=43,∴a +c =8 3. 答案:8312.在△ABC 中,a =2b cos C ,则△ABC 的形状为________.解析:由正弦定理,得a =2R ·sin A ,b =2R ·sin B , 代入式子a =2b cos C ,得 2R sin A =2·2R ·sin B ·cos C , 所以sin A =2sin B ·cos C , 即sin B ·cos C +cos B ·sin C =2sin B ·cos C , 化简,整理,得sin(B -C )=0. ∵0°<B <180°,0°<C <180°, ∴-180°<B -C <180°, ∴B -C =0°,B =C . 答案:等腰三角形13.在△ABC 中,A =60°,a =63,b =12,C=30°则a +b +csin A +sin B +sin C =________,c =________.解析:由正弦定理得a +b +c sin A +sin B +sin C=a sin A =63sin60°=12,又S △ABC =12bc sin A ,∴12×12×sin60°×c =183,∴c =6.答案:12 614.已知△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,a =1,则a -2b +csin A -2sin B +sin C=________.解析:由∠A ∶∠B ∶∠C =1∶2∶3得,∠A =30°,∠B =60°,∠C =90°,∴2R =a sin A =1sin30°=2,又∵a =2R sin A ,b =2R sin B ,c =2R sin C ,∴a -2b +c sin A -2sin B +sin C =2R sin A -2sin B +sin Csin A -2sin B +sin C =2R =2. 答案:215.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________.解析:依题意,sin C =223,S △ABC =12ab sin C =43,解得b =2 3. 答案:2316.在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.解析:∵b sin C =43×12=23且c =2, ∴c <b sin C ,∴此三角形无解. 答案:0 17.如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110°,航行半小时后船到达C 点,观测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是多少解:在△ABC 中,BC =40×12=20, ∠ABC =140°-110°=30°,∠ACB =(180°-140°)+65°=105°, 所以∠A =180°-(30°+105°)=45°, 由正弦定理得AC =BC ·sin ∠ABC sin A =20sin30°sin45°=102(km).即货轮到达C 点时,与灯塔A 的距离是10 2 km.18.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =23,sin C 2cos C 2=14,sin B sin C =cos 2A2,求A 、B 及b 、c .解:由sin C 2cos C 2=14,得sin C =12,又C ∈(0,π),所以C =π6或C =5π6.由sin B sin C =cos 2A2,得sin B sin C =12[1-cos(B +C )], 即2sin B sin C =1-cos(B +C ),即2sin B sin C +cos(B +C )=1,变形得 cos B cos C +sin B sin C =1,即cos(B -C )=1,所以B =C =π6,B =C =5π6(舍去),A =π-(B +C )=2π3.由正弦定理a sin A =b sin B =csin C ,得b =c =a sin Bsin A =23×1232=2.故A =2π3,B =π6,b =c =2.19.(2009年高考四川卷)在△ABC 中,A 、B 为锐角,角A 、B 、C 所对应的边分别为a 、b 、c ,且cos 2A =35,sin B =1010.(1)求A +B 的值;(2)若a -b =2-1,求a ,b ,c 的值. 解:(1)∵A 、B 为锐角,sin B =1010,∴cos B =1-sin 2B =31010.又cos 2A =1-2sin 2A =35,∴sin A =55,cos A =255, ∴cos(A +B )=cos A cos B -sin A sin B =255×31010-55×1010=22.又0<A +B <π,∴A +B =π4.(2)由(1)知,C =3π4,∴sin C =22.由正弦定理:a sin A =b sin B =csin C 得5a =10b =2c ,即a =2b ,c =5b .∵a -b =2-1,∴2b -b =2-1,∴b =1. ∴a =2,c = 5.20.△ABC 中,ab =603,sin B =sin C ,△ABC 的面积为153,求边b 的长.解:由S =12ab sin C 得,153=12×603×sin C ,∴sin C =12,∴∠C =30°或150°. 又sin B =sin C ,故∠B =∠C .当∠C =30°时,∠B =30°,∠A =120°.又∵ab =603,a sin A =bsin B ,∴b =215. 当∠C =150°时,∠B =150°(舍去). 故边b 的长为215.余弦定理1.在△ABC 中,如果BC =6,AB =4,cos B =13,那么AC 等于( )A .6B .26C .3 6D .46 解析:选A.由余弦定理,得 AC =AB 2+BC 2-2AB ·BC cos B= 42+62-2×4×6×13=6.2.在△ABC 中,a =2,b =3-1,C =30°,则c 等于( ) D .2解析:选B.由余弦定理,得c 2=a 2+b 2-2ab cos C =22+(3-1)2-2×2×(3-1)cos30° =2, ∴c = 2.3.在△ABC 中,a 2=b 2+c 2+3bc ,则∠A 等于( ) A .60° B .45° C .120° D .150°解析:选∠A =b 2+c 2-a 22bc =-3bc 2bc =-32, ∵0°<∠A <180°,∴∠A =150°. 4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则∠B 的值为( ) 或5π6 或2π3解析:选D.由(a 2+c 2-b 2)tan B =3ac ,联想到余弦定理,代入得cos B =a 2+c 2-b 22ac =32·1tan B =32·cos B sin B .显然∠B ≠π2,∴sin B =32.∴∠B =π3或2π3.5.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( ) A .a B .b C .c D .以上均不对解析:选·a 2+c 2-b 22ac +b ·b 2+c 2-a 22bc =2c 22c =c .6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .由增加的长度决定 解析:选A.设三边长分别为a ,b ,c 且a 2+b 2=c 2. 设增加的长度为m ,则c +m >a +m ,c +m >b +m ,又(a +m )2+(b +m )2=a 2+b 2+2(a +b )m +2m 2>c 2+2cm +m 2=(c +m )2, ∴三角形各角均为锐角,即新三角形为锐角三角形.7.已知锐角三角形ABC 中,|AB →|=4,|AC →|=1,△ABC 的面积为3,则AB →·AC →的值为( ) A .2 B .-2 C .4 D .-4解析:选△ABC =3=12|AB →|·|AC →|·sin A =12×4×1×sin A ,∴sin A =32,又∵△ABC 为锐角三角形,∴cos A =12,∴AB →·AC →=4×1×12=2.8.在△ABC 中,b =3,c =3,B =30°,则a 为( ) B .23 或2 3 D .2解析:选C.在△ABC 中,由余弦定理得b 2=a 2+c 2-2ac cos B ,即3=a 2+9-33a , ∴a 2-33a +6=0,解得a =3或2 3.9.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________.解析:∵2B =A +C ,A +B +C =π,∴B =π3. 在△ABD 中,AD =AB 2+BD 2-2AB ·BD cos B= 1+4-2×1×2×12= 3. 答案:310.△ABC 中,sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10,求最大角的度数. 解:∵sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10, ∴a ∶b ∶c =(3-1)∶(3+1)∶10.设a =(3-1)k ,b =(3+1)k ,c =10k (k >0), ∴c 边最长,即角C 最大.由余弦定理,得cos C =a 2+b 2-c 22ab =-12, 又C ∈(0°,180°),∴C =120°. 11.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =53,则边c 的值为________.解析:S =12ab sin C ,sin C =32,∴C =60°或120°.∴cos C =±12,又∵c 2=a 2+b 2-2ab cos C ,∴c 2=21或61,∴c =21或61. 答案:21或6112.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________. 解析:由正弦定理a ∶b ∶c =sin A ∶sin B ∶sin C =2∶3∶4, 设a =2k (k >0),则b =3k ,c =4k ,cos B =a 2+c 2-b 22ac =2k 2+4k 2-3k 22×2k ×4k=1116, 同理可得:cos A =78,cos C =-14,∴cos A ∶cos B ∶cos C =14∶11∶(-4). 答案:14∶11∶(-4)13.在△ABC 中,a =32,cos C =13,S △ABC =43,则b =________.解析:∵cos C =13,∴sin C =223.又S △ABC =12ab sin C =43,即12·b ·32·223=43,∴b =2 3.答案:2314.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则AB →·BC →的值为________.解析:在△ABC 中,cos B =AB 2+BC 2-AC 22AB ·BC=49+25-362×7×5=1935,∴AB →·BC →=|AB →|·|BC →|·cos(π-B )=7×5×(-1935)=-19.答案:-1915.已知△ABC 的三边长分别是a 、b 、c ,且面积S =a 2+b 2-c 24,则角C =________. 解析:12ab sin C =S =a 2+b 2-c 24=a 2+b 2-c 22ab ·ab 2 =12ab cos C ,∴sin C =cos C ,∴tan C =1,∴C =45°.答案:45°16.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________. 解析:设三边长为k -1,k ,k +1(k ≥2,k ∈N ),则⎩⎪⎨⎪⎧ k 2+k -12-k +12<0k +k -1>k +1⇒2<k <4,∴k =3,故三边长分别为2,3,4,∴最小角的余弦值为32+42-222×3×4=78.答案:7817.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-23x +2=0的两根,且2cos(A +B )=1,求AB 的长.解:∵A +B +C =π且2cos(A +B )=1,∴cos(π-C )=12,即cos C =-12.又∵a ,b 是方程x 2-23x +2=0的两根,∴a +b =23,ab =2. ∴AB 2=AC 2+BC 2-2AC ·BC ·cos C=a 2+b 2-2ab (-12)=a 2+b 2+ab =(a +b )2-ab=(23)2-2=10,∴AB =10. 18.已知△ABC 的周长为2+1,且sin A +sin B =2sin C .(1)求边AB 的长;(2)若△ABC 的面积为16sin C ,求角C 的度数.解:(1)由题意及正弦定理得 AB +BC +AC =2+1,BC +AC =2AB ,两式相减,得AB =1.(2)由△ABC 的面积12BC ·AC ·sin C =16sin C ,得BC ·AC =13,由余弦定理得cos C =AC 2+BC 2-AB 22AC ·BC=AC +BC 2-2AC ·BC -AB 22AC ·BC=12, 所以C =60°.19.在△ABC 中,BC =5,AC =3,sin C =2sin A .(1)求AB 的值; (2)求sin(2A -π4)的值.解:(1)在△ABC 中,由正弦定理AB sin C =BC sin A ,得AB =sin C sin A BC =2BC =2 5.(2)在△ABC 中,根据余弦定理,得cos A =AB 2+AC 2-BC 22AB ·AC=255, 于是sin A =1-cos 2A =55.从而sin 2A =2sin A cos A =45,cos 2A =cos 2 A -sin 2 A =35.所以sin(2A -π4)=sin 2A cos π4-cos 2A sin π4=210.20.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.解:由正弦定理,得sin C sin B =c b .由2cos A sin B =sin C ,有cos A =sin C 2sin B =c 2b .又根据余弦定理,得cos A =b 2+c 2-a 22bc ,所以c 2b =b 2+c 2-a 22bc ,即c 2=b 2+c 2-a 2,所以a =b .又因为(a +b +c )(a +b -c )=3ab ,所以(a +b )2-c 2=3ab ,所以4b 2-c 2=3b 2,所以b =c ,所以a =b =c ,因此△ABC 为等边三角形.。
正弦定理余弦定理题型总结

正弦定理余弦定理题型总结一、利用正弦定理求解三角形(已知两角和一边)1. 题目。
在△ ABC中,已知A = 30^∘,B = 45^∘,a = 2,求b的值。
2. 解析。
根据正弦定理(a)/(sin A)=(b)/(sin B)。
已知A = 30^∘,sin A=sin30^∘=(1)/(2);B = 45^∘,sin B=sin45^∘=(√(2))/(2),a = 2。
代入正弦定理可得b=(asin B)/(sin A)=(2×frac{√(2))/(2)}{(1)/(2)} = 2√(2)。
二、利用正弦定理求解三角形(已知两边和其中一边的对角)1. 题目。
在△ ABC中,a = 3,b = 4,A = 30^∘,求B的值。
2. 解析。
由正弦定理(a)/(sin A)=(b)/(sin B)。
已知a = 3,b = 4,A = 30^∘,sin A=sin30^∘=(1)/(2)。
则sin B=(bsin A)/(a)=(4×frac{1)/(2)}{3}=(2)/(3)。
因为b > a,所以B有两解,B=arcsin(2)/(3)或B = π-arcsin(2)/(3)。
三、利用余弦定理求解三角形(已知三边求角)1. 题目。
在△ ABC中,a = 3,b = 4,c = 5,求C的值。
2. 解析。
根据余弦定理cos C=frac{a^2+b^2-c^2}{2ab}。
把a = 3,b = 4,c = 5代入可得:cos C=frac{3^2+4^2-5^2}{2×3×4}=(9 + 16-25)/(24)=0。
因为0^∘,所以C = 90^∘。
四、利用余弦定理求解三角形(已知两边和夹角求第三边)1. 题目。
在△ ABC中,a = 2,b = 3,C = 60^∘,求c的值。
2. 解析。
根据余弦定理c^2=a^2+b^2-2abcos C。
已知a = 2,b = 3,C = 60^∘,cos C=cos60^∘=(1)/(2)。
(完整版)解三角形之正弦定理与余弦定理

正弦定理与余弦定理教学目标掌握正弦定理和余弦定理的推导,并能用它们解三角形.正余弦定理及三角形面积公式.教学重难点掌握正弦定理和余弦定理的推导,并能用它们解三角形.知识点清单一.正弦定理:1.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即 R Cc B b A a 2sin sin sin ===(其中R 是三角形外接圆的半径) 2.变形:1)sin sin sin sin sin sin a b c a b c C C++===A +B +A B . 2)化边为角:C B A c b a sin :sin :sin ::=; ;sin sin B A b a = ;sin sin C B c b = ;sin sin CA c a = 3)化边为角:C R cB R b A R a sin 2,sin 2,sin 2===4)化角为边:;sin sin b a B A = ;sin sin c b C B =;sin sin ca C A = 5)化角为边: Rc C R b B R a A 2sin ,2sin ,2sin === 3. 利用正弦定理可以解决下列两类三角形的问题:①已知两个角及任意—边,求其他两边和另一角;例:已知角B,C,a ,解法:由A+B+C=180o ,求角A,由正弦定理;sin sin B A b a = ;sin sin CB c b = ;sin sin CA c a =求出b 与c ②已知两边和其中—边的对角,求其他两个角及另一边。
例:已知边a,b,A,解法:由正弦定理BA b a sin sin =求出角B,由A+B+C=180o 求出角C ,再使用正弦定理CA c a sin sin =求出c 边4.△ABC 中,已知锐角A ,边b ,则①A b a sin <时,B 无解; ②A b a sin =或b a ≥时,B 有一个解;③b a A b <<sin 时,B 有两个解。
正余弦定理题型

正余弦定理题型小结题型一:已知两边及一边对角且角为锐角时需讨论(1)满足A =45°,a =2,c =6的△ABC 的个数为________.练习:(1)a=4,b=5,A=030(两解);(2)a=5,b=4,A=060(一解)方法汇总:方法一:大边对大角;方法二:利用高h=bsinA 与a 的讨论 方法三:利用余弦讨论题型二:利用正弦定理解三角形 例一:在△ABC 中,若B=045,,2a b =则C=变式一:在△ABC 中,若c=2,A=0120,a=32,则B=变式二:在△ABC 中,A,B,C 的对边为a,b,c,a=2,b=2,sinB+cosB=2,则A 的大小为变式三:在△ABC 中,A,B,C 的对边为a,b,c, B=3π,cosA=54,b=3 (1)求sinC;(2)求△ABC 面积。
变式四:在△ABC 中,A,B,C 的对边为a,b,c,A=2B,sinB=33,(1)求cosA 的值;(2)b=2,求边a,c 的长。
题型三:利用正余弦定理进行边角转化 例:在△ABC 中,若A=2B,则ba的取值范围为变式一:在△ABC 中,B=060,AC=3,则AB+2BC 的最大值变式二:(新课标)已知a,b,c 分别为△ABC 三个内角A,B,C 的对边c=3asinC-ccosA.(1)求角A 的大小; (2)若a=2, △ABC 的面积为3,求b,c.题型四:利用余弦定理解三角形 例:在△ABC 中,b=1,c=3,C=32π,则a=变式一:在△ABC 中,若a=2,b+c=7,cosB=-41,则b=变式二:(12辽宁)在△ABC 中,角A,B,C 的对边为a,b,c ,a A b B A a 2cos sin sin 2=+,(1)求ab ;(2)若2223c b a =+求B 。
题型五:利用余弦定理进行边角转化例1:在△ABC 中,角A,B,C 的对边为a,b,c ,若ac B b c a 3tan )(222=-+,则角B 的值为( )例2、在∆ABC 中,三边a ,b ,c 与面积s 的关系式为222),s a b c =+-则角C 为A 30B 45C 60D 90变式一:在△ABC中,角A,B,C 的对边为a,b,c ,且C b c B c b A a s i n )2(s i n )2(s i n 2+++=,(1)求A 的值。
(完整版)正弦定理和余弦定理典型例题(最新整理)

【答案】根据余弦定理可得:
cos A b2 c2 a2 8 8 4 3 4 3
2bc
22 2 6 2 2
∵ 0 A 180 , ∴ A 30 ;
∴由正弦定理得: sin C c sin A
6 2 sin 30
6 2
.
a
2
4
【变式 2】在 ABC 中,已知 B 750 , C 600 , c 5 ,求 a 、 A .
【答案】 A 1800 (B C) 1800 (750 600 ) 450 ,
根据正弦定理
a
5
,∴ a 5
6
.
sin 45o sin 60o
3
【变式 3】在 ABC 中,已知 sin A : sin B : sin C 1: 2 : 3 ,求 a : b : c 【答案】根据正弦定理 a b c ,得 a : b : c sin A : sin B : sin C 1: 2 : 3 .
【答案】根据三角形内角和定理, C 1800 (A B) 1800 (32.00 81.80) 66.20 ;
根据正弦定理,
b
asin B sin A
42.9sin81.80 sin32.00
80.1(cm)
;
根据正弦定理,
c
asinC sin A
42.9sin 66.20 sin32.00
74.1(cm).
sin A sin B sin C
例 2.在 ABC中,b 3, B 60, c 1,求: a 和 A , C .
思路点拨: 先将已知条件表示在示意图形上(如图),可以确定先用正弦定理求出角 C ,然后用三角形 内角和求出角 A ,最后用正弦定理求出边 a .
正弦定理和余弦定理知识点与题型归纳

●高考明方向掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.★备考知考情1.利用正、余弦定理求三角形中的边、角问题是高考考查的热点.2.常与三角恒等变换、平面向量相结合出现在解答题中,综合考查三角形中的边角关系、三角形形状的判断等问题.3.三种题型都有可能出现,属中低档题. 一、知识梳理名师一号P62知识点一 正弦定理其中R 为△ABC 外接圆的半径变形1:2sin ,2sin ,2sin ,===a R A b R B c R C 变形2:sin ,sin ,sin ,222===a b c A B C R R R变形3:∶∶∶∶sinA sinB sinC=a b c 注意:补充关于边的齐次式或关于角的正弦的齐次式均可利用正弦定理进行边角互化;知识点二 余弦定理222222222222222222cos ,22cos ,2cos ,cos ,22cos .cos .2⎧+-=⎪⎧=+-⎪+-⎪⎪=+-⇔=⎨⎨=+-⎪⎪⎩+-⎪=⎪⎩b c a A bc a b c bc A a c b b a c ac B B ac c a b ab C a b c C ab 注意:补充1关于边的二次式或关于角的余弦均可考虑利用余弦定理进行边角互化;2勾股定理是余弦定理的特例3在∆ABC 中,222090︒︒<+⇔<<a b c A用于判断三角形形状名师一号P63问题探究 问题3判断三角形形状有什么办法判断三角形形状的两种途径:一是化边为角;二是化角为边, 并常用正弦余弦定理实施边、角转换.知识点三 三角形中常见的结论△ABC 的面积公式有:①S =错误!a ·hh 表示a 边上的高;②S =错误!ab sin C =错误!ac sin B =错误!bc sin A =错误!;--知两边或两边的积及其夹角可求面积③S =错误!ra +b +cr 为内切圆半径.补充1++=A B C π2在三角形中大边对大角,大角对大边.3任意两边之和大于第三边,任意两边之差小于第三边.4有关三角形内角的常用三角函数关系式sin()sin ,cos()cos ,tan()tan sin cos ,cos sin 2222+=+=-+=-++==B C A B C A B C A B C A B C A 利用++=A B C π及诱导公式可得之5在△ABC 中的几个充要条件:名师一号P63问题探究 问题4sin A >sin B 错误!>错误! a >b A >B .补充 cos cos A B A B >⇔<若R ∈、αβ或2k απβπ=-+k Z ∈或2k αβπ=-+k Z ∈45套之7--196锐角△ABC 中的常用结论 ∆ABC 为锐角三角形⇔02<<、、A B C π4.解斜三角形的类型名师一号P63问题探究 问题1利用正、余弦定理可解决哪几类问题在解三角形时,正弦定理可解决两类问题:1已知两角及任一边,求其它边或角;2已知两边及一边的对角,求其它边或角.情况2中结果可能有一解、二解、无解,应注意区分.余弦定理可解决两类问题:1已知两边及夹角或两边及一边对角的问题;2已知三边问题.a b A补充已知两边和其中一边的对角如,,用正弦定理或余弦定理均可名师一号P63问题探究问题2选用正、余弦定理的原则是什么若式子中含有角的余弦或边的二次式,要考虑用余弦定理;若遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.补充:一、正弦定理推导必修5证明思路:转化到特殊情形----直角三角形中二、余弦定理推导必修52011年陕西高考考查余弦定理的证明18.本小题满分12分叙述并证明余弦定理;2222cos a b c bc A =+-, 2222cos b c a ca B =+-,2222cos c a b ab C =+-.证明:证法一 如图,2c BC = ()()AC AB AC AB =-•-即2222cos a b c bc A =+-同理可证 2222cos b c a ca B =+-,证法二 已知ABC ∆中,,,A B C 所对边分别为,,,a b c ,以A 为原点,AB 所在直线为x 轴建立直角坐标系,则(cos ,sin ),(,0)C b A b A B c ,∴222222222||(cos )(sin )cos 2cos sin a BC b A c b A b A bc A c b A ==-+=-++222cos b c bc A =+-,即 2222cos a b c bc A =+-同理可证 2222cos b c a ca B =+-,二、例题分析:一利用正、余弦定理解三角形例1.1名师一号P62 对点自测1在△ABC 中,A =60°,B =75°,a =10,则c 等于A .5错误!B .10错误! D .5错误!解析 由A +B +C =180°,知C =45°,由正弦定理得:错误!=错误!.即错误!=错误!. ∴c =错误!.注意:已知两角及任一边,求其它边或角----正弦定理,解唯一例1.2名师一号P62 对点自测2在△ABC 中,若a =3,b =错误!,A =错误!,则C 的大小为________.解析 由正弦定理可知sin B =错误!=错误!=错误!,所以B =错误!或错误!舍去,因为a >b 即A =错误!> B 所以B =错误!所以C =π-A -B =π-错误!-错误!=错误!.一解变式1: 在△ABC 中,若b =3,a =错误!,A =错误!, 则C 的大小为________.答案: sin B >1无解变式2:在ABC ∆中,已知45︒===a b B , 解ABC ∆.答案:60,75,︒︒+===A C c或120,15,2︒︒-===A C c两解变式3:求边c注意:知道两边和其中一边的对角如,,a b A 解三角形 可用正弦定理先求出角B 也可用余弦定理先求出边c 再求解;两种方法均须注意解的个数可能有一解、二解、无解,应注意区分.练习:补充2009山东文17已知函数x x x x f sin sin cos 2cossin 2)(2-+=ϕϕ ππϕ=<<x 在)0(处取最小值; I 求ϕ的值;Ⅱ在ABC ∆中,c b a ,,分别是角A,B,C 的对边,已知,23)(,2,1===A f b a 求角C; 解析 Ⅰfx =2sinx 1cos cos sin sin 2x x ϕϕ++- =sinx+ϕ.因为 fx 在x =π时取最小值,所以 sin π+ϕ=-1,故 sin ϕ=1.又 0<ϕ<π,所以ϕ=2π, Ⅱ由Ⅰ知fx=sinx+2π=cosx. 因为fA=cosA=3,且A 为△ABC 的角, 所以A =6π. 由正弦定理得 sinB =sin b A a =22, 又b >a, 当4π=B 时,,12746πππππ=--=--=B A C 当43π=B 时,.12436πππππ=--=--=B A C 综上所述,12127ππ==C C 或例2. 补充若满足条件060=C ,a BC AB ==,3的ABC ∆有两个,求a 的取值范围. 32<<a注意:判断三角形解的个数常用方法:1在ABC ∆中,已知,,A a b ;构造直角三角形判断 2利用余弦定理判断一元二次方程正根个数 勿忘大边对大角判断已知两边及其中一边对角,判断三角形解的个数的方法:①应用三角形中大边对大角的性质以及正弦函数的值域判断解的个数.②在△ABC 中,已知a 、b 和A ,以点C 为圆心,以边长a 为半径画弧,此弧与除去顶点A 的射线AB 的公共点的个数 即为三角形的个数,解的个数见下表:图示已知a 、b 、A ,△ABC 解的情况.ⅰA 为钝角或直角时解的情况如下:ⅱA 为锐角时,解的情况如下:③运用余弦定理转化为关于一元二次方程 正根个数问题练习:已知ABC ∆中,若22,2==b a ,且三角形有两解,求角A 的取值范围;答案:由条件知b sin A <a ,即2错误!sin A <2, ∴sin A <错误!,∵a <b ,∴A <B ,∴A 为锐角,∴0<A <错误!.例3.1名师一号P62 对点自测3在△ABC 中,a =错误!,b =1,c =2,则A 等于A .30°B .45°C .60°D .75° 解析 由余弦定理得:cos A =错误!=错误!=错误!,∵0<A <π,∴A =60°.注意:已知三边,求其它边或角---余弦定理例3.2名师一号P63 高频考点例122014·新课标全国卷Ⅱ钝角三角形ABC的面积是错误!,AB=1,BC=错误!,则AC=A.5 C.2 D.1解:由题意知S=错误!AB·BC·sin B,△ABC即错误!=错误!×1×错误!sin B,解得sin B=错误!,∴B=45°或B=135°.当B=45°时,AC2=AB2+BC2-2AB·BC·cos B=12+错误!2-2×1×错误!×错误!=1.此时AC2+AB2=BC2,△ABC为直角三角形,不符合题意;当B=135°时,AC2=AB2+BC2-2AB·BC·cos B=12+错误!2-2×1×错误!×错误!=5,解得AC=错误!.符合题意.故选B.注意:已知两边夹角,求其它边或角---余弦定理小结:已知与待求涉及三边和一角的关系---余弦定理例4.1名师一号P63 高频考点例112014·江西卷在△ABC中,内角A,B,C所对的边分别是a,b,c,若3a=2b,则错误!的值为A.-错误!C.1解:∵3a=2b,∴由正弦定理得错误!=错误!=错误!.∴错误!=错误!,∴错误!=2×错误!-1=2×错误!-1=错误!-1=错误!.例4.2名师一号P62 对点自测已知△ABC三边满足a2+b2=c2-错误!ab,则此三角形的最大内角为__________.解析∵a2+b2-c2=-错误!ab,∴cos C=错误!=-错误!,故C=150°为三角形的最大内角.注意:1关于边的齐次式或关于角的正弦的齐次式均可利用正弦定理进行边角互化;2关于边的二次式或关于角的余弦均可考虑利用余弦定理进行边角互化.注意等价转换练习:2010·天津理在△ABC中,内角A,B,C的对边分别是a,b,c,若a2-b2=错误!bc,sin C=2错误!sin B,则A=A.30°B.60°C.120°D.150°解:由余弦定理得:cos A=错误!,由题知b2-a2=-错误!bc,c2=2错误!bc,则cos A=错误!, 又A∈0°,180°,∴A=30°,故选A.注意:已知三边比例关系---余弦定理二三角形的面积例1.1名师一号P62 对点自测62014·福建卷在△ABC中,A=60°,AC=4,BC=2错误!,则△ABC的面积等于________.解析由题意及余弦定理得cos A=错误!=错误!=错误!,解得c=2.所以S=错误!bc sin A=错误!×4×2×sin60°=2错误!.故答案为2错误!.注意:a b A解三角形可用正知道两边和其中一边的对角如,,弦定理先求出角B也可用余弦定理先求出边c再求解;两种方法均须注意解的个数本例用余弦求边更快捷.例1.2名师一号P63 高频考点例32014·浙江卷在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a≠b,c=错误!,cos2A-cos2B=错误!sin A cos A-错误! sin B cos B.1求角C的大小;2若sin A=错误!,求△ABC的面积.解:1由题意得错误!-错误!=错误!sin2A-错误!sin2B,即错误!sin2A-错误!cos2A=错误!sin2B-错误! cos2B,sin错误!=sin错误!.由a≠b,得A≠B,又A+B∈0,π.得2A-错误!+2B-错误!=π,即A+B=错误!,所以C=错误!.2由c=错误!,sin A=错误!,错误!=错误!,得a=错误!.由a<c,得A<C,从而cos A=错误!,故sin B=sin A+C=sin A cos C+cos A sin C=错误!.所以△ABC的面积为S=错误!ac sin B=错误!.规律方法三角形面积公式的应用原则1对于面积公式S=错误!ab sin C=错误!ac sin B=错误! bc sin A,一般是已知哪一个角就使用哪一个公式.2与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化.三三角形形状的判定例1.1名师一号P63 高频考点例2在△ABC中a,b,c分别为内角A,B,C的对边,且2a sin A =2b+c sin B+2c+b sin C.1求A的大小;2若sin B+sin C=1,试判断△ABC的形状.解:1由已知,根据正弦定理得2a2=2b+c·b+2c+bc,即a2=b2+c2+bc.由余弦定理得a2=b2+c2-2bc cos A,故cos A=-错误!,∵0<A<180°,∴A=120°.2由1得sin 2A =sin 2B +sin 2C +sin B sin C =错误!.又sin B +sin C =1,解得sin B =sin C =错误!.∵0°<B <60°,0°<C <60°,故B =C =30°,A =120°.∴△ABC 是等腰钝角三角形.法二:因为A =120°,且A +B +C=180°所以sin B +sin C =1即sin60°-C +sin C =1 可求得C=30°例1.2补充根据所给条件,判断△ABC 的形状.1若a cos A =b cos B ,则△ABC 形状为________. 2若错误!=错误!=错误!,则△ABC 形状为________. 解析:1 解法一: 由正弦定理得sinA cos A =sinB cos B 即sin2A =sin2B22A B ∴= 或 22A B π=-A B ∴= 或 2A B π+= ∴△ABC 是等腰三角形或直角三角形.解法二:由余弦定理得a cos A =b cos Ba ·错误!=b ·错误!a 2c 2-a 4-b 2c 2+b 4=0,∴a 2-b 2c 2-a 2-b 2=0∴a 2-b 2=0或c 2-a 2-b 2=0∴a =b 或c 2=a 2+b 2∴△ABC是等腰三角形或直角三角形.2由正弦定理得错误!=错误!=错误!即tan A=tan B=tan C,∵A、B、C∈0,π,∴A=B=C,∴△ABC为等边三角形.注意:利用正、余弦定理进行边角互化1关于边的齐次式或关于角的正弦的齐次式均可利用正弦定理进行边角互化;2关于边的二次式或关于角的余弦均可考虑利用余弦定理进行边角互化;规律方法依据已知条件中的边角关系判断三角形的形状时,主要有如下两种方法:1利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.2利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B+C=π这个结论.加加练P9 第6题∆中,已知ABC∆为则ABCA.等边三角形B.等腰直角三角形C.锐角三角形D.钝角三角形答案:B计时双基练P252 第2题四三角形的综合问题例1.补充 在△ABC 中,sinC-A=1,sinB=31. Ⅰ求sinA 的值;Ⅱ设AC=错误!,求△ABC 的面积.解:Ⅰ由2C A π-=,且C A B π+=-,∴42B A π=-,∴sin sin()sin )42222B B B A π=-=-, ∴211sin (1sin )23A B =-=,又sin 0A >,∴sin A = Ⅱ如图,由正弦定理得sin sin AC BC B A=∴sin 31sin 3AC A BC B ===, 又sin sin()sin cos cos sin C A B A B A B =+=+∴11sin 223ABC S AC BC C ∆=••==注意:关注三角形内角和、特殊角、三角恒等变换公式、 知两边夹角求面积公式的选择;例2.补充已知ABC ∆中,角A B C 、、所对的边 A BC分别为a b c 、、,3B π∠=,b =求a c +的取值范围解法一:正弦定理结合三角最值 当且仅当62A ππ+=即3A π=时等号成立 法二:余弦定理结合不等式 由2222cos b a c ac B =+-得2228a c ac =+-即()2283a c ac =+-a c ∴+≤当且仅当a c =时等号成立 又三角形两边之和大于第三边注:这是一道好题,刚好都能运用“正余弦定理求解最值问题”的两种主要方法解决; 小结:借助正弦定理,转化为角的正弦值,利用三角函数最值求解借助余弦定理,转化为边的关系,利用均值不等式求解余弦定理注意两数和差与这两数的平方和、两数的积 的关系的运用练习:加加练P11 第11题已知△ABC 中,外接圆半径是1,且满足()()222sin sin sin sin A C A B b -=-,则△ABC 面积的最大值为答案:4计时双基练P251 第6题补充已知向量(sin ,1)2A m =-,()2,cos()nBC =+, ,,A B C 为锐角..ABC ∆的内角,其对应边为a ,b ,c . Ⅰ当m n ⋅取得最大值时,求角A 的大小;Ⅱ在Ⅰ成立的条件下,当a =,求22b c +的取值范围. 解:Ⅰ2(sin 212sin 22sin 2cos 2sin2)cos(sin 22--=++-=+=+-=⋅A A A A A C B A nm 0,0,0sin 2242A A A ππ<<∴<<∴<<,1sinA ∴=时,即A π=时,m n ⋅取得最大值,∴A π=正弦定理:2sin sin sin ===a b c R A B C其中R 为△ABC 外接圆的半径 22442cos 22cos(2)3sin 2cos 242sin(23b c B B B B B π+=---=-+=-ABC ∆为锐角三角形★注意:∆ABC 为锐角三角形⇔02<<、、A B C π讲评:1、计时双基练 P252 基础11---多个三角形问题2014·湖南卷如图,在平面四边形ABCD 中,AD =1,CD =2,AC =错误!.1求cos ∠CAD 的值;2若cos ∠BAD =-错误!,sin ∠CBA =错误!,求BC 的长.解 1由余弦定理可得cos ∠CAD =错误!=错误!=错误!,∴cos ∠CAD =错误!.2∵∠BAD 为四边形内角,∴sin ∠BAD >0且sin ∠CAD >0,则由正余弦的关系可得sin ∠BAD =错误!=错误!,且sin ∠CAD =错误!=错误!,由正弦的和差角公式可得sin ∠BAC =sin ∠BAD -∠CAD=sin ∠BAD cos ∠CAD -sin ∠CAD cos ∠BAD=错误!×错误!-错误!×错误!=错误!+错误!=错误!, 再由△ABC 的正弦定理可得错误!=错误!BC =错误!×错误!=3.2、45套之7--192---方程的思想课后作业一、计时双基练P251基础1-6;课本P63变式思考1、3补充练习1、2、3二、计时双基练P251基础7-11;培优1-4课本P63变式思考2三、课本P64典例、※对应训练补充练习4、5预习 第七节补充练习:1、2009山东文17已知函数x x x x f sin sin cos 2cos sin 2)(2-+=ϕϕ ππϕ=<<x 在)0(处取最小值; I 求ϕ的值;Ⅱ在ABC ∆中,c b a ,,分别是角A,B,C 的对边,已知,23)(,2,1===A f b a 求角C;解析Ⅰfx =2sinx 1cos cos sin sin 2x x ϕϕ++- =sinx+ϕ.因为 fx 在x =π时取最小值,所以 sin π+ϕ=-1,故 sin ϕ=1. 又 0<ϕ<π,所以ϕ=2π, Ⅱ由Ⅰ知fx=sinx+2π=cosx. 因为fA=cosA=3,且A 为△ABC 的角, 所以A =6π. 由正弦定理得 sinB =sin b A a =22, 又b >a,当4π=B 时,,12746πππππ=--=--=B A C 当43π=B 时,.12436πππππ=--=--=B A C 综上所述,12127ππ==C C 或 2、 已知ABC ∆中,若22,2==b a ,且三角形有两解,求角A 的取值范围;答案:由条件知b sin A <a ,即2错误!sin A <2,∴sin A <错误!,∵a <b ,∴A <B ,∴A 为锐角,∴0<A <错误!.3、已知△ABC 中,∠A =60°,BC=2错误!,则其外接圆面积为__________.答案:4π★注意:勿忘正弦定理中三角形各边与对角正弦的比为外接圆直径sin sin in 2s a b c A B R C=== R 为三角形外接圆半径 4、在四边形ABCD 中,∠B =∠D =90°,∠A =60°, AB =4,AD =5,则AC 的长为B .2错误!解析 如图,连结AC ,设∠BAC =α,则AC ·cos α=4,AC ·cos60°-α=5,两式相除得,错误!=错误!,展开解得,tan α=错误!∵α为锐角,∴cos α=错误!∴AC =错误!=2错误!解法二:补充△ABD 中,由余弦定理得21BD =由∠B =∠D =90°知AC 为△ABD 的外接圆直径由正弦定理得2127sin sin 620BD AC R A ︒====5、已知向量(sin ,1)2A m =-,()2,cos()nBC =+, ,,A B C 为锐角..ABC ∆的内角,其对应边为a ,b ,c .Ⅰ当m n ⋅取得最大值时,求角A 的大小; Ⅱ在Ⅰ成立的条件下,当a =, 求22b c +的取值范围. 解:Ⅰ2(sin 212sin 22sin 2cos 2sin2)cos(sin 22--=++-=+=+-=⋅A A A A A C B A nm 0,0,0sin 2242A A A ππ<<∴<<∴<<,1sinA ∴=时,即A π=时,m n ⋅取得最大值,∴A π=正弦定理:2sin sin sin ===a b c R A B C其中R 为△ABC 外接圆的半径 22442cos 22cos(2)2cos 242sin(23b c B B B B B π+=---=-+=-∆ABC 为锐角三角形⇔02<<、、A B C π6、2013年广州二模文数 第17题某单位有A 、B 、C 三个工作点,需要建立一个公共无线网络发射点O ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为80AB =m ,70BC =m ,50CA =m .假定A 、B 、C 、O 四点在同一平面上.1求BAC ∠的大小;2求点O 到直线BC 的距离.答案13BAC π∠=23m 课后作业三、计时双基练P251基础1-6;课本P63变式思考1补充练习1、3、例2四、计时双基练P251基础7-11;培优1-4课本P63变式思考3补充练习2三、课本P63变式思考2课本P64典例、※对应训练补充练习4、5预习 第七节。
(完整版)解三角形之正弦定理与余弦定理

正弦定理与余弦定理教学目标掌握正弦定理和余弦定理的推导,并能用它们解三角形正余弦定理及三角形面积公式.教学重难点掌握正弦定理和余弦定理的推导,并能用它们解三角形知识点清单一.正弦定理:1. 正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即a b c2R(其中R是三角形外接圆的半径)sin A sin B si2.变形:1) a b c a b csin sin si nC sin sin si nC2)化边为角:a :b: c sin A: sin B :s in C -a si nA.b sin B a sin AJb sin Bc sin C c sin C '3)化边为角:a 2Rsin A, b 2Rsi nB, c 2Rs inC4)化角为边:sin A a ;J sin B b ; si nA aJ7sin B b sin C c sin C c5)化角为边:sin A a sin B b si nC c2R‘2R'2R3.利用正弦定理可以解决下列两类三角形的问题:①已知两个角及任意一边,求其他两边和另一角; 例:已知角B,C,a,解法:由A+B+C=18°0,求角A,由正弦定理-Sn) - Sn^; b sin B c sin C a sin A;求出b与cc sin C②已知两边和其中一边的对角,求其他两个角及另一边。
例:已知边a,b,A,解法:由正弦定理旦血求出角B,由A+B+C=180求出角C,再使用正b sin B弦定理旦泄求出c边c sin C4. △ ABC中,已知锐角A,边b,贝U①a bsin A时,B无解;②a bsinA或a b时,B有一个解;③ bsin A a b 时,B 有两个解。
如:①已知A 60 ,a 2,b2, 3 ,求B (有一个解) ②已知A 60 ,b 2,a23,求B (有两个解)注意:由正弦定理求角时,注意解的个数。
第8讲 正弦定理和余弦定理5种常见题型(解析版)

第8讲 正弦定理和余弦定理5种常见题型【考点分析】考点一:三角形中常用知识①任意三角形的内角和为180°;三条边满足:两边之和大于第三边,两边之差小于第三边.②大边对大角,小边对小角,B A b a B A sin sin >⇔>⇔>,所以在ABC ∆中B A B A sin sin >>是的充要条件①在锐角ABC ∆中,一定有A C C B B A cos sin ,cos sin ,cos sin >>>,即一个角的正弦值一定大于另一个角的余弦值,从而可以得到锐角ABC ∆中,一定有C B A C B A cos cos cos sin sin sin ++>++ 考点二:正弦定理在一个三角形中,各边和它所对角的正弦的比相等,即R CcB b A a 2sin sin sin ===. 考点三:由正弦定理推出的几个结论 ①a ∶b ∶c =sin A ∶sin B ∶sinC .①B R C B R B A R a sin 2,sin 2,sin 2===③由等比性质和圆的性质可知,a sin A =b sin B =c sin C =a +b +c sin A +sin B +sin C =2R .其中,R 为△ABC 外接圆的半径.④A <B ⇔a <b ⇔sin A <sin B .考点四:由三角形性质和诱导公式导出的几个结论 ①22,ππ=++=++C B A C B A , 所以()()C C B A sin sin sin =-=+π,同理()A C B sin sin =+,()B C A sin sin =+,()()C C B A cos cos cos -=-=+π,同理()A C B cos cos -=+,()B C A cos cos -=+, ()()C C B A tan tan tan -=-=+π,同理()A C B tan tan -=+,()B C A tan tan -=+,所以2cos 22sin 2sin C C B A =⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛+π,同理2cos 2sin A C B =⎪⎭⎫ ⎝⎛+,2cos 2sin B C A =⎪⎭⎫ ⎝⎛+, 考点五:三角形面积公式S ①ABC =12 ah (h 表示边a 上的高) ;S ①ABC =12ab sin C =12bc sin A =12ac sin B ;由正弦定理可得RabcR c ab C ab S ABC 4221sin 21===∆ C B A R C B R A R C ab S ABC sin sin sin 2sin sin 2sin 221sin 212=⋅==∆ 海伦公式:()()()c p b p a p p S ABC ---=∆,其中()c b a p ++=21三角形面积和内切圆半径的关系:()r c b a S ABC ⋅++=∆21(其中r 为三角形内切圆的半径)【题型目录】题型一:正弦定理运用 题型二:余弦定理运用题型三:三角形面积公式运用 题型四:正弦定理解答题 题型五:余弦定理解答题【典型例题】题型一: 正弦定理运用【例1】在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若1sin 3A =,a =3b =,则sin B =( ). A .23BC2D.3【例2】在①ABC 中,已知4sin sin sin a b cA B C+-=+-,则其外接圆的直径为______.【分析】设ABC 外接圆半径为【详解】设ABC 外接圆半径为由正弦定理可得:sina sin sinbc B +--所以ABC 外接圆直径为故答案为:4.【例3】在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c .若a =2b =,60A =︒,则sin B = .【答案】721【解析】由正弦定理可得B b A a sin sin =,即B sin 2237=,所以721sin =B 【例4】在ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,若A ∠:B ∠:1C ∠=:2:3,则a :b :c =( ) A .1:2:3 B .3:2:1 C .21 D .12【答案】43π=B 【解析】由正弦定理可得R BbA a 2sin sin ==,可得B R b A R a sin 2,sin 2==,所以0cos sin 2sin sin 2=+B A R A B R ,即0cos sin sin sin =+B A A B ,因0sin ≠A ,所以0cos sin =+B B ,所以1tan -=B ,因()π,0∈B ,所以43π=B 【例6】ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c .已知sin sin (sin cos )B A C C +- 0=,2a =,c =C =A .12π B .6π C .4π D .3π【答案】B【解析】由()C A B +=sin sin ,可得()sin sin (sin cos )0A C A C C ++-=,所以sin cos cos sin sin sin sin cos 0A C A C A C A C ++-=,即cos sin sin sin 0A C A C +=,因0sin ≠C ,所以0cos sin =+A A ,所以1tan -=A ,因()π,0∈A ,所以43π=A ,由正弦定理可得CcA a sin sin =,即C sin 2222=,所以21sin =C ,所以6π=C【例7】在ABC △中,90ABC ∠=︒,4AB =,3BC =,点D 在线段AC 上,若45BDC ∠=︒,则BD =___________,cos ABD ∠=___________.【答案】5,10【解析】如图,在ABD △中,由正弦定理有:sin sin AB BD ADB BAC =∠∠,而3π4,4AB ADB =∠=,5AC ,34sin ,cos 55BC AB BAC BAC AC AC ∠==∠==,所以5BD =ππcos cos()cos cos sin sin 4410ABD BDC BAC BAC BAC ∠=∠-∠=∠+∠=.【例8】在ABC △中,角A ,B ,C 的对边分别为,,.若ABC △为锐角三角形,且满足sin (12cos )2sin cos cos sin B C A C A C +=+,则下列等式成立的是A .B .C .2A B =D .2B A =【答案】A【解析】由题意知sin()2sin cos 2sin cos cos sin A C B C A C A C ++=+, 所以2sin cos sin cos 2sin sin 2B C A C B A b a =⇒=⇒=, 故选A.【例9】ABC ∆的内角,,A B C 的对边分别为,,a b c ,若4cos 5A =,5cos 13C =,1a =,则b = . 【答案】2113【解析】因为45cos ,cos 513A C ==,且,A C 为三角形的内角,所以312sin ,sin 513A C ==,63sin sin[π()]sin()sin cos cos sin 65B AC A C A C A C =-+=+=+=,又因为sin sin a bA B=,所以a b c 2a b =2b a =sin 21sin 13a Bb A ==. 【例10】在锐角三角形ABC 中,若sin 2sin sin A B C =,则tan tan tan A B C 的最小值是 . 【答案】8.【解析】,又,因此即最小值为8. 【题型专练】1.设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c.若a =1sin 2B =,6C π=,则b = . 【答案】1=b【解析】由1sin 2B =,6C π=,可得6B π=,所以32π=A ,由正弦定理可得Bb A a sin sin =,即21233b=,所以1=b2.在锐角①ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,R 是①ABC 的外接圆半径,且cos cos b a C c A ++=,则B =( ) A .π6B .π4C .π3D .2π3sin sin()2sin sin tan tan 2tan tan A B+C B C B C B C ==⇒+=tan tan tan tan tan 1B+CA=B C -tan tan tan tan tan tan tan 2tan tan tan tan tan 8,A B C A B C A B C A B C =++=+≥≥3.在,内角所对的边长分别为,,a b c .若sin cos a B C +sin cos 2c B A b =,且a b >,则B ∠=A .B .C .D .【答案】A【解析】由题意知1sin sin sin sin sin cos sin 2A B C C B A B +=,即1sin sin sin cos 2A C C A += 所以()1sin 2A C +=,所以21sin =B ,因a b >,所以6π=B 故选A.4.设①ABC 的内角A , B , C 所对的边分别为a ,b ,c ,若,则①ABC 的形状为A .锐角三角形B .直角三角形C .钝角三角形D .不确定【答案】B【解析】由题意知sin cos sin cos sin sin B C C B A A +=,即()sin sin sin B C A A += 所以sin 1A =,所以2π=A故选B5.ABC ∆的三个内角A ,B ,C 所对的边分别为a ,b ,c ,2sin sin cos a A Bb A +=,则=abA .B .CD【答案】D【解析】由题意知2sin sin sin sin cos A A B B A A +=,即()22sin sin cos B A A A+=所以sin B A =,所以a b 2=,所以2=ab故选D6.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,若2cos cos cos b B a C c A =+,则B = 【答案】3π 【解析】由题意知2sin cos sin cos sin cos B B A C C A =+,即()2sin cos sin sin B B A C B =+=ABC ∆,,A B C 6π3π23π56πcos cos sin b C c B a A +=所以1cos 2B =,所以3π=B7.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .已知60C =,b =3c =,则A =_______.【答案】︒=75A【解析】由正弦定理可得BbC c sin sin =,即B sin 6233=,所以22sin =B ,所以︒=45B ,因π=++C B A ,所以︒=75A8.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若2a b ==,sin cos B B +=A 的大小为 . 【答案】6π=A【解析】因为sin cos 4B B B π⎛⎫+=+= ⎪⎝⎭()0,B π∈,所以42B ππ+=,所以4B π=,又因为sin sin a b A B =,所以sin 2A =1sin 2A =,因为b a <,所以6π=A 题型二:余弦定理运用 【例1】在①ABC 中,cos C =23,AC =4,BC =3,则tan B =( )A B .C .D .【答案】C【分析】设,,AB c BC a CA b ===22222cos 916234933c a b ab C c =+-=+-⨯⨯⨯=∴=2221cos sin tan 29a c b B B B ac +-==∴===故选:C【例2】在ABC △中,cos25C =,1BC =,5AC =,则AB =A .BCD .【解析】因为223cos 2cos 121,255C C ⎛=-=⨯-=- ⎝⎭所以22232cos 125215325AB BC AC BC AC C AB ⎛⎫=+-⋅=+-⨯⨯⨯-== ⎪⎝⎭,则 A.【例3】①ABC 的内角A 、B 、C 的对边分别为a 、b 、c .已知a =2c =,2cos 3A =,则b =A B C .2 D .3【答案】D 【解析】2222452cos 2223b c a b A bc b +-+-===⨯⨯,所以b b 8332=-,即03832=--b b故()133b =-或舍去. 【例4】在 ABC 中,a b c ,,分别是角A B C ,,的对边,222c ab a b +=+,则角C 的正弦值为( )A B C .12D .1【例5】已知ABC 的三边之比为3:5:7,则最大角为( ) A .2π3B .3π4C .5π6D .7π12,由条件结合余弦定理可求ABC 的最大角不妨设ABC 的三边满足因为ABC 的三边之比为由ABC 中最大边所对的角最大,可得ABC 的最大内角为C ∠22291cos 222a c x C +-+===-,又()0,πC ∠∈所以【例6】在ABC 中,内角A ,B ,C 所对的边分别为,,a b c .已知()()22232cos b c b c a abc C -+-=.则tan A =( )AB .CD .【例7】黄金三角形有两种,一种是顶角为36°的等腰三角形,另一种是顶角为108°的等腰三角形.其中顶角为36°,这种黄金三角形被认为是最美的三角形.根据这些信息,则cos36︒=( )A B C D【例8】设的内角所对边的长分别为.若,则则角_____. 【答案】4【分析】由3sin 5sin A B =,可得35a b =,因a c b 2=+,设3=b ,则7,5==c a ,结合余弦定理:222cos 2a b c C ab+-=,可得2135249925cos -=⨯⨯-+=C ,解得:23C π= 【例9】在锐角ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,若222a c b +=,则B ∠=_________;若sin 2sin sin A B C =,则tan tan tan A B C 的最小值_________. 而此时ABC 为等腰直角三角形,与题设矛盾,故ABC ∆,,A B C ,,a b c 2b c a +=3sin 5sin ,A B =C =【题型专练】1.在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若1,a b c ===B =_________. 【答案】5π6##150︒2.在ABC 中,角,,A B C 的对边分别是,,a b c ,sin cos 1sin 2C C C +=-.若()2248a b a b +=+-,则边c 的值为______.1##1(0,πC ∈即sin 2C -sin C ∴=cos C ∴=3.在ABC △中,π4B ,BC 边上的高等于13BC ,则cos A ( )(A (B (C )1010 (D )31010【答案】C【解析】设BC 边上的高为AD ,则3BC AD =,所以AC =,AB =.由余弦定理,知222222cos210AB AC BC A AB AC +-===-⋅,故选C .4.在①ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a =b =2,A =60°,则sin B =___________,c =___________.【答案】7,3【解析】由正弦定理得sinsin a A b B =,所以πsin sin 3B == 由余弦定理得22222cos ,742,3a b c bc A c c c =+-∴=+-∴=(负值舍去). 5.在ABC 中,已知120B =︒,AC 2AB =,则BC =( )A .1 BCD .3【答案】D【分析】设,,AB c AC b BC a ===,结合余弦定理:2222cos b a c ac B =+-可得:21942cos120a a =+-⨯⨯, 即:22150a a +-=,解得:3a =(5a =-舍去), 故3BC =.6.已知锐角的内角的对边分别为,223cos A +cos20A =,,,则A .B .C .D .【答案】D【分析】由题意得2223cos 2cos 10A A +-=,即225cos 10A -=,因为锐角三角形,所以51cos =A ,结合余弦定理:222cos 2b c a A bc+-=,可得b b ⨯⨯-+=624936512 即:2450152b b -=-,解得:5b =(135b =-舍去) 故选:D.7.设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且2a =,1cos 4C =-,3sin 2sin A B =,则c =________. 【答案】4【分析】由3sin 2sin A B =,可得32a b =,所以3=b ,结合余弦定理:222cos 2a b c C ab+-=,可得32294412⨯⨯-+=-c ,解得:4c = 题型三: 三角形面积公式运用【例1】记ABC 的内角A ,B ,C 的对边分别为a ,b ,c60B =︒,223a c ac +=,则b =________.【答案】【分析】由题意,1sin 24ABCSac B ac ===, 所以224,12ac a c =+=,所以22212cos 122482b ac ac B =+-=-⨯⨯=,解得b =(负值舍去).故答案为:【例2】ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知2b =,6B π=,4Cπ,则ABC ∆的ABC ∆,,A B C ,,a b c 7a =6c =b =10985ABC ∆A .2+B 1C .2-D 1【答案】B【详解】试题分析:根据正弦定理,,解得,,并且,所以【例3】ABC 的内角,,A B C 的对边分别为,,a b c .若π6,2,3b ac B ===,则ABC 的面积为__________.【答案】【分析】由余弦定理得2222cos b a c ac B =+-,所以2221(2)2262c c c c +-⨯⨯⨯=,即212c =,解得c c ==-,所以2a c ==11sin 22ABC S ac B ∆==⨯= 【例4】已知ABC 的角A ,B ,C 的对边分别为a ,b ,c ,且::2:3:4a b c =,则ABC 的面积为( )A 2B 2C .212aD .212b【例5】已知△ABC ,AB =AC =4,BC =2. 点D 为AB 延长线上一点,BD =2,连结CD ,则△BDC 的面积是______,cos ∠BDC =_______.【解析】取BC 中点E ,由题意:AE BC ⊥,①ABE 中,1cos 4BE ABC AB ∠==,①1cos ,sin 4DBC DBC ∠=-∠==,①1sin 22BCD S BD BC DBC =⨯⨯⨯∠=△. ①2ABC BDC ∠=∠,①21cos cos 22cos 14ABC BDC BDC ∠=∠=∠-=,解得cos BDC ∠=或cos BDC ∠=(舍去).综上可得,①BCD 面积为2,cos 4BDC ∠=.【例6】ABC △的内角A B C ,,的对边分别为a ,b ,c ,若ABC △的面积为2224a b c+-,则C =A .π2 B .π3 C .π4 D .π6【答案】C【解析】由题可知2221sin 24ABCa b c S ab C +-==△,所以2222sinC a b c ab +-=, 由余弦定理2222cos a b c ab C +-=,得sin cos C C =,因为()0,πC ∈,所以π4C =,故选C. 【例7】①ABC 的内角A B C ,,的对边分别为a b c ,,,已知sin sin 4sin sin b C c B a B C +=,2228b c a +-=,则①ABC 的面积为________.【分析】因为sin sin 4sin sin b C c B a B C +=,结合正弦定理可得sin sin sin sin 4sin sin sin B C C B A B C +=, 可得1sin 2A =,因为2228b c a +-=, 结合余弦定理2222a b c bccosA =+-,可得2cos 8bc A =,所以A 为锐角,且cos A =,从而求得bc =,所以ABC ∆的面积为111sin 222S bc A ===. 【例8】在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .点D 为BC 的中点,π1,3AD B ==,且ABCc =( )A .1B .2C .3D .4【题型专练】1.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,已知ABC ∆的面积为2b c -=,1cos 4A =-,则a 的值为 . 【答案】34【分析】详解:由1cos 4A =-,可得215cos 1sin 2=-=A A ,因1sin 2ABC S bc A ∆=,所以12bc =,所以12=bc ,由余弦定理可得()4124244222cos 222222-=-+=-+-=-+=a bc a bc c b bc a c b A ,解得34=a2.钝角三角形ABC 的面积是12,1AB =,BC =AC =A .5BC .2D .1 【答案】B【分析】因11sin 22ABC S ac B ∆==,所以111sin 22B ⨯=,所以22sin =B ,所以434ππ或=B , 当4π=B 时,22212212cos 2222=⨯⨯-+=-+=b ac b c a B ,解得1=b ,此时2π=A ,不合题意; 当43π=B 时,22212212cos 2222-=⨯⨯-+=-+=b ac b c a B ,解得5=b ,此时5=AC . 3.在ABC ∆中,a ,b ,c 分别为内角A ,B ,C 所对的边长,若2c =2()6a b -+,3C π=,则ABC ∆的面积是A .3B .239C .233 D .33 【答案】C【分析】由余弦定理可得()21226222cos 2222222=-+-=-+-=-+=ab c ab c ab c ab b a ab c b a C ,解得6=ab因11sin 622ABC S ab C ∆==⨯=4.在ABC ∆中,60A ∠=︒,1b =,ABC S ∆=,则2sin 2sin sin a b cA B C++=++( )ABCD.【答案】A1sin 424ABC S bc A c ∆====利用余弦定理得到:2222cos 116413a b c bc A a =+-=+-=∴=正弦定理:sin sin sin a b cA B C==故2sin 2sin sin sin a b c a A B C A ++===++ 故选A5.在①AB C 中,若2221()4ABCS b c a =+-,则A =( ) A .90° B .60°C .45°D .30°ABCS=222b c bc +1,又A 6.已知ABC 中,设角A 、B 、C 所对的边分别为a 、b 、c ,ABC 的面积为S ,若()223sin 2sin sin sin 2sin sin B C A A B C +=+,则2Sb 的值为( ) A .14B .12C .1D .2【答案】B【分析】首先根据正弦定理将等式中的角转化成边得:222322sin b c a bc A +=+,通过余弦定理可将等式化简0b >,c 又2b c c +综上所述:故得:b c+7.在ABC 中,已知π24B C ∠=∠=,AC =4,则ABC 的面积为( ) A .2 B .)21C .4D .)41题型四: 正弦定理解答题【例1】在ABC 中,角,,A B C 所对的边分别为,,a b ccos C c =-. (1)求角B ; (2)若3cos 5C =,4BD DC =,ABD △的面积为75,求c 的值.为ABC 的内角,得2cos 2B =,为ABC 的内角,所以)解:已知4BD DC =,则BD 114sin 225ABDSAB BD B c a ==⋅由3cos 5C =,可得sin 1cos =-C )sin sin cos4A B C π∴=+=【例2】在ABC 中,已知30A =,120B =,5b =, (1)求c 的值; (2)求①ABC 的面积.)30A =︒,sin sin c C =532, , 11531253sin 5223212bc A . 【例3】已知三角形ABC 中,内角A ,B ,C 所对边分别为a ,b ,c ,且(2)cos cos 0a c B b C --=. (1)求角B ;(2)若b =2,求a c +的取值范围.①22()416,a c b +≤=即4a c +≤,当且仅当2a c ==时取等,又2a c b +>=,①a c +的取值范围为(]2,4. 【题型专练】1.在锐角ABC 中,角,,A B C 所对的边分别为,,a b c . 已知2sin 0b A = (1)求角B 的大小; (2)若2,4a A π==,求ABC 的面积. 所以ABC 的面积2.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且()()22cos 2cos 2Ca c A Cb b +++=.(1)求B ;(2)如图,若D 为ABC 外一点,且712BCD π∠=,AB AD ⊥,1AB =,AD =sin BDC ∠.并求BC .2222132BDABAD,tan ABD ∠π3ABD =,所以CBD ABC ABD ∠=∠-∠=7πBCD =,所以πBDC BCD CBD ∠=-∠-∠3.在锐角ABC 中,角A B C ,,所对的边为a b c ,,,且()cos 1cos a B b A ⋅=+. (1)证明:2A B =(2)若2b =,求a 的取值范围.4.已知ABC 中,角A B C ,,的对边分别为,,a b c ,π4A =,cos cos b C cB -. (1)求()sin BC -的值;(2)若a =ABC 的面积.ABCS=题型五: 余弦定理解答题【例1】在ABC 中,内角,,A B C 所对的边分别为,,a b c ,且满足()2cos cos b a C c A -=. (1)求角C ;(2)已知7a b +=,ABC ,求ABC 的边AB 上的高h .)解:在ABC 中,cos A ,根据正弦定理得sin cos C =cos sin C C =cos sin C +)解:在ABC 中,33, 342=, 根据余弦定理得2cos ab C ABCS=11h ∴=【例2】如图,在平面四边形ABCD 中,90,60,23,4DAB DCB ABC AB AD ∠∠∠=====.(1)求cos DBC ∠的值; (2)求AC 的长度. )60cos60cos sin60sin ABD ABD ABD -∠=∠+∠ 7321714=; 90=,所以cos 33BC BD DBC ∠=⋅=,在ABC 中,由余弦定理得:【例3】在ABC 中,2220b c a bc +-+=,sin C =,a = (1)求A ∠的大小; (2)求ABC 的面积. 【答案】(1)所以ABC 的面积【例4】如图,在ABC 中,已知2AB =,AC =45BAC ∠=︒,BC 边上的中线为AM .(1)求AM 的值; (2)求sin BAM ∠.在ABC 中,利用余弦定理求,在ABM ,△,由此列方程求在ABM 中由余弦定理求)由余弦定理,得22cos AB AC AB AC +-⋅BM CM =在ABM 中,由余弦定理,得222BM AM AB BMA BM AM +-=⋅ACM △中,由余弦定理,得2CM CMA =BMA ∠与∠2)在ABM 中,由余弦定理,得【例5】在①ABC 中,已知222)ABC S a b c =+-△. (1)求角C 的大小; (2)求sin sin A B +的最大值. ABCS =转化为同一个角表示,然后根据两角和的正弦定理可得答案.ABCS=sin C20A <<当π6A +=sin sin A ∴+【题型专练】1.在ABC 中,a ,b ,c 分别为内角A ,B ,C cos B b -,ABC 的面积214S c =.(1)求C ; (2)求sin sin AB的值.ABCS=,根据正弦定理即可求出2a -2.已知ABC 的三个角A 、B 、C 的对边分别是a 、b 、c ,且满足)2222sin ab C a b c +-.(1)求C ;(2)若4a =,5b =,求点C 到边AB 的距离.ABC S =3.在①2cos22cos 12B B +=;①2sin tan b A a B =;()()sin sin sin a c A c A B b B -++=,这三个条件中任选一个,补充在下面的横线上,并加以解答.已知ABC 的内角,,A B C 所对的边分别是,,a b c ,若 .(1)求角B ;(2)若2b =,且ABCABC 的周长.4.记ABC 的内角A ,B ,C 所对的边分别是a ,b ,c .已知22cos cos 1c B b C bc b c ++=+.(1)求角A 的大小;(2)若点D 在边BC 上,AD 平分BAC ∠,2AD =,且2b c =,求a .5.已知ABC 的内角,,A B C 的对边分别为,,a b c ,)2222sin ab C b c a =+-. (1)求A ;(2)若34b c =,且a b +=ABC 的面积. 所以ABC 的面积。
正弦定理和余弦定理

正弦定理和余弦定理1. 正弦定理:a sinA =b sinB =csinC =2R(其中R 为△ABC 外接圆的半径).2. 余弦定理a 2=b 2+c 2-2bccosA ,b 2=a 2+c 2-2accosB ;c 2=a 2+b 2-2abcosC 或cosA =b 2+c 2-a 22bc,cosB =a 2+c 2-b 22ac ,cosC =a 2+b 2-c 22ab.3. 三角形中的常见结论 (1) A +B +C =π.(2) 在三角形中大边对大角,大角对大边:A>B a>b sinA>sinB. (3) 任意两边之和大于第三边,任意两边之差小于第三边. (4) △ABC 的面积公式① S =12a ·h(h 表示a 边上的高);② S =12absinC =12acsinB =12bcsinA =abc4R ;③ S =12r(a +b +c)(r 为内切圆半径);④ S =P (P -a )(P -b )(P -c ),其中P =12(a +b +c).例题解析题型1 正弦定理解三角形例1 在△ABC 中,a =3,b =2,B =45°.求角A 、C 和边c. 解:由正弦定理,得a sinA =b sinB ,即3sinA =2sin45°, ∴ sinA =32. ∵ a>b ,∴ A =60°或A =120°.当A =60°时,C =180°-45°-60°=75°,c =bsinCsinB =6+22;当A =120°时,C =180°-45°-120°=15°,c =bsinCsinB =6-22.变式训练在△ABC 中,(1) 若a =4,B =30°,C =105°,则b =________.(2) 若b =3,c =2,C =45°,则a =________.(3) 若AB =3,BC =6,C =30°,则∠A =________. 答案:(1) 22 (2) 无解 (3) 45°或135°解析:(1) 已知两角和一边只有一解,由∠B =30°,∠C =105°,得∠A =45°.由正弦定理,得b =asinB sinA =4sin30°sin45°=2 2.(2) 由正弦定理得sinB =bsinC C =32>1,∴ 无解.(3) 由正弦定理BC sinA =AB sinC ,得6sinA =312,∴ sinA =22.∵ BC>AB ,∴ A>C ,∴ ∠A =45°或135°. 题型2 余弦定理解三角形例2 在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且cosB cosC =-b2a +c .(1) 求角B 的大小;(2) 若b =13,a +c =4,求△ABC 的面积. 解:(1) 由余弦定理知:cosB =a 2+c 2-b 22ac ,cosC =a 2+b 2-c 22ab .将上式代入cosB cosC =-b 2a +c ,得a 2+c 2-b 22ac ·2ab a 2+b 2-c 2=-b 2a +c, 整理得a 2+c 2-b 2=-ac.∴ cosB =a 2+c 2-b 22ac =-ac 2ac =-12.∵ B 为三角形的内角,∴ B =23π.(2) 将b =13,a +c =4,B =23π代入b 2=a 2+c 2-2accosB ,得b 2=(a +c)2-2ac -2accosB ,∴ 13=16-2ac ⎝⎛⎭⎫1-12,∴ ac =3. ∴ S △ABC =12acsinB =334.例3(2014·南京期末)在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,已知c =2,C =π3. (1) 若△ABC 的面积等于3,求a 、b ;(2) 若sinC +sin(B -A)=2sin2A ,求△ABC 的面积. 解:(1) 由余弦定理及已知条件,得a 2+b 2-ab =4. 因为△ABC 的面积等于3,所以12absinC =3,得ab =4.联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,ab =4, 解得a =2,b =2.(2) 由题意得sin(B +A)+sin(B -A)=4sinAcosA ,所以sinBcosA =2sinAcosA. 当cosA =0时,A =π2,所以B =π6,所以a =433,b =233.当cosA ≠0时,得sinB =2sinA ,由正弦定理得b =2a ,联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,b =2a , 解得a =233,b =433.所以△ABC 的面积S =12absinC =233.题型3 三角形形状的判定例4 在△ABC 中,a 、b 、c 分别表示三个内角∠A 、∠B 、∠C 的对边,如果(a 2+b 2)sin(A -B)=(a 2-b 2)sin(A +B),判断三角形的形状.解:已知等式可化为a 2[sin(A -B)-sin(A +B)]= b 2[-sin(A +B)-sin(A -B)], ∴ 2a 2cosAsinB =2b 2cosBsinA.由正弦定理得sin 2AcosAsinB =sin 2BcosBsinA , ∴ sinAsinB(sinAcosA -sinBcosB)=0,∴ sin2A =sin2B.由0<2A<2π,0<2B<2π得2A =2B 或2A =π-2B ,即△ABC 为等腰或直角三角形.例5已知△ABC 中,b·cosC c ·cosB =1+cos2C1+cos2B ,试判断△ABC 的形状.解:由已知,得1+cos2C 1+cos2B =2cos 2C 2cos 2B =cos 2C cos 2B =b·cosCc ·cosB , ∴cosC cosB =bc. 由正弦定理知b c =sinB sinC ,∴ sinB sinC =cosCcosB .∴ sinCcosC =sinBcosB ,即sin2C =sin2B ,因为∠B 、∠C 均为△ABC 的内角.所以2∠C =2∠B 或2∠C +2∠B =180°,所以∠B =∠C或∠B +∠C =90°,故三角形为等腰或直角三角形.题型4 正弦定理、余弦定理的综合应用 例6 在△ABC 中,A 、B 、C 所对的边分别是a 、b 、c ,且bcosB 是acosC 、ccosA 的等差中项.(1) 求B 的大小; (2) 若a +c =10,b =2,求△ABC 的面积.解:(1) 由题意,得acosC +ccosA =2bcosB.由正弦定理,得sinAcosC +cosAsinC =2sinBcosB ,即sin(A +C)=2sinBcosB.∵ A +C =π-B ,0<B <π, ∴ sin(A +C)=sinB ≠0. ∴ cosB =12,∴ B =π3.(2) 由B =π3,得a 2+c 2-b 22ac =12,即(a +c )2-2ac -b 22ac =12,∴ ac =2.∴ S △ABC =12acsinB =32.1. (2013·安徽)设△ABC 的内角A 、B 、C 所对边的长分别为a 、b 、c ,若b +c =2a ,3sinA=5sinB ,则角C =________.2. (2013·贵州)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,已知b =2,B =π6,C =π4,则△ABC 的面积为________. 3. (2013·盐城期末)在△ABC 中,若9cos2A -4cos2B =5,则BCAC=________.4. 已知△ABC 中,∠B =45°,AC =4,则△ABC 面积的最大值为________.5. (2014·南通一模)在△ABC 中,a 、b 、c 分别为角A 、B 、C 所对的边,且c =-3bcosA ,tanC =34.(1) 求tanB 的值;(2) 若c =2,求△ABC 的面积.6、 (2014·苏州期末)在△ABC 中,设角A 、B 、C 的对边分别为a 、b 、c ,且acosC +12c =b.(1) 求角A 的大小;(2) 若a =15,b =4,求边c 的大小.7. 在△ABC 中,∠A 、∠B 、∠C 所对的边长分别是a 、b 、c. (1) 若c =2,C =π3,且△ABC 的面积为3,求a 、b 的值;(2) 若sinC +sin(B -A)=sin2A ,试判断△ABC 的形状.8. 在△ABC 中,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,若a =1,b =2,cosC =14.求:(1) △ABC 的周长; (2) cos(A -C)的值.1、答案:2π3解析:根据正弦定理,3sinA =5sinB 可化为3a =5b ,又b +c =2a ,解得b =3a 5,c =7a5.令a =5t(t>0),则b =3t ,c =7t ,在△ABC 中,由余弦定理得cosC =a 2+b 2-c 22ab =25t 2+9t 2-49t 22×5t ×3t =-12,所以C =2π3.2、答案:3+1解析:∵ b =2,B =π6,C =π4,∴ 由正弦定理得b sin π6=c sin π4,解得c =2 2.又A=π-(B +C)=7π12,S △ABC =12bcsinA =12×2×22×6+24=3+1.3、答案:23解析:由9cos2A -4cos2B =5,得9(1-2sin 2A)=5+4(1-2sin 2B),得9sin 2A =4sin 2B ,即3sinA =2sinB.由正弦定理得BC AC =sinA sinB =23.4、答案:4+42解析:AC 2=AB 2+BC 2-2AB·BC·cos45°,即16=c 2+a 2-2ac·cos45°, 则有2ac -2ac·cos45°≤16, 即ac ≤81-cos45°=16(2+2)2=8(2+2).S max =12acsin45°=24×8(2+2)=4+4 2.5、(1) 由正弦定理,得sinC =-3sinBcosA ,即sin(A +B)=-3sinBcosA.所以sinAcosB +cosAsinB =-3sinBcosA.从而sinAcosB =-4sinBcosA.因为cosAcosB ≠0,所以tanAtanB=-4. 又tanC =-tan(A +B)=tanA +tanB tanAtanB -1,由(1)知,3tanB 4tan 2B +1=34,解得tanB =12. (2) 由(1),得sinA =25,sinB =15,sinC =35.由正弦定理,得a =csinAsinC =2×2535=453.所以△ABC 的面积为12acsinB =12×453×2×15=43.6、(1) 用正弦定理,由acosC +12c =b ,得sinAcosC +12sinC =sinB.∵ sinB =sin (A +C)=sinAcosC +cosAsinC , ∴ 12sinC =cosAsinC. ∵ sinC ≠0,∴ cosA =12.∵ 0<A<π,∴ A =π3.(2) 用余弦定理,得a 2=b 2+c 2-2bccosA. ∵ a =15,b =4, ∴ 15=16+c 2-2×4×c ×12.即c 2-4c +1=0. 则c =2±3.7、(1) ∵ c =2,C =π3,∴ 由余弦定理c 2=a 2+b 2-2abcosC ,得a 2+b 2-ab =4.又△ABC的面积为3,∴ 12absinC =3,即ab =4.联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,ab =4, 解得a =2,b =2.(2) 由sinC +sin(B -A)=sin2A ,得sin(A +B)+sin(B -A)=2sinAcosA ,即2sinBcosA =2sinAcosA ,∴ cosA ·(sinA -sinB)=0,∴ cosA =0或sinA -sinB =0.当cosA =0时,∵ 0<A <π,∴ A =π2,△ABC 为直角三角形;当sinA -sinB =0时,得sinB =sinA ,由正弦定理得a =b ,即△ABC 为等腰三角形.∴ △ABC 为等腰三角形或直角三角形.8、(1) 因为c 2=a 2+b 2-2abcosC =1+4-4×14=4.所以c =2.所以△ABC 的周长为a +b +c =1+2+2=5. (2) 因为cosC =14,所以sinC =1-cos 2C =1-⎝⎛⎭⎫142=154.所以sinA =asinCc =1542=158. 因为a <c ,所以A <C ,故A 为锐角, 所以cosA =1-sin 2A =1-⎝⎛⎭⎫1582=78. 所以cos(A -C)=cosAcosC +sinAsinC =78×14+158×154=1116.。
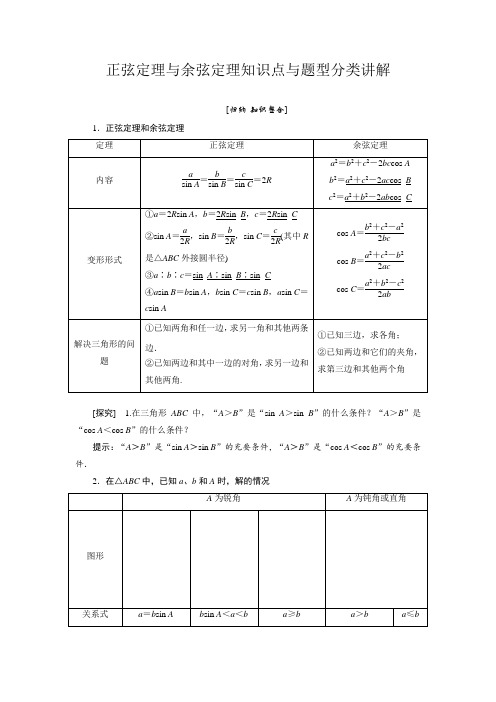
正弦定理与余弦定理知识点与题型分类讲解
正弦定理与余弦定理知识点与题型分类讲解[归纳·知识整合]1.正弦定理和余弦定理[探究] 1.在三角形ABC中,“A>B”是“sin A>sin B”的什么条件?“A>B”是“cos A<cos B”的什么条件?提示:“A>B”是“sin A>sin B”的充要条件,“A>B”是“cos A<cos B”的充要条件.2.在△ABC中,已知a、b和A时,解的情况[探究] 2.如何利用余弦定理判定三角形的形状?(以角A为例)提示:∵cos A与b2+c2-a2同号,∴当b 2+c 2-a 2>0时,角A 为锐角,若可判定其他两角也为锐角,则三角形为锐角三角形;当b 2+c 2-a 2=0时,角A 为直角,三角形为直角三角形; 当b 2+c 2-a 2<0时,角A 为钝角,三角形为钝角三角形.[自测·牛刀小试]1.(教材习题改编)在△ABC 中,若a =2,c =4,B =60°,则b 等于( ) A .23 B .12 C .27D .28解析:选A 由余弦定理得b 2=a 2+c 2-2ac cos B , 即b 2=4+16-8=12,所以b =2 3.2.(教材习题改编)在△ABC 中,a =15,b =10,A =60°,则cos B 等于( ) A .-223B.223 C .-63D.63解析:选D ∵a sin A =b sin B ,∴15sin 60°=10sin B ,∴sin B =23×32=33.又∵a >b ,A =60°, ∴B <60°,∴cos B =1-sin 2B =63. 3.△ABC 中,a =5,b =3,sin B =22,则符合条件的三角形有( ) A .1个 B .2个 C .3个D .0个解析:选B ∵a sin B =102,∴a sin B <b =3<a =5, ∴符合条件的三角形有2个.4.在△ABC 中,a =32,b =23,cos C =13,则△ABC 的面积为________.解析:∵cos C =13,∴sin C =223,∴S △ABC =12ab sin C =12×32×23×223=4 3.答案:4 35.在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c .若b =2a sin B ,则角A 的大小为________.解析:由正弦定理得sin B =2sin A sin B ,∵sin B ≠0, ∴sin A =12,∴A =30°或A =150°.答案:30°或150°[例1] (2012·浙江高考)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且b sin A =3a cos B .(1)求角B 的大小;(2)若b =3,sin C =2sin A ,求a ,c 的值. [自主解答] (1)由b sin A =3a cos B 及正弦定理 a sin A =bsin B,得sin B =3cos B , 所以tan B =3,所以B =π3.(2)由sin C =2sin A 及a sin A =csin C ,得c =2a .由b =3及余弦定理b 2=a 2+c 2-2ac cos B , 得9=a 2+c 2-ac . 所以a =3,c =2 3. ———————————————————正、余弦定理的选用原则解三角形时,有时可用正弦定理,也可用余弦定理,应注意用哪一个定理更方便、简捷.在解题时,还要根据所给的条件,利用正弦定理或余弦定理合理地实施边和角的相互转化.1.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知cos A -2cos C cos B =2c -a b .(1)求sin Csin A的值; (2)若cos B =14,△ABC 的周长为5,求b 的长.解:(1)由正弦定理,设a sin A =b sin B =c sin C=k ,则2c -a b =2k sin C -k sin A k sin B =2sin C -sin Asin B, 所以cos A -2cos C cos B =2sin C -sin A sin B,即(cos A -2cos C )sin B =(2sin C -sin A )cos B , 化简可得sin(A +B )=2sin(B +C ). 又因为A +B +C =π,所以sin C =2sin A . 因此sin Csin A =2.(2)由sin Csin A=2得c =2a . 由余弦定理及cos B =14得b 2=a 2+c 2-2ac cos B =a 2+4a 2-4a 2×14=4a 2.所以b =2a .又a +b +c =5,从而a =1.因此b =2.[例2] 在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)·sin(A +B ),试判断△ABC 的形状. [自主解答] ∵(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ), ∴b 2[sin(A +B )+sin(A -B )]= a 2[sin(A +B )-sin(A -B )], ∴2sin A cos B ·b 2=2cos A sin B ·a 2, 即a 2cos A sin B =b 2sin A cos B .法一:由正弦定理知a =2R sin A ,b =2R sin B , ∴sin 2A cos A sin B =sin 2B sin A cos B , 又sin A ·sin B ≠0,∴sin A cos A =sin B cos B , ∴sin 2A =sin 2B .在△ABC 中,0<2A <2π,0<2B <2π, ∴2A =2B 或2A =π-2B ,∴A =B 或A +B =π2.∴△ABC 为等腰或直角三角形. 法二:由正弦定理、余弦定理得: a 2b b 2+c 2-a 22bc =b 2a a 2+c 2-b 22ac,∴a 2(b 2+c 2-a 2)=b 2(a 2+c 2-b 2),∴(a 2-b 2)(a 2+b 2-c 2)=0, ∴a 2-b 2=0或a 2+b 2-c 2=0. 即a =b 或a 2+b 2=c 2.∴△ABC 为等腰或直角三角形.若将条件改为“sin B =cos A sin C ”,试判断△ABC 的形状. 解:∵sin B =cos A ·sin C , ∴b =b 2+c 2-a 22bc ·c ,即b 2+a 2=c 2,∴△ABC 为直角三角形.———————————————————1.三角形形状的判断思路判断三角形的形状,就是利用正、余弦定理等进行代换、转化,寻求边与边或角与角之间的数量关系,从而作出正确判断.(1)边与边的关系主要看是否有等边,是否符合勾股定理等; (2)角与角的关系主要是看是否有等角,有无直角或钝角等. 2.判定三角形形状的两种常用途径①通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断;②利用正弦定理、余弦定理,化角为边,通过代数恒等变换,求出三条边之间的关系进行判断.2.在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b -c )sin B +(2c -b )sin C .(1)求角A 的大小;(2)若sin B +sin C =3,试判断△ABC 的形状. 解:∵2a sin A =(2b -c )sin B +(2c -b )sin C , 得2a 2=(2b -c )b +(2c -b )c ,即bc =b 2+c 2-a 2, ∴cos A =b 2+c 2-a 22bc =12,∴A =60°.(2)∵A +B +C =180°, ∴B +C =180°-60°=120°.由sin B +sin C =3,得sin B +sin(120°-B )=3,∴sin B +sin 120°cos B -cos 120°sin B = 3. ∴32sin B +32cos B =3,即sin(B +30°)=1. 又∵0°<B <120°,30°<B +30°<150°, ∴B +30°=90°,即B =60°.∴A =B =C =60°,∴△ABC 为正三角形.[例3] (2012·山东高考)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知sin B (tan A +tan C )=tan A tan C .(1)求证:a ,b ,c 成等比数列; (2)若a =1,c =2,求△ABC 的面积S .[自主解答] (1)证明:在△ABC 中,由于sin B (tan A +tan C )=tan A tan C , 所以sin B ⎝⎛⎭⎫sin A cos A +sin C cos C =sin A cos A ·sin C cos C , 因此sin B (sin A cos C +cos A sin C )=sin A sin C , 所以sin B sin(A +C )=sin A sin C . 又A +B +C =π,所以sin(A +C )=sin B ,因此sin 2B =sin A sin C . 由正弦定理得b 2=ac , 即a ,b ,c 成等比数列.(2)因为a =1,c =2,所以b =2,由余弦定理得cos B =a 2+c 2-b 22ac =12+22-22×1×2=34,因为0<B <π,所以sin B =1-cos 2B =74, 故△ABC 的面积S =12ac sin B =12×1×2×74=74.———————————————————三角形面积公式的应用原则(1)对于面积公式S =12ab sin C =12ac sin B =12bc sin A ,一般是已知哪一个角就使用哪一个公式.(2)与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化.3.(2012·新课标全国卷)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a cos C +3a sin C -b -c =0.(1)求A ;(2)若a =2,△ABC 的面积为3,求b ,c .解:(1)由a cos C +3a sin C -b -c =0及正弦定理得 sin A cos C +3sin A sin C -sin B -sin C =0. 因为B =π-A -C ,所以3sin A sin C -cos A sin C -sin C =0. 由于sin C ≠0,所以sin ⎝⎛⎭⎫A -π6=12. 又0<A <π,故A =π3.(2)△ABC 的面积S =12bc sin A =3,故bc =4.而a 2=b 2+c 2-2bc cos A ,故b 2+c 2=8. 解得b =c =2.1条规律——三角形中的边角关系在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC 中,A >B ⇔a >b ⇔sin A >sin B .2个原则——选用正弦定理或余弦定理的原则在解有关三角形的题目时,要有意识地考虑用哪个定理更适合,或是两个定理都要用,要抓住能够利用某个定理的信息.一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.2种途径——判断三角形形状的途径根据所给条件确定三角形的形状,主要有两种途径:(1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角转换. 2个防范——解三角形应注意的问题(1)在利用正弦定理解已知三角形的两边和其中一边的对角求另一边的对角,进而求出其他的边和角时,有时可能出现一解、两解或无解,所以要进行分类讨论.(2)在判断三角形形状时,等式两边一般不要约去公因式,应移项提取公因式,以免漏解.答题模板——利用正、余弦定理解三角形[典例] (2012·江西高考)(本小题满分12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知A =π4,b sin ⎝⎛⎭⎫π4+C -c sin ⎝⎛⎭⎫π4+B =a . (1)求证:B -C =π2;(2)若a =2,求△ABC 的面积.[快速规范审题]第(1)问1.审条件,挖解题信息观察条件:A =π4,b sin ⎝⎛⎭⎫π4+C -c sin ⎝⎛⎭⎫π4+B =a ――――――――→数式中既有边又有角,应统一sin B sin ⎝⎛⎭⎫π4+C -sin C sin ⎝⎛⎭⎫π4+B =sin A . 2.审结论,明确解题方向 观察所求结论:求证:B -C =π2――――――――――→应求角B -C 的某一个三角函数值sin(B -C )=1或cos(B -C )=0.3.建联系,找解题突破口考虑到所求的结论只含有B ,C ,因此应消掉sin B ·sin ⎝⎛⎭⎫π4+C -sin C sin ⎝⎛⎭⎫π4+B =sin A 中的角A =4π借助−−−−→A sin B sin ⎝⎛⎭⎫π4+C -sin C sin ⎝⎛⎭⎫π4+B =22――――――――――→利用两角和与差的三角函数公式sin(B -C )=1―――――――――――→要求角的值,还应确定角的取值范围由0<B ,C <3π4,解得B -C =π2. 第(2)问1.审条件,挖解题信息观察条件:a =2,A =π4,B -C =π2―――――――→可求B ,C 的值 B =5π8,C =π8. 2.审结论,明确解题方向观察所求结论:求△ABC 的面积――――――→应具有两边及其夹角由a sin A =b sin B =c sin C ,得b =2sin 5π8,c =2sin π8.3.建联系,找解题突破口△ABC 的边角都具备―――――→利用面积公式求结论S =12bc sin A = 2sin 5π8sin π8=2cos π8sin π8=12. [准确规范答题](1)证明:由b sin ⎝⎛⎭⎫π4+C -c sin ⎝⎛⎭⎫π4+B =a ,应用正弦定理,得sin B sin ⎝⎛⎭⎫π4+C -sin C sin ⎝⎛⎭⎫π4+B =sin A ,sin B ⎝⎛⎭⎫22sin C +22cos C -sin C 22sin B +22cos B =22,⇨(3分) 整理得sin B cos C -cos B sin C =1, 即sin(B -C )=1,⇨(5分) 由于0<B ,C <34π,从而B -C =π2.⇨(6分)(2)B +C =π-A =3π4,因此B =5π8,C =π8.⇨(8分)由a =2,A =π4,得b =a sin B sin A =2sin 5π8,c =a sin C sin A =2sin π8,⇨(10分)所以△ABC 的面积S =12bc sin A =2sin 5π8sin π8=2cos π8sin π8=12.⇨(12分)[答题模板速成]解决解三角形问题一般可用以下几步解答:⇒⇒一、选择题(本大题共6小题,每小题5分,共30分)1.(2012·上海高考)在△ABC 中,若sin 2A +sin 2B <sin 2C ,则△ABC 的形状是( ) A .钝角三角形 B .直角三角形 C .锐角三角形D .不能确定解析:选A 由正弦定理得a 2+b 2<c 2,故cos C =a 2+b 2-c 22ab<0,所以C 为钝角.2.(2012·广东高考)在△ABC 中,若∠A =60°,∠B =45°,BC =32,则AC =( ) A .4 3 B .2 3 C. 3D.32解析:选B 由正弦定理得:BC sin A =AC sin B ,即32sin 60°=AC sin 45°,所以AC =3232×22=2 3.3.在△ABC 中,AC =7,BC =2,B =60°,则BC 边上的高等于( ) A.32 B.332 C.3+62D.3+394解析:选B 由余弦定理得:(7)2=22+AB 2-2×2AB ·cos 60°,即AB 2-2AB -3=0,得AB =3,故BC 边上的高是AB sin 60°=332. 4.在△ABC 中 ,角A ,B ,C 所对边的长分别为a ,b ,c ,若a 2+b 2=2c 2,则cos C 的最小值为( )A.32B.22C.12 D .-12解析:选C 由余弦定理得a 2+b 2-c 2=2ab cos C ,又c 2=12(a 2+b 2),得2ab cos C =12(a 2+b 2),即cos C =a 2+b 24ab ≥2ab 4ab =12.5.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,已知8b =5c ,C =2B ,则cos C =( )A.725 B .-725C .±725D.2425解析:选A 由C =2B 得sin C =sin 2B =2sin B cos B ,由正弦定理及8b =5c 得cos B =sin C 2 sin B =c 2b =45,所以cos C =cos 2B =2cos 2 B -1=2×⎝⎛⎭⎫452-1=725. 6.在△ABC 中,AB =3,AC =1,B =30°,则△ABC 的面积等于( ) A.32B.34C.32或 3 D.32或34解析:选D 依题意与正弦定理得AB sin C =AC sin B ,sin C =AB ·sin B AC =32,C =60°或C =120°.当C =60°时,A =90°,△ABC 的面积等于12AB ·AC =32;当C =120°时,A =30°,△ABC 的面积等于12AB ·AC ·sin A =34.因此,△ABC 的面积等于32或34.二、填空题(本大题共3小题,每小题5分,共15分)7.(2012·福建高考)已知△ABC 的三边长成公比为2的等比数列,则其最大角的余弦值为________.解析:依题意得,△ABC 的三边长分别为a ,2a,2a (a >0),则最大边2a 所对的角的余弦值为a 2+(2a )2-(2a )22a ·2a=-24.答案:-248.(2013·佛山模拟)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且cos A =35,cosB =513,b =3,则c =________.解析:由题意知sin A =45,sin B =1213,则sin C =sin(A +B )=sin A cos B +cos A sin B =5665,所以c =b sin C sin B =145.答案:1459.在△ABC 中,D 为边BC 的中点,AB =2,AC =1,∠BAD =30°,则AD 的长度为________.解析:延长AD 到M ,使得DM =AD ,连接BM 、MC ,则四边形ABMC 是平行四边形.在△ABM 中,由余弦定理得BM 2=AB 2+AM 2-2AB ·AM ·cos ∠BAM ,即12=22+AM 2-2·2·AM ·cos 30°,解得AM =3,所以AD =32. 答案:32三、解答题(本大题共3小题,每小题12分,共36分)10.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,已知cos(A -C )+cos B =1,a =2c ,求C .解:由B =π-(A +C ),得cos B =-cos(A +C ).于是cos(A -C )+cos B =cos(A -C )-cos(A +C )=2sin A sin C , 由已知得sin A sin C =12.①由a =2c 及正弦定理得sin A =2sin C .② 由①②得sin 2C =14,于是sin C =-12(舍去),或sin C =12.又a =2c ,所以C =π6.11.(2012·江苏高考)在△ABC 中,已知AB ·AC =3BA ·BC . (1)求证:tan B =3tan A ; (2)若cos C =55,求A 的值. 解:(1)因为AB ·AC =3BA ·BC ,所以AB ·AC ·cos A =3BA ·BC ·cos B ,即AC ·cos A =3BC ·cos B ,由正弦定理知AC sin B =BCsin A,从而sin B cos A =3sin A cos B ,又因为0<A +B <π,所以cos A >0,cos B >0, 所以tan B =3tan A . (2)因为cos C =55,0<C <π, 所以sin C =1-cos 2C =255,从而tan C =2,于是tan[π-(A +B )]=2, 即tan(A +B )=-2,亦即tan A +tan B 1-tan A tan B =-2.由(1)得4tan A 1-3tan 2A =-2,解得tan A =1或-13,因为cos A >0,故tan A =1,所以A =π4.12.(2012·浙江高考)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B =5cos C .(1)求tan C 的值;(2)若a =2,求△ABC 的面积.解:(1)因为0<A <π,cos A =23,得sin A =1-cos 2A =53.又5cos C =sin B =sin (A +C ) =sin A cos C +cos A sin C =53cos C +23sin C . 所以tan C = 5.(2)由tan C =5,得sin C =56,cos C =16. 于是sin B =5cos C =56. 由a =2及正弦定理a sin A =csin C ,得c = 3.设△ABC 的面积为S ,则S =12ac sin B =52.1.若△ABC 的内角A 、B 、C 所对的边a 、b 、c 满足(a +b )2-c 2=4,且C =60°,则ab 的值为( )A.43 B .8-4 3 C .1D.23解析:选A 由(a +b )2-c 2=4, 得a 2+b 2-c 2+2ab =4.① 由余弦定理得a 2+b 2-c 2=2ab cos C =2ab cos 60°=ab ,② 将②代入①得ab +2ab =4,即ab =43.2.若△ABC 的内角A ,B ,C 满足6sin A =4sin B =3sin C ,则cos B =( ) A.154B.34C.31516D.1116 解析:选D 依题意,结合正弦定理得6a =4b =3c ,设3c =12k (k >0),则有a =2k ,b =3k ,c =4k ,由余弦定理得cos B =a 2+c 2-b 22ac =(2k )2+(4k )2-(3k )22×2k ×4k=1116.3.在△ABC 中,sin 2A ≤sin 2B +sin 2C -sin B ·sin C ,则A 的取值范围是( )A.⎝⎛⎦⎤0,π6B.⎣⎡⎭⎫π6,π C.⎝⎛⎦⎤0,π3 D.⎣⎡⎭⎫π3,π解析:选C 由已知及正弦定理,有a 2≤b 2+c 2-bc .而由余弦定理可知,a 2=b 2+c 2-2bc cos A ,于是b 2+c 2-2bc cos A ≤b 2+c 2-bc ,可得cos A ≥12.注意到在△ABC 中,0<A <π,故A ∈⎝⎛⎦⎤0,π3. 4.已知A 、B 、C 为△ABC 的三个内角,其所对的边分别为a 、b 、c ,且2cos 2A2+cos A=0.(1)求角A 的值;(2)若a =23,b +c =4,求△ABC 的面积.解:(1)由2cos 2A2+cos A =0,得1+cos A +cos A =0,即cos A =-12,∵0<A <π,∴A =2π3.(2)由余弦定理得,a 2=b 2+c 2-2bc cos A ,A =2π3,则a 2=(b +c )2-bc ,又a =23,b +c =4, 有12=42-bc ,则bc =4, 故S △ABC =12bc sin A = 3.。
正余弦定理知识点及题型归纳

解三角形 一.正弦定理:A a sin =B bsin =C c sin =2R ,其中R 是三角形外接圆半径.正弦定理的如下变形常在解题中用到 1.(1) a=2RsinA (2) b=2RsinB (3) c=2RsinC 2.(1) sinA=a/2R (2) sinB=b/2R (3) sinC=c/2R 3.a :b :c=sinA :sinB:sinC二.余弦定理:1. a^2 = b^2 + c^2 - 2·b ·c ·cosA2. b^2 = a^2 + c^2 - 2·a ·c ·cosB3. c^2 = a^2 + b^2 - 2·a ·b ·cosC 余弦定理的如下变形常在解题中用到1. cosC = (a^2 + b^2 - c^2) / (2·a ·b)2. cosB = (a^2 + c^2 - b^2) / (2·a ·c)3. cosA = (c^2 + b^2 - a^2) / (2·b ·c ) 三.余弦定理和正弦定理的面积公式S △ABC =21absinC=21bcsinA=21acsinB(常用类型:已知三角形两边及其夹角)判断三角形的形状有两种途径:(1)将已知的条件统一化成边的关系,用代数求和法求解(2)将已知的条件统一化成角的关系,用三角函数法求解三.解三角形的实际应用测量中相关的名称术语仰角:视线在水平线以上时,在视线所在的垂直平面内,视线与水平线所成的角叫做仰角。
俯角:视线在水平线以下时,在视线所在的垂直平面内,视线与水平线所成的角叫俯角方向角:从指定方向线到目标方向的水平角(一)已知两角及一边解三角形例1已知在△ABC中,c=10,A=45°,C=30°,求a、b和B.(二)已知两边和其中一边对角解三角形例2在△ABC中,已知角A,B,C所对的边分别为a,b,C,若a=2√3,b =√6,A=45°,求边长C(三)已知两边及夹角,解三角形例3△ABC中,已知b=3,c=33,B=30°,求角A,角C和边a.例四:在△ABC中,若∠B=30°, AB=2, AC=2, 则△ABC的面积是例五.判断三角形的形状(1)正弦定理判断在△ABC中,若a2tan B=b2tan A,试判断△ABC的形状.(2)余弦定理判断在△ABC 中,若b 2sin 2C +c 2sin 2B =2bc cos B cos C ,试判断三角形的形状.例六 判断解得个数不解三角形,判断下列三角形的解的个数: (1)a=5,b=4,A=120度(2)a=7,b=14,A=150度(3)a=9,b=10,A=60度(4)c=50,b=72,C=135度考试类型一、求解斜三角形中的基本元素指已知两边一角(或二角一边或三边),求其它三个元素问题,进而求出三角形的三线(高线、角平分线、中线)及周长等基本问题. 1、ABC ∆中,3π=A ,BC =3,则ABC ∆的周长为( )A .33sin 34+⎪⎭⎫⎝⎛+πB B .36sin 34+⎪⎭⎫ ⎝⎛+πB C .33sin 6+⎪⎭⎫ ⎝⎛+πB D .36sin 6+⎪⎭⎫⎝⎛+πB2、 在ΔABC 中,已知66cos ,364==B AB ,AC 边上的中线BD =5,求sin A 的值. 3、在△ABC 中,角A ,B ,C 所对的边长分别为a ,b ,c ,若∠C=120°,c=2a ,则 A.a >b B.a <b C. a =b D.a 与b 的大小关系不能确定 4、在△ABC 中,内角A,B,C 的对边分别是a,b,c ,若223a b bc -=,sin 23sin C B =,则A=(A )030 (B )060 (C )0120 (D )0150 5、在ABC ∆中,a=15,b=10,A=60°,则cos B = A -223 B 223C -63D 636、在△ABC 中,若b = 1,c =3,23C π∠=,则a = 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦定理和余弦定理
一、题型归纳
<一>利用正余弦定理解三角形
【例1】在△ABC 中,已知a =3,b =2,B=45°,求A 、C 和c .
】
【例2】设ABC ∆的内角A 、B 、C 的对边长分别为a 、b 、c ,且32b +32c -32a 2b c .
(Ⅰ) 求sinA 的值; (Ⅱ)求2sin()sin()
44
1cos 2A B C A ππ
+++-的
值.
【练习1】 (2011·北京)在△ABC 中,若b =5,∠B =π
4,tan A =2,
则sin A =________;a =________.
【练习2】在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且
cos B
cos C
=-b 2a +c
.
—
(1)求角B 的大小;
(2)若b =13,a +c =4,求△ABC 的面积.
[
<二>利用正余弦定理判断三角形的形状
【例3】1、在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)sin C ,试判断△ABC
的形状.
2、在△ABC 中,在ABC ∆中,a,b,c 分别是角A 、B 、C 所对的边,bcosA =a cosB ,则ABC ∆三角形的形状为__________________
3、在△ABC 中,在ABC ∆中,a,b,c 分别是角A 、B 、C 所对的边,若cosA
cosB
=b a
, 则ABC ∆三角形的形状为___________________ *
【练习】1、在△ABC 中,2
cos 22A b c c
+=(,,a b c 分别为角,,A B C 的对边),
则△ABC 的形状为( )
A 、正三角形
B 、直角三角形
C 、等腰三角形或直角三角形
D 、等腰直角三角形
2、已知关于x 的方程2
2
cos cos 2sin 02
C
x x A B -⋅+=的两根之和等于两根之积的一半,则ABC ∆一定是( )
A 、直角三角形
B 、钝角三角形
C 、等腰三角形
D 、等边三角形
3、在△ABC 中,2222
()sin()()sin()a b A B a b A B +-=-+,则△ABC
的形状为__________
4、在△ABC 中,若a cos A =b cos B =c
cos C ;则△ABC 是( ).
A .直角三角形
B .等边三角形 |
C .钝角三角形
D .等腰直角三角形
<三>正余弦定理与三角形的面积
【例4】△ABC 中,
,,a b c 分别为,,A B C ∠∠∠的对边.如果c a b +=2,B ∠=30°,△ABC 的面积为2
3
,那么b =( )
A 、
B
、
B 、31+ C
、 D 、3
2+
【练习】已知ABC △
1
,且sin sin A B C +=. (1)求边AB 的长; (2)若ABC △的面积为1sin 6
C ,求角C 的度数.
-
【例5】设O 是锐角ABC ∆的外心,若
75=∠C ,且COA BOC AOB ∆∆∆,,的面积满足关系:COA BOC AOB S S S ∆∆∆=+3,求A ∠
{
【练习】已知O 是锐角三角形ABC 的外心,△BOC ,△COA ,△AOB 的面积满足关系:
COA BOC AOB S S S ∆∆∆=+2
(1)
(2)
推算tanAtanC 是否为定值?说明理由;
$
(2)求证:tanA ,tanB ,tanC 也满足关系:B
C A tan 2tan tan =+
<四>利用正余弦定理解决最值问题
【例6】在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,设S 为△ABC 的面积,满足()
222
4
3c b a S -+=
\
(1)求角C 的大小; (2)求sinA+sinB 的最大值.
【练习】1、已知锐角ABC △中,角,,A B C 的对边分别为c b a ,,,且
2
223tan b c a ac
B -+=
;
()
1求B
∠;
()
2求函数
()sin 2sin cos f x x B x =+0,2x π⎛⎫
⎡⎤∈ ⎪⎢⎥⎣
⎦⎝
⎭
的最大值
;
2、设ABC ∆的内角C B A ,,所对的边分别为,,,c b a 且b c C a =+2
1
cos .
(1)求角A 的大小;
(2)若1=a ,求ABC ∆的周长l 的取值范围.
>
<五>正余弦定理与向量的运算
【例
7】已知向量1
(sin ,1),(3cos ,)2
a x
b x =-=-,函数
()()2f x a b a =+⋅-.
(1)求函数()f x 的最小正周期T ;
(2)已知a 、b 、c 分别为ABC ∆内角A 、B 、C 的对边, 其中A 为锐
角,4a c ==,且()1f A =,求,A b 和ABC ∆的面积S .
】
【练习】1、在ABC ∆中,已知3AB AC BA BC =.
(1)求证:tan 3tan B A =; (2)若cos 5
C =,求A 的值.
;
2、在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足cos
25
A =,3A
B A
C ⋅=.
(I )求ABC ∆的面积;
;
(II )若1c =,求a 的值.
二、课后作业:
1、在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.
2、在△ABC 中,C B C B A sin sin 2sin sin sin 2
22++=,则A 等于( )
A 、60°
B 、45°
C 、120
D 、135°
3、若(c b a ++)(a c b —+)=bc 3,且C B A cos sin 2sin =, 那么ΔABC 是_____________.
4、在锐角△ABC 中,BC =1,B =2A ,则AC
cos A
的值等于______,AC 的取值范围为________
5、在ABC ∆中,若135
cos ,53sin ==B A ,则C cos 的值为_________ABC
∆的形状为_____
6、ABC ∆的面积是30,内角,,A B C 所对边长分别为,,a b c ,12
cos 13
A =。
(1)求A
B A
C ⋅。
(2)若1c b -=,求a 的值。
