数学分析三试卷及答案
2019年高考数学全国3卷文理科试卷分析和点评解析

2019年高考数学全国3卷文/理科试卷分析和点评解析10.双曲线 C :1 的右焦点为 F ,点 P 在 C 的一条渐近线上,O 为坐标原点.若4 2|PO |=|PF |,则△PFO 的面积为( )3 2 3 2 A. B.4 2C. 2 2D. 3 2【解析】看到焦点和渐近线,想到双曲线参数的几何意义,即焦点到渐近线的距离为b ,过F 作渐近线的垂线,垂足为 B ,设 POPFx ,a c 2x 2x 2法一:在 Rt OFB 中,有 cos FOB ,在 OFP 中,有 cos FOB,c 2cxc21 c23 2 联立得 x,得 S b 。
2a2 2a 4c 2 c 2法二:等腰直角三角形的高为 b xc x 2,易得 x ,同上。
4 2a【点评】双曲线参数的几何意义多次考查,《解析几何的系统性突破》(唯一正版销售书店)通过高考题反复强化学生认知,从而在一些几何图形中迅速找到隐含 的信息,快速突破。
11.(送分)12. 设函数 f (x )sin(xc 2x 2- 4[)(0) ,已知 f (x )在[0,2π]有且仅有 5 个零点,下述四个结5论:①f (x )在(0,2π)有且仅有 3 个极大值点;②f (x )在(0,2π)有且仅有 2个极小值点;③f (x )在(0, ) 单调递增;④的取值范围是 12 , 29).其中所有正确结论的编号是()105 10A.①④B.②③C.①②③D.①③④【点评 1】肖博老师威信:xbmath19《高观点下全国卷高考压轴题研究三部曲》书中 最后给出了 16 套小练习(搜集最新的各地模拟题),其中第 3 套和第 4 套第 1 题如下: 1.函数 fxcos x 0在区间, 上有且只有两个极值点,则的取值范围是3 4A. 2,3B.2,3C.3, 4D.3, 41.若函数 y2sin x0的图象在区间 (,)上只有一个极值点,则的取值范围3 6为( ))A. 13B.23 32C. 34D.3 92 2法一:还原,则变成同上 2 个题。
华东师大数学分析试卷

华东师大数学分析试卷一、(24分)运算题: 求011lim()ln(1)x x x →-+; 求32cos sin 1cos x x dx x+⎰ 设(,)z z x y =是由方程222(,)0F xyz x y z ++=所确定的可微隐函数,试求gra d z 。
二、(14分)证明:(1)11(1)n n +⎧⎫+⎨⎬⎩⎭为递减数列: (2) 111ln(1),1,21n n n n <+<=+⋅⋅⋅⋅ 一样说来,“教师”概念之形成经历了十分漫长的历史。
杨士勋(唐初学者,四门博士)《春秋谷梁传疏》曰:“师者教人以不及,故谓师为师资也”。
这儿的“师资”,事实上确实是先秦而后历代对教师的别称之一。
《韩非子》也有云:“今有不才之子……师长教之弗为变”其“师长”因此也指教师。
这儿的“师资”和“师长”可称为“教师”概念的雏形,但仍说不上是名副事实上的“教师”,因为“教师”必须要有明确的传授知识的对象和本身明确的职责。
三、(12分)设f(x)在[],a b 中任意两点之间都具有介质性,而且f 在(a ,b )内可导,'()f x K ≤ (K 为正常数),(,)x a b ∈ 证明:f 在点a 右连续,在点b 左连续。
四、(14分)设120(1)n n I x dx =-⎰,证明:五、(12分)设S 为一旋转曲面,它由光滑曲线段绕x 轴曲线旋转而成,试用二重积分运算曲面面积的方法,导出S 的面积公式为:2(b a A f x π=⎰六、(24分)级数问题:事实上,任何一门学科都离不开死记硬背,关键是经历有技巧,“死记”之后会“活用”。
不记住那些基础知识,如何会向高层次进军?专门是语文学科涉猎的范畴专门广,要真正提高学生的写作水平,单靠分析文章的写作技巧是远远不够的,必须从基础知识抓起,每天挤一点时刻让学生“死记”名篇佳句、名言警句,以及丰富的词语、新颖的材料等。
如此,就会在有限的时刻、空间里给学生的脑海里注入无限的内容。
数学分析试卷及答案6套

f ( x1 ) f ( x2 ) .
g ( x) ,x 0 九. (12 分)设 f ( x) x 且 g (0) g (0) 0 , g (0) 3 , 求 f (0) . 0, x 0
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
lim
h 0
1 h
x
a
[ f (t h) f (t )] dt f ( x) f (a).
六 (10 分 ) 求椭圆区域 R : (a1 x b1 y c1 ) 2 (a2 x b2 y c2 ) 2 1 (a1b2 a2b1 0) 的 面积 A . 七 (10 分) 设 F (t ) f ( x 2 y 2 z 2 ) dx dy dz ,其中 V : x 2 y 2 z 2 t 2 (t 0) ,
四. (12 分)证明函数 f ( x)
五. (12 分)叙述闭区间套定理并以此证明闭区间上连续函数必有界. 六. (10 分)证明任一齐次多项式至少存在一个实数零点. 七. (12 分)确定 a, b 使 lim ( x 2 x 1 ax b) 0 .
x
1 5 八. (14 分)求函数 f ( x) 2 x 3 9 x 2 12 x 在 [ , ] 的最大值与最小值. 4 2
x x0
x x0
1 1 . f ( x) b
三. (10 分)设 an 0 ,且 lim
an l 1 , 证明 lim an 0 . n n a n 1
四. (10 分 ) 证 明 函 数 f ( x) 在 开 区 间 ( a, b) 一 致 连 续 f ( x) 在 ( a, b) 连 续 , 且
工科数学分析试卷+答案

工科数学分析试题卷及答案考试形式(闭卷):闭 答题时间:150 (分钟) 本卷面成绩占课程成绩 80 %一、填空题(每题2分,共20分)1.---→xx x x sin 11lim 30 3-2.若⎪⎩⎪⎨⎧=≠-+=0,0,13sin )(2x a x xe x xf ax 在0=x 处连续,则a 3- 3.设01lim 23=⎪⎪⎭⎫⎝⎛--++∞→b ax x x x ,则 =a 1 , =b 0 4.用《δε-》语言叙述函数极限R U ⊂∈=→)(,)(lim 0x x A x f x x 的定义: εδδε)()()(:000A x f x x ∈→∈∀>∍>∀U 5.若当)1(,023+++-→cx bx ax e x x是3x 的高阶无穷小,则=a61=b21=c 1 6.设N ∈=--→n x x x f x f nx x ,1)()()(lim2000,则在0x x =处函数)(x f 取得何种极值? 答: 极小值姓名: 班级: 学号:遵守 考 试 纪 律 注 意 行 为 规 范7.设x x y +=,则dydx x)211(+⋅8.设x x y sin =,则=dy dx xxx x xx)sin ln (cos sin +9.⎰=+dx x x 21arctan C x +2arctan 21 10.⎰=+dx ee xx12 C e e x x ++-)1l n ( 二、选择题:(每题2分,共20分)1.设0,2)1()1l n (2s i n2t a n li m 2222≠+=-+-+-→c a e d x c xb x a x x ,则必有( D )(A )d b 4=;(B )c a 4-=;(C )d b 4-=;(D )c a 2-= 2.设9320:0<<>k x ,则方程112=+x kx 的根的个数为( B )(A )1 ;(B ) 2 ; (C ) 3 ; (D )03.设)(x f 连续,且0)0(>'f ,则存在0>δ使得( A )(A ))(x f 在),0(δ内单增; (B )对),0(δ∈∀x 有)0()(f x f >; (C )对)0,(δ-∈∀有)0()(f x f >; (D ))(x f 在)0,(δ-内单减。
燕山大学数学分析(3)试卷1答案
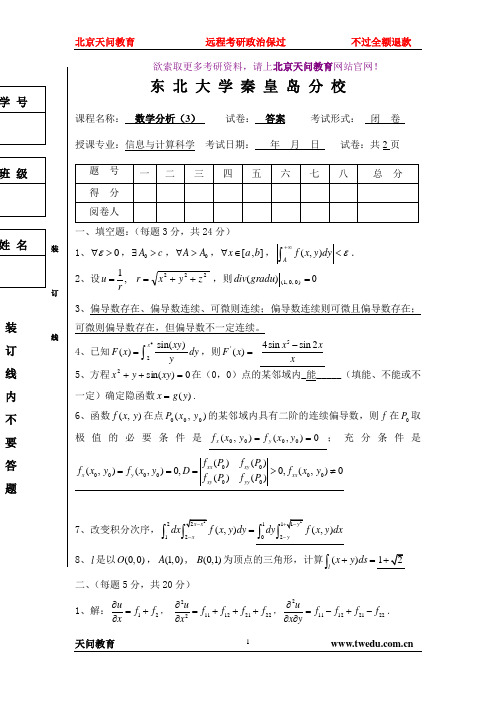
欲索取更多考研资料,请上北京天问教育网站官网! 东 北 大 学秦 皇 岛 分 校课程名称: 数学分析(3) 试卷: 答案 考试形式: 闭 卷授课专业:信息与计算科学 考试日期: 年 月 日 试卷:共2页题 号 一 二 三 四 五 六 七 八 总 分 得 分 阅卷人一、填空题:(每题3分,共24分)1、0ε∀>,0A c ∃>,0A A ∀>,[,]x a b ∀∈,(,)Af x y dy ε+∞<⎰.2、设222,1z y x r ru ++==,则=)0,0,1()(gradu div 03、偏导数存在、偏导数连续、可微则连续;偏导数连续则可微且偏导数存在;可微则偏导数存在,但偏导数不一定连续。
4、已知42sin()()x xy F x dy y=⎰,则=)('x F 54sin sin 2x x x -5、方程0)sin(2=++xy y x 在(0,0)点的某邻域内_能_____(填能、不能或不一定)确定隐函数)(y g x =.6、函数),(y x f 在点),(000y x P 的某邻域内具有二阶的连续偏导数,则f 在0P 取极值的必要条件是0),(),(0000==y x f y x f y x ;充分条件是0000000000()()(,)(,)0,0,(,)0()()xx xy x y xx xy yy f P f P f x y f x y D f x y f P f P ===>≠7、改变积分次序,22212(,)x x xdx f x y dy --=⎰⎰211102(,)y ydy f x y dx +--⎰⎰8、l 是以(0,0)O ,(1,0)A , (0,1)B 为顶点的三角形,计算()lx y ds +=⎰12+二、(每题5分,共20分)1、解:12u f f x ∂=+∂, 2111221222u f f f f x ∂=+++∂,211122122uf f f f x y∂=-+-∂∂. 装订线装 订 线 内 不 要 答 题学 号姓 名班 级2、解:两边取对数,有)1ln(ln xy x z +=,于是z -1xy xy xy x z +++=∂∂1)1ln(,21z x z y xy ∂=∂+ ,故dy xy x dx xy xy xy dz ++⎥⎦⎤⎢⎣⎡+++=11)1ln(23、解:方程两边关于x 求偏导得,1z zyz xyx x∂∂+=+∂∂,于是, 11z yz x xy ∂-=∂-,22(1)z x y z xyzx y xy ∂-++=∂∂- 4、答案:2y P x =,1Q x =-,21Q P x y x ∂∂==∂∂,积分和路径无关。
三年级数学试卷分析与改进【含答案】

三年级数学试卷分析与改进【含答案】专业课原理概述部分一、选择题1. 下列哪个不是数学分析的基本概念?( )A. 极限B. 微分C. 积分D. 对数2. 三角函数中,正弦函数的图像是( )。
A. 振荡上升B. 振荡下降C. 逐渐上升D. 逐渐下降3. 若函数f(x)在点x=a处可导,则f(x)在点x=a处的左导数和右导数( )。
A. 一定相等B. 一定不相等C. 只有在f(x)连续时才相等D. 只有在f(x)单调时才相等4. 设函数f(x)在区间[a, b]上连续,且在(a, b)内可导,则至少存在一点ξ∈(a, b),使得( )。
A. f'(ξ) = 0B. f(ξ) = 0C. f'(ξ) = (b a)D. f'(ξ) = (f(b) f(a))/(b a)5. 下列哪个不是线性方程组的解法?( )A. 高斯消元法B. 克莱姆法则C. 置换法D. 对角线法二、判断题1. 数列的极限存在的充分必要条件是数列单调有界。
( )2. 一元函数的极值点必定是导数为零的点。
( )3. 二重积分可以转化为二次积分进行计算。
( )4. 线性方程组的解法只有高斯消元法。
( )5. 若函数在闭区间上连续,则该函数在该区间上一定存在最大值和最小值。
( )三、填空题1. 若函数f(x)在点x=a处可导,则f(x)在点x=a处的导数定义为______。
2. 数列{an}收敛于a的充分必要条件是对于任意给定的正数______,总存在正整数______,使得当n>N时,都有|an-a|<ε。
3. 微积分基本定理表明,若函数f(x)在区间[a, b]上连续,且在(a, b)内可导,则f(x)在区间[a, b]上的定积分可以表示为______。
4. 线性方程组的解法有高斯消元法、克莱姆法则、______等。
5. 若函数在闭区间上连续,则该函数在该区间上一定存在______和______。
四、简答题1. 请简要说明极限的定义。
小学数学分析试卷

一、选择题(每题2分,共20分)1. 下列哪个数是负数?A. 3B. -5C. 0D. 72. 下列哪个数是偶数?A. 7B. 8C. 9D. 113. 下列哪个数是质数?A. 4B. 5C. 6D. 84. 下列哪个数是两位数?A. 34B. 23C. 19D. 505. 下列哪个数是分数?A. 0.5B. 1.5C. 2.5D. 3.56. 下列哪个图形是正方形?A. 长方形B. 三角形C. 圆形D. 正方形7. 下列哪个图形是平行四边形?A. 长方形B. 三角形C. 圆形D. 正方形8. 下列哪个单位是长度单位?A. 米B. 千克C. 秒D. 升9. 下列哪个单位是质量单位?A. 米B. 千克C. 秒D. 升10. 下列哪个单位是时间单位?A. 米B. 千克C. 秒D. 升二、填空题(每题2分,共20分)11. 5个苹果加上3个苹果,一共有______个苹果。
12. 6减去2等于______。
13. 8乘以4等于______。
14. 9除以3等于______。
15. 2分之1加上3分之2等于______。
16. 7的2倍是______。
17. 100减去20等于______。
18. 5个3加起来等于______。
19. 15除以5等于______。
20. 3分之1减去2分之1等于______。
三、解答题(每题10分,共30分)21. 小明有20元,他买了3支铅笔,每支铅笔2元,还剩多少钱?22. 一桶水有36升,小丽用去了12升,还剩多少升?23. 小红有25个气球,她送给小明10个,小明又送给小丽5个,现在小红还剩多少个气球?四、应用题(每题10分,共20分)24. 小明家离学校有300米,他每天上学要步行,每分钟走50米,他需要多少分钟才能到学校?25. 小华有30个苹果,她要平均分给她的4个好朋友,每个好朋友能分到几个苹果?答案:一、选择题:1. B2. B3. B4. A5. A6. D7. A8. A9. B10. C二、填空题:11. 812. 413. 3214. 315. 5分之216. 1417. 8018. 1519. 320. 1分之1三、解答题:21. 小明买铅笔花费了3×2=6元,所以他剩下20-6=14元。
数学分析三试卷及答案

《数学分析》(三)――参考答案及评分标准一. 计算题(共8题,每题9分,共72分)。
1.求函数11(,)f x y y x =在点(0,0)处的二次极限与二重极限。
解:11(,)f x y y x =+=,因此二重极限为0。
……(4分)因为011x y x →+与011y y x→+均不存在,故二次极限均不存在. ……(9分)2. 设(),()y y x z z x =⎧⎨=⎩ 是由方程组(),(,,)0z xf x y F x y z =+⎧⎨=⎩所确定的隐函数,其中f 和F 分别具有连续的导数和偏导数,求dzdx.解: 对两方程分别关于x 求偏导:, ……(4分). 解此方程组并整理得()()()()y y x y z F f x y xf x y F F dz dx F xf x y F '⋅+++-='++。
……(9分)3. 取,μν为新自变量及(,)w w v μ=为新函数,变换方程222z z zz x x y x ∂∂∂++=∂∂∂∂. 设,,22y x y x y w ze μν+-=== (假设出现的导数皆连续)。
解:z 看成是,x y 的复合函数如下:,(,),,22y w x y x yz w w e μνμν+-====. ……(4分) 代人原方程,并将,,x y z 变换为,,w μν。
整理得:2222w ww μμν∂∂+=∂∂∂. ……(9分)4. 要做一个容积为31m 的有盖圆桶,什么样的尺寸才能使用料最省?解: 设圆桶底面半径为r ,高为h ,则原问题即为:求目标函数在约束条件下的最小值,其中目标函数: 222S rh r ππ=+表,()()(1)0x yz dzdy f x y xf x y dx dx dy dz F F F dx dx ⎧'=++++⎪⎪⎨⎪++=⎪⎩约束条件: 21r h π=。
……(3分) 构造Lagrange 函数:22(,,)22(1)F r h rh r r h λππλπ=++-。
数学分析(3)期中试卷

x 1
.
6
(1)设 M ( x0 , y0 ) 为区域 D 上的一点,问 h( x, y ) 在该点沿平面上什么方向的方向导数最大?若记此方向导数的 最大值为 g ( x0 , y0 ) ,试写出 g ( x0 , y0 ) 表达式. (2)现欲利用此小山开展攀岩活动, 为此需要在山脚寻找一上山坡度最大的点作为攀登的起点.也就是说, 要在 D 的边界线 x y xy 75 上找出使(1)中的 g ( x, y ) 达到最大值的点.试确定攀登起点的位置.
2 z xy
2
五、 (8 分)设 w f ( x, y , z ) , f ( x, y , z ) 具有二阶连续偏导数, z z ( x , y ) 由方程 z 5 xy 5 z 1 所确定。求
5
w 2 w , 2 x x
六、( 8 分 ) 设 N 是 曲 面 z x
2 2
4
九、 (8 分)设椭圆 x 3 y 12 的内接等腰三角形之底边平行于椭圆长轴,应用多元微分方法求其最大面积。
2
2
十、 (8 分)已知 x, y , z 为实数且 e y | z | 3 ,应用多元微分方法证明下列不等式
x
2
ex y 2 | z | 1
5
十一、 (8 分)应用含参积分理论计算积分
z 二、(10 分)已知函数 f ( x, y , z ) ( ) ,求 grad f (1,1,1) 与 d f (1,1,1)
x y
1
1
三、 (8 分)已知
x y ( ) ,其中 为可微函数,试计算 z z
x
z z y x y
四、 (8 分)设 z f (2 x y , y sin x ) ,其中 f (u , v ) 具有连续的二阶偏导数,求
南开大学数学分析 2008-2012年考研真题及答案解析

目录Ⅰ历年考研真题试卷 (2)南开大学2008年招收攻读硕士学位研究生入学考试试卷 (2)南开大学2009年招收攻读硕士学位研究生入学考试试卷 (4)南开大学2010年招收攻读硕士学位研究生入学考试试卷 (6)南开大学2011年招收攻读硕士学位研究生入学考试试卷 (8)南开大学2012年招收攻读硕士学位研究生入学考试试卷 (10)Ⅱ历年考研真题试卷答案解析 (12)南开大学2008年招收攻读硕士学位研究生入学考试试卷答案解析 (12)南开大学2009年招收攻读硕士学位研究生入学考试试卷答案解析 (19)南开大学2010年招收攻读硕士学位研究生入学考试试卷答案解析 (28)南开大学2011年招收攻读硕士学位研究生入学考试试卷答案解析 (36)南开大学2012年招收攻读硕士学位研究生入学考试试卷答案解析 (44)Ⅰ历年考研真题试卷南开大学2008年招收攻读硕士学位研究生入学考试试卷考试专业:陈省身数学研究所基础数学、概率论与数理统计、应用数学;数学科学学院基础数学、计算数学、概率论与数理统计、应用数学、生物信息学、统计学专业考试科目:701数学分析一、计算题1.求极限2.求和3.已知4.设则x=?5.设区域,计算二、设x1>-6,证明数列收敛,并求其极限。
三、设,并且使得,求证,使得四、设f(x)在[α,+∞)一致连续且广义积分收敛,求证五、设f(x)在(-∞,+∞)可微,并且满足,其中0<m<1。
认取实数证明级数收敛。
六、证明:函数项级数(1)在(0,+∞)收敛,但不一致收敛;(2)和函数f(x)在(0,+∞)任意次可导七、作变换,将方程变换为ω关于自变量u、v的方程。
八、求由曲面将球体分成两部分的体积之比(α>0)。
九、设f(x)是(0,+∞)上具有二阶连续导数的正函数,且,有界,则。
数学分析 测试试卷及答案

综合测试试卷一一、 计算题(本大题共15小题,每小题2分,共30分)1、xx x tan 01lim ⎪⎭⎫⎝⎛+→; 2、()x x x 2cot lim 0→ ;3、设a 为非零常数,则xx a x a x ⎪⎭⎫ ⎝⎛-+∞→lim ;4、⎪⎭⎫ ⎝⎛--+∞→n n n n n 3lim ; 5、xx x ex e111lim +-+→;6、⎪⎪⎭⎫⎝⎛++∞→x x x x 2sin 3553lim 2; 7、⎪⎭⎫ ⎝⎛+++++++++∞→n n n n n n n n n 2222211lim ;8、()x x x sin 2031lim +→;9、⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+∞→x x x x 11ln sin 31ln sin lim ; 10、()()x x x x x x +++→1ln cos 11cossin 3lim20 ; 11、20211limx x x x --++→; 12、⎪⎭⎫ ⎝⎛-→x x x x tan 11lim 20; 13、()3021ln arctan limx xx x +-→ ;14、若0>a ,0>b 为常数,则xxx x ba 302lim ⎪⎪⎭⎫⎝⎛+→;15、⎪⎪⎭⎫⎝⎛++++++∞→n n n n n n πππcos 12cos 1cos 11lim。
. 二、单项选择题(本大题共5小题,每小题2分,共10分)16、xx x x sin sinlim10→的值为( ) A. 1; B. ∞; C.不存在; D. 0.17、=+--+→232231x x x x x lim ( )A. 3;B. 4-;C. 1;D. 1-.18、 =⎪⎭⎫ ⎝⎛-∞→xx x 211lim ( )A.e 2;B. 2-e; C. 2e ; D.e2. 19、若22222=--++→x x bax x x lim ,则必有( ) A. 82==b a ,; B. 52==b a ,;C. 80-==b a ,; D. 82-==b a ,. 20、当+→0x 时,以下四式中为无穷小量的是( )A. x x 1sin ;B. x e 1; C. x ln ; D. x xsin 1.21、当+→0x 时,以下四式中为无穷大量的是( ) A. 12--x; B.xx sec sin +1; C. xe -; D. x e 1. 22、=→xx x x cos sinlim10( ) A.不存在; B. 0; C. 1; D. ∞.23、()=-→xx x cos tan lim 02π( )A.0;B. 1;C. ∞;D. 不存在. 24、=⎪⎭⎫⎝⎛--→1110x x e x lim ( )A.0;B. 21;C. ∞;D.21-. 25、()=+→xx x ex 10lim ( )A.e ;B. 1;C. 2e ; D. 2.三、计算题(本大题共3小题,每小题17分,共51分)26、623lim 2232--++-→x x xx x x ; 27、()11lim 22--+∞→x x x . 28、38231lim x x x +---→. 29、⎪⎪⎭⎫ ⎝⎛+--∞→1212lim 223x x x x x . 30、n n n n n !2lim ∞→. 31、()()()503020152332lim++-∞→x x x x . 32、设)(a f '存在,且0>)(a f ,求xx a f x a f ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+∞→)(lim 1.33、xx x x ⎪⎭⎫ ⎝⎛+∞→1lim . 34、11lim 31--→x x x . 35、xx x cos lim 00+→. 36、xx x x 10arcsin lim ⎪⎭⎫⎝⎛→. 37、()x x x x cos 1sin 1ln lim 0-+→. 38、201sin lim x x →. 39、21cos lim x x x ⎪⎭⎫ ⎝⎛∞→. 40、121lim +∞→+++p p p p n n n ,0>p .41、()1ln lim0-+→xx e x.42、dx xx an nn ⎰+∞→1sin lim.(提示:先用积分中值定理:()()a b f dx x f ba-=⎰ξ)(,[]b a ,∈ξ)综合测试试卷一参考答案一、计算题(本大题共15小题,每小题2分,共30分) 1、1; 2、21; 3、a e 2;4、2;5、1-;6、56;7、21;8、6e ;9、2;10、23;11、41-;12、31; 13、61-; 14、()23ab ; 15、22π。
三年级数学试卷分析

1.低年级学生加强学习习惯和主动学习能力的培养。
2.大力加强数学知识与现实生活的联系,本领注重知识形成投资过程与能力发展并重。
三年级较难分析(三)
此次数学试题较强体现了《新课程ห้องสมุดไป่ตู้准》的新理念和目标体系。具有如下特点:
1.内容全面,覆盖广泛。各部分分值权重股合理课程标准指出:人人获得必须的数学知识,不同的人得到不同的产业发展。本卷注重考查了学生基础知识的掌握、基本能力的培植情况,也适当考查了相应学生学习过程。 试题内容全面,共计六个大题。
二大题,选择员。其中1小题,一定有一个是(红球),大部分学生凿的是A答案有,C答案也有,没有经过仔细想。
五大题,同学们敲定的很好。
六大题,解答员。共5小题。绝大多数学生完成的很好。
四、对试卷的评价:随着课改的深入,考试评价的形式和内容也在做相应的改变,突现了对学生动手能力和联系实际解决问题能力的关注;在发展性上,积极谋求试题呈现形式的多样性,加大联系生活实际的的考查力度。不但考察学生基础知识及口算、笔算能力又观摩考察了学生家长的观察、分析、及解决问题的能力和动手能力,确实审题考察了学生认真审题及细心答题的习惯。
五、从答卷全卷情况看教与学存在的主要问题:从试卷各种不同题型的抽样统计分析发现,学生基本常识坚实掌握较为牢固。学生书写大部分较为整洁,格式相对规范,反映出教师对学生书写习惯培养的重视,学生崇天相对较活,解决问题的能力有巨大的提高。但从答卷中也可以看出,学生在做题细心各方面,仍有欠缺,需要继续加强。
从试卷各种不同题型填空题的抽样统计分析发现,学生基本知识掌握较为扎实。学生书写大部分较为整洁,格式相对规范,反映出教师对学生书写习惯培养的重视,学生学得相对较活,解决困难的不小能力有很大的提高。但从答卷中也可以看出,学生在做题细心方面,仍有欠缺,需要继续加强。
数学分析试卷

数学分析试卷第十三章函数项级数应用题第十三章函数项级数计算题1.设S(某)=nen某某>0,计算积分ln3ln2S(t)dt2..判断级数(1)n某nn1某n(某>0)的敛散性.第十三章函数项级数计算题答案1.nen某在[ln2,ln3]上连续且一致收敛它在[ln2,ln3]可逐积分(得4分)ln3(t)dtln3nen某d某ln2(得6分)n1ln2=[(1)n(1)n23]111(得8分)n111211232.对交错级数(1)nn由莱布尼兹判别法知它收敛(得3分)而某n1某n当某>1时,单增有界;某=1时,值为12;当某<1时,单降为界(得6分)故由阿贝尔判别法知(1)n某nnn收敛(得8分)1某第十三章函数项级数填空题1.f)某nn(某n=1,2,…{fn(某)}在[0,1]上的极限函数是__________2n2某0某12n2.f某)2n2n2n(某12n某1n的极限函数是________________________10n某1第十三章函数项级数填空题答案01.f(某)10某1某12.f0第十三章函数项级数证明题1.证明:函数f(某)=inn某n3在(-,)有连续的导函数.(10分)某2.设f0(某)在[a,b]上连续,定义函数序列fn+1(某)=fn(t)dt,n0,1,2,,a证明fn(某)在[a,b]上一致收敛.(10分)3.设f(某)在[12,1]上的连续函数,那么当f(某)在[n12,1]有界且f(1)=0时,{某f(某)}在[4.设fn(某)n某1n某2212,1]上一致收敛.(10分)求证1)对任给的0<1,fn(某)在[,1]上一致收敛.2)fn(某)在(0,1]上不一致收敛(12分)5.若在区间I上,对任何自然数n,|un(某)|vn(某),证明:当vn(某)在I上一收敛时级数n1u(某)在I上也一致收敛,且绝对收敛.(11分)nn1第十三章函数项级数证明题答案1.证:(inn某n3)con某n2而inn某n3con某n21n2(得2分)由而由1n2收敛知1n3()在(-,)上一致收敛(得2分)inn某n3inn某n3及1n3收敛知收敛(得6分)(又inn某3ncon某n2)=con某n2(得8分)con某n2在(-,)上连续且con某n2在(-,)上一致收敛在(-,)上连续.(得10分)2.证:f0(某)在[a,b]上连续.f0(某)m(得3分)2从而f1(某)m(某a)m(ba)(得5分)f2(某)某am(ta)dtm2!(ba)(得6分)2fn(某)m(ba)n!nn(得8分)n又n1(ba)n!收敛.limm(ba)n!n0(得9分)从而fn(某)一致收敛.(得10分)n03.证明:f(某)M且lim某f(某)nf(1)n,某1,某1(得3分)而f(1)=0,故lim某f(某)0(得5分)n又由于f(某)在某=1处连续,故0,0.当1-某1时,f(某)f(1)f(某)(得7分)从而当某[,1)时,某f(某)0(1)M0(得8分)21nn当某[1,1]时,某f(某)0f(某)(得9分)因此,某f(某)一致收敛.(得10分)nn4.证明:先求极限函数f(某)某(0,1]易知lim(1)因为|fn(某)f(某)|=对某0取N=[1n某1n某22n某1n某222n0即f(某)=0(得2分)1n2n1n2nn22(得4分)2]则当n>N时1n2对某[,1]必有|fn(某)-f(某)|按定义有fn(某)在[,1]上一致收敛(得6分)(2)因为dfn(某)d某n(1n某)(1n某)22222对每个自然数n,某n=1n是fn(某)的唯一极大值点.因而必是连续函数fn(某)在[0,1]的最大值点(得9分)显然也是它在(0,1]的最大值点,所以upfn(某)f(某)0某1=ma某(0某1)fn(某n)fn()1n某n222n某113故fn(某)在(0,1]不一致收敛(得12分)5.证先证一致收敛性,对>0,由vn(某)在I上一致收敛,存在N(),当n>N时,对自然数p和某I vn1(某)vn2(某)vnp(某)(得5分)于是un1(某)unp(某)un1(某)unp(某)vn1(某)vnP(某)(得8分)对自然数p和某I成立即un(某)在I上一致收敛(得10分)又un(某)vn(某)某I故un(某)在I上绝对收敛(得11分)第十三章函数项级数选择题1.设an(某)在(a,b)内任何区间(a1,b1)(an1面哪个结论是错误的()(A)可逐项求导(B)可逐项求积(C)极限与求和可交换顺序(D)级数收敛2.下列函数列在所示区间D上不一致收敛的是()(A)fn(某)(C)fn(某)n某某21n2D=(-1,1)(B)fn(某)某1n某22D=(-,+)D=[0,+)(D)fn(某)n某D=[0,10]第十三章函数项级数选择题答案1.C2.C第十四章幂级数选择题1.n1某2nn的收敛区间为()(A)(-1,0)(B)[0,1](C)[-1,1](D)(-1,1)2.f(某)=ln(2+某)展开成某的幂级数是()(A)ln2+(1)n1n1某nnn2(B)ln2(1)n1n1某nnn24(C)1+(1)n1某n(1)n1ln2某nn1n(D)n1n(2)3.函数f(某)=e某2展开成某的幂级数为()23(A)1+某+某某32!3!(B)1-某+某22!某3!某4某6(C)1+某2+(D)1-某2+某4某62!3!2!3!4.已知ann某在某=-2处收敛,则在某=3/2处此级数n1(A)收敛(B)发散(C)可能收敛(D)可能发散5.级数(11n2nn)(某1)的收敛半径R=n1(A)1(B)e(C)e1(D)e26..级数某nn1n2的收敛域为()(A)(-1,1)(B)(-1,1](C)[-1,1)(D)[-1,1]7.下述展开式正确的是()2(A)e某1某某2某nn某R(B)e某1某某2某n2!n!某[-1,1](C)e某1某某2某n2!n!某R(D)e=1+1+11123n8.下列级数在所示区间上不一致收敛的是()(A)某n某[-r.r](r>0)(B)某nn2(n1)!n1n2某[0,1](1)n12(C)某n某(-,)(D)n0n1(1某2)n1某n9..级数某nn1n的收敛域为()5。
三年级数学试卷分析与改进【含答案】

三年级数学试卷分析与改进【含答案】专业课原理概述部分一、选择题1. 下列哪个不是数学分析的基本概念?( )A. 极限B. 微分C. 矩阵D. 积分2. 三角函数中的正弦函数是周期函数,其周期为?( )A. πB. 2πC. π/2D. 2π/33. 若函数f(x)在区间[a, b]上连续,则其在[a, b]上一定( )。
A. 可导B. 可积C. 有界D. 单调4. 下列哪种方法不是求解线性方程组的方法?( )A. 高斯消元法B. 克莱姆法则C. 穷举法D. 矩阵求逆法5. 若函数f(x) = x^3 3x在x=0处的导数为-2,则f(x)在x=0处的( )。
A. 极大值B. 极小值C. 驻点D.拐点二、判断题1. 数列极限的定义中,n趋向于无穷大时,数列必须趋近于一个确定的值。
()2. 一元函数的泰勒公式在任何区间上都成立。
()3. 若矩阵A的行列式为0,则A一定不可逆。
()4. 欧拉公式是复变函数中的一个重要公式,它表达了复指数函数与三角函数之间的关系。
()5. 三角函数的和差化积公式可以用于简化任意角度的三角函数计算。
()三、填空题1. 一元函数f(x)在x=a处可导,则其在x=a处的导数定义为______。
2. 若函数f(x)在区间[a, b]上可积,则其在[a, b]上的定积分表示为______。
3. 矩阵的______表示矩阵的列向量或行向量线性相关。
4. 三角函数中,正弦函数和余弦函数的周期都是______。
5. 若函数f(x)在区间[a, b]上单调增加,则其在[a, b]上的导数______。
四、简答题1. 简述泰勒公式的定义及其在数学分析中的应用。
2. 解释罗尔定理的内容及其在函数研究中的作用。
3. 什么是行列式?它在矩阵理论中有什么重要意义?4. 简述导数的定义及其几何意义。
5. 解释定积分的定义及其在物理学中的应用。
五、应用题1. 设函数f(x) = x^3 3x,求f(x)在x=2处的二阶导数。
《数学分析III》期末试卷+参考答案

《数学分析(III )》试题2005.1一.在球面上找点,满足,,,使得该球面在点处的切平面与三个坐标平面围成的四面体的体积最小。
1222=++z y x ),,(0000z y x P 00>x 00>y 00>z 0P二.求球面()被平面2222a z y x =++0>a 4a z =与2az =所夹部分的面积。
三.计算二重积分()∫∫+Ddxdy x y x 24,其中是由D x 轴,直线x y =以及曲线1=+y x ,2=+y x 所围成的平面闭区域。
四.计算三重积分∫∫∫,其中。
Ωdxdydz e z ||}1|),,({222≤++=Ωz y x z y x五. 计算曲线积分∫+Lds z y 222,其中L 是球面()与平面2222a z y x =++0>a y x =相交而成的圆周。
六.计算曲面积分,其中∫∫Σ++dxdy z dzdx y dydz x 222Σ为锥面在平面与()之间的部分,定向为下侧。
222z y x =+0=z h z =0>h七.设是右半平面j i λλ)()(2),(24224y x x y x xy y x A +−+=}0|),({>=x y x D 上的向量场,试确定常数λ,使得为上函数的梯度场,并求出。
),(y x A D ),(y x u ),(y x u八.将|(sin |)(x x f =ππ≤≤−x )展开为Fourier 级数,并分别求级数∑∞=−12141n n ,()∑∞=−122141n n的和。
九.设∫∞++=12)1(cos )(dt t t xtx f ,),(∞+−∞∈x 。
(1)证明积分∫∞++12)1(cos dt t t xt关于x 在),(∞+−∞上一致收敛; (2)证明;0)(lim =+∞→x f x (3)证明在上一致连续。
)(x f ),(∞+−∞《数学分析(III )》试题答案2005.1一.(本题满分10分)33000===z y x 。
《数学分析III》期末考试卷及参考答案05

第 1 页 共 6 页数学分析下册期末试题及参考答案05一、 填空题(第1题每空2分,第2、3、4、5、6题每题4分,共26分)1、已知、已知 22xy u e-=,,则u x¶¶= ,uy¶=¶ , du = ;2、cos sin x ar y br q q =ìí=î,则(,)J r q = ;3、设L :cos sin x a t y b t=ìí=î 0t p ££,则22()Lx y ds +ò= ;4、120(,)ydyf x y dx òò交换积分顺序后为:交换积分顺序后为: ; 5、2221x y I x ydxdy +£=òò= ;6、令设222L x y a +=:,则Lydx xdy -=ò . 第 2 页 共 6 页二、判断题(对的打√,错的打×,每空3分,共15分)1、若函数(,)z f x y =的重极限和两个累次极限都存在,的重极限和两个累次极限都存在,则他们必相等;则他们必相等; ( )2、若函数(,)z f x y =在00(,)x y 可微,则(,)z f x y =在点00(,)x y 一定连续;一定连续; ( )3、若函数(,)z f x y =在闭区域D 上连续,则函数(,)z f x y =在D 上可积;上可积; ( )4、(,,)P x y z 是定义在双侧曲面S 上的函数,则上的函数,则(,,)(,,)SSP x y z dxdy P x y z dxdy =-òòòò; ( )5、若函数(,)z f x y =的偏导数在00(,)x y 的邻域内存在,则(,)f x y 在点00(,)x y 可微;( )三、计算题(第3、6题各7分,其余每题8分,共46分)1、求曲面22z x y =+与22z x y =+所围立体的体积. 得 分分 阅卷人阅卷人得 分分 阅卷人阅卷人第 3 页 共 6 页2、计算222VI x y z dxdydz =++òòò,其中V 是由222x y z z ++=-所围成的区域. 3、利用二重积分计算椭圆面:22221x y a b+£的面积的面积任教姓学考生答题不得过此线密封线课教师:学班号:名:号:装订线第 4 页 共 6 页4、计算第二型曲面积分:1SI dxdy z =òò,其中S 是椭球面2222221x y z a b c ++=的外侧. 5、计算22()SI x y ds =+òò,其中S 为立体221x y z +££的边界曲面.第 5 页 共 6 页6、利用高斯公式计算235SI xdydz ydzdx zdxdy =++òò,其中S 是单位球面2221x y z ++=的外侧. 四、证明题(四、证明题(66分)1、证明(3sin )(cos )x y dx x y dy ++是全微分,并求原函数(,)u x y得 分分 阅卷人阅卷人 考生答题不得过此线密封线任课教师:教学班号:姓名:学号:装订线得 分分 阅卷人阅卷人第 7 页 共 6 页1、求曲面22z x y =+与22z x y =+所围立体的体积 解:设所求体积为V,V,则则2222[()]xyD V x y x y dxdy =+-+òò,其中,22:1xy D x y +£(3分),令cos ,sin x r y r q q ==,则xy D 可表示为:02,01r q p ££££(4分),所以,,所以, 21200()V d r r rdr pq =-òò(5分)=6p (8分)分)2、计算222VI x y z dxdydz =++òòò,其中V 是由222x y z z ++=-所围成的区域解:令sin cos ,sin sin ,cos x r y r z r j q j q j ===(2分), 则V 可表示为:02,,0cos 2r pq p j p j ££££££-(4分),所以, 222VI x y z dxdydz =++òòò=2cos 3002sin d d r dr ppjp q j j -òòò(5分) =10p(8分)3、利用二重积分计算椭圆面:22221x y a b+£的面积解:设所求面积为S,则Ds dxdy =òò,其中D 为:22221x y a b +£(2分),令cos ,sin x ar y br q q ==(3分),则D 可表示为:02,01r q p ££££(4分),所以, 2100S d abrdr pq =òò(5分),所以S ab p =(7分). 4、计算第二型曲面积分:1S I dxdy z =òò,其中S 是椭球面2222221x y z a b c ++=的外侧解:记1S 为椭球面0z ³的一侧,2S 为椭球面0z £的一侧,则的一侧,则12111S S SI dxdy dxdy dxdy z z z ==+òòòòòò(2分),则12,S S 在xoy 面上的投影都是2222:1xy x y D a b +£(3分),所以222222221111xyxyDD I dxdy dxdy x y x y c c aba b =------òòòò22221x y c a b --21dr c r-=4ab cp(,则221x y z z ++=22x y =+,则2212x y z z ++=(22222)+2)+=(12)2p +23Sxdydz ydzdx +òò235Sxdydz ydzdx =++òò分),所以10I =D 44033p p ´=分)分)则y x ==¶¶,所以第 9 页 共 6 页则00(,)(3sin )(cos )3cos x yM Mu x y x y dx x y dy xdx x ydy =++=+òòòò(5分)分)=23sin 2x x y +(6分)(说明:原函数可以直接观察得出!)五、应用题(五、应用题(77分) 一页长方形白纸,要求印刷面积占2Acm ,并使所留页边空白为:上部与下部宽度之和为:a b h +=cm,左部与右部宽度之和为:c d r +=cm (A,r,h 为已知数),求页面的长(y)和宽(x),使它的面积最小.解:由题意,目标函数与约束条件分别为xy S =与.))(( , ,A h y r x h y r x =-->>(1分)作Lagrange 函数],))([(A h y r x xy L ---+=l (2分)则有分)则有ïîïíì=---==-+==-+=.0))(( ,0)( ,0)(A h y r x L r x x L h y y L yx l l l (3分)分) 由此解得由此解得, , 111r h Ah x y r l l l l l æö===-+ç÷ç÷++èø(5分)分) 于是有于是有. ,h rAhy r h Arx +=+=(6分)分)根据问题的实际意义知,此时页面的面积是最小的根据问题的实际意义知,此时页面的面积是最小的..(7分)分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数学分析》(三)――参考答案及评分标准一. 计算题(共8题,每题9分,共72分)。
1.求函数11(,)f x y y x =在点(0,0)处的二次极限与二重极限.解:11(,)f x y y x ==,因此二重极限为0.……(4分)因为011x y x →+与011y y x→+均不存在,故二次极限均不存在。
……(9分)2. 设(),()y y x z z x =⎧⎨=⎩ 是由方程组(),(,,)0z xf x y F x y z =+⎧⎨=⎩所确定的隐函数,其中f 和F 分别具有连续的导数和偏导数,求dzdx.解: 对两方程分别关于x 求偏导:, ……(4分)。
解此方程组并整理得()()()()y y x y z F f x y xf x y F F dz dx F xf x y F '⋅+++-='++. ……(9分)3. 取,μν为新自变量及(,)w w v μ=为新函数,变换方程222z z zz x x y x ∂∂∂++=∂∂∂∂。
设,,22y x y x y w ze μν+-=== (假设出现的导数皆连续).解:z 看成是,x y 的复合函数如下:,(,),,22y w x y x yz w w e μνμν+-====。
……(4分) 代人原方程,并将,,x y z 变换为,,w μν。
整理得:2222w ww μμν∂∂+=∂∂∂。
……(9分)4. 要做一个容积为31m 的有盖圆桶,什么样的尺寸才能使用料最省? 解: 设圆桶底面半径为r ,高为h ,则原问题即为:求目标函数在约束条件下的最小值,其中目标函数: 222S rh r ππ=+表,()()(1)0x yz dzdy f x y xf x y dx dx dy dz F F F dx dx ⎧'=++++⎪⎪⎨⎪++=⎪⎩约束条件: 21r h π=。
……(3分) 构造Lagrange 函数:22(,,)22(1)F r h rh r r h λππλπ=++-。
令 22420,20.r hF h r rh F r r πππλππλ=++=⎧⎨=+=⎩ ……(6分) 解得2h r =,故有r h == 由题意知问题的最小值必存在,当底面半径为r =高为h =时,制作圆桶用料最省。
……(9分)5. 设322()y x yy F y e dx -=⎰,计算()F y '.解:由含参积分的求导公式332222322222()32y y x yx y x yxy x yx y y yyF y e dx x e dx y e ye ----=='⎛⎫'==-+- ⎪⎝⎭⎰⎰ ……(5分)327522232y x y y y y x e dx y e ye ---=-+-⎰375222751222y y y x yy y e ye e dx y ---=--⎰。
……(9分)6. 求曲线222222x y xyab c ⎛⎫+= ⎪⎝⎭所围的面积,其中常数,,0a b c >.解:利用坐标变换cos ,sin .x a y b ρθρθ=⎧⎨=⎩由于0xy ≥,则图象在第一三象限,从而可以利用对称性,只需求第一象限内的面积。
(),0,02πρθθρ⎧⎪Ω=≤≤≤≤⎨⎪⎩。
……(3分) 则(,)2(,)x y V d d ρθρθΩ∂=∂⎰⎰122sin cos 2002ab c d ab d πθθθρρ⎛⎫ ⎪⎝⎭=⎰⎰……(6分)22220sin cos a b d c πθθθ=⎰2222a b c =. ……(9分)7. 计算曲线积分352Lzdx xdy ydz +-⎰,其中L 是圆柱面221x y +=与平面3z y =+的交线(为一椭圆),从z 轴的正向看去,是逆时针方向. 解: 取平面3z y =+上由曲线L 所围的部分作为Stokes 公式中的曲面∑,定向为上侧,则∑的法向量为()cos ,cos ,cos 0,αβγ⎛= ⎝。
……(3分)由Stokes 公式得352Lzdx xdy ydz +-⎰cos cos cos 352dS x y z z x y αβγ∑∂∂∂=∂∂∂-⎰⎰dS ∑= ……(6分)221x y +≤=⎰⎰2π= ……(9分)8. 计算积分S yzdzdx ⎰⎰,S 为椭球2222221x y z a b c ++=的上半部分的下侧.解:椭球的参数方程为sin cos ,sin sin ,cos x a y b z c ϕθϕθϕ===,其中02,0,2πθπϕ≤≤≤≤且2(,)sin sin (,)z x ac ϕθϕθ∂=∂。
……(3分)积分方向向下,取负号,因此,yzdzdx ∑=⎰⎰22322sin cos sin d bac d ππθϕϕθϕ-⎰⎰……(6分)222320sin sin cos bac d d ππθθϕϕϕ=-⎰⎰24abcπ=-……(9分)二. 证明题(共3题,共28分)。
9.(9分) 讨论函数3222422,0()0,0xy x y x y f x x y ⎧+≠⎪+=⎨⎪+=⎩在原点(0,0)处的连续性、可偏导性和可微性.解:连续性:当220x y +≠时,2242424()022xy x y y yf x y x y x y +=⋅≤⋅=→++,当()(),0,0x y →, 从而函数在原点()0,0处连续。
……(3分)可偏导性:()()()00,00,00,0lim0x x f x f f x∆→+∆-==∆,()0,0y f ()()00,00,0lim0y f y f y∆→+∆-==∆,即函数在原点()0,0处可偏导。
……(5分)3f f x f y∆-∆-∆=不存在,从而函数在原点()0,0处不可微。
……(9分) 10.(9分)(9分)设(),F x y满足:(1)在(){}00,,D x y x x a y y b=-≤-≤上连续,(2)()00,0F x y=,(3)当x固定时,函数(),F x y是y的严格单减函数。
试证:存在0δ>,使得在{}x x xδδI=-<上通过(),0F x y=定义了一个函数()y y x=,且()y y x=在δI上连续。
证明:(i)先证隐函数的存在性。
由条件(3)知,(),F x y在[]00,y b y b-+上是y的严格单减函数,而由条件(2)知()00,0F x y=,从而由函数(),F x y的连续性得()00,0F x y b->,()00,0F x y b+<。
现考虑一元连续函数(),F x y b-。
由于()00,0F x y b->,则必存在1δ>使得(),0F x y b->,x∀∈01(,)O xδ。
同理,则必存在2δ>使得(),0F x y b+<,x∀∈02(,)O xδ。
取12min(,)δδδ=,则在邻域(,)O xδ内同时成立(),0F x y b->,(),0F x y b+<。
……(3分)于是,对邻域(,)O xδ内的任意一点x,都成立(),0F x y b->,(),0F x y b+<。
固定此x,考虑一元连续函数(),F x y。
由上式和函数(),F x y关于y的连续性可知,存在(),F x y的零点[]00,y y b y b∈-+使得(),F x y=0。
而(),F x y关于y严格单减,从而使(),F x y=0的y是唯一的。
再由x的任意性,证明了对:δI=(,)O xδ内任意一点,总能从(),0F x y=找到唯一确定的y与x相对应,即存在函数关系:f x y→或()y f x=。
此证明了隐函数的存在性。
……(6分) (ii)下证隐函数()y f x=的连续性。
设*x是:δI=(,)O xδ内的任意一点,记()**:y f x=。
对任意给定的0ε>,作两平行线*y yε=-,*y yε=+。
由上述证明知()**,0F x y ε->, ()**,0F x y ε+<。
由(),F x y 的连续性,必存在*x 的邻域*(,)O x δ使得()*,0F x y ε->, ()*,0F x y ε+<, *(,)x O x δ∀∈。
对任意的*(,)x O x δ∈,固定此x 并考虑y 的函数(),F x y ,它关于y 严格单减且()*,0F x y ε->, ()*,0F x y ε+<。
于是在()**,y y εε-+内存在唯一的一个零点y 使(),0F x y =,即 对任意的*(,)x O x δ∈,它对应的函数值y 满足*y y ε-<。
这证明了函数()y f x =是连续的。
……(9分)11.(10分)判断积分1011sin dx x xα⎰在02α<<上是否一致收敛,并给出证明。
证明:此积分在02α<<上非一致收敛。
证明如下:作变量替换1x t=,则1201111sin sin dx tdt x x t αα+∞-=⎰⎰。
……(3分)不论正整数n 多么大,当[]3,2,244t A A n nππππ⎡⎤'''∈++⎢⎥⎣⎦时,恒有sin t ≥。
……(5分)因此,2211sin 2A A A A tdt dt t tαα''''--''≥⎰⎰ ……(7分)A ''=≥2043424n αππ-≥→>⎛⎫+ ⎪⎝⎭,当2α→-时。
因此原积分在02α<<上非一致收敛。
……(10分) 注:不能用Dirichlet 判别法证明原积分是一致收敛的。
原因如下:尽管对任意的1B >积分1sin B tdt ⎰一致有界,且函数21tα-关于x 单调,但是当x →+∞时,21t α-关于()0,2α∈并非一致趋于零。
事实上,取,t n = 相应地取12nα=-,则112111lim lim 10lim t n n nn t n n α-→∞→∞→∞===>,并非趋于零。
《 数学分析[3] 》模拟试题一、解答下列各题(每小题5分,共40分)1、 设),ln(y x z +=求y z yx z x∂∂+∂∂;2、,32,24,23,sin 2232t s z t s y t s x x yz u -=-=+==求t us u ∂∂∂∂,3、设),sin(y x eu x-=求y x u ∂∂∂2在点)1,2(π处的值;4、求由方程2222=+++z y x xyz 所确定的函数),(y x z z =在点)1,0,1(-处的全微分dz ;5、求函数)ln(222z y x u ++=在点)2,2,1(-M 处的梯度)2,2,1(-gradu ; 6、求曲面32=+-xy e z z在点(1,2,0)处的切平面和法线方程; 7、计算积分:dx x e e xx ⎰∞+---02;8、计算积分:⎰⎰-=1102xy dyedx I ;二、(10分)求内接于椭球1222222=++c z b y a x 的最大长方体的体积,长方体的各个面平行于坐标面。
