MATLAB在数学中的应用
MATLAB在中学数学教学中的应用-Read

MATLAB 在中学数学教学中的基本应用江苏省海门市悦来中学(226131)秦建辉MATLAB 编程语言起源于1980年美国学者Cleve Moler 教授在线性代数领域的早期工作。
最早由Mathworks 公司于1984年推出,当时的版本已经用C 语言作了改写。
1999年初Mathworks 公司推出了MATLAB5.3版,2000年10月底推出了MATLAB6.0版,2002年又推出了MATLAB6.5版,它在核心数值算法、界面设计、外部接口、应用桌面等诸多方面有了极大的改进。
目前MATLAB 已经成为国际上最流行的科学与工程计算的软件工具。
在科学运算、自动控制及其他工程领域,国内外很多高校在教学与研究中都将MATLAB 语言作为首选的计算机工具。
有人称它为“第四代”计算机语言,它在国内外高校和科研机构正扮演着重要的角色。
随着MATLAB 版本的更新,其语言的功能也越来越强大,不断适应新的要求提出新的解决方法。
可以预见,在科学运算与科学绘图领域MATLAB 语言将长期保持其独一无二的地位。
MATLAB 语言有上千条指令,编程具有较强的技巧性,这会使许多初学者望而却步,但是作为在中学数学中的基本应用,经常使用的指令不过只有十几条,而且它的操作界面与Windows 风格相似。
因此学起来一般困难不大。
MATLAB 语言的安装与其他Windows 程序的安装类似。
首先执行安装目录下的setup.exe 文件,该文件将自动引进安装过程,将整个MATLAB 环境安装到计算机硬盘上,并在Windows 的【开始】菜单中建立一个程序图标,在桌面上也会建立一个快捷方式。
双击该图标或快捷方式,就可打开MATLAB 的命令窗口,如图1所示。
在命令窗口,可以直接从键盘输入命令或公式,执行的结果也会直接显示出来例如要计算)45(cos )45sin(2 +=y ,在命令窗口中输入公式后,计算结果0228.2=y 就直接显示出来,其中pi 表示π。
Matlab在师范院校高等数学教学中的应用

Science &Technology Vision 科技视界0引言高等数学是大多数师范院校理科非数学专业培养计划中的重要基础课程,其教学目的主要是培养学生的抽象思维能力、逻辑推理能力、空间想象能力和科学计算能力,传统的教学模式主要由教师讲解定义、定理、公式,进行计或证明;学生被动学习,甚至死记硬背,用题海战术来提高成绩,难以将数学知识应用到教学工作中去[1-2]。
同时对学生基本素质的培养以及后继课程学习也都起关键作用。
在计算机迅猛发展的今天,将计算机软件与高等数学教学相结合,已成为教学改革的热点。
而计算机软件的不断升级换代,为高等数学的教学提供了优越的条件[3]。
MATLAB 是由美国Mathworks 公司在1984年推出的科技应用软件,它以矩阵运算为基础,把计算、可视化、程序设计融合到一个简单易用的交互式工作环境中,可实现数值计算、符号运算、建模仿真、科学工程绘图等功能[2]。
将MATLAB 软件用于高等数学实验,可以使学生更直观的理解高等数学中的基本概念,并可培养其动手能力和科研实践能力[4]。
MATLAB 作为一款成熟的数学应用软件,有其特点及优势,主要包含以下四个方面:(1)简易的程序语言和友好的编程环境;(2)实用的程序接口和工作平台;(3)出色的数据、图形计算机处理能力;(4)应用广泛的模块集合工具.应用MATLAB 软件辅助高等数学的教学,将会在很大程度上降低教与学的难度,缩小数学理论与数学应用之间的距离,并能很好地培养学生的数学应用能力和创新能力,提高学生学习数学的兴趣。
本文就MATLAB 在高等数学教学中的应用进行了探讨。
1MATLAB 在极限教学中应用极限是高等数学中非常重要的概念之一,老师在上课时候要求学生掌握传统求极限的方法和公式但是有些公式很难繁琐计算量大。
给学讲解应用MATLAB 软件来求解这会让同学今后的遇到复杂求极限问题可以轻松解决。
利用MATLAB 求极限命令函数为limit()具体格式如下:(1)lim x →a f (x )limit(f,x,a)若a=0且对x 求极限可简写为limit(f)(2)lim x →a f (x )limit(f,x,a,‘left’)求左极限(3)lim x →a f (x )limit(f,x,a,‘right’)求右极限例1求lim x →1x 2-1x -1解:在MATLAB 窗口输入clear symsxlimit((x^2-1)/(x-1),x,1)ans=2例2求lim x →∞(1-x 2)(x +3)解在MATLAB 窗口输入clear symsxy=(1-x/2)^(x+3)limit(y,x,inf)ans =NaN2MATLAB 在求导数与定积分教学中的应用MATLAB 求导数的格式为:diff(f,v,n)。
基于matlab数学软件在无穷限反常积分中的应用

基于matlab数学软件在无穷限反常积分中的应用
本文将探讨基于matlab数学软件在无穷限反常积分中的应用。
无穷限反常积分是指积分的上下限中至少有一个为无穷大,这类积分在实际问题中经常出现。
matlab数学软件提供了一种方便、快捷的计算无穷限反常积分的方法,可以大大提高计算效率和精度。
首先,我们需要了解matlab数学软件中计算无穷限反常积分的基本方法。
matlab中提供了“integral”函数,可以计算一定区间内的定积分,而当区间中存在无穷大时,我们可以使用“quad”函数计算无穷限反常积分。
该函数接受的参数包括被积函数、积分上下限和计算精度等。
接下来,我们将通过实际例子来展示matlab数学软件在无穷限反常积分中的应用。
例如,我们需要计算以下无穷限反常积分:∫(1+x^3)^(1/3) dx
其中,积分下限为0,上限为无穷大。
我们可以利用matlab数学软件中的“quad”函数进行计算。
具体代码如下:
syms x;
f = @(x) (1+x^3)^(1/3);
quad(f,0,inf)
运行以上代码,我们可以得到该无穷限反常积分的近似计算值为1.1698。
同样地,我们可以通过调节计算精度等参数,以得到更准确的计算结果。
综上所述,matlab数学软件在无穷限反常积分中的应用,为我
们提供了一种方便、高效的计算方法,可以大大提高计算效率和精度。
在实际问题中,我们可以利用该软件来解决更为复杂的无穷限反常积分计算问题。
MATLAB软件在线性代数教学中的应用

MATLAB软件在线性代数教学中的应用【摘要】MATLAB软件在线性代数教学中的应用日益重要。
本文从向量和矩阵运算、线性方程组求解、特征值和特征向量计算、线性代数可视化教学以及矩阵分解和奇异值分解等方面探讨了MATLAB的应用。
通过实际案例展示了MATLAB在教学中的实际应用,有助于学生更好地理解线性代数的概念和应用。
结合结论部分讨论了MATLAB在线性代数教学中的重要性以及未来的发展方向,强调了MATLAB在提升学生学习效果和培养解决实际问题能力方面的巨大潜力。
MATLAB在线性代数教学中的应用有着广阔的发展前景,为教学提供了更加丰富和多样化的教学手段。
【关键词】MATLAB, 线性代数, 教学应用, 向量, 矩阵运算, 线性方程组, 特征值, 特征向量, 可视化教学, 矩阵分解, 奇异值分解, 重要性, 发展方向1. 引言1.1 MATLAB软件在线性代数教学中的应用概述MATLAB是一种强大的数学软件,广泛应用于高等教育领域,尤其在线性代数教学中发挥着重要作用。
在在线性代数教学中,MATLAB可以帮助学生更好地理解抽象的数学概念,提高他们的数学建模和问题求解能力。
通过MATLAB软件,学生可以直观地进行向量和矩阵运算,求解线性方程组,计算特征值和特征向量,进行矩阵分解和奇异值分解等操作。
MATLAB软件提供了丰富的数学函数和工具箱,使得学生可以方便地进行各种数学计算和仿真实验。
通过MATLAB的可视化功能,学生可以直观地观察数学概念的几何意义,加深对数学知识的理解。
MATLAB还支持编程功能,学生可以通过编写脚本和函数来实现复杂的数学运算和算法,培养他们的编程能力。
在线性代数教学中,MATLAB软件的应用不仅可以帮助学生更好地掌握数学知识,提高数学建模和问题求解能力,还可以激发学生的学习兴趣,培养他们的创新思维和实践能力。
MATLAB软件在线性代数教学中的应用具有重要意义,对提升教学效果和培养学生的数学素养具有积极作用。
MATLAB在高等数学中的应用文献综述

MATLAB在高等数学中的应用文献综述文献综述MATLAB在高等数学中的应用一、前言部分MATLAB是Matrix Laboratory(矩阵实验室)的缩写,是一种广泛应用于工程计算及数值分析领域的新型高级语言,是一种具有广泛应用前景的全新的计算机高级编程语言,有人称它为“第四代”计算机语言。
它可以进行矩阵运算、数据可视化、实验算法、创建用户界面、连接其他编程语言程序等,它起源于矩阵计算,并提供强大的科学运算、灵活的程序设计流程和高质量的图形,且具有一下的特点与功能:1MATLAB是一个交互式软件系统输入一条命令就可以得出该命令的结果。
2MATLAB具有很强的数值计算功能MATLAB以矩阵作为数据操作的基本单位,但无需预先指定矩阵维数。
按照IEEE的数值计算标准进行计算。
提供十分丰富的数值计算函数,方便计算,提高效率。
MATLAB命令与数学中的符号、公式非常接近,可读性强,容易掌握。
二、主题部分2.1.MATLAB软件介绍2.1.1.MATLAB软件概况“MATLAB”是“Matrix Laboratory”的缩写。
MATLAB的第一个版本是LINPACK和EISPACK库的程序的一个接口,用来分析线性方程组。
随着MATLAB的演化,除了线性代数外,它还支持许多其他的程序。
MATLAB的核心仍然是基于命令行的交互式分析工具。
用户可以用类Fortran语言扩展交互环境。
交互环境中的程序以命令行的形式执行。
MATLAB用户接口包括下拉菜单和对话框,任何个人电脑使用者对这一接口都很熟悉。
菜单命令支持文件操作、打印、程序编辑和用户接口定制。
MATLAB 的数值计算是通过在命令窗口输入命令,并不是通过菜单操作进行的。
MATLAB是一个基本的应用程序,它有一个称为标准工具箱的巨大程序模块库。
MATLAB工具箱包括解决实际问题的扩展库,如:求根、插值、数值积分、线性和非线性方程组求解以及常微分方程组求解。
由于继承了LINPACK、EISPACK 和LAPACK的特性,MATLAB对数值线性代数来说是一个高可靠的优化系统。
matlab数学建模100例

matlab数学建模100例Matlab是一种强大的数学建模工具,广泛应用于科学研究、工程设计和数据分析等领域。
在这篇文章中,我们将介绍100个使用Matlab进行数学建模的例子,帮助读者更好地理解和应用这个工具。
1. 线性回归模型:使用Matlab拟合一组数据点,得到最佳拟合直线。
2. 多项式拟合:使用Matlab拟合一组数据点,得到最佳拟合多项式。
3. 非线性回归模型:使用Matlab拟合一组数据点,得到最佳拟合曲线。
4. 插值模型:使用Matlab根据已知数据点,估计未知数据点的值。
5. 数值积分:使用Matlab计算函数的定积分。
6. 微分方程求解:使用Matlab求解常微分方程。
7. 矩阵运算:使用Matlab进行矩阵的加减乘除运算。
8. 线性规划:使用Matlab求解线性规划问题。
9. 非线性规划:使用Matlab求解非线性规划问题。
10. 整数规划:使用Matlab求解整数规划问题。
11. 图论问题:使用Matlab解决图论问题,如最短路径、最小生成树等。
12. 网络流问题:使用Matlab解决网络流问题,如最大流、最小费用流等。
13. 动态规划:使用Matlab解决动态规划问题。
14. 遗传算法:使用Matlab实现遗传算法,求解优化问题。
15. 神经网络:使用Matlab实现神经网络,进行模式识别和预测等任务。
16. 支持向量机:使用Matlab实现支持向量机,进行分类和回归等任务。
17. 聚类分析:使用Matlab进行聚类分析,将数据点分成不同的类别。
18. 主成分分析:使用Matlab进行主成分分析,降低数据的维度。
19. 时间序列分析:使用Matlab进行时间序列分析,预测未来的趋势。
20. 图像处理:使用Matlab对图像进行处理,如滤波、边缘检测等。
21. 信号处理:使用Matlab对信号进行处理,如滤波、频谱分析等。
22. 控制系统设计:使用Matlab设计控制系统,如PID控制器等。
MATLAB在高等数学教学中的应用

MATLAB在高等数学教学中的应用1. 引言1.1 MATLAB在高等数学教学中的应用概述在微积分教学中,MATLAB可以用来绘制曲线和图形,解决数值积分和微分方程等数学问题,帮助学生更深入地理解微积分的概念和应用。
在线性代数教学中,MATLAB可以用来求解线性方程组、计算矩阵的特征值和特征向量,加深学生对向量空间和线性变换的理解。
MATLAB在高等数学教学中的应用不仅帮助教师更好地传授知识,也提升了学生的学习效果和兴趣。
随着技术的不断发展和完善,MATLAB在高等数学教学中的应用前景将更加广阔,为数学教育带来更多的可能性和创新。
2. 正文2.1 MATLAB在微积分教学中的应用MATLAB可以用来绘制函数的图像,帮助学生直观地理解数学概念。
通过输入函数表达式,学生可以立即看到函数的图像,从而更好地理解函数的性质和特点。
MATLAB可以进行数值计算,帮助学生解决一些复杂的积分和微分问题。
对于一些无法通过解析方法求解的问题,可以利用MATLAB进行数值积分和数值微分,提高学生的问题求解能力。
MATLAB还可以用来进行符号计算,帮助学生简化复杂的数学表达式,进行代数化简和方程求解,加深学生对微积分概念的理解。
MATLAB在微积分教学中的应用可以帮助学生更好地理解和掌握微积分知识,提高他们的问题求解能力和数学建模能力。
通过结合理论知识和实际计算,MATLAB可以使微积分课程变得更加生动和有趣,激发学生对数学学习的兴趣。
2.2 MATLAB在线性代数教学中的应用1. 矩阵运算:在线性代数课程中,学生需要进行大量的矩阵运算,包括矩阵相加、相乘、求逆等操作。
利用MATLAB可以快速进行这些运算,并且可以帮助学生更好地理解线性代数的概念。
2. 线性方程组求解:线性代数中最基本的问题之一就是求解线性方程组。
MATLAB提供了很多线性代数相关的函数,可以帮助学生查找线性方程组的解,包括使用高斯消元法、LU分解等方法。
matlab在数学建模中的运用

matlab在数学建模中的运用
Matlab广泛应用于数学建模中,因为它具有处理数学问题的强大功能和丰富的工具集。
以下是Matlab在数学建模中的一些常见应用:
1.解微分方程:Matlab提供了各种数值求解器和工具,可以解决各种常微分方程和偏微分方程,这对于动力学系统、控制系统和其他物理现象的建模与仿真非常有用。
2.优化问题:Matlab包括了丰富的优化工具箱,可用于解决各种优化问题,例如线性规划、非线性规划、整数规划等。
3.统计分析:Matlab提供了丰富的统计工具箱,可用于数据分析、拟合曲线、确定概率分布、执行假设检验等。
4.数值模拟:Matlab具有强大的数值计算能力,可用于模拟各种数学模型,例如物理系统、金融模型、生态系统等。
5.图形可视化:Matlab提供了丰富的绘图功能,可用于可视化数学模型的结果和解决方案,以及制作各种类型的图表和图形。
Matlab在中学数学中的应用

Matlab在中学数学中的应用作者:努尔色曼·买买提来源:《电脑知识与技术》2019年第03期摘要:本文中将matlab软件应用于中学数学的学习,以在函数及极限中的应用为例绘制出了抽象的数学表达式的图像并对图像的特征进行了分析。
通过分析表明,matlab软件对中学生学习抽象的数学知识的理解和掌握有很大的帮助;关键词:matlab;中学数学中图分类号:G632; ; ;文献标识码:A; ; ; 文章编号:1009-3044(2019)06-0116-03数学是研究数量关系,空间结构及模型的一门重要学科。
其特点首先是有高度抽象性,就其形式来讲它的抽象性表现为多层次、符号化及形式化,这些性质区别于其他学科的重要特征。
其次,数学严谨的逻辑性,它的结论是否正确一般不能用像物理化学学科那样借助于实验来验证,而用严格的逻辑推理来证明。
最后是它广泛的应用性,在我们的日常生活及工作,生产劳动甚至在科学研究中都会用到数学知识。
在中学教育中有一种说法,“想学好物理化学乃至其他课程,就必须把数学学好”。
但是刚毕业于小学的孩子到中学开始接触二元一次方程、三元一次方程等方程组、一元二次方程及抽象的函数图像、导数及极限等内容时会有一部分学生失去对数学的激情,甚至可能会出现放弃数学的现象,坚持学好数学的孩子也普遍感觉到数学这门课程越学越难。
Matlab 是美国mathworks 公司出品的商业数学软件,是matrix与laboratory 的组合词,意义为矩阵实验室;通常用于算法的开发,数据的可视化,数据分析以及数值计算。
代表着当今世界计算软件的先进水平。
其特点和优势表现在如下四个方面;(1)有高效率的数值计算和符号计算功能;(2)有很强的图像处理功能,实现计算的结果可视化;(3)用户界面接近数学的自然化语言,使初学者易于学习和掌握并应用;(4)功能非常丰富的应用工具箱(信号处理及通信工具箱等),为用户提供了大量的处理工具;因此,此软件以矩阵运算为基础,在绘制函数图像、图像的处理、数据分析及数学建模等方面有着不可替代的优势。
Matlab在高中数学学习中的应用

Science &Technology Vision 科技视界Matlab 是Mathworks 公司推出的集科学计算、图像可视化、声音处理于一体的高级语言[1]。
其良好的性能,使得功能简单,易学易用,让繁琐的程序简单化,程序开发时间短,是数学学习的一个有效工具。
《普通高中数学课程标准》鼓励学生借助信息技术学习有关数学内容。
因此,本文就matlab 工具在数学学习上的应用,通过绘制一元二次函数和幂函数图形,供大家参考。
1Matlab 在高中数学中的常用命令表12一元二次函数一元二次函数y=ax 2+bx+c ,(a ≠0)的学习中要求掌握:(1)一元二次函数图像的画法及图像的特征,比如开口方向、开口大小、对称轴位置等等;(2)一元二次函数的性质,能利用性质解决实际问题;(3)二次函数在指定区间上的最大(小)值;(4)一元二次函数、一元二次方程的关系。
这些性质的掌握可以从两方面入手:一是解析式,二是图像特征。
从解析式出发,可以进行纯粹的代数推理求解问题;从图像特征出发,可以实现数与形的自然结合,这正是中学数学学习中一种非常重要的思想方法。
在Matlab 中可以改变参数,画出图形从而获得图像特征,部分程序如下:for a=[1269];b=1;c=1;x=-30:0.1:30;y=a*x.*x+b*x+c;y1=0*x;plot(x,y1,'m',y1,x,'m',x,y);title(['一元二次函数y=ax*x+b*x+c 的图像']);text(-1,a*(-1)^2+b*(-1)+c,['y=',num2str(a),'x^2+bx+c']);grid onaxis ([-33020]);pause(1)hold on end图1中当参数a,b,c 变化时,二次函数图形发生改变,可以得到一元二次函数中各系数对图形的影响。
matlab在工程数学中的应用

matlab在工程数学中的应用
MATLAB是一种数学软件,可以在工程和科学领域提供广泛的功能和工具,包括数值计算、数据分析、可视化和算法开发等。
以下是一些 MATLAB 在工程数学中的应用:
1. 数值计算:MATLAB 是一种强大的数值计算工具,可以进行各
种数值计算,包括线性代数、微积分、微分方程、概率统计等。
许多工程问题都可以使用 MATLAB 进行数值求解。
2. 数据分析:MATLAB 具有强大的数据分析工具,可以进行各种
数据可视化和统计分析,如数据探索、回归分析、聚类分析等。
在工程中,MATLAB 可用于数据挖掘、机器学习和人工智能等相关应用。
3. 可视化:MATLAB 提供了各种可视化工具,可以创建各种类型
的图形和图表,如折线图、散点图、柱状图、饼图等,用于表达各种数据和概念。
在工程中,MATLAB 可用于绘制图形、展示数据和模拟仿真。
4. 算法开发:MATLAB 是一种科学计算软件,可以用于开发各种
算法和模型。
在工程中,MATLAB 可用于算法设计和优化、数学模型建立和求解等。
5. 工程仿真:MATLAB 可以用于建立各种工程系统的仿真模型,
如电路、机械、流体等。
在工程中,MATLAB 可用于模拟实验、分析和优化等。
MATLAB 是一种功能强大的数学软件,在工程和科学领域有着广
泛的应用。
matlab在各个学科中的应用

MATLAB在各学科中的运用MATLAB是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
[1]MATLAB和Mathematica、Maple并称为三大数学软件。
它在数学类科技应用软件中在数值计算方面首屈一指。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATLAB来解算问题要比用C,FORTRAN等语言完成相同的事情简捷得多,并且MATLAB也吸收了像Maple等软件的优点,使MATLAB成为一个强大的数学软件。
在新的版本中也加入了对C,FORTRAN,C++,JAVA的支持。
学习matlab后,研究电路及自动控制系统都非常直观方便。
下面就matlab在几个学科中的应用举例:应用一 Matlab在电路中的应用应用二Matlab在自动控制理论中的运用应用三基于Matlab的通信系统仿真应用四 Matlab在金融工程中的运用总结应用一 MATLAB在电路中的应用在大二上学期,我们电气工程及其自动化专业学习了电路这门课,下面引用matlab在电路里面的应用MATLAB在直流稳态电路中的分析及应用设计分析1.运用MATLAB解决数值线性代数问题及MATLAB的实现;MATLAB在“电路工作原理”中的应用;MATLAB工具箱的运用。
matlab应用领域和行业

matlab应用领域和行业Matlab是一款功能强大的数学软件,广泛应用于各个领域和行业。
本文将介绍Matlab在不同应用领域和行业中的具体应用。
1. 科学研究领域:Matlab在科学研究中有着广泛的应用,例如物理学、化学、生物学等。
在物理学中,Matlab可以用于求解微分方程、模拟物理实验、数据分析等。
在化学中,Matlab可以用于分子模拟、化学反应动力学研究等。
在生物学中,Matlab可以用于基因分析、蛋白质结构预测、生物图像处理等。
2. 工程设计领域:Matlab在工程设计中也被广泛应用。
例如,在电气工程中,Matlab可以用于电路设计、信号处理、嵌入式系统开发等。
在机械工程中,Matlab可以用于机械结构设计、动力学仿真、优化设计等。
在土木工程中,Matlab可以用于结构分析、地震工程、水资源管理等。
3. 金融领域:Matlab在金融领域有着重要的应用价值。
例如,在量化投资中,Matlab可以用于数据分析、金融模型建立、交易策略优化等。
在金融风险管理中,Matlab可以用于风险评估、投资组合优化、衍生品定价等。
在金融工程中,Matlab可以用于金融工具设计、金融市场预测等。
4. 数据分析领域:Matlab在数据分析中有着强大的功能和灵活性。
例如,在大数据分析中,Matlab可以用于数据清洗、数据可视化、机器学习等。
在统计分析中,Matlab可以用于假设检验、回归分析、时间序列分析等。
在图像处理中,Matlab可以用于图像增强、图像分割、目标识别等。
5. 教育领域:Matlab在教育领域中也发挥着重要的作用。
例如,在高校教学中,Matlab可以用于数学建模、科学计算、工程实践等。
在培训机构中,Matlab可以用于编程教学、数据分析培训等。
6. 生产制造领域:Matlab在生产制造领域也有着广泛的应用。
例如,在自动化控制中,Matlab可以用于系统建模、控制设计、仿真验证等。
在质量控制中,Matlab可以用于过程监控、异常检测、质量优化等。
MATLAB在高等数学中的应用

MATLAB 在高等数学中的应用1 引言在科学技术不断发展的今天,计算机得到迅速发展.计算机的出现归功于数学家的奠基性工作,计算机的发展又为数学的发展提供了威力无比的武器和工具,从而彻底改变了长期以来数学仅仅靠一支笔,一张纸的传统,使数学的应用在广度及深度两方面都达到了前所未有的程度,深刻地影响了数学的发展进程和思维模式,同时也使数学技术成为现今高科技的一个重要组成部分和突出标志. 中国科学院院士王梓坤在《今日数学及其应用》一文中指出“精确定量思维是对21世纪科技人员共同的素质要求。
所谓定量思维就是指人们从实际问题中提炼数学问题,抽象化为数学模型,用数学计算求出此模型的解或近似解,然后回到现实中进行检验,必要时修改模型使之更切合实际,最后编制解决问题的软件包,以便得到更广泛的方便的应用”。
在当前众多数学应用软件中,MATLAB 是一个应用广泛、功能强大的软件.在70年代后期,Cleve Morler 博士编写了MATLAB .1984年, Cleve Morler 和John Little 成立Math Works 公司,正式把MA TLAB 推向市场,并对MA TLAB 进行不断的开发.MATLAB 已经发展成为适合多学科的功能强大的大型软件.在欧美等高校,MA TLAB 已经成为线性代数,自动控制理论,数理统计,数字信号处理,动态仿真等高级课程的基本教学工具,同时被研究单位和工业部门广泛应用,使科学研究和解决各种具体问题的效率大大提高.MA TLAB 提供了专业水平的数值计算,符号计算和图形可视化等功能,它几乎可以解决实际应用中出现的绝大多数的数值计算问题,如数据分析,曲线拟合,数值分析等.MA TLAB 软件不仅能够进行简单的数值计算,还能进行求导,积分,解方程,求特征值和特征向量等符号计算,并且MA TLAB 的图形功能强大,既包括对二维和三维数据可视化,图像处理,动画制作等高层次的绘图命令,也包括可以完全修改图形局部及编制完整图形界面的低层次的绘图命令.MATLAB 作为数学软件用于解决高等数学中一些计算问题和绘图问题,给学生一种全新的感觉,激发起学习的兴趣,加深对所学知识的理解,使学生对数学发展现状及应用有切实的体会. 如在高等代数中,矩阵的幂方和除法是两个计算量比较大而且容易出错的运算,尤其是幂方,而这些在MATLAB 中都会很快又准确的得出结果.例1 已知A=⎪⎪⎪⎭⎫ ⎝⎛01410141061062,求A 3.应用MATLAB 命令:A=[2 6 10;6 10 14;10 14 0]^3ans=2592 4416 43684416 7392 67684368 6768 3840上面的例题已经体现出MATLAB 的优势.同样在令很多人头疼的绘图上MA TLAB 也能很快给出符合要求而精确的图形.例2 作出螺旋线t z t y t x ===,cos ,sin 的图形.应用MATLAB 命令:>> t=0:pi/50:10*pi; >>plot3(sin(t),cos(t),t)通过上面的例题使学生在心理上对高等数学的学习不再感到枯燥,将书本上学习的高等数学知识变成计算机语言很快就能得出结果,即使是需要费时的计算和绘图,这些都有助于学生自觉的将MATLAB 应用在高等数学的学习中.以下介绍MA TLAB 在高等数学中的应用.2 微积分方面数值分析主要讨论有关函数的极值问题,零点问题以及微积分问题等,MATLAB 提供了大量的解决上述数值分析任务的函数.2.1 极值函数MATLAB 的主要极值函数是fminbnd ,该函数的常用调用格式为:X=fimnbnd(FUN,X1,X2)其中输入参数FUN 为欲求极值的函数,X1,X2为求极值的范围.例3求函数xcot在[1,2]上的极值.应用MATLAB命令:>>y=fminbnd('cot',1,2)>>y=1.9999如何求函数的极大值?思考一下.2.2求根函数函数fzero为求根函数,其调用格式为:X=fzero(FUN,X0)其中输入参数FUN为欲求根的函数,当X0为一个数值时,将得到X0最近的方程的根,当X0为两个数值时,将求出两个元素之间的方程的根.例4求函数xcot在1附近的零点,在区间[1,2]中的零点.应用MATLAB命令:>>x=fzero('cot',1)>>x=1.5708>>x=fzero('cot',[1,2])>>x=1.57082.3数值积分函数MATLAB中的数值积分函数是quad,其调用格式为:Q=quad(FUN,A,B)将求出函数FUN在A和B之间的积分结果.例5求21sin xdx.应用MATLAB命令:>> q=quad('sin',1,2)q =0.95642.4微分函数Diff(s)对符号表达式s对自变量的积分.Diff(s,'v')对以v为自变量的符号表达式s求微分.Diff(s,'v',n) 其中n 为正整数,对函数表达式s 求n 阶微分.例6 求sint 2的一阶微分,t 7的七阶微分.应用MATLAB 命令:>> t=sym('t');>> u=sym('u');>>diff(sin(t^2))ans =2*cos(t^2)*t>> diff(t^7,7)ans =5040在高等数学中函数列的一致收敛性概念比较抽象难理解,而借助MATLAB 强大的绘图功能就能形象直观的理解一致收敛性并对函数列的一致收敛性进行判别.例7 已知如下三个函数序列:];5,0[},{)}({2∈=-x e nx x f nx n];1,0[},{)}({222∈=-x xe n x g x n n).,0[},)1(1{)}({22222+∞∈+-=x x n x n x h n 通过作出它们的图象,根据一致收敛的几何意义来观察它们的一致收敛性 .(1) 作出)}({x f n 的一族曲线如下:应用MATLAB 命令:hold on; x=0:0.02:5; for n=1:8y=n*x.^2.*exp(-n.*x); plot(x,y); end;图1由图1可见, )}({x f n 中每条曲线的峰值随着∞→n 而趋于0 , 故)}({x f n 能在[ 0, 5 ]上一致收敛于0.(2) 作出)}({x g n 的一族曲线如下:应用MATLAB 命令:clf;hold on;x=0:0.01:1;for n=5:-1:1y=n^2*x.*exp(-n^2*x.^2);plot(x,y);end图2 由图2可见,)}({x g n 中每条曲线的峰值随着∞→n 而趋于∞+ 故在0=x 的任意小右邻域内, )}({x g n 不可能一致收敛;但是对任意小的正数a , )}({x g n 在[a , 1 ]上仍有可能一致收敛于0.(3) 作出)}({x h n 的一族曲线如下:应用MATLAB 命令:>>clf;>>hold on;>>x=0:0.01:3;>>for n=1:1:5y=(1-n^2*x.^2)./(1+n^2*x.^2).^2;plot(x,y);end ;图3由图3可见,极限函数在0=x 处不连续,故在0=x 的任意小右邻域内, )}({x h n 不可能一致收敛;但在任何),0[),[+∞⊂+∞a 上,)}({x h n 仍有可能一致收敛于0.在高等数学中幂级数求和函数手算比较困难,应用MATLAB 求和函数就会很快求出和函数.例8 求幂级数∑∞=-2)1(k kk k x 的和函数S2.应用MATLAB 命令:syms k xS2=symsum('x^k/k/(k-1)',k,2,inf)S2 = 1/2*x^2*(2/x*(-log(1-x)/x-1)*(x-1)-1/(x-1)*(-2*x+2))S2=simplify(S2) (将S2简化)S2 = -log(1-x)*x+log(1-x)+x在上面的例题中应用MATLAB 对高等数学中出现的一些复杂计算和函数项序列一致收敛进行判别,体现了MATLAB 在高等数学中的应用.3 矩阵MATLAB 的数学能力大部分是从它的矩阵函数中派生出来的,在MA TLAB 中提供了丰富的矩阵运算函数,包括所有的标准的线性代数中使用到的矩阵函数.3.1 计算行列式、秩Det 计算矩阵行列式的值Rank 函数计算矩阵的秩. n=1n=5例9 A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1097591086781075675,求|A|,rank(A). 应用MATLAB 命令:>> A=[5 7 6 5 ;7 10 8 7;6 8 10 9;5 7 9 10];>> det(A)ans =1>> rank(A)ans =43.2 特征值的计算eig (A) 计算矩阵的特征值如果A是n n *矩阵,若λ满足AX=λX,则称λ为A的特征值.例10 A= ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛86109638715435442 ,求A 的特征值. 应用MATLAB 命令: >>A=[2 4 4 5;3 4 5 1;7 8 3 6;9 10 6 8];>>eig=(A)ans =20.4983-3.4064-1.31331.2214如果还要求特征向量,则可以用eig (A)函数的第一个返回值得到.应用MATLAB 命令:>> [X,D]=eig(A)X =-0.3659 -0.6486 0.7050 0.4314-0.2674 -0.2135 -0.6239 -0.7569-0.5175 0.6321 0.2781 0.0644-0.7258 0.3664 -0.1905 0.4868D =20.4983 0 0 00 -3.4064 0 00 0 -1.3133 00 0 0 1.2214在MATLAB 中特征值和特征向量的求解过程体现了矩阵作为MA TLAB 的基本计算单位在进行矩阵运算时是很简便的.4 方程和方程组“方程是很多工程和科学工作的发动机”.若干世纪以来,工程师和科学家们花了大量的时间用于求解方程(组).数学家研究各种各样的方程求解方法.MATLAB 为求解方程(组)提供了便利条件.4.1 方程MA TLAB 的命令输入格式:solve('eqn1','eqn2'…,'eqnN','var1','var2',…'varN')其中eqni 表示第i 个方程,vari i 表示第i 个变量,i=1,2,…,N .在求解多项式方程时还可以用MATLAB 函数roots(p),其中p 是多项式的系数按降幂排列所形成的n+1维列向量,它能够给出全部根(包括重根).避免在高等数学日常计算中出现的丢根情况.例11 求解多项式方程0189=++x x .应用MATLAB 命令:>> P=[1,1,0,0,0,0,0,0,0,1];>> roots(P)ans =-1.2131-0.9017 + 0.5753i-0.9017 - 0.5753i-0.2694 + 0.9406i-0.2694 - 0.9406i0.4168 + 0.8419i0.4168 - 0.8419i0.8608 + 0.3344i0.8608 - 0.3344i4.2 方程组4.2.1 线性方程组除了使用MA TLAB 函数solve 以外,还可以用其他MATLAB 命令.如将线性方程组写成矩阵形式A*X=b ,其中A为m*n 阶方阵,X 和b 均为n 阶列向量.例12 解线性方程组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛852*********X=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛514351804366 .应用MATLAB 命令: >> A=[1 2 3;4 5 6;7 8 0;2 5 8];>>b=[366 804 351 514]';>> x=A\bx =247.9818-173.1091114.92734.2.2 非线性方程组非线性方程组可以用solve( )函数进行求解,一般给出的是数值解,也可以用fsolve( )进行求解,输入格式为fsolve('FUN',X0)其中FUN 表示M 文件函数,X0表示变量的初始点.下面用MATLAB 求解一个比较复杂的非线性方程组.例13 解非线性方程组⎪⎩⎪⎨⎧=-++=+-+=-++05012307ln sin 32z y x z x z y x y .应用MATLAB 命令:function eq=nxxf(x)global number;number=number+1;eq(1)=sin(x(1))+x(2)^2+log(x(3))-7;eq(2)=3*x(1)+2^x(2)-x(3)^3+1;eq(3)=x(1)+x(2)+x(3)-5;global number;number=0;y=fsolve('nxxf',[1,1,1])y =0.5991 2.3959 2.00505 微分方程微分方程是高等数学中一个比较重要的分支,它的应用也比较广泛,使用MATLAB 软件就可以方便地求出它的各种形式的解.5.1 解析解求微分方程的解析解的MATLAB 命令:dsolve('eqn1','eqn2',…,'x')其中'eqni'表示第i 个方程,'x'表示微分方程组中的自变量.除了用MA TLAB 求解一阶微分方程外,也可以解决较复杂的二阶微分方程.例14 求解二阶微分方程2x y ''x +y '2/1,/2)2/(),2/(,0)(22==-'==-+n y y y n x πππ.应用MA TLAB 命令:>> dsolve('D2y+(1/x)*Dy+(1-(1/2)^2/x^2)*y=0','y(pi/2)=2','Dy(pi/2)=(-2/pi)','x')ans =2^(1/2)*pi^(1/2)/x^(1/2)*sin(x)5.2 数值解在没有解析解的情况下就要求数值解.求解微分方程(组)数值解,用2阶龙格-库塔公式和4阶龙格-库塔公式,其程序为:[t,y]=ode23('F',ts,y0,options) [t,y]=ode45('F',ts,y0,options)其中F 为由微分方程(组)写成的M 文件名.例15 求方程0)(222=-+'+''y n x y x y x 的数值解.应用MATLAB 命令: function f=jie3(x,y)f=[y(2);-y(2)/x+((1/2)^2/x^2-1)*y(1)]; >> [x,y]=ode23('jie3',[pi/2,pi],[2,-2/pi]) x = 1.5708 1.6074 1.7645 1.9215 2.0786 2.2357 2.3928 2.5499 2.7069 2.8640 3.0211 3.1416 y =2.0000 -0.6366 1.9758 -0.6869 1.8518 -0.8879 1.6982 -1.0631 1.5192 -1.2108 1.3193 -1.3293 1.1032 -1.4174 0.8756 -1.4744 0.6416 -1.5002 0.4060 -1.4951 0.1735 -1.46020.0002 -1.4140>> y1=y(:,1);>> y2=y(:,2);>> plot(x,y1,x,y2,'r'),gtext('y1'),gtext('y2')6插值MATLAB中的插值函数为interpl( ),其调用格式为yi=interpl(x,y,xi,'method')其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量.'method'表示采用的插值方法.MA TLAB提供的插值方法有几种:'nearest'最邻近插值;'linear'线性插值;'spline'三次样条插值;'cubic'立方插值.用MATLAB插值做一个数学实验.O)例16 在一天24小时内,从零点开始每间隔2小时测得的环境温度数据为(C12,9,9,1,0,18,24,28,27,25,20,18,15,13,推测中午1点(即13点)时的温度.应用MATLAB命令:>> x=0:2:24;>> y=[12 9 9 10 18 24 28 27 25 20 18 15 13];>> x1=13;>> y1=interp1(x,y,x1,'spline')y1 =27.8725O所以,中午1点时的温度大约为27.8725C若要得到一天24小时的温度曲线,只需继续键入:应用MATLAB命令:>> xi=0:1/3600:24;>> yi=interp1(x,y,xi,'spline');>> plot(x,y,'o',xi,yi)7曲线拟合MATLAB中的拟合函数为polyfit( ),其调用格式为:Polyfit(X,Y,n)执行该函数将产生一个n阶多项式P,并且使得P(X)=Y.例17下表展示了来自1985年以来第x年从中国进口到美国的(以百万美元计数)值y (a)求一能近似该数据的线性函数y=b+mx.(b)对每个y求lny,并利用y和lny的值求一个能近似该数据的线性函数lny=b+mx.e的指数函数.(c)利用(b)中的方程求一个能拟合该数据的形为y=a kx年1985 1986 1987 1988 1989 1990 1991第x年0 1 2 3 4 5 6进口值y 3862 4771 6293 8511 11990 15237 18976应用MATLAB命令:(a)线性拟合x=[0:6];>> y=[3862 4771 6293 8511 11990 15237 18976];>> plot(x,y,'o')>> hold on>> f1=polyfit(x,y,1)f1 =1.0e+003 *2.5704 2.2374 >> y1=polyval(f1,x); >> plot(x,y1,'r')线性拟合函数拟合效果(b) 对数线性拟合 f2=polyfit(x,log(y),1) f2 =0.2765 8.2275 >> y2=polyval(f2,x); >> hold on >> plot(x,log(y),'o') >> plot(x,y2,'k')对数线性函数拟合效果(c) 由(b)可知,xey 2756.05.3742plot(x,y,'o')>> hold on>> plot(x,3742.5*exp(0.2756*x))指数拟合效果由拟合效果知指数函数拟合较好.8数学实验数学实验是对实际生活中的数学问题的解决,提出问题并进行探究、思考、分析等思维活动,最终理解并解决问题,提出想法借助于数学软件实现.培养学生的独立能力和创新精神.波音公司飞机最佳定价策略[2](P46-48)全球最大的飞机制造商—波音公司自1955年推出波音707开始.成功地开发了一系列的喷气式客机.问题:讨论该公司对一种新型客机最优定价策略的数学模型.(1) 问题分析定价策略涉及到诸多因素,这里考虑以下主要因素:价格、竞争对手的行为、出售客机的数量、波音公司的客机制造量、制造成本、波音公司的市场占有率等等因素。
Matlab软件在高等学校数学类课程中的作用及应用共4页文档

Matlab软件在高等学校数学类课程中的作用及应用Matlab是一种具有科学计算功能的应用软件,包括符号运算、数值运算、图像处理、统计分析及编程可视化等功能。
其特点是语句简单、功能强大。
自1984年推出正式版本以来,该软件已被越来越多的学者应用于科学研究工作中。
随着网络计算机技术的发展、多媒体教学的普及,电脑已成为教学过程中常用的辅助教学工具之一,使得将Matlab软件引入课堂教学过程更容易实现。
数学是进行科学研究的重要工具,高等数学、线性代数、概率论和数理统计是高等院校理工类和经管类专业学生必修的三门数学类基础课程,是学生学好其他基础课和专业课的基础。
高等数学课程在这三门数学课程中又是“重中之重”,也是绝大多数专业学生报考硕士研究生的必考课程。
刚刚经历高考进入高等学校的学生都知道高等数学课程的重要性,但突然面对抽象的符号、严密的逻辑、高深的理论,许多学生都望而却步,逐渐失去了学习的兴趣。
本学期,我系组建了一个Matlab软件兴趣小组,定期开展活动,活动内容主要是向学生介绍Matlab软件的基本使用方法,引导学生将Matlab 软件应用到数学类课程中,解决一些实际问题。
兴趣小组中的学生,基本上是大学二年级的学生,活动中所选取的内容都是学生上课过程中碰到的知识点。
一 Matlab软件在数学课堂教学中的作用1.激发学生的学习兴趣为了培养学生的学习积极性,要尽量地将抽象变得直观,变成学生能看得见、摸得着的东西,最直接的方法就是图形展示。
Matlab软件具有强大的图形处理功能,能形象直观地展现空间几何关系,在教学中展示复杂的函数图形,曲面、曲线相对位置变化,甚至利用动画模拟空间曲线、曲面和立体图形的生成过程,使原本难以想象的空间图形变得具体生动。
编程过程中还可以改变参数,使图形画面亮丽多彩,营造了一种轻松的课堂氛围。
例如,在利用定积分计算旋转体的体积一节中,首先介绍的是旋转体的概念,如果仅通过教师口述旋转体的定义,缺乏感官的刺激,容易使学生感到枯燥乏味。
Matlab在高等数学中的几点应用
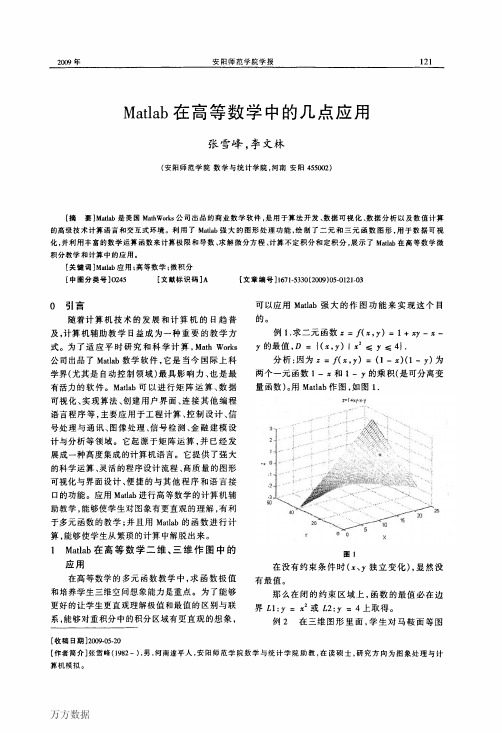
Abstract:Matlab,a commercial ma山ematical software from MathWorks Corporation of USA,is used in the high—
level technical computing language and.interactive environment for algorithm development,data visualization,data
及,计算机辅助教学日益成为一种重要的教学方 式。为了适应平时研究和科学计算,Math Works 公司出品了Matlab数学软件,它是当今国际上科 学界(尤其是自动控制领域)最具影响力、也是最 有活力的软件。Matlab可以进行矩阵运算、数据 可视化、实现算法、创建用户界面、连接其他编程 语言程序等,主要应用于工程计算、控制没计、信 号处理与通讯、图像处理、信号检测、金融建模设 计与分析等领域。它起源于矩阵运算,并已经发 展成一种高度集成的计算机语言。它提供了强大 的科学运算、灵活的程序设计流程、高质量的图形 可视化与界面设计、便捷的与其他程序和语言接 口的功能。应用Matlab进行高等数学的计算机辅 助教学,能够使学生对图象有更直观的理解,有利 于多元函数的教学;并且用Matlab的函数进行计 算,能够使学生从繁琐的计算中解脱出来。
分析:因为z=f(戈,Y)=(1一石)(1一Y)为 两个一元函数l一戈和1一Y的乘积(是可分离变 量函数)。用Matlab作图,如图1.
围l
在没有约束条件时(扒Y独立变化),显然没 有最值。
那么在闭的约束区域上,函数的最值必在边 界L1:Y=名2或L2:Y:4上取得。
例2 在三维图形里面,学生对马鞍面等图
化,并利用丰富的数学运算函数来计算极限和导数、求解微分方程、计算不定积分和定积分,展示了Matlab在高等数学微
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB在微分方程中的应用
12级通信一班张丹丹1202301039
摘要:MATLAB的强大功能也是大学的数学教育中是相当重视其学习重要性的原因之一。
它能将运用者从繁杂的计算束缚中解救出来,把更多的精神投入到数学的基本含义的理解上,因此,它逐渐成为大学生们课程中的规范和重要工具。
MATLAB在信息论、高等数学与代数中作图和教学中的应用,从而充分体现了MATLAB功能的强大,特别是绘图功能,矩阵运算,数值分析运算。
借助MATLAB的运用,使学习者对数学的欣赏得以向群众普及,这对数学文明的传递具有重要意义。
以下主要从数学中的解微分方程及其应用的角度来思考。
关键字:MATLAB介绍解微分方程绘图应用
一、MATLAB
(一)MATLAB简介
MATLAB(Matrix Laboratory,矩阵实验室)是MathWorks公司开发的,目前国际上最流行,应用最广泛的科学与工程计算软件。
它集成二维和三维图形功能,已完成相应数值可视化的工作,并且提供了一种交互式的高级编程语言-M语言,利用M语言可以通过编写脚本或则函数文件实现用户自己的算法。
MATLAB是目前发展最快的软件之一,其在多线程计算、视频图像算法等方面更加突出,能够从Symbolic math Toolbox 中生成Simscape语言方程,SimulMATLABink 中增加了Simulink PLC Coder。
(二)MATLAB的功能与特点
MATLAB集科学与工程计算机、图形可视化、多媒体处理于一体,并提供了Windows 图形界面设计方法。
MATLAB语言有以下特点:
起点高
2.人机界面友好,编程效率高
3.强大而智能化的作图功能
4.智能化程度高
5.Simulink动态仿真功能
二.Matlab求解微分方程
求微分方程(组)解析解的命令
应用dsolve函数求解方程(‘方程1’,‘方程2’,…,‘方程n’,‘初始条件’,‘自变量’)
例1 求du/dt=1+u^2的通解.
输入命令:dsolve('Du=1+u^2','t')
结果:u = tg(t+c1)
例2.求微分方程的特解. x’(t)=2x-3y+3z
y’(y)=4x-5y+3z
Z’(t)=4x-4y+2z
输入命令:
[x,y,z]=dsolve('Dx=2*x-3*y+3*z',
'Dy=4*x-5*y+3*z','Dz=4*x-4*y+2*z', 't');
x=simple(x) % 将x化简
y=simple(y)
z=simple(z)
结果为:x = (c1-c2+c3+c2e -3t-c3e-3t)e2t
y = -c1e-4t+c2e-4t+c2e-3t-c3e-3t+c1-c2+c3)e2t
z = (-c1e-4t+c2e-4t+c1-c2+c3)e2t
三.应用MATLAB解微积分方程及其图形绘制
在MATLAB中,使用函数可以把一个大的任务分解成比较小的任务,使得程序模块化,每个函数完成的定的功能,通过函数的调用完成整个过程。
微积分课程中引入matlab软件,并力争与教学的相关内容进行有机结合。
使malab作为一个重要工具,既能在数学课程的某些内容处理上发挥作用,也能为其它后续基础课程如《线性代数》《概率论与数理统计》《复变函数》等中涉及的微积分问题与matlab相结合。
1.应用function函数来声明调用:
以此来调用是M函数文件中必须有的,而且函数名应该与文件名一致。
而且应用相关的流程控制结构和表达式实现。
2.这里主要应用ode23,ode45求解非刚性标准形式的一阶常微分方程组的初值问题解的MATLAB常用程序.在解含n个未知数的方程组时,x0和x均为n维向量,M文件中的待解方程组应以x的分量形式写出.使用MATLAB软件求数值解时,高阶微分方程必须等价地变换成一阶微分方程组.
例3 解微分方程y1’=y2y3
Y2’=-y1y3
Y3’=-0.5y1y2
Y1(0)=0,y(0)=1,y(3)=1
解1)解题程序如下:
function dy=rigid(t,y)
dy=zeros(3,1);
dy(1)=y(2)*y(3);
dy(2)=-y(1)*y(3);
dy(3)=-0.51*y(1)*y(2);
2)取t0=0,tf=12,输入命令:
[T,Y]=ode45('rigid',[0 12],[0 1 1]);
plot(T,Y(:,1),'-',T,Y(:,2),'*',T,Y(:,3),'+')
3)结果如图
(图中,y1的图形为实线,y2的图形为“*”线,y3的图形为“+”线)
例4 dx^2/dt^2-1000(1-x^2)dx/dt-x=0
X(0)=2,x’(0)=0
1.解题程序如下:
function dy=vdp1000(t,y)
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=1000*(1-y(1)^2)*y(2)-y(1);
2.取t0=0,tf=3000,输入命令:
[T,Y]=ode15s('vdp1000',[0 3000],[2 0]);
plot(T,Y(:,1),'-')
3.结果如图
三.MATLAB在实例中的应用
例1、导弹追踪问题
设位于坐标原点的甲舰向位于x轴上点A(1, 0)处的乙舰发射导弹,导弹头始终对准乙舰.如
果乙舰以最大的速度v0(是常数)沿平行于y轴的直线行驶,导弹的速度是5v0,求导弹运行的曲线方程.又乙舰行驶多远时,导弹将它击中?
1.解题思路:假设导弹在t时刻的位置为P(x(t), y(t)),乙舰位于Q(1,v0t).
由于导弹头始终对准乙舰,故此时直线PQ就是导弹的轨迹曲线弧OP在点P处的切线,
即有y’=(v0t-y)/(1-x) 即v0t=(1-x)y’+y
2. 又根据题意,弧OP的长度为AQ的5倍
因此导弹运动轨迹的参数方程为:
3. 解导弹运动轨迹的参数方程
x’(t)= 5(1-x)
((1-x)^2+(t-y)^2)^1/2
y’(t)= 5(t-y)
((1-x)^2+(t-y)^2)^1/2
x(0)=0,y(0)=0
建立m-文件eq2.m如下:
function dy=eq2(t,y)
dy=zeros(2,1);
dy(1)=5*(1-y(1))/sqrt((1-y(1))^2+(t-y(2))^2);
dy(2)=5*(t-y(2))/sqrt((1-y(1))^2+(t-y(2))^2);
取t0=0,tf=2,建立主程序chase2.m如下:
[t,y]=ode45('eq2',[0 2],[0 0]);
Y=0:0.01:2;
plot(1,Y,'-')
hold on
plot(y(:,1),y(:,2),'*')
当x=1时y=5/24,即当乙舰航行到点(1,5/24)处时被导弹击中.
被击中时间为:t=y/v0=5/24v0. 若v0=1, 则在t=0.21处被击中.
4.轨迹图如下
四、学习的心得
通过十几周MATLAB学习过程中,涉及到很多数学模型,数学公式以及线性代数中一些概念问题,在老师的耐心指导下,加上通过讲解例题让我们更加的理解和应用MATLAB,在刚开始的过程中,我发现自己对MATLAB工具不能熟练,常常做到最后一个才走,但这更加坚定了我要好好学习专业课的决心,遇到不懂的问题,及时向老师求解。
通过一学期的努力,无论在MATLAB这个软件的应用,还是高数、线性代数等知识点都有了明显的提高。
尽管MATLAB的微积分的具体内容老师并没讲太多,但是由于我对其的兴趣,我自学了这方面知识,并且做出这份报告,我之所以有这样的能力,全应该感谢老师的不懈鼓励和栽培。
以后也会更加努力将MATLAB应用于实际生活中。
五、参考文献
[1]姜启源,大学数学实验的MATLAB求解【M】.北京:清华大学出版,2005.8
[2]陈阳泉,初等运用数学效果的MATLAB求解。
北京大学清华出版社,2007.6
[3]高等数学(第六版)上册同济大学数学系编
[4] MATLAB实用教程(第三版)郑阿奇主编2006.9。
