数字电路的逻辑运算.ppt
合集下载
数字逻辑电路与系统设计课件

计数器
用于计数和控制时序,常用于实现定时器和分频器。
移位器
用于二进制数据的移位操作,常用于数据格式化和数据传输。
顺序脉冲发生器
用于产生一定规律的顺序脉冲信号,常用于控制电路的工作流程。
04
数字系统设计
数字系统概述
数字系统的基本概念
数字系统是指使用离散的二进制数字信号进行信息处理的系统。它主要由逻辑 门电路、触发器、寄存器、加法器等基本元件组成,具有精度高、稳定性好、 易于大规模集成等优点。
实现逻辑功能
根据状态转换图,实现相应的 逻辑功能。
确定设计目标
明确设计时序逻辑电路的目的 和要求,如实现特定的功能、 达到一定的性能指标等。
设计状态转换图
根据设计要求,设计状态转换 图,确定状态和输出。
验证设计
通过仿真或实验验证设计的正 确性和可行性。
常用时序逻辑电路
寄存器
用于存储二进制数据,常用于数据传输和数据处理。
集成化和智能化技术的发展,为数字 系统的设计带来了新的机遇和挑战。
数字系统的智能化是当前的一个重要 趋势,它使得数字系统能够具有更强 的自适应性、智能性和灵活性。
THANKS FOR WATCHING
感谢您的观看
分析输入和输出信号的逻辑关系,确定电路的功 能。
真值表和逻辑表达式
通过列出所有输入组合和对应的输出值,得到真 值表,并根据真值表推导出逻辑表达式。
3
逻辑功能描述
根据逻辑表达式或真值表,描述组合逻辑电路的 逻辑功能。
组合逻辑电路的设计
明确设计要求:确定输入和 输出信号,以及电路要实现 的功能。
根据功能要求,逐一确定每 个输入组合对应的输出值。
自底向上的设计方法
用于计数和控制时序,常用于实现定时器和分频器。
移位器
用于二进制数据的移位操作,常用于数据格式化和数据传输。
顺序脉冲发生器
用于产生一定规律的顺序脉冲信号,常用于控制电路的工作流程。
04
数字系统设计
数字系统概述
数字系统的基本概念
数字系统是指使用离散的二进制数字信号进行信息处理的系统。它主要由逻辑 门电路、触发器、寄存器、加法器等基本元件组成,具有精度高、稳定性好、 易于大规模集成等优点。
实现逻辑功能
根据状态转换图,实现相应的 逻辑功能。
确定设计目标
明确设计时序逻辑电路的目的 和要求,如实现特定的功能、 达到一定的性能指标等。
设计状态转换图
根据设计要求,设计状态转换 图,确定状态和输出。
验证设计
通过仿真或实验验证设计的正 确性和可行性。
常用时序逻辑电路
寄存器
用于存储二进制数据,常用于数据传输和数据处理。
集成化和智能化技术的发展,为数字 系统的设计带来了新的机遇和挑战。
数字系统的智能化是当前的一个重要 趋势,它使得数字系统能够具有更强 的自适应性、智能性和灵活性。
THANKS FOR WATCHING
感谢您的观看
分析输入和输出信号的逻辑关系,确定电路的功 能。
真值表和逻辑表达式
通过列出所有输入组合和对应的输出值,得到真 值表,并根据真值表推导出逻辑表达式。
3
逻辑功能描述
根据逻辑表达式或真值表,描述组合逻辑电路的 逻辑功能。
组合逻辑电路的设计
明确设计要求:确定输入和 输出信号,以及电路要实现 的功能。
根据功能要求,逐一确定每 个输入组合对应的输出值。
自底向上的设计方法
数字逻辑电路 PPT课件

TTL电路具有较快的开关速度,较强的抗 干扰能力以及足够大的输出摆幅,所以是目前 在各个领域包括医学电子设备中使用最广泛的 逻辑电路系统。实际的集成门电路比这里的要 复杂些,在输出端还有放大器和跟随器,用来 保证逻辑电平符合要求,增加负载能力。
在一个实际的数字系统中,往往需要能实现多种
多样逻辑功能的门电路,只有一种与非门作为基本单 元使用起来显然是不方便的。在TTL门电路的系列产 品中,常用的还有或非门、与或非门、与门、或门等 等。虽然门电路的种类很多,但它们或者是由与非门 稍加改动得到的,或者是由与非门中的若干部分组合 成的,有的就是与非门的一部分。如,与非门只有一 个输入端时成了非门;在与非门后再连一个非门成了 与门;在与非门前面对于每个输入端各接一个非门成 了或门。可以说与非门可以完成一切逻辑运算。因此, 只要掌握与非门典型电路的工作原理和分析方法,就 不难对其它形式的门电路进行分析了。
2. 或门电路 上图为简单的具有两个输入端的二极管或门电路、常用
逻辑符号、逻辑表达式及真值表。 其中A、B分别为两个输入端,F为输出端。这种电路之
所以能实现或运算,是因为输出端的电平被最高电平的输入 端钳位,只要输入端有一个高电平时,输出就是高电平。也 就是说输入有一个为1时,输出即为1。输入端全为0时,输 出才为0。
阐述逻辑控制、脉冲计数和数字显示的基本原 理,介绍常用的计数器和A/D、D/A转换器。
主要内容
第一节 基本逻辑电路 第二节 双稳态触发器 第三节 脉冲的计数和显示 第四节 数模和模数转换
第一节 基本逻辑电路
所谓逻辑是指“条件”与“结果”的 关系。逻辑电路(logic circuit)是用电路的 输入信号反映“条件”,用电路的输出信 号反映“结果”。电路的输出与输入之间 构成一定的逻辑关系。
在一个实际的数字系统中,往往需要能实现多种
多样逻辑功能的门电路,只有一种与非门作为基本单 元使用起来显然是不方便的。在TTL门电路的系列产 品中,常用的还有或非门、与或非门、与门、或门等 等。虽然门电路的种类很多,但它们或者是由与非门 稍加改动得到的,或者是由与非门中的若干部分组合 成的,有的就是与非门的一部分。如,与非门只有一 个输入端时成了非门;在与非门后再连一个非门成了 与门;在与非门前面对于每个输入端各接一个非门成 了或门。可以说与非门可以完成一切逻辑运算。因此, 只要掌握与非门典型电路的工作原理和分析方法,就 不难对其它形式的门电路进行分析了。
2. 或门电路 上图为简单的具有两个输入端的二极管或门电路、常用
逻辑符号、逻辑表达式及真值表。 其中A、B分别为两个输入端,F为输出端。这种电路之
所以能实现或运算,是因为输出端的电平被最高电平的输入 端钳位,只要输入端有一个高电平时,输出就是高电平。也 就是说输入有一个为1时,输出即为1。输入端全为0时,输 出才为0。
阐述逻辑控制、脉冲计数和数字显示的基本原 理,介绍常用的计数器和A/D、D/A转换器。
主要内容
第一节 基本逻辑电路 第二节 双稳态触发器 第三节 脉冲的计数和显示 第四节 数模和模数转换
第一节 基本逻辑电路
所谓逻辑是指“条件”与“结果”的 关系。逻辑电路(logic circuit)是用电路的 输入信号反映“条件”,用电路的输出信 号反映“结果”。电路的输出与输入之间 构成一定的逻辑关系。
数字电路ppt课件

主要的工具是逻辑代数,电路的功能用真值表、
逻辑表达式及波形图表示。
3
模拟电路研究的问题
基本电路元件: 基本模拟电路:
•晶体三极管 •场效应管 •集成运算放大器
• 信号放大及运算 (信号放大、功率放大) • 信号处理(采样保持、电压比较、有源滤波) • 信号发生(正弦波发生器、三角波发生器、…)
4
数字电路研究的问题
长中含反, 去掉反。
A B(A A) A B
例如:A ABC DE A BC DE
被吸收
32
3.混合变量的吸收: AB AC BC AB AC
证明: AB AC BC
1
AB AC (A A)BC
正负相对, 余全完。
AB AC ABC ABC AB AC
BA BD BC
38
吸收
例如: AB AC BCD AB AC BC BCD AB AC BC AB AC
33
五、摩根定理
AB AB AB AB
还有更多变量
可以用列真值表的方法证明:
A
B A•B A • B A
B AB
00 01
1
11
01 01
1
01
10 01
0
11
11 10
0
00
34
反演定理:将函数式 F 中所有的
C
开关断为逻辑“0”
E
F
灯亮为逻辑“1”
灯灭为逻辑“0”
20
E
真值表 AB 00 00 01 01 10 10 11 11
A B C
CF 00 11 01 11 01 11 01 11
真值表特点: 任1 则1, 全0则0。
数字逻辑课件——逻辑代数

AB(1 C ) AC (1 B)
AB AC
(由互补律) (由分配律) (由交换律) (由分配律)
(由0-1律)
1818
定理3(右)的证明:
左边:( A B)( A C)(B C) ( AA AB AC BC )(B C ) (由分配律)
( AB AC BC )(B C )
(2) 证明方法
A BC ABC ABC A BC
上述各定律的证明的基本方法是真值表法,即分别列出等 式两边逻辑表达式的真值表,若两个真值表完全一致,则 表明两个逻辑表达式相等,定律便得到证明,
对偶规则的存在,使得需要证明的公式数减少了一半。
1212
例如,证明反演律,
A
B
A B AB
AB A B
0
0
1
1
1
1
1
0
0
0
1
1
0
1
0
0
1
1
1
1
0
0
0
0
第二列和第三列在变量A,B的所有四种取值组合 下结果完全一致,因而得证。
类似地,第四列和第五列在变量A,B的所有四种 取值组合下结果完全一致,因而得证。
1313
普通代数的一些定律和定理不能错误地“移植” 到逻辑代数中。
例如,在普通代数中,把等式两边相同的项消去, 等式仍成立,但在逻辑代数中则不然,请看下例:
A ( A A)B
= A + 1·B =A+B 定理2(右)的证明:
A( A B) AA AB
= 0 + AB = AB
(由定理1) (由分配律) (由互补律) (由0-1律)
(由分配律) (由互补律) (由0-1律)
AB AC
(由互补律) (由分配律) (由交换律) (由分配律)
(由0-1律)
1818
定理3(右)的证明:
左边:( A B)( A C)(B C) ( AA AB AC BC )(B C ) (由分配律)
( AB AC BC )(B C )
(2) 证明方法
A BC ABC ABC A BC
上述各定律的证明的基本方法是真值表法,即分别列出等 式两边逻辑表达式的真值表,若两个真值表完全一致,则 表明两个逻辑表达式相等,定律便得到证明,
对偶规则的存在,使得需要证明的公式数减少了一半。
1212
例如,证明反演律,
A
B
A B AB
AB A B
0
0
1
1
1
1
1
0
0
0
1
1
0
1
0
0
1
1
1
1
0
0
0
0
第二列和第三列在变量A,B的所有四种取值组合 下结果完全一致,因而得证。
类似地,第四列和第五列在变量A,B的所有四种 取值组合下结果完全一致,因而得证。
1313
普通代数的一些定律和定理不能错误地“移植” 到逻辑代数中。
例如,在普通代数中,把等式两边相同的项消去, 等式仍成立,但在逻辑代数中则不然,请看下例:
A ( A A)B
= A + 1·B =A+B 定理2(右)的证明:
A( A B) AA AB
= 0 + AB = AB
(由定理1) (由分配律) (由互补律) (由0-1律)
(由分配律) (由互补律) (由0-1律)
数字逻辑教学课件 数字电路2-4
4. 中规模组合逻辑部件 掌握典型集成电路的外部功能、扩展、应用。
–数据选择器:根据地址码的要求,从多路输入信号中 选择其中一路输出。
选择数据
应用:
并 —> 串
实现组合逻辑
–译码器:特定意义信息的二进制代码翻译出来,常用的 有二进制译码器、二-十进制译码器、数码显示译码器。
片选、地址译码
应用:
实现数据分配
0110 1 0110
7+5=12
=(0001 0010)8421
75 0111
0101 1100
0110 1 0010
一旦需要修正,则8421码必有进位输出。
判 9 加 6 修正电路:
1)当有进位输出 或 2) 当和数>9;
应修正让其产生进位,且加(0110);
设计两个一位8421BCD码加法电路应由三部分组成。
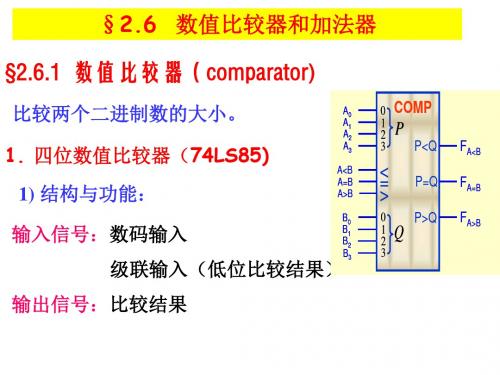
§2.6 数值比较器和加法器
§2.6.1 数值比较器(comparator)
比较两个二进制数的大小。
A0
A1
A2
1. 四位数值比较器(74LS85)
A3
A<B
1) 结构与功能:
A=B A>B
B0
输入信号:数码输入
B1 B2
级联输入(低位比较结果)B3
输出信号:比较结果
0 COMP
1 2
P
3 P<Q FA<B
奇校验位(监督位): P C1 C2 C2 Cn 1
74LS280
A B C EVEN D
E F ODD G H
“1” I
奇校验位
3) 校验位产生 / 校验检测
D0
D7
片1奇校验 位产生器
课件数字电路.ppt

将开关接通记作1,断开记作0;灯亮记作1,灯 灭记作0。可以作出如下表格来描述与逻辑关系:
功能表
开关 A 开关 B 灯 Y
A
断开 断开
灭
0
断开 闭合
灭
0
1
闭合 断开
灭
1
闭合 闭合 亮
BY
00 真 10 值
00 表
11
两个开关均接通时,灯才会 Y=A•B
亮。逻辑表达式为:
实现与逻辑的电路称为与门。
对偶定理:如果两个逻辑式相等,则它们的对偶 式也相等。
利用对偶规则,可以使要证明及要记忆的公 式数目减少一半。
逻辑函数及其表示方法
逻辑函数
如果以逻辑变量作为输入,以运算结果作为 输出,当输入变量的取值确定之后,输出的取值 便随之而定。输出与输入之间的函数关系称为逻 辑函数。Y=F(A,B,C,…)
反演定理 对于任何一个逻辑表达式Y,如果将表达式中
的所有“·”换成“+”,“+”换成“·”,“0” 换成“1”,“1”换成“0”,原变量换成反变量, 反变量换成原变量,那么所得到的表达式就是函 数Y的反函数Y′(或称补函数)。这个规则称为反 演定理。
对偶定理
对于任何一个逻辑表达式Y,如果将表达式 中的所有“·”换成“+”,“+”换成“·”,“0” 换成“1”,“1”换成“0”,而变量保持不变,则 可得到的一个新的函数表达式 YD, YD称为Y的对偶 式。
基本公式
0-1
律:
A A
0 A 1 A
A 1 1 A 0 0
互补律: A A 1 A A 0
分别令A=0及 A=1代入这些 公式,即可证 明它们的正确 性。
重叠律: A A A A A A
数字逻辑课件

数字信号 u t
特点是脉冲式的,只有两种状态: 有脉冲和无脉冲。 一般我们用高电平代表有脉冲,低电平代表无脉 冲----正逻辑 当然也可以反过来定义----负逻辑
研究数字电路时注重电路输出、
输入间的逻辑关系,因此不能采用 模拟电路的分析方法。主要的分析 工具是逻辑代数,时序图,逻辑电 路图等。
2 1 0
位权
一个十进制数 N可以表示成加权和的形式: D:decimal
( N )D
n 1 i m
取值
ai 10i
权重
若用电子电路进行十进制数运算, 必须要有十个电路状态与十个数码相对 应。这样将在技术上带来许多困难,电 路复杂,运算速度慢,而且很不经济。 早期的模拟计算机就是如此。
• 方法: 整数部分 • --从低位(小数点左边第一位)开始,每三位二进制数分为一组, 最后不足三位的前面补零,每组用一位等价的八进制数来代替; 小数部分 • --从高位(小数点右边第一位)开始,每三位二进制数分为一组, 最后不足三位的后面补零,然后按顺序写出对应的八进制数。
• 例:将二进制数(10111101.01110111)2转换为八进制数。
开关合为逻辑1开关断为逻辑0灯亮为逻辑1灯灭为逻辑0非逻辑逻辑反非逻辑真值表非逻辑关系非逻辑关系表示式与非逻辑真值表与非逻辑表达式与非逻辑表达式ab或非逻辑真值表或非逻辑表达式或非逻辑表达式cdab两输入变量ab不同时输出y为1而ab相同时输出y为0两输入变量ab相同时输出y为1而ab不同时输出y为0yyaabb运算类型逻辑表达式功能说明相同为1不同为0abcdabcdab与非逻辑或非逻辑与或非逻辑异或逻辑同或逻辑复合逻辑关系小结乘运算规则
t
对模拟信号进行传输、 处理的电子线路称为 模拟电路。
数电-数字逻辑基础幻灯片PPT

2.复合逻辑运算 在逻辑代数中,由基本的与、或、非逻辑运算可以实现多种复合逻辑运算。
A
B & Y1 A•B
A
A
B
Y1
B
Y1
A B
≥1
Y2 AB
A B
+ Y2
A B
Y2
A 1 Y3 A
A
Y3
A
Y3
(a)国际符号
(b)曾用符号 (c)美国符号
A B
&
Y4 A • B
A B
A B
≥ 1 Y5 A B
A
&
A
F
F
B
B
(a)
(b)
OC门逻辑符号
(a) 国际符号;
(b) 惯用符号
OC门除了可以“线与”连接外,还可以用来驱动感性负载或实现电平转换。 例如,在图的电路中,EC=10V时,F的输出高电平就从3.6V变成了10V。
+ EC
& A
F B
& C D
OC门的线与电路
(3)三态门
三态门也称TS门(Three State Gate), 是在TTL逻辑电路的基础上增加一个 使能端EN而得到的。当EN=0时,TTL与非门不受影响,仍然实现与非门功 能;当EN=1时,TTL与非门的V4、V5将同时截止,使逻辑门输出处于高阻 状态。因此,三态门除了具有普通逻辑门的高电平(逻辑1)和低电平( 逻辑0)两种状态之外,还有第三种状态——高阻抗状态,也称开路状态 或Z状态。三态门的逻辑符号和真值表分别如图1-6和表1-5所示。国际 符号中的倒三角形“▽”表示逻辑门是三态输出,EN为“使能”限定符 ,输入端的小圆圈表示低电平有效(有的三态门也可能没有小圆圈,说明 EN是高电平有效)。
数字电子技术-逻辑门电路PPT课件

在电路中的应用。
或非门(NOR Gate)
逻辑符号与真值表
描述或非门的逻辑符号,列出其对应的真值表, 解释不同输入下的输出结果。
逻辑表达式
给出或非门的逻辑表达式,解释其含义和运算规 则。
逻辑功能
阐述或非门实现逻辑或操作后再进行逻辑非的功 能,举例说明其在电路中的应用。
异或门(XOR Gate)
逻辑符号与真值表
01
02
03
Байду номын сангаас
04
1. 根据实验要求搭建逻辑门 电路实验板,并连接好电源和
地。
2. 使用示波器或逻辑分析仪 对输入信号进行测试,记录输
入信号的波形和参数。
3. 将输入信号接入逻辑门电 路的输入端,观察并记录输出
信号的波形和参数。
4. 改变输入信号的参数(如频 率、幅度等),重复步骤3, 观察并记录输出信号的变化情
THANKS
感谢观看
低功耗设计有助于提高电路效率和延长设 备使用寿命,而良好的噪声容限则可以提 高电路的抗干扰能力和稳定性。
扇入扇出系数
扇入系数
指门电路允许同时输入的最多 信号数。
扇出系数
指一个门电路的输出端最多可 以驱动的同类型门电路的输入 端数目。
影响因素
门电路的输入/输出电阻、驱动 能力等。
重要性
扇入扇出系数反映了门电路的驱动 能力和带负载能力,对于复杂数字 系统的设计和分析具有重要意义。
实际应用
举例说明非门在数字电路中的应用, 如反相器、振荡器等。
03
复合逻辑门电路
与非门(NAND Gate)
逻辑符号与真值表
描述与非门的逻辑符号,列出其 对应的真值表,解释不同输入下
或非门(NOR Gate)
逻辑符号与真值表
描述或非门的逻辑符号,列出其对应的真值表, 解释不同输入下的输出结果。
逻辑表达式
给出或非门的逻辑表达式,解释其含义和运算规 则。
逻辑功能
阐述或非门实现逻辑或操作后再进行逻辑非的功 能,举例说明其在电路中的应用。
异或门(XOR Gate)
逻辑符号与真值表
01
02
03
Байду номын сангаас
04
1. 根据实验要求搭建逻辑门 电路实验板,并连接好电源和
地。
2. 使用示波器或逻辑分析仪 对输入信号进行测试,记录输
入信号的波形和参数。
3. 将输入信号接入逻辑门电 路的输入端,观察并记录输出
信号的波形和参数。
4. 改变输入信号的参数(如频 率、幅度等),重复步骤3, 观察并记录输出信号的变化情
THANKS
感谢观看
低功耗设计有助于提高电路效率和延长设 备使用寿命,而良好的噪声容限则可以提 高电路的抗干扰能力和稳定性。
扇入扇出系数
扇入系数
指门电路允许同时输入的最多 信号数。
扇出系数
指一个门电路的输出端最多可 以驱动的同类型门电路的输入 端数目。
影响因素
门电路的输入/输出电阻、驱动 能力等。
重要性
扇入扇出系数反映了门电路的驱动 能力和带负载能力,对于复杂数字 系统的设计和分析具有重要意义。
实际应用
举例说明非门在数字电路中的应用, 如反相器、振荡器等。
03
复合逻辑门电路
与非门(NAND Gate)
逻辑符号与真值表
描述与非门的逻辑符号,列出其 对应的真值表,解释不同输入下
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
掉!也称 吸收律
证明: A(A+B )=A·A+A·B =A+A·B =A(1+B) =A
5. AB+A′C+BC = AB+A′C AB+A′C+BCD = AB+A′C
B B BB
EEEE
电路图
YYYY
AAA接、、通BB都、都断B接断开通开,,,灯灯灯不亮不亮。亮。。
A断开、B接通,灯不亮。
将开关接通记作1,断开记作0;灯亮记作1,灯 灭记作0。可以作出如下表格来描述与逻辑关系:
功能表
开关 A 开关 B 灯 Y
A
断开 断开
灭
0
断开 闭合
灭
0
1
闭合 断开
灭
1
闭合 闭合 亮
异或逻辑的运算规则:
0⊕0= 0 0⊕1= 1 1⊕0= 1 1⊕1= 0
A⊕0= A A⊕1= A′ A⊕A′= 1 A⊕A= 0
4、同或运算:逻辑表达式为:
Y AB AB =A⊙B
A BY
0
01
0
10
1
00
1
11
真值表
A
=
Y
B
同或门的逻辑符号
异或和同或互为反运算
L=A+B
同或逻辑的运算规则:
BY
00 真 10 值
00 表
11
两个开关均接通时,灯才会 Y=A•B
亮。逻辑表达式为:
实现与逻辑的电路称为与门。
与门的逻辑符号:
A
&
Y Y=A•B
B
二、或逻辑(或运算)
或逻辑:当决定事件(Y)发生的各种条件A,B,
C,…)中,只要有一个或多个条件具备,事件(Y)
就发生。表达式为:Y=A+B+C+…
A A
B) A B) A
B B
求证: (17式) A+BC=(A+B)(A+C)
证明:右边 =(A+B)(A+C)
课
=AA+AB+AC+BC
本 上
=A +A(B+C)+BC
用
真
=A(1+B+C)+BC
值
表
=A • 1+BC
证
明
=A+BC =左边
二、常用公式
1. A+AB = A 2. A+A′B= A+B A(A′+B)= AB
A′+AB= A′+B A′(A+B)= A′B
注: 红色变量被吸收 掉!统称 吸收律
证明:
A+A′B =(A+A′) •(A+B) ;分配律
=1•(A+B) =A+B
A+BC=(A+B)(A+C)
3. AB+AB ′= A (A+B ) (A+B′ )= A
4. A(A+B )= A 注: 红色变量被吸收
1
10
真值表
A
&
Y
B
与非门的逻辑符号
L=A+B
2、或非运算:
逻辑表达式为:Y (A B)
A
BY
0
01
0
10
1
00
1
10
真值表
A
≥1
Y
B
或非门的逻辑符号
L= A+ B
3、异或运算:逻辑表达式为:
Y AB AB A B
A BY
0
00
0
11
1
01
1
10
真值表
A
=1
Y
B
异或门的逻辑符号
0 ⊙ 0= 1 0 ⊙ 1= 0 1 ⊙ 0= 0 1 ⊙ 1= 1
A ⊙ 0= A′ A ⊙ 1= A A ⊙ A′= 0 A ⊙ A= 1
5、 与或非运算:逻辑表达式为:
Y (A B C D)
A
& ≥1
B
Y
C
D
与或非门的逻辑符号
§2.3 逻辑代数的基本公式和常用公式
一、基本公式
互补律: A A 1 A A 0
分别令A=0及 A=1代入这些 公式,即可证 明它们的正确 性。
重叠律: A A A A A A
还原律(双重否定律): ( A) A
亦称 非非律
3.基本定理
交换律:
A
A
B B BB
A
A
利用真值表很容易证 明这些公式的正确性。 如证明A·B=B·A:
条件(A)满足时,事件不发生;条件不满足,事件反
而发生。表达式为:Y=A′
真功能值表表
R
A开关 A Y灯 Y
E
A Y 0 断开 1亮
电路图
1 闭合 0灭
实现非逻辑的电路称为ຫໍສະໝຸດ 门。非门的逻辑符号:A1
Y
Y=A′
常用的逻辑运算
1、与非运算:
逻辑表达式为: Y (A B)
A
BY
0
01
0
11
1
01
成绩评定:平时10%,实验30%,期末考 试60%
逻辑代数基础
§2.1 §2.2 §2.3 §2.4
数字电路的基础知识 逻辑代数及其运算规则 逻辑函数表示方法 逻辑函数的化简
§2.1 概述
在数字电路中,主要研究的是电路的输入输出之 间的逻辑关系,因此数字电路又称逻辑电路,其研究 工具是逻辑代数(布尔代数或开关代数)。
数字电路与EDA技术
使用教材: 潘松 黄继业 EDA技术实用教 程(第三版)北京 科学出版社 2007 参考书目:刘昌华 数字逻辑EDA设计与实 践 国防工业出版社 阎石. 数字电子技术基础(第五版). 高等 教育出版社 2006.5 王毓银主编,数字电路逻辑设计,高等教 育出版社,1999;
考核方式:期末考试时间为120分钟,闭卷, 具体考试时间至少提前1周通知学生。
功真能 值表 表
A
开A关 A 开关BB
Y灯 Y
B E
断0开 断开0
0灭
Y
断0开 闭合1
1亮
闭1合 断开0
1亮
电路图
闭1合 闭合1
1亮
两个开关只L要=A有B一个接通,灯 就会亮。逻辑表达式为:
Y=A+B
实现或逻辑的电路称为或门。 或门的逻辑符号:
A
≥1
B
Y=A+B
三、非逻辑(非运算)
非逻辑:指的是逻辑的否定。当决定事件(Y)发生的
结合律:
( (
A A
B) B)
C
C
A
(B A
C) (B
C)
A B AB BA 00 0 0 01 0 0
分配律:
A
A
(B B
C) C
A (A
B B)
A (A
C C)
1 1
0 1
0 1
0 1
反演律(摩根定律):
( (
逻辑变量:用字母表示,取值只有0和1。 此时,0和1不再表示数量的大小, 只代表两种不同的状态。
§2.2 逻辑代数中的三种基本运算
一、与逻辑(与运算)
与逻辑:仅当决定事件(Y)发生的所有条件(A, B,C,…)均满足时,事件(Y)才能发生。表达 式为Y:=ABC…
例:开关A,B串联控制灯泡Y
AAAA
1.常量之间的关系
与运算:0 0 0 0 1 0 1 0 0 11 1 或运算:0 0 0 0 1 1 1 0 1 1 1 1
非运算:1 0
0 1
请特别注意与普 通代数不同之处
2.基本公式
0-1
律:
A A
0 A 1 A
A 1 1 A 0 0
证明: A(A+B )=A·A+A·B =A+A·B =A(1+B) =A
5. AB+A′C+BC = AB+A′C AB+A′C+BCD = AB+A′C
B B BB
EEEE
电路图
YYYY
AAA接、、通BB都、都断B接断开通开,,,灯灯灯不亮不亮。亮。。
A断开、B接通,灯不亮。
将开关接通记作1,断开记作0;灯亮记作1,灯 灭记作0。可以作出如下表格来描述与逻辑关系:
功能表
开关 A 开关 B 灯 Y
A
断开 断开
灭
0
断开 闭合
灭
0
1
闭合 断开
灭
1
闭合 闭合 亮
异或逻辑的运算规则:
0⊕0= 0 0⊕1= 1 1⊕0= 1 1⊕1= 0
A⊕0= A A⊕1= A′ A⊕A′= 1 A⊕A= 0
4、同或运算:逻辑表达式为:
Y AB AB =A⊙B
A BY
0
01
0
10
1
00
1
11
真值表
A
=
Y
B
同或门的逻辑符号
异或和同或互为反运算
L=A+B
同或逻辑的运算规则:
BY
00 真 10 值
00 表
11
两个开关均接通时,灯才会 Y=A•B
亮。逻辑表达式为:
实现与逻辑的电路称为与门。
与门的逻辑符号:
A
&
Y Y=A•B
B
二、或逻辑(或运算)
或逻辑:当决定事件(Y)发生的各种条件A,B,
C,…)中,只要有一个或多个条件具备,事件(Y)
就发生。表达式为:Y=A+B+C+…
A A
B) A B) A
B B
求证: (17式) A+BC=(A+B)(A+C)
证明:右边 =(A+B)(A+C)
课
=AA+AB+AC+BC
本 上
=A +A(B+C)+BC
用
真
=A(1+B+C)+BC
值
表
=A • 1+BC
证
明
=A+BC =左边
二、常用公式
1. A+AB = A 2. A+A′B= A+B A(A′+B)= AB
A′+AB= A′+B A′(A+B)= A′B
注: 红色变量被吸收 掉!统称 吸收律
证明:
A+A′B =(A+A′) •(A+B) ;分配律
=1•(A+B) =A+B
A+BC=(A+B)(A+C)
3. AB+AB ′= A (A+B ) (A+B′ )= A
4. A(A+B )= A 注: 红色变量被吸收
1
10
真值表
A
&
Y
B
与非门的逻辑符号
L=A+B
2、或非运算:
逻辑表达式为:Y (A B)
A
BY
0
01
0
10
1
00
1
10
真值表
A
≥1
Y
B
或非门的逻辑符号
L= A+ B
3、异或运算:逻辑表达式为:
Y AB AB A B
A BY
0
00
0
11
1
01
1
10
真值表
A
=1
Y
B
异或门的逻辑符号
0 ⊙ 0= 1 0 ⊙ 1= 0 1 ⊙ 0= 0 1 ⊙ 1= 1
A ⊙ 0= A′ A ⊙ 1= A A ⊙ A′= 0 A ⊙ A= 1
5、 与或非运算:逻辑表达式为:
Y (A B C D)
A
& ≥1
B
Y
C
D
与或非门的逻辑符号
§2.3 逻辑代数的基本公式和常用公式
一、基本公式
互补律: A A 1 A A 0
分别令A=0及 A=1代入这些 公式,即可证 明它们的正确 性。
重叠律: A A A A A A
还原律(双重否定律): ( A) A
亦称 非非律
3.基本定理
交换律:
A
A
B B BB
A
A
利用真值表很容易证 明这些公式的正确性。 如证明A·B=B·A:
条件(A)满足时,事件不发生;条件不满足,事件反
而发生。表达式为:Y=A′
真功能值表表
R
A开关 A Y灯 Y
E
A Y 0 断开 1亮
电路图
1 闭合 0灭
实现非逻辑的电路称为ຫໍສະໝຸດ 门。非门的逻辑符号:A1
Y
Y=A′
常用的逻辑运算
1、与非运算:
逻辑表达式为: Y (A B)
A
BY
0
01
0
11
1
01
成绩评定:平时10%,实验30%,期末考 试60%
逻辑代数基础
§2.1 §2.2 §2.3 §2.4
数字电路的基础知识 逻辑代数及其运算规则 逻辑函数表示方法 逻辑函数的化简
§2.1 概述
在数字电路中,主要研究的是电路的输入输出之 间的逻辑关系,因此数字电路又称逻辑电路,其研究 工具是逻辑代数(布尔代数或开关代数)。
数字电路与EDA技术
使用教材: 潘松 黄继业 EDA技术实用教 程(第三版)北京 科学出版社 2007 参考书目:刘昌华 数字逻辑EDA设计与实 践 国防工业出版社 阎石. 数字电子技术基础(第五版). 高等 教育出版社 2006.5 王毓银主编,数字电路逻辑设计,高等教 育出版社,1999;
考核方式:期末考试时间为120分钟,闭卷, 具体考试时间至少提前1周通知学生。
功真能 值表 表
A
开A关 A 开关BB
Y灯 Y
B E
断0开 断开0
0灭
Y
断0开 闭合1
1亮
闭1合 断开0
1亮
电路图
闭1合 闭合1
1亮
两个开关只L要=A有B一个接通,灯 就会亮。逻辑表达式为:
Y=A+B
实现或逻辑的电路称为或门。 或门的逻辑符号:
A
≥1
B
Y=A+B
三、非逻辑(非运算)
非逻辑:指的是逻辑的否定。当决定事件(Y)发生的
结合律:
( (
A A
B) B)
C
C
A
(B A
C) (B
C)
A B AB BA 00 0 0 01 0 0
分配律:
A
A
(B B
C) C
A (A
B B)
A (A
C C)
1 1
0 1
0 1
0 1
反演律(摩根定律):
( (
逻辑变量:用字母表示,取值只有0和1。 此时,0和1不再表示数量的大小, 只代表两种不同的状态。
§2.2 逻辑代数中的三种基本运算
一、与逻辑(与运算)
与逻辑:仅当决定事件(Y)发生的所有条件(A, B,C,…)均满足时,事件(Y)才能发生。表达 式为Y:=ABC…
例:开关A,B串联控制灯泡Y
AAAA
1.常量之间的关系
与运算:0 0 0 0 1 0 1 0 0 11 1 或运算:0 0 0 0 1 1 1 0 1 1 1 1
非运算:1 0
0 1
请特别注意与普 通代数不同之处
2.基本公式
0-1
律:
A A
0 A 1 A
A 1 1 A 0 0
