河海大学_土力学_课后习题答案
土力学_河海大学课后部分思考题答案

1、什么叫土?土是怎样形成的?粗粒土和细粒土的组成有何不同?土是松散颗粒的堆积物。
地球表层的整体岩石在大气中经受长期风化作用后形成形状不同,大小不一的颗粒,这些颗粒在不同的自然环境条件下堆积(或经搬运沉积),即形成了通常所说的土。
粗粒土中粒径大于0.075㎜的粗粒组质量多于总质量50%,细粒土中粒径小于0.075㎜的细粒组质量多于或等于总质量50%。
2、何谓土的级配?土的粒径分布曲线是怎样绘制的?为什么粒径分布曲线用半对数坐标? 土中各种大小的粒组中土粒的相对含量称为土的级配。
粒径分布曲线是以土粒粒径为横坐标(对数比例尺),小于某粒径土质量占试样总质量的百分数为纵坐标绘制而成的曲线。
由于土的粒径相差悬殊,因此横坐标用对数坐标表示,以突出显示细小颗粒粒径。
3、 土的粒径分布曲线的特征可以用哪两个系数来表示?它们定义又如何?粒径分布曲线的特征可用不均匀系数u C 和曲率系数c C 来表示。
式中:d 10,d 30和d 60为粒径分布曲线上小于某粒径的土粒含量分别为10%,30%和60%时所对应的粒径。
4、 如何利用土的粒径分布曲线来判断土的级配的好坏?土的级配的好坏可由土中的土粒均匀程度和粒径分布曲线的形状来决定,而土粒的均匀程度和曲线的形状又可用不均匀系数和曲率系数来衡量,对于纯净的砾、砂,当u C 大于或等于5,而且c C 等于1~3时,它的级配是良好的;不能同时满足上述条件时,它的级配是不良的。
5、 何谓粘性土的稠度?粘性土随着含水率的不同可分为几种状态?各有何特性?稠度是指粘性土的干湿程度或在某一含水率下抵抗外力作用而变形或破坏的能力,是粘性土最主要的物理状态指标。
随含水率的不同可分为流态、可塑态、半固态和固态。
流态时含水率很大,不能保持其形状,极易流动;可塑态时土在外力作用下可改变形状但不显著改变其体积,也不开裂,外力卸除后仍能保持已有的形状;半固态时粘性土将丧失其可塑性,在外力作用下不产生较大的变形且容易破碎。
土力学河海课后习题答案

⼟⼒学河海课后习题答案⼟⼒学河海课后习题答案Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】⼟⼒学课后习题与答案第⼀章思考题11-1 什么叫⼟⼟是怎样形成的粗粒⼟和细粒⼟的组成有何不同1-2 什么叫残积⼟什么叫运积⼟他们各有什么特征1-3 何谓⼟的级配⼟的粒径分布曲线是怎样绘制的为什么粒径分布曲线⽤半对数坐标1-4 何谓⼟的结构⼟的结构有哪⼏种类型它们各有什么特征1-5 ⼟的粒径分布曲线的特征可以⽤哪两个系数来表⽰它们定义⼜如何1-6 如何利⽤⼟的粒径分布曲线来判断⼟的级配的好坏1-7 什么是吸着⽔具有哪些特征1-8 什么叫⾃由⽔⾃由⽔可以分为哪两种1-9 什么叫重⼒⽔它有哪些特征1-10 ⼟中的⽓体以哪⼏种形式存在它们对⼟的⼯程性质有何影响1-11 什么叫的物理性质指标是怎样定义的其中哪三个是基本指标1-12 什么叫砂⼟的相对密实度有何⽤途1-13 何谓粘性⼟的稠度粘性⼟随着含⽔率的不同可分为⼏种状态各有何特性1-14 何谓塑性指数和液性指数有何⽤途1-15 何谓⼟的压实性⼟压实的⽬的是什么1-16 ⼟的压实性与哪些因素有关何谓⼟的最⼤⼲密度和最优含⽔率1-17 ⼟的⼯程分类的⽬的是什么1-18 什么是粗粒⼟什么叫细粒⼟习题11-1有A 、B 两个图样,通过室内实验测得其粒径与⼩于该粒径的⼟粒质量如下表所⽰,试绘出它们的粒径分布曲线并求出u C 和c C 值。
⽐重为,求试样的含⽔率、孔隙⽐、孔隙率、饱和密度、浮密度、⼲密度及其相应的重度。
1-3 某⼟样的含⽔率为%密度为 3g/cm ,⼟粒⽐重为,若设孔隙⽐不变,为使⼟样完全饱和,问100 3cm ⼟样中应该加多少⽔1-4 有⼟料1000g,它的含⽔率为%,若使它的含⽔率增加到%,问需要加多少⽔1-5 有⼀砂⼟层,测得其天然密度为3g/cm ,天然含⽔率为%,⼟的⽐重为,烘⼲后测得最⼩孔隙⽐为,最⼤孔隙⽐为,试求天然孔隙⽐e 、饱和含⽔率和相对密实度D ,并判别该砂⼟层处于何种密实状态。
土力学_河海大学课后部分思考题答案

1、什么叫土?土是怎样形成的?粗粒土和细粒土的组成有何不同?土是松散颗粒的堆积物。
地球表层的整体岩石在大气中经受长期风化作用后形成形状不同,大小不一的颗粒,这些颗粒在不同的自然环境条件下堆积(或经搬运沉积),即形成了通常所说的土。
粗粒土中粒径大于0.075㎜的粗粒组质量多于总质量50%,细粒土中粒径小于0.075㎜的细粒组质量多于或等于总质量50%。
2、何谓土的级配?土的粒径分布曲线是怎样绘制的?为什么粒径分布曲线用半对数坐标? 土中各种大小的粒组中土粒的相对含量称为土的级配。
粒径分布曲线是以土粒粒径为横坐标(对数比例尺),小于某粒径土质量占试样总质量的百分数为纵坐标绘制而成的曲线。
由于土的粒径相差悬殊,因此横坐标用对数坐标表示,以突出显示细小颗粒粒径。
3、 土的粒径分布曲线的特征可以用哪两个系数来表示?它们定义又如何?粒径分布曲线的特征可用不均匀系数u C 和曲率系数c C 来表示。
式中:d 10,d 30和d 60为粒径分布曲线上小于某粒径的土粒含量分别为10%,30%和60%时所对应的粒径。
4、 如何利用土的粒径分布曲线来判断土的级配的好坏?土的级配的好坏可由土中的土粒均匀程度和粒径分布曲线的形状来决定,而土粒的均匀程度和曲线的形状又可用不均匀系数和曲率系数来衡量,对于纯净的砾、砂,当u C 大于或等于5,而且c C 等于1~3时,它的级配是良好的;不能同时满足上述条件时,它的级配是不良的。
5、 何谓粘性土的稠度?粘性土随着含水率的不同可分为几种状态?各有何特性?稠度是指粘性土的干湿程度或在某一含水率下抵抗外力作用而变形或破坏的能力,是粘性土最主要的物理状态指标。
随含水率的不同可分为流态、可塑态、半固态和固态。
流态时含水率很大,不能保持其形状,极易流动;可塑态时土在外力作用下可改变形状但不显著改变其体积,也不开裂,外力卸除后仍能保持已有的形状;半固态时粘性土将丧失其可塑性,在外力作用下不产生较大的变形且容易破碎。
河海大学-土力学学课后习题答案完整版

(1) B 试样
d10 0.0015mm d30 0.003mm d60 0.0066mm
Cu
d60 d10
0.0066 0.0015
4.4
Cc
(d30 )2 d10d60
0.0032 0.0015 0.0066
0.91
1-2 解:
已知: m =15.3g mS =10.6g G S =2.70
饱和 S r =1
又知: mw m mS 15.3-10.6=4.7g
(1) 含水量
mw = 4.7 =0.443=44.3% mS 10.6
(2) 孔隙比
e G S 0.443 2.7 1.20
Sr
1.0
(3) 孔隙率
e 1.2
0.545 54.5%
1 e 11.2
(4) 饱和密度及其重度
(2) 对 B 土进行分类
① 由粒径分布曲线图,查得粒径大于 0.075 ㎜的粗粒含量大于 50%,所以 B
土属于粗粒土;
② 粒径大于 2 ㎜的砾粒含量小于 50%,所以 B 土属于砂类,但小于 0.075
㎜的细粒含量为 28%,在 15%~50%之间,因而 B 土属于细粒土质砂;
③ 由于 B 土的液限为 24.0%,塑性指数 I p 24 14 10 ,在 17 ㎜塑性图上
d d g 1.2310 12.3kN / m3
1-3 解:
d
1
1.60
1 0.06
1.51g / cm3
e s 1 Gs w 1 2.70 1.0 1 0.79
d
d
1.51
e 0.79 sat Gs 2.70 29.3%
m V 1.60100 ms 1 1 1 0.06 150.9g
土力学(河海大学第二版)第1章答案
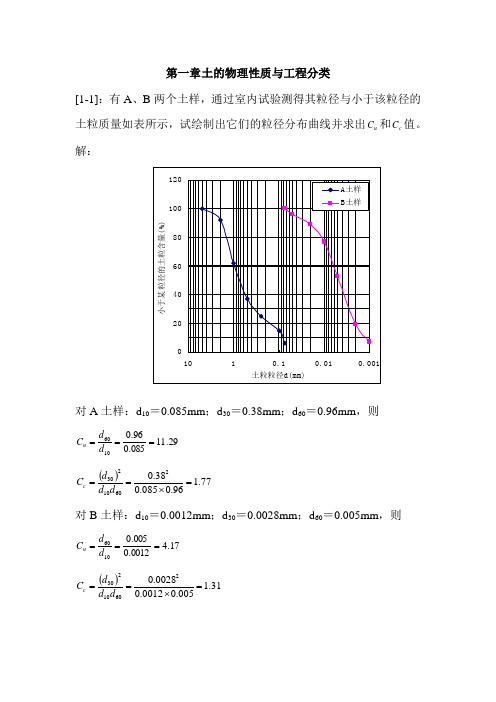
第一章 土的物理性质与工程分类[1-1]:有A 、B 两个土样,通过室内试验测得其粒径与小于该粒径的土粒质量如表所示,试绘制出它们的粒径分布曲线并求出u C 和c C 值。
解:对A 土样:d 10=0.085mm ;d 30=0.38mm ;d 60=0.96mm ,则 29.11085.096.01060===d d C u()77.196.0085.038.026010230=⨯==d d d C c对B 土样:d 10=0.0012mm ;d 30=0.0028mm ;d 60=0.005mm ,则 17.40012.0005.01060===d d C u()31.1005.00012.00028.026010230=⨯==d d d C c[1-2]从地下水位以下某粘土层中取出一土样做试验,测得其质量为15.3g ,烘干后质量为10.6g ,土粒比重为2.70。
求试样的含水量、孔隙比、孔隙率、饱和密度、浮密度、干密度、及其相应的重度。
解:(1) 已知:m =15.3g, m s =10.6g, G s =2.70, S r =100%, 则m w =m-m s =4.7gSr =100% 37.417.4cm m V V w w w v ====ρw s s s V m G ρ=393.3170.26.10cm V s =⨯= V=V s +V v =8.63(2) %3.44%1006.107.4%100=⨯=⨯=s w m m w 20.193.37.4===s v V V e %5.54%10063.87.4%100=⨯=⨯=V V n v 3/77.163.83.15cm g V m sat ===ρ; 3/73.1m kN g sat sat =⨯=ργ 3/77.0cm g w sat =-='ρρρ; 3/5.7m kN g =⨯'='ργ3/23.163.86.10cm g V m s d ===ρ; 3/1.12m kN g d d =⨯=ργ [1-3]某土样的含水率为6.0%,密度为1.60g/cm 3,土粒比重为2.70,若设孔隙比不变,为使土样饱和,问100cm 3土样中应加多少水? 解:已知 w=6.0%, ρ=1.60g/cm 3, G s =2.70, e 1=e 2, V=100cm 3 g V m 160==ρg w m m s 94.150%0.611601=+=+= g w m m s w 06.9==390.55170.294.150cm G m V w s s s =⨯==ρ 310.44cm V V V s v =-=所以,饱和时土中水总重为:g V m w v wsat 10.44==ρ需加入的水重为:g m m m w wsat w 04.3506.910.44=-=-=∆[1-4]有土料1000g ,它的含水率为6%,若使它的含水率增加16%。
河海大学_土力学习题答案

河海土力学课后习题与答案土力学答案第一章思考题11-1 土是松散颗粒的堆积物。
地球表层的整体岩石在大气中经受长期风化作用后形成形状不同,大小不一的颗粒,这些颗粒在不同的自然环境条件下堆积(或经搬运沉积),即形成了通常所说的土。
粗粒土中粒径大于0.075㎜的粗粒组质量多于总质量50%,细粒土中粒径小于0.075㎜的细粒组质量多于或等于总质量50%。
1-2 残积土是指岩石经风化后仍留在原地未经搬运的堆积物。
残积土的明显特征是,颗粒多为角粒且母岩的种类对残积土的性质有显著影响。
母岩质地优良,由物理风化生成的残疾土,通常是坚固和稳定的。
母岩质地不良或经严重化学风化的残积土,则大多松软,性质易变。
运积土是指岩石风化后经流水、风和冰川以及人类活动等动力搬运离开生成地点后的堆积物。
由于搬运的动力不同,分为坡积土、冲积土、风积土、冰碛土和沼泽土等。
坡积土一般位于坡腰或坡脚,上部与残积土相连,颗粒分选现象明显,坡顶粗坡下细;冲积土具有一定程度的颗粒分选和不均匀性;风积土随风向有一定的分选性,没有明显层里,颗粒以带角的细砂粒和粉粒为主,同一地区颗粒较均匀,黄土具有湿陷性;冰碛土特征是不成层,所含颗粒粒径的范围很宽,小至粘粒和粉粒,大至巨大的漂石,粗颗粒的形状是次圆或次棱角的有时还有磨光面;沼泽土分为腐植土和泥炭土,泥炭土通常呈海绵状,干密度很小,含水率极高,土质十分疏松,因而其压缩性高、强度很低而灵敏度很高。
1-3 土中各种大小的粒组中土粒的相对含量称为土的级配。
粒径分布曲线是以土粒粒径为横坐标(对数比例尺),小于某粒径土质量占试样总质量的百分数为纵坐标绘制而成的曲线。
由于土的粒径相差悬殊,因此横坐标用对数坐标表示,以突出显示细小颗粒粒径。
1-4 土的结构是指土的物质组成(主要指土里,也包括孔隙)在空间上的相互排列及土粒间联结特征的总和。
土的结构通常包括单粒、分散、絮状三种结构。
单粒结构比较稳定,孔隙所占的比例较小。
土力学河海大学第二版所有章节完整答案精

O、A、B点为0;
E点:kPa h w w 60 231(10=++⨯==γσ
绘图如下:
[2-3]甲乙两个基础,它们的尺寸和相对位置及每个基底下的基底净压力如图所示,求甲基础O点下2m处的竖向附加应力。
解:甲基础O点下2m处的竖向附加应力由基础甲、乙共同引起,计算中先分别计算甲、乙基础在该点引起的竖向附加应力,然后叠加。(1甲基础在O点下2m处引起的竖向附加应力:
1-5解:
(1 31.77
1.61/110.098d g cm w ρρ=
==++ ∴ 02.71.0
1110.681.61s s w d d G e ρρρρ⨯=-=-=-=
(2 00.68
25.2%2.7sat s e G ω===
(3 max 0max min 0.940.68
0.540.940.46
(1 B试样
100.0015d mm = 300.003d mm = 600.0066d mm =
60100.00664.40.0015u d C d === 22
301060( 0.0030.910.00150.0066
c d C d d ===⨯
1-3解:
31.60
1.51/110.06d g cm ρρω=
土力学(河海大学第二版所有章节完整答案
第一章土的物理性质指标与工程分类
1-1解:
(1 A试样
100.083d mm = 300.317d mm = 600.928d mm =
60100.92811.180.083u d C d === 22
301060( 0.3171.610.0830.928
土力学(河海大学第二版)所有章节完整课后习题答案

土力学(河海大学第二版)所有章节完整答案第一章 土的物理性质指标与工程分类1-1 解:(1) A 试样100.083d mm = 300.317d mm = 600.928d mm =60100.92811.180.083u d C d === 22301060()0.317 1.610.0830.928c d C d d ===⨯ (1) B 试样100.0015d mm = 300.003d mm = 600.0066d mm =60100.0066 4.40.0015u d C d === 22301060()0.0030.910.00150.0066c d C d d ===⨯ 1-2 解:已知:m =15.3g S m =10.6g S G =2.70饱和 ∴r S =1又知:wSm m m =-= 15.3-10.6=4.7g(1) 含水量 w Sm mω==4.710.6=0.443=44.3% (2) 孔隙比 0.443 2.71.201.0Sre G Sω⨯===(3) 孔隙率1.20.54554.5%11 1.2e e η====++ (4) 饱和密度及其重度32.7 1.21.77/11 1.2Ssat w G e g cm e ρρ++===++ 31.771017.7/sat sat g kN m γρ=⨯=⨯=(5) 浮密度及其重度3' 1.77 1.00.77/sat w g cm ρρρ=-=-= 3''0.77107.7/g kN m γρ=⨯=⨯= (6) 干密度及其重度32.7 1.01.23/11 1.2S w d G g cm e γρ⨯===++31.231012.3/d d g kN m γρ=⨯=⨯= 1-3 解:31.601.51/110.06d g cm ρρω===++ ∴ 2.70 1.01110.791.51s s w d d G e ρρρρ⨯=-=-=-= ∴ 0.7929.3%2.70sat s e G ω===1.60100150.91110.06s m V m g ρωω⨯====+++∴ (29.3%6%)150.935.2w s m m g ω∆=∆=-⨯=1-4 解:w Sm mω=w Sm m m =-sSm m mω=-∴ 1000940110.06s m m g ω===++0.16ω∆=∴ 0.16940150w s m m g ω∆=∆=⨯=1-5 解:(1)31.771.61/110.098d g cm w ρρ===++∴ 0 2.7 1.01110.681.61s s w d d G e ρρρρ⨯=-=-=-= (2) 00.6825.2%2.7sat s e G ω=== (3) max 0max min 0.940.680.540.940.46r e e D e e --===--1/32/3r D <<∴ 该砂土层处于中密状态。
土力学-河海课后习题答案2

土力学课后习题与答案第一章思考题11-1 什么叫土?土是怎样形成的?粗粒土和细粒土的组成有何不同?1-2 什么叫残积土?什么叫运积土?他们各有什么特征?1-3 何谓土的级配?土的粒径分布曲线是怎样绘制的?为什么粒径分布曲线用半对数坐标?1-4 何谓土的结构?土的结构有哪几种类型?它们各有什么特征?1-5 土的粒径分布曲线的特征可以用哪两个系数来表示?它们定义又如何?1-6 如何利用土的粒径分布曲线来判断土的级配的好坏?1-7 什么是吸着水?具有哪些特征?1-8 什么叫自由水?自由水可以分为哪两种?1-9 什么叫重力水?它有哪些特征?1-10 土中的气体以哪几种形式存在?它们对土的工程性质有何影响?1-11 什么叫的物理性质指标 是怎样定义的?其中哪三个是基本指标?1-12 什么叫砂土的相对密实度?有何用途?1-13 何谓粘性土的稠度?粘性土随着含水率的不同可分为几种状态?各有何特性?1-14 何谓塑性指数和液性指数?有何用途?1-15 何谓土的压实性?土压实的目的是什么?1-16 土的压实性与哪些因素有关?何谓土的最大干密度和最优含水率?1-17 土的工程分类的目的是什么?1-18 什么是粗粒土?什么叫细粒土? 习题11-1有A 、B 两个图样,通过室内实验测得其粒径与小于该粒径的土粒质量如下表所示,试绘出它们的粒径分布曲线并求出u C 和c C 值。
质量为10.6g ,土粒比重为2.70,求试样的含水率、孔隙比、孔隙率、饱和密度、浮密度、干密度及其相应的重度。
1-3 某土样的含水率为6.0%密度为1.60 3g/cm ,土粒比重为2.70,假设设孔隙比不变,为使土样完全饱和,问100 3cm 土样中应该加多少水?1-4 有土料1000g,它的含水率为6.0%,假设使它的含水率增加到16.0%,问需要加多少水?3g/cm ,天然含水率为9.8%,土的比重为2.70,烘干后测得最小孔隙比为0.46,最大孔隙比为0.94,试求天然孔隙比e 、饱和含水率和相对密实度D ,并判别该砂土层处于何种密实状态。
河海大学_土力学_课后习题答案

河海大学_土力学_课后习题答案思考题2 2-1土体的应力,按引起的原因分为自重应力和附加应力两种;按土体中土骨架和土中孔隙(水、气)的应力承担作用原理或应力传递方式可分为有效应力和孔隙应(压)力。
有效应力是指由土骨架传递(或承担)的应力。
孔隙应力是指由土中孔隙流体水和气体传递(或承担)的应力。
自重应力是指由土体自身重量所产生的应力。
附加应力是指由外荷(静的或动的)引起的土中应力。
2-2 自重应力是指由土体自身重量所产生的应力。
由静水位产生的孔隙水应力称为静孔隙水应力。
土体自重应力应由该点单位面积上土柱的有效重量来计算,如果存在地下水,且水位与地表齐平或高于地表,则自重应力计算时应采用浮重度,地下水位以下的土体中还存在静孔隙水应力。
2-3 附加应力是指由外荷(静的或动的)引起的土中应力。
空间问题有三个附加应力分量,平面问题有两个附加应力分量。
计算地基附加应力时,假定地基土是各向同性的、均匀的、线性变形体,而且在深度和水平方向上都是无限的。
2-4 实际工程中对于柔性较大(刚度较小)能适应地基变形的基础可以视为柔性基础。
对于一些刚度很大不能适应地基变形的基础可视为刚性基础。
柔性基础底面压力的分布和大小完全与其上的荷载分布于大小相同;刚性基础下的基底压力分布随上部荷载的大小、基础的埋深和土的性质而异。
2-5 基地中心下竖向附加应力最大,向边缘处附加应力将减小,在基底面积范围之外某点下依然有附加应力。
如果该基础相邻处有另外的荷载,也会对本基础下的地基产生附加应力。
2-6 在计算地基附加应力时,假定地基土是各向同性的、均质的、线性变形体,而且在深度的水平方向上都是无限的,这些条件不一定同时满足,因而会产生误差,所以计算结果会经常与地基中实际的附加应力不一致。
2-7 有效应力是指由土骨架传递(或承担)的应力。
孔隙应力是指由土中孔隙流体水和气体传递(或承担)的应力。
静孔隙水应力:习题22-1 解:根据图中所给资料,各土层交界面上的自重应力分别计算如下:cz0 0urhwwcz1 1h1 18.5'cz2 1h1 cz2 1h1 cz3 1h1 cz4 1h1 2-2解:23kPa7kPa55 (2 03h 37 1 8 122h 'h2' 55 222h 'h2 '2 'h3 221 0 )1kPa65 (1 946 5 10 )3kPa9 22kPa1 11h 'h2 '2 'h3 3'h 2249 2(1 9.5 10 )土的最大静孔隙水应力为:u0 rwhw 10 6 60kPa FV P G P GAd 2106基底压力:2 0 63 __ 3(1 62kN46 6pmpmaxinFvl b(16el)0.3178.k1Pa) 95.k9Pa6基底静压力:pn pmin r0d 95.9 17 1.0 78.9kPa pt pmaxpmin178.1 95. 98k2P.2 a只有前两章的,不过包括所有的思考题① 求O点处竖向附加应力由:m lzo12 n z 0 0 KS 0.250 0bb.5 4KSpn 4 0.25 78.9 78.9kPa b 1.5 0.5 n zb 0.5pt2由:m l0 Kt1 0 Kt2 0.2500 2 0.2582.2220.55kPazo2 2Kt1由:m lpt20 zo3 2Kt2bzo4 2KS4pt22 n z 2 0.25b82.22.50 KS4 0.250 020.55kPaz0 z01 z02 z03 z04 120kPa②求A点下4m处竖向附加应力由:m lzA16 4 n z 4 2.7 KS 0.103 6bb.52KSpn 2 0.1036 78.9 16.35kPa0.67 Kt 0.0695b662Ktpt 2 0.0695 82.2 11.4258kPa1.50.25 n z4由:m lzA2③zA zA1 zA2 16.35 11.4258 27.78kPa求B点下4m处竖向附加应力由:m l zB11.33 KS 0.1412b3b32KSpn 2 0.1412 78.9 22.28kPapt20.141282.225.80kPa3 1 n z 4zB2 KS由:m lzB3 Kt1pt2pt231 n z82.2282.221.33 Kt1 0.058 5Kt2 0.08260.0585 0.08262.39kPa3.39kPazB2 Kt2zB zB1 zB2 zB3 zB4 33.86kPa2-3 解:2-4 解:① 求自重应力zM 1h1 1'h2 19 4 (20 9.8) 1 86.19kPa zN zM 3'h3 86.19 (18.5 9.8) 3 112.26kPa 第三章思考题3 3-1水在土中的渗透速度与试样两端水平面间的水位差成正比,而与渗径长度成反比,即:v khLki 即为达西定律。
土力学_河海大学中国大学mooc课后章节答案期末考试题库2023年

土力学_河海大学中国大学mooc课后章节答案期末考试题库2023年1.1856年法国科学家达西对砂土的渗透性进行了研究,并提出了著名的达西定律。
有关达西渗透定律,以下哪项陈述是正确的?答案:达西定律的适用条件为土中渗流为层流2.UU试验通常被用来模拟透水性弱的黏土地基受到建筑物的快速荷载或土坝在快速施工中被剪破的情况,在UU试验剪切过程中,试样的含水率答案:不变3.在安徽马鞍山某地区有一无限长无黏性土坡与水平面成α角,土的重度γ=19kN/m3,内摩擦角φ =30°,求安全系数F s =1.2时,α角的容许值为答案:25.7°4.在滁宁高速公路施工过程中常常要求严格控制路基填土的压实度,而土的压实度与压实功能密切相关。
则当压实功能越大时,它如何影响土的最大干密度(r dmax)与最优含水率(w op)?答案:r dmax越大, w op越小5.土的单向固结理论是由太沙基教授于1923年提出,以下哪项不是太沙基单向固结理论的基本假定答案:固结过程中,土的渗透系数随孔隙比变化6.瑞典条分法又称为费伦纽斯法(Felenius,1927),因其计算结果偏于安全,在工程上有着很广泛的应用。
下列关于瑞典条分法的描述中只有________是正确的答案:假定土条侧面上作用力对土坡稳定性没有影响7.在我国南海表层广泛分布着黏土矿物。
黏土矿物是次生矿物中数量最多的一种,它是由各种硅酸盐矿物分解形成的含水铝硅酸盐矿物。
以下哪种矿物不是常见的黏土矿物?答案:石英8.现从南京市江宁区某施工现场取回一些土试样,其质量与体积分别为125g与75cm3,烘干后其质量为107g,假设土粒比重为2.7,试求该试样的饱和度()答案:50.9%9.取浙江台州某地区土样进行三轴压缩试验,测得土样剪破时的孔隙水应力为负值,则此时其有效应力圆在总应力圆的答案:右边10.南京市某住宅小区地基土的天然重度与饱和重度分别为18kN/m3与20kN/m3,地下水位处于地表以下3m,则地表以下5m深度处土的自重应力为____。
河海大学 土力学 课后习题答案

河海土力学课后习题与答案第一章思考题11-1 什么叫土?土是怎样形成的?粗粒土和细粒土的组成有何不同? 1-2 什么叫残积土?什么叫运积土?他们各有什么特征?1-3 何谓土的级配?土的粒径分布曲线是怎样绘制的?为什么粒径分布曲线用半对数坐标? 1-4 何谓土的结构?土的结构有哪几种类型?它们各有什么特征?1-5 土的粒径分布曲线的特征可以用哪两个系数来表示?它们定义又如何? 1-6 如何利用土的粒径分布曲线来判断土的级配的好坏? 1-7 什么是吸着水?具有哪些特征?1-8 什么叫自由水?自由水可以分为哪两种? 1-9 什么叫重力水?它有哪些特征?1-10 土中的气体以哪几种形式存在?它们对土的工程性质有何影响? 1-11 什么叫的物理性质指标 是怎样定义的?其中哪三个是基本指标? 1-12 什么叫砂土的相对密实度?有何用途?1-13 何谓粘性土的稠度?粘性土随着含水率的不同可分为几种状态?各有何特性? 1-14 何谓塑性指数和液性指数?有何用途? 1-15 何谓土的压实性?土压实的目的是什么?1-16 土的压实性与哪些因素有关?何谓土的最大干密度和最优含水率? 1-17 土的工程分类的目的是什么?1-18 什么是粗粒土?什么叫细粒土? 习题11-1有A 、B 两个图样,通过室内实验测得其粒径与小于该粒径的土粒质量如下表所示,试绘出它们的粒径分布曲线并求出u C 和c C 值。
率、饱和密度、浮密度、干密度及其相应的重度。
1-3 某土样的含水率为6.0%密度为1.603g/cm ,土粒比重为2.70,若设孔隙比不变,为使土样完全饱和,问100 3cm 土样中应该加多少水?1-4 有土料1000g,它的含水率为6.0%,若使它的含水率增加到16.0%,问需要加多少水? 1-5 有一砂土层,测得其天然密度为1.773g/cm ,天然含水率为9.8%,土的比重为2.70,烘干后测得最小孔隙比为0.46,最大孔隙比为0.94,试求天然孔隙比e 、饱和含水率和相对密实度D ,并判别该砂土层处于何种密实状态。
土力学河海大学第三版课后习题答案

土力学河海大学第三版课后习题答案Chapter 1: 土的性质和分类1.1 土力学的定义土力学是研究土体在外力作用下物理力学性质的学科,包括了土体的性质、分类和力学性质等方面。
1.2 土的组成和性质土的主要组成成分有固体颗粒、水和空气。
固体颗粒主要有砂粒、粉粒和黏粒。
土的性质包括颗粒大小、颗粒的形状、颗粒的强度和颗粒间的摩擦角等。
1.3 土的分类根据土的颗粒大小将土分为砂土、粉土和黏土。
砂土颗粒大小在0.05mm-2mm之间,粉土颗粒大小在0.002mm-0.05mm之间,黏土颗粒大小小于0.002mm。
1.4 土质的影响因素土质的影响因素有颗粒大小、颗粒形状、颗粒强度、颗粒内摩擦角、颗粒间摩擦角等。
这些因素决定了土质的力学性质,如强度、压缩性、渗透性等。
Chapter 2: 土的压缩性和渗透性2.1 土的压缩性土的压缩性是指土在受到外力压缩时的体积变化性质。
土的压缩性主要包括压缩指数、压缩变形和压缩曲线等。
2.2 土的渗透性土的渗透性是指土体中水分移动的能力。
土的渗透性受到土的孔隙结构和土的颗粒特性的影响。
常用的衡量土的渗透性的指标有渗透系数和渗透曲线。
Chapter 3: 土的剪切行为3.1 土的剪切强度土的剪切强度是指土体在剪切力作用下抵抗变形的能力。
常用的剪切强度指标有内摩擦角和剪切强度参数等。
3.2 剪切试验剪切试验是用来测定土体的剪切强度和确定剪切曲线的一种试验。
常用的剪切试验方法有直剪试验和三轴剪切试验。
3.3 剪切带剪切带是指在土体剪切过程中形成的裂缝。
剪切带的形成与土体的剪切强度、土的性质和剪切应力等因素有关。
Chapter 4: 土的变形和应力状态4.1 土的变形土体在受到外力作用下会发生变形。
土体的变形包括弹性变形和塑性变形。
弹性变形是可回复的,塑性变形是不可回复的。
4.2 应力状态应力状态是指土体中各个点所受到的应力,包括垂向应力和切向应力。
常用的应力状态有均匀应力状态和非均匀应力状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 思考题2 2-1土体的应力,按引起的原因分为自重应力和附加应力两种;按土体中土骨架和土中孔隙(水、气)的应力承担作用原理或应力传递方式可分为有效应力和孔隙应(压)力。
有效应力是指由土骨架传递(或承担)的应力。
孔隙应力是指由土中孔隙流体水和气体传递(或承担)的应力。
自重应力是指由土体自身重量所产生的应力。
附加应力是指由外荷(静的或动的)引起的土中应力。
2-2 自重应力是指由土体自身重量所产生的应力。
由静水位产生的孔隙水应力称为静孔隙水应力。
土体自重应力应由该点单位面积上土柱的有效重量来计算,如果存在地下水,且水位与地表齐平或高于地表,则自重应力计算时应采用浮重度,地下水位以下的土体中还存在静孔隙水应力。
2-3 附加应力是指由外荷(静的或动的)引起的土中应力。
空间问题有三个附加应力分量,平面问题有两个附加应力分量。
计算地基附加应力时,假定地基土是各向同性的、均匀的、线性变形体,而且在深度和水平方向上都是无限的。
2-4 实际工程中对于柔性较大(刚度较小)能适应地基变形的基础可以视为柔性基础。
对于一些刚度很大不能适应地基变形的基础可视为刚性基础。
柔性基础底面压力的分布和大小完全与其上的荷载分布于大小相同;刚性基础下的基底压力分布随上部荷载的大小、基础的埋深和土的性质而异。
2-5 基地中心下竖向附加应力最大,向边缘处附加应力将减小,在基底面积范围之外某点下依然有附加应力。
如果该基础相邻处有另外的荷载,也会对本基础下的地基产生附加应力。
2-6 在计算地基附加应力时,假定地基土是各向同性的、均质的、线性变形体,而且在深度的水平方向上都是无限的,这些条件不一定同时满足,因而会产生误差,所以计算结果会经常与地基中实际的附加应力不一致。
2-7 有效应力是指由土骨架传递(或承担)的应力。
孔隙应力是指由土中孔隙流体水和气体传递(或承担)的应力。
静孔隙水应力:wwuhr =习题22-1 解:根据图中所给资料,各土层交界面上的自重应力分别计算如下: 00cz σ=11118.5237cz h kPa σγ==⨯=21122'3718155cz h h kPa σγγ=+=+⨯= 2112222''55(2010)165cz h h h kPa σγγγ=++=+-⨯= 311222233'''65(1910)392cz h h h h kPa σγγγγ=+++=+-⨯= 41122223344''''92(19.510)2111cz h h h h h kPa σγγγγγ=++++=+-⨯= 土的最大静孔隙水应力为:010660w w u r h kPa ==⨯=2-2解:2106206312466V G F P G P Ad kN γ=+=+=+⨯⨯⨯= 基底压力:m a x mi n178.16246660.3(1)(1)95.9636v p k P aF e p k P a l bl⨯=±=±=⨯ 基底静压力:min 095.917 1.078.9n p p r d kPa =-=-⨯= ma xm i n178.195.982.2t p p pk P a=-=-=① 求O 点处竖向附加应力 由:321.5lm b === 001.5z n b === 0.2500S K = ∴ 1440.2578.978.9zo S n K p kPa σ==⨯⨯= 由: 1.50.53lm b === 001.5zn b === 10t K = 20.2500t K = ∴ 21202t zo t p K σ== 3282.2220.2520.5522t zo t p K kP a σ==⨯⨯=由:321.5lm b=== 001.5z n b === 40.2500S K = ∴ 4482.2220.2520.5522t zo S p K kP a σ==⨯⨯=∴ 001020304120z z z z z kPa σσσσσ=+++=②求A 点下4m 处竖向附加应力 由:641.5lm b === 42.71.5z n b === 0.1036S K = ∴ 1220.103678.916.35zA S n K p kPa σ==⨯⨯=由: 1.50.256lm b === 40.676zn b === 0.0695t K =∴ 2220.069582.211.4258zA t t K p kPa σ==⨯⨯=∴ 1216.3511.425827.78zA zA zA kPa σσσ=+=+=③求B 点下4m 处竖向附加应力 由:313lm b === 41.333z n b === 0.1412S K =∴ 1220.141278.922.28zB S n K p kPa σ==⨯⨯=282.20.1412 5.8022t zB Sp K kP a σ==⨯=由:313lm b === 41.333zn b=== 10.0585t K = 20.0826t K =∴ 3182.20.0585 2.3922t zB t p K kP a σ==⨯= 2282.20.0826 3.3922t zB t p K kP a σ==⨯=∴ 123433.86zB zB zB zB zB kPa σσσσσ=+++=2-3 解: 2-4 解:① 求自重应力1112'194(209.8)186.19zM h h kPa σγγ=+=⨯+-⨯= 33'86.19(18.59.8)3112.26zN zM h kPa σσγ=+=+-⨯= 第三章 思考题3 3-1水在土中的渗透速度与试样两端水平面间的水位差成正比,而与渗径长度成反比,即:ki Lh kv == 即为达西定律。
达西定律只有当渗流为层流的的时候才能适用,其使用界限可以考虑为:0.1/≤=ηρvd weR3-2室内测定土的渗透系数的方法可分为常水头试验和变水头试验两种。
常水头法是在整个试验过程中水头保持不变,适用于透水性强的无粘性土;变水头法在整个试验过程中,水头是随着时间而变化的,适用于透水性弱的粘性土。
3-3 流网具有下列特征:(1) 流线与等势线彼此正交;(2) 每个网格的长度比为常数,为了方便常取1,这时的网格就为正方形或曲边正方形; (3) 相邻等势线间的水头损失相等; (4) 各溜槽的渗流量相等。
3-4 按照渗透水流所引起的局部破坏的特征,渗透变形可分为流土和管涌两种基本形式。
流土是指在渗流作用下局部土体表面隆起,或土粒群同时起动而流失的现象,它主要发生在地基或土坝下游渗流出处。
管涌是指在渗流作用下土体中的细土粒在粗土粒形成的孔隙通道中发生移动并被带出的现象,主要发生在砂砾土中。
3-5 土体抵抗渗透破坏的能力称为抗渗强度,通常已濒临渗透破坏时的水力梯度表示,一般称为临界水力梯度或抗渗梯度。
流土的临界水力梯度:)1)(1(n G is cr--=, 该式是根据竖向渗流且不考虑周围土体的约束作用情况下推得的,求得的临界水力梯度偏小,建议按下式估算:[])1()1(79.0)1()1(2420CD n n niLcr+----=;管涌土的临界水力梯度:ddG in s cr2052)1)(1(2.2--=3-6在静水条件下,孔隙水应力等于研究平面上单位面积的水柱重量,与水深成正比,呈三角形分布;在稳定渗流作用下,当有向下渗流作用时,孔隙水应力减少了h wγ,当有向上渗流作用时,孔隙水应力增加了h wγ。
一旦流网绘出以后,渗流场中任一点的孔隙水应力即可由该点的测压管中的水柱高度乘以水的重度得到。
当计算点位于下游静水位以下时,孔隙水应力由静孔隙水应力和超静孔隙水应力组成。
3-7不相同。
由达西定律求出的渗透速度是一种假想平均流速,因为它假定水在土中的渗透是通过整个土体截面来进行的。
而实际上,渗透水不仅仅通过土体中的孔隙流动,因此,水在土体中的实际平均流速要比由达西定律求得的数值大得多。
3-8一、假定在渗流作用下单元体的体积保持不变,水又是不可压缩的,则单位时间内流入单元体的总水量必等于流出的总水量,即:)()(y y y x x x y x d yq q d xq q q q ∂∂+÷∂∂+=÷二、假定土是各向同性的,即x k 等于y k ,则02222=∂∂+∂∂yh xh土的渗透系数不是各向同性的。
第四章 思考题4 4-1地基土内各点承受土自重引起的自重应力,一般情况下,地基土在其自重应力下已经压缩稳定,但是,当建筑物通过其基础将荷载传给地基之后,将在地基中产生附加应力,这种附加应力会导致地基土体的变形。
4-2压缩系数v a 是指单位压力增量所引起的空隙比改变量,即e~p 压缩曲线的割线的坡度,pe p p e e a v ∆∆-=--=1221;压缩指数c C 是指e~lgp 曲线直线段的坡度,即:)lg(lg lg 111221p p p e p p e e C c ∆+∆-=--=;回弹再压缩指数s C 是指回弹再压缩曲线(在e~lgp 平面内)直线段的坡度;体积压缩系数v m 定义为土体在单位应力作用下单位体积的体积变化,其大小等于)1(1e a v +; 压缩模量s E 定义为土体在无侧向变形条件下,竖向应力与竖向应变之比,其大小等于v m 1,即;z z s E σ=。
4-3在无侧向变形条件下的土层压缩量计算公式要求土层均质,且在土层厚度范围内压力是均匀分布的,因此厚土层一般要求将地基土分层。
没有必要。
4-4 前式更准确些,因为压缩系数常取为100kPa 至200kPa 范围内的值。
4-5因为地基土的压缩是由外界压力在地基中一起的附加应力所产生的,当基础有埋置深度d 时,应采用基底静压力d n p p γ-=去计算地基中的附加应力。
4-6 有4-7 事先对地基堆载预压,能使地基在荷载作用下完成瞬时沉降和住固结沉降,将减少建筑物修盖之后的最终沉降量。
4-8在荷载施加的瞬时,由于孔隙水来不及排出,加之水被认为是不可压缩的,因而,附加应力全部由水来承担。
经过时间t ,孔隙水应力不断消散,有效应力逐渐增加。
当t 趋于无穷大时,超静孔隙水应力全部消散,仅剩静孔隙水应力,附加应力全部转化为有效应力。
饱和土的固结过程就是超静孔隙水应力逐渐转化为附加有效应力的过程。
在这种转化过程中,任一时刻任一深度上的应力始终遵循着有效应力原理,即:'σ+=u p 。
4-9 不对 4-10 正常固结土和超固结土虽然有相同的压力增量,但其压缩量是不同的,正常固结土的压缩量要比超固结土的大。
