4因式分解方法(七年级)
浙教版七年级数学下册因式分解(无答案)
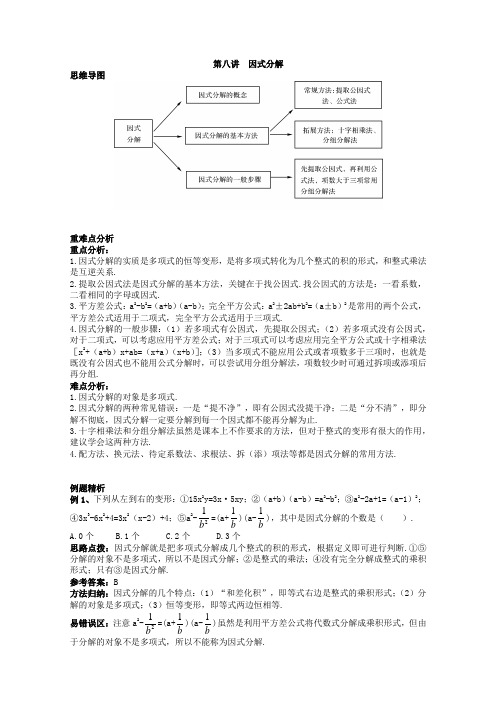
第八讲 因式分解思维导图重难点分析重点分析:1.因式分解的实质是多项式的恒等变形,是将多项式转化为几个整式的积的形式,和整式乘法是互逆关系.2.提取公因式法是因式分解的基本方法,关键在于找公因式.找公因式的方法是:一看系数,二看相同的字母或因式.3.平方差公式:a 2-b 2=(a+b )(a-b );完全平方公式:a 2±2ab+b 2=(a±b)2是常用的两个公式,平方差公式适用于二项式,完全平方公式适用于三项式.4.因式分解的一般步骤:(1)若多项式有公因式,先提取公因式;(2)若多项式没有公因式,对于二项式,可以考虑应用平方差公式;对于三项式可以考虑应用完全平方公式或十字相乘法[x 2+(a+b )x+ab=(x+a )(x+b )];(3)当多项式不能应用公式或者项数多于三项时,也就是既没有公因式也不能用公式分解时,可以尝试用分组分解法,项数较少时可通过拆项或添项后再分组.难点分析:1.因式分解的对象是多项式.2.因式分解的两种常见错误:一是“提不净”,即有公因式没提干净;二是“分不清”,即分解不彻底,因式分解一定要分解到每一个因式都不能再分解为止.3.十字相乘法和分组分解法虽然是课本上不作要求的方法,但对于整式的变形有很大的作用,建议学会这两种方法.4.配方法、换元法、待定系数法、求根法、拆(添)项法等都是因式分解的常用方法.例题精析例1、下列从左到右的变形:①15x 2y=3x·5xy;②(a+b )(a-b )=a 2-b 2;③a 2-2a+1=(a-1)2;④3x 3-6x 2+4=3x 2(x-2)+4;⑤a 2-21b =(a+b 1)(a-b1),其中是因式分解的个数是( ). A.0个 B.1个 C.2个 D.3个思路点拨:因式分解就是把多项式分解成几个整式的积的形式,根据定义即可进行判断.①⑤分解的对象不是多项式,所以不是因式分解;②是整式的乘法;④没有完全分解成整式的乘积形式;只有③是因式分解.参考答案:B方法归纳:因式分解的几个特点:(1)“和差化积”,即等式右边是整式的乘积形式;(2)分解的对象是多项式;(3)恒等变形,即等式两边恒相等.易错误区:注意a 2-21b =(a+b 1)(a-b1)虽然是利用平方差公式将代数式分解成乘积形式,但由于分解的对象不是多项式,所以不能称为因式分解.例2、分解因式:(1)-4+x2;(2)-4x2y+4xy2-y3;(3)9(a-b)2-4(a+b)2;(4)3a2+bc-3ac-ab;(5)16x4-8x2y2+y4.思路点拨:(1)交换两个加数的位置,即可运用平方差公式;(2)提取公因式-y,即可运用完全平方公式;(3)首先运用平方差公式,再对括号内的式子进行整理即可;(4)首先要合理分组,再运用提公因式法完成因式分解;(5)先运用完全平方公式因式分解,再运用平方差公式因式分解.解题过程:(1)原式=x2-4=(x+2)(x-2).(2)原式=-y(4x2-4xy+y2)=-y(2x-y)2.(3)原式=(3a-3b+2a+2b)(3a-3b-2a-2b)=(5a-b)(a-5b).(4)原式=(3a2-3ac)+(bc-ab)=3a(a-c)-b(a-c)=(3a-b)(a-c).(5)原式=(4x2-y2)2=(2x+y)2(2x-y)2.方法归纳:本题考查了用公式法、分组分解法分解因式,熟练掌握公式结构是解答本题的关键,合理分组也很重要.易错误区:第(2)题要先提取公因式,第(4)题要合理分组,第(5)题要分解彻底.例3、分解因式:x2-120x+3456.分析:由于常数项数值较大,则采用将x2-120x变为差的平方的形式进行分解,这样简便易行:原式=x2-2×60x+3600-3600+3456=(x-60)2-144=(x-60+12)(x-60-12)=(x-48)(x-72).请按照上面的方法分解因式:x2+42x-3528.思路点拨:先把x2+42x-3528转化为x2+2×21x+441-441-3528,因为前三项符合完全平方公式,将x2+2×21x+441作为一组,然后进一步分解.解题过程:原式=x2+2×21x+441-441-3528=(x+21)2-3969=(x+21+63)(x+21-63)=(x+84)(x-42).方法归纳:本题考查的是用分组分解法分解因式,关键是将原式转化为完全平方的形式,然后分组分解.解题时要求同学们要有构造意识和想象力.易错误区:本题主要方法是配方法,关键是将x2+42x配成完全平方式,配上的数应该是42的一半的平方,不要配成42的平方.例4、阅读下列材料并解答问题:因为(x+a)(x+b)=x2+(a+b)x+ab,所以对于二次项系数为1的二次三项式x2+px+q的因式分解,就是把常数项q分解成两个数的积且使这两个数的和等于p,即若有a,b两数满足a·b=q 且a+b=p,则有x2+px+q=(x+a)(x+b).例如:分解因式x2+5x+6.解:∵2×3=6,2+3=5,∴x2+5x+6=(x+2)(x+3).再如:分解因式x2-5x-6.解:∵-6×1=-6,-6+1=-5,∴x2-5x-6=(x-6)(x+1).同学们,阅读完上述文字后,你能完成下面的题目吗?试试看.分解因式:(1)x2+7x+12;(2)x2-7x+12;(3)x2+4x-12;(4)x2-x-12.思路点拨:发现规律:二次项系数为1的二次三项式x2+px+q的因式分解,就是把常数项q分解成两个数的积且使这两个数的和等于p,则x2+px+q=(x+a)(x+b).解题过程:(1)∵3×4=12,3+4=7,∴原式=(x+3)(x+4).(2)∵(-3)×(-4)=12,-3+(-4)=-7,∴原式=(x-3)(x-4).(3)∵6×(-2)=-12,6+(-2)=4,∴原式=(x+6)(x-2).(4)∵(-4)×3=-12,-4+3=-1,∴原式=(x-4)(x+3).方法归纳:本题考查用十字相乘法分解因式,是x2+(a+b)x+ab型式子的因式分解的应用,应掌握x2+(a+b)x+ab=(x+a)(x+b).易错误区:注意系数的符号,将常数项分解成两个数的积的时候要将符号考虑周全.例5、阅读下面的材料,解答下列问题:材料1:公式法(平方差公式、完全平方公式)是因式分解的一种基本方法.如对于二次三项式a2+2ab+b2,可以逆用乘法公式将它分解成(a+b)2的形式,我们称a2+2ab+b2为完全平方式.但是对于一般的二次三项式,就不能直接应用完全平方公式了,我们可以在二次三项式中先加上一项,使其配成完全平方式,再减去这项,使整个式子的值不变,于是有:x2+2ax-3a2=x2+2ax+a2-a2-3a2=(x+a)2-(2a)2=(x+3a)(x-a).材料2:因式分解:(x+y)2+2(x+y)+1.解:将“x+y”看成一个整体,令x+y=A,则原式=A2+2A+1=(A+1)2.再将“A”还原,得:原式=(x+y+1)2.上述解题用到的是“整体思想”,整体思想是数学解题中常见的一种思想方法,请你解答下列问题:(1)根据材料1,把c2-6c+8分解因式;(2)结合材料1和材料2完成下面各题:①分解因式:(a-b)2+2(a-b)+1;②分解因式:(m+n)(m+n-4)+3.思路点拨:(1)利用已知结合完全平方公式以及平方差公式分解因式得出答案;(2)①直接利用完全平方公式分解因式得出答案;②利用已知结合完全平方公式以及平方差公式分解因式得出答案.解题过程:(1)c2-6c+8=c2-6c+32-32+8=(c-3)2-1=(c-3+1)(c-3-1)=(c-2)(c-4). (2)①(a-b)2+2(a-b)+1=(a-b+1)2.②设m+n=t,则t(t-4)+3=t2-4t+3=t2-4t+22-22+3=(t-2)2-1=(t-1)(t-3),∴(m+n)(m+n-4)+3=(m+n-1)(m+n-3).方法归纳:本题主要考查了用公式法分解因式以及整体换元思想,熟练应用公式是解题关键. 易错误区:完全平方公式是配方的基本公式,特别注意配方是根据a2+2ab+b2来配常数,即若二次项系数是1,则常数项配一次项系数一半的平方,不是一次项系数的平方.探究提升例、分解因式:(1)4x3-31x+15;(2)x3+5x2+3x-9;(3)2a4-a3-6a2-a+2.思路点拨:(1)需把-31x拆项成-x-30x,再分组分解;(2)把x3+5x2+3x-9拆项成(x3-x2)+(6x2-6x)+(9x-9),再提取公因式因式分解;(3)先分组分解因式,再用拆项法把因式分解彻底.解题过程:(1)原式=4x3-x-30x+15=x(2x+1)(2x-1)-15(2x-1)=(2x-1)(2x2+x-15)=(2x-1)(2x-5)(x+3).(2)原式=(x3-x2)+(6x2-6x)+(9x-9)=x2(x-1)+6x(x-1)+9(x-1)=(x-1)(x2+6x+9)=(x-1)(x+3)2.(3)原式=a3(2a-1)-(2a-1)(3a+2)=(2a-1)(a3-3a-2)=(2a-1)(a3+a2-a2-a-2a-2)=(2a-1)[a 2(a+1)-a (a+1)-2(a+1)]=(2a-1)(a+1)(a 2-a-2)=(a+1)2(a-2)(2a-1).方法归纳:本题考查用公式法、分组分解法、十字相乘法、提取公因式法等方法进行因式分解,同时都应用了“拆项”、“添项”,所以难度较大.易错误区:本题是通过拆项法因式分解,拆项要围绕因式分解的基本方法进行,主要是为了出现公因式或可以应用公式,不能盲目去拆.走进重高1.【潍坊】将下列多项式因式分解,结果中不含有因式a+1的是(). A.a 2-1 B.a 2+a C.a 2+a-2 D.(a+2)2-2(a+2)+12.【贺州】将m 3(x-2)+m (2-x )分解因式的结果是 .3.【大庆】已知a+b=3,ab=2,求代数式a 3b+2a 2b 2+ab 3的值.4.先阅读第(1)题的解答过程,再解答第(2)题.(1)已知多项式2x 3-x 2+m 有一个因式是2x+1,求m 的值.解法一:设2x 3-x 2+m=(2x+1)(x 2+ax+b ),则2x 3-x 2+m=2x 3+(2a+1)x 2+(a+2b )x+b.比较系数得⎪⎩⎪⎨⎧==+=+m,b 0,2b a -1,12a 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧===.21m ,21b -1,a ∴m=21.解法二:设2x 3-x 2+m=A·(2x+1)(A 为整式).由于上式为恒等式,为方便计算取x=-21,2×-(21)3-(-21)2+m=0,故m=21.(2)已知x 4+mx 3+nx-16有因式x-1和x-2,求m ,n 的值.高分夺冠1.分解因式:(1)x4-1-4x2-4x;(2)x5+x+1;(3)a2-b2+4a+2b+3.2.因为(x+2)(x-1)=x2+x-2,所以(x2+x-2)÷(x-1)=x+2,这说明x2+x-2能被x-1整除,同时也说明多项式x2+x-2有一个因式为x-1,另外当x=1时,多项式x2+x-2的值为0.利用上述阅读材料求解:(1)已知x-2能整除x2+kx-16,求k的值;(2)已知(x+2)(x-1)能整除2x4-4x3+ax2+7x+b,试求a,b的值.无答案)4.已知x,y为正整数,并且xy+x+y=71,x2y+xy2=880,求3x2+8xy+3y2的值.。
七年级下《因式分解》(苏科版)-课件

一元二次方程的求解
求解一元二次方程
因式分解法是求解一元二次方程的一种常用方法。通过将方程$ax^2 + bx + c = 0$因 式分解为$(x - x_1)(x - x_2) = 0$,可以得到方程的解$x_1$和$x_2$。
判断解的合理性
在得到一元二次方程的解后,可以通过因式分解法判断解的合理性。例如,对于方程 $x^2 - 4 = 0$,因式分解为$(x + 2)(x - 2) = 0$,得到解$x = 2$和$x = -2$,这两
因式分解的历史与发展
古代数学中的因式分解
01
在古代数学中,因式分解就已经有了一些初步的应用,如中国
的《九章算术》等。
近现代因式分解的发展
02
ห้องสมุดไป่ตู้
随着数学的发展,因式分解的方法和技巧也得到了不断的完善
和发展,出现了许多新的方法和技巧。
因式分解在现代数学中的应用
03
因式分解是代数中的基本技能之一,它在代数学、几何学、方
例子
$2x^2 + 5x - 3 = (2x - 1)(x + 3)$
03
因式分解的应用与 实例
代数式的化简
代数式化简
通过因式分解,可以将复杂的代数式简化,使其更易于计算 和理解。例如,将多项式$x^2 - 4$因式分解为$(x + 2)(x 2)$,可以更方便地处理后续的运算。
简化计算过程
因式分解可以简化计算过程,减少不必要的复杂运算。例如 ,在计算$(x + 3y)(x - y)$时,通过因式分解可以快速得到结 果$x^2 + 2xy - 3y^2$。
因式分解的重要性
01
02
专题4.1 因式分解(提公因式法与运用公式法)(学生版)

专题4.1 因式分解(提公因式法与运用公式法)1.了解整式乘法与因式分解之间的互逆关系;2.会用提公因式法分解因式;3.会用运用公式法分解因式。
知识点01 因式分解的概念【知识点】因式分解的定义:把一个多项式化成了几个整式的积的形式,这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式。
【知识拓展1】辨别因式分解与整式乘法例1.(2024·江苏常州·期中)下列等式由左边到右边的变形中,属于因式分解的是( ) A .2(1)(1)1a a a +-=- B .43222186?3x y x y x y -=- C .221(2)1x x x x ++=++ D .2269(3)a a a -+=-【即学即练】1.(2024·广东禅城·期末)下列各式从左到右的变形中,是因式分解的为( ). A .()x a b ax bx -=- B .()()222111x y x x y -+=-++C .()()2111x x x -=+-D .()ax bx c x a b c ++=+【知识拓展2】应用因式分解的概念求参数例2.(2024·山东中区·初二期中)已知多项式x 2+ax ﹣6因式分解的结果为(x +2)(x +b ),则a +b 的值为( ) A .﹣4 B .﹣2C .2D .4【即学即练】1.(2024·贵州铜仁·初二期末)多项式26x mx ++可因式分解为()()23x x --,则m 的值为 ( ) A .6B .5±C .5D .5-2.(2024·江西昌江·景德镇一中初一期末)已知,,m n p 为实数,若1,4x x -+均为多项式32x mx nx p+++的因式,则2286m n p --+=__________.【知识拓展3】错题正解例3.(2024·上海市八年级期中)甲乙两个同学分解因式x 2+ax +b 时,甲看错了b ,分解结果为(x +2)(x +4),乙看错了a ,分解结果为(x +1)(x +9),则2a +b =_____. 【即学即练】1.(2024·张家界市初二期中)甲、乙两个同学分解因式x 2+ax+b 时,甲看错了b ,分解结果为(x+2)(x+4);乙看错了a ,分解结果为(x+1)(x+9),则a -b 的值是__________.知识点02 因式分解的方法(一)提公因式法【知识点】①提公因式法:pa +pb +pc =p (a +b +c );注意:挖掘隐含公因式;有时,公因式有显性完全相同类型,也有隐性互为相反数的类型。
上海初中七上因式分解260题(学生版)

【因式分解方法总览】版块一 基本方法因式分解的四种基本方法:一提二代三组四叉1. 【提】提公因式法:一次提净,注意符号确定公因式的方法:系数——取多项式各项系数的最大公约数;字母(或多项式因式)——取各项都含有的字母(或多项式因式)的最低次幂. 2. 【代】公式法因式分解中常用的公式:⑴平方差公式:22()()a b a b a b −=+− ⑵完全平方公式:2222()a ab b a b ±+=±⑶三元平方公式:2222222()a b c ab ac bc a b c +++++=++ ⑷三次方公式:①3322()()a b a b a ab b +=+−+;3322()()a b a b a ab b −=−++ ②3223333()a a b ab b a b +++=+;3223333()a a b ab b a b −+−=− ③()()3332223a b c abc a b c a b c ab bc ca ++−=++++−−− ⑸n 次方公式:①()()12321n n n n n n n a b a b a a b a b ab b −−−−−−=−+++++(n 为正整数) ②()()12321n n n n n n n a b a b a a b a b ab b −−−−−−=+−+−+−(n 为正偶数) ③()()12321n n n n n n n a b a b a a b a b ab b −−−−−+=+−+−−+(n 为正奇数)3. 【组】分组分解法分组分解法:通过分组,各组内可以用提公因式法或者公式法进行因式分解. 4. 【叉】十字相乘法与双十字相乘法⑴十字相乘法:适用范围:形如2ax bx c ++的二次三项式设()()21122ax bx c a x c a x c ++=++,则:12a a a =,12c c c =,1221a c a c b +=; 写成十字交叉的形式,即:12a x a x 12c c ; 口诀:降幂排列,首尾分解,交叉相乘,求和凑中.【注】若24b ac −不是一个平方数,那么二次三项式2ax bx c ++就不能在有理数范围内分解.⑵双十字相乘法适用范围:形如22Ax Bxy Cy Dx Ey F +++++的二次多项式 条件:①12A a a =,12C c c =,12F f f =②1221a c a c B +=,1221c f c f E +=,1221a f a f D += 即: 1a x 1c y 1f2a x 2c y 2f则()()22111222Ax Bxy Cy Dx Ey F a x c y f a x c f +++++=++++步骤:①用十字相乘法分解二次三项式()()221122Ax Bxy Cy a x c y a x c y ++=++,用十字交叉线表示(共两列);②用十字相乘法分解二次三项式()()21122Cy Ey F c y f c y f ++=++,继续用十字交叉线表示,即把常数项F 分解成两个因式填在第三列上;③用十字相乘法分解二次三项式2Ax Dx F ++,检验是否等于()()1122a x f a x f ++,若相等,则双十字相乘法分解因式成功.应用情况:⑴二元二次式(22Ax Bxy Cy Dx Ey F +++++);⑵三元二次齐次式(222Ax Bxy Cy Dxz Eyz Fz +++++); ⑶四次五项式(43243210a x a x a x a x a ++++).版块二 拓展方法因式分解的六种拓展方法:拆添项与配方、主元、换元、试根、待定系数、轮换对称式 1. 拆添项与配方法⑴拆、添项⇒分组⇒提、代; ⑵配方法⇒配完全平方式⇒平方差公式 2. 主元法步骤:选(二次三项式)→排(降幂排列)→叉(十字相乘法) 3. 换元法整体思想:化繁为简,本质不变4. 因式定理与试根法⑴余数定理:x c −除()f x ,余数为()f c ;⑵因式定理:若()0f c =,则x c −为()f x 的因式;若x c −为()f x 的因式,则()0f c =;⑶试根法:设()1110n n n n f x a x a x a x a −−=++++为整系数多项式若存在有理数c 满足()0f c =,则pc q=;其中:p 为0a 的因数,q 为n a 的因数;()f x 含有因式()qx p −;特别地,当1n a =时,c p =为整数.【注】常见技巧:若多项式各项系数和为0,则1一定为根. 5. 待定系数法步骤:设(待定系数)→(展)→等(对应项系数相等) 【注】待定系数法往往会有多种情况,需逐一验证. 6. 轮换对称式⑴判定多项式是否为轮换对称式;⑵试根:选定一个字母为主元,利用因式定理确定因式,并写出相关同型式 对于关于x ,y ,z 的轮换对称式,最常见的试根情况有:常见的齐次轮换对称式:【基础篇】1. 分解因式:22462x xy y +−2. 分解因式:242ab a b a bm an −++3. 分解因式:26312m mn mn −−4. 分解因式:()()32226a b c a c b −−−5. 分解因式:22223a b abc ab c −+−6. 分解因式:44332232722436x y z x y z x y z +−7. 分解因式:()()23262x a b xy a b +−+8. 分解因式:()()221n n x a b y b a +−+−9. 解方程:()()()()45303315453033160x x x x ++−++=11. 分解因式:()()()()22x y x y x y x y +−++−12. 分解因式:23361412abc a b a b −−+13. 分解因式:32461512a a a −+−14. 分解因式:4325286x y z x y −15. 分解因式:322618m m m −+−16. 分解因式:22224()x a x a x +−−17. 分解因式:2316()56()m m n n m −+−18. 分解因式:3223224612x y x y x y −+−20. 分解因式:(23)(2)(32)(2)a b a b a b b a +−−+−21. 分解因式:()()()213223x x x −−+− 22. 分解因式:2121()()m m p q q p +−−+−23. 分解因式:429ax ay −24. 分解因式:322x x x ++25. 分解因式:()2m p q p q −−+26. 分解因式:()()229m n m n +−−27. 分解因式:2229166824a b c ab ac bc ++−+−28. 分解因式:322333x x y xy y +++29. 分解因式:()222224a b a b +−30. 计算:2221999100033⎛⎫⎛⎫− ⎪ ⎪⎝⎭⎝⎭31. 计算:()22221052100595−⨯−+32. 计算:22221111111123410⎛⎫⎛⎫⎛⎫⎛⎫−−−− ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭33. 分解因式:()()()33x y x y xy y x −−−−−34. 已知5a b +=,3ab =,求代数式32232a b a b ab −+的值.35. 分解因式:()()22924a b a b +−−36. 分解因式:53182a a −+37. 分解因式:()()22229a a b x y +−+38. 分解因式:8881a b −39. 分解因式:322206045x x y xy −+−40. 分解因式:()2222224x y z x y +−−41. 分解因式:338a b +42. 分解因式:75()()a b b a −+−43. 分解因式:2243()27()x x y y x −−−44. 分解因式:22(5)2(5)(3)(3)m n n m n m n m +−+−+−45. 分解因式:44244()4p q p q +−46. 分解因式:222()4()4x x x x +−++47. 分解因式:22(23)9(1)x x +−−48. 分解因式:22223(2)27a a b a b +−49. 分解因式:222222(35)(53)a b a b −−+−50. 分解因式:22222(91)36a b a b +−−51. 分解因式:1xy x y −+−52. 分解因式:2ma mb m mn na nb −+++−53. 分解因式:434164a a a +−−54. 分解因式:26432xy yz x xz −+−55. 分解因式:322288a a b b a −+−56. 分解因式:3223636x x y x z xyz +−−57. 分解因式:ax by bx ay −−+58. 分解因式:32acx bcx adx bd +++59. 分解因式:42244a x ax a −+−60. 分解因式:()()22ax by bx ay ++−61. 分解因式:()()2221ab x x a b +++62.分解因式:()()()211y y m m −−−+63.分解因式:32232x x xy y y −+−−64.分解因式:3254222x x x x x −−++−65. 分解因式:()()2222ab x y xy a b −+−66. 已知3210x x x +++=,求20082000199625x x x ++的值.67. 分解因式:()()22114m n mn −−+68. 分解因式:()()()222222a b b c c a a b c +++++−−−69. 分解因式:22(1)12a b b b −−+−70. 分解因式:(1)(2)6x x x −−−72. 分解因式:241194n n m x x y +−+73. 分解因式:5544()x y x y xy +−+74. 分解因式:2222()()()()a b a c c d b d +++−+−+75. 分解因式:325153x x x −−+76. 分解因式:2226923ax a xy xy ay −+−77. 分解因式:222221x y z x z y z −−+78. 分解因式:22221a b a b −−+79. 分解因式:251539a m am abm bm −+−81. 分解因式:2910x x −−82. 分解因式:()238x x −−83. 分解因式:2367928x x −+84. 分解因式:21166x x −−+85. 分解因式:()()222211224x x x x −−−+86. 分解因式:2222360x y xyz z −+87. 分解因式:222536x y xyz z −−89. 分解因式:22310x xy y +−90. 分解因式:2672x x −+91. 分解因式:2121115x x −−92. 分解因式:256x x −++93. 分解因式:26136x x −+94. 分解因式:2273x x ++95. 分解因式:2253x x −+96. 分解因式:222064xy y x −++98. 分解因式:2273320x x −−99. 分解因式:2612x x −+−100. 分解因式:2214425x y xy +−101. 分解因式:22672x xy y −+102. 分解因式:22121115x xy y −−103. 分解因式:2358x x +−104. 分解因式:2212197x xy y −+105. 分解因式:2212()11()()2()x y x y x y x y +++−+−107. 分解因式:2(2)8(2)12a b a b −−−+108. 分解因式:222()14()24x x x x +−++109. 分解因式:()233x m n x mn +++110. 分解因式:2()()x a b c x a b c +++++【提高篇】1. 分解因式:321246n n n y y y +++−+−2. 分解因式:222232284163915a b x a x a b −−3. 分解因式:()()()()2223326a b x y b c a b x y b c ++−++4.分解因式:()()()()56m x y a b c n y x b a c −−++−−−5.分解因式:()()()()()()22322132212123x x x x x x x −+−−+++−6.计算:20.1737 2.017530201.7⨯+⨯+7.分解因式:()()()()()21222n n n x y x z x y y x y z +−−−−+−−8. 分解因式:8684279a a −9. 分解因式:32233111248x y x y x y −+−10. 分解因式:()()2232p p q p p q +−+11. 分解因式:()()()()322522322n n x y x y −−−−−12. 分解因式:()()()1232n n n a x y b y x c y x ++−−−+−13. 分解因式:()()13122n n n x x x x +−−−14. 分解因式:23229632x y x y xy ++15.分解因式:3222524261352xy z xy z x y z −++16.分解因式:212146n m n m a b a b ++−−(m 、n 为大于1的自然数)17.分解因式:23423232545224()20()8()x y z a b x y z a b x y z a b −−−+−18.分解因式:()()2121510n n a a b ab b a +−−−(n 为正整数)19.分解因式:2122()()()2()()n n n x y x z x y y x y z +−−−−+−−(n 为正整数)20. 分解因式:322()()()()()x x y z y z a x z z x y x y z x y x z a +−+−+−−+−−−−21. 分解因式:229312554a ab b −+22. 分解因式:2222()4()4()m n m n m n +−−+−23. 分解因式:()()()24c a b c a b −−−−24. 分解因式:()()24422a a b c b c −+++25. 分解因式:()()222122x x x x −++−26. 分解因式:()()24222222x a b x a b −++−27. 分解因式:77x y xy −28. 分解因式:5131214242n n n n n n x y x y x y −−+−+−+−29. 分解因式:3333a b c abc ++−30. 分解因式:3223332x x y xy y +++31. 分解因式:()()()()333333ax by ay bx a b x y +++−++32. 分解因式:()()2222224c b d a ab cd −+−−−33. 已知2471−可被40到50之间的两个整数整除,求这两个数.34. 求证:22823x xy y −−是两个整系数多项式的平方差.35. 分解因式:222139x xy y −+−36. 分解因式:444222222222a b c a b b c c a ++−−−37. 分解因式:81644x −38. 计算:()12351721n −⨯⨯⨯+39.分解因式:44()()a x a x +−−40.分解因式:2224244a b c ab ac bc +++−−41.分解因式:()()()()ab c d c d cd a b a b +−++−42.分解因式:()()3211x y xy x y ++−−−43.分解因式:2222x yz axyz yz xy xz az ++−−−44. 分解因式:()()222x b c d y d b c c d b +−−−−−+−45. 分解因式:322222422x x z x y xyz xy y z −−++−46. 分解因式:()()3322332a b a b a b ++++++47. 分解因式:432234a a a b ab b b ++++−48. 分解因式:()()()bc b c ca c a ab a b ++−++49. 分解因式:()222231b a x ab x +−−50. 分解因式:224632x xy ax a x y +−+−−51. 分解因式:222221x y z xy z +−−−−52. 分解因式:()222223691x y x y −+−53.分解因式:2222224x y x z y z z −−+54.分解因式:232232a b abc d ab cd c d −+−55.分解因式:22224946a b c d ac bd −+−++56.分解因式:221x ax x ax a +++−−57.分解因式:222332154810ac cx ax c +−−58.分解因式:22abx bxy axy y +−−59.分解因式:()()x x z y y z +−+60. 分解因式:333333()()()a b b c c a a b c ++++++++61.分解因式:3322()()ax y b by bx a y +++62.分解因式:2231()b a x abx +−−63.分解因式:22(3)(43)x ab x a b −+−64.分解因式:2222()()ab c d a b cd −−−65.分解因式:3254222x x x x x −−++−66.分解因式:222(1)()ab x x a b +++67.分解因式:222222()()ax by ay bx c x c y ++−++68.分解因式:()()()bc b c ca c a ab a b ++−−+69. 分解因式:()222124m x mx m −−−+70.分解因式:2222(48)3(48)2x x x x x x ++++++71.分解因式:2222()abcx a b c x abc +++72.分解因式:2222(4)8(4)15x x x x x x ++++++73.分解因式:2222222(61)5(61)(1)2(1)x x x x x x ++++++++74.分解因式:2()2a b x ax a b −+++75.分解因式:2222()3103x a b x a ab b ++−+−76.分解因式:()221999199911999x x −−−77.分解因式:22276212x xy y x y −++−−78.分解因式:22121021152x xy y x y −++−+79.分解因式:22534x y x y −+++80.分解因式:226731385x xy y x y −−++−81.分解因式:224434103x xy y x y −−−+−82.分解因式:22344883x xy y x y +−+−−83.分解因式:2265622320x xy y x y −−++−84.分解因式:226136222320x xy y x y −++−+85.分解因式:22223345a b c ab ac bc +++++86.分解因式:222311642x xy y xz yz z −+−−−87.分解因式:222695156x xy y xz yz z −+−++88.分解因式:2222372x y z xy yz xz −−+++89.分解因式:22265622320x xy y xz yz z −−−−−90.分解因式:222695156x xy y xz yz z −+−++91.分解因式:332x x ++92.分解因式:3234x x +−93.分解因式:9633x x x ++−94.分解因式:432433x x x x ++++95. 分解因式:432234232a a b a b ab b ++++96. 分解因式:444a b +97. 分解因式:44x +98. 分解因式:12631x x −+99. 分解因式:841x x ++100. 分解因式:422411x x y y −+101. 分解因式:4224(1)(1)(1)x x x ++−+−102. 分解因式:22(1)(1)4m n mn −−+103. 分解因式:412323x x −+104. 分解因式:42511x x −+105. 分解因式:444m n +106. 分解因式:422241x x ax a −++−107. 分解因式:2284025a ax xy y −−−108. 分解因式:22a ax xy y ++−109. 分解因式:2232x mx mx x −+−+110. 分解因式:()2232x a x a b b −−+−111. 分解因式:()()()2212121a a b a a b −−+−−112. 分解因式:22226x ax bx a ab b +−−−+113. 分解因式:4222x ax x a a −++−114. 分解因式:()32322x x a x a −++−115. 分解因式:222232x y x y xy xy x y ++++++116. 分解因式:22222a b ab ab a b ++−−−117. 分解因式:3222222x x y x z xz xyz y z yz −+−−++118. 分解因式:()()()2222abc a b c b c a c a b ++++++119. 分解因式:32539x x x ++−120. 分解因式:32256x x x +−−121. 分解因式:32694x x x −+−122. 分解因式:3210x x x +−−123. 分解因式:3487x x −−124. 分解因式:432262x x x x −−−+125. 分解因式:343115x x −+126. 分解因式:3292624x x x +++127. 分解因式:32252x x x −−−128. 分解因式:22(1)(2)12x x x x ++++−129. 分解因式:2222(48)3(48)2x x x x x x ++++++130. 分解因式:222(231)22331x x x x −+−+−131. 分解因式:2(2)(3)(4)(6)42x x x x x ++++−132. 分解因式:4(1)(21)(31)(41)6x x x x x ++−−+133. 分解因式:()()22216112a a a a a ++−++134. 分解因式:()()2254272x x x x −+−−−135. 分解因式:2244661124864x y x y x y −+−136. 分解因式:168243528x x y y −−137. 分解因式:()()222224x xy y xy x y ++−+138. 求证:(2016)(2017)(2018)(2019)1n n n n +++++是一个完全平方数.139. 计算:(472)(692)(8112)...(199419972)(362)(582)(7102) (199319962)⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+140. 计算:44444444(1064)(1864)(2664)(3464)(664)(1464)(2264)(3064)++++++++141. 分解因式:432227447x x x x −−−+142. 分解因式:435159x x x ++−143. 多项式32226x x x k +−+有一个因式是21x +,求k 的值.144. 若()()x a x b k −−−中含有因式x b +,求用a 、b 表示k 的式子.145. 21y x −+是2244xy x y k −−−的一个因式,求k 的值.146. 设多项式324715ax bx x +−−含有因式31x +、23x −,试试将此多项式因式分解.147. 已知关于x 、y 的二次式22754324x xy my x y ++−+−可分解为两个一次因式的乘积,求m 的值.148. 多项式2256x axy by x y ++−++的一个因式是2x y +−,试确定a b +的值.149. 已知225x x ++是42x ax b ++的一个因式,求a b +的值.150. 若多项式432511x x x mx n −+++能被2(1)x −整除,求m n +的值.。
七年级数学:因式分解精讲,建议收藏

七年级数学:因式分解精讲,建议收藏七年级数学中,因式分解是一个非常重要的知识点,它涉及到整式的运算、方程的解法、计算规律的探究等等,因此十分值得我们重视。
本文将详细介绍因式分解的概念、方法和技巧,并给出一些练习建议,帮助同学们深入理解这一知识点。
一、因式分解的概念及意义因式分解指将一个多项式拆分成乘积的形式,其中每一项被称为因式。
例如,$6x^2+9x$可以分解为$3x(2x+3)$,其中$3x$和$2x+3$为因式。
因式分解的意义主要有以下几个方面:1.方便进行乘法和约简运算。
通过因式分解,我们可以将一个式子化简为形式更简洁、易于计算的形式,从而更便于进行乘法和约简运算。
2.解决方程和不等式。
在解方程和不等式的时候,需要将复杂的多项式转化为等式或不等式的形式,此时因式分解可以派上用场,将式子转化为乘积形式后更易于解决。
3.发现规律和应用。
在一些求和、计算公式等问题中,由于形式过于复杂,我们难以直接进行分析和求解,此时可以采用因式分解的方法,将式子变形为更易于分析和计算的形式,帮助我们发现规律和应用。
二、因式分解的方法和技巧因式分解的方法和技巧有很多种,下面将介绍一些常见的方法和技巧。
1.公因式法。
公因式法是最基础的因式分解方法,即找出多项式中所有项的公因式,并将其提取出来。
例如,$4x^2-12x=4x(x-3)$,其中4x是公因式。
2.配方法。
在多项式中,有些项之间存在着一些值得注意的关系,例如$ab+ac$中的$a$可以因式分解成公因式$a(b+c)$。
此外,常用的配方法还有平方差公式和差平方公式等。
3.分组分解法。
分组分解法指将多项式中的项按一定的方法分组,然后再分别因式分解,并试图将各组得到的乘积合并。
这种方法在多项式中具有广泛的应用。
4.因式定理。
因式定理是在分组分解的基础上得到的一种方法,它可以直接得到多项式的因式拆分结果,是一种快捷有力的因式分解方法。
三、练习建议掌握任何一门学科都需要多加练习,数学也不例外。
第4章 因式分解-开放与探究:因式分解的六种常见方法习题课件

分类训练 9.分解因式:x4+14. 【点拨】本题直接分解因式很困难,考虑到添加辅助项使其符合 公式特征,因此将原式添上 x2 与-x2 两项后,便可通过分组使 其符合平方差公式的结构特征,从而将原多项式进行因式分解.
浙教版 七年级下
第四章 因式分解
开放与探究(四) 因式分解的六种常见方法
习题链接
提示:点击 进入习题
1B 2C 3 见习题 4 见习题
5 见习题
6 见习题 7 见习题 8 见习题 9 见习题 10 见习题
答案显示
习题链接
提示:点击 进入习题
11 见习题 12 见习题 13 见习题 14 见习题
答案显示
分类训练 6.分解因式:(x+3)(x+4)+(x2-9).
解:原式=(x+3)(x+4)+(x+3)(x-3) =(x+3)[(x+4)+(x-3)] =(x+3)(2x+1).
【点拨】解此题时,表面上看不能分解因式,但通过局部分解后, 发现有公因式可以提取,从而将原多项式分解因式.
分类训练 7.把下列各式分解因式: (1)x(x+4)+4;
分类训练 13.分解因式:x2-y2-4x+6y-5.
【点拨】这里巧妙地把-5 拆成 4-9.“凑”成(x2-4x+4)和 (y2-6y+9)两个整体,从而运用公式法分解因式.
解:原式=(x2-4x+4)-(y2-6y+9) =(x-2)2-(y-3)2 =(x+y-5)(x-y+1).
分类训练
解:原式=(x+y)2-4(x+y)+4=(x+y-2)2.
苏教版数学七年级下期末复习三---因式分解

苏教版数学七年级下期末复习三---因式分解一、知识点:1、因式分解:(1)把一个多项式写成几个整式的积的形式叫做多项式的因式分解。
(2)多项式的乘法与多项式因式分解的区别,简单地说:乘法是积.化和.,因式分解是和.化积.。
(3)因式分解的方法:①提公因式法;②运用公式法。
2、因式分解的应用:(1)提公因式法:如果多项式的各项含有公因式,那么就可以把这个公因式提出来。
把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法。
(2)公因式:多项式ab+ac+ad的各项ab、ac、ad都含有相同的因式a,a称为多项式各项的公因式。
(3)用提公因式法时的注意点:①公因式要提尽,考虑的顺序是,先系数,再单独字母,最后多项式。
如:4a2(a-2b)-18ab(a-2b)=2a(a-2b)(2a-9b);②当多项式的第一项的系数为负数时,把“-”号作为公因式的负号写在括号外,使括号内的第一项的系数为正。
如:-2m3+8m2-12m= -2.m(m2-4m+6);③提公因式后,另一个多项式的求法是用原多项式除以公因式。
(4)运用公式法的公式:①平方差公式:a2-b2=(a+b)(a-b)②完全平方公式:a2+2ab+b2=(a+b)2a2-2ab+b2=(a-b)2(5)因式分解的步骤和要求:把一个多项式分解因式时,应先提公因式...,注意公因式要提尽..,然后再应用公式,如果是二项式考虑用平方差公式,如果是三项式考虑用完全平方公式,直到把每一个因式都分解到不能再分解为止。
如:-2x5y+4x3y3-2xy5=-2xy(x4-2x2y2+y4) =-2xy(x2-y2)(x2+y2)=-2xy(x+y)(x-y)(x2+y2) 二、举例:例1:分解因式:(1)(a+b)2-2(a+b) (2)a(x-y)+b(y-x)+c(x-y) (3)(x+2)2-9 (4)4(a+b)2-9(a-b)2(5)80a2(a+b)-45b2(a+b)(6)(x2-2xy)2+2y2(x2-2xy)+y4(7)(m+n)2-4(m+n)+4 (8)x4-81 (9)(x+y)2-4(x2-y2)+4(x-y)2(10)16a4-8a2+1 (11)(x2+4)2-16x2(12)12422---yyx例2:计算:(1)20042-4008×2005+20052(2)9.92-9.9×0.2+0.01(3)22200120031001-(4)(1-221)(1-231)(1-241) (1)291)(1-2101) 例3:观察下列算式回答问题:32-1=8×1 52-1=24=8×3 72-1=48=8×692-1=80=8×10 ………问:根据上述的式子,你发现了什么?你能用数学式子来说明你的结论是正确的吗?例4:解答题:(1)已知x2-y2=-1 ,x+y=21,求x-y 的值。
12.2因式分解的方法(第1课时 提公因式法)(课件)七年级数学上册(沪教版2024)

=4 a ( x - y )+2 b ( x - y )
=2( x - y )(2 a + b ).
7.先分解因式,再计算求值:
(1)4 x ( m -2)-3 x ( m -2)2,其中 x =1, m =3;
【解】4 x ( m -2)-3 x ( m -2)2
=(2 x + y )(2 x -3 y +3 x )=(2 x + y )(5 x -3 y ).
+ = ,
+ = ,
∵
∴
∴原式=3×(-2)=-6.
− = − .
+ = ,
14. 试说明817-279-913能被45整除.
【解】因为817-279-913=328-327-326
2)( a +4).将 a =-2代入,得原式=(-2-2)×(-2+
4)=-8.
分层练习-巩固
8. 计算320-318×6的值是( A
)
A. 319
B. 318
C. 3 2
D. 0
9. [新考法 数形结合法]△ ABC 的三边长分别为 a , b , c ,
且 a +2 ab = c +2 bc ,则△ ABC 是(
提取公因式法.
新知探究
如何将6 2 + 9因式分解?
先找出6 2 + 9各项的公因式,再用提取公因式法因式分解. 这个整式有两项
6 2 与9, 这两项的系数6与9有最大公因数3,这两项的字母部分 2 与都含
有字母和, 且和的最低次数都是1,因此可提取公因式3,得
− = ,
= ,
所以
解得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4讲因式分解方法
多项式的因式分解是代数式恒等变形的基本形式之一.初中数学教材中主要介绍了提取公因式法、运用公式法、分组分解法和十字相乘法.本讲是对因式分解的方法、技巧和应用作进一步的介绍.
1.运用公式法
在整式的乘、除中,我们学过若干个乘法公式,现将其反向使用,即为因式分解中常用的公式,例如:
(1)a2-b2=(a+b)(a-b); (2)a2±2ab+b2=(a±b)2;
(3)a3+b3=(a+b)(a2-ab+b2); (4)a3-b3=(a-b)(a2+ab+b2).
下面再补充几个常用的公式:
(5)a2+b2+c2+2ab+2bc+2ca=(a+b+c)2
(6)a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca);
(7)a n-b n=(a-b)(a n-1+a n-2b+a n-3b2+…+ab n-2+b n-1)其中n为正整数;
(8)a n-b n=(a+b)(a n-1-a n-2b+a n-3b2-…+ab n-2-b n-1),其中n为偶数;
(9)a n+b n=(a+b)(a n-1-a n-2b+a n-3b2-…-ab n-2+b n-1),其中n为奇数.
运用公式法分解因式时,要根据多项式的特点,根据字母、系数、指数、符号等正确恰当地选择公式.
例1 分解因式:
(1)-2x5n-1y n+4x3n-1y n+2-2x n-1y n+4; (2)x3-8y3-z3-6xyz;
(3)a2+b2+c2-2bc+2ca-2ab; (4)a7-a5b2+a2b5-b7.
例2分解因式:x15+x14+x13+…+x2+x+1.
2.拆项、添项法
因式分解是多项式乘法的逆运算.在多项式乘法运算时,整理、化简常将几个同类项合并为一项,或将两个仅符号相反的同类项相互抵消为零.在对某些多项式分解因式时,需要恢复那些被合并或相互抵消的项,即把多项式中的某一项拆成两项或多项,或者在多项式中添上两个仅符合相反的项,前者称为拆项,后者称为添项.拆项、添项的目的是使多项式能用分组分解法进行因式分解.
例3 分解因式:(1)x3-9x+8 (2) a5+a+1
例4 分解因式:
(1)x9+x6+x3-3; (2)(m2-1)(n2-1)+4mn;
例5:分解因式:
(1)(x+1)4+(x2-1)2+(x-1)4; (2)a3b-ab3+a2+b2+1.
换元法指的是将一个较复杂的代数式中的某一部分看作一个整体,并用一个新的字母替代这个整体来运算,从而使运算过程简明清晰.
例6 分解因式:(x2+x+1)(x2+x+2)-12.
例7 分解因式:(x2+3x+2)(4x2+8x+3)-90.
例8 分解因式:(x2+4x+8)2+3x(x2+4x+8)+2x2.
例9分解因式:6x4+7x3-36x2-7x+6.
例10 分解因式:(1)x3-4x2+6x-4. (2)x3-5x2+9x-6
例11分解因式:(1)9x4-3x3+7x2-3x-2. (2)2x3-13x2+3
例12求一个关于x的二次多项式,它的二次项系数为1,它被x-3除余1,且它被x-1除和被x-2除所得的余数相同。
5.双十字相乘法
例13 分解因式:
(1)x2-3xy-10y2+x+9y-2; (2)x2-y2+5x+3y+4;
(3)xy+y2+x-y-2; (4)6x2-7xy-3y2-xz+7yz-2z2.
6.待定系数法
待定系数法是数学中的一种重要的解题方法,应用很广泛,这里介绍它在因式分解中的应用.在因式分解时,一些多项式经过分析,可以断定它能分解成某几个因式,但这几个因式中的某些系数尚未确定,这时可以用一些字母来表示待定的系数.由于该多项式等于这几个因式的乘积,根据多项式恒等的性质,两边对应项系数应该相等,或取多项式中原有字母的几个特殊值,列出关于待定系数的方程(或方程组),解出待定字母系数的值,这种因式分解的方法叫作待定系数法.
例14 分解因式:
(1)x2+3xy+2y2+4x+5y+3. (2)x4-2x3-27x2-44x+7.
7.分组分解法:
例15 4x4+4x3-9x2-x+2;。
