差分方程、滞后运算
差分方程滞后运算与动态模型

(3)如果 1,差分方程描绘的变 量序列仍然是非收敛序列,但这种特 殊情况下的差分方程对应一个专门的 名称,叫做随机游走过程。
图2.2(a)
1.2
经过以上分析,可以得出结论:一阶差分方 0.8 程中的一阶滞后项的系数的大小关键性地决定了 差分方程的求解结果。实际上,这个系数的取值 0.4 也关键性地决定了时间序列变量的动态走势特征。
滞后算子运算还符合标准的“结合律” 与“交换律”等如下运算法则: 0 (1) L 1 ( 2 )对任何常数 A 取滞后运算还等于原 常数,即 Lp A = A。 (3)结合与分配律,即 p q p q yt - p + yt -q = L yt L yt (L L )yt
p yt p t
要从高阶向一阶转化,首先定义几个 常用矩阵: t yt p1 p 1 2 0 y 1 0 0 0 t 1 Yt yt 2 F 0 1 0 0 et 0 yt ( p 1) 0 0 0 1 0 p p p1
14
yt 0.8 yt 1 t
图2.2(f)
40 20 0 -20 -40 5 10 15 20 25 30
15
yt 1.2 yt 1 t
2.2
动态乘数与脉冲响应函数
2.2.1 动态乘数(dynamic multiplier) 2.2.2 脉冲响应函数(impulse
当 1 0 时,如(e)情形,动态 乘数的取值正负号交替变化,但是这些 动态乘数的绝对值是呈现逐渐递减至0 的,这种情形经常被形象地称作“震荡 式衰减”。 这样,对于 1的情况,从脉 冲响应函数图来看,随机扰动因素对序 列 yt 的冲击将最终消失,而对应的一 阶差分方程在这种情况下就是一个稳定 的系统。
具有超前和滞后的二阶差分方程的边值问题

直接验证可知, D 是正定矩阵,记它的特征值为 λ j > 0, j = 1, 2, , k 。不妨设
λ1 ≤ λ2 ≤ ≤ λk
k 泛函 J 满足 Palais-Smale 条件 ( 简称 P.S. 条件 ) ,如果对任意的序列 u ( k ) ⊂ E ,若 J u ( )
定义 2.1 设 E 是实的 Banach 空间, J ∈ C1 ( E , ) ,即 J 是定义在 E 上的连续 Fréchet 可微的泛函,称
x0 0, xk 0, ∆= = +1
(1.7)
下解的存在性。 在参考文献[12]中,作者讨论了以下二阶差分方程
0, n ∈ (1, k ) , ∆ (ϕ p ( un −1 ) ) + f ( n, un +1 , un , un −1 ) =
在边值条件
∆u = 0, uk= 0, 0 +1
(1.8)
包含下列方程
f ( t , u ( t + 1) , u ( t ) , u ( t − 1) ) , t ∈ ,
(1.3)
在参考文献[1]中, Smets 和 Willem 得到了类似方程(1.3)格动力系统孤立波解的存在性, 而且方程(1.3)
0, t ∈ , ( p ( t ) ϕ ( u ′) )′ + f ( t , u ( t ) ) =
2. 变分框架及基本引理
为了运用临界点理论,我们将建立(1.1)~(1.2)的变分框架并给出一些必要的引理。 定义 k 上的内积如下:
k
u, v =
∑ un vn ,∀u, v ∈ k
n =1
1
(2.1)
由 k 上的内积可以诱导空间 k 上的范数:
差分方程简介

差分方程简介
汇报人:
contents
目录
• 差分方程的基本概念 • 差分方程的求解方法 • 差分方程的应用 • 差分方程的局限性 • 差分方程的发展历程与未来趋势 • 差分方程的实际案例分析
01
差分方程的基本概念
定义与例子
• 差分方程是描述离散序列变化的方程式。例如,考虑一个数列{an},我们可以写出一个差分方程:a{n+1} = 2a_n + 3。
应用
经济学中的差分方程模型适用于预测经济指标的未来趋势 、政策效应分析等。然而,由于现实世界中的复杂性,该 模型可能不适用于所有经济情况。
THANKS
感谢观看
公式法
公式法的原理
01
通过差分方程的解的公式直接计算出解。公式法的步骤 Nhomakorabea02
根据差分方程的特点,寻找解的公式,然后代入初值计算出解
。
公式法的优缺点
03
公式法适用于某些特定类型的差分方程,但不适用于所有类型
的差分方程,需要具体问题具体分析。
计算机方法
计算机方法的原理
利用计算机强大的计算能力,通过编程等方法求解差分方程。
人群、感染人群和免疫人群之间的转换。这些因素都可以通过差分方程来描述 。 • 数学方程:常见的传染病模型如SIR模型,其差分方程为 S(t+1) = S(t) b*S(t)*I(t)/N(t), I(t+1) = I(t) + b*S(t)*I(t)/N(t) - d*I(t), R(t+1) = R(t) + d*I(t),其中S表示易感人群,I表示感染人群,R表示免疫人群,b表示感染率 ,d表示疾病死亡率。 • 应用:传染病模型适用于预测疾病的传播趋势、评估公共卫生干预措施的效果 等。然而,由于现实世界中的复杂性,该模型可能不适用于所有疾病传播情况 。
差分方程知识点总结

差分方程知识点总结一、差分方程的概念差分方程是指用差分运算符号(Δ)表示的方程。
差分运算符Δ表示的是某一变量在两个连续时间点的变化量。
差分方程通常用于描述离散时间下的变化规律,比如时间序列、离散动力系统等。
二、常见的差分方程1. 一阶线性差分方程一阶线性差分方程的一般形式为:y(t+1) - y(t) = a*y(t) + b,其中a和b为常数。
一阶线性差分方程常常用于描述某一变量在不同时间点之间的线性变化规律。
2. 二阶线性差分方程二阶线性差分方程的一般形式为:y(t+2) - 2*y(t+1) + y(t) = a*y(t) + b,其中a和b为常数。
二阶线性差分方程通常用于描述某一变量在不同时间点之间的二阶线性变化规律。
3. 线性非齐次差分方程线性非齐次差分方程的一般形式为:y(t+1) - a*y(t) = b,其中a和b为常数。
线性非齐次差分方程通常用于描述某一变量在不同时间点之间的线性变化规律,并且受到外部条件的影响。
4. 滞后差分方程滞后差分方程的一般形式为:y(t+1) = f(y(t)),其中f为某一函数。
滞后差分方程通常用于描述某一变量在不同时间点之间的非线性变化规律。
5. 差分方程组差分方程组是指由多个差分方程组成的方程组。
差分方程组通常用于描述多个变量之间的变化规律,比如混合动力系统、多变量时间序列等。
三、差分方程的解法1. 特征根法特征根法是解一阶或二阶线性差分方程的一种常用方法。
通过求解特征方程,可以求得差分方程的通解。
2. 递推法递推法是解一阶或二阶非齐次差分方程的一种常用方法。
通过递推关系,可以求得差分方程的特解。
3. Z变换法Z变换法是解一阶或二阶差分方程的一种常用方法。
通过对差分方程进行Z变换,可以将其转换为等价的代数方程,然后求解其解。
4. 数值解法对于复杂的差分方程,通常采用数值解法求解。
数值解法包括Euler法、Runge-Kutta法、递推法等,通过迭代计算逼近差分方程的解。
已知因果系统的差分方程y

已知因果系统的差分方程y
因果系统的差分方程是描述其输入和输出之间的关系的数学表达式。
在这个方程中,输入信号的当前值与过去的值相关,而输出信号的当前值
则取决于输入信号的当前值和过去的值。
一个典型的因果系统的差分方程可以写成以下的形式:
y[n] = b0*x[n] + b1*x[n-1] + b2*x[n-2] + ... + bk*x[n-k] -
a1*y[n-1] - a2*y[n-2] - ... - an*y[n-k]
其中,y[n]是输出信号的当前值,x[n]是输入信号的当前值,b0、b1、b2、..、bk是输入信号的权重系数,a1、a2、..、an是输出信号的权重
系数,k是滞后阶数。
这个差分方程的含义是,当前时刻的输出值等于输入信号当前值与过
去的几个输入信号值的加权和,再减去输出信号当前值与过去的几个输出
信号值的加权和。
第一个例子是一个简单的滞后系统,它的差分方程可以写成:
y[n]=x[n-1]
这个方程的含义是,当前时刻的输出值等于输入信号上一个时刻的值。
这个系统只有一个滞后阶数,没有权重系数。
它的输出信号直接取决于输
入信号的过去值。
第二个例子是一个带有权重系数的差分方程,它可以写成:
y[n]=0.5*x[n]+0.3*x[n-1]+0.2*x[n-2]-0.6*y[n-1]-0.7*y[n-2]
这个方程的含义是,当前时刻的输出值等于输入信号当前值和过去两个输入信号值的加权和,再减去输出信号过去两个时刻的值的加权和。
输入信号的权重系数为0.5、0.3和0.2,输出信号的权重系数为-0.6和-0.7、这个系统的输入和输出信号都有两个滞后阶数。
时间序列练习题

如果没有特别说明,在本练习中~,,t i i d ε,()()()2t t 0,,0,t E Var E t τεεσεετ===≠ 一、填空题1.时间序列{}2,5,9的二阶差分为_________.2.时间序列{}t ε经过一阶差分后序列均值为_________,方差为_________________3.对于时间序列t X ,∆表示差分运算,则111d d d t t t X X X ---∆=∆-∆表示_____阶差分。
4.差分方程1t t t y y w φ-=+的j 期动态乘子为________________.5.差分方程01122t t t t y y y φφφε--=+++的特征方程为___________,特征根为_____6.差分方程01122t t t t y y y φφφε--=+++可用滞后算子表示成()t t L y εΦ=,则()L Φ=___________.7.差分方程01122t t t t y y y φφφε--=+++稳定的条件是方程特征根落在单位圆_____,将方程表示成滞后算子形式()2121t t L L y φφε--=,如果想要差分方程稳定,则其辅助方程21210z z φφ--=的根落在单位圆________。
8.一般来说,对于n 阶差分方程的解有两部分组成,其中含有n 个互相独立的任意常数的解称为差分方程的_____,不含有任意常数的解称为差分方程的_____。
9.差分方程11t t t y y φε-=+稳定的条件为________。
10.AR (1)模型150.5t t t y y ε-=++的均值为___________,自方差为_______,自协方差函数满足齐次差分方程______________。
11.MA (1)模型150.5t t t y εε-=+-的均值为________,自方差为_________,一阶自协方差为________,其它为_______。
3.4.差分方程简介

故原方程的通解为
(2)方程对应的特征方程为 λ 1= 0 ,其特征根为 λ =1 ,于是齐次方
* 程的通解为 yi = C 。设方程的特解为: yi = Acos π i + Bsin π i 2 2
将其代入原方程可解得 A = B = 1 2 故原方程的通解为
yi = C 1 (cos π i + sin π i) 2 2 2
λn + Pλn1 ++ P 1λ + P = 0 1 n n
(3.4.3)
方程(3.4.3)称为(3.4.2)的特征方程。若 λ1, λ2 ,, λn 是(3.4.3)的 n 个不同的根,则 Y (i) = λ1 ,Y2 (i) = λ2 ,,Yn (i) = λn 就是(3.4.2)的 n 个 1
r 1+ P ++ P 1 n
是稳定的条件与对应的齐次方程(3.4.2)完全相同。
此外,对于 n 维向量 yi 和 n× m 常数矩阵 A 构成的一阶线性差分方程组
yi +1 + Ayi = 0
其 平 衡点 稳 定的 条 件是 矩阵 A 的特 征 根
λi ( i =1,2,, n) 均有 λi <1 。 即均在复平面上的
(3)
若 Y1 (i) ,…,Yn (i) 是方程(3.4.2) n 个线性
无关的解,则它们的线性组合 C1Y (i) ++ CnYn (i) 1 就是 (3.4.2)的通解。 Y1 (i) ,…, Yn (i) 称为(3.4.2) 的一组基本解。 (4) 若 C1Y (i) ++ CnYn (i) 是 (3.4.2) 的通解, y *(i) 是 1 非齐次方程(3.4.1)的一个特解,则
计量经济学:平稳时间序列分析-差分方程与延迟算子

[c112 c222
c
p
2 p
]t
2
[c113
c223
c
p
3 p
]t 3
1
0
i
1
1ip1
2ip2 p1
i
p2 i
i2
i
p 1 i
p
因为 i 是矩阵F的特征值,它满足 ip 1ip1 2ip2 p1i p 0
ip p1
i
iipp12
Fti
ip
2
i
i
p3
iti
i2
i
i
1
即 ti 是与矩阵F的特征值 i 相对应的特征向量。
11 0
f (t1)
11
1
f (1)
11 t 1
t
其中
f ( j)
11
c11j
c22j
cppj
证明:只需证
ci
p
p1 i
k1(i k )
k i
令
iipp12
ti
ip
3
则
i
1
1 2 3
1
0
0
Fti
0
1
0
0 0 0
p1
0 0
p
0 0
iipp12 ip3
Jij
0i j
0
C1 j1 ji i j
0
C 2 j2 ji
C1 j1 ji
0
ni 1
C j
ni 2
C j
jni 1 i
jni 2 i
i j
例如,考察有重根的二阶差分方程
F
j
M
j
差分方程

第八讲 差分方程模型一、差分方程介绍规定t 只取非负整数。
记为变量在t 点的取值,则称t y y t t t y y y −=Δ+1为的一阶向前差分,简称差分,称Δ为的二阶差分。
类似地,可以定义的阶差分。
t y t t t t t y t t y y y y y y +−=Δ−Δ=ΔΔ=+++12122)(t y t y n t ny Δ由及的差分给出的方程称为的差分方程,其中含的最高阶差分的阶数称为该差分方程的阶。
差分方程也可以写成不显含差分的形式。
例如,二阶差分方程也可改写成t y t 、t y t y t y 02=+Δ+Δt t t y y y 012=+−++t t t y y y 。
满足一差分方程的序列称为差分方程的解。
类似于微分方程情况,若解中含有的独立常数的个数等于差分方程的阶数时,称此解为该差分方程的通解。
若解中不含任意常数,则称此解为满足某些初值条件的特解。
t y 称如下形式的差分方程)(110t b y a y a y a t n t n t n =+++−++L (1) 为阶常系数线性差分方程,其中是常数,n n a a a ,,,10L 00≠a 。
其对应的齐次方程为0110=+++−++t n t n t n y a y a y a L (2)容易证明,若序列与均为(2)的解,则也是方程(2)的解,其中为任意常数。
若是方程(2)的解,是方程(1)的解,则也是方程(1)的解。
)1(t y )2(t y )2(2)1(1t tt y c y c y +=21,c c )1(t y )2(t y )2()1(t t t y y y +=方程(1)可用如下的代数方法求其通解: (I )先求解对应的特征方程(3)00110=+++−a a a n nL λλ(II )根据特征根的不同情况,求齐次方程(2)的通解。
(i )若特征方程(3)有n 个互不相同的实根n λλ,,1L ,则齐次方程(2)的通解为t n n t c c λλ++L 11 (为任意常数)n c c ,,1L (ii )若λ是特征方程(3)的重根,通解中对应于k λ的项为t k k tc c λ)(11−++L ,),,1(k i c i L =为任意常数。
2020版金融计量学:时间序列分析视角(第三版)教学课件第3章第1节

无论是脉冲响应函数还是累积脉
冲响应函数,其根本特性都由一阶滞
后项系数 决定。
图3.3(a)
0.8 0.4 0.0 -0.4 -0.8
0
5
10
15
20
(a) 0.3
图3.3(b)
0.8 0.4 0.0 -0.4 -0.8
0
5
10
15
20
(b) 0.8
图3.3(c)
1.2 0.8 0.4 0.0 -0.4 -0.8
金融计量学
第三章 差分方程、滞后运算与 动态模型
3.1 一阶差分方程 3.2 动态乘数与脉冲响应函数 3.3 高阶差分方程 3.4 滞后算子与滞后运算法
2
3.1 一阶差分方程
3.1.1 差分方程的定义
yt yt1 t (3.1)
一个差分方程就是指将一个变量的 当期值定义为它的前一期和一个当期 的随机扰动因素的函数。模型(3.1) 等式的右侧只有因变量的一次滞后期 出现,这样的差分方程称为一阶差分 方程。
0
5
10
15
20
(c) 1.0
图3.3(d)
40 30 20 10
0 -10
0
5
10
15
20
(d) 1.2
图3.3(e)
1.2 0.8 0.4 0.0 -0.4 -0.8 -1.2
0
5
10
15
20
(e) 0.8
图3.3(f)
40 30 20 10
0 -10 -20 -30 -40
0
5
10
15
20
(f) 1.2
图3-3非常清晰地显示出,不同的
第七节差分方程

第七节 差分方程对连续型变量而言,我们常常回导致到微分方程的问题. 对离散型变量将导致一类的问题.一、差分的定义定义 设)(x y y =是一个函数, 自变量从x 变化到x +1, 这时函数的增量记为)()1(x y x y y x -+=∆, 我们趁这个量为)(x y 在点x 步长为1的一阶差分,简称为)(x y 的一阶差分. 为了方便我们也记)(),1(1x y y x y y x x =+=+,即x x x y y y -=∆+1.称x x x x x x x x y y y y y y y y +-=---=∆∆+++++121122)()()(为)(x y 二阶差分,简记为x y 2∆.同样记)(2x y ∆∆为x y 3∆,并称为三阶差分.一般记)(1x n x n y y -∆∆=∆,称为n 阶差分.且有i n x i ni i n x ny C y -+=-=∆∑)1(0. 性质: 当a,b,C 是常数, y x 和z x 是函数时,(1) Δ(C )=0;(2) Δ(Cy x )= C Δ(y x );(3) Δ(ay x + b z x )= a Δy x + b Δ z x ;(4) Δ(y x z x )= z x+1Δy x +y x Δ z x = y x+1Δz x +z x Δy x ;(5) 1111++++∆-∆=∆-∆=⎪⎪⎭⎫ ⎝⎛∆x x x x x x x x x x x x x xz z z y y z z z z y y z z y . 例 已知),0(≠=x x y x α求Δ(y x ).解 Δ(y x )= ααx x -+)1(.特别, 当n 为正整数时, Δ(y x )= i n n i i n x C-=∑1, 阶数降了一阶.推论 若m, ,n 为正整数时, m,> n P(x)为n 次多项式,则0)(=∆x P m .例 已知),10(≠<=a a y x x 求Δ(y x ).解 Δ(y x )= )1(1-=-+a a a a x x x .二、差分方程定义 设是含有未知函数差分的等式,称为差分方程。
差分方程公式总结

差分方程公式总结嘿,咱们来聊聊差分方程这玩意儿!差分方程,听起来是不是有点让人头大?其实啊,它没那么可怕。
先来说说啥是差分方程。
简单来讲,就是含有未知函数差分的方程。
就像我们解普通方程一样,只不过这里的主角变成了差分。
比如说,有个一阶差分方程:$y_{n+1} - y_{n} = f(n)$ 。
这就表示相邻两个时刻函数值的差和自变量之间的关系。
咱们来仔细瞅瞅它的公式。
一阶线性常系数差分方程的一般形式是:$y_{n+1} + ay_{n} = f(n)$ ,这里的$a$是个常数。
求解它的办法有很多,像迭代法啦、特征根法啦。
拿迭代法来说,假设初始值是$y_0$ ,那么就可以一步一步地算下去:$y_1 = -ay_0 + f(0)$ ,$y_2 = -ay_1 + f(1)$ ,以此类推。
再说说特征根法。
先求出特征方程$r + a = 0$的根$r$ ,要是特征根不同,那通解就是$y_n = C_1r_1^n + C_2r_2^n$ ;要是特征根相同,通解就是$y_n = (C_1 + C_2n)r^n$ 。
我还记得之前给学生讲差分方程的时候,有个小家伙一脸懵地看着我,问:“老师,这东西到底有啥用啊?”我笑着跟他说:“你想想啊,咱们预测人口增长、经济发展,都可能用到差分方程呢。
”然后我给他举了个例子,假设一个城市每年的人口增长数量是上一年人口数量的10%,初始人口是 10 万,那咱们就可以用差分方程来算算未来几年的人口。
小家伙听了,眼睛一下子亮了起来,好像突然发现了新大陆。
二阶线性常系数差分方程也有它的一套公式和解法。
一般形式是$y_{n+2} + ay_{n+1} + by_{n} = f(n)$ 。
求解的时候还是先看特征方程,不过这次是$r^2 + ar + b = 0$ 。
在实际应用中,差分方程可太有用啦。
比如在金融领域,分析股票价格的波动;在工程领域,预测系统的稳定性。
总之,差分方程虽然看起来有点复杂,但只要咱们掌握了它的公式和方法,就能在很多地方派上用场。
金融计量学张成思Lectu

对于季度频率数据,年度化的增 长率计算公式为:
100% ln( Pt )4 400% ln( Pt )
Pt 1
Pt 1
zhangcs@
对于月度频率数据,年度化的增 长率计算公式是:
100% ln( Pt )12 1200% ln( Pt )
Pt 1
组具有相同特性的随机变量。
zhangcs@
FX ,Y (x, y;) Pr( X x,Y y)
1.2.3 随机分布: X和Y的联合分布可定义为: FX ,Y (x, y;) Pr( X x,Y y)
其中: 为联合分布函数中的参数。假定 X与Y的联合概率密度函数为 fx,y (x, y;), 并且严格有定义,则有:
Pt 1
zhangcs@
其中: 表t : 示N (0, 2 ) t 2
1.2.2 随机变量与随机过程 例如:
yt c xt t t N (0, 2 )
其中:t N (0, 2 )表示t服从均值为0、 方差为 2的正态分布。注意,在很多教
量随机变量分布的尖峰程度或平坦程度。
zhangcs@
考虑随机变量t iid (0, 2 ),则有
E t 0
E
(t
E[ t
])2
var[ t
]
E[
2 t
]
2
E
(t
E[ t
])3
E[
3 t
]
E
(t
E[ t
])4
FX (x;) Pr( X x;)
zhangcs@
FX (x;) Pr( X x;) 这一公式在统计学中也称为X的累积 分布函数,其取值范围在0与1之间。虽然 CDF的概念稍微有些抽象,但是其在金融 计量学中有着广泛的应用,特别是在计算
差分方程

第九节差分方程迄今为止,我们所研究的变量基本上是属于连续变化的类型. 但在经济管理或其它实际问题中,大多数变量是以定义在整数集上的数列形式变化的,银行中的定期存款按所设定的时间等间隔计息,国家财政预算按年制定等等. 通常称这类变量为离散型变量. 对这类变量,我们可以得到在不同取值点上的各离散变量之间的关系,如递推关系等. 描述各离散变量之间关系的数学模型称为离散型模型. 求解这类模型就可以得到各离散型变量的运行规律. 本节将介绍在经济学和管理科学中最常见的一种离散型数学模型—差分方程.内容分布图示★引言★差分的概念★例1-5★差分方程的概念★例6 ★例7★一阶常系数线性齐次差分方程★一阶常系数线性非齐次差分方程★例9-14 ★例15 ★例16 ★二阶常系数线性差分方程★ 二阶常系数线性齐次差分方程的通解★ 例17★ 例18★ 例19★ 二阶常系数线性非齐次差分方程的特解 ★例20-23差分方程在经济学中的应用 ★ 模型1 ★ 模型2★模型3★ 内容小结★ 课堂练习★ 习题8-9 ★ 返回内容要点:一、 差分的概念与性质一般地,在连续变化的时间范围内,变量y 关于时间t的变化率是用dtdy 来刻画的;对离散型的变量y ,我们常取在规定的时间区间上的差商ty ∆∆来刻画变量y 的变化率. 如果选择1=∆t ,则)()1(t y t y y -+=∆可以近似表示变量y 的变化率. 由此我们给出差分的定义.定义1 设函数).(t y yt= 称改变量tt y y-+1为函数ty 的差分,也称为函数ty 的一阶差分, 记为ty ∆, 即tt t y y y -=∆+1 或)()1()(t y t y t y -+=∆.一阶差分的差分称为二阶差分ty 2∆, 即tt t t y y y y ∆-∆=∆∆=∆+12)(.2)()(12112t t t t t t t y y y y y y y +-=---=+++++类似可定义三阶差分, 四阶差分,……),(),(3423t t t t y y y y ∆∆=∆∆∆=∆一般地,函数ty 的1-n 阶差分的差分称为n 阶差分,记为tny ∆,即t n t n t ny y y 111-+-∆-∆=∆i n t in ni i y C -+=∑-=)1( 二阶及二阶以上的差分统称为高阶差分.差分的性质: (1)tt y C Cy ∆=∆)();(为常数C(2) ;)(t t t t z y z y ∆±∆=±∆(3);)(1t t t t t t z y y z z y ∆+∆=⋅∆+(4)tt tt t t t t z z z y y z z y ⋅∆-∆=⎪⎪⎭⎫ ⎝⎛∆+1).0(≠t z二、差分方程的概念定义2 含有未知函数ty 的差分的方程为差分方程.差分方程的一般形式:0),,,,,(2=∆∆∆t nt t t y y y y t F或.0),,,,,(21=+++n t t t t y y y y t G差分方程中所含未知函数差分的最高阶数称为该差分方程的阶. 差分方程的不同形式可以互相转化.定义3 满足差分方程的函数称为该差分方程的解. 如果差分方程的解中含有相互独立的任意常数的个数恰好等于方程的阶数, 则称这个解为该差分方程的通解.我们往往要根据系统在初始时刻所处的状态对差分方程附加一定的条件,这种附加条件称为初始条件, 满足初始条件的解称为特解.定义4 若差分方程中所含未知函数及未知函数的各阶差分均为一次的, 则称该差分方程为线性差分方程.线性差分方程的一般形式是)()()()(1111t f y t a y t a y t a y t n t n n t n t =+++++--++其特点是tn t n t y y y ,,,1 +++都是一次的.三、一阶常系数线性差分方程一阶常系数线性差分方程的一般形式为)(1t f P yy tt =-+(9.1)其中, P 为非零常数,)(t f 为已知函数. 如果,0)(=t f 则方程变为1=-+t t Py y (9.2)方程(9.2)称为一阶常系数线性齐次差分方程, 相应地,方程(9.1)称为一阶常系数线性非齐次差分方程.一阶常系数线性齐次差分方程的通解 一阶常系数线性非齐次差分方程定理1 设ty 为方程(9.2)的通解,*ty 为方程(9.1)的一个特解,则*tt ty y y+=为方程(9.1)的通解.(1)C t f =)( (C 为非零常数) (2)tCb t f =)( (C , b 为非零常数且1≠b )四、二阶常系数线性差分方程二阶常系数线性差分方程的一般形式:)(12t f byayy tt t =++++(9.9)其中b a ,均为常数, 且,0≠b )(x f 是已知函数. 当0)(=x f 时, 方程(9.9)变为12=++++t t t by ay y (9.10)方程(9.10)称为二阶常系数线性齐次差分方程,相应地,方程(9.9)称为二阶常系数线性非齐次差分方程.定理2 设ty 为方程((9.10)的通解,*ty 为方程(9.9)的一个特解, 则*tt ty y y+=为方程(9.9)的通解.二阶常系数线性齐次差分方程的通解 特征方程2=++b aλλ(9.11)二阶常系数线性非齐次差分方程的特解和通解 仅考虑方程(9.9)中的)(x f 取某些特殊形式的函数时的情形.(1))()(t Px f m=(其中)(t Pm是t 的m 次多项式), 方程(9.9)具有形如)(*t R t ym kt=的特解, 其中)(t Rm为t 的m 次待定多项式.五、 差分方程在经济学中的应用采用与微分方程完全类似方法,我们可以建立在经济学中的差分方程模型,下面举例说明其应用.1.“筹措教育经费”模型某家庭从现在着手, 从每月工资中拿出一部分资金存入银行, 用于投资子女的教育, 并计算20年后开始从投资账户中每月支取1 000元, 直到10年后子女大学毕业并用完全部资金. 要实现这个投资目标, 20年内要总共筹措多少资金? 每月要在银行存入多少钱? 假设投资的月利率为0.5%, 为此, 设第t 个月, 投资账户资金为,ta 每月存资金为b 元, 于是20年后, 关于,ta 的差分方程模型为1000)005.1(1-=+t t a a (9.11)且.,00120x a a==二、价格与库存模型本模型考虑库存与价格之间的关系 设)(t P 为第t 个时段某类产品的价格,)(t L 为第t 个时段的库存量. L 为该产品的合理库存量. 一般情况下, 如果库存量超过合理库存, 则该产品的售价要下跌, 如果库存量低于合理库存, 则该产品售价要上涨, 于是有方程)(1t t t L L k P P -=-+ (9.13)其中k 为比例常数.三、国民收入的稳定分析模型本模型主要讨论国民收入与消费和积累之间的关系问题.设第t 期内的国民收入ty 主要用于该期内的消费tG , 再生产投资tI 和政府用于公共设施的开支G (定为常数), 即有GI C y t t t ++= (9.17)又设第t 期的消费水平与前一期的国民收入水平有关, 即)10(1<<=-A Ay C t t (9.18)第t 期的生产投资应取决于消费水平的变化, 即有)(1--=t t t C C B I (9.19)由方程(9.17), (9.18), (9.19)合并整理得GBAyy B A y t t t =++---21)1( (9.20)于是, 对应A , B , G 以及,,0y y可求解方程, 并讨论国民收入的变化趋势和稳定性.例题选讲:差分的概念与性质例1(讲义例1)设,2t y t=求).(),(),(32t t t y y y ∆∆∆例2(讲义例2)设.1),1()2)(1()0()(=+---=tn t t t t t n 求)(n t ∆.例3(讲义例3)求ttt y 32⋅=的差分.例4 设,22t ty += 求.,,32t t ty y y∆∆∆例5 试改变差分方程023=∆+∆t t y y 的形式.差分方程的概念例6(讲义例4)试确定下列差分方程的阶..735)2(;0)1(15423=+=+-++--+t t t t t y y y y y例7(讲义例5)指出下列等式哪一个是差分方程, 若是, 进一步指出是否为线性方程..432)2(;33)1(12=+-+=∆-++t t t tt t y y y a y y一阶常系数线性差分方程例8(讲义例6)求差分方程031=-+t t y y 的通解. 例9(讲义例7)求差分方程231-=-+t t y y 的通解.例10(讲义例8)求差分方程tt t y y⎪⎭⎫⎝⎛=-+233211在初始条件5=y时的特解.例11(讲义例9)求差分方程2134ty y t t =-+的通解.例12 求差分方程ty yt t πsin 341=++的通解. 例13 求差分方程 ty y t t 231+=-+满足初始条件5=y的特解.例14(讲义例10)求差分方程tt t t y y4221+=++的通解.例15 设某产品在时期t 的价格, 供给量与需求量分别为tt S P ,与),2,1,0( =t Dt. 1当121+=t t P S,tt t t D S P D =+-=-3,5421时, 求证(1) 由3,2,1推出差分方程.221=++t t P P(2) 已知0P , 求上述差分方程的解.例16(讲义例11)在农业生产中, 种植先于产出及产品出售一个适当的时期, t 时期该产品的价格tP 决定着生产者在下一时期愿意提供市场的产量tt P S ,1+还决定着本期该产品的需求量,tQ 因此有1,-+-=-=t t t t dP c S bP a Q (a , b , c , d 均为正的常数)求价格随时间变动的规律. 二阶常系数线性差分方程例17(讲义例12)求差分方程04312=--++t t t y y y 的通解. 例18(讲义例13)求差分方程04412=++++t t t y y y 的通解. 例19(讲义例14)求差分方程04212=+-++t t t y y y 的通解.例20 求差分方程 12212=-+++t t t y y y 的通解及0,010==y y的特解.例21(讲义例15)求差分方程ty y y t t t =-+++4312的通解.例22(讲义例16)求差分方程tt t t y y y 23212⋅=++++的通解.例23 求差分方程tt t t y y y⎪⎭⎫⎝⎛-=++++214112的通解.差分方程在经济学中的应用课堂练习 1.求差分方程21ty yt t =-+的通解.2.求差分方程ty y y t t t =-+++4312的通解.3.求差分方程tt t t y y y57612⨯=-+++的通解.。
《金融计量学》教学大纲(本科)
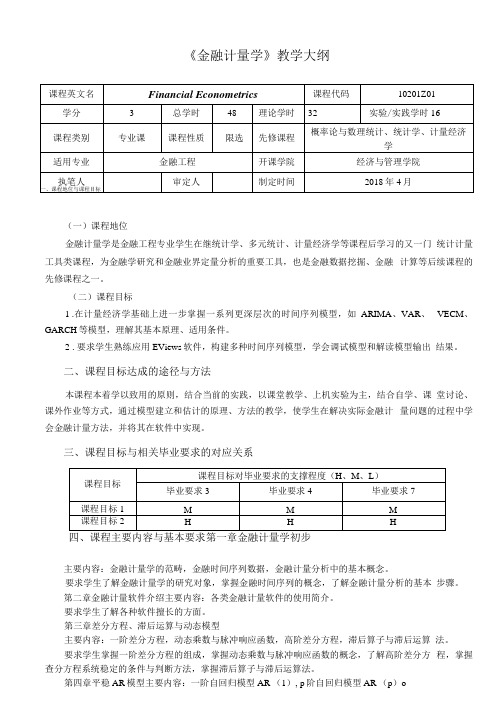
《金融计量学》教学大纲(一)课程地位金融计量学是金融工程专业学生在继统计学、多元统计、计量经济学等课程后学习的又一门统计计量工具类课程,为金融学研究和金融业界定量分析的重要工具,也是金融数据挖掘、金融计算等后续课程的先修课程之一。
(二)课程目标1.在计量经济学基础上进一步掌握一系列更深层次的时间序列模型,如ARIMA、VAR、VECM、GARCH等模型,理解其基本原理、适用条件。
2.要求学生熟练应用EViews软件,构建多种时间序列模型,学会调试模型和解读模型输出结果。
二、课程目标达成的途径与方法本课程本着学以致用的原则,结合当前的实践,以课堂教学、上机实验为主,结合自学、课堂讨论、课外作业等方式,通过模型建立和估计的原理、方法的教学,使学生在解决实际金融计量问题的过程中学会金融计量方法,并将其在软件中实现。
三、课程目标与相关毕业要求的对应关系四、课程主要内容与基本要求第一章金融计量学初步主要内容:金融计量学的范畴,金融时间序列数据,金融计量分析中的基本概念。
要求学生了解金融计量学的研究对象,掌握金融时间序列的概念,了解金融计量分析的基本步骤。
第二章金融计量软件介绍主要内容:各类金融计量软件的使用简介。
要求学生了解各种软件擅长的方面。
第三章差分方程、滞后运算与动态模型主要内容:一阶差分方程,动态乘数与脉冲响应函数,高阶差分方程,滞后算子与滞后运算法。
要求学生掌握一阶差分方程的组成,掌握动态乘数与脉冲响应函数的概念,了解高阶差分方程,掌握查分方程系统稳定的条件与判断方法,掌握滞后算子与滞后运算法。
第四章平稳AR模型主要内容:一阶自回归模型AR (1), p阶自回归模型AR (p)o要求学生掌握自回归模型的定义,掌握自协方差和自相关函数的定义与计算,掌握判断自回归过程平稳的条件。
第五章平稳ARMA模型主要内容:移动平均过程(MA),自回归移动平均过程(ARMA),部分自相关函数,自相关性检验。
要求学生掌握MA的定义、ARMA定义、部分自相关函数的定义,掌握偏自相关函数和自相关函数在各种模型下的图形特征,掌握ARMA滞后节数的初步判断,掌握自相关的Q检验和LM检验。
【推荐】滞后算子D在求解差分方程中的应用

滞后算子D在求解差分方程中的应用第l8卷第1期2OO6年3月郑州铁路职业技术学院Journalof:~engzhouRailwayV ocationalCollegeV o1.18No.1Mar.2006滞后算子D在求解差分方程中的应用王学力赵新颖(郑州铁路职业技术学院河南郑州450052)摘要:在求解差分方程时,有五种方法可以来求解.其中转移算子法完整地描述了离散系统的输入输出关系.转移算子有两个:超前算子和滞后算子,一些书中用到的都是超前算子,在这里提出了滞后算子的算法.关键词:差分方程转移算子法滞后算子求解差分方程的方法有五种:1.递推法;2.时域经典法;3.全响应法(分别求零输入响应与零状态响应);4.变换域方法;5.转移算子法.其中转移算子法可以完整地描述离散系统的输入输出关系,或者说集中反映了系统对输入序列的传输特性,所以掌握转移算子法非常重要.那么转移算子是指什么呢?滞后算子和超前算子通称转移(传输)算子.超前算子Ef(n+1)=En)f(n+m)=Emf(n)滞后算子Df(n一1)=Dt'(n)f(n—rn)Iy~f(n)一,问题的提出在我们所参阅的所有参考书中,见到的只是用超前算子求解差分方程,所以我们想有滞后算子的概念, 同样也可以用滞后算子来求解差分方程,所以我们进行了推导和总结.这种方法是N阶差分方程的一般形式:any(n-N)+QN—l(n—N+1)+A+aff(n一1)+ooy(n)=bx(n—M)+y(n—N一1)+A+blx(n-1)+box(n)我们用D来表示一个延时算子,差分方程用算子表示:(DN+oN—lOs一+A+aiD+oo)y(n)=(bD+bM.lDM+A+b1D+bo)x(n)可以改写为Y㈤=器如㈤烈uJ注意,H(D)的分子,分母算子多项式表示运算关系,不是简单的代数关系,不可随便约去.二,定义系统的转移(传输)算子=等等如先将H(D)做部分分式展开,设H(D)的分母多项式为单根.DIN+QN.1ON+A+chD+oo=(D一(11)(D—a2)A (D—QN)=+=量=(D)+Hl(D)+A+(D)=乏}王(D)h(n)=H(D)8(n)=i兰Pl8(n)=(n)(3)(3)式中任一子系统的传输算子为Hi(D)=(4)由此得到任一子系统差分方程,并对其中任一子系统的传输算子求hi(n)hj(n)=8(n)(5)hi(n一1)一i(n)=&8(n-1)(6)用初始条件等效法h(~1)=0当n=0,hi(一1)一aihi(0)=A占(一1)=O,解出h(O)=0当n--l,hi(0)一oihf(1)=Ai占(0),解出hi(1)=一/ni同理hi(1)一i(2)=Ai艿(1)解得:hi(2)=一/Qi,由此得出hiIn]的一般形式为hi(n)=一Aiai一"n≥1=一Aiai~u(n一1)(7)代人(3)式,h[n]的一般形式为h(n)=一ZQi~u(n一1)(8)收稿日期:2005—09—25作者简介:王学力(1963一)男,河南信阳人,郑州铁路职业技术学院铁道分院电子技术应用研究所讲师.赵新颖(1978一)女,河北衡水人,郑州铁路职业技术学院铁道分院信息工程系助教. 5l对应不同的转移算子H[D],有不同的h(n)序列与之对应,如下表所示.表转移算子H(D)与h(n)序列对应表H(D)h(n)A(n)1—一(n+1)u(n)D—a1D一一e-k(n+I)Tu(n)DD—a—a一"u(n一1)旦眦一(n+1)u(n一1)(D—a)三,举例验证算法的正确性例l已知某系统的差分方程y(n)一5y(n一1)+6y(n一2)=X(n)一3x(n一2),求系统的脉冲响应h(n).解:①滞后算子算法:(1—5D+6D2)y(n)=(1—3D2)x(n)H(D)=l43一-y+1一1h(n)=一{占(n)一n一u(n)+2×3nu(n)=8(n)+(2×3"一2"一)u(n一1)②超前算子算法:(E2—5E+6)y(n)=(E2—3)x(n)H(E)=E2-3=l++(上接第48页)多媒体课件中的音乐,是为了烘托气氛,演染情绪,增强艺术感染力的,为了深化教学主题,描写背景, 激发联想,组合画面,转换时空,强化节奏等,应根据课件内容,选择相应的乐曲.在使用上要注意它的不独立,不显露和不完整性.(2).正确把握解说,音响和音乐三者的关系.'通常情况下,解说表意,音响表实,音乐表情,解说占主要位置,音响和音乐是对解说和画面内容的补充和呼应.三种声音互相配合,能创造出一种多层面,立体感的总体效果,使多媒体课件能得到更好的烘托,渲染和深化.2.视觉元素的把握.视觉元素是构成多媒体课件语言的主要内容,它是多媒体课件中能看到的所有图片,按钮,动画,影像, 52h(n)=8(n)+(2×3"一2"一)u(n一1)例2已知某系统的差分方程y(n)一y(n一1)一2y(n一2)=x(n),求系统的脉冲响应h(n).解:①滞后算子算法:(1一D一2D2)y(n)=x(n)H(D)==一+h(n)={音(一1)"u(n)+詈(2)"}u(n)②超前算子算法:(E2一E一2)y(n)=E2x(n)一H(E)==?++h(n):占(n)+4×n-lu(n一1)一{(一1)n一-un一1)={{(一1)"u[n]+昔(2)"}u(n)四,结论通过以上两例题可以看出,滞后算子和超前算子两种算法是等价的,都能得到相同的结论.两种算法都基于首先要记住转移算子H(D)与h(n)序列对应表.至于用哪种算法,可以根据自己的情况来决定.参考文献[1]昊大正.信号与线性系统分析[M].北京:高等教育出版社, [责任编辑:张磊]字幕等画面的集合.多媒体课件是否引人人胜,生动形象,艺术性的画面起着不可低估的作用,因而,需要有良好的美术素养的制作者来进行美术设计.3.程序设计的把握.制作一个多媒体课件,常常由多个成员共同开发完成,因此开发时.不但要对设计中的细节给予注意,而且还要注意总体设计统一性,即:(1)思体设计要由专人完成.(2)软件的应用要具有通用性,在绝大多数计算机上都可以运行,课件中的各种文件格式必须是g-m格式. (3)交互性要强.为了适应各层次用户的需要,对每个步骤,既能让用户根据提示进入下一步程序.也能在用户不能正确操作时,给出正确操作钧演示或提示. (4)实现网络化.[责任编辑:赵伟]。
(完整版)总结版:滞后算子,推荐文档

第二章 滞后算子及其性质滞后算子是对时间序列进行动态线性运算的主要工具,利用滞后算子可以使得一些非线性运算非常简洁。
§2.1 基本概念时间序列是以观测值发生的时期作为标记的数据集合。
一般情况下,我们是从某个特定的时间开始采集数据,直到另一个固定的时间为止,我们可以将获得的数据表示为:),,,(21T y y y 如果能够从更早的时间开始观测,或者观测到更晚的时期,那么上面的数据区间可以进一步扩充。
相对而言,上述数据只是一个数据的片段,整个数据序列可以表示为:+∞=-∞==t t t T y y y y }{),,,,,,(21 例2.1 几种代表性的时间序列(1) 时间趋势本身也可以构成一个时间序列,此时:;t y t =(2) 另一种特殊的时间序列是常数时间序列,即:,是常数,这种时间的取值c y t =c 不受时间的影响;(3) 在随机分析中常用的一种时间序列是高斯白噪声过程,表示为:,t t y ε=是一个独立随机变量序列,每个随机变量都服从分布。
+∞=-∞=t t t }{ε),0(2σN 时间序列之间也可以进行转换,类似于使用函数关系进行转换。
它是将输入时间序列转换为输出时间序列。
例2.2 几种代表性的时间序列转换(1) 假设是一个时间序列,假设转换关系为:,这种算子是将一个时间序t x t t x y β=列的每一个时期的值乘以常数转换为一个新的时间序列。
(2) 假设和是两个时间序列,算子转换方式为:,此算子是将两个时t x t w t t t w x y +=间序列求和。
定义2.1 如果算子运算是将一个时间序列的前一期值转化为当期值,则称此算子为滞后算子,记做。
即对任意时间序列,滞后算子满足:L t x(1)1)(-≡t t x x L 类似地,可以定义高阶滞后算子,例如二阶滞后算子记为,对任意时间序列,二2L t x 阶滞后算子满足:(2)22)]([)(-=≡t t t x x L L x L 一般地,对于任意正整数,有:k(3)k t t k x x L -=)(命题2.1 滞后算子运算满足线性性质:(1) )()(t t x L x L ββ=(2) )()()(t t t t w L x L w x L +=+证明:(1) 利用滞后算子性质,可以得到:)()(1t t t x L x x L βββ==-(2)End)()()(11t t t t t t w L x L w x w x L +=+=+--由于滞后算子具有上述运算性质和乘法的交换性质,因此可以定义滞后算子多项式,它的作用是通过它对时间序列的作用获得一个新的时间序列,并且揭示这两个时间序列之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因此若给定初始值y0,yt 就可以由 t的序列来表示。
6
如果y0没有给定,则 y0 y1 0 ( y2 1 ) 0 y2 1 0
2
y0 yt
m 1
y m 1 j
系数的 后面的图即描绘了一阶差分方程中不同 -0.4 所对应的 yt 序列的动态路径。
0.0 -0.8 5 10 15 20 25 30
yt 0.3 yt 1 t
图2.2(b)
1.0 0.5 0.0 -0.5 -1.0 5 10 15 20 25 30
11
yt 0.8 yt 1 t
j 1 j j 1
一阶差分方程的动态乘数的表达式可以写成 yt j t
j
2.2.2 脉冲响应函数 从动态乘数的定义可知,对应每 一个时期跨度j,有一个对应的动态乘 数,那么如果将不同时期跨度j的动态 乘数按j从小到大的顺序摆放在一起, 形成一个路径,就成为了脉冲响应函 数。
累积脉冲响应函数:
3
yt yt 1 t
图2.1 美国CPI环比通胀率
16 U.S. CPI Inflation 12
8 % 4
0
-4
1950
1960
1970
1980
1990
2000
2010
1948年1季度-2010年3季度
原始数据来源:Fred Data, Federal Reserve Bank of St. Louis,经 作者计算。
一些差分运算常用的表达式:
yt yt 1 ( 1) yt 1 t
yt yt yt 1
(yt ) yt ( yt yt 1 ) ( yt 1 yt 2 )
2
5
2.1.2 一阶差分方程的求解(反复迭代 法):
如果y0是给定的,则 y1 y0 1 y2 y1 2 ( y0 1 ) 2 2 y0 1 2 y3 y2 3 3 y0 21 2 3 yt yt 1 t t y0 t 11 t 2 2 t t y0 i t i
yt j yt j yt j yt j j j 1 j 2 1 t t 1 t 2 t j
累积脉冲响应函数用来衡量随机扰动 因素出现永久性变化后,即 t , t 1 ,, t j 都 变化一个单位,对 yt j 造成的影响和冲击 情况。
图2.2(c)
1 0 -1 -2 -3 5 10 15 20 25 30
12
yt yt 1 t
图2.2(d)
0 -50 -100 -150 -200 5 10 15 20 25 30
13
yt 1.2 yt 1 t
图2.2(e)
2 1 0 -1 -2 5 10 15 20 25 30
2.2
动态乘数与脉冲响应函数
2.2.1 动态乘数(dynamic multiplier) 2.2.2 脉冲响应函数(impulse
response function, IRF)
2.2.1 动态乘数 对于yt yt 1 t 而言, 动态乘数可以定义为 yt j 动态乘数 = , j 0, 1, 2 t
j j 0
m
t m 1
y m 1 t i
i i 0
7
t m
1
可以观察到, t m 1 (1)如果 1 ,那么 的取值随 着m的不断增大而减小,最终减为0, 此时 yt 称为收敛序列。 t m 1 1 (2)如果 ,那么 的取值随 着m的不断增大将不会逐渐减小为0, 而是趋近于无穷大。此时 yt 称为非收 敛序列。
(3)如果 1,差分方程描绘的变 量序列仍然是非收敛序列,但这种特 殊情况下的差分方程对应一个专门的 名称,叫做随机游走过程(random Walk process)。
图2.2(a)
1.2
经过以上分析,可以得出结论:一阶差分方 0.8 程中的一阶滞后项的系数的大小关键性地决定了 差分方程的求解结果。实际上,这个系数的取值 0.4 也关键性地决定了时间序列变量的动态走势特征。
从模型可知,如果 1 条件满 足,在极限情况下,累积脉冲响应函 1 数就等于 。 1 无论是脉冲响应函数还是累积脉 冲响应函数,其根本特性都由一阶滞 后项系数 决定。
图2.3(a)
0.8 0.4 0.0 -0.4 -0.8 0 5
(a)
0.3
10
15
20
图2.3(b)
0.8 0.4 0.0 -0.4 -0.8 0 5
当 1 0 时,如(e)情形,动态 乘数的取值正负号交替变化,但是这些 动态乘数的绝对值是呈现逐渐递减至0 的,这种情形经常被形象地称作“震荡 式衰减”。 这样,对于 1的情况,从脉 冲响应函数图来看,随机扰动因素对序 列 yt 的冲击将最终消失,而对应的一 阶差分方程在这种情况下就是一个稳定 的系统。
(e)
0.8
图2.3(f)
40 30 20 10 0 -10 -20 -30 -40 0 5 10 15 20
(f) 1.2
图2-3非常清晰地显示出,不同的 取值,对应的脉冲响应函数图表现非常 不同。归纳来说: 在 0 1 的情况下,如(a)和(b)情 形,体现在脉冲响应函数中的动态乘数 随时间跨度j的增加而呈现几何式递减并 最终趋近于0的趋势。
再来考察其它可能的情况: 首先,如果 1 ,如(c),动态 乘数始终等于1,而不管时间跨度j如 一个单位的变化将导 何变化。这样, 致序列 yt 永久性地变化一个单位。
其次,对于 1的情况,(d)描绘了对应 例子的脉冲响应函数图,可以看出,动态乘数随 时间跨度j的增加呈现几何式上升趋势。而当 1 时,动态乘数表现出震荡式不断上升的变化。可 见,在 1 的条件下,对应的一阶差分方 程为不稳定系统。 因此,如果脉冲响应函数图呈现出不断下降 的趋势,这说明由差分方程刻画的时间序列是收 敛的,否则该时间序列是发散或者是随机游走的 。
14
yt 0.8 yt 1 t
图2.2(f)
40 20 0 -20 -40 5 10 15 20 25 30
15
yt 1.2 yt 1 t
►我们可以看出,一阶差分方程的滞后项系 数大小可以判断出时间序列变量的收敛与 发散特征。 ►在金融计量分析中,我们还可以通过观察 时间序列变量的走势来初步判断该时间序 列的收敛与发散特征,以及如何构建时间 序列模型。
在 j=0这种特殊情况下, 动态乘数也经常 被称为影响乘数(impact multiplier), yt 影响乘数 = t
另外, yt yt 1 t 也可以写成 yt j yt 1 t t 1 t j 1 t i
金融计量学
张成思
第二讲
2.1 2.2 2.3 2.4
差分方程、滞后运算与 动态模型
一阶差分方程 动态乘数与脉冲响应函数 高阶差分方程 滞后算子与滞后运算法
2
2.1 一阶差分方程 2.1.1 差分方程的定义 (2.1) 一个差分方程就是指将一个变量的 当期值定义为它的前一期和一个当期 的随机扰动因素的函数。模型(2.1) 等式的右侧只有因变量的一次滞后期 出现,这样的差分方程称为一阶差分 方程。
(b)
10
0.815Fra bibliotek20图2.3(c)
1.2 0.8 0.4 0.0 -0.4 -0.8 0 5
(c)
1.0
10
15
20
图2.3(d)
40 30 20 10 0 -10 0 5 10 15 20
(d)
1.2
图2.3(e)
1.2 0.8 0.4 0.0 -0.4 -0.8 -1.2 0 5 10 15 20
