非线性动力学-分岔图-混沌-程序
非线性动力学中的混沌与分岔现象

非线性动力学中的混沌与分岔现象混沌现象的介绍混沌现象是非线性动力学中一个重要的研究课题,它描述了一种似乎随机的、无规律可循的运动状态。
在混沌现象的研究中,人们发现了一些特征,如灵敏依赖于初始条件、无周期运动和封闭轨道等。
混沌现象的研究对于理解自然界中的复杂系统行为具有重要的意义。
混沌现象最早是由美国数学家Edward Lorenz于20世纪60年代发现的。
他在研究气象学中的大气运动方程时,意外地发现了不确定性的现象。
这个发现被称为“蝴蝶效应”,即当一个蝴蝶在巴西振动翅膀时,可能引发一系列的气流变化,最终导致美国得克萨斯州的一个龙卷风的形成。
这个例子说明了混沌现象中初始条件的微小变化可能引起系统运动的巨大变化。
混沌现象的数学表示混沌现象可以用一些非线性动力学方程描述。
这些方程通常包含了一些非线性项,使得系统的演化不再是简单的线性叠加。
一个经典的混沌系统方程是Lorenz方程:\\frac{{dx}}{{dt}} = \\sigma(y - x),\\frac{{dy}}{{dt}} = x(\\rho - z) - y,\\frac{{dz}}{{dt}} = xy - \\beta z其中,x、y和z是系统的状态变量,t是时间。
σ、ρ和β是一些常数,它们决定了系统的性质。
这个方程描述了一个三维空间中的运动,这种运动就是混沌现象。
分岔现象的介绍分岔现象是混沌现象的一个重要特征,它描述了系统参数发生微小变化时,系统行为的剧烈变化。
简单来说,分岔现象就是系统从一个稳定的演化状态变成多个稳定状态的过程。
分岔现象的经典例子是Logistic映射。
Logistic映射是一种常用的非线性映射,它用于描述生物种群的增长。
Logistic映射的公式为:x_{n+1} = r \\cdot x_n \\cdot (1 - x_n)其中,x_n是第n个时刻的种群密度,x_{n+1}是下一个时刻的种群密度,r是系统的参数,它决定了种群的增长速度。
第七章 非线性动力学与混沌 讲义

2. 线性化方程组的解及其稳定性
12
111 21 1
122 222
试探解:1 Aet ,2 Bet
11
21
12
22
A B
0
ij
( fi x j
)0
11 12 0 21 22
2 T 0
T 11 22
系数矩阵的迹
11 22 12 21 系数行列式的值
特征根
❖ 刘式达,刘式适,《非线性动力学和复杂 现象》,气象出版社,1989
§7.1 引言
一. “非线性动力学”的表观含义
数学上:
f (x) ax b
f
(x)
ax2
bx
c
线性 非线性
定义:力或微分方程含有坐标或速度的非线性项的系 统,称为非线性动力学系统,反之称为线性动力学系统。
例:
mx kx 2x2
1. 定态解 xi 0 i 1,2, , n
x2
平衡点,奇点
x1
2. 发散解
xi 之一或几个随时间无限地偏离初值 x2
爆炸,散射
x1
3. 振荡解
既不趋于无穷大,也不终止于某一点,而是在一定区域内不断变化。
❖ 周期振荡
❖ 准周期振荡
x2 闭合曲线
x1
x2 非闭合曲线
x1
❖ 混沌
相轨迹没有确定的形状周 期、貌似随机的运动。
1,2 T
T 2 4 2
特征矩阵
A1 B1
A2 B2
1 c1 A1e1t c2 A2e2t
2
c1B1e1t
c2 B2e2t
渐进稳定
临界情况 不稳定
1,2 T
T 2 4 2
描述混沌的指标

描述混沌的指标全文共四篇示例,供读者参考第一篇示例:混沌是一种无序、不可预测、非线性的动态系统,其表现形式复杂多样,难以准确描述和预测。
混沌系统的行为被认为是由一组变量组成的动力学系统所确定的,这些变量之间相互作用复杂而多样,导致系统的行为呈现出随机性和不可预测性。
混沌的数学模型通常采用分形几何、非线性动力学等方法来描述,其中包括了许多指标来表征混沌系统的性质和特征。
一、分岔图分岔图是一种描述混沌系统的重要指标,其通过展示系统响应在某个参数值的变化过程中发生的分支现象。
在分岔图中,横轴通常表示参数值,纵轴表示系统的状态变量,通过对参数值进行逐步调节,可以观察到系统状态之间的跳变和分支。
通过分岔图可以很直观地看出系统从有序状态向混沌状态的过渡过程,以及该过程中出现的周期倍增、分岔分叉等现象。
二、李雅普诺夫指数李雅普诺夫指数是一种度量混沌系统稳定性的指标,它描述了系统状态在相空间中的指数级增长或收缩速度。
通过计算系统状态变化的李雅普诺夫指数,可以评估系统的灵敏度和混沌程度。
正的李雅普诺夫指数表明系统存在混沌行为,而负的李雅普诺夫指数则表示系统会最终趋于稳定。
通过计算系统的李雅普诺夫指数,可以揭示混沌系统的动力学特性和演化规律。
三、分形维数分形维数是一种描述混沌系统几何形状复杂度的指标,它用来度量系统表面或轮廓的复杂程度。
由于混沌系统的分形结构具有无穷细节、无限重复的特点,因此分形维数可以很好地描述混沌系统的自相似性和随机性。
通过计算系统的分形维数,可以分析系统的几何形状、自相似性和空间分布特征,从而揭示混沌系统的内在结构和演化规律。
四、收敛性混沌系统的收敛性是描述系统最终状态的稳定性和确定性的重要指标。
在混沌系统中,初始条件的微小变化可能会导致系统最终状态的巨大差异,这种现象被称为“蝴蝶效应”。
通过分析系统在不同初始条件下的收敛性,可以评估系统的稳定性和可靠性,从而为系统的控制和优化提供重要参考。
混沌系统具有无序、不可预测、非线性等特点,其行为复杂多样,具有自相似性和随机性。
34-非线性动力学、分叉与混沌理论-摘要

升温和激振力共同作用下弹性梁的动力稳定性
王春妮2) 李世荣
(兰州理工大学理学院,兰州 730050)
1)
计及几何非线性和外阻尼效应,利用Harmilton原理推导出了弹性梁大振幅振动的动力学控制方 程,研究了两端不可移简支梁在横向周期载荷和非均匀热载荷共同作用下的非线性动力学行为。采 用 Galerkin变分原理将问题的非线性偏微分方程转化化为二自由度的Harmilton系统,利用Melnikov 方法解析判别了均匀升温下系统发生混沌运动的临界条件。采用数值识别方法计算出均匀升温及非 均匀升温下系统运动的 Lyapunov指数,绘出了反映系统运动特征的相平面图、位移波形图以及功率 谱图,讨论了在横向周期载荷一定时,不同热载荷对梁的非线性动力学行为的影响。结果表明:均 匀升温时,如果热轴力小于梁的静态热屈曲临界温度载荷,则梁只做周期运动;当热轴力超过临界 载荷后梁的运动出现混沌运动特征。非均匀升温时,当周期热载荷的最大值小于梁的静态热屈曲临 界温度载荷时,振动系统仍然不会发生混沌运动;相反,当周期热载荷的最大值大于梁的静态热屈 曲临界温度载荷后,虽然周期热载荷在某些时刻会小于零,但由于热载荷频率的影响,系统同样可 能发生混沌运动。
刘彦琦1) 张 伟
(北京工业大学机电学院,北京 100022 )
考虑几何非线性,黏弹性材料的本构关系采用 Kelvin 模型描述。考虑稳态张力有一个周期扰 动的情况,即可以表示为 P P P1 cos t ,同时考虑系统的外阻尼。利用 Hamilton 原理建立了 0 黏弹性传动带在三维空间的横向非线性动力学方程,并且面内横向振动方程与面外横向振动方程是 相互耦合的。然后,对黏弹性传动带的偏微分动力学方程进行 Galerkin 截断,得到了常微分方程。 数值模拟是探索黏弹性传动带系统动力学特性的有效方法。最后,根据实际工程情况选取系统参数, 利用四阶 Runge-Kutta 法对得到的常微分方程组进行数值模拟。模拟结果表明黏弹性传动带系统在 三维空间存在周期和混沌运动,并且通过调节参数激励运动状态可以相互演化。 关键词 黏弹性传动带,混沌动力学,非线性,横向振动
描述混沌的指标

描述混沌的指标全文共四篇示例,供读者参考第一篇示例:混沌是一个具有高度不确定性和复杂性的系统状态,常被描述为无序的、难以理解的状态。
在科学研究和实践中,我们常常需要寻找一些指标来描述混沌系统的特征,以便更好地理解和分析混沌现象。
下面将介绍一些常用的描述混沌的指标。
1. Lyapunov指数:Lyapunov指数是描述混沌系统的一个重要指标,它是衡量系统状态变化速率的指标。
当系统的Lyapunov指数为正时,系统将呈现混沌状态;当Lyapunov指数为负时,系统将呈现稳定状态。
通过计算Lyapunov指数,可以判断系统是否处于混沌状态。
2. 分形维数:分形维数是描述混沌系统结构的一个重要指标,它反映了系统结构的复杂程度。
分形维数越高,系统结构越复杂。
通过计算分形维数,可以揭示混沌系统的结构特征。
3. 自相关函数:自相关函数是描述混沌系统时间演化规律的一个重要指标,它反映了系统状态之间的相关性。
通过分析系统的自相关函数,可以揭示混沌系统的时间演化规律。
4. 峰谱特性:峰谱是描述混沌系统频率分布特性的一个重要指标,它反映了系统在不同频率上的能量分布。
通过分析系统的峰谱特性,可以了解混沌系统的频率分布规律。
以上是一些常用的描述混沌的指标,它们可以帮助我们更好地理解和分析混沌系统的特征。
在实际应用中,我们可以根据具体问题选择合适的指标来描述混沌现象,从而更好地理解混沌系统的特性。
混沌系统是一种具有复杂性和不确定性的系统,通过研究混沌系统的特征和规律,有助于我们更好地理解自然界的复杂现象。
【此为创作文章,仅供参考】。
第二篇示例:混沌理论最早由美国数学家爱德华·洛伦茨提出,它描述了一类非线性动力系统的行为特征。
混沌系统的演化非常敏感于初始条件,即所谓“蝴蝶效应”,微小的扰动可能导致系统的行为出现巨大的变化。
由于混沌系统的复杂性和不可预测性,其研究领域涉及到物理、天文、生物、社会和经济等方方面面。
在混沌系统中,我们需要一些指标来描述系统的混沌程度。
非线性动力学-分岔图-混沌-程序
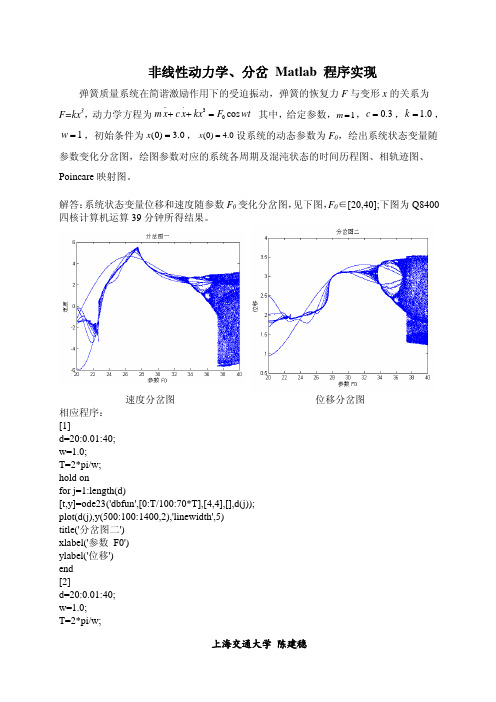
非线性动力学、分岔Matlab 程序实现弹簧质量系统在简谐激励作用下的受迫振动,弹簧的恢复力F与变形x的关系为F=kx3,动力学方程为...3cosm x c x kx F wt++=其中,给定参数,1m=,0.3c=, 1.0k=,1w=,初始条件为(0) 3.0x=,.(0) 4.0x=设系统的动态参数为F0,绘出系统状态变量随参数变化分岔图,绘图参数对应的系统各周期及混沌状态的时间历程图、相轨迹图、Poincare映射图。
解答:系统状态变量位移和速度随参数F0变化分岔图,见下图,F0∈[20,40];下图为Q8400四核计算机运算39分钟所得结果。
速度分岔图位移分岔图相应程序:[1]d=20:0.01:40;w=1.0;T=2*pi/w;hold onfor j=1:length(d)[t,y]=ode23('dbfun',[0:T/100:70*T],[4,4],[],d(j));plot(d(j),y(500:100:1400,2),'linewidth',5)title('分岔图二')xlabel('参数F0')ylabel('位移')end[2]d=20:0.01:40;w=1.0;T=2*pi/w;上海交通大学 陈建稳hold onfor j=1:length(d)[t,y]=ode23('dbfun',[0:T/100:70*T],[4,4],[],d(j));plot(d(j),y(500:100:1400,1),'linewidth',5)title('分岔图一')xlabel('参数F0')ylabel('速度')endM函数文件:dbfun.mfunction ydot=dbfun(t,y,flag,d)w=1;c=0.3;ydot=[y(2);-y(1)^3-c*y(2)+d*cos(w*t)];上海交通大学 陈建稳。
分叉与混沌_非线性动力学的发展与应用

刊 增 》 学 力
年 5 9 1
7 ! 1 0
Hale Waihona Puke A 子的 Z A 和 l
区 引 吸
于 位 从
域 区 色 白
2 1 图 任 的 中
状 始 初 何
始 开 态
被 动 运 的
A 到 引 吸
.
反 个 一 从
阴 于 位 跳 凹 势
任 的 中 影 个 一 另 至
状 始 初 何 的 凹 势
.
相 ; l
在 存 能 已 子 引
清 分 要 点 动 不
凡 滋
区 渡
始 开 态 运 则 规 无
被 运 的 而 从 动
A 到 引 吸 了 成 形
但 : 引 吸 沌 混
时 O 笋 A 当 这 子
可 球 小 吸 沌 混 种
,
,
.
加 。 H 由 吸 性 种 各
M 和 s e 的 子 引 同 不 质
验 实 n o 区 引 吸 的
所 置 装 各 究 研 找 即 (
0 2 1 实 证 子 种 区 引 吸 出
的 性 形 地 格
.
说 子 引 吸
或 子 引 以 可 A
沌 混 作 看
,
流 不 的 中
间 空 相 在 集 紧 变
n R A
,
中 即 引 吸 的 : 集
= A 指 是 区
,
A o a 咔 t 当
被 有 所 时
到 引 吸
点 的 A
,
.
沌 混 称
一 8 子 引 吸
} {
, 再 x 引 吸 的
, ‘ ^ 奇 为 区
} o a
区 引 吸 怪 振 迫 强 摆 ) a ( Z
非线性动力学中的混沌现象分析

非线性动力学中的混沌现象分析随着科技的进步,越来越多的系统在现实中被建立和研究。
而系统的复杂性增加,非线性动力学中的混沌现象也就显示出了特殊的表现。
在本文中,我们将主要介绍非线性动力学中的混沌现象以及相关的分析方法。
一. 混沌现象及其表现方式混沌现象是指一种非周期而又具有明显连续性的运动状态,它的变化看似毫无规律,但又似乎有着一定的规律可循。
混沌现象常常出现在一些比较复杂的系统中,例如气象系统、流体动力学、化学反应系统以及经济市场等。
混沌现象具有以下的表现方式:1. 敏感依赖性:混沌现象中微小的初始条件变化,往往会带来显著的结果差异。
2. 周期模糊性:混沌现象中周期的边界变得模糊不清,因为在不同的时间尺度上,周期的长度是不同的。
3. 统计规律性:混沌现象中有一些统计特性,例如自相似性、分形性等。
二. 分析混沌现象的基本方法针对混沌现象,人们提出了很多不同的分析方法。
以下是一些常用的分析方法。
1. 动力学系统的非线性微分方程建模:混沌现象常常可以从非线性动力学微分方程模型进行分析,在此基础上可以进一步分析系统的稳定性、周期行为、混沌现象等。
2. Poincare截面方法:该方法定义了一个截面,并将系统的运动状态在这个截面上投影,从而观察系统的周期性、混沌性等特征。
3. Lyapunov指数方法:该方法可以量化混沌现象中的灵敏度依赖,用于对比不同的混沌现象。
4. 分岔图法:该方法用于分析系统中出现的状态转换和稳定性变化。
5. 局部方差方法:该方法用于检测时间序列中的小尺度混沌性,并可以对其进行定量分析。
三. 混沌现象在实际中的应用混沌现象在生活中的应用十分广泛,下面主要介绍一些例子。
1. 加密传输:混沌信号可以用于加密通信,这是因为混沌信号的本性可以使得被传输的信息难以被窃取。
2. 噪声控制:利用混沌现象控制系统中的噪声,可以提高系统信噪比和精度,从而增强该系统的可靠性。
3. 脑电信号分析:可以运用混沌现象对脑电信号进行分析,以提高对脑部疾病和认知状态的诊断和研究。
第七章 非线性动力学与混沌 讲义

二. 决定性系统与不可预测性
1. 力学决定论及其伟大成就
x m F (x, x, t ) x x 0 , x x 0
t t0
x(t ), x(t )
存在且唯一, 可预测性
1757年,哈雷慧星(Hally comet)按预测回归。 1846年,海王星在预言的位置被发现。 今天,日月蚀的准确预测,宇宙探测器的成功发射与回收。
ij (
f i )0 x j
11 12 0 21 22
T 11 22 系数矩阵的迹 11 22 12 21 系数行列式的值
A1 B 1 A2 B2
T 0
2
特征根
1, 2
T T 2 4 2
xi f i ( x1 , x2 ,, xn )
i 1,2,, n
优点:
四. 相空间(相图)的概念
相空间,也就是状态空间,是由广义坐标和广义动量(速度) 张成的空间,也称相宇。相空间中运动状态的变化轨迹称为相图。
弹簧振子 通解
x 0 x
2 0
x A cos( 0t ) x1 x A0 sin(0t ) x2
设想一位智者在某一瞬间得知激励大自然所有力及组成它的物体 的相互位置,如果这位智者又能对众多的数据进行分析,把宇宙间最 庞大的物体和最轻微的原子的运动凝聚在一个公式中,没有什么事物 是不确定的,将来就像过去一样清晰地展现在眼前。
——拉普拉斯(Laplace,法国数学家,1749-1827)
2. 力学决定论不断受到挑战
x1 x, x2 x
x3 cos t , x4 x3
[经济学]非线性动力学浑沌说课讲解
![[经济学]非线性动力学浑沌说课讲解](https://img.taocdn.com/s3/m/fc77ec380812a21614791711cc7931b765ce7b48.png)
朱照宣,1987年,牛顿《原理》三百年祭
• “《原理》发表以来的三百年,牛顿力学经历了两 个阶段。前280年是一阶段。那时认为由运动微 分方程所确定的动态总是确定性的。……后20年 则是另一个阶段。以卡姆定理(KAM)为代表的浑 沌理论提示了决定论和随机论之间、牛顿力学和 统计力学之间没有不可逾越的界线。 ……不仅大 量粒子的系统要用统计力学,两个自由度的保守 系统运动也得用统计力学,连掷骰子本身也既是 决定论的又是概率论的。它从根本上为牛顿力学 摘除了‘机械论’的帽子。”(朱照宣 1987, 第12页)
费格尔
(Herbert Feigl,1902-1988)说
“A causes B” or “A is the cause of B” means that wherever and whenever A occurs it is followed (or attended) by B. Since a precise repetition of A may not be feasible (or discoverable), a less stringent formulation would use something like a mathematical limit process: The more the actual condition A' approximates the conceived (ideal) condition A, the more actual effect B' will approximate the (ideal) effect B.
• There are systems whose trajectories do not monotonically approximate any ideal state. They are sensitive dependence to initial conditions.
非线性微分方程的分岔和混沌现象

非线性微分方程的分岔和混沌现象非线性微分方程是自然科学中经典的研究对象之一。
在广泛的自然现象和实验研究时,非线性微分方程都是用来描述这些现象的数学工具。
但是,非线性微分方程的动力学特性非常复杂,包括分岔、混沌等现象。
这些现象对于科学家而言是非常重要而且有很多有趣的数学理论成果与实际应用。
在本文中,我们将探讨非线性微分方程的分岔和混沌现象的一些基本概念与数学理论。
一、非线性微分方程的分岔现象分岔现象是指一个系统中的某些参数发生变化时,该系统的稳定性质发生变化。
特别是当这些参数逐渐变化到一定的“临界点”时,系统的稳定性质突然发生改变,这种现象叫做分岔。
通常,这个临界点称为临界参数值。
分岔现象是非线性微分方程的一个根本动力学现象,在自然科学中有着广泛的应用。
1. 常见的分岔类型非线性微分方程的分岔有许多类型,其中比较常见的有:鞍点分岔、极小极大分岔、超过阈值分岔、分支分岔等。
鞍点分岔是指由一个稳定的状态发生分裂从而出现两个不同状态的现象。
这种分岔是由一个简单稳定节点与一个鞍点相遇时产生的。
极小极大分岔是指当参数发生微小的变化时,极小值点和极大值点突然出现的现象。
超过阈值分岔是指当参数超过某些阈值时,系统从一个极限环突变到一个新的解的现象。
分支分岔是指在参数空间中出现分支条件,这通常在响应系统行为的外部变量出现周期性变化时会发生。
2. 分岔的重要性分岔现象对于非线性微分方程而言是非常重要的,因为它可以揭示系统的稳定性和动力学性质。
而且,正是由于分岔现象才使得非线性微分方程在自然科学领域中有着广泛的应用。
例如,在物理领域中,分岔现象可以帮助我们研究光学、空气动力学、气象学等领域中的不同系统。
在生物学领域中,分岔现象可以帮助我们研究細胞過程中的周期性行为、神经行为、化學反應等。
在经济学领域中,分岔现象可以帮助我们理解市場泡沫、动态平衡等问题。
二、非线性微分方程的混沌现象混沌现象是指某些动力学系统(如非线性微分方程)的随时间演化的状态具有无限的、不可预测的细节。
非线性动力学与混沌理论

非线性动力学与混沌理论1. 引言在自然界中存在着许多复杂的系统,这些系统往往由大量相互作用的因素构成,并且呈现出复杂的非线性行为。
线性动力学已经无法很好地描述这些系统的行为,因此非线性动力学应运而生。
非线性动力学研究的对象是如何描述和预测这些复杂系统的行为,其中混沌现象是非线性动力学中一个极为重要的研究内容。
2. 非线性动力学基础非线性动力学是一门研究非线性系统行为的学科,它将微分方程和离散映射等数学工具运用到实际问题中。
相较于线性动力学,非线性动力学包含更加复杂和丰富的现象,如周期运动、共振、混沌等。
常见的非线性现象包括倍增现象、吸引子、分岔现象等。
3. 混沌现象及其特征混沌是一种似乎随机但实际上具有确定性规律的运动形式。
混沌系统表现出对初值极其敏感的特征,即所谓“蝴蝶效应”。
混沌系统的特征包括:确定性、不可预测性、灵敏依赖于初值、分形结构等。
混沌现象被广泛应用于信息加密、随机数生成、优化算法等领域。
4. 混沌理论的发展历程混沌理论产生于1970年代,起初是由洛伦兹(Lorenz)提出的天气系统中的混沌解。
随后,人们开始关注混沌现象在不同领域中的普遍存在,并逐渐建立起混沌理论框架。
混沌理论在探索系统内部复杂行为规律方面取得了重要进展。
5. 混沌系统建模与分析方法建立混沌系统的数学模型是研究混沌现象的首要任务之一。
常见的混沌系统包括Logistic映射、Henon映射、Lorenz系统等。
分岔图、极大Lyapunov指数、Poincare截面等方法被广泛用于对混沌系统进行分析和研究。
6. 混沌在实际应用中的价值混沌理论不仅仅是一种学术研究,更被广泛应用于各个领域。
在通信加密领域,利用混沌信号进行信息加密传输;在金融市场中,利用混沌理论预测股市走势;在生物医学领域,通过模拟生物体内复杂系统行为等方面都有重要应用。
7. 结语总而言之,非线性动力学与混沌理论作为一门交叉学科,在解释和描述复杂系统行为方面发挥着关键作用。
混沌效应非线性混沌电路(精)

混沌效应一、实验名称 非线性电路振荡周期的分岔与混沌二、实验原理⒈分岔与混沌 ⑴ 逻辑斯蒂映射考虑一条单位长度的线段,线段上的一点用0和1之间的数x 表示。
逻辑斯蒂映射是)1(x kx x -→其中k 是0和4之间的常数。
迭代这映射,我们得离散动力学系统 )1(1n n n x kx x -=+ ,0=n ,1,2…我们发现:①当k 小于3时,无论初值是多少经过多次迭代,总能趋于一个稳定的不动点; ②当k 大于3时,随着k 的增大出现分岔,迭代结果在两个不同数值之间交替出现,称之为周期2循环;k 继续增大会出现4,8,16,32…周期倍化级联;③很快k 在58.3左右就结束了周期倍增,迭代结果出现混沌,从而无周期可言。
④在混沌状态下迭代结果对初值高度敏感,细微的初值差异会导致结果巨大区别,常把这种现象称之为“蝴蝶效应”。
⑤迭代结果不会超出0~1的范围称为奇怪吸引子。
以上这些特点可用图示法直观形象地给出。
逻辑斯蒂映射函数是一条抛物线,所以先画一条)1(x kx y -=的抛物线,再画一条x y =的辅助线,迭代过程如箭头线所示(图1)。
图 1—A 不动点 图1—B 分岔周期2 图1—C 混沌 图1—D 蝴蝶效应图1⑵逻辑斯蒂映射的分岔图 以k 为横坐标,迭代200次以后的x 值为纵坐标,可得到著名的逻辑斯蒂映射分岔图。
X 0X A X B图2逻辑斯蒂映射的分岔图。
k 从2.8增大到4。
⒉ 非线性负阻电路振荡周期的分岔与混沌 ⑴非线性电路与非线性动力学实验电路如图3所示。
它由有源非线性负阻器件R ;LC 振荡器和移相器三部分构成。
图中只有一个非线性元件R ,它是一个有源非线性负阻器件;电感器L 和电容器C2组成一个损耗可以忽略的振荡回路;可变电阻Rv1+Rv2和电容器C1串联将振荡器产生的正弦信号移相输出。
较理想的非线性元件R 是一个三段分段线性元件。
图4所示的是该电阻的伏安特性曲线,从特性曲线显示加在此非线性元件上的电压与通过它的电流极性是相反的。
理论力学第28章非线性振动分岔混沌

• Ford J教授认为:20世纪科学将永远被铭记的只有三件事, 那就是相对论,量子力学和混沌。混沌学的出现是20世纪 的第三次科学革命。
• 孔丘(前551~前479)在《易经》中写道:“易有太极, 是生两仪,两仪生四象,四象生八卦,八卦定吉凶,吉凶 生大业。” 孔丘包含了朴素的倍周期分岔通向混沌道路 的思想。
• 李耳和孔丘的思想都是猜想没有经过严格的数学证明。而 在近代,全世界最早给出混沌的第一个严格数学定义的人 是美籍华人李天岩。他和约克教授在1975年12月份那期 《美国数学月刊》上发表了一篇论文,题为“周期3意味 着混沌”。在这篇文章中,他们正式提出混沌一词,并给 出它的定义和一些有趣的性质。
件; • b.当出现分岔时,系统的拓扑结构随参数变化的情况,
即分岔的定性性态的研究; • c.计算分岔解,尤其是平衡点和极限环,并分析其稳定
性; • d.考察不同分岔的相互作用问题,以及分岔与混沌,分
形等其他动力学现象的关系。
28.2.3普适开折的保持性、转迁集
用近似方法分析非线性振动问题时,会 得到响应方程。该方程是分析非线性振动 系统分岔解的基本方程,又称分岔方程。 需计算分岔方程的转迁集和分岔图,以便 完成非线性振动问题的分岔分析。如果所 求得的分岔方程不是普适开折,则需对之 进行识别,并进行普适开折,然后再求转 迁集和分岔图。
f 有m 周期点。如果 n 按Sarkovskii序大于 m ,则 f 有 n 周期点。其中自然数的 Sarkovskii是指如下的先后排列:
3, 5, 7, , 2n 1, 2n 3,
非线性动力学与混沌理论

非线性动力学与混沌理论非线性动力学与混沌理论是研究复杂系统行为的重要工具和方法。
它们的发展源于对线性系统理论的不足,能够更好地描述和解释自然界中的复杂现象。
本文将介绍非线性动力学与混沌理论的基本概念、发展历程以及在不同领域中的应用。
非线性动力学基础动力学系统动力学系统是指随时间演化的物理、化学或生物系统。
它可以用一组微分方程或差分方程来描述系统的演化规律。
传统的线性动力学系统假设系统的行为是可预测和稳定的,但在实际应用中,许多系统都表现出复杂、不可预测的行为。
非线性动力学非线性动力学研究非线性系统,即系统中存在非线性关系或非线性项的动力学系统。
与线性系统不同,非线性系统的行为更加复杂,可能出现周期运动、混沌现象等。
非线性动力学通过研究系统的稳定性、周期解、混沌现象等来揭示系统内在的规律和行为。
混沌理论混沌理论是非线性动力学的一个重要分支,研究的是混沌现象及其产生的机制。
混沌现象指的是一个看似随机、无序的运动,但实际上具有确定性的演化规律。
混沌系统对初始条件极其敏感,微小的扰动可能导致完全不同的演化轨迹。
混沌理论通过分析系统的吸引子、分岔图、Lyapunov指数等来描述和解释混沌现象。
非线性动力学与混沌理论的发展历程非线性动力学与混沌理论的发展可以追溯到19世纪末20世纪初。
以下是一些重要的里程碑事件:1887年,皮埃尔·路易·库齐奥(Pierre Louis Marie Henri Couette)发现了流体在两个旋转圆柱之间出现的不稳定现象,这被认为是非线性动力学研究的起点之一。
1963年,爱德华·洛伦兹(Edward Lorenz)提出了著名的洛伦兹方程,揭示了天气系统中可能存在的混沌现象。
1975年,本杰明·曼德尔布罗特(Benoit Mandelbrot)提出了分形几何的概念,为混沌理论的发展提供了新的视角。
1980年代,混沌理论得到了广泛的关注和研究,许多重要的混沌系统被发现和研究,如洛伦兹吸引子、Rössler系统等。
非线性电路振荡周期的分岔与混沌实验讲解

图3非线性电路原理图图4非线性负阻器件R的伏安曲线图3电路的非线性动力学方程为:
11211( dVc C G Vc Vc gVc dt
=--
2212( L dVc C G Vc Vc i dt
=-+ 2Vc dt
di L L -=式中,导纳12V V G R R =+, 1C V和2C V分别表示加在1C和2C上的电压, L i表示流过电感器L的电流, g表示非线性电阻R的导纳。
1(x kx x -→
其中k是0和4之间的常数。迭代这映射,我们得离散动力学系统
1(1n n n x kx x -=+ , 0=n , 1, 2„
我们发现:①当k小于3时,无论初值是多少经过多次迭代,总能趋于一个稳定的不动点; ②当k大于3时,随着k的增大出现分岔,迭代结果在两个不同数值之间交替出现,称之为周期2循环; k继续增大会出现4, 8, 16, 32„周期倍化级联; ③很快k在58. 3左右就结束了周期倍增,迭代结果出现混沌,从而无周期可言。④在混沌状态下迭代结果对初值高度敏感,细微的初值差异会导致结果巨大区别,常把这种现象称之为“蝴蝶效应”。⑤迭代结果不会超出0~1的范围称为奇怪吸引子。
图5图6
图7实际非线性混沌电路图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非线性动力学、分岔Matlab 程序实现
弹簧质量系统在简谐激励作用下的受迫振动,弹簧的恢复力F与变形x的关系为
F=kx3,动力学方程为
...
3
cos
m x c x kx F wt
++=其中,给定参数,1
m=,0.3
c=, 1.0
k=,
1
w=,初始条件为(0) 3.0
x=,.(0) 4.0
x=设系统的动态参数为F0,绘出系统状态变量随参数变化分岔图,绘图参数对应的系统各周期及混沌状态的时间历程图、相轨迹图、Poincare映射图。
解答:系统状态变量位移和速度随参数F0变化分岔图,见下图,F0∈[20,40];下图为Q8400四核计算机运算39分钟所得结果。
速度分岔图位移分岔图
相应程序:
[1]
d=20:0.01:40;
w=1.0;
T=2*pi/w;
hold on
for j=1:length(d)
[t,y]=ode23('dbfun',[0:T/100:70*T],[4,4],[],d(j));
plot(d(j),y(500:100:1400,2),'linewidth',5)
title('分岔图二')
xlabel('参数F0')
ylabel('位移')
end
[2]
d=20:0.01:40;
w=1.0;
T=2*pi/w;
上海交通大学 陈建稳
hold on
for j=1:length(d)
[t,y]=ode23('dbfun',[0:T/100:70*T],[4,4],[],d(j));
plot(d(j),y(500:100:1400,1),'linewidth',5)
title('分岔图一')
xlabel('参数F0')
ylabel('速度')
end
M函数文件:dbfun.m
function ydot=dbfun(t,y,flag,d)
w=1;c=0.3;
ydot=[y(2);
-y(1)^3-c*y(2)+d*cos(w*t)];
上海交通大学 陈建稳。
