2021版中考数学基础过关:第12课时~二次函数-ppt课件
合集下载
中考数学总复习 第一板块 基础知识过关 第12课时 二次函数数学课件

tí)点1
(mìng
tí)点2
(mìng
tí)点3
命题点4
命题点5
命题点6
命题点7
(2)点(-1,y1),(2,y2)不在对称轴的同一侧,不能直接利用二次函数的增减性
来判断y1,y2的大小,可先根据抛物线关于对称轴的对称性,再用二次函数的增减
性即可.
设抛物线经过点(0,y3),因为抛物线对称轴为直线x=1,
答案:B
12/9/2021
第十八页,共三十页。
命题
命题
命题
(mìng
tí)点1
(mìng
tí)点2
(mìng
tí)点3
命题点4
命题点5
12/9/2021
第十九页,共三十页。
命题点6
命题点7
命题
命题
命题
(mìng
tí)点1
(mìng
tí)点2
(mìng
tí)点3
命题点4
命题点4
命题点6
命题点5
命题点7
【例5】 已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说
法正确的是(
)
A.有最小值-5,最大值0
B.有最小值-3,最大值6
C.有最小值0,最大值6
D.有最小值2,最大值6
解析:由二次函数的图象,得当x=-5时,y=-3;
当x=-2时,y=6;当x=0时,y=2.
∵-5≤x≤0,∴-3≤y≤6.故选B.
易知a<0,b>0,c>0,又因为4a+b=0,
所以8a+7b+2c=-2b+7b+2c=5b+2c>0,所以③正确;
(mìng
tí)点2
(mìng
tí)点3
命题点4
命题点5
命题点6
命题点7
(2)点(-1,y1),(2,y2)不在对称轴的同一侧,不能直接利用二次函数的增减性
来判断y1,y2的大小,可先根据抛物线关于对称轴的对称性,再用二次函数的增减
性即可.
设抛物线经过点(0,y3),因为抛物线对称轴为直线x=1,
答案:B
12/9/2021
第十八页,共三十页。
命题
命题
命题
(mìng
tí)点1
(mìng
tí)点2
(mìng
tí)点3
命题点4
命题点5
12/9/2021
第十九页,共三十页。
命题点6
命题点7
命题
命题
命题
(mìng
tí)点1
(mìng
tí)点2
(mìng
tí)点3
命题点4
命题点4
命题点6
命题点5
命题点7
【例5】 已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说
法正确的是(
)
A.有最小值-5,最大值0
B.有最小值-3,最大值6
C.有最小值0,最大值6
D.有最小值2,最大值6
解析:由二次函数的图象,得当x=-5时,y=-3;
当x=-2时,y=6;当x=0时,y=2.
∵-5≤x≤0,∴-3≤y≤6.故选B.
易知a<0,b>0,c>0,又因为4a+b=0,
所以8a+7b+2c=-2b+7b+2c=5b+2c>0,所以③正确;
2021年中考数学第十二讲 二次函数的图像和性质(33PPT)

【解析】(1)∵抛物线y=ax2-2ax-3+2a2=a(x-1)2+2a2-a-3.
∴抛物线的对称轴为直线x=1.
(2)∵抛物线的顶点在x轴上,
∴2a2-a-3=0,解得a=3 或a=-1,
2
∴抛物线为y= 3x2-3x+3或y=-x2+2x-1.
2
2
(3)∵抛物线的对称轴为x=1,则Q(3,y2)关于x=1对称点的坐标为(-1,y2),
(x-5)2+2上有两个点(x1,y1)和(x2,y2),若x1>x2>5,则
y1____>__y2.
高频考点·疑难突破
考点一 二次函数的图象和性质 【示范题1】(2020·常德中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下 列结论: ①b2-4ac>0;②abc<0; ③4a+b=0;④4a-2b+c>0. 其中正确结论的个数是 ( B ) A.4 B.3 C.2 D.1
二、二次函数y=ax2+bx+c(a≠0)的图象与性质
1.当a>0时
(1)开口方向:向上. (2)顶点坐标: (__2_ba_,4ac b2 ).
4a
(3)对称轴:直线_x_____2b_a_.
(4)增减性:当x<- b 时,y随x的增大而___减__小____;
2a
当x>- b 时,y随x的增大而___增__大____.
考点三 二次函数与方程、不等式
【示范题3】(2020·贵阳中考)已知二次函数y=ax2+bx+c的图象经过(-3,0)与
(1,0)两点,关于x的方程ax2+bx+c+m=0(m>0)有两个根,其中一个根是3.则关于x
初三数学《二次函数的认识》PPT课件
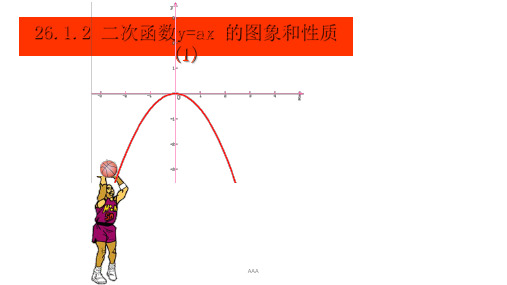
(2)抛物线
y
2 3
x
2在x轴的
下
方(除顶点外),在对称轴的
左侧,y随着x的 增大而增大 ;在对称轴的右侧,y随着x的
增大而减小 ,当x=0时,函数y的值最大,最大值是 0 ,
当x 0时,y<0.
AAA
y=ax2 性质简单运用
3、已知抛物线y=ax2经过点A(-2,-8)。 (1)求此抛物线的函数解析式; (2)判断点B(-1,- 4)是否在此抛物线上。 (3)求出此抛物线上纵坐标为-6的点的坐标。
y 2x2
y=ax2 性质简单运用
1、根据左边已画好的函数图象填空:
y 2 x2 3
(1)抛物线y=2x2的顶点坐标是(0,0), 对称轴是 y轴 ,在 对称轴的右 侧, y随着x的增大而增大;在对称轴的左 侧, y随着x的增大而减小,当x= 0 时, 函数y的值最小,最小值是 0 ,抛物 线y=2x2在x轴的 上 方(除顶点外)。
2
3
函数y=ax2的图象,以后叫做 抛物线y=ax2
y 2x2
抛物线y=ax2(a>0)性质:
– 对称性如何?
y=x²
– 位于哪些象限?
– 函数的最大、最小值?
– 顶点坐标? – 开口方向以及大小如何? – 增减性如何?
y 2 x2 3
AAA
二次函数y=ax2的性质
y=ax2
a>0
a<0
位置
17
解(1)把(-2,-8)代入y=ax2,得-8=a(-2)2, 解出a= -2,所求函数解析式为y= -2x2.
(2)因为42(1)2,所以点B(-1 ,-4) 不在此抛物线上。
(3)由-6=-2x2 ,得x2=3, x 3
二次函数的课件ppt课件ppt课件

二次函数的极坐标表示
二次函数$y = ax^{2} + bx + c$在极 坐标系下的表示为$r = a\cos^{2}\theta + b\cos\theta + c$。
05
二次函数的应用实例
生活中的二次函数应用
打篮球的抛物线
篮球运动员投篮时,篮球的运动 轨迹可以近似为二次函数。通过 调整投篮角度和力度,可以最大
数是偶函数。
03
二次函数的公式与运算
二次函数的公式
标准的二次函数公式
y = ax^2 + bx + c,其中a、b、c为系数,且a≠0。
顶点式
y = a(x-h)^2 + k,其中(h,k)为顶点坐标。
交点式
y = a(x-x1)(x-x2),其中x1、x2为与x轴的交点坐标。
二次函数的运算规则
解
根据顶点式,可知顶点坐标为(1.5, -0.75);根据交点式,可知 与x轴的交点坐标为(2.5, 0)和(2.5, 0);与y轴的交点坐标为(0, 5)。
例题2
已知二次函数y = -3x^2 + 6x + 9,求函数的对称轴和最小值。
04
二次函数的图像变换
平移变换
水平平移
二次函数$y = ax^{2} + bx + c$ 向右平移$m$个单位,得到新的 二次函数$y = a(x - m)^{2} + b(x - m) + c$。
垂直平移
二次函数$y = ax^{2} + bx + c$ 向上平移$n$个单位,得到新的 二次函数$y = ax^{2} + bx + c + n$。
二次函数$y = ax^{2} + bx + c$在极 坐标系下的表示为$r = a\cos^{2}\theta + b\cos\theta + c$。
05
二次函数的应用实例
生活中的二次函数应用
打篮球的抛物线
篮球运动员投篮时,篮球的运动 轨迹可以近似为二次函数。通过 调整投篮角度和力度,可以最大
数是偶函数。
03
二次函数的公式与运算
二次函数的公式
标准的二次函数公式
y = ax^2 + bx + c,其中a、b、c为系数,且a≠0。
顶点式
y = a(x-h)^2 + k,其中(h,k)为顶点坐标。
交点式
y = a(x-x1)(x-x2),其中x1、x2为与x轴的交点坐标。
二次函数的运算规则
解
根据顶点式,可知顶点坐标为(1.5, -0.75);根据交点式,可知 与x轴的交点坐标为(2.5, 0)和(2.5, 0);与y轴的交点坐标为(0, 5)。
例题2
已知二次函数y = -3x^2 + 6x + 9,求函数的对称轴和最小值。
04
二次函数的图像变换
平移变换
水平平移
二次函数$y = ax^{2} + bx + c$ 向右平移$m$个单位,得到新的 二次函数$y = a(x - m)^{2} + b(x - m) + c$。
垂直平移
二次函数$y = ax^{2} + bx + c$ 向上平移$n$个单位,得到新的 二次函数$y = ax^{2} + bx + c + n$。
初三二次函数ppt课件ppt课件

轴是$x = - \frac{b}{2,利用描点法可以 绘制出二次函数的图像。
与x轴交点
当$\Delta > 0$时,二次函数的 图像与x轴有两个交点;当
$\Delta = 0$时,二次函数的图 像与x轴只有一个交点;当
$\Delta < 0$时,二次函数的图 像与x轴没有交点。
理解二次函数的基本 概念和图像表示。
能够运用二次函数解 决实际问题。
掌握二次函数的性质 ,包括开口方向、顶 点坐标和对称轴。
课程计划
通过PPT演示,引导学生了解 二次函数的概念和图像表示。
通过例题讲解,帮助学生掌握 二次函数的性质和应用。
组织课堂练习和讨论,加深学 生对二次函数的理解和应用能 力。
二次函数的表达式
01
02
03
表达式
二次函数的表达式为$y = ax^{2} + bx + c$,其中 $a \neq 0$。
各项的意义
$a$是二次项系数,$b$ 是一次项系数,$c$是常 数项。
如何确定表达式
通过已知条件,利用待定 系数法可以确定二次函数 的表达式。
二次函数的图像
图像特点
二次函数的图像是一个抛物线, 其顶点坐标是$( - \frac{b}{2a}, \frac{4ac - b^{2}}{4a})$,对称
06
参考资料
初三二次函数ppt课件
初三二次函数的概念
介绍二次函数的基本定义、表达式和 图像特征。
初三二次函数的图像和性质
详细描述了如何绘制二次函数的图像 ,并分析了图像的开口方向、顶点坐 标、对称轴和增减性等性质。
初三二次函数的实际应用
通过实例和练习题,展示了二次函数 在解决实际问题中的应用,如最值问 题、行程问题等。
与x轴交点
当$\Delta > 0$时,二次函数的 图像与x轴有两个交点;当
$\Delta = 0$时,二次函数的图 像与x轴只有一个交点;当
$\Delta < 0$时,二次函数的图 像与x轴没有交点。
理解二次函数的基本 概念和图像表示。
能够运用二次函数解 决实际问题。
掌握二次函数的性质 ,包括开口方向、顶 点坐标和对称轴。
课程计划
通过PPT演示,引导学生了解 二次函数的概念和图像表示。
通过例题讲解,帮助学生掌握 二次函数的性质和应用。
组织课堂练习和讨论,加深学 生对二次函数的理解和应用能 力。
二次函数的表达式
01
02
03
表达式
二次函数的表达式为$y = ax^{2} + bx + c$,其中 $a \neq 0$。
各项的意义
$a$是二次项系数,$b$ 是一次项系数,$c$是常 数项。
如何确定表达式
通过已知条件,利用待定 系数法可以确定二次函数 的表达式。
二次函数的图像
图像特点
二次函数的图像是一个抛物线, 其顶点坐标是$( - \frac{b}{2a}, \frac{4ac - b^{2}}{4a})$,对称
06
参考资料
初三二次函数ppt课件
初三二次函数的概念
介绍二次函数的基本定义、表达式和 图像特征。
初三二次函数的图像和性质
详细描述了如何绘制二次函数的图像 ,并分析了图像的开口方向、顶点坐 标、对称轴和增减性等性质。
初三二次函数的实际应用
通过实例和练习题,展示了二次函数 在解决实际问题中的应用,如最值问 题、行程问题等。
中考数学总复习 第三单元 函数 第12课时 二次函数数学课件

2
第十九页,共二十五页。
高频考向探究
拓考向
[2017·通州一模] 如图 12-5,在平面直角坐标系 xOy 中,点 A,B,C
满足二次函数 y=ax2+bx 的表达式,则对该二次函数的系数 a 和
b 判断正确的是 (
)
图 12-5
A.a>0,b>0
B.a<0,b<0
C.a>0,b<0
D.a<0,b>0
[答案] D
内容(nèiróng)总结
UNIT THREE。第 12 课时 二次函数。【注意】 确定抛物线平移后所得新抛物线的函数解析式最好利用顶
点式,利用顶点的平移来研究图象的平移,但要注意平移前后a的值不变.。[答案] 1.B 2.A。高频考向探究
(tànjiū)。(2)求二次函数的图象的对称轴和顶点坐标
高频考向探究
2.在平面直角坐标系中,把一条抛物线先向上平移 3 个单位长
度,然后绕原点旋转 180°得到抛物线 y=x2+5x+6,则原抛物线的
解析式是 (
5 2 11
2
4
B.y=- x+
5 2 1
2
4
D.y=- x+
A.y=- xC.y=- x-
)
5 2 11
2
4
5 2 1
+
2
4
第二十三页,共二十五页。
在对称轴的左侧,即当 x<- 时,y 随 x 的增大
2a
性质
增大而减小;在对称轴的右侧,即当 x>-
b
2a
2a
b
而增大;在对称轴的右侧,即当 x>- 时,y 随 x 的
第十九页,共二十五页。
高频考向探究
拓考向
[2017·通州一模] 如图 12-5,在平面直角坐标系 xOy 中,点 A,B,C
满足二次函数 y=ax2+bx 的表达式,则对该二次函数的系数 a 和
b 判断正确的是 (
)
图 12-5
A.a>0,b>0
B.a<0,b<0
C.a>0,b<0
D.a<0,b>0
[答案] D
内容(nèiróng)总结
UNIT THREE。第 12 课时 二次函数。【注意】 确定抛物线平移后所得新抛物线的函数解析式最好利用顶
点式,利用顶点的平移来研究图象的平移,但要注意平移前后a的值不变.。[答案] 1.B 2.A。高频考向探究
(tànjiū)。(2)求二次函数的图象的对称轴和顶点坐标
高频考向探究
2.在平面直角坐标系中,把一条抛物线先向上平移 3 个单位长
度,然后绕原点旋转 180°得到抛物线 y=x2+5x+6,则原抛物线的
解析式是 (
5 2 11
2
4
B.y=- x+
5 2 1
2
4
D.y=- x+
A.y=- xC.y=- x-
)
5 2 11
2
4
5 2 1
+
2
4
第二十三页,共二十五页。
在对称轴的左侧,即当 x<- 时,y 随 x 的增大
2a
性质
增大而减小;在对称轴的右侧,即当 x>-
b
2a
2a
b
而增大;在对称轴的右侧,即当 x>- 时,y 随 x 的
初中数学九年级PPT课件二次函数可编辑全文

2
解:根据题意,得
k
1 2
0
①
2k 2 k 1 2
②
由①,得 k 1
2
由②,得
k1
1 2
,
k
2
1
∴
k 1
二.抛物线y=ax2+bx+c的特征与a、 b、c的符号:
(1)a决定开口方向:aa
0, 0,
开口向上, 开口向下;
((32))a与c决b定决抛定物对线称轴与位y轴置交:点aa,,位bb异 同置号 号, ,在 在yy轴 轴右 左侧 侧; ,
4a+2b+c=0
c=3
36a-6b+c=0
解得:
a=Leabharlann 1 4b= -1c=3
所以二次函数的解析式为: y 1 x2 x 3 4
顶点式:
解:因为二次函数的对称轴为x=-2,所以可设函 数的解析式为:y=a(x+2)2+k,把点(2,0) (0,3)代入可得:
16a+k=0
4a+k=3
解得
a=
例2、函数
y 1 x2 x 2
2
3
的开口方向
向上
,
顶点坐标是 ( 1 , 1 ) 6
,对称轴方程是 x 1.
解:a 1 ,b 1, c 2
2
3
a 0,
开口向上
又 b 2a
1 2
1
1
2
4ac b2
4 1 2 12 23
1
4a
4 1
6
2
∴ 顶点坐标为: (1, 1 ) 6
对称轴方程是: x 1
1 4
k=4 所以二次函数的解析式为:y 1 x2 x 3
解:根据题意,得
k
1 2
0
①
2k 2 k 1 2
②
由①,得 k 1
2
由②,得
k1
1 2
,
k
2
1
∴
k 1
二.抛物线y=ax2+bx+c的特征与a、 b、c的符号:
(1)a决定开口方向:aa
0, 0,
开口向上, 开口向下;
((32))a与c决b定决抛定物对线称轴与位y轴置交:点aa,,位bb异 同置号 号, ,在 在yy轴 轴右 左侧 侧; ,
4a+2b+c=0
c=3
36a-6b+c=0
解得:
a=Leabharlann 1 4b= -1c=3
所以二次函数的解析式为: y 1 x2 x 3 4
顶点式:
解:因为二次函数的对称轴为x=-2,所以可设函 数的解析式为:y=a(x+2)2+k,把点(2,0) (0,3)代入可得:
16a+k=0
4a+k=3
解得
a=
例2、函数
y 1 x2 x 2
2
3
的开口方向
向上
,
顶点坐标是 ( 1 , 1 ) 6
,对称轴方程是 x 1.
解:a 1 ,b 1, c 2
2
3
a 0,
开口向上
又 b 2a
1 2
1
1
2
4ac b2
4 1 2 12 23
1
4a
4 1
6
2
∴ 顶点坐标为: (1, 1 ) 6
对称轴方程是: x 1
1 4
k=4 所以二次函数的解析式为:y 1 x2 x 3
二次函数课件ppt

总结与回顾
主要知识点回顾
01 02
二次函数的定义
二次函数是一种特殊的函数形式,表达式为y = ax^2 + bx + c,其中a 、b、c为常数,a≠0。它的图像为抛物线,具有开口方向、顶点、对称 轴等特征。
二次函数的性质
二次函数具有极值、单调性、最值等性质,这些性质在解决实际问题中 有着广泛的应用。
二次函数的性质
开口方向
总结词
指二次函数图像的向上或向下方 向。
详细描述
二次函数开口方向取决于二次项 系数a的正负。当a>0时,开口向 上;当a<0时,开口向下。
顶点坐标
总结词
指二次函数图像的最高或最低点坐标。
详细描述
二次函数的顶点坐标通常由二次项系数a、一次项系数b及常数项c决定,一般表 达式为(-b/2a,(4ac-b^2)/4a)。
逐步深入学习
学习二次函数要由浅入深,从基础知识点开始学习,逐步深入掌握其 应用方法,提高自己的解题能力和思维水平。
对未来的展望
拓展应用领域
二次函数是数学中一个非常重要的概念,其应用领域广泛,未来可以将其应用到各个领域 中,如物理学、经济学、工程学等。
深化研究
二次函数还有许多未被探索的领域和性质,未来可以通过不断深化研究来发现新的理论和 应用成果。
学习目标
01
02
03
04
理解二次函数的基本概念和形 式。
掌握二次函数的图像和性质。
学会应用二次函数解决实际问 题。
熟悉二次函数与一元二次方程 的关系。
CHAPTER 02
二次函数的基本概念
二次函数定义
形如y=ax^2+bx+c(a、b、c为常数,a≠0)的函数称为二次函数。 其中x为自变量,y为因变量。
主要知识点回顾
01 02
二次函数的定义
二次函数是一种特殊的函数形式,表达式为y = ax^2 + bx + c,其中a 、b、c为常数,a≠0。它的图像为抛物线,具有开口方向、顶点、对称 轴等特征。
二次函数的性质
二次函数具有极值、单调性、最值等性质,这些性质在解决实际问题中 有着广泛的应用。
二次函数的性质
开口方向
总结词
指二次函数图像的向上或向下方 向。
详细描述
二次函数开口方向取决于二次项 系数a的正负。当a>0时,开口向 上;当a<0时,开口向下。
顶点坐标
总结词
指二次函数图像的最高或最低点坐标。
详细描述
二次函数的顶点坐标通常由二次项系数a、一次项系数b及常数项c决定,一般表 达式为(-b/2a,(4ac-b^2)/4a)。
逐步深入学习
学习二次函数要由浅入深,从基础知识点开始学习,逐步深入掌握其 应用方法,提高自己的解题能力和思维水平。
对未来的展望
拓展应用领域
二次函数是数学中一个非常重要的概念,其应用领域广泛,未来可以将其应用到各个领域 中,如物理学、经济学、工程学等。
深化研究
二次函数还有许多未被探索的领域和性质,未来可以通过不断深化研究来发现新的理论和 应用成果。
学习目标
01
02
03
04
理解二次函数的基本概念和形 式。
掌握二次函数的图像和性质。
学会应用二次函数解决实际问 题。
熟悉二次函数与一元二次方程 的关系。
CHAPTER 02
二次函数的基本概念
二次函数定义
形如y=ax^2+bx+c(a、b、c为常数,a≠0)的函数称为二次函数。 其中x为自变量,y为因变量。
云南省中考数学总复习函数第12课时二次函数的图象与性质课件
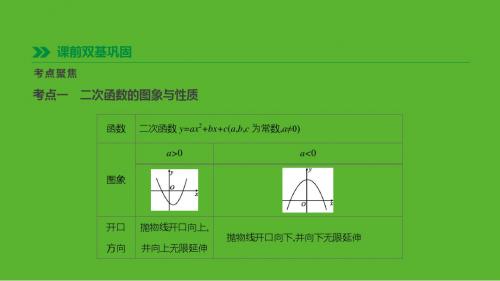
4������������ -������ 2 4������
������
时,
课前双基巩固
考点二 二次函数的解析式的确定
一般方法:待定系数法 条件 抛物线上任意三个点的坐标 抛物线的顶点坐标 抛物线与 x 轴两交点的坐标 方程设法 一般式:y=ax2+bx+c(a≠0) 顶点式:y=a(x-h)2+k(a≠0) 交点式:y=a(x-x1)(x-x2)(x1,x2 是二次函数的图象与 x 轴交点的横坐 标,a≠0)
(3)方法一:设抛物线的解析式为 y=a(x+1)(x-3), 把 C(0,-3)代入得 a×1×(-3)=-3,解得 a=1, ∴这个二次函数的解析式为 y=(x+1)(x-3)=x2-2x-3. ������ = 1, ������-������ + ������ = 0, 方法二:由题意知 9������ + 3������ + ������ = 0,解得 ������ = -2, ������ = -3, ������ = -3, ∴这个二次函数的解析式为 y=x2-2x-3.
[答案] B [解析] 由图象可知,当 x=1 时, 函数值取得最大值,最大值为 a+b+c,故 ①正确;因为抛物线经过点 B(-1,0),所以 当 x=-1 时,y=a-b+c=0,故②错误;因为该 函数图象与 x 轴有两个交点 A,B,所以 b2-4ac>0,故③错误;因为点 A 与点 B 关 于直线 x=1 对称,所以 A(3,0),根据图象
(4)y1>y2>y3.
高频考向探究
针对训练
1.在二次函数 y=x2-2x-3 的图象中,若 y 随 x 的增大而增大,则 x 的取值范围是( C ) A.x<1 B.x<-1 C.x>1 D.x>-1
������
时,
课前双基巩固
考点二 二次函数的解析式的确定
一般方法:待定系数法 条件 抛物线上任意三个点的坐标 抛物线的顶点坐标 抛物线与 x 轴两交点的坐标 方程设法 一般式:y=ax2+bx+c(a≠0) 顶点式:y=a(x-h)2+k(a≠0) 交点式:y=a(x-x1)(x-x2)(x1,x2 是二次函数的图象与 x 轴交点的横坐 标,a≠0)
(3)方法一:设抛物线的解析式为 y=a(x+1)(x-3), 把 C(0,-3)代入得 a×1×(-3)=-3,解得 a=1, ∴这个二次函数的解析式为 y=(x+1)(x-3)=x2-2x-3. ������ = 1, ������-������ + ������ = 0, 方法二:由题意知 9������ + 3������ + ������ = 0,解得 ������ = -2, ������ = -3, ������ = -3, ∴这个二次函数的解析式为 y=x2-2x-3.
[答案] B [解析] 由图象可知,当 x=1 时, 函数值取得最大值,最大值为 a+b+c,故 ①正确;因为抛物线经过点 B(-1,0),所以 当 x=-1 时,y=a-b+c=0,故②错误;因为该 函数图象与 x 轴有两个交点 A,B,所以 b2-4ac>0,故③错误;因为点 A 与点 B 关 于直线 x=1 对称,所以 A(3,0),根据图象
(4)y1>y2>y3.
高频考向探究
针对训练
1.在二次函数 y=x2-2x-3 的图象中,若 y 随 x 的增大而增大,则 x 的取值范围是( C ) A.x<1 B.x<-1 C.x>1 D.x>-1
初三二次函数课件ppt课件

02
二次函数的解析式
一般式
总结词
最通用的二次函数形式,包含三个系数a、b和c。
详细描述
一般式为y=ax^2+bx+c,其中a、b和c为实数,且a≠0。它可以表示任意二次 函数,通过调整系数a、b和c的值,可以改变函数的形状、开口方向和大小。
顶点式
总结词
包含顶点坐标的二次函数形式。
详细描述
顶点式为y=a(x-h)^2+k,其中(h,k)为抛物线的顶点坐标。通过顶点式可以直接 读出顶点的坐标,并且可以快速判断抛物线的开口方向和对称轴。
伸缩变换
总结词
伸缩变换是指二次函数的图像在平面坐标系中沿x轴或y轴方向进行缩放。
详细描述
伸缩变换包括沿x轴方向的伸缩和沿y轴方向的伸缩。沿x轴方向的伸缩是指将图像在x轴方向上放大或 缩小,对应的函数变换是将x替换为kx(k>1表示放大,0<k<1表示缩小)。沿y轴方向的伸缩是指将图 像在y轴方向上放大或缩小,对应的函数变换是将y替换为ky(k>1表示放大,0<k<1表示缩小)。
利用二次函数求面积
详细描述
通过设定一个变量为常数,将 二次函数转化为一次函数,再 根据一次函数的性质求出面积 。
总结词
几何图形面积
详细描述
在几何图形中,如矩形、三角 形、圆等,可以利用二次函数
来求解面积。
生活中的二次函数问题
总结词
生活中的二次函数
总结词
实际应用案例
详细描述
在生活中,许多问题都可以用二次函数来 描述和解决,如速度、加速度、位移等物 理量之间的关系。
二次函数的图像
总结词
二次函数的图像是一个抛物线,其形 状由系数$a$决定。
初三二次函数课件ppt

已知抛物线$y = ax^2 + bx + c$ 经过点$(0,3)$和$(3,0)$,且顶点 在第四象限,求抛物线的方程。
综合习题
综合习题1
已知抛物线$y = x^2 - 2x - 3$与直线$y = 2x + k$相交于点$(x_1, y_1)$和$(x_2, y_2)$,求证:$x_1 cdot x_2 < 0$。
位移变换会改变二次函数的开口方向、开口大小和顶 点位置,但不会改变顶点位置。
04
CATALOGUE
二次函数的实际应用
最大值与最小值问题
总结词
求二次函数的最值
详细描述
通过配方法或顶点式,找到二 次函数的对称轴,从而确定函 数的最大值或最小值。
总结词
求最值时的参数条件
详细描述
根据二次函数的开口方向和顶 点位置,确定参数的取值范围 ,确保函数取得最大值或最小
顶点式二次函数解析式
总结词
顶点式二次函数解析式是 $y=a(x-h)^2+k$,其中 $(h, k)$ 是函数的顶点。
详细描述
顶点式二次函数解析式是二次函数的一种特殊形式,其中 $(h, k)$ 是函数的顶点 。这个解析式可以很方便地表示函数的顶点和对称轴,并且可以很容易地转化为 一般二次函数解析式。
配方式二次函数解析式
总结词
配方式二次函数解析式是 $y=a(xh)^2+k$,其中 $h$ 和 $k$ 是常数,可 以通过配方将一般二次函数转化为这种 形式。VSFra bibliotek详细描述
配方式二次函数解析式可以通过配方将一 般二次函数转化为这种形式,其开口方向 和开口大小也可以通过调整 $a$ 和 $(h, k)$ 来改变。这种形式的二次函数在解决 实际问题中经常被使用。
综合习题
综合习题1
已知抛物线$y = x^2 - 2x - 3$与直线$y = 2x + k$相交于点$(x_1, y_1)$和$(x_2, y_2)$,求证:$x_1 cdot x_2 < 0$。
位移变换会改变二次函数的开口方向、开口大小和顶 点位置,但不会改变顶点位置。
04
CATALOGUE
二次函数的实际应用
最大值与最小值问题
总结词
求二次函数的最值
详细描述
通过配方法或顶点式,找到二 次函数的对称轴,从而确定函 数的最大值或最小值。
总结词
求最值时的参数条件
详细描述
根据二次函数的开口方向和顶 点位置,确定参数的取值范围 ,确保函数取得最大值或最小
顶点式二次函数解析式
总结词
顶点式二次函数解析式是 $y=a(x-h)^2+k$,其中 $(h, k)$ 是函数的顶点。
详细描述
顶点式二次函数解析式是二次函数的一种特殊形式,其中 $(h, k)$ 是函数的顶点 。这个解析式可以很方便地表示函数的顶点和对称轴,并且可以很容易地转化为 一般二次函数解析式。
配方式二次函数解析式
总结词
配方式二次函数解析式是 $y=a(xh)^2+k$,其中 $h$ 和 $k$ 是常数,可 以通过配方将一般二次函数转化为这种 形式。VSFra bibliotek详细描述
配方式二次函数解析式可以通过配方将一 般二次函数转化为这种形式,其开口方向 和开口大小也可以通过调整 $a$ 和 $(h, k)$ 来改变。这种形式的二次函数在解决 实际问题中经常被使用。
初三二次函数课件ppt

详细描述
图像法是通过绘制二次函数的图 像,观察其开口方向、对称轴、 顶点坐标等特征,从而求解二次 函数的解析式。
05
实际应用案例
生活中的二次函数应用
自由落体运动
在物理学中,自由落体运动可以用二 次函数来描述。物体下落时,下落的 高度与时间的平方成正比,即h = 1/2gt^2,其中g是重力加速度。
一次函数的应用
一次函数可以用于解决一些实际问 题,如速度、成本、时间等。
一次函数与二次函数的关系
一次函数与二次函数的区别
一次函数是一条直线,而二次函数是一个抛物线。
一次函数与二次函数的联系
二次函数可以看作是由两个一次函数组成的,其中一个一次函数的系数为0。
二次函数的意义与重要性
二次函数的意义
二次函数是函数中的一种,一般形如y=ax^2+bx+c(a,b,c是常数,a≠0),其中x 是自变量,y是因变量。
二次函数的对称轴与开口方向
对称轴:直线$x = \frac{b}{2a}$,是二次函数图像
的对称轴
开口方向:取决于二次项系数a ,a>0时开口向上,a<0时开口
向下
以上是初三二次函数课件的相关 内容。
04
二次函数的求解方法
配方法
详细描述:配方法是通过配方的 方式,将二次函数的一般形式转 化为顶点式或直接用配方法求出 抛物线的顶点坐标及对称轴。
$y = a(x - x_{1})(x - x_{2})$
二次函数的图像性质
开口方向
取决于二次项系数a,a>0时开口向上,a<0时开口向下
对称轴
直线$x = -\frac{b}{2a}$
顶点坐标
$(-\frac{b}{2a}, f(-\frac{b}{2a}))$
图像法是通过绘制二次函数的图 像,观察其开口方向、对称轴、 顶点坐标等特征,从而求解二次 函数的解析式。
05
实际应用案例
生活中的二次函数应用
自由落体运动
在物理学中,自由落体运动可以用二 次函数来描述。物体下落时,下落的 高度与时间的平方成正比,即h = 1/2gt^2,其中g是重力加速度。
一次函数的应用
一次函数可以用于解决一些实际问 题,如速度、成本、时间等。
一次函数与二次函数的关系
一次函数与二次函数的区别
一次函数是一条直线,而二次函数是一个抛物线。
一次函数与二次函数的联系
二次函数可以看作是由两个一次函数组成的,其中一个一次函数的系数为0。
二次函数的意义与重要性
二次函数的意义
二次函数是函数中的一种,一般形如y=ax^2+bx+c(a,b,c是常数,a≠0),其中x 是自变量,y是因变量。
二次函数的对称轴与开口方向
对称轴:直线$x = \frac{b}{2a}$,是二次函数图像
的对称轴
开口方向:取决于二次项系数a ,a>0时开口向上,a<0时开口
向下
以上是初三二次函数课件的相关 内容。
04
二次函数的求解方法
配方法
详细描述:配方法是通过配方的 方式,将二次函数的一般形式转 化为顶点式或直接用配方法求出 抛物线的顶点坐标及对称轴。
$y = a(x - x_{1})(x - x_{2})$
二次函数的图像性质
开口方向
取决于二次项系数a,a>0时开口向上,a<0时开口向下
对称轴
直线$x = -\frac{b}{2a}$
顶点坐标
$(-\frac{b}{2a}, f(-\frac{b}{2a}))$
二次函数 ppt课件

面积是 S ( 单位:m2 ). BC 是(45 - 3x)cm
0<45 - 3x≤20
(1) 求 S 与 x 的函数关系式及x的取值范围;
-45<- 3x ≤ -25
S =AB ·BC
解:(1) S = x(45 - 3x) = -3x2 + 45x
(
≤ x < 15 ).
≤ x < 15
(2) 当AB的长为5m时,围成的面积是多少?
⑦ y=(x+3)²-x²
⑤ y
x2
2x
二次项系数:-1
一次项系数:-2
常数项:0
不是,x的最
高次数是3.
不是、化简以
后是一次函数
1
④ y 2
x
不是,等式右
边是分式.
二次函数关系式 二次项系数 一次项系数 常数项
b=0时,二次函数
为y=ax²+c (a≠ 0 )
y=3-2x²
-2
0
3
y=x2
1
0
0
∴ m = 3.
∴当 m = 3 时,该函数是二次函数,
解析式为:y = (32+3)x3
5)x+32,
2-2×3-1
+(3-
即y = 12x2-2x+9.
例3 如图,用长为 45 m 的篱笆,一面利用墙 ( 墙的最大可用长度是 20 m ),
围成中间有一道篱笆的矩形花圃,设花圃的一边长 AB 是 x ( 单位:m ),
比较
关系式
y=6x2
1
2
1
2
m= n2- n
y=20x2+40x+20
相同点
是
都是函数
2021届中考数学复习课件:第12课时 二次函数的图象和性质(一)(共37张PPT)

第12课时 二次函数的图象和性质(一)
知识梳理
y=ax2+bx+c(a、b、c为常数,a≠0)
1.一般地,形如
___________________
的函数叫做二次函数. 当a__=__0____,b___≠__0___时,是一次函
数.
2.二次函数y=ax2+bx+c的图象是抛___物__线___,对称轴是
第一部分 数与代数
三 函数
第12课时 二次函数的图象和性质(一)
课时目标
1. 通过对实际问题的分析,体会二次函数的意义.
2. 会用描点法画出二次函数的图象,通过图象了解二次函数的性 质.
3. 会用配方法将二次函数的解析式化为y=a(x-h)2+k的形式,并 能由此得到二次函数图象的顶点坐标,知道图象的开口方向,会画 出图象的对称轴,知道二次函数的增减性,并掌握二次函数图象的 平移规律.
直线x=- b
(- b ,4ac b2 )
_________2_a___,顶点坐标是_______2_a______4_a___________.
第12课时 二次函数的图象和性质(一)
知识梳理
3.抛物线的开口方向由a确定,当a>0时,开口__向__上____;当 a<0时,开口__向___下___.|a|越大,开口越___小_____.
第12课时 二次函数的图象和性质(一)
考点演练
考点三 同一坐标系下二次函数与其他函数图象的共存问题
方法归纳
多种函数图象在同一平面直角坐标系中的识别, 一般可以先确定其中一种函数的图象(如一次函数、反比例函数), 再根据函数图象得到该函数解析式中字母的特点, 最后结合二次函数图象的开口方向、对称轴或图象经过的特殊点 对各选项进行逐一观察, 从而得出结论.
2021届初三数学中考复习 二次函数基础复习课 课件(共13张PPT)

准确应用 公式
灵活选择 方法
转化思想+方程思想+数形结合+分类讨论
真▶题▶演▶练
1.在平面直角坐标系xOy中,已知抛物线 y=x2-2bx+1 . (1)若此抛物线经过点(-2,-2),求b的值; (2)写出抛物线的顶点坐标(用含b的式子表示).
真▶题▶演▶练
2.已知抛物线y=ax2+bx+3a与y轴交于点P,将点P向右平 移4个单位得到点Q,点Q也在抛物线上. (1)抛物线的对称轴是直线x=____________; (2)用含a的代数式表示b.
真▶题▶演▶练
3.已知抛物线 y ax2 bx a 2(a 0)与x轴交于点 A( x1 , 0) 点 B( x2 , 0)(点A在点B的左侧),抛物线的对称轴为直 线 x 1. (1)若点A的坐标为 (3, 0) ,求抛物线的表达式及点B 的坐标; (2)C是第三象限的点,且点C 的横坐标为-2,若抛物
(1)用含有a的代数式表示b; (2)求抛物线顶点M 的坐标;
(1)二次项系数与一次项系数关系确定 (2)顶点横坐标确定
当解析式中含有两个待定字母时,需两个条件 才能使解析式确定.
对▶点▶演▶练
练习:在平面直角坐标系xOy中,抛物线 y=ax2+bx+3与 y 轴 交于点A,将点A向右平移3个单位长度,得到点B, 点B在抛物线上. (1)直接写出抛物线的对称轴是________; (2)用含a的代数式表示b;
0
4a
使问题得解.
(4) 0
对▶点▶演▶练 练习:已知抛物线 y ax2 2ax 3a2 4.
(1)该抛物线的对称轴为___________; (2)若该抛物线最低点的纵坐标为析
