概率论与数理统计05常见连续型分布
高等教育自学考试 概率论与数理统计期末自学 复习重要知识点

概率论与数理统计期末复习重要知识点第二章知识点:1.离散型随机变量:设X 是一个随机变量,如果它全部可能的取值只有有限个或可数无穷个,则称X 为一个离散随机变量。
2.常用离散型分布:(1)两点分布(0-1分布): 若一个随机变量X 只有两个可能取值,且其分布为12{},{}1(01)P X x p P X x p p ====-<<,则称X 服从12,x x 处参数为p 的两点分布。
两点分布的概率分布:12{},{}1(01)P X x p P X x pp ====-<<两点分布的期望:()E X p =;两点分布的方差:()(1)D X p p =-(2)二项分布:若一个随机变量X 的概率分布由式{}(1),0,1,...,.k kn k n P x k C p p k n -==-=给出,则称X 服从参数为n,p 的二项分布。
记为X~b(n,p)(或B(n,p)).两点分布的概率分布:{}(1),0,1,...,.k k n kn P x k C p p k n -==-= 二项分布的期望:()E X np =;二项分布的方差:()(1)D X np p =-(3)泊松分布:若一个随机变量X 的概率分布为{},0,0,1,2,...!kP X k ek k λλλ-==>=,则称X 服从参数为λ的泊松分布,记为X~P (λ)泊松分布的概率分布:{},0,0,1,2,...!kP X k ek k λλλ-==>=泊松分布的期望:()E X λ=;泊松分布的方差:()D X λ=4.连续型随机变量:如果对随机变量X 的分布函数F(x),存在非负可积函数()f x ,使得对于任意实数x ,有(){}()xF x P X x f t dt-∞=≤=⎰,则称X 为连续型随机变量,称()f x 为X 的概率密度函数,简称为概率密度函数。
5.常用的连续型分布: (1)均匀分布:若连续型随机变量X 的概率密度为⎪⎩⎪⎨⎧<<-=其它,0,1)(bx a a b x f ,则称X 在区间(a,b )上服从均匀分布,记为X~U(a,b)均匀分布的概率密度:⎪⎩⎪⎨⎧<<-=其它,0,1)(b x a a b x f 均匀分布的期望:()2a bE X +=;均匀分布的方差:2()()12b a D X -= (2)指数分布:若连续型随机变量X 的概率密度为00()0xe xf x λλλ-⎧>>=⎨⎩,则称X 服从参数为λ的指数分布,记为X~e (λ)指数分布的概率密度:00()0xe xf x λλλ-⎧>>=⎨⎩指数分布的期望:1()E X λ=;指数分布的方差:21()D X λ=(3)正态分布:若连续型随机变量X的概率密度为22()2()x f x x μσ--=-∞<<+∞则称X 服从参数为μ和2σ的正态分布,记为X~N(μ,2σ)正态分布的概率密度:22()2()x f x x μσ--=-∞<<+∞正态分布的期望:()E X μ=;正态分布的方差:2()D X σ=(4)标准正态分布:20,1μσ==,2222()()x t xx x e dtϕφ---∞=标准正态分布表的使用: (1)()1()x x x φφ<=--(2)~(0,1){}{}{}{}()()X N P a x b P a x b P a x b P a x b b a φφ<≤=≤≤=≤<=<<=-(3)2~(,),~(0,1),X X N Y N μμσσ-=故(){}{}()X x x F x P X x P μμμφσσσ---=≤=≤={}{}()()a b b a P a X b P Y μμμμφφσσσσ----<≤=≤≤=-定理1: 设X~N(μ,2σ),则~(0,1)X Y N μσ-=6.随机变量的分布函数: 设X 是一个随机变量,称(){}F x P X x =≤为X 的分布函数。
随机变量及其分布例题和知识点总结

随机变量及其分布例题和知识点总结在概率论与数理统计中,随机变量及其分布是非常重要的概念。
理解和掌握它们对于解决各种概率问题至关重要。
接下来,我们将通过一些具体的例题来深入探讨随机变量及其分布的相关知识。
一、随机变量的概念随机变量是指定义在样本空间上的实值函数。
简单来说,就是对于随机试验的每一个可能结果,都对应着一个实数。
例如,抛一枚硬币,正面记为 1,反面记为 0,那么这个结果就可以用一个随机变量 X 来表示。
二、随机变量的分类随机变量主要分为离散型随机变量和连续型随机变量。
离散型随机变量的取值是有限个或者可列个。
比如,抛骰子出现的点数就是一个离散型随机变量。
连续型随机变量的取值是某一区间内的所有实数。
例如,某地区一天的气温可以看作是一个连续型随机变量。
三、离散型随机变量的分布1、概率分布列离散型随机变量 X 的概率分布列就是列出 X 所有可能取值以及对应的概率。
例如,随机变量 X 表示抛两次硬币正面出现的次数,X 可能取值为0、1、2,其概率分布列为:| X | 0 | 1 | 2 ||||||| P | 1/4 | 1/2 | 1/4 |2、常见的离散型分布(1)二项分布在 n 重伯努利试验中,设每次试验中事件 A 发生的概率为 p,那么在 n 次试验中事件 A 恰好发生 k 次的概率为:\P(X=k) = C_n^k p^k (1-p)^{nk}\例如,一批产品的次品率为 01,从中抽取 10 个,其中次品的个数X 服从二项分布 B(10, 01)。
(2)泊松分布若随机变量 X 服从参数为λ的泊松分布,记为 X ~P(λ),其概率分布为:\P(X=k) =\frac{e^{\lambda}\lambda^k}{k!}\泊松分布常用于描述在一定时间或空间内稀有事件发生的次数。
例题 1某工厂生产的产品废品率为 005,从产品中随机抽取 100 个,求废品个数不超过 5 个的概率。
解:设废品个数为 X,X 服从二项分布 B(100, 005)。
连续型随机变量及其分布

2
2
a
大家应复习有关积分的方法与公式。
请看P.40-41:例9;例10.
概率论与数理统计
数学与计算科学学院 徐 鑫
三、几种重要的连续型随机变量 1、均匀分布
定义2 设连续型随机变量X具有概率密度
f
(x)
b
1
a
,
a x b,
0, 其它,
则称随机变量X服从区间(a,b)上的均匀分布,记为
X ~ U (a,b).
到x的一块面积;
概率论与数理统计
数学与计算科学学院 徐 鑫
概率密度的几何意义
b
P{a X b} f (x)dx
xx
a
f (x)dx f (x)x.
概率论与数理统计 x
数学与计算科学学院 徐 鑫
注意 对于任意可能值 a ,连续型随机变量取 a
的概率等于零.即 P{X a} 0.
证明
数学与计算科学学院 徐 鑫
均匀分布的概率密度的图形
均匀分布的特点是:随机变量X落入(a,b)中任意等长 度的小区间内的概率都相等;此概率与子区间的长度 成正比,而与子区间的起点无关。
x0 x0
(3).P{X>0.1}=1-P{X≤0.1}=1-F(0.1)
=1-(1-e-0.1λ)= e-0.1λ;
或P{X>0.1}=
f (x)dx
ex dx
e x
|
0.1
e 0.1
0.1
0.1
概率论与数理统计
数学与计算科学学院 徐 鑫
练习 设随机变量X的概率密度为
f
(x)
2
0,
求X的分布函数。
P{ X
a}
概率论与数理统计连续型随机变量及其概率分布ppt课件

0 x
则t , dt d
1-(x)
x1
2
3
F(x) 1
(t )2
1 x e
2 2
dt
x
2
e 2 d
( x )
2
2
4. P{a X b} (b ) ( a )
P{X b} (b ) P{X a} 1 (a )
例6
设 X ~ N(1,4) , 求 P (0 X 1.6)
解:X 的密度函数为
f
x
1 10
e
x 10
0
x0 x0
令:B={ 等待时间为10-20分钟 }
则 PB P10 X 20
20
1
x
e 10 dx
10 10
x
e 10
20
e 1
e 2
0.2325
10
例5 假定一大型设备在任何长为 t 的时间内发生
故障的次数 N( t ) 服从参数为t 的Poisson分布,
P(2
X
4)
4
2
2
2
2
(0)
0.3
2
0.8
P( X 0) 0.2
解二 图解法
0.2 0.15
0.1 0.05
0.3 0.2
-2
2
4
6
由图 P( X 0) 0.2
例 3 原理
设 X ~ N ( , 2), 求 P(| X | 3 )
解 P(| X | 3 ) P( 3 X 3 )
应用场合:
若随机变量X在区间(a,b)内等可能的取值,则
X ~ U a,b
例3 秒表的最小刻度差为0.01秒. 若计时精度 是取最近的刻度值, 求使用该秒表计时产生的 随机误差X 的概率密度, 并计算误差的绝对值 不超过0.004秒的概率.
概率论与数理统计-随机变量及其分布

解
直接对上式求导有
二、连续型随机变量函数的分布
81
例 18
解
二、连续型随机变量函数的分布
82
定理 1
定理 2
83
总结/summary
离散型随机变量:分布律
分 二项分布、泊松分布、几何
随 布 分布
机 变
函 数
连续型随机变量:密度函数
量 均匀分布、指数分布、正态
分布
随机变量函数的分布
84
谢谢观赏
46
47
目录/Contents
2.1 随机变量及其分布 2.2 常用的离散型随机变量 2.3 常用的连续型随机变量 2.4 随机变量函数的分布
48
目录/Contents
2.3 常用的连续型随机变量
一、均匀分布 二、指数分布 三、正态分布
一、均匀分布
49
一、均匀分布
50
一、均匀分布
51
一、均匀分布
15
定义3
(1)非负性 (2)规范性
三、离散型随机变量及其分布律
16
换句话说,如果一个随机变量只可能取有限个 值或可列无限个值, 那么称这个随机变量为(一维) 离散型随机变量.
一维离散型随机变量的分布律也可表示为:
三、离散型随机变量及其分布律
17
例2
求
三、离散型随机变量及其分布律
18
解
四、连续型随机变量及其密度函数
2.1 随机变量及其分布 2.2 常用的离散型随机变量 2.3 常用的连续型随机变量 2.4 随机变量函数的分布
73
目录/Contents
2.4 随机变量函数的分布 一、离散型随机变量函数的分布 二、连续型随机变量函数的分布
常见的连续型随机变量

02 均匀分布
定义和性质
定义
均匀分布是一种连续型概率分布,在 概率论和统计学中,均匀分布也叫矩 形分布,它是对称概率分布,在相同 长度间隔的分布概率是等可能的。
性质
均匀分布具有等可能性、对称性、均 匀性等特点。其分布函数是一条斜线 ,概率密度函数是一个常数。
概率密度函数和分布函数
概率密度函数
均匀分布的概率密度函数是一个常 数,表示为f(x) = 1/(b-a),其中a 和b是区间的端点,x属于[a, b]。
伽玛分布的概率密度函数具有指数函数和幂函数的乘积形式,形状 参数和尺度参数分别控制分布的形状和尺度。
性质
伽玛分布具有可加性,即多个独立同分布的伽玛随机变量的和仍然 服从伽玛分布。
贝塔分布
定义
贝塔分布是一种在[0,1]区间上的连续型概率分布,常用于描述比例、概率等随机变量的分布情况。
概率密度函数
贝塔分布的概率密度函数具有幂函数和Beta函数的乘积形式,形状参数控制分布的形状。
跨学科交叉融合
连续型随机变量的研究涉及数学、统 计学、计算机科学等多个学科领域。 未来,跨学科交叉融合将成为推动连 续型随机变量研究发展的重要趋势。 通过整合不同学科的优势和资源,我 们可以更深入地理解连续型随机变量 的本质和规律,为解决实际问题提供 更有效的手段和方法。
THANKS FOR WATCHING
均匀分布
在某一区间内,每个取值的可能性都 相等。
03
指数分布
描述某些随机事件发生的时间间隔的概率分 布,如放射性元素的衰变时间、电话交换台
的呼叫间隔时间等。
05
04
正态分布
一种钟形曲线分布,具有广泛的应用 背景,如自然和社会科学中的各种测 量误差、产品质量控制等。
概率论与数理统计中的三种重要分布

概率论与数理统计中的三种重要分布摘要:在概率论与数理统计课程中,我们研究了随机变量的分布,具体地研究了离散型随机变量的分布和连续型随机变量的分布,并简单的介绍了常见的离散型分布和连续型分布,其中二项分布、Poisson 分布、正态分布是概率论中三大重要的分布。
因此,在这篇文章中重点介绍二项分布、Poisson 分布和正态分布以及它们的性质、数学期望与方差,以此来进行一次比较完整的概率论分布的学习。
关键词:二项分布;Poisson 分布;正态分布;定义;性质一、二项分布二项分布是重要的离散型分布之一,它在理论上和应用上都占有很重要的地位,产生这种分布的重要现实源泉是所谓的伯努利试验。
(一)泊努利分布[Bernoulli distribution ] (两点分布、0-1分布)1.泊努利试验在许多实际问题中,我们感兴趣的是某事件A 是否发生。
例如在产品抽样检验中,关心的是抽到正品还是废品;掷硬币时,关心的是出现正面还是反面,等。
在这一类随机试验中,只有两个基本事件A 与A ,这种只有两种可能结果的随机试验称为伯努利试验。
为方便起见,在一次试验中,把出现A 称为“成功”,出现A 称为“失败” 通常记(),p A P = ()q p A P =-=1。
2.泊努利分布定义:在一次试验中,设p A P =)(,p q A P -==1)(,若以ξ记事件A 发生的次数,则⎪⎪⎭⎫⎝⎛ξp q 10~,称ξ服从参数为)10(<<p p 的Bernoulli 分布或两点分布,记为:),1(~p B ξ。
(二)二项分布[Binomial distribution]把一重Bernoulli 试验E 独立地重复地进行n 次得到n 重Bernoulli 试验。
定义:在n 重Bernoulli 试验中,设(),()1P A p P A q p ===-若以ξ记事件A 发生的次数,则ξ为一随机变量,且其可能取值为n ,,2,1,0 ,其对应的概率由二项分布给出:{}k n kk n p p C k P --==)1(ξ,n k ,,3,2,1,0 =,则称ξ服从参数为)10(,<<p p n 的二项分布,记为),(~p n B ξ。
概率论与数理统计随机变量及其分布

2.2 离散型随机变量及其概率分布
二项分布的图形特点: (1)当(n+1)p不为整数时,二项概率 P{X=k}在k=[(n+1)p]时达到最大值 (2)当(n+1)p为整数时,二项概率 P{X=k}在k=(n+1)p和k=(n+1)p-1时达
“未命中目标”;它们都可用(0-1)分布来描述.(0-1)分
布是实际中经常用到的一种分布.
2.2 离散型随机变量及其概率分布
二项分布:若一个随机变量X的概率分布由式
给P出{x,则k称} X服C从nk p参k (数1为pn),np的k , 二k 项0分,1布,..。., n记. 为X~b(n,p)(或
到最大值 讲课本例3和例4 注意二项分布b(n,p)和两点分布的关系
2.2 离散型随机变量及其概率分布
在实际中,我们经常要计算n次独立重 复的贝努利试验中恰好k次成功的概 率 Cnk pk (1 p)nk ,至少有次成功的概
n
率为 Cni pi (1 p)ni 等,当n很大时,要计 i 1
算出它们的确切数值很不容易,那我们 应该怎么做呢?
P{a
xi
b}
P{ {X axi b
xi}}
axi b
pi
而且X所成的任何事件的概率都能够求出来,
P{X I} P{X xi} pi
xi I
xi I
2.2 离散型随机变量及其概率分布
3 常用离散分布
两点分布(0-1分布):若一个随机变量X只有两个可能取值, 且其分布为
概率论与数理统计第五版答案

概率论与数理统计第五版答案第一章简介本章主要介绍概率论与数理统计的基本概念和研究对象,并概述了本书的组织结构和学习方法。
1.1 概率论与数理统计的基本概念概率论是研究不确定现象的数学分支,数理统计是利用概率论的方法进行统计分析的科学。
概率论研究的对象是随机现象及其概率规律,而数理统计研究的是通过对样本数据的分析来推断总体特征和进行决策。
1.2 概率论的基本思想概率论的基本思想是根据已知信息推断未知信息的可能性。
它主要包括两个方面:经典概率和统计概率。
经典概率是指通过理论计算得出的概率值,统计概率是通过观察数据进行统计分析得出的概率值。
1.3 数理统计的基本思想数理统计的基本思想是根据样本数据推断总体特征,并进行决策。
它包括描述统计和推断统计两个部分。
描述统计是对样本数据的整理、加工和展示;推断统计是通过样本数据来推断总体特征,并给出相应的置信区间或检验结果。
1.4 本书的结构和学习方法本书一共分为五个部分,分别是概率基础、随机变量及其分布、数理统计基础、参数估计与检验、方差分析与回归分析。
每个部分都有相应的章节和习题。
本书的学习方法包括理论学习和实践练习相结合。
在学习理论知识的同时,通过习题的解答来巩固和应用所学的知识。
第二章概率基础本章介绍了概率的基本性质和运算法则,并讲解了概率模型和条件概率的概念。
2.1 概率的基本性质概率具有非负性、规范性和可列可加性三个基本性质。
非负性指概率的取值范围为[0,1];规范性指必然事件的概率为1,不可能事件的概率为0;可列可加性指若事件A1、A2…是两两互斥事件,则它们的概率之和等于它们的并事件的概率。
2.2 概率的运算法则概率的运算法则包括加法法则和乘法法则。
加法法则是指若事件A和B互斥,则它们的概率之和等于它们的并事件的概率;乘法法则是指若事件A和B相互独立,则它们的概率之积等于它们的联合事件的概率。
2.3 概率模型概率模型是指用概率分布来描述随机现象的数学模型。
概率论与数理统计 2.3连续型随机变量

称X服从参数为 ,的正态分布或 高斯分布,记为 X~N( , 2) f(x) 1 (1)关于直线x 对称; 1 2 ( 2)最大值为 ; 2 ( 3)在x 处有拐点. o x 可求得X的分布函数为: ( t )2 x 1 2 2 F ( x) dt e 2
1 2
x
u2 2
du (x源自) (4) a<b, X~N( , 2) ,有: b a P(a X b) ( ) ( )
例7 设X~N(3,4),试求:
(1) P(2<X≤5) (2) P(2<X<7)
(3)若P(X>c)=P(X≤c),求c的值
0
得 P(X=a)=0
故: (1) P(A)=0 A是不可能事件 (2) 连续型随机变量X落在区间的概率 与区间是否包含端点无关 即: P(a<X≤b)=P(a≤X<b) =P(a<X<b) =P(a≤X≤b)
例1 设连续型随机变量X的概率密度为 f(x)=Ae-|x| , <x<+ 试求: (1)常数A (2) P(0<X<1) (3) X的分布函数
24
p P( X 10) 1 P( X 10)
1
10 0
1 e dx 1 e 5
x 5
x 5 10 0
| e
2
由于顾客每次去银行都是独立的,Y~B(5,p)
因此Y的分布律为
P (Y k ) C p (1 p )
k 5 k 5 k 2 5 k 2k
解: =3, =2
( x 3 ) 又 F ( x ) ( ) 2
陈国华等主编概率论与数理统计第五章习题解答

x>0 x≤0
(α > 0, β > 0)
a a 1 1 1 dx = ∫ cos(tx) ⋅ dx + ∫ sin(tx) ⋅ dx −a −a −a 2a 2a 2a 1 1 1 = ⋅ sin(tx) |a sin(at ) x =− a = at 2a t t −1 (2)参数为 λ 的指数分布的特征函数为, φ X (t ) = (1 − i ) ,参数为 λ 的指数分布可看做
1
π (1 + x 2 )
(−∞ < x < +∞) ;
⎧A ⎪ (D) X i 的概率函数为 : g ( x) = ⎨ x 3 ⎪0 ⎩
x ≥1 x <1
(i = 1,2,3, ) .
答案:CABAD 三.解答题
1.一颗骰子连续掷 4 次,点数总和记为 X ,估计 p (10 < X < 18) .
3.已知随机变量 X 的数学期望为 10,方差 DX 存在且 P (−20 < X < 40) ≤ 0.1 ,则
DX ≥ . 4.设 X 1 , X 2 , , X n, 为独立同分布的随机变量序列,且 X i (i = 1,2, ) 服从参数为 2 的
指数分布,则 n → ∞ 当时, Yn =
1 n 2 ∑ X i 依概率收敛于 n i =1
1 1 ln n + ln n = 0 2 2
n
DX n = EX n = ln n
n 1 1 D ( Xi) = 2 ∑ 2 n n i =1
2
∑ ln i → 0(n → ∞)
i =1
根据马尔可夫大数定律, {X n } 服从大数定律。
3 、 已 知 随 机 变 量 X 和 Y 的 数 学 期 望 、 方 差 以 及 相 关 系 数 分 别 为 E ( X ) = E (Y ) = 2 ,
概率论与数理统计--- 边缘分布

即 X 服从参数λ=0.5 的指数分布.
7
二、二维离散型随机变量的边缘分布 二维离散型随机变量(X,Y)的分布律 的分布律 二维离散型随机变量 为: P{X=xi,Y=yj}=pij (i, j=1,2,…) ∞ 则: P{X=xi}=P{X=xi,Y<+∞}
= ∑ P{ X = xi , Y = y j }
x2 a2
x2 + y2 ≤ 1 上的均匀分布, 设(X,Y)服从椭圆域 a 2 ) 上的均匀分布,求 b2
∫−∞
同理可得 2 y2 y ≤ b; − π fY ( y) = b 1 b2 ,
0, y >b.
a
x2 a2
0,
| x| >a,
X 与Y 不服从 均匀分布
a− x
x x 关于X 的边缘概率密度为 则(X,Y = ∫−∞ [∫+(t)dtu y)dy]du 为 )关于 X ∞ f边缘概率密度 F (x) = −∞ f −∞ ( , X
fX (x) = ∫
∞ + f (x, y)dy −∞
(X,Y) 关于 的边缘分布函数为 关于Y
F ( y) = ∫ Y
+ ∞ [ f (x,v)dx]dv −∞ −∞ y
e = 2π
∫
+∞
−∞
1 e 2 1− ρ
( y − ρ x )2 − 2 ( 1− ρ 2 )
dy
y−ρ x = t ,得: 得 令 2 x2 − 1− ρ e 2 f X ( x) = 2π
∫
+∞
−∞
e
t2 − 2
dt
e =
x2 − 2
连续型随机变量与分布

连续型随机变量与分布随机变量是概率论和数理统计中的重要概念之一,它描述了试验结果的不确定性。
随机变量可以分为离散型和连续型两种。
在本文中,我们将重点讨论连续型随机变量及其分布。
一、连续型随机变量的定义连续型随机变量是指其取值范围为连续的实数集合的随机变量。
与之相对应的是离散型随机变量,其取值范围为有限或可列的数集。
举例来说,假设我们研究某地每天降雨的量,用X表示降雨量。
如果我们用毫升作为单位,X可以取任意实数值,包括小数。
这种情况下,X就是一个连续型随机变量。
二、连续型随机变量的概率密度函数对于连续型随机变量X,我们不能像离散型随机变量那样用概率质量函数来描述其概率分布,因为连续型随机变量可能取无限个实数取值。
为了描述连续型随机变量的概率分布,我们引入了概率密度函数(Probability Density Function,简称PDF)。
概率密度函数f(x)满足以下两个条件:1. 非负性:对于任意实数x,有f(x)≥0;2. 归一性:∫f(x)dx = 1,其中积分范围为整个样本空间。
概率密度函数f(x)表示了随机变量X落在无穷小区间(x, x+dx)内的概率。
具体而言,对于一个事件A,其对应的概率可以通过计算f(x)在该区间上的积分得到。
三、连续型随机变量的分布函数与离散型随机变量相似,连续型随机变量也有分布函数(Distribution Function),又称为累积分布函数(Cumulative Distribution Function,简称CDF)。
对于连续型随机变量X,其分布函数F(x)定义为:F(x) = P(X ≤ x),表示X小于等于x的概率。
分布函数具有以下性质:1. 非减性:对于任意实数x1 < x2,有F(x1) ≤ F(x2);2. 右连续性:对于任意实数x0,有F(x0) = lim(x→x0⁺)F(x)。
通过分布函数,我们可以计算随机变量X落在任意区间上的概率。
概率论与数理统计公式(完整精华版)
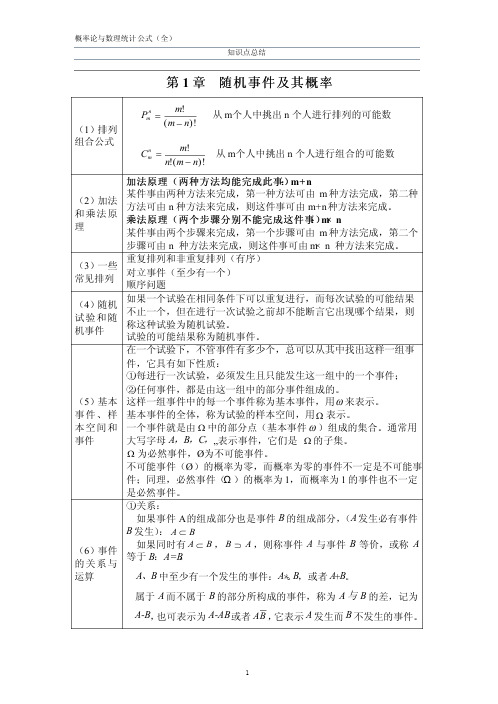
(6)事件 的关系与 运算
加法原理(两种方法均能完成此事:)m+ n 某件事由两种方法来完成,第一种方法可由 m 种方法完成,第二种 方法可由 n 种方法来完成,则这件事可由 m+n 种方法来完成。 乘法原理(两个步骤分别不能完成这件事:)m× n 某件事由两个步骤来完成,第一个步骤可由 m 种方法完成,第二个 步骤可由 n 种方法来完成,则这件事可由 m× n 种方法来完成。 重复排列和非重复排列(有序)
1° f (x) 0。
2°
+¥ -¥
f
(
x)dx
=
1。
4
概率论与数理统计 公式(全)
知识点总结
(3)离 散与连 续型随 机变量 的关系 (4)分 布函数
P(X = x) » P(x < X £ x + dx) » f (x)dx
积分元 f (x)dx 在连续型随机变量理论中所起的作用与 P(X = xk) = pk 在离散型随机变量理论中所起的作用相类似。
②任何事件,都是由这一组中的部分事件组成的。
这样一组事件中的每一个事件称为基本事件,用w 来表示。
基本事件的全体,称为试验的样本空间,用 W 表示。
一个事件就是由 W 中的部分点(基本事件 w )组成的集合。通常用
大写字母 A,B,C,„表示事件,它们是 W 的子集。
W 为必然事件,Ø为不可能事件。 不可能事件(Ø)的概率为零,而概率为零的事件不一定是不可能事 件;同理,必然事件(Ω )的概率为 1,而概率为 1 的事件也不一定 是必然事件。
①关系: 如果事件 A的组成部分也是事件 B 的组成部分,(A 发生必有事件
B 发生): A Ì B 如果同时有 A Ì B , B A ,则称事件 A 与事件 B 等价,或称 A
概率论与数理统计+第五章+大数定律及中心极限定理+练习题答案

〖填空题〗例5.1(棣莫佛-拉普拉斯定理) 设某种电气元件不能承受超负荷试验的概率为0.05.现在对100个这样的元件进行超负荷试验,以X 表示不能承受试验而烧毁的元件数,则根据中心极限定理{}≈≤≤105X P.分析 不能承受试验而烧毁的元件数X ~),(p n B .根据棣莫佛-拉普拉斯定理,X 近似服从正态分布),(npq np N ,其中n =100,p =0.05,q =0.95.因此{}.4890.0)0()29.2(29.275.45075.451075.450105105=-≈⎭⎬⎫⎩⎨⎧≤-≤=⎭⎬⎫⎩⎨⎧-≤-≤=⎭⎬⎫⎩⎨⎧-≤-≤-=≤≤ΦΦX X npq np npq np X npq np X P P P P例5.2(棣莫佛-拉普拉斯定理)设试验成功的概率p =20%,现在将试验独立地重复进行100次,则试验成功的次数介于16和32次之间的概率Q ≈ .分析 以n ν表示100次独立重复试验成功的次数,则)20.0 100(~,B nν,且4)1(20=-===p np np n n ννD E ,.因此试验成功的次数介于16和32次之间的概率{}[][],84.08413.019987.0)1(1)3()1()3(42032420420163216=--=--=--≈⎭⎬⎫⎩⎨⎧-≤-≤-=≤≤=ΦΦΦΦννn n Q P P 其中)(u Φ是标准正态分布函数.例5.3(棣莫佛-拉普拉斯定理) 将一枚均匀对称的硬币接连掷10000次,则正面恰好出现5000次的概率≈α.分析 正面出现的次数ν)5.0 , 10000(~B ,2500,5000==ννD E .根据局部定理,有008.025012D 1}5000{≈=≈==ππνναP .例5.10(辛钦大数定律) 将一枚色子重复掷n 次,则当∞→n 时,n 次掷出点数的算术平均值n X 依概率收敛于 7/2 .分析 设n X X X ,,,21 是各次掷出的点数,它们显然独立同分布,每次掷出点数的数学期望等于7/2.因此,根据辛钦大数定律,n X 依概率收敛于7/2.5.2. (1)121;(2)90;(3)21;(4)))((λλ-Φx n〖选择题〗例5.11(中心极限定理) 设随机变量n X X X ,,,21 相互独立,n n X X X S +++= 21,则根据列维-林德伯格中心极限定理,当n 充分大时n S 近似服从正态分布,只要n X X X ,,,21(A) 有相同期望和方差. (B) 服从同一离散型分布.(C) 服从同一指数分布. (D) 服从同一连续型分布. [ C ]分析 应选(C ).列维-林德伯格中心极限定理的条件是:随机变量n X ,,X ,X 21相互独立同分布, 并且其数学期望和方差存在.由于有相同的数学期望未必有相同分布,可见(A)不满足定理条件.满足(B)和(D)的随机变量i X 的数学期望或方差未必存在,故(B)和(D)也不满足定理条件.于是,只有(C)成立(指数分布的数学期望和方差都存在).例5.14(大数定律)下列命题正确的是(A) 由辛钦大数定律可以得出切比雪夫大数定律. (B) 由切比雪夫大数定律可以得出辛钦大数定律. (C) 由切比雪夫大数定律可以得出伯努利大数定律.(D) 由伯努利大数定律可以得出切比雪夫大数定律. [ C ]分析 应选(C ).切比雪夫大数定律的条件是:随机变量 ,,,,21n X X X 两两独立,并且存在常数C ,使),,,2,1( n i C X i=≤D ;这样的常数C 对于选项(C )存在.伯努利大数定律可以表述为:假设随机变量 ,,,,21n X X X 独立同服从参数为p 的0-1分布,则p X n ni i n =-∑=∞→11lim P ;对于服从参数为p 的0-1分布随机变量 ,,,,21n X X X ,显然),,,2,1(41)1( n i p p X i =≤-=D .从而满足服从切比雪夫大数定律的条件.此外,(A ),(B )和(D )显然不成立.5.1. (1)A ;(2)C ;(3)C ;(4)A〖计算题〗例5.16(棣莫佛-拉普拉斯定理) 设n ν是n 次伯努利试验成功的次数,p (0<p <1)是每次试验成功的概率,n f n n ν=是n 次独立重复试验成功的频率,设n 次独立重复试验中,成功的频率f n 对概率p 的绝对偏差不小于Δ的概率{}α∆=≥-p f n P . (5.10)试利用中心极限定理,(1) 根据∆和n 求α的近似值; (2) 根据α和n 估计∆的近似值; (3) 根据α∆和估计n . 解 变量n ν服从参数为),(p n 的二项分布.记p q -=1,则由(5.7)知,当n 充分大时nν近似服从正态分布),(npq np N .因此,近似地有{}{},,~)1,0(~α∆ν∆ν∆να=≥≈⎭⎬⎫⎩⎨⎧≥-=⎭⎬⎫⎩⎨⎧≥-=≥--u U pq n npqnp p n p f N npqnpU n n n n n P P P P(5.11)其中U 是服从)1,0(N 的随机变量,而αu 是)1,0(N 水平α双侧分位数(附表2).故(5.12)(1) 已知n 和∆,求α.利用附表1,可以由(5.11)求出α的值(附表1).例如,若(5.12)式左侧等于1.96,则05.0≈α.亦可由下式求α的近似值.有. 12 1 ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=⎭⎬⎫⎩⎨⎧<-≈⎭⎬⎫⎩⎨⎧≥-=pq n pq n U pq n npq np n ∆Φ∆∆ναP P (5.13) 进而由)1,0(N 分布函数)(x Φ的数值表(附表1)最后求出α的值.(2) 已知n 和α,求∆.由(*)和41≤pq ,可见nu n pqu 2αα∆≤≈; (5.14) (3) 已知α和∆,求n .由(5.12)和pq ≤1/4,可见2⎪⎭⎫⎝⎛≈∆αu pq n 或2241⎪⎭⎫ ⎝⎛≥⎪⎭⎫ ⎝⎛≥∆∆ααu pq u n . (5.15)例5.17(棣莫佛-拉普拉斯定理) 假设某单位交换台有n 部分机,k 条外线,每部分机呼叫外线的概率为p .利用中心极限定理,解下列问题:(1) 设n =200,k =30,p =0.12,求每部分机呼叫外线时能及时得到满足的概率α的近似值. (2) 设n =200,p =0.12,问为使每部分机呼叫外线时能及时得到满足的概率α≥95%,至少需要设置多少条外线?(3) k =30,p =0.12,问为使每部分机呼叫外线时能及时得到满足的概率α≥95%,最多可以容纳多少部分机?解 设n ν——n 部分机中同时呼叫外线的分机数,k ——外线条数,则n ν服从参数为(n , p )的二项分布,=np24,npq =21.12.当n 充分大时,根据棣莫佛-拉普拉斯中心极限定理,近似地)1 ,0(~N npqnpU n n -=ν.(1) 设n =200,k =30,p =0.12,每部分机呼叫外线时能及时得到满足的概率{}(). 9049.031.112.21243012.21243030≈=⎪⎭⎫⎝⎛-≈⎭⎬⎫⎩⎨⎧-≤-=≤=ΦΦνναnpqnp n n P P (2) 设n =200,p =0.12,k ——至少需要设置的外线条数,则{}.,; 31.562412.216449.1 1.644912.212495.012.212412.2124≈+⨯≥≥-≥⎪⎭⎫⎝⎛-≈⎭⎬⎫⎩⎨⎧-≤-=≤=k k k k npq np k n n ΦνναP P即至少需要设置32外线.(3) 设k =30,p =0.12,且每部分机呼叫外线时能及时得到满足的概率≥α95%.由{}95.01056.012.0301056.012.03030≥⎪⎭⎫⎝⎛-≈⎭⎬⎫⎩⎨⎧-≤-=≤=n n n n npq np n n ΦνναP P , 6449.11056.012.030≥-n n.09004857.70144.0 6449.11056.012.0302=+-≥-n n nn,,它有两个实根:3310431,7972.18821==n n ;经验证33104312=n 为增根,由此得n ≈188.797,即最多可以容纳188部分机.例5.20(列维-林德伯格定理) 设n X X X ,,,21 是独立同分布随机变量,n X 是其算术平均值.考虑概率{}α∆μ=≥-n X P , (5.16)其中μ=iX E ()n i .,2,1 =,()0>∆∆和α(0<α<1)是给定的实数.试利用中心极限定理,根据给定的,(1) ∆和n ,求α的近似值; (2) α和n ,求∆的近似值;(3)α∆和,估计n .解 式(5.16)中的三个数),,(α∆n 相互联系又相互制约:其中的任意两个可以完全决定第三个.不过,明显地表示出它们之间的关系一般并不容易.假如n 充分大,则利用(5.9)式可以(近似地)表示出α∆,,n 之间的关系.易见μ=nX E ,X n 2σ=D .(1) 已知∆和n ,求α-1的近似值:{}⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛≈⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤-=≤-=-σ∆Φσ∆Φσ∆σμ∆μαn n n n X X n n P P 1. (2) 已知α和n ,求∆的近似值.由(5.17)式可得nu σ∆α ≈.(3) 已知α∆和,求n 的近似值.由(5.18)有2⎪⎭⎫⎝⎛≈∆σαu n .例5.21(列维-林德伯格定理) 某保险公司接受了10000电动自行车的保险,每辆每年的保费为12元.若车丢失,则车主得赔偿1000元.假设车的丢失率为0.006,对于此项业务,试利用中心极限定理,求保险公司:(1) 亏损的概率α;(2) 一年获利润不少于40000元的概率β; (3) 一年获利润不少于60000元的概率γ.解 设X 为需要赔偿的车主人数,则需要赔偿的金额为X Y1.0=(万元);保费总收入C =12万元.易见,随机变量X 服从参数为(n ,p )的二项分布,其中 n =10000,p =0.006;60==np X E ,)1(p np X -=D =59.64.由棣莫佛-拉普拉斯定理知,随机变量X 近似服从正态分布)64.59,60(N ;随机变量Y 近似服从正态分布)5964.0,6(N .(1) 保险公司亏损的概率{}0)77.7(177.75964.065964.06125964.0612≈-=⎭⎬⎫⎩⎨⎧>-=⎭⎬⎫⎩⎨⎧->-=>=ΦαY Y Y P P P .(2) 保险公司一年获利润不少于4万元的概率{}{}.9952.0)59.2(5964.0685964.068412=≈⎭⎬⎫⎩⎨⎧-≤-=≤=≥-=ΦβY Y Y P P P (3) 保险公司一年获利润不少于6万元的概率{}{}.5.0)0(05964.066612=≈⎭⎬⎫⎩⎨⎧≤-=≤=≥-=ΦγY Y Y P P P例5.22(棣莫佛-拉普拉斯定理) 假设伯努利试验成功的概率为5%.利用中心极限定理估计,进行多少次试验才能以概率80%使成功的次数不少于5次.解 设n 是所需试验的次数,每次试验成功的概率p =0.05.以n ν表示n 次伯努利试验成功的次数,则),(~p n B nν,npq np n n ==ννD E ,,其中p q -=1;由棣莫佛-拉普拉斯定理,知对于充分大的n ,随机变量n ν近似服从正态分布),(npq np N .查)1,0(N 分位数表,可见()()8416.018416.080.0--==ΦΦ.因此{}().8416.01)1(51)1(5)1(5.080.0--=⎪⎪⎭⎫⎝⎛---≈⎭⎬⎫⎩⎨⎧--≥--=≥=ΦΦννp np np p np np p np np n n P P.,),(025)8416.010()1(8416.058416.0)1(522222≈++--≈--≈--n n p p np np p np np将05.0=p 代入上列方程,的关于n 的一元二次方程:0255354.00025.02≈+-n n ,其根为79.6837.14521==n n ,.经验证79.682=n 为增根,舍去2n ,取37.1451461=>=n n .于是,至少需要进行146次试验才能以概率80%保障成功的次数不少于5次.例5.26(列维-林德伯格定理) 生产线组装每件产品的时间服从指数分布.统计资料表明,每件产品的平均组装时间为10分钟.假设各件产品的组装时间互不影响.试利用中心极限定理,(1) 求组装100件产品需要15到20小时的概率Q ;(2) 求以概率0.95在16个小时内最多可以组装产品的件数. 解 以)100,,2,1( =iX i 表示第i 件产品的组装时间.由条件知)100,,2,1( =i X i 独立同服从指数分布.由指数分布的数字特征和条件“每件产品的平均组装时间为10分钟”,可见10=i X E ;由于i X 服从指数分布,可见()2210==i i X X E D .(1) 因为n =100充分大,故由列维-林德伯格定理,知100件产品组装的时间10021X X X T n +++= 近似服从()210100 10100⨯⨯,N ,因此{}.8156.0)8413.01(9973.0)1( )2( 21010010100112009002=--=--≈⎭⎬⎫⎩⎨⎧≤⨯⨯-≤-=≤≤=ΦΦT T Q n n P P(2) 16小时即960分钟.需要求满足{}95.0960=≤n T P 的n .由列维-林德伯格定理,知当n 充分大时,n nX X X T +++= 21近似服从()nn N 210 10,,故由{}, 101096010109601010960950⎪⎭⎫⎝⎛-≈⎭⎬⎫⎩⎨⎧-≤-=≤=n n n n n n T T .n n ΦP P 可见95.0)645.1( ≈Φ.因此645.11010960≈-nn. (*)由此得关于n 的一元二次方程09606025.1947010022≈+-n n ,其解为53.11318.8121≈≈n n ,,其中53.1132≈n 不满足式(*),因此53.1132≈n 为增根,故应舍去.于是,以概率0.95在16个小时内最多可以组装81~82件产品.例5.27(列维-林德伯格定理) 将n 个观测数据相加时,首先对小数部分按“四舍五入”舍去小数位后化为整数.试利用中心极限定理估计,(1) 试当n =1500时求舍位误差之和的绝对值大于15的概率;(2) 估计数据个数n 满足何条件时,以不小于90%的概率,使舍位误差之和的绝对值小于10的数据个数n .解 设)1500,,2,1( =iX i 是第i 个数据的舍位误差;由条件可以认为)1500,,2,1( =i X i 独立且都在区间]5.0 5.0[,-上服从均匀分布,从而12/10==i i X X D E ,.记n n X X X S +++= 21为n 个数据的舍位误差之和,则12/0n S S n n==D E ,.根据列维-林德伯格中心极限定理,当n 充分大时n S 近似服从)12/0(n N ,.记)(x Φ为)1,0(N 分布函数.(1) 由于12n S n近似服从标准正态分布,可见{}.1802.02)]34.1(1[34.112/150012/15001512/150015150015001500=⨯-≈⎭⎬⎫⎩⎨⎧>=⎭⎬⎫⎩⎨⎧>=>ΦS S S P P P(2) 数据个数n 应满足条件:{}.90.012/1012/10=⎭⎬⎫⎩⎨⎧≤=≤n n S S n n P P 由于12n S n近似服从)1,0(N ,可见51.4436449.11210 6449.112/102≈⎪⎪⎭⎫ ⎝⎛≈,n . 于是,当n >443时,才能使误差之和的绝对值小于10的概率不小于90%. 〖证明题〗例5.35(棣莫佛-拉普拉斯定理) 利用列维-林德伯格定理,证明棣莫佛-拉普拉斯定理.证明 设随机变量n X X X ,,,21 相互独立,同服从0-1分布;,,,,,npq S np S X X X S n i pq X p X n n n n i i ==+++====D E D E 21),,2,1(其中p q-=1. n X X X ,,,21 满足列维-林德伯格定理的条件:n X X X ,,,21 独立同分布且数学期望和方差存在,当n 充分大时近似地n n X X X S +++= 21~),(npq np N .4.55(证明不等式) 设X 是任一非负(离散型或连续型)随机变量,已知X的数学期望存在,而0>ε是任意实数,证明不等式{}εεXX E P ≤≥.证明 (1) 设X 是离散型随机变量,其一切可能值为}{i x ,则{}.}{1}{}{}{11εεεεεεεXx X x x X x x Xx XX iiii x i i x i ix i x i E P P P P P ==≤=≤====≥∑∑∑∑≥≥≥(2) 设X 是连续型随机变量,其概率密度为)(x f ,则{}.d )(1d )(1d )(0εεεεεεXx x f x x x f x x x f X E P ≤≤≤=≥⎰⎰⎰∞∞∞例4.00(切比雪夫不等式) 设事件A 出现的概率为=p 0.5,试利用切比雪夫不等式,估计在1000次独立重复试验中事件A 出现的次数在450到550次之间的概率α. 解 设n ν是1000次独立重复试验中事件A 出现的次数,则.,),,2505.010005005.010005.0 1000(~2=⨯==⨯=X X B n D E ν由用切比雪夫不等式,知{}{}.9.050250150|550|5504502=-≥≤-=≤≤=n n νναP P 例5.3. 设随机变量X 的数学期望为μ,方差为2σ,(1)利用切比雪夫不等式估计:X 落在以μ为中心,σ3为半径的区间 内的概率不小于多少?(2)如果已知),(~2σμN X ,对上述概率,你是否可得到更好的估计?解:(1)()()()0.88899131)3()3(222=-=-≥<-=<-σσσσμσX D X P X E X P (2)()()⎪⎪⎭⎫⎝⎛<-=<-DX DX X E X P X E X P σσ3)3( ()0.99743322=≈⎪⎪⎭⎫⎝⎛<-=⎰∞--dt e DX X E X P t例5.4. 利用切比雪夫不等式来确定,当抛掷一枚均匀硬币时,需抛多少次,才能保证 正面出现的频率在0.4至0.6之间的概率不小于90%,并用正态逼近去估计同一问题。
2.4连续型随机变量及其概率密度函数

概率论与数理统计Probability and Statistics —概率论与数理统计教学组—2.4 连续型随机变量及其概率密度函数第2章随机变量及其分布学习要点常见的连续型随机变量的分布连续型随机变量及概率密度函数:;:例3 在区间(0,5)上随机取一数X ,(1)写出X 的概率密度函数和分布函数;(2)该数X 的取值不小于2的概率为多少?解(1)随机变量X 在区间(0,5)上服从均匀分布,故其概率密度函数和分布函数为1,05()50,x f x ,其他 000,()(),05551,5x x x dt x F x f x dx x x(2)随机变量X 的取值不小于2,即25521()03{2}55P X d f x dx dx x 或 23{2}1{2}1{2}1(2)155P X P X P X F . 连续型随机变量及概率密度函数例4 设顾客在银行窗口接受服务的时间(单位:分)服从参数为0.1的指数分布. 如果某人刚好在你前面到窗口接受服务,试求你将等待(1)不超过10分钟,(2)10分钟到20分钟之间的概率.解 令X 表示顾客在银行窗口接受服务的时间,则X 的概率密度为101,0()100,0xe xf x x 101001011010001(1){10}()0()110x x P X f x dx dx e dx e e ; 202012101010101(2){1020}10x x P X e dx e e e .连续型随机变量及概率密度函数人们编制了()x的函数表,可供查用. 例如,可查(1.12)0.86864.连续型随机变量及概率密度函数例5 设随机变量X ~(3,9)N ,求:(1) {25},{36};P X P X (2)确定常数a ,使得{}{}P X a P X a .解 (1)令3~(0,1)3X Y N2335312{25}{}{}33333X P X P P Y2121()()()[1()]0.3779,3333393333{36}{9}{3}{}{}3333X X P X P X P X P P{2}{2}1(2)(2)2[1(2)]0.0456.P Y P Y(2) 由 {}{}P X a P X a ,得 1{}{}P X a P X a33131{}{},()33232X a a P X a P ,3=03a 所以,即有3a .连续型随机变量及概率密度函数例6随机变量~(0,1)X N ,求0.005z 和0.0052z .解 0.0050.005{}1{}0.005P X z P X z , 0.005{}0.995P X z ,即 0.005()0.995z , 查表可得, 0.005 2.575z . 另外 0.0050.00252z z ,即 0.0025()10.00250.9975z ,查表可得, 0.0025 2.81z ,也就是 0.00522.81z .x()x 0y 0.0025z 0.005=0.002520.0025z 2连续型随机变量及概率密度函数小结连续型随机变量及其概率密度函数连续型随机变量及其概率密度常见的连续型随机变量的分布Harbin Engineering University。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) 正态分布
若随机变量 X 的概率密度函数为
f(x)
1
(x)2
e 22
2
x
, 为常数, 0
则称 X服从参数为 , 2 的正态分布 记作 X~ N ( , 2 )
正态分布是德国数学家高斯在研究误差理论时得到的, 故正态分布也称为高斯分布.
整理ppt 17
f (x) 的性质:
1. 图形关于直线 x = 对称, 即f ( + x) = f ( - x)
1 15
0
0≤x≤15 其他
15
1
P (8 X 1) 5 8f(x )d x 1(1 5 5 8 ) 0 .47
整理ppt 9
(2) 指数分布 若 X的概率密度函数为
ex, x0
f (x) 0,
其他 > 0 为常数
则称X服从参数为 的指数分布,记作
X~E()
整理ppt 10
* 显然 f (x)0 ,且
*
f(x )d x
e x d x 1
0
整理ppt 11
容易求得,指数分布的分布函数为
1ex, x0 F(x)0, x 0
整理ppt 12
P(a X b) bexdx a F(b) F(a)
ea eb 应用场合 用指数分布描述的实例有:
随机服务系统中的服务时间
电话问题中的通话时间
为什么叫“正态”分布
正态分布密度呈现“中间高,两头低”的形态, 它描述了自然界大量存在的随机现象,所以正态分布 是自然界的一种“正常状态 ( normal )”的分布.
正态分布具有许多良好的性质,许多分布可用 正态分布来近似,在数理统计中解决实际问题时用 得最多的就是正态分布或与正态分布有关.
整理ppt 22
状不变化,只是位置不同。
— 形状参数
固定 ,对于不同的 ,f ( x) 的形状不同.
若 1< 2 则
1
21
1
22
前者取
附近值的概率更大。
整理ppt 20
整理ppt 21
服从正态分布的指标有什么特点
一般说,若影响某一数量指标的随机因素很多,而每 个因素所起的作用都不太大,则这个指标服从正态分布.
当 axb时
x
x
F (x) f(x)d x 0d x0
F (x )xf(x )d x a 0 d x x 1d x x a
ab a b a
整理ppt 6
当 xb 时
x
a
b1
x
F ( x )f( x ) d x 0 d x d x 0 d 1 x
a b a b
即
0
xa
F(x)
xa ba
axb
1
xb
整理ppt 7
f ( x)
a
b
F( x)
a
b 整理ppt
x
x
8
例2 宁波的363路公共汽车每隔15分钟一趟,
若一乘客到某站点的时间是随机的,问其候车时间 超过8分钟的概率是多少?
解 设X为候车时间,则X在[0,15]上服从均匀分布, 其概率密度函数为
f
(x)
气象中的月平均气温、湿度、降水量等 整理ppt 24
(4) 标准正态分布N (0,1)
密度函数 (x)
1
x2
e2
2
x
分布函数 (x)
1
t2
e 2dt
2
其值有专门的表供查. 25
且在 x = 时, f (x) 取得最大值
1 2
2. 在 x = ± 时, 曲线 y = f (x) 在对应的
点处有拐点
3. 曲线 y = f (x) 以 x 轴为渐近线
4. 曲线 y = f (x) 的图形呈单峰状 整理ppt 18
• 正态分布图象
整理ppt 19
— 位置参数
即固定 , 对于不同的 , 对应的 f (x)的形
第二章
随机变量及其分布
整理ppt 1
第三讲
常见的连续性 随机变量的分布
整理ppt 2
导读内容
1、常用连续型随机变量的分布有哪些?它 们的概率密度函数是怎样的?
2、均匀分布、正态分布和指数分布有哪些 重要应用?如何解决实际问题?请查找资 料举例说明。
整理ppt 3
常见的连续性随机变量的分布
(1) 均匀分布 若X的概率密度函数为
(2) P(XX)P(X P (X ,X ) )
整理ppt 15
P(X) P(X )
e3() e3
e3
由 e3 P(X ) ,知元件寿命至少为β的概率等于已 使用时间为α的条件下,剩余寿命至少为β的概率, 这一性质被称为指数分布的无记忆性.
故又把指数分布称为“永远年轻”的分 布
整理ppt 16
高尔顿钉板试验
这是什么曲线?
-8 -7 -6 -5 -4 -3 -2 -1 1O 2 3 4 5 6 7 8
整理ppt
x
23
可用正态变量描述的实例极多:
各种测量的误差; 炮弹弹着点; 工厂产品的尺寸; 农作物的收获量;
海洋波浪的高度; 金属线抗拉强度; 一个地区的家庭年收入; 一个班的某门课程的考试成绩; 成年人的各种生理指标: 身高、体重、血压、视力、智商等
1 f (x) ba
0
(a x b) 其他
则称X服从区间( a , b)上的均匀分布或称X服从
参数为 a , b的均匀分布,记作
X~U(a,b)
整理ppt 4
* 显然 f (x)0,且
b
f(x)dx
1 dx 1
a ba
* 对于 a,b 中任一子区间 c,d ,有
d
P (cXd)
d
x dc
无线电元件的寿命
指数分布 常作为各种“寿命”
动物的寿命
整理ppt
分布的近似
13
例3 假设某元件的寿命服从参数 = 0.0015的指数
分布,求它使用1000小时后还没有坏的概率.
解 设X为该元件的寿命,则
P(X 1000) f (x)dx 1000 0.0015e0.0015xdx e1.5 1000 0.223
整理ppt 14
例 4: 设某种电子元件的寿命 X(以年记)服从参 数λ=3 的指数分布,求
(1) 寿命在 0.5 年和 1 年之间的概率; (2) 设已经正常使用了α年,求还能够继续使用 β年的概率.
解(1)P(0.5X1) 0 1 .5 3 e 3 x d x e 3 x 1 0 .5 e 1 .5 e 3
cba ba
即 X落在 a中,b任 一子区间 中c的,d概 率只与区间长度
有关,而与位置无关,这反映了某种“等可能性”,即 在
区间 上a,b“ 等可能取值”
整理ppt 5
例1:设连续型随机变量X在[a,b]上服从均匀分布, 求其分布函数.
解 因为
1
f
(
x)
b
a
0
(a x
