安培环路定理(精)
合集下载
安培环路定理
安培环路定理
静电场
1
E dS
S
0
q内有源场Fra bibliotekLE dl 0
保守场
恒定磁场
SB dS 0
无源场
LB dl ?
一、 安培环路定理
以无限长直电流的磁场为例说明
1、圆形积分回路
选在垂直于长直载流导线的平面内,以导线与平面
交点o为圆心,半径为 r 的圆周路径 L,其指向与电流
成右旋关系。
练习:如图,流出纸面的电流为 2I ,流进纸面的电 流为 I ,则下述各式中那一个是正确的?
( A)
B• L1
dl
2
0I
(C )
B • dl
L3
0I
(B)
B• L2
dl
0I
( D)
B • dl
L4
0I
2I •
L1 I
L2
L3
L4
(D)
二、安培环路定理的应用
B • dl 0 Ii
...............
B
I
2)选取回路
作矩形安培环路,如图 规定:顺时针绕向为正
M
NB
++++++++++++
P
LO
N O p M
l B d l M B d l N B d l O B d l P B d l
B MN 利用安培环路定理求 B
B MN 0nMNI
B 0nI
方向可由右手螺旋法定。 无限长直螺线管内为均匀磁场
3、求螺线环内的磁感应强度
已知:I 、N、R1、R2
N——导线总匝数
静电场
1
E dS
S
0
q内有源场Fra bibliotekLE dl 0
保守场
恒定磁场
SB dS 0
无源场
LB dl ?
一、 安培环路定理
以无限长直电流的磁场为例说明
1、圆形积分回路
选在垂直于长直载流导线的平面内,以导线与平面
交点o为圆心,半径为 r 的圆周路径 L,其指向与电流
成右旋关系。
练习:如图,流出纸面的电流为 2I ,流进纸面的电 流为 I ,则下述各式中那一个是正确的?
( A)
B• L1
dl
2
0I
(C )
B • dl
L3
0I
(B)
B• L2
dl
0I
( D)
B • dl
L4
0I
2I •
L1 I
L2
L3
L4
(D)
二、安培环路定理的应用
B • dl 0 Ii
...............
B
I
2)选取回路
作矩形安培环路,如图 规定:顺时针绕向为正
M
NB
++++++++++++
P
LO
N O p M
l B d l M B d l N B d l O B d l P B d l
B MN 利用安培环路定理求 B
B MN 0nMNI
B 0nI
方向可由右手螺旋法定。 无限长直螺线管内为均匀磁场
3、求螺线环内的磁感应强度
已知:I 、N、R1、R2
N——导线总匝数
安培环路定理

1
2
I
B1
2
1 2
0i
0i
I
3 B2 0
B3 0i
1
2
I
B1 B3 0
3
I
B2 0i
作业:练习三
例6 已知无限长圆桶上均匀分布电荷,面密度σ,角初 速度ω0 , 角加速度β,求t时刻内部旳磁感应强度
解:相当于密绕螺线管
B 0nI
nI 为单位长度旳电流,
nI 2 R 1 (0 t) / 2 R(0 t)
围电流时,B矢量沿 该闭合曲线旳线积分 为零。
4、闭合曲线内包围多根载流导线电流
I2 I1
S
B dl L
L (B1 B2 ... Bn ) dl
IN
L
L
B1
dl
L B2 dl
... L Bn dl
0 I1 0 I2 ... 0 I N
N
B dl L
3、磁场分布
n, I
Bin 均匀分布
外部磁场 Bout 0 内部磁场: Bin 0nI 0 j
通电稀疏螺线管空间旳磁场 通电密绕螺线管空间旳磁场
例2 求密绕载流螺线绕环内旳磁场
解:1 对称性分析;环内B 线为同心圆,环外 B为零。
2 选环路。
Bdl L
2 π RB
0 NI
B 0 NI
(1) 分析磁场旳对称性,判断B旳方向;
(2) 选择合适旳闭合回路,含方向;
(3) 求出 B dl ? 和 0 I ?
L
L内
(4) 利用
B dl
L
0 I ,求出B旳值。
L内
环路L旳选择:
(1) L上旳B大小相等,方向相同或B与dl 平行或垂直。
9.4安培环路定理
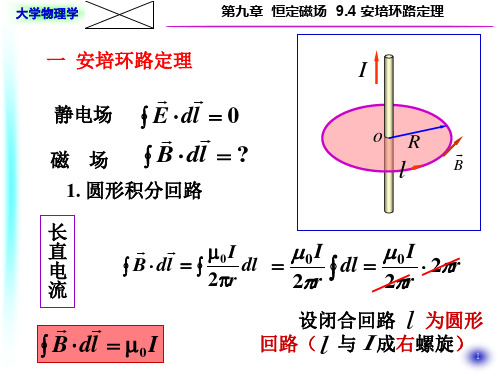
电流在回路之外
d
I
B1
r1
dl1
B2
dl2
r2
l
B1
0I
2π r1
,
B2
0I
2π r2
B1
dl1
B2
dl2
0I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
3
大学物理学
第九章 恒定磁场 9.4 安培环路定理
多电流情况
I1
I2
I3
l
B B1 B2 B3
Bdl
l
0(I2
I3)
推广:
➢ 安培环路定理
n
B dl 0 Ii
i 1
4
大学物理学
第九章 恒定磁场 9.4 安培环路定理
安培环路定理
n
B dl 0 Ii
i 1
一闭合即路在径真的空积的分稳的恒值磁,场等中于,磁0感乘应以强该度闭合B 路沿径任
所包围的各电流的代数和.
注意
电流 I 正负的规定 :I 与 L 成右螺旋时, I 为正;反之为负.
➢ 分析对称性
电流分布 磁场分布
轴对称
I R
26
大学物理学
l
第九章 恒定磁场 9.4 安培环路定理
B 的方向判断如下:
r
dS1
O
dS2
dB
dB2 dB1
P
27
大学物理学
第九章 恒定磁场 9.4 安培环路定理
➢ 作积分环路并计算环流
如图 r R
B • dl Bdl 2rB
➢
利用安培环路定理求
说 明
B • dl 0 Ii 0 (I2 I3 )
安培环路

B d l B d cos l Brd 0I 0 I d B dl rd 2π 2πr
d
l
I
dl
B
r
I r1
r2
l
B d l B d l 0 1 1 2 2 结论: d l 0 B
l
(3) 多电流情况
I1
B 0nI
无限长载流螺线管内部磁场处处相等 , 外部磁场为零.
2、求无限长载流圆柱导体内外的磁场。设圆柱体半 径为R,面上均匀分布的总电流为I。 I
解:沿圆周L的B环流为
(L )
R
I d l B 2 r 0 内 B
dB
P
dB d B
当 r R 时 , I I B 2 r I 内 0 0I B 2 r I 2 当 r R 时 , I r 内 2 R r2 I 0 B2 r I B r 0 2 2 R 2 R
d l I 0 B
l
R
l
I
B
若电流反向时,则:
I 0 l B dl 2πRl dl 0I
对任意形状的回路 B 0 I 2 r
I
l 2 I 0 B d l d 结论: B d l I 0 l 0 l 2 0I 0 I (2) 闭合曲线不包围长直电流: B2 B1 B2 2 π r2 2 π r1 B1 μ μ 0I 0I B d l1 d φ B dφ l2 d φ 1 2 d dl 2 π 2 π 2 dl1
dB1
解 1)对称性分析 2)选取回路 设:面电流密度为j
d dB
P
安培环路定理

l
r R, B d l 0 I
l
第10章 稳恒磁场
10–2 安培环路定理
12
例10.2 如图所示,一无限大导体薄平板垂直于纸 面放置,其上有方向指向读者的电流,通过与电流 方向垂直的单位长度的电流大小为i,求其磁场分布 .
第10章 稳恒磁场
10–2 安培环路定理
13
解:
ab cd l
a b c d
b c d a B dl B dl B dl B dl B dl 0li
L
2Bl 0li
1 B 0i 2
以上结果说明:在无限大均匀平面电流两侧的磁场 是匀强磁场,且大小相等、方向相反.其磁感应线在 无限远处闭合,与电流亦构成右螺旋关系.
L L
2 rB 0 I
0 I B (r R ) 2 r
2)圆柱体内任一点Q
I 2 L B d l 2 rB 0 R2 r 0 Ir B (r R2 安培环路定理
10
B
的方向与
r R,
第10章 稳恒磁场
10–2 安培环路定理
B d l 0 ( I1 I1 I1 I 2 )
L
I1 I1
L
I2 I 3 I1
( 0 I1 I 2)
问 1) B是否与回路 L 外电流有关? 2)若 B d l 0 ,是否回路 L上各处 B 0? L 是否回路 L 内无电流穿过?
第10章 稳恒磁场
r R,
I
I 构成右手螺旋关系 0 Ir B 2 2 R 0 I B 2 r
0 I 2 R
r R, B d l 0 I
l
第10章 稳恒磁场
10–2 安培环路定理
12
例10.2 如图所示,一无限大导体薄平板垂直于纸 面放置,其上有方向指向读者的电流,通过与电流 方向垂直的单位长度的电流大小为i,求其磁场分布 .
第10章 稳恒磁场
10–2 安培环路定理
13
解:
ab cd l
a b c d
b c d a B dl B dl B dl B dl B dl 0li
L
2Bl 0li
1 B 0i 2
以上结果说明:在无限大均匀平面电流两侧的磁场 是匀强磁场,且大小相等、方向相反.其磁感应线在 无限远处闭合,与电流亦构成右螺旋关系.
L L
2 rB 0 I
0 I B (r R ) 2 r
2)圆柱体内任一点Q
I 2 L B d l 2 rB 0 R2 r 0 Ir B (r R2 安培环路定理
10
B
的方向与
r R,
第10章 稳恒磁场
10–2 安培环路定理
B d l 0 ( I1 I1 I1 I 2 )
L
I1 I1
L
I2 I 3 I1
( 0 I1 I 2)
问 1) B是否与回路 L 外电流有关? 2)若 B d l 0 ,是否回路 L上各处 B 0? L 是否回路 L 内无电流穿过?
第10章 稳恒磁场
r R,
I
I 构成右手螺旋关系 0 Ir B 2 2 R 0 I B 2 r
0 I 2 R
安培环路定理

(1)管内:取L矩形回路 abcda
边在轴上,两边与轴平行,另
aP b
两个边垂直于轴。
LB dl Bab ab Bcd cd Bab ab
e
Q
f
0I 0nI ab
d
c
∞
B内 onI 其方向与电流满足右手螺旋.
(2)管外 :
取回路efbae同理可证,无限长直螺线管外任一点的磁场为
A(rQ )
0I 2
ln
r Q
r P
A(rP )
A(rQ
)
0I 2
ln
r Q
r
-I
r P
P
两式相加,得:
A(rP )
A(rQ )
0I 2
ln
rQ rP
rP rQ
0I 2
ln
rP rP
A(rP )
A(rQ )
0I 2
ln
r P
r P
若选Q点的矢势为零,则
A(rP )
0I 2
ln
r P
r P
例2.一无限长载流圆柱导体,半径为R, 电流I均匀分布
ldr
0I 2
l
ln
rQ r
A(rP ) A(rQ )
0I 2
ln
rQ rP
+I
Q
若选Q点的矢势为零,则
A(rp
)
0I 2
ln
rQ rP
r P
注意:若选Q点在无穷远处或导线
上,磁矢势将无意义.
讨论:两根平行的载流直导线,电流大 小相等方向相反,求磁矢势.
选Q点在两直线电流之间垂线的中点处.
A(rP )
B dS 0
11.4 安培环路定理

I
B // dl
环路内电流代数和为:
2
r 0 B dl B 2 r R 2 I
0 2
R
r
I r 2 r 2 I I 2 R R
L
0 I B r r 2 2R
2.圆柱体外一点 r > R 区域
I
在圆柱体外作一环路,
B dl Bdl cos
L 0
1. I 为环路内的电流代数和。
只与环路内的电流有关, B dl 2.环流
而与环路外电流无关。
3. B为环路上一点的磁感应强度,它与环路内外电流 都有关。
若 B dl 0 并不一定说明环路上各点的 B 都为 0。 若 B dl 0 环路内并不一定无电流。
L
I
B
0 I
要求环路上各点 B 大小相等,B 的方向 与环路方向一致, B // dl , cos 1
dl
或 Bdl ,
五、解题方法
cos 0
环路要经过所研究的场点。
1.场对称性分析; 2.选取环路; 3.确定环路内电流的代数和 I ; 4.应用环路定理列方程求解。 应用环路定理求 B 要比毕萨定律简 单,但只适用于具有高度对称的场。
B
I
左边:
L
B dl
L
r
L
Bdl cos
由于环路上各点的 B 大小相等; 且 B // dl ;θ=0
0 I B dl 2r 0 I 2r L
I 向下时为负值。
L B dl 0 I 左边=右边定理成立。
当环路为任意形状时:
B dl B2r 0 I
安培环路定理

i
i
nabI
利用安培环路定理求
............... B
B ab 0 nabI
0 nI B 0 内 外
a
d
b
c
I
计算环流
利用安培环路定理求 B
B dl 0 NI
0 NI 内 B 2r 外 0 R1、R2 R1 R2
D.若
静电场
稳恒磁场
B dl 0 I i
i
E dl 0
电场有保守性,它是 保守场,或有势场
磁场没有保守性,它是 非保守场,或无势场
1 s E dS 0 qi
电力线起于正电荷、 止于负电荷。 静电场是有源场
B dS 0
B dl 0 I
2、任意积分回路
B dl B cos dl
0 I cos dl 2r
0 I rd 2r
0 I 2 2
.
I
r
d
B dl
B dl 0 I
3、回路不环绕电流
B dl
r
练习:同轴的两筒状导线通有等值反向的电流I,
求 B的分布。
(1) r R1 , B 0
0 I ( 2) R1 r R2 , B 2r
R2
R1
I
r I
(3) r R2 , B 0
如图所示, 将半径为R的无限长薄圆柱管沿轴向割去 一宽度为a的狭缝, x轴穿过该狭 缝,且a << R, 电流沿轴向 均匀分布,单位长度的电流为i, 则轴线上任意点处的磁感 应强度的大小和方向为:
i
nabI
利用安培环路定理求
............... B
B ab 0 nabI
0 nI B 0 内 外
a
d
b
c
I
计算环流
利用安培环路定理求 B
B dl 0 NI
0 NI 内 B 2r 外 0 R1、R2 R1 R2
D.若
静电场
稳恒磁场
B dl 0 I i
i
E dl 0
电场有保守性,它是 保守场,或有势场
磁场没有保守性,它是 非保守场,或无势场
1 s E dS 0 qi
电力线起于正电荷、 止于负电荷。 静电场是有源场
B dS 0
B dl 0 I
2、任意积分回路
B dl B cos dl
0 I cos dl 2r
0 I rd 2r
0 I 2 2
.
I
r
d
B dl
B dl 0 I
3、回路不环绕电流
B dl
r
练习:同轴的两筒状导线通有等值反向的电流I,
求 B的分布。
(1) r R1 , B 0
0 I ( 2) R1 r R2 , B 2r
R2
R1
I
r I
(3) r R2 , B 0
如图所示, 将半径为R的无限长薄圆柱管沿轴向割去 一宽度为a的狭缝, x轴穿过该狭 缝,且a << R, 电流沿轴向 均匀分布,单位长度的电流为i, 则轴线上任意点处的磁感 应强度的大小和方向为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温州大学物理与电子信息学院
二.安培环路定理
思考3:当P1和P2分别无限趋近于面S的时候,它们 对应的立体角如何?
2 1 4
问题4:这里的正负号是如何确定的? 与两个回路的方向相关 如果两个回路不连套,则环绕安培回路一周的立体 角回到原来地方,其积分为零。 对于多个载流回路情况,只需要采用叠加原理即可 因此,定理得证。
I3
l
温州大学物理与电子信息学院
二.安培环路定理
练习2:如图所示,移动电流I3,哪里物理量变化?
B dl 0 I i 0 ( I 2 I 3 )
?
改 变
?
不 变
I4
I1 I 2
I3
l
位置移动
温州大学物理与电子信息学院
三.环路定理应用
当场源分布具有高度对称性时,利用安培环路定理 计算磁感应强度: 例题2:无限长载流圆柱导体 已知:I、R 电流沿轴向,在截面上均匀分布
I
0
R
利用安培环路定理求 B
r
B
2rB 0 I 0 I B 2r
温州大学物理与电子信息学院
三.环路定理应用
作积分环路并计算环流
如图 r R
I R
B dl Bdl 2rB
B dl 0 I
利用安培环路定理求B
I
(L) (L内)
其中电流方向和环路L的环绕方向满足右手螺旋 的为正,反之为负。(请看教材P105)
温州大学物பைடு நூலகம்与电子信息学院
二.安培环路定理
2. 定理证明 如图板书所示,安培环路连套载流回路,在安培 环路靠近载流回路的上下两面取两点P1和P2,将 环路分为两部分,则: P2 P1 B dl B dl B dl
二.安培环路定理
1. 定理表述
思考2:静电场有环路定理 E l 0 d 的环路积分结果会如何呢? B dl ?
磁场
磁感应强度沿任何闭合环路L的线积分,等于穿 过该环路所有电流的代数和的 0 倍。用数学公 式表达为: B dl 0 I
r
α
Idl
B
dB
L
L
0 Idl r 4r 3
温州大学物理与电子信息学院
一.毕奥定理复习
2. 复习例题 例题1:无限长载流线圈L,其电流为I,其所包围的 曲面对空间某点P张开的立体角为 ,则证明它 0 I L 在P点激发的磁场为 B 4
在不改变面积的情况下,移动线圈改变r即可得到 微分。因此,下面我们对线圈移动一个小距离 dl 0 I dl r 同时,观察毕奥定理 B 3 4 r L 要出现面积相关的量,则 dl dl r 0 I dl r dl 0 I 0 I B dl 3 3 4 L r 4 L r 4
安培环路定理
毕奥定理复习
安培环路定理 环路定理应用
温州大学物理与电子信息学院
一. 毕奥定理复习
1. 基本步骤 a. 任取电流元Idl, 求出其在 场点 P 产生的磁感dB的大小 dB p 与方向; b. 分析dB方向是否变化: 若不 变,直接积分; 若变化, 则要将 dB 适当 = 的分解 , 对各分量分 别积分, 然后再合成起来. p
温州大学物理与电子信息学院
一.毕奥定理复习
因为闭合曲面的立体角为零,则: 0 0 I 即: d 因此: B dl d 4 又因为: d dl 0 I 所以: B 4
温州大学物理与电子信息学院
I
R
分析对称性
电流分布
轴对称
磁场分布
温州大学物理与电子信息学院
三.环路定理应用 B 的方向判断如下:
r
l
dS1
O
d B2
dB
P
dB1
dS 2
温州大学物理与电子信息学院
三.环路定理应用
作积分环路并计算环流
如图
rR B dl Bdl 2rB
B dl 0 I
1 1 2 2
问题2:当P1和P2分别无限趋近于面S的时候,穿过 S面的回路L2的积分为零,为什么? 该回路长度趋近于零,而磁感应强度有限且连续。 问题3:当P1和P2分别无限趋近于面S的时候,穿过 S面的回路L1的积分为多少? P2 P2 0 I 0 I 0 I P1 ( L1 ) 4 dl P1 ( L1 ) 4 d 4 2 1
P 1 ( L1 ) P2 ( L2 )
(L)
0 I 根据例题1的结论: B 4 0 I 则有: B dl dl 4 (L) (L)
温州大学物理与电子信息学院
二.安培环路定理
则有:
(L)
P2 B dl
1
P 0 I dl B dl P ( L ) 4 P (L )
B
0
I 2 0 r 2 R 0 Ir B 2R 2
r
温州大学物理与电子信息学院
温州大学物理与电子信息学院
二.安培环路定理
练习1:如图所示,安培回路包围住的电流代数?
B dl 0 I i 0 ( I 2 I 3 )
由 环 路 内 电 流 决 定 环 路 所 包 围 的 电 流
由环 环路 路上 内的 外磁 电感 流应 产强 生度
I4
I1 I 2
解: 如图所示,根据毕奥萨划 dl
尔定理,P点的磁感应强度有
思考1:根据立体角的定义,将结果和 目前情况联系起来?
0 I dl r B 3 4 r L
r
P
温州大学物理与电子信息学院
一.毕奥定理复习
根据立体角定义,线圈面积 S r0 2 对P点张开的立体角为: r 问题1:要出现梯度或者说微分,对线圈有何要求?
二.安培环路定理
思考3:当P1和P2分别无限趋近于面S的时候,它们 对应的立体角如何?
2 1 4
问题4:这里的正负号是如何确定的? 与两个回路的方向相关 如果两个回路不连套,则环绕安培回路一周的立体 角回到原来地方,其积分为零。 对于多个载流回路情况,只需要采用叠加原理即可 因此,定理得证。
I3
l
温州大学物理与电子信息学院
二.安培环路定理
练习2:如图所示,移动电流I3,哪里物理量变化?
B dl 0 I i 0 ( I 2 I 3 )
?
改 变
?
不 变
I4
I1 I 2
I3
l
位置移动
温州大学物理与电子信息学院
三.环路定理应用
当场源分布具有高度对称性时,利用安培环路定理 计算磁感应强度: 例题2:无限长载流圆柱导体 已知:I、R 电流沿轴向,在截面上均匀分布
I
0
R
利用安培环路定理求 B
r
B
2rB 0 I 0 I B 2r
温州大学物理与电子信息学院
三.环路定理应用
作积分环路并计算环流
如图 r R
I R
B dl Bdl 2rB
B dl 0 I
利用安培环路定理求B
I
(L) (L内)
其中电流方向和环路L的环绕方向满足右手螺旋 的为正,反之为负。(请看教材P105)
温州大学物பைடு நூலகம்与电子信息学院
二.安培环路定理
2. 定理证明 如图板书所示,安培环路连套载流回路,在安培 环路靠近载流回路的上下两面取两点P1和P2,将 环路分为两部分,则: P2 P1 B dl B dl B dl
二.安培环路定理
1. 定理表述
思考2:静电场有环路定理 E l 0 d 的环路积分结果会如何呢? B dl ?
磁场
磁感应强度沿任何闭合环路L的线积分,等于穿 过该环路所有电流的代数和的 0 倍。用数学公 式表达为: B dl 0 I
r
α
Idl
B
dB
L
L
0 Idl r 4r 3
温州大学物理与电子信息学院
一.毕奥定理复习
2. 复习例题 例题1:无限长载流线圈L,其电流为I,其所包围的 曲面对空间某点P张开的立体角为 ,则证明它 0 I L 在P点激发的磁场为 B 4
在不改变面积的情况下,移动线圈改变r即可得到 微分。因此,下面我们对线圈移动一个小距离 dl 0 I dl r 同时,观察毕奥定理 B 3 4 r L 要出现面积相关的量,则 dl dl r 0 I dl r dl 0 I 0 I B dl 3 3 4 L r 4 L r 4
安培环路定理
毕奥定理复习
安培环路定理 环路定理应用
温州大学物理与电子信息学院
一. 毕奥定理复习
1. 基本步骤 a. 任取电流元Idl, 求出其在 场点 P 产生的磁感dB的大小 dB p 与方向; b. 分析dB方向是否变化: 若不 变,直接积分; 若变化, 则要将 dB 适当 = 的分解 , 对各分量分 别积分, 然后再合成起来. p
温州大学物理与电子信息学院
一.毕奥定理复习
因为闭合曲面的立体角为零,则: 0 0 I 即: d 因此: B dl d 4 又因为: d dl 0 I 所以: B 4
温州大学物理与电子信息学院
I
R
分析对称性
电流分布
轴对称
磁场分布
温州大学物理与电子信息学院
三.环路定理应用 B 的方向判断如下:
r
l
dS1
O
d B2
dB
P
dB1
dS 2
温州大学物理与电子信息学院
三.环路定理应用
作积分环路并计算环流
如图
rR B dl Bdl 2rB
B dl 0 I
1 1 2 2
问题2:当P1和P2分别无限趋近于面S的时候,穿过 S面的回路L2的积分为零,为什么? 该回路长度趋近于零,而磁感应强度有限且连续。 问题3:当P1和P2分别无限趋近于面S的时候,穿过 S面的回路L1的积分为多少? P2 P2 0 I 0 I 0 I P1 ( L1 ) 4 dl P1 ( L1 ) 4 d 4 2 1
P 1 ( L1 ) P2 ( L2 )
(L)
0 I 根据例题1的结论: B 4 0 I 则有: B dl dl 4 (L) (L)
温州大学物理与电子信息学院
二.安培环路定理
则有:
(L)
P2 B dl
1
P 0 I dl B dl P ( L ) 4 P (L )
B
0
I 2 0 r 2 R 0 Ir B 2R 2
r
温州大学物理与电子信息学院
温州大学物理与电子信息学院
二.安培环路定理
练习1:如图所示,安培回路包围住的电流代数?
B dl 0 I i 0 ( I 2 I 3 )
由 环 路 内 电 流 决 定 环 路 所 包 围 的 电 流
由环 环路 路上 内的 外磁 电感 流应 产强 生度
I4
I1 I 2
解: 如图所示,根据毕奥萨划 dl
尔定理,P点的磁感应强度有
思考1:根据立体角的定义,将结果和 目前情况联系起来?
0 I dl r B 3 4 r L
r
P
温州大学物理与电子信息学院
一.毕奥定理复习
根据立体角定义,线圈面积 S r0 2 对P点张开的立体角为: r 问题1:要出现梯度或者说微分,对线圈有何要求?
