厦门大学《应用多元统计分析》习题第04章 判别分析
厦门大学《应用多元统计分析》试题A答案

一、判断题 1. 正确
( ) 证明: ∀c = c1, c2 ,"cp ,
∑∑ c′∑c =
cic jσ ij
ji
= ∑∑cic j [E(Xi − E(Xi ))(Xj − E(Xj ))]
ji
= E⎢⎡∑c j (Xi − E(Xi ))∑ci (Xj − (E Xj ))⎥⎤
=
(n
−1)[
(n −1) p
n(X − μ0 )′S−1
n(X − μ0 )]
八、
( ) ( ) 在典型相关分析中 X (1) =
X
(1)
1
,
X
(1)
2
"
X
(1)
p
′
,
X
(2)
=
X 1(2 ) ,
X
(2
2
)
"
X
(2
q
)
′
是
两个相互关联的随机向量,分别在两组变量中选取若干有代表性的综合变量 Ui、Vi,使
计算共因子的方差贡献得:
g12
=
λ1
= 1.9633;
g
2 2
=
0.6795;
g 32
=
0.3572 ,分别为公共因子
F1, F2 ,
F
对X
的贡
献,是衡量每个公共因子的相对重要性的尺度。
三、解:先求三元总体 X 的协方差阵 ∑ 的特征根,
σ2 −λ ∑ −λE = ρσ 2
0
ρσ 2 σ2 −λ
ρσ 2
−00.7.6439749⎟⎟⎞⎜⎜⎜⎛ 1.9633 − 0.1772⎟⎠⎜⎜⎝ 0.4479 ⎟⎞ − 0.3812⎟ − 0.1059⎟⎠
R语言版应用多元统计分析判别分析

应用多元统计分析第4章 判别分析- 1-•判别分析是用于判断样品所属类型的一种统计方法。
•判别分析方法处理的问题看起来与聚类分析方法有些类似,似乎都是要将观察值进行分类,但是它们的使用前提是不同的。
•判别分析是根据某些指标的已有数据(或称为训练样本)对所研究的对象建立判别函数,并进行分类的一种多变量分析方法,也称之为“有监督的分类方法”。
•进行判别归类时,由假设前提、判别依据及处理手法的不同可采用不同的判别方法。
如距离判别、贝叶斯(Bayes)判别、费希尔(Fisher)判别等。
概念和方法l判别分析概念l判别分析方法是在已知的分类之下,对新的样品,利用某判别准则,来判定其属于哪个类。
判别分析(Discriminat Analysis)是多元分析中用于判别样品所属类型的一种统计分析方法。
主要内容判别分析的目的和意义几种判别分析方法和性质包括:距离判别法、Bayes判别法、Fisher判别法R语言程序中有关判别分析的算法4•定义4.1设 是从均值向量为 ,协方差阵为 的总体G 中抽取的两个样品,则 与 之间的马氏距离定义为•样品 与总体G 之间的马氏距离为•两总体的距离判别•设总体 和 的均值向量分别为 和 ,协方差阵分别为 和 ,x 是一个新样品,现在要判断x 来自哪一个总体。
可计算x 到两个总体的马氏距离的平方 和 ,并按照下列进行判别• 当两个总体的方差相等,即 时,该判别准则可以进行简化。
• 1. 当 时的线性判别•此时•其中 是两个总体均值的平均值。
令••其中 ,则 。
因此判别准则可简化为:其中称 为判别函数,由于它是 的线性函数,故又称它为线性判别函数。
•在实际中,总体的均值向量 和协方差阵 一般都是未知的,此时可用样本均值向量 和样本协方差阵 来代替。
设 是来自总体 的样品, 是来自总体 的样品,则样品均值向量和样品离差阵为• 的由两个总体样品构成的无偏估计为• 2. 当 时的非线性判别•此时判别函数为 与 之差,即•由于这个 是x 的二次函数,故又称它为二次判别函数或非线性判别函数。
《应用多元统计分析》试题答案

《应用多元统计分析》试题答案一、填空题1. 多元统计分析中,研究多个变量的协方差结构的方法是__________。
答案:主成分分析2. 在多元正态分布中,若两个变量线性相关,则它们的协方差__________。
答案:不为零3. 在因子分析中,因子载荷矩阵表示的是__________与__________之间的相关关系。
答案:变量公共因子4. 聚类分析中,类内平方和与类间平方和的比值越大,说明聚类效果__________。
答案:越好5. 在判别分析中,贝叶斯判别准则的基本思想是__________。
答案:最小化误判概率二、选择题1. 以下哪个方法不属于多元统计分析的范畴?A. 主成分分析B. 聚类分析C. 线性规划D. 因子分析答案:C2. 在多元正态分布中,以下哪个统计量可以用来检验变量间的线性关系?A. 相关系数B. 协方差C. 卡方统计量D. F统计量答案:D3. 在因子分析中,以下哪个指标用来衡量公共因子对变量的解释程度?A. 因子载荷B. 特征值C. 贡献率D. 累计贡献率答案:C4. 聚类分析中,以下哪种聚类方法属于层次聚类法?A. K-means聚类B. 动态聚类C. 系统聚类D. 密度聚类答案:C5. 在判别分析中,以下哪个指标可以用来衡量判别效果?A. 判别系数B. 判别函数C. 误判概率D. 准确率答案:C三、简答题1. 简述主成分分析的基本思想及其在多元统计分析中的应用。
答案:主成分分析的基本思想是将多个变量通过线性变换,转化为少数几个互相独立的主成分,以简化数据结构。
主成分分析在多元统计分析中的应用非常广泛,如数据降维、特征提取、因子分析等。
2. 简述因子分析的基本步骤。
答案:因子分析的基本步骤如下:(1)计算变量间的相关系数矩阵;(2)求解特征值和特征向量,确定公共因子个数;(3)求解因子载荷矩阵,进行因子旋转;(4)计算因子得分,进行进一步分析。
3. 简述聚类分析的基本思想及其在多元统计分析中的应用。
应用多元统计分析习题解答 第四章

第四章判别分析4.1 简述欧几里得距离与马氏距离的区别和联系。
答:设p维欧几里得空间中的两点X=和Y=。
则欧几里得距离为。
欧几里得距离的局限有①在多元数据分析中,其度量不合理。
②会受到实际问题中量纲的影响。
设X,Y是来自均值向量为,协方差为的总体G中的p维样本。
则马氏距离为D(X,Y)=。
当即单位阵时,D(X,Y)==即欧几里得距离。
因此,在一定程度上,欧几里得距离是马氏距离的特殊情况,马氏距离是欧几里得距离的推广。
4.2 试述判别分析的实质。
答:判别分析就是希望利用已经测得的变量数据,找出一种判别函数,使得这一函数具有某种最优性质,能把属于不同类别的样本点尽可能地区别开来。
设R1,R2,…,Rk 是p 维空间R p 的k 个子集,如果它们互不相交,且它们的和集为,则称为的一个划分。
判别分析问题实质上就是在某种意义上,以最优的性质对p 维空间构造一个“划分”,这个“划分”就构成了一个判别规则。
4.3 简述距离判别法的基本思想和方法。
答:距离判别问题分为①两个总体的距离判别问题和②多个总体的判别问题。
其基本思想都是分别计算样本与各个总体的距离(马氏距离),将距离近的判别为一类。
①两个总体的距离判别问题设有协方差矩阵∑相等的两个总体G 1和G 2,其均值分别是μ1和μ 2,对于一个新的样品X ,要判断它来自哪个总体。
计算新样品X 到两个总体的马氏距离D 2(X ,G 1)和D 2(X ,G 2),则X,D 2(X ,G 1)D 2(X ,G 2)X,D 2(X ,G 1)> D 2(X ,G 2,具体分析,2212(,)(,)D G D G -X X111122111111111222111211122()()()()2(2)2()-----------''=-----''''''=-+--+'''=-+-X μΣX μX μΣX μX ΣX X ΣμμΣμX ΣX X ΣμμΣμX ΣμμμΣμμΣμ11211212112122()()()2()22()2()---''=-++-'+⎛⎫=--- ⎪⎝⎭''=--=--X ΣμμμμΣμμμμX ΣμμX μααX μ 记()()W '=-X αX μ 则判别规则为X,W(X)X,W(X)<0②多个总体的判别问题。
多元统计分析判别分析(方法步骤分析总结)

判别分析:实验步骤:1.在SPSS窗口中选择:分析-分类-判别,将变量导入自变量框中,group导入分组变量中,选择定义范围,最小为1最大为3,并选择一起输入自变量,点击继续2.点击统计量,描述性中选择“均值”,“单变量”和”Box”,选择函数系数中的“Fisher”“未标准化”,矩阵中选择“组内相关”,点击继续3.点击分类点击继续4.点击“保存”,三个框均选中,点击继续5.点击确定实验结果分析:1.表1 组统计量看各个总体在均值等指标上的值是否接近,若接近说明各类之间在该指标差异不大表2表3 汇聚的组内矩阵若自变量之间存在高度相关,则判别分析价值不大,但并不严格,允许出现一定的相关表4 协方差矩阵的均等性的箱式检验检验结果p值>0.05时,说明协方差矩阵相等,可以进行bayes检验表5表7由表7可知,两个Fisher 判别函数分别为1123456212345674.99 1.861 1.6560.8770.7980.098 1.57929.4820.867 1.1550.3560.0890.0540.69y X X XX X X y X X X X X X =--+-+++=--+--++表8 结构矩阵该表是原始变量与典型变量(标准化的典型判别函数)的相关系数,相关系数的绝对值越大,说明原始变量与这个判别函数的相关性越强由表9可知各类别重心的位置,通过计算观测值与各重心的距离,距离最小的即为该观测值的分类。
第一类:11234565317.2143.9153.190.153.011.0189.3F X X X X X X =--+-+++2. 将各样品的自变量值代入上述三个Bayes 判别函数,得到函数值。
比较函数值,哪个函数值比较大就可以判断该样品判入哪一类下面是赠送的保安部制度范本,不需要的可以编辑删除谢谢!保安部工作制度一、认真贯彻党的路线、方针政策和国家的法津法规,按照####年度目标的要求,做好####的安全保卫工作,保护全体人员和公私财物的安全,保持####正常的经营秩序和工作秩序。
《应用多元统计分析》第04章-判别分析

04
判别分析的实例与演示
数据来源与预处理
数据来源
判别分析所使用的数据通常来源于实际研究或调查,这些数据可能涉及到多个 变量和观测样本。
数据预处理
在应用判别分析之前,需要对数据进行预处理,包括数据清洗、缺失值处理、 异常值检测与处理、数据标准化等步骤,以确保数据的质量和可靠性。
2. 建立判别模型
选择合适的变量,并进行数据清理和预处 理,包括缺失值处理、异常值检测与处理 等。
选择合适的判别分析方法,如线性判别分析 (LDA)或二次判别分析(QDA),并利用 已知分类的数据来估计判别函数。
3. 模型评估
4. 应用模型
使用诸如混淆矩阵、准确率、召回率等指 标来评估模型的性能,并可能进行交叉验 证。
目的
通过建立判别函数,使得不同类别之 间的差异尽可能大,而同一类别内的 差异尽可能小。
判别分析与聚类分析的区别
01
判别分析基于已知分类数据, 目标是建立预测分类的规则; 而聚类分析则是将未知分类的 数据进行归类。
02
判别分析要求对各变量之间的 相关性进行建模,而聚类分析 则更注重数据之间的距离或相 似性。
总结词
两总体判别分析是一种基本的判别分析方法,用于根据已知分类的数据集构建判别函数,从而对新数据进行分类。
详细描述
两总体判别分析通常用于解决二分类问题,其基本思想是通过选择一组特征变量,使得不同类别的样本在这组变 量上的均值差异最大,同时使同类样本之间的离散度最小。判别函数通常采用线性或非线性形式,通过最小化分 类错误率来构建。
对特征选择敏感
判别分析的特征选择可能对结果 影响较大,如果选择不合适的特 征,可能会导致分类效果不佳。
(完整版)多元统计分析课后练习答案

第1章 多元正态分布1、在数据处理时,为什么通常要进行标准化处理?数据的标准化是将数据按比例缩放,使之落入一个小的特定区间。
在某些比较和评价的指标处理中经常会用到,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。
其中最典型的就是0-1标准化和Z 标准化。
2、欧氏距离与马氏距离的优缺点是什么?欧氏距离也称欧几里得度量、欧几里得度量,是一个通常采用的距离定义,它是在m 维空间中两个点之间的真实距离。
在二维和三维空间中的欧氏距离的就是两点之间的距离。
缺点:就大部分统计问题而言,欧氏距离是不能令人满意的。
每个坐标对欧氏距离的贡献是同等的。
当坐标表示测量值时,它们往往带有大小不等的随机波动,在这种情况下,合理的方法是对坐标加权,使变化较大的坐标比变化较小的坐标有较小的权系数,这就产生了各种距离。
当各个分量为不同性质的量时,“距离”的大小与指标的单位有关。
它将样品的不同属性之间的差别等同看待,这一点有时不能满足实际要求。
没有考虑到总体变异对距离远近的影响。
马氏距离表示数据的协方差距离。
为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。
优点:它不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关。
由标准化数据和中心化数据计算出的二点之间的马氏距离相同。
马氏距离还可以排除变量之间的相关性的干扰。
缺点:夸大了变化微小的变量的作用。
受协方差矩阵不稳定的影响,马氏距离并不总是能顺利计算出。
3、当变量X1和X2方向上的变差相等,且与互相独立时,采用欧氏距离与统计距离是否一致?统计距离区别于欧式距离,此距离要依赖样本的方差和协方差,能够体现各变量在变差大小上的不同,以及优势存在的相关性,还要求距离与各变量所用的单位无关。
如果各变量之间相互独立,即观测变量的协方差矩阵是对角矩阵, 则马氏距离就退化为用各个观测指标的标准差的倒数作为权数的加权欧氏距离。
多元统计分析课后习题解答第四章

习题解析
• 题目:简述多元统计分析的基本思想 答案:多元统计分析是通过对多个变量进行综合分析,揭示数据之间的内在关 系和规律,进而解决实际问题的方法。其基本思想包括多变量综合分析、多变量分类分析、多变量预测分析等。
• 答案:多元统计分析是通过对多个变量进行综合分析,揭示数据之间的内在关系和规律,进而解决实际问题的方法。其基本 思想包括多变量综合分析、多变量分类分析、多变量预测分析等。
汇报人:XX
多元统计分析的 方法和技术广泛 应用于各个领域, 如心理学、经济 学、医学等。
多元统计分析的 基本步骤包括数 据收集、数据探 索、模型选择、 模型拟合和模型 评估等。
多元统计分析的基本思想
综合多个变量进行全面分析,以揭示数据之间的内在联系和规律 强调变量之间的交互作用和协同效应,以实现更准确的预测和推断 通过对数据的降维处理,简化复杂数据集,提取关键信息
• 题目:解释因子分析的基本思想。 答案:因子分析是一种探索性统计分析方法,其基本思想是通过寻找隐藏在多个变量背后的共 同因子来解释变量之间的相互关系。通过因子分析,可以揭示数据的基本结构,简化数据的复杂性,并加深对数据内在规律的认识。 • 答案:因子分析是一种探索性统计分析方法,其基本思想是通过寻找隐藏在多个变量背后的共同因子来解释变量之间的相互关系。通 过因子分析,可以揭示数据的基本结构,简化数据的复杂性,并加深对数据内在规律的认识。
厦门大学《应用多元统计分析》习题第05章 聚类分析
5.11 下表是 2003 年我国省会城市和计划单列市的主要经济指标:人均
GDP x1(元)、人均工业产值 x2 (元)、客运总量 x3(万人)、货运总量 x4 (万 吨)、地方财政预算内收入 x5 (亿元)、固定资产投资总额 x6 (亿元)、在岗 职工占总人口的比例 x7 (%)、在岗职工人均工资额 x8(元)、城乡居民年底 储蓄余额 x9 (亿元)。试通过统计分析软件进行系统聚类分析,并比较何种
思考与练习
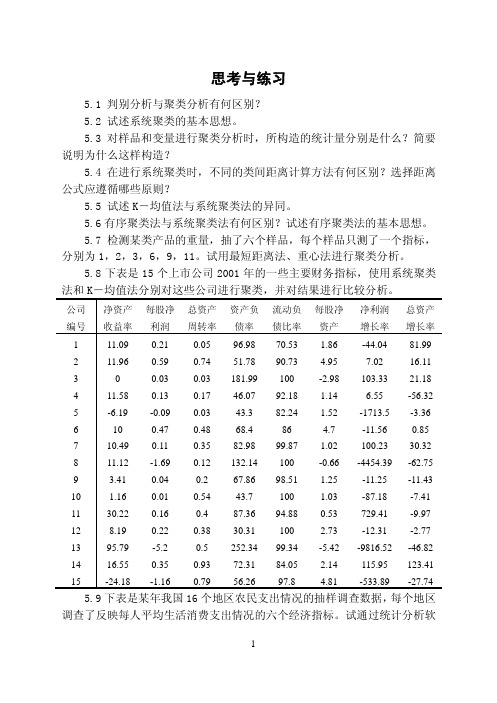
5.1 判别分析与聚类分析有何区别? 5.2 试述系统聚类的基本思想。 5.3 对样品和变量进行聚类分析时,所构造的统计量分别是什么?简要 说明为什么这样构造? 5.4 在进行系统聚类时,不同的类间距离计算方法有何区别?选择距离 公式应遵循哪些原则? 5.5 试述 K-均值法与系统聚类法的异同。 5.6 有序聚类法与系统聚类法有何区别?试述有序聚类法的基本思想。 5.7 检测某类产品的重量,抽了六个样品,每个样品只测了一个指标, 分别为 1,2,3,6,9,11。试用最短距离法、重心法进行聚类分析。 5.8 下表是 15 个上市公司 2001 年的一些主要财务指标,使用系统聚类 法和 K-均值法分别对这些公司进行聚类,并对结果进行比较分析。
2
大连 长春 哈尔滨 上海 南京 杭州 宁波 合肥 福州 厦门 南昌 济南 青岛 郑州 武汉 长沙 广州 深圳 南宁 海口 重庆 成都 贵阳 昆明 西安 兰州 西宁 银川 乌鲁木齐 南宁 海口
29145 18630 14825 46586 27547 32667 32543 10621 22281 53590 14221 23437 24705 16674 21278 15446 48220 191838 8176 16442 7190 17914 11046 16215 13140 14459 7066 11787 22508 31886 26433
应用多元统计分析之判别分析

励志人生 好好学习
第二节 距离判别法
一 马氏距离的概念 二 距离判别的思想及方法
三 判别分析的实质
励志人生 好好学习
一、马氏距离的概念
励志人生 好好学习
图4.1
励志人生 好好学习
励志人生 好好学习
为此,我们引入一种由印度著名统计学家马哈拉诺比斯( Mahalanobis, 1936)提出的“马氏距离”的概念。
判别函数就有几个判别得分变量; Probabilities of group membership:存放样品属于各组的
Bayes后验概率值。
将对话框中的三个复选框均选中,单击Continue按钮返回。
励志人生 好好学习
图4.5 Save子对话框 6. 返回判别分析主界面,单击OK按钮,运行判别分析过程 。
励志人生 好好学习
励志人生 好好学习
第五节 实例分析与计算机实现
这一节我们利用SPSS对Fisher判别法和Bayes判别法进行计 算机实现。
为研究某地区人口死亡状况,已按某种方法将15个已知地区 样品分为3类,指标含义及原始数据如下。试建立判别函数 ,并判定另外4个待判地区属于哪类?
图4.4 Classify…子对话框
励志人生 好好学习
5. 单击Save按钮,指定在数据文件中生成代表判别分组结果 和判别得分的新变量,生成的新变量的含义分别为:
Predicted group membership:存放判别样品所属组别的值; Discriminant scores:存放Fisher判别得分的值,有几个典型
法就是为了解决这些问题而提出的一种判别方法。
励志人生 好好学习
一、Bayes判别的基本思想
多元统计分析——判别分析共88页PPT

的总体G抽得的两个观测值,则称 d 2 ( x ,y ) ( x y ) 1 ( x y )
为X与Y之间的Mahalanobis距离
样本X和Gi类之间的马氏距离定义为X与Gi类 重心间的距离:
d 2 ( x , G i ) ( x i ) 1 ( x i )i 1 , 2 , , k
多元统计分析——判别分析
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
它产生于20世纪30年代。近年来,在自然科 学、社会学及经济管理学科中都有广泛的应用。 判别分析的特点是根据已掌握的、历史上每个类 别的若干样本的数据信息,总结出客观事物分类 的规律性,建立判别公式和判别准则。然后,当 遇到新的样本点时,只要根据总结出来的判别公 式和判别准则,就能判别该样本点所属的类别。
(二)两个总体距离判别法
1、方差相等
先考虑两个总体的情况,设有两个协差阵相同 的p维正态总体,对给定的样本Y,判别一个样本Y到 底是来自哪一个总体,一个最直观的想法是计算Y到 两个总体的距离。故我们用马氏距离来指定判别规 则,有:
yG1,如d2y,G1d2y,G2, yG2,如d2y,G2d2y,G1
.69479 .80234 .70620 .83420 .35312 .32019 .34442 .09012
多元统计分析判别分析

和
。距离判别的实1质就是:给出空间 的一个划分 2和 ,如果样品 落入 之中,
则判定
;如果样品 落入 之中,则判定
Rm
Rm
D1 D2
D1
D2
。
X
D1
X G1
X D2
X G2
B.
时的判别方法
1
2
1 2
•
W(X)
W ( X ) ( X ) ( X ) ( X ) ( X ) 当 时,根据判别准则(T1)式,1 我们同样的给出判别函数 为 T 1
显著性检验
3.1 距离判别
距离判别的基本思想:样品 X离•哪个总体的距离最近,就判断 X 属于哪个总体。
T
X (x , x ,, x ) R 中这,里两的点“距离”是通与常意T义下的距离(欧几里得距1 离:2 在 m 维欧m 几里得空间 Y ( y , y ,, y ) 的欧1 几2里)得吗距?离m,也就是通常我们所说的距离为
(
)……(4)
P( j | i) f ( X )dX j i 实际上,(4)式的几何意义是很D明j 显i的,见图2。
图2表示的是两个正态总体的误判概率示意图。
•
误判概率的估计方法有以下几种: (1)利用训练样本为检验集,用判别方法对训练样本进行判断,统计误判的样本个数,计
算误判样本占总样本的比例,并作为误判概率的估计值; (2)当训练样本足够大时,从训练样本中预留一部分作为检验集,并记录判错的比率,作
n 总训练样本数,该方法要求训练样本是通过随机抽样得到的;
3.假定
。
i
q n i i
i
n n n n 1 2
k
n是
q1 q2 qk 1/ k
厦门大学应用多元统计分析第判别分析

AB 102 52 125 ; CD 12 102 101
如果我们将长度单位变为 mm,那么,有
AB 102 502 2600 ; CD 12 1002 10001
量纲的变化,将影响欧氏距离计算的结果。
为此,我们引入一种由印度著名统计学家马哈拉诺比斯 (Mahalanobis, 1936)提出旳“马氏距离”旳概念。
其
中
μ
1 2
(μ1
μ2)
是
两
个
总
体
均
值
的
平
均
值
,
α Σ1 (μ1 μ 2 ) ,记 W (X) α(X μ)
(4.5)
则判别规则(4.4)式可表示为
X X
G1 G2
, ,
如果 如果
W (X) 0 W (X) 0
(4.6)
这里称W (X) 为两总体距离判别的判别函数,由于它是 X 的线性
设 X 和 Y 是来自均值向量为 μ ,协方差为 Σ( 0) 的总体 G
中的 p 维样本,则总体 G 内两点 X 与 Y 之间的马氏距离定
义为
D2 (X, Y) (X Y)Σ1(X Y) (4.2)
定义点 X 到总体 G 的马氏距离为
D2 (X,G) (X μ)Σ1(X μ)
(4.3)
一 Bayes鉴别旳基本思想 二 Bayes鉴别旳基本措施
从上节看距离鉴别法虽然简朴,便于使用。但是该措施也有 它明显旳不足之处。
第一,鉴别措施与总体各自出现旳概率旳大小无关;
第二,鉴别措施与错判之后所造成旳损失无关。Bayes鉴别 法就是为了处理这些问题而提出旳一种鉴别措施。
一、Bayes鉴别旳基本思想
多元统计分析应用 第四章课后习题

第四章判别分析习题4.8(1)根据数据建立贝叶斯判别函数,并根据此判别函数对原样本进行回判。
(2)现有一新品牌的饮料在该超市试销,其销售价格为3.0,顾客对其口味评分为8,信任度评分平均为5,试预测该饮料的销售情况。
将数据导入SPSS,分析得到以下结果:1.典型判别函数的特征函数的特征值表表1-1 特征值表表1-1所示是典型判别函数的特征值表,只有两个判别函数,所以特征值只有2个。
函数1的特征值为17.791,函数2的特征值为0.720,判别函数的特征值越大,说明函数越具有区别判断力。
函数1方差的累积贡献率高达96.1%,且典型相关系数为0.973,而函数2方差的贡献率仅为3.9%,典型相关系数为0.647。
由此,说明函数1的区别判断力比函数2的强,函数1更具有区别判断力。
2.Wilks检验结果表1-2 Wilks 的Lambda上表中判别函数1和判别函数2的Wilks’Lambda值为0.031,判别函数2的Wilks’Lambda值为0.581。
“1到2”表示两个判别函数的平均数在三个类间的差异情况,P值=0.002<0.05表示差异达到显著水平“2”表示在排除了第一个判别函数后,第二个判别函数在三个组别间的差异情况,P值=0.197>0.05表示判别函数2未达到显著水平。
3.建立贝叶斯判别函数表1-3 贝叶斯判别法函数系数上表为贝叶斯判别函数的系数矩阵,用数学表达式表示各类的贝叶斯判别函数为:第一组:F1=-81.843-11.689X1+12.97X2+16.761X3第二组:F2=-94.536-10.707X1+13.361X2+17.086X3第三组:F3=-17.499-2.194X1+4.960X2+6.447X3将新品牌饮料样品的自变量值分别代入上述三个贝叶斯判别函数,得到三个函数值为:F1=65.271,F2=65.661,F3=47.884比较三个值,可以看出F2=65.661最大,据此得出新品牌饮料样品应该属于第二组,即该饮料的销售情况为平销。
应用多元统计分析课后答案

第二章2.1.试叙述多元联合分布和边际分布之间的关系。
解:多元联合分布讨论多个随机变量联合到一起的概率分布状况,12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数,而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布,其概率密度函数的维数小于p 。
2.2设二维随机向量12()X X '服从二元正态分布,写出其联合分布。
解:设12()X X '的均值向量为()12μμ'=μ,协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭,则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。
2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1a x b ≤≤,2c x d ≤≤。
求(1)随机变量1X 和2X 的边缘密度函数、均值和方差; (2)随机变量1X 和2X 的协方差和相关系数; (3)判断1X 和2X 是否相互独立。
(1)解:随机变量1X 和2X 的边缘密度函数、均值和方差;112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd cc d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 12122222()()2[()2()]()()()()dd cc d c x a x b a t x a t dt b a d c b a d c ------=+----⎰2212122222()()[()2()]1()()()()d cdcd c x a x b a t x a t b a d c b a d c b a------=+=----- 所以由于1X 服从均匀分布,则均值为2b a +,方差为()212b a -。
多元统计分析课后习题解答_第四章

第四章 判别分析4、1 简述欧几里得距离与马氏距离得区别与联系。
答: 设p 维欧几里得空间中得两点X =与Y =。
则欧几里得距离为。
欧几里得距离得局限有①在多元数据分析中,其度量不合理。
②会受到实际问题中量纲得影响。
设X,Y 就是来自均值向量为,协方差为得总体G 中得p 维样本。
则马氏距离为D(X,Y)=。
当即单位阵时,D(X,Y)==即欧几里得距离。
因此,在一定程度上,欧几里得距离就是马氏距离得特殊情况,马氏距离就是欧几里得距离得推广。
4、2 试述判别分析得实质。
答:判别分析就就是希望利用已经测得得变量数据,找出一种判别函数,使得这一函数具有某种最优性质,能把属于不同类别得样本点尽可能地区别开来。
设R1,R2,…,Rk 就是p 维空间R p 得k 个子集,如果它们互不相交,且它们得与集为,则称为得一个划分。
判别分析问题实质上就就是在某种意义上,以最优得性质对p 维空间构造一个“划分”,这个“划分”就构成了一个判别规则。
4、3 简述距离判别法得基本思想与方法。
答:距离判别问题分为①两个总体得距离判别问题与②多个总体得判别问题。
其基本思想都就是分别计算样本与各个总体得距离(马氏距离),将距离近得判别为一类。
①两个总体得距离判别问题设有协方差矩阵∑相等得两个总体G 1与G 2,其均值分别就是μ1与μ 2,对于一个新得样品X ,要判断它来自哪个总体。
计算新样品X 到两个总体得马氏距离D 2(X,G 1)与D 2(X,G 2),则X ,D 2(X ,G 1)D 2(X ,G 2)X ,D 2(X ,G 1)> D 2(X ,G 2, 具体分析,111122111111111222111211122()()()()2(2)2()-----------''=-----''''''=-+--+'''=-+-X μΣX μX μΣX μX ΣX X ΣμμΣμX ΣX X ΣμμΣμX ΣμμμΣμμΣμ记 则判别规则为X ,W(X) X ,W(X)<0②多个总体得判别问题。
应用多元统计分析课后答案暴强整理

第二章2.1 试述多元联合分布和边缘分布之间的关系。
设X =(X 1,X 2,⋯X p )′是p 维随机向量,称由它的q 〔<p 〕个分量组成的子向量X(i)=(X i1,X i2,⋯X iq )′的分布为X 的边缘分布,相对地把X 的分布称为联合分布。
当X 的分布函数为F (x 1,x 2,⋯x p )时,X (1)的分布函数即边缘分布函数为F (x 1,x 2,⋯x p )=P(X 1≤x 1,⋯X q ≤x q ,X q+1≤∞,⋯X p ≤∞) = F (x 1,x 2,⋯x q ,∞,⋯∞)当X 有分布密度f 〔x 1,x 2,⋯x p 〕那么X (1)也有分布密度,即边缘密度函数为:f 〔x 1,x 2,⋯x q 〕=∫⋯+∞−∞∫f (x 1,x 2,⋯x p )dx q+1⋯d +∞−∞x p2.2 设随机向量X =(X 1,X 2)′服从二元正态分布,写出其联合分布密度函数和X 1,X 2各自的边缘密度函数。
联合分布密度函数12πσ1σ2(1−ρ2)1/2exp{−12(1−ρ2)[(x 1−μ1)2σ12−2ρ(x 1−μ1)(x 2−μ2)σ1σ2+f (x 1,x 2)=(x 2−μ2)2σ22]} , x 1>0,x 2>00 , 其他(x 1−μ1)2σ12−2ρ(x 1−μ1)(x 2−μ2)σ1σ2+(x 2−μ2)2σ22=(x 1−μ1)2σ12−2ρ(x 1−μ1)(x 2−μ2)σ1σ2+(x 2−μ2)2σ22+ρ2(x 1−μ1)2σ12−ρ2(x 1−μ1)2σ12=[ρ(x 1−μ1)σ1−(x 2−μ2)σ2]2+(1−ρ2)(x 1−μ1)2σ12所以指数局部变为−12{[11√1−ρ2σ1−22√1−ρ2σ2]2+(x 1−μ1)2σ12}令t=22√1−ρ2σ2−11√1−ρ2σ1 ∴dt =√1−ρ2σ22∴f (x 1)=∫f (x 1,x 2)+∞−∞dx 2=12πσ1σ2(1−ρ2)1/2exp{−(x 1−μ1)22σ12∫exp(+∞−∞−12t 2√1−ρ22dt =√2πσexp[−(x 1−μ1)22σ12] √2πσexp[−(x 1−μ1)22σ12] , x 1>0f (x 1)=0 ,其他 同理, √2πσ2exp[−(x 2−μ2)22σ22] , x 2>0f (x 2)=0 ,其他2.3 随机向量X =(X 1,X 2)′的联合分布密度函数为f (x 1,x 2)=2[(d−c )(x 1−a )+(b−a )(x 2−c )−2(x 1−a)(x 2−c)(b−a)2(d−c)2,其中,a ≤x 1≤b,c ≤x 2≤d 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考与练习
4.1 简述欧氏距离与马氏距离的区别和联系。
4.2 试述判别分析的实质。
4.3 简述距离判别法的基本思想和方法。
4.4 简述Bayes 判别法的基本思想和方法。
4.5 简述Fisher 判别法的基本思想和方法。
4.6 试析距离判别法、Bayes 判别法和Fisher 判别法的异同。
4.7 设有两个二元总体和,从中分别抽取样本计算得到
1G 2G (1)(2)53 5.8 2.1,,12 2.17.6p x x S ⎛⎞⎛⎞⎛⎞===⎜⎟⎜⎟⎜⎟−⎝⎠⎝⎠⎝⎠
假设,试用距离判别法建立判别函数和判别规则。
样品1=ΣΣ2(6,0)x ′=应属于哪个总体?
4.8 某超市经销十种品牌的饮料,其中有四种畅销,三种滞销,三种平销。
下表是这十种品牌饮料的销售价格(元)和顾客对各种饮料的口味评分、信任度评分的平均数。
销售情况 产品序号 销售价格 口味评分 信任度评分
畅销
1 2.
2 5 8 2 2.5 6 7
3 3.0 3 9
4 3.2 8 6 平销
5 2.8 7
6 6 3.5 8
7 7 4.
8
9 8 滞销
8 1.7 3 4 9 2.2 4 2 10 2.7 4 3
⑴ 根据数据建立贝叶斯判别函数,并根据此判别函数对原样本进行回判。
1
⑵ 现有一新品牌的饮料在该超市试销,其销售价格为3.0,顾客对其口味的评分平均为8,信任评分平均为5,试预测该饮料的销售情况。
4.9 银行的贷款部门需要判别每个客户的信用好坏(是否未履行还贷责任),以决定是否给予贷款。
可以根据贷款申请人的年龄(1X )、受教育程度(2X )、现在所从事工作的年数(3X )、未变更住址的年数(4X )、收入(5X )、负债收入比例(6X )、信用卡债务(7X )、其它债务(8X )等来判断其信用情况。
下表是从某银行的客户资料中抽取的部分数据,⑴根据样本资料分
别用距离判别法、Bayes 判别法和Fisher 判别法建立判别函数和判别规则。
⑵某客户的如上情况资料为(53,1,9,18,50,11.20,2.02,3.58),对其进行信用好坏的判别。
目前信用好坏
客户序号
1X 2X 3X 4X 5X 6X 7X 8X
已履行还贷责任
1 23 1 7
2 31 6.600.34 1.71
2 34 1 17
3 59 8.00 1.81 2.91 3 42 2 7 23 41 4.600.9
4 .94 4 39 1 19
5 48 13.10 1.93 4.3
6 5 35 1 9 1 34 5.000.40 1.30 未履行还
贷责任
6 3
7 1 1 3 24 15.10 1.80 1.82 7 29 1 13 1 42 7.40 1.46 1.65
8 32 2 11 6 75 23.307.76 9.72
9 28 2 2 3 23 6.400.19 1.29 10 26 1 4 3 27 10.50
2.47 .36
4.10 从胃癌患者、萎缩性胃炎患者和非胃炎患者中分别抽取五个病人进行四项生化指标的化验:血清铜蛋白()1X 、蓝色反应()2X 、尿吲哚乙酸
(3
)X 和中性硫化物()4
X ,数据见下表。
试用距离判别法建立判别函数,并
根据此判别函数对原样本进行回判。
2
类别 病人序号
1X 2X 3X 4X
胃癌患者 1 228 134 20 11 2 245 134 10 40 3 200 167 12 27 4 170 150 7 8 5 100 167 20 14 胃炎患者
萎缩性 6 225 125 7 14 7 130 100 6 12 8 150 117 7 6 9 120 133 10 26 10 160 100 5 10 非胃炎患者 11 185 115 5 19 12 170 125 6 4 13 165 142 5 3 14 135 108 2 12 15 100 117 7 2
3。
