2017.1实变函数期末试卷A卷
实变函数期末考试题

实变函数期末考试题考试题目:本次实变函数期末考试题旨在考察学生对实变函数的理解、分析和应用能力。
考试时间为120分钟,共分为两部分,选择题和解答题。
请同学们仔细阅读每个问题,并在考试纸上作答。
祝各位同学好运!第一部分:选择题选择题共有10道题,每题4分,共40分。
请在A、B、C、D四个选项中选择正确答案,并填涂在答题纸上。
1. 设函数f(x) = x^2 + 2x - 1,那么f'(x)的导函数是:A. 2x + 2B. 2x + 1C. 2x - 1D. 2x + 22. 实变函数f(x) = e^x,则f''(x)的导函数是:A. e^xB. e^x - 1C. e^x + 1D. e^x + e^x3. 设函数f(x) = 3x^2 + 5,那么f(0)的值为:A. 5B. 3C. 0D. 84. 函数f(x) = |x - 2|的定义域为:A. (2, +∞)B. (-∞, 2)C. [2, +∞)D. (-∞, +∞)5. 函数f(x) = log(2x - 1)的定义域为:A. (1/2, +∞)B. (-∞, 1/2)C. [1/2, +∞)D. (-∞, +∞)6. 函数f(x) = sin(2x)的最小正周期为:A. πB. 2πC. π/2D. π/47. 函数f(x) = arctan(x)的值域为:A. (-∞, +∞)B. (-π/2, π/2)C. (-π/4, π/4)D. [0, π/2)8. 设函数f(x) = ln(x),则f'(x)的导数为:A. 1/xB. xC. x - 1D. 1/(x - 1)9. 函数f(x) = x^3在闭区间[0, 1]上的最大值为:A. 27B. 9C. 1D. 310. 函数f(x) = sqrt(x)在闭区间[0, 4]上的最小值为:A. 0B. 1C. 2D. 4第二部分:解答题解答题共有3道题,共60分。
实变函数A卷(解答).docx
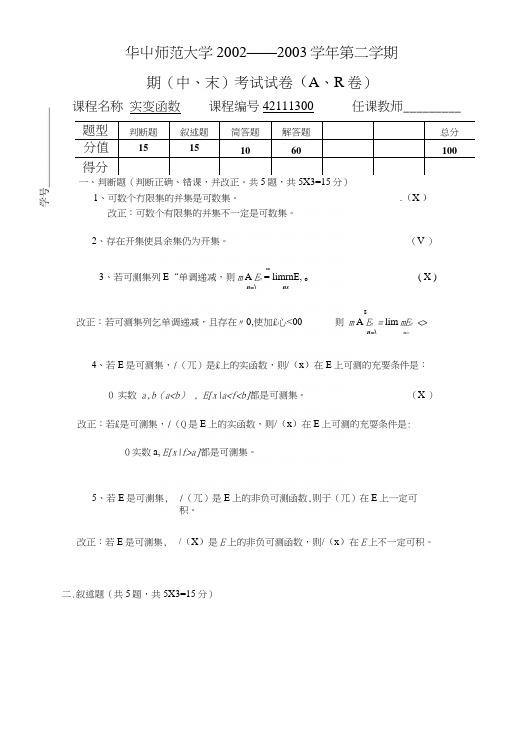
华屮师范大学2002——2003学年第二学期期(中、末)考试试卷(A、R卷)课程名称实变函数课程编号42111300 任课教师_________题型判断题叙述题简答题解答题总分分值151********得分一、判断题(判断正确、错课,并改正。
共5题,共5X3=15分)1、可数个冇限集的并集是可数集。
.(X )改正:可数个有限集的并集不一定是可数集。
2、存在开集使具余集仍为开集。
(V )co3、若可测集列E“单调递减,则m A E n = limrnE, o( X )n=\ ns改正:若可测集列乞单调递减,且存在〃0,使加£心<008则m A E n = lim mE n <>n=\n—4、若E是可测集,/(兀)是£上的实函数,则/(x)在E上可测的充要条件是:0 实数a,b(a<b) , E[x\a<f<b]都是可测集。
(X )改正:若£是可测集,/(Q是E上的实函数,则/(x)在E上可测的充耍条件是: 0实数a, E[x\f>a]都是可测集。
5、若E是可测集, /(兀)是E上的非负可测函数,则于(兀)在E上一定可积。
改正:若E是可测集, /(X)是E上的非负可测函数,则/(x)在E上不一定可积。
二.叙述题(共5题,共5X3=15分)1、集合的对等。
答:设A、B是两个集合,若A、BZ间存在一一对应,则称A与B对等。
2、可测集。
答:设E u R”,如果对任意T uR”,总有mV=/77*(Tn£) + m*(Tn£c),则称E为可测集。
3、可测集与几型集的关系。
答:设E为可测集,则存在人型集F,使F uE且加E二加F、加(E — F) = O。
4、叶果洛夫定理。
答:设mE < +oo , { f n(x))为E上儿乎处处有限的可测函数列,/(兀)也为E上儿乎处处有限的可测函数,如果AU)^/(x) a.e.于E,则对任意£>0,存在可测了集E£^E 使在E&上,f n (兀)一致收敛于/*(兀),而m{E-E G)< 8 o5、九(兀)在可测集E上依测度收敛于/(兀)的定义。
实变函数期末考试题库

《实变函数》期末考试试题汇编目录《实变函数》期末考试模拟试题(一) (2)《实变函数》期末考试模拟试题(二) (7)《实变函数》期末考试模拟试题(三) (13)《实变函数》期末考试模拟试题(四) (18)《实变函数》期末考试模拟试题(五) (27)《实变函数》期末考试模拟试题(六) (30)《实变函数》期末考试模拟试题(七) (32)《实变函数》期末考试模拟试题(八) (36)《实变函数》期末考试模拟试题(九) (41)《实变函数》期末考试模拟试题(十) (47)《实变函数》期末考试题(一) (57)《实变函数》期末考试题(二) (63)《实变函数》期末考试模拟试题(一)(含解答)一、选择题(单选题)1、下列集合关系成立的是( A )(A )(\)A B B A B ⋃=⋃ (B )(\)A B B A ⋃= (C )(\)B A A A ⋃⊆ (D )(\)B A A ⊆ 2、若n E R ⊂是开集,则( B )(A )E E '⊂ (B )E 的内部E = (C )E E = (D )E E '= 3、设P 是康托集,则( C )(A )P 是可数集 (B )P 是开集 (C )0mP = (D )1mP = 4、设E 是1R 中的可测集,()x ϕ是E 上的简单函数,则( D ) (A )()x ϕ是E 上的连续函数 (B )()x ϕ是E 上的单调函数 (C )()x ϕ在E 上一定不L 可积 (D )()x ϕ是E 上的可测函数5、设E 是n R 中的可测集,()f x 为E 上的可测函数,若()d 0Ef x x =⎰,则( A )(A )在E 上,()f z 不一定恒为零 (B )在E 上,()0f z ≥ (C )在E 上,()0f z ≡ (D )在E 上,()0f z ≠ 二、多项选择题(每题至少有两个或两个以上的正确答案) 1、设E 是[0,1]中的无理点全体,则(C 、D )(A )E 是可数集 (B )E 是闭集 (C )E 中的每一点都是聚点 (D )0mE > 2、若1E R ⊂至少有一个内点,则( B 、D )(A )*m E 可以等于零 (B )*0m E > (C )E 可能是可数集 (D )E 是不可数集3、设[,]E a b ⊂是可测集,则E 的特征函数()E X x 是 (A 、B 、C ) (A )[,]a b 上的简单函数 (B )[,]a b 上的可测函数 (C )E 上的连续函数 (D )[,]a b 上的连续函数4、设()f x 在可测集E 上L 可积,则( B 、D )(A )()f z +和()f z -有且仅有一个在E 上L 可积 (B )()f z +和()f z -都在E 上L 可积 (C )()f z 在E 上不一定L 可积 (D )()f z 在E 上一定L 可积5、设()f z 是[,]a b 的单调函数,则( A 、C 、D )(A )()f z 是[,]a b 的有界变差函数 (B )()f z 是[,]a b 的绝对连续函数 (C )()f z 在[,]a b 上几乎处处连续 (D )()f z 在[,]a b 上几乎处处可导 三、填空题(将正确的答案填在横线上)1、设X 为全集,A ,B 为X 的两个子集,则\A B=C A B ⋂ 。
实变函数(复习资料_带答案)资料

集。
0, 开集 G E,使 m* (G E)
,则 E 是可测
(第 7 页,共 19 页)
3. (6 分)在 a, b 上的任一有界变差函数 f ( x) 都可以表示为 两个增函数之差。
5. (8 分)设 f ( x) 在 E a,b 上可积,则对任何 0 ,必存
b
在 E 上的连续函数 ( x) ,使 | f ( x) (x) | dx . a
E
四、解答题 (8 分× 2=16 分) .
1、(8分)设 f (x)
x2, x为无理数 ,则 f ( x) 在 0,1 上是否 R
1, x为有理数
可积,是否 L 可积,若可积,求出积分值。
五、证明题 (6 分× 4+10=34 分) . 1、(6 分)证明 0,1 上的全体无理数作成的集其势为 c
可测集;
二. 填空题 (3 分× 5=15 分)
1、设 An
11 [ , 2 ], n 1,2,
,则 lim An
_________。
nn
n
2、设 P 为 Cantor 集,则 P
o
,mP _____,P =________。
3、设 Si 是一列可测集,则 m i 1 Si ______ mSi i1 4、鲁津定理:
4.(8 分)设函数列 fn (x) ( n 1,2, ) 在有界集 E 上“基本上” 一致收敛于 f ( x) ,证明: fn (x) a.e.收敛于 f ( x) 。
2. x
E , 则存在 E中的互异点列
{
xn },
使 lim n
xn
x ……… .2
分
xn E, f ( xn ) a ………………… .3 分
实变函数期末考试卷A卷资料

(3)因为 xnxnxxnnxnxxnnx2121sin121222132221)(xF 显然)(xF在]1,0[上可积。于是由Lebesgue控制收敛定理,有 0sin1)(limsin1)(lim10322211032221dxnxxnnxLdxnxxnnxRnn 2. 设为有理数,的无理数;为小于的无理数为大于xxxxxxf,01,;1,)(2试计算]2,0[)(dxxf。 解:因为有理数集的测度为零,所以 2)(xxf ..ea 于]1,0[, xxf)( ..ea 于]2,1[。 于是 ]2,1[]1,0[]2,0[)()()(dxxfdxxfdxxf dxxdxx211026112331 四、证明题(每题8分,共40分) 1. 证明:)()(11nnnnAAAA
Hale Waihona Puke 实变函数 一、 判断题(每题2分,共20分) 1.若A是B的真子集,则必有BA。 (×) 2.必有比a小的基数。 (√) 3.一个点不是E的聚点必不是E的内点。 (√) 4.无限个开集的交必是开集。 (×) 5.若E,则0*Em。 (×) 6.任何集nRE都有外测度。 (√) 7.两集合的基数相等,则它们的外测度相等。 (×) 8.可测集的所有子集都可测。 (×) 9.若)(xf在可测集E上可测,则)(xf在E的任意子集上也可测。(×) 10.)(xf在E上可积必积分存在。 (×) 1.设E为点集,EP,则P是E的外点.( × ) 2.不可数个闭集的交集仍是闭集. ( × ) 3.设nE是一列可测集,且1,1,2,,nnEEn则1()lim().nnnnmEmE(× ) 4.单调集列一定收敛. (√ ) 5.若()fx在E上可测,则存在F型集,()0FEmEF,()fx在F上连续.( × )
证明:)(1nnAA(AnnA1c) )(1cnnAA =)(1cnnAA )(1nnAA 2. 设M是直线上一族两两互不相交的非空开区间组成的集合,证明M是至多可列集。 证明:由有理数集的稠密性可知,每一个开区间中至少有一个有理数,从每个开区间中取定一个有理数,组成一个集合A。因为这些开区间是互不相交的,所以此有理数集A与开区间组成的集合M是一一对应的。则A是有理数集的子集,故至多可列,所以M也是至多可列集。 3. 证明:若0Em,则E为可测集。 证明:对任意点集T,显然成立着 )()(cETmETmTm。 另一方面,因为0Em,而EET,所以EmETm)(,于是)(ETm0。又因为cETT,所以)(cETmTm,从而 )()(cETmETmTm。 总之,)()(cETmETmTm。故E是可测集。 4. 可测集E上的函数)(xf为可测函数充分必要条件是对任何有理数r,集合])([rxfE是可测集。
实变函数(复习资料,带答案)

《实变函数》试卷一一、单项选择题(3分×5=15分) 1、下列各式正确的是( )(A )1lim n k n n k n A A ∞∞→∞===⋃⋂; (B )1lim n k n k n n A A ∞∞==→∞=⋂⋃;(C )1lim n k n n k nA A ∞∞→∞===⋂⋃; (D )1lim n k n k nn A A ∞∞==→∞=⋂⋂;2、设P 为Cantor 集,则下列各式不成立的是( ) (A )=P c (B) 0mP = (C) P P ='(D) P P =3、下列说法不正确的是( )(A) 凡外侧度为零的集合都可测(B )可测集的任何子集都可测(C) 开集和闭集都是波雷耳集 (D )波雷耳集都可测 4、设{}()n f x 是E 上的..a e 有限的可测函数列,则下面不成立的是( )(A )若()()n f x f x ⇒, 则()()n f x f x → (B){}sup ()n nf x 是可测函数(C ){}inf ()n nf x 是可测函数;(D )若()()n f x f x ⇒,则()f x 可测5、设f(x)是],[b a 上有界变差函数,则下面不成立的是( )(A) )(x f 在],[b a 上有界 (B) )(x f 在],[b a 上几乎处处存在导数(C ))('x f 在],[b a 上L 可积 (D)⎰-=b aa fb f dx x f )()()('二. 填空题(3分×5=15分)1、()(())s s C A C B A A B ⋃⋂--=_________2、设E 是[]0,1上有理点全体,则'E =______,oE =______,E =______.3、设E 是n R 中点集,如果对任一点集T 都_________________________________,则称E 是L 可测的 4、)(x f 可测的________条件是它可以表成一列简单函数的极限函数.(填“充分”,“必要”,“充要”)5、设()f x 为[],a b 上的有限函数,如果对于[],a b 的一切分划,使_____________________________________,则称()f x 为[],a b 上的有界变差函数。
(完整版)实变函数(复习资料_带答案)

《实变函数》试卷一一、单项选择题(3分×5=15分) 1、下列各式正确的是( )(A )1lim n k n n k n A A ∞∞→∞===⋃⋂; (B )1lim n k n k n n A A ∞∞==→∞=⋂⋃;(C )1lim n k n n k nA A ∞∞→∞===⋂⋃; (D )1lim n k n k nn A A ∞∞==→∞=⋂⋂;2、设P 为Cantor 集,则下列各式不成立的是( )(A )=P c (B) 0mP = (C) P P =' (D) P P =ο3、下列说法不正确的是( )(A) 凡外侧度为零的集合都可测(B )可测集的任何子集都可测(C) 开集和闭集都是波雷耳集 (D )波雷耳集都可测 4、设{}()n f x 是E 上的..a e 有限的可测函数列,则下面不成立的是( )(A )若()()n f x f x ⇒, 则()()n f x f x → (B){}sup ()n nf x 是可测函数(C ){}inf ()n nf x 是可测函数;(D )若()()n f x f x ⇒,则()f x 可测5、设f(x)是],[b a 上有界变差函数,则下面不成立的是( )(A) )(x f 在],[b a 上有界 (B) )(x f 在],[b a 上几乎处处存在导数(C ))('x f 在],[b a 上L 可积 (D)⎰-=b aa fb f dx x f )()()('二. 填空题(3分×5=15分)1、()(())s s C A C B A A B ⋃⋂--=_________2、设E 是[]0,1上有理点全体,则'E =______,oE =______,E =______.3、设E 是n R 中点集,如果对任一点集T 都_________________________________,则称E 是L 可测的4、)(x f 可测的________条件是它可以表成一列简单函数的极限函数.(填“充分”,“必要”,“充要”)5、设()f x 为[],a b 上的有限函数,如果对于[],a b 的一切分划,使_____________________________________,则称()f x 为[],a b 上的有界变差函数。
(完整版)实变函数期末考试卷A及参考答卷

2011—2012学年第1学期数计学院09级数学与应用数学专业(1、2班)《实变函数》期末考试卷(A)考生考试诚信承诺书在我填写考生信息后,表示我已阅读和理解《龙岩学院考试纪律与违纪处分办法》的有关规定,承诺在考试中自觉遵规守纪,如有违反将接受处理;我保证在本科目考试中,本人所提供的个人信息是真实、准确的。
考生签名:实变函数期末考试卷(A )2009级本科1、2班用 考试时间2012年01月 04日一 填空题(每小题3分,满分24分) 1 我们将定义在可测集qE ⊂上的所有L 可测函数所成的集合记为()M E .任取()f M E ∈,都可以确定两个非负可测函数:()()()(),0,0,0.f x x E f fx x E f +∈>⎧=⎨∈≤⎩当时当时 和()()()()0,0,,0.x E f fx f x x E f -∈>⎧=⎨-∈≤⎩当时当时分别称为f 的正部和负部。
请你写出()()(),,f x fx f x +-和()f x 之间的关系:()f x =,()f x =。
2 上题()M E 中有些元素ϕ被称为非负简单函数,指的是:12k E E E E =是有限个互不相交的可测集的并集,在i E 上()i x c ϕ≡(非负常数)(1,2,,i k =).ϕ在E 上的L 积分定义为:()Ex dx ϕ=⎰,这个积分值可能落在区间中,但只有当时才能说ϕ是L 可积的。
3 若()f M E ∈是非负函数,则它的L 积分定义为:()Ef x dx =⎰,这个积分值可能落在区间中,但只有当时才能说f 是L 可积的。
4 ()M E 中的一般元素f 称为是积分确定的,如果f +和f -, 即()Efx dx +⎰和()E f x dx -⎰的值;但只有当时才能说f 是L 可积的,这时将它的积分定义为:()Ef x dx =⎰。
5 从()M E 中取出一个非负函数列(){}n f x ,则法图引理的结论是不等式:;如果再添上条件和就试卷 共 8 页 第 2 页得到列维定理的结论:。
实变函数_周其生_实变函数试卷一及答案

《实变函数》试卷一一、单项选择题(3分×5=15分)1、1、下列各式正确的是( )(A )1lim n k n n k n A A ∞∞→∞===⋃⋂; (B )1lim n k n k n n A A ∞∞==→∞=⋂⋃;(C )1lim n k n n k nA A ∞∞→∞===⋂⋃; (D )1lim n k n k nn A A ∞∞==→∞=⋂⋂;2、设P 为Cantor 集,则下列各式不成立的是( ) (A )=P c (B) 0mP = (C) P P ='(D) P P =3、下列说法不正确的是( )(A) 凡外侧度为零的集合都可测(B )可测集的任何子集都可测 (C) 开集和闭集都是波雷耳集 (D )波雷耳集都可测4、设{}()n f x 是E 上的..a e 有限的可测函数列,则下面不成立的是( ) (A )若()()n f x f x ⇒, 则()()n f x f x → (B) {}sup ()n nf x 是可测函数(C ){}inf ()n nf x 是可测函数;(D )若()()n f x f x ⇒,则()f x 可测5、设f(x)是],[b a 上有界变差函数,则下面不成立的是( ) (A) )(x f 在],[b a 上有界 (B) )(x f 在],[b a 上几乎处处存在导数 (C ))('x f 在],[b a 上L 可积 (D) ⎰-=b aa fb f dx x f )()()('二. 填空题(3分×5=15分)1、()(())s s C A C B A A B ⋃⋂--=_________2、设E 是[]0,1上有理点全体,则'E =______,oE =______,E =______.3、设E 是n R 中点集,如果对任一点集T 都有_________________________________,则称E 是L 可测的4、)(x f 可测的________条件是它可以表成一列简单函数的极限函数. (填“充分”,“必要”,“充要”)5、设()f x 为[],a b 上的有限函数,如果对于[],a b 的一切分划,使_____________________________________________________,则称()f x 为[],a b 上的有界变差函数。
实变函数期末考试题库

《实变函数》期末考试试题汇编目录《实变函数》期末考试模拟试题(一) (2)《实变函数》期末考试模拟试题(二) (7)《实变函数》期末考试模拟试题(三) (13)《实变函数》期末考试模拟试题(四) (18)《实变函数》期末考试模拟试题(五) (27)《实变函数》期末考试模拟试题(六) (30)《实变函数》期末考试模拟试题(七) (32)《实变函数》期末考试模拟试题(八) (36)《实变函数》期末考试模拟试题(九) (41)《实变函数》期末考试模拟试题(十) (47)《实变函数》期末考试题(一) (57)《实变函数》期末考试题(二) (63)《实变函数》期末考试模拟试题(一)(含解答)一、选择题(单选题)1、下列集合关系成立的是( A )(A )(\)A B B A B ⋃=⋃ (B )(\)A B B A ⋃= (C )(\)B A A A ⋃⊆ (D )(\)B A A ⊆ 2、若nE R ⊂是开集,则( B )(A )E E '⊂ (B )E 的内部E = (C )E E = (D )E E '= 3、设P 是康托集,则( C )(A )P 是可数集 (B )P 是开集 (C )0mP = (D )1mP = 4、设E 是1R 中的可测集,()x ϕ是E 上的简单函数,则( D )(A )()x ϕ是E 上的连续函数 (B )()x ϕ是E 上的单调函数 (C )()x ϕ在E 上一定不L 可积 (D )()x ϕ是E 上的可测函数5、设E 是nR 中的可测集,()f x 为E 上的可测函数,若()d 0Ef x x =⎰,则( A )(A )在E 上,()f z 不一定恒为零 (B )在E 上,()0f z ≥ (C )在E 上,()0f z ≡ (D )在E 上,()0f z ≠ 二、多项选择题(每题至少有两个或两个以上的正确答案) 1、设E 是[0,1]中的无理点全体,则(C 、D )(A )E 是可数集 (B )E 是闭集 (C )E 中的每一点都是聚点 (D )0mE > 2、若1E R ⊂至少有一个内点,则( B 、D )(A )*m E 可以等于零 (B )*0m E > (C )E 可能是可数集 (D )E 是不可数集3、设[,]E a b ⊂是可测集,则E 的特征函数()E X x 是 (A 、B 、C ) (A )[,]a b 上的简单函数 (B )[,]a b 上的可测函数 (C )E 上的连续函数 (D )[,]a b 上的连续函数4、设()f x 在可测集E 上L 可积,则( B 、D )(A )()f z +和()f z -有且仅有一个在E 上L 可积 (B )()f z +和()f z -都在E 上L 可积 (C )()f z 在E 上不一定L 可积 (D )()f z 在E 上一定L 可积5、设()f z 是[,]a b 的单调函数,则( A 、C 、D )(A )()f z 是[,]a b 的有界变差函数 (B )()f z 是[,]a b 的绝对连续函数 (C )()f z 在[,]a b 上几乎处处连续 (D )()f z 在[,]a b 上几乎处处可导 三、填空题(将正确的答案填在横线上)1、设X 为全集,A ,B 为X 的两个子集,则\A B=C A B ⋂ 。
实变函数期末考试卷A及参考答卷

实变函数期末考试卷(A )2009级本科1、2班用 考试时间2012年01月 04日一 填空题(每小题3分,满分24分) 1 我们将定义在可测集qE ⊂上的所有L 可测函数所成的集合记为()M E .任取()f M E ∈,都可以确定两个非负可测函数:()()()(),0,0,0.f x x E f fx x E f +∈>⎧=⎨∈≤⎩当时当时 和()()()()0,0,,0.x E f fx fx x E f -∈>⎧=⎨-∈≤⎩当时当时分别称为f 的正部和负部。
请你写出()()(),,f x fx f x +-和()f x 之间的关系:()f x =,()f x =。
2 上题()M E 中有些元素ϕ被称为非负简单函数,指的是:试卷 共 8 页 第 2 页12k E E E E =是有限个互不相交的可测集的并集,在i E 上()i x c ϕ≡(非负常数)(1,2,,i k =).ϕ在E 上的L 积分定义为:()Ex dx ϕ=⎰,这个积分值可能落在区间中,但只有当时才能说ϕ是L 可积的。
3 若()f M E ∈是非负函数,则它的L 积分定义为:()Ef x dx =⎰,这个积分值可能落在区间中,但只有当时才能说f 是L 可积的。
4 ()M E 中的一般元素f 称为是积分确定的,如果f +和f -, 即()Efx dx +⎰和()E f x dx -⎰的值;但只有当时才能说f是L 可积的,这时将它的积分定义为:()Ef x dx =⎰。
5 从()M E 中取出一个非负函数列(){}n f x ,则法图引理的结论是不等式:;如果再添上条件和就得到列维定理的结论:。
6 设f 和()1,2,n f n =都是()M E 中的可测函数,满足()()lim n n f x f x a e →∞= 于E 或n f f ⇒两个条件之一。
或 (1);(2)。
7 富比尼定理的表述过程比较长,但它给出了定义在两个可测子集,pqA B ⊂⊂上的笛卡尔积P qA B +⨯⊂上的可测函数()(),f P f x y =的积分可化为累次积分的条件却非常简单。
2017.1实变函数期末试卷A卷

浙江师范大学2016-2017学年第一学期《实变函数》期末试卷——A 卷考试类别:考试(必修)使用学生:数学14级考试时间:90分钟考试日期:2017/01/11⋆说明:考生应将全部答案都写在答题纸上,否则作无效处理.(一)填空题(每空2分,共20分).1.设A n =¦(1+1k)k1≤k ≤n ©,则lim n →∞A n =,lim n →∞A n =.2.设E =¦(x ,y ,z ) x 2+y 2+z 2<1©⊂R 3,则m (E )=,∂E =,E ′=.3.设E ⊂R n .根据定义,E 的外测度m ∗(E )=;E 为可测集是指;非负可测函数f (x )在E 上的Lebesgue 积分为.4.设有集合列A k,令B =∞Y k =1A k =A 1×A 2×···×A k ×···,若A k =2(∀k ≥1),则B =.5.设m (E )<∞,且f k (x )依测度收敛于0,则limk →∞ZE11+|f k (x )|dx =.(二)辨析题(以下各论述若正确请证明,若不正确请说明原因.每小题6分,共18分).1.黎曼函数为R (x )=(1q,x =pq∈(0,1)∩Q ,其中p ,q ∈N 且(p ,q )=1,0,x =0,1和x ∈(0,1)\Q ,则R (x )在[0,1]上可测.2.函数列f k (x )=χ(0,k )(x )在E =(0,+∞)上几乎处处收敛,“基本上”一致收敛(近一致收敛),且依测度收敛.3.设E ⊂R n,则m ∗(E )=inf ¦m (G ) G 为R n 中开集,且G ⊃E ©.(三)简答与计算题(每小题7分,共14分).1.请叙述可测函数与连续函数的区别与联系,不必证明.12.计算:limk →∞Z(0,+∞)1(1+x k )k·x 1kdx .(四)证明题(注:从以下六题中选四题作答,每题12分,共48分).1.若f (x )是可测集E 上的实值函数,证明:f (x )在E 上可测⇐⇒对于R 中的任一开集G ,f −1(G )是可测集.2.若f k (x )在E 上同时依测度收敛于f (x )与g (x ),则f (x )与g (x )几乎处处相等.3.设f (x )在E 上非负可测,若ZEf (x )dx =0,则f (x )=0,a .e .x ∈E .4.设f k (x )为E 上的可积函数列.若存在E 上可积函数F (x ),使得|f k (x )|≤F (x ),a .e .x ∈E ,则ZE lim k →∞f k (x )dx ≥limk →∞ZEf k (x )dx .5.若 E k是R n 中递增可测集合列,f (x )是E 上非负可测函数,E =∞[k =1E k ,则Z Ef (x )dx =limk →∞ZE kf (x )dx .6.设f (x )和f k (x )(k ≥1)都是R 上可积函数.若ZR|f k (x )−f (x )|dx ≤1k 2(k ≥1),则 f k (x ) 在R 上几乎处处收敛于f (x ).2。
实变函数期末考试题库

实变函数期末考试题库一、选择题1. 下列函数符合实变函数的定义的是:()A. f(x) = x^2 - 5x + 6, x ∈ [0, ∞)B. f(x) = √(x + 2), x ∈ (-∞, 3]C. f(x) = 1/x, x ∈ (-∞, 0)D. f(x) = |x|, x ∈ R2. 实变函数的定义域是指函数所能取的值的范围。
下列函数的定义域是:()A. f(x) = 2x + 1, x ∈ ZB. f(x) = √(x^2 - 4), x ∈ RC. f(x) = log(x), x ∈ (-∞, ∞)D. f(x) = 1/(x - 2), x ∈ R - {2}3. 下列函数中,连续性具有间断点的是:()A. f(x) = 3x - 2, x ∈ (-∞, 10)B. f(x) = |x|, x ∈ RC. f(x) = {x^2, x < 0; 2x, x ≥ 0}, x ∈ RD. f(x) = 1/x, x ∈ (-∞, 0) U (0, ∞)4. 设f(x)和g(x)为两个实变函数,下列函数中不是实变函数的是:()A. f(x) + g(x)B. f(x)g(x)C. f(x)/g(x), g(x) ≠ 0D. g(f(x))5. 若f(x)为实变函数,则下列函数中一定是实变函数的是:()A. f(x)/xB. √f(x)C. ∣f(x)∣D. f(x + 1)二、填空题1. 若f(x)在x = a处连续,则f(x)在x = a处一定是__________函数。
答:连续2. 设f(x) = 2x^2 + bx +1,若f(x)在x = -1处连续,则b的取值范围是__________。
答:33. 设f(x) = (x - 1)/(x + 3) + e^x,则f(x)的定义域是__________。
答:(-∞, -3) U (-3, ∞)4. 设函数f(x) = |2x - 5|,则f(x)在点x = ________处不连续。
实变函数期末复习资料试卷

)
(第 13页,共 24页)
∞ (C) m⎛ ∩ En ⎞ ⎜n ⎟ < lim mEn ;(D)以上都不对 ⎝ =1 ⎠ n → ∞
5、设 f(x)是 [ a, b] 上绝对连续函数,则下面不成立的是( (A) f (x) 在 [ a, b] 上的一致连续函数 (C) f ( x ) 在 [ a, b] 上 L 可积 得 分 二. 填空题(3 分×5=15 分) 1、设集合 N ⊂ M ,则 M − ( M − N) = 2、设 P 为 Cantor 集,则 P = 3 、 设 E 是 _________
∞ ⎞ ______ ∞ mS 3、设 {Si } 是一列可测集,则 m ⎛ ∪ S ⎜ i =1 i ⎟ ∑ i ⎝ ⎠ i =1
o
4、 ______________________________________________________ 鲁津定理: _______________________________________________________________ 5、 设 F ( x) 为 [ a , b ] 上的有限函数, 如果_________________________________ _______________________________________________________________ ______________________________则称 F ( x) 为 [ a , b ] 上的绝对连续函数。
考 生
安庆师范学院
第
实变函数期末考试卷A

实变函数期末考试卷A附件一东 南 大 学 考 试 卷(A 卷)课程名称 实变函数 考试学期 11-12-2 得分 适用专业 数学系 考试形式 闭卷 考试时间长度 120分钟 (开卷、半开卷请在此写明考试可带哪些资料) 卷无一. (10分)试叙述可数集的定义,并分别给出一个可数集合和一个不可数集的例子。
二. (10 分)叙述勒贝格外测度的定义,并证明可数集的外测度为零.三. (10分)设E 是可测集,证明存在E 的一列单调增加的闭子集列1E,n n F F +⊂⊂n 1,∀≥ 使得 n mE=lim nmF →∞.四. (10 分)(1)试给出有界闭区间上有界函数Riemann 可积的充分必要条件。
(2)给出一个Lebesgue 可积但Riemann 不可积的例子。
五. (10分)(1) 叙述依测度收敛的定义。
(2) 若在E 上,()()n f x f x ⇒, ()()n g x g x ⇒, 证明()f x 和()g x 在E 上几乎处处相等。
六.(10分)叙述有界变差函数和绝对连续函数的定义,并分别给出一个例子。
七.(10分)设n f (x)在 E 上Lebesgue 可积。
如果lim |()|0nE n f x dx →∞→⎰, 证明存在子列kn {f }在E 上几乎处处收敛于零。
八. (10分)(1)试叙述Fatou 引理;(2)求下列极限: 20arctan()lim 1n nx dxx +∞→∞+⎰九.设()f x 在[,]a b 上Lebesgue 可积。
(1) 若()x φ是[,]a b 上的有界可测函数,证明()()f x x φ在[,]a b 上是Lebesgue 可积的。
(2) 如果对[,]a b 上的任意有界可测函数()x φ,总有()()0baf x x dx φ=⎰成立. 证明()f x 在[,]a b 上几乎处处为零。
(3) 如果对任意连续函数()x φ总有 ()()0b a f x x dx φ=⎰成立,证明上述(2)中结论仍然成立。
实变函数期末考试卷A及参考答卷

实变函数期末考试卷A及参考答卷Document number:NOCG-YUNOO-BUYTT-UU986-1986UT2011—2012学年第1学期数计学院09级数学与应用数学专业(1、2班) 《实变函数》期末考试卷(A)试卷共 8 页第 1 页考生考试诚信承诺书在我填写考生信息后,表示我已阅读和理解《龙岩学院考试纪律与违纪处分办法》的有关规定,承诺在考试中自觉遵规守纪,如有违反将接受处理;我保证在本科目考试中,本人所提供的个人信息是真实、准确的。
考生签名:实变函数期末考试卷(A )2009级本科1、2班用 考试时间2012年01月 04日一 填空题(每小题3分,满分24分) 1 我们将定义在可测集qE ⊂上的所有L 可测函数所成的集合记为()M E .任取()f M E ∈,都可以确定两个非负可测函数:()()()(),0,0,0.f x x E f fx x E f +∈>⎧=⎨∈≤⎩当时当时 和()()()()0,0,,0.x E f fx f x x E f -∈>⎧=⎨-∈≤⎩当时当时分别称为f 的正部和负部。
请你写出()()(),,f x fx f x +-和()f x 之间的关系:()f x =,()f x =。
2 上题()M E 中有些元素ϕ被称为非负简单函数,指的是:12k E E E E =是有限个互不相交的可测集的并集,在i E 上()i x c ϕ≡(非负常数)(1,2,,i k =).ϕ在E 上的L 积分定义为:()Ex dx ϕ=⎰,这个积分值可能落在区间中,但只有当时才能说ϕ是L 可积的。
3 若()f M E ∈是非负函数,则它的L 积分定义为:()Ef x dx =⎰,这个积分值可能落在区间中,但只有当时才能说f是L 可积的。
4 ()M E 中的一般元素f 称为是积分确定的,如果f +和f -,即()Efx dx +⎰和()E f x dx -⎰的值;但只有当时才能说f 是L 可积的,这时将它的积分定义为:()Ef x dx =⎰。
《实变函数》期末题

1《实变函数》期末练习题及答案一、单项选择题1.下列集合关系成立的是( )A ()\B A A =∅ B ()\A B A =∅C ()\A B B A =D ()\B A A B =2.若n R E ⊂是开集,则( )A E E '⊂B 0E E =C E E =DE E '= 4.设(){}n f x 是E 上一列非负可测函数,则( )A ()()lim lim n n E E n n f x dx f x dx →∞→∞≤⎰⎰B ()()lim lim n n E E n n f x dx f x dx →∞→∞≤⎰⎰C ()()lim lim n n E En n f x dx f x dx →∞→∞≤⎰⎰D ()()lim lim n nE E n n f x dx f x →∞→∞≤⎰⎰5.下列集合关系成立的是( )A cc A A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭ B ccA A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭ C cc A A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭ D ccA A αααα∈Λ∈Λ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭6.若n R E ⊂是闭集,则( )A E E '=B E E '⊂C E E '⊂D 0E E =7.设E 为无理数集,则( )A E 为闭集B E 是不可测集C mE =+∞D 0mE = 9.下列集合关系成立的是( )A cc A A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭ B ccA A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭ C ccA A αααα∈Λ∈Λ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭ D cc c A A αααα∈Λ∈Λ⎛⎫= ⎪⎝⎭210.设n R E ⊂,则( )A E E ⊃B E E '⊂C E E '⊂DE E =11.设P 为康托集,则( )A P 是可数集B 0mP =C P 是不可数集D P 是开集 13.下列集合关系成立的是( )A 若AB ⊂则c c B A ⊂ B 若A B ⊂则c c A B ⊂C 若A B ⊂则A B B =D 若A B ⊂则A B B =14.设n R E ⊂,则( )A ()E E = B 0E E ⊃ C E E '⊂ D E E '⊂ 15.设(){},001E x x =≤≤,则( )A 1mE =B 0mE =C E 是2R 中闭集DE 是2R 中完备集 16.设()f x ,()g x 是E 上的可测函数,则( )A ()()E x f x g x ⎡⎤≥⎣⎦不一定是可测集B ()()E x f x g x ⎡⎤≠⎣⎦是可测集C ()()E x f x g x ⎡⎤≤⎣⎦是不可测集D ()()E x f x g x ⎡⎤=⎣⎦不一定是可测集 17.下列集合关系成立的是( )(A )(\)A B B A B = (B )(\)A B B A = (C )(\)B A A A ⊆ (D )\B A A ⊆ 18. 若()n E R ⊆是开集,则 ( )(A )E 的导集E ⊆ (B )E 的开核E = (C )E E = (D )E 的导集E = 19. 设P 的康托集,则(A )P 为可数集 (B )P 为开集 (C )0mP = (D )1mP = 20、设E 是1R 中的可测集,()x ϕ是E 上的简单函数,则 ( )3(A )()x ϕ是E 上的连续函数 (B )()x ϕ是E 上的单调函数 (C )()x ϕ在E 上一定不L 可积 (D )()x ϕ是E 上的可测函数 21.下列集合关系成立的是( )(A )()()()A B C A B A C = (B )(\)A B A =∅ (C )(\)B A A =∅ (D )A B A B ⊆ 22. 若()n E R ⊆是闭集,则 ( )(A )0E E = (B )E E = (C )E E '⊆ (D )E E '= 23. 设Q 的有理数集,则( )(A )0mQ > (B )Q 为闭集 (C )0mQ = (D )Q 为不可测集24.设E 是n R 中的可测集,()f x 为E 上的可测函数,若()0Ef x dx =⎰,则 ( )(A )在E 上,()f x 不一定恒为零 (B )在E 上,()0f x ≥ (C )在E 上,()0f x ≡ (D )在E 上,()0f x ≠二、填空题1.设,A B 为集合,则()\A B B _A B (用描述集合间关系的符号填写) 2.设A 是B 的子集,则A _B (用描述集合间关系的符号填写) 3.如果E 中聚点都属于E ,则称E 是_集 4.有限个开集的交是_集5.设1E 、2E 是可测集,则()12m E E _12mE mE +(用描述集合间关系的符号填写) 6.设n E ⊂ 是可数集,则*m E _07.设()f x 是定义在可测集E 上的实函数,如果1a ∀∈ ,()E x f x a ⎡⎤≥⎣⎦是_,则称()f x 在E 上可测8.可测函数列的上极限也是_函数9.设()()n f x f x ⇒,()()n g x g x ⇒,则()()n n f x g x +⇒_410.设()f x 在E 上L 可积,则()f x 在E 上_11.设,A B 为集合,则()\B A A _A (用描述集合间关系的符号填写) 12.设{}211,2,A k k =-= ,则A _a (其中a 表示自然数集N 的基数) 13.设n E ⊂ ,如果E 中没有不属于E ,则称E 是_集 14.任意个开集的并是_集15.设1E 、2E 是可测集,且12E E ⊂,则1mE _2mE 16.设E 中只有孤立点,则*m E _017.设()f x 是定义在可测集E 上的实函数,如果1a ∀∈ ,()E x f x a ⎡⎤<⎣⎦是_,则称()f x 在E 上可测18.可测函数列的下极限也是_函数19.设()()n f x f x ⇒,()()n g x g x ⇒,则()()n n f x g x ⇒_20.设()n x ϕ是E 上的单调增收敛于()f x 的非负简单函数列,则()Ef x dx =⎰_21.设,A B 为集合,则()\A B B _B22.设A 为有理数集,则A _a (其中a 表示自然数集N 的基数) 23.设n E ⊂ ,如果E 中的每个点都是内点,则称E 是_集 24.有限个闭集的交是_集 25.设n E ⊂ ,则*m E _026.设E 是n 中的区间,则*m E _E 的体积27.设()f x 是定义在可测集E 上的实函数,如果1a ∀∈ ,()E x f x a ⎡⎤≤⎣⎦是_,则称()f x 在E 上可测28.可测函数列的极限也是_函数29.设()()n f x f x ⇒,()()n g x g x ⇒..a e ,则()n f x _()g x30.设()n f x 是E 上的非负可测函数列,且单调增收敛于()f x ,由勒维定理,有()Ef x dx =⎰_31.设,A B 为集合,则()\B A B A _A B32.设A 为无理数集,则A _c (其中c 表示自然数集[]0,1的基数)533.设n E ⊂ ,如果E 中没有不是内点的点,则称E 是_集 34.任意个闭集的交是_集35.设n E ⊂ ,称E 是可测集,如果n T ∀⊂ ,()**m T m T E =+ _ 36.设E 是外测度为零的集合,且F E ⊂,则*m F _037.设()f x 是定义在可测集E 上的实函数,如果1a ∀∈ ,()E x a f x b ⎡⎤≤<⎣⎦是_,(a b ≤)则称()f x 在E 上可测38.可测函数列的上确界也是_函数39.设()()n f x f x ⇒,()()n g x g x ⇒..a e ,则()()n n f x g x ⇒_40.设()()n f x f x ⇒,那么由_定理,(){}n f x 有子列()k n f x ,使()()k n f x f x →..a e 于E 41.设,A B 为两个集合,则__c A B A B - .42.设n E R ⊂,如果E 满足E E '⊆(其中E '表示E 的导集),则E 是____集.43.若开区间(,)αβ为直线上开集G 的一个构成区间,则(,)αβ满(i)_______________(ii)__________.44.设A 为无限集.则A 的基数__A a (其中a 表示自然数集N 的基数). 45.设12,E E 为可测集, 2mE <+∞,则1212(\)__m E E mE mE -. 46.设()f x 是定义在可测集E 上的实函数,若对任意实数a ,都有[()]E x f x a >是______,则()f x 是E 上的可测函数.47.设0x 是E (R ⊆)的内点,则*__0m E .48.设{}()n f x 为可测集E 上的可测函数列,且()(),n f x f x x E ⇒∈,则由______定理可知得,存在{}()n f x 的子列{}()kn f x ,使得.()()()ka en f x f x x E →∈.49.设()f x 为可测集E (n R ⊆)上的可测函数,则()f x 在E 上的L 积分值不一定存在且|()|f x 在E 上____________L 可积.50.若()f x 是[,]a b 上的绝对连续函数,则()f x ____[,]a b 上的有界变差函数. 51.设,A B 为集合,则___(\)A B B A A52.设n E R ⊂,如果E 满足0E E =(其中0E 表示E 的内部),则E 是_____集653.设G 为直线上的开集,若开区间(,)a b 满足(,)a b G ⊆且,a G b G ∉∉,则(,)a b 必为G 的________区间54.设{|2,}A x x n n ==为自然数,则A 的基数____ a (其中a 表示自然数集N 的基数) 55.设,A B 为可测集,B A ⊆且mB <+∞,则__(\)mA mB m A B -56.设()f x 是可测集E 上的可测函数,则对任意实数,()a b a b <,都有[()]E x a f x b <<是______ 57.若()E R ⊆是可数集,则__0mE 58.设{}()n f x 为可测集E 上的可测函数列,()f x 为E 上的可测函数,如果.()()()a en f x f x x E →∈,则()()n f x f x ⇒ x E ∈_________59. 设()f x 为可测集()n E R ⊆上的非负可测函数,则()f x 在E 上的L 积分值_________ 60.若()f x 是[,]a b 上的有界变差函数,则()f x 必可表示成两个_______________________ 61.设B 是1R 中无理数集,则=B 。
2017级第一学期《高等数学》期末考试试卷(A类)

2017级第一学期《高等数学》期末考试试卷 (A 类)一、单项选择题(本题共15分,每小题3分)1. 下列曲线中必有渐近线的是 ( )(A )cos =+y x x ; (B )2cos =+y x x ;(C )1cos =+y x x ; (D )21cos =+y x x。
2. 平面221x y z +-=与直线212122x y z ---==-的夹角是 ( ) (A )8arcsin 9; (B )8arccos 9; (C )4arcsin 9; (D )4arccos 9。
3. 若21()|1|2()d f x x f x x -=-+⎰,则()f x 等于 ( ) (A )1()|1|2f x x =-+; (B )()|1|1f x x =--; (C )3()|1|5f x x =-+; (D )3()|1|5f x x =--。
4. 下列选项中,肯定不是某个二阶常系数线性微分方程的一组解的是 ( )(A )e x x +,22e x x --,2e x x -+;(B )e e x x x -+,2+e x x xe x -,e e x x x x -+;(C )e 1x x -+,2x -,e x x -; (D )(e 1)x x +,e 2e x x x --,+2+2e x x xe x -。
5. 对于命题:① 设函数f 在R 上可积,则f 在R 上连续的充要条件是变上限积分 0()()d xx f t t Φ=⎰在R 上可导; ② 若R 上的单调函数f 有原函数,则对于任意取定的常数a 和b ,必存在 ξ∈R , 使得()d ()()ba f x x fb a ξ=-⎰, 下述选项正确的是 ( )(A )①错误,②正确; (B )①正确,②错误;(C )①和②均正确; (D )①和②均错误。
二、填空题(每小题3分,共15分)6. 设可导函数()=y f x 由方程cos()ln 1+-=xy y x 确定,则2lim [()1]n n f n→∞-=___________。
实变函数试题库参考答案

实变函数试题库参考答案(共37页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《实变函数》试题库及参考答案(完整版)选择题1,下列对象不能构成集合的是:( )A 、全体自然数B 、0,1 之间的实数全体C 、[0, 1]上的实函数全体D 、全体大个子2、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{全体小个子}D 、{x :x>1}3、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{x :x>1}D 、{全体胖子}4、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{x :x>1}D 、{全体瘦子}5、下列对象不能构成集合的是:( )A 、{全体小孩子}B 、{全体整数}C 、{x :x>1}D 、{全体实数}6、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体大人}C 、{x :x>1}D 、{全体整数}7、设}1:{ααα≤<-=x x A , I 为全体实数, 则ααA I∈⋃= ( ) A 、(-1, 1) B 、(-1, 0) C 、(-∞, +∞) D 、(1, +∞)8、设}1111:{ix i x A i -≤≤+-=, N i ∈, 则i i A ∞=⋃1= ( ) A 、(-1, 1) B 、(-1, 0) C 、[0, 1] D 、[-1, 1]9、设}110:{ix x A i +≤≤=, N i ∈, 则i i A ∞=⋂1= ( ) A 、(0, 1) B 、[0, 1] C 、[0, 1] D 、(0, +∞)10、设}1211:{ix i x A i +<<-=, N i ∈, 则i i A ∞=⋃1= ( ) A 、[1, 2] B 、(1, 2) C 、 (0, 3) D 、(1, 2)11、设}23:{+≤≤=i x i x A i , N i ∈, 则i i A ∞=⋂1= ( ) A 、(-1, 1) B 、[0, 1] C 、Φ D 、{0}12、设}11:{ix i x A i <<-=, N i ∈, 则i i A ∞=⋂1= ( ) A 、(-1, 1) B 、[0, 1] C 、Φ D 、{0}13、设]1212,0[12--=-n A n , ]211,0[2nA n +=, N n ∈,则=∞→n n A lim ( )A 、[0, 2]B 、[0, 2]C 、[0, 1]D 、[0, 1]14、设]1212,0[12--=-n A n , ]211,0[2nA n +=, N n ∈, 则=∞→n n A lim ( ) A 、[0, 2]B 、[0, 2]C 、[0, 1]D 、[0, 1]15、设),0(n A n =, N n ∈, 则=∞→n n A lim ( )A 、ΦB 、[0, n]C 、RD 、(0, ∞)16、设)1,0(nA n =, N n ∈, 则=∞→n n A lim ( ) A 、(0, 1)B 、(0, n1) C 、{0} D 、Φ 17、设)1,0(12nA n =-, ),0(2n A n =, N n ∈, 则=∞→n n A lim ( )A 、ΦB 、(0, n1) C 、(0, n) D 、(0, ∞) 18、设)1,0(12nA n =-, ),0(2n A n =, N n ∈, 则=∞→n n A lim ( )A 、ΦB 、(0, n1) C 、(0, n) D 、(0, ∞) 19、设A 、B 、C 是三个集合, 则A-(A-B)= ( )A 、B B 、AC 、A ⋂BD 、A ⋃B20、设A 、B 、C 是三个集合, 则A-(B ⋃C)= ( )A 、(A-B)⋂(A-C)B 、(A-B)⋃(A-C)C 、A ⋂BD 、A ⋂C21、设A 、B 、C 是三个集合, 则A-(B ⋂C)= ( )A 、(A-B)⋂(A-C)B 、(A-B)⋃(A-C)C 、A ⋂BD 、A ⋂C22、设A 、B 、S 是三个集合, 且S A ⊂, S B ⊂, 则)(B A C s -= ( )A 、BC A C s s ⋃ B 、B C A C s s ⋂ C 、B A C s ⋃D 、B A C s ⋂23、设A 、B 、S 是三个集合, 且S A ⊂, S B ⊂, 则)(B A C s ⋃= ( )A 、BC A C s s ⋃ B 、B C A C s s ⋂ C 、B A C s ⋃D 、B C A s ⋃24、设A 、B 、C 是三个集合, 则A-(B-C) = ( )A 、 A ⋃C-B B 、 A-B-C C 、 (A-B)⋃(A ⋂C)D 、 C-(B-A)25、集合E 的全体内点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包26、集合E 的全体聚点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包27、集合E 的全体边界点和内点所成的集合是E 的 ( )A 、开核B 、边界C 、导集D 、闭包28、E-E '所成的集合是 ( )A 、开核B 、边界C 、外点D 、{E 的全体孤立点}29、E 的全体边界点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包30、设点P 是集合E 的边界点, 则 ( )A 、P 是E 的聚点B 、P 是E 的孤立点C 、P 是E 的内点D 、P 是CE 的边界点31、设)3,2()1,0(⋃=G , 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(21, 1) C 、[0, 1] D 、(0, 2) 32、设)1,0(1=G , )2,21()0,1(2⋃-=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 2)C 、(-1, 21) D 、(-1, 2) 33、设)4,0(1=G , )4,3()1,0(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(3, 4)C 、(0, 4)D 、 (1, 4)34、设)1,0(1=G , )4,3()2,1(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 3)C 、(0, 4)D 、(1, 4)35、设)2,0(1=G , )4,3()2,1(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 2)C 、(1, 2)D 、(1, 4)36、设)2,1()1,0(1⋃=G , )23,21()0,1(2⋃-=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(21, 23) B 、(1, 2) C 、(0, 1) D 、(-1, 0) 37、若B A ⊂ ,则下列命题错误的是: ( )A 、B A ⊂ B 、A '⊂B 'C 、B A ∂⊂∂D 、B A ⊂38、若C B A =⋃, 则下列命题正确的是:( )A 、 CB A =⋃ B 、 A '⋃B '=C ' C 、C B A ∂=∂⋃∂D 、{A 的孤立点}⋃{B 的孤立点}={C 的孤立点}39、若C B A =⋂, 则下列命题错误的是:( )A 、 CB A =⋂ B 、C '⊂ A '⋂B ' C 、C B A =⋂D 、{A 的孤立点}⋂{B 的孤立点}={C 的孤立点}40、设CA 是A 的余集,则下列命题正确的是:( )A 、 )()(CA A C =B 、)(CA A ∂=∂C 、C(A ')=(CA )'D 、CA A C =)(41、设A -B=C, 则下列命题正确的是:( )A 、CB A ∂=∂-∂ B 、C B A =- C 、A '-B '=C 'D 、{A 的孤立点}-{B 的孤立点}={C 的孤立点}42、 (2-4-1-2) 下列命题错误的是:( )A 、A 是闭集B 、A '是闭集C 、A ∂是闭集D 、 A 是闭集43、若A 是闭集,B 是开集,则A -B 是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断44、若A 是开集,B 是闭集,则A -B 是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断45、若}{n A 是一开集列,则n n A ∞=⋃1是:( ) A 、开集 B 、闭集 C 、既非开集又非闭集 D 、无法判断46、若}{n A 是一开集列,则n n A ∞=⋂1是:( ) A 、开集 B 、闭集 C 、既非开集又非闭集 D 、无法判断47、若}{n A 是一闭集列,则n n A ∞=⋃1是:( ) A 、开集 B 、闭集 C 、既非开集又非闭集 D 、无法判断48、若}{n A 是一闭集列,则n n A ∞=⋂1是:( ) A 、开集 B 、闭集 C 、既非开集又非闭集 D 、无法判断49、若]1,0[ Q E =,则=mE ( )A 、0B 、1C 、2D 、350、下述结论( )正确.A 、E m E m **>B 、E m E m *≥*C 、E m E m **<D 、E m E m **≤51、下列说法正确的是( )A 、xx f 1)(=在(0,1)有限 B 、xx f 1)(=在)1,21(无界 C 、⎪⎩⎪⎨⎧=∞+∈=0,]1,0(,1)(x x x x f ,在[0,1]有限 D 、⎪⎩⎪⎨⎧=∈=0,1]1,0(,1)(x x x x f ,在[0,1]有界 52、函数列n n x x f =)(在[0,1]上( )于0.A 、a ,e 一致收敛B 、收敛C 、一致收敛D 、基本上一致收敛53、设E 是[0,1]中的不可测集,⎩⎨⎧-∈-∈=E x E x x f ]1,0[,1,1)( 则下列函数在[0,1]上可测的是( ).A 、)(x fB 、)(x f +C 、|)(|x fD 、)(x f -54、若)(x f 可测,则它必是( ).A 、连续函数B 、单调函数C 、简单函数D 、简单函数列的极限55、若Q E -=]1,0[,则=mE ( )A 、0B 、1C 、2D 、356、下列说法不正确的是( )A 、E 的测度有限,则E 必有界B 、E 的测度无限,则E 必无界C 、有界点集的测度有限D 、n R 的测度无限57、(4-4-2-1)下述论断正确的是( )A 、x x f tg )(=在)4,0(π无界 B 、⎪⎩⎪⎨⎧=∞+∈=2,)2,0[,tg )(ππx x x x f 在]2,0[π有限 C 、⎪⎩⎪⎨⎧=∈=2,1)2,0[,tg )(ππx x x x f 在]2,0[π有界 D 、x x f tg )(=在)2,0(π有限58、函数列n n x x f )21()(=在[0, 2]上( )于0. A 、收敛 B 、一致收敛 C 、基本上一致收敛 D 、.一致收敛59、设⎩⎨⎧-∈-∈=Ex x E x x x f ]1,0[,,)(其中E 是[0,1]的不可测集,则下列函数在[0, 1]可测的是( ).A 、|)(|x fB 、)(x fC 、)(x f +D 、)(x f -60、一个函数在其定义域中的( )点处都是连续的.A 、边界点B 、内点C 、聚点D 、孤立点.61、0P 是康托尔(cantor )集,则=0mP ( )A 、0B 、1C 、2D 、362、设A 是B 的真子集,则( )A 、B m A m **< B 、B m A m **≤C 、B m A m **>D 、B m A m **≥63、下列说法正确的是( )A 、x x f ctg )(=在)2,4(ππ无界 B 、⎪⎩⎪⎨⎧=∞+∈=0,]2,0(ctg )(x x x x f π在]2,0[π有限C 、⎪⎩⎪⎨⎧=∈=0,1]2,0(ctg )(x x xx f π在]2,0[π有界 D 、x x f ctg )(=在)2,0(π有限64、函数列n n n x x f 2)(=在]21,0[上( )于0. A 、收敛 B 、一致收敛、 C 、基本上一致收敛 D 、a. e.一致收敛65、设E 是[0, 1]上的不可测集,⎩⎨⎧-∈-∈=Ex xE x x x f ]1,0[)(22则下列函数在[0, 1]可测的是( ). A 、)(x f B 、)(x f + C 、|)(|x f D 、)(x f -66、设E 为可测集,则下列结论中正确的是( )A 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n 一致收敛于)(x fB 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n 基本上一致收敛于)(x fC 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n ⇒)(x fD 、若)}({x f n 在E 上基本上一致收敛于)(x f ,则)(x f n a , e 收敛于)(x f67、G 表示康托尔(cantor )集在[0,1]中的余集,则mG=( ) A 、0 B 、1 C 、2 D 、368、设21,S S 都可测,则21S S ( )A 、可测B 、不可测C 、可能可测也可能不可测D 、以上都不对 69、下列说法正确的是( ) A 、x x f sec )(=在)4,0(π上无界B 、x x f sec )(=在)4,0(π上有限C 、⎪⎩⎪⎨⎧=∞+∈=2)2,0[sec )(ππx x xx f 在]2,0[π上有限 D 、⎪⎩⎪⎨⎧=∈=21)2,0[sec )(ππx x x x f 在]2,0[π上有界 70、函数列n n n x x f 3)(=在]31,0[上( )于0 A 、收敛 B 、一致收敛 C 、基本上一致收敛 D 、a. e.一致收敛71、设⎩⎨⎧-∈∈-=E x x Ex x x f ]1,0[,,)(33,其中E 是[0, 1]上的不可测集,则( )在[0, 1]可测.A 、)(x f 、B 、)(x f +C 、)(x f -D 、|)(|x f 72、关于连续函数与可测函数,下列论述中正确的是( )A 、它们是同一概念B 、a , e 有限的可测函数是连续函数C 、a , e 有限的可测函数是基本上连续的函数D 、a , e 有限的可测函数是a , e 连续的函数 73、()=-)2,1()1,0( m ( ) A 、1、 B 、2 C 、3 D 、4 74、A 可测,B 是A 的真子集,则( )A 、mB mA ≥ B 、B m mA *≥C 、B m mA *=D 、以上都不对 75、下列说法正确的是( ) A 、21)(x x f =在(0, 1)有限、 B 、21)(xx f =在]1,21[无界C 、⎪⎩⎪⎨⎧=∞+∈=0,]1,0(,1)(2x x x x f 在[0, 1]有限D 、⎪⎩⎪⎨⎧=∈=1,1]1,0(,1)(2x x x x f 在[0, 1]有界76、函数列x x f n n sin )(=在]2,0[π上( )于0.A 、收敛B 、基本上一致收敛C 、一致收敛D 、a. e.一致收敛77、设⎩⎨⎧-∈∈-=Ex x Ex x x f ]1,0[,,)(22其中E 是[0, 1]上的不可测集,则( )在[0, 1]上是可测的.A 、|)(|x fB 、)(x fC 、)(x f +D 、)(x f - 78、关于简单函数与可测函数下述结论不正确的是( )A 、简单函数一定是可测函数B 、简单函数列的极限是可测函数C 、简单函数与可测函数是同一概念D 、简单函数列的极限与可测函数是同一概念79、()=-]3,2()1,1[ m ( ) A 、1 B 、2 C 、3 D 、4 80、L 可测集类,对运算( )不封闭.A 、可数和B 、有限交C 、单调集列的极限D 、任意和. 81、下列说法正确的是( ) A 、31)(x x f =在)1,21(无界 B 、31)(xx f =在)1,0(有限C 、⎪⎩⎪⎨⎧=∞+∈=0]1,0(1)(3x x xx f 在[0, 1]有限 D 、⎪⎩⎪⎨⎧=∈=01]1,0(1)(3x x xx f 在[0, 1]有界82、函数列x x f n n cos )(=在]2,0[π上( )于0.A 、基本一致收敛B 、收敛C 、一致收敛D 、a. e.一致收敛83、设E 是]2,0[π中的不可测集,⎪⎩⎪⎨⎧-∈-∈=E x x E x x x f ]2,0[,sin ,sin )(π则下列函数在]2,0[π上可测的是( ).A 、)(x fB 、|)(|x fC 、)(x f +D 、)(x f - 84、关于依测度收敛,下列说法中不正确的是( )A 、依测度收敛不一定一致收敛B 、依测度收敛不一定收敛C 、若)}({x f n 在E 上.收敛于.有限的可测函数)(x f ,则)()(x f x f n ⇒D 、若)()(x f x f n ⇒,则存在子列)}({x f i n a. e.收敛于)(x f85、设)(x f 是可测集E 上的非负可测函数,则)(x f ( )A 、必可积B 、必几乎处处有限C 、必积分确定D 、不一定积分确定 86、设)(x f 在可测集E 上可积,则在E 上( )A 、)(x f +与)(x f -只有一个可积B 、)(x f +与)(x f -皆可积C 、)(x f +与)(x f -不一定可积D 、)(x f +与)(x f -至少有一个不可积 87、设0=mE (Φ≠E ),)(x f 是E 上的实函数,则下面叙述正确的是( )A 、)(x f 在E 上不一定可测B 、)(x f 在E 上可测但不一定可积C 、)(x f 在E 上可积且积分值为0D 、)(x f 在E 上不可积 88、)(x f 在可测集E 上)(L 可积的必要条件是,)(x f 为( )A 、连续函数B 、几乎处处连续函数C 、单调函数D 、几乎处处有限的可测函数89、设)(x D 为狄立克雷函数,则⎰=10)()(dx x D L ( )A 、 0B 、 1C 、1/2D 、不存在 90、设)(x f 为Cantor 集的特征函数,则⎰=10)()(dx x f L ( )A 、 0B 、 1/3C 、2/3D 、 1 填空题1、设A 为一集合,B 是A 的所有子集构成的集合;若A =n, 则B =2、设A 为一集合,B 是A 的所有子集构成的集合;若A 是一可数集, 则B =3、若c A =, c B =, 则=⋃B A4、若c A =, B 是一可数集, 则=⋃B A5、若c A =, n B =, 则=⋃B A6、若}{n A 是一集合列, 且c A n =, =⋃∞=n n A 17、若I A ∈αα}{是任意集族, 其中I 是指标集, 则ααA I∈⋂=8、若I A ∈αα}{是任意集族, 其中I 是指标集, 则ααA I∈⋃=9、若I A ∈αα}{是任意集族, 其中I 是指标集, S 是一集合, 则)(ααA C IS ∈⋂=10、若I A ∈αα}{是任意集族, 其中I 是指标集, S 是一集合, 则)(ααA C IS ∈⋃=11、若}{n A 是任意一个集合列, 则=∞→n n A lim12、若}{n A 是任意一个集合列, 则=∞→n n A lim13、欧氏空间n R 中, 任意两点),,(21n x x x x =, ),,(21n y y y y =的距离d(x, y)=14、C[a, b]空间中,任意两元素x(t), y(t) 的距离 d(x, y)= 15、2l 空间中, 任意两元素 ),,,(21 n x x x x =, ),,(21 n y y y y =的距离 d(x, y)=16、欧氏空间2R 中, 任意两点),(21x x x =, ),(21y y y =的距离 d(x, y)= 17、欧氏空间3R 中, 任意两点),,(321x x x x =, ),,(321y y y y =的距离d(x, y)=18、欧氏空间4R 中, 任意两点),,,(4321x x x x x =, ),,,(4321y y y y y =的距离d(x,y)=19、设2R X =,}1:),{(22<+=y x y x E ,则E =20、设3R X =, }1:),,{(222<++=z y x z y x E , 则E =21、设2R X =,}1:),{(22<+=y x y x E ,则E ∂= 22、设2R X =,}1:),{(22<+=y x y x E ,则E '=23、设3R X =, }1:),,{(222<++=z y x z y x E , 则 E ∂= 24、设3R X =, }1:),,{(222<++=z y x z y x E , 则E '= 25、设A= [0, 1] , B = [3, 4] , 则 d(A, B) = 26、设C 是康托完备集, G= [0, 1]-C , 则d (C, G) = 27、设C 是康托完备集, 则C 的半径)(C δ=28、两个非空集合A, B 距离的定义为 d (A, B ) = 29、一个非空集合A 的直径的定义为)(A δ= 30、设A = [0, 1] ⋂Q, 则)(A δ=31、nR E ⊂,对每一列覆盖E 的开区间 ∞=⊃1i i E I ,定义=E m *________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江师范大学2016-2017学年第一学期《实变函数》期末试卷——A 卷
考试类别:考试(必修)使用学生:数学14级考试时间:90分钟
考试日期:2017/01/11
⋆说明:考生应将全部答案都写在答题纸上,否则作无效处理.
(一)填空题(每空2分,共20分).1.设A n =¦
(1+
1k
)k
1≤k ≤n ©,则lim n →∞
A n =
,lim n →∞
A n =
.2.设E =¦(x ,y ,z ) x 2
+y 2+z 2<1©⊂R 3,则m (E )=
,∂E =
,E ′=
.
3.设E ⊂R n .根据定义,E 的外测度m ∗(E )=;E 为可测集是指
;非负可测函数f (x )在E 上
的Lebesgue 积分为.
4.设有集合列
A k
,令B =
∞Y k =1
A k =A 1×A 2×···×A k ×···,若A k =2(∀k ≥1),则
B =
.
5.设m (E )<∞,且f k (x )依测度收敛于0,则lim
k →∞
Z
E
1
1+|f k (x )|
dx =
.
(二)辨析题(以下各论述若正确请证明,若不正确请说明原因.每小题6分,共18分).
1.黎曼函数为R (x )=
(
1q
,x =
p
q
∈(0,1)∩Q ,其中p ,q ∈N 且(p ,q )=1,
0,x =0,1和x ∈(0,1)\Q ,
则R (x )在[0,1]上可测.
2.函数列f k (x )=χ(0,k )(x )在E =(0,+∞)上几乎处处收敛,“基本上”一致收敛(近一致收敛),且依测度收敛.
3.设E ⊂R n
,则m ∗
(E )=inf ¦
m (G ) G 为R n 中开集,且G ⊃E ©.
(三)简答与计算题(每小题7分,共14分).
1.请叙述可测函数与连续函数的区别与联系,不必证明.
1
2.计算:lim
k →∞
Z
(0,+∞)
1
(1+x k )k
·x 1k
dx .(四)证明题(注:从以下六题中选四题作答,每题12分,共48分).
1.若f (x )是可测集E 上的实值函数,证明:f (x )在E 上可测⇐⇒对于R 中的任一开集G ,f −1(G )是可测集.
2.若
f k (x )
在E 上同时依测度收敛于f (x )与g (x ),则f (x )与g (x )几乎处处相等.
3.设f (x )在E 上非负可测,若
Z
E
f (x )dx =0,则f (x )=0,a .e .x ∈E .
4.设
f k (x )
为E 上的可积函数列.若存在E 上可积函数F (x ),使得|f k (x )|≤F (x ),a .e .x ∈E ,则
Z
E lim k →∞
f k (x )dx ≥lim
k →∞
Z
E
f k (x )dx .
5.若 E k
是R n 中递增可测集合列,f (x )是E 上非负可测函数,E =
∞[k =1
E k ,则Z E
f (x )dx =lim
k →∞
Z
E k
f (x )dx .
6.设f (x )和f k (x )(k ≥1)都是R 上可积函数.若Z
R
|f k (x )−f (x )|dx ≤
1
k 2
(k ≥1),则 f k (x ) 在R 上几乎处处收敛于f (x ).
2。
