实验四控制系统的稳定性分析
控制系统的稳定性分析

自动控制原理
其中系数 b1 , b2 , b3 等;根据
下列公式计算:
b1
a1a 2 a 0a 3 a1
b2
a1a 4 a 0a 5 a1
b3
a1a 6 a 0a 7 a1
同样的方法可以计算c;d;e等各行的系数
自动控制原理
注意:
在展开的阵列中;为简化其后的数值计算;可用一个正整数去除 或乘某一个整行;并不影响稳定性结论; 劳斯判据还说明:方程式5 4中;其正实部特征根数;等于劳斯阵列中第一列的系数改变的次数;
自动控制原理
从乃氏图上看;Gjw不包围1;j0点
G ( jw ) 1
稳定
G ( jw )
G ( jw )
不稳定
自动控制原理
2 若开环系统不稳定;有p个零点在右半平面;q的零点在原点;npq个 零点在左半平面 则
argD K(jw)(n2pq)2
如果闭环是稳定的;则
argDb(jw)n 2
故
a r g 1 G (jw ) n ( n 2 p q ) p q
F是新引进的函数;其分母是系统开环特征多项式;分子是闭环特征多 项式;
对于非单位反馈系统;开环传递函数为
GsG' sHsM DK Kss
自动控制原理
2 乃奎斯特队稳定判据 1 若开环是稳定的;则根据米哈依洛夫定理
argDk
jwn
2
如果闭环系统稳定;有
于是
argDb
jwn
2
arg1G (jw )0o
0
0
a n1 0
0
an2 an
自动控制原理
系统稳定的充要条件是:主行列式
式 1,2, n1 ;均大于零;即
计算机控制系统性能分析

南京邮电大学自动化学院实验报告课程名称:计算机控制系统实验名称:计算机控制系统性能分析所在专业:自动化学生姓名:**班级学号:B************: ***2013 /2014 学年第二学期实验一:计算机控制系统性能分析一、 实验目的:1.建立计算机控制系统的数学模型;2.掌握判别计算机控制系统稳定性的一般方法3.观察控制系统的时域响应,记录其时域性能指标;4.掌握计算机控制系统时间响应分析的一般方法;5.掌握计算机控制系统频率响应曲线的一般绘制方法。
二、 实验内容:考虑如图1所示的计算机控制系统图1 计算机控制系统1. 系统稳定性分析(1) 首先分析该计算机控制系统的稳定性,讨论令系统稳定的K 的取值范围; 解:G1=tf([1],[1 1 0]);G=c2d(G1,0.01,'zoh');//求系统脉冲传递函数 rlocus(G);//绘制系统根轨迹Root LocusReal AxisI m a g i n a r y A x i s-7-6-5-4-3-2-1012-2.5-2-1.5-1-0.500.511.522.5将图片放大得到0.750.80.850.90.9511.051.11.151.21.25-0.15-0.1-0.050.050.10.15Root LocusReal AxisI m a g i n a r y A x i sZ 平面的临界放大系数由根轨迹与单位圆的交点求得。
放大图片分析: [k,poles]=rlocfind(G)Select a point in the graphics window selected_point = 0.9905 + 0.1385i k =193.6417 poles =0.9902 + 0.1385i 0.9902 - 0.1385i 得到0<K<193(2) 假设不考虑采样开关和零阶保持器的影响,即看作一连续系统,讨论令系统稳定的K 的取值范围; 解:G1=tf([1],[1 1 0]); rlocus(G1);-1.2-1-0.8-0.6-0.4-0.200.2-0.8-0.6-0.4-0.20.20.40.60.8Root LocusReal AxisI m a g i n a r y A x i s由图片分析可得,根轨迹在S 平面左半面,系统是恒稳定的,所以: 0<K<∞(3) 分析导致上述两种情况下K 取值范围差异的原因。
线性系统的稳定性分析实验报告

线性系统的稳定性分析实验报告本实验旨在对线性系统的稳定性进行分析,包括定义稳定性、利用极点分布法分析稳定性、利用本征模态分析稳定性、以及使用Matlab进行稳定性分析等内容。
一、实验背景稳定性是控制系统研究中一个非常重要的概念,它与系统的性能、可靠性、控制策略等密切相关。
简而言之,稳定性就是指当输入信号发生变化时,系统能否在一定时间范围内维持稳定状态。
对于线性系统,稳定性的分析可以通过系统的传递函数、本征模态等途径进行求解。
二、实验设备(1)计算机(2)Matlab软件三、实验过程及结果1.定义稳定性在控制系统稳定性分析中,一般都是针对线性时不变系统进行讨论。
对于线性时不变系统,我们可以采用两种常用的定义方法来判断其稳定性:(1)定义1:系统是稳定的,当且仅当系统的输入信号有界时,系统的输出信号也有界。
(2)定义2:系统是稳定的,当且仅当系统的特征方程所有极点的实部均小于0。
2.利用极点分布法分析稳定性极点分布法是一种常用的线性时不变系统稳定性分析方法,通过计算系统的特征方程的极点分布来判断系统的稳定性。
例如,现有一个传递函数为G(s)= 1/ (s+1)(s-2)的系统,可以写出系统的特征方程:s^2-s-2=0求解特征方程,得到系统的两个极点为s1=2,s2=-1,其中s2=-1的实部小于0,符合定义2的稳定性判断标准,因此该系统是稳定的。
3.利用本征模态分析稳定性本征模态是指一组特定的正交基,通过它们可以表示出系统的任意初始状态和任意输入下的响应。
因此,本征模态分解法是一种可以用来分析线性可逆系统稳定性的工具。
例如,现有一个传递函数为G(s)= 1/(s+3)的系统,对应的状态空间方程为:x(t+1)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)其中,A=[-3],B=[1],C=[1],D=0。
求解系统的本征值,得到该系统的特征根为-3,证明该系统是非常稳定的。
因此,该系统满足定义2的稳定性判断标准。
仿真实验线性系统稳定性分析报告.doc

实验四 Stability analysis of linear systems线性系统稳定性分析一、实验目的1.通过响应曲线观测特征参量ζ和n ω对二阶系统性能的影响。
2.熟练掌握系统的稳定性的判断方法。
二、基础知识及MATLAB 函数注意:routh ()和hurwitz ()不是MATLAB 中自带的功能函数,(在共享文件夹里有劳斯判据和赫尔维茨判据的m 文件,把其中的routh.m 和hurwitz .m 放到MATLAB 文件夹下的work 文件夹中才能运行)。
1)直接求根判稳roots()控制系统稳定的充要条件是其特征方程的根均具有负实部。
因此,为了判别系统的稳定性,就要求出系统特征方程的根,并检验它们是否都具有负实部。
MATLAB 中对多项式求根的函数为roots()函数。
若求以下多项式的根24503510234++++s s s s ,则所用的MATLAB 指令为: >> roots([1,10,35,50,24])ans =-4.0000 -3.0000 -2.0000 -1.0000特征方程的根都具有负实部,因而系统为稳定的。
2)劳斯稳定判据routh ()劳斯判据的调用格式为:[r, info]=routh(den)该函数的功能是构造系统的劳斯表。
其中,den 为系统的分母多项式系数向量,r 为返回的routh 表矩阵,info 为返回的routh 表的附加信息。
以上述多项式为例,由routh 判据判定系统的稳定性。
>> syms EPS den=[1,10,35,50,24]; ra=routh(den,EPS) r=1 35 24 10 50 0 30 24 0 42 0 0 24 0 0 info=[ ]由系统返回的routh 表可以看出,其第一列没有符号的变化,系统是稳定的。
3)赫尔维茨判据hurwitz ()赫尔维茨的调用格式为:H=hurwitz (den )。
实验四三阶系统的瞬态响应及稳定性分析

实验四三阶系统的瞬态响应及稳定性分析引言:实际工程中经常遇到三阶系统,对三阶系统的瞬态响应及稳定性进行分析能够帮助我们更好地设计和优化控制系统。
本实验旨在通过实验,研究三阶系统的瞬态响应及稳定性,并加深对其理论知识的理解和掌握。
实验一:三阶系统的瞬态响应1.实验目的:通过三阶系统的瞬态响应实验,观察系统的输出响应情况,了解系统的动态特性。
2.实验仪器:示波器、波形发生器、三阶系统实验箱3.实验原理:三阶系统的瞬态响应是指系统在初始状态发生突变时,输出的响应情况。
三阶系统的瞬态响应主要涉及到系统阶跃响应、系统脉冲响应。
4.实验步骤:a.将波形发生器的正弦波信号输入三阶系统实验箱。
b.设置示波器的观测通道,将示波器的探头连接到三阶系统实验箱的输出端口。
c.调节波形发生器的频率和幅度,观察示波器上得到的输出响应波形。
5.数据处理:a.根据示波器上输出的响应波形,可以观察到系统的超调量、调整时间等指标,根据公式可以计算得到这些指标的具体数值。
b.将实验得到的数据记录下来,进行分析和比较。
1.实验目的:通过三阶系统的稳定性分析实验,了解系统的稳定性及稳定性判据。
2.实验仪器:示波器、三阶系统实验箱3.实验原理:三阶系统的稳定性是指系统在初始状态发生突变或受到外部扰动时,系统是否能够回到稳定状态。
常见的稳定性分析方法包括极点判据、频率响应法等。
4.实验步骤:a.将示波器的探头连接到三阶系统实验箱的输出端口。
b.调节系统的输入信号,观察示波器上得到的系统输出响应波形。
c.根据观察到的输出波形,分析系统的稳定性。
5.数据处理:a.根据实验得到的数据和观察到的波形,可以从输入输出关系中提取出系统的稳定性信息,比如振荡频率、稳定的输出值等。
b.根据提取出的信息,判断系统的稳定性。
实验三:实验结果和分析1.通过实验一,我们可以观察到三阶系统的瞬态响应,并根据输出波形,计算得到系统的超调量、调整时间等指标。
通过对比不同输入频率和幅度下的响应波形,可以分析系统的动态特性。
实验四三阶系统的瞬态响应及稳定性分析-一剖析
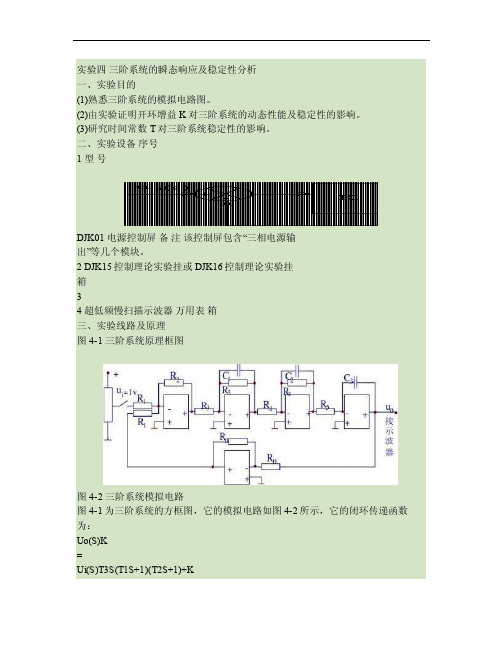
实验四三阶系统的瞬态响应及稳定性分析一、实验目的(1)熟悉三阶系统的模拟电路图。
(2)由实验证明开环增益K对三阶系统的动态性能及稳定性的影响。
(3)研究时间常数T对三阶系统稳定性的影响。
二、实验设备序号1 型号DJK01 电源控制屏备注该控制屏包含“三相电源输出”等几个模块。
2 DJK15控制理论实验挂或DJK16控制理论实验挂箱34 超低频慢扫描示波器万用表箱三、实验线路及原理图4-1 三阶系统原理框图图4-2 三阶系统模拟电路图4-1为三阶系统的方框图,它的模拟电路如图4-2所示,它的闭环传递函数为:Uo(S)K=Ui(S)T3S(T1S+1)(T2S+1)+K该系统的特征方程为:T1T2T3S³+T3(T1+T2)S²+T3S+K=0其中K=R2/R1,T1=R3C1,T2=R4C2,T3=R5C3。
若令T1=0.2S,T2=0.1S,T3=0.5S,则上式改写为S3+15S2+50S+100K=0用劳斯稳定判据,求得该系统的临界稳定增益K=7.5。
这表示K>7.5时,系统为不稳定;K<7.5时,系统才能稳定运行;K=7.5时,系统作等幅振荡。
除了开环增益K对系统的动态性能和稳定性有影响外,系统中任何一个时间常数的变化对系统的稳定性都有影响,对此说明如下:令系统的剪切频率为ωc,则在该频率时的开环频率特性的相位为:ϕ(ωc)= - 90° - tg-¹T1ωc - tg-¹T2ωc 相位裕量γ=180°+ϕ(ωc)=90°- tg-¹T1ωc- tg-¹T2ωc 由上式可见,时间常数T1和T2的增大都会使γ减小。
四、思考题(1)为使系统能稳定地工作,开环增益应适当取小还是取大?(2)系统中的小惯性环节和大惯性环节哪个对系统稳定性的影响大,为什么?(3)试解释在三阶系统的实验中,输出为什么会出现削顶的等幅振荡?(4)为什么图3-2和图4-1所示的二阶系统与三阶系统对阶跃输入信号的稳态误差都为零?(5)为什么在二阶系统和三阶系统的模拟电路中所用的运算放大器都为奇数?五、实验方法图4-1所示的三阶系统开环传递函数为KT3S(T1S+1)(T2S+1)(1)按K=10,T1=0.2S, T2=0.05S, T3=0.5S的要求,调整图4-2中的相应参数。
系统响应及系统稳定性实验报告

系统响应及系统稳定性实验报告系统响应及系统稳定性实验报告引言:系统响应和系统稳定性是控制论中重要的概念。
在工程和科学领域中,我们经常需要对系统的响应和稳定性进行评估和分析,以便设计和优化控制系统。
本实验旨在通过实际测量和数据分析,探讨系统响应和系统稳定性的相关概念。
一、实验背景控制系统是由输入、输出和系统本身组成的。
系统响应是指系统对输入信号的反应。
而系统稳定性则是指系统在长时间运行中是否趋于稳定状态。
了解系统的响应和稳定性对于设计和优化控制系统至关重要。
二、实验目的1. 了解系统响应和系统稳定性的概念和定义。
2. 掌握测量系统响应和稳定性的方法和技巧。
3. 分析实验数据,评估系统的响应和稳定性。
三、实验装置和方法本实验使用了一个简单的电路系统作为示例。
实验装置包括一个信号发生器、一个电路板和一个示波器。
实验步骤如下:1. 将信号发生器连接到电路板的输入端,设置合适的频率和振幅。
2. 将示波器连接到电路板的输出端,用于测量输出信号。
3. 通过改变信号发生器的输入信号,观察并记录系统的响应。
四、实验结果与数据分析在实验中,我们通过改变信号发生器的输入信号频率和振幅,记录了系统的输出信号。
根据实验数据,我们可以绘制出系统的频率响应曲线和幅频特性曲线。
1. 频率响应曲线频率响应曲线是描述系统对不同频率输入信号的响应的曲线。
通过绘制频率响应曲线,我们可以观察到系统对于不同频率信号的增益和相位变化。
从实验数据中绘制的频率响应曲线中,我们可以观察到系统在低频时具有较高的增益,而在高频时增益逐渐降低。
2. 幅频特性曲线幅频特性曲线是描述系统对不同幅度输入信号的响应的曲线。
通过绘制幅频特性曲线,我们可以观察到系统对于不同幅度信号的增益变化。
从实验数据中绘制的幅频特性曲线中,我们可以观察到系统在低幅度信号时具有较高的增益,而在高幅度信号时增益逐渐饱和。
五、系统稳定性分析系统稳定性是指系统在长时间运行中是否趋于稳定状态。
自控实验报告四离散系统的稳定性分析

实验四离散系统的稳定性分析一、实验目的1.掌握香农定理,了解信号的采样保持与采样周期的关系。
2.掌握采样周期对采样系统的稳定性影响。
二、实验设备PC 机一台,TD-ACC+(或TD-ACS)教学实验系统一套。
三、实验原理及内容本实验采用“采样-保持器”LF398 芯片,它具有将连续信号离散后以零阶保持器输出信号的功能。
其管脚连接图如 5.1-1 所示,采样周期 T 等于输入至 LF398 第 8 脚 (PU) 的脉冲信号周期,此脉冲由多谐振器 (由 MC1555 和阻容元件构成) 发生的方波经单稳电路 (由 MC14538 和阻容元件构成) 产生,改变多谐振荡器的周期,即改变采样周期。
图 5.1-2 是 LF398 采样-保持器功能的原理方块图。
1.信号的采样保持:电路如图 5.1-3 所示。
连续信号 x(t) 经采样器采样后变为离散信号 x*(t),香农 (Shannon) 采样定理指出,离散信号 x*(t)可以完满地复原为连续信号条件为:2.闭环采样控制系统(1) 原理方块图图 5.1-4 所示闭环采样系统的开环脉冲传递函数为:从式(5.1-4) 知道,特征方程式的根与采样周期T有关,若特征根的模均小于1,则系统稳定,若有一个特征根的模大于1,则系统不稳定,因此系统的稳定性与采样周期T的大小有关。
四、实验步骤1.准备:将信号源单元的“ST”的插针和“+5V”插针用“短路块”短接。
2.信号的采样保持实验步骤(1) 按图 5.1-3 接线。
检查无误后开启设备电源。
(2) 将正弦波单元的正弦信号 (将频率调为 2.5HZ) 接至 LF398 的输入端“IN1”。
(3) 调节信号源单元的信号频率使“S”端的方波周期为 20ms 即采样周期 T = 20ms。
(4) 用示波器同时观测 LF398 的 OUT1 输出和IN1 输入,此时输出波形和输入波形一致。
(5) 改变采样周期,直到 200ms,观测输出波形。
系统稳定性分析实验报告

一、实验目的1. 理解系统稳定性的基本概念和稳定性判据。
2. 掌握控制系统稳定性分析的方法和步骤。
3. 分析系统开环增益和时间常数对系统稳定性的影响。
4. 通过实验验证稳定性分析方法的有效性。
二、实验原理系统稳定性分析是自动控制理论中的一个重要内容,主要研究系统在受到扰动后能否恢复到原来的稳定状态。
根据系统传递函数的极点分布,可以将系统分为稳定系统和不稳定系统。
稳定系统在受到扰动后,其输出会逐渐恢复到原来的平衡状态;而不稳定系统在受到扰动后,其输出会发散,无法恢复到原来的平衡状态。
三、实验仪器1. 自动控制系统实验箱一台2. 计算机一台3. 数据采集卡一台四、实验内容1. 系统模拟电路搭建根据实验要求,搭建一个典型的控制系统模拟电路,如图1所示。
电路中包含一个比例积分(PI)控制器和一个被控对象。
被控对象可以用一个一阶环节表示,传递函数为G(s) = K / (Ts + 1),其中K为开环增益,T为时间常数。
图1 系统模拟电路图2. 系统稳定性分析(1)观察系统的不稳定现象在实验箱上设置不同的K和T值,观察系统在受到扰动后的响应情况。
当K值较大或T值较小时,系统容易产生增幅振荡,表现为不稳定现象。
(2)研究系统开环增益和时间常数对稳定性的影响通过改变K和T的值,观察系统稳定性的变化。
分析以下情况:1)当K值增加时,系统稳定性降低,容易出现增幅振荡;2)当T值减小时,系统稳定性降低,容易出现增幅振荡;3)当K和T同时改变时,系统稳定性受到双重影响。
(3)验证稳定性分析方法的有效性使用劳斯-赫尔维茨稳定性判据,分析系统传递函数的极点分布,判断系统是否稳定。
将实验得到的K和T值代入传递函数,计算特征方程的根,判断系统稳定性。
五、实验步骤1. 搭建系统模拟电路,连接实验箱和计算机。
2. 设置实验箱参数,调整K和T的值。
3. 观察系统在受到扰动后的响应情况,记录数据。
4. 使用劳斯-赫尔维茨稳定性判据,分析系统稳定性。
系统稳定性分析的仿真实验

系统稳定性分析的仿真实验一、实验目的:1.加深了解系统稳定性概念。
2.掌握使用Matlab 分析系统稳定性。
3.掌握使用Matlab 分析系统的频率特性二、实验设备:Matlab三、实验内容:1、已知控制系统开环传递函数为:17.18.01.023+++s s s K ,用Nyquist 稳定判据判定开环放大系数K 为10和50时闭环系统的稳定性。
2、已知控制系统开环传递函数为:()11.0)12.0(++s s s K ,取K =10,要求: ①绘制系统Bode 图,求出频域性能指标,并判断系统的稳定性;②改变开环增益K 值,分析K 变化对开环对数幅频、相频特性曲线的影响;③根据给出的稳定裕量,作K 参数设计,并评估系统性能。
四、实验步骤:实验内容一进入Matlab 命令窗口:1、当K=10时,输入命令num=[10]; %分子系数den=[0.1,0.8,1.7,1]; %分母系数g1=tf(num,den); %建立系统多项式模型nyquist(g1) %绘制Nyquist 图分析开环系统Nyquist 图,曲线是否包围(-1,j0)点?因此闭环系统稳定吗?2、当K=50时,输入命令num=[50]; %分子系数den=[0.1,0.8,1.7,1]; %分母系数g2=tf(num,den); %建立系统多项式模型nyquist(g2) %绘制Nyquist 图分析开环系统Nyquist 图,曲线顺时针包围(-1,j0)点几圈?表明闭环系统稳定性如何?有几个右半s 平面的极点?实验内容二K=10 K=50曲线未包围(-1,j0)点曲线包围(-1,j0)点一圈实验内容二①K=10,程序运行结果和图示可知,幅值裕度k= 1.5000 ,即 db;相位穿越频率wg=7.0711 rad/s;相角裕度r= 11.4304 ;幅值穿越频率wc= 5.7154 rad/s 。
②改变K值,分别取K为K1,K2,K3值时,观察系统的开环对数幅频、相频特性曲线的变化,分析K值变化对其影响。
河北大学自动控制原理实验四报告含结果分析

实验4 频率响应分析一 实验要求掌握应用MATLAB 绘制系统Bode 图和Nyquist 图的方法,并通过系统的Bode 图和Nyquist 图分析系统的动态性能、稳定性和相对稳定性。
二 实验步骤1 系统Nyquist 曲线的绘制(1)掌握系统极坐标(Nyquist )图绘制的函数nyquist()及其参数的使用方法。
(可通过help 方法)(2)在Matlab 中输入课本162页例5-14的程序,观察并记录结果。
利用Nyquist 稳定判据判断该系统的稳定性。
(3)在Matlab 中输入课本162-163页例5-15的程序,观察并记录结果(包括系统函数和Nyquist 图),利用Nyquist 稳定判据判断该系统的稳定性。
(4)在Matlab 中输入下面例子的程序,观察并记录结果,利用轴函数axis ()绘出在一定区域内的曲线,或用放大镜工具放大,进行稳定性分析。
例:已知系统的开环传递函数为101781000)(230+++=s s s s G 绘制系统的Nyquist 图,并利用Nyquist 稳定判据判断该系统的稳定性。
Matlab 命令窗口输入: >> num=[1000];>> den=[1 8 17 10];>> nyquist(num,den);grid2 系统Bode 图的绘制(1)掌握系统对数频率特性曲线(Bode )图绘制的函数bode()及其参数的使用方法。
(可通过help 方法) (2)在Matlab 中输入课本164页例5-16的程序,观察并记录结果。
计算系统稳定裕量(相角稳定裕量和增益稳定裕量)分析系统的稳定性。
(3)在Matlab 中输入课本164-165页例5-17的程序,观察并记录结果。
并分析阻尼系数对系统幅频特性和相频特性的影响。
三 思考题1 已知系统的开环传递函数为 12.124.22420)(230+++=s s s s G (1)绘制系统的开环零极图、Nyquist 图,并利用Nyquist 稳定判据判断该系统的稳定性。
系统稳定性分析实验报告

系统稳定性分析实验报告系统稳定性分析实验报告一、引言系统稳定性是指系统在一定条件下能够保持平衡或者回归到平衡状态的能力。
在工程领域中,系统稳定性是一个重要的指标,它直接影响着系统的可靠性和安全性。
为了更好地理解和评估系统的稳定性,我们进行了一系列的实验,并对实验结果进行了分析。
二、实验目的本次实验的目的是通过对不同系统的稳定性进行分析,探究系统在不同条件下的行为,并深入研究系统的稳定性特征。
通过实验,我们希望能够提供有关系统稳定性的定量指标,并为系统设计和优化提供参考。
三、实验方法1. 实验设备:我们使用了一台实验室提供的系统稳定性测试设备,该设备能够模拟不同条件下的系统行为。
2. 实验步骤:首先,我们选择了多个不同类型的系统进行实验,包括机械系统、电子系统和化学反应系统等。
然后,我们根据实验设备的要求,设置不同的参数和条件,观察系统的稳定性表现,并记录相关数据。
3. 数据分析:我们对实验数据进行了统计和分析,包括系统的响应时间、波动范围、稳定性指标等。
通过对比不同系统和不同条件下的数据,我们得出了一些初步的结论。
四、实验结果与分析1. 不同系统的稳定性表现:根据实验数据,我们发现不同类型的系统在稳定性方面存在一定的差异。
机械系统通常具有较好的稳定性,其响应时间相对较长,波动范围较小;而电子系统的稳定性较差,响应时间较短,波动范围较大。
化学反应系统的稳定性则受到反应物浓度、温度等因素的影响。
2. 系统稳定性指标:我们通过对实验数据的分析,提出了一些系统稳定性的指标,如系统的稳定性系数、稳定性指数等。
这些指标可以用于评估系统的稳定性水平,并为系统设计和优化提供依据。
3. 系统稳定性的影响因素:我们还分析了系统稳定性的影响因素,包括系统结构、参数设置、外界干扰等。
通过对这些因素的研究,我们可以更好地理解系统的稳定性特征,并采取相应的措施提高系统的稳定性。
五、实验结论通过对不同系统的稳定性进行实验和分析,我们得出了以下结论:1. 系统的稳定性与系统类型密切相关,不同类型的系统在稳定性方面表现出不同的特点。
自动控制原理实验四-线性定常控制系统的稳定分析

实验四线性定常控制系统的稳定分析
一、实验目的
(1)深刻理解反馈对系统稳定性的作用和影响;
(2)深刻理解系统类型对系统稳定性的影响的规律;
(3)深刻理解零点对系统稳定性无影响;
(4)理解系统参数对系统稳定性的影响。
二、实验原理及内容:
1.单位反馈对系统稳定性的影响
(1) 已知开环系统结构图如图4-1所示。
R (S
其中W(S)分别为:(a )1()0.11W s s =+和(b )1()0.2
W s s =- (2)闭环系统单位负反馈形式为:
图4-2 闭环系统
其中W(S)同(1)。
通过观察两组W (S )在开环和闭环两种形式下系统的零、极点分布和单位阶跃响应曲。
控制理论实验报告

一、实验目的1. 理解控制理论的基本概念,掌握控制系统的基本组成和分类。
2. 掌握控制系统稳定性分析的方法,如奈奎斯特稳定判据、劳斯稳定判据等。
3. 学会应用MATLAB软件进行控制系统仿真,分析系统的性能指标。
4. 培养动手能力和实际操作技能,提高对控制理论的理解和应用能力。
二、实验原理控制理论是研究系统在输入信号作用下,输出信号与期望信号之间关系的一门学科。
控制系统一般由控制器、被控对象和反馈环节组成。
本实验主要研究线性定常系统的稳定性分析和性能指标分析。
三、实验器材1. MATLAB软件2. 控制系统仿真模块3. 控制系统仿真数据四、实验步骤1. 稳定性分析(1)根据实验要求,设计一个控制系统,并绘制系统的开环传递函数。
(2)利用奈奎斯特稳定判据,判断系统的稳定性。
具体步骤如下:①绘制系统的开环传递函数的幅相特性曲线。
②计算系统的开环增益K和相位裕度。
③在复平面上绘制K的轨迹,判断系统是否稳定。
(3)利用劳斯稳定判据,判断系统的稳定性。
具体步骤如下:①将系统的开环传递函数写成标准形式。
②根据劳斯稳定判据,计算系统的特征根。
③判断系统的稳定性。
2. 性能指标分析(1)根据实验要求,设计一个控制系统,并绘制系统的闭环传递函数。
(2)利用MATLAB软件进行控制系统仿真,获取系统的性能指标。
(3)分析系统的性能指标,如上升时间、超调量、稳态误差等。
3. 结果分析(1)根据奈奎斯特稳定判据和劳斯稳定判据,判断系统的稳定性。
(2)分析系统的性能指标,如上升时间、超调量、稳态误差等。
五、实验结果与分析1. 稳定性分析根据奈奎斯特稳定判据和劳斯稳定判据,本实验所设计的控制系统均为稳定系统。
2. 性能指标分析(1)上升时间:系统从初始状态到达期望状态所需的时间。
(2)超调量:系统输出信号超过期望信号的最大幅度。
(3)稳态误差:系统输出信号在稳态时与期望信号之间的差值。
根据实验结果,本实验所设计的控制系统具有较快的上升时间、较小的超调量和较小的稳态误差,满足实验要求。
自动控制原理实验报告--控制系统的稳定性和稳态误差

本科实验报告课程名称:自动控制原理实验项目:控制系统的稳定性和稳态误差实验地点:多学科楼机房专业班级:学号:学生姓名:指导教师:2012 年5 月15 日一、实验目的和要求:1.学会利用MATLAB 对控制系统的稳定性进行分析; 2.学会利用MATLAB 计算系统的稳态误差。
二、实验内容和原理:1.利用MATLAB 描述系统数学模型如果系统的的数学模型可用如下的传递函数表示nn n m m m a s a s b s b s b s U s Y s G ++++++==-- 11110)()()( 则在MATLAB 下,传递函数可以方便的由其分子和分母多项式系数所构成的两个向量惟一确定出来。
即num=[b 0,b 1 ,…, b m ]; den=[1,a 1,a 2 ,…,a n ]例2-1 若系统的传递函数为5234)(23+++=s s s s G 试利用MA TLAB 表示。
当传递函数的分子或分母由若干个多项式乘积表示时,它可由MA TLAB 提供的多项式乘法运算函数conv( )来处理,以获得分子和分母多项式向量,此函数的调用格式为 p=conv(p1,p2)其中,p1和p2分别为由两个多项式系数构成的向量,而p 为p1和p2多项式的乘积多项式系数向量。
conv( )函数的调用是允许多级嵌套的。
例2-2 若系统的传递函数为)523)(1()66(4)(232++++++=s s s s s s s s G试利用MA TLAB 求出其用分子和分母多项式表示的传递函数。
2.利用MATLAB 分析系统的稳定性在分析控制系统时,首先遇到的问题就是系统的稳定性。
判断一个线性系统稳定性的一种最有效的方法是直接求出系统所有的极点,然后根据极点的分布情况来确定系统的稳定性。
对线性系统来说,如果一个连续系统的所有极点都位于左半s 平面,则该系统是稳定的。
MATLAB 中根据特征多项式求特征根的函数为roots( ),其调用格式为r=roots(p) 其中,p 为特征多项式的系数向量;r 为特征多项式的根。
控制系统的稳定性分析实验报告

控制系统的稳定性分析实验报告一、实验目的1.了解控制系统的稳定性分析方法。
2.通过实验,掌握系统稳态误差、系统阻尼比、系统根轨迹等稳态分析方法。
3.掌握控制系统的稳定性分析实验步骤。
二、实验原理1.系统稳态误差分析系统稳态误差是指系统在达到稳态时,输出与输入之间的偏差。
对于稳态误差的分析,可以采用开环传递函数和闭环传递函数进行分析。
开环传递函数:G(s)闭环传递函数:G(s)/(1+G(s)H(s))其中,H(s)为系统的反馈环节,G(s)为系统的前向传递函数。
稳态误差可以分为静态误差和动态误差。
静态误差是指系统在达到稳态时,输出与输入之间的偏差;动态误差是指系统在达到稳态时,输出与输入之间的波动。
2.系统阻尼比分析系统阻尼比是指系统在达到稳态时,振荡的阻尼程度。
阻尼比越大,系统越稳定;阻尼比越小,系统越不稳定。
系统阻尼比的计算公式为:ζ=1/(2ξ)其中,ξ为系统的阻尼比,ζ为系统的阻尼比。
3.系统根轨迹分析系统根轨迹是指系统的极点随着控制参数变化而在复平面上的轨迹。
根轨迹分析可以用来判断系统的稳定性和性能。
系统的根轨迹可以通过以下步骤进行绘制:(1)确定系统的传递函数G(s)(2)将G(s)写成标准形式(3)计算系统的极点和零点(4)绘制系统的根轨迹三、实验步骤1.系统稳态误差分析实验(1)将系统的开环传递函数和闭环传递函数写出。
(2)通过实验,测量系统的静态误差和动态误差。
(3)根据静态误差和动态误差的测量结果,计算系统的稳态误差。
2.系统阻尼比分析实验(1)通过实验,测量系统的振荡频率和衰减周期。
(2)根据振荡频率和衰减周期的测量结果,计算系统的阻尼比。
3.系统根轨迹分析实验(1)将系统的传递函数写成标准形式。
(2)计算系统的极点和零点。
(3)绘制系统的根轨迹,并根据根轨迹的形状,判断系统的稳定性和性能。
四、实验结果分析通过实验,我们可以得到系统的稳态误差、阻尼比和根轨迹等数据。
根据这些数据,我们可以分析系统的稳定性和性能,并对系统进行优化。
自动控制原理实验1-6

⾃动控制原理实验1-6实验⼀MATLAB 仿真基础⼀、实验⽬的:(1)熟悉MATLAB 实验环境,掌握MATLAB 命令窗⼝的基本操作。
(2)掌握MATLAB 建⽴控制系统数学模型的命令及模型相互转换的⽅法。
(3)掌握使⽤MATLAB 命令化简模型基本连接的⽅法。
(4)学会使⽤Simulink 模型结构图化简复杂控制系统模型的⽅法。
⼆、实验设备和仪器 1.计算机;2. MATLAB 软件三、实验原理函数tf ( ) 来建⽴控制系统的传递函数模型,⽤函数printsys ( ) 来输出控制系统的函数,⽤函数命令zpk ( ) 来建⽴系统的零极点增益模型,其函数调⽤格式为:sys = zpk ( z, p, k )零极点模型转换为多项式模型[num , den] = zp2tf ( z, p, k ) 多项式模型转化为零极点模型 [z , p , k] = tf2zp ( num, den )两个环节反馈连接后,其等效传递函数可⽤feedback ( ) 函数求得。
则feedback ()函数调⽤格式为: sys = feedback(sys1, sys2, sign )其中sign 是反馈极性,sign 缺省时,默认为负反馈,sign =-1;正反馈时,sign =1;单位反馈时,sys2=1,且不能省略。
四、实验内容:1.已知系统传递函数,建⽴传递函数模型2.已知系统传递函数,建⽴零极点增益模型3.将多项式模型转化为零极点模型12s 2s s 3s (s)23++++=G )12()1()76()2(5)(3322++++++=s s s s s s s s G 12s 2s s 3s (s)23++++=G )12()1()76()2(5)(3322++++++=s s s s s s s s G4. 已知系统前向通道的传递函数反馈通道的传递函数求负反馈闭环传递函数5、⽤系统Simulink 模型结构图化简控制系统模型已知系统结构图,求系统闭环传递函数。
控制系统的稳定性分析实验报告
1.连接被测量典型环节的模拟电路。电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入,将纯积分电容两端连在模拟开关上。检查无误后接通电源。
2.启动计算机,在桌面双击图标[自动控制实验系统]运行软件。
3.在实验项目的下拉列表中选择实验三[控制系统的稳定性分析]控Βιβλιοθήκη 系统的稳定性分析一、实验目的
1.观察系统的不稳定现象。
2.研究系统开环增益和时间常数对稳定性的影响。
二、实验仪器
1.自动控制系统实验箱一台
2.计算机一台
三、实验内容
系统模拟电路图如图
系统模拟电路图
其开环传递函数为:
G(s)=10K/s(0.1s+1)(Ts+1)
式中K1=R3/R2,R2=100K,R3=0~500K;T=RC,R=100K,C=1f或C=0.1f两种情况。
五、实验数据
1模拟电路图
2.画出系统增幅或减幅振荡的波形图。
C=1uf时:
R3=50K K=5:
R3=100KK=10
R3=200KK=20:
等幅振荡:R3=220k:
增幅振荡:R3=220k:
R3=260k:
C=0.1uf时:
R3=50k:
R3=100K:
R3=200K:
5.取R3的值为50K,100K,200K,此时相应的K=10,K1=5,10,20。观察不同R3值时显示区内的输出波形(既U2的波形),找到系统输出产生增幅振荡时相应的R3及K值。再把电阻R3由大至小变化,即R3=200k,100k,50k,观察不同R3值时显示区内的输出波形,找出系统输出产生等幅振荡变化的R3及K值,并观察U2的输出波形。
控制系统仿真实验四

实验四:控制系统的时域分析一,实验目的1、使用MATLAB 分析系统的稳定性及稳态性能。
2、分析系统的暂态性能并会计算暂态性能指标。
二、实验内容1、已知系统的闭环传递函数为:38440014020200)(234++++=S S G S S S ,分析系统的稳定性,并求该系统的单位阶跃响应曲线。
>> num=[200];>> den=[1 20 140 400 384];>> [z,p]=tf2zp(num ,den);>> ii=find(real(p)>0);n1=length(ii);>> if(n1>0)disp('The Unstable Poles are:');disp(p(ii));else disp('System is Stable');endSystem is Stable>>step(num,den)2、已知离散系统5.08.06.1)(22+--=Z Z Z Z Z φ,求该系统的单位阶跃响应曲线。
>> num=[1.6 -1 0];>> den=[1 -0.8 0.5];>> dstep(num,den);3、控制系统的状态空间模型为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡.3.2.1x x x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--17120100010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡x x x 321+u ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100 []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=x x x y 321132,求该系统在[0,3]区间上的单位脉冲响应曲线。
>> A=[0 1 0;0 0 1;0 -12 -17];B=[0;0;1];C=[2 3 1];D=0;>> impulse(A,B,C,D)4、已知控制系统模型为:u x x x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡10961021.2.1,[]⎥⎦⎤⎢⎣⎡=x x y 2111,求系统在y=sint 时的响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四 控制系统的稳定性分析
班级:电信171
姓名:陈远 学号:1700506163
一、 实验目的
1、 了解系统的开环增益和时间常数对系统稳定性的影响;
2、 研究系统在不同输入下的稳态误差的变化;
二、 实验内容 已知系统开环传递函数为:)
1)(11.0(10)(++=Ts s s K s G 1、 分析开环增益K 和时间常数T 对系统稳定性及稳态误差的影响。
(1) 取T=0.1,令K=1,2,3,4,5,绘制相应的阶跃响应曲线,分析开环增益K 的变化
对系统阶跃响应和稳定性的影响。
(2) 在K=1(系统稳定)和K=2(系统临界稳定)两种情况下,分别绘制T=0.1和T=0.01
时系统的阶跃响应,分析时间常数T 的变化对系统阶跃响应和稳定性的影响。
提示:
由开环传递函数转换为闭环传递函数可以使用反馈连接函数feedback ,举例
如下:
Gopen=tf (num ,den ) %建立开环传递函数
Gclose=feedback (Gopen ,1,-1) %建立闭环传递函数
2、 分析系统在不同输入时的稳态误差。
取K=1,T=0.01,改变系统输入r ,使r 分别为单位阶跃函数、单位斜坡函数
和单位加速度函数,观察系统在不同输入下的响应曲线及相应的稳态误差。
提示:
lsim 函数可用来绘制系统在任意自定义输入下的响应曲线,用法如下:
lsim (sys ,input ,t ) %其中sys 是待求的系统,input 是自定义的输入信号,t 是时间。
例如:
G1=tf (num ,den )
t=0:0.01:5
u1=t ;
lsim (G1, u1,t )
三、 实验结果:
(1)取T=0.1,令K=1,2,3,4,5,绘制相应的阶跃响应曲线。
MATLAB代码:
K=1时系统的阶跃响应曲线:
K=3时系统的阶跃响应曲线:
K=5时系统的阶跃响应曲线:
分析:随着增益系数的K的增加,系统将趋于不稳定,其中K=2是临界状态
(2)在K=1(系统稳定)和K=2(系统临界稳定)两种情况下,分别绘制T=0.1和T=0.01时系统的阶跃响应
MATLAB代码
K=1(系统稳定)时系统的阶跃响应曲线:(绿色是T=0.1,红色是T=0.01)
K=2(系统临界稳定)时系统的阶跃响应曲线:(黄色是T=0.1,蓝色是T=0.01)
分析:时间常数T减小时,系统的动态性能得到改善。
取K=1,T=0.01,改变系统输入r,使r分别为单位阶跃函数、单位斜坡函数和单位加速度函数,观察系统在不同输入下的响应曲线及相应的稳态误差。
MATLAB代码:
输入r为单位斜坡信号时的响应曲线:
分析:r为单位阶跃信号时,系统对于单位阶跃响应输入可以实现无差跟踪;r为单位斜坡信号时,系统对于单位斜坡输入可以跟踪,但存在一定的稳态误差;r为单位加速度信号时,系统对于单位加速度输入随时间的推移,误差越来越大,即不能跟踪。
四、实验心得:
通过本次实验如何用MATLAB对系统的稳定性分析;开环增益系数K影响系统的稳定性,K 减小,系统的稳定性增加;当时开环增益系数K一定时时,时间常数T 减小时,系统动态性能得到改善。
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
