真值表与等价公式
第二课合式公式真值表等价置换定理

2、符号化下列命题
例1、除非你努力,否则你将失败。 解:设P:你努力 Q:你失败 则符号化为 P Q 或 Q P 例2、仅当你走我将留下。 解:设P:你走 Q:我留下 则符号化为 Q P 例3、(1)只要充分考虑一切论证,就能得到可靠见解。 (2)只有充分考虑一切论证,才能得到可靠见解。 解:设P:我们充分考虑一切论证 Q:我们得到可靠见解 则符号化为 (1) P Q (2) Q P
定义:命题演算的合式公式 • 基础 (1) 单个命题变元本身ห้องสมุดไป่ตู้个合式公式;
约定 (1) • 归纳 (2) 如果 A最外层的括号可以省去 是一个合式公式,那么 A也是一个合式公式; (2) 运算符优先次序: , ∧, ∨, B) , (3) 如果 A、 B是合式公式,那么( A∧ B)、( A∨ 、 (A B)、 (A ⇄ B)都是合式公式;
对应于所有可能的真值指派,A、B的真值都相同。又称 为两命题公式逻辑相等。记为:A B 思考: ((P Q) ( P ∨ Q))在真值表中值有何特征?
例2 :永真式和永假式 P T T F F 定义3 Q T F T F PP T T T T Q∧Q F F F F
永真式(重言式)
翻译总结
(1)首先找出原子命题 (2)根据命题含义翻译,不可拘泥于句子形式 一些固定搭配:
•不可兼或:
命题公式真值表
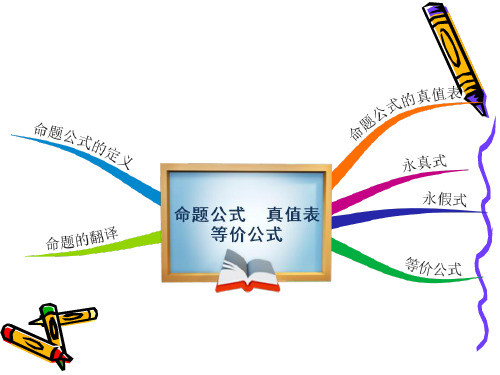
说明:
(1)命题变元是没有真假值的,只有当命题变元用 确定的命题代入时,才得到一个命题,命题的真值 依赖于代换变元的那些命题的真值;
1-3 命题公式与翻译
(2) 不是所有由命题变元 ,常元 ,联结词和括号组成的字符串 都能成为命题公式.例如, P , P (Q ) 等不是命题公式.
定义 1-3.1 命题演算的合式公式,规定为: (1)单个命题变元本身是一个合式公式; (2)如果 A 是合式公式,那么 A 是合式公式; (3)如果 A 和 B 是合式公式,那么
1-3 命题公式与翻译
2、命题的翻译
练习 将下列命题符号化: (1)她既聪明又用功. (2)他虽聪明但不用功. (3)虽然这次语文考试的题目很难,但是王丽还是取得了好成绩. (4)张三或李四都可以做这件事. (5)一公安人员审查一起案件,事实如下,请将案件事实符 号化: 张三或李四盗窃了机房的一台电脑,若是张三所为,则作案 时间不能发生在午夜前;若李四的证词正确,则午夜时机房 的灯未灭; 若李四证词不正确,则作案时间发在午夜前; 午夜时机房的灯全灭了.
分配律
P (Q R) ( P Q) ( P R)
吸收律
P ( P Q) P , P ( P Q) P
1-4 真值表与等价公式
4.基本等价公式
德·摩根律 同一律 零律 否定律 (互补律) 条件式转化律 双条件转化律
( P Q) P Q , ( P Q) P Q
1-3 命题公式与翻译
1、命题公式(合式公式)
定义 1 由命题变元、常元、联结词、括号以规定的格式联结 起来的字符串称为命题公式,也称合式公式.命题公式中的命 题变元称为命题公式的分量.
例如,若 P 和 Q 是命题变元, 则下面式子均是命题公式
离散数学课件真值表和等价公式PPT文档16页

离散数学课件真值表和等价公式
1、 舟 ቤተ መጻሕፍቲ ባይዱ 遥 以 轻飏, 风飘飘 而吹衣 。 2、 秋 菊 有 佳 色,裛 露掇其 英。 3、 日 月 掷 人 去,有 志不获 骋。 4、 未 言 心 相 醉,不 再接杯 酒。 5、 黄 发 垂 髫 ,并怡 然自乐 。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
离散数学-----命题逻辑

离散数学-----命题逻辑逻辑:是研究推理的科学。
公元前四世纪由希腊的哲学家亚里斯多德首创。
作为一门独立科学,十七世纪,德国的莱布尼兹(Leibniz)给逻辑学引进了符号, 又称为数理逻辑(或符号逻辑)。
逻辑可分为:1. 形式逻辑(是研究思维的形式结构和规律的科学,它撇开具体的、个别的思维内容,从形式结构方面研究概念、判断和推理及其正确联系的规律。
)→数理逻辑(是用数学方法研究推理的形式结构和规律的数学学科。
它的创始人Leibniz,为了实现把推理变为演算的想法,把数学引入了形式逻辑中。
其后,又经多人努力,逐渐使得数理逻辑成为一门专门的学科。
)2. 辩证逻辑(是研究反映客观世界辩证发展过程的人类思维的形态的。
)一、命题及其表示方法1、命题数理逻辑研究的中心问题是推理,而推理的前提和结论都是表达判断的陈述句,因而表达判断的陈述句构成了推理的基本单位。
基本概念:命题:能够判断真假的陈述句。
命题的真值:命题的判断结果。
命题的真值只取两个值:真(用T(true)或1表示)、假(用F(false)或0表示)。
真命题:判断为正确的命题,即真值为真的命题。
假命题:判断为错误的命题,即真值为假的命题。
因而又可以称命题是具有唯一真值的陈述句。
判断命题的两个步骤:1、是否为陈述句;2、是否有确定的、唯一的真值。
说明:(1)只有具有确定真值的陈述句才是命题。
一切没有判断内容的句子,无所谓是非的句子,如感叹句、祁使句、疑问句等都不是命题。
(2)因为命题只有两种真值,所以“命题逻辑”又称“二值逻辑”。
(3)“具有确定真值”是指客观上的具有,与我们是否知道它的真值是两回事。
2、命题的表示方法在书中,用大写英文字母A,B,…,P,Q或带下标的字母P1,P2,P3 ,…,或数字(1),*2+, …,等表示命题,称之为命题标识符。
命题标识符又有命题常量、命题变元和原子变元之分。
命题常量:表示确定命题的命题标识符。
命题变元:命题标识符如仅是表示任意命题的位置标志,就称为命题变元。
1-4真值表与等价公式

第一章 数理逻辑 1-4 真值表与等价公式
10
2、等价公式-证明(真值表法)
例题 5 证明 PQ(PQ)(QP)
第一章 数理逻辑 1-4 真值表与等价公式
11
2、等价公式-汇总
下面的命题定理(表1-4.8)都可以用真值表 予以验证:
对合律 等幂律 结合律 交换律 分配律 吸收律 德·摩根律 同一律 零律 否定律
从真值表可见,上述两个命题公式在分量的不同 指派下,其对应的真值与另一命题公式完全相同。
同理如: (PQ)(PQ)与PQ。
第一章 数理逻辑 1-4 真值表与等价公式
9
2、等价公式-概念
定义:1-4.2 给定两个命题公式A和B,设P1, P2,…,Pn为所有出现于A和B中的原子变元, 若给P1,P2,…,Pn任一组真值指派, A和B的 真值都相同,则称A和B是等价的或逻辑相等。 记作AB。
PQ F F F T
(PQ) (PQ) T F F T
6
第一章 数理逻辑 1-4 真值表与等价公式
1、真值表
例题4 给出(PQ)(PQ)的真值表 公式不论命题变元做何种指派,其真值永为真, 我们把这类公式记为T。
P Q PQ (PQ) P Q PQ T T T F F T F F T F F F F T T T F F T T F T F T F T T T (PQ)( PQ) T T T T
第一章 数理逻辑 1-4 真值表与等价公式
18
第一章 数理逻辑 1-4 真值表与等价公式
16
小结
真值表
完整性
等价公式
等价公式表1-4.8 等价置换
命题公式(合式公式)证明方法
列真值表法 利用等价公式
命题公式真值表

定义 1-3.1 命题演算的合式公式,规定为: (1)单个命题变元本身是一个合式公式; (2)如果 A 是合式公式,那么 A 是合式公式; (3)如果 A 和 B 是合式公式,那么
A B , A B , A B , A B 是合式公式;
(4)当且仅当能够有限次地应用(1)、(2)、(3) 所得到的包含命题变元,联结词和括号的字符串 是合式公式.
T F F T
1-4 真值表与等价公式
(5) ( P Q) (P Q) 的真值表为:
P
Q
PQ
P
Q
( P Q)
P Q
( P Q) (P Q)
T T F F
T F T F
T F F F
F F T T
F T F T
F T T T
F T T T
T T T T
1-4 真值表与等价公式
1.真值表
定义1-4.1 在命题公式中,对于分量指派真值的各种可能 组合,就确定了这个命题公式的各种真值情况,把它汇列成 表,就是命题公式的真值表.
例 2 构造下列命题公式的真值表: (1) P Q ; (3) ( P Q) P ; (5) ( P Q) (P Q) . (2) P Q ; (4) ( P Q) (P Q) ;
1-4 真值表与等价公式
解 (1)
P Q 的真值表为:
P
Q
P Q
T T F F
T F T F
T F T T
(2)
P Q 的真值表为:
P
Q
P Q
T T F F
T F T F
T F T T
1-4 真值表与等价公式
第1章 命题逻辑(二)

p,q的极小项为:p∧q,p∧¬ q,¬ p∧q,p∧¬ q
两个命题变元的极小项共4(=22)个, 三个命题变元的极小项 共8(=23)个, …。一般地说,n个命题变元共有2n个极小项。
1.5.2 主析取范式
极小项有下列的性质: ⑴每个极小项只有一个成真赋值,且各极小项的成真赋值 互不相同。极小项和它的成真赋值构成了一一对应的关系。
1.5.2 主析取范式
真值表法:即用真值表求主析取范式。 用真值表求主析取范式的步骤如下: ① 构造命题公式的真值表。
② 找出公式的成真赋值对应的极小项。
③ 这些极小项的析取就是此公式的主析取范式。
1.5.2 主析取范式
【例1.24】用真值表法,求(p→q)→r的主析取范式。 解:表1.15是(p→q)→r的真值表 p 0 0 0 0 1 1 1 1 q 0 0 1 1 0 0 1 1 r 0 1 0 1 0 1 0 1 表1.15 p→q 1 1 1 1 0 0 1 1 (p→q)→r 0 1 0 1 1 1 0 1
1.5.2 主析取范式
矛盾式无成真赋值,因而主析取范式不含任何极小项, 将矛盾式的主析取范式记为0。 重言式无成假赋值,因而主析取范式含2n (n为公式中命题
变元的个数)个极小项。
可满足式,它的主析取范式中极小项的个数一定小于等于 2n。
1.5.3主合取范式
定义1.5.7 在基本和中,每个变元及其否定不同时存在, 但两者之一必须出现且仅出现一次,这样的基本和叫作布 尔析取,也叫大项或极大项。 两个变元p,q构成的极大项为: p∨q,p∨¬q,¬p∨q,¬p∨¬q 三个命题变元p,q,r构成的极大项为: p∨q∨r, p∨q∨¬r, p∨¬q∨r, p∨¬q∨¬r, ¬p∨q∨r,¬p∨q∨¬r,¬p∨¬q∨r,¬p∨¬q∨¬r 两个命题变元的极大项共4(=22)个, 三个命题变元的极大 项共8(=23)个, …。一般地说,n个变元共有2n个极大项。
1-3命题公式与翻译1-4真值表与等价公式解析

PQR TTT TTF TFT TFF FTT FTF FFT FFF
Q∨R T T T F T T T F
P → (Q∨R) T T T F T T T T
P17(1) (C) (P ∨Q) (Q ∨P)
PQ TT TF FT FF
P ∨Q T T T F
Q ∨P T T T F
(P ∨Q) (Q ∨P) T T T T
命题符号化步骤: ❖(1)分成原子命题 ❖(2)用大写字母代替命题 ❖(3)按题意用联结词
自然语言的语句用Wff 形式化注意方面:
① 要准确确定原子命题,并将其形式化。 ② 要选用恰当的联结词,尤其要善于识别自然语 言中的联结词(有时它们被省略),否定词的位置要 放准确。
③ 必要时可以进行改述,即改变原来的叙述方式, 但要保证表达意思一致。
FF T
T
F
T
T
T
❖ 可以看出,有一类公式不论命题变元作何种 指派,其真值永为真(假),记为T(F)。
❖ 在真值表中,命题公式真值的取值数目,决 定于分量的个数。一般说来,n个命题变元组 成的命题公式共有2n种真值情况。
练习 17页(1)a, c, e 18页(6)
P17 (1)求下列复合命题的真值表 (a) P → (Q∨R)
若设 P:你努力。 Q:你失败。 本命题可表示为:
┐P→Q
例题6 张三或李四都可以做这件事。
解 这个命题的意义是: 张三可以做这件事,并且李四也可以做这件事。 若设
P:张三可以做这事。 Q:李四可以做这 事。 本命题可表示为:
P∧Q
例题7 (1)2是素数,这是假的。
(2) 2与4都是素数,这是不对的。 解 若设
④ 需要的括号不能省略,而可以省略的括号, 在需要提高公式可读性时亦可不省略。
真值表与等价公式

y
n
P∨ R
S
W
执行程序段W的条件为:( p r)
例1-16 化简下列各式
(1) ( p q) ( p q)
解: ( p q) ( p q)
p (q q)
p 1 p
(2) ((p q) (p (q r))) (p q) (p r)
0
q p
0 1 0 0
(q p) p
1 0 1 1
例1-10 构造公式 (( p q) r) p 的真值表。 解:
Pqr
000 001 010 011 1 00 101 1 10 111
p q r
0
1
0
0
0
1
0
0
0
1
0
0
1
1
1
0
( p q) r ((p q) r) p
1
0
0
1.3.3 等价公式
从真值表中可以发现,两个有相同命题分量但结 构不同的命题公式,对其分量真值的不同指派,其真 值总相同,如:
例1-12 构造下列命题公式的真值表。 (1)构造命题公式 p q, p q和q p 的真值表。 (2)构造命题公式( p q) (p q)和p q 的真值表。 解(1)
联结词归化
其中包含否定、合取和析取联结词的等价命题公式称为 命题定律,包含条件和双条件联结词的等价命题公式 称为联结词归化。
交换律 E1
A B B A AB B A
结合律 E2 ( A B ) C A ( B C ) ( A B)C A(BC )
分配律 E3 A ( B C ) ( A B ) ( A C )
(p r) (q r) (p q) r ( p q) r
2真值表等值式

7
二、重言式与矛盾式
定理1 任意两个重言式的合取(或析取)仍然是重 言式。 定理2 一个重言式,对同一个命题变元均用任何公 式置换,其结果仍然是重言式。
8
三、等值式及其基本等值式
定义1 若等价式AB是重言式,则称A与B等值(逻 辑相等),记作AB,并称AB是等值式。 定理2.1 AB为重言式,当且仅当A、B具有相同 的真值表。
12
四、公式等值演算与置换规则
1. 等值演算——由已知的等值式推演出新的等值式 的过程 2. 等值演算的基础: (1) 等值关系的性质:自反性、对称性、传递性 (2) 基本的等值式 (3) 置换规则 3. 置换规则 设 (A) 是含公式 A 的命题公式,(B) 是用公式 B 置换(A) 中所有的 A 后得到的命题公式 若 BA,则 (B)(A)
pq (pq) 1 1 0 1 0 0 1 0
(pq)q 0 0 0 0
成假赋值:00,01,10,11; 无成真赋值
5
真值表的作用:
求出公式的全部成真赋值与成假赋值, 区别不同 公式间的关联,判断公式的类型。
6
二、重言式与矛盾式
定义1 设A为任一命题公式, (1) 若A在它的任何赋值下均为真, 则称A为重言式或 永真式; (2) 若A在它的任何赋值下均为假, 则称A为矛盾式或 永假式; (3) 若A不是矛盾式, 则称A是可满足式.
等值演算在计算机硬件设计,开关理论和电子元 器件中都占据重要地位。
17
五、 ,与 ,间的区别
, 是联结词 , 是逻辑符号,表明公式的取值情况。
18
第二讲 真值表、等值演算
主要内容
一、真值表及其作用
二、重言式与矛盾式的定义和相关结论
证明两个命题公式等价的方法

证明两个命题公式等价的方法1. 用真值表呀!就像看地图找宝藏一样,通过列出两个命题公式在各种情况下的真假值,来清楚地看出它们是不是等价的。
比如说“P→Q”和“¬P∨Q”,画个真值表一看,嘿,不就明了啦!2. 可以运用逻辑等价式呀!这就像是给公式穿上合适的衣服,让它们呈现出相同的模样。
比如“¬(P∧Q)”和“¬P∨¬Q”,用那些等价式一转化,哇,原来它们是一伙的呀!比如咱说“A 或者B”和“非 A 则B”,这不就能轻易发现它们其实是一样的嘛。
3. 构造证明呀!就如同警察破案一样,一步一步找到两者等价的证据。
假设一个命题,然后从这个命题推出另一个命题,反过来也行呀,不就证明它们等价啦。
就像“如果今天下雨,那么地会湿”和“地没湿,那么今天没下雨”,仔细一想,不就是一回事嘛!4. 语义理解也很重要哇!把命题放到具体的情境中去理解,看看是不是表达的是同一个意思。
像“所有人都爱音乐”和“不存在不爱音乐的人”,这么一想,可不就是等价的嘛,太明显啦!5. 举例说明呀!找个简单易懂的例子让它们现出原形。
好比“小红要么在教室,要么在操场”和“小红不在教室就一定在操场”,这不是很直白嘛!6. 数学归纳法有时候也能派上用场呢!就像爬楼梯一样,一步一步验证。
比如一些和自然数有关的命题公式,用这个方法就能很好地证明它们等价。
哎呀,就像“当 n 为奇数时,这个式子成立,当 n 为偶数时也成立”,多妙呀!7. 反证法也可以试试嘛!假设它们不等价,然后推出矛盾,这不就说明它们其实是等价的嘛。
就好像说“这不是这样的”,结果发现说不通,那就只能是等价的咯。
比如“如果天气好,我们就去爬山”和“我们没去爬山,那肯定天气不好”,想想是不是这么回事呀!我的观点结论就是:这些方法都很实用呀,都能有效地证明两个命题公式等价,大家可以根据具体情况选择合适的方法来大显身手呀!。
第一章 3 真值表与等价公式

00 1
1
1
1
01 0
0
1
0
10 0
1
0
0
11 1
1
1
1
2021/1/13
15
1.4 真值表与等价公式
例4 判断公式 P(QR)、(P∧Q)R是否等价。
P QR 0 00 0 01 0 10 0 11 1 00 1 01 1 10 1 11
P∧Q 0 0 0 0 0 0 1 1
Q R P (Q R) (P ∧ Q) R
P Q P Q
11
双条件转化律
P Q P Q Q P
12
逆否律
P Q Q P
13
2021/1/13
17
1.4 真值表与等价公式
2、等值演算法(Equivalent Caculation)
重要的等价式(补充):
14. 双条件否定等价式:PQ ¬P¬Q
15. 归谬律:
(PQ)(P¬Q) ¬P
定义1-4.1 设P1,P2, … ,Pn是出现在公式A中的全部 的命题变元,给P1, P2 ,…, Pn 各指定一个真值, 称为对A的一个真值指派或赋值(Assigment)或解 释。若指定的一组值使A的真值为真(假),称这组 值为A的成真(假)指派.
2021/1/13
5
1.4 真值表与等价公式
离散数学
(Discrete Mathematics)
2021/1/13
1
1.4 真值表与等价公式
复习 符号化命题:我们不能既划船又跑步
P:我们划船
Q:我们跑步
翻译
A:
B:
PQ
00 0
1
1
C:
离散数学第1章命题公式与翻译 真值表与等价公式

这个合式公式的定义,是以递归形式给出的,其 中(1)称为基础,(2)(3)称为归纳,(4)称为界限。
按照定义,下列公式都是合式公式: ┐(P∧Q),┐(P→Q),(P→(P∨┐Q), (((P→Q)∧(Q→R)) (S T)) 而 (P→Q)→(∧Q),(P→Q,(P∧Q)→Q) 等都不是合式公式。
在这里,请注意和的区别与联系: 区别:
是逻辑联结词,它出现在命题公式中;
不是逻辑联结词,它表示两个命题公式的一种
关系,不属于这两个公式的任何一个公式中的符 号。
2、等价公式的证明方法: ⑴真值表法
例题5 证明 P Q (P→Q) ∧(Q→P) 证明 列出其值表 表 1-4.7
注意
由表1-4.4 (表1-4.2)可以看出,有一类公式不论命 题变元作何种指派,其真值永为真(假),我们把这 类公式记为T(F)。 在真值表中,命题公式真值的取值数目,决定于 分量(命题变元)的个数。例如,由2个命题变元 组成的命题公式共有四种可能的真值,由3个命题 变元组成的命题公式共有八种真值。一般说来,n 个命题变元组成的命题公式共有2n种真值情况。
同理(P∧Q)∨(┐P∧┐Q)与P 同,如表1-4.6所示。 表1-4.6 P Q P T T T F F T F F T F F T Q
Q对应的真值相
(P∧Q)∨(┐P∧┐Q) T F F T
二、等价公式
1.定义
定义1-4.2 给定两个命题公式A和B,设P1, P2,……,Pn为所有出现于A和B中的原子变 元,若给P1,P2,……,Pn任一组真值指派, A和B的真值都相同,则称A和B是等价的或逻 辑相等。记作A B。
P T T F F
命题公式真值表
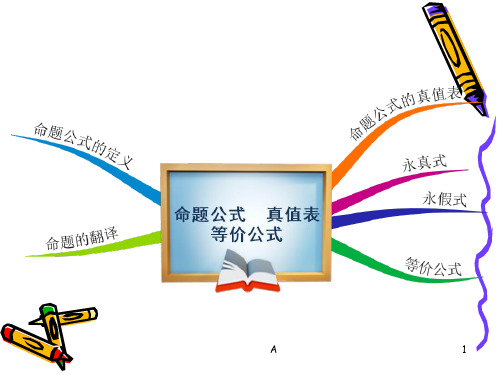
(4) (P Q) (P Q);
(5) (P Q) (P Q).
A
6
1-4 真值表与等价公式
解 (1) P Q 的真值表为:
P
Q
T
T
T
F
F
T
F
F
P Q
T F T T
(2) P Q 的真值表为:
P
Q
PQ
T
T
T
T
F
F
F
T
T
F
F
T
A
7
1-4 真值表与等价公式
(3) (P Q) P 的真值表为:
(1)单个命题变元本身是一个合式公式;
(2)如果 A 是合式公式,那么 A是合式公式;
(3)如果 A 和 B 是合式公式,那么
A B , A B , A B, A B 是合式公式;
(4)当且仅当能够有限次地应用(1)、(2)、(3)
所得到的包含命题变元,联结词和括号的字符串
是合式公式.
A
3
1-3 命题公式与翻译
A 中的 X 用Y 置换,所得公式 B 与公式 A 等价,即 A B .
例 4 证明: Q (P (P Q)) Q P
例 5 证明下列等价式
(1) (P Q) (P Q) P ;
(2) P (Q R) Q (P R) .
练习 证明 P (Q R) (P Q) R
A
14
1-4 真值表与等价公式
例 6 化简下列命题公式: (1) P (P (Q P)) (2) (P Q) (Q P)
说明:
(1)命题变元是没有真假值的,只有当命题变元用 确定的命题代入时,才得到一个命题,命题的真值 依赖于代换变元的那些命题的真值;
合式公式真值表等价置换定理 第二课

1 ∧ 2 ∧ 3 ⇔T 变换为( ∧…… ∧ ) ∨ ( ∧…… ∧ ) 的形式 排除( ∧…… ∧ ) 中Pi ∧ Pj的可能即可。A2, C1, D ¬ (( P → Q ) ∧ P ) ⇔ T
Q ∨ ¬ (( P → Q ) ∧ P ) ⇔ Q ∨ ¬ (( ¬ P ∨ Q ) ∧ P ) ⇔ Q ∨ ¬ (( ¬ P ∧ P ) ∨ ( Q ∧ P )) ⇔ Q ∨ ¬ (Q ∧ P ) ⇔ Q ∨ (¬ Q ∨ ¬ P ) ⇔
2、等价定理与常用等价式 、 定理: 和 是两个命题公式 是两个命题公式, 当且仅当A 定理:A和B是两个命题公式,A ⇔ B当且仅当 当且仅当 证明: 证明 (1)由A ⇔ B 知,在所有可能的真值指派下,A、B的真值总是 相同的,从而,A ↔ B是一个重言式。 (2)由A ↔ B为重言式, 可知:在所有可能的真值指派下,A、 B的真值总是相同的,所以A ⇔ B。 注意:“当且仅当” 注意: 当且仅当” 的证明需要分为 仅当” “当”和“仅当” 两个部分 B是一个重言式。 是一个重言式。 是一个重言式
对应于所有可能的真值指派, 、 的真值都相同 的真值都相同。 对应于所有可能的真值指派,A、B的真值都相同。又称 为两命题公式逻辑相等。记为: 为两命题公式逻辑相等。记为:A ⇔ B 思考: ((P →Q) ( P ∨ Q))在真值表中值有何特征? 思考 ( ) )
例2 :永真式和永假式 P T T F F 定义3 定义 Q T F T F ¬P∨P ∨ T T T T
2. 命题演算的合式公式 • 基础 (1). 单个命题变元本身是个合式公式;
约定(1)最外层的括号可以省去 • 归纳 约定 如果A是一个合式公式,那么 A也是一个合式公 (2). 最外层的括号可以省去 式; (2)运算符优先次序: , ∧, ∨, →, 运算符优先次序: 运算符优先次序
常用的命题等价公式

0
成立
练习 :用真值表判断下列等价公式是否成立 1 (1)p (q r ) ( p q ) r 成立
p 0 0 0 0 1 1 1 1 q 0 0 1 1 0 0 1 1 r 0 1 0 1 0 1 0 1 q→r 1 p∧q 0 p→(q → r) ( p∧q )→ r 1 1 1 1 1 1 1 1 0 1 1 1 1 1
证明 1):( p q) r (p q ) r ( (p q ) r ( p q ) r ( q p ) r
(2) p q r p r q r
(2) p q r p r q r
(2)( p q) p q r 解 : ( p q) p q r (p q) p q r (p p) (q p) q r 0 (q p) q r (q p) q r (q p) q r (q p) q r q p q r 1 r 0 r 0 该公式是永假式
练习4:利用基本等价公式判断下列公式的类型
(1) ( p q ) q p (2)( p q) p q r 解(1): p q) q p (
( p q ) q p (p q ) (q q ) p ( p q ) 0 p ( p q ) p (p q ) p ( p q ) p p q p 1 该公式是永真式
由于日本和中国不能并列第一,日本不能既第一又第三, 韩国和日本不能并列第三,即第一、第三和第四为0,所以 (R1 Q 3 P 1 R3) 1 ⑷
1-3命题公式与翻译1-4真值表与等价公式

定义1-3.1 命题演算的合式公式(wff),规定为:
(1)单个命题变元(常元)本身是一个合式公式。
(2)如果A是合式公式,那么┐A是合式公式。
(3)如果A和B是合式公式,那么(A∧B),(A∨B), (A→B)和(A B)都是合式公式。 (4)当且仅当能够有限次地应用(1)、(2)、(3)所得到 的包含命题变元,联结词和括号的符号串是合式公 式。
P17(1) (C) (P ∨Q) P T T F F Q T F T F P ∨Q T T T F Q ∨P T T T F
(Q ∨P)
(P ∨Q) (Q ∨P)
T T T T
P17(1) (e) (P →(Q→R) )→((P→Q) →(P→R)) 设S (P →(Q→R) )→((P→Q) →(P→R))
离散数学
Discrete Mathematics
课程回顾
命题:命题的定义、真值、分类及其表示。 命题联结词: 否定、合取、析取、条件、双条件。
P Q ┐P P∧Q P∨Q P→Q P Q
T T
T F F T
F
F T
T
F F
T
T T
T
F T
T
F F
F F
T
F
F
T
T
第一章 命题逻辑第2讲
1—3 命题公式与翻译 1—4 真值表与等价公式 要求:理解合式公式及两个合式公式等价 的定义,熟悉真值表与命题定律,会证明 等价公式。 重点:合式公式的定义,两个合式公式等价 的定义,命题定律。 难点:推证等价公式。
例题4
给出┐(P∧Q) (┐P∨┐Q)的真值表。
解
P Q ┐P T T T F F T F F F F T T ┐Q F T F T P∧Q T F F F ┐(P∧Q) ┐P∨┐Q F T T T F T T T ┐(P∧Q) T T T T ┐P∨┐Q)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( p q) r
联结词归化 联结词归化 结合律 德.摩根公式 联结词归化
例1-15 已知程序流程图如下,试化简该流程。 解:运行S程序段的条件: p∨(¬p∧r) 运行W程序段的条件: ¬p∧¬r
S S W
y
P
பைடு நூலகம்
n
y
R
n
经过等价变换: p (p r ) ( p p) ( p r )
交换律 E1
A B B A A B B A
结合律 E2
( A B ) C A ( B C ) ( A B ) C A ( B C )
分配律 E3
A ( B C ) ( A B ) ( A C )
A ( B C ) ( A B ) ( A C )
0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 1 0 1 1
练习:Q∧(P→Q)→Q
1.3.2 命题公式的分类 从真值表中可以发现,某些命题公式不论其分量 真值作何指派,其真值总为真,或者总为假。 例1-11 构造下列命题的真值表。
思考:命题公式是命题吗?为 什么?
解答:命题公式不一定是命题。
因为命题公式没有确定的真值。
把符号命题翻译成自然语言命题: 这种翻译比较简单,只要求用词准确,力求保 持原命题的意思。 例 设 A: 今天下雨。 B: 今天下雪。 C: 今天天晴。试把下列命题翻译成自然语言: 1) ┐(A∧B) 2) C↔ (┐A∧┐B) 3) A∨B→┐C 解 :1) 说今天下雨且下雪是不对的。 2) 今天天晴当且仅当今天既不下雨又不下雪。 3) 如果今天下雨或者下雪, 今天就不是晴天。
0 0 0 1 1 0 0 0 1 0 0 1
pq
1 0 0 1
1.3.1命题公式的等价
定义1-11 给定两个命题公式A和B,设 p1 , p2 ,, pn 是所有出现在A和B中的命题分量,若对 p1 , p2 ,, pn 的任一组真值指派,A和B的真值都相同,则称A 和B等价或逻辑相等。记为A ⇔B 。
德· 摩根律 E10
( A B ) A B ( A B ) A B
联结词归化 E11 E12 E13 E14 E15
A B A B
A B ( A B ) ( B A)
A ( B C ) ( A B ) C A B B A
P 0 0 1 1 q 0 1 0 1
p q
1 1 0 0 1 0 1 0
pq
p q
1 1 0 1
1 1 0 1
q p 1 1 0 1
解(2)
P 0 0 1 1 q p q 0 1 1 1 1 0 0 0 1 1 0 0
p q p q ( p q) (p q)
定理1-3 设X是命题公式A的子公式,若X⇔Y,如 果将A中的X用Y置换,所得的公式B与命题公式 A等价。 证明: 因为在相应分量的任一种真值指派下,X和Y的 真值都相同,用Y置换X后,公式B与A在相应分 量的真值指派下,其真值仍相同,所以A⇔B 。
例1-13 推导证明吸收律 p ( p q) p 。 证明:
P 0 0 1 1 q 0 1 0 1
p
1 1 0 0
q p
0 1 0 0
(q p) p
1 0 1 1
例1-10 构造公式 (( p q) r ) p 的真值表。 解: p q r ( p q) r (( p q) r ) p P q r
1.3.3
等价公式
从真值表中可以发现,两个有相同命题分量但结 构不同的命题公式,对其分量真值的不同指派,其真 值总相同,如: 例1-12 构造下列命题公式的真值表。 (1)构造命题公式 p q, p q和q p 的真值表。 (2)构造命题公式 ( p q) (p q)和p q 的真值表。 解(1)
证明:根据定义,因为任何重言式不论分量 真值作何指派,其真值总为真,而两个真 值为真的命题的合取或析取一定为真。
练习
1.判别下列命题公式中哪些是重言式?矛盾式?偶然式? 1 重言式 ① (P→Q)↔(¬Q→¬P) ② (P→Q)∧(Q →P)→(¬P∧Q) ( P Q ) 偶然式 ③ (P↔Q)→(P∧Q→P) 1 重言式
第一章 命题逻辑
第三讲
回
一、命题公式
顾
命题公式也称命题演算的合式公式(Well form formula,简写为wff)。 定义1-6 命题公式的递归定义如下: (1)单个的命题常元或命题变元是命题公式; (2)如果A是一个命题公式,则 (┐A)也是命题公式; (3)如果A和B都是命题公式,则(A∧B)、(A∨B)、 (A→B)、(A↔B)也是命题公式; (4)当且仅当有限次地应用(1)、(2)、(3)所得 到的符号串是命题公式。
1 ( p r) ( p r)
p r ( p r )
( 执行程序段S的条件为: p r )
S
y
P∨ R
n
W
执行程序段W的条件为:( p r )
例1-16 化简下列各式 (1) ( p q) ( p q) 解: ( p q) ( p q)
例如:对于命题公式: ( p q) r
( p, q, r ) (1,1,1)就是其一个解释
在这个解释下( p q ) r为真, 把(1,1,1)称为( p q ) r的一个成真赋值
同样( p, q, r ) (1,0,0)也是其一个解释
但此时( p q) r为假, 从而(1,0,0)是( p q) r的一个成假赋值
同一律 分配律 零 律 同一律
( p q) r
联结词规化 分配律 德.摩根公式
(2)p (q r ) ( p q) r 证明: p (q r )
p (q r )
p (q r ) (p q) r
( p q) r
逻辑等价 "与双条件联结词"的区别: " "
1." " 是 一 种 联 结 词S T是 命 题 公 式其 中 的 " 是 逻 辑 , , " 运 算, 其 结 果 仍 是 一 个 命 题 式 ; 而" " 则 是 描 述 两 个 命 题 公 公 式S和T之 间 的 一 种 关 系 等 价, 其 结 果 不 是 命 题 公 式
( p (q (q r ))) (( p q) ( p r ))
( A B ) A B
1.3.4 命题公式的等价演算 在算术运算中,我们可以根据运算符的优先次 序,将算术表达式中某一部分用其结果代替,得 到的新表达式与原表达式相等。在命题演算中, 我们同样可以用命题公式某一部分的等价命题公 式代入,所得的新命题公式与原公式等价,这个 过程称为置换。置换时要求被置换部分应该是命 题合式公式。 定义1-12 如果X是命题公式A的一部分,且X本身 是一个合式公式,则称X为公式A的子公式。
2. 要 判 断 两 个 命 题 公 式 和T是 否 等 价使 用S T S , 是 不 可 能 做 到 的 而 可 以 通 过 计 算S T是 否 是 ,然 永真式来判断
常用的命题等价公式有:
联结词归化
其中包含否定、合取和析取联结词的等价命题公式称为 命题定律,包含条件和双条件联结词的等价命题公式 称为联结词归化。
公式的分类 设A为一个命题公式,则:
1 若A在它的所有解释下都为 真, 则称A为永真式(也称为重言式) 2 若A在它的所有解释下都为 假, 则称A为永假式(也称为矛盾式)
3 若A在它的至少一个解释下为真, 则称A为可满足式(也称偶然式)
很显然,永真式一定是 可满足式
定理1-1 任何两个重言式的合取或析取仍然是 一个重言式。
0 0 1 1
解(3) p q 0 0 0 0 0 1 0 1 1 0 1 0 1 1 1 1
0 1 0 1
r 0 1 0 1 0 1 0 1
1 1 0 1
p→q 1 1 1 1 0 0 1 1
0 0 1 0
¬r 1 0 1 0 1 0 1 0
0 0 0 0
( p→q)∧¬r 1 0 1 0 0 0 1 0
(1) ( p ( p q)) q
(2) ( p q) q (3) ( p q) r 解(1) p q p→q 0 0 1 1 0 1 0 1 1 1 0 1
p∧(p→q)
0 0 0 1
(p∧ (p→q))→q
1 1 1 1
解(2)
p q p→q ¬(p→q) ¬(p→q)∧ q
p (q q)
p 1
p
(2) (( p q) (p (q r ))) (p q) (p r ) 解: (( p q) (p (q r ))) (p q) (p r )
(( p q) ( p (q r ))) ( p q) ( p r )
同一律 E4
A 0 A
A A 1
A1 A
A A 0
互否律 E5
双否律 E6 等幂律 E7 零一律 E8 吸收律 E9
A A
A A A A A A
A1 1
A 0 0
A ( A B ) A A ( A B ) A
( A B) A B
从真值表中可知,命题公式 p q, p q和q p
( 等价;p q) (p q)和p q 等价。
