3.2代数式的值ppt
合集下载
人教版(2024)数学七年级上册 3.2.2求代数式的值 课件(共16张PPT)

(1)用式子表示图中阴影部分的面积 x2 7x 14;
(2)当 x 4 时,图中阴影部分的面积为___5_8____;
3.如图所示,用含有a的式子表示阴影部分的面积,并计算当a=6cm 时阴影部分的面积.(π取3) 解:由图形可知,阴影部分的面积可以表示为:
a • a 1 • ( a )2 a2 a2
获取新知
探究点3 体积公式的应用 问题:回顾常见的体积公式 1.正方体的体积= 边长3 2.长方形的体积= 长×ቤተ መጻሕፍቲ ባይዱ×高 3.圆柱体的体积= 底面积×高
例题讲解
例3.一个长方体纸箱的长是a,宽与高都是b,用代数式表示这个纸箱 的体积V. 当a=60cm,b=40 cm时,求这个纸箱的体积.
解:因为长方体纸箱的长是a,宽与高都是b, 所以这个纸箱的体积V=ab². 当a=60 cm,b=40时, V=ab²=60×40²=60×1600=96000(cm3).
解:(1)因为两段直道的长为2a,两段弯道组成一个圆,它的直径为b,周长为πb. 所以这条跑道的周长为2a+πb. (2)当a=67.3m,b=52.6m时,2a+b=2X67.3+3.14X52.6≈300(m). 答:这条跑道的周长约为300m.
获取新知
探究点2 面积公式的应用 问题:回顾常见图形的面积公式 1.三角形的面积= 底×高÷2 2.正方形的面积= 边长2 3.长方形的面积= 长×宽 4.圆的面积= π×半径2
1 ab-πr²= 1×10×17.3-3.14×22=86.5-12.56 =73.94(cm2).
2
2
答:这个三角尺的面积是73.94cm2.
跟踪训练
1.填空题:(1)若a、b分别表示平行四边形的底和高,则面积S=_a_b_; 当a=2 cm,b=3cm时,S=__6___cm2. (2)若a,b分别表示梯形的上底和下底,h表示梯形的高,则面积S=
(2)当 x 4 时,图中阴影部分的面积为___5_8____;
3.如图所示,用含有a的式子表示阴影部分的面积,并计算当a=6cm 时阴影部分的面积.(π取3) 解:由图形可知,阴影部分的面积可以表示为:
a • a 1 • ( a )2 a2 a2
获取新知
探究点3 体积公式的应用 问题:回顾常见的体积公式 1.正方体的体积= 边长3 2.长方形的体积= 长×ቤተ መጻሕፍቲ ባይዱ×高 3.圆柱体的体积= 底面积×高
例题讲解
例3.一个长方体纸箱的长是a,宽与高都是b,用代数式表示这个纸箱 的体积V. 当a=60cm,b=40 cm时,求这个纸箱的体积.
解:因为长方体纸箱的长是a,宽与高都是b, 所以这个纸箱的体积V=ab². 当a=60 cm,b=40时, V=ab²=60×40²=60×1600=96000(cm3).
解:(1)因为两段直道的长为2a,两段弯道组成一个圆,它的直径为b,周长为πb. 所以这条跑道的周长为2a+πb. (2)当a=67.3m,b=52.6m时,2a+b=2X67.3+3.14X52.6≈300(m). 答:这条跑道的周长约为300m.
获取新知
探究点2 面积公式的应用 问题:回顾常见图形的面积公式 1.三角形的面积= 底×高÷2 2.正方形的面积= 边长2 3.长方形的面积= 长×宽 4.圆的面积= π×半径2
1 ab-πr²= 1×10×17.3-3.14×22=86.5-12.56 =73.94(cm2).
2
2
答:这个三角尺的面积是73.94cm2.
跟踪训练
1.填空题:(1)若a、b分别表示平行四边形的底和高,则面积S=_a_b_; 当a=2 cm,b=3cm时,S=__6___cm2. (2)若a,b分别表示梯形的上底和下底,h表示梯形的高,则面积S=
3.2代数式的值课件人教版数学七年级上册(1)

3. 如图,在长为 a m,宽为 b m的长方形地块中,空白部分均为四分 之一圆.
(1)试用含 a , b 的式子表示阴影部分的面积;(结果保留π)
(2)若 a =9, b =4,求阴影部分的面积.(π取3.14) 答:阴影部分的面积为10.88 m2.
1. 若 a =2, b =-1,则 a +2 b +3的值为( B ) A. -1 B. 3 C. 5 D. 6
(3)根据(2)中的猜想,当 n =300时,用了多少根小木棒? (3)当 n =300时,12 n +8( n -1)=12×300+8×(300-1)=5 992. 答:当 n =300时,用了5 992根小木棒.
密码中的数学
字母 a b c d e f g h I j k l m 序号1 2 3 4 5 6 7 8 9 10 11 12 13 字母n o p q r s t u v w x y z 序号14 15 16 17 18 19 20 21 22 23 24 25 26
答:当蟋蟀1 min叫的次数是80时,该地当5=0,则6y-2x2-6的值为( D )
A. 4
B. -4
C. 16
D. -16
7. 一块三角尺的形状和尺寸如图所示,直角边的边长为a,圆孔的 半径为r.
(1)求阴影部分的面积S;
(2)当a=4 cm,r=1 cm时,求S的值.(π取3. 14)
5. 在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有 如下的近似关系:用蟋蟀1 min叫的次数除以7,然后再加上3,就近似地 得到该地当时的温度(℃).若用x表示蟋蟀1 min叫的次数.
(1)用含x的代数式表示该地当时的温度;
(2)当蟋蟀1 min叫的次数是80时,该地当时的温度约是多少?(结果保 留整数)
数学人教版(2024版)七年级初一上册 3.2 代数式的值 课件02

果可以说:当n=10时,代数式18+2(n-1)的值是36;当n=15时,代数式
18+2(n-1)的值是46;等等.
一般地,用数值代替代数式里的字母,按照代数式中的运算关系计算得出
的结果,叫做代数式的值.
讲授新课
求代数式的值的步骤:
(1)写出条件:当……时;
(2)抄写代数式;
(3)代入数值;
(4)计算.
解:专卖店A:购买足球数不超过10个时,所需要的费用为130x元;
超过10个时,所需要的费用为130×10+100(x-10)=(100x+300)元;
专卖店B:所需要的费用为110x元;
当堂检测
7.某校体育社团计划购买一些足球,该社团负责人去两家足球专卖店对足
球的价格进行了了解:
专卖店A:购买足球数不超过10个时,每个130元;超过10个时,超过的
(1)x = 15,y = 12;
解: 当 x = 15,y = 12时,
原式 = 2×15+3 × 12
= 66;
(2)x = 1,y
1
= .
2
解:当 x = 1,y
原式 = 2 ×
7
= .
2
1
= 时,
2
1
1+3×
2
讲授新课
典例精析
例2.根据下列 a,b
2
的值,分别求代数式a - 的值:
(1)a = 4,b = 12;
部分每个100元.
专卖店B:无论购买多少个,每个110元.
(2)若体育社团要购买20个足球,去哪家专卖店比较合算?请说明理由.
解:专卖店A:当x=20时,100x+300=100×20+300=2300元,
七年级数学上册3.2代数式的值ppt课件

若第一位同学报出的数用x表示,请用代数式表示出这一 过程.
x →x+1 →(x+1)2 →(x+1)2-1
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
代数式的值
问题引导
问题 某礼堂第1排有18个座位,往后每排比前一排多2个座 位.问:
(2)当a=2,b=-1,c=-3时, (a+b+c)2=(2-1-3)2=4.
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
例2 某企业去年的年产值为 a亿元,今年比去年增长了10%. 如果明年还能按这个速度增长,请你预测一下,该企业明年的 年产值将能达到多少亿元?如果去年的产值是2亿元,那么预 计明年的年产值是多少亿元?
数
果叫做代数式的值.
式
的
值
直接代入求值
应 用
列代数式求值 整体代入求值
1.代入 步 2.计算 骤
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
典例精析 例1 当a=2,b=-1,c=-3时,求下列代数式的值: (1) b2-4ac; (2) (a+b+c)2.
3.2 代数式的值(课件)人教版(2024)数学七年级上册

处于平衡. 测得x 与y 的几组对应数据如下表:
x/g 0
2
4
6 10
y/mm 10 14 18 22 30
中考风向标
由表中数据的规律可知,当x=20 时,y=___5_0___.
中考风向标
试题评析:本题考查学生根据提供的数据总结规律 并用代数式表示,然后求代数式值的能力,综合性 较强. 当秤盘放入2 g 物品时,秤砣所挂位置与提纽的距离 为10+2×2=14(mm);
中考风向标
当秤盘放入4 g 物品时,秤砣所挂位置与提纽的距离 为10+2×4 =1 8(mm); 当秤盘放入6 g 物品时,秤砣所挂位置与提纽的距离 为10+2×6 =2 2(mm); 当秤盘放入1 0 g 物品时,秤砣所挂位置与提纽的距 离为10+2×1 0 =3 0(mm); ……
中考风向标
5. [新视角 结论开放题]写一个只含有字母a的代数式,使 得这个代数式中不论a取何值,该代数式的值总是负数, 你写的代数式是_-__a_2_-__1_(答__案__不__唯__一__)_ .
综合素养训练
6. [立德树人 红色旅游]赓续红色文化,传承红色基 因. 学校组织学生参加红色研学活动,共有m 名教师 与n 名学生参加.学校咨询了A,B 两家旅行社,两 家旅行社给出了不同的报价如下,A旅行社:教师全 价,80元/ 人,学生半价,40元/ 人;B旅行社:全部 成员,六折优惠,即48元/ 人.两家旅行社提供的服 务项目与服务质量相同.
综合应用创新
题型 4 根据变化规律求值
例 8 [新考法 归纳法]如图3.2-3 是按照一定规律摆放棋子组 成的图案,照这样的规律摆下去,请解答下列问题:
综合应用创新
解题秘方:
综合应用创新
数学人教版(2024版)七年级初一上册 3.2 代数式的值 课件03

原式 = 2×15+3×12
= 66;
(2)x = 1,y
1
= .
2
解:当 x = 1,y
原式 =
7
= .
2
1
= 时,
2
1
2×1+3×
2
例题讲解
例2.根据下列 a,b
2
的值,分别求代数式a - 的值:
(1)a = 4,b = 12;
解:(1)当 a = 4,b =
(2)a = -3,b = 2.
7上数学
人教版2024
第三章
3.2
代数式
代数式的值
学习目标
1.通过现实情境的学习能解释代数式的意义和作用.
2.由字母取值准确求出代数式的值.
3.会利用代数式求值推断代数式所反映的规律.
新课引入
周末,妈妈为小明买了双舒适
又美观的运动鞋,但小明在鞋
的标识上并没有找到自己的鞋
码. 你能读懂标识上的信息吗?
直接代值法的步骤:
(1)写出条件:当……时;
(2)抄写代数式;
(3)代入数值;
(4)计算.
注意:数字间相乘关系要加入乘号;当代入负数时要添上括号
例题讲解
例3.如图,某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,
其中直道的长为 a,半圆形弯道的直径为 b.
(1)用代数式表示这条跑道的周长;
∴原式=5×(-5)2-3×(-5)-60
=125+15-60
=80.
7.物体自由下落的高度 h(m)和下落时间 t(s)的关系,在地球上大约是:h
= 4.9 t2,在月球上大约是:h = 0.8 t2.
= 66;
(2)x = 1,y
1
= .
2
解:当 x = 1,y
原式 =
7
= .
2
1
= 时,
2
1
2×1+3×
2
例题讲解
例2.根据下列 a,b
2
的值,分别求代数式a - 的值:
(1)a = 4,b = 12;
解:(1)当 a = 4,b =
(2)a = -3,b = 2.
7上数学
人教版2024
第三章
3.2
代数式
代数式的值
学习目标
1.通过现实情境的学习能解释代数式的意义和作用.
2.由字母取值准确求出代数式的值.
3.会利用代数式求值推断代数式所反映的规律.
新课引入
周末,妈妈为小明买了双舒适
又美观的运动鞋,但小明在鞋
的标识上并没有找到自己的鞋
码. 你能读懂标识上的信息吗?
直接代值法的步骤:
(1)写出条件:当……时;
(2)抄写代数式;
(3)代入数值;
(4)计算.
注意:数字间相乘关系要加入乘号;当代入负数时要添上括号
例题讲解
例3.如图,某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,
其中直道的长为 a,半圆形弯道的直径为 b.
(1)用代数式表示这条跑道的周长;
∴原式=5×(-5)2-3×(-5)-60
=125+15-60
=80.
7.物体自由下落的高度 h(m)和下落时间 t(s)的关系,在地球上大约是:h
= 4.9 t2,在月球上大约是:h = 0.8 t2.
代数式的值ppt课件
ab
1.08,女儿成年后的身高=
女身高的经验公式:儿子成年后的身高=
2
0.923a b
,其中a为父亲身高,b为母亲身高,单位:m.
2
(1)七年级男生小刚的爸爸身高为1.72m,妈妈身高为1.65m,试预测小刚成年
后的身高;
(2)根据公式,预测一下自己的身高.
ab
1.08中,
解: (1)将a=1.72,b=1.65,代入
3.2代数式的值
名人屋
三百多年前的法国数学家韦达第一个
有意识地、系统地使用字母来表示数,用
字母代替数的思想就是代数思想,自从韦
达把字母当作符号来表示数之后,数学获
得了飞速发展,人们称韦达——“代数学
之父”。
情境导入
为了开展体育活动,学校准备添置一些足球,如果每个班级配3个足球,
学校另外留8个,n个班级一共需要多少个足球? (3n+8)个
1
求代数式的值的概念
定 义:
像这样,用数值代替代数式中的字母,按照代数
式中给出的运算计算出的结果,叫做代数式的值.这
个过程叫做求代数式的值.
随堂练习
1.人体血液的质量约占人体体重的6%~7.5%.
(1) 如果某人体重是a kg,那么他的血液质量大约在什么
范围内?
(2) 亮亮体重是35kg,他的血液质量大约在什么范围内?
➢ 用数值代替代数式中的字母,按照代数式中指明
的运算,计算出结果.
代
数
式
注意:
➢ 字母的值变化,代数式的值随之变化;
➢ 字母的值确定,代数式的值随之确定.
家庭作业
教科书第 85~86页(习题3.3)
第1、4、6题
逐渐增大
1.08,女儿成年后的身高=
女身高的经验公式:儿子成年后的身高=
2
0.923a b
,其中a为父亲身高,b为母亲身高,单位:m.
2
(1)七年级男生小刚的爸爸身高为1.72m,妈妈身高为1.65m,试预测小刚成年
后的身高;
(2)根据公式,预测一下自己的身高.
ab
1.08中,
解: (1)将a=1.72,b=1.65,代入
3.2代数式的值
名人屋
三百多年前的法国数学家韦达第一个
有意识地、系统地使用字母来表示数,用
字母代替数的思想就是代数思想,自从韦
达把字母当作符号来表示数之后,数学获
得了飞速发展,人们称韦达——“代数学
之父”。
情境导入
为了开展体育活动,学校准备添置一些足球,如果每个班级配3个足球,
学校另外留8个,n个班级一共需要多少个足球? (3n+8)个
1
求代数式的值的概念
定 义:
像这样,用数值代替代数式中的字母,按照代数
式中给出的运算计算出的结果,叫做代数式的值.这
个过程叫做求代数式的值.
随堂练习
1.人体血液的质量约占人体体重的6%~7.5%.
(1) 如果某人体重是a kg,那么他的血液质量大约在什么
范围内?
(2) 亮亮体重是35kg,他的血液质量大约在什么范围内?
➢ 用数值代替代数式中的字母,按照代数式中指明
的运算,计算出结果.
代
数
式
注意:
➢ 字母的值变化,代数式的值随之变化;
➢ 字母的值确定,代数式的值随之确定.
家庭作业
教科书第 85~86页(习题3.3)
第1、4、6题
逐渐增大
3.2代数式的值利用公式列代数式并求值(课件)2024-2025学年人教版七年级数学上册

用代数式表示只需要表示一次数量关系,其余代入数值即可, 直接计算需要每一次都梳理数量关系,因此用代数式更简便 3.完成课本81页练习1题.
如图,正方形ABCD和正方形ECGF的边长分别为a和6,点C,D,E在 一条直线上,点B,C,G在一条直线上,将阴影部分的面积记为S阴影. (1)试用含a的代数式表示S阴影; (2)当a=12时,比较S阴影与△BGF的面积的大小.
请同学们回忆学过的三角形面积公式, 由底和高为数过渡到底和高为字母,引入新课.
情境导入 某工厂生产了一种T型零件,该零件由两个长方形组成,其尺寸如图 所示.
(1)用含x,y的式子表示T型零件的周长; (2)用含x,y的式子表示T型零件的面积;
1.请同学们阅读课本80-81页,并思考以下问题. 2.研读课本80页例3.
同学们,今天我们学习了用公式列代数式并进行计算,在 课上大家通过动手计算体会到了利用代数式解决问题的简 便,大家在未来的学习中要继续不断探索,体会数学在我 们生活中的重要作用.
教材习题:完成课本81页练习2,3题. 实践性作业:利用我们学过的几何图形 公式两人一组互相画图练习,列出代数 式并计算.
小组展示
越展越优秀
提疑惑:你有什么疑惑?
知识点:利用公式列代数式并求值(重难点)
(1)在同一个式子或具体问题中,每一个字母只能代表一个量. (2)要注意书写的规范性,用字母表示数以后,在含有字母与数的
乘法中,通常将“×”简写作“·”或者省略不写. (3)在数和表示数的字母的乘积中,一般把数写在字母的前面. (4)含有字母的除法,一般不用“÷”,而是写成分数的形式.
例2:如图,某长方形广场的四角都有一块边长为 x米的正方形草地.若长方形的长为a米,宽为b米. (1)请用代数式表示阴影部分的面积; (2)若长方形广场的长为300米,宽为200米,正方形草地的边长为10
如图,正方形ABCD和正方形ECGF的边长分别为a和6,点C,D,E在 一条直线上,点B,C,G在一条直线上,将阴影部分的面积记为S阴影. (1)试用含a的代数式表示S阴影; (2)当a=12时,比较S阴影与△BGF的面积的大小.
请同学们回忆学过的三角形面积公式, 由底和高为数过渡到底和高为字母,引入新课.
情境导入 某工厂生产了一种T型零件,该零件由两个长方形组成,其尺寸如图 所示.
(1)用含x,y的式子表示T型零件的周长; (2)用含x,y的式子表示T型零件的面积;
1.请同学们阅读课本80-81页,并思考以下问题. 2.研读课本80页例3.
同学们,今天我们学习了用公式列代数式并进行计算,在 课上大家通过动手计算体会到了利用代数式解决问题的简 便,大家在未来的学习中要继续不断探索,体会数学在我 们生活中的重要作用.
教材习题:完成课本81页练习2,3题. 实践性作业:利用我们学过的几何图形 公式两人一组互相画图练习,列出代数 式并计算.
小组展示
越展越优秀
提疑惑:你有什么疑惑?
知识点:利用公式列代数式并求值(重难点)
(1)在同一个式子或具体问题中,每一个字母只能代表一个量. (2)要注意书写的规范性,用字母表示数以后,在含有字母与数的
乘法中,通常将“×”简写作“·”或者省略不写. (3)在数和表示数的字母的乘积中,一般把数写在字母的前面. (4)含有字母的除法,一般不用“÷”,而是写成分数的形式.
例2:如图,某长方形广场的四角都有一块边长为 x米的正方形草地.若长方形的长为a米,宽为b米. (1)请用代数式表示阴影部分的面积; (2)若长方形广场的长为300米,宽为200米,正方形草地的边长为10
3.2 第1课时 求代数式的值 课件(共19张PPT) 人教版七年级数学上册

同学们,我们一起来玩一个游戏.老师随意说出一个数字,我们一条龙来做这个游戏,规则如下: 用字母x来表示这个数.
游戏导入
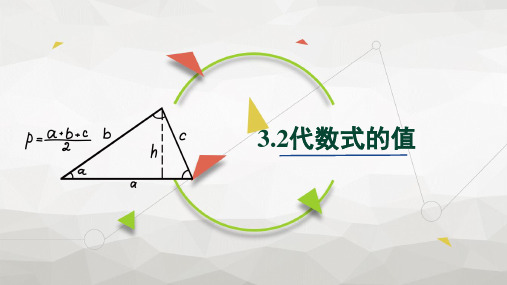
同学们,你们知道自己身体的健康状况吗?营养学家用身体质量指数来判断人体的健康状况,这个指数是人体质量m(千克)除以人体身高h(米)的平方所得商.你能用含m,h的代数式表示身体质量指数P吗?再通过计算判断一下你的身体健康状况.
情境导入
身体质量指数
18.5~23.9
低于18.5
高于23.9
身体健康状况
健康
不健康的瘦
不健康的胖
1.请同学们阅读课本79-80页内容.2.拿出小正方形纸卡动手操作并思考.(1)用同样大小的正方形纸片,按以下方式拼大正方形,第n个大正方形是由______个小正方形拼成的.(2)当n=4时,即拼成第4个大正方形,需要小正方形____个;(3)当n=10 时,即拼成第 10 个大正方形,需要小正方形____个;(4)当n=30 时,即拼成第 30个大正方形,需要小正方形____个.
【题型一】求代数式的值
例1:已知|a|=4,|b|=7,且a-b>0,则a+b的值为( )A.11 B.3或11 C.-3或-11 D.3或-11
C
变式: 已知两个代数式:①m2-2mn+n2;②(m-n)2.(1)当m=3,n=4时,分别求出①与②的值;(2)当m=10,n=-10时,分别求出①与②的值;(3)根据(1)与(2)的结果,你可得出什么结论?请直接写出来.
A
D
B
1.定义:用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值.当字母取不同的数值时,代数式的值一般也不同.2.求代数式的值的步骤:(1)写出条件:当……时;(2)抄写代数式;(3)代入数值;(4)计算.
游戏导入
同学们,你们知道自己身体的健康状况吗?营养学家用身体质量指数来判断人体的健康状况,这个指数是人体质量m(千克)除以人体身高h(米)的平方所得商.你能用含m,h的代数式表示身体质量指数P吗?再通过计算判断一下你的身体健康状况.
情境导入
身体质量指数
18.5~23.9
低于18.5
高于23.9
身体健康状况
健康
不健康的瘦
不健康的胖
1.请同学们阅读课本79-80页内容.2.拿出小正方形纸卡动手操作并思考.(1)用同样大小的正方形纸片,按以下方式拼大正方形,第n个大正方形是由______个小正方形拼成的.(2)当n=4时,即拼成第4个大正方形,需要小正方形____个;(3)当n=10 时,即拼成第 10 个大正方形,需要小正方形____个;(4)当n=30 时,即拼成第 30个大正方形,需要小正方形____个.
【题型一】求代数式的值
例1:已知|a|=4,|b|=7,且a-b>0,则a+b的值为( )A.11 B.3或11 C.-3或-11 D.3或-11
C
变式: 已知两个代数式:①m2-2mn+n2;②(m-n)2.(1)当m=3,n=4时,分别求出①与②的值;(2)当m=10,n=-10时,分别求出①与②的值;(3)根据(1)与(2)的结果,你可得出什么结论?请直接写出来.
A
D
B
1.定义:用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值.当字母取不同的数值时,代数式的值一般也不同.2.求代数式的值的步骤:(1)写出条件:当……时;(2)抄写代数式;(3)代入数值;(4)计算.
3.2 代数式的值第2课时 利用公式列代数式并求值 课件 人教版(2024)数学七年级上册

第三章 代数式
3.2 代数式的值
第2课时 利用公式列代数式并求值
目录页
讲授新课
当堂练习
课堂小结
新课导入
新课导入
教学目标
教学重点
1.把同类事物中的数量关系用公式表示出来.(重点)2.在解决有关实际问题时,能够用这些公式列出代数式并求值.(难点)
1.小Q从家里到学校所需要花费的时间是0.5h,他的速度是vkm/h,那么他从家里到学校的路程S如何表示?
THANKS
2.在1中的问题中,你使用的是哪个公式?
S=0.5v
3.除了上述提到的公式,你还知道哪些公式呢?
路程=速度×时间
面积公式:圆、长方形、正方形、三角形等
生活中的公式
体积公式:长方、正方体等
讲授新课
典例精讲
归纳总结
(1)用代数式表示该跑道的周长;
(1)求阴影部分的面积S;
一块三角为r.
2ab﹣πb2
解:(2)当a=7,b=2,π取3时,2abπb2=2×7×23×22+=16(平方米), 答:草地的面积是16平方米.
当堂练习
当堂反馈
即学即用
1. 铜钱是我国的早期货币,外圆内方的构造彰显了数学之美,铜钱外部的圆半径为a,方形边长为b,下列表示铜钱阴影部分的面积的式子是( )A.2π(ab) B.πa2b2 C.π(b2a2) D.2π(ba)
B
2. 有长为L的篱笆,利用它和房屋的一面墙围成如图形状的长方形园子,园子的宽为t,则所围成的园子面积为( )A.(L)t B.(Lt)t C.(t)t D.(L2t)t
D
3. 如图,一截钢管外半径是R cm,内半径是r cm,高为a cm.(1)用含有R,r,a的代数式表示钢管的体积;(2)若R=10,r=8,a=20,求钢管的体积(π取3.14,结果保留整数).
3.2 代数式的值
第2课时 利用公式列代数式并求值
目录页
讲授新课
当堂练习
课堂小结
新课导入
新课导入
教学目标
教学重点
1.把同类事物中的数量关系用公式表示出来.(重点)2.在解决有关实际问题时,能够用这些公式列出代数式并求值.(难点)
1.小Q从家里到学校所需要花费的时间是0.5h,他的速度是vkm/h,那么他从家里到学校的路程S如何表示?
THANKS
2.在1中的问题中,你使用的是哪个公式?
S=0.5v
3.除了上述提到的公式,你还知道哪些公式呢?
路程=速度×时间
面积公式:圆、长方形、正方形、三角形等
生活中的公式
体积公式:长方、正方体等
讲授新课
典例精讲
归纳总结
(1)用代数式表示该跑道的周长;
(1)求阴影部分的面积S;
一块三角为r.
2ab﹣πb2
解:(2)当a=7,b=2,π取3时,2abπb2=2×7×23×22+=16(平方米), 答:草地的面积是16平方米.
当堂练习
当堂反馈
即学即用
1. 铜钱是我国的早期货币,外圆内方的构造彰显了数学之美,铜钱外部的圆半径为a,方形边长为b,下列表示铜钱阴影部分的面积的式子是( )A.2π(ab) B.πa2b2 C.π(b2a2) D.2π(ba)
B
2. 有长为L的篱笆,利用它和房屋的一面墙围成如图形状的长方形园子,园子的宽为t,则所围成的园子面积为( )A.(L)t B.(Lt)t C.(t)t D.(L2t)t
D
3. 如图,一截钢管外半径是R cm,内半径是r cm,高为a cm.(1)用含有R,r,a的代数式表示钢管的体积;(2)若R=10,r=8,a=20,求钢管的体积(π取3.14,结果保留整数).
3.2代数式的值 课件(共17张PPT)-人教版(2024)初中数学七年级上册

目录
目录
直接代入法:把已知字母的值,直接代入代数式,
并按原来的运算顺序计算求值.
2 求代数式的值
目录
例3 已知x+y=5,xy=2,求代数式(x+y)2-5xy的值.
解:因为x+y=5,xy=2,
所以(x+y)2-5xy=52-5×2=25-10=15.
目录
3
例4 已知2y-x=3 , 求代数式6-2x+4y的值.
2
求代数式的值
例2
目录
如图,已知长方体的高为h,底面是边长为a的正
方形.当h=3,a=2时,求其体积V
解:因为V=a2h,
所以 当h=3,a=2时,
V=a2h=22×3=12,
2
求代数式的值
练一练: 当x= -3时,求x2-3x+5的值.
解:当x=-3时,
x2-3x+5=(-3)2-3×(-3)+5=23.
不相同
n
1
2
3
4
5n+6
11
16
21
n2
1
4
9
26
16
31
25
从上面我们可以看到,对代数式中的字母代入不同的值,都可
以求出代数式相应的值.一个代数式,可以看做一个计算程序.
1
求代数式的值的概念
目录
定 义:
像这样,用数值代替代数式中的字母,按照代数
式中给出的运算计算出的结果,叫做代数式的值.这
个过程叫做求代数式的值.
解:6-2x+4y=6+4y-2x=6+2(2y-x),
因为2y-x=3,将其代入上式中,可得:
3.2代数式的值课件2024-2025学年人教版七年级数学上册++

半径作两个四分之一圆.
(1)用代数式表示阴影部分的面积;
(2)当a=10,b=4时,求阴影部分的面积(结果保留π).
1 2
【解析】(1)阴影部分的面积为ab- πb .
2
(2)当a=10,b=4时,
1 2
1
ab- πb =10×4- π×42=40-8π.
2
2
知识点1
求代数式的值
1.若x的相反数是-3,则代数式2x-1的值是( C )
高分别为a cm,b cm,30 cm的箱子(其中a>b),准备采用如图①,②所示的两种打包方式,
所用打包带的总长(不计接头处的长)分别记为l1,l2.
(1)求图①中打包带的总长l1、图②中打包带的总长l2分别是多少?(用含a,b的式子表
示)
(2)当a=70,b=50时,计算两种打包方式所用打包带总长各是多少?并判断哪一种打包
即长方形中空白部分的面积为24.
5.若m2+mn=-1,n2-3mn=10,则代数式m2+7mn-2n2的值为________.
-21
【解析】因为m2+mn=-1,n2-3mn=10,
所以原式=(m2+mn)-2(n2-3mn)=-1-20=-21.
6.当x=2时,代数式ax3+bx+1的值为6,那么当x=-2时,这个代数式的值是( B )
因为560>520,所以题图②方式更节省.
8.当a=3,b=-1时,
(1)求代数式a2-b2和(a+b)(a-b)的值.
(2)猜想这两个代数式的值有何关系?
(3)根据(1)(2),请你用简便方法算出a=2 026,b=2 025时,a2-b2的值.
3.2 代数式的值(课件)七年级数学上册(人教版2024)

这样的式子为代数式.
单独的一个数或字母也是代数式,例如5,t都是代数式.
合作探究
在解决具体问题时,列出代数式后,往往还需要求出所需的数值. 思考下面的问题: 为了开展体育活动,学校要购置一批排球,每班配5个, 学校另外留20个,学校总共需要购置多少个排球?
合作探究
问题:为了开展体育活动,学校要购置一批排球,每班配 5个,学校另外留20个,学校总共需要购置多少个排球?
1. 一个长方体纸箱的长是a,宽与高都是b,用代数式表示这个纸箱 的体积V. 当a=60 cm,b=40 cm时,求这个纸箱的体积.
解:这个纸箱的体积V=a·b·b=a·b2.
当a=60 cm,b=40 cm时, 这个纸箱的体积V=60×40×40=96000. 答:这个纸箱的体积V=a·b2. 当a=60 cm,b=40 cm时,这个纸箱的体积是96000 cm3.
布置作业
P82:习题3.2:第3题,第4题; P82:习题3.2:第6题,第7题.
(2)当a=67.3 m,b=52.6 m时, 2a+πb=2×67.3+3.14×52.6≈300 (m). 因此,这条跑道的周长约为300 m.
典例分析
例4:一个三角尺的形状和尺寸如图所示,用代数式表示这个三角尺 的面积S. 当a=10 cm,b=17.3 cm,r=2 cm时,求这个三角尺的面 积(π取3.14). 分析:三角尺的面积=三角形的面积-圆的面积. 根据三角形、圆的面积公式可以求出三角尺的面积.
当堂巩固
2. 如图,用代数式表示圆环的面积.当R=15 cm,r=10 cm时,求圆环 的面积(π取3.14).
解:这个圆环的面积S=πR2- πr2= π(R2- r2).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题教学
例1、当a=2,b=-1,c=-3时,求下列 代数式的值: (1) b2-4ac
(2) (a+b+c)2
解:(1)当a=2,b=-1,c=-3时
b2-4ac=-1 ( ) 2-4×2 × ( -3=1+24=25 )
(2)当a=2,b=-1,c=-3时
a b c 2 1 3 4
答:第10排、第15排、第23排各有36个, 46个,62个座位.
我们看到,当n取不同数值时,代数 式 2n+16的计算结果也不同,以上结 果说明:当n=10时,代数式2n+16的 值是36;当n=15时,代数式2n+16的 值是46;等等。
一般地,用数值代替代数式里的字母, 按照代数式中的运算关系计算得出的结果, 叫做代数式的值。
一般地,第n排是第1排的后(n-1)排,它 的座位数应比第1排多2(n-1)个, 即为 18+2(n-1) 答:第n排有18+2(n-1)个座位。
(2)第10排、第15排、第23排各有多少个座位?
解:当n=10时,18+2(n-1)=18+2×(10-1)=36; 当n=15时,18+2(n-1)=18+2×(15-1)=46; 当n=23时,18+2(n-1)=18+2×(23-1)=62;
4.若梯形的上底为a,下底为b,高为h,则梯形
面积为
1 a b h 2 ;当a=2cm,b=4cm,h=3cm
2
时梯形的面积为 9 c m .
整体代入法
2 2
2 y 5 3 x 6 y 4 例3.若 x 的值为7,求代数式 的值。 y 2 解:由 x 2 y 5 7, 得 x2
(2)当x=-2, 2 2 2 4 4 4 16 16 3 2 2 2 2 x 2 xy y 2 2 2 4 4 4 16 16 4
1.21a=1.21×2=2.42 (亿元)
答:该企业明年的年产值 能达到1.21a亿元.有去年的年 产值是2亿元,可预计明年的年产值是2.42 亿元.
思考: 2 判断题: 1 1 1 2 ( )①当 x 时, 3x 3 3 2 4 2 2 2 ( )②当 x 2时,3 x 3 2 1 如何改正呢?
2 2
例题教学
例2、某企业去年的年产值为 a亿元,今年比去年 增长了10%。如果明年还能按这个速度增长,请你预 测一下,该企业明年的年产值将能达到多少亿元?如 果去年的产值是2亿元,那么预计明年的年产值是多 少亿元?
解:由题意可得,今年的产值为a(1+10%)亿元, 于是明年的产值为 a(1+10%)(1+10%) =1.21a(亿元) 当a=2时,
雄鹰选择蓝天,必与狂风为邻; 海鸥选择大海,定与风浪共舞; 而你选择了成功,必与辛劳为伴, 才与幸福结缘!
重庆市黔江中学校 韩乐远
一、座位问题
某礼堂第1排有18个座位,往后每排比前 一排多2个座位,问: (1)第n排有多少个座位?(用含n的代 数式表示) (2)第10排、第15排、第23排各有多少 个座位?
解:
∵2x2+3x-5= 8
∴2x2+3x=13 ∴4x2+6x=26 即 4x2+6x-15= 26-15 =11
练习:
2 (1)若 x ,则 x1 16 ; 14 2 (2) 若 x ,则 x 1 1 24 ; 15 x 10 y 8 ; 5 y4,则 2 (3) 若 x 5 y4 ,则 2 x 7 10 y 15 ; (4) 若 x 2 2 2 x 6 x 10 3 x 5 4 8 ; (5) 若 x ,则 1 (6) 若 ,则 x 1/4 ; 4 x x y x y x y 2 -3.5 2 ,则 (7) 若 x y x y
(1)第n排有多少个座位?(用含n的代数式表示) 解:(1)第2排比第1排多2个座位,它的座位 数应为18+2=20; 第3排比第2排多2个座位,它的座位数应为 20+2=22;
也可以这样考虑:第3排是第1排的后2排,它的座位数 应比第1排多2×2个,
即为 18+2×2=22; 类似的,第4排是第1排的后3排,它的座位数应 比第1排多2×3个, 即为18+2×3=24;
3.根据下列各组x、y 的值,分别求出代数式 2 2 2 与 2 x 2 xy y 的值: x 2 xy y
(1)x=2,y=3;(2)x=-2,y=-4。
解: (1)当x=2,y=3时,
2 2
2 2
2 2 2 3 3 4 12 9 2 x 2 xy y 2 2 2 2 x 2 xy y 2 2 2 3 3 4 12 9 1
x y
辅助未知数法 m 2 ,求 1.已知 n
3m 2 n 3 m 2 n 的值.
2.已知 xyz ,求 : : 1 : 2 : 3
3x 2 y z 2x 3y z
的值.
已知几个字母的比值时,设每份为k
五、小结本节课内容:
一、求代数式的值的步骤: (1)代入,(2)计算; 二、求代数式的值的注意事项: (1)代入数值前应先指明字母的取值把 “当„„时”写出来。 (2)如果字母的值是负数、分数,代 入时应加上括号; (3)代数式中省略了的乘号,代入数 值后必须添上乘号。 (4)相同的代数式可以看作一个整体— —整体代换.
2
1 3 1 3 x 3 3 4 4 2
2
3 x 3 2 3 4 1 2
2 2
求代数式的值方法归纳:
一、求代数式的值的步骤: (1)代入,将字母所取的值代入代数式中; (2)计算,按照代数式指明的运算进行,计算出结果 二、注意的几个问题: (1)由于代数式的值是由代数式中的字母所取的 值确定的,所以代入数值前应先指明字母的取值 ,把“当„„时”写出来。 (2)如果字母的值是负数、分数,代入时应加上 括号; (3)代数式中省略了乘号时,代入数值以后必须 添上乘号。
2 2
3 x 6 y 4
2
=3 x2y2 +4
(逆用乘法分配律)
3 2 4 10
(1)、已知:2x-y=3, 2(2x-y)-3 =2×3-3 =3 那么4x-3-2y=____________________
(2)、已知:2x2+3x-5的值是8,
求代数式4x2+6x-15的值。
