第四章物质结构第一节原子结构学习资料
原子的结构

(2)不同电子层的表示及能量关系
电子层数 1 2 3 4 5 6 7
各电子 字母代号 K L M N O P Q
层由内 到外 离核远近
由_近__到_远__
能量高低
由_低__到_高__
பைடு நூலகம்
【情境·思考】 洋葱是我们非常熟悉的一种蔬菜,洋葱切开后,我们会 看到里面一层一层地呈现,电子层模型就类似于切开的 洋葱。请思考:
【巧判断】
(1)某种硫原子的中子数是18,则其质量数是34。(
) 提示:√。硫的质子数为16,根据质量数=质子数+中子 数可知,硫的质量数为34。
二、核外电子排布 1.电子层 (1)概念:在多电子原子里,把电子运动的_能__量__不__同__的 区域简化为_不__连__续__的__壳__层__,称作电子层。
(2)电子层最多容纳的电子数 ①各电子层最多容纳_2_n_2个电子。如K、L、M、N层最 多容纳的电子数分别为_2_、__8_、__1_8_、__3_2_。 ②最外层电子数目最多不能超过_8_个(K层为最外层时不 能超过_2_个)。 ③次外层最多能容纳的电子数不超过_1_8_个。
3.原子核外电子排布的表示方法 (1)原子结构示意图。
第四章 物质结构 元素周期律 第一节 原子结构与元素周期表
第1课时 原 子 结 构
一、原子的构成 1.构成
2.质量数
(1)概念:质子和中子的相对质量都近似为1,忽略电子 的质量,将原子核内所有_质__子__和_中__子__的相对质量取近
似整数值相加,所得的数值叫做质量数。 (2)关系:质量数(A)=_质__子__数__(_Z_)_+_中__子__数__(_N_)_
知识点 核外电子的分层排布 【重点释疑】 1.原子核外电子排布规律及其之间的关系
2019人教版新教材高中化学必修一第四章重点知识点归纳总结( 物质结构元素周期律)

第四章物质结构元素周期律第一节原子结构与化学周期表一、原子结构1、原子的构成原子由原子核和核外电子组成(原子核包括质子和中子),质子带正电,电子带负电,中子中立不带电。
2、质量数(1)概念:将核内所有质子和中子的相对质量取近似整数值相加,所得的数值。
(2)构成原子的粒子间的两个关系①质量数(A)=质子数(Z)+中子数(N)②质子数=核电荷数=核外电子数3、原子的表示方法如作为相对原子质量标准的126C表示质子数为6,质量数为12的碳原子。
4、粒子符号(A Z X±b n±m)中各数字的含义5、原子核外电子排布的表示方法(1)原子结构示意图用小圆圈和圆圈内的符号及数字表示原子核及核内质子数,弧线表示各电子层,弧线上的数字表示该电子层上的电子数。
以钠原子为例:(2)离子结构示意图①金属元素原子失去最外层所有电子变为离子时,电子层数减少一层,形成与上一周期的稀有气体元素原子相同的电子层结构(电子层数相同,每层上所排的电子数也相同)。
如Mg:→Mg2+:。
②非金属元素的原子得电子形成简单离子时,形成和同周期的稀有气体元素原子相同的电子层结构。
如F :→F-:。
Na+与稀有气体Ne 的核外电子排布相同;Cl-与稀有气体Ar 的核外电子排布相同。
二、元素在周期表1、周期的分类与包含元素类别周期序数行序数核外电子层数包含元素种数起止元素短周期1112H ~He 2228Li ~Ne 3338Na ~Ar 长周期44418K ~Kr 55518Rb ~Xe 66632Cs ~Rn 77732Fr ~Og2、族的分类16个族分为7个主族、7个副族、1个第Ⅷ族和1个0族。
3、元素周期表中的方格中各符号的意义注:元素周期表记忆口诀横行叫周期,现有一至七;三四分长短,四长副族现;竖行称作族,总共十六族;Ⅷ族最特殊,三列是一族;二三分主副,先主后副族;镧锕各十五,均属ⅢB族。
4、元素在周期表中的位置与原子结构的相互推断(1)元素的位置与原子结构的关系(2)短周期元素原子结构与位置的关系①族序数等于周期数的元素有H、Be、Al。
高中化学新人教版必修1第4章 第1节(第1课时)原子结构与元素周期表 教案_06

第一节原子结构与元素周期表微观角度探索元素之间的内在联系,进一步认识了元素性质及其递变规律,并通过研究粒子间的相互作用,认识化学反应的本质;逐步建立了结构决定性质的观念。
教师:元素周期表揭示了元素间的内在联系,使元素构成了一个较为系统的体系。
元素周期表的建立成为化学发展史上的重要的里程碑之一。
教师提问:20世纪初,原子结构的奥秘被揭示后,人们对元素周期表的认识更加完善。
那么,原子结构与元素周期表之间有怎样的关系呢?教师:引出本节课学习内容在老师的带领下,对问题进行思考。
引出本节课内容。
简单的思维训练能够让学生不害怕对本节课知识点学习,感悟本节课的知识点。
讲授新课教师利用多媒体设备向学生投影出下面【新课讲解】原子结构教师:原子由原子核和核外电子构成,原子核由质子和中子构成。
记录笔记,认真倾听。
通过书写和口述帮助学生对知识点进行记忆。
【新课讲解】质量数【新课讲解】原子结构教师:在含有多个电子的原子力,电子分别在能量不同的区域内运动。
把不同的区域简化为不连续的壳层,也称作电子层。
(有人把这种电子层模型比拟为洋葱式结构)。
分别用n=1,2,3,4,5,6,7或K、L、M、N、O、P、Q来表示从内到外的电子层。
【新课讲解】原子结构中的电子层【思考讨论】教师:在多电子原子中,电子的能量是不相同的。
那么在离核较近的区域内运动的电子能量较低,在离核较远的区域内运动的电子能量较高。
由于原子中的电子是处在原子核的引力场中,电子总是从内层排起,当一层充满后再填充下一层。
那么,每个电子层最多可以排布多少个电子呢?答案:根据Na元素的核外电子排布,我们可以发现,K层最多可以排布2个电子,L层最多可以排布8个电子。
记录笔记,认真倾听。
老师和同学一起讨论,思考问题。
老师和同学一起讨论,思考通过书写和口述帮助学生对知识点进行记忆。
通过讨论,帮助同学对知识点的掌握。
通过讨论,加深对知识点的印【思考讨论】下表是稀有气体元素原子的电子层排布,根据表格回答问题。
高中化学第四章物质结构元素周期律第一节原子结构与元素周期律第3课时原子结构与元素的性质必修第一册
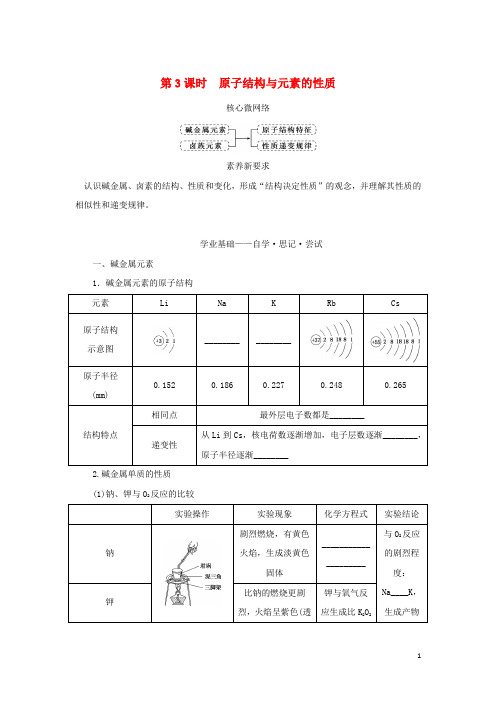
第3课时原子结构与元素的性质核心微网络素养新要求认识碱金属、卤素的结构、性质和变化,形成“结构决定性质”的观念,并理解其性质的相似性和递变规律。
学业基础——自学·思记·尝试一、碱金属元素1.碱金属元素的原子结构2.碱金属单质的性质(1)钠、钾与O2反应的比较特别提醒(1)做碱金属化学性质实验时,碱金属一般取绿豆大小为宜。
若用量过多,实验时易发生危险。
在使用前,要用滤纸吸干钾、钠等金属表面的煤油。
(2)碱金属在空气中加热与O2反应,Li与O2反应生成Li2O,Na与O2反应生成Na2O2,K 与O2反应生成KO2,Rb和Cs遇空气立即燃烧,生成更复杂的产物。
改变反应条件,K也能与O2反应生成K2O、K2O2。
(2)钾、钠与H2O反应的比较特别提醒(1)碱金属单质与H2O反应,生成强碱和H2,Li反应剧烈(但比Na弱),Rb和Cs遇H2O 立即燃烧、爆炸。
(2)由于Li、Na、K能与O2和H2O反应,故实验室中Na、K保存在煤油中,Li(密度比煤油的小)常保存在石蜡中。
(3)碱金属与盐溶液反应时,可以看作是碱金属先与H2O反应生成碱和H2,而非直接与盐发生置换反应。
(4)碱金属中还原性最强的是Cs,还原性最弱的是Li。
3.碱金属元素的原子结构与性质的关系二、卤族元素1.卤族元素的原子结构2.卤素单质的性质(1)物理性质特别提醒(1)Cl2易液化。
(2)常温下,Br2是唯一呈液态的非金属单质;Br2易挥发,实验室中将溴单质密封保存,并加水液封以减少挥发。
(3)I2为紫黑色固体,易升华,淀粉遇碘变为蓝色。
(4)卤素单质在水中的溶解度不大,但易溶于CCl4等有机溶剂(都能与水反应,其中F2与水能完全反应)。
(2)化学性质①与H2反应a.填写下表:b.得出结论:从F2到I2,与H2反应所需要的条件逐渐________,反应剧烈程度依次________,生成气态氢化物的稳定性依次________。
《原子结构》原子结构与元素周期表课件 图文

年代 1911年
模型
卢瑟福 原子 模型
观点或理论
在原子的中心有一个带正电 荷的核,它的质量几乎等于 原子的全部质量,电子在它 的周围沿着不同的轨道运转, 就像行星环绕太阳运转一样。
年代 1913年
模型
玻尔原子 模型
1926~ 1935年
电子云 模型
观点或理论
电子在原子核外空间的一定 轨道上绕核做高速圆周运动。
(8)内层电子总数是最外层电子数2倍的原子有Li、P。 (9)电子层数与最外层电子数相等的原子有H、Be、Al 。 (10)电子层数是最外层电子数2倍的原子是Li。 (11)最外层电子数是电子层数2倍的原子有He、C、S。 (12)最外层电子数是电子层数3倍的原子是O。
【迁移·应用】 1.(2019·南京师大附中高一检测)下列各原子结构示 意图中所表示的核外电子排布正确的是 ( )
【解析】选D。A原子的M层比B原子的M层少3个电子,B 原子的L层电子数恰为A原子L层电子数的2倍,说明A、B 为第二、第三周期元素;L层最多排8个电子,B原子的L 层电子数恰为A原子L层电子数的2倍,说明B原子的L层 有8个电子,A原子的L层有4个电子,故A是碳原子;A原子 的M层比B原子的M层少3个电子,故B为铝原子。
2.用A+、B-、C2-、D、E、F和G分别表示含有18个电子 的七种微粒(离子或分子),请回答: (1)A元素是________,B元素是________,C元素是 ________(用元素符号表示)。 (2)D是由两种元素组成的双原子分子,其分子式是 ________。
知识点 核外电子的分层排布 【重点释疑】 1.原子核外电子排布规律及其之间的关系
2.原子核外电子排布的表示方法 (1)原子结构示意图。
第4章 物质结构元素周期律 第1节 基础课时 18原子结构

原子结构学 习 任 务1.知道原子的结构及构成原子的粒子间的关系;根据原子核外电子排布规律,能画出1~20号元素的原子结构示意图。
培养学生“微观探析与证据推理”的核心素养。
2.了解预测、假设、模型等方法在研究原子结构中的作用,培养学生“证据推理与模型认知”的核心素养。
一、原子的构成 1.构成原子⎩⎨⎧原子核⎩⎪⎨⎪⎧ 质子相对质量近似为1,带1个单位 正电荷中子相对质量近似为1,不带电核外电子带1个单位负电荷2.质量数(1)概念:质子和中子的相对质量都近似为1,如果忽略电子的质量,将原子核内所有质子和中子的相对质量取近似整数值相加,所得的数值叫作质量数。
(2)关系:质量数(A)=质子数(Z)+中子数(N)。
3.原子结构模型的演变一种中子数为9的氧原子的质量数为多少?核外电子数为多少?其二价氧离子的质量数为多少?核外电子数为多少?[提示] 17,8,17,10(正确的打“√”,错误的打“×”)(1)原子呈电中性,其质量主要集中在原子核上。
( )(2)相对原子质量就是质量数。
( )(3)任何粒子的质子数等于电子数。
( )(4)阳离子的质量数等于其中的质子数与中子数之和。
( )[答案] (1)√ (2)× (3)× (4)√二、原子的核外电子排布1.电子层(1)概念:在含有多个电子的原子里,电子分别在能量不同的区域内运动。
我们把不同的区域简化为不连续的壳层,也称作电子层。
(2)不同电子层的表示及能量关系各电子层由内到外电子层数 1 2 3 4 5 6 7 字母代号K L M N O P Q 离核远近由近到远能量高低由低到高(1)能量最低原理核外电子总是优先排布在能量最低的电子层里,然后再由里往外排布在能量逐步升高的电子层里,即按K→L→M→N……顺序排列。
(2)电子层最多容纳的电子数①第n层最多容纳2n2个电子。
如K、L、M、N层最多容纳电子数分别为2、8、18、32。
01-第一节 原子结构与元素周期表-课时1 原子结构高中化学必修一人教版

最外层电子数2倍的原子有Li、Si;内层电子总数是最外层电子数2倍的原子
有Li、P。
(3)电子层数与最外层电子数相等的原子有H、Be、Al;电子层数是最
外层电子数2倍的原子是Li、Ca;最外层电子数是电子层数2倍的原子有He、
C、S;最外层电子数是电子层数3倍的原子是O。
有些元素不一定满足此规律,错误。
.
5.有 X + 和 Y − 两种元素的简单离子,若它们的电子层结构相同,则下
列关系正确的是( C )
A. − = +
B. − = −
C.核电荷数:Y < X
D.质子数:Y > X
【解析】 因两种离子的电子层结构相同,则它们的核外电子数相同,且
用含In的导电玻璃。已知In是第49号元素,质量数为115,下列有关In原
子的说法不正确的是( D )
A.原子核外有49个电子
B.该原子可表示为115
49 In
C.质子数为49
D.中子数为115
【解析】 原子中:质量数=质子数+中子数,质子数=核外电子数=原子序数。
D项,In原子的中子数为115 − 49 = 66,错误。
N2 H4 + 2H2 O2
N2 ↑ +4H2 O。
7.已知X、Y、Z、W四种元素中,X是宇宙中最丰富的元素;Y元素原子最
外层电子数是内层电子总数的2倍;Z元素原子最外层电子数比次外层电子
数多4;W元素原子最外层有1个电子,其阳离子与Z的简单阴离子核外电
子总数相同。请完成下列问题。
(1)W元素的原子结构示意图为_____________;由X、Z元素形成的10电
第四章 物质结构 元素周期律 知识点【新教材】人教版(2019)高中化学必修一

第四章物质结构元素周期律一、原子结构1、质量数(A)=质子数(Z)+中子数(N)质子数=原子序数=核电荷数=核外电子数2.原子核外电子的排布规律:①电子总是尽先排布在能量最低的电子层里;②各电子层最多容纳的电子数是2n2;③最外层电子数不超过8个(K层为最外层不超过2个),次外层不超过18个,倒数第三层电子数不超过32个。
电子层:一(能量最低)二三四五六七对应表示符号: K L M N O P Q 3.元素、核素、同位素元素:具有相同核电荷数的同一类原子的总称。
核素:具有一定数目的质子和一定数目的中子的一种原子。
同位素:质子数相同而中子数不同的同一元素的不同原子互称为同位素。
(对于原子来说)二、元素周期表编排原则:①按原子序数递增的顺序从左到右排列②将电子层数相同......的各元素从左到右排成一横行..。
(周期序数=原子的电子层数)③把最外层电子数相同..。
........的元素按电子层数递增的顺序从上到下排成一纵行主族序数=原子最外层电子数三、元素周期律1.元素周期律:元素的性质(核外电子排布、原子半径、主要化合价、金属性、非金属性)随着核电荷数的递增而呈周期性变化的规律。
元素性质的周期性变化实质是元素原子核外电子排布的周期性变化...................的必然结果。
水化物(12)变化规律碱性减弱,酸性增强—第ⅠA族碱金属元素:Li Na K Rb Cs Fr (Fr是金属性最强的元素,位于周期表左下方)第ⅦA族卤族元素:F Cl Br I At (F是非金属性最强的元素,位于周期表右上方)★判断元素金属性和非金属性强弱的方法:(1)金属性强(弱)——①单质与水或酸反应生成氢气容易(难);②氢氧化物碱性强(弱);③相互置换反应(强制弱)Fe+CuSO4=FeSO4+Cu。
(2)非金属性强(弱)——①单质与氢气易(难)反应;②生成的氢化物稳定(不稳定);③最高价氧化物的水化物(含氧酸)酸性强(弱);④相互置换反应(强制弱)2NaBr+Cl2=2NaCl+Br2。
人教版高中化学必修第一册精品课件 第四章 第一节 原子结构与元素周期表-第1课时 原子结构

34 8
知新
致用
1.某元素的原子结构示意图为 (C )
。下列关于该元素的说法不正确的是
2.某粒子的结构示意图为 A.核外电子数为18 C.属于带负电荷的粒子
,关于该粒子的说法不正确的是( D ) B.核外有3个电子层 D.在化学反应中易得电子
3.根据下列叙述,写出元素名称,并画出原子结构示意图。
道尔顿 汤姆孙 卢瑟福 玻尔
电子云
致用
C
B
A
A.54
B.56
C.58
D.137
02
考点二 原子(或离子)核外电子排布 的表示
导入
微量元素在人体内含量极微小,但具有强大的生物学作用,它们参与酶、核酸等 的代谢过程等。世界卫生组织公布了14种人体必需微量元素,包括氟、硒、碘、硅、 铁、铜、锰、锌、钴、钼、铬、镍、钒、锡。
序号
信息
元素名称 原子结构示意图
(1)
_硅___
____________
(2) B元素原子最外层电子数是次外层电子数的1.5倍 _硼___
__________
序号 (3) (4)
信息
续表 元素名称 原子结构示意图
_钠___
___________
_氧___
__________
第四章 物质结构 元素周期律
第一节 原子结构与元素周期表
第1课时 原子结构
1 考点一 原子核外电子的分层排布及规律 2 考点二 原子(或离子)核外电子排布的表示
1.知道原子的结构及构成原子的微粒间的关系,了解人类对原子结构认识的逐 素养 步深入的过程,发展宏观辨识与微观探析的学科核心素养。 目标 2.能利用粒子结构图式(如结构示意图)描述粒子,能从微观角度认识原子的
_新教材高中化学第四章物质结构元素周期律第一节第一课时原子结构核素课件新人教版必修第一册

→F-:
。
[名师点拨] (1)最外层电子数排满 8 个(He 为 2 个)形成稳定结构,不易得失电子、化学性 质稳定。 (2)原子核外电子排布规律是相互联系、相互制约的,不能孤立地理解或应用其 中一部分。如 M 层不是最外层时,其容纳的电子数最多为 18 个,当 M 层为最外 层时,其容纳的电子数最多为 8 个。 (3)原子形成离子时,核外电子数发生变化,但核内质子数不变。
提示:Na+
与稀有气体 Ne 的核外电子排布相同;Cl-
与稀有气
体 Ar 的核外电子排布相同。
1.电子层 在含有多个电子的原子中,电子分别在能量不同的区域内运动。我们把不同的区
域简化为不连续的壳层,也称作电子层。
2.核外电子的分层排布 在多电子原子中,电子的能量是不相同的。能量较低的,通常在离核较近的区域
第四章 物质结构 元素周期律
第一节 原子结构与元素周期表
第一课时 原子结构 核素
[素养发展目标]
1.从微观视角认识原子的构成,了解元素、核素、同位素的含义。 2.了解原子核外电子排布规律,能画出 1~20 号元素的原子结构示意图,能根据
原子的结构特征确定元素,促进宏观辨识与微观探析化学核心素养的发展。
解析:4200Ca 和4220Ca 是质子数相同、中子数不同的两种核素,二者互为同位素,不 属于同素异形体。
答案:B
3.(1)下列原子:162C、174N、11H、2113Na、21H、4200Ca、4109K、31H、164C 中,元素有________ 种,核素有________种,互为同位素的有________。 (2)18O2 与 16O2,二者的关系是________(填“互为同位素”“互为同素异形体”或 “属于同一种物质”)。 解析:(1)题目提供的 9 种原子共 9 种核素,6 种元素,其中11H、21H、31H,126C、164C 分别互为同位素。 (2)18O2 和 16O2 是分子,属于同一种物质。 答案:(1)6 9 11H、21H、31H;126C、146C (2)属于同一种物质
第一节 原子结构和元素周期表

击
考纲网络
网络构建
梳理判断
栏 目 链 接
梳理基础
一、原子结构
1.构成原子的微粒及其应用
梳理基础
2.微粒之间的关系。
A 原子组成符号为________ ,其中A表示________ 质量数 ,Z表示________ 质子数 。 ZX
(4)包含很多信息的符号:
梳理基础
二、核外电子排布
1.排布方式。 分层 排布的。 多电子原子核外的电子是________
电子层序数 电子层符号 离核距离 电子能量 1 ____ K 2 ____ L 3 ____ M 4 ____ N 5 O 6 P 7 Q
近 到____ 远 由____ 低 到____ 高 由____
梳理基础
(3)镧系:位于元素周期表第六周期中,从57号元素镧到
71号元素镥,共15种元素。 (4)锕系:位于元素周期表第七周期中,从89号元素锕到 103号元素铹,共15种元素。
梳理基础
正确的打“√”,错误的打“×”。 1.18 g H2O中所含的质子数为10NA( √ ) 2.S2-的结构示意图为 ( × ) ( √ )
梳理基础
(1)分区。
①分界线:沿着元素周期表中铝、锗、锑、钋与硼、硅、砷、碲、
砹的交界处画一条斜线,即为金属元素区和非金属元素区分界线 (氢元素除外)。 ②各区位置:分界线左面为金属元素区,分界线右面为非金属元 素区。
③分界线附近元素的性质:既表现金属元素的性质,又表现非金
属元素的性质。 (2)过渡元素:位于元素周期表中部,从ⅢB族到ⅡB族10个纵列, 共六十多种元素,这些元素都是金属元素。
梳理基础
2.排布规律。 (1) 电子一般总是首先排在能量 ______ 最低 的电子层里,即最先排 在________ 第1层 ,当________ 第1层 排满后,再排________ 第2层 ,依次类推。 (2)每层最多容纳的电子数为______( 2n2 n代表电子层数)。 (3) 最外层电子数不超过 ____ 8 个 (K 层为最外层时,最多不超过
高中化学—— 原子结构

注意:原子结构示意图中质子数等于核外电子数, 而离子结构示意图中质子 数与核外电子数不相等。
阴离子的核外电子数=质子数+电荷数 阳离子的核外电子数=质子数-电荷数
核外电子排布的表示方法
思考与交流
【思考1】当M层上有电子时,L层上的电子是否已排满? 由于L电子层能量比M层低,故电子先排满L层后再排M层;因此,当M层上有电 子时,L层上一定排布8个电子。
原子的诞生
大爆炸 2h后诞生 大量的_氢___,少量的__氦___,极少量的__锂___ 原子核的融合反应 其他元素
科学史话-原子结构模型的演变
英国化学家 道尔顿
英国物理学家 汤姆生
英国科学家 卢瑟福
丹麦物理学家 玻尔
奥地利物理学家 薛定谔
实心球模型 葡萄干蛋糕模型 行星太阳模型 玻尔原子模型 电子云模型
【思考与交流】如果是离子,各微粒数如何变化?
粒子符号
23 11
Na+
3177Cl-
质子数 (Z) 11 17
质量数(A) 23 37
中子数(N) 12 20
电荷数 1 1
核外电子数 10 18
阳离子:核外电子数=质子数-电荷数 阴离子:核外电子数=质子数+电荷数
原子核外电子的排布
电子层
在含有多个电子的原子里,电子分别在 能量不同的区域内运动。在多电子原子里, 把电子运动的能量不同的区域简化为不连 续的壳层,称作电子层。
课堂练习
1.某元素原子的最外层电子数是次外层的m倍(m为大于1的整数),则该原子的核
外电子总数为( C )
A.2m
B.2m+10
C.2m+2
D.m+2
高中化学必修一 第四章第一节 物质结构与元素周期表20202021学年新)解析版)

第四章物质结构元素周期律第一节原子结构与元素周期表本章内容是继氧化还原反应和离子反应之后又一个化学的理论知识点,通过本章的学习可以体会化学也是有规律可循的,本节内容是本章的基础,也是整个周期表周期律的基础,这一节学不好,就很难体会化学上结构决定性质的奥秘,也就很难体会化学的规律性,本节内容共有13个重点内容,静下心来慢慢体会吧!一、核外电子排布的表示方法(1)原子结构示意图①小圆圈和圆圈内的符号及数字表示原子核及核内质子数。
②弧线表示电子层。
③弧线内数字表示该层中的电子数。
(2)离子结构示意图①当主族中的金属元素原子失去最外层所有电子变为离子时,电子层数减少一层,形成与少一个电子层的稀有气体元素原子相同的电子层结构。
②非金属元素的原子得电子形成简单离子时,形成与电子层数相同的稀有气体元素原子相同的电子层结构。
(2020·上海市奉贤区奉城高级中学高一期末)有四种微粒的结构示意图,下列叙述中错误的是()它们属于不同种元素它们的核外电子排布相同它们都是离子它们都具有稀有气体原子的稳定结构【答案】C【分析】根据结构示意图分析可得,四种微粒分别为O2-、Ne、Mg2+和Al3+。
【详解】由分析可知,它们属于不同元素,故A不选;根据结构示意图,它们的核外电子排布相同,故B不选;由分析可知,第二种微粒不是离子,是氖原子,故C选;稀有气体原子最外层有8个电子(氦有2个),是稳定结构,第二种微粒就是Ne,其他几种微粒都和Ne的原子结构相同,故D不选;故选C。
二、明确符号A Z X±c n±m中各个字母的含义并了解它们之间的关系(1)质量数(A)=质子数(Z)+中子数(N),质量数可近似地代替原子的相对原子质量。
(2)原子的核外电子总数=质子数=核电荷数=原子序数。
(3)阳离子M n+的核外电子数=质子数-n;阴离子N n-的核外电子数=质子数+n。
(2020·福建南安市·高一期中)科学研究表明,月球上有丰富的He资源,可开发利用作未来的新型能源。
高中化学第四章物质结构元素周期律第一节原子结构与元素周期律第课时原子结构课件新人教版必修第一册

答案:A
解析:A元素原子的次外层电子数只能是2,最外层电子数是4,A的原子序数 为6;B元素的内层电子总数只能是2,最外层电子数为6,B的原子序数为8;C元 素原子有3个电子层,L层必有8个电子,M层有4个电子,C的原子序数为14;D 的阳离子与B的阴离子(即O2-)电子层结构相同,D为Na,原子序数为11;故原子 序数:C>D>B>A。
阳离子(Rm+) 阴离子(Rm-)
质子数>电子数 质子数<电子数
质子数=电子数+m 质子数=电子数-m
(3)数量关系。 原子序数=质子数
目标2 核外电子排布规律应用 例2表示某微粒的结构示意图,下列说法不正确的是( ) A.表示的原子只能为Ne B.表示的金属阳离子有3种 C.表示的微粒对应的元素一定为非金属元素 D.表示的微粒有2个电子层
2.离子结构示意图 (1)当主族中的金属元素原子失去最外层所有电子变为离子时,电子 层数减少一层,形成与上一周期的稀有气体原子相同的电子层结构。
如:
(2)非金属元素的原子得电子形成简单离子时,形成和稀有气体原子 相同的电子层结构。 如:
1~20号元素原子核外电子排布特征 (1)最外层电子数为1的原子有H、Li、Na、K。 (2)最外层电子数为2的原子有He、Be、Mg、Ca。 (3)最外层电子数与次外层电子数存在倍数关系的情况 ①最外层电子数=次外层电子数的原子:Be、Ar。 ②最外层电子数=次外层电子数2倍的原子:C。 ③最外层电子数=次外层电子数3倍的原子:O。 ④最外层电子数=次外层电子数4倍的原子:Ne。 ⑤最外层电子数=次外层电子数12的原子:Li、Si。
(新教材)【人教版】必修一(化学)原子结构与元素周期表

12
2.质量数
(1)概念:质子和中子的相对质量都近似为1,忽略电子 的质量,将原子核内所有_质__子__和_中__子__的相对质量取近
似整数值相加,所得的数值叫做质量数。 (2)关系:质量数(A)=_质__子__数__(_Z_)_+_中__子__数__(_N_)_
【巧判断】 (1)某种硫原子的中子数是18,则其质量数是34。( ) 提示:√。硫的质子数为16,根据质量数=质子数+中子 数可知,硫的质量数为34。
2.用A+、B-、C2-、D、E、F和G分别表示含有18个电子 的七种微粒(离子或分子),请回答: (1)A元素是________,B元素是________,C元素是 ________(用元素符号表示)。 (2)D是由两种元素组成的双原子分子,其分子式是 ________。
【规律方法】1~18号元素中12类原子结构的特点 (1)最外层电子数为1的原子有H、Li、Na。 (2)最外层电子数为2的原子有He、Be、Mg。 (3)最外层电子数与次外层电子数相等的原子有Be、Ar 。
(4)最外层电子数是次外层电子数2倍的原子是C。 (5)最外层电子数是次外层电子数3倍的原子是O。 (6)最外层电子数是次外层电子数4倍的原子是Ne。 (7)次外层电子数是最外层电子数2倍的原子有Li、Si 。
【素养提升】 如图所示为原子核外电子运动的三维立体图:
图中所有电子均已画出。
(1)该图所描述的是哪种元素的原子? 提示:该原子共8个电子,故属于氧元素。
(2)请用另一种形式表示该元素原子的电子排布。 提示:
【备选要点】等电子粒子 (1)利用元素排布寻找“10电子”微粒的方法
(2)利用元素排布寻找“18电子”微粒的方法
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
课件1:4.1.4原子结构与元素性质

3.递变性
(1)物理性质
F2
Cl2
Br2
I2
颜色:浅黄―绿―色――黄―绿―色―――深―红―棕―色――紫→―液―体――――固→体 逐渐__升__高____
水溶性:反―应――――溶―解―――溶―解――――微→溶 逐渐__减__小____
密度: ――――――――――――――→ 逐渐增大
第四章 物质结构 元素周期律
解析 根据同主族元素性质的递变规律,从金属锂到金属钫随原子序数的递增 ,原子半径逐渐增大,元素的金属性逐渐增强,最高价氧化物对应的水化物的碱性 逐渐增强,与水反应的剧烈程度逐渐增强,与氧气反应的产物越来越复杂,可以产 生过氧化物、超氧化物等。
第四章 物质结构 元素周期律
第四章 物质结构 元素周期律
①与 H2 反应:X2+H2一=定==条==件2HX ②与变价金属(如 Fe)反应 2Fe+3X2===2FeX3X=F、Cl、Br
Fe+X2===FeX2X=I ③与 H2O 反应 X2+H2O HX+HXOX=Cl、Br、I
2F2+2H2O===4HF+O2
第四章 物质结构 元素周期律
知识点二 卤族元素(★★★)
1.原子结构
元素
核电 荷数
氟(F)
9
原子结构 示意图
氯(Cl) 17
最外层 电子数
__7___
电子 层数
原子 半径
2
从上到下
由__小____到
3
__大____
第四章 物质结构 元素周期律
元素
核电 荷数
原子结构 示意图
溴(Br) 35
碘(I)
53
最外层 电子数
电子 层数
原子 半径
第四章 物质结构 元素周期律
高一化学人教版2019必修第一册 4.1原子结构与元素 周期表(知识点)

第四章物质结构元素周期律第一节原子结构与元素周期表1.认识原子的构成,了解原子核外电子排布规律,能画出1~20号元素的原子结构示意图。
2.能从原子结构的角度理解元素周期表的编排原则,能进行元素在周期表中的位置与原子结构之间的相互推导。
3.了解元素周期表的发展历程及现行元素周期表的结构。
4.知道元素、核素、同位素、A Z X的含义,并能比较它们的不同。
5.知道碱金属元素、卤族元素的结构和性质,能从原子结构角度解释同主族元素性质的递变规律。
6.能设计实验方案,探究同主族元素性质的递变性7.巩固原子的构成,加深对核素、同位素概念的理解,熟练掌握核电荷数、质子数、中子数、质量数之间的关系。
8.熟练掌握元素周期表的结构,能用原子结构理论解释同族元素性质的相似性和递变性。
知识点一原子的构成知识点二原子核外电子排布知识点三元素周期表的编排原则与结构知识点一原子的构成1.构成原子的微粒及其性质2.质量数(1)概念:将原子核内所有质子和中子的相对质量取近似整数值相加,所得的数值叫做质量数,常用A 表示。
(2)构成原子的粒子间的两个关系①质量数(A)=质子数(Z)+中子数(N)。
②质子数=核电荷数=核外电子数。
3.元素(1)概念:具有相同质子数(核电荷数)的一类原子的总称。
(2)决定元素种类的是质子数。
4.核素(1)概念:具有一定数目质子和一定数目中子的一种原子。
表示方法:A Z X。
(2)实例原子符号(A Z X)原子名称氢元素的原子核质子数(Z)中子数(N)11H氕1021H或D氘1131H或T氚125.同位素(1)概念:质子数相同而中子数不同的同一元素的不同原子互称为同位素(即同一元素的不同核素互称为同位素)。
“同位”是指核素的质子数相同,在元素周期表中占有相同的位置。
例如:氢元素有11H、21H、31H三种核素;碳元素有126C、136C、146C等核素;氧元素有168O、178O和188O三种核素;铀元素有23492U、23592U、23892U等核素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
波函数(Ψ)即原子轨道是薛定谔方程的合理解,从 求解薛定锷方程得到的波函数(Ψ)本身不能与任何 可以观察的物理量相联系,但波函数的平方︱Ψ︱2可 以反映电子在空间某位置上单位体积内出现的几率大 小,即几率密度,因而一般用︱Ψ︱2表示电子在核外 空间某单位体积内出现的几率,即电子出现的几率密 度。波函数Ψ(x,y,z)表征电子的运动状态,并且 用它的模的平方|Ψ|2表示单位体积内电子在核外空间 某处出现的几率,即几率密度,所以电子云实际上就 是|Ψ|2在空间的分布。
解薛定谔方程解出一个波函数,就得 到一条原子轨道;但要使其是合理解, 需要指定三个量子数n,L,m为一定值 ;另外,原子光谱的精细结构表明,电 子还有另一种运动形式,称为“自旋运 动”,用自旋量子数mS表示,n,L,m, mS称为四个量子数。
主量子数n、角量子数 l、磁量子数m、自旋 量子数mS。
连续光谱:色带无明显的分界线,为连 续波长光。
线状光谱:谱线是分立的,有明显的分 界。
1. 氢光谱和玻尔理论 (1)氢光谱: 在可见光区有分立谱线:
氢原子光谱特征:①不连续的,线状的;②有规律。
碱金属原子的光谱也有类似规律。
(2)Bohr理论
氢光谱与经典的物理学解释相互矛盾。1913 年波尔以普朗克的量子理论和爱因斯坦的光子学 说为基础建立了原子模型。
波动性的表征:波长、频率、衍射干涉等 ;
粒子性的表征:速度、质量、动量等。 1927年,法国de Broglie设想电子也具有波动 性。很快被电子衍射实验所证实。 可见,高速运动的电子,在原子中的运动规律必 然与Байду номын сангаас观物体不同。
应用Ni晶体进行电子衍射
实验,证实电子具有波动性。
3、 测不准原理
1927年德国物理学家海森堡指出:对微观粒子,不能同时准 确测出它在某一瞬间的运动速率(或动量)和位置。
x ·px h
位置误差 动量误差
表明:微观粒子的运动只能使用统计规律描 述,即几率描述。
4.波粒二象性的统计解释
海森堡测不准原理,否定了玻尔提出的原子结 构模型。通过电子衍射实验人们发现,如果用 较强的电子流,在较短的时间得到电子衍射图 像,若电子流很弱,弱到电子一个一个通过小 孔到达底片上,每个电子到达后,都只会在底 片上留下一个感光点,当感光点不是很多的时 候,这些点并不能完全重合,从底片上看不出 电子落点具有规律性。这说明单个或少量的电 子并不能表现出波性,某一个电子经过小孔后, 究竟落在底片的哪个位置上,是无法准确预言 的;但是,只要衍射时间足够长, 大量感光点 在底片上同样会形成一张完整的衍射图像,显 示了电子的波动性。
2、原子轨道的角度分布图
注意:此处的原子轨道绝不是玻尔理论的 原子轨道,而是指电子的一种空间运动 状态,指用统计的方法,可在所代表的 区域内找到核外运动的该电子,而该电 子在此区域内(即这一轨道)中的运动 是随机的、测不准地出现的。波函数本 身没有具体物理意义,它的物理意义通 过|ψ|2来理解。
二、 核外电子状态
1、波函数和Schrödinger方程 2、原子轨道的角度分布图
3.电子云的角度分布图
4.电子云的径向分布图 5、四个量子数
(1) 主量子数n (2) 角量子数 l
(3) 磁量子数m (4)自旋量子数mS
1、波函数和Schrödinger方程
量子力学用薛定谔方程(二阶偏微分)来描述具 有波粒二相性的微观粒子的运动状况。
量子理论:物质吸收和发射能量是量子化的。
光子学说:光既有波动性又有粒子性,即:
光量子的能量 Ehv
光量子的动量
p h
h为普朗克常6数.6, 2610-34J s
两式将光子的波动粒 性子 和性定量的联系。 起来
(2)Bohr理论
要点:
①电子在符合量子化条件的轨道上绕核运动,这些轨道称 为稳定轨道,电子在稳定轨道上运动不释放能量;
3.电子云的角度分布图
(1)电子云 解薛定锷方程得到的波函数(Ψ) 不能与任何可以观察的物理量相联系,但︱Ψ︱2
可以反映电子在空间某单位体积内出现的几率大
小,即几率密度,因而一般用︱Ψ︱2表示电子在
核外空间某单位体积内出现的几率,即电子出现 的几率密度。
为了形象化的表示核外电子运动的几率密度, 用小黑点分布的疏密来表示。小黑点较密的地方 ,表示几率密度较大,单位体积内出现的机会多 。用这种方法来描述电子在核外出现的几率密度 分布所得的空间图像称为电子云。因此,电子云
4.波粒二象性的统计解释
电子等微观粒子运动的波动性,是大量微观粒 子运动的统计性规律的表现。就大量粒子的行 为而言,在空间某点波的强度大,则电子在该 点处单位微体积内出现的几率、即几率密度大; 反之,空间某点波的强度小,则电子在该点处 单位微体积内出现的几率、即几率密度小。所 以,空间任何一点电子波的强度和电子在该处 单位微体积内出现的几率密切相关。根据微观 粒子波粒二象性的统计解释,人们建立了一种 全新的力学体系——量子力学,用来对微观粒 子的运动状态进行研究。
是原子中电子几率密度︱Ψ︱2分布的具体形象。
电子云是一种形象化的描绘。
3.电子云的角度分布图
这二图有所不同:
的角度分布图有正、负,(不是代表电荷 的正负;与成键有关);
2 图--电子云角度分布图均正, 且“瘦” 些.(平方的结果)。
但二张图都能表示电子运动状况角度分布的 情况,从而了解原子轨道的形状及空间伸展方 向。
第四章物质结构第一节原子结构
按其模型:
1.原子光谱应是连续光谱 ;
2.电子运动,发射电磁波 ,能量渐失,直到原子湮 灭。但事实并非如此!每 种原子都有线状光谱。( 光谱分析就是根据特征线 状光谱定性、定量的)
[评述] 根据电磁学:原子将毁灭,所产 生的光谱应为连续光谱。
光谱:光通过分光镜后形成的色带(谱 线)。
每个特定解Ψ表示电子运动的一稳定状态,用“轨 道”名称,称Ψ为原子轨道。
[说明]:
22282m(EV)
x2 y2 z2
h2
①方程的解Ψ并非具体数值,而是一函数关系;
②须同时引入三个限制条件,即三个量子数, Ψ才具有 确定的物理意义;换句话说,一组量子数确定后,对应 Ψ和相应的能量确定,该电子的运动状态确定。
②轨道离核越远,能量越大; 基态: 电子尽可能处于能量最低轨道的状态; 激发态:获得能量,电子跃迁到能量高轨道的状态。 ③脱离供给能量体系,激发态不稳定,电子将从高能级回
到较低能级,以光子形式放出能量。 △E=hν
[简评]是结构理论的重大突破,但对原子结构复杂性仍认 识不够。
2、微观粒子的波粒二象性
