16-5驻波解析
驻波的名词解释

驻波的名词解释多导体元件在电流激励下,发生极化而产生强烈震荡。
这种由于强烈震荡引起的频率为两倍以上原来基本谐振频率的新的谐振现象称作驻波。
驻波是交流电路中不希望出现的一种特殊情况,因此它有时也被成为“电网的疲劳”或“噪声”。
1、驻波是指沿着两个相反方向的振动,其间没有能量传递,即所谓正弦波的余弦分量为零;但实际上总存在各次谐波之间和每对正弦波与其余弦之间都有能量传递。
这样就形成了叠加后的合成波,通常叫做驻波。
当系统受到周期性外力扰动时,如果只考虑正负半周期内的变化,则该扰动将会使得某些地点附近的导线处于暂时的最大位移状态,并且往复运行至初始位置(图1a),从而造成了所谓的共振,此时电压、电流表示值会突然增高很多,甚至超过额定数值,同时伴随着响亮的蜂鸣声,这便是我们平时说的电容器爆裂,属于驻波的一种现象。
2、驻波是一种稳定状态,任何含有两个独立正弦分量的信号均可看作是两个单边带信号相乘的结果,用一个函数y=a+bx来描述,即y=a×b+bx,这里a,b, c是三个角频率。
例: y=a×b+bx,则当它取正弦波形式时, x=(0, 0),当它取余弦波形式时, x=(a/2,-a/2)。
3、驻波又名行波,当干扰源激励电气设备时,电感L上将会出现行波干扰,即输入信号的行波部份通过电感L后,回到输入端再返回电源负载,另一部分直接进入电源负载,这种类型的干扰会导致设备误工作。
4、对于三相桥式整流电路,由于三相负载的不平衡,经常会在负载A相上产生很强的行波磁场,影响负载的正常工作,给负载的安全运行构成威胁,因此必须采取措施抑制行波磁场。
5、对于功率放大器等电子设备,主要应注意防止前级对后级的干扰。
6、功率分配不合理。
7、铁心饱和。
8、电源供电电压过低。
9、整机散热效果差。
10、驱动电路调试质量不好。
11、负荷特性畸变。
12、铁芯连接松弛。
13、静态开关电容失效。
14、印刷板阻抗匹配不良。
10.5驻波

对于光学中的光波
光密媒质:折射率n较大的媒质。 n1 光疏媒质:折射率n较小的媒质。 n2
若波由 光疏媒质=>光密媒质,则有半波损失
例题:平面简谐波在距一反射面B为L处的振动规
律为
y = Acost
,设波速为 u ,反射时有半波损失,求入射波及反 射波的表达式。
1 2 3 4 5x
(2) 相邻两波节之间的质点运动同向,故驻波的运动是一段一
段的运动。
“驻”含义之二:
驻波不传播相位
四、驻波的能量
• 合能流密度为 wu + w (− u ) = 0
“驻”含义之三: 驻波不传播能量
t=0
t=T 4
t=T 2
势能 动能
波腹 波节 /4
能量 流动
势能
五、半波损失 绳子在固定端反射
y
y
1 2 3 4 5x 1 2 3 4 5x
y
t=0
1 2 3 4 5x
“驻”含义之一: 驻波不传播振动状态
y
t=T/4
1 2 3 4 5x
y
波腹
t=T/2
1 2 3 4 5x
波节
y
t=3T/4
12 3
4 5x
驻波
波腹
波节
驻波
波腹
波节
二、驻波的表达式
y
y1
=
A cos (t
−
x) u
= y1 + y2 = A cos (t
§10.5 驻波 音叉实验
一、驻波的形成
t=0
y
u
t=T/4
y
u
1 2 3 4 5x 1 2 3 4 5x
选修3测试题及答案解析

选修3测试题及答案解析一、单项选择题(每题2分,共50分)1. 以下哪项不是选修3中的内容?A. 机械振动B. 电磁感应C. 量子力学D. 热力学答案:C解析:量子力学是选修3-5的内容,而非选修3。
2. 简谐运动的振动周期与振幅的关系是:A. 正比B. 反比C. 无关D. 无法确定答案:C解析:简谐运动的振动周期只与振动系统本身的性质有关,与振幅无关。
3. 阻尼振动中,振幅逐渐减小的原因是:A. 摩擦力B. 空气阻力C. 外部驱动力减小D. 系统内部能量耗散答案:D解析:阻尼振动中,由于系统内部能量的耗散,振幅会逐渐减小。
4. 以下哪个选项是正确的机械波传播速度公式?A. v = fλB. v = f/λC. v = λ/fD. v = √(G/ρ)答案:D解析:机械波的传播速度v与介质的密度ρ和弹性模量G有关,公式为v = √(G/ρ)。
5. 声波属于哪种类型的波?A. 横波B. 纵波C. 表面波D. 驻波答案:B解析:声波是纵波,介质中的质点振动方向与波的传播方向相同。
6. 以下哪个选项是正确的多普勒效应描述?A. 波源与观察者相对静止时,观察者接收到的波频率不变B. 波源远离观察者时,观察者接收到的波频率变高C. 波源靠近观察者时,观察者接收到的波频率变低D. 波源与观察者相对运动时,观察者接收到的波频率不变答案:A解析:当波源与观察者相对静止时,观察者接收到的波频率与波源发出的频率相同。
7. 以下哪个选项是正确的光的干涉现象描述?A. 两束光波相遇时,波峰与波峰相遇,波谷与波谷相遇,形成亮条纹B. 两束光波相遇时,波峰与波谷相遇,形成暗条纹C. 两束光波相遇时,波峰与波峰相遇,波谷与波谷相遇,形成暗条纹D. 两束光波相遇时,波峰与波峰相遇,波谷与波谷相遇,形成亮条纹答案:D解析:光的干涉现象中,当两束光波相遇时,波峰与波峰相遇,波谷与波谷相遇,形成亮条纹。
8. 以下哪个选项是正确的光的衍射现象描述?A. 光波通过小孔或障碍物时,会发生弯曲B. 光波通过小孔或障碍物时,不会发生弯曲C. 光波通过小孔或障碍物时,只会发生反射D. 光波通过小孔或障碍物时,只会发生折射答案:A解析:光波通过小孔或障碍物时,会发生弯曲,形成衍射现象。
大学物理学(课后答案)第5-6章
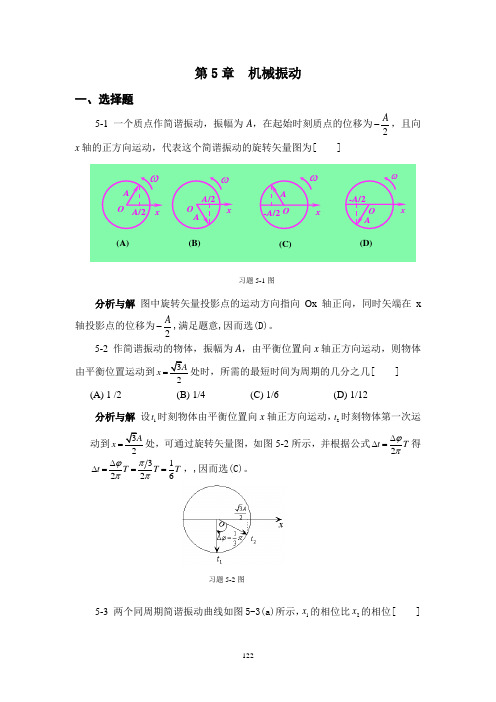
第5章 机械振动一、选择题5-1 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为2A-,且向x 轴的正方向运动,代表这个简谐振动的旋转矢量图为[ ]分析与解 图中旋转矢量投影点的运动方向指向Ox 轴正向,同时矢端在x轴投影点的位移为2A-,满足题意,因而选(D)。
5-2 作简谐振动的物体,振幅为A ,由平衡位置向x 轴正方向运动,则物体由平衡位置运动到32Ax =处时,所需的最短时间为周期的几分之几[ ] (A) 1 /2 (B) 1/4 (C) 1/6 (D) 1/12分析与解 设1t 时刻物体由平衡位置向x 轴正方向运动,2t 时刻物体第一次运动到32A x =处,可通过旋转矢量图,如图5-2所示,并根据公式2t T ϕπ∆∆=得31226t T T T ϕπππ∆∆===,,因而选(C)。
5-3 两个同周期简谐振动曲线如图5-3(a)所示,1x 的相位比2x 的相位[ ]O O OO A Axxx(A) (B)(D)(C)A /2-A /2 A /2 -A /2A Aωωωωx习题5-1图习题5-2图(A) 落后2π(B) 超前2π(C) 落后π (D) 超前π分析与解 可通过振动曲线作出相应的旋转矢量图(b ),正确答案为(B )。
5-4 一弹簧振子作简谐振动,总能量为E ,若振幅增加为原来的2倍,振子的质量增加为原来的4倍,则它的总能量为[ ](A) 2E (B) 4E (C) E (D) 16E 分析与解 因为简谐振动的总能量2p k 12E E E kA =+=,因而当振幅增加为原来的2倍时,能量变为原来的4倍,因而答案选(B)。
5-5 两个同振动方向、同频率、振幅均为A 的简谐振动合成后,振幅仍为A ,则这两个简谐振动的相位差为[ ](A) 60 (B) 90 (C) 120 (D) 180分析与解 答案(C )。
由旋转矢量图可知两个简谐振动的相位差为 120时,合成后的简谐运动的振幅仍为A 。
驻波经典知识介绍

λ
的同频率谐振动。 的同频率谐振动。
三、驻波的特点
1.频率特点:由图及方程知,各质元以同一频率作简 1.频率特点:由图及方程知, 频率特点 谐振动。 谐振动。 2.振幅特点: 2.振幅特点 振幅特点: x (1)各点的振幅 有关, (1)各点的振幅 2Acos(2π λ ) 和位置 x 有关,振幅 大小按余弦规律随 x 变化 (2)波节 有些点始终静止, 波节: (2)波节:有些点始终静止,这些点称作波节
实际中驻波的形成 实际的驻波可由入射到媒质界面上的行波和它 的反射波叠加而成。 的反射波叠加而成。 1.波在固定端的反射 (如一端固定的弹性绳) 1.波在固定端的反射 如一端固定的弹性绳) 反射点是波节(和固定点情况吻合) 反射点是波节(和固定点情况吻合)。 2.波在自由端的反射 2.波在自由端的反射 反射点是波腹。 反射点是波腹。 问题 在两个介质分界面上将如何 ?
驻波的能量被“封闭” 驻波的能量被“封闭”在相邻波节和波腹间的 λ 的范围内,在此范围内有能量的反复流动, /4 的范围内,在此范围内有能量的反复流动,但能 量不能越过波腹和波节传播, 量不能越过波腹和波节传播,驻波没有单向的能量传 输。 形成驻波的两个行波的能流密度数值相等,方 形成驻波的两个行波的能流密度数值相等, 向相反,因此它们叠加而成的驻波能流密度为零, 向相反,因此它们叠加而成的驻波能流密度为零, 驻波不传播能量 ---“驻”字的第三层含义。 ---“ 字的第三层含义。
二 、驻波方程
设两列沿同一直线相向传播的同振幅相干波, 设两列沿同一直线相向传播的同振幅相干波, 取两波在空间某点引起振动,同时达到最大为起始时刻, 取两波在空间某点引起振动,同时达到最大为起始时刻, 该点为坐标原点. 该点为坐标原点. y1 u x 入射波 y 1 = A cos 2π t − x
液体表面驻波的演示和驻波波长的测量

液体表面驻波的演示和驻波波长的测量卢桂林;钟浩源;谭铝平;翟若迅;白在桥【摘要】将液体平铺在透明亚克力平板上,在表面张力的作用下得到均匀的液膜.驱动平板上下振动,在合适的频率下可在液膜表面得到稳定的驻波图样.通过光学方法将驻波图样投影到屏幕上,适当地调制投影光源,可以显示不同相位的驻波峰值图样.利用自制装置演示了不同形状液膜的驻波,测量了驻波波长,并得到液体毛细波的色散关系.【期刊名称】《物理实验》【年(卷),期】2019(039)005【总页数】5页(P29-33)【关键词】驻波;波长;毛细波;色散关系【作者】卢桂林;钟浩源;谭铝平;翟若迅;白在桥【作者单位】北京师范大学物理学系,北京100875;北京师范大学物理学系,北京100875;北京师范大学物理学系,北京100875;北京师范大学物理学系,北京100875;北京师范大学物理学系,北京100875【正文语种】中文【中图分类】O353.5在物理教学中,水波经常被用来演示一般的波动规律,比如波的干涉和衍射. 水波的定量测量比较复杂[1-4],一般需要水槽和造波装置[5-6]. 本文提出简便的水波驻波观察和测量方法:将透明亚克力平板切割成一定形状和尺寸的承液板,把液体铺在承液板上,在表面张力作用下形成1层液膜,将驱动承液板放置在振动台上,使之上下微幅振动. 在合适的驱动频率下,液膜表面可形成稳定的驻波图样. 由于没有水槽壁的摩擦,波在液膜边界的反射系数更高,产生的驻波图样更完整、清晰. 该方法既可以演示不同形状液膜的驻波图样,也可以定量测量液体毛细波的色散关系,进而得到液体的表面张力系数.1 理论分析1.1 水波的色散关系水波的回复力包括重力和表面张力,水波的波速与波长和水深都有关系. 水波振幅比较小时,忽略高阶效应,线性水波的色散关系为(1)其中,ω为角频率,k为波数,g,σ,ρ,h分别为重力加速度、液体表面张力系数、液体密度和液体深度. (1)式的推导可参见文献[7].与空气中的声波或真空中的光波不同,水波的ω不与k成正比,这说明水波有色散,相速度与群速度不相等,它们随波长的改变而改变. 对于长波(k→0),表面张力可以忽略,此时称为重力波. 如果水深远小于波长,则有近似无色散,但波速与成正比. 如果水深远大于波长,则对于短波重力可以忽略,此时称为毛细波. 如果深度足够,满足tanh (kh)≈1,则有1.2 驻波图样用前述的方法得到的水膜厚度约为3 mm,而平板的尺度在10 cm,因此除了弧形的边缘部分,水膜可认为厚度均匀. 液膜上驻波图案对应于水波方程在给定边界条件下的本征函数. 但边界条件的数学形式并不容易确定,精确的驻波形式不易计算. 不过驻波产生的机制并不复杂:水波在液膜边界反射改变方向,不同行进方向的行波叠加而形成驻波. 对于几种简单形状的液膜,可以结合实验现象写出其驻波形式. 对于正方形水膜,驻波形式为u(x,y,t)=C[cos (kx)+cos (ky)]cos (ωt).(2)对于正三角形或正六边形水膜,驻波形式为(3)其中(ki,qi)=k[cos (iπ/3),sin (iπ/3)],C为常量. 这里ω和k满足色散关系(1)式,而且只能取由液膜形状确定的离散值.为便于理解,用Matlab画出2种驻波图样,见图1和图2. 图中黄色代表波峰,蓝色代表波谷,随时间推移,波峰和波谷位置周期性互换.图1 正方形水膜上的驻波图样(a)t=0(b)t=π图2 正三角形和正六边形水膜上的驻波图样需要指出的是,对于正方形水膜上的驻波,峰值点和谷值点各形成正方点阵,每套点阵相差1个平移,空间周期都是λ=2π/k. 而正三角形或正六边形水膜上的驻波图样则不然,峰值和谷值形成的点阵形状并不相同,分别为正三角形点阵和类似蜂窝状网格.1.3 驻波成像由于液体透明而且驻波的振幅很小,不便于直接观察. 1束平行光透过液膜,液膜表面波可以看成若干凸透镜(波峰)与凹透镜(波谷)的组合,其中凸透镜可以使光束会聚,在观察屏上形成亮点或亮线(见图3).图3 水波波峰成像示意图假设液膜按(2)式振动. 当cos (ωt)=1时,振幅达到最大,此时原点处有1个峰值.当x,y趋于0时,所以液面最大的曲率为对应最短的焦距为其中n=1.33为水的折射率. 若fmin=16 cm,代入实验的典型值k=1 000 m-1,得到振幅2c=0.038 mm,远小于液膜厚度.2 实验装置和实验方法2.1 实验装置实验装置包括振动台、液膜和投影光路3部分,实物图和示意图分别见图4和图5.由于实验需要的振幅很小,选用4个4寸低音扬声器作为振动源. 用1块挖去4个圆孔的平板将扬声器的相对位置固定,并放置在装有调平地脚的平台上. 信号发生器输出正弦波,经功率放大器后串联通过4个扬声器,保证它们同步振动. 将边长16 cm的正方体支架的4个脚分别放在4个扬声器的振膜上. 平台和支架均由透明亚克力板切割粘接制成.承液板用透明亚克力板切割而成. 虽然液膜的厚度不能调节,但由于激光切割的便利性,水膜的形状和尺寸很容易改变,方便研究边界形状对液膜驻波图样的影响. 将承液板放在正方体支架的上表面. 支架内部放置倾斜角为45°的平面反射镜. 支架前表面粘1张硫酸纸作为投影屏,如图5所示.图4 实验装置实物图图5 实验装置示意图实验用激光做投影光源. 激光经扩束和平面镜反射后从正上方垂直照射到液膜上,然后经过正方体支架内部的反射镜,投射在屏上. 屏到液膜的光路约为16 cm. 由于视觉暂留现象,如果保持光源常亮,人眼看到的图案是不同振动相位的叠加效果.为了克服视觉暂留,实验采用的激光器有输出调制功能. 采用与振动信号同频率而且相位差和宽度都可调的脉冲信号调制激光输出,可以观察到特定相位的驻波图案,同时也提高了显示图像的对比度.2.2 实验方法在完成水平调节以及液膜准备之后,操作步骤为:1)保持光源常亮,调节振动台驱动信号频率,找到液膜共振频率,调节驱动振幅,使投影屏上的图案尽量清晰.2)将光源调制信号频率调至振动台频率,调节相位延迟与脉冲宽度,观察液膜振幅最大时刻对应的驻波图样,完成需要的测量.重复步骤1)和2),完成一系列共振模式的观察和测量.为了实验方便,并提高测量精确度,利用摄像头采集图像,并用LabVIEW编写控制和测量程序. 图6为LabVIEW程序的前面板,主要分为5个区域:Ⅰ区为摄像头采集到的成像图,由于使用激光的波长为532 nm,程序做了简单的图像处理,只显示绿色分量,这样可以滤除环境杂光. Ⅱ区为控制部分,通过VISA控制信号发生器,调节振源频率、振幅、振源与光源调制信号的频率差、调制信号的相位和占空比. Ⅲ区控制图像的测量区域,在采集图像的特定位置选取矩形区域. 程序将所选区域的光强按垂直方向求和,得到一维光强分布. 然后对数据进行低通滤波(相当于长时间取平均),结果在Ⅳ区用图形显示,图中每个峰值代表Ⅰ中矩形框中的1条亮线. 图形显示控件有若干光标,左右移动可以对峰值定位. 光标位置坐标在Ⅴ区显示.图6 控制测量前面板在做图像测量之前需要进行长度定标. 定标采用图7所示的定标板,由多条平行的透光缝组成,缝间距为5 mm. 将定标板放液膜的位置,测量图像中亮条纹的位置,定出标度系数.图7 定标狭缝板3 结果与分析3.1 驻波演示图8为不加光源调制时一些液膜上的驻波投影图,其中正方形板得到正方形网格,圆形板得到同心圆圈,三角形和六边形板均得到正六边形蜂窝状网格加中心亮点图案.(a)正方形板 (b)圆形板(c)六边形板 (d)三角形板图8 未经激光调制的成像图用与振源同频率、占空比为10%的脉冲调制光源输出,在合适的相位差下,得到清晰的驻波图案,结果见图9. 与不加调制的图像相比,调制后的图案更清晰、对比度更高. 图9(a)和9(b)中亮线数目减半. 图9(c)和9(d)中,正三角形和正六边形板的图案由图8(c)和8(d)分裂为六边形蜂窝状网格和三角形格点2套图案,这与Matlab模拟结果一致.(a)正方形板 (b)圆形板(c)六边形板(d)三角形板图9 经激光调制的成像图3.2 驻波波长测量使用正方形液膜,调节振源频率得到一系列共振,记录信号发生器频率f,并从对应驻波图案中测出波长λ(定标系数为0.087 3 mm/pixel). 自来水和肥皂水的测量结果见表1.表1 水波的频率与波长f自/Hzλ自/mmf肥/Hzλ肥/mm239.270217.724258.663296.241 307.552355.658 337.233385.037 366.772414.971396.455444.646 435.917484.401 465.619514.064 495.339553.950554.901603.762 624.455633.569 664.308714.134753.901823.598自来水和肥皂水的色散关系曲线见图10. 由于液膜深度在3 mm左右,测量区间的波数满足tanh (kh)≈1,按照拟合测量数据,得到自来水和肥皂水的表面张力系数分别为5.00×10-2N/m和2.55×10-2N/m. 该结果与用拉脱法测得的结果基本一致.用ω2-gk与k做双对数图,拟合结果见图11. 自来水数据的斜率为3.03,肥皂水数据的斜率为3.38,斜率与理论值基本符合. 自来水的数据与理论更符合,这可能是肥皂水表面张力系数小,低频时容易引起非线性效应造成的.图10 自来水和肥皂水的色散曲线图11 ln (ω2-gk)与lnk的关系4 结束语直接观察铺在透明亚克力板上的水膜(相当于1颗扁平的大水滴)上的驻波,通过光学方法将驻波图样投影在屏幕上,可以演示不同的驻波图案,并且可以测量毛细波的色散关系. 承液板容易加工成不同的形状与尺寸,方便进行设计性实验,探究液膜边界对波动的影响. 通过光源调制,可显示不同时刻的驻波图样. 基于图像的测量系统,操作简便而且结果比较准确. 与克拉尼图形实验相互参照,该装置可用来演示二维驻波,也可以作为液体表面张力系数的测量装置,引入大学物理实验教学.【相关文献】[1] 丁力,娄昊楠,吕景林,等. 水波频闪法测量液体表面张力系数[J]. 大学物理实验,2005,18(3):8-10.[2] 杨泓,谯楷耀,阮承宗. 水波色散关系测量方法探讨[J]. 大学物理,2016,35(10):52-55.[3] Behroozi F, Perkins A . Direct measurement of the dispersion relation of capillary waves by laser interferometry [J]. American Journal of Physics, 2006,74(1):957-961.[4] Ströbel B. Demonstrati on and study of the dispersion of water waves with a computer-controlled ripple tank [J]. American Journal of Physics, 2011,79(6):581-590.[5] 钱小匀,张进治,安艳伟,等. 基于光学投影的智能化水波演示仪[J]. 物理实验,2016,36(12):12-15.[6] 欧阳丽婷,杨旭东,刘敏蔷,等. 水面驻波演示仪[J]. 物理实验,2016,36(2):26-28.[7] 吴秀芳. 水面波的几何结构及色散关系[J]. 大学物理,1989,8(11):10-14.。
大学物理课后习题答案(第五章) 北京邮电大学出版社

习题五5-1 振动和波动有什么区别和联系?平面简谐波动方程和简谐振动方程有什么不同?又有什么联系?振动曲线和波形曲线有什么不同?解: (1)振动是指一个孤立的系统(也可是介质中的一个质元)在某固定平衡位置附近所做的往复运动,系统离开平衡位置的位移是时间的周期性函数,即可表示为)(t f y =;波动是振动在连续介质中的传播过程,此时介质中所有质元都在各自的平衡位置附近作振动,因此介质中任一质元离开平衡位置的位移既是坐标位置x ,又是时间t 的函数,即),(t x f y =. (2)在谐振动方程)(t f y =中只有一个独立的变量时间t ,它描述的是介质中一个质元偏离平衡位置的位移随时间变化的规律;平面谐波方程),(t x f y =中有两个独立变量,即坐标位置x 和时间t ,它描述的是介质中所有质元偏离平衡位置的位移随坐标和时间变化的规律.当谐波方程)(cos u xt A y -=ω中的坐标位置给定后,即可得到该点的振动方程,而波源持续不断地振动又是产生波动的必要条件之一.(3)振动曲线)(t f y =描述的是一个质点的位移随时间变化的规律,因此,其纵轴为y ,横轴为t ;波动曲线),(t x f y =描述的是介质中所有质元的位移随位置,随时间变化的规律,其纵轴为y ,横轴为x .每一幅图只能给出某一时刻质元的位移随坐标位置x 变化的规律,即只能给出某一时刻的波形图,不同时刻的波动曲线就是不同时刻的波形图.5-2 波动方程y =A cos [ω(u x t -)+0ϕ]中的u x表示什么?如果改写为y =A cos (0ϕωω+-u x t ),u x ω又是什么意思?如果t 和x 均增加,但相应的[ω(u x t -)+0ϕ]的值不变,由此能从波动方程说明什么?解: 波动方程中的u x /表示了介质中坐标位置为x 的质元的振动落后于原点的时间;u x ω则表示x 处质元比原点落后的振动位相;设t 时刻的波动方程为)cos(0φωω+-=u xt A y t则t t ∆+时刻的波动方程为])()(cos[0φωω+∆+-∆+=∆+u x x t t A y t t其表示在时刻t ,位置x 处的振动状态,经过t ∆后传播到t u x ∆+处.所以在)(u x t ωω-中,当t ,x 均增加时,)(u x t ωω-的值不会变化,而这正好说明了经过时间t ∆,波形即向前传播了t u x ∆=∆的距离,说明)cos(0φωω+-=u xt A y 描述的是一列行进中的波,故谓之行波方程.5-3 波在介质中传播时,为什么介质元的动能和势能具有相同的位相,而弹簧振子的动能和势能却没有这样的特点?解: 我们在讨论波动能量时,实际上讨论的是介质中某个小体积元dV 内所有质元的能量.波动动能当然是指质元振动动能,其与振动速度平方成正比,波动势能则是指介质的形变势能.形变势能由介质的相对形变量(即应变量)决定.如果取波动方程为),(t x f y =,则相对形变量(即应变量)为x y ∂∂/.波动势能则是与x y ∂∂/的平方成正比.由波动曲线图(题5-3图)可知,在波峰,波谷处,波动动能有极小(此处振动速度为零),而在该处的应变也为极小(该处0/=∂∂x y ),所以在波峰,波谷处波动势能也为极小;在平衡位置处波动动能为极大(该处振动速度的极大),而在该处的应变也是最大(该处是曲线的拐点),当然波动势能也为最大.这就说明了在介质中波动动能与波动势能是同步变化的,即具有相同的量值.题5-3图对于一个孤立的谐振动系统,是一个孤立的保守系统,机械能守恒,即振子的动能与势能之和保持为一个常数,而动能与势能在不断地转换,所以动能和势能不可能同步变化. 5-4 波动方程中,坐标轴原点是否一定要选在波源处? t =0时刻是否一定是波源开始振动的时刻? 波动方程写成y =A cos ω(u xt -)时,波源一定在坐标原点处吗?在什么前提下波动方程才能写成这种形式?解: 由于坐标原点和开始计时时刻的选全完取是一种主观行为,所以在波动方程中,坐标原点不一定要选在波源处,同样,0=t 的时刻也不一定是波源开始振动的时刻;当波动方程写成)(cos u xt A y -=ω时,坐标原点也不一定是选在波源所在处的.因为在此处对于波源的含义已做了拓展,即在写波动方程时,我们可以把介质中某一已知点的振动视为波源,只要把振动方程为已知的点选为坐标原点,即可得题示的波动方程.5-5 在驻波的两相邻波节间的同一半波长上,描述各质点振动的什么物理量不同,什么物理量相同?解: 取驻波方程为vtx A y απλπcos 2cos 2=,则可知,在相邻两波节中的同一半波长上,描述各质点的振幅是不相同的,各质点的振幅是随位置按余弦规律变化的,即振幅变化规律可表示为xA λπ2cos2.而在这同一半波长上,各质点的振动位相则是相同的,即以相邻两波节的介质为一段,同一段介质内各质点都有相同的振动位相,而相邻两段介质内的质点振动位相则相反.5-6 波源向着观察者运动和观察者向波源运动都会产生频率增高的多普勒效应,这两种情况有何区别?解: 波源向着观察者运动时,波面将被挤压,波在介质中的波长,将被压缩变短,(如题5-6图所示),因而观察者在单位时间内接收到的完整数目(λ'/u )会增多,所以接收频率增高;而观察者向着波源运动时,波面形状不变,但观察者测到的波速增大,即B v u u +=',因而单位时间内通过观察者完整波的数目λu '也会增多,即接收频率也将增高.简单地说,前者是通过压缩波面(缩短波长)使频率增高,后者则是观察者的运动使得单位时间内通过的波面数增加而升高频率.题5-6 图多普勒效应5-7 一平面简谐波沿x 轴负向传播,波长λ=1.0 m ,原点处质点的振动频率为ν=2. 0 Hz ,振幅A =0.1m ,且在t =0时恰好通过平衡位置向y 轴负向运动,求此平面波的波动方程.解: 由题知0=t 时原点处质点的振动状态为0,000<=v y ,故知原点的振动初相为2π,取波动方程为])(2cos[0φλπ++=xT t A y 则有]2)12(2cos[1.0ππ++=x t y)224cos(1.0πππ++=x t m5-8 已知波源在原点的一列平面简谐波,波动方程为y =A cos(Cx Bt -),其中A ,B ,C为正值恒量.求:(1)波的振幅、波速、频率、周期与波长;(2)写出传播方向上距离波源为l 处一点的振动方程; (3)任一时刻,在波的传播方向上相距为d 的两点的位相差. 解: (1)已知平面简谐波的波动方程)cos(Cx Bt A y -=(0≥x )将上式与波动方程的标准形式)22cos(λππυxt A y -=比较,可知: 波振幅为A ,频率πυ2B =,波长C πλ2=,波速C Bu ==λυ, 波动周期B T πυ21==. (2)将l x =代入波动方程即可得到该点的振动方程)cos(Cl Bt A y -=(3)因任一时刻t 同一波线上两点之间的位相差为)(212x x -=∆λπφ将d x x =-12,及C πλ2=代入上式,即得Cd =∆φ.5-9 沿绳子传播的平面简谐波的波动方程为y =0.05cos(10x t ππ4-),式中x ,y 以米计,t 以秒计.求:(1)波的波速、频率和波长;(2)绳子上各质点振动时的最大速度和最大加速度; (3)求x =0.2m 处质点在t =1s 时的位相,它是原点在哪一时刻的位相?这一位相所代表的运动状态在t =1.25s 时刻到达哪一点? 解: (1)将题给方程与标准式)22cos(x t A y λππυ-=相比,得振幅05.0=A m ,频率5=υ1-s ,波长5.0=λm ,波速5.2==λυu 1s m -⋅.(2)绳上各点的最大振速,最大加速度分别为ππω5.005.010max =⨯==A v 1s m -⋅ 222max 505.0)10(ππω=⨯==A a 2s m -⋅(3)2.0=x m 处的振动比原点落后的时间为08.05.22.0==u x s故2.0=x m ,1=t s 时的位相就是原点(0=x ),在92.008.010=-=t s 时的位相,即 2.9=φπ.设这一位相所代表的运动状态在25.1=t s 时刻到达x 点,则825.0)0.125.1(5.22.0)(11=-+=-+=t t u x x m5-10 如题5-10图是沿x 轴传播的平面余弦波在t 时刻的波形曲线.(1)若波沿x 轴正向传播,该时刻O ,A ,B ,C 各点的振动位相是多少?(2)若波沿x 轴负向传播,上述各点的振动 位相又是多少?解: (1)波沿x 轴正向传播,则在t 时刻,有题5-10图对于O 点:∵0,0<=O O v y ,∴2πφ=O对于A 点:∵0,=+=A A v A y ,∴0=A φ 对于B 点:∵0,0>=B B v y ,∴2πφ-=B 对于C 点:∵0,0<=C Cv y ,∴23πφ-=C (取负值:表示C B A 、、点位相,应落后于O 点的位相)(2)波沿x 轴负向传播,则在t 时刻,有对于O 点:∵0,0>'='O O v y ,∴2πφ-='O对于A 点:∵0,='+='A A v A y ,∴0='A φ 对于B 点:∵0,0<'='B B v y ,∴2πφ=B 对于C 点:∵0,0>'='C C v y ,∴23πφ='C (此处取正值表示C B A 、、点位相超前于O 点的位相)5-11 一列平面余弦波沿x 轴正向传播,波速为5m ·s -1,波长为2m ,原点处质点的振动曲线如题5-11图所示. (1)写出波动方程;(2)作出t =0时的波形图及距离波源0.5m 处质点的振动曲线.解: (1)由题5-11(a)图知,1.0=A m ,且0=t 时,0,000>=v y ,∴230πφ=,又5.225===λυuHz ,则ππυω52==题5-11图(a)取 ])(cos[0φω+-=u xt A y ,则波动方程为)]235(5cos[1.0ππ+-=x t y m(2) 0=t 时的波形如题5-11(b)图题5-11图(b) 题5-11图(c)将5.0=x m 代入波动方程,得该点处的振动方程为)5cos(1.0)235.05.055cos(1.0πππππ+=+⨯-=t t y m如题5-11(c)图所示.5-12 如题5-12图所示,已知t =0时和t =0.5s 时的波形曲线分别为图中曲线(a)和(b) ,波沿x 轴正向传播,试根据图中绘出的条件求: (1)波动方程;(2)P 点的振动方程.解: (1)由题5-12图可知,1.0=A m ,4=λm ,又,0=t 时,0,000<=v y ,∴20πφ=,而25.01==∆∆=t x u 1s m -⋅,5.042===λυu Hz ,∴ππυω==2故波动方程为]2)2(cos[1.0ππ+-=x t y m(2)将1=P x m 代入上式,即得P 点振动方程为tt y ππππcos 1.0)]22cos[(1.0=+-=m题5-12图5-13 一列机械波沿x 轴正向传播,t =0时的波形如题5-13图所示,已知波速为10 m ·s -1,波长为2m ,求: (1)波动方程;(2) P 点的振动方程及振动曲线; (3) P 点的坐标;(4) P 点回到平衡位置所需的最短时间. 解: 由题5-13图可知1.0=A m ,0=t 时,0,200<=v A y ,∴30πφ=,由题知2=λm ,10=u 1s m -⋅,则5210===λυuHz∴ ππυω102==(1)波动方程为]3)10(10cos[.01ππ+-=x t y m题5-13图(2)由图知,0=t 时,0,2<-=P P v A y ,∴34πφ-=P (P 点的位相应落后于0点,故取负值)∴P 点振动方程为)3410cos(1.0ππ-=t y p (3)∵πππ34|3)10(100-=+-=t x t ∴解得67.135==x m (4)根据(2)的结果可作出旋转矢量图如题5-13图(a),则由P 点回到平衡位置应经历的位相角题5-13图(a)πππφ6523=+=∆∴所属最短时间为121106/5==∆=∆ππωφt s5-14 如题5-14图所示,有一平面简谐波在空间传播,已知P 点的振动方程为P y =A cos(0ϕω+t ).(1)分别就图中给出的两种坐标写出其波动方程; (2)写出距P 点距离为b 的Q 点的振动方程.解: (1)如题5-14图(a),则波动方程为])(cos[0φω+-+=u xu l t A y如图(b),则波动方程为题5-14图])(cos[0φω++=u xt A y(2) 如题5-14图(a),则Q 点的振动方程为 ])(cos[0φω+-=u bt A A Q如题5-14图(b),则Q 点的振动方程为])(cos[0φω++=u bt A A Q5-15 已知平面简谐波的波动方程为)24(cos x t A y +=π(SI).(1)写出t =4.2 s 时各波峰位置的坐标式,并求此时离原点最近一个波峰的位置,该波峰何时通过原点?(2)画出t =4.2 s 时的波形曲线. 解:(1)波峰位置坐标应满足ππk x t 2)24(=+解得 )4.8(-=k x m (,2,1,0±±=k …) 所以离原点最近的波峰位置为4.0-m . ∵u xt t t ωωππ+=+24 故知2=u 1s m -⋅,∴2.024.0=-='∆t s ,这就是说该波峰在2.0s 前通过原点,那么从计时时刻算起,则应是42.02.4=-s ,即该波峰是在4s 时通过原点的.题5-15图(2)∵2,4==u πω1s m -⋅,∴12===ωπλuuT m ,又0=x 处,2.4=t s 时,ππφ8.1642.40=⨯=A A y 8.02.44cos 0-=⨯=π又,当A y -=时,πφ17=x,则应有πππ1728.16=+x解得 1.0=x m ,故2.4=t s 时的波形图如题5-15图所示5-16 题5-16图中(a)表示t =0时刻的波形图,(b)表示原点(x =0)处质元的振动曲线,试求此波的波动方程,并画出x =2m 处质元的振动曲线. 解: 由题5-16(b)图所示振动曲线可知2=T s ,2.0=A m ,且0=t 时,0,000>=v y ,故知20πφ-=,再结合题5-16(a)图所示波动曲线可知,该列波沿x 轴负向传播,且4=λm ,若取])(2cos[0φλπ++=xT t A y题5-16图则波动方程为]2)42(2cos[2.0ππ-+=x t y5-17 一平面余弦波,沿直径为14cm 的圆柱形管传播,波的强度为18.0×10-3J ·m -2·s -1,频率为300 Hz ,波速为300m ·s -1,求 : (1)波的平均能量密度和最大能量密度?(2)两个相邻同相面之间有多少波的能量? 解: (1)∵ u w I =∴53106300100.18--⨯=⨯==u I w 3m J -⋅ 4max 102.12-⨯==w w 3m J -⋅(2)νπλπωud w d w V W 224141=== 7251024.9300300)14.0(41106--⨯=⨯⨯⨯⨯=πJ 5-18 如题5-18图所示,1S 和2S 为两相干波源,振幅均为1A ,相距4λ,1S 较2S 位相超前2π,求:(1) 1S 外侧各点的合振幅和强度; (2) 2S 外侧各点的合振幅和强度解:(1)在1S 外侧,距离1S 为1r 的点,1S 2S 传到该P 点引起的位相差为πλλππφ=⎥⎦⎤⎢⎣⎡+--=∆)4(2211r r0,0211===-=A I A A A(2)在2S 外侧.距离2S 为1r 的点,1S 2S 传到该点引起的位相差.)4(2222=-+-=∆r r λλππφ2121114,2A A I A A A A ===+=5-19 如题5-19图所示,设B 点发出的平面横波沿BP 方向传播,它在B 点的振动方程为t y π2cos 10231-⨯=;C 点发出的平面横波沿CP 方向传播,它在C 点的振动方程为)2cos(10232ππ+⨯=-t y ,本题中y 以m 计,t 以s 计.设BP =0.4m ,CP =0.5 m ,波速u =0.2m ·s -1,求:(1)两波传到P 点时的位相差;(2)当这两列波的振动方向相同时,P 处合振动的振幅;*(3)当这两列波的振动方向互相垂直时,P 处合振动的振幅.解: (1))(2)(12BP CP ---=∆λπϕφφ)(BP CP u --=ωπ 0)4.05.0(2.02=--=ππ题5-19图(2)P 点是相长干涉,且振动方向相同,所以321104-⨯=+=A A A P m(3)若两振动方向垂直,又两分振动位相差为0,这时合振动轨迹是通过Ⅱ,Ⅳ象限的直线,所以合振幅为33122211083.210222--⨯=⨯==+=A A A A m5-20 一平面简谐波沿x 轴正向传播,如题5-20图所示.已知振幅为A ,频率为ν波速为u . (1)若t =0时,原点O 处质元正好由平衡位置向位移正方向运动,写出此波的波动方程;(2)若从分界面反射的波的振幅与入射波振幅相等,试写出反射波的波动方程,并求x 轴上 因入射波与反射波干涉而静止的各点的位置.解: (1)∵0=t 时,0,000>=v y ,∴20πφ-=故波动方程为]2)(2cos[ππ--=u x t v A y m题5-20图(2)入射波传到反射面时的振动位相为(即将λ43=x 代入)2432πλλπ-⨯-,再考虑到波由波疏入射而在波密界面上反射,存在半波损失,所以反射波在界面处的位相为πππλλπ-=+-⨯-2432若仍以O 点为原点,则反射波在O 点处的位相为 ππλλπ25432-=-⨯-,因只考虑π2以内的位相角,∴反射波在O 点的位相为2π-,故反射波的波动方程为]2)(2cos[ππυ-+=u x t A y 反此时驻波方程为]2)(2cos[ππυ--=u x t A y ]2)(2cos[ππυ-++u x t A)22cos(2cos 2ππυπυ-=t u x A故波节位置为2)12(22πλππυ+==k x u x故4)12(λ+=k x (,2,1,0±±=k …)根据题意,k 只能取1,0,即λλ43,41=x 5-20 一驻波方程为y =0.02cos20x cos750t (SI),求:(1)形成此驻波的两列行波的振幅和波速;(2)相邻两波节间距离.解: (1)取驻波方程为t u x A y πυπυ2cos 2cos2=故知01.0202.0==A m 7502=πυ,则πυ2750=, 202=u πυ∴5.37202/7502202=⨯==πππυu 1s m -⋅ (2)∵314.01.020/2====πυπυυλu m 所以相邻两波节间距离 157.02==∆λx m5-22 在弦上传播的横波,它的波动方程为1y =0.1cos(13t +0.0079x ) (SI)试写出一个波动方程,使它表示的波能与这列已知的横波叠加形成驻波,并在x =0处为波 节.解: 为使合成驻波在0=x 处形成波节,则要反射波在0=x 处与入射波有π的位相差,故反射波的波动方程为)0079.013cos(1.02π--=x t y5-23 两列波在一根很长的细绳上传播,它们的波动方程分别为1y =0.06cos(t x ππ4-)(SI), 2y =0.06cos(t x ππ4+)(SI).(1)试证明绳子将作驻波式振动,并求波节、波腹的位置;(2)波腹处的振幅多大?x =1.2m 处振幅多大?解: (1)它们的合成波为)4cos(06.0)4cos(06.0t x x y ππππ++-= t x ππ4cos cos 12.0=出现了变量的分离,符合驻波方程特征,故绳子在作驻波振动.令ππk x =,则k x =,k=0,±1,±2…此即波腹的位置; 令2)12(ππ+=k x ,则21)12(+=k x ,,2,1,0±±=k …,此即波节的位置. (2)波腹处振幅最大,即为12.0m ;2.1=x m 处的振幅由下式决定,即 097.0)2.1cos(12.0=⨯=π驻A m5-24 汽车驶过车站时,车站上的观测者测得汽笛声频率由1200Hz 变到了1000 Hz ,设空气中声速为330m ·s -1,求汽车的速率.解: 设汽车的速度为s v ,汽车在驶近车站时,车站收到的频率为01υυs v u u -= 汽车驶离车站时,车站收到的频率为02υυs v u u +=联立以上两式,得3010012001000120030021211=+-⨯=+-=υυυυυu1s m -⋅ 5-25 两列火车分别以72km ·h -1和54 km ·h -1的速度相向而行,第一列火车发出一个600 Hz的汽笛声,若声速为340 m ·s -1,求第二列火车上的观测者听见该声音的频率在相遇前和相遇后分别是多少?解: 设鸣笛火车的车速为201=v 1s m -⋅,接收鸣笛的火车车速为152=v 1s m -⋅,则两者相遇前收到的频率为 66560020340153400121=⨯-+=-+=υυv u v u Hz两车相遇之后收到的频率为54160020340153400121=⨯+-=+-=υυv u v u Hz。
驻波——精选推荐

驻波驻波(standing wave)频率和振幅均相同、振动方向一致、传播方向相反的两列波叠加后形成的波。
波在介质中传播时其波形不断向前推进,故称行波;上述两列波叠加后波形并不向前推进,故称驻波。
例如,如图所示,一弦线的一端与音叉一臂相连,另一端经支点O并跨过滑轮后与一重物相连。
音叉振动后在弦线上产生一自左向右传播的行波,传到支点O 后发生反射,弦线中产生一自右向左传播的反射波,当弦长接近1/2波长的整数倍时。
两列波叠加后弦线上各点的位移为(设音叉振动规律为u=Acosωt)u(x,t)=2Asin(x)sin(ωt )=A(x)sin(ωt),弦线上每个固定的点均作简谐运动,但不同点的振幅不同,由x值决定。
振幅为零的点称为波节,振幅最大处称为波腹。
波节两侧的振动相位相反。
相邻两波节或波腹间的距离都是半个波长。
在行波中能量随波的传播而不断向前传递,其平均能流密度不为零;但驻波的平均能流密度等于零,能量只能在波节与波腹间来回运行。
测量两相邻波节间的距离就可测定波长。
各种乐器,包括弦乐器、管乐器和打击乐器,都是由于产生驻波而发声。
为得到最强的驻波,弦或管内空气柱的长度L必须等于半波长的整数倍,即,k为整数,λ为波长。
因而弦或管中能存在的驻波波长为,相应的振动频率为,υ为波速。
k=1时,,称为基频,除基频外,还可存在频率为kn1的倍频。
入射波(推进波)与反射波相互干扰而形成的波形不再推进(仅波腹上、下振动,波节不移动)的波浪,称驻波。
驻波多发生在海岸陡壁或直立式水工建筑物前面。
紧靠陡壁附近的海水面随时间虽作周期性升降,海水呈往复流动,但并不向前传播,水面基本上是水平的,这就是由于受岸壁的限制使入射波与反射波相互干扰而形成的。
波面随时间作周期性的升降,每隔半个波长就有一个波面升降幅度为最大的断面,称为波腹;当波面升降的幅度为0时的断面,称为波节。
相邻两波节间的水平距离仍为半个波长,因此驻波的波面包含一系列的波腹和波节,腹节相间,波腹处的波面的高低虽有周期性变化,但此断面的水平位置是固定的,波节的位置也是固定的。
驻波理解

音响与驻波
现在许多人在家庭装修时都会考虑购买音响,而音响技术 中有一个最难对付的祸害--驻波。下面我们来讨论一下音 响学中的驻波。 声音虽然是纵波,但它与横波一样同样存在驻波现象。波 节两边的质点在某一时刻涌向波节,使波节附近成为质点 密集区,半周期后,又向两边散开,使波节附近成为质点 稀疏区,相邻节点附近质点的密集和稀疏情况正好相反。 类比水波,对于声波,假设它在一个密闭的矩形房间里传 播。考虑两堵平行的墙壁,对于恒定的波源,特定频率的 波,某些恒定的点会成为波腹和波节。在波节的点就始终 听不到这一频率的声音,而在波腹的点声音频率特别高。 实际上,不管声源在什么地方,只要有二个平行平面存在, 声音最终都会在平行的二个面之间来回反射。所以,凡是 两个平行面间的距离是某些频率的半波长或半波长的整数 倍,那么,这些频率都是这个房间的驻波频率。这些频率 在空间的各点会表现出非常不同的性质。
右行波 左行波
合成后,弦上的运动为
y y1 y2 2 A cos(kx
合成后的波称为驻波
2 1
2
) cos( t
2 1
2
)
由图可以看出: 各点离平衡位置 的距离保持不变, 经过T/4,各点 位移改变符号。 于是,我们所见 的驻波与行波不 同,没有位相的 逐点不同和逐点 传播。
在无线电技术中,驻波有重要的 应用。 在发射过程中要使无线电波以尽 量大的功率传输。 只有阻抗完全匹配,才能达到最 大功率传输。这在高频更重要! 发射机、传输电缆(馈线)、天 线阻抗都关系到功率的传输。驻 波比就是表示馈线与天线匹配情 形。 不匹配时,发射机发射的电波将 有一部分反射回来,在馈线中产 生反射波,反射波到达发射机, 最终产生为热量消耗掉。接收时, 也会因为不匹配,造成接收信号 不好。
横波和纵波横波质元的振动方向与波动的传播方向垂直纵波

§16-2 平面简谐波 波动方程
简谐波:谐振动在弹性媒质中的 传播所构成的波
----波源和媒质中各质元 作同频率的谐振动
波动方程:描述波动沿波线传 播的解析表达式
一.平面简谐波的波动方程
设波源在原点O作谐振动
y 0 (t) A c ot s y
u
P
Ox
x
原点的振动状态传输到
x 处的 P点需时间 x / u
r1 P r2
y 1 A 1 co t s 2r 1 ( 1 )S 2 y 2 A 2 co t 2 sr 2 (2 )
P点的合振动为
yy1y2Acost ()
其中
A A 1 2A 2 22A 1A 2co 2 s1 (2r2 r1)
tgA A11cso in s1 1(( 2 2rr1 1)) A A2 2csion s22(( 22rr22))
y B 2 2c co2 o 2s(t(t s0 .0 [1 5 )) 0 ] 100
以B点y为坐2标c原o点2s的(t[波动x)方程为 ]
vB
d yB dt
4su in21 (t00)
100
vB
4
max
§16-3 波的能量 波的强度
媒质质点振动 波传播
媒质弹性形变
一.波的能量
动能
势能
9 23
x=9m时,其振动方程
y(t)610 2cost ()m
96
yt(=x 3)s时,6 波1 形 方2 0c 程 o2 s (x)m
波峰处有 cos2(3 x)118
3 18
2 x2k
3 18
得 x (1 2 3k )6k 0 , 1 , 2
----各波峰的位置坐标
驻波

y反B
t l A cos[ 2π( ) π] T
反射波的波动方程
t l (l x) y反 A cos[ 2π( ) π 2π ] T
t x t x y A cos(2π 21π 2π ) A cos 2π( ) T T
反
将l = 5 代入上式得
x x y y1 y2 A cos( t 2 π ) A cos( t 2 π )
驻波方程 y 2 A cos(
2π
x)cost
三、驻波的特征 讨论: 驻波方程 y 2 A cos 2 π 1.振幅分布 振幅: 2 A cos 2π
x
o
cos t
面反射,设反射处有半波损失,反射波的振幅近似 等于入射波振幅。求: (1)反射波的波动方程; (2)驻波方程; (3)在原点O到反射点B之间各个波节和波腹的 位置坐标。 入射波 P B x x O l 反射波
解:(1)入射波在B点的振动方程
y 入B
t l A cos 2π( ) T
反射波在B点的振动方程
波腹处
sin
2π
x 1
2π
π x (2k 1) , 2
(k 0, 1, 2, , 9)
x ( 2k 1)
4
1 3 5 7 9 11 13 15 17 19 x , , , , , , , , , 4 4 4 4 4 4 4 4 4 4
§16-5
驻 波
驻波:两列振幅相同,在同一直线上沿相反方向 传播的相干波,叠加形成的特殊干涉现象。 一、驻波形成
B
A
波 节 波 腹
10-5(新)驻波
驻波
例 已知弦线上入射波在 x l 处发生反射,反射 点为自由端,若波在传播和反射过程中振幅不变,入射 波波函数为 y1 A cos(t 2π x ) ,求反射波波函数. 解2:入射波和反射波在 B 点振动同相位(自由端)
y1 A cos(t 2π x )
反射波在O点振动与入射波 在O点振动相位落后
l
码子
1 基频 n 1 1 2l
谐频
T
262 Hz
第十章 波动
n T n 1 n 2l
23
物理学
第五版
10-5 驻波 例 如图一向右传播的简谐波在 t 时刻的波形BC 为波密媒质的反射面,则反射波在 t 时刻的波形图为:
A
o A
练习
y
uБайду номын сангаас
B
p
答:(B)
A
A
y
u
T 0.05s
26
第十章 波动
物理学
第五版
10-5 例 已知: y 0.040sin 5 π x cos40 π t
驻波
3)求在 0 t 0.050 s 内的什么时刻,线上所有点横 向速度为零? 解 令 cos 40 π t 1
1,2) 则 40 π t k π (k 0,
4
y
4
波腹
3 4
2
5 4
x
第十章 波动
物理学
第五版
10-5 驻波 2)相邻两波节之间质点振动同相位,任一波节 两侧振动相位相反,在波节处产生 的相位跃变 . (与行波不同,无相位的传播).
π
x y 2 A cos 2π cos 2π t 例 x 为波节 4
《驻波多普勒效应》PPT课件

振源
软 绳
当 形 成 驻 波 时
自由端反射 总出现波腹
2. 半波损失
固定端反射 总出现波节
y
波疏介质 波密介质
入射波
驻波
O
x
反射波
2
由波疏介质向波密介质入射并
反射时, 在界面处, 反射波的振动 相位总是与入射波的振动相位相 反, 即差了 ; 若形成驻波, 界面处 一定出现波节.
相位差, 相当于波程差了λ/2,称 为“半波损失”.
整波形的数目.
uR u uS 0
uS
Su
波源
uR
观察者
R
(1) 观察者接近波源 uR 0
S
O
uR
6.7.1 波源静止, 观察者以速度 uR 相对于介质运动
R
u
uR u
s
uR u uS 0
(1) 观察者接近波源
uR 0
S
观察者在单位时间
内接收到的波形数:
R
u
uR
u uR
u /W
u
uR u
请观察在反射点入射波和反射波两振动的相位关系
波 疏 介 质
u
较 小
波 密 介 质
u
较 大
当波从波疏介质垂直入射到波密介质,被反射到 波疏介质时形成波节. 入射波与反射波在此处的相位
π 时时相反, 即反射波在分界处产生相位跃变 ,相当
于出现了半个波长的波程差,称半波损失.
请观察在反射点入射波和反射波两振动的相位关系
2
本征频率
νn
n
u 2L
n 1,2,3,
2. 一端固定一端自由的弦驻波
L (n 1 ) n , n 1,2,
驻波的概述

即
y1
Acos(2 t
2
x)
y2
A c os(2 t
2
x)
两波相遇,其合成波为
y
y1
y2
A c os(2 t
2
x)
A c os(2 t
2
x)
2Acos 2 x cos2 t (x) (t)
变量分离 2
2、驻波特征
① 振幅分布的特点
➢波线上各点都在自己平衡位置附近作周期为T的谐振动,各
x
0
Dy2
A c os2
t T
x
解:反射波的传播方向与入射波方向相反,反射点为波节, 说明有半波损失。
故应选 (D)
12
例 5-10 某时刻驻波波形曲线如图所示,则a,b两点位相差是
(A)
a
(B) 2
A
b
(C)5 4
o
(D) 0
A
2
9
8
解:由驻波位相分布特点知,同一波节两侧各点的位相相反。
5
/4
(x) >0 (x) < 0 3/4
5/4
相邻两个波节之间的所有各点振动位相相同,同步振动。任 一波节两侧的点,振动位相正好相反,相差π ,
──即驻波干涉中,介质各点的振动位相分段相同,相 邻两段位相相反。
6
③、驻波能量分布特点:
y(t t, x x) 2Acos2 (x x) cos2 (t t) y(t, x)
驻波的概述
一、驻波现象
在同一介质中,两列振幅相同的相干平面简谐波,在同一 直线上沿相反方向传播时叠加形成的波,称为驻波。
P
A
B
m
绳上的驻波
16_07_波的叠加原理 波的干涉 驻波

相邻两波腹的距离: xk 1 xk 振动的相位关系
2
相邻两节点之间的各点为一段,同一段上各质点振动 的相一致,相邻两段上各点振动的相相反。如图 XCH004_038 所示。 驻波的能量:形成驻波时,没有振动状态和能量的定向传播
1 A2 2u 2 1 2 2 —— 负向波的能流密度: I 2 ( u ) A u 2
2
x y1 A cos[2 ( t ) 1 ] y A cos[2 ( t x ) ] 2 2
合成波 y y1 y2 A cos[2 ( t
x
x ) 1 ] A cos[2 ( t ) 2 ]
t x ) ,在 x 0 处发生反射,反射点为节点。求: T
t x ) ] T
t x t x ) A cos[2 ( ) ] T T x t y 2 A sin 2 sin 2 T x 3) 波腹位置: 2 (2k 1) —— x (2k 1) 2 4 y A cos 2 ( x (2n 1)
4
—— 驻波只在-X 空间形成
波节位置: 2
x
k , x k
2
—— x n
2
REVISED TIME: 09-10-7
-4-
CREATED BY XCH
普通物理学_程守洙_第十六章 机械波和电磁波_20090921
4 行波的叠加和群速度 不同频率的简谐波叠加后,合成波不再是简谐波 —— 复波 图 XCH004_149 为两列频率分别为 1 and
REVISED TIME: 09-10-7
16--6驻波

解释: 解释: C a a
v F
u
C
v F
C’ v
结论; v b质点 要带动 向上运 结论; 质点b要带动 要带动a向上运 v F' 作为反射波的波
动b却受一反作用力 F' 却受一反作用力
F'
源C’点的位移总 点的位移总 C’给C一作用力 不 是与入射波在C’ 一作用力,C’不 是与入射波在C 给 一作用力 而给C一反作用力 动,而给 一反作用力 v 点的位移反向。 点的位移反向。 点产生一 F' ,使C’点产生一 --半波反射。 --半波反射 半波反射。 向下的反向位移。 向下的反向位移。
2
O1m+mP=8 λ,O1P=3 λ,求(1)两列波分别在P点引起 的振动的振动方程;(2)P点的合振幅(设介质无吸 收)
2.一平面简谐波沿x轴正向传播,如图所示,振幅为 A,频率为ν,传播速度为v, (1)t=0时,在原点O处的质元由平衡位置向x轴正方向运 动,试写出此波的波函数; (2)若经分界面反射的波的振幅和入射波的振幅相等, 试写出反射波的波函数,并求在x轴上因入射波和反射 波叠加而静止的各点的位置。
>0
λ π x 3π ≤ 2π ≤ 2 λ 2
2Acos 2π
x
λ
<0
节点两侧质点反相
总之:相邻两节点间的质点同相, 总之:相邻两节点间的质点同相,节点两侧质 点反相。 点反相。 纵驻波: 纵驻波: X 节点 3)驻波的能量 Y X 节点
驻波中的能流密度为零, 驻波中的能流密度为零,实际上是系统的一 种稳定的振动状态。 种稳定的振动状态。
1.0 0.5 0 1.0 0.5 0 1.0 0.5 0 1.0 0.5 0 0 1000
电磁波衰减

[吸收系数]absorption coefficient 又称“衰减系数”当电磁波进入岩石中时,由于涡流的热能损耗,将使电磁波的强度随进入距离的增加而衰减,这种现象又称为岩石对电磁波的吸收作用。
吸收或衰减系数β的大小和电磁波角频率ω、岩石导电率σ、岩石导磁率μ、岩石介电系数ε有关,1)1(2222-+=δωσμεωβ。
在导体中则简化为:2ωμσβ=。
第十六章机械波和电磁波振动状态的传播就是波动,简称波.激发波动的振动系统称为波源16-1机械波的产生和传播1. 机械波产生的条件(1)要有作机械振动的物体,亦即波源.(2)要有能够传播这种振动的介质波源处质点的振动通过弹性介质中的弹性力,将振动传播开去,从而形成机械波。
波动(或行波)是振动状态的传播,是能量的传播,而不是质点的传播。
◆ 质点的振动方向和波的传播方向相互垂直,这种波称为横波.◆ 质点的振动方向和波的传播方向相互平行,这种波称为纵波.2.波阵面和波射线● 在波动过程中,振动相位相同的点连成的面称为波阵面(wave surface)● 波面中最前面的那个波面称为波前(wave front)● 波的传播方向称为波线(wave line)或波射线波面波线平面波球面波3. 波的传播速度由媒质的性质决定与波源情况无关● 液体和气体中纵波传播速度B-介质体变弹性模量ρ-介质密度●在固体中G-介质切变模量Y-介质杨氏模量4.波长和频率● 一个完整波的长度,称为波长.● 波传过一个波长的时间,叫作波的周期● 周期的倒数称为频率.振动曲线波形曲线图形研究对象某质点位移随时间变化规律某时刻,波线上各质点位移随位置变化规律物理意义由振动曲线可知周期T. 振幅A 初相φ0某时刻方向参看下一时刻由波形曲线可知该时刻各质点位移,波长λ,振幅 A只有 t=0 时刻波形才能提供初相某质点方向参看前一质点特征对确定质点曲线形状一定曲线形状随 t 向前平移16-2 平面简谐波波动方程● 前进中的波动,称为行波.● 描述介质中各质点的位移随时间变化的数学函数式称为行波的波动表式(或波动方程)设坐标原点的振动为:O 点运动传到 p 点需用时相位落后所以 p点的运动方程:1.平面简谐波的波动表式定义 k 为角波数又因此下述表达式等价:为波的相位● 波在某点的相位反映该点媒质的“运动状态”,所以简谐波的传播也是媒质振动相位的传播。
EMI测试仪器简述课件
天线
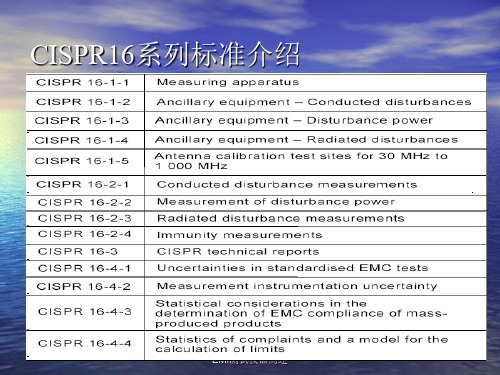
4.天线的增益 天线增益是用来衡量天线朝一个特定方向收发信号的能力.一般来说, 增益的提高主要依靠减小垂直面向辐射的波瓣宽度,而在水平面上保 持全向的辐射性能。表征天线增益的参数有dBd和dBi。dBi是相对于点 源天线的增益,在各方向的辐射是均匀的;dBd相对于对称阵子天线的 增益dBi=dBd+2.15。相同的条件下,增益越高,电波传播的距离越远。
功率 5.CISPR 16-1-4:无线电骚扰和抗扰度测量设备 辅助设备 辐射
骚扰
EMI测试仪器简述
EMI测试接收机
1.参考标准:CISPR16-1-1:2006+A1:2006+A2:2007 2.频率范围:9KHz-18GHz(Band A:9KHz-150KHz, Band B:150KHz-30MHz,
2.1.50ohm/50uH+5ohm V型AMN Freq. Range: 9KHz-150KHz
2.2. 50ohm/50uH V型AMN Freq. Range: 150KHz-30MHz
2.3. 50ohm/5uH+1ohm V型AMN Freq. Range: 150KHz-100MHz
2.4. 150ohm V型AMN Freq. Range: 150KHz-30MHz
2.5. 150ohm △型AMN Freq. Range: 150KHz-30MHz
EMI测试仪器简述
人工电源网络AMN
2.输出阻抗:50ohm 3.当输出阻抗为50ohm时,RF Att.=10dB,VSWR<=1.2-1dB 4.阻抗的模和相角 5.隔离 6.电流负载能力和串联电压降
EMI测试仪器简述
者脉冲调制骚扰测量。
驻波精品文档

实验结果分析:通 过波形图分析驻波 的特点和影响因素
实验步骤
准备实验器材: 包括弦线、振 动测量仪器、 信号发生器等
安装弦线:将 弦线固定在两 个端点上,确
保弦线绷紧
信号发生器连 接:将信号发 生器连接到弦 线上,以产生
振动信号
振动测量:使 用振动测量仪 器测量弦线的 振动幅度和频
率
数据记录与分 析:记录实验 数据,并进行 分析,以得出
弦的振动与琴弓 的摩擦产生音乐
不同弦乐器利用 不同长度的弦产 生不同音调
电磁波的传播
无线通信:利用驻波实现信号传输 雷达系统:通过驻波进行目标探测和定位 卫星通信:利用驻波实现地球与卫星之间的信号传输 电磁波的传播方式:驻波是其中的一种重要形式,具有特定的传播特性
地震波传播
地震波传播原理
地震波传播的衰减规律
驻波
汇报人:XX
目录
01 02 03 04 05
驻驻驻驻驻 波波波波波 的的的的的 形特应实未 成点用验来
研发 究展
01
驻波的形成
波的干涉现象
波的干涉定义:两列或两 列以上的波在空间相遇时 发生叠加,形成新的波动 现象。
形成条件:频率相同、振 动方向相同、相位差恒定。
干涉现象:在波的干涉区 域内,某些点的振动加强 ,某些点的振动减弱,形 成稳定的强弱分布。
输和存储方式。
在特定频率下产生共振
驻波的特点之一是在 特定频率下产生共振。
驻波的能量在空间中 分布均匀,不会向外
传播。
驻波的振幅和相位在空 间中保持不变,只在特
定频率下产生共振。
驻波的频率与产生它 的振源的频率相同。
03
驻波的应用
ห้องสมุดไป่ตู้
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2 2 2π 2 dEp 2dVA sin x cos t
x) sin 2 t
波节处动能始终为0
16.6 驻波
当波节点间质点振幅最大时: y A B
A O -A A O -A A O -A A O -A
A O -A
B
P
C
P
P
(A)
(B) P ( D)
P (C)
16.6 驻波
例7.6 有一平面简谐波
y入
向右传播,在距坐标原点O为l=5λ的B点被垂直界面反射, 设反射处有半波损失,反射波的振幅近似等于入射波振 幅。求: 入射波 P B (1)反射波波动方程 X x O l (2)驻波方程 反射波 (3)在原点O到反射点B之间各个波节和波腹的坐标。 解(1)入射波在B点的振动方程
16.6 驻波
16.6.4 弦线上的驻波与简正模式
在两端拉紧、绳长为L 的弦上的波经两端 反射后在弦上形成驻波,两端点均为波节。
n 驻波波长必须满足条件 l n , n 1,2,3,... 2 u 2l ——不连续 n n n
n
2l
这些频率称为弦振动的本征频率,对应的 振动方式称为简正模式。 最低的频率称为基频,其它整倍数频率为谐频。
2u
在右端即x=l/2处,
l y 2 A cos[ (t ) 2 ] A cos( t ) 2u l 2 2u
y2=Acos ( t + )
16.6 驻波
y y1 y2
x l y 1 A cos[ (t )] u 2u x l y2 A cos[ (t ) ] u 2u
dEk 2dVA cos (
2 2 2
2π
1 y 2 2 π 2 2 2 dEp EdV ( ) 2dVA sin x cos2 t 2 x
x) sin t
2
16.6 驻波
dEk 2dVA cos (
2 2 2
2π
(1) cos t = ±1 各质点的位移达到最大,dEk为零, 势能 dEp 不为零。波节处势能最大;在波腹处势 能最小。势能集中在波节附近。
演示程序:弦线上的驻波
16.6 驻波
两端固定的弦振 动的简正模式
一端固定一端自由 的弦振动的简正模式
ln
n
2
n 1,2,
l
1 n l (n ) n 1,2, 2 2
1
2
l
1
4
2 2 l 2
33 l 2
32 l 4 53 l 4
16.6 驻波
笛中的驻波
2π y2 A cos( t x)
2π x) A cos( t 2π x)
x)
A cos( t
2 A cos
2π
x cos t
16.6 驻波
演示程序:驻波
y 2 A cos
2π
x cos t
O
16.6 驻波
16.5.2 驻波的特征 2π y 2 A cos x cos t
小 结
波腹处质点的振幅最大;波节处质点始终静止。
在波节两侧质点的振动相位相反,振动的速度方 向相反;在相临两波节之间质点的振动相位相同, 振动的速度方向相同。 驻波中能量没有向前传播。
2l 三、弦线上的驻波与简正模式 n n
16.6 驻波
例:图中画出一向右传播的简谐波 在t时刻的波形图,BC为波密介质 的反射面,波由P点反射,则反射 波在t时刻的波形图为:
t x A cos 2( ) T
y入B
t l A cos 2( ) T
16.6 驻波
y入B
y反B
t l A cos 2( ) T
t l A cos[ 2( ) ] T
反射波在B点的振动方程
反射波的表达式
t l (l x) y反 A cos[ 2( ) 2 ] T t x y反 A cos( 2 21 2 ) T t x A cos 2( ) T
(2) 驻波的表达式为
t x t x y y入 y反 A cos 2π( ) A cos 2π( ) T T 2π 2π 2 A sin x sin t T
16.6 驻波
(3) 驻波波节 2π sin x0
2π
x kπ
点O 到点B 之间的波节
k x 2
2π
反射波的表达式
(l x)
t l (l x) y反 A cos 2π( ) π 2π T
16.6 驻波
反射波的表达式
t x 2l y反 A cos 2π( ) π T
l=5
t x y反 A cos[ 2π( ) 21π] T t x y反 A cos 2π( ) T
x y1 A cos[ (t ) 1 ] u
设左行波的波动表达式(以绳的中心为坐标原点)
x y2 A cos[ (t ) 2 ] u
16.6 驻波
l 绳的中心为坐标原点,在左端 x 2 y1 =Acos t
l y1 A cos[ (t ) 1 ] A cos t 2u l 1
L (2n 1)
n
4
n=1 n=2
2L n 2n 1 u u n (2n 1) n 4L
基频: 第一谐频
n=3
n=4
n 1, 2,3.
Second harmonics
u 1 4L
3u 2 4L
5u 3 4L
16.6 驻波
一、驻波的形成 沿x 轴正、反两方向传播的两列简谐波,如 果它们的振动频率和振幅都相同,初相差恒定, 就会叠加形成驻波 。 二、驻波的特征
势能曲线 X
驻波的能量在相邻的波腹和波节间往复变化, 在相邻的波节间发生动能和势能间的转换,动能 主要集中在波腹,势能主要集中在波节。.
驻波中能量没有向前传播 驻波是媒质的一种特殊运动状态,它是稳定态
演示程序:驻波的能量
16.6 驻波
16.5.3 半波损失
Z = u 媒质的特性阻抗 波密媒质: Z 值较大 波疏媒质: Z 值较小
xk
2
,
k 0,1,2,3,...
x (2k 1) , 4
k 0,1,2,3,...
相邻波腹(节)间距
2 相邻波腹和波节间距 4
演示程序:驻波的波腹和波节
16.6 驻波
二、驻波的相位
y 2 A cos
2π
在波节x = /4两侧
x cos t
左侧:/4 x /4 2 A cos
2π
2π
x0
x0
右侧:/4 x 3/4
2 A cos
在波节两侧,质点的振动相位相反,振动 的速度方向相反; ——在波节处产生的相位跃变 在相临两波节之间,质点的振动相位相同, 振动的速度方向相同。
演示程序 :驻波的相位
16.6 驻波
16.6 驻波
16.5 驻波
16.5.1 驻波的形成 16.5.2 驻波的特征 16.5.3 半波损失 16.5.4 弦线上的驻波与简正模式
16.6 驻波
当海浪从悬崖或码头反射的时候,能看到它与 入射波叠加后形成一个固定的浪头,这就是驻波
16.6 驻波
16.5.1 驻波的形成
驻波的形成 沿x 轴正、反两方向传播的两列简谐波,如果它 们的振动频率和振幅都相同,初相差恒定,就会叠加 形成驻波
16.6 驻波
(2)驻波的表达式为
y y入 y反
t x t x A cos 2( ) A cos 2( ) T T 2 2 2 A sin x sin t T 2 (3)波节处 sin x0 2 x k, (k 0,1,2, ,10) k x 2
选择题. 某时刻驻波波形曲线如图所示,则a,b两 点处振动的相位差是
√
A. π
B. π/ 2
C. 0
D. 无法确定
y
o
a
b
x
16.6 驻波
三、驻波的能量
体积元dV 的振动动能和弹性势能
1 1 y 2 2 dEk (dm) v ( dV )( ) 2 t 2 1 y 2 1 2 y 2 dEp EdV ( ) dVu ( ) 2 x 2 x 2π y 2 A cos x cos t
2π
2π
16.6 驻波
例题* 两人各执长为l 的绳的一端,以相同的角 频率和振幅在绳上激起振动,右端的人的振动比 左端的人的振动相位超前,试以绳的中心为坐标 原点描写合成驻波。由于绳很长,可不考虑反射。 绳上的波速设为u 。 解 设左端的振动为y1 =Acos t,则右端的振动 为 y2=Acos ( t + )。 设右行波的波动表达式(以绳的中心为坐标原点)
16.6 驻波
波疏
波密媒质:反射点出现波节
u1 u2
1 2
1u1 2u 2
2
即在反射点反射波的相位有 突变
——半波损失
16.6 驻波
波密
波疏媒质: 反射点出现波腹
u1
u2
