第3章佳逼近多项式
第3章数值分析---最佳平方逼近

它可表示为
Tn ( x) cos( n arccos x),
x 1.
(2.10)
若令 x cos , 则 Tn ( x) cos n , 0 .
7
3.3.1
最佳平方逼近及其计算
对 f ( x) C[a, b] 及 C[a, b] 中的一个子集
span{0 ( x), 1 ( x), , n ( x)}
0
(1 x 2 )dx 0.426d1 0.934d 0 0.0026.
0
1
最大误差 ( x)
max
0 x 1
* 1 x 2 S1 ( x) 0.066.
14
3.3.2
用正交函数族作最佳平方逼近
设 f ( x) C[a, b], span{0 ( x), 1 ( x), , n ( x)},
就是在区间 [ , ] 上的正交函数族.
5
勒让德多项式 P59-61
P ,P 利用上述递推公式就可推出 0 ( x) 1 1 ( x) x,
2 P ( x ) ( 3 x 1) / 2, 2
3 P ( x ) ( 5 x 3 x) / 2, 3
4 P 30 x 2 3) / 8, 4 ( x) (35 x
det G(0 , 1 ,, n ) 0 ( P56)
* 于是方程组(3.3)有唯一解 ak ak
(k 0,1, , n),
* * S * ( x) a0 0 ( x ) an n ( x).
10
若取 k ( x) x k , ( x) 1, f ( x) C[0, 1], 则要在 H n
计算方法最佳一致逼近多项式切比雪夫多项式ppt课件

0,1,2,… , n)
轮流取得最大值1和最小值 1,{xk }称为交错点组。
- 1 x4
x 3
x2 0
x 1
x0 1
证: 将xk
cos
kπ n
,
(k
1,2,… , n)
代入Tn(x)的表达式,得到
Tn(x)
cos[narccos(cos
kπ )] n
cos[kπ]
(1)k
1
T2(x) T1(x)
多项式,且 max | f(x)
-1 x 1
Ln(x)
|
1 2n(n 1)!
||
f (n 1) (x)
||
证明:
max
-1 x 1
|
f(x)
Ln(x)
|
(n
1 1)!
||
f(n1)(x)
||||
(x
x0 )(x
x1) … (x
xn)
||
(n
1 1)!
||
f (n 1) (x)
||||
1 2n
xn )
|
要使 max 1 x 1
|
(x
x0 )(x
x1) … (x
xn )
|
取极小值, 只需令:
(x x0 )(x x1) … (x xn)
1 2n
Tn1(x),
最佳一致 逼近0的 多项式
而上式成立的充分必要条件是x0, x1,…xn是切比雪夫 多项式的0点。
将Lagrange插值多项式Ln(x)的节点取为Tn1(x) 的0点 :
cos[(2k
1)π] 2
0 (k
1,2, … , n)
图为T11(x)的零点,一共有11个
计算方法最佳一致逼近多项式切比雪夫多项式

路漫漫其修远兮, 吾将上下而求索
2020年4月11日星期六
内容
1. 函数逼近的基本概念 2. 切比雪夫多项式 3. 最佳一致逼近多项式 4. 切比雪夫多项式在函数逼近中的应用 5. 利用切比雪夫多项式的0点构造最佳逼近多
项式的例子
路漫漫其修远兮, 吾将上下而求索
y
y=L (x)
路漫漫其修远兮, 吾将上下而求索
一致逼近的几何意义
x Home
切比雪夫多项式
路漫漫其修远兮, 吾将上下而求索
切比雪夫(Chebyshev)多项式
• 切比雪夫多项式在逼近理论中有重要的应用 • 。切比雪夫多项式的0点可以用于构造具有最佳
一致逼近性质的插值多项式。
切比雪夫多项式的(简单)定义:
三、切比雪夫多项式在函数逼近中的应用
希望构造最高次幂xn 系数为1 的多项式:
路漫漫其修远兮, 吾将上下而求索
…
三、切比雪夫多项式在函数逼近中的应用
证明比较复杂,省略。
路漫漫其修远兮, 吾将上下而求索
这个定理的 结论非常重要
怎样才能使得拉格朗日插值多项式成为最佳逼近 ?
…
偏差估计
路漫漫其修远兮, 吾将上下而求索
吾将上下而求索
(5)切比雪夫多项式的极值点 …
路漫漫其修远兮, 吾将上下而求索
…
1
T2(x )
T1(x
)
-1
1
T3(x ) 路漫漫其修远兮,
吾将上下而求索
T4(x )
-1
T3(x)有3个0值点,4个极值点
总结: Tn(x)具有很好的性质。
y
x
Tn(x)是n阶多项式,具有n个0点,n+1个极值点;有 界[-1, 1]; T1(x), T3(x),…只含x的奇次项,是奇函数
最佳一致逼近多项式3.3

定理说明任意连续函数都可以用多项式来近似 3.3.1 基本概念及其理论
Bn ( f , x) =
f ( x) −
* pn ( x)
∞
=
max a≤ x≤b
f
n k =0* ( x ) − p n ( x ) n= kmin f n − k ( x) )− p k ( x ) = k xp n ((x1∈ Pn x )
f ( x) − pn ( x)
pn(x) 在[a,b]上的偏差。 为 f (x) 与 是点到集合的距离
p n ∈Pn pn ∈P a ≤ x ≤b
E n = inf {∆( f , pn )} = inf max f ( x ) − pn ( x )
称为f (x)在 [a, b]上与 Pn 的偏差。 定义2
f ( x 0 ) − p n ( x 0 ) = ∆ ( f , pn ) = f ( x ) − pn ( x )
称 x 0为 p n ( x )的偏差点 .
∞
f ( x 0 ) − pn ( x 0 ) = − E n
f ( x 0 ) − pn ( x 0 ) = E n
负偏差点 正偏差点
正负偏差点有多少? 有什么特点?
−1≤ x ≤1
p2 ( x ) − 3ax 4+3bx3+ c 2 3 = ( x) = 2 x x= x − x
3
⇓ 3次多项式!
(1 − a ) 2 ( 2 − b ) (1 + c ) max f ( x ) − p2 ( x ) = 2 max x + x + x− −1≤ x ≤1 −1≤ x ≤1 2 2 2
是两点之间的距离
∆( f , p n ) ≥ 0
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
第三章-2-最佳平方逼近

性质 5 设 k k 0是 [a, b] 上带权 (x) 的正交多项式
族,则n(x) (n>0) 有n个单重实根,且都位于 区间[a, b] 内。
几类重要的正交多项式 Legendre 多项式 Chebyshev 多项式
第二类 Chebyshev 多项式
Laguerre 多项式 Hermite 多项式
Chebyshev 多项式
切比雪夫多项式的性质:
(1) 递推公式: Tn1 ( x ) 2 xTn ( x ) Tn1 ( x )
cos(n+1) + cos(n-1) = 2cos cosn x = cos
mn 0, 1 T ( x )T ( x ) n m (Tn , Tm ) dx π / 2, m n 0 (2) 正交性: 2 1 1 x π, mn0 n T ( x ) ( 1) Tn ( x) (3) 奇偶性: n
性质1 性质2
n ( x)
为首一 n 次多项式。 [a, b] 上带权 (x) 的正交多
是 k k 0
项式族,且
H n span 0 ,1,...,n
性质 3 正交。
n ( x) 与所有次数不高于n-1次的多项式
正交多项式性质
性质 4
此 k k 0 满足如下三项递推公式:
数值分析及计算软件
第三章
函数逼近与计算
3.3 最 佳 平 方 逼 近 及正交多项式
最佳平方逼近问题:
若存在 Pn* ( x )H n , 使得
|| f ( x) Pn ( x) ||2 inf || f ( x) Pn ( x) ||2 ,
第三章 参数多项式的插值与逼近

第三章 参数多项式的插值与逼近2009年8月29日10时35分 1本章内容•几何不变性与参数变换•参数多项式插值与逼近的基本概念•参数多项式插值曲线与逼近曲线•张量积曲面•参数双三次曲面片2009年8月29日10时35分 22009年8月29日10时35分 3第一节 几何不变性和参数变换 • 一、几何不变性:1、定义:指曲线曲面不依赖于坐标系的 选择,或者说在旋转与平移变化下不变 的性质。
2、曲线曲面的基表示: 0 n i i i P a j = = å r r 其中: 为矢量系数,修改它可以改变曲线曲面的形状i a r i j 为单参数(表示曲线时)或双参数(表示曲面时) 的基函数,决定曲线曲面的几何性质2009年8月29日10时35分 43、基表示的分类:(1)规范基表示:即满足Cauchy 条件 也称权性。
这种表示下,曲线 (面)上的点是矢量系数的一个重心组 合,重心坐标是基函数。
其中 一、几何不变性:0 1n i i j = º å 我们常见的线性插值就是一种规范基表示。
(2)部分规范基表示:即满足 0 1,0 ki i k n j = º£< å 如: 01 () p u a a u =+ r r r 0 1j =一、几何不变性:(3)非规范基表示:除规范基表示和部分规范基表示以外的其它基表示。
4、基表示与几何不变性的关系:曲线曲面的规范基表示具有仿射不变性, 其余两种只具有几何不变性。
5、几何不变性的意义: (1)方便局部坐标与整体坐标之间的转换;(2)便于平移和旋转变换;(3)节省了计算量。
2009年8月29日10时35分 5• 1、概述• 曲线的参数域总是有界的。
• 曲线的参数可能有某种几何意义,也可能没有。
• 曲线的参数化:即确定曲线上的点与参数域中的参数值之间的一种对应关系。
• 这种对应关系可以是一一对应的,也可以不是一一对应的,后者称为奇点(Singularpoint),如曲线的自交点。
第3章 函数逼近1 (最佳一致逼近)

上求切比雪夫交错组 在[ 1, 1]上求切比雪夫交错组 t1, …, tn+1 } 。 上求切比雪夫交错组{
最佳一致逼近多项式
目标: 目标:
要在H n中求Pn ( x )逼近f ( x ) ∈ C [a , b], 使其误差 || f ( x ) Pn ( x ) ||∞ = inf || f ( x ) Pn ( x ) ||∞
定理 3.3 的最佳逼近多项式,则 若P ( x ) ∈ H n 是 f ( x ) ∈ C [a , b] 的最佳逼近多项式 则P ( x ) 同时存在正、负偏差点. 同时存在正、负偏差点 证明:用反证法,设只有正偏差点。 证明:用反证法,设只有正偏差点。 设 || Pn y || ∞ = max ] | Pn ( x ) y ( x ) | = E n x∈[ a , b 而对于所有的 x∈[a, b] 都有 Pn ( x ) y ( x ) > E n ∈
-En≤pn*(x)-f(x)≤ En, -En≤qn(x)-f(x)≤ En (x)(x)所以- ≤(p 所以-En≤(pn*(x)+qn(x))/2 -f(x)≤En * 这说明 pn ( x) + qn ( x) pn ( x) = 2 也是对函数f(x)∈C a,b]的最佳一致逼近元. f(x)∈C[ 也是对函数f(x)∈C[a,b]的最佳一致逼近元. 现设误差曲线函数pn(x)-f(x)在区间[a,b] 在区间[ 现设误差曲线函数 (x)-f(x)在区间 a,b] 上的一个交错点组为{x 上的一个交错点组为{x1, x2,…, xn+2} ,为此 , En=|f(xk)-pn(xk)| =1/2|(f(xk)-pn*(xk))+(f(xk)-qn(xk))|.
第三章 函数逼近与计算

其中,H n 表示由所有次数不超过n的代数多项式
构成的线性空间。
这就是
C a,b
空间中的最佳一致逼近问题。
四、C a , b 上最佳一致逼近多项式的存在性
定理2(Borel定理)
对任意的 f x C a , b , 在 H n 中都存在对
* f x 的最佳一致逼近多项式,记为 pn x ,使得
对于函数类 A 中给定的函数 f x ,要求在另一类较简
单的且便于计算的函数类 B A 中寻找一个函数 P x ,使
P x 与
f x 之差在某种度量意义下最小。
A 通常为区间
注:本章中所研究的函数类
a,b
上的连续函数,记做 C a , b ;而函数类 B 通常是代数多项式或三角多项式。
采用
b
a
f x P x dx f x P x
2
2
作为度量误差“大小”标准的函数逼近称为最佳平 方逼近或均方逼近。
§2
定义
最佳一致逼近
对于任意 设函数 f x 是区间 a , b 上的连续函数, 给定的 ,如果存在多项式 P x ,使不等式
4、交错点组
定义 若函数 f x 在其定义域的某一区间 a , b
上存在 n 个点
xk , k
1, 2 , ..., n ,
f
使得
,
1
f
xk
f
max f
f
x
x
k 1, 2,..., n;
2
xk
xk 1 , k
§3.2最佳一致逼近多项式

5 5
第三章 函数逼近与计算
5、最佳逼近多项式
假定 f ( x ) C[a, b],若存在 Pn* ( x ) H n使
( f , Pn* ) E n
则称Pn*(x)是f(x)在[a, b]上的最佳一致逼近多项式 或最小偏差逼近多项式。
定理3.3
f x 是区间 a, b 上的连续函数,Pn* x 是 设
* f x 的n次最佳一致逼近多项式, f x Pn x 必同时 则
存在正负偏差点。
y
y f x En
y Pn* ( x )
y f x En
O
a
1313
第三章 函数逼近与计算
几何意义
y
N
y P x 1
M
D
Q
O
a
x2
b
x
© §2 2009, Henan Polytechnic University 最佳一致逼近多项式
1414
第三章 函数逼近与计算
例3.1
求函数 f ( x) 1 x 2 在区间[0,1]上的最佳一致逼近多项式。 f (b) f (a ) 解 a1 2 1 0.414 ba x2 由 f ' ( x2 ) 2 1 0.414 2 1 x2 2 2 1 x2 2 2 x2 ( 2 1) 即 得 2 2 1 x2
第二节 最佳一致逼近多项式
1
第三章 函数逼近与计算
3.2.1 最佳一致(Chebyshev)逼近多项式的存在性 H n span 1, x,, x n } { 令
第3章 函数逼近与计算

0 ( x) 1
2 2 ( x , ) ( x , 1 ) 2 0 2 ( x) x 0 1 ( x) (0 , 0 ) (1 , 1 )
1 1 ( 0 , 0 ) ln dx ln xdx 1 0 0 x 1
( x, 0 )
b
a
f 2 ( x)dx
函数的平方模满足 (1) 20,而且2=0(x)=0;
(2) c2=|c|2;
(3) +g22+g2 (4) (,g)2 g2
权函数 考虑到(x)在区间[a,b]上各点的函数值比重不同, 常引进加权形式的定义
什么是函数逼近
对函数类A中给定的函数 f(x),记作f(x)∈A,
要求在另一类简单的便于计算的函数类 B
中求函数 p(x)∈B ,使 p(x)与 f(x)的误差在 某种意义下最小.函数类A通常是区间[a, b] 上的连续函数,记作C[a, b],称为函数逼近空 间;而函数B通常为n次多项式,有理函数或分
续函数空间---- C[a, b]
3.1 函数逼近的基本概念
1)线性无关
设集合S是数域P上的线性空间,元素x1,x2,…,xn∈S, 如果存在不全为零的数a1,a2,…,an∈P,使得
a1 x1 a2 x2 ... an xn 0,
则称x1,x2,…,xn线性相关.
关的.
若 0 ( x), n1 ( x)
n n ! d ~ 2 n P ( x ) [( x 1 ) ]. n n ( 2n)! dx
勒让德多项式的性质
(1)正交性
m n; 0, 1 1 Pn ( x) Pm ( x)dx 2 , m=n. 2n 1
§3 最佳平方逼近多项式

若f ( x) C[a, b], span{0 ( x),1 ( x),n ( x)},
若函数组 0 ( x),1 ( x), n ( x)满足条件
则
方程组
0, 当i j ( i , j ) ( j , j ), 当i j
( 0 , 0 ) a 0 ( f , 0 ) a ( f , ) ( , ) 1 1 1 1 ( n , n ) an ( f , n )
* a 展开,而系数 k (k 1,2,, n)
按下式计算
ak ( f ( x),k ( x)) /(k ( x),k ( x)) ; (k 0,1,, n)
得级数
a k k ( x) k 0
* 称为f(x)的广义傅立叶(Foureir)级数,系数 ak (k 1,2,, n)
( x)
1 1 x2
,k 0 ( (Tk Tk ) ) ,k 0 2
1 1 x
2
由切比雪夫(Chebyshev)镇多项式作最佳平方逼近
Cn ( x ) ak Tk ( x ) k 0 n
其中
( f , T0 ) 1 a (T0 , T0 )
f P*
2 2
事实上,
f P
2 2
( f P, f P )
*
( f P* P* P, f Pn P* P)
( f P * , f P* ) ( P* P, P * P ) 2( f P * , P * P )
* 因为(f P ,P P) (f P , ( a j a j) j ( x) ) * * * j 0
最佳一致逼近多项式

P ( x) = 0.955 + 0.414 x 1 误差限为 max 1 + x − P ( x) ≤ 0.045 1
∞
在[a, b]上一致成立。
3.2 最佳一致逼近多项式
• 最佳一致逼近多项式 是讨论 f∈C[a, b],在Hn=span{1,x,…xn}中求 多项式 P* (x) , 使其误差 n
|| f − P || = max | f (x) − P (x) |= min || f − Pn ||
* n ∞ a≤x≤b * n Pn ∈Hn
什么是函数逼近
对函数类A中给定的函数 记作f(x)∈ 对函数类 中给定的函数 f(x),记作 ∈A, 记作 要求在另一类简单的便于计算的函数类 B p(x)∈ ,使 p(x)与 f(x)的误差在 中求函数 p(x)∈B ,使 p(x)与 f(x)的误差在 某种意义下最小.函数类 通常是区间 某种意义下最小 函数类A通常是区间 b] 函数类 通常是区间[a, 上的连续函数,记作 上的连续函数 记作C[a, b],称为函数逼近空 记作 称为函数逼近空 而函数B通常为 次多项式,有理函数 间;而函数 通常为 次多项式 有理函数,分 而函数 通常为n次多项式 有理函数, 段低次多项式或三角多项式等. 段低次多项式或三角多项式等
k a≤x≤b
( σ=±1, k =1,2,3)
最佳逼近 - 正交多项式、最佳逼近
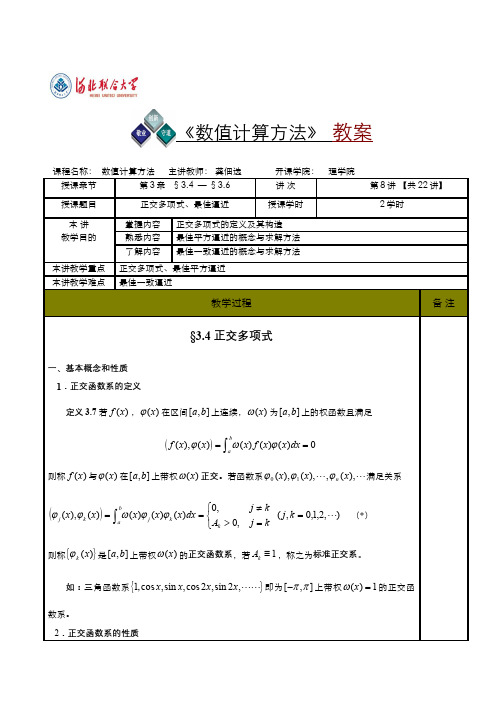
2
(x)
x2
1 3
3
(
x)
x3
3 5
x
4
(x)
x4
6 7
x2
+
3 35
5
(x)
x5
10 9
x3
+
5 21
x
6
(
x)
x6
15 11
x4
+
5 11
x
2
5 231
7
(x)
x7
231 143
x5
+
105 143
x3
35 429
x
3.正交多项式的性质
(1){0 (x),1(x),,n (x)} 线性无关;
(2)任何 n 次多项式均可表示为0 (x),1 (x),,n (x),的线性组合;
(4)
Pn (x) 的最高次项系数为 an
(2n)! 2n (n!)2
,显然最高项系数为
1 的勒让德多项式为
~
Pn (x)
n! (2n)!
dn dx n
[( x
2
1)n
]
;
(5) Pn (x) 在区间[1,1] 内有 n 个不同的实零点。
勒让德多项式的由来:
勒让德微分方程:
(1
-
x2)
d
2P(x) dx2
称为逼近的误差或余项。 这里必须表明两点:其一是函数类 M 的选取。何为简单函数?在数值分析中所谓简单函数
主要是指可以用四则运算进行计算的函数,最常用的有多项式及有理分式函数;其二是如何确
定 P 与 f 之间的度量。 定义 3.9 设函数 f (x) 是区间[a, b] 上的连续函数,对于任意给定的 "e 0 ,如果存在多项
最佳一致逼近多项式

( f , p n ) E n,
*
( 3 .3 ) 或
则称 p n ( x ) 是 f ( x ) 在 [ a , b ]上的 n 次 最佳一致逼近多项式 最小偏差逼近多项式 ,简称 最佳逼近多项式
*
*
.
定理 2 若 f ( x ) C [ a , b ],
*
则总存在 p n ( x ) H n , 使得 。
证明:令 ( x ) | P ( x ) f ( x ) |, 则 ( x ) 连续,因而可以达到最 即存在 x 0 , 使得 ( x 0 ) max ( x ) || P ( x ) f ( x ) || 。
a xb
大值,
这说明 x 0 是 P ( x ) 的一个偏差点,不妨设 由于 P ( x ) 是最佳逼近多项式,则
三、最佳一致逼近多项式
1.零次最佳一致逼近多项式 对于n=0的P0(x)有: P0(x) =(M+m)/2 其中M、m分别为f (x) 的最大值和最小值。 ∵f(x)C[a,b],由闭区间上连续函数性质;在[a,b]上存在两点x1,x2 使f (x1)=M, f (x2)=m, 即:x1,x2为偏差点(负,正)使:
axb
f (x)
n
(x)
即在H中 (x)与f(x)之差的绝对值的最大值是最小的,H中 任一ψ (x)与f(x)之差的绝对值都比它大,这样的 (x)为 f(x)在H中的最佳一致逼近函数。
定义1
设 f ( x ) C [ a , b ],
pn ( x ) H n , 称
a xb
逼近多项式
推论2 设f(x)C[a,b],则f(x)在Hn中的最佳一致逼近多项 式Pn(x),就是f (x)在[a,b]上的某个n次Lagrange插 值多项式。 证明∵Pn(x)有n+2个偏差点,亦即使f (x) -Pn (x)在[a,b]上至少 有n+2个点交替换正负号,亦就是说f(x) Pn(x)=0在[a,b]上有n+1 个根存在n+1个点:a x0<…< xn b使f (xi) Pn (xi)=0 即:f (xi)=Pn(xi) (i =0,1,2,…,n) , 所以,以此作为插值条件可得 到Pn(x),因此,Pn(x)就是以x0,x1,…,xn为插值节点的n次值多项 式。 切比雪夫定理不仅给出了最佳一致逼近多项式的特征, 并从理论上给出了寻找最佳一致逼近多项式的方法:
3.3最佳一致逼近多项式

( 1, k 1,2,3).
12
由于 f ( x) 在 [a, b]上不变号, 故 f ( x) 单调, f ( x) a1 在 (a, b)内只有一个零点,记为 x2, 于是
且点 xk cos
k (k 0,1, , n) 是 Tn ( x)的切比雪夫交错点组, n
8
由定理5可知,区间 [1, 1] 上 x n 在 H n 1 中最佳逼近多项式
为 Pn*1 ( x), 即 ( x) 是与零的偏差最小的多项式. n
定理得证.
9
例3 求 f ( x) 2 x3 x 2 2 x 1 在 [1, 1]上的最佳2次逼 近多项式. 解 由题意,所求最佳逼近多项式 P2* ( x) 应满足
5
使 P( x), 用反证法,若存在 Q( x) H n , Q( x)
f ( x) Q( x)
f ( x ) P( x ) .
由于
P( x) Q( x) [ P( x) f ( x)] [Q( x) f ( x)]
在点 x1 , x2 ,, xn 2 上的符号与 P( xk ) f ( xk )(k 1,, n 2) 一致, 故 P( x) Q( x) 也在 n 2 个点上轮流取“+”、“-”号. 由连续函数性质,它在 [a, b] 内有 n 1 个零点,但因
于是得 1 x 2 的最佳一次逼近多项式为
P 1 ( x) 0.955 0.414 x,
即
1 x 2 0.955 0.414 x, 0 x 1;
计算方法最佳一致逼近多项式-切比雪夫多项式专题培训课件

cos(nθθs )c in o(snθθ )si
co s1 () n θ cos(θ n s θi) nc(o θ n
Tn(x)在 1,[1]上有的 n个 零不 点同 xk co(s22k 1 n)π , (k1,2 …,,n)
证:将xk
cos(2k 1)π, 2n
(k
1,2,…, n)
代入Tn(x)的表达式,得到
Tn(x)
cos[narccso(cos(2k 1)π)] 2n
cos[(2k 1)π] 2
计算方法最佳一致
逼近多项式-切比 雪夫多项式
内容
1. 函数逼近的基本概念 2. 切比雪夫多项式 3. 最佳一致逼近多项式 4. 切比雪夫多项式在函数逼近中的应用 5. 利用切比雪夫多项式的0点构造最佳逼近多
项式的例子
函数逼近的基本概念
第3章 函数逼近与曲线拟合
§1 函数逼近的基本概念
一、函数逼近与函数空间
实际应用需要使用简单函数逼近已知复杂函数。
函数逼近问题: 对于函数类A中给定函的数
f(x),要求在另一类较简单便的于计算的函
数类
BA
B
A
中找一个函数p(,x使) p(x)与f(x的) 误差在某
种度量意义下达到最. 小
定1 理(Weaisesrf)s(若 tx rC ) [b a],则 ,ε0, 多项式 使p得 (x),
得知:情况a)如 为果 奇n数,则n2(xT)只含n的偶, 次方 Tn1(x)只含x的偶方 数, 次从而左n端 1(xT)只含x的偶; 次 情况b)如果n为,偶则数2xn(Tx)只含x的奇, 次Tn方 1(x) 只含x的奇次方,左从端而 nT1(x)只含x的奇次方
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y ( ) ( x xi ) ( n + 1)! i 0
( n +1 ) n
达到极小?
在[ 1, 1]上求{ x1, …, xn } 使得 wn( x) ( x xi ) i 1 的||wn|| 最小。
v 2.1
n
wn ( x) xn Pn1 ( x) ,要使||w || 最小就意味着 注意到 n
考虑三角函数 cos(n ) 在[ 0, ] 上的 n + 1 个极值点。
k k 当 n ( k 0, 1, ... , n) 时, cos(n )交错达到极大值 1 和极
n k 0
小值 1 ,且存在系数 a0, …, an 使得 cos(n ) ak (cos )k
y
y y ( x) + En
y Pn ( x)
可见Pn(x) 是 y(x)的 某一个插值多项式
y y ( x) y y ( x) En
v 2.0
如何确定
插值节点{ x0, …, xn }
x
0
的位臵,使得Pn(x) 刚好是 y 的OUAP ? 即,使插值余项
| Rn ( x ) |
{ tk }称为切比雪夫交错组 /* Chebyshev alternating sequence */
P79 Th.5 若 y C[a, b] ,则 n 次OUAP 唯一。P80 推论1
由Chebyshev定理可推出:Pn(x) y(x) 在定义域上至少变号 n+1 次,故至少有 n+1 个根。
Tn(x)为 n 次多项式,首项系数为 2n1。且T2n(x)只含 x 的 偶 次幂, T2n+1(x)只含x 的 奇 次幂。
OKOK, I think it’s enough for us… What’s our target again?
v 3.1 v 3.0
在[ 1, 1]上求切比雪夫交错组{ t1, …, tn+1 } 。 在[ 1, 1]上求函数 xn 的n1阶 OUAP。
P2 ( x) 1.013+ 0.851x + 0.839x
2
v 2.0 n如何确定插值节点{
Pn(x),则插值余项的上界可达极小
M 2 n ( n + 1)!
。
注:
上界最小不表示| Rn(x)|最小,故Pn(x)严格意义上只是y(x)
的近似最佳逼近多项式; a+b ba x + t ,则 对于一般区间 x [a, b] ,可作变量替换 2 2 t [ 1 , 1 ] ,这时
j 0 n
n
j 0
i 0,1, n
即 ( 0 , 0 ) ( 0 , 1 ) ( 1 , 0 ) ( 1 , 1 ) ( , ) ( , ) n 1 n 0 ( 0 , n ) c0 ( 0 , f ) ( 1 , n ) c1 ( 1 , f ) ( n , n ) cn ( n , f )
证() M, * M
f
2 2
( f , f )
( f + , f + )
* * * *
( f * , f * ) + 2( f * , * ) + ( * , * )
=0
f
* 2 2
+ f
* 2
2
* 2 2
为最佳平方逼近
()用反证法 设 * M为f ( x )的最佳平方逼近函数,但存在
M使得( f * , ) a 0
记( , ) b 0( ) 2 a a a * * * f ( f , f ) b 2 b b
令 x = cos( ) ,则 x [ 1 , 1 ]。
Tn 的重要性质:
Tn ( x ) cos(n ) cos(n· cos x ) 称为Chebyshev多项式 arc
k t k cos ( k 0, 1, ... , n) 时,Tn (t k ) 交错取到极大值 1 当 n 1
1 0
( 0 , 1 ) ( 1 , 0 )
1 0
1
0
( 0 , f ) e x dx e 1 ( 1 , f ) xe x dx 1
1 0
1 xdx 2
( 2 , f ) x 2 e x dx e 2
1 0
1 1 / 2 1 / 3 c1 e 1 1 / 2 1 / 3 1 / 4 c 2 1 1 / 3 1 / 4 1 / 5 c e 2 3
v 2.1
= {首项系数为1的 nx阶多项式 0, …, xn }的位臵,使得Pn(x) 刚 /*monic polynomials of degree n */ } y ( n+1) ( ) n 好是 y 的OUAP ?即,使插值余项 | Rn ( x ) | ( x xi ) ( n + 1)! i 0 达到极小? 取{ x0, …, xn } 为Tn+1(x)的n+1个零点,做 y 的插值多项式
Tn+1 ( t )
( b a ) n+1 2 2 n+1
Tn+1 ( t )
即以 xk
a+b ba 2k + 1 + cos 为插值节点 (k=0,…, n), 2 2 2n + 2
y ( n+1) ( ) (b a )n+1 得Pn(x),余项 Rn ( x ) Tn+1 (t ) 有最小上界。 2 n +1 (n + 1)! 2
a xb
则称Pn ( x )为f ( x )的n次最佳一致逼近多项式
偏差
也称为minimax problem。
/deviation/
若 P( x0 ) y( x0 ) || P y || ,则称 x0 为 偏差点。
直接构造 OUAP 的确比较困难,不妨换个角度,先 考察它应该具备的性质。有如下结论:
wn+1 ( x) wn+1 ( a+b + ba t ) ( a+b + ba t x0 )...(a+b + ba t xn ) 2 2 2 2 2 2
b a n +1 2 b a n +1 1 2 2n
( t t 0 )...(t t n )
最佳平方逼近多项式
定义:定义范数 f
2
( f , f ) , 则最佳平方逼近
可描述为:f ( x ) C [a , b], M为C [a , b]的子空间, 选择 ( x ) M,使得 f
2
( f , f )为最小
定理2:C [a , b]是内积空间,M是其有限维子空间, f ( x ) C [a , b],M中 * ( x )是f ( x )的最佳平方逼近 函数的 f *与M中任一元正交
v 3.0
在[ 1, 1]上求函数 xn 的n1阶 OUAP。
由Chebyshev定理可推出:Pn1(x) 关于xn 有n+1个偏 差点,即wn(x)在 n+1个点上交错取极大、极小值。
v 3.1
在[ 1, 1]上求切比雪夫交错组{ t1, …, tn+1 } 。
切比雪夫多项式 /Chebyshev polynomials/
OUAP 存在,且必同时有 偏差点。P79 Th.4 (Chebyshev定理)Pn 是 y 的OUAP Pn 关于 y 在定义域 上至少有n+2个交错的 偏差点。
k 即存在点集 a t1 <…< tn+2 b 使得 Pn (tk ) y(tk ) (1) || Pn y ||
a a * ( f , f ) b b =a =b 2 2a a * * * ( f , f ) ( f , ) + 2 ( , ) b b 2 a2 * * 2 f f 2 2 b
*
不是最佳平方逼近函数 ,矛盾
Tn ( x ) 可见:若取 w n ( x ) n1 ,则wn在[ 1 , 1 ]上有 n+1 个极 2
值点{ tk },也即Pn1(x) = xn wn(x)关于xn在[ 1 , 1 ]上有 n+1个交错偏差点{ tk } 。 v3.0 OK
n
在[ 1, 1]上求{ x1, …, xn } 使得 wn( x) ( x xi ) 的 i 1 ||wn|| 最小。 1 1 n min || wn || n1 Tn ( x ) n 1 || Pn1 ( x) x || 取最小值 w n n 2 2 { x1, …, xn } 即为 Tn(x)的n个零点。
n j 0
求解出c0 , c1 ,cn即可得 * c j j ( x )
例:设f ( x ) e , x [0,1],求最佳二次平方逼近
x
多项式P2 ( x ) c0 + c1 x + c2 x
2
解:M span 1, x, x 2
( 0 , 0 ) 1dx 1
和极小值1,即 Tn (tk ) (1)k || Tn ( x) ||
当 xk cos
