§6矢量在轴上的投影(射影)

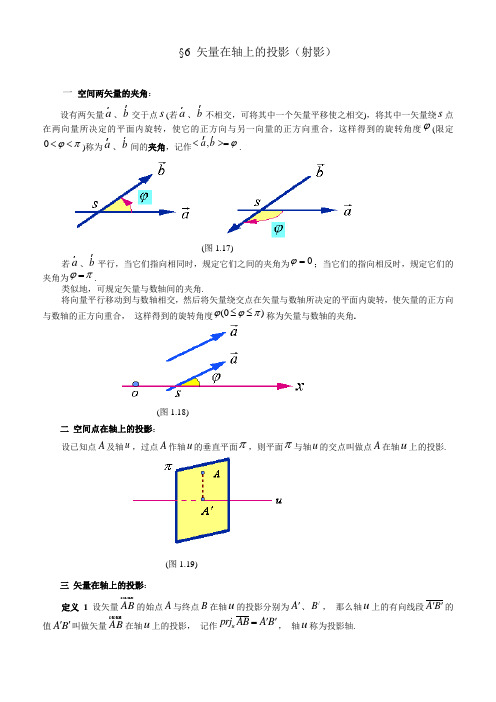
§6 矢量在轴上的投影（射影）
一 空间两矢量的夹角：
设有两矢量a 、b 交于点s (若a 、b 不相交，可将其中一个矢量平移使之相交)，将其中一矢量绕s 点在两向量所决定的平面内旋转，使它的正方向与另一向量的正方向重合，这样得到的旋转角度ϕ(限定0ϕπ<<)称为a 、b 间的夹角，记作,a b ϕ<>=.
(图1.17) 若a 、b 平行，当它们指向相同时，规定它们之间的夹角为0ϕ=；当它们的指向相反时，规定它们的夹角为ϕπ=.
类似地，可规定矢量与数轴间的夹角.
将向量平行移动到与数轴相交，然后将矢量绕交点在矢量与数轴所决定的平面内旋转，使矢量的正方向与数轴的正方向重合， 这样得到的旋转角度(0)ϕϕπ≤≤称为矢量与数轴的夹角.
(图1.18)
二 空间点在轴上的投影：
设已知点A 及轴u ，过点A 作轴u 的垂直平面π，则平面π与轴u 的交点叫做点A 在轴u 上的投影.
(图1.19)
三 矢量在轴上的投影：
定义1 设矢量AB 的始点A 与终点B 在轴u 的投影分别为A '、/
B ， 那么轴u 上的有向线段A B ''的值A B ''叫做矢量AB 在轴u 上的投影， 记作u prj AB A B ''=， 轴u 称为投影轴.
(图1.20) 这里，A B ''的值''A B 是这样的一个数：
(1)、''''||||A B A B =即， 数A B ''的绝对值等于向量A B ''的模.
(2)、当A B ''的方向与轴u 的正向一致时，0A B ''>；当A B ''的方向与u 轴的正向相反时，0A B ''<.
四 投影定理：
定理1 矢量AB 在轴u 上的投影等于矢量的模||AB 乘以轴u 与矢量AB 的夹角ϕ的余弦.即
prj AB AB u =cos ϕ, (1.6-1)
(图1.21)
证 过矢量AB 的始点A 引轴'u ，且轴'u 与轴u 平行且具有相同的正方向，那未轴u 与向量AB 的夹角等于轴'u 与向量的夹角，而且有
u u prj AB prj AB '=
prj AB AB AB u '=''=cos ϕ
故 prj AB AB u =cos ϕ 由上式可知：矢量AB 在轴u 上的投影是一个数值，而不是矢量. 当非零矢量AB 与投影轴u 成锐角时， 向量AB 的投影为正.
定理2 对于任何矢量,a b 都有
()u u u prj a b prj a prj b +=+. (1.6-2)
证 取,AB a BC b ==，那么AC a b =+，设'''
,,A B C 分别是,,A B C 在轴l 上的投影，那么显然有
''''''AC A B B C =+，
因为
'''''',,l l l AC prj AC A B prj AB B C prj BC === 所以 u u u prj AC prj AB prj BC =+， 即 ()u u u prj a b prj a prj b +=+.
类似地可证下面的定理：
定理3 对于任何矢量a 与任何实数λ有
u u prj a prj a λλ=. (1.6-3)。