辽宁省朝阳市普通高中2018届高三第一次模拟考试数学(

合集下载

2018届辽宁省朝阳市普通高中高三第一次模拟考试文综试卷(扫描版)

朝阳市普通高中2018年高三第一次模拟考试地理参考答案及评分标准1-5 ACDBC 6-11 BDDABC36．（24分）(1)土地面积大，发展空间广阔；人口数量多，劳动力充足；有4所百强高校，科技实力强；客、货吞吐量大，交通便捷，运输能力强。

（答对3点得6分）弊：与其它三区相比，人均GDP较小，经济实力相对较低；第三产业比重稍低，产业结构需进一步优化；五百强公司数量较少，大型企业的竞争力较差。

（6分）(2)利于推动内地与港澳的深化合作；利于粤港澳大湾区产业分工与合作；利于发挥港澳的独特优势，提升该地区在国家经济发展和对外开放中的地位；利于发挥其对全国的辐射、引领和示范作用。

（答对3点得6分）(3)推进基础设施建设，共建宜居宜业宜游的优质生活圈；提升市场一体化水平，加大投资、贸易、人员往来；提高科技水平，提高国际竞争力；加强协作与融合，支持重大合作平台建设；加快制造业转型升级，重点培育新型产业，形成新型产业集群。

（答对3点得6分）37.(22分)（1）年降水量西部多，东部少；（2 分）西部处于来自海洋的盛行西风的迎风坡（雨区），东部处于背风坡（雨影区）。

（4 分）（2）W岛地处太平洋，冬季浩瀚的海洋对气温有巨大的调节作用；（2 分）东（北）部有高大山脉的阻挡，受北极冷空气的影响较小；（2 分）沿岸海区有暖流流经，增温作用明显。

（2 分）（3）（与热带雨林相比，）W岛纬度较高，气温较低，适合冷杉、云杉等针叶树种生长；（3分）阴雨天气较多、森林茂密，日照时间相对较短，（3分）低矮的阔叶植物因光照不足而分布稀少，但高大的冷杉、云杉等针叶树却能够获得较好的光照，成为主要树种。

（4分）41.（10分）(1)独特的人文景观；清新优雅的校园风光；悠久而深厚的文化内涵和校园特有的书香氛围；以参观校园、体验高校学习生活为主题的旅游活动。

（任答三点即可得6分）(2)不利影响：干扰高校正常的教学秩序；增加高校周边的交通压力；加剧校园环境污染；加快校园基础设施的耗损。

辽宁省朝阳市2018届高三第一次模拟考试理数试题(考试版)

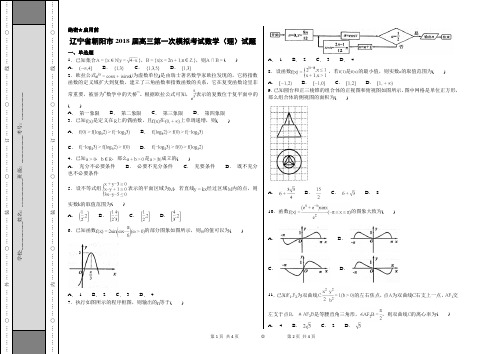
第1页共4页 ◎ 第2页共4页绝密★启用前辽宁省朝阳市2018届高三第一次模拟考试数学（理）试题一、单选题 1．已知集合，，则( ) A ．B ．C ．D ．2．欧拉公式(为虚数单位)是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里非常重要，被誉为“数学中的天桥”。

根据欧拉公式可知，表示的复数位于复平面中的( )A ．第一象限 B．第二象限 C ．第三象限 D ．第四象限 3．已知是定义在上的偶函数，且在上单调递增，则( )A ．B ．C ．D ．4．已知，，那么是成立的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．设不等式组表示的平面区域为，若直线经过区域内的点，则实数的取值范围为() A ．B ．C ．D ．6．已知函数的部分图象如图所示，则的值可以为( )A ． 1B ． 2C ． 3D ． 47．执行如图所示的程序框图，则输出的等于( )A ． 1B ． 2C ．3 D ．4 8．设函数，若是的最小值，则实数的取值范围为( )A ．B ．C ．D ．9．已知圆台和正三棱锥的组合体的正视图和俯视图如图所示，图中网格是单位正方形，那么组合体的侧视图的面积为( )A ．B ．C ．D ． 810．函数的图象大致为( )A ．B ．C ．D ．11．已知为双曲线的左右焦点，点为双曲线右支上一点，交左支于点，是等腰直角三角形，，则双曲线的离心率为( )A ． 4B ．C ． 2D ．第3页共4页◎第4页共4页12．已知台风中心位于城市东偏北(为锐角)度的150公里处，以公里/小时沿正西方向快速移动，小时后到达距城市西偏北(为锐角)度的200公里处，若，则( )A．B．80C．100D．125二、填空题13．设函数在内可导，其导函数为，且，则____________．14．已知平面向量，，若，则实数____________．15．在圆上任取一点，则该点到直线的距离的概率为________________．16．已知函数，若，，且，则________．三、解答题17．已知等比数列的前项和为，满足，．(1)求的通项公式；(2)记，求的最大值．18．某校为了推动数学教学方法的改革，学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班，每班各40人，甲班按原有模式教学，乙班实施教学方法改革．经过一年的教学实验，将甲、乙两个班学生一年来的数学成绩取平均数再取整，绘制成如下茎叶图，规定不低于85分(百分制)为优秀，甲班同学成绩的中位数为74．(1)求的值和乙班同学成绩的众数；(2)完成表格，若有以上的把握认为“数学成绩优秀与教学改革有关”的话，那么学校将扩大教学改革面，请问学校是否要扩大改革面？说明理由．19．如图，四棱锥中，底面，为直角梯形，与相交于点，，，，三棱锥的体积为9．(1)求的值；(2)过点的平面平行于平面，与棱，，，分别相交于点，求截面的周长．20．已知椭圆的下顶点为，右顶点为，离心率，抛物线的焦点为，是抛物线上一点，抛物线在点处的切线为，且．(1)求直线的方程；(2)若与椭圆相交于，两点，且，求的方程．21．已知函数，其中为自然对数的底数．(1)若在处取到极小值，求的值及函数的单调区间；(2)若当时，恒成立，求的取值范围．22．在平面直角坐标系中，曲线的参数方程为(为参数)，以坐标原点为极点，轴非负半轴为极轴建立极坐标系．(1)求的极坐标方程；(2)若直线的极坐标方程分别为，，设直线与曲线的交点为，，，求的面积．23．已知．(1)当时，求不等式的解集；(2)对于任意实数，不等式成立，求实数的取值范围．。

东北三省辽宁省实验中学等三校2018届高三一模文科数学试卷(含答案)

哈尔滨师大附中、东北师大附中、辽宁省实验中学2018年高三第一次联合模拟考试文科数学试卷第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合*2,A x x x N，2,B y y x x R，则A B( )A.0x x B.1x x C.1,2 D.0,1,22.已知复数z满足12i z i，i为虚数单位，则z等于( )A.1iB.1iC.1122i D.1122i3.在下列向量中，可以把向量3,1a表示出来的是( )A.10,0e，23,2e B.11,2e，23,2eC.13,5e，26,10e D.13,5e，23,5e4.在区间0,3上任取一个实数x，则22x的概率是( )A.23B.12C.13D.145.抛物线24y x的焦点到准线的距离为( )A.2B.1C.14D.186.已知,a b都是实数，p：直线0x y与圆222x a y b相切；q：2a b，则p是q的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》，执行该程序框图若输出的4a，则输入的,a b不可能为( )A.4，8B.4，4C.12，16D.15，188.已知函数sin3f x x，则下列说法不正确的是( )A.f x的一个周期为2B.f x向左平移3个单位长度后图象关于原点对称C.f x在7,66上单调递减 D.f x的图象关于56x对称9.函数af x xx(其中a R)的图象不可能是( )A B C D10.如图所示是一个三棱锥的三视图，则此三棱锥的外接球的体积为( )A.43B.32C.556D.611.设双曲线222210,0x ya ba b的两条渐近线与直线2axc分别交于,A B两点，F为该双曲线的右焦点，若6090AFB∠°°，则该双曲线离心率e的取值范围是( )A.1,2B.23,3 C.2,2D.23,2312.已知函数21221221xx xx f xx，1cos g x a x x R ，若对任意的12,x x R ，都有12f x g x ，则实数a 的取值范围为( )A.0,2B.RC.2,0D.,20,二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若直线l平面，平面平面，则直线l 与平面的位置关系为_____________.14.若实数,x y 满足不等式组0103xx y x y，则32y x的取值范围是_____________.15.甲、乙、丙三人中只有一人做了好事，他们各自都说了一句话，而且其中只有一句真话。

朝阳市第一高级中学2018-2019学年上学期高三期中数学模拟题

朝阳市第一高级中学2018-2019学年上学期高三期中数学模拟题班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1．在正方体1111ABCD A B C D -中，M 是线段11A C 的中点，若四面体M ABD -的外接球体积为36p ，则正方体棱长为（）A ．2B ．3C ．4D ．5【命题意图】本题考查以正方体为载体考查四面体的外接球半径问题，意在考查空间想象能力和基本运算能力．2．已知不等式组⎪⎩⎪⎨⎧≥+≤+≥-1210y x y x y x 表示的平面区域为D ，若D 内存在一点00(,)P x y ,使001ax y +<，则a 的取值范围为（）A ．(,2)-∞B ．(,1)-∞C ．(2,)+∞D ．(1,)+∞ 3．已知集合{}{2|5,x |y ,A y y x B A B ==-+===（）A ．[)1,+∞B ．[]1,3C ．(]3,5D ．[]3,5【命题意图】本题考查二次函数的图象和函数定义域等基础知识，意在考查基本运算能力． 4．记,那么ABC D5． ABC ∆的外接圆圆心为O ，半径为2，OA AB AC ++为零向量，且||||OA AB =，则CA 在BC 方向上的投影为（）A ．-3 B． C ．3 D6．在ABC ∆中，10a =，60B =，45C =，则等于（）A．10 B．1) C1 D．7．高考临近，学校为丰富学生生活，缓解高考压力，特举办一场高三学生队与学校校队的男子篮球比赛．由于爱好者众多，高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队．首发要求每个班至少1人，至多2人，则首发方案数为（） A ．720 B ．270 C ．390 D ．3008．设F 为双曲线22221(0,0)x y a b a b-=>>的右焦点，若OF 的垂直平分线与渐近线在第一象限内的交点到另一条渐近线的距离为1||2OF ，则双曲线的离心率为（）A ．B ．3C ．D ．3【命题意图】本题考查双曲线方程与几何性质，意在考查逻辑思维能力、运算求解能力、方程思想． 9．已知,,a b c 为ABC ∆的三个角,,A B C 所对的边，若3cos (13cos )b C c B =-，则s i n :s i n C A =（） A ．2︰3 B ．4︰3 C ．3︰1 D ．3︰2 【命题意图】本题考查正弦定理、余弦定理，意在考查转化能力、运算求解能力． 10．已知全集为R ，且集合}2)1(log |{2<+=x x A ，}012|{≥--=x x x B ，则)(B C A R 等于（） A ．)1,1(- B ．]1,1(- C ．)2,1[ D ．]2,1[【命题意图】本题考查集合的交集、补集运算，同时也考查了简单对数不等式、分式不等式的解法及数形结合的思想方法，属于容易题. 11．已知()(2)(0)x b g x ax a e a x =-->，若存在0(1,)x ∈+∞，使得00()'()0g x g x +=，则b a的取值范围是（）A ．(1,)-+∞B ．(1,0)- C. (2,)-+∞ D ．(2,0)- 12．在ABC ∆中，22tan sin tan sin A B B A =，那么ABC ∆一定是（）A ．锐角三角形B ．直角三角形C ．等腰三角形D ．等腰三角形或直角三角形二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知数列{}n a 的首项1a m =，其前n 项和为n S ，且满足2132n n S S n n ++=+，若对n N *∀∈，1n n a a +<恒成立，则m 的取值范围是_______．【命题意图】本题考查数列递推公式、数列性质等基础知识，意在考查转化与化归、逻辑思维能力和基本运算能力．14．等比数列{a n }的前n 项和S n ＝k 1＋k 2·2n （k 1，k 2为常数），且a 2，a 3，a 4－2成等差数列，则a n ＝________． 15．设平面向量()1,2,3,i a i =，满足1ia =且120a a ⋅=，则12a a += ，123a a a ++的最大值为 .【命题意图】本题考查平面向量数量积等基础知识，意在考查运算求解能力.16．已知n S 是数列1{}2n n -的前n 项和，若不等式1|12n n n S λ-+<+｜对一切n N *∈恒成立，则λ的取值范围是___________．【命题意图】本题考查数列求和与不等式恒成立问题，意在考查等价转化能力、逻辑推理能力、运算求解能力．三、解答题（本大共6小题，共70分。

东北三省三校2018届高三第一次模拟考试数学(文)试题有答案AlUPAq

哈尔滨师大附中、东北师大附中、辽宁省实验中学2018年高三第一次联合模拟考试文科数学试卷第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合{}*2,A x x x N =≤∈，{}2,B y y x x R ==∈，则A B =I ( ) A.{}0x x ≥B.{}1x x ≥C.{}1,2D.{}0,1,22.已知复数z 满足()12i z i +=，i 为虚数单位，则z 等于( ) A.1i -B.1i +C.1122i - D.1122i + 3.在下列向量中，可以把向量()3,1a =-r 表示出来的是( ) A.()10,0e =u r ，()23,2e =u u rB.()11,2e =-u r ，()23,2e =u u rC.()13,5e =u r ，()26,10e =u u rD.()13,5e =-u r ，()23,5e =-u u r4.在区间()0,3上任取一个实数x ，则22x <的概率是( ) A.23B.12C.13D.145.抛物线24y x =的焦点到准线的距离为( ) A.2B.1C.14D.186.已知,a b 都是实数，p ：直线0x y +=与圆()()222x a y b -+-=相切；q ：2a b +=，则p 是q 的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件7.如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》，执行该程序框图若输出的4a =，则输入的,a b 不可能为( )A.4，8B.4，4C.12，16D.15，188.已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭，则下列说法不正确的是( )A.()f x 的一个周期为2πB.()f x 向左平移3π个单位长度后图象关于原点对称 C.()f x 在7,66ππ⎡⎤⎢⎥⎣⎦上单调递减D.()f x 的图象关于56x π=-对称 9.函数()af x x x=+(其中a R ∈)的图象不可能是( )ABCD10.如图所示是一个三棱锥的三视图，则此三棱锥的外接球的体积为( )A.43π3556π11.设双曲线()222210,0x y a b a b -=>>的两条渐近线与直线2a x c=分别交于,A B 两点，F 为该双曲线的右焦点，若6090AFB <<∠°°，则该双曲线离心率e 的取值范围是( ) A.(2B.23⎫+∞⎪⎪⎝⎭C.)2,2D.232⎝ 12.已知函数()()()21221221x x x x f x x --⎧-+-≤⎪=⎨->⎪⎩，()()1cos g x a x x R =-∈，若对任意的12,x x R ∈，都有()()12f x g x ≤，则实数a 的取值范围为( ) A.[]0,2B.RC.[]2,0-D.(][),20,-∞-+∞U二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若直线l ⊥平面β，平面α⊥平面β，则直线l 与平面α的位置关系为_____________. 14.若实数,x y 满足不等式组01030x x y x y ≥⎧⎪-+≤⎨⎪+-≤⎩，则32y x +-的取值范围是_____________.15.甲、乙、丙三人中只有一人做了好事，他们各自都说了一句话，而且其中只有一句真话。

英语-辽宁省朝阳市普通高中2018届高三第一次模拟考试

辽宁省朝阳市普通高中2018届高三第一次模拟考试英语试题第一部分听力（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. When are the two speakers going to the school?A. On Saturday’s morning.B. On Sunday’s afternoon.C. On Saturday’s afternoon.2. Where does the man come from?A. America.B. England.C. Japan.3. What does the woman suggest the man do?A. Not smoke so heavily.B. Give up smoking.C. Take more exercise.4. What is the woman looking for?A. A friend’s house.B. A restaurant.C. A single room for night.5. When does the Boeing 747 leave for New York?A. At 8:05.B. At 8:45.C. At 8:55.第二节（共15小题；每小题1.5分,满分22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6至第7题。

6. What will the two speakers do this weekend?A. See a science fiction film.B. Go dancing at the Friendship Hotel.C. Have a meal in a Sichuan restaurant.7. How much will the two speakers spend on the film?A. ￥9.B. ￥6.C. ￥3.听第7段材料，回答第8至第9题。

数学文卷·2018届辽宁省朝阳市高三第一次模拟考试

A． B． C. D．
第Ⅱ卷（共90分）
二、填空题（每题5分，满分20分，将答案填在答题纸上）
13.设变量、满足约束条件，则最大值是．
14.抛物线：（）的准线与轴的交点为，过点作的两条切线，切点分别为，，则．
15.矩形中，，，平面，，，分别是，的中点，则四棱锥的外接球表面积为．
（2）由（1）知直线平面，故，到平面等距离
下面求到平面的距离，设这个距离是
由平面平面，，知平面，考虑三棱锥的体积：
因正方形边长为，所以
在中求得；在中求得，在中求得
于是可得的面积为，∴由得，，解得
故点到平面的距离为
19.（1）“成绩少于分”的频率
④的高度
21.已知函数（常数）.
（1）讨论的单调性；
（2）设是的导函数，求证： .
请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.
22.在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，圆的极坐标方程为，直线的参数方程为为参数，直线和圆交于，两点.
三、解答题
17.（1），且，∴ ．
．
（2）由（1）可得．
由正弦定理得，即，解得 .
在中，，，所以．
18.证明：（1）∵四边形和四边形都是正方形
∴ 且
∴四边形是平行四边形
连结交于，连结，则是中点.
∵ 是的中点，∴ 是边的中位线，，
注意到在平面外，在平面内，∴直线平面
附1：“ 列联表 ”的卡方统计量公式：
附2：卡方（）统计量的概率分布表：

2018届辽宁朝阳市三校协作体高三下学期第一次联合模拟考试文科数学试题及答案

2018学年度下学期三校协作体高三第一次联合模拟考试数学试卷（文史类）第I 卷（选择题, 共60分）一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．)1. 集合⎭⎬⎫⎩⎨⎧>+-=031x x xP ，{}24x y x Q -==，则=Q PA ．]2,1(B ．]2,1[C ．(,3)(1,)-∞-+∞D ．)2,1[ 2. 等差数列{}n a 的前n 项和为n S ，且3S =6，1a =4，则公差d 等于A ．1B ．35 C ．2-D ．33. 在ABC ∆中，3=AB ，1=AC ， 30=∠B ，ABC ∆的面积为23，则=∠CA ．30 B ． 45 C ． 60 D ． 754. 下列函数在),0(+∞上为减函数的是 A ．1--=x y B ．xe y = C ．)1ln(+=x yD ．)2(+-=x x y5. 设定义在R 上的奇函数()f x 满足)0(4)(2>-=x x x f ，则0)2(>-x f 的解集为A ．(4,0)(2,)-+∞ B ．(0,2)(4,)+∞ C ．(,0)(4,)-∞+∞D ．(4,4)-6. 将函数()()ϕ+=x x f 2sin 的图象向左平移8π个单位，所得到的函数图象关于y 轴对称，则ϕ的一个可能取值为A ．43π B ．4π C ．0D ．4π-7. 给出下列关于互不相同的直线m 、l 、n 和平面α、β的四个命题：① 若α⊂m ，A l =α ，点m A ∉，则l 与m 不共面；② 若m 、l 是异面直线，α//l ，α//m ，且l n ⊥，m n ⊥，则α⊥n ； ③ 若α//l ，β//m ，βα//，则m l //；④ 若α⊂l ，α⊂m ，A m l = ，β//l ，β//m ，则βα//，其中为真命题的是A ．①③④B ．②③④C ．①②④D ．①②③8. 变量x 、y 满足条件⎪⎩⎪⎨⎧->≤≤+-111x y y x ，则22)2(y x +-的最小值为 A ．223 B ．5 C ．29D ．59. 如图， AOB ∆为等腰直角三角形，1=OA ，OC 为斜边AB 的高，P 为线段OC 的中点，则AP A ．1- B ．81-C ．41- D ．21-10. 如图，四棱锥ABCD P -中， 90=∠=∠BAD ABC ，AD BC 2=，PAB∆和PAD ∆都是等边三角形，则异面直线CD 与PB 所成角的大小为A ． 90B ． 75C ．60D ．4511. 已知抛物线C ：x y 82=的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若QF PF 3=，则QF=BDCPAAA ． 25 B ． 38 C ． 3 D ． 612. 设xx f lg )(=，若函数ax x f x g -=)()(在区间)4,0(上有三个零点，则实数a 的取值范围是A ．10,e ⎛⎫ ⎪⎝⎭B ．lg 2lg ,2e e ⎛⎫ ⎪⎝⎭C ． lg 2,2e ⎛⎫ ⎪⎝⎭D ．lg 20,2⎛⎫ ⎪⎝⎭正视图侧视图第Ⅱ卷（非选择题, 共90分）二、填空题（本大题共4小题，每小题5分，共20分，将答案填在答题卡相应的位置上．）13. 正项等比数列{}n a 中，42=a ，164=a ，则数列{}n a 的前9项和等于．14. 它的体积为．15. 已知椭圆C ：2211612x y +=，点M与C 的焦点不重合，若M 关于C 的两焦点的对称点分别为P ，Q ，线段MN 的中点在C 上，则||||PN QN += ． 16．定义：如果函数)(x f y =在定义域内给定区间],[b a 上存在0x )(0b x a <<，满足ab a f b f x f --=)()()(0，则称函数)(x f y =是],[b a 上的“平均值函数”，0x 是它的一个均值点，例如2x y =是]1,1[-上的平均值函数，0就是它的均值点．现有函数mx x x f +=3)(是]1,1[-上的平均值函数，则实数m 的取值范围是．三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．）俯视图17.（本小题满分12分）设ABC ∆是锐角三角形，三个内角A ，B ，C 所对的边分别记为a ，b ，c ，并且)3sin()3sin()sin )(sin sin (sin B B B A B A +-=+-ππ.（Ⅰ）求角A 的值；（Ⅱ）若12=⋅AC AB ，72=a ，求b ，c （其中c b <）． 18.（本小题满分12分）已知数列}{n a 满足)(3)1)(1(11++-=--n n n n a a a a ，21=a ，令11-=n n a b . （Ⅰ）证明：数列}{n b 是等差数列；（Ⅱ）求数列}{n a 的通项公式．19.（本小题满分12分）ABC ∆为等腰直角三角形，4==BC AC ， 90=∠ACB ，D 、E 分别是边AC 和AB 的中点，现将ADE ∆沿DE 折起，使面ADE ⊥面DEBC ，H 是边AD 的中点，平面BCH 与AE 交于点I ．（Ⅰ）求证：IH//BC ；（Ⅱ）求三棱锥HIC A -的体积.AHICDBE20.（本小题满分12分）如图，抛物线1C ：px y 22=与椭圆2C ：1121622=+y x 在第一象限的交点为B ，O 为坐标原点，A 为椭圆的右顶点，OAB ∆的面积为368.（Ⅰ）求抛物线1C 的方程；（Ⅱ）过A 点作直线l 交1C 于C 、D 两点，求OCD ∆面积的最小值．21.（本小题满分12分）设函数)1(ln )(2-+=x b x ax x f )0(>x ，曲线)(x f y =过点)1,(2+-e e e ，且在点)0,1(处的切线方程为0=y .（Ⅰ）求a ，b 的值；（Ⅱ）证明：当1≥x 时，2)1()(-≥x x f ；（Ⅲ）若当1≥x 时，2)1()(-≥x m x f 恒成立，求实数m 的取值范围．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-1：几何证明选讲如图，四边形ABCD 是⊙O 的内接四边形，延长BA 和CD 相交于点P ，41=PBPA ，21=PC PD . （Ⅰ）求BCAD 的值；（Ⅱ）若BD 为⊙O 的直径，且1=PA ，求BC 的长．23.（本小题满分10分）选修4-4：坐标系与参数方程已知在平面直角坐标系xOy 中，直线l 的参数方程是P⎪⎪⎩⎪⎪⎨⎧+==242222t y t x （t 是参数），以原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程)4cos(2πθρ+=.（Ⅰ）判断直线l 与曲线C 的位置关系；（Ⅱ）设M 为曲线C 上任意一点，求y x +的取值范围．24.（本小题满分10分）选修4-5：不等式选讲已知函数212)(--+=x x x f .（Ⅰ）解不等式0)(≥x f ；（Ⅱ）若存在实数x ，使得a x x f +≤)(，求实数a 的取值范围．三校协作体高三第一次联合模拟考试数学试卷（文史类）答案及评分标准一、选择题：二、填空题：13. 1022 14. 83π 15. 16 16. 3(3,]4--三、解答题： 17.解：(Ⅰ)B B B B B A 22sin )sin 21cos 23()sin 21cos 23(sin +-⋅+= 43)sin (cos 4322=+=B B ， 23sin =∴A ，3π=∴A ． ………………………… 6分(Ⅱ) 12cos ==⋅A b AC AB ，24=∴bc ，又bc c b A bc c b a 3)(cos 22222-+=-+=，10=+∴c b ，c b < ，4=∴b ，6=c ．………………………… 12分18.解：(Ⅰ) [])1()1(3)1)(1(11---=--++n n n n a a a a ，3111111=---∴+n n a a ，即311=-+n n b b ，{}n b ∴是等差数列． (6)分(Ⅱ)11=b ，3231+=∴n b n ，………………………… 10分231+=-n a n ，25++=∴n n a n ．………………………… 12分19. (Ⅰ)因为D 、E 分别是边AC 和AB 的中点，所以BC ED //，因为⊂BC 平面BCH ，⊄ED 平面BCH ，所以//ED 平面BCH因为⊄ED 平面BCH ，⊂ED 平面AED ，平面BCH⋂平面HI AED =所以HI ED // 又因为BC ED //，所以IH //BC . …………………………………… 6分 (Ⅱ)211121=⨯⨯=∆AICS 高2=CD3122131=⨯⨯=V …………………………………… 12分20. 解: (Ⅰ)因为OAB∆的面积为368,所以364=B y ，……………2分代入椭圆方程得)364,34(B ，抛物线的方程是：x y 82= (6)分(Ⅱ) 直线CD 斜率不存在时，OCD S ∆=；直线CD 斜率存在时，设直线CD 方程为(4)y k x =-，带入抛物线，得28320ky y k --=121162OCD S OA y y ∆=-=>，综上OCDS ∆最小值为. (12)分21.解：(Ⅰ)()2ln f x a x ax b '=++，(1)0f a b '=+= ，22()(1)(1)f e ae b e a e e =+-=-+21e e =-+ 1=∴a ，1-=b ． (4)分(Ⅱ)2()ln 1f x x x x =-+，设22()ln g x x x x x =+-，(1)x ≥，()2ln 1g x x x x '=-+(())2ln 0g x x ''=>，∴)(x g '在[)+∞,0上单调递增，∴()(1)0g x g ''≥=，∴)(x g 在[)+∞,0上单调递增，∴()(1)0g x g ≥=．∴2()(1)f x x ≥-．………………………………8分（Ⅲ）设22()ln (1)1h x x x x m x =---+，()2ln 2(1)1h x x x x m x '=+---，(Ⅱ) 中知22ln (1)1(1)x x x x x x ≥-+-=-，∴ln 1x x x ≥-，∴()3(1)2(1)h x x m x '≥---，①当023≥-m 即23≤m 时，0)(≥'x h ，)(x h ∴在[1,)+∞单调递增，()(1)0h x h ∴≥=，成立．②当03<-m 即23>m 时，()2ln (12)(1)h x x x m x '=---，(())2ln 32h x x m ''=+-，令(())0h x '=，得232021m x e-=->，当[)01,x x ∈时，()(1)0h x h ''<=，)(x h ∴在[)01,x 上单调递减()(1)0h x h ∴<=，不成立．综上，23≤m ．………………………………12分22. (Ⅰ)由PAD ∠=PCB ∠，A A ∠=∠，得PAD ∆与PCB ∆相似，设,PA x PD y ==则有24x yy y x=⇒=，所以2AD x BC y == ………………………………5分 (Ⅱ)90C ∠=，4,PA PC ===10分23.解：(Ⅰ)直线l 的普通方程为0x y -+=曲线C 的直角坐标系下的方程为22((1x y -++=圆心到直线0x y -+=的距离为51d >所以直线l 与曲线C 的位置关系为相离. (5)分(Ⅱ)设cos ,sin )M θθ+，则cos sin )4x y πθθθ⎡+=+=+∈⎣.……………10分24. (Ⅰ)① 当12x ≤-时，1223x x x --+≥⇒≤-，所以3x ≤-② 当102x -<<时，12123x x x ++≥⇒≥，所以为φ③ 当0x ≥时，121x x +≥⇒≥，所以1x ≥综合①②③不等式的解集为(][),31,-∞-⋃+∞……………5分(Ⅱ)即12122122ax x a x x +-≤+⇒+-≤+ 由绝对值的几何意义，只需11322aa -≤+⇒≥-…………………10分。

高三数学辽宁省朝阳市普通高中2018年高三第一次模拟考试试题理科数学及参考答案

辽宁省朝阳市普通高中2018年高三第一次模拟考试数学试题(理)一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.若集合{|0}A y y =≥,AB B =,则集合B 不可能是( )A.{|0}y y x ≥B.1{|()}2R xy y x =∈， C.{|lg 0}y y x x =>，D.∅2.设复数z 满足(1i)1z -=(i 是虚数单位)，则||z 等于( )B.2C.12 D.23.按照程序框图(如图所示)执行，第3个输出的数是( )A.6B.5C.4D.34.已知数列{}n a 的通项公式262n a n =-,若使此数列的前n 项和n S 最大，则n 的值为( )A.12B.13C.12 或13D.145.《九章算术》是我国古代内容即为丰富的数学名著，书中有如下问题：“今有刍凳，下广三丈，袤四丈，上袤二丈，无广，高二丈，问：积几何？”其意思为：“今有底面为矩形的屋脊状的锲体，下底面宽3 丈，长4 丈，上棱长2 丈，高2 丈，问：它的体积是多少？”已知1 丈为10 尺，该锲体的三视图如图所示，在该锲体的体积为( )A.10000 立方尺B.11000 立方尺C.12000 立方尺D.13000 立方尺6.将函数π3sin(2)3y x =+的图象向右平移π3个单位长度后，再将所得图象上各点的纵坐标不变，横坐标压缩到原来的12倍，最终所得图象对应的函数的最小正周期为( ) A.π6 B.π2 C.5π6D.2π 7.设中心在原点、焦点在x 轴上的双曲线的焦距为12,圆22(6)20x y -+= 与该双曲线的渐近线相切，点P 在双曲线上，若点P 到焦点1F 的距离是9,则点P 到2F 的距离是( )A.17 或1B.13 或5C.13D.178.一个含有5 项的等比数列，其中每一项都是小于100 的正整数，这5 项的和为121,如果S 是数列中奇数项之和，则S 等于( )A.90B.91C.118D.1219.某地流行一种游戏，如图一是一长方形纸盒，高为4,宽为3,纸盒底部是一个“心形”图案，如图二所示，“心形”图案是由上边界1C (虚线L 上方部分)与下边界2C (虚线L 下方部分)围成，曲线1C 是函数45y x =的图象，曲线2C 是函数27y x =的图象，游戏者只需向纸盒内随机投掷一颗瓜子，若瓜子落在“心形”图案内部即可获奖，则一次游戏获奖的概率为( )A.π1627- B.π1-2427 C.π1-1227 D.π24+123510.从20名男同学和30名女同学中选4人去参加一个会议，规定男女同学至少各有1人参加，下面是不同的选法种数的三个算式：①112203048C C C ；②444502030C -C -C ；③132231203020302030C C +C C +C C .则其中正确算式的个数是( )A.0B.1C.2D.311.已知定义在R 上的奇函数()f x 可导，设其导函数为()f x '，当(0)x ∈-∞，时，恒有()()xf x f x '<-，令()()F x xf x =，则满足(3)(21)F F x >-的实数x 的取值范围是( )A.()21-，B.112⎛⎫- ⎪⎝⎭，C.122⎛⎫⎪⎝⎭， D.()12-， 12.在ABC △中，G 为ABC △的重心，过G 点的直线分别交AB ，AC 于P ，Q 两点，且AP hAB =，AQ k AC =，则1625h k +的最小值( )A.27B.81C.66D.41 二、填空题：每题5分，满分20分.13.设变量x 、y 满足约束条件2211x y x y x y -≤⎧⎪-≥-⎨⎪+≥⎩，则2z x y =+最大值是 .14.抛物线C ：22y px =(0p >)的准线与x 轴的交点为M ，过点M 作C 的两条切线，切点分别为P ，Q ，则PMQ ∠= .15.矩形ABCD 中，4AB =，2BC =，PA ⊥平面ABCD ，2PA =，E ，F 分别是AB ，DC 的中点，则四棱锥P EBCF -的外接球表面积为 . 16.函数1()sin (sin cos )2f x x x x =+-在区间π(π)2a a ，(01a <<)上有且仅有一个零点，则实数a 的取值范围是.三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17. 在ABC△中，已知45A=︒，4 cos5B=.(1)求cos C的值；(2)若10BC=，D为AB的中点，求CD的长.18. 在如图所示的几何体ABCDEF中，平面ABCD⊥平面ABEF，四边形ABCD和四边形ABEF都是正方形，且边长为2，Q是AD的中点.(1)求证：直线AE∥平面FQC；(2)求二面角A FC B--的大小.19. 为了调查学生数学学习的质量情况，某校从高二年级学生(其中男生与女生的人数之比为9:11)中，采用分层抽样的方法抽取n名学生依期中考试的数学成绩进行统计.根据数学的分数取得了这n名同学的数据，按照以下区间分为八组：①[3045)，，②[4560)，，③[6075)，，④[7590)，，⑤[90105)，，⑥[105120)，，⑦[120135)，，⑧[135150)，得到频率分布直方图如图所示.已知抽取的学生中数学成绩少于60分的人数为5人.(1)求n 的值及频率分布直方图中第④组矩形条的高度；(2)如果把“学生数学成绩不低于90分”作为是否达标的标准，对抽取的n 名学生，完成下列22⨯列联表：据此资料，你是否认为“学生性别”与“数学成绩达标与否”有关？(3)若从该校的高二年级学生中随机抽取3人，记这3人中成绩不低于120分的学生人数为X ，求X 的分布列、数学期望和方差附1：“22⨯列联表a b c d ”的卡方统计量公式：22()()()()()()a b c d ad bc K a b c d a c b d +++-=++++附2：卡方(2K )统计量的概率分布表：2()0.0500.0100.0013.841 6.63510.828P K k k≥20. 已知椭圆C ：22221x y a b+=(0a b >>)的左右焦点分别为1F ，2F 且2F 关于直线0x y a -+=的对称点M 在直线320x y +=上. (1)求椭圆的离心率；(2)若过焦点2F 垂直x 轴的直线被椭圆截得的弦长为3，斜率为12的直线l 交椭圆于A ，B 两点，问是否存在定点P ，使得PA ，PB 的斜率之和为定值？若存在，求出所有满足条件的P 点坐标；若不存在，说明理由.21. 已知函数2211()()ln 24f x x ax x x ax =--+(常数0a >).(1)讨论()f x 的单调性；(2)设()f x '是()f x 的导函数，求证：3()4e ln x f x a x -'<-.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，圆C 的极坐标方程为π)4ρθ=-，直线l 的参数方程为1x t y t =-⎧⎨=+⎩t 为参数，直线l 和圆C 交于A ，B 两点.(1)求圆C 的直角坐标方程；(2)设l 上一定点(01)M ，，求MA MB ⋅的值.23.已知函数()3f x x m =--，且()0f x ≥的解集为(2][4)-∞-+∞，， (1)求m 的值；(2)若R x ∃∈，使得()2f x t x ≥+-成立，求实数t 的取值范围.【参考答案】一、选择题1-5:CABCA 6-10:BDBCC 11-12：DA 二、填空题 13.10 14.π2 15.44π 16.1159()(]8488，，三、解答题 17.解：(1)4cos 5B =，且(0180)B ∈，，∴3sin 5B ==. cos cos(180)cos(135)C A B B =--=-243cos135cossin135sin 2525B B =+=-+10=(2)由(1)可得sin C =.由正弦定理得sin sin BC ABA C =AB =，解得14AB =. 在BCD △中，7BD =，22247102710375CD =+-⨯⨯⨯=，所以CD =18.证明：(1)∵且AF BE ∥，AD BC ∥AF 与AD 交于点A ，BE 与BC 交于点B∴平面ADF ∥平面BCE ，∴几何体ADF BCE -是三棱柱又平面ABCD ⊥平面ABEF ，AB BC ⊥，∴AB ⊥平面BCE ，故几何体ADF BCE -是直三棱柱(1)四边形ABCD 和四边形ABEF 都是正方形，所以EF AB DC ∥∥且EF AB DC ==，所以四边形DCEF 为矩形；于是，连结DE 交FC 于P ，连结PQ ，P 是DE 中点，又Q 是AD 的中点，故PQ 是边AE 的中位线，PQ AE ∥，注意到AE 在平面FQC 外，PQ 在平面FQC 内，∴直线AE ∥平面FQC(2)由于平面ABCD ⊥平面ABEF ，AB BC ⊥，∴BC ⊥平面ABEF ，所以BC BE ⊥. 于是AB ，BC ，BE 两两垂直.以BA ，BC ，BE 所在直线分别为x ，y ，z 轴建立空间直角坐标系，因正方形边长为2，且Q 为AD 中点，所以(210)Q ，，，(202)F ，，，(020)C ，，，(000)B ，，，于是(020)BC =，，，(202)BF =，，，设平面BFC 的法向量为()m x y z =，，则0m BC m BF ⎧⋅=⎪⎨⋅=⎪⎩，解之得(101)m =-，，，同理可得平面AFC 的法向量(110)n =，，， ∴1cos 2m n =，记二面角B FC A --的大小为θ，依题意知，θ为锐角，1cos 2θ=，π3θ= 即求二面角B FC A --的大小为π319. 解：(1)“成绩少于60分”的频率511()151001500375n n =+⋅⇒= ④的高度[7590)，的率距内频组151530151515151()150037537550601003001/12515-++++++== (2)按照“男生”和“女生”分层抽样在容量为100的样本中，“男生”人数910045911=⨯=+，“女生”人数1110055911=⨯=+“达标”即“成绩不低于90分”的频数1111()15100755060100300=+++⨯⨯= 据此可填表如下：据表可得卡方统计量22100(30104515)1004555752533K ⨯-⨯==⨯⨯⨯ 3.030 3.841=< 故有不足95%的把握认为“学生性别”与“数学成绩达标与否”有关可以认为它们之间没有关联(3)“成绩不低于120分”的频率111()151003005=+⨯=因高二年级的学生数远超过样本容量,故从该年级抽取任意1人的概率都可认为是15 从而1~(3)5X B ，则031464(0)()()55125P X ===，12148(1)()()55125P X 4===211412(2)()()55125P X ===，30141(3)()()55125P X === 故X 的分布列为：01236448121125125125125XP数学期望13()355E X =⨯=方差1112()3(1)5525D X =⨯⨯-=20. 解：(1)依题知2(0)F c ，，设00()M x y ，，则001y x c =--且00022x c y a +-+=，解得00x ay a c =-⎧⎨=+⎩，即()M a a c -+，∵M 在直线320x y +=上，∴32()0a a c -++=，2a c =，∴12c e a == (2)由(1)及题设得：12c a =且223b a =，∴2a =，b 22143x y +=设直线l 方程为12y x t =+，代入椭圆方程消去y 整理得2230x tx t ++-=. 依题0∆>，即24t <设11()A x y ，，22()B x y ，，则12x x t +=-，2123x x t =-如果存在()P m n ，使得PA PB k k +为定值，那么PA PB k k +的取值将与t 无关 1212PA PBy n y n k k x m x m --+=+--223()2323n m t mn t mt m -+-=++-，令223()2323n m t mn M t mt m -+-=++- 则223()32302Mt mM m n t m M M mn ++-+--+=为关于2(4)t t <的恒等式∴03223M n m mn =⎧⎪⎪=⎨⎪=⎪⎩，解得132m n =⎧⎪⎨=⎪⎩或132m n =-⎧⎪⎨=-⎪⎩综上可知，满足条件的定点P 是存在的，坐标为3(1)2--，及3(1)2，21. 解：(1)()()ln f x x a x '=-(0x >，0a >)画出y x a =-(0a >)及ln y x =(0x >)的图象，它们的零点分别为a 和1 ①当01a <<时，()f x 在(0)a ，↑，(1)a ↓，，(1)+∞↑， ②当1a =时，()f x 在(1)+∞↑，③当1a >时，()f x 在(01)↑，，(1)a ↓，，()a +∞↑， (2)因()()ln ln ln f x x a x x x a x '=-=-要证3()4e ln x f x a x -'<-，需证3ln 4e x x x -<(0x >)法1.即证32ln 4e x x x x-<(0x >)设ln ()xF x x =(0x >)，324e ()xG x x-=(0x >)一方面21ln ()xF x x -'=(0x >)()F x ⇒在(0e)↑，，(e )+∞↓，则1()(e)eF x F =≤① 另一方面，334(2)e ()x x G x x --'=(0x >)()G x ⇒在(02)↓，，(2)+∞↑，则1()(2)eG x G =≥②据①②()()F x G x ⇒≤有因①的取等条件是e x =，②的取等条件是2x =故()()F x G x <，即32ln 4e x x x x-<(0x >)，即3()4e ln x f x a x -'<- 法2先证1ln ex x ≤(0x >)(差函数) 进而21ln ex x x ≤(0x >) 再证2314e ex x -≤(差函数或商函数) 说明等号不成立故3ln 4e x x x -<(0x >)成立.22.解：(1)π)cos 4ρθθθ=-=2sin 2cos θθ=- ∴22sin 2cos ρρθρθ=-∴2222x y y x +=-∴22(1)(1)2x y ++-=(2)直线l的参数方程可化为1x y ⎧'=⎪⎪⎨⎪'=+⎪⎩t '为参数代入22(1)(1)2x y ++-=，得22(1))2''++=化简得：210t ''-=∴121t t ''⋅=-∴121MA MB t t ''=⋅= 23.解：(1)不等式30x m --≥的解集为(3][3)m m -∞-⋃++∞，，又∵()30f x x m =--≥的解集为(2][4)-∞-⋃+∞，， ∴34m +=，32m -=-∴1m =(2)∵x ∃∈R ，使得()2f x t x ≥+-成立∴R x ∃∈，使得132x t x --≥+-∴R x ∃∈，123x x t ---≥+ 令11()12231212x g x x x x x x -≤⎧⎪=---=-<≤⎨⎪>⎩∴x ∃∈R ，123x x t ---≥+∴max 3()1t g x +≤=∴2t ≤-.。

辽宁省朝阳市普通高中2018届高三第一次模拟考试数学(理)试卷(扫描版).doc

朝阳市 2018 年普通高中高三第一次模拟考试数学 (理)参考答案及评分标准一、选择题 :CABCA BDBCC D A2 15： 44 1 15 9二、填空题 13： 10 16(8,4) ∪(8,8]14：三、解答题：17：（Ⅰ） cos B4,且B(0 ,180 ) ，∴ sin B1 cos 2B355． ---------3 分cosC cos(180 A B) cos(135B)cos135 cos B sin135 sin B2 4 23 2． --------------6 分2 52 510（Ⅱ）由（Ⅰ）可得 sin C 1cos 2 B1 (2 )2 7 2 ． --------------8 分10AB10 10BCAB，解得 AB14 ． -----------10 分由正弦定理得，即27 sin Asin C2210104在 BCD 中， BD7， CD2721022 7 37，所以 CD37 ．-----12518. 证明 (1): ∵ 且AF ∥ BE,AD ∥ BCAF 与 AD 交于点 A,BE 与 BC 交于点 B∴平面 ADF ∥平面 BCE,∴几何体 ADF-BCE 是三棱柱 ,,,,2 分又平面 ABCD ⊥平面 ABEF,AB ⊥ BC,∴ AB ⊥平面 BCE,故几何体ADF-BCE 是直三棱柱; ,,,,,,4 分（1）四边形 ABCD 和四边形 ABEF 都是正方形，所以 EF ∥ AB ∥DC 且 EF=AB=DC ，所以四边形 DCEF 为矩形； ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,2 分于是，连结 DE 交 FC 于 P, 连结 PQ, P 是 DE 中点 , 又 Q 是 AD 的中点 , 故 PQ 是边 AE 的中位线 ,PQ∥AE ，注意到 AE 在平面 FQC 外 ,PQ 在平面 FQC 内 , ∴直线 AE ∥平面 FQC; ,,,,, 6 分 (2) 由于平面 ABCD ⊥平面 ABEF,AB ⊥BC,∴ BC ⊥平面 ABEF ，所以 BC ⊥ BE.于是 AB ，BC ， BE两两垂直。

2018年朝阳高三一模文科数学试题及答案

2018年朝阳高三一模文科数学试题及答案D三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15. （本小题满分13分）已知数列{}n a 的前n 项和n S 满足21n n S a =-*()n ∈N .（Ⅰ）求123,,a a a 的值;（Ⅱ）若数列{}n b 满足112,n n n b b a b +==+,求数列{}n b 的通项公式.16. （本小题满分13分）在ABC 中,已知5sin 5A =,2cos b a A =.（Ⅰ）若5ac =,求ABC 的面积;（Ⅱ）若B 为锐角,求sin C 的值.17. （本小题满分13分）某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:性别选考方案确定情况物理化学生物历史地理政治选考方案确定的有6人 6 6 3 1 2 0 男生选考方案待确定的有8人 5 4 0 1 2 1选考方案确定的有10人8 9 6 3 3 1 女生选考方案待确定的有6人 5 4 0 0 1 1（Ⅰ）试估计该学校高一年级确定选考生物的学生有多少人？（Ⅱ）写出选考方案确定的男生中选择“物理、化学和地理”的人数.（直接写出结果）（Ⅲ）从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.18. （本小题满分14分）如图1,在梯形ABCD 中,//,1,3,BC AD BC AD BE AD ==⊥于E ,1BE AE ==.将ABE 沿BE 折起至A BE ',使得平面A BE '⊥平面BCDE （如图2）,M 为线段A D '上一点.（Ⅰ）求证:A E CD '⊥;（Ⅱ）若M 为线段A D '中点,求多面体A BCME '与多面体MCDE 的体积之比;（Ⅲ）是否存在一点M ,使得//A B '平面MCE ?若存在,求A M '的长.若不存在,请说明理由.19. （本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=>>的离心率为22,且过点2(1,2. （Ⅰ）求椭圆C 的方程;（Ⅱ）过椭圆C 的左焦点的直线1l 与椭圆C 交于,A B 两点,直线2l 过坐标原点且直线1l 与2l 的斜率互为相反数,直线2l 与椭圆交于,E F 两点且均不与点,A B 重合,设直线AE 的斜率为1k ,直线BF 的斜率为2k ,证明:12k k +为定值.20. （本小题满分13分）已知函数ln 1()()x f x ax a x-=-∈R . （Ⅰ）若0a =,求曲线()y f x =在点(1,(1))f 处的切线方程;（Ⅱ）若1a <-,求函数()f x 的单调区间;（Ⅲ）若12a <<,求证:()1f x <-.北京市朝阳区2018届高三下学期3月综合练习（一模）数学（文）试题第I 卷（选择题共40分）一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集为实数集R ,集合22{|30},{|log 0}A x xx B x x =-<=>, 则()A B =R（A ）(,0](1,)-∞+∞ （B ）(0,1]（C ）[3,)+∞（D ）∅ 【答案】C【解析】本题考查集合的运算.集合2{|30}{|(3)0}{|03}A x xx x x x x x =-<=-<=<<, 集合222{|log 0}{|log log 1}{|1}B x x x x x x =>=>=>.所以{|0A x x =≤R 或3}x ≥,所以(){|3}A B x x =≥R ,故选C .2. 在复平面内,复数i 1i z=+所对应的点位于（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限【答案】A【解析】本题考查复数的运算与坐标表示.i i(1i)1i 1i (1i)(1i)2z -+===++-,在复平面内对应的点为11(,)22,在第一象限,故选A . 3. 已知平面向量(,1),(2,1)x x ==-a b ,且//a b ,则实数x 的值是（A ）1-（B ）1 （C ）2 （D ）1-或2 【答案】D【解析】本题考查平面向量的平行的坐标运算.由(,1),(2,1)x x ==-ab ,且//a b ,可以得到(1)2x x -=, 即22(2)(1)0x x x x --=-+=,所以1x =-或2x =,故选D .4. 已知直线m ⊥平面α,则“直线n m ⊥”是“//n α”的（A ）充分但不必要条件（B ）必要但不充分条件（C ）充要条件（D ）既不充分又不必要条件【答案】B【解析】本题考查线面位置关系的判定、性质与充分必要条件.（充分性）当m α⊥且n m ⊥时,我们可以得到//n α或n α⊂（因为直线n 与平面α的位置关系不确定）,所以充分性不成立;（必要性）当//n α时,过直线n 可做平面β与平面α交于直线a ,则有//n a .又有m α⊥,则有m a ⊥,即m n ⊥.所以必要性成立,故选B .5. 已知F 为抛物线2:4C y x =的焦点,过点F 的直线l 交抛物线C 于,A B 两点,若||8AB =,则线段AB 的中点M 到直线10x +=的距离为（A ）2（B ）4 （C ）8 （D ）16 【答案】B【解析】本题考查抛物线的定义.如图,抛物线24y x =的焦点为(1,0)F ,准线为1x =-,即10x +=.分别过,A B 作准线的垂线,垂足为,C D ,则有||||||||||8AB AF BF AC BD =+=+=.过AB 的中点M 作准线的垂线,垂足为N ,则MN 为直角梯形ABDC 中位线, 则1||(||||)42MN AC BD =+=,即M 到准线1x =-的距离为4.故选B . 6. 某四棱锥的三视图如图所示,则该四棱锥的体积等于（A ）13（B ）23（C ）12（D ）34 【答案】A【解析】本题考查三视图还原和锥体体积的计算抠点法:在长方体1111ABCD A B C D -中抠点,1.由正视图可知:11C D 上没有点;2.由侧视图可知:11B C 上没有点;3.由俯视图可知:1CC 上没有点;4.由正（俯）视图可知:,D E 处有点,由虚线可知,B F 处有点,A 点排除.由上述可还原出四棱锥1A BEDF -,如右图所示,111BEDF S =⨯=四边形,1111133A BEDF V -=⨯⨯=. 故选A .7. 函数2πsin 12()12x f x x x=-+的零点个数为（A ）0（B ）1 （C ）2 （D ）4 【答案】C【解析】本题考查函数零点.2πsin 12(),12x f x x x=-+定义域为(,0)(0,)-∞+∞, 通分得:()22π2sin 122(1)x x x f x x x --=+, 设()1π2sin 2f x x x =,()221f x x =+, ()()12f x f x =时,()0f x =,画出大致图象如下.易发现()()12112f f ==,即()1f x 与()2f x 交于点()1,2A , 又()1πππcos 2sin 22f x x x x '=⋅+,()22f x x '=, ()()12112f f ''∴==即点A 为公切点,∴点A 为()0,+∞内唯一交点,又()()12,f x f x 均为偶函数,∴点()1,2B -也为公切点,∴,A B 为交点,()f x 有两个零点.故选C8. 某学校举办科技节活动,有甲、乙、丙、丁四个团队参加“智能机器人”项目比赛,该项目只设置一个一等奖.在评奖揭晓前,小张、小王、小李、小赵四位同学对这四个参赛团队获奖结果预测如下:小张说:“甲或乙团队获得一等奖”;小王说:“丁团队获得一等奖”;小李说:“乙、丙两个团队均未获得一等奖”;小赵说:“甲团队获得一等奖”.若这四位同学中只有两位预测结果是对的,则获得一等奖的团队是（A）甲（B）乙（C）丙（D）丁【答案】D【解析】本题考查学生的逻辑推理能力.1.若甲获得一等奖,则小张、小李、小赵的预测都正确,与题意不符;2.若乙获得一等奖,则只有小张的预测正确,与题意不符;3.若丙获得一等奖,则四人的预测都错误,与题意不符;4.若丁获得一等奖,则小王、小李的预测正确,小张、小赵的预测错误,符合题意.故选D.第Ⅱ卷（非选择题共110分）二、填空题:本大题共6小题,每小题5分,共30分.m 则输出k的值为______.9. 执行如图所示的程序框图,若输入5,【答案】4【解析】本题考查程序框图.m k初始 5 0第一次9 1第二次17 2第三次33 3第四次 65 4第四次时,6550>,所以4k =.10. 双曲线2214x y -=的焦距为______;渐近线方程为______. 【答案】125,2y x =± 【解析】本题考查双曲线的基本量.由题知224,1,a b ==故2225c a b =+=,焦距:225c =,渐近线:12b y x x a =±=±. 11. 已知圆22:2410C x y x y +--+=内有一点(2,1),P 经过点P 的直线l 与圆C交于,A B 两点,当弦AB 恰被点P 平分时,直线l 的方程为______.【答案】1y x =-【解析】本题考查直线与圆的位置关系.圆22:(1)(2)4C x y -+-=,弦AB 被P 平分,故PCAB ⊥, 由(2,1),(1,2)P C 得1pc lk k ⋅=-即1l k =,所以直线方程为1y x =-.12. 已知实数,x y 满足1010,1x y x y y +-≥⎧⎪--≤⎨⎪≤⎩若(0)z mx y m =+>取得最小值的最优解有无数多个,则m 的值为______.【答案】1【解析】本题考查线性规划.:l y mx z =-+,0m -<,z 取得最小值,则直线l 的截距最小,最优解有无数个,即l 与边界重合,故1m =.13. 函数()sin()f x A x ωϕ=+π(0,0,)2A ωϕ>><的部分图象如图所示,则______;ϕ=______.ω=【答案】4;63π-【解析】本题考查三角函数的图象与性质.由图可知,0,6,22x x x x πωϕππωϕ⎧=+=-⎪⎪⎨⎪=+=⎪⎩解得4,63πϕω=-=. 14. 许多建筑物的地板是用正多边形的砖板铺成的（可以是多种正多边形）.如果要求用这些正多边形的砖板铺满地面,在地面某一点（不在边界上）有k 块砖板拼在一起,则k 的所有可能取值为______.【答案】3,4,5,6【解析】本题考查逻辑推理与多边形的性质.由题意知只需这k 块砖板的角度之和为360︒即可.显然3k ≥,因为任意正多边形内角小于180︒;且6k ≤,因为角度最小的正多边形为正三角形,360660︒︒=. 当3k=时,3个正六边形满足题意; 当4k=时,4个正方形满足题意; 当5k=时,3个正三角形与2个正方形满足题意; 当6k =时,6个正三角形满足题意.综上,所以k 可能为3,4,5,6.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15. （本小题满分13分）已知数列{}n a 的前n 项和n S 满足21n n S a =-*()n ∈N .（Ⅰ）求123,,a a a 的值;（Ⅱ）若数列{}n b 满足112,n n n b b a b +==+,求数列{}n b 的通项公式.【解析】（Ⅰ）由题知11121,S a a ==-得11a =,221221,S a a a =-=+得2112,a a =+=3312321,S a a a a =-=++得31214a a a =++=,（Ⅱ）当2n ≥时,1121,21,n n n n S a S a --=-=-所以1121(21)n n n n n a S S a a --=-=---,得122n n n a a a -=-,即12n n a a -=,{}n a 是以11a =为首项,2为公比的等比数列,则12n n a -=.当2n ≥时,1211()()n n n b b b b b b -=+-++-1212n a a a -=++++,111(12)22112n n a ---=+=+-,经验证:111221b -==+,综上:121n n b -=+.16. （本小题满分13分）在ABC 中,已知5sin 5A =,2cos b a A =.（Ⅰ）若5ac =,求ABC 的面积;（Ⅱ）若B 为锐角,求sin C 的值.解:（Ⅰ）由正弦定理得sin sin A a B b=,因为2cos b a A =, 所以sin 2sin cos B A A =,cos =02b A a >, 因为5sin 5A =,所以25cos 5A =, 所以5254sin 2555B =⨯⨯=, 114sin 52225ABC S ac B ==⨯⨯=. （Ⅱ）由（Ⅰ）知4sin 5B =, 因为B 为锐角,所以3cos 5B =. sin =sin(π)sin()C A B A B --=+sin cos cos sin A B A B =+532545555=⨯+⨯ 115=25 17. （本小题满分13分）某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表: 性别选考方案确定情况物理化学生物历史地理政治男生选考方案确定的有6人6 6 3 1 2 0 选考方案待确定的有8人 5 4 0 1 2 1女生选考方案确定的有10人8 9 6 3 3 1 选考方案待确定的有6人 5 4 0 0 1 1（Ⅰ）试估计该学校高一年级确定选考生物的学生有多少人？（Ⅱ）写出选考方案确定的男生中选择“物理、化学和地理”的人数.（直接写出结果）（Ⅲ）从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.【解析】（Ⅰ）设该学校选考方案确定的学生中选考生物的学生为,x因为在选考方案确定的学生的人中,选生物的频率为3+63=,8+6+10+610所以选择生物的概率约为3,10所以选择生物的人数约为3420=12610x =⨯人. （Ⅱ）2人.（Ⅲ）设选择物理、生物、化学的学生分别为123,,,A A A选择物理、化学、历史的学生为1B ,选择物理、化学、地理的学生分别为12,,C C所以任取2名男生的基本事件有1223311112(,),(,),(,),(,),(,)A A A A A B B C C C13213212(,),(,),(,),(,)A A A B A C B C112131(,),(,),(,)A B A C A C1122(,),(,)A C A C12(,)A C所以两名男生所学科目相同的基本事件共有四个,分别为12231213(,),(,),(,),(,),A A A A C C A A 概率为4.1518. （本小题满分14分）如图1,在梯形ABCD 中,//,1,3,BC AD BC AD BE AD ==⊥于E ,1BE AE ==.将ABE 沿BE 折起至A BE ',使得平面A BE '⊥平面BCDE （如图2）,M 为线段A D '上一点.（Ⅰ）求证:A E CD '⊥;（Ⅱ）若M 为线段A D '中点,求多面体A BCME '与多面体MCDE 的体积之比;（Ⅲ）是否存在一点M ,使得//A B '平面MCE ?若存在,求A M '的长.若不存在,请说明理由.【解析】（Ⅰ）在梯形ABCD 中,因为BE AE ⊥,所以'A E BE ⊥, 平面'A BE ⊥平面BCDE ,BE =平面'A BE 平面BCDE , 'A E ⊂平面'A BE ,'A E ∴⊥平面BCDE ,CD ⊂平面BCDE ,'A E CD ∴⊥.（Ⅱ）M 为'A D 中点,M ∴到底面BCDE 的距离为1'2A E ,在梯形ABCD 中,1121122DCE S DE BE =⋅=⨯⨯=,111'326M DCE DCE V A E S -=⋅⋅=,'11'36A BCE BCE V A E S -=⋅⋅=.'A E DE ⊥,∴在'Rt A DE 中,'12A EM S =,'A E ⊥平面BCDE ,'A E ⊂平面'A DE ,∴平面'A DE ⊥平面BCDE ,,BE ED ⊥平面'A DE 平面BCDE ED =,//BC AD ,C ∴到平面'A DE 的距离为1BE =.''1136C A EM A EM V BE S -∴=⋅⋅=,'''13A BCME CA EM A BCE V V V =+=多面体多面体多面体. ':2:1A BCME MCDE V V ∴=多面体多面体.（Ⅲ）连结BD 交CE 于O ,连结OM ,在四边形BCDE 中,//BC DE ,BOC DOE ∴∽,23OD BD ∴=, '//A B 平面CME ,平面'A BD 平面CEM OM =, '//A B OM ∴,在'A BD 中,//'OM A B ,'1'3A M BO A D BD ∴==, '1,2,'A E DE A E ED ==⊥, ∴在'Rt A ED 中,'5A D =5'3A M ∴=.19. （本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=>>的离心率为22,且过点2(1,2. （Ⅰ）求椭圆C 的方程;（Ⅱ）过椭圆C 的左焦点的直线1l 与椭圆C 交于,A B 两点,直线2l 过坐标原点且直线1l 与2l 的斜率互为相反数,直线2l 与椭圆交于,E F 两点且均不与点,A B 重合,设直线AE 的斜率为1k ,直线BF 的斜率为2k ,证明:12k k +为定值.【解析】（Ⅰ）由题可得222222222121c aa b a b c ⎧=⎪⎪⎪⎪⎨+=⎪⎪⎪⎪=+⎩,解得211a b c ⎧=⎪=⎨⎪=⎩. 所以椭圆C 的方程为2212x y +=. （Ⅱ）由题知直线1l 斜率存在,设11122:(1),(,),(,)l y k x A x y B x y =+.联立22(1)22y k x x y =+⎧⎨+=⎩, 消去y 得2222(12)4220k x k x k +++-=,由题易知0∆>恒成立, 由韦达定理得22121222422,1212k k x x x x k k-+=-=++,因为2l 与1l 斜率相反且过原点,设2:l y kx =-,3333(,),(,)E x y F x y --,联立2222y kx x y =-⎧⎨+=⎩, 消去y 得22(12)20k x +-=,由题易知0∆>恒成立, 由韦达定理得232212x k --=+, 则1323121323y y y y k k x x x x -++=+-+13231323(1)(1)k x kx k x kx x x x x +++-=+-+ 132323131323(1)()(1)()()()x x x x x x x x k x x x x ++++-+-=⋅-+ 212312132322()()x x x x x k x x x x +++=⋅-+ 2222213232(22)224121212()()k k k k k k x x x x -⨯-+++++=⋅-+0=所以12k k +为定值0.20. （本小题满分13分）已知函数ln 1()()x f x ax a x -=-∈R .（Ⅰ）若0a =,求曲线()y f x =在点(1,(1))f 处的切线方程; （Ⅱ）若1a <-,求函数()f x 的单调区间;（Ⅲ）若12a <<,求证:()1f x <-.解:（Ⅰ）若0a =,则(1)1f =-,22ln (),(1)2xf x f x -''==,所以()f x 在点(1,1)-处的切线方程为230x y --=. （Ⅱ）222ln (0,),().ax xx f x x --'∈+∞=令2()2ln g x ax x =--,则221()ax g x x --'=.令()0g x '=,得12x a =±-依题意102a ->)由()0g x '>,得12x a >-由()0g x '<,得102x a <<-所以,()g x 在区间12a -上单调递减,在区间1(,)2a -+∞上单调递增所以,min 151().222g x g a a =-=--因为1a <-,所以1110,ln 0222a a <-<-<.所以()0g x >,即()0f x '>.所以函数()f x 的单调递增区间为(0,)+∞.（Ⅲ）由0,()1x f x ><-,等价于ln 11x ax x --<-,等价于21ln 0ax x x -+->.设2()1ln h x ax x x =-+-,只须证()0h x >成立. 因为2121()21,12,ax x h x ax a x x --'=--=<<由()0h x '=,得2210ax x --=有异号两根. 令其正根为0x ,则200210ax x --=.在0(0,)x 上()0h x '<,在0(,)x +∞上()0h x '> 则()h x 的最小值为20000()1ln h x ax x x =-+-00011ln 23ln .2x x x x x +=-+--=- 又13(1)220,()2()30,222ah a h a ''=->=-=-< 所以01 1.2x << 则0030,ln 0.2x x ->-> 因此003ln 0,2x x -->即0()0.h x >所以()0h x >. 所以()1f x <-.。

2018年高三最新朝阳区高三第一次统一考试数学试卷(理

朝阳区高三第一次统一考试数学试卷(理科)一、选择题:(1) 设全集U=R，集合M={ x | x >0 }，N={x| x2≥x }，则下列关系中正确的是（）A．M∩N∈M B．M∪N⊆MC．(C U M)∪(C U N)=φD．(C U N)∩M⊆M(2)在△ABC中，sin2A=sin2B是A=B的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件(3) 已知a、b是两条不重合的直线，α、β是两个不重合的平面，给出四个命题：①a∥b，b∥α，则a∥α；②a、b⊂α，a∥β，b∥β，则α∥β；③a与α成30°的角，a⊥b，则b与α成60°的角；④a⊥α，b∥α，则a⊥b.其中正确命题的个数是（）A．4个B．3个C．2个D．1个（4）已知等比数列{a n}的前n项和为S n，S3=3，S6=27，则此等比数列的公比q等于（）A. 2B.-2C.12D. -12(5)从4位男教师和3位女教师中选出3位教师，派往郊区3所学校支教，每校1人.要求这3位教师中男、女教师都要有，则不同的选派方案共有（）A．210种B．186种C．180种D．90种(6) 已知函数f(x)=-在区间M上的反函数是其本身，则M可以是（）A．[-2，2] B．[-2，0] C．[0，2] D．[-2，0)(7) 已知椭圆焦点是F1、F2，P是椭圆上的一个动点，过点F2向∠F1PF2的外角平分线作垂线，垂足为M，则点M的轨迹是（）A. 圆B．椭圆C. 直线D．双曲线的一支(8) 已知计算机中的某些存储器有如下特性：若存储器中原有数据个数为m个，则从存储器中取出n个数据后，此存储器中的数据个数为m-n个；若存储器中原有数据为m个，则将n个数据存入存储器后，此存储器中的数据个数为m+n个.现已知计算机中A、B、C三个存储器中的数据个数均为0，计算机有如下操作：第一次运算：在每个存储器中都存入个数不小于2的数据；第二次运算：从A存储器中取出2个数据，将这2个数据存入B存储器中；第三次运算：从C存储器中取出1个数据，将这1个数据存入B存储器中；第四次运算：从B存储器中取出与A存储器中个数相同的数据，将取出的数据存入A存储器，则这时B 存储器中的数据个数是（）A . 8B . 7C . 6D . 5二、填空题:(9) 设复数z 1=1+2i ，z 2=2-i ，则12z z 等于． (10) 若(1-ax )6的展开式中x 4的系数是240，则实数a 的值是 .(11)圆x 2+y 2+4x -2y +4=0上的点到直线x -y -1=0的最大距离与最小距离的差为 . (12) 已知一个球与一个二面角的两个半平面都相切，若球心到二面角的棱的距离是5，切点到二面角棱的距离是1，则球的表面积是，球的体积是 . (13)已知向量a = (2，3)，|b |a ∥b ，则|a |= ，b 的坐标是. (14)已知函数f (x )=|1|(1),3(1),x x x x +<⎧⎨-+⎩≥且不等式f (x )≥a 的解集是(]2-∞-，∪[0，2]，则实数a 的值是 . 三、解答题:(15)（本小题满分13分）已知a = (cos x ，sin x )，b = (-cos x ，cos x )，函数f (x )= 2a ·b +1. (Ⅰ)求函数f (x )的最小正周期；(Ⅱ) 当x ∈[0，2π]时，求f (x )的单调减区间. (16)（本小题满分13分）甲、乙两支篮球队进行比赛，已知每一场甲队获胜的概率为0.6，乙队获胜的概率为0．4，每场比赛均要分出胜负. 比赛时采用三场两胜制，即先取得两场胜利的球队胜出. (Ⅰ)求甲队以二比一获胜的概率；(Ⅱ)求乙队获胜的概率； (Ⅲ)若比赛采用五场三胜制，试问甲获胜的概率是增大还是减小，请说明理由. (17)（本小题满分13分）如图，棱长为1的正四面体ABCD 中，E 、F 分别是棱AD 、CD 的中点，O 是点A 在平面BCD 内的射影.(Ⅰ)求直线EF 与直线BC 所成角的大小； (Ⅱ)求点O 到平面ACD 的距离； (Ⅲ) 求二面角A-BE-F 的大小.· ABCDEFO(18)（本小题满分13分）已知函数f (x )= x 3+ax 2+bx +c 在x =1处有极值，f (x )在x =2处的切线l 不过第四象限且斜率为1，坐标原点到切线l的距离为2． (Ⅰ) 求a 、b 、c 的值； (Ⅱ) 求函数y = f (x )在区间[-1，32]上的最大值和最小值． (19)（本小题满分14分）已知双曲线的中心在原点O ，右焦点为(,0)F c ，P 是双曲线右支上任意一点，且OFP∆（Ⅰ）若点P 的坐标为(2，求此双曲线的离心率；（Ⅱ）若26(1)OF FP c ⋅=，当OP 取得最小值时，求此双曲线的方程. (20)（本小题满分14分）已知数列{}n a 的前n 项和为n S ，点,n S n n⎛⎫⎪⎝⎭在直线11122y x =+上．数列{}n b 满足2120n n n b b b ++-+=*()n N ∈，且311b =，前9项和为153．（Ⅰ）求数列{}n a 、{}n b 的通项公式；（Ⅱ）设3(211)(21)n n n c a b =--，数列{}n c 的前n 项和为n T ，求使不等式57n k T >对一切*n N ∈都成立的最大正整数k 的值；（Ⅲ）设**(21, ),() (2, ).n n a n l l N f n b n l l N ⎧=-∈⎪=⎨=∈⎪⎩是否存在*m N ∈，使得(15)5()f m f m +=成立？若存在，求出m 的值；若不存在，请说明理由．朝阳区高三第一次统一考试数学试卷答案(理科)一.选择题（1）D （2）B （3） D （4）A （5）C （6）B （7）A （8）D 二.填空题（9）i （10）±2 （11）2 （12）16π 323π（13（-4，-6）或（4，6）（14）1三.解答题(15) 解：(Ⅰ)因为f (x )= 2a ·b +1 = 2(cos x ，sin x )·(-cos x ，cos x )+1=2(-cos 2x + sin x cos x ) +1 ……………………………………2分 =1-2cos 2x + 2sin x cos x=sin2x -cos2x ……………………………………4分x -4π) ……………………………………6分所以f (x )的最小正周期是T=22π= π. ……………………………………7分(Ⅱ)依条件得2k π+2π≤2x -4π≤2k π+32π(k ∈Z). ………………………………9分解得k π+38π≤x ≤k π+78π(k ∈Z). ……………………………………11分又x ∈[0，2π]，所以38π≤x ≤78π，118π≤x ≤158π.即当x ∈[0，2π]时，f (x )的单调减区间是[38π，78π]，[118π，158π]. …………13分(16) 解： (Ⅰ)甲队以二比一获胜，即前两场中甲胜1场，第三场甲获胜，其概率为P 1=12C ×0.6×0.4×0.6=0.288. ……………………………………4分(Ⅱ)乙队以2：0获胜的概率为 20.40.40.16P '=⨯=；乙队以2：1获胜的概率为 1220.40.60.40.192P C ''=⨯⨯=∴乙队获胜的概率为 P 2=0.42+12C ×0.4×0.6×0.4=0.16+0.192=0.352. …………………8分(Ⅲ)若三场两胜，则甲获胜的概率P 3=0.62+12C ×0.6×0.4×0.6=0.36+0.288=0.648或P 3=1- P 2=1-0.352=0.648；若五场三胜，则甲获胜的概率P 3′=0.63+23C ×0.62×0.4×0.6+24C ×0.62×0.42×0.6=0.216+0.2592+0.21836=0.68256. ……………………………………12分 ∵P 3< P 3′,∴采用五场三胜制，甲获胜的概率将增大. ……………………………………13分 (17) 方法一：(Ⅰ)因为E 、F 分别是棱AD 、CD 的中点，所以EF ∥AC .所以∠BCA 是EF 与BC 所成角.∵正四面体ABCD ，∴△ABC 为正三角形，所以∠BCA=60°.即EF 与BC 所成角的大小是60°. ……………………………………3分 (Ⅱ)解法1：如图，连结AO ，AF ，因为F 是CD 的中点，且△ACD ，△BCD 均为正三角形，所以BF ⊥CD ，AF ⊥CD . 因为BF ∩AF=F ，所以CD ⊥面AFB . 因为CD 面ACD ，所以面AFB ⊥面ACD . 因为ABCD 是正四面体，且O 是点A 在面BCD 内的射影，所以点O 必在正三角形BCD 的中线BF 上. 在面ABF 中，过O 做OG ⊥AF ，垂足为G ，所以OG ⊥面ACD .即OG 的长为点O 到面ACD 的距离. 因为正四面体ABCD 的棱长为1，在△ABF 容易求出，OF=，AO=3因为△AOF ∽△OGF ，故由相似比易求出所以点O 到平面ACD 的距离是· A B CD E FO G· ABCDEFO9……………………………………8分解法2：如图，连结AO ，CO ，DO ，所以点O 到平面ACD 的距离就是三棱锥 O-ACD 底面ACD 上的高h . 与解法1同理容易求出所以V A -COD =1312·.因为V O -ACD =V A -COD ，所以36= V O -ACD =13·h ·(12·2·1) .解得h(Ⅲ) 设△ABD 中，AB 边的中线交BE 于H ，连结CH ，则由ABCD 为正四面体知 CH ⊥面ABD .设HD 的中点为K ，则FK ∥CH . 所以FK ⊥面ABD .在面ABD 内，过点K 作KN ∥AD ， KN 交BE 于M ，交AB 于N ，因为BE ⊥AD ，所以NM ⊥BE. 连结FM ，所以FM ⊥BE.所以∠NMF 是所求二面角的平面角. 因为FK=12CH=12MK=12ED=14AD=14，所以tan ∠FMK=FK MK. HKM· A BCDEFON所以tan ∠NMF=tan (π-∠FMK)=-3. 所以所求二面角的大小为π-arctan3. ……………………………………13分（或者由正四面体的对称性，可转求二面角C —BF —E 的大小）方法二：如图，以点A 在面BCD 的射影O 为坐标原点，有向直线OA 为z 轴，有向直线BF 为y 轴，x过点O 与DC 平行方向.因为正四面体ABCD 的棱长为1，所以可以求出各点的坐标依次为：O(0，0，0)，A(0，0，B(0，0)C(12，6，0)，D(-12，6，0)， E(-14，12，6，F(0，6，0).(Ⅰ)因为EF =(14，，=(12，，0)，又EF ·=14×12+0=18+18=14，且|EF |=12||=12，||=1，所以cos 〈EF ，BC 〉=14112=12.所以EF 与BC 所成角的大小是60°. ……………………………………3分 (Ⅱ) 因为AC =(12，)， AD =(-12，设平面ACD 的一个法向量为F ACD = (x 1，y 1，z 1)，由AC ·F ACD =0，AD ·F ACD =0，解得F ACD = (0，2，22). CD因为OF =(0，6，0)，OF ·F ACD =33，| F ACD|=2，所以点O 到平面ACD 的距离等于d =ACD ACD OF ⋅F F =33×3=…………8分(Ⅲ)因为AB =(0，-33，，AD =(-12，，，设平面ABD 的一个法向量为F ABD = (x 2，y 2，z 2)， AB ·F ABD =0，AD ·F ABD =0，可得一个法向量F ABD = (-6，-2， 1).同理可以求出平面BEF 的一个法向量为F BEF = (26，0，3). 因为F ABD ·F BEF =-9，|F ABD |=3，|F BEF|= 所以co s β=ABD BEF ABD BEF ⋅F F F F=所以二面角A-BE-F 的大小为arccos (-)=π-…………13分 (18) 解：(I) 由f (x )= x 3+ax 2+bx +c ，得f ′(x )= 3x 2+2ax +b ． ………………………2分∵x =1时f (x )有极值，∴f ′(1)= 3+2a +b =0． ① ∵f (x )在x =2处的切线l 的斜率为1，∴f ′(2)= 12+4a +b =1． ②由①②可解得a = -4，b =5． ……………………………………4分设切线l 的方程为y =x + m ，由坐标原点（0，0）到切线l的距离为2，可得m =±1，又切线不过第四象限，所以m =1，切线方程为y =x +1． ……………………………6分 ∴ 切点坐标为(2，3)，∴f (2)=8-16+10+c =3，所以c =1．故a = -4，b =5，c =1． ……………………………………7分（Ⅱ）由（Ⅰ）知f (x )= x 3-4x 2+5x +1，f ′(x )= 3x 2-8x +5=(x -1)(3x -5)．∵x ∈[-1，32]，∴ 函数f (x )在区间[-1，1]上递增，在3(1,]2上递减 . ………9分又f (-1)=-9，f (1)=3，f (32)=238， ……………………………………12分∴f(x)在区间[-1，32]上的最大值为3，最小值为-9．……………………………13分(19)解：（Ⅰ）设所求的双曲线的方程为22221(0,0) x ya ba b-=>>，则1||22OF=，∴c=……………………………………1分∴22222b c a a=-=-．……………………………………2分由点P在双曲线上，∴224312a a-=-，解得21a=，……5分∴离心率cea==……………………………………6分（Ⅱ）设所求的双曲线的方程为22221(0,0)x ya ba b-=>>，11(,)P x y，则11(,)FP x c y=-. ……………………………………7分∵OFP∆112OF y=∴1y=……8分∵26(1)OF FP c⋅=-, ∴21()1)OF FP x c c c⋅=-=.解得13x=. ……………………………………9分∵22OP x=, …………………………11分当且仅当c=. …………………………………12分此时P.由此得2222221,3a ba b⎧-=⎪⎨⎪+=⎩解得2212ab⎧=⎨=⎩或2263ab⎧=⎨=-⎩（舍）.故所求双曲线的方程为2212y x -=. …………………………………14分(20)解：（Ⅰ）由题意，得11122n S n n =+，即211122n S n n =+．故当2n ≥时，1n n n a S S -=-=2111()22n n +2111[(1)(1)]22n n --+-5n =+．注意到1n =时，116a S ==，而当1n =时，56n +=，所以， *5 ()n a n n N =+∈． ………………………………………3分又2120n n n b b b ++-+=，即211n n n n b b b b +++-=-*()n N ∈，所以{}n b 为等差数列，于是379()1532b b +=．而311b =，故723b =，2311373d -==-，因此，33(3)32n b b n n =+-=+，即32n b n =+*()n N ∈．………………5分（Ⅱ）3(211)(21)n n n c a b =--3[2(5)11][2(32)1]n n =+-+-1111(21)(21)22121n n n n ⎛⎫==- ⎪-+-+⎝⎭．所以，12n n T c c c =+++1111111112335572121n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦11122121nn n ⎛⎫=-= ⎪++⎝⎭． ………………………………………8分由于112321n n n n T T n n ++-=-++10(23)(21)n n =>++，因此n T 单调递增，故min 1()3n T =．令1357k >，得19k <，所以 max 18k =． …………………………………10分（Ⅲ）**+5 (21, ),()3 2 (2, ).n n l l N f n n n l l N ⎧=-∈⎪=⎨+=∈⎪⎩ ① 当m 为奇数时，15m +为偶数．此时(15)3(15)2347f m m m +=++=+，5()5(5)525f m m m =+=+，所以347m +525m =+，11m =． …………………………………12分 ② 当m 为偶数时，15m +为奇数．此时(15)15520f m m m +=++=+，5()5(32)1510f m m m =+=+，所以20m +1510m =+，*57m N =∉（舍去）．综上，存在唯一正整数11m =，使得(15)5()f m f m +=成立．…………………………………14分。