2014年上城区一模数学试卷(含答案)

合集下载

2014年杭州市杭州中考一模试卷汇编

2014-2015杭州市中考一模试卷汇编2014年杭州市西湖区中考数学一模试卷 (2)2014年杭州市上城区中考数学一模试卷 (11)2014年杭州市下城区一模测试卷 (16)2014杭州市拱墅区中考数学一模试卷 (23)2014年杭州市滨江区一模测试卷 (29)2014年杭州市西湖区中考数学一模试卷一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的4个选项中，只有一个是正确的，请把正确选项前的字母在答题卡中相应的方框内涂黑，注意可以用多种不同的方法来选取正确答案。

1、)3(2)3(12-⨯--÷结果为（）A.18B.-10C.2D.18 2、如图，⊙O 是△ABC 的外接圆，∠OBC=40°，则∠A 的度数为（）A.40°B.50°C.80°D.100°3、已知a+1<b,且c 为非零实数，则可得（）A.bc ac <B.22bc ac < C.bc ac > D.22bc ac >4、将一个半径为6，圆心角为120°的扇形围城圆锥的侧面（无重叠），则圆锥的侧面积为（）A.6B.12C.6πD.12π 5、要使抛物线1632+-=x x y 平移后经过点（1,4），则可以将此抛物线（）A.向下平移2个单位B.向上平移6个单位C.向右平移1个单位D.向左平移2个单位6、同一平面内，若两圆圆心距是1与1，则两圆的位置关系是（）A.内含B.外离C.相交D.内切7、一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6，投两次骰子，设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为P0，P1，P2，P3，则P0，P1，P2，P3中最大的是（）A. P0B. P1C. P2D. P38、某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道，为尽量减少施工对交通造成的影响，实施施工时“……”，设实际每天铺设管道x米，则可得方程300030001510x x-=-，根据此情景，题中用“……”表示的缺失的条件应补为（）A.每天比原计划多铺设10米，结果延期15天才完成B.每天比原计划少铺设10米，结果延期15天才完成C.每天比原计划多铺设10米，结果提前15天才完成D.每天比原计划少铺设10米，结果提前15天才完成9、二次函数2y ax bx c=++的图象开口向上，对称轴为直线x=-2，图象经过（1,0），则下列结论中，正确的一项是（）A.c>0B.4ac-b2>0C.9a+c>3bD.5a>b10、如图，Rt△OAB的顶点O与坐标原点重合，角AOB=90°，AO=3BO，当AO=3BO，当A点在反比例函数y=9/x（x>0）的图象上移动时，B点坐标满足的函数解析式为（）A.y=-1/x（x<0）B.y=-3/x（x<0）C.y=-1/3x （x<0）D.y=-1/9x（x<0）二．认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案．11、如图，CD 是⊙O 的直径，弦AB CD ⊥于点H ，若30D ∠=︒，1CH cm =，则AB =_____________.12、如图，在ABC ∆中，D ，E 分别是AB 和AC 的中点，F 是延长线BC 上一点，1CF =，DF 交CE 于点G ，且EG CG =，则BC =__________．13、如图，一架2.5米长的梯子AB 斜靠在竖直的墙AC 上，开始时B 到墙C 的距离为0.7米，若梯子的顶端从A 处沿墙AC 下滑的距离与点B 向外移动的距离相等，则下滑的距离是__________米．14、设直线27y x k =-++与直线43y x k =+-的交点为M ，若点M 在第一象限或第二象限，则k 的取值范围是__________．15、如图，是一个无盖玻璃容器的三视图，其中俯视图是一个正六边形，A 、B 两点均在容器顶部．现有一只小甲虫在容器外A 点正下方距离顶部5cm 处，要爬到容器内B 点正下方距离底部5cm 处，则这只小甲虫最短爬行距离是__________cm ．16、如图，将二次函数2y x m =-（其中0m >）的图像在x 轴下方的部分沿x 轴翻转，图像的其余部分保持不变，形成新的图像记为1y ，另有一次函数y x b =+的图像记为2y ，则以下说法：①当1m =，且1y 与2y 恰有三个交点时b 有唯一值为1；②当2b =，且1y 与2y 恰有两个交点时，4m >或704m <<； ③当m b =时，1y 与2y 至少有2个交点，且其中一个为(0,)m ；④当m b =-时，1y 与2y 一定有交点．其中正确说法的序号为__________．三、全面答一答（本题有7个小题，共66分）解答应写出文字说明，证明过程或推演步骤。

2014年杭州市上城区初一新生素质统一测试数学试卷(含答案)

2014年杭州市上城区初一新生素质统一测试数学试卷(含答案)2014年杭州市上城区初一新生素质统一测试数学试卷考生须知：本试卷分试题卷和答题卷两部分，满分100分，考试时间100分钟。

答题时，不能使用计算器，在答题卷指定位置内写明校名、姓名和班级，填涂考生号。

所有答案都做在答题卡标定的位置上，请务必注意试题序号和答题序号相对应。

一、细心计算（共35分）1.（8分）40 × _______% = 100，直接写出结果。

答：2504.2 ÷ 2.1 = 3 + 0.3 ÷ 2 = 1答：12.（18分）计算下面各题，能简便计算的要简便计算：5.9 + 1.6）÷ 2.5答：2.51.5 - 0.6）×（3 - 1.8）答：0.543.解方程：x + x = 20答：x = 1050% × x - 30 = 52答：x = 164二、谨慎填空（共28分）4.（2分）24分 = _______ 时 6600千克 = _______ 吨答：1.6，6.60.8公顷 = _______ 平方米 3.2立方分米 = _______ 毫升。

答：8000，32005.（3分）某市2013年小麦的总产量为二亿五千零四万零三百千克，这个数写作 _______，改用“万”作单位记作_______，用四舍五入法省略“亿”后面的尾数约是 _______。

答：xxxxxxxx，2504，2504.06.（2分）两位数“2□”是2和3的公倍数，□里的数是_______，这个两位数与36的最大公因数是 _______。

答：6，187.（1分）XXX买5只茶杯，付了80元，找回m元，一只茶杯 _______ 元。

答：168.（4分）3 ÷ 5 = _______ × 100%答：609.（3分）直线上A点表示的数是 _______，B点表示的数写成小数是 _______，C点表示的数写成分数是 _______。

2014年上城区科学一模试题

2014年杭州市各类高中招生文化考试上城区一模试卷科学考生须知1．本试卷满分为180分，考试时间为120分钟。

2．答题前，在答题纸上写学校、姓名、座位号、准考证号。

3．必须在答题纸的对应位置上答题，写在其它地方无效，答题方式详见答题纸上的说明。

4．考试结束后，只上交答题纸。

试题卷一、选择题（每小题4分，共24分，每小题只有一个选项符合题意）1．分析下列实验操作正确的是A．稀释浓硫酸B．称量氢氧化钠固体C．测定溶液的pH D．a处进气收集H2 2．某家庭式空气净化器在工作时会释放出臭氧(O3)，利用其强氧化性杀菌消毒并转化为无污染的氧气。

下列分析合理的是A．O3的强氧化性是由O3结构决定的B．等质量的O3与O2所含的原子个数不同C．O3转化为O2是分解反应D．O3与O2的化学性质完全相同3. 下列对人体出现异常状况所作的分析或处置正确的是A．吃海鲜时出现皮肤奇痒等过敏反应，过敏原在医学上称为抗体B．吞噬细胞对病菌的吞噬作用，属于保卫人体的第一道防线C．异型血输血时主要考虑受血者血清是否会使供血者红细胞发生凝集D．当人体大腿体表大血管破裂出血时，要按住破裂血管的近心端止血4. 泡菜的制作需要使用乳酸菌进行发酵，制作泡菜的坛子需加水密封，使用的清水必须进行高温煮沸、冷却、加盐等步骤。

下列关于泡菜制作过程的分析正确的是A.乳酸菌是一种单细胞真菌，它的细胞内没有成形的细胞核B.坛子加水密封的目的是使乳酸菌进行无氧呼吸产生酒精C.清水高温煮沸,加盐等步骤是为了杀死原有的杂菌及抑制其生长D.泡菜发酵中乳酸菌会抑制其他微生物生长的现象属于种内斗争5. 海边滩涂上正在举办一场别开生面的“骑泥马”比赛。

比赛的人们双手握住泥马上的横档，一只脚跪在泥马上，另一只脚在滩涂上蹬，泥马就在滩涂上疾行如飞。

以下说法正确的是A.使用泥马，增大了人与滩涂的接触面积，增大了压强B.使用泥马，增大了人对滩涂的压力，增大了压强C.若将泥马与滩涂的接触面积增大，则泥马下陷的深度更深D.在泥马与滩涂的接触面积不变的情况下，选择轻质泥马更有利于比赛6. 小吴与小徐用如图装置研究光的反射定律，有关实验操作与目的不合理的是A．沿ON前后转动板F或E，可研究反射光线与入射光线是否在同一平面B．改变OB与法线的夹角，可研究反射角与入射角大小关系C．观察每一次入射光线与反射光线的位置，可说明它们分居法线两侧D．若光沿BO入射，反射光线沿OA射出，可说明光路可逆二、选择题（每小题3分，共48分，每小题只有一个选项符合题意）7．在沼气、石油、医用酒精、钢、干冰、熟石灰中属于含有碳元素的混合物有几种A．3种B．4种C．5种D．6种8. 近年来，城郊农民利用海拔500米以上高山进行蔬菜种植，向城市居民提供安全放心的高山蔬菜，深受市民喜欢，下列关于高山蔬菜的说法错误的是A．高山上温度低，不利于蔬菜光合作用B．高山上氧气少，不利于蔬菜呼吸作用C．高山上污染少，蔬菜内含有害物质少D．高山上温差大，蔬菜积累有机物较多9. 转基因水稻是利用转基因技术把水稻中本来没有的基因转入到水稻中，使水稻具有抗虫、抗除草剂、抗病害等新的性状。

问酷网2014年浙江省杭州市上城区中考数学一模试卷

更多试题试卷答案尽在问酷网2014年浙江省杭州市上城区中考数学一模试卷参考答案与试题解析一、仔细选一选（本题有10小题，每小题3分，共30分）C D3．（3分）（2014•上城区一模）为了证明命题“任何偶数都是8的整数倍”是假命题，下列各数中可以作为反例的是4．（3分）（2009•梧州）如图，正方形ABCD中，E为AB的中点，AF⊥DE于点O，则等于（）C D∴AE=∴5．（3分）（2014•上城区一模）已知（﹣1，y1），（﹣0.5，y2），（1.7，y3）是直线y=﹣9x+b（b为常数）上的三个6．（3分）（2014•海拉尔区模拟）将一个有45°角的三角板的直角顶点C放在一张宽为5cm的纸带边沿上，另一个顶点B在纸带的另一边沿上，测得∠DBC=30°，则三角板的最大边的长为（）7．（3分）（2014•上城区一模）近四年杭州经济发展驶入快车道，某公司近四年的销售也取得较大突破，如图1反映的是该公司2006﹣2009年每年的投资额统计图，图2反映的是该公司2006﹣2009年每年的利润率统计图（利润率=×100%），观察图1、图2提供的信息．下列说法：①该公司2007年获得的利润最多；②该公司2007年获得的利润率最高；③从2006年到2009年四年的投资总额为730万元；④该公司计划2010年获得的利润与2009年持平，利润率不低于近四年的最高值，那么该公司2010年投资额约为172万元．=1778．（3分）（2014•上城区一模）关于x的二次函数y=（x﹣m）2﹣1的图象与x轴交于A，B两点，与y轴交于点C．下b==9．（3分）（2014•上城区一模）如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上，若sin∠DFE=，则tan∠EBF的值为（）C D，可得DFE=，∴EBF=10．（3分）（2013•资阳）如图，抛物线y=ax2+bx+c（a≠0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a﹣b+c，则P的取值范围是（）﹣﹣二、认真填一填（本题有6小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案．11．（4分）（2014•上城区一模）的值为1．，12．（4分）（2014•海拉尔区模拟）一组数据2，3，4，x中，如果众数为2，则中位数是 2.5．13．（4分）（2014•上城区一模）如图是一个直三棱柱及其主视图和俯视图，在△EFG中，∠FEG=90°，EF=6cm，EG=8cm，该三棱柱的高是7cm，则它的侧面积为168cm2．=1014．（4分）（2014•上城区一模）如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点，OM⊥AB于点M，若OM=，则∠CBD的度数为30°．OM=，OAM=15．（4分）（2014•上城区一模）已知矩形ABCD的对角线AC，BD的长度是关于x的方程x2﹣px+p+3=0的两个实数根，则此矩形面积的最大值是．ACS=ACAC，故答案为：≤16．（4分）（2014•上城区一模）如图，点A，B在直线MN上，AB=20厘米，⊙A，⊙B的半径均为2厘米．⊙B以每秒4厘米的速度自右向左运动，与此同时，⊙A的半径也不断增大，其半径r（厘米）与时间t（秒）之间的关系式为r=2+t（t≥0）．若点B出发t秒后两圆相切，则时间t的值是或4或或8．t=，t=或三．全面答一答（本题有7小题，共66分）17．（6分）（2014•上城区一模）化简：（﹣）÷，并回答：原代数式的值能等于1吗？为什么？﹣]=[]••18．（8分）（2014•上城区一模）已知方程组的解满足x＞0，y＞0，求整数a的值．，19．（8分）（2014•上城区一模）如图，已知Rt△ABC中，∠C=90°．（1）作∠BAC的角平分线AD交BC边于D，以AB边上一点O为圆心，过A，D两点作⊙O（不写作法，保留作图痕迹）（2）设（1）中⊙O的半径为r，若AB=4，∠B=30°，求r的值．，CD=AD=AO=r=．20．（10分）（2013•苏州）如图，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点分别位于小正方形的顶点上．（1）现以D，E，F，G，H中的三个点为顶点画三角形，在所画的三角形中与△ABC不全等但面积相等的三角形是△DFG或△DHF或△EGF（只需要填一个三角形）（2）先从D，E两个点中任意取一个点，再从F，G，H三个点中任意取两个不同的点，以所取得这三个点为顶点画三角形，求所画三角形与△ABC面积相等的概率（用画树状图或列表格求解）．×=，面积相等的概率为．21．（10分）（2014•上城区一模）如图，在▱ABCD中，E为BC边上一点，且AB=AE．（1）求证：△ABC≌EAD；（2）若AE平分∠DAB，∠EAC=20°，求∠AED的度数．中，22．（12分）（2014•上城区一模）我们知道，y=x的图象向右平移1个单位得到y=x﹣1的图象，类似的，y=（k≠0）的图象向左平移2个单位得到y=（k≠0）的图象．请运用这一知识解决问题．如图，已知反比例函数y=的图象C与正比例函数y=ax（a≠0）的图象l相交于点A（1，m）和点B．（1）写出点B的坐标，并求a的值；（2）将函数y=的图象和直线AB同时向右平移n（n＞0）个单位长度，得到的图象分别记为C1和l1，已知图象C1经过点M（3，2）．①分别写出平移后的两个图象C1和l1对应的函数关系式；②直接写出不等式+4≤ax的解集．y=的图象向右平移，y=不等式可理解为比较y=y=y=个单位长度，得到的图象；解不等式得：=2的图象与正比例函数的图象向右平移y=2=y=，所以不等式为，结合图象知解集23．（12分）（2014•上城区一模）如图，在平面直角坐标系中，直线y=﹣x+与x轴，y轴分别交于点A，点B，动点P（a，b）在第一象限内，有点P向x轴，y轴所作的垂线PM，PN（垂足为M，N）分别于直线AB相交于点E，点F，当点P（a，b）运动时，矩形PMON的面积为定值1．（1）求∠OAB的度数；（2）求证：△AOF∽△BEO；（3）当点E，F都在线段AB上时，由三条线段AE，EF，BF组成一个三角形，记此三角形的外接圆面积为S1，△OEF 的面积为S2．试探究：S1+S2是否存在最小值？若存在，请求出该最小值；若不存在，请说明理由．OA=OB=，b BE=a OA=OB=，∴，，AM=EM=﹣4BN=FN=4EF•=（PF OMPF OM（=（，时，﹣（﹣+2当=a=b=2（﹣+22。

2014市中一模数学试题

2014年初三年级学业水平考试模拟一
数学试题2014、4
本试题分第1卷（选择题）和第Ⅱ卷（非选择题）两部分，第1卷共2页，满分为45分；第1I卷共6页，满分为75分．本试题共8页，满分为120分．考试时间为120分钟，答卷前，请考生务必将自己的姓名、准考证号、座号、考试科目涂写在答题卡上，并同时将考点、姓名、准考证号、座号填写在试卷规定的位置．考试结束后，将本试卷和答题卡一并交回．本考试不允许使用计算器，
16.3a（x＋y）（x－y）17. 1518.OD=OB（或∠A=∠C或∠D=∠B）
19.atan40°20. 9 21.
22.(1) (2)
23.（1）证明：∵ED⊥AB
∴∠EDB=900...............1分
在Rt△ECB和Rt△EDB中
∴Rt△ECB≌Rt△EDB（HL）……2分
∵S△EOM ，S△AON ……………8分
∴S△EOM=S△AON，
∵AN和ME边上的高相等，
∴AN=ME……………………………………………9分
27.解：（1）PN＝ PM
证明：略…………………………3分
（2）解：①如图2，PN＝PM…………4分
如图2：在Rt△ABC中，过点P作PE⊥AB于E，PF⊥BC于点F
质地完全相同且充分洗匀），那么员工小胡抽到去以地的概率是多少？
(3)若有一张车票，小王、小李都想要，决定采取抛掷一枚各面分别标有1，2，3，4的正四面体骰子的方法来确定，具体规则是；“每人各抛掷一次，若小王掷得着地一面的数字比小李掷得着地一面的数字小，车票给小王，否则给小李”，试用“列表法或画树状图”的方法分析，这个规则对双方是否公平？
其中正确的是( )
A．①②B．①②④C．③④D．①②③④

杭州市上城区中考数学一模试题含答案

杭州市初中毕业升学文化考试上城区一模试卷数学考生须知1.本科目试卷分试题卷和答题卷两部分,满分120分,考试时间100分钟.2.答题前,考生务必用黑色水笔或签字笔填写学校、班级、姓名、座位号、考号.3.所有答案都必须做在答题卷标定的位置上,务必注意试题序号和答题序号相对应.4.考试结求后,上交试题卷和答题卷.试题卷一、选择题:本大题有10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合趣目要求的 1.-5的相反数是（）A.5B.51 C.5 D.512.浙江省陆域面积为101800平方千米。

数据101800用科学记数法表示为（） A.1.018×104 B.1.018×105 C.10.18×105 D.0.1018×1063.下列运算正确的是（） A.（a 4）3=a 7 B.a 6÷a 3=a 2 C.（3ab ）3=9a 3b 3 D.-a 5·a 5=-a 104. 四张分别画有平行四边形、菱形、等边三角形、圆的卡片，它们的背面都相同。

现将它们背面朝上，从中任取一张，卡片上所画图形恰好是中心对称图形的概率是（） A. 43 B.1 C.21 D.415. 若代数式832+=x M ，x x N 422+=，则M 与N 的大小关系是（） A. N M ≥ B.N M ≤ C.N M > D.N M <6.下表是某校合唱团成员的年龄分布，对于不同的x ，下列关于年龄的统计量不会发生改变的是（） A.平均数、中位数 B.众数、方差 C.平均数、方差 D ．众数、中位数年龄/岁13 14 15 16 频数5 15 x 10- x7.如图，⊙O 的半径OC 与弦AB 交于点D ，连结OA ，AC ，CB ，BO ，则下列条件中，无法判断四边形OACB 为菱形的是（） A. ∠DAC=∠DBC=30。

2014年杭州上城区新思维数学期末模拟卷全套

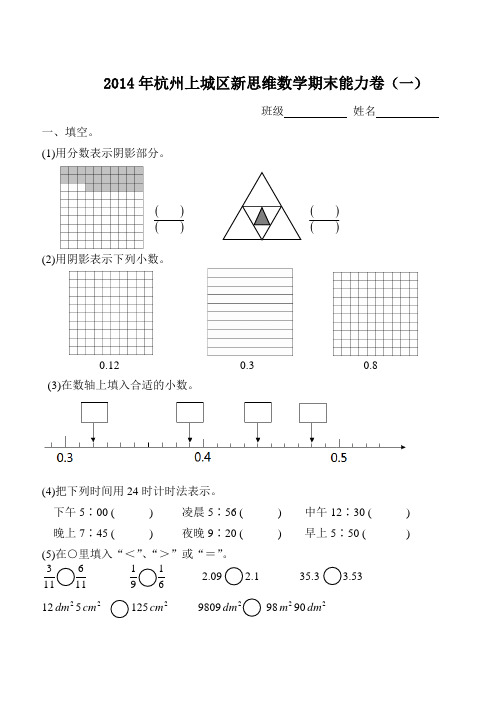
2014年杭州上城区新思维数学期末能力卷（一）班级姓名一、填空。

(1)用分数表示阴影部分。

(2)用阴影表示下列小数。

0.12 0.3 0.8 (3)在数轴上填入合适的小数。

(4)把下列时间用24时计时法表示。

下午5∶00 ( ) 凌晨5∶56 ( ) 中午12∶30 ( ) 晚上7∶45 ( ) 夜晚9∶20 ( ) 早上5∶50 ( ) (5)在○里填入“＜”、“＞”或“＝”。

113 116 91 61 2.09 2.1 122dm 52cm 1252cm 9809dm 982m 902dm()() ()()(6)在括号里填上合适的数。

400平方厘米=( )平方分米 10平方米=( )平方分米 2400平方分米=( )平方米 1200平方米=( )平方分米 (7) 6.37由（）个1、（）个0.1、（）个0.01组成。

(8)平年全年有（）天；闰年全年有（）天。

(9)2005年10月12日上午9时，我国自行研制的神舟六号载人飞船顺利升空，2005年10月17日凌晨4时33分成功着陆。

“神舟六号”飞行的总时间是（）天（）时（）分。

(10)小明到外婆家住了两个月正好是62天，是（）月和（）月。

(11)在表格里填数。

二、计算。

1. 口算。

7200÷9= 24×50= 15×40= 160÷40= 450÷90= 2400÷8= 200÷4= 44×10= 0.02+2.14= 520÷40= 15×60= 11×5= 2.5+3.1= 4.5－4.2= 1.3+3.7= 63÷7×8= 52+52= 41+41+43= 148－142+143= 91×3= 2. 列竖式计算。

75×28 780÷80 56×39 520÷403. 递等式计算。

2014年杭州市小学升初中质量检测模拟-数学试卷(含答案)

2014年杭州市小学升初中入学质量检测模拟-数学试卷一、填空．1．（1分）月球表面白天的平均温度是零上126℃，记作_________℃，夜间的平均温度为零下150℃，记作_________℃．2．（3分）将827.4、﹣1.13、、9.49、275、3.63%填到下面适当的横线里．截至2013年底，武汉市户籍总人口约_________万，较上一年同期减少_________万人，增长率为_________%．武汉市已处于人口老龄化快速发展期．2013年末较2012年同期增长_________全武汉市100周岁以上老人有_________人，其中，男性占_________．3．（2分）3、按要求填数，用小数表示是_________米，用分数表示是_________米．4．（2分）在0.36、13.6%、36、3.6、3.06这五个数中，最大的数是_________，最小的数是_________．5．（2分）3m370dm3=_________m3 2.15小时=_________小时_________分．6．（3分）0.75=_________：_________=_________=_________%7．（2分）18和12的最大公因数是_________，12和_________互质数．8．（2分）观察，是从_________面看到的形状．是从_________面看到的形状．9．（2分）学军小学六（1）班6名同学身高的分别是：1.33米、1.45米、1.46米、1.52米、1.52米、1.52米．这6名同学身高的中位数是_________，众数是_________．10．（1分）区田径队从采荷第二小学的3名男生中选2人，从4名女生中选2人参加区田径队集训，一共有_________种选法．二、判断．11．（1分）﹣1、﹣2、0、3、5都是整数．_________．12．（1分）非0自然数的倒数都比1小．_________．13．（1分）因为钝角两边张开的角度大，所以钝角比锐角大．_________．14．（1分）如图，甲乙两阴影部分的面积相等．_________．15．（1分）当圆的直径和正方形的边长相等时，正方形的面积比圆的面积大．_________．三、选择．四、计算题21．（8分）直接写出得数．+×+= ﹣= ÷= （×=22．（12分）选择合适的方法计算．1422÷÷（+﹣24 ﹣（+）÷．23．（6分）求未知数X．+=12 12+3x=38．24．（6分）看图列式计算（1）福州地铁2号线．（2）已知BE=6dm，EC=4dm．求图中阴影部分的面积．五、活动乐园25．（4分）在如图的方框中，画一个底5cm，面积5cm2的三角形．26．（4分）根据信息在方格图中标出学校、公园和博物馆的位置．（1）学校位于（2，3）．（2）从学校向北走800m，再向东走1200m到达公园．（3）博物馆在学校东偏北30°的方向上，与学校相距500m．六、生活园地27．（5分）王畅计划15天看完一本书．实际每天看8页，结果推迟3天才看完．这本书共有多少页？28．（5分）汉江全长1532千米，比苏伊士运河全长的8倍还多148千米．苏伊士运河全长多少千米？29．（5分）上海和武汉相距925千米，两车同时从两地出发，相向而行，出发4小时正好行驶了全程的80%．已知从武汉开出的汽车每小时行驶90千米，问从上海开出的汽车每小时行驶多少千米？30．（5分）如图是丰裕粮仓示意图．如果每立方米稻谷重600千克，这个粮仓可储存稻谷多少千克？31．（5分）一种糖水，按糖和水1：19配制而成．如果要配制这样糖水250克，需要糖多少千克？32．（5分某学校初一年级共有525人，分成三个兴趣小组开展课外活动，已知第一小组人数的是第二小组人数的，第二小组人数的是第三小组人数的，则这三个小组各有多少人？2013年小学升初中学生素质质量检测-数学试卷参考答案与试题解析一、填空．1．（1分）月球表面白天的平均温度是零上126℃，记作+126℃，夜间的平均温度为零下150℃，记作﹣150℃．2．（3分）将827.4、﹣1.13、、9.49、275、3.63%填到下面适当的横线里．截至2011年底，市户籍总人口约827.4万，较上一年同期减少9.49万人，增长率为﹣1.13%．武汉市已处于人口老龄化快速发展期．2011年末较2010年同期增长 3.63%全武汉市100周岁以上老人有275人，其中，男性占．人，其中，男性占．3．（2分）（2012•汉阳区）3、按要求填数，用小数表示是0.06米，用分数表示是米．、、，4．（2分）在0.36、13.6%、36、3.6、3.06这五个数中，最大的数是36，最小的数是13.6%．5．（2分）3m370dm3= 3.07m3 2.15小时=2小时9分．6．（3分）0.75=3：4==75%化成分数并化简是，根据比与分数的关系，就是=75%，7．（2分）18和12的最大公因数是6，12和5互质数．8．（2分）观察，是从上面看到的形状．是从侧面看到的形状．是从上面看到的形状．9．（2分兴华小学六（1）班6名同学身高的分别是：1.33米、1.45米、1.46米、1.52米、1.52米、1.52米．这6名同学身高的中位数是 1.49米，众数是 1.52米．10．（1分）区田径队从思雅小学的3名男生中选2人，从4名女生中选2人参加区田径队集训，一共有18种选法．×二、判断．11．（1分）﹣1、﹣2、0、3、5都是整数．正确．12．（1分）非0自然数的倒数都比1小．错误．13．（1分）因为钝角两边张开的角度大，所以钝角比锐角大．正确．14．（1分）如图，甲乙两阴影部分的面积相等．√．15．（1分）当圆的直径和正方形的边长相等时，正方形的面积比圆的面积大．√．三、选择．倍．缩小到原数的的小数点向右移动两位后，再向左移动三位得到的数缩小到原数的；×=30四、计算题21．（8分）直接写出得数．+×+= ﹣= ÷= （×=（）××，（）×=，+=，﹣=，÷=，×22．（12分）选择合适的方法计算．1422÷÷（+﹣24 ﹣（+）÷．÷÷）+﹣）24+×﹣（+）÷，23．（6分）求未知数X．+=1212+3x=38．）等式的两边同时减去，然后等式的两边同时除以即可；）先计算+﹣=12，，÷=÷；x=；+3x=3824．（6分）看图列式计算（1）武汉地铁2号线．（2）已知BE=6dm，EC=4dm．求图中阴影部分的面积．，还剩﹣五、活动乐园25．（4分）在如图的方框中，画一个底5cm，面积5cm2的三角形．26．（4分）根据信息在方格图中标出学校、公园和博物馆的位置．（1）学校位于（2，3）．（2）从学校向北走800m，再向东走1200m到达公园．（3）博物馆在学校东偏北30°的方向上，与学校相距500m．六、生活园地27．（5分）王畅计划15天看完一本书．实际每天看8页，结果推迟3天才看完．这本书共有多少页？28．（5分）汉江全长1532千米，比苏伊士运河全长的8倍还多148千米．苏伊士运河全长多少千米？29．（5分）上海和武汉相距925千米，两车同时从两地出发，相向而行，出发4小时正好行驶了全程的80%．已知从武汉开出的汽车每小时行驶90千米，问从上海开出的汽车每小时行驶多少千米？30．（5分）如图是丰裕粮仓示意图．如果每立方米稻谷重600千克，这个粮仓可储存稻谷多少千克？×31．（5分）一种糖水，按糖和水1：19配制而成．如果要配制这样糖水250克，需要糖多少千克？=×32．（5分）某学校初一年级共有525人，分成三个兴趣小组开展课外活动，已知第一小组人数的是第二小组人数的，第二小组人数的是第三小组人数的，则这三个小组各有多少人？根据第一小组人数的是第二小组人数的，可知第一小组和第二小组人数的比是是第三小组人数的，可知第二小组人数和第三小组人数的比是×=120×=180×=225。

人教版九年级数学上册二次函数y=ax2+bx+c的图象和性质(教师版)

1．函数y=ax2+bx+c图象和性质四、典例探究总结： 1. 二次函数y=ax 2+bx+c 图象的画法：（1）“化”：化成顶点式；（2）“定”：确定开口方向、对称轴、顶点坐标；（3）“画”：列表、描点、连线. 2. 利用配方法将二次函数y=ax 2+bx+c 化为顶点式后，可求出二次函数的顶点坐标和最值，顶点坐标是（﹣，），并在顶点处取到最值. 当a ＜0时，最大值是；当a ＞0时，最小值是． 3. 在二次函数y=ax 2+bx+c 中，（1）当a>0时，在对称轴x=-2b a 的左侧，y 随着x 的增大而减小，在对称轴的右侧，y 随着x 的增大而增大；（2）当a ＜0时，在对称轴 x=-2b a的左侧，y 随着x 的增大而增大，在对称轴的右侧，y 随着x 的增大而减小．练1（2015•峨眉山市一模）对二次函数y=3x 2﹣6x 的图象性质，下列说法不正确的是（）A ．开口向上B ．对称轴为x=1C ．顶点坐标为（1，﹣3）D ．最小值为3练2（2014•黄陂区模拟）二次函数y=2x 2﹣4x+5，当x=____时，y 有最小值为______；若y 随x 的增大而减小，则x 的范围为____________．2．已知二次函数y=ax²+bx+c的顶点、对称轴求参数或解析式【例2】（2013秋•青羊区校级期中）若二次函数y=x2﹣2x+c图象的顶点在x轴上，则c等于（）A．﹣1 B．1 C．D．2总结：二次函数y=ax2+bx+c（a≠0）的顶点坐标是（﹣，），根据顶点坐标结合已知条件列方程求参数的值即可．练3 （2015•虹口区一模）若抛物线y=2x2-mx-m的对称轴是直线x=2，则m=_________.练4（2015•奉贤区一模）若抛物线y=x2+mx-1的顶点横坐标为1，那么m的值为______________.一、选择题1．（2015•开县模拟）将抛物线+2x+1的顶点坐标为（）A．（2，3）B．（﹣2，﹣3）C．（﹣2，﹣1）D．（2，﹣3）2．（2014秋•新疆期中）已知抛物线y=x2﹣8x+c的顶点在x轴上，则c等于（）A．4 B．8 C．﹣4 D．163．（2015•黔南州）二次函数y=x2﹣2x﹣3的图象如图所示，下列说法中错误的是（）A．函数图象与y轴的交点坐标是（0，﹣3）B．顶点坐标是（1，﹣3）C．函数图象与x轴的交点坐标是（3，0）、（﹣1，0）D．当x＜0时，y随x的增大而减小4．（2013秋•绍兴期末）关于二次函数y=x2﹣4x+3，下列说法错误的是（）A．当x＜1时，y随x的增大而减小B．它的图象与x轴有交点C．当1＜x＜3时，y＞0 D．顶点坐标为（2，﹣1）5.（2015•大庆模拟）若点A（2，y1），B（﹣3，y2），C（﹣1，y3）三点在抛物线y=x2﹣4x﹣m的图象上，则y1、y2、y3的大小关系是（）A．y1＞y2＞y3B．y2＞y1＞y3C．y2＞y3＞y1D．y3＞y1＞y26.（2015•巴中模拟）若直线y=ax+b（a≠0）在第二、四象限都无图象，则抛物线y=ax2+bx+c（）A．开口向上，对称轴是y轴B．开口向下，对称轴平行于y轴C．开口向上，对称轴平行于y轴D．开口向下，对称轴是y轴二、填空题7．（2011秋•平江区校级月考）抛物线化成顶点式是__________．8.（2015•长宁区一模）已知二次函数y=ax2﹣（a+1）x﹣2，当x＞1时，y的值随x的值增大而增大，当x＜1时，y的值随x的值增大而减小，则实数a的值为___________．9．（2015•黄冈中学自主招生）二次函数y=x2+2ax+a在﹣1≤x≤2上有最小值﹣4，则a的值为______．三、解答题10.（2014秋•上城区期末）已知二次函数y=-2x2+4x+6.（1）求函数图象的顶点坐标、对称轴和与坐标轴交点的坐标，并画出函数的大致图象.（2）自变量x在什么范围内，y随x的增大而增大？何时y随x的增大而减小？并求出函数的最大值或最小值.11．（2015•建邺区一模）已知函数y=x2+（2m+1）x+m2﹣1．（1）m为何值时，y有最小值0；（2）求证：不论m取何值，函数图象的顶点都在同一直线上．典例探究答案：【例1】【解析】根据五点画出二次函数y=﹣x2+4x+5的图象，根据图象即可回答（1）（2）（3）（4）（5）的问题．解：列表：x …0 1 2 3 4 …y … 5 8 9 8 5 …描点、连线可得如图所示抛物线．（1）由y=﹣x2+4x+5=﹣（x﹣2）2+9可知，对称轴为直线x=2，顶点坐标为（2，9），取到最大值，为9；故答案为：x=2，（2，9），大，9；（2）由图象可知：与x轴、y轴的交点坐标分别为（﹣1，0），（5，0）和（0，5）；故答案为：（﹣1，0）（5，0）和（0，5）；（3）当x＜2时，y随x的增大而增大，当x＞2时，y随x的增大而减小；故答案为：x＜2，x＞2．（4）当0≤x＜3时，函数y的值为5≤x≤9．故答案为：5≤x≤9（5）当0＜y＜5时，自变量x的值为﹣1＜x＜0或4＜x＜5．故答案为：﹣1＜x＜0或4＜x＜5．点评：本题考查了二次函数的图象的作法以及二次函数的性质，正确理解函数图象的作法及函数的性质是关键．练1．【解析】首先根据二次项系数判断开口方向，然后把y=3x2﹣6x转化为y=3（x﹣1）2﹣3，进而得到对称轴、顶点坐标以及最值．解：∵二次函数y=3x2﹣6x二次项系数为a=3，∴开口向上，A选项正确；∵y=3x2﹣6x=3（x﹣1）2﹣3，∴对称轴为x=1，顶点坐标为（1，﹣3），B、C正确；∴当x=1时有最小值为﹣3，D选项错误；故选：D．点评：本题主要考查了二次函数的性质，解答本题的关键是熟练掌握二次函数图象的顶点坐标，对称轴以及开口方向等.练2．【解析】把此二次函数化为顶点式或直接用公式法求其最值即可．根据抛物线的增减性填空．解：∵二次函数y=2x 2﹣4x+5可化为y=2（x ﹣1）2+3，∴当x=1时，二次函数y=2x 2﹣4x+5的最小值是3，∵抛物线的对称轴是x=1，抛物线的开口方向向上，∴当x ＜1时，y 随x 的增大而减小．故答案是：1；3；x ＜1．点评：本题考查了二次函数的性质．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．【例2】【解析】抛物线的顶点在x 轴上，那么抛物线顶点坐标中的纵坐标为0，即=0；然后将已知的a 、b 的值代入上式中，即可求得c 的值．解：根据题意，得=0，将a=1，b=﹣2代入得=0，所以c=1．故本题选B ．点评：此题考查了顶点坐标的表示方法，解题的关键是理解题意．练3．【解析】根据二次函数的对称轴公式列方程求解即可.解：由题意得，解得m=8. 故答案为：8.点评：本题考查了二次函数的性质，熟记对称轴的求法是解题的关键.练4 【解析】根据抛物线的顶点公式求解即可. 解：由题意得，121m -=⨯，解得m=-2. 故答案为：-2.点评：本题考查了二次函数的性质，熟记顶点坐标公式是解题的关键.课后小测答案：一、选择题1．【解析】已知抛物线的解析式是一般式，用配方法转化为顶点式，根据顶点式的坐标特点，直接写出顶点坐标．解：∵+2x+1=﹣（x2﹣4x）+1=﹣（x﹣2）2+3，∴顶点坐标是（2，3）．故选A．点评：此题主要考查了二次函数的性质，二次函数y=a（x﹣h）2+k的顶点坐标为（h，k），对称轴为x=h，此题还考查了配方法求顶点式．2．【解析】顶点在x轴上，所以顶点的纵坐标是0．据此作答．解：根据题意，得=0，解得c=16．故选：D．点评：本题考查求抛物线顶点纵坐标的公式，比较简单．3. 解：A、∵y=x2﹣2x﹣3，∴x=0时，y=﹣3，∴函数图象与y轴的交点坐标是（0，﹣3），故本选项说法正确；B、∵y=x2﹣2x﹣3=（x﹣1）2﹣4，∴顶点坐标是（1，﹣4），故本选项说法错误；C、∵y=x2﹣2x﹣3，∴y=0时，x2﹣2x﹣3=0，解得x=3或﹣1，∴函数图象与x轴的交点坐标是（3，0）、（﹣1，0），故本选项说法正确；D、∵y=x2﹣2x﹣3=（x﹣1）2﹣4，∴对称轴为直线x=1，又∵a=1＞0，开口向上，∴x＜1时，y随x的增大而减小，∴x＜0时，y随x的增大而减小，故本选项说法正确；故选：B．点评：本题考查了二次函数的性质，抛物线与坐标轴的交点坐标，掌握二次函数的性质是解决本题的关键．4．【解析】根据二次函数的性质解题．解：在函数y=x2﹣4x+3中a=1＞0，∴此函数图象开口向上；又∵a=1，b=﹣4，c=3，∴﹣=2，=﹣1．∴顶点坐标是（2，﹣1），且对称轴是x=2，∴故D正确；∴令x2﹣4x+3=0，解得x1=1，x2=3，∴此函数图象和x轴有交点，求交点坐标是（1，0）；（3，0）．故B正确；当x＜1时，即说明x的取值范围在对称轴的左边，∴y随x的增大而减小，故A正确；当1＜x＜3时，y的值在x轴下方，∴y＜0，故C错误．故选：C．点评：考查二次函数图象开口方向、顶点坐标、对称轴与增减性．5.【解析】先求出二次函数y=x2﹣4x﹣m的图象的对称轴，然后判断出A（2，y1），B（﹣3，y2），C（﹣1，y3）在抛物线上的位置，再根据二次函数的增减性求解．解：∵二次函数y=x2﹣4x﹣m中a=1＞0，∴开口向上，对称轴为x=﹣=2，∵A（2，y1）中x=2，∴y1最小，又∵B（﹣3，y2），C（﹣1，y3）都在对称轴的左侧，而在对称轴的左侧，y随x得增大而减小，故y2＞y3．∴y2＞y3＞y1．故选：C．点评：本题考查了二次函数的性质．关键是（1）找到二次函数的对称轴；（2）掌握二次函数y=ax2+bx+c（a≠0）的图象性质．6. 【解析】先由直线y=ax+b（a≠0）在第二、四象限，得出a＞0，b=0，再判断抛物线的开口方向和对称轴．解：∵直线y=ax+b（a≠0）在第二、四象限，∴a＞0，b=0，则抛物线y=ax2+bx+c开口方向向上，对称轴x=0，即y轴．故选A．点评：本题考查了一次函数和二次函数的图象与其系数的关系，先由一次函数的图象判断出a、b的正负，再根据二次函数的性质进行判断．二、填空题7．【解析】利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．解：由原抛物线方程，得y=（x2+2x）+，即y=（x2+2x+1）+﹣，∴y=（x+1）2+3；故答案是：y=（x+1）2+3．点评：本题考查了二次函数的解析式的三种形式：（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；（2）顶点式：y=a（x﹣h）2+k；（3）交点式（与x轴）：y=a（x﹣x1）（x﹣x2）．8.【解析】根据二次函数的增减性，结合条件可求得抛物线的对称轴方程，可得到关于a 的方程，可求得答案．解：∵y=ax2﹣（a+1）x﹣2，∴其对称轴方程为x=，又当x＞1时，y的值随x的值增大而增大，当x＜1时，y的值随x的值增大而减小，∴其对称轴为x=1，∴=1，解得a=1，故答案为：1．点评：本题主要考查抛物线的对称轴及增减性，掌握在对称轴两侧的增减性相反是解题的关键．9．【解析】分三种情况考虑：对称轴在x=﹣1的左边，对称轴在﹣1到2的之间，对称轴在x=2的右边，当对称轴在x=﹣1的左边和对称轴在x=2的右边时，可根据二次函数的增减性来判断函数取最小值时x的值，然后把此时的x的值与y=﹣4代入二次函数解析式即可求出a的值；当对称轴在﹣1到2的之间时，顶点为最低点，令顶点的纵坐标等于﹣4，列出关于a的方程，求出方程的解即可得到满足题意a的值．解：分三种情况：当﹣a＜﹣1即a＞1时，二次函数y=x2+2ax+a在﹣1≤x≤2上为增函数，所以当x=﹣1时，y有最小值为﹣4，把（﹣1，﹣4）代入y=x2+2ax+a中解得：a=5；当﹣a＞2即a＜﹣2时，二次函数y=x2+2ax+a在﹣1≤x≤2上为减函数，所以当x=2时，y有最小值为﹣4，把（2，﹣4）代入y=x2+2ax+a中解得：a=﹣＞﹣2，舍去；当﹣1≤﹣a≤2即﹣2≤a≤1时，此时抛物线的顶点为最低点，所以顶点的纵坐标为=﹣4，解得：a=或a=＞1，舍去．综上，a的值为5或．故答案为：5或点评：此题考查二次函数的增减性和二次函数最值的求法，是一道综合题．求二次函数最值时应注意顶点能否取到．三、解答题10. 分析：（1）根据函数解析式可求出顶点坐标、对称轴及与坐标轴的交点；根据二次函数的顶点、对称轴及与y轴的交点可画出图象；（2）根据确定的对称轴及顶点坐标确定其增减性即可.解：（1）∵y= -2x2+4x+6= -2（x2-2x+1-1）+6=-2(x-1)2+8，∴顶点坐标为（1，8），对称轴为x=1；令y= -2x2+4x+6=0，解得x=-1或x=3，∴抛物线与x轴的交点为（-1，0）和（3，0）；令x=0,则y=6，∴抛物线与y轴的交点为（6，0），大致图象为：（2）∵开口向下且对称轴为x=1,∴当x＜1时，y随x的增大而增大；当x＞1时，y随x的增大而减小；函数值有最大值，为8.点评：本题考查了二次函数的性质，解题的关键是能够确定函数的对称轴及顶点坐标以及抛物线与坐标轴的交点坐标.11．【解析】（1）直接将y=0代入=0求出即可；（2）首先求出函数顶点坐标，设顶点在直线y1=kx+b上，代入函数解析式求出k，b的值即可．（1）解：当y=0时，===0，解得：m=﹣；（2）证明：函数y=x2+（2m+1）x+m2﹣1的顶点坐标为：（﹣，）设顶点在直线y1=kx+b上，则﹣k+b=，故﹣mk=﹣m，解得：k=1，b=，不论m取何值，该函数图象的顶点都在直线y1=x﹣上．点评：此题主要考查了二次函数的性质以及二次函数最值求法，得出k的值是解题关键．。

2014-2015学年浙江省杭州市上城区八年级(下)期末数学试卷答案加解析

2014-2015学年浙江省杭州市上城区八年级（下）期末数学试卷一、仔细选一选（本题有10个小题，每小题3分，共30分．每题只有一个是正确答案）1．（3分）代数式在实数范围内有意义，则x的取值范围为（）A．x≥1 B．x≥﹣1 C．x≥D．x≥﹣2．（3分）用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（）A．有一个内角小于90° B．有一个内角小于或等于90°C．每一个内角都小于90°D．每一个内角都大于90°3．（3分）已知反比例函数y=（k＞0）的图象上有两点A（1，m），B（2，n），则m与n的大小关系是（）A．m＞n B．m＜n C．m=n D．不能确定4．（3分）某商店四月份的利润为6.3万元，此后两个月进入淡季，利润均以相同的百分比下降，至六月份利润为5.4万元．设下降的百分比为x，由题意列出方程正确的是（）A．5.4（1+x）2=6.3 B．5.4（1﹣x）2=6.3 C．6.3（1+x）2=5.4 D．6.3（1﹣x）25．（3分）小张参加招考公务员考试，本次参加招考的总人数是1600名，规定：按考试成绩从高到低排列，前800名通过笔试，小张想知道自己是否通过笔试，他最应该了解的考试成绩统计量是（）A．平均数B．中位数C．众数D．标准差6．（3分）已知a是实数，则一元二次方程x2+ax﹣4=0的根的情况是（）A．没有实数根 B．有两个相等的实数根C．有两个不相等的实数根D．根据a的值来确定7．（3分）如果=﹣1，则a与b的大小关系为（）A．a＞b B．b＞a C．a≥b D．b≥a8．（3分）如图，在平面直角坐标系中，点A是x轴正半轴上的一定点，点P是反比例函数y=（x＞0）图象上的一个动点，PB⊥y轴于点B，当点P的横坐标的值逐渐减小时，四边形OAPB的面积将会（）A．逐渐减小B．逐渐增大C．不变D．先减小后增大9．（3分）一艘快艇的航线如图所示，从O港出发，1小时后回到O港，若行驶中快艇的速度保持不变，AB∥x轴，则快艇驶完AB这段路程所用的时间为（）（取的值为1.4）A．26分B．25分C．24分D．23分10．（3分）如图，已知正六边形ABCDEF的边长为2，G，H分别是AF和CD的中点，P 是GH上的动点，连接AP，BP，则AP+BP的最小值为（）A．4 B．+2 C．+1 D．2二、完整填一填（本题有6个小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案．11．（4分）一个多边形的内角和为900°，则这个多边形的边数为．12．（4分）在直角坐标系中，点A（3，4）和点B（a，b）关于原点成中心对称，则a﹣b 的值为．13．（4分）已知（x2+y2）2+5（x2+y2）﹣6=0，则x2+y2的值为．14．（4分）如图，一张矩形纸片ABCD，沿AF折叠，点B恰好落在CD边上的点E处，已知CD为10cm，DE：EC=3：2，则FC的长度为cm．15．（4分）已知点P是反比例函数y=图象上的一个动点，在y轴上取点Q，使得△OPQ 为等腰直角三角形，则符合条件的Q点的坐标为．16．（4分）如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=．下列结论：①△APD≌△AEB；②点B到直线AE的距离为；③EB⊥ED；④S△APD+S△APB=1+；⑤S正方形ABCD=4+．其中正确结论的序号是．三、全面答一答（本题有8个小题，共66分）解答需要用文字或符号说明演算过程或推演步骤，如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以．17．（6分）计算．（1）3﹣（﹣6）（2）（2+3）2．18．（6分）解方程．（1）3x2﹣x﹣4=0（2）（x﹣1）2=4（x﹣5）2．19．（8分）小明、小华参加了学校射击队训练，下表是他们在最近一次选拔赛上的成绩（环）：选手第1次第2次第3次第4次第5次第6次第7次第8次小明57610710109小华879106978（1）根据提供的数据填写下表：平均数（环）众数（环）中位数（环）小明10小华88（2）若学校欲从两人中选发挥比较稳定的一人参加市中学生运动会，你认为选谁去比较合适？请说明理由．20．（8分）如图，在Rt△ABC中，CE是斜边AB上的中线，CD∥AB，且CD=CE，求证：（1）四边形CDEB是平行四边形；（2）四边形AECD是菱形．21．（8分）如图，在△ABC中，∠B=90°，AB=6cm，BC=8cm，点P从点A出发，以1cm/s 的速度沿AB边向点B移动，以此同时，点Q从点C出发，以2cm/s的速度沿CB边向点B移动，如果P，Q同时出发，经过几秒，△PBQ的面积等于8cm2？22．（8分）如图，在直角坐标系中，一次函数y=﹣x+b与反比例函数y=的图象交于A，B两点，已知A（﹣1，a）．（1）求一次函数的解析式；（2）求B点的坐标；（3）结合图象，直接写出当﹣x+b＞时，x的取值范围．23．（10分）如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，AH=2，连结CF．（1）若DG=2，求证：四边形EFGH为正方形；（2）若DG=6，求△FCG的面积．24．（12分）在直角坐标系中，已知反比例函数y=（k≠0）图象经过点D（5，1），且BD⊥y轴，垂足为B，点C是第三象限图象上的动点，过C作CA⊥x轴，垂足为A，连接AB，BC．（1）求k的值；（2）若△BCD的面积是10，求直线CD的解析式；（3）判断AB与CD的位置关系，并说明理由．2014-2015学年浙江省杭州市上城区八年级（下）期末数学试卷参考答案与试题解析一、仔细选一选（本题有10个小题，每小题3分，共30分．每题只有一个是正确答案）1．（3分）（2015春•上城区期末）代数式在实数范围内有意义，则x的取值范围为（）A．x≥1 B．x≥﹣1 C．x≥D．x≥﹣【分析】二次根式有意义的条件就是被开方数是非负数，即可求解．【解答】解：根据题意得：x﹣1≥0，解得x≥1．故选A【点评】主要考查了二次根式的意义和性质．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．2．（3分）（2015春•上城区期末）用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（）A．有一个内角小于90° B．有一个内角小于或等于90°C．每一个内角都小于90°D．每一个内角都大于90°【分析】至少有一个角不小于90°的反面是每个角都小于90°，据此即可假设．【解答】解：用反证法证明：在四边形中，至少有一个角不小于90°，应先假设：四边形中的每个角都小于90°．故选：C．【点评】此题考查了反证法，解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．3．（3分）（2015春•上城区期末）已知反比例函数y=（k＞0）的图象上有两点A（1，m），B（2，n），则m与n的大小关系是（）A．m＞n B．m＜n C．m=n D．不能确定【分析】将点A、B的坐标分别代入已知反比例函数解析式，分别求得m、n的值，然后再来比较它们的大小即可．【解答】解：∵反比例函数y=，且k＞0，它的图象经过A（1，m），B（2，n）两点，∴m=k＞0，n=＞0，∴m＞n．故选A．【点评】本题考查了反比例函数图象上点的坐标特征．经过函数的某点一定在函数的图象上．4．（3分）（2015春•上城区期末）某商店四月份的利润为6.3万元，此后两个月进入淡季，利润均以相同的百分比下降，至六月份利润为5.4万元．设下降的百分比为x，由题意列出方程正确的是（）A．5.4（1+x）2=6.3 B．5.4（1﹣x）2=6.3 C．6.3（1+x）2=5.4 D．6.3（1﹣x）2【分析】根据题意可得出5月份的利润为：6.3（1﹣x），6月份的利润为：6.3（1﹣x）（1﹣x），再由两个月内将利润降到5.4万元，可得出方程．【解答】解：由题意得，5月份的利润为：6.3（1﹣x），6月份的利润为：6.3（1﹣x）（1﹣x），故可得方程：6.3（1﹣x）2=5.4．故选D．【点评】此题考查了由实际问题抽象一元二次方程的知识，关键是根据题意的降低百分率表示出每个月的开支，难度一般．5．（3分）（2015春•上城区期末）小张参加招考公务员考试，本次参加招考的总人数是1600名，规定：按考试成绩从高到低排列，前800名通过笔试，小张想知道自己是否通过笔试，他最应该了解的考试成绩统计量是（）A．平均数B．中位数C．众数D．标准差【分析】根据题意可得：由中位数的概念，即最中间一个或两个数据的平均数．参赛选手要想知道自己是否能通过考试，只需要了解自己的成绩以及全部成绩的中位数，比较即可．【解答】解：由于前一半的人可通过考试，要判断是否通过考试，故应知道中位数．故选B．【点评】此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．6．（3分）（2015•平定县一模）已知a是实数，则一元二次方程x2+ax﹣4=0的根的情况是（）A．没有实数根 B．有两个相等的实数根C．有两个不相等的实数根D．根据a的值来确定【分析】判断上述方程的根的情况，只要看根的判别式△=b2﹣4ac的值的符号就可以了．【解答】解：△=a2﹣4×1×（﹣4）=a2+16＞0，∴方程有两个不相等的实数根．故选C．【点评】本题考查了一元二次方程根的判别式的应用．总结一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．7．（3分）（2015春•上城区期末）如果=﹣1，则a与b的大小关系为（）A．a＞b B．b＞a C．a≥b D．b≥a【分析】根据=﹣1，推得=b﹣a，所以b﹣a＞0，据此推得b＞a 即可．【解答】解：∵=﹣1，∴=﹣1，∴=b﹣a，∵b﹣a＞0，∴b＞a，则a与b的大小关系为：b＞a．故选：B．【点评】此题主要考查了二次根式的性质和化简，要熟练掌握，解答此题的关键是要明确化简二次根式的步骤：①把被开方数分解因式；②利用积的算术平方根的性质，把被开方数中能开得尽方的因数（或因式）都开出来；③化简后的二次根式中的被开方数中每一个因数（或因式）的指数都小于根指数2．8．（3分）（2015春•上城区期末）如图，在平面直角坐标系中，点A是x轴正半轴上的一定点，点P是反比例函数y=（x＞0）图象上的一个动点，PB⊥y轴于点B，当点P的横坐标的值逐渐减小时，四边形OAPB的面积将会（）A．逐渐减小B．逐渐增大C．不变D．先减小后增大【分析】由双曲线y=（x＞0）设出点P的坐标，运用坐标表示出四边形OAPB的面积函数关系式即可判定．【解答】解：设点P的坐标为（x，），∵PB⊥y轴于点B，点A是x轴正半轴上的一个定点，∴四边形OAPB是个直角梯形，∴四边形OAPB的面积=（PB+AO）•BO=（x+AO）•=2+=2+2AO•，∵AO是定值，∴四边形OAPB的面积是个增函数，即点P的横坐标逐渐减小时四边形OAPB的面积逐渐增大．故选：B．【点评】本题主要考查了反比例函数系数k的几何意义，解题的关键是运用点的坐标求出四边形OAPB的面积的函数关系式．9．（3分）（2015春•上城区期末）一艘快艇的航线如图所示，从O港出发，1小时后回到O港，若行驶中快艇的速度保持不变，AB∥x轴，则快艇驶完AB这段路程所用的时间为（）（取的值为1.4）A．26分B．25分C．24分D．23分【分析】根据∠AOD=45°，∠BOD=45°，AB∥x轴，△AOB为等腰直角三角形，OA=OB，根据AB=，设行驶OA所用的时间为a分钟，则行驶OB所用的时间为a分钟，行驶AB所用的时间为a分钟，根据从O港出发，1小时后回到O港，得到a+a+a=60，求出a的值即可解答．【解答】解：如图，∵∠AOD=45°，∠BOD=45°，∴∠AOD=90°，∵AB∥x轴，∴∠BAO=∠AOC=45°，∠ABO=∠BOD=45°，∴△AOB为等腰直角三角形，OA=OB，∴AB=，设行驶OA所用的时间为a分钟，则行驶OB所用的时间为a分钟，行驶AB所用的时间为a分钟，∵从O港出发，1小时后回到O港，∴a+a+a=60，解得：a=，a=24，故选：C．【点评】本题考查了等腰直角三角形，解决本题的关键是熟悉等腰直角三角形的性质．10．（3分）（2015春•上城区期末）如图，已知正六边形ABCDEF的边长为2，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP+BP的最小值为（）A．4 B．+2 C．+1 D．2【分析】易知点B关于GH的对称点为点E，连接AE交GH于点P，那么有PB=PE，AP+BP=AE最小．又易知△AEF为等腰三角形，∠AFE=120°，则作FM⊥AE于点M，易求得AM=EM=，从而AE=2．【解答】解：利用正多边形的性质可得点B关于GH的对称点为点E，连接AE交GH于点P，那么有PB=PE，AP+BP=AE最小．又易知△AEF为等腰三角形，∠AFE=120°，则作FM⊥AE于点M，∵∠AFE=120°，AF=EF，∴∠FAE=∠FEA=30°，AM=EM，在RT△AFM中，AF=2，∴AM=AF=，∴AM=EM=，从而AE=2，故AP+BP的最小值为2．故选D．【点评】此题主要考查了正多边形的以性质及轴对称最短路线问题，作出辅助线构建直角三角形是解题的关键．二、完整填一填（本题有6个小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案．11．（4分）（2009•巴中）一个多边形的内角和为900°，则这个多边形的边数为7．【分析】本题根据多边形的内角和定理和多边形的内角和等于900°，列出方程，解出即可．【解答】解：设这个多边形的边数为n，则有（n﹣2）×180°=900°，解得：n=7，∴这个多边形的边数为7．故答案为：7．【点评】本题主要考查多边形的内角和定理，解题的关键是根据已知等量关系列出方程从而解决问题．12．（4分）（2015春•上城区期末）在直角坐标系中，点A（3，4）和点B（a，b）关于原点成中心对称，则a﹣b的值为1．【分析】首先根据点A（3，4）和点B（a，b）关于原点成中心对称，可得a=﹣3，b=﹣4，然后把a、b的值代入，求出a﹣b的值为多少即可．【解答】解：∵点A（3，4）和点B（a，b）关于原点成中心对称，∴a=﹣3，b=﹣4，∴a﹣b=﹣3﹣（﹣4）=1．故答案为：1．【点评】此题主要考查了关于原点对称的点的坐标，要熟练掌握，解答此题的关键是要明确：两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点是P′（﹣x，﹣y）．13．（4分）（2015春•上城区期末）已知（x2+y2）2+5（x2+y2）﹣6=0，则x2+y2的值为1．【分析】先设x2+y2=t，则方程即可变形为t2+5t﹣6=0，解方程即可求得t即x2+y2的值．【解答】解：设x2+y2=t，则原方程可化为：t2+5t﹣6=0即（t+6）（t﹣1）=0∴t=﹣6（舍去）或t=1，即x2+y2=1．故答案是：1．【点评】本题主要考查了换元法解一元二次方程，即把某个式子看作一个整体，用一个字母去代替它，实行等量替换．14．（4分）（2015春•上城区期末）如图，一张矩形纸片ABCD，沿AF折叠，点B恰好落在CD边上的点E处，已知CD为10cm，DE：EC=3：2，则FC的长度为3cm．【分析】由矩形的性质和折叠的性质得出∠C=∠D=90°AE=AB=10cm，EF=BF，由勾股定理求出AD，得出BC，设FC=xcm，则EF=BF=（8﹣x）cm，根据勾股定理得出方程，解方程即可．【解答】解：，∵四边形ABCD是矩形，∴∠C=∠D=90°，AB=CD=10cm，BC=AD，根据折叠的性质得：AE=AB=10cm，EF=BF，∵DE：EC=3：2，∴DE=6cm，EC=4cm，∴AD===8（cm），∴BC=8cm，设FC=xcm，则EF=BF=（8﹣x）cm，根据勾股定理得：FC2+EC2=EF2，即x2+42=（8﹣x）2，解得：x=3，∴FC=3cm．故答案为：3．【点评】本题考查了矩形的性质、翻折变换的性质、勾股定理；熟练掌握矩形的性质和翻折变换的性质，并能进行推理计算是解决问题的关键．15．（4分）（2015春•上城区期末）已知点P是反比例函数y=图象上的一个动点，在y 轴上取点Q，使得△OPQ为等腰直角三角形，则符合条件的Q点的坐标为（0，2）、（0，﹣2）、（0，4）或（0，﹣4）．【分析】根据题意，分两种情况：（1）当∠AQP=90°时；（2）当∠APQ=90°时；根据△OPQ 为等腰直角三角形，判断出符合条件的所有Q点的坐标有哪些即可．【解答】解：（1）当∠AQP=90°时，∵△OPQ为等腰直角三角形，∴OQ=PQ，∴点P（a，b）的横坐标、纵坐标相等，∴a=b，ab=4，解得或∴Q点的坐标为（0，2）或（0，﹣2）．（2）当∠APQ=90°时，∵△OPQ为等腰直角三角形，∴OP=PQ，∴点P（a，b）的横坐标、纵坐标相等，∴a=b，ab=4，解得或∴OP=，PQ=2，∵△OPQ为等腰直角三角形，∴OQ=2=4，∴Q点的坐标为（0，4）或（0，﹣4）．综上，可得符合条件的Q点的坐标为：（0，2）、（0，﹣2）、（0，4）或（0，﹣4）．故答案为：（0，2）、（0，﹣2）、（0，4）或（0，﹣4）．【点评】（1）此题主要考查了反比例函数图象上点的坐标的特征，要熟练掌握，解答此题的关键是要明确：①图象上的点（x，y）的横纵坐标的积是定值k，即xy=k；②双曲线是关于原点对称的，两个分支上的点也是关于原点对称；③在xk图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．（2）此题还考查了等腰直角三角形的性质和应用，要熟练掌握，解答此题的关键是要明确：等腰直角三角形是一种特殊的三角形，具有所有三角形的性质，还具备等腰三角形和直角三角形的所有性质．即：两个锐角都是45°，斜边上中线、角平分线、斜边上的高，三线合一，等腰直角三角形斜边上的高为外接圆的半径R ，而高又为内切圆的直径．16．（4分）（2012•深圳二模）如图，在正方形ABCD 外取一点E ，连接AE 、BE 、DE ．过点A 作AE 的垂线交DE 于点P ．若AE=AP=1，PB=．下列结论：①△APD ≌△AEB ；②点B 到直线AE 的距离为；③EB ⊥ED ；④S △APD +S △APB =1+；⑤S 正方形ABCD =4+．其中正确结论的序号是 ①③⑤ ．【分析】①首先利用已知条件根据边角边可以证明△APD ≌△AEB ；②由①可得∠BEP=90°，故BE 不垂直于AE 过点B 作BF ⊥AE 延长线于F ，由①得∠AEB=135°所以∠EFB=45°，所以△EFB 是等腰Rt △，故B 到直线AE 距离为BF=，故②是错误的；③利用全等三角形的性质和对顶角相等即可判定③说法正确；④由△APD ≌△AEB ，可知S △APD +S △APB =S △AEB +S △APB ，然后利用已知条件计算即可判定； ⑤连接BD ，根据三角形的面积公式得到S △BPD =PD ×BE=，所以S △ABD =S △APD +S △APB +S△BPD=2+，由此即可判定．【解答】解：由边角边定理易知△APD ≌△AEB ，故①正确；由△APD ≌△AEB 得，∠AEP=∠APE=45°，从而∠APD=∠AEB=135°，所以∠BEP=90°，过B 作BF ⊥AE ，交AE 的延长线于F ，则BF 的长是点B 到直线AE 的距离，在△AEP 中，由勾股定理得PE=，在△BEP 中，PB=，PE=，由勾股定理得：BE=，∵∠PAE=∠PEB=∠EFB=90°，AE=AP ， ∴∠AEP=45°，∴∠BEF=180°﹣45°﹣90°=45°， ∴∠EBF=45°， ∴EF=BF ，在△EFB 中，由勾股定理得：EF=BF=，故②是错误的；因为△APD ≌△AEB ，所以∠ADP=∠ABE ，而对顶角相等，所以③是正确的；由△APD ≌△AEB ， ∴PD=BE=，可知S △APD +S △APB =S △AEB +S △APB =S △AEP +S △BEP =+，因此④是错误的；连接BD ，则S △BPD =PD ×BE=，所以S △ABD =S △APD +S △APB +S △BPD =2+，所以S 正方形ABCD =2S △ABD =4+．综上可知，正确的有①③⑤．【点评】此题分别考查了正方形的性质、全等三角形的性质与判定、三角形的面积及勾股定理，综合性比较强，解题时要求熟练掌握相关的基础知识才能很好解决问题．三、全面答一答（本题有8个小题，共66分）解答需要用文字或符号说明演算过程或推演步骤，如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以． 17．（6分）（2015春•上城区期末）计算．（1）3﹣（﹣6）（2）（2+3）2．【分析】（1）先把各二次根式化为最简二次根式，然后去括号后合并即可；（2）利用完全平方公式计算．【解答】解：（1）原式=3﹣2+2=3；（2）原式=12+12+45=57+12．【点评】本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．18．（6分）（2015春•上城区期末）解方程．（1）3x2﹣x﹣4=0（2）（x﹣1）2=4（x﹣5）2．【分析】（1）方程利用因式分解法求出解即可；（2）方程利用直接开平方法求出解即可．【解答】解：（1）分解因式得：（3x﹣4）（x+1）=0，解得：x1=，x2=﹣1；（2）开方得：x﹣1=2（x﹣5）或x﹣1=﹣2（x﹣5），解得：x1=9，x2=．【点评】此题考查了解一元二次方程﹣因式分解法，熟练掌握因式分解的方法是解本题的关键．19．（8分）（2015春•上城区期末）小明、小华参加了学校射击队训练，下表是他们在最近一次选拔赛上的成绩（环）：选手第1次第2次第3次第4次第5次第6次第7次第8次小明57610710109小华879106978（1）根据提供的数据填写下表：平均数（环）众数（环）中位数（环）小明10小华88（2）若学校欲从两人中选发挥比较稳定的一人参加市中学生运动会，你认为选谁去比较合适？请说明理由．【分析】（1）小明的平均数=分；将小明的成绩由小到大排列为5、6、7、7、9、10、10、10则中位数为=8；小华的众数为7，8，9；（2）首先求出小明的方差=3.5，小华的方差=1.5，小明和小华成绩的平均数均为8分，但小华的方差比小明的小，且大于等于8分的次数小华比小明的多，所以让小华去；或小明成绩总体上呈现上升趋势，且后几次的成绩均高于8分，所以让小明去较合适．【解答】解：（1）平均数（环）众数（环）中位数（环）小明8108小华87，8，98（2）小明的方差=3.5，小华的方差=1.5，小明和小华成绩的平均数均为8分，但小华的方差比小明的小，且大于等于8分的次数小华比小明的多，所以让小华去；或小明成绩总体上呈现上升趋势，且后几次的成绩均高于8分，所以让小明去较合适．【点评】本题考查了平均数，中位数、众数及方差的概念，理解它们的概念是解决本题的关键．20．（8分）（2015春•上城区期末）如图，在Rt△ABC中，CE是斜边AB上的中线，CD ∥AB，且CD=CE，求证：（1）四边形CDEB是平行四边形；（2）四边形AECD是菱形．【分析】（1）首先根据直角三角形斜边上的中线等于斜边的一半得到AE=CE=BE，从而得到CD=BE，利用一组对边平行且相等证得四边形CDEB是平行四边形；（2）首先判定四边形AECD是平行四边形，然后根据邻边相等得到四边形AECD是菱形．【解答】证明：（1）∵Rt△ABC中，CE是斜边AB上的中线，∴AE=CE=BE，∵CD=CE，∴CD=BE，∵CD∥AB，∴四边形CDEB是平行四边形；（2）∵CD=AE，∴四边形AECD是平行四边形，∵AE=CE，∴四边形AECD为菱形．【点评】本题考查了平行四边形的判定、菱形的判定，解题的关键是能够熟练掌握菱形及平行四边形的判定定理，难度不大．21．（8分）（2015春•上城区期末）如图，在△ABC中，∠B=90°，AB=6cm，BC=8cm，点P从点A出发，以1cm/s的速度沿AB边向点B移动，以此同时，点Q从点C出发，以2cm/s的速度沿CB边向点B移动，如果P，Q同时出发，经过几秒，△PBQ的面积等于8cm2？【分析】设P、Q同时出发，x秒钟后，AP=xcm，PB=（6﹣x）cm，BQ=（8﹣2x）cm，此时△PCQ的面积为：×（8﹣2x）（6﹣x），令该式=8，由此等量关系列出方程求出符合题意的值．【解答】解：设xs后，可使△PCQ的面积为8cm2．由题意得，AP=xcm，PB=（6﹣x）cm，BQ=（8﹣2x）cm，则（6﹣x）•（8﹣2x）=8，整理，得x2﹣10x+16=0，解得x1=2，x2=8（不合题意舍去）．所以P、Q同时出发，2s后可使△PBQ的面积为8cm2．【点评】本题主要考查一元二次方程的应用，关键在于根据三角形面积公式找出等量关系列出方程求解．22．（8分）（2015春•上城区期末）如图，在直角坐标系中，一次函数y=﹣x+b与反比例函数y=的图象交于A，B两点，已知A（﹣1，a）．（1）求一次函数的解析式；（2）求B点的坐标；（3）结合图象，直接写出当﹣x+b＞时，x的取值范围．【分析】（1）把A（﹣1，a）代入y=求出a，得到点A的坐标，把点A的坐标代入y=﹣x+b求出b，得到一次函数的解析式；（2）把解出的一次函数y=﹣x+b与反比例函数y=组成方程组，解方程组得到答案；（3）根据函数图象确定当﹣x+b＞时，x的取值范围．【解答】解：（1）∵A（﹣1，a）在y=的图象上，∴a=4，则A（﹣1，4），又A（﹣1，4）在一次函数y=﹣x+b图象上，∴1+b=4，解得，b=3，∴一次函数的解析式为：y=﹣x+3；（2）由题意得，，解得，，，∴B点的坐标为：（4，﹣1）；（3）从图象可以看出，当x＜﹣1或0＜x＜4时，﹣x+b＞．【点评】本题综合考查一次函数与反比例函数的图象与性质，同时考查用待定系数法求函数解析式，先由点的坐标求函数解析式，然后解由解析式组成的方程组求出交点的坐标，体现了数形结合的思想．23．（10分）（2015春•上城区期末）如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，AH=2，连结CF．（1）若DG=2，求证：四边形EFGH为正方形；（2）若DG=6，求△FCG的面积．【分析】（1）通过证明Rt△DHG≌△AEH，得到∠DHG=∠AEH，从而得到∠GHE=90°，然后根据有一个角为直角的菱形为正方形得到四边形EFGH为正方形；（2）作FQ⊥CD于Q，连结GE，如图，利用AB∥CD得到∠AEG=∠QGE，再根据菱形的性质得HE=GF，HE∥GF，则∠HEG=∠FGE，所以∠AEH=∠QGF，于是可证明△AEH ≌△QGF，得到AH=QF=2，然后根据三角形面积公式求解．【解答】（1）证明：∵四边形EFGH为菱形，∴HG=EH，∵AH=2，DG=2，∴DG=AH，在Rt△DHG和△AEH中，，∴Rt△DHG≌△AEH，∴∠DHG=∠AHE，∵∠AEH+∠AHE=90°，∴∠DHG+∠AHE=90°，∴∠GHE=90°，∵四边形EFGH为菱形，∴四边形EFGH为正方形；（2）解：作FQ⊥CD于Q，连结GE，如图，∵四边形ABCD为矩形，∴AB∥CD，∴∠AEG=∠QGE，即∠AEH+∠HEG=∠QGF+∠FGE，∵四边形EFGH为菱形，∴HE=GF，HE∥GF，∴∠HEG=∠FGE，∴∠AEH=∠QGF，在△AEH和△QGF中，∴△AEH≌△QGF，∴AH=QF=2，∵DG=6，CD=8，∴CG=2，∴△FCG的面积=CG•FQ=×2×2=2．【点评】本题考查了正方形的判定与性质：正方形的判定没有固定的方法，只要判定既是矩形又是菱形就可以判定；正方形具有平行四边形、矩形、菱形的所有性质．也考查了菱形和矩形的性质．24．（12分）（2015春•上城区期末）在直角坐标系中，已知反比例函数y=（k≠0）图象经过点D（5，1），且BD⊥y轴，垂足为B，点C是第三象限图象上的动点，过C作CA ⊥x轴，垂足为A，连接AB，BC．（1）求k的值；（2）若△BCD的面积是10，求直线CD的解析式；（3）判断AB与CD的位置关系，并说明理由．【分析】（1）把点D的坐标代入双曲线解析式，进行计算即可得解；（2）先根据点D的坐标求出BD的长度，再根据三角形的面积公式求出点C到BD的距离，然后求出点C的纵坐标，再代入反比例函数解析式求出点C的坐标，然后利用待定系数法求一次函数解析式解答；（3）根据题意求出点A、B的坐标，然后利用待定系数法求出直线AB的解析式，可知与直线CD的解析式k值相等，所以AB、CD平行．【解答】解：（1）∵比例函数y=（k≠0）图象经过点D（5，1），∴k=5×1=5；（2）设点C到BD的距离为h，∵点D的坐标为（5，1），DB⊥y轴，∴BD=5，=×5•h=10，∴S△BCD解得h=4，∵点C是双曲线第三象限上的动点，点D的纵坐标为1，∴点C的纵坐标为1﹣4=﹣3，∴=﹣3，解得x=﹣，∴点C的坐标为（﹣，﹣3），设直线CD的解析式为y=kx+b，则，解得，所以，直线CD的解析式为y=x﹣2；（3）AB∥CD．理由如下：∵CA⊥x轴，DB⊥y轴，设点C的坐标为（c，），点D的坐标为（5，1），∴点A、B的坐标分别为A（c，0），B（0，1），设直线AB的解析式为y=mx+n，则，解得，所以，直线AB的解析式为y=﹣x+1，设直线CD的解析式为y=ex+f，则，解得，∴直线CD的解析式为y=﹣x+，∵AB、CD的解析式k都等于﹣，∴AB与CD的位置关系是AB∥CD．【点评】本题是对反比例函数的综合考查，主要利用了待定系数法求函数解析式，三角形的面积的求解，待定系数法是求函数解析式最常用的方法，一定要熟练掌握并灵活运用．参与本试卷答题和审题的老师有：1987483819；gbl210；守拙；sjzx；放飞梦想；王学峰；sdwdmahongye；HLing；dbz1018；家有儿女；Liuzhx；gsls；sks；sd2011；知足长乐（排名不分先后）菁优网2017年5月26日。

2014年浙江省杭州市上城区中考一模英语试题及答案

2014年杭州各类高中招生文化考试上城区一模试卷英语(2014.4.18)一、完形填空On a trip to California, my family stopped for lunch. As we walked towards the entrance to the restaurant, a man, with a messy beard and ___1___ hair, jumped up from a bench outside the restaurant and opened the door for us. Paying no attention to his ___2____, he greeted us in a friendly way.Once inside, my daughters said in a low voice, “Mom, he ____3___.”After we ordered our lunch, I explained, telling the the kids to look beyond the dirt. We then watched other ___4___ come into the restaurant but many took no notice of him. Seeing this rudeness truly ___5___me. The day I became a mother, I had determined to set a good example to my children. Yet sometimes being a good example was ____6___, especially when things didn’t go right. After our meal arrived, I realized I had left my car-sick pills in the car, so I went back to the car to get them.Just then, the “doorman”was opening the door for a couple. They ___7___ him without even noticing his presence. Letting them in first, I said a loud “thank you” to ___8___ as I went out.When I returned, we talked a bit. He said he was not allowed inside ___9___ he bought food. I went back and asked our waitress to ___10___ one soup and sandwich. The kids looked puzzed as they had already eaten. But when I told them his story and said the ___11___ was for the “doorman”, they smiled. When it was time to continue our ___12___, I found the “doorman” enjoying his meal. Upon seeing me, he stood up and thanked me heartily with tears in his eyes.Back in the car, I fell into deep thought. While we can’t choose many things in life, we can choose __13___ to show gratitude. I said thanks to a man who had __14___held open a door for me, and also said thanks for that opportunity to teach my children by ___15____.( )1.A.dirty B.clean C.pretty D.shiny( )2.A.appearance B.happiness C.illness D.carelessness( )3.A.smokes B.shouts C.smells D.smiles( )4.A.travelers B.visitors C.passengers D.customers( )5.A.taught B.upset C.troubled D.surprised( )6.A.tiring B.amazing C.difficult D.successful( )7.A.waited for B.rushed past C.stopped by D.returned to( )8.A.him B.them C.myself D.themselves( )9.A.before B.since C.though D.unless( )10.A.buy B.add C.show D.borrow( )11.A.order B.money C.note D.service( )12.A.meal B.talk C.trip D.story( )13.A.where B.when C.how D.why( )14.A.actually B.truly C.really D.simply( )15.A.journey B.example C.lesson D.experience二、单项选择( )1.Which of the following phonetic transcription is right for the word “breakfast”?A. ['breikfəst]B. ['brekfəst]C. ['brikfəst]D. ['brækfəst]( )2.If you travel in _______ India, you can use English everywhere.A.aB.anC.theD./( )3.Though it rained heavily, it didn’t make much _______ to the game.A.progressB.troubleC.differenceD.sense( )4.I often see lights in that empty house. So you think I ______ report it to the police?A.canB.mayC.willD.should()5.He jumped to his feet, thinking that the planes were going to ________.A.take offB.keep offC.get offD.turn off( )6.The rock band is going on a world tour in ______they will perform in different cities.A.thatB.whichC.whomD.where( )7.It seems some students would like to start work as soon as possible, _____ they can help provide better lives for their parents.A.as ifB.so thatC.even thoughD.now that( )8.Sorry, there is no Yangzhou Fried Rice now. It _____ only for lunch and supper.A.servesB.servedC.is servedD.is serving( )9.The _____ kids learn to be independent, the better it is for their future.tertestC.earlierD.earliest( )10.Here on the bag it ______ that they were invented by a chef called George Crum.A.saysB.writesC.speaksD.notices( )11.However, if you don’t take these talen shows too _______, they are fun to watch.A.clearlyB.carefullyC.seriouslyD.excitedly( )12.He said that he had waited for ________.A.one and a half hoursB.one and half hourC.one and the half hourD.one and half an hour ( )13.Pushy parents are _____ new, but now parents seem to push their children a lot more.A.somethingB.nothingC.anythingD.everything( )14.You can’t imagine ______ when you read it in the newspaper.A.the story is how movingB.how is the story movingC.how moving is the storyD.how moving the story is( )15.—If I speak this way, could you hear me clearly? --__________A.Go ahead.B.Never mind.C.I hope not.D.What for?三、阅读理解AYou know that eating a suitable diet and getting plenty of exercise help make your body healthy and strong. But did you know that there are ways to make your brain healthier and smarter?Studies show that when the brains is forced to do something new, it creates new neural (神经元) pathways. The more pathways you have, the faster you can think and the better memory you will have. Wonderful steps towards a smarter brain are as follows:Choose proper TV programsWatching an average TV show needs very little brain power and brings the same result as giving no care to physical exercise. Your brain will become weak just as your muscles do,if you watch TV, choose something educational and full of information.TravelTraveling to a new country forces you to see and do things in a new way, making your brains more active.Learning a new languageA new language learner usually uses different learning methods. Learning a language sharpens yourbrain and helps you prevent memory problems in later years.Master a new subjectEach week, choose an animal, a bird or a fish, and read everything you can about it. Go on learning unitl you become an expert on the subject.Use your non-dominant handIf you are right-handed,use your left hand for everyday activities, or use your right hand if you are left-handed. Doing familiar things in a new way will cause your brain to create new neural networks.Read oftenAs you read, take the time to look up people or places that aren’t familiar. Reading can enlarge your vocabulary if you search for words and expressions that you don’t know.Calculate while you shopAs you put things in your shopping bag, total everything in your head. See how close you get to the actual total.Play video gamesStudies have found that some video games force you to use critical decision-making skills and can even improve students’ math grades.So get into the habit of challenging your brain, and make yourself smarter!( )1.The passage can most probably be found in a _____book.A.historyB.travelC.scienceD.story( )2.The underlined word “it” in the second paragraph refers to _________.A.the brainB.the studyC.the neural pathwayD.something new( )3.According to the passage,there are _____ ways to make your brain smartr besides traveling and reading often.A.fiveB.sixC.eightD.ten( )4.While you are reading, you should _______.A.read as loudly as possibleB.look up something unfamiliarC.read as quickly as you canD.read from the beginning to the end( )5.Which of the following statements is TRUE according to the passage?A.Playing video games is bad for your study and your health.ing calculators a lot can make you smarter when you are a child.C.Watching something educational on TV needs very little brain power.D.Writing with the right hand can make the left-handed smarter.BFor many years, a small percentage of homeowners have fixed solar panels (太阳能板) on their rooftops. Those panels collect some of the sun’s energy and either change it into electricity or use it to heat water. Until recently, the panels were too expensive for average homeowners, and their designs were not attractive. Thanks to new advances, however, solar panels for homes are becoming cheaper and less large and heavy. Now more homeowners are considering using them.Stores begin to sell Solar panelsLast fall furniture retailer(零售商) IKEA began selling solar panels in its U.K. stores. IKEA has brought the DIY solar choice to the public. While shopping for furniture, shoppers could not add a box or two of solar panels to their shopping cart (购物车). IKEA is partnering with a company. The company deals with fixing and servcing of the solar panels on the roofs. So it is easy for customers to change from old energy system to solar system. If all goes well, IKEA plans to begin selling the panels in other countries soon.Stylish solar panelsSolTech, a Swedish company, offers a really great solar-power solution. Instead of flat panels, SolTech covers the panels with a special glass tile. And the shape of the glass tile fits traditional tiled roof designs. SolTech recently offers solar systems that heat the home’s air or water. And it also offers one solar system that produces electricity.______________New technology has turned windows into solar panels. SolarWindow technology enables see-through windows to produce electricity after the glass surface is added with a special coating. Amazingly, SolarWindow can produce electricity in low-light conditons and can even turn indoor, man-made light into electricity! Since buildings are getting taller and about 60 percent of an office building’s surface is covered with windows, solar window could become a very popular way for people to produce energy and save money.Turning your home –business-into a solar-powered one is a choice that’s becoming a lot more attractive these days!( )1.This passage mainly talks about ______.A.fashion showsB.life in the UKC. a technologyD.different opinions( )2.The reason why only a few homeowners used solar panels is that they are __________.A.cheap but heavyB.attractive but expensiveC.light and smallD.dear and not attractive()3.The DIY solar choice has been brought to the public so that _______.A.the IKEA stores can sell more furniture in the U.K.B.it is possible to make more panels in other countries.C.more people will choose to use a new energy system.D.people can get solar panels for free after buying furniture.( )4.The best title for the fourth paragraph is __________.A.Making new kinds of windownsB.Turning windows into solar panelsC.Changing our homes into panelsD.Adding electricity to the windows( )5.The author’s attitude towards solar panels is _________.A.positiveB.negative D.uncertain D.questioningC下面五个家庭或个人正在考虑各自的活动安排。

2024年浙江省杭州市上城区中考数学一模试卷及答案解析

2024年浙江省杭州市上城区中考数学一模试卷一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（3分）下列各数中，最小的数是（）A．﹣3B．﹣1C．0D．32．（3分）杭州亚运会主会场莲花体育场有固定座位80800个，其中数字80800用科学记数法表示为（）A．8.08×104B．80.8×103C．808×102D．0.808×1053．（3分）如图所示的几何体是由6个大小相同的小正方体组成，则该物体的俯视图是（）A．B．C．D．4．（3分）下列计算正确的是（）A．a2•a4＝a8B．2a3﹣a3＝aC．（ab2）3＝a3b6D．5．（3分）如图，转盘中8个扇形的面积都相等，涂色的为灰色部分，其余为白色部分，任意转动这个转盘1次，当转盘停止转动时，指针落在灰色区域的概率是（）A．B．C．D．6．（3分）《孙子算经》中有这样一道题，大意为：今有100头鹿，每户分一头鹿后，还有剩余，将剩下的鹿按每3户共分一头，恰好分完，问：有多少户人家？若设有x户人家，则下列方程正确的是（）A．x+3＝100B．C．x+3x＝100D．7．（3分）在平面直角坐标系中，一次函数y＝x+a（a≠0）的图象如图所示，若y＝ax+1的图象与x轴交于（m，0），则下列判断正确的是（）A．m＜﹣1B．﹣1＜m＜0C．0＜m＜1D．m＞18．（3分）如图，在△ABC中，点D为BC边上的中点，点E为AC边上的三等分点（AE＜EC），连结AD，BE，交点为F，过D作DG∥EF，已知△AEF的面积为4，则S△ABC为（）A．144B．120C．60D．489．（3分）二次函数y1＝x2+bx+c（b，c是常数）过（﹣2，0），（m，0）两个不重合的点，一次函数y2＝x+d过（m，0）和二次函数的顶点，则m的值为（）A．﹣1B．0C．1D．210．（3分）如图，在⊙O中，将沿弦AB翻折，使恰好经过圆心O，C是劣弧AB上一点．已知AE ＝2，tan∠CBA＝，则AB的长为（）A．B．6C．D．二、填空题：本大题有6小题，每题3分，共18分．11．（3分）在实数范围内分解因式：2x2﹣8＝．12．（3分）不等式2x+2≤4的最大整数解是．13．（3分）如图，在菱形ABCD中，AC、BD为对角线，AE平分∠CAB，若∠CAE＝32°，则∠ABC的度数为°．14．（3分）第19届杭州亚运会会徽如图1所示，名为“潮涌”，象征着新时代中国特色社会主义大潮的涌动和发展．其主体部分可以看成如图2的几何图形，小明测量得OB＝2cm，OA＝5cm，∠BOC＝120°．则图2中的阴影部分的面积为cm2.（结果保留π）15．（3分）如图，是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形组成的一个大正方形．（1）连接BF，若F恰为AG中点，则∠BFG的度数为°；（2）连接CF，若△ABF与△FEC的面积相等，DF＝2，则AF的长为．16．（3分）如图，在△OAB中，边OA在y轴上．反比例函数y＝（x＞0）的图象恰好经过点B，与边AB交于点C．若BC＝3AC，S△OAB＝10．则k的值为．三、解答题：本大题有8个小题，共72分.解答应写出文字说明、证明过程或演算步骤．17．（6分）先化简，再求值：（2a﹣b）2﹣（b2﹣3ab），其中a＝﹣1，b＝2．18．（6分）今年是农历龙年，假期里学校组织学生进行龙灯制作活动，每班精选一项进行年级评选，校学生会组织对同学的作品按10分制进行评分，成绩（单位：分）均为不低于6的整数．对每个班的成绩进行整理，并绘制统计表，信息如表：八年级10个班成绩统计表成绩/分678910班级个数13a b1已知八年级各班成绩只有一个众数为9分，且a、b均为正整数．请根据以上信息，完成下列问题：（1）a＝，b＝；（2）八年级成绩的中位数为分；（3）若年级均分高于8.5分，则认定该年级在活动中荣获“优秀组织奖”，请判断本次活动八年级能否获得“优秀组织奖”．19．（8分）光线从空气射入水中会发生折射现象（如图1），我们把称为折射率（其中α代表入射角，β代表折射角）．明明制作了一个测算液体折射率的装置．光线从点A按固定角度从空气射入液面（介质），如图2，装入某液体（介质），使光线折射后恰好落到点C，直线GH为法线．已知∠1＝53°，液面高度CF为12cm，正方形ABCD的边长为30cm．（参考数据：，，，，，（1）求PE的长；（2）求该液体（介质）的折射率n．20．（8分）如图，反比例函数的图象与直线y＝ax交于点D（1，4），点A是线段OD上的一个动点，过点A作y轴的垂线分别交反比例函数图象和y轴于点B和点C．（1）求k和a的值；（2）根据图象直接写出的自变量x的取值范围；（3）当AB长为时，求点A的坐标．21．（10分）如图，点D为△ABC的边AC上一点，延长BD至点F，使得CF∥AB，点E在线段BC上，且DE∥AB，AB＝4，CF＝6．（1）若AD＝3，求CD的长．（2）若∠ABC＝60°，BD平分∠ABC，求BD的长．22．（10分）某校开展劳动实践活动，九（1）班分配得到一块如图所示的边长为8米的正方形菜地ABCD ，由于场地调整，现将菜地改成周长不变的长方形菜地AEGH ，两块菜地的重叠部分为矩形ABFE ，不重叠两块是矩形CDEF 和矩形BHGF ，设AE 长为x 米，EG 长为y 米．（1）求y 关于x 的函数表达式；（2）求矩形BHGF 面积的最大值；（3）九（1）班的亮亮同学说：“矩形CDEF 面积一定不小于矩形BHGF 的面积”，请你判断他的说法是否正确，并说明理由．23．（12分）综合与实践主题任务“我的校园我做主”草坪设计入项探究环节任务背景学校举办“迎五一，爱劳动”主题实践活动，九（2）班参加校园美化设计任务：校园内有一块宽为31米，长为40米的矩形草坪，在草坪上设计两条小路，具体要求：（1）矩形草坪每条边上必须有一个口宽相等的路口；（2）两条小路必须设计成平行四边形；驱动任务一九（2）班各个实践小组的设计方案汇总后，主要有甲、乙、丙三种不同的方案（如图1）：（1）直观猜想：方案中小路的总面积大小关系：S 甲S 乙，S甲S 丙；（请填“相等”或“不相等”）深入探究驱动任务二验证猜想：各个实践小组用如表格进行研究：方案纵向小路面积横向小路面积纵横交叉面积小路总面积乙方案31x 40x 甲方案31x 40x 丙方案31x40x（2）请用含x 的代数式表示甲方案中小路总面积：；驱动任务三（3）如果甲种方案除小路后草坪总面积约为1170平方米．请计算两条小路的宽度是多少？拓展探究驱动任务四为了深入研究，各个小组选择丙方案（如图2）进行研究．若两条小路与矩形两组对边所夹锐角∠BGF ＝∠AEF ＝θ．（4）若θ＝60°时，用含x 的代数式拓表示四边形FHPQ 的边长FH ；（5）若x ＝1时，请用含θ的三角函数表示两条路重叠部分四边形FHPQ 的面积，并写出sin θ取值范围．24．（12分）如图，△ABC 内接于⊙O ，点D为弦AB 的中点，连接DO 、OB ，延长DO 交弦AC 的延长线于点E ，DE 与弦BC 交于点F ，DE 与⊙O 交于点G ，已知AB ＝6，DG ＝9．（1）求⊙O 的半径；（2）求证：∠E ＝∠OBC ；（3）若OF ＝3，求CF 的长．2024年浙江省杭州市上城区中考数学一模试卷参考答案与试题解析一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【分析】根据正数大于0，0大于负数，以及两个负数比较大小方法判断即可．【解答】解：∵﹣3＜﹣1＜0＜3，∴最小的数为﹣3．故选：A．【点评】此题考查了有理数的大小比较，熟练掌握有理数大小比较方法是解本题的关键．2．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数；当原数的绝对值＜1时，n是负整数．【解答】解：80800＝8.08×104．故选：A．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．3．【分析】根据从上边看得到的图形是俯视图，可得答案．【解答】解：从上边看，底层靠左侧是一个小正方形，上层是四个小正方形．故选：C．【点评】本题考查了简单组合体的三视图，从上边看得到的图形是俯视图．4．【分析】根据同底数幂的乘法、合并同类项、积的乘方及分式的运算逐一判断即可．【解答】解：A．a2•a4＝a6，故本选项不符合题意；B.2a3﹣a3＝a3，故本选项不符合题意；C．（ab2）3＝a3b6，故本选项符合题意；D.1÷（a+b）＝，故本选项不符合题意．故选：C．【点评】本题主要考查同底数幂的乘法、合并同类项、幂的乘方及积的乘方，熟练掌握以上知识点是解题的关键．5．【分析】首先确定在图中阴影区域的面积在整个面积中占的比例，根据这个比例即可求出指针落在灰色区域的概率．【解答】解：∵圆被等分成8份，其中灰色区域占2份，∴指针落在灰色区域的概率为．故选：B．【点评】本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．6．【分析】根据“今有100头鹿，每户分一头鹿后，还有剩余，将剩下的鹿按每3户共分一头，恰好分完”，即可列出关于x的一元一次方程，此题得解．【解答】解：根据题意得：x+x＝100．故选：D．【点评】本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．7．【分析】先根据函数图象判断出a的取值范围，用a表示出m的值，再用取特殊值法即可得出结论．【解答】解：由函数图象可知，﹣1＜a＜0，∵y＝ax+1的图象与x轴交于（m，0），∴当y＝0时，ax+1＝0，∴x＝﹣，∴m＝﹣，令a＝﹣0.5，则﹣a＝0.5，∴﹣＝＝2＞1，∴m＞1．故选：D．【点评】本题考查的是一次函数的性质及一次函数的图象，熟知一次函数的图象与系数的关系是解题的关键．8．【分析】由点D为BC边上的中点，得到S△ABC＝2S△ACD，由平行线等分线段定理推出AF＝FD，得到EF是△ADG的中位线，因此EF＝DG，由△AFE∽△ADG，推出＝＝，求出S△ADG ＝16，由S△ADG＝S△ACD，得到△ACD的面积＝24，于是得到S△ABC＝2S△ACD＝48．＝4S△AFE【解答】解：∵点D为BC边上的中点，＝2S△ACD，∴S△ABC∵DG∥EF，BD＝CD，∴CG＝EG，∵E为AC边上的三等分点（AE＜EC），∴CE＝2AE，∴AE＝EG＝CG，∵EF∥DG，∴AF＝FD，∴EF是△ADG的中位线，∴EF＝DG，∵FE∥DG，∴△AFE∽△ADG，∴＝＝，∵△AEF的面积为4，＝4S△AFE＝16，∴S△ADG∵AG＝AC，＝S△ACD，∴S△ADG∴△ACD的面积＝24，＝2S△ACD＝48．∴S△ABC故选：D．【点评】本题考查相似三角形的判定和性质，三角形中位线定理，关键是由平行线等分线段定理推出EF是△ADG的中位线，由△AFE∽△ADG，推出＝＝，9．【分析】依据题意，由抛物线过（﹣2，0），（m，0），从而可得抛物线的对称轴是直线x＝﹣＝，且有4﹣2b+c＝0，故有b＝2﹣m，c＝2b﹣4＝﹣2m，进而顶点为（，），再结合一次函数y2＝x+d过（m，0）和二次函数的顶点，即可求出m．【解答】解：由题意，∵抛物线过（﹣2，0），（m，0），∴抛物线的对称轴是直线x＝﹣＝，4﹣2b+c＝0．∴b＝2﹣m．∴c＝2b﹣4＝﹣2m．∴顶点为（，）．又一次函数y2＝x+d过（m，0）和二次函数的顶点，∴m+d＝0，且+d＝．∴﹣m＝﹣．∴m＝0或m＝﹣2（舍去）．∴m＝0．故选：B．【点评】本题主要考查了二次函数的图象与性质，解题时要熟练掌握并能灵活运用是关键．10．【分析】连接EO并延长交⊙O于点H，连接AH，过点O作OF⊥AB于F，延长OF交⊙O于点G，连接OB，根据圆周角定理求出∠EAH＝90°，解直角三角形求出AH＝4，根据勾股定理求出EH＝2，根据垂径定理求出AB＝2BF，根据折叠的性质得，OF＝GF，再根据勾股定理求解即可．【解答】解：连接EO并延长交⊙O于点H，连接AH，过点O作OF⊥AB于F，延长OF交⊙O于点G，连接OB，∵EH是⊙O的直径，∴∠EAH＝90°，∴tan∠AHE＝，∵∠AHE＝∠CBA，tan∠CBA＝，∴tan∠AHE＝tan∠CBA＝，∴＝，∵AE＝2，∴AH＝4，∴EH＝＝2，∴⊙O的半径为，∴OG＝OB＝，∵OG⊥AB于F，∴AB＝2BF，根据折叠的性质得，OF＝GF，∴OF＝OG＝，∴BF＝＝，∴AB＝，故选：C．【点评】此题考查了圆周角定理、折叠的性质、垂径定理、解直角三角形等知识，熟练运用圆周角定理、折叠的性质、垂径定理并作出合理的辅助线构建直角三角形是解题的关键．二、填空题：本大题有6小题，每题3分，共18分．11．【分析】首先提取公因式2，然后利用平方差公式继续分解，即可求得答案．【解答】解：2x2﹣8＝2（x2﹣4）＝2（x+2）（x﹣2）．故答案为：2（x+2）（x﹣2）．【点评】此题考查了在实数范围内分解因式的知识．此题比较简单，注意因式分解的步骤为：一提公因式；二看公式．在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止．12．【分析】解不等式求得x的范围，再该范围内可得其最大整数解．【解答】解：移项、合并，得：2x≤2，系数化为1，得：x≤1，∴不等式的最大整数解为1，故答案为：1．【点评】本题考查的是一元一次不等式的整数解，熟知不等式的基本性质是解答此题的关键．13．【分析】由角平分线定义得到∠CAB＝2∠CAE＝2×32°＝64°，由菱形的性质推出AB＝BC，得到∠ACB＝∠CAB＝64°，即可求出∠ABC＝180°﹣64°×2＝52°．【解答】解：∵AE平分∠CAB，∴∠CAB＝2∠CAE＝2×32°＝64°，∵四边形ABCD是菱形，∴AB＝BC，∴∠ACB＝∠CAB＝64°，∴∠ABC＝180°﹣64°×2＝52°．故答案为：52．【点评】本题考查菱形的性质，关键是由菱形的性质推出AB＝BC，得到∠ACB＝∠CAB＝64°．14．【分析】根据S阴影部分＝S扇形AOD﹣S扇形BOC计算即可；【解答】解：S阴影部分＝S扇形AOD﹣S扇形BOC＝﹣＝7π（cm2）故答案为：7π．【点评】本题考查扇形的面积，解题的关键是掌握扇形面积公式．15．【分析】（1）根据全等三角形的性质得到AF＝BG，得到AF＝FG，推出△BGF是等腰直角三角形，根据等腰直角三角形的性质得到结论；（2）设FG＝HG＝EF＝EH＝x，由题意得，AG＝CE＝DF＝BH＝2，得到AF＝BG＝2﹣x，根据题意列方程即可得到结论．【解答】解：（1）由题意得，△ADF≌BAG，∴AF＝BG，∵F恰为AG中点，∴AF＝FG，∴BG＝FG，∴△BGF是等腰直角三角形，∴∠BFG＝45°，故答案为：45；（2）∵四边形EFGH是正方形，∴FG＝HG＝EF＝EH，设FG＝HG＝EF＝EH＝x，由题意得，AG＝CE＝DF＝BH＝2，∴AF＝BG＝2﹣x，∵若△ABF与△FEC的面积相等，∴，∴（2﹣x）2＝2x，∴x＝3﹣或x＝3+（不合题意舍去），∴FG＝3﹣，∴AF＝2﹣（3﹣）＝﹣1，故答案为：﹣1．【点评】本题考查了勾股定理的证明，全等三角形的性质，正方形的性质，等腰直角三角形的判定和性质，正确地识别图形是解题的关键．16．【分析】根据BC＝3AC，S△OAB＝10可得S△COB＝，再根据反比例函数k值的几何意义列出方程求出k即可．＝10．【解答】解：∵BC＝3AC，S△OAB＝＝，△COB设点C（m，），则B（4m，），＝S梯形BCDE＝，∵S△COB∴，解得：k＝4．故答案为：4．【点评】本题考查了反比例函数k值的几何意义，熟练掌握反比例函数k值的几何意义是关键．三、解答题：本大题有8个小题，共72分.解答应写出文字说明、证明过程或演算步骤．17．【分析】利用整式的相应的法则对式子进行化简，再代入相应的值运算即可．【解答】解：（2a﹣b）2﹣（b2﹣3ab）＝4a2﹣4ab+b2﹣b2+3ab＝4a2﹣ab，当a＝﹣1，b＝2时，原式＝4×（﹣1）2﹣（﹣1）×2＝4+2＝6．【点评】本题主要考查整式的混合运算，解答的关键是对相应的运算法则的掌握．18．【分析】（1）根据八年级各班成绩只有一个众数为9分，且a、b均为正整数和表格中的数据，可以得到a、b的值；（2）根据表格中的数据，可以得到八年级成绩的中位数；（3）先计算出八年级成绩的平均数，再与8.5比较大小即可．【解答】解：（1）∵八年级各班成绩只有一个众数为9分，且a、b均为正整数，∴b＝4，则a＝10﹣1﹣3﹣4﹣1＝1，故答案为：1，4；（2）由表格可得，八年级的中位数为：（8+9）÷2＝17÷2＝8.5（分），故答案为：8.5；（3）由表格可得，八年级的平均分为：（6×1+7×3+8×1+9×4+10×1）÷10＝8.1（分），∵8.1＜8.5，∴本次活动八年级不能获得“优秀组织奖”．【点评】本题考查众数、中位数、平均数，解答本题的关键是明确题意，求出相应的数据．19．【分析】（1）根据题目条件，先说明各个小四边形都是矩形，AG＝EP，在Rt△AGP中，利用直角三角形的边角间关系求出AG；（2）先利用线段的和差关系求出PF，再在Rt△CHP中利用直角三角形的边角间关系求出∠2的正弦，最后利用求折射率的公式得结论．【解答】解：∵正方形ABCD的边长为30cm，∴AD＝CD＝30cm．由题意知：液面平行于底垂直于AB、CD两边，法线垂直于液面，∴四边形AEGP、DGPF、CFPH、EPHB都是矩形．∴PE＝AG，GP＝CD﹣CF＝30﹣12＝18（cm）．（1）在Rt△AGP中，∵tan∠APG＝，∴PE＝AG＝tan∠APG•GP＝tan53°•18≈×18＝24（cm）．（2）∵四边形AEGP、DGPF、CFPH、EPHB都是矩形，∴CH＝GD＝AD﹣AG＝6（cm），在Rt△PCH中，∵CP＝＝＝6．∴sin∠2＝＝＝．∴n＝≈＝．【点评】本题考查了解直角三角形，掌握直角三角形的边角间关系、勾股定理、正方形的性质、矩形的性质和判定等知识点是解决本题的关键．20．【分析】（1）将D点坐标代入两个解析式可得k、a值；（2）根据函数图象和点D横坐标可得不等式的解集；（3）先确定两个函数解析式，再设A（m，4m）则B（m+，4m），根据点B在反比例函数图象上，列出关于m的方程解出m值即可知道点A坐标．【解答】解：（1）∵反比例函数的图象与直线y＝ax交于点D（1，4），∴k＝4，a＝4，（2）根据图像可知，的自变量x的取值范围为：0＜x＜1．（3）由（1）可知，反比例函数解析式为y＝，正比例函数解析式为：y＝4x，设A（m，4m）则B（m+，4m），∵点B在反比例函数图象上，∴4m（m+）＝4，解得m＝或m＝﹣2（舍去），∴A（，2）．【点评】本题考查了反比例函数与一次函数的交点问题，交点坐标满足两个函数解析式是关键．21．【分析】（1）由△ABD∽△CFD，得到AD：CD＝AB：CF，即可求出CD的长．（2）过E作EH⊥BD于H，由平行线的性质，等腰三角形的性质，锐角的正弦推出BD＝2DH＝DE，由△CDE∽△CAB，△BDE∽△BFC，推出+＝1，即可求出DE＝，于是得到BD＝DE ＝．【解答】解：（1）∵AB∥CF，∴△ABD∽△CFD，∴AD：CD＝AB：CF，∴3：CD＝4：6，∴CD＝4.5．（2）过E作EH⊥BD于H，∵DE∥AB，∴∠BDE＝∠ABD，∵BD平分∠ABC，∴∠ABD＝∠CBD＝∠ABC＝×60°＝30°，∴∠BDE＝∠DBE＝30°，∴DE＝BE，∴BD＝2DH，∵cos∠EDH＝cos30°＝＝，∴DH＝DE，∴BD＝2DH＝DE，∵CF∥AB，DE∥AB，∴DE∥CF，∴△CDE∽△CAB，△BDE∽△BFC，∴＝，＝，∴+＝+＝1，∵AB＝4，CF＝6，∴DE＝，∴BD＝DE＝．【点评】本题考查相似三角形的判和性质，等腰三角形的判定和性质，关键是由△ABD∽△CFD，得到AD：CD＝AB：CF；由△CDE∽△CAB，△BDE∽△BFC推出+＝1，由等腰三角形的性质，锐角的余弦得到BD＝DE．22．【分析】（1）根据长方形的周长公式解答即可；（2）用含x的代数式分别表示出矩形BHGF的长和宽，根据长方形的面积公式写出其面积表达式，利用二次函数求最值的方法求解即可；（3）利用作差法判断两个面积的大小即可．【解答】解：（1）根据长方形的周长公式，得2（x+y）＝8×4，即y＝﹣x+16，∴y关于x的函数表达式为y＝﹣x+16．（2）∵EF＝8，∴FG＝y﹣8＝﹣x+8，＝FG•BF＝（﹣x+8）x＝﹣（x﹣4）2+16，∴S矩形BHGF∴当x＝4时，矩形BHGF面积最大，最大值为16米2．（3）他的说法正确．理由如下：∵CD＝8，DE＝8﹣x，＝CD•DE＝8（8﹣x）＝64﹣8x，∴S矩形CDEF﹣S矩形BHGF＝64﹣8x﹣（﹣x+8）x＝（x﹣8）2≥0，∴S矩形CDEF≥S矩形BHGF．∴S矩形CDEF【点评】本题考查一次函数的应用、矩形和正方形的性质，掌握矩形和正方形的性质及其周长和面积公式、二次函数求最值的方法是解题的关键．23．【分析】（1）应用平移的性质即可求得答案；（2）根据小路总面积＝横向小路面积+纵向小路面积﹣重叠部分的面积，即可得出答案；（3）表达出草地面积，建立方程求解即可；（4）连接FH，过点F作FM∥AD，交KH于M，由∠AEF+∠AGF＝180°，得出四边形AEFG是圆内接四边形，进而可得∠A +∠EFG ＝180°，即∠EFG ＝90°，再运用解直角三角形即可求得答案；（5）连接FM 、PM 、PQ 、FQ ，过点F 作FM ∥AD ，交KH 于M ，可证得四边形FHPQ 是正方形，边长为sin θ，即可得出正方形FHPQ 的面积；当G 与A 重合时，θ最小，即sin θ的值最小，而sin θ的最大值为1，即可求出答案．【解答】解：（1）如图1，∵S 甲＝40×31﹣（40﹣x ）（31﹣x ）＝71x ﹣x 2，S 乙＝40×31﹣（40﹣x ）（31﹣x ）＝71x ﹣x 2，S 丙＝40×31﹣（40﹣x ）（31﹣x ）＝71x ﹣x 2，∴S 甲＝S 乙＝S 丙，故答案为：相等，相等；（2）S 甲＝40x +31x ﹣x 2＝71x ﹣x 2（平方米），故答案为：（71x ﹣x 2）平方米；（3）由题意得：（40﹣x ）（31﹣x ）＝1170，解得：x 1＝1，x 2＝70（不符合题意，舍去），答：两条小路的宽度是1米；（4）如图2，连接FH ，过点F 作FM ∥AD ，交KH 于M ，∵∠BGF ＝∠AEF ＝θ＝60°，∠BGF +∠AGF ＝180°，∴∠AEF +∠AGF ＝180°，∴四边形AEFG 是圆内接四边形，∴∠A +∠EFG ＝180°，∵∠A ＝90°，∴∠EFG ＝90°，∵EF ∥KH ，∴∠FHM ＝∠EFG ＝90°，∵FM ∥AD ，∴∠EFM ＝∠AEF ，∵EF ∥KH ，∴∠FMH＝∠EFM，四边形EFMK是平行四边形，∴∠FMH＝∠AEF＝60°，FM＝EK＝x，∴FH＝FM•sin∠FMH＝x•sin60°＝x（米）；（5）如图3，连接FM、PM、PQ、FQ，过点F作FM∥AD，交KH于M，则四边形EFMK是平行四边形，∴FM＝EK＝1，∠FMH＝∠AEF＝θ，∵FH∥PQ，FQ∥PH，∴四边形FHPQ是平行四边形，由（4）知：∠AFE＝90°，∴∠QFH＝90°，∴四边形FHPQ是矩形，在Rt△FMH中，FH＝FM•sinθ＝sinθ，同理可得FQ＝sinθ，∴FH＝FQ，∴四边形FHPQ是正方形，∴两条路重叠部分四边形FHPQ的面积为sin2θ平方米；如图4，当G与A重合时，∵∠DAR+∠ARD＝90°，∠DAR+∠AEF＝90°，∴∠ARD＝∠AEF＝θ，此时θ最小，即sinθ的值最小，∵CR＝1，∴DR＝31﹣1＝30，在Rt△ADR中，AR＝＝＝50，∴sinθ＝＝＝，∴≤sinθ≤1．【点评】本题是解直角三角形应用问题，考查了矩形的判定和性质，正方形的判定和性质，直角三角形的性质，解直角三角形等，解题关键是理解题意，熟练运用解直角三角形解决问题．24．【分析】（1）利用垂径定理得到OD⊥AB，AD＝DB＝3，设⊙O的半径为r，利用勾股定理列出方程解答即可；（2）延长BO交⊙O于点K，连接CK，利用直径所对的圆周角是直角和直角三角形的性质解答即可；（3）连接OC，利用相似三角形的判定与性质求得OE＝，利用勾股定理求得BF，再利用相似三角形的判定与性质解答即可．【解答】（1）解：∵点D为弦AB的中点，O为圆心，AB＝6，∴OD⊥AB，AD＝DB＝3，设⊙O的半径为r，则OB＝OG＝r，OD＝DG﹣OG＝9﹣r，∵BD2+OD2＝OB2，∴32+（9﹣r）2＝r2，∴r＝5．∴⊙O的半径为5；（2）证明：延长BO交⊙O于点K，连接CK，如图，∵BK为⊙O的直径，∴∠BCK＝90°，∴∠OBC+∠K＝90°．∵OD⊥AB，∴∠E+∠A＝90°．∵∠A＝∠K，∴∠E＝∠OBC；（3）解：连接OC，∵OC＝OB，∴∠OCB＝∠OBC，∵∠E＝∠OBC，∴∠OCB＝∠E．∵∠COF＝∠EOC，∴△COF∽△EOC，∴，∴，∴OE＝．∴EF＝OE﹣OF ＝．由（1）知：OB＝OC＝5，OD＝4，∴DF＝OD+OF＝7，∴BF＝＝．∵∠E＝∠OBC，∠CFE＝∠OFB，∴△CFE∽△OFB，∴，∴，∴CF＝．【点评】本题主要考查了圆的有关性质，垂径定理，圆周角定理，直角三角形的性质，勾股定理，相似三角形的判定与性质，等腰三角形的性质，连接直径所对的圆周角和利用勾股定理列出方程解答是解题的关键。