正方体展开图和三视图

合集下载

小学六年级立体图形三视图及展开图

立体图形三视图及展开图一、知识点(一)三视图在观察物体的时候，我们往往可以从不同的角度进行观察，角度不同，看到的风景就会不同。

比如：我们可以从正面看、上面看、左面看，看到的图形分别称为正视图、俯视图和左视图，并且容易发现：正面看和后面看，上面看和下面看，左面看和右面看得到的图形是相同的。

对于较复杂的立体图形，通过三视图法往往可以很方便地计算出表面积(二)正方体的展开图展开后由上、下、左、右、前、后六个正方形面组成，这六个正方形面的面积都相等，我们采用不同的剪开方法，共可以得到下面(三)长方体的展开图：观察上图可以发现，长方体的展开图由6个长方形组成，相对面的面积相等，即S上＝S下＝长×宽，S左＝S右＝宽×高，S前＝S后＝长×高。

(四)判断图形折叠后能否围成长方体或正方体的方法判断一个图形折叠后能否围成正方体或长方体，首先，要依据它们各自展开图的特点判断；其次，可以运用空间想象或实际操作进一步判断。

二、题型(一)展开图与对立面【例1.1】水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如下图，是一个正方体的平面展开图，若图中的“似”表示正方体的前面，“锦”表示右面，“程”表示下面。

则“祝”、“你”、“前”分别表示正方体的________________________。

【答案】后面、上面、左面【解析】易知“你”、“程”相对，“前”、“锦”相对，“祝”、“似”相对，因此“祝”、“你”、“前”分别表示正方体的后面、上面、左面。

【例1.2】一个数学玩具的包装盒是正方体，其表面展开图如下。

现在每方格内都填上相应的数字。

已知将这个表面展开图沿虚线折成正方体后，相对面的两数之和为“3”，则填在A、B、C内的三个数字依次是___________。

【答案】3、1、2【解析】面上的数是“0”，与“B”相对的面上的数是“2”，与“C"相对的面上的数是“1”。

正方体11种平面展开图(精心整理)

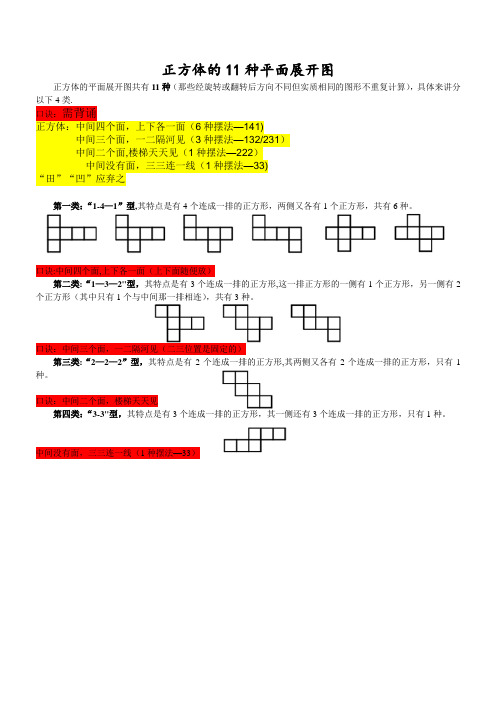
正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类.
口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法—141)
中间三个面，一二隔河见（3种摆法—132/231）
中间二个面,楼梯天天见（1种摆法—222）
中间没有面，三三连一线（1种摆法—33)
“田”“凹”应弃之
第一类：“1-4—1”型,其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀:中间四个面,上下各一面（上下面随便放）
第二类:“1—3—2"型，其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类:“2—2—2”型，其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3-3"型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法—33）。

正方体展开图ppt

正方体有11种不同的展开方式，这些展开方式可以通过不同的方式切割和展开正方体的面得到。
02
正方体展开图的种类
1-4-1型
总结词
该类型展开图有一个面是正方形，其它四个面是长方形，且这四个长方形在展开图中呈一字排列。
详细描述
在1-4-1型正方体展开图中，一个面是正方形，代表正方体的一个面。另外四个面是长方形，且这四个长方形在展开图中呈一字排列，代表正方体的另外四个面。这种类型的展开图在正方体展开中比较常见。
03
正方体展开图的制作方法
手工制作
总结词
手工制作正方体展开图需要一定的空间想象能力和手工技巧，但可以自由发挥创意，制作出独一无二的作品。
详细描述
手工制作正方体展开图通常使用纸、布等材料，通过剪裁、折叠、粘贴等步骤，将正方体展开成平面图形。在制作过程中，需要注意保持各面的几何形状和比例，以确保最终能够正确还原成正方体。
利用实物模型
总结词
利用实物模型制作正方体展开图是一种直观且易于理解的方法，可以帮助初学者更好地理解正方体的几何性质和展开原理。
详细描述
实物模型可以采用纸盒、塑料等材料制作，通过切割、折叠、粘贴等步骤，将正方体展开成平面图形。利用实物模型可以更加直观地展示正方体的几何特征和展开过程，但制作过程相对繁琐，需要一定的耐心和细心。
详细描述
在2-3-1型正方体展开图中，两个面是正方形，代表正方体的两个相邻的面。另外三个面是长方形，代表正方体的另外三个面。这种类型的展开图在正方体展开中也比较常见。
2-2-2型
总结词
该类型展开图有两个面是正方形，另外两个面是长方形，还有两个面是三角形。
VS
详细描述
在2-2-2型正方体展开图中，两个面是正方形，代表正方体的两个相邻的面。另外两个面是长方形，代表正方体的另外两个相对的面。还有两个面是三角形，这种类型的展开图在正方体展开中也比较常见。

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

正方体展开图和三视图的初步认识

正方体展开图和三视图的初步认识1．认识立体图形和平面图形我们常见的立体图形有长方体、正方体、球、圆柱、圆锥，此外，棱柱，棱锥也是常见的几何体。

我们常见的平面图形有正方形、长方形、三角形、圆2. 立体图形和平面图形关系立体图形问题常常转化为平面图形来研究，常常会采用下面的作法（1）画出立体图形的三视图立体图形的的三视图是指正视图（从正面看）、左视图（从左面看）、俯视图（从上面看）得到的三个平面图形。

（2）立体图形的平面展开图常见立体图形的平面展开图圆柱、圆锥、三棱柱、三棱锥、正方体（共十一种）知识梳理知识梳理1 正方体的侧面展开图（共十一种）分类记忆：第一类，中间四连方，两侧各一个，共六种。

第二类，中间三连方，两侧各有一、二个，共三种。

第三类，中间二连方，两侧各有二个，只有一种。

第四类，两排各三个，只有一种。

知识梳理2 常见立体图形的平面展开图1. 棱柱：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱。

两个互相平行的平面叫做棱柱的底面，其余各面叫做棱柱的侧面。

两个侧面的公共边叫做棱柱的侧棱。

侧面与底的公共顶点叫做棱柱的顶点，不在同一个面上的两个顶点的连线叫做棱柱的对角线，两个底面的距离叫做棱柱的高。

棱柱的底面可以是三角形，四边形，五边形……我们把这样的棱柱叫分别叫做三棱柱、四棱柱、五棱柱……棱柱的表面展开图是两个完全相同的多边形（作底面）和几个长方形（作侧面）2. 棱锥：一般地，有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥。

棱锥中的多边形叫做棱锥的底面。

棱锥中除底面以外的各个面都叫做棱锥的侧面。

相邻侧面的公共边叫做棱锥的侧棱。

棱锥中各个侧面的公共顶点叫做棱锥的顶点。

棱锥的顶点到底面的距离叫做棱锥的高。

棱锥中过不相邻的两条侧棱的截面叫做对角面。

棱锥的底面可以是三角形、四边形、五边形……我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱锥……棱锥的展开图是由一个多边形（作底）和几个三角形（作侧面）组成的。

正方体的11种展开图课件

正方体展开图
.
1
将正方体剪开展成一个平面图形。
.
2
• 1、在正方体的相对的面上标上相同的数字
• 2、在展开的过程中注意你剪开了几条棱？
.
3
“一四一”
型
.
4
“二三一” 型
“三三” 型
“二二二”
.型
5
判断下列图形能不能折成正方体？
(1)
(2)
.
7
(3)
.
8
(4)
.
9
(5)
.
10
(6 )
开始时我们已经在正方体的相对的面上标上相同的数字，现在观察一下这些数字在展开图中有什么规律？
.
25
“一四一”
型
.
26
“二三一” 型
“三三” 型
“二二二”
型 .
27
考考你下图是正方体的表面展开图。
1、如果“你”在前面，那么谁在后面？
了！太棒你们
.
28
2、“坚”在下，“就”在后，“胜”、 “利”在哪里？
坚
持就是
胜
利
.
29
.
30
圆柱
圆锥
.
31
三棱锥
四棱锥 .
五棱锥
32
感谢亲观看此幻灯片，此课件部分内容来源于网络，如有侵权请及时联系我们删除，谢谢配合！
.
11
(7 )
.
12
(8)
.
13
(9)
.
14
பைடு நூலகம்10 )
.
15
(11)
.
16
(12 )
.
17

《正方体展开图》课件

连续性
总结词
正方体展开图展示了正方体的连续变化过程。
详细描述
正方体展开图不仅展示了正方体的各个面，还通过连续的图形变化展示了正方体的形成过程。这种连续性使得正方体展开图具有动态感，能够让人们更加直观地理解正方体的形成和变化过程。
稳定性
要点一
总结词
正方体展开图具有稳定性，能够清晰地表达出正方体的结构和特征。
REPORT
《正方体展开图》 ppt课件
CATALOG
DATE
ANALYSIS
SUMMARY
目录
CONTENTS
• 正方体的基本性质 • 正方体的展开图种类 • 正方体展开图的特性 • 正方体展开图的制作方法 • 正方体展开图的应用
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
特殊型展开图
总结词
不包含在正方体的11种展开图中的特殊类型。
详细描述
这种类型的展开图在正方体的11种展开图中并不常见，其形状和结构相对较为特殊。这种展开图的特点是需要学生具备更强的空间想象能力和分析能力，才能理解和掌握。同时，这种展开图也是考试中经常出现的一种类型，需要学生特别注意。
REPORT
制作步骤包括在三维建模软件中创建正方体模型、导出STL文件、3D打印等。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
正方体展开图的应用
在几何教学中的应用
帮助学生理解立体几何
正方体展开图可以帮助学生更好地理解立体几何的概念，通过将三维图形展开成二维图形，可以让学生更好地理解空间关系和几何形状。

正方体的平面展开图及三视图练习

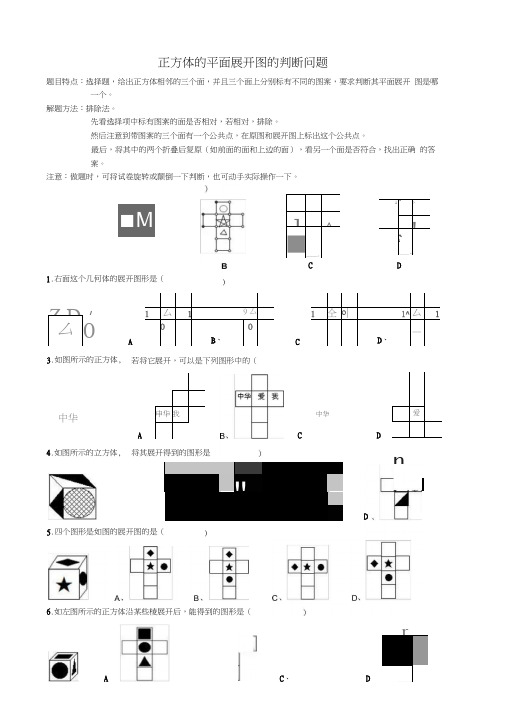
正方体的平面展开图的判断问题题目特点：选择题，给出正方体相邻的三个面，并且三个面上分别标有不同的图案，要求判断其平面展开图是哪一个。

解题方法：排除法。

先看选择项中标有图案的面是否相对，若相对，排除。

然后注意到带图案的三个面有一个公共点，在原图和展开图上标出这个公共点。

最后，将其中的两个折叠后复原（如前面的面和上边的面），看另一个面是否符合，找出正确的答案。

注意：做题时，可将试卷旋转或颠倒一下判断，也可动手实际操作一下。

1.右面这个几何体的展开图形是（■M111△■1 ---------------- 1 111 ■>'A 1■ ________ d ■Z D /厶 0/1厶19厶OB 、 O1仝 o|1^ 厶1D 、—3.如图所示的正方体, 若将它展开，可以是下列图形中的（中华申华我4.如图所示的立方体, 中华■■"■■■爱nC 、r□)CDA 、C、A 、C 、将其展开得到的图形是)D 、5.四个图形是如图的展开图的是（6.如左图所示的正方体沿某些棱展开后，能得到的图形是（A 、D、D 、2.如图几何体的展开图形最有可能是（7.将如图所示表面带有图案的正方体沿某些棱展开后，得到的图形是（C 、& 一个三面带有标记的正方体，如果把它展开，应是下列展开图形中的（■，押9.下图右边四个图形中，哪个是左边立体图形的展开图？（# # fflIB 、 _C 、 L 」D 、 L I I10 .如图，有一个正方体纸盒，在它的三个侧面分别画有三角形、正方形和圆，现用一把剪刀沿着它的棱剪开成一个平面图形，则展开图可以是（11.将如图正方体的相邻两面上各画分成九个全等的小正方形，并分别标上）1.下面简单几何体的左视图是（）.2.如图所示，右面水杯的俯视图是（D 、B 、）C 、) 0、X 两符号.若下列有一图B 、C 、C .D .AB C 正面DA .9、如图：是由几个小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置小立方块的个数。

(完整版)正方体11种平面展开图

正方体的11种平面展开图正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

注：①将长方体、正方体展开：无论怎么剪，都要剪7条棱。

②“隔”的原理：相对的面如果在同一行或同一排，中间一定只隔一个面；相对的面如果不在同一行或同一排，中间可以隔着一些面。

③长方体、正方体中各面的关系：相对、相邻。

每个面都有1个相对的面，4个相邻的面。

注：立体图中相对的面在展开图中符合“隔”的原理，而相邻的面在展开图中不符合“隔”的原理。

④长方体、正方体中最多可以同时看到三个面，且这三个面都是相邻的面。

⑤要区分好是从“立体图”到“展开图”，还是从“展开图”到“立体图”：互逆正方体、长方体展开图⑥长方体（不包含正方体）最多有1组相对的面是正方形；当有2组相对的面是正方形时，长方体就变成了正方体（特殊的长方体）。

长方体（不包含正方体）的6个面中，最多有4个面的面积相等；12条棱中，最多有8条棱长度相等。

（即2个相对的面是正方形，其余四个面变为完全相同的长方形。

）⑦正方体的棱长扩大a倍：棱长和扩大a倍，表面积扩大a2倍，体积扩大a3倍。

（给出其中一个，要能将其余的都求出来）⑧常见的平方、立方（需熟记在心）12=1 22=4 32=9 42=16 52= 25 62=36 72=49 82=64 92=81 ……13=1 23=8 33=27 43=64 53= 125 63=216 ……。

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

《正方体展开图》课件

《正方体展开图》ppt课件
目录
• 正方体的基本性质 • 正方体的展开图种类 • 正方体展开图的制作方法 • 正方体展开图的运用 • 正方体展开图的注意事项
01
CATALOGUE
正方体的基本性质
正方体的定义
总结词
正方体的定义
详细描述
正方体是一种三维几何体，它具有六个面，每个面都是一个正方形，所有的面都相等且相对。
正方体的结构特征
总结词
正方体的结构特征
详细描述
正方体的结构特征包括其顶点、面、棱等元素。正方体的每个顶点都是三条棱的交点，每个面都是一个正方形，且所有的面都相等。
正方体的性质定理
总结词
正方体的性质定理
详细描述
正方体的性质定理包括其对称性、内角和、外角和等性质。正方体具有高度的对称性，其内角和为360度，外角和也为360度。
05
CATALOGUE
正方体展开图的注意事项
展开后形状的稳定性
01
展开后的形状应保持稳定，不易发生变形或扭曲，以确保正确的展示效果。
02
在设计展开图时，应充分考虑结构的稳定性，选择合适的材料和工艺，以确保展开后的形状能够持久保持。
制作过程中的误差控制
在制作过程中，应严格控制误差，确保展开图的尺寸、角度和形状与实际需求相符。
详细描述
这种展开图将正方体的六面体分为两个部分，每部分展开成独立的平面图形，两部分相对而立。这种展开图可以更清楚地展示正方体的内部结构和特点。
三合一型展开图
总结词
正方体的六面体展开成三个相互连接的平面图形。
VS
详细描述
这种展开图将正方体的六面体分为三个部分，每部分展开成独立的平面图形，三个部分相互连接形成一个整体。这种展开图可以更全面地展示正方体的内部结构和特点，同时也可以更好地理解正方体的空间关系和几何特性。

(全)正方体平面展开图PPT资料

谢谢观看
补上缺少的一面,使展开图可以折成正方形.
平移〞左〞或〞右〞可以得到如下图形
通过上面得到的正方体平面展开图你得到什么规律?
补上缺少的一面,使展开图可以折成正方形.
补上缺少的一面,使展开图可以折成正方形.
下列图形能折叠成正方形吗?
(3)
(4)
补上缺少的一面,使展开图可以折成正方形.
补上缺少的一面,使展开图可以折成正方体.
正方体平面展开图
后左下右
前
上后后左下右前
通过上面得到的正方体平面展开图你得到什么规律?
平移〞左〞或〞右〞可以得到如下图形
上平移〞左〞或〞右〞可以得到如下图形
补上缺少的一面,使展开图可以折成正方形.
上
后补上缺少的一面,使展开图可以折成正方形.
下列图形能折叠成正方形吗? 补上缺少的一面,使展开图可以折成正方形.
下列图形能折叠成正方形ຫໍສະໝຸດ ?补上缺少的一面,使展开图可以折成正方形.
补上缺少的一面,使展开图可以折成正方形.
下列图形能折叠成正方形吗?
平移〞左〞或〞右〞可以得到如下图形补上缺少的一面,使展开图可以折成正方形.
(2)
下列图形能折叠成正方形吗?
补通上过缺上少面的得一到(1面的)正,使方展体开平图面可展以开折图成你正得方到形什. 么规律?
左
上
前右
上右下列图形能折叠成正方形吗?
补上缺少的一面,使展开图可以折成正方形. 通过上面得到的正方体平面展开图你得到什么规律?
后
下列图形能折叠成正方形吗?
后通过上面得到的正方体平面展开图你得到什么规律?
下
右
左上右后
下
前

正方体展开图和三视图

一、正方体展开图共11种，为方便大家记忆，总结如下：1．“141型”，中间一行4个作侧面，上下两个各作为上下底面，•共有6种基本图形。

2．“231型”，中间3个作侧面，共3种基本图形。

3．“222”型，两行只能有1个正方形相连。

4．“33”型，两行只能有1个正方形相连。

二、会判断哪两个面相对三、典型题目分析1、（2005·四川省）如图是一个正方体表面展开图，如果正方体相对的面上标注的值相等，那么x= ，y=2、下左图中，欲使相对两个面的数字互为相反数，则A=_____,B=____,C=___3、下右图中，哪两个数字相对？4、如图是立方体的表面展开图，要求折成立方体后，使得6在前，2在右，那么哪个面在上？5、有一个正方体，在它的各个面上分别写了①、②、③、④、⑤、⑥。

甲、乙、丙三位同学从三个不同的角度去观察此正方体，结果如下图，问这个正方体各个面的对面的是什么数？四、三视图⑥ ②④甲②③ ① 乙④ ③ ⑤ 丙562 1 34在生活中和数学中，对于不是很复杂的物体，如图所示通常从三个方向看，并画出图形，就可以大致搞清这个物体的外观了，这就是我们的课本是给出的：练习：1.如图,桌面上放着一个圆锥和一个长方体,其中俯视图形应该是( )2.下图是一个立体图形的三视图,请根据视图说出立体图形的名称( )从上面看从左面看从正面看主视图左视图俯视图A.圆柱B.圆台C.圆锥D.无法确定3.下列立体图形中有哪些图形的三视图都一样( ) A.圆柱 B.四面体 C.圆台 D.球4. 下面是由7块小正方体木块堆成的物体,从三个方向看到的图形如下,请同学们说出哪一个是主视图?哪一个是左视图?哪一个是俯视图?5:请同学们画出下列几何体的三视图6下图是几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,________图是这个几何体的主视图( )7图是由几个小立方体所搭几何体的俯视图，小正方形中的数字表示在该位置小正方体的个数。