初中三角函数公式及其定理

初中数学三角函数公式汇总,没有比这更全的!

01定义式02函数公式倒数关系：①②③商数关系：①②平方关系：①②③03诱导公式公式1：设为任意角，终边相同的角的同一三角函数的值相等：公式2：设为任意角，与的三角函数值之间的关系：公式3：任意角与的三角函数值之间的关系：公式4：与的三角函数值之间的关系：公式5：与的三角函数值之间的关系：公式6：及与的三角函数值之间的关系：记背诀窍：奇变偶不变，符号看象限，即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。

形如2k×90°±α，则函数名称不变。

04基本公式【和差角公式】◆ 二角和差公式◆ 三角和公式【和差化积公式】口诀：正加正，正在前，余加余，余并肩，正减正，余在前，余减余，负正弦．【积化和差公式】【倍角公式】◆ 二倍角公式◆ 三倍角公式◆ 四倍角公式sin4a=-4*[cosa*sina*(2*sina^2-1)]cos4a=1+(-8*cosa^2+8*cosa^4)tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)◆ 五倍角公式◆ 半角公式（正负由所在的象限决定）◆ 万能公式◆ 辅助角公式◆ 余弦定理◆ 三角函数公式算面积定理：在△ABC中，其面积就应该是底边对应的高的1/2，不妨设BC边对应的高是AD，那么△ABC的面积就是AD*BC*1/2。

而AD是垂直于BC的，这样△ADC就是直角三角形了，显然，由此可以得出，AD=ACsinC，将这个式子带回三角形的计算公式中就可以得到：，同理，即可得出三角形的面积等于两邻边及其夹角正弦值的乘积的一半。

◆ 公式：若△ABC中角A，B，C所对的三边是a,b,c：则S△ABC=1/2absinC=1/2bcsinA=1/2acsinB.◆ 反三角函数反三角函数主要是三个：y＝arcsin(x)，定义域[-1,1] ，值域[-π/2,π/2]y=arccos(x)，定义域[-1,1] ，值域[0,π]y=arctan(x)，定义域(-∞,+∞)，值域(-π/2,π/2)sinarcsin(x)=x,定义域[-1,1],值域【-π/2,π/2】◆ 反三角函数公式:arcsin(-x)=-arcsinxarccos(-x)=π－arccosxarctan(-x)=-arctanxarccot(-x)=π－arccotxarcsin x+arccosx=π/2=arctanx+arccotx sin(arcsinx)=x=cos(arccosx) =tan(arctanx)=cot(arccotx)当x∈〔—π/2，π/2〕时，有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2，π/2),arctan(tanx)=xx∈(0，π),arccot(cotx)=x x〉0,arctanx=arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2，π/2),则arctanx+arctany=arctan(x+y/1-xy)。

初中三角函数公式及定理大全

初中三角函数公式及定理大全1、正弦定理：在三角形中，各边和它所对的角的正弦的比相等，即a/sinA=b/sinB=c/sinC=2R 。

（其中R为外接圆的半径），2、第一余弦定理：三角形中任意一边等于其他两边以及对应角余弦的交叉乘积的和，即a=c cosB + b cosC。

初中三角函数公式及定理大全1锐角三角函数定义:锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec)，余割(csc)都叫做角A的锐角三角函数。

正弦(sin)：对边比斜边，即sinA=a/c余弦(cos)：邻边比斜边，即cosA=b/c正切(tan)：对边比邻边，即tanA=a/b余切(cot)：邻边比对边，即cotA=b/a正割(sec)：斜边比邻边，即secA=c/b余割(csc)：斜边比对边，即cscA=c/a初中三角函数公式及定理大全2互余角的关系sin(π-α)=cosα, cos(π-α)=sinα,tan(π-α)=cotα, cot(π-α)=tanα.积的关系sinα=tanα·cosαcosα=cotα·sinαtanα=sinα·secαcotα=cosα·cscαsecα=tanα·cscαcscα=secα·cotα初中三角函数公式及定理大全3平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)倒数关系tanα·cotα=1sinα·cscα=1cosα·secα=1初中三角函数公式及定理大全4三角函数的和差化积公式sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)。

初中数学三角函数公式

初中数学三角函数公式三角函数的公式：1. 余弦定理：\cos A＝\frac{b^2 + c^2 - a^2}{2bc}；2. 正弦定理：\sin A＝\frac{\sqrt{a^2 - b^2 - c^2}}{2bc}；3. 梯形公式：S＝\frac{1}{2} a \times b \sin C；4. 两边和定理：a\sin A＝b\sin B＝c\sin C；5. 余切定理：\tan A＝\frac{1}{\sin A}\；6. 正切定理：\cot A＝\frac{1}{\tan A}\；三角函数的概念问题可以追溯到古希腊人。

他们考虑了三角函数如何影响几何形状和外形，从而得到了代表三角形的几个基本函数，即正弦函数、余弦函数和正切函数。

三角函数在很多领域有着广泛的用途，比如在地理学和天文学中，它们帮助计算地球上特定地点的坐标，确定太阳位置等等；在单元电路中它们可以用来计算电流和电压；在许多工程应用中，它们可以用来计算房屋的张力，测量角度等等。

三角函数的公式有多种，主要有：1. 余弦定理：它有助于计算三角形的两个角的余弦值，当我们知道该三角形的三条边的长度的时候：余弦定理的表达式为：\cos A＝\frac{b^2 + c^2 -a^2}{2bc}；2. 正弦定理：它可以帮助我们计算三角形三个角度中其中一个角度的正弦值，以及三角形三条边的关系：正弦定理的表达式：\sin A＝\frac{\sqrt{a^2 - b^2 - c^2}}{2bc}；3. 梯形公式：它可以帮助我们计算出三角形的面积，它有两种表示形式：一：根据三角形三条边的长度，可以表示为：S＝\frac{1}{2} a \times b \sin C；二：根据三角形的三个内角的度数，可以表示为：S＝\frac{abc}{4R}；4. 两边和定理：它可以帮助我们计算出一个三角形的面积，这个定理可以用来得出三角形三个角度两条边之间的关系：两边和定理的表达式为：a\sin A＝b\sin B＝c\sin C；5. 余切定理：它可以帮助我们计算出三角形的余切值，当我们知道角的正弦值时：余切定理的表达式为：\tan A＝\frac{1}{\sin A}\；6. 正切定理：它可以帮助我们计算出三角形的正切值，当我们知道角的余弦值时：正切定理的表达式：\cot A＝\frac{1}{\tan A}\；以上这些定理和公式都是三角函数中最重要最常用的，因为三角函数具有广泛的应用，所以必须熟悉这些定理和公式，以便于灵活地应用。

三角函数怎么算

三角函数怎么算
譬如：
1、已知直角三角形的两条直角边,求斜边。

方法就是：利用勾股定理：斜边=根号（两条直角边的平方和）。

2、已知直角三角形的一个锐角a及其对边,求斜边。

方法就是：利用正弦函数：斜边=（角a的对边）/sina。

3、已知直角三角形的一个锐角a及其邻边,求斜边。

方法就是：利用余弦函数：斜边=（角a的'邻边）/cosa。

4、已知直角三角形的面积及斜边上的高,求斜边。

方法就是：利用三角形的面积公式：斜边=（2倍三角形的面积）/斜边上的高。

1、勾股定理：c^2=a^2 b^2。

2、三角函数：c=a/cosb或c=b/cosa。

c=a/sina或c=b/sinb。

(表明：斜边c，直角边a、b。

与其对着的角分别为直角c，锐角a、b)。

直角三角形的斜边的长度可以使用毕达哥拉斯定理找到，该定理表示斜边长度的平方等于另外两边长度的平方和。

三角函数公式及其定理

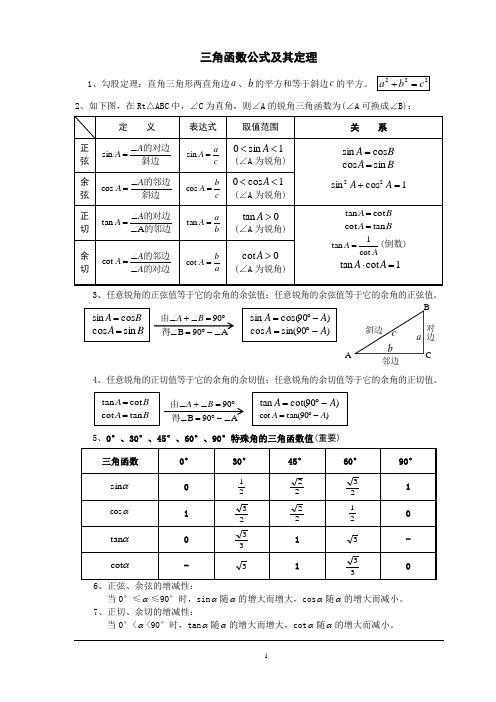
三角函数公式及其定理1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。

4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。

5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。

7、正切、余切的增减性：当0°<α<90°时，tan α随α的增大而增大，cot α随α的增大而减小。

A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 C A90B 90∠-︒=∠︒=∠+∠得由B A1、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。

依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。

(注意：尽量避免使用中间数据和除法)2、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。

用字母i 表示，即hi l=。

坡度一般写成1:m 的形式，如1:5i =等。

把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。

3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。

如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。

4、指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角。

如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）。

(完整)初中常用三角函数公式

(完整)初中常用三角函数公式初中常用三角函数公式
三角函数是数学中常见的概念，它们在初中阶段的数学研究中起着重要的作用。

以下是一些常用的三角函数公式：
1. 正弦函数公式：
- 正弦函数的定义：在直角三角形中，对于一个锐角角度A，正弦函数的值等于对边与斜边的比值，可以表示为sin(A) = 对边/斜边。

2. 余弦函数公式：
- 余弦函数的定义：在直角三角形中，对于一个锐角角度A，余弦函数的值等于邻边与斜边的比值，可以表示为cos(A) = 邻边/斜边。

3. 正切函数公式：
- 正切函数的定义：在直角三角形中，对于一个锐角角度A，正切函数的值等于对边与邻边的比值，可以表示为tan(A) = 对边/邻边。

4. 余切函数公式：
- 余切函数的定义：在直角三角形中，对于一个锐角角度A，余切函数的值等于邻边与对边的比值，可以表示为cot(A) = 邻边/对边。

5. 正割函数公式：
- 正割函数的定义：在直角三角形中，对于一个锐角角度A，正割函数的值等于斜边与邻边的比值，可以表示为sec(A) = 斜边/邻边。

6. 余割函数公式：
- 余割函数的定义：在直角三角形中，对于一个锐角角度A，余割函数的值等于斜边与对边的比值，可以表示为csc(A) = 斜边/对边。

这些公式是初中数学中常用的三角函数公式，它们可以用来解决与三角函数相关的各种问题。

熟练掌握这些公式并灵活运用，有助于提高数学解题能力和理解几何概念的能力。

初中三角函数公式大全

初中三角函数公式大全一、正弦定理在任意三角形ABC中，我们可以利用正弦定理计算三角形的边与角之间的关系。

正弦定理的表达式如下：a/sinA = b/sinB = c/sinC其中a、b、c表示三角形的三条边的长度，A、B、C表示对应的内角。

利用正弦定理，我们可以求解出任意一个角的大小，或者求解出任意一条边的长度。

二、余弦定理余弦定理和正弦定理类似，也是用于计算三角形的边与角之间的关系。

余弦定理的表达式如下：c² = a² + b² - 2abcosCb² = a² + c² - 2accosBa² = b² + c² - 2bccosA其中a、b、c表示三角形的三条边的长度，A、B、C表示对应的内角。

余弦定理可以帮助我们计算三角形边的长度，特别是当已知两边和它们之间的夹角时。

三、正切公式对于任意角度θ，我们可以利用正切公式计算其正切值：tanθ = sinθ/cosθ正切公式可以帮助我们计算角度的正切值，常常用于解决与直角三角形相关的问题。

四、倍角公式倍角公式是用来计算角度的二倍角的三角函数值。

倍角公式的表达式如下：sin2θ = 2sinθcosθcos2θ = cos²θ - sin²θtan2θ = (2tanθ)/(1-tan²θ)五、半角公式半角公式是用来计算角度的一半或二分之一角的三角函数值。

半角公式的表达式如下：sin(θ/2) = ±√[(1-cosθ)/2]cos(θ/2) = ±√[(1+cosθ)/2]tan(θ/2) = ±√[(1-cosθ)/(1+cosθ)]半角公式可以帮助我们计算角度的一半或二分之一角的三角函数值。

六、常用的三角函数关系在学习三角函数时，我们需要掌握一些常用的三角函数关系。

这些关系可以帮助我们在不同的三角函数之间进行转换。

(完整版)初中数学公式定理大全

一、锐角三角函数：初中数学公式定理大全sin A =∠A 的对边cos A =∠A 的邻边① ∠A 是 Rt △ABC 的任一锐角，则∠A 的正弦：tan A = ∠A 的对边斜边，∠A 的余弦：斜边，∠A 的正切：∠A 的邻边；并且 sin 2A ＋cos 2A ＝1． 0＜sin A ＜1，0＜cos A ＜1，tan A ＞0． ∠A 越大，∠A 的正弦和正切值越大，余弦值反而越小．② 余角公式：sin(90º－A )＝cos A ，cos(90º－A )＝sin A ．铅垂高度=ℎ ℎ③ 斜坡的坡度：i ＝水平宽度 ④ 特殊角的三角函数值：l ．设坡角为 α，则 i ＝tan α＝l ． l二、二次函数： y = ） 1.定义：一般地，如果，那么 y 叫做 x 的二次函数. 2. 抛物线的三要素：开口方向、对称轴、顶点.①a 的符号决定抛物线的开口方向：当a > 0时，开口向上；当a < 0时，开口向下；|a |相等，抛物线的开口大小、形状相同。

②平行于 y 轴（或重合）的直线记作x = ℎ，特别地，y 轴记作直线x = 0。

y = ax 2 + bx + c = a(x + b )2 + 4ac ‒ b2(‒ b , 4ac ‒ b 2) x = ‒ b（1）公式法：2a4a，∴顶点是 2a4a，对称轴是直线2a（2）配方法：运用配方的方法，将抛物线的解析式化为y = a (x ‒ ℎ)2+ k 的形式，得到顶点为(h,k)，对称轴是直线x = ℎ（3）运用抛物线的对称性：由于抛物线是以对称轴为轴的轴对称图形，对称轴与抛物线的交点是顶点。

(x ，y ) (x ，y ) x = x 1 + x 2 若已知抛物线上两点 1 、 2 （及 y 值相同），则对称轴方程可以表示为：2 4.抛物线y = ax 2 + bx + c 中，a ,b ,c 的作用（1）a 决定开口方向及开口大小，这与y = ax 2中的a 完全一样. b a y = ax 2 + bx + c x =‒ bb = 0 （2）和共同决定抛物线对称轴的位置.由于抛物线的对称轴是直线 2a ，故：① 时，对b > 0a b< 0 a称轴为 y 轴；②a （即、b 同号）时，对称轴在 y 轴左侧；③a （即、b 异号）时，对称轴在 y 轴右侧.（3）c 的大小决定抛物线y = ax 2+ bx + c 与 y 轴交点的位置. 当x = 0时，y=c ，∴抛物线y = ax 2+ bx + c 与 y 轴有且只有一个交点（0，c ）① c = 0，抛物线经过原点; ②c > 0,与 y 轴交于正半轴；③c < 0,与 y 轴交于负半轴b < 0α以上三点中，当结论和条件互换时，仍成立。

【初中数学】三角形与三角函数公式大全

【初中数学】三角形与三角函数公式大全【—三角形与三角函数】三角形中任意一边等于其他两边以及对应角余弦的交叉乘积的和，即a=ccosb+bcosc。

三角形与三角函数1、正弦定理：在三角形中，各边和它所对的角的正弦的比相等，即a/sina=b/sinb=c/sinc=2r.(其中r为外接圆的半径)2.切线定理（纳皮尔类比）：三角形任意两边的差和之比等于相应半角上的差和之比，即（a-b）/（a+b）=Tan[（a-b）/2]/Tan[（a+b）/2]=Tan[（a-b）/2]/cot（C/2）三、三角形中的恒等式：对于任何非直角三角形，比如ABC，总有Tana+tanb+Tanc=tanatanbtanc证明：已知（a+b）=（π-C）所以tan(a+b)=tan(π-c)然后（Tana+tanb）/（1-tanatanb）=（Tanπ-Tanc）/（1+TanπTanc）整理可得tana+tanb+tanc=tanatanbtanc类似地，我们同样也可以求证:当α+β+γ=nπ(n∈z)时，总有tanα+tanβ+tanγ=tanαtanβtanγ域和范围sin(x),cos(x)的定义域为r，值域为[-1,1]。

Tan（x）的定义域是x，它不等于π/2+Kπ（K）∈ z），值域为r。

cot(x)的定义域为x不等于kπ(k∈z),值域为r。

y=a·sin（x）+B·cos（x）+C的取值范围为[C-√ （a+b），C+√ （a+b）]三角函数的画法以y=SiNx的图像为例，获得y=asin的（ωx+φ）图像：方法一：Y=SiNx→ [左移]（φ>0）/右移（φ<0）oooφO单位]→ y=sin（x）+φ）→ 【纵坐标保持不变，横坐标扩展到原来的（1/ω）】→y=sin（ωx+φ）→ [纵坐标更改为原始a 倍（伸长[a>1]/缩短[0]方法二：Y=SiNx→ [纵坐标保持不变，横坐标扩展到原来的（1/ω）]→y=sinωX→ 【向左移动】（φ>0）/向右移动（φ<0）oφo/ω[单位]→ y=sin（ωx+φ）→ [纵坐标更改为原始a倍（伸长[a>1]/缩短[0]温馨提示：三角形中任何一边的平方等于其它两边的平方之和减去这两边与它们夹角的余弦的积的2倍，即a^2=b^2+c^2-2bc·cosa。

初中三角函数公式及定理大全

初中三角函数的公式有半角公式sin(A/2)=±√((1-cosA)/2)、倍角公式Sin2A=2SinA*CosA、两角和与差公式Sin2A=2SinA*CosA、平方关系公式sin²α+cos²α=1、倒数关系公式tanα·cotα=1等等。

1初中数学三角函数公式锐角三角函数公式sinα=∠α的对边/斜边cosα=∠α的邻边/斜边tanα=∠α的对边/∠α的邻边cotα=∠α的邻边/∠α的对边2倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注：SinA^2是sinA的平方sin2(A))2初中三角函数正切定理公式在平面三角形中，正切定理说明任意两条边的和除第一条边减第二条边的差所得的商等于这两条边的对角的和的一半的正切除第一条边对角减第二条边对角的差的一半的正切所得的商。

正切定理：(a+b)/(a-b)=tan((α+β)/2)/tan((α-β)/2)。

3初中三角函数余弦定理定义：对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

对于边长为a、b、c而相应角为A、B、C的三角形，有：a^2=b^2+c^2-2bc·cosAb^2=a^2+c^2-2ac·cosBc^2=a^2+b^2-2ab·cosC也可表示为：cosC=(a^2+b^2-c^2)/2abcosB=(a^2+c^2-b^2)/2accosA=(c^2+b^2-a^2)/2bc这个定理也可以通过把三角形分为两个直角三角形来证明。

如果这个角不是两条边的夹角，那么三角形可能不是唯一的(边-边-角)。

要小心余弦定理的这种歧义情况。

延伸定理：第一余弦定理(任意三角形射影定理)设△ABC的三边是a、b、c，它们所对的角分别是A、B、C，则有：a=b·cosC+c·cosB，b=c·cosA+a·cosC，c=a·cosB+b·cosA。

三角函数定理公式大全

三角函数定理1.诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = - sin(a)sin(π - a) = sin(a)cos(π - a) = - cos(a)sin(π + a) = - sin(a)cos(π + a) = - cos(a)2.两角和与差的三角函数sin(a + b) = sin(a)cos(b) + cos(α)sin(b) cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)] tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)] 3.和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2]sin(a) - sin(b) = 2sin[(a - b)/2]cos[(a + b)/2]cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2]cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2]4.积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)]cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]5.二倍角公式sin(2a) = 2sin(a)cos(a)cos 2a = cos2a - sin2a = 2cos2a - 1= 1 - 2sin2a6.半角公式sin2a = （1 – cos 2a）/ 2cos2a = （1 + cos 2a）/ 2tan a = [1 – cos 2a] /sin 2a = sin 2a / [1 + cos 2a ] 7.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)]三角函数公式三角函数是数学中属于初等函数中的超越函数的一类函数。

三角公式总结正弦定理余弦定理诱导公式二倍角公式半角公式积化和差公式和差化积公式

三角公式总结正弦定理余弦定理诱导公式二倍角公式半角公式积化和差公式和差化积公式三角公式是解决三角形问题的基本工具，包括正弦定理、余弦定理、诱导公式、二倍角公式、半角公式、积化和差公式和和差化积公式等。

下面我们详细介绍这些公式。

1. 正弦定理（Sine Rule）：在一个三角形ABC中，边长a、b、c与其对应的角A、B、C满足如下关系：a/sinA = b/sinB = c/sinC这个公式可以用于求解已知三角形任意两边及其夹角，求解三角形内外角和的问题。

2. 余弦定理（Cosine Rule）：在一个三角形ABC中，边长a、b、c 与其对应的角A、B、C满足如下关系：a^2 = b^2 + c^2 - 2bc*cosAb^2 = a^2 + c^2 - 2ac*cosBc^2 = a^2 + b^2 - 2ab*cosC这个公式可以用于求解已知三角形两边及其夹角，求解三角形内外角和的问题。

3. 诱导公式（Tangent Addition Formula）：对于角A和角B，有如下关系：tan(A+B) = (tanA + tanB) / (1 - tanA*tanB)tan(A-B) = (tanA - tanB) / (1 + tanA*tanB)这个公式可以用于求解角的和与差的正切值。

4. 二倍角公式（Double Angle Formula）：对于角A，有如下关系：sin(2A) = 2*sinA*cosAcos(2A) = cos^2(A) - sin^2(A)tan(2A) = 2*tanA / (1 - tan^2(A))这个公式可以用于求解角的两倍角的正弦、余弦和正切值。

5. 半角公式（Half Angle Formula）：对于角A，有如下关系：sin(A/2) = ±√[(1 - cosA) / 2]cos(A/2) = ±√[(1 + cosA) / 2]tan(A/2) = ±√[(1 - cosA) / (1 + cosA)]这个公式可以用于求解角的半角的正弦、余弦和正切值。

三角函数定义及三角函数公式大全

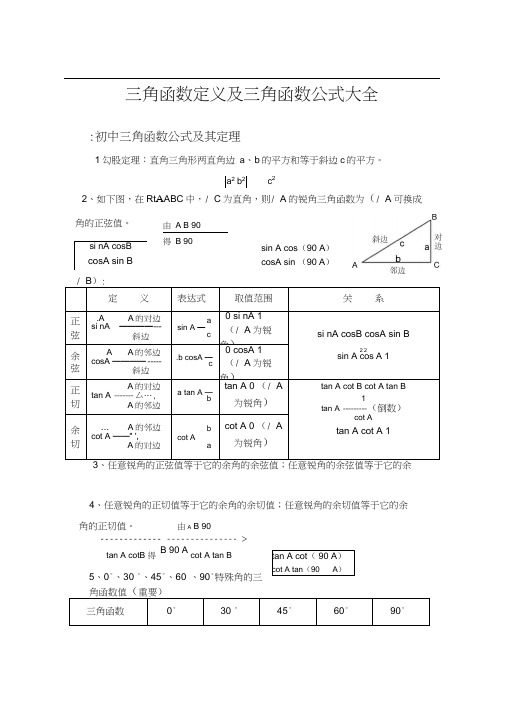
三角函数定义及三角函数公式大全:初中三角函数公式及其定理1勾股定理：直角三角形两直角边 a 、b 的平方和等于斜边c 的平方。

2、如下图，在Rt A ABC 中，/ C 为直角，则/ A 的锐角三角函数为（/ A 可换成/ B ）:定义表达式取值范围关系正弦 .AA 的对边 si nA ———— --- 斜边 asin A —c0 si nA 1 （/ A 为锐角） si nA cosB cosA sin B2 2sin A cos A 1余弦 A A 的邻边 cosA ———— ----- 斜边 .b cosA —c 0 cosA 1（/ A 为锐角）正切 A 的对边 tan A -------厶…,A 的邻边 a tan A —btan A 0 （/ A 为锐角） tan A cot B cot A tan B1tan A --------- （倒数）cot Atan A cot A 1余切 … A 的邻边 cot A ——“ ‘, A 的对边bcot Aacot A 0 （/ A 为锐角）4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。

由A B 90------------- --------------- >tan A cotB 得B 90 Acot A tan B5、0°、30 °、45°、60°、90°特殊角的三角函数值重要）三角函数0° 30 ° 45° 60° 90°a 2b 2c 2角的正弦值。

si nA cosBcosA sin B由 A B 90 得 B 90tan A cot （ 90 A ）cot A tan （90A ）sin A cos （90 A ） cosA sin （90 A ）sin 0 12""2~ 1cos 12近21~20 tan 0旦31 -cot - 13当0°< < 90°时，sin随的增大而增大，cos随的增大而减小7、正切、余切的增减性：当0° < <90°时，tan随的增大而增大，cot随的增大而减小。

三角函数定理公式大全

三角函数定理1.诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = - sin(a)sin(π - a) = sin(a)cos(π - a) = - cos(a)sin(π + a) = - sin(a)cos(π + a) = - cos(a)2.两角和与差的三角函数sin(a + b) = sin(a)cos(b) + cos(α)sin(b) cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)] tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)] 3.和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2]sin(a) - sin(b) = 2sin[(a - b)/2]cos[(a + b)/2]cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2]cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2]4.积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)]cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]5.二倍角公式sin(2a) = 2sin(a)cos(a)cos 2a = cos2a - sin2a = 2cos2a - 1= 1 - 2sin2a6.半角公式sin2a = （1 – cos 2a）/ 2cos2a = （1 + cos 2a）/ 2tan a = [1 – cos 2a] /sin 2a = sin 2a / [1 + cos 2a ] 7.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)]三角函数公式三角函数是数学中属于初等函数中的超越函数的一类函数。

三角函数三角形公式

三角函数三角形公式一、正弦定理正弦定理是三角形中的重要定理之一。

它可以帮助我们计算任意三角形的边长和角度。

正弦定理的表达式为：a/sinA = b/sinB = c/sinC其中，a、b、c分别表示三角形的三条边的长度，A、B、C表示三个对应的角度。

例如，我们可以利用正弦定理来计算一个三角形的边长。

假设我们已知一个三角形的两条边的长度分别为5cm和8cm，夹角为30°。

我们可以利用正弦定理来求第三边的长度。

根据正弦定理的公式，我们可以得到：5/sin30° = 8/sinB通过移项，我们可以得到：sinB = (8*sin30°)/5利用三角函数表，我们可以得到sin30°的值为0.5。

代入公式，我们可以求得sinB的值为0.8。

通过反函数，我们可以得到角度B的值为53.13°。

因此，我们可以得出结论，第三边的长度为10cm。

二、余弦定理余弦定理也是三角形中的重要定理之一。

它可以帮助我们计算三角形的边长和角度。

余弦定理的表达式为：c^2 = a^2 + b^2 - 2ab*cosC其中，a、b、c分别表示三角形的三条边的长度，C表示夹角的角度。

例如，我们可以利用余弦定理来计算一个三角形的角度。

假设我们已知一个三角形的两条边的长度分别为3cm和4cm，夹角为60°。

我们可以利用余弦定理来求第三边的长度。

根据余弦定理的公式，我们可以得到：c^2 = 3^2 + 4^2 - 2*3*4*cos60°通过计算，我们可以得到c^2的值为19。

因此，第三边的长度c为√19 cm。

三、正切定理正切定理是三角形中的另一个重要定理。

它可以帮助我们计算三角形的边长和角度。

正切定理的表达式为：tanA = (b*sinC)/(a - b*cosC)其中，a、b分别表示三角形的两条边的长度，A表示夹角的角度，C表示另一个角度。

例如，我们可以利用正切定理来计算一个三角形的角度。

三角函数定义及三角函数公式大全

三角函数定义及三角函数公式大全一：初中三角函数公式及其定理1、勾股定理：直角三角形两直角边a、b的平方和等于斜边c2、如下图，在Rt△ABC中，∠C为直角，则∠A的锐角三角函数为(∠A可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。

4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余A90B90∠-︒=∠︒=∠+∠得由BA对边C角的正切值。

5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。

7、正切、余切的增减性：当0°<α<90°时，tan α随α的增大而增大，cot α随α的增大而减小。

1、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。

依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。

(注意：尽量避免使用中间数据和除法)2、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。

用字母i 表示，即hi l=。

坡度一般写成1:m 的形式，如1:5i =等。

把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。

3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。

如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。

4、指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角。

如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）。

三角函数常用公式和定理

三角函数常用公式和定理1．常见三角不等式： ⑴若(0,)2x π∈，则sin tan x x x <<.⑵ 若(0,)2x π∈，则1sin cos x x <+≤⑶ |sin ||cos |1x x +≥.2．同角三角函数的基本关系式：22sin cos 1θθ+=，tan θ=θθcos sin ，tan 1cot θθ⋅=. 3．正弦、余弦的诱导公式：(奇变偶不变,符号看象限)212(1)sin ,sin()2(1)s ,n n n n co n απαα-⎧-⎪+=⎨⎪-⎩为偶数为奇数 212(1)s ,s()2(1)sin ,n n co n n co n απαα+⎧-⎪+=⎨⎪-⎩为偶数为奇数 4．和角与差角公式：sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±= ;tan tan tan()1tan tan αβαβαβ±±= . 22sin()sin()sin sin αβαβαβ+-=-(平方正弦公式);22cos()cos()cos sin αβαβαβ+-=-.sin cos a b αα+=)αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan b aϕ= ). 5．二倍角公式及降幂公式： sin 22sin cos ααα=22tan 1tan αα=+. 2222cos 2cos sin 2cos 112sin ααααα=-=-=-221tan 1tan αα-=+.22tan tan 21tan ααα=-. sin 21cos 2tan 1cos 2sin 2ααααα-==+ 221cos 21cos 2sin ,cos 22αααα-+== 6．三倍角公式：3sin 33sin 4sin 4sin sin()sin()33ππθθθθθθ=-=-+. 3cos34cos 3cos 4cos cos()cos()33ππθθθθθθ=-=-+.323tan tan tan 3tan tan()tan()13tan 33θθππθθθθθ-==-+-. 7．三角函数的周期公式：函数sin()y x ωϕ=+，x ∈R 及函数cos()y x ωϕ=+，x ∈R(A,ω,ϕ为常数，且A ≠0，ω＞0)的周期2T πω=；函数tan()y x ωϕ=+，,2x k k Z ππ≠+∈(A,ω,ϕ为常数，且A≠0，ω＞0)的周期T πω=. 三角函数的图像：8．正弦定理：2sin sin sin a b c R A B C===.(R 为△ABC 外接圆的半径), 2sin ,2sin ,2sin :::sin :sin a R A b R B C R C a b c sinA B C ===→=。

三角函数定义及三角函数公式大全

三角函数定义及三角函数公式大全-CAL-FENGHAI.-(YICAI)-Company One1三角函数定义及三角函数公式大全一：初中三角函数公式及其定理1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。

4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。

5、0°、30°、45°、60°、90°特殊角的三角函数值(重要) A90B 90∠-︒=∠︒=∠+∠得由B A邻边CA90B 90∠-︒=∠︒=∠+∠得由B Aαsin02122231αcos12322210αtan03313-αcot-31330当0°≤α≤90°时，sinα随α的增大而增大，cosα随α的增大而减小。

7、正切、余切的增减性：当0°<α<90°时，tanα随α的增大而增大，cotα随α的增大而减小。

1、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。

依据：①边的关系：222cba=+；②角的关系：A+B=90°；③边角关系：三角函数的定义。

(注意：尽量避免使用中间数据和除法)2、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)。

用字母i表示，即hil=。

坡度一般写成1:m的形式，如1:5i=等。

把坡面与水平面的夹角记作α(叫做坡角)，那么tanhilα==。

3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。

如图3，OA、OB、OC、OD的方向角分别是：45°、135°、225°。