333点到直线、两平行线间的距离OK

合集下载

3.3.3 ~3.3.4点到直线的距离两平行线间的距离

小结(1)若给出的直线方程不是一般式，则应先把方程化为一般式，再利用公式求距离．(2)若点P在直线上，点P到直线的距离为零，距离公式仍然适用．
训练1求过点M(－2,1)且与A(－1,2)，B(3,0)两点距离相等的直线的方程．
【探究点二】两条平行直线间的距离
导引设直线l1∥l2，如何求l1与l2间的距离？
(1)求直线l的方程；
(2)若直线m与l平行，且点P到直线m的距离为3，求直线m的方程．
1．点到直线的距离即是点与直线上点连线的距离的最小值，利用点到直线的距离公式，解题时要注意把直线方程化为一般式．当直线与坐标轴垂直时可直接求之．
2．利用点到直线的距离公式可求直线的方程，有时需结合图形，数形结合，会使问题更加清晰．
3．已知两平行直线间的距离，即可利用公式d＝求解，也可在已知直线上取一点，转化为点到直线的距离.
例2已知直线l1：2x－7y－8＝0，l2：6x－21y－1＝0，l1与l2是否平行？若平行，求l1与l2间的距离．
小结(1)求两平行线间的距离可以转化为求点到直线的距离，也可以应用公式．
(2)应用两平行线间的距离公式d＝时，两直线方程必须是一般形式，而且x，y的系数对应相等．
训练2(1)求直线2x＋11y＋16＝0关于点P(0,1)对称的直线方程．
[问题情境]
构成平面图形的基本元素为点和直线，就距离而言有两点之间的距离，点到直线的距离及两条直线之间的距离．上节课我们已经学习了两点之间的距离，本节我们来研究点到直线的距离及两条直线之间的距离．
【探究点一】点到直线的距离
问题1两点间的距离公式是什么？
答已知点P1(x1，y1)，P2(x2，y2)，则|P1P2|＝.
鸡西市第十九中学学案
2015年（）月（）日班级姓名

点到直线的距离公式及两条平行直线间的距离(人教A版2019选修一高二数学

由光的性质可知，光线从O到P的路程即为AP的长度|AP|，由
A(4,3)，P(－4,3)知，|AP|＝4－(－4)＝8，
∴光线从O经直线l反射后到达P点所走过的路程为8.
[方法技巧]
光线的入射、反射的问题以及在某定直线取点，使它与两定点
距离之和最小这类问题均属于点关于直线对称的问题．
(1)点 A(x0，y0)关于直线 l：Ax＋By＋C＝0 的对称点 M(x，y)，
yx－－yx00·(－AB )＝－1AB≠0
可由方程组 A·x＋x0＋B·y＋y0＋C＝0
2
2
求得．
(2)常用对称的特例有： ①A(a，b)关于 x 轴的对称点为 A′(a，－b)； ②B(a，b)关于 y 轴的对称点为 B′(－a，b)； ③C(a，b)关于直线 y＝x 的对称点为 C′(b，a)； ④D(a，b)关于直线 y＝－x 的对称点为 D′(－b，－a)； ⑤P(a，b)关于直线 x＝m 的对称点为 P′(2m－a，b)； ⑥Q(a，b)关于直线 y＝n 的对称点为 Q′(a,2n－b)．
[方法技巧] 点到直线的距离的求解方法
(1)求点到直线的距离时，只需把直线方程化为一般式方程，直接应用点到直线的距离公式求解即可．
(2)对于与坐标轴平行(或重合)的直线 x＝a 或 y＝b，求点到它们的距离时，既可以用点到直线的距离公式，也可以直接写成 d＝ |x0－a|或 d＝|y0－b|.
解析：设与直线x＋3y－5＝0垂直的直线的方程为3x－y＋m＝ 0，
则由点到直线的距离公式知： d＝|3×3－2＋1－－01＋2 m|＝|m－103|＝35 10. 所以|m－3|＝6，即m－3＝±6. 得m＝9或m＝－3，故所求直线l的方程为3x－y＋9＝0或3x－y－3＝0. 答案：3x－y＋9＝0或3x－y－3＝0

333点到直线、两平行线间的距离

两条平行直线间的距离是指夹在两条平行直
线间的公垂线段的长.
y
P l1
d C1 - C2 A2 B2
l2
Q
o
x
例7、求证：两条平行线l1:Ax+By+C1=0与
l2: Ax+By+C2=0的距离是
d
ቤተ መጻሕፍቲ ባይዱ
C1 - C2
A2 B2
例7、求证：两条平行线l1:Ax+By+C1=0与
l2: Ax+By+C2=0的距离是 d C1 - C2
§3.3. 3 点到直线的距离
两点间的距离公式是什么？
已知平面上两点P1(x1,y1)， P2(x2,y2)，如何求P1 P2的距离| P1 P2 |呢?
y P1(x1,y1) Q(x2,y1)
P2(x2,y2)
o
x
| P1P2 | (x2 x1)2 ( y2 y1)2
特别地,原点O与任一点P(x, y)的距离:
y
A2 B2
P
l1 证明：B l2
0时，在l1上取一点P
0，-
C1 B
，
o
Q
x
则P到l2的距离d
A
0
B
C1 B
C2
A2 B2
注意:两直线方程的 A,B应相同
C1 C2 A2 B2
B 0时，则A 0，同理可证它们之间的距离为 d C1 C2
A2 B2
练习2
14 53
1.平行线2x-7y+8=0和2x-7y-6=0的距离是___5_3__;
d RS PR • PS PR • PS
d RS
d Ax0 By0 C A2 B2

3.3.3点到直线的距离和3.3.4两平行线间的距离学案

y
A
h C
O
B
探究二。两平行线间的距离公式的应用。探究二。两平行线间的距离公式的应用。公式的应用例 3、已知直线 l1 : 3 x − 4 y − 8 = 0, l2 : 3 x − 4 y + 2 = 0 ，求 l1 与 l2 间的距离。
x
例 4、已知直线 l1 : 2 x − 7 y − 8 = 0, l2 : 6 x − 21 y − 1 = 0 ， l1 与 l2 是否平行？若平行，求 l1 与 l2 间的距离。
当 A=0 时，公式。
合作探究
探究一。点到直线的距离公式的应用。探究一。点到直线的距离公式的应用。距离公式的应用例 1、求点 P0 ( −1, 2) 到直线 l : 3 x = 2 的距离。
例 2、已知点 A(1,3), B (3,1), C ( −1, 0) ，求 ∆ABC 的面积。（如下图）
探究三。距离公式的综合应用。探究三。距离公式的综合应用。例 5.求经过点 P（1，2）的直线，且使 A（2，3），B（0，-5）到它的距离相等的直线方程。
1
连南民族高级中学“学案导学”课堂教学活页学案执笔人：雷训福审阅人：姚尹赞时间：09 年 12 月 16 日课堂达标课堂达标 [一层练习：一层练习]：一层练习 1.已知点 A（ a ，6）到直线 3 x －４ y ＝2 的距离 d=4，则 a 的值为 2.求点 p(3, −2) 到下列直线的距离：（1） y =
连南民族高级中学“学案导学”课堂教学活页学案执笔人：雷训福审阅人：姚尹赞时间：09 年 12 月两平行线间的距离学案 3.3.3 点到直线的距离和 3.3.4 两平行线间的距离学案
学习目标：学习目标：

新课标人教A版数学必修2全部课件：3.3.3点到直线、两平行线间的距离

y
P (x0,y0) y=y1
Q (x0,y1)
y
(x1,y0)
Q
P(x0,y0) x x=x1
o
x
o
PQ = y 0 - y 1
Page 3
PQ = xΒιβλιοθήκη 0 - x 1练习15
(1)点P(-1,2)到直线3x=2的距离是______. 3
4
(2)点P(-1,2)到直线3y=2的距离是______. 3
§3.3. 3
点到直线的距离
Page 1
点到直线的距离
如图，P到直线l的距离，就是指从点P到直线l 的垂线段PQ的长度，其中Q是垂足. y
P
l
Q
o x
思考：已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎
样求点P到直线l的距离呢?
Page 2
当A=0或B=0时,直线方程为y=y1或x=x1的形式.
的距离公式是
d =
Ax
0
+ By A
2
0
+ C
2
+ B
当A=0或B=0时,公式仍然成立.
2.两条平行线Ax+By+C1=0与
Ax+By+C2=0的距离是
d = C1 - C A
Page 12
2 2
2
+ B
练习4
1.点A(a,6)到直线x+y+1=0的距离为4，求a的值. 2.求过点A（－1,2），且与原点的距离等于的直线方程 .
2.两平行线3x-2y-1=0和6x-4y+2=0的距离是____. 13
2 13

点到直线的距离公式两条平行直线间的距离

点到直线的距离公式两条平行直线间的距离要计算点到直线的距离，我们需要知道直线的方程以及点的坐标。

一般来说，直线的方程可以用一般式（Ax + By + C = 0）或截距式（y = mx + b）表示。

点的坐标通常以（x，y）的形式给出。

我们以一般式为例来介绍如何计算点到直线的距离。

假设我们有一个直线的一般式方程为Ax+By+C=0，点的坐标为（x0，y0）。

要计算这个点到直线的距离，我们可以使用以下公式：距离=，Ax0+By0+C，/√(A²+B²)下面我们来详细解释这个公式。

首先，我们可以通过将点的坐标代入直线方程得到：Ax0+By0+C=0根据这个等式，我们可以得到点在直线上的投影点(xp，yp)：xp = x0 - (A(Ax0 + By0 + C) / (A² + B²))yp = y0 - (B(Ax0 + By0 + C) / (A² + B²))接下来，我们可以计算这两个点之间的距离。

使用两点间距离公式：距离= √((xp - x0)² + (yp - y0)²)代入xp和yp的值，我们可以得到：距离=√((x0-(A(Ax0+By0+C)/(A²+B²))-x0)²+(y0-(B(Ax0+By0+C)/(A²+B²))-y0)²)化简这个表达式，我们可以得到：距离= √((A²(x0 - xp)² + B²(y0 - yp)²) / (A² + B²))因为xp和yp是点到直线上的投影点，所以(x0 - xp)是点到投影点的水平距离，(y0 - yp)是点到投影点的垂直距离。

因此，我们可以将上述公式进一步简化为：距离= √((A²(x0 - xp)² + B²(y0 - yp)²) / (A² + B²))最后，我们可以再次替换xp和yp的值，将它们表示为点的坐标和直线方程：距离=√((A²(x0-(x0-(A(Ax0+By0+C)/(A²+B²))))²+(B²(y0-(y0-(B(Ax0+By0+C)/(A²+B²))))²)/(A²+B²))进一步简化，我们可以得到最终的公式：距离=，Ax0+By0+C，/√(A²+B²)这就是点到直线的距离公式。

两点间的距离点到直线的距离两平行线间的距离

§3.3.2两点间的距离，点到直线的距离，两平行线间的距离基础知识过关检测姓名评价1. 两点间的距离两点()111,P x y ,()222,P x y 间的距离12PP =. （1）当直线12PP 平行于轴时,12PP =；（2）当直线12PP 平行于轴时,12PP =；（3）当12,P P 中有一个是原点时,不妨设在原点,则12PP =；（4）当12,P P 在直线y kx b =+上时,12PP =.（1）直线方程应为一般式，若给出其他形式，应先化成一般式再用公式.例如求()00,P x y 到直线y kx b =+的距离，应先把直线方程化为，得d =.（2）点在直线上时，点到直线的距离为零，公式仍然适用，故应用公式时不必判定点与直线的位置关系.（3）直线方程0Ax By C ++=中0A =或0B =时，公式也成立，也可以用下列方法求点到直线的距离.①()00,P x y 到x a =的距离d =； ②()00,P x y 到y b =的距离d =.4.已知ABC ∆的顶点A(2,3),B(-1,0),C(2,0),则ABC ∆的周长是( )A.2B.3+2C.6+3D.6+105.一条线段的长是5个单位，它的一个端点是A （2，1），另一个端点B 的横坐标是-1，则点B 的纵坐标是（）A.-3B.5C.-1或-3D.-3或56.若轴上的点M 到原点的距离与到点N （5，-3）的距离相等，则M 点的坐标是（）A.（-2，0）B.（1，0）C.（23，0）D.（3.4，0） 7.已知ABC ∆的顶点坐标为A(7,8)、B(10,4)、C(2,-4),则BC 边上的中线AM 的长为_____________. 8.点(2,1)到直线:220l x y -+=的距离为( )A.52B.52C.56D.0 9.已知()(),20a a >到直线:30l x y -+=的距离为1，则的值为（）A.-1B.+1C.2-1D.2+110.两条平行线1:3470l x y +-=和2:34120l x y +-=的距离为（）A.3B.2C.1D.21 11.分别过点A （-2，1）和点B （3，-5）的两条直线均垂直于轴，则这两条直线的距离为__________.能力提升1. 两平行直线，分别过点P （-1，3），Q （2，-1）它们分别绕P ，Q 旋转，但始终保持平行，则，之间的距离的取值范围是（）A ．()0,+∞ B.（0，5） C.(]0,5D.( 2. 点(4cos ,3sin )P θθ到直线60x y +-=的距离的最小值等于.3. 与直线210x y ++=. 4. 过原点且与两定点)2,3(),1,1(--B A 距离相等的直线的方程为. 5. 已知ABC ∆的三个顶点坐标是A （1，-1），B （-1，3），C （3，0）. （1）判定ABC ∆的形状；（2）求ABC ∆的面积.6. 试在直线40x y -+=上求一点，使它到点M （-2，-4）、N （4，6）的距离相等.7. 已知三条直线()1:200l x y a a -+=<2:4210l x y -++=3:10l x y +-= ，若与的距离是（1）求的值；（2）能否找到一点使得同时满足下列三个条件:①是第一象限的点；②点到的距离是点到的距离的12；若能，求点坐标；若不能，说明理由.§3.3.2两点间的距离，点到直线的距离，两平行线间的距离基础知识过关检测姓名评价1. 两点间的距离两点()111,P x y ,()222,P x y 间的距离12PP =. （1）当直线12PP 平行于轴时,12PP =；（2）当直线12PP 平行于轴时,12PP =；（3）当12,P P 中有一个是原点时,不妨设在原点,则12PP =；（4）当12,P P 在直线y kx b =+上时,12PP =.（1）直线方程应为一般式，若给出其他形式，应先化成一般式再用公式.例如求()00,P x y 到直线y kx b =+的距离，应先把直线方程化为，得d =.（2）点在直线上时，点到直线的距离为零，公式仍然适用，故应用公式时不必判定点与直线的位置关系.（3）直线方程0Ax By C ++=中0A =或0B =时，公式也成立，也可以用下列方法求点到直线的距离.①()00,P x y 到x a =的距离d =； ②()00,P x y 到y b =的距离d =.4.已知ABC ∆的顶点A(2,3),B(-1,0),C(2,0),则ABC ∆的周长是( C )A.2B.3+2C.6+3D.6+105.一条线段的长是5个单位，它的一个端点是A （2，1），另一个端点B 的横坐标是-1，则点B 的纵坐标是（ D ）A.-3B.5C.-1或-3D.-3或56.若轴上的点M 到原点的距离与到点N （5，-3）的距离相等，则M 点的坐标是（ D ）A.（-2，0）B.（1，0）C.（23，0）D.（3.4，0） 7.已知ABC ∆的顶点坐标为A(7,8)、B(10,4)、C(2,-4),则BC 边上的中线AM 的长为_____________. 8.点(2,1)到直线:220l x y -+=的距离为( B )A.52B.52C.56D.0 9.已知()(),20a a >到直线:30l x y -+=的距离为1，则的值为（ A ）A.-1B.+1C.2-1D.2+110.两条平行线1:3470l x y +-=和2:34120l x y +-=的距离为（ C ）A.3B.2C.1D.21 11.分别过点A （-2，1）和点B （3，-5）的两条直线均垂直于轴，则这两条直线的距离为__________.能力提升1. 两平行直线，分别过点P （-1，3），Q （2，-1）它们分别绕P ，Q 旋转，但始终保持平行，则，之间的距离的取值范围是（）A ．()0,+∞ B.（0，5） C.(]0,5 D.( 解析:最大值为P ，Q 的距离，即5，选C2. 点(4cos ,3sin )P θθ到直线60x y +-=的距离的最小值等于.解析:222|6)sin(5|2|6sin 3cos 4|≥-+=-+=φθθθd3. 与直线210x y ++=的距离为5.解析:02=+y x 或022=-+y x4. 过原点且与两定点)2,3(),1,1(--B A 距离相等的直线的方程为.解析: 直线过线段AB 的中点或平行于直线AB ，故方程为02=+y x 或043=+y x 5. 已知ABC ∆的三个顶点坐标是A （1，-1），B （-1，3），C （3，0）. （1）判定ABC ∆的形状；（2）求ABC ∆的面积.解：（1）如图，△ABC法一：∵|AB |=[]22)1(3)11(--+--=20=2，|AC |=[]22)1(0)13(--+-=，|BC |=[]22)30()1(3-+--=25=5，∴|AB |2+|AC |2=|BC |2，即△ABC 是以A 为直角顶点的直角三角形. 法二：∵k AB =11)1(3----=-2，k AC =13)1(0--- = 21，∴k AB ·k AC =-1，∴AB ⊥AC ，∴△ABC 是以A 为直角顶点的直角三角形. （2）∵∠A =90°， ∴S △ABC =21|AB |·|AC |=5. 规律方法：判定三角形形状的依据是三角形的分类标准，由边的分类或角的分类进行解决. 6. 试在直线40x y -+=上求一点，使它到点M （-2，-4）、N （4，6）的距离相等. 解：法一：由直线x -y +4=0，得y =x +4，点P 在该直线上. ∴可设P 点的坐标为（a ，a +4）. 由已知|PM |=|PN |， ∴[][]22)4(4)2(--++--a a=22)64()4(-++-a a ,22)8()2(+++a a =22)2()4(-+-a a .∴（a +2）2+（a +8）2=（a -4）2+（a -2）2.解得a =-23，从而a +4=-23+4=25. ∴P （-23，25）.法二：由于|PM |=|PN |，∴点P 在线段MN 的垂直平分线上. 由于k MN =)2(4)4(6----=610=35， ∴线段MN 的垂直平分线的斜率为k =-53. 又MN 的中点为（1，1），∴线段MN 的垂直平分线的方程为y -1=-53（x -1），即y =-53x +58. 又∵点P 在直线x -y +4=0上，∴点P 为直线x -y +4=0与y =-53x +58的交点. 由⎪⎩⎪⎨⎧+-==+-,5853,04x y y x得⎪⎪⎩⎪⎪⎨⎧=-=.25,23y x∴点P 的坐标为（-23，25）. 7. 已知三条直线()1:200l x y a a -+=<2:4210l x y -++=3:10l x y +-= ，若与的距离是（1）求的值；（2）能否找到一点使得同时满足下列三个条件:①是第一象限的点；②点到的距离是点到的距离的12；若能，求点坐标；若不能，说明理由.【解题思路】由三个条件可列三个方程或不等式，最终归结为混合组是否有解的问题[解析]（1）21:20,32l x y d a --===⇒=(2)设00(,)P x y 同时满足三个条件由②得：设00(,)P x y 在':20l x y C -+=131126C C =⇒==或则有00001311202026x y x y -+=-+=或------------（1）=000240320x y x ⇒-+=+=或--------------（2）由①得 000,0x y >> ----------------（3）解由（1）（2）（3）联立的混合组得 00137,.918x y == 所以137(,)918P 【名师指引】（1）在条件比较多时，思路要理顺；（2）解混合组时，一般是先解方程，再验证不等式成立。

3.3.3~3.3.4 点到直线的距离~两条平行直线间的距离

时，利用 yx－－yx00·－AB＝－1，
可以求点P′的坐标.
x0＋x y0＋y A· 2 ＋B· 2 ＋C＝0，
对称问题的解决，要充分利用对称的几何性质，同时还要注意运算的策
略和方法，所以说对称问题充分体现了直观想象和数学运算的数学核心
素养.
3 达标检测
PART THREE
1.已知原点O(0,0)，则点O到直线x＋y＋2＝0的距离等于
解 3y＝4可化为3y－4＝0，则点 P(2，－3)到该直线的距离为|－30×2＋3－324|＝133. ③x＝3.
解 x＝3可化为x－3＝0，则点 P(2，－3)到该直线的距离为|2－1 3|＝1.
(2)求过点M(－1,2)，且与点A(2,3)，B(－4,5)距离相等的直线l的方程.
反思
感悟 (1)应用点到直线的距离公式时应注意的三个问题 ①直线方程应为一般式，若给出其他形式应化为一般式. ②点P在直线l上时，点到直线的距离为0，公式仍然适用. ③直线方程Ax＋By＋C＝0，当A＝0或B＝0时公式也成立，但由于直线是特殊直线(与坐标轴垂直)，故也可用数形结合求解. (2)用待定系数法求直线方程时，首先考虑斜率不存在是否满足题意.
A.1
√B.2
C. 1 2
D.4
解析由两条直线平行可得－34＝－m6 ，解得 m＝8.由两条平行线间的距离公式得 d＝ |－332＋－472|＝2.
(3)已知直线l1，l2是分别经过A(1,1)，B(0，－1)两点的两条平行直线，当l1，l2间的距离最大时，直线l1的方程是__x_＋__2_y－__3_＝__0__.
解析当两条平行直线与A，B两点的连线垂直时，两条平行直线间的距离最大. 因为A(1,1)，B(0，－1).

333-334点到直线的距离-两条平行直线间的距离更新

典型例题
例1 求点P(-1,2)到直线 ①2x+y-10=0； ②3x=2的距离。
y
P(-1,2)
用公式验证，结果怎样？
O
x l:3x=2
变1式 .点 P（ mn,m)到直x 线 y1的距离等 mn
2020/6/15
典型例题
例2 已知点A(1，3),B(3，1),C(-1,0)，求三角形 ABC的面积
2020/6/15
小结
• 1.点到直线距离公式
d Ax0 By0 C
A2 B2
注意：化为一般式．
• 2.特殊情况
y
y y1 y1
x x1
|y1-y0|
y0 P0 (x0,y0)
|x1-x0|
2020/6/15
O
x0
x1
x
典型例题
求平行线2x-7y+8=0与2x-7y-6=0的距离。
y
l1:2x-7y-8=0
y
P
l
Q
P（x0，y0）
x
l:Ax+By+C=0
O
Q(x, y)满足:
xB2x0 AB0 yAC
Ax+By+C=0
A2 B2
B x-Ay-Bx0+Ay0=0
yAB0xB0yBC
2020/x 6y/15 x y0 0 A B((A AA A 0 02 x 2 x B B B B0 2 0 2y y C C))
y 3 A (1,3)
还有其他方法吗
？
2
1h
B (3,1)
-1
O 1 2 3x
C (-1,0)
2020/6/15
典型例题

点到直线的距离公式两条平行线间距离(课件)(人教A版2019选择性必修第一册)

A．8
B．2 2
C． 2
D．16
(2)若 P(x，y)在直线 x＋y－4＝0 上，则 x2＋y2－2x－4y＋5的最小值为多少？
(1)A 解析：x2＋y2＝(x－0)2＋(y－0)2 表示点(x，y)与原点(0,0)的距离的平方，故等价
于原点(0,0)到直线 x＋y－4＝0 的距离的平方，即 d＝ 4 ＝2 2，∴d2＝8，故选 A． 2
当堂达标
2.两条平行线 l1：3x＋4y－2＝0，l2：9x＋12y－10＝0 间的距离等于( )
7
7
4
2
A.5
B.15
C.15
D.3
C 解析：l1 的方程可化为 9x＋12y－6＝0，由平行线间的距离公式得 d＝|－962＋＋11202|＝145.
当堂达标
3.已知 O 为原点，点 P 在直线 x＋y－1＝0 上运动，那么|OP|的最小值为( )
经典例题
题型一点到直线的距离
跟踪训练1
已知点(a，2)(a>0)到直线 l：x－y＋3＝0 的距离为 1，则 a＝( )
A. 2
B．2－ 2 C. 2－1
D. 2＋1
C 解析：由点到直线的距离公式得： 1|2a＋－（2＋－31|）2＝|a＋21|＝1， ∴|a＋1|＝ 2. ∵a>0， ∴a＝ 2－1.故选 C.
√
)
小试牛刀
2.原点到直线 x＋2y－5＝0 的距离为( )
A．1
B. 3
C．2
D. 5
D 解析：利用点到直线的距离公式可得：原点到直线 x＋2y－5＝0 的距离
d＝|0＋120＋－252|＝ 5.
3.两条平行线 l1：3x＋4y－7＝0 和 l2：3x＋4y－12＝0 的距离为( )

2.3.3 点到直线的距离公式~2.3.4 两条平行直线间的距离(解析版)..

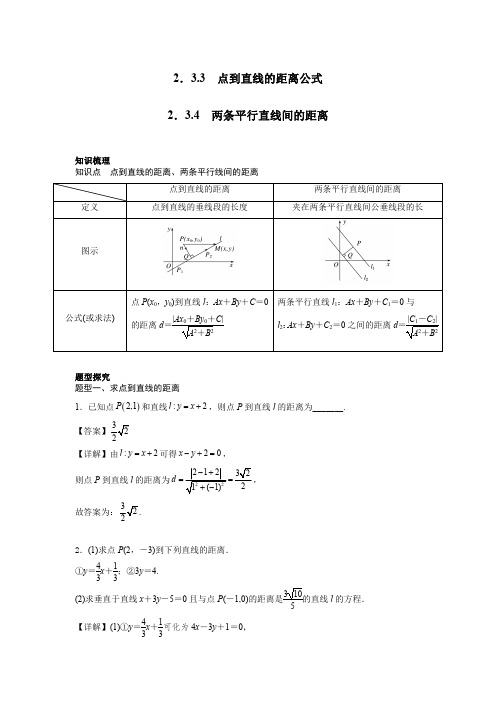
2．3.3点到直线的距离公式2．3.4两条平行直线间的距离知识梳理知识点点到直线的距离、两条平行线间的距离点到直线的距离两条平行直线间的距离定义点到直线的垂线段的长度夹在两条平行直线间公垂线段的长图示公式(或求法)点P (x 0，y 0)到直线l ：Ax ＋By ＋C ＝0的距离d ＝|Ax 0＋By 0＋C |A 2＋B 2两条平行直线l 1：Ax ＋By ＋C 1＝0与l 2：Ax ＋By ＋C 2＝0之间的距离d ＝|C 1－C 2|A 2＋B 2题型探究题型一、求点到直线的距离1．已知点()2,1P 和直线:2l y x =+，则点P 到直线l 的距离为_______.【答案】322【详解】由:2l y x =+可得20x y -+=，则点P 到直线l 的距离为222123221(1)d -+==+-，故答案为：322.2．(1)求点P (2，－3)到下列直线的距离．①y ＝43x ＋13；②3y ＝4.(2)求垂直于直线x ＋3y －5＝0且与点P (－1,0)的距离是3105的直线l 的方程．【详解】(1)①y ＝43x ＋13可化为4x －3y ＋1＝0，则点P (2，－3)到该直线的距离为|4×2－3×(－3)＋1|42＋(－3)2＝185.②3y ＝4可化为3y －4＝0，则点P (2，－3)到该直线的距离为|－3×3－4|02＋32＝133.(2)设与直线x ＋3y －5＝0垂直的直线的方程为3x －y ＋m ＝0，则由点到直线的距离公式知，d ＝|3×(－1)－0＋m |32＋(－1)2＝|m －3|10＝3105.所以|m －3|＝6，即m －3＝±6.得m ＝9或m ＝－3，故所求直线l 的方程为3x －y ＋9＝0或3x －y －3＝0.题型二、由点到直线的距离求参数或范围1．已知(2,0),(4,)-A B a 两点到直线:3410l x y -+=的距离相等，则=a （）A ．2B ．92C ．2或8-D ．2或92【答案】D【详解】因为(2,0),(4,)-A B a 两点到直线:3410l x y -+=的距离相等，所以有22223(2)0(4)13441134523(4)3(4)a a a ⨯-+⨯-+⨯-+=⇒-=⇒=+-+-，或92a =，故选：D2．已知直线():22l y k x =-+，当k 变化时，点()1,2P -到直线l 的距离的取值范围是（）A ．[)0,∞+B ．[]0,2C ．[]0,3D ．[)0,3【答案】D【详解】由题意知直线():22l y k x =-+过定点()2,2A ，且不与x 轴垂直，当直线():22l y k x =-+经过点()1,2P -时，，点()1,2P -到直线l 的距离最小为0，当过点()2,2A 的直线垂直于x 轴时，点()1,2P -到该直线的距离最大,最大值为3，如图示：由于():22l y k x =-+的斜率存在，故点()1,2P -到直线l 的距离小于3，即点()1,2P -到直线l 的距离的取值范围是[)0,3，故选：D.3．已知点()M a b ，在直线34200x y +-=上,则22a b +的最小值为_____.【答案】4【详解】根据题意知，22a b +表示原点到直线34200x y +-=上的点的距离，∴22a b +大于等于原点到直线34200x y +-=的距离，原点到直线34200x y +-=的距离为2045=，∴224a b + ，∴22a b +的最小值为4．故答案为：4．题型三、两平行线间的距离1．直线120l x y ++=：与直线22210l x y +-=：之间的距离为_________.【答案】524【详解】因为直线120l x y ++=：与直线22210l x y +-=：平行,而直线22210l x y +-=：可化为2102l x y +-=：，故直线120l x y ++=：与直线22210l x y +-=：之间的距离为1|2()|52242d --==，故答案为：5242．两条平行直线34120x y +-=与8110ax y ++=之间的距离为（）A ．235B ．2310C ．72D ．27【答案】C【详解】因为直线34120x y +-=与直线8110ax y ++=平行,所以8113412a =≠-,解得6a =,将68110x y ++=化为113402x y ++=,所以两平行直线34120x y +-=与113402x y ++=之间的距离为2211|12|72234--=+.故选：C3．若直线230x y +-=与直线420++=x y a 之间的距离不大于5，则实数a 的取值范围为（）A ．4a ≤B ．164a -≤≤C ．416a -≤≤D ．16a ≤或4a ≥【答案】B【详解】直线230x y +-=化为4260x y +-=，则两直线之间的距离226542a d +=≤+，即610a +≤，解得164a -≤≤.所以实数a 的取值范围为164a -≤≤.故选：B.4．过点(1,0)A 的直线1l 与过点(1,4)B -的直线2l 平行，且它们之间的距离为2，求直线1l 和2l 的方程．【答案】1:10l x y +-=，2:30l x y +-=；或1:770l x y +-=，2:730l x y ++=【详解】当两直线的斜率不存在时，方程分别为1x =，1x =-，此时它们之间的距离为2，不满足题意；当两直线的斜率存在时，设方程分别为(1)y k x =-与()14=++y k x ，即kx y k 0--=，40kx y k -++=．它们之间的距离为2，22421+∴=+k k ，化简得287=0++k k ，解得1k =-，或7k =-，∴这两条直线的方程为1:10l x y +-=，2:30l x y +-=；或1:770l x y +-=，2:730l x y ++=题型四、距离的综合应用1．两条互相平行的直线分别过点A (6,2)和B (－3，－1)，并且各自绕着A ，B 旋转，如果两条平行直线间的距离为d .求：(1)d 的变化范围；(2)当d 取最大值时，两条直线的方程．【详解】(1)如图，显然有0<d ≤|AB |.而|AB |＝(6＋3)2＋(2＋1)2＝310.故所求的d 的变化范围为(0,310]．(2)由图可知，当d 取最大值时，两直线与AB 垂直．而k AB ＝2－(－1)6－(－3)＝13，所以所求直线的斜率为－3.故所求的直线方程分别为y －2＝－3(x －6)和y ＋1＝－3(x ＋3)，即3x ＋y －20＝0和3x ＋y ＋10＝0.2．已知△ABC 的顶点坐标为A (1,1)，B (m ，m )，C (4,2)，1<m <4.当m 为何值时，△ABC 的面积S 最大？【详解】|AC |＝(4－1)2＋(2－1)2＝10，直线AC 的方程为y －12－1＝x －14－1，即x －3y ＋2＝0.因为点B (m ，m )到直线AC 的距离d ＝|m －3m ＋2|12＋(－3)2，所以△ABC 的面积S ＝12|AC |·d ＝12|m －3m ＋2|＝12|m －322－14|.因为1<m <4，所以1<m <2，所以0<|m －322－14|≤14，0<S ≤18.所以当m ＝32，即m ＝94时，△ABC 的面积S 最大．跟踪训练1．点(1，2)到直线:3450l x y ++=的距离为___．【答案】165【详解】由点线距离公式有(1，2)到直线:3450l x y ++=的距离为22|31425|16534⨯+⨯+=+.故答案为：1652．在第一象限的点()1,A a 到直线4310x y +-=的距离为3，则a 的值为__________．【答案】4【详解】()1,A a 在一象限，所以0a >，点()1,A a 到直线4310x y +-=的距离为3，则43135a +-=，解得：4a =或6a =-.因为0a >，所以4a =.故答案为：4.3．在平面角坐标系xOy 中，直线l ：(21)10k x ky -++=，则当实数k 变化时，原点O 到直线l 的距离的最大值为_____________．【答案】5【详解】由直线(21)10k x ky -++=可化为(1)(2)0x k x y -++=，联立方程组1020x x y -=⎧⎨+=⎩，解得x 1,y 2==-，即直线过定点(1,2)P -，由于直线(21)10k x ky -++=经过定点(1,2)P -，又221(2)5OP =+-=所以原点到直线l 的距离的最大值为5.4．已知点(,)M a b 在直线3410x y +=上，则22a b +的最小值为______【答案】2【详解】由点(,)M a b 在直线上得3410x y +=上，且22a b +表示点M 与原点的距离∴22a b +的最小值为原点到直线3410x y +=的距离，即2210234d ==+∴22a b +的最小值为2故答案为25．两条平行线4310x y +-=与8630x y ++=之间的距离是___________.【答案】12【详解】直线4310x y +-=可化为8620x y +-=，又直线8620x y +-=与直线8630x y ++=的距离为22|3(2)|8+6--，所以平行线4310x y +-=与8630x y ++=之间的距离是12，故答案为：12.6．已知直线1l ：10ax y ++=，2l ：10x ay ++=．若12l l ∥，则=a ___________，此时1l 与2l 之间的距离为___________．【答案】1-2【详解】直线1l ：10ax y ++=，2l ：10x ay ++=．若12l l ∥，所以10a a ⋅-=，解得1a =±，当1a =时，1l ：10x y ++=，2l ：10x y ++=，此时1l 与2l 重合，故舍去；当1a =-时，1l ：10x y -++=，2l ：10x y -+=，此时1l 与2l 平行；故1a =-；若12l l ∥，即1l ：10x y -++=，即1l ：10x y --=，2l ：10x y -+=，所以1l 与2l 之间的距离为()()2211211--=+-.故答案为：1-，2.7．若直线1:21l y x =-与直线2l 平行，且它们之间的距离等于5，则直线2l 的方程为___________.【答案】240x y -+=或260x y --=【详解】设直线2:2l y x b =+，将直线1l 与直线2l 化为一般式可得1:210l x y --=，2:20l x y b -+=，故它们之间的距离为22152(1)b +=+-，解得4b =或6-，故直线2l 的方程为240x y -+=或260x y --=.故答案为：240x y -+=或260x y --=.8．已知直线l 1，l 2是分别经过A (1,1)，B (0，－1)两点的两条平行直线，当l 1，l 2间的距离最大时，直线l 1的方程是________．【答案】x ＋2y －3＝0【详解】当两条平行直线与A ，B 两点的连线垂直时，两条平行直线间的距离最大．因为A (1,1)，B (0，－1)．所以k AB ＝－1－10－1＝2，所以两条平行直线的斜率为－12，所以直线l 1的方程为y －1＝－12(x －1)，即x ＋2y －3＝0.高分突破1．与点()21M ,之间的距离为2，且在x 轴上的截距为4的直线是（）A ．4x =B ．34120x y --=C ．4x =或34120x y --=D ．4y =或34120x y --=【答案】C【详解】4x =与()21M ,的距离为2，在x 轴上的截距为4，故4x =符合要求；对于直线34120x y --=，有22|324112|23(4)d ⨯-⨯-==+-且0y =时4x =，故也符合要求；4y =与()21M ,的距离为3且x 轴无交点，不符合要求.∴4x =、34120x y --=都是与点()21M ,距离为2且在x 轴上的截距为4的直线.故选：C2．直线1l ：230x y --=与2l ：3610x y -+-=之间的距离为（）A ．455B ．253C ．4515D ．5【答案】B【详解】由3610x y -+-=可得1203x y -+=，即1l 与2l 平行，故1l 与2l 之间的距离为2231331(252)--=+-.故选：B.3．已知直线330x y +-=和610x my ++=互相平行，则它们之间的距离是（）A ．4B ．1020C ．104D ．71020【答案】D【详解】由直线平行可得360m -=，解得2m =，则直线方程为6210x y ++=，即1302x y ++=，则距离是221371022031+=+.故选：D.4．冰糖葫芦是中国传统小吃，起源于南宋.由山楂串成的冰糖葫芦如图1所示，若将山楂看成是大小相同的圆，竹签看成一条线段，如图2所示，且山楂的半径（图2中圆的半径）为2，竹签所在的直线方程为20x y +=，则与该串冰糖葫芦的山楂都相切的直线方程为（）A ．220x y +±=B ．250x y +±=C ．240x y +±=D ．2250x y +±=【答案】D【详解】由题可设与该串冰糖葫芦的山楂都相切的直线方程为20x y c ++=，则22221c =+，∴25c =±，∴与该串冰糖葫芦的山楂都相切的直线方程为2250x y +±=.故选：D.5．①点()3,2P -到直线:34210l x y +-=的距离是___________.②两平行直线3210x y --=和6430x y --=间的距离是___________.【答案】41326【详解】①()3,2,:34210P l x y -+-=；则点P 到直线l 的距离()22334221204534d ⨯+⨯--===+.②6430x y --=即为33202x y --=，所以两平行直线3210x y --=和6430x y --=间的距离22311322632d -==+.6．点P 为直线3420x y +=-上任意一个动点，则P 到点(3,1)-的距离的最小值为___________.【答案】3【详解】由题意得当点P 和点(3,1)-的连线和直线3420x y +=-垂直时距离最小，此时距离等于点(3,1)-到直线3420x y +=-的距离()223341233(4)⨯-⨯-+=+-，故P 到点(3,1)-的距离的最小值为3.故答案为：3.7．点(2,3)P 到直线(1)30mx m y +-+=的距离等于4，则实数m ___________.【答案】47或4【详解】由题意可得：22|23(1)3|4(1)m m m m +-+=⇒+-2103267m m -+=，解得47=m 或4．故答案为：47或4．8．两平行线1:340l x y m ++=与2:680l x y n ++=之间的距离为______．【答案】210m n -【详解】因为直线1:340l x y m ++=，即为1:6820l x y m ++=，所以两平行直线1:340l x y m ++=与2:680l x y n ++=之间的距离为22221068m n m n d --==+.故答案为：210m n-.9．设3450x y +-=，则22x y +的最小值是___________.【答案】1【详解】22xy +表示直线3450x y +-=上任意点(,)P x y 到原点的距离的平方，显然原点到直线3450x y +-=上的点的最小距离就是原点到直线3450x y +-=的距离，即2203045134d ⨯+⨯-==+，所以22x y +的最小值是2211d ==.故答案为：110．已知ABC 的三个顶点的坐标为()3,3A 、()2,2B -、()7,1C -，试求：(1)BC 边上的高所在的直线方程；(2)ABC 的面积．【答案】(1)360x y --=；(2)24【详解】(1)因为2112(7)3BC k --==---，则BC 边上的高的斜率为3，又经过A 点，故方程为()333y x -=-，化简得360x y --=．(2)()2227(21)310BC =++--=，直线BC 方程为12(2)3y x +=--，整理得340x y ++=，则A 到BC 的距离为223334161013+⨯+=+，则ABC 的面积为11631024210⨯⨯=.11．求与直线3240x y -+=平行且距离等于3的直线．【答案】3243130x y -++=或3243130x y -+-=.【详解】设所求直线方程为320x y m -+=，由()22|4|332m -=+-，得4313m =+或4313m =-，所以与直线3240x y -+=平行且距离等于3的直线方程为3243130x y -++=或3243130x y -+-=.12．两平行直线1l ，2l 分别过()1,0A ，()0,5B .(1)1l ，2l 之间的距离为5，求两直线方程；(2)若1l ，2l 之间的距离为d ，求d 的取值范围.【答案】(1)12:0,:5l y l y ==或12:51250,:512600l x y l x y --=-+=；(2)(0,26⎤⎦【详解】(1)当1l ，2l 斜率不存在时，易知12:1,:0l x l x ==，1l ，2l 之间的距离为1，不合题意；当1l ，2l 斜率存在时，设斜率为k ，则12:(1),:5l y k x l y kx =--=，化为一般式得1:0l kx y k --=，2:50l kx y -+=，由1l ，2l 之间的距离为5，可得()22551k k --=+-，解得0k =或512k =，当0k =时，12:0,:5l y l y ==；当512k =时，12:51250,:512600l x y l x y --=-+=.故两直线方程为12:0,:5l y l y ==或12:51250,:512600l x y l x y --=-+=.(2)如图：当1l ，2l 旋转到和AB 垂直时，1l ，2l 之间的距离d 最大为()2210(05)26-+-=，当1l ，2l 旋转到和AB 重合时，距离为0，又两平行直线1l ，2l 不重合，故(0,26d ⎤∈⎦.13．已知直线1:320l x y ++=与2:20l mx y n ++=平行，且直线1l 与直线2l 之间的距离为10，求m 、n 的值．【详解】因为直线1:320l x y ++=与2:20l mx y n ++=平行，所以2312m n =≠，解得6m =，4n ¹，又因为直线1l 与直线2l 之间的距离为10，所以2241062n -=+，解得24n =或16n =-.综上，m 的值为6；n 的值为24或16-.14．已知(4,3)A -､(2,1)B -和直线:4320l x y +-=，若坐标平面内存在一点P ，使PA PB =，且点P 到直线l 的距离为2，求点P 的坐标.【详解】设点P 的坐标为(,)a b .∵(4,3)A -，(2,1)B -，所以线段AB 的中点M 的坐标为(3,2)-.而AB 所在直线的斜率31142AB k -+==--，∴线段AB 的垂直平分线方程为23y x +=-，即50x y --=.∵点(,)P a b 在直线50x y --=上，∴50a b --=……①；又点(,)P a b 到直线4320x y +-=的距离为2，∴22432243a b +-=+，即43210a b +-=±……②.联立①②，解得1,4,a b =⎧⎨=-⎩或27,78.7a b ⎧=⎪⎪⎨⎪=-⎪⎩故所求点P 的坐标为(1,4)-或278,77⎛⎫- ⎪⎝⎭.故答案为(1,4)-或278,77⎛⎫- ⎪⎝⎭15．已知平行四边形ABCD ，(1,2)A 、(2,4)B 、1(,5)2C ，求：(1)点D 的坐标及点A 到直线CD 的距离；(2)平行四边形ABCD 的面积．【详解】(1)设点00(,)D x y ，则有线段BD 的中点坐标为00(1,2)22x y ++，依题意，线段AC 中点坐标为37(,)42，由平行四边形性质知：0031247222x y ⎧+=⎪⎪⎨⎪+=⎪⎩，解得001,32x y =-=，所以点D 的坐标为1(,3)2D -；直线CD 的斜率53211()22k -==--，直线CD 的方程为152()2y x -=-，即240x y -+=，所以点(1,2)A 到直线CD 的距离22|2124|4552(1)d ⨯-+==+-.(2)由（1）知，线段CD 长2211||()(35)522CD =--+-=，所以平行四边形ABCD 的面积45||545S CD d =⋅=⨯=.。

点到直线的距离,两平行直线的距离

点到直线的距离，两平行直线的距离【学习目标】1. 了解点到直线距离公式的推导，熟练掌握点到直线距离公式2. 会用点到直线距离公式求解两平行线距离.【重难点】重点：点到直线距离公式；两平行线距离公式难点：直线距离公式的推导自主学习案【知识梳理】1. 点P (x 0，y 0)到直线l ：Ax + By + C = 0的距离公式为________________2. 两条平行直线间的距离的求法：转化为求点到直线的距离，即在其中任意一条直线上任取一点，就是这两条平行直线间的距离3. 两平行线间的距离公式：两平行线间的距离d ，已知1l ：Ax + By + C 1= 0 2l ：Ax + By + C 2= 0 则d= _________________【预习自测】1. 原点到直线02623=-+y x 的距离是______________.2. 点)2,1(0-P )到直线l ：23=x 的距离是_____，点)2,1(0-P )到直线l ：23=y 的距离是____。

3. 平行直线1l ：0872=+-y x ，2l ：0172=+-y x 的距离为_____________。

【合作探究】例1 已知点A (1，3)，B (3，1)，C(–1，0)，求三角形ABC 的面积.例2．求过点M(–2， 1)且与A(–7，2)，B(3，0)两点距离相等的直线的方程.例3：若两条平行直线1l ：ax ＋2y ＋2＝0 ，2l ：3x －y ＋d ＝0的距离为10，求a 与d 的值.例4. 等腰直角三角形ABC 的直角顶点C 和顶点B 都在直线2x + 3y – 6 = 0上，顶点A 的坐标是(1，–2).求边AB 、AC 所在直线方程.【当堂检测】1、点)5,0(到直线x y 2=的距离是（） A. 25 B. 5 C. 23 D. 25 2.若点),3(a 到直线043=-+y x 的距离是1，则a 的值是___________3、已知直线1l ：0323=-+y x 和直线2l ：016=++my x 互相平行，求它们之间的距离。

333点到直线的距离334两平行线间的距离20121025

d Ax0 By0 C A2 B2
yl
Q
P0
O
x
二、点到直线的距离例1. 求点P0(0, 5)到直线y＝2x的距离. 例2. 已知点A(1, 3)，B(3, 1)，C(－1, 0)，求△ABC的面积.
练习1. 已知A(2, 1)，直线BC的方程是 x＋y＝1，求△ABC的BC边上的高.
l P0Q
直线P0Q的斜率
直线 l 的方程
直线P0Q的方程
交点
点 P0的坐标
点Q 的坐标
两点间距离公式
点P0、Q 之间的距离 P0Q（ P0 到l 的距离）
点到直线的距离
回忆建立两点间的距离公式的过程．
首先求出两条与坐标轴平行的线段的长度，然后利用勾股定理求出这两点间的距离（斜边长）．
y
P2
53 53
两条平行线间的距离可以化归为点到直线的距离去求.
两条平行直线间的距离：
两条平行直线间的距离是指夹在两条平行直线间
的公垂线段的长.
y
P l1
两条平行线
l2
l1:Ax+By+C1=0与 l2:Ax+By+C2=0
Q
o
x
的距离是
d
C1 - C2
A2 B2
二、两条平行直线间的距离
例3. 已知直线l1：2x－7y－8＝0， l2：6x－21y－1＝0，
3.3.3《点到直线的距离》 3.3.4《两平行线间的距离》
复习引入
两点间的距离公式是什么？
已知点 P1x1, y1，P2 x2, y2 ，则
P1P2 x2 x1 2 y2 y12 .
y
P2
N2

3..3..3点到直线的距离和两条平行直线间的距离

3.3.3点到直线的距离【教学目标】1.让学生掌握点到直线的距离公式，并会求两条平行线间的距离.2.引导学生构思距离公式的推导方案，培养学生观察、分析、转化、探索问题的能力，鼓励创新.培养学生勇于探索、善于研究的精神，学会合作.WSGg45LRBS【重点难点】教学重点:点到直线距离公式的推导和应用.教学难点:对距离公式推导方法的感悟与数学模型的建立.【教学过程】导入新课思路1.点P(0,5>到直线y=2x的距离是多少？更进一步在平面直角坐标系中,如果已知某点P的坐标为(x0,y0>,直线l的方程是Ax+By+C=0,怎样由点的坐标和直线的方程直接求点P到直线l的距离呢?这节课我们就来专门研究这个问题.WSGg45LRBS思路2.我们已学习了两点间的距离公式，本节课我们来研究点到直线的距离.如图1,已知点P(x0,y0>和直线l:Ax+By+C=0，求点P 到直线l的距离(为使结论具有一般性，我们假设A、B≠0>.WSGg45LRBS图1新知探究提出问题①已知点P(x0,y0>和直线l:Ax+By+C=0，求点P到直线l的距离.你最容易想到的方法是什么?各种做法的优缺点是什么?WSGg45LRBS②前面我们是在A、B均不为零的假设下推导出公式的，若A、B中有一个为零，公式是否仍然成立？③回顾前面证法一的证明过程，同学们还有什么发现吗？(如何求两条平行线间的距离>活动：①请学生观察上面三种特殊情形中的结论:(ⅰ>x0=0,y0=0时，d=；(ⅱ>x0≠0,y0=0时，d=；(ⅲ>x0=0,y0≠0时，d=.观察、类比上面三个公式，能否猜想：对任意的点P(x0,y0>，d=?学生应能得到猜想：d=.启发诱导：当点P不在特殊位置时，能否在距离不变的前提下适当移动点P到特殊位置，从而可利用前面的公式？(引导学生利用两平行线间的距离处处相等的性质，作平行线，把一般情形转化为特殊情形来处理>WSGg45LRBS证明：设过点P且与直线l平行的直线l1的方程为Ax+By+C1=0，令y=0，得P′(,0>.∴P′N=. (*>WSGg45LRBS∵P在直线l1:Ax+By+C1=0上,∴Ax0+By0+C1=0.∴C1=-Ax0-By0.代入(*>得|P′N|=即d=,.②可以验证，当A=0或B=0时，上述公式也成立.③引导学生得到两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离d=.证明：设P0(x0,y0>是直线Ax+By+C2=0上任一点，则点P0到直线Ax+By+C1=0的距离为d=.WSGg45LRBS又Ax0+By0+C2=0,即Ax0+By0=-C2，∴d=.讨论结果：①已知点P(x0,y0>和直线l:Ax+By+C=0，求点P到直线l的距离公式为d=.②当A=0或B=0时，上述公式也成立.③两条平行线Ax+By+C1=0与Ax+By+C2=0的距离公式为d=.应用示例例1 求点P0(-1，2>到下列直线的距离：(1>2x+y-10=0;(2>3x=2.解:(1>根据点到直线的距离公式得d=.(2>因为直线3x=2平行于y轴，所以d=|-(-1>|=.点评：例1(1>直接应用了点到直线的距离公式，要求学生熟练掌握；(2>体现了求点到直线距离的灵活性，并没有局限于公式.WSGg45LRBS变式训练点A(a，6>到直线3x－4y=2的距离等于4，求a的值.解:=4|3a-6|=20a=20或a=.例2 已知点A(1，3>，B(3，1>，C(-1，0>，求△ABC的面积.解:设AB边上的高为h，则S△ABC=|AB|·h.|AB|=，AB边上的高h就是点C到AB的距离.AB边所在的直线方程为,即x+y-4=0.点C到x+y-4=0的距离为h=，因此，S△ABC=×=5.点评：通过这两道简单的例题，使学生能够进一步对点到直线的距离理解应用，能逐步体会用代数运算解决几何问题的优越性.WSGg45LRBS变式训练求过点A(-1,2>,且与原点的距离等于的直线方程.解:已知直线上一点，故可设点斜式方程，再根据点到直线的距离公式,即可求出直线方程为x＋y－1=0或7x＋y＋5=0.WSGg45LRBS 例3 求平行线2x-7y+8=0和2x-7y-6=0的距离.解:在直线2x-7y-6=0上任取一点,例如取P(3,0>,则点P(3,0>到直线2x-7y+8=0的距离就是两平行线间的距离.因此,WSGg45LRBS d=.点评:把求两平行线间的距离转化为点到直线的距离.变式训练求两平行线l1:2x+3y-8=0,l2:2x+3y-10=0的距离.答案：.解:点O(0，0>关于直线l:2x-y+1=0的对称点为O′(-,>，则直线MO′的方程为y-3=x.直线MO′与直线l:2x-y+1=0的交点P(>即为所求，相应的||PO|-|PM||的最大值为|MO′|=.课堂小结通过本节学习，要求大家：1.掌握点到直线的距离公式，并会求两条平行线间的距离.2.构思距离公式的推导方案，培养学生观察、分析、转化、探索问题的能力，鼓励创新.培养学生勇于探索、善于研究的精神，学会合作.WSGg45LRBS3.本节课重点讨论了平面内点到直线的距离和两条平行线之间的距离，后者实际上可作为前者的变式应用.当堂检测导学案当堂检测【板书设计】一、点到直线距离公式二、例题例1变式1例2变式2【作业布置】课本习题3.3 A组9、10；B组2、4及导学案课后练习与提高3.3.3 点到直线的距离课前预习学案一、预习目标让学生掌握点到直线的距离公式，并会求两条平行线间的距离二、学习过程预习教材P117~ P119，找出疑惑之处问题1．已知平面上两点，则的中点坐标为，间的长度为 .WSGg45LRBS 问题2．在平面直角坐标系中，如果已知某点的坐标为，直线的方程是，怎样用点的坐标和直线的方程直接求点到直线的距离呢?WSGg45LRBS5分钟训练1.点<0，5）到直线y=2x的距离是( >A. B. C.D.WSGg45LRBS2.两条平行直线3x+4y-2=0,3x+4y-12=0之间的距离为________________.WSGg45LRBS3.已知点(a,2>(a＞0>到直线l：x-y+3=0的距离为1,则a的值等于( >A. B. C.D.答案：C三．提出疑惑同学们，通过你的自主学习，你还有那些疑惑，请填在下面的表格中课内探究学案一、学习目标1．理解点到直线距离公式的推导，熟练掌握点到直线的距离公式；2．会用点到直线距离公式求解两平行线距离3．认识事物之间在一定条件下的转化.用联系的观点看问题学习重点:点到直线距离公式的推导和应用.学习难点:对距离公式推导方法的感悟与数学模型的建立二、学习过程知识点1：已知点和直线，则点到直线的距离为：.注意：⑴点到直线的距离是直线上的点与直线外一点的连线的最短距离；⑵在运用公式时，直线的方程要先化为一般式.问题1：在平面直角坐标系中，如果已知某点的坐标为，直线方程中，如果，或，怎样用点的坐标和直线的方程直接求点P到直线的距离呢并画出图形来.WSGg45LRBS例分别求出点到直线的距离.问题2：求两平行线：，：的距离.知识点2：已知两条平行线直线，，则与的距离为注意：应用此公式应注意如下两点：<1）把直线方程化为一般式方程；<2）使的系数相等.典型例题例1 求点P0(-1，2>到下列直线的距离：(1>2x+y-10=0;(2>3x=2.变式训练点A(a，6>到直线3x－4y=2的距离等于4，求a的值.例2 已知点A(1，3>，B(3，1>，C(-1，0>，求△ABC的面积变式训练求两平行线l1:2x+3y-8=0,l2:2x+3y-10=0的距离当堂检测课本本节练习.拓展提升问题：已知直线l:2x-y+1=0和点O(0，0>、M(0，3>，试在l 上找一点P，使得||PO|-|PM||的值最大，并求出这个最大值.WSGg45LRBS.学习小结1.点到直线距离公式的推导过程，点到直线的距离公式，能把求两平行线的距离转化为点到直线的距离公式课后巩固练习与提高30分钟训练1.点<3,2）到直线l:x-y+3=0的距离为( >A. B. C.D.WSGg45LRBS2.点P(m-n,-m>到直线=1的距离为( >A. B. C.D.3.点P在直线x+y-4=0上，O为坐标原点，则|OP|的最小值为( >A. B. C.D.2WSGg45LRBS4.到直线2x+y+1=0的距离为的点的集合为( >A.直线2x+y-2=0B.直线2x+y=0WSGg45LRBSC.直线2x+y=0或直线2x+y-2=0D.直线2x+y=0或直线2x+y+2=0WSGg45LRBS5.若动点A、B分别在直线l1：x+y-7=0和l2：x+y-5=0上移动,则AB的中点M到原点的距离的最小值为( >WSGg45LRBSA. B. C.D.WSGg45LRBS6.两平行直线l1、l2分别过点P1(1,0>、P2(1,5>,且两直线间的距离为５，则两条直线的方程分别为l1：_________________,l2：_______________.WSGg45LRBS7.已知直线l过点A(-2,3>,且点B(1,-1>到该直线l的距离为3，求直线l的方程.8.已知直线l过点(1,1>且点A(1,3>、B(5,-1>到直线l的距离相等，求直线l的方程.9.已知三条直线l1：2x-y+a=0(a＞0>,直线l2：4x-2y-1=0和直线l3：x+y-1=0,且l1与l2的距离是.WSGg45LRBS(1>求a的值.(2>能否找到一点P,使得P点同时满足下列3个条件:①P是第一象限的点；②P点到l1的距离是P到l2的距离的；③P点到l1的距离与P点到l3的距离之比是？若能,求P点的坐标;若不能,请说明理由.WSGg45LRBS参考答案1.解读:由点到直线的距离公式可得d=.答案：C2.解读:nx+my-mn=0，由点到直线的距离公式，得.答案：A3.解读:根据题意知|OP|最小时，|OP|表示原点O到直线x+y-4=0的距离.即根据点到直线的距离公式，得.WSGg45LRBS答案：B4.解读:根据图形特点，满足条件的点的集合为直线，且该直线平行于直线2x+y+1=0，且两直线间的距离为.设所求直线的方程为2x+y+m=0,根据平行线间的距离公式，得｜m-1｜=1，解得m=2或m=0.WSGg45LRBS故所求直线的方程为2x+y=0或2x+y+2=0.答案：D8.解：直线l平行于直线AB时，其斜率为k=kAB==-1，即直线方程为y=-(x-1>+1x+y-2=0；直线l过线段AB的中点M(2,1>时也满足条件，即直线l的方程为y=1.WSGg45LRBS综上，直线l的方程为x+y-2=0或y=1.9.解：(1>根据题意得：l1与l2的距离d=a=3或a=-4(舍>.(2>设P点坐标为(x0,y0>,则x0＞0,y0＞0.若P点满足条件②,则2×｜8x0-4y0+12｜=｜4x0-2y0-1｜, 8x0-4y0+12=4x0-2y0-1或8x0-4y0+12=-(4x0-2y0-1>4x0-2y0+13=0或12x0-6y0+11=0; ①WSGg45LRBS若P点满足条件③,则｜2x0-y0+3｜=｜x0+y0-1｜, 2x0-y0+3=x0+y0-1或2x0-y0+3=-(x0+y0-1>,x0-2y0+4=0或3x0+2=0;②WSGg45LRBS由①②得解得故满足条件的点P为(-3,>或(>或(>或(>.申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

3-3-4点到直线的距离两平行线间的距离精品文档

第三章 3.3 3.3.3、3.3.4
成才之路 ·数学 ·人教A版 · 必修2
方法二：因为直线y＝6平行于x轴，所以d＝|6－(－2)|＝8. (3)因为直线x＝4平行于y轴，所以d＝|4－3|＝1.
第三章 3.3 3.3.3、3.3.4
成才之路 ·数学 ·人教A版 · 必修2
规律总结：针对这个类型的题目一般先把直线的方程化为一般式，然后直接利用点到直线的距离公式求得．对于与坐标轴平行的直线x＝a或y＝b，求点到它们的距离时，既可以用点到直线的距离公式，也可以直接写成d＝|x0－a|或d＝|y0－ b|.
成才之路 ·数学 ·人教A版 · 必修2
规律总结：求两条平行直线间的距离的基本思路是：(1) 在一条直线上取一点，再求这一点到直线的距离即可，即将求平行线间距离转化为求点到直线的距离．也可以在两条直线外取一点，再求这一点分别到这两条直线的距离，若这一点夹在两条平行线之间，则所求的距离为它们的和；若这一点在两条平行线之外，所求距离为它们的差．
成才之路 ·数学 ·人教A版 · 必修2
点(1，－5)到直线2x－y－2＝0的距离d＝________. [答案] 5 [解析] d＝|2×12－2＋－－51－2 2|＝ 5.
第三章 3.3 3.3.3、3.3.4
成才之路 ·数学 ·人教A版 · 必修2
2．两条平行直线间的距离 (1)定义：夹在两条平行直线间公垂线段的长叫做这两条平行直线间的距离． (2)求法：转化为求点．到．直．线．的距离，即在其中任意一条直线上任取一点，这点到另一条直线的距离就是这两条平行直线间的距离．
第三章 3.3 3.3.3、3.3.4
成才之路 ·数学 ·人教A版 · 必修2
[破疑点](1)使用两条平行直线间的距离公式的前提条件： ①把直线方程化为直线的一般式方程； ②两条直线方程中x，y系数必须分别相等． (2)求两条平行直线间的距离通常转化为其中一条直线上任意一点到另一条直线的距离，且两平行线间距离与其中一条直线上点的选取无关．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

d | Ax0 By0 C | A2 B2
例1 求点 P0 1，2到直线 l : 3x 2的距离．
解： d 3 1 2 5
32 02
3
点到直线的距离：
P0(x0,y0)到直线l:Ax+By+C=0的距离：
d | Ax0 By0 C | A2 B2
练习1
1、求点A（-2，3）到直线3x+4y+3=0的距离.
x
思考：已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎
样求点P到直线l的距离呢?
当A=0或B=0时,直线方程为 y=y1或x=x1的形式.
y y=y1
o
P (x0,y0)
Q(x0,y1) x
y (x1,y0)
Q
P(x0,y0)
o
x
PQ = y0 - y1
x=x1 PQ = x0 - x1
o
Q
x
则P到l2的距离d
A
0
B
C1 B
C2
A2 B2
注意:两直线方程的 A,B应相同
C1 C2 A2 B2
B 0时，则A 0，同理可证它们之间的距离为 d C1 C2
A2 B2
练习2
14 53
1.平行线2x-7y+8=0和2x-7y-6=0的距离是___5_3__;
2 13
A2 + B2
当A=0或B=0时,公式仍然成立.
2.两条平行线Ax+By+C1=0与 Ax+By+C2=0的距离是
d=
C1 - C2 A2 + B2
§3.3. 3 点到直线的距离
两点间的距离公式是什么？
已知点 P1x1, y1，P2 x2, y2 ，则
P1P2 x2 x1 2 y2 y12 .
y
P2
N2
M2
O
Q
M1 x N1 P1
点到直线的距离
如图，P到直线l的距离，就是指从点P到直线l 的垂线段PQ的长度，其中Q是垂足.
y
P
l
Q
o
下面设A≠0,B ≠0, 我们进一步探求点到直线的距离公式:
[思路一] 利用两点间距离公式:
y
P
l
Q
o
x
[思路二] 构造直角三角形求其高.
y
PR : y y0
PS : x x0
R
By0 A
C
,
y0
S
Ax0 B
C
,
x0
R
P(x0,y0)
PR Leabharlann By0 ACx0
Ax0 By0 C A
2.两平行线3x-2y-1=0和6x-4y+2=0的距离是_1_3__.
练习3
1、点A(a,6)到直线x+y+1=0的距离为4，求a的值.
2
2、求过点A（－1,2），且与原点的距离等于 2 的直线方程 .
小结
1.平面内一点P(x0,y0) 到直线Ax+By+C=0 的距离公式是 d = Ax 0 + By 0 + C
2. 求点B（-5，7）到直线12x+5y+3=0的距离.
3、求点P0（-1，2）到直线2x+y-10=0的距离.
例2:已知点A(1,3),B(3,1),C(-1,0),求的A面BC积
解 : 如图, 设AB边上的高为h, 则
SABC
1 2
|
AB | h
y
A
| AB | (3 1)2 (1 3)2 2 2
AB边上的高h就是点C到AB的距离
h
AB边所在直线的方程为
C
y-3 x 1
即x y 4 0
O
1-3 31
h | 1 0 4 | 5
12 12
2
因此, SABC
12 2
2
5 5 2
B
x
两条平行直线间的距离：
两条平行直线间的距离是指夹在两条平行直
线间的公垂线段的长.
y
P l1
l2
Q
o
x
例7、求证：两条平行线l1:Ax+By+C1=0与
l2: Ax+By+C2=0的距离是
d
C1 - C2
A2 B2
例7、求证：两条平行线l1:Ax+By+C1=0与
l2: Ax+By+C2=0的距离是 d C1 - C2
y
A2 B2
P
l1 证明：B l2
0时，在l1上取一点P
0，-
C1 B
，
Q
PS
Ax0 B
C
y0
Ax0 By0 C B
O
S
x RS
L:Ax+By+C=0
设 PQ d,由三角形面积公式得
PR2 PS 2 A2 B2 A B Ax0 By0 C
d RS PR • PS PR • PS
d RS
d Ax0 By0 C A2 B2
点到直线的距离：
P0(x0,y0)到直线l:Ax+By+C=0的距离：