普通物理学-力学-平面简谐波
大学物理学课件-平面简谐波规律

y 波形曲线
0
t = t0
x
大学物理学
章目录 节目录 上一页 下一页
5.2 平面简谐波规律
3、如x、t 均变化,波函数表示波形沿传播方向
的运动情况
t 时刻,x处质点的相位
(t x )
u
t 时t 刻, x 处 质Δx点的相位
dWk
1 2
A2 2
sin
2
(t
x u
)dV
2) 介质元的弹性势能:
dW p
1 2
k(dy
)2
dW p1 2来自A2 2sin2(t
x u
) dV
dWk
3) 介质元的总能量:
dW
dWk
dWp
A2 2
sin2
(t
x u
)
dV
大学物理学
章目录 节目录 上一页 下一页
5.2 平面简谐波规律
dW
dWk
dWp
(t
1)] 8
在下列情况下试求波函数(设波速为u):
(1) 以 A 为原点; (2) 以 B 为原点;
x1
x
BA
(3) 若u沿x 轴负向,以上两种情况又如何?
解: (1)在x轴上任取一点P ,
该点振动方程为:
yp
Acos[4π
(t
x u
1)] 8
x1
u
x
BA P
波函数为: y(x,t) Acos[4π (t x 1)] u8
y Acos[t kx ]
k 2
大学物理学
章目录 节目录 上一页 下一页
普通物理学 §11-02 平面简谐波的波函数

v y t
2
角波数 k
x u ) ]
2π
A sin[ (t
2
a
y t
2
A cos[ (t
x u
) ]
11 – 2 平面简谐波的波函数
二
波函数的物理意义
x u ) ] A cos[ 2 π ( t T x )]
1 (t
x1 u ) 2π ( t T x1
2 (t
x2 u
) 2π (
t T
x2
)
波程差
x 21 x 2 x 1
2π x
)
12 1 2 2 π
x 2 x1
2π
x 21
11 – 2 平面简谐波的波函数 例1 已知波动方程如下,求波长、周期和波速.
y ( 5 cm ) cos π [( 2.50s
-1
) t ( 0 . 01 cm
-1
) x ].
解:方法一(比较系数法).
y A cos 2π ( t T x
)
把题中波动方程改写成
y ( 5 cm ) cos 2π [( 2.50 2 s )t (
y (1 . 0 ) cos[ 2 π ( t 2 .0 x 2 .0 ) π 2 ]
t 1 .0 s
y (1 . 0 ) cos[
π 2
π x]
波形方程
y /m
(1 . 0 ) sin( π x )
1.0
o
-1.0
2.0
t 1 . 0 s 时刻波形图
第二节 平面简谐波波动方程

§ 9.2 平面简谐波的波动方程一、平面简谐波波动方程简谐波:如果波源和介质中的各质点都持续地作简谐振动,这种波称为简谐波。
平面简谐波:波面为平面的简谐波。
平面简谐波也称为一维简谐波,其表达式也称波函数(wave function)沿+x 方向传播的一维简谐波 (波速u ,振动角频率为ω),假设媒质无吸收(质元振幅均为A )介质中任一质点(坐标为 x )相对其平衡位置的位移(坐标为 y )随时间的变化关系,即 称为波动方程。
设O 点处质点的振动方程为波线上坐标为x 的任意点P 处质点的振动方程振动从O 点传到P 点所需的时间为t 时刻点 P 的振动与 t-x/u 时刻点O 的振动状态相同,只是落后了Δt 点P 振动方程 式中称上式为沿x 轴正向传播的平面简谐波的波动方程(,)y x t cos O y A tω=(,)P y f x t ==?x t u∆=cos ()P xy A t uω=-2πων=u λν=xo任一点p参考点a波速u波方程的其它表示式讨论:(1)如果原点的初相位不为零设:点O振动方程则:波动方程为(2)如果平面简谐波沿x轴负方向传播则P点处质点相位比O点处质点的相位超前波动方程为二、波动方程的物理意义由从几方面讨论1 当x 一定时(设x =x0,即考察波线上某一点x0) 给出x =x0处质点的振动方程即x0处质元的振动表达式,表示x处的质点在各个不同的时刻位移随时间的变化情况,由它画出的曲线是x0处质元的振动曲线。
2 当t一定时(设t = t0,即在某一时刻t0),给出t= t0时刻各质点的位移y分布情况反映t0时刻各不同x处质元的位移状况,即同一时刻x轴上各个质点离开它们平c o s2π()xy A tνλ=-[]c o sOy A tωϕ=+c o s[2π()]xy A tνϕλ=-+c o s[2π()]xy A tνϕλ=++c o s[2π()]xy A tνϕλ=-+()y y t=()y y x=c o s[2π()]xy A tνϕλ=-+2c o s()y A t xπωλ=-c o s()xy A tuωϕ⎡⎤=-+⎢⎥⎣⎦c o s()xy A tuωϕ⎡⎤=++⎢⎥⎣⎦c o s()xy A tuωϕ⎡⎤=-+⎢⎥⎣⎦衡位置的位移分布,由它画出的曲线即t 0时刻的波形曲线。
平面简谐波概念
O
-A
x
P
x
P点比O点超前时间 反向波波函数
y
O
P
x
x
以波线上x0处点为参考点
y
则Q点处质点的振动方程为 A x0 Q
O -A
x
P
x
Q点的任一振动状态传到P点,需要时间
则波动方程:
其中:x xo u
— 表示x处质元的振动落后(或超前)xo处质元
振动的时间
(
x u
xo
)
—
表示x处质元的振动落后(或超前)于xo处质元
u
(2).y Acos[(t x ) ]
u
(3).y Acos[(t x a ) ]
u
(3)
(1)x b (2)x b (3)x a b
[例] 已知: T 4S 求:P点的振动方程
Y(cm) 0.2 •
解:yP
Aco(s t
平面简谐波
一、平面简谐波概念 所有质点作谐振且波面为平面的波 二、平面简谐波的波动方程:y=f(x,t)
描述媒质中各质点位移y随各点平衡位置x和时间t变化 的函数关系
源
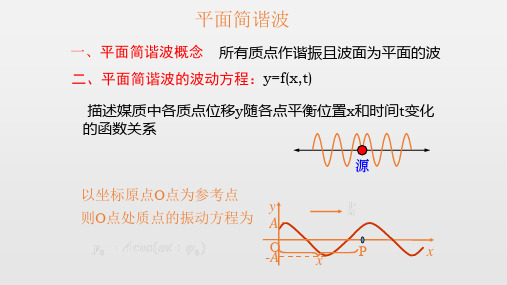
以坐标原点O点为参考点
则O点处质点的振动方程为
y A
O -A
x
P
x
O点的任一振动状态传到P点,需要时间
y A
正向波波函数(波动方程)
(2)同一时刻,沿波线各质元振动状态不同,各质元相位 依次落后
*u
=
T
=
u由介质的性质决定
T T振
振 由振源决定.
得波动方程:
当x确定: y(t)——x处质元的振动方程 当t确定: y(x)——t时刻的波形
16_02_平面简谐波 波动方程

x1 点的振动方程: y1 (t ) 0.01cos[200 (t
1 ) ] ( m ) —— x 1 m 400 2
1 ) ] 2 1 (200 t ) [200 (t 2 400 2
2 1
3)
REVISED TIME: 09-10-7
-2-
CREATED BY XCH
普通物理学_程守洙_第十六章 机械波和电磁波_20090921
波数 波数 —— 波线单位长度内波的数目: k
2
x
—— 将 2 k 代入 y ( x, t ) A cos[2 ( t 3 波动方程 简谐波的波函数: y ( x, t ) A cos[ (t 对时间的二阶偏微分: 对坐标的二阶偏微分: 则:
2) 距波源 x2 2m 和 x1 1m 的两点间的振动相差
x2 点的振动方程: y2 (t ) 0.01cos(200 t ) ( m) —— x 0 2
REVISED TIME: 09-10-7 -4CREATED BY XCH
普通物理学_程守洙_第十六章 机械波和电磁波_20090921
x x0 ) 0 ] u
例题 04 如图 XCH004_135_00 所示的是一平面简谐波在 t 0 时刻的波形图,设该简谐波的频率 为 250 Hz ,且此时质点 P 的运动方向向下,求: 1) 该波的波函数; 2) 在距原点 O 为 100 m 处质点的振动方程与质点速度表达式。
x u
x u
x ) 0 ] —— 波动方程,或波函数 u 2 , uT T
—— 波函数既是时间的周期性函数,又是空间的周期性函数。 波函数的几种表示:利用关系: 2
2平面简谐波

y( x, t ) = A cos[ωt −
2πx
+ ϕ0 ]
注:若u沿x轴负向,P点的振动领先: 轴负向, 点的振动领先: 2πx y( x, t ) = A cos[ωt + + ϕ0 ] λ
x y ( x, t ) = A cos[ω (t + ) + ϕ 0 ] u x y( x, t ) = A cos[2π (νt + ) + ϕ0 ] λ 2π ′ y( x, t ) = Acos[ ( x + ut) + ϕ0 ] λ ′ y( x, t ) = A cos[k ( x + ut) + ϕ0 ] y u x x o P
.
o
r u
x0
.
a
λ
∆x
p
λ
点的相位比a落后 解2:p点的相位比 落后: 2 π ∆ x = 2 π ( x − x 0 ) : 点的相位比 落后: a点的振动方程:ya = A cos[ωt + ϕ ′)] 点的振动方程: 点的振动方程 即得波动方程: 即得波动方程:
y p = A cos[ωt −
五、惠更斯原理
1. 波动的描述:( )波函数 (2)几何描述 波动的描述:( :(1) ) 几个概念: 几个概念:
(1) 波面:振动相位相同的 波面: 点组成的面称波面。 点组成的面称波面。波面是 平面的波称为平面波,波面 平面的波称为平面波, 是球面的波称为球面波。 是球面的波称为球面波。 (2) 波前 波阵面 :传播过 波前(波阵面 波阵面): 程中处在最前面的那个波面 称为波前或波阵面。 称为波前或波阵面。
11-02 平面简谐波

点间的距离 .
π(2.5t 1.0x1) π(2.5t 1.0x2 ) 2π
x2 x1 2.0 m
周期为相位传播一个波长所需的时间.
π(2.5t1 1.0x1) π(2.5t2 1.0x2 )
x2 x1 2.0 m
T t2 t1 0.8 s
位移和速度分别为:
o
x0 Acos 0
-1.0
v0 A sin 0
y(x,
t
)
O
π 2
Acos[
(t
x u
)
O
]
0.1cos[ π(t 2x) π] (m)
2
2
t 1.0 s
2.0 x / m
Ao
O
y
11 – 2 平面简谐波
第十一章 机械波和电磁波
讨 论 1)给出下列波函数所表示的波的传播方向
函 数
y(x,
t)
A cos [ (t
x u
)
O
]
u 沿x 轴负向
11 – 2 平面简谐波
第十一章 机械波和电磁波
如果已知距原
A
y
u
x
点为 xQ 的点Q的
振动规律
O Q*
A xQ
P*
x
点 Q 振动方程 yQ A cos(t Q )
波
y(x,
t)
Acos[(t
x
xQ u
)
Q
]
u 沿 x轴正向
11 – 2 平面简谐波
第十一章 机械波和电磁波
一 平面简谐波的波动表达式
简谐波:在均匀的、无吸收的介质中,波源作 简谐运动时,在介质中所形成的波 .
平面简谐波

解 根据题意设波源的振动方程为
y
0.01cos
200
t
x 400
0
vy00
0 0
即0.021csoins00
0 0
0
2
故
y
0.01cos
200
t
x 400
2
(1)B 和A 两点之间的振动相位差为
200
t
2 400
2
200
t
1 400
2
2
(2)以B 为坐标原点时有
t x
T
(t, x) (t t, x x)
x ut
讨论:如图简谐 波以余弦函数表示,
求 O、a、b、c 各点
振动初相位.
(π ~ π )
t =0 A y
Oa
A
A
O
y o π
O
A
O
y
a
π 2
O A
u
b c
A
y
y
t=T/4
x
b 0
c
π 2
讨论
1.同一波线上两个不同点的振动相位差
x 2 x
程、2)波函数。
2 y(102 m)
22
o
2
yo
t(s)
2 102 cos(2π t )m
4
A
oA2 y
π
3
t 0,x 0 y A 2 v 0
波函数
y 2 102 cos[2π( t x ) π ]m 44 3
x 0.5m 处质点的振动方程
y 1.0cos(π t π)m
y
y/m
3
1.0
3*
2
4
6.1平面简谐波

5
Oy50.0c 5o21s.(0t[1x)]t(s)
2 0.8 2
例、已知一沿x轴负方向传播的平面简谐波,在
t=1/3s时的波形曲线如图所示,且周期T=2s,(1)
写出O点的振动方程; (2)写出P点的振动方程;
(3)O、P两点间的距离;(4)写出波动方程。
标准形式
T 2 0.04s 50
u50m 0 /s
波函数为 uT 2m 0
例 一平面简谐波沿 Ox轴正方向传播,
已知振幅A1.0m,T 2.0s,λ2.0m. 在 t 0
时坐标原点处的质点在平衡位置沿 Oy 轴正向 运动. 求:(1)波函数;
(2) x0.5m处质点的振动方程.
y(x,t)Aco2 stx y(x,t)A co ts(kx)其中 k2
沿x
轴负方向传播的平面简谐波的表达式
y
u
o
P
x
x
O 点简谐运动方程:
y0A co ts
P 点的运动方程为:
yAcos(tux)
波函数的意义:
OP 0.7m
y(cm)
3
P
1
2
10
P
1 6
O
5
P
60cm
yP 0 .1 co t s /(6 )
u
3
O
2
3
O
yO0.1cots()
x(cm)
y0.1cos(t[x))
0.6
例、一平面简谐波沿x轴正方向传播,波速
为u,振幅为A、角频率为。设t=t0时刻的
y P ( t) A co t t s '
平面简谐波

平面简谐波
平面简谐波是一种由沿着同一方向运动的波源发出的波,可以被描述为振幅在空间内
相等且经过同一时间周期的波形。
这种波形通常由正弦或余弦函数表示,因此也被称为正
弦波或余弦波。
平面简谐波的传播方向通常被称为波矢方向,其振幅通常被称为波矢大小。
当平面简
谐波从波源处发出时,其速度通常已知,并且可以通过波长和频率的关系来计算。
平面简谐波最常见的应用是在电磁波的传播过程中,尤其是在无线通信和雷达系统中。
电磁波可以经过不同的介质(如空气,水和金属)传播,但在这些介质中都遵循平面简谐
波的基本原理。
在无线通信中,发射器会产生一个特定频率的平面简谐波,该波会经由空气传播到接
收器,接收器会接收并处理信号。
这种方式是无线通信的基础,也是电视和电台广播的基
本工作原理。
平面简谐波在其他领域中也很常见。
例如,在音频系统中,声波可以被描述为正弦波。
通过理解平面简谐波的基本原理,我们可以更好地理解波的传播,并使用它来实现各种实
用的应用。
大学物理 平面简谐波

x
一维平面简谐波
y
A
u
振 动 方 O 向
-A
1 2 3 4 5 6 7 8 9 10111213 1415 16 1718192021 22 23
x
一维平面简谐波
y
A
u
振 动 方 O 向
-A
1 2 3 4 5 6 7 8 9 10111213 1415 16 1718192021 22 23
x
一维平面简谐波
y
A
u
振 动 方 O 向
-A
1 2 3 4 5 6 7 8 9 10111213 1415 16 1718192021 22 23
x
一维平面简谐波
y
A
u
振 动 方 O 向
-A
1 2 3 4 5 6 7 8 9 10111213 1415 16 1718192021 22 23
x
波传播的是振动状态(相位)
x
一维平面简谐波
y
A
u
振 动 方 O 向
-A
1 2 3 4 5 6 7 8 9 10111213 1415 16 1718192021 22 23
x
一维平面简谐波
y
A
u
振 动 方 O 向
-A
1 2 3 4 5 6 7 8 9 10111213 1415 16 1718192021 22 23
x
一维平面简谐波
一维平面简谐波
y
A
u
振 动 方 O 向
-A
1 2 3 4 5 6 7 8 9 10111213 1415 16 1718192021 22 23
x
一维平面简谐波
平面简谐波

12.2 平面简谐波简谐波 谐振动在介质中的传播 (介质中各质点作同 频率、同振幅的谐振动)。
平面简谐波 说明 (1) 复杂的波可分解为一系列简谐波; (2) 平面简谐波各处振幅相同。
平面简谐波齐鲁工业大学·2014 1波面为平面的简谐波 。
一、平面简谐波的波函数设 O 点振动方程为 y0 = A cos(ωt + ϕ0 ) yG uPx 经过 Δ t = x / u 时间,O 点振动相位传播到任一点P,所以 P 点振动的相位比 O 点落后Δϕ = ω ⋅ Δt = ωx / uO.xP 点 t 时刻的相位为ωt + ϕ0 − Δϕ = ωt + ϕ0 − ωx u所以 P 点振动方程,亦即波函数为 x y ( x, t ) = A cos[ω (t − ) + ϕ0 ] u齐鲁工业大学·2014 2x y ( x, t ) = A cos[ω (t − ) + ϕ 0 ] u x y ( x, t ) = A cos[2 π(νt − ) + ϕ 0 ]波 函 数 其它形式讨论t x y ( x, t ) = A cos[2 π( − ) + ϕ 0 ] T λ 2π y ( x, t ) = A cos[ (ut − x) + ϕ 0 ]λλ(1) 当x=x0时,y = y (t) 是 x0 处振动方程; (2) 当 t=t0 时,y = y (x) 表示 t0 时刻各个质点的位移。
y t x0 处质点的振动方程齐鲁工业大学·2014y x t0 时刻的波形曲线3x (3) 波函数 y ( x, t ) = A cos[ω (t − ) + ϕ 0 ] y ut1时刻 波形t1+Δt时刻波形t1 时刻,x1 处质点的位移为 x1 y ( x1 , t1 ) = A cos[ω (t1 − ) + ϕ 0 ] uuΔtx1 x2x ut2 (= t1+Δt) 时刻,x2 (= x1+Δx) 处质点的位移为x2 y ( x2 , t 2 ) = A cos[ω (t 2 − ) + ϕ 0 ] u Δx x1 = A cos{ ω [( t1 − ) + ( Δ t − )] + ϕ 0 } u u 若 Δx = uΔt ,则有 y ( x1 , t1 ) = y ( x2 , t 2 ) 。
平面简谐波

dx
dt k
2 / T 2 / T
p
• 波传播过程中,波的等相位面是以速率
p / T 沿波传播方向推进的。
• 对于平面简谐波,波相速等于波速。
三、平面简谐波的波动方程
以最简形式的正向波为例,波函数为:
y( x, t) Acos( t-kx) Acos[(t x )]
u
2 y x 2
y( x, t) Acos( t kx)
(2) 给定 t = t0 时
y( x, t0 ) Acos( t0-kx)
——表示 t0 时刻的波形
y
u
y1
o
x1
t0时刻的波形曲线
x
二、平面简谐波的物理意义
y( x, t) Acos( t kx)
(3) 在 x 与 t 都变化时
y(x x, t t) Acos[(t t k(x x)]
1 u2
2 y t 2
(对正、负向波均成立)
三、平面简谐波的波动方程
一般平面波均可表示为平面简谐波的线性叠加。
y C1 y1 C2 y2
2y 1 2y x2 u2 t 2
平面波方程
意
对坐标x和时间t 的关系满足平面波方程的任 何物理量,必以平面波的形式沿x轴传播,
义 且传播速度为u.
三、平面简谐波的波动方程
u P
x
随堂练习
3、简谐波沿x轴正向传播,频率为=0.5Hz, 波速为u=18ms-1, t=0.5s时刻的波形如图,求 波函数。
y 0.1
x 0.05
y(x,t) Acos(t kx 0)
欢迎网上答疑
(1) 若某物理量(设为 )在三维空间中以平面波形式
北京化工大学 普通物理学 2-2 平面简谐波的波函数

2 – 2 平面简谐波的波函数 波函数
第2章 机械波
y A
O
v u
P
x y = A cos ω (t − ) u
振动方程: 点 O 振动方程:
*
−A
x
λ
x
y o = A cos ω t x = 0 ,ϕ = 0
相位落后法
落后的相位 ∆ 的相位: 点 P 比点 O 落后的相位: ϕ = ϕ p −ϕO
第2章 机械波
波线上各点的简谐运动图
2 – 2 平面简谐波的波函数
第2章 机械波
x t x y = A s[2 π( − ) + ϕ ] u T λ
2、当t 一定时,波函数表示该时刻波线上各 、 一定时, 点相对其平衡位置的位移,即此刻的波形. 点相对其平衡位置的位移,即此刻的波形 波具有空间的周期性) y ( x, t ) = y ( x + λ , t ) (波具有空间的周期性)
2 – 2 平面简谐波的波函数
第2章 机械波
解:方法二(由各物理量的定义解之)。 方法二(由各物理量的定义解之)。 波长是指同一时刻 波长是指同一时刻 点间的距离。 点间的距离。
-1
t
,波线上相位差为 2π 的两
-1 -1
π [(2.50s )t − (0.01cm ) x1 ] −π [(2.50s )t −
y
u
t = t′
x
2 – 2 平面简谐波的波函数
第2章 机械波
解:由波沿 x轴正向传播定出 t = t ′ 时,x=0 轴正向传播定出 处的点将离开平衡位置向y轴负向运动 轴负向运动。 处的点将离开平衡位置向 轴负向运动。 由旋转矢量法可得此时相位为 2 。 y
2019普通物理PPT课件10.2 平面简谐波.ppt

解 根据题意设波源的振动方程为
x y 0.01cos 200 t 0 400
y0 0 v0 0
0.01cos 0 0 0 即 2 2 sin 0 0 x 故 y 0.01cos 200 t 400 2
T
250m s 1
(2)质元的振动速度为 y v 0.02 25 sin 25t 0.1 x m s 1 t 其最大值为 1 vmax 0.02 25 1.57m s (3)将t =1s代入波动方程得 y 0.02 cos 25 0.1 x m y
y x v A sin t t u
1 1 x 2 2 2 2 dEk (dm)v ( dV ) A sin t 2 2 u
质元因变形而具有的势能等于动能
即dE p dEk
质元的总能量为
dE dE p dEk
由图可见t1时刻x1处的振动状态与t1+t 时刻x1+x 处的振动状态完全相同,即相位 相同. x1 x1 x t1 t1 t u u
x u t
t1时刻x1处质元的振动相位在t1+t 时刻 传至x1+x 处,相位的传播速度为u
解(1)设o 点的振动方程为 y A cos t 0
y0 0 A cos 0 0 因为 即 v0 0 A sin 0 0
所以原点o 的振动相位为 0 2 (2)波动方程为 x y A cos t u 2
设在均匀媒质中,垂直于波速的方向的 面积为S ,已知平均能量密度为 w ,则 平均能流密度为
《物理学教学课件》6-2平面简谐波的运动方程

波动传播时,介质中 的各点的振动加速度 是相同的,只是相位 不同。
波动传播时,介质中 的各点的振动速度是 相同的,只是相位不 同。
平面波的应用
电磁波
无线电波、微波、可见光、不可见光(含紫外线和红外线)、X射线和伽马射 线等。
声波
可闻声、次声和超声。
02
平面简谐波的运动方程
BIG DATA EMPOWERS TO CREATE A NEW
通过将波动方程中的波动函数进 行傅里叶变换,得到平面简谐波
的运动方程。
推导过程中涉及到的数学公式和 物理量较多,需要有一定的数学
和物理基础。
平面简谐波的运动方程理解
平面简谐波的运动方程描述了波在空间中的分布和传播规律。
通过求解平面简谐波的运动方程,可以得到波在空间中的分布情况,如波长、振幅、 相位等。
电磁波的应用
电磁波在通信、雷达、导航、天文观测等 领域有着广泛的应用。例如,无线电波可 以用于长距离通信和广播,微波可以用于 卫星通信和雷达测距等。
06
总结与思考
BIG DATA EMPOWERS TO CREATE A NEW
ERA
本章重点回顾
平面波的概念
平面波是波动传播过程中,波 面始终保持平面的波。
思考题
波动方程的求解方法有哪些?如何选择合适的求 解方法?
习题
利用不同的求解方法求解波动方程,并比较结果。
思考题
波的能量传播有何特点?如何理解能流密度和能 流方向的概念?
习题
计算一维平面波的能流密度和能流方向,并分析其物理 意义。
THANKS
感谢观看
平面波的波动方程
描述了波在传播过程中,任意 时刻任意一点的振动位移、速 度和加速度。
§10.2 平面简谐波方程

(波具有空间的周期性)
动画演示
二、平面简谐波方程的物理意义
3 若 x,t 均变化,波函数表示波形沿传播方
向的运动情况(行波).
y
u
t1 时刻
t1 t 时刻
O
x
u/T v/k
x
(k 2 / )
三、平面简谐波方程的多种表示形式
y Acos[ (t
x u
)
0
]
振动方程为: yP Acos(t 0 )
则平面简谐波方程为:
y
A cos[ (t
x
x0 u
)
0 ]
二、平面简谐波方程的物理意义
y
A cos[ (t
x u
)
0 ]
1.如果 x = x0
y
波函数变为
t T
y(x0
,t)
Acos[(t
x0 u
)
0
]
表示x0点的简谐振动规律(独舞)。
x) u
0
]
2 y t 2
A
2
cos[ ( t
x) u
0
]
2 y x 2
2
A u2
cos[ ( t
x u
)
0
]
波动方程:
2 y t 2
u2
2 y x 2
习题类型
1)已知波动方程,求波长、频率、波速。
2)已知某点振动状态,求波函数、某点 的振动方程。
y(x0,t) y(x0,t T ) (波具有时间的周期性)
动画演示
平面简谐波函数
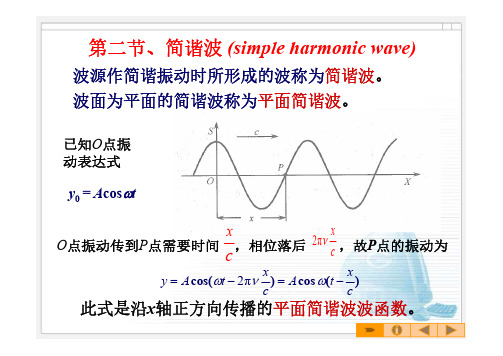
第二节、简谐波(simple harmonic wave)波源作简谐振动时所形成的波称为简谐波。
波面为平面的简谐波称为平面简谐波。
已知O 点振动表达式y 0= A cos tO 点振动传到P 点需要时间,相位落后,故P 点的振动为c xc x π2)(cos )cos(cx t A c x t A y π2此式是沿x 轴正方向传播的平面简谐波波函数。
医学物理学由 、 、T 、 和c 之间关系,,,得平面简谐波函数的另一些形式π2π2 T c Tc y A t T x y A t x y A t kx y A t xcos ()cos ()cos()cos()222 式中称为波数,表示在2 米内所包含的完整波的数目。
π2k医学物理学波函数的物理意义1. 当x 一定时,波函数表示了距原点为x 处的质点在不同时刻的位移。
即x 处质点的振动方程。
2. 当t 一定时,波函数表示了给定时刻Ox 轴上各质点的位移分布情况。
3. 当t 和x 都变化时,波函数表示了所有质点的位移随时间变化的整体情况。
p tTy O 4. x 前的负号表示波沿x 轴正方向传播,称为右行波;若波沿x 轴负方向传播,负号改为正号,即为左行波。
p c x y O x医学物理学一般情况下坐标原点的振动应写为)cos( t A y 0平面简谐波波函数为)π2cos( xt A y医学物理学例1: 以y = 0.040 cos 2.5 t m 的形式作简谐振动的波源,在某种介质中以100 m s -1的速率传播。
(1) 求平面简谐波函数;(2) 求在波源起振后1.0 s 、距波源20 m 处质点的位移、速度和加速度。
解:(1)以波源为原点、传播方向为x 轴正方向,根据题意知:A = 0.040 m , = 2.5 rad s 1,c = 100 m s 1)(cos cxt A y 波函数为m100520400)(.cos .x t y 所以(2) 在x = 20 m 处质点振动表示为y = 0.040 cos 2.5 (t 0.20) m= 0.040 cos (2.5 t 0.50 ) m医学物理学在波源起振后1.0 s 时的位移为y = 0.040 cos 2.0 m = 4.0 10 2 m速度为0s m π0.2sin 040.0π5.2)20.0(π5.2sin d d 1- t A t yv 加速度为2-2-2222s m 5.2s m 0.2cos 040.0)5.2()20.0(5.2cos d d t A t ya 式中负号表示加速度的方向与位移的方向相反。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22
例4:某平面简谐波沿X轴正向传播,t=T/4的波形如图,若振动用余弦
函数表示,写出图中各点处质元的初相值
解:沿波速方向各质元相位依次落后, 由旋转矢量图易于确定
为: φ0= , 振动表达式为 y(0, t ) A cos( t ) Y x u b y o
a b
如: O点处质元 t =0时, y0=-A, v0>0.由旋矢图得其振动初相
Y
u
P
o
X
x
y =y (x, t )
3
已知x0点处质元的谐振动表达式为 y=y(x0,t )=Acos(ωt+φ)
记 任一点 x 处质元的谐振动表达式为
此式即为平面简谐波的表达式, 即 波的运动学方程
GL.普物-力学-Ch.10-波动 2
Y
u
x
P
X
o
③推导(以实例介绍)
y( x 0, t ) A cos( t o )
①位置(或 位移) 波线上 xm 处质元在 t 时刻的位置 (或 xm处质元相对平衡
位置的位移)
y = y(x=xm , t )
例如:某正向平面简谐行波的表式为 2 x ) y( x, t ) A cos( t x ) A cos( t 0 0 u
则波线上 xm处质元 t 时刻的位置(或 相对平衡位置的位移)为
v xm ( t )
d y( x ,t ) dt
x xm
注意:质元的速度为其运动速度,勿与波速 u 混淆
③质元的加速度
波线上 xm 处质元的加速度方程为
a xm (t )
d2 y( x ,t ) dt
2
x xm
d v( x ,t ) dt
x xm
举例说明之
GL.普物-力学-Ch.10-波动 2 9
3.平面简谐波的波形图
时刻 t 一定,波的表式给出了该 t 时刻波线上各点处质元的 位置分布, 称之为该 t 时刻的波形方程 如图, y ~ x 曲线为 t 时刻某平面简谐波波形曲线
Y
O
u
X
t 时刻波形曲线
GL.普物-力学-Ch.10-波动 2
10
波形的传播的图示
Y
O
u
x
x =u t
X
t
t + t
1.建立波动的表达式
①依据
• 直接、间接知任一波线上某个质元的简谐振动方程 • 知波速的信息(显然其为常量)
由此导出平面简谐波的运动学方程—波的表达式
GL.普物-力学-Ch.10-波动 2 2
② 模式
取OXY坐标系: X 轴为横、纵波的波线, 波速沿其正或反向 对横波、纵波质元的振动皆以Y 轴描述
GL.普物-力学-Ch.10-波动 2 13
三维平面简谐波的动力学波动方程为
2 1 r , t 2 r , t 2 2 u t
在OXYZ系下波动方程为
2 1 x, y, z , t 2 x, y, z , t 2 u t2
式中: ψ(x, y, z)为波函数(即 波的表达式)
解(1):作旋矢图,由该图知P点处质元的振动初相为 =
由图可见振动周期为 T= 4s
则有
=2/T= /2
YP
A
则P点处质元的振动表达式为
yP A cos( t ) 2
GL.普物-力学-Ch.10-波动 2
xP
-A
O
t =1 t =0
20
解(2):t 时刻P点处质元的振动表达式为 yP A cos( 2 t ) 波沿负向传播, 前方任意点x处质元 t 时刻的振动,为 P点处 质元(tt )时刻的振动,即: YP t o 1 y ( x , t ) y ( t t )
c
d
x
xa
o xd x0
xc
t =0 t =T/4
该波表达式为 y( x , t ) A cos( t (2 x ) ) t =0时的旋矢图 则图中各点处质元的初相为
0
a 2 b 0 c 2 d
23
GL.普物-力学-Ch.10-波动 2
可见波形的传播的情况
也可见波线上一系列质元的位移情况
GL.普物-力学-Ch.10-波动 2
11
4. 波程差、相位差
如图,波程差为
Δx x 2 x1
Δx
与之相应的相位差为 2
该式也是波程差与相位差的关系式
Y
O
u
x1
X
u
x2 x2 x1
Y
O
X
GL.普物-力学-Ch.10-波动 2
解(2): 将 t =1.0(s)代入 ①式,则得此时刻的波形方程为 1.0 x y( x ) 1.0cos[2 ( ) ] 1.0cos( x )
2.0 4.0 2 2 2
y( x ) 1.0sin
2
x ②
由②式可画出 t = 1.0(s)时刻的波形如下图所示:
或解:由波的表达式确定各振动初相
由图知O点处质元 t =0时, y0=-A, v0>0. 则其振动初相为 φ0=, • O点处质元振动表式为 y(0, t ) A cos( t ) u
Δ PO=2
GL.普物-力学-Ch.10-波动 2
xO xP
0
xP xO 10m
15
作旋矢图,由该图可见:
2 Δ PO 6 2 3 xP xO Δ PO 2 2 10 2 3
则该平面简谐波的波长为
O点
1 2
Y
3
O
6
12
5.平面简谐波的动力学方程—波动方程
(即 微分方程形式)
y 1 y 2 2 2 x u t
2 2
x 例如由波的表达式 y A cos [ ( t ) ] u 2 2 y x 2 A 2 cos [ ( t ) ] u u x 有 2 y A 2 cos [ ( t x ) ] 2 u t 则得出上述微分方程形式的波动方程
p
x d d x t ( x ) 0 u u
则波的表达式为
x
x
Y
u d X
P
o
dx y( x , t ) A cos[ ( t )] 2 u 或 y( x , t ) A cos[ t ] 2
GL.普物-力学-Ch.10-波动 2 21
u
x 0 ) A cos( t
x 0 )
2 • 式中
k k 称为 “(角)波数”, 为2π 弧度内的波形数
• 其他情形下平面简谐波表式的推导,与以上两例的方法类同 要熟练掌握平面简谐波表式的推导方法
GL.普物-力学-Ch.10-波动 2 7
2.质元的位置(或 位移)、速度和加速度
t x 解(1):取波的表达式为 y A cos[2 ( ) ] T
式中, 为坐标原点处质元振动初相,由所给的初态知
2
则该正向平面简谐波表达式为
t x y A cos[2 ( ) ] ① T 2
GL.普物-力学-Ch.10-波动 2 17
(i)知波速u沿X轴正向; 原点O处质元振动表达式为 P点比O点处质元振动落后的时间间隔Δt 为 x t ( x ) 0 u P点比O点处质元振动落后的相位为
x ( x ) t u
GL.普物-力学-Ch.10-波动 2 4
可见:在 t+ Δt 时刻,P点处质元与t 时刻O点质元振动状态相同 在 t 时刻,P点处质元与tΔt 时刻O点质元振动状态相同
结论:可用tΔt 时刻O点处质元振动方程 y(0, tΔt ),作为
P点处质元 t 时刻的振动方程,即为波表式 y(x, t )
即
y(x, t)= y(0, tΔt )
式中
Δt(x)=x/u >0
y( x, t ) y(0, t t ) A cos (t t ) o
§10-2.平面简谐波
行波(traveling waves): 波形以波速沿波线行进的波 简谐波 :简谐振动的传播形成的行波(介质均匀、无吸收、
足够大. 波源及介质各质元以一定的时间差重复 波源的简谐振动)
平面(球、柱面)简谐波
波面是平面(球、柱面)的简谐波 (显然,平面简谐波是一维简谐波) 一般形式的波,大都可分解为一系列简谐波;
P点比O点处质元振动落后的Δt 为
x t ( x ) 0 u u x
P
u
x x x 0
Y
o
X
则此负向平面简谐行波的表达式为
y( x , t ) y(0, t t ) A cos (t t ) 0
2 y( x , t ) A cos( t x 0 ) A cos( t x 0 ) u
P点
=30(m)
GL.普物-力学-Ch.10-波动 2 16
例2:某平面简谐波沿X轴正向传播,已知 A=1.0(m), T = 2.0(s),
= 4.0(m). t =0 时坐标原点处质元在平衡位置,沿 Y 轴正向
运动. 求:(1) 波的表达式; (2) t= 1.0s 时波形方程,并画出 波形图; (3) x = 1.0(m)处质元振动表达式,并画出振动图线
u 为波速
2 2 2 2 x, y, z + + 2 2 x y z2
