【100所名校】2018届宁夏银川唐徕回民中学高三下学期第四次模拟考文科综合地理试题(解析版)
宁夏银川唐徕回民中学高三下学期第四次模拟考文科综合历史试题
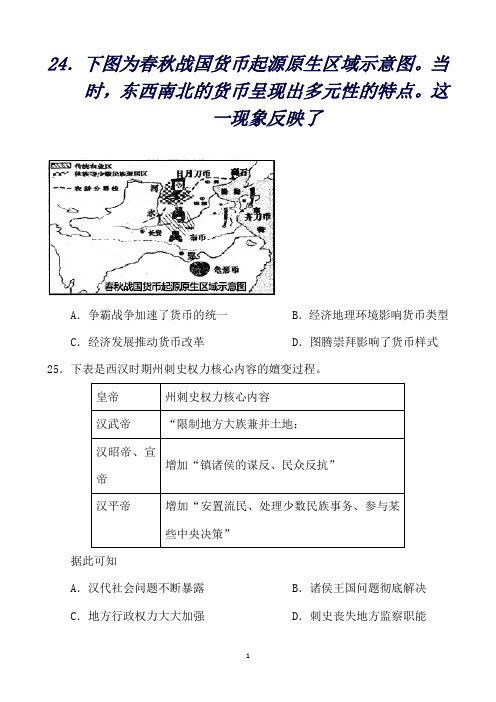
24.下图为春秋战国货币起源原生区域示意图。
当时,东西南北的货币呈现出多元性的特点。
这一现象反映了A.争霸战争加速了货币的统一 B.经济地理环境影响货币类型C.经济发展推动货币改革 D.图腾崇拜影响了货币样式25.下表是西汉时期州刺史权力核心内容的嬗变过程。
据此可知A.汉代社会问题不断暴露B.诸侯王国问题彻底解决C.地方行政权力大大加强D.刺史丧失地方监察职能26. 1904年,中国科举史上进行最后一科会试:第一场考中国治史论五篇,体现出注重现实、着眼改革的思想:第二场考各国政治艺学策五道,关于当时内政外交的重要问题:第三场考《四书》《五经》义,这次考试A. 折射了中国近代化的艰难努力B. 客观上为辛亥革命奠定了人才基础C. 标志着清末新政上升到新阶段D. 体现了中国教育的半殖民地特点27.由于这场战争,江、浙及赣、皖、鲁一带官绅商贾为避兵燹,竞相逃往上海,上海的外国人和中国富商把值钱的东西放在船上随时逃跑,英法租界的洋人组建防御工事和巡逻队保护自身的安全。
这场“战争”指的是A.太平天国运动B.义和团运动C.北伐战争 D.淞沪会战28.从下表曹操历史形象描述的变化可以得出A.史家不可能客观描述历史事实B.史家身份立场会影响历史书写C.史家调查考证难以揭示历史真相D.史家观念变化较少影响历史书写29.抗日战争期间,《大公报》在报导某次战役时写道:“(1938)年3月31日午,敌虽鼓其余勇,但已无能为力,并逐渐坠入我大规模歼灭战之圈套中,鲁南伟大之歼灭战场面已揭开序幕,精彩节目,自当陆续其后也”。
据此判断,当时《大公报》报导的这次战役应是A.淞沪会战 B.平型关大捷C.台儿庄战役 D.百团大战30.下图反映了新中国某一时期连续十年国内工农业生产总值的变化情况。
对图中“C—D”阶段经济发展状况分析正确的是A.“大跃进”运动促使农业产值提升B.国民经济调整的任务已经基本完成C.国企改革推动了轻重工业比例协调D.家庭联产承包责任制取得明显成效31.下图为1949—2013年《人民日报》有关“对外援助”报道中的援助事由统计,由此可见,20世纪80年代对外援助A.带有明显的不结盟色彩B.由政治导向为主转向多元需求C.被报道的数量日趋减少D.以援助亚非拉革命为主要目标32.罗马法学家盖尤斯认为交易“不需要任何特殊语言或文字,只需要实施交易行为的人们相互同意”,但如果交易物有缺陷则必须宣明,否则购买者可以取消买卖。
2018届宁夏银川唐徕回民中学高三下学期第四次模拟考文科综合历史试题(解析版)

2018届宁夏银川唐徕回民中学高三下学期第四次模拟考文科综合历史试题(解析版)1. 下图为春秋战国货币起源原生区域示意图。
当时,东西南北的货币呈现出多元性的特点。
这一现象反映了A. 争霸战争加速了货币的统一B. 经济地理环境影响货币类型C. 经济发展推动货币改革D. 图腾崇拜影响了货币样式【答案】B【解析】材料表明春秋战国时期,各诸侯国纷纷铸造自己的货币,货币形式多样,北部农业发达,货币形式与农业生产密切相关;东南部地区手工业发达,货币形式与手工业紧密联系,由此可知,B符合题意;材料没有涉及货币统一,A不正确;材料没有涉及货币改革,C不正确;材料没有涉及图腾崇拜,D不正确。
2. 下表是西汉时期州刺史权力核心内容的嬗变过程。
据此可知A. 汉代社会问题不断暴露B. 诸侯王国问题彻底解决C. 地方行政权力大大加强D. 刺史丧失地方监察职能【答案】A【解析】根据材料可知,刺史权力由督察郡国到“镇压诸侯的谋反、民众反抗” “安置流民、处理少数民族事务、参与某些中央决策”,表明汉代社会问题不断暴露,刺史的权力不断扩大,A正确;B材料信息无法体现,排除;材料反映的是刺史权力的不断扩大,无法体现地方行政权力大大加强,排除C;材料反映的是刺史的权力在监察郡国的基础上不断增加权力,D错误。
3. 1904年,中国科举史上进行最后一科会试:第一场考中国治史论五篇,体现出注重现实、着眼改革的思想:第二场考各国政治艺学策五道,关于当时内政外交的重要问题:第三场考《四书》《五经》义,这次考试A. 折射了中国近代化的艰难努力 B. 客观上为辛亥革命奠定了人才基础C. 标志着清末新政上升到新阶段D. 体现了中国教育的半殖民地特点【答案】A【解析】材料“体现出注重现实、着眼改革的思想”“考各国政治艺学策五道,关于当时内政外交的重要问题”可以看出涉及到一些关注现实的问题,结合所学,1901年《辛丑条约》签订,中国完全沦为半殖民地半封建社会,清朝统治危机日益加深,1904年科举考试的内容表明清朝仍在为近代化艰难努力,A正确;1904年科举考试的内容涉及到关注现实,着眼改革,有利于引导更多的知识分子关注社会现实问题,但辛亥革命的人才主要不是来源于科举考试,B错误;材料无法体现1904年科举考试标志着清末新政上升到新阶段,排除C;材料表明科举考试关注现实和传统儒学,和半殖民地无关,D错误。
苏联的社会主义建设和经济全球化趋势

苏俄苏联全球趋势1.(2018年全国Ⅲ卷文综历史12)12. 1959年,苏共二十一大讨论通过了七年经济计划,规定7年内工业生产总值提高80%,其中发电量、钢铁产量都要求成倍增长。
这反映出七年经济计划A. 未能摆脱斯大林模式B. 是应对马歇尔计划的举措C. 是新经济政策的延续D. 加强了国家对经济的控制【答案】A2.(2018年江苏单科历史18)18. 1957年,苏联进行工业体制改革,撤销汽车工业部、机器制造部等7个全联盟部,保留了航空工业部、无线电工业部等6个全联盟部,在地方设立了105个经济行政区,把被撤的全联盟部所管辖的企业移交给相应的经济行政区。
上述举措的主要意图是A. 从根本上突破斯大林模式B. 摒弃优先发展重工业的政策C. 适度扩大地方经济自主权D. 削弱公有制经济的主导地位【答案】C3.(内蒙古赤峰二中2018届高三最后一模文科综合历史试题)学者钱乘旦认为,“现代化”是一个中性概念……现代化的执行方式可以姓“资”,也可以姓“社”,甚至出现更复杂的属性。
下列不能体现“现代化复杂属性”的是A. 苏俄新经济政策B. 苏联斯大林模式C. 美国罗斯福新政D. 中国的改革开放【答案】B4.(宁夏银川一中2018届高三第四次模拟考试文科综合历史试卷)苏联国民生产总值(GNP)在1928年至1952年间增加了3.5倍,这一发展速度超过了同一时期其它任何国家。
苏联在全球工业总产量中所占的份额从1921年的1.5%增长到了1939年的10%。
上述变化的主要原因是A. 新经济政策活跃了市场经济和自由贸易B. 斯大林体制利于集中人力物力发展生产C. 集体农庄大大提高了农民的生产积极性D. 工业化方针提出使国家优先发展重工业【答案】B5.(黑龙江省哈尔滨师范大学附属中学2018届高三第四次模拟考试文综历史试题)20世纪30年代的苏联私人土地只占耕地总面积的3%-5%,却生产了25%-30%的苏联农产品。
这反映出当时的苏联A. 鼓励私人农场发展B. 集体农庄生产效率较低C. 忽视农业重视工业D. 受到全球经济危机影响【答案】B6.(宁夏银川唐徕回民中学2018届高三下学期第四次模拟考文科综合历史试题)苏联作家爱伦堡在《解冻》(1954年发行)里中写到:“窗外是一片激动人心的情景。
(解析版)宁夏银川市唐徕回民中学2018届高三下学期第四次模拟考数学(理)试题

银川唐徕回民中学2017~2018学年度第二学期高三年级第四次模拟考试数学试卷(理科)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合,则A. [-2,-1]B. [-1,2)C. [-1,1]D. [1,2)【答案】A【解析】分析:化简集合,利用数轴法计算可得.详解:因为,所以:故选A.点睛:集合是每年高考的必考题,属于得分题,一般以小题的形式出现,解题时应注意区别符号,避免混淆出错..2. 设复数,则下列命题中错误的是A. B.C.在复平面上对应的点在第一象限D.的虚部为【答案】D【解析】分析:将复数化简整理得,依次验证A、B、C、D四个选项,可知D错误.详解:,知复数的虚部为1,故选D.点睛:复数问题是高考数学中的常考题型,属于得分题,解题思路通常是通过解方程或者化简等方式将复数整理成的形式,再进行复数的分类、复数的几何意义、复数的模、共轭复数等相关问题的求解.3. 等差数列前项和为,若,是方程的两根,则()A. B. C. D.【答案】C 【解析】【详解】分析:由根与系数关系可得,由等差数列性质可求得,根据等差数列的性质,即可求出结果.详解:由根与系数关系可得,由等差数列性质可求得,根据等差数列的性质.故选C.点睛:本题考查根与系数关系与等差数列的中项性质,当数列为等差数列,利用跟与系数关系中和的关系,当数列为等比数列时,利用根的乘法关系. 4. 已知两个单位向量和夹角为,则向量在向量方向上的投影为( )A.B. C.D.【答案】D 【解析】【详解】分析:由投影公式列出式子,结合两个向量的模、夹角与乘积,即可求出结果. 详解:,则向量在向量方向上的投影为:.故选D.点睛:本题考查投影公式以及向量的数量积和单位向量,注意题目中隐含的单位向量的模为1,同时由于角度与长度都为特殊值,所以本题也可以使用坐标的方式解.5. 我国古代数学著作《九章算术》中,其意是:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问:米几何?右图是源于其思想的一个程序框图,若输出的(单位:升),则输入的值为A. 6B. 7C. 8D. 9【答案】C【解析】分析:执行程序框图,得到输出值,令,可得. 详解:阅读程序框图,初始化数值,循环结果执行如下:第一次:成立,;第二次:成立,;第三次:成立,;第四次:不成立,输出,解得.故选C.点睛:解决循环结构程序框图问题的核心在于:第一,要确定是利用当型还是直到型循环结构;第二,要准确表示累计变量;第三,要注意从哪一步开始循环,弄清进入或终止的循环条件、循环次数.6. 已知实数满足则的取值范围是()A. B. C. D.【答案】D【解析】【详解】分析:的意义为可行域内的点与原点的距离,画出可行域,根据几何图像中的距离,结合点到直线的距离公式,即可求出范围.详解:根据题意作出可行域:此区域为开放区域,所以距离可以无限大,由图像可知最近距离为原点到直线的距离,所以由点到直线距离公式可得:最短距离.故选D.点睛:本题考查线性规划中的非线性目标函数,要与几何公式相结合,用几何意义求解,常见的非线性目标函数由距离型,斜率型以及距离平方型.7. 一个棱锥的三视图如图(单位:),则该棱锥的表面积是()A. B.C. D.【答案】A【解析】【详解】分析:由三视图可知该棱锥侧面为两个全等的等腰三角形和一个与另外两个不同的等腰三角形,底面与俯视图轮廓相同.由三视图的边长可得各条棱长,通过棱长求面积即可. 详解:由三视图可将该几何体还原,如图所示为其某方向上的直观图.由三视图的边长,该几何体可分为如下四个三角形:由勾股定理等性质计算得:,,所以四个面的面积分别为2、2、、,所以表面积为,故选A.点睛:三视图题型需将三视图还原,注意各个面之间的位置关系,一般边长要通过勾股定理以及三角形的性质求得,必要时可将立体图形放至长方体中切割得到.8. 的三个内角分别为,,,则“”是“,,成等差数列”的()A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】C【解析】【详解】分析:由三角形内角和,可列出A、B、C三个角的关系,进而由等差中项的知识判断为等差数列.详解:由,则,所以A、B、C成等差数列,为充分条件,由A、B、C成等差数列,所以,由内角和公式可得,为必要条件.故选C.点睛:本题考查充分必要条件,与三角形内角和以及等差数列的性质结合,根据题意列式即可.9. 已知甲、乙、丙三人中,一人是军人,一人是工人,一人是农民.若乙的年龄比农民的年龄大;丙的年龄和工人的年龄不同;工人的年龄比甲的年龄小,则下列判断正确的是A. 甲是军人,乙是工人,丙是农民 B. 甲是农民,乙是军人,丙是工人C. 甲是农民,乙是工人,丙是军人D. 甲是工人,乙是农民,丙是军人【答案】A【解析】丙的年龄和工人的年龄不同;工人的年龄比甲的年龄小,则甲丙均不是工人,故乙是工人;乙的年龄比农民的年龄大,即工人的年龄比农民的年龄大,而工人的年龄比甲的年龄小,故甲不是农民,则丙是农民;最后可确定甲是军人.本题选择A选项.10. 有名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙、丙两位同学不能相邻,则不同的站法有()A. 种B. 种C. 种D. 种【答案】B【解析】首先将甲排在中间,乙、丙两位同学不能相邻,则两人必须站在甲的两侧,选出一人排在左侧,有:种方法,另外一人排在右侧,有种方法,余下两人排在余下的两个空,有种方法,综上可得:不同的站法有种.本题选择B选项.11. 已知函数.将的图象向左平移个单位长度后所得的函数为偶函数,则关于函数,下列命题正确的是()A. 函数在区间上有最小值B. 函数在区间上单调递增C. 函数的一条对称轴为D. 函数的一个对称点为【答案】B【解析】【详解】分析:求出函数平移后的解析式,由偶函数的性质求出参数,判断最值、单调区间、对称轴、对称中心时需将结论代入原函数,根据的图像与性质判断正确与否. 详解:由题意知平移后的解析式为:,因为此函数为偶函数,所以y轴为其对称轴之一,所以将代入可得,解得:,由的取值范围可得,所以原解析式为,A选项,将区间代入函数,可得,根据图像可知无最值,B选项,将区间代入函数,可得,根据图像知函数单调递增,C选项,将代入函数,可得,所以应为对称中心的横坐标,D选项,将代入函数,可得,所以应为对称轴与x轴交点.故选B.点睛:本题综合考查函数图像的变换以及对称轴、对称中心、单调区间、最值等知识点,需要明确解题思路,注意结合图像解题,会更容易理解.12. 已知抛物线()与双曲线(,)有相同的焦点,点是两条曲线的一个交点,且轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是()A. B. C. D.【答案】B【解析】【详解】分析:因为抛物线与双曲线有相同的焦点,所以可得p与c之间的关系,因为轴,则点A的坐标可以由抛物线求出,将其代入双曲线方程,再由a、b、c之间的关系,可求出离心率,由离心率公式可得,即斜率的值,由斜率求出倾斜角的范围.详解:因为抛物线与双曲线焦点相同,所以,因为与x轴垂直,所以可求得点A的坐标为,将其代入双曲线方程可得:,因为,代入上式可得:,化简得:,两边同时除以得:,解得或(舍),设渐近线斜率为k,由,解得,所以倾斜角应大于,所以区间可能是,故选B.点睛:本题主要考查抛物线与双曲线的几何性质,由焦点与公共点建立系数之间的联系,渐近线斜率与离心率有关,所以由系数求出离心率并求得斜率,与特殊倾斜角的斜率作对比,求出倾斜角取值范围.二、填空题:本题共4小题,每小题5分,共20分.13. 计算定积分__________.【答案】ln2【解析】由题意结合微积分基本定理可得:.故答案为:.14. 在的展开式中,含项的系数为,则实数的值为______.【答案】-1【解析】【详解】分析:由二项展开式求出该项的表达式,根据系数为-10,即可求出结果.详解:由二项展开式公式可知项为,所以,解得.点睛:本题考查二项式定理,熟练掌握公式,求值即可,要注意区分二项式系数与某项系数的区别.15. 已知向量的夹角为,,,则=_______.【答案】【解析】分析:欲求的值,可先求的值,展开代入可得.详解:由已知,,点睛:本题的核心是通过利用已知向量(向量的坐标、模、夹角)来线性表示求的值,再间接求,本题的易错点在于忘记将的值开平方.16. 已知函数,若方程有两个解,则实数的取值范围是______.【答案】【解析】【详解】分析:由分段函数的分段区间进行分类讨论,当时,易解得只有一个解,则当时也只有一个零点,根据二次函数性质,求出只有一个零点时参数的取值范围.详解:当时,令,解得,所以只有一个解,则时,只有一个解,令,即在时,只有一个解,即函数在此区间内只有一个零点.因为函数对称轴为,且图像开口朝上,所以时函数单调递减,所以根据函数性质,当时,函数值小于0,即,解得:.点睛:本题考查函数零点与方程的解,要熟练掌握零点与解得关系,以及二次函数的有关性质,二次函数中求根的情况要综合考虑对称轴以及单调性,所以简单示意图对解题有非常大的帮助.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17. 已知函数的一个零点是.(1)求实数的值;(2)设,若,求的值域.【答案】(1)a=1;(2).【解析】【详解】分析:(1)令即可求得结果;(2)将原解析式代入,结合二倍角公式、辅助角公式等求得,将x的范围带入解析式,结合三角函数图像的性质即可求出值域.详解:(Ⅰ)解:依题意,得即……3分解得.(Ⅱ)解:由(Ⅰ)得.…8分.由得当即时,取得最大值2,当即时,取得最小值-1.所以的值域是点睛:本题主要考查三角恒等变形及求值域问题,要熟练掌握倍角公式以及辅助角公式,学会通过结合图像,数形结合的方式解题.18. 如图,在四棱锥中,四边形为正方形,平面,,是上一点,且.(1)求证:平面;(2)求直线与平面所成角的正弦值.【答案】(1)见解析;(2).【解析】试题分析:(1)连接,由线面垂直的性质定理可得,且,故平面,,又,利用线面垂直的判断定理可得平面.(2)法1:由(1)知平面,即是直线与平面所成角,设,则,,,结合几何关系计算可得,即直线与平面所成角的正弦值为.法2:取为原点,直线,,分别为,,轴,建立坐标系,不妨设,结合(1)的结论可得平面得法向量,而,据此计算可得直线与平面所成角的正弦值为.试题解析:(1)连接,由平面,平面得,又,,∴平面,得,又,,∴平面.(2)法1:由(1)知平面,即是直线与平面所成角,易证,而,不妨设,则,,,在中,由射影定理得,可得,所以,故直线与平面所成角的正弦值为.法2:取为原点,直线,,分别为,,轴,建立坐标系,不妨设,则,,,由(1)知平面得法向量,而,∴.故直线与平面所成角的正弦值为.19. 针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:岁以下岁以上(含岁)(1)在所有参与调查的人中,用分层抽样的方法抽取个人,已知从持“不支持”态度的人中抽取了人,求的值;(2)在持“不支持”态度的人中,用分层抽样的方法抽取人看成一个总体,从这人中任意选取人,求岁以下人数的分布列和期望;(3)在接受调查的人中,有人给这项活动打出的分数如下:,,,,,,,,,,把这个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过概率.【答案】(1)120;(2)见解析;(3).【解析】试题分析:(1)由题意可知参与调查的总人数为,结合分层抽样的概念计算可得.(2)由题意可知抽取的人中,岁以下与岁以上人数分别为人,人,则,计算相应的概率值有,,,,据此可得分布列,计算相应的期望为.(3)总体的平均数为,则与总体平均数之差的绝对值超过的数有,,,由古典概型计算公式可得满足题意的概率值为.试题解析:(1)参与调查的总人数为,其中从持“不支持”态度的人数中抽取了人,所以.(2)在持“不支持”态度的人中,岁以下及岁以上人数之比为,因此抽取的人中,岁以下与岁以上人数分别为人,人,,,,,,.(3)总体的平均数为,那么与总体平均数之差的绝对值超过的数有,,,所以任取个数与总体平均数之差的绝对值超过的概率为.20. 椭圆的离心率为,其右焦点到椭圆外一点的距离为,不过原点....的直线与椭圆相交于,两点,且线段的长度为.(1)求椭圆C的方程;(2)求面积的最大值.【答案】(1);(2).【解析】【详解】分析:(1)由离心率、两点间距离公式、椭圆系数关系可列方程组,即可求得结果;(2)设直线的方程,与椭圆方程联立,求得弦长,再求出原点到直线的距离,根据三角形求面积的方法求得面积表达式,由二次函数性质可得三角形面积的最大值.详解:(Ⅰ)设椭圆右焦点为,则由题意得得或(舍去)所以椭圆方程为.(Ⅱ):因为线段的长等于椭圆短轴的长,要使三点能构成三角形,直线不过原...点.,则弦不能与轴垂直,故可设直线的方程为(),由消去,并整理,得.设,,又,所以,因为,所以,即所以,即,因为,所以.又点到直线的距离,因为,所以所以,即的最大值为.点睛:本题主要考查直线与椭圆关系,掌握基本的解题套路,会用弦长公式及韦达定理,会根据解析式求最值,设直线方程时注意直线的限定条件.21. 设函数,(为常数),.曲线在点处的切线与轴平行(1)求的值;(2)求的单调区间和最小值;(3)若对任意恒成立,求实数的取值范围.【答案】(1)k=1;(2)的单调递减区间为,单调递增区间为,最小值为;(3).【解析】【详解】分析:(1)由曲线切线斜率的性质,令,即可求出k值;(2)给函数求导,球池导函数零点,根据单调性判断的方法,结合定义域,求出单调区间,根据单调性,求出最值;(3)问题为恒成立问题,所以要取最小值,即取最大值时成立即可.详解:(Ⅰ),因为曲线在点处的切线与轴平行,所以,所以.(Ⅱ),定义域为令得,当变化时,和的变化如下表由上表可知的单调递减区间为,单调递增区间为,最小值为。
宁夏银川市唐徕回民中学2017-2018学年高考数学四模试卷(文科) Word版含解析

宁夏银川市唐徕回民中学2017-2018学年高考数学四模试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={﹣1,0,1,2,3},B={x|x2﹣2x>0},则A∩B=( )A.{3} B.{2,3} C.{﹣1,3} D.{0,1,2}2.若复数(α∈R,i为虚数单位)是纯虚数,则实数α的值为( )A.﹣6 B.﹣4 C.4 D.63.“∃x∈R,x2﹣2x+1<0”的否定是( )A.∃x∈R,x2﹣2x+1≥0 B.∃x∈R,x2﹣2x+1>0C.∀x∈R,x2﹣2x+1≥0 D.∀x∈R,x2﹣2x+1<04.某几何体的三视图如图所示,图中三个正方形的边长均为2,则该几何体的体积为( )A.B.8﹣2πC.πD.8﹣π5.已知双曲线(a>0)的离心率为,则a的值为( ) A.B.C.D.6.如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )A.85,84 B.84,85 C.86,84 D.84,867.如图给出的是计算的值的程序框图,其中判断框内应填入的是( )A.i≤2013 B.i≤2015 C.i≤2017 D.i≤20198.设2a=5b=m,且,则m=( )A.B.10 C.20 D.1009.已知函数f(x)=asinωxcosωx+cos2ωx(a>0,ω>0)的最小正周期为,最小值为﹣,将函数f(x)的图象向左平移φ(φ>0)个单位后,得到的函数图象的一条对称轴为x=,则φ的值不可能为( )A.B.C.D.10.如图过拋物线y2=2px(p>0)的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则拋物线的方程为( )A.y2=x B.y2=3x C.y2=x D.y2=9x11.已知a>0,x,y满足约束条件,若z=2x+y的最小值为1,则a=( )A.B.C.1 D.212.设x1,x2分别是方程xa x=1和xlog a x=1的根(其中a>1),则x1+2x2的取值范围( ) A.(2,+∞)B.表示不超过x的最大整数,观察下列等式:.按照此规律第n个等式的等号右边的结果为__________.三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.17.已知数列{a n}的前n项和为S n=n2(Ⅰ)求通项公式a n;(Ⅱ)令b n=a2n+3求{b n的前n项和T n.18.如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE.19.某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.(Ⅰ)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;(Ⅱ)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.20.椭圆C:+=1(a>b>0)的离心率为,其左焦点到点P(2,1)的距离为.(Ⅰ)求椭圆C的标准方程;(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.21.已知函数f(x)=e x﹣ax﹣1(a>0,e为自然对数的底数)(1)求函数f(x)的最小值;(2)若f(x)≥0对任意的x∈R恒成立,求实数a的值;(3)在(2)的条件下,证明:1+++…+>ln(n+1)(n∈N*)请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题记分.作答时请在答题卡涂上题号.选修4-1:几何证明选讲22.如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.(Ⅰ)求证:AD∥OC;(Ⅱ)若圆O的半径为2,求AD•OC的值.选修4-4:坐标系与参数方程23.在直角坐标系xOy中,圆C的参数方程为(θ为参数).(1)以原点为极点、x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;(2)已知A(﹣2,0),B(0,2),圆C上任意一点M(x,y),求△ABM面积的最大值.选修4-5:不等式选讲24.已知函数f(x)=k﹣|x﹣3|,k∈R,且f(x+3)≥0的解集为.(Ⅰ)求k的值;(Ⅱ)若a、b、c是正实数,且,求证:.宁夏银川市唐徕回民中学2015届高考数学四模试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={﹣1,0,1,2,3},B={x|x2﹣2x>0},则A∩B=( )A.{3} B.{2,3} C.{﹣1,3} D.{0,1,2}考点:交集及其运算.专题:集合.分析:求出B中不等式的解集确定出B,找出A与B的交集即可.解答:解:由B中不等式变形得:x(x﹣2)>0,解得:x<0或x>2,即B={x|x<0或x>2},∵A={﹣1,0,1,2,3},∴A∩B={﹣1,3},故选:C.点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.若复数(α∈R,i为虚数单位)是纯虚数,则实数α的值为( )A.﹣6 B.﹣4 C.4 D.6考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:把已知复数利用复数代数形式的乘除运算化简,然后由实部等于0且虚部不等于0求得a的值.解答:解:∵=为纯虚数,∴,解得:a=﹣6.故选:A.点评:本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.3.“∃x∈R,x2﹣2x+1<0”的否定是( )A.∃x∈R,x2﹣2x+1≥0 B.∃x∈R,x2﹣2x+1>0C.∀x∈R,x2﹣2x+1≥0 D.∀x∈R,x2﹣2x+1<0考点:的否定.专题:常规题型.分析:对于含有量词的的否定,要对量词和结论同时进行否定,“∃”的否定为“∀”,“<”的否定为“≥”即可求解解答:解解:∵“存在性”的否定一定是“全称”∴“∃x∈R,x2﹣2x+1<0”的否定是∀x∈R,x2﹣2x+1≥0故选C.点评:本题考查了含有量词的的否定,要注意对量词和结论同时进行否定,属于基础题.4.某几何体的三视图如图所示,图中三个正方形的边长均为2,则该几何体的体积为( )A.B.8﹣2πC.πD.8﹣π考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:根据三视图可判断正方体的内部挖空了一个圆锥,该几何体的体积为23﹣×π×12×2运用体积计算即可.解答:解:∵几何体的三视图可得出:三个正方形的边长均为2,∴正方体的内部挖空了一个圆锥,∴该几何体的体积为23﹣×π×12×2=8,故选:D点评:本题考查了空间几何体的三视图,运用求解几何体的体积问题,关键是求解几何体的有关的线段长度.5.已知双曲线(a>0)的离心率为,则a的值为( )A.B.C.D.考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:直接利用双曲线求出半焦距,利用离心率求出a即可.解答:解:双曲线,可得c=1,双曲线的离心率为:,∴,解得a=.故选:B.点评:本题考查双曲线的离心率的求法,双曲线的简单性质的应用.6.如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )A.85,84 B.84,85 C.86,84 D.84,86考点:茎叶图.专题:概率与统计.分析:根据所给的茎叶图,看出七个数据,根据分数处理方法,去掉一个最高分93和一个最低分79后,把剩下的五个数字求出平均数和众数.解答:解:由茎叶图知,去掉一个最高分93和一个最低分79后,所剩数据84,84,86,84,87的平均数为(84+84+86+84+87)=85;众数为:84.故选:A.点评:本题主要考查茎叶图的有关知识,茎叶图、平均数和方差属于统计部分的基础知识,也是2015届高考的新增内容,考生应引起足够的重视,确保稳拿这部分的分数.7.如图给出的是计算的值的程序框图,其中判断框内应填入的是( )A.i≤2013 B.i≤2015 C.i≤2017 D.i≤2019考点:程序框图.专题:算法和程序框图.分析:根据流程图写出每次循环i,S的值,和,比较即可确定退出循环的条件,得到答案.解答:第1次循环:i=2,S=;第2次循环:i=4,S=;第3次循环:i=6,S=;…第1007次循环:i=2014,S=;此时,设置条件退出循环,输出S的值.由程序知道,i=2,4,6,…2014都应该满足条件,i=2016不满足条件,故判断框内可填入i≤2015.故选:B.点评:本题主要考察程序框图和算法,属于基本知识的考查.8.设2a=5b=m,且,则m=( )A.B.10 C.20 D.100考点:指数式与对数式的互化;对数的运算性质.专题:计算题;压轴题.分析:直接化简,用m代替方程中的a、b,然后求解即可.解答:解:,∴m2=10,又∵m>0,∴.故选A点评:本题考查指数式和对数式的互化,对数的运算性质,是基础题.9.已知函数f(x)=asinωxcosωx+cos2ωx(a>0,ω>0)的最小正周期为,最小值为﹣,将函数f(x)的图象向左平移φ(φ>0)个单位后,得到的函数图象的一条对称轴为x=,则φ的值不可能为( )A.B.C.D.考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:利用二倍角的正弦和余弦化简,由已知求得a的值,然后由平移后函数图象的对称轴为x=得到φ的值,则答案可求.解答:解:f(x)=asinωxcosωx+cos2ωx=ωx2ωx.=sin(2ωx+φ)+.依题意可得:,∴a2+3=12,∵a>0,∴a=3.故f(x)=2ωx+cosωx+=.故=,∴ω=2.即f(x)=,将函数f(x)的图象向左平移φ(φ>0)个单位后,得到的函数图象的一条对称轴为x=,即4(+φ)+=k,即φ=.∴φ的值不可能为.故选:B.点评:本题考查了函数y=Asin(ωx+φ)的图象和性质,考查了函数图象的平移,是中档题.10.如图过拋物线y2=2px(p>0)的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则拋物线的方程为( )A.y2=x B.y2=3x C.y2=x D.y2=9x考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,根据抛物线定义可知|BD|=a,进而推断出∠BCD的值,在直角三角形中求得a,进而根据BD∥FG,利用比例线段的性质可求得p,则抛物线方程可得.解答:解:如图分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,则由已知得:|BC|=2a,由定义得:|BD|=a,故∠BCD=30°,在直角三角形ACE中,∵|AF|=3,|AC|=3+3a,∴2|AE|=|AC|∴3+3a=6,从而得a=1,∵BD∥FG,∴,求得p=,因此抛物线方程为y2=3x,故选:B点评:本题主要考查了抛物线的标准方程.考查了学生对抛物线的定义和基本知识的综合把握.11.已知a>0,x,y满足约束条件,若z=2x+y的最小值为1,则a=( )A.B.C.1 D.2考点:简单线性规划.专题:不等式的解法及应用.分析:先根据约束条件画出可行域,设z=2x+y,再利用z的几何意义求最值,只需求出直线z=2x+y过可行域内的点B时,从而得到a值即可.解答:解:先根据约束条件画出可行域,设z=2x+y,将最大值转化为y轴上的截距,当直线z=2x+y经过点B时,z最小,由得:,代入直线y=a(x﹣3)得,a=故选:B.点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.线性规划中的最优解,通常是利用平移直线法确定.12.设x1,x2分别是方程xa x=1和xlog a x=1的根(其中a>1),则x1+2x2的取值范围( ) A.(2,+∞)B.专题:概率与统计.分析:根据几何概型的概率公式进行求解即可得到结论.解答:解:如果∠AEB为直角,动点E位于以AB为直径的圆上(如图所示).要使∠AMB为锐角,则点M位于正方形内且半圆外(如图所示的阴影部分);因为半圆的面积为,正方形的面积为4×4=16,所以满足∠AMB为锐角的概率.故答案为:1﹣点评:本题主要考查几何概型的概率公式的应用,根据几何概型的概率公式是解决本题的关键.16.对于实数x,表示不超过x的最大整数,观察下列等式:.按照此规律第n个等式的等号右边的结果为2n2+n.考点:归纳推理.专题:推理和证明.分析:由表示不超过x的最大整数,分别研究等式的左边和右边,归纳出规律即可求出第n个等式的等号右边的结果.解答:解:因为表示不超过x的最大整数,所以=1,=2,…,因为等式:,,,…,所以第1个式子的左边有3项、右边1+1+1=1×3=3,第2个式子的左边有5项、右边2+2+2+2+2=2×5=10,第3个式子的左边有7项、右边3×7=21,则第n个式子的左边有(2n+1)项、右边=n(2n+1)=2n2+n,故答案为:2n2+n.点评:本题考查了归纳推理,难点在于发现其中的规律,考查观察、分析、归纳能力.三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.17.已知数列{a n}的前n项和为S n=n2(Ⅰ)求通项公式a n;(Ⅱ)令b n=a2n+3求{b n的前n项和T n.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:(Ⅰ)运用a1=S1=1,n>1时,a n=S n﹣S n﹣1,计算即可得到通项公式a n;(Ⅱ)运用数列求和方法:分组求和,分别运用等差数列和等比数列的求和公式的运用,即可得到所求和.解答:解:(Ⅰ)数列{a n}的前n项和为S n=n2则a1=S1=1,a n=S n﹣S n﹣1=n2﹣(n﹣1)2=2n﹣1,(n≥2),综上可得a n=2n﹣1;(Ⅱ)b n=a2n+3=4n﹣1+32n﹣1,则前n项和T n=(3+4n﹣1)n+=(2n﹣1)n+(9n﹣1).点评:本题考查数列的通项和求和的关系,主要考查等差数列和等比数列的求和公式的运用,属于中档题.18.如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE.考点:平面与平面垂直的判定;直线与平面平行的判定.专题:空间位置关系与距离.分析:(I)根据线面平行的判定定理证出即可;(II)根据面面垂直的判定定理证明即可.解答:证明:(I)∵O是AC的中点,E是PC的中点,∴OE∥AP,又∵OE⊂平面BDE,PA⊄平面BDE.∴PA∥平面BDE.(II)∵PO⊥底面ABCD,PO⊥BD,又∵AC⊥BD,且AC∩PO=O∴BD⊥平面PAC,而BD⊂平面BDE,∴平面PAC⊥平面BDE点评:本题考查了线面平行的判定定理,面面垂直的判定定理,是一道基础题.19.某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.(Ⅰ)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;(Ⅱ)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.考点:古典概型及其概率计算公式;频率分布直方图.专题:概率与统计.分析:(Ⅰ)根据频率分布直方图,求出每个矩形的面积,即每组的概率,每组的中值乘以每组的频率之和即这100名学生参加选拔测试的平均成绩;(Ⅱ)利用频率分布直方图计算分数在∴所求椭圆C的方程为:.(Ⅱ)设A(x1,y1),B(x2,y2),由得(3+4k2)x2+8mkx+4(m2﹣3)=0,△=64m2k2﹣16(3+4k2)(m2﹣3)>0,化为3+4k2>m2.∴,.y1y2=(kx1+m)(kx2+m)==.∵以AB为直径的圆过椭圆的右顶点D(2,0),k AD•k BD=﹣1,∴,∴y1y2+x1x2﹣2(x1+x2)+4=0,∴.化为7m2+16mk+4k2=0,解得m1=﹣2k,.,且满足3+4k2﹣m2>0.当m=﹣2k时,l:y=k(x﹣2),直线过定点(2,0)与已知矛盾;当m=﹣时,l:y=k,直线过定点.综上可知,直线l过定点,定点坐标为.点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、圆的性质、两点间的距离公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.21.已知函数f(x)=e x﹣ax﹣1(a>0,e为自然对数的底数)(1)求函数f(x)的最小值;(2)若f(x)≥0对任意的x∈R恒成立,求实数a的值;(3)在(2)的条件下,证明:1+++…+>ln(n+1)(n∈N*)考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性.专题:导数的综合应用.分析:(1)通过对函数f(x)求导,讨论f(x)的单调性可得函数f(x)的最小值;(2)根据条件可得g(a)=a﹣alna﹣1≥0,讨论g(a)的单调性即得结论;(3)由(2)得e x≥x+1,即ln(x+1)≤x,通过令(k∈N*),可得(k=1,2,…,n),然后累加即可.解答:解:(1)由题意a>0,f′(x)=e x﹣a,令f′(x)=e x﹣a=0,解得x=lna,先当x∈(﹣∞,lna)时,f′(x)<0;当x∈(lna,+∞)时,f′(x)>0.即f(x)在(﹣∞,lna)上单调递减,在(lna,+∞)上单调递增,所以f(x)在x=lna处取得极小值,且为最小值,其最小值为f(lna)=e lna﹣alna﹣1=a﹣alna﹣1;(2)∵f(x)≥0对任意的x∈R恒成立,∴在x∈R上,f min(x)≥0,由(1),设g(a)=a﹣alna﹣1,则g(a)≥0,令g′(a)=1﹣lna﹣1=﹣lna=0,解得a=1,易知g(a)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,∴g(a)在a=1处取得最大值,而g(1)=0.因此g(a)≥0的解为a=1,即a=1;(3)由(2)得e x≥x+1,即ln(x+1)≤x,当且仅当x=0时,等号成立,令(k∈N*),则,即,所以(k=1,2,…,n),累加,得1+++…+>ln(n+1)(n∈N*).点评:本题考查函数的最值,单调性,通过对表达式的灵活变形是解决本题的关键,属于中档题.请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题记分.作答时请在答题卡涂上题号.选修4-1:几何证明选讲22.如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.(Ⅰ)求证:AD∥OC;(Ⅱ)若圆O的半径为2,求AD•OC的值.考点:与圆有关的比例线段;平行线分线段成比例定理.专题:选作题;推理和证明.分析:(Ⅰ)要证明AD∥OC,我们要根据直线平行的判定定理,观察已知条件及图形,我们可以连接OD,构造出内错角,只要证明∠1=∠3即可得证.(Ⅱ)因为⊙O的半径为1,而其它线段长均为给出,故要想求AD•OC的值,我们要将其转化用半径相等或相关的线段积的形式,结合(Ⅰ)的结论,我们易证明Rt△BAD∽Rt△ODC,根据相似三角形性质,不们不难得到转化的思路.解答:(Ⅰ)证明:如图,连接BD、OD.∵CB、CD是⊙O的两条切线,∴BD⊥OC,∴∠2+∠3=90°又AB为⊙O直径,∴AD⊥DB,∠1+∠2=90°,∴∠1=∠3,∴AD∥OC;(Ⅱ)解:AO=OD,则∠1=∠A=∠3,∴Rt△BAD∽Rt△ODC,∵圆O的半径为2,∴AD•OC=AB•OD=8.点评:根据求证的结论,使用分析推敲证明过程中所需要的条件,进而分析添加辅助线的方法,是平面几何证明必须掌握的技能,大家一定要熟练掌握,而在(2)中根据已知条件分析转化的方向也是解题的主要思想.解决就是寻找解题的思路,由已知出发,找寻转化方向和从结论出发寻找转化方向要结合在一起使用.选修4-4:坐标系与参数方程23.在直角坐标系xOy中,圆C的参数方程为(θ为参数).(1)以原点为极点、x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;(2)已知A(﹣2,0),B(0,2),圆C上任意一点M(x,y),求△ABM面积的最大值.考点:简单曲线的极坐标方程;参数方程化成普通方程.专题:坐标系和参数方程.分析:(1)圆C的参数方程为,通过三角函数的平方关系式消去参数θ,得到普通方程.通过x=ρcosθ,y=ρsinθ,得到圆C的极坐标方程.(2)求出点M(x,y)到直线AB:x﹣y+2=0的距离,表示出△ABM的面积,通过两角和的正弦函数,结合绝对值的几何意义,求解△ABM面积的最大值.解答:解:(1)圆C的参数方程为(θ为参数)所以普通方程为(x﹣3)2+(y+4)2=4.,x=ρcosθ,y=ρsinθ,可得(ρcosθ﹣3)2+(ρsinθ+4)2=4,化简可得圆C的极坐标方程:ρ2﹣6ρcosθ+8ρsinθ+21=0.(2)点M(x,y)到直线AB:x﹣y+2=0的距离为△ABM的面积所以△ABM面积的最大值为点评:本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化、平面内直线与曲线的位置关系等内容.本小题考查考生的方程思想与数形结合思想,对运算求解能力有一定要求.选修4-5:不等式选讲24.已知函数f(x)=k﹣|x﹣3|,k∈R,且f(x+3)≥0的解集为.(Ⅰ)求k的值;(Ⅱ)若a、b、c是正实数,且,求证:.考点:绝对值不等式的解法;二维形式的柯西不等式.专题:不等式的解法及应用.分析:(Ⅰ)由题意可得|x|≤k的解集为,(k>0),由绝对值不等式的解法,即可求得k=1;(Ⅱ)将k=1代入,再由乘1法,可得a+2b+3c=(a+2b+3c)(++),展开运用基本不等式即可得证.解答:(Ⅰ)解:f(x+3)≥0的解集为,即为|x|≤k的解集为,(k>0),即有=,解得k=1;(Ⅱ)证明:将k=1代入可得,++=1(a,b,c>0),则a+2b+3c=(a+2b+3c)(++)=3+(+)+(+)+(+)≥3+2+2+2=3+2+2+2=9,当且仅当a=2b=3c,上式取得等号.则有.点评:本题考查绝对值不等式的解法以及不等式的证明,注意运用不等式和方程的转化思想,运用添1法和基本不等式是解题的关键.。
2018年高考历史真题与模拟题类编:专题10-苏俄苏联全球趋势(含答案)

考点一:俄国十月革命01.(2018年海南卷单科历史20)20.在俄国十月革命期间,布尔什维克党最初主张废除地主土地所有制、一切土地国有化,后随着形势的发展,又调整为全部土地归国家所有并交给农民使用。
这一调整( )A.促成了苏维埃的成立B.争取了农民对革命的支持C.推动了民主革命的深入 D.瓦解了临时政府的阶级基础【答案】B【解析】俄国二月革命期间,起义群众建立的政权被称为“苏维埃”,而不是十月革命期间才建立,故A项错误;据材料“全部土地归国家所有并交给农民使用”,通过解决农民的土地问题,争取了农民对革命的支持,故B项正确;俄国十月革命属于社会主义革命,不是资产阶级民主革命,故C项错误;临时政府的阶级基础是资产阶级,与布尔什维克党争取农民阶级支持无关,故D项错误。
02.(陕西省2018届高三年级第十二次模拟文综历史试题)《全球通史》载:“1917年3月至11月是临时政府和苏维埃之间为权力而斗争的时期。
在这场斗争中,临时政府处于极其不利的地位。
”“临时政府处于极其不利的地位”的主要原因是A. 罗曼诺夫王朝的被推翻B. 其反对“全部政权归苏维埃”C. 经济危机导致工人罢工D. 其拒绝停战也拒不分配土地【答案】D点睛:注意题目中的“1917年3月至11月”这个时间。
03.(江苏省盐城市2018届高三下学期第三次模拟考试历史试题)二月革命后,以列宁为首的布尔什维克党人提出了“和平、土地、面包”的口号,这最简单的口号直击人心。
三月份,布尔什维克党只有2万多名党员,到了十月革命前,成为35万人的大党。
由此说明当时A. 退出一战的俄国急需土地和面包B. 民意成为革命发展的助推力C. 布尔什维克政党获得了执政地位D. 实现向社会主义的和平过渡【答案】B点睛:排除法是做选择题的一个重要技巧。
有些题目不是很容易直接得出正确选项,就比较适合用排除法,一般是排除:不符合史实的选项(比如时间、空间等);不符合逻辑的选项(比如,让选择“原因”,那就需要排除掉属于结果的选项);明显和题目所给的信息不一致或者相反的选项;说法过于绝对的选项需要慎重对待,很多时候也是该排除掉的选项。
宁夏银川高三4月高中教学质量检测(图片)——文综(文综)

银川市2018年高三质量检测文科综合试卷地理试题答案36.(24分)(1)地面起伏较小;地势东北部、西北部、西南部高,中部、东南部低。
(4分)(2)泵站将水位较低的河水抽到地势较高的干渠;(2分)干渠将灌溉用水分配给灌渠;(2分)灌渠将水引入农田灌溉;(2分)排水渠将灌溉余水或洪水排入水位较低的下游河道。
(2分)(3)降水不稳定,有旱涝灾害,(2分)农业技术落后,(2分)经济条件差,(2分)机械化水平低。
(2分)(4)改良作物品种,(2分)提高机械化水平,(2分)改良种植技术,(2分)提高复种指数。
(2分)(任答两点得4分,其它合理答案亦可酌情给分)37.(22分)(1)缩短收货时间;(2分)购物价格低;(2分)用户体验好。
(2分)(2)德国经济发达,是我国出口商品的重要市场;(2分)地处欧洲中部,地理位置优越;(2分)是中欧铁路的重要枢纽,(2分)德国交通网络发达,便于货物迅速运往欧洲各国。
(2分)(3)西欧面积较小且以平原为主,水陆交通便利,对仓库的需求量小;(2分)经济发达区,地价高,建仓成本高。
(2分)储量大,剩余货物难处理。
(2分)原有商业庞大完善,竞争激烈。
(2分)43. 不要用手触摸钟乳石及石笋及岩壁,避免破坏萤火虫的生长环境;(2分)在萤火虫洞洞穴内必须保持宁静;(2分)全程禁止使用相机及录像机,避光以免影响萤火虫捕食生长;(2分)必须跟着团队一同行动以便向导照顾,避免在湿黑的萤火虫洞洞穴内发生意外;(2分)禁烟保持空气清新。
(2分)任答五点即可,其它合理答案亦可酌情给分。
44.对流层顶部或平流层,不受云层云系影响,(3分)白色食盐粉末反射太阳辐射,减少到达地面太阳辐射,从而缓解全球变暖状况。
(3分)食盐中的氯离子可能破坏臭氧层,(2分)二氧化硫可能加剧酸雨危害。
(2分)政治选择答案12-----16 CDDAC 17-----21 DCBAB 22----23 BA38.必要性:①农业是国民经济的基础,解决好“三农”问题是全部工作的重中之重;②是全面建成小康社会的要求、是社会主义本质的要求、是共同富裕的要求;③有利于加快转变农业经济发展方式、优化农村经济结构、增加农民收入、提高人民生活水平。
2018年宁夏银川市唐徕回民中学高考数学四模试卷(文科)-教师用卷

2018年宁夏银川市唐徕回民中学高考数学四模试卷(文科)副标题一、选择题(本大题共12小题,共60.0分)1.若复数是虚数单位是纯虚数,则其虚部为A. B. C. 3 D. 3i【答案】C【解析】解:是纯虚数,,即.复数的虚部为,故选:C.利用复数代数形式的乘除运算化简,由实部为0且虚部不为0列式求得a,则虚部可求.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.2.集合,0,,若,则A. B. C. D.【答案】B【解析】解:集合,0,,若,则,解得,又.故选:B.根据交集的定义得出关于t的方程,求出t的值,再化简本题考查了交集的定义和对数的运算问题,是基础题.3.函数的最大值是A. 1B. 2C. 3D. 4【答案】B【解析】解:函数,,.函数的最大值为:2.故选:B.直接利用两角和与差的三角函数化简函数的表达式,利用正弦函数的值域求解即可.本题考查两角和与差的三角函数,三角函数的最值的求法,基本知识的考查.4.如框为某程序语言,则该程序语言执行的是函数的功能.A. B. C. D.【答案】C【解析】解:根据如图所示的程序语言知,该程序语言执行的是函数,即的功能.故选:C.分析如图所示的程序语言知该程序执行的是分段函数,即绝对值函数.本题考查了程序语言的应用问题,是基础题.5.已知实数x,y满足,则目标函数的最小值为A. B. C. D.【答案】C【解析】解:作出实数x,y满足如图阴影部分的可行域,由得,当目标函数平移到点A时,直线在y轴上的截距最大,即z取最小值,即的最小值为.故选:C.先画出约束条件的可行域,再将可行域中各个角点的值依次代入目标函数,不难求出目标函数的最小值.本题主要考查线性规划的基本知识,用图解法解决线性规划问题时,利用线性规划求函数的最值时,关键是将目标函数赋予几何意义.6.已知数列,,且,,设的前n项和为,则A. 62B. 60C. 58D. 56【答案】A【解析】解:,,.则.故选:A.由,,可得利用等比数列的求和公式即可得出.本题考查了等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.7.已知双曲线:的一条渐近线与直线垂直,则双曲线的离心率为A. B. C. D.【答案】C【解析】解:双曲线:的一条渐近线与直线互相垂直,,得到.双曲的离心率.故选:C.由双曲线:的一条渐近线与直线互相垂直,利用相互垂直的直线的斜率之间的关系和离心率的计算公式即可得出.熟练掌握双曲线的渐近线、相互垂直的直线的斜率之间的关系和离心率的计算公式是解题的关键.8.函数的部分图象是A. B. C. D.【答案】A【解析】解:由于,,故函数是偶函数,排除B,D;又当时,,,,故排除C,故选:A.根据函数的奇偶性排除BD,再根据x的变化趋势排除C.本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力,属于中档题.9.某四棱锥的三视图如图所示,该四棱锥的表面积为A. 17B. 22C.D.【答案】D【解析】解:由三视图知:几何体为四棱锥,如图:其中平面ABCD,,底面ABCD为矩形,,,几何体的表面积为故选:D.几何体为四棱锥,结合直观图判断几何体的结构特征及相关几何量的数据,把数据代入棱锥的体积公式计算.本题考查了由三视图求几何体的体积,根据三视图判断几何体的结构特征及数据所对应的几何量是解题的关键.10.已知命题p:若函数在上存在零点,则;命题q:若,则在处取得极值,下列命题为真命题的是A. B. C. ¬ D. ¬【答案】C【解析】解:命题p是假命题,由函数的零点存在性定理,函数是连续不断的函数时,且,在区间内存在零点,但是反之不成立命题q是假命题,因为如果在处取得极值,则,同样,反之不成立,要想取极值,必须在处两侧导数值异号才可以.A选项,为真,必须p,q中最少有一个是真命题才可以,不符合题意.B选项,为真,必须p,q两个都是真命题才可以,不符合题意.C选项,¬为真,必须p,¬中最少有一个是真命题才可以,符合题意.D选项,¬为真,必须¬,q中都是真命题才可以,不符合题意.故选:C.p:函数零点存在性定理的辨析,定理反之不成立,故p是假命题:是函数极值存在问题,有极值与导数值为0之间不是充要条件,故q是假命题.本题考查了简易逻辑的有关判定、函数零点问题、函数极值问题,考查了推理能力与计算能力,属于基础题.11.已知函数,则使得成立的x的取值范围是A. B.C. D.【答案】B【解析】解:函数,当时,,函数,在上是减函数,使得成立,可得,解得.则使得成立的x的取值范围是.故选:B.求出函数的导数,判断函数的单调性,然后转化求解不等式即可.本题主要考察函数的单调性,并根据单调性判断函数的取值,属于中档题.12.某中学为了调查高三女生的健康状况,从高三年级随机选取8名女学生,得到其身高和体重数据如表:经计算得知,身高预报体重的回归方程为,相关系数的平方.有下列四种判断:身高x每增加1个单位,体重y就大约增加个单位越接近于1,表示回归的效果越好女学生的体重差异有是由身高引起的女学生的身高解释了的体重变化正确的是A. B. C. D.【答案】D【解析】解:根据身高预报体重的回归方程为,相关系数的平方;对于,身高x每增加1个单位,体重y就大约增加个单位,正确;对于,越接近于1,表示回归的拟合效果越好,正确;对于,由知,女学生的体重差异有是由身高引起的,正确;对于,由的意义知,女学生的身高解释了的体重变化,正确;综上,正确的命题序号是.故选:D.根据身高预报体重的回归方程和即相关系数的平方,对题目中的命题判断正误即可.本题考查了线性回归方程与相关系数的平方的定义和应用问题,是基础题.二、填空题(本大题共4小题,共20.0分)13.椭圆的左焦点为______.【答案】【解析】解:椭圆,可得,,则,所以椭圆的左焦点为.故答案为:.直接利用椭圆的方程,转化求解即可.本题考查椭圆的简单性质的应用,是基本知识的考查.14.函数在点处的切线方程为______.【答案】【解析】解:根据题意,函数,则,其导数,则,则切线的斜率,故函数在点处的切线方程为,即;故答案为:.根据题意,由函数的解析式计算可得的值,计算其导数,求出的值,即可得切线的斜率,由直线的点斜式方程可得切线的方程,变形即可得答案.本题考查利用导数计算函数的切线方程,关键是掌握导数的几何意义.15.不等式的解集为______.【答案】或【解析】解:根据题意,,则,解可得或,即不等式的解集为或故答案为:或.根据题意,原不等式可以变形为,由一元二次不等式的解法计算可得答案.本题考查其他不等式的解法,关键是将变形.16.如图,已知平行四边形ABCD中,E,M分别为DC的两个三等分点,F,N分别为BC的两个三等分点,,,则______.【答案】90【解析】解:平行四边形ABCD中,E,M分别为DC的两个三等分点,F,N分别为BC的两个三等分点,,,,,解得,,,.故答案为:90.由,,列出方程组,求出,再由,,得到,由此能求出结果.本题考查平行四边形的对角线的平方和的求法,考查向量加法定理等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.三、解答题(本大题共7小题,共82.0分)17.如图,气球A相对于BC所在地平面的高度是h,前方有一座桥梁,气球A带有一个测角器,试用测角仪器测得适当的角用字母表示,用测得的角度及h表示河流的宽度BC.【答案】解:如图所示,中,,测角器测得,则,中,,测角器测得,则,河流的宽度为.【解析】根据图形,利用直角三角形的边角关系,即可求出BC的值.本题考查了直角三角形中边角关系的应用问题,是基础题.18.如图,在四棱锥中,侧面PAB为等边三角形且垂直于底面ABCD,.证明:;若的面积为,求四棱锥的体积.【答案】证明:取AB中点O,连结PO,在四棱锥中,侧面PAB为等边三角形且垂直于底面ABCD,,平面ABCD,平面ABCD,,,,平面PAB,平面PAB,.解:以O为原点,OA为x轴,过O作AD的平行线为y轴,OP为z轴,建立空间直角坐标系,设,则4a,,2a,,0,,2a,,4a,,,,的面积为,,解得,,,梯形四棱锥的体积梯形.【解析】取AB中点O,连结PO,推导出平面ABCD,从而,再求出,从而平面PAB,由此能证明.以O为原点,OA为x轴,过O作AD的平行线为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出四棱锥的体积.本题考查线线垂直的证明,考查满四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系的应用,考查运算求解能力,考查函数与方程思想,是中档题.19.某班级50名学生的考试分数x分布在区间内,设分数x的分布频率是,且求实数b的值;估算班级的考试平均分数;考试成绩采用“5分制”,规定:考试分数在内的成绩记为1分,考试分数在内的成绩记为2分,考试分数在内的成绩记为3分,考试分数在内的成绩记为5分用分层抽样的方法,在50名学生中选取成绩为1分,2分及3分中随机抽取6人,再从这6人中抽出2人,试分析这2人的成绩之和为4分的概率与成绩之和为3分或6分的概率哪个较大将频率视为概率?班级的平均成绩分由题意知:考试成绩记为1分,2分,3分,4分,5分的频率分别是,,,,,考试成绩记为1分、2分、3分的分别可以抽出1人,记为,2人记为B,,3人记为D、E、,再从这面人中抽出2人,基本事件为:AB,AC、AD、AE、AF、BC、BD、BE、BF、CD、CE、CF、DE、EF,共15个,成绩之和为4的有:AD、AE、AF、BC,共4个,这2人的成绩之和为4分的概率.成绩之和为3的有:AB,AC,共2个,人的成绩之和为3分的概率.成绩之和为6的有:DE,DF,EF,共3个,人的成绩之和为6分的概率.这2人的成绩之和为4分的概率较大.【解析】考试分数x的分布频率是,列出方程,能求出b的值.利用考试分数x的分布频率是,能求出班级的考试平均分数.考试成绩记为1分,2分,3分,4分,5分的频率分别是,,,,,考试成绩记为1分、2分、3分的分别可以抽出1人,记为,2人记为B,,3人记为D、E、,再从这面人中抽出2人,利用列举法能求出这2人的成绩之和为4分的概率较大.本题考查实数值、平均数、概率的求法及应用,涉及到分布频率、概率、平均值、概率等基础知识,考查函数与方程思想、集合思想,是中档题.20.已知圆F方程为,顶点在原点,焦点在y轴上的抛物线C过点,求抛物线C的方程;是否存在倾斜角为的直线l,使得直线l与圆F交于C,D,与抛物线C相交于点A,从左到右依次排列为A,C,D,,且?若存在,求出的取值范围;若不存在,请说明理由.【答案】解:顶点在原点,焦点在y轴上的抛物线C过点,可设抛物线的方程为,即有,可得抛物线的方程为;假设存在倾斜角为的直线l,使得直线l与圆F交于C,D,与抛物线C相交于点A,B,且,设直线l的方程为,圆F方程为的圆心为,半径为1,由圆和直线相交可得,可得,设AB的中点为H,由,可得H也为CD的中点,即,联立直线l和抛物线,可得,则,,中点H的坐标为,由,可得,解得,代入可得,代入可得,即为,则存在这样的直线l,且,满足题意.【解析】由题意设抛物线的方程为,代入可得p,进而得到所求抛物线的方程;假设存在倾斜角为的直线l,使得直线l与圆F交于C,D,与抛物线C相交于点A,B,且,设直线l的方程为,可得AB的中点H即为CD的中点,运用联立直线方程和抛物线的方程,由判别式大于0和中点坐标公式,求得H的坐标,由F到直线的距离小于半径,和,运用斜率之积为,求得t,解不等式可得k的范围,即为所求.本题考查抛物线的方程的求法和运用,考查直线和圆的位置关系、直线和抛物线方程联立,运用判别式和韦达定理,考查不等式的解法,属于中档题.21.已知函数,.求函数的单调区间及极值;求函数的零点个数.【答案】解:,,,令,解得,当时,,函数单递减,当时,,函数单递增,当时,函数有极小值,即,无极大值,在上为减函数,在为增函数,由可得,,,当时,,函数单调递增,当时,,函数单调递减,,,且与无交点,函数没有零点.【解析】先求导,再根据导数和函数的单调性和极值的关系即可求出;由可得,对求导,求出函数的最大值,即可判断函数的零点个数的个数.本题考查了导数和函数的单调性和极值最值的关系,以及函数零点的个数,考查了运算能力和转化能力,属于中档题.22.已知直线为参数,为参数,Ⅰ当时,求与的交点坐标;Ⅱ过坐标原点O做的垂线,垂足为A,P为OA中点,当变化时,求P点的轨迹的参数方程,并指出它是什么曲线.【答案】解:Ⅰ当时,的普通方程为,的普通方程为.联立方程组,解得与的交点为.Ⅱ的普通方程为.则OA的方程为,联立可得,;A点坐标为,故当变化时,P点轨迹的参数方程为:为参数,P点轨迹的普通方程.故P点轨迹是圆心为,半径为的圆.【解析】先消去参数将曲线与的参数方程化成普通方程,再联立方程组求出交点坐标即可,设,利用中点坐标公式得P点轨迹的参数方程,消去参数即得普通方程,由普通方程即可看出其是什么类型的曲线.本题主要考查直线与圆的参数方程,参数方程与普通方程的互化,利用参数方程研究轨迹问题的能力.23.设函数.画出的图象;求的解集.【答案】解:,其图象见下图.,不等式可化为,,;,不等式可化为,,;,不等式可化为,,;综上所述,不等式的解集为或.【解析】去掉绝对值,写成分段函数形式,作出函数的图象.分类讨论以去掉绝对值号,即可解关于x的不等式.本题考查了绝对值函数的应用及数形结合的思想方法应用,属于中档题.。
宁夏银川一中2018届高三第四次模拟考试文科综合试卷

绝启用前2018年普通高等学校招生全国统一考试文科综合能力测试( 银川一中第四次模拟考试 )本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第42~47题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.考生必须按照题号在答题卡各题号相对应的答题区域(黑色线框)内作答,写出草稿纸上、超出答题区域或非题号对应的答题区域的答案一律无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的题目涂黑。
第Ⅰ卷本卷共35个小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符号题目要求的。
读浙江省2000年和2016年省外流入人口分年龄的性别比(每百名女性人口相对应的男性人口数)情况折线图(图1),完成1-2题。
1.2016年,浙江省省外流入人口中A.男性人口仍占多数B.性别比最大的年龄段是40-44岁C.少年儿童的性别比低于老年人D.迁入人口性别比随年龄增大而下降2.与2000年比,2016年中年女性人口大量流入,其影响因素可能包括①行业需求②交通运输③工程建设④家庭需要A.①②B.①④C.②③D.③④第二次世界大战后,荷兰西部港口小镇罗曾堡(51.90°N,4.25°E)工业发展迅速,为此于1960年修建了一条新的入运河——卡兰运河,分担原有南北向运河的运输压力,运河建成后,承担着繁重的运输任务,大型船只川流不息。
1980年,在卡兰运河一侧河岸修建了一座高墙。
2018年宁夏银川市唐徕回民中学高考数学四模试卷(文科)

2018年宁夏银川市唐徕回民中学高考数学四模试卷(文科)副标题题号一二三总分得分一、选择题(本大题共12小题,共60.0分)1.若复数(i是虚数单位)是纯虚数,则其虚部为()A. -6B. -6iC. 3D. 3i2.集合M={0,2t},N={,0,},若M∩N={0,},则t=()A. B. log48 C. D.3.函数f(x)=sin x+cos x的最大值是()A. 1B. 2C. 3D. 44.如框为某程序语言,则该程序语言执行的是()函数的功能.A. y=xB. y=-xC. y=|x|D. y=-|x|5.已知实数x,y满足,则目标函数的最小值为()A. B. C. D.6.已知数列{a n},{b n},且,,设b n的前n项和为S n,则S5=()A. 62B. 60C. 58D. 567.已知双曲线Γ:(a>0,b>0)的一条渐近线与直线3x-2y+1=0垂直,则双曲线Γ的离心率为()A. B. C. D.8.函数f(x)=-cos x•lg|x|的部分图象是()A. B. C. D.9.某四棱锥的三视图如图所示,该四棱锥的表面积为()A. 17B. 22C.D.10.已知命题p:若函数f(x)在(a,b)上存在零点,则f(a)•f(b)<0;命题q:若g'(x0)=0,则g(x)在x0处取得极值,下列命题为真命题的是()A. p∨qB. p∧qC. p∨(¬q)D. (¬p)∧q11.已知函数f(x)=sin x-x,则使得成立的x的取值范围是()A. (-1,1)B. (-∞,-1)C. (-∞,-1)∪(1,+∞)D. (1,+∞)12.某中学为了调查高三女生的健康状况,从高三年级随机选取8名女学生,得到其身高和体重数据如表:编号12345678身高/cm165165157170175165155170体重/kg4857505464614359经计算得知,身高预报体重的回归方程为=0.849x-85.712,R2(相关系数的平方)≈0.64.有下列四种判断:①身高x每增加1个单位,体重y就大约增加0.849个单位②R2越接近于1,表示回归的效果越好③女学生的体重差异有64%是由身高引起的④女学生的身高解释了64%的体重变化正确的是()A. ①B. ①②C. ①②③D. ①②③④二、填空题(本大题共4小题,共20.0分)13.椭圆的左焦点为______.14.函数f(x)=e x+1在点(-1,f(-1))处的切线方程为______.15.不等式(2-x)(x+3)(x2+1)≤0的解集为______.16.如图,已知平行四边形ABCD中,E,M分别为DC的两个三等分点,F,N分别为BC的两个三等分点,=25,=43,则=______.三、解答题(本大题共7小题,共82.0分)17.如图,气球A相对于BC所在地平面的高度是h,前方有一座桥梁,气球A带有一个测角器,试用测角仪器测得适当的角(用字母表示),用测得的角度及h表示河流的宽度BC.18.如图,在四棱锥P-ABCD中,侧面PAB为等边三角形且垂直于底面ABCD,AB=BC=AD.∠BAD=∠ABC=90°.(1)证明:PA⊥BC;(2)若△PCD的面积为,求四棱锥P-ABCD的体积.19.某班级50名学生的考试分数x分布在区间[50,100]内,设分数x的分布频率是f(x),且(1)求实数b的值;(2)估算班级的考试平均分数;(3)考试成绩采用“5分制”,规定:考试分数在[50,60)内的成绩记为1分,考试分数在[60,70)内的成绩记为2分,考试分数在[70,80)内的成绩记为3分,考试分数在[90,100)内的成绩记为5分.用分层抽样的方法,在50名学生中选取成绩为1分,2分及3分中随机抽取6人,再从这6人中抽出2人,试分析这2人的成绩之和为4分的概率与成绩之和为3分或6分的概率哪个较大(将频率视为概率)?20.已知圆F方程为x2+(y-2)2=1,顶点在原点,焦点在y轴上的抛物线C过点P(1,1),(1)求抛物线C的方程;(2)是否存在倾斜角为α的直线l,使得直线l与圆F交于C,D,与抛物线C相交于点A,B(从左到右依次排列为A,C,D,B),且|AC|=|DB|?若存在,求出tanα的取值范围;若不存在,请说明理由.21.已知函数f(x)=x lnx,.(1)求函数f(x)的单调区间及极值;(2)求函数h(x)=f(x)-g(x)的零点个数.22.已知直线C1(t为参数),C2(θ为参数),(Ⅰ)当α=时,求C1与C2的交点坐标;(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.23.设函数f(x)=|x-1|+|2x+4|.(1)画出y=f(x)的图象;(2)求f(x)≥2x+5的解集.答案和解析1.【答案】C【解析】解:∵=是纯虚数,∴,即a=-6.∴复数的虚部为,故选:C.利用复数代数形式的乘除运算化简,由实部为0且虚部不为0列式求得a,则虚部可求.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.2.【答案】B【解析】解:集合M={0,2t},N={,0,},若M∩N={0,},则2t=2,解得t=,又log48=log22=.故选:B.根据交集的定义得出关于t的方程,求出t的值,再化简log48.本题考查了交集的定义和对数的运算问题,是基础题.3.【答案】B【解析】解:函数f(x)=sinx+cosx=2sin(x+),y=sinx∈[-1,1],2sin(x+)∈[-2,2].函数的最大值为:2.故选:B.直接利用两角和与差的三角函数化简函数的表达式,利用正弦函数的值域求解即可.本题考查两角和与差的三角函数,三角函数的最值的求法,基本知识的考查.4.【答案】C【解析】解:根据如图所示的程序语言知,该程序语言执行的是函数y=,即y=|x|的功能.故选:C.分析如图所示的程序语言知该程序执行的是分段函数,即绝对值函数.本题考查了程序语言的应用问题,是基础题.5.【答案】C【解析】解:作出实数x,y满足如图阴影部分的可行域,由得A(,),当目标函数平移到点A时,直线z=x-y在y轴上的截距最大,即z取最小值,即z=x-y的最小值为-.故选:C.先画出约束条件的可行域,再将可行域中各个角点的值依次代入目标函数z=x-y,不难求出目标函数z=x-y的最小值.本题主要考查线性规划的基本知识,用图解法解决线性规划问题时,利用线性规划求函数的最值时,关键是将目标函数赋予几何意义.6.【答案】A【解析】解:∵,,∴b n=2n.则S5=2+22+……+25==26-2=62.故选:A.由,,可得b n=2n.利用等比数列的求和公式即可得出.本题考查了等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.7.【答案】B【解析】解:双曲线Γ:(a>0,b>0)的一条渐近线与直线3x-2y+1=0互相垂直,×(-)=-1,得到=.双曲线Γ的离心率e=.故选:B.由双曲线Γ:(a>0,b>0)的一条渐近线与直线3x-2y+1=0互相垂直,利用相互垂直的直线的斜率之间的关系和离心率的计算公式即可得出.熟练掌握双曲线的渐近线、相互垂直的直线的斜率之间的关系和离心率的计算公式是解题的关键.8.【答案】A【解析】解:由于f(x)=-cosx•lg|x|,∴f(-x)=-cos(-x)•lg|-x|=-cosx•lg|x|=f(x),故函数f(x)是偶函数,排除B,D;又当x→0时,lg|x|→-∞,cosx→1,∴f(x)→+∞,故排除C,故选:A.根据函数的奇偶性排除BD,再根据x的变化趋势排除C.本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力,属于中档题.9.【答案】D【解析】解:由三视图知:几何体为四棱锥,如图:其中SA⊥平面ABCD,SA=3,底面ABCD为矩形,AD=4,AB=2,∴几何体的表面积为4×2+=22+2故选:D.几何体为四棱锥,结合直观图判断几何体的结构特征及相关几何量的数据,把数据代入棱锥的体积公式计算.本题考查了由三视图求几何体的体积,根据三视图判断几何体的结构特征及数据所对应的几何量是解题的关键.10.【答案】C【解析】解:命题p是假命题,由函数的零点存在性定理,函数f(x)是连续不断的函数时,且f(a)•f(b)<0,在区间(a,b)内存在零点,但是反之不成立.命题q是假命题,因为如果g(x)在x=x0处取得极值,则g'(x0)=0,同样,反之不成立,要想取极值,必须在x=x0处两侧导数值异号才可以.A选项,p∨q为真,必须p,q中最少有一个是真命题才可以,不符合题意.B选项,p∧q为真,必须p,q两个都是真命题才可以,不符合题意.C选项,p∨(¬q)为真,必须p,¬q中最少有一个是真命题才可以,符合题意.D选项,(¬p)∧q为真,必须¬p,q中都是真命题才可以,不符合题意.故选:C.p:函数零点存在性定理的辨析,定理反之不成立,故p是假命题.q:是函数极值存在问题,有极值与导数值为0之间不是充要条件,故q是假命题.本题考查了简易逻辑的有关判定、函数零点问题、函数极值问题,考查了推理能力与计算能力,属于基础题.11.【答案】B【解析】解:函数f(x)=sinx-x,当x>0时,f′(x)=cosx-1≤0,函数f(x)=sinx-x,在x>0上是减函数,使得成立,可得,解得x<-1.则使得成立的x的取值范围是(-∞,-1).故选:B.求出函数的导数,判断函数的单调性,然后转化求解不等式即可.本题主要考察函数的单调性,并根据单调性判断函数的取值,属于中档题.12.【答案】D【解析】解:根据身高预报体重的回归方程为=0.849x-85.712,R2(相关系数的平方)≈0.64;对于①,身高x每增加1个单位,体重y就大约增加0.849个单位,正确;对于②,R2越接近于1,表示回归的拟合效果越好,正确;对于③,由R2≈0.64知,女学生的体重差异有64%是由身高引起的,正确;对于④,由R2的意义知,女学生的身高解释了64%的体重变化,正确;综上,正确的命题序号是①②③④.故选:D.根据身高预报体重的回归方程和R2(即相关系数的平方),对题目中的命题判断正误即可.本题考查了线性回归方程与R2(相关系数的平方)的定义和应用问题,是基础题.13.【答案】(- ,0)【解析】解:椭圆,可得 a=3,b=2,则 c= ,所以椭圆的左焦点为(- ,0).故答案为:(- ,0).直接利用椭圆的方程,转化求解即可.本题考查椭圆的简单性质的应用,是基本知识的考查.14.【答案】y=x+2【解析】解:根据题意,函数 f(x)=ex+1,则 f(-1)=e-1+1=e0=1,其导数 f′(x)=ex+1,则 f′(-1)=e-1+1=e0=1,则切线的斜率 k=1,故函数 f(x)=ex+1 在点(-1,f(-1))处的切线方程为 y-1=(x+1),即 y=x+2;故答案为:y=x+2.根据题意,由函数的解析式计算可得 f(-1)的值,计算其导数,求出 f′(-1)的值,即可得切线的斜率,由直线的点斜式方程可得切线的方程,变形即可得 答案. 本题考查利用导数计算函数的切线方程,关键是掌握导数的几何意义.15.【答案】{x|x≤-3 或 x≥2}【解析】解:根据题意,x2+1>0,则(2-x)(x+3)(x2+1)≤0⇒(2-x)(x+3)≤0⇒(x-2)(x+3) ≥0, 解可得 x≤-3 或 x≥2, 即不等式的解集为{x|x≤-3 或 x≥2}故答案为:{x|x≤-3 或 x≥2}.根据题意,原不等式可以变形为(x-2)(x+3)≥0,由一元二次不等式的解法计 算可得答案. 本题考查其他不等式的解法,关键是将(2-x)(x+3)(x2+1)≤0 变形. 16.【答案】90【解析】第 11 页,共 18 页解:∵平行四边形 ABCD 中,E,M 分别为 DC的两个三等分点,F,N 分别为 BC 的两个三等分点,=25,=43,∴,∴,解得| |2+| |2=45,=()2=| |2+| |2+2| |•| |cos∠BAD,| |2=()2=| |2+| |2+2| |•| |cos∠ABC=| |2+| |2-2| |•| |cos∠BAD,∴=2(| |2+| |2)=90.故答案为:90.由=25,=43,列出方程组,求出| |2+| |2=45,再由=| |2+| |2+2| |•| |cos∠BAD,| |2=| |2+| |2-2| |•| |cos∠BAD,得到=2(| |2+| |2),由此能求出结果.本题考查平行四边形的对角线的平方和的求法,考查向量加法定理等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.第 12 页,共 18 页17.【答案】解:如图所示,Rt△ABM 中,AM=h,测角器测得∠BAM=α, 则 BM=AMtanα=htanα, Rt△ACM 中,AM=h,测角器测得∠CAM=β, 则 CM=AMtanβ=htanβ, ∴河流的宽度为 BC=CM-BM=htanβ-htanα=h(tanβ-tanα). 【解析】根据图形,利用直角三角形的边角关系,即可求出 BC 的值.本题考查了直角三角形中边角关系的应用问题,是基础题.18.【答案】证明:(1)取 AB 中点 O,连结 PO, ∵在四棱锥 P-ABCD 中,侧面 PAB 为等 边三角形且垂直于底面 ABCD, ∴PO⊥AB,∴PO⊥平面 ABCD, ∵BC⊂平面 ABCD,∴PO⊥BC, ∵∠BAD=∠ABC=90°.∴AB⊥BC, ∵AB∩PO=O,∴BC⊥平面 PAB, ∵PA⊂平面 PAB,∴PA⊥BC. 解:(2)以 O 为原点,OA 为 x 轴,过 O 作 AD 的平行线为 y 轴,OP 为 z 轴, 建立空间直角坐标系,设 AB=BC= AD=2a,则 D(a,4a,0),C(-a,2a,0),P(0,0, a),=(-a,2a,- ), =(a,4a,- ),cos<>===,∴sin<>==,∵△PCD 的面积为 解得 a=1,,∴S△PCD==,第 13 页,共 18 页∴S 梯形 ABCD===6,PO=,∴四棱锥 P-ABCD 的体积 VP-ABCD==【解析】=3 .(1)取 AB 中点 O,连结 PO,推导出 PO⊥平面 ABCD,从而 PO⊥BC,再求出AB⊥BC,从而 BC⊥平面 PAB,由此能证明 PA⊥BC.(2)以 O 为原点,OA 为 x 轴,过 O 作 AD 的平行线为 y 轴,OP 为 z 轴,建立空间直角坐标系,利用向量法能求出四棱锥 P-ABCD 的体积.本题考查线线垂直的证明,考查满四棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系的应用,考查运算求解能力,考查函数与方程思想,是中档题.19.【答案】解:(1)依题意频率分布表如下:分数[50,60) [60.70)[70.80)[80,90) [90,100)成绩12345频率0.10.20.3b-1.6b-1.8∵f(5)+f(6)+f(7)+f(8)+f(9)=1,∴b=1.9 (2)班级的平均成绩 =55×0.1+65×0.2+75×0.3+85×0.3+95×0.1=76(分) (3)由题意知: 考试成绩记为 1 分,2 分,3 分,4 分,5 分的频率分别是 0.1,0.2,0.3,0.3,0.1, 考试成绩记为 1 分、2 分、3 分的分别可以抽出 1 人,(记为 A),2 人(记为 B,C), 3 人(记为 D、E、F), 再从这面人中抽出 2 人,基本事件为: AB,AC、AD、AE、AF、BC、BD、BE、BF、CD、CE、CF、DE、EF,共 15 个, 成绩之和为 4 的有:AD、AE、AF、BC,共 4 个,∴这 2 人的成绩之和为 4 分的概率 p1= . 成绩之和为 3 的有:AB,AC,共 2 个,∴2 人的成绩之和为 3 分的概率 p2= .成绩之和为 6 的有:DE,DF,EF,共 3 个,∴2 人的成绩之和为 6 分的概率 p3= = .∴这 2 人的成绩之和为 4 分的概率较大. 【解析】(1)考试分数 x 的分布频率是 f(x),列出方程,能求出 b 的值. (2)利用考试分数 x 的分布频率是 f(x),能求出班级的考试平均分数.第 14 页,共 18 页(3)考试成绩记为 1 分,2 分,3 分,4 分,5 分的频率分别是 0.1,0.2,0.3,0.3,0.1,考试成绩记为 1 分、2 分、3 分的分别可以抽出 1 人,(记为 A),2 人(记为B,C),3 人(记为 D、E、F),再从这面人中抽出 2 人,利用列举法能求出这 2人的成绩之和为 4 分的概率较大.本题考查实数值、平均数、概率的求法及应用,涉及到分布频率、概率、平均值、概率等基础知识,考查函数与方程思想、集合思想,是中档题.20.【答案】解:(1)顶点在原点,焦点在 y 轴上的抛物线 C 过点 P(1,1),可设抛物线的方程为 x2=2py, 即有 1=2p,可得抛物线的方程为 x2=y; (2)假设存在倾斜角为 α 的直线 l,使得直线 l 与圆 F 交于 C,D, 与抛物线 C 相交于点 A,B,且|AC|=|DB|, 设直线 l 的方程为 y=kx+t, 圆 F 方程为 x2+(y-2)2=1 的圆心为(0,2),半径为 1,由圆和直线相交可得<1,可得 2-<t<2+,①设 AB 的中点为 H,由|AC|=|DB|, 可得 H 也为 CD 的中点,即 FH⊥l, 联立直线 l 和抛物线 x2=y,可得 x2-kx-t=0, 则△=k2+4t>0,②x1+x2=k,中点 H 的坐标为( ,t+ ),由 FH⊥l,可得- • =t+ -2,解得 t= - ,代入②可得 k2<6, 代入①可得 k2<3, 即为- <k< , 则存在这样的直线 l,且 tanα∈(- , ),满足题意. 【解析】(1)由题意设抛物线的方程为 x2=2py,代入(1,1)可得 p,进而得到所求抛物 线的方程; (2)假设存在倾斜角为 α 的直线 l,使得直线 l 与圆 F 交于 C,D,与抛物线 C 相交于点 A,B,且|AC|=|DB|, 设直线 l 的方程为 y=kx+t,可得 AB 的中点 H 即为 CD 的中点,运用联立直线第 15 页,共 18 页方程和抛物线的方程,由判别式大于 0 和中点坐标公式,求得 H 的坐标,由 F 到直线的距离小于半径,和 FH⊥l,运用斜率之积为-1,求得 t,解不等式可得 k 的范围,即为所求. 本题考查抛物线的方程的求法和运用,考查直线和圆的位置关系、直线和抛 物线方程联立,运用判别式和韦达定理,考查不等式的解法,属于中档题. 21【. 答案】解:(1)∵(f x)=xlnx,x>0, ∴f′(x)=1+lnx, 令 f′(x)=0,解得 x= ,当 x∈(0, )时,f′(x)<0, 函数单调递减, 当 x∈( ,+∞)时,f′(x)>0, 函数单调递增, ∴当 x= 时,函数有极小值,即 f( )=- ,无极大值,f(x)在(0, )上为减函数,在( ,+∞)为增函数,(2)由(1)可得 f(x)min=- ,∵g(x)= - ,∴g′(x)=- , 当 0<x<1 时,g′(x)>0,函数 g(x)单调递增, 当 1<x<+∞时,g′(x)<0,函数 g(x)单调递减, ∴g(x)max=g(1)= - =- ,∴f(x)min≥g(x)max,且 <1 ∴y=f(x)与 y=g(x)无交点, ∴函数 h(x)=f(x)-g(x)没有零点. 【解析】(1)先求导,再根据导数和函数的单调性和极值的关系即可求出;第 16 页,共 18 页(2)由(1)可得 f(x)min=- ,对 g(x)求导,求出函数 g(x)的最大值,即可判断 函数 h(x)=f(x)-g(x)的零点个数的个数. 本题考查了导数和函数的单调性和极值最值的关系,以及函数零点的个数,考查了运算能力和转化能力,属于中档题.22【. 答案】解:(Ⅰ)当 α= 时,C1 的普通方程为,C2 的普通方程为 x2+y2=1.联立方程组,解得 C1 与 C2 的交点为(1,0).(Ⅱ)C1 的普通方程为 xsinα-ycosα-sinα=0①. 则 OA 的方程为 xcosα+ysinα=0②, 联立①②可得 x=sin2α,y=-cosαsinα; A 点坐标为(sin2α,-cosαsinα),故当 α 变化时,P 点轨迹的参数方程为:,P 点轨迹的普通方程 故 P 点轨迹是圆心为 【解析】. ,半径为 的圆.(I)先消去参数将曲线 C1 与 C2 的参数方程化成普通方程,再联立方程组求出 交点坐标即可, (II)设 P(x,y),利用中点坐标公式得 P 点轨迹的参数方程,消去参数即得普 通方程,由普通方程即可看出其是什么类型的曲线. 本题主要考查直线与圆的参数方程,参数方程与普通方程的互化,利用参数 方程研究轨迹问题的能力.23.【答案】解:(1)f(x)=|x-1|+|2x+4|=,其图象见下图.第 17 页,共 18 页(2)x≤-2,不等式可化为-3x-3≥2x+5,∴x ,∴x≤-2; -2<x<1,不等式可化为 x+5≥2x+5,∴x≤0,∴-2<x≤0; x≥1,不等式可化为 3x+3≥2x+5,∴x≥2,∴x≥2; 综上所述,不等式的解集为{x|x≥2 或 x≤0}. 【解析】(1)去掉绝对值,写成分段函数形式,作出函数的图象. (2)分类讨论以去掉绝对值号,即可解关于 x 的不等式 f(x)≥2x+5. 本题考查了绝对值函数的应用及数形结合的思想方法应用,属于中档题.第 18 页,共 18 页。
宁夏银川唐徕回民中学2018届高三下学期第四次模拟考数学文试题 含答案 精品

银川唐徕回民中学2017~2018学年度第二学期高三年级第四次模拟考试数学试卷(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~23题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只 有一项是符合题目要求的.1.若复数i i a 213++(i 是虚数单位)是纯虚数,则其虚部为( ) A. -6 B. -6i C. 3 D. 3i2. 集合M={0,2t },N={22-,0,22},若M ∩N={0,22},则t =( ) A. 2 B. log 48 C. 43 D. 41 3. 函数x x y cos sin 3+=的最大值为( )A. 2B. 3C. 1D. 44. 右框为某程序语言,则该程序语言执行的是( )函数的功能.A. x y =B. x y -=C. ||x y =D. ||x y -=5. 已知实数y x ,满足⎪⎩⎪⎨⎧≤-+≥-≤-01020y x y x y x ,则目标函数y x z -=23的最小值为( ) A. 21 B. 41 C. 61- D. 41- 6. 已知数列{}{}n n b a ,,且)(*N n n a n ∈=,n a b n 2=,设n b 的前n 项和为n S ,则5S =( )A. 62B. 60C. 58D. 567. 已知双曲线Γ:12222=-bx a y (a >0,b >0)的一条渐近线与直线0123=+-y x 垂直,则双 曲线Γ的离心率为( ) A. 25 B. 213 C. 313 D. 413 8. 函数()||lg cos x x x f ⋅-=的部分图象是( )9. 某四棱锥的三视图如图所示,该四棱锥的表面积为( )A. 17B. 22C. 13214+D. 13222+10. 已知命题p :若函数()x f 在(b a ,)上存在零点,则()()0<⋅b f a f ;命题q :若()00='x g ,则()x g 在0x处取得极值,下列命题为真命题的是( )A. q p ∨B. q p ∧C. )(q p ⌝∨D. q p ∧⌝)( 11. 已知函数()x x x f -=sin ,则使得())21(2f f x >成立的x 的取值范围是( )A. (-1,1)B.(-∞,-1)C.(-∞,-1)∪(1,+∞)D.(1,+∞) 12. 某中学为了调查高三女生的健康状况,从高三年级随机选取8名女学生,得到其身高和体重数据如下表:有下列四种判断:①身高x 每增加1个单位,体重y 就大约增加0.849个单位②R 2越接近于1,表示回归的效果越好③女学生的体重差异有64%是由身高引起的④女学生的身高解释了64%的体重变化 A. ① B. ①② C. ①②③ D. ①②③④ 第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:( 本大题共4小题,每小题5分)13. 椭圆14922=+y x 的左焦点为___________. 14. 函数()1+=x e x f 在点(-1,f (-1))处的切线方程为__________.15. 不等式()()()01322≤++-x x x 的解集为_____________. 16. 如图,已知平行四边形ABCD 中,E ,M 分别为DC 的两个三等分点,F ,N 分别为BC 的两个三等分点,⋅=25,⋅=43,则22||||+=___________.三、解答题(本大题共5小题,共70分。
宁夏银川市唐徕回民中学高三下学期第四次模拟考试语文试题 Word版含答案

一、现代文阅读(9分,每小题3分)艺术操作是艺术创造才能的一个重要方面。
在艺术意象的生产过程中,艺术操作一方面是意象形成不可或缺的一个重要因素,另一方面又赋予意象以最终的形式符号,将意象孕育的成果物化为现实的可传达的艺术品。
表面看来,艺术操作纯然是一种外在的技艺,实际不然。
在艺术家准备操作时,心中的意象不一定已经非常清晰、完善,靠着操作运动,意象才逐渐鲜明、完整并得以最后定型、完成。
郑板桥讲他画竹的体会:“江馆清秋,晨起看竹,烟光日影霜气皆浮动于疏枝密枝之间。
胸中勃勃遂有画意。
其实胸中之竹,并非眼中之竹也。
因而磨墨展纸,落笔倏作变相,手中之竹又不是胸中之竹也。
”“胸中之竹”之所以不同于“眼中之竹”,是因为经过了艺术家的意象孕育和改造,这一目了然;而“手中之竹”又不同于“胸中之竹”,则常为人忽视。
其实,这是艺术家把心中孕育的意象用艺术操作加以表达并且用特定形式符号将之凝定下来。
因此,不能轻视艺术操作,它是意象孕育的继续与完成。
艺术操作是意象创造的有机组成部分和深化,人们应当重视艺术操作中的技能,因为所有的艺术操作作为一种实践活动,作为主体本质力量的对象化,是离不开特定的技能的。
一定意义上也可以说,艺术操作就是艺术技能的运用与发挥。
各种不同门类的艺术,由于其形式符号及传达媒介的不同,各有不同的操作和技能。
对于外行,由于不能掌握其操作技能,就不可能进入艺术的创作过程,即使有了“胸中之竹”,也变不成“手中之竹”。
因此,操作技能是艺术创作中极为重要的环节。
然而,如果离开艺术意象的创作过程,孤立地追求操作技能,就会沦为匠艺。
如一些广告画,就技能角度看,是符合“画”的要求的,然而缺乏艺术不可少的灵气,所以算不上真正的艺术。
这就涉及艺术创造中“技”与“道”的关系问题。
这里所谓的“道”是指艺术创造过程中自由无碍、充满生气的最高境界。
操作技能经过长期训练,娴熟自如,艺术家就能将它们化为自己的血肉,与对象世界亲密无间,从而进入“道”的自由境界。
宁夏银川2018届高三4月高中教学质量检测文综地理试题 含答案

宁夏银川市2018届高三4月高中教学质量检测文综地理试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3. 回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4. 考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷本卷共35小题。
每小题4分,共140分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
穿堂风也叫过堂风,是气象学中一种空气流动的现象,是流动于建筑物内部空间的风。
我国许多地区民居设计都充分考虑了穿堂风。
下为我国西南山区的传统民居景观图和该民居穿堂风示意图。
据此完成1-3题。
1. 图示中石质地面在增强“穿堂风”中的主要作用是A. 增加地面的平整度,便于通风B. 减少下渗,增强湿度C. 增加房屋前后温差D. 降低夜晚时庭院温度,便于纳凉2. 现代民居建筑若想利用穿堂风,以下设计合理的是A. 利用厨房、卫生间做进风口B. 房屋的朝向为东西向C. 减少东西向墙面的长度D. 在前后居室间墙上设窗或门洞3. 与空调冷风相比大多数人更喜欢穿堂风,主要是因为穿堂风A. 不消耗能源B. 风频与人体自然频率接近C. 风力恒定D. 风向恒定植被覆盖度指某一地域植物(包括叶,茎、枝)垂直投影面积与该地域面积之比,用百分数表示;它能够在一定程度上代表植被的生长状态和生长趋势。
下图示意我国某平原植被生长期内乔木林地和粮食作物耕地生态区植被覆盖度变化趋势,据此完成4-5题。
4. 该平原林地地带性植被可能是A. 常绿硬叶林B. 常绿阔叶林C. 落叶阔叶林D. 亚寒带针叶林5. 该地耕地生态区生长期内植被覆盖度出现双峰值的主要原因是A. 不同作物的主要生长期不同B. 同一作物有两个生长旺盛期C. 耕地生态区的田间管理不同D. 同一作物不同时期叶片大小不同珊瑚礁是成千上万的由碳酸钙组成的珊瑚虫的骨骼在数百年至数千年的生长过程中形成的,珊瑚虫生长的最佳环境是温度22-30℃、盐度34%-36%,水深不超过50米的海水,近年来,澳大利亚大堡礁因珊瑚礁内珊瑚虫逐渐死亡出现大规模白化现象,超过90%的珊瑚礁受到影响。
宁夏银川唐徕回民中学2018届高三下学期第四次模拟考理科综合试卷

银川唐徕回民中学2017~2018学年度第二学期第四次模拟考试高三年级理科综合试卷可能用到的相对原子质量:H-1 C-12 N-14 O-16 S-32 Ca-40 Ni-59 Cu-64 Ba-137第Ⅰ卷(必做,共126分)一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.关于细胞生命历程的叙述,正确的是A. 衰老的生物体中,细胞都处于衰老状态B. 原癌基因与抑癌基因在人体的正常细胞中不表达C. 细胞凋亡有利于多细胞生物体维持内部环境的稳定D. 细胞分裂间期完成DNA的复制和染色体数目的加倍2.为研究酶的催化效率,进行了相关实验,实验结果如下图所示。
据图分析,下列叙述错误..的是A. 增加酶浓度后m值将变大B. 曲线1和2说明酶具有高效性C. 曲线1和3说明酶具有催化作用D. 该实验需要控制温度等无关变量3.下列关于人体内环境与稳态的叙述,正确的是A.浆细胞能够特异性识别抗原B.肾小管细胞和下丘脑神经分泌细胞能够选择性表达抗利尿激素受体基因C.寒冷环境下正常机体通过各种途径减少散热,使散热量低于产热量D.饥饿时,血液流经肝脏后血糖浓度会升高4.下列关于生物实验操作、原理的说法中,不正确...的是A.糖类与斐林试剂在水浴加热的条件下生成砖红色沉淀B. 探究温度对酶活性影响实验中,不应选用过氧化氢酶C.T2噬菌体侵染大肠杆菌实验中,保温时间过短或过长,都会影响实验结果D. 探究生长素类似物促进扦插枝条生根的最适浓度实验中,必须设置空白对照5.下列关于遗传与进化的说法,错误..的是A.不同组织细胞中,可能有相同的基因进行表达B.不同tRNA分子中,可能含有相同的密码子C.判断生物进化及新物种形成的依据依次是种群的基因频率是否改变、是否产生生殖隔离D.AaBb(黄圆)x aabb(绿皱),后代表现型及比例为黄圆:绿皱:黄皱:绿圆=1:1:1:1,则说明控制黄圆绿皱的基因遵循基因的自由组合定律6.关于种群、群落和生态系统的叙述,正确的是A. 种群内的个体在水平方向的分布构成了群落的水平结构B. 环境容纳量也称K值,是指一定空间中种群的最大数量C. 生物多样性只包括物种多样性和生态系统多样性D. 捕食者的存在客现上起到促进被捕食者种群发展的作用7.下列有关化学与能源开发、环境保护、生产生活等的说法正确的是A. 开发利用可燃冰是缓解能源紧缺的唯一途径B. 将“地沟油”制成肥皂,可以提高资源的利用率C. 将聚氯乙烯制成食品保鲜膜和食品包装袋D. 在食品中大量添加苯甲酸钠等防腐剂,延长其保质期8.向100mL 0.1mol·L-1的AlCl3溶液中,加入1mol·L-1的NaOH溶液VmL后,再滴加1mol·L-1的盐酸.滴加盐酸的体积与生成的沉淀的质量有如图所示关系.则加入的NaOH溶液的体积V为A.10mLB. 30mLC. 40mLD. 50mL9.下列有机反应无论怎样调整反应物的用量,都只能生成一种物质的是A. 甲烷和Cl2混合后在光照条件下反应B. 甲苯与Br2发生反应C. 乙炔和H2的加成反应D. 乙烯与HCl的加成反应10.某烃R的结构简式如图所示: , 它的二氯代物有A. 4种B. 11种C. 12种D. 13种11.某原电池装置如图所示.下列有关叙述正确的是。
宁夏银川一中2018届高三第四次模拟考试数学(文)试卷(精编含解析)

2018年普通高等学校招生全国统一考试文科数学( 银川一中第四次模拟考试)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知,集合,集合,若,则A. 1B. 2C. 4D. 8【答案】A【解析】【分析】由题设有,因此,故可求出.【详解】因为,故,所以,故,又,因此,故选A.【点睛】本题考察集合的元素性质,属于基础题,解题时注意元素的确定性、互异性、唯一性的应用. 2. 若复数,复数,则A. B. C. D.【答案】B【解析】【分析】先计算,再求.【详解】,故,故选B.【点睛】本题考察复数的概念与运算,涉及到乘法运算和复数的模,为基础题.3. 已知命题:,,则:A. ,B. ,C. ,D. ,【答案】C【解析】【分析】全称命题的否定是存在性命题,按规则写出其否定即可.【详解】命题的否定为:.故选C.【点睛】一般地,全称命题“”的否定为“”,而存在性命题“”的否定为“”.4. 设,,,则A. B. C. D.【答案】A【解析】试题分析:因为,所以,应选A.考点:指数函数对数函数幂函数的图象和性质及运用.5. 函数的大致图象为A. B.C. D.【答案】C【解析】由,得,解得,.故函数的图象与轴的两个交点坐标为,,排除B、D.又,排除A,故选C.6. 地的天气预报显示,地在今后的三天中,每一天有强浓雾的概率为,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生0—9之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:则这三天中至少有两天有强浓雾的概率近似为A. B. C. D.【答案】D【解析】由随机数表可知,满足题意的数据为978,479,588,779,据此可知,这三天中至少有两天有强浓雾的概率近似为选D.7. 我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是A. B.C. D.【答案】D【解析】【分析】此算法为循环结构,共循环7次,故①处填判断语句,②填取半计算,③填循环控制变量的变化方式. 【详解】算法为循环结构,循环7次,每次对长度折半计算,也就是,因此②填,又①填判断语句,需填,③填.故选D.【点睛】本题考察算法中的循环结构,属于基础题.此类问题,注意循环的次数,如本题7天后木棍的长度为尺,故需执行7次,由此判断出循环所需次数.8. 已知实数,满足,则的最大值为A. 1B. 2C. 4D. 8【答案】B【解析】【分析】画出可行域,算出可行域中的点到的距离的最大值即可.【详解】可行域如图所示:又表示可行域中的点与之间连线的长度,其最大值为与之间连线的长度,其大小为,故选B.【点睛】在二次一次不等式组的条件下考虑二元目标函数的最值问题,往往需要利用线性规划来处理,注意寻找二元目标函数的几何意义,常见的二元目标函数有:(1),表示;与定点的连线的斜率;(2),表示与定点之间的距离.9. 某四棱锥的三视图如图所示,其中正视图是斜边为等腰直角三角形,侧视图和俯视图均为两个边长为1的正方形,则该四棱锥的高为A. B. 1 C. D.【答案】A【解析】几何体是是如图放置的四棱锥,是正方体中切除一个三棱柱,再切除一个三棱锥所得到的几何体,该正方体的棱长为1,高为到平面的距离,此距离为,故选A.10. 将函数y=sin(2x+φ)的图像沿x轴向左平移个单位后,得到一个偶函数的图像,则φ的一个可能取值为A. B. C. 0 D.【答案】B【解析】试题分析:由题意得关于轴对称,所以的一个可能取值为,选B.考点:三角函数图像变换【思路点睛】三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母x而言. 函数y=Asin(ωx+φ),x∈R是奇函数⇔φ=kπ(k∈Z);函数y=Asin(ωx+φ),x∈R是偶函数⇔φ=kπ+(k∈Z);函数y=Acos(ωx+φ),x∈R是奇函数⇔φ=kπ+(k∈Z);函数y=Acos(ωx+φ),x∈R是偶函数⇔φ=kπ(k∈Z);视频11. 已知数列的首项,满足,则A. B. C. D.【答案】C【解析】【分析】由,两式相加可得,利用“累加法”可得结果.【详解】,,两式相加有;且,,,故答案为C.【点睛】由数列的递推公式求通项常用的方法有:(1)等差数列、等比数列(先根据条件判定出数列是等差、等比数列);(2)累加法,相邻两项的差成等求和的数列可利用累加求通项公式;(3)累乘法,相邻两项的商是能求出积的特殊数列时用累乘法求通项;(4)构造法.12. 已知函数函数恰有一个零点,则实数的取值范围为A. B.C. D.【答案】C【解析】分析:作出f(x)的函数图象,根据图象判断m的值.详解:令g(x)=0得f(x)=m,作出y=f(x)的函数图象如图所示:由图象可知当m<0或<m≤4时,f(x)=m只有一解.故答案为:C点睛:本题有两个解题技巧,一是分离参数法,高中数学中经常用到分离参数法,在有的问题中可以提高解题效率,优化解题. 二是数形结合处理零点问题,零点问题是高中数学中的一个重要问题,处理它常用的就是数形结合,非常直观地形象地看到图像的零点的个数情况.在今后的学习中,大家注意灵活使用.二、填空题:本大题共4小题,每小题5分.13. 若双曲线的渐近线与圆相切,则的渐近线方程为__________.【答案】【解析】【分析】先求出渐近线的方程,利用圆心到渐近线的距离为半径计算即可.【详解】渐近线方程为:.因为渐近线与圆相切,故,所以,故渐近线方程为.填.【点睛】一般地,求双曲线的渐近线的方程,可以把等号右边的常数变为即可,同理共渐近线的双曲线的标准方程可假设为.14. 已知{a n}是等差数列,a1=1,公差d≠0,S n为其前n项和,若a1,a2,a5成等比数列,则S8=________.【答案】64【解析】因为a1,a2,a5成等比数列,则=a1·a5,即(1+d)2=1×(1+4d),解得d=2.所以a n=1+(n-1)×2=2n-1,a8=2×8-1=15,S8==4×(1+15)=64.视频15. 已知向量,,,则实数的值为____________.【答案】16【解析】【分析】原数量积等价为,用坐标代入计算即可得的值.【详解】由题设有,所以,故,填.【点睛】本题考察数量积的坐标运算,属于基础题.16. 设正实数满足,则的最小值为__________.【答案】1【解析】【分析】把化为,再用基本不等式求最小值.【详解】因为,所以,由基本不等式有,当且仅当即时取等号,故所求最小值为,故填1.【点睛】应用基本不等式求最值时,要注意“一正二定三相等”,如果代数式中没有和为定值或积为定值,我们需要对代数式变形以便有和或积为定值的局部结构.注意对取等条件的验证.三、解答题:解答应写出文字说明,证明过程或演算步骤.17. 已知函数的图象过点.(1)求m的值;(2)在△ABC中,角A、B、C的对边分别是a、b、c,若ccosB+bcosC=2acosB,求的取值范围.【答案】(1);(2)【解析】试题分析:(Ⅰ)利用二倍角公式和配角公式化简函数解析式,代点求值;(Ⅱ)利用正弦定理将边角关系转化为角角关系,进而求出,再利用角的范围和三角函数的性质进行求解.试题解析:(Ⅰ)由因为点在函数的图象上,所以.(Ⅱ)因为所以所以即又因为所以所以又因为所以所以;令,,所以的取值范围是.18. 在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标和,制成下图,其中“”表示甲村贫困户,“”表示乙村贫困户.若,则认定该户为“绝对贫困户”,若,则认定该户为“相对贫困户”,若,则认定该户为“低收入户”;若,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.(1)从乙村的50户中随机选出一户,求该户为“绝对贫困户”的概率;(2)从甲村所有“今年不能脱贫的非绝对贫困户”中任选2户,求选出的2户均为“低收入户”的概率;(3)试比较这100户中,甲、乙两村指标的方差的大小(只需写出结论).【答案】(1);(2);(3)见解析【解析】试题分析:(1)由图知,在乙村户中,指标的有户,根据古典概型概率公式可得结果;(2)利用列举法可得,所有可能的结果组成的基本事件有个,其中两户均为“低收入户”的事件共有个,根据古典概型概率公式可得选出的户均为“低收入户”的概率;(3) 由图可知,这户中甲村指标的方差大于乙村指标的方差..试题解析:(1)由图知,在乙村50户中,指标的有15户,所以,从乙村50户中随机选出一户,该户为“绝对贫困户”的概率为.(2)甲村“今年不能脱贫的非绝对贫困户”共有6户,其中“相对贫困户”有3户,分别记为,,.“低收入户”有3户,分别记为,,,所有可能的结果组成的基本事件有:,,,,,, , , ,, , ,,,.共15个,其中两户均为“低收入户”的共有3个, 所以,所选2户均为“低收入户”的概率.(3)由图可知,这100户中甲村指标的方差大于乙村指标的方差.【方法点睛】本题主要考查古典概型概率公式的应用,属于难题,利用古典概型概率公式求概率时,找准基本事件个数是解题的关键,基本亊件的探求方法有 (1)枚举法:适合给定的基本事件个数较少且易一一列举出的;(2)树状图法:适合于较为复杂的问题中的基本亊件的探求.在找基本事件个数时,一定要按顺序逐个写出:先,….,再,…..依次….… 这样才能避免多写、漏写现象的发生. 19. 如图,在长方形中,,,现将沿折起,使折到的位置且在面的射影恰好在线段上.(1)证明:; (2)求三棱锥的表面积.【答案】(1)见解析;(2)【解析】试题分析:(Ⅰ)由平面,可得,结合,可得平面,由此可得,又∴平面;又平面,所以;(Ⅱ)在中,由(Ⅰ)得,,∴,,∴∴,而的面积都可以利用直角三角形面积公式求得,四个三角形面积相加即可得结果. 试题解析:(Ⅰ)由题知平面,又平面,∴;又且,∴平面;又平面,∴;又且,∴平面;又平面,所以.(Ⅱ)在中,由(Ⅰ)得,,∴,∴∴在中,,,∴,在中,∴,∴,所以三棱锥的表面积为20. 已知椭圆的左、右焦点分别为、,点在椭圆上,有,椭圆的离心率为;(1)求椭圆的标准方程;(2)已知,过点作斜率为k(k>0)的直线与椭圆交于,不同两点,线段的中垂线为,记的纵截距为,求的取值范围.【答案】(1);(2)【解析】【分析】(1)根据椭圆的定义得到的值,再根据离心率得到的值,从而计算出即得椭圆方程.(2)设,联立直线方程和椭圆方程,利用韦达定理算出的中点坐标(用表示),再计算中垂线的直线方程,从而得到,而由直线与椭圆相交可得,最后利用导数求的取值范围.【详解】(1)因为,所以,所以,因为,所以,所以,所以椭圆的标准方程为.(2)由题意可知直线的斜率存在,设:,,,联立直线与椭圆,消去得,·,,·又,解得:,·故.设,的中点为,则,,所以:,即,化简得:,令,得,,,当时,恒成立,所以在上为增函数,所以.【点睛】求椭圆的标准方程,可以用定义法或待定系数法确定基本量.直线与椭圆位置关系中的对称问题,需要联立方程组并消元,再用韦达定理把要求解的目标表示成关于斜率的代数式,最后再利用导数或不等式等工具讨论该代数式的性质.21. 已知函数.(1)若,求曲线在点处的切线方程;(2)若,恒成立,求实数的取值范围;【答案】(1);(2)【解析】试题分析:(1)当时,,∴,∴切线的斜率,又,即可得曲线在点处的切线方程;(2),,因为,恒成立,所以在上恒成立,令,求导研究单调性得出,即可得实数的取值范围.试题解析:(1)当时,,∴,∴切线的斜率,又,∴在点处的切线方程为,即.(2)∵,∴,∵,恒成立,∴在上恒成立,令,则,当时,;当时,,∴在上单调递减,在上单调递增,∴,∴,即实数取值范围为.点睛:本题处理不等式恒成立问题选用了变量分离的方法,先再式子两边同除以x简化表达式,通过构造新函数研究函数的最值即可得出参数范围.22. 在平面直角坐标系中,以原点为极点,以轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线1的极坐标方程为:.(1)若曲线的参数方程为:(为参数),求曲线的直角坐标方程和曲线的普通方程;(2)若曲线的参数方程为(为参数),,且曲线与曲线的交点分别为P、Q,求的取值范围.【答案】(1),;(2)【解析】分析:第一问首先应用极坐标与平面直角坐标的转换关系,求得曲线的直角坐标方程,之后对曲线的参数方程进行消参,求得其普通方程;第二问将曲线的参数方程代入的方程,得到关于的关系式,利用韦达定理求得两个和与两根积的值,之后应用参数的几何意义以及题中所求得的范围,最后借助于对三角函数值域的求解求得结果.详解:(1)曲线的直角坐标方程为:曲线的普通方程为:(2)将的参数方程:代入的方程:得:由的几何意义可得:点睛:该题所考查的是有关极坐标方程与平面直角坐标方程的转化,参数方程与普通方程的转化,直线与曲线相交时,有关线段的长度问题与直线的参数方程中参数的几何意义,以及韦达定理的应用,并且借助于三角形函数来完成,要注意关于角的范围是通过判别式大于零所求得的.23. 已知函数.(1)若,解不等式;(2)若不等式对任意的实数恒成立,求的取值范围.【答案】(1);(2)【解析】分析:第一问先将代入解析式,之后应用零点分段法将绝对值不等式转化为若干个不等式组,最后取并集即可得结果;第二问将恒成立问题转化为最值问题来处理,应用绝对值的性质,将不等式的左边求得其最小值,之后将其转化为关于b的绝对值不等式,利用平方法求得结果.详解:(1)所以解集为:.(2)所以的取值范围为:.点睛:该题考查的是有关绝对值不等式的求解问题,在解题的过程中,需要用到零点分段法求绝对值不等式的解集,再者对于恒成立问题可以向最值来转化,而求最值时需要用到绝对值不等式的性质,之后应用平方法求解即可得结果.。
银川唐徕回中第二学期高三年级四模考试.doc

银川唐徕回中2014~2015学年度第二学期高三年级四模考试数学试卷(理科)(考试时间:120分钟;满分:150分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知i 为虚数单位,则复数iiz 325+-=在复平面内表示的点位于( ) A .第四象限 B .第三象限C .第二象限D .第一象限2.函数()2212+++=x x x x f 的值域是( ) A .21(-,)21 B .-∞(,)21-∪21[,)∞+C .21[-,]21 D .[-1,1]3.已知等差数列{}n a 的公差为()0≠d d ,且32131063=+++a a a a ,若8=m a ,则m 的值 为( ) A .12 B .8C .6D .44.已知样本:10 8 6 10 13 8 10 12 11 7 891191291011 1211那么频率为0.2的范围是( )A .5.5~ 7.5B .7.5~ 9.5C .9.5~ 11.5D .11.5 ~ 13.55.在()()()5043111x x x ++++++Λ的展开式中,3x 的系数为( )A .351C B .450CC .451CD .447C6.由曲线x y =,直线2-=x y 及y 轴所围成的封闭图形的面积为( )A .316 B. 310C. 4D. 67.设m ,n 是两条不同的直线,βα,是两个不同的平面,则下列命题不正确的是( ) A .βαβα⊥⇒⊥n m n m ////,, B .αα⊥⇒⊥n n m m //, C .βαβα⊥⇒⊂⊂⊥m n n m ,, D .n m n m m ////⇒=⊂βααβI ,,8. 一个算法的程序框图如图所示,如果输入的x 的值为2014, 则输出的i 的结果为( ) A .3 B. 5C. 6D. 89. 假如清华大学给某市三所重点中学7个自主招生的推荐名额, 则每所中学至少分到一个名额的方法数为( ) A .10 B. 15 C. 21 D. 30 10.函数()12sin cos 442f x x x ππ⎛⎫⎛⎫=+-- ⎪ ⎪⎝⎭⎝⎭在y 轴右侧的零点按横坐标从小到大依次记为123,,,P P P L ,则24P P 等于( )A. πB. 2πC. 3πD. 4π11.已知F 1、F 2为双曲线C :22221x y a b-=的左、右焦点,P 为双曲线C 右支上一点,且PF 2⊥F 1F 2,PF 1与y 轴交于点Q ,点M 满足123F M MF =u u u u r u u u u r,若MQ ⊥PF 1,则双曲线C 的离心率为( )A. 2B. 3C.232+ D.262+ 12. 设10e x <<,记()()()()ln ln ,lg lg ,ln lg ,lg ln a x b x c x d x ====则,,,a b c d 的大小关系( )A. a b c d <<<B. c d a b <<<C. c b d a <<<D. b d c a <<<二、填空题:(本大题共4小题,每小题5分,共20分)13. 若等边△ABC 的边长为1,平面内一点M 满足,则= .14.若各项均为正数的等比数列{n a }满足123a a a =5,789a a a =10,则192021a a a =________.15. 点P(x ,y )在不等式组⎪⎩⎪⎨⎧+≥≤+≥130x y y x x 表示的平面区域内,若点P(x ,y )到直线()01>-=k kx y 的最大距离为22,则k = .16. 已知点F 为抛物线28y x =-的焦点,O 为原点,点P 是抛物线准线上一动点,A 在抛物线上,且4AF =,则PA PO +的最小值是 .三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.17.(本小题满分12分)在△ABC 中,已知A=4π,255cos B =.(I )求cosC 的值;(Ⅱ)若BC=25,D 为AB 的中点,求CD 的长. 18.(本小题满分12分)实验中学的三名学生甲、乙、丙参加某大学的自主招生考核测试,在本次考核中只有合格和优秀两个等次,若考核为合格,则授予10分降分资格;考核为优秀,授予20分降分资格。
宁夏银川2018届高三4月高中教学质量检测文科综合试题。含答案

宁夏银川2018届高三4月高中教学质量检测文科综合试题。
含答案银川市2018年高三质量检测文科综合试卷地理试题答案:36.(24分)1)该地地面起伏较小,东北部、西北部、西南部高,中部、东南部低。
(4分)2)该地泵站将水位较低的河水抽到地势较高的干渠,干渠将灌溉用水分配给灌渠,灌渠将水引入农田灌溉,排水渠将灌溉余水或洪水排入水位较低的下游河道。
(2分)3)该地降水不稳定,有旱涝灾害,农业技术落后,经济条件差,机械化水平低。
(2分)4)可以通过改良作物品种,提高机械化水平,改良种植技术,提高复种指数来改善该地的农业生产。
(任答两点得4分,其它合理答案亦可酌情给分)37.(22分)1)该物流系统可以缩短收货时间,购物价格低,用户体验好。
(2分)2)德国经济发达,是我国出口商品的重要市场,地处欧洲中部,地理位置优越,是中欧铁路的重要枢纽,德国交通网络发达,便于货物迅速运往欧洲各国。
(2分)3)由于西欧面积较小且以平原为主,水陆交通便利,对仓库的需求量小;经济发达区,地价高,建仓成本高,储量大,剩余货物难处理,原有商业庞大完善,竞争激烈。
(2分)43.参观萤火虫洞洞穴时,不要用手触摸钟乳石及石笋及岩壁,避免破坏萤火虫的生长环境,在萤火虫洞洞穴内必须保持宁静,全程禁止使用相机及录像机,避光以免影响萤火虫捕食生长,必须跟着团队一同行动以便向导照顾,避免在湿黑的萤火虫洞洞穴内发生意外,禁烟保持空气清新。
(任答五点即可,其它合理答案亦可酌情给分)44.在对流层顶部或平流层,由于不受云层云系影响,可以使用白色食盐粉末反射太阳辐射,减少到达地面太阳辐射,从而缓解全球变暖状况。
(3分)但是食盐中的氯离子可能破坏臭氧层,二氧化硫可能加剧酸雨危害。
(2分)政治选择答案:13-16 CDDAC,17-21 DCBAB,22-23 BA。
38.农业作为国民经济的基础,解决“三农”问题是当前最重要的任务。
同时,全面建设小康社会、实现共同富裕也需要发展农业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018届宁夏银川唐徕回民中学高三下学期第四次模拟考文科综合地理试题地理注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第I 卷(选择题)一、选择题组青海省共和县塔拉滩(图甲)以戈壁沙丘为主,是黄河上游风沙危害最严重地区之一。
2011~2017年,塔拉滩地区大力发展光伏产业,建成数十个光伏企业集聚的产业园。
光伏产业发展促进了生态改善,植被不断恢复,沙丘移动明显减缓。
但植被恢复对光伏发电效率产生了不利影响,为此园区引入牧羊业(图乙),形成了良性循环。
读下图,完成下列各题。
1.塔拉滩地区面临的主要生态环境问题是( )A. 水土流失B. 草场退化C. 土地盐碱化D. 森林破坏2.光伏产业促进了塔拉滩的植被生长,关键是因为太阳能电池板( )A. 阻挡风沙,减弱风力侵蚀B. 反射阳光,改善光照条件C. 吸收热量,增加土壤温度D. 减弱蒸发,提高土壤水分 3.光伏产业园区引入牧羊业,有利于( ) A. 减缓沙丘移动速度 B. 提高水电发电量 C. 提高土地利用率 D. 增加植被覆盖率 2014年上海市建设用地开发强度为46%,已超过东京、香港等国际大都市,“十三五”期间上海市将“人口天花板”设定为2500万。
下图为“2001-2017年上海市人口变化图”回答下列各题。
4.影响上海市人口“天花板"的主要因素是( ) A. 土地资源 B. 水资源 C. 生物资源 D. 矿产资源 5.上海市( ) A. 常住外来人口增长率先增后减 B. 2017年常住外来人口约占15% C. 户籍人口基本保持稳定 D. 常住人口持续快速增加 传统经济发展模式的转变推动了企业区位偏好的改变,时间价值成为影响企业决策的重要因素,机场周边地区成为驱动城市经济增长的新型经济空间。
下图示意北京首都机场(距市中心25千米)附近制造业、物流业、金融业和商务服务业(咨询、广告、中介等)的分布密度。
读下图,完成下列各题。
此卷只装订不密封班级姓名准考证号考场号座位号6.图中表示物流业分布密度变化的曲线是()A. ①B. ②C. ③D. ④7.在该区域内空间布局最灵活的产业是()A. ①B. ②C. ③D. ④8.该区域的制造业最可能是()A. 玩具制造业B. 生物制药业C. 电力工业D. 钢铁工业下图示意伏尔加河三角洲位置变化及里海海平面变化,结合相关知识,完成下列各题。
9.1900~1978年伏尔加河三角洲变化的特点有()①增速先慢后快②向东南方向扩展③面积不断增大④坡度逐渐趋缓A. ①②B. ①③C. ②③D. ②④10.2000年该三角洲的前缘位置可能位于()A. 甲处B. 乙处C. 丙处D. 丁处11.若在该河中上游修建大型水库,将导致河口及附近水域()A. 河口盐碱化加剧B. 生物多样性增加C. 三角洲面积缩小D. 水位季节变化增大第II卷(非选择题)二、综合题12.阅读图文材料,完成下列要求。
俄罗斯亚马尔半岛(下图)油气资源储量丰富,已探明天然气储量1.3万亿立方米。
2016年,俄罗斯、中国、法国在此进行世界最大的液化天然气(LNG)项目开发。
液化天然气是将气态天然气经超低温液化而成,是地球上最干净的化石能源,其体积约为同等质量气态天然气的1/625,使用特殊船只运輸。
亚马尔项目工程釆取模块化建设方案,整个项目设施由模块组成,不同种类的模块在全球多地制造完成后运往亚马尔半岛,随后在现场进行组装。
其中85%的模块由中国企业承揽建造,仅一年工期便完成项目设施建设。
2017年12月,项目正式投产,俄罗斯在世界液化天然气市场中的比例随之达到10%。
随着北极航道的逐步开辟,亚马尔项目成为“冰上丝绸之路”中俄合作的经典范例。
(1)简析在亚马尔开展液化天然气项目的优势条件。
(2)分析亚马尔液化天然气项目采取模块化建设的主要原因。
(3)因受海况条件影响,冬季运往中国的液化天然气运输船需向西绕行欧洲并经过大西洋、印度洋和太平洋。
试分析其主要原因。
(4)简述亚马尔项目对俄罗斯能源开发的积极影响。
13.阅读图文材料,完成下列要求。
港珠澳大桥主体工程已经全线贯通,预计将在2018年7月1日前正式通车。
大桥通车将推动粤港澳大湾区建设成为更具活力的经济区、宜居宜业宜游的优质生活圈和内地与港澳深度合作的示范区,打造国际一流湾区和世界级城市群。
下图为粤澳港大湾区和港珠澳大桥示意图。
下表为粤港澳大湾区与世界其他大湾区基本情况对比表。
(1)从自然角度,分析港珠澳大桥建设面临的困难。
(2)与其他世界三大湾区相比,指出粤港澳大湾区的优势条件。
(3)对比其他湾区,粤港澳大湾区建设成世界级大湾区需要采取哪些措施。
(4)分析粤港澳大湾区建设对我国社会经济发展的影响。
14.(旅游地理)2017年8月8日九寨沟风景区因7级地震关闭,2018年3月8日正式对外开放。
本次开放的特点:①不是全景开放,只开放了沟口到长海沿途景观,其中长海、五彩池、诺日朗瀑布(如图)、树正群海、双龙海5个景点为徒步游览(以前可以坐车)。
②实行专车专导,团队游览方式,实行原车原回(以前是滚动发车路边招手即上)。
③全年限流,每天限量2000人/天,(以前是旺季限流,人数是4万/天),并必须实名先预约,现场实名验票。
④实行了新的票价,2018年全年110元/张,观光车90元/人。
(以前是旺季220元/人,淡季80元/人)。
⑤目前接待对象仅限旅行社组织的团队游客,且旅行社必须为游客购买意外保险。
说说九寨沟风景区本次对外开放调整的主要目的。
15.(环境保护)2018年3月29日一则视频引人关注,河北一灌农田水井像往常一样,往外流出泛红的井水,再沿着沟渠淌进农田,而不远处就是一家化工厂。
事件发生后,“生态环境部”4月21日发布消息,通报了河北省宁晋县“红水浇地”案件的调查进展,并称当地公安机关已依法对该企业4名负责人和直接责任人实施刑事拘留。
宁晋县政府已聘请专业机构开展水土修复工作。
试分析“红水浇地”产生的危害并提出防止类似事件发生的主要措施。
2018届宁夏银川唐徕回民中学高三下学期第四次模拟考文科综合地理试题地理答案1.B2.D3.C【解析】1.根据材料所述“青海省共和县塔拉滩(图甲)以戈壁沙丘为主,是黄河上游风沙危害最严重地区之一。
”可推断,该处主要的生态环境问题应为草场退化,土地沙化,B正确。
而水土流失、土地盐碱化,森林破坏都不属于该地区的生态环境问题,A、C、D错。
2.据图乙可知:太阳能板遮挡的地方,草类茂盛,结合该地区干旱多风沙的自然环境可知,该地区植被生长的限制性因素主要是水分。
太阳能板阻挡太阳光,产生“阴坡效应”,减少土壤水分蒸发,可以使植被更好地生长,D正确;排除ABC。
3.光伏产业是一种占地面积广大的产业,在发展光伏产业的同时能够发展牧羊,充分利用了土地资源。
再加上太阳能板阻挡光照,减少蒸发,草类茂盛,为牧羊提供了极为有利的条件。
C正确;牧羊会减少植被覆盖,从而加快沙丘移动,减少河流流量,降低发电量,所以ABD错。
4.A5.C【解析】4.人口“天花板”是指一个地区人口规模上限,上海市土地面积小,城市化速度快,城市用地紧张,所以限制上海市人口“天花板”的主要因素是土地资源,A正确。
BCD错。
5.由题可知,户籍人口=常住人口-常住外来人口,观察柱状图变化可推测出户籍人口比较稳定,C正确;常住外来人口率波动明显,并不是先增后减,A错;2017年常住外来人口的增长率为15%,而人口约占总人口的27%,由900/2400+900可得,B错。
由图可知,常住人口呈缓慢增长状态,而不是持续快速增加,D错。
【点睛】该题主要考察人口问题,弄清“常住人口”“常住外来人口”“户籍人口”几个概念的关系。
搞清楚图表里的人口数量轴和增长率轴,不可混淆。
6.D7.A8.B【解析】6.物流业要求交通便利,应在距机场近的范围内密度最大,距机场远,交通条件差,密度小。
图中表示物流业分布密度变化的曲线是①,在机场附近密度最大,A对。
B、C、D错。
7.商业服务业包括咨询、广告、中介等,需要广泛分布到各处,布局最灵活。
该区域内空间布局最灵活的产业是④,距机场远近对密度影响不大,D对。
其它受机场距离影响较大,布局不够灵活,A、B、C错。
8.该区域的制造业需要靠近飞机场,说明产品需要进行航空运输。
产品特点是轻薄短小,附加值高,最可能是生物制药业,C对。
电力工业产品不需要空运,A错。
钢铁工业是笨重产品,不适宜空运,B错。
玩具制造业体积较大,附加值低,不宜空运,D错。
9.C10.B11.A【解析】9.从左图可以看出伏尔加河三角洲从1900—1978年的变化是:面积扩大;增速减缓;向东南方向扩展,综合各点C正确;从图中读不出坡度变化,④错。
10.由右图可知,里海2000年的海平面高度与1920-1940之间高度一致,所以2000年时该三角洲的前缘位置应位于1920-1940年之间,即乙处,B正确。
11.在河流上游修建水库,会对下游水文特征产生影响,尤其使入湖水量减少,湖泊水位下降,含盐量增加,河口盐碱化加剧,A正确。
入湖水量减少,会导致生物多样性减少;湖泊水位下降,三角洲面积增大,BC错;水库具有调节作用,水位季节变化减小,D错。
【点睛】突破该题的关键在于把左右两图进行对比,尤其对于第2题至关重要。
另外需要清楚伏尔加河和里海的关系,以及修建水库的一般意义,对于做此类题目十分重要。
12.((1)亚马尔天然气储量丰富,油气资源充足;北极地区低温环境,有利于天然气液化;北极航道交通便利;国际市场广阔。
(2)气候严寒,冻土广布,且冬季昼长较短,施工环境恶劣;人口稀少,基础设施不完善,模块化建设利于减少建设成本,加快建设时间,提高工程效率。
(3)通往欧洲的航线纬度较低,且受暖流影响,受海冰影响小。
(或通往中国的航线纬度较高,且受寒流影响,受海冰影响大。
(4)对天然气进行深加工,增加能源附加值;提高俄罗斯液化天然气产能,强化俄罗斯在世界液化天然气市场中的地位;天然气外运采用船运与管道结合的方式,优化俄罗斯天然气输出结构。
【解析】(1)工业区位条件应从资源、交通、市场、科技、劳动力等方面分析。
据材料可知,俄罗斯亚马尔半岛油气资源储量丰富;液化天然气是将气态天然气经超低温液化而成,据图可知,北极地区低温环境,有利于天然气液化;据图可知,随着北极航道的逐步开辟,北极航道交通便利;据材料知俄罗斯在世界液化天然气市场中的比例随之达到10%,国际市场广阔。
