山东省济南市长清区2018届九年级数学第一次模拟考试试题
山东省济南市长清区九年级数学第一次模拟考试试题(扫

山东省济南市长清区2018届九年级数学第一次模拟考试试题九年级数学参考答案一、选择题(每题4分,共48分)二、填空题(每题4分,共24分)13.x(x+y) 14.> 15.6 16.7 17.100 18.-24 19、解:(1)原式=32……2分=1-…………3分(2) 原式=a2-6+2a-a2………2分,=2a-6………3分20.(1)解①得:x<4………1分≥………2分解②得:x2所以原不等式组的解集是2≤x<4………3分(2)由x2-4x+3=0得(x-1)(x-3)=0………1分∴x-1=0或x-3=0………2分∴x1=1,x2=3………3分21.(1)解:∵BC∥OD∴∠B=∠AOD………1分∵AB是直径,∴∠ACB=90。
,………2分(3)画树状图为:共有6种等可能的结果数,其中一男生一女生的结果数为4, ………6分所以刚好抽到一男生一女生的概率3264==P .………8分 23.解:设购买了荔枝x 千克,则购买芒果(30-x)千克.………1分根据题意列方程得:26x+22(30-x)=708,………4分,解得:x=12,30-x=18.………7分答:购买了无核荔枝12千克,购买鸡蛋芒果18千克.…8分24.解:∵∠CBF=60°, ∠CAF=30°,∠CBF=∠CAF+∠BFA∴∠BFA=30°……………………3分∴AB=BF ,∵AB=800米∴AB=BF=800米……………………4分∵∠BCF=90°,∠CBF=60°,答:竖直高度CF 约为680米.……………………8分25. (1)∵点A(2,3)在y=mx 的图象上∴m=6,∴反比例函数的解析式为:y=x6,............2分 ∵B(−3,n)在反比例函数图象上,∴n=6÷(-3)=−2,∵A(2,3),B(−3,−2)两点在y=kx+b 上,∴⎩⎨⎧+-=-+=b k b k 3223解得:⎩⎨⎧==11b k ∴一次函数的解析式为:y=x+1;……4分 (2)−3<x<0或x>2;……6分 (3)以BC 为底,则BC 边上的高AE 为3+2=5,∴S △ABC=21×2×5=5.……10分 26.(1)CE=AF ;……1分证明:在正方形ABCD,等腰直角三角形CEF 中,FD=DE,CD=CA,∠ADC=∠EDF=90∘ ∴∠ADF=∠CDE ,∴△ADF ≌△CDE ,∴CE=AF.……4分(2)∵DE=1,AE=7,CE=3,∴CE=AF=3,EF=2,……5分∵AE2+EF2=7+2=9,AF2=9,即AE2+EF2=AF2∴△AEF为直角三角形,……7分∴∠BEF=90∘∴∠AED=∠AEF+DEF=90∘+45∘=135∘;……8分(3)∵M是AB中点,∴MA=21AB=21AD,∵AB∥CD,∴21===DCAMOCOAODOM,……9分在Rt△DAM中,DM=5222=+AMAD∴DO=354,∵OF=35,∴DF=5,……10分∵∠DFN=∠DCO=45∘,∠FDN=∠CDO,∴△DFN∽△DCO,……11分373543535445,=-=-=∴=∴=∴=∴DNCDCNDNDNDODNDCDF……12分27.(1)∵C(0,4),∴OC=4.∵OA=OC=4OB,∴OA=4,OB=1,∴A(4,0),B(−1,0),设抛物线解析式:y=a(x+1)(x−4),∴4=−4a,∴a=−1.∴y=−x2+3x+4.……3分(2)存在. ……4分作PN⊥x轴交AC于N,求得AC的解析式为y=-x+4 ……5分设P(x,−x2+3x+4),则N(x,-x+4),得PN=(−x2+3x+4)-(-x+4)=−x2+4x……6分S△PAC=21PN×4=2PN=2(−x2+4x)=-2(x-2)2+8……7分∴P点坐标为(2,6)时ΔPAC面积的最大值,最大面积是8…………8分(3)Q(0,0),(-4,0),()()0,244,0,244-+. ……12分。
2018年山东省济南市长清区中考数学一模试卷带解析答案

D.x<1
10. (4 分)抛物线 y=2(x+3)2+1 的顶点坐标是( A. (3,1) B. (3,﹣1) C. (﹣3,1)
D. (﹣3,﹣1)
11. (4 分)如图,直线 y=﹣
x+2 与 x 轴、y 轴分别交于 A、B 两点,把△AOB )
沿直线 AB 翻折后得到△AO′B,则点 O′的坐标是(
25. (10 分) 如图, 一次函数 y=kx+b 与反比例函数 y= 的图象相交于 A (2, 3) , B(﹣3,n)两点. (1)求一次函数与反比例函数的解析式; (2)根据所给条件,请直接写出不等式 kx+b> 的解集; (3)过点 B 作 BC⊥x 轴济南市长清区中考一模数学试卷
一、选择题(本大题共 12 小题,每小题 4 分,共 48 分。在每小题给出的四个 选项中,只有一项是符合题目要求的) 1. (4 分)2018 的相反数是( A.8102 B.﹣2018 ) C. D.2018 )
A. (
,3)
B. (
,
)
C. (2,2
)
D. (2
,4)
12. (4 分)如图,抛物线 y=ax2+bx+c 的对称轴是 x=﹣1,且过点( ,0) ,有 下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0; ⑤a﹣b≥m(am﹣b) ;其中所有正确的结论有( )个
B.1.008×106
5. (4 分)下列图案中既是中心对称图形,又是轴对称图形的是(
A.
B.
C.
D. )
6. (4 分)如图所示的几何体是由 4 个相同的小正方体组成.其主视图为(
2018年山东省济南市长清区中考一模数学试卷和答案PDF
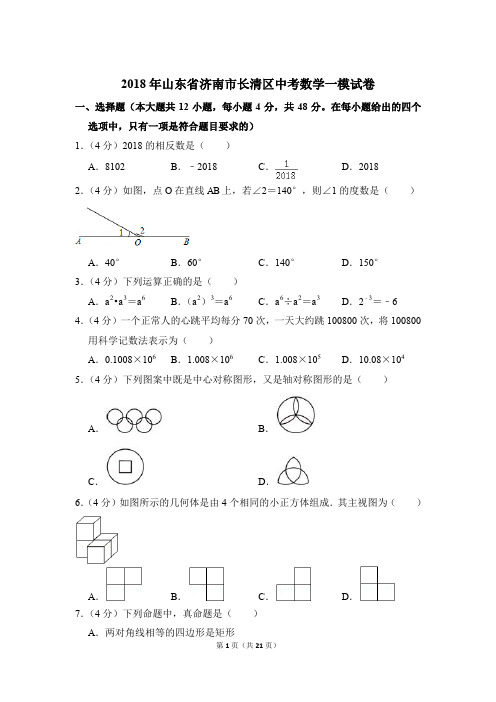
22. (8 分)为进一步推广“阳光体育”大课间活动,高新中学对已开设的 A 实 心球,B 立定跳远,C 跑步,D 排球四种活动项目的学生喜欢情况进行调查, 随机抽取了部分学生,并将调查结果绘制成图 1,图 2 的统计图,请结合图中 的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计 图补充完整; (2)随机抽取了 3 名喜欢“跑步”的学生,其中有 2 名男生,1 名女生,现从 这 3 名学生中任意抽取 2 名学生,请用画树状图或列表的方法,求出刚好抽 到一男生一女生的概率. 23. (8 分)春节期间,某超市出售的桂圆和芒果,单价分别为每千克 26 元和 22 元,李叔叔购买这两种水果共 30 千克,共花了 708 元,请问李叔叔购买这两 种水果各多少千克?
第 4 页(共 21 页)
24. (10 分)如图,在一次空中搜寻中,水平飞机的飞机观测到在点 A 俯角为 30°方向的 F 点处有疑似飞机残骸的物体 (该物体视为静止) , 为了便于观察, 飞机继续向前飞行了 800 米到达 B 点, 此时测得点 F 在点 B 俯角为 60°的方 向上, 请你计算当飞机飞临 F 点的正上方点 C 时 (点 A、 B、 C 在同一直线上) , 竖直高度 CF 约为多少米?(结果保留整数,参考数值: ≈1.7)
D.x<1
10. (4 分)抛物线 y=2(x+3)2+1 的顶点坐标是( A. (3,1) B. (3,﹣1) C. (﹣3,1)
D. (﹣3,﹣1)
11. (4 分)如图,直线 y=﹣
x+2 与 x 轴、y 轴分别交于 A、B 两点,把△AOB )
沿直线 AB 翻折后得到△AO′B,则点 O′的坐标是(
2018年中考第1次模拟考试数学试卷(含答案)

2018年初三第一次模拟考试数学试题一、选择题(本大题共16题,1-8小题,9-16小题,每题3分,共40分) 1.如图,数轴上表示-2的相反数的点是( ) A.点P B.点Q C.点M D.点N 2.下列运算正确的是( ) A.9=±3B. 532)(m m =C. 532a a a =⋅D.222)(y x y x +=+3.如图,AD 与BC 相交于点O,AB//CD,如果∠B =20°,∠D =40° ,那么∠BOD 为( ) A. 40° B.50° C.60° D.70°4.估计18-的值在( )A. 0到1之间B. 1到2之间C.2到3之间D. 3至4之间 5.用配方法解一元二次方程0542=-+x x ,此方程可变形( ) A. 9)2(2=+xB. 9)2(2=-xC. 1)2(2=+xD. 1)2(2=-x6.下列各因式分解正确的是( ) A.22)1(12-=-+x x xB.)2)(2()2(22+-=-+-x x xC.)2)(2(43-+=-x x x x xD.22)1(22++=+x x x7.若a>b,则下列式子一定成立的是( )A.0>+b aB. 0>-b aC.0>abD.0>ba8.△ABC 中,已知AB=8,∠C=90°,∠A=30°,DE 是中位线,则DE 的长是( ) A. 4B. 5C.32D. 29.若关于x 的一元一次不等式组⎩⎨⎧>-<-001a x x 无解,则a 的取值范围是( )A.1≥aB.1>aC. 1≤aD.1-<a 10.已知点A ),(11y x ,B ),(22y x 是反比例函数xy 2=图像上的点,若210x x >>,则一定成立的是( ) A.021>>y yB.210y y >>C.210y y >>D.120y y >>11.如图是王老师去公园锻炼及原路返回家的距离y (千米)与时间t (分钟)之间的函数图像,根据图像信息,下列说法正确的是( ) A. 王老师去时所用时间少于回家的时间 B. B. 王老师在公园锻炼了40分钟C. 王老师去时走上坡路,回家时走下坡路D. D.王老师去时速度比回家时的速度慢12.如图,CD 是Rt △ABC 斜边AB 边上的高,将△BCD 沿CD 折叠,B 点恰好落在AB 的中点E 处,则∠A 等于( ) A. 60° B.45° C. 30° D.25° 13.如图,在Rt △ABC 中,∠C =90°,AC=4cm ,BC=6cm ,动点P 从点C 沿CA,以1cm/s 的速度向点A 运动,同时动点O 从点C 沿CB,以2cm/s 的速度向点B 运动,其中一个动点运动到终点时,另一个动点也停止运动。
济南市2018年中考数学模拟综合检测试卷(一)含答案.docx

济南市 2018 年中考数学模拟综合检测试卷(一)含答案济南市 2018 年中考数学模拟综合检测卷 ( 一)一、选择题1.下列各数中,比 3 大的数是 ( )1A.-3B.- |3|C.πD.2 22.如图所示的工件是由两个长方体构成的组合体,则它的主视图是( )3.据媒体报道,我国最新研制的“察打一体”无人机的速度极快,经测试最高速度可达 204 000 米/ 分,这个数用科学记数法表示,正确的是 ( )A.204×10B.20.4 ×1043C.2.04 ×105D.2.04 ×1064.下列选项中,哪个不可以得到l 1∥l2()A.∠ 1=∠ 2B.∠ 2=∠3C.∠ 3=∠ 5D.∠ 3+∠ 4=180°5.下列汽车标志中,既是轴对称图形又是中心对称图形的是( )a46.计算a+2-a2+2a的结果是()2a-2a-4A. a B.a-2 C. a D.a2+2a7.函数 y =x+1 与 y=ax+b(a ≠0) 的图象如图所示,这两个函数12图象的交点在 y 轴上,那么使 y1,y2的值都大于 0 的 x 的取值范围是( )A.x>- 1B.x>2C.x<2D.- 1<x<28.赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30 天) 每天健步走的步数 ( 单位:万步 ) ,将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )A.1.2,1.3B.1.4 ,1.3C.1.4,1.35D.1.3 ,1.39.如图,在矩形 ABCD中,AB=2,AD= 2,以点 A 为圆心, AD的长为半径的圆交 BC边于点 E,则图中阴影部分的面积为( )A.22-1-πB.22-1-π32C.22-2-πD.22-1-π2410.如图所示,在△ ABC中, AD⊥BC于点 D,CE⊥AB 于点 E,且 BE3=2AE,已知 AD=33,tan ∠BCE=3,那么 CE等于 ( )A.2 3 B .3 3-2 C .5 2 D .4 311.函数 y=x3-3x 的图象如图所示,则以下关于该函数图象及其性质的描述正确的是 ( )A.函数最大值为2B.函数图象最低点为(1 ,- 2)C.函数图象关于原点对称D.函数图象关于y 轴对称12.如图, E,F 分别是正方形 ABCD的边 CD,AD上的点,且 CE=DF,AE,BF相交于点 O,下列结论: (1)AE =BF;(2)AE ⊥BF;(3)AO=OE;(4)S=S中,正确的有 ( )△AOB四边形 DEOFA.4 个B.3 个C.2 个D.1 个二、填空题13.计算: 3tan 60 °-12=________.14.分解因式: (a -b) 2-4b2=________.15.小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏( 每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等 ) ,则飞镖落在阴影区域的概率是 ________.16.如图,△ ABC内接于⊙ O,∠ ACB=90°,∠ ACB的角平分线交⊙O于D.若 AC=6,BD=5 2,则 BC的长为 ________.1317.如图,函数 y=x和 y=-x的图象分别是 l 1和 l 2. 设点 P在 l 1上,PC⊥x轴,垂足为 C,交 l 2于点 A,PD⊥y轴,垂足为 D,交 l 2于点 B,则△ PAB的面积为 ______.18.如图,在平面直角坐标系 xOy 中,矩形 OABC 的边 OA ,OC 分别在x 轴和 y 轴上, OC =3,OA =2 6,D 是 BC 的中点,将△ OCD 沿直线OD 折叠后得到△ OGD ,延长 OG 交 AB 于点 E ,连接 DE ,则点 G 的坐标为 ________.三、解答题2x>3x +2,19.解不等式组: 2x +1 x 23 ≤2-3.20.如图,AB 是⊙O 的直径, CA 与⊙O 相切于点 A ,连接 CO 交⊙O 于点 D ,CO 的延长线交⊙O 于点 E ,连接 BE ,BD ,∠ ABD =25°,求∠C 的度数.21. “母亲节”前夕,某商店根据市场调查,用 3 000 元购进第一批盒装花,上市后很快售完,接着又用 5 000 元购进第二批这种盒装花,已知第二批所购花的盒数是第一批所购花盒数的 2 倍,且每盒花的进价比第一批的进价少 5 元.求第一批盒装花每盒的进价是多少元?22.如图,在四边形 ABCD中, BD为一条对角线, AD∥BC, AD=2BC, ∠ABD=90°, E 为 AD的中点,连接 BE.(1)求证:四边形 BCDE为菱形;(2)连接 AC,若 AC平分∠ BAD,BC=1,求 AC的长.23.近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为进一步普及环保和健康知识,我市某校举行了“建设大美济南,关注环境保护”的知识竞赛,竞赛结果分为四个等级 (A. 不及格, B. 及格, C.良好, D. 优秀 ) ,并将调查结果绘制成了如下两幅不完整的统计图.请根据统计图回答下列问题:(1)这次被调查的学生共有多少人;(2)请将统计图 2 补充完整;(3)统计图 1 中 A 项目对应的扇形的圆心角是多少度;(4)已知该校共有学生 5 000 人,请根据调查结果估计该校成绩优秀的学生人数.24.如图,已知正比例函数和反比例函数的图象都经过点M(-2,-1),且 P(-1,- 2) 为双曲线上的一点,点 Q为坐标平面上一动点,PA垂直于 x 轴, QB垂直于 y 轴,垂足分别是A,B.(1)写出正比例函数和反比例函数的表达式;(2)当点 Q在直线 MO上运动时,直线 MO上是否存在这样的点 Q,使得△ OBQ与△ OAP面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.25. 如图 1,在平行四边形 ABCD中,AB=12,BC=6,AD⊥BD.以 AD 为斜边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED =90°.(1)求△ AED的周长;(2)若△ AED以每秒 2 个单位长度的速度沿 DC向右平行移动,得到△A0E0D0,当点E0 恰好在BC上时停止移动,设运动时间为t秒,△A0E0D0与△ BDC重叠的面积为S,请直接写出S 与 t 之间的函数关系式,并写出 t 的取值范围;(3)如图 2,在(2) 中,当△ AED移动至△ BEC的位置时,将△ BEC绕点C 按顺时针方向旋转α(0°<α<90°),在旋转过程中,B的对应点为 B1,E 的对应点为 E1,设直线 B1E1与直线 BE交于点 P、与直线 CB 交于点 Q.是否存在这样的α,使△ BPQ为等腰三角形?若存在,求出α 的度数;若不存在,请说明理由.26.在平面直角坐标系中,已知抛物线经过A(-4,0) ,B(0,-4) ,C(2,0) 三点.(1)求抛物线的表达式;(2)若点 M为第三象限内抛物线上的一动点,点 M的横坐标为 m,△AMB 的面积为 S,求 S关于 m的函数关系式,并求出S 的最大值;(3)若点 P 是抛物线上的动点,点 Q是直线 y=- x 上的动点,判断有几个位置能够使得以点 P,Q,B,O 为顶点的四边形为平行四边形?直接写出相应的点 Q的坐标.参考答案1. C 2.A 3.C 4.C 5.D 6.C 7.D 8.B 9.B 10.D11.C12.B113. 314.(a -3b)(a +b) 15. 416.8 17.86 6 318.( 5 ,5)2x>3x +2,①19.解: 2x +1 x 23 ≤2-3. ②由①得 x<-2,由②得 x ≤- 6,∴不等式组的解集为 x ≤- 6. 20.解:∵∠ ABD =25°, ∴∠ AOD =2∠ABD =50°.∵CA 与⊙O 相切于点 A ,OA 是半径,∴OA ⊥AC ,∴∠ C =90°-∠ AOD =40°.21.解:设第一批盒装花的进价是 x 元/ 盒,则2×3 000 5 000x = x -5 , 解得 x =30,经检验, x =30 是原方程的根.答:第一批盒装花每盒的进价是 30 元.22.(1) 证明:∵E 为 AD 的中点, AD =2BC ,∴ BC =ED.∵AD ∥BC, ∴四边形 BCDE 是平行四边形.又∵E 为 AD 的中点,∴ BE = ED.∴四边形 BCDE是菱形.(2) 解:∵ AD∥BC, AC平分∠ BAD,∴∠ BAC=∠ DAC=∠ BCA,∴ BA= BC=1.1∵AD= 2BC=2,∴ sin∠ADB=2,∠ ADB=30°,∴∠ DAC=30°,∠ADC=60°.在Rt△ACD中, AD=2,CD=1,∴ AC= 3.23.解:(1) 由题图知 C等级的人数有 140,占调查总人数的 28%,则调查总人数是 140÷28%= 500.(2)A 等级的人数为 500-75-140-245=40.(3)40 ÷500×100%= 8%,360°× 8%=28.8 °.答: A等级对应的扇形的圆心角是28.8 °.(4)245÷500×100%= 49%,5 000 ×49%= 2 450(人) .答:该校成绩优秀的学生大约有 2 450人.k24.解:(1)设反比例函数的表达式为y=x(k ≠0) ,正比例函数的表达式为y=k′x,∵正比例函数和反比例函数的图象都经过点M(-2,- 1) ,k∴- 1=-2,- 1=- 2k′,1∴k=2,k′=2.12∴正比例函数的表达式为y=2x,反比例函数的表达式为y=x.(2)当点 Q在直线 MO上运动时,假设在直线 MO上存在这样的点 Q(x,112x) ,使得△ OBQ与△ OAP的面积相等,则B(0 ,2x) .111∴2·x·2x=2×2×1.解得 x=± 2.1当x=2 时,2x=1;1当x=- 2 时,2x=- 1.∴存在点 Q(2,1) 或( -2,- 1) .25.解: (1) ∵四边形 ABCD是平行四边形,∴AD= BC=6.在Rt△ADE中, AD=6,∠ EAD=30°,∴AE=AD·cos 30 °= 33,DE=AD·sin 30 °= 3,∴△ AED的周长为 6+3 3+3=9+3 3.(2)在△ AED向右平移的过程中:( Ⅰ) 当 0≤t ≤1.5 时,如图,此时重叠部分为△D0NK.∵DD0=2t ,∴ ND0=DD0·sin30°= t ,NK=ND·tan 30 °=3t ,11 3 2∴S=S△D0NK=2ND0·NK=2t ·3t =2 t .( Ⅱ) 当1.5 <t≤4.5时,如图,此时重叠部分为四边形D0E0KN.∵AA0=2t ,∴A0B=AB-AA0=12- 2t ,1∴A0N=2A0B=6-t,3NK=A0N·tan 30 °=3 (6 -t) .∴S=S 四边形 D0E0 KN=S△A0D0E0-S△A0NK113=2×3×3 3-2×(6 -t) ×3 (6 -t)3233=-6 t +23t -2 .综上所述, S与 t 之间的函数关系式为3 2t ,0≤t ≤1.5 ,S=-6 t 2+2 3t -323,1.5<t ≤4.5.(3)存在α,使△ BPQ为等腰三角形.理由如下:∵∠ BQP=∠B1QC,∠ QBP=∠QB1C,∴△ BPQ∽△B1CQ.3故当△ BPQ为等腰三角形时,△B1QC也为等腰三角形.( Ⅰ) 如图,当 QB=QP时,则QB1=QC,∴∠B1CQ=∠B1=30°,即∠ BCB1=30°. ∴ α=30°.( Ⅱ) 当 BQ=BP时,则 B1Q=B1C,如图,点 Q在线段 B1E1的延长线上,∵∠B1=30°,∴∠B1CQ=∠B1QC=75°,即∠ BCB1=75°. ∴ α=75°.综上所述,存在α=30°或 75°时,△ BPQ为等腰三角形.26.解: (1) 设抛物线的表达式为 y=ax2+bx+c(a ≠0) ,将 A,B,C三点代入得116a-4b+c=0,a=2,c=- 4,解得b=1,4a+2b+c=0,c=- 4,1 2∴函数表达式为y=2x +x-4.(2)∵M点的横坐标为 m,且点 M在抛物线上,121 1 21∴M(m,2m+m-4),∴ S=S△AOM+S△OBM-S△AOB=2×4( -2m-m+4)+2 122×4×( - m)-2×4×4=- m-4m=- (m+2)+4.∵- 4<m<0,∴当 m=- 2 时, S 有最大值为 S=4.12(3) 设 P(x ,2x -x+4) ,当 OB为边时,∵ PB∥OQ,∴Q的横坐标的绝对值等于P的横坐标的绝对值,∴ Q(x,- x) .由PQ=OB,得| -x-( 1x2+x-4)| =4,2解得 x=0( 舍去 ) 或 x=- 4 或 x=- 2±2 5.当 BO为对角线时,点A 与点 P 重合, OP=4,∴BQ= PO=4,即点 Q的横坐标为 4,∴ Q(4,- 4) .综上 Q(-4,4) 或( -2+2 5,2-2 5) 或( -2-2 5,2+25) 或(4 ,-4) .。
初中数学 山东省济南市长清区九年级数学复习调查考试(一模)考试题考试卷及答案

xx学校xx学年xx学期xx 试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:-6的绝对值是A.-6 B. C.6 D.试题2:如图所示的几何体的左视图是试题3:下列多项式中,能用公式法分解因式的是A. B. C. D.试题4:近年来,随着交通网络的不断完善,我市近郊游持续升温。
据统计,在今年“五一”期间,某风景区接待游览的人数约为20.3万人,这一数据用科学记数法表示为A.人B.人C.人D.人试题5:评卷人得分下列运算中,正确的是A. B. C. D.试题6:不等式8-2x>0的解集在数轴上表示正确的是试题7:化简:的结果是A. B. C. D.试题8:甲、乙、丙三个旅行团的游客人数都相等,且每团游客的平均年龄都是32岁,这三个团游客年龄的方差分别是,,,导游小王最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选A.甲团 B.乙团 C.丙团 D.甲或乙团试题9:如图,正三角形ABC内接于圆O,动点P在圆周的劣弧AB上,且不与A,B重合,则∠BPC等于A. 30oB. 60oC. 90oD. 45o试题10:如图,在□ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于A. 1.5cmB. 2cmC. 2.5cmD. 3cm试题11:已知二次函数的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是A .(1,0) B. (-1,0) C.(2,0) D.(-2,0)试题12:已知一次函数,从中随机取一个值,从中随机取一个值,则该一次函数的图象经过二、三、四象限的概率为A. B. C. D.试题13:如图,双曲线与直线交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程的解为A.-3,1 B.-3,3 C.-1,1 D.-1,3试题14:如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为,则的值为A.16B.17C. 18D.19试题15:如图,已知直线l:,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为A.(0,64)B.(0,128)C.(0,256)D.(0,512)试题16:计算:-20120=1111111111试题17:不等式组的解集是______________.试题18:一块直角三角板放在两平行直线上,如图所示,∠1+∠2=___________度.试题19:若反比例函数的图象上有两点,,则______(填“”或“”或“”).试题20:如图,已知点A(1,1)、B (3,2),且P为x轴上一动点,则△ABP的周长的最小值为.试题21:如图,菱形ABCD中,AC =8,BD=6,将△ABD沿AC方向向右平移到△A′B′D′的位置,若平移距离为2,则阴影部分的面积为_________试题22:化简:试题23:解方程组:试题24:(1)如图,点、、、在同一条直线上,,,.求证:.试题25:如图,在梯形ABCD中,AD∥BC,∠B =90°,AD=2,BC =5,tan C =.求腰AB的长.试题26:某市体育中考现场考试内容有三项:50米跑为必测项目;另外在立定跳远和实心球中选一项,在坐位体前屈和1分钟跳绳中选一项.(1)每位考生有__________种选择方案;(2)若用……等字母分别表示上述各种方案,请用画树状图或列表的方法求小明与小刚选择同一种方案的概率.试题27:八年级学生到距离学校15千米的农科所参观,一部分学生骑自行车先走,过了40分钟后,其余同学乘汽车出发,结果两者同时到达.若汽车的速度是骑自行车同学速度的3倍,求骑自行车同学的速度.试题28:如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.(1)求证:≌.(2)把向左平移,使与重合,得,交于点.请判断AH与ED 的位置关系,并说明理由.(3)求的长.试题29:如图,在平面直角坐标系中,直线=分别与轴,轴相交于两点,点是轴的负半轴上的一个动点,以为圆心,3为半径作.(1)连结,若,试判断与轴的位置关系,并说明理由;(2)当为何值时,以与直线=的两个交点和圆心为顶点的三角形是正三角形?试题30:如图1,抛物线与轴交于两点,与轴交于点,连结AC,若(1)求抛物线的解析式;(2)抛物线对称轴上有一动点P,当时,求出点的坐标;(3)如图2所示,连结,是线段上(不与、重合)的一个动点.过点作直线,交抛物线于点,连结、,设点的横坐标为.当t为何值时,的面积最大?最大面积为多少?试题1答案:C试题2答案:A试题3答案:D试题4答案:B试题5答案:B试题6答案:C试题7答案: A试题8答案: C试题9答案: B试题10答案: B试题11答案: D试题12答案: A试题13答案: A试题14答案: B试题15答案: C试题16答案: 1试题17答案:<x≤1 试题18答案:90试题19答案:<试题20答案:+试题21答案:7.5试题22答案:解:原式==试题23答案:,解:①+②得:,∴,把代入①得:,解得:,∴方程组的解集是:.试题24答案:证明:∵∴.在和中,∴∴.试题25答案:解:(1)如图①,作DE⊥BC于E,∵AD∥BC,∠B=90°,∴∠A=90°.又∠DEB=90°,∴四边形ABED是矩形.(能判断出矩形即可得分)∴BE=AD=2,∴EC=BC-BE=3.在Rt△DEC中,DE= EC·t a n C ==4.试题26答案:解:(1)4(2)用代表四种选择方案.解法一:用树状图分析如下:解法二:用列表法分析如下:A B C D小刚小明A(A,A)(A,B)(A,C)(A,D)B(B,A)(B,B)(B,C)(B,D)C(C,A)(C,B)(C,C)(C,D)D(D,A)(D,B)(D,C)(D,D)(每列对一组1分)共有16中情况,小明和小刚选择同种方案的情况有4种(小明与小刚选择同种方案)=.试题27答案:解:设骑自行车同学的速度为x千米/小时,由题意得-=解之得:x=15经验,x=15是原方程的解答:骑自行车同学的速度为15千米/小时.试题28答案:解:(1)由已知正方形ABCD得AD =DC,又∵AE=CF∴.(2)AH⊥ED理由:由(1)和平移性质可知,∵,∴∴.即AH⊥ED(3)由已知AE=1,AD=2,∴,∴即,∴.(注:用三角形相似解的,计算ED,判定相似,求解AG各得1分)试题29答案:解:(1)与轴相切.直线与轴交于,与轴交于,,…由题意,.在中,,等于的半径,与轴相切.(2)设与直线交于两点,连结.当圆心在线段上时,作于.为正三角形,,∵,∴AB=∴.当圆心在线段延长线上时,同理可得,当或时,以与直线的两个交点和圆心为顶点的三角形是正三角形.试题30答案:解:(1)∵抛物线过点. ∴又∵∴,即又∵点A在抛物线上.∴0=12+b×1+2,b=-3∴抛物线的解析式为:(2)过点作对称轴的垂线,垂足为,∴.∴∵∴∴,即,解得或∴点的坐标为(,)或(,). (备注:可以用勾股定理或相似解答)(3)易得直线的解析式为,∵点是直线和线段的交点,∴点的坐标为的坐标为∴∴∴∴当时,最大值为1.。
2018年山东省济南市长清区中考数学模拟试卷(3月份)

2018年山东省济南市长清区中考数学模拟试卷(3月份)一、选择题(本题共48分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的.1. (4分)16的算术平方根为()A. 土4B. 4C. - 4D. 82. (4分)中国移动数据中心IDC项目近日在高新区正式开工建设,该项目规划建设规模12.6万平方米,建成后将成为山东省最大的数据业务中心.其中126000 用科学记数法表示应为()A. 1.26X 106B. 12.6X 104C. 0.126X 106D. 1.26X 1053. (4分)从棱长为2a的正方体零件的一角,挖去一个棱长为a的小正方体,得到一个如图所示的零件,则这个零件的俯视图是()6(4分)下列计算中,正确的是(则/A等于(A. 2a+3b=5abB. (3a3)2=6a6C.A. 30°B. 35°C. 40°D. 505. (4分)下面的图形中,既是轴对称图形又是中心对称图形的是()他选中创新能力试题的概率是()A ,十B.「C.匸D .丄9. (4分)《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其 中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱,问 人数、物价各是多少?设合伙人数为 x 人,物价为y 钱,以下列出的方程组正确10. (4分)如图,直径为10的。
A 经过点C 和点0,点B 是y 轴右侧。
A 优弧11. (4分)如图,在菱形 ABCD 中,AB=6,Z DAB=60,AE 分别交BC 、BD 于点 E 、F ,CE=2连接CF,以下结论:①厶ABF ^A CBF ;②点E 到AB 的距离是励; ③tan /DCF=J :④厶ABF 的面积为二「;.其中一定成立的有几个( )7. (4分)化简A. B. ab-a 2 C. -h D.-2 aab 等于( ) a 8. (4分)某学校组织知识竞赛,共设 20道试题,其中有关中国优秀传统文化 试题10道,实践应用题4道,创新能力题6道.小捷从中任选一道试题作答, 的是( ) A . \y-7m~4C.ry-8z=3 1B.D.12. (4分)如图,Rt A ABC中/ C=90°, / BAC=30, AB=8,以血为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A- B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFg A ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是()1 F E CAG A(D f)二、填空题(本题共6小题,每小题4分,共24分)13. (4 分)计算:2-1+ . - = .14. _______________________________ (4 分)分解因式a3- 6a2+9a= .15. (4分)某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人, 16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是 ________ 岁. 16. (4分)如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长为 _______ m .i e20 m 2 * * ** 2聲 < 4 * ■ 17. (4分)如图,D , E 分别是△ ABC 的边AB BC 上的点,且 DE// AC, AE 、CD相交于点 0,若 & DOE : S\ COA =1 : 16,贝U S A BDE 与 S^CDE 的比是 _____18. (4分)如图,△ ABC 的三个顶点分别为 A (1, 2), B (1, 3), C (3, 1), 若反比例函数y 二在第一象限内的图象与厶 ABC 有公共点,贝U k 的取值范围 20. (6分)(1)如图1,在矩形ABCD 中,点O 在边AB 上,/ AOC=Z BOD,求 证:AO=OEB(2)如图2, AB 是。
3月2018届九年级第一次模拟大联考(山东卷)数学卷(考试版)

数学试题 第1页(共6页) 数学试题 第2页(共6页)绝密★启用前|学科网试题命制中心2018届九年级第一次模拟大联考【山东卷】数 学(考试时间:120分钟 试卷满分:120分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
5.考试范围:中考全部内容。
第Ⅰ卷一、选择题(本大题共15小题,每小题3分,共45分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.在–1,0,2,–3这四个数中,绝对值最小的数是 A .–1B .0C .2D .–32.据央视报道:2017年,在经济下行压力很大的情况下,按照年人均纯收入2300元的农村扶贫标准计算,我国农村贫困人口将比上年减少1650万人,这一成就来之不易.将“1650万”用科学记数法表示是 A .1.65×103 B .165×105C .1.65×107D .0.165×1083.在下面四个几何体中,主视图与俯视图都是圆的为A .B .C .D .4.在平面直角坐标系中,点P (–2,x 2+1)所在的象限是 A .第一象限 B .第二象限C .第三象限D .第四象限5.如图,AB ∥CD ,已知∠BED =64°,BC 平分∠ABE,则∠ABC 的度数是A .16°B .32°C .64°D .116°6.下列运算正确的是 A .–2(a –b )=–2a –b B .–2(a –b )=–2a +bC .–2(a –b )=–2a –2bD .–2(a –b )=–2a +2b7.方程–13+x =2x 的解是 A .–13 B .13C .1D .–18.若x 1,x 2是方程x 2–2mx +m 2–m –1=0的两个根,且x 1+x 2=1–x 1x 2,则m 的值为A .–1或2B .1或–2C .–2D .19.P 是⊙O 外一点,PA 、PB 分别交⊙O 于C 、D 两点,已知AB 、CD 的度数别为88°、32°,则∠P 的度数为A .26°B .28°C .30°D .32°10.如图,两个转盘分别自由转动一次,当停止转动时,两个转盘的指针都指向2的概率为A .12B .14C .18D .116。
山东省济南市2018年最新九年级学业水平数学模拟试卷(一)及答案

2018年济南市九年级学业水平模拟考试数学试题考试时间:120分钟满分150分第I 卷(选择题共48分)一、选择题(本大题共12小题,每小题4分,共48分。
在每小题列出的四个选项中,只有一项是符合题目要求的。
)1.-2的绝对值是()A.2 B.-2 C.21D.-212.2017年济南市GDP 总量实现历史性突破,生产总值达386000000000元,首次跃居全市第二。
将386000000000用科学计数法表示为()A.3.86×1010B.3.86×1011C.3.86×1012D.3.86×1093.下图是由4个相同的正方体搭成的几何体,则其俯视图是A .B .C .D .4.下列运算正确的是()A .x 2+x 3=x 5B .(x ﹣2)2=x 2﹣4C .(x 3)4=x 7D .2x 2⋅x 3=2x 55.如图,AB ∥DE ,FG ⊥BC 于F ,∠CDE=40°,则∠FGB=()A .40°B .50°C .60°D .70°6.关于x 的一元二次方程mx 2﹣(m+1)x+1=0有两个不等的整数根,第5题图m 为整数,那么m 的值是()A .﹣1B .1C .0D .±17.在△ABC 中,∠C=90°,BC=2,sinA=,则边AC 的长是()A .B .3C .D .第8题图8.二次函数y=ax 2+bx+c (a≠0)的图象如图所示,则下列结论中正确的是()A .a >0B .c <0C .当﹣1<x <3时,y >0D .当x≥1时,y 随x 的增大而增大9.下列说法正确的是()A .“明天降雨的概率是60%”表示明天有60%的时间都在降雨。
2018届济南市长清区中考第一次模拟考试数学试卷含答案
2018届济南市长清区中考第一次模拟考试数学试卷含答案本试卷满分为150分一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.2018的相反数是( )A .2018B .-12018C .12018D .-20182.如图,点O 在直线AB 上,若∠2=140°,则∠1的度数是( )A .40°B .60°C .140°D .150°21CBA3.下列运算正确的是( )A .a 2·a 3=a 6B .(a 2)3=a 6C .a 6÷a 2=a 3D .2-3=-6 4.将100800用科学记数法表示为A .0.1008×106B .1.008×106C .10.08×104D .1.008×1055.下列图案中既是中心对称图形,又是轴对称图形的是( )A B CD6.如图所示的几何体是由4个相同的小正方体组成,其主视图为( )A B C D7.下列命题中,真命题是 ( )A .两对角线相等的四边形是矩形B .两对角线互相平分的四边形是平行四边形则表示“跳绳个数”这组数据的中位数和众数分别是( )A .170,160B .180,160C .170,180D .160,2009.如图,一次函数y 1=x +b 与一次函数y 2=kx +4的图象交于点P (1,3),则关于x 的不等式x +b >kx +4的解集是( ) A .x >-2 B .x >0C .x >1D .x <1y 2 10.抛物线 y =2(x +3)2+1的顶点坐标是( )A .(3, 1)B .(-3,-1)C .(-3,1)D .(3, -1)11.如图,直线y =-33x +2与x 轴,y 轴分别交于A ,B 两点,把△AOB 沿着直线AB 翻折后得到△AO ′B ,则点O ′ 的坐标是( ) A .(3,3)B .(2,23)C .(3,3)D .(23,4)B12.如图,抛物线y =ax 2+bx +c 的对称轴是x =-1.且过点(12,0),有下列结论:①abc >0;②a -2b +4c =0;③25a -10b +4c =0;④3b +2c >0;⑤a -bm ≥(am -b );其中所有正确的结论有( )个. A .2个 B .3个 C .4个D .5个二、填空题(本大题共6个小题,每题4分,共24分.把答案填在题中的横线上)14.比较大小:5-12 ________ 12. 15.在一个不透明的盒子中有12个白球,若干个黄球,它们除了颜色不同外,其余均相同,若从中随机摸出一个球是黄球的概率是13,则黄球有 _____ 个.16.若代数式1x -2和32x +1的值相等,则x = _____ .17.如图,在圆内接四边形ABCD 中,O 为圆心,∠BOD =160°,则∠BCD 的度数是 _____ .D三、解答题(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤)19.(本题满分6分,每小题3分)(1)计算:tan 60°+(5-1)0-12; (2)化简:(a +3)(a -3)+a (2-a )20.(本题满分6分,每小题3分)(1)解不等式组:⎩⎨⎧x -3<14x -4≥x +2; (2)解方程:x 2-4x +3=021.(本题满分6分)如图,AB 是⊙O 的直径,AD 是⊙O 的切线,点C 在⊙O 上,BC ∥OD ,AB =2,OD =3. (1)求证:ΔACB ∽ΔDAO . (2)求BC 的长.22.(本小题满分8分)为进一步推广“阳光体育”大课间活动,长清区某中学对已开设的A 实心球,B 立定跳远,C 跑步,D 排球四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:(1)本次共调查了 名学生; (2)将两个统计图补充完整;(3)随机抽取了3名喜欢“跑步”的学生,其中有2名男生,1名女生,现从这3名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到一男生一女生的概率.23.(本小题满分8分)春节期间,某超市出售的荔枝和芒果,单价分别为每千克26元和22元,李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?24.(本小题满分10分)如图,在一次空中搜寻中,水平飞行的飞机观测到在点A 俯角为30°方向的F 点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B 点,此时测得点F 在点B 俯角为60°的方向上,请你计算当飞机飞临F 的正上方点C 时(点A 、B 、C 在同一直线上),竖直高度CF 约为多少米?(结果保留整数,参考数值:3≈1.7)25.(本小题满分10分)如图,一次函数y =kx +b 与反比例函数y =mx 的图象交于A (2,3),B (-3,n )两点.(1)求一次函数与反比例函数的表达式;(2)根据所给条件,请直接写出不等式kx +b >mx 的解集______________;(3)过点B 作BC ⊥x 轴,垂足为C ,求S △AB C .26.(本小题满分12分)已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;(2)在(1)的条件下,若DE=1,AE=7,CE=3,求∠AED的度数;(3)若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=53,求CN的长.图1图2F27.(本小题满分12分)如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.(1)求抛物线的函数表达式;(2)在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.(3)在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.C C备用图九年级数学参考答案一、选择题(每题4分,共48分)二、填空题(每题4分,共24分)13.x(x+y) 14.>15.616.717.10018.-242……2分19、解:(1)原式=3=1-…………3分(2) 原式=a2-6+2a-a2………2分,=2a-6………3分20.(1)解①得:x<4………1分≥………2分解②得:x2所以原不等式组的解集是2≤x<4………3分(2)由x2-4x+3=0得(x-1)(x-3)=0………1分∴x-1=0或x-3=0………2分∴x1=1,x2=3………3分21.(1)解:∵BC∥OD∴∠B=∠AOD………1分∵AB是直径,∴∠ACB=90。
山东省济南市长清区2018届九年级数学上学期12月抽测试题新人教版

山东省济南市长清区2018届九年级数学上学期12月抽测试题本试题共6页,满分为150分,考试时间为120分钟。
第I 卷(选择题 共60分)一.选择题(本大题共15个小题,每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列立体图形中,俯视图是正方形的是( )A .B .C .D .2.在Rt ABC △中,90C ∠=︒,∠B=60°,则cos B 的值是( )123.已知△ABC ∽△A ´B ´C ´,且21=''B A AB ,则S △ABC :S △A ´B ´C ´为( ) A .1:2 B .2:1 C .1:4 D .4:1 4.反比例函数x3-y =的图象位于( ) A .第一、三象限 B .第二、四象限 C .第一、二象限D .第三、四象限5.三角形在正方形网格纸中的位置如图所示,则sin α的值是( )A.43B.34C.53D.54 6.反比例函数x2y =的图象上有两个点为(x 1,y 1),(x 2,y 2),且x 1<x 2<0,则下列关系成立的是( )A .y 1>y 2B .y 1<y 2C .y 1=y 2D .不能确定7.如图,函数-x y =与函数x4-y =的图象相交于A 、B 两点,过A 、B 两点分别作y 轴的垂线,垂足分别为点C 、D ,则四边形ACBD 的面积为( )A .2B .4C .6D .88第5题图( )9.如图,一艘海轮位于灯塔P 的北偏东方向55°,距离灯塔为2 海里的点A 处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB 长是( )A .2 海里B.2sin55°海里C .2cos55°海里 D.2tan55°海里10.在x 2□2xy□y 2的空格□中,分别填上“+”或“﹣”,在所得的代数式中,能构成完全平方式的概率是( )A .1B .43C .21D .4111.某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5 m 的同学的影长为1.35 m ,由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图,他们测得地面部分的影长为3.6 m ,建筑物上的影长为1.8 m ,则树的高度为( )A .5.4 mB .5.8 mC .5.22 mD .6.4 m第11题图 第12题图 第13题图12.如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,在DC 的延长线上取一点E ,连接OE 交BC 于点F ,已知AB=4,BC=6,CE=2,则CF 的长等于( )A.1B.1.5C.2D.313.如图,将正方形OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1,3),则点B 的坐标为( )A .(3-1,13+) B .(3-,13+)C .(﹣1,13+)D .(﹣1,3)14.如图,△OAC 和△BAD 都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=x6在第一象限的图象经过点B ,则△OAC 与△BAD 的面积之差S △OAC ﹣S △BAD 为( )A .36B .12C .6D .3第14题图 第15题图15.如图,正方形ABCD 中,点E 是AD 边中点,BD 、CE 交于点H ,BE 、AH 交于点G ,则下列结论:①AG ⊥BE ;②BG=4GE ;③S △BHE =S △CHD ;④∠AHB=∠EHD . 其中正确的个数是( )A .1B .2C .3D .4第Ⅱ卷(非选择题 共90分)二、填空题(本大题共6个小题.每小题4分,共24分.把答案填在题中横线上.)16.若21y =x ,则yx x +=________. 17.如图,点D,E 分别在AB,AC 上,且∠ABC=∠AED.若DE=4,AE=5,BC=8,则AB 的长为.18.反比例函数x1-a 2y =的图象有一支位于第二象限,则常数a 的取值范围是.19.在一个暗盒中放有若干个白色球和2个黑色球(这些球除颜色外无其他区别),若从中随机取出1个球是白色球的概率是53,则在暗盒中随机取出2个球都是白色球的概率是________. 20.如图,在平行四边形ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则S △DEF =3,则平行四边形ABCD 的面积是____________ .第20题图 第21题图21.在平面直角坐标系的第一象限内,边长为1的正方形ABCD 的边均平行于坐标轴,A 点的坐标为(a ,a ).如图,若曲线)0(3>=x xy 与此正方形的边有交点,则a 的取值范围是.三、解答题(本大题共7个小题.共66分.解答应写出文字说明、证明过程或演算步骤.) 22.(每小题4分,共8分)(1012cos 454π-+︒+(-2);(2)在直角三角形ABC 中,已知∠C =90°,∠A =60°,BC =3,求AC .第17题图23.(本小题8分)某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.求:(1)取出纸币的总额是30元的概率;(2)取出纸币的总额可购买一件55元的商品的概率.24.(本小题8分)如图,某校教学楼AB 的后面有一建筑物CD ,当光线与水平面的夹角是22︒时,教学楼在建筑物的墙上留下高2m 的影子CE ;而当光线与地面的夹角是45︒时,教学楼顶A 在地面上的影子F 与墙角C 有13m 的距离(B 、F 、C 在一条直线上).求教学楼AB 的高度.(参考数据:3sin 228︒≈,15cos2216︒≈,2tan225︒≈)25.(本小题9分)如图,正方形ABCD 中,M 为BC 上一点,F 是AM 的中点,EF ⊥AM ,垂足为F ,交AD 的延长线于点E ,交DC 于点N . (1)求证:△ABM ∽△EFA ; (2)若AB=12,BM=5,求DE 的长.26.(本小题9分)如图,已知一次函数b kx y +=1的图象与反比例函数xy m2=的图象的两个交点是A (-2,-4),C (4,n ),与y 轴交于点B ,与x 轴交于点D .(1)求反比例函数xy m2=和一次函数b kx y +=1的解析式; (2)连结OA ,OC ,求△AOC 的面积.(3)直接写出一次函数值大于反比例函数值的自变量x 的取值范围。
(汇总3份试卷)2018年济南市中考数学毕业升学考试一模试题

中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.如图,已知△ABC 中,∠C=90°,AC=BC=2,将△ABC 绕点A 顺时针方向旋转60°到△AB′C′的位置,连接C′B ,则C′B 的长为( )A .2-2B .32C .3-1D .1【答案】C 【解析】延长BC′交AB′于D ,根据等边三角形的性质可得BD ⊥AB′,利用勾股定理列式求出AB ,然后根据等边三角形的性质和等腰直角三角形的性质求出BD 、C′D ,然后根据BC′=BD -C′D 计算即可得解.【详解】解:延长BC′交AB′于D ,连接BB ',如图,在Rt △AC′B′中,AB′=2AC′=2,∵BC′垂直平分AB′,∴C′D=12AB=1, ∵BD 为等边三角形△ABB′的高,∴BD=3AB′=3, ∴BC′=BD -C′D=3-1.故本题选择C.【点睛】熟练掌握勾股定理以及由旋转60°得到△ABB′是等边三角形是解本题的关键.2.设点()11A ,x y 和()22B ,x y 是反比例函数k y x=图象上的两个点,当1x <2x <时,1y <2y ,则一次函数2y x k =-+的图象不经过的象限是A .第一象限B .第二象限C .第三象限D .第四象限 【答案】A【解析】∵点()11A ,x y 和()22B ,x y 是反比例函数k y x =图象上的两个点,当1x <2x <1时,1y <2y ,即y 随x 增大而增大,∴根据反比例函数k y x =图象与系数的关系:当0k >时函数图象的每一支上,y 随x 的增大而减小;当0k <时,函数图象的每一支上,y 随x 的增大而增大.故k <1. ∴根据一次函数图象与系数的关系:一次函数1y=k x+b 的图象有四种情况:①当1k 0>,b 0>时,函数1y=k x+b 的图象经过第一、二、三象限;②当1k 0>,b 0<时,函数1y=k x+b 的图象经过第一、三、四象限;③当1k 0<,b 0>时,函数1y=k x+b 的图象经过第一、二、四象限;④当1k 0<,b 0<时,函数1y=k x+b 的图象经过第二、三、四象限.因此,一次函数2y x k =-+的1k 20=-<,b=k 0<,故它的图象经过第二、三、四象限,不经过第一象限.故选A .3.如图,矩形 ABCD 的边 AB=1,BE 平分∠ABC ,交 AD 于点 E ,若点 E 是 AD 的中点,以点 B 为圆心,BE 长为半径画弧,交 BC 于点 F ,则图中阴影部分的面积是( )A .2-4πB .324π-C .2-8πD .324π- 【答案】B【解析】利用矩形的性质以及结合角平分线的性质分别求出AE ,BE 的长以及∠EBF 的度数,进而利用图中阴影部分的面积=S ABCD 矩形-S ABE -S EBF 扇形,求出答案.【详解】∵矩形ABCD 的边AB=1,BE 平分∠ABC ,∴∠ABE=∠EBF=45°,AD ∥BC ,∴∠AEB=∠CBE=45°,∴2 ,∵点E 是AD 的中点,∴AE=ED=1,∴图中阴影部分的面积=S ABCD 矩形 −S ABE −S EBF 扇形 =1×2−123-24π 故选B.【点睛】此题考查矩形的性质,扇形面积的计算,解题关键在于掌握运算公式4.下列调查中,调查方式选择合理的是( )A .为了解襄阳市初中每天锻炼所用时间,选择全面调查B .为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择全面调查C .为了解神舟飞船设备零件的质量情况,选择抽样调查D .为了解一批节能灯的使用寿命,选择抽样调查【答案】D【解析】A .为了解襄阳市初中每天锻炼所用时间,选择抽样调查,故A 不符合题意;B .为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择抽样调查,故B 不符合题意;C .为了解神舟飞船设备零件的质量情况,选普查,故C 不符合题意;D .为了解一批节能灯的使用寿命,选择抽样调查,故D 符合题意;故选D .5.世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.0000000076克,将数0.0000000076用科学记数法表示为( )A .7.6×10﹣9B .7.6×10﹣8C .7.6×109D .7.6×108【答案】A【解析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10n -,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:将0.0000000076用科学计数法表示为97.610-⨯.故选A.【点睛】本题考查了用科学计数法表示较小的数,一般形式为a×10n -,其中110a ≤<,n 为由原数左边起第一个不为0的数字前面的0的个数所决定.6.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t (分钟),所走的路程为s (米),s 与t 之间的函数关系如图所示,下列说法错误的是( )A.小明中途休息用了20分钟B.小明休息前爬山的平均速度为每分钟70米C.小明在上述过程中所走的路程为6600米D.小明休息前爬山的平均速度大于休息后爬山的平均速度【答案】C【解析】根据图像,结合行程问题的数量关系逐项分析可得出答案.【详解】从图象来看,小明在第40分钟时开始休息,第60分钟时结束休息,故休息用了20分钟,A正确;小明休息前爬山的平均速度为:28007040=(米/分),B正确;小明在上述过程中所走的路程为3800米,C错误;小明休息前爬山的平均速度为:70米/分,大于休息后爬山的平均速度:380028002510060-=-米/分,D正确.故选C.考点:函数的图象、行程问题.7.如图,⊙O 是等边△ABC 的外接圆,其半径为3,图中阴影部分的面积是()A.πB.32πC.2πD.3π【答案】D【解析】根据等边三角形的性质得到∠A=60°,再利用圆周角定理得到∠BOC=120°,然后根据扇形的面积公式计算图中阴影部分的面积即可.【详解】∵△ABC 为等边三角形,∴∠A=60°,∴∠BOC=2∠A=120°,∴图中阴影部分的面积= 21203360π⨯=3π. 故选D .【点睛】本题考查了三角形的外接圆与外心、圆周角定理及扇形的面积公式,求得∠BOC=120°是解决问题的关键.8.如图,BD 为⊙O 的直径,点A 为弧BDC 的中点,∠ABD =35°,则∠DBC =( )A .20°B .35°C .15°D .45°【答案】A 【解析】根据∠ABD =35°就可以求出AD 的度数,再根据180BD ︒=,可以求出AB ,因此就可以求得ABC ∠的度数,从而求得∠DBC【详解】解:∵∠ABD =35°,∴的度数都是70°,∵BD 为直径,∴的度数是180°﹣70°=110°,∵点A 为弧BDC 的中点,∴的度数也是110°, ∴的度数是110°+110°﹣180°=40°,∴∠DBC ==20°, 故选:A .【点睛】本题考查了等腰三角形性质、圆周角定理,主要考查学生的推理能力.9.已知抛物线y =ax 2+bx+c (a <0)与x 轴交于点A (﹣1,0),与y 轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n ),则下列结论:①4a+2b <0; ②﹣1≤a≤23-; ③对于任意实数m ,a+b≥am 2+bm 总成立;④关于x 的方程ax 2+bx+c =n ﹣1有两个不相等的实数根.其中结论正确的个数为( ) A .1个B .2个C .3个D .4个 【答案】C【解析】①由抛物线的顶点横坐标可得出b=-2a ,进而可得出4a+2b=0,结论①错误;②利用一次函数图象上点的坐标特征结合b=-2a 可得出a=-3c ,再结合抛物线与y 轴交点的位置即可得出-1≤a≤-23,结论②正确; ③由抛物线的顶点坐标及a <0,可得出n=a+b+c ,且n≥ax 2+bx+c ,进而可得出对于任意实数m ,a+b≥am 2+bm 总成立,结论③正确;④由抛物线的顶点坐标可得出抛物线y=ax 2+bx+c 与直线y=n 只有一个交点,将直线下移可得出抛物线y=ax 2+bx+c 与直线y=n-1有两个交点,进而可得出关于x 的方程ax 2+bx+c=n-1有两个不相等的实数根,结合④正确.【详解】:①∵抛物线y=ax 2+bx+c 的顶点坐标为(1,n ),∴-2b a=1, ∴b=-2a ,∴4a+2b=0,结论①错误;②∵抛物线y=ax 2+bx+c 与x 轴交于点A (-1,0),∴a-b+c=3a+c=0,∴a=-3c . 又∵抛物线y=ax 2+bx+c 与y 轴的交点在(0,2),(0,3)之间(包含端点),∴2≤c≤3,∴-1≤a≤-23,结论②正确; ③∵a <0,顶点坐标为(1,n ),∴n=a+b+c ,且n≥ax 2+bx+c ,∴对于任意实数m ,a+b≥am 2+bm 总成立,结论③正确;④∵抛物线y=ax 2+bx+c 的顶点坐标为(1,n ),∴抛物线y=ax 2+bx+c 与直线y=n 只有一个交点,又∵a <0,∴抛物线开口向下,∴抛物线y=ax 2+bx+c 与直线y=n-1有两个交点,∴关于x 的方程ax 2+bx+c=n-1有两个不相等的实数根,结合④正确.故选C .【点睛】本题考查了二次函数图象与系数的关系、抛物线与x轴的交点以及二次函数的性质,观察函数图象,逐一分析四个结论的正误是解题的关键.10.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形共有()个〇.A.6055 B.6056 C.6057 D.6058【答案】D【解析】设第n个图形有a n个O(n为正整数),观察图形,根据各图形中O的个数的变化可找出"a n=1+3n(n 为正整数)",再代入a=2019即可得出结论【详解】设第n个图形有a n个〇(n为正整数),观察图形,可知:a1=1+3×1,a2=1+3×2,a3=1+3×3,a4=1+3×4,…,∴a n=1+3n(n为正整数),∴a2019=1+3×2019=1.故选:D.【点睛】此题考查规律型:图形的变化,解题关键在于找到规律二、填空题(本题包括8个小题)11.已知x=2是关于x的一元二次方程kx2+(k2﹣2)x+2k+4=0的一个根,则k的值为_____.【答案】﹣1【解析】把x=2代入kx2+(k2﹣2)x+2k+4=0得4k+2k2﹣4+2k+4=0,再解关于k的方程,然后根据一元二次方程的定义确定k的值即可.【详解】把x=2代入kx2+(k2﹣2)x+2k+4=0得4k+2k2﹣4+2k+4=0,整理得k2+1k=0,解得k1=0,k2=﹣1,因为k≠0,所以k的值为﹣1.故答案为:﹣1.【点睛】本题考查了一元二次方程的定义以及一元二次方程的解,能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.12.因式分解:3x3﹣12x=_____.【答案】3x(x+2)(x﹣2)【解析】先提公因式3x,然后利用平方差公式进行分解即可.【详解】3x3﹣12x=3x(x2﹣4)=3x(x+2)(x﹣2),故答案为3x(x+2)(x﹣2).【点睛】本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.13.如图所示,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的大小是_____.【答案】40°【解析】根据外角的概念求出∠ADC的度数,再根据垂直的定义、四边形的内角和等于360°进行求解即可得.【详解】∵∠ADE=60°,∴∠ADC=120°,∵AD⊥AB,∴∠DAB=90°,∴∠B=360°﹣∠C﹣∠ADC﹣∠A=40°,故答案为40°.【点睛】本题考查了多边形的内角和外角,掌握四边形的内角和等于360°、外角的概念是解题的关键.14.如图,已知点C为反比例函数6yx=-上的一点,过点C向坐标轴引垂线,垂足分别为A、B,那么四边形AOBC的面积为___________.【答案】1【解析】解:由于点C为反比例函数6yx=-上的一点,则四边形AOBC的面积S=|k|=1.故答案为:1.15.半径为2的圆中,60°的圆心角所对的弧的弧长为_____.【答案】2π3【解析】根据弧长公式可得:602180π⨯⨯=23π,故答案为23π.16.如图,在正六边形ABCDEF的上方作正方形AFGH ,联结GC,那么GCD∠的正切值为___.【答案】31+【解析】延长GF与CD交于点D,过点E作EM DF⊥交DF于点M,设正方形的边长为a,则,CD GF DE a===解直角三角形可得DF,根据正切的定义即可求得GCD∠的正切值【详解】延长GF与CD交于点D,过点E作EM DF⊥交DF于点M,设正方形的边长为a,则,CD GF DE a===AF//CD,90,CDG AFG∴∠=∠=1209030,EDM∠=-=3cos30,DM DE=⋅=23,DF DM a∴==)331,DG GF FD a a a∴=+==()3131tan.aGDGCDCD a∠===3 1.【点睛】考查正多边形的性质,锐角三角函数,构造直角三角形是解题的关键.17.A .如果一个正多边形的一个外角是45°,那么这个正多边形对角线的条数一共有_____条. B .用计算器计算:7•tan63°27′≈_____(精确到0.01).【答案】20 5.1【解析】A 、先根据多边形外角和为360°且各外角相等求得边数,再根据多边形对角线条数的计算公式计算可得;B 、利用计算器计算可得.【详解】A 、根据题意,此正多边形的边数为360°÷45°=8,则这个正多边形对角线的条数一共有8(83)2⨯-=20, 故答案为20;B 、7•tan63°27′≈2.646×2.001≈5.1,故答案为5.1.【点睛】本题主要考查计算器-三角函数,解题的关键是掌握多边形的内角与外角、对角线计算公式及计算器的使用.18.如图,⊙O 的半径为6,四边形ABCD 内接于⊙O ,连接OB ,OD ,若∠BOD=∠BCD ,则弧BD 的长为________.【答案】4π【解析】根据圆内接四边形对角互补可得∠BCD+∠A=180°,再根据同弧所对的圆周角与圆心角的关系以及∠BOD=∠BCD ,可求得∠A=60°,从而得∠BOD=120°,再利用弧长公式进行计算即可得.【详解】解:∵四边形ABCD 内接于⊙O ,∴∠BCD+∠A=180°,∵∠BOD=2∠A ,∠BOD=∠BCD ,∴2∠A+∠A=180°,解得:∠A=60°,∴∠BOD=120°,∴BD 的长=41812060ππ=⨯, 故答案为4π.【点睛】本题考查了圆周角定理、弧长公式等,求得∠A 的度数是解题的关键.三、解答题(本题包括8个小题)19.已知m 是关于x 的方程2450x x -=+的一个根,则228m m +=__【答案】10【解析】利用一元二次方程的解的定义得到245m m +=,再把228m m + 变形为()224m m +,然后利用整体代入的方法计算 .【详解】解:m 是关于x 的方程2450x x +-=的一个根,2450m m ∴+-=,245m m ∴+=,()2228242510m m m m ∴+=+=⨯=.故答案为 10 .【点睛】本题考查了一元二次方程的解: 能使一元二次方程左右两边相等的未知数的值是一元二次方程的解 . 20.某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x 米. 若平行于墙的一边长为y 米,直接写出y 与x 的函数关系式及其自变量x的取值范围.垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大值.【答案】112.1【解析】试题分析:(1)根据题意即可求得y 与x 的函数关系式为y=30﹣2x 与自变量x 的取值范围为6≤x <11;(2)设矩形苗圃园的面积为S ,由S=xy ,即可求得S 与x 的函数关系式,根据二次函数的最值问题,即可求得这个苗圃园的面积最大值.试题解析:解:(1)y=30﹣2x (6≤x <11).(2)设矩形苗圃园的面积为S ,则S=xy=x (30﹣2x )=﹣2x 2+30x ,∴S=﹣2(x ﹣7.1)2+112.1,由(1)知,6≤x <11,∴当x=7.1时,S 最大值=112.1,即当矩形苗圃园垂直于墙的一边的长为7.1米时,这个苗圃园的面积最大,这个最大值为112.1.点睛:此题考查了二次函数的实际应用问题.解题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.21.6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:血型 A B AB O人数10 5(1)这次随机抽取的献血者人数为人,m=;补全上表中的数据;若这次活动中该市有3000人义务献血,请你根据抽样结果回答:从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?【答案】(1)50,20;(2)12,23;见图;(3)大约有720人是A型血.【解析】(1)用AB型的人数除以它所占的百分比得到随机抽取的献血者的总人数,然后用B型的人数除以抽取的总人数即可求得m的值;(2)先计算出O型的人数,再计算出A型人数,从而可补全上表中的数据;(3)用样本中A型的人数除以50得到血型是A型的概率,然后用3000乘以此概率可估计这3000人中是A型血的人数.【详解】(1)这次随机抽取的献血者人数为5÷10%=50(人),所以m=1050×100=20,故答案为50,20;(2)O型献血的人数为46%×50=23(人),A型献血的人数为50﹣10﹣5﹣23=12(人),补全表格中的数据如下:血型 A B AB O 人数12 10 5 23 故答案为12,23;(3)从献血者人群中任抽取一人,其血型是A型的概率=126 5025,3000×625=720,估计这3000人中大约有720人是A型血.【点睛】本题考查了扇形统计图、统计表、概率公式、用样本估计总体等,读懂统计图、统计表,从中找到必要的信息是解题的关键;随机事件A 的概率P (A )=事件A 可能出现的结果数除以所有可能出现的结果数.22.先化简,后求值:(1﹣11a +)÷(2221a a a a -++),其中a =1. 【答案】11a a +-,2. 【解析】先根据分式的混合运算顺序和运算法则化简原式,再将a 的值代入计算可得. 【详解】解:原式=()()2111111a a a a a a -+⎛⎫-÷ ⎪++⎝⎭+ ()()2111a a a a a +=+- 11a a +=-, 当a =1时, 原式=3131+-=2. 【点睛】本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则.23.2018年“植树节”前夕,某小区为绿化环境,购进200棵柏树苗和120棵枣树苗,且两种树苗所需费用相同.每棵枣树苗的进价比每棵柏树苗的进价的2倍少5元,每棵柏树苗的进价是多少元.【答案】15元.【解析】首先设每棵柏树苗的进价是x 元,则每棵枣树苗的进价是(2x -5)元,根据题意列出一元一次方程进行求解.【详解】解:设每棵柏树苗的进价是x 元,则每棵枣树苗的进价是(2x -5)元.根据题意,列方程得:200=120(25)x x -, 解得:x=15答:每棵柏树苗的进价是15元.【点睛】此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.24201(1)6tan 303π-︒⎛⎫--+- ⎪⎝⎭解方程:544101236x x x x -++=-- 【答案】 (1)10;(2)原方程无解.【解析】(1)原式利用二次根式性质,零指数幂、负整数指数幂法则,以及特殊角的三角函数值计算即可求出值;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【详解】(1)原式=323169+-⨯+=10;(2)去分母得:3(5x﹣4)+3x﹣6=4x+10,解得:x=2,经检验:x=2是增根,原方程无解.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.25.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+1.求抛物线的表达式;在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.【答案】(1)y=﹣x2+2x+1;(2)P (97,127);(1)当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.【解析】(1)先求得点B和点C的坐标,然后将点B和点C的坐标代入抛物线的解析式得到关于b、c的方程,从而可求得b、c的值;(2)作点O关于BC的对称点O′,则O′(1,1),则OP+AP的最小值为AO′的长,然后求得AO′的解析式,最后可求得点P的坐标;(1)先求得点D的坐标,然后求得CD、BC、BD 的长,依据勾股定理的逆定理证明△BCD为直角三角形,然后分为△AQC∽△DCB和△ACQ∽△DCB两种情况求解即可.【详解】(1)把x=0代入y=﹣x+1,得:y=1,∴C(0,1).把y=0代入y=﹣x+1得:x=1,∴B(1,0),A(﹣1,0).将C(0,1)、B(1,0)代入y=﹣x2+bx+c得:9303b cc-++=⎧⎨=⎩,解得b=2,c=1.∴抛物线的解析式为y=﹣x2+2x+1.(2)如图所示:作点O 关于BC 的对称点O′,则O′(1,1).∵O′与O 关于BC 对称,∴PO=PO′.∴OP+AP=O′P+AP≤AO′.∴OP+AP 的最小值=O′A=()()221330--+-=2. O′A 的方程为y=3344x + P 点满足33443y x y x ⎧=+⎪⎨⎪=+⎩﹣解得:97127x y ⎧=⎪⎪⎨⎪=⎪⎩所以P (97 ,127) (1)y=﹣x 2+2x+1=﹣(x ﹣1)2+4,∴D (1,4).又∵C (0,1,B (1,0),∴2,25∴CD 2+CB 2=BD 2,∴∠DCB=90°.∵A (﹣1,0),C (0,1), ∴OA=1,CO=1.∴13AO CD CO BC ==. 又∵∠AOC=DCB=90°,∴△AOC ∽△DCB .∴当Q 的坐标为(0,0)时,△AQC ∽△DCB .如图所示:连接AC ,过点C 作CQ ⊥AC ,交x 轴与点Q .∵△ACQ为直角三角形,CO⊥AQ,∴△ACQ∽△AOC.又∵△AOC∽△DCB,∴△ACQ∽△DCB.∴CD ACBD AQ=,即21025=,解得:AQ=3.∴Q(9,0).综上所述,当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.【点睛】本题考查了二次函数的综合应用,解题的关键是掌握待定系数法求二次函数的解析式、轴对称图形的性质、相似三角形的性质和判定,分类讨论的思想.26.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.【答案】证明见试题解析.【解析】试题分析:首先根据∠ACD=∠BCE得出∠ACB=∠DCE,结合已知条件利用SAS判定△ABC和△DEC 全等,从而得出答案.试题解析:∵∠ACD=∠BCE ∴∠ACB=∠DCE 又∵AC=DC BC=EC ∴△ABC≌△DEC ∴∠A=∠D考点:三角形全等的证明中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.估算9153+÷的运算结果应在( ) A .2到3之间B .3到4之间C .4到5之间D .5到6之间【答案】D【解析】解:9153+÷=35+ ,∵2<5<3,∴35+在5到6之间.故选D . 【点睛】此题主要考查了估算无理数的大小,正确进行计算是解题关键.2.如图,正比例函数11y k x =的图像与反比例函数22k y x =的图象相交于A 、B 两点,其中点A 的横坐标为2,当12y y >时,x 的取值范围是( )A .x <-2或x >2B .x <-2或0<x <2C .-2<x <0或0<x <2D .-2<x <0或x >2【答案】D 【解析】先根据反比例函数与正比例函数的性质求出B 点坐标,再由函数图象即可得出结论.【详解】解:∵反比例函数与正比例函数的图象均关于原点对称,∴A 、B 两点关于原点对称,∵点A 的横坐标为1,∴点B 的横坐标为-1,∵由函数图象可知,当-1<x <0或x >1时函数y 1=k 1x 的图象在22k y x=的上方, ∴当y 1>y 1时,x 的取值范围是-1<x <0或x >1.故选:D .【点睛】本题考查的是反比例函数与一次函数的交点问题,能根据数形结合求出y 1>y 1时x 的取值范围是解答此题的关键.3.如图,圆弧形拱桥的跨径12AB =米,拱高4CD =米,则拱桥的半径为( )米A.6.5B.9C.13D.15【答案】A【解析】试题分析:根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O.连接OA.根据垂径定理和勾股定理求解.得AD=6设圆的半径是r,根据勾股定理,得r2=36+(r﹣4)2,解得r=6.5考点:垂径定理的应用.4.中国幅员辽阔,陆地面积约为960万平方公里,“960万”用科学记数法表示为()A.0.96×107B.9.6×106C.96×105D.9.6×102【答案】B【解析】试题分析:“960万”用科学记数法表示为9.6×106,故选B.考点:科学记数法—表示较大的数.5.对于一组统计数据1,1,6,5,1.下列说法错误的是()A.众数是1 B.平均数是4 C.方差是1.6 D.中位数是6【答案】D【解析】根据中位数、众数、方差等的概念计算即可得解.【详解】A、这组数据中1都出现了1次,出现的次数最多,所以这组数据的众数为1,此选项正确;B、由平均数公式求得这组数据的平均数为4,故此选项正确;C、S2=15[(1﹣4)2+(1﹣4)2+(6﹣4)2+(5﹣4)2+(1﹣4)2]=1.6,故此选项正确;D、将这组数据按从大到校的顺序排列,第1个数是1,故中位数为1,故此选项错误;故选D.考点:1.众数;2.平均数;1.方差;4.中位数.6.如图1,在△ABC中,AB=BC,AC=m,D,E分别是AB,BC边的中点,点P为AC边上的一个动点,连接PD,PB,PE.设AP=x,图1中某条线段长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是()A .PDB .PBC .PED .PC【答案】C 【解析】观察可得,点P 在线段AC 上由A 到C 的运动中,线段PE 逐渐变短,当EP ⊥AC 时,PE 最短,过垂直这个点后,PE 又逐渐变长,当AP=m 时,点P 停止运动,符合图像的只有线段PE ,故选C.点睛:本题考查了动点问题的函数图象,对于此类问题来说是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.7.某种品牌手机经过二、三月份再次降价,每部售价由1000元降到810元,则平均每月降价的百分率为( )A .20%B .11%C .10%D .9.5% 【答案】C【解析】设二,三月份平均每月降价的百分率为x ,则二月份为1000(1)x -,三月份为21000(1)x -,然后再依据第三个月售价为1,列出方程求解即可.【详解】解:设二,三月份平均每月降价的百分率为x .根据题意,得21000(1)x -=1.解得10.1x =,2 1.9x =-(不合题意,舍去).答:二,三月份平均每月降价的百分率为10%【点睛】本题主要考查一元二次方程的应用,关于降价百分比的问题:若原数是a ,每次降价的百分率为a ,则第一次降价后为a (1-x );第二次降价后后为a (1-x )2,即:原数x (1-降价的百分率)2=后两次数. 8.在半径等于5 cm 的圆内有长为53cm 的弦,则此弦所对的圆周角为A .60°B .120°C .60°或120°D .30°或120° 【答案】C【解析】根据题意画出相应的图形,由OD ⊥AB ,利用垂径定理得到D 为AB 的中点,由AB 的长求出AD 与BD 的长,且得出OD 为角平分线,在Rt △AOD 中,利用锐角三角函数定义及特殊角的三角函数值求出∠AOD 的度数,进而确定出∠AOB 的度数,利用同弧所对的圆心角等于所对圆周角的2倍,即可求出弦AB 所对圆周角的度数.【详解】如图所示,∵OD⊥AB,∴D为AB的中点,即AD=BD=532,在Rt△AOD中,OA=5,AD=53 2,∴sin∠AOD=5332=52,又∵∠AOD为锐角,∴∠AOD=60°,∴∠AOB=120°,∴∠ACB=12∠AOB=60°,又∵圆内接四边形AEBC对角互补,∴∠AEB=120°,则此弦所对的圆周角为60°或120°.故选C.【点睛】此题考查了垂径定理,圆周角定理,特殊角的三角函数值,以及锐角三角函数定义,熟练掌握垂径定理是解本题的关键.9.如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G,下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE=12S△CEF,其中正确的是()A.①③B.②④C.①③④D.②③④【答案】C【解析】①通过条件可以得出△ABE≌△ADF,从而得出∠BAE=∠DAF,BE=DF,由正方形的性质就可以得出EC=FC ,就可以得出AC 垂直平分EF ,②设BC=a ,CE=y ,由勾股定理就可以得出EF 与x 、y 的关系,表示出BE 与EF ,即可判断BE+DF 与EF 关系不确定;③当∠DAF=15°时,可计算出∠EAF=60°,即可判断△EAF 为等边三角形,④当∠EAF=60°时,设EC=x ,BE=y ,由勾股定理就可以得出x 与y 的关系,表示出BE 与EF ,利用三角形的面积公式分别表示出S △CEF 和S △ABE ,再通过比较大小就可以得出结论.【详解】①四边形ABCD 是正方形,∴AB ═AD ,∠B=∠D=90°.在Rt △ABE 和Rt △ADF 中,AE AF AB AD=⎧⎨=⎩, ∴Rt △ABE ≌Rt △ADF (HL ),∴BE=DF∵BC=CD ,∴BC-BE=CD-DF ,即CE=CF ,∵AE=AF ,∴AC 垂直平分EF .(故①正确).②设BC=a ,CE=y ,∴BE+DF=2(a-y )y ,∴BE+DF 与EF 关系不确定,只有当y=()a 时成立,(故②错误).③当∠DAF=15°时,∵Rt △ABE ≌Rt △ADF ,∴∠DAF=∠BAE=15°,∴∠EAF=90°-2×15°=60°,又∵AE=AF∴△AEF 为等边三角形.(故③正确).④当∠EAF=60°时,设EC=x ,BE=y ,由勾股定理就可以得出:(x+y)2+y 2=x)2∴x 2=2y (x+y )∵S △CEF =12x 2,S △ABE =12y(x+y),∴S △ABE =12S △CEF .(故④正确). 综上所述,正确的有①③④,故选C .【点睛】本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,等边三角形的性质的运用,三角形的面积公式的运用,解答本题时运用勾股定理的性质解题时关键.10.《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱,问人数、物价各是多少?设合伙人数为x 人,物价为y 钱,以下列出的方程组正确的是( )A .8374y x y x -=⎧⎨-=⎩B .8374y x x y -=⎧⎨-=⎩C .8374x y y x -=⎧⎨-=⎩D .8374x y x y -=⎧⎨-=⎩【答案】C 【解析】分析题意,根据“每人出8钱,会多3钱;每人出7钱,又会差4钱,”可分别列出方程.【详解】设合伙人数为x 人,物价为y 钱,根据题意得8x-y 3y 7x 4=⎧⎨-=⎩故选C【点睛】本题考核知识点:列方程组解应用题.解题关键点:找出相等关系,列出方程.二、填空题(本题包括8个小题)11.在Rt △ABC 中,∠C =90°,AB =2,BC sin2A =_____. 【答案】12【解析】根据∠A 的正弦求出∠A =60°,再根据30°的正弦值求解即可.【详解】解:∵sin 2BC A AB == ∴∠A =60°, ∴1sinsin 3022A ︒==. 故答案为12. 【点睛】本题考查了特殊角的三角函数值,熟记30°、45°、60°角的三角函数值是解题的关键.12.如图,直线y 1=kx+n (k≠0)与抛物线y 2=ax 2+bx+c (a≠0)分别交于A (﹣1,0),B (2,﹣3)两点,那么当y 1>y 2时,x 的取值范围是_____.【答案】﹣1<x<2【解析】根据图象得出取值范围即可.【详解】解:因为直线y1=kx+n(k≠0)与抛物线y2=ax2+bx+c(a≠0)分别交于A(﹣1,0),B(2,﹣3)两点,所以当y1>y2时,﹣1<x<2,故答案为﹣1<x<2【点睛】此题考查二次函数与不等式,关键是根据图象得出取值范围.13.将抛物线y=2x2平移,使顶点移动到点P(﹣3,1)的位置,那么平移后所得新抛物线的表达式是_____.【答案】y=2(x+3)2+1【解析】由于抛物线平移前后二次项系数不变,然后根据顶点式写出新抛物线解析式.【详解】抛物线y=2x2平移,使顶点移到点P(﹣3,1)的位置,所得新抛物线的表达式为y=2(x+3)2+1.故答案为:y=2(x+3)2+1【点睛】本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.14.已知关于x方程x2﹣3x+a=0有一个根为1,则方程的另一个根为_____.【答案】1【解析】分析:设方程的另一个根为m,根据两根之和等于-ba,即可得出关于m的一元一次方程,解之即可得出结论.详解:设方程的另一个根为m,根据题意得:1+m=3,解得:m=1.故答案为1.点睛:本题考查了根与系数的关系,牢记两根之和等于-ba是解题的关键.15.抛物线y=(x+1)2 - 2的顶点坐标是______ .。
2018济南市学业水平考试数学一摸试题

.(用含 a,h
的代数式表示)
数学试题第 5页(共 6 页)
【灵活应用】 如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了 一个面积最大的矩形(∠B 为所剪出矩形的内角),求该矩形的面积. 【实际应用】 如图④,现有一块四边形的木板余料 ABCD,经测量 AB=50cm,BC=108cm,CD=60cm, 且 tanB=tanC= 4 ,木匠徐师傅从这块余料中裁出了顶点 M,N 在边 BC 上且面积最大的矩形
第 I 卷(选择题共 48 分)
注意事项: 第Ⅰ卷为选择题,每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑;
如需改动,用橡皮擦干净后,再选涂其他答案标号.答案写在试卷上无效. 一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分.在每小题给出的四个选项中,只有
一项是符合题目要求的.) 1. 7 的相反数是
交 CA 延长线于点 E,连接 AD,BD.
C
(1)△ABD 的面积是___________;
(2)求证:DE 是⊙O 的切线; (3)求线段 DE 的长.
A
O
B
E
D
26.(本小题满分 12 分) 【探索发现】
如图①,是一张直角三角形纸片,∠C=60°,小明想从中剪出一个以∠B 为内角且面积最
大的矩形,经过多次操作发现,当沿着中位线 DE,EF 剪下时,矩形的面积最大,经证明发
数学试题第 6页(共 6 页)
在点 P 运动过程中,若⊙P 与直线 y x 4 有且只有 3 次相
切时,则定值 R 为
.
第 18 题图
三、解答题:(本大题共 9 个小题,共 78 分.解答应写出文字说明、证明过程或演算步骤.) 19.(本小题满分 6 分)
解析:山东省济南市长清第五中学2018届九年级1月月考数学试题(解析版)

山东省济南市长清第五中学2018届九年级1月月考数学试题一.选择题(12×4分)1. 如图,由几个相同的小正方体搭成的一个几何体,它的左视图为()A. B. C. D.【答案】A【解析】解:从左面看易得第一层有3个正方形,第二层最左边有一个正方形.故选A.点睛:本题考查了三视图的知识,左视图是从物体的左面看得到的视图.2. 为估计池塘两岸A、B间的距离,晓明在池塘一侧选取了一点P,测得P A=16m,PB=12m,那么AB间的距离不可能是()A. 5mB. 15mC. 20mD. 28m【答案】D【解析】解:∵P A、PB、AB能构成三角形,∴P A﹣PB<AB<P A+PB,即4m<AB<28m.故选D.点睛:已知三角形的两边,则第三边的范围是:大于已知的两边的差,而小于两边的和.3. 如图,在△ABC中, 若DE∥BC , ,DE=4cm,则BC的长为( )A. 8cmB. 12cmC. 11cmD. 10cm【答案】B【解析】试题分析:因为=,所以,又因为DE∥BC,所以, 因为DE=4cm,所以,所以BC=12cm,故选:B.考点:平行线分线段成比例定理4. 如图,A、B是数轴上的两点,在线段AB上任取一点C,则点C到表示-1的点的距离不大于...2的概率是()A. B. C. D.【答案】D【解析】解:∵AB间距离为5,点C到表示-1的点的距离不大于2的点是﹣3到1之间的点,满足条件的点组成的线段的长是4,∴其概率为,故选D.点睛:此题考查了概率公式,关键是求出点C到表示-1的点的距离不大于2的点在线段的长,用到的知识点为:概率=相应的线段长与总线段长之比.5. 一次函数y=(m—1)x+m2的图象过点(0,4),且y随x的增大而增大,则m的值为()A. -2B. 2C. 1D. -2或2【答案】B【解析】试题分析:把(0,4)代入解析式得,,解得m=,因为y随x的增大而增大,所以m-1>0,所以m=-2舍去,只取m=2.故选:B.考点:待定系数法求一次函数解析式;一次函数的性质.6. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=在同一坐标系中的大致图象是()A. B. C. D.【答案】C【解析】解:由二次函数图象可知a>0,c>0,由对称轴x=>0,可知b<0,当x=1时,a+b+c<0,即b+c<0,所以正比例函数y=(b+c)x经过二四象限,反比例函数图象经过一三象限,故选C.点睛:本题主要考查二次函数图象的性质、一次函数的图象的性质、反比例函数图象的性质,关键在于通过二次函数图象推出a、b、c的取值范围.7. 如图,直线与反比例函数(x>0)、(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则的值为()A. 2B. 3C. 4D. 5【答案】D【解析】解:由题意得,点C的坐标(t,﹣),点B的坐标(t,),BC=,则()×t=3,解得k=5,故选D.点睛:本题考查的是反比例函数系数k的几何意义,利用函数解析式表示出点的横纵坐标的关系是解题的关键.8. 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为()A. B. C. D.【答案】A【解析】解:连结AD,如图,∵∠A=90°,AB=6,AC=8,∴BC==10,∵点D为边BC的中点,∴DA=DC=5,∴∠1=∠C,∵∠MDN=90°,∠A=90°,∴点A、D在以MN为直径的圆上,∴∠1=∠DMN,∴∠C=∠DMN,在Rt△ABC中,cos C=,∴cos∠DMN=.故选A.点睛:本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了直角三角形斜边上的中线性质.9. 在平面直角坐标系中,将抛物线先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为()A. B. C. D.【答案】C【解析】试题分析:图象的平移法则为:上加下减,左加右减.考点:函数的图象平移.10. 抛物线的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为()A. (4,-1)B. (0,-3)C. (-2,-3)D. (-2,-1)【答案】A【解析】解:∵抛物线y=x2﹣4x+3可化为:y=(x﹣2)2﹣1,∴其顶点坐标为(2,﹣1),∴向右平移2个单位得到新抛物线的解析式,所得抛物线的顶点坐标是(4,﹣1).故选A.点睛:本题考查的是二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.11. .二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是()A. 1个B. 2个C. 3个D. 4个【答案】C【解析】解:∵抛物线和x轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2<0,∴①正确;∵对称轴是直线x=﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,∴4a+c>2b,∴②错误;∵把x=1代入抛物线得:y=a+b+c<0,∴2a+2b+2c<0,∵=﹣1,∴b=2a,∴3b+2c<0,∴③正确;∵抛物线的对称轴是直线x=﹣1,∴y=a﹣b+c的值最大,即把x=m(m≠﹣1)代入得:y=am2+bm+c<a﹣b+c,∴am2+bm+b<a,即m(am+b)+b<a,∴④正确;即正确的有3个,故选C.点睛:此题主要考查了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax2+bx+c=0的解的方法,同时注意特殊点的运用.12. 如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是()A. B. C. D.【答案】B【解析】当点N在AD上时,即0≤x≤1,,点N在CD上时,即1≤x≤2,,y随x的增大而增大,所以排除A. D;当N在BC上时,即2≤x≤3,,开口方向向下。
2018年3月济南市长清区中考数学模拟试卷(有答案)最新精选

山东省济南市长清区2018届中考模拟试卷(3月)数学一、单选题1.16的算术平方根为()A. ±4B.4C.﹣4D.8【答案】B【考点】算术平方根【解析】【解答】16的算术平方根为 4.故答案为:B.【分析】根据算术平方根的意义可得16的算术平方根为4.2.中国移动数据中心IDC项目近日在高新区正式开工建设,该项目规划建设规模12.6万平方米,建成后将成为山东省最大的数据业务中心.其中126000用科学记数法表示应为()A. 1.26×106B. 12.6×104C. 0.126×106D. 1.26×105【答案】D【考点】科学记数法—表示绝对值较大的数【解析】【解答】根据科学记数法的表示形式(a×10n,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数)可得:126000=1.26×105.故答案为:D.【分析】任何一个绝对值大于或等于1的数都可表示为a 的形式,其中n=整数位数-1。
则126000=1.26.3.从棱长为2a的正方体零件的一角,挖去一个棱长为a的小正方体,得到一个如图所示的零件,则这个零件的俯视图是()A. B. C. D.【答案】B【考点】简单几何体的三视图【解析】【解答】俯视图是从上面往下看到的图形,从上面往下看到的是大正方形的左下角有一个小正方形,故答案选B.【分析】俯视图是从上面往下看到的图形,由图知;从上面往下看到的是大正方形的左下角有一个小正方形.4.如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于()A. 30°B. 35°C. 40°D. 50°【答案】C【考点】平行线的性质【解析】【解答】解:如图,∵直线m∥n,∴∠1=∠3,∵∠1=70°,∴∠3=70°,∵∠3=∠2+∠A,∠2=30°,∴∠A=40°,故选C.【分析】首先根据平行线的性质求出∠3的度数,然后根据三角形的外角的知识求出∠A的度数.5.下面的图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.【答案】A【考点】轴对称图形,中心对称及中心对称图形【解析】【解答】B、D选项是轴对称图形但不是中心轴对称图形,C选项不是轴对称图形;故答案为:A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018济南市长清区九年级第一次模拟考试数学试题本试卷满分为150分一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.2018的相反数是( )A .2018B .-12018C .12018D .-20182.如图,点O 在直线AB 上,若∠2=140°,则∠1的度数是( )A .40°B .60°C .140°D .150°21CBA3.下列运算正确的是( )A .a 2·a 3=a 6B .(a 2)3=a 6C .a 6÷a 2=a 3D .2-3=-6 4.将100800用科学记数法表示为A .0.1008×106B .1.008×106C .10.08×104D .1.008×1055.下列图案中既是中心对称图形,又是轴对称图形的是( )A B C D 6.如图所示的几何体是由4个相同的小正方体组成,其主视图为( )A B C D7.下列命题中,真命题是 ( )A .两对角线相等的四边形是矩形B .两对角线互相平分的四边形是平行四边形则表示“跳绳个数”这组数据的中位数和众数分别是( )A .170,160B .180,160C .170,180D .160,2009.如图,一次函数y 1=x +b 与一次函数y 2=kx +4的图象交于点P (1,3),则关于x 的不等式x +b >kx +4的解集是( )A .x >-2B .x >0C .x >1D .x <1y 2 10.抛物线 y =2(x +3)2+1的顶点坐标是( )A .(3, 1)B .(-3,-1)C .(-3,1)D .(3, -1)11.如图,直线y =-33x +2与x 轴,y 轴分别交于A ,B 两点,把△AOB 沿着直线AB 翻折后得到△AO ′B ,则点O ′ 的坐标是( ) A .(3,3)B .(2,23)C .(3,3) D .(23,4)12.如图,抛物线y =ax 2+bx +c 的对称轴是x =-1.且过点(12,0),有下列结论:①abc >0;②a -2b +4c =0;③25a -10b +4c =0;④3b +2c >0;⑤a -bm ≥(am -b );其中所有正确的结论有( )个. A .2个 B .3个 C .4个 D .5个二、填空题(本大题共6个小题,每题4分,共24分.把答案填在题中的横线上) 13.分解因式:x 2+xy =____________. 14.比较大小:5-12 ________ 12. 15.在一个不透明的盒子中有12个白球,若干个黄球,它们除了颜色不同外,其余均相同,若从中随机摸出一个球是黄球的概率是13,则黄球有 _____ 个.16.若代数式1x -2和32x +1的值相等,则x = _____ . 17.如图,在圆内接四边形ABCD 中,O 为圆心,∠BOD =160°,则∠BCD 的度数是 _____ .D三、解答题(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤) 19.(本题满分6分,每小题3分)(1)计算:tan60°+(5-1)0-12; (2)化简:(a +3)(a -3)+a (2-a )20.(本题满分6分,每小题3分) (1)解不等式组:⎩⎨⎧x -3<14x -4≥x +2; (2)解方程:x 2-4x +3=021.(本题满分6分)如图,AB 是⊙O 的直径,AD 是⊙O 的切线,点C 在⊙O 上,BC ∥OD ,AB =2,OD =3. (1)求证:ΔACB ∽ΔDAO . (2)求BC 的长.22.(本小题满分8分)为进一步推广“阳光体育”大课间活动,长清区某中学对已开设的A实心球,B立定跳远,C跑步,D排球四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:(1)本次共调查了名学生;(2)将两个统计图补充完整;(3)随机抽取了3名喜欢“跑步”的学生,其中有2名男生,1名女生,现从这3名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到一男生一女生的概率.23.(本小题满分8分)春节期间,某超市出售的荔枝和芒果,单价分别为每千克26元和22元,李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?24.(本小题满分10分)如图,在一次空中搜寻中,水平飞行的飞机观测到在点A 俯角为30°方向的F 点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B 点,此时测得点F 在点B 俯角为60°的方向上,请你计算当飞机飞临F 的正上方点C 时(点A 、B 、C 在同一直线上),竖直高度CF 约为多少米?(结果保留整数,参考数值:3≈1.7)25.(本小题满分10分)如图,一次函数y =kx +b 与反比例函数y =m x的图象交于A (2,3),B (-3,n )两点. (1)求一次函数与反比例函数的表达式;(2)根据所给条件,请直接写出不等式kx +b >m x的解集______________; (3)过点B 作BC ⊥x 轴,垂足为C ,求S △AB C .26.(本小题满分12分)已知:正方形ABCD ,等腰直角三角板的直角顶点落在正方形的顶点D 处,使三角板 绕点D 旋转.(1)当三角板旋转到图1的位置时,猜想CE 与AF 的数量关系,并加以证明;(2)在(1)的条件下,若DE =1,AE =7,CE =3,求∠AED 的度数;(3)若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=53,求CN的长.图1图2F27.(本小题满分12分)如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.(1)求抛物线的函数表达式;(2)在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.(3)在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.备用图九年级数学参考答案一、选择题(每题4分,共48分)二、填空题(每题4分,共24分)13.x(x+y) 14.> 15.6 16.7 17.100 18.-2419、解:(1)原式=32……2分=1-…………3分 (2) 原式=a 2-6+2a -a 2………2分,=2a -6………3分20.(1)解①得:x <4………1分解②得:x 2≥………2分所以原不等式组的解集是2≤x <4………3分 (2)由x 2-4x +3=0得(x -1)(x -3)=0………1分∴x -1=0或x -3=0………2分 ∴x 1=1,x 2=3………3分21.(1)解:∵BC ∥OD ∴∠B =∠AOD ………1分∵AB 是直径,∴∠ACB =90。
,………2分22.(1)150………2分; (2)C 跑步人数是60人,图略.………4分 (3)画树状图为:共有6种等可能的结果数,其中一男生一女生的结果数为4, ………6分所以刚好抽到一男生一女生的概率3264==P .………8分 23.解:设购买了荔枝x 千克,则购买芒果(30-x )千克.………1分根据题意列方程得:26x +22(30-x )=708,………4分, 解得:x =12,30-x =18.………7分答:购买了无核荔枝12千克,购买鸡蛋芒果18千克.…8分 24.解:∵∠CBF =60°, ∠CAF =30°,∠CBF =∠CAF +∠BFA∴∠BFA =30°……………………3分∴AB =BF , ∵AB =800米∴AB =BF =800米……………………4分∵∠BCF =90°,∠CBF =60°,答:竖直高度CF 约为680米.……………………8分25. (1)∵点A (2,3)在y =mx 的图象上∴m =6, ∴反比例函数的解析式为:y =x6,............2分∵B (−3,n )在反比例函数图象上,∴n =6÷(-3)=−2, ∵A (2,3),B (−3,−2)两点在y =kx +b 上,∴⎩⎨⎧+-=-+=b k b k 3223解得:⎩⎨⎧==11b k ∴一次函数的解析式为:y =x +1;……4分(2)−3<x <0或x >2;……6分(3)以BC 为底,则BC 边上的高AE 为3+2=5,∴S △ABC =21×2×5=5.……10分 26.(1)CE =AF ;……1分证明:在正方形ABCD ,等腰直角三角形CEF 中,FD =DE ,CD =CA ,∠ADC =∠EDF =90∘ ∴∠ADF =∠CDE ,∴△ADF ≌△CDE ,∴CE =AF .……4分 (2)∵DE =1,AE =7,CE =3, ∴CE =AF =3,EF =2,……5分∵AE 2+EF 2=7+2=9,AF 2=9,即AE 2+EF 2=AF 2∴△AEF 为直角三角形,……7分 ∴∠BEF =90∘∴∠AED =∠AEF +DEF =90∘+45∘=135∘;……8分(3)∵M 是AB 中点,∴MA =21AB =21AD , ∵AB ∥CD ,∴21===DC AM OC OA OD OM ,……9分 在Rt △DAM 中,DM =5222=+AM AD∴DO =354,∵OF =35,∴DF =5,……10分 ∵∠DFN =∠DCO =45∘,∠FDN =∠CDO ,∴△DFN ∽△DCO ,……11分373543535445,=-=-=∴=∴=∴=∴DN CD CN DN DN DO DN DC DF ……12分 27.(1)∵C (0,4),∴OC =4. ∵OA =OC =4OB ,∴OA =4,OB =1, ∴A (4,0),B (−1,0),设抛物线解析式:y =a (x +1)(x −4),∴4=−4a ,∴a =−1.∴y =−x 2+3x +4.……3分 (2)存在. ……4分作PN ⊥x 轴交AC 于N ,求得AC 的解析式为y =-x +4 ……5分设P (x ,−x 2+3x +4),则N (x ,-x +4),得PN =(−x 2+3x +4)-(-x +4)=−x 2+4x ……6分S △PAC =21PN ×4=2PN =2(−x 2+4x )=-2(x -2)2+8……7分 ∴P 点坐标为(2,6)时ΔPAC 面积的最大值,最大面积是8…………8分 (3)Q (0,0),(-4,0),()()0,244,0,244-+. ……12分。
