2015年下学期八年级数学竞赛试题
初二数学竞赛试题7套整理版(含答案)

初二数学竞赛试题7套整理版(含答案)初二数学竞赛试题7套整理版(含答案)第一套试题1. 某数与它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.2. 有一个矩形,长是宽的3倍,如果长再加上宽再加上1的和等于50,求矩形的长和宽各是多少?解:设矩形的宽为x,则长为3x,根据题意可得方程 3x + x + 1 = 50,化简得 4x + 1 = 50,解得 x = 12,所以长为3 * 12 = 36,宽为12.3. 某个数的三次方减去它自身等于608,求这个数是多少?解:设这个数为x,根据题意可得方程 x^3 - x = 608,化简得 x^3 - x - 608 = 0,因此需求解该方程的解x.4. 甲数和乙数之和是300,甲数比乙数大30,求甲数和乙数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 x + y = 300,x - y = 30,联立这两个方程可以解得甲数x和乙数y.5. 家长购买某品牌的饮料,每瓶售价为5元,如果购买10瓶,优惠50%,那么需要支付的价格是多少?解:购买10瓶优惠50%,相当于购买5瓶的价格,所以需要支付 5 * 10 * (1 - 50%) = 25元.第二套试题1. 学校图书馆购买300本新书,若图书馆中已有书籍500本,现将这些书按每排放10本的方式摆放,共需要多少排?解:新书300本加上原有书籍500本,共计800本书,每排放10本,所以需要 800 / 10 = 80排.2. 小明每天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,求他一天中运动的总时长是多少分钟?解:小明一天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,总时长为 30 + 25 + 40 = 95分钟.3. 甲、乙两人开始一起钓鱼,甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,如果他们一起钓了45分钟,那么他们一共钓到了多少条鱼?解:甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,他们一起钓了45分钟,所以甲和乙一共钓到了 2 * 45 + 1 * 45 = 135 条鱼.4. 某商品原价100元,现在打8折,过了一段时间后再降价,降到原价的85%,现在这个商品的售价是多少?解:原价100元,打8折后为 100 * (1 - 80%) = 80元,再降到原价的85%为 80 * 85% = 68元.5. 某人的年收入为12000元,每月生活费占月收入的1/5,那么这个人每月的生活费用是多少元?解:年收入12000元,月收入为 12000 / 12 = 1000元,生活费占收入的1/5,所以生活费用为 1000 * 1/5 = 200元.第三套试题1. 甲、乙两个人合作修一个房子,甲一个人修需要8天,乙一个人修需要12天,问他们一起修需要多少天?解:甲一个人修需要8天,乙一个人修需要12天,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8天.2. 甲购买一本书花费了原价的3/4,折后价格为60元,问这本书的原价是多少?解:折后价格为60元,花费原价的3/4,所以原价为 60 / (3/4) = 80元.3. 甲、乙两人比赛,甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,问谁的平均速度更快?解:甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒,平均速度为 (60 + 50 + 40) / 3 = 50 秒/轮;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,平均速度为 (55 + 45 + 35) / 3 = 45 秒/轮;所以甲的平均速度更快.4. 一只小狗每小时能跑5公里,一只小猫每小时能跑8公里,如果它们从同一地点同时出发并分别向东和西跑,4小时后它们相距了多少公里?解:小狗每小时能跑5公里,4小时后跑了5 * 4 = 20公里,小猫每小时能跑8公里,4小时后跑了8 * 4 = 32公里,所以它们相距了 32 -20 = 12 公里.5. 三个连续的偶数相加的和是60,求这三个数分别是多少?解:设第一个偶数为x,那么第二个偶数为x + 2,第三个偶数为x+ 4,根据题意可得方程 x + (x + 2) + (x + 4) = 60,求解该方程可得x及其对应的三个连续偶数.第四套试题1. 一个数的2倍加上5等于13,求这个数是多少?解:设这个数为x,根据题意可得方程 2x + 5 = 13,解得 x = 4.2. 甲乙两数相差22,乙数的2倍与甲数的3倍之和等于70,求甲、乙两数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 y - x = 22,2y + 3x= 70,联立这两个方程可以解得甲数x和乙数y.3. 一辆汽车以每小时80千米的速度行驶,行驶了1小时20分钟后停下来休息,求这段时间内汽车行驶的路程?解:汽车以每小时80千米的速度行驶,1小时20分钟共1.33 小时,所以汽车行驶的路程为 80 * 1.33 = 106.4 千米.4. 甲、乙两个人一起做一件工作,甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成需要的时间为 1/(1/4 + 1/6) = 2.4小时.5. 一个数加上它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.第五套试题1. 一条宽10米的路,两边分别种植了向阳向每排7棵树或9棵树,每棵树之间距离相等,而且与路两边相邻树之间距离也相等,问道路中间最宽的地方有多宽?解:分别种植7棵树和9棵树,每棵树之间距离相等,所以道路中间最宽的地方为两排树之间的距离.2. 一个数与4的乘积减去2等于18,求这个数是多少?解:设这个数为x,根据题意可得方程 4x - 2 = 18,解得 x = 5.3. 甲、乙、丙三人合作种田,甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,问他们三个人一起种地需要多少天?解:甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,他们一起种地需要的时间为 1/(1/10 + 1/12 + 1/15) =4.8天.4. 某人共有100元,买了一本书花掉了原价的3/5,剩下的钱还能买另一本原价为80元的书吗?解:100元买了一本书花掉了原价的3/5,剩下的钱为 100 * (1 - 3/5) = 40元,剩下的钱不足以购买另一本80元的书.5. 一团面粉重800克,其中水分为15%,求这团面粉中水分的重量是多少克?解:面粉重800克,其中水分为15%,所以水分的重量为800 * 15% = 120克.第六套试题1. 一个数与它的五分之一之和的和是40,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/5)x + x = 40,化简得7/5x = 40,解得 x = 28.57.2. 甲、乙两个人分别完成一项工作需要的时间比为2:5,如果他们一起完成这项工作需要3小时,求乙单独完成这项工作需要多少时间?解:甲、乙两个人分别完成一项工作需要的时间比为2:5,设甲单独完成需要的时间为x,乙单独完成需要的时间为y,根据题意可得方程 2x + 5x = 3,解得 y = 7.5.3. 有两个相交的圆,圆心之间的距离为8,两圆的半径分别为5和3,求两圆相交的弦的长度是多少?解:两个圆的半径分别为5和3,圆心之间的距离为8,利用勾股定理可以求得两圆相交的弦的长度.4. 甲乙两个人一起做一件工作,甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成需要的时间为 1/(1/10 + 1/15) = 6小时.5. 甲给乙20元,乙给丙30元,丙给甲10元,这三个人一共交易了多少元?解:甲给乙20元,乙给丙30元,丙给甲10元,所以一共交易了20 + 30 + 10 = 60元.第七套试题1. 某数比它的2/3小12,求这个数是多少?解:设这个数为x,根据题意可得方程 x - (2/3)x = 12,化简得 1/3x = 12,解得 x = 36.2. 甲、乙两个人一起修一条路,甲单独修需要8小时,乙单独修需要12小时,也有可能甲的速度是乙的倍数,问他们一起修需要多少小时?解:甲单独修需要8小时,乙单独修需要12小时,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8小时.3. 某品牌的衣服原价为200元,现在打折8折,过了一段时间后再降价,降到原价的85%,现在这件衣服的售价是多少?解:原价200元,打8折后为 200 * (1 - 80%) = 160元,再降到原价的85%为 160 * 85% = 136元.4. 甲、乙两个人一起做工,甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,问他们一起做一份工作需要多少时间?解:甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,他们一起做一份工作需要的时间为 1/(1/3 + 1/4) = 12/7小时.5. 某人的年收入为12000元,每月花销占收入的1/4,那么这个人每月的花销是多少元?解:年收入12000元,。
2015全国初中数学联赛初二试题

(初二年级)
第二试(A)
(3月22日上午9﹕50——11﹕20)
考生注意:本试共三个大题,第一题20分,第二、三题各25分,全卷满分70分.
一、(本题满分20分)
求所有的两位数 ,使得 的末两位数字构成的数恰好为 .
二、(本题满分25分)
在四边形 中, , , = ,求 .
2015年全国初中数学联合竞赛试题
(初二年级)
第一试(A)
(3月22日上午8﹕30——9﹕30)
考生注意:1.本试两个大题共10个小题,全卷满分70分.
2.用圆珠笔或钢笔作答.
3.解题书写不要超出装订线.
一、选择题(本题满分42分,每小题7分)
本题共有6个小题,每题均给出了代号为A,B,C,D的四个答案,其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得7分;不选、选错或选出的代号字母超过一个(不论是否写在括号内),一律得0分.
1.若 ,则 ()
A.3 B. 4 C. 5 D. 6
2.设实数 满足: , ,则
()
A.9 B. 6 C. 3 D. 0
3.锐角△ 中, 边的中垂线和 的角平分线相交于点 .若 , ,则 =( )
A.24°B.28°C.30°D.36°
4.三边长均为整数且周长为24的三角形的个数为()
A.11 B.12 C.17 D.18
三、(本题满分25分)已知 为实数,对任何满足 的实数 ,都有 成立,则 的最大值为.
3.设 是小于100的正整数且使 是6的倍数,则符合条件的所有正整数 的和是.
4.将数字1,2,3,……,34,35,36填在6×6的方格中,每个方格填一个数字,要求每行数字从左到右是从小到大的顺序,则第三列所填6个数字的和的最小值为.
八年级数学竞赛题
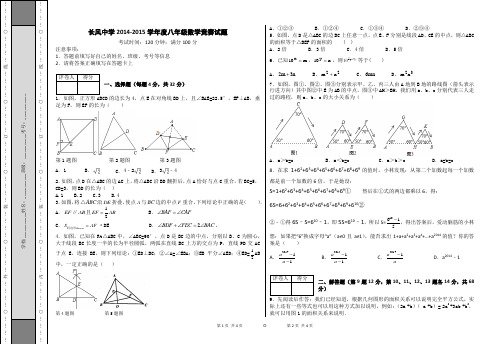
○…………外…………订…………___________考号:______○…………内…………订…………长风中学2014-2015学年度八年级数学竞赛试题考试时间:120分钟;满分100分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题(每题4分,共32分)的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()第1题图第2题图第3题图A.1 B. C.4﹣2 D.3﹣42.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合,若BC=5,CD=3,则BD的长为()A.1B.2C.3D.43使点A与BC边的中点F重合,下列结论中正确的是().A B.BAF CAF∠=∠C.ADFES AF=四边形·DE D.2BDF FEC BAC∠+∠=∠,4.如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④中,一定正确的是()第4题图第5题图A.①②③ B.①②④ C.①③④ D.②③④5.如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,则△ABC的面积等于△BEF的面积的 ( )A.2倍 B.3倍 C.4倍 D.5倍6.已知m10x=,n10y=,则2310x y+等于( )A、n3m2+ B、22nm+ C、mn6 D、32nm7.如图,图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进方向)其中图②中E为AB的中点,图③中AH>BH,我们用a、b、c分别代表三人走过的路程,则a、b、c的大小关系为()A.a>b=c B.a<b=c C.a>b>c D.a=b=c8.在求1+62+63+64+65+66+67+68+69的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:S=1+62+63+64+65+66+67+68+69①然后在①式的两边都乘以6,得:6S=6+62+63+64+65+66+67+68+69+610②②﹣①得6S﹣S=610﹣1,即5S=610﹣1,所以想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?你的答案是()A B C D.a2014﹣1二、解答题(第9题12分,第10、11、12、13题各14分,共68分)际上还有一些等式也可以用这种方式加以说明,例如:(2a +b)( a +b)= 2a2 +3ab +b2,就可以用图1的面积关系来说明.第1页共4页◎第2页共4页第3页 共4页 ◎ 第4页 共4页(1)根据图2写出一个等式 ; (2)已知等式:(x +1)(x +3)=x 2 + 4x + 3,请你画出一个相应的几何图形加以说明(模仿图1或图2画出图形即可).10.问题:在△ABC 中,AB=AC ,∠A=100°,BD 为∠B 的平分线,探究AD 、BD 、BC 之间的数量关系.请你完成下列探究过程:(1)观察图形,猜想AD 、BD 、BC 之间的数量关系为 .(2)在对(1)中的猜想进行证明时,当推出∠ABC=∠C=40°后,可进一步推出∠ABD=∠DBC= 度.(3)为了使同学们顺利地解答本题(1)中的猜想,小强同学提供了一种探究的思路:在BC 上截取BE=BD ,连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路,画出图形,在此基础上对(1)中的猜想加以证明.也可以选用其它的方法证明你的猜想.11.已知正方形ABCD 的对角线AC 与BD 交于点O ,点E 、F 分别是OB 、OC 上的动点, (1)如果动点E 、F 满足BE=CF (如图):①写出所有以点E 或F 为顶点的全等三角形(不得添加辅助线); ②证明:AE ⊥BF ;(2)如果动点E 、F 满足BE=OF (如图),问当AE ⊥BF 时,点E 在什么位置,并证明你的结论.12.阅读下列题目的解题过程:已知a 、b 、c 为∆ABC 的三边,且满足a c b c a b 222244-=-,试判断∆ABC 的形状.解:a cbc a b A 222244-=-()2222222222()()()()()ABC c a b a b a b B c a b C ∆∴-=+-∴=+∴是直角三角形问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: (2)错误的原因为: (3)本题正确的结论为:13.在等腰直角△ABC 中,∠BAC=90°,AB=AC ,(1)如图1,点D 、E 分别是AB 、AC 边的中点,AF ⊥BE 交BC 于点F ,连结EF 、CD 交于点H.求证,EF ⊥CD ;(2)如图2,AD=AE ,AF ⊥BE 于点G 交BC 于点F ,过F 作FP ⊥CD 交BE 的延长线于点P ,试探究线段BP,FP,AF 之间的数量关系,并说明理由.图1 图2。
2015年全国初中数学联赛初二年级试题答案

)
A.9. 【答】A.
B.6.
C.3.
D.0.
∵ a b c 3, a b c 4 ,
2 2 2
∴
a 2 b2 b2 c 2 c 2 a 2 4 c 2 4 a 2 4 b2 (2 c) (2 a) (2 b) 2c 2a 2b 2c 2a 2b
第一试(A)
一、选择题: (本题满分 42 分,每小题 7 分) 1. 若 x2 y 2 2 z 2 xy 2 yz 2 x 2 0 ,则 x y z A.3. 【答】C.
2 2 2
(
)
B.4.
C.5.
2 2
D.6.
2
∵ x y 2 z xy 2 yz 2 x 2 0 ,∴ 2 x 2 y 4 z 2 xy 4 yz 4 x 4 0 , ∴ ( x 2 xy y ) ( x 4 x 4) ( y 4 yz 4 z ) 0 ,
2 2 2 2 2
∴ ( x y) ( x 2) ( y 2 z) 0 ,∴ x y 2 , z 1 ,∴ x y z 5.
2 2 2
2. 设实数 a, b, c 满足: a b c 3 , a b c 4 ,则
2 2 2
a 2 b2 b2 c 2 c 2 a 2 ( 2c 2a 2b
∵ 2n 3n 2 是 6 的倍数,∴ m 1 是 3 的倍数,∴ m 3k 1 或 m 3k 2 ,其中 k 是非负整数.
2 2
∴ n 2(3k 1) 6k 2 或 n 2(3k 2) 6k 4 ,其中 k 是非负整数. ∴符合条件的所有正整数 n 的和是(2+8+14+…+86+92+98)+(4+10+16+…+82+88+94) =1634. 4.将数字 1,2,3,……,34,35,36 填在 6×6 的方格中,每个方格填一个数字,要求每行数字从 左到右是从小到大的顺序,则第三列所填 6 个数字的和的最小值为______. 【答】63. 设第三列所填 6 个数字按从小到大的顺序排列后依次为 A , B , C , D , E , F . 因为 A 所在行前面需要填两个比 A 小的数字, 所以 A 不小于 3; 因为 B 所在行前面需要填两个比 B 小 的数字,且 A 及 A 所在行前面两个数字都比 B 小,所以 B 不小于 6. 同理可知: C 不小于 9, D 不小于 12, E 不小于 15, F 不小于 18. 因此,第三列所填 6 个数字之和 A + B + C + D + E + F 3 6 9 12 15 18 63 . 如图即为使得第三列所填 6 个数字之和取得最小值的一种填法(后三列的数字填法不唯一). 1 4 7 10 13 16 2 5 8 11 14 17 3 6 9 12 15 18 19 25 22 26 31 32 20 27 23 28 34 33 21 29 24 30 35 36 第 3 页(共 6 页)
2015年全国初中数学联赛(初二组)初赛试卷(含答案)(完整资料).doc

(2)若 ,求PM的值。
2015年全国初中数学联赛(初二组)初赛试题
参考解答
一、选择题
1.D.
2.C.
3.A 延长FD至点G,使得DG=BE.显然△ABE≌△ADG.
∴AE=AG.易证△FAG≌△FAE. ∴FG=FE. ∴△ECF的周长=CF+FE+EC=CF+FG+EC=CF+FD+DG+EC=(CF+FD)+(BE+EC)=CD+BC=2.选A.
C、2或 D、2或
6、已知2015年3月13日是星期五,则 天之后是星期( )
A、一 、二C、三D、四
二、填空题(本题满分28分,每小题7分)
7、计算: .
8、已知 ,则 的值为.
9、如图,在四边形ABCD中, , , , , ,则BD的值为.
10、如果关于x的不等式组 的整数解仅为1,2,3,那么适合这个不等式组的整数a,b组成的有序数对(a,b)的个数为.
10.12. 即是 .因为原不等式组的整数解仅为1,2,3,所以 即 .所以 可以取9,10,11共3个数, 可以取1,2,3,4共4个数. 所以适合原不等式组的整数 组成的有序数对 的个数为 个.
三、解答题
11.解:∵a2+2ab+b2-6a-6b+9=0,……………………………………..…………………5分
∵AP=PC,CM=ME, ∴PM∥ 且PM= .………………………………….……….20分
∴PQ=PM, PQ⊥PM.
∴△MPQ为等腰直角三角形.
∴PM=PQ=2.5. .…………………………………………………………………………….25分
(完整版)2015年全国初中数学联合竞赛试题及参考答案

2015年全国初中数学联合竞赛试题第一试(A )一、选择题(每小题7分,共42分)1.设实数a ,b ,c 满足:3a b c ++=,2224a b c ++=,则222222222a b b c c ac a b +++++=---( ) A. 0B. 3C. 6D. 92.若抛物线2y x bx c =++与x 轴只有一个公共点,且过点A (m ,n ),B (m -8,n ),则n =( )A. 8B. 12C. 16D. 243.矩形ABCD 中,AD =5,AB =10,E 、F 分别为矩形外的两点,BE =DF =4,AF =CE =3,则EF =( ) A. B .15 CD.4.已知O 为䝐标原点,位于第一象限的点A 在反比例函数1(0)y x x=>的图象上,位于第二象限的瀹B 在反比例函数4(0)y x x=-<的图象上且OA ⊥OB ,则tan ∠ABO 的值为( ) A .12B.2 C .1 D .25.已知实数x (y 满足关系式1xy x y --=,则22x y +的最小值为( )A.3-B.6-C .1 D.6+6.设n 是小于100的正整数且使2535n n +-是15的倍数,则符合条件的所有正整数n 的和是( ) A .285 B .350 C .540 D .635 二、填空题(每小题7分,共28分)7.设a ,b 是一元二次方程210x x --=的两根,则32234a b a ++的值为 . 8.从三边长均为整数且周长为24的三角形中任取一个,它是直角三角形 的概率为 .9.已知锐角△ABC 的外心为O ,AO 交BC 于D ,E 、F 分别为△ABD 、 △ACD 的外心,若AB >AC ,EF =BC ,则∠C -∠B = .10.将数字1,2,3,…,34,35,36填在6×6的方格中,每个方格填一个数字,要求每行数字从左到右是从小到大的顺序,则第三列所填6个数字的和的最小值为 .第一试(B )一、选择题(每小题7分,共42分)1.设实数a ,b ,c 满足:3a b c ++=,2224a b c ++=,则222222222a b b c c a c a b+++++=---( )A. 12B. 9C. 6D. 32.若抛物线2y x bx c =++与x 轴只有一个公共点,且过点A (m ,n ),B (m -8,n ),则n =( )A. 8B. 12C. 16D. 243.矩形ABCD 中,AD =5,AB =10,E 、F 分别为矩形外的两点,BE =DF =4,AF =CE =3,则EF =( ) A. B .15CD.4.已知实数x ,y 满足关系式223x xy y ++=,则2()x y -的最大值为( )A .3B .6C .9D .125.已知O 为坐标原点,位于第一象限的点A 在反比例函数1(0)y x x=>的图象上,位于第二象限的点B 在反比例函数4(0)y x x=-<的图象上,且OA ⊥OB ,则tan ∠ABO 的值为( ) A .12BC .1D .26.设n 是小于100的正整数且使2232n n --是6的倍数,则符合条件的所有正整数n 的和是( ) A .784B .850C .1536D .1634二、填空题(每小题7分,共28分)7.设a ,b 是一元二次方程210x x --=的两根,则32234a b a ++的值为 . 8.三边长均为整数且周长为24的三角形的个数为 .9.C 、D 两点在以AB 为直径的半圆周上,AD 平分∠BAC ,AB =20, AD=AC 的长为 .10.在圆周上按序摆放和为15的五个互不相等的正整数a ,b ,c ,d ,e ,使得ab +bc +cd +de +ea最小,则这个最小值为 .ABCD EF第二试(A )1.(20分)关于xx 有且仅有一个实数根,求实数m 的取值范围. 2.(25分)如图,圆内接四边形ABCD 的对角线AC 、BD 交于点E ,且AC ⊥BD ,AB =AC . 过点D 作DF ⊥BD ,交BA 的延长线于点F ,∠BFD 的平分线分别交AD 、BD 于点M 、N . (1)证明:∠BAD =3∠DAC ; (2)如果BF DF CDBD AC-=,证明:MN =MD .3.(25分)设正整数m ,n 满足:关于x 的方程()()x m x n x m n ++=++至少有一个正整数解,证明:222()5m n mn +<.第二试(B )1.(20分)若正数a ,b 满足ab =1,求11112M a b=+++的最小值. 2.(25分)如图,圆内接四边形ABCD 的对角线AC 、BD 交于点E ,且AC ⊥BD ,AB =AC =BD . 过点D 作DF ⊥BD ,交BA 的延长线于点F ,∠BFD 的平分线分别交AD 、BD 于点M 、N . (1)证明:∠BAD =3∠DAC ;(2)如果MN =MD ,证明:BF =CD +DF .3.(25分)若关于x 的方程2343410x x k -+-=至少有一个正整数根,求满足条件的正整数k 的值.2015年全国初中数学联合竞赛试题参考答案第一试(A )1. 解:D. 提示:∵3a b c ++=,2224a b c ++=,∴222222222444(2)(2)(2)222222a b b c c a c a b c a b c a b c a b +++---++=++=+++++------6()9a b c =+++=.2. 解:C. 提示:依题意,有22(8)(8)n m bm c m b m c =++=-+-+,于是可得82b m =-. ∵抛物线2y x bx c =++与x 轴只有一个公共点,∴240b c -=,∴221(4)4c b m ==-.因此222(82)(4)16n m bm c m m m m =++=+-+-=.3. 解:C. 提示:易知∠AFD =∠BEC =90°,△BEC ≌△DF A ,∴∠DAF =∠BCE . 延长F A ,EB 交于点G . ∵∠GAB =90°-∠DAF =∠ADF ,∠GBA =90°-∠CBE =∠BCE =∠DAF ,∴△BGA ∽△AFD ,且∠AGB =90°,∴AG =8,BG =6, ∴GF =11,GE =10,∴EF ==4. 解:A. 提示:过点A 、B 分别作AC ⊥x 轴,BD ⊥x 轴,垂足为C 、D . 由OA ⊥OB 得∠AOB =90°,于是可得△AOC ∽△OBD ,∴12OAABO OB∠===. 5. 解:B. 提示:设x y t +=,则由题设条件可知11xy x y t =++=+, ∴x ,y 是关于m 的一元二次方程210m tm t -++=的两个实数根, 于是有:24(1)0t t ∆=-+≥,解得2t ≥+2t ≤-又∵22222()22(1)(1)3x y x y xy t t t +=+-=-+=--,∴当2t =-1x y ==22x y +取得最小值,最小值为2(21)36--=-6. 解:D. 提示:∵2535n n +-是15的倍数, ∴25|(535)n n +-,∴5|3n ,∴5|n . 设5n m =(m 是正整数),则2222535125155120155(1)n n m m m m m +-=+-=++-.∵2535n n +-是15的倍数,∴21m -是3的倍数,∴31m k =+或32m k =+,其中k 是非负整数.∴5(31)155n k k =+=+或5(32)1510n k k =+=+,其中k 是非负整数.∴符合条件的所有正整数n 的和是(5203550658095)(102540557085)635++++++++++++=. 7. 解:11. 提示:∵a ,b 是一元二次方程210x x --=的两根, ∴1ab =-,1a b +=,21a a =+,21b b =+, ∴332222343423(1)42(1)3362a b a b b a a b b a a b a++=++=++++=+++ 3(1)3626()511a a b a b =++++=++=.8. 解:112. 提示:设三角形的三边长为a ,b ,c (a b c ≥≥), 则324a a b c ≥++=,2()24a a b c <++=,∴812a ≤<,故a 的可能取值为8,9,10或11,满足题意的数组(a ,b ,c )可以为: (8,8,8),(9,9,6),(9,8,7),(10,10,4),(10,9,5),(10,8,6), (10,7,7),(11,11,2),(11,10,3),(11,9,4),(11,8,5),(11,7,6). 共12组,其中,只有一组是直角三角形的三边长,∴所求概率为112. 9. 解:60°. 提示:作EM ⊥BC 于点M ,FN ⊥BC 于点N ,FP ⊥EM 于点P . ∵E 、F 分别为△ABD 、△ACD 的外心, ∴M 、N 分别为BD 、CD 的中点.又EF =BC ,∴PF =MN =12BC =12EF ,∴∠PEF =30°.又EF ⊥AD ,EM ⊥BC ,∴∠ADC =∠PEF =30°. 又∠ADC =∠B +∠BAD =∠B +12(180°-2∠C )=90°+∠B -∠C ,∴∠C -∠B =90°-∠ADC =60°.10. 解:63. 提示:设第三列所填6个数字按从小到大的顺序排列后依次为A ,B ,C ,D ,E ,F .∵A 所在行前面需要填两个比A 小的数字,∴A 不小于3; ∵B 所在行前面需要填两个比B 小的数字,且A 及A 所在行前面两个数字都比B 小,∴B 不小于6.同理可知:C 不小于9,D 不小于12,E 不小于15,F 不小于18.因此,第三列所填6个数字之和A +B +C +D +E +F ≥3+6+9+12+15+18=63.如图即为使得第三列所填6个数字之和取得最小值的一种填法(后三列的数字填法不唯一).ABCD E F G第一试(B )1. 解:B. 提示:∵3a b c ++=,2224a b c ++=,∴222222222444(2)(2)(2)222222a b b c c a c a b c a b c a b c a b +++---++=++=+++++------6()9a b c =+++=.2. 解:C. 提示:依题意,有22(8)(8)n m bm c m b m c =++=-+-+,于是可得82b m =-. ∵抛物线2y x bx c =++与x 轴只有一个公共点,∴240b c -=,∴221(4)4c b m ==-.因此222(82)(4)16n m bm c m m m m =++=+-+-=.3. 解:C. 提示:易知∠AFD =∠BEC =90°,△BEC ≌△DF A ,∴∠DAF =∠BCE . 延长F A ,EB 交于点G . ∵∠GAB =90°-∠DAF =∠ADF ,∠GBA =90°-∠CBE =∠BCE =∠DAF ,∴△BGA ∽△AFD ,且∠AGB =90°,∴AG =8,BG =6, ∴GF =11,GE =10,∴EF ==4. 解:D. 提示:设x y t -=,则x y t =+,代入题设等式得22()()3y t y t y y +++++=,整理得223330y ty t ++-=. 由判别式22(3)12(3)3t t ∆=--≥得t -≤22()12x y t -=≤. 5. 解:A. 提示:过点A 、B 分别作AC ⊥x 轴,BD ⊥x 轴,垂足为C 、D . 由OA ⊥OB 得∠AOB =90°,于是可得△AOC ∽△OBD ,∴12OAABO OB∠===. 6. 解:D. 提示:∵2232n n --是6的倍数, ∴22|(232)n n --,∴2|3n ,∴2|n .设2n m =(m 是正整数),则2222232862662(1)n n m m m m m --=--=-+-. ∵2232n n --是6的倍数,∴21m -是3的倍数,∴31m k =+或32m k =+,其中k 是非负整数.∴2(31)62n k k =+=+或2(32)64n k k =+=+,其中k 是非负整数. ∴符合条件的所有正整数n 的和是(2814869298)(41016828894)1634++++++++++++=L L . 7. 解:11. 提示:∵a ,b 是一元二次方程210x x --=的两根, ∴1ab =-,1a b +=,21a a =+,21b b =+, ∴332222343423(1)42(1)3362a b a b b a a b b a a b a++=++=++++=+++ 3(1)3626()511a a b a b =++++=++=.8. 解:12. 提示:设三角形的三边长为a ,b ,c (a b c ≥≥), 则324a a b c ≥++=,2()24a a b c <++=,∴812a ≤<,故a 的可能取值为8,9,10或11, 满足题意的数组(a ,b ,c )可以为: (8,8,8),(9,9,6),(9,8,7),(10,10,4),(10,9,5),(10,8,6), (10,7,7),(11,11,2),(11,10,3),(11,9,4),(11,8,5),(11,7,6). 共12组,∴三边长均为整数且周长为24的三角形的个数为12. 9. 解:4. 提示:连接OD 、OC ,作DE ⊥AB 于E ,OF ⊥AC 于F .∵AD 平分∠BAC ,∴∠DOB =2∠BAD =∠OAC .又OA =OD ,∴△AOF ≌△ODE ,∴OE =AF ,∴AC =2OF =2OE .设AC =2x ,则OE =AF =x . 在Rt △ODE中,由勾股定理得DE ==在Rt △ADE 中,AD 2=DE 2+AE 2,即222(100)(10)x x =-++,解得x =2.∴AC =2x =4.10. 解:37. 提示:和为15的五个互不相等的正整数只能是1,2,3,4,5.注意到五个数在圆周上是按序摆放的,且考虑的是和式ab bc cd de ea ++++,不妨设a =5.如果1和5的位置不相邻,不妨设c =1(如图2),此时的和式为155P b b d ed e =++++; 交换1和b 的位置后,得到如图3的摆法, 此时的和式为255P b bd ed e =++++.∵1255(5)(1)0P P b dbd d b -=+--=-->,∴12P P >.因此,交换1和b 的位置使得1和5相邻(如图3)以后,和式的值会变小. 如图3,如果d =2,此时的和式为35225P b b e e =++++;交换e 和2的位置以后,得到如图4的摆法,此时的和式为45210P b be e =++++. ∵342510(5)(2)0P P b e be b e -=+--=-->,∴34P P >. 因此,交换e 和2的位置使得2和5相邻以后和式的值会变小. 如果b =2,此时的和式为55225P d ed e =++++;交换e 和2的位置以后,得到如图5的摆法,此时的和式为65210P e ed d =++++. ∵5625104(2)0P P e e e -=+--=->,∴56P P >.因此,交换e 和2的位置使得2和5相邻以后和式的值会变小. 综上可知:1和2摆在5的两边(如图5)时,和式的值会变小.AB CD E F Gd d d de 图1 图2 图3 图4 图5当d =3,e =4时,和式的值为754126103P =++++=; 当d =4,e =3时,和式的值为853*******P =++++=. 因此,所求最小值为37.第二试(A )1. 解:将所给方程记为方程①,显然有2x m ≥且1x ≥.若0m <x ,此时方程①无解,不符合题意,故0m ≥.方程①变形得x两边平方后整理得2242x m +-=- 再平方,整理得228(2)(4)m x m -=-.显然,应该有02m ≤<,并且此时方程①只可能有解x =将x =1=-,化简整理得???,于是有403m ≤≤,此时方程①有唯一解x =.综上所述,所求实数m 的取值范围为403m ≤≤. 2. 证明:(1)在BE 上取一点P ,使得∠BAP =∠DAC , 则△BAP ≌△CAD ,∴AP =AD . 又AE ⊥PD ,∴△ADE ≌△APE ,∴∠P AE =∠DAE ,∴∠P AE =∠BAP =∠DAC ,∴∠BAD =3∠DAC .(2)设∠DAC =α,则∠BAC =2α,∠BAD =3α,∠NDM =90°-α. 在FB 上截取FQ =FD ,连接QD ,则BQ =BF -FQ =BF -FD .又BF DF CD BD AC -=,∴BQ CD BD AC=. 又∠QBD =∠DCA ,∴△QBD ∽△DCA ,∴∠QDB =∠DAC .又∵∠DBC =∠DAC ,∴∠QDB =∠DBC ,∴QD ∥BC ,∴∠FQD =∠ABC . 又AB =AC ,∠BAC =2α,∴∠ABC =90°-α,∴∠FQD =90°-α. 又FQ =FD ,∴∠BFD =2α.∵FN 平分∠BFD ,∴∠AFM =α,∴∠NMD =∠AMF =∠BAD -∠AFM =3α-α=2α, ∴∠MND =180°-∠NMD -∠NDM =90°-α=∠MDN ,∴MN =MD .3. 证明:方程即2(1)0x m n x mn m n ++-+--= ①,方程①的判别式222(1)4()()42()1()2()1m n mn m n m n mn m n m n m n ∆=+----=+-+++=-+++.不妨设m n ≥,由题设可知,整系数方程①至少有一个正整数解,∴∆应为完全平方数. 注意到222()2()1(1)4(1)m n m n m n n m n ∆=-+++=-++>-+,22()2()1(3)(488)m n m n m n m n ∆=-+++=-+--+,若4880m n -+>,即22m n >-,则2(3)m n ∆<-+,从而有22(1)(3)m n m n -+<∆<-+,故只可能2(2)m n ∆<-+, 即22()2()1(2)m n m n m n -+++=-+,整理得332m n =-, 这与m ,n 均为正整数矛盾.因此22m n ≤-,从而可得2m n <,∴2mn<. 又∵112m n >>,∴有1()(2)02m m n n --<,整理即得222()5m n mn +<.第二试(B )1. 解:∵1ab =,∴1b a=, ∴2111111211211211212321a aM a b a a a a a a a a =+=+=+=+-=-++++++++++. 设232a a N a++=,则22333N a a =++=+++当a .∴103N <≤=-111(32M N=-≥--=.因此,当a =2b =时,11112M a b=+++取得最小值2. 2. 证明:(1)在BE 上取一点P ,使得∠BAP =∠DAC , 则△BAP ≌△CAD ,∴AP =AD .又AE ⊥PD ,∴△ADE ≌△APE ,∴∠P AE =∠DAE , ∴∠P AE =∠BAP =∠DAC ,∴∠BAD =3∠DAC . (2)设∠DAC =α,则∠BAC =2α,∠BAD =3α. ∵AC ⊥BD ,∴∠NDM =90°-α.∵MN =MD ,∴∠MND =∠MDN =90°-α, ∴∠NMD =180°-∠MND -∠NDM =2α,∴∠AMF =2α, ∴∠AFM =∠BAD -∠AMF =3α-2α=α.FN 平分∠BFD ,∴∠BFD =2∠AFM =2α.在FB 上截取FQ =FD ,连接QD ,则∠FQD =90°-α. 又AB =AC ,∠BAC =2α,∴∠ABC =90°-α,∴∠FQD =∠ABC , ∴QD ∥BC ,∴∠QDB =∠DBC .又∵∠DBC =∠DAC ,∴∠QDB =∠DAC .又∵DB =AC ,∠QBD =∠DCA ,∴△QBD ∽△DCA ,∴BQ =CD , ∴BF =BQ +FQ =CD +DF .3. 解:设方程的两个根为x 1,x 2,且x 1为正整数, 则1234x x +=,12341x x k =-.由1234x x +=知2134x x =-,∴ x 2也是整数.由k 为正整数及12341x x k =-可知20x >,∴x 2是正整数. 注意到121212(1)(1)134(1)x x x x x x k ++=+++=+, ∴1217|(1)(1)x x ++,∴117|(1)x +或217|(1)x +.若117|(1)x +,则由112134x x x +≤+=知:1117x +=或1134x +=. 当1117x +=时,116x =,218x =,此时3411618k -=⨯,k 无整数解; 当1134x +=时,133x =,21x =,此时341331k -=⨯,解得k =1. 若217|(1)x +,同样可得k =1. ∴满足条件的正整数k =1.。
2015年全国初中数学联合竞赛试题及参考答案

2015年全国初中数学联合竞赛试题第一试(A )一、选择题(每小题7分,共42分)1.设实数a ,b ,c 满足:3a b c ++=,2224a b c ++=,则222222222a b b c c ac a b +++++=---( ) A. 0B. 3C. 6D. 92.若抛物线2y x bx c =++与x 轴只有一个公共点,且过点A (m ,n ),B (m -8,n ),则n =( )A. 8B. 12C. 16D. 243.矩形ABCD 中,AD =5,AB =10,E 、F 分别为矩形外的两点,BE =DF =4,AF =CE =3,则EF =( ) A. B .15 CD.4.已知O 为䝐标原点,位于第一象限的点A 在反比例函数1(0)y x x=>的图象上,位于第二象限的瀹B 在反比例函数4(0)y x x=-<的图象上且OA ⊥OB ,则tan ∠ABO 的值为( ) A .12B.2 C .1 D .25.已知实数x (y 满足关系式1xy x y --=,则22x y +的最小值为( )A.3-B.6-C .1 D.6+6.设n 是小于100的正整数且使2535n n +-是15的倍数,则符合条件的所有正整数n 的和是( ) A .285 B .350 C .540 D .635 二、填空题(每小题7分,共28分)7.设a ,b 是一元二次方程210x x --=的两根,则32234a b a ++的值为 . 8.从三边长均为整数且周长为24的三角形中任取一个,它是直角三角形 的概率为 .9.已知锐角△ABC 的外心为O ,AO 交BC 于D ,E 、F 分别为△ABD 、 △ACD 的外心,若AB >AC ,EF =BC ,则∠C -∠B = .10.将数字1,2,3,…,34,35,36填在6×6的方格中,每个方格填一个数字,要求每行数字从左到右是从小到大的顺序,则第三列所填6个数字的和的最小值为 .第一试(B )一、选择题(每小题7分,共42分)1.设实数a ,b ,c 满足:3a b c ++=,2224a b c ++=,则222222222a b b c c a c a b+++++=---( )A. 12B. 9C. 6D. 32.若抛物线2y x bx c =++与x 轴只有一个公共点,且过点A (m ,n ),B (m -8,n ),则n =( )A. 8B. 12C. 16D. 243.矩形ABCD 中,AD =5,AB =10,E 、F 分别为矩形外的两点,BE =DF =4,AF =CE =3,则EF =( ) A. B .15CD.4.已知实数x ,y 满足关系式223x xy y ++=,则2()x y -的最大值为( )A .3B .6C .9D .125.已知O 为坐标原点,位于第一象限的点A 在反比例函数1(0)y x x=>的图象上,位于第二象限的点B 在反比例函数4(0)y x x=-<的图象上,且OA ⊥OB ,则tan ∠ABO 的值为( ) A .12BC .1D .26.设n 是小于100的正整数且使2232n n --是6的倍数,则符合条件的所有正整数n 的和是( ) A .784B .850C .1536D .1634二、填空题(每小题7分,共28分)7.设a ,b 是一元二次方程210x x --=的两根,则32234a b a ++的值为 . 8.三边长均为整数且周长为24的三角形的个数为 .9.C 、D 两点在以AB 为直径的半圆周上,AD 平分∠BAC ,AB =20, AD=AC 的长为 .10.在圆周上按序摆放和为15的五个互不相等的正整数a ,b ,c ,d ,e ,使得ab +bc +cd +de +ea最小,则这个最小值为 .ABCD EF第二试(A )1.(20分)关于xx 有且仅有一个实数根,求实数m 的取值范围. 2.(25分)如图,圆内接四边形ABCD 的对角线AC 、BD 交于点E ,且AC ⊥BD ,AB =AC . 过点D 作DF ⊥BD ,交BA 的延长线于点F ,∠BFD 的平分线分别交AD 、BD 于点M 、N . (1)证明:∠BAD =3∠DAC ; (2)如果BF DF CDBD AC-=,证明:MN =MD .3.(25分)设正整数m ,n 满足:关于x 的方程()()x m x n x m n ++=++至少有一个正整数解,证明:222()5m n mn +<.第二试(B )1.(20分)若正数a ,b 满足ab =1,求11112M a b=+++的最小值. 2.(25分)如图,圆内接四边形ABCD 的对角线AC 、BD 交于点E ,且AC ⊥BD ,AB =AC =BD . 过点D 作DF ⊥BD ,交BA 的延长线于点F ,∠BFD 的平分线分别交AD 、BD 于点M 、N . (1)证明:∠BAD =3∠DAC ;(2)如果MN =MD ,证明:BF =CD +DF .3.(25分)若关于x 的方程2343410x x k -+-=至少有一个正整数根,求满足条件的正整数k 的值.2015年全国初中数学联合竞赛试题参考答案第一试(A )1. 解:D. 提示:∵3a b c ++=,2224a b c ++=,∴222222222444(2)(2)(2)222222a b b c c a c a b c a b c a b c a b +++---++=++=+++++------6()9a b c =+++=.2. 解:C. 提示:依题意,有22(8)(8)n m bm c m b m c =++=-+-+,于是可得82b m =-. ∵抛物线2y x bx c =++与x 轴只有一个公共点,∴240b c -=,∴221(4)4c b m ==-.因此222(82)(4)16n m bm c m m m m =++=+-+-=.3. 解:C. 提示:易知∠AFD =∠BEC =90°,△BEC ≌△DF A ,∴∠DAF =∠BCE . 延长F A ,EB 交于点G . ∵∠GAB =90°-∠DAF =∠ADF ,∠GBA =90°-∠CBE =∠BCE =∠DAF ,∴△BGA ∽△AFD ,且∠AGB =90°,∴AG =8,BG =6, ∴GF =11,GE =10,∴EF ==4. 解:A. 提示:过点A 、B 分别作AC ⊥x 轴,BD ⊥x 轴,垂足为C 、D . 由OA ⊥OB 得∠AOB =90°,于是可得△AOC ∽△OBD ,∴12OAABO OB∠===. 5. 解:B. 提示:设x y t +=,则由题设条件可知11xy x y t =++=+, ∴x ,y 是关于m 的一元二次方程210m tm t -++=的两个实数根, 于是有:24(1)0t t ∆=-+≥,解得2t ≥+2t ≤-又∵22222()22(1)(1)3x y x y xy t t t +=+-=-+=--,∴当2t =-1x y ==22x y +取得最小值,最小值为2(21)36--=-6. 解:D. 提示:∵2535n n +-是15的倍数, ∴25|(535)n n +-,∴5|3n ,∴5|n . 设5n m =(m 是正整数),则2222535125155120155(1)n n m m m m m +-=+-=++-.∵2535n n +-是15的倍数,∴21m -是3的倍数,∴31m k =+或32m k =+,其中k 是非负整数.∴5(31)155n k k =+=+或5(32)1510n k k =+=+,其中k 是非负整数.∴符合条件的所有正整数n 的和是(5203550658095)(102540557085)635++++++++++++=. 7. 解:11. 提示:∵a ,b 是一元二次方程210x x --=的两根, ∴1ab =-,1a b +=,21a a =+,21b b =+, ∴332222343423(1)42(1)3362a b a b b a a b b a a b a++=++=++++=+++ 3(1)3626()511a a b a b =++++=++=.8. 解:112. 提示:设三角形的三边长为a ,b ,c (a b c ≥≥), 则324a a b c ≥++=,2()24a a b c <++=,∴812a ≤<,故a 的可能取值为8,9,10或11,满足题意的数组(a ,b ,c )可以为: (8,8,8),(9,9,6),(9,8,7),(10,10,4),(10,9,5),(10,8,6), (10,7,7),(11,11,2),(11,10,3),(11,9,4),(11,8,5),(11,7,6). 共12组,其中,只有一组是直角三角形的三边长,∴所求概率为112. 9. 解:60°. 提示:作EM ⊥BC 于点M ,FN ⊥BC 于点N ,FP ⊥EM 于点P . ∵E 、F 分别为△ABD 、△ACD 的外心, ∴M 、N 分别为BD 、CD 的中点.又EF =BC ,∴PF =MN =12BC =12EF ,∴∠PEF =30°.又EF ⊥AD ,EM ⊥BC ,∴∠ADC =∠PEF =30°. 又∠ADC =∠B +∠BAD =∠B +12(180°-2∠C )=90°+∠B -∠C ,∴∠C -∠B =90°-∠ADC =60°.10. 解:63. 提示:设第三列所填6个数字按从小到大的顺序排列后依次为A ,B ,C ,D ,E ,F .∵A 所在行前面需要填两个比A 小的数字,∴A 不小于3; ∵B 所在行前面需要填两个比B 小的数字,且A 及A 所在行前面两个数字都比B 小,∴B 不小于6.同理可知:C 不小于9,D 不小于12,E 不小于15,F 不小于18.因此,第三列所填6个数字之和A +B +C +D +E +F ≥3+6+9+12+15+18=63.如图即为使得第三列所填6个数字之和取得最小值的一种填法(后三列的数字填法不唯一).ABCD E F G第一试(B )1. 解:B. 提示:∵3a b c ++=,2224a b c ++=,∴222222222444(2)(2)(2)222222a b b c c a c a b c a b c a b c a b +++---++=++=+++++------6()9a b c =+++=.2. 解:C. 提示:依题意,有22(8)(8)n m bm c m b m c =++=-+-+,于是可得82b m =-. ∵抛物线2y x bx c =++与x 轴只有一个公共点,∴240b c -=,∴221(4)4c b m ==-.因此222(82)(4)16n m bm c m m m m =++=+-+-=.3. 解:C. 提示:易知∠AFD =∠BEC =90°,△BEC ≌△DF A ,∴∠DAF =∠BCE . 延长F A ,EB 交于点G . ∵∠GAB =90°-∠DAF =∠ADF ,∠GBA =90°-∠CBE =∠BCE =∠DAF ,∴△BGA ∽△AFD ,且∠AGB =90°,∴AG =8,BG =6, ∴GF =11,GE =10,∴EF ==4. 解:D. 提示:设x y t -=,则x y t =+,代入题设等式得22()()3y t y t y y +++++=,整理得223330y ty t ++-=. 由判别式22(3)12(3)3t t ∆=--≥得t -≤22()12x y t -=≤. 5. 解:A. 提示:过点A 、B 分别作AC ⊥x 轴,BD ⊥x 轴,垂足为C 、D . 由OA ⊥OB 得∠AOB =90°,于是可得△AOC ∽△OBD ,∴12OAABO OB∠===. 6. 解:D. 提示:∵2232n n --是6的倍数, ∴22|(232)n n --,∴2|3n ,∴2|n .设2n m =(m 是正整数),则2222232862662(1)n n m m m m m --=--=-+-. ∵2232n n --是6的倍数,∴21m -是3的倍数,∴31m k =+或32m k =+,其中k 是非负整数.∴2(31)62n k k =+=+或2(32)64n k k =+=+,其中k 是非负整数. ∴符合条件的所有正整数n 的和是(2814869298)(41016828894)1634++++++++++++=.7. 解:11. 提示:∵a ,b 是一元二次方程210x x --=的两根, ∴1ab =-,1a b +=,21a a =+,21b b =+, ∴332222343423(1)42(1)3362a b a b b a a b b a a b a++=++=++++=+++ 3(1)3626()511a a b a b =++++=++=.8. 解:12. 提示:设三角形的三边长为a ,b ,c (a b c ≥≥), 则324a a b c ≥++=,2()24a a b c <++=,∴812a ≤<,故a 的可能取值为8,9,10或11, 满足题意的数组(a ,b ,c )可以为: (8,8,8),(9,9,6),(9,8,7),(10,10,4),(10,9,5),(10,8,6), (10,7,7),(11,11,2),(11,10,3),(11,9,4),(11,8,5),(11,7,6). 共12组,∴三边长均为整数且周长为24的三角形的个数为12. 9. 解:4. 提示:连接OD 、OC ,作DE ⊥AB 于E ,OF ⊥AC 于F .∵AD 平分∠BAC ,∴∠DOB =2∠BAD =∠OAC .又OA =OD ,∴△AOF ≌△ODE ,∴OE =AF ,∴AC =2OF =2OE .设AC =2x ,则OE =AF =x . 在Rt △ODE中,由勾股定理得DE ==在Rt △ADE 中,AD 2=DE 2+AE 2,即222(100)(10)x x =-++,解得x =2.∴AC =2x =4.10. 解:37. 提示:和为15的五个互不相等的正整数只能是1,2,3,4,5.注意到五个数在圆周上是按序摆放的,且考虑的是和式ab bc cd de ea ++++,不妨设a =5.如果1和5的位置不相邻,不妨设c =1(如图2),此时的和式为155P b b d ed e =++++; 交换1和b 的位置后,得到如图3的摆法, 此时的和式为255P b bd ed e =++++.∵1255(5)(1)0P P b d bdd b -=+--=-->,∴12P P >.因此,交换1和b 的位置使得1和5相邻(如图3)以后,和式的值会变小. 如图3,如果d =2,此时的和式为35225P b b e e =++++;交换e 和2的位置以后,得到如图4的摆法,此时的和式为45210P b be e =++++. ∵342510(5)(2)0P P b e be b e -=+--=-->,∴34P P >. 因此,交换e 和2的位置使得2和5相邻以后和式的值会变小. 如果b =2,此时的和式为55225P d ed e =++++;交换e 和2的位置以后,得到如图5的摆法,此时的和式为65210P e ed d =++++. ∵5625104(2)0P P e e e -=+--=->,∴56P P >.因此,交换e 和2的位置使得2和5相邻以后和式的值会变小. 综上可知:1和2摆在5的两边(如图5)时,和式的值会变小.AB CD E F Gd d d de 图1 图2 图3 图4 图5当d =3,e =4时,和式的值为754126103P =++++=; 当d =4,e =3时,和式的值为853*******P =++++=. 因此,所求最小值为37.第二试(A )1. 解:将所给方程记为方程①,显然有2x m ≥且1x ≥.若0m <x ,此时方程①无解,不符合题意,故0m ≥.方程①变形得x两边平方后整理得2242x m +-=- 再平方,整理得228(2)(4)m x m -=-.显然,应该有02m ≤<,并且此时方程①只可能有解x =将x =1=-,化简整理得,于是有403m ≤≤,此时方程①有唯一解x =.综上所述,所求实数m 的取值范围为403m ≤≤. 2. 证明:(1)在BE 上取一点P ,使得∠BAP =∠DAC , 则△BAP ≌△CAD ,∴AP =AD . 又AE ⊥PD ,∴△ADE ≌△APE ,∴∠P AE =∠DAE ,∴∠P AE =∠BAP =∠DAC ,∴∠BAD =3∠DAC .(2)设∠DAC =α,则∠BAC =2α,∠BAD =3α,∠NDM =90°-α. 在FB 上截取FQ =FD ,连接QD ,则BQ =BF -FQ =BF -FD .又BF DF CD BD AC -=,∴BQ CD BD AC=. 又∠QBD =∠DCA ,∴△QBD ∽△DCA ,∴∠QDB =∠DAC .又∵∠DBC =∠DAC ,∴∠QDB =∠DBC ,∴QD ∥BC ,∴∠FQD =∠ABC . 又AB =AC ,∠BAC =2α,∴∠ABC =90°-α,∴∠FQD =90°-α. 又FQ =FD ,∴∠BFD =2α.∵FN 平分∠BFD ,∴∠AFM =α,∴∠NMD =∠AMF =∠BAD -∠AFM =3α-α=2α, ∴∠MND =180°-∠NMD -∠NDM =90°-α=∠MDN ,∴MN =MD .3. 证明:方程即2(1)0x m n x mn m n ++-+--= ①,方程①的判别式222(1)4()()42()1()2()1m n mn m n m n mn m n m n m n ∆=+----=+-+++=-+++.不妨设m n ≥,由题设可知,整系数方程①至少有一个正整数解,∴∆应为完全平方数. 注意到222()2()1(1)4(1)m n m n m n n m n ∆=-+++=-++>-+,22()2()1(3)(488)m n m n m n m n ∆=-+++=-+--+,若4880m n -+>,即22m n >-,则2(3)m n ∆<-+,从而有22(1)(3)m n m n -+<∆<-+,故只可能2(2)m n ∆<-+, 即22()2()1(2)m n m n m n -+++=-+,整理得332m n =-, 这与m ,n 均为正整数矛盾.因此22m n ≤-,从而可得2m n <,∴2mn<. 又∵112m n >>,∴有1()(2)02m m n n --<,整理即得222()5m n mn +<.第二试(B )1. 解:∵1ab =,∴1b a=, ∴2111111211211211212321a aM a b a a a a a a a a =+=+=+=+-=-++++++++++. 设232a a N a++=,则22333N a a =++=+++当a .∴103N <≤=-111(32M N=-≥--=.因此,当a =2b =时,11112M a b=+++取得最小值2. 2. 证明:(1)在BE 上取一点P ,使得∠BAP =∠DAC , 则△BAP ≌△CAD ,∴AP =AD .又AE ⊥PD ,∴△ADE ≌△APE ,∴∠P AE =∠DAE , ∴∠P AE =∠BAP =∠DAC ,∴∠BAD =3∠DAC . (2)设∠DAC =α,则∠BAC =2α,∠BAD =3α. ∵AC ⊥BD ,∴∠NDM =90°-α.∵MN =MD ,∴∠MND =∠MDN =90°-α, ∴∠NMD =180°-∠MND -∠NDM =2α,∴∠AMF =2α, ∴∠AFM =∠BAD -∠AMF =3α-2α=α.FN 平分∠BFD ,∴∠BFD =2∠AFM =2α.在FB 上截取FQ =FD ,连接QD ,则∠FQD =90°-α. 又AB =AC ,∠BAC =2α,∴∠ABC =90°-α,∴∠FQD =∠ABC , ∴QD ∥BC ,∴∠QDB =∠DBC .又∵∠DBC =∠DAC ,∴∠QDB =∠DAC .又∵DB =AC ,∠QBD =∠DCA ,∴△QBD ∽△DCA ,∴BQ =CD , ∴BF =BQ +FQ =CD +DF .3. 解:设方程的两个根为x 1,x 2,且x 1为正整数, 则1234x x +=,12341x x k =-.由1234x x +=知2134x x =-,∴ x 2也是整数.由k 为正整数及12341x x k =-可知20x >,∴x 2是正整数. 注意到121212(1)(1)134(1)x x x x x x k ++=+++=+, ∴1217|(1)(1)x x ++,∴117|(1)x +或217|(1)x +.若117|(1)x +,则由112134x x x +≤+=知:1117x +=或1134x +=. 当1117x +=时,116x =,218x =,此时3411618k -=⨯,k 无整数解; 当1134x +=时,133x =,21x =,此时341331k -=⨯,解得k =1. 若217|(1)x +,同样可得k =1. ∴满足条件的正整数k =1.。
2015 年全国初中数学联合竞赛试题参考答案及评分标准

AB AC , EF BC ,则 C B ____________.
【答】 60 .
E
作 EM BC 于点 M , FN BC 于点 N , FP EM 于点 P .
∵ E 、 F 分别为△ ABD 、△ ACD 的外心,∴ M 、 N 分别为 BD 、CD 的中
点.又 EF BC ,∴ PF MN 1 BC 1 EF ,∴ PEF 30 .
6. 设 n 是小于 100 的正整数且使 5n2 3n 5 是 15 的倍数,则符合条件的所有正整数 n 的和是( )
A.285. 【答】D.
B.350.
C.540.
D.635.
∵ 5n2 3n 5 是 15 的倍数,∴ 5 | (5n2 3n 5) ,∴ 5 | 3n ,∴ 5 | n ,设 n 5m ( m 是正整数),
∴符合条件的所有正整数 n 的和是(2+8+14+…+86+92+98)+(4+10+16+…+82+88+94)
=1634. 二、填空题:(本题满分 28 分,每小题 7 分) 1.题目和解答与(A)卷第 1 题相同. 2. 三边长均为整数且周长为 24 的三角形的个数为________. 【答】12.
C E
B
G
∴ GF 11, GE 10 ,∴ EF GE2 GF 2 221 .
4. 已知 O 为坐标原点,位于第一象限的点 A 在反比例函数 y 1 (x 0) 的图象上,位于第二象限的 x
点 B 在反比例函数 y 4 (x 0) 的图象上,且 OA OB ,则 tan ABO 的值为 x
同理可知: C 不小于 9, D 不小于 12, E 不小于 15, F 不小于 18.
因此,第三列所填 6 个数字之和 A + B + C + D + E + F 3 6 9 12 15 18 63.
2015年广东省陆丰市八年级数学竞赛题

1 八年级数学竞赛题(本卷满分100分,时间90分钟)班级:姓名:评分:一、填空题(每小题3分,共39分)1、将五个分数:23,58,1523,1017,1219;由小到大或由大到小排列,排在中间位置的分数是2、5397除以一个质数,所得的余数是15,则这个质数是3、观察下列运算:12=1;22=1+3;32=1+3+5;42=1+3+5+7;52=1+3+5+7+9;则n 2= (n 为正整数)。
4、x 表示a 与b 的和的平方,y 表示a 与b 的平方的和,则a=7,b=-5时,x-y 的值是5、计算:19961997×19971996-19961996×19971997=6、计算:1-2+3-4+5-6+7-8+……+4999-5000=7、计算:|11992-11991 |+|11993-11992 |-|11993-11991 |=8、计算:1234567892-1234567882=9、如果用四则运算的加法与除法定义一种新的运算,记为★,对任意有理数a 、b ;a ★b=a +b2,那么计算(1★9)★(9★5)=10、有含盐8%的盐水40kg ,要配成含盐20%的盐水,需要加盐 kg 。
11、分解因式:x 4+x 2y 2+y 4=12、已知x a-b =y b-c =zc-a ,则x +y +z=D OB CA13题图13、如图所示,∠AOC=∠BOD=150°,若∠AOD=3∠BOC,则∠BOC=二、计算与化简(每小题7分,共21分)14、试比较3111与1714的大小。
15、若3x2m+5n+9+4y4m-2n-7=2是关于x,y的二元一次方程,求(n+1)1995+m的值。
16、化简:3-2 2 +5-2 6 +7-212 +9-220 +11-230 +13-242+15-256 +17-2722。
八年级下数学竞赛试题(含答案)

八年级(下)数学期末竞赛测试卷一、选择题(每小题3分,共30分)1、下列多项式中能用完全平方公式分解的是( ) A.x 2-x +1 B.1-2xy +x 2y 2 C.a 2+a +21D.-a 2+b 2-2ab 2、不等式组⎩⎨⎧>-≥-04012x x 的整数解为( )A.1个B.2个C.3个D.4个 3、下列各分式中,与分式ba a--的值相等的是 ( ) A 、b a a -- B 、b a a + C 、a b a - D 、-ab a -4、.若分式34922+--x x x 的值为0,则x 的值为( )A . 3-B .3或3-C .3D .无法确定5、某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为82=甲x 分,82=乙x 分;2452=甲s ,1902=乙s ,那么成绩较为整齐的是( ) A .甲班 B .乙班 C .两班一样整齐 D .无法确定6、某天同时同地,甲同学测得1 m 的测竿在地面上影长为0.8 m ,乙同学测得国旗旗杆在地面上的影长为9.6 m ,则国旗旗杆的长为( )A .10 mB .12 mC .13 mD .15 m7、如图,△ABC 中,D 、E 分别是AB 、AC 上的点,DE ∥BC ,DE =1,BC =3,AB =6,则AD 的长为( )A .1B .1.5C .2D .2.5(第7题图) (第9题图)8、赵强同学借了一本书,共280页,要在两周借期内读完.当他读了一半时,发现平均每天要多读21页才能在借期内读完.他读前一半时,平均每天读多少页?如果设读前一半时,平均每天读x 页,则下面所列方程中,正确的是( ) A .1421140140=-+x x B .1421280280=++x x C .1421140140=++x x D .1211010=++x x 9、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2米,桌面距离地面1米.若灯泡距离地面3米,则地面上阴影部分的面积为( )A .0.36π平方米B .0.81π平方米C .2π平方米D .3.24π平方米10.下列从左到右的变形是因式分解的是( ) A.(x+1)(x-1)=x 2-1 B. a 2b =a ·ab C.ab-a-b+1=(a-1)(b-1) D.m 2-2m-3=m(m-2-m3)二、填空题(每小题3分,共24分)11、已知:线段AB=10cm ,C 为AB 有黄金分割点,AC>BC ,则AC=_________. 12、不等式(a -b )x>a -b 的解集是x <1,则a 与b 的大小关系是________. 13、已知x 1,x 2,x 3的标准差是2,则数据2x 1+3,2x 2+3,2x 3+3的方差是 .. 14、计算机生产车间制造a 个零件,原计划每天造x 个,后为了供货需要,每天多造了b 个,则可提前______________天完成。
2015香河县八年级数学能力竞赛试题及答案

2015年 香 河 县八 年 级 数 学 竞 赛 试 题学校 姓名 辅导教师 (时间2015.5.21上午9:00---11:00)一、选择题(共10小题,每小题3分,满分30分.以下每小题的四个选项中有且只有一个选项是正确的.请将正确选项的代号填在括号里.不填、多填或错填均得零分)1.已知式子1)1)(8(-+-x x x 的值为0,则x 的值为 ( ) A .±1 B .-l C .8 D .-1或82.如果0<+b a ,且0>b ,那么2a 与2b 的关系是 ( )A .2a ≥2bB .2a >2bC .2a ≤2bD .2a <2b3.已知x 是实数, 则πππ1-+-+-x x x 的值是 ( )A .π11-B .π11+ C .11-π D .无法确定的4 如图1,在矩形ABCD 中,AB=8,BC=4,将矩形沿AC 折叠,则重叠部分△AFC 的面积为 ( )方程A .12B .10C .8D .65.已知△ABC 是锐角三角形,且∠A >∠B >∠C ,则下列结论中错误的是 ( )A .∠A >60°B .∠C <60° C .∠B >45°D .∠B +∠C <90° 6.如图2,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE=a ,AF=b ,若S EFGH =32,则a b -等于( ) A .22 B .32 C .23 D .33 7. 如果823+++bx ax x 有两个因式x+1和x+2,则a +b =( ).A .7B .8C .15D .2l待定系数或代根-1和-2解出a,b图2图18. 如图3,△ABC 中,AD 是∠BAC 内的一条射线,BE ⊥AD ,且△CHM 可由△BEM 旋转而得,延长CH 交AD 于F ,则下列结论错误的是( )A .BM=CMB .FM=21EH C .CF ⊥AD D . FM ⊥BC 9. 有2015个数排成一行,其中任意相邻的三个数中,中间的数总等于前后两数的和,若第一个数是1,第二个数是-1,则这2015个数的和是 ( )6个一循环A .-2B .-1C .0D .210.用8个相同的小正方形搭成一个几何体,其从上面看如图4所示,那么这个几何体的从左面看一定不是( )C二、填空题(共11小题,每小题3分,满分33分)11.一条线段的长为a ,若要使3a —l ,4a +1,12-a 这三条线段组成一个三角形,则a 的取值范围是 .1.5<a <512.等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形底边的长为 .5cm13. 如图是重叠的两个直角三角形,将其中一个直角三角形沿BC 方向平移BE 距离就得到此图,已知AB=8cm,BE=4cm ,DH=3cm,则图中阴影部分的面积是_____.26cm 2 14.已知点P 在直角坐标系中的坐标为(0,1),O 为坐标原点,∠QPO =150°,且P 到Q 的距离为2,则Q 的坐标为 .(1,1+3)(﹣1,1+3)15.己知a 2=a +1,求代数式a 5-5a +2的值 .5 代入降次16. 如果式子a a ---11)1( 根号外的因式移入根号内,化简的结果为 .﹣1-a图4 图3图517.假期学校组织360名师生外出旅游,某客车出租公司有两种大客车可供选择:甲种客车每辆车有40个座,租金400元;乙种客车每辆车有50个座,租金480元。
八年级下数学竞赛试题(含答案)

八年级(下)数学期末竞赛测试卷一、选择题(每小题3分,共30分)1、下列多项式中能用完全平方公式分解的是( ) A.x 2-x +1 B.1-2xy +x 2y 2 C.a 2+a +21D.-a 2+b 2-2ab 2、不等式组⎩⎨⎧>-≥-04012x x 的整数解为( )A.1个B.2个C.3个D.4个 3、下列各分式中,与分式ba a--的值相等的是 ( ) A 、b a a -- B 、b a a + C 、a b a - D 、-ab a -4、.若分式34922+--x x x 的值为0,则x 的值为( )A . 3-B .3或3-C .3D .无法确定5、某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为82=甲x 分,82=乙x 分;2452=甲s ,1902=乙s ,那么成绩较为整齐的是( ) A .甲班 B .乙班 C .两班一样整齐 D .无法确定6、某天同时同地,甲同学测得1 m 的测竿在地面上影长为0.8 m ,乙同学测得国旗旗杆在地面上的影长为9.6 m ,则国旗旗杆的长为( )A .10 mB .12 mC .13 mD .15 m7、如图,△ABC 中,D 、E 分别是AB 、AC 上的点,DE ∥BC ,DE =1,BC =3,AB =6,则AD 的长为( )A .1B .1.5C .2D .2.5(第7题图) (第9题图)8、赵强同学借了一本书,共280页,要在两周借期内读完.当他读了一半时,发现平均每天要多读21页才能在借期内读完.他读前一半时,平均每天读多少页?如果设读前一半时,平均每天读x 页,则下面所列方程中,正确的是( ) A .1421140140=-+x x B .1421280280=++x x C .1421140140=++x x D .1211010=++x x 9、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2米,桌面距离地面1米.若灯泡距离地面3米,则地面上阴影部分的面积为( )A .0.36π平方米B .0.81π平方米C .2π平方米D .3.24π平方米10.下列从左到右的变形是因式分解的是( ) A.(x+1)(x-1)=x 2-1 B. a 2b =a ·ab C.ab-a-b+1=(a-1)(b-1) D.m 2-2m-3=m(m-2-m3)二、填空题(每小题3分,共24分)11、已知:线段AB=10cm ,C 为AB 有黄金分割点,AC>BC ,则AC=_________. 12、不等式(a -b )x>a -b 的解集是x <1,则a 与b 的大小关系是________. 13、已知x 1,x 2,x 3的标准差是2,则数据2x 1+3,2x 2+3,2x 3+3的方差是 .. 14、计算机生产车间制造a 个零件,原计划每天造x 个,后为了供货需要,每天多造了b 个,则可提前______________天完成。
八年级下数学竞赛试题(含答案)

八年级(下)数学期末竞赛测试卷一、选择题(每小题3分,共30分)1、下列多项式中能用完全平方公式分解的是( ) A.x 2-x +1 B.1-2xy +x 2y 2 C.a 2+a +21D.-a 2+b 2-2ab 2、不等式组⎩⎨⎧>-≥-04012x x 的整数解为( )A.1个B.2个C.3个D.4个 3、下列各分式中,与分式ba a--的值相等的是 ( ) A 、b a a -- B 、b a a + C 、a b a - D 、-ab a -4、.若分式34922+--x x x 的值为0,则x 的值为( )A . 3-B .3或3-C .3D .无法确定5、某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为82=甲x 分,82=乙x 分;2452=甲s ,1902=乙s ,那么成绩较为整齐的是( ) A .甲班 B .乙班 C .两班一样整齐 D .无法确定6、某天同时同地,甲同学测得1 m 的测竿在地面上影长为0.8 m ,乙同学测得国旗旗杆在地面上的影长为9.6 m ,则国旗旗杆的长为( )A .10 mB .12 mC .13 mD .15 m7、如图,△ABC 中,D 、E 分别是AB 、AC 上的点,DE ∥BC ,DE =1,BC =3,AB =6,则AD 的长为( )A .1B .1.5C .2D .2.5(第7题图) (第9题图)8、赵强同学借了一本书,共280页,要在两周借期内读完.当他读了一半时,发现平均每天要多读21页才能在借期内读完.他读前一半时,平均每天读多少页?如果设读前一半时,平均每天读x 页,则下面所列方程中,正确的是( ) A .1421140140=-+x x B .1421280280=++x x C .1421140140=++x x D .1211010=++x x 9、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2米,桌面距离地面1米.若灯泡距离地面3米,则地面上阴影部分的面积为( )A .0.36π平方米B .0.81π平方米C .2π平方米D .3.24π平方米10.下列从左到右的变形是因式分解的是( ) A.(x+1)(x-1)=x 2-1 B. a 2b =a ·ab C.ab-a-b+1=(a-1)(b-1) D.m 2-2m-3=m(m-2-m3)二、填空题(每小题3分,共24分)11、已知:线段AB=10cm ,C 为AB 有黄金分割点,AC>BC ,则AC=_________. 12、不等式(a -b )x>a -b 的解集是x <1,则a 与b 的大小关系是________. 13、已知x 1,x 2,x 3的标准差是2,则数据2x 1+3,2x 2+3,2x 3+3的方差是 .. 14、计算机生产车间制造a 个零件,原计划每天造x 个,后为了供货需要,每天多造了b 个,则可提前______________天完成。
2015年佳荣中学八年级数学知识竞赛考试试题

2015年佳荣中学八年级数学竞赛试题一、选择题:(每小题3分,共60分) 1、-2013的倒数是( ) A 、2013 B 、20131 C 、20131 D 、1 2、我国最长河流长江全长约6300千米,用科学记数法表示为( )千米. A 、63×102 B 、6.3×102 C 、6.3×103 D 、6.3×104 3、下列各式中,对于任意实数a 都成立的是( ) A 、7a >5a B 、a >-a C 、a 71< a 51D 、5-a <7-a 4、如图1,AB=16cm ,C 为AB 上一点,且AC : CB = 3 : 5,M 、N 分别为AC 、AB 的中点,则MN =( )A 、4cmB 、5cmC 、5.5cmD 、6cm5、一个正方形的边长增加2厘米,它的周长增加( )厘米。
A 、2 B 、4 C 、6 D 、86、在圆柱、圆锥和正方体中,侧面展开图是长方形的有( ) A 、0个 B 、1个 C、2个 D 、3个 7、如图2,已知AD // BC ,∠B = 30°,DB 平分∠ADE , 则∠ADE 的大小是( )A 、30°B 、45°C 、60°D 、75°(图2)(图1)8、下列各组数中,相等的是( )A 、(-1 ) 3和1B 、(-1 ) 2和-1C 、2)1(-和-1D 、-(-1 ) 和|-1| 9、为了搞活经济、商场将一种商品A 按标价的9折出售(即优惠10%),仍可获利润10%,若商品标价33元,那么该商品的进价是( )A 、31元B 、30.2元C 、29.7元D 、27元 10、若两个角的和与这两个角的差互补,则这两个角一定满足的条件是( )A 、一个锐角一个钝角B 、必有一个是直角C 、两个角都是直角D 、两个角都是钝角 11、实数701 在( )A 、7与8之间B 、8与9之间C 、9与10之间D 、10与11之间 12、如图3,△ABC 是等边三角形,BP = AQ ,则∠CRP 的度数为( ) A 、30° B 、45° C 、60° D 、75°13、如果a 2+ b 2+ 2c 2+ 2ac -2bc = 0,则a+ b =( )A 、0B 、1C 、-1D 、不能确定14、若三角形两边分别是5和7,则三角形的周长不可能是( )A 、23B 、18C 、17D 、1415、有个人买了头牛用了100元,卖出为200元,再买进为300元,再卖出为400 元,问:共赚了多少?.( )A 、100B 、200C 、300D 、40016、一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是( )A 、5B 、6C 、7D 、8(图3)17、有4位小朋友暑假互相通一次电话,他们一共打了多少( )次电话。
2015年八年级数学竞赛试题

D
E
A
O B F
C
2015 年下八年级数学竞赛
—3—
学校________________ 班级_________________ 姓名__________________ 学号________________ ---------------------------------------------------密--------------------------------------------------------------------------封-------------------------------------------------------------------------线--------------------------------------
21、某商店准备购进甲、乙两种商品.已知甲商品每件进价 15 元,售价 20 元;乙商 品每件进价 35 元,售价 45 元. (1)若该商店同时购进甲、乙两种商品共 100 件,恰好用去 2700 元,求购进甲、乙 两种商品各多少件?(6 分) (2)若该商店准备用不超过 3100 元购进甲、乙两种商品共 100 件,且这两种商品全 部售出后获利不少于 890 元,问应该怎样进货,才能使总利润最大,最大利润是多少? (利润=售价﹣进价) (8 分)
上海市黄浦区2015年初中数学竞赛试题(含答案)

2015年黄浦区初中数学竞赛(满分120分,用时:80分钟)(注意:请将答案填写在右边表格中)1.已知一组分数1324,2324,3324,…,68324,69324,其中最简分数有 个.2.在直角△ABC 中,∠C =90°,若261+=BC AC ,则cos B = .3.如果44x y === .4.方程013=-++y x x 的整数解()y x ,是 .5.已知n 是正整数,定义n n ⨯⨯⨯⨯= 321!,设!2015!3!2!1++++= m ,则m 的末两位数字是 .6.记[]x 表示不超过实数x 的最大整数(如[]21.2=,[]11=).如果实数a 满足()3345=-+-aa a a a ,那么[]=a .7.在四边形ABCD 中,AD ∥BC ,∠ABC =80°,AB =AD =BC 21,CH ⊥AB 于点H ,联结DH ,则∠CHD = .°8.已知梯形ABCD ,AD ∥BC ,:1:3AD BC =,M 、N 分别是AB 、CD 上的点,且:3:2AM MB =,若MN 将梯形ABCD 分成两部分的面积比为3:1,则:DN NC = .9.设1232015,,,,x x x x 为实数,且满足123201512320151232015x x x x x x x x x x x x =-=-=123201420151x x x x x =-=,则2000x = .10.四边形ABCD 两对角线的交点为O ,用四种颜色给AOB ∆、BOC ∆、COD ∆、DOA ∆染色,使得有公共边的三角形不同色,那么有___________种染色方法.11.设D 为△ABC 内一点,使得∠BAD =∠BCD ,且∠BDC =90°,已知AB =5,BC =6,M 为AC 的中点,则DM = .12.若m =m 的最大值是 .(答案填写在此表格内)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年下学期八年级数学竞赛试题
时量:120分钟 满分:120分
一、选择题(共8道小题,每小题4分,满分32分)
1.已知大家以相同的效率做某件工作,a 人做b 天可以完工,若增加c 人,则提前完工的天数为( )
A .ab b a c -+
B .b b a c -+
C .ab b a c -+
D .b
b a c
-+ 2.已知13m m +=,则221
m m
+的值是( )
A .9
B .11
C .7
D .1 3.如图,ABC △的面积为1cm 2
,AP 垂直B ∠的平分线BP 于P ,则PBC △的面积为( )
A .0.4 cm
2
B .0.5 cm 2
C .0.6 cm 2
D .0.7 cm 2
4.在等腰ABC △中,AB AC =,其周长为20cm ,则AB 边的取值范围是( )
A .1cm <A
B <4cm B .5cm <AB <10cm
C .4cm <AB <8cm
D .4cm <AB <10cm
5.已知m ,n 为常数,若0mx n +>的解集为1
3
x <,则0n x m -<的解集是( ) A .x >3 B .x <3 C .x >﹣3 D .x <﹣3
6.若方程组4143x y k x y +=+⎧⎨+=⎩的解满足条件01x y <+<,则k 的取值范围是( )
A .﹣4<k <1
B .﹣4<k <0
C .0<k <9
D .k >﹣4
7.下列说法中正确的是( )
A .0.9的算术平方根是0.3
B 4
C .﹣0.6是0.36的平方根
D . 4
8.计算
2015
2016
--⋅
的结果是( )
A .﹣1
B .1
C
D 二、填空题(共7道小题,每小题4分,满分28分)
9.若x 取整数,则使分式67
23x x -+的值为整数的x 的值有 个.
10.若3927a b ⋅=,则()2
2a b -+= .
11.在ABC △中,若20A B C ∠-∠-∠=︒,则A ∠= 度.
12.已知关于x,y的方程组
3
25
x y a
x y a
-=+
⎧
⎨
+=
⎩
的解满足0
x y
>>,化简3
a a
+-=
_______________.
13
.化简:
⎛
-=
⎝
.
14
5
=,则x的取值范围是.
15
m的平方根,则m=.
三、解答题(共六道小题,每小题10分,满分60分)
16.先化简,再求值:
2
22
1121
x x x x
x x x x
-
⎛⎫
-÷
⎪
---+
⎝⎭
,其中x是不等式组
13
22
124
x
x
+
⎧
≤
⎪
⎨
⎪-<
⎩
的整数解.
17.
求2
yz x
-
的平方根.
18.若a,b
是一等腰三角形的两边长,且满足等式4
b-,
试求此等腰三角形的周长.
19.如图,在ABC △中,45ABC ∠=︒,CD AB ⊥,BE AC ⊥,垂足分别为D ,E ,F 为BC 中点,BE 与DF ,DC 分别交于点G ,H ,线段BH 与AC 相等吗?若相等给予证明,若不相等请说明理由.
20.去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件. (1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货
A E
C
H
D B
G
F
车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
21.在四边形ABCD中,AD BC
=,E为AB边上一点,
∠=︒,AB BC
∥,90
ABC
=.连接DE交对角线AC于H,连接BH.
∠=︒,且AE AD
15
BCE
(1)求证:AC ED
⊥;
(2)求证:ACD ACE
△≌△;
(3)试判断CDE
△的形状,并说明理由.
参考答案
16.解:
=
×
﹣
×
=1﹣
=,……4分
∵, 由①得:x ≤2,由②得:x >﹣,
∴原不等式组的解集是:﹣<x ≤2,…………………………………………………6分 ∴原不等式组的整数解是:﹣1,0,1,2,…………………………………………7分 又∵(x ﹣1)(x+1)x ≠0∴x ≠±1且x ≠0,∴x=2,……………………………………9分 ∴原式=
=.………………………………………………………………………10分
170=,
0=0=,∴1x =,3y =-.……………………………4分
2
2420z z +++=,
∴2
440z z ++=,即()2
20z +=,∴2z =-,……………………………8分
∴()()232214yz x -=-⨯--⨯=,∴2yz x -的平方根是2±.……………10分
18.解:根据题意得,3a ﹣6≥0且2﹣a ≥0,………………………………………………2分
解得a ≥2且a ≤2,所以a =2,b =4,………………………………………………5分 ①a =2是腰长时,三角形的三边分别为2、2、4,
∵2+2=4,∴不能组成三角形,……………………………………………………7分 ②a =2是底边时,三角形的三边分别为2、4、4,
能组成三角形,周长=2+4+4=10,…………………………………………………9分 所以此等腰三角形的周长为10.………………………………………………………10分 19.解:线段BH 与AC 相等.理由如下:…………………………………………………1分
∵∠BDC=∠BEC=∠CDA=90°,∠ABC=45°,
∴∠BCD=∠ABC=45°,∠A+∠DCA=90°,∠A+∠ABE=90°,………………3分
∴DB=DC,∠ABE=∠DCA.……………………………………………………5分
∵在△DBH与△DCA中,,
∴△DBH≌△DCA(AAS),……………………………………………………8分
∴BH=AC.…………………………………………………………………………10分20.解:(1)设饮用水有x件,则蔬菜有(x﹣80)件.
x+(x﹣80)=320,……………………………………………………………1分
解这个方程,得x=200.
∴x﹣80=120.…………………………………………………………………2分
答:饮用水和蔬菜分别为200件和120件;…………………………………3分(2)设租用甲种货车m辆,则租用乙种货车(8﹣m)辆.得:
,…………………………………………………5分
解这个不等式组,得2≤m≤4.
∵m为正整数,
∴m=2或3或4,………………………………………………………………6分
安排甲、乙两种货车时有3种方案.设计方案分别为:
①甲2辆,乙6辆;②甲3辆,乙5辆;③甲4辆,乙4辆; (7)
分
(3)3种方案的运费分别为:①2×400+6×360=2960(元);
②3×400+5×360=3000(元);③4×400+4×360=3040(元);……………9分
∴方案①运费最少,最少运费是2960元. (10)
分
21.解:(1)∵AD∥BC,∠ABC=90°,∴∠BAD=90°,
又∵AB=BC,∴∠BAC=45°,∴∠CAD=∠BAD﹣∠BAC=90°﹣45°=45°,
∴∠BAC=∠CAD,∴AH⊥ED,即AC⊥ED;……………………………3分(2)由(1)证得∠ABC=90°,AB=BC,
∴∠BAC=∠ACB=45°,又∵∠BAD=90°,∴∠BAC=∠DAC,
在△ACD和△ACE中,,∴△ACD≌△ACE(SAS);…6分
(3)△CDE为等边三角形.理由如下:
∵∠BCE=15°,
∴∠BEC=90°﹣∠BCE=90°﹣15°=75°,
∴∠CED=180°﹣∠BEC﹣∠AED=180°﹣75°﹣45°=60°,
又由(2)知CD=CE,
∴△CDE为等边三角形,……………………………………………………10分。
