培优四边形测试题
第四章:平行四边形培优训练试题

第四章:平行四边形培优训练试题一.选择题:(本题共10小题,每小题3分,共30分)温馨提示:每一题的四个答案中只有一个是正确的,请将正确的答案选择出来!1.下列图形中,既是中心对称图形,又是轴对称图形的是( )2.平行四边形一边的长是12cm ,则这个平行四边形的两条对角线长可以是( ) A .4cm 或6cmB .6cm 或10cmC .12cm 或12cmD .12cm 或14cm3.如图,在ABCD 中,对角线AC ,BD 相交于点O ,E 、F 是对角线AC 上的两点,给出下列四个条件,其中不能判定四边形DEBF 是平行四边形的有( ) A .AE CF =B .DE BF =C .ADE CBF ∠=∠D .ABE CDF ∠=∠4.若用反证法证明:若0a b >>,则a b >,需假设( )A .a b <B .a b >C .a b ≤D .a b ≥5.如图,在平行四边形ABCD 中,M 是CD 的中点,2AB BC =,BM a =,AM b =,则CD 的长为( ) A .2+ab B .2b a +C .abD .22a b + 6.如图,在平行四边形ABCD 中,已知,,,过BC 的中点E 作,垂足为F ,与DC 的延长线相交于点H ,则的面积是( ) A .38B .312C .314D .3187.一个多边形除了一个内角外,其余各内角之和为,则这个内角的度数为( ) A. 0120 B.0130 C. 0135D.01508.如图,在平行四边形ABCD 中,延长CD 到E ,使DE =CD ,连接BE 交AD 于点F ,交AC 于点G .下列结论,①DE =DF ;②AG =GF :③AF =DF :④BG =GC ;⑤BF =EF ,其中正确的有( )个 A .1B .2C .3D .49.如图,四边形ABCD 中.,,BD 为的平分线,,,F 分别是BD ,AC 的中点,则EF 的长为( )A. 1 B .5.1 C. 2 D . 5.210.如图,已知在▱ABCD 中,分别以AB ,AD 为边分别向外作等边三角形ABE 和等边三角形ADF ,延长CB 交AE 于点G ,点G 在点A ,E 之间,连接CE ,CF ,EF ,则下列结论不一定正确的是( ) A .△CDF ≌△EBCB .∠CDF =∠EAFC .△ECF 是等边三角形D .CG ⊥AE二.填空题(本题共6小题,每题4分,共24分) 温馨提示:填空题必须是最简洁最正确的答案!11.一个多边形的内角和等于1800°,则该多边形的边数n 等于12.在平面直角坐标系中,若▱ABCD 的三个顶点坐标分别是A (m ,﹣n )、B (2,3)、C (﹣m ,n ),则点D 的坐标是13.用反证法证明“三角形中必有一个内角不小于60°”,应当先假设这个三角形中________ 14.在ABCD 中,BE AD ⊥于E ,BF CD ⊥于F ,若60EBF ︒∠=,且3AE =,2DF =,则EC =_______15.如图,在▱ABCD 中,对角线AC 与BD 相交于点E ,∠AEB =45°,BD =2,将△ABC 沿AC 所在直线翻折180°到其原来所在的同一平面内,若点B 的落点记为B ′,则DB ′的长为________ 16.如图,在梯形ABCD 中,AD ∥BC ,AD =6,BC =16,E 是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒2个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动.当运动时间________秒时,以点P ,Q ,E ,D 为顶点的四边形是平行四边形.三.解答题(共6题,共66分)温馨提示:解答题应将必要的解答过程呈现出来!17(本题6分)如图,在ABCD 中,ABC ∠和BCD ∠的角平分线BE 与CE 相交于点E ,且点E恰好落在AD 上;(1)求证:222BE CE BC += ;(2)若2AB =,求ABCD 的周长.18(本题8分).如图,在四边形ABCD 中,AB =CD ,BF =DE ,AE ⊥BD ,CF ⊥BD ,垂足分别为E 、F . (1)求证:△ABE ≌△CDF ;(2)若AC 与BD 交于点O ,求证:AO =CO .19(本题8分)如图,在ABCD 中,过点B 作BM AC ⊥,交AC 于点E ,交CD 于点M ,过点D 作DN AC ⊥,交AC 于点F ,交AB 于点N .(1)求证:四边形BMDN 是平行四边形;(2)已知125AF EM ==,,求AN 的长.20(本题10分)已知如图,四边形ABCD 为平行四边形,AD=a ,AC 为对角线,BM ∥AC ,过点D 作 DE ∥CM ,交AC 的延长线于F ,交BM 的延长线于E .(1)求证:△ADF ≌△BCM ;(2)若AC=2CF ,∠ADC=60°,AC ⊥DC ,求四边形ABED 的面积(用含a 的代数式表示).21.(本题10分)在平行四边形ABCD 中,点E 是AD 边上的点,连接BE . (1)如图1,若BE 平分∠ABC ,BC =8,ED =3,求平行四边形ABCD 的周长;(2)如图2,点F 是平行四边形外一点,FB =C D .连接BF 、CF ,CF 与BE 相交于点G ,若∠FBE +∠ABC=180°,点G 是CF 的中点,求证:2BG +ED =B C .22(本题12分)如图1,在平面直角坐标系中,点A 的坐标是(0,8),点B 的坐标是(6,0),点C 为AB 的中点,动点P 从点A 出发,沿AO 方向以每秒1个单位的速度向终点O 运动,同时动点Q 从点O 出发,以每秒2个单位的速度沿射线OB 方向运动;当点P 到达点O 时,点Q 也停止运动.以CP ,CQ 为邻边构造▱CPDQ ,设点P 运动的时间为t 秒. (1)点C 的坐标为 ,直线AB 的解析式为 . (2)当点Q 运动至点B 时,连结CD ,求证://CD AP .(3)如图2,连结OC ,当点D 恰好落在△OBC 的边所在的直线上时,求所有满足要求的t 的值.23.(本题12分)如图所示,在ABCD 中,对角线AC ,BD 相交于点O ,5cm OA =,E ,F 为直线BD 上的两个动点(点E ,F 始终在ABCD 的外面),且11,22DE OD BF OB ==,连结AE ,CE ,CF ,AF .(1)求证:四边形AFCE 为平行四边形.(2)若11,33DE OD BF OB ==,上述结论还成立吗?若11,DE OD BF OB n n==呢? (3)若CA 平分BCD ∠,60AEC ∠=,求四边形AECF 的周长.第四章:平行四边形培优训练试题答案三.选择题:(本题共10小题,每小题3分,共30分)温馨提示:每一题的四个答案中只有一个是正确的,请将正确的答案选择出来!1.答案:A解析:A、既是轴对称图形,也是中心对称图形,故此选项符合题意;B、不是轴对称图形,是中心对称图形,故此选项不合题意;C、既不是轴对称图形,也又是中心对称图形,故此选项不合题意;D、是轴对称图形,不是中心对称图形,故此选项不合题意.故选:A.2.答案:D解析:∵四边形ABCD是平行四边形,∴OA=12AC,OB=12BD,A、∵AC=4cm,BD=6cm,∴OA=2cm,OB=3cm,∴OA+OB=5cm<12cm,不能组成三角形,故不符合;B、∵AC=6cm,BD=10cm,∴OA=3cm,OB=5cm,∴OA+OB=8cm<12cm,不能组成三角形,故不符合;C、∵AC=12cm,BD=12cm,∴OA=6cm,OB=6cm,∴OA+OB=12cm=12cm,不能组成三角形,故不符合;D、∵AC=12cm,BD=14cm,∴OA=6cm,OB=7cm,∴OA+OB=13cm>12cm,能组成三角形,故符合;故选D.3.答案:B解析:A 、∵AE CF =, ∴AO=CO ,由于四边形ABCD 是平行四边形,则BO=DO , ∴四边形DEBF 是平行四边形;B 、不能证明四边形DEBF 是平行四边形;C 、∵四边形ABCD 是平行四边形, ∴AD=BC ,∠DAE=∠BCF ,又∠ADE=∠CBF , ∴△DAE ≌△BCF (ASA ),∴AE=CF ,同A 可证四边形DEBF 是平行四边形; D 、同C 可证:△ABE ≌△CDF (ASA ), ∴AE=CF ,同A 可证四边形DEBF 是平行四边形; 故选:B .4.答案:C解析:反证法证明“若a >b >0a b >a b ≤,故选:C .5.答案:D解析:∵M 为CD 中点, ∴CM=DM=12CD=12AB=BC=AD , ∴∠DAM=∠DMA ,∠CBM=∠CMB , ∵四边形ABCD 是平行四边形, ∴AD ∥BC , ∴∠C+∠D=180°,∴∠C=2∠DMA ,∠D=2∠CMB , ∴∠DMA+∠CMB=12(∠C+∠D )=90°, ∴∠AMB=180°-(∠DMA+∠CMB )=90°即△MAB为直角三角形,∵BM=a,AM=b,∴CD=AB=2222MA MB a b+=+,故选:D.6.答案:A解析:∵四边形ABCD是平行四边形,∴8==BCAD,CDAB//,6==CDAB,∵E为BC中点,∴4==CEBE,∵060=∠B,ABEF⊥,∴030=∠FEB,∴2=BF,由勾股定理得:32=EF,∵CDAB//,∴ECHB∠=∠,在BFE∆和CHE∆中,⎪⎩⎪⎨⎧∠=∠=∠=∠CEHBEFCEBEECHB∴△BFE≌△CHE(SAS),∴32==EHEF,2==BFCH,∵31621=⨯=∆FHDHSDHF,∴3821==∆∆DHFDEFSS.故选A.7.答案:B解析;设这是一个n边形,这个内角的度数为x度.∵()x n +=⨯-025701802,∴()0293018025701802-=-⨯-=n n x ,∵01800<<x ,∴00018029301800<-<n ,解得:2.172.16<<n ,又n 为正整数, ∴17=n ,所以多边形的内角和为()02700180217=⨯-,即这个内角的度数是00013025702700=-. 故选B .8.答案:B解析:∵四边形ABCD 是平行四边形, ∴AB ∥CD ,AB =CD ,即AB ∥CE , ∴∠ABF =∠E , ∵DE =CD , ∴AB =DE ,在△ABF 和△DEF 中,∵⎪⎩⎪⎨⎧=∠=∠∠=∠DE AB DFE AFB E ABF , ∴△ABF ≌△DEF (AAS ), ∴AF =DF ,BF =EF ; 可得③⑤正确, 故选:B .9.答案:A解析:∵BC AC ⊥, ∴090=∠ACB ,∵4,3==AC BC , ∴5=AB , ∵BC AD //,∴DBC ADB ∠=∠,∵BD 为ABC ∠的平分线, ∴CBD ABD ∠=∠, ∴ADB ABD ∠=∠, ∴5==AD AB ,连接BF 并延长交AD 于G , ∵BC AD //∴BCA GAC ∠=∠, ∵F 是AC 的中点, ∴CF AF =,∵CFB AFG ∠=∠, ∴△AFG ≌△CFB(ASA), ∴3,===BC AG FG BF , ∴235=-=DG , ∵E 是BD 的中点, ∴121==DG EF . 故选:A .10.答案:D解析:(1)∵四边形ABCD 是平行四边形, ∴∠ADC=∠ABC ,AD=BC ,CD=AB , ∵△ABE 、△ADF 都是等边三角形, ∴AD=DF ,AB=EB ,∠ADF=∠ABE=60°, ∴DF=BC ,CD=BE ,∠CDF=360°-∠ADC-60°=300°-∠ADC ,∠EBC=360°-∠ABC-60°=300°-∠ABC , ∴∠CDF=∠EBC ,∴△CDF ≌△EBC (SAS ),故A 中结论正确; (2)∵在平行四边形ABCD 中,∠DAB=180°-∠ADC ,∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC , 又∵∠CDF=300°-∠ADC , ∴∠CDF=∠EAF ,故B 中结论正确;(3)∵在△CDF和△EAF中,DF=AF,∠CDF=∠EAF,DC=AB=AE,∴△CDF≌△EAF,∴EF=CF,∵△CDF≌△EBC,∴CE=CF,∴EF=CE=CF,∴△ECF是等边三角形,故C正确;(4)∵△ABE是等边三角形,∴∠ABE=60°,∴当CG⊥AE时,∠ABG=30°,则此时∠ABC=180°-∠ABG=150°,∵由题中条件无法确定∠ABC的度数,∴D中结论不一定成立.故选D.四.填空题(本题共6小题,每题4分,共24分)温馨提示:填空题必须是最简洁最正确的答案!11.答案:12解析:因为多边形的内角和公式为(n﹣2)•180°,所以(n﹣2)×180°=1800°,解得n=12.则该多边形的边数n等于12.故答案为:12.12.答案:(﹣2,﹣3)解析:∵A(m,﹣n),C(﹣m,n),∴点A和点C关于原点对称,∵四边形ABCD是平行四边形,∴D和B关于原点对称,∵B(2,3),∴点D的坐标是(﹣2,﹣3).故答案为(﹣2,﹣3)13.答案:三角形中每一个内角都小于60°解析: 用反证法证明“三角形中必有一个内角不小于60°”时,应先假设三角形中每一个内角都小于60°.故答案为:三角形中每一个内角都小于60°14.解析:∵BE⊥AD,BF⊥CD,∴∠BFD=∠BED=∠BFC=∠BEA=90°,∵∠EBF=60°,∴∠D=120°,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠BCD=∠A=60°,∵在△ABE中,∠ABE=30°,∴AB=2AE=2×3=6,∴CD=AB=6,=∴CF=CD-DF=6-2=4,∵在△BFC中,∠CBF=30°,∴BC=2CF=2×4=8,∴=15.答案:2解析:连结BB′.根据已知条件和折叠的性质易知△BB′E是等腰直角三角形且∠BEB′=90°.∵BD=2,所以BE=1,∴BB′=2.又∵BE=DE,B′E⊥BD,∴B ′E 是BD 的中垂线, ∴DB ′=BB ′=216.答案:2或143解析:由已知梯形,当Q 运动到E 和B 之间,设运动时间为t ,则得:162t 2-=6-t , 解得:t=143, 当Q 运动到E 和C 之间,设运动时间为t ,则得:162-2t=6-t , 解得:t=2, 故当运动时间t 为2或143秒时,以点P ,Q ,E ,D 为顶点的四边形是平行四边形. 故答案为2或143三.解答题(共6题,共66分)温馨提示:解答题应将必要的解答过程呈现出来!17解析:()1BE CE 、分别平分ABC ∠和BCD ∠12EBC ABC ∴∠=∠,12ECB BCD ∠=∠ ABCD//AB CD ∴180ABC BCD ∴∠+∠=90EBC ECB ∴∠+∠=︒90BEC ∴∠=222BE CE BC ∴+=()2ABCD//,2AD BC CD AB ∴==EBC AEB ∴∠=∠BE 平分ABC ∠EBC ABE ∴∠=∠ AEB ABE ∴∠=∠AB AE =∴同理可证DE DC =122DE AE AD ===∴ ()24212ABCDC∴=⨯+=18.解析:(1)∵BF=DE , ∴BF EF DE EF -=-, 即BE=DF ,∵AE ⊥BD ,CF ⊥BD , ∴∠AEB=∠CFD=90°, 在Rt △ABE 与Rt △CDF 中,AB CDBE DF =⎧⎨=⎩, ∴Rt ABE Rt CDF ∆∆≌(HL ); (2)如图,连接AC 交BD 于O , ∵Rt ABE Rt CDF ∆∆≌, ∴ABE CDF ∠=∠, ∴//D AB C ,∵=D AB C ,∴四边形ABCD 是平行四边形, ∴AO CO =.19.解析:(1)∵四边形ABCD 是平行四边形, ∴CDAB .∵BM AC DN AC ⊥⊥,, ∴DNBM ,∴四边形BMDN 是平行四边形.(2)∵四边形ABCD ,BMDN 都是平行四边形,∴AB CDDM BN CD AB ==,,∥, ∴CM AN MCE NAF =∠=∠,. 又∵90CEM AFN ∠=∠=︒, ∴()CEM AFN AAS ≌, ∴5FN EM ==. 在Rt AFN 中,222212513AN AF FN =+=+=.20.解析:(1)在平行四边形ABCD 中,则AD =BC ,AD//BC , ∵AC ∥BM ,∴∠AFD =∠E ,∠DAF=∠ACB , ∵CM ∥DE ,∴∠BMC =∠E , ∴∠BMC =∠AFD , ∵AC ∥BM , ∴∠ACB=∠MBC , ∴∠FAD =∠MBC , 则在△ADF 与△BCM 中.BMC AFD FAD MBC AD BC ∠∠⎧⎪∠∠⎨⎪⎩===,∴△ADF ≌△BCM (AAS ). (2)解:在△ACD 中, ∵AC ⊥CD ,∠ADC =60°, ∴CD =12AD =12a , 则AC, ∵AC=2CF , ∴, ∴AF =AC CF -=24a a -=4a , 又由△ADF ≌△BCM ,可得BM=4a , 又∵DE ∥CM ,BM ∥AC , ∴CFEM 为平行四边形, ∴, ∴, 又∵AC ⊥DC , ∴DC 为△ADF 高, 又∵△ADF ≌△BCM , ∴△ADF 的高的长度等于DC , S ABED =S △ADF +S ABEF =12•AF •CD +12(AF +BE )•CD =12×4a ×12 a +12(4aa )×12a=53a2.21.解析:(1)∵四边形ABCD是平行四边形,∴AD=BC=8,AB=CD,AD∥BC,∴∠AEB=∠CBE,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABE=∠AEB,∴AB=AE,∵AE=AD﹣ED=BC﹣ED=8﹣3=5,∴AB=5,∴平行四边形ABCD的周长=2AB+2BC=2×5+2×8=26;(2)连接CE,过点C作CK∥BF交BE于K,如图2所示:则∠FBG=∠CKG,∵点G是CF的中点,∴FG=CG,在△FBG和△CKG中,∵FBG CKGBGF KGCFG CG∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△FBG≌△CKG(AAS),∴BG=KG,CK=BF=CD,∵四边形ABCD是平行四边形,∴∠ABC=∠D,∠BAE+∠D=180°,AB=CD=CK,AD∥BC,∴∠DEC=∠BCE,∠AEB=∠KBC,∵∠FBE+∠ABC=180°,∴∠FBE+∠D=180°,∴∠CKB+∠D=180°,∴∠EKC=∠D,∵∠BAE+∠D=180°,∴∠CKB=∠BAE,在△AEB和△KBC中,∵BAE CKBAEB KBCAB CK∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEB≌△KBC(AAS),∴BC=EB,∴∠KEC=∠BCE,∴∠KEC=∠DEC,在△KEC和△DEC中,∵KEC DECEKC DCK CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△KEC≌△DEC(AAS),∴KE=ED,∵BE=BG+KG+KE=2BG+ED,∴2BG+ED=BC.22.解析:(1)∵点A的坐标是(0,8),点B的坐标是(6,0),点C为AB的中点,∴点C(3,4),设直线AB的解析式为:y=kx+b,由题意可得:8068bk=⎧⎨=+⎩,解得:438kb⎧=-⎪⎨⎪=⎩,∴直线AB的解析式为:y=﹣43x+8;故答案为:(3,4),y=﹣43x+8;(2)如图1,连接CD,∵四边形CBDP是平行四边形,∴CB//PD,BC=PD,∵点C为AB的中点,∴AC=BC,∴PD=AC,∴四边形ACDP是平行四边形,∴CD//AP;(3)如图2,过点D作DF⊥AO于F,过点C作CE⊥BO于E,∵四边形PCQD是平行四边形,∴CQ=PD,PD//CQ,∴∠QCP+∠DPC=180°,∵AO//CE,∴∠OPC+∠PCE=180°,∴∠FPD=∠ECQ,又∵∠PFD=∠CEQ=90°,∴△PDF≌△CQE(AAS),∴DF=EQ,PF=CE,∵点C(3,4),点P(0,8﹣t),点Q(2t,0),∴CE=PF=4,EQ=DF=2t﹣3,∴FO=8﹣t﹣4=4﹣t,∴点D(2t﹣3,4﹣t),当点D落在直线OB上时,则4﹣t=0,即t=4,当点D落在直线OC上时,∵点C(3,4),∴直线OC解析式为:y=43x,∴4﹣t=43(2t﹣3),∴t=24 11,当点D落在AB上时,∵四边形PCQD是平行四边形,∴CD与PQ互相平分,∴线段PQ的中点(t,82t-)在CD上,∴82t-=﹣43t+8,∴t=245;综上所述:t=4或2411或245.23.解析:(1)证明:四边形ABCD 是平行四边形,OA OC ∴=,OB OD =.12DE OD =,12BF OB =,DE BF ∴=,OE OF ∴=,∴四边形AFCE 为平行四边形.(2)13DE OD =,13BF OB =,DE BF ∴=,OE OF ∴=,∴四边形AFCE 为平行四边形. ∴上述结论成立,由此可得出结论:若1DE OD n =,1BF OB n =,则四边形AFCE 为平行四边形.(3)在ABCD 中,//AD BC ,DAC BCA ∴∠=∠. CA 平分BCD ∠,BCA DCA ∴∠=∠, DCA DAC ∴∠=∠, AD CD ∴=. OA OC =, OE AC ∴⊥,OE ∴是AC 的垂直平分线, AE CE ∴=.60AEC ∠=︒,ACE ∴∆是等边三角形,210AE CE AC OA cm ∴====,()()22101040AECF C AE CE cm ∴=+=⨯+=四边形.。
特殊的四边形培优

特殊的四边形培优1.如图,已知在菱形ABCD中,DE⊥AB,DF⊥BC,垂足分别为E、F,且AE=BE,则∠EDF=______度.1.如图,四边形ABCD是正方形,△BDE是等边三角形,EF⊥DF,则∠BEF=________3.如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE 的长为_______FB CA DE4. 如图,在菱形ABCD 中,AB=4a ,E 在BC 上,BE=2a ,∠BAD=120°,P 点在BD 上,则PE+PC 的最小值为( )5.如图,矩形AEFG 与矩形APQK 的周长都等于120cm,求△ABC 的周长6.如图,在矩形ABCD 中,M ,N 分别是AD ,DC 边的中点,AN 与MC 交于P 点,若∠MCB=∠NBC+33°,那么∠MPA 的大小是( )1. 边长为25cm 的正方形纸片,AD 上有一点P ,且AP=66cm,将这纸片折叠使B 落在P 上,则折痕的长是________2. 已知直角三角形ABCD 中,∠C=90°,AC=3,BC=5,以AB 为边向外作正方形ABEF 求此正方形KGP E BC中心O到C点的距离OC的长________3.如图,已知在矩形ABCD中,E为CB延长线上一点,CE=AC,F是AE的中点.(1)求证BF⊥DF(2)若AB=8,AD=6,求DF的长10.如图,已知三角形ABC中,AB=AC,点M为BC 的中点,MG⊥BA于G,MD⊥AC于D,GF⊥AC于点E,GF与DF相交于点F,(1)求证:四边形HGMD是菱形(2)若∠GMD=120°,求证:从M点向所对的HG 和HD边引出的两条垂线MK和MQ分别平分这两条线段.E FQKDG11.如图,将一矩形的每一内角三等分,连接靠近同一边上的两三等分线所交成4交点组成四边形EFGH,试判断四边形EFGH形状12.在正方形ABCD中,AK和AN是∠A内的两射线,BK⊥AK,BL⊥AN,DM⊥AK,DN⊥AN,试求KL=MN1.在锐角△ABC中,BE是高,CF是中线,若∠ACF=30°则BE:CF=________2.如图,D、E、F分别是△ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P、Q两点,则PQ:BE=______.3.如图,△ABC中,∠BAC=120°,以AB,AC为边分别向形外作正三角形ABD和正三角形ACE,M为AD中点,N为AE中点,P为BC中点,求∠MPN的度数.4.凸五边形ABCDE中,∠ABC=∠AED=90°,∠CAD=30°,∠BAE=70°,F是CD中点,且FB=FE,则∠BAC=_________.5.已知:如图所示,在△ABC中,D、G分别为AB、AC上的点,且BD=CG,M、N分别是BG、CD的中点,过MN的直线交AB于点P,交AC于点Q,求证:AP=AQ。
四边形专项训练题(培优)

四边形专项训练题(培优)一.选择题(共10小题)1.四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是()A.1B.C.D.2.如图,在▱ABCD中,一定正确的是()A.AD=CD B.AC=BD C.AB=CD D.CD=BC3.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌()A.等边三角形B.正方形C.正五边形D.正六边形4.如图,在▱ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为()A.5B.4C.3D.25.如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F 的坐标为(2,3),则图象最低点E的坐标为()A.(,2)B.(,)C.(,)D.(,2)6.如图,在△ABC中,AB=AC,△DBC和△ABC关于直线BC对称,连接AD,与BC相交于点O,过点C作CE⊥CD,垂足为C,与AD相交于点E,若AD=8,BC=6,则的值为()A.B.C.D.7.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF 的边长为()A.2mm B.2mm C.2mm D.4mm8.如图,在正五边形ABCDE中,以AB为边向内作正△ABF,则下列结论错误的是()A.AE=AF B.∠EAF=∠CBF C.∠F=∠EAF D.∠C=∠E9.依据所标数据,下列一定为平行四边形的是()A.B.C.D.10.如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是()A.若OB=OD,则▱ABCD是菱形B.若AC=BD,则▱ABCD是菱形C.若OA=OD,则▱ABCD是菱形D.若AC⊥BD,则▱ABCD是菱形二.填空题(共10小题)11.四边形具有不稳定性.如图,矩形ABCD按箭头方向变形成平行四边形A'B'C'D',当变形后图形面积是原图形面积的一半时,则∠A'=.12.正十二边形的一个内角的度数为.13.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接P A,以P A,PC为邻边作平行四边形P AQC,连接PQ,则PQ长度的最小值为.14.如图,在正六边形ABCDEF中,M,N是对角线BE上的两点.添加下列条件中的一个:①BM=EN;②∠F AN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN是平行四边形的是(填上所有符合要求的条件的序号).15.如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC与BD交于点O,E为OB 中点,F为AD中点,连接EF,则EF的长为.16.如图,CD是△ABC的角平分线,过点D分别作AC,BC的平行线,交BC于点E,交AC于点F.若∠ACB=60°,CD=4,则四边形CEDF的周长是.17.七边形一共有条对角线.18.小张同学家要装修,准备购买两种边长相同的正多边形瓷砖用于铺满地面.现已选定正三角形瓷砖,则选的另一种正多边形瓷砖的边数可以是.(填一种即可)19.如图,在四边形ABCD中,连接AC,∠ACB=∠CAD.请你添加一个条件,使AB=CD.(填一种情况即可)20.如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED 是菱形,这个条件可以是.(写出一个即可)三.解答题(共8小题)21.同学们在探索“多边形的内角和”时,利用了“三角形的内角和”.请你在不直接运用结论“n边形的内角和为(n﹣2)•180°”计算的条件下,利用“一个三角形的内角和等于180°”,结合图形说明:五边形ABCDE的内角和为540°.22.如图,在▱ABCD中,点E、F分别是边AB、CD的中点.求证:AF=CE.23.小惠自编一题:“如图,在四边形ABCD 中,对角线AC ,BD 交于点O ,AC ⊥BD ,OB =OD .求证:四边形ABCD 是菱形”,并将自己的证明过程与同学小洁交流.小惠:证明:∵AC ⊥BD ,OB =OD ,∴AC 垂直平分BD .∴AB =AD ,CB =CD ,∴四边形ABCD 是菱形.小洁: 这个题目还缺少条件,需要补充一个条件才能证明.若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.24.如图,已知五边形ABCDE 是正五边形,连接AC 、AD .证明:∠ACD =∠ADC .25.如图,四边形ABCD 为菱形,E 为对角线AC 上的一个动点(不与点A ,C 重合),连接DE 并延长交射线AB 于点F ,连接BE .(1)求证:△DCE ≌△BCE ;(2)求证:∠AFD =∠EBC .26.如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB中点,连结CE.(1)求证:四边形AECD为菱形;(2)若∠D=120°,DC=2,求△ABC的面积.27.如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为点E,F,且BE=DF,∠ABD=∠BDC.求证:四边形ABCD是平行四边形.28.如图,在△ABC中,AD⊥BC于点D,E,F分别是AC,AB的中点,O是DF的中点,EO的延长线交线段BD于点G,连结DE,EF,FG.(1)求证:四边形DEFG是平行四边形.(2)当AD=5,tan∠EDC=时,求FG的长.。
2021年中考复习数学 几何专项:四边形 培优训练(含答案)

2021中考数学几何专项:四边形培优训练一、选择题1. 如图,菱形ABCD中,∠D=150°,则∠1=()A.30°B.25°C.20°D.15°2. 如图,将▱ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为()A. 66°B. 104°C. 114°D. 124°3. 如图,菱形ABCD的周长为8 cm,高AE长为cm,则对角线AC和BD长之比为()A.1∶2B.1∶3C.1∶D.1∶4. 若一个正多边形的每一个外角都等于40°,则它是()A.正九边形B.正十边形C.正十一边形D.正十二边形5. 如图,在▱ABCD中,对角线AC与BD交于点O.若增加一个条件,使▱ABCD 成为菱形,下列给出的条件不正确...的是()A. AB=ADB. AC⊥BDC. AC=BDD. ∠BAC=∠DAC6. 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是()A .∠DAB ′=∠CAB′ B .∠ACD =∠B′CDC .AD =AE D .AE =CE7. 如图,正方形ABCD 的边长为9,将正方形折叠,使顶点D 落在BC 边上的点E 处,折痕为GH ,若BE ∶EC =2∶1,则线段CH 的长是( ) A . 3 B . 4 C . 5 D . 68. 如图,在正方形ABCD 中,AC 为对角线,E 为AB 上一点,过点E 作EF ∥AD ,与AC 、DC 分别交于点G 、F ,H 为CG 的中点,连接DE 、EH 、DH 、FH.下列结论:①EG =DF ;②∠AEH +∠ADH =180°;③△EHF ≌△DHC ;④若AE AB =23,则3S △EDH =13S △DHC ,其中结论正确的有( ) A . 1个 B . 2个 C . 3个 D . 4个9. 如图,把正方形纸片ABCD 沿对边中点所在的直线对折后展开,折痕为MN ,再过点B 折叠纸片,使点A 落在MN 上的点F 处,折痕为BE.若AB 的长为2,则FM 的长为( ) A . 2 B . 3 C . 2 D . 110. 已知在平面直角坐标系中放置了5个如图X3-1-10所示的正方形(用阴影表示),点B 1在y 轴上,点C 1、E 1、E 2、C 2、E 3、E 4、C 3在x 轴上.若正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3,则点A 3到x 轴的距离是( )A.3+318 B.3+118C.3+36 D.3+16二、填空题11. 以正方形ABCD的边AD为边作等边三角形ADE,则∠BEC的度数是.12. 如图,在▱ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为________.13. 如图,含30°角的三角尺的直角边AC,BC分别经过正八边形的两个顶点,则∠1+∠2=________°.14. 如图,正方形ABCD的面积为3 cm2,E为BC边上一点,∠BAE=30°,F 为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于________cm.15. 七巧板是一种古老的中国传统智力游戏,被誉为“东方魔板”.由边长为4的正方形ABCD可以制作一副如图①所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图②所示的“拼搏兔”造型(其中点Q,R分别与图②中的点E,G重合,点P 在边EH 上),则“拼搏兔”所在正方形EFGH的边长是.三、解答题16. 如图,在四边形ABCD 中,AB ∥CD ,AD ⊥CD ,∠B=45°,延长CD 到点E ,使DE=DA ,连接AE. (1)求证:AE=BC ;(2)若AB=3,CD=1,求四边形ABCE 的面积.17. ABC 的三条中线分别为AD 、BE 、CF ,H 为BC 边外一点,且BHCF为平行四边形,求证:AD EH ∥.ABCDE FH18. 如图,将矩形ABCD 沿AF 折叠,使点D 落在BC 边的点E 处,过点E 作EG ∥CD 交AF 于点G ,连接DG . (1)求证:四边形EFDG 是菱形;(2)探究线段EG 、GF 、AF 之间的数量关系,并说明理由; (3)若AG =6,EG =25,求BE 的长.19. 如图,在菱形ABCD 中,AB =5,sin ∠ABD=55,点P 是射线BC 上一点,连接AP 交菱形对角线BD 于点E ,连接EC . (1)求证:△ABE ≌△CBE ;(2)如图①,当点P 在线段BC 上时,且BP =2,求△PEC 的面积;(3)如图②,当点P 在线段BC 的延长线上时,若CE ⊥EP ,求线段BP 的长.20. 如图,求证:四边形两组对边中点连线与两对角线中点连结这三条线共点.OE FLHNMDCB A2021中考数学 几何专项:四边形 培优训练-答案一、选择题 1. 【答案】D2. 【答案】C 【解析】设∠ACD =x ,∠B =y ,则根据题意可列方程组⎩⎨⎧x +y +44°=180°180°-y -(44°-x )=44°,解得y =114°.3. 【答案】D[解析]由菱形ABCD 的周长为8 cm 得边长AB=2 cm .又高AE 长为cm ,所以∠ABC=60°,所以△ABC ,△ACD 均为正三角形,AC=2 cm ,BD=2AE=2 cm .故对角线AC 和BD 长之比为1∶,应选D .4. 【答案】A[解析] 由于正多边形的外角和为360°,且每一个外角都相等,因此边数=360°40°=9.5. 【答案】C 【解析】邻边相等的平行四边形是菱形,所以A 正确;对角线互相垂直的平行四边形是菱形,所以B 正确;对角线相等的平行四边形是矩形,所以C 错误;由∠BAC =∠DAC 可得对角线是角平分线,所以D 正确.6. 【答案】D 【解析】∵四边形ABCD 为矩形,∴AB ∥CD ,∴∠ACD =∠BAC ,由折叠的性质可得∠BAC =∠EAC, ∴∠ACD =∠EAC ,∴AE =CE .7. 【答案】B 【解析】设CH =x ,∵BE ∶EC =2∶1,BC =9,∴EC =3,由折叠可知,EH =DH =9-x ,在Rt △ECH 中,由勾股定理得:(9-x )2=32+x 2,解得:x =4.序号 逐项分析 正误① 在正方形ABCD 中,AB =BC =CD =DA ,∠DAB =∠B =∠BCD =∠CDA =90°,∠ACB =∠ACD =45°,∵EF ∥AD ,∴四边形EFDA 、四边形EFCB 是矩形,∴∠EFC =∠ADC =90°,EF =DC ,在Rt △CGF 中,∠ACD =45°,∴GF =CF ,∴EF -GF =CD -CF ,即EG =DF√② ∵△GFC 是等腰直角三角形,H 是CG 的中点,∴GH =FH ,∠HGF =∠GFH =45°,∴∠EGH =∠DFH =135°,又由①知EG =DF ,∴△EGH ≌△DFH (SAS),∴∠HEF =∠FDH ,∵∠AEH =∠AEF +∠HEF =90°+∠HEF ,∠ADH =∠ADC-∠FDH =90°-∠FDH ,∴∠AEH +∠ADH =180° √③ 由②可知EH =DH ,FH =CH ,又∵EF =DC ,∴△EHF ≌△DHC (SSS)√④ ∵△EGH ≌△DFH ,∴EH =DH ,∠EHG =∠DHF ,∴∠EHG +∠AHD =∠DHF +∠AHD =90°,即∠EHD =∠AHF =90°,∴△EHD 为等腰直角三角形,∵AE AB =23,∴设AE =2x ,√9. 【答案】B【解析】∵AB =2,∴BF =2,又∵BM =12BC =1,由勾股定理得FM =FB 2-BM 2= 3.10. 【答案】⎝⎛⎭⎪⎫72,0D 解析:过小正方形的一个顶点D 3作FQ ⊥x 轴于点Q ,过点A 3作A 3F ⊥FQ 于点F .∵正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3, ∴∠B 3C 3E 4=60°,∠D 1C 1E 1=30°,∠E 2B 2C 2=30°, ∴D 1E 1=12D 1C 1=12,∴D 1E 1=B 2E 2=12, ∴cos30°=B 2E 2B 2C 2=12B 2C 2,解得:B 2C 2=33.∴B 3E 4=36,cos30°=B 3E 4B 3C 3.解得:B 3C 3=13. 则D 3C 3=13.根据题意得出:∠D 3C 3Q =30°,∠C 3D 3Q =60°,∠A 3D 3F =30°, ∴D 3Q =12×13=16,FD 3=D 3A 3·cos30°=13×32=36.则点A3到x轴的距离FQ=D3Q+FD3=16+36=3+16.二、填空题11. 【答案】30°或150°[解析]如图①,∵△ADE是等边三角形,∴DE=DA,∠DEA=∠1=60°.∵四边形ABCD是正方形,∴DC=DA,∠2=90°.∴∠CDE=150°,DE=DC,∴∠3=(180°-150°)=15°.同理可求得∠4=15°.∴∠BEC=30°.如图②,∵△ADE是等边三角形,∴DE=DA,∠1=∠2=60°,∵四边形ABCD是正方形,∴DC=DA,∠CDA=90°.∴DE=DC,∠3=30°,∴∠4=(180°-30°)=75°.同理可求得∠5=75°.∴∠BEC=360°―∠2―∠4―∠5=150°.故答案为30°或150°.12. 【答案】110°【解析】∵四边形ABCD是平行四边形,∴CD∥AB,∴∠CAB=∠1=20°,∵BE ⊥AB交对角线AC于点E,∴∠ABE=90°,∴∠2=∠CAB+∠ABE=20°+90°=110°.13. 【答案】180 [解析] 正八边形的每一个内角为(8-2)×180°8=135°,所以∠1+∠2=2×135°-90°=180°.14. 【答案】233或33 【解析】如解图,过N 作NG ⊥AB ,交AB 于点G ,∵四边形ABCD 为正方形,∴AB =AD =NG = 3 cm ,在Rt △ABE 中,∠BAE =30°,AB = 3 cm ,∴BE =1 cm ,AE =2 cm ,∵F 为AE 的中点,∴AF =12AE =1 cm ,在Rt △ABE 和Rt △NGM 中,⎩⎨⎧AB =NGAE =NM ,∴Rt △ABE ≌Rt △NGM(HL ),∴BE =GM ,∠BAE =∠MNG =30°,∠AEB =∠NMG =60°,∴∠AFM =90°,即MN ⊥AE ,在Rt △AMF 中,∠FAM =30°,AF =1 cm ,∴AM =AF cos 30°=132=233cm ,由对称性得到AM′=BM =AB -AM =3-233=33 cm ,综上,AM 的长等于233或33 cm .解图15. 【答案】4[解析]如图,连接EG ,作GM ⊥EN 交EN 的延长线于M.在Rt △EMG 中,∵GM=4,EM=2+2+4+4=12,∴EG===4,∴EH==4.三、解答题16. 【答案】解:(1)证明:∵AD ⊥CD ,AB ∥CD , ∴∠ADE=∠DAB=90°.∵AD=DE ,∴∠E=∠DAE=45°, ∴∠EAB=135°.∵∠B=45°,∴∠B +∠EAB=180°, ∴AE ∥BC ,∴四边形ABCE 是平行四边形, ∴AE=BC.(2)由(1)知AB=CE , ∵CD=1,AB=3, ∴DE=2. ∵AD=DE , ∴AD=2,∴S 四边形ABCE =3×2=6.17. 【答案】此题解法很多,仅供两种解法参考.方法一:连结DE 、DH .(如图1) ∵四边形BHCF 为平行四边形 ∴CH BF AF ==且CH AF ∥由中位线可得12DE AB AF == ∴CH DE =∴四边形DECH 为平行四边形 ∴DH CE ∥且DH CE AE == ∴四边形DHEA 为平行四边形 ∴AD EH ∥图1HFED CBA方法二:连结DE .(如图2)通过中位线和平行四边的性质可得 DE HC =,AB DE HC ∥∥∴AED ECH ∠=∠又∵AE EC =显然ADE EHC ∆∆≌∴DAE HEC ∠=∠∴AD EH ∥ A B C DE FH图218. 【答案】 8955(1)【思路分析】根据折叠的性质,易得DF =EF ,DG =EG ,∠AFD =∠AFE ,再由EG ∥DC ,可得∠EGF =∠AFD ,从而得出EG =EF.根据四条边都相等的四边形是菱形得证;证明:由折叠的性质可得,EF =FD ,∠AEF =∠ADF =90°,解图∠EFA =∠DFA ,EG =GD.(1分)∵EG ∥DC ,∴∠DFA =∠EGF ,∴∠EFA =∠EGF ,(2分)∴EF =EG =FD =GD ,∴四边形EFDG 是菱形.(3分)(2)【思路分析】由(1)可知EG =EF ,连接DE ,则DE 与GF 相互垂直平分,证得Rt △FHE ∽Rt △FEA ,列比例式,结合FH =12GF 得到EG 、GF 、AF 的关系;解:如解图,连接ED ,交AF 于点H ,∵四边形EFDG 是菱形,∴DE ⊥AF ,FH =GH =12GF ,EH =DH =12DE.(4分)∵∠FEH =∠FAE =90°-∠EFA ,∴Rt △FEH ∽Rt △FAE ,∴EF FH =AF EF ,即EF 2=FH·AF ,∴EG 2=12GF·AF.(5分)(3)【思路分析】把AG ,EG 代入(2)中的关系式,求得GF ,AF 的值,根据勾股定理求得AD ,DE ,再证Rt △ADF ∽Rt △DCE ,可求出EC ,从而可求出BE 的值.解:∵AG =6,EG =25,EG 2=12GF·AF , ∴(25)2=12(6+GF)·GF ,∴GF =4,∴AF =10.(6分)∵DF =EG =25,∴AD =BC =AF 2-DF 2=45,DE =2EH =2EG 2-(12GF )2=8.(7分) ∵∠CDE +∠DFA =90°,∠DAF +∠DFA =90°,∴∠CDE =∠DAF ,∴Rt △ADF ∽Rt △DCE ,(8分)∴EC DF =DE AF ,即EC 25=810, ∴EC =855,∴BE =BC -EC =AD -EC =45-855=1255.(9分)19. 【答案】(1)证明:∵四边形ABCD 是菱形,∴AB =BC ,∠ABE =∠CBE .在△ABE 和△CBE 中,AB =BC ,∠ABE =∠CBE ,BE =BE ,∴△ABE ≌△CBE (SAS);(2)解:如解图①,连接AC 交BD 于点O ,分别过点A 、E 作BC 的垂线,垂足分别为点H 、F ,解图①∵四边形ABCD 是菱形,∴AC ⊥BD ,∵AB =5,sin ∠ABD =55,∴AO =OC =5,∴BO =OD =25, ∴AC =25,BD =45, ∵12AC ·BD =BC ·AH ,即12×25×45=5AH ,∴AH =4,∵AD ∥BC ,∴△AED ∽△PEB , ∴AE PE =AD BP, ∴AE +PE PE =AD +BP BP ,即AP PE =5+22=72,∴AP =72PE ,又∵EF ∥AH ,∴△EFP ∽△AHP ,∴EF AH =PE AP ,∴EF =PE AP ·AH =PE 72PE×4=87,∴S △PEC =12PC ·EF =12×(5-2)×87=127;(3)解:如解图②,连接AC 交BD 于点O ,解图②∵△ABE ≌△CBE ,CE ⊥PE ,∴∠AEB =∠CEB =45°,∴AO =OE =5,∴DE =OD -OE =25-5=5,BE =3 5.∵AD ∥BP ,∴△ADE ∽△PBE ,∴AD BP =DE BE ,∴5BP =535, ∴BP =15.20. 【答案】方法一:设N H M L F E ,,,,,分别为AB BC CD DA AC BD ,,,,,的中点,要证明EF LH ,,及MN 三线共点.因为LF DC ∥且12LF DC =, 所以EF DC ∥且12EF DC =,LF EH ∥且LF EH =,从而四边形EHFL 为平行四边形,故LH 与EF 互相平分.设LH 与EF 的交点为O ,则LH 经过EF 中点O (当然也是LH 中点).同理,MN 也过EF 中点O .所以,EF ,LH ,MN 三线共点于O . 说明:本题证明的关键是平行四边形EHFL 的获得(它是通过三角形中位线定理来证明的).由此可见,在某些四边形的问题中,通过构造平行四边形去解题是一种常用的技巧.请看下例.方法二:应用中点公式法可设()11A x y ,,()()()223344B x y C x y D x y ,,,,, 那么AC 线段的中点坐标为131322x x y y F ++⎛⎫⎪⎝⎭,,BD 线段的中点坐标为242422x x y y E ++⎛⎫ ⎪⎝⎭, 那么EF 线段的中点坐标为1234123422x x x x y y y y ++++++⎛⎫⎪⎝⎭, 同理可得:MN LH ,的中点坐标也为1234123422x x x x y y y y ++++++⎛⎫ ⎪⎝⎭, 所以可知:EF ,LH ,MN 三线共点于O。
人教版 八年级数学下册 18.1 平行四边形 培优训练(含答案)

人教版 八年级数学 18.1 平行四边形 培优训练一、选择题(本大题共8道小题)1. 以三角形的三个顶点作平行四边形,最多可以作( ) A .2个 B .3个 C .4个 D .5个2. 如图,将▱ABCD 沿对角线AC 折叠,使点B 落在点B′处.若∠1=∠2=44°,则∠B 为( )A . 66°B . 104°C . 114°D . 124°3. 如图,平行四边形ABCD 的周长是26 cm ,对角线AC 与BD 交于点O ,AC ⊥AB ,E 是BC 中点,△AOD 的周长比△AOB 的周长多3 cm ,则AE 的长度为( ) A . 3 cm B . 4 cm C . 5 cm D . 8 cm4. 如图,ABCD 中,AB=2,AD=4,对角线AC ,BD 相交于点O ,且E ,F ,G ,H 分别是AO ,BO ,CO ,DO 的中点,则下列说法正确的是A .EH=HGB .四边形EFGH 是平行四边形C .AC ⊥BDD .△ABO 的面积是△EFO 的面积的2倍5. 在平行四边形ABCD 中,点1A 、2A 、3A 、4A 和1C 、2C 、3C 、4C 分别为AB 和CD 的五等分点,点1B 、2B 和1D 、2D 分别是BC 和DA 的三等分点,已知四边形4242A B C D 的面积为1,则平行四边形ABCD 面积为( )A .2B .35C .53D .156. (2019▪广西池河)如图,在△ABC中,D ,E 分别是AB ,BC 的中点,点F 在DE 延长线上,添加一个条件使四边形ADFC 为平行四边形,则这个条件是A .∠B=∠FB .∠B=∠BCFC .AC=CFD .AD=CF7.已知四边形的四条边长分别是a b c d ,,,,其中a b ,为对边,并且满足222222a b c d ab cd +++=+则这个四边形是( )A .任意四边形B .平行四边形C .对角线相等的四边形D .对角线垂直的四边形8.(2020·临沂)如图,P 是面积为S 的ABCD 内任意一点,PAD ∆的面积为1S ,PBC ∆的面积为2S ,则( )A.122SS S +>B.122SS S +<C.212SS S += D.21S S +的大小与P 点位置有关二、填空题(本大题共8道小题)9. 如图所示,四边形ABCD 的对角线相交于点O ,若AB ∥CD ,请添加一个条件________(写一个即可),使四边形ABCD 是平行四边形.10.(2020·牡丹江)如图,在四边形ABCD 中,AD//BC ,在不添加任何辅助线的情况下,请你添加一个条件__________________,使四边形ABCD 是平行四边形(填一个即可).11. 已知平行四边形ABCD 的周长为60cm ,对角线AC 、BD 相交于O 点,AOB ∆的周长比BOC ∆的周长多8cm ,则AB的长度为cm .OD CBA12. 如图所示,在▱ABCD中,∠C =40°,过点D 作AD 的垂线,交AB 于点E ,交CB 的延长线于点F ,则∠BEF 的度数为__________.13. (2020·凉山州)如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,OE ∥AB 交AD 于点E .若OA =1,△AOE 的周长等于5,则平行四边形ABCD 的周长等于 .O EDCB A14. 如图,在ABCD 中,E.F 是对角线AC 上两点,AE=EF=CD ,∠ADF=90°,∠BCD=63°,则∠ADE 的大小为__________.15. 如图,在▱ABCD中,E 为边CD 上一点,将△ADE 沿AE 折叠至△AD′E 处,AD ′与CE 交于点F ,若∠B =52°,∠DAE =20°,则∠FED′的大小为________.ABC16. 如图,一个平行四边形被分成面积为1S 、2S 、3S 、4S 四个小平行四边形,当CD 沿AB 自左向右在平行四边形内平行滑动时.① 14S S 与23S S 的大小关系为.② 已知点C 与点A 、B 不重合时,图中共有 个平行四边形,S 4S 3S 2S 1(3)DCBA三、解答题(本大题共4道小题) 17. (2020·重庆B 卷)如图,在平行四边形ABCD 中,AE ,CF 分别平分∠BAD 和∠DCB ,交对角线BD 于点E ,F . (1)若∠BCF =60°,求∠ABC 的度数; (2)求证:BE =DF .18. 如图所示,P 为平行四边形ABCD 内一点,求证:以AP 、BP 、CP 、DP 为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB 和BC .DPCBA19. (2020·泰安)(12分)若△ABC 和△AED 均为等腰三角形,且∠BAC ﹦∠EAD﹦90°.(1)如图(1),点B 是DE 的中点,判断四边形BEAC 的形状,并说明理由;(2)如图(2),若点G 是EC 的中点,连接GB 并延长至点F ,使CF ﹦CD . 求证:①EB ﹦DC ,②∠EBG ﹦∠BFC .GFABCDEABCDE20. 如图,AC 是平行四边形ABCD 较长的一条对角线,点O 是ABCD 内部一点,OE AB ⊥于点E ,OF AD ⊥于点F ,OG AC ⊥于点G ,求证:AE AB AF AD AG AC ⋅+⋅=⋅.人教版 八年级数学 18.1 平行四边形 培优训练-答案一、选择题(本大题共8道小题) 1. 【答案】B2. 【答案】C 【解析】设∠ACD =x ,∠B =y ,则根据题意可列方程组⎩⎨⎧x +y +44°=180°180°-y -(44°-x )=44°,解得y =114°.3. 【答案】B【解析】在▱ABCD 中,AD =BC ,AB =CD ,BO =DO ,∵平行四边形ABCD 的周长为26 cm ,∴AB +BC =13 cm ,又∵△AOD 的周长比△AOB 的周长多3 cm ,∴AD -AB =BC -AB =3 cm ,解得AB =5 cm ,BC =8 cm ,又AB ⊥AC ,E 是BC 的中点,∴AE =BE =CE =12BC =4 cm.4. 【答案】B【解析】∵E,F,G,H分别是AO,BO,CO,DO的中点,在ABCD中,A B=2,AD=4,∴EH=12AD=2,HG=1122CD=AB=1,∴EH≠HG,故选项A 错误;∵E,F,G,H分别是AO,BO,CO,DO的中点,∴EH=1122AD BC FG==,∴四边形EFGH是平行四边形,故选项B正确;由题目中的条件,无法判断AC和BD是否垂直,故选项C错误;∵点E、F分别为OA和OB的中点,∴EF=12AB,EF∥AB,∴△OEF∽△OAB,∴214AEFOABS EFS AB⎛⎫==⎪⎝⎭,即△ABO的面积是△EFO的面积的4倍,故选项D错误,故选B.5. 【答案】C6. 【答案】B【解析】∵在△ABC中,D,E分别是AB,BC的中点,∴DE是△ABC的中位线,∴DE=12 AC.A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.故选B.7. 【答案】B8. 【答案】C【解析】可以利用割补法对平行四边形进行分割,然后使分割后的图形与PAD ∆的面积1S ,PBC ∆的面积2S 发生关联,然后求出其数量关系,如下图,过点P 作AD 的平行线,分别交ABCD 的边于点M 、N :2111(21222)AMND MbCN AMND MbCN SS S S S S S =+++==.二、填空题(本大题共8道小题) 9. 【答案】AD ∥BC (答案不唯一) 【解析】根据平行四边形的判定,在已有AB ∥DC 的条件下,可再加另一组对边平行即可证得它是平行四边形,即加“AD ∥BC”.10. 【答案】AD=BC【解析】当添加条件AD=BC 时,根据一组对边平行且相等的四边形是平行四边形,可得四边形ABCD 是平行四边形.11. 【答案】19【解析】如图,AOB ∆的周长为AB AO BO ++,BOC ∆的周长为BC BO CO ++ 由平行四边形的对角线互相平分可得()()8AB AO BO BC BO CO AB BC ++-++=-= ∴6082194AB +⨯==.12. 【答案】50°【解析】在平行四边形ABCD 中,AB ∥CD ,AD ∥BC ,∴∠FBA=∠C =40°,∵FD ⊥AD ,∴∠ADF =90°,∵AD ∥BC ,∴∠F =∠ADF =90°,∴∠BEF =180°-90°-40°=50°.13. 【答案】16【解析】∵四边形ABCD 是平行四边形,∴OA =OC ,AB =CD ,AD =BC .∵OE ∥AB ,∴OE 是△ACD 的中位线.∴AE =12AD ,OE =12CD .∵OA =1,△AOE 的周长等于5,∴AE +OE =4.∴AD +CD =8.∴平行四边形ABCD 的周长=16.故答案为16.14. 【答案】21° 【解析】设∠ADE=x ,∵AE=EF ,∠ADF=90°,∴∠DAE=∠ADE=x ,DE=12AF=AE=EF ,∵AE=EF=CD ,∴DE=CD , ∴∠DCE=∠DEC=2x ,∵四边形ABCD 是平行四边形,∴AD ∥BC , ∴∠DAE=∠BCA=x ,∴∠DCE=∠BCD ﹣∠BCA=63°﹣x ,∴2x=63°﹣x ,解得x=21°,即∠ADE=21°; 故答案为:21°.15. 【答案】36°【解析】∵在▱ABCD 中,∠D =∠B =52°,∴∠AEF =∠DAE +∠D =20°+52°=72°,∴∠AED =180°-∠AEF =108°,由折叠的性质得,∠AED ′=∠AED =108°,∴∠FED ′=∠AED′-∠AEF =108°-72°=36°.16. 【答案】①1423S S S S =;②9三、解答题(本大题共4道小题)17. 【答案】(1)解: ∵CF 平分∠BCD ,∴∠BCD =2∠BCF .∵∠BCF =60°,∴∠BCD =2×60°=120°.∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠ABC +∠BCD =180°. ∴∠ABC =180°-120°=60°.(2)证明:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,∠BAD =∠DCB .∴∠ABE =∠CDF .∵AE ,CF 分别平分∠BAD 和∠DCB ,∴∠BAE =12∠BAD =12∠DCB =∠DCF .在△ABE 和△CDF 中,∵∠ABE =∠CDF ,AB =CD ,∠BAE =∠DCF , ∴△ABE ≌△CDF . ∴BE =DF .18. 【答案】如图所示,将PAB ∆平移至QDC ∆的位置,易证DQ AP =,CQ BP =,则四边形DPCQ 恰好是一个以AP 、BP 、CP 、DP 为边的四边形,并且它的对角线恰好等于平行四边形ABCD 的两条邻边.QDPCBA19. 【答案】(1)证明:四边形BEAC 是平行四边形. 理由如下:∵△EAD 为等腰三角形且∠EAD ﹦90°, ∴∠E ﹦45°.∵B 是DE 的中点, ∴AB ⊥DE . ∴∠BAE ﹦45°.∵△ABC 为等腰三角形且∠BAC ﹦90°, ∴∠CBA ﹦45°. ∴∠BAE ﹦∠CBA . ∴BC ∥EA . 又∵AB ⊥DE ,∴∠EBA ﹦∠BAC ﹦90°. ∴BE ∥AC .∴四边形BEAC 是平行四边形.(2)证明:①∵△AED 和△ABC 为等腰三角形, ∴AE ﹦AD ,AB ﹦AC . ∵∠EAD ﹦∠BAC ﹦90°,∴∠EAD +∠DAB ﹦∠BAC +∠DAB .即∠EAB ﹦∠DAC . ∴△AEB ≌△ADC . ∴EB ﹦DC .②延长FG 至点H ,使GH ﹦FG . ∵G 是EC 中点,∴EG ﹦CG .又∠EGH ﹦∠FGC , ∴△EHG ≌△CFG ,∴∠BFC ﹦∠H ,CF ﹦EH . 又∵CF ﹦CD , ∴BE ﹦CF . ∴BE ﹦EH .∴∠EBG ﹦∠H . ∴∠EBG ﹦∠BFC .AB CDEEDCBA FGH20. 【答案】如图所示,,分别过点B 、C 、D 作直线AO 的垂线,EG CP DL ∥∥、Q 、N 为垂足;分别过B 、D 作AC 的垂线,L 、K 为垂足. 显然,A 、E 、O 、G 、F 五点共圆,AO 是直径.由DN AO ⊥,CQ AO ⊥,BM AO ⊥,DC AB ∥且DC AB =可知NQ AM =. 已知AF AD AN AO ⋅=⋅,AE AB AM AO ⋅=⋅, 则AF AD AE AB ⋅+⋅ AN AO AM AO =⋅+⋅ ()AO AN AM =+ ()AO AN NQ =+ AO AQ =⋅ AG AC =⋅故AE AB AF AD AG AC ⋅+⋅=⋅.点评:ab cd ef +=类型的问题一般要转化为ab mn =型的问题(当然,如果能够使用勾股定理、余弦定理等,大家也可以踊跃尝试),把握了这一点,就能及时调整思路,确保解题不会误入歧途.图(1)图(2)。
平行四边形培优

平行四边形性质培优一:角的题型。
1、在▱ABCD中,∠A:∠B:∠C:∠D可能是()A.1:2:3:4B.2:3:2:3C.2:2:1:1D.2:3:3:22.▱ABCD中,∠B=5∠A,则∠C的度数为3.已知▱ABCD中,∠A+∠C=240°,则∠B的度数是4.在▱ABCD中,∠A﹣∠B=40°,则∠C的度数为5.如图,▱ABCD与▱DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为二:周长题型。
1.如图,平行四边形ABCD的周长为8,△AOB的周长比△BOC的周长多2,求:AB边的长。
2.在▱ABCD中,O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E,若▱ABCD的周长为22cm,则△CDE的周长为3、如图,▱ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为10,则▱ABCD的周长为4.如图,EF过▱ABCD的对角线的交点O,交AD于点E,交BC于点F.若▱ABCD的周长为10,OE=1,线则四边形EFCD的周长为5、如图所示,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,∠EAF=45∘,且AE+AF=32求平行四边形ABCD的周长。
6、如图所示,在平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为12,△FCB的周长为22,则FC的长为_________.三:面积题型。
1、如图,□ABCD的两条对角线相交于点O,E,F分别是边CD,BC的中点,图中与△BCE面积相等的三角形(不包括△BCE)共有_______个.2,如图,E是□ABCD中AB边上的任意一点,连接CE、DE,DE与对角线AC 相交于点F,则下列结论中不正确的是()A.S△ADE=S△BCEB.S△ACD=S△ABCB..S△CDE=S△ABC D.S△CDE=S△ADE+S△BCE3、如图,四边形ABCD、BEFD、EGHD均为平行四边形,其中C.F两点分别在EF、GH上。
第十八章四边形综合测试题-学而思培优

第十八章综合测试题(满分100分,时间90分钟)一 、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是正确的)下列图形中,周长不是32的图形是( ).2.菱形和矩形一定都具有的性质是( ).A .对角线相等B .对角线互相垂直C .对角线互相平分D .对角线互相平分且相等3.如下图所示,一正方形的纸片经三次折叠后,用剪子剪掉虚线部分,则展开后的图形是( ).4.如右图所示,四边形ABCD 中,F E BC AD 、,>分别是AB 、CD 的中点,AD 、BC 的延长线分别与EF 的延长线交于H 、G ,则( ).BGE AHE A ∠>∠. BGE AHE B ∠=∠. BGE AHE C ∠<∠.BGE AHE D ∠∠与.的大小关系不确定5.如右图所示,0为平行四边形ABCD 对角线AC 、BD 的交点,EF 经过点0,且与边AD 、BC 分别交于点E 、F ,若,DE BF =则图中的全等三角形最多有( ). A .8对 B .6对 C .5对 D .4对6.将正方形ABCD 折叠,使顶点A 与CD 边上的点M 重合,折痕交AD 于点E ,交BC 于点F ,边AB 折叠后与BC 边交于点G (如下图所示).如果,2:1:=MC DM 则=⋅EM DM DE ::( )25:24:7.A 5:3:4.B 13:12:5.C 17:15:8.D7.时钟的表面为圆形,在它的圆周上有12个用于表示整点的等分点.以这些等分点为顶点的矩形共有( ).A.6个 B .12个 C.15个 D .18个8.如右图所示,已知四边形ABCD 是正方形,点E 在BC 上,且,41BC CE =点F 是CD 的中点,延长AF 与BC 的延长线交于点M .以下结论:;CM AB =①+=AB AE ②④③四边形;41;ABCF AEF S s CE =∆090=∠AFE 其中正确的结论的个数有( ).A .1个B .2个C .3个D .4个9.如右图所示,已知△ABC 的面积为1,连接△ABC 三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,第2013个三角形的面积为( )20111.A 2021.B 201141.c 201241.D10.已知正方形纸片的边长为18,若将它按下图所示方法折成一个正方体纸盒,则纸盒的边(棱)长是( ).6.A 23.B 29.C 32.D二、填空题{本火题共10小题,每小题2分,共20分)11.如下左图所示,在菱形ABCD 中,点E 是AB 上的一点,连接DE 交AC 于点O ,连接BO ,且,50oAED =∠则=∠CBO 度.12.如下中图所示,四边形ABCD 中,AD BE BC AB CDA ABC ⊥==∠=∠,,90于点E ,且四边形ABCD 的面积为8,则=BE13.如下右图所示,用边长为1的正方形材料制作的七巧板拼成一幅土家摆手舞图案,其中舞者头部占整个身体面积的14.如下左图所示,AB∥CD,E ,F 分别为AC ,BD 的中点,若,3,5==CD AB 则EF 的长是15.如下中图所示,在梯形ABCD 中,C B BC AD ∠∠与,//互余,,13,5==BC AD M 、N 分别为AD 、BC的中点,则MN 的长为16.平行四边形两邻边的长分别为16和20,两条长边间的距离为8,则两一条短边间的距离为 .17.如下右图所示,在等腰梯形ABCD 中,AD∥BC,点E 是BC 的中点,点F 是AC 上的一个动点.若四边形AECD 是菱形,△ABE 的周长为6cm ,则BF+EF 的最小值是 cm.18.如右图所示,有位农场主有一大片田地,其形状恰好是一个平行四边形,并且在对角线BD 上有一口水井E.农场主临死前留下遗嘱,把两块三角形的田地(即图7中阴影部分)给小儿子,剩下的全部给大儿子,至于水井E ,正好两儿子共用,由于平行四边形两边长不同,所以遗嘱公布之后,亲友们七嘴八 舌,议论纷纷,认为这个分配不公平,那么你认为 .(填“公平”或“不公平”)理由是19.如下左图所示,在矩形ABCD 中,E 、F 分别是边AD 、BC 的中点,点G 、H 在DC 边上,且.31DC GH = 若,16,15==BC AB 则图中阴影部分面是20.如下右图所示,在△ABC 中,CE 、CF 分别平分,//,//,CE AF CF AE ACD ACB ∠∠和直线EF 分别交AB 、AC 于点M 、N.若,,,c AB b AC a BC ===且,b c a >>则ME 的长为三、解答题(2l 题5分,22-24题每题7分,25~27题每题8分)21.如下图所示,在DABCD 中,两条对角线相交于点0,点E 、F 、G 、H 分别是OA 、OB 、OC 、OD 的中点,以图中的任意四点(即点A 、B 、C 、D 、E 、F 、G 、H 、0中的任意四点)为顶点画两种不同的平行四边形.22.有一块形状如下图所示的玻璃,AE∥BC,不小心把DEF 部分打碎,现在只测得70BC ,30==cm AB,150,60, =∠=∠C B cm 请根据测得的数据求出AD 的长.23.如下图所示,分别以Rt△ABC 的直角边AC 及斜边AB 向外作等边△ACD 、等边△ABE.已知,,30AB EF BAC ⊥=∠ 垂足为F ,连接DF.(1)试说明;EF AC =(2)求证:四边形ADFE 是平行四边形.24.如下图所示,在四边形ABCD 中,F E DC AB 、,=分别是AD 、BC 的中点,G 、H 分另0是BD 、AC 的中点,猜一猜EF 与GH 的位置关系,并证明你的结论.25.用右图所示的图形拼成一个9×9的正方形,但中央留出一个3×3的正方形.26.如下图所示,正方形ABCD 被两条与边平行的线段EF 、GH 分割成4个小矩形,P 是EF 与GH 的交点,若矩形PFCH 的面积恰是矩形AGPE 面积的2倍,试确定∠HAF 的大小,并证明你的结论.27.如下图所示,在△ABC 中,,90=∠C 点M 在BC 上,且BM =AC ,点N 在AC 上,且AM MC AN ,=与BN 相交于点P.求证:.45=∠BPM。
中考数学培优(含解析)之平行四边形含答案
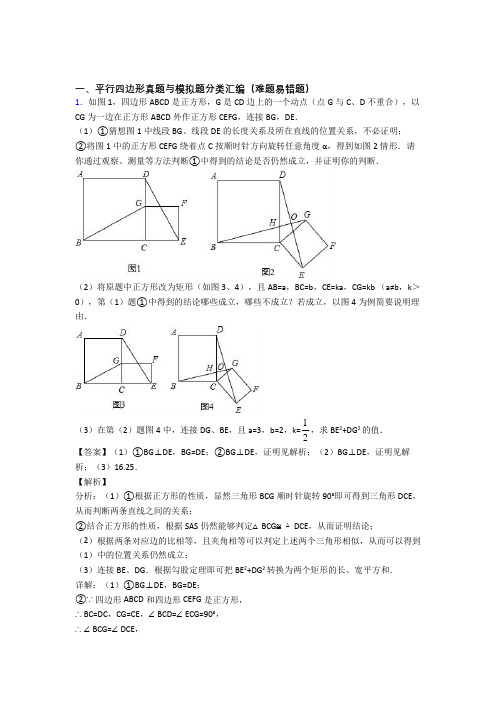
一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.(1)①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并证明你的判断.(2)将原题中正方形改为矩形(如图3、4),且AB=a,BC=b,CE=ka,CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图4为例简要说明理由.(3)在第(2)题图4中,连接DG、BE,且a=3,b=2,k=12,求BE2+DG2的值.【答案】(1)①BG⊥DE,BG=DE;②BG⊥DE,证明见解析;(2)BG⊥DE,证明见解析;(3)16.25.【解析】分析:(1)①根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系;②结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论;(2)根据两条对应边的比相等,且夹角相等可以判定上述两个三角形相似,从而可以得到(1)中的位置关系仍然成立;(3)连接BE、DG.根据勾股定理即可把BE2+DG2转换为两个矩形的长、宽平方和.详解:(1)①BG⊥DE,BG=DE;②∵四边形ABCD和四边形CEFG是正方形,∴BC=DC,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,∴△BCG≌△DCE,∴BG=DE,∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(2)∵AB=a,BC=b,CE=ka,CG=kb,∴BC CG b==,DC CE a又∵∠BCG=∠DCE,∴△BCG∽△DCE,∴∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(3)连接BE、DG.根据题意,得AB=3,BC=2,CE=1.5,CG=1,∵BG⊥DE,∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25.点睛:此题综合运用了全等三角形的判定和性质、相似三角形的判定和性质以及勾股定理.2.如图1,正方形ABCD的一边AB在直尺一边所在直线MN上,点O是对角线AC、BD 的交点,过点O作OE⊥MN于点E.(1)如图1,线段AB与OE之间的数量关系为.(请直接填结论)(2)保证点A始终在直线MN上,正方形ABCD绕点A旋转θ(0<θ<90°),过点 B作BF⊥MN于点F.①如图2,当点O、B两点均在直线MN右侧时,试猜想线段AF、BF与OE之间存在怎样的数量关系?请说明理由.②如图3,当点O、B两点分别在直线MN两侧时,此时①中结论是否依然成立呢?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.③当正方形ABCD绕点A旋转到如图4的位置时,线段AF、BF与OE之间的数量关系为.(请直接填结论)【答案】(1)AB=2OE;(2)①AF+BF=2OE,证明见解析;②AF﹣BF=2OE 证明见解析;③BF ﹣AF=2OE,【解析】试题分析:(1)利用直角三角形斜边的中线等于斜边的一半即可得出结论;(2)①过点B作BH⊥OE于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBH,然后利用“角角边”证明△AOE和△OBH全等,根据全等三角形对应边相等可得OH=AE,OE=BH,再根据AF-EF=AE,整理即可得证;②过点B作BH⊥OE交OE的延长线于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBH,然后利用“角角边”证明△AOE和△OBH全等,根据全等三角形对应边相等可得OH=AE,OE=BH,再根据AF-EF=AE,整理即可得证;③同②的方法可证.试题解析:(1)∵AC,BD是正方形的对角线,∴OA=OC=OB,∠BAD=∠ABC=90°,∵OE⊥AB,∴OE=12 AB,∴AB=2OE,(2)①AF+BF=2OE证明:如图2,过点B作BH⊥OE于点H∴∠BHE=∠BHO=90°∵OE⊥MN,BF⊥MN∴∠BFE=∠OEF=90°∴四边形EFBH为矩形∴BF=EH,EF=BH∵四边形ABCD为正方形∴OA=OB,∠AOB=90°∴∠AOE+∠HOB=∠OBH+∠HOB=90°∴∠AOE=∠OBH∴△AEO≌△OHB(AAS)∴AE=OH,OE=BH∴AF+BF=AE+EF+BF=OH+BH+EH=OE+OE=2OE.②AF﹣BF=2OE证明:如图3,延长OE,过点B作BH⊥OE于点H∴∠EHB=90°∵OE⊥MN,BF⊥MN∴∠AEO=∠HEF=∠BFE=90°∴四边形HBFE为矩形∴BF=HE,EF=BH∵四边形ABCD是正方形∴OA=OB,∠AOB=90°∴∠AOE+∠BOH=∠OBH+∠BOH∴∠AOE=∠OBH∴△AOE≌△OBH(AAS)∴AE=OH,OE=BH,∴AF﹣BF=AE+EF﹣HE=OH﹣HE+OE=OE+OE=2OE③BF﹣AF=2OE,如图4,作OG⊥BF于G,则四边形EFGO是矩形,∴EF=GO,GF=EO,∠GOE=90°,∴∠AOE+∠AOG=90°.在正方形ABCD中,OA=OB,∠AOB=90°,∴∠AOG+∠BOG=90°,∴∠AOE=∠BOG.∵OG⊥BF,OE⊥AE,∴∠AEO=∠BGO=90°.∴△AOE≌△BOG(AAS),∴OE=OG,AE=BG,∵AE﹣EF=AF,EF=OG=OE,AE=BG=AF+EF=OE+AF,∴BF﹣AF=BG+GF﹣(AE﹣EF)=AE+OE﹣AE+EF=OE+OE=2OE,∴BF﹣AF=2OE.3.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系;(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由(3)若|CF﹣AE|=2,EF=23,当△POF为等腰三角形时,请直接写出线段OP的长.【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP62 23.【解析】【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再根据直角三角形斜边中线等于斜边一半即可得OF=OE;(2)如图2中,延长EO交CF于K,由已知证明△ABE≌△BCF,△AOE≌△COK,继而可证得△EFK是等腰直角三角形,由等腰直角三角形的性质即可得OF⊥EK,OF=OE;(3)分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】(1)如图1中,延长EO交CF于K,∵AE⊥BE,CF⊥BE,∴AE∥CK,∴∠EAO=∠KCO,∵OA=OC,∠AOE=∠COK,∴△AOE≌△COK,∴OE=OK,∵△EFK是直角三角形,∴OF=12EK=OE;(2)如图2中,延长EO交CF于K,∵∠ABC=∠AEB=∠CFB=90°,∴∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,∴∠BAE=∠CBF,∵AB=BC,∴△ABE≌△BCF,∴BE=CF,AE=BF,∵△AOE≌△COK,∴AE=CK,OE=OK,∴FK=EF,∴△EFK是等腰直角三角形,∴OF⊥EK,OF=OE;(3)如图3中,点P在线段AO上,延长EO交CF于K,作PH⊥OF于H,∵|CF﹣AE|=2,EF=23,AE=CK,∴FK=2,在Rt△EFK中,tan∠FEK=33,∴∠FEK=30°,∠EKF=60°,∴EK=2FK=4,OF=12EK=2,∵△OPF是等腰三角形,观察图形可知,只有OF=FP=2,在Rt△PHF中,PH=12PF=1,HF=3,OH=2﹣3,∴OP=()2212362+-=-.如图4中,点P在线段OC上,当PO=PF时,∠POF=∠PFO=30°,∴∠BOP=90°,∴OP=33OE=33,综上所述:OP6223.【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等,综合性较强,正确添加辅助线是解题的关键.4.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E 是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形ADBC的面积.【答案】(1)见解析;(2)S平行四边形ADBC=32.【解析】【分析】(1)在Rt△ABC中,E为AB的中点,则CE=12AB,BE=12AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD//BC,则四边形BCFD是平行四边形.(2)在Rt△ABC中,求出BC,AC即可解决问题;【详解】解:(1)证明:在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°,在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°,∵E为AB的中点,∴AE=BE,又∵∠AEF=∠BEC,∴△AEF≌△BEC,在△ABC中,∠ACB=90°,E为AB的中点,∴CE=12AB,BE=12AB,∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°,又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°,又∵∠D=60°,∴∠AFE=∠D=60°,∴FC∥BD,又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC,∴四边形BCFD是平行四边形;(2)解:在Rt△ABC中,∵∠BAC=30°,AB=6,∴BC=AF=3,AC=33∴S平行四边形BCFD=3×3393,S△ACF=12×3×3332,S平行四边形ADBC=32.【点睛】本题考查平行四边形的判定和性质、直角三角形斜边中线定理、等边三角形的性质、解直角三角形、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.5.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.(1)证明:BE=CF.(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.【答案】(1)见解析;(2)43;(3)见解析【解析】试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.试题解析:(1)证明:连接AC,∵∠1+∠2=60°,∠3+∠2=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=∠ADC=60°∵四边形ABCD是菱形,∴AB=BC=CD=AD,∴△ABC、△ACD为等边三角形∴∠4=60°,AC=AB,∴在△ABE和△ACF中,,∴△ABE≌△ACF.(ASA)∴BE=CF.(2)解:由(1)得△ABE≌△ACF,则S△ABE=S△ACF.故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值.作AH⊥BC于H点,则BH=2,S四边形AECF=S△ABC===;(3)解:由“垂线段最短”可知,当正三角形AEF的边AE与BC垂直时,边AE最短.故△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.由(2)得,S△CEF=S四边形AECF﹣S△AEF=﹣=.点睛:本题考查了菱形每一条对角线平分一组对角的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了三角形面积的计算,本题中求证△ABE≌△ACF是解题的关键.6.如图,在平行四边形ABCD中,AD⊥DB,垂足为点D,将平行四边形ABCD折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度7.(感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.(应用)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,菱形CEFG的面积是_______.(只填结果)【答案】见解析【解析】试题分析:探究:由四边形ABCD 、四边形CEFG 均为菱形,利用SAS 易证得△BCE ≌△DCG ,则可得BE=DG ;应用:由AD ∥BC ,BE=DG ,可得S △ABE +S △CDE =S △BEC =S △CDG =8,又由AE=3ED ,可求得△CDE 的面积,继而求得答案.试题解析:探究:∵四边形ABCD 、四边形CEFG 均为菱形,∴BC=CD ,CE=CG ,∠BCD=∠A ,∠ECG=∠F .∵∠A=∠F ,∴∠BCD=∠ECG .∴∠BCD-∠ECD=∠ECG-∠ECD ,即∠BCE=∠DCG .在△BCE 和△DCG 中,BC CD BCE DCG CE CG ⎧⎪∠∠⎨⎪⎩=== ∴△BCE ≌△DCG (SAS ),∴BE=DG .应用:∵四边形ABCD 为菱形,∴AD ∥BC ,∵BE=DG ,∴S △ABE +S △CDE =S △BEC =S △CDG =8,∵AE=3ED ,∴S △CDE =1824⨯= , ∴S △ECG =S △CDE +S △CDG =10∴S 菱形CEFG =2S △ECG =20.8.(1)问题发现:如图①,在等边三角形ABC 中,点M 为BC 边上异于B 、C 的一点,以AM 为边作等边三角形AMN ,连接CN ,NC 与AB的位置关系为 ; (2)深入探究:如图②,在等腰三角形ABC 中,BA=BC ,点M 为BC 边上异于B 、C 的一点,以AM 为边作等腰三角形AMN ,使∠ABC=∠AMN ,AM=MN ,连接CN ,试探究∠ABC 与∠ACN 的数量关系,并说明理由;(3)拓展延伸:如图③,在正方形ADBC 中,AD=AC ,点M 为BC 边上异于B 、C 的一点,以AM 为边作正方形AMEF ,点N 为正方形AMEF 的中点,连接CN ,若BC=10,CN=2,试求EF 的长.【答案】(1)NC ∥AB ;理由见解析;(2)∠ABC=∠ACN ;理由见解析;(3)241;【解析】分析:(1)根据△ABC ,△AMN 为等边三角形,得到AB=AC ,AM=AN 且∠BAC=∠MAN=60°从而得到∠BAC-∠CAM=∠MAN-∠CAM ,即∠BAM=∠CAN ,证明△BAM ≌△CAN ,即可得到BM=CN .(2)根据△ABC ,△AMN 为等腰三角形,得到AB :BC=1:1且∠ABC=∠AMN ,根据相似三角形的性质得到AB AC AM AN=,利用等腰三角形的性质得到∠BAC=∠MAN ,根据相似三角形的性质即可得到结论; (3)如图3,连接AB ,AN ,根据正方形的性质得到∠ABC=∠BAC=45°,∠MAN=45°,根据相似三角形的性质得出BM AB CN AC=,得到BM=2,CM=8,再根据勾股定理即可得到答案. 详解:(1)NC ∥AB ,理由如下:∵△ABC 与△MN 是等边三角形,∴AB=AC ,AM=AN ,∠BAC=∠MAN =60°,∴∠BAM=∠CAN ,在△ABM 与△ACN 中, AB AC BAM CAN AM AN =⎧⎪∠=∠⎨⎪=⎩, ∴△ABM ≌△ACN (SAS ),∴∠B=∠ACN=60°,∵∠ANC+∠ACN+∠CAN=∠ANC+60°+∠CAN=180°,∴∠ANC+∠MAN+∠BAM=∠ANC+60°+∠CAN=∠BAN+∠ANC=180°,∴CN ∥AB ;(2)∠ABC=∠ACN ,理由如下: ∵AB AM BC MN==1且∠ABC=∠AMN , ∴△ABC ~△AMN ∴AB AC AM AN=, ∵AB=BC , ∴∠BAC=12(180°﹣∠ABC ), ∵AM=MN∴∠MAN=12(180°﹣∠AMN ), ∵∠ABC=∠AMN ,∴∠BAC=∠MAN ,∴∠BAM=∠CAN ,∴△ABM ~△ACN ,∴∠ABC=∠ACN ;(3)如图3,连接AB ,AN , ∵四边形ADBC ,AMEF 为正方形,∴∠ABC=∠BAC=45°,∠MAN=45°,∴∠BAC ﹣∠MAC=∠MAN ﹣∠MAC即∠BAM=∠CAN ,∵AB AM BC AN == ∴AB AC AM AN=, ∴△ABM ~△ACN ∴BM AB CN AC =,∴CN AC BM AB ==cos45°=2,∴=, ∴BM=2,∴CM=BC ﹣BM=8,在Rt △AMC ,==,∴EF=AM=241.点睛:本题是四边形综合题目,考查了正方形的性质、等边三角形的性质、等腰三角形的性质、全等三角形的性质定理和判定定理、相似三角形的性质定理和判定定理等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.9.如图,AB 为⊙O 的直径,点E 在⊙O 上,过点E 的切线与AB 的延长线交于点D ,连接BE ,过点O 作BE 的平行线,交⊙O 于点F ,交切线于点C ,连接AC(1)求证:AC 是⊙O 的切线;(2)连接EF ,当∠D= °时,四边形FOBE 是菱形.【答案】(1)见解析;(2)30. 【解析】【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案.【详解】(1)证明:∵CD 与⊙O 相切于点E ,∴OE CD ⊥,∴90CEO ∠=︒,又∵OC BE ,∴COE OEB ∠=∠,∠OBE=∠COA∵OE=OB ,∴OEB OBE ∠=∠,∴COE COA ∠=∠,又∵OC=OC ,OA=OE ,∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒,又∵AB 为⊙O 的直径,∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形,∴OF=OB=BF=EF ,∴OE=OB=BE ,∴OBE ∆为等边三角形,∴60BOE ∠=︒,而OE CD ⊥,∴30D ∠=︒.故答案为30.【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.10.如图1,若分别以△ABC 的AC 、BC 两边为边向外侧作的四边形ACDE 和BCFG 为正方形,则称这两个正方形为外展双叶正方形.(1)发现:如图2,当∠C =90°时,求证:△ABC 与△DCF 的面积相等.(2)引申:如果∠C ≠90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;(3)运用:如图3,分别以△ABC 的三边为边向外侧作的四边形ACDE 、BCFG 和ABMN 为正方形,则称这三个正方形为外展三叶正方形.已知△ABC 中,AC =3,BC =4.当∠C =_____°时,图中阴影部分的面积和有最大值是________.【答案】(1)证明见解析;(2)成立,证明见解析;(3)18.【解析】试题分析:(1)因为AC=DC ,∠ACB=∠DCF=90°,BC=FC ,所以△ABC ≌△DFC ,从而△ABC 与△DFC 的面积相等;(2)延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q .得到四边形ACDE ,BCFG 均为正方形,AC=CD ,BC=CF ,∠ACP=∠DCQ .所以△APC ≌△DQC .于是AP=DQ.又因为S△ABC=12 BC•AP,S△DFC=12FC•DQ,所以S△ABC=S△DFC;(3)根据(2)得图中阴影部分的面积和是△ABC的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.所以S阴影部分面积和=3S△ABC=3×12×3×4=18.(1)证明:在△ABC与△DFC中,∵{AC DCACB DCFBC FC∠∠===,∴△ABC≌△DFC.∴△ABC与△DFC的面积相等;(2)解:成立.理由如下:如图,延长BC到点P,过点A作AP⊥BP于点P;过点D作DQ⊥FC于点Q.∴∠APC=∠DQC=90°.∵四边形ACDE,BCFG均为正方形,∴AC=CD,BC=CF,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,∴∠ACP=∠DCQ.∴{APC DQCACP DCQAC CD∠∠∠∠===,△APC≌△DQC(AAS),∴AP=DQ.又∵S△ABC=12BC•AP,S△DFC=12FC•DQ,∴S△ABC=S△DFC;(3)解:根据(2)得图中阴影部分的面积和是△ABC的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,∴当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.∴S阴影部分面积和=3S△ABC=3×12×3×4=18.考点:四边形综合题。
人教版-八年级数学下册-第18章-平行四边形培优练习(含答案)

人教版八年级数学下册第18章平行四边形培优练习(含答案)一、单选题(共有9道小题)1.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是().A.测量对角线是否相互平分B.测量两组对边是否分别相等C.测量一组对角是否都为直角D.测量其中三角形是否都为直角2.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()…A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形3.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AD=2,则AC的长是()《A.2 B.4 C..4.下列说法正确的是()A.有一组对角是直角的四边形一定是矩形B.有一组邻角是直角的四边形一定是矩形C.对角线互相平分的四边形是矩形,D.对角互补的平行四边形是矩形5.下列命题是假命题的是()A.四个角相等的四边形是矩形 B.对角线相等的平行四边形是矩形C.对角线垂直的四边形是菱形 D.对角线垂直的平行四边形是菱形6.在Rt△ABC中,∠ACB=90°,AC=BC,CD是斜边AB的中线,若AB=,则点D到BC的距离为()D.27.下列命题是真命题的有()①对顶角相等;%ODBA②两直线平行,内错角相等;③两个锐角对应相等的两个直角三角形全等; ④有三个角是直角的四边形是矩形;⑤平分弦的直径垂直于弦,并且平分弦所对的弧。
A .1个 B .2个 C .3个 D .4个8.如图,已知点P 是矩形ABCD 内一点(不含边界),设1=PADθ∠,2=PBA θ∠,3=PCB θ∠,4=PDC θ∠,若∠APB =80°,∠CPD =50°,则( )A .1423()()30+-+=θθθθ︒B .2413()()40+-+=θθθθ︒>C .1234()()70+-+=θθθθ︒D .1234()()180+++=θθθθ︒9.如图,四边形ABCD 是矩形,AB=6cm ,BC=8cm ,把矩形沿直线BD 折叠,点C 落在点E 处,BE 与AD 相交于点F ,连接AE.下列结论中结论正确的个数有 ( ) ①△FBD 是等腰三角形; ②四边形ABDE 是等腰梯形; ③图中有6对全等三角形; ④四边形BCDF 的周长为532; ⑤AE 的长为145cm.|A .2个B .3个个D .5个二、填空题(共有8道小题)10.如图,□ABCD 的对角线相交于点O ,请你添加一个条件 (只添一个即可),使□ABCD 是矩形.11.如图,在矩形ABCD 中,AB <BC ,AC,BD 相交于点O ,则图中等腰三角形的个数是__。
八年级数学下《四边形》培优练习卷

八年级数学下《四边形》培优练习卷一、选择题1.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线互相垂直的四边形D.对角线相等的四边形2.如图,在△ABC,∠ACB=90°中,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,求四边形A CEB的周长。
A.4 B.10+ 4 C. 10+2 D. 23.在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE= ( )A.30° B.22.5° C.15° D.以上都不对4.如图,将矩形ABCD沿AE折叠,若∠BAD'=30°,则∠AED' 等于 ( )A.30° B.45° C.60° D.75°第6题5.如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是 ( ) A.1.6 B.2.5 C.3 D.3.46.平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD五等分点,点B1,B2和D1,D2分别是BC和DA三等分点,若四边形A4B2C4D2面积为1.则平行四边形ABCD面积为 ( )A.2 B.35C.53D.157.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EB的长为()A.1 B.4C.4﹣2D.4﹣4第7题二、填空题8.在□ABCD中,一角的平分线把一条边分成3 cm和4 cm两部分,则□ABCD的周长为______.9.矩形的两条对角线的夹角为60°,一条对角线与较短边的和为15,则较长边的长为_______.10.已经△ABC中,∠C=90°,C=10,a:b=3:4 ,则a= b=11.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE、BF.当∠ACB为度时,四边形ABFE为矩形.第11题第12题第13题第14题12.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F.连接CE,则CE的长是_______.13.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是_______厘米.14.如图,△ABC中,∠A的平分线交BC于点D,过点D作DE⊥AC,DF⊥AB,垂足分别为E,F,下面四个结论:①∠AFE=∠AEF;②AD垂直平分EF;③CEBFSSCEDBFD=∆∆;④EF∥BC.其中正确的是_______.15.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,7=∆ABCS,DE=2,AB=4,则AC长为.三、解答题16.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.(1)证明:四边形EGFH是平行四边形;(2)在(1)的条件下,若EF⊥BC,且EF=BC,证明:平行四边形EGFH是正方形.17.已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.(1)求证:△ACE≌△ABD;(2)若AC=8,CD=1,求ED的长.18.如图,四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、CD分别交于点E、F.求证:∠BEN=∠NFC. (提示:连结AC并取中点)19.如图,在Rt⊿ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿边AB向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿边BC向点C以1.5cm/s的速度运动.(1)20s后,点P与点Q相距 cm.(2)在(1)的条件下,若P、Q两点同时在直线PQ上相向而行,多少秒后,两点相遇?(3)多少秒后,AP=CQ?20.△ABC中,∠ACB=90°,AC=BC,AB=2.现将一块三角板的直角顶点放在AB的中点D处,两直角边分别与直线..AC、直线..BC相交于点E、F.我们把DE⊥AC时的位置定为起始位置(如图1),将三角板绕点D顺时针方向旋转一个角度α (0°<α<90°).(1)在旋转过程中,当点E在线段AC上,点F在线段BC上时(如图2),①试判别△DEF的形状,并说明理由;②判断四边形ECFD的面积是否发生变化,并说明理由.(2)设直线..ED交直线..BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形?若存在,求出CG的长,若不存在,说明理由;D DEADEDA。
中考数学培优专题复习平行四边形练习题及详细答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.(1)用尺规将图1中的△ABC分割成两个互补三角形;(2)证明图2中的△ABC分割成两个互补三角形;(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为、、的三角形,并计算图3中六边形DEFGHI的面积.②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.【答案】(1)作图见解析(2)证明见解析(3)①62;②6【解析】试题分析:(1)作BC边上的中线AD即可.(2)根据互补三角形的定义证明即可.(3)①画出图形后,利用割补法求面积即可.②平移△CHG到AMF,连接EM,IM,则AM=CH=BI,只要证明S△EFM=3S△ABC即可.试题解析:(1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.(2)如图2中,延长FA到点H,使得AH=AF,连接EH.∵四边形ABDE,四边形ACGF是正方形,∴AB=AE,AF=AC,∠BAE=∠CAF=90°,∴∠EAF+∠BAC=180°,∴△AEF和△ABC是两个互补三角形.∵∠EAH+∠HAB=∠BAC+∠HAB=90°,∴∠EAH=∠BAC,∵AF=AC,∴AH=AB,在△AEH和△ABC中,∴△AEH≌△ABC,∴S△AEF=S△AEH=S△ABC.(3)①边长为、、的三角形如图4所示.∵S△ABC=3×4﹣2﹣1.5﹣3=5.5,∴S六边形=17+13+10+4×5.5=62.②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,∵AM∥CH,CH⊥BC,∴AM⊥BC,∴∠EAM=90°+90°﹣x=180°﹣x,∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x,∴∠EAM=∠DBI,∵AE=BD,∴△AEM≌△DBI,∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,∴△DBI和△ABC是互补三角形,∴S△AEM=S△AEF=S△AFM=2,∴S△EFM=3S△ABC=6.考点:1、作图﹣应用与设计,2、三角形面积2.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t 秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.【答案】(1)见解析;(2)能,t=10;(3)t=152或12.【解析】【分析】(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;(3)△DEF为直角三角形,分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】解:(1)证明:∵在Rt△ABC中,∠C=90°﹣∠A=30°,∴AB=12AC=12×60=30cm,∵CD=4t,AE=2t,又∵在Rt△CDF中,∠C=30°,∴DF=12CD=2t,∴DF=AE;(2)能,∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,∴当t=10时,AEFD是菱形;(3)若△DEF为直角三角形,有两种情况:①如图1,∠EDF=90°,DE∥BC,则AD=2AE,即60﹣4t=2×2t,解得:t=152,②如图2,∠DEF=90°,DE⊥AC,则AE=2AD,即2t2(604t)=-,解得:t=12,综上所述,当t=152或12时,△DEF为直角三角形.3.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)请问EG与CG存在怎样的数量关系,并证明你的结论;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.【详解】(1)CG=EG.理由如下:∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,同理.在Rt△DEF中,EG=12FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG.∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=12MC,∴EG=CG.(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.∵G为CM中点,∴EG=CG,EG⊥CG【点睛】本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.4.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).【答案】(1)作图参见解析;(2)作图参见解析.【解析】试题分析:(1)过点O向线段OM作垂线,此直线与格点的交点为N,连接MN即可;(2)根据勾股定理画出图形即可.试题解析:(1)过点O向线段OM作垂线,此直线与格点的交点为N,连接MN,如图1所示;(2)等腰直角三角形MON面积是5,因此正方形面积是20,如图2所示;于是根据勾股定理画出图3:考点:1.作图﹣应用与设计作图;2.勾股定理.5.(问题情境)在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)(变式探究)(1)当点P在CB延长线上时,其余条件不变(如图3),试探索PD、PE、CF之间的数量关系并说明理由;请运用上述解答中所积累的经验和方法完成下列两题:(结论运用)(2)如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD =16,CF=6,求PG+PH的值.(迁移拓展)(3)在直角坐标系中,直线l1:y=-43x+8与直线l2:y=﹣2x+8相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为2.求点P的坐标.【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】(﹣1,6),(1,10)【解析】【变式探究】连接AP,同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得;【结论运用】过点E作EQ⊥BC,垂足为Q,根据勾股定理和矩形的性质解答即可;【迁移拓展】分两种情况,利用结论,求得点P到x轴的距离,再利用待定系数法可求出P的坐标.【详解】变式探究:连接AP,如图3:∵PD⊥AB,PE⊥AC,CF⊥AB,且S△ABC=S△ACP﹣S△ABP,∴12AB•CF=12AC•PE﹣12AB•PD.∵AB=AC,∴CF=PD﹣PE;结论运用:过点E作EQ⊥BC,垂足为Q,如图④,∵四边形ABCD是长方形,∴AD=BC,∠C=∠ADC=90°.∵AD=16,CF=6,∴BF=BC﹣CF=AD﹣CF=5,由折叠可得:DF=BF,∠BEF=∠DEF.∴DF=5.∵∠C=90°,∴DC2222-=-8.DF CF106∵EQ⊥BC,∠C=∠ADC=90°,∴∠EQC=90°=∠C=∠ADC.∴四边形EQCD是长方形.∴EQ=DC=4.∵AD∥BC,∴∠DEF=∠EFB.∵∠BEF=∠DEF,∴∠BEF=∠EFB.∴BE=BF,由问题情境中的结论可得:PG+PH=EQ.∴PG+PH=8.∴PG+PH的值为8;迁移拓展:如图,由题意得:A(0,8),B(6,0),C(﹣4,0)∴AB226810,BC=10.∴AB=BC,(1)由结论得:P1D1+P1E1=OA=8∵P1D1=1=2,∴P1E1=6 即点P1的纵坐标为6又点P1在直线l2上,∴y=2x+8=6,∴x=﹣1,即点P1的坐标为(﹣1,6);(2)由结论得:P2E2﹣P2D2=OA=8∵P2D2=2,∴P2E2=10 即点P1的纵坐标为10又点P1在直线l2上,∴y=2x+8=10,∴x=1,即点P1的坐标为(1,10)【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点,利用面积法列出等式是解决问题的关键.6.菱形ABCD中、∠BAD=120°,点O为射线CA上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.(1)如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;(2)如图②,点O在CA的延长线上,且OA=13AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;(3)点O在线段AC上,若AB=6,BO=27,当CF=1时,请直接写出BE的长.【答案】(1)CA=CE+CF.(2)CF-CE=43AC.(3)BE的值为3或5或1.【解析】【分析】(1)如图①中,结论:CA=CE+CF.只要证明△ADF≌△ACE(SAS)即可解决问题;(2)结论:CF-CE=43AC.如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.只要证明△FOG≌△EOC(ASA)即可解决问题;(3)分四种情形画出图形分别求解即可解决问题.【详解】(1)如图①中,结论:CA=CE+CF.理由:∵四边形ABCD是菱形,∠BAD=120°∴AB=AD=DC=BC,∠BAC=∠DAC=60°∴△ABC,△ACD都是等边三角形,∵∠DAC=∠EAF=60°,∴∠DAF=∠CAE,∵CA=AD,∠D=∠ACE=60°,∴△ADF≌△ACE(SAS),∴DF=CE,∴CE+CF=CF+DF=CD=AC,∴CA=CE+CF.(2)结论:CF-CE=43 AC.理由:如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.∵∠GOC=∠FOE=60°,∴∠FOG=∠EOC,∵OG=OC,∠OGF=∠ACE=120°,∴△FOG≌△EOC(ASA),∴CE=FG,∵OC=OG,CA=CD,∴OA=DG,∴CF-EC=CF-FG=CG=CD+DG=AC+13AC=43AC,(3)作BH⊥AC于H.∵AB=6,AH=CH=3,∴BH=33,如图③-1中,当点O在线段AH上,点F在线段CD上,点E在线段BC上时.∵7,∴22OB BH=1,∴OC=3+1=4,由(1)可知:CO=CE+CF,∵OC=4,CF=1,∴CE=3,∴BE=6-3=3.如图③-2中,当点O在线段AH上,点F在线段DC的延长线上,点E在线段BC上时.由(2)可知:CE-CF=OC,∴CE=4+1=5,∴BE=1.如图③-3中,当点O在线段CH上,点F在线段CD上,点E在线段BC上时.同法可证:OC=CE+CF,∵OC=CH-OH=3-1=2,CF=1,∴CE=1,∴BE=6-1=5.如图③-4中,当点O在线段CH上,点F在线段DC的延长线上,点E在线段BC上时.同法可知:CE-CF=OC,∴CE=2+1=3,∴BE=3,综上所述,满足条件的BE的值为3或5或1.【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,等边三角形的性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.7.如图,在正方形ABCD中,对角线AC与BD交于点O,在Rt△PFE中,∠EPF=90°,点E、F分别在边AD、AB上.(1)如图1,若点P与点O重合:①求证:AF=DE;②若正方形的边长为23,当∠DOE=15°时,求线段EF的长;(2)如图2,若Rt△PFE的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP 时,证明:PE=2PF.【答案】(1)①证明见解析,②2;(2)证明见解析.【解析】【分析】(1)①根据正方形的性质和旋转的性质即可证得:△AOF≌△DOE根据全等三角形的性质证明;②作OG⊥AB于G,根据余弦的概念求出OF的长,根据勾股定理求值即可;(2)首先过点P作HP⊥BD交AB于点H,根据相似三角形的判定和性质求出PE与PF的数量关系.【详解】(1)①证明:∵四边形ABCD是正方形,∴OA=OD,∠OAF=∠ODE=45°,∠AOD=90°,∴∠AOE+∠DOE=90°,∵∠EPF=90°,∴∠AOF+∠AOE=90°,∴∠DOE=∠AOF,在△AOF和△DOE中,OAF ODE OA ODAOF DOE ===∠∠⎧⎪⎨⎪∠∠⎩, ∴△AOF ≌△DOE ,∴AF=DE ;②解:过点O 作OG ⊥AB 于G ,∵正方形的边长为23, ∴OG=12BC=3, ∵∠DOE=15°,△AOF ≌△DOE ,∴∠AOF=15°,∴∠FOG=45°-15°=30°,∴OF=OG cos DOG∠=2, ∴EF=22=22OF OE +;(2)证明:如图2,过点P 作HP ⊥BD 交AB 于点H ,则△HPB 为等腰直角三角形,∠HPD=90°,∴HP=BP ,∵BD=3BP ,∴PD=2BP ,∴PD=2HP ,又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,∴∠HPF=∠DPE ,又∵∠BHP=∠EDP=45°,∴△PHF ∽△PDE , ∴12PF PH PE PD ==, ∴PE=2PF .【点睛】 此题属于四边形的综合题.考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理.注意准确作出辅助线是解此题的关键.8.如图,AB 为⊙O 的直径,点E 在⊙O 上,过点E 的切线与AB 的延长线交于点D ,连接BE ,过点O 作BE 的平行线,交⊙O 于点F ,交切线于点C ,连接AC(1)求证:AC 是⊙O 的切线;(2)连接EF ,当∠D= °时,四边形FOBE 是菱形.【答案】(1)见解析;(2)30.【解析】【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案.【详解】(1)证明:∵CD 与⊙O 相切于点E ,∴OE CD ⊥,∴90CEO ∠=︒,又∵OC BE ,∴COE OEB ∠=∠,∠OBE=∠COA∵OE=OB ,∴OEB OBE ∠=∠,∴COE COA ∠=∠,又∵OC=OC ,OA=OE ,∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒,又∵AB 为⊙O 的直径,∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形,∴OF=OB=BF=EF ,∴OE=OB=BE ,∴OBE ∆为等边三角形,∴60BOE ∠=︒,而OE CD ⊥,∴30D ∠=︒.故答案为30.【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.9.如图1,矩形ABCD 中,AB=8,AD=6;点E 是对角线BD 上一动点,连接CE ,作EF ⊥CE 交AB 边于点F ,以CE 和EF 为邻边作矩形CEFG ,作其对角线相交于点H .(1)①如图2,当点F 与点B 重合时,CE= ,CG= ;②如图3,当点E 是BD 中点时,CE= ,CG= ;(2)在图1,连接BG ,当矩形CEFG 随着点E 的运动而变化时,猜想△EBG 的形状?并加以证明; (3)在图1,CG CE的值是否会发生改变?若不变,求出它的值;若改变,说明理由; (4)在图1,设DE 的长为x ,矩形CEFG 的面积为S ,试求S 关于x 的函数关系式,并直接写出x 的取值范围.【答案】(1)245,185,5,154 ;(2)△EBG 是直角三角形,理由详见解析;(3)34 ;(4)S=34x 2﹣485x+48(0≤x≤325). 【解析】【分析】(1)①利用面积法求出CE ,再利用勾股定理求出EF 即可;②利用直角三角形斜边中线定理求出CE ,再利用相似三角形的性质求出EF 即可;(2)根据直角三角形的判定方法:如果一个三角形一边上的中线等于这条边的一半,则这个三角形是直角三角形即可判断;(3)只要证明△DCE ∽△BCG ,即可解决问题;(4)利用相似多边形的性质构建函数关系式即可;【详解】(1)①如图2中,在Rt △BAD 中,BD=22AD AB +=10, ∵S △BCD =12•CD•BC=12•BD•CE , ∴CE=245.CG=BE=2224186()=55-. ②如图3中,过点E 作MN ⊥AM 交AB 于N ,交CD 于M .∵DE=BE ,∴CE=12BD=5, ∵△CME ∽△ENF ,∴CM EN CE EF=, ∴CG=EF=154, (2)结论:△EBG 是直角三角形.理由:如图1中,连接BH .在Rt △BCF 中,∵FH=CH ,∴BH=FH=CH ,∵四边形EFGC 是矩形,∴EH=HG=HF=HC ,∴BH=EH=HG ,∴△EBG 是直角三角形.(3)F 如图1中,∵HE=HC=HG=HB=HF ,∴C 、E 、F 、B 、G 五点共圆,∵EF=CG ,∴∠CBG=∠EBF ,∵CD ∥AB ,∴∠EBF=∠CDE ,∴∠CBG=∠CDE ,∵∠DCB=∠ECG=90°,∴∠DCE=∠BCG ,∴△DCE ∽△BCG , ∴6384CG BC CE DC ===. (4)由(3)可知: 34CG CD CE CB ==, ∴矩形CEFG ∽矩形ABCD , ∴2264CEFG ABCD S CE CE S CD ==矩形矩形(), ∵CE 2=(325-x )2+245)2,S 矩形ABCD =48, ∴S 矩形CEFG =34[(325-x )2+(245)2]. ∴矩形CEFG 的面积S=34x 2-485x+48(0≤x≤325). 【点睛】 本题考查相似三角形综合题、矩形的性质、相似三角形的判定和性质、勾股定理、直角三角形的判定和性质、相似多边形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形或直角三角形解决问题,属于中考压轴题.10.在正方形ABCD 中,动点E ,F 分别从D ,C 两点同时出发,以相同的速度在直线DC ,CB 上移动.(1)如图①,当点E 自D 向C ,点F 自C 向B 移动时,连接AE 和DF 交于点P ,请你写出AE 与DF 的位置关系,并说明理由;(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不须证明)(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;(4)如图④,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F 的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP 的最小值.【答案】(1)AE=DF,AE⊥DF;(2)是;(3)成立,理由见解析;(4)CP=QC﹣QP=.【解析】试题分析:(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;(2)是.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,所以AE⊥DF;(3)成立.由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF;(4)由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD 的中点为Q,连接QC交弧于点P,此时CP的长度最小,再由勾股定理可得QC的长,再求CP即可.试题解析:(1)AE=DF,AE⊥DF.理由:∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.在△ADE和△DCF中,,∴△ADE≌△DCF(SAS).∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.∴AE⊥DF;(2)是;(3)成立.理由:由(1)同理可证AE=DF,∠DAE=∠CDF延长FD交AE于点G,则∠CDF+∠ADG=90°,∴∠ADG+∠DAE=90°.∴AE⊥DF;(4)如图:由于点P在运动中保持∠APD=90°,∴点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,在Rt△QDC中,QC=,∴CP=QC﹣QP=.考点:四边形的综合知识.。
八下数学《平行四边形》培优试卷-(A4含答案)

《平行四边形》竞赛试题总分120分,时间120分钟一、填空题(共9小题,每小题3分,满分27分)1.在矩形ABCD中,已知两邻边AD=12,AB=5,P是AD边上异于A和D的任意一点,且PE⊥BD,PF⊥AC,E、F分别是垂足,那么PE+PF=_________.2.如图,BD是平行四边形ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需要增加的一个条件是_________.(填一个即可)3.如图,已知矩形ABCD,对角线AC、BD相交于O,AE⊥BD于E,若AB=6,AD=8,则AE=____.4.如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.(1)四边形ADEF是_________;(2)当△ABC满足条件_________时,四边形ADEF为菱形;(3)当△ABC满足条件_________时,四边形ADEF不存在.1题2题3题4题5.已知一个三角形的一边长为2,这边上的中线为1,另两边之和为1+,则这两边之积为________.6.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,图中有_________对四边形面积相等;它们是_________.7.如图,菱形ABCD的对角线AC、BD相交于O,△AOB的周长为3+,∠ABC=60°,则菱形ABCD的面积为_________.8.如图,矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于E,若∠EAO=15°,则∠BOE 的度数为_________度.9.如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为_________.6题7题8题9题二、选择题(共9小题,每小题3分,满分27分)10.如图,▱ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD于E,若DE=2AB,则∠AED的大小是()A.60°B.65°C.70°D.75°10题11题12题13题11.如图,正△AEF的边长与菱形ABCD的边长相等,点E、F分别在BC、CD上,则∠B的度数是()A.70°B.75°C.80°D.95°12.如图,正方形ABCD外有一点P,P在BC外侧,并在平行线AB与CD之间,若PA=,PB=,PC=,则PD=()A.2B.C.3D.13.如图,平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54°,则∠B=()A.54°B.60°C.66°D.72°14.四边形ABCD的四边分别为a、b、c、d,其中a、c为对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是()A.两组角分别相等的四边形B.平行四边形C.对角线互相垂直的四边形D.对角线相等的四边形15.周长为68的长方形ABCD被分成7个全等的长方形,如图所示,则长方形ABCD的面积为()A.98 B.196 C.280 D.28415题16题16.如图,菱形花坛ABCD的边长为6m,∠A=120°,其中由两个正六边形组成的图形部分种花,则种花部分图形的周长为()A.12m B.20m C.22m D.24m17.在凸四边形ABCD中,AB∥CD,且AB+BC=CD+DA,则()A.A D>BC B.A D<BCC.A D=BC D.A D与BC的大小关系不能确定18.已知四边形ABCD,从下列条件中:(1)AB∥CD;(2)BC∥AD;(3)AB=CD;(4)BC=AD;(5)∠A=∠C;(6)∠B=∠D.任取其中两个,可以得出“四边形ABCD是平行四边形"这一结论的情况有()A.4种B.9种C.13种D.15种三、解答题(共10小题,满分66分)19.如图,在△ADC中,∠BAC=90°,AD⊥BC,BE、AF分别是∠ABC、∠DAC的平分线,BE和AD 交于G,求证:GF∥AC.20.设P为等腰直角三角形ACB斜边AB上任意一点,PE垂直AC于点E,PF垂直BC于点F,PG垂直EF于点G,延长GP并在其延长线上取一点D,使得PD=PC,试证:BC⊥BD,且BC=BD.21.如图,在等腰三角形ABC中,延长AB到点D,延长CA到点E,且AE=BD,连接DE.如果AD=BC=CE=DE,求∠BAC的度数.22.如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.(1)求证:△ACD≌△CBF;(2)点D在线段BC上何处时,四边形CDEF是平行四边形且∠DEF=30°.23.如图,在Rt△ABC中,AB=AC,∠A=90°,点D为BC上任一点,DF⊥AB于F,DE⊥AC于E,M 为BC的中点,试判断△MEF是什么形状的三角形,并证明你的结论.24.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.25.如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.26.阅读下面短文:如图①,△ABC是直角三角形,∠C=90°,现将△ABC补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个矩形ACBD和矩形AEFB(如图②)解答问题:(1)设图②中矩形ACBD和矩形AEFB的面积分别为S1、S2,则S1_________S2(填“>”“=”或“<”).(2)如图③,△ABC是钝角三角形,按短文中的要求把它补成矩形,那么符合要求的矩形可以画_________个,利用图③把它画出来.(3)如图④,△ABC是锐角三角形且三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出_________个,利用图④把它画出来.(4)在(3)中所画出的矩形中,哪一个的周长最小?为什么?27.如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,N在AC上,且AN=MC,AM与BN相交于P,求证:∠BPM=45°.28.如图,在锐角△ABC中,AD、CE分别是BC、AB边上的高,AD、CE相交于F,BF的中点为P,AC 的中点为Q,连接PQ、DE.(1)求证:直线PQ是线段DE的垂直平分线;(2)如果△ABC是钝角三角形,∠BAC>90°,那么上述结论是否成立?请按钝角三角形改写原题,画出相应的图形,并给予必要的说明.参考答案与试题解析一、填空题(共9小题,每小题4分,满分36分)1.在矩形ABCD中,已知两邻边AD=12,AB=5,P是AD边上异于A和D的任意一点,且PE⊥BD,PF⊥AC,E、F分别是垂足,那么PE+PF=.考点:矩形的性质;等腰三角形的性质。
数学平行四边形的专项培优练习题含详细答案

F 点移动到 F'的距离是 10 t,
在 Rt△ F'NF 中, NF = 1 , NF 3
∴ FN=t,F'N=3t, ∵ MH'=FN=t, EM=NG'=15﹣F'N=15﹣3t,
在 Rt△ DMH'中,
MH 4 , EM 3
∴ t 4, 15 3t 3
∴ t=4,
∴ EM=3,MH'=4,
CD DM
设 AM=x,则 x a , a bx
整理得:x2﹣bx+a2=0, ∵ b>2a,a>0,b>0, ∴ △ =b2﹣4a2>0, ∴ 方程有两个不相等的实数根,且两根均大于零,符合题意, ∴ 当 b>2a 时,存在∠ BMC=90°, (3)不成立. 理由:若∠ BMC=90°, 由(2)可知 x2﹣bx+a2=0, ∵ b<2a,a>0,b>0, ∴ △ =b2﹣4a2<0, ∴ 方程没有实数根, ∴ 当 b<2a 时,不存在∠ BMC=90°,即(2)中的结论不成立. 考点:1、相似三角形的判定与性质;2、根的判别式;3、矩形的性质
(1)试猜想 AE 与 GC 有怎样的关系(直接写出结论即可);
(2)将正方形 DEFG 绕点 D 按顺时针方向旋转,使点 E 落在 BC 边上,如图 2,连接 AE 和
CG.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
(3)在(2)中,若 E 是 BC 的中点,且 BC=2,则 C,F 两点间的距离为
(2)将正方形 EFGH 沿射线 FB 的方向以每秒 10 个单位的速度匀速平移,得到正方形
E1F1G1H1,在平移过程中边 F1G1 始终与 y 轴垂直,设平移的时间为 t 秒(t>0). ①当点 F1 移动到点 B 时,求 t 的值; ②当 G1,H1 两点中有一点移动到直线 DE 上时,请直接写出此时正方形 E1F1G1H1 与△ APE 重叠部分的面积.
特殊平行四边形综合题(培优)

特殊平行四边形综合题(培优)一.选择题(共9小题)1.如图.任意四边形ABCD中,E,F,G,H分别是各边上的点,对于四边形E,F,G,H的形状,小聪进行了探索,下列结论错误的是()A.E,F,G,H是各边中点,且AC=BD时,四边形EFGH是菱形B.E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH是矩形C.E,F,G,H不是各边中点,四边形EFGH可以是平行四边形D.E,F,G,H不是各边中点,四边形EFGH不可能是菱形2.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点.若AC=8,BD=6,则四边形EFGH的面积为()A.14B.12C.24D.483.依次连接四边形ABCD的四边中点得到的图形是正方形,则四边形ABCD的对角线需满足()A.AC=BD B.AC⊥BDC.AC=BD且AC⊥BD D.AC⊥BD且AC与BD互相平分4.顺次连接正方形各边中点所成的四边形的面积与原正方形的面积之比为()A.1:B.1:C.1:3D.1:25.如图,正方形ABCD中,AE=BF,下列说法中,正确的有()①AF=DE;②AF⊥DE;③AO=OF;④S△AOD=S四边形BEOF.A.1个B.2个C.3个D.4个6.顺次连接凸四边形各边中点所得到的四边形是正方形时,原四边形对角线需满足的条件是()A.对角线相等且垂直B.对角线相等C.对角线垂直D.一条对角线平分另一条对角线7.如图,矩形ABCD中,对角线AC,BD交于点O,如果∠ADB=35°,那么∠AOB的度数为()A.35°B.45°C.70°D.110°8.下列命题中,正确的是()A.一组对边平行且另一组对边相等的四边形是平行四边形B.两组邻边分别相等的四边形是平行四边形C.两组对边分别平行的四边形是平行四边形D.对角线互相垂直的四边形是平行四边形9.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=6,则OC=()A.12B.C.6D.3二.填空题(共21小题)10.如图,点A、B、C为平面内不在同一直线上的三点.点D为平面内一个动点.线段AB,BC,CD,DA的中点分别为M、N、P、Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④存在无数个中点四边形MNPQ是正方形.所有正确结论的序号是.11.如图,点A,B,C为平面内不在同一直线上的三点,点D为平面内一个动点,线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④中点四边形MNPQ不可能是正方形;所有结论正确的序号是.12.如图,点A,B,C为平面内不在同一直线上的三点.点D为平面内一个动点.线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④存在两个中点四边形MNPQ是正方形.所有正确结论的序号是.13.如图,四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形EFGH为矩形,应添加的条件是.14.小明作生成“中点四边形”的数学游戏,具体步骤如下:(1)任画两条线段AB、CD,且AB与CD交于点O,O与A、B、C、D任意一点均不重合.连接AC、BC、BD、AD,得到四边形ACBD;(2)分别作出AC、CB、BD、DA的中点A1,B1,C1,D1,这样就得到一个“中点四边形”.①若AB⊥CD,则四边形A1B1C1D1的形状一定是,这样作图的依据是.②请你再给出一个AB与CD之间的关系,并写出在该条件下得到的“中点四边形”A1B1C1D1的形状.15.如图,矩形ABCD中,AD=a,AB=b,依次连接它的各边中点得到第一个四边形E1F1G1H1,再依次连接四边形E1F1G1H1的各边中点得到第二个四边形E2F2G2H2,按此方法继续下去,得到的第n个四边形E n F n G n H n的面积等于.16.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第4个图形中直角三角形的个数有个;第2014个图形中直角三角形的个数有个.17.已知:四边形ABCD的面积为1.如图1,取四边形ABCD各边中点,则图中阴影部分的面积为;如图2,取四边形ABCD各边三等分点,则图中阴影部分的面积为;…;取四边形ABCD各边的n(n为大于1的整数)等分点,则图中阴影部分的面积为.18.梯形的高为4cm,中位线长为5cm,则梯形的面积为cm2.19.如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边,其中正确结论的序号是.形DEOF20.若梯形的面积为12cm2,高为3cm,则此梯形的中位线长为cm.21.已知一个梯形的面积为22cm2,高为2cm,则该梯形的中位线的长等于cm.22.如图,正方形ABCD中,O是AC的中点,E是AD上一点,连接BE,交AC于点H,作CF⊥BE于点F,AG⊥BE于点G,连接OF,则下列结论中,①AG=BF;②OF平分∠CFG;⑤CF﹣BF=EF;④GF=OF,正确的有.(填序号)23.如图,点E是正方形ABCD的对角线BD上一点.EF⊥BC,EG⊥CD,垂足分别是F,G,GF=5,则AE=.24.如图,平行四边形ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,AC=6,BD=10,则OE的长为.25.如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=2,BC=5,则DE =.26.如图,菱形ABCD的边长为2,∠BAD=60°,点E是AD边上一动点(不与A,D重合),点F是CD边上一动点,DE+DF=2,则∠EBF=°,△BEF面积的最小值为.27.在平面直角坐标系xOy中,菱形ABCD的四个顶点都在坐标轴上.若A(﹣4,0),B (0,﹣3),则菱形ABCD的面积是.28.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,使得点D落在点D'处,则FC=.29.如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+.其中正确结论的序号是.30.在数学家吴文俊主编的《“九章算术”与刘徽》一书中,小宇同学看到一道有趣的数学问题:古代数学家刘徽使用“出入相补”原理,即割补法,把筝形转化为与之面积相等的矩形,从而得到“筝形的面积等于其对角线乘积之半”.(说明:一条对角线垂直平分另一条对角线的四边形是筝形)请根据如图完成这个数学问题的证明过程.证明:证明:S筝形ABCD=S△AOB+S△AOD+S△COB+S△COD.易知,S△AOD=S△BEA,S△COD=S△BFC,由等量代换可得:S筝形ABCD=S△AOB++S△COB+=S矩形EFCA=AE•AC=•.三.解答题(共30小题)31.在正方形ABCD中,P是边BC上一动点(不与点B、C重合),E是AP的中点,过点E作MN⊥AP,分别交AB、CD于点M,N.(1)判定线段MN与AP的数量关系,并证明;(2)连接BD交MN于点F.①根据题意补全图形;②用等式表示线段ME,EF,FN之间的数量关系,直接写出结论.32.如图,已知在四边形中,AC⊥BD交于点O,E、F、G、H分别是四边上的中点,求证:四边形EFGH是矩形.33.我们规定:一组邻边相等且对角互补的四边形叫做“完美四边形”.(1)在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美”四边形的是(请填序号);(2)在“完美”四边形ABCD中,AB=AD,∠B+∠D=180°,连接AC.①如图1,求证:AC平分∠BCD;小明通过观察、实验,提出以下两种想法,证明AC平分∠BCD:想法一:通过∠B+∠D=180°,可延长CB到E,使BE=CD,通过证明△AEB≌△ACD,从而可证AC平分∠BCD;想法二:通过AB=AD,可将△ACD绕点A顺时针旋转,使AD与AB重合,得到△AEB,可证C,B,E三点在一条直线上,从而可证AC平分∠BCD.请你参考上面的想法,帮助小明证明AC平分∠BCD;②如图2,当∠BAD=90°,用等式表示线段AC,BC,CD之间的数量关系,并证明.34.如图,在等边△ABC中,作∠ACD=∠ABD=45°,边CD、BD交于点D,连接AD.(1)请直接写出∠CDB的度数;(2)求∠ADC的度数;(3)用等式表示线段AD、BD、CD三者之间的数量关系,并证明.35.如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是.36.在正方形ABCD中,点E是边BC上的中点,在边CD上取一点F,使得AE平分∠BAF.(1)依题意补充图形;(2)小玲画图结束后,通过观察、测量,提出猜想:线段AF等于线段BC与线段CF 的和.小玲把这个猜想与同学们进行交流.通过讨论,形成了证明该猜想的几种想法:想法1:考虑到AE平分∠BAF,且∠B=90°.若过点E作EM⊥AF,则易证AM=AB =BC.这样,只需证明FM=FC即可.因∠EMF=∠C=90°,证FM=FC即证EF平分∠MEC,所以连接EF.想法2:考虑到E是BC中点,若延长AE,交DC的延长线于点G,则易证CG=AB,则CF+BC=CF+CG=FG.要证AF=BC+CF,只需证F A=FG即可.想法3:小米在课外小组学习了梯形中位线的相关知识,考虑到正方形ABCD所以有BC =AB,因此BC+CF=AB+CF,是梯形上、下底之和,结合“E是BC中点”,易联想到梯形中位线的性质,从而解决问题.…请你参考上面的想法,帮助小玲证明AF=BC+CF.(一种方法即可)37.已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).(1)四边形EFGH的形状是,证明你的结论;(2)当四边形ABCD的对角线满足条件时,四边形EFGH是矩形;(3)你学过的哪种特殊四边形的中点四边形是矩形?.38.(1)如图1,正方形ABCD中,E、F分别是BC、CD边上的点,且满足BE=CF,连接AE、BF交于点H..请直接写出线段AE与BF的数量关系和位置关系;(2)如图2,正方形ABCD中,E、F分别是BC、CD边上的点,连接BF,过点E作EG⊥BF于点H,交AD于点G,试判断线段BF与GE的数量关系,并证明你的结论;(3)如图3,在(2)的条件下,连接GF、HD.求证:①FG+BE≥BF;②∠HGF=∠HDF.39.已知:如图,梯形ABCD中,AD∥BC,AD+BC=10,M是AB的中点,MD⊥DC,D 是垂足,sin∠C=,求梯形ABCD的面积.40.如图,在正方形ABCD中,点E、F分别在BC、CD上,BE=CF,连接AE、BF相交于点G.现给出了四个结论:①AE=BF;②∠BAE=∠CBF;③BF⊥AE;④AG=FG.请在这些结论中,选择一个你认为正确的结论,并加以证明.结论:.41.如图,在梯形ABCD中,AD∥BC,∠B=∠ACD.(1)请再写出图中另外一对相等的角;(2)若AC=6,BC=9,试求梯形ABCD的中位线的长度.42.已知:如图,梯形ABCD中,AB∥CD,中位线EF长为20,AC与EF交于点G,GF ﹣GE=5.求AB、CD的长.43.已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.(1)如果点E、F分别为AB、DC的中点,如图.求证:EF∥BC,且EF=;(2)如果,如图,判断EF和BC是否平行,并用a、b、m、n的代数式表示EF.请证明你的结论.44.如图,在正方形ABCD中,点E在线段CB的延长线上,连接AE,并将线段AE绕点E 顺时针旋转90°,得到线段FE,连接AF,BD,CF,线段AF与线段BD相交于点M.(1)请写出∠ECF的度数,并给出证明;(2)求证:点M是线段AF的中点;(3)直接写出线段CF,BM和AD的数量关系.45.四边形ABCD是正方形,将线段CD绕点C逆时针旋转2α(0°<α<45°),得到线段CE,CE=CD,连接DE,过点B作BF⊥DE交DE的延长线于点F,连接BE.(1)依题意补全图1;(2)直接写出∠FBE的度数;(3)连接AF,用等式表示线段AF与DE的数量关系,并证明.46.在正方形ABCD中,P是射线CB上的一个动点,过点C作CE⊥AP于点E,射线CE 交直线AB于点F,连接BE.(1)如图1,当点P在线段CB上时(不与端点B,C重合).①求证:∠BCF=∠BAP;②求证:EA=EC+EB;(2)如图2,当点P在线段CB的延长线上时(BP<BA),依题意补全图2并用等式表示线段EA,EC,EB之间的数量关系.47.如图,在正方形ABCD中,点E是直线AC上任意一点(不与点A,C重合),过点E 作EF⊥BE交直线CD于点F,过点F作FG⊥AC交直线AC于点G.(1)如图1,当点E在线段AC上时,猜想EG与AB的数量关系;(2)如图2,当点E在线段AC的延长线上时,补全图形,并判断(1)中EG与AB的数量关系是否仍然成立.如果成立,请证明;如果不成立,请说明理由.48.已知正方形ABCD,点E是直线BC上一点(不与B,C重合),∠AEF=90°,EF交正方形外角的平分线CF所在的直线于点F.(1)如图1,当点E在线段BC上时,①请补全图形,并直接写出AE,EF满足的数量关系;②用等式表示CD,CE,CF满足的数量关系,并证明.(2)当点E在直线BC上,用等式表示线段CD,CE,CF之间的数量关系(直接写出即可).49.如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB',FD′相交于点O.简单应用:(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是.(2)请你结合图1写出一条完美筝形的性质.(3)当图3中的∠BCD=120°时,∠AEB′=.(4)当图2中的四边形AECF为菱形时,对应图③中的“完美筝形”有(写出筝形的名称:例筝形ABCD).50.在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明:CE=CF;(2)若∠ABC=90°,G是EF的中点(如图2),求出∠BDG的度数;(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.51.在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作射线EF.(1)若∠DAB=60°,EF∥AB交BC于点H,请在图1中补全图形,并判断四边形ABHE 的形状;(2)如图2,若∠DAB=90°,EF与AB相交,在EF上取一点G,使得∠EGB=∠EAB,连接AG,请在图2中补全图形,猜想线段EG,AG,BG之间的数量关系,并证明你的结论;(3)如图3,若∠DAB=α(0°<α<90°),EF与AB相交,在EF上取一点G,使得∠EGB=∠EAB,连接AG.请在图3中补全图形(要求:尺规作图,保留作图痕迹),直接写出线段EG,AG,BG之间的数量关系(用含α的式子表示).52.如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形.根据学习平行四边形性质的经验,小文对筝形的性质进行了探究.(1)小文根据筝形的定义得到筝形边的性质是;(2)小文通过观察、实验、猜想、证明得到筝形角的性质是“筝形有一组对角相等”.请你帮他将证明过程补充完整.已知:如图,在筝形ABCD中,AB=AD,CB=CD.求证:.证明:(3)小文连接筝形的两条对角线,探究得到筝形对角线的性质是.(写出一条即可)53.如果一个四边形ABCD满足AB=AD且BC=CD,则称四边形ABCD为筝形.(1)如图1,连接筝形ABCD的对角线AC、BD交于点H,求证:AC⊥BD.(2)求证:筝形ABCD的面积S=AC•BD.(3)如图2,在筝形ABCD中,AB=AD=5,BC=CD,BD=8,过点B作BF⊥CD于点,交AC于点E,过点F作FM⊥AB于点M,若四边形ABED是菱形,求FM的长.54.已知,在菱形ABCD中,∠ADC=60°,点F为CD上任意一点(不与C、D重合),过点F作CD的垂线,交BD于点E,连接AE.(1)①依题意补全图1;②线段EF、CF、AE之间的等量关系是.(2)在图1中将△DEF绕点D逆时针旋转,当点F、E、C在一条直线上(如图2).线段EF、CE、AE之间的等量关系是.写出判断线段EF、CE、AE之间的等量关系的思路(可以不写出证明过程)55.在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠P AB=α.(1)依题意补全图1;(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.56.在菱形ABCD中,∠ABC=60°,点P在对角线BD上,点Q在直线AD上,且∠CPQ =120°.(1)如图1,若点P为菱形ABCD的对角线的交点.①依题意补全图1;②猜想PC与PQ的数量关系并加以证明;(2)如图2,若∠CPD=80°,连接CQ,写出求∠PQD度数的思路.57.在菱形ABCD中,∠ADC=120°,点E是对角线AC上一点,连接DE,∠DEC=50°,将线段BC绕点B逆时针旋转50°并延长得到射线BF,交ED的延长线于点G.(1)依题意补全图形;(2)求证:EG=BC;(3)用等式表示线段AE,EG,BG之间的数量关系:.58.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B 重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC =AM;(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.59.请阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,点A、B、E在同一条直线上,P是线段DF的中点,连接PG、PC.若∠ABC=∠BEF=60°,探究PG与PC的位置关系及数量关系.小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题:(1)直接写出上面问题中线段PG与PC的位置关系及的值;(2)如图2,在正方形ABCD和正方形BEFG中,点A、B、E在同一条直线上,P是线段DF的中点,连接PG、PC,探究PG与PC的位置关系及数量关系;(3)将图2中的正方形BEFG绕点B顺时针旋转,原问题中的其他条件不变(如图3),你在(2)中得到的两个结论是否发生变化?写出你的猜想并加以证明.60.在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.(1)如图1,求证:ME=MF;(2)如图2,点G是线段BC上一点,连接GE、GF、GM,若△EGF是等腰直角三角形,∠EGF=90°,求AB的长;(3)如图3,点G是线段BC延长线上一点,连接GE、GF、GM,若△EGF是等边三角形,则AB=.。
四边形经典培优提高题

四边形一.选择题(共16小题)★★★1.如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于()A.7 B.8 C.12 D.14★★★2.如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB、OC,点E在线段BC上(点E不与点B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为()A.6 B.1.5 C .D .★★★3.如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是()A.12cm2B.24cm2C.48cm2D.60cm2★★★4.如图,线段AB 的长为,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH 的对角线交点为O,连接OB,则线段BO的最小值为()A .B.15 C .D.30★★★5.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是()A.1或9 B.3或5 C.4或6 D.3或6★★★6.如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为()A.2B .C.2D.31★★★7.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是()A.4.8 B.5 C.6 D.7.2★★★8.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为()A.(3,1)B.(3,)C.(3,)D.(3,2)9.如图,在▱ABCD中,对角线AC与BD交于点O,若增加一个条件,使▱ABCD成为菱形,下列给出的条件不正确的是()A.AB=AD B.AC⊥BD C.AC=BD D.∠BAC=∠DAC★★★10.已知菱形OABC在平面直角坐标系的位置如图所示,顶点A (5,0),OB=4,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为()A.(0,0)B.(1,)C.(,)D.(,)★★★11.如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为()A.5 B.7 C.8 D .二.填空题(共3小题)★★★12.如图,AC是四边形ABCD的对角线,∠B=90°,∠ADC=∠ACB+45°,BC=AB +,2若AC=CD,则边AD 的长为.★★★13.如图,正方形ABCD的长为8cm ,E 、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH,则四边形EFGH面积的最小值是cm2.★★★14.已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是.15.如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是.★★★16.如图所示,在平面直角坐标系中,矩形ABCD 定点A、B在y轴、x轴上,当B在x轴上运动时,A随之在y轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为.17.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于度.★★★18.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为.★★★19.如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF=AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有条.★★★20.如图,在正方形ABCD中,AB=6,点E在边CD上,DE=DC,连接AE,将△ADE3沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG 的周长是.★★★21.如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于cm.★★★22.如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于.23.有一面积为5的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为.12.正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE=.则四边形ABFE′的面积是.24.如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是.★★★25.如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A 恰好落在直线l上,则DF的长为.26.如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(4,3),∠CAO的平分线与y轴相交于点D,则点D的坐标为.427.如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=.28.如图,矩形ABCD中,对角线AC=2,E为BC边上一点,BC=3BE,将矩形ABCD沿AE 所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB=.★★★29.如图,在矩形ABCD中,AD=4,点P是直线AD上一动点,若满足△PBC是等腰三角形的点P有且只有3个,则AB的长为.★★★30.如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP 的底边长是.★★★31.如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为.32.如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6,则FG的长为.533.如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE ,则=.34.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=.35.有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2=.★★★36.如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为.★★★37.如图,在平面直角坐标系xOy中,边长为2的正方形OCBA,点A、C分别在x轴、y轴上,把正方形绕点O逆时针旋转α 度后得到正方形OC1B1A1(0<α<90)﹒(1)直线OB的表达式是;(2)在直线OB上找一点P(原点除外),使△PB1A1为等腰直角三角形,则点P的坐标是.★★★38.如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE 的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=cm.★★★39.如图,E、F是正方形ABCD的边AD上有两个动点,满足AE=DF,连接CF交BD于G,连接BE交AG于点H,若正方形的边长为3,则线段DH长度的最小值是.★★★40.如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH 的中点P所经过的路线围成的图形的面积为.★★★41.如图,在正方形ABCD中,AB=,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,6AP=.★★★42.如图,正方形ABCD和正方形CEFG 中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.★★★43.如图,矩形ABCD中,AB=6,BC=4,点E在AB上,EF⊥DC于点F,在边AD,DF,EF,AE上分别存在点M,N,P,Q,这四点构成的四边形与矩形BCFE全等,则DM的长度为.★★★44.如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是.★★★45.如图,矩形ABCD,对角线AC,BD相交于点O,点E是边CD上一动点,已知AC=10,CD=6,则OE的最小值是.★★★46.如图,线段AB的长为10cm,点D在AB上,△ACD为等边三角形,过点D作DP ⊥CD,点G是DP上不与点D重合的一动点,作矩形CDGH.记矩形CDGH的对角线交点为O,连接OA、OB,(1)∠OAB=度;(2)线段BO的最小值为cm.★★★47.如图,在矩形ABCD中,AB=2,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为时,△CDF是等腰三角形.7★★★48.如图,矩形ABCD中,AD=6,CD=6+,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是.★★★49.如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是.★★★50.如图,在Rt△ABC中,∠BAC=90°,AB=AC=,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1,矩形PDFE的面积为S2,运y=S1+S2,则y与x的关系式是.★★★51.如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为.★★★52.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是.★★★53.如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是矩形,顶点A、B、C、8D的坐标分别为(﹣1,0),(5,0),(5,2),(﹣1,2),点E(3,0)在x轴上,点P在CD边上运动,使△OPE为等腰三角形,则满足条件的P点有个.★★★54.如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE 折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为.★★★55.矩形ABCD中,AB=10,BC=4,Q为AB边的中点,P为CD边上的动点,且△AQP 是腰长为5的等腰三角形,则CP的长为.★★★56.如图,在矩形ABCD中,BC=6,CD=8,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B的对应点B′落在矩形ABCD对角线上时,BP=.★★★57.如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为.★★★59.如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为.★★★60.如图,已知菱形ABCD的两条对角线长分别是3和4,点M、N分别是边BC、CD9的中点,点P是对角线上的一点,则PM+PN的最小值是.★★★61.如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为.★★★62.如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是.★★★63.如图,在菱形ABCD中,sin∠D=,E,F分别是AB和CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC是直角三角形时,CP的长为.★★★64.如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF= 60°,连接EF,则△AEF的面积最小值是.三.解答题(共11小题)★★★65.如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.(1)求证:四边形AEPQ为菱形;(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?1066.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.(1)求证:四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.★★★67.如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.(1)试探究BE与BF的数量关系,并证明你的结论;(2)求EF的最大值与最小值.★★★68.如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.(1)当AN平分∠MAB时,求DM的长;(2)连接BN,当DM=1时,求△ABN的面积;(3)当射线BN交线段CD于点F时,求DF的最大值.69.如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.(1)求证:MD=ME;(2)填空:①若AB=6,当AD=2DM时,DE=;②连接OD,OE,当∠A的度数为时,四边形ODME是菱形.1170.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.★★★71.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6,∠BAD=60°,且AB>6.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值;(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.12。
第18章《平行四边形》单元培优训练卷 原卷

第18章《平行四边形》单元培优训练卷一、选择题1.(2021春•抚远市校级期末)下列说法中,正确的是()A.对角线互相垂直且相等的四边形是正方形B.对角线互相垂直的四边形是菱形C.对角线互相垂直的四边形是平行四边形D.对角线相等的平行四边形是矩形2.(2022秋•泰山区期末)如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形()A.OA=OC,OB=OD B.AB=CD,AO=COC.AB=CD,AD=BC D.∠BAD=∠BCD,AB∠CD3.(2022秋•深圳期末)要检验一个四边形画框是否为矩形,可行的测量方法是()A.测量四边形画框的两个角是否为90°B.测量四边形画框的对角线是否相等且互相平分C.测量四边形画框的一组对边是否平行且相等D.测量四边形画框的四边是否相等4.(2022秋•任城区期末)已知,在平行四边形ABCD中,∠A的平分线分BC成4cm和3cm两条线段,则平行四边形ABCD的周长为()cm.A.11B.22C.20D.20或225.(2021秋•青羊区期末)如图,菱形ABCD中,AC=6,BD=8,AH∠BC于点H,则AH=()A.24B.10C.D.6.(2022•湘西州)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH∠AB于点H,连接OH,OH=4,若菱形ABCD的面积为32,则CD的长为()A.4B.4C.8D.87.(2022•苏州模拟)如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P.则下列结论不成立的是()A.AE=DF B.PC=PDC.AE∠DF D.S∠ADP=S四边形PFBE8.(2022春•东平县校级月考)如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E 作EG∠AD交CD于点G,过点F作FH∠AB交BC于点H,EG与FH交于点O,当四边形AEOF与四边形CGOH 的周长之差为12时,AE的值为()A.5.5B.4C.2D.69.(2022春•新罗区校级月考)如图,在∠ABCD中,AD=2AB,F是AD的中点,作CE∠AB,垂足E在线段AB 上(E不与A、B重合),连接EF、CF,则下列结论中正确个数是()∠∠DCF=∠BCD;∠EF=CF;∠S∠BEC<2S∠CEF;∠∠DFE=4∠AEFA.4B.3C.2D.110.(2022秋•渠县校级期末)如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任一点,PQ∠BC于点Q,PR∠BE于点R,则PQ+PR的值是()A.B.C.D.二、填空题11.(2022秋•碑林区校级期末)如图,菱形ABCD的周长是40cm,对角线AC为10cm,则菱形相邻两内角的度数分别为.12.如图,在平行四边形ABCD中,点M为边AD上一点,2AM=3MD,点E、F分别是BM、CM的中点,若EF =5,则AM的长为.13.(2022秋•锦江区期末)小颖将能够活动的菱形学具活动成为图1所示形状,并测得AC=5,∠B=60°,接着,她又将这个学具活动成为图2所示正方形,此时A'C'的长为.14.(2022秋•朝阳区校级期末)如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于.15.(2022秋•朝阳区校级期末)如图,Rt∠ABC中,∠ACB=90°,∠B=30°,.点D为边AB上一个动点,作DE∠BC、DF∠AC,垂足为E、F,连结EF.则EF长度的最小值为.16.(2022秋•平桂区期末)如图,在长方形ABCD中,AB=8,GC=,AE平分∠BAG交BC于点E,E是BC 的中点,则AG的长为.三、解答题17.(2022秋•南关区校级期末)如图,在平行四边形ABCD中,E,F是对角线BD上两个点,且BE=DF.(1)求证:AE=CF;(2)若AD=AE,∠DFC=140°,求∠DAE的度数.18.如图,在正方形ABCD中,点E是对角线AC上的一点,点F在BC的延长线上,且BE=EF.(1)求证:DE=EF;(2)若BE=3,求DF的长.19.(2022秋•平遥县期末)如图,已知平行四边形ABCD中,延长AB至点E,使BE=AB,连接BD和CE.(1)求证:∠DAB∠∠CBE(2)请你给图中平行四边形ABCD补充适当的条件,使四边形DBEC成为菱形;请结合补充条件证明;20.(2023•黔江区一模)如图,在∠ABCD中,对角线AC,BD交于点O,E是AD上一点,连接EO并延长,交BC于点F.连接AF,CE,EF平分∠AEC.(1)求证:四边形AFCE是菱形;(2)若∠DAC=60°,AC=2,求四边形AFCE的面积.21.(2022•苏州模拟)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是OA,OC的中点.(1)求证:四边形DEBF是平行四边形;(2)∠对角线AC,BD满足时,四边形DEBF是矩形;∠对角线AC,BD满足时,四边形DEBF是菱形.22.(2022春•杭州期中)已知:如图,在正方形ABCD中,E,F分别是BC,CD上的点,AE、BF相交于点P,并且AE=BF.(1)如图1,判断AE和BF的位置关系?并说明理由;(2)若AB=8,BE=6,求BP的长度;(3)如图2,FM∠DN,DN∠AE,点F在线段CD上运动时(点F不与C、D重合),四边形FMNP是否能否成为正方形?请说明理由.23.(2022春•梅江区期末)如图,矩形ABCD中,AB=6cm,BC=8cm,E、F是对角线AC上的两个动点,分别从A、C同时出发,相向而行,速度均为2cm/s,运动时间为t(0≤t≤5)秒.(1)若G、H分别是AB、DC的中点,且t≠2.5,求证:以E、G、F、H为顶点的四边形始终是平行四边形.(2)在(1)的条件下,当t为何值时,以E、G、F、H为顶点的四边形为矩形?(3)若G、H分别是折线A﹣B﹣C,C﹣D﹣A上的动点,分别从A、C开始,与E、F相同的速度同时出发,当t为何值时,以E、G、F、H为顶点的四边形为菱形?请直接写出t的值.。
浙教版2022-2023学年八下数学第四章 平行四边形 培优测试卷(解析版)

浙教版2022-2023学年八下数学第四章 平行四边形 培优测试卷(解析版)一、选择题(本大题有10小题,每小题3分,共30分) 下面每小题给出的四个选项中,只有一个是正确的.1.以下分别是回收、节水、绿色包装、低碳4个标志,其中是中心对称图形的是( ).A .B .C .D .【答案】C【解析】A 、此图形不是中心对称图形,故本选项不符合题意; B 、此图形不是中心对称图形,故此选项不符合题意; C 、此图形是中心对称图形,故此选项符合题意;D 、此图形不是中心对称图形,故此选项不符合题意. 故答案为:C .2.已知平行四边形ABCD 中,∠A +∠C =240°,则∠B 的度数是( ) A .100° B .60° C .80° D .160° 【答案】B【解析】∵四边形ABCD 为平行四边形, ∴∠A=∠C ,∠A+∠B =180°. 又∵∠A+∠C=240°, ∴∠A=∠C=120°, ∠B=180°-∠A=60°. 故答案为:B3.多边形边数从n 增加到n +1,则其内角和( ) A .增加180° B .增加360° C .不变 D .减少180° 【答案】A【解析】n 边形的内角和是(n -2)•180°,边数增加1,则新的多边形的内角和是(n+1-2)•180°. 则(n+1-2)•180°-(n -2)•180°=180°. 故它的内角和增加180°. 故答案为:A .4.如图,平行四边形ABCD 的对角线AC 与BD 相交于点O ,AB∠AC .若AC =6,BD =10,则AB 的长是( )A .3B .4C .5D .6 【答案】B【解析】∵四边形ABCD 是平行四边形,BD =10,AC =6, ∴AO =OC =12AC =3,BO =DO =12BD =5,又∵AB∠AC , ∴∠BAC =90°,∴AB =√BO 2−AO 2=√52−32=4, 故答案为:B . 5.用反证法证明,“在∠ABC 中,∠A 、∠B 对边是a 、b ,若∠A <∠B ,则a <b .”第一步应假设( ) A .a >b B .a =b C .a≤b D .a≥b【答案】D【解析】根据反证法步骤,第一步应假设a <b 不成立,即a≥b . 故答案为:D.6.如图,点E 、F 分别是∠ABCD 边AD 、BC 的中点,G 、H 是对角线BD 上的两点,且BG=DH .则下列结论中错误的是( )A .GF =EHB .四边形EGFH 是平行四边形C .EG =FHD .EH ⊥BD【答案】D【解析】连接EF 交BD 于点O ,在平行四边形ABCD 中,AD=BC ,∠EDH=∠FBG , ∵E 、F 分别是AD 、BC 边的中点,∴DE=BF=12BC ,∠EDO=∠FBO ,∠DOE=∠BOF ,∴∠EDO∠∠FBO , ∴EO=FO ,DO=BO , ∵BG=DH , ∴OH=OG ,∴四边形EGFH 是平行四边形, ∴GF=EH ,EG=HF ,故答案为:A 、B 、C 不符合题意; ∵∠EHG 不一定等于90°,∴EH∠BD 错误,D 符合题意; 故答案为:D .7.如图,在四边形ABCD 中,点P 是对角线BD 的中点,点E 、F 分别是AB 、CD 的中点,AD=BC ,∠CBD=30°,∠ADB=100°,则∠PFE 的度数是( )A .15°B .25°C .30°D .35°【答案】D【解析】∵点P 是BD 的中点,点E 是AB 的中点, ∴PE 是∠ABD 的中位线, ∴PE=12AD ,PE∠AD ,∴∠EPD=180°-∠ADB=80°, 同理可得,PF=12BC ,PE∠BC ,∴∠FPD=∠CBD=30°, ∵AD=BC , ∴PE=PF ,∴∠PFE=12×(180°-110°)=35°,故答案为:D .8.如图, ▱EFGH 的四个顶点分别在 ▱ABCD 的四条边上, QF ∥AD ,分别交EH 、CD 于点P 、Q 过点P 作 MN ∥AB ,分别交AD 、BC 于点M 、N ,若要求 ▱EFGH 的面积,只需知道下列哪个四边形的面积( )A .四边形AFPMB .四边形MPQDC .四边形FBNPD .四边形PNCQ【答案】C【解析】如图,连接PG ,FN ,∵∠EFGH ,∴S △FPG =12S ▱EFGH ,∵FQ ∥BC ,∴S △FPN =S △FPG , 又∵MN∠AB ,∴四边形FBNP 为平行四边形,∴S △FPN =S △FPG =12S ▱FBNP∴S ▱FBNP =S ▱EFGH ,∴要求∠EFGH 的面积,只需要知道四边形FBNP 的面积. 故答案为:C.9.如图,已知□OABC 的顶点A ,C 分别在直线 x =1 和 x =4 上,O 是坐标原点,则对角线OB 长的最小值为( )A .3B .4C .5D .6 【答案】C【解析】过点B 作BD⊥直线x=4,交直线x=4于点D ,过点B 作BE⊥x 轴,交x 轴于点E ,直线x=1与OC 交于点M ,与x 轴交于点F ,直线x=4与AB 交于点N ,如图:∵四边形OABC是平行四边形,∴⊥OAB=⊥BCO,OC⊥AB,OA=BC.∵直线x=1与直线x=4均垂直于x轴,∴AM⊥CN,∴四边形ANCM是平行四边形,∴⊥MAN=⊥NCM,∴⊥OAF=⊥BCD.∵⊥OFA=⊥BDC=90°,∴⊥FOA=⊥DBC.在⊥OAF和⊥BCD中,⊥FOA=⊥DBC,OA=BC,⊥OAF=⊥BCD,∴⊥OAF⊥⊥BCD,∴BD=OF=1,∴OE=4+1=5,∴OB=√OE2+BE2.由于OE的长不变,所以当BE最小时,OB取得最小值,最小值为OB=OE=5.故答案为:C.10.如图,∠ ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=12BC,连接OE.下列结论:①∠ADO=30°;②S ∠ ABCD=AB·AC;③OB=AB;④S四边形OECD=32S∠AOD,其中成立的个数为()A.1个B.2个C.3个D.4个【答案】B【解析】∵四边形ABCD为平行四边形,∠ADC=60°,∴OA=OC,OB=OD,∠ABC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠DAE=60°,∴△ABE是等边三角形,∴AB=AE=BE,∠AEB=60°,∵AB=12BC,∴BE=12BC,∴CE=BE=AE,∴∠ACE=∠CAE=30°,∴∠OAB=90°,∠OAD=30°,∴在Rt△AOB中,OB>OA,OB>AB,则结论③不成立;∴OD >OA ,∴∠ADO ≠∠OAD ,即∠ADO ≠30°,结论①不成立; ∵∠OAB =90°,即AB ⊥AC ,∴S ▱ABCD =AB ⋅AC ,则结论②成立; 设平行四边形ABCD 的面积为8a(a >0), 则S △AOD =S △COD =S △BOC =14S ▱ABCD =2a ,∵BE =CE ,∴S △BOE =S △COE =12S △BOC =a ,∴S 四边形OECD =S △COE +S △COD =3a =32S △AOD ,结论④成立;综上,成立的个数为2个, 故答案为:B .二、填空题(本大题有6小题,每小题4分,共24分)要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.11.一个多边形的内角和与外角和的和为2160∠,则这个多边形的边数为 . 【答案】12【解析】设这个多边形的边数是n , (n -2)•180°+360°=2160°, 解得n=12. 故答案为:12.12.在平面直角坐标系中,已知A 、B 、C 、D 四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),若一次函数y=mx -6m 的图象将四边形ABCD 的面积分成1:3两部分,则m 的值为 .【答案】−35或−6【解析】∵直线y=mx -6m 经过定点B (6,0),A 、B 、C 、D 四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),∴CD∠AB ,CD=8-2=6= AB , ∴四边形ABCD 是平行四边形,∴S∠ADC= S∠ADC=12S 平行四边形ABCD ,又∵直线y=mx -6m 把平行四边形ABCD 的面积分成1:3的两部分.∴直线y=mx -6m 经过AD 的中点M (1,3)或经过CD 的中点N (5,6), ∴m -6m=3或5m -6m=6,∴m=-35或-6,故答案为:-35或-6.13.如图,△ABC 是边长为1的等边三角形,取BC 边中点E ,作ED ∥AB ,EF ∥AC ,ED ,EF 分别交AC ,AB 于点D ,F ,得到四边形EDAF ,它的面积记作S 1;取BE 中点E 1,作E 1D 1∥FB ,E 1F 1∥EF ,E 1D 1,E 1F 1分别交EF ,BF 于点D 1,F 1,得到四边形E 1D 1FF 1,它的面积记作S 2……照此规律作下去,则S n = .【答案】√322n+1【解析】∵∠ABC 是边长为1的等边三角形,∴∠ABC 的高为:√12−(12)2=√32,∴S △ABC =12×1×√32=√34,∵DE 、EF 分别是∠ABC 的中位线,∴AF =12AC =12,∴S 1=12S △ABC =√38,同理可得S 2=√38×14;…,∴S n =√38×(14)n−1=√322n+1;故答案为:√322n+1.14.如图, ΔABC 和 ΔDEC 关于点C 成中心对称,若 AC =1 , AB =2 , ∠BAC =90° ,则 AE 的长是 .【答案】2√2【解析】∵∠DEC 与∠ABC 关于点C 成中心对称, ∴DC=AC=1,DE=AB=2,∴在Rt∠EDA 中,AE 的长是:AE =√AD 2+DE 2=√(DC +AC)2+DE 2=√(1+1)2+22=2√2 . 故答案为: 2√2 . 15.已知:如图,线段AB =6cm ,点P 是线段AB 上的动点,分别以AP 、BP 为边在AB 作等边△APC 、等边△BPD ,连接CD ,点M 是CD 的中点,当点P 从点A 运动到点B 时,点M 经过的路径的长是 cm .【答案】3【解析】如图,分别延长AC,BD交于H,过点M作GN∠AB分别交AH于G,BH于N,∵∠APC、∠BPD都是等边三角形,∴∠A=∠B=∠DPB=∠CPA=60°,∴AH∠PD,BH∠CP,∴四边形CPDH是平行四边形,∴CD与HP互相平分,∴M是PH的中点,故在P运动过程中,M始终在HP的中点,所以M的运动轨迹即为∠HAB的中位线,即线段GN,∴GN=12AB=3cm,故答案为:3.16.如图,把含45∘,30∘角的两块直角三角板放置在同一平面内,若AB//CD,AB=CD=√6则以A,B,C,D为顶点的四边形的面积是.【答案】3+2√3【解析】延长CO,交AB于点E,由题意可知:∠BAO=45°,∠CDO=30°∵AB//CD,AB=CD=√6∴四边形ABCD为平行四边形∵OC∠CD∴CE∠AB∴S∠AOB+S∠COD= 12AB·OE+12CD·OC= 12AB·(OE+OC)= 12AB·CE= 12S平行四边形ABCD∴S平行四边形ABCD=2(S∠AOB+S∠COD)在Rt∠AOB中,AO2+BO2=AB2=6,AO=BO解得:AO=BO= √3在Rt∠COD中,∠CDO=30°,OC2+CD2=OD2∴OD=2OC,OC2+6=(2OC)2解得:OC= √2,∴S∠AOB= 12AO·BO= 32,S∠COD=12CD·OC= √3∴S平行四边形ABCD=2(S∠AOB+S∠COD)=2×(32+√3)= 3+2√3故答案为:3+2√3.三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)解答应写出文字说明,证明过程或推演步骤.17.如图,在▱ABCD中,点E、F在对角线AC上,且AE=CF,连接BF、DE.求证:BF=DE,BF∥DE.【答案】解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴∠DAC=∠BCA.又∵AE=CF,∴△DAE≌△BCF(SAS),∴BF=DE,∠DEA=∠BFC.∴∠DEC=∠BFA.∴BF∥DE.18.如图,在∠ABCD中,点E在边AD上,连接EB并延长至F,使BF=BE;连接EC并延长至G,使CG=CE,连接FG,点H为FG的中点,连接DH,AF.(1)若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)求证:四边形AFHD为平行四边形.【答案】(1)解:∵四边形ABCD是平行四边形,∴∠BAE=∠BCD=70°,AD∠BC,∵∠DCE=20°,AB∠CD,∴∠CDE=180°﹣∠BAE=110°,∴∠DEC=180°﹣∠DCE﹣∠CDE=50°;(2)解:∵四边形ABCD是平行四边形,∴AD=BC,AD∠BC,∵BF=BE,CG=CE,∴BC是∠EFG的中位线,∴BC∠FG ,BC =12FG ,∵H 为FG 的中点, ∴FH =12FG ,∴BC∠FH ,BC =FH , ∴AD∠FH ,AD =FH ,∴四边形AFHD 是平行四边形.19.如图,∠ABC 中,点D ,E 分别是边AB ,AC 的中点,过点C 作CF∠AB 交DE 的延长线于点F ,连接BE .(1)求证:四边形BCFD 是平行四边形.(2)当AB =BC 时,若BD =2,BE =3,求AC 的长. 【答案】(1)证明:∵点 D ,E 分别是边 AB ,AC 的中点, ∴DE∠BC . ∵ CF∠AB ,∴四边形 BCFD 是平行四边形;(2)解:∵AB =BC ,E 为 AC 的中点, ∴BE∠AC .∵AB =2DB =4, BE =3, ∴AE =√42−32=√7 ∴AC =2AE =2√720.如图,在 5×5 的方格纸中,每个小正方形的边长均为1,A ,B 两点均在小正方形的顶点上,请按下列要求,在图1,图2,图3中各画一个四边形(所画四边形的顶点均在小正方形的项点上)(1)在图1中画四边形 ABCD ,使其为中心对称图形,但不是轴对称图形; (2)在图2中画以A ,B ,M ,N 为顶点的平行四边形,且面积为5;(3)在图3中画以A ,B ,E ,F 为顶点的平行四边形,且其中一条对角线长等于3. 【答案】(1)解:如图1中,四边形ABCD 即为所求作.(2)解:如图2中,四边形ABMN即为所求作. (3)解:如图3中,四边形ABEF即为所求作. 21.如图,在▱ABCD中,E,F是对角线AC上的两点,且AE=CF.(1)求证:四边形BEDF是平行四边形;(2)若AB⊥BF,AB=8,BF=6,AC=16.求线段EF长.【答案】(1)证明:连接BD交AC于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵AE=CF,∴OE=OF,∵OB=OD,∴四边形BEDF是平行四边形.(2)解:在Rt△ABF中,AF=√AB2+BF2=√82+62=10,∵AC=16,∴CF=AC−AF=16−10=6,∵AE=CF,∴AE=6,∴EF=AF−AE=10−6=4.22.如图,已知:在∠ABCD中,AE∠BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.(1)求证:G 为CD 的中点.(2)若CF =2.5,AE =4,求BE 的长.【答案】(1)证明:∵点F 为CE 的中点,∴CF=12CE , 在∠ECG 与∠DCF 中,∵∠2=∠1, ∠C =∠C , CE =CD ,∴∠ECG∠∠DCF (AAS ),∴CG=CF= 12CE. 又CE=CD , ∴CG=12CD , 即G 为CD 的中点; (2)解:∵CE=CD ,点F 为CE 的中点,CF=2.5,∴DC=CE=2CF=5,∵四边形ABCD 是平行四边形,∴AB=CD=5,∵AE∠BC ,∴∠AEB=90°,在Rt∠ABE 中,由勾股定理得:BE=√52−42=3.23.如图,平行四边形ABCD 中,AE 平分∠BAD ,交BC 于点E ,且AB =AE ,延长AB 与DE 的延长线交于点F .下列结论中:求证:(1)∠ABE 是等边三角形;(2)∠ABC ∠∠EAD ;(3)S △ABE =S △CEF .【答案】(1)证明:∵ABCD 是平行四边形∴AD∠BC ,AD=BC ,∴∠EAD=∠AEB ,又∵AE 平分∠BAD ,∴∠BAE=∠DAE ,∴∠BAE=∠BEA ,∴AB=BE ,∵AB=AE ,∴∠ABE 是等边三角形;(2)证明:∵∠ABE 是等边三角形∴∠ABE=∠EAD=60∠,∵AB=AE ,BC=AD ,∴∠ABC∠∠EAD(SAS)(3)证明:∵∠FCD 与∠ABC 等底(AB=CD)等高(AB 与CD 间的距离相等),∴S∠FCD=S∠ABC ,又∵∠AEC与∠DEC同底等高,∴S∠AEC=S∠DEC,∴S∠ABE=S∠CEF24.我们规定:有一组邻边相等,且这组邻边的夹角为60°的凸四边形叫做“准筝形”.(1)如图1,在四边形ABCD中,∠A+∠C=270°,∠D=30°,AB=CB,求证:四边形ABCD是“准筝形”;(2)如图2,在“准筝形”ABCD中,AB=AD,∠BAD=∠BCD=60°,BC=4,CD=3,求AC的长;(3)如图3,在∠ABC中,∠A=45°,∠ABC=120°,AB=3-√3,设D是∠ABC所在平面内一点,当四边形ABCD是“准筝形”时,请直接写出四边形ABCD的面积.【答案】(1)证明:在四边形ABCD中,∠A+∠B+∠C+∠D=360°,∵∠A+∠C=270°,∠D=30°,∴∠B=360°-(∠A+∠C+∠D)=360°-(270°+30°)=60°,∵AB=BC,∴四边形ABCD是“准筝形”;(2)解:以CD为边作等边∠CDE,连接BE,过点E作EF∠BC于F,如图2所示:则DE=DC=CE=3,∠CDE=∠DCE=60°,∵AB=AD,∠BAD=∠BCD=60°,∴∠ABD是等边三角形,∴∠ADB=60°,AD=BD,∴∠ADB+∠BDC=∠CDE+∠BDC,即∠ADC=∠BDE,在∠ADC和∠BDE中,{AD=BD∠ADC=∠BDEDC=DE,∴∠ADC∠∠BDE(SAS),∴AC=BE,∵∠BCD=∠DCE=60°,∴∠ECF=180°-60°-60°=60°,∵∠EFC =90°,∴∠CEF =30°,∴CF =12CE =32 , 由勾股定理得:EF =√CE 2−CF 2=√32−(32)2=3√32 , BF =BC +CF =4+32=112, 在Rt∠BEF 中,由勾股定理得:BE =√BF 2+EF 2=√(112)2+(3√32)2=√37 , ∴AC =√37 ;(3)解:四边形ABCD 的面积为3√32或9+3√32 或 92+3√3. 【解析】(3)过点C 作CH∠AB ,交AB 延长线于H ,如图3所示:设BH =x ,∵∠ABC =120°,CH 是∠ABC 的高线,∴∠BCH =30°,∴HC =√3x ,BC =2BH =2x ,又∵∠A =45°,∴∠HAC 是等腰直角三角形,∴HA =HC ,∵AB =3-√3 ,∴√3x =3-√3+x ,解得:x =√3,∴HC =√3x =3,BC =2√3 ,∴AC = √2 HC =3 √2 ,当AB =AD =3- √3 ,∠BAD =60°时,连接BD ,过点C 作CG∠BD ,交BD 延长线于点G ,过点A 作AK∠BD ,如图4所示:则BD =3-√3 ,∠ABD =60°,BK =12AB =12(3-√3 ), ∵∠ABC =120°,∴∠CBG =60°=∠CBH ,在∠CBG 和∠CBH 中, {∠CGB =∠CHB =90°∠CBG =∠CBH BC =BC,∴∠CBG∠∠CBH (AAS ),∴GC =HC =3,在Rt∠ABK 中,由勾股定理得:AK =√AB 2−BK 2 =√(3−√3)2−[12(3−√3)]2 = 3√3−32, ∴S ∠ABD = 12 BD•AK = 12×(3-√3 )×3√3−32 =6√3−92, S ∠CBD = 12 BD•CG = 12×(3-√3 )×3=9−3√32, ∴S 四边形ABCD = 6√3−92 + 9−3√32 = 3√32; ②当BC =CD =2√3 ,∠BCD =60°时,连接BD ,作CG∠BD 于点G ,AK∠BD 于K ,如图5所示:则BD =2√3 ,CG =√32 BC =√32×2√3 =3,AK =3√3−32 , ∴S ∠BCD =12 BD•CG =12×2√3×3=3√3, S ∠ABD =12BD•AK =12×2√3×3√3−32=9−3√32, ∴S 四边形ABCD =3√3+9−3√32=9+3√32 ; ③当AD =CD =AC =3√2,∠ADC =60°时,作DM∠AC 于M ,如图6所示:则DM =√32AD =√32×3√2 =3√62 , ∴S ∠ABC =12AB•CH =12×(3-√3)×3=9−3√32, S ∠ADC = 12 AC•DM =12×3√2×3√62=9√32, ∴S 四边形ABCD =9−3√32+ 9√32=92+3√3. 综上所述,四边形ABCD 的面积为3√32或9+3√32 或 92+3√3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《四边形综合测试题》
一、选择题
1、如图,在平行四边形ABCD 中,过对角线BD 上一点P 作EF ∥AB ,GH ∥AD ,与各边交点分别为E 、F 、G 、H ,则图中面积相等的平行四边形的对数为( ) A .3 B .4
C .5
D .6
( 第一题)
( 第二题) ( 第四题)
2、如图,在▱ABCD 中,分别以AB 、AD 为边向外作等边△ABE 、△ADF ,延长CB 交AE 于点G ,点G 在点A 、E 之间,连接CE 、CF ,EF ,则以下四个结论一定正确的是:①△CDF ≌△EBC ;②∠CDF=∠EAF ;③△ECF 是等边△;④CG ⊥AE ( ) A .只有①②
B .只有①②③
C .只有③④
D .①②③④
3、如图,在平行四边形ABCD 中,按下列条件得到的四边形EFGH 不一定是平行四边形的是( )
A .
B .
C .
D .
4、如图,平行四边形ABCD 中,∠ABD=30°,AB=4,AE ⊥BD ,CF ⊥BD ,且E 、F 恰好是BD 的三等分点,又M 、N 分别是AB ,CD 的中点,那么四边形MENF 的面积是( ) A .3
3
B .
3
C .3
2
D .
2
5、如图,菱形ABCD 的对角线的长分别为2和5,P 是对角线AC 上任一点(点P 不与点A 、C 重合)且PE ∥BC 交AB 于E ,PF ∥CD 交AD 于F ,则阴影部分的面积是( ) A .2 B .
2
5
C .3
D .
3
5
( 第五题)
( 第六题) ( 第七题)
6、如图,在正方形ABCD 中,点O 为对角线AC 的中点,过点0作射线OM 、ON 分别交AB 、BC 于点E 、F ,且∠EOF=90°,BO 、EF 交于点P .则下列结论中:
(1)图形中全等的三角形只有两对;(2)正方形ABCD 的面积等于四边形OEBF 面积的4倍; (3)BE+BF=2 0A ;(4)AE 2+CF 2=20P•OB .正确的结论有(
)个.
A .1
B .2
C .3
D .4
7、已知:如图,在正方形ABCD 外取一点E ,连接AE 、BE 、DE .过点A 作AE 的垂线交DE 于点P .若AE=AP=1,PB=
5.下列结论:①△APD ≌△AEB ;②点B 到直线AE 的距离为2 ;③EB ⊥ED ;④S
△APD
+S △APB =1+
6 ;⑤S
正方形
ABCD
=4+
6.其中正确结论的序号是(
)
A .①③④
B .①②⑤
C .③④⑤
D .①③⑤
8、如图,在等腰Rt △ABC 中,∠C=90°,AC=8,F 是AB 边上的中点,点D ,E 分别在AC ,BC 边上运动,且保持AD=CE .连接DE ,DF ,EF .在此运动变化的过程中,下列结论:
①△DFE 是等腰直角三角形;②四边形CDFE 不可能为正方形,
③DE 长度的最小值为4;④四边形CDFE 的面积保持不变;⑤△CDE 面积的最大值为8. 其中正确的结论是( ) A .①②③
B .①④⑤
C .①③④
D .③④⑤
9、如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;...,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( ) .
A. 669
B. 670
C.671
D. 672
10、如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,∠BEG>60°,现沿直线EG 将纸
片折叠,使点B 落在纸片上的点H 处,连接AH ,则与∠BEG 相等的角的个数为( ) A .4 B .3 C .2 D .1
11、如图,在矩形ABCD 中,AB=12cm ,BC=6cm ,点E 、F 分别在AB 、CD 上,将矩形ABCD 沿EF 折叠,使点A 、D 分别落在矩形ABCD 外部的点A’,D’处,则整个阴影部分图形的周长..为( ) A .18cm
B .36cm
C .40cm
D .72cm
12、在等腰梯形ABCD 中,AD=AB=
2
1
BC=1,点E 是AD 上一点,点F 是AB 上一点,且AE=BF ,连接CE 、DF ,交于点P .在下列结论中:(1)∠EDF=∠DCE ;(2)∠DPC=72°;(3)
S 四边形AEPF =S △DPC ;(4)当E 为AD 中点时,
S 四边形FBCP =
2
3
.正确的个数有( )
A .1
B .2
C .3
D .4
第九题图
B
A
G
C
D
H
E
(第十题图)
( 第十一题) ( 第十二题)
二、填空题
13、如图,已知平行四边形ABCD ,E 是AB 延长线上一点,连结DE 交BC 于点F ,在不添加任何辅助线的情况下,请补充一个条件,使CDF BEF △≌△,这个条件是 .(只要填一个)
14、如图,在□ABCD 中,对角线AC 、BD 相交于点O ,如果AC=14,BD=8,AB=x ,那么x 的取值范围是 .
15、如图,矩形ABCD 中,AB =8cm ,BC =4cm ,E 是DC 的中点,BF =
4
1
BC ,则四边形DBFE 的面积为 16、如图,活动衣帽架由三个菱形组成,利用四边形的不稳定性,调整菱形的内角α,使衣帽架拉伸或收缩,当菱形的边长为18cm ,α=1200时,A 、B 两点的距离为
cm.
( 第十六题)
( 第十八题)
17、如图,在平面直角坐标系中,边长为1的正方形OA 1B 1C 的对角线 A 1C 和OB 1交于点M 1;以M 1A 1
为对角线作第二个正方形A 2A 1B 2M 1,对角线A 1M 1和A 2B 2交于点M 2;以M 2A 1为对角线作第三个正方形A 3A 1B 3M 2,对角线A 1M 2和A 3B 3交于点M 3;……依此类推,这样作的第n 个正方形对角线交点M n 的坐标为 .
18、已知如图正方形ABCD 的C 、D 的两个顶点在双曲线y= x
10
的第一象限分支上,顶点A 、B 分别在x 、y 轴上,则此正方形的边长等于
三、解答题
19、已知边长为4的正方形ABCD ,顶点A 与坐标原点重合,一反比例函数图象过顶点C ,动点P 以每秒1个单位速度从点A 出发沿AB 方向运动,动点Q 同时以每秒4个单位速度从D 点出发沿正方形的边DC-CB-BA 方向顺时针折线运动,当点P 与点Q 相遇时停止运动,设点P 的运动时间为t .
(1)求出该反比例函数解析式.
(2)连接PD ,当以点Q 和正方形的某两个顶点组成的三角形和△PAD 全等时,求点Q 的坐标. ( 第十九题) (3)用含t 的代数式表示以点Q 、P 、D 为顶点的三角形的面积s ,并指出相应t 的取值范围.
A
B
E
F
D
C
第13题
(十五题)
20、如图,一次函数y=-3
1
x-2的图象分别交x 轴、y 轴于A 、B 两点,P 为AB 的中点,PC ⊥x 轴于点C ,延长PC 交反比例函数y= x
k
(x <0)的图象于点D ,且OD ∥AB , (1)求k 的值;
(2)连OP 、AD ,求证:四边形APOD 是菱形.
21、如图,在等腰梯形ABCD 中,AB ∥DC ,AD=BC=5,DC=7,AB=13,点P 从A 点出发,以3个单位长度/秒的速度沿AD ⇒DC 向终点C 运动,同时点Q 从点B 出发,以1个单位长度/秒的速度沿BA 向点A 运动,当有一点到达终点时,P 、Q 就同时停止运动.设运动的时间为t 秒.
(1)用t 的代数式表示P 的运动路程
,Q 的运动路程 ;(2)则梯形ABCD 的面积是
;
(3)若四边形PQBC 为平行四边形,则t=
秒
22、如图,正方形ABCD 中,AC 是对角线,今有较大的直角三角板,一边始终经过点B ,直角顶点P 在射线AC 上移动,另一边交DC 于Q .(1)如图1,当点Q 在DC 边上时,猜想并写出PB 与PQ 所满足的数量关系;并加以证明; (2)如图2,当点Q 落在DC 的延长线上时,猜想并写出PB 与PQ 满足的数量关系,请证明你的猜想.
23、在图1到图3中,点O 是正方形ABCD 对角线AC 的中点,△MPN 为直角三角形,∠MPN=90°.正方形ABCD 保持不动,△MPN 沿射线AC 向右平移,平移过程中P 点始终在射线AC 上,且保持PM 垂直于直线AB 于点E ,PN 垂直于直线BC 于点F .
(1)如图1,当点P 与点O 重合时,OE 与OF 的数量关系为
; (2)如图2,当P 在线段OC 上时,猜想OE 与OF 有怎样的数量关系与位置关系?并对你的猜想结果给予证明; (3)如图3,当点P 在AC 的延长线上时,OE 与OF 的数量关系为
;位置关系为
.。
