2019高考数学二轮复习小题专项练习(二)平面向量、复数与框图(无答案)理
高考数学二轮复习小题专项练习(二)平面向量、复数与框图理

高考数学二轮复习 小题专项练习(二)平面向量、复数与框图理一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2021·成都第三次诊断性检测]若复数z =a +i 1-i(i 是虚数单位)为纯虚数,则实数a 的值为( )A .-2B .-1C .1D .22.[2021·银川一中第二次模拟考试]若两个单位向量a ,b 的夹角为120°,则|2a +b|=( )A .2B .3C. 2D.33.[2021·合肥市高三第三次教学质量检测]运行如图所示的程序框图,则输出的s 等于( )A .-10B .-3C .3D .14.[2021·山东沂水期中]若复数z =i20201-i 2(i 为虚数单位),则z 的共轭复数z -=( ) A .1+i B .iC .-12i D.12i 5.[2021·百校联盟四月联考]设复数z 满足z -i z =3+i ,则z -=( ) A.15+25i B .-15+25iC.15-25i D .-15-25i6.[2021·河南新乡第三次模拟测试]已知复数z1,z2在复平面内对应的点分别为(2,-1),(0,-1),则z1z2+|z2|=( )A .2+2iB .2-2iC .-2+iD .-2-i7.[2021·宁夏六盘山高三年级第三次模拟]执行下面的程序框图,则输出K 的值为( )C .100D .1018.[2021·安徽池州一中5月月考]设点O 在△ABC 的内部,且有AD →=32(OB →+OC →),则△ABC 的面积与△BOC 的面积之比为( )A .3 B.13 C .2 D.129.[2021·银川一中第二次模拟]20世纪70年代,流行一种游戏——角谷猜想,规则如下:任意写出一个自然数n ,按照以下的规律进行变换:假如n 是个奇数,则下一步变成3n +1;假如n 是个偶数,则下一步变成n 2,这种游戏的魅力在于不管你写出一个多么庞大的数字,最后必定会落在谷底,更准确地说是落入底部的循环,而永久也跳不出那个圈子.下列程序框图确实是依照那个游戏而设计的,假如输出的i 值为6,则输入的n 值为( )A .5B .16C .5或32D .4或5或3210.[2021·河南洛阳第三次统考]在△ABC 中,点P 满足BP→=2PC →,过点P 的直线与AB ,AC 所在直线分别交于点M ,N ,若AM→=mAB →,AN →=nAC→(m>0,n>0),则m +2n 的最小值为( ) A .3 B .4宋以后,京师所设小学馆和武学堂中的教师称谓皆称之为“教谕”。
高考数学平面向量及复数专项训练试题、参考答案

高考数学平面向量及复数专项训练试题一、选择题(本题每小题5分,共60分)1.设向量(cos 23,cos67),(cos53,cos37),a b a b =︒︒=︒︒⋅=则 ( )AB .12C .D .12-2.如果复数212bi i-+(其中i 为虚数单位,b 为实数)的实部和虚部是互为相反数,那么b 等于( )A B .23C .2D . 23-3.220041i i i ++++的值是 ( ) A .0 B .1- C .1 D .i 4.若(2,3)a =-, (1,2)b =-,向量c 满足c a ⊥,1b c ⋅=,则c 的坐标是 ( ) A .(3,2)- B .(3,2) C .(3,2)-- D .(3,2)- 5.使4()a i R +∈(i 为虚数单位)的实数a 有( ) A .1个 B .2个 C .3个D .4个6.设e 是单位向量,3,3,3AB e CD e AD ==-=,则四边形ABCD 是( )A .梯形B .菱形C .矩形D .正方形7.已知O 、A 、B 三点的坐标分别为(0,0)O ,(3,0)A ,(0,3)B ,点P 在线段AB 上,且(0AP t AB =≤t ≤1),则OA OP ⋅的最大值为( )A .3B .6C .9D .128.已知2,1a b ==,a 与b 的夹角为60︒,则使向量a b λ+与2a b λ-的夹角为钝角的实数λ的取值范围是 ( )A . (,1-∞--B . (1)-++∞C . (,1(13,)-∞--++∞D . (11--+9.若z 为复数,下列结论正确的是 ( )A .若12,z z C ∈且120z z ->且12z z >B .22z z =C .若0,z z -=则z 为纯虚数D .若2z 是正实数,那么z 一定是非零实数10.若sin 211)i θθ-++是纯虚数,则θ的值为 ( ) A .2()4k k Z ππ-∈ B .2()4k k Z ππ+∈ C .2()4k k Z ππ±∈ D .()24k k Z ππ+∈11.已知△ABC 的三个顶点的A 、B 、C 及平面内一点P 满足PA PB PC AB ++=,下列结论中正确的是 ( ) A .P 在△ABC 内部 B .P 在△ABC 外部 C .P 在AB 边所在直线上 D .P 是AC 边的一个三等分点 12.复数z 在复平面上对应的点在单位圆上,则复数21zz+ ( )A .是纯虚数B .是虚数但不是纯虚数C .是实数D .只能是零 二、填空题(本题每小题4分,共16分)13.已知复数z 满足等式:2||212z zi i -=+,则z= .14.把函数)2245y x x =-+的图象按向量a 平移后,得到22y x =的图象,且a ⊥b ,(1,1)c =-,4b c ⋅=,则b =_____________。
全国高考数学第二轮复习 专题升级训练2 平面向量、复数、框图及合情推理 理
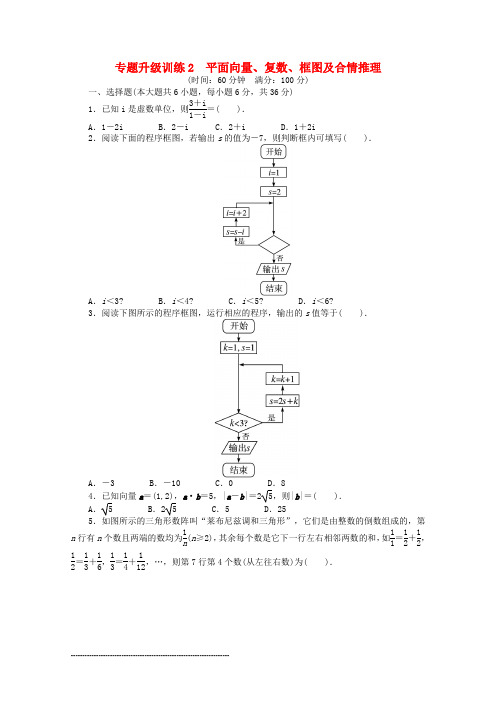
专题升级训练2 平面向量、复数、框图及合情推理(时间:60分钟 满分:100分)一、选择题(本大题共6小题,每小题6分,共36分)1.已知i 是虚数单位,则3+i1-i=( ).A .1-2iB .2-iC .2+iD .1+2i2.阅读下面的程序框图,若输出s 的值为-7,则判断框内可填写( ).A .i <3?B .i <4?C .i <5?D .i <6?3.阅读下图所示的程序框图,运行相应的程序,输出的s 值等于( ).A .-3B .-10C .0D .84.已知向量a =(1,2),a ·b =5,|a -b |=25,则|b |=( ). A . 5 B .2 5 C .5 D .255.如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n 行有n 个数且两端的数均为1n (n ≥2),其余每个数是它下一行左右相邻两数的和,如11=12+12,12=13+16,13=14+112,…,则第7行第4个数(从左往右数)为( ).A .1140B .1105C .160D .1426.已知两点A (1,0),B (1,3),O 为坐标原点,点C 在第二象限,且∠AOC =5π6,=2+(R)OC OA OB λλ-∈,则λ=( ).A .-12B .12C .-1D .1二、填空题(本大题共3小题,每小题6分,共18分) 7.两点等分单位圆时,有关系为sin α+sin(π+α)=0;三点等分单位圆时,有关系为sin α+sin ⎝ ⎛⎭⎪⎫α+2π3+sin ⎝⎛⎭⎪⎫α+4π3=0.由此可以推知:四点等分单位圆时的相应正确关系为__________.8.已知向量a ,b 满足|b |=2,a =(6,-8),a 在b 方向上的投影是-5,则a 与b 的夹角为__________.9.在四边形ABCD 中,()=1,1AB DC =,113···||||||BA BC BD BA BC BD +=,则四边形ABCD 的面积为__________.三、解答题(本大题共3小题,共46分.解答应写出必要的文字说明、证明过程或演算步骤)10.(本小题满分15分)已知函数()11335x x f x --=,()11335x x g x -+=.(1)证明f (x )是奇函数;(2)分别计算f (4)-5f (2)g (2),f (9)-5f (3)g (3)的值,由此概括出涉及函数f (x )和g (x )对所有不等于0的实数x 都成立的一个等式,并证明.11.(本小题满分15分)已知向量a =(cos θ,sin θ),θ∈[0,π],向量b =(3,-1).(1)若a ⊥b ,求θ的值;(2)若|2a -b |<m 恒成立,求实数m 的取值范围.12.(本小题满分16分)已知向量a =(cos θ,sin θ)和b =(2-sin θ,cos θ),θ∈⎣⎢⎡⎦⎥⎤11π12,17π12. (1)求|a +b |的最大值;(2)若|a +b |=4105,求sin 2θ的值.参考答案一、选择题1.D 解析:∵3+i 1-i =(3+i)(1+i)(1-i)(1+i)=3+3i +i +i22=1+2i ,∴选D.2.D 解析:i =1,s =2; s =2-1=1,i =1+2=3; s =1-3=-2,i =3+2=5; s =-2-5=-7,i =5+2=7.因输出s 的值为-7,循环终止,故判断框内应填“i <6?”,故选D. 3.D4.C 解析:∵|a -b |2=(a -b )2=20,∴|a|2+|b|2-2a·b =20.(*)又a =(1,2),a·b =5,∴(*)式可化为5+|b |2-10=20,∴|b |2=25,∴|b |=5.5.A 解析:由“第n 行有n 个数且两端的数均为1n (n ≥2)”可知,第7行第1个数为17,由“其余每个数是它下一行左右相邻两数的和”可知,第7行第2个数为16-17=142,同理,第7行第3个数为130-142=1105,第7行第4个数为160-1105=1140.6.B 解析:如图所示:∠AOC =5π6,根据三角函数的定义,可设C ⎝ ⎛⎭⎪⎫-32r ,12r .∵=2+OC OA OB λ-,∴⎝ ⎛⎭⎪⎫-32r ,12r =(-2,0)+(λ,3λ),∴⎩⎪⎨⎪⎧-32r =λ-2,12r =3λ,解得λ=12.二、填空题7.sin α+sin ⎝ ⎛⎭⎪⎫α+π2+sin(α+π)+sin ⎝⎛⎭⎪⎫α+3π2=0 解析:由类比推理可知,四点等分单位圆时,α与α+π的终边互为反向延长线,α+π2与α+3π2的终边互为反向延长线,如图.8.120° 解析:由题意得,|a |·cos〈a ,b 〉=-5,即cos 〈a ,b 〉=-12,∴〈a ,b 〉=120°.9. 3 解析:由AB DC ==(1,1),可得|=||=2AB DC 且四边形ABCD 是平行四边形,再由113···||||||BA BC BD BA BC BD +=可知D 在∠ABC 的角平分线上,且以BA 及BC 上单位边长为边的平行四边形的一条对角线长PB =3,因此∠ABC =π3,所以AB =BC ,S ▱ABCD =AB ·BC ·sin∠ABC =2×2sin π3= 3.三、解答题10.(1)证明:f (x )的定义域为(-∞,0)∪(0,+∞), 又11113333()()()()55x x x x f x f x -------==-=-,故f (x )是奇函数.(2)解:计算知f (4)-5f (2)g (2)=0,f (9)-5f (3)g (3)=0,于是猜测f (x 2)-5f (x )g (x )=0(x ∈R 且x ≠0).证明:()()()2211113333332550555x x x x x x f x f x g x -----+-⨯⋅=-=.11.解:(1)∵a ⊥b ,∴3cos θ-sin θ=0,得tan θ= 3.又θ∈[0,π],∴θ=π3.(2)∵2a -b =(2cos θ-3,2sin θ+1),∴|2a -b |2=(2cos θ-3)2+(2sin θ+1)2=8+8⎝ ⎛⎭⎪⎫12sin θ-32cos θ=8+8sin ⎝ ⎛⎭⎪⎫θ-π3. 又θ∈[0,π],∴θ-π3∈⎣⎢⎡⎦⎥⎤-π3,2π3.∴sin ⎝ ⎛⎭⎪⎫θ-π3∈⎣⎢⎡⎦⎥⎤-32,1. ∴|2a -b |2的最大值为16.∴|2a -b |的最大值为4. 又|2a -b |<m 恒成立,∴m >4.12.解:(1)a +b =(cos θ-sin θ+2,cos θ+sin θ), |a +b |=(cos θ-sin θ+2)2+(cos θ+sin θ)2=4+22(cos θ-sin θ)=4+4cos ⎝⎛⎭⎪⎫θ+π4=21+cos ⎝⎛⎭⎪⎫θ+π4. ∵θ∈⎣⎢⎡⎦⎥⎤11π12,17π12,∴7π6≤θ+π4≤5π3, ∴-32≤cos ⎝ ⎛⎭⎪⎫θ+π4≤12. ∴|a +b |max = 6.(2)由已知|a +b |=4105,得cos ⎝⎛⎭⎪⎫θ+π4=35,sin 2θ=-cos 2⎝⎛⎭⎪⎫θ+π4 =1-2cos 2⎝ ⎛⎭⎪⎫θ+π4=1-2×925=725.。
高考数学(理科)二轮专题:第一篇专题二第2练 平面向量、复数

第2练 平面向量、复数(限时45分钟,满分80分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2019·兰州二诊)复数z =(1+i)2,则|z |= A .0B .1C .2D .3解析 由题得z =2i ,所以|z |=2.故选C. 答案 C2.(2019·长春期末)(2+2i)(1-2i)= A .4-2iB .-2iC .4+2iD.2i解析 由题意,根据复数的运算(2+2i)(1-2i)=2+2-2i =4-2i.故选A. 答案 A3.(2019·全国卷Ⅱ)设z =i(2+i),则z -= A .1+2iB .-1+2iC .1-2iD .-1-2i解析 z =i(2+i)=2i +i 2=-1+2i ,所以z -=-1-2i.故选D. 答案 D4.(2019·全国卷Ⅰ)设复数|z -i|=1,z 在复平面内对应的点为(x ,y ),则 A .(x +1)2+y 2=1 B .(x -1)2+y 2=1 C .x 2+(y -1)2=1D .x 2+(y +1)2=1解析 设z =x +y i ,故而|z -i|=|x +(y -1)i|=x 2+(y -1)2=1,化简得x 2+(y -1)2=1.故选C.答案 C5.(2019·全国卷Ⅱ)已知向量a =(2,3),b =(3,2),则|a -b |= A. 2B .2C .5 2D .50解析 由已知a -b =(2,3)-(3,2)=(-1,1),所以|a -b |=(-1)2+12= 2.故选A.答案 A6.(2019·昆明一检)设向量a =(x -1,x ),b =(-1,2),若a ∥b ,则x = A .-32B .-1C.23D.32解析 ∵a ∥b ,∴2(x -1)+x =0,∴ x =23.故选C.答案 C7.(2019·全国卷Ⅰ)已知非零向量a ,b 满足|a |=2|b |,且(a -b )⊥b ,则a 和b 的夹角为 A.π6B.π3C.2π3D.5π6解析 ∵(a -b )⊥b ,∴(a -b )·b =a ·b -b 2=|a |·|b |cos θ-|b |2=0,将|a |=2|b |代入可得cosθ=12,即夹角为π3.故选B.答案 B8.(2019·合肥质检)若向量a ,b 的夹角为120°,|a |=1,|a -2b |=7,则|b |= A.12B.72C .1D .2解析 因为|a -2b |2=|a |2+4|b |2-4|a ||b |cos 〈a ,b 〉, 又〈a ,b 〉=120°,|a |=1,|a -2b |=7,所以7=1+4|b |2+2|b |,解得|b |=-32(舍去)或|b |=1.故选C.答案 C9.(2019·烟台二模)已知a ,b 均为单位向量,其夹角为θ,则“θ∈⎝⎛⎭⎫π3,π”是“|a-b |>1”的A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件解析 因为|a -b |>1⇒(a -b )2>1⇒a 2-2a ·b +b 2>1⇒1-2×1×1cos θ+1>1⇒cos θ<12⇒θ∈⎝⎛⎦⎤π3,π,所以“θ∈⎝⎛⎭⎫π3,π”是“|a -b |>1”的充分不必要条件.故选B. 答案 B10.(2019·晋城二模)已知向量a ,b 满足2a +b =(1,2m ),b =(1,m ),且a 在b 方向上的投影是255,则实数m =A .士2B .2C .± 5D. 5解析 因为向量a ,b 满足2a +b =(1,2m ),b =(1,m ),所以a =⎝⎛⎭⎫0,m 2,a ·b =m 22,|b |(|a |cos θ)=1+m 2·255=a ·b =m 22,所以5m 4-16m 2-16=0,即(5m 2+4)(m 2-4)=0,解得m =±2.故选A.答案 A11.(2019·长春质监)已知向量a =(cos θ-2,sin θ),其中θ∈R ,则|a |的最小值为 A .1B .2C. 5D .3解析 因为a =(cos θ-2,sin θ),所以|a |=(cos θ-2)2+sin 2θ=1-4cos θ+4 =5-4cos θ,因为θ∈R ,所以-1≤cos θ≤1, 故|a |的最小值为5-4=1.故选A. 答案 A12.(2019·南昌二模)已知△ABC 中,AB =2,B =π4,C =π6,点P 是边BC 的中点,则AP →·BC →等于A .1B .2C .3D .4解析 在△ABC 中,由正弦定理a sin A =b sin B =c sin C 得AB sin C =AC sin B ,即212=AC22,解得AC=22,因为AP →=AB →+AC →2,BC →=AC →-AB →,所以AP →·BC →=AB →+AC →2·(AC →-AB →)=12(AC →2-AB →2)=12(8-4)=2.故选B.答案 B二、填空题(本大题共4小题,每小题5分,共20分) 13.(2019·宁德质检)复数z =1+2i1-i的实部为________. 解析 复数z =1+2i 1-i =(1+2i )(1+i )(1-i )(1+i )=-1+3i2=-12+32i ,则复数z 的实部为-12.答案 -1214.(2019·开封三模)设向量a =(x ,x +1),b =(1,2),且a ∥b ,则x =________. 解析 由题得2x -(x +1)=0,所以x =1. 答案 115.(2019·石家庄二模)在平行四边形ABCD 中,已知AB =1,AD =2,∠BAD =60°,若CE →=ED →,DF →=2FB →,则AE →·AF →=________.解析 由题意,如图所示,设AB →=a ,AD →=b ,则|a |=1,|b |=2,又由CE →=ED →,DF →=2FB →,所以E 为CD 的中点,F 为BD 的三等分点, 则AE →=b +12a ,AF →=b +23(a -b )=23a +13b ,所以AE →·AF →=⎝⎛⎭⎫12a +b ·⎝⎛⎭⎫23a +13b =13a 2+56a ·b +13b 2=13×12+56×1×2cos 60°+13×22=52. 答案 5216.(2019·泰安二模)如图,在△ABC 中,∠BAC =π3,AD →=2DB →,P 为CD 上一点,且满足AP →=mAC →+12AB →,若△ABC 的面积为23,则|AP →|的最小值为________.解析 因为△ABC 的面积为23, 所以12|AB ||AC |sin A =23,∴12|AB ||AC |sin π3=23,|AB ||AC |=8, 因此AB →·AC →=|AB →||AC →|cos π3=4,因为AP →=mAC →+12AB →=mAC →+34AD →,所以m +34=1,m =14因此|AP →|2=⎪⎪⎪⎪14AC →+12AB →2=116AC →2+14AB →2+14AC →·AB →=116|AC →|2+14|AB →|2+1≥2×14|AC →|·12|AB →|+1=3, 当且仅当2|AC →|=|AB →|=4时取等号 即|AP →|≥3,|AP →|的最小值为 3. 答案 3。
高考数学二轮复习小题专项练习(二)平面向量复数与框图理

高考数学二轮复习小题专项练习(二)平面向量复数与框图理一、选择题:本大题共12小题,每题5分,共60分.在每题给出的四个选项中,只要一项为哪一项契合标题要求的.1.[2021·成都第三次诊断性检测]假定双数z =a +i 1-i(i 是虚数单位)为纯虚数,那么实数a 的值为( )A .-2B .-1C .1D .22.[2021·银川一中第二次模拟考试]假定两个单位向量a ,b 的夹角为120°,那么|2a +b |=( )A .2B .3C. 2D. 33.[2021·合肥市高三第三次教学质量检测]运转如下图的顺序框图,那么输入的s 等于( )A .-10B .-3C .3D .14.[2021·山东沂水期中]假定双数z =i 20201-i2(i 为虚数单位),那么z 的共轭双数z -=( )A .1+iB .iC .-12i D.12i 5.[2021·百校联盟四月联考]设双数z 满足z -i z=3+i ,那么z -=( ) A.15+25i B .-15+25i C.15-25i D .-15-25i 6.[2021·河南新乡第三次模拟测试]双数z 1,z 2在复平面内对应的点区分为(2,-1),(0,-1),那么z 1z 2+|z 2|=( )A .2+2iB .2-2iC .-2+iD .-2-i7.[2021·宁夏六盘山高三年级第三次模拟]执行下面的顺序框图,那么输入K 的值为( )A .99B .98C .100D .1018.[2021·安徽池州一中5月月考]设点O 在△ABC 的外部,且有AD →=32(OB →+OC →),那么△ABC 的面积与△BOC 的面积之比为( )A .3 B.13C .2 D.129.[2021·银川一中第二次模拟]20世纪70年代,盛行一种游戏——角谷猜想,规那么如下:恣意写出一个自然数n ,依照以下的规律停止变换:假设n 是个奇数,那么下一步变成3n +1;假设n 是个偶数,那么下一步变成n 2,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后肯定会落在谷底,更准确地说是落入底部的循环,而永远也跳不出这个圈子.以下顺序框图就是依据这个游戏而设计的,假设输入的i 值为6,那么输入的n 值为( )A .5B .16C .5或32D .4或5或3210.[2021·河南洛阳第三次统考]在△ABC 中,点P 满足BP →=2PC →,过点P 的直线与AB ,AC 所在直线区分交于点M ,N ,假定AM →=mAB →,AN →=nAC →(m >0,n >0),那么m +2n 的最小值为( )A .3B .4C.83D.10311.[2021·成都毕业班第三次诊断检测]P 为△ABC 所在平面内一点,AB →+PB →+PC →=0,|PC →|=|PB →|=|AB →|=2,那么△PBC 的面积等于( ) A. 3 B .2 3C .3 3D .4 312.[2021·山东日照高三校际结合考试]在△ABC 中,点D 是线段BC 上恣意一点,M是线段AD 的中点,假定存在实数λ和μ,使得BM →=λAB →+μAC →,那么λ+μ=( )A .2B .-2C.12 D .-12二、填空题:本大题共4小题,每题5分,共20分,把答案填在题中的横线上.13.[2021·内蒙古北重三中第九次调研]双数z =1+i +i 2+…+i 10,那么双数z 在复平面内相应的点为________.14.[2021·江西赣州顺应性考试]|a |=1,|b |=2,a ·(b -a )=0,那么向量a 与b 的夹角为________.15.[2021·哈尔滨三中模拟]我国现代数学著作«孙子算经»中有这样一道算术题:〝今有物不知其数,三三数之剩一,五五数之剩三,七七数之剩六,问物几何?〞人们把此类标题称为〝中国剩余定理〞.假定正整数N 除以正整数m 后的余数为n ,那么记为N ≡n (mod m ),例如10≡2(mod4).现将该效果以顺序框图给出,执行该顺序框图,那么输入的n 等于________.16.[2021·江苏东台中学质量监测]向量a ,b ,c 满足a +b +c =0,且a 与b 的夹角的正切值为-12,b 与c 的夹角的正切值为-13,|b |=1,那么a ·c 的值为________.。
2019年高考数学二轮复习专题一常考小题点1.4平面向量题专项练课件文

D 重合,
∴点 D 在 CB 的延长线上.故选 D.
C.2
D.54
解析 ∵a=(m,2),b=(2,-1),且a⊥b,∴a·b=2m-2=0,∴m=1, ∴a=(1,2),2a-b=(0,5),|2a-b|=5. 又a+b=(3,1),a·(a+b)=1×3+2×1=5,
∴ |2������-������|
������·(������+������)
13.(2018全国Ⅲ,文13)已知向量a=(1,2),b=(2,-2),c=(1,λ).若
1
c∥(2a+b),则λ=
2.
解析 2a+b=2(1,2)+(2,-2)=(4,2),c=(1,λ),
由c∥(2a+b),得4λ-2=0,得λ=
1 2
.
14.(2018北京,文9)设向量a=(1,0),b=(-1,m).若a⊥(ma-b),则
∴由 p·a=12,得|p|×1×cosπ3 = 12,即|p|=1.
12.(2018 浙江,9)已知 a,b,e 是平面向量,e 是单位向量.若非零向量 a
与 e 的夹角为π3,向量 b 满足 b2-4e·b+3=0,则|a-b|的最小值是( A )
A. 3-1
B. 3+1
C.2
D.2- 3
2019高考数学(理)通用版二轮精准提分练习:第一篇第2练 复数与平面向量Word版含解析

第2练 复数与平面向量[明晰考情] 1.命题角度:复数的四则运算和几何意义;以平面图形为背景,考查平面向量的线性运算、平面向量的数量积.2.题目难度:复数题目为低档难度,平面向量题目为中低档难度.考点一 复数的概念与四则运算要点重组 (1)复数:形如a +b i(a ,b ∈R )的数叫做复数,其中a ,b 分别是它的实部和虚部,i 为虚数单位.若b =0,则a +b i 为实数;若b ≠0,则a +b i 为虚数;若a =0且b ≠0,则a +b i 为纯虚数.(2)复数相等:a +b i =c +d i ⇔a =c 且b =d (a ,b ,c ,d ∈R ). (3)共轭复数:a +b i 与c +d i 共轭⇔a =c ,b =-d (a ,b ,c ,d ∈R ).(4)复数的模:向量OZ →的模r 叫做复数z =a +b i(a ,b ∈R )的模,记作|z |或|a +b i|,即|z |=|a +b i|=r =a 2+b 2(r ≥0,r ∈R ).(5)复数的四则运算类似于多项式的四则运算,复数除法的关键是分子分母同乘分母的共轭复数.1.(2018·全国Ⅰ)设z =1-i1+i +2i ,则|z |等于( )A.0B.12 C.1 D. 2答案 C解析 ∵z =1-i 1+i +2i =(1-i )2(1+i )(1-i )+2i =-2i2+2i =i ,∴|z |=1.故选C.2.已知a ,b ∈R ,i 是虚数单位.若a -i 与2+b i 互为共轭复数,则(a +b i)2等于( ) A.5-4i B.5+4i C.3-4i D.3+4i 答案 D解析 由已知得a =2,b =1,即a +b i =2+i , ∴(a +b i)2=(2+i)2=3+4i.故选D.3.已知i 是虚数单位,a ,b ∈R ,则“a =b =1”是“(a +b i)2=2i ”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件答案 A解析 当a =b =1时,(a +b i)2=(1+i)2=2i , 反过来(a +b i)2=a 2-b 2+2ab i =2i , 则a 2-b 2=0,2ab =2,解得a =1,b =1或a =-1,b =-1.故“a =b =1”是“(a +b i)2=2i ”的充分不必要条件,故选A.4.复数(m 2-3m -4)+(m 2-5m -6)i 是虚数,则实数m 的取值范围是__________. 答案 {m |m ≠6且m ≠-1}解析 根据题意知,m 2-5m -6≠0,即(m -6)(m +1)≠0,所以m ≠6且m ≠-1. 考点二 复数的几何意义 要点重组 (1)复数z =a +b i 一一对应复平面内的点Z (a ,b )(a ,b ∈R ). (2)复数z =a +b i(a ,b ∈R )一一对应平面向量OZ →.5.设a ∈R ,若(1+3i)(1+a i)∈R (i 是虚数单位),则a 等于( ) A.3 B.-3 C.13 D.-13答案 B解析 (1+3i)(1+a i)=1+a i +3i -3a , ∵(1+3i)(1+a i)∈R ,∴虚部为0,则a +3=0,∴a =-3.6.已知z =(m +3)+(m -1)i 在复平面内对应的点在第四象限,则实数m 的取值范围是( ) A.(-3,1) B.(-1,3) C.(1,+∞) D.(-∞,-3) 答案 A解析 由复数z =(m +3)+(m -1)i 在复平面内对应的点在第四象限,得⎩⎪⎨⎪⎧m +3>0,m -1<0,解得-3<m <1,故选A.7.如图,在复平面内,复数z 1,z 2对应的向量分别是OA →,OB →,则|z 1+z 2|=_______.答案 2解析 由题意知,z 1=-2-i ,z 2=i , ∴z 1+z 2=-2,∴|z 1+z 2|=2.8.已知复数z =i +i 2+i 3+…+i 2 0191+i ,则复数z 在复平面内对应的点位于第______象限.答案 二解析 因为i 4n +k =i k (n ∈Z ),且i +i 2+i 3+i 4=0,所以i +i 2+i 3+…+i 2 019=i +i 2+i 3=i -1-i =-1,所以z =-11+i =-(1-i )(1+i )(1-i )=-12(1-i)=-12+12i ,对应的点为⎝⎛⎭⎫-12,12,在第二象限. 考点三 平面向量的线性运算方法技巧 (1)向量加法的平行四边形法则:共起点;三角形法则:首尾相连;向量减法的三角形法则:共起点连终点,指向被减.(2)已知O 为平面上任意一点,则A ,B ,C 三点共线的充要条件是存在s ,t ,使得OC →=sOA →+tOB →,且s +t =1,s ,t ∈R .(3)证明三点共线问题,可转化为向量共线解决.9.(2018·全国Ⅰ)在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB →等于( ) A.34AB →-14AC → B.14AB →-34AC →C.34AB →+14AC →D.14AB →+34AC → 答案 A解析 作出示意图如图所示.EB →=ED →+DB →=12AD →+12CB →=12×12(AB →+AC →)+12(AB →-AC →)=34AB →-14AC →.故选A.10.如图,在△ABC 中,N 是AC 边上一点,且AN →=12NC →,P 是BN 上的一点,若AP →=mAB→+29AC →,则实数m 的值为( )A.19B.13 C.1 D.3 答案 B解析 ∵AN →=12NC →,∴AN →=13AC →,∴AP →=mAB →+29AC →=mAB →+23AN →.又B ,N ,P 三点共线,∴m +23=1,∴m =13.11.如图,在正方形ABCD 中,M ,N 分别是BC ,CD 的中点,若AC →=λAM →+μBN →,则λ+μ等于( )A.2B.83C.65D.85答案 D解析 方法一 如图以AB ,AD 为坐标轴建立平面直角坐标系,设正方形边长为1,AM →=⎝⎛⎭⎫1,12,BN →=⎝⎛⎭⎫-12,1,AC →=(1,1).∵AC →=λAM →+μBN →=λ⎝⎛⎭⎫1,12+μ⎝⎛⎭⎫-12,1=⎝⎛⎭⎫λ-μ2,λ2+μ, ∴⎩⎨⎧λ-μ2=1,λ2+μ=1,解得⎩⎨⎧λ=65,μ=25,故λ+μ=85.方法二 以AB →,AD →作为基底, ∵M ,N 分别为BC ,CD 的中点,∴AM →=AB →+BM →=AB →+12AD →,BN →=BC →+CN →=AD →-12AB →,∴AC →=λAM →+μBN →=⎝⎛⎭⎫λ-μ2AB →+⎝⎛⎭⎫λ2+μAD →, 又AC →=AB →+AD →,因此⎩⎨⎧λ-μ2=1,λ2+μ=1,解得⎩⎨⎧λ=65,μ=25.所以λ+μ=85.12.已知a ,b 为单位向量,且a ⊥(a +2b ),则|a -2b |=________. 答案7解析 由a ⊥(a +2b )得a ·(a +2b )=0,∴|a |2+2a ·b =0,得2a ·b =-1,∴|a -2b |2=(a -2b )2=a 2-4a ·b +4b 2=|a |2-4a ·b +4|b |2=1+2+4=7,∴|a -2b |=7. 考点四 平面向量的数量积方法技巧 (1)向量数量积的求法:定义法,几何法(利用数量积的几何意义),坐标法. (2)向量运算的两种基本方法:基向量法,坐标法.13.已知向量a =(1,2),b =(1,0),c =(3,4),若λ为实数,(b +λa )⊥c ,则λ的值为( ) A.-311 B.-113 C.12 D.35答案 A解析 b +λa =(1,0)+λ(1,2)=(1+λ,2λ),又c =(3,4),且(b +λa )⊥c ,所以(b +λa )·c =0,即3(1+λ)+2λ×4=3+3λ+8λ=0,解得λ=-311.14.(2017·全国Ⅱ)已知△ABC 是边长为2的等边三角形,P 为平面ABC 内一点,则P A →·(PB →+PC →)的最小值是( ) A.-2 B.-32 C.-43 D.-1答案 B解析 方法一 (解析法)建立坐标系如图①所示,则A ,B ,C 三点的坐标分别为A (0,3),B (-1,0),C (1,0).设P 点的坐标为(x ,y ),图①则P A →=(-x ,3-y ), PB →=(-1-x ,-y ), PC →=(1-x ,-y ),∴P A →·(PB →+PC →)=(-x ,3-y )·(-2x ,-2y ) =2(x 2+y 2-3y )=2⎣⎡⎦⎤x 2+⎝⎛⎭⎫y -322-34≥2×⎝⎛⎭⎫-34=-32.当且仅当x =0,y =32时,P A →·(PB →+PC →)取得最小值,最小值为-32.故选B. 方法二 (几何法)如图②所示,PB →+PC →=2PD →(D 为BC 的中点),则P A →·(PB →+PC →)=2P A →·PD →.图②要使P A →·PD →最小,则P A →与PD →方向相反,即点P 在线段AD 上,则(2P A →·PD →)min =-2|P A →||PD →|, 问题转化为求|P A →||PD →|的最大值.又当点P 在线段AD 上时,|P A →|+|PD →|=|AD →|=2×32=3,∴|P A →||PD →|≤⎝⎛⎭⎪⎫|P A →|+|PD →|22=⎝⎛⎭⎫322=34, ∴[P A →·(PB →+PC →)]min =(2P A →·PD →)min =-2×34=-32.故选B.15.(2016·全国Ⅲ)已知向量BA →=⎝⎛⎭⎫12,32,BC →=⎝⎛⎭⎫32,12,则∠ABC 等于( )A.30°B.45°C.60°D.120° 答案 A解析 |BA →|=1,|BC →|=1,cos ∠ABC =BA →·BC →|BA →||BC →|=32.又∵0°≤∠ABC ≤180°, ∴∠ABC =30°.16.(2016·浙江)已知向量a ,b ,|a |=1,|b |=2.若对任意单位向量e ,均有|a ·e |+|b ·e |≤6,则a ·b 的最大值是________. 答案 12解析 由已知可得6≥|a ·e |+|b ·e |≥|a ·e +b ·e |=|(a +b )·e |, 由于上式对任意单位向量e 都成立. ∴6≥|a +b |成立.∴6≥(a +b )2=a 2+b 2+2a ·b =12+22+2a ·b . 即6≥5+2a ·b ,∴a ·b ≤12.∴a ·b 的最大值为12.1.(2017·全国Ⅰ)设有下面四个命题: p 1:若复数z 满足1z ∈R ,则z ∈R ;p 2:若复数z 满足z 2∈R ,则z ∈R ; p 3:若复数z 1,z 2满足z 1z 2∈R ,则z 1=z 2; p 4:若复数z ∈R ,则z ∈R . 其中的真命题为( )A.p 1,p 3B.p 1,p 4C.p 2,p 3D.p 2,p 4 答案 B解析 设z =a +b i(a ,b ∈R ),z 1=a 1+b 1i(a 1,b 1∈R ),z 2=a 2+b 2i(a 2,b 2∈R ).对于p 1,若1z ∈R ,即1a +b i =a -b i a 2+b 2∈R ,则b =0,即z =a +b i =a ∈R ,所以p 1为真命题;对于p 2,若z 2∈R ,即(a +b i)2=a 2+2ab i -b 2∈R ,则ab =0.当a =0,b ≠0时,z =a +b i =b i ∉R ,所以p 2为假命题;对于p 3,若z 1z 2∈R ,即(a 1+b 1i)(a 2+b 2i)=(a 1a 2-b 1b 2)+(a 1b 2+a 2b 1)i ∈R ,则a 1b 2+a 2b 1=0.而z 1=z 2,即a 1+b 1i =a 2-b 2i ⇔a 1=a 2,b 1=-b 2.因为a 1b 2+a 2b 1=0⇏a 1=a 2,b 1=-b 2,所以p 3为假命题;对于p 4,若z ∈R ,即a +b i ∈R ,则b =0⇒z =a -b i =a ∈R ,所以p 4为真命题.故选B. 2.在△ABC 中,有如下命题,其中正确的是________.(填序号) ①AB →-AC →=BC →; ②AB →+BC →+CA →=0;③若(AB →+AC →)·(AB →-AC →)=0,则△ABC 为等腰三角形; ④若AB →·BC →>0,则△ABC 为锐角三角形. 答案 ②③解析 在△ABC 中,AB →-AC →=CB →,①错误;若AB →·BC →>0,则B 是钝角,△ABC 是钝角三角形,④错误.3.已知向量a =(1,2),b =(1,1),且a 与a +λb 的夹角为锐角,则实数λ的取值范围是__________.答案 ⎝⎛⎭⎫-53,0∪()0,+∞ 解析 a +λb =(1+λ,2+λ),由a ·(a +λb )>0,可得λ>-53.又a 与a +λb 不共线,∴λ≠0. 故λ>-53且λ≠0.解题秘籍 (1)复数的概念是考查的重点,虚数及纯虚数的意义要把握准确.(2)复数的运算中除法运算是高考的热点,运算时要分母实数化(分子分母同乘以分母的共轭复数),两个复数相等的条件在复数运算中经常用到.(3)注意向量夹角的定义和范围.在△ABC 中,AB →和BC →的夹角为π-B ;向量a ,b 的夹角为锐角要和a ·b >0区别开来(不要忽视向量共线情况,两向量夹角为钝角类似处理).1.设i 是虚数单位,则复数i 3-2i 等于( )A.-iB.-3iC.iD.3i 答案 C解析 i 3-2i =-i -2ii2=-i +2i =i.故选C.2.(2017·山东)已知a ∈R ,i 是虚数单位.若z =a +3i ,z ·z =4,则a 等于( ) A.1或-1 B.7或-7 C.- 3 D. 3 答案 A解析 ∵z ·z =4,∴|z |2=4,即|z |=2. ∵z =a +3i ,∴|z |=a 2+3=2,∴a =±1. 故选A.3.设i 是虚数单位,则复数2i1-i 在复平面内所对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限 答案 B 解析2i 1-i =2i (1+i )(1-i )(1+i )=2i (i +1)2=-1+i ,由复数的几何意义知,-1+i 在复平面内的对应点为(-1,1),该点位于第二象限,故选B.4.(2018·安庆模拟)在△ABC 中,点D 是边BC 上任意一点, M 是线段AD 的中点,若存在实数λ和μ,使得BM →=λAB →+μAC →,则λ+μ等于( ) A.12 B.-12 C.2 D.-2 答案 B解析 因为点D 在边BC 上,所以存在t ∈R , 使得BD →=tBC →=t (AC →-AB →).因为M 是线段AD 的中点,所以BM →=12(BA →+BD →)=12(-AB →+tAC →-tAB →)=-12(t +1)AB →+12tAC →.又BM →=λAB →+μAC →,所以λ=-12(t +1),μ=12t ,所以λ+μ=-12.5.“复数z =3+a ii 在复平面内对应的点在第三象限”是“a ≥0”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 D解析 由题意得z =a -3i ,若z 在复平面内对应的点在第三象限,则a <0,故选D.6.(2018·通州期末)△ABC 的外接圆的圆心为O ,半径为1,若OA →+AB →+OC →=0,且|OA →|=|AB →|,则CA →·CB →等于( ) A.32 B.3 C.3 D.2 3 答案 C解析 ∵OA →+AB →+OC →=0,∴OB →=-OC →,故点O 是BC 的中点,且△ABC 为直角三角形, 又△ABC 的外接圆的半径为1,|OA →|=|AB →|,∴BC =2,AB =1,CA =3,∠BCA =30°, ∴CA →·CB →=|CA →||CB →|·cos 30°=3×2×32=3.7.已知a >0,⎪⎪⎪⎪a +i i =2,则a 等于( )A.2B. 3C. 2D.1 答案 B解析 ⎪⎪⎪⎪a +i i =⎪⎪⎪⎪-a i +11=(-a )2+1=2,即a 2=3.又∵a >0,∴a = 3.8.(2018·浙江)已知a ,b ,e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为π3,向量b满足b 2-4e ·b +3=0,则|a -b |的最小值是( ) A.3-1 B.3+1 C.2 D.2- 3答案 A解析 ∵b 2-4e ·b +3=0, ∴(b -2e )2=1, ∴|b -2e |=1.如图所示,把a ,b ,e 的起点作为公共点O ,以O 为坐标原点,向量e 所在直线为x 轴,则b 的终点在以点M (2,0)为圆心,1为半径的圆上,|a -b |就是线段AB 的长度.要求|AB |的最小值,就是求圆上动点到定直线的距离的最小值,也就是圆心M 到直线OA 的距离减去圆的半径长,因此|a -b |的最小值为3-1. 故选A.9.设x ,y 为实数,且x 1-i +y 1-2i =51-3i ,则x +y =______.答案 4解析 由题意得x 2(1+i)+y 5(1+2i)=510(1+3i),∴(5x +2y )+(5x +4y )i =5+15i ,∴⎩⎪⎨⎪⎧ 5x +2y =5,5x +4y =15,∴⎩⎪⎨⎪⎧x =-1,y =5,∴x +y =4. 10.若点M 是△ABC 所在平面内的一点,且满足5AM →=AB →+3AC →,则△ABM 与△ABC 的面积之比为________. 答案 35解析 设AB 的中点为D ,由5AM →=AB →+3AC →,得3AM →-3AC →=2AD →-2AM →,即3CM →=2MD →.故C ,M ,D 三点共线,如图所示,MD →=35CD →, 也就是△ABM 与△ABC 对于边AB 的两高之比为3∶5,则△ABM 与△ABC 的面积之比为35. 11.(2018·德阳诊断)已知i 为虚数单位,实数x ,y 满足(x +2i)i =y -i ,则|x -y i|=______. 答案 5解析 ∵(x +2i)i =y -i ,∴-2+x i =y -i ,∴⎩⎪⎨⎪⎧x =-1,y =-2, 则|x -y i|=|-1+2i|= 5.12.已知AB →⊥AC →,|AB →|=1t ,|AC →|=t ,若点P 是△ABC 所在平面内的一点,且AP →=AB →|AB →|+4AC →|AC →|,则PB →·PC →的最大值为________.答案 13解析 以点A 为坐标原点,AB →,AC →所在直线分别为x 轴,y 轴,建立如图所示的平面直角坐标系,则A (0,0),B ⎝⎛⎭⎫1t ,0,C (0,t ),AB →=⎝⎛⎭⎫1t ,0,AC →=(0,t ), AP →=AB →|AB →|+4AC →|AC →|=t ⎝⎛⎭⎫1t ,0+4t (0,t )=(1,4), ∴点P (1,4),则PB →·PC →=⎝⎛⎭⎫1t -1,-4·(-1,t -4)=17-⎝⎛⎭⎫1t +4t ≤17-21t·4t =13, 当且仅当1t =4t ,即t =12时取“=”, ∴PB →·PC →的最大值为13.。
2019高考数学二轮复习 第一部分 送分专题 第2讲 平面向量练习 理

第2讲 平面向量一、选择题1.已知向量a ,b 不共线,c =ka +b (k ∈R),d =a -b .如果c ∥d ,那么( ) A .k =1且c 与d 同向 B .k =1且c 与d 反向 C .k =-1且c 与d 同向 D .k =-1且c 与d 反向解析:由c ∥d ,则存在λ使c =λd ,即ka +b =λa -λb ,∴(k -λ)a +(λ+1)b =0,又a 与b 不共线,∴k -λ=0,且λ+1=0, ∴k =-1,此时c =-a +b =-(a -b )=-d .故c 与d 反向,选D. 答案:D2.已知a 与b 是两个不共线向量,且向量a +λb 与-(b -3a )共线,则λ的值为( )A .1B .-1 C.13D .-13解析:由题意知a +λb =-k (b -3a )=-kb +3ka ,∴⎩⎪⎨⎪⎧3k =1,λ=-k ,解得⎩⎪⎨⎪⎧k =13,λ=-13.答案:D3.若向量a =(1,1),b =(1,-1),c =(-1,2),则c 等于( ) A .-12a +32bB.12a -32bC.32a -12b D .-32a +12b解析:设c =xa +yb ,则(-1,2)=x (1,1)+y (1,-1)=(x +y ,x -y ),∴⎩⎪⎨⎪⎧x +y =-1,x -y =2,解得⎩⎪⎨⎪⎧x =12,y =-32,则c =12a -32b .答案:B4.已知△ABC 的三个顶点A ,B ,C 及所在平面内一点P 满足PA →+PB →+PC →=AB →,则点P 与△ABC 的关系为( )A .P 在△ABC 内部B .P 在△ABC 外部 C .P 在边AB 上D .P 在边AC 上解析:由PA →+PB →+PC →=AB →=PB →-PA →,得2 PA →+PC →=0, ∴CP →=2 PA →,即CP →∥PA →,∴C 、P 、A 三点共线. 答案:D5.已知向量a ,b ,c 中任意两个都不共线,并且a +b 与c 共线,b +c 与a 共线,那么a +b +c 等于( ) A .a B .b C .cD .0解析:设a +b =λc ,b +c =μa ,则a -c =λc -μa , 所以(1+μ)a =(1+λ)c , 因为a ,c 不共线, 所以μ=λ=-1, 所以a +b +c =0.故选D. 答案:D6.设向量a ,b 满足|a |=|b |=1,a ·b =-12,则|a +2b |=( )A. 2B. 3C. 5D.7解析:|a +2b |2=a 2+4a ·b +4b 2=1+4×⎝ ⎛⎭⎪⎫-12+4=3,∴|a +2b |= 3. 答案:B7.设x ∈R ,向量a =(x,1),b =(1,-2),且a ⊥b ,则|a +b |=( ) A. 5 B.10 C .2 5D .10解析:∵a ⊥b ,∴a ·b =0,即x -2=0,x =2,∴a +b =(3,-1), ∴|a +b |=10. 答案:B8.已知向量a =(1,3),b =(3,m ),若向量a ,b 的夹角为π6,则实数m =( )A .2 3 B. 3 C .0D .- 3解析:a ·b =|a ||b |cos π6,则3+3m =2·9+m 2·32,(3+m )2=9+m 2,解得m = 3.答案:B9.已知△ABC 外接圆的半径为1,圆心为O .若|OA →|=|AB →|,且2 OA →+AB →+AC →=0,则CA →·CB →等于( ) A. 3 B .2 3 C.32D .3解析:因为2 OA →+AB →+AC →=0,所以(OA →+AB →)+(OA →+AC →)=0,即OB →+OC →=0,所以O 为BC 的中点,故△ABC 为直角三角形,∠A 为直角,又|OA |=|AB |,则△OAB 为正三角形,|AC →|=3,|AB →|=1,CA →与CB →的夹角为30°,由数量积公式可知CA →·CB →=3×2cos 30°=3×2×32=3.选D. 答案:D10.在△ABC 中,设AC →2-AB →2=2 AM →·BC →,那么动点M 的轨迹必经过△ABC 的( ) A .垂心 B .内心 C .外心D .重心解析:设BC 边中点为D ,∵AC →2-AB →2=2 AM →·BC →,∴(AC →+AB →)·(AC →-AB →)=2 AM →·BC →,即AD →·BC →=AM →·BC →,∴MD →·BC →=0,则MD →⊥BC →,即MD ⊥BC ,∴MD 为BC 的垂直平分线,∴动点M 的轨迹必经过△ABC 的外心,故选C. 答案:C11.若OP →=OA →+λ⎝ ⎛⎭⎪⎪⎫AB →|AB →|+AC →|AC →|(λ>0),则点P 的轨迹经过△ABC 的( )A .重心B .垂心C .外心D .内心解析:AB→|AB →|,AC→|AC →|分别表示与AB →,AC →方向相同的单位向量,记为AE →,AF →.以AE →,AF →为邻边作▱AEDF ,则▱AEDF 为菱形. ∴AD 平分∠BAC 且AB →|AB →|+AC→|AC →|=AD →.∴OP →=OA →+λ⎝ ⎛⎭⎪⎪⎫AB →|AB →|+AC →|AC →|=OA →+λ AD →.∴AP →=λ AD →.∵λ>0,∴点P 的轨迹为射线AD (不包括端点A ). ∴点P 的轨迹经过△ ABC 的内心. 答案:D12.已知|a |=2|b |≠0,且关于x 的函数f (x )=13x 3+12|a |x 2+a ·bx 在R 上有极值,则向量a 与b 的夹角的范围是( )A.⎣⎢⎡⎭⎪⎫0,π6B.⎝ ⎛⎦⎥⎤π6,πC.⎝⎛⎦⎥⎤π3,πD.⎝⎛⎭⎪⎫π3,23π解析:设a 与b 的夹角为θ. ∵f (x )=13x 3+12|a |x 2+a ·bx ,∴f ′(x )=x 2+|a |x +a ·b . ∵函数f (x )在R 上有极值,∴方程x 2+|a |x +a ·b =0有两个不同的实数根, 即Δ=|a |2-4a ·b >0, ∴a ·b <a 24, 又∵|a |=2|b |≠0,∴cos θ=a ·b |a ||b |<a 24a 22=12,即cos θ<12,又∵θ∈[0,π], ∴θ∈⎝ ⎛⎦⎥⎤π3,π,故选C. 答案:C 二、填空题13.已知向量a 与b 的夹角为60°,且a =(-2,-6),|b |=10,则a ·b =__________. 解析:由a =(-2,-6),得|a |=-22+-62=210,则a ·b =|a ||b |cos 60°=210·10·12=10.答案:1014.如图所示,已知∠B =30°,∠AOB =90°,点C 在AB 上,OC ⊥AB ,用OA →和OB →来表示向量OC →,则OC →等于__________.解析:根据三角形三边关系:AC →=14AB →,OC →=OA →+AC →=OA →+14AB →=OA →+14(OB →-OA →)=34OA →+14OB →.答案:34OA →+14OB →15.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,重心为G ,若a GA →+b GB →+33c GC →=0,则A =__________.解析:由G 为△ABC 的重心知GA →+GB →+GC →=0,则GC →=-GA →-GB →,因此a GA →+b GB →+33c (-GA →-GB →)=⎝ ⎛⎭⎪⎫a -33c GA →+⎝ ⎛⎭⎪⎫b -33c GB →=0,又GA →,GB →不共线,所以a -33c =b -33c =0,即a =b =33c .由余弦定理得cos A =b 2+c 2-a 22bc =c 22×33c2=32,又0<A <π,所以A =π6.答案:π616.已知正方形ABCD 的边长为2,点E 在边DC 上,且DE →=2 EC →,DF →=12(DC →+DB →),则BE →·DF→=__________.解析:如图,以B 为原点,BC 所在直线为x 轴,AB 所在直线为y 轴建立平面直角坐标系,则B (0,0),E ⎝ ⎛⎭⎪⎫2,23,D (2,2).由DF →=12(DC →+DB →),知F 为BC 的中点,则F (1,0),BE →=⎝ ⎛⎭⎪⎫2,23,DF →=(-1,-2), ∴BE →·DF →=-2-43=-103.10答案:-3。
2019年最新高考数学二轮复习 专题能力训练3 平面向量与复数 理(考试专用)

专题能力训练3 平面向量与复数一、能力突破训练1.设有下面四个命题p1:若复数z满足∈R,则z∈R;p2:若复数z满足z2∈R,则z∈R;p3:若复数z1,z2满足z1z2∈R,则z1=;p4:若复数z∈R,则∈R.其中的真命题为()A.p1,p3B.p1,p4C.p2,p3D.p2,p42.设a,b是两个非零向量,则下列结论一定成立的为()A.若|a+b|=|a|-|b|,则a⊥bB.若a⊥b,则|a+b|=|a|-|b|C.若|a+b|=|a|-|b|,则存在实数λ,使得b=λaD.若存在实数λ,使得b=λa,则|a+b|=|a|-|b|3.(2018全国Ⅲ,理2)(1+i)(2-i)=()A.-3-iB.-3+iC.3-iD.3+i4.在复平面内,若复数z的对应点与的对应点关于虚轴对称,则z=()A.2-iB.-2-iC.2+iD.-2+i5.已知向量a=(1,-1),b=(-1,2),则(2a+b)·a=()A.-1B.0C.1D.26.(2018浙江,4)复数(i为虚数单位)的共轭复数是 ()A.1+iB.1-iC.-1+iD.-1-i7.已知菱形ABCD的边长为a,∠ABC=60°,则=()A.-a2B.-a2C.a2D.a28.已知非零向量m,n满足4|m|=3|n|,cos<m,n>=.若n⊥(t m+n),则实数t的值为()A.4B.-4C.D.-9.如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=,I2=,I3=,则()A.I1<I2<I3B.I1<I3<I2C.I3<I1<I2D.I2<I1<I310.(2018全国Ⅲ,理13)已知向量a=(1,2),b=(2,-2),c=(1,λ).若c∥(2a+b),则λ= .11.在△ABC中,∠A=60°,AB=3,AC=2.若=2=λ(λ∈R),且=-4,则λ的值为.12.设a∈R,若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a= .13.已知a,b∈R,(a+b i)2=3+4i(i是虚数单位),则a2+b2= ,ab= .14.设D,E分别是△ABC的边AB,BC上的点,|AD|=|AB|,|BE|=|BC|.若=λ1+λ2(λ1,λ2为实数),则λ1+λ2的值为.二、思维提升训练15.在△ABC中,已知D是AB边上一点,+λ,则实数λ=()A.-B.-C.D.16.已知,||=,||=t.若点P是△ABC所在平面内的一点,且,则的最大值等于()A.13B.15C.19D.2117.已知两点M(-3,0),N(3,0),点P为坐标平面内一动点,且||·||+=0,则动点P(x,y)到点M(-3,0)的距离d的最小值为()A.2B.3C.4D.618.已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是,最大值是.19.在任意四边形ABCD中,E,F分别是AD,BC的中点,若=λ+μ,则λ+μ= .20.已知a∈R,i为虚数单位,若为实数,则a的值为.专题能力训练3平面向量与复数一、能力突破训练1.B解析p1:设z=a+b i(a,b∈R),则R,所以b=0,所以z∈R.故p1正确;p2:因为i2=-1∈R,而z=i∉R,故p2不正确;p3:若z1=1,z2=2,则z1z2=2,满足z1z2∈R,而它们实部不相等,不是共轭复数,故p3不正确;p4:实数的虚部为0,它的共轭复数是它本身,也属于实数,故p4正确.2.C解析设向量a与b的夹角为θ.对于A,可得cos θ=-1,因此a⊥b不成立;对于B,满足a⊥b 时|a+b|=|a|-|b|不成立;对于C,可得cos θ=-1,因此成立,而D显然不一定成立.3.D解析 (1+i)(2-i)=2+i-i2=3+i.4.D解析=2+i所对应的点为(2,1),它关于虚轴对称的点为(-2,1),故z=-2+i.5.C解析∵2a+b=(1,0),又a=(1,-1),∴(2a+b)·a=1+0=1.6.B解析=1+i,∴复数的共轭复数为1-i.7.D解析如图,设=a,=b.则=()=(a+b)·a=a2+a·b=a2+a·a·cos60°=a2+a2=a2.8.B解析由4|m|=3|n|,可设|m|=3k,|n|=4k(k>0),又n⊥(t m+n),所以n·(t m+n)=n·t m+n·n=t|m|·|n|cos<m,n>+|n|2=t×3k×4k+(4k)2=4tk2+16k2=0.所以t=-4,故选B.9.C解析由题图可得OA<AC<OC,OB<BD<OD,∠AOB=∠COD>90°,∠BOC<90°,所以I2=>0,I1=<0,I3=<0,且|I1|<|I3|,所以I3<I1<0<I2,故选C.10解析 2a+b=2(1,2)+(2,-2)=(4,2),c=(1,λ),由c∥(2a+b),得4λ-2=0,得λ=11解析=2,)=又=,∠A=60°,AB=3,AC=2,=-4,=3×2=3,()=-4, 即=-4,4-9+3=-4,即-5=-4,解得λ=12.-1解析∵(1+i)(a+i)=a-1+(a+1)i∈R,∴a+1=0,即a=-1.13.52解析由题意可得a2-b2+2ab i=3+4i,则解得则a2+b2=5,ab=2.14解析由题意)=-,故λ1=-,λ2=,即λ1+λ2=二、思维提升训练15.D解析如图,D是AB边上一点,过点D作DE∥BC,交AC于点E,过点D作DF∥AC,交BC于点F,则因为+,所以=由△ADE∽△ABC,得,所以,故λ=16.A解析以点A为原点,所在直线分别为x轴、y轴建立平面直角坐标系,如图,则A(0,0),B,C(0,t),=(1,0),=(0,1),=(1,0)+4(0,1)=(1,4),∴点P的坐标为(1,4),=(-1,t-4),=1--4t+16=-+17≤-4+17=13.当且仅当=4t,即t=时取“=”,的最大值为13.17.B解析因为M(-3,0),N(3,0),所以=(6,0),||=6,=(x+3,y),=(x-3,y).由||·||+=0,得6+6(x-3)=0,化简得y2=-12x,所以点M是抛物线y2=-12x 的焦点,所以点P到M的距离的最小值就是原点到M(-3,0)的距离,所以d min=3.18.42解析设向量a,b的夹角为θ,由余弦定理得|a-b|=,|a+b|=,则|a+b|+|a-b|=令y=,则y2=10+2[16,20],据此可得(|a+b|+|a-b|)max==2,(|a+b|+|a-b|)min==4.即|a+b|+|a-b|的最小值是4,最大值是219.1解析如图,因为E,F分别是AD与BC的中点,所以=0,=0.又因为=0,所以①同理由①+②得,2+()+()=, 所以).所以λ=,μ=所以λ+μ=1.20.-2解析i为实数,∴-=0,即a=-2.。
(通用版)2019版高考数学二轮复习 专题检测(二)平面向量 理(普通生,含解析)

专题检测(二)平面向量一、选择题1.设a=(1,2),b=(1,1),c=a+k b。
若b⊥c,则实数k的值等于()A.-错误!B.-错误!C.错误! D。
错误!解析:选A 因为c=a+k b=(1+k,2+k),又b⊥c,所以1×(1+k)+1×(2+k)=0,解得k=-错误!.2.已知向量a=(1,1),2a+b=(4,2),则向量a,b的夹角的余弦值为()A。
错误! B.-错误!C.错误! D.-错误!解析:选C 因为向量a=(1,1),2a+b=(4,2),所以b=(2,0),则向量a,b的夹角的余弦值为错误!=错误!。
3.已知在平面直角坐标系中,点A(0,1),向量错误!=(-4,-3),错误!=(-7,-4),则点C的坐标为()A.(11,8) B.(3,2)C.(-11,-6) D.(-3,0)解析:选C 设C(x,y),∵在平面直角坐标系中,点A(0,1),向量错误!=(-4,-3),错误!=(-7,-4),∴错误!=错误!+错误!=(-11,-7),∴错误!解得x=-11,y=-6,故C(-11,-6).4.在等腰梯形ABCD中,错误!=-2错误!,M为BC的中点,则错误!=()A。
12错误!+错误!错误! B.错误!错误!+错误!错误!C。
错误!错误!+错误!错误! D.错误!错误!+错误!错误!解析:选B 因为错误!=-2错误!,所以错误!=2错误!.又M是BC的中点,所以错误!=错误!(错误!+错误!)=错误!(错误!+错误!+错误!)=错误!错误!=错误!错误!+错误!错误!。
5.(2019届高三·武汉调研)设非零向量a,b满足|2a+b|=|2a-b|,则( )A.a⊥b B.|2a|=|b|C.a∥b D.|a|<|b|解析:选A 法一:∵|2a+b|=|2a-b|,∴(2a+b)2=(2a-b)2,化简得a·b=0,∴a⊥b,故选A.法二:记c=2a,则由|2a+b|=|2a-b|得|c+b|=|c-b|,由平行四边形法则知,以向量c,b为邻边的平行四边形的对角线相等,∴该四边形为矩形,故c⊥b,即a⊥b,故选A.6.已知错误!=(2,1),点C(-1,0),D(4,5),则向量错误!在错误!方向上的投影为() A.-错误! B.-3错误!C.错误! D.3错误!解析:选C 因为点C(-1,0),D(4,5),所以错误!=(5,5),又错误!=(2,1),所以向量错误!在错误!方向上的投影为|错误!|cos〈错误!,错误!>=错误!=错误!=错误!。
专题10 平面向量与复数(二)-高考数学(文)二轮复习单元过关测试

2019高考数学(文)二轮单元复习过关测试单元测试10 平面向量与复数(二)(120分钟 150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.复平面内表示复数z =i(-2+i)的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】C【解析】∵z =i(-2+i)=-1-2i ,∴复数z =-1-2i 所对应的复平面内的点为Z (-1,-2),位于第三象限. 故选C .2.已知a ,b 是两个非零向量,且|a +b |=|a |+|b |,则下列说法正确的是 ( )A .a +b =0B .a =bC .a 与b 共线反向D .存在正实数λ,使a =λb 【答案】D【解析】因为a ,b 是两个非零向量,且|a +b |=|a |+|b |.则a 与b 共线同向,故D 正确. 3.复数1+2i 2-i =( )A .iB .1+iC .-iD .1-i 【答案】A【解析】 法一:1+2i2-i=1+2i 2+i 2-i2+i =5i5=i.法二:1+2i 2-i =i 1+2i i 2-i =i 1+2i2i +1=i.4.若a ,b ,c 均为单位向量,且a·b =0,(a -c )·(b -c )≤0,则|a +b -c |的最大值为( )A .2-1B .1C . 2D .2【答案】B【解析】因为|a |=|b |=|c |=1,a·b =0,所以|a +b |2=a 2+b 2+2a·b =2,故|a +b |= 2.展开(a -c )·(b -c )≤0,得a·b -(a +b )·c +c 2≤0,即0-(a +b )·c +1≤0,整理,得(a +b )·c ≥1.而|a +b -c |2=(a +b )2-2(a +b )·c +c 2=3-2(a +b )·c , 所以3-2(a +b )·c ≤3-2×1=1. 所以|a +b -c |2≤1,即|a +b -c |≤1.5.已知A (-1,-1),B (m ,m +2),C (2,5)三点共线,则m 的值为( )A .1B .2C .3D .4【答案】A【解析】 AB ―→=(m ,m +2)-(-1,-1)=(m +1,m +3),AC ―→=(2,5)-(-1,-1)=(3,6), ∵A ,B ,C 三点共线,∴AB ―→∥AC ―→, ∴3(m +3)-6(m +1)=0, ∴m =1.故选A .6.若z =4+3i ,则z|z |=( ) A .1 B .-1 C .45+35iD .45-35i 【答案】D【解析】 ∵z =4+3i ,∴z =4-3i ,|z |=42+32=5,∴z|z |=4-3i 5=45-35i. 7.设a ,b 是向量,则“|a |=|b |”是“|a +b |=|a -b |”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】D【解析】 若|a |=|b |成立,则以a ,b 为邻边的平行四边形为菱形.a +b ,a -b 表示的是该菱形的对角线,而菱形的两条对角线长度不一定相等,所以|a +b |=|a -b |不一定成立,从而不是充分条件;反之,若|a +b |=|a -b |成立,则以a ,b 为邻边的平行四边形为矩形,而矩形的邻边长度不一定相等,所以|a |=|b |不一定成立,从而不是必要条件.故“|a |=|b |”是“|a +b |=|a -b |”的既不充分也不必要条件. 8.已知i 为虚数单位,复数z =i2+i 的虚部为 ( )A .-15B .-25C .15D .25【答案】D【解析】复数z =i2+i=i 2-i 2+i 2-i =1+2i 5=15+25i ,则其虚部为25,故选D .9.在平面直角坐标系中,已知O 是坐标原点,A (3,0),B (0,3),C (cos α,sin α),若|OA →+OC →|=13,α∈(0,π),则OB →与OC →的夹角为( )A .π6B .π3C .23π D .56π 【答案】A【解析】由题意,得OA →+OC →=(3+cos α,sin α),所以|OA →+OC →|=3+cos α2+sin 2α=10+6cos α=13, 即cos α=12,因为α∈(0,π),所以α=π3,C ⎝ ⎛⎭⎪⎫12,32.设OB →与OC →的夹角为θ,则cos θ=OB →·OC →|OB →|·|OC →|=3233×1=32.因为θ∈[0,π],所以θ=π6.10.已知直线ax +by +c =0与圆O :x 2+y 2=1相交于A ,B 两点,且AB =3,则OA →·OB →的值是 ( ) A .-12B .12C .-34D .0【答案】A11已知1-i2z=1+i(i 为虚数单位),则复数z =( )A .1+iB .1-iC .-1+iD .-1-i【答案】D 【解析】由1-i2z=1+i ,得z =1-i21+i=-2i 1+i =-2i 1-i1+i 1-i=-1-i ,故选D . 12.已知向量a ,b 的夹角为60°,且|a |=2,|b |=3,设OA →=a ,OB →=b ,OC →=m a -2b ,若△ABC 是以BC 为斜边的直角三角形,则m =( )A .-4B .3C .-11D .10【答案】C【解析】a ·b =2×3×cos 60°=3,AB →=OB →-OA →=b -a ,AC →=OC →-OA =(m -1)a -2B .∵AB ⊥AC ,∴AB →·AC →=0, 即(b -a )·[(m -1)a -2b ]=0,∴(1-m )a 2-2b 2+(m -1)a ·b +2a ·b =0, 即4(1-m )-18+3(m -1)+6=0, 解得m =-11.故选C .二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上) 13.已知两个平面向量a ,b 满足|a |=1,|a -2b |=21,且a 与b 的夹角为120°,则|b |=________. 【答案】2【解析】 由|a -2b |=21得a 2-4a·b +4b 2=21.即1+2|b |+4|b |2=21,解得|b |=2或|b |=-52(舍).14.已知点A ,B ,C 满足|AB →|=3,|BC →|=4,|CA →|=5,则AB →·BC →+BC →·CA →+CA →·AB →=________. 【答案】-25【解析】由|AB →|2+|BC →|2=|CA →|2得∠B =90°,cos C =45,cos A =35,AB →·BC →=0,BC →·CA →=4×5×⎝ ⎛⎭⎪⎫-45=-16,CA →·AB →=5×3×⎝ ⎛⎭⎪⎫-35=-9,所以AB →·BC →+BC →·CA →+CA →·AB →=-25.15.如图,菱形ABCD 的边长为2,∠BAD =60°,M 为DC 的中点,若N 为菱形内任意一点(含边界),则AM →·AN →的最大值为________.【答案】9【解析】由平面向量的数量积的几何意义知,AM →·AN →等于AM →与AN →在AM →方向上的投影之积,所以(AM →·AN →)max =AM →·AC →=⎝ ⎛⎭⎪⎫12AB →+AD →·(AB →+AD →)=12AB →2+AD →2+32AB →·AD →=9.16.已知a ,b ∈R ,i 是虚数单位,若(1+i)(1-b i)=a ,则ab的值为________. 【答案】2【解析】∵(1+i)(1-b i)=1+b +(1-b )i =a ,又a ,b ∈R ,∴1+b =a 且1-b =0,得a =2,b =1,∴a b=2.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分) 在直角坐标系xOy 中,已知点A (1,1),B (2,3),C (3,2),点P (x ,y )在△ABC三边围成的区域(含边界)上,且OP →=mAB →+nAC →(m ,n ∈R ). (1)若m =n =23,求|OP →|;学_科网(2)用x ,y 表示m -n ,并求m -n 的最大值. 【答案】(1)|OP →|=22;(2)1令y -x =t ,由图知,当直线y =x +t 过点B (2,3)时,t 取得最大值1,故m -n 的最大值为1.12分18.(12分) 设向量a =(3sin x ,sin x ),b =(cos x ,sin x ),x ∈⎣⎢⎡⎦⎥⎤0,π2.(1)若|a |=|b |,求x 的值;(2)设函数f (x )=a ·b ,求f (x )的最大值. 【答案】 (1)x =π6;(2)f (x )的最大值为32.【解析】(1)由|a |2=(3sin x )2+(sin x )2=4sin 2x ,|b |2=(cos x )2+(sin x )2=1, 及|a |=|b |,得4sin 2x =1.3分 又x ∈⎣⎢⎡⎦⎥⎤0,π2,从而sin x =12,所以x =π6. 5分(2)f (x )=a ·b =3sin x ·cos x +sin 2x =32sin 2x -12cos 2x +12=sin ⎝⎛⎭⎪⎫2x -π6+12,8分当x =π3∈⎣⎢⎡⎦⎥⎤0,π2时,sin ⎝ ⎛⎭⎪⎫2x -π6取最大值1.所以f (x )的最大值为32.12分19.(12分) 复数z 1=3a +5+(10-a 2)i ,z 2=21-a+(2a -5)i ,若z 1+z 2是实数,求实数a 的值. 【答案】a =3.20.(12分) 已知函数f (x )=a ·b ,其中a =(2cos x ,-3sin 2x ),b =(cos x,1),x ∈R .(1)求函数y =f (x )的单调递减区间;(2)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,f (A )=-1,a =7,且向量m =(3,sin B )与n =(2,sin C )共线,求边长b 和c 的值. 【答案】 (1)f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π-π6,k π+π3(k ∈Z );(2)b =3,c =2.【解析】(1)f (x )=a ·b =2cos 2x -3sin 2x =1+cos 2x -3sin 2x =1+2cos ⎝ ⎛⎭⎪⎫2x +π3,2分令2k π≤2x +π3≤2k π+π(k ∈Z ),解得k π-π6≤x ≤k π+π3(k ∈Z ),∴f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π-π6,k π+π3(k ∈Z ).5分(2)∵f (A )=1+2cos ⎝⎛⎭⎪⎫2A +π3=-1,∴cos ⎝⎛⎭⎪⎫2A +π3=-1. 7分 又π3<2A +π3<7π3,∴2A +π3=π,即A =π3. 9分∵a =7,由余弦定理得a 2=b 2+c 2-2bc cos A =(b +c )2-3bc =7. ①∵向量m =(3,sin B )与n =(2,sin C )共线, ∴2sin B =3sin C .由正弦定理得2b =3c , ② 由①②可得b =3,c =2.12分21.(12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知向量m =(cos A ,cos B ),n =(a,2c -b ),且m∥n .(1)求角A 的大小.(2)若a =4,求△ABC 面积的最大值.【答案】(1)A =π3;(2)△ABC 面积的最大值为4 3.【解析】 (1)因为m∥n , 所以a cos B -(2c -b )cos A =0, 由正弦定理得sin A cos B -(2sin C -sin B )cos A =0,所以sin A cos B +sin B cos A =2sin C cos A , 所以sin(A +B )=2sin C cos A , 因为A +B +C =π, 所以sin C =2sin C cos A , 因为0<C <π,所以sin C >0, 所以cos A =12,因为0<A <π,所以A =π3.(2)由余弦定理得a 2=b 2+c 2-2bc cos A , 所以16=b 2+c 2-bc ≥2bc -bc =bc , 因此bc ≤16,当且仅当b =c =4时,等号成立; 因此△ABC 的面积S =12bc sin A ≤43,因此△ABC 面积的最大值为4 3.22.(12分)已知平面上的两个向量OA →,OB →满足|OA →|=a ,|OB →|=b ,且OA →⊥OB →,a 2+b 2=4.向量OP →=xOA →+yOB →(x ,y ∈R ),且a 2⎝ ⎛⎭⎪⎫x -122+b 2⎝ ⎛⎭⎪⎫y -122=1.(1)如果点M 为线段AB 的中点,求证:MP →=⎝ ⎛⎭⎪⎫x -12OA →+⎝ ⎛⎭⎪⎫y -12OB →.(2)求|OP →|的最大值,并求出此时四边形OAPB 面积的最大值.(2)设点M 为线段AB 的中点,则由OA →⊥OB →,知|M A →|=|MB →|=|MO →|=12|AB →|=1.又由(1)及a 2⎝ ⎛⎭⎪⎫x -122+b 2⎝ ⎛⎭⎪⎫y -122=1, 得|MP →|2=|OP →-OM →|2=⎝ ⎛⎭⎪⎫x -122OA →2+⎝ ⎛⎭⎪⎫y -122OB →2 =a 2⎝ ⎛⎭⎪⎫x -122+b 2⎝ ⎛⎭⎪⎫y -122=1. 所以|MP →|=|MA →|=|MB →|=|MO →|=12|AB →|=1,所以P ,O ,A ,B 四点都在以M 为圆心,1为半径的圆上.所以当且仅当OP 是直径时,|OP →|max =2,这时四边形OAPB 为矩形,则S四边形OAPB=|OA →|·|OB →|=ab ≤a 2+b 22=2,当且仅当a =b =2时,四边形OAPB 的面积最大,最大值为2.。
(新课标)天津市2019年高考数学二轮复习 专题能力训练3 平面向量与复数 理

专题能力训练3 平面向量与复数一、能力突破训练1.设有下面四个命题p1:若复数z满足∈R,则z∈R;p2:若复数z满足z2∈R,则z∈R;p3:若复数z1,z2满足z1z2∈R,则z1=;p4:若复数z∈R,则∈R.其中的真命题为()A.p1,p3B.p1,p4C.p2,p3D.p2,p42.设a,b是两个非零向量,则下列结论一定成立的为()A.若|a+b|=|a|-|b|,则a⊥bB.若a⊥b,则|a+b|=|a|-|b|C.若|a+b|=|a|-|b|,则存在实数λ,使得b=λaD.若存在实数λ,使得b=λa,则|a+b|=|a|-|b|3.(2018全国Ⅲ,理2)(1+i)(2-i)=()A.-3-iB.-3+iC.3-iD.3+i4.在复平面内,若复数z的对应点与的对应点关于虚轴对称,则z=()A.2-iB.-2-iC.2+iD.-2+i5.已知向量a=(1,-1),b=(-1,2),则(2a+b)·a=()A.-1B.0C.1D.26.(2018浙江,4)复数(i为虚数单位)的共轭复数是 ()A.1+iB.1-iC.-1+iD.-1-i7.已知菱形ABCD的边长为a,∠ABC=60°,则=()A.-a2B.-a2C.a2D.a28.已知非零向量m,n满足4|m|=3|n|,cos<m,n>=.若n⊥(t m+n),则实数t的值为()A.4B.-4C.D.-9.如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=,I2=,I3=,则()A.I1<I2<I3B.I1<I3<I2C.I3<I1<I2D.I2<I1<I310.(2018全国Ⅲ,理13)已知向量a=(1,2),b=(2,-2),c=(1,λ).若c∥(2a+b),则λ= .11.在△ABC中,∠A=60°,AB=3,AC=2.若=2=λ(λ∈R),且=-4,则λ的值为.12.设a∈R,若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a= .13.已知a,b∈R,(a+b i)2=3+4i(i是虚数单位),则a2+b2= ,ab= .14.设D,E分别是△ABC的边AB,BC上的点,|AD|=|AB|,|BE|=|BC|.若=λ1+λ2(λ1,λ2为实数),则λ1+λ2的值为.二、思维提升训练15.在△ABC中,已知D是AB边上一点,+λ,则实数λ=()A.-B.-C.D.16.已知,||=,||=t.若点P是△ABC所在平面内的一点,且,则的最大值等于()A.13B.15C.19D.2117.已知两点M(-3,0),N(3,0),点P为坐标平面内一动点,且||·||+=0,则动点P(x,y)到点M(-3,0)的距离d的最小值为()A.2B.3C.4D.618.已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是,最大值是.19.在任意四边形ABCD中,E,F分别是AD,BC的中点,若=λ+μ,则λ+μ= .20.已知a∈R,i为虚数单位,若为实数,则a的值为.专题能力训练3平面向量与复数一、能力突破训练1.B解析p1:设z=a+b i(a,b∈R),则R,所以b=0,所以z∈R.故p1正确;p2:因为i2=-1∈R,而z=i∉R,故p2不正确;p3:若z1=1,z2=2,则z1z2=2,满足z1z2∈R,而它们实部不相等,不是共轭复数,故p3不正确;p4:实数的虚部为0,它的共轭复数是它本身,也属于实数,故p4正确.2.C解析设向量a与b的夹角为θ.对于A,可得cos θ=-1,因此a⊥b不成立;对于B,满足a⊥b 时|a+b|=|a|-|b|不成立;对于C,可得cos θ=-1,因此成立,而D显然不一定成立.3.D解析 (1+i)(2-i)=2+i-i2=3+i.4.D解析=2+i所对应的点为(2,1),它关于虚轴对称的点为(-2,1),故z=-2+i.5.C解析∵2a+b=(1,0),又a=(1,-1),∴(2a+b)·a=1+0=1.6.B解析=1+i,∴复数的共轭复数为1-i.7.D解析如图,设=a,=b.则=()=(a+b)·a=a2+a·b=a2+a·a·cos60°=a2+a2=a2.8.B解析由4|m|=3|n|,可设|m|=3k,|n|=4k(k>0),又n⊥(t m+n),所以n·(t m+n)=n·t m+n·n=t|m|·|n|cos<m,n>+|n|2=t×3k×4k+(4k)2=4tk2+16k2=0.所以t=-4,故选B.9.C解析由题图可得OA<AC<OC,OB<BD<OD,∠AOB=∠COD>90°,∠BOC<90°,所以I2=>0,I1=<0,I3=<0,且|I1|<|I3|,所以I3<I1<0<I2,故选C.10解析 2a+b=2(1,2)+(2,-2)=(4,2),c=(1,λ),由c∥(2a+b),得4λ-2=0,得λ=11解析=2,)=又=,∠A=60°,AB=3,AC=2,=-4,=3×2=3,()=-4, 即=-4,4-9+3=-4,即-5=-4,解得λ=12.-1解析∵(1+i)(a+i)=a-1+(a+1)i∈R,∴a+1=0,即a=-1.13.52解析由题意可得a2-b2+2ab i=3+4i,则解得则a2+b2=5,ab=2.14解析由题意)=-,故λ1=-,λ2=,即λ1+λ2=二、思维提升训练15.D解析如图,D是AB边上一点,过点D作DE∥BC,交AC于点E,过点D作DF∥AC,交BC于点F,则因为+,所以=由△ADE∽△ABC,得,所以,故λ=16.A解析以点A为原点,所在直线分别为x轴、y轴建立平面直角坐标系,如图,则A(0,0),B,C(0,t),=(1,0),=(0,1),=(1,0)+4(0,1)=(1,4),∴点P的坐标为(1,4),=(-1,t-4),=1--4t+16=-+17≤-4+17=13.当且仅当=4t,即t=时取“=”,的最大值为13.17.B解析因为M(-3,0),N(3,0),所以=(6,0),||=6,=(x+3,y),=(x-3,y).由||·||+=0,得6+6(x-3)=0,化简得y2=-12x,所以点M是抛物线y2=-12x 的焦点,所以点P到M的距离的最小值就是原点到M(-3,0)的距离,所以d min=3.18.42解析设向量a,b的夹角为θ,由余弦定理得|a-b|=,|a+b|=,则|a+b|+|a-b|=令y=,则y2=10+2[16,20],据此可得(|a+b|+|a-b|)max==2,(|a+b|+|a-b|)min==4.即|a+b|+|a-b|的最小值是4,最大值是219.1解析如图,因为E,F分别是AD与BC的中点,所以=0,=0.又因为=0,所以①同理由①+②得,2+()+()=, 所以).所以λ=,μ=所以λ+μ=1.20.-2解析i为实数,∴-=0,即a=-2.。
2019版高考数学二轮复习课件+训练:自测过关卷(二)平面向量、复数、算法、推理与证明理

自测过关卷(二) 平面向量、复数、算法、推理与证明组——高考题点全面练A (对应配套卷P 163)1.(2019届高三·惠州调研)若=2-i (i 为虚数单位),则复数z 在复平面内对应z1+i的点在( )A .第一象限B .第二象限C .第三象限D .第四象限解析:选A 由题意知z =(1+i )(2-i )=3+i ,其在复平面内对应的点的坐标为(3,1),在第一象限.2.向量a ,b 满足a +b =(-1,5),a -b =(5,-3),则b =( )A .(-3,4) B .(3,4)C .(3,-4)D .(-3,-4)解析:选A 由a +b =(-1,5),a -b =(5,-3),得2b =(-1,5)-(5,-3)=(-6,8),所以b =(-6,8)=(-3,4).123.(2018·开封模拟)复数z =,则( )2-1+iA .z 的共轭复数为1+iB .z 的实部为1C .|z |=2D .z 的虚部为-1解析:选D 因为z ===-1-i ,所以复数z 的实部和2-1+i 2 -1-i-1+i -1-i虚部均为-1,=-1+i ,|z |=,故选D.z 24.(2018·石家庄质检)当n =4时,执行如图所示的程序框图,则输出S 的值为( )A .9B .15C .31D .63解析:选C 由程序框图可知,k =1,S =1,S =1+2=3,k =2;S =3+22=7,k =3;S =7+23=15,k =4;S =15+24=31,k =5,退出循环,输出的S 的值为31,故选C.5.已知在平面直角坐标系中,点A (0,1),向量=(-4,-3),=(-7,-4),AB ―→ BC ―→则点C 的坐标为( )A .(11,8)B .(3,2)C .(-11,-6)D .(-3,0)解析:选C 设C (x ,y ),∵在平面直角坐标系中,点A (0,1),向量=(-4,-3),=(-7,-4),AB ―→ BC ―→∴=+=(-11,-7),AC ―→ AB ―→ BC ―→∴Error!解得x =-11,y =-6,故C (-11,-6).6.(2018·益阳、湘潭调研)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例.若输入n ,x 的值分别为3,3,则输出v 的值为( )A .15B .16C .47D .48解析:选D 执行程序框图,n =3,x =3,v =1,i =2≥0,v =1×3+2=5,i =1≥0,v =5×3+1=16,i =0≥0,v =16×3+0=48,i =-1<0,退出循环,输出v 的值为48.7.(2018·全国卷Ⅱ)为计算S =1-+-+…+-,设计了如图所示的程序框1213141991100图,则在空白框中应填入( )A .i =i +1B .i =i +2C .i =i +3D .i =i +4解析:选B 由题意可将S 变形为S =-,则由S =N -T ,得N =1+(1++…+)(++…+)+…+,T =++…+.据此,结合N =N +,T =T +易知在空白框中应填入i =i 13199121411001i 1i +1+2.故选B.8.(2018·全国卷Ⅰ)在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则=( )EB ―→A.-B.-34AB ―→ 14AC ―→14AB ―→ 34AC ―→C.+D.+34AB ―→ 14AC ―→14AB ―→ 34AC ―→解析:选A 法一:作出示意图如图所示.=+=+EB ―→ ED ―→ DB ―→ 12AD ―→ 12CB―→=×(+)+(-)=-.故选A.1212AB ―→ AC ―→ 12AB ―→ AC ―→ 34AB ―→ 14AC ―→法二:不妨设△ABC 为等腰直角三角形,且∠A =,AB =AC =1.建立π2如图所示的平面直角坐标系,则A (0,0),B (1,0),C (0,1),D ,E .故=(1,0),=(0,1),(12,12)(14,14)AB ―→ AC ―→=(1,0)-=,EB ―→(14,14)(34,-14)即=-.EB ―→ 34AB ―→ 14AC ―→9.(2018·茂名一模)甲、乙、丙三人参加某公司的面试,最终只有一人能够被该公司录用,得到面试结果以后,甲说:丙被录用了;乙说:甲被录用了;丙说:我没被录用.若这三人中仅有一人说法错误,则下列结论正确的是( )A .丙被录用了B .乙被录用了C .甲被录用了D .无法确定谁被录用了解析:选C 假设甲说的是真话,即丙被录用,则乙说的是假话,丙说的是假话,不成立;假设甲说的是假话,即丙没有被录用,则丙说的是真话,若乙说的是真话,即甲被录用,成立,故甲被录用;若乙被录用,则甲和乙的说法都错误,不成立.故选C.10.在△ABC 中,|+|=|-|,AB =2,AC =1,E ,F 为BC 的三等分点,AB ―→ AC ―→ AB ―→ AC ―→则·=( )AE ―→ AF ―→A. B.89109C. D.259269解析:选B 由|+|=|-|知⊥,以A 为坐标原点,,AB ―→ AC ―→ AB ―→ AC ―→ AB ―→ AC ―→ AB ―→ AC―→的方向分别为x 轴、y 轴的正方向建立平面直角坐标系,则A (0,0),B (2,0),C (0,1),不妨设E ,F ,则·=·=+=.(43,13)(23,23)AE ―→ AF ―→ (43,13)(23,23)892910911.(2018·昆明适应性检测)我国南北朝时期的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上,提出下面的体积计算原理(祖暅原理):“幂势既同,则积不容异”.“幂”是截面面积,“势”是几何体的高.意思是:若两个等高几何体在同高处的截面面积总相等,则这两个几何体的体积相等.现有一旋转体D (如图1所示),它是由抛物线y =x 2(x ≥0),直线y =4及y 轴围成的封闭图形绕y 轴旋转一周形成的几何体,旋转体D 的参照体的三视图如图2所示,利用祖暅原理,则旋转体D 的体积是( )A.B .6π16π3C .8πD .16π解析:选C 由三视图知参照体是一个直三棱柱,其体积V =×4×4×π=8π,故旋12转体D 的体积为8π,故选C.12.(2018·南昌调研)已知A ,B ,C 是圆O :x 2+y 2=1上的动点,且AC ⊥BC ,若点M的坐标是(1,1),则| ++|的最大值为( )MA ―→ MB ―→ MC ―→A .3B .4C .3-1D .3+122解析:选D 法一:∵A ,B ,C 是圆O :x 2+y 2=1上的动点,且AC ⊥BC ,∴设A (cos θ,sin θ),B (-cos θ,-sin θ),C (cos α,sin α),其中0≤θ<2π,0≤α<2π,∵M (1,1),∴++=(cos θ-1,sin θ-1)+(-cos θ-1,-sin θ-1)MA ―→ MB ―→ MC ―→+(cos α-1,sin α-1)=(cos α-3,sin α-3),∴|++|=MA ―→ MB ―→ MC ―→cos α-3 2+ sin α-3 2=cos 2α-6cos α+9+sin 2α-6sin α+9= ,19-62sin (α+π4)当且仅当sin =-1时,|++|取得最大值,最大值为=3(α+π4)MA ―→ MB ―→ MC ―→ 19+62+1.2法二:连接AB ,∵AC ⊥BC ,∴AB 为圆O 的直径,∴+=2,MA ―→ MB ―→ MO ―→∴|++|=|2+|≤|2|+||=2+||,MA ―→ MB ―→ MC ―→ MO ―→ MC ―→ MO ―→ MC ―→ 2MC ―→ 易知点M 与圆上动点C +1,2∴||≤+1,∴|++|≤3+1,故选 D.MC ―→ 2MA ―→ MB ―→ MC ―→213.(2017·浙江高考)已知a ,b ∈R ,(a +b i)2=3+4i(i 是虚数单位),则a 2+b 2=________,ab =________.解析:∵(a +b i)2=a 2-b 2+2ab i ,a ,b ∈R ,∴Error!⇒Error!⇒Error!∴a 2+b 2=2a 2-3=5,ab =2.答案:5 214.(2018·潍坊统一考试)已知单位向量e 1,e 2,且〈e 1,e 2〉=,若向量a =e 1-2e 2,π3则|a|=________.解析:因为|e 1|=|e 2|=1,〈e 1,e 2〉=,所以|a|2=|e 1-2e 2|2=1-4|e 1|·|e 2|cos π3+4=1-4×1×1×+4=3,即|a|=.π3123答案:315.(2018·南昌模拟)已知13+23=2,13+23+33=2,13+23+33+43=2,…,(62)(122)(202)若13+23+33+43+…+n 3=3 025,则n =________.解析:13+23=2=2,(62)(2×32)13+23+33=2=2,(122)(3×42)13+23+33+43=2=2,(202)(4×52)…由此归纳可得13+23+33+43+…+n 3=2,[n n +1 2]因为13+23+33+43+…+n 3=3 025,所以2=3 025,[n n +1 2]即n 2(n +1)2=(2×55)2,解得n =10.答案:1016.在矩形ABCD 中,AB =2,AD =1.边DC 上的动点P (包含点D ,C )与CB 延长线上的动点Q (包含点B )满足| |=||,则·的最小值为________.DP ―→ BQ ―→ PA ―→ PQ ―→解析:以点A 为坐标原点,分别以AB ,AD 所在直线为x 轴,y 轴建立如图所示的平面直角坐标系,设P (x,1),Q (2,y ),由题意知0≤x ≤2,-2≤y ≤0.∵||=||,∴|x |=|y |,∴x =-y .DP ―→ BQ ―→∵=(-x ,-1),=(2-x ,y -1),PA ―→ PQ ―→∴·=-x (2-x )-(y -1)=x 2-2x -y +1=x 2-x +1=2+,PA ―→ PQ ―→ (x -12)34∴当x =时,·取得最小值,为.12PA ―→ PQ ―→34答案:34组——高考达标提速练B (对应配套卷P164)1.(2018·福州模拟)若复数的模为,则实数a =( )a1+i22A .1B .-1C .±1D .±2解析:选C 法一:==-i ,a1+ia 1-i 1+i 1-i a 2a2∵=,a1+i22∴=,(a 2)2+(-a 2)222解得a =±1.故选C .法二:∵=,∴=,∴|a|=1,|a1+i |22|a |222解得a =±1.故选C .2.已知a ∈R ,复数z =,若=z ,则a =( )a -i 1+iiz A .1 B .-1C .2D .-2解析:选B ∵z ===+a -1=(a -1)-(a +a -i 1+i i a +1+ a -1 i i a +1i1)i ,∴=(a -1)+(a +1)i.z 又∵=z ,∴a +1=0,得a =-1.z 3.已知向量m =(t +1,1),n =(t +2,2),若(m +n)⊥(m -n),则t =( )A .0 B .-3C .3D .-1解析:选B 法一:由(m +n)⊥(m -n)可得(m +n)·(m -n)=0,即m 2=n 2,故(t +1)2+1=(t +2)2+4,解得t =-3.法二:m +n =(2t +3,3),m -n =(-1,-1),∵(m +n)⊥(m -n),∴-(2t +3)-3=0,解得t =-3.4.在△ABC 中,∠ABC =90°,AB =6,点D 在边AC 上,且2=,则·AD ―→ DC ―→ BA ―→ BD―→的值是( )A .48B .24C .12D .6解析:选B 法一:由题意得,·=0,·=·(-)=|BA ―→ BC ―→ BA ―→ CA ―→ BA ―→ BA ―→ BC ―→|2=36,∴·=·(+)=·=0+×36=24. BA ―→ BA ―→ BD ―→ BA ―→ BC ―→ CD ―→ BA ―→(+23)23法二:(特例法)若△ABC 为等腰直角三角形,建立如图所示的平面直角坐标系,则A (6,0),C (0,6).由2=,得D (4,2).AD ―→ DC ―→∴·=(6,0)·(4,2)=24.BA ―→ BD ―→5.(2017·全国卷Ⅰ)设有下面四个命题:p 1:若复数z 满足∈R ,则z ∈R ;1z p 2:若复数z 满足z 2∈R ,则z ∈R ;p 3:若复数z 1,z 2满足z 1z 2∈R ,则z 1=2;z p 4:若复数z ∈R ,则∈R.z 其中的真命题为( )A .p 1,p 3 B .p 1,p 4C .p 2,p 3D .p 2,p 4解析:选B 设复数z =a +b i(a ,b ∈R),对于p 1,∵==∈R ,1z1a +b i a -b i a 2+b 2∴b =0,∴z ∈R ,∴p 1是真命题;对于p 2,∵z 2=(a +b i)2=a 2-b 2+2ab i ∈R ,∴ab =0,∴a =0或b =0,∴p 2不是真命题;对于p 3,设z 1=x +y i(x ,y ∈R),z 2=c +d i(c ,d ∈R),则z 1z 2=(x +y i)(c +d i)=cx -dy +(dx +cy )i ∈R ,∴dx +cy =0,取z 1=1+2i ,z 2=-1+2i ,z 1≠2,z ∴p 3不是真命题;对于p 4,∵z =a +b i ∈R ,∴b =0,∴=a -b i =a ∈R ,z ∴p 4是真命题.6.(2018·郑州第一次质量预测)执行如图所示的程序框图,若输出的结果是7,则判断框内m 的取值范围是( )A .(30,42]B .(30,42)C .(42,56]D .(42,56)解析:选A k =1,S =2,k =2;S =2+4=6,k =3;S =6+6=12,k =4;S =12+8=20,k =5;S =20+10=30,k =6;S =30+12=42,k =7,此时不满足S =42<m ,退出循环,所以30<m ≤42,故选A.7.(2018·开封一模)我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )A .i <7?,s =s -,i =2i1iB .i ≤7?,s =s -,i =2i1iC .i <7?,s =,i =i +1s2D .i ≤7?,s =,i =i +1s2解析:选D 由题意及程序框图可知第一次剩下,第二次剩下,…,由此得出第712122次剩下,可得①为i ≤7?,②s =,③i =i +1.故选D.127s28.(2019届高三·南宁摸底联考)已知O 是△ABC 内一点,++=0,·OA ―→ OB ―→ OC ―→ AB ―→ =2且∠BAC =60°,则△OBC 的面积为( )AC ―→A. B.333C.D.3223解析:选A ∵++=0,∴O 是△ABC 的重心,于是S △OBC =S △ABC .∵·OA ―→ OB ―→ OC ―→ 13AB ―→=2,∴||·||·cos ∠BAC =2,∵∠BAC =60°,∴||·||=4.∴S △ABC =AC ―→ AB ―→ AC ―→ AB ―→ AC ―→||·||sin ∠BAC =,∴△OBC 的面积为.12AB ―→AC ―→3339.(2019届高三·广元调研)二维空间中,圆的一维测度(周长)l =2πr ,二维测度(面积)S =πr 2,三维空间中,球的二维测度(表面积)S =4πr 2,三维测度(体积)V =πr 3,应43用合情推理,若四维空间中,“超球”的三维测度V =8πr 3,则其四维测度W =( )A .2πr 4B .3πr 4C .4πr 4D .6πr 4解析:选A 对于二维空间中,圆的一维测度(周长)l =2πr ,二维测度(面积)S =πr 2,(πr 2)′=2πr .三维空间中,球的二维测度(表面积)S =4πr 2,三维测度(体积)V =πr 3,′=43(43πr 3)4πr 2.四维空间中,“超球”的三维测度V =8πr 3,∵(2πr 4)′=8πr 3,∴“超球”的四维测度W =2πr 4.10.如图,直线EF 与平行四边形ABCD 的两边AB ,AD 分别交于E ,F 两点,且交其对角线于K ,其中,=,=, =λAE ―→ 25AB ―→ AF ―→ 12AD ―→ AK ―→ AC―→,则λ的值为( )A. B.2927C. D.2523解析:选A 因为=,=,AE ―→ 25AB ―→ AF ―→ 12AD ―→则=,=2,AB ―→ 52AE ―→AD ―→ AF ―→由向量加法的平行四边形法则可知=+,AC ―→ AB ―→ AD ―→所以=λ=λ(+)=λ=λ+2λ,由E ,F ,K 三点共AK ―→ AC ―→ AB ―→ AD ―→ (52+2)52AE ―→ AF ―→线可得λ+2λ=1,52所以λ=.2912.(2017·浙江高考)如图,已知平面四边形ABCD ,AB ⊥BC ,AB =BC =AD =2,CD =3,AC 与BD 交于点O .记I 1=·,I 2=·,I 3=·,则( )OA ―→OB ―→ OB ―→ OC ―→ OC ―→ OD ―→A .I 1<I 2<I 3B .I 1<I 3<I 2C .I 3<I 1<I 2D .I 2<I 1<I 3解析:选C 法一:如图所示,四边形ABCE 是正方形,F 为正方形的对角线的交点,易得AO <AF ,而∠AFB =90°,∴∠AOB 与∠COD 为钝角,∠AOD 与∠BOC 为锐角.根据题意,I 1-I 2=·-·=·(-)=·=|OA ―→ OB ―→ OB ―→ OC ―→ OB ―→ OA ―→ OC ―→ OB ―→ CA ―→ OB―→|·||cos ∠AOB <0,CA ―→∴I 1<I 2,同理得,I 2>I 3,作AG ⊥BD 于G ,又AB =AD ,∴OB <BG =GD <OD ,而OA <AF =FC <OC ,∴||·||<||·||,OA ―→ OB ―→ OC ―→ OD ―→ 而cos ∠AOB =cos ∠COD <0,∴·>·,即I 1>I 3,OA ―→ OB ―→ OC ―→ OD ―→∴I 3<I 1<I 2.法二:如图,建立平面直角坐标系,则B (0,0),A (0,2),C (2,0).设D (m ,n ),由AD =2和CD =3,得Error!从而有n -m =>0,∴n >m .54从而∠DBC >45°,又∠BCO =45°,∴∠BOC 为锐角.从而∠AOB 为钝角.故I 1<0,I 3<0,I 2>0.又OA <OC ,OB <OD ,故可设=-λ1 (λ1>1),=-λ2 (λ2>1),OD ―→ OB ―→ OC ―→ OA ―→从而I 3=·=λ1λ2·=λ1λ2I 1,OC ―→ OD ―→ OA ―→ OB ―→又λ1λ2>1,I 1<0,I 3<0,∴I 3<I 1,∴I 3<I 1<I 2.13.已知复数z 满足z +|z |=3+i ,则z =________.解析:设z =a +b i ,其中a ,b ∈R ,由z +|z |=3+i ,得a +b i +=3+i ,由a 2+b 2复数相等可得Error!解得Error!故z =+i.43答案:+i4314.我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问:米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S =1.5(单位:升),则输入k 的值为________.解析:模拟程序的运行,可得n =1,S =k ,满足条件n <4,执行循环体,n =2,S =k -=;k 2k 2满足条件n <4,执行循环体,n =3,S =-=;k 2k23k3满足条件n <4,执行循环体,n =4,S =-=,k 3k34k4此时,不满足条件n <4,退出循环,输出S 的值为,k4由题意可得=1.5,解得k =6.k4答案:615.(2018·长春质检)有甲、乙二人去看望高中数学老师张老师,期间他们做了一个游戏,张老师的生日是m 月n 日,张老师把m 告诉了甲,把n 告诉了乙,然后张老师列出来如下10个日期供选择:2月5日,2月7日,2月9日,5月5日,5月8日,8月4日,8月7日,9月4日,9月6日,9月9日.看完日期后,甲说:“我不知道,但你一定也不知道.”乙听了甲的话后,说:“本来我不知道,但现在我知道了.”甲接着说:“哦,现在我也知道了.”请问,张老师的生日是________.解析:根据甲说的“我不知道,但你一定也不知道”,可排除5月5日、5月8日、9月4日、9月6日、9月9日;根据乙听了甲的话后说的“本来我不知道,但现在我知道了”,可排除2月7日、8月7日;根据甲接着说的“哦,现在我也知道了”,可以得知张老师生日为8月4日.答案:8月4日16.(2018·郑州质检)已知△ABC 中,点D 满足2+=0,过D 的直线l 与直线AB ,ACBD ―→ CD ―→分别交于点E ,F ,=λ,=μ.若λ>0,μ>0,则λ+μ的最小值为AE ―→ AB ―→ AF ―→ AC ―→________.解析:因为2+=0,所以=,所以=+=+=BD ―→ CD ―→ BD ―→ 13BC ―→ AD ―→ AB ―→ BD ―→ AB ―→ 13BC ―→+(-)=+.因为D ,E ,F 三点共线,所以可设=x +(1-x )AB ―→ 13AC ―→ AB ―→ 23AB ―→ 13AC ―→ AD ―→ AE ―→=xλ+(1-x )μ,所以xλ+(1-x )μ=+,根据平面向AF ―→ AB ―→ AC ―→ AB ―→ AC ―→ 23AB ―→ 13AC ―→量基本定理,得xλ=,(1-x )μ=,所以x =,1-x =,所以+=1,所以λ+μ=231323λ13μ23λ13μ(λ+μ)=3++≥,当且仅当λ=μ=时等号成立.故λ+13(2λ+1μ)132μλλμ3+22322+23μ的最小值为.3+223答案:.3+223。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小题专项练习(二) 平面向量、复数与框图
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.[2018·成都第三次诊断性检测]若复数z =a +i
1-i
(i 是虚数单位)为纯虚数,则实数a
的值为( )
A .-2
B .-1
C .1
D .2
2.[2018·银川一中第二次模拟考试]若两个单位向量a ,b 的夹角为120°,则|2a +b |=( )
A .2
B .3 C. 2 D. 3
3.[2018·合肥市高三第三次教学质量检测]运行如图所示的程序框图,则输出的s 等于( )
A .-10
B .-3
C .3
D .1
4.[2018·山东沂水期中]若复数z =i
2018
-
2
(i 为虚数单位),则z 的共轭复数z -
=
( )
A .1+i
B .i
C .-12i D.12
i
5.[2018·百校联盟四月联考]设复数z 满足
z -i z
=3+i ,则z -
=( ) A.15+25i B .-15+25i C.15-25i D .-15-25
i 6.[2018·河南新乡第三次模拟测试]已知复数z 1,z 2在复平面内对应的点分别为(2,-1),(0,-1),则z 1z 2
+|z 2|=( )
A .2+2i
B .2-2i
C .-2+i
D .-2-i
7.[2018·宁夏六盘山高三年级第三次模拟]执行下面的程序框图,则输出K 的值为( )
A .99
B .98
C .100
D .101
8.[2018·安徽池州一中5月月考]设点O 在△ABC 的内部,且有AD →=32
(OB →+OC →
),则△
ABC 的面积与△BOC 的面积之比为( )
A .3 B.1
3
C .2 D.1
2
9.[2018·银川一中第二次模拟]20世纪70年代,流行一种游戏——角谷猜想,规则如下:任意写出一个自然数n ,按照以下的规律进行变换:如果n 是个奇数,则下一步变成3n +1;如果n 是个偶数,则下一步变成n
2
,这种游戏的魅力在于无论你写出一个多么庞大的
数字,最后必然会落在谷底,更准确地说是落入底部的循环,而永远也跳不出这个圈子.下列程序框图就是根据这个游戏而设计的,如果输出的i 值为6,则输入的n 值为( )
A .5
B .16
C .5或32
D .4或5或32
10.[2018·河南洛阳第三次统考]在△ABC 中,点P 满足BP →=2PC →
,过点P 的直线与AB ,
AC 所在直线分别交于点M ,N ,若AM →=mAB →,AN →=nAC →
(m >0,n >0),则m +2n 的最小值为( )
A .3
B .4 C.83 D.103
11.[2018·成都毕业班第三次诊断检测]已知P 为△ABC 所在平面内一点,AB →+PB →+PC →
=0,|PC →|=|PB →|=|AB →
|=2,则△PBC 的面积等于( )
A. 3 B .2 3 C .3 3 D .4 3
12.[2018·山东日照高三校际联合考试]在△ABC 中,点D 是线段BC 上任意一点,M
是线段AD 的中点,若存在实数λ和μ,使得BM →=λAB →+μAC →
,则λ+μ=( )
A .2
B .-2 C.12 D .-12
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中的横线上.
13.[2018·内蒙古北重三中第九次调研]已知复数z =1+i +i 2+…+i 10
,则复数z 在复平面内相应的点为________.
14.[2018·江西赣州适应性考试]已知|a |=1,|b |=2,a ·(b -a )=0,则向量a 与b 的夹角为________.
15.[2018·哈尔滨三中模拟]我国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之剩一,五五数之剩三,七七数之剩六,问物几何?”人们把此类题目称为“中国剩余定理”.若正整数N 除以正整数m 后的余数为n ,则记为N ≡n (mod m ),例如10≡2(mod4).现将该问题以程序框图给出,执行该程序框图,则输出的n 等于________.
16.[2018·江苏东台中学质量监测]已知向量a ,b ,c 满足a +b +c =0,且a 与b 的
夹角的正切值为-12,b 与c 的夹角的正切值为-1
3
,|b |=1,则a ·c 的值为________.。
