2012年广东外语外贸大学附设外语学校高三数学寒假作业(数学文)1

合集下载

广东外语外贸大学附设外语学校高三数学寒假作业1 文

数学寒假作业（数学文）1数学文本试卷分第一部分（选择题）和第二部分（非选择题），共8页。

试题1至4页，答题卷5至8页。

满分150分。

考试用时120分钟。

参考公式：锥体的体积公式13V Sh =，其中S 是锥体的底面积，h 是锥体的高．如果事件A 、B 互斥，那么()()()P A B P A P B +=+．第一部分（选择题，共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 复数i m m m z )1()32(2-+-+=为纯虚数,则实数m 的值为:A.1B.1-或3C.3-或1D.3-2．若函数()f x =A ，函数()lg(1)g x x =-,[2,11]x ∈的值域为B ，则AB 为A.(,1]-∞B.(,1)-∞C. [0,1]D.[0,1) 3. 已知平面直角坐标系内的点A(1,1),B(2,4),C(-1,3),AC AB ⋅的值为: A.-4 B.4 C.-8 D.84. 等比数列{}n a 中,2a =4,1617=a ,则5463a a a a +的值是: A.1 B.2 C.21 D.415. 曲线32x x y -=在1-=x 的处的切线方程为A.02=-+y xB.02=++y xC.02=+-y xD.02=--y x6. 如果实数y x ,满足:⎪⎩⎪⎨⎧≥+≤-+≤+-010201x y x y x ，则目标函数y x z +=4的最大值为 A.2B.3C.27 D.47．下列有关命题的说法正确的是A ．“21x =”是“1=x ”的充分不必要条件B ．“1x =-”是“2560x x --=”的必要不充分条件．C ．命题“x R ∃∈，使得210x x ++<”的否定是：“x R ∀∈，均有210x x ++<”．D ．命题“若x y =，则sin sin x y =”的逆否命题为真命题． 8.已知一个正三棱锥P-ABCA.399B.54C.527 D.3369．椭圆22221x y a b+=（a >0b >）的左、右焦点分别是12F F ，，过2F 作倾斜角为120的直线与椭圆的一个交点为M ，若1MF 垂直于x 轴，则椭圆的离心率为A．2．2(2 C D ．10.已知函数1(),()12x x f x g x x +==+，若()()f x g x >，则实数x 的取值范围是（） A (,1)(0,1)-∞- B 1(,1)(0,-+-∞- C 15(1,0)()-+-+∞ D 1(1,0)(0,-+- 第二部分（非选择题，共100分）二、填空题：本大题共4小题，每小题5分，满分20分．其中14~15题是选做题，考生只能选做一题，二题全答的，只计算前一题得分．11．已知α是第二象限角，21sin =α，则=+)4sin(πα ．12.已知流程图如右图所示,该程序运行后,为使输出的b 值为16，则循环体的判断框内①处应填______. 13.已知数列{n a }的通项公式是22++=kn n a n ,若对于n *∈N ，都有n a >+1n a 成立，则实数k 的取值范围是．选做题:(14,15两题只需选答其中一题,两题都答者按第14题给分)14.极坐标系中,曲线4sin ρθ=-和cos 1ρθ=相交于点A,B,则AB =______.15.如图,已知:△ABC 内接于圆O ，点D 在OC 的延长线上， AD 是⊙O 的切线，若o30=∠B ,2=AC ,则OD 的长为 .A12题三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．（解答请写在答题卷上）16.(12分)已知向量)2cos ,(cos ),1,sin 2(x x x =-=,定义函数OQ OP x f ⋅=)(. (Ⅰ)求函数)(x f 的表达式,并指出其最大最小值;(Ⅱ)在锐角△ABC 中,角A,B,C 的对边分别为c b a ,,,且1)(=A f ,8=bc , 求△ABC 的面积S.17．（本小题满分12分）a 、b 是常数，关于x 的一元二次方程023)(2=++++abx b a x 有实数解记为事件A ．⑴若a 、b 分别表示投掷两枚均匀骰子出现的点数，求)(A P ； ⑵若R a ∈、R b ∈，66≤+≤-b a 且66≤-≤-b a ，求)(A P ．18.(14分)如图,在四棱锥ABCD P -中,ABCD PA 底面⊥,PBAo 120=∠BCD ,BC ⊥AB,CD ⊥AD,BC=CD=PA=a,(Ⅰ)求证:平面PBD ⊥平面PAC.(Ⅱ)求四棱锥P-ABCD 的体积V;19.(14分)已知常数a 、b 、c 都是实数，函数c bx x a x x f +++=2323)(的导函数为)(x f '(Ⅰ)设)0(),1(),2('='='=f c f b f a ，求函数f(x)的解析式；(Ⅱ)设 ()()()f x x x γβ'=--，且12γβ<≤<,求(1)(2)f f '⋅'的取值范围；20.(14分)已知圆O:222=+y x 交x 轴于A,B 两点,曲线C 是以AB 为长轴,离心率为22的椭圆,其左焦点为F,若P 是圆O 上一点,连结PF,过原点O 作直线PF 的垂线交直线x=-2于点Q.(Ⅰ)求椭圆C 的标准方程；(Ⅱ)若点P 的坐标为(1,1),求证:直线PQ 与圆O 相切； (Ⅲ)试探究:当点P 在圆O 上运动时(不与A 、B 重合),直线PQ 与圆O 是否保持相切的位置关系?若是,请证明；若不是,请说明理由.21.(14分)在数列{}n a 中，1111,30(2)n n n n a a a a a n --=+-=≥(Ⅰ)证明:}1{na 是等差数列; (Ⅱ)求数列{}n a 的通项； (Ⅲ)若11n n a a λλ++≥对任意2n ≥的整数恒成立，求实数λ的取值范围.数学寒假作业（数学文）数学文参考答案一、选择题：本大题共10小题，每小题5分，共50分．1．D 2．C 3． B 4． C 5．B 6． C 7． D 8．A 9．A 10．D 二、填空题： 11．462-， 12．3 13． ),3(+∞-14.三、解答题：本大题共6小题，满分80分．16.(Ⅰ))42sin(22cos 2sin )2cos ,(cos )1,sin 2()(π-=-=⋅-=⋅=x x x x x x x f ……4分 2,2:)(-∴的最大最小值分别是x f . ………6分(Ⅱ)∵f(A)=1, ∴22)42sin(=-πA ∴4342442ππππ=-=-A A 或 ………8分 ∴24ππ==A A 或,又△ABC 为锐角三角形,所以4π………10分 ∵bc=8,∴△ABC 的面积2222821sin 21=⋅⋅==A bc S ………12分17．⑴方程有实数解，0)23(4)(2≥+⨯-+abb a ，即1222≥+b a ……1分依题意，1=a 、2、3、4、5、6，1=b 、2、3、4、5、6，所以，“投掷两枚均匀骰子出现的点数”共有3666=⨯种结果……2分当且仅当“1=a 且1=b 、2、3”，或“2=a 且1=b 、2”，或“3=a 且1=b ”时，1222≥+b a 不成立......5分，所以满足1222≥+b a 的结果有30)123(36=++-种 (5)分，从而653630)(==A P ……6分．⑵在平面直角坐标系aOb 中，直线6±=+b a 与6±=+b a 围成一个正方形……7分正方形边长即直线6=+b a 与6-=+b a 之间的距离为26266=+=d ……8分正方形的面积722==d S ……10分，圆1222=+b a 的面积为π12/=S ……10分圆在正方形内部……12分，所以66721272)(/ππ-=-=-=S S S A P ……12分．18. (Ⅰ)连结AC,∵BC=CD,AB=AD,∴AC ⊥BD, ………2分PBACD又PA ⊥平面ABCD,且ABCD BD 平面⊂ ∴PA ⊥BD ………3分又PA ∩AC=A, ∴BD ⊥平面PAC ………4分又BDP BD 平面⊂ ∴平面PBD ⊥平面PAC ………6分(Ⅱ)依题意得∠CBD=∠CDB=300,又BC ⊥AB,CD ⊥AD,所以∠DBA=∠BDA=600又BC=CD=a ，∴a BD 3= ∴△ABD 是边长为3的正三角形 ……9分∴PA S S V ABD BCD ⋅+=∆∆)(31a AB AD CD BC ⋅⋅⋅⋅+⋅⋅⋅=)60sin 21120sin 21(31032233)32323(61a a a a =⋅⨯+=………14分 19.(Ⅰ)解：b ax x x f ++='2)(．⎪⎩⎪⎨⎧==++=++∴cb b b a ab a 124，解得：⎩⎨⎧-==-=31c b a ．…5分 33213)(23---=∴x x x x f ． (7)分 (2)()()()f x x x γβ'=--．又 12,(1)(1)(1)0,(2)(2)(2)0f f γβγβγβ<≤<∴'=-->'=--> ………10分 [][])2)(1()2)(1()2)(2)(1)(1()2()1(ββγγβγβγ--⋅--=----='⋅'∴f f2212121()()2216γγββ-+--+-≤⋅=161)2()1(0≤'⋅'<∴f f ………14分20.(14分)解:(Ⅰ)因为a e ==,所以c=1,则b=1,所以椭圆C 的标准方程为2212x y += ………5分(Ⅱ)∵P(1,1),∴12PF k =,∴2OQ k =-,∴直线OQ 的方程为y=-2x, ∴点Q(-2,4)…7分∴1PQ k =-,又1OP k =,∴1k k PQ O P -=⊥,即OP ⊥PQ,故直线PQ 与圆O 相切 ……10分(Ⅲ)当点P 在圆O 上运动时,直线PQ 与圆O 保持相切 ………11分证明:设00(,)P x y(0x ≠则22002y x =-,所以001PFy k x =+,01OQ x k y +=-,E所以直线OQ 的方程为001x y x y +=-所以点Q(-2,0022x y +) ………12分所以002200000000000022(22)22(2)(2)PQx y y y x x x xkx x y x y y +--+--====-+++,又0OPy k x =……13分所以1k k PQ O P -=⊥,即OP ⊥PQ,故直线PQ 始终与圆O 相切. ………14分 21.解:(Ⅰ)将1130(2)n n n n a a a a n --+-=≥整理得：1113(2)n n n a a --=≥ ………3分所以}1{na 是以1为首项,3为公差的等差数列. ………4分(Ⅱ)由(Ⅰ)可得:113(1)32n n n a =+-=-，所以132n a n =-………8分(Ⅲ)若11n n a a λλ++≥恒成立，即3132n n λλ++≥-恒成立………9分整理得：(31)(32)3(1)n n n λ+-≤- 令(31)(32)3(1)n n n c n +-=-1(34)(31)(31)(32)(31)(34)33(1)3(1)n n n n n n n n c c n n n n ++++-+--=-=-- ………12分因为2n ≥，所以上式0>，即{}n c 为单调递增数列，所以2c 最小，2283c =，所以λ的取值范围为28(,]3-∞ ………14分.精品资料。

广东省2012届高三数学文科仿真模拟卷1

广东省2012届高三数学文科仿真模拟卷1第Ⅰ卷（选择题共50分）一．选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．若复数(1)(1)i ai ++(,a R i ∈是虚数单位）是纯虚数，则a =A ．1-B ．0C ．1D ．2 2．设等差数列{n a }的前n 项和为n S ，若515S =,则3a =A. 3B. 4C. 5D.63．双曲线14222-=-y x 的渐近线方程为A ．x y 2±=B ．y x 2±=C ．x y 22±= D ．y x 22±=4．给出下列四个命题,其中假命题是A ．命题“若0m >，则方程20x x m +-=有实数根”的逆否命题为：“若方程20x x m +-=无实数根，则0m ≤”.B ．“1x =”是“2320x x -+=”的充分不必要条件.C ．若命题p :,10x R x x ∈++<2存在使得,:,10p x R x x ⌝∈++≥2则存在都有. D ．若“p q 且”为假命题，则,p q 中至少有一个为假命题.5．设,m n 是两条不同的直线，,,αβγ是三个不同的平面。

有下列四个命题：①若,,m m βαβα⊂⊥⊥则； ②若//,,//m m αβαβ⊂则； ③若,,,n n m m αβαβ⊥⊥⊥⊥则； ④若,,αγβγαβ⊥⊥⊥则. 其中正确命题的序号是A ．①③B ．①②C ．③④D ．②③6．某公司2006～2011年的年利润x (单位：百万元)与年广告支出y (单位：百万元)的统计资料支出y 0.62 0.74 0.81 0.89 1 1.11根据统计资料，则A.利润中位数是16，x 与y 有正线性相关关系B.利润中位数是17，x 与y 有正线性相关关系C.利润中位数是17，x 与y 有负线性相关关系D.利润中位数是18，x 与y 有负线性相关关系7．欧阳修《卖油翁》中写到：（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿. 可见“行行出状元”，卖油翁的技艺让人叹为观止. 若铜钱是直径为3cm 的圆，中间有边长为1cm 的正方形孔，若随机向铜钱上滴一滴油（油滴的大小忽略不计），则油滴正好落入孔中的概率是A. π94B. 43πC. 94πD. 34π8．若右边的程序框图输出的S 是30，则条件①可为 A ．3n ≤ B ．4n ≤C ．5n ≤D ．6n ≤9．已知变量,x y 满足条件10290x x y x y ≥⎧⎪-≤⎨⎪+-≤⎩，若目标函数z ax y =+仅在点(3,3)处取得最小值，则a 的取值范围是A ．10a -<<B ．01a <<C ．1a <-D ．1a <-或1a >10．已知椭圆C ：22221x y a b +=（0a b >>）32，过右焦点F 且斜率为k （0k >）的直线与C 相交于A 、B 两点，若3AF FB =.则k = A 2 B ．1 C ．3 D ． 2第Ⅱ卷（非选择题共100分）二．填空题（本题5小题，每小题5分，共25分.把答案填在答题卡的相应位置） 11．若三点(1,3),(,0),(0,1)A B a C 共线,则a 的值等于 .12．△ABC 的三个内角A 、B 、C 所对边的长分别为a 、b 、c ，已知2,3a b ==，则sin sin()AA C =+ .13．已知奇函数()f x 满足(2)(),(0,1)f x f x x +=-∈且当时，()2xf x =，则72()f 的值为 .14．给出下列六种图象变换方法：①图象上所有点的横坐标缩短到原来的，纵坐标不变； ②图象上所有点的横坐标伸长到原来的2倍，纵坐标不变； ③图象向右平移个单位； ④图象向左平移个单位； ⑤图象向右平移个单位； ⑥图象向左平移个单位.请用上述变换中的两种变换，将函数sin y x =的图象变换到函数y ＝sin(2x＋)的图象，那么这两种变换的序号依次是 (填上一种你认为正确的答案即可). 15．（考生注意：请在下列三题中任选一题作答，若多做，按所做的第一题评分）A ．（不等式选做题）若不等式121a x x -≤+对一切非零实数x 恒成立，则实数a 的取值范围是 . B ．（几何证明选做题）如图，圆O 的直径AB =8，C 为圆周上一点，BC =4，过C 作圆的切线，过A 作直线的垂线AD ，D 为垂足，AD 与圆O 交于点E ，则线段 AE 的长为 .C ．（坐标系与参数方程选做题）在平面直角坐标系xOy 中，已知圆5cos 1:5sin 2x C y θθ=-⎧⎨=+⎩（θ为参数）和直线46:32x t l y t =+⎧⎨=--⎩（为参数），则直线截圆C所得弦长为 .三．解答题（本题6小题，共75分。

2012年师大附中高考模拟卷文科数学

实用文档2012年师大附中高考模拟卷文科数学一、选择题1、程序框图如右图，若5n =，则输出的S 值为A. 30B. 50C. 62D. 662、已知向量(,1)a m =,(1,)b n =,若a ∥b ,则22m n +的最小值为A.0B. 1C.2D. 33、双曲线2244x y -=的离心率为A.5 B.3 C ．43 D.54、设全集{}1,2,3,4,5,6,7,8U =，集合{1,2,3,5}A =，{2,4,6}B =，则下图中的阴影部分表示的集合为A ．{}2B ．{}4,6C ．{}1,3,5D ．{}4,6,7,8实用文档5、在区间[,]22ππ-上随机取一个数x,则cos x的值介于12到1之间的概率为A.13B.2πC.12D.236、在△ABC 中，∠BAC =90º，D 是BC 的中点，AB =4，AC =3，则AD BC ⋅= A.7- B.72-C. 72D. 77、已知函数sin (0)y ax b a =+>的图象如图所示，则函数log ()a y x b =+的图象可能是A. B. C. D.8、如右图所示，圆和直角AOB 的两边相切，直线OP 从OA 处开始，绕点O 匀速旋转（到OB 处为止）时，所扫过的圆内阴影部分的面积S 是t 的函数，它的图象大致为S t S tS tSt ABCDBPAS实用文档9、“{}2log n a 为等差数列”是 “{}n a 为等比数列”的 A. 充分非必要条件 B. 必要非充分条件C. 充要条件D. 既非充分也非必要条件10、一个几何体的正视图与侧视图相同，均为右图所示，则其俯视图可能是11、函数()y f x =的定义域为[1,0)(0,1]-，其图像上任一点(,)P x y 满足221x y +=①函数()y f x =一定是偶函数；②函数()y f x =可能既不是偶函数，也不是奇函数； ③函数()y f x =可以是奇函数；④函数()y f x =如果是偶函数，则值域是[0,1)或(1,0]- 其中正确命题的序号是A. ①③B. ②③C. ③④D. ②③④12、下列命题中，错误．．的是 A. 平行于同一平面的两个不同平面平行A BCD实用文档B. 一条直线与两个平行平面中的一个相交，则必与另一个平面相交C.若直线l 与平面α相交但不垂直，则经过该直线l 有且只有一个平面β与α垂直D.若直线l 不平行平面α，则在平面α内不存在与l 平行的直线二、填空题13、若对于定义在R 上的函数f (x ) ,其图象是连续不断的，且存在常数λ(∈λR)，使得对任意实数x 都有 f (x +λ) +λf (x ) = 0成立，则称f (x ) 是一个“λ—伴随函数”. 有下列关于“λ—伴随函数”的结论：①f (x ) =0 是常数函数中唯一个“λ—伴随函数”；② f (x ) = x 2是一个“λ—伴随函数”； ③ “21—伴随函数”至少有一个零点. 其中不正确．．．的序号是______.14、若i 为虚数单位，则(1)i i -= .15、若实数,x y 满足10,0,x y x -+≤⎧⎨≤⎩，则22x y +的最小值是 .16、若[0,],x π∀∈ 不等式1sin 02x x m --<恒成立，则m 的取值范围为 .三、解答题 17、某园林局对1000株树木的生长情况进行调查，其中杉树 600株，槐树400株 .现用分层抽样方法从这1000株树木中随机抽取100株，杉树与槐树的树干周长（单位：cm ）的抽查结果如下表：实用文档(I)求x ，y 值及估计槐树树干周长的众数；（Ⅱ）如果杉树的树干周长超过60cm 就可以砍伐，请估计该片园林可以砍伐的杉树有多少株？（Ⅲ）树干周长在30cm 到40cm 之间的4株槐树有1株患虫害，现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.18、如图，圆1C :()222x a y r -+=()0r >与抛物线2C ：22x py =()0p >的一个交点M ()1,2，且抛物线在点M 处的切线过圆心1C . （Ⅰ）求1C 和2C 的标准方程；（Ⅱ）若点N 为抛物线2C 上的一动点，求11C N C M •的取值范围．实用文档19、如图，从点1(0,0)P 做x 轴的垂线交曲线xy e =于点1(0,1),Q 曲线在1Q 点处的切线与x 轴交于点2P ，再从2P 做x 轴的垂线交曲线于点2Q ，依次重复上述过程得到一系列点：1122,;,......;,,n n P Q P Q P Q 记n P (,0)n x ，*(,)()n x n n Q x e n N ∈.（Ⅰ）求点n Q 处的切线方程，并指出1n x +与n x 的关系；（Ⅱ）求112233...nn PQ PQ PQ PQ ++++20、已知椭圆2212x y +=的左、右焦点为1F 、2F ，上顶点为A ，直线1AF 交椭圆于B . 如图所示沿x 轴折起，使得平面12AF F ⊥平面12BF F . 点O 为坐标原点. ( I ) 求三棱锥12A F F B -的体积；（Ⅱ）线段2BF 上是否存在点M ，使得AM OB ⊥，若存在，请在图1中指出点M 的坐标；若不存在，请说明理由.YXOB AFF AO BXF F MY 图1图2实用文档21、已知函数32()f x x ax bx =++ (0)x ≠只有一个零点3x =. （Ⅰ）求函数()f x 的解析式；（Ⅱ）若函数'()()ln g x f x m x =+在区间(0,2)上有极值点，求m 取值范围；（Ⅲ）是否存在两个不等正数,s t ()s t <，当[,]x s t ∈时，函数32()f x x ax bx =++的值域也是[,]s t ，若存在，求出所有这样的正数,s t ；若不存在，请说明理由；22、如图某河段的两岸可视为平行，为了测量该河段的宽度，在河段的一岸边选取两点A 、B ，观察对岸的点C,测得105CAB ∠=，45CBA ∠=,且100AB =米. （1）求sin105；（2）求该河段的宽度.CA B以下是答案一、选择题1、 C2、 C3、 A4、 B5、 D6、 B7、 B8、 D9、A10、B11、B12、D 实用文档实用文档二、填空题 13、 ①②14、 1i +15、1216、6m π>-三、解答题17、解：（Ⅰ）按分层抽样方法随机抽取100株，可得槐树为40，杉树60株606192114x ∴=---=，40420610y =---=. 估计槐树树干周长的众数为45CM（Ⅱ）1460014060⨯=，估计该片园林可以砍伐的杉树有140株（Ⅲ）设4株树为1B 、2B 、3B 、D ，设D 为有虫害的那株，基本事件为：（12,B B ）（13,B B ）（1,B D ）（21,B B ）（23,B B ）（2,B D ）（31,B B ）（32,B B ）（3,B D ）（1,D B ）（2,D B ）（3,D B ）设事件A:排查的树木恰好为2株，事件A 包含（1,B D ）（2,B D ）（3,B D ）3种31()124P A ∴==18、解（Ⅰ）把M ()1,2代入2C ：()022>=p py x 得2=p ，故2C ：y x 42= 由241x y =得x y 21'=，从而2C 在点M 处的切线方程为21-=-x y 令0=y 有1=x ，圆心1C （1，0），又M ()1,2在圆1C 上所以()22112r =+-，解得22=r ，故1C ：()2122=+-y x实用文档（Ⅱ）设N ()y x ,，则()11,C N x y =-，()11,1C M =，所以111C N C M x y •=+-，2221411(2)244x x y x y x x =∴+-=+-=+-,又因为x R ∈所以11C N C M •的取值范围为[2,)-+∞。

广东外语外贸大学附设外语学校2012年高一数学寒假作业

数学科寒假作业班级姓名质量评价一、选择题.1. 已知全集}41|{},32|{,>-<=≤≤-==x x x B x x A R U 或，那么=)(B C A UA 、}42|{<≤-x xB 、}43|{≥≤x x x 或C 、}12|{-<≤-x xD 、}31|{≤≤-x x2.过点（1，0）且与直线x-2y-2=0平行的直线方程是（）（A ）x-2y-1=0 (B)x-2y+1=0 (C)2x+y-2=0 （D ）x+2y-1=0 3. 已知A （-1,2），B （2，-2），则直线AB 的斜率是（）A.34-B.43-C. 34D. 434. 直线y x b =+平分圆228280x y x y +-++=的周长，则b = （）A ．3B ．5C ．－3D ．－55. 设函数⎪⎩⎪⎨⎧>-+≤-=)1(,23)1(,21)(22x x x x x x f ，则=))3(1(f f （）A 、128127B 、128127-C 、81D 、1616. 直线023=++y x 的倾斜角是（）A.300B. 600C. 900D. 12007. 直线2)1(0122=+-=++y x y x 与圆的位置关系是（）A ．相切B ．相交C ．相离D ．不能确定8. 若01x <<，则2x，12x⎛⎫⎪⎝⎭，()0.2x 之间的大小关系为（） A 、2x <()0.2x<12x⎛⎫ ⎪⎝⎭ B 、2x<12x⎛⎫⎪⎝⎭<()0.2x C 、12x⎛⎫ ⎪⎝⎭<()0.2x < 2x D 、()0.2x< 12x⎛⎫⎪⎝⎭< 2x9、方程3log 3=+x x 的解所在的区间是（）A 、)1,0(B 、)2,1(C 、)3,2(D 、),3(+∞10、设)(x f 为定义在R 上的奇函数，当为常数）（时b b x x f x x++=≥22)(,0，则=-)1(f （）A 、3-B 、1-C 、1D 、3二、填空题.11. 已知,,,S A B C 是球O 表面上的点，SA ABC ⊥平面，AB BC ⊥，1SA AB ==，BC =则球O 的表面积等于。

广东外语外贸大学附设外语学校高三数学寒假作业（数学理）1

数学寒假作业（数学理）1一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1. 已知集合A 、B 满足A B A =，那么下列各式中一定成立的是（）A. A BB. B AC. AB B = D. A B A =2．设条件,0:;0:2≥+>a a q a p 条件那么p 是q 的什么条件（）A ．充分非必要条件B ．必要非充分条件C ．充分且必要条件D ．非充分非必要条件3.若12a b，则（）（A ）22aba （B ）22abb（C ）2log ()1ab （D ）2log ()2ab4．已知双曲线)0,0(,12222>>=-b a by a x 的一条渐近线方程为x y 34=，则双曲线的离心率为（）A ．34 B ．35 C ．45 D ．235. 设向量a ，b 满足：||3=a ，||4=b ，0⋅=a b ．以a ，b ，-a b 的模为边长构成三角形，则它的边与半径为1的圆的公共点个数最多为( ) A ．3 B.4 C ．5D ．66．为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)，已知加密规则如图所示，例如，明文1,2,3,4对应密文5,7,18,16. 当接收方收到密文14,9, 23,28时，则解密得到的明文为（）A ．4,6,1,7B ．7,6,1,4C ．6,4,1,7D ．1,6,4,77.在棱长均为2的正四棱锥P ABCD -中，点E 为PC 的中点，则下列命题正确的是输入a,b,c,d22234m a b n b c p c d q d←+←+←+←输出m,n,p,q 结束开始第7题图（）.（A ）BE ∥平面PAD ，且BE 到平面PAD 3（B ）BE ∥平面PAD ，且BE 到平面PAD 的距离为263（C ）BE 与平面PAD 不平行，且BE 与平面PAD 所成的角大于30︒（D ）BE 与平面PAD 不平行，且BE 与平面PAD 所成的角小于30︒8．已知)(x f 是业义在R 上的不恒为零的函数，且对于任意实数R ∈b a ,满足：)()2(,2)2(),()()(*∈==+=⋅N n n f a f a bf b af b a f n n ，)(2)2(5*∈=N n b nn n 考察下列结论：网①);1()0(f f =②数列{a n }为等比例数列；③数列{b n }为等差数列。

广东省2012届高三全真模拟卷数学文 14

广东省2012届高三全真模拟卷数学文科14一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的1、如图所示，U 表示全集，则用A 、B 表示阴影部分正确的是( )A.)(B A C UB. B C A C U UC. )(B A C UD. B A 2、函数()2sin()2f x x π=+在其定义域上是( )A.奇函数B. 偶函数C. 增函数D. 减函数 3、等差数列{}为则中，593,19,7a a a a n ==（）.A 、13B 、12C 、11D 、104、原命题：“设2,,ac b a R c b a 则若、、>∈＞bc ”以及它的逆命题，否命题、逆否命题中，真命题共有（）个.A. 0B. C . 2 D. 4 5、已知正方形ABCD 边长为1，则AB BC AC ++=( ) A. 0 B. 2 C .2 D. 226、一个正方体的体积是8，则这个正方体的内切球的表面积是（） A 、π8 B 、π6 C 、π4 D 、π7、方程0Ax By C ++=表示倾斜角为锐角的直线，则必有( ) A. 0AB > B. 0AB < C . 0BC > D. 0BC <8、若焦点在x 轴上的椭圆 1222=+m y x 的离心率为21，则m =（）.A 、23 B 、3 C 、38 D 、329、在空间直角坐标系xyz O -中，过点(4,2,3)--M 作直线OM 的垂线，则直线与平面Oxy 的交点(,,0)P x y 的坐标满足条件( ) A ．42290+-=x y B ．42290-+=x y C ．42290++=x y D ．42290--=x y10、已知()f x 是定义在R 上的不恒为零的函数，且对于任意的a 、b ∈R ，满足()f ab =()()af b bf a +，(2)2f =，(2)n n f a n =（n *∈N ），(2)2n n n f b =（n *∈N ）.考查下列结论：①(0)(1)f f =；②()f x 为偶函数；③数列{}n a 为等比数列；④{}n b 为等差数列。

广东外语外贸大学附设外语学校高二数学寒假作业文科

广东外语外贸大学附设中山外语学校2011~2012学年高二上学期寒假作业1—数学（文科）一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1.“a ＞0”是“2a ＞0”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2. 不等式0652≤+--x x 的解集为（）A.}16|{-≤≥x x x 或B.}61|{≤≤-x xC.}16|{≤≤-x xD.}16|{≥-≤x x x 或3．设数列{}n a 的前n 项和2n S n =，则8a 的值为（）A. 15B. 16C. 49D.64 4. 在ABC ∆中,8,60,75a B C ︒︒===,则b = ( )A．D.3235.下列命题正确的个数有（）①若,1>a 则11<a ②若b a >，则ba 11< ③对任意实数a ，都有a a ≥2 ④若22bc ac >，则b a >A ．1个 B.2个 C.3个 D.4个 6．过点（3，－2）且与椭圆24x 03692=-+y 有相同焦点的椭圆方程是（）A ．1101522=+y x B ．110522=+y x C ．1151022=+y x D ．1102522=+y x 7．下列说法错误．．的是 ( ) A ．如果命题“p ⌝”与命题“p 或q ”都是真命题，那么命题q 一定是真命题B.命题p ：022,0200≤++∈∃x x R x ,则022,:2>++∈∀⌝x x R x pC ．命题“若b a ,都是偶数，则b a +是偶数”的否命题是“若b a ,都不是偶数，则b a +不是偶数”D ．特称命题 “R x ∈∃，使2240x x -+-=”是假命题8.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是（） A.54 B. 53 C. 52 D. 51 9．给出命题：“已知a 、b 、c 、d 是实数，若,a b c d a c b d ≠≠+≠+且则”.对原命题、逆命题、否命题、逆否命题而言，其中真命题（） A.0个 B.1个 C.2个 D.4个10.设,x y 满足约束条件12x y y x y +≤⎧⎪≤⎨⎪≥-⎩,则3zx y =+的最大值为（）CA ． 5 B.3 C. 7 D. -811. 椭圆1244922=+y x 上一点P 与椭圆的两个焦点1F 、2F 的连线互相垂直，则△21F PF 的面积为( )A ．20B ．22C ．24D ．28 12．在△ABC 中，cos cos A aB b=，则△ABC 一定是( )A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等边三角形二、填空题：(本大题共4小题，每小题4分，共16分．把答案填写在题中横线上)． 13．已知{}n a 是公比为2的等比数列，则1234a a a a ++的值为 .14. 椭圆1422=+y m x 的焦距为2，则m 的值为 . 15．已知命题p ：23,x x R x >∈∀；命题q ：ABC ∆中，ab c b a =-+222，则3π=C ，则命题（p ⌝）且q 的真假性的是 .16.已知,x y R +∈，且满足134x y +=，则xy 的最大值为 .三、解答题：(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤). 17.（本小题满分12分）设函数2()f x x ax b =-+若不等式()0f x <的解集是{}|23x x <<，求不等式012>+-ax bx 的解集.18．(本小题满分12分)已知数列{}n a 是一个等差数列，且21a =，55a =-.（Ⅰ）求{}n a 的通项n a ；（Ⅱ）求{}n a 前n 项和n S 的最大值．19．(本小题满分12分)已知命题p ：关于x 的不等式01)1(2≤+-+x a x 的解集为空集φ；命题q ：函数x a y )1(-=为增函数，若命题q p ∧为假命题，q p ∨为真命题，求实数a 的取值范围. 20．（本小题满分12分）在锐角ABC △中，内角A B C ，，对边的边长分别是a b c ，，，且A c a sin 23⋅=, （Ⅰ）求角C ;（Ⅱ）若边3=a ， ABC △的面积等于233，求边长b .21．（本小题满分12分）已知椭圆的焦点是)0,1(),0,1(21F F -,P 为椭圆上一点，且||21F F 是||1PF 和||2PF 的等差中项.（Ⅰ）求椭圆的方程；（Ⅱ）求21F PF ∆面积的最大值及此时点P 的坐标.22．（本小题满分12分）已知椭圆22122:1(0)x y C a b a b+=>>的长轴长为1e =，椭圆2C 与1C 有共同的短轴.（Ⅰ）求椭圆1C 的方程;（Ⅱ）若2C 与直线l ：02=+-y x 有两个不同的交点，求椭圆的离心率2e 的取值范围.广东外语外贸大学附设中山外语学校2011~2012学年高二上学期寒假作业2—数学（文科）一、选择题（本大题共10小题，每小题5分，共50分. 每小题各有四个选择支，仅有一个选择支正确. 请用2B 铅笔把答题卡中所选答案的标号涂黑．）1.在ABC ∆中，角A ，B ，C 的对边长分别为,,a b c ，0075,60,8===C B a ,则=b （）A. 64B. 34C. 24D.3322．命题“若ab =0,则a =0或b =0”的逆否命题是（）A ．若a =0或b =0,则ab =0B ．若0≠ab ，则0≠a 或0≠bC ．若0≠a 且0≠b ,则0≠abD ．若0≠a 或0≠b ，则0≠ab 3．设c b a >>,则下列不等式一定成立的是（）A.c b c a >B.ac ab >C.cb a 111<< D.c b c a ->- 4．已知{}n a是等比数列，141a a ==，3a =（） A.2± B.2 C.2- D.45．抛物线23y x =的焦点坐标是（）A ．3(,0)4B ．3(0,)4C ．1(,0)12D ．1(0,)126．已知等差数列{}n a 的前n 项和为n S ，若4518a a =-，则8S 等于（）A ．72B ．54C ．36D ．187．在平面直角坐标系中，不等式组,040⎪⎩⎪⎨⎧≤≥+-≥+a x y x y x （a 是常数）表示的平面区域面积是9，那么实数a 的值为（）A ．223+B ．－223+C ．－5D ．18．若函数m mx mx x x f 3)(23++-=在)1,0(A. 0<mB. 3<mC. 3>mD. 30<<m 9．如图，椭圆与双曲线有公共焦点1F 、2F ，它们在第一象限的交点为A ,且21AF AF ⊥，02130=∠F AF ，则椭圆与双曲线的离心率的倒数和为（）A ．23B ．3C ．2D ．110．某商场对某种商品搞一次降价促销活动，现有四种降价方案. 方案Ⅰ：先降价x %,后降价y %；方案Ⅱ：先降价y %,后降价x %；方案Ⅲ：先降价2y x +%,后降价2yx +%；方案Ⅳ：一次性降价)(y x +%（其中50,0<<y x ）.在上述四种方案中，降价最少的是（）A ．方案ⅠB ．方案ⅡC ．方案ⅢD ．方案Ⅳ 二、填空题（本大题共4小题，每小题5分，共20分．请把答案填在答题卡中相应的位置上．）11．如果方程22112x y m m +=++表示双曲线，那么m 的取值范围是。

2012年广东某外语外贸大学附设外语学校英语真卷

2012年广东某外语外贸大学附设外语学校英语真卷（时间：50分钟满分：100分）听力部分略。

（20分）笔试部分（80分）Ⅰ. Multiple choice.（选择最佳答案。

10%）（）1. May I your bike?—Sorry, I it to Mary yesterday.A. keep; borrowedB. borrow; repairedC. use; lentD. lend; returned（）2. Mike and Tom, did you enjoy on Christmas Day?A. myselfB. yourselvesC. ourselvesD. themselves（）3. Jim likes apples a lot, he doesn’t like oranges at all.A. andB. orC. butD. so（）4. I think it’s a fine day a walk.A. ofB. forC. withD.to（）5. book on the desk is English book.A. The; anB. The; aC. A; anD. A; /（）6. Who can good English in your class?A. sayB. tellC. talkD. speak（）7. We are going to do some at the weekend.A. cleanB. cleansC. to cleanD. cleaning（）8. There are only students in the classroom. Where are the others?A. a fewB. a littleC. littleD. few（）9. Amy makes fewer mistakes than Frank. She does her homework .A. more carelesslyB. more carefullyC. more carefulD. more careless（）10. How much does the ticker from Shanghai to Beijing?A. takeB. costC. spendD. payⅡ. Rewrite the sentences as required.（按要求改写句子。

【高三数学试题精选】2018年广东外语外贸大学附设外语学校高三数学寒假作业(数学文)1(含答案)

2018年广东外语外贸大学附设外语学校高三数学寒假作业
（数学文）1(含答案)
5
数学寒假作业（数学）1
数学
本试卷分第一部分（选择题）和第二部分（非选择题），共8页。

试题1至4页，答题卷5至8页。

满分150分。

考试用时14 B4 c-8 D8
4 等比数列中, =4, ,则的值是
A1 B2 c D
5 曲线在的处的切线方程为
A B c D
6 如果实数满足，则目标函数的最大值为
A2 B3 c D4
7．下列有关命题的说法正确的是
A．“ ”是“ ”的充分不必要条
B．“ “是“ ”的必要不充分条．
c．命题“ 使得”的否定是“ 均有”．
D．命题“若，则”的逆否命题为真命题．
8已知一个正三棱锥P-ABc的主视图如图所示，则此正三棱锥的侧面积为
A B54 c D
9．椭圆（）的左、右焦点分别是，过作倾斜角为的直线与椭圆的一个交点为，若垂直于轴，则椭圆的离心率为
A． B． c． D．
10已知函数，若，则实数的取值范围是（）
A B
c D。

2012-2013学年高三数学寒假作业2 含答案

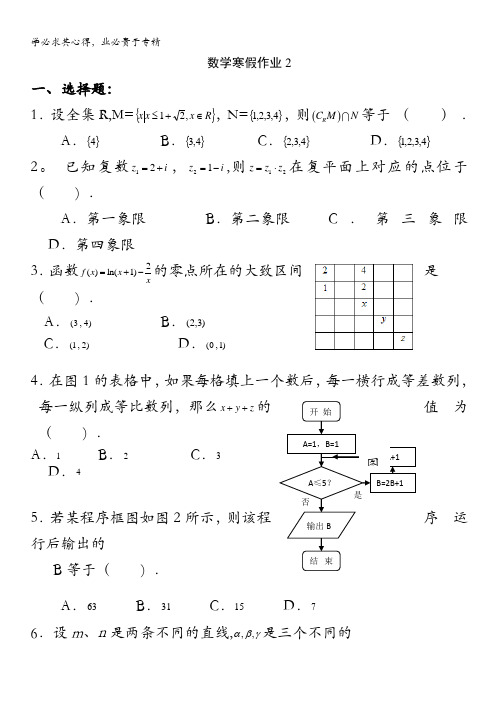
数学寒假作业2一、选择题：1．设全集R,M={}Rx x x ∈+≤,21，N={}4,3,2,1，则()RC M N 等于（）．A ．{}4B ．{}4,3C ．{}4,3,2D ．{}4,3,2,12。

已知复数iz +=21，i z-=12,则21z z z ⋅=在复平面上对应的点位于（ ) ．A ．第一象限B ．第二象限C ．第三象限D ．第四象限是3．函数2()ln(1)f x x x=+-的零点所在的大致区间（ ) ．A ．(3,4)B ．)3,2(C ．(1,2)D ．(0,1)4．在图1的表格中，如果每格填上一个数后，每一横行成等差数列，每一纵列成等比数列，那么z y x ++的值为（ ) ．A ．1B ．2C ．3D ．45．若某程序框图如图2所示，则该程序运行后输出的B 等于（ ) ．A ．63B ．31C ．15D ．76．设m 、n 是两条不同的直线,,,αβγ是三个不同的开始A=1，B=1A=A+1 B=2B+1A ≤5？输出B结束是否图平面,给出下列四个命题: ①若m ⊥α，n //α，则m n ⊥ ②若αβ//,βγ//,m ⊥α，则m ⊥γ ③若m //α，n //α，则m n // ④若αγ⊥，βγ⊥，则//αβ其中正确命题的序号是（）．A 、①和②B 、②和③C 、③和④D 、①和④7.则该几何体的表面积为（ )A 。

6+3+π B 。

18+3+π4C 。

18+23+πD. 32+π8.已知0(,)|y x y y ⎧⎫≥⎧⎪⎪Ω=⎨⎨≤⎪⎪⎩⎩，直线2y mx m =+y =有两个不同的交点，它们围成的平面区域为M ，向区域Ω上随机投一点A,点A落在区域M 内的概率为()P M ,若2()[,1]2P M ππ-∈，则实数m 的取值范围为（ ) ．A ．1[,1]2B ．C ．D ． [0,1]二、填空题：本大题共7小题,考生作答6小题，每小题5分，满分30分．正视图侧视图俯视图9。

广东外语外贸大学附设外语学校高三数学寒假作业1 理

数学寒假作业（数学理）1一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.中国教考资源网 1. 已知集合A 、B 满足A B A =，那么下列各式中一定成立的是（）A. A BB. B AC. AB B = D. A B A =2．设条件,0:;0:2≥+>a a q a p 条件那么p 是q 的什么条件（）A ．充分非必要条件B ．必要非充分条件中国教考资源网C ．充分且必要条件D ．非充分非必要条件中国教考资源网3.若102a b <<<，则（）（A ）22aba> （B ）22abb> （C ）2log ()1ab >- （D ）2log ()2ab <-4．已知双曲线)0,0(,12222>>=-b a by a x 的一条渐近线方程为x y 34=，则双曲线的离心率为（）A ．34 B ．35 C ．45 D ．235. 设向量a ，b 满足：||3=a ，||4=b ，0⋅=a b ．以a ，b ，-a b 的模为边长构成三角形，则它的边与半径为1的圆的公共点个数最多为( ) A ．3 B.4 C ．5D ．66．为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)，已知加密规则如图所示，例如，明文1,2,3,4对应密文5,7,18,16. 当接收方收到密文14,9, 23,28时，则解密得到的明文为（）A ．4,6,1,7B ．7,6,1,4C ．6,4,1,7D ．1,6,4,77.在棱长均为2的正四棱锥P ABCD -中，点E 为PC 的中点，则下列命题正确的是（）. （A ）BE ∥平面PAD ，且BE 到平面PADE DCBAP第7题图（B ）BE ∥平面PAD ，且BE 到平面PAD的距离为3（C ）BE 与平面PAD 不平行，且BE 与平面PAD 所成的角大于30︒ （D ）BE 与平面PAD 不平行，且BE 与平面PAD 所成的角小于30︒8．已知)(x f 是业义在R 上的不恒为零的函数，且对于任意实数R ∈b a ,满足：)()2(,2)2(),()()(*∈==+=⋅N n n f a f a bf b af b a f n n ，)(2)2(5*∈=N n b n n n 中国教考资源网考察下列结论：网①);1()0(f f =②数列{a n }为等比例数列；中国教考资源网③数列{b n }为等差数列。

2012届高三数学寒假作业

2012届高三数学寒假作业
各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢
2012届高三数学寒假作业三
一、填空题(14×5′=70′)
1. 已知全集为实数集，，则.
2.复数(i是虚数单位)的虚部为.
3.设向量a，b满足：，，则.
4. 角的顶点在原点，始边与x轴正半轴重合，点P 是角终边上一点，则= .
5.在平面直角坐标系xoy中，直线与直线互相垂直的充要条件是m= .
6.函数的最小正周期是.
7.抛掷甲、乙两枚质地均匀且四面上分别标有1，2，3，4的正四面体，其底面落于桌面，记所得的数字分别为x，y，则为整数的概率是.
8.为了解高中生用电脑输入汉字的水平，随机抽取了部分学生进行每分钟
输入汉字个数测试，下图是根据抽样测试后的数据绘制的频率分布直方图，其中每分钟输入汉字个数的范围是[50，150]，样本数据分组为[50，70)，[70，90)，[90，110)，[110，130)，[130，150]，已知样本中每分钟输入汉字个数小于90的人数是36，则样本中每分钟输入汉字个数大于或等于70个并且小于130个的人数是.
9.运行如图所示程序框图后，输出的结果是.
10.已知直线与曲线相切，则的值为.
11. 关于直线和平面，有以下四个命题：
①若，则;②若，则;
各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢。

广东省广东外语外贸大学附属外国语学校2023-2024学年高二下学期期中考试数学试卷(含简单答案)

广东外语外贸大学附属外国语学校2023-2024学年高二下学期期中考试数学试题考试范围：第五六七章；考试时间：120分钟；满分：150分注意事项：1.选择题作答请用2B 铅笔写在答题卡上，修改时用橡皮擦干净．笔答题作答必须用黑色墨迹签字笔或钢笔填写在相对应的答题框内，不得超出答题框.2.保持答题卡卡面清洁，不要折叠，不要弄破.3.在每页考生信息框中填写姓名及考生号.第I 卷（选择题）一､单选题：本题共8小题，每小题5分，共40分．在每小题给出的选项中，只有一项是符合题目要求的.1. 已知函数f (x )的图象如图所示，下列数值的排序正确的是（）A. B. C. D. 2. 2023年杭州亚运会吉祥物组合为“江南忆”，出自白居易的“江南忆，最忆是杭州”，名为“琮琮”、“莲莲”、“宸宸”的三个吉祥物，是一组承载深厚文化底蕴的机器人为了宣传杭州亚运会，某校决定派4名志愿者将这三个吉祥物安装在学校科技广场，每名志愿者只安装一个吉祥物，且每个吉祥物至少有一名志愿者安装，若志愿者甲只能安装吉祥物“宸宸”，志愿者乙不能安装吉祥物“宸宸”则不同的安装方案种数为（）A. 6B. 12C. 10D. 143. 函数的最小值为（）A. B. C.D. (2)(3)(3)(2)f f f f <'<-'(3)(3)(2)(2)f f f f <-'<'(3)(2)(3)(2)f f f f <'<-'(3)(2)(2)(3)f f f f ''-<<()[]11e ,3,4x y x x +=+∈-22e -55e 54e 1e --4. 已知某地市场上供应的灯泡中，甲厂产品占，乙厂产品占，甲厂产品的合格率是，乙厂产品的合格率是，则从该地市场上买到一个合格灯泡的概率是（）A. B. C. D.5. 从1，2，3，4，5中任取2个不同的数，记事件为“取到的2个数之积为偶数”，事件为“取到的2个数之和为偶数”，则（）A.B.C.D.6. 某三甲医院组织安排4名男主任医师和3名女主任医师到3家不同的区级医院支援，要求每家区级医院至少安排2人且必须有1名女主任医师，则不同的安排方法有（）A. 216种B. 108种C. 72种D. 36种7. 设函数与是定义在同一区间上的两个函数，若对任意的，都有，则称与在上是“密切函数”，区间称为“密切区间”，设函数与在上是“密切函数”，则实数m 的取值范围是（）A. B. C. D. 8. 若对一切正实数恒成立，则实数的取值范围是（）A B. C. D. 二､多选题：本题共3小题，共18分．在每小题给出的选项中，有多项符合题目要求.9. 下列说法中不正确的有（）A. B. 函数的切线与函数可以有两个公共点C. 若，则是函数的极值点D. 函数的减区间为10. 下列各式中，不等于是（）A. B. C.D. 11. 下列说法正确的是（）.的60%40%90%80%0.540.320.840.86A B ()|P B A =18171625()f x ()g x [],a b [],x a b ∈()()1f x g x -≤()f x ()g x [],a b [],a b ()ln f x x =()1mx g x x -=1,e e ⎡⎤⎢⎥⎣⎦[]2,2e -1,2e ⎡⎤⎢⎥⎣⎦1,1e e e ⎡⎤-+⎢⎥⎣⎦[]1,1e e -+2ln 2x t e x t +≥-x t 1(,e-∞1(,]2-∞1+2⎡⎫-∞⎪⎢⎣⎭，(,]e -∞ππsin cos44'⎛⎫= ⎪⎝⎭()y f x =()00f x '=0x ()f x ()ln2f x x x =-(),1-∞!n 11n n n A --⋅m mn nA C ⋅11n n A ++m n mn n mA A --⋅A. 已知随机变量X ，Y ，满足，且X 服从正态分布，则B 已知随机变量X 服从二项分布，则C. 已知随机变量X 服从正态分布，且，则D. 已知随机变量X 服从两点分布，且，令，则第II 卷（非选择题）三､填空题：本题共3小题，每小题5分，共15分.12. 在的展开式中，的系数为15，则________.13. 丝瓜的主要用途是作为蔬菜被人们食用，除此之外，丝瓜成熟后里面的网状纤维（丝瓜络）可代替海绵用于洗刷灶具及家具，其肉、籽、花、藤、叶等也具有一定的药用作用．已知一种白玉香丝瓜成熟后的长度近似服从正态分布，某蔬菜种植基地新摘下一批成熟白玉香丝瓜，整理后发现长度在23cm 以上（含23 cm ）的白玉香丝瓜有320根，则此次摘下的白玉香丝瓜约有______根．（结果保留整数，若，则，，）14. 对于函数，若其定义域内恰好存在两个不同非零实数，使得成立，则称函数为M 函数．若函数为M 函数，则实数a 的取值范围是____________．四､解答题：本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤.15. 已知函数.（1）求曲线在点处的切线的方程；（2）求函数的极值.16. 某外语学校的一个社团中有7名同学，其中2人只会法语；2人只会英语，3人既会法语又会英语，现选派3人到法国的学校交流访问．（1）在选派的3人中恰有2人会法语的概率；.的24X Y +=(3,1)N 1()2E Y =15,3B ⎛⎫ ⎪⎝⎭80(3)243P X ==(4,1)N (5)0.1587P X ≥=(35)0.6826P X <<=(0)0.6,(1)0.4P X P X ====32Y X =-(2)0.6P Y =-=5(1)(1)x ax ++2x =a ()20,9N ()2,X N μσ:()0.6827P X μσμσ-<<+≈()220.9545P X μσμσ-<<+≈()330.9973P X μσμσ-<<+≈()y f x =12,x x ()()121211,f x f x x x ==()f x ()xef x a=()21xx x f x e +-=()y f x =()()0,0f ()y f x =（2）在选派的3人中既会法语又会英语的人数X 的分布列和数学期望．17. （1）求的展开式中的常数项；（2）若，求：①②.18. 某校有一个露天的篮球场和一个室内乒乓球馆为学生提供锻炼场所，甲、乙两位学生每天上下午都各花半小时进行体育锻炼，近50天天气不下雨的情况下，选择体育锻炼情况统计如下：上下午体育锻炼项目的情况（上午，下午）（篮球，篮球）（篮球，乒乓球）（乒乓球，篮球）（乒乓球，乒乓球）甲20天15天5天10天乙10天10天5天25天假设甲、乙选择上下午锻炼的项目相互独立，用频率估计概率.（1）分别估计一天中甲上午和下午都选择篮球的概率，以及甲上午选择篮球的条件下，下午仍旧选择篮球的概率；（2）记为甲、乙在一天中选择体育锻炼项目的个数，求的分布列和数学期望；（3）假设A 表示事件“室外温度低于10度”，表示事件“某学生去打乒乓球”，，一般来说在室外温度低于10度的情况下学生去打乒乓球的概率会比室外温度不低于10度的情况下去打乒乓球的概率要大，证明：.19. 设函数，其中为常数，且.（1）讨论函数的单调性；（2）设函数，是函数的两个极值点，证明：.6212x x ⎛⎫- ⎪⎝⎭()62212012121x x a a x a x a x ++=++++ 02412a a a a ++++ 123122312a a a a ++++ X X ()E X B ()0P A >(|)(|)P A B P A B >1()ln 1f x a x x =++a 0a >()f x ()()ln F x f x x a =+12,x x ()f x ()()1214ln 2F x F x +<-广东外语外贸大学附属外国语学校2023-2024学年高二下学期期中考试数学试题简要答案第I卷（选择题）一､单选题：本题共8小题，每小题5分，共40分．在每小题给出的选项中，只有一项是符合题目要求的.【1题答案】【答案】B【2题答案】【答案】C【3题答案】【答案】D【4题答案】【答案】D【5题答案】【答案】B【6题答案】【答案】A【7题答案】【答案】A【8题答案】【答案】C二､多选题：本题共3小题，共18分．在每小题给出的选项中，有多项符合题目要求.【9题答案】【答案】ACD【10题答案】【答案】BC【11题答案】【答案】ACD第II 卷（非选择题）三､填空题：本题共3小题，每小题5分，共15分.【12题答案】【答案】或1【13题答案】【答案】2017【14题答案】【答案】四､解答题：本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤.【15题答案】【答案】（1）；（2）极小值为，极大值为.【16题答案】【答案】（1）（2）分布列略；【17题答案】【答案】（1）（2）①；②【18题答案】【答案】（1）0.4；（2）分布列略，182（3）证明略【19题答案】【答案】（1）答案略；（2）证明略..32-1,0e⎛⎫- ⎪⎝⎭210x y --=e -25e47()97E X =240365437447。

广东省高三数学寒假作业(六)

一、选择题1．已知θ是三角形的一个内角，且sinθ、cosθ是关于x 的方程2x 2＋px －1＝0的两根，则θ等于A ．B ．C ．D ．2．定义运算22mn m mn n =--，则cos sin66ππ=（）A ．1324- B ．1324-- C ．314+ D ．314-3．已知向量(cos ,sin ),(cos ,sin )a b ααββ==，并且满足关系：3ka b a kb+=-(0k >）,则><b a ,的最大值为 ( )A ．6πB ．3π C ．65π D ．32π 4．已知α为第二象限角，3sin 5α=，则sin 2α=（）. A ．2524-B ．2512-C ．2512 D ．2524 5．设tan ,tan αβ是方程2320x x -+=的两个根，则tan()αβ+的值为 A ．－3 B ．－1 C ．1D ．36．sin 163°sin 223°＋sin 253°sin 313°等于( )A ．－12B ．12C ．－32D ．327．已知α是第二象限角，且sin(53)-=+απ，则tan2α的值为( ) A ．54 B ．723-C ．724D ．724-8．已知COS(+α6π)－sin α= 332，则sin(α－π67)的值是( )A ．－ 332B ．332 C ．－ 32D ．32 二、填空题9．已知53)4sin(=-x π，则x 2sin 的值为10．已知)0,2(),2,0(,135sin ,34)tan(πβπαββα-∈∈-==-，则tan α=______．11．在△ABC 中，若2cos c a B =，则△ABC 的形状为12．若α是锐角，且1sin(),cos 63παα-=则的值是。

13．已知0<α<2π<β<π，cos α＝35，sin(α＋β)＝3-5，则cos β的值为________．14．化简计算：1tan1951tan(15)+︒=+-︒ _.三、解答题15．在ABC ∆中，角C B A ，，所对的边分别为c b a ，，，且满足C a A c cos sin =.()I 求角C 的大小； ()II 求⎪⎭⎫ ⎝⎛+-4cos sin 3πB A 的最大值，并求取得最大值时角B A ，的大小.16．（本小题满分12分）已知,,A B C 是三角形ABC ∆三内角，向量()()1,3,cos ,sin m n A A =-=，且1m n ⋅=(1）求角A ； (2）若221sin 23cos sin BB B+=--，求tan B 。

广东省高三数学寒假作业(一)

广东省2014届高三寒假作业（二）数学一、选择题 1．函数f （x ）=cos2x 在区间[－3，3]上的零点的个数为（）A ．3B ．4C ．5D ．62．函数（）A ．B ．C ．D ．3．对于函数，下列结论中正确的是：A ．当上单调递减B ．当上单调递减C ．当上单调递增D ．上单调递增 4．设函数则( )A ．在区间内均有零点B ．在区间内均无零点C ．在区间内无零点，在区间内有零点D ．在区间内有零点，在区间内无零点 5．方程330x x --=的实数解落在的区间是A ．[1,0]-B ．[0,1]C ．[1,2]D ．[2,3]6．用“二分法”求函数()3222f x x x x =+--的一个正实数零点，其参考数据如下：()12f =- ()1.50.625f = ()1.250.984f =-()1.3750.260f =- ()1.43750.162f = ()1.406250.054f =-那么方程32220x x x +--=的一个近似根（精确到0.1）为 () A ． 1.2B ． 1.3C ． 1.4D ． 1.57．方程22xx =的解的个数是（）A ．0B ．1C ．2D ．38．已知a 为实数，且3220,a a a +-+=则8910(1)(1)(1)a a a +++++的值是： A ．－3 B ．3 C ．－1 D ．1 二、填空题9．若a>3，则函数f （x ）=x 2－ax+1在区间（0，2）上恰好有个零点 10．已知，则的最大值是．11．函数的零点个数是________．12．若方程()lg 2lg 1kx x =+仅有一个实根，那么k 的取值范围是 .13．已知整数12,32012,,...,x x x x 满足：①12n x -≤≤，1,2,...,2012;n =②1220122010;x x x ++⋅⋅⋅+=③2221220122012.x x x ++⋅⋅⋅+=则333122012x x x ++⋅⋅⋅+的值是 . 14．若函数b x a x ax x f +-+-=||)3(2||31)(23有六个不同的单调区间，则实数a 的取值范围是．三、解答题15． (本题满分16分) 如图，开发商欲对边长为的正方形地段进行市场开发，拟在该地段的一角建设一个景观，需要建一条道路（点分别在上），根据规划要求的周长为．(1）设，求证：； (2）欲使的面积最小，试确定点的位置．16．（本题满分12分）已知某公司生产某品牌服装的年固定成本为10万元，每生产一千件，需要另投入2.7万元.设该公司年内共生产该品牌服装千件并全部销售完，每千件的销售收入为万元，且.(Ｉ）写出年利润（万元）关于年产量（千件）的函数关系式；(Ⅱ）年生产量为多少千件时，该公司在这一品牌服装的生产中所获年利润最大？17．（本小题满分12分）某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比．已知投资1万元时两类产品的收益分别为0.125万元和0.5万元（如图）．(1）分别写出两种产品的收益与投资额的函数关系；(2）该家庭现有20万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大收益，其最大收益是多少万元？18．（本小题满分12分）设某物体一天中的温度T 是时间t 的函数：32()(0)T t at bt ct d a =+++≠，其中温度的单位是℃，时间单位是小时，0t =表示12:00，t 取正值表示12:00以后．若测得该物体在8:00的温度是8℃，12:00的温度为60℃，13:00的温度为58℃，且已知该物体的温度在8:00和16:00有相同的变化率． (1）写出该物体的温度T 关于时间t 的函数关系式；(2）该物体在10:00到14:00这段时间中（包括10:00和14:00），何时温度最高，并求出最高温度；(3）如果规定一个函数()f x 在区间1212[]()x x x x <，上的平均值为21211()x x f x dx x x -⎰，求该物体在8:00到16:00这段时间内的平均温度．19．商店出售茶壶和茶杯，茶壶单价为每个20元，茶杯单价为每个5元，该店推出两种促销优惠办法：(1）买1个茶壶赠送1个茶杯；(2）按总价打9.2折付款。

广东省深圳外国语学校高三数学考前模拟试题文【会员独享】

深圳外国语学校2012届文科最后一次周测数学试卷（注意：请将答案填在答题卡上）一、选择题（本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．在复平面内，复数ii21+对应的点位于（） A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限2．设全集==A R U ,(2){|21},{|ln(1)}x x x B x y x -<==-，则右图中阴影部分表示的集合为 ( )A ．{|1}x x ≥B ．{|12}x x ≤<C ．{|01}x x <≤D ．{|1}x x ≤3．已知平面向量(3,1),(,3)x ==-a b ，若a ∥b ，则实数x 等于（） A ． 1- B ． 1 C ． 9- D ．94. 某学校有教师150人，其中高级教师15人，中级教师45人，初级教师90人. 现按职称分层抽样选出30名教师参加教工代表大会, 则选出的高、中、初级教师的人数分别为（）A ．5,10,15B ．5,9,16C ．3,10,17D ．3,9,185．阅读右面的程序框图，则输出的S 等于A ．40B ．20C ．32D ．386. 已知()f x 是定义在R 上的函数，并满足()(2)2,f x f x +=- 当12x <<时，()f x x =，则(5.5)f =（）A ．1.5B ． 1.5-C ．5.5D ． 5.5- 7．函数),52sin(2)(ππ+=xx f 对任意的,R x ∈都有)()()(21x f x f x f ≤≤成立，则21x x -的最小值为（）A ．4B ．4πC ．2πD ． 28．设[][]0,3,0,4∈∈x y ，则点M 落在不等式组：23000+-≤⎧⎪≥⎨⎪≥⎩x y x y 所表示的平面区域内的概率等于( )(第5题)A ．112 B. 316 C. 516 D. 139．函数在定义域内可导，若(1)y f x =+是偶函数，且当时，'()01f x x <-，设a=， b = ,)3(f c =，则()A ．.c b a <<B ． a b c <<C ．b a c <<D ．a c b <<10．已知椭圆221169x y +=的左、右焦点分别1F ，2F ，点A 在椭圆上，且A ，1F ，2F 是一个直角三角形的三个顶点，则点A 到x 轴的距离为（） A ．95 B ． 94 C． 3二、填空题（本大题共5小题．考生作答4小题．每小题5分，满分20分，请把正确答案填在题中横线上）（一）必做题（11～13题）11．设γβα,,是三个不重合的平面，l 是直线，给出下列命题： ①若γββα⊥⊥,，则γα⊥； ②若l 上两点到α的距离相等，则α//l ； ③若βαβα⊥⊥则,//,l l④若.//,//,,//βαββαl l l 则且⊄其中所有正确命题的编号是 .12．已知,322322=+ ,833833=+,15441544=+, ,66tat a =+t a ,均为正实数，类比以上等式，可推测t a ,的值，则=+t a ．13．设n S 是等差数列{}n a 的前n 项和.若3173=S S ，则=76S S. （二）选做题（14、15题，考生只能从中选做一题） 14. （坐标系与参数方程选做题）直线112,:2x t l y t=+⎧⎨=+⎩()t 为参数与直线22cos ,:sin x s l y s αα=+⎧⎨=⎩()s 为参数平行，则直线2l 的斜率为 .15．（几何证明选讲选做题）如图，在△ABC 中，AB =AC ，以BC为直径的半圆O 与边AB 相交于点D ，切线DE ⊥AC ，垂足为O点E ．则AECE=_______________．三、解答题（本大题共6小题，共80分，解答写出必要的文字说明、演算过程及步骤） 16.（本小题满分12分）已知()2sin(2)16f x x π=++（x R ∈）（Ⅰ）将函数()f x 的图象按向量(16π=-，）a 平移后，得到()g x 的图象，写出函数()g x 的表达式；（Ⅱ）已知ABC ∆的三个内角A 、B 、C 的对边分别为a 、b 、c ，若()32A f =，且2a =，求ABC ∆的面积的最大值．17．（本小题满分13分）对某校高一年级学生参加社区服务次数进行统计，随机抽取M 名学生作为样本，得到这M 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下：（Ⅰ）求出表中,M p 及图中a 的值；（Ⅱ）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间[10,15)内的人数；（Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间[20,25)内的概率.18．（本小题满分13分）如图1，三棱柱是111C B A ABC -直三棱柱，它的三视图如图2所示（N 为11C B 中点）. （Ⅰ）求证：MN//平面11A ACC ；（Ⅱ）求证：MN ⊥平面BC A 1；（Ⅲ）求三棱锥1B A NC -的体积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 ， 2
开始 a=1,b=1
．
12.已知流程图如右图所示,该程序运行后,为使输出的 b 值为 16，则循环体的判断框内①处应填______. 13. 已知数列 { a n } 的通项公式是 a n n 2 kn 2 , 若对于 n N ，都有 a n 1 a n 成立，则实数 k 的取值范围是．
x3 a 2 x bx c 的导函数为 f ( x ) 3 2
(Ⅰ)设 a f ( 2), b f (1), c f (0) ，求函数 f(x)的解析式； (Ⅱ)设 f ( x ) ( x )( x ) ，且 1 2 ,求 f (1) f (2) 的取值范围；
C ( 1, 0) (
1 5 ) 2
第二部分（非选择题，共 100 分）二、填空题：本大题共 4 小题，每小题 5 分，满分 20 分．其中 14~15 题是选做题，考生只能选做一题，二题全答的，只计算前一题得分． 11．已知是第二象限角， sin 则 sin(
) 4
2 2
B
9．椭圆
x2 y2 1（ a b 0 ）的左、右焦点分别是 F1，F2 ，过 F2 作倾斜角为 120 的直 a 2 b2 线与椭圆的一个交点为 M ，若 MF1 垂直于 x 轴，则椭圆的离心率为
A． 2 3 B． 2(2 3) C．
10. 已知函数 f ( x ) （ A ）
2 2 20.(14 分)已知圆 O: x y 2 交 x 轴于 A,B 两点,曲线 C 是以 AB 为长轴,离心率为 2 的
2
椭圆,其左焦点为 F,若 P 是圆 O 上一点,连结 PF,过原点 O 作直线 PF 的垂线交直线 x=-2 于点 Q. (Ⅰ)求椭圆 C 的标准方程； (Ⅱ)若点 P 的坐标为(1,1),求证:直线 PQ 与圆 O 相切； (Ⅲ)试探究:当点 P 在圆 O 上运动时(不与 A、B 重合), 直线 PQ 与圆 O 是否保持相切的位置关系?若是,请证明；若不是,请说明理由. A F O B x Q y P
E
3a
∴△ABD 是边长为 3 的正三角形
……9 分
1 ( S BCD S ABD ) PA 3 1 1 1 ( BC CD sin 120 0 AD AB sin 60 0 ) a 3 2 2 1 3 2 3 3 3 ( a 3a 2 ) a a 6 2 2 3
2 2
66 2
6 2 ……8 分
P
72 ……10 分，圆 a 2 b 2 12 的面积为 S / 12 ……10 分
B C
A
圆在正方形内部……12 分，所以 P ( A)
S S / 72 12 6 ……12 分． S 72 6
………2 分 ∴PA⊥BD ………3 分 ………4 分 ………6 分
D
C
B
O
A
三、解答题：本大题共 6 小题，满分 80 分．解答须写出文字说明、证明过程和演算步骤．（解答请写在答题卷上） 16.(12 分)已知向量 OP ( 2 sin x , 1), OQ (cos x , cos 2 x ) ,定义函数 f ( x ) OP OQ . (Ⅰ)求函数 f ( x ) 的表达式,并指出其最大最小值; (Ⅱ)在锐角△ABC 中,角 A,B,C 的对边分别为 a, b, c ,且 f ( A) 1 , bc 8 , 求△ABC 的面积 S.
2
A.1 则 A B为 A. ( ,1]
B. 1 或 3
C. 3 或 1
D. 3
2．若函数 f ( x ) 1 x 的定义域为 A，函数 g ( x ) lg( x 1) , x [2,11] 的值域为 B，
B. ( ,1)
C. [0,1]
D. [0,1)
3. 已知平面直角坐标系内的点 A(1,1),B(2,4),C(-1,3), AB AC 的值为: A.-4 B.4 C.-8 D.8 4. 等比数列 an 中, a2 =4, a 7 A.1
数学寒假作业（数学文）1 数学文
本试卷分第一部分（选择题）和第二部分（非选择题），共8页。试题1至4页，答题卷5至8页。满分150分。考试用时120分钟。参考公式：锥体的体积公式 V
1 Sh ，其中 S 是锥体的底面积， h 是锥体的高． 3
如果事件 A 、 B 互斥，那么 P ( A B ) P ( A) P ( B ) ．第一部分（选择题，共 50 分）一、选择题：本大题共 10 小题，每小题 5 分，共 50 分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 复数 z (m 2m 3) (m 1)i 为纯虚数,则实数 m 的值为:
21.(14 分)在数列 {an } 中， a1 1,3an an 1 an an 1 0( n 2) (Ⅰ)证明: {
1 } 是等差数列; an
(Ⅱ)求数列 {an } 的通项； (Ⅲ)若 an
1 对任意 n 2 的整数恒成立，求实数的取值范围. an 1
……4 ) 4
f ( x )的最大最小值分别是 : 2 , 2 .
(Ⅱ)∵f(A)=1, ∴ 2A ∴ sin(2 A
………6 分
Байду номын сангаас
2 ) 4 2
………8 分 ………10 分

4

4
或2 A

4

∴A
或A ,又△ABC 为锐角三角形,所以 4 2 4
1 1 2 bc sin A 8 2 2 2 2 2

a≤① 是 b=2
b
否
输出 b
a=a+1
12 题
结束
选做题:(14,15 两题只需选答其中一题,两题都答者按第 14 题给分)
14.极坐标系中,曲线 4sin 和 cos 1 相交于点 A,B, 则 AB =______. 15.如图,已知:△ABC 内接于圆 O，点 D 在 OC 的延长线上， AD 是⊙O 的切线，若 B 30 o , AC 2 ,则 OD 的长为 .
A.2 B.3 C.
7 2
D.4
7．下列有关命题的说法正确的是
2 A． “ x 1 ”是“ x 1 ”的充分不必要条件
B． “ x 1 ”是“ x 2 5 x 6 0 ”的必要不充分条件． C．命题“ x R ，使得 x x 1 0 ”的否定是： “ x R ，均有 x x 1 0 ” ． D．命题“若 x y ，则 sin x sin y ”的逆否命题为真命题． 8.已知一个正三棱锥 P-ABC 的主视图如图所示，则此正三棱锥的侧面积为 A. 9 39 B.54 C. 27 5 D. 36 3 A C 3 3 P 6
数学寒假作业（数学文）数学文参考答案一、选择题：本大题共 10 小题，每小题 5 分，共 50 分． 1．D 2．C 3． B 4． C 5．B 6． C 7． D 8．A 9．A 10．D 15. 4
二、填空题： 11．
2 6 ， 12．3 4
13． ( 3, )
14. 2 3
三、解答题：本大题共 6 小题，满分 80 分． 16.( Ⅰ ) f ( x) OP OQ (2 sin x,1) (cos x, cos 2 x) sin 2 x cos 2 x 2 sin( 2 x 分
3 4
∵bc=8,∴△ABC 的面积 S
………12 分
17．⑴方程有实数解， ( a b) 2 4 (3
ab ) 0 ，即 a 2 b 2 12 ……1 分 2
依题意， a 1 、 2 、 3 、 4 、 5 、 6 ， b 1 、 2 、 3 、 4 、 5 、 6 ，所以， “投掷两枚均匀骰子出现的点数”共有 6 6 36 种结果……2 分当且仅当“ a 1 且 b 1 、 2 、 3 ” ，或“ a 2 且 b 1 、 2 ” ，或“ a 3 且 b 1 ”时，所以满足 a 2 b 2 12 的结果有 36 (3 2 1) 30 种…… a b 2 12 不成立……5 分， 30 5 5 分，从而 P ( A) ……6 分． 36 6 ⑵在平面直角坐标系 aOb 中，直线 a b 6 与 a b 6 围成一个正方形……7 分正方形边长即直线 a b 6 与 a b 6 之间的距离为 d 正方形的面积 S d
0
18. (Ⅰ)连结 AC,∵BC=CD,AB=AD,∴AC⊥BD, 又 PA⊥平面 ABCD,且 BD 平面ABCD 又 PA∩AC=A, 又 BD 平面BDP ∴BD⊥平面 PAC ∴平面 PBD⊥平面 PAC
0
(Ⅱ)依题意得∠CBD=∠CDB=30 ,又 BC⊥AB,CD⊥AD,所以∠DBA=∠BDA=60 又 BC=CD=a，∴ BD ∴V
x x 1 ，若 f ( x) g ( x) ，则实数 x 的取值范围是 , g ( x) 1 x 2 1 5 ) 2
3 3
D．
12 2 3 11
( , 1) (0,1) 1 5 , ) 2
B ( , 1) (0, D ( 1, 0) (0,
f ( x)
x3 1 2 x 3x 3 ．…… 3 2
又 1 2, f (1) (1 )(1 ) 0, f (2) (2 )(2 ) 0 分
………10