第5讲 表的建立和操作
第 5 讲 图和表的运用

第 5 讲图表和参考文献的使用规范一、表格与插图的使用规范(一)图表的编序1、论文中的图和表要编序。
如果只有一个图或一张表,无需编序。
2、图和表要分开编序,图统一编序,表格另外统一编序。
3、无论是表还是图,编序都有两种方法。
(1)统一编序。
如:表1、表2等;或图1、图2。
(2)逐章单独编序。
如:表2.1、表2.2等;或图2.1、图2.2等。
不论采用哪种方式,表和图以及公式的编序方式要统一。
编号必须连续。
(二)图表的结构1、表格(1)表的结构要简洁。
(2)表格中各栏都应标注量和相应的单位。
(3)表格内数字须上下对齐。
(4)相邻栏内的数值相同时,不能用“同上”、“同左”和其它类似用词,应一一重新标注。
(5)表号和表标题置于表格上方中间位置。
2、插图(1)插图要精选。
(2)图号必须连续。
(3)仅有一图时,在图标题前加“附图”字样。
(4)一幅图有若干分图时,分图用a,b,c,……标出。
(5)图号和图标题置于图下方中间位置。
3、公式(1)论文中重要的或者后文中须重新提及的公式应注序号,序号应加圆括号。
序号一律用阿拉伯数字连续编序,如:(2);或逐章编序,如:(2.2)。
(2)序号排在版面右侧,且距右边距离相等。
(3)公式与序号之间不加虚线。
4、数字的用法(1)公历世纪、年代、年、月、日、时间和各种计数、计量,均用阿拉伯数字。
(2)年份不能简写。
例如,10年,应2010年。
数值的有效数字应全部写出。
5、计量单位按国家计量局规定使用。
课堂练习:2000-2009年外资对华投资一览表二、参考文献使用规范参考文献是毕业论文(设计)不可缺少的组成部分,也是作者对他人知识成果的承认和尊重。
(一)参考文献排列顺序参考文献应按文中引用出现的顺序列出,一般不少于10篇,附于文末。
(二)参考文献排列编号方法按论文中参考文献出现的先后顺序用阿拉伯数字连续编号,如[1]、[2]、[3]等数码表示,并将序号在正文中作为上角标。
参考文献采用五号、仿宋体、1.5倍行距打印。
第五讲 全国矿产地数据库

LOGO
图2 数据库关系示意图
LOGO
3、由项目综合技术组组织对各单位矿产地数据 库进行汇总,建立全国矿产地空间数据库。内容 包括: 数据库的拼接和合并; 数据库检查和修正; 全国矿产地数据库的集成; 建立全国矿产地数据库查询、检索等应用系统; 建立全国矿产地数据库信息共享服务体系。
LOGO
二、数据库结构和数据库关系
1、数据库结构 矿产地属性数据库的内容初步拟包括矿产地11个数据文件,156个属性数 据项(详见《矿产地数据库建设工作指南》修订版)。11个数据文件分别是: (1)矿产地基本情况,包括矿产地编号、矿种、矿产地名、交通位置、 地理经度、地理纬度、矿床成因类型、共生矿、伴生矿、矿床规模、成矿时 代、三级成矿带、四级成矿带、地质工作程度和开采情况15个数据项。 (2)矿区地质情况,包括矿产地编号、矿区大地构造位置、岩石地层单位、 侵入岩、火山岩、变质岩、地质构造特征、围岩蚀变、年龄测定方法种类、 同位素地质年龄、采样位置、样品编号、稳定同位素分析方法和稳定同位素 地球化学14个数据项。 (3)矿体特征,包括矿产地编号、矿体数、主矿体数、矿体形状、矿体埋 深、矿体走向、矿体倾向、矿体倾角、矿体侧伏方向、矿体长度、矿体斜长、 矿体厚度、氧化带深度、矿石自然类型、矿石结构、矿石构造、矿石的矿物 组成、矿石品位、矿石品级、伴生有益组分、矿石工业特征和矿石工业类型 22个数据项。 (4)煤矿产特征,包括矿产地编号、含煤地层、含煤层数、可采煤层层数、 可采煤层累计厚度、煤层总厚度、煤层型别、宏观煤炭类型、工业牌号(煤 类)、煤层倾向、煤层倾角、埋藏深度、煤层顶板、煤层底板、露天开采、 矿井瓦斯、自燃倾向等级和地温状况18个数据项。
第五讲个案工作的过程

(一)做好会谈前的准备
1.回顾 • 翻阅机构过去接待当事人的记录,避免会谈中重复一 些信息。熟知当事人的情况能让他感到受尊重,有助
于建立相互信任的专业关系。翻阅资料时工作者要保
持价值中立,持非评判的态度,避免偏见的形成。
2.电话记录 • 当事人寻求帮助,会事先打电话给机构进行询问和预 约,机构工作人员会做一个电话预约记录,工作者可
(1)介绍机构的服务范围,告诉当事人机构可以做什么 和不能做什么,为不适合本机构的服务对象提供转介 服务;
(2)清楚告诉当事人,问题的解决需要双方共同的努力 ,减低当事人的依赖心理。
(三)初步评估当事人的需要及问题
1.当事人的求助意愿如何?主动或者被动? 2.当事人的主要问题是什么?怎么产生的?当事人期望达到什么目 的和需要什么结果? 3.当事人曾经为此寻求过什么帮助?自己努力做过什么努力? 4.服务机构所掌握的资源或工作者自己的能力能否为其提供服务? 5.机构对当事人的要求和当事人对机构和工作员的期望是否可以相 互协调?
6.信息提供 • 考虑提供的信息对解决案主的问题是否有积极的或正向 的作用;提供的信息要准确可靠,讲明信息的出处。 7.直接干预 • 危机干预,一般用于案主处在危机状态下,在法律赋予
权力的范围内,工作者采取一些直接的干预行动。
(三)注意事项
• 计划和协议为基础,但应根据案主的实际情况及其变 化开展工作。 • 善于运用案主本人的社会资源。 • 进行阶段性检查和评估。 • 妥善处理与案主的专业关系
2.服务的内容以及采用的方法;
3.双方应该享有的权利和义务; • 如:工作者遵守职业伦理,对案主的问题保密;案主完 成工作者布置的家庭作业,保证个案辅导的时限等。 4.服务的时间、地点和次数;
高考数学一轮复习 第八章 立体几何 第5讲 简单几何体的再认识(表面积与体积)教学案 理
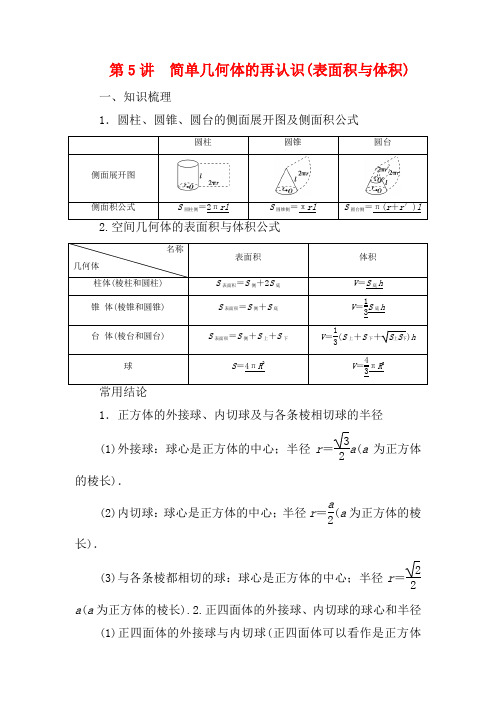
第5讲 简单几何体的再认识(表面积与体积)一、知识梳理1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrl S 圆锥侧=πrlS 圆台侧=π(r +r ′)l名称几何体表面积体积柱体(棱柱和圆柱) S 表面积=S 侧+2S 底 V =S 底h 锥 体(棱锥和圆锥) S 表面积=S 侧+S 底 V =13S 底h台 体(棱台和圆台)S 表面积=S 侧+S 上+S 下V =13(S 上+S 下+S 上S 下)h球S =4πR 2V =43πR 31.正方体的外接球、内切球及与各条棱相切球的半径 (1)外接球:球心是正方体的中心;半径r =32a (a 为正方体的棱长).(2)内切球:球心是正方体的中心;半径r =a2(a 为正方体的棱长).(3)与各条棱都相切的球:球心是正方体的中心;半径r =22a (a 为正方体的棱长).2.正四面体的外接球、内切球的球心和半径(1)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分).(2)外接球:球心是正四面体的中心;半径r =64a (a 为正四面体的棱长).(3)内切球:球心是正四面体的中心;半径r =612a (a 为正四面体的棱长).二、教材衍化1.已知圆锥的表面积等于12π cm 2,其侧面展开图是一个半圆,则底面圆的半径为________.解析:S 表=πr 2+πrl =πr 2+πr ·2r =3πr 2=12π, 所以r 2=4,所以r =2. 答案:2 cm 2.如图,将一个长方体用过相邻三条棱的中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体体积的比为________.解析:设长方体的相邻三条棱长分别为a ,b ,c ,它截出棱锥的体积V 1=13×12×12a ×12b ×12c =148abc ,剩下的几何体的体积V 2=abc -148abc =4748abc ,所以V 1∶V 2=1∶47.答案:1∶47 一、思考辨析判断正误(正确的打“√”,错误的打“×”) (1)多面体的表面积等于各个面的面积之和.( ) (2)锥体的体积等于底面积与高之积.( )(3)球的体积之比等于半径比的平方.( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差.( )(5)长方体既有外接球又有内切球.( )答案:(1)√(2)×(3)×(4)√(5)×二、易错纠偏常见误区|K(1)不能把三视图正确还原为几何体而错解表面积或体积;(2)考虑不周忽视分类讨论;(3)几何体的截面性质理解有误;(4)混淆球的表面积公式和体积公式.1.已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则该四棱锥的体积为________m3.解析:根据三视图可知该四棱锥的底面是底边长为2 m,高为1 m的平行四边形,四棱锥的高为 3 m.故该四棱锥的体积V=1 3×2×1×3=2(m3).答案:22.将一个相邻边长分别为4π,8π的矩形卷成一个圆柱,则这个圆柱的表面积是________.解析:当底面周长为4π时,底面圆的半径为2,两个底面的面积之和是8π;当底面周长为8π时,底面圆的半径为4,两个底面的面积之和为32π.无论哪种方式,侧面积都是矩形的面积32π2,故所求的表面积是32π2+8π或32π2+32π.答案:32π2+8π或32π2+32π3.已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为________.解析:因为过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为22,底面圆的直径为22,所以该圆柱的表面积为2×π×(2)2+22π×22=12π.答案:12π4.一个球的表面积是16π,那么这个球的体积为________. 解析:设球的半径为R ,则由4πR 2=16π,解得R =2,所以这个球的体积为43πR 3=323π.答案:323π空间几何体的表面积(师生共研)(1)(2020·河南周口模拟)如图,在三棱柱ABC A 1B 1C 1中,AA 1⊥底面ABC ,AB ⊥BC ,AA 1=AC =2,直线A 1C 与侧面AA 1B 1B 所成的角为30°,则该三棱柱的侧面积为( )A .4+4 2B .4+43C .12D .8+42(2)(2020·四川泸州一诊)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )A .(5+2)πB .(4+2)πC .(5+22)πD .(3+2)π【解析】 (1)连接A 1B .因为AA 1⊥底面ABC ,则AA 1⊥BC ,又AB ⊥BC ,AA 1∩AB =A ,所以BC ⊥平面AA 1B 1B ,所以直线A 1C 与侧面AA 1B 1B 所成的角为∠CA 1B=30°.又AA 1=AC =2,所以A 1C =22,BC = 2.又AB ⊥BC ,则AB =2,则该三棱柱的侧面积为22×2+2×2=4+42,故选A.(2)因为在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2,所以将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB =1,高为BC -AD =2-1=1的圆锥,所以该几何体的表面积S =π×12+2π×1×2+π×1×12+12=(5+2)π.故选A.【答案】 (1)A (2)A空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(3)旋转体的表面积问题注意其侧面展开图的应用. 1.在如图所示的斜截圆柱中,已知圆柱底面的直径为40 cm ,母线长最短50 cm ,最长80 cm ,则斜截圆柱的侧面面积S =________cm 2.解析:将题图所示的相同的两个几何体对接为圆柱,则圆柱的侧面展开图为矩形.由题意得所求侧面展开图的面积S=12×(50+80)×(π×40)=2 600π(cm2).答案:2 600π2.已知一几何体的三视图如图所示,它的主视图与左视图相同,则该几何体的表面积为________.解析:由三视图知,该几何体是一个正四棱柱与半球的组合体,且正四棱柱的高为2,底面对角线长为4,球的半径为2,所以该正四棱柱的底面正方形的边长为22,该几何体的表面积S=1 2×4π×22+π×22+22×2×4=12π+16.答案:12π+16空间几何体的体积(多维探究)角度一直接利用公式求体积(2020·山东省实验中学模拟)我国古代《九章算术》里,记载了一个“商功”的例子:今有刍童,下广二丈,袤三丈,上广三丈,袤四丈,高三丈.问积几何?其意思是:今有上下底面皆为长方形的草垛(如图所示),下底宽2丈,长3丈,上底宽3丈,长4丈,高3丈.问它的体积是多少?该书提供的算法是:上底长的2倍与下底长的和与上底宽相乘,同样下底长的2倍与上底长的和与下底宽相乘,将两次运算结果相加,再乘以高,最后除以6.则这个问题中的刍童的体积为( )A.13.25立方丈B.26.5立方丈C.53立方丈D.106立方丈【解析】 由题意知,刍童的体积为[(4×2+3)×3+(3×2+4)×2]×3÷6=26.5(立方丈),故选B.【答案】 B角度二 割补法求体积《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何?刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1),那么该刍甍的体积为( )A .4B .5C .6D .12【解析】 如图所示,由三视图可还原得到几何体ABCDEF ,过E ,F 分别作垂直于底面的截面EGH 和FMN ,可将原几何体切割成三棱柱EHG FNM ,四棱锥E ADHG 和四棱锥F MBCN ,易知三棱柱的体积为12×3×1×2=3,两个四棱锥的体积相同,都为13×1×3×1=1,则原几何体的体积为3+1+1=5.故选B.【答案】 B角度三 等体积法求体积(2020·贵州部分重点中学联考)如图,在直四棱柱ABCD A 1B 1C 1D 1中,底面ABCD 是平行四边形,点E 是棱BB 1的中点,点F 是棱CC 1上靠近C 1的三等分点,且三棱锥A 1AEF 的体积为2,则四棱柱ABCD A 1B 1C 1D 1的体积为( )A .12B .8C .20D .18【解析】 设点F 到平面ABB 1A 1的距离为h ,由题意得V A 1AEF=V F A 1AE .又V F A 1AE =13S △A 1AE ·h =13×⎝ ⎛⎭⎪⎫12AA 1·AB ·h =16(AA 1·AB )·h =16S 四边形ABB 1A 1·h =16V ABCD A 1B 1C 1D 1,所以V ABCD A 1B 1C 1D 1=6V A 1AEF =6×2=12.所以四棱柱ABCD A 1B 1C 1D 1的体积为12.故选A.【答案】 A(1)处理体积问题的思路①“转”:指的是转换底面与高,将原来不易求面积的底面转换为易求面积的底面,或将原来不易看出的高转换为易看出并易求解长度的高;②“拆”:指的是将一个不规则的几何体拆成几个简单的几何体,便于计算;③“拼”:指的是将小几何体嵌入一个大几何体中,如将一个三棱锥复原成一个三棱柱,将一个三棱柱复原成一个四棱柱,这些都是拼补的方法.(2)求空间几何体的体积的常用方法①公式法:对于规则几何体的体积问题,可以直接利用公式进行求解;②割补法:把不规则的图形分割成规则的图形,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算其体积;③等体积法:一个几何体无论怎样转化,其体积总是不变的.如果一个几何体的底面面积和高较难求解时,我们可以采用等体积法进行求解.等体积法也称等积转化或等积变形,它是通过选择合适的底面来求几何体体积的一种方法,多用来解决有关锥体的体积,特别是三棱锥的体积.1.(2020·江西上饶二模)已知下图为某几何体的三视图,则其体积为( )A .π+23B .π+13C .π+43D .π+34解析:选C.几何体为半圆柱与四棱锥的组合体(如图),半圆柱的底面半径为1,高为2,四棱锥的底面为边长为2的正方形,高为1,故几何体的体积V =12×π×12×2+13×22×1=π+43.故选C.2.(2019·高考全国卷Ⅲ)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD A 1B 1C 1D 1挖去四棱锥O EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,AB =BC =6 cm ,AA 1=4 cm.3D 打印所用原料密度为0.9 g/cm 3.不考虑打印损耗,制作该模型所需原料的质量为________g.解析:由题易得长方体ABCD A 1B 1C 1D 1的体积为6×6×4=144(cm 3),四边形EFGH 为平行四边形,如图所示,连接GE ,HF ,易知四边形EFGH 的面积为矩形BCC 1B 1面积的一半,即12×6×4=12(cm 2),所以V四棱锥O EFGH =13×3×12=12(cm 3),所以该模型的体积为144-12=132(cm 3),所以制作该模型所需原料的质量为132×0.9=118.8(g).答案:118.8球与空间几何体的接、切问题(多维探究) 角度一 外接球(1)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .3π4C.π2D .π4(2)已知三棱锥S ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S ABC的体积为9,则球O 的表面积为________.【解析】 (1)设圆柱的底面圆半径为r ,则r 2=12-⎝ ⎛⎭⎪⎫122=34,所以,圆柱的体积V =34π×1=3π4,故选B.(2)设球O 的半径为R ,因为SC 为球O 的直径,所以点O 为SC 的中点,连接AO ,OB ,因为SA =AC ,SB =BC ,所以AO ⊥SC ,BO ⊥SC ,因为平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,所以AO ⊥平面SCB ,所以V S ABC =V A SBC =13×S △SBC ×AO =13×(12×SC ×OB )×AO ,即9=13×(12×2R ×R )×R ,解得R =3,所以球O 的表面积为S =4πR2=4π×32=36π.【答案】 (1)B (2)36π角度二 内切球(1)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,表面积为S 1,球O 的体积为V 2,表面积为S 2,则V 1V 2的值是__________,S 1S 2=________. (2)已知棱长为a 的正四面体,则此正四面体的表面积S 1与其内切球的表面积S 2的比值为________.【解析】 (1)设圆柱内切球的半径为R ,则由题设可得圆柱O 1O 2的底面圆的半径为R ,高为2R ,所以V 1V 2=πR 2·2R 43πR 3=32.S 1S 2=2πR ·2R +2πR 24πR 2=32. (2)正四面体的表面积为S 1=4×34×a 2=3a 2,其内切球半径r 为正四面体高的14,即r =14×63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2πa 26=63π. 【答案】 (1)32 32 (2)63π解决与球有关的切、接问题,其通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程是:1.(2020·四川成都一诊)如图,在矩形ABCD 中,EF ∥AD ,GH ∥BC ,BC =2,AF =FG =BG =1.现分别沿EF ,GH 将矩形折叠使得AD 与BC 重合,则折叠后的几何体的外接球的表面积为( )A .24πB .6π C.163π D .83π 解析:选C.由题意可知,折叠后的几何体是底面为等边三角形的三棱柱,底面等边三角形外接圆的半径为23× 12-⎝ ⎛⎭⎪⎫122=33.因为三棱柱的高为BC =2,所以其外接球的球心与底面外接圆圆心的距离为1,则三棱柱外接球的半径为R =⎝ ⎛⎭⎪⎪⎫332+12=233,所以三棱柱外接球的表面积S =4πR 2=16π3.故选C.2.(2020·黑龙江哈尔滨师范大学附属中学模拟)在底面是边长为2的正方形的四棱锥P ABCD 中,点P 在底面的射影H 为正方形ABCD 的中心,异面直线PB 与AD 所成角的正切值为2.若四棱锥P ABCD 的内切球半径为r ,外接球的半径为R ,则r R=( ) A.23B .25 C.12D .13解析:选B.如图,取E ,F 分别为AB ,CD 的中点,连接EF ,PE ,PF .由题意知,P ABCD 为正四棱锥,底面边长为2.因为BC ∥AD ,所以∠PBC 即为异面直线PB 与AD 所成的角.因为∠PBC 的正切值为2,所以四棱锥的斜高为2,所以△PEF 为等边三角形,则正四棱锥P ABCD 的内切球的半径r 即为△PEF 的内切圆的半径,为33. 设O 为正四棱锥外接球的球心,连接OA ,AH .由题可得AH =2,PH = 3.在Rt △OHA 中,R 2=(2)2+(3-R )2,解得R =536, 所以r R =25. 确定球心位置的三种方法决定球的几何要素是球心的位置和球的半径,在球与其他几何体的结合问题中,通过位置关系的分析,找出球心所在的位置是解题的关键,不妨称这个方法为球心位置分析法.方法一 由球的定义确定球心若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体外接球的球心.(1)长方体或正方体的外接球的球心是其体对角线的中点;(2)正三棱柱的外接球的球心是上、下底面中心连线的中点;(3)直三棱柱的外接球的球心是上、下底面三角形外心连线的中点;(4)正棱锥的外接球球心在其高上,具体位置可通过建立直角三角形运用勾股定理计算得到;(5)若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( )A.16π B.20πC.24πD.32π【解析】已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,可求得底面边长为2,故球的直径为22+22+42=26,则半径为6,故球的表面积为24π,故选C.【答案】C方法二构造长方体或正方体确定球心(1)正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥,可将三棱锥补形成长方体或正方体;(2)同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥,可将三棱锥补形成长方体或正方体;(3)若已知棱锥含有线面垂直关系,则可将棱锥补形成长方体或正方体;(4)若三棱锥的三个侧面两两垂直,则可将三棱锥补形成长方体或正方体.如图,边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为( )A. 2 B.6 2C.112D.52【解析】易知四面体A′EFD的三条侧棱A′E,A′F,A′D 两两垂直,且A′E=1,A′F=1,A′D=2,把四面体A′EFD补成从顶点A′出发的三条棱长分别为1,1,2的一个长方体,则长方体的外接球即为四面体A′EFD的外接球,球的半径为r=1 212+12+22=62.故选B.【答案】B方法三由性质确定球心利用球心O与截面圆圆心O′的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质,确定球心.正三棱锥ABCD内接于球O,且底面边长为3,侧棱长为2,则球O的表面积为________.【解析】如图,M为底面△BCD的中心,易知AM⊥MD,DM=1,AM= 3.在Rt△DOM中,OD2=OM2+MD2,即OD2=(3-OD)2+1,解得OD=23 3,故球O的表面积为4π×⎝⎛⎭⎪⎪⎫2332=163π.【答案】163π[基础题组练]1.圆柱的底面积为S ,侧面展开图是一个正方形,那么圆柱的侧面积是( )A .4πSB .2πSC .πSD .233πS 解析:选A.由πr 2=S 得圆柱的底面半径是S π,故侧面展开图的边长为2π·S π=2πS ,所以圆柱的侧面积是4πS ,故选A. 2.已知圆锥的高为3,底面半径长为4,若一球的表面积与此圆锥的侧面积相等,则该球的半径长为( ) A .5B .5C .9D .3解析:选B.因为圆锥的底面半径R =4,高h =3,所以圆锥的母线l =5,所以圆锥的侧面积S =πRl =20π.设球的半径为r ,则4πr 2=20π,所以r =5,故选B.3.(2020·安徽黄山一模)如图所示为某几何体的三视图,则几何体的体积为( )A.12B .1 C.32D .3 解析:选B.由主视图可得如图的四棱锥P ABCD ,其中平面ABCD ⊥平面PCD .由主视图和俯视图可知AD =1,CD =2,P 到平面ABCD 的距离为32. 所以四棱锥P ABCD 的体积为V =13×S 长方形ABCD ×h =13×1×2×32=1.故选B.4.(2020·河南郑州三模)某几何体的三视图如图所示,则该几何体的体积为( )A.5π3B .4π3 C.π3D .2π3 解析:选D.几何体是半个圆柱挖去半个圆锥所形成的,如图,由题意可知几何体的体积为:12×12·π×2-13×12×12·π×2=2π3.故选D. 5.(2020·广东茂名一模)在长方体ABCD A 1B 1C 1D 1中,四边形ABCD 是边长为2的正方形,D 1B 与DC 所成的角是60°,则长方体的外接球的表面积是( )A .16πB .8πC .4πD .42π解析:选A.如图,在长方体ABCD A 1B 1C 1D 1中,因为DC ∥AB ,所以相交直线D 1B 与AB 所成的角是异面直线D 1B 与DC 所成的角.连接AD 1,由AB ⊥平面ADD 1A 1,得AB ⊥AD 1,所以在Rt △ABD 1中,∠ABD 1就是D 1B 与DC 所成的角,即∠ABD 1=60°,又AB =2,AB =BD 1cos 60°,所以BD 1=AB cos 60°=4,设长方体ABCD A 1B 1C 1D 1外接球的半径为R ,则由长方体的体对角线就是长方体外接球的直径得4R 2=D 1B 2=16,则R =2,所以长方体外接球的表面积是4πR 2=16π.故选A.6.一个四棱锥的侧棱长都相等,底面是正方形,其主视图如图所示,则该四棱锥的侧面积是________.解析:因为四棱锥的侧棱长都相等,底面是正方形,所以该四棱锥为正四棱锥,如图,由题意知底面正方形的边长为2,正四棱锥的高为2, 取正方形的中心O ,AD 的中点E ,连接PO ,OE ,PE ,可知PO 为正四棱锥的高,△PEO 为直角三角形,则正四棱锥的斜高PE =22+12= 5.所以该四棱锥的侧面积S =4×12×2×5=4 5. 答案:457.已知圆锥SO ,过SO 的中点P 作平行于圆锥底面的截面,以截面为上底面作圆柱PO ,圆柱的下底面落在圆锥的底面上(如图),则圆柱PO 的体积与圆锥SO 的体积的比值为________.解析:设圆锥SO 的底面半径为r ,高为h ,则圆柱PO 的底面半径是r 2,高为h 2, 所以V 圆锥SO =13πr 2h ,V 圆柱PO =π⎝ ⎛⎭⎪⎫r 22·h 2=πr 2h 8,所以V 圆柱PO V 圆锥SO =38. 答案:388.已知正三棱锥的高为1,底面边长为23,内有一个球与四个面都相切,则棱锥的内切球的半径为________.解析:如图,过点P 作PD ⊥平面ABC 于点D ,连接AD 并延长交BC 于点E ,连接PE ,因为△ABC 是正三角形,所以AE 是BC 边上的高和中线,D 为△ABC 的中心.因为AB =BC =23,所以S △ABC =33,DE =1,PE = 2.所以S 表=3×12×23×2+33=36+3 3. 因为PD =1,所以三棱锥的体积V =13×33×1= 3. 设球的半径为r ,以球心O 为顶点,三棱锥的四个面为底面,把正三棱锥分割为四个小棱锥,则r =3336+33=2-1. 答案:2-19.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P ,Q 在正视图中所示位置,P 为所在线段的中点,Q 为顶点,求在几何体表面上,从P 点到Q 点的最短路径的长.解:(1)由三视图知该几何体是由一个圆锥与一个圆柱组成的组合体,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=12(2πa )·(2a )=2πa 2, S 圆柱侧=(2πa )·(2a )=4πa 2,S 圆柱底=πa 2,所以S 表=2πa 2+4πa 2+πa 2=(2+5)πa 2.(2)沿P 点与Q 点所在母线剪开圆柱侧面,如图.则PQ =AP 2+AQ 2=a 2+(πa )2=a 1+π2,所以从P 点到Q 点在侧面上的最短路径的长为a 1+π2.10.如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1)证明:平面AEC ⊥平面BED ;(2)若∠ABC =120°,AE ⊥EC ,三棱锥E ACD 的体积为63,求该三棱锥的侧面积.解:(1)证明:因为四边形ABCD 为菱形,所以AC ⊥BD . 因为BE ⊥平面ABCD ,所以AC ⊥BE .故AC ⊥平面BED .又AC 平面AEC , 所以平面AEC ⊥平面BED .(2)设AB =x ,在菱形ABCD 中,由∠ABC =120°,可得AG =GC=32x ,GB =GD =x 2.因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =32x .由BE ⊥平面ABCD ,知△EBG 为直角三角形,可得BE =22x .由已知得,三棱锥E ACD 的体积V 三棱锥E ACD =13×12·AC ·GD ·BE=624x 3=63,故x =2.从而可得AE =EC =ED = 6.所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为 5. 故三棱锥E ACD 的侧面积为3+2 5.[综合题组练])1.如图,以棱长为1的正方体的顶点A 为球心,以2为半径作一个球面,则该正方体的表面被球面所截得的所有弧长之和为( )A.3π4 B .2π C.3π2D .9π4解析:选C.正方体的表面被该球面所截得的弧长是相等的三部分,如图,上底面被球面截得的弧长是以A 1为圆心,1为半径的圆周长的14,所以所有弧长之和为3×2π4=3π2.故选C.2.(2020·江西萍乡一模)如图,网格纸上小正方形的边长为1,粗线画的是某几何体的三视图,则该几何体的体积为( )A.236 B .72C.76D .4解析:选A.由三视图可得,该几何体是如图所示的三棱柱ABB 1DCC 1,挖去一个三棱锥E FCG 所形成的,故所求几何体的体积为12×(2×2)×2-13×⎝ ⎛⎭⎪⎫12×1×1×1=236. 故选A.3.(2020·福建厦门外国语学校模拟)已知等腰直角三角形ABC 中,∠ACB =90°,斜边AB =2,点D 是斜边AB 上一点(不同于点A ,B ).沿线段CD 折起形成一个三棱锥A CDB ,则三棱锥A CDB 体积的最大值是( )A .1B .12C.13D .16解析:选D.设AD =x ,将△ACD 折起使得平面ACD ⊥平面BCD .在△ACD 中,由面积公式得12CD ·h 1=12AD ·1(h 1为点A 到直线CD 的距离),则h 1=x1+(x -1)2.由题易知h 1为点A 到平面BCD 的距离,故三棱锥A CDB 体积为V =13S △BCD ·h 1=13×⎝ ⎛⎭⎪⎫12BD ·1·h 1=16·2x -x 2x 2-2x +2,x ∈(0,2).令t =x 2-2x +2,则t ∈[1,2),故V =16·2-t 2t =16·⎝ ⎛⎭⎪⎫2t -t .由于2t -t 是减函数,故当t =1时,V取得最大值为16×(2-1)=16.故选D.4.设A ,B ,C ,D 是同一个半径为4的球的球面上的四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为( )A .12 3B .183C .24 3D .543解析:选B.如图,E 是AC 的中点,M 是△ABC 的重心,O 为球心,连接BE ,OM ,OD ,BO .因为S △ABC =34AB 2=93,所以AB =6,BM =23BE=23AB 2-AE 2=2 3.易知OM ⊥平面ABC ,所以在Rt △OBM 中,OM =OB 2-BM 2=2,所以当D ,O ,M 三点共线且DM =OD +OM 时,三棱锥D ABC 的体积取得最大值,且最大值V max =13S △ABC ×(4+OM )=13×93×6=18 3.故选B. 5.如图所示,已知三棱柱ABC A 1B 1C 1的所有棱长均为1,且AA 1⊥底面ABC ,则三棱锥B 1ABC 1的体积为________.解析:三棱锥B 1ABC 1的体积等于三棱锥A B 1BC 1的体积,三棱锥A B 1BC 1的高为32,底面积为12,故其体积为13×12×32=312.答案:3126.已知半球O 的半径r =2,正三棱柱ABC A 1B 1C 1内接于半球O ,其中底面ABC 在半球O 的大圆面内,点A 1,B 1,C 1在半球O 的球面上.若正三棱柱ABC A 1B 1C 1的侧面积为63,则其侧棱的长是________.解析:依题意O 是正三角形ABC 的中心,设AB =a ,分析计算易得0<a <23,AO =33a ,在Rt △AOA 1中,A ′O =r =2,则AA 1=r 2-AO 2=4-a 23,所以正三棱柱ABC A 1B 1C 1的侧面积S =3a ·AA 1=3a4-a 23=3-a 43+4a 2=63,整理得a 4-12a 2+36=0,解得a 2=6,即a =6,此时侧棱AA 1= 2.答案:27.如图,正方体ABCD A 1B 1C 1D 1的棱长为1,P 为BC 边的中点,Q 为线段CC 1上的动点,过点A ,P ,Q 的平面截正方体所得的截面为S ,当CQ =1时,S 的面积为________.解析:当CQ =1时,Q 与C 1重合.如图,取A 1D 1,AD 的中点分别为F ,G .连接AF ,AP ,PC 1,C 1F ,PG ,D 1G ,AC 1,PF .因为F 为A 1D 1的中点,P 为BC 的中点,G 为AD 的中点, 所以AF =FC 1=AP =PC 1=52,PG 綊CD ,AF 綊D 1G .由题意易知CD 綊C 1D 1,所以PG 綊C 1D 1,所以四边形C 1D 1GP 为平行四边形, 所以PC 1綊D 1G ,所以PC 1綊AF , 所以A ,P ,C 1,F 四点共面, 所以四边形APC 1F 为菱形.因为AC 1=3,PF =2,过点A ,P ,Q 的平面截正方体所得的截面S 为菱形APC 1F ,所以其面积为12AC 1·PF =12×3×2=62.答案:628.已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为515,则该圆锥的侧面积为________.解析:如图所示,设S 在底面的射影为S ′,连接AS ′,SS ′.△SAB 的面积为12·SA ·SB ·sin ∠ASB =12·SA 2·1-cos 2∠ASB =1516·SA 2=515,所以SA 2=80,SA =4 5.因为SA 与底面所成的角为45°,所以∠SAS ′=45°,AS ′=SA ·cos 45°=45×22=210.所以底面周长l =2π·AS ′=410π,所以圆锥的侧面积为12×45×410π=402π.答案:402π。
计算机基础第5讲 WORD基本操作(1)

50
首字下沉
“插入”选项卡“文本”任务组“首字下沉” 按钮
51
目录
“引用”选项卡 “目录”任务组 “目录”按钮
目录
选择创建的目录 “目录”按钮 “插入目录”选 项
目录
单击“选项”按钮将打开“目录选项”对话框,设置 采用目录形式的样式内容。
行首 下一行 上一行 段尾 段首
26
键盘选定文本
Shift+PageDown Shift+PageUp Ctrl+shift+Home
Ctrl+shift+End Alt+ctrl+Shift+PageDown Ctrl+A
下一屏 上一屏 文档开始处
文档结尾处 窗口结尾 包含整篇文档
27
删除文本 :
查找功能只用于在文本中定位,而对文 本不做任何修改。利用Word 2010的查找命令 可在文档中快速找到所需要的内容、带特殊 格式的文本及特殊字符。查找有两种方式: 常规查找和高级查找。
34
35
36
37
38
公式的输入
“插入”选项卡的“符号”任务组中的“公式 ”命令
39
字符格式设置
使用“字体”任务组
2.预览打印文档及打印
单击“文件”标签,在选项卡中单击“打印”选 项,在最右侧的窗格中将能够预览打印效果 (Ctrl+P)
边框和底纹
1.添加边框 “页面布局”选项卡“页面背景”任务组“页面边框” 按钮。
2.添加装饰线
边框和底纹
3.为文字添加边框
4.为文字添加底纹
分栏
“页面布局”选项卡“页面设置”任务组“分栏” 按钮
单链表的基本运算

建表结束*/ { c=getchar(); if(c!=’$’) { s=(Node*)malloc(sizeof(Node)); /*建立新结点 s*/ s->data=c; s->next=L->next; /*将 s 结点插入表头*/ L->next=s; } else flag=0;
3. 结果判断 如找到第 i 个结点,则返回结点 p;
如表查完未找到,则返回空。
【算法描述】
Node * Get (LinkList L, int i) / * 在带头结点的单链表 L 中查找第 i 个结点,若找到(1≤i≤n),则返回 该结点的存储位置; 否则返回 NULL * / { int j;
【算法描述】
int ListLength(LinkList L)
/*求带头结点的单链表 L 的长度*/
{ Node *p;
p=L->next;
j=0; /*用来存放单链表的长度*/
while(p!=NULL)
{
p=p->next;
j ++;
}
return j; /*j 为求得的单链表长度*/
} /* ListLength */
H
∧
s r
(a)初始化的空表
C1 ∧
(b)申请新结点并赋值
s 指向新申请的结点空间;
s->data:=C1
H
c1 ∧
r
(c)插入第一个结点
s
① r->next=s;
c1 H
系统工程第五讲--ISM(解释结构模型)

系统⼯程第五讲--ISM(解释结构模型)第五讲解释结构模型法本章学习要点解释结构模型法是⽤于分析教育技术研究中复杂要素间关联结构的⼀种专门研究⽅法,作⽤是能够利⽤系统要素之间已知的零乱关系,揭⽰出系统的内部结构。
解释结构模型法的具体操作是⽤图形和矩阵描述出各种已知的关系,通过矩阵做进⼀步运算,并推导出结论来解释系统结构的关系.本章介绍了解释结构模型的基本概念;论述了解释结构模型法应⽤的具体步骤;以“⽹络化学习与传统学习的差异分析”为案例说明解释结构模型法在教育技术研究中的具体应⽤。
通过本章的学习,应了解解释结构模型的基本概念,明确有向图、邻接矩阵和可达矩阵的含义,掌握解释结构模型法应⽤的步骤,熟练运⽤解释结构模型法分析解决教育技术研究中的具体问题。
本章内容结构系统结构的有向图⽰法有向图的矩阵描述邻接矩阵的性质可达矩阵系统要素分析建⽴邻接矩阵进⾏矩阵运算,求出可达矩阵对可达矩阵进⾏分解差异特征要素分析要素强弱分析解释结构模型分析WBT的层级模型与因果关系分析第⼀节解释结构模型法的基本概念定义:解释结构模型法(InterpretativeStructuralModellingMethod,简称ISM⽅法)ISM⽅法是现代系统⼯程中⼴泛应⽤的⼀种分析⽅法,它在揭⽰系统结构,尤其是分析教学资源内容结构和进⾏学习资源设计与开发研究、教学过程模式的探索等⽅⾯具有⼗分重要作⽤,它也是教育技术学研究中的⼀种专门研究⽅法。
⼀、系统结构的有向图⽰法有向图形——是系统中各要素之间的联系情况的⼀种模型化描述⽅法。
它由节点和边两部分组成节点——利⽤⼀个圆圈代表系统中的⼀个要素,圆圈标有该要素的符号;边——⽤带有箭头的线段表⽰要素之间的影响。
箭头代表影响的⽅向。
例1:在教育技术应⽤中的计算机辅助教学(CAI)其过程可以简单表⽰为:教师设计CAI课件提供给学⽣⾃主学习,CAI课件通过计算机向学⽣显⽰教学内容,并对学⽣提问,学⽣根据计算机的提问作出反应回答。
2023年高考历史一轮复习(部编版新高考) 第5讲 课题11 从明朝建立至清朝前中期的统治

设立
大学士替皇帝浏览百官奏章,草拟处理意见,称为“_票__拟__”
职责
内阁
皇帝在票拟的基础上,用红笔正式批复奏章,称为 “批红”
机构
内廷宦官机构司礼监
宦官
获得协助甚至代理皇帝批红的权力,还负责提督东厂,控制 专权 权力
材料导读
材料的第一层着重说明了阁臣的特点(从地位、权限、德性和业务方面); 第二层论述了其对明代政治建设的作用(从皇帝个人意志与国家机构职 能间的关系,但还要看到内阁的实质)。 根据材料并结合所学知识,概括明朝内阁阁臣的特点和内阁对明代政 治建设的意义。 试答:_特__点__:__政__治__地__位__有__所__提__高__;__拥__有__票__拟__之__权__,__但__没__有__决__策__权__,__也__ _不__负__责__执__行__;__德__性__高__尚__、__政__治__业__务__精__湛__、__学__识__渊__博__,__但__品__级__较__低__;__处__ _理__事__务__较__为__公__平__、__客__观__。_
管理对外贸易事务;严厉禁止民间船只出海贸易
外部危机——
这种闭关自守的政策,无法适应新的外部环境,
评价
闭关锁国
中国逐渐落ቤተ መጻሕፍቲ ባይዱ于世界潮流
返回
强化关键能力
1.提炼信息 明清君主专制中央集权的强化
角度1 专制皇权的进一步发展——明代内阁制 材料 阁臣至仁宣,以部院职、兼公孤衔,地位骤显。也以票拟之预政 形式,在明最高行政权力运行过程中之裁决权、执行权间构成一个中介 程序。仁宣以来,阁臣多进士资格,翰林起身,识达大体,谙熟政令。 且综理庶务,少掺杂各部门本位之偏狭,平章政事,更能拿出较为公允 贴切之意见,其缓冲君主个人意志与国家机构职能之对立,调整国家机 器合理运行之作用是显而易见的。——姜德成《明代内阁制浅议》
第五讲 实例演示-钢混组合梁1

第五讲实例演示-钢混组合梁1 第五讲实例演示,钢混组合梁桥的计算一、结构尺寸:某桥为34米简支钢混组合梁桥,如下图所示,横桥向由多片梁组成,梁中到中间距7.3米,取其中一片梁计算。
钢梁裸梁高1.4米,顶板(含翼缘)宽5.5米,底板4.374米,底板厚0.025米,腹板厚0.016~0.02米。
二次浇注混凝土厚0.20米。
图1钢混组合箱梁桥构造图二、设计计算参数:1. 设计荷载:城 - A级。
2. 车道数:2车道。
3. 结构重力:一期恒载:结构自重混凝土γ=25KN/m3;钢γ=100KN/m3二期恒载:桥面铺装(t=100mm)防撞栏杆: 8 KN/m(一侧)5.温度影响力:温度条件考虑按规范取值(JTGD60—2004 4.3.10条)整体均匀温差+15?、-30?。
梯度温度正温差A=400mm,T1=16.4?,T2=6?;负温差A=400mm, T1= -8.2?,T2=-3?。
7.收缩徐变影响力:按新设计规范取用。
三、计算方法选用1本系统包含三种算法 :1. 平面梁单元算法。
2. 梁格法。
3(膜、板、八节点非协调块单元算法。
这里我们选用第三种算法。
模型的建立主要有两大步骤:(1)和建立梁单元计算模型类似,通过输入单元集、材料、截面、积分方法等参数建立网格划分控制信息;(2)执行网格划分。
网格划分控制信息的建立分以下几种情况:1、当桥的内横梁及边横梁垂直于桥中线(对于弯桥横梁沿径向),开始建模时,可完全按单根梁模型来建,建完后定义一下每个梁单元的积分方法,再执行网格划分,基本的空间块单元模型便可建立。
在建立单根梁模型时,梁可以位于桥的中线,此时需定义梁为中纵梁;梁也可定位于桥的边缘,此时需定义梁为边纵梁。
2、对于其它异型桥,网格划分控制信息建立有两种方式:(1)梁边缘控制法;(2)腹板节点控制法。
具体可参照说明书。
在本例题中,由于桥为直桥且等宽,因此建立起单根梁模型后就可以执行网格划分。
总体建模思路是:(1)不考虑横隔板将主梁模型建立起来;(2)按基本类似的步骤在主梁模型上增加横隔板或先单独建立横隔板模型文件再将该文件合并到主梁模型中。
数据库系统原理及应用教程课后答案苗雪兰第5讲

2.基于3NF的数据库设计方法
基于3NF的数据库设计方法是由S·Atre提出的结构 化设计方法,其基本思想是在需求分析的基础上, 确定数据库模式中的全部属性和属性间的依赖关系, 将它们组织在一个单一的关系模式中,然后再分析 模式中不符合3NF的约束条件,将其进行投影分解, 规范成若干个3NF关系模式的集合。
2.概念结构设计阶段
概念设计是把用户的信息要求统一到一个整体逻辑 结构中,此结构能够表达用户的要求,是一个独立 于任何DBMS软件和硬件的概念模型。
3.逻辑结构设计阶段
逻辑设计是将上一步所得到的概念模型转换为某个 DBMS所支持的数据模型,并对其进行优化。
15
现有应用 、未来应 用
数据分析
转换规范,规范 化理论DBMS要 求
需求分析的结果是否准确的反映了用户的实际 要求,将直接影响到后面各个阶段的设计,并 影响到设计结果是否合理和实用。
经验证明,由于设计要求的不正确或误解,直 到系统测试阶段才发现许多错误,则纠正起来 要付出很大代价。
因此,必须高度重视系统的需求分析。
19
6.2.1 需求分析的任务 从数据库设计的角度来看,需求分析的任务是:
用户的行为总是使数据库的内容发生变化,所以行为 设计是动态的,行为设计又称为动态模型设计。
6.1.1.3 数据库设计的特点
在70年代末80年代初,人们为了研究数据库设计方法 学的便利,曾主张将结构设计和行为设计两者分离, 随着数据库设计方法学的成熟和结构化分析、设计方 法的普遍使用,人们主张将两者作一体化的考虑,这 样可以缩短数据库的设计周期,提高数据库的设计效 率。
《数据库及其应用》教案-Access数据库应用技术(第4版)-崔洪芳-清华大学出版社

数据库及其应用教案选用教材:1.《Access数据库应用技术》崔洪芳主编,清华大学出版社2.《Access数据库应用技术实验教程》崔洪芳主编,清华大学出版社2020年9月23日目录第1讲数据库基本概念第2讲关系模型与关系的规范化第3讲Access系统简介、数据库的创建第4讲数据表的创建第5讲数据表的编辑第6讲选择查询的建立第7讲查询设计器的使用第8讲SQL查询的建立第9讲窗体向导的使用第10讲窗体设计视图的操作第11讲报表第12讲宏第13讲VBA模块第14讲流程控制语句第15讲循环和过程调用第1讲数据库基本概念【教学目标】了解数据、数据管理、以及数据管理技术的主要发展阶段。
理解数据库、数据库管理系统的基本概念和作用。
了解数据模型的作用以及经典的数据模型。
通过实例说明,了解数据库在信息社会的应用价值,明确本课程的研究内容和学习目标。
【教学内容】第1章数据库基础1.1 数据库基本概念1.1.1 数据与信息1.1.2 计算机数据管理技术的发展1.1.3 数据库的概念与特点1.1.4 数据库系统体系结构1.1.5 数据库系统与数据库管理系统1.2 数据模型1.2.1 数据模型的概念1.2.2 四种数据模型1.2.3 概念模型与E-R图【重点难点】1、数据库管理系统的定义(DBMS);2、数据模型的意义。
【教学方法】教师讲授与学生自主学习、协作探究相结合。
【思政元素】以我们学校数据库技术的应用为例,介绍数据库在我们生活中的广泛应用,从清早去食堂刷卡的校园一卡通,到学生查看考试成绩的教务管理系统,学校图书馆的管理系统,教学辅助的学习通,考试使用的考试系统等,介绍数据库技术在我们生活学习中的广泛应用,展示我国计算机技术的巨大发展,培养学生热爱祖国,关注学校的发展,满足学生不断增长的精神文化需求。
【教学进程】本章节作为课程第一节课,概念较多,特别对于非计算机专业学生而言,许多计算机领域的专业词汇理解上较为困难,教师讲授时应注意尽量将概念用通俗的语言进行转换,并加以身边的例子辅助说明,并对重点要掌握的概念加以强调,同时不强求所有内容的完全理解,例如对于数据库的3级模式结构可以只要求学生简单记忆便可,这样适度降低学生的理解难度,增强学生学好这门课程的信心。
第5讲 实验:描绘小灯泡的伏安特性曲线
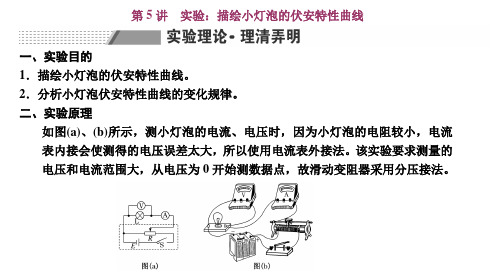
次数 1
2
3
4
5
6
7
U/V 0.20 0.60 1.00 1.40 1.80 2.20 2.70
I/mA 80 155 195 227 255 279 310
请你根据表中实验数据 在如图所示坐标系中作 出灯泡的 U-I 图线。
(3)由图像得出该灯泡的额定电压应为________ V;这一结果大于 1.22 V,其原因是 ______________________________________________________________。 解析:(1)根据 P=I2R,估算出灯泡的额定电流大约是 600 mA,因 此电流表应选 A2;本实验要描绘出灯泡的 U-I 图线,需要测量多组 数据,因此滑动变阻器应采用分压式接法,所以应选阻值较小的 R1; 小灯泡电阻较小,电流表应外接。原理图如图甲所示。
变阻器应采用分压式接法。 3.闭合开关 S 前,滑动变阻器的触头应移到使小灯泡分得电压为 0 的一端,使开
关闭合时小灯泡的电压能从 0 开始变化,而且实验过程中不要超过其额定电压。 七、误差分析 1.由于电压表不是理想电表,内阻并非无穷大,对电路的影响会带来误差,电流
表外接,由于电压表的分流,使测得的电流值大于真实值。 2.测量时读数带来误差。 3.在坐标纸上描点、作图带来误差。
第 5 讲 实验:描绘小灯泡的伏安特性曲线
一、实验目的 1.描绘小灯泡的伏安特性曲线。 2.分析小灯泡伏安特性曲线的变化规律。 二、实验原理
如图(a)、(b)所示,测小灯泡的电流、电压时,因为小灯泡的电阻较小,电流 表内接会使测得的电压误差太大,所以使用电流表外接法。该实验要求测量的 电压和电流范围大,从电压为 0 开始测数据点,故滑动变阻器采用分压接法。
第5讲 样式表

第5讲样式表样式是控制文本块或段落外观的一组格式属性,使用样式可以格式化文本,可以设置一篇文档的格式。
在DW中,样式包括HTML样式和CSS样式。
●HTML样式是DW自身携带的工具,帮助用户进行文本格式的设置。
HTML样式实际上是一系列HTML格式标记的组合,用于一次对文本对象进行多个方面的格式设置,例如,如果将文字设置为宋体,3号,加粗,倾斜,按照传统的方法必须进行4次格式化设置,如果使用DW的HTML样式功能,将这4次格式化操作组合成一个HTML样式,并以合适的名字命名,下次当需要对文本应用这些格式时,只需要应用该HTML样式即可。
●CSS样式(层叠样式单)用来进行网页风格设计,通过设立样式表,可以统一控制HTML中各标记的显示属性,通过只修改一个文件就可以改变一批网页的外观和格式(css样式可以控制多个文本的文本格式,当css样式被更新时,所有使用css样式的文档也自动随着更新)。
1、HTML样式:“窗口->HTML样式”把HTML样式面板选出来HTML样式面板“新建样式”右键点击选“新建”点击面板上的“新建样式”图标或右键点击选“新建”(看上图),在“定义HTML样式”中就可以对HTML样式进行设置了。
几个留意的地方1)应用到:选中应用到选定的范围还是段落2)当应用:当HTML应用到文本上,会出现两种情况:覆盖型样式和添加型样式。
“清除现有样式”指如原来已经有样式了,当应用这一样式时,会把原有的样式清除,再应用选定的样式。
“添加到现有样式”就是在原有样式基础上再进行添加应用一个样式。
所以看出HTML样式其实的设置不是太多内容,只是些字体,大小,颜色,样式之类的。
创建好HTML样式后,在“HTML样式”面板就可以看到刚创建好的样式了,name前面的a表明是应用到选定范围,+指是添加到现有样式。
2)编辑、复制和删除HTML样式如果觉得样式不满意,想继续编辑的话可以直接双击要编辑的样式即可,或者右键点击选“编辑”。
第五讲 面向对象分析与设计(Object-oriented Analysis and Design)

4 面向对象软件工程
OOA强调直接针对问题域中客观存在的各项事物设立OOA模 型中的对象。另外,OOA模型也保留了问题域中事物之间关 系的原貌。 OOD包括两方面的工作,一是把OOA模型直接搬到OOD,作为 OOD的一个部分;另外是针对具体实现中的人机界面、数据 存储、任务管理等因素补充一些与实现有关的部分。这些 部分与OOA采用相同的表示法和模型结构。 在OOA->OOD->OOP这一软件工程的过程系列中,在OOA和OOD 阶段对系统需要设立的每个对象类及其内部构成与外部关 系都达到透彻的认识和清晰的描述, OOP工作就是用同一 种面向对象的编程语言把OOD模型中的每个成分书写出来: 用具体的数据结构来定义对象的属性,用具体的语句来实 现操作流程图所表示的算法。
第五讲 面向对象分析与设计 (Object-oriented Analysis and Design)
Welcome to Software Engineering Lecture 5 Zhang Jiannan jiannanz@
目标
熟悉面向对象方法的基本知识;
熟悉 UML的基础知识;
assemble() …
结构化设计中模块和模块之间的关系,被紧紧局限于 信息流,试图通过信息流及其转换来认识系统,这限 制了对模块之间众多关系的表达和体现,如继承、依 赖。
结构化与面向对象
流水线式的过程处理与人们日常处理问题的方式不一 致。随着时间流逝,软件工程师越来越注重系统整体 关系的表示和数据模型技术(把数据结构与过程看作 一个独立功能模块)。程序定律被重新认识: 程序 = (过程+数据结构) 这样的思想符合现实世界中的事物特征,我们区分事 务主要依靠就是事物各式各样的特征,包括事物不同 的属性和特定的行为。 集成化的软件开发方法--面向对象方法产生。
数据结构考研讲义 第五章 图

第四章图4.1图的概念1.图的定义图是由一个顶点集V和一个弧集R构成的数据结构。
2.图的重要术语;(1)无向图:在一个图中,如果任意两个顶点构成的偶对(v,w)∈E是无序的,即顶点之间的连线是没有方向的,则称该图为无向图。
(2)有向图:在一个图中,如果任意两个顶点构成的偶对(v,w)∈E是有序的,即顶点之间的连线是有方向的,则称该图为有向图。
(3)无向完全图:在一个无向图中,如果任意两顶点都有一条直接边相连接,则称该图为无向完全图。
在一个含有n个顶点的无向完全图中,有n(n-1)/2条边。
(4)有向完全图:在一个有向图中,如果任意两顶点之间都有方向互为相反的两条弧相连接,则称该图为有向完全图。
在一个含有n个顶点的有向完全图中,有n(n-1)条边。
(5)稠密图、稀疏图:若一个图接近完全图,称为稠密图;称边数很少(e<nlogn)的图为稀疏图。
(6)顶点的度、入度、出度:顶点的度(degree)是指依附于某顶点v的边数,通常记为TD(v)。
在有向图中,要区别顶点的入度与出度的概念。
顶点v的入度是指以顶点为终点的弧的数目,记为ID(v);顶点v出度是指以顶点v为始点的弧的数目,记为OD(v)。
TD(v)=ID(v)+OD(v)。
(7)边的权、网图:与边有关的数据信息称为权(weight)。
在实际应用中,权值可以有某种含义。
边上带权的图称为网图或网络(network)。
如果边是有方向的带权图,则就是一个有向网图。
(8)路径、路径长度:顶点vp到顶点vq之间的路径(path)是指顶点序列vp,vi1,vi2,…,vim,vq.。
其中,(vp,vi1),(vi1,vi2),…,(vim,.vq)分别为图中的边。
路径上边的数目称为路径长度。
(9)简单路径、简单回路:序列中顶点不重复出现的路径称为简单路径。
除第一个顶点与最后一个顶点之外,其他顶点不重复出现的回路称为简单回路,或者简单环。
(10)子图:对于图G=(V,E),G’=(V’,E’),若存在V’是V的子集,E’是E的子集,则称图G’是G的一个子图。
word表格制作教案模板(共9篇)

word表格制作教案模板(共9篇)轻松制作表格教案课题:Word表格制作教学目标:知识目标:了解表格中的基本概念,掌握表格的创建、编辑与调整。
能力目标:能够熟练完成表格的制作。
情感目标:培养学生的审美能力,自主思考与学习能力,使其在探索中进步。
教学重点:表格的创建、编辑与修饰教学难点:表格的编辑与调整教学方法:讲授法、演示法、任务驱动法学法:思考、讨论、练习教具准备:计算机、课件及多媒体设备教学内容及过程:课题引入:同学们,在我们日常生活、工作中往往会用到表格,例如:上课要用到的课程表,考试结束后的成绩单,求职时的个人简历等等(用第1张幻灯片展示提到的几种表格)。
这些表格让我们非常清晰、有条理化的看到相关信息。
那么这些表格是怎么制作的呢?这就是本节课我们要学习的内容—word表格制作(展示第2张幻灯片)。
讲授新课:一、表格的创建1、认识表格在学习之前我们先来认识表格。
(利用表进行讲解,展示第3张幻灯片。
)我们来看一下表格由哪些部分组成?行线:表格中水平的线列线:表格中垂直的线单元格:行列交叉的矩形框,表格中容纳数据的基本单元。
行:水平方向的单元格组成了行列:垂直方向的单元格组成了列二、轻松制作表格:1.创建表格2.编辑表格3.修饰表格2、创建表格的方法(教师边演示边讲解,展示第5张幻灯片)方法一:使用菜单创建表格(展示第6张幻灯片)操作如下:(1)打开文档,调整好光标位置;(2)单击“表格”菜单的“插入”子菜单中的“表格”项,打开“插入表格”对话框;(3)在“插入表格”对话框中设置表格参数;在[列数]和[行数]文本框分别用于设置所创建的表格的列数与行数;(4)单击“确定”按钮。
方法二:使用“插入表格”按钮创建表格(展示第7张幻灯片)操作如下:(1)首先要启动word;(2)调整好光标的位置,使它正好位于要插入表格的地方。
(3)将鼠标放在[常用]工具栏的[插入表格]按钮上,按下这个按钮,将出现一个示意网格。
第5讲 用例建模

2 识别参与者(Actor)
从需求中识别参与者
参与者:在系统之外,通过系统边界与系统进 行有意义交互的任何事物
要点:任何事物
任何事物举例:小人与圣小猪-1
如果我开发一个猪圈自动供食供水系统 ,猪的 前蹄触发一个开关系统就供食或供水。很显然 这里的参与者是小猪。通常,用例图中的参与 者用一个小人表示。
场景1:某企业要求开发一个企业信息管理 系统,并与原来已有的库存系统相连接
系统之外,重点明确新老系统间的接口
场景2:某企业要求开发一个企业信息管理 系统,并把原来已有的库存管理系统加以 改造,成为企业信息管理系统的一部分
系统之内,新系统存在一个“改造库存系统” 用例,工作量要比上述大很多
参与者的命名
涉众无法直接提供需求的现象
涉众无法陈述自己的需要
涉众说的是解决方案而不是需求
涉众难以构想新的工作方法
涉众的利益矛盾
涉众抵制变更
“最好也要有”—过度的要求
需求引发新的需求
获取需求的技巧——需求启发技术
技巧 描述 直接观察个人工作的情况,以发现现存的实践方 实地观察 式和问题,提供最直观的业务细节,但耗时 访谈 从个人处收集特定信息,直接沟通,信息真实性 特定群体 对一组人员进行调查,以便了解工作态度和共同 看法 调查 收集详细数据和统计意义上比较重要的数据,可 问卷调查 以获得匿名答复 用户指导 让最终用户告诉你,他们是如何实现业务流程的 原型制作 模拟一个无法直接测试的系统,便于沟通 记录用户完成任务的方式,便于了解用户习惯, 统计版本 及时改进
多,反之则包含的功能越少。
合作学习记记法内外圈第5讲

第五讲合作学习的基本理论一、学习目标1.了解与合作学习相关的主要理论。
2.了解哪些理论对自己的教育观点产生了影响。
3.掌握“记记法”和“内外圈”两种合作学习策略。
4.学会“提问-应答提问”的合作技能。
二、学习材料《合作学习的理论》三、合作学习方式(一)记记法1.记记法的操作步骤(1)组成4-6人组。
(2)桌面上摆放题卡,题卡正面是问题,背面是答案。
(3)A向其他成员出示卡片正面的问题,其他学员抢答。
(4)交换角色,B、C、D分别向其他学员出示卡片正面的问题,其他成员抢答。
2.记记法的操作要领(1)每张题卡上只能有一道题,答案应是唯一的。
(2)答题人对某一问题只可以答一次。
(3)题卡上的题可以是教师提供,也可以由学生自主设定。
(4)可使用抢答,也可以使用指定答题人的方式进行。
3.记记法的运用适用于记忆和理解层面的认知活动。
(二)内外圈1.内外圈的操作步骤(1)小组中一半成员组成内圈,面朝外,还有一半成员组成外圈,面对内圈。
外圈中的每个人都应面对内圈的一个人。
(2)面对面的两个人进行交流。
(3)外圈的人轮换位置,面对内圈中另外一个人。
(4)面对面继续交流。
2.内外圈的操作要领(1)组成内外圈时,可以是本组的一半成员是内圈,另外一半成员是外圈,也可以跨组组成内外圈,即,一个组为内圈,另外一个组为外圈,甚至可以由女生做内圈,男生做外圈。
(2)已经先讨论完的可以举手示意,当内外圈中大多数成员都已经讨论完,统一由一名成员指挥轮换。
(3)全部轮换并讨论完毕后,由组长向教师示意,经教师许可后方可入座。
3.内外圈的运用(1)这是合作学习中用于高水平思维活动的一种合作策略。
(2)主要适用于分析、评价和创造性的认知活动。
(3)也可以用于对他人的学习指导,即,内圈每人负责成为一个学习内容的专家,反复教授外圈的同学。
四、合作技能(一)提问1.“什么”、“为什么”、“怎么做”是问话的三件宝。
2.尽量问对方开放性问题,这样不会给对方带来紧张感,也给对方留下展示自己才能的机会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5讲表的建立与操作西南民族大学教师: 肖明xm0928@第5讲表的建立和操作5.1 表结构的建立与基本操作5.2 数据表的基本操作5.1 表结构的建立与基本操作5.1.1 数据表的结构5.1.2 表结构建立5.1.3 表结构的基本操作库数据库表文件对应一个关系,由表结构(关系模式)和记录(元组)数据两部分组成。
如:学生.DBF•表名:表名可以由字母、数字或下划线组成,系统自动给出的扩展名为.DBF•表头:由若干标题栏目构成,每栏对应表的一列,也称为一个字段(属性),涉及字段名、数据类型、宽度。
•表的内容:括由若干行组成,每行反映一个对象的各方面情况,称为表的一个记录。
创建一个表时,首先要设计和建立表结构,然后再输入数据。
设计表结构,即根据具体情况定义表中各个字段的属性,包括字段名,字段类型、字段宽度,对数值型还有小数位数。
如,上表的结构为:学生(学号C(8),姓名C(8),性别C(2),出生年月D,入校总分N(3),三好生L,特长M,照片G)。
•字段名:用于标识字段,以字母、汉字或下划线开头,自由表字段名最长10个字符,数据表可达128个字符。
•字段类型与宽度:字段类型应与将要存储的信息类型相匹配,其宽度必须能容纳将要显示的信息内容;对数值型应根据具体情况指定小数位数。
应记住各种常用类型的固定宽度和取值范围。
•说明:备注型字段宽度为4个字节,用于存储指向备注内容存放的地址。
备注内容存放在与表同名的.FPT文件中,其随表的打开而自动打开。
通用型字段宽度为4个字节,用于存储指向.FPT文件中想念通用型字段的地址。
小数点与正负号在字段宽度中占一位可指定字段是否接受空值(NULL),其不同于零、空字符串,是一个不存在的值。
•说明:数据表文件名,支持长文件名,但文件名中不可以使用空格、*或?号等。
因为系统已经设定了A、B、C、…、J十个单字母和W11、W12、W13、…、W225作为数据库工作区的别名,所以用户不要用它们作为数据库名或数据表名,否则会引起操作上的错误。
5.1.2 表结构建立•命令方式:格式1:CREATE[[盘符][路径]<新表文件名>|?]功能:打开”表设计器”,创建一个新的表文件结构. 说明:①若未指定盘符、路径则默认为当前盘的当前目录中创建数据表②使用?参数时,系统会打开一对话框,要求用户输入表的文件名,此时应注意存放目录。
•命令方式:格式2:CREATE TABLE[盘符][路径]<新表文件名>(<字段名1> <类型>(<长度[,小数位数]>)[,<字段名2><类型>(<长度>) …]) 功能:不进入”表设计器”,直接创建一个新的表文件结构.例:若输入以下命令:CREATE TABLE 学生(学号C(8),姓名C(8),性别C(2),入校总分N(3))则可以建立一个包含学号、姓名、性别、入校总分的新表。
•菜单方式:步骤:“文件”菜单→“新建”→“表”→“新建文件”按钮→“创建”对话框为文件取名→进入表设计器•项目方式:步骤:“项目管理器”→“数据”选项卡→“自由表”→“新建”→“新表”向导→创建”对话框取名→进入表设计器•设定默认目录:格式:SET DEFAULT TO [<盘符>][<路径>]功能: 设定操作的默认目录.例: SET DEFAULT TO D:\VFP\TABLE则以后操作中D:\VFP\TABLE为当前默认目录。
•建立表结构示例:(菜单方式)步骤:单击“文件”菜单→选择“新建”→选择“表”→单击“新建文件”按钮→在“创建”对话框中,选择保存在“D:\VFP\TABLE”文件夹中,为表取名为“学生.DBF”,再单击“保存”按钮,将弹出“表设计器”对话框,选择“字段”选项卡→在“字段名”中输入“学号”→按TAB键切换到“类型”列,选择C型→按TAB键切换到“宽度”列,输入10→按TAB键换到“索引”列→按TAB键换到“NULL”列→按TAB键换下行“字段名”一列→…•建立表结构示例:(菜单方式)说明:在“字段名”列左面有上下双箭头的按钮,拖动可改变字段的次序。
在设定字段属性时,可用光标键,上下左右移动光标,但注意不要按回车键,否则将结束结构的设定。
要删除一个字段,可选定该字段后单击“删除”按钮;要插入一个字段,可选定某字段后单击“插入”按钮,新字段将插入在当前字段之前。
字段属性设定完成后,单击“确定”按钮或回车后,将弹出一对话框询问“现在输入数据记录吗?”可在此输入记录数据,也可选否,以后再添加记录数据,但表结构已产生。
•立即型追加数据:环境:当表结构建立完成,出现询问框后选择’是’,即可出现一编辑窗口,在此可输入数据.说明:①逻辑型字段只接受T,Y,F,N四个字母之一(不论大小写).②日期型字段的默认格式是”mm/dd/yy”.③输入备注型字段数据时,需先将光标移到该字段,再按Ctrl+Pgdn或鼠标双击memo即可打开备注型字段编辑窗口,在此可输入内容,完毕后按Ctrl+W退出且保存,memo变为Memo. Esc或Ctrl+Q放弃.④通用型的输入与备注型类似, 存储后gen显示为Gen.5.1.3 表结构的基本操作A. 表的打开与关闭B. 表结构的查看与修改C. 表结构的复制A. 表的打开格式:USE [<表文件名>|?][EXCLUSIVE|SHARED] 菜单:“文件”→“打开”→“表”→文件名→“确定”功能:在当前工作区中打开指定的表文件。
说明:①EXCLUSIVE表独占,SHARED表共享打开。
②打开该表前,会自动关闭当前工作区已打开的表,相应.FPT会同时打开。
③打开后,记录指针指向首记录。
A. 表的关闭格式1:USE功能:关闭当前工作区已打开的表文件格式2:CLOSE ALL功能:关闭所有工作区中的各类文件,但不释放内存变量格式3:CLOSE <文件类型>功能:关闭指定的相应类型文件,如:CLOSE TABLES [ALL] 格式4:CLEAR ALL功能:关闭所有工作区中的各类文件,并且释放内存变量格式5:QUIT功能:关闭所有工作区中的各类文件,释放内存变量且返加操作系统。
B. 表结构的查看与修改•表结构的显示格式:LIST/DISPLAY STRUCTURE [TO <PRINTER [PROMPT]>|<FILE 文件名>]功能:对打开的表结构以列表或分屏方式显示或输出 说明:①TO PRINTER输出到打印机,PROMPT进行设置②<TO 文件名> 输出到文件。
B. 表结构的查看与修改格式: MODIFY STRUCTURE菜单:“显示”→“表设计器”功能:打开表设计器对话框,修改当前表文件结构。
说明:①必须先打开表。
②修改操作:插入、删除③不要同时修改同一字段的两项内容,否则易造成数据丢失,应退出后再进入修改。
C. 数据表结构的复制格式1: COPY STRUCTURE TO <表文件名> [FIELDS<字段名表>][[WITH]CDX][DATABASE 数据库名[NAME 表名]] 功能: 用当前选择的表结构创建一个新的数据表结构 说明: ①FIELDS<字段名表>用于选择欲复制的字段②WITH CDX表示同时创建同名复合索引文件③DATABASE 数据库名[NAME 表名]表示在一个数据库中创建一张表结构。
例:USE 学生COPY STRUCTURE TO STU FIELDS 学号,姓名,性别D. 表的复制格式: COPY TO <新表文件名>[范围] [FOR/WHILE<条件>][FIELDS<字段名表>]功能: 用当前表的结构和内容支创建一个既有结构又有内容的新表文件说明:①范围、条件、字段名表的作用5.2 数据表的基本操作5.2.1 表记录指针5.2.2 表记录的命令操作5.2.3 逻辑表的设置5.2.4 表与数组间的传送•记录指针的定位格式1:GO[TO][n|TOP|BOTTOM]功能:将记录指针移到指定位置说明:①n为数值表达式,移到记录号为n的记录②TOP:移到首记录③BOTTOM:移到末记录•记录指针的定位格式2:SKIP[±n]功能:将记录指针正向或反向移动n条记录 说明:①参数为正时,向文件末尾移动②参数为负时,向文件头移动③缺省参数时,等同于参数为1②注意超过范围时的情况5.2.2 表记录的命令操作A. 表记录查看B. 记录的追加C. 记录的批量追加D. 复制表中的数据至其它类型的文件E. 表记录的删除与恢复F. 表数据的替换•表记录的显示格式1:LIST/DISPLAY [[FIELDS] <字段名表>][范围][FOR<条件>][WHILE<条件>][OFF][TO <文件名>|PRINTER[PROMPT]]功能:对满足条件的当前表记录以列表或分屏方式显示或输出说明:①FOR条件与WHILE条件②有OFF参数,不显示记录号•表记录的显示格式2:BROWSE [[FIELDS] <字段名表>][FOR<条件>][REST]功能:打开浏览窗口,显示、浏览和修改记录数据。
说明:①有REST参数,指针定位在当前窗口②通过“显示”菜单中的“浏览”和“编辑”可在两种格式间切换③可通过浏览窗口左下角的窗口分割器将窗口分为两个区B. 记录的追加•直接追加记录:格式1:APPEND [BLANK]功能:在已打开的表的末尾追加一条或多条记录. 说明:无BLANK参数时,将进入编辑窗口,用户可追加多条记录,操作同前;带BLANK时,将在表未尾直接追加一空白记录,且不进入编辑窗口.C. 记录的批量追加•直接追加记录:格式2:APPEND FROM[<文件名>|?][FIELDS<字段名表>][FOR<条件>][[DELIMITED WITH <“分隔符”>|CHAR<分隔符>]|[SDF] 功能:将其它表(或文本文件或电子表格)中的记录追加到当前表的末尾.说明:DELIMITED WITH <“分隔符”>用于指定文本文件中各字段间的隔符号;SDF说明源文件为标准文本格式,即数据按字段宽度排列,不使用分隔符。
D. 复制表中数据至其它类型文件格式: COPY TO <文件名> [范围][FOR/WHILE<条件>] [FIELDS<字段名表>][[WITH] CDX][SDF|DELIMITED WITH <“分隔符”>]菜单:“文件”→“导出”→“…”选择导出文件与类型→“选项”设定条件→“确定”功能: 用当前表的结构和内容支创建一个既有结构又有内容的新文件说明:①范围、条件、字段名表的作用②WITH CDX表示同时创建一个结构索引文件③SDF与DELIMITED的作用同APPEND FROM命令•为记录做删除标记(鼠标方式)步骤:打开”浏览”窗口→单击欲删除记录左边的小方框→出现黑色小方块(删除标记)说明:①再次单击黑色小方块,可取消删除标记②若欲彻底删除,须从”表”菜单中选择”彻底删除”,会出现询问,选择”是”即可.③若欲设置删除范围与条件,可在”删除”对话框中设置.•为记录做删除标记(命令方式)格式:DELETE[范围][FOR<条件>][WHILE<条件>]功能:对当前表中指定范围内满足条件的记录前加删除标记.说明:若范围与条件缺省, 则仅对当前记录前加删除标记•逻辑删除记录的恢复格式:RECALL[范围][FOR<条件>][WHILE<条件>]功能:对当前表中指定范围内满足条件的记录去掉删除标记.菜单:打开”浏览”窗口→”表”→”恢复删除”或打开”浏览”窗口→单击每个欲恢复记录前的小黑方块•物理删除记录格式1:PACK功能:从物理上删除当前表中带有删除标记的记录. 菜单:打开”浏览”窗口→”表”→”恢复删除” 格式2:ZAP功能:从物理上删除当前表中所有记录.说明:上述命令删除的记录不可再恢复•记录的修改格式1:EDIT [FIELDS <字段名表>][范围][<条件>] 功能:打开编辑窗口,供用户修改满足条件记录的指定字段。
