习题课3
辽宁工业大学高数习题课(3)

ln sin x 【例2】计算 lim 2 x ( 2 x )
2
分析 当 x 0 分子分母均趋近于0, 为 型, 用洛必达法则计算. 解:
ln sin x lim 2 x ( 2 x )
2
0 0
( 0 型)
0
cos x lim x sin x [ 4( 2 x )]
1
【例4】计算 lim x 2 e x
x 0
2
分析 当 x 0 时, 函数式为 0 型,
1
0 将其化为 0
或
型.
解:
lim x 2 e x ( 0 型)
2
x 0
1
ex l im x0 1 x2
1
2
(
型)
e lim
x 0
x2
2 3 1 x x2 lime . 2 x 0 3 x
拉格朗日型余项 佩亚诺型余项
Rn ( x) 0[( x x0 )n ]
2.麦克劳林公式
f (0) f ( n ) ( 0) 2 f ( x ) f (0) f (0)( x x0 ) ( x x0 ) ( x x0 )n Rn ( x ) 2! n!
所以
f (1) 8, f (1) 5, f ( 1) 0,
f ( 1) 6.
f ( ) ( x 1) 2 一阶泰勒公式为 f ( x ) f ( 1) f ( 1)( x 1) 2!
8 5( x 1) 3( 1)( x 1)
0 0
二、泰勒公式
1.泰勒公式
f ( x0 ) f ( n ) ( x0 ) 2 f ( x ) f ( x0 ) f ( x0 )( x x0 ) ( x x0 ) ( x x0 )n Rn ( x ) 2! n!
高分子习题课(1-3)

f kd=2.0×10-9
第三章 自由基聚合
R p kp( fk d kt
Kp Kt
ν 2(fk kp
d
)
1/2
[I]
1/2
[M]
1 2
0 .0 3 3 5 4 1
[M]
1/2
kt)
[I]
1/2
V=3750
第三章 自由基聚合
设苯的浓度为[S],在1L苯乙烯-苯的理想溶液中, 有:V苯+V苯乙烯=1000(mL)
第二章 缩聚和逐步聚合
反应程度(参与反应的基团数占起始基团数的分数)
P = N 0- N N0 =1 - N N0
N0 起始二元酸和二元醇的分子总数 N
为时间t 时的体系中的聚酯分子数
聚合度
Xn =
结构单元数目 大分子数
= Xn = N 1 P -
N0
1
第二章 缩聚和逐步聚合
不可逆线形缩聚动力学
M1010=374 M0=338/2=169
n
第二章 缩聚和逐步聚合
假设对癸二胺的反应程度P=1,
在1g1010盐中:
胺基摩尔数: 游离羧基摩尔数为: 羧基摩尔数:
等于KOH的摩尔数
第二章 缩聚和逐步聚合
酸值
第三章 自由基聚合
引发剂分解动力学
Rd d[I ] dt kd [I ]
例4.尼龙1010是根据1010盐中过量的癸二酸控制分子量的。 如果要求合成尼龙1010的分子量为20000,问尼龙1010盐 的酸值(以mg KOH/g 1010盐计算)应是多少?
1010盐 尼龙1010 NH3+(CH2)10NH3OOC(CH2)8COOC O (C H 2 ) 8 C O N H (C H 2 ) 10 N H
随机过程及应用习题课三

随机过程及应用习题课三11. 设()cos ,X t A B t t =+-∞<<+∞,其中A 和B 为相互独立均服从(0,1)N 的随机变量.(1)证明{(),}X t t -∞<<+∞为正态过程;(2)求其一维、二维概率密度和一维、二维特征函数.2. 设{(),(,)}X t t ∈-∞+∞是均值函数为0,自相关函数()(,)/2X R s t s t s t =+-- 的正态过程,证明1()()Y t X t =,0t >,2()(),0Y t X t t =-≥是相互独立的正态过程。
3. 设0{()}W t +∞是参数为2σ的维纳过程,试证明1()0()0tW t W t tt ?>?'=??=?是参数为2σ的维纳过程。
4. 设{(),0}W t t ≥是参数为2σ的维纳过程,证明12()()0t W t c W t c=?≥是参数为2σ的维纳过程。
5. 设{(),0}W t t ≥是参数为2σ的维纳过程,证明2()()W t W t =-是参数为2σ的维纳过程。
6. 设{(),0}W t t ≥是参数为2σ的维纳过程,证明3,0()()()0t W t W t a W a a ≥=+->是参数为2σ的维纳过程7. 设{(),0}W t t ≥是参数为2σ的维纳过程,令231()0()00t W t W t tt ?>?'=??=? (1)(){},0W t t '≥是否为正态过程;(2)(){},0W t t '≥是否为维纳过程。
8. 设{(),0}X t t ≥是具有零均值和协方差(,)C s t 的正态过程,则对于任意的非负数,s t 和τ,证明:(1)2[()](,)()E X t C t t D t ==;(2)222[()]2(,)2()D X t C t t D t ==;2(3)222cov((),())2(,)X s X t C s t =;(4)[()()](,)E X t X t C t t ττ+=+;(5)2[()()](,)(,)(,)D X t X t C t t C t t C t t ττττ+=++++;(6)cov[()(),()()](,)(,)(,)(,)X s X s X t X t C s t C s t C s t C s t ττττττ++=+++++ 9. 设{(),0}W t t ≥是参数24σ=的维纳过程,令(3)(1),(4)(2).X W W Y W W =-=-求:()D X Y +和cov(,).X Y10. 设0{()}W t +∞是为参数为2σ的Wiener 过程,求下列过程的均值函数和自相关函数。
第六章习题课线性代数 (3)

性指数, 并且秩相同.应选(B).
例 8 用正交变换化二次型 f (x1, x2 , x3 ) x12 2x22 3x32 4x1x2 4x2 x3 为标准形, 并求
出该正交变换.
1
解
二次型的对应矩阵为
A
2
2 2
0 2
.则由
A
的特征方程
0 2 3
解得 a 3.于是
5 A 1
1 5
3 3 .
3 3 3
5 1 3 I A 1 5 3 ( 4)( 9) ,
3 3 3
所以 A 的特征值为 1 0, 2 4, 3 9 .
(2)由(1)知存在正交矩阵 P , 使得
注 用正交变换 X PY 化二次型为标准形, 这类题若要求写出正交变换 X UY , 计
5
算量大.若只要求知道结果, 即仅需知道标准形, 则计算量不大.在解答中要注意区分和判 断.
例 12 已知二次曲面方程 x2 ay2 z2 2bxy 2xz 2yz 4 可以经过正交变换
绕 y 轴旋转而成的空间曲面的性质, 可以得到该曲面可
y2
由
4
z2
1绕 y 轴旋转而成,
也可由
x2
y2 4
1绕 y 轴旋转而成.
x 0
z 0
例6
空间曲线
x2 y2 4
所属曲线类型是
.
z c
解 该曲线可由平行与 xoy 平面的一平面 z c 截双曲柱面 x2 y2 4 所得, 为双曲线.
解
二次型
f
高等数学习题课(3)中值定理与导数的应用

(3)
中值定理与导数的应用
第二课 中值定理与导数应用
I. 目的要求 ⒈ 理解罗尔定理、拉格朗日定理,了解柯西定理; 会用中值定理解决诸如方程根的存在性、不等 式证明等问题; ⒉ 了解泰勒定理的条件、结论及余项,掌握函数 ex , sinx, cosx, ln(1+x), (1+x)α的麦克劳 林公式; ⒊ 熟练掌握用洛必达法则求不定型极限的方法; ⒋ 熟练掌握求函数单调区间、极值、凹凸区间、 拐点的方法,并会用其证明一些相关问题。
证:由条件易知F (x)在 [1,2]上满足罗尔定理条件, 则 (1,2),使 F(1) 0 又 F(x) 2(x 1) f (x) (x 1)2 f (x) 在 [1,1]上连续,在(1,1)内可导,且 F(1) F(1) 0 由罗尔定理, (1, 1) (1, 2) 使 F() 0 #
(a 0)有极值,试证:曲线y f (x) 在点(a, f (a))处的
切线经过坐标原点。 证:曲线 y f (x) 在 (a, f (a)) 处的切线方程为
y f (a) f (a)(x a)
即 y f (a)x [ f (a) a f (a)]
由条件 (x) 在 x a 点有极值,且易知(x)在 x a 点可导
x
2
分析:只需证明 sin x x 0 3 cos x
证:令
f
(x)
sin x 3 cos x
x
sin
1
x cos 3
x
x
,显见
f
(0)
0;
f
(x)
cos
2 3
x
1 sin
2
x
4
cos 3
x
电路分析第3、4章习题课

图5
6. 图6 所示线性网络N只含电阻,若IS1=8A, IS2=12A,Ux为80V,若IS1=8A,IS2=4A,Ux为0.求: IS1=IS2=10A时,Ux是多少?
图6
7. 用戴维南定理求图7 电路中流过 20 kΩ电阻的电 流及 a 点电压 Ua.
图7
8. 图8(a)所示电路,输入电压为20V,U2=12.5V, 若将网络N短路,如图(b)所示,短路电流I为10mA, 试求网络N在AB端的戴维南等效电路
+
2U1
- 2V
(a)
-
(b )
图11
12. 如图12所示,RL为何值时能获得最大功率,并 求最大功率。 10 + a + Uoc
2A
UR 20
UR 20 – + - 20V – b
图12
练习
1. 列出图1-1所示电路的网孔方程、节点方程。
+ uS 6 -
R6 2
uS2 +
1 R1
uS1 +
电路分析习题课(3—4章)
1. 电路如图1 所示 用网孔分析法求 I A 并求受控源 提供的功率 PK .
图1
2. 电路如图所示,用网孔分析法求4Ω电阻的功率。
图2
3. 试用结点分析法求解图3中的 U1及受控源的功率。
图3
4. 试列出为求解图4 所示电路中 Uo所需的结点方程。
图4
5. 电路如图5 所示,用叠加定理求Ix
图8
9. 求图9 所示电路的戴维南等效电路。
图9
10. 用戴维南定理求图10所示电路中2A电流源上的电 压U 。
15Ω 5Ω I
15Ω
5I
+
3章习题课

s1 2
z − z 0 = 2 x, p = p 0 , u = u 0
设杯中速度为V,管中速度为u,
V d ⇒ V = u ( )2 , 4 4 D ∂V ∂u (h − x + h + x) + l + 2 gx = 0 ∂t ∂t =u
p + ρ ′g ∆h = p0 + ρ g ∆h, 则 p0 − p = ( ρ ′ − ρ)g ∆h, 2 ( ρ ′ − ρ ) g ∆h = (
∴u =
ρ
ρ′ − 1)2 g ∆h ρ
ρ ′ / ρ = 13600 / 800, ∆h = 60mm = 0.06m,
∴ u = 4.3391m / s
2 p1 + ρ (v1
2 − v2 ) / 2
= 17.6×103 +1000 (1.422 − 3.182 ) / 2 ×
= 17.2 ×10 3
(Pa)
3.所取控制体受力分析 进、出口控制面上得总压力:
P2 = p 2 A2 = 17.2 × 10 3 ×
P = p1 A1 = 17.6×10 × ×0.32 = 12.43 1 4 π
2 根据射出水流轨迹: x = Vt 1 x 1 2 ⇒ h − y = g h − y = gt 2 V 2
整理得: 解得:
4 y (h − y ) = x 2 ,即 y (4 − y ) = 1
y = 2± 3
3-18解:
u = u m (1 −
r 1 r n r ) ⇒ Q = ∫ u 2πrdr = um 2πR 2 ∫ (1 − η ) nηdη (令:η = ) 0 0 R R
氧化还原习题课(3、4课时)讲解

第3课时氧化还原反应热点专题训练【典型例题】例1.某种飞船以N2H4和N2O4为动力源,发生反应:2N2H4+N2O4===3N2+4H2O,反应温度可高达2 700 ℃,对于该反应,下列说法正确的是()A.该反应属于置换反应B.N2H4是氧化剂C.N2O4是还原剂D.N2既是氧化产物又是还原产物例2.某反应中有反应物和生成物共5种物质:S、H2S、HNO3、NO和H2O。
已知水是反应产物之一。
(1)该反应中的还原剂是__________。
(2)该反应中的还原产物是______________。
(3)写出该反应的化学方程式,并用双线桥法标出电子转移的方向和数目_______________。
(4)若反应过程中转移了0.3 mol电子,则生成水的质量是______________。
【随堂训练】1.事实上,许多氧化物在一定条件下能与Na2O2反应,且反应极有规律,如Na2O2+SO2===Na2SO4,2Na2O2+2SO3===2Na2SO4+O2,据此你认为下列反应方程式中不正确的是() A.Na2O2+N2O3===NaNO2+NaNO3 B.Na2O2+2NO2===2NaNO2+O2C.Na2O2+N2O4===2NaNO3D.2Na2O2+2Mn2O7===4NaMnO4+O22. 制备氰氨基化钙的化学方程式为CaCO3+2HCN===CaCN2+CO↑+H2↑+CO2↑,在反应中A.氢元素被氧化,碳元素被还原B.HCN是氧化剂,CaCO3是还原剂C.CaCN2是氧化产物,H2是还原产物D.CO为氧化产物,H2为还原产物3.火法炼铜首先要焙烧黄铜矿,其反应为2CuFeS2+O2===Cu2S+2FeS+SO2下列说法正确的是(双选)()A.SO2既是氧化产物又是还原产物B.CuFeS2仅作还原剂,硫元素被氧化D.每转移1.2 mol电子,有0.2 mol硫被氧化【典型例题】例1.MnO-4+H2O2+________===Mn2++O2↑+H2O例2.(1)在NaOH的环境中,Cl2与NaI反应,每l mol NaI完全反应转移6 mol电子,写出反应的化学方程式:_________________________________________________________________。
哈工大集合论习题课-第三章 关系习题课(学生)

习 题 课例1设{,,}A a b c =,给出A 上的一个二元关系,使其同时不满足自反性、反自反性、对称性、反对称和传递性的二元关系,并画出R 的关系图。
解:{(,),(,),(,),(,)}R a a b c c b a c =,关系图如图所示。
例2 设X 是一个集合,X =n ,求:1.X 上的二元关系有多少?()22n 2. X 上的自反的二元关系有多少? 3. X 上的反自反的二元关系有多少?解:因为把所有的反自反的二元关系的每个都加上对角线上的序对,就变成了自反的关系,因此,自反的与反自反的个数一样多。
即22nn-4. X 上的对称的二元关系有多少?2222n n n nn -++=,故共有222n n+个对称的关系。
5. X 上的反对称的二元关系有多少?22(32)n n n -∙6. X 上既是自反的也是反自反的二元关系的个数;(0)个7.X 上既不是自反的也不是反自反的二元关系有多少?2(2(22))n nn --解:解:可用容斥原理来计算设B 表示所有自反关系构成的集合,C 表示所有反自反关系构成的集合,则22nnB C -==。
而B C φ=,故B C B C =+,从而CC B C S B C S B C =-=--2222222222222(22)n n n n n n n n n n n ----=--=-=-于是,既不是自反的,也不是反自反关系共有22(22)n nn --个。
8.自反的且对称的关系有多少?[此结果与“反自反的且对称的关系有多少?”是一样多]即有222n n -(对角线上全去掉)9.自反的或对称的关系有多少?解:设B 表示自反关系的集合,C 表示对称关系的集合,则自反或对称关系的集合为:22222222n n n n nnB C B C B C +--=+-=+-。
10.X 上既是反自反的也是反对称的二元关系的个数为:223n n -;11.X 上既是对称的也是反对称的关系个数;解:X 上既是对称的也是反对称的关系X R I ⊆,故有2n 。
高数A习题课(3)_

′ 故仅当a = 2, b = −1 f− (1) = f+ (1)即f (x)在x =1 时′ 处可导 , 综上,当a = 2, b = −1 f (x)在(− ∞,∞)可导 时 + 。
例5 求下列函数的导数: 求下列函数的导数:
dy ()由方程sin( xy) + ln( y − x) = x确定y是x的函数 求 1 , dx 方程两边对x求导,得 解 1 cos(xy)( y + xy′) + ( y′ −1) =1 ( ) * y−x
解
由 件 f (0) = 0, 条 知
f (x) − f (0) ϕ(a + bx) −ϕ(a − bx) f ′(0) = lim = lim x→0 x→0 x −0 x −0 [ϕ(a + bx) −ϕ(a)] ⋅ b + lim [ϕ(a −bx) −ϕ(a)] ⋅ b = lim x→0 x→0 bx − bx
dy d d sinxlnx x ) ∴ = (sinx) + (e dx dx dx = (sinx) (ln sin x + x cot x) + x
x sinx
sin x (cos x ln x + ). x
例2
求下列函数在指定点处的导数: 求下列函数在指定点处的导数:
1−sin x () = arcsinx ⋅ 1 y , 求 ′(0). f 1+ sin x
3
′ 7.证 明: f (x)在 a, b]上可导 设 [ ,且 + (a) f− (b) < 0,则 f′ 至 ∃一 ξ ∈(a, b),使 ′(ξ ) = 0. 少 个 f 8.设f (x)在 a, b]上连续 [ ,在 a, b)可 ( 导, f (a) = 且 f (b) = 0, 证 至少 一个 ∈(a, b), 使 (ξ ) + f ′(ξ ) = 0. ∃ ξ f
地学模型课程课后习题3

序号 水土流失面积 y 土壤含氮量 x 1 0.8 6.6 2 1.4 5.2 3 2.0 4.8 4 2.7 3.9 5 3.3 3.7 6 4.1 3.2 7 5.6 2.4 8 6.5 2.3 9 7.1 2.1 10 7.7 2.3 11 8.3 1.7 12 9.2 1.5
14.某地区连续 13 年的农业总产值(亿元)资料见下表,试计算其自相关系 数,并拟合一级自回归模型,并预测 2005 年的农业总产值。
第三章 地理学中的经典统计分析方法
课后习题
1.什么是相关系数?单相关系数、 偏相关系数和复相关系数在计算上有什么 联系?三者在检验上有什么区别? 2.什么是秩相关系数?试比较单相关系数和秩相关系数。 3.什么是地理回归分析?相关分析和回归分析的联系和区别是什么? 4.什么是地理过程时间序列?地理时间序列分析在地理学中有什么用途? 5.什么是多元回归模型?多元回归模型和一元回归模型相比有什么特点? 6.什么是系统聚类分析?系统聚类方法有几种?其距离是如何计算的? 7.什么是主成分分析?主成分分析的步骤有哪些? 8.什么是马尔可夫预测方法?使用马尔可夫预测法进行地理预测时所要遵 循的基本要求是什么? 9.是否所有的马尔可夫过程都存在终极状态?为什么? 10.趋势面分析的基本原理是什么?除了多项式形式以外,是否可以用其它 函数形式拟合趋势面?为什么? 11.某地区粮食产量(t)与受灾面积(hm2)的历年数据见下表,试计算二 者之间的相关系数,并对相关系数进行检验(а=0.5) 。
习题 3.15
年度 季度 用电量(单位:10 4KW) 1 435 2 2217 2002 3 3756 4 394 1 488 2 2687 2003 3 4396 4 406 1 667 2 3076 20004 年的 7 项经济统计指标数据见下表。 (1)试用最短距离聚类法对 45 个城市综合实力进行系统聚类分析,并画出 聚类谱系图; (2)试用主成分分析法对 45 个城市 7 项经济指标进行主成分分析,并分析 其综合实力; (3)以第一、二、三主成分为变量,进行聚类分析,结果又怎样呢?
新概念英语第二册课后练习题答案详解(第3课)

新概念英语第二册课后练习题答案详解(第3课)新概念英语第二册课后习题Lesson 31. c根据课文能够判断出作者不喜欢写明信片,但他很想收到别人寄来的明信片,所以应该选c.d. doesn’t like postcards 不喜欢明信片,和课文的含义不符合,所以不选d.2. a根据课文最后两句话能够判断出:作者作出的“一项重大决定”是给他的朋友们写明信片,不过还是一张没有写成,所以应该选a.3. ca. at 表示在小的地点和空间;b. to 表示方向;d. on 表示在……上;只有c. in 表示在大的空间和地方,如城市国家等,所以选c.4. a只有选a. Who taught ,这句问话才与回答相配。
5. d只有选d. in a friendly way(以友好的方式)才能说明前一句He was a friendly waiter,也合乎语法和逻辑。
而其他3个 a. friend(朋友), b. as friends(作为朋友),c. like friends(像朋友一样)在语法上都讲不通。
6. b本句的时态是一般过去时,应该用动词的过去式形式;a. reads 是第3人称蛋单数现在时形式;c. red 词意思不符合;d. reading 是现在分词形式;b. read 过去式和现在式形式相同,发音不同。
所以只有选b.7. ca. the hole 词意思不对;b. the ball 和 d. all of 不合乎习惯用法; 英语中不用the all day, all of day 这样一来的短语。
只有选c. all 才能使句中的词组all day 同前一句中的the whole day 意思相同。
8. c句中的waiter 是“饭店服务员”的意思,他通常在饭店工作,而不在a. public garden(公园),b. shop(商店),d. private house(私宅) 工作,所以选c. restaurant.9. b只有b. borrowed 才与前一句中的lent相对应,而其他3个选择都不是。
球习题课(3).许兴华

E
Firstpage首页 upward return next last 铃
件 件
E
件
o1
C
A
B
o
o2
N S E 许E V 课
兴T华
Firstpage首页 upward return next last 铃
件
[应用举例]
key
例 3 . 正 四 面 体 的 棱 为 2, 个 顶 点 长 四 在同一球面上, 此球的表面积为( 则 A) A.3π B.4π C.3 3 D.6π π
2
3
A
o
3
A
C
2
(2R) ( 3) ( 3) ( 3) V 4 R3 9 . 3 2
2 2
3
B
2
C
B
N S E 许E V 课
兴T华
Firstpage首页 upward return next last 铃
件
o1
C
B
o
o2
N S E 许E V 课
兴T华
Firstpage首页 upward return next last 铃
A●
●
B●
●
O1
·
●
D
N S E 许E V 课
兴T华
Firstpage首页 upward return next last 铃
件
解:设四面体为ABCD, 1为其外接球心. O 球半径为R, O为A在平面BCD上 的射影, M为CD的中点.连接1, BO
return
2, AO AB BO 3 2 2 2
1
(key)
return
物理化学傅献彩习题课-第二、三、四章
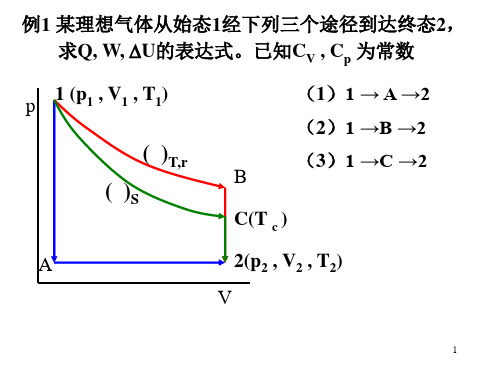
8.卡诺循环过程包括——、——、———、———。 9.理想气体在等温下向真空膨胀,则ΔU=———,ΔH=—— ——,ΔS————。 10.在隔离系统中发生某剧烈化学反应,使系统的温度及压力 皆明显升高,则系统的:ΔS—;ΔU—;ΔH——;ΔA—; Δ G——。(填>0,=0,<0或无法确定。) 11.使一个过程的熵变等于零,应满足的条件是—————— ——————————。 12.给自行车打气时,把气筒内的空气作为系统,打气筒、橡 皮管和轮胎均不导热,则该过程中Q—0,W—0。 13.理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨 胀到达相同的终态压力,则终态的温度T可逆——T不可逆;V可 逆—V不可逆;ΔH可逆—ΔH不可逆。 14.在恒熵、恒容、不做非膨胀功的封闭系统中,当热力学函 数——到达最——值的状态为平衡状态。 15
13
填空题
1.Qv=ΔU应用条件是__________, _________, __________。
2.纯物质完美晶体___________________时熵值为零。 3.热力学第三定律的普朗克说法的数学表达式是——。
4.熵增原理表述为
_______________________________________________________ _________________________________。 5.物理量Q、T、P、V、W、U、H、S、A、G ,其中属于状态函数 的是————;与过程有关的是————;状态函数中属于容 量性质的是—————;属于强度性质的是————。 6.节流膨胀过程是————,膨胀后温度将———。 7.热力学第二定律的经典表述之一是——-————————; 其数学表达公式是——————————。
椐,因 W = 0 ∴ −W ≤ − ∆vapA ∴ ∆vapA < 0,过程不可逆 ∵ 过程不恒压,不能用 ∆vapG 来判别
高数A(2)习题课(3)向量代数

将 cos 2 2 cos 1代入并整理得
2
cos ( 2 cos 1) 0
2 2
解得
2
或
( . 不合) 4 4
3
故向量的方向余弦为
0 , 0 1或
1 2
,
1 2
, 0
所求向量为(
0 , 0, 2)或(
2, 2,) 0
三、
典型例题讲析
2 3
即ab=ca.
同理可证ab=bc.
充分性:由条件ab=bc=ca知,三向量a,b,c共面, 于是有不全为0的1,2,3,使得1a+2b+3c=0 在上式两边与a,b作叉积得 2ab+3ac=0, 1ab+3cb =0 ∴ 1= 2= 3且非零。于是得a+b+c=0。
1 42
cos
1
(为什么不是
42
1 42
?)
如图,过B作PA的平行向量BD交PC于D,显然 |PB|= |BD|=3.于是PD=PB+BD=PB+3/7PA
而 PD 2 PB cos
6 42
C D
B
故 PC
PC
PD
3 42 6/ 42
P
PD
A
PD
解:显然1与2不平行,过其交线的一切平面方程 (除2外)均可表示为 2x -y +1 +( x +2y +z+1)=0 (1) 显然3是上述方程中取1的结果,即1、2、 3 属同一平面束。
将P(1,0,1)的坐标代入(1)式解得=-1
习题课(3)

习题课(3)1. 仪表系统的数学模型是进行特性分析的基础,可分为时域模型、(频域模型和离散模型。
2. 仪表系统的时域模型采用微分方)来描述仪表的输入输出关系;离散模型采用差分方程来描述仪表的输入输出关系;而频域模型采用传递函数/频响函数来描述系统的传输特性。
3. 变送器是自动控制系统中的检测还价,它将被控变量变换成统一标准的模拟信号或数字信号,输送至显示控制仪表或计算机系统。
变送器的理想输入输出关系式为:m in m in)m ax (m inm ax m in y y y x x x x y +---= 4. 变送器使用前必须进行零点和量程的检验或调整。
量程调整的目的是使变送器的输出信号上限y max 与测量范围的上限x max 相对应。
零点调整的目的是使使变送器的输出信号下限y min 与测量下限的x min 相对应.。
测量下限不是0时,称为零点迁移,x min >0,为零点正迁移,x min <0为零点付迁移。
5. 变送器二线制信号传输方式:是用二根导线同时传输变送器所需要的电源和输出电流信号,电源、负载电阻和变送器串联连接。
种类变送器称为二线制变送器。
6. 现场总线通信方式由微处理器(CPU )、通信控制单元和媒体访问单元组成的电路实现,其原理图如下:7.如图所示力矩平衡式变送器原理,写出力矩平衡方程式:Fi·di+F0·d0≈Ff·df。
8.如图所示平衡式电桥变送器原理,写出电动势平衡方程式:其主要应用在以(电压或电流)为输出的变送器中。
9.如图所示不平衡式电桥变送器原理,写出电动势平衡方程式:。
其主要应用在以电阻变化为输出的变送器中。
10.如图所示电桥式自动平衡显示仪表测量电路。
(1)简述其工作原理。
(2)令电桥左右两臂的阻值之比为:32R Rr+'=γ,说明仪表的电压测量灵敏度与其值大小的关系(定性说明),(3)简述在实际应用中,对不同量程仪表进行不同电桥左右两臂的阻值之比的设计。
第三节速度习题课

题型1:关于过桥(山洞、隧道等)的问题
例1: 一列长 360 m的火车,匀速
通过一个长 1800 m的隧道,如果 该火车的时速是 54km/h ,请问: (2)火车全部在山洞内运行的时间 是多少?
练习1:
一列长150m的火车用5min时间匀速通 过一座长度为7350m的大桥,求火车通 过大桥时速度为多少千米/时?
s v
o
t
o
t
匀速直线运动
匀变速直线运动
[练习3] 课外活动时,小明和小华均在操作 上沿直线进行跑步训练.在某次训练中,他 们通过的路程和时间的关生系如右图所示, 则下列说法中正确的是( ) A.两人都做匀速直线运动 B.两人都不 是做匀速直线运动 C.前2s内,小明跑得较快 D.全程中,两 人跑步的平均速度相同
第三节
运动的描述
习题课
s 在匀速直线运动中对 v 的讨论 t
①.v与s不成正比、v与t不成反比. 即v与s、t无关 ②. ∵v不变 ∴s与t成正比
③.v只与s/t比值大小有关
在《龟兔赛跑》的故事中,乌龟和兔子同时从起点 出发,当兔子远远超过乌龟时,便骄傲地睡起了大 觉,当它醒来后,发现乌龟已悄悄地爬到了终点。 在龟兔赛跑的全程中,下列说法正确的是(C) A.乌龟的速度始终大于兔子的速度 B.兔子的速度始终大于乌龟的速度 C.乌龟的平均速度大于兔子的平均速度 D.兔子的平均速度大于乌龟的平均速度
练习: 某物体在前一半路程的平均速度是4m/s,后一 半路程的平均速度是 5m/s. 则全程的平均速度是 多大?
一辆汽车在与铁路平行的公路上行驶,追 赶一列长320m的列车。已知汽车的速度 是54km/h,火车的速度是36 km/h,问汽 车从列车尾部到全部超越列车需多少时间?
人教部编版七年级历史上册第3课 远古的传说练习题

第3课远古的传说练习题一、选择题1.“中华开国五千年,神州轩辕自古传。
创造指南车,平定蚩尤乱……”这是孙中山对“人文初祖”黄帝的评价。
与“平定蚩尤乱”有关的战役是()A. 牧野之战B. 涿鹿之战C. 城濮之战D. 巨鹿之战2.2018年4月5日,清明公祭轩辕黄帝典礼在陕西省黄陵县黄帝陵举行。
约一万名海内外中华儿女怀着崇敬之情共同祭拜,下列有关他的叙述正确的是()①建造宫室、车船,制作兵器、衣裳②让部下发明文字、算术③他是我国第一个封建帝王,被称为“人文始祖”④妻子嫘祖发明养蚕抽丝技术A. ①②④B. ①②③C. ②③④D. ①②③④3.“务农桑,筑宫室,初定家邦;创文字,造舟车,走出洪荒;……巍巍先祖功德,绵绵万世流芳。
”孙中山先生的这篇祭文写的是传说中的()A. 炎帝B. 黄帝C. 蚩尤D. 禹4.“神农因天之时,分地之利,制耒耜,教民农耕。
”材料中的“神农”是()A. 炎帝B. 黄帝C. 尧D. 舜5.研究中国古代史多有“传说时代”的概念,传说主要是神话和祖先传说,这些内容被后人用文字记录下来,描绘的就是远古传说时代。
下列关于远古传说有误的是()A. 尧舜“禅让”B. 炎帝尝百草发明医药C. 黄帝在“阪泉之野”大战中打败蚩尤D. 大禹治水6.炎黄子孙不忘本,两岸和平一家亲。
山岳巍巍,河海殇殇,缅怀祖德,永矢弗忘!海外华人常称自己为“炎黄子孙”是因为()A. 他们都是黄皮肤B. 是从中国大陆移民的人C. 中华民族的主体是由黄炎部落联盟发展而来的D. 全部是黄帝和炎帝的后代7.相传,黄帝建造宫室,制作衣裳,还教人们挖井,发明舟车,为后世的衣食住行奠定了基础.这些神话传说,反映了()A. 后人对华夏始祖黄帝的尊敬B. 黄帝有许多发明流传于世C. 黄帝是我国古代伟大的发明家D. 黄帝堪称我国古代帝王的杰出代表8.相传炎帝教民耕种,制作工具,种植五谷,制作陶器等;传说黄帝建造宫室,制作衣裳,发明弓箭和指南车,命下属创造文字、制作音律、发明算盘。
第三章 初等矩阵及习题课 3

r2 5r3
0 3 2 1 0 4 6 0 2 0 0 0 1 1 3
2 r2 2) 1 0 0 3 ( 0 1 0 2 3 , r3 1) ( 0 0 1 1 3 2 3 X 2 3 . 1 3
等于把 A的第 j 行乘 k 加到第 i 行上 (ri krj ).
2013-7-17 14
6. 类似地,以 En (ij (k )) 右乘矩阵 A,其结果相当于 把 A 的第i列乘 k 加到第 j 列上 (c j kci ).
1 0 0 0 01 k 0 第 i 行 Amn En (i, j ) 1 , i , j , n 1n 0 01 0 第 j 行 0 0 01 nn 1 , i , j k i , n
2013-7-17 2
矩阵的初等列变换也有三种:
1. 对调 矩阵 A中第 i , j 两列,即 (ci c j );
2. 将矩阵 A中第 i列乘非零常数
k,即 ( kci );
3. 将矩阵 A中第 j列乘常数 k加至第 i列, 即 (ci kc j ).
2013-7-17 3
二、初等矩阵的概念
8
初等矩阵的性质
初等矩阵均可逆且其逆阵仍为初等矩阵
1. 变换 ri r j 的逆变换是其本身, 则E ( i , j )1 E ( i , j ) ; 1 2. 变换 ri k 的逆变换为 ri , k 1 1 则 E ( i ( k )) E ( i ( )); k 3. 变换 ri krj 的逆变换为 ri ( k )r j, 1 则 E ( ij( k )) E ( ij( k )) .
