第一章空间几何体测试卷

合集下载

第一章空间几何体测试题及答案

空间几何体检测题（时间 120分钟分数150分）一、选择题（本大题共12小题，每小题5分，共60分）1、一个长方体的长、宽、高分别为3，8，9，若在上面钻一个圆柱形孔后其表面积没有变化，则孔的半径为（）A. 3 B .8 C. 9 D. 3或8或92、要使圆柱的体积扩大8倍，有下面几种方法：①底面半径扩大4倍，高缩小21倍；②底面半径扩大2倍，高缩为原来的98；③底面半径扩大4倍，高缩小为原来的2倍；④底面半径扩大2倍，高扩大2倍；⑤底面半径扩大4倍，高扩大2倍，其中满足要求的方法种数是（） A. 1 B. 2 C. 3 D. 43、在用斜二测画法画水平放置的平面图形直观图时，与轴不平行的线段的大小（） A. 变大 B. 变小 C. 一定改变 D. 可能不变4、向高为H 的水瓶中匀速注水，注满为止，如果注水量V 与水深h 的函数关系如下面左图所示，那么水瓶的形状是（）5、设正方体的全面积为24，那么其内切球的体积是（） A. π6 B.π34 C. π38D. π3326、圆锥的表面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为（） A. 1200B. 1500C. 1800D. 24007、四棱柱有两个侧面互相平行，并且这两个侧面的面积之和为S ，它们的距离为h ，那么这个四棱柱的体积是（） A. Sh B.21Sh C. 31Sh D. 2Sh 8、长方体的一个顶点上三条棱的边长分别为3、4、5，且它的八个顶点都在同一个球面上，这个球的表面积是（）A. 220πB. 225πC. π50D. π200 9、如图所示的直观图的平面图形ABCD 是（） A. 任意梯形 B. 直角梯形 C. 任意四边形 D. 平行四边形10、体积相等的球和正方体，它们的表面积的大小关系是（）A. 正方体球S S >B. 正方体球S S =C. 正方体球S S <D. 不能确定11、正三棱锥的底面边长为a ，高为a 66，则此棱锥的侧面积等于（） A.432a B. 232a C. 4332a D.233 2a 12、一个圆台的上、下底面面积分别是12cm 和492cm ，一个平行底面的截面面积为252cm ，m 则这个截面与上、下底面的距离之比是( )A. 2: 1B. 3: 1C. 2: 1D. 3: 1二、填空题（本题共4小题，每小题4分，共16分）11、轴截面是等边三角形的圆锥，它的侧面展开图的圆心角等于12、一个圆柱的底面直径和高都等于一个球的直径，则这个圆柱的体积与球的体积之比为13、把一根长4m ，直径1m 的圆木锯成底面为正方形的方木，则方木的体积为 14、三棱柱C B A ABC '''-的底面是边长为1cm 的正三角形，侧面是长方形，侧棱长为4cm ，一个小虫从A 点出发沿表面一圈到达A '点，则小虫所行的最短路程为 cm 三、解答题（本题共6小题，第17-21题每题12分，第22题14分，共74分）17、一个容器的盖子用一个正四棱台和一个球焊接而成，球的半径为R ，正四棱台的上、下底面边长分别为R R 35.2和，斜高为R 6.0（1）求这个容器盖子的表面积（用R 表示，焊接处对面积的影响忽略不记）；（2）若cm R 2=，为盖子涂色时所用的涂料每kg 4.0可以涂21m ，计算100个这样的盖子约需涂料多少kg （精确到kg 1.0）18、直平行六面体的底面是菱形，两个对角面的面积分别为1Q ,2Q ,求直平行六面体的侧面积19、画出下面实物的三视图20、一个圆锥底面半径为R ，高为R 3 ，求此圆锥的内接正四棱柱表面积的最大值21、如果棱台的两底面积分别是S S '、，中截面（过棱台高的中点且平行于底面的截面）的面积是0S 求证： S S S '+=0222、已知正三棱锥ABC S -,一个正三棱柱的一个底面的三个顶点在棱锥的三条侧棱上，另一底面在正三棱锥的底面上，若正三棱锥的高为15cm ，底面边长为12cm ，内接正三棱柱的侧面积为120cm2，（1）求正三棱柱的高；（2）求棱柱上底面截的小棱锥与原棱锥侧面积的比参考答案：二、填空题13、1800 14、3：2 15、 2 3m 16、 5三、解答题17、（1）2)485.21(R S π+= (2)约需kg 6.0 18、22212Q Q S +=19、略20、当内接正四棱柱的底面边长是163-R 时表面积有最大值为1662-R21、略 22、（1）正三棱柱的高为10cm 或5cm （2）1:9或4:9。

(完整版)高一数学必修2第一章空间几何体测试题(答案)

则四边形 EFGH 是
；
②若 AC BD ，则四边形 EFGH 是
．
三、解答题：解答应写出文字说明、证明过程或演算步骤 (共 76 分 )．
15．（ 12 分）将下列几何体按结构分类填空
①集装箱；②油罐；③排球；④羽毛球；⑤橄榄球；⑥氢原子；⑦魔方；
⑧金字塔；⑨三棱镜；⑩滤纸卷成的漏斗；○ 11 量筒；○12 量杯；○13 十字架．
（ 1）具有棱柱结构特征的有
；（ 2）具有棱锥结构特征的有
；
（ 3）具有圆柱结构特征的有
；（ 4）具有圆锥结构特征的有
；
（ 5）具有棱台结构特征的有
；（ 6）具有圆台结构特征的有
；
（ 7）具有球结构特征的有
；（ 8）是简单集合体的有
；
（ 9）其它的有
．
16．（ 12 分）已知： a ,b ,a b A, P b, PQ // a.求证： PQ .．
C．③④
3．棱台上下底面面积分别为 16 和 81,有一平行于底面的截面面积为
（） D ． ①②③④
36,则截面戴的两棱台高
的比为
（）
A ．1∶ 1
B． 1∶ 1
C． 2∶ 3
D ．3∶4
4．若一个平行六面体的四个侧面都是正方形 ,则这个平行六面体是
（）
A ．正方体
B．正四棱锥
C．长方体
D ．直平行六面体
2la
Q1 2 Q2 2
S侧 4al 2 Q12 Q2 2
19．解：设 A1B1C1D1 是棱台 ABCD －A2B2C2D 2 的中截面，延长各侧棱交于
P 点.
a
∵ BC=a ，B2C2=b ∴ B1C1=

高一数学第一章空间几何体综合试题及答案

人教A 必修2第一章空间几何体综合试题一、选择题（每道题5分）1．有一个几何体的三视图如下图所示；这个几何体可能是一个( )．主视图左视图俯视图(第1题)A ．棱台B ．棱锥C ．棱柱D ．正八面体2．如果一个水平放置的平面图形的斜二测直观图是一个底角为45°；腰和上底均为1的等腰梯形；那么原平面图形的面积是( )．A ．2＋2B ．221＋C ．22＋2D ．2＋13．棱长都是1的三棱锥的表面积为( )．A ．3B ．23C ．33D ．434．长方体的一个顶点上三条棱长分别是3；4；5；且它的8个顶点都在同一球面上；则这个球的表面积是( )．A ．25πB ．50πC ．125πD ．都不对5．正方体的棱长和外接球的半径之比为( )．A ．3∶1B ．3∶2C ．2∶3D ．3∶36．在△ABC 中；AB ＝2；BC ＝1.5；∠ABC ＝120°；若使△ABC 绕直线BC 旋转一周；则所形成的几何体的体积是( )．A ．29πB ．27πC ．25πD ．23π 7．若底面是菱形的棱柱其侧棱垂直于底面；且侧棱长为5；它的对角线的长分别是9和15；则这个棱柱的侧面积是( )．A ．130B ．140C ．150D ．1608．半径为R 的半圆卷成一个圆锥；则它的体积为（）A ．324RB ．38RC ．324RD ．38R9．下列关于用斜二测画法画直观图的说法中；错误．．的是( )．A．用斜二测画法画出的直观图是在平行投影下画出的空间图形B．几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C．水平放置的矩形的直观图是平行四边形D．水平放置的圆的直观图是椭圆10．如图是一个物体的三视图；则此物体的直观图是( )．(第10题)二、填空题（每道题5分）11．一个棱柱至少有______个面；面数最少的一个棱锥有________个顶点；顶点最少的一个棱台有________条侧棱．12．若三个球的表面积之比是1∶2∶3；则它们的体积之比是_____________．13．正方体ABCD－A1B1C1D1 中；O是上底面ABCD的中心；若正方体的棱长为a；则三棱锥O－AB1D1的体积为_____________．14．如图；E；F分别为正方体的面ADD1A1、面BCC1B1的中心；则四边形BFD1E在该正方体的面上的射影可能是___________(第14题)15．已知一个长方体共一顶点的三个面的面积分别是2、3、6；则这个长方体的对角线长是___________；它的体积为___________．16．一个直径为32厘米的圆柱形水桶中放入一个铁球；球全部没入水中后；水面升高9厘米则此球的半径为_________厘米．三、解答题（17题；18；19各15分；20题25分）17．有一个正四棱台形状的油槽；可以装油190 L；假如它的两底面边长分别等于60 cm 和40 cm；求它的深度．18．如图；在四边形ABCD中；∠DAB＝90°；∠ADC＝135°；AB＝5；CD＝22；AD＝2；求四边形ABCD绕AD旋转一周所成几何体的表面积及体积．(第18题)19．已知圆台的上下底面半径分别是2,5；且侧面面积等于两底面面积之和；求该圆台的母线长.20．养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用)；已建的仓库的底面直径为12 m；高4 m；养路处拟建一个更大的圆锥形仓库；以存放更多食盐；现有两种方案：一是新建的仓库的底面直径比原来大4 m(高不变)；二是高度增加4 m(底面直径不变)．(1)分别计算按这两种方案所建的仓库的体积；(2)分别计算按这两种方案所建的仓库的表面积；(3)哪个方案更经济些？第一章空间几何体参考答案一、选择题1．A解析：从俯视图来看；上、下底面都是正方形；但是大小不一样；可以判断可能是棱台．2．A解析：原图形为一直角梯形；其面积S ＝21(1＋2＋1)×2＝2＋2． 3．A解析：因为四个面是全等的正三角形；则S 表面＝4×43＝3． 4．B解析：长方体的对角线是球的直径； l ＝2225＋4＋3＝52；2R ＝52；R ＝225；S ＝4πR 2＝50π． 5．C 解析：正方体的对角线是外接球的直径．6．D解析：V ＝V 大－V 小＝31πr 2(1＋1.5－1)＝23π． 7．D解析：设底面边长是a ；底面的两条对角线分别为l 1；l 2；而21l ＝152－52；22l ＝92－52；而21l ＋22l ＝4a 2；即152－52＋92－52＝4a 2；a ＝8；S 侧面＝4×8×5＝160．8.A 2312,,,22324R r R r h V r h R πππ===== 9．B 解析：斜二测画法的规则中；已知图形中平行于 x 轴的线段；在直观图中保持原长度不变；平行于 y 轴的线段；长度为原来的一半．平行于 z 轴的线段的平行性和长度都不变．10．D解析：从三视图看底面为圆；且为组合体；所以选D.二、填空题11．参考答案：5；4；3．解析：符合条件的几何体分别是：三棱柱；三棱锥；三棱台．12．参考答案：1∶22∶33．r 1∶r 2∶r 3＝1∶2∶3；31r ∶32r ∶33r ＝13∶(2)3∶(3)3＝1∶22∶33．13．参考答案：361a ．解析：画出正方体；平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点；三棱锥O －AB 1D 1的高h ＝33a ；V ＝31Sh ＝31×43×2a 2×33a ＝61a 3．另法：三棱锥O －AB 1D 1也可以看成三棱锥A －OB 1D 1；它的高为AO ；等腰三角形OB 1D 1为底面．14．参考答案：平行四边形或线段．15．参考答案：6；6．解析：设ab ＝2；bc ＝3；ac ＝6；则V = abc ＝6；c ＝3；a ＝2；b ＝1； l ＝1＋2＋3＝6．16．参考答案：12．解析：V ＝Sh ＝πr 2h ＝34πR 3；R ＝32764×＝12．三、解答题17．参考答案：V ＝31(S ＋S S ′＋S )h ；h ＝S S S S V ′＋′＋3＝6001＋4002＋60030001903×＝75．18．参考答案：S 表面＝S 下底面＋S 台侧面＋S 锥侧面＝π×52＋π×(2＋5)×5＋π×2×22＝(60＋42)π． V ＝V 台－V 锥＝31π(21r ＋r 1r 2＋22r )h －31πr 2h 1 ＝3148π． 19．解2229(25)(25),7l l ππ+=+=20．解：(1) 参考答案：如果按方案一；仓库的底面直径变成16 m ；则仓库的体积V 1＝31Sh ＝31×π×(216)2×4＝3256π(m 3)．如果按方案二；仓库的高变成8 m ；则仓库的体积V 2＝31Sh ＝31×π×(212)2×8＝3288π(m 3)． (2) 参考答案：如果按方案一；仓库的底面直径变成16 m ；半径为8 m ．棱锥的母线长为l ＝224＋8＝45；仓库的表面积S 1＝π×8×45＝325π(m 2)．如果按方案二；仓库的高变成8 m ．棱锥的母线长为l ＝226＋8＝10；仓库的表面积S 2＝π×6×10＝60π(m 2)．(3) 参考答案：∵V 2＞V 1；S 2＜S 1；∴方案二比方案一更加经济些．。

高一数学必修2第一章空间几何体测试题(答案)

第一章章节测试题YC、选择题：1不共面的四点可以确定平面的个数为 A . 2个 B . 3个 2•利用斜二测画法得到的 ① 三角形的直观图-② 正方形的直观图一定是菱形； ③ 等腰梯形的直观图可以是平行四边形;④ 菱形的直观图一定是菱形 • 以上结论正确的是 A .①② B .① 3.棱台上下底面面积分别为 16和81,有的比为 A . 1 : 1 B . 1 : 1 C . 2 : 3B .a 丄丫且B 丄丫A . Ucm 229.将一圆形纸片沿半径剪开为两个扇形，其圆心角之比为 3 : 4.再将它们卷成两个圆锥侧面，则两圆锥体积之比为 ()A . 3 : 4B . 9 : 16C . 27 : 64D .都不对10 .将边长为a 的正方形ABCD 沿对角线AC 折起，使BD = a ，则三棱锥D — ABC 的体积为( )二、填空题： 11.螺母是由和两个简单几何体构成的.4.若一个平行六面体的四个侧面都是正方形 A .正方体 B .正四棱锥，则这个平行六面体是 C .长方体 ( D .直平行六面体5.已知直线a 、 b 与平面a 、B 、丫，下列条件中能推出a//B 的是( )C .4个 D .无法确定( )C . ③④D .①②③④平行于底面的截面面积为 36,则截面戴的两棱台高C . a a, b B, a /bD . a a, b a, a //B, b//B6. 如图所示，用符号语言可表达为( A . aQ ( 3 = m , n a, m d n =A B . adf 5 = m , n€ a, m d n = AC . adf 5 = m , n a, A m , AD . adf 3 = m , n € a, A € m , A €7. 下列四个说法 ① a//a, b a 则 a 〃 b ③a a,贝V a//a 其中错误的说法的个数是 ) AC* n Vi n-41b② a da= P , b a ，则 a 与b \④ a 〃 a, b // a,贝y a 〃 bA . 1个B . 2个C . 3个D . 4个&正六棱台的两底边长分别为 1cm,2cm,高是1cm,它的侧面积为a 3 3 a 12 、'‘3 3 C . a 12 丘 3D . a12则正三棱锥的体积是_______________________ .14.空间四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA 的中点.①若AC=BD ,则四边形EFGH是___________________________________________ ；②若AC BD，则四边形EFGH是 ___________________________________________三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分).15.( 12分)将下列几何体按结构分类填空①集装箱；②油罐；③排球；④羽毛球；⑤橄榄球；⑥氢原子；⑦魔方；⑧金字塔；⑨三棱镜；⑩滤纸卷成的漏斗；O 11量筒；量杯；03十字架.(1)具有棱柱结构特征的有 ____________ ； (2)具有棱锥结构特征的有____________(3)具有圆柱结构特征的有 ____________ ； (4)具有圆锥结构特征的有____________(5)具有棱台结构特征的有 ____________ ； (6)具有圆台结构特征的有____________(7)具有球结构特征的有 ______________ ； ( 8)是简单集合体的有_______________ ；(9)其它的有 ________________ .17. (12分)正四棱台的侧棱长为3cm，两底面边长分别为1cm和5cm，求体积.18. (12分)直平行六面体的底面是菱形，两个对角面面积分别为Q1, Q2，求直平行六面体的侧面积.B1 又 a 与重合 PQ17•解：正四棱台 ABCD A 1B 1C 1D 1O i , 0是两底面的中心 AC i 2 , AC 5 2 A i O i 」AO 2 5、2 2参考答案(五)一、 CBCDA ACADD .二、 ii .正六棱柱，圆柱；i2. 48cm 3; i3. —(2 . 3) . i . 3a 2 ； i4.菱形，矩形i2三、 i5.⑴①⑦⑨；⑵⑧；⑶(11);⑷⑩；5)(14)；。

2019-2020年高中数学必修二第一章《空间几何体》整章测试卷及答案解析

第 1 页共 10 页 2019-2020年高中数学必修二
第一章《空间几何体》整章测试卷
第Ⅰ卷(选择题，共60分)
一、选择题(本大题共12小题，每题5分，共60分)
1．下列说法不正确的是( )
A ．圆柱的侧面展开图是一个矩形
B ．圆锥的过轴的截面是一个等腰三角形
C ．直角三角形绕它的一条边旋转一周形成的曲面围成的几何体是圆锥
D ．圆台平行于底面的截面是圆面
答案 C
2．如图所示的直观图的原平面图形是(
)
A ．任意三角形
B ．直角梯形
C ．任意四边形
D ．平行四边形
答案 B
3．三视图如图所示的几何体是(
)
A ．三棱锥
B ．四棱锥
C ．四棱台
D ．三棱台
答案 B
4．下图中的图形经过折叠不能围成棱柱的是(
)
答案 D。

第一章--空间几何体-单元测试题-学生用卷

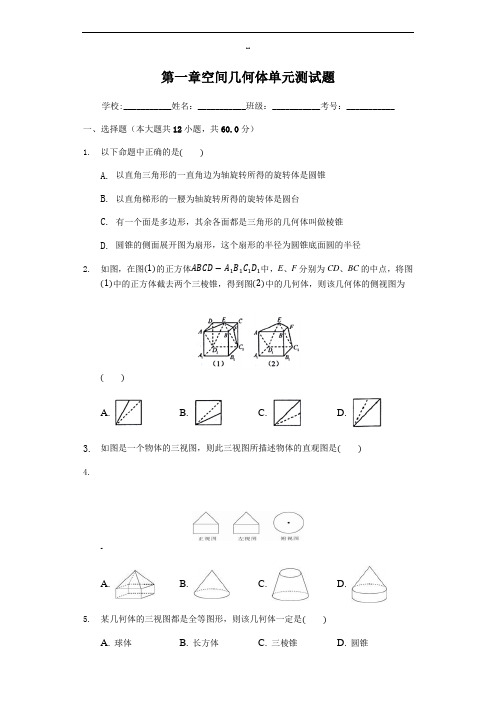
…第一章空间几何体单元测试题学校:___________姓名：___________班级：___________考号：___________一、选择题（本大题共12小题，共60.0分）1.以下命题中正确的是( )A. 以直角三角形的一直角边为轴旋转所得的旋转体是圆锥B. 以直角梯形的一腰为轴旋转所得的旋转体是圆台C. 有一个面是多边形，其余各面都是三角形的几何体叫做棱锥D. 圆锥的侧面展开图为扇形，这个扇形的半径为圆锥底面圆的半径2.如图，在图(1)的正方体ABCD−A1B1C1D1中，E、F分别为CD、BC的中点，将图(1)中的正方体截去两个三棱锥，得到图(2)中的几何体，则该几何体的侧视图为( )A. B. C. D.3.如图是一个物体的三视图，则此三视图所描述物体的直观图是( )4.~A. B. C. D.5.某几何体的三视图都是全等图形，则该几何体一定是( )A. 球体B. 长方体C. 三棱锥D. 圆锥6.如图所示，是一个正方体的表面展开图，则图中“2”所对的面是( )7.A. 1B. 7C. 快D. 乐8.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原来的图形是( )A. B. C.D.9.$10.已知某三棱锥的三视图如图所示，图中的3个直角三角形的直角边长度已经标出，则在该三棱锥中，最短的棱和最长的棱所在直线的成角余弦值为( )A. 13B. √55C. 12D. 2311.如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )12.A. 20πB. 24πC. 28πD. 32π13.如图，是水平放置的△OAB的直观图，则△OAB的周长为( )14.A.10+2√13B. 3√2C. 10+4√13D. 1215.{16.一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个等腰直角三角形，则该几何体外接球的体积为( )A. √32π B. √32C. 3πD. 317.如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3，则它的表面积是( )A. 17πB. 18πC. 20πD. 28π18.在封闭的直三棱柱ABC−A1B1C1内有一个体积为V的球，若AB⊥BC，AB=6，BC=8，AA1=3，则V的最大值是( )A. 4πB. 9π2C. 6π D. 32π3:二、填空题（本大题共4小题，共20.0分）19.一个圆锥的母线长为20cm，母线与轴的夹角为30∘，则圆锥的高为______cm．20.已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为______ ．15．若某几何体的三视图(单位：cm)如图所示，则此几何体的体积是__________cm3.16、如图，已知正方体ABCD−A1B1C1D1的棱长为2，E，F分别是A1B1，CC1的中点，过D1，E，F作平面D1EGF交BB1于G.给出以下五个结论：①EG//D1F；②BG=3GB1；③平面D1EGF⊥平面CDD1C1；④直线D1E与FG的交点在直线B1C1上；.其中正确的结论有______ (填上所有正确结论⑤几何体ABGEA1−DCFD1的体积为416的序号)三、解答题（本大题共5小题，共60.0分）17、(10分)画出下列空间几何体的三视图．！18、(12分)一空间几何体的三视图如图所示．(1)求该几何体的体积；(2)求表面积．19、(12分)现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P−A1B1C1D1，下部的形状是正四棱柱ABCD−A1B1C1D1(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍．(1)若AB=6m，PO1=2m，则仓库的容积是多少？(2)若正四棱锥的侧棱长为6m，则当PO1为多少时，仓库的容积最大？/20、(12分)一块边长为10cm的正方形铁块按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器．(1)试把容器的容积V表示为x的函数(2)若x=6，求图2的主视图的面积21、(12分)如图，在底半径为5，高为10的圆锥中内接一个圆柱，(1)写出圆柱的高h与圆柱的底面半径r的关系式(2)当内接圆柱的底面半径为何值时，圆柱的表面积有最大值，最大值是多少？22.(12分)降水量是指水平地面上单位面积降雨水的深度．今用上口直径为38 cm，底面直径为24 cm，深为35 cm的圆台形水桶来测量水量．若在一次降雨过程中，用此桶盛得的雨水正好是桶深的，则其降水量是多少？(精确到1 mm)。

空间几何体测试题及答案

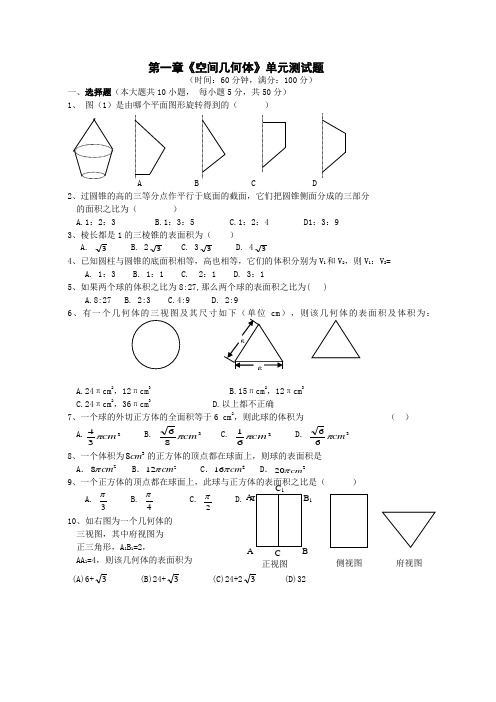
第一章《空间几何体》单元测试题（时间：60分钟，满分：100分）一、选择题（本大题共10小题，每小题5分，共50分）1、图（1）是由哪个平面图形旋转得到的（）A B C D2、过圆锥的高的三等分点作平行于底面的截面，它们把圆锥侧面分成的三部分的面积之比为（）A.1：2：3B.1：3：5C.1：2：4 D1：3：93、棱长都是1的三棱锥的表面积为（）A. 3B. 23C. 33D. 434、已知圆柱与圆锥的底面积相等，高也相等，它们的体积分别为V1和V2，则V1：V2=A. 1：3B. 1：1C. 2：1D. 3：15、如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:96A.24πcm2，12πcm3B.15πcm2，12πcm3C.24πcm2，36πcm3D.以上都不正确7、一个球的外切正方体的全面积等于6 cm2，则此球的体积为（）A.334cmπ B. 386cmπ C. 361cmπ D. 366cmπ8、一个体积为38cm的正方体的顶点都在球面上，则球的表面积是A．28cmπ B．212cmπ C．216cmπ D．220cmπ9、一个正方体的顶点都在球面上，此球与正方体的表面积之比是（）A.3π B.4π C.2π D. π10、如右图为一个几何体的三视图，其中府视图为正三角形，A1B1=2，AA1=4，则该几何体的表面积为(A)6+3 (B)24+3 (C)24+23 (D)32A B1C正视图侧视图府视图二、填空题（本大题共4小题，每小题5分，共20分）11. 长方体的共顶点的三个侧面面积分别为3，5，15，则它的体积为12.一个半球的全面积为Q，一个圆柱与此半球等底等体积，则这个圆柱的全面积是______.13、球的半径扩大为原来的2倍,它的体积扩大为原来的 _________ 倍.14、一个圆柱和一个圆锥的母线相等，底面半径也相等，则侧面积之比是_________.三、解答题（本大题共3小题，每小题10分，共30分）15.将圆心角为1200，面积为3 的扇形， 16. （如图）在底半径为2母线长为4的作为圆锥的侧面，求圆锥的表面积和体积. 圆锥中内接一个高为3的圆柱，求圆柱的表面积*16、如图，在四边形ABCD中，，，，，AD=2，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.参考答案：1.A ；2.B ；3.A ；4.D ；5.C ；6.A ；7.C ；8.B ；9.C ；10.C.11.15；12.910Q；13.8；14.2：1 15.解:l=3,R=1；S=4π；V=322π.16.R=1,h=3,S=2π+2π3.17.S=60π+4π2;V=52π-38π=3148π.。

数学必修2第一章空间几何体测试题

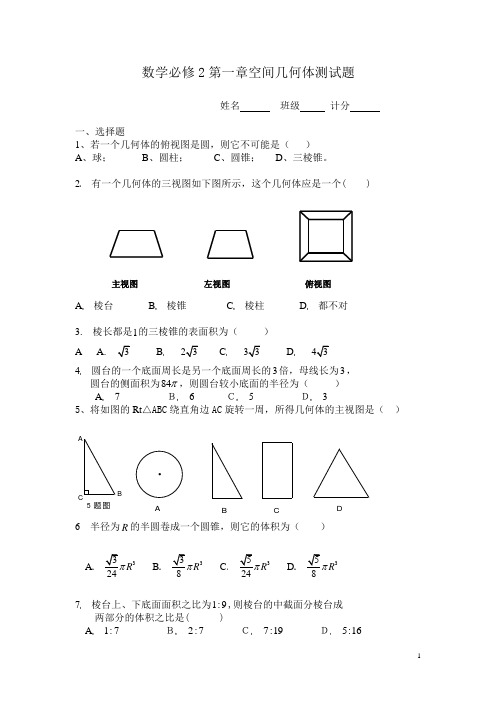
数学必修2第一章空间几何体测试题姓名班级计分一、选择题1、若一个几何体的俯视图是圆，则它不可能是（）A 、球；B 、圆柱；C 、圆锥；D 、三棱锥。

2 有一个几何体的三视图如下图所示，这个几何体应是一个( )A 棱台B 棱锥C 棱柱D 都不对3. 棱长都是1的三棱锥的表面积为（）A A.BCD4 圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为（） A 7 Ｂ 6 Ｃ5 Ｄ 35、将如图的Rt △ABC 绕直角边AC 旋转一周，所得几何体的主视图是（）∙D C B A 题图 6 半径为R 的半圆卷成一个圆锥，则它的体积为（）A324R B38R C324R D38R7 棱台上、下底面面积之比为1:9,则棱台的中截面分棱台成两部分的体积之比是( )A 1:7 Ｂ 2:7 Ｃ 7:19 Ｄ 5:16主视图左视图俯视图8．图（1）是由哪个平面图形旋转得到的（）A B C D9．已知圆柱与圆锥的底面积相等，高也相等，它们的体积分别为1V和2V，则12:V V=（）A. 1:3B. 1:1C. 2:1D. 3:110．有一个几何体的三视图及其尺寸如下（单位cm），则该几何体的表面积及体积为：A. 224cmπ，212cmπ B. 215cmπ，212cmπC. 224cmπ，236cmπ D.以上都不正确二、填空题11 等体积的球和正方体,它们的表面积的大小关系是S球___S正方体12若三个球的表面积之比是1:2:3，则它们的体积之比是_____________13．图（1）为长方体积木块堆成的几何体的三视图，此几何体共由________块木块堆成;图（2）中的三视图表示的实物为_____________14 如图，,E F 分别为正方体的面11A ADD 、面11B BCC 的中心，则四边形 E BFD 1在该正方体的面上的射影可能是____________15、正方体的全面积为18cm 2，则它的体积是____________16.一个半球的全面积为Q ，一个圆柱与此半球等底等体积，则这个圆柱的全面积是 .17．球的半径扩大为原来的2倍,它的体积扩大为原来的 _________ 倍.18．一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为_________厘米.19．已知棱台的上下底面面积分别为4,16，高为3,则该棱台的体积为___________。

高中数学必修2第一章《空间几何体》基础测试卷

俯视图正视图必修二第一章《空间几何体》基础测试卷一、选择题：1．右面三视图所表示的几何体是( )． A ．三棱锥 B ．四棱锥 C ．五棱锥 D ．六棱锥2.边长为a 正四面体的表面积是（）A 、34a； B 、312a ；C 、24a ；D 2。

3.一个球的体积和表面积在数值上相等，则该球半径的数值为( )． A ．1B ．2C ．3D ．44.已知一个铜质的五棱柱的底面积为16cm 2,高为4cm ，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（） A. 2cm; B.cm 34; C.4cm; D.8cm 。

5.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示，则这个棱柱的体积为（）A.6.长方体的一个顶点上的三条棱长分别为3、4、5，且它的8个顶点都在同一个球面上，则这个球的表面积是（）A 、25π；B 、50π；C 、125π；D 、都不对。

7.正方体的全面积为a,它的顶点都在球面上，则这个球的表面积是（） A.3aπ; B.2aπ; C.a π2; D.a π3.8.长方体的三个侧面面积分别为9，6，2，则长方体的体积是（） A 、36；B 、36；C 、11；D 、12。

9.圆锥的表面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为（） A 、1200；B 、1500；C 、1800；D 、240010．已知圆台的上下底面半径分别为1和2，高为1，则该圆台的全面积为( )A ．32πB ．(5＋32)π C.5＋323πD ．5＋22π正视图侧视图俯视图二、填空题：11．已知圆锥的母线长为2，高为3，则该圆锥的侧面积是_______12．一个长方体的长、宽、高之比为2：1：3，全面积为88cm2，则它的体积为___________．13. 两个球的表面积之比是1：16，这两个球的体积之比为________14．一个与球心距离为2的平面截球所得的圆面面积为π，则球的表面积为_________;15.右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是16. 圆柱的侧面展开图是边长分别为2,a a的矩形，则圆柱的体积为 .17.底面直径和高都是4cm的圆柱的侧面积为 cm2。

第一章空间几何体检测试题 Word版含解析

第一章空间几何体检测试题(时间:120分钟满分:150分)一、选择题(本大题共10小题,每小题4分,共40分)1.下列说法正确的是( D )(A)有两个面平行,其余各面都是四边形的几何体叫棱柱(B)有两个面平行,其余各面都是平行四边形的几何体叫棱柱(C)各侧面都是正方形的四棱柱一定是正方体(D)九棱柱有9条侧棱,9个侧面,侧面均为平行四边形解析:选项A,B都不正确,反例如图所示.选项C也不正确,上、下底面是全等的菱形,各侧面是全等的正方形的四棱柱不是正方体.根据棱柱的定义知选项D正确.2.有一个正三棱锥和一个正四棱锥,它们所有的棱长都相等,把这个三棱锥的一个侧面重合在正四棱锥的一个侧面上,则所得到的这个几何体是( D )(A)底面为平行四边形的四棱柱(B)五棱锥(C)无平行平面的六面体(D)斜三棱柱解析:正三棱锥A BEF和正四棱锥B CDEF的一个侧面重合后,平面BCD和平面AEF平行,其余各面都是四边形,故该组合体是斜三棱柱.3.如图,△ABC为正三角形,AA′∥BB′∥CC′,CC′⊥平面ABC, 3AA′=BB′=CC′=AB,则多面体ABC A′B′C′的正视图是( D )解析:由题知AA′<BB′<CC′,正视图为D.4.如果一个水平放置的平面图形的斜二测直观图是如图所示的直角梯形,其中O′A′=2,∠B′A′O′=45°,B′C′∥O′A′.则原平面图形的面积为( A )(A)3 (B)6(C) (D)解析:因为O′A′=2,∠B′O′A′=∠B′A′O′=45°,所以O′B′=,又B′C′∥O′A′,所以∠C′B′O′=45°,∠O′C′B′=90°,所以B′C′=1,所以原图形为梯形,其上底为1,下底为2,高为2,所以S==3.5.已知长方体的表面积是24 cm2,过同一顶点的三条棱长之和是6 cm,则它的体对角线长是( D )(A) cm (B)4 cm(C)3 cm (D)2 cm解析:设长方体的长、宽、高分别为a,b,c,由题意可知,2(ab+bc+ac)=24,①a+b+c=6,②②2-①可得a2+b2+c2=12,所以长方体的体对角线的长为==2,故选D.6.一个几何体的三视图如图所示(单位:cm),那么此几何体的表面积(单位:cm2)是( C )(A)102 (B)128 (C)144 (D)184解析:由三视图知几何体为正四棱锥,且底面正方形的边长为8,斜高为5,其直观图如图,所以几何体的表面积S=82+4××8×5=144.故选C.7.若圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V1和V2,则V1∶V2等于( C )(A)3∶2 (B)2∶1 (C)3∶1 (D)1∶1解析:因为V1=S底·h,V2=S底·h,所以V1∶V2=3∶1.故选C.8.某几何体的三视图如图所示(单位:cm),则该几何体的体积是( C )(A)8 cm3(B)12 cm3(C) cm3(D) cm3解析:该几何体的体积V=V四棱柱+V四棱锥,故V=23+×22×2=(cm3).9.某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)( A )(A) (B)(C) (D)解析:由三视图知,原工件为圆锥,要使正方体新工件的体积最大,则正方体下底面在圆锥底面上,上底面是平行于圆锥底面的截面圆的内接正方形,过正方体的顶点作轴截面如图,且AB为上底面正方形的对角线,设正方体的棱长为a,则AB=a,又圆锥的高为=2,所以=,得a=,正方体体积为V=a3=,圆锥的体积为×π×12×2=,故原工件的材料利用率为=,选A.10.如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE和△BEC分别沿ED,EC向上折起,使A,B重合于点P,则三棱锥P DCE的外接球的体积为( C )(A) (B)(C) (D)解析:因为ABCD为等腰梯形,AB=2DC,E为AB的中点,所以AD=DE= CE=BC,又∠DAB=60°,所以△ADE,△DCE,△CEB均为边长为1的正三角形,故翻折后的三棱锥P DCE为正四面体,其高PO1==,设球的半径为R,所以R2=(-R)2+()2,得R=,所以V=π.故选C.二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)11.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于cm3,表面积等于 cm2.解析:根据三视图画出几何体,显然是将一个长方体割去两个三棱锥,所以体积V=--=2×2×4-××2×2×2-××2×2×2=(cm3).S表面积=2×4×2+×2×2×2+×4×2×2+×2××2=(28+ 4) cm2.☆答案☆:(28+4)12.某几何体的三视图如图所示,其中俯视图中的弧线是半径为1的四分之一个圆弧,则该几何体的表面积为,体积为.解析:由已知中的三视图可得该几何体为柱体,底面面积为1×1-π=1-,底面周长为1+1+π,柱体的高为1,故该几何体的表面积S=2×(1-)+(1+1+π)×1=4.体积为(1-)×1=1-.☆答案☆:4 1-13.一个空间几何体的三视图(单位:cm)如图所示,则侧视图的面积为cm2,该几何体的体积为cm3.解析:该几何体的直观图为半个圆锥和一个三棱锥,侧视图是底边长为2 cm,高为1 cm的三角形,所以面积为 1 cm2,空间几何体的体积为×1×1+××π×12×1=(+) cm3.☆答案☆:1 (+)14.已知三棱锥O ABC中,OA,OB,OC两两互相垂直,OC=1,OA=x,OB=y,且x+y=4,则此三棱锥体积的最大值是.解析:由题意可知该三棱锥的体积为×xy×1=x(4-x)=-(x-2)2+.由于0<x<4,则当x=2时,该三棱锥的体积最大,且最大值为.☆答案☆:15.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是.解析:作出直观图如图所示,由题意计算得到BG=4,AF=CD=3,AG=CG=5,比较可得任意两个顶点间距离的最大值是3.☆答案☆:316.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则正方体的体积为,这个球的体积为.解析:设正方体的棱长为a,则6a2=18,所以a=.所以正方体的体积为3.设球的半径为R,则由题意知2R==3,所以R=.故球的体积V=πR3=π×()3=π.☆答案☆:3π17.如图,网格纸上小正方形的边长为2,粗线画出的是某多面体的三视图,则该几何体的各个面的面积的最大值为.解析:构造棱长为2的正方体,由三视图,可知该几何体为如图所示的三棱锥P ABC,其中点A为相应棱的中点.因为S△ABC=S△PAB=×1×2=1,S△PBC=×(2)2=2,S△PAC=×PC×=×2×=.因为2>>1,所以该几何体的各个面的面积的最大值为2.☆答案☆:2三、解答题(本大题共5小题,共74分)18.(本小题满分14分)已知某几何体的三视图如图所示.(1)画出该几何体的直观图;(2)求该几何体的表面积.解:(1)几何体的直观图如图.(2)由(1)知该几何体是底面边长为4,高为2的同底的正四棱柱与正四棱锥的组合体,易求得棱锥的斜高h′=2,其表面积S=42+4×4×2+(×4×2)×4=48+16.19.(本小题满分15分)如图,长方体ABCD A1B1C1D1中,AB=12,BC=10, AA1=8,过点A1,D1的平面α与棱AB和CD分别交于点E,F,四边形A1EFD1为正方形.(1)在图中请画出这个正方形(不必写作法),并求AE的长;(2)问平面α右侧部分是什么几何体,并求其体积.解:(1)正方形A1EFD1如图所示.因为A1E=A1D1=AB=10,A1A=8,在Rt△A1AE中,由勾股定理知AE=6.(2)平面α右侧部分几何体是以A1EBB1为底面的直四棱柱,由棱柱体积公式得V=×(6+12)×8×10=720.20.(本小题满分15分)一几何体按比例绘制的三视图如图所示(单位:m).(1)试画出它的直观图;(2)求它的表面积和体积.解:(1)直观图如图所示.(2)由(1)直观图可知该几何体是长方体被截去一个角得到的,且该几何体的体积是以A1A,A1D1,A1B1为棱的长方体的体积的.在直角梯形AA1B1B中,作BE⊥A1B1,垂足为E,则AA1EB是正方形,所以AA1=BE=1.在Rt△BEB1中,BE=1,EB1=1,所以BB1=.所以几何体的表面积S=+2++S正方形ABCD+ =1+2×(1+2)×1+1×+1+1×2=(7+)m2.体积V=×1×2×1=(m3).所以该几何体的表面积为(7+)m2,体积为 m3.21.(本小题满分15分)有一个倒圆锥形的容器,它的轴截面是正三角形,在这个容器内注入水,并且放入一个半径是r的钢球,这时球面恰好与水面相切,那么将球从圆锥形容器中取出后,水面高是多少?解:如图,作出截面,因轴截面是一个正三角形,根据切线的性质知当球在容器内时,水面的深度为3r,水面半径为r,则容器内水的体积为V=V圆锥-V球=π·(r)2·3r-πr3=πr3.将球取出后,设容器中水的深度为h,则水面圆的半径为,从而容器内水的体积为V′=π··h=πh3,由V=V′,可得h=r.22.(本小题满分15分)已知圆柱OO1的底面半径为2,高为4.(1)求从下底面圆周上一点出发环绕圆柱侧面一周到达上底面的最短路径长;(2)若平行于轴OO1的截面ABCD将底面圆周截去四分之一,求截面面积;(3)在(2)的条件下,设截面将圆柱分成的两部分中较小部分为Ⅰ,较大部分为Ⅱ,求VⅠ∶VⅡ(体积之比).解:(1)将侧面沿过该点的母线剪开铺平得到一个矩形,邻边长分别是4π和4,则从下底面圆周上一点出发环绕侧面一周到达上底面的最短路径长即为此矩形的对角线长4.(2)连接OA,OB,因为截面ABCD将底面圆周截去,所以∠AOB=90°,因为OA=OB=2,所以AB=2,而截面ABCD是矩形且AD=4,所以S矩形ABCD=8.(3)依题知V圆柱=Sh=16π,三棱柱AOB DO1C的体积是8,则VⅠ+8=V圆柱=4π,所以VⅠ=4π-8,而VⅡ=V圆柱-VⅠ=12π+8,于是VⅠ∶VⅡ=.。

2021_2022学年高中数学第一章空间几何体测评作业含解析

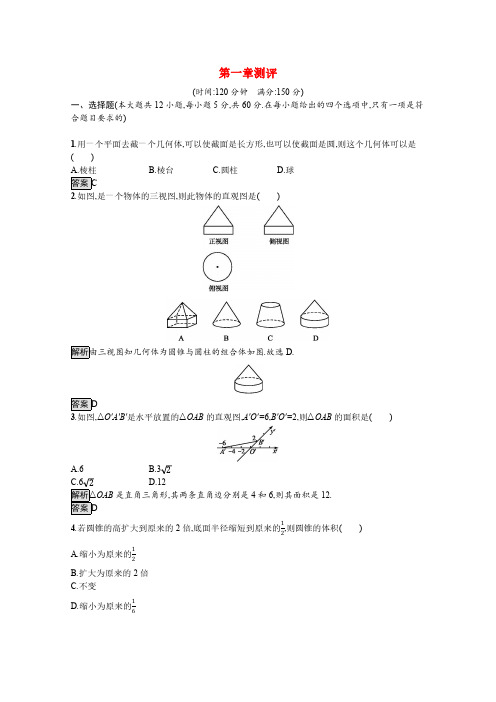
三棱柱 A1B1C1-ABC 的体积为 V2,则 V1∶V2=
.
解析因为 D,E 分别是 AB,AC 的中点,所以 S△ADE∶S△ABC=1∶4.
又 F 是 AA1 的中点,所以 A1 到底面的距离 H 为 F 到底面距离 h 的 2 倍,
1
即三棱柱 A1B1C1-ABC 的高是三棱锥 F-ADE 高的 2 倍,所以 V1∶V2=3 △
A.434π
B.4894π
C.81π
4
D.16π
解析如图,设 PE 为正四棱锥 P-ABCD 的高,则正四棱锥 P-ABCD 的外接球的球心 O 必在其高 PE 所在的直线上,延长 PE 交球面于一点 F,连接 AE,AF.
由球的性质可知△PAF 为直角三角形且 AE⊥PF,又底面边长为 4, ∴AE=2 2,PE=6,
A.13 + 23π
B.1
3
+
2π
3
C.1 + 2π
36
D.1+ 2π
6
解析由三视图可知,四棱锥为底面边长为 1 的正方形,高为 1.其体积 V1=13×12×1=13.
设球的半径为 R,因为四棱锥的底面是半球底面的内接正方形,故 2R= 2,即 R= 2.
2
所以半球的体积为
V2=12
×
4πR3=1
在 Rt△MCN 中,MN= 2 + 2=2 5. 答案 B 8.某几何体的三视图如图所示,则此几何体的体积为( )
A.2
B.1
C.4
D.8
3
3
3
解析该几何体为三棱锥,其直观图如图所示,体积 V=13× 12×2×2 ×2=43.
答案 C 9.如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边 BD 长为 2;侧视图为一直角三角形;俯视图为一直角梯形,且 AB=BC=1,则此几何体的体积是( )

第一章空间几何体单元检测(原卷版)

2
）已知圆锥的表面积为 6，且它的侧面展开图是一个半圆，则这个圆锥的底面半
径为( )
A. 2 π
B. 1 π
C. 2π
D. π
12．（2019 年石家庄期中）已知三棱锥 SABC 的所有顶点都在球 O 的球面上，△ABC 是边长为 1 的正
三角形，SC 为球 O 的直径，且 SC＝2，则此棱锥的体积为( )
20．（2019 年汉台区期中）(本小题满分 12 分)正三棱锥 SABC 的侧面积是底面积的 2 倍，它的高 SO＝ 3，求此正三棱锥的表面积．
21．（2019 年牡丹江期中）(本小题满分 12 分)已知正三棱锥的高为 1，底面边长为 2 6，其内有一个球和该三棱锥的四个面都相切．
(1)求球的半径； (2)求棱锥的表面积.
D．棱柱的各条棱都相等
2．棱锥的侧面和底面可以都是( )
A．三角形
B．四边形
C．五边形
D．六边形
3．（2018 年厦门模拟）如图 1 所示的组合体，其构成形式是( )
图1 A．左边是三棱台，右边是圆柱 B．左边是三棱柱，右边是圆柱 C．左边是三棱台，右边是长方体 D．左边是三棱柱，右边是长方体 4．（2019 年汕头月考）如下所示的直观图是将正方体模型放置在你的水平视线的左下角而绘制的，其中正确的是( )
A. 2 6
B. 3 6
C. 2 3
D. 2 2
二、填空题(本大题共 4 小题，每小题 5 分，共 20 分．把答案填在题中横线上) 13．（2019 年南京期中）若一个圆台的母线长为 l，上、下底面半径分别为 r1，r2，且满足 2l＝r1＋r2，其侧面积为 8π，则 l＝________. 14．（2019 年广安期末）已知 H 是球 O 的直径 AB 上一点，AH∶HB＝1∶2，AB⊥平面α，H 为垂足，α 截球 O 所得截面的面积为π，则球 O 的表面积为________． 15．（2019 年邢台模拟）在棱长为 a 的正方体 ABCDA1B1C1D1 中，EF 是棱 AB 上的一条线段，且 EF＝ b(b<a)．若 Q 是 CD 上的动点，则三棱锥 Q D1EF 的体积为________.

【优质文档】第1章空间几何体单元测试卷及参考答案

________ cm3.
15．已知各顶点都在一个球面上的正四棱柱高为
4，体积为 16，则这个球的表面积是 ________．
16.一个水平放置的圆柱形储油桶 (如图所示 )，桶内有油部分所在圆弧占底面
圆周长的 1，则油桶直立时，油的高度与桶的高度的比值是 4
________ ．
三、解答题
17．某个几何体的三视图如图所示 ( 单位： m)，
()
A ．①②
B ．②③
C ．①③
D ．①②
3．如图所示的正方体中， M 、N 分别是 AA1、CC1 的中点，作四边形 D1MBN ，
则四边形 D1MBN 在正方体各个面上的正投影图形中，不可能出现的是
()
4．如图所示的是水平放置的三角形直观图， D ′是△ A′B′ C′中 B′C′边上的一点，且 D ′ 离 C′比 D ′离 B′近，又 A′ D′∥ y′轴，那么原△ ABC 的 AB、AD 、AC 三条线段中 ( ) A ．最长的是 AB，最短的是 AC B ．最长的是 AC，最短的是 AB C．最长的是 AB，最短的是 AD D ．最长的是 AD ，最短的是 AC
图 2，则该几何体按图 2 所示方向的侧视图为选项图中的
()
11．圆锥的表面积是底面积的 3 倍，那么该圆锥的侧面展开图扇形的圆心角为
()
A ． 120 °
B ．150 °
C． 180 °
D． 240 °
12．已知三棱锥 S－ ABC 的所有顶点都在球 O 的球面上， △ ABC 是边长为 1 的正三角形，
为球 O 的直径，且 SC＝ 2，则此棱锥的体积为
2 A. 6
3 B. 6
2 C. 3