辐射换热2011
合集下载
第十一章辐射换热
dA1dA2
结果查有关手册（书327页表）
28
2）代数法：
利用角系数的定义及性质, 通
过代数运算确定角系数。
图(a)、(b)： X1,2 1
A1 X1,2 A2 X 2,1
X 2,1
图(c) ：X1,2
X1,2a
A2a A1
A1 A2
图(d) ：X1,2 X 2,1 1
三个非凹表面构成的封闭空腔
25
假设表面1、2都是黑体表面，根据辐射强度的定义，
单位时间内从dA1发射到dA2上的辐射能为
d12
Lb1dA1
cos1
dA2
cos2
r2
Eb
dA1
cos1
dA2
cos2
r2
Eb1
cos1 cos2 r2
dA1dA2
从整个表面1发射到表面2的辐射能为
12
A1
A2
Eb1
cos1 cos2 r2
根据辐射力与辐射强度的关系可求得
E L cosd L cos sindd
2
2
2
/2
L0 d 0 sincosd L
16
11-3 实际物体的辐射特性，基尔霍夫定律
1. 实际物体的发射特性
发射率（黑度）： E
Eb
发射率反映了物体发射辐射能的能力的大小。
光发谱射发率射与率光（谱光发谱射黑率度之）间：的关 系为EEb
一些材料对黑体辐射的吸 收比随黑体温度的变化。
22
3. 基尔霍夫（G.R.Kirchhoff）定律
基尔霍夫定律揭示了物体吸收辐射能的能力与发 射辐射能的能力之间的关系，其表达式为
,,T ,,T
传热学 第九章 辐射换热的计算
灰体——多次反射、吸收
9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
任意位置的两个黑体表面1、2，从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
任意位置的两个黑体表面1、2，从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
《辐射换热》PPT课件 (2)
普朗特定律，维恩位移定律， 斯忒藩-波耳兹曼定律，兰贝特定律。
11-2-1 普朗特定律
1. 辐射力和光谱辐射力
辐射力 (Emissive power) 单位时间单位面积物体表面向半球空间的所
有方向发射全部波长范围的辐射能的总量，称为 该物体表面的辐射力。E，W/m2
光谱辐射力 (Emissive power) 单位时间单位面积物体表面向半球空间的
A1
A2
cos1 cos2 r 2
dA1dA2
1
X 2,1 A2 A1
A2
cos1 cos2 r 2
dA1dA2
几何量
2. 角系数的性质 非自见面的角系数等于0。
X 1,1 0
角系数的相对性
A1 X1,2 A2 X 2,1
角系数的完整性
封闭空腔中：
X1,1 X1,2 1
1
X1,1 X1,2 X1,3 X1,4 X1,5 1
结论
✓ 同一温度下，吸收辐射能力愈强的物体， 发射辐射能的能力也愈强。
✓ 同一温度下，黑体的辐射能力最强。
✓ 对于灰体： (T) (T)
不适于太阳辐射的吸收。
11—4 辐射换热的计算方法
假设
➢ 进行辐射换热的物体表面之间是
不参与辐射换热的介质或真空；
➢ 参与辐射换热的物体表面为漫射灰体
或黑体表面；
发射，吸收 辐射能
T1
q 1,net
q
2,net
T
2
➢ 两物体温度不同时，高温物体失去热量； ➢ 两物体温度相同时，辐射换热量为零。
11-1-1 吸收，反射和透过
1 吸收比，反射比和透过比
投入辐射G： 单位时间投射到单位面积物体表面上
11-2-1 普朗特定律
1. 辐射力和光谱辐射力
辐射力 (Emissive power) 单位时间单位面积物体表面向半球空间的所
有方向发射全部波长范围的辐射能的总量，称为 该物体表面的辐射力。E，W/m2
光谱辐射力 (Emissive power) 单位时间单位面积物体表面向半球空间的
A1
A2
cos1 cos2 r 2
dA1dA2
1
X 2,1 A2 A1
A2
cos1 cos2 r 2
dA1dA2
几何量
2. 角系数的性质 非自见面的角系数等于0。
X 1,1 0
角系数的相对性
A1 X1,2 A2 X 2,1
角系数的完整性
封闭空腔中：
X1,1 X1,2 1
1
X1,1 X1,2 X1,3 X1,4 X1,5 1
结论
✓ 同一温度下，吸收辐射能力愈强的物体， 发射辐射能的能力也愈强。
✓ 同一温度下，黑体的辐射能力最强。
✓ 对于灰体： (T) (T)
不适于太阳辐射的吸收。
11—4 辐射换热的计算方法
假设
➢ 进行辐射换热的物体表面之间是
不参与辐射换热的介质或真空；
➢ 参与辐射换热的物体表面为漫射灰体
或黑体表面；
发射，吸收 辐射能
T1
q 1,net
q
2,net
T
2
➢ 两物体温度不同时，高温物体失去热量； ➢ 两物体温度相同时，辐射换热量为零。
11-1-1 吸收，反射和透过
1 吸收比，反射比和透过比
投入辐射G： 单位时间投射到单位面积物体表面上
11、辐射换热计算PPT课件
第十一章 辐射换热计算
1
角系数Fij的定义： 离开表面i的辐射被表面j所拦截的份额
5
热电比拟
电路图
示意图
电势差 电阻 电流
热网络图
6
例1：
7
图(2-3) 两个表面空腔的辐射换热
8
9
例2：
10
12
图2-4 例题2的辐射网络示意图
11
12
13
14
15
？
37
38
同情形下，没有辐射遮热板时的热阻为：
39
由上式可以看出，有辐射遮热板的 热阻比无辐射遮热板的热阻大 (n+1) 倍。
40
若两种情况下，换热表面的温度相同， 则：
41
§2.3 辐射对温度测量的影响
42
当把温度计放在气流中测量温度时， 感受元件所指示的是温度取决于感受 元件上的总的能量平衡。 如图(2-9)所示:
部分资料从网络收集整 理而来，供大家参考，
感谢您的关注！
43
图(2-9) 温度计测温
44
45
从上式可知，温度计指示的温度并 非是气体的真实温度，而是温度计 进行对流和辐射换热的平衡温度。 因此会造成测量误差，有时误差甚 至会很大。
46
例4
图(2-4) 用热电偶测量气流温度的示意图 47
48
49
50
51
52
53
54
The End
55
16
图(2-5)
17
18
19
图2-6 矩形的角系数
20
21
22
23
24
§2.2 辐射遮热板(辐射屏)
减少两个特定的表面之间辐射换 热的方法之一是采用高反射率的 材料。
1
角系数Fij的定义： 离开表面i的辐射被表面j所拦截的份额
5
热电比拟
电路图
示意图
电势差 电阻 电流
热网络图
6
例1：
7
图(2-3) 两个表面空腔的辐射换热
8
9
例2：
10
12
图2-4 例题2的辐射网络示意图
11
12
13
14
15
？
37
38
同情形下，没有辐射遮热板时的热阻为：
39
由上式可以看出，有辐射遮热板的 热阻比无辐射遮热板的热阻大 (n+1) 倍。
40
若两种情况下，换热表面的温度相同， 则：
41
§2.3 辐射对温度测量的影响
42
当把温度计放在气流中测量温度时， 感受元件所指示的是温度取决于感受 元件上的总的能量平衡。 如图(2-9)所示:
部分资料从网络收集整 理而来，供大家参考，
感谢您的关注！
43
图(2-9) 温度计测温
44
45
从上式可知，温度计指示的温度并 非是气体的真实温度，而是温度计 进行对流和辐射换热的平衡温度。 因此会造成测量误差，有时误差甚 至会很大。
46
例4
图(2-4) 用热电偶测量气流温度的示意图 47
48
49
50
51
52
53
54
The End
55
16
图(2-5)
17
18
19
图2-6 矩形的角系数
20
21
22
23
24
§2.2 辐射遮热板(辐射屏)
减少两个特定的表面之间辐射换 热的方法之一是采用高反射率的 材料。
辐射换热原理
辐射换热原理
辐射换热是指热能通过电磁波的辐射传递或交换。
辐射换热不需要介质的存在，它可以在真空中传播。
辐射换热的原理是热辐射，即热能以电磁波的形式从高温物体传递到低温物体。
热辐射的波长范围从长波红外线到短波紫外线，其中短波辐射的能量较高，长波辐射的能量较低。
热辐射是由物体内部来自分子振动和电子跃迁的能量转化为电磁波产生的。
物体的温度越高，分子振动和电子跃迁所产生的电磁波的能量越高，波长越短。
这意味着高温物体会发出较多能量较高的短波辐射，而低温物体则会发出能量较低的长波辐射。
辐射换热的传热速率取决于物体的温度差、表面性质和形状等因素。
通过控制物体的表面特性，如涂层、颜色和纹理，可以调节辐射换热的效率。
此外，辐射换热还受到物体之间的距离的影响，较近的物体之间的辐射换热效率更高。
辐射换热在日常生活中广泛应用，例如太阳能、红外线加热、热辐射扇等。
它也是火焰、火炬和电炉等热能传递的重要机制。
2011热动传热学内蒙古科技大学考试范围
2011热动传热学考试范围2-47 核反应堆的辐射防护壁因受γ射线的照射而发热，这相当于防护壁内有ax e -Φ=Φ0 的内热源，其中0Φ 是X=0的表面上的发热率，a 为已知常数。
已知x=0处t=t1,x=δ处t=2t ,试导出该防护壁中温度分布的表达式及最高温度的所在位置。
导热系数λ为常数。
解：由题意导热微分方程0022=Φ+-axe dx t d λ又x=0处t=t1,x=δ处t=2t积分并结合边界条件可得λδλλλδ2012020210a t x a e a t t a e t a ax Φ++Φ-Φ+--Φ=--令0=dx dt可得：当()⎥⎦⎤⎢⎣⎡-+Φ--=-δδλδa e t t a a x a 1ln 1021时，t 最大。
2-52 在外径为25mm 的管壁上装有铝制的等厚度环肋，相邻肋片中心线之间的距离s=9.5mm,环肋高H=12.5mm,厚δ＝0.8mm 。
管壁温度200=w t ℃，流体温度90=f t ℃，管壁及肋片与流体之间的表面传热系数为110)./(2K m W 。
试确定每米长肋片管（包括肋片及基管部分）的散热量。
解：2521003.1;9.122/m A A mm H H -⨯='==+='δδ查表得238=λW/(m.K)()31.0)(2/1223=⎥⎦⎤⎢⎣⎡'A h H λmm H r r mm r 4.25;5.12121='+='=从图查得，88.0=f η肋片两面散热量为：()Wt t h r r f w 15.372120=-⎪⎭⎫ ⎝⎛-'=Φπ 肋片的实际散热量为：Wf 7.320=Φ=Φη两肋片间基管散热量：()1051;021.921===-=Φ's n W s r t t h f w π总散热量为()W n Z 8.4382=Φ'+Φ=Φ2-76 刚采摘下来的水果，由于其体内葡萄糖的分解而具有“呼吸”作用，结果会在其表面析出C2O ,水蒸气，并在体内产生热量。
传热学第八章辐射换热的计算
02
辐射换热的计算方法
辐射换热的基本公式
斯蒂芬-玻尔兹曼方程
描述了物体在任意温度下的辐射功率，是辐射换热的基本公式。
辐射力方程
表示物体发射和吸收的辐射能与物体表面温度和周围环境温度之间 的关系。
辐射传递方程
表示在给定温度和光谱发射率下，物体表面发射和吸收的辐射能与 物体表面温度之间的关系。
辐射换热的角系数法
表面传热系数的计算方法
通过实验测定或经验公式计算表面传热系数， 需要考虑表面粗糙度和涂层的影响。
表面传热系数的应用
适用于简化模型或近似计算中的辐射换热计算。
辐射换热的积分方程法
积分方程的建立
根据斯蒂芬-玻尔兹曼方程和边界条件建立积分方程。
积分方程的求解方法
采用数值方法求解积分方程，如有限元法、有限差分 法等。
太阳能利用
通过优化太阳能集热器的设计，提高太阳能辐射的吸收和 转换效率，降低太阳能利用成本，有助于减少化石能源的 消耗和碳排放。
05
辐射换热的发展趋势与展 望
新型材料的辐射换热特性研究
总结词
随着科技的发展，新型材料不断涌现，对新型材料的辐射换热特性研究成为当 前热点。
详细描述
新型材料如碳纳米管、石墨烯等具有独特的物理和化学性质，其辐射换热特性 与传统材料有所不同。研究这些新型材料的辐射换热特性有助于发现新的传热 机制，提高传热效率。
感谢观看
THANKS
传热学第八章辐射 换热的计算
目 录
• 辐射换热的基本概念 • 辐射换热的计算方法 • 辐射换热的实际应用 • 辐射换热的优化与控制 • 辐射换热的发展趋势与展望
01
辐射换热的基本概念
定义与特性
定义
传热学第5章辐射换热(Radiation Heat Transfer)
5.1辐射的基本概念
由于起因不同，物体发射电磁波的波长也不同，可分为：
5.1辐射的基本概念
由于起因不同，物体发射电磁波的波长也不同，可分为：
λ<0.38μm 紫外线、X射线、γ射线 0.38<λ<0.76μm 可见光 0.76<λ<1000μm 红外线
0.76<λ<4μm 近红外 4<λ<1000μm 远红外 λ>1000μm 无线电波
J2
Eb2
12 A 2
Φ1,2
Φ2
5.6无限大灰体间辐射换热特性
第五章第一次作业 8—1，8—4，8—6，8—15，8—23
5.7 漫射表面间的角系数
角系数 X a,b —在两表面间介质是透明的情况下，由一个漫射表面 a 发出的辐射能落到另一个表 b 上的百分数为 a 表面 对 b 表面的角系数。
讨论：
如果两个表面均为黑体表面，1 2 1 ，表面热阻为零，
只有空间辐射热阻，J Eb 。
如果 1 为凸表面， X1,2 1
Rt
1 A1
1
1
A1 A2
1 2
2
如果
A1
A2 ：Rt
1 A1
1
1
1 2
1
（相当于无限大平板）
如果 A1 A2 ：
A1 A2
0，Rt
1
A1
，Φ
A11 Eb1
5.2黑体辐射的基本定律
四、兰贝特定律
定向辐射强度——单位时间、单位立体角单位可见辐射面 积的辐射能量。
I dΦ( )
dAcosd
微元立体角
d
dAc r2
sin dd
5.2黑体辐射的基本定律
第四节辐射换热
q=E-AE0
热平衡时T=T0，由q=0得：
E-AE0=0 或 E/A=E0
• 结论： 从基尔霍夫定律可得出如下结论： 1）物体的辐射力愈大，吸收率也就愈大。 即善于发射的物体必善于吸收； 2）实际物体的吸收率总是小于1，所以在同 温度下绝对黑体的辐射力最大。 3）在热平衡条件下，任意物体对绝对黑体 辐射的吸收率等于同温度下该物体的黑度。
• 基尔霍夫定律 基尔霍夫定律的内容：任何物体的辐射力 和吸收率之比值与物体的性质无关，而恒 等于同温度下绝对黑体的辐射力。
E1 A1 E2 A2 E3 A3 E 0
注：该定理只对于平衡的热辐射适用。
• 推倒过程 如图：表面1和表面2 其中1为黑体 根据推倒可得： 表面2辐射换热的差额为
• 如果电子产品装在箱内，则通过箱壁传入 的太阳辐射热可近似计算为：
Q12 0 . 047 KS s E s As
K是箱体的传热系数
思考题： • 试从辐射换热的角度分析，在进行表面组 装回流焊接时，为什么选用热风炉比选用 红外炉对焊接质量更为有利？ • 试从辐射换热角度分析，在对表面贴装元 件进行回流焊接时，为什么某些元件有时 会出现冷焊或过热等焊接缺陷？
• 斯蒂芬-玻尔兹曼定律（四次方定律） 斯蒂芬-玻尔兹曼定律内容：物体的辐射力E 与其绝对温度T的四次方成正比。
E C(
对于黑体，有：
T 100
)
4
W/m2
(4-3)
E0 C0 (
式中：C0=5.67W/（m2·4） K
T 100
)
4
黑度
是指实际物体的辐射力与同温度下 黑体的辐射力之比 ，即实际物体吸收 率的大小。
第四节 辐射换热
辐射换热
三、维恩位移定律 由
dEb λ = 0 → Ebλ max dλ
→
λmax ⋅ T = 2.8967 ×10 −3 (m ⋅ K )
利用维恩定律，可测得 后反求黑体表面温度。 利用维恩定律，可测得λmax 后反求黑体表面温度。 实际物体光谱辐射力按波长的分布规律不完全符合 普朗克定律, 但大趋势一致。 普朗克定律 但大趋势一致。 在工业温度范围内（ 以下） 在工业温度范围内（2000 K以下）, 热辐射波长在 以下 0.38 ~100µm , 且大部分能量在 0.76 ~20µm 的红 外线区段。 外线区段。
∆Eb = Eb ( λ1 −λ2 ) = Fb ( λ1 −λ2 ) Eb = ( Fb ( 0−λ2 ) − Fb ( 0−λ1 ) ) Eb
Fbλ ——黑体 在 0至λ波段区间的辐射力占同温度 黑体 下黑体全波辐射力的百分比。 下黑体全波辐射力的百分比。 Fbλ = f（λT） （ ） 四、基尔霍夫定律 实际物体表面的黑度（发射率） 单色黑度。 1. 实际物体表面的黑度（发射率）、单色黑度。 黑度： 黑度：
P.209 图11.5为 为 放大的局部图： 放大的局部图：
讨论： 讨论： 1）T↑→Ebλ↑→Eb↑； ） ； 2）λ→0 或λ→∞，Ebλ→0； ） →0 → →0； 的波长记为λ 3）对应 Ebλmax 的波长记为 max 越小。 向移动。即T↑，λmax越小。 向移动。
， T↑→λmax 向短波方
11－3 角系数 －
一、角系数及其特性 1. 角系数
X 1, 2 Φ1− 2 = Φ1
式中
上的部分 Φ1− 2 ——A1发出的能量中落到 A2上的部分； 发出的总能量。 Φ1 —— A1发出的总能量。
角系数是几何参数, 通常认为表面不透明,介质透明 介质透明。 角系数是几何参数 通常认为表面不透明 介质透明。 2. 角系数的特性 相对性（互换性）： ① 相对性（互换性）： X 1, 2 A1 = X 2,1 A2
辐射换热2011_PPT课件
注意： X21X2a,1X2b,1
角系数的完整性
角系数的可加性
15
第四章 辐射换热
（4）等值性 （5）非凹面
X1,2 X1,2'
X11 0
例4.1 求X21,X11
X 12
A2 A1
X111X121A A12
2’ 2 1
1 2
16
第四章 辐射换热
例4.2 求X12,X21,X22,X11
1 3
X12A A13
A1(Eb1 Eb2) 1 1 1
1 2
③若 1为非凹表面
A1 0 A2
12 1A 1(E b1E b2)
24
第四章 辐射换热
三、遮热板
1
2
q121 11E b1X 11E 2 b21 22
Eb1Eb2
11121
E b1
J1
1 1
若加一板3（ 3 ）
1A1
q12 11
1
Eb1 Eb2
T328.69K
33
第四章 辐射换热
第4章小结：
1、吸收比、反射比、穿透比、光谱辐射力、总辐射力、定 向辐射强度 2、黑体辐射基本定律（ planck’s law, Wien’s displacement
law, Stefan-Boltzman’s law , Lambert’s law )
3、发射率，吸收比，灰体，基尔霍夫定律
表面 1发出的热 表面 2发出的热
辐射到达表面 2 辐射到达表面 1
的部分
的部分
A1,T1,11
12
(Eb1
1
Eb2 )
A1 X 12
空间热阻
E b1
Eb2
角系数的完整性
角系数的可加性
15
第四章 辐射换热
（4）等值性 （5）非凹面
X1,2 X1,2'
X11 0
例4.1 求X21,X11
X 12
A2 A1
X111X121A A12
2’ 2 1
1 2
16
第四章 辐射换热
例4.2 求X12,X21,X22,X11
1 3
X12A A13
A1(Eb1 Eb2) 1 1 1
1 2
③若 1为非凹表面
A1 0 A2
12 1A 1(E b1E b2)
24
第四章 辐射换热
三、遮热板
1
2
q121 11E b1X 11E 2 b21 22
Eb1Eb2
11121
E b1
J1
1 1
若加一板3（ 3 ）
1A1
q12 11
1
Eb1 Eb2
T328.69K
33
第四章 辐射换热
第4章小结：
1、吸收比、反射比、穿透比、光谱辐射力、总辐射力、定 向辐射强度 2、黑体辐射基本定律（ planck’s law, Wien’s displacement
law, Stefan-Boltzman’s law , Lambert’s law )
3、发射率，吸收比，灰体，基尔霍夫定律
表面 1发出的热 表面 2发出的热
辐射到达表面 2 辐射到达表面 1
的部分
的部分
A1,T1,11
12
(Eb1
1
Eb2 )
A1 X 12
空间热阻
E b1
Eb2
传热学第十章辐射换热计算
22
概念汇总:
1.角系数：表面1发出的辐射能落到表面2上的份额 称为表面1对表面2的角系数。记为：X1，2。 2.空间辐射热阻：
1 A1 X 1, 2
3.对于性质均匀且服从兰贝特定律的表面，其角系 数是纯几何因子。 4.角系数的相对性： A1X1，2=A2X2，1 5.角系数的完整性： X i , j
表面辐射热阻
13
2）灰体辐射换热网络
以上分析表明：物体间的辐射换热量与辐射力之差成正比， 与辐射热阻成反比。辐射热阻分为两大类：一类是辐射角 系数起主要作用的空间辐射热阻，一类是表面黑度起主要 作用的表面辐射热阻。因此，各种形式的辐射换热都可以 用类似于电路网络的相应辐射换热网络描述和计算。 辐射换热等效网络的特点：表面辐射热阻是各表面同温
L dA 1 cos d
A2
dA 1 E 1 cos dA 2 cos
( E 1 / ) cos d
j 1 n
1 （对于封闭系统的n个表面）
6.角系数的可加性：
X1，2+3=X1，2+X1，3 ；
X 1 2,3 A1 A1 2 X 1,3 A2 A1 2 X 2,3
23
思考题和典型习题分析 :
1.试述角系数的定义。“角系数是一个纯几何因子”的结论是 在什么前提下得出的？ 答：表面1发出的辐射能落到表面2上的份额称为表面1对表面2的 角系数。“角系数是一个纯几何因子”的结论是在物体表面性质 及表面温度均匀、物体辐射服从兰贝特定律的前提下得出的。 2.角系数有哪些特性？这些特性的物理背景是什么？ 答：角系数有相对性，完整性和可加性。相对性是在两物体处于 热平衡时，净辐射换热量为零的条件下导得的；完整性反映了一 个由几个表面组成的封闭系统中，任一表面所发生的辐射能必全 部落到封闭系统的各个表面上；可加性是说明从表面1发出而落 到表面2上的总能量等于落到表面2上各部份的辐射能之和。
概念汇总:
1.角系数：表面1发出的辐射能落到表面2上的份额 称为表面1对表面2的角系数。记为：X1，2。 2.空间辐射热阻：
1 A1 X 1, 2
3.对于性质均匀且服从兰贝特定律的表面，其角系 数是纯几何因子。 4.角系数的相对性： A1X1，2=A2X2，1 5.角系数的完整性： X i , j
表面辐射热阻
13
2）灰体辐射换热网络
以上分析表明：物体间的辐射换热量与辐射力之差成正比， 与辐射热阻成反比。辐射热阻分为两大类：一类是辐射角 系数起主要作用的空间辐射热阻，一类是表面黑度起主要 作用的表面辐射热阻。因此，各种形式的辐射换热都可以 用类似于电路网络的相应辐射换热网络描述和计算。 辐射换热等效网络的特点：表面辐射热阻是各表面同温
L dA 1 cos d
A2
dA 1 E 1 cos dA 2 cos
( E 1 / ) cos d
j 1 n
1 （对于封闭系统的n个表面）
6.角系数的可加性：
X1，2+3=X1，2+X1，3 ；
X 1 2,3 A1 A1 2 X 1,3 A2 A1 2 X 2,3
23
思考题和典型习题分析 :
1.试述角系数的定义。“角系数是一个纯几何因子”的结论是 在什么前提下得出的？ 答：表面1发出的辐射能落到表面2上的份额称为表面1对表面2的 角系数。“角系数是一个纯几何因子”的结论是在物体表面性质 及表面温度均匀、物体辐射服从兰贝特定律的前提下得出的。 2.角系数有哪些特性？这些特性的物理背景是什么？ 答：角系数有相对性，完整性和可加性。相对性是在两物体处于 热平衡时，净辐射换热量为零的条件下导得的；完整性反映了一 个由几个表面组成的封闭系统中，任一表面所发生的辐射能必全 部落到封闭系统的各个表面上；可加性是说明从表面1发出而落 到表面2上的总能量等于落到表面2上各部份的辐射能之和。
热工基础 第11章 辐射换热
立体角即为某一方向的空间占总空间的大小。
§11.1.4 定向辐射强度
立体角定义：球面面积除以球半径的平方， 单位：sr(球面度)
c r2
dAc rd r sin d
d
dAc r2
sin d d
称为经度角， 称为纬度角（方位角）
§11.1.4 定向辐射强度
定向辐射强度I 定义：
单位时间内、单位可见辐射面积向（ ， ）
辐射力从总体上表征物体发射辐射能本领的大小。 在热辐射的整个波谱内不同波长发出的辐射能是 不同的，如图，每条曲线下的面积表示相应温度 下黑体的辐射力。
§11.1.4 辐射力和光谱辐射力
光谱辐射力 E λ ： 单位时间内，单位波长范围内 ( 包含某一给定波长 ) ，物体的单
位表面积向半球空间发射的能量。单位：W
§11.2.2 Stefan-Boltzmann 定律
Eb
0
Eb
d
0
e
c
2
c15
(T )
1
d
T 4
Eb
C0
(T 100
)4
式中， σ= 5.67×10-8 w/(m2K4)，是Stefan-Boltzmann常 数。
外界投射到物体表面的总能量φ中被物体反射的部分Qρ与Q的比值。 当ρ＝1时称绝对白体。 穿透比τ：
外界投射到物体表面的总能量φ中被物体穿透的部分Qτ与Q的比值。
当τ＝1时称绝对透明体。
由能量守恒定律：α＋ρ＋τ＝1
黑体、镜体(或白体)和透明体都是假定的理想物体。
§11.1.2 吸收比、反射比、穿透比
第11章 辐射换热
第11章 辐射换热
一、基本内容： 1、热辐射的基本概念及黑体辐射三大定律； 2、实际物体的辐射及吸收特性； 3、辐射换热的基耳霍夫定律。
§11.1.4 定向辐射强度
立体角定义：球面面积除以球半径的平方， 单位：sr(球面度)
c r2
dAc rd r sin d
d
dAc r2
sin d d
称为经度角， 称为纬度角（方位角）
§11.1.4 定向辐射强度
定向辐射强度I 定义：
单位时间内、单位可见辐射面积向（ ， ）
辐射力从总体上表征物体发射辐射能本领的大小。 在热辐射的整个波谱内不同波长发出的辐射能是 不同的，如图，每条曲线下的面积表示相应温度 下黑体的辐射力。
§11.1.4 辐射力和光谱辐射力
光谱辐射力 E λ ： 单位时间内，单位波长范围内 ( 包含某一给定波长 ) ，物体的单
位表面积向半球空间发射的能量。单位：W
§11.2.2 Stefan-Boltzmann 定律
Eb
0
Eb
d
0
e
c
2
c15
(T )
1
d
T 4
Eb
C0
(T 100
)4
式中， σ= 5.67×10-8 w/(m2K4)，是Stefan-Boltzmann常 数。
外界投射到物体表面的总能量φ中被物体反射的部分Qρ与Q的比值。 当ρ＝1时称绝对白体。 穿透比τ：
外界投射到物体表面的总能量φ中被物体穿透的部分Qτ与Q的比值。
当τ＝1时称绝对透明体。
由能量守恒定律：α＋ρ＋τ＝1
黑体、镜体(或白体)和透明体都是假定的理想物体。
§11.1.2 吸收比、反射比、穿透比
第11章 辐射换热
第11章 辐射换热
一、基本内容： 1、热辐射的基本概念及黑体辐射三大定律； 2、实际物体的辐射及吸收特性； 3、辐射换热的基耳霍夫定律。
辐射换热优秀课件
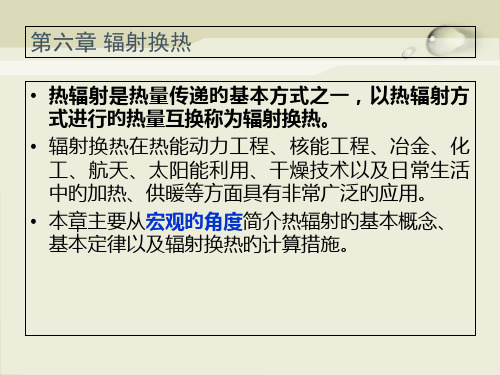
3. 基尔霍夫定律
• 物体吸收辐射能旳能力与发射辐射能旳能力之间旳关系
, ,T , ,T
吸收辐射能旳能力愈强旳物体，发射辐射能旳 能力也就愈强。 在温度相同旳物体中，黑体吸收辐射能旳能力 最强，发射辐射能旳能力也最强。
• 对于漫射体，辐射特征与方向无关，基尔霍夫定律体 现式为
T T
• 立体角
半径r旳球面上面积 A 与球心所相应空间角度
A
r2
立体角旳单位叫球面度，用Sr表达。
半个球面所相应旳立体角为2 Sr。
dA2 rd rsind r 2sindd
d
dA2 r2
sindd
辐射强度
• 单位时间内从单位投影面积（可会面积）所发 出旳包括在单位立体角内旳辐射能。
L , d
Eb
C15
eC2 / T 1
—波长，m；
T—热力学温度，K； C1—普朗克第一常数，C1= 3.743×10-16 Wm2 ; C2—普朗克第二常数， C2 = 1.439×10-2 mK。
黑体旳光谱辐射力
可见光
光谱辐射力随波长和温度旳变化特点：
• 温度愈高，同一波长下旳光谱辐射力愈大； • 在一定旳温度下，黑体旳光谱辐射力随波长连续
对于金属，表面层厚度只有1m旳量级； 对于绝大多数非金属材料，表面层厚度不大于
1mm。
所以，对于固体和液体，能够以为对热辐射旳 透射比为零:
1
为了简化问题，定义某些理想物体。 •镜体（或白体）:
反射比 = 1旳物体
•绝对透明体:
透射比 = 1旳物体。
物体表面对热辐射旳反射 • 镜反射
物体表面粗糙尺度不不小于投射辐射能旳波长. 例如高度抛光旳金属表面
辐射换热
（2）角系数的完整性 对于N个表面包围并形成一个封 闭腔，根据角系数的定义有
X
j 1
N
i, j
X i ,1 X i ,2 X i ,i X i , N 1
（3）角系数的可加性（分解性）
A1Eb1 X 1,2 A1Eb1 X 1,2 a A1Eb1 X 1,2b X 1,2 X 1,2 a X1,2b A2 Eb2 X 2,1 A2a Eb2 X 2a,1 A2b Eb2 X 2b,1 A2 X 2,1 A2a X 2a,1 A2b X 2b,1
辐射网络法：
N J J N Ebi J i i j i Ai X i , j J i J j 1 i 1 j 1 j 1 Ai i Ai X i , j
24
Ebi J i i 1 i Ai i
Ji J j 1 j 1 Ai X i , j
A1 X1,2 Eb1 Eb2 A2 X 2,1 Eb1 Eb2 Eb1 Eb2 1 1,2 --空间辐射热阻 1 A1 X 1,2 A1 X 1,2
注意： 1，2 是两个任意位置的黑体表面1、2之间 直接的辐射换热量，没考虑其它表面的影响。
16
对两个黑体表面构成封闭腔，两表面间的 净交换热量：
封闭空腔内任意一个表面i 净损失的辐射热流量等 于该表面与所有表面交换的辐射热流量的代数和，即
Ebi J i Ai X i , j J i J j i 1 i j 1 Ai i n
N
1 J i Ebi 1 X i , j ( J i J j ) i j 1
X 1,1 X 2,2 X 4,4 0
11-4辐射换热的计算
对于灰体，表面 与外界的净换热量Q1为以放出为正： 1
Q1 J1 G1 A1
其中，G1
J1 1 Eb1 1 1
J1 1Eb1 Eb1 J1 热势差 Q1 J1 A1 1 1 1 1 表面热阻 1 A1
2013年1月18日星期五
华北电力大学能源与动力工程学院 工程热物理教研室
Heat transfer (3)角系数的计算
Q12 1 cos1 cos 2 1).积分法：利用式 X 12 dA1 dA2计算 2 E1 A1 A1 A1 A2 R
教材中给出了几种几何系统角系数的计算公式 也可查典型几何体系角系数的线图，并利用角系数的特性进行计算 2).代数法：利用角系数的定义及性质, 通过代数运算确定角系数。 图(a)、(b)：
n n
Ebi J i n J k J i 0 1 i k 1 1 A AX i i i ik
i 1 2， n ，3......
上式表明，在辐射换热网络 中，流向Ji点的热流量为0。N 个表面组成的封闭空腔有n个 节点，可列出n个方程，求出 n个未知数， J1、 J2、…… Jn， 从而求解换热网络。
1 1 Eb1 A 1 1
J1
1 A1 X 12
J2
1 2 2 A2 Eb 2
1 A1 X 13
J3
1 A2 X 23 1 3 3 A3
Eb 3
2013年1月18日星期五
华北电力大学能源与动力工程学院 工程热物理教研室
Heat transfer
几点说明：
①.对于不封闭的空间，向外界敞开的截面可以用假想表面来封闭， 并且常常可以处理成黑体表面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Eb1
A1 , T1 , 1 1
( Eb1 Eb 2 ) 12 1 A1 X 12
Eb 2
1 A1 X 12
21
空间热阻
第四章
辐射换热
二、两灰表面间辐射换热
Eb1
E1
Eb 2
E2
两黑表面
两灰表面
22
第四章
辐射换热
1.有效辐射，投入辐射，自身辐射
自身辐射:E1 投入辐射:G1 有效辐射: J1 E1 G1 2.表面的净辐射
Eb
（1） （2） 成立条件: ①1为黑体 ②热平衡
推论：
2o 灰体
E Eb
1o 善于辐射的物体也善于吸收。黑体辐射力Eb最大， 也最大。
13
第四章
辐射换热
§4.4 角系数
一、定义
X 1, 2 表面1对表面2的投入辐射1 2 表面1的辐射1
表面1 表面2
对于灰表面，角系数是几何因子
第四章
辐射换热
非导电体材料的光谱吸收 比同波长的关系
二、吸收比
1.光谱吸收比
吸收的某一特定波长的能量 投入的某一特定波长的能量
如： 温室效应 2.(总)吸收比 吸收的能量 投入的能量(投入辐射) 物体表面的吸收比取决于吸收表面 与发射表面的物质种类、表面温度 和表面状况。
三、灰体（gray body）
2
16
第四章
辐射换热
例4.2
1 3 2
求X12,X21,X22,X11
X 12 A3 A1
A3 A1
A3 X 21 A2
X 22 1 A3 A2
X 11 1
17
第四章
辐射换热
例4.3 三个非凹表面
X 12 X 13 1 X X 1 23 21 X 31 X 32 1 A1 X 12 A2 X 21 A1 X 13 A3 X 31 A2 X 23 A3 X 32
1 1 5 A1 X 12 0.2 9 9
1 1 5 1 A1 X 13 0.8 9 36 A2 X 23
5 36
Eb 3 J 3
32
第四章
辐射换热
Eb1
1 36
地板损失的热流量：
12 Eb1 Eb 2 9 1 1 1 36 5 5 5 36 36 36 Eb1 Eb 2 159 .9 W 13 54
Eb1
1 1 1 A1
J1
1 A1 X 12
J2
1 2 2 A2
A2
Eb 2
X 11 0, X 12 1
A1
Eb1 Eb 2 A1 ( Eb1 Eb 2 ) 12 1 1 1 1 2 1 A1 1 1 1 A1 A1 X 12 2 A2 1 A2 2
定义：
Const
11
工业上， 0.76 ~ 20 m 可以作为灰体。
第四章
辐射换热
四、Krichhoff’s law 1859年
板1—黑体，板2—任意物体
2.表面： q 热平衡
E2 2 Eb
E2 E
q E2 2 Eb 0
E3
3
2
②若1为非凹表面,而且
A1 ( Eb1 Eb 2 ) A1 1 12 1 1 A2 1
1
2
③若 1为非凹表面
A1 0 A2
12 1 A1 ( Eb1 Eb 2 )
24
第四章
辐射换热
1
2
三、遮热板
Eb1 Eb 2 Eb1 Eb 2 q12 1 1 1 1 2 1 1 1 1 X 12 2 1 2
4、兰贝特定律 Lambert’s law
黑体的定向辐射强度为常数。
Eb L
9
第四章
辐射换热
§4.3 实际物体的辐射与吸收特性
一、黑度 半球总黑度
E (T ) (T ) Eb (T )
E Eb 0T
4
物体表面的发射率取决于物质种类、表面温度和表面状况。
10
例如：雪对可见光 0.05, 0.95 对红外线
0.95, 0.05
4
第四章
辐射换热
§4.2 黑体辐射的基本定律
一、黑体 1 人工黑体b-black 二、基本概念
1.光谱辐射力
E Eb
W / m3
单位时间内，单位波长范围内(包含某一给定波长)，物体的单 位表面积向半球空间发射的能量。
J1 J 2
1 A1 X 1, 2
Eb
1 A
J1
J1
1 A1 X 1, 2
J2
27
第四章
辐射换热
1 1 1 A1
二、求解步骤
1.画等效网络图 2.列节点方程
E J J J1 J 3 J1 J1 : b1 1 2 0 1 1 1 1 1 A1 A1 X 12 A1 X 13 Eb 2 J 1 J 1 J 2 J 3 J 2 J2 : 0 1 2 1 1 2 A2 A1 X 12 A2 X 23 J3 : Eb1 J1 J1 J 3 J 2 J 3 0 1 3 1 1 A1 X 13 A2 X 23 3 A3
J1
G1
灰表面
J1 E1 1 ( Eb1 J1 ) q1 J1 G1 J1 1 1 1 1
Eb1
Eb1 J1 1 q1 A1 1 1 1 A1
表面热阻
G1
黑表面
23
第四章
辐射换热
3.两灰表面辐射换热 Eb1 Eb 2 12 1 1 1 1 2 1 A1 A1 X 12 2 A2 ①若1为非凹表面
二、角系数的计算
1.积分法 2.查图 3.代数法
14
第四章
辐射换热
角系数性质 （1）相对性（互换性）
A X1, 2 A2 X 2,1 1
（2）完整性 对于封闭系统:
X1,1 X1, 2 X1,3 X1, n X1,i 1
i 1 n
角系数的完整性
（3）可加性 注意：
对于大多数的固体和液体： 0, 1
对于不含颗粒的气体：
0, 1
3
第四章
辐射换热
三、理想物体
1. 黑体
1
镜面反射
2.白体（镜体） 1
漫反射
3.透明体
注意：
1
1.黑体，白体，透明体是对热射线而言的（非可见光） 2. , , 与投入辐射有关。
Eb1
J1
1 A1 X 12
J2
1 2 2 A2
Eb 2
1 A1 X 13
J3
1 A2 X 23
1 3 3 A3
Eb 3
1 3
2
28
第四章
辐射换热
3.求解方程组，得
J1 , J 2 , J 3
4.计算每个表面的净辐射热流量和两表面之间的净辐射热流量
Ji J j Ebi J i i , ij 1 i 1 Ai X ij i Ai
c1
5
式中，λ— 波长，m ；
① 0, , Eb 0
② 0.1~100μm ③T↑, Eb↑
7
第四章
辐射换热
2. 维恩位移定律 Wien’s displacement law
m T 2.9 10 3 m K
如太阳辐射：
m 0.5m
所以太阳表面温度
2.9 10 T 5800 K 6 0.5 10
8
3
第四章
辐射换热
3. 斯忒藩-玻耳兹曼定律Stefan-Boltzman’s law
Eb 0T
4
0 5.67 10 8 W m 2 k 4
T W / m c0 100
2
4
c0 5.67
J2
1 2 2 A2
Eb 2
2.重辐射面（绝热面）
3 Eb 3 J 3 1 3 3 A3
1 A1 X 13
1 A2 X 23
1 3 Eb3 J 3 3 0 3 A3
Eb 3 J 3
仍有３个未知量
J1 , J 2 , J 3
30
第四章
辐射换热
例4.7 ：一房间，地板T1=293K，天花板T2=286K，四周 墙壁绝热，黑度均为0.8。
Eb1
1 1 1 A1
J1
1 A1 X 12
J2
1 2 2 A2
Eb 2
1
2
3
1 A1 X 13
J3
1 A2 X 23
1 3 3 A3
Eb 3
29
第四章
辐射换热
1 1 1 A1
三、 特例
Eb1
J1
1 A1 X 12
J2
1 2 2 A2
Eb 2
1.某一表面为黑表面（３表面）
1
3
2
Eb1
1 1 1 A1
J1
1 A1 X 13
J3
1 3 3 A3
Eb 3
1 3 3 A3
J3
1 A2 X 32
J2
1 2 2 A2
Eb 2
25
第四章
辐射换热
§4.6 多表面系统辐射换热计算
A1 , T1 , 1 1
( Eb1 Eb 2 ) 12 1 A1 X 12
Eb 2
1 A1 X 12
21
空间热阻
第四章
辐射换热
二、两灰表面间辐射换热
Eb1
E1
Eb 2
E2
两黑表面
两灰表面
22
第四章
辐射换热
1.有效辐射，投入辐射，自身辐射
自身辐射:E1 投入辐射:G1 有效辐射: J1 E1 G1 2.表面的净辐射
Eb
（1） （2） 成立条件: ①1为黑体 ②热平衡
推论：
2o 灰体
E Eb
1o 善于辐射的物体也善于吸收。黑体辐射力Eb最大， 也最大。
13
第四章
辐射换热
§4.4 角系数
一、定义
X 1, 2 表面1对表面2的投入辐射1 2 表面1的辐射1
表面1 表面2
对于灰表面，角系数是几何因子
第四章
辐射换热
非导电体材料的光谱吸收 比同波长的关系
二、吸收比
1.光谱吸收比
吸收的某一特定波长的能量 投入的某一特定波长的能量
如： 温室效应 2.(总)吸收比 吸收的能量 投入的能量(投入辐射) 物体表面的吸收比取决于吸收表面 与发射表面的物质种类、表面温度 和表面状况。
三、灰体（gray body）
2
16
第四章
辐射换热
例4.2
1 3 2
求X12,X21,X22,X11
X 12 A3 A1
A3 A1
A3 X 21 A2
X 22 1 A3 A2
X 11 1
17
第四章
辐射换热
例4.3 三个非凹表面
X 12 X 13 1 X X 1 23 21 X 31 X 32 1 A1 X 12 A2 X 21 A1 X 13 A3 X 31 A2 X 23 A3 X 32
1 1 5 A1 X 12 0.2 9 9
1 1 5 1 A1 X 13 0.8 9 36 A2 X 23
5 36
Eb 3 J 3
32
第四章
辐射换热
Eb1
1 36
地板损失的热流量：
12 Eb1 Eb 2 9 1 1 1 36 5 5 5 36 36 36 Eb1 Eb 2 159 .9 W 13 54
Eb1
1 1 1 A1
J1
1 A1 X 12
J2
1 2 2 A2
A2
Eb 2
X 11 0, X 12 1
A1
Eb1 Eb 2 A1 ( Eb1 Eb 2 ) 12 1 1 1 1 2 1 A1 1 1 1 A1 A1 X 12 2 A2 1 A2 2
定义：
Const
11
工业上， 0.76 ~ 20 m 可以作为灰体。
第四章
辐射换热
四、Krichhoff’s law 1859年
板1—黑体，板2—任意物体
2.表面： q 热平衡
E2 2 Eb
E2 E
q E2 2 Eb 0
E3
3
2
②若1为非凹表面,而且
A1 ( Eb1 Eb 2 ) A1 1 12 1 1 A2 1
1
2
③若 1为非凹表面
A1 0 A2
12 1 A1 ( Eb1 Eb 2 )
24
第四章
辐射换热
1
2
三、遮热板
Eb1 Eb 2 Eb1 Eb 2 q12 1 1 1 1 2 1 1 1 1 X 12 2 1 2
4、兰贝特定律 Lambert’s law
黑体的定向辐射强度为常数。
Eb L
9
第四章
辐射换热
§4.3 实际物体的辐射与吸收特性
一、黑度 半球总黑度
E (T ) (T ) Eb (T )
E Eb 0T
4
物体表面的发射率取决于物质种类、表面温度和表面状况。
10
例如：雪对可见光 0.05, 0.95 对红外线
0.95, 0.05
4
第四章
辐射换热
§4.2 黑体辐射的基本定律
一、黑体 1 人工黑体b-black 二、基本概念
1.光谱辐射力
E Eb
W / m3
单位时间内，单位波长范围内(包含某一给定波长)，物体的单 位表面积向半球空间发射的能量。
J1 J 2
1 A1 X 1, 2
Eb
1 A
J1
J1
1 A1 X 1, 2
J2
27
第四章
辐射换热
1 1 1 A1
二、求解步骤
1.画等效网络图 2.列节点方程
E J J J1 J 3 J1 J1 : b1 1 2 0 1 1 1 1 1 A1 A1 X 12 A1 X 13 Eb 2 J 1 J 1 J 2 J 3 J 2 J2 : 0 1 2 1 1 2 A2 A1 X 12 A2 X 23 J3 : Eb1 J1 J1 J 3 J 2 J 3 0 1 3 1 1 A1 X 13 A2 X 23 3 A3
J1
G1
灰表面
J1 E1 1 ( Eb1 J1 ) q1 J1 G1 J1 1 1 1 1
Eb1
Eb1 J1 1 q1 A1 1 1 1 A1
表面热阻
G1
黑表面
23
第四章
辐射换热
3.两灰表面辐射换热 Eb1 Eb 2 12 1 1 1 1 2 1 A1 A1 X 12 2 A2 ①若1为非凹表面
二、角系数的计算
1.积分法 2.查图 3.代数法
14
第四章
辐射换热
角系数性质 （1）相对性（互换性）
A X1, 2 A2 X 2,1 1
（2）完整性 对于封闭系统:
X1,1 X1, 2 X1,3 X1, n X1,i 1
i 1 n
角系数的完整性
（3）可加性 注意：
对于大多数的固体和液体： 0, 1
对于不含颗粒的气体：
0, 1
3
第四章
辐射换热
三、理想物体
1. 黑体
1
镜面反射
2.白体（镜体） 1
漫反射
3.透明体
注意：
1
1.黑体，白体，透明体是对热射线而言的（非可见光） 2. , , 与投入辐射有关。
Eb1
J1
1 A1 X 12
J2
1 2 2 A2
Eb 2
1 A1 X 13
J3
1 A2 X 23
1 3 3 A3
Eb 3
1 3
2
28
第四章
辐射换热
3.求解方程组，得
J1 , J 2 , J 3
4.计算每个表面的净辐射热流量和两表面之间的净辐射热流量
Ji J j Ebi J i i , ij 1 i 1 Ai X ij i Ai
c1
5
式中，λ— 波长，m ；
① 0, , Eb 0
② 0.1~100μm ③T↑, Eb↑
7
第四章
辐射换热
2. 维恩位移定律 Wien’s displacement law
m T 2.9 10 3 m K
如太阳辐射：
m 0.5m
所以太阳表面温度
2.9 10 T 5800 K 6 0.5 10
8
3
第四章
辐射换热
3. 斯忒藩-玻耳兹曼定律Stefan-Boltzman’s law
Eb 0T
4
0 5.67 10 8 W m 2 k 4
T W / m c0 100
2
4
c0 5.67
J2
1 2 2 A2
Eb 2
2.重辐射面（绝热面）
3 Eb 3 J 3 1 3 3 A3
1 A1 X 13
1 A2 X 23
1 3 Eb3 J 3 3 0 3 A3
Eb 3 J 3
仍有３个未知量
J1 , J 2 , J 3
30
第四章
辐射换热
例4.7 ：一房间，地板T1=293K，天花板T2=286K，四周 墙壁绝热，黑度均为0.8。
Eb1
1 1 1 A1
J1
1 A1 X 12
J2
1 2 2 A2
Eb 2
1
2
3
1 A1 X 13
J3
1 A2 X 23
1 3 3 A3
Eb 3
29
第四章
辐射换热
1 1 1 A1
三、 特例
Eb1
J1
1 A1 X 12
J2
1 2 2 A2
Eb 2
1.某一表面为黑表面（３表面）
1
3
2
Eb1
1 1 1 A1
J1
1 A1 X 13
J3
1 3 3 A3
Eb 3
1 3 3 A3
J3
1 A2 X 32
J2
1 2 2 A2
Eb 2
25
第四章
辐射换热
§4.6 多表面系统辐射换热计算