第9章辐射换热的计算
辐射传热的计算

2. 斯狄芬-玻耳兹曼定律(维恩位移定律)
3. 兰贝特定律
4.基尔霍夫定律
基本原理: 1.辐射换热的分析与计算(四大部分)
2.遮热板原理的分析与计算
5.67 (1T010
)4
( T2 100
1 1 1
)
4
B(T14
T24 )
1 2
1 2
有板3时,对稳态有: q1,2’=q1,3=q3,2;其中q1,3=B(T14-T34)
图11 遮热板
q3,2=B(T34-T24);而q1,3+q3,2=B(T14-T34)+B(T34-T24)=B(T14-T24)= q1,2
这些都是用减少发射率(吸收比)的方法来削弱换热的例子。
在实际工程应用中,多采用遮热板来减少辐射换热的方法。
所谓遮热板,是指插入两个辐射换热表面之间以削弱辐射 换热的薄板。
如图11所示
假设 1 2 3 只考虑单位面积
无板3时,
q1,2
(Eb1 Eb2 ) 1 1 1
A11 A1 X1,2 A2 2
2. 三灰表面间的辐射换热
应用电学中的基尔霍夫定律, 可列出节点的热流方程:
J1 :
Eb1 J1
1 1
J2
1
J1
J3
1
J1
0
1 A1
A1 X1,2 A1 X1,3
J2 :
Eb2 J 2
12
J1 J2 1
J3 J2 1
0
辐射能的百分数随之而异,从而
影响到换热量。
传热学-第9章-辐射传热的计算

A2
cos1 cos2 r 2
dA1dA2
X 2,1
1 A2
A1
A2
cos1 cos2 r 2
dA1dA2
则有: A1 X1,2 A2 X 2,1
2
平面1
2
凸面1
3. 角系数的完整性
封闭空腔中: A2 两表面组成封闭空腔:
X1,1 X1,2 1
A1
多表面组成封闭空腔:
Eb 2
1 2
A11 A1 X1,2 A2 2
或:
1,2
(1
A1(Eb1 Eb2 ) 1) 1 A1 (
1
1)
1
X1,2 A2 2
1,2 s A1(Eb1 Eb2 )
系统黑度
两漫灰表面间的辐射换热网络图
Φ 1,2
Eb1
1 1 J1 1
J2 1 2
解:作辅助面A3(非自见面):
A2
A3
则: X1,2 X1,3 , X 2,1 X 2,3
A1
由角系数的相对性: A1 X1,3 A3 X 3,1
得: X1,3
A3 A1
X 3,1
A3 A1
X1,2
X 1,1
1
X 1, 2
1
A3 A1
同理:X 2,3
A3 A2
X 3,2
A11
A1 X1,2
A2 2
节点J3:
Eb3 J 3
13
J1 J3 1
J2
J3 1
0
A3 3
A1 X1,3 A2 X 2,3
3. 求解代数方程组,计算各表面的有效辐射。
《传热学》第9章-辐射换热的计算

J = E + ρG = εEb + (1 − α )G
漫灰表面之间的辐射换热
单位面积的辐射换热量=?
应该等于有效辐射与投入辐射之差
Φ= A
也等于自身辐射力与吸收的投入辐射能之差
J− Φ A
G = εEb
α =ε
− αG
Φ
=
Aε 1−ε
X
1,
2
1 ε1
− 1
+1+
X
2.1
1 ε2
− 1
= ε s A1 X1,2 (Eb1 − Eb2 )
εs
=
X
1,
2
1 ε1
−1 + 1 +
X
2.1
1 ε2
− 1 −1
系统黑度
6
两个漫灰表面构成的封闭空腔中的辐射换热
两块平行壁面构成的封闭空腔
角系数的曲线图
(a)平行的等面积矩形
(c)垂直的两个矩形
2 角系数的性质
(1) 相对性 (2) 完整性
A1 X 1,2 = A2 X 2,1
-互换性
封闭空腔的所有表面的角系数之和等于1
n
∑ X i , j = X i ,1 + X i ,2 +L+ X i ,i +L + X i ,n = 1
j =1
黑体辐射
Lb
=
Eb π
角系数的定义式
∫ ∫ Φ1→2 =
A1
A2
Eb1
cosθ1 cosθ 2 πr 2
传热学 第九章 辐射换热的计算

9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
任意位置的两个黑体表面1、2,从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
9、炉内辐射传热计算解析

(, s) L,s eks
L ,0
(, s) 0
气体的光谱发射率 (, s) 1 eks
第九章 炉内辐射传热计算
二、介质的吸收率和黑度
介质的吸收率
a 1 ekaS
ka炉内辐射介质的吸收衰减系数,m-1;S炉内辐射层有效厚度,m。 对于灰体,介质的黑度等于其吸收率
a 1 ekaS
第九章 炉内辐射传热计算
2
[1
1
syn f
(T2 )4 ] T1
第九章 炉内辐射传热计算
二、炉内传热计算公式
• 辐射传热量
Q R
F
syn
f
0T14
kW
syn f
syn
syn (1 syn)
1
syn
0.32ka R
1
1• 烟气放热量Qre fBcal
(Q
ef f
If )
BcalVCavTth
(1
Tf Tth
气带入的热量)
Q
ef f
Qf
100 q3 q4 q6 100 q4
Qa
kJ / kg
Qa
( f
f
pcs
)
I
0 ha
( f
pcs
)I
0 ca
kJ / kg
引入烟气平均热容的概念计算理论燃烧温度:炉内烟气在理论燃烧 温度至炉膛出口温度区间内的平均热容。
I V (c ),
Q
e f
f
I f
VC av (Tth
T f)
VC
av
Q
ef f
Tth
I f T f
Q
ef f
VC avTth
[工学]第9章 辐射换热的计算备份
![[工学]第9章 辐射换热的计算备份](https://img.taocdn.com/s3/m/3516d9fd7f1922791688e837.png)
根据上图可以很容易写出两表面间的辐射换热量:
1, 2
Eb1 Eb 2 1 1 1 1 2 1 A1 X 1, 2 A1 2 A2
2019/1/29
50-22
网络法求解多表面封闭系统辐射换热步骤: (以三个漫灰表面构成的封闭空腔为例)
A3, T3, ε3
1 3 3 A3
1, 2 2,1
1, 2
Eb1 Eb 2 1 1 1 1 2 1 A1 X 1, 2 A1 2 A2
50-14
2019/1/29
1, 2
Eb1 Eb 2 1 1 1 1 2 1 A1 X 1, 2 A1 2 A2
A1 X 1,2 ( Eb1 Eb 2 )
2019/1/29
可见,黑体系统计算 角系数是关键
50-11
二、 有效辐射(灰体) 为避免多次吸收和反射带来的复杂性,引入有效辐射 投入辐射:单位时间内投射到表面单位面积的总辐射能, 记为G 有效辐射:单位时间内离开表面单位面积的总辐射能, 记为J
J1 E1 1G1 1Eb1 (1 1 )G1
1, 2 J1 J 2 1 A1 X 1, 2
相当于 电势差 相当于 电阻 2 1
2 1 2
50-20
2019/1/29
E J b 1 A
表面辐射热阻
空间辐射热阻
1, 2
J1 J 2 1 A1 X 1, 2
2、网络法求解辐射换热 辐射换热等效单元电路图 Φ
Eb
1 A
2 1
2019/1/29
1 2 1 2
50-13
1,2 A1J1 X1,2 A2 J 2 X 2,1
辐射换热的计算

X d 2 ,1 =
(4) 面对面的角系数
∫A
X d 2,d 1
1
(9-3b)
对面A 的角系数X 以及面A 对面A 的角系数X 面A1对面A2的角系数X1,2以及面A2对面A1的角系数X2,1分 别为
1 cos1 cos2dA dA2 1 1 X1,2 = ∫A ∫A = ∫A ∫A Xd1,d 2dA 1 2 A A πr 1 1
X 1, 2
A1 + A2 A3 = 2 A1
图9-10 三个非凹表面 组成的封闭系统
若系统横截面上三个表面的断面长度分别为l1,l2和
l3,则上式可写为
X 1, 2
l1 + l2 l3 = 2l1
见图9 11, ②交叉线法 见图 9-11, 假设两个 表面垂直于纸面方向很长, 表面垂直于纸面方向很长 , 作辅 助线ac bd,组成封闭腔 则有: ac和 组成封闭腔。 助线ac和bd,组成封闭腔。则有: 根据完整性和上面的公式, 根据完整性和上面的公式,有:
A1
∫
A1
πLb1dA1
∫ ∫ =
A1 A2
Lb1cos1dA2 cos 2 dA1 A1πLb1r 2
1 cos1cos 2 dA2 = ∫ ∫ dA1 2 A1 A1 A2 πr 1 = ∫ ∫ X d 1,d 2 dA1 A1 A1 A2
2. 角系数性质 根据角系数的定义和诸解析式,可导出角系数的代数性质。 根据角系数的定义和诸解析式,可导出角系数的代数性质。 (1) 相对性 由式(8-2a)和(8-2b)可以看出 由式(8-2a)和(8-2b)可以看出 (8
X d 1, d 2
X d 2, d 1
Lb1 cos 1dA1d dA2 cos 1 cos 2 = = E b1dA1 π r2
传热学重点、题型讲解第九章辐射换热计算

第九章 辐射换热计算 第一节 黑表面间的辐射换热一、任意位置两非凹黑表面间的辐射换热1.黑表面间的辐射换热图9-1 任意位置两非凹黑表面的辐射换热122dA dA b1111d d cos d ΦI A θω-= E b1=πI b1; 2221cos d d rA θω=12212dA dA b1122cos cos d d d πΦE A A r θθ-=21212dA dA b2122cos cos d d d πΦE A A r θθ-=12122122212dA ,dA dA dA dA dA b1b2122cos cos d d d ()d d πΦΦΦE E A A r θθ--=-=- 1212122121,2dA ,dA b1b2122cos cos d ()d d πA A A A ΦΦE E A A r θθ==-⎰⎰⎰⎰ (9-1)2.角系数12121122b1122dA dA 12dA ,dA 22dA b11cos cos d d d cos cos πd d d πE A A Φr X A ΦE A r θθθθ-===12122121122dA dA 2dA A 12dA ,A 22dA dA d d cos cos d d d πA A ΦΦX A ΦΦr θθ--===⎰⎰12121211122dA dAA A121,2122A A1dcos cos1d dπA AA AΦΦX A AΦΦA rθθ--===⎰⎰⎰⎰(9-2a)212212AAA1,2ddπcoscos121212AArAΦΦXAA⎰⎰==-θθ(9-2b)21,212,1AXAX=(9-3)3.辐射空间热阻图9-2 辐射空间热阻21,2b2b112,1b2b12,1)()(AXEEAXEEΦ-=-=(9-4)b1b21,21,211E EΦX A-=Φ1,2=(E b1-E b2)A = σb(T14- T24)A二、封闭空腔诸黑表面间的辐射换热图9-3 多个黑表面组成的空腔图9-4 三个黑表面组成空腔的辐射网络图9-5 例9-1附图:,1,2,,1ni i i i n i j j ΦΦΦΦΦ==++⋅⋅⋅⋅⋅⋅=∑将上式除以i Φ,按角系数定义,可得,1,2,n ,11ni i i i j j X X X X ==++⋅⋅⋅⋅⋅⋅=∑(9-5)∑∑∑∑====-=-==nj nj i j i nj i j i i j i nj j i i A X E A X E A X E E ΦΦ11,bj 1,bi ,bj bi 1,)(∑=-=nj j i j i i A X E A E Φ1,bj bi (9-6)【例9-1】∑=-=311,b 1b11j j j j A X E A E Φ (a )∑=-=312,b 2b22j j j j A X E A E Φ (b )0313,b 3b33=-=∑=j j j j A X E A E Φ (c )02,21,22,11,1====X X X X13,23,1==X X31,313,1A X A X =32,323,2A X A X =213,11,33,223/210.252A r X X X A r ππ==⨯==13,32,31,3=++X X X5.03,3=X033,3b323,2b213,1b13b3=---A X E A X E A X E A E4b b T E σ=2424143T T T +=T 3=415.6K 或者142.6℃1b11b11,11b22,12b33,1344b11b31,3111344311b 244()()()100100473415.61 5.67()()1801.0W 2100100b ΦE A E X A E X A E X A E A E X A A T T T T AC σπ=---=-=-⎡⎤=-⎢⎥⎣⎦⎡⎤=⨯⨯⨯-=⎢⎥⎣⎦【讨论】π411212121=+=+=∑A A A A A AR 4444b1b2121,2()π 5.67 4.73 3.13)1801.0W 4/π4b E E T T ΦRσ--===⨯⨯-=∑(第二节 灰表面间的辐射换热一、有效辐射图9-6 有效辐射示意图图9-7 辐射表面热阻1.有效辐射J 1=ε1E b1+ρ1G 1=ε1E b1+(1-α1)G 1 W/m 2(a )2. 辐射表面热阻11b111111G E G J A Φαε-=-= W/m 2 (b ) 1111b11b111111)(1A J E J E A Φεεεε--=--= W (9-7)二、组成封闭腔的两灰表面间的辐射换热图9-8 两个灰表面组成封闭腔的辐射换热网络图9-9 空腔与内包壁面间的辐射换热22212,1111b2b12,1111A A X A E E Φεεεε-++--=W (9-8a ))11(1)11()(2212,112b 1b 12,1-++--=εεA A X E E A Φ 1,2112()W s b b X A E E ε=- (9-8b ))11()11(1121,212,1s -+-+=εεεX X1.无限大平行灰平壁的辐射换热A 1=A 2=A ,且X 1,2=X 2,1=1,)(111)(4241b s 212b b12,1T T A E E A Φ-=-+-=σεεε W (9-9)1121s -+=εεε2.其中一个表面为平面或凸表面的辐射换热)11(1)(22112b 1b 12,1-+-=εεA A E E A Φ W (9-10)A 2 >>A 1,且ε2的数值较大Φ1,2=ε1 A 1(E b1-E b2)W (9-11)三、封闭空腔中诸灰表面间的辐射换热1.网络法求解图9-10三个灰表面组成封闭腔辐射换热网络图9-11 例9-4附图图9-12 例题9-5附图节点1013,11312,1121111b1=-+-+-A X J J A X J J A J E εε (a )节点2 011123,22321,2212222b2=-+-+--A X J J A X J J A J E εε (b )节点3 011132,33231,3313333b3=-+-+--A X J J A X J J A J E εε (c )【例9-4】X 1,2= X 2,1=0.38X 1,3=X 2,3=1-X 1,2=1-0.38=0.62计算网络中的各热阻值:A 1=A 2=π⨯0.32=0.283m 21.14283.02.02.011111=⨯-=-A εε m -23.5283.04.04.011222=⨯=--A εε m -23.9283.038.01112,1=⨯=A X m -27.5283.062.011123,213,1=⨯==A X A X m -2流入每个节点的电流总和等于零07.53.91.141b3121b1=-+-+-J E J J J E 07.53.93.52b3212b2=-+-+-J E J J J E 202447731067.5484b1=⨯⨯==-T E b σW/m 235445001067.5484b2=⨯⨯==-T E b σW/m24593001067.5484b3=⨯⨯==-T E b σW/m 2J 1=5129 W/m 2 J 2=2760W/m 2b1111112024451291072W 114.1E J ΦA εε--===- b22222235442760148W 1 5.3E J ΦA εε--===-312()(1072148)1220W ΦΦΦ=-+=-+=-【例9-5】1.1411111=-=A R εεm -23.512222=-=A R εεm -23.9112,12,1==A X R m -27.5113,13,23,1===A X R R m -2E b1=20244W/m 2 E b2=3544W/m 2∑++++=23,23,12,11111R R R R R R =14.1+5.243.57.57.513.911=+++m -2b1b21,2202443544682W 24.5E E ΦR --===∑J 1=E b1-Φ1,2⨯R 1=20244-682⨯14.1=10627.8 W/m 2J 2=E b2+Φ1,2⨯R 2=3544+682⨯5.3=7185.6 W/m 2J 3=(J 1+J 2)/2=8893.2 W/m 2J 3=G 3=E b3=σ b T 341/41/4b3388893.2629K5.6710b E T σ-⎛⎫⎛⎫=== ⎪⎪⨯⎝⎭⎝⎭2. 值解法图9-13 例9-6(a )(b )附图及其辐射换热网络∑==ni i j i i j j A X J G A 1,j j εα=∑=-+=ni i j i i j j j j j j A X J A E A J 1,b )1(εε(9-12)∑∑===ni i j i j n i i j i i X J A A X J 1,1,b ,1(1)nj j j j i j i i J E J X εε==+-∑(9-13)4b 1,11j j j j jni i j i T J X J σεεε⎥⎥⎦⎤⎢⎢⎣⎡-=--∑=(9-14)4111,121,231,31,b 1114212,122,232,32,b 2221,12,231()()111()()11n n n n n n n J X J X J X J X T J X J X J X J X T J X J X J X εσεεεσεε-+++⋅⋅⋅+=--+-++⋅⋅⋅+=--⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅++4,3,b 1()()11n n n n n n n J X T εσεε⎫⎪⎪⎪⎪⎬⎪⎪⎪+⋅⋅⋅+-=⎪--⎭ (9-15)ii i i i i A J E Φεε--=1b i =1,2,…n (9-16)【例9-6】1,11,21,31,400.150.540.31X X X X ====、、、;2,12,22,32,40.2500.500.25X X X X ====、、、;3,13,23,33,40.270.140.320.27X X X X ====、、、;4,14,24,34,40.310.150.540X X X X ====、、、;4432198.267.5931.054.015.010⨯⨯=---J J J J 4432183.267.5425.05.0525.0⨯⨯=--+-J J J J4432186.267.5427.068.414.027.0⨯⨯=-+--J J J J 4432184.267.55.15.254.015.031.0⨯⨯=+---J J J JJ 1=440.45 W/m 2; J 2=370.28 W/m 2; J 3=382.69 W/m 2 ; J 4=380.80 W/m 2。
辐射换热的计算

角系数的完整性
3、角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
A 1 E b 1 X 1 ,2 A 1 E b 1 X 1 ,2 a A 1 E b 1 X 1 ,2 b
X1,2X1,2aX1,2b
如把表面2进一步分成若干小块,则有
AX AX (1 2 ) (1 2 ) ( ,3 4 )(3 4 )( 3 4 ) ,(1 2 )
A X AX (1 2) (1 2),3 3 3 ,(1 2) A X AX 2 2 ,(3 4 ) (3 4 ) (3 4 ),2
A2X2,3A3X3,2
注:利用这样的分析方法,扩大线图的使用,可以得出很多几何结构简单的角系数
图8-5 三个非凹表面组成的封闭系统
由角系数完整性
X1,2 X1,3 1 X2,1 X2,3 1 X3,1 X3,2 1
由角系数相对性
A1X1,2 A2X2,1 A1X1,3 A3X3,1 A2X2,3 A3X3,2
A1
A2
A3
三表面封闭空间 角系数的确定
上述方程解得: X 1,2
A1 A2 2A1
A3
X 1,3
A1 A3 2A3
A2
X 2,3
A2 A3 2A2
A1
由于垂直纸面方向的长度相同,则有:
X 1,2
l1 l2 2 l1
l3
X 1,3
l1 l3 2 l1
l2
X
2 ,3
l2
l3 l1 2 l2
(2)任意两个非凹表面间的角系数 如图所示表面和假定在垂直于纸面的方向上表面的长度 是无限延伸的,只有封闭系统才能应用角系数的完整性, 为此作辅助线ac和bd,与ab、cd一起构成封闭腔。
第九章 辐射换热计算

即黑体的有效辐射就是黑体的 本身辐射.
二.组成封闭腔的两灰表面间的辐射换热
1,2 A1J1 X1,2 A2 J 2 X 2,1
(J1 J 2 ) X1,2 A1
(J1 J2 ) 1
X1,2 A1
J1
(J1 J2 ) 1
X 2,1 A2 1,2
J2
11 X1,2 A1 X 2,1 A2
X 2,1
1 A2
A1
A2
cos1 cos2 r 2
dA2dA1
A1 X 1,2 A2 X 2,1
角系数互换性
3. 辐射空间热阻
1,2 (Eb1 Eb2 )
A2
A1
cos1 cos2 r 2
dA1dA2
(Eb1 Eb2 ) X1,2 A1
(Eb1 Eb2 ) X 2,1 A2
第九章 辐射换热计算
§9-1 黑体间的辐射换热
一、任意位置两非凹黑体表面间的辐射换热 1.两黑体表面之间的辐射换热
T1
(c) T2
讨论:两黑体表面任意放置,彼此可见
p dA2
由dA1 dA2的辐射能:
dA1dA2 Ib1 dA1 cos1d1
d1
dA2
c os 2
r2
Eb1 Ib1
n2 θ2
解: 这是三个灰表面间的辐射换热问题。因大 房间壁的表面积A3很大,其表面热阻可取为零, 即
13 0 3 A3
J3 Eb3
但3 0
计算网络中的各热阻值:
A1 A2 0.32 0.283 m2
1 1 1 0.2 14.4m2 1A1 0.2 0.283
1 2 1 0.4 5.3m2 2 A2 0.4 0.283
第9章 辐射传热的计算(杨世铭,陶文栓,传热学,第四版,答案)
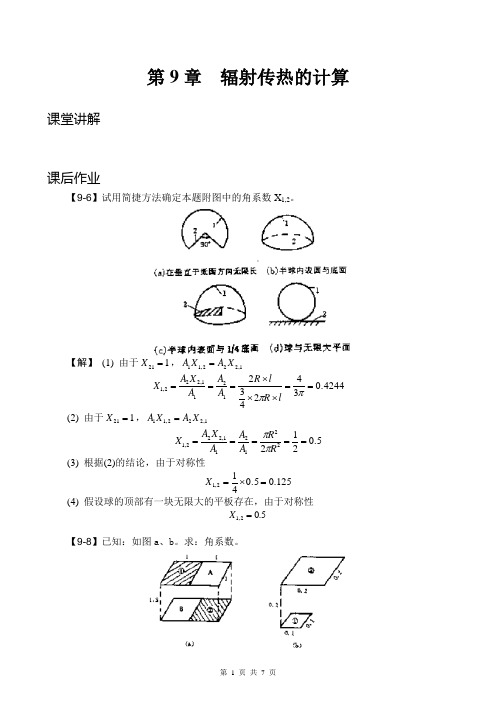
第9章 辐射传热的计算课堂讲解课后作业【9-6】试用简捷方法确定本题附图中的角系数X 1,2。
【解】 (1) 由于121=X ,1,222,11X A X A =0.42443424321211,222,1==⨯⨯⨯===ππl R l R A A A X A X(2) 由于121=X ,1,222,11X A X A =0.5212221211,222,1=====R R A A A X A X ππ (3) 根据(2)的结论,由于对称性125.00.5412,1=⨯=X(4) 假设球的顶部有一块无限大的平板存在,由于对称性0.52,1=X【9-8】已知:如图a 、b 。
求:角系数。
【解】(a) A,2A B A,A 1,21B 1,12B A,1A 1X A X A X A X A X A +++=+++由于对称性,则()1,21B 1,11,21B 1,12B A,1A 1222X A X A X A X A X A +=+=+++。
1A 12A A =+ ,1,2B 1,2B A,1X X X +=∴++B 1,2B A,11,2X X X -=++X =1,Y =2175.01,2=X(b) 扩充图(b),得1'由扩充图可知,2.021,='X ,由于对称性,可得:05.042.04121,1,2==='X X 1,222,11X A X A =2.005.041,21211,222,1=⨯===X A A A X A X【9-18】一管状电加热器内表面温度为900K 、ε=1,试计算从加热表面投入到圆盘上的总辐射能(见附图)。
【解】表面2发出而落到表面1上的辐射能应为2,11b 1X E A =Φ; 按角系数的对称性,1,222,11X A X A =;做虚拟表面3及4,则可有4,21,23,2X X X +=,即4,23,21,2X X X -=,其中3,2X ,4,2X 为两平行圆盘间辐射角系数。
第9章_辐射传热的计算

几何分析法、形状分解法
9.1.1 角系数的定义及计算假定
定义: 表面i发出的辐射能中
落到表面j上的百分数,
称为表面i对表面j的角
系数,记为Xi,j
研究表面是漫射的
1,2
A1 ( Eb1 1 A1
Eb2 ) ( 1 1)
s
A1 ( Eb1
Eb2 )(9
15)
1 A2 2
其中,系统黑度为:
s
1
1 A1 ( 1
1)
2、
A1
1
1(如两无限大平行平板),则有 :
A2
2
A2
1,2
A1 ( Eb1 Eb2 ) (9 16 ) 1 1 1
典型实例: 1 2
例:q、Φ的计算(P408--410)
例9-2:液氮储存容器单位面积散热量q的计算 ——简化成两无限大平行平板处理
例9-3:置于方形砖槽道内的钢管辐射热损失Φ的计算 ——直接用公式(9-15)或近似采用A1/A2≈0 模型
例9-4:圆筒形埋地式加热炉热损失Φ的计算* (同类型问题:热金属板中的孔壁对外辐射)
b.垂直于纸面方向 为足够长
结果: X1,2
A1 A2 A3 2 A1
L1 L2 L3 2 L1
(2)交叉线法
条件:a.二个表面均为非凹 表面;
b.垂直于纸面方向为 足够长
结果:X1,2
(ad
bc) (ac 2ab
bd)
交叉线之和 不交叉线之和 2 表面1的断面长度
3、根据已知几何关系的角系数, 推出其他几何关系 的角系数----也称形状分解法 实例:例题9-1
第9章 辐射换热计算

画热阻网络图
辐射面 吸热面
书P229例9-1
8
重辐射面-----即两重性
从温度上看,可以将其视为黑体;
从能量上看,可以将其当作反射率为1的表面。
所以重辐射表面是在一定条件下的黑体或白体。
因为重辐射面的温度与其它表面的温度不同, 所以重辐射面的存在改变了辐射能的方向分布。重 辐射面的几何形状、尺寸及相对位置将影响整个系 统的辐射换热。
14
三种特殊情形 (1) 表面1为凸面或平面,此时,X1,2=1,于是
1,2 A1 ( Eb1 Eb 2 ) 1 A1 1 1 1 A2 2
T1 4 T2 4 s A1 5.67 100 100
Eb 2 J1 J1 J 2 J 3 J 2 J 4 J 2 0 1 2 1 1 1 2 A2 A2 X 2,1 A2 X 2,3 A2 X 2.4
Eb3 J 3 J1 J 3 J 2 J 3 J 4 J 3 0 1 3 1 1 1 3 A3 A3 X 3,1 A3 X 3,2 A3 X 3,4
2
§9-1 黑表面间的辐射传热
一、任意位置两非凹黑表面间的辐射传热
dA1投射到dA2的辐射能(即dA2吸收的):
A2
2
2
d A2
n1
对于黑体: Eb1 I b1 立体角定义中的面积为与法线垂直的面积 代入得: dA2投射到dA1的辐射能 (即dA2发射的)
1
r
n2
1
dA 1
A 1
任意位置的两表面间的 辐射换热
按电学原理,并联的等效电阻Req为
1 Req 1 1 1 1 1 A1 X 1, 2 A1 X 1,3 A2 X 2,3
传热学第九章辐射换热的计算

遮热罩的热平衡表达式
4 4 2 h T T TT f 3 3 3 2
联立求解以上两式可求得测温误差 Tf T ,结果为 44 K。可见,加 1 遮热罩后,相对测温误差由未加遮热罩的14.4%降低到4.4% 。
i 1 n
图9-2 角系数的完 整性
上式称为角系数的完整性。若表面1为非凹表面时,X1,1 = 0。
(3) 可加性
3 角系数的计算方法
4 求解角系数的方法通常有直接积分法、代数分析法。
(1) 直接积分法 dA1对A2角系数为:
X d 1 , 2
A 2
d 1 , d 2
d 1
9.3
辐射换热应用举例
1、控制表面热阻强化或削弱辐射换热:比如涂层(不同辐射 表面涂层的效果不同,为什么?举例说明); 2、控制空间热阻强化或削弱辐射换热:比如遮热板; 3、遮热板的原理。
遮热板的主要作用就是削弱辐射换热。下面以两块靠得很近
的大平壁间的辐射换热为例来说明遮热板的工作原理。 没有遮热板时,两块平 壁间的辐射换热有 2 个 表面辐射热阻、 1 个空 间辐射热阻。 在两块平壁之间加一块大 小一样、表面发射率相同 的遮热板3 如果忽略遮热板的导热热阻,则总辐射热阻增加了1倍, 辐射换热量减少为原来的1/2,即 12
d 1 , d 2 d 1
A 2
d 1 , d 2 X
A 2
A1对A2角系数为:
1 cos cos d A d A 1 2 1 2 1 X X d A 1 , 2 d 1 , d 2 1 2 A A A A A A r 1 1
1 2 1 2
第九章—辐射换热计算

第九章 辐射换热计算重点:角系数的特点、性质及其计算,表面热阻、空间热阻及有效辐射的概念,两个及多个漫灰表面辐射换热的计算方法,辐射换热的强化与削弱,气体辐射的特点。
影响辐射换热的因素有:表面温度、表面的几何特性(大小、形状)、表面的相对位置,表面的辐射性质。
本章只对黑体表面和漫灰表面作分析。
第一节 黑表面间的辐射换热1-1 任意位置两非凹黑表面间的辐射换热 一、两黑表面间的辐射换热设有两个任意放置的非凹黑体表面,面积分别为1A 、2A ,温度分别为1T 、2T 。
从表面上分别取微元面积1dA 、2dA ,两者的距离为r ,两表面的法线与连线r 间的夹角分别为:1θ,2θ。
微面积1dA 投射到微元面积2dA 的辐射能为:111cos 121ωθd dA I b dA dA ⋅⋅⋅=Φ-黑体服从兰贝特定律:11b b I E ⋅=π ⇒ 21221c o sc o s 121dA dA rE b dA dA ⋅⋅⋅⋅=Φ-πθθ 2221cos rdA d θω=同理,从微面积2dA 投射到微元面积1dA 的辐射能为:21221cos cos 212dA dA r E b dA dA ⋅⋅⋅⋅=Φ-πθθ微面积1dA 和2dA 之间的辐射换热量为:21221cos cos 2121dA dA rE E b b dA dA ⋅⋅⋅⋅-=Φπθθ)(、 黑体表面1A 和2A 之间的辐射换热量为:⎰⎰⎰⎰⋅⋅⋅⋅-=Φ=Φ122112212122121cos cos A A b b A A dA dA dA dA r E E πθθ)(、、二、角系数(angle factor or view factor )角系数:表示一表面发出的辐射能中直接落到另一表面上的百分数。
21、X —称为1A 对2A 的角系数,表示1A 辐射的能量落到2A 上的百分数。
12、X —称为2A 对1A 的角系数角系数中的第一个角码指发射体,第二个角码指受射体。
第九章:炉内辐射传热计算

6. 参数确定
(1)水冷壁结构特性
水冷壁-管中心线所在平面 敷设卫燃带的水冷壁-卫燃带向火侧
有效容积
炉膛的底部-冷灰斗1/2处的水平面面积 炉膛出口-后屏第一排管中心线所在平面 炉膛高度-炉膛底部至炉膛出口中部水平面垂直距离
10
第二节 炉膛传热计算
(1)水冷壁结构特性
包覆有效容积的炉墙面积F
x:角系数 投射到受热面的热量 投射到壁面的热量
第二节 炉膛传热计算
(4)炉膛黑度
含义:表征火焰有效辐射的假想黑度
表达:与火焰黑度εsyn有关
syn f
syn
syn (1 syn )
13
第二节 炉膛传热计算
ka:辐射减弱系数(1/(m·MPa))
(4)炉膛黑度
p:炉膛内压力(0.1MPa)
s:辐射层有效厚度(m)
含义:表征炉内高温介质的辐射能力
100 q3 q4 q6 10膛传热计算
(2)准则方程 辐射传热公式
Q
F
T syn
4
f
01
烟气放热公式
Q
BcalVCav (Tth
T
'' f
)
辐射传热=烟气放热
1=
T1 Tth
"=
f
T
" f
Tth
T1介于 Tth与Tf”之间
1=C1 (
" f
)n
M:经验系数
表达: syn 1 eka ps
火焰 黑度
组成
气体 固体
三原子气体:CO2、H2O、SO2等
二原子气体:N2、O2、H2等
灰分颗粒 燃煤
焦炭颗粒 燃油和燃气:炭黑颗粒
辐射传热的计算

1,2 J1 A1 X1,2 - J 2 A2 X 2,1
1,2 A1 X1,2 J1 - J 2 =A2 X 2,1 J1 - J 2
J1 J 2 J1 J 2 1,2 1 A1 X 1,2 1 A2 X 2,1
类似于欧姆定律,满足势差、阻力和流的关系
A1 X12 =A2 X 21
b(12) A 1 X12 Eb1 Eb2 =A 2 X 21 Eb1 Eb2
第9章 辐射传热的计算
9.1 辐射传热的角系数/角系数的性质
性质2:角系数的完整性
X i ,1 X i ,2
X i ,n
= X i , j
X 1,2
ad bc ac bd
2ab
X 1,2
交叉线长度之和 非交叉线长度之和 2倍表面 1的横断面线段长度
——交叉线法
第9章 辐射传热的计算
9.1 辐射传热的角系数/角系数的计算
第9章 辐射传热的计算
9.2 两表面封闭系统的辐射传热/封闭腔模型
两个黑体表面之间的净换热量
对只有两个黑体表面换热的封闭系统,二者一致 对任意位置的两个表面,二者不相等
“半球空间”概念的引入 “封闭腔模型”的重要性
第9章 辐射传热的计算
9.2 两表面封闭系统的辐射传热/封闭腔模型
封闭腔应包括的表面: ——能接受研究表面发射的 辐射能的其他所有表面
——能将辐射能投射到研究
X12
离开表面1并投落到表面2上的辐射能 离开表面1的总辐射能
同样可定义X2,1
传热学-辐射传热的计算

X1,2
=
A1 + A2 − 2A1
A3
X1,3
=
A1 + A3 − 2A1
A2
X 2,3
=
A2
+ A3 − 2A2
A1
相对性
A1 X1,2 = A2 X 2,1 A1 X1,3 = A3 X 3,1 A2 X 2,3 = A3 X 3,2
三个非凹表面组成的封闭系统
由于垂直纸面方向的长度相同,则有:
从表面内部观察,该表面与外界的辐射
换热量应为: q = E1 − α1G1
J1
=
q
+
E1 − α1
q
=
E1 α1
−
⎛ ⎜ ⎝
1 α1
−
1
⎞ ⎟
q
⎠
注意:式中的各个量均是对
J
=
E α
−1−α α
q
=
Eb
−
(1 ε
−1)q
同一表面而言的,而且以向 外界的净放热量为正值。
9.2.3 两漫灰表面组成的封闭腔的辐射传热
n
∑ Φ1 = Φ1− j j =1
∑ ∑ Φ n 1− j
Φ j =1
1
=
n
x1− j = 1
j =1
X1,1 + X1,2 + X1,3 + + X1,n = 1
9.1.2 角系数的性质
1.角系数的相对性
两个有限大小表面之间角系数的相对性 Φ1,2 = A1 Eb1 X 1,2 − A2 Eb2 X 2,1
E b1 − +1
Eb2 + 1− ε2
ε 1 A1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传热学 Heat Transfer
对于两平行的黑体大平壁(A1=A2 =A),若略 去周边溢出的辐射热量,可以认为: X1, 2= X2, 1=1,
且由斯蒂芬-波尔兹曼定律知Eb=σbT4,此时:
传热学 Heat Transfer
传热学 Heat Transfer
一.积分法
直接用角系数的公式进行积分得出。
X dA1,A2
A2
cos
θ1 π
cos r2
θ
2
dA2
R2 2πxdx
A2 π (R2 x 2 )2
R2 D/ 2
dx 2
0 (R2 x2 )2
D2
4R2 D2
此法太烦,有人做成图表,供查阅P242、243图
三、多个黑体表面间的辐射换热
如图所示为n个黑体表面组成了封闭空腔。 1、封闭空腔某一黑体表面的净换热量:
2、角系数的完整性:
注意: 对于平面或凸表面等于0,对于凹面不等于0。
传热学 Heat Transfer
计算黑表面与所有其他黑表面的辐射换热:
n
n
i i, j (Ebi Ebj ) X i, j Ai
传热学 Heat Transfer
未加遮热板时: 在板间加入遮热板后:
【例9-7】
传热学 Heat Transfer
第三节 角系数的确定方法
漫射表面间的辐射换热计算,必须先要 知道它们之间的辐射角系数。求角系数 的常用方法有: (1)直接积分法 (2)数值计算方法 (3)图解方法 (4)代数方法 (5)几何投影方法(单位球法), 这里主要介绍积分法和代数法。
第九章 辐射换热计算
传热学 Heat Transfer
本章教学内容
9.1 黑体表面间的辐射换热 9.2 灰体表面间的辐射换热 9.3 角系数的确定方法 9.4 气体辐射的特点
传热学 Heat Transfer
第一节 黑表面间的辐射换热
辐射换热的推动力:诸表面之间温度不同
影响辐射换热的因素:物体表面的温度,表面形 状及尺寸,表面间相对位置,表面的辐射及吸收 特性。
面间可以断开,不连接空间热阻。 ⑷若某表面绝热,则其为浮动热势,不与接地相连。
称绝热表面或重辐射面。 ⑸再根据辐射换热热阻网络图进行辐射换热计算。
传热学 Heat Transfer
2、黑体表面辐射换热的计算
⑴两黑体表面:
⑵三个黑体表面:
传热学 Heat Transfer
3、绝热表面
绝热表面又称重辐射表面,是指绝热良好,因而在由 多个表面组成的辐射换热体系中净得失热量为零的表 面。
⑵表面间的换热量:
传热学 Heat Transfer
⑶有效辐射的确定
应用电学的基尔霍夫定律—流入每个结点的电流(即热流)总和 为零,联立求解。
传热学 Heat Transfer
网络法的基本步骤
1) 分析封闭系统组成及各表面性质; 2) 画等效电路图; 3) 列出各节点的热流(电流)方程组; 4) 求解方程组,以获得各个节点的有效辐射; 5) 利用公式 i E1bi计 J算i i 每个表面的净辐
传热学 Heat Transfer
传热学 Heat Transfer
传热学 Heat Transfer
注意:查图时,严格按图示确定X、Y、Z的值。
传热学 Heat Transfer
二.代数法
代数法是以角系数的性质为基础的。
1、角系数的性质
互换性:
完整性:
分解性:(如图所示)
传热学 Heat Transfer
A2 X 2.3 A3 X 3.2
六个方程六个未知数可解
四、封闭空腔网络法
1、封闭空腔网络法
首先所有表面必须形成封闭空腔。
然后根据以下原则绘出辐射换热热阻网络图, 如图所示分别为两个和三个黑体表面组成封 闭空腔时辐射换热热阻网络图。
传热学 Heat Transfer
网络法要点:
⑴每个表面是一个结点,其热势为Eb ⑵每两个表面间连接一个相应的空间热阻。 ⑶若某角系数为0,即空间热阻→∞,则相应两个表
d Φ 2 dA1 dA2
d Φ 2 dA2 dA1
(
Eb1
Eb2
)
cos
1 cos2
πr 2
dA1dA2
Φ1,2
d Φ 2 dA1 ,dA2 A1A2
(Eb1 Eb2 )
A1A2
cos1 cos2
πr 2
dA1dA2
传热学 Heat Transfer
传热学 Heat Transfer
第二节 (漫-)灰体表面间的辐射换热
一、有效辐射及有效投射
(漫-)灰体表面间的辐射换热比较复杂,无论是表面辐射出去 还是投射到表面的能量均包括自身辐射和其他表面辐射的 能量。
为处理问题方便,定义: 有效辐射:离开某表面单位面积上的辐射能量,J,W/m2。 有效投射:到达某表面单位面积上的辐射能量,G,W/m2。 有效辐射把表面的自身发射和对外来投射的反射合并起来考虑。
实用价值:如各种加热炉、工业窑炉,如果炉墙隔热 比较好,就可以近似视为绝热面。
对于有一个重辐射面的三表面辐射换热体系来说,来 自高温表面1的热流必定等于流向低温表面2的热流。 而重辐射表面3的“电位”是“浮动”的,它的数值
取决于左右两个空间热阻的相对大小。
传热学 Heat Transfer
传热学 Heat Transfer
⑴板1的本身辐射
⑵对板1的投入辐射即为板2的有效辐射 ⑶板1的反射辐射 ⑷板1的有效辐射 ⑸板2的有效辐射 ⑹板1、2间的辐射换热量
传热学 Heat Transfer
2、两个以上表面间的辐射换热
以三个漫-灰表面组成封闭空腔为例,其辐射换热热阻网络 如图所示。 ⑴表面的净换热量:
传热学 Heat Transfer
二、表面热阻
1、净辐射换热量
表面有效辐射为:
则该表面净辐射换热量为:
传热学 Heat Transfer
2 表面热阻
对于漫-灰表面,α=ε。合并上述两式,有:
即为表面热阻。 它只与物体表面辐射和吸收特性 有关。图为辐射换热热阻网络图。
传热学 Heat Transfer
从物理本质看,重辐射面本身没有净得失热量, 但是它对整个体系的换热状况产生了明显的影 响。它为1、2两个表面之间的辐射热交换提供 了另一条并联途径。
存在重辐射表面时,辐射换热求解将简化,只 需用热阻串并联的办法就可以解出来。
传热学 Heat Transfer
【例9-1】:有一半球形容器r=1m,底部的圆 形面积上有温度为200℃的辐射表面和温度为 40℃的吸热表面2,它们各占圆形面积之半。1、 2表面均系黑表面,容器壁面3是绝热表面。试计 算表面1、2之间的辐射换热和容器壁3的温度。
传热学 Heat Transfer
遮热板原理
对于两个无限大平面组成的封闭系统,其单位表面积换热量为:
q1,2
σb(T14 T24 ) 11
1
ε1 ε2
现在在两面之间插入一块发射率为ε3 的遮热板, 这样就组成了两个换热系统,如图所示.
传热学 Heat Transfer
稳态时有:
q1,3
分析对象:黑表面、漫-灰表面
实际物体分析中的假定:物体表面⑴为恒温表面; ⑵为漫-灰表面;⑶之间气体为透明体。
辐射换热阻力:空间热阻和表面热阻两大类。
辐射换热计算中最有效、应用最普遍的方法是封 闭空腔网络法。
传热学 Heat Transfer
一、两黑体表面间的辐射换热
非凹黑表面:辐射能量不会被自己吸收,遵循兰贝特定律。
发射面被分解: 受射面被分解:
传热学 Heat Transfer
三、举例
例1:三个非凹表面构成的封闭系统,如图
完整性:
X 1.2 X 1.3 1
X
2.1
X 2.3
1
X 3.1 X 3.2 1
相对性:
A1 X1.2 A2 X 2.1
A1
X
1.3
A3 X 3.1
解:
角系数:
传热学 Heat Transfer
表面1、2之间没有直接辐射换热,仅是依靠绝热表 面3间接地进行辐射换热,其换热量为:
传热学 Heat Transfer
根据辐射换热热阻网络图的特点,存在以下关系:
Eb3 Eb1 Eb2 Eb3
1
1
X 3,1 A3
X 3,2 A3
从而得到容器壁3的温度
到表面2上的百分数。是无量纲量。
角系数的互换性
传热学 Heat Transfer
分析角系数:
仅表示离开某表面的辐射能中到达另一表面的百 分数,而与另一表面的系数能力无关。
是一个纯粹的几何量,仅取决于表面的大小和相 对位置,与辐射物体是否是黑体无关。
前提条件: 物体表面为漫射表面; 物体表面的辐射物性均匀,即温度均匀、发射 率及反射比均匀。
b (T14 T24 )
1 1 1
1 3
q Βιβλιοθήκη 3,2q11,
2
b (T34 T24 )
11 1
3 2
q1,3 q3,2
2 3
q1,2
1 b (T14
2 11
T24 ) 1
1 2
可见,与没有遮热板时相比,辐射换热量减小了一半。当 加入n块与壁面发射率相同的遮热板,则换热量将减少到 原来的1/(n+1)。即遮热板层数越多,遮热效果越好。
