包装盒——长方体和正方体
《包装盒》PPT教学课件(第1课时)

两个正方体拼成一个长方体后,有 2 个面的 8 条棱因为互相重合不 再作数,所以长方体的棱长之和是 12 + 12–8 = 16(条)正方体的棱长 之和,所以正方体的棱长是 3 cm,两个正方体的棱长之和是 72 cm。
随堂小测
1. 判断正误。
(1)长方体每个面有 4 条棱,6 个面共有 24 条棱。 ( ) (2)一个长方体,如果有 2 个面是正方形,那么其他的 4 个面是完全
相同的。 ( ) (3)正方体的 6 个面一定都是正方形。 ( ) (4)正方体是一种特殊的长方体。 ( )
2. 正方体和长方体的关系可以表示为( B. )
正方体 长方体
A.
长方体 正方体
B.
正方体 长方体
C.
3. 在下面的平面图形中找出 6 个面,使它们围成下面的长方体。
2 cm
4 cm
2 cm
4 cm
2 cm
①
②
③
④
2 cm 3 cm
3 cm
1.5 cm
1.5 cm
⑧⑤⑥来自⑦4 cm3 cm
4 cm
规范解答:
这六个面是( ①②④⑤⑥⑧ )。
课后作业 对应的本节课后练习题
包装盒——长方体和正方体
第1课时
-.
情境导入
长方体有哪些特征? 你能提出什么问题? 正方体有哪些特征?
长方体有6个面,它们是长方形(有 时有两个相对的面是正方长形方)体,相对的
面…完…全相同。正方体是特殊的长方体。 长方体有8可个以顶用点,右1图2条表棱示,正按方长度体
可以分成3组,和相长对方的4体条正的棱方关长…体度…系相。等。
顶点
长正两线三点相点长作宽正的方方个叫条叫交的度长、方长正形正度体体面作棱作于三,方高方。方都体相相一条分棱顶。体体相相正长6的交交个棱别。点有有等对个。6方正正是8长的的顶的叫。个的个面面体方方 特、顶完2,有形体 殊点个全它面、哪的是与面们相12是些长特长完同条完全特方殊方棱全,相征体的体相每同同?呢长有条的棱?方什棱面相 的 1长我形么2对 长 度条们,联的 度 都棱正整系棱相 相的4理方与条等 等一体区长棱棱下是别。不?
五年级上册《第三单元 包装盒——长方体和正方体》单元测试卷及答案
五年级上册《第三单元包装盒——长方体和正方体》单元测试卷及答案一、选择题(共5题,共计20分)1、用1000个小正方块拼成一个大正方体,如果拿走顶点处的一个小正方块,它的表面积与原来相比()。
A.增加了B.减少了C.不变D.无法确定2、一个菜窖能容纳6m3白菜,这个菜窖的( )是6m3。
A.体积B.容积C.表面积3、如下图,不能围成正方体的是().A. B. C. D.4、体积是()A.105B.108C.110D.1205、一个玻璃鱼缸,装满水后水是50升,这个鱼缸的()是50升。
A.体积B.重量C.容积二、填空题(共8题,共计24分)6、用一根长132厘米的铁丝围成一个正方体的模型,棱长应是________厘米,如果围成一个长方体的模型,长、宽、高的和是________厘米。
7、用一根长96厘米的铁丝焊成一个最大的正方体框架,再糊上纸做成正方体,则这个正方体的表面积是________,体积是________.8、把一个棱长2分米的正方体分成两个相同的长方体,每个长方体的体积是________立方分米,表面积是________平方分米。
9、一个长方体木块,高2.4cm,平行于底面截成两个长方体后,表面积比原来增加了100cm2。
原长方体木料的体积是________ cm3。
10、如图:从一张长方形纸剪下一个正方体的展开图,做成一个纸盒。
这个纸盒的表面积是________平方厘米。
这张长方形纸的面积是________平方厘米。
11、用铁丝焊接一个长方体框架,同一个顶点的三根铁丝分别长15cm、12cm、6cm,焊接这个长方体框架一共用________cm铁丝(接头处忽略不计)。
12、一间教室的长是8米,宽是7米,高是3.5米。
要粉刷教室的屋顶和四面墙壁,除去黑板和门窗的面积24.8平方米,需要粉刷的面积是________平方米.13、一个长方体长8厘米,宽6厘米,高4厘米,体积是________立方厘米.一个长方体长20分米,宽和高都是5分米,体积是________立方分米.三、判断题(共4题,共计8分)14、一个玻璃容器的体积与容积相等。
青岛版六三制五年级下册数学单元测试卷第七单元 包装盒——长方体和正方体(含答案)

五年级下册数学单元测试卷-第七单元包装盒——长方体和正方体-青岛版六三制(含答案)一、选择题(共5题,共计20分)1、做一个长方体纸盒,需要多少硬纸板,是求长方体的()。
①体积②容积③表面积A.体积B.容积C.表面积2、一个长4dm宽3dm,高5dm的长方体鱼缸,倒入水后量得水深3.5dm,倒入的水是()L。
A.60B.52.5C.423、用一根60cm长的铁丝,可以焊成长8cm,宽4cm,高( )cm长方体框架。
A.2B.3C.4D.54、长方体的6个面()。
A.一定都是长方形B.一定都是正方形C.可能有长方形也可能有正方形5、用棱长1cm的小正方体拼成一个稍大的正方体,至少要用()个小正方体。
A.4B.8C.16二、填空题(共8题,共计24分)6、一个正方体的棱长之和为48dm,它的表面积是________,它的体积是________.7、如图,在一个长15cm,宽10cm,水面高度为10cm的长方体容器中,放入一个西红柿后(完全浸没),水面高度上升到12cm(没有溢出).西红柿的体积是________cm3.8、食堂的张师傅把4升油平均装进8个油壶里,平均每个油壶装________毫升。
9、把一个正方体木块锯成两个完全一样的长方体,结果表面积增加了32厘米2,原正方体木块的表面积是________,体积是________。
10、一块长方体蛋糕长4dm,宽3dm,厚0.9dm。
小明把它平均分成6块长方体形状的小蛋糕,每块小蛋糕的体积是________。
11、棱长总和为60厘米的正方体的表面积是________平方厘米,体积是________立方厘米。
12、用60分米的铁条焊成一个正方体的框架,那么这个正方体的棱长是________厘米。
13、正方体的棱长扩大3倍,棱长和扩大________倍,表面积扩大________倍,体积扩大________倍。
三、判断题(共4题,共计8分)14、棱长为6cm的正方体.它的表面积和体积相等。
《包装盒———长方体和正方体的认识》一等奖创新教案

《包装盒———长方体和正方体的认识》一等奖创新教案创新教案:包装盒,长方体和正方体的认识教学目标:1.认识长方体和正方体的概念及特点。
2.了解长方体和正方体在包装行业中的应用。
3.培养学生观察、分析和解决问题的能力。
教学准备:1.教师准备长方体和正方体的实物模型或图片。
2.学生准备笔和纸。
3.教师准备一个包装盒的实物。
教学过程:Step1:导入(5分钟)教师出示一个包装盒,让学生观察并回答以下问题:1.这是什么东西?2.它的形状是什么样的?3.你们家里有类似的东西吗?教师引导学生注意到包装盒是一个长方体的形状。
Step2:认识长方体和正方体(10分钟)教师出示长方体和正方体的实物模型或图片,并进行解释:长方体:有6个面,每个面都是一个矩形,相邻的面彼此平行且相等。
正方体:有6个面,每个面都是一个正方形,相邻的面彼此平行且相等。
教师和学生一起讨论并总结长方体和正方体的特点。
Step3:观察、测量和比较(15分钟)教师在班里找一些包装盒,让学生每人拿到一个,然后对包装盒进行观察。
学生注意以下内容:1.包装盒的形状是长方体还是正方体?2.包装盒的长、宽、高分别是多少?3.包装盒的长、宽、高之间有什么关系?学生测量各自包装盒的长、宽、高,并将数据记录下来。
Step4:数据整理和归纳(15分钟)学生将测得的数据整理到表格里,并进行讨论和比较。
学生注意到包装盒的长、宽、高都是相互平行且相等的。
教师引导学生总结:包装盒是一个长方体或正方体,它的长、宽、高是相互平行且相等的。
Step5:包装盒的应用(10分钟)教师出示一些包装盒的实物或图片,并让学生观察。
学生讨论并回答以下问题:1.你们发现了哪些包装盒?2.这些包装盒有哪些特点?3.为什么包装盒大多是长方体和正方体的形状?教师引导学生思考和讨论包装盒为什么多是长方体和正方体的形状,以及长方体和正方体在包装行业中的应用。
Step6:创意设计(20分钟)教师告诉学生今天的最终任务是设计一个自己的包装盒。
五年级上册数学2.包装盒-长方体和正方体测试卷 青岛版五四制_含答案

五年级上册数学单元测试-2.包装盒-长方体和正方体一、单选题1.长、宽、高分别是9cm,8cm,7cm的长方体的表面积()棱长是9厘米的正方体表面积.A. 小于B. 大于C. 等于2.要做一个无盖的长方体玻璃鱼缸,长60厘米,宽50厘米,高40厘米,至少要用( )平方厘米的玻璃。
A. 14800B. 11800C. 128003.一根长方体木料锯下10厘米长的一段后,正好剩下一个棱长3厘米的正方体.原来这根木料的体积是()A. 27立方厘米B. 117立方厘米C. 2197立方厘米4.将一块正方体形状的橡皮泥捏成长方体,长方体和正方体()A. 体积相等,表面积不相等B. 体积不相等,表面积相等C. 体积和表面积都相等D. 体积和表面积都不相等5.表面积是24平方厘米的正方体,体积是( )立方厘米。
A. 4B. 8C. 246.一个长方体,长、宽、高都扩大为原来的2倍,它的()扩大为原来的8倍.A. 表面积B. 体积C. 棱长和7.用一根60cm长的铁丝,可以焊成长8cm,宽4cm,高( )cm长方体框架。
A. 2B. 3C. 4D. 5二、判断题8.如果一个长方体和一个正方体的棱长之和相等,那么它们的表面积一定相等。
9.正方体的12条棱都相等。
10.一个长方体的长,宽,高都扩大2倍,它的表面积就扩大8倍。
11.将8个棱长是1厘米的小正方体拼成一个大正方体,拼成的大正方体的表面积是24平方厘米。
12.一个长方体,长、宽、高都扩大2倍,体积也扩大2倍三、填空题13.在横线上填充.表面积和体积的计算方法不同.如计算正方体的表面积是:________×________×6.计算正方体的体积是________×________×________14.正方体的棱长之和是36厘米,正方体的表面积是________平方厘米,体积是________立方厘米.15.一个正方体的棱长之和是48分米,它的体积是________立方分米.16.一块砖长24厘米,宽1.2分米,厚6厘米,它的体积是________立方分米17.挖一个长和宽都是5m的长方体水池,要使水池的容积是50m3,应该挖________米深。
五年级数学下册第7单元包装盒__长方体和正方体第2课时长方体和正方体的表面积青岛版六三制

长方体的表面积 =(长×宽+长×高+宽×高)×2
合作探索
归纳总结:
长方体的表面积=长×宽×2+长×高× 2+宽×高×2或长方体的表面积=(长×宽+长×高+宽× 高)×2
5cm
合作探索
做一个化妆品盒子至少需要多少平方厘米纸板?
7 包装盒——长方体和正方体
第2课时 长方体和正方体的表面积
情景导入
5cm 30cm
50cm 5cm
制作这样一个电 脑包装箱至少需 要多少平方厘米 纸板?
做一个化妆品盒 子至少需要多少 平方厘米纸板?
从根图据中这,些你信能息知,道你哪能些提数出学包装箱至少需要多少平方厘米纸板?
前、后面: 50×30×2 = 3000(平方厘米) 左、右面: 20×30×2 = 1200(平方厘米) 上、下面: 50×20×2 = 2000(平方厘米)
总 面 积: 3000+1200+2000 = 6200(平方厘米)
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2
先求前面、右面和上面3个面的面积之和。 (50×30 + 20×30 + 50×20)× 2
合作探索
制作这样一个电脑包装箱至少需要多少平方厘米纸板?
先求前面、右面和上
30cm
面3个面的面积之和。
(50×30 + 20×30 + 50×20)× 2
50cm
=(1500 + 600 + 1000)×2 =3100×2 = 6200(平方厘米)
答:至少需要6200平方厘米的纸板。
青岛版6年制数学五年级下册《七、包装盒——长方体和正方体》练习题含答案
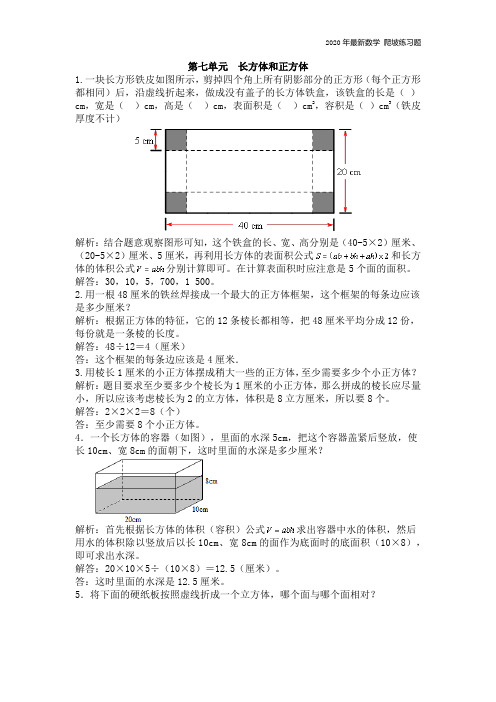
第七单元长方体和正方体1.一块长方形铁皮如图所示,剪掉四个角上所有阴影部分的正方形(每个正方形都相同)后,沿虚线折起来,做成没有盖子的长方体铁盒,该铁盒的长是()cm,宽是()cm,高是()cm,表面积是()cm2,容积是()cm3(铁皮厚度不计)解析:结合题意观察图形可知,这个铁盒的长、宽、高分别是(40-5×2)厘米、(20-5×2)厘米、5厘米,再利用长方体的表面积公式和长方体的体积公式分别计算即可。
在计算表面积时应注意是5个面的面积。
解答:30,10,5,700,1 500。
2.用一根48厘米的铁丝焊接成一个最大的正方体框架,这个框架的每条边应该是多少厘米?解析:根据正方体的特征,它的12条棱长都相等,把48厘米平均分成12份,每份就是一条棱的长度。
解答:48÷12=4(厘米)答:这个框架的每条边应该是4厘米.3.用棱长1厘米的小正方体摆成稍大一些的正方体,至少需要多少个小正方体?解析:题目要求至少要多少个棱长为1厘米的小正方体,那么拼成的棱长应尽量小,所以应该考虑棱长为2的立方体,体积是8立方厘米,所以要8个。
解答:2×2×2=8(个)答:至少需要8个小正方体。
4.一个长方体的容器(如图),里面的水深5cm,把这个容器盖紧后竖放,使长10cm、宽8cm的面朝下,这时里面的水深是多少厘米?解析:首先根据长方体的体积(容积)公式求出容器中水的体积,然后用水的体积除以竖放后以长10cm、宽8cm的面作为底面时的底面积(10×8),即可求出水深。
解答:20×10×5÷(10×8)=12.5(厘米)。
答:这时里面的水深是12.5厘米。
5.将下面的硬纸板按照虚线折成一个立方体,哪个面与哪个面相对?解析:通过实验可以看到带有标号的面7与10,面8与11,面9与12是相对的面。
解答:面7与10,面8与11,面9与12是相对的面。
五年级下册数学教案-七 包装盒——长方体和正方体-青岛版.doc

五年级下册数学教案-七包装盒——长方体和正方体-青岛版教学目标1.了解长方体和正方体的形状和特点。
2.能够正确地计算长方体和正方体的表面积和体积。
3.能够合理地选择包装盒,计算出所需的纸张面积。
教学重点1.长方体和正方体的表面积和体积的计算。
2.包装盒的选择和计算。
教学难点1.包装盒的不同形状对纸张面积的影响的计算。
2.运用所学知识解决实际问题。
教学过程导入活动用四根木棒和六个饼干,分别搭成一个长方体和一个正方体。
让学生观察并描述两种图形的特点。
新课呈现1.展示长方体和正方体的图片,讲解两种图形的特点,并介绍表面积和体积的概念和计算公式。
2.让学生在小组内利用套形体的方法,自行制作长方体和正方体的模型,并测量它们的长、宽、高,然后计算出它们的表面积和体积。
3.讲解包装盒的不同形状对纸张面积的影响,并引导学生讲述自己在买包装盒时遇到的问题。
4.设计一个情境:学校要将一些书籍用包装盒装起来,让学生合理地选择包装盒和计算所需的纸张面积,然后在课堂上进行演示。
练习活动1.让学生互相检查自己制作的模型的表面积和体积,帮助彼此发现和纠正错误。
2.给学生一组数据,让他们自己选择合适的包装盒,并计算出所需的纸张面积。
总结归纳让学生自己总结今天学到的知识,比如长方体和正方体的特点和计算公式,包装盒的形状对纸张面积的影响以及如何合理地选择包装盒。
作业布置布置作业:练习册10页,11题。
要求学生识别图形并计算出表面积和体积,并在完成作业后将答案与大家分享。
常见问题解答Q: 如何判断一个图形是长方体还是正方体?A: 长方体的形状非常长,而正方体的形状则非常正方形。
一个图形的长、宽、高相等时,就是一个正方体;否则就是一个长方体。
Q: 如何计算包装盒需要的纸张面积?A: 首先需要测量出包装盒的长、宽、高。
然后按照包装盒的不同形状选择合适的计算公式进行计算。
最后将表面积相加,得出需要的纸张面积。
参考资料1.《新版小学数学课程标准实验教材》(人教版)2.《青岛版小学数学》五年级下册。
五年级上册数学课件 三 包装盒——长方体和正方体|青岛版(五年制) (共19张PPT)

寻找方法
切一切、摆 一摆、数一 数、算一算。
归纳结论
猜想、验证、总 结体积公式: v=abh
返回
解决问题、解释应用
运用公式求出长方体的 体积,解决求饮料箱体 积的问题。
产生新问题
是不是所有立方 体的体积都等于 底面积乘高。
三、综合应用
1.填一填。 3m2=( 300 )dm2 5000cm2=( 50 )dm2 0.05m3=( 50 )dm3=( 50000 )cm3 3560mL=( 3.56 )L=( 3.56)dm3 0.32m3=( 320 )L
二、系统梳理
意义
长 方 体 长方体 或正方 体6个面 的总面 积,叫 做它的 表面积。 正 方 体
返回
长方体和正方体的表面积
展开图
计算方法
上 后 下 前
长×宽×2+长×高×2+宽×高×2 (长×宽+长×高+宽×高)×2
后 左 下 右上
前
棱长×棱长×6 或棱长2×6
二、系统梳理
长方体和正方体的体积和容积
正方体
长方体
返回
二、系统梳理
长方体和正方体的特征
名称 个数
面
形状
长方体
正方体
6个
6个
6个面都是长方形(可能有 两个相对的面是正方形), 相对的面完全相同。
6个面都是正 方形,6个面 完全相同。
条数 棱
长度
顶点返回个数 Nhomakorabea12条
相对的4条棱长度相等(可 能有8条棱长度相等)
8个
12条
12条棱长 度相等
8个
意义
常用单位
单位间的关系
物体所占空间 计量体积要用体积单位。常用 1立方米=1000立方分米 体 的大小,叫做 的体积单位有:立方厘米、立 1立方分米=1000立方厘米 积 物体的体积。 方分米和立方米,可以分别写
《包装盒——长方体和正方体》 学习任务单

《包装盒——长方体和正方体》学习任务单一、学习目标1、理解长方体和正方体的特征,包括面、棱、顶点的数量和特征。
2、掌握长方体和正方体的表面积和体积的计算方法。
3、能够运用所学知识解决与包装盒相关的实际问题,如设计合适的包装盒尺寸以节省材料。
4、培养空间想象力和逻辑思维能力,提高对数学在实际生活中应用的认识。
二、学习内容1、长方体和正方体的认识长方体的面:一般为长方形(特殊情况下有两个相对的面是正方形),相对的面面积相等。
正方体的面:都是正方形,且面积都相等。
长方体和正方体的棱:相对的棱长度相等。
顶点:长方体和正方体都有 8 个顶点。
2、表面积的计算长方体的表面积=(长×宽+长×高+宽×高)× 2正方体的表面积=棱长×棱长× 63、体积的计算长方体的体积=长×宽×高正方体的体积=棱长×棱长×棱长4、实际应用如何根据物品的尺寸选择合适的包装盒,以达到节省空间和材料的目的。
计算包装盒所需材料的面积和体积,考虑材料的厚度等实际因素。
三、学习资料1、教材相关章节:详细介绍长方体和正方体的概念、性质及应用。
2、在线课程:通过网络平台搜索相关的数学课程视频,加深对知识点的理解。
3、数学辅导书籍:提供更多的例题和练习题,巩固所学知识。
四、学习方法1、观察法:通过观察实际的长方体和正方体物体,如纸盒、魔方等,直观地理解其特征。
2、实践操作:动手制作长方体和正方体模型,亲身体验面、棱、顶点的特点。
3、计算练习:通过大量的练习题,熟练掌握表面积和体积的计算方法。
4、案例分析:分析实际生活中的包装盒案例,将理论知识应用于实际问题的解决。
五、学习活动1、观察身边的长方体和正方体物品,记录它们的尺寸,并计算表面积和体积。
2、小组合作,设计一个包装盒,要求满足一定的物品存放需求,并计算所需材料的面积和体积。
3、参加线上或线下的数学讨论活动,分享自己在学习过程中的心得和疑惑。
包装盒长方体和正方体的体积

长方体的底面积=_长__×_长
正方体的体积=_棱__长__×__棱__长__×_棱__长_
正方体的底面积=_棱__长__×__棱__长___
长方体(正方体)的体积=____底__面__积__×__高___
V=Sh
0.06平方米
一根长方体木料,长5米,横截面的面积
是0.06平方米。这根木料的体积是多少?
20×4×5 =400(m³)
36.8×18.9×9.3
7.3×4×22
642.4cm³=642.4毫升
=29.2×22 =642.4(cm³)
答:这桶清洁剂 有642.4毫升。
4000 0.85 2.78
1400 0.045
2170
96(8×8) = 96÷ 64 =1.5(m)
答:这个沙雕底 座的高是1.5米。
七 包装盒
方法一:切成小 正方体数一数
方法二:用小正 方体摆一摆。
表示高的数,除了表示3厘米 高3 高外,还表示出摆了3层.
表示宽的数,除了表示2厘米
宽2 宽外,还表示出摆了2排.
长6
表示长的数,除了表示6厘米长外,还表 PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ PPT论坛: 语文课件:/kejian/yuw en/
地理课件:/kejian/dili/
历史课件:/kejian/lish i/
示出一排摆了6个1厘米的正方体.
一排摆出6个1厘米的正方体 一共摆了2排
一共摆3层
长/厘米 宽/厘米 高/厘米 体积/厘米
6×2 × 3=
36
长方体的体积正好等于它的长、宽、高的乘积.
五年级上册数学单元测试卷-第三单元 包装盒——长方体和正方体-青岛版五四制(含答案)

五年级上册数学单元测试卷-第三单元包装盒——长方体和正方体-青岛版五四制(含答案)一、选择题(共5题,共计20分)1、将三个完全一样的正方体拼成一个大长方体之后,表面积()。
A.不变B.增加了C.减少了D.无法判断2、把一个棱长为4dm的正方体,切成两个相同的长方体,表面积()。
A.减少了16dm 2B.增加了16dm 2C.增加了32 dm 23、如图,将纸片折起来可以做成一个正方体,这个正方体6号面的对面是()号面。
A.2B.3C.4D.54、一个长方体中有4个面相同,那么其余的两个面()。
A.一定是长方形B.一定是正方形C.可能是长方形或正方形5、一个棱长是4cm的正方体,把它锯成3个相等的长方体,表面积增加了()cm2。
A.16B.32C.64二、填空题(共8题,共计24分)6、挖一个长50米,宽40米,深2米的长方体蓄水池,占地面积是________平方米,如果在它的四壁和底面抹水泥,抹水泥的面积是________平方米,最多能容纳________立方米的水.7、一瓶娃哈哈饮料的净含量是150毫升,________瓶饮料最接近1升。
8、一个长方体长、宽、高分别扩大4倍,表面积扩大________倍。
9、五(3)中队计划选举中队长,他们做了一个棱长为40m的正方体投票箱,现在要在投票箱的每条棱上粘贴胶带纸,一共需要________ cm胶带纸。
10、看图计算长方体、正方体的表面积________.(单位:厘米)11、在长方体中,两个面相交的边叫做棱.长方体有________条棱,一组相对的________条棱的长度________.12、一个长方体,长、宽、高分别是8cm、7cm和5cm,从中截去一个最大的正方体后,剩下的体积是________.13、一个棱长为2cm的正方体,如果把它的棱长扩大到原来的4倍,那么它的表面积扩大到原来的________倍,体积扩大到原来的________倍.三、判断题(共4题,共计8分)14、正方体、长方体、圆柱体、圆锥的体积都等于底面积乘高.()15、可以围成一个正方体。
七 包装盒——长方体和正方体

七包装盒——长方体和正方体长方体的6个面中,相对的两个面完全相同。
长方体的摆放方式不同,长、宽、高也不同。
正方体是特殊的长方体。
计算长方体某个面的面积时,注意根据相对的4条棱的长度相等,把长方体的长、宽、高对应到要计算的面上。
对于看不到的面要利用“相对的两个面完全相同”转化到能看到的面上。
1分米=10厘米,两个正方体的棱长相等,体积就相等。
棱长是10厘米的正方体里有10×10×10=1000(个)棱长为1厘米的正方体,棱长是10厘米的正方体,体积是1000立方厘米。
1.立方分米........立方厘米....=.1000用同样的方法可推出:1.立方米........立方分米...=.10002.容积及容积单位之间的进率(1)容积的意义:容器所能容纳物体的体积,叫作它们的容积。
(2)容积单位有升和毫升,分别用字母L和mL表示。
计量物体的大小一般用体积单位,计量液体的体积常用容积单位。
(3)1.立方分米....毫...1.升.=.1000....=.1.升.1.立方厘米....=.1.毫升升.四、长方体和正方体的体积1.推导体积公式(1)计算一个物体的体积的大小,就要看这个物体含有“体积单位”的数量。
把上图中的长方体和正方体切成以1立方厘米为体积单位的小正方体,数出含有“体积单位”的数量就知道了它们的体积大小。
(2)通过切割发现,长方体所含小正方体体积单位的个数,同它本身的长、宽、高有一定关系,每排小正方体的个数相当于长方体的长;排数相当于长方体的宽;层数相当于长方体的高。
所含体积单位的个数正好等于长方体长、宽、高的积。
2.长方体、正方体的体积公式长方体的体积.....。
......:.V=abh ......=.长.×.宽.×.高.,.用字母表示正方体的体积..,.用字母表......×.棱长..×.棱长......=.棱长示.:.V=a...3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体和正方体的认识
教学目的:
1、让学生通过动手、观察、合作、交流等活动认识长方体、正方体,知道长方体和正方体的面、棱、顶点以及长、宽、高〔或棱长〕的含义,掌握长方体和正方体的根本特征。
理解长方体和正方体之间的关系。
2、〔1〕学生在观察与操作中掌握长、正方体的特征,在活动中进步学生的理论才能。
〔2〕学生在观察、比拟、发现长方体、正方体间的联络与区别。
3、让学生体会立体图形学习与实际生活的严密联络,感受其价值,增强数学学习的兴趣和团结合作的才能。
教学重、难点
认识长方体、正方体的面、棱的特征,并理解长方体、正方体间的联络与区别。
教学具准备:
老师:课件、长方体模型、正方体模型、表格
学生:长方体和正方体实物
教学过程:
一、创设情境,激发兴趣。
今天这节课我们就来认识长方体和正方体。
(板书课题)
师:请同学们来回忆:我们在生活中见过哪些物体的形状类似于长方体或正方体?
二、引导探究,理解新知
〔一〕初步感知,建立表象
1、整体认识长方体的面、棱、顶点。
引导学生看一看、摸一摸、说一说等,同时结合电脑演示去初步感知。
〔1〕师:看老师手里的这个图形,他是什么图形?〔长方体〕你先看到的是什么?〔面〕
请你用手摸一摸,有什么感觉?〔平平的〕介绍长方体上平平的局部叫作长方体的面。
(2)师边指边说:长方体两个面相交的局部叫做长方体的棱。
请你找出长方体的棱。
(3)指导学生观察:三条棱相交的地方叫作长方体的顶点。
用手摸摸看。
〔二〕探究长方体的特征
1、独立观察、小组合作探究长方体特征。
师:刚刚我们认识了长方体的面、棱和顶点,如今小组合作:
小组合作要求:以小组为单位,通过看一看,摸一摸,数一数,量一量,想一想等活动,自主研究长方体的体征,并完成灰白单一。
温馨提示:同学们,在数长方体的面、棱、顶点的数目时,不要拿着长方体乱转,要想一想怎样数比拟好,不重复,不遗漏。
〔老师巡视指导学生观察〕
2、汇报交流,归纳长方体的特征。
〔课件一步步出示问题及答案〕在汇报交流时注意:
(1)引导学生按照一定顺序数面、棱、顶点的个数。
在数棱的数目时,假如学生不理解相对的棱,老师要引导学生认识相对的棱。
(2)学生介绍长方体面及棱的特征后老师分别再用课件演示加深理解。
〔3〕让学生指一指特殊的长方体中哪些面是一样的,哪些棱的长度相等。
3、拿出学具按照表格中的问题完好说一说长方体的特征。
4、师小结:通过刚刚的观察、探究,我们知道长方体是由6个长方形,特殊情况有两个相对的面是正方形围成的立体图形,在一个长方体中,相对的面完全一样,相对的棱长度相等。
〔三〕认识长方体的长、宽、高。
长方体的棱可以分为几组?每组有几条?每一组棱的长度怎么样?
生1:长方体的12条棱可以分成3组,每组4条,每一组棱的长度都相等。
生2:我们分为4组,相交于一个顶点的3条棱为一组。
2、认识长、宽、高。
〔1〕师:通过刚刚的动手操作,我们把12条棱有分为了3组,每组4条,他们的长度相等;
有分为4组,相交于一个顶点的3条棱为一组,他们的长度不相等。
〔2〕师:像这样相交于同一个顶点的三条棱的长度,分别叫做长方体的长、宽、高。
习惯上,把面向我们程度的棱称为长,左右的棱称为宽,竖着的棱称为高。
3、认识不同位置放置的长方体的长、宽、高。
横着、竖着、侧着摆放长方体框架,分别让学生指它的长、宽、高。
〔四〕探究正方体,发现它的特征
师:想一想:假如将长方体的长、宽、高调整,使长、宽、高相等,会
得到什么形体呢?〔老师演示将长方体变成一个正方体〕它也叫立方体。
它有什么特征呢?〔出示自学提纲〕:
1、正方体有几个面?大小怎样?
2、正方体有几条棱?长短有什么关系?
3、正方体有几个顶点?
请同学们带着这几个问题,自主研究正方体的体征,并完成汇报单二。
拿出学具按照表格中的问题完好说一说正方体的特征。
〔五〕、引导辨析,掌握本质
1.认识长方体、正方体的关系
多媒体动态演示,比拟分析。
提醒出长方体和正方体的内在联络,得出:正方体是特殊的长方体。
三、稳固练习,拓展进步〔电脑出示〕
四、全班小结:这节课,你有哪些收获?〔知识、学法、兴趣〕
五、板书设计
长方体和正方体
长方体正方体
面 6个 6个
都是长方形〔特殊都是正方形
时2个向对面是正方形〕 6个面完全一样
向对面完全一样
棱 12条 12条
分为三组,每组长度 12条棱长度都相等
都相等
顶点 8个 8个。
