第三章 量子力学初步 - 山东大学
《原子物理学》(褚圣麟)第三章 量子力学初步

波程差:
n 2 d sin ( 2 n 1) 2
当 2 d sin n 时加强----布拉格公式。
第3章 量子力学初步
可见,当、满足此式时,测得电流的极大值。
对于通过电压V加速的电子:
1 . 225 nm V ( 伏特 )
n 1, 2
第3章 量子力学初步
1.实验装置
第3章 量子力学初步
2.实验结果 (1)当V不变时,I与的 关系如图 不同的,I不同;在有 的上将出现极值。
(2)当不变时,I与V的 关系如图 当V改变时,I亦变;而 且随了V周期性的变化
V
第3章 量子力学初步
3.实验解释 晶体结构:
第3章 量子力学初步
又
d
2x
p x p
2x
2x p x p h
x p x h / 2
x p x h / 2
第3章 量子力学初步 狭缝对电子束起了两种作用:一是将它的坐标限制在缝 宽d的范围内,一是使电子在坐标方向上的动量发生了 变化。这两种作用是相伴出现的,不可能既限制了电子
p / 2
E t / 2
第3章 量子力学初步 三、讨论 1.不确定关系只适用于微观粒子 例1: 设电子与 的子弹均沿x方向运动, m 0 . 01 kg 测定x 坐标所能达到的最大准确度。 0 .01 % , 精确度为 m / s ,求 x 500
dW ( x , y , z , t ) ( x , y , z , t ) dV
讨 论
1.波恩的波函数几率解释是量子力学基本原理之一 2.经典波振幅是可测量,而波函数是不可测量,可测是几率 3.单缝、双缝干涉实验在1961年前是假想实验
第三章 量子力学初步

2
求出本征函数ψ 的表 达式和本征值E的数值
求解微分方程,需要利用一定的边界条件
1、一维简谐振子势
1 2 1 2 2 • 势能 V ( x) kx m x 2 2
哈密顿方程为:
势能函数是 一条抛物线
V ( x)
d 2 ( x) 1 2 kx ( x) E ( x) 2 2m dx 2
X<0区域内薛定谔方程的通解:
I ( x) Ae
ik1x
Be
ik1x
b) x>0 区域 V(x)=V0 薛定谔可以写为:
d 2 2 ( x) 2m(V0 E ) 2 ( x ) k 2 2 2 ( x) 2 2 dx
其通解为:
2m(V0 E ) k 2
2 2
n奇 a n n A 0 B (1) B 0 ( ) A cos B sin n偶 2 2 2 A (1) B 0 A 0
n奇 a n n A 0 B (1) B 0 ( ) A cos B sin n偶 2 2 2 A (1) B 0 A 0
2
2)不存在n=0的波函数,零点能不为零:
E1
2
2
2ma 2
为什么?这是由粒子的波动性所决定的,由不确定原理:
xp
2
势阱中的位置不确定量为Δx≈a
p
进一步确定 本征函数
2a
不可能有
p0
nx nx ( x) A cos B sin a a
当 x
a 时,依据边界条件,有 2
通解为
( x) A cos kx B sin kx
量子力学初步

镍单晶
将
换成以 表达,得 实验结果:
1.65×10 –10 (m)
的电子
2.15A
按德布罗意公式推算,具有动能
的德布罗意波长的理论值为 1.67×10 –10 (m)
该实验首次证实了电子具有波动性。
电子衍射附图一 1927年,G.P.汤姆孙等令一电子束通过薄铝箔,结果发现,
同X射线一样,也能得到清晰的电子衍射图样。
出的概率(见后面章
节)。
试应用不确定关系分别估算下述电子和子弹的位置不确定量 质量 某原子中的电子 m e = 9.1×10 – 31 kg 某飞行中的子弹 m = 0.01 kg 速度
例题一
v = 500 m / s
子
速度不确定量
v e = 2×10 6 m / s △v e = 0.1 v e
光子的行为不能用经典粒子的运动状态参量描述和准确预测;
光波在空间某处的强度反映了光子在该处附近出现的概率。
光子衍射 在光的衍射实验中,摄像记录弱光入射的几个不 同曝光阶段的衍射图样,并进行比较,可以发现, 在衍射图样中较亮的地方,光子出现的概率较大。
单 缝 衍 射 像
圆孔衍射像
物质波假设
光,具有波粒二象性,是否一切物质都具有波粒二象性呢?
波函数具有统计意义,其函数性质应具备三个标准条件:
波函数标准条件 波函数的三个标准条件:
连续 单值 有限
因概率不会在某处发生突变,故波函数必 须处处连续; 因任一体积元内出现的概率只有一种,故 波函数一定是单值的;
因概率不可能为无限大,故波函数必须是 有限的;
以一维波函数为例,在下述四种函数曲线中,只有一种符合标准条件
这说明原子光谱有一定宽度,实验已经证实这一点。 ▲ 存在不确定关系的一对物理量互称共轭物理量。
山东大学量子力学 第三章 量子力学中的力学量

n ˆ [ Ht ] i
(13)复共轭算符
算符Û的复共轭算符 Û*就是把Û表达式中 的所有量换成复共轭.
例如: 坐标表象中
ˆ * ( i ) * p ˆ i p
三.力学量算符与力学量算符的构成
1. 量子力学中某一力学量总是与一个厄米 算符对应(一个基本假定) 2. 力学量算符的构成
2
角动量算符:
Lr p
ˆ yˆ ˆ zˆ ˆ L p z p L px x ˆ pz x z y y
ˆ ˆ ˆ2 ˆ2 ˆ2 2 ˆ L L L Lx Ly Lz
ˆ xˆ L py y ˆ px z
一 个基本假定(P56)
ˆ 如果一粒子处在力学量F对应的厄米算符 F
F (r , p),
构成规则为:先写出某一力学量的经典表示式
pˆ, 然后将其中的 P换为算符
就到得此力学量的算符,即
ˆ ˆ ˆ ˆ ˆ F (r , p) F F (r , p) F (r ,i)
3. 力学量算符都是厄米算符
如坐标算符、动量算符、哈密顿算符、角动量算符等。
动能算符个基本假定p56如果一粒子处在力学量f对应的厄米算符中那么测量这个力学量f时就有确定值这个值就是这个本征态一动量算符一动量算符2动量本征方程3箱归一化二角动量算符二角动量算符1角动量算符的形式2角动量本征方程3角动量算符的对易关系4角动量升降阶算符返回一动量算符使用波函数在无穷远处趋于零的边界条件
是任意波函数, ˆx p ˆ x x i xp
对易 关系
显然二者结果不相等,所以:
ˆ x i 记为 x, p
同理可证其它坐标算符 与共轭动量满足 写成通式: ˆy p ˆ y y i yp ˆz p ˆ z z i zp
03第三章 量子力学初步(甲型)

Lord Kelvin
• 第Th一e f朵irs乌t c云am伴e 随int着o e光xi的ste波nc动e w理it论h t而he来,这 一un理du论lat由ory菲th涅eo耳ry和of托li马gh斯t, a·n杨d博wa士s 所dea建lt立wi;th 它by隐Fr含esn着el这an样d的Dr问. T题ho:m地as 球Yo如un何g;在it 弹inv性ol介ved 质the中qu运es动tio,n,例ho如w从co本ul质d t上he说ea这rth种m介ov质e 就是 发thr光ou的gh以an太e?lastic solid, such as essentially is
• 坚and信L热ig和ht 光(都19是00运)动形式的动 • 力Th学e b理ea论uty的a优nd雅cl和ea清rne晰ss,of目th前e
由dy于nam被i两cal朵th乌eo云ry,遮w蔽hic而h 暗ass淡er无ts 光heat and light to be modes of motion, is at present obscured by two clouds.
• 假设相互间只能以热辐射的 形式交换能量
• 每一个物体向外辐射能量, 也吸收其它物体辐射到其表 面的能量
• 温度低的,辐射小,吸收大; 温度高的,辐射大,吸收小
• 经过一个过程后,所有物体的 温度相同,达到热平衡
• 热平衡时,每一个物体辐射的 能量等于其吸收的能量
• 热平衡状态下,吸收本领大, 辐射本领也大
• 基尔霍夫热辐射定律:热平衡 状态下物体的辐射本领与吸收 本领成正比,比值只与T,ν有 关。
E( ,T ) f ( ,T ) 吸收大,辐射也大。 A( ,T )
f ( ,T ) 是普适函数,与物质无关 应当通过实验测量 f ( ,T )
量子力学[第三章量子力学中的力学量] 山东大学期末考试知识点复习
![量子力学[第三章量子力学中的力学量] 山东大学期末考试知识点复习](https://img.taocdn.com/s3/m/b54c1b87a0116c175f0e48a5.png)
第三章量子力学中的力学量1.力学量算符(1)力学量的描述(r)满足正交归一性关系本征函数之间具有正交性.归一化的本征函数ψn其集合具有完备性以后我们总是默认力学量算符的本征函数是归一化的,除非另有说明。
(2)力学量的测量(x)中测量对力学量Q的测量结果为力学量算符的本征值,在本征态ψn.在一般状态ψ中测量Q得到一个概率分布,测出第n个力学量Q得到唯一值qn的概率为本征值qn其中称为概率幅,按照概率论,在状态ψ中力学量Q的期望值为上式等价于这说明我们常用的波函数实质就是测量力学量x时所得到的概率幅。
(3)两个力学量的关系2.力学量的演化(1)力学量的演化规律(2)守恒量3.中心势场问题(1)角动量算符在球坐标中,角动量z分量和角动量平方算符分别为(θ,ψ)称为球谐函数,满足正式中l为角量子数,m为磁量子数,归一化的Ylm交归一性关系具体形式和性质参见附录A的公式(A2—9)。
(2)中心势场的定态薛定谔方程质量为m的粒子在中心势场U(r)中运动,哈密顿算符为(r)满足定态薛定谔方程的径向部分上式中径向本征函数Rnl定义约化的径向本征函数Unl (r)=rRnl(r),(3—20)式化为称为约化的径向方程.与约化的径向本征函数对应的归一化条件为在一般情况下,能量由主量子数n和角量子数l共同确定,即E=Enl,与磁量子数m无关,因此能级简并度为2l+1.(3)径向概率分布和角向概率分布(4)氢原子情况假设原子核不动,取为坐标原点,电子运动的势场为U(r)=-es2/r.当能量E<0时,系统处于束缚定态,能量本征值为其中径向函数Rnl(r)的具体形式参见附录A.由于能量仅与主量子数n有关,因此能级简并度为如果考虑氢原子核的运动,上述公式中的电子质量me 应修正为折合质量mμ=me mp/(me+mp);对于核电荷为Z的类氢离子,能量本征值应改变为Z2En,径向函数变为Rnl(Zr)。
原子物理学课后习题详解第3章(褚圣麟)

第三章 量子力学初步3.1 波长为οA 1的X 光光子的动量和能量各为多少? 解:根据德布罗意关系式,得:动量为:12410341063.6101063.6----∙∙⨯=⨯==秒米千克λhp 能量为:λ/hc hv E==焦耳151083410986.110/1031063.6---⨯=⨯⨯⨯=。
3.2 经过10000伏特电势差加速的电子束的德布罗意波长?=λ 用上述电压加速的质子束的德布罗意波长是多少?解:德布罗意波长与加速电压之间有如下关系:meV h 2/=λ 对于电子:库仑公斤,19311060.11011.9--⨯=⨯=e m把上述二量及h 的值代入波长的表示式,可得:οοολA A A V 1225.01000025.1225.12===对于质子,库仑公斤,19271060.11067.1--⨯=⨯=e m ,代入波长的表示式,得:ολA 319273410862.2100001060.11067.1210626.6----⨯=⨯⨯⨯⨯⨯⨯=3.3 电子被加速后的速度很大,必须考虑相对论修正。
因而原来ολA V25.12=的电子德布罗意波长与加速电压的关系式应改为:ολA V V)10489.01(25.126-⨯-=其中V 是以伏特为单位的电子加速电压。
试证明之。
证明:德布罗意波长:p h /=λ对高速粒子在考虑相对论效应时,其动能K 与其动量p 之间有如下关系:222022c p c Km K =+而被电压V 加速的电子的动能为:eV K =2200222/)(22)(c eV eV m p eV m ceV p +=+=∴因此有:2002112/c m eV eVm h p h +⋅==λ一般情况下,等式右边根式中202/c m eV 一项的值都是很小的。
所以,可以将上式的根式作泰勒展开。
只取前两项,得:)10489.01(2)41(260200V eVm h c m eV eVm h -⨯-=-=λ 由于上式中οA VeV m h 25.122/0≈,其中V 以伏特为单位,代回原式得: ολA V V)10489.01(25.126-⨯-=由此可见,随着加速电压逐渐升高,电子的速度增大,由于相对论效应引起的德布罗意波长变短。
3第三章量子力学初步2

一维无限深势阱中粒子如何运动?
它的波函数如何?能量如何?
解:由于粒子做一维运动,所以有
2
d2 dx2
由于势能 U (x)中不显含时间,故用定态薛定谔方程求解。
因此一维定态薛定谔方程为
2
2
d 2(x)
dx2
U (x)(x)
E(x)
方程的解为定态解 (x,t) (x)ei Et
1.方程的通解
2
2
d 2(x)
子初始时刻的状态 (r0 , t0 ) 。原则上说,只要通过薛 定谔方程,就可以求出任意时刻的状态 (r ,t) 。
4.薛定谔方程中有虚数单位i,所以 (r,t) 一般是复数
形式。 (r ,t) 表示概率波, (r , t) 2 是表示粒子在时刻t、
在空间某处出现的概率。因而薛定谔方程所描述的状态
(x, y, z,t) 2 即波的强度表示t时刻、(x、y、z)处发现 电子的几率密度。如果 (x, y,大z,t,) 2 则电子出现几率大,
因而电子出现的目也多,此处为衍射极大值处;反之,
如果
小,则电子出现几率小,电子出现的数目也
少,此 (处x,为y, z衍,t)射2 极小值处。
W (x, y, z,t) 2 * 表示t时刻、(x、y、z)处发现粒
x 0 x p x h / 2 px
二、不确定关系
1927年,海森堡首先推导出不确定关系 :
x p x / 2 y p y / 2 z p z / 2
p / 2 E t / 2
三、讨论 1.不确定关系只适用于微观粒子
例1:设电子与 m 0.01 kg的子弹均沿x方向运动, x 500m,/精s 确度
原子物理学教学大纲
《原子物理学》课程教学大纲(54学时)(理论课程)一课程说明(一)课程概况课程中文名称:《原子物理学》课程英文名称:Atomic Physics课程编码:3910252109开课学院:理学院适用专业/开课学期:物理学、应用物理学/第四学期学分/周学时:3/3《原子物理学》是物理学专业的一门重要专业核心必修课程,属于专业发展课程。
原子物理学是研究介于分子和原子核两层次间物质结构的科学,研究这一层次是由什么组成,组成物是怎样运动和发生相互作用的。
原子物理学的发展为量子力学的建立奠定了基础,它上承经典物理,下接量子力学,属于近代物理的范畴,随着科学技术的发展,原子物理学在许多领域得到广泛地应用和拓展。
《原子物理学》是《量子力学》、《固体物理学》等近代物理课程的基础学科,学习本课程必须先修《高等数学》、《力学》、《电磁学》和《光学》。
(二)课程目标1. 使学生初步建立描述微观世界的物理图像,掌握原子、原子核的结构和运动规律,了解粒子物理中的有关知识,为今后继续学习量子力学、固体物理学、近代物理实验等课程打下坚实基础。
2. 掌握研究原子物理问题的基本方法,明确如何由分析实验结果出发,建立物理模型,进而建立物理理论体系的过程,培养学生分析问题和解决问题的能力。
3. 使学生了解一些正在发展的学科前沿,扩大视野,引导学生勇于思考、乐于探索发现,培养其良好的科学素质。
培养学生辩证唯物主义世界观。
(三)学时分配二教学方法和手段以启发式教学为主,学生自学为辅。
教学中要注重理论教学中穿插背景材料、物理学史的教学,注重物理思想、物理方法的教学,注重把学科前沿引入经典内容的教学中,提倡学生课外查阅文献了解学科前沿。
三教学内容第一章原子的基本状况(含绪论)(4学时)一、教学目标1.了解原子物理学的发展历史及原子物理学研究的内容、方法和手段;2.掌握原子的静态性质;3.掌握原子的核式模型及实验基础、卢瑟福散射公式;4.了解对两种主要的原子模型的定性半定量分析、核式模型的意义及经典物理在其中遇到的困难。
第三章量子力学初步

2
(
t
-
r
cos
)
C
y
写成复数形式:
r
e e 2
i
(
r
cos
t
)
0
2 i(kr- t )
0
rn
考虑到关系式,则有:
B
i ( pr-Et )
0e
x A
8
上式就是物质波的波函数。历史上对物质波的解释有多种, 其中三种主要的解释如下:
(a) 波是基本的,粒子是由许多波组合而成的一个波包, 波包的速度就是粒子的速度,波包的运动表现出粒子的性 质。
(x) (x)
(x) (x)
V
◆ 思考题: 一个粒子在如图所示的两个 无限高势壁间运动,求解体系 的波函数和能量。
V=
V=
I
II
V=0 II
a
x
28
§3.3 简谐振子
简谐振子是物理学经常遇到的一个典型模型,物质结构中 原子和分子的振动均可视为简谐运动。
经典物理学对简谐振子的定义为:作简谐运动的物体受到 的力与他的位移x成正比,而他的方向与位移方向相反,即
H(r) E(r)
波函数标准条件 ⊙体系的波函数为
i Et
(r, t) (r)e
20
⊙波函数的归一化问题。由于
(r, t) * (r, t) (r) * (r)
所以只要求对定态波函数归一化即可。
⊙体系的几率密度。由于
dW
d
w (r, t)
* (r, t) (r) * (r)
对定态体系,几率密度是不随时间变化的。
15
2
2m
2
V
i
t
2
章3 量子力学初步(3)
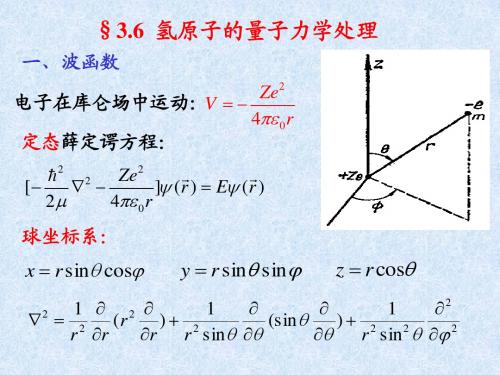
能量是量子化的,自然得出。
E 0时 E取任何值都能使R满足标准条件的解。
2.角量子数 l 和角动量量子化
L l (l 1) l 0,1,2n 1
ˆ L2Y ( , ) l (l 1)2Y ( , )
角动量是量子化的,自然得出。 3.磁量子数m和空间量子化
三、电子云
用小黑点的密或稀形象地表示空间各处概率密度的相 对大小,概率大的地方黑点浓密,概率小的地方黑点稀 疏,称它们为“电子云” 电子在原子核外很小的空间内作高速运动,其运动 规律跟一般物体不同,它们没有确定的轨道。因此,我 们不能同时准确地测定电子在某一时刻所处的位置和运 动的速度,也不能描画出它的运动轨迹。因此,人们常 用一种能够表示电子在一定时间内在核外空间各处出现 机会的模型来描述电子在核外的运动。在这个模型里, 某个点附近的密度表示电子在该处出现机会的大小。密 度大的地方,表明电子在核外空间单位体积内出现的机 会多;密度小的地方,表明电子在核外空间单位体积内 出现的机会少。由于这个模型很像在原子核外有一层疏 密不等的“云”,所以,人们形象地把它叫做“电子 云”。
阅读参考文献
(1)张哲华、刘莲君编 《量子力学与原子物理学》(武汉大学
出版社)第一章实验基础:光的波粒二象性、第二章量子力学原 理(1):波函数及薛定谔方程部分。 (2)曾谨言著《量子力学》(上)(科学出版社)第一章量子 力学的诞生部分。 (3)苟清泉编《原子物理学》(高等教育出版社)相关部分。 (4)顾建中编《原子物理学》(高教出版社)相关部分。
作 业 题
(1)电子显微镜中的电子从静止开始通过电势差为U
的静电场加速后,其德布罗意波长为0.4埃,求加速电
势差。(上海大学2002)
(2)试画出时l=2电子轨道角动量在磁场中空间量子化
《原子物理学》(褚圣麟)第三章 量子力学初步

3.2 测不准原理
一、电子的单缝衍射(1961年,约恩逊成功的做出)
电子以速度沿着y轴射向A 屏,其波长为 h p ,经 过单缝发生衍射,缝宽为d, 到达C屏。第一级暗纹的位
置:d sin
x方向上,粒子坐标的不确定度
为
x d
2
单缝衍射时,粒子位置和动量的确定度
粒子动量的不确定度为
px p sin
p
h
n
k
式中, 2 :角频率n; :传播方向上的单位矢量
k
2
n
:波矢量
h 1.0545881034 J s
2
粒子的德布罗意波长: h h
p m
1.当 ~ c 时,m m0
12 / c2
2.当 c
时m, mo
1
m
经过电场加速的电子: 1 m 2 eV
2
h
h 12.25 埃
m 2eV / m 2emV V (伏特)
适用条件:(1)电子,(2)非相对论(U不能太大)。
四、德布罗意假设的实验验证
德布罗意曾指出由于实物粒子的波粒二象性,当加速后的电 子穿过晶体时,将会发生电子波的衍射现象。
1925年戴维孙-革末在一次偶然的真空破坏事故,使镍棒样 品被氧化,为了还原,他们对镍加热,结果形成了镍的单晶结 构,即将镍单晶化,镍的晶格成了电子衍射的光栅。从而当电 子穿过镍单晶时,观察到电子的衍射图象,测量了电子波的波 长,证实了德布罗意假设。
E h
p h
E, P , --------光的波粒二象性
光的波粒二象性是否具有更深刻的普遍意义? 1924年,年轻的法国物理学家德布罗意反向思考了这一问题 在向巴黎大学理学院提交的题为《量子理论的比较》的博士 论文中提出了所有粒子都具有波动性的假设。他指出:“在整 个世纪以来,人们在辐射理论上,比起关注波动的研究方法 来,是过于忽视了粒子的研究方法;在实物理论上,是否发 生了相反的错误呢?是否我们关于粒子的图象想的太多,而过 分忽视了波的图象?”于是他将光的波粒二象性大胆地赋予了 电子这样的实物粒子上,即承认实物粒子也具有波粒二象性。
量子力学初步

来表示。这是量子力学的一个很重要的特点。
数学运 算符号
劈形算符
拉普拉 斯算符
力 学 量 算 符 统称 举 例
位矢算符
动量算符 动能算符
哈密顿算符
含动、势能
若 作用在某函数 上的效果
和 与某一常量 的乘积相当,
即
则
称为 的 本征值
称为 的 本征函数
所描述的状态称为 本征态
真 空 或 介 质
电子云
纵向 分辨率 达 0.005 n m
横向
分辨率达 0.1 n m
续上
电 子
沿XY逐行扫描的同时,自控系统根据反馈
测 信号调节针尖到样ห้องสมุดไป่ตู้表层原子点阵的距离,
控 使 保持不变。针尖的空间坐标的变化
及 反映了样品表面原子阵列的几何结构及起
数 伏情况。经微机编码可显示表面结构图像。
(1887-1961获1)933年诺贝尔物理学奖
含时薛定谔方程
若粒子所在的
势场只是空间函数
即
,则
对应于一个可能态
有一个能量定值
定态薛定谔方程
定态薛定谔方程
定态 波函数
解释: 若 故
时间的函数
由
则
可分离变量,写成
得 定态薛定谔方程
常量
对应一个可能
空间的函数 态有一常量
此外,对
解得 将常量 归入 定态波函数
由 (4)以区 上向 结势 论垒 都能运 不动 对流。 密度分布取决于空
概率密度分布取决于空间
间各点的波强的绝对值。 Si (111)表面 7×7 元胞的STM图像
7 ×10 -16 eV
各点波强的比例,并非取
量子力学 - 山东师范大学.

1 2 ' 21'
在1(x)和 2 (x)不为0处(不包含1(x)和 2 (x)节点 区域)用1 2 除上式,则有
19
1' 2', 1 2
'ຫໍສະໝຸດ 即 ln
1 2
常数由渐近条件来决定。
对于束缚态,有x 时,1、 2 0,
常数 0。
故对两束缚态波函数,有下列关系:
1 2 ' 21'
关于此定理的应用,有定理7:
18
定理7:设粒子在规则势场中运动(V (x)无奇点), 如存在束缚态,则必定是不简并的。
证明:[分析]证明是否简并,只要设E有两个态, 看此两态相等即可。
氢原子中的电子就是在三维库仑势阱中运动, 不过“阱壁”不是直立的,而是按-1/r分布。近 来,人们设计制作了一种具有“量子阱”的半 导体器件,它具有介观(介于宏观与微观)尺寸的 势阱,阱宽约在10nm上下。这种材料具有若干 特性,已用于制造半导体激光器、光电检测器、 双稳态器件等。
24
③势垒 V(x)
0 a
15
得 '(a 0 ) '(a 0 )
2m
lim
a
dx[E V (x)] (x)
2 0 a
由于 [E V (x)] (x) 有限,积分区间 2 0,故
右端为 0。
可见 '(a 0 ) '(a 0 ),即 '(x)在a处连续
如无确定的宇称 有简并,即 (x)也是方程的一个不同于 (x)但同属于
能量 E。
11
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 量子力学初步
一、学习要点
1.德布罗意假设:
(1)内容: ,
(2)试验验证:戴维孙-革末试验
电子 =(?)
2.测不准关系: , ;
3.波函数及其统计解释、标准条件、归一化条件
(4)基于德布罗意假设得出的公式 ?的适用条件是:
A.自由电子,非相对论近似; B.一切实物粒子,非相对论近似;
C.被电场束缚的电子,相对论结果; D带电的任何粒子,非相对论近似
(5)如果一个原子处于某能态的时间为10-7S,原子这个能态能量的最小不确定数量级为(以焦耳为单位):
A.10-34; B.10-27; C.10-24; D.10-30
(6)将一质子束缚在10-13cm的线度内,则估计其动能的量级为:
A. eV; B. MeV; C. GeV, D.10-20J
(7)按量子力学原理,原子状态用波函数来描述. 不考虑电子自旋,对氢原子当有确定主量子数n时,对应的状态数是:
A.2n; B.2n+1; C.n2; D.2n2
(8)按量子力学原理,原子状态用波函数来描述.不考虑电子自旋,对氢原子当确定后,对应的状态数为:
A.n2; B.2n; C.; D.2+1
(9)按原子力学原理,原子状态用波函数来描述.考虑电子自旋,对氢原子当确定后,对应的状态数为:
(2)德布罗意假设可归结为下列关系式:
A .E=h, p=; B.E=,P=; C. E=h ,p=; D. E= ,p=
(3)为使电子的德布罗意假设波长为100埃,应加多大的加速电压:
A.11.51106V; B.24.4V; C.24.4105V; D.15.1V
描述电子空间运动的三个量子数的名称、取值范围、所表征的物理量表达式
二、基本练习
1.楮书 P113习题①②③
2.选择题
(1)为了证实德布罗意假设,戴维孙-革末于1927年在镍单晶体上做了电子衍射实验从而证明了:
A.电子的波动性和粒子性 B.电子的波动性 C.电子的粒子性 D.所有粒子具有二项性
(2)请回答测不准关系的主要内容和物理实质.
(3)为什么说德布罗意是量子力学的创始人?贡献如何?
(4)何谓定态?定态波函数具有何种形式?
(5)波函数满足标准条件是什么?写出波函数的归一化条件.
4.计算题
(1)电子显微镜中的电子从静止开始通过电势差为的静电场加速后,其德布罗意波长为,求加速电势差.
A.2(2+1); B.2+1; C. n; D.n2
(10)按量子力学原理,原子状态用波函数来描述.考虑自旋对氢原子当m确定后对应的状态数为:
A.1; B.2; C.2+1; D. n
3.简答题
(1)波恩对波函数作出什么样的解释?
薛定谔方程、定态薛定谔方程、定态波函数、定态
4量子力学对氢原子的处理
=0 1 2 3 4 ... 电 子 态 ... 原 子 态 ... 能量,=1.2.3......
轨道投影角动量 ,称轨道磁量子数,表征轨道角动量对外场方向的取向,轨道角动量对外场方向的投影图
(2)试画出时电子轨道角动量在磁场中空间量子化示意图,并标出电子轨道角动量在外磁场方向的投影的各种可能值.
读书以过目成诵为能,最是不济事。——郑板桥
