北京市西城区2014 — 2015学年度第一学期期末试卷高一数学普通校(试题)

合集下载

2014-2015学年北京市西城区高三上期末考试文科数学试卷

2014-2015学年北京市西城区高三上期末考试文科数学试卷一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合要求的．1．设集合A ＝{1，2，3，4，5}，B ＝{x|（x−1）（x−4）＜0}，则A ∩B ＝（）A 、{1，2，3，4}B 、{2，3}C 、{1，2，3}D 、{2，3，4}2．在实数范围内，下列不等关系不恒成立的是（）A 、x 2≥0B 、a 2＋b 2≥2ab C 、x ＋1＞x D 、|x ＋1|＞|x|3．下列函数中，既是偶函数又在（0，＋∞）上是单调递增函数的是（）A 、y ＝lgxB 、y ＝−x 2＋3C 、y ＝|x|−1D 、y ＝3x4．命题“存在实数x ，使x ＞1”的否定是（）A 、对任意实数x ，都有x ＞1B 、不存在实数x ，使x ≤1C 、对任意实数x ，都有x ≤1D 、存在实数x ，使x ≤15．已知{a n }是等差数列，a 1＋a 2＝4，a 7＋a 8＝28，则公差等于（）A 、2B 、4C 、6D 、86．已知a ，b 为不相等的两个正数，且lgab ＝0，则函数y ＝a x 和y ＝b x 的图象之间的关系是（）A 、关于原点对称B 、关于y 轴对称C 、关于x 轴对称D 、关于直线y ＝x 对称7．已知a ，b 是实数，则“a ＞0且b ＞0”是“a ＋b ＞0且ab ＞0”的（）A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件8．过曲线C ：y ＝x1（x ＞0）上一点P （x 0，y 0）作曲线C 的切线，若切线的斜率为−4，则x 0等于（）A 、2B 、21C 、4D 、419．已知函数f （x ）＝⎪⎩⎪⎨⎧≤+->-12111x a x x x 在R 上满足：对任意x 1≠x 2，都有f （x 1）≠f （x 2），则实数a 的取值范围是（）A 、（−∞，2]B 、（−∞，−2]C 、[2，＋∞）D 、[−2，＋∞）10．已知函数f （x ）＝xe x ，给出下列结论： ①（1，＋∞）是f （x ）的单调递减区间；②当k ∈（−∞，e1）时，直线y ＝k 与y ＝f （x ）的图象有两个不同交点； ③函数y ＝f （x ）的图象与y ＝x 2＋1的图象没有公共点．其中正确结论的序号是（）A 、①②③B 、①③C 、①②D 、②③二、填空题：本大题共6小题，每小题5分，共30分．把答案填在题中横线上．11．若x ∈R ＋，则x ＋x 4的最小值为____________． 12．log 22＋lne ＝____________．13．不等式xx 12-＞1的解集为____________． 14．已知定义在R 上的奇函数f （x ）满足f （x−2）＝f （x ），且当x ∈[1，2]时，f （x ）＝x 2−3x＋2，则f （6）＝____________；f （21）＝____________． 15．函数f （x ）＝lnx−21x 2的极值是____________． 16．个人取得的劳务报酬，应当交纳个人所得税．每月劳务报酬收入（税前）不超过800元不用交税；超过800元时，应纳税所得额及税率按下表分段计算：（注：应纳税所得额单次超过两万，另有税率计算方法．）某人某月劳务报酬应交税款为800元，那么他这个月劳务报酬收入（税前）为_________元．三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．17．设函数f （x ）＝log 2（x 2−2x−8）的定义域为A ，集合B ＝{x|（x−1）（x−a ）≤0}．（Ⅰ）若a ＝−4，求A ∩B ；（Ⅱ）若集合A ∩B 中恰有一个整数，求实数a 的取值范围．18．已知数列{a n }是等差数列，S n 为其前n 项和，a 1＝−6，S 3＝S 4．（Ⅰ）求{a n }的通项公式；（Ⅱ）设b n ＝2＋4，求数列{b n }的前n 项和．19．已知函数f （x ）＝x 2−2mx ＋3．（Ⅰ）当m ＝1时，求函数f （x ）在区间[−2，2]上的最大值和最小值；（Ⅱ）若函数f （x ）在区间[1，＋∞）上的值恒为正数，求m 的取值范围．20．已知函数f （x ）＝（a−x ）e x ＋1，其中a ＞0．（Ⅰ）求函数f （x ）的单调区间；（Ⅱ）证明函数f （x ）只有一个零点．21．某人销售某种商品，发现每日的销售量y （单位：kg ）与销售价格x （单位：元/kg ）满足关系式y ＝⎪⎩⎪⎨⎧≤≤-<<-+-159617796)9(61502x x x x a x ，其中a 为常数．已知销售价格为8元/kg 时，该日的销售量是80kg ．（Ⅰ）求a 的值；（Ⅱ）若该商品成本为6元/kg ，求商品销售价格x 为何值时，每日销售该商品所获得的利润最大．22．已知函数f （x ）＝lnx ＋x−21mx 2．（Ⅰ）当m ＝2时，求函数f （x ）的极值点；（Ⅱ）若关于x 的不等式f （x ）≤mx−1恒成立，求整数m 的最小值．。

北京市西城区2014 — 2015学年高三(文)第一学期期末试卷

北京市西城区2014 — 2015学年度第一学期期末试卷高三数学（文科） 2015.1第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合1,0,1,2{}A -=，2{|}B x x x =>，则集合A B = （）（A ）{1,0,1}-（B ）{1,2}-（C ）{0,1,2}（D ）{1,1,2}-【答案】B 【解析】“0x ∀>”的否定为“0x ∃>”，“2log 2x x >”的否定为“2log 2x x ≤” 所以，p ⌝为：2log 0,2x x x ∃>≤ 故答案为：B 【考点】全称量词与存在性量词【难度】 13．在∆ABC 中，角A ，B ，C 所对的边分别为a ，b ，c . 若A 为锐角，2a b =，sin B =，则（）【答案】B 【解析】{}01B x x x =<>或，所以{}1,2A B =-故答案为：B 【考点】集合的运算【难度】 12．设命题p ：2log 0,2x x x ∀>>，则p ⌝为（）（A ）2log 0,2x x x ∀>< （B ）2log 0,2x x x ∃>≤ （C ）2log 0,2x x x ∃>< （D ）2log 0,2x x x ∃>≥（A ）3A π= （B ）6A π=（C）sin 3A =（D ）2sin 3A =【答案】A 【解析】由正弦定理得sin sin a b A B =，所以sin 2sin A aB b==，所以sin A =。

因为ABC ∆为锐角三角形，所以3A π=故答案为：A【考点】正弦定理【难度】 14．执行如图所示的程序框图，输出的x 值为（）（A ）4 （B ）5 （C ）6 （D ）7【答案】C【解析】3x =时，328y ==，833<； 4x =时，4216y ==，1643<； 5x =时，5232y ==，3253<；6x =时，6264y ==，6463>，输出6x =。

北京市西城区-第一学期期末考试高三数学理及答案

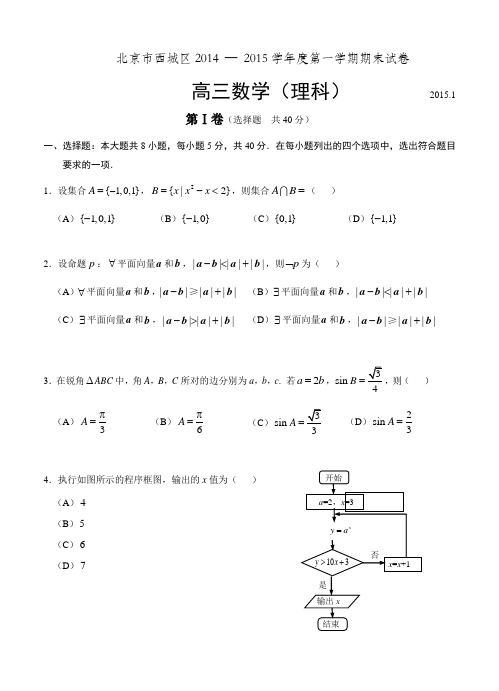
北京市西城区2014 — 2015学年度第一学期期末试卷高三数学（理科） 2015.1第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合1,0,1{}A -=，2{|2}B x x x =-<，则集合A B =（）（A ）{1,0,1}-（B ）{1,0}-（C ）{0,1}（D ）{1,1}-3．在锐角∆ABC 中，角A ，B ，C 所对的边分别为a ，b ，c . 若2a b =，sin B =，则（）（A ）3A π= （B ）6A π=（C）sin 3A =（D ）2sin 3A =4．执行如图所示的程序框图，输出的x 值为（）（A ）4 （B ）5 （C ）6 （D ）72．设命题p ：∀平面向量a 和b ，||||||-<+a b a b ，则p ⌝为（）（A ）∀平面向量a 和b ，||||||-+≥a b a b （B ）∃平面向量a 和b ，||||||-<+a b a b （C ）∃平面向量a 和b ，||||||->+a b a b （D ）∃平面向量a 和b ，||||||-+≥a b a b5．设函数()3cos f x x b x =+，x ∈R ，则“0b =”是“函数()f x 为奇函数”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件8. 设D 为不等式组1,21,21x y x y x y ---+⎧⎪⎨⎪⎩≤≥≤表示的平面区域，点(,)B a b 为坐标平面xOy 内一点，若对于区域D内的任一点(,)A x y ，都有1OA OB ⋅≤成立，则a b +的最大值等于（）（A ）2 （B ）1 （C ）0（D ）36．一个四棱锥的三视图如图所示，那么对于这个四棱锥，下列说法中正确的是（）（A（B ）最长棱的棱长为3（C ）侧面四个三角形中有且仅有一个是正三角形（D ）侧面四个三角形都是直角三角形7. 已知抛物线2:4C y x =，点(,0)P m ，O 为坐标原点，若在抛物线C 上存在一点Q ，使得90OQP ，则实数m 的取值范围是（）（A ）(4,8) （B ）(4,) （C ）(0,4)（D ）(8,)侧(左)视图正(主)视图俯视图第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分． 9. 复数2i12iz -=+，则||z = _____．10．设12,F F 为双曲线C ：2221(0)16x y a a -=>的左、右焦点，点P 为双曲线C 上一点，如果12||||4PF PF -=，那么双曲线C 的方程为____；离心率为____.11．在右侧的表格中，各数均为正数，且每行中的各数从左到右成等差数列，每列中的各数从上到下成等比数列，那么x y z ++=______．12．如图，在ABC ∆中，以BC 为直径的半圆分别交AB ，AC 于点E ，F ，且2AC AE =，那么AFAB=____；A ∠= _____．13．现要给4个唱歌节目和2个小品节目排列演出顺序，要求2个小品节目之间恰好有3个唱歌节目，那么演出顺序的排列种数是______. （用数字作答）14. 设P ，Q 为一个正方体表面上的两点，已知此正方体绕着直线PQ 旋转（）角后能与自身重合，那么符合条件的直线PQ 有_____条.三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤． 15．（本小题满分13分）2 x3ya321258zE FCB A已知函数()cos cos 442x x xf x =+, x ∈R 的部分图象如图所示. （Ⅰ）求函数()f x 的最小正周期和单调递增区间；（Ⅱ）设点B 是图象上的最高点，点A 是图象与x 轴的交点，求BAO ∠tan 的值.16．（本小题满分13分）现有两种投资方案，一年后投资盈亏的情况如下：（1）投资股市：（2）购买基金：（Ⅰ）当4p时，求q 的值；（Ⅱ）已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资，如果一年后他们中至少有一人获利的概率大于45，求p 的取值范围；（Ⅲ）丙要将家中闲置的10万元钱进行投资，决定在“投资股市”和“购买基金”这两种方案中选择一种，已知12p，16q ，那么丙选择哪种投资方案，才能使得一年后投资收益的数学期望较大？给出结果并说明理由．如图，在四棱柱1111D C B A ABCD -中，A A 1⊥底面ABCD ，90BAD ∠=，BC AD //，且122A A AB AD BC ==== ，点E 在棱AB 上，平面1A EC 与棱11C D 相交于点F .（Ⅰ）证明：1A F ∥平面1B CE ；（Ⅱ）若E 是棱AB 的中点，求二面角1A EC D --的余弦值；（Ⅲ）求三棱锥11B A EF -的体积的最大值.18．（本小题满分13分）已知函数2()(0)f x ax bx a =->和()ln g x x =的图象有公共点P ，且在点P 处的切线相同.（Ⅰ）若点P 的坐标为1(,1)e-，求,a b 的值；（Ⅱ）已知a b =，求切点P 的坐标.19．（本小题满分14分）已知椭圆C ：2211612x y +=的右焦点为F ，右顶点为A ，离心率为e ，点(,0)(4)P m m >满足条件||||FA e AP =. （Ⅰ）求m 的值；（Ⅱ）设过点F 的直线l 与椭圆C 相交于M ，N 两点，记PMF ∆和PNF ∆的面积分别为1S ，2S ，求证：12||||S PM S PN =.B CDA B 1C 1E FA 1 D 1设函数()(9)f x x x =-，对于任意给定的m 位自然数0121m m n a a a a -=（其中1a 是个位数字，2a 是十位数字，），定义变换A ：012()()()()m A n f a f a f a =+++. 并规定(0)0A =．记10()n A n =，21()n A n =，， 1()k k n A n -=，．（Ⅰ）若02015n =，求2015n ；（Ⅱ）当3m ≥时，证明：对于任意的*()m m ∈N 位自然数n 均有1()10m A n -<；（Ⅲ）如果*010(,3)m n m m <∈≥N ，写出m n 的所有可能取值.（只需写出结论）北京市西城区2014 — 2015学年度第一学期期末高三数学（理科）参考答案及评分标准2015.1一、选择题：本大题共8小题，每小题5分，共40分.1．C 2．D 3．A 4．C 5．C 6．D 7．B 8．A 二、填空题：本大题共6小题，每小题5分，共30分.9．1 10．221416x y -=11．17412．12 π313．9614．13注：第10，12题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分. 其他正确解答过程，请参照评分标准给分. 15．（本小题满分13分）（Ⅰ）解：因为()cos cos 442x x xf x =+cos 22x x=+ ……………… 2分=π2sin()26x +， ……………… 4分所以 2π4π12T ==. 故函数()f x 的最小正周期为4π. ……………… 6分由题意，得πππ2π2π2262x k k -++≤≤，解得4π2π4π4π+33k x k -≤≤，所以函数()f x 的单调递增区间为4π2π[4π,4π+],()33k k k -∈Z . ……………… 9分（Ⅱ）解：如图过点B 作线段BC 垂直于x由题意，得33π4TAC ==，2=BC ，所以2tan 3πBC BAO AC ∠==.16．（本小题满分13分）（Ⅰ）解：因为“购买基金”后，投资结果只有“获利”、“不赔不赚”、“亏损”三种，且三种投资结果相互独立，所以p +13+q =1. ……………… 2分又因为14p，所以q =512． ……………… 3分（Ⅱ）解：记事件A 为 “甲投资股市且盈利”，事件B 为“乙购买基金且盈利”，事件C 为“一年后甲、乙两人中至少有一人投资获利”， ……………… 4分则CAB AB AB ，且A ，B 独立.由上表可知， 1()2P A ，()P B p .所以()()()()P C P AB P AB P AB ……………… 5分111(1)222p pp1122p . ……………… 6分因为114()225P C p ，所以35p. ……………… 7分又因为113p q ，0q ≥，所以23p ≤.所以3253p ≤. ……………… 8分（Ⅲ）解：假设丙选择“投资股票”方案进行投资，且记X 为丙投资股票的获利金额（单位：万元），所以随机变量X 的分布列为：…………… 9分则113540(2)2884EX =⨯+⨯+-⨯=. ……………10 分假设丙选择“购买基金”方案进行投资，且记Y 为丙购买基金的获利金额（单位：万元），所以随机变量Y 的分布列为：…………… 11分则111520(1)2366EY =⨯+⨯+-⨯=. …………… 12分因为EX EY >，所以丙选择“投资股市”，才能使得一年后的投资收益的数学期望较大．……… 13分17．（本小题满分14分）（Ⅰ）证明：因为1111D C B A ABCD -是棱柱，所以平面ABCD ∥平面1111A B C D .又因为平面ABCD 平面1A ECF EC =，平面1111A B C D 平面11A ECF A F =，所以1A F ∥EC . …………………2分又因为1A F ⊄平面1B CE ，EC ⊂平面1B CE ，所以1A F ∥平面1B CE . …………………4分（Ⅱ）解：因为1AA ⊥底面ABCD ，90BAD ∠=，所以1AA ，AB ，AD 两两垂直，以A 为原点，以AB ，AD ，1AA 分别为x 轴、y 轴和z 轴，如图建立空间直角坐标系. …………………5分则1(0,0,2)A ，(1,0,0)E ，(2,1,0)C ，所以 1(1,0,2)A E =-,1(2,1,2)AC =-. 设平面1A ECF 的法向量为(,,),m x y z = 由10A E m ⋅=，10AC m ⋅=, 得20,220.x z x y z -=⎧⎨+-=⎩令1z =,得(2,2,1)m =-. …………………7分又因为平面DEC 的法向量为(0,0,1)n =， …………………8分所以1cos ,3||||m n m n m n ⋅<>==⋅，由图可知，二面角1A EC D --的平面角为锐角，所以二面角1A EC D --的余弦值为13. …………………10分（Ⅲ）解：过点F 作11FM A B ⊥于点M ,因为平面11A ABB ⊥平面1111A B C D ，FM ⊂平面1111A B C D , 所以FM ⊥平面11A ABB ,所以11111113B A EF F B A E A B E V V S FM --∆==⨯⨯ …………………12分1222323FM FM ⨯=⨯⨯=. 因为当F 与点1D 重合时，FM 取到最大值2（此时点E 与点B 重合），所以当F 与点1D 重合时，三棱锥11B A EF -的体积的最大值为43. ………………14分18.（本小题满分13分）（Ⅰ）解：由题意，得21()1e e ea bf =-=-， …………………1分且()2f x ax b '=-，1()g x x'=， …………………3分由已知，得11()()e ef g ''=，即2e eab -=，解得22e a =，3e b =. …………………5分（Ⅱ）解：若a b =，则()2f x ax a '=-，1()g x x'=，设切点坐标为(,)s t ，其中0s >,由题意，得 2ln as as s -=， ① 12as a s-=， ② …………………6分由②，得 1(21)a s s =-，其中12s ≠，代入①，得 1ln 21s s s -=-. （*） …………………7分因为 10(21)a s s =>-，且0s >，所以 12s >. …………………8分设函数 1()ln 21x F x x x -=--，1(,)2x ∈+∞，则 2(41)(1)()(21)x x F x x x ---'=-. …………………9分令()0F x '= ，解得1x =或14x =(舍). …………………10分当x 变化时，()F x '与()F x 的变化情况如下表所示，…………………12分所以当1x =时，()F x 取到最大值(1)0F =，且当1(,1)(1,)2x ∈+∞时()0F x <. 因此，当且仅当1x =时()0F x =.所以方程（*）有且仅有一解1s =.于是 ln 0t s ==，因此切点P 的坐标为(1,0). …………………13分19．（本小题满分14分）（Ⅰ）解：因为椭圆C 的方程为 2211612x y +=，所以 4a =,b =2c =, ………………2分则 12c e a ==，||2FA =，||4AP m =-. ………………3分因为 ||21||42FA AP m ==-，所以 8m =. ………………5分（Ⅱ）解：若直线l 的斜率不存在，则有 21S S =，||||PM PN =，符合题意. …………6分若直线l 的斜率存在，则设直线l 的方程为)2(-=x k y ，),(11y x M ，),(22y x N .由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得 2222(43)1616480k x k x k +-+-=， ……………… 7分可知 0>∆恒成立，且 34162221+=+k k x x ，3448162221+-=k k x x . ……………… 8分因为 8)2(8)2(8822112211--+--=-+-=+x x k x x k x y x y k k PN PM ……………… 10分 )8)(8()8)(2()8)(2(211221----+--=x x x x k x x k )8)(8(32)(102212121--++-=x x k x x k x kx 0)8)(8(323416103448162212222=--++⋅-+-⋅=x x k k k k k k k ，所以 MPF NPF ∠=∠. ……………… 12分因为PMF ∆和PNF ∆的面积分别为11||||sin 2S PF PM MPF =⋅⋅∠， 21||||sin 2S PF PN NPF =⋅⋅∠， ……………… 13分所以12||||S PM S PN =. ……………… 14分20．（本小题满分13分）（Ⅰ）解：114082042n =+++=，2201434n =+=，3182038n =+=，418826n =+=，5141832n =+=，6181432n =+=，……所以 201532n =． ……………… 3分（Ⅱ）证明：因为函数2981()(9)()24f x x x x =-=--+，所以对于非负整数x ，知()(9)20f x x x =-≤.（当4x =或5时，取到最大值）… 4分因为 12()()()()m A n f a f a f a =+++，所以 ()20A n m ≤． ……………… 6分令 1()1020m g m m -=-，则31(3)102030g -=-⨯>．当3m ≥时，11(1)g()1020(1)1020910200m m m g m m m m --+-=-+-+=⨯->，所以 (1)g()0g m m +->，函数()g m ，（m ∈N ，且3m ≥）单调递增．故 g()g(3)0m >≥，即11020()m m A n ->≥．所以当3m ≥时，对于任意的m 位自然数n 均有1()10m A n -<. …………………9分（Ⅲ）答：m n 的所有可能取值为0，8，14，16，20，22，26，28，32，36，38．…………………14分。

北京市西城区2014-2015学年度高二上学期期末考试数学试题(文科)

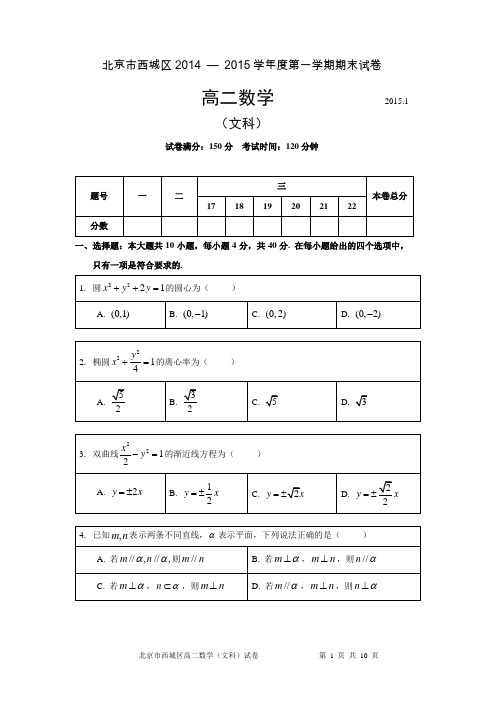
北京市西城区2014 —2015学年度第一学期期末试卷高二数学2015.1（文科）试卷满分：150分考试时间：120分钟一、选择题：本大题共10小题，每小题4分，共40分. 在每小题给出的四个选项中，只有一项是符合要求的.二、填空题：本大题共6小题，每小题5分，共30分. 把答案填在题中横线上. 11. 抛物线24y x =的准线方程为_______________.12. 命题“2,20x x x ∃∈-<R ”的否定是_____________________. 13. 右图是一个四棱锥的三视图，则该四棱锥的体积为_______.14. 圆心在直线y x =上，且与x 轴相切于点(2,0) 的圆的方程为____________________.15. 已知F 为双曲线22:14y C x -=的一个焦点，则点F 到双曲线C 的一条渐近线的距离为__________. 16. “降水量”是指从天空降落到地面上的液态或固态（经融化后）降水，未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以m m 为单位.为了测量一次降雨的降水量，一个同学使用了如图所示的简易装置：倒置的圆锥. 雨后，用倒置的圆锥接到的雨水的数据如图所示，则这一场雨的降水量为 m m .三、解答题：本大题共6小题，共80分. 解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分13分）如图，四边形ABCD 为矩形，AD ⊥平面ABE ，90AEB ∠=o，F 为CE 上的点. （Ⅰ）求证：//AD 平面BCE ；（Ⅱ）求证：AE ⊥BF ．正（主）视图侧（左）视图俯视图AEBCD F18.（本小题满分13分）已知△ABC 三个顶点的坐标分别为(0,0)A ，(4,0)B ，(3,1)C . （Ⅰ）求△ABC 中AC 边上的高线所在直线的方程；（Ⅱ）求△ABC 外接圆的方程.19.（本小题满分14分）如图，已知直三棱柱111ABC A B C -中，AB BC =，E 为AC 中点. （Ⅰ）求证：1//AB 平面1BC E ；（Ⅱ）求证：平面1BC E ⊥平面11ACC A .20.（本小题满分13分）如图，,A B 是椭圆22:13x W y +=的两个顶点，过点A 的直线与椭圆W 交于另一点C .（Ⅰ）当AC 的斜率为31时，求线段AC 的长；（Ⅱ）设D 是AC 的中点，且以AB 为直径的圆恰过点D . 求直线AC 的斜率.AB CEA 1B 1C 121.（本小题满分13分）如图，四棱锥P ABCD -中，底面ABCD 为矩形，平面PCD ⊥平面ABCD ，且3PD PC BC ===，CD =E 为PB 中点.（Ⅰ）求三棱锥P BCD -的体积；（Ⅱ）求证：CE ⊥平面PBD ；（Ⅲ）设M 是线段CD 上一点，且满足2DM MC =，试在线段PB 上确定一点N ，使得//MN 平面PAD ，并求出BN 的长.22.（本小题满分14分）已知,A B 是抛物线24y x =上的不同两点，弦AB （不平行于y 轴）的垂直平分线与x 轴交于点P .（Ⅰ）若直线AB 经过抛物线24y x =的焦点，求,A B 两点的纵坐标之积；（Ⅱ）若点P 的坐标为(4,0)，弦AB 的长度是否存在最大值？若存在，求出其最大值；若不存在，请说明理由.PABCDE M·北京市西城区2014 — 2015学年度第一学期期末试卷高二数学（文科）参考答案及评分标准2015.1一、选择题：本大题共10小题，每小题4分，共40分.1.B2.B3.D4. C5. D6.D7.A8. A9.C 10. C 二、填空题：本大题共6小题，每小题5分，共30分.11. 1x =- 12. 2,20x x x ∀∈-≥R 13.8314. 22(2)(2)4x y -+-= 15. 2 16. 1三、解答题：本大题共6小题，共80分. 17. （本小题满分13分）（Ⅰ）证明：因为四边形ABCD 为矩形，所以//AD BC . ………………2分又因为BC ⊂平面BCE ，AD ⊄平面BCE ， ………………4分所以//AD 平面BCE . ………………5分（Ⅱ）证明：因为AD ⊥平面ABE ，BC AD //，所以BC ⊥平面ABE ，则BC AE ⊥ . ………………7分又因为90AEB ∠=o，所以AE BE ⊥. ………………9分所以AE ⊥平面BCE . ………………11分又BF ⊂平面BCE ， ………………12分所以AE BF ⊥. ………………13分18. （本小题满分13分）解：（Ⅰ）因为(0,0)A ，(3,1)C ，所以直线AC 的斜率为13k =， ………………2分又AC 边上的高所在的直线经过点(4,0)B ，且与AC 垂直，所以所求直线斜率为3-， ………………4分所求方程为03(4)y x -=--，即 3120x y +-=. ………………5分（Ⅱ）设△ABC 外接圆的方程为220x y Dx Ey F ++++=, ………………6分AEBCDF因为点(0,0)A ，(4,0)B ，(3,1)C 在圆M 上，则2220,440,3130.F D F D E F =⎧⎪++=⎨⎪++++=⎩………………9分解得4D =-，2E =，0F =. ………………12分所以△ABC ∆外接圆的方程为22420x y x y +-+=. ………………13分19. （本小题满分14分）（Ⅰ）证明：连结1CB ，与1BC 交于点F ，连结EF . ………………1分因为三棱柱111ABC A B C -是直三棱柱，所以四边形11BCC B 是矩形，点F 是1B C 中点. ………………3分又E 为AC 中点，所以1//EF AB . …………5分因为EF ⊂平面1BC E ，1AB ⊄平面1BC E ，所以1//AB 平面1BC E . ………………7分（Ⅱ）证明：因为AB BC =，E 为AC 中点，所以BE AC ⊥. ………………9分又因为三棱柱111ABC A B C -是直三棱柱，所以1CC ⊥底面ABC ，从而1CC BE ⊥. ………………11分所以BE ⊥平面11ACC A . ………………12分因为BE ⊂平面1BC E ， ………………13分所以平面1BC E ⊥平面11ACC A . ………………14分20. （本小题满分13分）解：（Ⅰ）由已知(0,1)A -，直线AC 的方程为13y x 1=-. ………………1分由221,313y x x y 1⎧=-⎪⎪⎨⎪+=⎪⎩ 得2230x x -=， ………………2分解得32x =或0x =（舍）， ………………3分所以点C 的坐标为31(,)22-， ………………4分所以2AC ==. ………………5分ABCEA 1B 1C 1F（Ⅱ）依题意，设直线AC 的方程为1y kx =-，0k ≠.由221,13y kx x y =-⎧⎪⎨+=⎪⎩ 得22(31)60k x kx +-=， ………………7分解得2631kx k =+或0x =（舍）， ………………8分所以点C 的横坐标为2631kk +，设点D 的坐标为00(,)x y ，则02331kx k =+， ………………9分0021131y kx k -=-=+， ………………10分因为以AB 为直径的圆恰过点D ，所以1OD =，即222231()()13131k k k -+=++. ………………11分整理得23k 1=， ………………12分所以k =. ………………13分21. （本小题满分13分）（Ⅰ）解：由已知3PD PC ==，CD =△PCD 是等腰直角三角形，90CPD ∠=o. ………………1分因为平面PCD ⊥平面ABCD ，底面ABCD 为矩形，BC CD ⊥，所以BC ⊥平面PCD . ………………2分三棱锥P BCD -的体积1119()3322PCD V S BC PC PD BC ∆=⨯=⨯⨯⨯=. ………………4分（Ⅱ）证明：由（Ⅰ）知，BC ⊥平面PCD ，所以BC ⊥PD .因为90CPD ∠=o，即PD PC ⊥，所以PD ⊥平面PBC . ………………5分因为CE ⊂平面PBC ，所以PD CE ⊥. ………………6分因为PC BC =，E 为PB 中点，所以CE PB ⊥， ………………7分因为PD PB P =I ，所以CE ⊥平面PBD . ………………8分（Ⅲ）解：在面PCD 上，过M 作//MF PD 交PC 于F .在面PBC 上，过F 作//FN BC 交PB 于N ，连结MN . ………………9分因为//MF PD ，MF ⊄平面PAD ，PD ⊂平面PAD ，PABCDE M· FN所以//MF 平面PAD .因为////FN BC AD ，FN ⊄平面PAD ，AD ⊂平面PAD ，所以//FN 平面PAD .所以平面//MNF 平面PAD . ………………10分从而，//MN 平面PAD . ………………11分由所作可知，△CMF 为等腰直角三角形，CM =所以1CF =，2PF =. ………………12分△PNF ,△PBC 均为等腰直角三角形，所以PN =PB =所以N 为线段PB 上靠近点B 的三等分点，且BN =. ………………13分22. （本小题满分14分）解：（Ⅰ）抛物线24y x =的焦点为(1,0)F ， ………………1分依题意，设直线AB 方程为(1)y k x =-，其中0k ≠. ………………2分将24y x =代入直线方程，得2(1)4y y k =-，整理得2440ky y k --=， ………………4分所以4A B y y =-，即,A B 两点的纵坐标之积为4-. ………………5分（Ⅱ）设:(0)AB y kx b k =+≠，11(,)A x y ，22(,)B x y .由24,y x y kx b⎧=⎨=+⎩ 得222(24)0k x kb x b +-+=. ………………6分由222241616416160k b kb k b kb ∆=+--=->，得1kb <. ………………7分所以12242kb x x k -+=，2122b x x k=. ………………8分设AB 中点坐标为00(,)x y ，则120222x x kb x k +-==， 002y kx b k=+=， ………………9分所以弦AB 的垂直平分线方程为2212()kby x k k k--=--，令0y =，得222kbx k -=+. ………………10分由已知2224kb k-+=，即222k kb =-. ………………11分AB ======……………12分当2112k =，即k =AB 的最大值为6. ………………13分当k =b =；当k =b =均符合题意.所以弦AB 的长度存在最大值，其最大值为6. ………………14分。

【数学】北京市西城区(普通校)2014-2015学年高一上学期期末考试

北京市西城区2014 — 2015学年度第一学期期末试卷高一数学试卷满分：150分考试时间：120分钟 A 卷 [必修模块4] 本卷满分：100分一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.1．已知(0,2π)α∈，且sin 0<α，cos 0>α，则角α的取值范围是（）（A ）π(0,)2（B ）π(,π)2（C ）3π(π,)2（D ）3π(,2π)22．已知向量(2,8)=a ，(4,2)=-b ．若2=-c a b ，则向量=c （）（A ）(0,18)（B ）(8,14)（C ）(12,12)（D ）(4,20)-3．已知角α的终边经过点(3,4)P -，那么sin =α（）（A ）35（B ）45-（C ）34（D ）34-4．在△ABC 中，D 是BC 的中点，则AD =（）（A ）1()2AB AC + （B ）1()2AB AC - （C ）1()2AB BC +（D ）1()2AB BC -5．函数2(sin cos )y x x =-的最小正周期为（）（A ）2π（B ）3π2（C ）π（D ）π26．如果函数cos()y x =+ϕ的一个零点是3π，那么ϕ可以是（）（A ）6π （B ）6π-（C ）3π（D ）3π-7．如图，在矩形ABCD 中，2AB =，BC =， E 是CD 的中点，那么AE DC ⋅=（）（A ）4（B ）2（C （D ）18．当[0,π]x ∈时，函数()cos f x x x =的值域是（）（A ）[2,1]-（B ）[1,2]-（C ）[1,1]-（D ）[-9．为得到函数πcos()6y x =+的图象，只需将函数sin y x =的图象（）（A ）向左平移π3个单位（B ）向右平移π3个单位（C ）向左平移2π3个单位（D ）向右平移2π3个单位10．已知a ，b 为单位向量，且m ⋅=a b ，则||t +a b ()t ∈R 的最小值为（）（A （B ）1（C ）||m（D二、填空题：本大题共6小题，每小题4分，共24分. 把答案填在题中横线上. 11．若向量(1,2)=a 与向量(,1)=-λb 共线，则实数=λ_____． 12．已知α是第二象限的角，且5sin 13α=，则cos =α_____． 13．若(,)22ππ∈-θ，且tan 1>θ，则θ的取值范围是_____． 14．已知向量(1,3)=a ，(2,1)=-b ，(1,1)=c ．若(,)=∈R c a +b λμλμ，则=λμ_____． 15．函数2()sin sin cos f x x x x =+⋅的最大值是_____． 16．关于函数()sin(2)()6f x x x π=-∈R ，给出下列三个结论：① 对于任意的x ∈R ，都有2()cos(2)3f x x π=-； ② 对于任意的x ∈R ，都有()()22f x f x ππ+=-；③ 对于任意的x ∈R ，都有()()33f x f x ππ-=+．其中，全部正确结论的序号是_____．三、解答题：本大题共3小题，共36分. 解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）已知tan 2=-α，其中(,)2π∈πα．（Ⅰ）求πtan()4-α的值；（Ⅱ）求sin 2α的值． 18．（本小题满分14分）已知向量(cos ,sin )=ααa，1(2=-b ，其中α是锐角．（Ⅰ）当30︒=α时，求||+a b ；（Ⅱ）证明：向量+a b 与-a b 垂直；（Ⅲ）若向量a 与b 夹角为60︒，求角α． 19．（本小题满分10分）已知函数()sin cos f x a x b x =+，其中a ∈Z ，b ∈Z ．设集合{|()0}A x f x ==，{|(())0}B x f f x ==，且A B =．（Ⅰ）证明：0b =；（Ⅱ）求a 的最大值．B 卷 [学期综合] 本卷满分：50分一、填空题：本大题共5小题，每小题4分，共20分. 把答案填在题中横线上. 1．已知集合{,}A a b =，则满足{,,}AB a b c =的不同集合B 的个数是_____．2．若幂函数y x =α的图象过点(4,2)，则=α_____．3．函数2lg ,0,()4,0,x x f x x x >⎧=⎨-<⎩的零点是_____．4．设()f x 是定义在R 上的偶函数，且()f x 在[0,)+∞上是减函数．若()(2)f m f >，则实数m 的取值范围是_____．5．已知函数()f x 的定义域为D ．若对于任意的1x D ∈，存在唯一的2x D ∈，使得M =成立，则称函数()f x 在D 上的几何平均数为M ．已知函数()31([0,1])g x x x =+∈，则()g x 在区间[0,1]上的几何平均数为_____．二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤. 6．（本小题满分10分）已知函数()(2)()f x x x a =-+，其中a ∈R ．（Ⅰ）若()f x 的图象关于直线1x =对称，求a 的值；（Ⅱ）求()f x 在区间[0,1]上的最小值． 7．（本小题满分10分）已知函数()23x x f x a b =⋅+⋅，其中,a b 为常数．（Ⅰ）若0ab >，判断()f x 的单调性，并加以证明；（Ⅱ）若0ab <，解不等式：(1)()f x f x +>． 8．（本小题满分10分）定义在R 上的函数()f x 同时满足下列两个条件： ① 对任意x ∈R ，有(2)()2f x f x +≥+；② 对任意x ∈R ，有(3)()3f x f x +≤+．设()()g x f x x =-．（Ⅰ）证明：(3)()(2)g x g x g x +≤≤+；（Ⅱ）若(4)5f =，求(2014)f 的值．北京市西城区2014 — 2015学年度第一学期期末试卷高一数学参考答案及评分标准 2015.1A 卷 [必修模块4] 满分100分一、选择题：本大题共10小题，每小题4分，共40分.1.D ；2.B ；3.B ；4.A ；5.C ；6.A ；7.B ；8.A ；9.C ； 10.D. 二、填空题：本大题共6小题，每小题4分，共24分.11.12-； 12.1213-； 13. (,)42ππ； 14.32；15.12+； 16. ① ② ③. 注：16题，少解不给分.三、解答题：本大题共3小题，共36分. 17.（本小题满分12分）（Ⅰ）解：因为 tan 2=-α，所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】 3=. 【 6分】（Ⅱ）解：由π(,π)2∈α，tan 2α=-，得sin α=，【 8分】cos α=. 【10分】所以 4sin 22sin cos 5==-ααα. 【12分】 18.（本小题满分14分）（Ⅰ）解：当30︒=α时，1)2=a ，【 1分】所以+a b =，【 2分】所以||+=a b = 【 4分】（Ⅱ）证明：由向量(cos sin )αα=，a，1(,22=-b ，得 1(cos ,sin 22+=-+ααa b ，1(cos ,sin 22-=+-ααa b ，由 π(0,)2∈α，得向量+a b ，-a b 均为非零向量. 【 5分】因为 222213()()||||(sin cos )()044+⋅-=-=+-+=ααa b a b a b ，【 7分】所以向量+a b 与-a b 垂直. 【 8分】（Ⅲ）解：因为||||1==a b ，且向量a 与b 夹角为60︒，所以 1||||cos 602︒⋅=⋅=a b a b . 【10分】所以 11cos 22-=αα，即 π1sin()62-=α. 【12分】因为 π02<<α，所以 πππ663-<-<α，【13分】所以 ππ66-=α，即3π=α. 【14分】 19.（本小题满分10分）（Ⅰ）证明：显然集合A ≠∅．设 0x A ∈，则0()0f x =．【 1分】因为 A B =，所以 0x B ∈，即 0(())0f f x =，所以 (0)0f =，【 3分】所以 0b =．【 4分】（Ⅱ）解：由（Ⅰ）得()sin f x a x =，a ∈Z ．① 当0a =时，显然满足A B =．【 5分】 ② 当0a ≠时，此时{|sin 0}A x a x ==；{|sin(sin )0}B x a a x ==，即{|sin ,}B x a x k k ==π∈Z ．【 6分】因为 A B =，所以对于任意x ∈R ，必有sin a x k ≠π (k ∈Z ，且0)k ≠成立．【 7分】所以对于任意x ∈R ，sin k x a π≠，所以 1k aπ>，【 8分】即 ||||a k <⋅π，其中k ∈Z ，且0k ≠．所以 ||a <π，【 9分】所以整数a 的最大值是3．【10分】B 卷 [学期综合] 满分50分一、填空题：本大题共5小题，每小题4分，共20分.1. 4；2.12； 3. 2-，1； 4. (2,2)-； 5. 2. 注：3题，少解得2分，有错解不给分. 二、解答题：本大题共3小题，共30分. 6.（本小题满分10分）（Ⅰ）解法一：因为2()(2)()(2)2f x x x a x a x a =-+=+--，所以，()f x 的图象的对称轴方程为22ax -=. 【 2分】由212a-=，得0a =. 【 4分】解法二：因为函数()f x 的图象关于直线1x =对称，所以必有(0)(2)f f =成立，【 2分】所以 20a -=，得0a =. 【 4分】（Ⅱ）解：函数()f x 的图象的对称轴方程为22ax -=. ① 当202a-≤，即 2a ≥时，因为()f x 在区间(0,1)上单调递增，所以()f x 在区间[0,1]上的最小值为(0)2f a =-. 【 6分】 ② 当2012a-<<，即 02a <<时，因为()f x 在区间2(0,)2a -上单调递减，在区间2(,1)2a-上单调递增，所以()f x 在区间[0,1]上的最小值为222()()22a a f -+=-. 【 8分】 ③ 当212a-≥，即 0a ≤时，因为()f x 在区间(0,1)上单调递减，所以()f x 在区间[0,1]上的最小值为(1)(1)f a =-+. 【10分】 7.（本小题满分10分）（Ⅰ）解：当0,0a b >>时，()f x 在R 上是增函数；当0,0a b <<时，()f x 在R 上是减函数；【 1分】证明如下：当0,0a b >>时，任取12,x x ∈R ，且12x x <，则210x x x ∆=->，则 212121()()(22)(33)x x x x y f x f x a b ∆=-=-+-.因为 122122,0(22)0x x x x a a <>⇒->；又122133,0(33)0x x x xb b <>⇒->，所以 21()()0y f x f x ∆=->，所以，当0,0a b >>时，()f x 在R 上是增函数.当0,0a b <<时，同理可得，()f x 在R 上是减函数. 【 5分】（Ⅱ）解：由(1)()2230x xf x f x a b +-=⋅+⋅>，得 32()2xb a >-. （*）【 6分】① 当0,0a b <>时，（*）式化为3()22xa b->，解得32log ()2ax b>-.【 8分】 ② 当0,0a b ><时，（*）式化为3()22xa b-<，解得32log ()2ax b<-.【10分】 8.（本小题满分10分）（Ⅰ）证明：因为()()g x f x x =-，所以(2)(2)2g x f x x +=+--，(3)(3)3g x f x x +=+--．由条件①，②可得(2)(2)2()22()()g x f x x f x x f x x g x +=+--≥+--=-=；③ 【 2分】 (3)(3)3()33()()g x f x x f x x f x x g x +=+--≤+--=-=． ④ 【 4分】所以(3)()(2)g x g x g x +≤≤+．（Ⅱ）解：由③得 (2)()g x g x +≥，所以(6)(4)(2)()g x g x g x g x +≥+≥+≥．【 6分】由④得 (3)()g x g x +≤，所以(6)(3)()g x g x g x +≤+≤．【 7分】所以必有(6)()g x g x +=，即()g x 是以6为周期的周期函数．【 8分】所以(2014)(33564)(4)(4)41g g g f =⨯+==-=．【 9分】所以(2014)(2014)20142015f g =+=．【10分】。

2014—2015学年度北京市西城区第一学期数学期中试题(附答案)

APNMO北京市西城区2014—2015学年度第一学期数学期中试题（附答案）第Ⅰ卷（选择题共30分）一、选择题(本题共30分，每小题3分) 1．下列因式分解结果正确的是（）。

A ．3221055(2)a a a a a +=+B ．249(43)(43)x x x -=+- C ．2221(1)a a a --=- D ．256(6)(1)x x x x --=-+2．如图，OP 平分∠MON，PA⊥ON 于点A ，点Q 是射线OM 上的一个动点，若PA=2，则PQ 的最小值为（）。

A. 1 B.2 C.3 D. 43．下列分式中，无论x 取何值，分式总有意义的是( )。

A ．211x +B ．21x x +C ．311x - D ．5x x -4.若分式2aa b+中的a 、b 的值同时扩大到原来的10倍，则分式的值（）。

A ．是原来的20倍 B ．是原来的10倍C ．是原来的110D ．不变 5．在数学活动课上，小明提出这样一个问题：如右图, ∠B =∠C = 90︒,E 是BC 的中点, DE 平分∠ADC, ∠CED = 35︒, 则∠EAB 的度数是 ( )。

A ．65︒B ．55︒C ．45︒D ．35︒6．某园林公司增加了人力进行园林绿化，现在平均每天比原计划多植树50棵，现在植树600棵所需的时间与原计划植树450棵所需的时间相同，如果设原计划平均每天植树x 棵，那么下面所列方程中，正确的是（）。

A ．x x 45050600=- B ．x x 45050600=+ C ．50450600+=x x D ．50450600-=x x 7．若分式112--x x 的值为0，则x 的值为（）。

A ．1B ．－1C ．0D ． 1±8．如果一个等腰三角形的两边长分别是4cm 和8cm ，那么此三角形的周长是（）。

A. 12cm B.16cm C. 20cm D. 16cm 或20cm 9.如图，在△ABC 中，BD 、CE 分别是AC 、AB 边上的中线，分别延长BD 、CE 到F 、G ，使DF ＝BD ，EG ＝CE ，则下列结论：①GA ＝AF ，②GA ∥BC ，③AF ∥BC ，④G 、A 、F 在一条直线上， ⑤A 是线段GF 的中点，其中正确的有（）。

北京市西城区2013-2014学年高一上学期期末考试数学试题(普通校试题

北京市西城区2013 — 2014学年度第一学期期末试卷高一数学 2014.1试卷满分：150分考试时间：120分钟A 卷 [必修模块4] 本卷满分：100分一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的. 1．若sin 0<α，且cos 0>α，则角α是（）（A ）第一象限的角（B ）第二象限的角（C ）第三象限的角（D ）第四象限的角2．已知向量1(1,0)=e ，2(0,1)=e ，那么122|+=|e e （）（A ）1（B （C ）2（D 3．若角α的终边经过点(1,2)P -，则tan =α（）（A （B ）（C ）2- （D ）12-4．已知正方形ABCD 的边长为1，则AB AC ⋅=（）（A （B ）1（C （D ）25．在平面直角坐标系xOy 中，函数2sin()6y x π=-的图象（）（A ）关于直线6x π=对称（B ）关于直线6x π=-对称（C ）关于点(,0)6π对称（D ）关于点(,0)6π-对称 6．已知非零向量,OA OB 不共线，且13BM BA =，则向量OM =（）（A ）1233OA OB +（B ）2133OA OB +（C ）1233OA OB -（D ）1433OA OB -7．已知函数1()cos 22f x x x =+，则()12f π=（）（A ）2（B ）2（C ）1（D 8．设a ，b 是两个非零向量，且+=-a b a b ，则a 与b 夹角的大小为（）（A ）120︒（B ）90︒（C ）60︒（D ）30︒9．已知函数()sin cos f x x x =ωω在区间[,]63ππ-上单调递增，则正数ω的最大值是（）（A ）32（B ）43（C ）34 （D ）2310．已知函数()cos(sin )f x x =，则下列结论中正确的是（）（A ）()f x 的定义域是[1,1]- （B ）()f x 的值域是[1,1]- （C ）()f x 是奇函数（D ）()f x 是周期为π的函数二、填空题：本大题共6小题，每小题4分，共24分. 把答案填在题中横线上. 11. sin()6π-=______.12. 若sin =α，且(0,)∈πα，则α=______. 13. 已知向量(1,3)=a ，(2,)k =-b ．若向量a 与b 共线，则实数k =_____. 14. 若tan 2=α，且32π∈(π,)α，则sin()2π+=α______. 15. 已知向量(cos ,sin )αα=a ，(cos ,sin )ββ=b ．若π,3〈〉=a b ，则c o s ()-=αβ_____. 16. 定义在R 上的非常值函数()f x 同时满足下述两个条件：① 对于任意的x ∈R ，都有2()()3f x f x π+=； ② 对于任意的x ∈R ，都有()()66f x f x ππ-=+.则其解析式可以是()f x =_____.（写出一个满足条件的解析式即可）三、解答题：本大题共3小题，共36分.解答应写出文字说明，证明过程或演算步骤.17. （本小题满分12分）已知3tan 4=-α. （Ⅰ）求πtan()4-α的值；（Ⅱ）求2sin 3cos 3sin 2cos --αααα的值.18.（本小题满分12分）已知函数2()sin 22cos2f x x x x =⋅．（Ⅰ）求()f x 的最小正周期；（Ⅱ）若[,]84x ππ∈，求()f x 的最大值与最小值．19.（本小题满分12分）如图，正六边形ABCDEF 的边长为1.,M N 分别是,BC DE 上的动点，且满足BM DN =.（Ⅰ）若,M N 分别是,BC DE 的中点，求AM AN ⋅的值；（Ⅱ）求AM AN ⋅的取值范围.B 卷 [学期综合] 本卷满分：50分一、填空题：本大题共5小题，每小题4分，共20分.把答案填在题中横线上. 1. 已知集合2{|430}A x x x =-+>，{|02}B x x =<≤，那么A B =_____.2. 已知2log 3a =，32b=，21log 3c =.将,,a b c 按从小到大排列为_____. 3. 若函数2()2f x x x =-在区间(,)a +∞上是增函数，则a 的取值范围是_____. 4. 函数12()|21|xf x x =--的零点个数为_____.5. 给定数集A .若对于任意,a b A ∈，有a b A +∈，且a b A -∈，则称集合A 为闭集合.给出如下四个结论：① 集合{4,2,0,2,4}A =--为闭集合； ② 集合{|3,}A n n k k ==∈Z 为闭集合； ③ 若集合12,A A 为闭集合，则12AA 为闭集合；④ 若集合12,A A 为闭集合，且1A R Ø，2A R Ø，则存在c ∈R ，使得12()c A A ∉.其中，全部正确结论的序号是_____.二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤. 6.（本小题满分10分）已知函数()log (2)1a f x x =+-，其中1a >.（Ⅰ）若()f x 在[0,1]上的最大值与最小值互为相反数，求a 的值；（Ⅱ）若()f x 的图象不经过第二象限，求a 的取值范围.7.（本小题满分10分）已知函数()|2|f x x x =-. （Ⅰ）解不等式()3f x <；（Ⅱ）设0a >，求()f x 在区间[0,]a 上的最大值.8.（本小题满分10分）设函数()f x ，()g x 的定义域分别为f g D D ，，且f g D D Ø.若对于任意f x D ∈，都有()()g x f x =，则称()g x 为()f x 在g D 上的一个延拓函数.给定2() 1 (01)f x x x =-<≤.（Ⅰ）若()h x 是()f x 在[1,1]-上的延拓函数，且()h x 为奇函数，求()h x 的解析式；（Ⅱ）设()g x 为()f x 在(0,)+∞上的任意一个延拓函数，且()g x y x=是(0,)+∞上的单调函数.（ⅰ）判断函数()g x y x=在(0,1]上的单调性，并加以证明；（ⅱ）设0s >，0t >，证明：()()()g s t g s g t +>+.北京市西城区2013 —2014学年度第一学期期末试卷一、选择题：本大题共10小题，每小题4分，共40分.1.D；2.D；3.C；4.B；5.C；6.A；7.A；8.B；9.C；10.D.二、填空题：本大题共6小题，每小题4分，共24分.11.12-；12.3π，或32π；13.6-；14.5-；15.12；16.sin3x等（答案不唯一）.注：12题，得出一个正确的结论得2分.三、解答题：本大题共3小题，共36分.17.（Ⅰ）解：因为3 tan4=-α，所以πtan tanπ4tan()π41tan tan4--=+⋅ααα【3分】7=-. 【6分】（Ⅱ）解：因为3 tan4=-α，所以2sin3cos2tan33sin2cos3tan2--=--αααααα【9分】1817=. 【12分】18.（Ⅰ）解：1cos4()2cos22xf x x x-=⋅1cos4422xx-=+【2分】1sin(4)62xπ=-+．【4分】因为242Tππ==，所以()f x的最小正周期是2π．【6分】（Ⅱ）解：由（Ⅰ）得，1 ()sin(4)62f x xπ=-+．因为84x ππ≤≤，所以 54366x πππ≤-≤，【 8分】所以 1sin(4)126x π≤-≤，【 9分】所以 131sin(4)622x π≤-+≤．【10分】所以，当6x π=时，()f x 取得最大值32；当4x π=时，()f x 取得最小值1．【12分】19.（本小题满分12分）（Ⅰ）解：如图，以AB 所在直线为x 轴，以A 为坐标原点建立平面直角坐标系. 【 1分】因为ABCDEF 是边长为1的正六边形，且,M N 分别是,BC DE 的中点，所以 5(,)44M ，1(2N ，【 3分】所以 5311848AM AN ⋅=+=. 【 4分】（Ⅱ）解：设BM DN t ==，则[0,1]t ∈.【 5分】所以(1,)22t M +，(1N t -. 【 7分】所以3(1)(1)22t AM AN t t ⋅=+⋅-+2112t t ++=-213(1)22t =--+ 【10分】当0t =时，AM AN ⋅取得最小值1；【11分】当1t =时，AM AN ⋅取得最大值32. 【12分】一、填空题：本大题共5小题，每小题4分，共20分.1.{|01}x x <<；2.c b a <<；3. [1,)+∞；4. 2；5.②④. 注：5题，选出一个正确的序号得2分，有错选不给分.6.（Ⅰ）解：函数()log (2)1a f x x =+-的定义域是(2,)-+∞. 【 1分】因为 1a >，所以 ()log (2)1a f x x =+-是[0,1]上的增函数. 【 2分】所以 ()f x 在[0,1]上的最大值是(1)log 31a f =-；最小值是(0)log 21a f =-.【 4分】依题意，得 log 31(log 21)a a -=--，【 5分】解得a =【 6分】（Ⅱ）解：由（Ⅰ）知，()log (2)1a f x x =+-是(2,)-+∞上的增函数. 【 7分】在()f x 的解析式中，令0x =，得(0)log 21a f =-，所以，()f x 的图象与y 轴交于点(0,log 21)a -. 【 8分】依题意，得(0)log 210a f =-≤，【 9分】解得 2a ≥. 【10分】 7.（Ⅰ）解：原不等式可化为22230x x x ≥⎧⎨--<⎩，，（1）或22230.x x x <⎧⎨-+>⎩，（2）【 1分】解不等式组（1），得 23x ≤<；解不等式组（2），得2x <. 【 3分】所以原不等式的解集为{|3}x x <. 【 4分】（Ⅱ）解：222,2,()|2|2, 2.x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩ 【 5分】① 当01a <<时，()f x 是[0,]a 上的增函数，此时()f x 在[0,]a 上的最大值是2()2f a a a =-+. 【 6分】② 当12a ≤≤时，()f x 在[0,1]上是增函数，在[1,]a 上是减函数，此时()f x 在[0,]a 上的最大值是(1)1f =. 【 7分】③ 当2a >时，令()(1)(2)10f a f a a -=-->，解得1a >. 所以，当21a <≤此时()(1)f a f ≤，()f x 在[0,]a 上的最大值是(1)1f =；当1a >此时()(1)f a f >，()f x 在[0,]a 上的最大值是2()2f a a a =-.【 9分】记()f x 在区间[0,]a 上的最大值为()g a ，所以222,01,()1,112,1a a a g a a a a a ⎧-+<<⎪⎪=≤≤+⎨⎪->+⎪⎩ 【10分】8.（Ⅰ）解：当0x =时，由()h x 为奇函数，得(0)0h =. 【 1分】任取[10)x ∈-，，则(01]x -∈，，由()h x 为奇函数，得22()()[()1]1h x h x x x =--=---=-+，【 2分】所以()h x 的解析式为221,01,()0,0,1,10.x x h x x x x ⎧-<≤⎪==⎨⎪-+-≤<⎩【 3分】（Ⅱ）解：（ⅰ）函数()g x y x=是(0,1]上的增函数. 【 4分】证明如下：因为()g x 为()f x 在(0,)+∞上的一个延拓函数，所以当(01]x ∈，时，2()()1g x f x x ==-. 记()()1()g x f x k x x x x x===-，其中(0,1]x ∈. 任取12,(0,1]x x ∈，且12x x <，则210x x x ∆=->，因为211221212112()(1)11()()()0x x x x y k x k x x x x x x x -+∆=-=---=>，所以函数()g x y x=是(0,1]上的增函数. 【 6分】（ⅱ）由()g x y x = 是(0,)+∞上的单调函数，且(0,1]x ∈时，()g x y x =是增函数，从而得到函数()g x y x= 是(0,)+∞上的增函数. 【 7分】因为 0s >，0t >，所以 s t s +>，s t t +>，所以()()g s t g s s t s+>+，即 ()()()s g s t s t g s ⋅+>+⋅. 【 8分】同理可得：()()()t g s t s t g t ⋅+>+⋅.将上述两个不等式相加，并除以s t +，即得 ()()()g s t g s g t +>+. 【10分】。

北京市西城区2014-2015学年度第一学期期末试卷高三数学(文科)

北京市西城区2014-2015学年度第一学期期末试卷高三数学(文科)一、选择题（共8小题；共40分）1. 设集合，，则集合 ______A. B. C. D.2. 设命题，，则为______A. ，B. ，C. ，D. ，3. 在锐角中，角，，所对的边分别为，，，若，，则______A. B. C. D.4. 执行如图所示的程序框图，输出的值为______A. B. C. D.5. 设函数的定义域为，则“ ”是“函数为奇函数”的______A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件6. 某天，甲要去银行办理储蓄业务，已知银行的营业时间为9：00 至17：00，设甲在当天13：00至 18：00 之间任何时间去银行的可能性相同，那么甲去银行且恰好能办理业务的概率是______A. B. C. D.7. 设抛物线的焦点为，过的直线与相交于，两点，记点到直线的距离为，则有______A. B.C. D.8. 如图，在空间四边形中，两条对角线，互相垂直，且长度分别为和，平行于这两条对角线的平面与边，，，分别相交于点，，，，记四边形的面积为，设，则______A. 函数的值域为B. 函数的最大值为C. 函数在上单调递减D. 函数满足二、填空题（共6小题；共30分）9. 复数，则 ______10. 设平面向量，满足，，，那么，的夹角 ______．11. 一个四棱锥的三视图如图所示，那么这个四棱锥最长棱的棱长为______．12. 设，为双曲线：的左、右焦点，且直线为双曲线的一条渐近线，点为上一点，如果，那么双曲线的方程为______；离心率为______．13. 某小学教师准备购买一些签字笔和铅笔盒作为奖品，已知签字笔每支元，铅笔盒每个元，花费总额不能超过元，为了便于学生选择，购买签字笔和铅笔盒的个数均不能少于个，那么该教师有______种不同的购买奖品方案．14. 设函数（1）如果，那么实数 ______；（2）如果函数有且仅有两个零点，那么实数的取值范围是______．三、解答题（共6小题；共78分）15. 已知函数，．（1）求函数的最小正周期；（2）判断函数在区间上是否为增函数?并说明理由．16. 已知数列满足，且其前项和．（1）求的值和数列的通项公式；（2）设数列为等比数列，公比为，且其前项和满足，求的取值范围．17. 如图，在四棱柱中，底面，．，且，．点在棱上，平面与棱相交于点．（1）求证：平面；（2）求证：平面；（3）写出三棱锥体积的取值范围．（结论不要求证明）18. 最近，张师傅和李师傅要将家中闲置资金进行投资理财．现有两种投资方案，且年后投资盈亏的情况如下：（i ）投资股市：投资结果获利不赔不赚亏损概率（ii ）购买基金：投资结果获利不赔不赚亏损概率（1）当时，求的值；（2）已知"购买基金"亏损的概率比"投资股市"亏损的概率小，求的取值范围；（3）已知张师傅和李师傅两人都选中了"购买基金"来进行投资，假设三种投资结果出现的可能性相同，求一年后他们两人中至少有一人获利的概率．19. 已知椭圆的右焦点为，右顶点为，离心率为，点满足条件．（1）求的值；（2）设过点的直线与椭圆相交于，两点，记和的面积分别为，，若，求直线的方程．20. 对于函数，，如果它们的图象有公共点，且在点处的切线相同，则称函数和在点处相切，称点为这两个函数的切点．设函数（），．（1）当，时，判断函数和是否相切?并说明理由；（2）已知，，且函数和相切，求切点的坐标；（3）设，点的坐标为，问是否存在符合条件的函数和，使得它们在点处相切?若点的坐标为呢?（结论不要求证明）答案第一部分1. B2. B3. A4. C5. B6. D7. A8. D第二部分9.10.11.12. ；13.14. 或；第三部分15. （1）因为所以函数的最小正周期．（2）结论：函数在区间上是增函数．理由如下：由，解得所以函数的单调递增区间为，．当时，知在区间上单调递增．所以函数在区间上是增函数．16. （1）由题意，得，，因为，，所以．解得．所以．当时，由，得．验证知时，符合上式，所以，．（2）由（1），得．因为，所以，解得．又因为，所以的取值范围是．17. （1）因为是棱柱，所以平面平面．又因为平面平面，平面平面，所以．又平面，平面．所以平面．（2）在四边形中，因为，，且，，，所以，．所以，所以，即，因为平面，平面．所以．因为在四棱柱中，，所以．又因为平面，，所以平面．（3）三棱锥的体积的取值范围是．18. （1）因为“购买基金”后，投资结果只有“获利”、“不赔不赚”、“亏损”三种，且三种投资结果相互独立，所以．又因为，所以．（2）由“购买基金”亏损的概率比“投资股市”亏损的概率小，得，因为，所以，解得．又因为，，所以．所以．（3）记事件为“一年后张师傅和李师傅两人中至少有一人获利”．用，，分别表示一年后张师傅购买基金“获利”、“不赔不赚”、“亏损”，用，，分别表示一年后李师傅购买基金“获利”、“不赔不赚”、“亏损”，则一年后张师傅和李师傅购买基金，所有可能的投资结果有种，它们是，，，，，，，，，所以事件包含的结果有种，它们是，，，，，因此一年后张师傅和李师傅两人中至少有一人获利的概率．19. （1）因为椭圆的方程为，所以，，，则，，．因为．所以．（2）若直线的斜率不存在，则有，不合题意．若直线的斜率存在，设直线的方程为，，．由得．可知恒成立，且，，因为和的面积分别为，．所以，即，所以，，则即，即，解得．所以直线的方程为或．20. （1）结论：当，时，函数和不相切．理由如下：由条件知，由，得又因为，，所以当时，，，所以对于任意的，，当，时，函数和不相切．（2）若，则，．设切点坐标为，其中．由题意，得由，得，代入，得因为，且．所以．设函数，，则．令，解得或（舍）．当变化时，与的变化情况如下表所示．所以当时，取到最大值，且当时，．因此，当且仅当时．所以方程有且仅有一解．于是．因此切点的坐标为．（3）当点的坐标为时，存在符合条件的函数和，使得它们在点处相切；当点的坐标为时，不存在符合条件的函数和，使得它们在点处相切．。

北京市西城区2014-2015学年度高三第一学期期末试数学文

北京市西城区2014 — 2015学年度第一学期期末试卷高三数学（文科） 2015.1第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合1,0,1,2{}A -=，2{|}B x x x =>，则集合AB =（）（A ）{1,0,1}- （B ）{1,2}- （C ）{0,1,2} （D ）{1,1,2}- 2．设命题p ：2log 0,2x x x ∀>>，则p ⌝为（）（A ）2log 0,2x x x ∀>< （B ）2log 0,2x x x ∃>≤ （C ）2log 0,2x x x ∃>< （D ）2log 0,2x x x ∃>≥3．在锐角∆ABC 中，角A ，B ，C 所对的边分别为a ，b ，c . 若2a b =，sin B =，则（）（A ）3A π=（B ）6A π= （C）sin A = （D ）2sin 3A =4．执行如图所示的程序框图，输出的x 值为（）（A ）4 （B ）5 （C ）6 （D ）75．设函数()y f x =的定义域为R ，则“(0)0f =”是“函数()f x 为奇函数”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件6. 某天，甲要去银行办理储蓄业务，已知银行的营业时间为9：00至17：00，设甲在当天13：00至18：00之间任何时间去银行的可能性相同，那么甲去银行恰好能办理业务的概率是（）（A ）13 （B ）34 （C ）58 （D ）457．设抛物线2:4W y x =的焦点为F ，过F 的直线与W 相交于A ，B 两点，记点F 到直线l ：1x =-的距离为d ，则有（）（A ）2||d AB ≥ （B ）2||d AB = （C ）2||d AB ≤ （D ）2||d AB <8. 如图，在空间四边形ABCD 中，两条对角线,AC BD 互相垂直，且长度分别为4和6，平行于这两条对角线的平面与边,,,AB BC CD DA 分别相交于点,,,E F G H ，记四边形EFGH 的面积为y ，设BEx AB=，则（）（A ）函数()y f x =的值域为(0,4] （B ）函数()y f x =的最大值为8（C ）函数()y f x =在2(0,)3上单调递减（D ）函数()y f x =满足()(1)f x f x =-第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分． 9. 复数i1iz =+，则||z =______.10．设平面向量,a b 满足||3=a ，||2=b ，3⋅=-a b ，那么,a b 的夹角θ=____.11．一个四棱锥的三视图如图所示，那么这个四棱锥最长棱的棱长为_____.12．设12,F F 为双曲线C ：22221(0,0)x y a b a b -=>>的左、右焦点，且直线2y x =为双曲线C 的一条渐近线，点P 为C 上一点，如果12||||4PF PF -=，那么双曲线C 的方程为____；离心率为_____.13. 某小学教师准备购买一些签字笔和铅笔盒作为奖品，已知签字笔每支5元，铅笔盒每个6元，花费总额不能超过50元. 为了便于学生选择，购买签字笔和铅笔盒的个数均不能少于3个，那么该教师有_______种不同的购买奖品方案.侧(左)视图正(主)视图俯视图A BE CD GH F14. 设函数3||, 1,()log , 1.x a x f x x x -⎧=⎨>⎩≤（1）如果(1)3f =，那么实数a =___；（2）如果函数()2y f x =-有且仅有两个零点，那么实数a 的取值范围是___.三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤． 15．（本小题满分13分）已知函数2π()12sin ()4f x x =--，x ∈R .（Ⅰ）求函数()f x 的最小正周期；（Ⅱ）判断函数()f x 在区间ππ[,]66-上是否为增函数？并说明理由.16．（本小题满分13分）已知数列{}n a 满足25a =，且其前n 项和2n S pn n =-．（Ⅰ）求p 的值和数列{}n a 的通项公式；（Ⅱ）设数列{}n b 为等比数列，公比为p ，且其前n 项和n T 满足55T S <，求1b 的取值范围．17．（本小题满分14分）如图，在四棱柱1111D C B A ABCD -中，A A 1⊥底面A B C D ，90BAD ∠=，BC AD //，且122A A AD BC ===，1AB =. 点E 在棱AB 上，平面1A EC 与棱11C D 相交于点F .（Ⅰ）求证：1A F ∥平面1BCE ；（Ⅱ）求证： AC ⊥平面11CDD C ；（Ⅲ）写出三棱锥11B A EF -体积的取值范围. （结论不要求证明）B CA 1 D 1 DA B 1C 1E F最近，张师傅和李师傅要将家中闲置资金进行投资理财. 现有两种投资方案，且一年后投资盈亏的情况如下：（1）投资股市：（2）购买基金：（Ⅰ）当2p =时，求q 的值；（Ⅱ）已知“购买基金”亏损的概率比“投资股市”亏损的概率小，求p 的取值范围；（Ⅲ）已知张师傅和李师傅两人都选择了“购买基金”来进行投资，假设三种投资结果出现的可能性相同，求一年后他们两人中至少有一人获利的概率．19．（本小题满分14分）已知椭圆C ：2211612x y +=的右焦点为F ，右顶点为A ，离心率为e ，点(,0)(4)Pmm >满足条件||||FA e AP =. （Ⅰ）求m 的值；（Ⅱ）设过点F 的直线l 与椭圆C 相交于M ，N 两点，记PMF ∆和PNF ∆的面积分别为1S ，2S ，若122S S =,求直线l 的方程.对于函数(),()f x g x ，如果它们的图象有公共点P ，且在点P 处的切线相同，则称函数()f x 和()g x 在点P 处相切，称点P 为这两个函数的切点. 设函数2()(0)f x ax bx a =-≠,()ln g x x =.（Ⅰ）当1a =-,0b =时, 判断函数()f x 和()g x 是否相切？并说明理由；（Ⅱ）已知a b =，0a >，且函数()f x 和()g x 相切，求切点P 的坐标；（Ⅲ）设0a >，点P 的坐标为1(,1)e-，问是否存在符合条件的函数()f x 和()g x ，使得它们在点P 处相切？若点P 的坐标为2(e ,2)呢？（结论不要求证明）北京市西城区2014 — 2015学年度第一学期期末高三数学（文科）参考答案及评分标准2015.1一、选择题：本大题共8小题，每小题5分，共40分.1．B 2．B 3．A 4．C 5．B 6．D 7．A 8．D 二、填空题：本大题共6小题，每小题5分，共30分.9．2 10．2π3 11. 12．221416x y -=13．9 14．2-或4 (1,3]- 注：第12，14题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分. 其他正确解答过程，请参照评分标准给分. 15．（本小题满分13分）（Ⅰ）解：因为2π()12sin ()4f x x =--πcos 2()4x =- ……………… 3分sin 2x =， ……………… 5分所以函数()f x 的最小正周期2ππ2T ==.……………… 7分（Ⅱ）解：结论：函数()f x 在区间ππ[,]66-上是增函数. ……………… 9分理由如下：由ππ2π22π22k x k -+≤≤，解得ππππ44k x k -+≤≤，所以函数()f x 的单调递增区间为ππ[π,π]44k k -+，()k ∈Z .……………… 12分当0=k 时，知)(x f 在区间ππ[,]44-上单调递增，所以函数()f x 在区间ππ[,]66-上是增函数. ……………… 13分16．（本小题满分13分）（Ⅰ）解：由题意，得11S p =-，242S p =-，因为 25a =，212S a a =+，所以 24215S p p =-=-+，解得 2p =. ……………… 3分所以 22n S n n =-．当2n ≥时，由1n n n a S S -=-， ……………… 5分得 22(2)[2(1)(1)]43n a n n n n n =-----=-. ……………… 7分验证知1n =时，1a 符合上式，所以43n a n =-，*n ∈N . ……………… 8分（Ⅱ）解：由（Ⅰ），得11(12)(21)12n n n b T b -==--. ……………… 10分因为 55T S <，所以 521(21)255b -<⨯-，解得 14531b <． ……………… 12分又因为10b ≠，所以1b 的取值范围是45(,0)(0,)31-∞． ……………… 13分17．（本小题满分14分）（Ⅰ）证明：因为1111D C B A ABCD -是棱柱，所以平面ABCD ∥平面1111A B C D . 又因为平面ABCD 平面1A ECF EC =，平面1111A BC D 平面11A ECF A F =，B CA 1 D 1DA B 1C 1E F所以 1A F ∥CE . …………………3分又 1A F ⊄平面1BCE ，CE ⊂平面1BCE ，所以 1A F ∥平面1BCE . …………………6分（Ⅱ）证明：在四边形ABCD 中，因为 90BAD ∠=，BC AD //,且BC AD 2=，2AD =，1AB =，所以 222112AC =+=，222112CD =+=. 所以 222AC CD AD +=，所以 90ACD ∠=，即AC CD ⊥. …………………7分因为 1A A ⊥平面ABCD AC ⊂，平面ABCD ，所以 1A A AC ⊥.因为在四棱柱1111D C B A ABCD -中，11//A A C C ，所以 1C C AC ⊥. …………………9分又因为 1,CD C C ⊂平面11CDD C ，1CDC C C =，所以 AC ⊥平面11CDD C . …………………11分（Ⅲ）解：三棱锥11B A EF -的体积的取值范围是12[,]33. …………………14分18．（本小题满分13分）（Ⅰ）解：因为“购买基金”后，投资结果只有“获利”、“不赔不赚”、“亏损”三种且三种投资结果相互独立，所以 p +13+q =1. ……………… 2分又因为 12p =，所以 q =61． ……………… 3分（Ⅱ）解：由“购买基金”亏损的概率比“投资股市”亏损的概率小，得 38q <， ……………… 4分因为 p +13+q =1，所以 2338q p =-<，解得 724p >. ……………… 7分又因为 113p q ++=，0q ≥，所以 23p ≤. 所以72243p ≤<. ……………… 8分（Ⅲ）解：记事件A 为 “一年后张师傅和李师傅两人中至少有一人获利”， ………… 9分用a ，b ，c 分别表示一年后张师傅购买基金“获利”、“不赔不赚”、“亏损”，用x ，y ，z 分别表示一年后李师傅购买基金“获利”、“不赔不赚”、“亏损”，则一年后张师傅和李师傅购买基金，所有可能的投资结果有339⨯=种，它们是：(,)a x ，(,)a y ，(,)a z ，(,)b x ，(,)b y ，(,)b z ，(,)c x ，(,)c y ，(,)c z ， ……………10分所以事件A 的结果有5种，它们是：(,)a x ，(,)a y ，(,)a z ，(,)b x ，(,)c x .…………… 11分因此这一年后张师傅和李师傅两人中至少有一人获利的概率5()9P A =. …………13分19．（本小题满分14分）（Ⅰ）解：因为椭圆C 的方程为 2211612x y +=，所以 4a =,b =2c , ………………2分则 12c e a ==，||2FA =，||4AP m =-. ………………3分因为 ||21||42FA AP m ==-，所以 8m =. ………………5分（Ⅱ）解：若直线l 的斜率不存在，则有 21S S =，不合题意. ………………6分若直线l 的斜率存在，设直线l 的方程为)2(-=x k y ，),(11y x M ，),(22y x N .由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x得 2222(43)1616480k x k x k +-+-=， ……………… 7分可知 0>∆恒成立，且 34162221+=+k k x x ，3448162221+-=k k x x . ……………… 8分因为PMF ∆和PNF ∆的面积分别为111||||2S PF y =⋅，221||||2S PF y =⋅,所以2||||212121=-==y yy y S S . ……………… 9分即 212y y -=.所以 221y y y -=+，2212221)(22y y y y y +-=-=， ……………… 11分则 22121)]2()2([2)2()2(-+--=-⋅-x k x k x k x k ，即 2212121)4(24)(2-+-=++-x x x x x x ，即 2222222)43416(2434162344816-+-=++⋅-+-k k k k k k ，解得 25±=k . ……………… 13分所以直线l 的方程为 )2(25-=x y 或 )2(25--=x y . ……………… 14分20．（本小题满分13分）（Ⅰ）解：结论：当1a =-,0b =时,函数()f x 和()g x 不相切. …………………1分理由如下：由条件知2()f x x =-，由()ln g x x =，得0x >，又因为 ()2f x x '=-，1()g x x'=， …………………2分所以当0x >时，()20f x x '=-<，1()0g x x '=>，所以对于任意的0x >，()()f x g x ''≠.当1a =-,0b =时,函数()f x 和()g x 不相切. …………………3分（Ⅱ）解：若a b =，则()2f x ax a '=-，1()g x x'=，设切点坐标为(,)s t ，其中0s >,由题意，得 2ln as as s -=， ①·11· 12as a s -=， ② …………………4分由②，得 1(21)a s s =-，代入①，得 1ln 21s s s -=-. （*） …………………5分因为 10(21)a s s =>-，且0s >，所以 12s >. 设函数 1()ln 21x F x x x -=--，1(,)2x ∈+∞，则 2(41)(1)()(21)x x F x x x ---'=-. …………………6分令()0F x '= ，解得1x =或14x =(舍). …………………7分当x 变化时，()F x '与()F x 的变化情况如下表所示，…………………8分所以当1x =时，()F x 取到最大值(1)0F =，且当1(,1)(1,)2x ∈+∞时()0F x <. 因此，当且仅当1x =时()0F x =.所以方程（*）有且仅有一解1s =.于是 ln 0t s ==，因此切点P 的坐标为(1,0). …………………9分（Ⅲ）解：当点P 的坐标为1(,1)e-时，存在符合条件的函数()f x 和()g x ，使得它们在点P 处相切； …………………11分当点P 的坐标为2(e ,2)时，不存在符合条件的函数()f x 和()g x ，使得它们在点P 处相切. …………………13分。

2014-2015学年北京市西城区七年级上学期期末考试数学试题(含答案)

5．若 x 1 ( y 2)2 0 ，则 (xy)2015 的值为（） 2
A. 1
B. 1
C. 2015
D. 2015
6．在下面四个几何体中，从左面看、从上面看分别得到的平面图形是长方形、圆，这个几何
体是（）
A
B
C
D
7．如图，将一个直角三角板 AOB 的顶点 O 放在直线 CD 上，
点
M，N 表示的有理数互为相反数，则图中表示绝对值最小的数的点是
A．点 M
B．点 N
C．点 P
D．点 Q
10．小明制作了一个正方体包装盒，他在这个正方体包装盒的上面设计
了一个“ ”标志，并在正方体的每个表面都画了黑色粗线，如右图
所示．在下列图形中，是这个正方体包装盒的表面展开图的是
A
B
C
D
二、填空题（本题共 20 分，第 11～14 题每小题 3 分，第 15～18 题每小题 2 分）
解：
22． 8 (12) 1 (2)3 (8) 3
59
5
解：
四、先化简，再求值（本题 5 分） 23． 2(3ab2 a3b) 3(2ab2 a3b) ，其中 a 1 ， b 4 ．
2 解：
五、解下列方程或方程组（本题共 10 分，每小题 5 分）
24． 4x 1 1 3x 1 ．
1．1883 年，德国数学家引入位于一条线段上的一些点的集合，他的做法如下：
取一条长度为 1 的线段，将它三等分，去掉中间一段，余下两条线段，达到第 1 阶段；
将剩下的两条线段再分别三等分，各去掉中间一段，余下四条线段，达到第 2 阶段；
再将剩四条线段，分别三等分，分别去掉中间一段，余下八条线段，达到第 3 阶段；

北京市西城区2014-2015学年度高二上学期期末考试数学试题(理科)

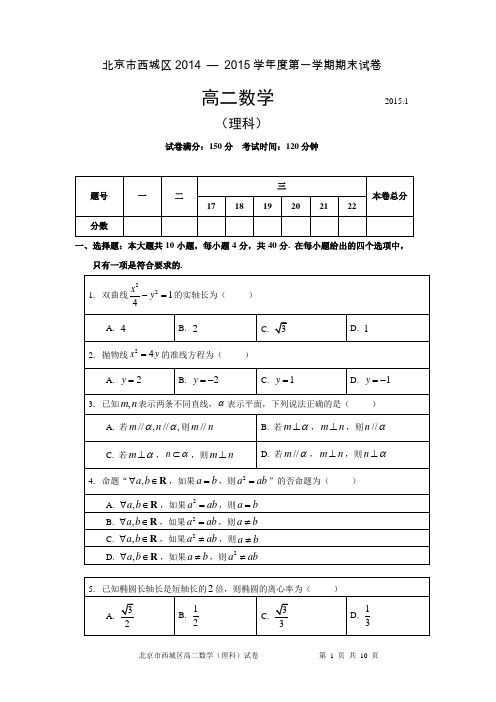
北京市西城区2014 —2015学年度第一学期期末试卷高二数学2015.1（理科）试卷满分：150分考试时间：120分钟一、选择题：本大题共10小题，每小题4分，共40分. 在每小题给出的四个选项中，只有一项是符合要求的.角角60角二、填空题：本大题共6小题，每小题5分，共30分. 把答案填在题中横线上.11. 命题“2,20x x x ∃∈-<R ”的否定是_______________.12. 空间向量(1,1,2)=--a ，(1,2,1)=--b ，(,,2)x y =-n ，且//n b . 则⋅a n =_______.13. 右图是一个四棱锥的三视图，则该四棱锥的体积为_______. 14. 已知F 为双曲线22:13xC y -=的一个焦点，则点F 到双曲线C 的一条渐近线的距离为_______.15. 由直线y x =上一点向圆22(4)1x y -+=引切线，则切线长的最小值为 . 16 .已知点(3,0)M 和点(3,0)N -，直线PM ，PN 的斜率乘积为常数a （0a ≠），设点P 的轨迹为C .给出以下几个命题：①存在非零常数a ，使C 上所有点到两点(4,0),(4,0)-距离之和为定值； ②存在非零常数a ，使C 上所有点到两点(0,4),(0,4)-距离之和为定值； ③不存在非零常数a ，使C 上所有点到两点(4,0),(4,0)-距离差的绝对值为定值； ④不存在非零常数a ，使C 上所有点到两点(0,4),(0,4)-距离差的绝对值为定值. 其中正确的命题是________.（填出所有正确命题的序号）三、解答题：本大题共6小题，共80分. 解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分13分）如图，四边形ABCD 为矩形，AD ⊥平面ABE ，90AEB ∠=o ， F 为CE 上的点.（Ⅰ）求证：//AD 平面BCE ；（Ⅱ）求证：AE ⊥BF ．正（主）视图侧（左）视图俯视图AEBCDF18.（本小题满分13分）已知三个点(0,0)A ，(4,0)B ，(3,1)C ，圆M 为△ABC 的外接圆. （Ⅰ）求圆M 的方程；（Ⅱ）设直线1y kx =-与圆M 交于,P Q两点，且PQ =k 的值.19.（本小题满分14分）在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面四边形ABCD 为直角梯形，//AD BC ，AD AB ⊥，2PA AD ==，1AB BC ==，Q 为PD 中点.（Ⅰ）求证：PD BQ ⊥；（Ⅱ）求直线BQ 与平面PCD 所成角的正弦值.20.（本小题满分14分）已知椭圆22:14x W y +=，直线l 过点(0,2)-与椭圆W 交于两点,A B ，O 为坐标原点.（Ⅰ）设C 为AB 的中点，当直线l 的斜率为32时，求线段OC 的长；（Ⅱ）当△OAB 面积等于1时，求直线l 的斜率.PAB CDQ21.（本小题满分13分）在如图所示的几何体中，四边形ABCD 是矩形，24AB BC ==,四边形CDEF 是等腰梯形，//EF DC ，2EF =，且平面ABCD ⊥平面CDEF ，AF CF ⊥. （Ⅰ）过BD 与AF 平行的平面与CF 交于点G . 求证：G 为CF 的中点；（Ⅱ）求二面角B AF D --的余弦值.22.（本小题满分13分）如图，曲线E 是由抛物线弧1E :x y 42=(203x ≤≤)与椭圆弧2E :12222=+by a x (a x ≤≤32)所围成的封闭曲线，且1E 与2E 有相同的焦点.（Ⅰ）求椭圆弧2E 的方程；（Ⅱ）设过点(1,0)F 的直线与曲线E 交于,A B 两点，1||r FA =,2||r FB =，且α=∠AFx (0α≤≤π)，试用αcos 表示1r ；并求21r r的取值范围.ABCDE F G北京市西城区2014 — 2015学年度第一学期期末试卷高二数学（理科）参考答案及评分标准2015.1一、选择题：本大题共10小题，每小题4分，共40分.1.A2.D3.C4. D5. A6. B7.A8. C9.C 10. A 二、填空题：本大题共6小题，每小题5分，共30分.11. 2,20x x x ∀∈-≥R 12. 2- 13.38 14. 116. ②④ 注:16题，仅选出②或④得3分；错选得0分. 三、解答题：本大题共6小题，共80分. 17. （本小题满分13分）（Ⅰ）证明：因为四边形ABCD 为矩形，所以//AD BC . ………………2分又因为BC ⊂平面BCE ，AD ⊄平面BCE ，………………4分所以//AD 平面BCE . ………………5分（Ⅱ）证明：因为AD ⊥平面ABE ，BC AD //，所以BC ⊥平面ABE ，则BC AE ⊥ . ………………7分又因为90AEB ∠=o，所以AE BE ⊥. ………………9分所以AE ⊥平面BCE . ………………11分又BF ⊂平面BCE ,所以AE BF ⊥. ………………13分 18. （本小题满分13分）（Ⅰ）设圆M 的方程为 220x y Dx Ey F ++++=, ………………1分因为点(0,0)A ，(4,0)B ，(3,1)C 在圆M 上，则2220,440,3130.F D F D E F =⎧⎪++=⎨⎪++++=⎩………………4分解得4D =-，2E =，0F =. ………………6分所以ABC ∆外接圆的方程为22420x y x y +-+=. ………………7分（Ⅱ）由（Ⅰ）圆M 的圆心为(2,1)-AEBCDF又PQ =所以圆M 的圆心到直线1y kx =-的距离为2.………………9分所以=………………11分解得215k =. k =. ………………13分19. （本小题满分14分）（Ⅰ）证明：因为PA ⊥平面ABCD ，所以PA AB ⊥PA AD ⊥，又AD AB ⊥，如图，建立以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴的空间直角坐标系. ………………2分由已知，2PA AD ==，1AB BC ==，//AD BC所以，(0,0,0)A ，(1,0,0)B ，(1,1,0)C ，(0,2,0)D ,(0,0,2)P ………………4分又Q 为PD 中点，所以(0,1,1)Q . 所以(0,2,2)PD =-，(1,1,1)BQ =-，所以0PD BQ ⋅=， ………………6分所以PD BQ ⊥. ………………7分（注：若第一问不用空间向量，则第一问4分）（Ⅱ）解：设平面PCD 的法向量为(,,)a b c =n ，则0PD ⋅=n ,0CD ⋅=n .又(1,1,0)CD =-，所以220b c a b -=⎧⎨-+=⎩， ………………9分令1c =，得1a b ==，所以(1,1,1)=n . ………………11分因此cos ,3BQ BQ BQ ⋅1〈〉===n n n， ………………13分所以直线BQ 与平面PCD 所成角的正弦值为31. ………………14分 20.（本小题满分14分）解：（Ⅰ）当直线l 的斜率为32时，直线l 的方程为22y x 3=-. ………………1分由222,214y x x y 3⎧=-⎪⎪⎨⎪+=⎪⎩ 得251260x x -+=， ………………2分设11(,)A x y ，22(,)B x y ，00(,)C x y .则12125x x +=， ………………3分所以点C 的坐标065x =，0031225y x =-=-， ………………4分所以OC ==. ………………5分（Ⅱ）设直线:2l y kx =-，由221,42x y y kx ⎧+=⎪⎨⎪=-⎩得22(14)16120k x kx +-+=， ………………6分所以222(16)48(14)16(43)k k k ∆=-+=- ………………7分1221614k x x k +=+，1221214x x k =+. ………………8分AB ===. ………………10分原点O 到直线l的距离d =. ………………11分所以△OAB 面积为1122AB d ==. 因为△OAB 面积等于1，1=， ………………12分解得k=， ………………13分带入判别式检验，符合题意，所以2k =±. ………………14分21. （本小题满分13分）（Ⅰ）证明：连接AC 交BD 于点H ，ABCD 为矩形，则H 为AC 中点，连接GH . ………………1分因为//AF 平面BDG ，平面ACF平面BDG GH =， ………………2分所以//AF HG . ………………3分所以G 为CF 的中点. ………………4分（Ⅱ）解：在平面CDEF 上作FO CD ⊥，垂足为O ，由于平面CDEF 为等腰梯形，所以1OC =，因为且平面ABCD ⊥平面DCFE ，所以FO ⊥平面ABCD ， ………………5分在平面ABCD 中，作OM CD ⊥，交AB 于M ，所以FO OM ⊥，如图，以O 为原点建立空间直角坐标系O xyz -. ………………6分则(2,3,0)A -，(2,1,0)B ，(0,1,0)C ，(0,3,0)D -. 设(0,0,)F h （0h >）. 因为AF CF ⊥，所以0AF CF ⋅=，即(2,3,)(0,1,)0h h -⋅-=，所以2030h -+=，解得h =………………7分设平面ABF 的法向量为(,,)a b c =n ，而(AF =-，(0,4,0)AB =，由0,0AF AB ⎧⋅=⎪⎨⋅=⎪⎩n n得230,40.a b b ⎧-++=⎪⎨=⎪⎩令2c =，解得a =0b =.所以(3,0,2)=n . (9)分由于(2,0,0)AD =-,(0,1CF =-, 所以0AD CF ⋅=，CF AD ⊥，又CF AF ⊥，所以CF ⊥平面ADF ，所以CF 为平面ADF 的法向量， ………………11分cos ,CF 〈〉===n . ………………12分由图知，二面角的平面角为钝角，所以二面角B AF D --的余弦值为7-. ………………13分22. （本小题满分13分）解：（Ⅰ）抛物线弧1E :x y 42=的焦点为(1,0)，且23x =时，283y =，所以2(3为椭圆上一点，又椭圆的焦点为(1,0),-(1,0)， ………………2分所以752433a ==+=. ………………3分所以2a =，2213b a =-=， ………………4分所以椭圆2E 的方程为22143x y +=（223x ≤≤）. ………………5分（Ⅱ）曲线E 由两部分曲线1E 和2E 组成，所以按A 在抛物线弧1E 或椭圆弧2E 上加以分类，由曲线E 的对称性,不妨设A 在x 轴上方(或x 轴上).当32=x 时，362±=y ，此时35=r ,51cos -=α；当1cos 51≤≤-α时，A 在椭圆弧2E 上，由题设知)sin ,cos 1(11ααr r A +，将A 点坐标代入13422=+y x 得，012)sin (4)cos 1(32121=-++ααr r ，整理得09cos 6)cos 4(1212=-+-ααr r ，解得αcos 231+=r 或2cos 31-=αr (舍去). ………………6分当51cos 1-≤≤-α时，A 在抛物线弧1E 上，由抛物线定义可得αcos 211r r +=，所以αcos 121-=r ， ………………7分综上，当51c o s 1-≤≤-α时，αcos 121-=r ；当1c o s 51≤≤-α时，αcos 231+=r .相应地，22(1cos(),sin())B r r αα++π+π，当1cos 15α≤≤时，B 在抛物线弧1E 上，所以222cos()r r α=++π，221cos r α=+， ………………8分当11cos 5α-≤≤时，B 在椭圆弧2E 上，根据图形的对称性，232cos r α=-. ………………9分所以，当51cos 1-≤≤-α时A 在抛物线弧1E 上,B 在椭圆弧2E 上，]911,1[)cos 111(323cos 2cos 1221∈-+=-⋅-=αααr r ； ………………10分当1cos 51≤≤α时A 在椭圆弧2E 上,B 在抛物线弧1E 上，]1,119[)cos 211(232cos 1cos 2321∈+-=+⋅+=αααr r ； ………………11分当51cos 51<<-α时A 、B 在椭圆弧2E 上，)911,119(cos 2cos 23cos 2cos 2321∈+-=-⋅+=ααααr r ； ………………12分综上，21r r 的取值范围是]911,119[. ………………13分。

北京市西城区2014-2015学年度第一学期期末高一数学(普通校试题)

北京市西城区2014 — 2015学年度第一学期期末试卷高一数学 2015.1试卷满分：150分考试时间：120分钟A 卷 [必修模块4] 本卷满分：100分一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.1．已知(0,2π)α∈，且sin 0<α，cos 0>α，则角α的取值范围是（）（A ）π(0,)2（B ）π(,π)2（C ）3π(π,)2（D ）3π(,2π)22．已知向量(2,8)=a ，(4,2)=-b ．若2=-c a b ，则向量=c （）（A ）(0,18)（B ）(8,14)（C ）(12,12)（D ）(4,20)-3．已知角α的终边经过点(3,4)P -，那么sin =α（）（A ）35（B ）45-（C ）34（D ）34-4．在△ABC 中，D 是BC 的中点，则AD =（）（A ）1()2AB AC + （B ）1()2AB AC - （C ）1()2AB BC +（D ）1()2AB BC -5．函数2(sin cos )y x x =-的最小正周期为（）（A ）2π（B ）3π2（C ）π（D ）π26．如果函数cos()y x =+ϕ的一个零点是3π，那么ϕ可以是（）（A ）6π （B ）6π-（C ）3π（D ）3π-7．如图，在矩形ABCD 中，2AB =，BC ， E 是CD 的中点，那么AE DC ⋅=（）（A ）4（B ）2（C （D ）18．当[0,π]x ∈时，函数()cos f x x x =的值域是（）（A ）[2,1]-（B ）[1,2]-（C ）[1,1]-（D ）[-9．为得到函数πcos()6y x =+的图象，只需将函数sin y x =的图象（）（A ）向左平移π3个单位（B ）向右平移π3个单位（C ）向左平移2π3个单位（D ）向右平移2π3个单位10．已知a ，b 为单位向量，且m ⋅=a b ，则||t +a b ()t ∈R 的最小值为（）（A （B ）1（C ）||m（D二、填空题：本大题共6小题，每小题4分，共24分. 把答案填在题中横线上. 11．若向量(1,2)=a 与向量(,1)=-λb 共线，则实数=λ_____． 12．已知α是第二象限的角，且5sin 13α=，则cos =α_____． 13．若(,)22ππ∈-θ，且tan 1>θ，则θ的取值范围是_____． 14．已知向量(1,3)=a ，(2,1)=-b ，(1,1)=c ．若(,)=∈R c a +b λμλμ，则=λμ_____． 15．函数2()sin sin cos f x x x x =+⋅的最大值是_____．16．关于函数()sin(2)()6f x x x π=-∈R ，给出下列三个结论：① 对于任意的x ∈R ，都有2()cos(2)3f x x π=-； ② 对于任意的x ∈R ，都有()()22f x f x ππ+=-；③ 对于任意的x ∈R ，都有()()33f x f x ππ-=+．其中，全部正确结论的序号是_____．三、解答题：本大题共3小题，共36分. 解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）已知tan 2=-α，其中(,)2π∈πα．（Ⅰ）求πtan()4-α的值；（Ⅱ）求sin 2α的值．18．（本小题满分14分）已知向量(cos ,sin )=ααa ，1(2=-b ，其中α是锐角．（Ⅰ）当30︒=α时，求||+a b ；（Ⅱ）证明：向量+a b 与-a b 垂直；（Ⅲ）若向量a 与b 夹角为60︒，求角α．19．（本小题满分10分）已知函数()sin cos f x a x b x =+，其中a ∈Z ，b ∈Z ．设集合{|()0}A x f x ==，{|(())0}B x f f x ==，且A B =．（Ⅰ）证明：0b =；（Ⅱ）求a 的最大值．B 卷 [学期综合] 本卷满分：50分一、填空题：本大题共5小题，每小题4分，共20分. 把答案填在题中横线上. 1．已知集合{,}A a b =，则满足{,,}AB a b c =的不同集合B 的个数是_____．2．若幂函数y x =α的图象过点(4,2)，则=α_____．3．函数2lg ,0,()4,0,x x f x x x >⎧=⎨-<⎩的零点是_____．4．设()f x 是定义在R 上的偶函数，且()f x 在[0,)+∞上是减函数．若()(2)f m f >，则实数m 的取值范围是_____．5．已知函数()f x 的定义域为D ．若对于任意的1x D ∈，存在唯一的2x D ∈，使得M =成立，则称函数()f x 在D 上的几何平均数为M ．已知函数()31([0,1])g x x x =+∈，则()g x 在区间[0,1]上的几何平均数为_____．二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤.6．（本小题满分10分）已知函数()(2)()f x x x a =-+，其中a ∈R ．（Ⅰ）若()f x 的图象关于直线1x =对称，求a 的值；（Ⅱ）求()f x 在区间[0,1]上的最小值． 7．（本小题满分10分）已知函数()23xxf x a b =⋅+⋅，其中,a b 为常数．（Ⅰ）若0ab >，判断()f x 的单调性，并加以证明；（Ⅱ）若0ab <，解不等式：(1)()f x f x +>．8．（本小题满分10分）定义在R 上的函数()f x 同时满足下列两个条件： ① 对任意x ∈R ，有(2)()2f x f x +≥+；② 对任意x ∈R ，有(3)()3f x f x +≤+．设()()g x f x x =-．（Ⅰ）证明：(3)()(2)g x g x g x +≤≤+；（Ⅱ）若(4)5f =，求(2014)f 的值．北京市西城区2014 — 2015学年度第一学期期末试卷高一数学参考答案及评分标准 2015.1A 卷 [必修模块4] 满分100分一、选择题：本大题共10小题，每小题4分，共40分.1.D ；2.B ；3.B ；4.A ；5.C ；6.A ；7.B ；8.A ；9.C ； 10.D . 二、填空题：本大题共6小题，每小题4分，共24分.11.12-； 12.1213-； 13. (,)42ππ； 14.32； 1516. ① ② ③. 注：16题，少解不给分.三、解答题：本大题共3小题，共36分. 17.（本小题满分12分）（Ⅰ）解：因为 tan 2=-α，所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】 3=. 【 6分】（Ⅱ）解：由π(,π)2∈α，tan 2α=-，得sin α=，【 8分】cos α=. 【10分】所以 4sin 22sin cos 5==-ααα. 【12分】18.（本小题满分14分）（Ⅰ）解：当30︒=α时，1)2=a ，【 1分】所以+a b =，【 2分】所以||+=a b = 【 4分】（Ⅱ）证明：由向量(cos sin )αα=，a ，1(,22=-b ，得 1(cos ,sin )22+=-+ααa b ，1(cos ,sin )22-=+-ααa b ，由 π(0,)2∈α，得向量+a b ，-a b 均为非零向量. 【 5分】因为 222213()()||||(sin cos )()044+⋅-=-=+-+=ααa b a b a b ，【 7分】所以向量+a b 与-a b 垂直. 【 8分】（Ⅲ）解：因为||||1==a b ，且向量a 与b 夹角为60︒，所以 1||||cos 602︒⋅=⋅=a b a b . 【10分】所以 11cos sin 222-+=αα，即 π1sin()62-=α. 【12分】因为 π02<<α，所以 πππ663-<-<α，【13分】所以 ππ66-=α，即3π=α. 【14分】19.（本小题满分10分）（Ⅰ）证明：显然集合A ≠∅．设 0x A ∈，则0()0f x =．【 1分】因为 A B =，所以 0x B ∈，即 0(())0f f x =，所以 (0)0f =，【 3分】所以 0b =．【 4分】（Ⅱ）解：由（Ⅰ）得()sin f x a x =，a ∈Z ．① 当0a =时，显然满足A B =．【 5分】 ② 当0a ≠时，此时{|sin 0}A x a x ==；{|sin(sin )0}B x a a x ==，即{|sin ,}B x a x k k ==π∈Z ．【 6分】因为 A B =，所以对于任意x ∈R ，必有sin a x k ≠π (k ∈Z ，且0)k ≠成立．【 7分】所以对于任意x ∈R ，sin k x a π≠，所以 1k aπ>，【 8分】即 ||||a k <⋅π，其中k ∈Z ，且0k ≠．所以 ||a <π，【 9分】所以整数a 的最大值是3．【10分】B 卷 [学期综合] 满分50分一、填空题：本大题共5小题，每小题4分，共20分.1. 4；2.12； 3. 2-，1； 4. (2,2)-； 5. 2. 注：3题，少解得2分，有错解不给分. 二、解答题：本大题共3小题，共30分. 6.（本小题满分10分）（Ⅰ）解法一：因为2()(2)()(2)2f x x x a x a x a =-+=+--，所以，()f x 的图象的对称轴方程为22ax -=. 【 2分】由212a-=，得0a =. 【 4分】解法二：因为函数()f x 的图象关于直线1x =对称，所以必有(0)(2)f f =成立，【 2分】所以 20a -=，得0a =. 【 4分】（Ⅱ）解：函数()f x 的图象的对称轴方程为22ax -=. ① 当202a-≤，即 2a ≥时，因为()f x 在区间(0,1)上单调递增，所以()f x 在区间[0,1]上的最小值为(0)2f a =-. 【 6分】② 当2012a-<<，即 02a <<时，因为()f x 在区间2(0,)2a -上单调递减，在区间2(,1)2a-上单调递增，所以()f x 在区间[0,1]上的最小值为222()()22a a f -+=-. 【 8分】 ③ 当212a-≥，即 0a ≤时，因为()f x 在区间(0,1)上单调递减，所以()f x 在区间[0,1]上的最小值为(1)(1)f a =-+. 【10分】7.（本小题满分10分）（Ⅰ）解：当0,0a b >>时，()f x 在R 上是增函数；当0,0a b <<时，()f x 在R 上是减函数；【 1分】证明如下：当0,0a b >>时，任取12,x x ∈R ，且12x x <，则210x x x ∆=->，则 212121()()(22)(33)x x x xy f x f x a b ∆=-=-+-.因为 122122,0(22)0x x x x a a <>⇒->；又122133,0(33)0x x x xb b <>⇒->，所以 21()()0y f x f x ∆=->，所以，当0,0a b >>时，()f x 在R 上是增函数.当0,0a b <<时，同理可得，()f x 在R 上是减函数. 【 5分】（Ⅱ）解：由(1)()2230x x f x f x a b +-=⋅+⋅>，得 32()2xb a >-. （*）【 6分】 ① 当0,0a b <>时，（*）式化为3()22xa b->，解得32log ()2ax b>-. 【 8分】 ② 当0,0a b ><时，（*）式化为3()22xab-<，解得32log ()2ax b<-. 【10分】8.（本小题满分10分）（Ⅰ）证明：因为()()g x f x x =-，所以(2)(2)2g x f x x +=+--，(3)(3)3g x f x x +=+--．由条件①，②可得(2)(2)2()22()()g x f x x f x x f x x g x +=+--≥+--=-=； ③ 【 2分】 (3)(3)3()33()()g x f x x f x x f x x g x +=+--≤+--=-=． ④ 【 4分】所以(3)()(2)g x g x g x +≤≤+．（Ⅱ）解：由③得 (2)()g x g x +≥，所以(6)(4)(2)()g x g x g x g x +≥+≥+≥．【 6分】由④得 (3)()g x g x +≤，所以(6)(3)()g x g x g x +≤+≤．【 7分】所以必有(6)()g x g x +=，即()g x 是以6为周期的周期函数．【 8分】所以(2014)(33564)(4)(4)41g g g f =⨯+==-=．【 9分】所以(2014)(2014)20142015f g =+=．【10分】。

北京市西城区2015届高三第一学期期末数学(文)试题(含答案)(word版)

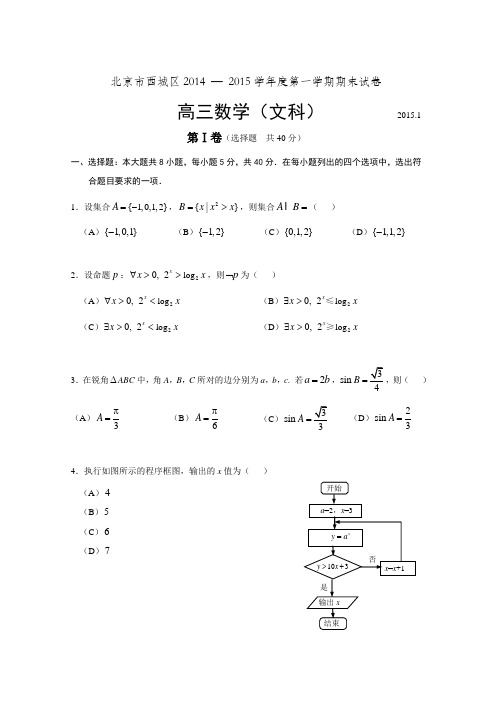
北京市西城区2014 — 2015学年度第一学期期末试卷高三数学（文科） 2015.1第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合1,0,1,2{}A -=，2{|}B x x x =>，则集合A B =（）（A ）{1,0,1}-（B ）{1,2}-（C ）{0,1,2}（D ）{1,1,2}-3．在锐角∆ABC 中，角A ，B ，C 所对的边分别为a ，b ，c . 若2a b =，sin B =，则（）（A ）3A π= （B ）6A π=（C）sin A =（D ）2sin 3A =4．执行如图所示的程序框图，输出的x 值为（）（A ）4 （B ）5 （C ）6 （D ）72．设命题p ：2log 0,2x x x ∀>>，则p ⌝为（）（A ）2log 0,2x x x ∀>< （B ）2log 0,2x x x ∃>≤ （C ）2log 0,2x x x ∃>< （D ）2log 0,2x x x ∃>≥5．设函数()y f x =的定义域为R ，则“(0)0f =”是“函数()f x 为奇函数”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件6. 某天，甲要去银行办理储蓄业务，已知银行的营业时间为9：00至17：00，设甲在当天 13：00至18：00之间任何时间去银行的可能性相同，那么甲去银行恰好能办理业务的概率是（）（A ）13 （B ）34 （C ）58 （D ）458. 如图，在空间四边形ABCD 中，两条对角线,AC BD 互相垂直，且长度分别为4和6，平行于这两条对角线的平面与边,,,AB BC CD DA 分别相交于点,,,E F G H ，记四边形EFGH 的面积为y ，设BEx AB=，则（）（A ）函数()y f x =的值域为(0,4] （B ）函数()y f x =的最大值为8（C ）函数()y f x =在2(0,)3上单调递减（D ）函数()y f x =满足()(1)f x f x =-7．设抛物线2:4W y x =的焦点为F ，过F 的直线与W 相交于A ，B 两点，记点F 到直线l ：1x =-的距离为d ，则有（）（A ）2||d AB ≥ （B ）2||d AB = （C ）2||d AB ≤ （D ）2||d AB <A BE CD GH F。

北京市西城区2013—2014学年度高一年级第一学期期末数学试卷(普通校试题)

北京市西城区2013 — 2014学年度第一学期期末试卷高一数学 2014.1试卷满分：150分考试时间：120分钟A 卷 [必修模块4] 本卷满分：100分一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的. 1．若sin 0<α，且cos 0>α，则角α是（）（A ）第一象限的角（B ）第二象限的角（C ）第三象限的角（D ）第四象限的角2．已知向量1(1,0)=e ，2(0,1)=e ，那么122|+=|e e （）（A ）1（B（C ）2（D3．若角α的终边经过点(1,2)P -，则tan =α（）（A （B ）（C ）2- （D ）12-4．已知正方形ABCD 的边长为1，则AB AC ⋅=（）（A ）2（B ）1（C（D ）25．在平面直角坐标系xOy 中，函数2sin()6y x π=-的图象（）（A ）关于直线6x π=对称（B ）关于直线6x π=-对称（C ）关于点(,0)6π对称（D ）关于点(,0)6π-对称6．已知非零向量,OA OB 不共线，且13BM BA =，则向量OM = （）（A ）1233OA OB + （B ）2133OA OB +（C ）1233OA OB - （D ）1433OA OB -7．已知函数1()cos 22f x x x =+，则()12f π=（）（A ）2 （B ）2（C ）1（D8．设a ，b 是两个非零向量，且+=-a b a b ，则a 与b 夹角的大小为（）（A ）120︒（B ）90︒（C ）60︒（D ）30︒9．已知函数()sin cos f x x x =ωω在区间[,]63ππ-上单调递增，则正数ω的最大值是（）（A ）32（B ）43（C ）34 （D ）2310．已知函数()cos(sin )f x x =，则下列结论中正确的是（）（A ）()f x 的定义域是[1,1]- （B ）()f x 的值域是[1,1]- （C ）()f x 是奇函数（D ）()f x 是周期为π的函数二、填空题：本大题共6小题，每小题4分，共24分. 把答案填在题中横线上. 11. sin()6π-=______.12. 若sin 2=α，且(0,)∈πα，则α=______. 13. 已知向量(1,3)=a ，(2,)k =-b ．若向量a 与b 共线，则实数k =_____. 14. 若tan 2=α，且32π∈(π,)α，则sin()2π+=α______. 15. 已知向量(cos ,sin )αα=a ，(cos ,sin )ββ=b ．若π,3〈〉=a b ，则cos()-=αβ_____. 16. 定义在R 上的非常值函数()f x 同时满足下述两个条件：① 对于任意的x ∈R ，都有2()()3f x f x π+=； ② 对于任意的x ∈R ，都有()()66f x f x ππ-=+.则其解析式可以是()f x =_____.（写出一个满足条件的解析式即可）三、解答题：本大题共3小题，共36分.解答应写出文字说明，证明过程或演算步骤. 17. （本小题满分12分）已知3tan 4=-α. （Ⅰ）求πtan()4-α的值；（Ⅱ）求2sin 3cos 3sin 2cos --αααα的值.18.（本小题满分12分）已知函数2()sin 22cos 2f x x x x =⋅．（Ⅰ）求()f x 的最小正周期；（Ⅱ）若[,]84x ππ∈，求()f x 的最大值与最小值．19.（本小题满分12分）如图，正六边形ABCDEF 的边长为1.,M N 分别是,BC DE 上的动点，且满足BM DN = .（Ⅰ）若,M N 分别是,BC DE 的中点，求AM AN ⋅的值；（Ⅱ）求AM AN ⋅的取值范围.B 卷 [学期综合] 本卷满分：50分一、填空题：本大题共5小题，每小题4分，共20分.把答案填在题中横线上. 1. 已知集合2{|430}A x x x =-+>，{|02}B x x =<≤，那么A B = _____. 2. 已知2log 3a =，32b=，21log 3c =.将,,a b c 按从小到大排列为_____. 3. 若函数2()2f x x x =-在区间(,)a +∞上是增函数，则a 的取值范围是_____. 4. 函数12()|21|xf x x =--的零点个数为_____.5. 给定数集A .若对于任意,a b A ∈，有a b A +∈，且a b A -∈，则称集合A 为闭集合.给出如下四个结论：① 集合{4,2,0,2,4}A =--为闭集合； ② 集合{|3,}A n n k k ==∈Z 为闭集合； ③ 若集合12,A A 为闭集合，则12A A 为闭集合；④ 若集合12,A A 为闭集合，且1A R Ø，2A R Ø，则存在c ∈R ，使得12()c A A ∉ . 其中，全部正确结论的序号是_____.二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤. 6.（本小题满分10分）已知函数()log (2)1a f x x =+-，其中1a >.（Ⅰ）若()f x 在[0,1]上的最大值与最小值互为相反数，求a 的值；（Ⅱ）若()f x 的图象不经过第二象限，求a 的取值范围.7.（本小题满分10分）已知函数()|2|f x x x =-. （Ⅰ）解不等式()3f x <；（Ⅱ）设0a >，求()f x 在区间[0,]a 上的最大值.8.（本小题满分10分）设函数()f x ，()g x 的定义域分别为f g D D ，，且f g D D Ø.若对于任意f x D ∈，都有()()g x f x =，则称()g x 为()f x 在g D 上的一个延拓函数.给定2() 1 (01)f x x x =-<≤.（Ⅰ）若()h x 是()f x 在[1,1]-上的延拓函数，且()h x 为奇函数，求()h x 的解析式；（Ⅱ）设()g x 为()f x 在(0,)+∞上的任意一个延拓函数，且()g x y x=是(0,)+∞上的单调函数.（ⅰ）判断函数()g x y x=在(0,1]上的单调性，并加以证明；（ⅱ）设0s >，0t >，证明：()()()g s t g s g t +>+.北京市西城区2013 — 2014学年度第一学期期末试卷高一数学参考答案及评分标准 2014.1A 卷 [必修模块4] 满分100分一、选择题：本大题共10小题，每小题4分，共40分.1.D ；2.D ；3.C ；4.B ；5.C ；6.A ；7.A ；8.B ；9.C ； 10.D . 二、填空题：本大题共6小题，每小题4分，共24分.11.12-； 12. 3π，或32π； 13.6-； 14.15.12； 16.sin3x 等（答案不唯一）. 注：12题，得出一个正确的结论得2分. 三、解答题：本大题共3小题，共36分. 17.（本小题满分12分）（Ⅰ）解：因为 3tan 4=-α，所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】 7=-. 【 6分】（Ⅱ）解：因为3tan 4=-α，所以2sin 3cos 2tan 33sin 2cos 3tan 2--=--αααααα 【 9分】 1817=. 【12分】18.（本小题满分12分）（Ⅰ）解：1cos 4()2cos 22xf x x x -=⋅1cos 442x x -=+ 【 2分】 1sin(4)62x π=-+．【 4分】因为 242T ππ==，所以()f x 的最小正周期是2π．【 6分】（Ⅱ）解：由（Ⅰ）得，1()sin(4)62f x x π=-+．因为 84x ππ≤≤，所以 54366x πππ≤-≤，【 8分】所以 1sin(4)126x π≤-≤，【 9分】所以 131sin(4)622x π≤-+≤．【10分】所以，当6x π=时，()f x 取得最大值32；当4x π=时，()f x 取得最小值1．【12分】19.（本小题满分12分）（Ⅰ）解：如图，以AB 所在直线为x 轴，以A 为坐标原点建立平面直角坐标系. 【 1分】因为ABCDEF 是边长为1的正六边形，且,M N 分别是,BC DE 的中点，所以 5(4M ，1(2N ，【 3分】所以 5311848AM AN ⋅=+= . 【 4分】（Ⅱ）解：设BM DN t ==，则[0,1]t ∈.【 5分】所以(1,)22t M +，(1N t -. 【 7分】所以3(1)(1)22t AM AN t t ⋅=+⋅-+2112t t ++=-213(1)22t =--+ 【10分】当0t =时，AM AN⋅取得最小值1；【11分】当1t =时，AM AN ⋅取得最大值32. 【12分】B 卷 [学期综合] 满分50分一、填空题：本大题共5小题，每小题4分，共20分.1.{|01}x x <<；2.c b a <<；3. [1,)+∞；4. 2；5.②④. 注：5题，选出一个正确的序号得2分，有错选不给分. 二、解答题：本大题共3小题，共30分.6.（本小题满分10分）（Ⅰ）解：函数()log (2)1a f x x =+-的定义域是(2,)-+∞. 【 1分】因为 1a >，所以 ()log (2)1a f x x =+-是[0,1]上的增函数. 【 2分】所以 ()f x 在[0,1]上的最大值是(1)log 31a f =-；最小值是(0)log 21a f =-. 【 4分】依题意，得 log 31(log 21)a a -=--，【 5分】解得a =. 【 6分】（Ⅱ）解：由（Ⅰ）知，()log (2)1a f x x =+-是(2,)-+∞上的增函数. 【 7分】在()f x 的解析式中，令0x =，得(0)log 21a f =-，所以，()f x 的图象与y 轴交于点(0,log 21)a -. 【 8分】依题意，得(0)log 210a f =-≤，【 9分】解得 2a ≥. 【10分】7.（本小题满分10分）（Ⅰ）解：原不等式可化为22230x x x ≥⎧⎨--<⎩，，（1）或22230.x x x <⎧⎨-+>⎩，（2）【 1分】解不等式组（1），得 23x ≤<；解不等式组（2），得2x <. 【 3分】所以原不等式的解集为{|3}x x <. 【 4分】（Ⅱ）解：222,2,()|2|2, 2.x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩ 【 5分】① 当01a <<时，()f x 是[0,]a 上的增函数，此时()f x 在[0,]a 上的最大值是2()2f a a a =-+. 【 6分】 ② 当12a ≤≤时，()f x 在[0,1]上是增函数，在[1,]a 上是减函数，此时()f x 在[0,]a 上的最大值是(1)1f =. 【 7分】③ 当2a >时，令()(1)(2)10f a f a a -=-->，解得1a >. 所以，当21a <≤此时()(1)f a f ≤，()f x 在[0,]a 上的最大值是(1)1f =；当1a >时，此时()(1)f a f >，()f x 在[0,]a 上的最大值是2()2f a a a =-.【 9分】记()f x 在区间[0,]a 上的最大值为()g a ，所以222,01,()1,112,1a a a g a a a a a ⎧-+<<⎪⎪=≤≤⎨⎪->+⎪⎩【10分】8.（本小题满分10分）（Ⅰ）解：当0x =时，由()h x 为奇函数，得(0)0h =. 【 1分】任取[1 0)x ∈-，，则(01]x -∈，，由()h x 为奇函数，得22()()[()1]1h x h x x x =--=---=-+，【 2分】所以()h x 的解析式为221,01,()0,0,1,10.x x h x x x x ⎧-<≤⎪==⎨⎪-+-≤<⎩【 3分】（Ⅱ）解：（ⅰ）函数()g x y x=是(0,1]上的增函数. 【 4分】证明如下：因为()g x 为()f x 在(0,)+∞上的一个延拓函数，所以当(01]x ∈，时，2()()1g x f x x ==-. 记()()1()g x f x k x x x x x===-，其中(0,1]x ∈. 任取12,(0,1]x x ∈，且12x x <，则210x x x ∆=->，因为211221212112()(1)11()()()0x x x x y k x k x x x x x x x -+∆=-=---=>，所以函数()g x y x=是(0,1]上的增函数. 【 6分】（ⅱ）由()g x y x = 是(0,)+∞上的单调函数，且(0,1]x ∈时，()g x y x =是增函数，从而得到函数()g x y x= 是(0,)+∞上的增函数. 【 7分】因为 0s >，0t >，所以 s t s +>，s t t +>，所以()()g s t g s s t s+>+，即 ()()()s g s t s t g s ⋅+>+⋅. 【 8分】同理可得：()()()t g s t s t g t ⋅+>+⋅.将上述两个不等式相加，并除以s t +，即得 ()()()g s t g s g t +>+. 【10分】。

北京市西城区2013-2014学年高一上学期期末考试数学试卷(普通校试卷)Word版含答案

北京市西城区2013 — 2014学年度第一学期期末试卷高一数学 2014.1试卷满分：150分考试时间：120分钟A 卷 [必修模块4] 本卷满分：100分一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的. 1．若sin 0<α，且cos 0>α，则角α是（）（A ）第一象限的角（B ）第二象限的角（C ）第三象限的角（D ）第四象限的角2．已知向量1(1,0)=e ，2(0,1)=e ，那么122|+=|e e （）（A ）1（B（C ）2（D3．若角α的终边经过点(1,2)P -，则tan =α（）（A （B ）（C ）2- （D ）12-4．已知正方形ABCD 的边长为1，则AB AC ⋅=（）（A （B ）1（C（D ）25．在平面直角坐标系xOy 中，函数2sin()6y x π=-的图象（）（A ）关于直线6x π=对称（B ）关于直线6x π=-对称（C ）关于点(,0)6π对称（D ）关于点(,0)6π-对称 6．已知非零向量,OA OB 不共线，且13BM BA =，则向量OM =（）（A ）1233OA OB +（B ）2133OA OB +（C ）1233OA OB - （D ）1433OA OB -7．已知函数1()cos 2f x x x =+，则()12f π=（）（A （B （C ）1（D8．设a ，b 是两个非零向量，且+=-a b a b ，则a 与b 夹角的大小为（）（A ）120︒（B ）90︒（C ）60︒（D ）30︒9．已知函数()sin cos f x x x =ωω在区间[,]63ππ-上单调递增，则正数ω的最大值是（）（A ）32（B ）43（C ）34 （D ）2310．已知函数()cos(sin )f x x =，则下列结论中正确的是（）（A ）()f x 的定义域是[1,1]- （B ）()f x 的值域是[1,1]- （C ）()f x 是奇函数（D ）()f x 是周期为π的函数二、填空题：本大题共6小题，每小题4分，共24分. 把答案填在题中横线上. 11. sin()6π-=______.12. 若sin =α，且(0,)∈πα，则α=______. 13. 已知向量(1,3)=a ，(2,)k =-b ．若向量a 与b 共线，则实数k =_____. 14. 若tan 2=α，且32π∈(π,)α，则sin()2π+=α______. 15. 已知向量(cos ,sin )αα=a ，(cos ,sin )ββ=b ．若π,3〈〉=a b ，则cos()-=αβ_____. 16. 定义在R 上的非常值函数()f x 同时满足下述两个条件：① 对于任意的x ∈R ，都有2()()3f x f x π+=； ② 对于任意的x ∈R ，都有()()66f x f x ππ-=+.则其解析式可以是()f x =_____.（写出一个满足条件的解析式即可）三、解答题：本大题共3小题，共36分.解答应写出文字说明，证明过程或演算步骤. 17. （本小题满分12分）已知3tan 4=-α. （Ⅰ）求πtan()4-α的值；（Ⅱ）求2sin 3cos 3sin 2cos --αααα的值.18.（本小题满分12分）已知函数2()sin 22cos 2f x x x x =+⋅．（Ⅰ）求()f x 的最小正周期；（Ⅱ）若[,]84x ππ∈，求()f x 的最大值与最小值．19.（本小题满分12分）如图，正六边形ABCDEF 的边长为1.,M N 分别是,BC DE 上的动点，且满足BM DN =.（Ⅰ）若,M N 分别是,BC DE 的中点，求AM AN ⋅的值；（Ⅱ）求AM AN ⋅的取值范围.B 卷 [学期综合] 本卷满分：50分一、填空题：本大题共5小题，每小题4分，共20分.把答案填在题中横线上. 1. 已知集合2{|430}A x x x =-+>，{|02}B x x =<≤，那么A B =_____.2. 已知2log 3a =，32b =，21log 3c =.将,,a b c 按从小到大排列为_____. 3. 若函数2()2f x x x =-在区间(,)a +∞上是增函数，则a 的取值范围是_____. 4. 函数12()|21|xf x x =--的零点个数为_____.5. 给定数集A .若对于任意,a b A ∈，有a b A +∈，且a b A -∈，则称集合A 为闭集合.给出如下四个结论：① 集合{4,2,0,2,4}A =--为闭集合； ② 集合{|3,}A n n k k ==∈Z 为闭集合； ③ 若集合12,A A 为闭集合，则12A A 为闭集合；④ 若集合12,A A 为闭集合，且1A R Ø，2A R Ø，则存在c ∈R ，使得12()c A A ∉.其中，全部正确结论的序号是_____.二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤. 6.（本小题满分10分）已知函数()log (2)1a f x x =+-，其中1a >.（Ⅰ）若()f x 在[0,1]上的最大值与最小值互为相反数，求a 的值；（Ⅱ）若()f x 的图象不经过第二象限，求a 的取值范围.7.（本小题满分10分）已知函数()|2|f x x x =-. （Ⅰ）解不等式()3f x <；（Ⅱ）设0a >，求()f x 在区间[0,]a 上的最大值.8.（本小题满分10分）设函数()f x ，()g x 的定义域分别为f g D D ，，且f g D D Ø.若对于任意f x D ∈，都有()()g x f x =，则称()g x 为()f x 在g D 上的一个延拓函数.给定2() 1 (01)f x x x =-<≤. （Ⅰ）若()h x 是()f x 在[1,1]-上的延拓函数，且()h x 为奇函数，求()h x 的解析式；（Ⅱ）设()g x 为()f x 在(0,)+∞上的任意一个延拓函数，且()g x y x=是(0,)+∞上的单调函数.（ⅰ）判断函数()g x y x=在(0,1]上的单调性，并加以证明；（ⅱ）设0s >，0t >，证明：()()()g s t g s g t +>+.北京市西城区2013 —2014学年度第一学期期末试卷高一数学参考答案及评分标准2014.1A卷[必修模块4] 满分100分一、选择题：本大题共10小题，每小题4分，共40分.1.D；2.D；3.C；4.B；5.C；6.A；7.A；8.B；9.C；10.D.二、填空题：本大题共6小题，每小题4分，共24分.11.12-；12.3π，或32π；13.6-；14.15.12；16.sin3x等（答案不唯一）.注：12题，得出一个正确的结论得2分.三、解答题：本大题共3小题，共36分.17.（本小题满分12分）（Ⅰ）解：因为3 tan4=-α，所以πtan tanπ4tan()π41tan tan4--=+⋅ααα【3分】7=-. 【6分】（Ⅱ）解：因为3 tan4=-α，所以2sin3cos2tan33sin2cos3tan2--=--αααααα【9分】1817=. 【12分】18.（本小题满分12分）（Ⅰ）解：1cos 4()2cos 22xf x x x -=+⋅1cos 442x x -=+ 【 2分】1sin(4)62x π=-+．【 4分】因为 242T ππ==，所以()f x 的最小正周期是2π．【 6分】（Ⅱ）解：由（Ⅰ）得，1()sin(4)62f x x π=-+．因为 84x ππ≤≤，所以 54366x πππ≤-≤，【 8分】所以 1sin(4)126x π≤-≤，【 9分】所以 131sin(4)622x π≤-+≤．【10分】所以，当6x π=时，()f x 取得最大值32；当4x π=时，()f x 取得最小值1．【12分】19.（本小题满分12分）（Ⅰ）解：如图，以AB 所在直线为x 轴，以A 为坐标原点建立平面直角坐标系. 【 1分】因为ABCDEF 是边长为1的正六边形，且,M N 分别是,BC DE 的中点，所以 5(4M ，1(2N ，【 3分】所以 5311848AM AN ⋅=+=. 【 4分】（Ⅱ）解：设BM DN t ==，则[0,1]t ∈.【 5分】所以(1)2t M +，(1N t -. 【 7分】所以3(1)(1)22t AM AN t t ⋅=+⋅-+2112t t ++=-213(1)22t =--+ 【10分】当0t =时，AM AN ⋅取得最小值1；【11分】当1t =时，AM AN ⋅取得最大值32. 【12分】B 卷 [学期综合] 满分50分一、填空题：本大题共5小题，每小题4分，共20分.1.{|01}x x <<；2.c b a <<；3. [1,)+∞；4. 2；5.②④. 注：5题，选出一个正确的序号得2分，有错选不给分. 二、解答题：本大题共3小题，共30分.6.（本小题满分10分）（Ⅰ）解：函数()log (2)1a f x x =+-的定义域是(2,)-+∞. 【 1分】因为 1a >，所以 ()log (2)1a f x x =+-是[0,1]上的增函数. 【 2分】所以 ()f x 在[0,1]上的最大值是(1)log 31a f =-；最小值是(0)log 21a f =-. 【 4分】依题意，得 log 31(log 21)a a -=--，【 5分】解得 a =【 6分】（Ⅱ）解：由（Ⅰ）知，()log (2)1a f x x =+-是(2,)-+∞上的增函数. 【 7分】在()f x 的解析式中，令0x =，得(0)log 21a f =-，所以，()f x 的图象与y 轴交于点(0,log 21)a -. 【 8分】依题意，得(0)log 210a f =-≤，【 9分】解得 2a ≥. 【10分】7.（本小题满分10分）（Ⅰ）解：原不等式可化为22230x x x ≥⎧⎨--<⎩，，（1）或22230.x x x <⎧⎨-+>⎩，（2）【 1分】解不等式组（1），得 23x ≤<；解不等式组（2），得2x <. 【 3分】所以原不等式的解集为{|3}x x <. 【 4分】（Ⅱ）解：222,2,()|2|2, 2.x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩ 【 5分】① 当01a <<时，()f x 是[0,]a 上的增函数，此时()f x 在[0,]a 上的最大值是2()2f a a a =-+. 【 6分】 ② 当12a ≤≤时，()f x 在[0,1]上是增函数，在[1,]a 上是减函数，此时()f x 在[0,]a 上的最大值是(1)1f =. 【 7分】③ 当2a >时，令()(1)(2)10f a f a a -=-->，解得1a >+. 所以，当21a <≤+时，此时()(1)f a f ≤，()f x 在[0,]a 上的最大值是(1)1f =；当1a >时，此时()(1)f a f >，()f x 在[0,]a 上的最大值是2()2f a a a =-.【 9分】记()f x 在区间[0,]a 上的最大值为()g a ，所以222,01,()1,112,1a a a g a a a a a ⎧-+<<⎪⎪=≤≤⎨⎪->+⎪⎩【10分】8.（本小题满分10分）（Ⅰ）解：当0x =时，由()h x 为奇函数，得(0)0h =. 【 1分】任取[1 0)x ∈-，，则(01]x -∈，，由()h x 为奇函数，得22()()[()1]1h x h x x x =--=---=-+，【 2分】所以()h x 的解析式为221,01,()0,0,1,10.x x h x x x x ⎧-<≤⎪==⎨⎪-+-≤<⎩【 3分】（Ⅱ）解：（ⅰ）函数()g x y x=是(0,1]上的增函数. 【 4分】证明如下：因为()g x 为()f x 在(0,)+∞上的一个延拓函数，所以当(01]x ∈，时，2()()1g x f x x ==-. 记()()1()g x f x k x x x x x===-，其中(0,1]x ∈. 任取12,(0,1]x x ∈，且12x x <，则210x x x ∆=->，因为211221212112()(1)11()()()0x x x x y k x k x x x x x x x -+∆=-=---=>，所以函数()g x y x=是(0,1]上的增函数. 【 6分】（ⅱ）由()g x y x = 是(0,)+∞上的单调函数，且(0,1]x ∈时，()g x y x =是增函数，从而得到函数()g x y x= 是(0,)+∞上的增函数. 【 7分】因为 0s >，0t >，所以 s t s +>，s t t +>，所以()()g s t g s s t s+>+，即 ()()()s g s t s t g s ⋅+>+⋅. 【 8分】同理可得：()()()t g s t s t g t ⋅+>+⋅.将上述两个不等式相加，并除以s t +，即得 ()()()g s t g s g t +>+. 【10分】。

2014 — 2015西城区学年度第一学期期末试卷高三【数学理】

北京市西城区2014 — 2015学年度第一学期期末试卷高三数学（理科）2015.1第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合，，则集合（）1,0,1{}A -=2{|2}B x x x =-<A B = （A ）{1,0,1}-（B ）{1,0}-（C ）{0,1}（D ）{1,1}-3．在锐角ABC 中，角A ，B ，C 所对的边分别为a ，b ，c . 若，，则∆2a b=sin B =（）（A ）3A π=（B ）6A π=（C）sin A =（D ）2sin 3A =2．设命题：平面向量和，，则为（）p ∀a b ||||||-<+a b a b p ⌝ （A ）平面向量和，∀a b ||||||-+≥a b a b （B ）平面向量和，∃a b ||||||-<+a b a b （C ）平面向量和，∃a b ||||||->+a b a b （D ）平面向量和，∃a b ||||||-+≥a b a b4．执行如图所示的程序框图，输出的x 值为（）（A ）4（B ）5（C ）6（D ）75．设函数，，则“”是“函数为奇函数”的（）()3cos f x x b x =+x ∈R 0b =()f x （A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件6．一个四棱锥的三视图如图所示，那么对于这个四棱锥，下列说法中正确的是（）（A（B ）最长棱的棱长为3（C ）侧面四个三角形中有且仅有一个是正三角形（D ）侧面四个三角形都是直角三角形7. 已知抛物线，点，O 为坐标原点，若在抛物线C 上存在一点，使得2:4C y x =(,0)P m Q ，则实数m 的取值范围是（）90OQP Ð= （A ）(4,8)（B ）(4,)+¥侧(左)视图正(主)视图俯视图8. 设D 为不等式组表示的平面区域，点为坐标平面内一点，若对于区域D1,21,21x y x y x y ---+⎧⎪⎨⎪⎩≤≥≤(,)B a b xOy 内的任一点，都有成立，则的最大值等于（）(,)A x y 1OA OB ⋅≤a b +（A ）2（B ）1（C ）0（D ）3第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分．9. 复数，则 _____．2i12iz -=+||z =10．设为双曲线C ：的左、右焦点，点P 为双曲线C 上一点，如果12,F F 2221(0)16x y a a -=>，那么双曲线C 的方程为____；离心率为____.12||||4PF PF -=11．在右侧的表格中，各数均为正数，且每行中的各数从左到右成等差数列，每列中的各数从上到下成等比数列，那么______．x y z ++=12．如图，在中，以为直径的半圆分别交，于ABC ∆BC AB AC 点，，且，那么____； _____．E F 2AC AE =AFAB =A ∠=13．现要给4个唱歌节目和2个小品节目排列演出顺序，要求2个小（C ）(0,4)（D ）(8,)+¥2x3ya321258z品节目之间恰好有3个唱歌节目，那么演出顺序的排列种数是______. （用数字作答）14. 设P ，Q 为一个正方体表面上的两点，已知此正方体绕着直线PQ 旋转（）角后能θ0<θ<2π与自身重合，那么符合条件的直线PQ 有_____条.三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．（本小题满分13分）已知函数, x ∈R 的部分图象如图所示.()cos cos 442x x xf x =+（Ⅰ）求函数的最小正周期和单调递增区间；()f x （Ⅱ）设点B 是图象上的最高点，点A 是图象与x 轴的交点，求的值.BAO ∠tan 16．（本小题满分13分）现有两种投资方案，一年后投资盈亏的情况如下：（1）投资股市：投资结果获利40%不赔不赚亏损20%概率121838（2）购买基金：投资结果获利20%不赔不赚亏损10%概率p13q（Ⅰ）当时，求q 的值；14p =（Ⅱ）已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资，如果一年后他们中至少有一人获利的概率大于，求的取值范围； 45p（Ⅲ）丙要将家中闲置的10万元钱进行投资，决定在“投资股市”和“购买基金”这两种方案中选择一种，已知，，那么丙选择哪种投资方案，才能使得一年后投资收益的数学12p =16q =期望较大？给出结果并说明理由．17．（本小题满分14分）如图，在四棱柱1111D C B A ABCD -中，A A 1⊥底面ABCD ，，BC AD //，且90BAD ∠= ，点E 在棱AB 上，平面与棱相交于点F .122A A AB AD BC ====1A EC 11C D （Ⅰ）证明：∥平面；1A F 1B CE （Ⅱ）若E 是棱AB 的中点，求二面角的余弦值；1A EC D --（Ⅲ）求三棱锥的体积的最大值.11B A EF -18．（本小题满分13分）已知函数和的图象有公共点P ，且在点P 处的切线相同.2()(0)f x ax bx a =->()ln g x x =（Ⅰ）若点P 的坐标为，求的值；1(,1)e-,a b （Ⅱ）已知，求切点P 的坐标.a b =19．（本小题满分14分）已知椭圆C ：的右焦点为F ，右顶点为A ，离心率为e ，点满足条件2211612x y +=(,0)(4)P m m >B D 1.||||FA e AP =（Ⅰ）求m 的值；（Ⅱ）设过点F 的直线l 与椭圆C 相交于M ，N 两点，记和的面积分别为，PMF ∆PNF ∆1S ，求证：.2S 12||||S PM S PN =20．（本小题满分13分）设函数，对于任意给定的位自然数（其中是个位数字，()(9)f x x x =-m 0121m m n a a a a -= 1a 2a 是十位数字，），定义变换：. 并规定．记 A 012()()()()m A n f a f a f a =+++ (0)0A =10()n A n =，，，，．21()n A n = 1()k k n A n -= （Ⅰ）若，求；02015n =2015n （Ⅱ）当时，证明：对于任意的*()m m ∈N 位自然数n 均有1()10m A n -<；3m ≥ （Ⅲ）如果，写出的所有可能取值.（只需写出结论）*010(,3)m n m m <∈≥N m n 北京市西城区2014 — 2015学年度第一学期期末高三数学（理科）参考答案及评分标准2015.1一、选择题：本大题共8小题，每小题5分，共40分.1．C2．D3．A4．C5．C 6．D 7．B 8．A二、填空题：本大题共6小题，每小题5分，共30分. 9． 10．1221416x y -=11．12．17412π313．14．9613注：第10，12题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分. 其他正确解答过程，请参照评分标准给分. 15．（本小题满分13分）（Ⅰ）解：因为()cos cos 442x x xf x =+……………… 2分cos 22x x=+=，……………… 4分π2sin()26x +所以 .2π4π12T ==故函数的最小正周期为. ……………… 6分()f x 4π由题意，得，πππ2π2π2262x k k -++≤≤解得，4π2π4π4π+33k x k -≤≤所以函数的单调递增区间为. ……………… 9分()f x 4π2π[4π,4π+],()33k k k -∈Z （Ⅱ）解：如图过点作线段垂直于B BC x 由题意，得，，33π4TAC ==2=BC 所以.2tan 3πBC BAO AC ∠==16．（本小题满分13分）（Ⅰ）解：因为“购买基金”后，投资结果只有“获利”、“不赔不赚”、“亏损”三种，且三种投资结果相互独立，所以++=1. ……………… 2分p 13q又因为， 14p = 所以=． ……………… 3分q 512（Ⅱ）解：记事件A 为 “甲投资股市且盈利”，事件B 为“乙购买基金且盈利”，事件C 为“一年后甲、乙两人中至少有一人投资获利”，……………… 4分则，且A ，B 独立. C AB AB AB = 由上表可知，，. 1()2P A =()P B p = 所以 ……………… 5分()()()()P C P AB P AB P AB =++111(1)222p p p =´-+´+ . ……………… 6分1122p =+ 因为，114()225P C p =+> 所以.……………… 7分35p > 又因为，，113p q ++=0q ≥ 所以.23p ≤ 所以.……………… 8分3253p ≤<（Ⅲ）解：假设丙选择“投资股票”方案进行投资，且记X 为丙投资股票的获利金额（单位：万元），所以随机变量的分布列为：X X402 P121838…………… 9分则. ……………10 分113540(2)2884EX =⨯+⨯+-⨯=假设丙选择“购买基金”方案进行投资，且记Y 为丙购买基金的获利金额（单位：万元），所以随机变量的分布列为：Y Y201-P121316…………… 11分则. …………… 12分111520(1)2366EY =⨯+⨯+-⨯= 因为，EX EY >所以丙选择“投资股市”，才能使得一年后的投资收益的数学期望较大．……… 13分17．（本小题满分14分）（Ⅰ）证明：因为1111D C B A ABCD -是棱柱，所以平面平面.ABCD ∥1111A B C D 又因为平面平面，平面平面，ABCD 1A ECF EC =1111A B C D 11A ECF A F =所以∥. …………………2分1A F EC 又因为平面，平面，1A F ⊄1B CE EC ⊂1B CE 所以∥平面. …………………4分1A F 1B CE （Ⅱ）解：因为⊥底面ABCD ，，1AA 90BAD ∠= 所以，，两两垂直，以A 为原点，以，，分别为轴、轴和1AA AB AD AB AD 1AA x y z 轴，如图建立空间直角坐标系. …………………5分则，，，1(0,0,2)A (1,0,0)E (2,1,0)C 所以 ,.1(1,0,2)A E =- 1(2,1,2)AC =- 设平面的法向量为(,,),m x y z =1A ECF由，,10A E m ⋅= 10AC m ⋅= 得20,220.x z x y z -=⎧⎨+-=⎩令,得. …………………7分1z =(2,2,1)m =-又因为平面的法向量为， …………………8分DEC (0,0,1)n =所以，1cos ,3||||m n m n m n ⋅<>==⋅由图可知，二面角的平面角为锐角，1A EC D --所以二面角的余弦值为. …………………10分（Ⅲ）1A EC D --13解：过点F 作于点,11FM A B ⊥M 因为平面⊥平面，平面,11A ABB 1111A B C D FM ⊂1111A B C D 所以平面,FM ⊥11A ABB 所以 …………………12分11111113B A EF F B A E A B E V V S FM --∆==⨯⨯.1222323FM FM ⨯=⨯⨯=因为当F 与点重合时，取到最大值2（此时点E 与点B 重合），1D FM 所以当F 与点重合时，三棱锥的体积的最大值为. ………………14分1D 11B A EF -4318.（本小题满分13分）（Ⅰ）解：由题意，得， …………………1分21(1e e ea bf =-=- 且，， …………………3分()2f x ax b '=-1()g x x'=由已知，得，即，11()(e ef g ''=2e eab -=解得，. …………………5分22e a =3e b =（Ⅱ）解：若，则，，a b =()2f x ax a '=-1()g x x'=设切点坐标为，其中,(,)s t 0s >由题意，得， ①2ln as as s -= ， ②…………………6分12as a s -= 由②，得，其中，1(21)a s s =-12s ≠代入①，得 .（*） …………………7分1ln 21s s s -=- 因为，且，1(21)a s s =>-0s > 所以 . …………………8分12s >设函数，，1()ln 21x F x x x -=--1(,)2x ∈+∞ 则 .…………………9分2(41)(1)()(21)x x F x x x ---'=- 令，解得或(舍).…………………10分()0F x '=1x =14x =当变化时，与的变化情况如下表所示，x ()F x '()F x x1(,1)21(1,)+∞()F x '+0-()F x ↗↘…………………12分所以当时，取到最大值，且当时.1x =()F x (1)0F =1(,1)(1,)2x ∈+∞ ()0F x < 因此，当且仅当时. 1x =()0F x = 所以方程（*）有且仅有一解.1s = 于是，ln 0t s ==因此切点P 的坐标为.…………………13分(1,0)19．（本小题满分14分）（Ⅰ）解：因为椭圆C 的方程为，2211612x y +=所以 ,,, ………………2分4a=b=2c ==则，，. ………………3分12c e a ==||2FA =||4AP m =-因为，||21||42FA AP m ==-所以 . ………………5分8m =（Ⅱ）解：若直线l 的斜率不存在，则有，，符合题意. …………6分21S S =||||PM PN =若直线l 的斜率存在，则设直线l 的方程为，，.)2(-=x k y ),(11y x M ),(22y x N 由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得， ……………… 7分2222(43)1616480k x k x k +-+-= 可知恒成立，且，. ……………… 8分0>∆34162221+=+k k x x 3448162221+-=k k x x 因为 ……………… 10分8)2(8)2(8822112211--+--=-+-=+x x k x x k x y x y k k PN PM)8)(8()8)(2()8)(2(211221----+--=x x x x k x x k)8)(8(32)(102212121--++-=x x kx x k x kx，0)8)(8(323416103448162212222=--++⋅-+-⋅=x x k k k k k k k 所以 . ……………… 12分MPF NPF ∠=∠ 因为和的面积分别为，PMF ∆PNF ∆11||||sin 2S PF PM MPF =⋅⋅∠， ……………… 13分21||||sin 2S PF PN NPF =⋅⋅∠ 所以. ……………… 14分12||||S PM S PN =20．（本小题满分13分）（Ⅰ）解：，，，，114082042n =+++=2201434n =+=3182038n =+=418826n =+=，，……5141832n =+=6181432n =+= 所以．……………… 3分201532n =（Ⅱ）证明：因为函数，2981()(9)(24f x x x x =-=--+所以对于非负整数，知.（当或5时，取到最大值）… 4分x ()(9)20f x x x =-≤4x = 因为， 12()()()()m A n f a f a f a =+++ 所以． ……………… 6分()20A n m ≤ 令，则．1()1020m g m m -=-31(3)102030g -=-⨯> 当时，，3m ≥11(1)g()1020(1)1020910200m m m g m m m m --+-=-+-+=⨯-> 所以，函数，（，且）单调递增．(1)g()0g m m +->()g m m ∈N 3m ≥ 故，即．g()g(3)0m >≥11020()m m A n ->≥ 所以当时，对于任意的位自然数均有.…………………9分3m ≥m n 1()10m A n -<（Ⅲ）答：的所有可能取值为0，8，14，16，20，22，26，28，32，36，38．m n …………………14分。

北京市西城区2014-2015学年七年级(上)期末考试数学试题及答案

北京市西城区2014— 2015学年度第一学期期末试卷七年级数学 2015.1试卷满分：100分，考试时间：100分钟一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．在1， 0，1-，2-这四个数中，最小的数是（）A. 2-B. 1-C. 0D. 12．2014年3月5日，李克强总理在政府工作报告中指出：2013年全国城镇新增就业人数约为13 100 000人，创历史新高．将数字13 100 000用科学记数法表示为 A ． 13.1×106B ．1.31×107C ．1.31×108D ．0.131×1083．下列计算正确的是（）A. 235a b ab +=B. 325a a a +=C. 2222a a a --=-D. 22271422a b a b a b -= 4．已知关于x 的方程225x m +=的解是2x =-，则m 的值为（）．A.12 B. 12- C. 92 D. 92- 5．若21(2)02x y -++=，则2015()xy 的值为（） A. 1 B. 1- C.2015- D. 20156．在下面四个几何体中，从左面看、从上面看分别得到的平面图形是长方形、圆，这个几何体是（）A B CD7．如图，将一个直角三角板AOB 的顶点O 放在直线CD 上，若∠AOC =35°，则∠BOD 等于 A ．155°B ．145°C ．65°D ． 55°8．在某文具店，一支铅笔的售价为1.2元，一支圆珠笔的售价为2元．该店在新年之际举行文具优惠销售活动，铅笔按原价打8折出售，圆珠笔按原价打9折出售，结果两种笔共卖出60支，卖得金额87元．设该铅笔卖出x 支，则可列得的一元一次方程为（） A ．0.8 1.20.92(60)87x x ⨯+⨯-= B ．0.8 1.20.92(60)87x x ⨯+⨯+= C ．0.920.8 1.2(60)87x x ⨯+⨯+= D ． 0.920.8 1.2(60)87x x ⨯+⨯-= 9．如图，四个有理数在数轴上的对应点M ，P ，N ， Q ，若点M ，N 表示的有理数互为相反数，则图中表示绝对值最小的数的点是A ．点MB ．点NC ．点PD ．点Q10．小明制作了一个正方体包装盒，他在这个正方体包装盒的上面设计了一个“ ”标志，并在正方体的每个表面都画了黑色粗线，如右图所示．在下列图形中，是这个正方体包装盒的表面展开图的是A BC D二、填空题（本题共20分，第11～14题每小题3分，第15～18题每小题2分） 11．4-的倒数是．12． “m 与n 的平方差”用式子表示为．14．已知多项式22x y +的值是3，则多项式224x y ++的值是． 15．写出一个只含有字母x ，y 的三次单项式．16．如图，已知线段AB =10cm ，C 是线段AB 上一点，D 的中点，E 是线段BC 的中点，则DE 的长是 cm ．17．如图，把一个圆平均分为若干份，然后把它们全部剪开，拼成一个近似的平行四边形．若这个平行四边形的周长比圆的周长增加了4cm ，则这个圆的半径是 cm ，拼成的平行四边形的面积是 cm 2．18．观察下列等式：12×231=132×21， 13×341=143×31， 23×352=253×32， 34×473=374×43， 62×286=682×26，……在上面的等式中，等式两边的数字分别是对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．（1）根据以上各等式反映的规律，使下面等式成为“数字对称等式”：52× = ×25；（2）设这类等式左边的两位数中，个位数字为a ，十位数字为b ，且2≤a +b ≤9，则用含a ，b 的式子表示这类“数字对称等式”的规律是．三、计算题（本题共16分，每小题4分）19． 3011(10)(12)-+--- 20．51(3)()(1)64-⨯-÷-解：解：21．21[1(10.5)][10(3)]3--⨯⨯-+- 22．312138()(2)(8)595⨯--⨯-+-⨯解：解：四、先化简，再求值（本题5分）23．23232(3)3(2)ab a b ab a b ---，其中12a =-，4b =．解：五、解下列方程或方程组（本题共10分，每小题5分）24．4131163x x --=-． 25．32105.x y x y +=⎧⎨-=⎩，解：解：六、解答题（本题6分）26．如图，∠A +∠B =90°，点D 在线段AB 上，点E 在线段AC 上，DF 平分∠BDE ，DF 与BC 交于点F ．（１）依题意补全图形；（２）若∠B +∠BDF =90°，求证：∠A =∠EDF ．证明：∵∠A +∠B =90°，∠B +∠BDF =90°，∴ (理由： ) ．又∵ ，∴∠BDF =∠EDF (理由： ) ． ∴∠A =∠EDF ．七、列方程或方程组解应用题（本题5分）27．电子商务的快速发展逐步改变了人们的购物方式，网购已悄然进入千家万户．李阿姨在某网店买了甲、乙两件商品，已知甲商品的价格比乙商品价格的2倍多108元，乙商品的价格比甲、乙两件商品总价的14少3元．问甲、乙两件商品的价格各多少元？解：八、解答题（本题8分）28．已知A，B，C三点在同一条数轴上．（1）若点A，B表示的数分别为－4，2，且12BC AB=，则点C表示的数是；（2）点A，B表示的数分别为m，n，且m＜n．①若AC－AB=2，求点C表示的数（用含m，n的式子表示）；②点D是这条数轴上的一个动点，且点D在点A的右侧（不与点B重合），当2AD AC=，14BC BD=，求线段AD的长（用含m，n的式子表示）．解：（1）点C表示的数是；（2）①②北京市西城区2014— 2015学年度第一学期期末试卷七年级数学附加题2015.1试卷满分：20分一、填空题（本题共7分，第1题5分，第2题2分）1．1883年，德国数学家格奥尔格·康托尔引入位于一条线段上的一些点的集合，他的做法如下：取一条长度为1的线段，将它三等分，去掉中间一段，余下两条线段，达到第1阶段；将剩下的两条线段再分别三等分，各去掉中间一段，余下四条线段，达到第2阶段；再将剩四条线段，分别三等分，分别去掉中间一段，余下八条线段，达到第3阶段；……；这样的操作一直继续下去，在不断分割舍弃过程中，所形成的线段数目越来越多，把这种分形，称做康托尔点集．下图是康托尔点集的最初几个阶段，当达到第5个阶段时，余下的线段的长度．．之和为；当达到第n个阶段时(n为正整数)，余下的线段的长度．．之和为．2．如图，足球的表面是由若干块黑皮和白皮缝合而成的，其中黑皮为正五边形，白皮为正六边形．已知黑皮和白皮共有32块，每块黑皮周围有5块白皮，每块白皮周围有3块黑皮，设缝制这样一个足球需要x块黑皮，y块白皮，那么根据题意列出的方程组是．二、解答题（本题共4分）3．（1）如图1，D 是线段BC 的中点，三角形ABC 的面积与三角形ABD 的面积比为；（2）如图2，将网格图中的梯形ABCD 分成三个三角形，使它们的面积比是1:2:3．4．设x 是有理数，我们规定：(0)0(0)x x x x +≥⎧=⎨<⎩，0(0)(0)x x x x ->⎧=⎨≤⎩．例如：33+=，(2)0+-=；30-=， (2)2--=-．解决如下问题：（1）填空： 1()2+= ， (1)--= ，x x +-+= ；（2）分别用一个含||,x x 的式子表示x +，x -．解：（1）1()2+= ， (1)--= ，x x +-+= ；（2）北京市西城区2014— 2015学年度第一学期期末试卷七年级数学参考答案及评分标准 2015.1一、选择题（本题共30分，每小题3分）三、计算题（本题共16分，每小题4分） 19．3011(10)(12)-+---解：3011(10)(12)-+---=30111012--+ ···························································································· 1分 =4221- ········································································································· 3分 =21 ················································································································· 4分20． 51(3)()(1)64-⨯-÷-解：51(3)()(1)64-⨯-÷-55364=-⨯÷ ···································································································· 2分 =54365-⨯⨯ ····································································································· 3分=2- ················································································································· 4分21． 21[1(10.5)][10(3)]3--⨯⨯-+-解：21[1(10.5)][10(3)]3--⨯⨯-+-=11[1(1)](109)23--⨯⨯-+ ······················································································ 1分 =5(1)(1)6-⨯- ··········································································································· 3分 =16- ·························································································································· 4分22．312138()(2)(8)595⨯--⨯-+-⨯ 解：312138()(2)(8)595⨯--⨯-+-⨯=1213888595-⨯+⨯-⨯ ···················································································· 2分=12388()559-++ ····························································································· 3分=8249-+=1239- ············································································································ 4分四、先化简，再求值（本题5分）23．23232(3)3(2)ab a b ab a b ---，其中12a =-，4b =．解：23232(3)3(2)ab a b ab a b ---=23236263ab a b ab a b --+ ·············································································· 2分 =3a b ··············································································································· 3分当12a =-，4b =时，原式31()42=-⨯ ···························································································· 4分12=- ······································································································· 5分五、解下列方程或方程组（本题共10分，每小题5分） 24．4131163x x --=-解：去分母，得 (41)62(31x x -=--． ························································ 1分去括号，得 41662x x -=-+． ····························································· 2分移项，得 46621x x +=++． ································································· 3分合并同类项，得 109x =． ······································································· 4分系数化1，得910x =． ················································································ 5分 25．32105.x y x y +=⎧⎨-=⎩，解：由②得 5x y =+．③ ················································································ 1分把③代入①，得 3(5)210y y ++=． ··························································· 2分解得 1y =-． ······························································································· 3分把1y =-代入③，得 5(1)4x =+-=． ····················································· 4分① ②所以，原方程组的解为 41.x y =⎧⎨=-⎩，································································ 5分六、解答题（本题6分）26．解：（1）补全图形，如图； ···································· 2分（2）证明：∵∠A +∠B =90°，∠B +∠BDF =90°， ∴ ∠A =∠BDF (理由：同角的余角相等 ) ． ·················································································· 4分又∵ DF 平分∠BDE ， ······················· 5分 ∴∠BDF =∠EDF (理由：角平分线定义 ) ． ·················································································· 6分 ∴∠A =∠EDF ．七、列方程或方程组解应用题（本题6分）27．解：设甲商品的价格x 元，乙商品价格y 元． ···················································· 1分由题意，得2108,1() 3.4x y y x y =+⎧⎪⎨=+-⎪⎩········································································ 3分解得300,96.x y =⎧⎨=⎩································································································ 5分答：甲商品的价格为300元，乙商品的价格为96元． ····························· 6分八、解答题（本题共8分）28．解：（1）﹣1，5； ·································································································· 2分（2）设点C 表示的数为x ，由m ＜n ，可得：点A 在点B 的左侧．AB n m =-．①由AC －AB =2，得AC ＞AB ．以下分两种情况：ⅰ) 当点C 在点B 的右侧时，如图1所示，此时AC = x －m ．∵AC －AB =2， ∴(x －m ) －(n －m ) =2．解得2x n =+．∴点C 表示的数为2n +． ····················································· 4分 ⅱ) 当点C 在点A 的左侧时，如图2所示，此时，AC =m －x ．∵AC －AB =2，∴（m －x ）－（n －m ） =2解得22x m n =--．∴点C 表示的数为22m n --．综上，点C 表示的数为2n +，22m n --． ························ 6分AB CEDBA 图1图2②由2AD AC =，可得：点C 为线段AD 上或点C 在点A 的左侧．当动点D 在线段AB 上时，无论点C 在何位置均不合题意；当动点D 在点B 的右侧时，以下分三种情况：ⅰ）当点C 在线段BD 的延长线上时，点C 为线段AD 的中点，当点C 在线段BD 上时，如图3所示． ∴33AD n m =-．ⅱ）当点C 在线段AB 上时，如图4所示．∴5533AD n m =-．ⅲ）当点C 在点A 左侧时，不合题意．综上所述，线段AD 的长为33n m -或5533n m -． ···························· 8分北京市西城区2014— 2015学年度第一学期期末试卷七年级数学附加题参考答案及评分标准 2015.1一、填空题（本题共7分，第1题5分，第2题2分）1．523⎛⎫⎪⎝⎭； ··················································································································· 3分23n⎛⎫⎪⎝⎭． ················································································································· 5分 2．32,53.x y x y +=⎧⎨=⎩·············································································································· 2分二、解答题（本题共13分，第3题6分，第4题7分）3．解：（1）2:1； ·········································································································· 3分（2）答案不唯一，如：···························································· 6分4．解：（1）1122+⎛⎫= ⎪⎝⎭，()111--=-，x x x +-+=； ················································ 3分（2）当x ≥0时，x x +=，x x =，∴2x xx ++=． CB DA 图4图3DBC当x ＜0时，0x +=， ∴2x xx ++=．综上所述，当x 为有理数时，2x xx ++=．当x ≥0时， 0x -=，∴2x xx --=．当x ＜0时，x x -=，x x =-∴2x xx --=；综上所述，当x 为有理数时，2x xx --=． ············································ 7分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。