广东省2014届高三寒假作业数学(三) Word版解析
2014年高考理科数学试题广东卷word版 含答案

2014年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.MN?{0,1,2}??1,0,1}NM?{ 1.已知集合,,则{?1,0,1}{?1,0,1,2}{?1,0,2}{0,1} D.C.A.B.(3?4i)z?25,则Z= Z满足2.已知复数3?4i3?4i?3?4i?3?4i A.C.B.D.y?x??x?y?1且z?2x?ymn yx,,则.若变量满足约束条件和的最大值和最小值分别为3??y??1?m?n?A.8B.7C.6D.52222yyxx??1??10?k?9,则曲线k的4与曲线.若实数满足k25?k259?9A.离心率相等 B.虚半轴长相等 C.实半轴长相等 D.焦距相等 ??1?1,0,a?a60?夹角的是成.已知向量,则下列向量中与5A.(-1,1,0)B.(1,-1,0) C.(0,-1,1)D.(-1,0,1)6.已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别是/%近视率小学生高中生3500名2000名5030 初中生4500名10O 初中年级高中小学10 D.100, B.100,20 C.200,10 A.200,20ll??l,,ll?l,lll,,l,则下面结论一定正确的满足,7.若空间中四条两两不同的直线4321233214是l/ll/?ll,,lll B.的位置关系不确定 C. A.D.既不垂直也不平行41414411????542,,3,0{1,,1}?i,A=1,?xx,x,,x,xx?件足条A集8.设合那中满么集合,i345123?x?xx?x?x?1?“”的元素个数为54231D.130B.90C.120 A.6030分.6小题,每小题5分,满分二、填空题:本大题共7小题,考生作答题)~(一)必做题(91352??x?1?x的解集为。
广东省高三数学寒假作业(一)

广东省2014届高三寒假作业(二)数学一、选择题 1.函数f (x )=cos2x 在区间[-3,3]上的零点的个数为( )A .3B .4C .5D .62.函数( )A .B .C .D .3.对于函数,下列结论中正确的是:A .当上单调递减B .当上单调递减C .当上单调递增D .上单调递增 4.设函数则( )A .在区间内均有零点B .在区间内均无零点C .在区间内无零点,在区间内有零点D .在区间内有零点,在区间内无零点 5.方程330x x --=的实数解落在的区间是A .[1,0]-B .[0,1]C .[1,2]D .[2,3]6.用“二分法”求函数()3222f x x x x =+--的一个正实数零点,其参考数据如下:()12f =- ()1.50.625f = ()1.250.984f =-()1.3750.260f =- ()1.43750.162f = ()1.406250.054f =-那么方程32220x x x +--=的一个近似根(精确到0.1)为 () A . 1.2B . 1.3C . 1.4D . 1.57.方程22xx =的解的个数是( )A .0B .1C .2D .38.已知a 为实数,且3220,a a a +-+=则8910(1)(1)(1)a a a +++++的值是: A .-3 B .3 C .-1 D .1 二、填空题9.若a>3,则函数f (x )=x 2-ax+1在区间(0,2)上恰好有 个零点 10.已知,则的最大值是 .11.函数的零点个数是________.12. 若方程()lg 2lg 1kx x =+仅有一个实根,那么k 的取值范围是 .13.已知整数12,32012,,...,x x x x 满足:①12n x -≤≤,1,2,...,2012;n =②1220122010;x x x ++⋅⋅⋅+=③2221220122012.x x x ++⋅⋅⋅+=则333122012x x x ++⋅⋅⋅+的值是 . 14.若函数b x a x ax x f +-+-=||)3(2||31)(23有六个不同的单调区间,则实数a 的取值范围是 .三、解答题15. (本题满分16分) 如图,开发商欲对边长为的正方形地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路(点分别在上),根据规划要求的周长为.(1)设,求证:; (2)欲使的面积最小,试确定点的位置.16.(本题满分12分)已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装千件并全部销售完,每千件的销售收入为万元,且.(I)写出年利润(万元)关于年产量(千件)的函数关系式;(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?17.(本小题满分12分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).(1)分别写出两种产品的收益与投资额的函数关系;(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?18.(本小题满分12分)设某物体一天中的温度T 是时间t 的函数:32()(0)T t at bt ct d a =+++≠,其中温度的单位是℃,时间单位是小时,0t =表示12:00,t 取正值表示12:00以后.若测得该物体在8:00的温度是8℃,12:00的温度为60℃,13:00的温度为58℃,且已知该物体的温度在8:00和16:00有相同的变化率. (1)写出该物体的温度T 关于时间t 的函数关系式;(2)该物体在10:00到14:00这段时间中(包括10:00和14:00),何时温度最高,并求出最高温度;(3)如果规定一个函数()f x 在区间1212[]()x x x x <,上的平均值为21211()x x f x dx x x -⎰,求该物体在8:00到16:00这段时间内的平均温度.19.商店出售茶壶和茶杯,茶壶单价为每个20元,茶杯单价为每个5元,该店推出两种促销优惠办法:(1)买1个茶壶赠送1个茶杯;(2)按总价打9.2折付款。
广东省广州市2014届高三调研测试数学理试题 Word版含答案

广州市2014届高三年级调研测试 试卷类型:A数 学(理 科) 2014.1本试卷共4页,21小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:锥体体积公式13V Sh =,其中S 为锥体的底面积,h 为锥体的高.一.选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i 为虚数单位, 则复数i2i-的模等于A B C D 2.设集合{}0322=--=x x x A ,{}12==x x B ,则B A 等于A .{}1-B .{}1,3C .{}1,1,3-D .R 3.已知向量(3,1)=a ,(,2)x =-b ,(0,2)=c ,若()⊥-a b c ,则实数x 的值为 A .43 B .34 C .34- D .43- 4.定义在R 上的函数()f x 满足2log (16), 0,()(1),0,x x f x f x x -≤⎧=⎨->⎩则()3f 的值为 A .4- B .2 C .2log 13 D .45.函数()()s i n fx A x ωϕ=+(0A >,0ω>,2πϕ<)的部分图象如图1所示,则函数()y f x =对应的解析式为A .sin 26y x π⎛⎫=+ ⎪⎝⎭B .sin 26y x π⎛⎫=- ⎪⎝⎭C .cos 26y x π⎛⎫=+⎪⎝⎭D .cos 26y x π⎛⎫=-⎪⎝⎭6.执行如图2的程序框图,如果输入的N 的值是6,那么输出的p 的值是A .15B .105C .120D .7207.若点(1,0)A 和点(4,0)B 到直线l 的距离依次为1和2,则这样的直线有A .1条B .2条C .3条D .4条8.对于实数a 和b ,定义运算“*”:a *2221, ,, .a ab a b b b ab a b ⎧-+-≤⎪=⎨->⎪⎩设()()21f x x =-*()1x -,且关于x 的方程为()()f x m m =∈R 恰有三个互不相等的实数根1x ,2x ,3x ,则321x x x ⋅⋅的取值范围是 A .1,032⎛⎫-⎪⎝⎭ B .1,016⎛⎫- ⎪⎝⎭ C .10,32⎛⎫ ⎪⎝⎭ D .10,16⎛⎫⎪⎝⎭二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题)9.在等比数列{}n a 中,若1323a a a =⋅,则4a = .10.若x ,y 满足约束条件0,0,1,3412,x y x y x y ≥⎧⎪≥⎪⎨-≥-⎪⎪+≤⎩则x y +的最大值为_______.ks5u11.如图3,设D 是图中边长为4的正方形区域,E 是D 内函数2y x =图象下方的点构成的区域.在D 内随机取一点,则该点落在E 中的概率为 .12.已知点P 在曲线4e 1x y =+(其中e 为自然对数的底数)上,α为曲线在点P 处的切线的倾斜角,则αtan 的取值范围是 .13.有4名优秀学生A ,B ,C ,D 全部被保送到甲,乙,丙3所学校,每所学校至少去一名,则不同的保送方案共有 种.(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图4,AC 为⊙O 的直径,OB AC ⊥,弦BN 交AC 于点M .若OC =1OM =,则MN 的长为 . 15.(坐标系与参数方程选讲选做题)若点(,)P x y 在曲线2cos sin x y θθ=-+⎧⎨=⎩(θ为参数,θ∈R )上,则y x 的取值范围是 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c,且cos 2A C +=. (1)求cos B 的值;(2)若3a =,b =c 的值.ks5u17.(本小题满分12分)空气质量指数PM2.5 (单位:3/m μg )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:从甲城市2013年9月份的30天中随机抽取15天的PM2.5日均浓度指数数据茎叶图如图5所示.(1)试估计甲城市在2013年9月份30天的空气质量类别为优或良的天数; (2)在甲城市这15个监测数据中任取2个,设X 为空气质量类别为优或良的天数,求X 的分布列及数学期望.18.(本小题满分14分)在如图6的几何体中,平面CDEF 为正方形,平面ABCD 为等腰梯形,AB ∥CD ,BC AB 2=,60ABC ︒∠=,AC FB ⊥.3 2 045 56 47 6 9 78 8 0 79 1 8 0 9 图5(1)求证:⊥AC 平面FBC ;(2)求直线BF 与平面ADE 所成角的正弦值.19.(本小题满分14分)已知数列{a n }满足135a =,1321n n n a a a +=+,*n ∈N .(1)求证:数列1 1 n a ⎧⎫-⎨⎬⎩⎭为等比数列; (2)是否存在互不相等的正整数m ,s ,t ,使m ,s ,t 成等差数列,且1m a -,1s a -,1t a -成等比数列?如果存在,求出所有符合条件的m ,s ,t ;如果不存在,请说明理由.20.(本小题满分14分)设函数()313f x x ax =-()0a >,()221g x bx b =+-. (1)若曲线()x f y =与()x g y =在它们的交点()c ,1处有相同的切线,求实数a ,b 的值; (2)当12ab -=时,若函数()()()h x f x g x =+在区间()0,2-内恰有两个零点,求实数a 的取值范围;(3)当1a =,0b =时,求函数()()()h x f x g x =+在区间[]3,+t t 上的最小值.21.(本小题满分14分)如图7,已知椭圆C 的方程为()222210x y a b a b +=>>,双曲线12222=-by a x 的两条渐近线为21,l l .过椭圆C 的右焦点F 作直线l ,使1l l ⊥,又l 与2l 交于点P ,设l 与椭圆C 的两个交点由上至下 依次为A ,B .(1)若1l 与2l 的夹角为60°,且双曲线的焦距为4,求椭圆C 的方程;(2)求||||AP FA 的最大值.图7广州市2014届高三年级调研测试 数学(理科)试题参考答案及评分标准说明:1.参考答案及评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)解:(1)在△ABC 中,A B C π++=.………………………………………………………………1分所以coscos22A C Bπ+-= …………………………………………………………………………2分sin2B ==.………………………………………………………………………3分所以2cos 12sin2BB =- ……………………………………………………………………………5分 13=.………………………………………………………………………………………7分(2)因为3a =,b =1cos 3B =,8 A由余弦定理2222cos b a c ac B =+-,………………………………………………………………9分得2210c c -+=.……………………………………………………………………………………11分解得1c =.……………………………………………………………………………………………12分17.(本小题满分12分)解:(1)由茎叶图可知,甲城市在2013年9月份随机抽取的15天中的空气质量类别为优或良的天数为5天.…………………………………………………………………………………………………1分所以可估计甲城市在2013年9月份30天的空气质量类别为优或良的天数为10天.…………2分 (2)X 的取值为0,1,2,………………………………………………………………………………3分因为()02510215C C 30C 7P X ===,………………………………………………………………………5分 ()11510215C C 101C 21P X ===,………………ks5u …………………………………………7分 ()20510215C C 22C 21P X ===.…………………………………………………………………………9分 所以X 的分布列为:所以数学期望321221170=⨯+⨯+⨯=EX . (12)分18.(本小题满分14分)(1)证明1:因为BC AB 2=,60ABC ︒∠=,在△ABC 中,由余弦定理可得BC AC 3=.……………………………………………………2分 所以222AC BC AB +=.所以BC AC ⊥. (3)分因为AC FB ⊥,BF BC B = ,BF 、BC ⊂平面FBC ,……………………10分所以⊥AC 平面FBC .………………………………………………………………………………4分证明2:因为60ABC ︒∠=,设BAC α∠=()0120α<<,则120ACB α∠=-.在△ABC 中,由正弦定理,得()sin sin 120BC ABαα=- .…………………………………………1分因为BC AB 2=,所以()sin 1202sin αα-=.整理得tan 3α=,所以30α= .…………………………………………………………………2分所以BC AC ⊥.………………………………………………………………………………………3分因为AC FB ⊥,BF BC B = ,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .………………………………………………………………………………4分(2)解法1:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C = ,所以⊥FC 平面ABCD .……………………………………………………6分取AB 的中点M ,连结MD ,ME ,因为ABCD 是等腰梯形,且BC AB 2=,60DAM ∠=,所以MD MA AD ==.所以△MAD 是等边三角形,且ME BF .…………………………7分取AD 的中点N ,连结MN ,NE ,则MN AD ⊥.………8分 因为MN ⊂平面ABCD ,ED FC ,所以ED MN ⊥. 因为AD ED D = ,所以MN ⊥平面ADE . ……………9分 所以MEN ∠为直线BF 与平面ADE 所成角. ……………10分 因为NE ⊂平面ADE ,所以MN ⊥NE .…………………11分因为2MN AD =,ME ==,…………………………………………12分在Rt △MNE中,sin MN MEN ME ∠==.……………………………………………………13分所以直线BF 与平面ADE所成角的正弦值为4.………ks5u …………………14分解法2:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C = ,所以⊥FC 平面ABCD .……………………………………………………6分所以CA ,CB ,CF 两两互相垂直,建立如图的空间直角坐标系xyz C -.………………………7分 因为ABCD 是等腰梯形,且BC AB 2=,60ABC ︒∠= 所以CB CD CF ==.不妨设1BC =,则()0,1,0B ,()0,0,1F,)A,1,022D ⎛⎫- ⎪ ⎪⎝⎭,1,,122E ⎛⎫- ⎪ ⎪⎝⎭, 所以()0,1,1BF =-,1,02DA ⎫=⎪⎪⎝⎭,()0,0,1DE =. (9)分设平面ADE 的法向量为=()x,y,z n ,则有0,0.DA DE ⎧⋅=⎪⎨⋅=⎪⎩ n n即0,20.y x z +=⎪=⎩ 取1x =,得=n ()1,是平面ADE 的一个法向量.………………………………………11分 设直线BF 与平面ADE 所成的角为θ,则sin cos ,4BF BF BF ⋅θ=〈〉===n nn.……………………………13分 所以直线BF 与平面ADE .………………………………………………14分19.(本小题满分14分) 解:(1)因为1321n n n a a a +=+,所以111233n n a a +=+.…………………………………………………1分 所以1111113n n a a +⎛⎫-=- ⎪⎝⎭.……………………………ks5u ……………………3分因为135a =,则11213a -=. (4)分所以数列11n a ⎧⎫-⎨⎬⎩⎭是首项为32,公比为31的等比数列.…………………………………………5分(2)由(1)知,112121333n n n a -⎛⎫-=⨯= ⎪⎝⎭,所以332nn n a =+.……………………………………7分 假设存在互不相等的正整数m ,s ,t 满足条件,则有()()()22,111.s m t m t s a a a +=⎧⎪⎨-=--⎪⎩……………………………………………………………………9分 由332n n n a =+与()()()2111s m t a a a -=--,得2333111323232s m t sm t ⎛⎫⎛⎫⎛⎫-=-- ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭.……………………………………………………10分 即232323343m tm t s s ++⨯+⨯=+⨯.……………………………………………………………11分因为2m t s +=,所以3323mts+=⨯.……………………………………………………………12分因为3323mts +≥=⨯,当且仅当m t =时等号成立,这与m ,s ,t 互不相等矛盾.……………………………………………………………………13分 所以不存在互不相等的正整数m ,s ,t 满足条件.……………………………………………14分 20.(本小题满分14分) 解:(1)因为()313f x x ax =-,()221g x bx b =+-, 所以()2f x x a '=-,()2g x bx '=.…………………………………………………………………1分因为曲线()x f y =与()x g y =在它们的交点()c ,1处有相同切线, 所以()()11g f =,且()()11g f '='。
广东省2013-2014学年高二寒假作业数学(三) Word版 含解析

广东省2013-2014学年高二寒假作业(三)数学一、选择题1.设,曲线在处的切线与轴的交点的纵坐标为,则( ) A .80 B .32 C .192D .2562.曲线在点处的切线方程是A .B .C .D .3.定义在R 上的可导函数f(x),已知y =e f ′(x)的图象如下图所示,则y =f(x)的增区间是A .(-∞,1)B .(-∞,2)C .(0,1)D .(1,2)4.已知函数()y f x =是定义在实数集R 上的奇函数,且当(,0)x ∈-∞时()()xf x f x '<-成立(其中()()f x f x '是的导函数),若a ,(1)b f =,2211(log )(log )44c f =则,,a b c 的大小关系是( )Ks5uA .c a b >>B .c b a >>C .a b c >>D .a c b >> 5.若函数的导函数在区间上是增函数,则函数在区间上的图象可能是( )A .B .C .D . 6.曲线3123y x =-在点(5(1,)3-处切线的倾斜角为( ) A . 6π B . 4π C . 34π D . 56π7.函数y=x 3-2ax+a 在(0,1)内有极小值,则实数a 的取值范围是 ( )A .(0,3)B .(-∞,3)C .(0,+∞)D .(0,32) 8.已知函数)0()(23≠+++=a d cx bx ax x f 的对称中心为00(,)M x y ,记函数)(x f 的导函数为)(/x f ,)(/x f 的导函数为)(//x f ,则有0)(0//=x f .若函数()323f x x x =-,则可求得1220122012f f ⎛⎫⎛⎫++⎪ ⎪⎝⎭⎝⎭4022...2012f ⎛⎫+ ⎪⎝⎭40232012f ⎛⎫+= ⎪⎝⎭A .4023B .4023-C .8046D .8046-9.若函数(1)4a x y e x -=+(x ∈R )有大于零的极值点,则实数a 范围是 ( )A .3a >-B .3a <-C .13a >-D .13a <-二、填空题10.过曲线上的点的切线的方程为,那么点坐标可能为____________.11. 曲线在处的切线方程为 .12.对于三次函数,给出定义:设是函数的导数,是的导数,若方程有实数解,则称点为函数的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”应对对称中心.根据这一发现,则函数的对称中心为 .13.函数=)x (f xx 4+,),0(x +∞∈的最小值为 三、解答题14.(本小题满分14分) 已知函数(Ⅰ)求函数的极值点;Ks5u(Ⅱ)若直线过点且与曲线相切,求直线的方程;(Ⅲ)设函数求函数在上的最小值.( )Ks5u15.(14分)已知函数(1)当时,求函数的单调区间;(2)函数在上是减函数,求实数a的取值范围. Ks5u16.(本小题满分14分)已知函数,.(其中为自然对数的底数),(Ⅰ)设曲线在处的切线与直线垂直,求的值;(Ⅱ)若对于任意实数≥0,恒成立,试确定实数的取值范围;(Ⅲ)当时,是否存在实数,使曲线C:在点处的切线与轴垂直?若存在,求出的值;若不存在,请说明理由.。
广东省惠州市2014届高三第三次调研考试数学理试卷Word版含答案

惠州市2014届高三第三次调研考试数 学(理科)本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
参考公式:如果事件A B 、互斥,那么()()()P A B P A P B +=+如果事件A B 、相互独立,那么()()()P AB P A P B =一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项符合题目要求.1. 若复数2(32)(1)a a a i -++-是纯虚数,则实数a 的值为( )A .1B .2C .1或2D .1-2.已知集合{|2}xS y y ==,集合{|ln(1)0}T x x =-<,则S T ⋂=( ) A .φ B .(0,2)C .(0,1)D . (1,2)3.设等比数列{}n a 的公比2q =,前n 项和为n S ,则=24a S(A .2B .4C .152D .1724. 执行右边的程序框图,若0.8p =,则输出的n =( )A .3B .4C .5D .65. 设椭圆22221(0,0)x y m n m n+=>>的右焦点与抛物线28y x =的焦点相同,离心率为12,则此椭圆的方程为( )A .2211612x y +=B .2211216x y +=C .2214864x y +=D .2216448x y +=6.某商场在国庆黄金周的促销活动中,对10月2日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时到12时的销售额为( )A . 6万元B .8万元C .10万元D .12万元7. 右图是一个几何体的三视图,根据图中数据可得该几何体的表面积是( )A .9πB .10πC .11πD .12π8.已知函数3()),f x x x =-则对于任意实数,(0)a b a b +≠, 则()()f a f b a b++的值为( )A .恒正 B.恒等于0 C .恒负 D. 不确定二、填空题(本大题共7小题,分为必做题和选做题两部分.每小题5分,满分30分) (一)必做题:第9至13题为必做题,每道试题考生都必须作答.9.设随机变量ξ服从正态分布(3,4)N ,若(23)(2)P a P a ξξ<-=>+,则a 的值为 .10. 已知向量(0,1,1)a =-,(4,1,0)b =,||29a b λ+=且0λ>,则λ= .11. 某班级要从4名男生、2名女生中选派4人参加社区服务,如果要求至少有1名女生,那么不同的选派方案种数为 .(用数字作答)12. 若0,0a b ≥≥,且当001x y x y ≥⎧⎪≥⎨⎪+≤⎩,,时,恒有1ax by +≤,则以a ,b 为坐标点(,)P a b 所形成的平面区域的面积等于 .13. 对于*n N ∈,将n 表示为1101102222k k k k n a a a a --=⨯+⨯+⋅⋅⋅+⨯+⨯,当i k =时,1i a =;当01i k ≤≤-时,i a 为0或1. 定义n b 如下:在n 的上述表示中,当012,,,,ka a a a ⋅⋅⋅中等于1的个数为奇数时,1nb =;否则0n b =.则3456b b b b +++= .俯视图正(主)视图 侧(左)视图FADBC(二)选做题:第14、15题为选做题,考生只选做其中一题,两题全答的,只计前一题的得分。
2014年数学三真题答案解析

解 区域D的图形如右图所示,面积
s=J:[—�-(-y)] dy
xy=-1
I: =(f —lny)
X
y=-x
=— 3 — ln 2. 2
( 1 1 、丿
1 2_
解
n+ 』二二 由于r xe2xdx =产(2x — 1) 1· =产(2a —
0
4
0
4
4
4,
得a
.1
=—
2
e- 1 (1 2)
2
解 如右图所示,则
因为nl-im=
lan+if = lim
I an f
n-=
(n+Z)(n+4) =
(n+1)(n+3)
l, 所以收敛半径R=
l.
=
=
当x = 士1时,因级数�(n+l)(n+3)及�(n+DCn+3)(— 1)"发散,
n�o
n�o
故收敛域为(- 1,1),
(沁
r。 t 设S(x)= �(n+1)(n+3)x勹X E(— 1,1)'
n -0
=
=
则 5 (t)dt= (n+3)x n+l= �(n+2)X n+I +�X n+l ,
n �O
n -0
n -0
其中�X n+l= n �O
l
X -x'
言 (�J: 勹二 (n+2)X n+l=
2
(n+2)t
n+ 1
dt)
= 1
(
l� x)'=
【名师原创 全国通用】2014-2015学年高三寒假作业 数学(三)Word版含答案

【原创】高三数学寒假作业(三)一、选择题,每小题只有一项是正确的。
1. 集合 {}{}{}1,2,3,4,5,1,2,3,|,A B C z z xy x A y B ====∈∈且,则集合C 中的元素个数为A.3 B .4 C .11 D .12 2.设集合}{{}2|11,|M x x N x x x =-<<=≤,则M N =( )A .[)0,1B .(]1,1-C .[)1,1-D .(]1,0-3.若命题p :0log ,2>∈∀x R x ,命题q :02,00<∈∃x R x ,则下列命题为真命题的是( )A. q p ∨B. q p ∧C. q p ∧⌝)(D.)(q p ⌝∨ 4.下列各组函数中,表示相等函数的是( ).A .y =55x 与yB .y =ln e x与y =eln xC .与y =x +3D .y =x 0与y =01x5.若函数f (x) (x ∈R)是奇函数,则( )A .函数f (x 2)是奇函数 B .函数 [f (x) ]2是奇函数 C .函数f (x)⋅x 2是奇函数 D .函数f (x)+x 2是奇函数6.设S n 是等差数列{a n }的前n 项和,已知a 2=3,a 6=11,则S 7等于. A .13 B .35 C .49 D .637.,则sin 2x =( )A8.过双曲线22221(0,0)x y a b a b-=>>的右顶点A 作斜率为1-的直线,该直线与双曲线的两条渐近线的交点分别为,B C .若12AB BC =,则双曲线的离心率是( ) A9.已知函数22log (log )a a y x x =-+对任意1(0,)2x ∈时都有意义,则实数a 的范围是( ) A.11322a ≤<B. 01a <<C.112a <<D. 1a >二、填空题10.设变量x ,y 满足约束条件250200x y x y x +-≤⎧⎪--≤⎨⎪≥⎩,则目标函数z =2x +3y +1的最大值为11.一个几何体的三视图如右图所示,则该几何体的体积为__ ___.12.在ABC ∆中,c b a ,,分别为角C B A ,,的对边,若b c a 322=-,且C A B si n co s 8si n =,则边b 等于 .13.如图,已知正方形ABCD 的边长为3,E 为DC 的中点,AE 与BD 交于点F ,则FD DE ⋅=uu u r uuu r________.FE DCB A三、计算题14.已知函数()2sin()cos f x x x π=-. (Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值. 15.(本题满分14分)如图,在正三棱柱ABC -A 1B 1C 1中,A 1AAC ,D ,E ,F 分别为线段AC ,A 1A ,C 1B 的中点. (1)证明:EF ∥平面ABC ; (2)证明:C 1E ⊥平面BDE .16.(本题满分12分)如图,椭圆C :22221(0)x y a b a b+=>>的右焦点为F ,右顶点、上顶点分别为点A 、B ,且||||AB BF =. (1)求椭圆C 的离心率;(2)若斜率为2的直线l 过点(0,2),且l 交椭圆C 于P 、Q 两点,OP OQ ⊥.求直线l 的方程及椭圆C 的方程.一、选择题1~5 CADDC 6~9 CCCA 二、填空题 10.10 11.23ABC DEC 1A 1B 1F12.4 13.32-三、计算题 14.(Ⅰ)∵()()2sin cos 2sin cos sin 2f x x x x x x π=-==, ∴函数()f x 的最小正周期为π.(Ⅱ)由2623x x ππππ-≤≤⇒-≤≤,∴sin 21x ≤≤,∴()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值为1,最小值为15.证明(1)如图,取BC 的中点G ,连结AG ,FG . 因为F 为C 1B 的中点,所以FG 1//2C 1C . 在三棱柱ABC -A 1B 1C 1中,A 1A //C 1C ,且E 为A 1A 的中点, 所以FG //EA .所以四边形AEFG 是平行四边形.所以EF∥AG.………………………… 4分因为EF平面ABC,AG平面ABC,所以EF∥平面ABC.………………………… 6分(2)因为在正三棱柱ABC-A1B1C1中,A1A⊥平面ABC,BD平面ABC,所以A1A⊥BD.因为D为AC的中点,BA=BC,所以BD⊥AC.因为A1A∩AC=A,A1A平面A1ACC1,AC平面A1ACC1,所以BD⊥平面A1ACC1.因为C1E平面A1ACC1,所以BD⊥C1E.………………………… 9分根据题意,可得EB=C1E=2,C1BAB,所以EB2+C1E2=C1B2.从而∠C1EB=90°,即C1E⊥EB.……………………… 12分因为BD∩EB=B,BD 平面BDE, EB平面BDE,所以C1E⊥平面BDE.………………………… 14分16.(1)由已知|||AB BF,,222445a b a+=,222244()5a a c a+-=,∴cea==.…………………………………………4分(2)由(Ⅰ)知224a b=,∴椭圆C:222214x yb b+=.设11(,)P x y,22(,)Q x y,直线l的方程为22(0)y x-=-,即220x y-+=.由22222222204(22)4014x yx x bx yb b-+=⎧⎪⇒++-=⎨+=⎪⎩,即2217321640x x b ++-=.22321617(4)0b b ∆=+⨯->⇔>123217x x +=-,21216417b x x -=.……8分 ∵ OP OQ ⊥,∴ 0OP OQ ⋅=,即12120x x y y +=,1212(22)(22)0x x x x +++=,121254()40x x x x +++=.从而25(164)128401717b --+=,解得1b =,∴ 椭圆C 的方程为2214x y +=.…………………………………………………12分。
2014年广州市普通高中毕业班综合测试(三)-文科数学

2014年广州市普通高中毕业班综合测试(三)数学(文科)说明:1.本训练题由广州市中学数学教学研究会高三中心组与广州市高考数学研究组共同编写,共24题.2.本训练题仅供本市高三学生考前冲刺训练用,希望在5月31日之前完成.3.本训练题与市高三质量抽测、一模、二模等数学试题在内容上相互配套,互为补充.四套试题覆盖了高中数学的主要知识和方法.1.在ABC ∆中,C =A +2π,sin A (1)求sin C 的值;(2)若BC =6,求ABC ∆的面积.2.已知函数f (x )=3sin(ωx +φ)(ω>0,02πϕ<<)的最小正周期为π,且其图象经过点(,0)3π.(1)求函数f (x )的解析式; (2)若函数g (x )=()212x f π+,α,β∈),0(π,且g (α)=1,g (β)=324,求g (α-β)的值.3.已知向量m =(sin x,1),n =(3A cos x ,A2cos 2x ) (A >0),函数f (x )=m ·n 的最大值为6.(1)求A 的值;(2)将函数y =f (x )的图象向左平移π12个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )在⎥⎦⎤⎢⎣⎡245,0π上的值域.4.如图,某测量人员为了测量珠江北岸不能到达的两点A,B之间的距离,他在珠江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,CD=CE=100m.(1)求△CDE的面积;(2)求A,B之间的距离.5.一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.(1)从袋中随机抽取一个球,将其编号记为a,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为b,求关于x的一元二次方程x2+2ax+b2=0有实根的概率;(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n.若以(m,n)作为点P的坐标,求点P落在区域0,50x yx y-≥⎧⎨+-<⎩内的概率.6.某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其质量(单位:克)是否合格,分别记录抽查数据,获得质量数据的茎叶图如图所示.(1)根据样品数据,计算甲、乙两个车间产品质量的均值与方差,并说明哪个车间的产品的质量较稳定;(2)若从乙车间6件样品中随机抽取两件,求所抽取的两件样品的质量之差不超过2克的概率.乙甲743112985241011127.某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率;(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成22⨯列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?附:22()n ad bc K -=,其中n a b c d =+++.8.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.(1)求选取的2组数据恰好是不相邻2天数据的概率;(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y 关于x 的线性回归方程ˆˆˆybx a =+; (3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?(参考公式:1221ˆˆˆ,ni ii ni i x y nx ybay bx x nx==-==--∑∑.)9.如图,三棱锥ABC P -中,PB ⊥底面ABC ,90BCA ∠=,4===CA BC PB ,E 为PC 的中点,M 为AB 的中点,点F 在PA 上,且2AF FP =. (1)求证:BE ⊥平面PAC ; (2)求证://CM 平面BEF ; (3)求三棱锥ABE F -的体积.10.如图,已知两个正四棱锥P -ABCD 与Q -ABCD 的高都是2,AB =4. (1)求证:PQ ⊥平面ABCD ; (2)求点P 到平面QAD 的距离.QBCPAD11.等腰梯形PDCB 中,DC ∥PB ,PB =3DC =3,PD =2,DA ⊥PB ,垂足为A ,将△P AD 沿AD 折起,使得P A ⊥AB ,得到四棱锥P -ABCD .(1)求证:平面P AD ⊥平面PCD ;(2)点M 在棱PB 上,平面AMC 把四棱锥P -ABCD 分成两个几何体,当这两个几何体的体积之比ABC M ACD PM V V --=45时,求证:PD //平面AMC .12.如图,三棱柱111ABC A B C -的侧棱1AA ⊥平面ABC ,ABC ∆为正三角形,侧面11AAC C 是正方形,E 是1A B 的中点,F 是棱1CC 上的点.(1)当E ABF V -=11AAC C 的边长; (2)当1A F FB +最小时,求证:1AE A FB ⊥平面.13.数列}{},{n n b a 满足:*112,2,2()n n n n a a a n b a n n +==+=-+∈N . (1)求数列}{n b 的通项公式;(2)设数列}{},{n n b a 的前n 项和分别为A n 、B n ,问是否存在实数λ,使得}{nB A nn λ+为等差数列?若存在,求出λ的值;若不存在,说明理由.14.设数列{}n a 满足12a =,248a a +=,且对任意*n ∈N ,函数1212()()cos sin n n n n n f x a a a x a x a x ++++=-++⋅-⋅满足()02f π'=.(1)求数列{}n a 的通项公式;(2)若122nn n a b a =+(),求数列{}n b 的前n 项和n S .15.根据如图所示的程序框图,将输出的x 、y 值依次分别记为122008,,,,,n x x x x ;122008,,,,,n y y y y .(1)求数列}{n x 的通项公式n x ;(2)求y 1和y 2,写出y n+1与y n 的关系式,并推导求出数列{y n }的一个通项公式y n ; (3)求*1122(,2008)n n n z x y x y x y n n =+++∈≤N .16.已知函数a R x a x f x,(21)(∈+=为常数),P 1(x 1,y 1),P 2(x 2,y 2)是函数y=f (x )图象上的两点.当线段P 1P 2的中点P 的横坐标为21时,P 的纵坐标恒为41.(1)求y=f (x )的解析式;(2)若数列{a n }的通项公式为*00()(,1,2,,)n na f n n n n =∈=N ,求数列{a n }的前n 0和0n S .17.已知椭圆C :()222210x y a b a b+=>>的离心率为12,12F F 、分别为椭圆C 的左、右焦点,若椭圆C 的焦距为2.(1)求椭圆C 的方程;(2)设M 为椭圆上任意一点,以M 为圆心,1MF 为半径作圆M ,当圆M 与直线 l 2a x c=:有公共点时,求△12MF F 面积的最大值.18.如图,已知(),0F c 是椭圆()2222:10x y C a b a b+=>>的右焦点,圆()222:F x c y a-+=与x 轴交于,D E 两点,其中E 是椭圆C 的左焦点.(1)求椭圆C 的离心率;(2)设圆F 与y 轴的正半轴的交点为B ,点A 是点D 关于y 轴的对称点,试判断直线AB 与 圆F 的位置关系;(3)设直线BF 与圆F 交于另一点G ,若BGD ∆的面积为C 的标准方程.19.已知动圆 C 过定点M(0,2),且在 x 轴上截得弦长为 4.设该动圆圆心的轨迹为曲线 E. (1)求曲线 E 的方程;(2)点 A 为直线 l :x -y -2 = 0 上任意一点,过 A 作曲线 C 的切线,切点分别为 P 、Q ,求△APQ 面积的最小值及此时点 A 的坐标.20.如图所示,已知A 、B 、C 是长轴长为4的椭圆E 上的三点,点A 是长轴的一个端点,BC 过椭圆中心O ,且0=⋅BC AC ,|BC |=2|AC |. (1)求椭圆E 的方程;(2)在椭圆E 上是否存点Q ,使得222|QB||QA|-=? 若存在,有几个(不必求出Q 点的坐标),若不存在,请说明理由.(3)过椭圆E 上异于其顶点的任一点P ,作2243O :x y +=图(6)y xBOE FD的两条切线,切点分别为M 、N ,若直线MN 在x 轴、y 轴上的截距分别为m 、n ,求证:22113m n +为定值.21.已知函数32()3f x ax bx x =+-()a b ∈R 、在点(1,(1))f 处的切线方程为20y +=. (1)求函数()f x 的解析式;(2)若对于区间[2,2]-上任意两个自变量的值1x ,2x 都有12()()f x f x c -≤,求实数c 的最小值;(3)若过点(2,)M m (2)m ≠可作曲线()y f x =的三条切线,求实数m 的取值范围.22.已知函数()ln f x ax x =-,ln ()xg x x=,它们的定义域都是(0,]e .(2.718e ≈)(1)当1a =时,求函数()f x 的最小值; (2)当1a =时,求证:17()()27f mg n >+对一切,(0,]m n e ∈恒成立; (3)是否存在实数a ,使得()f x 的最小值是3?如果存在,求出a 的值;如果不存在,说明理由.23.已知函数2()ln ,f x ax bx x =+-,a b ∈R .(1)设0a ≥,求()f x 的单调区间;(2)设0a >,且对于任意0x >,()(1)f x f ≥.试比较ln a 与2b -的大小.24.已知函数()ln f x x =,()g x x '=且(2)2g =.(1)设函数()()()F x ag x f x =-(其中0a >),若()F x 没有零点,求实数a 的取值范围; (2)若0p q >>,总有[()()]()()m g p g q pf p qf q ->-成立,求实数m 的取值范围.2014年广州市普通高中毕业班综合测试(三)参考答案1.(1)因为在ABC ∆中,C =A +2π, 所以A为锐角,且cos A ===. 所以sin C =sin(A +2π)=cosA=3(2)由正弦定理得sin sin BC AB A C =,所以sin sin BC CAB A===因为在ABC ∆中,C =A +2π, 所以C为钝角,且cos C ===. 因为在ABC ∆中,()B A C π=-+,所以1sin sin()sin cos cos sin (33333B AC A C A C =+=+=-+=. 所以ABC ∆的面积为111sin 223ABC S AB BC B ∆=⨯⨯=⨯=2.(1)因为函数f (x )的最小正周期为π,且ω>0,所以2πω=π,解得ω=2.所以f (x )=3sin(2x +φ). 因为函数f (x )的图象经过点(,0)3π,所以3sin (2)3πϕ⨯+=0,得23πϕ+=k π,k ∈Z ,即φ=k π-23π,k ∈Z . 由02πϕ<<,得φ=π3.所以函数f (x )的解析式为f (x )=3sin (2)3x π+.(2)依题意有g (x )=3sin [2()]2123x ππ⨯++=)2sin(3π+x =3cos x . 由g (α)=3cos α=1,得cos α=13,由g (β)=3cos β=324,得cos β=24.因为α,β∈),0(π,所以sin α=223,sin β=144.所以g (α-β)=3cos(α-β)=3(cos αcos β+sin αsin β)=3×⎪⎪⎭⎫ ⎝⎛⨯+⨯4143224231=2+474.3.(1)f (x )=m ·n =3A sin x cos x +A2cos 2x =A ⎪⎪⎭⎫ ⎝⎛+x x 2cos 212sin 23=A sin ⎪⎭⎫ ⎝⎛+62πx . 因为f (x )的最大值为6,且A >0,所以A =6. (2)由(1)知f (x )=6sin ⎪⎭⎫⎝⎛+62πx . 将函数y =f (x )的图象向左平移π12个单位后得到y =6sin ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+6122ππx =6sin ⎪⎭⎫ ⎝⎛+32πx 的图象;再将所得图象上各点横坐标缩短为原来的12倍,纵坐标不变,得到y =6sin ⎪⎭⎫ ⎝⎛+34πx 的图象.因此g (x )=6sin ⎪⎭⎫⎝⎛+34πx . 因为x ∈⎥⎦⎤⎢⎣⎡245,0π,所以4x +π3∈⎥⎦⎤⎢⎣⎡67,3ππ,≤-21sin ⎪⎭⎫ ⎝⎛+34πx 1≤,所以3-≤g (x )6≤. 所以g (x )在⎥⎦⎤⎢⎣⎡245,0π上的值域为[-3,6].4.(1)在△CDE 中,∠DCE =360°-90°-15°-105°=150°.所以△CDE 的面积为S △CDE =12CD ⨯CE ⨯sin150°=12⨯100⨯100⨯sin30°=2500(m 2).(2)连结AB .在Rt △ACD 中,AC =CD tan ∠ADC =100⨯tan 60°=1003(m). 在△BCE 中,∠CBE =180°-∠BCE -∠CEB =180°-105°-45°=30°.由正弦定理得BC sin ∠CEB =CEsin ∠CBE ,所以0sin 100sin 45sin sin 30CE CEB BC CBE ∠==∠=1002(m).在△ABC 中,由余弦定理得AB 2=AC 2+BC 2-2AC ·BC ·cos ∠ACB , 又cos ∠ACB =cos 15°=cos(60°-45°)=cos 60°cos 45°+sin 60°sin 45° =12×22+32×22=6+24, 所以AB 2=(1003)2+(1002)2-2⨯1003⨯1002⨯6+24=10000(2-3). 所以AB =1002-3(m),所以A ,B 之间的距离为1002- 3 m .5.(1)所有基本事件(a ,b )有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),共12种.因为关于x 的一元二次方程x 2+2ax +b 2=0有实根,所以△=4a 2-4b 2≥0,即a 2≥b 2. 记“关于x 的一元二次方程x 2+2ax +b 2=0有实根的概率”为事件A , 则事件A 包含的基本事件有:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),共6种.所以P(A)=61122=为所求. (2)所有基本事件(m ,n )有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16种. 记“点P 落在区域0,50x y x y -≥⎧⎨+-<⎩内”为事件B ,则事件B 包含的基本事件有:(1,1),(2,1),(2,2),(3,1),共4种. 所以P(B)=41164=为所求.6.(1)由茎叶图可知,甲车间样品的质量分别是107,111,111,113,114,122,乙车间样品的质量分别是108,109,110,112,115,124.()11071111111131141221136x =+++++=甲, ()11081091101121151241136x =+++++=乙.()()()()()()222222211071131111131111131131131141131221136S ⎡⎤=-+-+-+-+-+-⎣⎦甲21=, ()()()()()()222222211081131091131101131121131151131241136S ⎡⎤=-+-+-+-+-+-⎣⎦乙883=.因为x x =乙甲,22S S <乙甲,所以甲车间的产品的质量较稳定. (2)从乙车间6件样品中随机抽取两件,所有的基本事件有:(108,109),(108,110)(108,112),(108,115),(108,124),(109,110),(109,112),(109,115),(109,124),(110,112), (110,115),(110,124),(112,115),(112,124),(115,124),共15种.设事件A 表示“所抽取的两件样品的质量之差不超过2克”,则事件A 包含的基本事件有:(108,109),(108,110),(109,110),(110,112),共4种.所以()415P A =为所求. 7.(1)由已知得,样本中有“25周岁以上组”工人60名,“25周岁以下组”工人40名. 在样本中日平均生产件数不足60件的工人中, “25周岁以上组”工人有600.053⨯=(人),记为A 1,A 2,A 3; “25周岁以下组”工人有400.052⨯=(人),记为B 1,B 2. 从中随机抽取2名工人,所有可能的结果有: (A 1,A 2),(A 1,A 3),(A 2,A 3),(A 1,B 1),(A 1,B 2), (A 2,B 1),(A 2,B 2),(A 3,B 1),(A 3,B 2),(B 1,B 2),共10种. 其中至少有1名“25周岁以下组”工人的结果有: (A 1,B 1),(A 1,B 2),(A 2,B 1),(A 2,B 2),(A 3,B 1),(A 3,B 2),(B 1,B 2),共7种.所以所求的概率为710. (2)由频率分布直方图可知,在抽取的100名工人中, “25周岁以上组”中的生产能手有600.2515⨯=(人), “25周岁以下组”中的生产能手有400.37515⨯=(人). 据此可得22⨯列联表如下:假设0H :生产能手与工人所在的年龄组没有关系. 将22⨯列联表中的数据代入公式,计算得222()()()()(100(15251545)251.79604030701)4n ad bc K a b c d a c b d ⨯-==+++⨯-⨯=≈+⨯⨯⨯.当0H 成立时,2( 2.706)0.100P K ≥≈.因为1.79 2.706<,所以没有90%的把握认为“生产能手与工人所在的年龄组有关”. 8.(1)设“选取的2组数据恰好是不相邻2天数据”为事件A ,所有基本事件(m ,n )(其中m ,n 为12月份的日期数)有:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共有10种.事件A 包括的基本事件有:(1,3),(1,4),(1,5),(2,4),(2,5),(3,5),共有6种.所以53106)(==A P 为所求. (2)由数据,求得11131225302612,2733x y ++++====. 由公式,求得ˆˆˆ2.5,3ba y bx ==-=-. 所以y 关于x 的线性回归方程为ˆ 2.53yx =-. (3)当x =10时,ˆ 2.510322,222312y=⨯-=-=<. 同理,当x =8时,ˆ 2.58317,171612y=⨯-=-=<. 所以该研究所得到的线性回归方程是可靠的. 9.(1)∵⊥PB 底面ABC ,且⊂AC 底面ABC , ∴AC PB ⊥.由90BCA ∠=,可得CB AC ⊥. 又PBCB B =,∴AC ⊥平面PBC .又⊂BE 平面PBC ,∴AC BE ⊥.BC PB = ,E 为PC 中点,∴BE PC ⊥.又PC ⊂平面PAC ,AC ⊂平面PAC ,PCAC C =,∴BE ⊥平面PAC .(2)取AF 的中点G ,AB 的中点M ,连接,,CG CM GM . ∵E 为PC 中点,2FA FP =,∴//EF CG .∵CG ⊄平面,BEF EF ⊂平面BEF ,∴//CG 平面BEF . 同理可证//GM 平面BEF . 又CGGM G =,∴平面//CMG 平面BEF .又CD ⊂平面CDG ,∴//CD 平面BEF . (3)由(1)知BE ⊥平面PAC , 所以BE 是三棱锥B AEF -的高.由已知可得22=BE ,238213131=⋅⨯==∆∆PC AC S S PAC AEF . ∴三棱锥ABE F -的体积为93231=⋅==∆--BE S V V AEF AEF B ABE F .10.(1)取AD 的中点M ,连结PM ,QM . 因为P -ABCD 与Q -ABCD 都是正四棱锥, 所以AD ⊥PM ,AD ⊥QM ,从而AD ⊥平面PQM . 又⊂PQ 平面PQM ,所以PQ ⊥AD .同理PQ ⊥AB .又AD ⊂平面ABCD ,AB ⊂平面ABCD , AD AB A =,所以PQ ⊥平面ABCD . (2)连结OM ,则PQ AB OM 21221===. 所以∠PMQ =90°,即PM ⊥MQ .由(1)知AD ⊥PM ,所以PM ⊥平面QAD . 所以PM 的长是点P 到平面QAD 的距离.在Rt △PMO 中,22222222=+=+=OM PO PM .所以点P 到平面QAD 的距离为22.11.(1)因为在等腰梯形PDCB 中,DA ⊥PB , 所以在四棱锥P -ABCD 中,DA ⊥AB ,DA ⊥PA , 又PA ⊥AB ,且DC ∥AB ,所以DC ⊥PA ,DC ⊥DA ,QBCPADOMAB PMN又DA ⊂ 平面PAD ,PA ⊂平面PAD ,PA∩DA = A , 所以DC ⊥平面PAD .又DC ⊂平面PCD ,所以平面PAD ⊥平面PCD . (2)因为DA ⊥PA ,PA ⊥AB ,,,DAAB A DA AB ABCD =⊂平面,所以PA ⊥平面ABCD ,又PA ⊂ 平面PAB ,所以平面PAB ⊥平面ABCD . 过M 作MN ⊥AB ,垂足为N ,则MN ⊥平面ABCD .在原等腰梯形PDCB 中,DC ∥PB ,PB = 3DC = 3,DA ⊥PB , ∴PA = 1,AB = 2,1AD ==.设MN = h ,则1133M ABC ABC V S h h -∆=⋅=,1132P ABCD ABCD V S PA -∆=⋅=. ∴123PM ACD P ABCD M ABC hV V V ---=-=-.∵ABC M ACD PM V V --=45,∴152343h h -=,解得23h =. 在△PAB 中,23BM MN BP PA ==,∴21,33BM BP MP BP ==. 在梯形ABCD 中,连结BD 交AC 于点O ,连结OM . 易知△AOB ∽△DOC ,∴12DO DC OB AB ==. 故DO PMOB MB=,所以在平面PBD 中,有PD ∥MO . 又PD ⊄平面AMC ,MO ⊂平面AMC ,所以PD ∥平面AMC .12.(1)设正方形AA 1C 1C 的边长为x , 由于E 是1A B 的中点,△EAB 的面积为定值.1CC ∥平面1AA B ,∴点F 到平面EAB 的距离为定值,即点C 到平面1AA B 的距离为定值. 又E ABF F ABE V V --=,且13F ABE ABE V S h -∆=⋅即1132223x x x ⋅⋅⋅⋅=,38,2x x ∴==,所以正方形11AAC C 的边长为2.(2)将侧面11B BCC 展开到侧面11ACC A 得到矩形11A ABB . 连结B A 1交C C 1于点F ,此时点F 使得BF F A +1最小. 此时FC 平行且等于A A 1的一半,F ∴为C C 1的中点. 取AB 中点O ,连接OE,EF ,OC ,OEFC ∴为平行四边形, △ABC 为正三角形,∴OC AB ⊥. 又1AA ⊥平面ABC ,1OC AA ∴⊥. 因为1ABAA A =,OC ∴⊥平面1A AB .AE ⊂平面1A AB ,OC AE ∴⊥.又EF ∥OC ,AE EF ∴⊥.由于E 是1A B 的中点,所以1AE A B ⊥.又1A B ⊂平面1A FB ,EF ⊂平面1A FB ,1A B EF E =,所以1AE A FB ⊥平面.13.(1)由2,2-+=+-=n b a n a b n n n n 得.∵,21n a a n n +=+∴n n n n b b n b n b 21,22]2)1([211=-+=-++++即. ∴}{n b 是首项为21,3111公比为=+=+a b n 是等比数列.所以1)21(3-=n n b .(2)∵,2-+=n b a n n ∴2)3(-+=n n B A n n .又),211(6211)211(3n n n B -=--=∴n n n B n B A n n n 2)3()1(-++=+λλnn n )211)(1(623-++-=λ. 所以当且仅当}{,1nB A nnλλ+-=时为等差数列. 14.(1)因为1212()()cos sin n n n n n f x a a a x a x a x ++++=-++⋅-⋅,所以1212sin cos n n n n n f x a a a a x a x ++++'=-+-⋅-⋅().所以121()02n n n n f a a a a π+++'=-+-=.所以122n n n a a a ++=+,{}n a ∴是等差数列.因为12a =,248a a +=,所以34a =,1d =,2-111n a n n ∴=+⋅=+(). (2)因为111122121222n n n a n nb a n n +=+=++=++()()(), 所以111221221212n n n n S -++=+-()()211313122n n n n n n =++-=++-().15.(1)由框图,知数列2,1}{11+==+n n n x x x x 中,, ∴*12(1)21(,2008)n x n n n n =+-=-∈≤N . (2)由框图,y 1=2,y 2=8,知数列{y n }中,y n +1=3y n +2. ∴)1(311+=++n n y y ,∴1113,1 3.1n n y y y ++=+=+∴数列{y n +1}是以3为首项,3为公比的等比数列. ∴n y +1=3·3n -1=3n ,∴n y =3n -1(*,2008n n ∈≤N ).(3)z n =n n y x y x y x +++ 2211=1×(3-1)+3×(32-1)+…+(2n -1)(3n -1) =1×3+3×32+…+(2n -1)·3n -[1+3+…+(2n -1)] 记S n =1×3+3×32+…+(2n -1)·3n ,① 则3S n =1×32+3×33+…+(2n -1)×3n +1 ② ①-②,得-2S n =3+2·32+2·33+…+2·3n -(2n -1)·3n +1 =2(3+32+…+3n )-3-(2n -1)·3n +1=2×13·)12(331)31(3+-----n n n =113·)12(63++---n n n 63·)1(21--=+n n∴.33·)1(1+-=+n n n S 又1+3+…+(2n -1)=n 2, ∴12*(1)33(,2008)n n z n n n n +=-⋅+-∈≤N .16.(1)由)(x f y =的图象上得,21,212121+=+=x x a y a y 两式相加得21212121+++=x x a a ,化简得421=+xx a 恒成立. ,4,121=∴=+a x x ∴.241)(+=xx f (2)),1,,3,2,1(2120000-==-+n k n k n n k 000000()()11,()(),242k n k f f k n k n n f f n n -+-∴=+=由已知条件得即 00000001231()()()()(),n n nS f f f f f n n n n n -∴=+++++000000000012321()()()()()(),:n n n nS f f f f f f n n n n n n --∴=++++++两式相加得000000000000000112222112[()()][()()][()()][()()]2()n n n n n nS f f f f f f f f f n n n n n n n n n ----=+++++++++0111112(1)(1)2,22226f n =++++=-+⋅121300-=∴n S n .17.(1)因为22c =,且12c a =,所以1,2,c a b ==== 所以椭圆C 的方程为22143x y +=.(2)设点M 的坐标为()00,x y ,则2200143x y +=.因为()11,0F -,24a c=,所以直线l 的方程为4x =. 由于圆M 与l 由公共点,所以M 到l 的距离04x -小于或等于圆的半径R .因为()22221001R MF x y ==++,所以()()22200041x x y -≤++,即20010150y x +-≥.又因为2200314x y ⎛⎫=- ⎪⎝⎭,所以233101504x x -+-≥,解得0423x ≤≤. 当043x =时,0y =()12max122MF F S =⨯=. 18.(1)∵圆F 过椭圆C 的左焦点,把(—c,0)代入圆F 的方程,得224c a =,所以椭圆C 的离心率12c e a ==. (2)在方程()222x c y a -+=中, 令22220x y a c b ==-=得, 可知点B 为椭圆的上顶点. 由(1)知12c a =,得2,a c b ===,所以()0B .在圆F 的方程中,令0y =,可得点D 的坐标为()3,0c ,则点()3,0A c -.于是可得直线AB的斜率33AB k c ==,而直线FB的斜率FB k c==—Gy xBOAEFD1AB FD k k ⋅=-,∴直线AB 与圆F 相切.(3)DF 是BDG ∆的中线,22BDG BFD S S DF OB c ∆∆∴==⋅==22c ∴=,从而得28a =,26b =,∴椭圆C 的标准方程为22186x y +=. 19.(1)设动圆圆心坐标为 C (x ,y ), 根据题意得x 2 + (y -2) 2 = y 2 + 4化简得 x 2 = 4y ,所以曲线 E 的方程为x 2 = 4y . (2)设直线 PQ 的方程为 y = kx + b由 ⎩⎨⎧ x 2= 4yy = kx + b消去 y 得 x 2-4kx -4b = 0 设 P (x 1,y 1)、Q (x 2,y 2),则 x 1 + x 2 = 4k ,x 1x 2 = -4b ,且△ = 16k 2 + 16b . 以点 P 为切点的切线的斜率为y’ | x =x 1 = 12 x 1,其切线方程为 y -y 1 = 12 x 1 (x -x 1),即 y = 12 x 1x -14 x 12 ⇒ x 12-2x 1x + 4y = 0.由切线过 A (x 0,y 0) 得 x 12-2x 1x 0 + 4y 0 = 0, 同理 x 22-2x 2x 0 + 4y 0 = 0.∴x 1、x 2 是方程 x 2-2x 0 x + 4y 0 = 0的两个解. ∴x 1 + x 2 = 2x 0,x 1x 2 = 4y 0.所以 ⎩⎨⎧ x 0 =x 1 + x 22= 2k y 0 = x 1x 24 = -b所以 A (2k ,-b ) .由 A (x 0,y 0) 在直线 x -y -2 = 0 上, 则 2k + b -2 = 0,即 b = 2-2k .代入 △ = 16k 2 + 16b = 16k 2 + 32-32k = 16 (k -1) 2 + 16 > 0. ∴| PQ | = 1 + k 2 | x 1-x 2 | = 4 1 + k 2 k 2 + b . A (2k ,-b ) 到直线 PQ 的距离为 d = | 2k 2 + 2b |k 2 + 1 ,∴S △APQ = 12| PQ | d = 4 | k 2 + b | k 2 + b = 4 (k 2+ b ) 32= 4 (k 2-2k + 2) 32 = 4 [(k -1) 2+ 1] 32 .∴当 k = 1 时,S △APQ 最小,其最小值为 4,此时点 A 的坐标为 (2,0) .20.(1)依题意知,椭圆的长半轴长2a =,则A (2,0) .设椭圆E 的方程为14222=+by x .由椭圆的对称性知|OC |=|OB |,又∵0=⋅BC AC ,|BC |=2|AC |.∴AC ⊥BC ,|OC |=|AC | ∴△AOC 为等腰直角三角形. ∴点C 的坐标为(1,1),点B 的坐标为(-1,-1) . 将C 的坐标(1,1)代入椭圆方程得342=b ,∴所求的椭圆E 的方程为143422=+y x . (2)设在椭圆E 上存在点Q ,使得222|QB||QA|-=,设00Q(x ,y ),则()()()2222220000001126222|QB ||QA|x y x y x y .-=+++---=+-=即00320x y +-=,--------①又∵点Q 在椭圆E 上,∴2200340x y +-=,-----②由①式得0023y x =-代入②式并整理得:2007920x x -+=,-----③∵方程③的根判别式8156250∆=-=>,∴方程③有两个不相等的实数根,即满足条件的点Q 存在,且有两个. (3)设点11P(x ,y ),由M 、N 是O 的切点知,OM MP,ON NP ⊥⊥,∴O 、M 、P 、N 四点在同一圆上,且圆的直径为OP,则圆心为1122x y (,), 其方程为22221111224x y x y (x )(y )+-+-=,即22110x y x x y y +--=-----④即点M 、N 满足方程④,又点M 、N 都在O 上,∴M 、N 坐标也满足方程2243O :x y +=----⑤ ⑤-④得直线MN 的方程为1143x x y y +=. 令0y ,=得143m x =,令0x =得143n y =,∴114433x ,y m n ==. 又点P 在椭圆E 上,∴22443433()()m n +=,即2211334m n +=为定值. 21.(1)2()323f x ax bx '=+-.根据题意,得(1)2(1)0f f =-⎧⎨'=⎩,即323230a b a b +-=-⎧⎨+-=⎩,解得10a b =⎧⎨=⎩.所以3()3f x x x =-.(2)令()0f x '=,即2330x -=.得1x =-或1x =.因为(1)2f -=,(1)2f =-,所以当[2,2]x ∈-时,max ()2f x =,min ()2f x =-. 对于区间[2,2]-上任意两个自变量的值1x ,2x ,都有12max min ()()()()4f x f x f x f x -≤-=,所以4c ≥,所以c 的最小值为4.(3)因为点(2,)M m (2)m ≠不在曲线()y f x =上,所以可设切点为00(,)x y . 则30003y x x =-.因为200()33f x x '=-,所以切线的斜率为2033x -, 则曲线()y f x =在00(,)x y 处的切线方程为000()()y y f x x x '-=-, 即2300(33)2y x x x =--.又切线过点(2,)M m ,所以2300(33)22m x x =-⨯-,即32002660x x m -++=. 因为过点(2,)M m (2)m ≠可作曲线()y f x =的三条切线,所以关于0x 的方程32002660x x m -++=有三个不同的实数解. 所以函数32()266g x x x m =-++有三个不同的零点. 则2()612g x x x '=-.令()0g x '=,则0x =或2x =.则(0)0(2)0g g >⎧⎨<⎩,即6020m m +>⎧⎨-+<⎩,解得62m -<<.22.(1)当1a =时,()ln f x x x =-,11()1x f x x x-'=-=. 因为()f x 定义域是(0,]e ,当1x =时()0f x '=,当(0,1)x ∈时()0f x '<, 当(1,]x e ∈ 时()0f x '>,所以当1x =时,()f x 有最小值(1)1f =. (2)由(1)知,在1a =且(0,]x e ∈时,有()1f m ≥.又因为(0,]x e ∈,21ln ()0xg x x-'=≥,所以()g x 在区间(0,]e 上为增函数, 1110()() 2.727g x g e e ≤=<=,所以当(0,]n e ∈时,171017()1272727g n +<+=. 因为()1f m ≥,所以17()()27f mg n >+对一切,(0,]m n e ∈恒成立.(3)假设存在实数a ,使得()f x 的最小值是3,11()ax f x a x x-'=-=.当1a e≤时,因为(0,]x e ∈,所以1ax ≤,()0f x '≤,所以()f x 在(0,]e 上为减函数.所以当x e =时()f x 取最小值()13f e ae =-=,此时4a e=,矛盾,故舍去. 当1a e >时,令'()0f x <,得10x a <<;令'()0f x >,得1x e a<≤.所以()f x 在1(0,]a 上为减函数,在1(,]e a 上为增函数.所以当1x a =时,()f x 取最小值11()1ln 3f a a=-=,此时2a e =.所以假设成立,所以存在2a e =,使得()f x 的最小值是3.23.(1)由2()ln ,(0,)f x ax bx x x =+-∈+∞得221()ax bx f x x+-'=.①当0a =,1()bx f x x-'=. (ⅰ)若0b ≤,因为0x >,所以()0f x '<恒成立, 所以函数()f x 的单调减区间是(0,)+∞. (ⅱ)若0b >,当10x b<<时,()0f x '<,函数()f x 单调递减. 当1x b>时, ()0f x '>,函数()f x 单调递增. 所以函数()f x 单调递减区间是1(0,)b ,单调递增区间是1(,)b+∞.②当0a >时,令()0f x '=,得2210ax bx +-=.由280b a ∆=+>得1x =,2x =.显然10x <,20x >.当20x x <<时,()0f x '<,函数()f x 单调递减; 当2x x >时,()0f x '>,函数()f x 单调递增.所以函数()f x 单调递减区间是(0,4b a -,单调递增区间是()4b a-+∞.综上所述,当0a =,0b ≤时,函数()f x 的单调减区间是(0,)+∞;当0a =,0b >时,函数()f x 单调递减区间是1(0,)b ,单调递增区间是1(,)b+∞;当0a >时,函数()f x 单调递减区间是,单调递增区间是)+∞.(2)由题意,函数()f x 在处取得最小值,由(1)知4b a -是()f x 的唯一极小值点,所以14b a-+=,整理得21a b +=即12b a =-.ln (2)ln 2ln 24a b a b a a --=+=+-.令()ln 24g x x x =+-,则14()x g x x-'=.令()0g x '=,得14x =.当104x <<时,()0g x '>,()g x 单调递增; 当14x >时,()0g x '<,()g x 单调递减. 所以当14x =时,()g x 最大.所以11()()1ln 1ln 4044g x g ≤===-<.所以()0g a <,所以ln 240a a +-<,即ln (2)a b <-. 24.(1)由()g x x '=,可设21()2g x x c =+,又由(2)2g =,解得0c =,所以21()2g x x =.所以2()ln 2a F x x x =-,211'()(ax a F x ax x x x x x -=-==.因为0a >,()F x 的定义域为(0,)+∞,所以当时x >()0F x '>,0x <<时,()0F x '<.所以()F x 在是减函数,在)+∞上是增函数. 易知0x +→时,()F x →+∞;x →+∞时,()F x →+∞.因为()F x 没有零点,所以()F x 在(0,)+∞上的最小值是11ln 022F a =+>, 解得1a e >.所以a 的取值范围为1(,)e+∞. (2)原问题即0p q >>时,()()()()mg p pf p mg q qf q ->-恒成立. 令2()()()ln 2m h x mg x xf x x x x =-=-,则()h x 在(0,)+∞上为单调递增函数, 所以'()ln 10h x mx x =--≥在(0,)+∞上恒成立,即ln 1x m x+≥在(0,)+∞上恒成立. 令ln 1()x G x x +=,则2ln '()xG x x=-,所以当(0,1)x ∈时,()0G x '>;(1,),()0x G x '∈+∞<. 所以()G x 的最大值为(1)1G =,所以m 的取值范围为[1,)+∞.。
2014年高考广东理科数学试题及答案(word解析版)

2014年高考广东理科数学试题及答案(word解析版)2014年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)【2014年广东,理1,5分】已知集合{1,0,1}M =-,{0,1,2}N =,则M N =U ( ) (A ){1,0,1}- (B ){1,0,1,2}- (C ){1,0,2}- (D ){0,1} 【答案】B【解析】{1,0,1,2}M N =-U ,故选B . (2)【2014年广东,理2,5分】已知复数z 满足(34i)25z +=,则z =( ) (A )34i - (B )34i + (C )34i -- (D )34i -+ 【答案】A【解析】2525(34i)25(34i)=34i 34i (34i)(34i)25z --===-++-,故选A . (3)【2014年广东,理3,5分】若变量,x y 满足约束条件121y xx y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为M 和m ,则M m -=( ) (A )8 (B )7 (C )6 (D )5 【答案】C 【解析】画出可行域,易知在点(2,1)与(1,1)--处目标函数分别取得最大值3M =,与最小值3m =-,6M m ∴-=,故选C .(4)【2014年广东,理4,5分】若实数k 满足09k <<,则曲线221259x y k-=-与曲线221259x y k -=-的( ) (A )离心率相等 (B )虚半轴长相等 (C )实半轴长相等 (D )焦距相等 【答案】D【解析】09k <<Q ,90k ∴->,250k ->,从而两曲线均为双曲线,又25(9)34(25)9k k k +-=-=-+,两双曲线的焦距相等,故选D .(5)【2014年广东,理5,5分】已知向量()1,0,1a =-,则下列向量中与a 成60︒夹角的是( ) (A )()1,1,0- (B )()1,1,0- (C )()0,1,1- (D )()1,0,1- 【答案】B【解析】2222221210(1)1(1)0=++-⋅+-+,即这两向量的夹角余弦值为12,从而夹角为060,故选A . (6)【2014年广东,理6,5分】已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( ) (A )200,20 (B )100,20 (C )200,10 (D )100,10 【答案】A【解析】样本容量为(350045002000)2%200++⋅=,抽取的高中生近视人数为:20002%50%20⋅⋅=,故选A .(7)【2014年广东,理7,5分】若空间中四条两两不同的直线1234,,,l l l l ,满足12l l ⊥,23l l ⊥,34l l ⊥则下列结论一定正确的是( )(A )14l l ⊥ (B )14//l l (C )14,l l 既不垂直也不平行 (D )14,l l 的位置关系不确定 【答案】D【解析】平面中的四条直线,14l l ⊥,空间中的四条直线,位置关系不确定,故选D .(8)【2014年广东,理8,5分】设集合(){}12345=,,,,{1,0,1},1,2,3,4,5iA x x x x x x i ∈-=,那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为( )(A )60 (B )90 (C )120 (D )130 【答案】D【解析】12345x x x x x ++++可取1,2,3,和为1的元素个数为:1125C 10C =;和为2的元素个数为:122255C 40C A +=;和为3的元素个数为:1311225254C C C 80C C +=,故满足条件的元素总的个数为104080130++=,故选D .二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13) (9)【2014年广东,理9,5分】不等式125x x -++≥的解集为 .【答案】(][),32,-∞-+∞U【解析】数轴上到1与2-距离之和为5的数为3-和2,故该不等式的解集为:(][),32,-∞-+∞U . (10)【2014年广东,理10,5分】曲线52xy e -=+在点(0,3)处的切线方程为 .【答案】530x y +-=【解析】'55xy e -=-,'5x y =∴=-,∴所求切线方程为35y x -=-,即530x y +-=.(11)【2014年广东,理11】,5分从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为 . 【答案】16【解析】要使6为取出的7个数中的中位数,则取出的数中必有3个不大于6,另外3个不小于6,故所求概率为3671016C C=. (12)【2014年广东,理12,5分】在ABC ∆中,角,,A B C 所对应的边分别为,,a b c ,已知cos cos 2b C c B b +=,则a b = . 【答案】2【解析】解法一:由射影定理知cos cos b C c B a +=,从而2a b =,2ab ∴=. 解法二:由上弦定理得:sin cos sin cos 2sin B C C B B +=,即sin()2sin B C B +=,sin 2sin A B ∴=,即2a b =,2ab ∴=. 解法三:由余弦定理得:222222222a b c a c b b bab ac+-+-⋅+=,即224a ab=,2a b ∴=,即2ab =.(13)【2014年广东,理13,5分】若等比数列{}na 的各项均为正数,且510119122a a a a e +=,则1220ln ln ln a a a +++=L L .【答案】50【解析】1011912a a a a =Q ,51011a a e ∴=,设1220ln ln ln S a a a =+++L ,则20191ln ln ln S a a a =+++L , 51201011220ln 20ln 20ln 100S a a a a e ∴====,50S ∴=.(二)选做题(14-15题,考生只能从中选做一题)(14)【2014年广东,理14,5分】(坐标系与参数方程选做题)在极坐标系中,曲线1C 和2C 的方程分别为2sin cos ρθθ=和sin 1ρθ=,以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,则曲线1C 和2C 的交点的直角坐标为 .【答案】(1,1)【解析】1C 即2(sin )cos ρθρθ=,故其直角坐标方程为:2y x =,2C 的直角坐标系方程为:1y =,1C ∴与2C 的交点的直角坐标为(1,1).(15)【2014年广东,理15,5分】(几何证明选讲选做题)如图3,在平行四边形ABCD 中,点E 在AB 上且2EB AE =,AC 与DE 交于点,则CDF AEF ∆=∆的面积的面积. 【答案】9【解析】显然CDF AEF ∆∆:,∴22()()9CDF CDEB AE AEF AEAE∆+===∆的面积的面积.三、解答题:本大题共6题,共80分.解答应写出文字说明,证明过程或演算步骤. (16)【2014年广东,理16,12分】已知函数()sin(),4f x A x x R π=+∈,且53()122f π=. (1)求A 的值;(2)若3()()2f f θθ+-=,(0,)2πθ∈,求3()4f πθ-. 解:(1)5523()sin()sin 1212432f A A ππππ=+==,3323A ∴=⋅=. (2)由(1)得:()3sin()4f x x π=+,()()3sin()3sin()44f f ππθθθθ∴+-=++-+33(sin cos cos sin )3(sin()cos cos()sin )23cos sin 6cos 444442πππππθθθθθθ=++-+-===,6cos θ∴=,(0,)2πθ∈Q ,10sin θ∴=,331030()3sin()3sin()3sin 3444f πππθθπθθ∴-=-+=-==⨯=.(17)【2014年广东,理17,12分】随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.根据上述数据得到样本的频率分布表如下:分组 频数 频率 [25,30] 3 0.12 (30,35] 5 0.20 (35,40] 8 0.32 (40,45] 1n 1f (45,50] 2n 2f(1)确定样本频率分布表中121,,n n f 和2f 的值;(2)根据上述频率分布表,画出样本频率分布直方图;(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(]30,35的概率.解:(1)17n =,22n =,170.2825f ==,220.0825f ==. (2)频率分布直方图如下所示:(3)根据频率分布直方图,可得工人们日加工零件数落在区间(]30,35的概率为0.2,设日加工零件数落在区间(]30,35的人数为随机变量ξ,则(4,0.2)B ξ:,故4人中,至少有1人的日加工零件数落在区间(]30,35 的概率为:0441(0.2)(0.8)10.40960.5904C -=-=.(18)【2014年广东,理18,14分】如图4,四边形ABCD 为正方形,PD ⊥平面ABCD ,30DPC ∠︒=,AF PC ⊥于点F ,//FE CD ,交PD 于点E . (1)证明:CF ⊥平面ADF ;(2)求二面角D AF E --的余弦值. 解:(1)PD ⊥平面ABCD ,PD PCD ⊂,∴平面PCD ⊥平面ABCD ,平面PCD I 平面ABCD CD =,AD ⊂平面ABCD ,AD CD ⊥,AD ∴⊥平面PCD ,CF ⊂平面PCD ,CF AD ∴⊥,又AF PC ⊥,CF AF ∴⊥,,AD AF ⊂平面ADF ,AD AF A =I ,CF ∴⊥平面ADF .(2)解法一:过E 作//EG CF 交DF 于G ,CF ⊥Q 平面ADF ,EG ∴⊥平面ADF ,过G 作GH AF ⊥于H ,连EH则EHG ∠为二面角D AF E --的平面角,设2CD =,030DPC ∠=Q ,30CDF ∴∠=,从而1==12CF CD , 4CP =,EF DC Q ∥,DE CFDP CP∴=,即12=223,3DE ∴=,还易求得32EF =,3DF =,从而3332243DE EF EG DF ⋅⋅===,易得19AE =,7AF =,32EF =,19331922747AE EF EH AF ⋅⋅∴===,故22319363()()44747HG =-=,6347257cos 47319GH EHG EH ∴∠==⋅=.解法二:分别以DP ,DC ,DA 为x ,y ,z 轴建立空间直角坐标系,设2DC =,则(0,0,2)A ,(0,2,0)C ,(23,0,0)P ,设CF CP λ=u u u r u u u r ,则(23,22,0)F λλ-,DF CF ⊥u u u r u u u r Q ,可得14λ=,从而33(,0)2F ,易得 3(E ,取面ADF 的一个法向量为11(3,1,0)2n CP ==-u u r u u u r,设面AEF的一个法向量为2(,,)nx y z =u u r, 利用20n AE ⋅=u u r u u u r ,且20n AF ⋅=u u r u u u r ,得2n u u r可以是3),从而二面角的余弦值为121243257||||219n n n n ⋅==⋅⨯u u r u u r u u r u u u r . (19)【2014年广东,理19,14分】设数列{}na 的前n 和为nS ,满足2*1234,n n S na n n n N +=--∈,且315S =. (1)求123,,a a a 的值;(2)求数列{}na 的通项公式.解:(1)211222314127a S a a ==-⨯-⨯=- ①2122331212+=432424()204(15)20a a S a S a a a a =-⨯-⨯=---=---,12+8a a ∴= ②联立①②解得1235a a =⎧⎨=⎩,33121587a S a a ∴=--=-=,综上13a =,25a =,37a =.(2)21234nn Sna n n +=-- ③ ∴当2n ≥时,212(1)3(1)4(1)n n Sn a n n -=----- ④-③④并整理得:1216122n n n n aa n n+-+=+,由(1)猜想21nan =+,以下用数学归纳法证明:(ⅰ)由(1)知,当1n =时,13211a ==⨯+,猜想成立; (ⅱ)假设当n k =时,猜想成立,即21ka k =+,则当1n k =+时,212161211411(21)33232(1)1222222k k k k k k a a k k k k k k k k k+-+--=+=⋅+++=++=+=++,这就是说1n k =+时,猜想也成立,从而对一切n N *∈,21na n =+.(20)【2014年广东,理20,14分】已知椭圆2222:1(0)xy C a b ab+=>>的一个焦点为(5,0)5.(1)求椭圆C 的标准方程;(2)若动点0(,)P x y 为椭圆外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程.解:(1)5c =,55c e a ==3a ∴=,222954b a c =-=-=,∴椭圆C 的标准方程为:22194x y +=.(2)若一切线垂直x 轴,则另一切线垂直于y 轴,则这样的点P 共4个,它们的坐标分别为(3,2)-±,(3,2)±.若两切线不垂直与坐标轴,设切线方程为()y y k x x -=-,即0()y k x x y =-+,将之代入椭圆方程22194x y+=中并整理得:222(94)18()9()40k x k y kx x y kx ⎡⎤++-+--=⎣⎦,依题意,0∆=,即222200(18)()36()4(94)0k y kx y kx k ⎡⎤----+=⎣⎦,即224()4(94)0y kx k--+=, 2220000(9)240x k x y k y ∴--+-=,Q 两切线相互垂直,121k k∴=-,即2020419y x -=--,220013xy ∴+=,显然(3,2)-±,(3,2)±这四点也满足以上方程,∴点P 的轨迹方程为2213x y +=.(21)【2014年广东,理21,14分】设函数222()(2)2(2)3f x x x k x x k =+++++-2k <-.(1)求函数()f x 的定义域D (用区间表示);(2)讨论()f x 在区间D 上的单调性;(3)若6k <-,求D 上满足条件()(1)f x f >的x 的集合(用区间表示).解:(1)222(2)2(2)30x x k x x k +++++->,则221x x k ++> ① 或 223x x k ++<- ②由①得:2210x x k ++->,144(1)4(2)0k k ∆=--=->(2)k <-Q , ∴方程2210x x k ++-=的解为12k --,∴由2210x x k ++->得12x k <--12x k >--由②得2230x x k +++<,方程2230x x k +++=的判别式244(3)4(2)0k k ∆=-+=-->(2)k <-Q ,∴该方程的解为12k ---,由2230x x k +++<得1212k x k ----<-+--2k <-Q ,121211212k k k k ∴--<-----<-----(,12)(12,12)(12,)D k k k k ∴=-∞--------+---+-+∞U U .(2)设222(2)2(2)30u x x k x x k +++++->, 则3'221()2(2)(22)2(22)2f x u x x k x x -⎡⎤=-⋅⋅++⋅+++⎣⎦ 3222(1)(21)u x x x k -=-+⋅+++, (ⅰ)当(,12)x k ∈-∞--时,10x +<,221110x x k +++>+>,'()0f x ∴>;(ⅱ)当(12,1)x k ∈-----时,10x +<,221310x x k +++<-+<,'()0f x ∴<; (ⅲ)当(1,12)x k ∈--+--时,10x +>,221310x x k +++<-+<,'()0f x ∴>; (ⅳ)当(12,)x k ∈-+-+∞时,10x +>,221110x x k +++>+>,'()0f x ∴<. 综上,()f x 在D 上的单调增区间为:(,12),(1,12)k k -∞-----+--,()f x 在D 上的单调减区间为:(12,1),(12,)k k -----+-+∞.(3)设222(x)(2)2(2)3g x x k x x k =+++++-,由(1)知,当x D ∈时,()0g x >; 又2(1)(3)2(3)3(6)(2)g k k k k =+++-=++,显然,当6k <-时,(1)0g >, 从而不等式()(1)()(1)f x f g x g >⇔<,2222()(1)[(2)2(2)3][(3k)2(3)3]g x g x x k x x k k -=+++++--+++-22222[(2)(3k)]2[(2)(3)](3)(1)(225)x x k x x k k x x x x k =++-++++-+=+-+++,6k <-, 1421212311212142k k k k k k ∴--------<-<<----+--+--(ⅰ)当12x k <--时,(3)(1)0x x +->,∴欲使()(1)f x f >,即()(1)g x g <,亦即22250x x k +++<,即142142k x k ---<<---14212k x k ∴---<---(ⅱ)123k x ---<-时,(3)(1)0x x +->,22225(2)(5)3(5)0x x k x x k k k +++=++++<-++<,此时()(1)g x g <,即()(1)f x f >;(ⅲ)31x -<<时,(3)(1)0x x +-<,22253(5)0x x k k +++<-++<()(1)g x g ∴>不合题意;(ⅳ)112x k <<-+--时,(3)(1)0x x +->,22253(5)0x x k k +++<-++<,()(1)g x g ∴<,不合题意;(ⅴ)12x k >--时,(3)(1)0x x +->,∴欲使()(1)g x g <,则22250x x k +++<,即142142k x k ---<<---,从而12142k x k --<-+--.综上所述,()(1)f x f >的解集为: (()()(142,1212,31,1212,142k k k k k k ----------+-----+--U U U .。
广东省广州市广雅中学2014届高三第三次模拟数学文试题Word版含答案

广东省广州市广雅中学2014届高三第三次模拟数学文试题 考试时间:5月27日 命题:高三文数备课组本试卷分选择题和非选择题两部分,共4页,满分150分,考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的校名、姓名、考号填写在答题卡的密封线内。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在另发的答题卷各题目指定区域内的相应位置上;如需改动,先划掉原的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将答题卷和答题卡一并收回。
参考公式:柱体的体积公式sh V =,其中s 为柱体的底面积,h 为柱体的高。
锥体的体积公式sh V 31=,其中s 为锥体的底面积,h 为锥体的高。
一组数据n x x x ⋯⋯,,21的方差])()()[(12_2_22_12x x x x x x ns n -+⋯⋯+-+-=,其中_x 表示这组数据的平均数。
第一部分选择题(共50分)一.选择题(本大题共10道小题,每小题5分,满分50分。
在每小题给出的四个选项中有且只有一个是符合题目要求的)1.函数y =的定义域是( )A. )3,(-∞B. ]1,0(C. ]3,0(D.]3,(-∞ 2.下列函数中周期为π且图象关于直线3x π=对称的函数是( )A.2sin()23x y π=+B .2sin(2)6y x π=- C.2sin(2)6y x π=+ D.2sin()23x y π=- 3.已知i 是虚数单位,若31iiz+=-,则z 的共轭复数为( )A.12i -B.24i - - D.12i +4.阅读右面的程序框图,运行相应的程序,输出的结果为( )A.2- B .12C.1-D.2 5.已知等比数列{}n a 的前n 项和为n S ,且1S ,22S a +,3S 成等差数列,则数列{}n a 的公比为( ) A .1 B .2 C .12D .3 6.下列说法错误的是( )A.在统计学中,独立性检验是检验两个分类变量是否有关系的一种统计方法.B.线性回归方程对应的直线a x b yˆˆˆ+=至少经过其样本数据),,(11y x ),,(22y x ),(,33y x …),(n n y x 中的一个点.C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高.D.在回归分析中,相关指数2R 为98.0的模型比相关指数2R 为80.0的模型拟合的效果好.7.一个空间几何体的三视图如图所示,则这个几何体的表面积为( )A .61 B .23+ C .23 D .218.已知x 、y 满足231143x y x y +≥⎧⎪≤⎨⎪≤⎩,则12y z x -=+的取值范围为( )A .]32,0[B .]1,0[C .]32,(-∞D .),32[+∞ 9.已知定义域为)1,1(-的奇函数)(x f y =又是减函数,且0)9()3(2<-+-a f a f ,则a 的取值范围是( )A .(22,3)B .(3,10)C .(22,4)D .(-2,3)10.若集合A 具有以下性质:①0A ∈,1A ∈;②若,x y A ∈,则x y A -∈,且0x ≠时,1A x∈.则称集合A 是“好集”. (1)集合{}1,0,1B =-是好集; (2)有理数集Q 是“好集”; (3)设集合A 是“好集”,若,x y A ∈,则x y A +∈; (4)设集合A 是“好集”,若,x y A ∈,则必有xy A ∈;(5)对任意的一个“好集”A ,若,x y A ∈,且0x ≠,则必有yA x∈.则上述命题正确的个数是( )A.2个B.3个C.4个D.5个第二部分非选择题(100分)二、填空题:本大题共四小题,每小题5分,满分20分。
广东省2014届高三数学寒假作业(三)
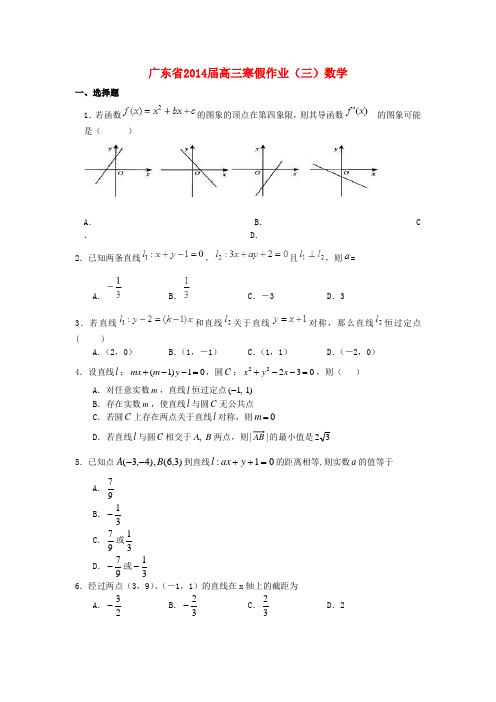
广东省2014届高三寒假作业(三)数学一、选择题 1.若函数的图象的顶点在第四象限,则其导函数的图象可能是( )A .B .C .D . 2.已知两条直线,且,则=A .B .C .-3D .3 3.若直线和直线关于直线对称,那么直线恒过定点( )A .(2,0)B .(1,-1)C .(1,1)D .(-2,0)4.设直线l :01)1(=--+y m mx ,圆C :03222=--+x y x ,则( )A .对任意实数m ,直线l 恒过定点)1 ,1(-B .存在实数m ,使直线l 与圆C 无公共点C .若圆C 上存在两点关于直线l 对称,则0=mD .若直线l 与圆C 相交于B A ,两点,则||AB 的最小值是325.已知点)3,6(),4,3(B A --到直线01:=++y ax l 的距离相等,则实数a 的值等于A .97 B .31-C .97或31D .97-或31-6.经过两点(3,9)、(-1,1)的直线在x 轴上的截距为A .23-B .32-C .32 D .27.已知直线1l :32+=x y ,直线2l 与1l 关于直线x y =对称,直线23l l ⊥,则3l 的斜率为( )A .21B . 21-C .-2D .28.直线02=++by ax ,当0,0<>b a 时,此直线必不过 ( ) A .第一象限 B .第二象限C .第三象限D .第四象限二、填空题9.若直线l :y="k" x 经过点,则直线l 的倾斜角为α = .10.一条直线的方向向量为(1,2)-,且过点(1,0),该直线的方程为 11. 已知直线l 的一个法向量为(2,3)n →=-,且经过点(2,3)-,则直线l 的方程是 . 12.直线0543=-+y x 到直线01543=++y x 的距离是13.若直线210ax y ++=与直线20x y +-=互相平行,那么a 的值等于 14.若直线过点,且与直线垂直,则直线的方程为___________.三、解答题15.(本小题满分12分)已知p :方程012=++mx x 有两个不等的负实根..., q :方程01)2(442=+-+x m x 无实根. 若p 或q 为真,p 且q 为假. 求实数m 的取值范围。
广东省2014届高三寒假作业数学(十) 解析

广东省2014届高三寒假作业(十)数学一、选择题 1.在△ABC中,若Ba b sin 2=,则A等于( )A006030或B 006045或C 060120或 D0015030或2.某船开始看见灯塔在南偏东30︒方向,后来船沿南偏东60︒的方向航行45km 后,看见灯塔在正西方向,则这时船与灯塔的距离是( )A .15kmB .30kmC . 15km D . km3.在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cosC 等于( )2A.32B.-31C.-31D.-44. △ABC 的内角A 、B 、C 的对边分别为a 、b 、c.若a 、b 、c 成等比数列,且2c a =,则cos B 等于( ) Ks5uA .41B .43C .42 D .325.在△ABC 中,角A ,B,C 所对的边分别为c b a ,,,若oC b a 120,2,1===,则CA sin sin 的值为( )A .7B .77 C .33 D .36.在O 点测量到远处有一物体在做匀速直线运动,开始时该物体位于P 点,一分钟后,其位置在Q 点,且90POQ ∠=o,再过二分钟后,该物体位于R 点,且60QOR ∠=o,则2tanOPQ ∠的值等于A .4BC .4 D .1二、填空题 7.在三角形中,,,,则的值为 。
8.已知ABC ∆的三个内角,,A B C 成等差数列,且1,4,AB BC ==,则边BC 上的中线AD 的长为__________;9. 在ABC ∆中,设角A ,B ,C 的对边分别为a ,b ,c ,已知2220bbc c --=,6a =,7cos 8A =,则b =______ 10.在△ABC 中,若,3))((bc a c b c b a =-+++则A =11.在△ABC 中,a,b ,c 是三个内角,A,B,C 所对的边,若131,7,cos ,4a b c B =+==-则b =()12.在△ABC 中,内角,,A B C 所对的边分别是,,a b c ,已知60B =︒,不等式0142<+-x x 的解集为{|}x a x c <<,则b =________________ ;三、解答题13.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,向量=(sinA,b+c ),=(a -c ,sinC -sinB),满足=(Ⅰ)求角B 的大小;(Ⅱ)设=(sin (C+),), =(2k,cos2A ) (k>1), 有最大值为3,求k 的值. Ks5u14.在中,分别是角的对边,,.(1)求的值;(2)若,求边的长.Ks5u15.(8分)在ABC ∆中,, , A B C∠∠∠所对的边分别为, , a b c ,已知4,5,a b c ==(1)求C ∠的大小; (4分) (2)求ABC ∆的面积.(4分)Ks5u16.在ABC∆中,角A,B,C的对边分别为,,a b c,且满足.cB-ba=coscos)2(C (Ⅰ)求角B的大小;(Ⅱ)若ABC|,2|的面积的最大值。
广东省2013-2014学年高一寒假作业数学(三) 解析

广东省2013-2014学年高一寒假作业(三)数学一、选择题1.函数33)(3--=x x x f 有零点的区间是( )A .(- 1 ,0)B .(0,1)C .(1,2)D .(2,3)2.对于函数,下列结论中正确的是:A .当上单调递减B .当上单调递减C .当上单调递增Ks5uD .上单调递增3.方程x 3-6x 2+9x -10=0的实根个数是( )A .3B .2C .1D .04.函数的图像大致形状是( )5.的解集是方程组⎩⎨⎧=+-=+0302y x y x ( ) A .{-1,2} B .(-1,2) C .{(-1,2)}D .{(x,y )|x= -1或y=2}6.方程31()02x x-=的根个数是( )A .0个B .1个C .2个D .无数个7.函数x 2x ln )x (f -=的零点所在的大致区间是()A .)2,1(B . )e ,2(C . )3,e (D . ),e (+∞8.某车间分批生产某种产品,每批的生产准备费用为800元。
若每批生产x 件,则平均仓储时间为8x 天,且每件产品每天的仓储费用为1元.为使平均每件产品的生产准备费用与仓储费用之和最小,每批应生产产品为( )A .60件B .80件C .100件D .120件二、填空题9.(5分)对于定义域和值域均为的函数,定义,,…,,n=1,2,3,….满足的点称为f 的阶周期点. (1)设则f 的阶周期点的个数是___________;(2)设则f 的阶周期点的个数是__________ .10.(5分)已知对于任意的a ∈R ,关于x 的方程14204xx a a b +---+=总有实根,则实数b 的取值范围是 .11.(5分) 已知函数21,0()1,0x x f x x x ⎧-<=⎨+≥⎩,若()3f m =,则实数m 的值为 . 12.(5分)已知⎩⎨⎧∉-∈=]1,0[,2]1,0[,1)(x x x x f ,若1)]([=x f f 时,∈x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省2014届高三 (三)数学一、选择题 1.若函数的图象的顶点在第四象限,则其导函数的图象可能是( )A .B .C .D . 2.已知两条直线,且,则=A .B .C .-3D .33.若直线和直线关于直线对称,那么直线恒过定点( )A .(2,0)B .(1,-1)C .(1,1)D .(-2,0)4.设直线l :01)1(=--+y m mx ,圆C :03222=--+x y x ,则( )A .对任意实数m ,直线l 恒过定点)1 ,1(-B .存在实数m ,使直线l 与圆C 无公共点C .若圆C 上存在两点关于直线l 对称,则0=mD .若直线l 与圆C 相交于B A ,两点,则||AB 的最小值是325.已知点)3,6(),4,3(B A --到直线01:=++y ax l 的距离相等,则实数a 的值等于A .97 B .31-C .97或31D .97-或31- Ks5u6.经过两点(3,9)、(-1,1)的直线在x 轴上的截距为A .23-B .32-C .32 D .27.已知直线1l :32+=x y ,直线2l 与1l 关于直线x y =对称,直线23l l ⊥,则3l 的斜率为( )A .21B . 21-C .-2D .28.直线02=++by ax ,当0,0<>b a 时,此直线必不过 ( ) A .第一象限 B .第二象限C .第三象限D .第四象限二、填空题9.若直线l :y="k" x 经过点,则直线l 的倾斜角为α = .10.一条直线的方向向量为(1,2)-,且过点(1,0),该直线的方程为 11. 已知直线l 的一个法向量为(2,3)n →=-,且经过点(2,3)-,则直线l 的方程是 . 12.直线0543=-+y x 到直线01543=++y x 的距离是13.若直线210ax y ++=与直线20x y +-=互相平行,那么a 的值等于 14.若直线过点,且与直线垂直,则直线的方程为___________.三、解答题15.(本小题满分12分)已知p :方程012=++mx x 有两个不等的负实根..., q :方程01)2(442=+-+x m x 无实根. 若p 或q 为真,p 且q 为假. 求实数m 的取值范围。
Ks5u16.(本小题满分14分)如图几何体,ABCD 是矩形,ABE AD 平面⊥,AE EB BC ==,F 为CE 上的点,且ACE BF 平面⊥.(1)求证:BCE AE 平面⊥; (2)求证:BFD AE 平面//. Ks5uAD17.(本小题满分14分)如图,长方体1111D C B A ABCD -中,1==AD AB ,21=AA ,P 为1DD 的中点。
PD 1C 1B 1A 1D CBA(1)求证:直线1BD ∥平面PAC ;(2)求证:平面PAC ⊥平面1BDD; (3)求证:直线1PB ⊥平面PAC 。
Ks5u18.已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点.(1)求AB边所在的直线方程;(2)求中线AM的长(3)求AB边的高所在直线方程.19.(本小题满10分) 设直线l 的方程为)(02)1(R a a y x a ∈=-+++. (1) 若l 在两坐标轴上的截距相等,求l 的方程; (2) 若l 不经过第二象限,求实数a 的取值范围. Ks5u20.(本小题14分)如图,在平面直角坐标系xoy 中,设点F(0, p)(p>0), 直线l : y= -p, 点P 在直线l 上移动,R 是线段PF 与x 轴的交点, 过R 、P 分别作直线1l 、2l ,使1l P F ⊥,2l l ⊥12l l Q = .(1) 求动点Q 的轨迹C 的方程;(2)在直线l 上任取一点M 做曲线C 的两条切线,设切点为A 、B ,求证:直线AB 恒过一定点.Ks5u广东省2014届高三寒假作业(三)数学一、选择题 1.C【解析】∵函数的图象的顶点在第四象限,∴,∴b<0.由的斜率为正,截距为负,故选C2.C【解析】根据题意,由于两条直线,且,则可知3+a=0,a=-3,故可知答案为选C. 3.C 【解析】直线,恒过定点(0,2), 设(0,2)关于直线的对称点为(a ,b ),所以,解得a=1,b=1,所以直线恒过定点(1,1).故选C .Ks5u 4.D【解析】由l :01)1(=--+y m mx 得:0y)m(x 1)-(-y =++,所以过定点)1- ,1(,选项A 错。
又定点)1- ,1(与圆心的距离为1小于半径2,所以定点在圆内,所以选项B 错。
若圆C 上存在两点关于直线l 对称,则直线过圆心,求得m=1,所以选项C 错。
当定点为AB 中点时,线段AB 最短,求得||AB 的最小值是32,所以选项D 对。
5.D 【解析】由1|136|1|14-3-|22+++=++⋅a a a a )(,解得:=a 97-或31- 6.A.【解析】直线l 的斜率为912,3(1)k -==--所以所求直线方程为12(1)y x -=+,令y=0,则32x =-,所以此直线在x 轴上的截距为32-. 7.C【解析】解:∵直线l 1:y=2x+3,l 2与l 1关于直线y=-x 对称,∴l 2的方程为-x=2(-y )+3,即 x -2y+3=0,∴l 2的斜率为12由直线l 3⊥l 2得:l 3的斜率是-2,故答案为C 8.D【解析】确定一条直线是否经过那个象限的问题,关键是看斜率的正负和截距的大小。
而根据已知条件可知a 2ax by 20y x b b ++=∴=--,则由斜截式方程可知直线中斜率k=ab-,纵截距为2b -,那么根据已知条件,0,0<>b a ,可知k=a b ->0, 2b->0,那么在坐标系中作图可知,图像必定不过第四象限,选D. 二、填空题9.【解析】因为直线l :y="k" x 经过点,所以,所以α =。
10.220x y +-=【解析】因为直线过点(1,0),且直线的方向向量为(1,2)-,则其斜率为-2,利用点斜式方程可知为220x y +-= 11.23130x y -+=【解析】因为根据题意可知直线l 的一个法向量为(2,3)n →=-,因此可知垂直于直线L 的直线斜率为32=-k ,直线L 的斜率为其负倒数,即为23那么利用点斜式可知直线L 的方程为3-y =((32)2)--x ,变形可知为23130x y -+=。
故答案为23130x y -+=12.4【解析】本试题主要是考查了两平行线之间的距离的求解。
d =,即直线0543=-+y x 到直线01543=++y x 的距离是4=,故答案为4.d =得到。
13.2【解析】本试题主要是考查了两条直线的位置关系的运用。
因为直线210ax y ++=与直线20x y +-=互相平行,因此斜率相等,直线20x y +-=的斜率为-1,直线210ax y ++=的斜率为a 2-,故有-1=a2-,解得a=2,故填写实数a 的值为2.解决该试题的关键是两直线的平行的充要条件是斜率相等,截距不同。
14.【解析】根据与已知直线垂直的直线系方程可设与与直线垂直的直线方程为2x+y+c=0,再把点(-1,3)代入,即可求出c 值,得到所求方程. 解:∵所求直线方程与直线垂直,∴设方程为2x+y+c=0,∵直线过点(-1,3),∴2×(-1)+3+c=0,∴c=-1∴所求直线方程为故答案为三、解答题15.m ∈(1,2]∪[3,+∞)【解析】由题意,p , q 中有且仅有一为真,一为假。
p 真⇔⎪⎩⎪⎨⎧>=<-=+>∆01002121x x m x x ⇔m>2, q 真⇔∆<0⇔1<m<3。
若p 假q 真,则⎩⎨⎧<<≤31,2m m ⇔1<m≤2; 若p 真q 假,则⎩⎨⎧≥≤>312m m m 或⇔m≥3。
综上所述:m ∈(1,2]∪[3,+∞). 16.(1)见解析(2)见解析【解析】(1)证明: ABE AD 平面⊥,BC AD //.∴ABE BC 平面⊥,则BC AE ⊥……………… (4分) 又 ACE BF 平面⊥,则BF AE ⊥∴BCE AE 平面⊥. ……………………… (8分)Ks5u(2)证明:依题意可知:G 是AC 中点ACE BF 平面⊥ 则BF CE ⊥,而BE BC =,∴F 是EC 中点. (12分) 在AEC ∆中,AE FG // ∴BFD AE 平面//. ………………(14分)17.(1)见解析(2)见解析(3)见解析【解析】解:(1)设AC 和BD 交于点O ,连PO ,由P ,O 分别是1DD ,BD 的中点,故PO//1BD ,所以直线1BD ∥平面PAC --(4分)(2)长方体1111D C B A ABCD -中,1==AD AB ,底面ABCD 是正方形,则AC ⊥BD又1DD ⊥面ABCD ,则1DD ⊥AC ,所以AC ⊥面1BDD ,则平面PAC ⊥平面1BDD(3)PC 2=2,PB 12=3,B 1C 2=5,所以△PB 1C 是直角三角形。
1PB ⊥PC ,同理1PB ⊥PA ,所以直线1PB ⊥平面PAC 。
18.(1)6110x y -+=(2)230x y +-=(3)6220x y +-=【解析】(1)先根据斜率公式求出AB 的斜率,写出点斜式方程再化成一般式即可.(2)先根据中点坐标公式求出中点M 的坐标,然后求出AM 的斜率,写出点斜式方程再化成一般式方程.(3)根据AB 的斜率可求出AB 边上的高的斜率,再根据它过点C ,从而可求出高线的点斜式方程,再化成一般式即可.19.(1) 02=++y x .(2) a≤-1.【解析】(Ⅰ)根据直线方程求出它在两坐标轴上的截距,根据它在两坐标轴上的截距相等,求出a 的值,即得直线l 方程.(Ⅱ)把直线方程化为斜截式为 y=-(a+1)x -a -2,若l 不经过第二象限,则a=-1 或 -(a+1)》0,-a -2≤0,由此求得实数a 的取值范围。
解:(1)当直线过原点时,该直线在x 轴和y 轴上的截距都为零,截距相等,∴2=a ,方程即03=+y x . ﹍﹍﹍﹍﹍﹍﹍2分若2≠a ,由于截距存在,∴ 212-=+-a a a , ﹍﹍﹍﹍﹍﹍﹍3分 即11=+a ,∴0=a , 方程即02=++y x . ﹍﹍﹍﹍﹍﹍﹍﹍5分(2)法一:将l 的方程化为2)1(-++-=a x a y , ﹍﹍﹍﹍﹍﹍﹍﹍7分∴欲使l 不经过第二象限,当且仅当()1020a a -+≥⎧⎪⎨-≤⎪⎩ ﹍﹍﹍﹍﹍﹍﹍9分 ∴a≤-1. 所以a 的取值范围是a≤-1. ﹍﹍﹍﹍﹍﹍10分法二:将l 的方程化为(x +y +2)+a(x -1)=0(a ∈R), ﹍﹍﹍﹍﹍﹍﹍7分它表示过l 1:x +y +2=0与l 2:x -1=0的交点(1,-3)的直线系(不包括x =1).由图象可知l 的斜率-(a +1)≥0时,l 不经过第二象限,∴a≤-1. ﹍﹍﹍﹍﹍﹍﹍﹍10分20.解:(1) 24(0)x py p =>. (2)见解析.【解析】(Ⅰ)先判断RQ 是线段FP 的垂直平分线,从而可得动点Q 的轨迹C 是以F 为焦点,l 为准线的抛物线;(Ⅱ)设M (m ,-p ),两切点为A (x 1,y 1),B (x 2,y 2),求出切线方程,从而可得x 1,x 2为方程x 2-2mx -4p 2=0的两根,进一步可得直线AB 的方程,即可得到直线恒过定点(0,p ); 解:(1)依题意知,点R 是线段FP 的中点,且RQ ⊥FP ,∴RQ 是线段FP 的垂直平分线. ∴PQ QF =. 故动点Q 的轨迹C 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)x py p =>.(2)设(,)M m p -,两切点为11(,)A x y ,22(,)B x y∴两条切线方程为x 1x=2p(y+y 1) ①x 2x=2p(y+y 2) ②对于方程①,代入点(,)M m p -, 又21114y x p=, 整理得:2211240x mx p --=, 同理对方程②有2222240x mx p --=, 即12,x x 为方程22240x mx p --=的两根.∴212122,4x x m x x p +==- ③设直线AB 的斜率为k ,2221211221211()4()4y y x x k x x x x p x x p--===+-- 所以直线AB 的方程为211211()()44x y x x x x p p-=+-,展开得:12121()44x x y x x x p p =+-,代入③得:2m y x p p =+,∴直线恒过定点(0,)p .。
