【数学】2014-2015年浙江省温州市十校联合体高三(上)期中数学试卷与答案(理科)
浙江温州十校联合体2014届高三上学期期中联考文科数学试卷(解析版)

浙江温州十校联合体2014届高三上学期期中联考文科数学试卷(解析版)一、选择题1()AC.{—2,0}【答案】C.【解析】{}{}{2211B x x x x x=-≤<>=<C.考点:1.函数的定义域;2.集合的运算.2x的值为()A.3 B C.0 D【答案】B.【解析】试题分析:由已知得是实数,B.考点:1.复数的概念;2.复数的运算.3.)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】D.【解析】既不充分也不必要条件,故选D.考点:充分条件、必要条件及充要条件的判断.4()ABCD【答案】B.【解析】试题分析:举反例:“正方体上下两地面与侧面的关系”考点:空间线面、面面平行与垂直位置关系的判断.5.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是()A【答案】B.【解析】试题分析:由三视图可知该几何体是三棱锥,其中底面是等腰直角三角形,直角边长为2,三棱锥的高为2B.考点:1.几何体的三视图;2.几何体体积的计算.6.()A B C D.2【答案】A.【解析】A.7()A BC【答案】B.【解析】试题分析:当时解.综上所述,不等式B.考点:简单不等式的解法.8分别为()A.B.C.D【答案】B.【解析】B.考点:1.平面向量数量积的坐标运算;2.三角函数的最值问题.9垂直,则此双曲线的离心率为()A.B.2 CD【答案】C.【解析】又横坐标为1,代入得再把代入考点:抛物线与双曲线简单的几何性质(焦点、离心率).10则关于()A.3 B.4 C.5 D.6【答案】A.【解析】考点:1.导数与函数的单调性、极值;2.函数的零点与方程的解;3.函数图象平移变换.11【解析】考点:求分段函数的值.二、填空题12.若程序框图如图所示,则该程序运行后输出的值是.【解析】考点:算法与程序框图.13.袋中共有6个除了颜色外完全相同的球,其中有1个红球, 2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于.【解析】1个红球, 2个白球和3个黑球.从袋中任取两个15种,两球颜色一白一黑:6考点:古典概型概率的计算.14所截得的弦长为.【解析】试题分析:由已知得圆的圆心到直线的距离为考点:直线和圆相交弦长的计算.15的取值范围是.【解析】作的平行线交于,过等分线段定理得因此,若则从而与,在边上;若则故考点:平面向量的几何意义.16的取值范围为.【解析】间上恒成立”区间上为减函数,考点:1.含参数的一元二次不等式的解法;2.含参数不等式中的参数取值范围问题;3.补集思想.17.若函数f(x)=x2+ax+2b在区间(0,1),(1,2)内各有一个零点,取值范围是.【解析】画出不等式组表示的平面区域如图阴影区域,2.考点:1.二次函数零点分布问题;2.简单的线性规划问题.三、解答题18.在△ABC中,内角A,B,C的对边分别为a,b,c,且满足 (2a-c)cosB=bcosC.(1)求角B的大小;(2)若b=6,求△ABC面积的最大值.【答案】【解析】试题分析:(1)(可以利用余弦定理把角化为边来求得大小);(2) 根据余弦定理试题解析:(1)(可以利用余弦定理把角化为边也可酌情给分)(2)(另解:可利用圆内接三角形,底边一定,当高经过圆心时面积最大).考点:1.利用正弦定理、余弦定理解三角形;2.求三角形的面积;3.均值不等式的应用.19.n项和记为S n,a1=t,点(S n,a n+1)在直线y=2x+1上,n∈N*.(1)(2)在(1)【答案】(1)当实数时,数列是等比数列;【解析】试题分析:(1)首先由已知两式相减整理得;(2) 由(1)得知试题解析:(14分所以当是等比数列.要使,分()(2)由(1) 9分12分分.考点:1.等差数列、等比数列通项公式的求法;2.用裂项法求数列的和.20.如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.(Ⅰ)证明EF//平面A1CD;(Ⅱ)证明平面A1CD⊥平面A1ABB1;(Ⅲ)求直线BC与平面A1CD所成角的正弦值.【答案】(Ⅰ)详见解题分析;(Ⅱ)详见解题分析;(Ⅲ)【解析】试题分析:(Ⅰ)如图,平面这可到;(Ⅱ)要证明平面为的中点,故,为此只要证明(Ⅲ)首先需找到或,过直点试题解析:(Ⅰ)证明:如图,且连接在中,分别为的中点,且//,又为的中点,可得且//即四边形为平行四边形,.又平面平面(Ⅱ)由于侧(Ⅲ)解:在平面,过作直线线,平面所成角.设棱长为,可得由∽,易得.在中,所以直平成角的正弦值为考点:1.空间线面平行的证明;2.空间面面垂直的证明;3.空间线面角的计算.21.A,B两点。
浙江省2014届理科数学复习试题选编22:等比数列(学生版)

浙江省2014届理科数学复习试题选编22:等比数列一、选择题1 .(浙江省温州十校联合体2013届高三期中考试数学(理)试题)已知321121,,,...,,...n n a a a a a a a -是首项为1,公比为2的等比数列,则数列{ a n }的第100项等于( )A .25050B .24950C .2100D .2992 .(浙江省黄岩中学2013年高三5月适应性考试数学(理)试卷 )已知等比数列{n a }的公比2=q ,且42a ,6a ,48成等差数列,则{n a }的前8项和为( )A .127B .255C .511D .10233 .(浙江省宁波市十校2013届高三下学期能力测试联考数学(理)试题)若方程250x x m -+=与2100x x n -+=的四个根适当排列后,恰好组成一个首项1的等比数列,则:m n 值为( )A .14B .12C .2D .44 .(浙江省一级重点中学(六校)2013届高三第一次联考数学(理)试题)已知数列}{n a 为等比数列,274=+a a ,865-=⋅a a ,则101a a +的值为 ( )A .7B .5-C .5D .7-5 .(浙江省宁波一中2013届高三12月月考数学(理)试题)已知等比数列{}n a 中,12345640,20a a a a a a ++=++=,则前9项之和等于( )A .50B .70C .80D .90 6 .(浙江省考试院2013届高三上学期测试数学(理)试题)设数列{a n }.( )A .若2n a =4n,n ∈N*,则{a n }为等比数列B .若a n a n +2=21n a +,n ∈N*,则{a n }为等比数列C .若a m a n =2m +n,m ,n ∈N*,则{a n }为等比数列 D .若a n a n +3=a n +1a n +2,n ∈N*,则{a n }为等比数列7 .(浙江省重点中学2013届高三上学期期中联谊数学(理)试题)设等比数列{}n a 的前n 项和为S n ,若3510=S S ,则=1015S S ( )A .2B .73C .83D.38 .(浙江省诸暨中学2013届高三上学期期中考试数学(理)试题)已知等比数列{}n a 中,各项都是正数,且2312,21,a a a 成等差数列,则8967a a a a ++等于 ( )A .21+B .21-C .223+D .223-9 .(浙江省湖州市2013年高三第二次教学质量检测数学(理)试题(word 版) )设n S 为等比数列{}n a 的前n 项和,若2580a a -=,则42S S = ( )A .8-B .5C .8D .1510.(浙江省杭州二中2013届高三年级第五次月考理科数学试卷)设n S 为等比数列{}n a 的前n 项和,0852=-a a ,则=24S S ( )A .5B .8C .8-D .1511.(浙江省海宁市2013届高三2月期初测试数学(理)试题)已知等比数列}{n a 前n 项和为n S ,则下列一定成立的是( )A .若01>a ,则02013<aB .若02>a ,则02014<aC .若01>a ,则02013>SD .若02>a ,则02014>S12.(浙江省宁波市鄞州中学2012学年高三第六次月考数学(理)试卷 )设等比数列{a n }的前n 项和为S n ,若10S :5S 2:1=,则15S :5S = ( )A .4:3B .3:2C .2:1D .3:1二、填空题13.(浙江省永康市2013年高考适应性考试数学理试题 )已知公比为q 的等比数列{}n b 的前n 项和n S 满足13223S S S +=,则公比q 的值为____;14.(浙江省2013年高考模拟冲刺(提优)测试一数学(理)试题)各项都是正数的等比数列{}n a 中,首项21=a ,前3项和为14,则654a a a ++值为_____________.15.(浙江省名校新高考研究联盟2013届高三第一次联考数学(理)试题)在各项均为正数的等比数列}{n a 中,若公比为32,且满足113a a ⋅=16,则=162log a _______.16.(浙江省金丽衢十二校2013届高三第二次联合考试理科数学试卷)等比数列{n a }的前n 项和为n S ,已知123,2,3S S S 成等差数列,则等比数列{n a }的公比为______17.(浙江省绍兴市2013届高三教学质量调测数学(理)试题(word 版) )已知实数1234,,,a a a a 依次构成公差不为零的等差数列.若去掉其中一个数后,其余三个数按原来顺序构成一个等比数列,则此等比数列的公比为______.18.(浙江省温州十校联合体2013届高三期中考试数学(理)试题)数列{}n a 是首项为1,公比为2的等比数列,则0123991001100210031004100100100101100........a C a C a C a C a C a C -+-+-+=_____.19.(浙江省绍兴一中2013届高三下学期回头考理科数学试卷)各项均为正偶数的数列1234,,,a a a a 中,前三项依次成公差为(0)d d >的等差数列,后三项依次成公比为q 的等比数列,若4188a a -=,则q 的所有可能的值构成的集合为____________.20.(浙江省杭州二中2013届高三6月适应性考试数学(理)试题)各项均为正数的等比数列{}n a 满足17648a a a ==,,若函数()231012310f x a x a x a x a x =+++⋅⋅⋅+的导数为()f x ',则1()2f '=__________.21.(浙江省重点中学2013届高三上学期期中联谊数学(理)试题)等比数列}{n a 的公比为q ,其前n 项的积为n T ,并且满足条件11a >,9910010a a ->,99100101a a -<-.给出下列结论:①01q <<;②9910110a a ⋅-<,③100T 的值是n T 中最大的;④使1n T >成立的最大自然数n 等于198.其中正确的结论是__________;22.(浙江省六校联盟2013届高三回头联考理科数学试题)设数列{}n a 的前n 项和为n S ,若数列{}n S 是首项和公比都是3的等比数列,则{}n a 的项公式n a =_________23.(浙江省温州市十校联合体2013届高三上学期期末联考理科数学试卷)已知等比数列}{n a 满足1129-+⋅=+n n n a a ,*N n ∈则数列}{n a 的前n 项和n S 为____.三、解答题24.(浙江省丽水市2013届高三上学期期末考试理科数学试卷)在等比数列{}n a 中,已知13a =,公比1q ≠,等差数列{}n b 满足1142133b a b a b a ===,,. (Ⅰ)求数列{}n a 与{}n b 的通项公式;(Ⅱ)记n n nn a b c +-=)1(,求数列{}n c 的前n 项和n S .25.(浙江省稽阳联谊学校2013届高三4月联考数学(理)试题(word 版) )已知数列{}n a 的前n 项和为n S ,满足2*.()n n a S n n N +=∈,记2.n n b a =- (I)求证:{}n b 是等比数列,并求{}n b 的前n 项和n B ;(II)求1122112()()()().n n n n n b B b b B b b B b n ---+-++-≥26.(浙江省一级重点中学(六校)2013届高三第一次联考数学(理)试题)已知数列{}n a 的前n 项和为n S ,且11,4a =*1()16n n ta S t +=+∈n N ,为常数. I ()若数列{}n a 为等比数列,求t 的值;II ()若14,lg n t b a +>-=n ,数列{}n b 前n 项和为n T ,当且仅当n=6时n T 取最小值,求实数t 的取值范围.浙江省2014届理科数学复习试题选编22:等比数列参考答案一、选择题 1. B 2. B 3. A 4. D 5. B 6. C 7. B 8. C 9. B 10. A 11. C 12. A 二、填空题 13. 2 14. 11215. 516. 31 17. 或218. 1 19. {}58 37,20.55421. ①②④22. 1323n n a -⎧=⎨⨯⎩(1)(2)n n =≥ 23. )12(3-n三、解答题24.解:(Ⅰ) 设等比数列{}n a 的公比为q ,等差数列{}n b 的公差为d .由已知得:2323,3q a q a ==,d b d b b 123,23,31341+=+==3411123333322=⇒⎩⎨⎧+=+=⇒⎩⎨⎧+=+=q d q dq d q d q 或 1=q (舍去) 所以, 此时 2=d所以,nn a 3=, 12+=n b n ┈┈┈┈┈┈┈┈┈┈┈┈(Ⅱ) 由题意得:n n n n n n n a b c 3)12()1()1(++-=+-=n n c c c S +++= 21n n n n n 333)12()1()12()1()97()53(21+++++-+--+++-++-=-当n 为偶数时,2323232311-+=-+=++n n S n n n当n 为奇数时,27232323)12()1(11--=-++--=++n n n S n n n所以,⎪⎪⎩⎪⎪⎨⎧---+=++)(2723)(232311为奇数时为偶数时n n n n S n n n ┈┈┈┈┈┈┈┈┈┈┈┈25.解:(I)∵2n n a S n +=, ∴ 112(1)(2)n n a S n n --+=-≥,两式相减得122n n a a -=+,11221(2)22(22)2n n n n n n b a a n b a a ----===≥--- {}n b ∴是等比数列.11111()1121,21,,2[1()]12212nn n a b a q B -=∴=-==∴==-- (II)原式=11223311()()()() n n n n n n b B b b B b b B b b B b ---+-+-++-222212311231()() n n n B b b b b b b b b --=++++-++++ 222211231() n n n B B b b b b --=-++++1111()118140142[1()]2[1()]12()()122323414n n n n n ---=---=-+-26. .解:I () 11....(1);....(2)1616n n n n t ta S a S +-=+=+1(1)(2):2(2)n n a a n +-=≥得2141616t ta S +=+=, 数列{}n a 为等比数列, 212a a ∴= 42,44tt +=∴= II ()2416t a +=,12(1)n n a a n +=>1*142()16n n t a n N -++∴=⋅∈ 1432,,+⋅⋅⋅n a a a a 成等比数列,1n a +n b =lg ,∴n 数列{b }是等差数列 数列{}n b 前n 项和为n T ,当且仅当n=6时n T 取最小值, 6700b b ∴<>且可得78011a a <<>且,27415:-<<-t t 的范围是解得。
2015届高考模拟高考(310)浙江温州市十校联合体高三期末考试(整理精校版)

2015届高考模拟高考(310)浙江温州市十校联合体高三期末考试高考模拟试卷0126 09:27::浙江省温州市十校联合体2015届高考模拟高三上学期期末考试语文试题一、语言文字运用。
(共23分,其中选择题每小题3分)1.下列词语中加点的字,注音正确的一组是()A. 阜盛(fù)墙垣(huán)操胜券(quàn)插科打诨(hùn)B. 玷污(diàn)媲美(bì)嗟来食(jiē)忍俊不禁(jìn)C. 倏忽(shū)瘦削(xiāo)舶来品(bó)牵强附会(qiǎng)D. 巨擘(bò)寥廓(liáo)炸酱面(zhá)胯下之辱(kuà)2.下列各句中,没有错别字的一项是()A. 近年来,一方面是大量待业人员寻工无着,另一方面是沿海地区许多企业招聘不到足够的人员,“就业难”与“用工荒”折射出我国产业转型时期的“就业之觞”。
B. 春暖花开,万物复苏,但恼人的“春季综合症”也接踵而至,虚弱无力、心情阴郁、对什么都提不起兴趣,这些都是其具体表现。
C. 又是地震,又是灾难,近期全球地震频烦,无数人在倾刻之间失去生命,灾难带来的断壁残垣以及残疾、孤儿现象让人心痛。
D. 在全国各大城市房价飙涨的背景下,房价越来越成为中低收入人群无法逾跃的屏障,拥有自己的房子也越来越成为难以企及的梦想。
3.下列各句中,加点的词语运用正确的一项是()A.他最近的状态一直不佳,接连几次考试都不理想,屡试不爽,心情糟透了。
B.以往经验表明,举办一次奥运会对于促进主办城市和所在国家在经济方面的发展,其效果会比平常好几倍,而对于整个体育产业的振兴和繁荣,更是为虎添翼。
C.苏杭山水果然名不虚传,秀色可餐,称之“人间天堂”实不为过。
D.一项社会调查显示,如果丈夫的收入低于妻子,一部分男性会感到自惭形秽,甚至无端地对自己进行心理折磨。
浙江省温州市十校联合体2023-2024学年高二下学期5月期中联考数学试题(含答案)

2023学年第二学期温州十校联合体期中联考高二年级数学学科试题考生须知:1.本卷共4页满分150分,考试时间120分钟.2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.3.所有答案必须写在答题纸上,写在试卷上无效.4.考试结束后,只需上交答题纸.选择题部分一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、设集合,若,则( )A .B .C .D .2、若函数是指数函数,则的值为( )A .2B .-2C .D .3、设复数,则复数的共轭复数的虚部是( )A .B .C .1D .-14、已知非负实数满足,则的最小值为( )A .B .2C .D .5、已知,则( )A .B .C .D .6、已知正方形的边长为2,若将正方形沿对角线折叠为三棱锥,则在折叠过程中,不能出现( )A .B .面面C .D .{}{}21,2,30A B xx mx ==+-=∣{}1A B = A B = {}3,1,2-{}1,2{}3,2-{}1,2,3()132x f x a a ⎛⎫=-⋅ ⎪⎝⎭12f ⎛⎫⎪⎝⎭-51i 1iz -=+z ii-,x y 1x y +=111x y++7395433sin 124πθ⎛⎫-= ⎪⎝⎭sin 23πθ⎛⎫+= ⎪⎝⎭7161818-716-ABCD ABCD BD A BCD -BD AC ⊥ABD ⊥BCDA BCD V -=AB CD⊥7、一个袋子中装有大小相同的5个小球,其中有3个白球,2个黑球,从中无放回地取出3个小球,摸到一个白球记2分,摸到一个黑球记1分,则总得分的数学期望等于( )A .5分B .4.8分C .4.6分D .4.4分8、已知,则( )A .B .C .D . 二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9、已知向量,则下列命题正确的是( )A .B .向量在向量上的投影向量为C.D .10、下列命题中正确的是( )A .已知随机变量,则B .已知随机变量,若函数为偶函数,则C .数据第80百分位数是8D .样本甲中有件样品,其方差为,样本乙中有件样品,其方差为,则由甲乙组成的总体样本的方差为11、定义在上的函数,满足,且当时,,则使得在上恒成立的可以是( )A .1B .2C .D .非选择题部分三、填空题:本大题共3小题,每小题5分,共15分.把答案填在题中的横线上.12、______.13、一位射击运动员向一个目标射击二次,记事件“第次命中目标”ξ1325321log 2,log 6,log 52x x x ===123x x x <<132x x x <<312x x x <<321x x x <<()()1,1,1,2a b ==a b +=ab 36,55⎛⎫ ⎪⎝⎭//a ba b⊥16,2X B ⎛⎫~ ⎪⎝⎭()216D X -=()2,N ξμσ~()(11)f x P x x ξ=-<<+0μ=1,3,4,5,7,8,10m 21s n 22s 2212m n s s m n m n⋅+⋅++R ()f x ()()12f x f x +=[)0,1x ∈()121f x x =--()4f x <(],m -∞m 9415455(1(1++-=i A =i,,则______.14、已知在三棱锥中,,点为三棱锥外接球上一点,则三棱锥的体积最大为______.四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15、(本题13分)在中,内角所对的边分别为,且(1)若,求的值;(2)若,且的面积为,求和的值.16、(本题15分)已知四棱锥面,底面为正方形,,为的中点.(1)求证:面;(2)求直线与面所成的角.17、(本题15分)已知的最小正周期为,(1)求的值;(2)若在上恰2个极值点和2个零点,求实数的取值范围.()()111,2,4i P A ==()()()()1112,1,24i i i i iP A A P A P A A i ++===∣∣()2P A =A BCD -,,8,6AB BD AC CD AB BD ⊥⊥==P A BCD -P ABD -ABC △A B C 、、,,a b c 8a b c ++=2,3b c ==cos A sin sin 3sin C B A +=ABC △9sin 2S A =b c ,S ABCD SA -⊥ABCD ABCD SA AB =E SD AE ⊥SCD BS SCD ()2cos cos (0)f x x x x ωωωω=->π23f π⎛⎫⎪⎝⎭()()12g x f x =+()0,m m18、(本题17分)为了了解高中学生课后自主学习数学时间(分钟/每天)和他们的数学成绩(y 分)的关系,某实验小组做了调查,得到一些数据(表一).编号12345学习时间3040506070数学成绩65788599108(1)求数学成绩与学习时间的相关系数(精确到0.001);(2)请用相关系数说明该组数据中与之间的关系可用线性回归模型进行拟合,并求出关于的回归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据:的方差为200(3)基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计,得到列联表(表二).依据表中数据及小概率值的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.没有进步有进步合计参与周末在校自主学习35130165未参与周末不在校自主学习253055合计60160220附:.x x yy x y x y x 1552211522820,435,38999,107.411540,i ii i i i i i x yy y x ======≈∑∑∑);22⨯0.001α=()()()ˆ1122211ˆˆ.n nni i i ii i nn i i i i x x y y x y nx yx y b r x nxx x a y b x ====⎧---⋅⎪⎪===⎪-⎨-⎪⎪⎪=-⎩∑∑∑∑nx y nx y-⋅=()()()()22()n ad bc a b c d a c b d χ-=++++0.100.050.0100.0050.0012.7063.8416.6357.87910.82819、(本题17分)已知(1)当时,解关于的不等式;(2)若有两个零点,求的值;(3)当时,的最大值,最小值为,若,求的取值范围.2023学年第二学期温州十校联合体期中联考高二年级数学学科参考答案一、选择题:本大题共8小题,每小题5分,共40分题号12345678答案ADCBCDBA二、选择题:本大题共8小题,每小题5分,共40分题号91011答案ABABCABC二、填空题:本大题共3小题,每小题5分,共15分12、152 13、 14、4015、(本题13分)(1),所以,于是(2)由,正弦定理得:.又,所以又,所以.于是16、(本题15分)(1)证明:面面又面(2)方法1:面点B 到面的距离就是点到面距离ααχ()()2,0f x x a x a a =-->1a =x ()0f x <()()g x f x a =+12,x x 12x x -[]1,1x ∈-()f x M m 4M m -≤a 5162,3b c ==3a =2221cos 23b c a A bc +-==sin sin 3sin C B A +=3b c a +=8a b c ++=6b c +=91sin sin 22S A bc A ==9bc =3b c ==SA ⊥AD ,ABCD SA CD CD CD ∴⊥⊥⊥ SCD AE CD ∴⊥,AE SD AE ⊥∴⊥ SCD//AB SCD SCD A SCD由(1)得点到面距离为.记线面角为方法2:设,则,线面角记为,方法3:设,以为轴,为轴,为轴建立直角坐标系,设面的法向量为则.令线面角记为,.方法4:将四棱锥还原为立方体,面为直线与面所成的角.记为,17、(本题15分)解析:(1)因为,由函数的最小正周期为,即,得,.(2),因为,A SCD 1122AE SD SB ==AE 1,sin 2BS θθ==1AB =16S BCDV -=122SCD S =⋅⋅=1136B SCD SCD S BCD V S h V --∴=⋅⋅==h ∴=1,sin 2h BS θθ==30θ∴= 2AB AD AS ===AB x AD y As z ()()()2,0,2,2,0,0,0,2,2SA CD SD =-==-SCD (),,n x y z =00n CD n SD ⎧⋅=⎨⋅=⎩0,x y z ∴==()10,1,1y z n ==∴= 1,sin cos 2n BS n BS θθα⋅===⋅30θ∴=︒//,BF AE BF ∴⊥SCD BSF ∴∠BS SCD 1,sin 2BF BS θθ==30θ∴= ()2cos cos f x x x x ωωω=-111cos2sin 22262x x x πωωω⎛⎫=--=-- ⎪⎝⎭()f x π22ππω=1ω=()12sin 2,1623f x x f ππ⎛⎫⎛⎫=--=- ⎪ ⎪⎝⎭⎝⎭()sin 2x 6g x π⎛⎫=-⎪⎝⎭()0,,2,2666x m x m πππ⎛⎫∈∴-∈-- ⎪⎝⎭要使在上恰有2个极值点和2个零点,则需,得18、(本题17分)(1),,又的方差为,(2)由(1)知r =0.996接近1,故与之间具有极强的线性相关关系,可用线性回归直线方程模型进行拟合:,,故当时,,故预测每天课后自主学习数学时间达到100分钟时的数学成绩为140.5分.(3)零假设为学生周末在校自主学习与成绩进步无关.根据数据,计算得到:因为,所以依据的独立性检验,可以认为“周末自主学习与成绩进步”有关.19、(本题17分)(1)当时,或所以或所以不等式的解集为(2)因为,所以当时,必有一零点记为),()g x ()0,m 32,262m πππ⎛⎤-∈ ⎥⎝⎦513612m ππ<≤3040506070505x ++++==435875y ==()1,2,3,,5i x i = ()52112005i i x x =-=∑10700.9961074r ==≈()()()55ˆ11251522820550871.0752001000iiiii i i i x x y y x y x yb x x===-⋅-⋅-⋅-⨯⨯====⨯∑-∑∑ˆˆ87 1.075033.5a y b x =-=-⨯=ˆ1.0733.5y x =+100x =140.5y =0H :()()()()222()220(251303530)11012.2216555601609n ad bc a b c d a c b d χ-⨯⨯-⨯===≈++++⨯⨯⨯12.2210.828>0.001α=1a =()()()()()12,1,12, 1.x x x f x x x x ⎧--≥⎪=⎨---<⎪⎩()()1201x x x ⎧--<⎨≥⎩()()1201x x x ⎧---<⎨<⎩1x <12x <<()0f x <()(),11,2-∞ ()()()()()2,,2,.x a x a a x a g x x a x a a x a ⎧--+≥⎪=⎨---+<⎪⎩()0g a a =>x a <()g x (1x所以当时,有且仅有一零点(记为),由得,故,当时,令,解得,所以(3)由知在上单调递增,在上单调递减,在上单调递增.当时,,解得,所以,当即时,,要使,分析可知需满足:,解得:;当即时,分析可知需满足:,解得:,又,综上可得,.故的取值范围为.x a ≥()g x 2x 302g a ⎛⎫= ⎪⎝⎭20,44a a a -+==26x =4x <()()4840x x ---+=16x =-12x x -=()()()()()2,,2,.x a x a x a f x x a x a x a ⎧--≥⎪=⎨---<⎪⎩()f x (),a -∞3,2a a ⎛⎫ ⎪⎝⎭3,2a ⎛⎫+∞ ⎪⎝⎭1a ≥()()11M m f f -=--()()()()1121124a a a a =---+----≤23a ≤a ∈∅12a a <<112a <<()()30,min 1,1,2M m f f f a ⎧⎫⎛⎫==-⎨⎬ ⎪⎝⎭⎩⎭4M m -≤()()01124a a +----≤12a <≤21a ≤12a ≤()()11M m f f -=--()()()()1121124a a a a =--+----≤12a ≤≤0a >0a <≤a ⎛ ⎝。
浙江省温州市十校联合体2015届高三上学期期初联考数学(文)试题 Word版含答案
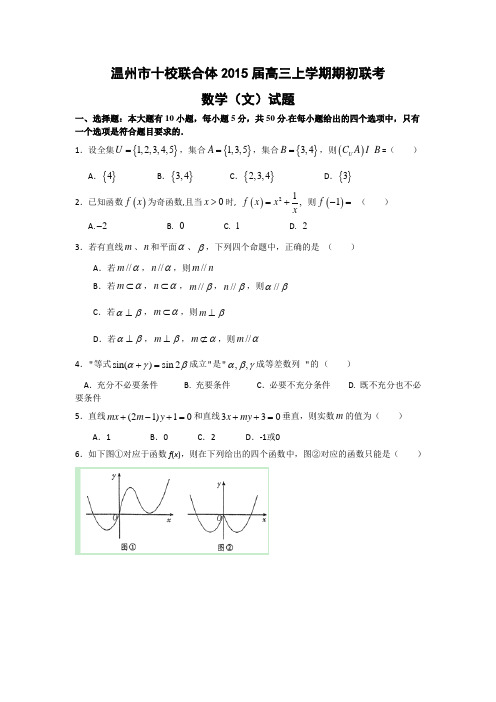
温州市十校联合体2015届高三上学期期初联考数学(文)试题一、选择题:本大题有10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.设全集{}1,2,3,4,5U =,集合{}1,3,5A =,集合{}3,4B =,则()U C A B =( )A .{}4B .{}3,4C .{}2,3,4D .{}3 2.已知函数()f x 为奇函数,且当0x >时, ()21,f x x x=+ 则()1f -= ( ) A.2-B. 0C. 1D. 23.若有直线m 、n 和平面α、β,下列四个命题中,正确的是 ( )A .若//m α,//n α,则//m nB .若m α⊂,n α⊂,//m β,//n β,则//αβC .若αβ⊥,m α⊂,则m β⊥D .若αβ⊥,m β⊥,m α⊄,则//m α4."等式sin()sin 2αγβ+=成立"是",,αβγ成等差数列 "的 ( )A .充分不必要条件 B. 充要条件 C .必要不充分条件 D. 既不充分也不必要条件5.直线(21)10mx m y +-+=和直线330x my ++=垂直,则实数m 的值为( ) A .1 B .0C .2D .-1或06.如下图①对应于函数f (x ),则在下列给出的四个函数中,图②对应的函数只能是( )A .y =f (|x |)B .y =|f (x )|C .y =f (-|x |)D .)(x f y -=7.若{}n a 为等差数列,n S 是其前n 项和,且S 15 =π10,则tan 8a 的值为( ) AB .C .D.8.过点(,0)引直线l与曲线y = 交于A,B 两点 ,O 为坐标原点,当△AOB的面积取最大值时,直线l 的斜率等于( )B.C.D.9.当x>3时,不等式x+11-x ≥a 恒成立,则实数a 的取值范围是( ) A .(-∞,3] B .[3,+∞) C .[72,+∞) D .(-∞, 72]10.如图,南北方向的公路l ,A 地在公路正东2 km 处,B 地在A 东偏北300方向23 km 处,河流沿岸曲线PQ上任意一点到公路l 和到A 地距离相等。
浙江省温州市十校联合体2015届高三上学期期中联考数学(文)试题 Word版含答案

2014学年第一学期十校联合体高三期中联考数 学 试 卷(文)(满分150分,考试时间:120分钟)一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.设集合U={1,2,3,4},A={1,2},B={2,4},则B)(A ⋂U C 等于( ) A.{1,4} B.{1,3,4} C.{2} D.{3}2.已知复数 z满足(1)1z i =+,则||z =( )A.21D.23.点(cos ,tan )P αα在第二象限是角α的终边在第三象限的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 4.设,αβ是两个不同的平面,l 是一条直线,以下命题正确的是( ) A.若,l ααβ⊥⊥,则l β⊂ B.若//,//l ααβ,则l β⊂C.若,//l ααβ⊥,则l β⊥D.若//,l ααβ⊥,则l β⊥ 5.已知}{n a 是等差数列,其前n 项和为n S ,若237a a -=,则4S =( ) A.15 B.14 C.13 D.126.已知向量b ,a 满足的夹角为与则向量且,)(,2||,1||⊥+==( ) 0000150.120.60.30.D C B A7.同时具有性质“①最小正周期是π,②图象关于直线3π=x 对称”的一个函数是 ( )A.)62sin(π+=xy B.)3cos(π+=x y C.)62cos(π-=x y D .)62sin(π-=x y 8.x ,y 满足约束条件⎪⎩⎪⎨⎧≥+-≤--≤-+.022,022,02y x y x y x 若ax y z -=取得最大值的最优解不唯一...,则实数a 的值为( ) A.21或-1 B.2或21C.2或1D.2或-1 9.已知函数()5f x x =-当19x ≤≤时,()1f x >有解,则实数m 的取值范围为( ) A.313<m B.5<m C.4<m D.5≤m10.已知椭圆22122:1(0)x y C a b a b+=>>与圆2222:C x y b +=,若在椭圆1C 上不存在点P ,使得由点P 所作的圆2C 的两条切线互相垂直,则椭圆1C 的离心率的取值范围是( )A.0,2⎛ ⎝⎭B.0,2⎛ ⎝⎭C.,1)2D.,1)2 二、填空题(本大题共7小题,每小题4分,共28分。
浙江省温州市十校联合体(温州中学等)2015届高三第一次月考数学(理)试题(解析版)

浙江省温州市十校联合体(温州中学等)2015届高三第一次月考数学(理)试题(解析版) 一.选择题:本大题共10题,每小题5分,共50分.1. 若全集{}2,1,0,1-=U ,{}22<∈=x Z x A ,则=A C U ( )A.{}2B.{}2,0C.{}2,1-D.{}2,0,1- 【知识点】补集及其运算.A1【答案解析】A 解析:∵x 2<2,∴﹣<x <,∴P={x ∈Z|x 2<2}={x|﹣<x <,x ∈Z|}={﹣1,0,1},又∵全集U={﹣1,0,1,2},∴∁U P={2}故选:A . 【思路点拨】先解出集合P ,然后根据补集的定义得出答案.【题文】2.已知a ,b 是实数,则“||||||b a b a -=-”是“0>ab ”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 【知识点】必要条件、充分条件与充要条件的判断.A2【答案解析】D 解析:若|a ﹣b|=|a|﹣|b|,不一定得到ab >0,比如a=b=0; ∴|a ﹣b|=|a|﹣|b|不是ab >0的充分条件;若ab >0,不一定得到|a ﹣b|=|a|﹣|b|,比如a=1,b=2; ∴|a ﹣b|=|a|﹣|b|不是ab >0的必要条件;综上得,|a ﹣b|=|a|﹣|b|是ab >0的既不充分又不必要条件.故选D .【思路点拨】|a ﹣b|=|a|﹣|b|得不到ab >0,比如a=b=0;ab >0得不到|a ﹣b|=|a|﹣|b|,比如a=1,b=2,所以“|a ﹣b|=|a|﹣|b|”是“ab >0”的既不充分也不必要条件.【题文】3.下列式子中成立的是( ) A .6log 4log 4.04.0< B .5.34.301.101.1> C .3.03.04.35.3< D . 7log 6log 67< 【知识点】幂函数的性质;指数函数单调性的应用.B6 B8【答案解析】D 解析:对于A :设函数y=log 0.4x ,则此函数单调递减∴log 0.44>log 0.46∴A选项不成立对于B :设函数y=1.01x ,则此函数单调递增∴1.013.4<1.013.5∴B 选项不成立对于C :设函数y=x 0.3,则此函数单调递增∴3.50.3>3.40.3∴C 选项不成立 对于D :设函数f (x )=log 7x ,g (x )=log 6x ,则这两个函数都单调递增∴log 76<log 77=1<log 67∴D 选项成立,故选D 。
浙江省温州市十校联合体2015届高三第一次月考数学(理)试题

浙江省温州市十校联合体2015届高三第一次月考数学(理)试题(完卷时间:120分钟, 满分:150分,本次考试不得使用计算器)一.选择题:本大题共10题,每小题5分,共50分.1. 若全集{}2,1,0,1-=U ,{}22<∈=x Z x A ,则=A C U ( )A.{}2B.{}2,0C.{}2,1-D.{}2,0,1-2.已知a ,b 是实数,则“||||||b a b a -=-”是“0>ab ”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件3.下列式子中成立的是 ( ) A .6log 4log4.04.0< B .5.34.301.101.1> C .3.03.04.35.3< D . 7log 6log 67< 4.在等差数列}{n a 中,有12876=++a a a ,则此数列的前13项之和为( ) A. 104 B.52 C .39 D .24 5.函数 2log 1()2xf x x x=--的图像为 ( )6.已知函数),cos()(),sin()(ππ+=-=x x g x x f 则下列结论中正确的是 ( )A .函数)()(x g x f y ⋅=的最小正周期为π2B .函数)()(x g x f y ⋅=的最大值为2C .将函数)(x f y =的图象向左平移2π单位后得)(x g y =的图象 D .将函数)(x f y =的图象向右平移2π单位后得)(x g y =的图象7. 已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数)sin(ϕω+=x y 图像的两条相邻的 对称轴,则ϕ= ( )A.π4B.π3C.π2D.3π48.在ABC ∆中,内角A,B,C 所对应的边分别为,,,c b a ,若,3,6)(22π=+-=C b a c则ABC ∆的面积为 ( ) A.3 B.239 C.233 D.33 9.已知等比数列}{n a 前n 项和为n S ,则下列一定成立的是 ( ) A .若03>a ,则02013<a B .若04>a ,则02014<a C .若03>a ,则02013>S D .若04>a ,则02014>S10.已知函数31,0()9,0x x f x xx x ⎧+>⎪=⎨⎪+≤⎩,若关于x 的方程()a x x f =+22有六个不同的实根, 则常数a 的取值范围是 ( ) A .(]2,8B .(]2,9C .()9,8D .(]8,9二.填空题:本大题共7小题,每小题4分,共28分 11.若函数xx x f 1)(+=,则)(x f 的定义域是 .12.已知等差数列{}n a 满足4,1231-==a a a ,则n a =_____________. 13.若31tan 1tan =-+αα,则=α2sin .14.已知平面向量()1,2a =, ()2,b m =-, 且//a b , 则b = 15.数列{}n a 前n 项和为n S ,已知113a =,且对任意正整数,m n ,都有m n m n a a a +=⋅, 若n S a <恒成立则实数a 的最小值为16.如图在平行四边形ABCD 中,已知8,5AB AD ==,3,2CP PD AP BP =⋅=, 则AB AD ⋅的值是17.具有性质)()1(x f xf -=-的函数,我们称其为满足“倒负”变换的函数,下列函数:(1)x x f 1)(-= (2)x x x f 1)(-=; (3);1)(x x x f += (4)⎪⎪⎩⎪⎪⎨⎧>-=<<=)1(1)1(0)10()(x xx x x x f ,其中不满足“倒负”变换的函数是 .三.解答题:本大题共5小题,共72分。
浙江省台州市十校联盟2023-2024学年高一下学期4月期中联考数学试题含答案

浙江省台州市十校联盟2023-2024学年高一下学期4月期中联考数学试题(答案在最后)考生须知:1.本卷共4页满分150分,考试时间120分钟.2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.3.所有答案必须写在答题纸上,写在试卷上无效.4.考试结束后,只需上交答题纸.选择题部分一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若(1i)i z -=,其中i 为虚数单位,则复数z 在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B 【解析】【分析】先求出复数z 的代数形式,然后可确定复数z 在复平面内对应的点的位置.【详解】()()()i 1i i 1i 11i 1i 1i 1i 222z +-+====-+--+.复数z 在复平面内对应的点为11,22⎛⎫- ⎪⎝⎭,在第二象限.故选:B.2.已知三角形ABC 中,角A ,B ,C 的对边分别为,,a b c ,若5,8,60a b C === ,则CA CB ⋅=A.-B.20- C.20D.【答案】C 【解析】【分析】由数量积的定义计算.【详解】cos cos 6020CA CB CA CB C ab ⋅===故选:C .3.ABC 内角A ,B ,C 的对边分别为a ,b ,c ,且π1,6a c B ===,则ABC 的面积为()A.2B.4C.D.【答案】B 【解析】【分析】直接由面积公式计算可得.【详解】依题意可得1113sin 12224ABC S ac B ==⨯=.故选:B4.已知向量(,3),(1,4),(2,1)a k b c === ,且(23)a b c -⊥,则实数k =A.92-B.0C.3D.152【答案】C 【解析】【详解】试题分析:由题意得,23(23,6),(2,1)a b k c -=--=,因为(23)a b c -⊥,所以(23)4660a b c k -⋅=--=,解得3k =,故选C.考点:向量的坐标运算.5.如图所示,矩形O A B C ''''是水平放置的一个平面图形的直观图,其中6cm O A ''=,2cm C D ''=,则原图形OABC 的面积是()2cm .A.12B.C.6D.【答案】D 【解析】【分析】求出直观图面积,根据直观图面积和原图面积之间的关系即可得答案.【详解】因为2cm C D ''=,由斜二测画法可知45D O A '''∠=o ,则45C O D '''∠= ,故O C D ''' 为等腰直角三角形,故2cm O C ''=,故矩形O A B C ''''的面积为26212(cm )S O A O C '''''=⨯=⨯=,所以原图形OABC的面积是212)4S ===,故选:D6.)A.12πB.9πC.3πD.43π3【答案】C 【解析】【分析】由圆锥侧面展开图得圆锥母线,高,再由体积公式计算.【详解】设圆锥的底面半径为r ,母线为l ,由于圆锥的侧面展开图是一个半圆面,则2ππr l =,所以2l r =,所以圆锥的高h ==,圆锥的体积为2211ππ3π33V r h ==⨯⨯⨯=.故选:C7.窗户,在建筑学上是指墙或屋顶上建造的洞口,用以使光线或空气进入室内.如图1,这是一个外框为正八边形,中间是一个正方形的窗户,其中正方形和正八边形的中心重合,正方形的上、下边与正八边形的上、下边平行,边长都是4.如图2,,A B 是中间正方形的两个相邻的顶点,P 是外框正八边形上的一点,则AB AP ⋅的最大值是()A.16+B.8C.8D.16【答案】A 【解析】【分析】利用平面向量数量积的定义,结合线段长即可得解.【详解】记正八边形右下角的两个顶点分别为,C D ,连接,BC BD ,由题意易得BCD △是等腰直角三角形,4CD =,则BC =不妨设,AP AB θ=,由于题目要求AB AP ⋅的最大值,故只考虑090θ︒≤<︒的情况,过P 作PE AB ⊥,垂足为E ,则cos AP AE θ=,又4AB =,所以cos 4AB AP AB AP AB AE AE θ⋅=== ,显然,当点P 与点C 重合时,AE取得最大值4AB BC +=+,所以AB AP ⋅的最大值为(4416⨯+=+.故选:A.8.在锐角ABC 中,角A ,B ,C 所对的边为a ,b ,c ,若sin sin cos cos 3sin B C A CA a c=+,且222sin sin sin sin sin A B C A B +-=⋅,则2c a b+的取值范围是()A. B.(6, C. D.2)【答案】D 【解析】【分析】由222sin sin sin sin sin A B C A B +-=⋅,结合正余弦定理求得角C ,继而由sin sin cos cos3sin B C A CA a c=+结合正余弦定理求出c =,再表示出4sin a A =,4sin b B =,利用三角函数的性质求得a b +的范围,即可求得答案.【详解】由222sin sin sin sin sin A B C A B +-=⋅,由正弦定理得222a b c ab +-=,即有2221cos 22a b c C ab +-==,而0,2C π⎛⎫∈ ⎪⎝⎭,则3C π=,又sin sin cos cos 3sin B C A CA a c=+,由正弦定理、余弦定理得,22222232223b c a a b c b bc ab a a c+-+-⋅=+,化简得:c =,由正弦定理有:4sin sin sin a b c A B C ====,即4sin a A =,4sin b B =,ABC 是锐角三角形且3C π=,有0,2A π⎛⎫∈ ⎪⎝⎭,20,32B A ππ⎛⎫=-∈ ⎪⎝⎭,解得,62A ππ⎛⎫∈⎪⎝⎭,因此24(sin sin )4sin sin 3⎡⎤⎛⎫+=+=+- ⎪⎢⎥⎝⎭⎣⎦a b A B A Aπ14sin cos sin 22⎛⎫=++ ⎪ ⎪⎝⎭A AA 6A π⎛⎫=+ ⎪⎝⎭,由,62A ππ⎛⎫∈ ⎪⎝⎭得:2,633A πππ⎛⎫+∈ ⎪⎝⎭,sin ,162A π⎛⎤⎛⎫+∈ ⎥ ⎪ ⎝⎭⎝⎦,所以2122)6=∈+⎛⎫+ ⎪⎝⎭c a bA π.故选:D二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.在复平面内,下列说法正确的是()A.2i 1-= B.2(i)1-=C.若a b >,则i i a b +>+ D.若复数z 满足20z <,则z 是纯虚数【答案】AD 【解析】【分析】利用复数的运算和性质判断ABD ;虚数无法比较大小判断C.【详解】对于A ,()()2i 111-=-⨯-=,故A 正确;对于B ,()222(i)1i 1-=-⨯=-,故B 不正确;对于C ,两个虚数不能比较大小,故C 不正确;对于D ,设()i ,R z a b a b =+∈,则()2222i 2i z a b a b ab =+=-+,20z <Q ,则22020a b ab ⎧-<⎨=⎩,解得00a b =⎧⎨≠⎩,故i z b =是虚数,故D 正确;故选:AD10.设ABC 的内角A,,B C 所对的边分别为a ,b ,c ,则下列结论正确的是()A.若2,3a b c ===,则32BA AC ⋅=B.若A B >,则sin sin A B >C .若45a b B ︒===,则60A ︒=D.若cos cos a A b B =,则ABC 为等腰三角形或直角三角形【答案】BD 【解析】【分析】A 选项,由余弦定理与数量积的定义计算;B 选项,由大角对大边和正弦定理判断;C 选项,由正弦定理解三角形;D 选项,由正弦定理与二倍角公式化简后判断.【详解】对于A ,2221cos 24b c a A bc +-==,而()3cos π2BA AC c b A ⋅=⋅⋅-=- ,故A 选项错误,对于B ,ABC 中,若A B >,则a b >,由正弦定理得:2sin 2sin R A R B >(R 为ABC 的外接圆半径),故sin sin A B >,B 选项正确,对于C ,由正弦定理sin sin a b A B =,得sin sin 2a B Ab ==,由a b >,则60A ︒=或120A =o ,C 选项错误对于D ,若cos cos a A b B =,则sin cos sin cos A A B B =,即sin2sin2A B =,得22A B =或2π2A B =-,故A B =或π2A B +=,ABC 为等腰三角形或直角三角形,D 选项正确.故选:BD11.在正四面体ABCD 中,若2AB =,M 为BC 的中点,下列结论正确的是()A.正四面体的体积为212B.正四面体外接球的表面积为6πC.如果点P 在线段DM 上,则()2AP CP +的最小值为43+D.正四面体ABCD 内接一个圆柱,使圆柱下底面在底面BCD 上,上底圆面与面ABD 、面ABC 、面ACD 均只有一个公共点,则圆柱的侧面积的最大值为2π3【答案】BCD 【解析】【分析】由正四棱锥的结构特征,应用棱锥的体积公式求体积,并确定外接球的半径求表面积,展开侧面,要使()2AP CP +最小,只需,,A P C 共线,结合余弦定理求其最小值,根据正四面体ABCD 内接一个圆柱底面圆与其中截面正三角形关系求半径、体高,应用二次函数性质求侧面积最大值.【详解】由正四面体各棱都相等,即各面都为正三角形,故棱长为2,如下图示,O 为底面中心,则,,D O M 共线,AO为体高,故2323BO BD =⨯⋅=,所以263AO ===,故正四面体的体积为111261322sin 6043233223AO BC BD ⋅⋅⋅⋅⋅︒=⨯⨯⨯⨯=,A 错误;由题设,外接球球心E 在AO 上,且半径r EA EB ==,所以222()r AO r BO =-+,则22843322AO BO r AO ++==,故外接球的表面积为234π4π6π2r =⨯=,B 正确;由题意知:将面AMD 与面CMD 沿MD 翻折,使它们在同一个平面,如下图示,所以2AD CD ==且cos 3DO BO ADM AD AD ∠===,sin 3AO ADM AD ∠==,又30CDM ∠=︒,而13cos cos()32326ADC ADM CDM ∠=∠+∠=⨯-⨯=,要使()2AP CP +最小,只需,,A P C 共线,则()2222min 2cos AP CP AC AD CD AD CD ADC +==+-⋅∠,所以()2min34(38(1)63AP CP -++=-=,C 正确;如下图,棱锥中一个平行于底面的截面所成正三角形的内切圆为正四面体ABCD 内接一个圆柱的上底面,若截面所成正三角形边长为(0,2)x ∈,则圆柱体的高)(1)23xx h AO -=⋅-=,圆柱底面半径为133326=⨯=r x x ,所以其侧面积2)(2)1)2π2π6333x x x S rh x ---==⨯⨯==,故当1x =时,max 3S =,D 正确.故选:BCD非选择题部分三、填空题:本大題共3小题,每小題5分,共15分(12題第一空2分第二空3分).12.平面向量,a b 中,已知()4,3a =- ,1= b ,且5a b ⋅= ,则a 与b 的夹角为______,向量b 的坐标为______.【答案】①.0##0︒②.43,55⎛⎫-⎪⎝⎭【解析】【分析】首先求出a ,设a 与b的夹角为θ,根据数量积的定义求出cos θ,从而确定θ,则b 为a 方向上的单位向量,从而得到ab a = ,即可得解.【详解】因为()4,3a =- ,所以5a = ,又1= b ,且5a b ⋅= ,设a 与b 的夹角为θ,则cos 15cos 5a b a b θθ⋅==⨯=,解得cos 1θ=,又[]0,πθ∈,所以0θ=,即a与b的夹角为0,所以a 与b共线同向,又1= b ,所以b 为a 方向上的单位向量,即()1434,3,555a b a ⎛⎫==-=- ⎪⎝⎭.故答案为:0;43,55⎛⎫-⎪⎝⎭13.若i 为虚数单位,复数z满足11i z ≤++≤1i z --的最大值为_______.【答案】【解析】【分析】利用复数的几何意义知复数z 对应的点Z 到点(1,1)C --的距离d 满足1d ≤≤1i z --表示复数z 对应的点Z 到点(1,1)P 的距离,数形结合可求得结果.【详解】复数z满足11z i ≤++≤()11i z ≤---≤即复数z 对应的点Z 到点(1,1)C --的距离d 满足1d ≤≤设(1,1)P ,1i z --表示复数z 对应的点Z 到点(1,1)P 的距离数形结合可知1i z --的最大值||||AP CP ==故答案为:3214.若G 为ABC 的重心,BG CG ⊥,则cos A 的最小值为_______.【答案】45【解析】【分析】根据BG CG ⊥,利用向量的数量积运算可得22225cos 0c b bc A +-=,再由均值不等式即可求出cos A 的最小值.【详解】如图,CG BG ⊥ ,CD BE ∴⊥,11()()22CD BE CA CB BA BC ⋅=+⋅+ ()()(2)(2)AC AB AC AB AC AB AB AC AB AC =-+-⋅-+-=--⋅- ()225AB AB AC AC AB AC=-⋅+⋅-⋅ ()22225cos c b bc A=-+-22225cos 0c b bc A ∴+-=222222224cos 555c b c b A bc bc +⋅∴=≥=,当且仅当b c =时,等号成立,cos A ∴的最小值为45.故答案为:45四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知i 是虚数单位,z 是z 的共轭复数.(1)若()202112i 44i i z +=+-,求复数z 和z ;(2)若复数()()221563i z m m m m =-++-是纯虚数,求实数m 的值.【答案】(1)2i z=+,z =(2)2【解析】【分析】(1)先化简,再求出复数z ,再求出模长;(2)由纯虚数的实部为零,虚部不为零求出结果即可.【小问1详解】因为20212020i i i i=⨯=由()202112i 44i i z +=+-.得()()()()43i 12i 43i 105i 2i 12i 12i 12i 5z +-+-====-++-.所以2i z =+,z ==【小问2详解】因为()()221563i z m m m m =-++-是纯虚数,所以2256030m m m m ⎧-+=⎨-≠⎩,解得2m =.16.已知向量()2,1a =r ,(),3b x = ,(),2c y = ,且//a b ,a c ⊥ .(1)求b 与c ;(2)若2m a b =- ,n a c =+ ,求向量m 与n的夹角的大小.【答案】(1)()6,3b = ,()1,2c =-r ;(2)3π4.【解析】【分析】(1)利用平行、垂直的坐标表示列方程,由此求得,x y ,进而求得b 与c.(2)利用向量夹角公式计算出cos ,m n ,进而求得向量m 与n 的夹角的大小.【详解】(1)由//a b r r 得,2310x ⨯-⨯=,所以6x =,即()6,3b = ,由a c ⊥得,2120y ⨯+⨯=,所以1y =-,即()1,2c =-r .(2)由(1)得()()()222,16,32,1m a b =-=-=-- ,()()()2,11,21,3n a c =+=+-= ,所以()()21135m n ⋅=-⨯+-⨯=- ,m ==n ==所以[]2cos ,0,2m n m n x m n π⋅===-∈ ,所以向量m ,n 的夹角为3π4.17.如图,AB 是圆柱OO '的一条母线,BC 过底面圆心O ,D 是圆O 上一点.已知5,3AB BC CD ===,(1)求该圆柱的表面积;(2)将四面体ABCD 绕母线AB 所在的直线旋转一周,求ACD 的三边在旋转过程中所围成的几何体的体积.【答案】(1)75π2(2)15π【解析】【分析】(1)由题意求出柱的底面圆的半径即可求解;(2)ACD 绕AB 旋转一周而成的封闭几何体的体积为两个圆锥的体积之差,结合圆锥体积公式求解即可【小问1详解】由题意知AB 是圆柱OO '的一条母线,BC 过底面圆心O ,且5AB BC ==,可得圆柱的底面圆的半径为52R =,则圆柱的底面积为221525πππ24S R ⎛⎫==⨯= ⎪⎝⎭,圆柱的侧面积为252π2π525π2S Rl ==⨯⨯=所以圆柱的表面积为12257522π25ππ42S S S =+=⨯+=.【小问2详解】由线段AC 绕AB 旋转一周所得几何体为以BC 为底面半径,以AB 为高的圆锥,线段AD 绕AB 旋转一周所得的几何体为BD 为底面半径,以AB 为高的圆锥,所以以ACD 绕AB 旋转一周而成的封闭几何体的体积为:22221111πππ55π4515π3333V BC AB BD AB =⋅⋅-⋅⋅=⋅⋅-⋅⋅=.18.在ABC 中,设A ,B ,C 所对的边分别为a ,b ,c ,已知sin cos b C B =.(1)求C 的大小;(2)若2a b +=,求边长c 的取值范围;(3)若4c =,求ABC 面积S 的最大值.【答案】(1)π3;(2)[1,2)(3)【解析】【分析】(1)已知条件由正弦定理边化角,利用两角和的正弦公式化简得tan C =,可得C 的大小;(2)由三角形两边之和大于第三边和余弦定理结合基本不等式,可得边长c 的取值范围;(3)由余弦定理和重要不等式得16ab ≤,代入面积公式求S 的最大值.【小问1详解】在ABC 中,sin cos b C B =,由正弦定理得:sin sin cos B C A C B =-,因为πA B C ++=,所以sin sin()sin cos sin cos A B C B C C B =+=+,所以sin sin cos B C A C B =-可化为sin sin cos sin cos sin cos )B C B C C B C B =+-,即sin sin cos B C B C =.因为(0,π)B ∈,所以sin 0B ≠,所以tan C =因为(0,π)C ∈,所以π3C =.【小问2详解】由三角形两边之和大于第三边可得:2c a b <+=,即2c <.由余弦定理得:2222cos c a b ab C =+-,即2222()3c a b ab a b ab =+-=+-.由基本不等式可得:a b +≥,所以22a b ab +⎛⎫≤ ⎪⎝⎭即22()14a b c +≥=,所以1c ≥.综上所述:12c ≤<.所以边长c 的取值范围为[1,2).【小问3详解】由余弦定理得222222cos c a b ab C a b ab =+-=+-,由重要不等式得2162c ab ab ab =≥-=,当且仅当4a b ==时取等号,1sin 24S ab C ab ∴==≤即S 最大值为19.如图,点P ,Q 分别是矩形ABCD 的边DC ,BC 上的两点,3AB =,2AD =.(1)若DP DC λ= ,CQ CB λ= ,01λ≤≤,求AP AQ ⋅ 的范围;(2)若π4PAQ ∠=,求AP AQ ⋅ 的最小值;(3)若2DP PC =,连接AP 交BC 的延长线于点T ,Q 为BC 的中点,试探究线段AB 上是否存在一点H ,使得THQ ∠最大.若存在,求BH 的长;若不存在,说明理由.【答案】(1)[]4,9(2)12(3)存在,BH =【解析】【分析】(1)借助向量的线性运算及数量积公式计算即可得;(2)建立平面直角坐标系后借助三角函数与基本不等式计算即可得(3)建立平面直角坐标系后,将THQ ∠最大转化为tan THQ ∠最大,借助()tan tan tan tan 1tan tan THB QHB THQ THB QHB THB QHB∠-∠∠=∠-∠=+∠⋅∠计算即可得.【小问1详解】由3AB =,2AD =,故3DP DC λλ== ,2CQ CB λλ== ,则22BQ λ=- ,()()AP AQ AD DP AB BQ AD AB AD BQ DP AB DP BQ ⋅=+⋅+=⋅+⋅+⋅+⋅ ()022233054λλλ=+-+⨯+=+,由01λ≤≤,故[]4,9AP AQ ⋅∈ ;【小问2详解】如图所示,以A 点为坐标原点,AB 为x轴,建立直角坐标系,设π0,4QAB α⎡⎤∠=∈⎢⎥⎣⎦,20tan 3α≤≤,则()3,3tan Q α,π2tan ,24P α⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,π1tan 6tan 6tan 66tan 41tan AP AQ ααααα-⎛⎫⋅=-+=⨯+ ⎪+⎝⎭1226tan 66tan 1121tan 1tan αααα⎛⎫=+-=++- ⎪++⎝⎭1212≥-=-,当且仅当2tan 11tan αα=++,即tan 1α=-时,等号成立,即AP AQ ⋅的最小值为12;【小问3详解】如图所示,以A 点为坐标原点,AB 为x 轴,建立直角坐标系,由题意可得()2,2P ,()3,1Q ,112TC AD ==,()3,1Q 即()3,3T ,假设存在点H ,使得THQ ∠最大,由π0,2THQ ⎡⎫∠∈⎪⎢⎣⎭,即有tan THQ ∠最大,设BH a =,当0a =时,角度为0,此时THQ ∠不可能最大,故0a ≠,则()()2tan tan tan tan 1tan tan 1TB QB BH TB QB THB QHB BH BH THQ THB QHB TB QB THB QHB BH TB QB BH BH-⋅-∠-∠∠=∠-∠===+∠⋅∠+⋅+⋅()223122333133a a a a a a ⋅-===≤+⨯++,当且仅当3a a=,即a =即存在,且BH =【点睛】关键点点睛:本题第三问的关键是引入变量BH ,结合建系法,再通过两角差的正切公式再结合基本不等式求出角度最大情况.。
2023-2024学年浙江省A9协作体高二(上)期中数学试卷【答案版】

2023-2024学年浙江省A9协作体高二(上)期中数学试卷一、单项选择题:(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.椭圆x 236+y 29=1上的一点P 到椭圆一个焦点的距离为5,则点P 到另一个焦点的距离为( )A .7B .5C .4D .12.已知向量a →=(﹣3,2,1),b →=(2,x ,4),且a →⊥b →,则实数x 的值是( ) A .1B .2C .3D .43.若直线l 的一个方向向量n →=(1,−√3),则l 的倾斜角为( ) A .30°B .60°C .120°D .150°4.已知圆C 1:x 2+y 2=1与圆C 2:(x +3)2+(y +4)2=16,则两圆的公切线条数为( ) A .1B .2C .3D .45.若直线4x +3y ﹣12=0与两坐标轴的交点为A 、B ,则以AB 为直径的圆的方程为( ) A .x 2+y 2﹣3x ﹣4y =0 B .x 2+y 2﹣4x ﹣3y =0C .x 2+y 2+3x +4y =0D .x 2+y 2+4x +3y =06.正方体ABCD ﹣A 1B 1C 1D 1中,二面角A ﹣B 1D 1﹣A 1的余弦值为( ) A .√32B .√63 C .√22D .√337.已知点F 为椭圆C :x 225+y 216=1的右焦点,点P 是椭圆C 上的动点,点Q 是圆M :(x +3)2+y 2=1上的动点,则|PF||PQ|的最小值是( )A .12B .29C .23D .838.如图,一束平行光线与地平面的夹角为60°,一直径为24cm 的篮球在这束光线的照射下,在地平面上形成的影子轮廓为椭圆,则此椭圆的离心率为( )A .√33B .√32C .√22D .12二、多项选择题:(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.直线l 经过点(2,﹣3),且在两坐标轴上的截距的绝对值相等,则直线l 的方程可能是( )A .3x +2y =0B .2x +3y =0C .x ﹣y ﹣5=0D .x +y +1=010.在空间直角坐标系Oxyz 中,点O (0,0,0),A (﹣2,﹣1,1),B (3,4,5),下列结论正确的有( ) A .|AB|=3√5B .向量OA →与OB →的夹角的余弦值为−√36C .点A 关于z 轴的对称点坐标为(﹣2,﹣1,﹣1)D .向量OA →在OB →上的投影向量为−110OB →11.如图,在四棱锥S ﹣ABCD 中,底面ABCD 为正方形,AB =2,SD ⊥底面ABCD ,点E 、F 分别为SC 、AB 的中点,若线段SD 上存在点G ,使得GE ⊥GF ,则线段SD 的长度可能值为( )A .3B .4C .5D .6 12.画法几何的创始人——法国数学家蒙日发现:在椭圆C :x 2a 2+y 2b 2=1(a >b >0)中,任意两条互相垂直的切线的交点都在同一个圆上,它的圆心是椭圆的中心,半径等于长、短半轴平方和的算术平方根,这个圆就称为椭圆C 的蒙日圆,其圆方程为x 2+y 2=a 2+b 2.已知椭圆C 的离心率为√63,点A ,B 均在椭圆C 上,直线l :bx +ay ﹣4=0,则下列描述正确的为( ) A .点A 与椭圆C 的蒙日圆上任意一点的距离最小值为bB .若l 上恰有一点P 满足:过P 作椭圆C 的两条切线互相垂直,则椭圆C 的方程为x 23+y 2=1C .若l 上任意一点Q 都满足QA →⋅QB →>0,则b >1D .若b =1,椭圆C 的蒙日圆上存在点M 满足MA ⊥MB ,则△AOB 面积的最大值为√32三、填空题:(本题共4小题,每小题5分,共20分.) 13.已知椭圆x 25+y 2k=1的一个焦点是(2,0),则k 的值为 .14.已知实数x ,y 满足x ﹣2y +4=0,则√x 2+y 2的最小值为 .15.已知点A ,B 分别为圆M :(x +4)2+(y ﹣1)2=1与圆N :(x ﹣2)2+(y ﹣7)2=4上的动点,点P 为x 轴上的动点,则|P A |+|PB |的最小值为 .16.已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为2,E ,F 分别为AA 1,A 1D 1的中点,点P 在正方体表面上运动,若直线D 1P ∥平面BEF ,则点P 的轨迹长度为 .四、解答题:(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(10分)已知直线x ﹣y ﹣1=0和直线x +2y +2=0的交点为P . (1)求过点P 且与直线x ﹣2y +1=0平行的直线方程; (2)若点P 到直线l :mx +y +m =0距离为√2,求m 的值.18.(12分)如图,直三棱柱ABC ﹣A 1B 1C 1,AC =BC =CC 1=2,AC ⊥BC ,点M 是线段AB 的中点. (1)证明:平面MCC 1⊥平面ABB 1A 1. (2)求异面直线CA 与B 1M 所成角的余弦值.19.(12分)已知圆C :(x ﹣3)2+(y ﹣4)2=4.(1)若直线l 过定点A (1,0)且与圆C 相切,求直线l 的方程; (2)若直线l :kx ﹣y ﹣2k +3=0与圆C 交于A ,B 两点,求|AB |的最小值.20.(12分)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的离心率e =√22,且椭圆C 经过点(1,√22).(1)求椭圆C 的标准方程;(2)过点P (2,0)且斜率不为零的直线与椭圆C 交于B ,D 两点,B 关于x 轴的对称点为A ,求证:直线AD 与x 轴交于定点Q .21.(12分)已知空间几何体ABCDEF ,底面ABCD 为菱形,∠DAB =60°,EF ∥AB ,AE =DE ,AB =2,EF =1,平面ADE ⊥平面ABCD ,BM →=13BF →,AN →=12AD →.(1)求证:EN ⊥BC ;(2)若直线AE 与平面ABCD 所成角为60°,求直线AM 与平面BCF 所成角的正弦值.22.(12分)已知椭圆T :x 24+y 2=1,F 1,F 2为椭圆的左右焦点,C ,D 为椭圆的左右顶点,直线l :y =12x +m 与椭圆T 交于A ,B 两点.(1)若m =−12,求|AB |;(2)设直线AD 和直线BC 的斜率分别为k 1,k 2,且直线l 与线段F 1F 2交于点M ,求k 1k 2的取值范围.2023-2024学年浙江省A9协作体高二(上)期中数学试卷参考答案与试题解析一、单项选择题:(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.椭圆x 236+y 29=1上的一点P 到椭圆一个焦点的距离为5,则点P 到另一个焦点的距离为( )A .7B .5C .4D .1解:椭圆x 236+y 29=1,所以a =6,2a =12,由椭圆的定义可知:椭圆上一点P 到椭圆的一个焦点的距离为5,则P 到另一个焦点的距离为:7. 故选:A .2.已知向量a →=(﹣3,2,1),b →=(2,x ,4),且a →⊥b →,则实数x 的值是( ) A .1B .2C .3D .4解:向量a →=(﹣3,2,1),b →=(2,x ,4),且a →⊥b →,则(﹣3)×2+2x +4=0,解得x =1. 故选:A .3.若直线l 的一个方向向量n →=(1,−√3),则l 的倾斜角为( ) A .30°B .60°C .120°D .150°解:由直线l 的方向向量可知直线的斜率k =−√31=−√3,设直线的倾斜角为α,0°≤α<180°, 即tan α=−√3,所以α=120°. 故选:C .4.已知圆C 1:x 2+y 2=1与圆C 2:(x +3)2+(y +4)2=16,则两圆的公切线条数为( ) A .1B .2C .3D .4解:圆C 1:x 2+y 2=1,其圆心坐标是(0,0),半径是1,圆C 2:(x +3)2+(y +4)2=16,其圆心坐标是(﹣3,﹣4),半径为4, C 1C 2=√(−3−0)2+(−4−0)2=5=4+1, ∴两个圆外切,所以圆C 1:x 2+y 2=1与圆C 2:(x +3)2+(y +4)2=16的公切线条数为3. 故选:C .5.若直线4x +3y ﹣12=0与两坐标轴的交点为A 、B ,则以AB 为直径的圆的方程为( ) A .x 2+y 2﹣3x ﹣4y =0B .x 2+y 2﹣4x ﹣3y =0C .x 2+y 2+3x +4y =0D .x 2+y 2+4x +3y =0解:直线4x +3y ﹣12=0与两坐标轴的交点为A 、B ,则A (3,0),B (0,4), 故|AB |=√(3−0)2+(0−4)2=5,以AB 为直径的圆的半径为52,点A ,B 的中点坐标为(32,2),故圆的方程为(x −32)2+(y −2)2=(52)2,化简整理可得,x 2+y 2﹣3x ﹣4y =0. 故选:A .6.正方体ABCD ﹣A 1B 1C 1D 1中,二面角A ﹣B 1D 1﹣A 1的余弦值为( ) A .√32B .√63C .√22D .√33解:取B 1D 1中点E ,连接A 1E ,AE ,由方体ABCD ﹣A 1B 1C 1D 1,可得A 1B 1=A 1D 1,AB 1=AD 1, ∴A 1E ⊥B 1D 1,AE ⊥B 1D 1,∴∠A 1EA 是二面角A ﹣B 1D 1﹣A 1的平面角, 设正方体ABCD ﹣A 1B 1C 1D 1的棱长为1, 则可得A 1E =√22,AE =√1+12=3√2,∴cos ∠A 1EA =A 1E AE =√22√32=√33. 故选:D .7.已知点F 为椭圆C :x 225+y 216=1的右焦点,点P 是椭圆C 上的动点,点Q 是圆M :(x +3)2+y 2=1上的动点,则|PF||PQ|的最小值是( )A .12B .29C .23D .83解:由椭圆的方程可得a =5,b =4,c =3, 设椭圆的左焦点F ',则|PF |=2a ﹣|PF '|=10﹣|PF '|, 由圆的方程可得圆心M 与F '重合,且半径为1,所以|PQ |=|PF '|+1, 所以|PF||PQ|=10−|PF′||PF′|+1=−(|PF′|+1)+11|PF′|+1=−1+11|PF′|+1,因为P 在椭圆上,所以a ﹣c ≤|PF '|≤a +c =5+3=8, 所以|PF||PQ|≥−1+118+1=29. 故选:B .8.如图,一束平行光线与地平面的夹角为60°,一直径为24cm 的篮球在这束光线的照射下,在地平面上形成的影子轮廓为椭圆,则此椭圆的离心率为( )A .√33B .√32C .√22D .12解:由题意如图所示:设BC =2b ,AB =2a ,∠CAB =60°, 即短轴长2b =24,长轴长2a =2b sin60°=4b 3,即a =2b3, 所以椭圆的离心率e =c a =√1−b 2a2=√1−34=12.故选:D .二、多项选择题:(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.直线l 经过点(2,﹣3),且在两坐标轴上的截距的绝对值相等,则直线l 的方程可能是( ) A .3x +2y =0B .2x +3y =0C .x ﹣y ﹣5=0D .x +y +1=0解:截距都为0时,即直线过原点,则直线的方程为y =−32x ,即3x +2y =0;当截距不为0时,且截距相等时,设直线的方程为x +y =a ,将点(2,﹣3)代入方程,可得2﹣3=a ,即a =﹣1,所以此时方程为x +y +1=0;当截距不为0时,且截距相反时,设直线的方程为x ﹣y =b ,将点(2,﹣3)代入方程,可得2﹣(﹣3)=b ,即b =5,所以此时方程为x ﹣y ﹣5=0. 故选:ACD .10.在空间直角坐标系Oxyz 中,点O (0,0,0),A (﹣2,﹣1,1),B (3,4,5),下列结论正确的有( ) A .|AB|=3√5B .向量OA →与OB →的夹角的余弦值为−√36C .点A 关于z 轴的对称点坐标为(﹣2,﹣1,﹣1)D .向量OA →在OB →上的投影向量为−110OB →解:点O (0,0,0),A (﹣2,﹣1,1),B (3,4,5), 则OA →=(﹣2,﹣1,1),OB →=(3,4,5),AB →=(5,5,4), |AB →|=√52+52+42=√66,故A 错误; cos <OA →,OB →>=OA →⋅OB →|OA →||OB →|=−5√6×5√2=−√36,故B 正确;点A 关于z 轴的对称点坐标为(2,1,1),故C 错误; OA →在OB →上的投影向量为:OA →⋅OB →|OB →|×OB →|OB →|=−550OB →=−110OB →,故D 正确.故选:BD .11.如图,在四棱锥S ﹣ABCD 中,底面ABCD 为正方形,AB =2,SD ⊥底面ABCD ,点E 、F 分别为SC 、AB 的中点,若线段SD 上存在点G ,使得GE ⊥GF ,则线段SD 的长度可能值为( )A .3B .4C .5D .6解:以D 为坐标原点,DA ,DC ,DS 为坐标轴建立如图所示的空间直角坐标系,设SD =2m (m >0),则F (2,1,0),E (0,1,m ),设G (0,0,x ),∴GE →=(0,1,m ﹣x ),GF →=(2,1,﹣x ),∵GE ⊥GF ,∴GE →•GF →=1﹣x (m ﹣x )=0, 即x 2﹣mx +1=0,因方程有解,∴Δ=m 2﹣4≥0,解得m ≥2,故SD ≥4. 故选:BCD .12.画法几何的创始人——法国数学家蒙日发现:在椭圆C :x 2a 2+y 2b 2=1(a >b >0)中,任意两条互相垂直的切线的交点都在同一个圆上,它的圆心是椭圆的中心,半径等于长、短半轴平方和的算术平方根,这个圆就称为椭圆C 的蒙日圆,其圆方程为x 2+y 2=a 2+b 2.已知椭圆C 的离心率为√63,点A ,B 均在椭圆C 上,直线l :bx +ay ﹣4=0,则下列描述正确的为( ) A .点A 与椭圆C 的蒙日圆上任意一点的距离最小值为bB .若l 上恰有一点P 满足:过P 作椭圆C 的两条切线互相垂直,则椭圆C 的方程为x 23+y 2=1C .若l 上任意一点Q 都满足QA →⋅QB →>0,则b >1D .若b =1,椭圆C 的蒙日圆上存在点M 满足MA ⊥MB ,则△AOB 面积的最大值为√32解:因为椭圆C 的离心率为√63, 所以e =ca =√63,① 又a 2=b 2+c 2,联立①②,可得a 2=3b 2,此时C 的蒙日圆方程为x 2+y 2=4b 2,对于选项A :因为原点O 到蒙日圆上任意一点的距离都为2b ,O 到椭圆上任意一点的距离最大值为a =√3b ,所以C 上任意一点A 与C 的蒙日圆上任意一点的距离最小值为(2−√3)b ,选项A 错误; 对于选项B :因为直线l 与蒙日圆:x 2+y 2=4b 2相切, 此时圆心O 到直线l 的距离d =4√a 2+b =42b=2b , 解得b =1, 则C 的方程为x 23+y 2=1,故选项B 正确;对于选项C :由蒙日圆的定义知,点Q 应在蒙日圆外, 所以直线l 与蒙日圆:x 2+y 2=4b 2相离, 此时圆心O 到直线l 的距离为d =4√a 2+b =42b >2b ,解得0<b <1,故选项C 错误;对于选项D :易知椭圆C 的方程为x 2+3y 2=3,蒙日圆方程为x 2+y 2=4, 不妨设M (x 0,y 0), 因为点M 在蒙日圆上,所以x 02+y 02=4,不妨设A (x 1,y 1),B (x 2,y 2),此时直线MA 的方程为x 1x +3y 1y =3,MB 的方程为x 2x +3y 2y =3, 将M (x 0,y 0)代入MA 、MB 方程中, 可得x 1x 0+3y 1y 0=3,x 2x 0+3y 2y 0=3, 所以直线AB 的方程为x 0x +3y 0y =3,联立{x 2+3y 2=3x 0x +3y 0y =3,消去y 并整理得(x 02+3y 02)x 2−6x 0x +(9−9y 02)=0,由韦达定理得x 1+x 2=6x 0x 02+3y 02,x 1x 2=9−9y 02x 02+3y 02, 所以|AB|=2(1+2y 02)2+y 02,因为原点O 到AB 的距离d ′=3√x 0+9y 0=3√0,所以S △AOB=12|AB|⋅d′=3√1+2y 022(2+y 02),不妨令t =√1+2y 02∈[1,3]此时S △AOB =3⋅t t 2+3=3⋅1t+3t, 因为t +3t ≥2√t ×3t=2√3, 所以S △AOB ≤√32,当且仅当t =3t ,即t =√3时,等号成立,故选项选项D 正确. 故选:BD .三、填空题:(本题共4小题,每小题5分,共20分.) 13.已知椭圆x 25+y 2k=1的一个焦点是(2,0),则k 的值为 1 .解:由椭圆的焦点坐标可知椭圆的焦点在x 轴上,所以a 2=5,b 2=k , 所以c 2=22=a 2﹣b 2=5﹣k ,解得k =1. 故答案为:1.14.已知实数x ,y 满足x ﹣2y +4=0,则√x 2+y 2的最小值为4√55. 解:因为x ﹣2y +4=0表示一条直线,√x 2+y 2表示直线上的点P (x ,y )到原点的距离, 所以√x 2+y 2的最小值是原点到直线的距离,即为d =|0−0+4|√1+(−2)=4√55.故答案为:4√55. 15.已知点A ,B 分别为圆M :(x +4)2+(y ﹣1)2=1与圆N :(x ﹣2)2+(y ﹣7)2=4上的动点,点P 为x 轴上的动点,则|P A |+|PB |的最小值为 7 .解:圆M :(x +4)2+(y ﹣1)2=1的圆心M (﹣4,1),半径r =1, 圆N :(x ﹣2)2+(y ﹣7)2=4的圆心N (2,7),半径r '=2,设M 关于x 轴的对称点M '(﹣4,﹣1),则|M 'N |=√(2+4)2+(7+1)2=10, 由题意A ,B 在两个圆上,所以|P A |+|PB |≥|M 'N |﹣r ﹣r '=10﹣r ﹣r '=10﹣1﹣2=7, 所以|P A |+|PB |的最小值为7. 故答案为:7.16.已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为2,E ,F 分别为AA 1,A 1D 1的中点,点P 在正方体表面上运动,若直线D 1P ∥平面BEF ,则点P 的轨迹长度为 2√5+3√2 . 解:根据题意,取CC 1的中点M ,BC 的中点N ,连接D 1M 、MN 、AN ,AD 1, 由于E ,F 分别为AA 1,A 1D 1的中点,则EF ∥AD 1, 又由M 、N 分别为CC 1、BC 的中点,则MN ∥AD 1, 则有EF ∥MN ,A 、D 1、M 、N 四点共面,又由E 为AA 1中点,M 为CC 1的中点,易得MD 1∥BE , 又由BE ⊂平面BEF ,且MD 1⊄平面BEF , 则得MD 1∥平面BEF ,又由EF ∥AD 1,EF ⊂平面BEF ,AD 1⫋平面BEF , 则AD 1∥平面BEF , AD 1∩MD 1=D 1,且AD 1⊂平面AD 1MN ,MD 1⊂平面AD 1MN 则有平面AD 1MN ∥平面BEF , 故P 的轨迹为梯形AD 1MN ,又由正方体ABCD ﹣A 1B 1C 1D 1的棱长为2,则AD 1=√4+4=2√2,MN =12AD 1=√2,AN =MD 1=√4+1=√5, 故点P 的轨迹长度为2√5+3√2. 故答案为:2√5+3√2.四、解答题:(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(10分)已知直线x ﹣y ﹣1=0和直线x +2y +2=0的交点为P . (1)求过点P 且与直线x ﹣2y +1=0平行的直线方程; (2)若点P 到直线l :mx +y +m =0距离为√2,求m 的值.解:(1)联立方程组{x −y −1=0x +2y +2=0,解得{x =0y =−1,所以点P (0,﹣1),又所求直线与直线x ﹣2y +1=0平行,设所求直线的的方程为:x ﹣2y +a =0, 将点P (0,﹣1)代入可得2+a =0,即a =﹣2, 则所求的直线方程x ﹣2y ﹣2=0; (2)点P 到l :mx +y +m =0的距离为d =|m⋅0+(−1)+m|√m 2+1=√2,解得m =﹣1. 即m 的值为1.18.(12分)如图,直三棱柱ABC ﹣A 1B 1C 1,AC =BC =CC 1=2,AC ⊥BC ,点M 是线段AB 的中点. (1)证明:平面MCC 1⊥平面ABB 1A 1. (2)求异面直线CA 与B 1M 所成角的余弦值.(1)证明:直三棱柱ABC ﹣A 1B 1C 1中,CC 1⊥平面ABC ,AB ⊂平面ABC ,∴AB ⊥CC 1, 又∵等腰Rt △ACB 中,点M 为AB 的中点,∴AB ⊥CM , 又∵CM ∩CC 1=C ,∴AB ⊥平面MCC 1, 又AB ⊂平面ABB 1A 1,∴平面MCC 1⊥平面ABB 1A 1;(2)解:取BC 中点N ,连结MN ,B 1N ,易知MN ∥CA , ∴∠B 1MN 即为异面直线CA 与B 1M 所成角,设为θ, 由题意可知MN =1,B 1N =√BB 12+(BC 2)2=√22+12=√5, B 1M =√BB 12+(AB2)2=√22+(2√22)2=√6, ∴由余弦定理可知cos θ=MN B 1M =16=√66.19.(12分)已知圆C :(x ﹣3)2+(y ﹣4)2=4.(1)若直线l 过定点A (1,0)且与圆C 相切,求直线l 的方程; (2)若直线l :kx ﹣y ﹣2k +3=0与圆C 交于A ,B 两点,求|AB |的最小值. 解:(1)C :(x ﹣3)2+(y ﹣4)2=4, 则圆心C (3,4),半径r =2,当直线斜率不存在时,直线l 的方程为x =1,满足题意. 当直线斜率存在时,设直线l :y =k (x ﹣1),即kx ﹣y ﹣k =0, 圆心C (3,4)到直线l 的距离为d =|3k−4−k|√k +1=2,得k =34,此时直线方程为34x −y −34=0,整理得3x ﹣4y ﹣3=0.所以直线l 的方程为3x ﹣4y ﹣3=0和x =1.(2)直线l 的方程可化为点斜式y ﹣3=k (x ﹣2),所以l 过定点P (2,3).又点P (2,3)在圆C 内,当直线l 与直线CP 垂直时,直线l 被圆截得的弦|AB |最小. 因为k CP =4−33−2=1,所以l 的斜率k =﹣1, 所以l 的方程为y ﹣3=﹣(x ﹣2),即x +y ﹣5=0, 因为|CP|=√(3−2)2+(4−3)2=√2,r =2, 此时|AB|=2√r 2−|CP|2=2√2 所以当k =﹣1时,|AB |的最小值为2√2. 20.(12分)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率e =√22,且椭圆C 经过点(1,√22).(1)求椭圆C 的标准方程;(2)过点P (2,0)且斜率不为零的直线与椭圆C 交于B ,D 两点,B 关于x 轴的对称点为A ,求证:直线AD 与x 轴交于定点Q .解:(1)由题意可得:{ e =ca =√22a 2=b 2+c 21a 2+12b 2=1,解得{a 2=2b 2=1,所以椭圆C 的方程为:x 22+y 2=1;证明:(2)设点B (x 1,y 1),D (x 2,y 2),则A (x 1,﹣y 1), 设直线PB 的方程为x =my +2,联立{x =my +2x 2+2y 2=2,整理可得(m 2+2)y 2+4my +2=0, 则y 1+y 2=−4m m 2+2,y 1y 2=2m 2+2,Δ=8m 2﹣16>0,得m 2>2, 由题意,直线AD 的方程为y =y 2+y 1x 2−x 1(x −x 2)+y 2, 令y =0,所以点Q 的横坐标x Q =x 1y 2+x 2y 1y 1+y 2=2my 1y 2y 1+y 2+2=1.所以直线AD 与x 轴交于定点Q (1,0).21.(12分)已知空间几何体ABCDEF ,底面ABCD 为菱形,∠DAB =60°,EF ∥AB ,AE =DE ,AB =2,EF =1,平面ADE ⊥平面ABCD ,BM →=13BF →,AN →=12AD →.(1)求证:EN ⊥BC ;(2)若直线AE 与平面ABCD 所成角为60°,求直线AM 与平面BCF 所成角的正弦值.(1)证明:∵AN →=12AD →,∴N 为AD 的中点, ∵AE =DE ,∴EN ⊥AD ,∵底面ABCD 为菱形,∴AD ∥BC , ∴EN ⊥BC ;(2)解:平面ADE ⊥平面ABCD ,平面ADE ∩平面ABCD =AD ,EN ⊥AD ,∴EN ⊥平面ABCD , ∴AE 与平面ABCD 所成角为∠EAN =60°,又AE =DE , 所以△ADE 为正三角形,故AE =DE =AD =2.以N 为坐标原点,分别以NA ,NB ,NE 为x ,y ,z 轴建立空间直角坐标系. A (1,0,0),B(0,√3,0),C(−2,√3,0),E(0,0,√3),F(−12,√32,√3),∵BM →=13BF →,∴可得M 点坐标为M(−16,5√36,√33) 所以AM →=(−76,5√36,√33), 设平面BCF 得法向量为n →=(x ,y ,z ),又BC →=(﹣2,0,0),BF →=(−12,−√32,√3), ∵{n →⋅BC →=0n →⋅BF →=0,即{2x =0−12x −√32y +√3z =0,可得n →=(0,2,1), 设直线AM 与平面BCF 所成角为θ,可得n →•AM →=−76×0+5√36×2+√33×1=2√3,|n →|=√02+22+12=√5,|AM →|=√4936+25×336+39=√343,∴sin θ=|cos <AM →,n →>|=|n →⋅AM→|n →|⋅|AM →||=2√35×√343=6√3√170=3√51085.22.(12分)已知椭圆T :x 24+y 2=1,F 1,F 2为椭圆的左右焦点,C ,D 为椭圆的左右顶点,直线l :y =12x +m 与椭圆T 交于A ,B 两点. (1)若m =−12,求|AB |;(2)设直线AD 和直线BC 的斜率分别为k 1,k 2,且直线l 与线段F 1F 2交于点M ,求k 1k 2的取值范围.解:(1)由椭圆的方程可得a =2,b =1,c =√3,则C (﹣2,0),D (2,0), 设A (x 1,y 1),B (x 2,y 2),联立{y =12x −12x24+y 2=1,整理可得:2x 2﹣2x ﹣3=0,Δ=(﹣2)2﹣4•2•(﹣3)=28>0,x 1+x 2=1,x 1x 2=−32,故弦长|AB |=√1+k 2•√(x 1+x 2)2−4x 1x 2=√1+14•√12−4×(−32)=√352; (2)联立直线l 与椭圆方程:{y =12x +m x24+y 2=1,整理可得:x 2+2mx +2m 2﹣2=0,Δ=4m 2﹣4(2m 2﹣2)>0,则m 2<2, 可得x 1+x 2=﹣2m ,x 1x 2=2m 2−2, 因为k 1k 2=y 1x 1−2y 2x 2+2=y 1(x 2+2)y 2(x 1−2)=(12x 1+m)(x 2+2)(12x 2+m)(x 1−2)=12x 1x 2+mx 2+x 1+2m 12x 1x 2+mx 1−x 2−2m , 将2m =﹣(x 1+x 2),x 1x 2=2m 2−2代入可得k 1k 2=m 2−1+(m−1)x 2m 2−1+(m+1)x 1=m−1m+1⋅m+1+x 2m−1+x 1,因为m ﹣1+x 2=﹣(m +1+x 1),所以k 1k 2=1−m 1+m,因为点M 在线段F 1F 2上,所以−2m ∈[−√3,√3],即m ∈[−√32,√32],代入k 1k 2=1−m 1+m,可得k 1k 2∈[7−4√3,7+4√3].。
浙江温州十校联合体2014届高三上学期期中联考理科数学试卷(解析版)

浙江温州十校联合体2014届高三上学期期中联考理科数学试卷(解析版)一、选择题1)A【答案】D 【解析】{0,1B =A . 考点:1.集合的运算;2.简单不等式的解法. 2是虚数单位),则 ( ) A ..1 D 【答案】B 【解析】试题分析:由已知(1i-纯虚数,A .考点:1.复数的概念;2.复数的运算.3三个命题中,假命题的个数是( )A.3 B .2 C .1 D .0 【答案】B 【解析】原命题为真命题,而互为逆否命题的两个命题同真同假,故它的逆否命题也为真命题.取它的否命题互为逆否命题,所以它的否命题也为假命题.故选B.考点:四种形式的命题(原命题、逆命题、否命题、逆否命题)及其真假关系.4 )A.3 B .4 C .6 D .8【答案】C . 【解析】 试题分析:由约束不等式组画图得可行域如图阴影区域,几何意义为直线的纵截距,由图可知,当直线最大值,此时( )A 【答案】D【解析】考点:一元二次不等式的解法.6 ( ) A a b ==B CD【答案】C . 【解析】 试题分析:a b ∴==,故A 正确;21b -=-()a b ∴+⊥Bcosa ab aa bb=⋅=⋅D 正确.对于C ,两向量的夹角范围为[]0,,πC 错误.综上所述选C . 考点:1.向量数量积的几何意义;2.向量的坐标运算.70.8450角,则)【答案】D .【解析】1)、图(2).图(1)图(2)1;当如图(2)位置时,在直角梯形中3)、图(4).图(3) 图(4)当如图(3)位置时,在中可求得(4)位置时,考点:1.空间线面角的计算;2.空间两点间距离.8( )ABCD【答案】B .【解析】B .考点:1.导数与函数的单调性;2.导数的几何意义.9值范围是( )A.【答案】D.【解析】试题分析:由已知得显然成故,从而A.B.C.D.【答案】B.【解析】有零点)A二、填空题11 . 【答案】5. 【解析】 065C -=. 考点:应用二项式定理求指定项的系数.12.程序框图(即算法流程图)如图所示,其输出结果是 .【答案】63.【解析】试题分析:输出63.考点:算法程序框图.13【答案】21.【解析】考点:1.等差数列的性质;214.A f为A到B的映射,f:x→x2,集合A有多少种不同情况.【答案】15.【解析】试题分析:由已知及映射的定义,可能是1对应1,11应2.故集合A考点:1.集合的定义;2.加法原理和乘法原理.15.向单位正交基底【解析】试题分析:由已知得解故考点:平面向量的数量积运算.16从左到右为P、Q、R,若PQ=3QR,则a【解析】知可得3X考点:1.三角函数的周期性;2.三角函数求值问题.17的取值范围为.【解析】18.已知定义域为R(1(2;(2)函数的单调递增区间为【解析】(2得函数的单调递增区间为考点:1.由三角函数的图像确定其解析式;2.三角恒等变换;3.三角函数的单调区间的求法.19.(14分)如图所示,机器人海宝按照以下程序运行○1从A出发到达点B或C或D,到达点B、C、D之一就停止;②每次只向右或向下按路线运行;④到达P时只向下,到达Q点只向右.(1)求海宝过点从A经过M到点B的概率,求海宝过点从A经过N到点C的概率;(2)记海宝到点B、C、D的事件分别记为X=1,X=2,X=3,求随机变量X的分布列及期望.【答案】(1)从A过M到B A过N到C【解析】试题分析:(1)从A过M到B,再有一次向下与一次向右组合,由乘法原理可得所求概率;同理从A过N到C,需要经过两次向下和两次向右的组合,由乘法原理可得所求概率为;(2)先分别求出;;量X的期望.(1)从A过M到B,先有两次向下,和有一次向下与一次向右组合其概率为从A过M到C(7分)(2) ;;;(14分)考点:1.独立重复试验型事件发生的概率的计算;2.离散型随机变量期望的计算.20足(1(2)若存在,请写出满足题意的其中一项;若不存在,请说明理由.【答案】(1)2)存在,的第5项.【解析】试题分析:(1为首项和公比均为(2)先假设存在,项满足题意,亦即,故2,因此只要取试题解析:(1(2分)当时,1,1n nb T-∴=两式相减得:,即:(6分)(8分)(2,取,则7(其它形如.(14分)考点:1.数列通项公式的求法;2.数列探究型问题的解法.21.已知椭圆C的中心为直角坐标系xOy的原点,焦点在s轴上,它的一个顶点到两个焦点的距离分别是7和1.(Ⅰ)求椭圆C的方程;(Ⅱ)若P为椭圆C上的动点,M为过P且垂直于xλ,求点M的轨迹方程,并说明轨迹是什么曲线.【答案】(Ⅰ)椭圆C的方程为;(Ⅱ)点M的轨迹方程为【解析】试题分析:(Ⅱ)由已知及点在椭圆上可得,整理得.注意到,令,得.需按M的轨迹为椭圆,这时需要注意试题解析:(Ⅰ)设椭圆长半轴长及半焦距分别为,由已知得(5分)(Ⅱ)其由已椭可得(7分)(i(9分)(ii分; (11分)(13分)当时,点的轨迹为中心在原点、长轴在轴上的椭圆. (15分)考点:1.椭圆方程的求法;2.轨迹方程的求法. 22(I(i(ii【答案】(I(Ⅱ)(i(ii )详见试题解析.【解析】试题分析:(I )首先求函数的定义域,再求的导数,令(Ⅱ)(i )先由已知条件,将问题转化(ii )先根据已知条试题解析:(I )解:函数的定义域为令时,(f x '(6分)(Ⅱ)(i∵在上恒成立,∴在上为减函数,∴实数的取值范围为(10分)(ii)证明:(12x x ∴+(15分)考点:1.导数与函数的单调性;2.利用导数求恒成立问题中的参数取值范围问题参数;3.利用导数证明不等式.。
浙江省温州市十校联合体2014-2015学年高二上学期期中联考化学试题

浙江省温州市十校联合体2014-2015学年高二上学期期中联考化学试题第Ⅰ卷(共50分)一、选择题(每小题只有一个正确答案,1-10题每题2分,11-20题每题3分,共50分)1.下列说法正确的是()A.热化学方程式中,如果没有注明温度和压强,表示反应热是在标准状况下测得的数据B.升高温度或加入催化剂,均可以改变化学反应的反应热C.据能量守恒定律,反应物的总能量一定等于生成物的总能量D.物质发生化学变化一定伴随着能量变化2.热化学方程式C(s)+H2O(g)CO(g)+H2(g);△H =+131.3kJ/mol表示()A.碳和水反应吸收131.3kJ能量B.1mol碳和1mol水反应生成一氧化碳和氢气,并吸收131.3kJ热量C.1mol固态碳和1mol水蒸气反应生成一氧化碳气体和氢气,并吸热131.3kJD.1个固态碳原子和1分子水蒸气反应吸热131.1kJ3. 下列说法正确的是()A.在铁片上镀铜时,若阴极增重3.2g,则电镀液中通过的电子的物质的量为0.1mol B.钢铁电化学腐蚀的两种类型主要区别在于水膜的PH不同,引起的负极反应不同C.参加反应的物质的性质是决定化学反应速率的重要因素D.电解饱和食盐水制烧碱采用离子交换膜法,可防止阴极区产生的Cl2进入阳极区4.工业上利用可逆反应N2(g)+3H2(g)⇌2NH3(g)合成氨,下列叙述正确的是()A.凡是放热反应都是自发的,因为吸热反应都是非自发的B.自发反应的的现象一定非常明显,非自发反应的熵一定减小C.常温下,反应C(s)+CO 2(g)2CO(g)不能自发进行,则该反应的ΔH>0D.反应2Mg(s)+CO2(g)=C(s)+2MgO(s)能自发进行,则该反应的ΔH>06.下列反应中符合图示能量变化的是()A.碳与二氧化碳化合成为一氧化碳 B.HCl分解为H2和Cl2C.Na与H2O反应 D.Ba(OH)2·8H2O和NH4Cl晶体混合反应7.下列说法或表示方法正确的是()A.催化剂能降低正反应的活化能,但不能改变逆反应的活化能B.在稀溶液中:H+(aq)+OH-(aq)=H2O(l);△H = –57.3kJ/mol,则含40.0 g NaOH的稀溶液与稀醋酸完全中和,放出小于57.3 kJ的热量C.由C(石墨)→C(金刚石);△H = +73 kJ/mol,可知金刚石比石墨稳定D.在101kPa时,2gH2完全燃烧生成液态水,放出285.8kJ热量,氢气燃烧的热化学方程式表示为:2H2(g)+O2(g)=2H2O(l);△H = –285.8kJ/mol8.恒温恒容,下列物理量不再发生变化时,不能说明A(s)+3B(g)2C(g)+D(g)已达平衡状态的()A.混合气体的压强 B.C的体积分数C.混合气体的密度 D.混合气体的平均相对分子质量9.下列有关化学反应速率的说法正确的是()A.用铁片和稀硫酸反应制取氢气时,改用98%的浓硫酸可以加快产生氢气的速率B.100mL2mol/L的盐酸跟锌片反应,加入适量的氯化钠溶液,反应速度减小C.SO2的催化氧化是一个放热的反应,所以升高温度,V逆加快,V正减慢D.对于CaCO3+2HCl===CaCl2+H2O+CO2↑不能用CaCO3的浓度变化来表示反应速率,但可用水的浓度变化来表示10.下列说法正确的是()A. 理论上任何放热的反应均能设计成为原电池B. 实验室研究反应条件对速率的影响,硫代硫酸钠稀溶液与稀硫酸反应Na2S2O3+H2SO4=S↓+SO2↑+Na2SO4+H2O,常根据产生气泡的快慢判断反应速率的快慢C. 恒温恒容,2molSO2(g)与1molO2(g)充分反应放出热量是aKJ,则该反应的热方程式是2SO2(g)+O2(g)2SO3(g) △H = -akJ/molD. 对于有气体参加的某放热反应,使用合适催化剂或增大压强(减小体积)均增加了单位体积内活化分子数目从而加快反应速率11. SF6是一种优良的绝缘气体,分子结构中只存在S-F键。
浙江省温州市十校联合体2014届高三上学期10月测试文科数学试卷(解析版)

浙江省温州市十校联合体2014届高三上学期10月测试文科数学试卷(解析版)一、选择题1.已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有 ( ) A.2个 B.4个 C.6个 D.8个【答案】B【解析】P.考点:1.集合的运算;2.集合的子集.2( ) A.0 B.1 C.2 D.3【答案】D【解析】考点:1.分段函数;2.指数、对数运算.3( )A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【答案】A【解析】成立的充分不必要条件.考点:1.充要条件;2.一元二次不等式解法.4( ) ABCD【答案】D【解析】.考点:三角函数图像变换.560 ( )【答案】C【解析】=.13考点:1.向量的模;2.数量积运算.6nA.18 B.20 C.21 D.22【答案】B【解析】考点:1.等差数列的通项,和式;2.等差数列性质(下标关系).7( )A B C D【答案】A【解析】试题分析:函)对称轴当考点:三角函数的对称轴.8k的取值范围是 ( )【答案】A 【解析】由此可知k考点:1.方程根与函数零点之间的关系;2.数形结合思想.9.若存在过点(1,0),【答案】A【解析】(1(2考点:1.导数的几何意义;2.切线的方程.10R上的奇函数,且当( )A.恒为负数B.恒为0 C.恒为正数D.可正可负【答案】C【解析】考点:1.函数的单调性;2.等差数列性质.二、填空题11【解析】考点:三角求值.12.在△A BC中,角A,B,C°,则角A=___.【解析】考点:1.解三角形;2.正弦定理.13___________.【解析】考点:利用导数求函数的最值.14.____.【解析】考点:1.函数零点;2.数形结合法的应用.BC=15, ,AB=2,AC=1,D是边BC____【解析】,所以试题分析:A C B C A C-考点:1.数量积运算;2.向量的线性表示.16则第60个数对是__________.【解析】试题分析:在平面直角坐标系中,将各点按顺序连线,如下图示:有(1,1)为第1项,(1,2)为第2项,(1,3)为第4项,…(1,11)为第56项,因此第60项为(5,7).考点:归纳推理17.【答案】0【解析】考点:1.“新定义”题型;2.数形结合思想.三、解答题18(1(2【答案】(2)证明详见解析.【解析】试题分析:(1)(2)通过数量积运算.试题解析:……7分(2)……14分考点:1.三点共线;2.数量积运算.19(1(2【答案】(2【解析】试题分析:(1)先利用二倍角公式化为一角一函数,再求单调区间;(2).试题解析:(1)4分分(2)分考点:1 函数的单调区间;2 三角化简求值20(1(2【答案】【解析】试题分析:(1(2试题解析:(1分分(2分分考点:1 数列的通项;2 数列的求和21(1(2值.(【答案】【解析】试题分析:(1)(2)试题解析:(1-5(2a,b。
浙江省温州市十校联合体2014届高三上学期期中联考数学(文)试题

一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. .已知集合2{|22},{|log (1)},M x x N x y x MN =-≤<==-则=( ▲ ) A .{|20}x x -≤<B .{|10}x x -<<C .{|12}x x <<D .{—2,0} 2. 复数31x i z i +=-(,x R i ∈是虚数单位)是实数,则x 的值为 (▲ )A .3B .-3C .0D 3.“a >b ”是“11a b<”的 ( ▲ ) A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件4.设,,αβγ是三个互不重合的平面,,m n 是两条不重合的直线,则下列命题中正确的是( ▲ )A .若,αββγ⊥⊥,则αγ⊥B .若//αβ,m β⊄,//m α,则//m βC .若αβ⊥,m α⊥,则//m βD .若//m α,//n β,αβ⊥,则m n ⊥5.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 ( ▲ )A .383cmB .343cmC .323cm D .313cm6.设n S 为等差数列{}n a 的前n 项和,8374,2S a a ==-,则9a = ( ▲ )A .6-B .4-C .2-D .27.设函数⎩⎨⎧<+≥+-=0,60,64)(2x x x x x x f ,则不等式)1()(f x f >的解集是 (▲ )A .),2()1,3(+∞⋃-B .),3()1,3(+∞⋃-C .),3()1,1(+∞⋃-D .)3,1()3,(⋃--∞8.已知向量(cos ,sin )a θθ=,向量(3,1)b =,则2a b -的最大值和最小值分别为(▲ )A. B .4,0 C .16,0 D.9. 已知抛物线x y 42=的焦点F 与双曲线12222=-b y a x 的一个焦点重合,它们在第一象限内的交点为T ,且TF 与x 轴垂直,则此双曲线的离心率为( ▲ )A . 23+B .2C .12+D .210.已知函数32()f x x ax bx c =+++有两个极值点12,x x ,若112()f x x x =<,则关于x 的方程23(())2()0f x af x b ++=的不同实根个数为 (▲ )A .3B .4C .5D .6 二、填空题(本大题共7小题,每小题4分,共28分) 11.已知函数23 (0)()log (0)x x f x x x ⎧≤=⎨>⎩则1[()]2f f = ▲ 12.若程序框图如图所示,则该程序运行后输出的值是▲13.袋中共有6个除了颜色外完全相同的球,其中有1个红球, 2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于 ▲14.若2222(0)a b c c +=≠,则直线0ax by c ++=被圆221x y +=所截得的弦长为 ▲ 。
浙江省温州市十校联合体2007-2008学年第一学期高三期末联考数学试题(文科)

浙江省温州市十校联合体2007-2008学年第一学期高三期末联考数学试卷(文科)第I 卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知集合{|A x = ||x ≤1},{|2B x =-≤x <12},则A B =( ) A 、{|2x -≤x ≤1} B 、{|1x -≤x <12}C 、{|2x -≤x <12}D 、{|2x -≤x <1-}2、已知等差数列{}n a 中,288a a +=,则该数列前9项和9S 等于 ( )A 、18B 、27C 、36D 、45 3、函数)0(12<-=x x y 的反函数为( )A 、)1(1<-=x x yB 、)1(1≤--=x x yC 、)1(1<--=x x yD 、)1(1≤-=x x y4、将2sin()36x y π=+的图象按向量(4a π=-,4)平移,则平移后所得图象的解析式为( ) A 、2sin()434x y π=++ B 、2sin()434x y π=--C 、2sin()4312x y π=-+D 、2sin()4312x y π=+-5、已知函数()f x 、()g x 定义在R 上,()()()h x f x g x =⋅,则“()f x 、()g x 均为奇函数”是“()h x 为偶函数”的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件 6、已知直线m 、n 及平面α,下列命题中的真命题是( ) A 、若m n ⊥,m α⊥,则n ∥α B 、若m ∥n ,m α⊥,则n ∥αC 、若m ∥α,n ∥α,则m ∥nD 、若m α⊥,n α⊥,则m ∥n7、若以连续掷两次骰子分别得到的点数m 、n 作为点P 的横、纵坐标,则点P 在直线5x y +=下方的概率是( )A 、13B 、14C 、16D 、1128、在231(3)2nx x-的展开式中含有常数项,则正整数n 的最小值是( )A 、4B 、5C 、6D 、79、函数|ln ||1|x y e x =--的图象大致是( )10、椭圆22221x y a b+=(a >b >0)的离心率为12e =,右焦点为F (c ,0),方程20ax bx c +-=的两个实根分别为1x ,2x ,则点12(,)P x x ( ) A 、必在圆222x y +=内 B 、必在圆222x y +=上 C 、必在圆222x y +=外D 、以上三种情形都有可能第II 卷(非选择题100分)二、填空题:本大题共7小题,每小题4分,共28分。
浙江省温州市十校联合体2015届高三上学期期中联考数学(理)试题 Word版含答案

2014学年第一学期十校联合体高三期中联考数 学(理) 试 卷(满分150分,考试时间:120分钟)第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合2{|20}A x x x =--<,{||1}B x x =<,则()A B =R ð( ) A.(1,2)B.(1,2]C.[1,2)D.[1,2]2.设x R ∈,则“1x <”是“2x ≠”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件 3.某几何体的三视图如图所示,且该几何体的体积是3, 则正视图中的x 的值是( ) A.2 B.92 C.32 D.34.设m n 、是两条不同的直线, αβ、是两个不同的平面,下列命题中错误的是( ) A.若m α⊥,//m n ,//n β,则αβ⊥ B.若αβ⊥,m α⊄,m β⊥,则//m α C.若m β⊥,m α⊂,则αβ⊥ D.若αβ⊥,m α⊂,n β⊂,则m n ⊥5.将函数π()2tan 36x f x ⎛⎫=+⎪⎝⎭的图象向左平移π4个单位,再向下平移1个单位,得到函数()g x 的图象,则()g x 的解析式为( )A.π()2tan()134x g x =+-B.π()2tan()134x g x =-+C.π()2tan()1312x g x =-+D.π()2tan()1312x g x =--6.设M (x 0,y 0)为抛物线C :x 2=8y 上一点,F 为抛物线C 的焦点,以F 为圆心,|FM |为半 径的圆和抛物线的准线相交,则y 0的取值范围是 ( ) A.(0,2) B.[0,2] C.(2,+∞) D.[2,+∞)7.设等差数列{}n a 的前n 项和为n S ,若675S S S >>,则满足01<+n n S S 的正整数n 的值为( )A.13B.12C.11D. 108.设函数()g x 是二次函数,2,||1(),||1x x f x x x ⎧≥=⎨<⎩,若函数[()]f g x 的值域是[0,)+∞,则函数(第3题图)正视图 侧视图x()g x 的值域是( )A.(,1][1,)-∞-+∞B.[0,)+∞C.(,1][0,)-∞-+∞D.[1,)+∞9.若X 是一个集合,τ是一个以X 的某些子集为元素的集合,且满足:①X 属于τ,φ属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X 上的一个拓扑.已知集合{}X a b c =,,,对于下面给出的四个集合τ: ①{{}{}{}}a c a b c τ=∅,,,,,; ②{{}{}{}{}}b c b c a b c τ=∅,,,,,,,; ③{{}{}{}}a a b a c τ=∅,,,,,; ④{{}{}{}{}}a c b c c a b c τ=∅,,,,,,,,. 其中是集合X 上的拓扑的集合τ的序号是( )A.①B.②C.②③D.②④10.设函数2()2,()ln 3x f x e x g x x x =+-=+-,若实数,a b 满足()()0f a g b ==,则( )A.()0()g a f b <<B.()0()f b g a <<C.0()()g a f b <<D.()()0f b g a <<第Ⅱ卷 (非选择题共100分)二、填空题(本大题共7小题,每小题4分,满分28分)11.已知函数,0,()ln ,0,x e x f x x x ⎧<=⎨>⎩则1[()]f f e =_______________.12.若点M (y x ,)为平面区域⎪⎩⎪⎨⎧≤≥++≥+-001012x y x y x 上的一个动点,则y x 2+的最大值是_______13.若数列{}n a 的前n 项和2133n n S a =+,则4a =___________14.已知cos sin 6⎛⎫-+ ⎪⎝⎭παα,则7sin 6⎛⎫+= ⎪⎝⎭πα .15.过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左焦点F 作圆x 2+y 2=a 24的切线,切点为E ,延长FE 交双曲线右支于点P ,若E 为PF 的中点,则双曲线的离心率为________.16.已知,a b 是单位向量,0a b =.若向量c 满足1,c a b c --=则的最大值是______ 17.函数{}()min 2f x x =-,其中{},min ,,a a ba b b a b≤⎧=⎨>⎩,若动直线y m =与函数()y f x =的图像有三个不同的交点,它们的横坐标分别为123,,x x x ,则123x x x ⋅⋅是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”______________三、解答题(本大题共5小题,满分72分。
浙江省温州十校联合体2015高三第一次适应性考试数学理

浙江省温州十校联合体2015高三第一次适应性考试数学理(完卷时间:120分钟, 满分:150分,本次考试不得使用计算器)一.选择题:本大题共10题,每小题5分,共50分.1. 若全集{}2,1,0,1-=U ,{}22<∈=x Z x A ,则=A C U ( )A.{}2B.{}2,0C.{}2,1-D.{}2,0,1-2.已知a ,b 是实数,则“||||||b a b a -=-”是“0>ab ”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件3.下列式子中成立的是 ( ) A .6log 4log4.04.0< B .5.34.301.101.1> C .3.03.04.35.3< D . 7log 6log 67< 4.在等差数列}{n a 中,有12876=++a a a ,则此数列的前13项之和为( ) A. 104 B.52 C .39 D .24 5.函数 2log 1()2xf x x x=--的图像为 ( )6.已知函数),cos()(),sin()(ππ+=-=x x g x x f 则下列结论中正确的是 ( )A .函数)()(x g x f y ⋅=的最小正周期为π2B .函数)()(x g x f y ⋅=的最大值为2C .将函数)(x f y =的图象向左平移2π单位后得)(x g y =的图象 D .将函数)(x f y =的图象向右平移2π单位后得)(x g y =的图象7. 已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数)sin(ϕω+=x y 图像的两条相邻的 对称轴,则ϕ= ( ) A.π4 B.π3 C.π2 D.3π48.在ABC ∆中,内角A,B,C 所对应的边分别为,,,c b a ,若,3,6)(22π=+-=C b a c则ABC ∆的面积为 ( ) A.3 B.239 C.233 D.33 9.已知等比数列}{n a 前n 项和为n S ,则下列一定成立的是 ( ) A .若03>a ,则02013<a B .若04>a ,则02014<a C .若03>a ,则02013>S D .若04>a ,则02014>S10.已知函数31,0()9,0x x f x xx x ⎧+>⎪=⎨⎪+≤⎩,若关于x 的方程()a x x f =+22有六个不同的实根, 则常数a 的取值范围是 ( ) A .(]2,8B .(]2,9C .()9,8D .(]8,9二.填空题:本大题共7小题,每小题4分,共28分 11.若函数xx x f 1)(+=,则)(x f 的定义域是 .12.已知等差数列{}n a 满足4,1231-==a a a ,则n a =_____________. 13.若31tan 1tan =-+αα,则=α2sin .14.已知平面向量()1,2a =, ()2,b m =-, 且//a b b = 15.数列{}n a 前n 项和为n S ,已知113a =,且对任意正整数,m n ,都有m n m n a a a +=⋅,若n S a <恒成立则实数a 的最小值为16.如图在平行四边形ABCD 中,已知8,5AB AD ==,3,2CP PD AP BP =⋅=, 则AB AD ⋅的值是17.具有性质)()1(x f xf -=-的函数,我们称其为满足“倒负”变换的函数,下列函数:(1)x x f 1)(-= (2)x x x f 1)(-=; (3);1)(x x x f += (4)⎪⎪⎩⎪⎪⎨⎧>-=<<=)1(1)1(0)10()(x xx x x x f ,其中不满足“倒负”变换的函数是 .三.解答题:本大题共5小题,共72分。
浙江温州2015届高三第一学期十校联合体期中联考数学(理)试卷

浙江温州2015届高三第一学期十校联合体期中联考数学(理)试卷(满分150分,考试时间:120分钟)第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合2{|20}A x x x =--<,{||1}B x x =<,则()A B =R ð( ) A.(1,2) B.(1,2] C.[1,2) D.[1,2]2.设x R ∈,则“1x <”是“2x ≠”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件 3.某几何体的三视图如图所示,且该几何体的体积是3, 则正视图中的x 的值是( ) A.2 B.92C.32D.34.设m n 、是两条不同的直线, αβ、是两个不同的平面,下列命题中错误的是( ) A.若m α⊥,//m n ,//n β,则αβ⊥ B.若αβ⊥,m α⊄,m β⊥,则//m α C.若m β⊥,m α⊂,则αβ⊥ D.若αβ⊥,m α⊂,n β⊂,则m n ⊥5.将函数π()2tan 36x f x ⎛⎫=+⎪⎝⎭的图象向左平移π4个单位,再向下平移1个单位,得到函数()g x 的图象,则()g x 的解析式为( )A.π()2tan()134x g x =+-B.π()2tan()134x g x =-+C.π()2tan()1312x g x =-+D.π()2tan()1312x g x =--6.设M (x 0,y 0)为抛物线C :x 2=8y 上一点,F 为抛物线C 的焦点,以F 为圆心,|FM |为半 径的圆和抛物线的准线相交,则y 0的取值范围是 ( ) A.(0,2) B.[0,2] C.(2,+∞) D.[2,+∞)7.设等差数列{}n a 的前n 项和为n S ,若675S S S >>,则满足01<+n n S S 的正整数n 的值为( ) A.13 B.12 C.11 D. 108.设函数()g x 是二次函数,2,||1(),||1x x f x x x ⎧≥=⎨<⎩,若函数[()]f g x 的值域是[0,)+∞,则函数()g x 的值域是(第3题图)正视图 侧视图x( )A.(,1][1,)-∞-+∞B.[0,)+∞C.(,1][0,)-∞-+∞D.[1,)+∞9.若X 是一个集合,τ是一个以X 的某些子集为元素的集合,且满足:①X 属于τ,φ属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X 上的一个拓扑.已知集合{}X a b c =,,,对于下面给出的四个集合τ:①{{}{}{}}a c a b c τ=∅,,,,,; ②{{}{}{}{}}b c b c a b c τ=∅,,,,,,,; ③{{}{}{}}a a b a c τ=∅,,,,,; ④{{}{}{}{}}a c b c c a b c τ=∅,,,,,,,,. 其中是集合X 上的拓扑的集合τ的序号是( )A.①B.②C.②③D.②④10.设函数2()2,()ln 3xf x e xg x x x =+-=+-,若实数,a b 满足()()0f a g b ==,则( ) A.()0()g a f b << B.()0()f b g a << C.0()()g a f b << D.()()0f b g a <<第Ⅱ卷 (非选择题共100分)二、填空题(本大题共7小题,每小题4分,满分28分)11.已知函数,0,()ln ,0,x e x f x x x ⎧<=⎨>⎩则1[()]f f e =_______________.12.若点M (y x ,)为平面区域⎪⎩⎪⎨⎧≤≥++≥+-001012x y x y x 上的一个动点,则y x 2+的最大值是_______13.若数列{}n a 的前n 项和2133n n S a =+,则4a =___________ 14.已知cos sin 6⎛⎫-+= ⎪⎝⎭παα,则7sin 6⎛⎫+= ⎪⎝⎭πα .15.过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左焦点F 作圆x 2+y 2=a 24的切线,切点为E ,延长FE 交双曲线右支于点P ,若E 为PF 的中点,则双曲线的离心率为________.16.已知,a b 是单位向量,0a b =.若向量c 满足1,c a b c --=则的最大值是______ 17.函数{}()min 2f x =-,其中{},min ,,a a ba b b a b≤⎧=⎨>⎩,若动直线y m =与函数()y f x =的图像有三个不同的交点,它们的横坐标分别为123,,x x x ,则123x x x ⋅⋅是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”______________三、解答题(本大题共5小题,满分72分。
2023-2024学年浙江省温州市十校联合体高一(上)期中数学试卷【答案版】

2023-2024学年浙江省温州市十校联合体高一(上)期中数学试卷一、选择题。
本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x |﹣1<x <1},B ={﹣1,0,1},则A ∩B =( ) A .{x |x <1}B .{0}C .{﹣1,0,1}D .{0,1}2.命题“∀x >0,x +1≥0“的否定是( ) A .∃x ≤0,x +1<0 B .∃x >0,x +1<0 C .∃x ≤0,x +1≥0D .∀x >0,x +1<03.已知定义在R 上的幂函数f (x ),则f (0)﹣f (1)=( ) A .0 B .﹣1 C .1D .不确定4.已知a =0.3﹣0.3,b =0.3﹣0.2,c =2﹣0.01,则下列正确的是( )A .c <b <aB .c <a <bC .b <a <cD .a <c <b5.对∀x ∈R ,恒有(a +b ﹣c )x +c =2成立,则a +b +c 的值为( ) A .1B .2C .4D .不能确定6.若“x 2﹣3x +2<0“是“x 2﹣(2a +1)x +a 2+a >0“的一个充分不必要条件,则a 的取值范围是( ) A .0<a <2B .a <0或a >2C .a ≤0或a ≥2D .1<a <27.已知x ,y 满足{3x −a =03x 2+2y 2+2a =0,则x 2+y 2的取值范围是( )A .[−94,92]B .[0,92]C .[−94,0]D .[0,4]8.如图,将边长为1的正方形ABCD 沿x 轴正向滚动,先以A 为中心顺时针旋转,当B 落在x 轴时,又以B 为中心顺时针旋转,如此下去,设顶点C 滚动时的曲线方程为y =f (x ),则下列说法错误的为( )A .f(1)=√2B .f (2023)=0C .f (x )=﹣x 2+4x ﹣3(2<x ≤3)D .f (x )在区间[2023,2025]单调递增二、选择题。
浙江省温州市十校联合体2023-2024学年高二下学期期中联考数学试题含答案

2023学年第二学期温州十校联合体期中联考高二年级数学学科试题(答案在最后)考生须知:1.本卷共4页满分150分,考试时间120分钟.2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.3.所有答案必须写在答题纸上,写在试卷上无效.4.考试结束后,只需上交答题纸.选择题部分一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}{}21,2,30A B x x mx ==+-=∣,若{}1A B ⋂=,则A B ⋃=()A.{}3,1,2- B.{}1,2 C.{}3,2- D.{}1,2,3【答案】A 【解析】【分析】由{}1A B ⋂=作出判断方程230x mx +-=有一个根是1,且2一定不是它的根,从而代入1x =,解得2m =,再解得{}1,3B =-,满足{}1A B ⋂=,从而可以计算出结果.【详解】因为{}1A B ⋂=,{}{}21,2,30A B xx mx ==+-=∣,所以方程230x mx +-=有一个根是1,且2一定不是它的根,则21130m +⋅-=,解得2m =,当2m =时,方程()()223310xx x x +-=+-=的根是1和3-,所以{}1,3B =-,满足{}1A B ⋂=,即{}{}{}1,21,31,2,3A B =-=- .故选:A.2.若函数1()(3)2xf x a a =-⋅是指数函数,则1()2f 的值为A.2B.-2C.-D.【答案】D【解析】【分析】根据指数函数的定义可得12a ﹣3=1,a >0,a ≠1,先求出函数解析式,将x 12=代入可得答案.【详解】解:∵函数f (x )=(12a ﹣3)•a x 是指数函数,∴12a ﹣3=1,a >0,a ≠1,解得a =8,∴f (x )=8x ,∴f (12)==,故选D .【点睛】本题主要考查了指数函数的定义:形如y =a x (a >0,a ≠1)的函数叫指数函数,属于考查基本概念.3.设复数51i 1iz -=+,则复数z 的共轭复数的虚部是()A.iB.i- C.1D.-1【答案】C 【解析】【分析】根据复数代数形式的除法运算化简复数z ,从而得到其共轭复数,再确定其虚部.【详解】因为()()()4251i 1i 1i 1ii 1i 1i 1i 1i i 1i z ----=====-++-⨯++,所以i z =,则复数z 的共轭复数的虚部是1.故选:C4.已知非负实数,x y 满足1x y +=,则111x y++的最小值为()A.73B.2C.95D.43【答案】B 【解析】【分析】依题意可得0x >且()12x y ++=,利用乘“1”法及基本不等式计算可得.【详解】因为非负实数,x y 满足1x y +=,显然0x ≠,则0x >,所以()12x y ++=,则()111111*********y x x y x y x y x y ⎛⎫⎛⎫+⎡⎤+=+++=++ ⎪ ⎪⎣⎦+++⎝⎭⎝⎭1222⎛≥+= ⎝,当且仅当11y xx y +=+,即1x =,0y =时取等号,所以111x y++的最小值为2.故选:B 5.已知π3sin 124θ⎛⎫-= ⎪⎝⎭,则πsin 23θ⎛⎫+= ⎪⎝⎭()A.716-B.18-C.18D.716【答案】B 【解析】【分析】利用诱导公式和二倍角公式求解值.【详解】2πππππ91sin 2sin 2cos212sin 1231221212168θθθθ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=-=--=-⨯- ⎪ ⎪ ⎪ ⎪⎢⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.故选:B6.已知正方形ABCD 的边长为2,若将正方形ABCD 沿对角线BD 折叠成三棱锥A BCD -则在折叠过程中,不可能出现()A.AB CD⊥ B.AC BD⊥ C.三棱锥A BCD -的体积为23D.平面ABD ⊥平面BCD【答案】A 【解析】【分析】根据题意,由线面垂直的性质定理即可判断AB ,由三棱锥的体积公式即可判断C ,由二面角的定义即可判断D.【详解】对于A ,若AB CD ⊥,因为BC CD ⊥,AB BC B CD ⋂=∴⊥面ABC ,所以CD AC ⊥,而2,2CD AD ==,即直角边长与斜边长相等,显然不对,故A 错;对于B ,取BD 中点O ,因为,AO BD CO BD ⊥⊥,AO CO O ⋂=所以BD ⊥面AOC ,所以BD AC ⊥,故B 对;对于C ,当折叠所成的二面角150o AOC ∠=时,顶点A 到底面BCD 的距离为2,此时1123323A BCD V Sh -==⨯⨯=,故C 对;对于D ,当沿对角线BD 折叠成直二面角时,有平面ABD ⊥平面CBD ,故D 对;故选:A7.一个袋子中装有大小相同的5个小球,其中有3个白球,2个黑球,从中无放回地取出3个小球,摸到一个白球记2分,摸到一个黑球记1分,则总得分ξ的数学期望等于()A.5分B.4.8分C.4.6分D.4.4分【答案】B 【解析】【分析】按白球的个数分类,然后换算成得分可能性,计算相应的概率,再用公式求出期望即可.【详解】设三个白球编号为1,2,3,黑球编号为4,5,i A 表示取到i 个白球,则1,2,3i =,所有取法为35A 60=种,则()1233231C C A 36010P A ==,()2133232C C A 3605P A ==,()333A 16010P A ==,ξ的可能取值为4,5,6,所以()331456 4.810510E ξ=⨯+⨯+⨯=,总得分ξ的数学期望等于4.8分,故选:B.8.已知1325321log 2,log 6,log 52x x x ===,则()A.123x x x <<B.132x x x << C.312x x x << D.321x x x <<【答案】A 【解析】【分析】先判断出11<x ,231,1x x >>,然后根据作差法结合基本不等式比较23,x x .【详解】由题意,133log 2log 31x =<=,255log 6log 51x =>=,32211log 5log 4122x =>=,由换底公式,32411ln 5ln 5log 5log 522ln 2ln 4x ====,()22354ln 4ln 6ln 5ln 6ln 5log 6log 5ln 5ln 4ln 5ln 4x x ⋅--=-=-=⋅,由于ln 4ln 6≠,根据基本不等式,()2222ln 4ln 6ln 24ln 25ln 4ln 6ln 5222+⎛⎫⎛⎫⎛⎫⋅<=<= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故230x x -<,即23x x <,于是123x x x <<.故选:A二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知向量()()1,1,1,2a b ==,则下列命题正确的是()A.+=a b B.向量a 在向量b 上的投影向量为36,55⎛⎫⎪⎝⎭C.//a bD.a b⊥【答案】AB 【解析】【分析】对于A :求得()2,3a b +=,结合模长公式分析判断;对于B :先求,a b b ⋅r r r ,结合投影向量的定义运算求解;对于C :根据向量平行的坐标表示分析判断;对于C :根据向量垂直的坐标表示分析判断.【详解】因为()()1,1,1,2a b ==,对于选项A :因为()2,3a b += ,所以a b +==r r ,故A 正确;对于选项B :因为3,a b b ⋅==r r r,所以向量a在向量b 上的投影向量为2336,555a b b b b ⎛⎫⋅⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭r r r r r ,故B 正确;对于选项C :因为1211⨯≠⨯,所以,a b不平行,故C 错误;对于选项D :因为111230⨯+⨯=≠,所以,a b不垂直,故D 错误;故选:AB.10.下列命题中正确的是()A.已知随机变量16,2X B ⎛⎫ ⎪⎝⎭,则()216D X -=B.已知随机变量()2,N ξμσ,若函数()(11)f x P x x ξ=-<<+为偶函数,则0μ=C.数据1,3,4,5,7,8,10第80百分位数是8D.样本甲中有m 件样品,其方差为21s ,样本乙中有n 件样品,其方差为22s ,则由甲乙组成的总体样本的方差为2212m n s s m n m n⋅+⋅++【答案】ABC 【解析】【分析】利用二项分布的方差公式及方差性质可判断A ,利用正态曲线的对称性可判断B ,根据百分位数的求法可判断C ,利用两组数据方差的特征可判断D.【详解】对于A ,因为16,2X B ⎛⎫~ ⎪⎝⎭,所以()1136222D X =⨯⨯=,()()2146D X D X -==,A 正确;对于B ,因为函数()(11)f x P x x ξ=-<<+为偶函数,所以()()f x f x -=,(11)(11)P x x P x x ξξ-<<+=--<<-+,所以区间()1,1x x -+和区间()1,1x x ---+是关于x μ=的对称区间,所以0μ=,B 正确;对于C ,因为780% 5.6⨯=,所以数据1,3,4,5,7,8,10第80百分位数是8,C 正确;对于D ,记样本甲,乙的平均数分别为,x y ,由甲乙组成的总体样本的平均数为ω,由甲乙组成的总体样本的方差为()()222212m n s x s y m n m n ωω⎡⎤⎡⎤⋅+-+⋅+-⎣⎦⎣⎦++,D 不正确.故选:ABC11.定义在R 上的函数()f x ,满足()()12f x f x +=,且当[)0,1x ∈时,()121f x x =--,则使得()4f x <在(],m ∞-上恒成立的m 可以是()A.1B.2C.94D.154【答案】ABC 【解析】【分析】根据题意,一步步转化到2[2,3)x +∈时,1[1,2)x +∈,则(2)2(1)4(1|21|)[0,4)f x f x x +=+=--∈,作函数()f x 的图象,结合图象可求出m 的最大值.【详解】由题意可知,如图所示当[0,1)x ∈时,122,12()12112,02x x f x x x x ⎧-≤<⎪⎪=--=⎨⎪≤<⎪⎩,即()[0,1]f x ∈;当1[1,2)x +∈时,[0,1)x ∈,故(1)2()2(1|21|)[0,2]f x f x x +==--∈;当2[2,3)x +∈时,1[1,2)x +∈,故(2)2(1)4(1|21|)[0,4]f x f x x +=+=--∈;令(2)4(1|21|)4f x x +=--=,解得0x =或12x =,所以22x +=或522x +=,所以m 的最大值为52.即52m ≤.故选:ABC.非选择题部分三、填空题:本大题共3小题,每小题5分,共15分.把答案填在题中的横线上.12.((5511+-=_______【答案】152【解析】【分析】利用二项式定理得到((55,11+-的展开式,求出相加得到答案.【详解】(2512350134555554551C C C C C C =++++++13045=+++,(((((((550123455555235141C C C C C C -+++++-=30451---=,故((55113045304515211+=++-++++=.故答案为:15213.一位射击运动员向一个目标射击二次,记事件=i A “第i 次命中目标”()()111,2,4i P A ==,()()()()1112,1,24i i i i i P A A P A P A A i ++===∣∣,则()2P A =______.【答案】516##0.3125【解析】【分析】根据条件概率公式及对立事件概率公式,全概率公式求解即可.【详解】由题意,()()221111()1122()42P A A P A A P A P A ===⨯=∣,所以12111()248P A A =⨯=.又()()2112112()()11()4P A A P A A P A A P A P A ===-∣,所以21113(14416P A A ⎛⎫=⨯-= ⎪⎝⎭,所以()22112135(()81616P A P A A P A A =+=+=.故答案为:51614.已知在三棱锥A BCD -中,,,8,6AB BD AC CD AB BD ⊥⊥==,点P 为三棱锥A BCD -外接球上一点,则三棱锥P ABD -的体积最大为______.【答案】40【解析】【分析】取AD 的中点O ,得到12OB OC AD ==,得出点O 为三棱锥A BCD -的外接球的球心,求得外接球的半径为12R AD =,结合点P 到平面ABD 的距离为R 时,此时P ABD -的体积最大,利用体积公式,即可求解.【详解】在三棱锥A BCD -中,由AB BD ⊥且8,6AB BD ==,可得10AD =,取AD 的中点O ,连接,OB OC ,因为AB BD ⊥,AC CD ⊥,可得12OB OC AD ==,所以点O 为三棱锥A BCD -的外接球的球心,其中AD 为外接球的直径,设外接球的半径为R ,可得152R AD ==,当点P 到平面ABD 的距离为R 时,此时三棱锥P ABD -的体积最大,体积的最大值为1111865403232V AB BD R =⨯⋅⨯=⨯⨯⨯⨯=.故答案为:40.四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且8a b c ++=(1)若2,3b c ==,求cos A 的值;(2)若sin sin 3sin C B A +=,且ABC 的面积为9sin 2S A =,求b 和c 的值.【答案】(1)1cos 3A =(2)3==b c 【解析】【分析】(1)利用余弦定理计算可得;(2)利用正弦定理将角化边得到3b c a +=,从而得到6b c +=,再由面积公式求出bc ,解得即可.【小问1详解】因为8a b c ++=,2,3b c ==,所以3a =,所以2222222331cos 22233b c a A bc +-+-===⨯⨯;【小问2详解】由sin sin 3sin C B A +=,由正弦定理得3b c a +=,又8a b c ++=,所以6b c +=,又91sin sin 22S A bc A ==,因为()0,πA ∈,所以sin 0A >,所以9bc =,解得3==b c (负值已舍去).16.已知四棱锥S ABCD -,SA ⊥面ABCD ,底面ABCD 为正方形,SA AB =,E 为SD 的中点.(1)求证:⊥AE 面SCD ;(2)求直线BS 与面SCD 所成的角.【答案】(1)证明见解析(2)30°【解析】【分析】(1)由线面垂直得到SA ⊥CD ,结合AD ⊥CD ,得到线面垂直,CD ⊥AE ,结合三线合一得到的AE SD ⊥,证明出线面垂直;(2)方法1:证明线面平行,得到点B 到面SCD 的距离就是点A 到面SCD 距离,且结合(1)得点A 到面SCD 距离为1122AE SD SB ==.从而求出直线BS 与面SCD 所成角的正弦值,得到答案;方法2:利用等体积法求出点B 到面SCD 的距离,进而得到直线BS 与面SCD 所成角的正弦值,得到答案;方法3:建立空间直角坐标系,求出平面SCD 的法向量,利用空间向量夹角的余弦值得到线面角的正弦值,得到答案:方法4:作出辅助线,并得到BF ⊥面SCD ,故BSF ∠为直线BS 与面SCD 所成的角,记为θ,根据边长关系得到1sin 2BF BS θ==,求出答案.【小问1详解】因为SA ⊥面ABCD ,CD ⊂平面ABCD ,所以SA ⊥CD ,因为四边形ABCD 为正方形,所以AD ⊥CD ,又SA AD A = ,,SA AD ⊂平面SAD ,故CD ⊥平面SAD ,因为AE ⊂平面SAD ,所以CD ⊥AE ,又SA AB =,故SA AD =,因为E 为SD 的中点,所以AE SD ⊥,因为CD SD D = ,,CD SD ⊂平面SCD ,故⊥AE 平面SCD ;【小问2详解】方法1:因为//AB CD ,AB ⊄平面SCD ,CD ⊂平面SCD ,所以//AB 平面SCD ,点B 到面SCD 的距离就是点A 到面SCD 距离,由勾股定理得SB SD ==,又SA AD =,由(1)得点A 到面SCD 距离为1122AE SD SB ==.记直线BS 与面SCD 所成角为θ,故1sin 2AE BS θ==,故30θ=︒;方法2:设1AB =,则1AD SA ==,SD ==故111113326S BCD BCD V S AS -=⋅=⨯⨯= ,且1121222SCD S CD SD =⋅=⨯= ,因为16B SCD S BCD V V --==,所以121366SCD S h h ⋅⋅== ,2h ∴=,记直线BS 与面SCD 所成角为θ,1sin 2h BS θ==,30θ∴= ;方法3:设2AB AD AS ===,以AB 为x 轴,AD 为y 轴,AS 为z 轴建立直角坐标系,()()()()()0,0,0,2,0,0,2,2,0,0,2,0,0,0,2A B C D S ,故()2,0,0CD =- ,()0,2,2SD =- ,设平面SCD 的法向量为(),,n x y z =,则()()()(),,2,0,020,,0,2,2220n CD x y z x n SD x y z y z ⎧⋅=⋅-=-=⎪⎨⋅=⋅-=-=⎪⎩ ,解得0x =,令1y =,则1z =,故()0,1,1n =,记直线BS 与面SCD 所成角为θ,1sin cos 2n BS n BSθα⋅===⋅ ,30θ∴=︒.方法4:将四棱锥还原为立方体,取TC 的中点F ,连接,,BF SF EF ,因为EF AB =且//EF AB ,故四边形ABFE 为平行四边形,故//BF AE ,由(1)知,⊥AE 平面SCD ,故BF ⊥面SCD ,BSF ∴∠为直线BS 与面SCD 所成的角,记为θ,且1122BF TC SB ==,故1sin 2BF BS θ==,30θ∴=︒.17.已知()2cos cos (0)f x x x x ωωωω=->的最小正周期为π,(1)求2π3⎛⎫ ⎪⎝⎭f 的值;(2)若()()12g x f x =+在()0,m 上恰有2个极值点和2个零点,求实数m 的取值范围.【答案】(1)1-(2)513π,π612⎛⎤ ⎥⎝⎦【解析】【分析】(1)利用二倍角公式及两角差的正弦公式化简,再结合周期求出ω,即可得到函数解析式,再代入计算可得;(2)首先得到()g x 解析式,再根据x 的范围求出π26x -的范围,最后根据正弦函数的性质得到3ππ22π26m <-≤,解得即可.【小问1详解】因为()2cos cos f x x x x ωωω=-11π1sin2cos2sin 222262x x x ωωω⎛⎫=--=-- ⎪⎝⎭,由函数()f x 的最小正周期为π且0ω>,即2ππ2ω=,解得1ω=,所以()1sin 262πf x x ⎛⎫=-- ⎪⎝⎭,所以24ππ1π1π1πsin sin πsin 133626262f ⎛⎫⎛⎫⎛⎫=--=+-=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.【小问2详解】由(1)可得()()πsin 2612g x x f x ⎛⎫==- ⎝+⎪⎭,因为()0,x m ∈,所以πππ2,2666x m ⎛⎫-∈-- ⎪⎝⎭,要使()g x 在()0,m 上恰有2个极值点和2个零点,则需3ππ22π26m <-≤,解得513ππ612m <≤,即实数m 的取值范围513π,π612⎛⎤ ⎥⎝⎦.18.为了了解高中学生课后自主学习数学时间(x 分钟/每天)和他们的数学成绩(y 分)的关系,某实验小组做了调查,得到一些数据(表一).编号12345学习时间x3040506070数学成绩y 65788599108(1)求数学成绩y 与学习时间x 的相关系数(精确到0.001);(2)请用相关系数说明该组数据中y 与x 之间的关系可用线性回归模型进行拟合,并求出y 关于x 的回归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据:555211122820,435,38999i i i i i i i x yy y ======∑∑∑,2107.411540,i x ≈的方差为200);(3)基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计,得到22⨯列联表(表二).依据表中数据及小概率值0.001α=的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.没有进步有进步合计参与周末在校自主学习35130165未参与周末不在校自主学习253055合计60160220附:()()()12221,ˆˆˆn n i ii i n i i n n i i n i i x x y y x y nxyb a y xb x x x nx ====---===--∑∑∑∑,()()nn i i i i x x y y x y nxy r ---=∑∑()()()()22()n ad bc a b c d a c b d χ-=++++.α0.100.050.0100.0050.001αχ 2.706 3.841 6.6357.87910.828【答案】(1)0.996(2)ˆ1.0733.5y x =+,140.5分(3)可以认为“周末自主学习与成绩进步”有关【解析】【分析】(1)根据公式计算即可;(2)利用最小二乘法求出回归方程,再令100x =即可得解;(3)根据公式求出2χ,再对照临界值表即可得解.【小问1详解】3040506070505x ++++==,435875y ==,又()1,2,3,,5i x i = 的方差为()52112005i i x x =-=∑,10700.9961074r ==≈;【小问2详解】由(1)知0.996r =接近1,故与之间具有极强的线性相关关系,可用线性回归直线方程模型进行拟合,5152222222152282055087ˆ 1.0730405060705505i i i i i x y x y b x x ==--⨯⨯===++++-⨯-∑∑, 87 1.075033.5ay bx =-=-⨯= ,故 1.0733.5y x =+,当100x =时, 140.5y =,故预测每天课后自主学习数学时间达到100分钟时的数学成绩为140.5分;【小问3详解】零假设为0H :学生周末在校自主学习与成绩进步无关.根据数据,计算得到:22220(251303530)11012.2216555601609χ⨯⨯-⨯==≈⨯⨯⨯因为12.2210.828>,所以依据0.001α=的独立性检验,可以认为“周末自主学习与成绩进步”有关.19.已知()()2,0f x x a x a a =-->(1)当1a =时,解关于x 的不等式()0f x <;(2)若()()g x f x a =+有两个零点12,x x ,求12x x -的值;(3)当[]1,1x ∈-时,()f x 的最大值M ,最小值为m ,若4M m -≤,求a 的取值范围.【答案】(1)()(),11,2-∞(2)12x x -=(3)30,4⎛- ⎝⎦.【解析】【分析】(1)将1a =代入,然后取消绝对值解不等式即可;(2)先根据题意取消绝对值,然后判断()g x 的单调性,由()0g a a =>,()()g x f x a =+有两个零点12,x x 可得302g a ⎛⎫= ⎪⎝⎭,进而求a 的值,从而利用()0g x =求12,x x 即可.(3)先取消绝对值写出单调性,易得()()20f a f a ==,()()3102a f f f ⎛⎫-<< ⎪⎝⎭,然后对1111,,22a a a ≤<>≥进行分类,分别求最大值M 和最小值为m 的值,从而由4M m -≤解不等式可得实数a 的取值范围.【小问1详解】当1a =时,()()()()()12,1,12, 1.x x x f x x x x ⎧--≥⎪=⎨---<⎪⎩()()1201x x x ⎧--<⎨≥⎩或()()1201x x x ⎧---<⎨<⎩,所以1x <或12x <<于是不等式()0f x <的解集为()(),11,2-∞ .【小问2详解】()()()()()2,2,x a x a a x a g x x a x a a x a ⎧--+≥⎪=⎨---+<⎪⎩,当x a ≥时,()2232g x x ax a a =-++的对称轴为32a x a =>,所以()g x 在3,2a a ⎡⎤⎢⎥⎣⎦单调递减,在3,2a ⎡⎤+∞⎢⎥⎣⎦上单调递增;当x a <时,()2232g x x ax a a =-+-+的对称轴为32a x a =>,所以()g x 在[],a -∞单调递增;综上所述,()g x 在[],a -∞上单调递增,在3,2a a ⎡⎤⎢⎥⎣⎦上单调递减,在3,2a ⎡⎤+∞⎢⎥⎣⎦上单调递增,又因为()0g a a =>,()()g x f x a =+有两个零点12,x x ,所以302g a ⎛⎫= ⎪⎝⎭,即204a a -+=又0a >,得4a =.于是()221236,41228,4x x x g x x x x ⎧--≥=⎨-+-<⎩,由()0g x =,解得16x =-,26x =,所以12x x -=.【小问3详解】()(2),()()(2),x a x a x a f x x a x a x a --≥⎧=⎨---<⎩,当0a >时,()f x 在(,]a -∞递增,在3,2a a ⎡⎤⎢⎥⎣⎦递减,在3,2a ⎛⎫+∞ ⎪⎝⎭递增,()(2)0f a f a ==,当1a ≥时,()f x 在[1,1]-上递增,所以(1)(1)(21)M f a a ==---,(1)(21)m a a =-++,由4M m -≤,得64a ≤,不满足1a ≥,当12a a <≤,即112a ≤<时,223(0)2,()24a f a f a =-=-,则3(0)()2f f a <,所以3(1)(0)()2f f f a -<<,则()0M f a ==,(1)(1)(21)m f a a =-=-++,由4M m -≤,得(1)(21)4a a ++≤,则22330a a +-≤,得33,44a ⎡---+∈⎢⎣⎦,所以133324a -+≤≤,当021a <<,即102a <<时,由223(0)2,()24a f a f a =-=-,则3(0)()2f f a <,所以3(1)(0)()2f f f a -<<,所以(1)(1)(21)M f a a ==--,(1)(1)(21)m f a a =-=-++,由4M m -≤,得2424a +≤,得2222a ⎡∈-⎢⎣⎦,所以102a <<,综上,a 的取值范围为3330,4⎛⎤ ⎥ ⎝⎦【点睛】关键点点睛:本题第(3)问解题的关键是先求出()f x 的单调性,再由()(2)0f a f a ==,分分1a ≥,12a a <≤和021a <<三种情况求出()f x 的最值,再由4M m -≤可求出a 的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年浙江省温州市十校联合体高三(上)期中数学试卷(理科)一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合A={x|x2﹣x﹣2<0},B={x||x|<1},则A∩(∁R B)=()A.(1,2) B.(1,2]C.[1,2) D.[1,2]2.(5分)设x∈R,则“x<1”是“x≠2”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件3.(5分)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是()A.2 B.C.D.34.(5分)设m、n是两条不同的直线,α、β是两个不同的平面,下列命题中错误的是()A.若m⊥α,m∥n,n∥β,则α⊥βB.若α⊥β,m⊄α,m⊥β,则m∥αC.若m⊥β,m⊂α,则α⊥βD.若α⊥β,m⊂α,n⊂β,则m⊥n5.(5分)将函数f(x)=2tan()的图象向左平移个单位,再向下平移1个单位,得到函数g(x)的图象,则g(x)的解析式为()A.g(x)=2tan(+)﹣1 B.g(x)=2tan(﹣)+1C.g(x)=2tan(﹣)+1 D.g(x)=2tan(﹣)﹣16.(5分)设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是()A.(0,2) B.[0,2]C.(2,+∞)D.[2,+∞)7.(5分)设等差数列{a n}的前n项和为S n,若S6>S7>S5,则满足S n•S n+1<0的正整数n的值为()A.10 B.11 C.12 D.138.(5分)设函数g(x)是二次函数,f(x)=,若函数f[g(x)]的值域是[0,+∞),则函数g(x)的值域是()A.(﹣∞,﹣1]∪[1,+∞)B.[0,+∞)C.(﹣∞,﹣1]∪[0,+∞)D.[1,+∞)9.(5分)若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:①X属于τ,ϕ属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X={a,b,c},对于下面给出的四个集合τ:①τ={∅,{a},{c},{a,b,c}};②τ={∅,{b},{c},{b,c},{a,b,c}};③τ={∅,{a},{a,b},{a,c}};④τ={∅,{a,c},{b,c},{c},{a,b,c}}.其中是集合X上的拓扑的集合τ的序号是()A.①B.②C.②③D.②④10.(5分)设函数f(x)=e x+x﹣2,g(x)=lnx+x2﹣3.若实数a,b满足f(a)=0,g(b)=0,则()A.g(a)<0<f(b)B.f(b)<0<g(a)C.0<g(a)<f(b)D.f(b)<g(a)<0二、填空题(本大题共7小题,每小题4分,满分28分)11.(4分)已知函数f(x)=,则f[f()]=.12.(4分)若点M(x,y)为平面区域上的一个动点,则x+2y的最大值是.13.(4分)若数列{a n}的前n项和S n=a n+,则a4=.14.(4分)已知,则=.15.(4分)过双曲线=1(a>0,b>0)的左焦点F(﹣c,0)(c>0),作圆x2+y2=的切线,切点为E,延长FE交双曲线右支于点P,若,则双曲线的离心率为.16.(4分)已知•是单位向量,•=0.若向量满足|﹣﹣|=1,则||的最大值是.17.(4分)(理)函数f(x)=min{2,|x﹣2|},其中min{a,b}=,若动直线y=m与函数y=f(x)的图象有三个不同的交点,它们的横坐标分别为x1,x2,x3,则x1•x2•x3是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”.三、解答题(本大题共5小题,满分72分.解答应写出文字说明、证明过程或演算步骤)18.(14分)已知函数f(x)=sin cos+cos2.(Ⅰ)求该函数图象的对称轴;(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b2=ac,求f (B)的取值范围.19.(14分)已知等差数列{a n}的各项均为正数,a1=3,a3=7,其前n项和为S n,{b n}为等比数列,b1=2,且b2S2=32.(Ⅰ)求a n与b n;(Ⅱ)若++…+≤x2+ax+1对任意正整数n和任意x∈R恒成立,求实数a 的取值范围.20.(14分)如图,已知四棱锥P﹣ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.(1)证明:AE⊥PD;(2)若PA=AB=2,求二面角E﹣AF﹣C的余弦值.21.(15分)已知椭圆E:+=1(a>b>0)的离心率e=,并且经过定点P(,).(Ⅰ)求椭圆E的方程;(Ⅱ)设A,B为椭圆E的左右顶点,P为直线l:x=4上的一动点(点P不在x 轴上),连AP交椭圆于C点,连PB并延长交椭圆于D点,试问是否存在λ,使=λS△BCD成立,若存在,求出λ的值;若不存在,说明理由.得S△ACD22.(15分)已知函数f(x)=﹣x2+2|x﹣a|.(Ⅰ)若函数y=f(x)为偶函数,求a的值;(Ⅱ)若,求函数y=f(x)的单调递增区间;(Ⅲ)当a>0时,若对任意的x∈[0,+∞),不等式f(x﹣1)≥2f(x)恒成立,求实数a的取值范围.2014-2015学年浙江省温州市十校联合体高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合A={x|x2﹣x﹣2<0},B={x||x|<1},则A∩(∁R B)=()A.(1,2) B.(1,2]C.[1,2) D.[1,2]【解答】解:由A中不等式变形得:(x﹣2)(x+1)<0,解得:﹣1<x<2,即A=(﹣1,2);由B中方程解得:﹣1<x<1,即B=(﹣1,1),∵全集为R,∴∁R B=(﹣∞,﹣1]∪[1,+∞),则A∩(∁R B)=[1,2),故选:C.2.(5分)设x∈R,则“x<1”是“x≠2”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件【解答】解:若“x<1”则“x≠2”成立,即充分性成立,若x=3满足“x≠2”,但x<1不成立,即必要性不成立,故“x<1”是“x≠2”的充分不必要条件,故选:A.3.(5分)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是()A.2 B.C.D.3【解答】解:根据三视图判断几何体为四棱锥,其直观图是:V==3⇒x=3.故选:D.4.(5分)设m、n是两条不同的直线,α、β是两个不同的平面,下列命题中错误的是()A.若m⊥α,m∥n,n∥β,则α⊥βB.若α⊥β,m⊄α,m⊥β,则m∥αC.若m⊥β,m⊂α,则α⊥βD.若α⊥β,m⊂α,n⊂β,则m⊥n【解答】解:若m⊥α,m∥n,n∥β,则由平面与平面垂直的判定定理得α⊥β,故A正确;若α⊥β,m⊄α,m⊥β,则由直线与平面平行的判定定理得m∥α,故B正确;若m⊥β,m⊂α,则由平面与平面垂直的判定定理得α⊥β,故C正确;若α⊥β,m⊂α,n⊂β,则m与n相交、平行或异面,故D错误.故选:D.5.(5分)将函数f(x)=2tan()的图象向左平移个单位,再向下平移1个单位,得到函数g(x)的图象,则g(x)的解析式为()A.g(x)=2tan(+)﹣1 B.g(x)=2tan(﹣)+1C.g(x)=2tan(﹣)+1 D.g(x)=2tan(﹣)﹣1【解答】解:将函数f(x)=2tan()的图象向左平移个单位,得=,再向下平移1个单位,得到函数g(x)=﹣1的图象,所以g(x)的解析式为g(x)=2tan(+)﹣1.故选:A.6.(5分)设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是()A.(0,2) B.[0,2]C.(2,+∞)D.[2,+∞)【解答】解:由条件|FM|>4,由抛物线的定义|FM|=y0+2>4,所以y0>2故选:C.7.(5分)设等差数列{a n}的前n项和为S n,若S6>S7>S5,则满足S n•S n+1<0的正整数n的值为()A.10 B.11 C.12 D.13【解答】解:∵S6>S7>S5,∴,∴a7<0,a6+a7>0.∴,=6(a6+a7)>0.∴满足S n•S n+1<0的正整数n的值为12.故选:C.8.(5分)设函数g(x)是二次函数,f(x)=,若函数f[g(x)]的值域是[0,+∞),则函数g(x)的值域是()A.(﹣∞,﹣1]∪[1,+∞)B.[0,+∞)C.(﹣∞,﹣1]∪[0,+∞)D.[1,+∞)【解答】解:∵f(x)=,又∵函数f[g(x)]的值域是[0,+∞),∴g(x)∈(﹣∞,﹣1]∪[0,+∞),又∵函数g(x)是二次函数,∴﹣∞与+∞不可能同时存在,故排除A、C;又∵要取到0;故选:B.9.(5分)若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:①X属于τ,ϕ属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X={a,b,c},对于下面给出的四个集合τ:①τ={∅,{a},{c},{a,b,c}};②τ={∅,{b},{c},{b,c},{a,b,c}};③τ={∅,{a},{a,b},{a,c}};④τ={∅,{a,c},{b,c},{c},{a,b,c}}.其中是集合X上的拓扑的集合τ的序号是()A.①B.②C.②③D.②④【解答】解:①τ={∅,{a},{c},{a,b,c}};而{a}∪{c}={a,c}∉τ,故①不是集合X上的拓扑的集合τ;②τ={∅,{b},{c},{b,c},{a,b,c}},满足:①X属于τ,∅属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ因此②是集合X上的拓扑的集合τ;③τ={∅,{a},{a,b},{a,c}};而{a,b}∪{a,c}={a,b,c}∉τ,故③不是集合X上的拓扑的集合τ;④τ={∅,{a,c},{b,c},{c},{a,b,c}}.满足:①X属于τ,∅属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ因此④是集合X上的拓扑的集合τ;故选:D.10.(5分)设函数f(x)=e x+x﹣2,g(x)=lnx+x2﹣3.若实数a,b满足f(a)=0,g(b)=0,则()A.g(a)<0<f(b)B.f(b)<0<g(a)C.0<g(a)<f(b)D.f(b)<g(a)<0【解答】解:①由于y=e x及y=x﹣2关于x是单调递增函数,∴函数f(x)=e x+x ﹣2在R上单调递增,分别作出y=e x,y=2﹣x的图象,∵f(0)=1+0﹣2<0,f(1)=e﹣1>0,f(a)=0,∴0<a<1.同理g(x)=lnx+x2﹣3在R+上单调递增,g(1)=ln1+1﹣3=﹣2<0,g()=,g(b)=0,∴.∴g(a)=lna+a2﹣3<g(1)=ln1+1﹣3=﹣2<0,f(b)=e b+b﹣2>f(1)=e+1﹣2=e﹣1>0.∴g(a)<0<f(b).故选:A.二、填空题(本大题共7小题,每小题4分,满分28分)11.(4分)已知函数f(x)=,则f[f()]=.【解答】解:∵函数f(x)=,∴f()=ln=﹣1,∴f[f()]=f(﹣1)=e﹣1=.故答案为:.12.(4分)若点M(x,y)为平面区域上的一个动点,则x+2y的最大值是1.【解答】解:作出不等式对应的平面区域,设z=x+2y,得y=﹣,平移直线y=﹣,由图象可知当直线y=﹣经过点A时,直线y=﹣的截距最大,此时z最大.由,得,即A(0,),此时z的最大值为z=0+2×=1,故答案为:113.(4分)若数列{a n}的前n项和S n=a n+,则a4=﹣8.【解答】解:由S n=a n+,得,解得:a1=1;取n=2得:,解得:a2=﹣2;取n=3得:,解得:a3=4;取n=4得:,解得:a4=﹣8.故答案为:﹣8.14.(4分)已知,则=.【解答】解:∵已知,∴+sinα=,即()=,∴sin(+α)=.∴=﹣sin(+α)=﹣,故答案为﹣.15.(4分)过双曲线=1(a>0,b>0)的左焦点F(﹣c,0)(c>0),作圆x2+y2=的切线,切点为E,延长FE交双曲线右支于点P,若,则双曲线的离心率为.【解答】解:∵,∴E为PF的中点,令右焦点为F′,则O为FF′的中点,则PF′=2OE=a,∵E为切点,∴OE⊥PF∴PF′⊥PF∵PF﹣PF′=2a∴PF=PF′+2a=3a在Rt△PFF′中,PF2+PF′2=FF′2即9a2+a2=4c2⇒所以离心率e=故答案为:.16.(4分)已知•是单位向量,•=0.若向量满足|﹣﹣|=1,则||的最大值是.【解答】解:∵•是单位向量,•=0.若向量满足|﹣﹣|=1,∴设=(1,0),=(0,1),=(x,y),则﹣﹣=(x﹣1,y﹣1),∵|﹣﹣|=1,∴(x﹣1)2+(y﹣1)2=1,故向量||的轨迹是在以(1,1)为圆心,半径等于1的圆上,∴||的最大值为,故答案为:17.(4分)(理)函数f(x)=min{2,|x﹣2|},其中min{a,b}=,若动直线y=m与函数y=f(x)的图象有三个不同的交点,它们的横坐标分别为x1,x2,x3,则x1•x2•x3是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”1.【解答】解:作出函数f(x)的图象如下图所示:由解得A(4﹣2,2﹣2),由图象可得,当直线y=m与f(x)图象有三个交点时m的范围为:0<m<2﹣2.不妨设0<x1<x2<2<x3,则由2=m得x 1=,由|x2﹣2|=2﹣x2=m,得x2=2﹣m,由|x3﹣2|=x3﹣2=m,得x3=m+2,且2﹣m>0,m+2>0,所以x1•x2•x3=×(2﹣m)×(2+m)=•m2•(4﹣m2)≤•=1,当且仅当m2=4﹣m2即m=时取得等号,所以x1•x2•x3存在最大值为1.故答案为:1.三、解答题(本大题共5小题,满分72分.解答应写出文字说明、证明过程或演算步骤)18.(14分)已知函数f(x)=sin cos+cos2.(Ⅰ)求该函数图象的对称轴;(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b2=ac,求f (B)的取值范围.【解答】解:(Ⅰ)由即即对称轴为…(6分)(Ⅱ)由已知b2=ac,∴,∴,∴,∴,∴1∴即f(B)的值域为.…(14分)19.(14分)已知等差数列{a n}的各项均为正数,a1=3,a3=7,其前n项和为S n,{b n}为等比数列,b1=2,且b2S2=32.(Ⅰ)求a n与b n;(Ⅱ)若++…+≤x2+ax+1对任意正整数n和任意x∈R恒成立,求实数a 的取值范围.【解答】解:(1)设{a n}的公差为d,由2d=a3﹣a1=7﹣3=4,d=2.∴a n=3+2(n﹣1)=2n+1设{b n}的公比为q,则b2=2q,又S2=a1+a2=3+5=8,代入b2S2=32,得16q=32,即q=2.∴;(2),∴++…+====,++…+≤x2+ax+1对任意正整数n和任意x∈R恒成立,等价于f(x)=x2+ax+1的最小值大于或等于,即,即a2≤1,解得﹣1≤a≤1.20.(14分)如图,已知四棱锥P﹣ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.(1)证明:AE⊥PD;(2)若PA=AB=2,求二面角E﹣AF﹣C的余弦值.【解答】(1)证明:∵四棱锥P﹣ABCD,底面ABCD为菱形,∠ABC=60°,E,F分别是BC,PC的中点,∴△ABC是等边三角形,∴AE⊥BC,∴AE⊥AD,∵PA⊥平面ABCD,AE⊂平面ABCD,∴AE⊥PA,∵AE∩AD=A,∴AE⊥平面PAD,∵PD⊂平面PAD,∴AE⊥PD.(2)解:由(1)知AE、AD、AP两两垂直,∴以A为坐标原点,建立如图所示的空间直角坐标系,∵E,F分别为BC,PC的中点,PA=AB=2,∴A(0,0,0),B(,﹣1,0),C(,1,0),D(0,2,0),P(0,0,2),E(,0,0),F(),∴,设平面AEF的一个法向量为,则取z1=﹣1,得=(0,2,﹣1),∵BD⊥AC,BD⊥PA,PA∩AC=A,∴BD⊥平面AFC,∴为平面AFC的一法向量.又,∴cos<>==.∵二面角E﹣AF﹣C为锐角,∴所求二面角的余弦值为.21.(15分)已知椭圆E:+=1(a>b>0)的离心率e=,并且经过定点P(,).(Ⅰ)求椭圆E的方程;(Ⅱ)设A,B为椭圆E的左右顶点,P为直线l:x=4上的一动点(点P不在x 轴上),连AP交椭圆于C点,连PB并延长交椭圆于D点,试问是否存在λ,使=λS△BCD成立,若存在,求出λ的值;若不存在,说明理由.得S△ACD【解答】解:(Ⅰ)∵椭圆E:+=1(a>b>0)的离心率e=,并且经过定点P(,),∴且,又c2=a2﹣b2解得:a2=4,b2=1,∴椭圆E的方程为(1)=λS△BCD成立(Ⅱ)存在λ=3,使得S△ACD设P(4,y0)(y0≠0),又A(﹣2,0),则故直线AP的方程为:,代入方程(1)并整理得:.由韦达定理:,即,∴,同理可解得:,∴,故直线CD的方程为y=k CD(x﹣x C)+y C,即,∴直线CD恒过定点E(1,0).∴.故λ=3.22.(15分)已知函数f(x)=﹣x2+2|x﹣a|.(Ⅰ)若函数y=f(x)为偶函数,求a的值;(Ⅱ)若,求函数y=f(x)的单调递增区间;(Ⅲ)当a>0时,若对任意的x∈[0,+∞),不等式f(x﹣1)≥2f(x)恒成立,求实数a的取值范围.【解答】解:(Ⅰ)解法一:因为函数f(x)=﹣x2+2|x﹣a|又函数y=f(x)为偶函数,所以任取x∈R,则f(﹣x)=f(x)恒成立,即﹣(﹣x)2+2|﹣x﹣a|=﹣x2+2|x﹣a|恒成立.…(3分)所以|x﹣a|=|x+a|恒成立,两边平方得:x2﹣2ax+a2=x2+2ax+a2所以4ax=0,因为x为任意实数,所以a=0…(5分)解法二(特殊值法):因为函数y=f(x)为偶函数,所以f(﹣1)=f(1),得|1﹣a|=|1+a|,得:a=0所以f(x)=﹣x2+2|x|,故有f(﹣x)=f(x),即f(x)为偶函数…(5分)(Ⅱ)若,则.…(8分)由函数的图象并结合抛物线的对称轴可知,函数的单调递增区间为(﹣∞,﹣1]和…(10分)(Ⅲ)不等式f(x﹣1)≥2f(x)化为﹣(x﹣1)2+2|x﹣1﹣a|≥﹣2x2+4|x﹣a|,即:4|x﹣a|﹣2|x﹣(1+a)|≤x2+2x﹣1(*)对任意的x∈[0,+∞)恒成立.因为a>0.①当0≤x≤a时,不等式(*)化为﹣4(x﹣a)+2[x﹣(1+a)]≤x2+2x﹣1,即x2+4x+1﹣2a≥0对任意的x∈[0,a]恒成立,∵函数g (x )=x 2+4x +1﹣2a 在区间[0,a ]上单调递增, ∴g (0)≥0,解得,∴…(12分)②a <x ≤1+a 时,不等式(*)化为4(x ﹣a )+2[x ﹣(1+a )]≤x 2+2x ﹣1, 即x 2﹣4x +1+6a ≥0对任意的x ∈(a ,1+a ]恒成立, 由①中知:函数h (x )=x 2﹣4x +1+6a 在区间(a ,1+a ]上单调递减,∴h (1+a )≥0,即a 2+4a ﹣2≥0,解得或.∴结合①的结论可得.…(14分)③x >1+a 时,不等式(*)化为4(x ﹣a )﹣2[x ﹣(1+a )]≤x 2+2x ﹣1, 即x 2+2a ﹣3≥0对任意的x ∈(a +1,+∞)恒成立, ∵函数φ(x )=x 2+2a ﹣3在区间(a +1,+∞)上单调递增, ∴φ(a +1)≥0, 即a 2+4a ﹣2≥0,解得或,结合②的结论可得:.综上所述得,a 的取值范围是.…(16分)赠送—高中数学知识点二次函数(1)一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=-③判别式:∆ ④端点函数值符号. ①k <x 1≤x 2 ⇔②x 1≤x 2<k ⇔xy1x 2x 0>a O∙ab x 2-=k 0)(>k f xy1x 2x O∙ab x 2-=k<a 0)(<k f③x 1<k <x 2 ⇔ af (k )<0)(<k f xy1x 2x 0>a O∙kx y1x 2x O∙k<a 0)(>k f④k 1<x 1≤x 2<k 2 ⇔⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔ f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1<x 1<k 2≤p 1<x 2<p 2 ⇔ 此结论可直接由⑤推出.(5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值 设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (Ⅰ)当0a >时(开口向上) ①若2b p a -<,则()m f p = ②若2b p q a ≤-≤,则()2b m f a =- ③若2b q a->,则()m f q =①若02b x a -≤,则()M f q = ②02b x a->,则()M f p =(Ⅱ)当0a <时(开口向下) ①若2b p a -<,则()M f p = ②若2b p q a ≤-≤,则()2b M f a =- ③若2b q a->,x>O-=f(p) f (q)()2b f a-x>O-=f (p)f (q)()2b f a-xxx则()M f q =①若02b x a -≤,则()m f q = ②02b x a->,则()m f p =.x<O-=f (p) f (q) ()2bf a-x<O-=f (p)f(q)()2b f a-x<O-=f (p)f(q)()2bf a-0xx<O-=f (p)f (q)()2b f a-x<O-=f (p)f (q)()2b f a-0x。
