北师大版高中数学必修二双基限时练16
北师大版高中数学必修一双基限时练16.docx

双基限时练(十六) 指数运算的性质基 础 强 化1.已知a >0,b >0,m ,n ∈R ,以下运算正确的是( ) A. a m ·a n =a mn B. (a m )n =a m +nC. a m b n =(ab )m +nD. ⎝ ⎛⎭⎪⎫b a m =b ma m 答案 D2.化简-a ·3a 的结果是( ) A. 5-a 2 B. -6-a 5 C.6-a 5D. -6a 5解析 由题意得a ≤0,故原式=(-a ) 12·a 13=-(-a ) 12(-a ) 13=-(-a ) 56=-6-a 5.答案 B3.下列各式运算错误的是( ) A. (-a 2b )2·(-ab 2)3=-a 7b 8B. (-a 2b 3)3÷(-ab 2)3=a 3b 3C. (-a 3)2·(-b 2)3=a 6b 6D. [(a 3)2·(-b 2)3]3=-a 18b 18 答案 C4.下列结论中正确的个数是( ) ①当a <0时,(a 2) 32=a 3; ②na n =|a |;③函数y =(x -2)12-(3x -7)0的定义域是[2,+∞); ④622=32. A. 0个 B. 1个 C. 2个D. 3个解析 对于①,∵a <0,∴a 3<0,而(a 2) 32>0,故①不对;对于②,当n 为奇数时显然不对;对于③函数的定义域为⎩⎪⎨⎪⎧x -2≥0,3x -7≠0,即⎣⎢⎡⎭⎪⎫2,73∪⎝ ⎛⎭⎪⎫73,+∞,故③也不对;对于④显然正确,故答案为B.答案 B5.设2x =8y +1,9y =3x -9,则x +y 的值为( ) A. 18 B. 21 C. 24 D. 27答案 D6.已知a -1a =3(a >0),则a 2+a +a -2+a -1的值等于( ) A .13-11B .11-13C .13+11D .11+13解析 由a -1a =3,得⎝⎛⎭⎪⎫a -1a 2=9,因此a 2+1a 2-2=9,故a 2+a-2=11. 又(a +a -1)2=a 2+a -2+2=11+2=13,且a >0,所以a +a -1=13.于是a 2+a +a -2+a -1=11+13.答案 D7.化简a3a -4-b 5b 的结果是________.解析 a3a -4-b 5b =a 3a 2+4-b5b 4=a +4-b .答案 a +4-b能 力 提 升8.设α,β是方程5x 2+10x +1=0的两根,则2α·2β=________,(2α)β=________.解析 ∵α,β是方程的两根,故α+β=-105=-2,αβ=15,故2α·2β=2α+β=2-2=14.(2α)β=2αβ=215 .答案 14 2159.解析答案 26310.计算下列各式:考 题 速 递13.已知m -x =5+2,则m 2x-1+m-2x m -3x +m 3x 的值为________.解析 ∵m -x =5+2,∴m 2x-1+m-2x m -3x +m 3x=(m x )2-m x m -x +(m -x )2(m x +m -x )[(m x )2-m x m -x +(m -x )2] =1m x +m -x =115+2+5+2=510. 答案 510。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练6

双基限时练(六)一、选择题1.下列说法错误的是()A.若一条直线与平面有无数个公共点,则这条直线在平面内B.若两个平面没有公共点,则两个平面互相平行C.直线与平面的位置关系有两种:相交、平行D.如果一条直线与平面只有一个公共点,那么这条直线和平面相交答案 C2.下列表示正确的是()A.直线l在平面α内,用符号表示为“l∈α”B.点A在直线l上,直线l在平面α内,用符号表示为“A∈l,lα”C.点A在平面α内,用符号表示为“Aα”D.直线l与平面α外,用符号表示为“l∉α”答案 B3.如果两条直线a和b没有公共点,那么a与b的位置关系是() A.共面B.平行C.异面D.平行或异面解析由两条直线的位置关系,可知答案为D.答案 D4.下面空间图形画法错误的是()解析画立体图时,被平面遮住的部分画成虚线或不画.答案 D5.分别在两相交平面内的两条直线的位置关系是()A.异面B.平行C.相交D.以上皆有可能答案 D6.一条直线与两条异面直线中的一条相交,则它与另一条的位置关系是()A.异面B.平行C.相交D.可能相交、平行,也可能异面解析一条直线与两条异面直线中的一条相交,它与另一条的位置关系有三种:平行、相交、异面,如图所示.答案 D二、填空题7.点A在直线l上,用符号表示为________;直线AB在平面β内,用符号可表示为________;平面α与平面β相交于直线l可表示为________.答案A∈l ABβα∩β=l8.如图是一个正方体表面的一种展开图,图中的四条线段AB,CD,EF,GH在原正方体中相互异面的有________对.解析如图所示,AB与GH异面,AB与CD异面,EF与GH异面.答案三9.若直线a,b都平行于平面α,则直线a,b的位置关系是________.解析直线a,b的位置关系有三种:相交、平行、异面,如图所示.三、解答题10.按照给出的要求,完成下面两个相交平面的作图,如图①②③④⑤⑥中的线段AB,分别是两个平面的交线.答案11.如图,在四棱锥P-ABCD中,写出互相异面的直线.解由异面直线的判定定理可知,互为异面的直线有AB与PD,AB与PC,AD与PB,AD与PC,DC与P A,DC与PB,BC与P A,BC与PD异面.12.如图,已知P∉平面ABC,P A≠PB,CM是AB上的中线,PN⊥AB 于N,求证:CM和PN是异面直线.证明证法1:假设CM和PN共面,则有下列两种情况:(1)若M、N重合,可得AN=BN,∴PN是线段AB的中垂线,∴P A=PB,与题设P A≠PB矛盾.(2)若M、N不重合,CM和PN共面,即PC与MN共面,可得P∈平面ABC,与题设P∉平面ABC矛盾.所以CM和PN是异面直线.证法2:∵CM是AB上的中线,∴CM平面ABC.又∵PN⊥AB于N,∴N∈平面ABC.∵P A≠PB,∴AN≠BN.∴N与M不重合,即N∉CM.又∵P∉平面ABC,∴CM和PN是异面直线.思维探究13.若a与b异面,c与b异面,试举例说明a与c的位置关系.解a与c可能相交、平行、异面,说明如下:在正方体ABCD-A1B1C1D1中,A1D1与AB异面,B1C1与AB异面,而A1D1∥B1C1;A1D1与AB异面,DD1与AB异面,而A1D1与DD1相交;A1D1与AB异面,CC1与AB异面,而CC1与A1D1异面,故与b异面的两条直线a,c可能相交、平行、异面.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练5
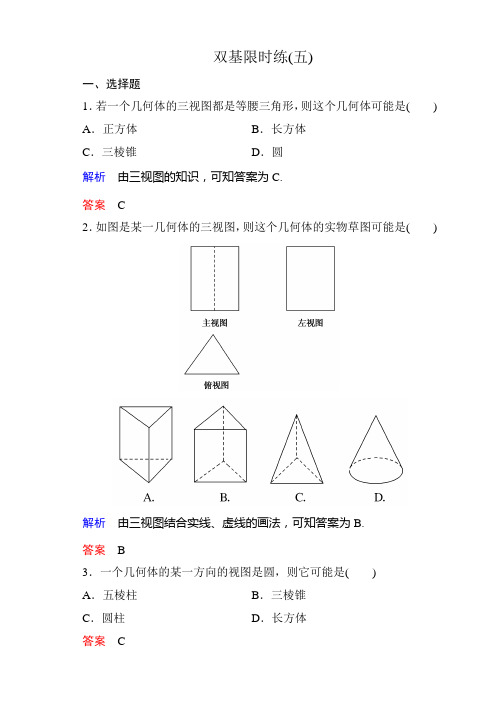
双基限时练(五)一、选择题1.若一个几何体的三视图都是等腰三角形,则这个几何体可能是() A.正方体B.长方体C.三棱锥D.圆解析由三视图的知识,可知答案为C.答案 C2.如图是某一几何体的三视图,则这个几何体的实物草图可能是()解析由三视图结合实线、虚线的画法,可知答案为B.答案 B3.一个几何体的某一方向的视图是圆,则它可能是()A.五棱柱B.三棱锥C.圆柱D.长方体答案 C4.某几何体的三视图如图所示,则该几何体是()A.棱台B.棱柱C.棱锥D.以上均不对解析由相似比,可知几何体的侧棱相交于一点.答案 A5.如果一个几何体的主视图和左视图都是矩形,则这个几何体可能是()A.长方体B.圆柱或正方体C.长方体或圆台D.长方体或圆柱解析正方体的三视图都是正方形;圆台的主视图、左视图都是等腰梯形,长方体和圆柱的主视图和左视图都是矩形.答案 D6.某几何体的主视图和左视图均如图所示,则该几何体的俯视图不可能是()解析若俯视图是A,则原几何体是两个圆柱的组合体;若俯视图是B,则原几何体是一个圆柱和一个四棱柱的组合体;若俯视图为D,则原几何体是一个底面为等腰直角三角形的直三棱柱和一个四棱柱的组合体,故选C.答案 C二、填空题7.如图所示,①②③是三个几何体的三视图,其中①对应的几何体为________,②对应的几何体为________,③对应的几何体为________.解析由三视图的知识,可知甲对应的几何体为圆柱,乙对应的几何体为三棱锥,丙对应的几何体为圆锥.答案圆柱三棱锥圆锥8.桌上放着一个半球,如图所示,则在它的三视图及右面看到的图形中,有三个图相同,这个不同的图应该是________.解析俯视图为圆,主视图与左视图均为半圆.答案俯视图9.如图是长和宽分别相等的两个矩形.给定下列三个命:①存在三棱柱,其主视图、俯视图如图;②存在四棱柱,其主视图、俯视图如图;③存在圆柱,其主视图、俯视图如图.其中是真命题的是________(只填写序号).解析如图①②③的主视图和俯视图都与原题相同.答案①②③三、解答题10.如图是简单组合体的三视图,想象它们表示的组合体的结构特征,并作适当描述.解由三视图可知该几何体是体育器材杠铃.11.根据下列几何体的三视图,画出该几何体的直观图.该几何体上面是一个圆锥,下面是一个倒置的圆台,如图②所示.9题解析图12.某建筑由相同的若干房间组成,该楼房的三视图如图所示,问:(1)该楼房有几层?从前往后最多要经过几个房间?(2)最高一层的房间在什么位置?请画出此楼房的大致形状.解(1)由主视图和左视图可以知道,该楼房有3层;由俯视图知道,从前往后最多要经过3个房间;(2)从主视图和左视图可以知道,最高一层的房间在左侧的最后一排的房间.楼房大致形状如图所示.思维探究13.如图所示,已知几何体的三视图,用斜二测画法画出它的直观图.解由三视图可知,该几何体下方是一个长方体,上方是以长方体的上底面为底面的四棱锥,其直观图的画法如下:(1)作出长方体的直观图ABCD-A1B1C1D1,如图a所示;(2)再以上底面A1B1C1D1的对角线交点为原点建立x′,y′,z′轴,如图b所示,在z′上取点V′,使得V′O′的长度为棱锥的高,连接V′A1,V′B1,V′C1,V′D1,得到四棱锥的直观图,如图b;(3)擦去辅助线和坐标轴,遮住部分用虚线表示,得到几何体的直观图,如图c.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练8

双基限时练(八)一、选择题1.在正方体ABCD—A1B1C1D1中,E,F,G,H分别为AB,BC,A1B1,B1C1的中点,下列结论错误的是()A.GH∥EFB.GH∥ACC.GE∥HFD.GB∥B1F解析GB与B1F异面.答案 D2.如图,点P,Q,R,S分别在正方体的四条棱上,且是所在棱的中点,则直线PQ与RS不平行的两个图是()A.①②B.②③C.③④D.①④解析③中的PQ与RS异面,④中的PQ与RS相交于一点,故选C.答案 C3.在四棱柱ABCD—A1B1C1D1中,底面ABCD为平行四边形(称这样的几何体为平行六面体),与AB共面也与CC1共面的棱的条数为() A.3 B.4C.5 D.6解析根据两条平行直线、两条相交直线确定一个平面,可得CD,BC,BB1,AA1,C1D1符合条件.答案 C4.在正方体ABCD—A1B1C1D1中,E,F,M,N分别为A1D1,A1B1,DC,BC的中点,下列说法中错误的是()A.EF∥MN B.AF∥C1MC.AF∥C1N D.AE∥C1N解析∵B1D1∥BD,MN∥BD,∴MN∥B1D1.又EF∥B1D1,∴MN∥EF,故A正确,如图取AD的中点G,连接D1G,GN,则D1C1綊GN,∴D1G∥C1N,而E,G为A1D1,AD的中点,∴AE∥D1G,∴AE∥C1N,故D正确,同理可证AF∥C1M,故B正确,而AF与C1N 异面.答案 C5.在正方体ABCD—A1B1C1D1中,E,F,M分别为A1B1,B1C1,BB1的中点,下列说法中错误的是()A .∠BA 1C 1=∠MEFB .∠A 1BC 1=∠EMF C .∠B 1EM =∠EA 1BD .∠EFM =∠A 1C 1F解析 由等角定理,可知A 、B 、C 均正确. 答案 D6.在三棱柱ABC -A 1B 1C 1中,E ,F 分别在AB ,AC 上,且AE =13AB ,AF =13AC ,则下列说法正确的是( )A .EF ⊥BB 1 B .EF ∥A 1B 1C .EF ∥B 1C 1D .EF ∥AA 1解析 ∵AE =13AB ,AF =13AC ,∴EF ∥BC ,又ABC -A 1B 1C 1为棱柱,∴BC ∥B 1C 1,∴EF ∥B 1C 1.答案 C 二、填空题7.如图所示,在空间四边形ABCD 中,E ,H 分别为AB ,AD 的中点,F ,G 分别是BC ,CD 上的点,且CF CB =CG CD =23,若BD =6 cm ,梯形EFGH 的面积为28 cm 2,则平行线EH ,FG 间的距离为________.解析 EH =3,FG =6×23=4,S EFGH =(EH +FG )h 2=28,得h =8(cm). 答案 8 cm8.用一个平面去截一个正方体,截面可能是________. 解析(注:这儿画了其中的特例来说明有这几种图形) 答案 三角形、四边形、五边形、六边形9.空间中两个角α,β且α,β的角的两边分别平行,且α=60°,则β=________.答案 60°或120° 三、解答题10.在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为棱CC 1和AA 1的中点.画出平面BED 1F 与平面ABCD 的交线.解 如图,在平面AA 1D 1D 内,延长D 1F ,DA .∵D 1F 与DA 不平行,∴D 1F 与DA 必相交于一点,设为P ,则P ∈D 1F ,P ∈DA .又∵D 1F ⊂平面BED 1F ,DA ⊂平面ABCD , ∴P ∈平面BED 1F ,且P ∈平面ABCD . 又∵B 为平面ABCD 与平面BED 1F 的公共点,∴连接PB ,则PB 即为平面BED 1F 与平面ABCD 的交线.11.如图,两个三角形ABC 和A ′B ′C ′的对应顶点的连线AA ′,BB ′,CC ′交于同一点O ,且AO OA ′=BO OB ′=CO OC ′=23.(1)求证:A ′B ′∥AB ,A ′C ′∥AC ,B ′C ′∥BC ; (2)求S △ABCS △A ′B ′C ′的值.解 (1)证明:∵AA ′与BB ′交于点O ,且 AO OA ′=BO OB ′=23,∴AB ∥A ′B ′.同理AC ∥A ′C ′,BC ∥B ′C ′.(2)∵A ′B ′∥AB ,AC ∥A ′C ′,且AB 和A ′B ′,AC 和A ′C ′方向相反,∴∠BAC =∠B ′A ′C ′. 同理∠ABC =∠A ′B ′C ′. 因此△ABC ∽△A ′B ′C ′,且AB A ′B ′=AO OA ′=23.∴S △ABCS △A ′B ′C ′=⎝ ⎛⎭⎪⎫232=49. 12.如图,E ,F ,G ,H 分别是三棱锥ABCD 的边AB ,BC ,CD ,DA 上的点,且AE EB =AH HD =λ,CF FB =CGGD =μ.(1)若λ=μ,判断四边形EFGH 的形状; (2)若λ≠μ,判断四边形EFGH 的形状; (3)若λ=μ=12,且EG ⊥HF ,求ACBD 的值.解 (1)∵AE EB =AHHD =λ,∴EH ∥BD ,且EH =λ1+λBD .①又∵CF FB =CG GD =μ,∴FG ∥BD ,且FG =μ1+μBD .②又λ=μ,∴EH 綊FG (公理4).因此λ=μ时,四边形EFGH 为平行四边形.(2)若λ≠μ,由①②,知EH ∥FG ,但EH ≠FG ,因此λ≠μ时,四边形EFGH 为梯形.(3)∵λ=μ,∴四边形EFGH 为平行四边形. 又∵EG ⊥HF ,∴四边形EFGH 为菱形. ∴FG =HG .∴BD =1+μμFG =3FG , AC =(λ+1)HG =32HG =32FG . ∴AC BD =12.思 维 探 究13.如图,一个梯形纸片ABCD ,AB ∥CD ,E ,F 分别是AD ,BC 的中点,将四边形ABFE 绕EF 旋转到A ′B ′FE 的位置,G ,H 分别为A ′D ,B ′C 的中点.求证:(1)四边形A ′B ′CD 是梯形; (2)四边形EFHG 是平行四边形.证明(1)∵四边形ABCD是梯形,AB∥CD,∴AB≠CD. ∵E,F分别为AD,BC的中点,∴EF∥AB,EF∥CD,旋转后A′B′∥EF.∴A′B′∥CD,且A′B′=AB≠CD.∴四边形A′B′CD是梯形.(2)由(1)知四边形A′B′CD是梯形,∴GH=12(A′B′+CD).又GH∥CD,∴EF∥GH.∵EF=12(AB+CD),∴EF綊GH. ∴四边形EFHG是平行四边形.。
北师大版高中数学必修2双基限时练:第二章+解析几何初

双基限时练(二十)一、选择题1.若直线l 1:ax +2y +6=0与直线l 2:x +(a -1)y +(a 2-1)=0平行而不重合,则a 等于( )A .-1或2B .-1C .2D .23解析 ∵l 1∥l 2,∴a 1=2a -1≠6a 2-1,得⎩⎨⎧a =-1,或a =2,a ≠1,且a ≠2,∴a =-1.答案 B2.已知过点A(-1,m)和B(m,5)的直线与3x -y -1=0平行,则m 的值为( )A .0B .12 C .2 D .10 解析 由题意k AB =5-m m +1=3,得m =12.答案 B3.下列说法中,正确的是( ) A .若直线l 1与l 2的斜率相等,则l 1∥l 2 B .若直线l 1与l 2互相平行,则它们的斜率相等C .直线l 1与l 2中,若一条直线的斜率存在,另一条直线的斜率不存在,则l 1与l 2一定相交D .若直线l 1与l 2的斜率都不存在,则l 1∥l 2解析 若l 1与l 2中一条直线的斜率存在,另一条直线的斜率不存在,则l 1与l 2不平行,故l 1与l 2一定相交.答案 C4.过点(-1,3),且平行于直线x -2y +3=0的直线方程为( ) A .x -2y +7=0 B .2x +y -1=0 C .x -2y -5=0D .2x +y -5=0解析 由点斜式y -3=12(x +1),得x -2y +7=0,故选A . 答案 A5.若两条直线2x -y +a =0和x -y2+b =0平行, 则a ,b 的取值可能是( )A .a =2,b =1B .a =52,b =54 C .a =0,b =0D .a =7,b =3解析 由两条直线平行,知满足A 1B 2=A 2B 1,且A 1C 2≠A 2C 1,可得a ≠2b ,故选D .答案 D6.若直线ax +by +c =0与直线y =tan α·x 平行,且sin α+cos α=0,则a ,b 满足( )A .a +b =1B .a -b =1C .a +b =0D .a -b =0解析 由sin α+cos α=0,得tan α=-1,又tan α=-ab , 即-ab =-1,得a =b ,即a -b =0. 答案 D 二、填空题7.若直线l :x +ay +2=0平行于直线2x -y +3=0,则直线l 在两坐标轴上的截距之和为________.解析 由x +ay +2=0与2x -y +3=0平行, 则1×(-1)=2a ,得a =-12, ∴l 为x -y2+2=0,令x =0,y =4, 令y =0,x =-2,∴l 在两坐标轴上的截距之和为4-2=2. 答案 28.若过A(4,a)与B(5,b)两点的直线与直线y =x +m 平行,则b -a =________.解析 由b -a5-4=1,得b -a =1.答案 19.与直线3x -2y +6=0平行且纵截距为9的直线方程为________. 解析 设直线l 的方程为3x -2y +b =0,令x =0,y =b2=9,得b =18,故所求的直线方程为3x -2y +18=0.答案 3x -2y +18=0 三、解答题10.求a 的值,使两直线x +ay =2a +2和ax +y =a +1平行. 解 由1a =a1,得a =±1,当a =1时,两直线的方程分别为x +y =4和x +y =2,两直线平行;当a =-1时,两直线方程为x -y =0和x -y =0重合,∴a 的值为1.11.已知直线l 1与直线l 2:x -3y +6=0平行,l 1与两坐标轴围成的三角形的面积是8,求直线l 1的方程.解 设l 1的方程为x -3y +c =0, 令y =0,得x =-c ,令x =0,得y =c3, 由题意,得12|-c|·|c3|=8,得c =±4 3.∴直线l 1的方程为x -3y +43=0,或x -3y -43=0.12.已知▱ABCD 的三个顶点A(0,1),B(1,0),C(4,3),求顶点D 的坐标. 解 设D(m ,n),由题意得AB ∥DC ,AD ∥BC ,∴k AB =k DC ,k AD =k BC,∴⎩⎪⎨⎪⎧0-11-0=3-n4-m,n -1m -0=3-04-1,得⎩⎪⎨⎪⎧m =3,n =4,∴D(3,4).思 维 探 究13.已知两条直线l 1:(a -1)x +2y +1=0,l 2:x +ay +3=0平行,求a 的值.解 ∵l 1∥l 2,∴a(a -1)-2=0,得a =-1或a =2.又当a =-1时,l 1:-2x +2y +1=0,l 2:x -y +3=0,此时l 1∥l 2,符合题意;当a =2时,l 1:x +2y +1=0,l 2:x +2y +3=0,此时l 1∥l 2,符合题意.∴a 的值为-1或2.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练1

双基限时练(一)一、选择题1.下面几何体的截面一定是圆面的是()A.圆柱B.圆锥C.球D.圆台答案 C2.下列说法正确的是()A.圆锥是直角三角形绕其一边旋转而成B.在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线C.圆柱的任意两条母线所在直线互相平行D.用一平面截圆锥,截面与底面之间的部分为圆台解析由旋转的过程,可知圆柱的任意两条母线所在直线互相平行.答案 C3.如图所示,观察下面四个几何体,其中判断正确的是()A.①是圆台B.②是圆台C.③是圆锥D.④是圆台答案 C4.如图①是由下面哪个平面旋转得到的()解析由旋转的知识,可知答案为C.答案 C5.一个圆锥的母线长为20 cm,母线与轴的夹角为30°,则圆锥的高为()A.10 3 cm B.20 3 cmC.20 cm D.10 cm解析由图可知,h=20cos30°=103(cm),答案为A.答案 A6.有下列四个命题:①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线可能相交也可能不相交;④圆锥的轴截面是等腰三角形.其中错误命题的个数是( ) A .1 B .2 C .3D .4解析 ①错,以矩形某一边为轴旋转才是圆柱,以对角线为轴旋转则不是圆柱;②错,以其直角边为轴旋转才是圆锥;③错,一定相交;④正确.答案 C 二、填空题7.圆台的两底面半径分别为2 cm 和5 cm ,母线长为310 cm ,则它的轴截面面积为________.解析 圆台的高h =(310)2-(5-2)2=9(cm), S 轴截面=(4+10)×92=63(cm 2). 答案 63 cm 28.用一张4 cm ×8 cm 的矩形硬纸卷成圆柱的侧面,接头忽略不计,则轴截面面积是________.解析 若圆柱的高为8 cm ,则2πr =4(cm), 2r =4π,轴截面面积S =8·4π=32π(cm 2), 若圆柱的高为4 cm ,则2πr =8(cm), 2r =8π,轴截面面积S =4·8π=32π(cm 2), 故答案为32π cm 2.答案 32π cm 29.一直角梯形上底长为1,下底长为3,高为2,现绕着直角梯形的下底旋转一周,所围成的几何体的轴截面的面积为________.解析 其轴截面由两部分组成其中一个为矩形,一个为三角形,S =4×1+12×4×2=8.答案 8 三、解答题 10.如图所示,已知梯形ABCD 中,AD ∥BC ,且AD <BC ,当梯形ABCD 绕AD 所在直线旋转一周时,其他各边旋转围成一个几何体,试描述该几何体的结构特征.解 如图所示,旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分而成的组合体.11.如果一个圆锥的侧面展开图是半圆,求这个圆锥的轴截面的顶角.解 设圆锥的底面半径为r ,母线长为l ,由题意,可得πl =2πr ,∴r =l2. ∴轴截面的顶角α满足 sin α2=r l =12,∴α2=30°.∴α=60°,即圆锥轴截面的顶角为60°.12.已知一个圆台的母线长是5 cm ,上、下底面的面积分别是9π cm 2和16π cm 2,求:(1)圆台的高;(2)截得此圆台的圆锥的母线长.解 (1)设圆台的上、下底面半径为r 、R ,高为h , 则r =3,R =4,h =l 2-(R -r )2=52-12= 26(cm);(2)设圆锥母线长为l ′,则l ′-l l ′=r R ,即l ′-5l ′=34,l ′=20(cm).思 维 探 究13.一个圆锥的底面直径为4,高为8,在其中有一个高为x 的内接圆柱.(1)用x 表示圆柱的轴截面面积; (2)当x 为何值时,S 最大.解 作出圆锥和内接圆柱的轴截面,设圆柱的底面半径为r . 由三角形相似可得x 8=2-r 2,得r =2-x4.(1)圆柱的轴截面面积S =2rx =2⎝ ⎛⎭⎪⎫2-x 4x =-12x 2+4x ,x ∈(0,8) (2)∵S =-12x 2+4x =-12(x -4)2+8,x ∈(0,8), ∴当x =4时,S 取得最大值8.。
北师大版高中数学必修2双基限时练:第一章++立体几何

双基限时练(二)一、选择题1.下列说法中正确的是()A.棱柱的各个面中,至少有两个面互相平行B.棱柱中两个互相平行的平面一定是棱柱的底面C.棱柱中侧棱的长叫做棱柱的高D.棱柱的侧面是矩形,但它的底面一定不是矩形解析据棱柱的概念,知答案为A.答案 A2.若棱台上、下底面的对应边之比为1:2,则上、下底面的面积之比为()A.1:2 B.1:4C.2:1 D.4:1解析面积之比等于对应边之比的平方,可知答案为B.答案 B3.棱台不一定具有的性质是()A.侧面都是梯形B.侧棱都相等C.两底面相似D.侧棱延长后交于一点解析据棱台的性质,知答案为B.答案 B4.以下命题正确的是()A.棱锥的各侧棱长相等B.棱柱的各侧面都是矩形C.棱台的各侧棱延长线相交于一点D.圆锥的母线长等于底面圆的周长答案 C5.一个正棱锥的底面边长与侧棱长相等,则该棱锥一定不是() A.三棱锥B.四棱锥C.五棱锥D.六棱锥解析由于正六边形的中心到顶点的距离与边长都相等,故正六棱锥的侧棱长大于底面边长.答案 D6.给出下列命题:①有两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱;②有一个面是多边形,其余各面都是三角形所围成的几何体是棱锥;③用一个平行于棱锥底面的平面去截棱锥,得到的几何体叫棱台.以上命题中真命题的个数为()A.0 B.1C.2 D.3解析对于①②不符合棱柱、棱锥的定义;对于③,用一个平行于棱锥底面的平面去截棱锥,得的几何体一个是棱台,另一个是棱锥,故③不正确.答案 A二、填空题7.四棱柱有________条侧棱;________个顶点;________个侧面.答案48 48.给出下列几个命题:①棱柱的侧面都是平行四边形;②棱锥的侧面为三角形,且所有侧面都有一个公共点;③棱台的侧棱所在直线均相交于一点;④将直角梯形绕着它的一条腰所在的直线旋转一周所得的几何体为圆台.其中正确的是________.解析①②③显然正确,对于④,只有当直角梯形绕着它的一条垂直于底边的腰所在的直线旋转一周时,所形成的几何体才是圆台,故④不正确.答案①②③9.已知正四棱锥V—ABCD,底面面积为16,一条侧棱长为211,则它的斜高为________.解析由S底=16,知底面边长为4,又侧棱长为211,故斜高h′=(211)2-22=210.答案210三、解答题10.如图所示的棱柱ABCD—A1B1C1D1为正四棱柱,用平面BCEF把该棱柱分成两部分后,各部分的几何体还是棱柱吗?如果是,是几棱柱?如果不是,说明理由.解∵ABCD—A1B1C1D1为正四棱柱,∴截面BCEF右边的部分是三棱柱BFB1—CEC1,截面BCEF左边的部分也是棱柱,是一个四棱柱ABF A1—DCED1.11.如图所示的几何体所有的棱长都相等,分析此几何体的面数,顶点数和棱数,并判断该几何体是不是棱柱、棱锥、棱台的一种.解该几何体有8个面,6个顶点,12条棱,它不满足棱柱、棱锥、棱台的定义,故不是棱柱,也不是棱锥,也不是棱台,但它是一个多面体.12.已知正三棱柱ABC-A1B1C1的底面边长为1,高为4,一动点从A 点出发,沿着三棱柱的侧面绕行一周到达点A1,求动点所经过的最短路程长.解将三棱柱沿AA1将侧面展开,如图所示其中AA′=3,A′A′1=4,∴AA′1=AA′2+A′A′21=32+42=5.∴动点所经过的最短路程长为5.思维探究13.已知底面是正方形,侧棱都相等的棱锥的高为3,侧棱长为7,求侧面等腰三角形底边上的高.解如图,在棱锥S-ABCD中,高OS=3,侧棱SA=SB=SC=SD =7,解Rt△SOA,得OA=2,则AC=4,∴AB=BC=CD=DA=2 2.作OE⊥AB于E,则E为AB中点.连接SE,则SE即为所求.由于SO⊥OE,在Rt△SOE中,∵OE=12BC=2,SO=3,∴SE= 5.∴棱锥侧面等腰三角形底边上的高为 5.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练10

双基限时练(十)一、选择题1.在空间中,下列命题正确的是()A.若a∥α,b∥a,则b∥αB.若a∥α,b∥α,aβ,bβ,则α∥βC.若α∥β,b∥α,则b∥βD.若α∥β,aα,则a∥β解析对于A,当a∥α,b∥a时,b可能在α内,故A不正确;对于B,a,b有可能平行,此时α∥\β,故B不正确;对于C,α∥β,b∥α,此时b 有可能在平面β内,故C不正确.答案 D2.平面α∥平面β,平面γ∥平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是()A.互相平行B.交于一点C.相互异面D.不能确定解析由面面平行的性质定理,可知答案为A.答案 A3.给出下列命题:①一条直线与另一条直线平行,它就和经过另一条直线的任何平面平行;②一条直线和一个平面平行,它就和这个平面内的所有直线平行;③经过两条异面直线a,b外一点,必有一个平面与a,b都平行;④经过两条异面直线中的一条,有且只有一个平面平行于另一条直线.其中正确的命题有()A.0个B.1个C.2个D.3个解析①因为两条平行直线可确定一个平面,其中的一条直线可能在另一条直线所在的平面内,故①不对;对于②,一条直线和一个平面平行,它和这个平面内的直线有的平行,有的异面,故②不对;③中,经过两条异面直线外一点P,可作a′∥a,b′∥b,a′∩b′=P,可确定一个平面,但有可能aα或bα,故③不正确;④显然正确,故选B.答案 B4.在正方体ABCD—A1B1C1D1中,E,F,G,H分别为棱AA1,BB1,CC1,DD1上的点,且E,F,G,H四点共面,则四边形EFGH一定是() A.平行四边形B.菱形C.不是菱形D.不一定是平行四边形解析据两平面平行的性质定理,可知EFGH一定为平行四边形.答案 A5.过长方体ABCD—A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有()A.4条B.6条C.8条D.12条解析与面BDD1B1平行的平面有EFGH,MNPQ,其中E,F,G,H,M,N,P,Q分别为棱的中点,每一个平面由中点构成的线有6条,据面面平行的性质定理,可知与面BDD1B1平行的线共有12条.答案 D6.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与面ABB1A1平行的直线的条数有()A.4 B.5C.6 D.7解析画出图形,结合图形作出判断.如图所示,E,F,G,H分别是所在棱的中点,显然EF,EH,HG,GF,EG,FH都与平面ABB1A1平行.答案 C二、填空题7.在正方体ABCD—A1B1C1D1中,M,N分别在AB1,BC1上,且AM=BN,那么①AC∥MN;②MN∥面ABCD;③MN∥面A1B1C1D1.其中正确的是________.解析如图,过M ,N 分别作MG ∥BB 1,NH ∥BB 1,分别交AB ,BC 于G ,H 两点.∴MG BB 1=AM AB 1=AG AB ,又NH CC 1=BN BC 1=BH BC ,又ABCD —A 1B 1C 1D 1为正方体,∴AB 1=BC 1,又AM=BN ,∴MG =NH ,AG =BH .故当G ,H 不是AB ,BC 的中点时,GH AC , 故①不正确,由MG 綊NH ,知MN ∥GH ,∴MN ∥面ABCD ,同理可得MN ∥面A 1B 1C 1D 1. 答案 ②③8.如图a ∥α,A 是α的另一侧的点,B ,C ,D ∈a ,线段AB ,AC ,AD 交α于E ,F ,G ,若BD =4,CF =4,AF =5,则EG =________.解析 由相似比EG BD =AF AC ,∴EG =AF ·BD AC =5×49=209. 答案 2099.如图,在四面体ABCD 中,若截面PQMN 是正方形,则在下列命题中,正确的是________.①AC ∥面PQMN ;②AC =BD ;③BD ∥面PQMN ;④AC ⊥BD 解析 由PQMN 为正方形,知PQ ∥MN , ∴PQ ∥面ADC .又PQ面ABC ,面ABC ∩面ADC =AC ,∴PQ ∥AC . ∴AC ∥面PQMN ,同理BD ∥面PQMN .故①③正确,又AC ∥MN ,BD ∥MQ ,MN ⊥MQ , ∴AC ⊥BD ,故④正确.∴正确的有①③④.答案①③④三、解答题10.如图,正三棱柱ABC—A1B1C1中,D是BC的中点.判断直线A1B 与平面ADC1的关系.解A1B∥面ADC1,证明如下:证法1:如图①,连接A1C交AC1于F,则F为A1C的中点.连接FD.∵D是BC的中点,∴DF∥A1B.又DF平面ADC1,A1B平面ADC1,∴A1B∥平面ADC1.证法2:如图②,取C1B1的中点D1,则AD∥A1D1,C1D∥D1B,∴AD∥平面A1D1B,且C1D∥平面A1D1B.又AD∩C1D=D,∴平面ADC1∥平面A1D1B.∵A1B平面A1D1B,∴A1B∥平面ADC1.11.如图,在直四棱柱ABCD—A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,DC=2,E,E1分别为AD,AA1的中点,F为AB的中点.求证:EE1∥面FCC1.证明∵ABCD—A1B1C1D1为直棱柱,∴DD1∥CC1.又CC1面ADD1A1,DD1面ADD1A1,∴CC 1∥面ADD 1A 1.又ABCD 为梯形,AB ∥CD ,AB =4,DC =2, F 为AB 的中点, ∴AF ∥DC ,且AF =DC .故四边形AFCD 为平行四边形,故FC ∥AD . 又AD面ADD 1A 1,FC面AD 1,∴FC ∥面ADD 1A 1. 又FC ∩CC 1=C , ∴面FCC 1∥面ADD 1A 1. 又EE 1面ADD 1A 1,∴EE 1∥面FCC 1.12.在四棱锥P —ABCD 中,底面ABCD 为矩形,E 为线段PD 上的点,F 为线段AB 上的点,且PE ED =BFF A ,试判断EF 与平面PBC 的关系,并证明.证明 EF ∥平面PBC .证明如下: 如图作FG ∥BC 交CD 于点G ,连接EG , 则BF F A =CGGD .∵PE ED =BF F A ,∴PE ED =CG GD . ∴PC ∥EG .又FG ∥BC ,BC ∩PC =C ,FG ∩GE =G , ∴平面PBC ∥平面EFG .又EF 平面PBC , ∴EF ∥平面PBC .思 维 探 究13.在三棱柱ABC -A 1B 1C 1中,点D 为AC 的中点,点D 1是A 1C 1上的一点.(1)当A 1D 1D 1C 1等于何值时,BC 1∥平面AB 1D 1?(2)当BC 1∥平面AB 1D 1时, 求证:平面BC 1D ∥平面AB 1D 1.解(1)A1D1D1C1=1.证明如下:如图,此时D1为线段A1C1的中点,连接A1B交AB1于O,连接OD1.由棱柱的定义知四边形A1ABB1为平行四边形,∴点O为A1B的中点.在△A1BC1中,点O,D1分别为A1B,A1C1的中点,∴OD1∥BC1.又∵OD1平面AB1D1,BC1平面AB1D1,∴BC1∥平面AB1D1,∴当A1D1D1C1=1时,BC1∥平面AB1D1.(2)证明:由(1)知,当BC1∥平面AB1D1时,点D1是线段A1C1的中点,则有AD∥D1C1,且AD=D1C1,∴四边形ADC1D1是平行四边形.∴AD1∥DC1.又∵DC1平面AB1D1,AD1平面AB1D1,∴DC1∥平面AB1D1.又∵BC1∥平面AB1D1,BC1平面BC1D,DC1平面BC1D,DC1∩BC1=C1,∴平面BC1D∥平面AB1D1.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练15

双基限时练(十五)一、选择题1.已知正四棱锥的侧棱长为23,高为3,则该棱锥的体积为( ) A .3 B .6 C .9D .18解析 设棱锥的底面边长为a ,则(23)2=32+⎝ ⎛⎭⎪⎫22a 2,∴a 22=3,∴a 2=6,V 锥=13a 2h =13×6×3=6. 答案 B2.已知一正四棱台的三视图如图所示,则该几何体的体积为( )A .624B .208C .131D .1313解析 由图可知,棱台的上底面边长为4,下底面边长为10,高为4,所以棱台的体积为V =13(S 上+S下+S 上·S 下)h =13×(16+100+40)×4=6243=208.答案 B3.直角梯形的一个内角为45°,下底为上底长的32倍,这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为(5+2)π,则旋转体的体积为( )A .2πB .4+23πC .5+23πD .73π解析 设该直角梯形的上底长为r ,下底长则为32r.该几何体为圆柱与圆锥的组合体.S 全=π×⎝ ⎛⎭⎪⎫r 22+πr 2+π2r ×22r =⎝ ⎛⎭⎪⎫54π+24πr 2=(5+2)π,∴r =2,∴V =V 圆柱+V 圆锥=73π. 答案 D4.在棱长为1的正方体上,分别用过公共顶点的三条棱的中点的平面截该正方体,则截去8个三棱锥后,剩下的多面体的体积是( )A .23B .76C .45D .56解析 V =1-8V 锥=1-8×13×12×12×12×12=56. 答案 D5.已知某个几何体的三视图如图所示,根据图中标明的尺寸(单位:cm )可得这个几何体的体积是( )A .40003 cm 3 B .80003 cm 3 C .2000 cm 3D .4000 cm 3解析 由三视图得几何体S -ABCD ,且面SCD ⊥面ABCD ,四边形ABCD 为正方形,作SE ⊥CD 于E ,得SE ⊥面ABCD ,SE =20 cm .∴V S -ABCD =13S ABCD ·SE =80003(cm 3). 答案 B6.图中的三个直角三角形是一个体积为20 cm 3的几何体的三视图,则该几何体的高为( )A .4B .12C .43D .24解析 由三视图可知该几何体为一个三棱锥S -ABC ,其中SA ⊥面ABC ,AB ⊥AC ,∴V =13S △ABC ·h =13×12×5×6×h =5h ,得h =4.答案 A 二、填空题7.用一张圆弧长为12π,半径为10的扇形纸片制作一个圆锥体,则这个圆锥体的体积是________.解析 由2πr =12π,得r =6,h =102-r 2=8,∴V 锥=13S 底·h =13π×62×8=96π. 答案 96π8.正四棱台的斜高与上、下底面边长之比为,体积为14 cm 3,则棱台的高为________.解析 设正四棱台上底为2a ,下底为8a ,斜高为5a ,则(5a)2=h 2+9a 2, ∴h 2=16a 2,∴h =4a ,又由棱台的体积公式求得h =2(cm ). 答案 2 cm9.在三棱锥P —ABC 中,三条侧棱PA ,PB ,PC 两两垂直,设PA =x ,PB =y ,PC =1,若x +y =4,则此三棱锥体积的最大值是________.解析 V =13×12xy =16xy =16x(4-x)=16(4x -x 2)=16×[-(x -2)2+4], ∴当x =2即x =y 时,V max =46=23. 答案 23 三、解答题10.将边长为a 的正方形ABCD 沿对角线AC 折起,使BD =a ,求三棱锥D —ABC 的体积.解取AC的中点M,连接BM,DM,∵BD=a,BM=22a,DM=22a,∴DM2+BM2=BD2.∴∠DMB=90°,又AD=DC,∴DM⊥AC.又AC∩BM=M,∴DM⊥面ABC.∴V=13S底·h=13×a22×22a=212a3.11.在下图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积. 解 (1)俯视图如下图所示.(2)所求多面体的体积V =V 长方体-V 三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843(cm 3).12.在正方体ABCD —A 1B 1C 1D 1中,O 为底面ABCD 的中心,若正方体的棱长为a.(1)求三棱锥O —AB 1D 1的体积; (2)求O 到平面AB 1D 1的距离. 解 (1)∵V O -AB 1D 1=V A —B 1D 1O , S △B 1D 1O =12B 1D 1·a =22a 2, 又AO ⊥面BDD 1B 1, 且AO =22a ,∴V A —B 1D 1O =V O —AB 1D 1=13×22a 2×22a =a 36. (2)∵AB 1=B 1D 1=AD 1=2a , ∴S △AB 1D 1=12B 1D 1·AB 1 sin 60°=32a 2, 设O 到平面AB 1D 1的距离为h. 由等积转化得13×32a 2h =a 36, ∴h =33a.思 维 探 究13.如图所示,在△ABC 中,∠ACB =90°,∠B =30°,AC =2,M 是AB 的中点,将△ACM 沿CM 折起,使A ,B 间的距离为22,求三棱锥A -BCM 的体积.解 由题意知在Rt △ABC 中,AB =4,BC =2 3. 又∵CM 为中线,∴MA =MB =MC =12AB =2.∴在三棱锥A -BCM 中,M 在面ABC 上的射影为△ABC 的外心. 又∵在折叠后的△ABC 中,AC =2,AB =22,BC =23, ∴AC 2+AB 2=BC 2,即折叠后的△ABC 也为直角三角形.取BC 的中点E ,连接ME ,则E 为点M 在面ABC 上的射影,即ME 的长为三棱锥M -ABC 的高.∵ME 为△MBC 的高,MB =MC =2,∠MBE =30°, ∴ME =12MB =1.∴V A -BCM =V M -ABC =13S △ABC ·ME =223.。
【名师点睛】高中数学北师大版必修2 第一章 立体几何初步双基限时练16(含解析)

双基限时练(十六)一、选择题1.设长方体的长、宽、高分别为2a ,a ,a ,其顶点都在一个球面上,则该球的表面积为( )A .3πa 2B .6πa 2C .12πa 2D .24πa 2解析 由题意得,2R =4a 2+a 2+a 2=6a , ∴R=62a ,∴球的表面积S =4πR 2=6πa 2. 答案 B2.已知某几何体的三视图如图所示,则其表面积为( )A .4πB .3πC .2πD .π解析 由三视图可知,该几何体为半径为1的半球体, ∴S 表=πr 2+2πr 2=3πr 2=3π. 答案 B3.若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积之比为( )A .1:2:3B .2:3:4C .3:2:4D .3:1:2解析 V 圆柱=2πR 3,V 圆锥=13πR 2·(2R)=2π3R 3,V 球=43πR 3.则体积之比为:2:23 :43即3:1:2.答案 D4.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A .6πB .43πC .46πD .63π解析 如图,设平面α截球O 所得圆的圆心为O 1,则|OO 1|=2,|O 1A|=1,∴球的半径R =|OA|=2+1= 3.∴球的体积V =43πR 3=43π.故选B .答案 B5.如图,正四棱锥P —ABCD 底面的四个顶点A ,B ,C ,D 在球O 的同一个大圆上,点P 在球面上,如果V P —ABCD =163,那么球O 的表面积是( )A .4πB .8πC .12πD .16π解析 由题意,可得AB =2R ,PO =R ,又V P —ABCD =13(2R)2R =163,得R =2,∴S 表=4πR2=16π.答案 D6.64个直径都为a4的球,记它们的体积之和为V 甲,表面积之和为S 甲,一个直径为a的球记其体积为V 乙,表面积为S 乙,则( )A .V 甲>V 乙,S 甲>S 乙B .V 甲<V 乙,S 甲>S 乙C .V 甲=V 乙,S 甲>S 乙D .V 甲=V 乙,S 甲<S 乙解析 V 甲=64×43π×⎝ ⎛⎭⎪⎫a 4×123=16πa 3,S 甲=64×4π×⎝ ⎛⎭⎪⎫a 82=4πa 2,V 乙=43π×⎝ ⎛⎭⎪⎫a 23=16πa 3,S 乙=4π×⎝ ⎛⎭⎪⎫a 22=πa 2,∴V 甲=V 乙,S 甲>S 乙. 答案 C 二、填空题7.一个正方体的各顶点均在同一球的球面上,若该球的体积为43π,则该正方体的表面积为________.解析 设正方体的棱长为a ,球的半径为r ,则2r =3a , ∴a=233r ,∵43πr 3=43π,∴r=3,∴a=2.∴S 表=6a 2=24. 答案 248.圆柱形容器的内壁底面半径为5 cm ,两个直径为5 cm 的玻璃小球都浸没于该容器的水中,若取出两个小球,则容器的水面将下降________.解析 由题意,得2×43π×⎝ ⎛⎭⎪⎫523=π×52×h,得h =53.答案 53cm9.一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都是在同一个球面上,且该六棱柱的高为3,底面周长为3,那么这个球的体积为________.解析 球的半径R =⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫362=1, 故V 球=43πR 3=43π.答案 43π三、解答题10.已知某几何体的三视图如图所示,求它的体积和表面积.解 由三视图可知该几何体是半径为1的球被挖出了18部分得到的几何体,∴其体积V=78V 球=78×43π×13=76π,S 表=78×4π×12+3×14π×12=174π. 11.一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,求这个圆锥的高与球的半径之比.解 如图,作出轴截面,设公共底面圆的半径为R ,圆锥的高为h.∴V 锥=13πR 2h ,V 半球=12·43πR 3.∵V 锥=V 半球,∴h=2R ,即h:R =2:1.12.桌面上有三个半径均为r 的小球,它们两两相切,现有第四个半径为r 的小球放在三个小球上面,且与这三个小球都相切,求第四个小球的球心离桌面的距离.解 如图所示,设桌面上三个小球的球心分别为O 1,O 2,O 3,第四个小球的球心为O 4.因每两个小球都相切,所以O 1,O 2,O 3,O 4构成一个棱长都为2r 且各面都全等的正三角形的三棱锥.设O 4在平面O 1O 2O 3的正投影为O ,则O 4到桌面的距离为O 4O +r. 连接O 3O ,由于O 为正三角形△O 1O 2O 3的中心,∴OO 3=23×32×2r=233r.∴O 4O =2-⎝⎛⎭⎪⎫233r 2=263r. 因此,第四个小球的球心离桌面的距离为⎝⎛⎭⎪⎫263+1r. 思 维 探 究13.已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的316,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为多少?解 如图,设球的半径为R ,圆锥底面半径为r ,由题意得πr 2=316×4πR 2.∴r=32R ,∴OO 1=12R. 体积较小的圆锥的高AO 1=R -12R =12R ,体积较大的圆锥的高BO 1=R +12R =32R.故这两个圆锥中,体积较小者的高与体积较大者的高的比值为13.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练3

双基限时练(三)一、选择题1.用斜二测画法画水平放置的平面图形的直观图,对其中两条线段结论错误的是()A.原来相交的仍相交B.原来垂直的仍垂直C.原来平行的仍平行D.原来共点的仍共点解析斜二测画法保平行,保相交,保平行线段的比,但不保垂直.答案 B2.如图所示的直观图中A′B′∥y′轴,B′C′∥A′D′∥x′轴,且B′C′≠A′D′.其对应的平面图形ABCD是()A.任意梯形B.直角梯形C.任意四边形D.平行四边形解析由直观图的画法,可知原四边形ABCD为直角梯形.答案 B3.一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,如图若O′B′=1,那么原△ABO的面积是()A.12B.22C. 2D .2 2解析 由斜二测画法,可知原三角形为直角三角形,且∠AOB =90°,OB =1,OA =2O ′A ′=22,∴S △AOB =12×1×22= 2. 答案 C 4.如图所示为等腰直角三角形,其中AB=AC=2,则△ABC的直观图的面积为()A.2 B. 2C.22D.2 2解析△ABC的直观图如图所示,则S△A′B′C′=12×2×1×sin45°=22.答案 C5.已知△A′B′C′为水平放置的△ABC的直观图,如图,则在△ABC 的三边及中线AD中,最长的线段是()A.AB B.ADC.BC D.AC解析由斜二测画法,可知原三角形ABC为直角三角形,AC为斜边,D为BC的中点,故AC>AD,故最长的线段为AC,故答案为D.答案 D6.已知等边三角形的边长为2,那么它的直观图的面积为()A.32B.34C.64D.62解析 如图①②分别为平面图与直观图,由②可知,A ′B ′=2,h ′=C ′O ′sin45°=32×22=64,S △A ′B ′C ′=12×64×2=64.答案 C 二、填空题7.在一等腰梯形ABCD 中,AB ∥DC ,∠A =45°,DC =2,AD =2,建立如图所示的直角坐标系,其中O 为AB 的中点,则其直观图的面积为________.解析 由图可知AB =DC +2AD cos45°=4,EO =2sin45°=1,其直观图如图所示,其中A ′B ′=4,C ′D ′=2,高h ′=E ′O ′.sin45°=24,∴S A ′B ′C ′D ′=(2+4)×242=324.答案 3248.一个水平放置的△ABC 的斜二测直观图如图所示,已知A ′C ′=3,B ′C ′=2,则AB 边上的中线的实际长度为________.解析 由斜二测画法,知△ABC 为直角三角形,AB =AC 2+BC 2=9+16=5,∴AB 边上的中线为52. 答案 529.如图所示,ABCD 为边长为2的正方形,其中B (2,2),则在斜二测画法中,直观图A ′B ′C ′D ′中B ′点到x ′轴的距离为________.解析 在直观图中,A ′B ′C ′D ′是有一个角为45°的平行四边形,B ′到x ′轴的距离为d =1×sin45°=22.答案 22三、解答题10.把下图水平放置的直观图P ′Q ′R ′S ′还原为真实图形.若S ′R ′=2,P ′Q ′=4,S ′P ′=2,S ′R ′∥P ′Q ′∥O ′x ′,P ′S ′∥O ′y ′,试求其真实图形PQRS 的面积.解 由斜二测画法,知P ′Q ′∥O ′x ′,P ′S ′∥O ′y ′,R ′S ′∥O ′x ′.故PQ ∥Ox ,PS ∥Oy ,RS ∥Ox ,且PS =2P ′S ′,PQ =P ′Q ′,RS =R ′S ′.故真实图形如图所示.由上知PQ =P ′Q ′=4,SR =S ′R ′=2,SP =2S ′P ′=4,且四边形PQRS 是直角梯形,其面积S =12(SR +PQ )·SP =12 (2+4)×4=12.11.已知正△ABC 的边长为a ,求△ABC 的平面直观图△A ′B ′C ′的面积.解 由斜二测画法可知,A ′B ′=AB =a ,O ′C ′=12OC =34a , 在图②中,作C ′D ′⊥A ′B ′于点D ′,则C ′D ′=22O ′C ′=68a ,所以S △A ′B ′C ′=12A ′B ′·C ′D ′=12×a ×68a =616a 2.12.画出长为5,宽为4,高为5的长方体的直观图.解 (1)画出x 轴,y 轴,z 轴三轴相交于O 点,使∠xOy =45°,∠xOz =90°,∠yOz =90°.(2)在x 轴上取OA =5,OC =2,过A 作AB ∥OC ,过C 作CB ∥OA ,则四边形OABC 为下底面.(3)在z 轴上取OO ′=5,过O ′作O ′x ′∥Ox ,O ′y ′∥Oy ,建立坐标系x ′O ′y ′,重复(2)的步骤作出上底面O ′A ′B ′C ′.(4)连接AA ′,BB ′,CC ′,OO ′,即得到长方体OABC -O ′A ′B ′C ′的直观图.思 维 探 究13.已知水平放置的三角形ABC 是正三角形,其直观图的面积为64a 2,求△ABC 的周长.解 图△ABC 是△A ′B ′C ′的原图形,设△ABC 的边长为x ,由斜二测画法,知A ′B ′=AB =x ,O ′C ′=12OC =34x ,作C ′D ′⊥A ′B ′,垂足为D ′,∵∠C ′O ′D ′=45°,∴C ′D ′=22O ′C ′=22×34x =68x ,∴S △A ′B ′C ′=12A ′B ′×C ′D ′=12x ×68x =616x 2. ∴616x 2=64a 2,∴x =2a , ∴△ABC 周长为3×2a =6a .。
北师大版高中数学必修2双基限时练:第一章++立体几何

双基限时练(十四)一、选择题1.圆柱的轴截面是边长为2的正方形,则圆柱的全面积为( ) A .6π B .4π C .2πD .4解析 由题可知,r =1,l =2,∴S 全=2πrl +2πr 2=6π. 答案 A2.一个圆锥的高为10,侧面展开图为半圆,则圆锥的侧面积为( ) A .200π B .2003 C .2003πD .200解析 设圆锥的底面半径为x ,则侧面母线长为x 2+102,又侧面展开图为半圆,∴2πx =πx 2+102,得x =1033. ∴S 圆锥侧=πrl =π×1033× 1003+102=2003π.即圆锥的侧面积为2003π. 答案 C3.若圆台的高为3,一个底面半径是另一个底面半径的2倍,其轴截面的一个底角为45°,则这个圆台的侧面积是( )A .27πB .272πC .92πD .362π解析 如图可知,2r 2=2r 1+6=4r 1,∴r1=3,r2=6.S圆台侧=π(r1+r2)l=π(6+3)×32=272π.答案B4.一个几何体的三视图中,主视图和左视图都是矩形,俯视图是等腰直角三角形(如图),根据图中标准的长度,可以计算出该几何体的表面积是()A.12+4 2 B.8+4 2C.2+8 2 D.6+4 2解析由三视图可知,该几何体为直三棱柱,其中底面为等腰直角三角形,直角边长为2,高为2,S表=2×12×2×2+(2+2+22)×2=12+42,故选A.答案A5.正四棱台两底面面积分别为4 cm2,64 cm2,侧棱长为37 cm,则棱台的高为()A.6 5 cm B.12 cmC.6 cm D.3 5 cm解析由题可知,棱台上、下底面边长分别为2,8,由侧棱长为37知,高h=(37)2-(42-2)2=63-18=35(cm),故选D.答案D6.一个棱锥的三视图如图所示,则该棱锥的表面积(单位:cm2)为()A.48+12 2 B.48+24 2C.36+12 2 D.36+24 2解析由三视图可知,该几何体是一个底面为直角三角形且顶点在底面上的射影为斜边的中点的三棱锥,如图,SE=5,SD=4,AC=62,AB=BC=6,∴S表=S△ABC+2S△SAB+S△ASC=12×6×6+2×12×5×6+12×62×4=48+12 2.答案A二、填空题7.若一个底面是正三角形的三棱柱的主视图如图所示,则其侧面积等于________.解析由图可知,此三棱柱的底面是一个边长为2的正三角形,此三棱柱的高为1,则此三棱柱的侧面积为2×1×3=6.答案 68.某个几何体的三视图是两个边长为2 cm的菱形和一个直径为2 cm 的圆,则该几何体的表面积为________.解析由三视图可知,该几何体为两个共底的圆锥,其中底面圆的半径为1,母线长为2,则该几何体的表面积S表=2πrl=2π×1×2=4π.答案4π9.已知一个几何体的三视图如图所示,则此几何体的表面积为________.解析由题可知,该几何体为圆柱、圆锥的组合体,S表=πa2+2πa·2a+πa·2a=5πa2+2πa2=(5+2)πa2.答案(5+2)πa2三、解答题10.已知一个圆台的轴截面的面积为F,母线与底面的夹角是30°,求圆台的侧面积.解如图是圆台的轴截面,设AO1=r,BO =R ,BE =R -r , AE =33(R -r), AB =233(R -r),由题意,得F =(R +r)33(R -r)=33(R 2-r 2). ∴R 2-r 2=3F.∴S 圆台侧=π(R +r)·233(R -r) =233π(R 2-r 2)=2πF. 11.如图,在三棱锥S —ABC 中,SA ⊥面ABC ,△ABC 是直角三角形,∠ACB =90°,∠ABC =30°,AC =1,SB =2 3.求三棱锥S —ABC 的表面积.解 ∵SA ⊥面ABC ,∴SA ⊥BC.又∠ACB =90°, ∴AC ⊥BC ,∴BC ⊥面SAC ,∴SC ⊥BC. ∴四个面都是直角三角形. ∵∠ABC =30°,AC =1,∴在Rt △ABC 中,AB =2,BC =3, 在Rt △SCB 中,SC =SB 2-BC 2=3,在Rt △SAB 中,SA =SB 2-AB 2=2 2. ∴S △SBC =12SC·BC =332, S △ABC =12AC·BC =32,S △SAB =12SA·AB =22,S △SAC =12SA·AC = 2.∴三棱锥的表面积S 表=S △ABC +S △SBC +S △SAB +S △SAC =23+3 2. 12.已知,在底面半径为2,母线长为4的圆锥中内接一个高为3的圆柱,求圆柱的表面积.解 圆锥的高h =42-22=23,设圆柱的底面半径为r ,由r 2=h -3h ,得圆柱的底面半径r =1,所以S 表面=2S 底面+S 侧面=2π+2π×3=2(1+3)π.思 维 探 究13.如图,在直三棱柱ABC -A 1B 1C 1中,AC =9,BC =12,AB =15,AA 1=12,点D 是AB 的中点.(1)求证:AC ⊥B 1C ; (2)求证:AC 1∥平面CDB 1; (3)求这个三棱柱的表面积.解 (1)证明:∵AB 2=AC 2+BC 2,∴∠ACB =90°,AC ⊥BC ,∵CC 1⊥AC ,CC 1∩BC =C ,∴AC ⊥面BB 1C 1C.∵B 1C 面BB 1C 1C ,∴AC ⊥B 1C.(2)证明:连接BC 1交B 1C 于点O ,连接OD. ∵四边形BB 1C 1C 为矩形,∴点O 为BC 1的中点. 又∵点D 为BA 的中点,∴OD ∥AC 1. ∵OD平面CDB 1,AC 1平面CDB 1,∴AC 1∥平面CDB 1.(3)S 表=(9+12+15)×12+2×12×9×12=540.。
北师大版高中数学必修2双基限时练:第二章+解析几何初

双基限时练(二十三)一、选择题1.点(1,1)到直线x -y =2的距离为( ) A.22 B .1 C. 2 D .2解析 d =|1-1-2|12+(-1)2= 2.答案 C2.过点A (4,a )和B (5,b )的直线与y =x +m 平行,则|AB |的值为( ) A .6 B. 2 C .2D .不确定解析 由k AB =b -a5-4=1,得b -a =1,即|AB |=(5-4)2+(b -a )2= 2.答案 B3.两条平行线4x +3y -1=0与8x +6y +3=0之间的距离是( ) A .2 B .1.5 C .1D .0.5解析 8x +6y +3=0,可化为4x +3y +32=0,d =⎪⎪⎪⎪⎪⎪32-(-1)32+42=12. 答案 D4.若两平行直线2x +y -4=0与y =-2x -k -2的距离不大于5,则k 的取值范围是( )A .[-11,-1]B .[-11,0]C .[-11,-6)∪(-6,-1]D .[-1,+∞) 解析 y =-2x -k -2可化为2x +y +k +2=0,由题意, 得|k +2+4|22+12=|k +6|5≤5,且k +2≠-4即k ≠-6得-5≤k +6≤5,即-11≤k ≤-1,且k ≠-6. 答案 C5.过点A (1,1)的直线l 与点B (2,4)的距离为5,则此直线l 的方程为( )A .x +2y -3=0B .x -2y +1=0C .x +2y -3=0或x -2y +1=0D .x -2y +1=0或2x +y -3=0解析 显然直线l 的斜率存在,设所求直线方程为 y -1=k (x -1),即kx -y +1-k =0. 由题意,得|2k -4+1-k |k 2+(-1)2= 5.得k =-2,或k =12.∴所求直线方程为2x +y -3=0,或x -2y +1=0. 答案 D6.过点P (0,1)且和A (3,3),B (5,-1)距离相等的直线的方程是( ) A .y =1 B .2x +y -1=0 C .y =1或2x +y -1=0 D .2x +y -1=0或2x +y +1=0解析 ∵k AB =3-(-1)3-5=-2,过P 与AB 平行的直线方程为y -1=-2(x -0),即:2x +y -1=0;又AB 的中点C (4,1),∴PC 的方程为y =1. 答案 C 二、填空题7.已知A (-1,2),B (3,b )的距离为42,则b =________. 解析 |AB |=[3-(-1)]2+(b -2)2=16+(b -2)2=42,得b =-2,或b =6. 答案 -2或68.已知点P 在直线5x +12y +6=0上,A 点坐标为(-3,2),则|P A |的最小值为________.解析 |P A |min 等于A 到直线5x +12y +6=0的距离,则点(-3,2)到直线的距离d =1513.答案 15139.已知点A (3,4),B (6,m )到直线3x +4y -7=0的距离相等,则实数m =________.解析 由题意,得|9+16-7|5=|18+4m -7|5, 得m =74,或m =-294. 答案 74或-294三、解答题10.若两条平行直线3x -2y -1=0和6x +ay +c =0之间的距离为21313,求c +2a 的值.解 由两条直线平行得a =-4,应用距离公式得|c +2|62+42=21313.解得|c+2|=4,所以c +2a =±4-4=±1.11.已知正方形的边长为25,中心(-3,-4),一边与直线2x +y +3=0平行,求正方形的各边所在的直线方程.解 设所求的直线方程为2x +y +b =0与x -2y +a =0, 由题意,可得|(-3)×2+(-4)+b |22+12=5,得b =15,或b =5, 由|-3-2×(-4)+a |12+(-2)2=5,得a =0,或a =-10. ∴所求的这四条直线方程为2x +y +15=0;2x +y +5=0;x -2y =0;x -2y -10=0.12.△ABC 的三个顶点A (-1,4),B (-2,-1),C (2,3). (1)求BC 边的高所在的直线方程; (2)求△ABC 的面积S .解 (1)设BC 边的高所在的直线为l . 又k BC =3-(-1)2-(-2)=1,∴k l =-1k BC =-1.又A (-1,4)在直线l 上,∴l 的方程为y -4=-(x +1),即x +y -3=0. (2)BC 所在直线为y +1=x +2,即x -y +1=0. 点A (-1,4)到BC 的距离d =|-1-4+1|12+(-1)2=2 2.又|BC |=(-2-2)2+(-1-3)2=42, 则S △ABC =12|BC |d =12×42×22=8.思 维 探 究13.直线l 1过点A (0,1),l 2过点B (5,0),如果l 1∥l 2,且l 1与l 2之间的距离为5,求l 1,l 2的方程.解 若直线l 1,l 2的斜率存在,设直线l 1,l 2的斜率为k . 由斜截式得l 1的方程为y =kx +1,即kx -y +1=0. 由点斜式得l 2的方程为y =k (x -5),即kx -y -5k =0.在直线l 1上取点A (0,1),点A 到直线l 2的距离d =|1+5k |1+k 2=5, 即25k 2+10k +1=25k 2+25,解得k =125.所以l 1的方程为12x -5y +5=0,l 2的方程为12x -5y -60=0. 若l 1,l 2的斜率不存在,则l 1的方程为x =0,l 2的方程为x =5,它们之间的距离为5,同样满足条件.故满足条件的直线方程为l 1:12x -5y +5=0,l 2:12x -5y -60=0或l 1:x =0, l 2:x =5.。
北师大版高中数学必修2双基限时练:第二章+解析几何初步(13套,含解析)双基限时练18

双基限时练(十八)一、选择题1.经过点(1,-3),倾斜角是150°的直线方程是( ) A .-3x +3y +9-3=0 B .3x +3y +9-3=0 C .3x -3y +9-3=0 D .3x +3y -9+3=0解析 由题可知,直线的斜率为k =tan 150°=-33,由点斜式,得y +3=-33(x -1),即3x +3y +9-3=0.答案 B2.直线3x +2y +6=0的斜率为k ,在y 轴上的截距为b ,则有( ) A .k =-32,b =3 B .k =-23,b =-2 C .k =-32,b =-3D .k =-23,b =-3解析 由3x +2y +6=0,得y =-32x -3,知k =-32,b =-3,答案为C .答案 C3.直线x -y +1=0与坐标轴围成的三角形的周长为( ) A . 2 B .2+ 2 C .2- 2D .22-2解析 令x =0,y =1,令y =0,x =-1,故三角形的周长l =1+1+12+12=2+2,选B . 答案 B4.已知直线l 的倾斜角为直线y =3x -1的倾斜角的一半,且直线l 过点(3,-4),则l 的方程为( )A .y +4=32(x -3) B .y +4=33(x +3) C .x -3y -3=0 D .x -3y -43-3=0解析 由题可知,k l =33,由点斜式可得l 的方程. 答案 D5.若直线l 过点(0,2),倾斜角的正弦值为45,则此直线方程为( ) A .4x -3y -6=0 B .4x -y +6=0C .4x -3y +6=0或4x +3y -6=0D .4x -3y -6=0或4x +3y +6=0 解析 设直线l 的倾斜角为θ,∵sin θ=45,∴tan θ=±43,故所求的直线方程为y -2=43(x -0),或y -2=-43(x -0). 即4x -3y +6=0,或4x +3y -6=0. 答案 C6.与直线3x -2y =0的斜率相等,且过点(4,-3)的直线方程为( ) A .y +3=32(x -4) B .y -3=32(x +4) C .y +3=23(x -4)D .y -3=23(x +4)解析 因直线3x -2y =0的斜率为32,由点斜式可知所求的直线方程为y +3=32(x -4).答案 A 二、填空题7.斜率与直线y =3x 的斜率相等,且过点(-4,3)的直线方程为________________.解析 由题可知,所求直线的斜率为3,故所求的直线方程为y -3=3(x +4),即3x -y +15=0.答案 3x -y +15=08.若直线l 的方程为y -a =(a -1)(x +2),且l 在y 轴上的截距为6,则a =________.解析 令x =0,得y =(a -1)×2+a =6,得a =83. 答案 839.已知一直线过点P(1,2),且斜率与直线y =-2x +3的斜率相等,则该直线方程是________.解析 由点斜式可得所求直线的方程. 答案 2x +y -4=0 三、解答题10.(1)求经过点(1,1),且与直线y =2x +7的斜率相等的直线方程; (2)已知直线l 过点(2,0),且与直线y =3(x -2)的夹角为30°,求直线l 的方程.解 (1)∵y =2x +7的斜率为k =2,∴所求直线的斜率k =2,又直线过点(1,1),由点斜式可得l 的方程为y -1=2(x -1),即y =2x -1.(2)∵直线y =3(x -2)的斜率为3, ∴其倾斜角为60°,又直线l 与y =3(x -2)的夹角为30°,∴直线l 的倾斜角可能为30°或90°,此时,斜率分别为33或不存在,又直线过(2,0),对应的直线方程分别为y =33(x -2),或x =2.11.已知直线l 的斜率为6,且被两坐标轴截得的线段长为37,求直线l 的方程.解 设所求的直线l 的方程为y =kx +b ,∵k =6, ∴方程为y =6x +b.令x =0,y =b ,令y =0,x =-b6,∴l 与x 、y 轴的交点分别为(-b6,0),(0,b).由题意,得⎝ ⎛⎭⎪⎫-b 62+b 2=37,得b =±6.∴直线l 的方程为y =6x±6.12.若A(a ,a 2),B(b ,b 2),且a +b =2,a ≠b ,直线l 过点(0,2),斜率与AB 两点连线的斜率相等,求直线l 的方程.解 k AB =b 2-a 2b -a =a +b =2,则直线l 的方程为y -2=2(x -0), 即2x -y +2=0.思 维 探 究13.求与两坐标轴围成的三角形的周长为9,且斜率为-43的直线方程. 解 设直线l 的方程为y =-43x +b.令x =0,得y =b ;令y =0,得x =34b.由题意,得|b|+34|b|+b 2+⎝ ⎛⎭⎪⎫34b 2=9.∴|b|+34|b|+54|b|=9,∴b =±3.∴所求直线方程为y =-43x +3或y =-43x -3,即4x +3y -9=0或4x +3y +9=0.。
北师大版高中数学必修2双基限时练:第二章+解析几何初步(13套,含解析)双基限时练27

双基限时练(二十七)一、选择题1.圆x2+y2=1与x2+y2-2x-2y=0的位置关系是()A.相交B.相离C.内含D.外切解析圆心距d=(1-0)2+(1-0)2=2<1+2,且d>2-1,可知答案为A.答案 A2.若x2+y2-2mx+4y+m2-5=0与x2+y2+2x-2y-2=0相外切,则m的值为()A.-5 B.3C.-5或3 D.以上均不对解析x2+y2-2mx+4y+m2-5=0可化为(x-m)2+(y+2)2=9,x2+y2+2x-2y-2=0可化为(x+1)2+(y-1)2=4,由题可知,(m+1)2+(-2-1)2=3+2,得m=-5,或m=3.答案 C3.过两圆(x+3)2+(y+2)2=13及(x+2)2+(y+1)2=9的交点的直线方程是()A.x+y+2=0 B.x+y-2=0C.5x+3y+2=0 D.5x+3y-2=0解析将两圆的方程相减.答案 A4.两圆x2+y2+2ax+2ay+2a2-1=0与x2+y2+2bx+2by+2b2-1=0的公共弦长的最大值为()A .2 2B .2 C. 2D .1解析 两圆相交弦所在的直线方程为x +y +a +b =0, ∴弦长=21-⎝ ⎛⎭⎪⎪⎫a -b 22. ∴当a =b 时弦长最大,最大值为2. 答案 B5.若圆x 2+y 2-ax +2y +1=0关于直线x -y =1对称的圆的方程为x 2+y 2=1,则实数a 的值为( )A .0B .1C .±2D .2解析 x 2+y 2-ax +2y +1=0的圆心为⎝ ⎛⎭⎪⎫a 2,-1,半径为|a |2,由题意,得⎩⎪⎨⎪⎧|a |2=1,-1-0a 2-0=-1,得a =2.答案 D6.圆x 2+y 2+4x -4y +7=0与圆x 2+y 2-4x +10y +13=0的公切线的条数是( )A .1B .2C .3D .4解析 两圆的圆心距d =(-2-2)2+(2+5)2=65,半径r 1=1,r 2=4,∴d >r 1+r 2,∴两圆相外离,故有4条公切线.答案 D二、填空题7.若圆x 2+y 2=4与圆x 2+y 2+2ay -6=0(a >0)的公共弦的长为23,则a =________.解析 由题可知,两圆的公共弦所在的直线方程为y =1a ,圆心O 到直线的距离为1a ,则由弦长公式(3)2+1a 2=4,得a =1.答案 18.若(x +1)2+y 2=4与(x -a )2+y 2=1相交,则a 的取值范围是________. 解析 由题可知(-1-a )2+(0-0)2∈(2-1,2+1),得-4<a <-2,或0<a <2. 答案 -4<a <-2,或0<a <29.若圆x 2+y 2=4和圆x 2+y 2+4x -4y +4=0关于直线l 对称,则直线l 的方程为________.解析由⎩⎨⎧x 2+y 2+4x -4y +4=0,①x 2+y 2=4,②①-②可得l 的方程为x -y +2=0. 答案 x -y +2=0 三、解答题10.已知圆C 1:x 2+y 2+2x +2y -8=0与圆C 2:x 2+y 2-2x +10y -24=0相交于A ,B 两点.(1)求公共弦AB 所在的直线方程;(2)求圆心在直线y =-x 上,且经过A ,B 两点的圆的方程.解 (1)由⎩⎪⎨⎪⎧x 2+y 2+2x +2y -8=0,x 2+y 2-2x +10y -24=0,得x -2y +4=0,所以公共弦AB 所在的直线方程为x -2y +4=0.(2)设所求的圆的方程为x 2+y 2+2x +2y -8+λ(x 2+y 2-2x +10y -24)=0①整理得(1+λ)x 2+(1+λ)y 2+(2-2λ)x +(2+10λ)y -8-24λ=0,圆心⎝⎛⎭⎪⎫λ-11+λ,-1+5λ1+λ,又圆心在y =-x 上, 即λ-11+λ=1+5λ1+λ,得λ=-12. 代入①得x 2+y 2+6x -6y +8=0.即所求的圆的方程为x 2+y 2+6x -6y +8=0.11.求通过直线2x -y +3=0与圆x 2+y 2+2x -4y +1=0的交点,且面积最小的圆的方程.解 解法1:设所求的圆的方程为x 2+y 2+2x -4y +1+λ(2x -y +3)=0, 配方得标准方程为(x +1+λ)2+⎝ ⎛⎭⎪⎫y -2-λ22=(1+λ)2+(4+λ)24-3λ-1. ∵r 2=54λ2+λ+4=54(λ+25)2+195, ∴当λ=-25时,半径r =195最小.∴所求面积最小的圆的方程为5x 2+5y 2+6x -18y -1=0. 解法2:设直线与圆的交点为A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧2x -y +3=0,x 2+y 2+2x -4y +1=0,消去y ,得5x 2+6x -2=0. ∴判别式Δ>0,AB 中点横坐标x 0=x 1+x 22=-35,纵坐标y 0=2x 0+3=95,即圆心C ⎝ ⎛⎭⎪⎫-35,95,半径r =12·|x 1-x 2|1+22= 195,∴所求面积最小的圆的方程为⎝ ⎛⎭⎪⎫x +352+⎝ ⎛⎭⎪⎫y -952=195.12.已知圆C 1:x 2+y 2-10x -10y =0和圆C 2:x 2+y 2+6x +2y -40=0相交于A ,B 两点,求公共弦AB 的长.解 解法1:由两圆方程相减,得公共弦AB 所在直线的方程为:4x +3y -10=0.由⎩⎪⎨⎪⎧ 4x +3y -10=0,x 2+y 2-10x -10y =0解得⎩⎪⎨⎪⎧ x =-2,y =6或⎩⎪⎨⎪⎧x =4,y =-2.令A (-2,6),B (4,-2). 故|AB |=(-2-4)2+(6+2)2=10.解法2:同法1,先求出公共弦所在直线l 的方程为4x +3y -10=0. 过C 1作C 1D ⊥AB 于D ,如图,圆C 1的圆心C 1(5,5),半径r 1=52,则|C 1D |=|20+15-10|5=5.∴|AB |=2|AD |=2C 1A 2-C 1D 2=250-25=10.思 维 探 究13.已知圆C 1:x 2+y 2-2ax -2y +a 2-15=0,C 2:x 2+y 2-4ax -2y +4a 2=0(a >0).试求a 为何值时,两圆C 1,C 2:(1)相切;(2)相交;(3)相离? 解 对圆C 1,C 2的方程,经配方后可得:C1:(x-a)2+(y-1)2=16,C2:(x-2a)2+(y-1)2=1,∴C1(a,1),r1=4,C2(2a,1),r2=1,∴|C1C2|=(a-2a)2+(1-1)2=a.(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切,当|C1C2|=r1-r2=3,即a=3时,两圆内切.(2)当3<|C1C2|<5,即3<a<5时,两圆相交.(3)当|C1C2|>5,即a>5时,两圆外离.。
北师大版高中数学必修2双基限时练:第二章+解析几何初

双基限时练(二十二)一、选择题1.直线3x +y -5=0与x +y -1=0的交点是( ) A .(2,-1) B .(-1,2) C .(-2,1) D .(-2,-1)解析由⎩⎨⎧3x +y -5=0,x +y -1=0,得⎩⎨⎧x =2,y =-1.答案 A2.若(-1,-2)为直线ax +3y +8=0与x -by =0的交点,则a ,b 的值分别为( )A .2,12 B .12,2 C .-2,-12D .-2,12解析 ∵(-1,-2)为两条直线的交点,∴⎩⎨⎧-a -6+8=0,-1+2b =0,得⎩⎪⎨⎪⎧a =2,b =12.答案 A3.若直线x +y +3m +2=0与x -y -5m +6=0的交点在第三象限,则m 的取值范围是( )A .12<m<4 B .-4<m<-12 C .m>4D .m<12解析由⎩⎨⎧x +y +3m +2=0,x -y -5m +6=0,得⎩⎨⎧x =m -4,y =-4m +2,由⎩⎨⎧m -4<0,-4m +2<0,得12<m<4.答案 A4.已知三条直线y =2x ,x +y =3,mx +ny +5=0交于一点,则坐标(m ,n)可能是( )A .(1,-3)B .(3,-1)C .(-3,1)D .(-1,3)解析由⎩⎨⎧y =2x ,x +y =3,得⎩⎨⎧x =1,y =2.由三条直线相交于一点,可知m ×1+n ×2+5=0即m +2n +5=0,结合选项可知A 项正确. 答案 A5.已知直线l 1:2x +y -10=0,l 2⊥l 1,且l 2过(-10,0),则l 1与l 2的交点坐标为( )A .(6,2)B .(2,-6)C .(-6,2)D .(2,6)解析 ∵kl 1=-2,l 2⊥l 1,∴kl 2=12. 又l 2过(-10,0),∴l 2:x -2y +10=0.由⎩⎨⎧x -2y +10=0,2x +y -10=0,得⎩⎨⎧x =2,y =6.答案 D6.无论k 为何值,直线(k +2)x +(1-k)y -5-4k =0都过一个定点,则这个定点的坐标为( )A .(1,3)B .(-1,3)C .(3,1)D .(3,-1)解析原直线可化为(2x +y -5)+k(x -y -4)=0,由⎩⎨⎧2x +y -5=0,x -y -4=0,得⎩⎨⎧x =3,y =-1.∴交点(3,-1). 答案 D 二、填空题7.直线l 1:3x +4y -5=0与直线l 2:2x -3y +8=0的交点坐标为________.解析由⎩⎨⎧3x +4y -5=0,2x -3y +8=0,得⎩⎨⎧x =-1,y =2.答案 (-1,2)8.经过直线x +y -1=0和x -y +1=0的交点,且与3x +2y +6=0垂直的直线方程为________.解析 所求的直线方程为x +y -1+λ(x -y +1)=0,即(λ+1)x -(λ-1)y +λ-1=0,k =λ+1λ-1,由k·⎝ ⎛⎭⎪⎫-32=-1,则λ+1λ-1=23,得λ=-5,故所求的直线方程为-4x +6y -6=0,即2x -3y +3=0.答案 2x -3y +3=09.已知l 1:x -y -1=0,l 2:2x -y +3=0,l 3:x +my -5=0,若l 1,l 2,l 3只有两个交点,则m =________.解析 ∵l 1与l 2相交,故只需l 1∥l 3,或l 2∥l 3即可,得m =-1,或m =-12.答案 -1或-12 三、解答题10.设直线l 经过2x -3y +2=0和3x -4y -2=0的交点,且与两坐标轴围成等腰直角三角形,求直线l 的方程.解 设所求的直线方程为(2x -3y +2)+λ(3x -4y -2)=0,整理得(2+3λ)x -(4λ+3)y -2λ+2=0由题意,得2+3λ3+4λ=±1,解得λ=-1,或λ=-57.∴所求的直线方程为x -y -4=0,或x +y -24=0.11.三条直线ax +2y +8=0,4x +3y =10和2x -y =10相交于一点,求a 的值.解 解方程组⎩⎪⎨⎪⎧ 4x +3y =10,2x -y =10得⎩⎪⎨⎪⎧x =4,y =-2,所以交点坐标为(4,-2).代入直线方程ax +2y +8=0,得a ×4+2×(-2)+8=0,解得a =-1.12.设直线l 的方程为(a +1)x +y +(2-a)=0(a ∈R ). (1)证明直线l 恒过定点;(2)若l 在两坐标轴上的截距相等,求直线l 的方程.解 (1)证明:直线l 的方程可化为(x -1)a +x +y +2=0(a ∈R )令⎩⎪⎨⎪⎧ x -1=0,x +y +2=0,得⎩⎪⎨⎪⎧x =1,y =-3.∴无论a 为任何实数,直线l 总经过定点(1,-3). (2)∵直线l 在两坐标轴上截距相等,l 的方程为 (a +1)x +y +2-a =0,∴l 的两截距一定存在,∴a ≠-1,令y =0,x =a -2a +1,令x =0,y =a -2,由a -2a +1=a -2,得a =2,或a =0. ∴所求直线l 的方程为3x +y =0,或x +y +2=0.思 维 探 究13.求经过两直线2x +y -8=0与x -2y +1=0的交点,且在y 轴上的截距为x 轴上截距的两倍的直线l 的方程.解 设所求的直线方程为2x +y -8+λ(x -2y +1)=0即:(2+λ)x +(1-2λ)y +λ-8=0,由题意得2+λ≠0且1-2λ≠0.令x >0,得y =λ-82λ-1;令y =0,得x =8-λ2+λ.由题意得2·8-λ1-2λ=8-λ2+λ,得λ=8或λ=-34.当λ=8时,直线方程为10x -15y =0,即2x -3y =0; 当λ=-34时,直线方程为:54x +52y -354=0,即x +2y -7=0. ∴所求的直线方程为2x -3y =0或x +2y -7=0.。
北师大版高中数学必修二双基限时练6.docx

双基限时练(六)一、选择题1.下列说法错误的是()A.若一条直线与平面有无数个公共点,则这条直线在平面内B.若两个平面没有公共点,则两个平面互相平行C.直线与平面的位置关系有两种:相交、平行D.如果一条直线与平面只有一个公共点,那么这条直线和平面相交答案 C2.下列表示正确的是()A.直线l在平面α内,用符号表示为“l∈α”B.点A在直线l上,直线l在平面α内,用符号表示为“A∈l,lα”C.点A在平面α内,用符号表示为“Aα”D.直线l与平面α外,用符号表示为“l∉α”答案 B3.如果两条直线a和b没有公共点,那么a与b的位置关系是()A.共面B.平行C.异面D.平行或异面解析由两条直线的位置关系,可知答案为D.答案 D4.下面空间图形画法错误的是()解析画立体图时,被平面遮住的部分画成虚线或不画.答案 D5.分别在两相交平面内的两条直线的位置关系是()A.异面B.平行C.相交D.以上皆有可能答案 D6.一条直线与两条异面直线中的一条相交,则它与另一条的位置关系是()A.异面B.平行C.相交D.可能相交、平行,也可能异面解析一条直线与两条异面直线中的一条相交,它与另一条的位置关系有三种:平行、相交、异面,如图所示.答案 D二、填空题7.点A在直线l上,用符号表示为________;直线AB在平面β内,用符号可表示为________;平面α与平面β相交于直线l可表示为________.答案A∈l ABβα∩β=l8.如图是一个正方体表面的一种展开图,图中的四条线段AB,CD,EF,GH在原正方体中相互异面的有________对.解析如图所示,AB与GH异面,AB与CD异面,EF与GH 异面.答案三9.若直线a,b都平行于平面α,则直线a,b的位置关系是________.解析直线a,b的位置关系有三种:相交、平行、异面,如图所示.答案相交、平行、异面三、解答题10.按照给出的要求,完成下面两个相交平面的作图,如图①②③④⑤⑥中的线段AB,分别是两个平面的交线.答案11.如图,在四棱锥P-ABCD中,写出互相异面的直线.解由异面直线的判定定理可知,互为异面的直线有AB与PD,AB与PC,AD与PB,AD与PC,DC与P A,DC与PB,BC与P A,BC与PD异面.12.如图,已知P∉平面ABC,P A≠PB,CM是AB上的中线,PN⊥AB于N,求证:CM和PN是异面直线.证明证法1:假设CM和PN共面,则有下列两种情况:(1)若M、N重合,可得AN=BN,∴PN是线段AB的中垂线,∴P A=PB,与题设P A≠PB矛盾.(2)若M、N不重合,CM和PN共面,即PC与MN共面,可得P∈平面ABC,与题设P∉平面ABC矛盾.所以CM和PN是异面直线.证法2:∵CM是AB上的中线,∴CM平面ABC.又∵PN⊥AB于N,∴N∈平面ABC.∵P A≠PB,∴AN≠BN.∴N与M不重合,即N∉CM.又∵P∉平面ABC,∴CM和PN是异面直线.思维探究13.若a与b异面,c与b异面,试举例说明a与c的位置关系.解a与c可能相交、平行、异面,说明如下:在正方体ABCD-A1B1C1D1中,A1D1与AB异面,B1C1与AB异面,而A1D1∥B1C1;A1D1与AB异面,DD1与AB异面,而A1D1与DD1相交;A1D1与AB异面,CC1与AB异面,而CC1与A1D1异面,故与b异面的两条直线a,c可能相交、平行、异面.。
人教B版高中数学必修二双基限时练16.docx

双基限时练(十六)基础强化1.下列命题正确的个数为()①若α是直线l的倾斜角,则α∈[0°,180°);②任何直线都存在倾斜角,但不一定存在斜率;③任何直线都存在斜率,但不一定存在倾斜角;④任何直线都存在倾斜角和斜率.A.1B.2C.3 D.4解析任何直线都存在倾斜角,但当倾斜角为90°时,斜率不存在.故正确的是①②.答案 B2.直线l过点P(-2,a),Q(a,4),若直线l的斜率为1,则a的值为()A.1 B.4C.1或4 D.1或-4解析k PQ=a-4-2-a=1,∴a-4=-2-a,∴a=1.答案 A3.已知直线y=(3a-1)x+2的倾斜角为钝角,则实数a的取值范围为( )A .a <13B .a >13C .a >3D .a <3解析 直线y =(3a -1)x +2的斜率为3a -1,∵该直线的倾斜角为钝角,∴3a -1<0,∴a <13.答案 A4.设点P 在y 轴上,点M 与点N 关于y 轴对称,若直线PM 的斜率为2,则直线PN 的斜率为( )A .2B .-2 C.12 D .-12解析 设P (0,y 0),M (a ,b ),则N (-a ,b ).∵k PM =y 0-b 0-a=2,∴y 0-b a =-2, ∴k PN =y 0-b 0-(-a )=-2. 答案 B5.已知M (1,2),N (4,3),直线l 过点P (2,-1)且与线段MN 相交,那么直线l 的斜率k 的取值范围是( )A .[-3,2]B.⎣⎢⎡⎦⎥⎤-13,12 C .(-∞,-3]∪[2,+∞)D.⎝ ⎛⎦⎥⎤-∞,-13∪⎣⎢⎡⎭⎪⎫12,+∞ 答案 C6.斜率为2的直线经过点(3,5),(a,7),(-1,b ),则a ,b 的值为( )A .a =4,b =0B .a =-4,b =-3C .a =4,b =-3D .a =-4,b =3 解析 7-5a -3=b -5-1-3=2,∴a =4,b =-3. 答案 C7.过原点引直线l ,使l 与连接A (1,1)和B (1,-1)两点间的线段相交,则直线l 的倾斜角θ的取值范围是__________.答案 0°≤θ≤45°或135°≤θ<180°8.已知直线l 1,l 2,l 3的斜率分别为k 1,k 2,k 3,如图所示,则k 1,k 2,k 3的大小关系为________.解析 由于l 3过二、四象限,故l 3的斜率小于0,l 1与l 2过一、三象限,故它们的斜率大于0,因为l 2倾斜角大于l 1的倾斜角,∴k 2>k 1>0.答案 k 2>k 1>k 3能 力 提 升9.已知点M (5,3)和点N (-3,2),若直线PM 和PN 的斜率分别为2和-74,则P 的坐标为________.解析 设P (x ,y ),则y -3x -5=2,y -2x +3=-74. ∴x =1,y =-5,故P (1,-5).答案 (1,-5)10.如图,已知A (3,2),B (-4,1),C (0,-1),求直线AB ,BC ,CA 的斜率,并判断这些直线的倾斜角是锐角还是钝角.解 直线AB 的斜率k AB =1-2-4-3=17; 直线BC 的斜率k BC =-1-10-(-4)=-12; 直线CA 的斜率k CA =-1-20-3=1. 由k AB >0及k CA >0知,直线AB 与CA 的倾斜角均为锐角;由k BC <0知,直线BC 的倾斜角为钝角.11.已知点A (3,4),在坐标轴上有一点B ,使得直线AB 的斜率等于2,求出点B 的坐标.解 如果点B 在x 轴上,可设B (x 0,0),x 0≠3.则直线AB 的斜率k =0-4x 0-3=2,解得x 0=1,即B (1,0);如果点B 在y 轴上,可设B (0,y 0),y 0≠4.则直线AB 的斜率k =y 0-40-3=2,解得y 0=-2,即B (0,-2).12.已知直线l :y =ax +2和两点A (1,4),B (3,1),当直线l 与线段AB 相交时,求实数a 的取值范围.解 如图所示,直线l 过定点C (0,2),直线BC 的斜率k CB =1-23-0=-13,直线AC 的斜率k CA =4-21-0=2,直线l 的斜率k l =a .当直线l 与线段AB 相交时,k CB ≤k l ≤k CA ,∴-13≤a ≤2.品 味 高 考13.下列四个命题:①一条直线向上的方向与x 轴正向所成的角,叫做这条直线的倾斜角②直线l 的倾斜角要么是锐角,要么是钝角③已知直线l 经过P 1(x 1,y 1),P 2(x 2,y 2)两点,则直线l 的斜率k=y 2-y 1x 2-x 1④若直线l 的方程是ax +by +c =0,则直线l 的斜率k =-a b .其中正确命题的个数是( )A .3B .2C .1D .0解析 根据倾斜角的定义知,①正确;倾斜角θ的范围为0°≤θ<180°,②不正确;当x 1=x 2时,直线P 1P 2的斜率k 不存在,不能用公式k =y 2-y 1x 2-x 1求解,③不正确;当b =0时,直线斜率不存在,④不正确.故选C.答案 C。
北师大版高中数学必修四双基限时练16.docx

双基限时练(十六) 向量的减法一、选择题1.如图,在▱ABCD 中,若|AB →+AD →|=|AB →-AD →|,则必有() A.AD →=0B.AB →=0或AD →=0C .ABCD 为矩形D .ABCD 为正方形解析 由|AB →+AD →|=|AB →-AD →|知|AC →|=|DB →|,即对角线相等,故ABCD 为矩形.答案 C2.如图D 为△ABC 中边AB 的中点,则CD →等于( )A. -BC →-BD →B. BC →+BD →C. BC →-BD →D. -BC →+DA →解析 CD →=BD →-BC →=DA →-BC →答案 D3.在平行四边形ABCD 中,AB →-CD →+BD →等于() A.DB → B.AD →C.AB →D.AC →解析 AB →-CD →+BD →=AB →+BD →+DC →=AC →.答案 D4.在四边形ABCD 中,设AB →=a ,AD →=b ,BC →=c ,则DC →=( )A. a -b +cB. b -(a +c )C. a +b +cD. b -a +c解析 ∵DC →=BC →-BD →=BC →-(AD →-AB →)=BC →+AB →-AD →=c +a-b答案 A5.下列各式中不能化简为PQ →的是( )A.AB →+P A →+BQ →B.AB →+PC →+BA →-QC →C.QC →-QP →+CQ →D.P A →+AB →-BQ →解析 对于A :AB →+P A →+BQ →=P A →+AB →+BQ →=PQ →;对于B :可化为AB →+BA →+PC →+CQ →=PQ →;对于C :可化为CQ →+QC →+PQ →=PQ →;对于D :P A →+AB →-BQ →=PB →-BQ →≠PQ →,故选D.答案 D6.已知△ABC 的三个顶点A 、B 、C 及平面内一点P 满足P A →+PB→=PC →,下列结论中正确的是( )A .P 在△ABC 的内部B .P 在△ABC 的边AB 上C .P 在AB 边所在直线上D .P 在△ABC 的外部解析 由P A →+PB →=PC →可得P A →=PC →-PB →=BC →,∴四边形PBCA 为平行四边形.可知点P 在△ABC 的外部.选D.答案 D二、填空题7.在边长为1的正三角形ABC 中,|AB →-BC →|的值为__________.解析 |AB →-BC →|=|-BA →-BC →|=|BA →+BC →|=2×32= 3. 答案38.如图所示,已知O 到平行四边形的三个顶点A ,B ,C 的向量分别为a ,b ,c ,则OD →=________.解析 OD →=OC →+CD →,又CD →=BA →=OA →-OB →=a -b ,∴OD →=c+a -b .答案 c +a -b9.已知菱形ABCD 的边长为2,求向量AB →-CB →+CD →的模为________.解析 ∵AB →-CB →+CD →=AB →+(CD →-CB →)=AB →+BD →=AD →,又|AD →|=2,∴|AB →-CB →+CD →|=2.答案 210.OA →+AB →-AC →+OC →+BD →-CD →+CO →+BO →的结果为________.解析 原式=OB →-AC →+BD →-CD →+BO →=CA →+BD →+DC →=CA →+BC →=BA →.答案 BA →三、解答题11.如图所示,已知OA →=a ,OB →=b ,OC →=c ,OD →=d ,OE →=e ,OF →=f ,试用a ,b ,c ,d ,e ,f 表示AC →,AD →,AD →-AB →,AB →+CF →,BF→-BD →,DF →+FE →+ED →.解 AC →=OC →-OA →=c -a ,AD →=OD →-OA →=d -a ,AD →-AB →=BD →=OD →-OB →=d -b ,AB →+CF →=OB →-OA →+OF →-OC →=b -a -c +f ,BF →-BD →=DF →=OF →-OD →=f -d ,DF →+FE →+ED →=0.12.如图所示,P 、Q 是△ABC 的边BC 上两点,且BP =QC .求证:AB →+AC →=AP →+AQ →.证明 AB →=AP →+PB →,AC →=AQ →+QC →,∴AB →+AC →=AP →+PB →+AQ →+QC →.∵PB →和QC →大小相等、方向相反,∴PB →+QC →=0,故AB →+AC →=AP →+AQ →+0=AP →+AQ →.13.若O 为△ABC 所在平面内一点,且满足|OB →-OC →|=|OB →+OC →-OA →-OA →|,试判断△ABC 的形状.解 由|OB →+OC →-OA →-OA →|=|AB →+AC →|,∵|OB →-OC →|=|CB →|,即|AB →+AC →|=|CB →|,由平行四边形法则,即BC 边上的中线等于BC 边上的一半.∴△ABC 为直角三角形.。
高中数学课时达标训练十六北师大版必修2

=3a.
1 3.解析:选 A ∵ f (2)= log3 22- 1 = log33-1=- 1,
2 ∴ f(f (2))= f(- 1)= 2e- 2= e2. 4.解析:选 B ∵2m= 7n= p,
∴ m= log2p, n= log7p.
11 1
1
又 -= - m n log2p log7p
lg 2 0.301 0 故 x= lg 1.08≈0.033 4≈ 9(年 ).
答:约经过 9 年,国民生产总值是 2011 年的两倍. 10.解:原方程可化为 2(lg x)2- 4lg x+ 1= 0, 设 t= lg x,则原方程化为 2t2- 4t +1=0.
1
∴
t1+
t2=
2,
t1t
2=
. 2
由已知 a,b 是原方程的两个根,
则 t1= lg a, t2=lg b,
1 即 lg a+ lg b= 2, lg a· lg b= ,
2
∴ lg(ab)· (logab+ logba)=(lg a+
lg b lg a lg b) lg a+ lg b
lg a+ lg b [ lg b 2+ lg a 2]
2 = logp2- logp7= logp7= 4,
2 ∴ p4= .∴ p=
7
5.解析: lg 5+ lg 20= lg( 5× 20)=
lg 10= 1.故填 1.
答案: 1
6.解析:∵ a> 0,
4 =,
9
马鸣风萧萧整理
》》》》》》》》》积一时之跬步 臻千里之遥程《 《《《《《《《《《《《
24 6.若 a> 0,a3= 9,则
= ________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双基限时练(十六)
一、选择题
1.设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )
A.3πa2B.6πa2
C.12πa2D.24πa2
解析由题意得,2R=4a2+a2+a2=6a,
∴R=
6
2
a,∴球的表面积S=4πR2=6πa2.
答案B
2.已知某几何体的三视图如图所示,则其表面积为( )
A.4πB.3π
C.2πD.π
解析由三视图可知,该几何体为半径为1的半球体,
∴S表=πr2+2πr2=3πr2=3π.
答案B
3.若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积之比为( )
A.1:2:3 B.2:3:4
C.3:2:4 D.3:1:2
解析V圆柱=2πR3,V圆锥=1
3πR2·(2R)=
2π
3
R3,
V球=4
3
πR3.则体积之比为:2:
2
3
:
4
3
即3:1:2.
答案D
4.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为2,则此球的体积为( )
A.6πB.43π
C.46πD.63π
解析 如图,设平面α截球O 所得圆的圆心为O 1,则|OO 1|=2,|O 1A|=1,∴球的半径R =|OA|=2+1= 3.
∴球的体积V =4
3
πR 3=43π.故选B .
答案 B
5.如图,正四棱锥P —ABCD 底面的四个顶点A ,B ,C ,D 在球O 的同一个大圆上,点P 在球面上,如果V P —ABCD =16
3,那么球O 的表面
积是( )
A .4π
B .8π
C .12π
D .16π
解析 由题意,可得AB =2R ,PO =R ,又V P —ABCD =13(2R)2R =16
3
,
得R =2,∴S 表=4πR 2
=16π.
答案 D
6.64个直径都为a
4的球,记它们的体积之和为V 甲,表面积之和
为S 甲,一个直径为a 的球记其体积为V 乙,表面积为S 乙,则( )
A .V 甲>V 乙,S 甲>S 乙
B .V 甲<V 乙,S 甲>S 乙
C .V 甲=V 乙,S 甲>S 乙
D .V 甲=V 乙,S 甲<S 乙
解析 V 甲=64×4
3π×⎝ ⎛⎭⎪⎫a 4×123=16πa 3,
S 甲=64×4π×⎝ ⎛⎭⎪⎫a 82
=4πa 2,
V 乙=4
3π×⎝ ⎛⎭⎪⎫a 23=16πa 3,
S 乙=4π×⎝ ⎛⎭
⎪⎫a 22
=πa 2,
∴V 甲=V 乙,S 甲>S 乙. 答案 C 二、填空题
7.一个正方体的各顶点均在同一球的球面上,若该球的体积为43π,则该正方体的表面积为________.
解析 设正方体的棱长为a ,球的半径为r ,则2r =3a , ∴a =233r ,∵43πr 3=43π,∴r =3,∴a =2.
∴S 表=6a 2=24. 答案 24
8.圆柱形容器的内壁底面半径为5cm ,两个直径为5cm 的玻璃
小球都浸没于该容器的水中,若取出两个小球,则容器的水面将下降________.
解析 由题意,得2×43π×⎝ ⎛⎭
⎪⎫523=π×52×h ,得h =5
3.
答案 5
3
cm
9.一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都是在同一个球面上,且该六棱柱的高为3,底面周长为3,那么这个球的体积为________.
解析 球的半径R =⎝ ⎛⎭
⎪⎪⎫322+⎝ ⎛⎭⎪
⎫362=1, 故V 球=43πR 3
=43π.
答案 4
3π
三、解答题
10.已知某几何体的三视图如图所示,求它的体积和表面积.
解 由三视图可知该几何体是半径为1的球被挖出了1
8部分得到
的几何体,∴其体积V =78V 球=78×43π×13
=76π,S 表=78×4π×12+
3×14π×12
=174
π. 11.一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,求这个圆锥的高与球的半径之比.
解 如图,作出轴截面,设公共底面圆的半径为R ,圆锥的高为h.
∴V锥=1
3
πR2h,V半球=
1
2
·
4
3
πR3.
∵V锥=V半球,
∴h=2R,即h:R=2:1.
12.桌面上有三个半径均为r的小球,它们两两相切,现有第四个半径为r的小球放在三个小球上面,且与这三个小球都相切,求第四个小球的球心离桌面的距离.
解如图所示,设桌面上三个小球的球心分别为O1,O2,O3,第四个小球的球心为O4.因每两个小球都相切,所以O1,O2,O3,O4构成一个棱长都为2r且各面都全等的正三角形的三棱锥.
设O4在平面O1O2O3的正投影为O,则O4到桌面的距离为O4O+r.
连接O3O,由于O为正三角形△O1O2O3的中心,
∴OO 3=23×32×2r =23
3r.
∴O 4O =
(2r )2
-⎝ ⎛⎭
⎪⎪
⎫233r 2=263r. 因此,第四个小球的球心离桌面的距离为⎝
⎛⎭
⎪
⎪⎫
263+1r. 思维探究
13.已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的3
16,则这两个圆
锥中,体积较小者的高与体积较大者的高的比值为多少?
解 如图,设球的半径为R ,圆锥底面半径为r ,由题意得πr 2
=3
16
×4πR 2.
∴r =32R ,∴OO 1=1
2
R.
体积较小的圆锥的高AO 1=R -12R =1
2
R ,体积较大的圆锥的高BO 1
=R +12R =3
2R.故这两个圆锥中,体积较小者的高与体积较大者的高的
比值为13
.。
