顺义区2017届高三第二次统练试题
北京市顺义区2017届高三第二次统练生物试题(含答案)
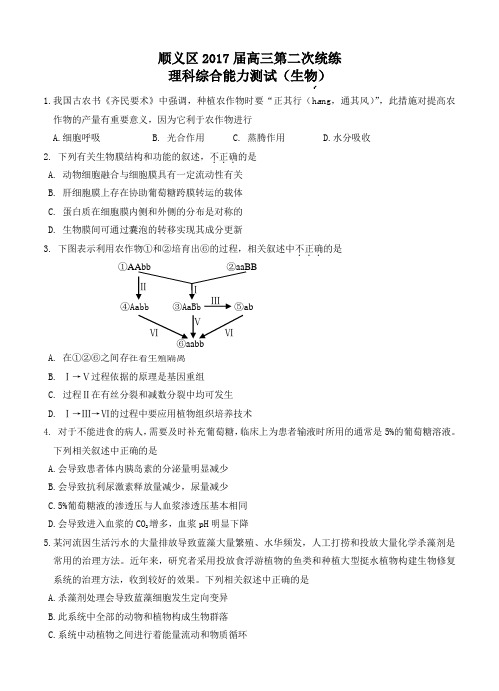
顺义区2017届高三第二次统练 理科综合能力测试(生物)1.我国古农书《齐民要术》中强调,种植农作物时要“正其行(h a ng ,通其风)”,此措施对提高农作物的产量有重要意义,因为它利于农作物进行 A.细胞呼吸B. 光合作用C. 蒸腾作用D.水分吸收2. 下列有关生物膜结构和功能的叙述,不正确...的是 A. 动物细胞融合与细胞膜具有一定流动性有关 B. 肝细胞膜上存在协助葡萄糖跨膜转运的载体 C. 蛋白质在细胞膜内侧和外侧的分布是对称的 D. 生物膜间可通过囊泡的转移实现其成分更新3. 下图表示利用农作物①和②培育出⑥的过程,相关叙述中不正确的是A. B. Ⅰ→Ⅴ过程依据的原理是基因重组 C. 过程Ⅱ在有丝分裂和减数分裂中均可发生 D. Ⅰ→Ⅲ→Ⅵ的过程中要应用植物组织培养技术4. 对于不能进食的病人,需要及时补充葡萄糖,临床上为患者输液时所用的通常是5%的葡萄糖溶液。
下列相关叙述中正确的是A.会导致患者体内胰岛素的分泌量明显减少B.会导致抗利尿激素释放量减少,尿量减少C.5%葡萄糖液的渗透压与人血浆渗透压基本相同D.会导致进入血浆的CO 2增多,血浆pH 明显下降5.某河流因生活污水的大量排放导致蓝藻大量繁殖、水华频发,人工打捞和投放大量化学杀藻剂是常用的治理方法。
近年来,研究者采用投放食浮游植物的鱼类和种植大型挺水植物构建生物修复系统的治理方法,收到较好的效果。
下列相关叙述中正确的是 A.杀藻剂处理会导致蓝藻细胞发生定向变异 B.此系统中全部的动物和植物构成生物群落 C.系统中动植物之间进行着能量流动和物质循环D.大型挺水植物与蓝藻竞争资源能减轻水华发生29. (16分)茶是中华民族的传统饮品,其活性成分能够影响人体的能量代谢和脂肪代谢,有一定的降脂减肥作用。
科研人员以大鼠为对象研究普洱茶的降脂效果,实验过程及结果如下。
注:食物利用率:体重增长量/摄食量X100% 脂肪系数:脂肪重量/体重X100%(1)上述实验中,需使用来配制普洱水提物的水溶液;A、B、C均为对照组,其中设置C组的目的是。
2016-2017学年度北京市顺义区高三第二学期第二次统练(二模)理综试卷及答案(精排版)

2016-2017学年度北京市顺义区高三第二学期第二次统练(二模)理综试卷及答案(精排版)顺义区2017届高三第二次统练理科综合能力测试1.我国古农书《齐民要术》中强调,种植农作物时要“正其行(h a ng,通其风)”,此措施对提高农作物的产量有重要意义,因为它利于农作物进行A.细胞呼吸B. 光合作用C. 蒸腾作用D.水分吸收2. 下列有关生物膜结构和功能的叙述,不正确...的是A. 动物细胞融合与细胞膜具有一定流动性有关B. 肝细胞膜上存在协助葡萄糖跨膜转运的载体C. 蛋白质在细胞膜内侧和外侧的分布是对称的D. 生物膜间可通过囊泡的转移实现其成分更新3. 下图表示利用农作物①和②培育出⑥的过程,相关叙述中不正确...的是A. 在①②⑥之间存在着生殖隔离B. Ⅰ→Ⅴ过程依据的原理是基因重组C. 过程Ⅱ在有丝分裂和减数分裂中均可发生D. Ⅰ→Ⅲ→Ⅵ的过程中要应用植物组织培养技术4. 对于不能进食的病人,需要及时补充葡萄糖,临床上为患者输液时所用的通常是5%的葡萄糖溶液。
下列相关叙述中正确的是 A.会导致患者体内胰岛素的分泌量明显减少 B.会导致抗利尿激素释放量减少,尿量减少Ⅴ ⑥aabb Ⅵ ④Aabb ③AaBb ⑤abⅡ Ⅲ Ⅰ Ⅵ ①AAbb②aaBBC.5%葡萄糖液的渗透压与人血浆渗透压基本相同D.会导致进入血浆的CO2增多,血浆pH明显下降5.某河流因生活污水的大量排放导致蓝藻大量繁殖、水华频发,人工打捞和投放大量化学杀藻剂是常用的治理方法。
近年来,研究者采用投放食浮游植物的鱼类和种植大型挺水植物构建生物修复系统的治理方法,收到较好的效果。
下列相关叙述中正确的是A.杀藻剂处理会导致蓝藻细胞发生定向变异B.此系统中全部的动物和植物构成生物群落C.系统中动植物之间进行着能量流动和物质循环D.大型挺水植物与蓝藻竞争资源能减轻水华发生6. 下列有关说法不正确...的是选项 A. B. C. D. 生活中的应用月饼袋内放有小袋铁粉口服补血剂(琥珀酸亚铁)并同时服维生C饼干包装盒内放有小袋硅胶肉制品中添加适量的亚硝酸钠作用铁粉有抗氧化的作用维生素C有防止Fe2+被还原的作用硅胶有吸水的作用亚硝酸钠有防腐的作用7. 氮元素在海洋中的循环,是整个海洋生态系统的基础和关键。
2017北京顺义高三二模【理】数学真题试卷
2017年北京市顺义区高考数学二模试卷(理科)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项)1.设集合A={x|x2﹣3x+2>0},B={x|3x﹣4>0},则A∩B=()A.(﹣2,﹣)B.(﹣2,)C.(1,)D.(2,+∞)2.执行如图所示的程序框图,则输出的s值为()A.B.C.D.3.已知向量=(1,),=(﹣1,),则∠BAC=()A.30°B.45°C.60°D.120°4.某四棱锥的三视图如图所示,则该四棱锥的侧面积为()A.8 B.8+4C.2+D.4+25.已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b垂直”是“平面α和平面β垂直”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件6.在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域中的点在直线x﹣2y﹣2=0上的投影构成的线段记为AB,则|AB|=()A.B.C.2 D.87.将函数y=sin(2x+)图象上的点M(θ,)(0<θ<)向右平移t(t >0)个单位长度得到点M′.若M′位于函数y=sin2x的图象上,则()A.θ=,t的最小值为B.θ=,t的最小值为C.θ=,t的最小值为D.θ=,t的最小值为8.某学校为了提高学生综合素质、树立社会主义荣辱观、发展创新能力和实践能力、促进学生健康成长,开展评选“校园之星”活动.规定各班每10人推选一名候选人,当各班人数除以10的余数大于7时再增选一名候选人,那么,各班可推选候选人人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为()A.y=[]B.y=[]C.y=[]D.y=[]二、填空题(本大题共6个小题,每小题5分,共30分)9.已知z=(a﹣2)+(a+1)i在复平面内对应的点在第二象限,则实数a的取值范围是.10.在(x2+)8的展开式中,x7的系数为.(用数字作答)11.已知{a n}为等差数列,S n为其前n项和,若a2=4,S8=﹣8,则a10=.12.在极坐标系中,圆ρ=﹣2cosθ的圆心C到直线2ρcosθ+ρsinθ﹣2=0的距离等于.13.已知抛物线y2=2px(p>0)的准线为l,若l与圆x2+y2+6x+5=0的交点为A,B,且|AB|=2.则p的值为.14.已知函数f(x)=,函数g(x)=f(x)﹣k.(1)当m=2时,若函数g(x)有两个零点,则k的取值范围是;(2)若存在实数k使得函数g(x)有两个零点,则m的取值范围是.三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤)15.在△ABC中,角A,B,C的对边分别为a,b,c,已知cosB+cosA=(I)求∠C的大小;(II)求sinB﹣sinA的最小值.16.春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中PM2.5浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化.2017年除夕18时和初一2时,国家环保部门对8个城市空气中PM2.5浓度监测的数据如表(单位:微克/立方米).(Ⅰ)求这8个城市除夕18时空气中PM2.5浓度的平均值;(Ⅱ)环保部门发现:除夕18时到初一2时空气中PM2.5浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹.从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;(Ⅲ)记2017年除夕18时和初一2时以上8个城市空气中PM2.5浓度的方差分别为s12和s22,比较s12和s22的大小关系(只需写出结果).17.如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.(I)求证:EM⊥AD;(II)求二面角A﹣BE﹣C的余弦值;(III)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为45°,若存在,求出的值;若不存在,说明理由.18.已知函数f(x)=pe﹣x+x+1(p∈R).(Ⅰ)当实数p=e时,求曲线y=f(x)在点x=1处的切线方程;(Ⅱ)求函数f(x)的单调区间;(Ⅲ)当p=1时,若直线y=mx+1与曲线y=f(x)没有公共点,求实数m的取值范围.19.已知椭圆E: +=1(a>b>0)经过点(﹣1,),其离心率e=.(Ⅰ)求椭圆E的方程;(Ⅱ)设动直线l:y=kx+m与椭圆C相切,切点为T,且l与直线x=﹣4相交于点S.试问:在x轴上是否存在一定点,使得以ST为直径的圆恒过该定点?若存在,求出该点的坐标;若不存在,请说明理由.20.设数列{a n}的前n项和为S n.若对∀n∈N*,总∃k∈N*,使得S n=a k,则称数列{a n}是“G数列”.(Ⅰ)若数列{a n}是等差数列,其首项a1=1,公差d=﹣1.证明:数列{a n}是“G 数列”;(Ⅱ)若数列{a n}的前n项和S n=3n(n∈N*),判断数列{a n}是否为“G数列”,并说明理由;(Ⅲ)证明:对任意的等差数列{a n},总存在两个“G数列”{b n}和{c n},使得a n=b n+c n(n∈N*)成立.2017年北京市顺义区高考数学二模试卷(理科)参考答案与试题解析一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项)1.设集合A={x|x2﹣3x+2>0},B={x|3x﹣4>0},则A∩B=()A.(﹣2,﹣)B.(﹣2,)C.(1,)D.(2,+∞)【考点】1E:交集及其运算.【分析】根据不等式的解法求出集合的等价条件,利用集合的基本运算进行求解即可.【解答】解:A={x|x2﹣3x+2>0}={x|x>2或x<1},B={x|3x﹣4>0}={x|x>},则A∩B={x|x>2},故选:D2.执行如图所示的程序框图,则输出的s值为()A.B.C.D.【考点】EF:程序框图.【分析】模拟执行程序框图,依次写出每次循环得到的s,k的值,当k=4时不满足条件k<4,退出循环,输出S的值即可得解.【解答】解:模拟执行程序框图,可得s=1,k=1满足条件k<4,执行循环体,k=2,s=1+满足条件k<4,执行循环体,k=3,s=1++满足条件k<4,执行循环体,k=4,s=1+++不满足条件k<4,退出循环,输出s的值为s=1+++=.故选:C.3.已知向量=(1,),=(﹣1,),则∠BAC=()A.30°B.45°C.60°D.120°【考点】9R:平面向量数量积的运算.【分析】方法一:判断△ABC为等边三角形,问题得以解决,方法二:根据向量的夹角公式计算即可【解答】解:方法一:∵=(1,),=(﹣1,),∴||=2,||=2,=﹣=(﹣2,0),∴||=2,∴△ABC为等边三角形,∴∠BAC=60°,方法二::∵=(1,),=(﹣1,),∴||=2,||=2,•=1×(﹣1)+×=2,∴cos∠BAC==,∵0°≤∠BAC≤180°,∴∠BAC=60°,故选:C .4.某四棱锥的三视图如图所示,则该四棱锥的侧面积为( )A .8B .8+4C .2+D .4+2【考点】L!:由三视图求面积、体积.【分析】首先还原几何体为四棱锥是直观图,根据图中数据求侧面积.【解答】解:由三视图得到几何体的直观图如图:四棱锥P ﹣ABCD ,其中OP=3,AB=CD=4,AD=BC=2,所以PE=,PF=,所以侧面积为2(S △PAB +S △PBC )=;故选:D .5.已知直线a ,b 分别在两个不同的平面α,β内.则“直线a 和直线b 垂直”是“平面α和平面β垂直”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【考点】2L :必要条件、充分条件与充要条件的判断.【分析】根据直线垂直和面面垂直的判定条件分别进行判断即可.【解答】解:当a⊥b时,满足条件,但此时α∥β,即充分性不成立,当平面α和平面β垂直时,直线a和b平行,则直线a和直线b垂直不一定成立,故必要性不成立,则“直线a和直线b垂直”是“平面α和平面β垂直”的既不充分也不必要条件,故选:D6.在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域中的点在直线x﹣2y﹣2=0上的投影构成的线段记为AB,则|AB|=()A.B.C.2 D.8【考点】7C:简单线性规划.【分析】作出不等式组对应的平面区域,利用投影的定义,利用数形结合进行求解即可.【解答】解:作出不等式组对应的平面区域如图:(阴影部分)区域内的点在直线x+y﹣2=0上的投影构成线段A′B′,由得A(﹣1,)由得B(2,﹣2),可得|AB|==,故选:B.7.将函数y=sin(2x+)图象上的点M(θ,)(0<θ<)向右平移t(t >0)个单位长度得到点M′.若M′位于函数y=sin2x的图象上,则()A.θ=,t的最小值为B.θ=,t的最小值为C.θ=,t的最小值为D.θ=,t的最小值为【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【分析】利用函数y A=sin(ωx+φ)的图象变换规律,得出结论.【解答】解:将函数y=sin(2x+)图象上的点M(θ,)(0<θ<)向右平移t(t>0)个单位长度得到点M′,故有sin(2θ+)=,∴θ=,点M′(θ+t,),即M′(+t,).若M′位于函数y=sin2x的图象上,则=sin2(+t),∴t的最小值为,故选:A.8.某学校为了提高学生综合素质、树立社会主义荣辱观、发展创新能力和实践能力、促进学生健康成长,开展评选“校园之星”活动.规定各班每10人推选一名候选人,当各班人数除以10的余数大于7时再增选一名候选人,那么,各班可推选候选人人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为()A.y=[]B.y=[]C.y=[]D.y=[]【考点】36:函数解析式的求解及常用方法.【分析】由题意,根据规定10推选一名代表,当各班人数除以10的余数大于7时再增加一名代表,即余数分别为8,9时可以增选一名代表,也就是x要进一位,所以最小应该加2.进而得到解析式.【解答】由题意,根据规定10推选一名代表,当各班人数除以10的余数大于7时再增加一名代表,即余数分别为8,9时可以增选一名代表,也就是x要进一位,所以最小应该加2.因此利用取整函数可表示为y=[];故选B.二、填空题(本大题共6个小题,每小题5分,共30分)9.已知z=(a﹣2)+(a+1)i在复平面内对应的点在第二象限,则实数a的取值范围是(﹣1,2).【考点】A4:复数的代数表示法及其几何意义.【分析】z=(a﹣2)+(a+1)i在复平面内对应的点在第二象限,可得,解得a范围.【解答】解:z=(a﹣2)+(a+1)i在复平面内对应的点在第二象限,∴,解得﹣1<a<2.则实数a的取值范围是(﹣1,2).故答案为:(﹣1,2).10.在(x2+)8的展开式中,x7的系数为7.(用数字作答)【考点】DB:二项式系数的性质.【分析】利用二项展开式的通项公式求出展开式的通项;令x的指数为7,求出r,即可求出展开式中x7的系数.=()r C8r x16﹣3r【解答】解:展开式的通项为T r+1令16﹣3r=7,解得r=3,故展开式中x7的系数是()3C83=7,故答案为:7.11.已知{a n}为等差数列,S n为其前n项和,若a2=4,S8=﹣8,则a10=﹣12.【考点】85:等差数列的前n项和.【分析】由已知条件,利用等差数列的通项公式和前n项和公式,建立方程组,求出首项和公差,由此能求出结果.【解答】解:等差数列{a n}的前n项和为S n,∵a2=4,S8=﹣8,设公差为d,∴,解得a1=6,d=﹣2,∴a10=6+9×(﹣2)=﹣12.故答案为:﹣1212.在极坐标系中,圆ρ=﹣2cosθ的圆心C到直线2ρcosθ+ρsinθ﹣2=0的距离等于.【考点】Q4:简单曲线的极坐标方程.【分析】圆ρ=﹣2cosθ化为直角坐标方程式,求出圆心C(﹣1,0),直线2ρcosθ+ρsinθ﹣2=0化为直角坐标方程,由此利用点到直线的距离公式能求出圆心C到直线的距离.【解答】解:圆ρ=﹣2cosθ,即ρ2=﹣2ρcosθ,化为直角坐标方程得:x2+y2=﹣2x,即(x+1)2+y2=1.∴圆心C(﹣1,0),∵直线2ρcosθ+ρsinθ﹣2=0,∴直线的直角坐标方程为2x+y﹣2=0,∴圆心C到直线的距离:d==.故答案为:.13.已知抛物线y2=2px(p>0)的准线为l,若l与圆x2+y2+6x+5=0的交点为A,B,且|AB|=2.则p的值为4或8.【考点】K8:抛物线的简单性质.【分析】求得圆心及半径,分类讨论,由A(﹣,),则丨AH丨=,丨AE丨=2,则丨EH丨=1,由丨EH丨+=丨OE丨或丨OE丨+丨EH丨=,即可求得p的值.【解答】解:抛物线y2=2px的焦点F(,0),准线x=﹣,准线与x轴相交于H,圆x2+y2+6x+5=0的标准方程(x+3)2+y2=4,则圆心E(﹣3,0),半径为2,假设抛物线的准线在圆心的左侧,由丨AB丨=2,则A(﹣,),则丨AH丨=,丨AE丨=2丨EH丨=1,则丨EH丨+=丨OE丨,即1+=3,则p=4,设抛物线的准线在圆心的右侧,由丨AB丨=2,则A(﹣,),则丨AH丨=,丨AE丨=2则丨OE丨+丨EH丨=,即3+1=,则p=8,∴p的值为4或8.故答案为:4或8.14.已知函数f(x)=,函数g(x)=f(x)﹣k.(1)当m=2时,若函数g(x)有两个零点,则k的取值范围是(4,8] ;(2)若存在实数k使得函数g(x)有两个零点,则m的取值范围是(﹣∞,0)∪(1,+∞).【考点】52:函数零点的判定定理.【分析】(1)分别画出y=f(x)与y=k的图象,如图所示,若函数g(x)有两个零点,由图象可得4<k≤8,(2)分类讨论,当m≥0时,只要m3>m2即可,当m<0都存在【解答】解:(1)当m=2时,分别画出y=f(x)与y=k的图象,如图所示,若函数g(x)有两个零点,由图象可得4<k≤8,故k的取值范围是(4,8](2)当m≥0时,y=x3在(﹣∞,m]为增函数,最大值为m3,y=x2在(m,+∞)为增函数,最小值为m2,若存在实数k使得函数g(x)有两个零点,则m3>m2,解得m>1,当m<0时,y=x2在(m,0)上为减函数,在(0,+∞)为增函数,故若存在实数k使得函数g(x)有两个零点,综上所述m的取值范围为(﹣∞,0)∪(1,+∞),故答案为:(1):(4,8],(2):(﹣∞,0)∪(1,+∞)三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤)15.在△ABC中,角A,B,C的对边分别为a,b,c,已知cosB+cosA=(I)求∠C的大小;(II)求sinB﹣sinA的最小值.【考点】HT:三角形中的几何计算.【分析】(I)由正弦定理,得.即cosC=,可得C=.(II)sinB﹣sinA=sin()﹣sinA=cos(A+)由A+B=,得A+,cos(A+)最小值为﹣1.即可得sinB﹣sinA的最小值【解答】解:(I)由正弦定理,得,.所以,,即.∵A+B+C=π,∴sin(A+B)=sinC.∴2cosC=,cosC=∵C∈(0,π),∴C=.(II)∵A+B+C=π∴A+B=∴sinB﹣sinA=sin()﹣sinA==cos(A+),∵A+B=,∴A,∴A+∴cos(A+)最小值为﹣1.即sinB﹣sinA的最小值为﹣1.16.春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中PM2.5浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化.2017年除夕18时和初一2时,国家环保部门对8个城市空气中PM2.5浓度监测的数据如表(单位:微克/立方米).(Ⅰ)求这8个城市除夕18时空气中PM2.5浓度的平均值;(Ⅱ)环保部门发现:除夕18时到初一2时空气中PM2.5浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹.从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;(Ⅲ)记2017年除夕18时和初一2时以上8个城市空气中PM2.5浓度的方差分别为s12和s22,比较s12和s22的大小关系(只需写出结果).【考点】CH:离散型随机变量的期望与方差;CG:离散型随机变量及其分布列.【分析】(Ⅰ)利用平均数的计算公式即可得出8个城市除夕18时空气中PM2.5浓度的平均值.(II)以上8个城市中禁止燃放烟花爆竹的有太原,上海,南京,杭州4个城市,随机变量X的所有可能取值为0,1,2,3.利用P(X=k)=,即可得出分布列,进而得到X 的数学期望EX .(III )<.【解答】解:(Ⅰ)8个城市除夕18时空气中PM2.5浓度的平均值==70.(Ⅱ)以上8个城市中禁止燃放烟花爆竹的有太原,上海,南京,杭州4个城市,随机变量X 的所有可能取值为0,1,2,3.P (X=k )=,可得:P (X=0)=,P (X=1)=,P (X=k )=,P (X=3)=.X 的分布列为:X 的数学期望EX=0×+1×+2×+3×=.(III )<.17.如图,正三角形ABE 与菱形ABCD 所在的平面互相垂直,AB=2,∠ABC=60°,M 是AB 的中点. (I )求证:EM ⊥AD ;(II )求二面角A ﹣BE ﹣C 的余弦值;(III )在线段EC 上是否存在点P ,使得直线AP 与平面ABE 所成的角为45°,若存在,求出的值;若不存在,说明理由.【考点】MI :直线与平面所成的角;MT :二面角的平面角及求法.【分析】(Ⅰ)推导出EM ⊥AB ,从而EM ⊥平面ABCD ,由此能证明EM ⊥AD . (Ⅱ)推导出EM ⊥MC ,MC ⊥AB ,从而MB 、MC 、ME 两两垂直,建立空间直角坐标系M﹣xyz,利用向量法能求出二面角A﹣BE﹣C的余弦值.(III)求出和平面ABE的法向量,利用向量法能示出在线段EC上存在点P,使得直线AP与平面ABE所成的角为45°,且=.【解答】证明:(Ⅰ)∵EA=EB,M是AB的中点,∴EM⊥AB,∵平面ABE⊥平面ABCD,平面ABE∩平面ABCD=AB,EA⊂平面ABE,∴EM⊥平面ABCD,AD⊂平面ABCD,∴EM⊥AD.解:(Ⅱ)∵EM⊥平面ABCD,∴EM⊥MC,∵△ABC是正三角形,∴MC⊥AB.∴MB、MC、ME两两垂直.建立如图所示空间直角坐标系M﹣xyz.则M(0,0,0),A(﹣1,0,0),B(1,0,0),C(0,,0),E(0,0,),=(﹣1,,0),=(﹣1,0,),设=(x,y,z)是平面BCE的一个法向量,则,令z=1,得=(),∵y轴与平面ABE垂直,∴=(0,1,0)是平面ABE的一个法向量.cos<>===,∴二面角A﹣BE﹣C的余弦值为.(III)假设在线段EC上存在点P,使得直线AP与平面ABE所成的角为45°.=(1,0,),=(0,),设==(0,﹣),(00≤λ≤1),则=,∵直线AP与平面ABE所成的角为45°,∴sin45°=|cos<>|===,由0≤λ≤1,解得,∴在线段EC上存在点P,使得直线AP与平面ABE所成的角为45°,且=.18.已知函数f(x)=pe﹣x+x+1(p∈R).(Ⅰ)当实数p=e时,求曲线y=f(x)在点x=1处的切线方程;(Ⅱ)求函数f(x)的单调区间;(Ⅲ)当p=1时,若直线y=mx+1与曲线y=f(x)没有公共点,求实数m的取值范围.【考点】6H:利用导数研究曲线上某点切线方程;6B:利用导数研究函数的单调性.【分析】(Ⅰ)求出当p=e时的函数f(x)的导数,可得切线的斜率和切点,运用点斜式方程即可得到所求切线的方程;(Ⅱ)求出f(x)的导数,讨论①当p≤0时,②当p>0时,由导数大于0,可得增区间;导数小于0,可得减区间;(Ⅲ)当p=1时,f(x)=e﹣x+x+1,直线y=mx+1与曲线y=f(x)没有公共点,等价于关于x的方程mx+1=e﹣x+x+1在(﹣∞,+∞)上没有实数解,即关于x的方程(m﹣1)x=e﹣x(*)在(﹣∞,+∞)上没有实数解.讨论当m=1,当m≠1时,通过方程的解和构造函数,求出导数和单调区间,可得值域,即可得到所求m的范围.【解答】解:(Ⅰ)当p=e时,f(x)=e1﹣x+x+1,可得导数f′(x)=﹣e1﹣x+1,∴f(1)=3,f′(1)=0,∴曲线y=f(x)在点x=1处的切线方程为y=3;(Ⅱ)∵f(x)=pe﹣x+x+1,∴f′(x)=﹣pe﹣x+1,①当p≤0时,f′(x)>0,则函数f(x)的单调递增区间为(﹣∞,+∞);②当p>0时,令f′(x)=0,得e x=p,解得x=lnp.则当x变化时,f′(x)的变化情况如下表:所以,当p>0时,f(x)的单调递增区间为(lnp,+∞),单调递减区间为(﹣∞,lnp).(Ⅲ)当p=1时,f(x)=e﹣x+x+1,直线y=mx+1与曲线y=f(x)没有公共点,等价于关于x的方程mx+1=e﹣x+x+1在(﹣∞,+∞)上没有实数解,即关于x的方程(m﹣1)x=e﹣x(*)在(﹣∞,+∞)上没有实数解.①当m=1时,方程(*)化为e﹣x=0,显然在(﹣∞,+∞)上没有实数解.②当m≠1时,方程(*)化为xe x=,令g(x)=xe x,则有g′(x)=(1+x)e x.令g′(x)=0,得x=﹣1,则当x变化时,g'(x)的变化情况如下表:当x=﹣1时,,同时当x趋于+∞时,g(x)趋于+∞,从而g(x)的值域为.所以当<﹣时,方程(*)无实数解,解得实数m的取值范围是(1﹣e,1).综合①②可知实数m的取值范围是(1﹣e,1].19.已知椭圆E: +=1(a>b>0)经过点(﹣1,),其离心率e=.(Ⅰ)求椭圆E的方程;(Ⅱ)设动直线l:y=kx+m与椭圆C相切,切点为T,且l与直线x=﹣4相交于点S.试问:在x轴上是否存在一定点,使得以ST为直径的圆恒过该定点?若存在,求出该点的坐标;若不存在,请说明理由.【考点】KL:直线与椭圆的位置关系.【分析】(Ⅰ)由题意可知:将点代入椭圆方程,利用椭圆的离心率公式即可求得a和b的值,即可求得椭圆方程;(Ⅱ)将直线方程代入椭圆方程,由△=0,求得4k2﹣m2+3=0,利用韦达定理及中点坐标公式,求得T点坐标,联立即可求得S点坐标,由•=0,根据向量数量积的坐标运算,可得,即可求得A点坐标,即可求得以ST为直径的圆恒过该定点(1,0).【解答】解:(Ⅰ)由点(1,)在椭圆上得,代入椭圆方程:,①﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣椭圆的离心率e==,则a=2c,a2=4c2,b2=3c2,②﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②代入①解得c2=1,a2=4,b2=3,故椭圆C的标准方程为;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)由,消去y,整理得(4k2+3)x2+8kmx+4m2﹣12=0;因为动直线l与椭圆C相切,即它们有且只有一个公共点T,可设T(x0,y0),m≠0,△=0,∴(8km)2﹣4×(4k2+3)×(4m2﹣12)=0,∴4k2﹣m2+3=0,③﹣﹣﹣﹣此时,x0==﹣=﹣,y0=kx0+m=,则T(﹣,).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣由,得S(4,4k+m).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣假设平面内存在定点满足条件,不妨设为点A.由图形对称性知,点A必在x轴上.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣设A(x1,0),则由已知条件知AS⊥AT,即•=0对满足③式的m,k恒成立.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣由=(4﹣x1,4k+m),=(﹣﹣x1,),由•=0得:﹣ +﹣4x1+x12++3=0,整理得(4x1﹣4)+x12﹣4x1+3=0,④﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣由②式对满足①式的m,k恒成立,则,解得x1=1.故平面内存在定点(1,0),使得以ST为直径的圆恒过该定点.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣20.设数列{a n}的前n项和为S n.若对∀n∈N*,总∃k∈N*,使得S n=a k,则称数列{a n}是“G数列”.(Ⅰ)若数列{a n}是等差数列,其首项a1=1,公差d=﹣1.证明:数列{a n}是“G 数列”;(Ⅱ)若数列{a n}的前n项和S n=3n(n∈N*),判断数列{a n}是否为“G数列”,并说明理由;(Ⅲ)证明:对任意的等差数列{a n},总存在两个“G数列”{b n}和{c n},使得a n=b n+c n(n∈N*)成立.【考点】8E:数列的求和;8H:数列递推式.【分析】(Ⅰ)根据G数列的定义证明即可,(Ⅱ)由,可以判断数列{a n}不是“G数列”,(Ⅲ)若d n=bn,(b为常数),可与判断数列{d n}是“G数列”,继而可以证明a n=b n+c n(n∈N*)成立.【解答】解:(1)证明:由题意a n=1+(n﹣1)(﹣1)=2﹣n,,若,则.所以,存在k∈N*,使得S n=a k.所以,数列{a n}是“G数列.(Ⅱ)首先a1=S1=3,当n≥2时,,所以当n=2时,9=2×3k﹣1,得k∉N*因此数列{a n}不是“G数列”.(Ⅲ)若d n=bn,(b为常数),则数列{d n}的前n项和是数列{d n}中的第项,因此数列{d n}是“G数列”.对任意的等差数列{a n},a n=a1+(n﹣1)d,(d为公差),设b n=na1,c n=(d﹣a1)(n﹣1),则a n=b n+c n,而数列{b n}和{c n}都是“G数列”.2017年6月15日。
市顺义高三二模数学理试题及答案

市顺义高三二模数学理试题及答案集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]顺义区2017届高三第二次统练 数学试卷(理科) 第一部分(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项)1. 设集合2{|320}A x x x =-+> ,{|340}B x x =->,则A B =A.4(2,)3--B.4(2,)3-C.4(1,)3D.(2,)+∞2.执行如图所示的程序框图,则输出的s 值为A.116 B.136 C.2512D. 2912 3.已知向量(1,3),(AB AC ==- , 则BAC=4. 某四棱锥的三视图如图所示,则该四棱锥的侧面积为∠A. 8B. 8410+ C. 21013+ D.410213+5. 已知直线a ,b 分别在两个不同的平面α,β内.则“直线a 和直线b 垂直”是“平面α和平面β垂直”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6. 在平面上,过点P 作直线l 的垂线所得的垂足称为点P 在直线l 上的投影.由区域200220x y x y x y +≥⎧⎪-≤⎨⎪-+≥⎩中的点在直线220x y --=上的投影构成的线段记为AB ,则│AB │=A .2C .D .8 7.将函数sin(2)6y x π=+图象上的点(,2M θ(0)4πθ<<向右平移(0)t t >个单位长度得到点'M .若'M 位于函数sin 2y x =的图象上,则 A.,12t πθ=的最小值为12πB. ,12t πθ=的最小值为6πC. ,6t πθ=的最小值为6πD. ,6t πθ=的最小值为12π8. 某学校为了提高学生综合素质、树立社会主义荣辱观、发展创新能力和实践能力、促进学生健康成长,开展评选“校园之星”活动.规定各班每10人推选一名候选人 ,当各班人数除以10的余数大于7时再增选一名候选人,那么,各班可推选候选人人数y 与该班人数x 之间的函数关系用取整函数[]y x =( []x 表示不大于x 的最大整数)可以表示为.[]10x A y = 2.[]10x B y += 3.[]10x C y += 4.[]10x D y +=第二部分(非选择题 共110分)二、填空题(本大题共6个小题,每小题5分,共30分)9.` 已知(2)(1)z a a i =-++在复平面内对应的点在第二象限,则实数a 的取值范围是 ________ .10.在281()2x x+的展开式中, 7x 的系数为________.(用数字作答) 11. 已知为等差数列,为其前项和,若24a =,88S =-,则10a =_______.12. 在极坐标系中,圆2cos ρθ=-的圆心C 到直线2cos sin 20ρθρθ+-=的距离 等于______.13. 已知抛物线22(0)y px p =>的准线为l ,若l 与圆22650x y x +++=的交点为,A B ,且AB =则p 的值为_______.{}n a n S n14.已知函数32,,(),.x x m f x x x m ⎧≤⎪=⎨>⎪⎩,函数()()g x f x k =-.(1)当2m =时,若函数()g x 有两个零点,则k 的取值范围是 ;(2)若存在实数k 使得函数()g x 有两个零点,则m 的取值范围是 .三、解答题(本大题共6小题,共80分. 解答应写出文字说明,证明过程或演算步骤)15.(本小题满分13分)在ABC △中,角A ,B ,C 的对边分别为,,a b c,已知cos cos .2cos a b B+A c c C= (I )求C ∠的大小;(II)求sin B A 的最小值.16. (本小题满分13分)春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化.2017年除夕18时和初一2时,国家环保部门对8个城市空气中浓度监测的数据如下表(单位:微克/立方米).(Ⅰ)求这8个城市除夕18时空气中浓度的平均值;(Ⅱ)环保部门发现:除夕18时到初一2时空气中浓度上升不超过100的城市都是"禁止燃放烟花爆竹"的城市, 浓度上升超过100的城市都未禁止燃放烟花爆竹.从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X ,求随机变量X 的分布列和数学期望;(Ⅲ) 记2017年除夕18时和初一2时以上8个城市空气中浓度的方差分别为21s 和22s ,比较21s 和22s 的大小关系(只需写出结果).17. (本小题满分14分)如图,正三角形ABE 与菱形ABCD 所在的平面互相垂直,2=AB ,︒=∠60ABC ,M 是AB 的中点.(I )求证:EM AD ⊥;(II )求二面角C BE A --的余弦值;(III )在线段EC 上是否存在点P ,使得直线AP 与平面ABE 所成的角为︒45,若存在,求出ECEP的值;若不存在,说明理由.18. (本小题满分14分)已知函数()1++=-x pe x f x ()R p ∈.(Ⅰ)当实数e p =时,求曲线()x f y =在点1=x 处的切线方程; (Ⅱ)求函数()x f 的单调区间;(Ⅲ)当1=p 时,若直线1+=mx y 与曲线()x f y =没有公共点,求实数m的取值范围.19.(本小题满分13分)已知椭圆:E ()012222>>=+b a b y a x 经过点3(1,)2-,其离心率21=e .BA CDEM(Ⅰ)求椭圆E 的方程;(Ⅱ)设动直线m kx y l +=:与椭圆C 相切,切点为T ,且l 与直线4-=x 相交于点S .试问:在x 轴上是否存在一定点,使得以ST 为直径的圆恒过该定点若存在,求出该点的坐标;若不存在,请说明理由.20.(本小题满分13分)设数列{}n a 的前n 项和为n S .若对n N *∀∈,总k N *∃∈,使得n k S a =,则称数列{}n a 是“G 数列”.(Ⅰ)若数列{}n a 是等差数列,其首项,公差1d =-.证明: 数列是“G 数列”;(Ⅱ)若数列{}n a 的前n 项和3()n n S n N *=∈,判断数列是否为“G数列”,并说明理由;(Ⅲ)证明:对任意的等差数列{}n a ,总存在两个“G 数列”和,使得().n n n a b c n N *=+∈成立.11=a }{n a }{n a }{n b }{n c顺义区2017届高三第二次统练数学试卷答案(理科)一、DCC D DBAB 二、9. (1,2)- 13. 4或8 14. (]8,4; ()()+∞∞-,10,三、15. 解(I )由正弦定理,得 sin sin ,sin sin a A b BcC c C==,---------------------------------1分所以,sin cos sin cos .sin 2cos A B B A C C+=即sin()sin A B C +=. -----------------------------------3分∵πA B C ++=,(),,0,π,A B C ∈∴()sin sin .A B C += -----------------------------------4分∴2cos C =cos C =-----------------------------------5分∵()0πC ∈,, ∴π6C =. -----------------------------------6分 (II )∵π,A B C ++=∴5π6A B +=. -----------------------------------7分∴5sin sin()6B A A A π-=-1cos 2A A A = -----------------------------------9分1cos 2A A =πcos()3A =+ . -----------------------------------11分 ∵5π6A B +=, ∴5(0,π)6A ∈,∴ππ7(,)336A π+∈. -----------------------------------12分∴πcos()3A +最小值为-1.即sin B A 的最小值为-1. -----------------------------------13分16.解:(Ⅰ)8个城市除夕18时空气中浓度的平均值708131351646102896675=+++++++=v .-------------------------------3分(Ⅱ)以上8个城市中禁止燃放烟花爆竹的有太原,上海,南京,杭州4个城市,---4分随机变量X 的所有可能取值为0,1,2,分0344381(0),14C C P X C === 1244386(1),14C C P X C === 2144386(2),14C C P X C === 3044381(3).14C C P X C === X 的分布列为:-----------------------------------------------------------------------9分X 的数学期望1661213012314141414142EX =⨯+⨯+⨯+⨯==. -------------11分(Ⅲ)21s <22s . ----------------------------------------------------------13分17.(Ⅰ)证明:∵EB EA =,M 是AB 的中点,∴.EM AB ⊥ --------------------------------------------------------------------1分∵平面⊥ABE 平面,ABCD -----------------------------------------------------2分平面 ABE 平面,ABCD AB =⊂EM 平面,ABE∴⊥EM 平面.ABCD -----------------------------------------------------------3分AD ⊂平面ABCD ,∴EM AD ⊥. -----------------------------------------------------------------4分 (Ⅱ)解:∵⊥EM 平面ABCD ,∴MC EM ⊥.显然△ABC 是正三角形, 则AB MC ⊥.∴ME MC MB ,,两两垂直.建立如图所示空间直角坐标系M xyz 分则)0,0,0(M ,)0,0,1(-A ,)0,0,1(B ,0,3,0(C )0,3,1(-=,(BE =-设),,(z y x =是平面BCE 的一个法向量则⎪⎩⎪⎨⎧=⋅=00m 即⎪⎩⎪⎨⎧=+-=+-0303z x y x 令1=z 得)1,1,3(=,--------------------------------------------------------------7分因为y 轴与平面ABE 垂直.所以(0,1,0)n =是平面ABE 的一个法向量.----------------------------------------8分cos ,5m n m n m n⋅<>===⨯------------------------------------------------9分所以二面角C BE A --的余弦值为55.------------------------------------------10分(III )解:假设在线段EC 上存在点P ,使得直线AP 与平面ABE 所成的角为︒45.)3,0,1(=,)3,3,0(-=,设)3,3,0(λλλ-==,])1,0[(∈λ则)33,3,1(λλ-=+=. ------------------------------------------------11分由sin 45cos ,1AP n AP n AP n⋅=<>===解得 23λ=----------------------------------------------------------------------------------13分 所以存在点P ,且23EP EC =.----------------------------------------------------------------14分18.解:(Ⅰ)当e p =时,()11++=+-x e x f x ,()11+-='+-x e x f ∴()31=f ,()01='f∴曲线()x f y =在点1=x 处的切线方程为3=y -----------------------------4分(Ⅱ)∵()1++=-x pe x f x ,∴()1+-='-x pe x f ---------------------------------5分①当0≤p 时,()0>'x f ,则函数()x f 在的单调递增区间为()+∞∞-,; -----------------------------------6分②当0>p 时,令()0f x '=,得p e x =,解得p x ln =.---------------------7分则当x 变化时,()x f '的变化情况如下表:------------------------------9分所以, 当0>p 时,()x f 的单调递增区间为 ()+∞,ln p , 单调递减区间为()p ln ,∞-. ------------------------------10分(Ⅲ)当1=p 时,()1++=-x e x f x ,直线1+=mx y 与曲线()x f y =没有公共点,等价于关于x 的方程11++=+-x e mx x 在()+∞∞-,上没有实数解, 即关于x 的方程()x e x m -=-1(*)在()+∞∞-,上没有实数解. ①当1=m 时,方程(*)化为0=-x e ,显然在()+∞∞-,上没有实数解. --------------------------------12分②当1≠m 时,方程(*)化为11-=m xe x ,令()x xe x g =,则有()()x e x x g +='1.令()0='x g ,得1-=x ,则当x 变化时,()g x '的变化情况如下表:当1x =-时,()min 1g x e=-,同时当x 趋于+∞时,()g x 趋于+∞,从而()g x 的值域为1,e⎡⎫-+∞⎪⎢⎣⎭. -----------------------------------13分所以当em 111-<-时,方程(*)无实数解,解得实数m 的取值范围是()1,1e -.综合①②可知实数m 的取值范围是(]1,1e -.----------------------------14分19.解:(Ⅰ)由点3(1,)2-在椭圆上得,221914a b+=-----------------① 依题设知2a c =,则223b c =. ----------------------------------②②代入①解得2221,4,3c a b ===故椭圆E 的标准方程为22143x y +=.---------------------------------4分(Ⅱ)由⎪⎩⎪⎨⎧=++=13422y x m kx y 消去y ,得()0124834222=-+++m kmx x k . -----------------------------------5分因为动直线l 与椭圆C 相切,即它们有且只有一个公共点T ,可设()00,y x T ,所以0≠m 且0=∆,即()()0124344642222=-+-m k m k ,化简得03422=+-m k ------------③此时,m k k km x 434420-=+-=,m m kx y 300=+=,所以点T 的坐标为43(,)k m m-. 由⎩⎨⎧+=-=m kx y x 4得()m k S +--4,4. -----------------------------------9分假设在x 轴上存在定点满足条件,不妨设为点()0,1x A .则由已知条件知AT AS ⊥,即0=•AT AS 对满足③式的k m ,恒成立.因为()m k x AS +---=4,41,⎪⎭⎫ ⎝⎛--=m x mk3,41,由0=•得0312********=+-+++m k x x m kx m k ,整理得()034441211=++++x x mkx --------④由④式对满足③式的k m ,恒成立,所以⎩⎨⎧=++=+0340441211x x x ,解得11-=x . 故在x 轴上存在定点()0,1-,使得以ST 为直径的圆恒过该定点.-----------------13分20.解(1)由题意1(1)(1)2na n n , ---------------------------1分(1)(1)2nn n S n, -----------------------------------2分若(1)(1)22nkn n S na k , -----------------------------------3分 则(1)22n n k n -=+-. 所以,存在*∈N k ,使得n k S a =.所以, 数列是“G 数列. ---------------------------------------4分{}n a(2)解:首先113a S ,当2≥n 时,1132--⨯=-=n n n n S S a ,所以⎩⎨⎧≥⨯==-2,321,31n n a n n , -----------------------------------6分 当2n =时,1923k -=⨯,得k N *∉因此数列{}n a 不是“G 数列”. ----------------8分 (3)若nd bn ,(b 为常数),则数列的前n 项和(1)2n n n S b +=是数列中的第(1)2n n +项,因此数列是“G 数列”. 对任意的等差数列,,(d 为公差),设1nb na ,1()(1)nc da n ,则nnna b c ,而数列,都是“G 数列”.--------------------------------13分{}n d {}n d {}n d {}n a 1(1)n a a n d {}n b {}n c。
2017届高三第二次教学质量检测数学理试题(12页有答案)

-1012}012}01}-101}-1012} 23B.5A.4C.D.3[+高三年级第二次教学质量检测试题理科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题共60分)一.选择题:本大题共12个小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={-2,,,,,B={x|-2<x≤2},则A B=A.{-1,,,B.{-1,,C.{-2,,,D.{-2,,,,2.复数2-i1+i对应的点在A.第一象限B.第二象限C.第三象限D.第四象限3.已知向量a=(2,-1),b=(3,x),若a⋅b=3,则x=A.3B.4C.5D.64.已知双曲线x2y2-a b23=1的一条渐近线方程为y=x,则此双曲线的离心率为457445.已知条件p:x-4≤6;条件q:x≤1+m,若p是q的充分不必要条件,则m的取值范围是A.(-∞,-1]B.(-∞,9]C.1,9]D.[9,∞)6.运行如图所示的程序框图,输出的结果S=A.14B.30C.62D.1268.已知α,β是两个不同的平面,l,m,n是不同的直线,下列命题不正确的是A.πA.332D.27.(x-1)n的展开式中只有第5项的二项式系数最大,则展开式中含x2项的系数是xA.56B.35C.-56D.-35...A.若l⊥m,l⊥n,m⊂α,n⊂α,则l⊥αB.若l//m,l⊂/α,m⊂α,则l//αC.若α⊥β,αβ=l,m⊂α,m⊥l,则m⊥βD.若α⊥β,m⊥α,n⊥β,,则m⊥n9.已知f(x)=sin x+3cos x(x∈R),函数y=f(x+ϕ)的图象关于直线x=0对称,则ϕ的值可以是πππB.C.D.263410.男女生共8人,从中任选3人,出现2个男生,1个女生的概率为1528,则其中女生人数是A.2人B.3人C.2人或3人D.4人11.已知抛物线y2=4x,过焦点F作直线与抛物线交于点A,B(点A在x轴下方),点A与1点A关于x轴对称,若直线AB斜率为1,则直线A B的斜率为12B.3C.12.下列结论中,正确的有①不存在实数k,使得方程x ln x-1x2+k=0有两个不等实根;2②已知△ABC中,a,b,c分别为角A,B,C的对边,且a2+b2=2c2,则角C的最大值为π6;③函数y=ln与y=ln tan x2是同一函数;④在椭圆x2y2+a2b2=1(a>b>0),左右顶点分别为A,B,若P为椭圆上任意一点(不同于A,B),则直线PA与直线PB斜率之积为定值.A.①④B.①③C.①②D.②④13.已知等比数列{a}的前n项和为S,且a+a=5n2414.已知实数x、y满足约束条件⎨y≥2,则z=2x+4y的最大值为______.⎪x+y≤6②若a∈(0,1),则a<a1+11-x是奇函数(第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分.第13题~21题为必考题,每个试题考生都必须做答.第22题、第23题为选考题,考生根据要求做答.二.填空题:本大题共4小题;每小题5分,共20分.5,a+a=,则S=__________.n13246⎧x≥2⎪⎩15.一个几何体的三视图如图所示,则这个几何体的外接球的半径为__________.16.下列命题正确是.(写出所有正确命题的序号)①若奇函数f(x)的周期为4,则函数f(x)的图象关于(2,0)对称;③函数f(x)=ln;三.解答题:本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分12分)在△ABC中,角A、B、C的对边分别为a,b,c,且a=3,b=4,B=A+高三理科数学试题和答案第3页共6页π2., 20 40 60 80 ,(1)求 cos B 的值;(2)求 sin 2 A + sin C 的值.18.(本小题满分 12 分)如图,三棱柱 ABC - A B C 中,侧棱 AA ⊥ 平面 ABC , ∆ABC 为等腰直角三角形,1 1 1 1∠BAC = 90 ,且 AA = AB , E , F 分别是 C C , BC 的中点.1 1(1)求证:平面 AB F ⊥ 平面 AEF ;1(2)求二面角 B - AE - F 的余弦值.119.(本小题满分 12 分)某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0 100],样本数据分组为第一组[0, ),第二组[20, ),第 三组 [40, ),第四组 [60, ),第五组 [80 100].(1)求直方图中 x 的值;(2)如果年上缴税收不少于 60 万元的企业可申请政策优惠,若共抽取企业 1200 家,试估计有多少企业可以申请政策优惠;(3)从所抽取的企业中任选 4 家,这 4 家企业年上缴税收少于 20 万元的家数记为 X ,求 X 的分布列和数学期望.(以直方图中的频率作为概率)= 1(a > b > 0) 经过点 P (2, 2) ,离心率 e = ,直线 l 的方程为 220.(本小题满分 12 分)已知椭圆 C : x 2 y 2+ a 2 b 22 2x = 4 .(1)求椭圆 C 的方程;(2)经过椭圆右焦点 F 的任一直线(不经过点 P )与椭圆交于两点 A , B ,设直线 AB 与l 相交于点 M ,记 P A , PB , PM 的斜率分别为 k , k , k ,问:是否存在常数 λ ,使得1 2 3k + k = λ k ?若存在,求出 λ 的值,若不存在,说明理由.12321.(本小题满分 12 分)已知函数 f ( x ) = ax + ln x ,其中 a 为常数,设 e 为自然对数的底数.(1)当 a = -1 时,求 f ( x ) 的最大值;(2)若 f ( x ) 在区间 (0, e ] 上的最大值为 -3 ,求 a 的值;(3)设 g ( x ) = xf ( x ), 若 a > 0, 对于任意的两个正实数 x , x ( x ≠ x ) ,1 2 1 2证明: 2 g ( x 1 + x 2) < g ( x ) + g ( x ) .1 2请考生在第 22、23 二题中任选一题做答,如果多做,则按所做的第一题记分.做答时,用⎪⎪ 5⎩17.解:(1)∵ B = A + , ∴ A = B -, ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 1 分 ==2B 铅笔在答题卡上把所选题目对应的题号涂黑.22.(本小题满分 10 分)选修 4-4:坐标系与参数方程⎧3 x =- t + 2 在直角坐标系 xOy 中,直线 l 的参数方程为 ⎨ ( t 为参数),以原点 O 为极点, x⎪ y = 4 t ⎪5轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为 ρ = a sin θ .(1)若 a = 2 ,求圆 C 的直角坐标方程与直线 l 的普通方程;(2)设直线 l 截圆 C 的弦长等于圆 C 的半径长的 3 倍,求 a 的值.23.(本小题满分 10 分)选修 4-5:不等式选讲已知函数 f ( x ) = 2x -1 + 2x + 5 ,且 f ( x ) ≥ m 恒成立.(1)求 m 的取值范围;(2)当 m 取最大值时,解关于 x 的不等式: x - 3 - 2x ≤ 2m - 8 .高三第二次质量检测理科数学答案一.ADABD CCABC CA二.13.631614.20 15. 61 16.①③ππ2 23 4 又 a = 3, b = 4 ,所以由正弦定理得 ,sin Asin B34所以, ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅3 分- cos B sin B所以 -3sin B = 4cos B ,两边平方得 9sin 2 B = 16cos 2 B ,3又 sin 2 B + cos 2 B = 1 ,所以 cos B = ± , ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 5 分5π 3而 B > ,所以 cos B = - . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 6 分2 53 4(2)∵ cos B = - ,∴ sin B = , ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 7 分5 5∴面 ABC ⊥ 面 BB C C..........2 分+ = 则 F (0,0,0) , A ( 22 2 2 2 2 1 ∵ B = A +π2,∴ 2 A = 2 B - π ,∴ sin 2 A = sin(2 B - π ) = - sin 2 B ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 8 分4 3 24= -2sin B cos B = -2 ⨯ ⨯ (- ) = ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 10 分5 5 25又 A + B + C = π ,∴ C = 3π 2- 2 B ,7 24 7 31∴ sin C = - cos 2 B = 1 - cos 2 B = .∴ sin 2 A + sin C = . (12)25 25 25 25分18.解答: (1)证明:∵ F 是等腰直角三角形 ∆ABC 斜边 BC 的中点,∴ AF ⊥ BC .又∵侧棱 AA ⊥ 平面ABC ,11 1∴ AF ⊥ 面 BB 1C 1C , AF ⊥ B 1F .…3 分设 AB = AA = 1 ,则1,EF= , .∴ B F 2 + EF 2 = B E 2 ,∴ B F ⊥ EF ........... 4 分1 11又 AF ⋂ EF = F ,∴ B F ⊥平面 AEF .…1而 B F ⊂ 面 AB F ,故:平面 AB F ⊥ 平面 AEF . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅5 分1 11(2)解:以 F 为坐标原点, FA , FB 分别为 x , y 轴建立空间直角坐标系如图,设 AB = AA = 1 ,12 2 1,0,0) , B (0, - ,1) , E (0, - , ) ,12 2 1 2 2AE = (- , - , ) , AB = (- , ,1) .… ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 6 分2 2 2 2 2由(1)知, B F ⊥平面 AEF ,取平面 AEF 的法向量:12m = FB = (0, ,1) . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 7 分14 4 256 4 4 4 644 4 64 4 4 64设平面 B AE 的法向量为 n = ( x , y , z ) ,1由取 x = 3 ,得 n = (3, -1,2 2) (10),分设二面角 B - AE - F 的大小为θ ,1则 cos θ=|cos <>|=| |= .由图可知θ 为锐角,∴所求二面角 B - AE - F 的余弦值为.… ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 12 分119.解答: 解:(I )由直方图可得: 20 ⨯ (x + 0.025 + 0.0065 + 0.003 ⨯ 2) = 1解得 x = 0.0125 .⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 2 分(II )企业缴税收不少于 60 万元的频率 = 0.003 ⨯ 2 ⨯ 20 = 0.12 , ∴1200 ⨯ 0.12 = 144 .∴1200 个企业中有144 个企业可以申请政策优惠.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 4 分(III ) X 的可能取值为 0,1,2,3,4 .由(I )可得:某个企业缴税少于 20 万元的概率 = 0.0125 ⨯ 20 = 0.25 =分1 3 81 1 3 27P ( X = 0) = C 0 ( )0 ( )4 = P ( X = 1) = C 1 ( )1 ( )3 = 41 3 27 1 3 3P ( X = 2) = C 2 ( )2 ( )2 = P ( X = 3) = C 3 ( )3 ( )1 =4 4 14 (5)X0 1 2 3 44 4 256∴ E ( X ) = 0 ⨯ 81+ = 1 ① 又e = , 所以 = = 4, a = 8,b 1 + 2k 2 1 + 2k 2, x x = x - 2 x - 22, k = k = 2k - 2 4 - 2 2P8125627 64 27 64 3 64 1 2561 3 1P ( X = 4) = C 4 ( )4 ( )0 =4...................................... 10 分............. 11 分27 27 3 1+ 1⨯ + 2 ⨯ + 3 ⨯ + 4 ⨯= 1. ....12 分25664 64 64 25620.解:(1)由点 P (2, 2) 在椭圆上得, 4 2 2 c 2 a 2 b 2 2 a 2②由 ①②得 c 2 2 2 = 4 ,故椭圆 C 的方程为 x 2 y 2+ = 1 ……………………..4 分 8 4(2)假设存在常数 λ ,使得 k + k = λ k .1 23由题意可设 AB 的斜率为k , 则直线AB 的方程为 y = k ( x - 2) ③代入椭圆方程x 2 y 2+ = 1 并整理得 (1+ 2k 2 ) x 2 - 8k 2 x + 8k 2 - 8 = 0 8 48k 2 8k 2 - 8设 A ( x , y ), B ( x , y ) ,则有 x + x = ④ ……………6 分 1 1 2 2 1 2 1 2在方程③中,令 x = 4 得, M (4,2 k ) ,从而 k = y 1 - 2 y 2 - 21 2 1,3 2= k - .又因为 A 、F 、B 共线,则有 k = k AF = k BF ,即有y当 a = -1 时, f ( x ) = - x + ln x , f ' ( x ) = -1 + 1①若 a ≥ - ,则 f ' ( x ) ≥ 0 ,从而 f ( x ) 在 (0, e ] 上是增函数,y1=2= k ……………8 分x - 2x - 21 2所以 k + k = 1 2 y - 2 y - 2 1 + 2 x - 2 x - 21 2= y y 1 11 +2 - 2( + )x - 2 x - 2 x - 2 x - 2 1 2 1 2= 2k - 2x 1 + x 2 - 4x x - 2( x + x ) + 41 212⑤ ……………10 分将④代入⑤得 k + k = 2k - 2 1 2 8k 2- 41 + 2k2 8k 2 - 8 8k 2- 2 + 41 + 2k2 1 + 2k 2= 2k - 2 ,又 k = k - 32 2 ,所以 k + k = 2k 1 2 3 . 故存在常数 λ = 2 符合题意…………12 分21.【解答】解:(1)易知 f ( x ) 定义域为 (0, +∞) ,1 - x= ,x x令 f ' ( x ) = 0 ,得 x = 1 .当 0 < x < 1 时, f ' ( x ) > 0 ;当 x > 1 时, f ' ( x ) < 0 . (2)分∴ f ( x ) 在 (0,1) 上是增函数,在 (1,+∞) 上是减函数.f ( x )max= f (1) = -1.∴函数 f ( x ) 在 (0, +∞) 上的最大值为 -1 . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 4 分(2)∵ f '( x ) = a + 1 1 1, x ∈ (0, e ], ∈ [ , +∞) .x x e1e∴ f ( x )max= f (e ) = ae + 1 ≥ 0 ,不合题意. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 5 分11② 若 a < - ,则由 f ' ( x ) > 0 ⇒ a +ex> 0 ,即 0 < x < -1a11由 f ' ( x ) < 0 ⇒ a +< 0 ,即 - < x ≤ e . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 6 分xa从而 f ( x ) 在 (0, - ) 上增函数,在 (- (3)法一:即证 2a ( x + x 2) + 2( 12 )ln( 222 2 x 2 x21 1a a, e ) 为减函数∴ f ( x ) max 1 1 = f (- ) = -1 + ln(- ) a a1 1令 -1 + ln(- ) = -3 ,则 ln(- ) = -2a a∴- 11= e -2 -e 2 < -a ,即 a = -e 2.∵ e ,∴ a = -e 2 为所求 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 8 分1 1 x + x x + x2 2 22 ) ≤ ax 2 + ax 2 + x ln x + x ln x 1 2 1 1 222a ( x + x ( x + x )21 2 )2 - ax 2 - ax 2 = a ⋅[ 1 21 2- x 2 - x 2 ]1 2( x - x )2= -a 1 2 2< 0 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 9 分另一方面,不妨设 x < x ,构造函数1 2k ( x ) = ( x + x )ln(1x + x12) - x ln x - x ln x ( x > x )1 1 1x + xx + x则 k ( x ) = 0 ,而 k ' ( x ) = ln 1 - ln x = ln 1 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 10 分1x + x由 0 < x < x 易知 0 < 11< 1 , 即 k ' ( x ) < 0 , k ( x ) 在 ( x , +∞) 上为单调递减且连续, 1x + x故 k ( x ) < 0 ,即 ( x + x )ln( 11) < x ln x + x ln x 1 1相加即得证⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 12 分1法二: g ' ( x ) = 2ax + 1 + ln x , g '' ( x ) = 2a + > 0.........9 分x故 g ' ( x ) 为增函数,不妨令 x > x 21令 h ( x ) = g ( x ) + g ( x ) - 2 g (1x + x12)( x > x )1h ' ( x ) = g '(x ) - g ' (x + x12) ......... 10 分易知 x > x + x x + x1 , 故h ' ( x ) = g '(x ) - g ' ( 12 2) > 0 (11)分而 h ( x ) = 0 , 知 x > x 时, h ( x ) > 0112(2)圆 C : x 2 + y - a ⎫2∴圆心 C 到直线的距离 d = 2- 8 得 a = 32 或 a = 32 ⎪ -4 x - 4, x < - 523.解 (1) f (x) = ⎨6, - 5⎩ 4 x + 4, x > 22 ≤ x ≤ ⎩3 - x - 2 x ≤4 ⎧ 3 ≤ x < 3 .所以,原不等式的解集为 ⎨⎧x x ≥ - ⎬ .故 h ( x ) > 0 , 即 2 g ( x 1 + x 2) < g ( x ) + g ( x )21 2 (12)分22.解 (1) a = 2 时,圆 C 的直角坐标方程为 x 2 + (y -1)2 = 1 ;直线 l 的普通方程为 4 x + 3 y - 8 = 0 . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 4 分⎛⎪ = ⎝ 2 ⎭a 2 4 ,直线 l : 4 x + 3 y - 8 = 0 ,∵直线 l 截圆 C 的弦长等于圆 C 的半径长的 3 倍,3a1 a5 = 2 ⨯ 2 ,11 .⎧2 ⎪1 ⎪2 ≤ x ≤ 2 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 2 分⎪1 ⎪ ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 7 分⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 10 分当 - 5 12 时,函数有最小值 6 ,所以 m ≤ 6 . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 5 分另解:∵ 2x -1 + 2x + 5 ≥ (2x -1) - (2x + 5) = -6 = 6 .∴ m ≤ 6 .(2)当 m 取最大值 6 时,原不等式等价于 x - 3 - 2x ≤ 4 ,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 6 分等价于 ⎨ x ≥ 3 ⎩ x - 3 - 2x ≤ 4 ⎧ x < 3 ,或 ⎨,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 8 分可得 x ≥ 3 或 - 11 ⎫ ⎩ 3 ⎭⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 10 分。
北京市顺义区2017届高三下学期第二次统练理综化学试题 【解析版】
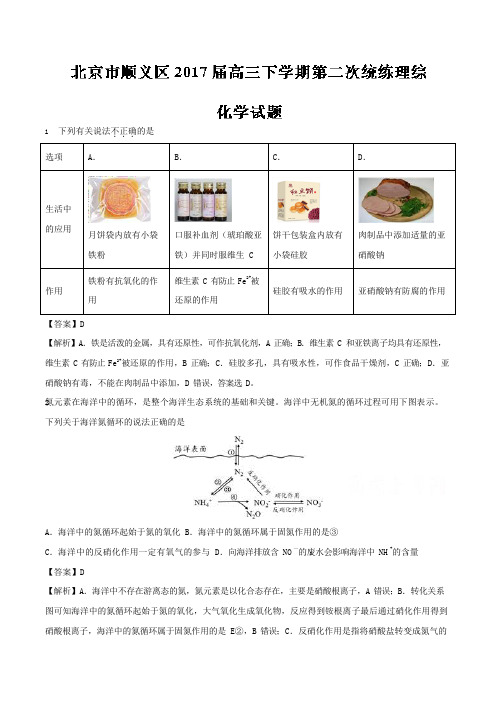
3 41. 下列有关说法不.正.确.的是选项A .B .C .D .生活中的应用月饼袋内放有小袋铁粉口服补血剂(琥珀酸亚铁)并同时服维生 C饼干包装盒内放有小袋硅胶肉制品中添加适量的亚硝酸钠作用铁粉有抗氧化的作用维生素 C 有防止 Fe 2+被还原的作用硅胶有吸水的作用亚硝酸钠有防腐的作用【答案】D【解析】A .铁是活泼的金属,具有还原性,可作抗氧化剂,A 正确;B .维生素 C 和亚铁离子均具有还原性, 维生素 C 有防止 Fe 2+被还原的作用,B 正确;C .硅胶多孔,具有吸水性,可作食品干燥剂,C 正确;D .亚硝酸钠有毒,不能在肉制品中添加,D 错误,答案选 D 。
2.氮元素在海洋中的循环,是整个海洋生态系统的基础和关键。
海洋中无机氮的循环过程可用下图表示。
下列关于海洋氮循环的说法正确的是A .海洋中的氮循环起始于氮的氧化B .海洋中的氮循环属于固氮作用的是③C .海洋中的反硝化作用一定有氧气的参与D .向海洋排放含 NO —的废水会影响海洋中 NH +的含量【答案】D【解析】A .海洋中不存在游离态的氮,氮元素是以化合态存在,主要是硝酸根离子,A 错误;B .转化关系图可知海洋中的氮循环起始于氮的氧化,大气氧化生成氧化物,反应得到铵根离子最后通过硝化作用得到硝酸根离子,海洋中的氮循环属于固氮作用的是 E②,B 错误;C .反硝化作用是指将硝酸盐转变成氮气的3 4 过程。
硝化作用是指氨在微生物作用下氧化为硝酸的过程,硝化细菌将氨氧化为硝酸的过程。
反硝化作用: 反硝化细菌在缺氧条件下,还原硝酸盐,释放出分子态氮(N 2)或一氧化二氮(N 2O )的过程,不一定有氧参加,C 错误;D .转化关系图中硝酸根离子增多,反硝化作用增强,向海洋排放含 NO -的废水会影响海洋中 NH +的含量,D 正确;答案选 D 。
3.C 和 H 2 在生产、生活、科技中是重要的燃料。
①2C(s)+O 2(g) ===2CO(g) ΔH 1=—220 kJ/mol②下列推断正确的是A .C(s) 的 燃 烧 热 110kJ/molB .2H 2(g)+O 2(g)===2H 2O(g)ΔH 1=+480kJ/molC .C(s)+H 2O(g)===CO(g)+H 2(g)ΔH 1=+130kJ/molD .欲分解 2molH 2O(l),至少需要提供 4×462kJ 的热量 【答案】C【解析】A .①中生成物是 CO ,不是 CO 2,不能据此计算碳的燃烧热,A 错误;B .反应 2H 2(g) + O 2(g)=2H 2O(g)的反应热 ΔH 1=4×462kJ/mol-496kJ/mol -2×436kJ/mol=-480 kJ/mol ,B 错误;C .根据盖斯定律(① -②)/2 即得到反应 C(s) + H 2O(g)=CO(g) + H 2(g) ΔH 1=+130 kJ/mol ,C 正确;D .气态水的能量高于液态水,因此欲分解 2 mol H 2O(l),需要提供的能量高于 4×462 kJ,D 错误,答案选 C 。
2017年北京市顺义区高考地理二模试卷(解析版)

2017年北京市顺义区高考地理二模试卷一.选择题气候学上以某地连续5天平均气温稳定≥10℃的第一天为春季的开始日期.5天平均气温稳定≥22℃第一日的前一天是春季的结束日期.当某区内70%以上县级气象站点进入春季,则该地区进入春季.图为我国1981年﹣﹣2010年间“春天”到来的脚步.读图回答1~3题.1.2月28日图中城市()A.北京比杭州白昼长B.北京比上海日出早C.南京比长沙日落晚D.兰州比上海正午太阳高度小2.图中“春天”的脚步()A.是指夏季风的移动节奏规律B.塔里木盆地入春早于同纬度地区是由于深居内陆C.青藏高原与大兴安岭入春晚的原因相同D.范围由区域内连续5天平均气温≥10℃的时段决定3.“春天”的脚步()A.与太阳直射点北移有关B.影响我国农业的耕作制度C.主要由人类生产活动决定D.出现的时间是固定不变的4.我国是一个自然灾害频发的国家.灾害类型多样给人们带来了生命和财产损失.依据所学判断出下面四个选项中,哪个反应的是地震灾害的内容.()A.它是一种发生范围广、频度高、强度大、危害大的灾害.在我国西多东少,主要有新疆、青藏、华北和台湾四个多发区,灾情却东重西轻.其分布基本上遵循活动性断裂带的分布,构造运动频繁,地壳脆弱地多发B.它主要发生在我国山区,地域上具有广泛和相对集中的分布特点.其中之一受连续降水、暴雨等激发,具有与降水相对一致的季节变化C.它是一种发生范围最广、频次高、持续时间最长的渐发性灾害.农牧业灾情重,工矿、城市危害巨大.主要分布在常年雨水较多的东部季风区,在我国有华北、华南、西南和江淮地区四个多发中心D.它是一种分布范围广、发生频繁、突发性强、损失大.据统计其造成的经济损失和人员伤亡在各种灾害中居第一位.其分布是东多西少;沿海多,内陆少;平原低地多,高原山地少;山脉东坡和南坡多.季风区多发,夏季多发2017年为“中国﹣﹣丹麦旅游年”.丹麦是发达的北欧工业国家.农牧渔业及食品加工业发达,有欧洲乳酪市场之称.丹麦环境优美,风能资源丰富,是旅游胜地.哥本哈根是丹麦首都,城市规划独具特色.图为丹麦地理位置和首都哥本哈根“手指规划”简图.读图,回答5~7题.5.图中“手指”为交通干线经过地区,“手指”之间的区域最可能规划为()A.工业与商业区B.别墅与港口区C.金融与贸易区D.农田与绿化区6.自1948年以来,该城市一直在按“手指”规划发展.此规划对城市发展所产生的积极影响,突出表现在8()A.避免地表硬化,减少城市内涝B.减缓热岛效应,改善宜居环境。
北京市顺义区2017-2018届高三二模语文试卷含答案

北京市顺义区2017--2018届高三二模语文一、本大题共7小题,共24分。
阅读下面材料,完成1—7题。
材料一幌子俗称酒帘,是古代酒店以其引人注目、招揽顾客的招牌,又称望子、酒旗等,最初是酒家使用的,后来加以引申,凡商店门面上展示形象性的行业标记,以图形、色彩、文字等视觉符号传达商品信息、辅助经营和招揽顾客的旗帜,统称为“幌子”,它是商家向消费者宣传生产或经营事项的标志。
招幌是伴随市场商业行为而兴起的,在我国有悠久的历史。
它的萌生和演化,反映了古代商品交换日趋繁荣的历史进程,也折射出古代社会的商业民俗。
周朝的市场管理由“司市”负责,在经营活动期间,要挂起旗帜表示开市。
可见早在三千年前的西周,已经使用旗帜作为市场运行的标志系统。
战国时期出现了正式意义上的幌子。
据《韩非子•外储说》载,“宋人有酤酒者,为酒甚美,悬帜甚高。
”这显然已是酒铺的标志,表明当时店家已懂得用高悬酒旗来招徕生意。
汉代商业经济有了较大发展,为招幌的发展奠定了基础。
东汉时卖药者就不乏以药葫芦为幌的。
唐代集市与商业贸易日趋发达,店铺标志在诗歌中有大量的描写,如白居易《曲江》:“细草岸西东,酒旗摇水风。
”杜牧更是在《江南春绝句》中将酒旗融入了“千里莺啼绿映红,水村山郭酒旗风”的如画美景中。
可见,在唐代商铺中已经广泛使用标志系统。
宋代市场经济更为活跃,商业城市的涌现,使旗帜商幌得以广泛地使用,商业类的标志愈加丰富。
此后,招幌的形式日趋丰富,我们可在明清时期游记、笔记、小说及年画作品中看到大量商铺招幌的描写或图像。
这表明明清时期招幌更加成熟。
民国之后,随着外来文化的进入及科技的发展,传统的招幌逐渐被霓虹灯所取代,在大街小巷中已经难觅其身影。
(取材于许大海文章)1.根据材料一,下列对招幌的解说,不当的一项是(3分)A.周代悬挂旗帜已成为市场运行的标志B.唐代经济发展,店铺已广泛使用招幌C.明清的招幌信息只保存在文字资料中D.民国时期传统的招幌被科技广告取代2.对材料一涉及的文学常识,表述有误的一项是(2分)A.《韩非子》,战国思想家韩非著,常用寓言故事阐明道理。
2017年北京市顺义区高考数学二模试卷(文科)

2017年北京市顺义区高考数学二模试卷(文科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共8小题,共40.0分)1.设集合A={x|x<1或x>2},B={x|3x-4>0},则A∩B=()A.(-,1)B.(,2)C.(1,)D.(2,+∞)【答案】D【解析】解:B={x|3x-4>0}={x|x>},则A∩B={x|x>2},故选:D根据集合交集的定义进行求解即可.本题主要考查集合的基本运算,根据集合的交集定义是解决本题的关键.2.下列函数中为奇函数的是()A.y=x2+2xB.y=ln|x|C.y=()xD.y=xcosx【答案】D【解析】解:A.函数y=x2+2x为非奇非偶函数,故本选项错误;B.函数y=ln|x|定义域不关于原点对称,非奇非偶函数,故本选项错误;C.函数y=()x不满足f(-x)=-f(x)不是奇函数,故本选项错误;D.f(-x)=-xcos(-x)=-xcosx=-f(x),则f(x)为奇函数,故本选项正确;故选:D.直接利用基本函数的奇偶性判断选项即可.本题主要考查函数奇偶性的判断,根据函数奇偶性定义是解决本题的关键.3.过原点且与圆x2+y2-4x+3=0相切的直线的倾斜角为()A.或B.或C.或D.或【答案】B【解析】解:由x2+y2-4x+3=0,得(x-2)2+y2=1,∴圆的圆心为(2,0),半径为1,设直线l的方程为kx-y=0,由圆与直线相切得:=1,解得k=.设直线l的倾斜角为θ(0≤θ<π),由tanθ=±,得θ=或.∴直线l的倾斜角为或.故选:B.由已知圆的方程求出圆心坐标和圆的半径,设出直线l的方程,由圆心到l的距离等于半径求得斜率,则直线l的倾斜角可求.本题考查了圆的切线方程,训练了点到直线的距离公式,考查了直线的倾斜角和斜率的关系,是中档题.4.执行如图所示的程序框图,则输出的s值为()A. B. C. D.【答案】C【解析】解:模拟执行程序框图,可得s=1,k=1满足条件k<4,执行循环体,k=2,s=1+满足条件k<4,执行循环体,k=3,s=1++满足条件k<4,执行循环体,k=4,s=1+++不满足条件k<4,退出循环,输出s的值为s=1+++=.故选:C.模拟执行程序框图,依次写出每次循环得到的s,k的值,当k=4时不满足条件k<4,退出循环,输出S的值即可得解.本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.5.已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b垂直”是“平面α和平面β垂直”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】D【解析】解:当a⊥b时,满足条件,但此时α∥β,即充分性不成立,当平面α和平面β垂直时,直线a和b平行,则直线a和直线b垂直不一定成立,故必要性不成立,则“直线a和直线b垂直”是“平面α和平面β垂直”的既不充分也不必要条件,故选:D根据直线垂直和面面垂直的判定条件分别进行判断即可.本题主要考查充分条件和必要条件的判断,借助于正方体,结合空间直线和平面的位置关系是解决本题的关键.6.已知向量=(1,),=(-1,),则∠BAC=()A.30°B.45°C.60°D.120°【答案】C【解析】解:方法一:∵=(1,),=(-1,),∴||=2,||=2,=-=(-2,0),∴||=2,∴△ABC为等边三角形,∴∠BAC=60°,方法二::∵=(1,),=(-1,),∴||=2,||=2,•=1×(-1)+×=2,∴cos∠BAC==,∵0°≤∠BAC≤180°,∴∠BAC=60°,故选:C.方法一:判断△ABC为等边三角形,问题得以解决,方法二:根据向量的夹角公式计算即可本题考查了向量的夹角公式和向量的坐标运算,属于基础题7.某四棱锥的三视图如图所示,则该四棱锥的侧面积为()A.8B.8+4C.4+2D.2+【答案】C【解析】解:由三视图得到几何体的直观图如图:四棱锥P-ABCD,其中OP=3,AB=CD=4,AD=BC=2,所以PE=,PF=,所以侧面积为2(S△PAB+S△PBC)=;故选:C.首先由三视图还原几何体,根据图中数据计算侧面斜高,进一步计算侧面积.本题考查了由几何体的三视图求侧面积;关键是正确还有几何体.8.某学校为了提高学生综合素质、树立社会主义荣辱观、发展创新能力和实践能力、促进学生健康成长,开展评选“校园之星”活动.规定各班每10人推选一名候选人,当各班人数除以10的余数大于7时再增选一名候选人,那么,各班可推选候选人人数y 与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为()A.y=[]B.y=[]C.y=[]D.y=[]【答案】B【解析】由题意,根据规定10推选一名代表,当各班人数除以10的余数大于7时再增加一名代表,即余数分别为8,9时可以增选一名代表,也就是x要进一位,所以最小应该加2.因此利用取整函数可表示为y=[];故选B.由题意,根据规定10推选一名代表,当各班人数除以10的余数大于7时再增加一名代表,即余数分别为8,9时可以增选一名代表,也就是x要进一位,所以最小应该加2.进而得到解析式.本题主要考查给定条件求函数解析式的问题,这里主要是要读懂读明白题意,再根据数学知识即可得到答案.对于选择题要会选择最恰当的方法.二、填空题(本大题共6小题,共30.0分)9.复数z=(1-i)(2+i)的实部为______ .【答案】3【解析】解:z=(1一i)(2+i)=1×2+i-2i-i2=3-i,所以复数z的实部是3.故答案为3.直接把两个复数采用多项式乘多项式运算即可.本题考查了复数的基本概念,考查了复数的乘法运算,是基础题.10.在△ABC中,a=7,b=8,c=5,则∠A= ______ .【答案】【解析】解:∵a=7,b=8,c=5,∴cos A===,∴由A∈(0,π),可得A=.故答案为:.由已知利用余弦定理可求cos A的值,结合A的范围即可得解.本题主要考查余弦定理的应用,根据三角函数的值求角,属于基础题.11.3-2,21.5,log23三个数中最大的数是______ .【答案】21.5【解析】解:3-2=,21.5>2,log23<2,∴3-2,21.5,log23三个数中最大的数是21.5,故答案为:21.5由于3-2=,21.5>2,log23<2,即可判断本题考查大小比较,掌握指数函数,对数函数的图象和性质时关键.12.若抛物线y2=8x上的点P到焦点的距离为6,则P到y轴的距离是______ .【答案】4【解析】解:∵抛物线y2=8x,则p=4,则焦点F(2,0),设P(x,y)由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,∴|MF|=6=x+2=6,∴x=4,P到y轴的距离4,故答案为:4.根据抛物线的焦半径公式,求得x+=6,即可求得x的值,求得P到y轴的距离.本题考查抛物线的性质,抛物线的焦半径公式,考查计算能力,属于基础题.13.在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域中的点在x轴上的投影构成的线段记为AB,则|AB|= ______ .【答案】3【解析】解:作出不等式组对应的平面区域如图:(阴影部分),区域内的点在直线x+y-2=0上的投影构成线段A′B′,由得A(-1,)由得B(2,-2),则|AB|=|2+1|=3,故答案为:3.作出不等式组对应的平面区域,利用投影的定义,利用数形结合进行求解即可.本题主要考查线性规划的应用,作出不等式组对应的平面区域,利用投影的定义以及数形结合是解决本题的关键.14.若直线l与曲线M(x0,y0)满足下列两个条件:(1)直线l在点M(x0,y0)处与曲线C相切;(2)曲线C在点M附近位于直线l的两侧,则称直线l在点M处“内切”曲线C.下列命题正确的是______ (写出所有正确命题的编号)①直线l:y=0在点M(0,0)处“内切”曲线C:y=x3②直线l:y=x在点M(0,0)处“内切”曲线C:y=sinx③直线l:y=x-1在点M(1,0)处“内切”曲线C:y=lnx.【答案】①②【解析】解:①,由y=x3,得y′=3x2,则y′|x=0=0,直线y=0是在点M(0,0)处的曲线C 的切线,又当x>0时y>0,当x<0时y<0,满足曲线C在M(0,0)附近位于直线y=0两侧,故命题①正确;②,由y=sinx,得y′=cosx,则y′|x=0=1,直线y=x是在点M(0,0)处的曲线的切线,满足曲线C在M(0,0)附近位于直线y=x两侧,故命题②正确;③,由y=lnx,得y′=,则y′|x=1=1,曲线在M(1,0)处的切线为y=x-1,由g(x)=x-1-lnx,得g′(x)=1-,当x∈(0,1)时,g′(x)<0,当x∈(1,+∞)时,g′(x)>0.则g(x)在(0,+∞)上有极小值也是最小值,为g(1)=0.即y=x-1恒在y=lnx的上方,不满足曲线C在点M附近位于直线l的两侧,故命题③错误.故答案为:①②.分别求出每一个命题中曲线C的导数,得到曲线在点M处的导数值,求出曲线在点M 处的切线方程,再由曲线在点M两侧的函数值与对应直线上点的值的大小判断是否满足条件(2),则正确的选项可求.本题考查命题的真假判断与应用,考查了利用导数研究过曲线上某点处的切线方程,综合考查导数的应用.三、解答题(本大题共6小题,共80.0分)15.已知函数f(x)=sinxcosx+cos(π-x)cosx(Ⅰ)求f(x)的最小正周期;(Ⅱ)求f(x)在区间[0,]上的最大值和最小值.【答案】解:函数f(x)=sinxcosx+cos(π-x)cosx化简可得:f(x)=sin2x-cos2x=sin2x cos2x-=sin(2x-)(Ⅰ)f(x)的最小正周期T=(Ⅱ)∵x∈[0,]上,∴2x-∈[,]当2x-=,即x=0时,函数f(x)取得最小值为.当2x-=,即x=时,函数f(x)取得最大值为1-.∴f(x)在区间[0,]上的最大值为1-,最小值为.【解析】(Ⅰ)利用二倍角以及辅助角公式基本公式将函数化为y=A sin(ωx+φ)的形式,再利用周期公式求函数的最小正周期.(Ⅱ)x∈[0,]上时,求出内层函数的取值范围,结合三角函数的图象和性质,即得f(x)的最大值和最小值.本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题.16.已知数列{a n}满足:a1=1,a n+1=2a n,数列{b n}满足:b1=3,b4=11,且{a n+b n}为等差数列.(I)求数列{a n}和{b n}的通项公式;(II)求数列{b n}的前n项和.【答案】解:(I)因为在数列{a n}中,a1=1,a n+1=2a n所以,=2,n∈N*,即数列{a n}是以首项为1,公比为2的等比数列.所以a n=2n-1设等差数列{a n+b n}的公差为d,由题意得:3d=(a4+b4)-(a1+b1)=(23+11)-(1+3)=15解得d=5,∴a n+b n=4+5(n-1)=5n-1,∴b n=5n-1-2n-1,(II)由(I)知b n=5n-1-2n-1,数列{5n-1}的前n项和为4n+=n2+n.数列{2n-1}的前n项和为=2n-1,所以,数列{b n}的前n项和n2+n-2n+1.【解析】(Ⅰ)利用等差数列、等比数列的通项公式先求得公差和公比,即可求数列的通项公式;(Ⅱ)利用分组求和的方法求解数列的和,由等差数列及等比数列的前n项和公式即可求解数列的和.本题考查了等差数列、等比数列的通项公式,考查了利用分组求和的方法求解数列的前n项和,是中档题.17.某高中学校为了解学生体质情况,从高一和高二两个年级分别随机抽取了40名男同学进行“引体向上”项目测试.样本的测试成绩均在0至30个之间,按照[0,5),[5,10),[10,15),[15,20),[20,25),[25,30]的分组分别作出频率分布直方图.记样本中高一年级的“引体向上”成绩的方差为s12,高二年级的“引体向上”成绩的方差为s22.(Ⅰ)已知该学校高二年级男同学有500人,估计该学校高二年级男同学引体向上成绩不少于10个的人数;(Ⅱ)从样本中高一年级的成绩不小于20个男同学中随机抽取2人,求至少有1人成绩在[25,30]中的概率.(Ⅲ)比较s12与s22的大小(只需写出结果).【答案】解:(Ⅰ)因为样本中高二年级男同学引体向上成绩不少于10个的频率为(0.08+0.04+0.01)×5=0.65,(2分)所以估计该学校高二年级男同学引体向上成绩不少于10个的人数为:500×0.65=325人.(4分)(Ⅱ)记“从样本中高一年级的成绩不小于20个的同学中随机抽取2人,至少有1人成绩在[25,30]中”为事件M,(5分)样本中高一年级的成绩在[20,25)的人数为40×0.02×5=4人,记这4名同学为A1,A2,A2,A4,样本中高一年级的成绩在[25,30]的人数为40×0.01×5=2人,记这两名同学为B1,B2,(6分)则从样本中高一年级的成绩不小于20个的同学中,随机抽取2人,所有可能的结果有15种,分别为:(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),(8分)事件M包含的结果有9种,分别是:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),所以至少有1人成绩在[25,30]中的概率P(M)=.(11分)(Ⅲ)>.(13分)【解析】(Ⅰ)先求出样本中高二年级男同学引体向上成绩不少于10个的频率,由此能估计该学校高二年级男同学引体向上成绩不少于10个的人数.(Ⅱ)记“从样本中高一年级的成绩不小于20个的同学中随机抽取2人,至少有1人成绩在[25,30]中”为事件M,样本中高一年级的成绩在[20,25)的人数为4人,记这4名同学为A1,A2,A2,A4,样本中高一年级的成绩在[25,30]的人数为2人,记这两名同学为B1,B2,由此利用列举法能求出至少有1人成绩在[25,30]中的概率.(Ⅲ)由频率分布直方图能比较,的大小.本题考查频率分布直方图的应用,考查概率的求法,涉及到频率分布直方图的性质、列举法,方差等基础知识,考查数据处理能力、运算求解能力,考查数形结合思想、集合思想,是基础题.18.如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.(I)求证:EM⊥AD;(II)求证:MN∥平面ADE;(III)求点A到平面BCE的距离.【答案】证明:(Ⅰ)∵EA=EB,M是AB的中点,∴EM⊥AB,(1分)∵平面ABE⊥平面ABCD,平面ABE∩平面ABCD=AB,EM⊂平面ABE,∴EM⊥平面ABCD,(4分)∵AD⊂平面ABCD,∴EM⊥AD.(5分)(Ⅱ)取DE的中点F,连接AF,NF,∵N是CE的中点.,∴NF CD,∵M是AB的中点,∴AM,∴NF AM,∴四边形AMNF是平行四边形,(7分)∴MN∥AF,(8分)∵MN⊄平面ADE,AF⊂平面ADE,∴MN∥平面ADE.(10分)解:(III)设点A到平面BCE的距离为d,由(I)知ME⊥平面ABC,BC=BE=2,MC=ME=,则CE=,BN==,(12分)∴,°=,∵V A-BCE=V E-ABC,(13分)即,解得d=,故点A到平面BCE的距离为.(14分)【解析】(Ⅰ)推导出EM⊥AB,从而EM⊥平面ABCD,由此能证明EM⊥AD.(Ⅱ)取DE的中点F,连接AF,NF,推导出四边形AMNF是平行四边形,从而MN∥AF,由此能证明MN∥平面ADE.(III)设点A到平面BCE的距离为d,由V A-BCE=V E-ABC,能求出点A到平面BCE的距离.本题考查线线垂直、线面平行的证明,考查点到平面的距离的求法,涉及到空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查数形结合思想,是中档题.19.已知函数f(x)=1+lnx-ae x(Ⅰ)若曲线y=f(x)在x=1处的切线与x轴平行,求实数a的值;(Ⅱ)若对任意x∈(0,+∞),不等式f(x)≤0恒成立,求实数a的取值范围.【答案】解:(Ⅰ)∵f(x)=1+lnx-ae x,∴f′(x)=-ae x,x∈(0,+∞).由于曲线y=f(x)在x=1处的切线与x轴平行,∴f′(1)=1-ae=0,解得,(Ⅱ)由条件知对任意x∈(0,+∞),不等式f(x)≤0恒成立,此命题等价于a≥对任意x∈(0,+∞)恒成立令,x∈(0,+∞).∴′=(-1-lnx),x∈(0,+∞).令g(x)=(-1-lnx),x∈(0,+∞).则g′(x)=--<0.∴函数g(x)在x∈(0,+∞)上单调递减.注意到g(1)=0,即x=1是g(x)的零点,而当x∈(0,1)时,g(x)>0;当x∈(1,+∞)时,g(x)<0.又e x>0,所以当∈(0,1)时,h′(x)>0;当x∈(1,+∞)时,h′(x)<0.则当x变化时,h′(x)的变化情况如下表:因此,函数h(x)在x∈(0,+∞),取得最大值,所以实数a≥.【解析】(Ⅰ)根据导数和几何意义即可求出,(Ⅱ)分离参数,构造函数,利用导数,求出函数的最值,即可求出参数的取值范围本题考查利用函数的最值求参数问题,解题时要认真审题,仔细解答,考查了等价转化思想及导数性质的合理运用,属于难题20.已知椭圆C:+=1(a>b>0)经过点(1,),离心率e=.(Ⅰ)求椭圆C的方程,(Ⅱ)设动直线l:y=kx+m与椭圆C相切,切点为T,且直线l与直线x=4相交于点S.试问:在坐标平面内是否存在一定点,使得以ST为直径的圆恒过该定点?若存在,求出该点的坐标;若不存在,请说明理由.【答案】解:(Ⅰ)由点(1,)在椭圆上得,代入椭圆方程:,①----------(1分)椭圆的离心率e==,则a=2c,a2=4c2,b2=3c2,②----------(2分)②代入①解得c2=1,a2=4,b2=3,故椭圆C的标准方程为;-----------(4分)(Ⅱ)由,消去y,整理得(4k2+3)x2+8kmx+4m2-12=0;因为动直线l与椭圆C相切,即它们有且只有一个公共点T,可设T(x0,y0),m≠0,△=0,∴(8km)2-4×(4k2+3)×(4m2-12)=0,∴4k2-m2+3=0,③----(6分)此时,x0==-=-,y0=kx0+m=,则T(-,).----------(7分)由,得S(4,4k+m).-------------------------------------------------------(8分)假设平面内存在定点满足条件,不妨设为点A.由图形对称性知,点A必在x轴上.-------------------------------------------------(9分)设A(x1,0),则由已知条件知AS⊥AT,即•=0对满足③式的m,k恒成立.-----------------------------------------(10分)由=(4-x1,4k+m),=(--x1,),由•=0得:-+-4x1+x12++3=0,整理得(4x1-4)+x12-4x1+3=0,④-----------------------(12分)由②式对满足①式的m,k恒成立,则,解得x1=1.故平面内存在定点(1,0),使得以ST为直径的圆恒过该定点.-----------------(14分)【解析】(Ⅰ)由题意可知:将点代入椭圆方程,利用椭圆的离心率公式即可求得a和b的值,即可求得椭圆方程;(Ⅱ)将直线方程代入椭圆方程,由△=0,求得4k2-m2+3=0,利用韦达定理及中点坐标公式,求得T点坐标,联立即可求得S点坐标,由•=0,根据向量数量积的坐标运算,可得,即可求得A点坐标,即可求得以ST为直径的圆恒过该定点(1,0).本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,中点坐标公式,向量数量积的坐标运算,考查计算能力,属于中档题.。
2017北京市顺义区高三(二模)地理

2017北京市顺义区高三(二模)地理气候学上以某地连续5天平均气温稳定≥10℃的第一天为春季的开始日期。
5天平均气温稳定≥22℃第一日的前一天是春季的结束日期。
当某区内70%以上县级气象站点进入春季,则该地区进入春季。
图1为我国1981年--2010年间“春天”到来的脚步。
读图回答1~3题。
1.2月28日图中城市A.北京比杭州白昼长B.北京比上海日出早C.南京比长沙日落晚D.兰州比上海正午太阳高度小2.图1中“春天”的脚步A.是指夏季风的移动节奏规律B.塔里木盆地入春早于同纬度地区是由于深居内陆C.青藏高原与大兴安岭入春晚的原因相同D.范围由区域内连续5天平均气温≥10℃的时段决定3.“春天”的脚步A.与太阳直射点北移有关 B.影响我国农业的耕作制度C.主要由人类生产活动决定 D.出现的时间是固定不变的4.我国是一个自然灾害频发的国家。
灾害类型多样给人们带来了生命和财产损失。
依据所学判断出下面四个选项中,哪个反应的是地震灾害的内容。
A.它是一种发生范围广、频度高、强度大、危害大的灾害。
在我国西多东少,主要有新疆、青藏、华北和台湾四个多发区,灾情却东重西轻。
其分布基本上遵循活动性断裂带的分布,构造运动频繁,地壳脆弱地多发。
B.它主要发生在我国山区,地域上具有广泛和相对集中的分布特点。
其中之一受连续降水、暴雨等激发,具有与降水相对一致的季节变化。
C.它是一种发生范围最广、频次高、持续时间最长的渐发性灾害。
农牧业灾情重,工矿、城市危害巨大。
主要分布在常年雨水较多的东部季风区,在我国有华北、华南、西南和江淮地区四个多发中心。
D.它是一种分布范围广、发生频繁、突发性强、损失大。
据统计其造成的经济损失和人员伤亡在各种灾害中居第一位。
其分布是东多西少;沿海多,内陆少;平原低地多,高原山地少;山脉东坡和南坡多。
季风区多发,夏季多发。
2017年为“中国--丹麦旅游年”。
丹麦是发达的北欧工业国家。
农牧渔业及食品加工业发达,有欧洲乳酪市场之称。
2017-2018届北京市顺义区高三第二次统练历史试题及答案

北京市顺义区2017-2018届高三4月第二次统练(二模)文科综合能力历史测试12.据史书记载,官员□□□□“掌邦国刑宪、典章之政令,以肃正朝列……。
”文中□□□□处缺失的官员身份应是A.御史大夫 B.刑部尚书 C.平章政事 D.军机大臣13.“惠遍农无乏,均输役不骚。
保兵知警守,吏禄绝色饕”该诗赞扬的是A.商鞅变法 B.北魏孝文帝改革 C.王安石变法 D.戊戌变法14. 以下对这两位思想家共同之处的分析,正确的是A. 都批判了君主专制统治B. 都是工业革命在思想领域的反映C. 都主张革命推翻君主制D. 都促成本国一场声势浩大的革命15. 下列各项史实与结论之间逻辑关系正确的是16. 凌青诗作:“粤海销烟扬我威,但悲港岛易英徽。
前仇旧恨今尽雪,只缘华夏已腾飞。
”诗中涉及的历史事件有①虎门销烟②签订《南京条约》③签订《马关条约》④香港回归史实结论A 孔子提出“仁者爱人”和“克己复礼”的主张孔子的思想确立了中国传统文化中的主流地位B 董仲舒的《春秋繁露》和《举贤良对策》等书籍儒学思想成为中国古代最为精致、完备的理论体系C 莎士比亚的戏剧《哈姆雷特》文艺复兴时期的人文主义精神在欧洲得到了弘扬D 马丁路德的《九十五条论纲》宗教改革在德国拉开了序幕,成为反对天主教会的思想运动A.①② B.②③④ C.①②④ D.①③④17.一位学者评价说:“当时知识分子不但没有全盘反传统,而且使不少被尘封或淹没了的传统重现光芒。
例如,不登大雅之堂的白话小说,成了中国文学史的重要内容;作为传统文化的民间文学,第一次真正进入了大学的学术殿堂。
”这一观点认为新文化运动A.反对旧道德崇尚现代文化 B.存在对旧文化的传承与创新C.充分肯定了文言文的价值 D.混淆了先进与落后的界限18. 《剑桥中华民国史》说:“如果它(指中共)在1922年和1923年选择单独作战而不与国民党联合,它可能干得更糟;如果它较早地为最后的决裂做好准备,它也许会干得更好。
2017-2018届北京市顺义区高三第二次统练政治试题及答案

北京市顺义区2017-2018届高三4月第二次统练(二模)文科综合能力政治测试“金鱼缸法则”即“透明效应”。
它是一种比喻,金鱼缸是玻璃做的,透明度很高,不论从哪个角度观察,里面的情况都一清二楚。
回答24~26题。
24.某市社保局召开局务会议时对媒体全程开放,并表示以后只要涉及民生的工作,都将向媒体公开。
“金鱼缸法则”在行政领域的试用是为了①让权力在阳光下运行②规范政府及其工作人员的行政行为③更好地保障公民的知情权和监督权④提高政府的行政效率A.①② B. ①④ C. ②③ D. ③④25. 某市在第二届人民代表大会常务委员会第三十六次会议上,设立了8个公民旁听席。
关于人大常委会,下列认识正确的是A.是最高国家权力机关B.其他国家机关由它产生,受它监督C.旁听是公民直接参与人大事务管理的途径D.享有立法权、决定权、任免权、监督权26.对自己的弱点缺陷是背靠背还是面对面,是检验一个人人格力量的试金石。
“透明效应”启示我们要A.生活的更现实一点,不要虚幻B.勇于面对自己的弱点,不要自我欺骗C.用发展的观点看问题,悉心保护新事物D.通过自我营造相反的事实,获得心理平衡27.图8漫画蕴含的哲理是A.天气可以影响人的心情B .下雨可能是坏事也可能是好事C.不同的问题要采取不同的解决办法D.人可以主动创造好心情图828. 某制药厂商如是说:应永远铭记,我们旨在救人,不在求利。
如果记住这一点,我们绝不会没有利润,记得越清楚,利润越大。
这说明①市场经济也是道德经济②企业要提高产品质量和服务水平③社会责任的担当可以带动企业利润的增长④企业经营的目的是利润A.①② B.①③ C.②④ D.③④在全党深入开展党的群众路线教育实践活动,是党的十八大作出的重大部署。
回答29、30题。
29. 党内脱离群众的现象大量存在,集中表现在图9中的“四风”上。
反“四风”从哲学层面上看A.发挥了正确意识的决定作用B.抓住了现阶段的主要矛盾C.坚持了正确价值观的导向作用D.体现了外因是事物发展的根源30.开展群众路线教育实践活动、除“四风”①体现了中国共产党的性质和宗旨②体现了我国的政党制度③坚持了人民的主体地位图9④是中国共产党执政的基本方式A.①③B.①④C.②③D.②④31.读书多了,容颜自然改变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
顺义区2017届高三第二次统练语文试题本试卷共28道小题,共150分。
考试时长150分钟。
答案请务必写在答题卡的相应位臵;作文请务必写在作文纸上。
一、本大题共9小题,共31分。
阅读下面材料,完成1—9题。
【材料一】所谓酒令,按新版《辞海》的说法:‚酒令,旧时饮酒时助兴取乐的游戏。
推一人为令官,余以听令轮流说诗词,或做其它游戏,违令或负者罚饮。
‛据考证,酒令之始可以上溯到周朝初年,鉴于商朝统治者溺酒亡国的教训,由周公以王命发布《酒诰》禁酒。
‚群饮,汝无佚,尽执拘以归于周,予其杀!‛起初本意是为了禁止酗酒而设酒令官。
在《诗〃小雅•宾之初筵》第五章中有‚凡此饮酒,或醉或否,既立之监,或佐之史‛的句子,这里的‚监‛‚史‛即令官,是为限制宴会上饮酒过度而设的执法官,对饮酒失仪妄言者要予以惩罚。
而后世所说的酒令与其本意恰恰相反,是劝人多饮酒的一种行乐手段、游艺活动。
从形式上看,酒令有多种多样,诗词曲文类(如作诗令、说诗令、回环令等);游戏类有拇战(或曰猜拳、划拳等)、猜枚、牙牌令、射覆、投壶、击鼓传花、占花名儿、拆字、联句等。
从内容上看,酒令有俗令和雅令、通令和筹令之分。
中国的酒令文化是一种特别、独有的酒俗。
‚酒令‛二字出现在历史资料文献中最早见于《后汉书〃贾逵传》:‚逵作酒令,学者宗之。
‛但在当时并没有广泛流行。
《梁书〃王规传》说:‚湘东王时为京尹,与朝士宴集,属规为酒令。
规从容对曰:‘自江左以来,未有此举。
’‛可见,南北朝时期,酒令并不风行。
它的流行大概始于唐玄宗发明的击鼓催花,从此就自上而下传播于民间。
唐代的酒令有许多种类,据唐人皇甫松《醉乡日月》记载,已有骰子令、旗幡令、上酒令、手势令、小酒令、杂法等多种,唐人的诗歌也多有反映,如白居易的‚筹插红螺碗,斛飞白玉卮。
碧筹攒彩碗,红袖拂骰盘‛,刘禹锡的‚杯停新令举,诗动彩笺忙‛等等。
同时,一系列的行令、酒约也制定出来。
《醉乡日月》的目录里便有‚饮论‛‚为宾‛‚律录事‛‚觥录事‛‚选徒‛‚令误‛‚逃席‛等各项内容。
宋代的情况与唐代差不多,只是更加丰富。
至于明清两代酒令则发展到了高峰,举凡世间事物,人物、花木、虫禽,曲牌、词牌、诗文、戏曲、小说、中药、丹令、八卦等等,无不入令。
(取材于姜南《浅析〈红楼梦〉中的酒令》)1.根据材料一,下列对“酒令”的理解,错误..的一项是(3分)A.据《酒诰》文字,对酗酒者可以处以极刑。
B.最初的“酒令”是劝人多饮酒的行乐手段。
C.据文献记载,东汉至南北朝酒令尚未流行。
D.明清两代,酒令内容丰富,几乎无不入令。
2.下列内容没有..在“材料一”中体现的是(3分)A.酒令的定义B.酒令的起源C.酒令的种类D.酒令的价值【材料二】中国古代文人,喜欢在各种场合显示学问与才能,以示风雅博洽。
唐代开始,雅令便在文人学士的酒席间流行开了,当时即有‚闲征雅令穷经史‛说法。
雅令的种类很多,如古文贯串令、词牌令、拆字令、四书令、飞花令等。
以下略举一二。
‚古文贯串令‛行令的格式大致如下:先说一句古文,接旧诗一句,再以一个骨牌(即‚牙牌‛‚宣和牌‛)名称和一支曲牌名称衔接,末以历书一句殿底。
这么一个长句,共同组成‚酒面‛,长句之间要上下照应,彼此关联,最后说出‚酒底‛。
‚酒底‛多为酒席间现成的花果名,再续古诗一句,诗句须有花果名相联。
《红楼梦》六十二回宝玉做生日,酒席间湘云和宝玉划拳,湘云赢了宝玉,要宝玉行一个‚古文贯串令‛,宝玉一时说不出,黛玉便道:‚你多喝一钟,我替你说。
‛宝玉真个喝了酒,听黛玉说道:‚落霞与孤鹜齐飞,风急江天过雁哀,却是一枝折脚雁,叫得人九回肠,这是鸿雁来宾。
‛说得大家笑了。
众人说:‚这一串子倒有些意思。
‛黛玉又拈了一个榛瓤,说酒底道:‚榛子非关隔院砧,何来万户捣衣声。
‛‚四书令‛是用‚四书‛中的句子组合而成的酒令,这种酒令在明清时期特别流行。
行令时具体要求又各有不同。
《重论文斋笔录》记载了清朝嘉庆年间一则‚四书令‛,很有特色。
这种酒令要求选用‚四书‛中的两个句子,上一句的末字和下一句的首字须合成一个药名,否则便要罚酒。
其佳构有:道不远人,参也鲁(人参);诸侯之宝三,七里之郭(三七);臧武仲以防,风乎舞雩(防风);不知为不知,母命之(知母);殷鉴不远,志于道(远志);颜路请子之车,前日于齐(车前);事亲为大,黄衣狐裘(大黄);长一身有半,夏日则饮水(半夏);与其弟辛,夷子思以易天下(辛夷)等等。
可见,不熟悉经书的文人是无法参与这种‚四书令‛的。
明清两朝科举制八股取士,当时的文人要参加科举考试就要死背经书,‚四书令‛正是在这种背景下流行开来的。
除了‚四书令‛,其它雅令也都具有一定的难度。
(取材于史双元《说酒令》)3.根据材料一、二,下列酒令不属于...“雅令”的一项是(2分)A.骰子令B.古文贯串令C.拆字令D.四书令4.对材料二“《红楼梦》酒令”一节内容的理解,不正确...的一项是(3分)A.黛玉所说的“酒面”,首句出自王勃《滕王阁序》。
B.“酒底”为席间干果榛子,“榛”与“砧”谐音。
C.贾宝玉因饮酒过量,故无法完成湘云规定的酒令。
D.黛玉的酒令不仅包含视觉的景象,还有听觉因素。
5.对材料一、二涉及的文学常识,表述有误..的一项是(3分)A.《小雅》是《诗经》中“二雅”之一。
“雅”即正,指朝廷正乐。
B.白居易是唐代“古文运动”倡导者,代表作有长诗《长恨歌》。
C.刘禹锡《陋室铭》运用托物言志的手法,表现了高尚的追求。
D.“四书”即《论语》《孟子》《大学》《中庸》,是儒家经典著作。
6.“飞花令”是雅令中的一种,最基本的飞花令诗句中必须含有“花”字,且对“花”字出现的位置有严格的要求。
这些诗可自作,也可背诵前人成句。
行令者先后相续,作不出、背不出或作错、背错时,由酒令官命其喝酒。
请根据你的背诵,完成下面的“飞花令”。
(诗句可以少于7个字;任选三句作答;6分)①花□□□□□□;②□花□□□□□;③□□花□□□□;④□□□花□□□;⑤□□□□花□□;⑥千树万树梨花开;⑦□□□□□□花;【材料三】唐宋时期,最具时代特色的助饮方式是行酒令助饮。
行酒令助饮多在巡(行)酒之后进行,它极大地调动了当时人们的饮酒情趣,唐宋酒令艺术的繁荣对唐宋饮酒之风的盛行起到了推波助澜的作用。
唐代,酒令开始作为一个专有名称,特指酒筵上那些决定饮者胜负的活动方式。
酒令在唐代形成后,很快就成为人们宴饮助兴的主要娱乐形式,从文人到百姓无不选择适应其活动的酒令来佐饮。
唐代的酒令名目繁多,但现在人们能够知道的大约只有20多种。
大多数唐代酒令至宋代时就已经失传了。
宋人多不解唐代酒令这一现象,说明唐宋两代的酒令有很大的变化。
唐宋两代的酒令及人们行令的差异主要表现在以下几点:首先,唐代酒令以器具令居多,宋代酒令以文字令居多。
唐代的器具令众多,如头盘(亦称投盘、骰盘)令、筹令等,这些酒令需要借助骰盘、筹箸等器具方能行令。
与唐代器具令居多不同,留传下来的宋代酒令多是文字令。
宋代文字令的盛行与宋代文人群体的迅速壮大密切相关。
由于宋代统治者采用重文轻武的政策,加大科举取士的力度,大大刺激了宋代文化的发展,使宋代的文人群体日益扩大,整个社会的文化水平有了较大的提高,人们进行文字游戏的技巧也比较娴熟。
酒酣耳热之际,宋人为后世留下了不少高水平的文字令。
其次,唐人行令强调胜负,宋人行令注重参与。
唐人尚武任侠,争强好胜,行酒令时也往往强调胜负,负者要罚酒。
唐人最喜欢在酒席上罚别人喝酒,有时看着对方醉倒而大乐不已。
受此风影响,人们千方百计去寻找罚酒的理由,以致于你惩我罚,毫无休止。
为公平处理因酒令而引起的纷争和更好地维持酒场秩序,唐人聚饮时常设酒纠(亦称席纠、觥使)。
与唐代相比,宋人行令更注重参与,不太计较胜负。
由于宋人行令不太强调胜负,酒席之上的纷争也大为减少,所以宋代酒纠的设臵也不如唐代那么普遍。
最后,唐人行令比较豪爽,宋人行令比较文雅。
唐人行令之所以比较豪爽,除了唐人普遍开放豁达之外,与唐代的酒令形式也不无关系。
由于唐代的器具令居多,行令时,人们的注意力随着骰盘、香球等器具的运动而转移,往往面目紧张情绪激动。
除器具令之外,唐代酒宴上还流行各种动作令。
与此相反,由于宋代的酒令多为文字令,需要的是口齿清晰地吐字讲谈,而不是如狂似颠地大呼小叫,加之宋人行令不太强调胜负,酒席之上的纷争也大为减少,因此宋人行令就显得比较谦和、随意和文雅。
(取材于刘朴兵《从酒宴习俗看唐宋社会变迁》)7.根据材料三,下列说法或推断不正确...的一项是(3分)A.唐宋时期酒令是人们宴饮助兴的主要娱乐形式。
B.宋代整体文化水平的提高也提高了酒令的水平。
C.宋人行令更注重参与,因此行错酒令不必罚酒。
D.唐人行令的豪爽与当时的风气及酒令形式相关。
8.下列诗句所描绘的内容,没有..表现唐人行令场面的一项是(3分)A.叫噪掷投盘,生狞摄觥使。
(元稹《元和五年》)B.翻醉衫袖抛小令,笑掷骰盘呼大采。
(白居易《就花枝》)C.隔座送钩春酒暖,分曹射覆蜡灯红。
(李商隐《无题》)D.葡萄美酒夜光杯,欲饮琵琶马上催。
(王翰《凉州词》)9.请结合上面三则材料,简要说明我国古代酒令的发展情况。
(5分)二、本大题共8小题,共25分。
阅读下面文言文完成10—17题人生在世,会当有业。
农民则计量耕稼,商贾则讨论货贿,工巧则致精器用,伎艺则沉思法术,武夫则惯习弓马,文士则讲议经书。
今多见士大夫耻涉农商,羞务工伎,射则不能穿札①,笔则才记姓名,饱食醉酒,忽忽无事,以此销日,以此终年。
或因家世余绪,得一阶半级,便自为足,全忘修学。
议论得失,蒙然张口,如坐云雾;公私宴集,谈古赋诗,塞默低头。
有识旁观,代其入地。
何惜数年勤学,长受一生愧辱哉!梁朝全盛之时,贵游子弟,多无学术,莫不熏衣剃面,傅粉施朱,驾长檐车,跟高齿履,从容出入,望若神仙;明经求第,则雇人答策,三九②公宴,则假手赋诗,当此之时,亦快士也。
及离乱之后,朝市迁革,铨衡选举,非复曩者之亲,当路秉权,不见昔时之党,求诸身而无所得,施之世而无所用,鹿独③戎马之间,转死沟壑之际,当此之时,诚驽材也。
有学艺者,触地而安。
以此观之,安可不自勉耶?若能常保数百卷书,千载终不为小人也。
有客难主人曰:‚吾见学备古今,才兼文武,身无禄位,妻子饥寒者,不可胜数,安足贵学乎?‛主人对曰:‚夫命之穷达,犹金玉木石也;修以学艺,犹磨莹雕刻也。
金玉之磨莹,自美于矿璞;木石之段块,自丑于雕刻。
安可言木石之雕刻,乃胜金玉之矿璞哉?不得以有学之贫贱,比于无学之富贵也。
且负甲为兵,咋笔为吏,身死名灭者如牛毛,特立杰出者如芝草,岂得同年而语矣。
且又闻之:生而知之者上,学而知之者次。
所以学者,欲其多知明达耳。
必有天才,拔群出类,为将则与孙武、吴起同术,执政则得管仲、子产之教,虽未读书,吾亦谓之学矣。
