指数函数、对数函数、幂函数图像与性质
幂函数、指数函数与对数函数(解析版))

幂函数、指数函数与对数函数知识方法扫描一、指数函数及其性质形如y =a x (a >0,a ≠1)的函数叫作指数函数,其定义域为R ,值域为(0,+∞).当0<a <1时,y =a x 是减函数,当a >1时,y =a x 为增函数,它的图像恒过定点(0,1).二、分数指数幂a 1n=na ,a m n=n a m ,a -n=1an ,a -mn =1na m三、对数函数及其性质对数函数y =log a x (a >0,a ≠1)的定义域为(0,+∞),值域为R ,图像过定点(1,0).它是指数函数y =a x (a >0,a ≠1)的反函数,所有性质均可由指数函数的性质导出.当0<a <1时,y =log a x 为减函数,当a >1时,y =log a x 为增函数.四、对数的运算性质(M >0,N >0)(1)a log M a =M (这是定义);(2)log a (MN )=log M a +log a N ;(3)log a MN=log a M -log a N ;(4)log a M n =n log a M ;(5)log a b =log c blog c a (a ,b ,c >0,a ,c ≠1)(换底公式).由以上性质(4)、(5)容易得到以下两条推论:1)log a mb n =n m log a b ;2)log a b =1log b a.典型例题剖析1已知x 1是方程x +lg x =10的根,x 2是方程x +10x =10的根,求x 1+x 2的值.【解法1】由题意得lg x 1=10-x 110x 2=10-x 2,表明x 1是函数y =lg x 与y =10-x 的交点的横坐标,x 2是函数y =10x 与y =10-x 的交点的横坐标.因为y =lg x 与y =10x 互为反函数,其图像关于y =x 对称,由y =10-x y =x 得,x =5y =5 ,所以x 1+x 22=5,所以x 1+x 2=10.【解法2】构造函数f (x )=x +lg x ,由x 1+lg x 1=10知f x 1 =10,x 2+10x 2=10即10x 2+lg10x 2=10,则f 10x 2 =10,于是f x 1 =f 10x 2 ,又f (x )为(0,+∞)上的增函数,故x 1=10x 2,x 1+x 2=10x 2+x 2=10.【解法3】由题意得x 1=1010-x 110-x 2=10x 2,两式相减有x 1+x 2-10=1010-x 1-10x 2.若x 1+x 2-10>0,则1010-x 1-10x 2>0,得10-x 1>x 2,矛盾;若x 1+x 2-10<0,则1010-x 1-10x 2<0,得10-x 1<x 2,矛盾;而当x 1+x 2=10时,满足题意.【评注】解法1巧妙地利用了数形结合的方法,解法2巧妙地利用了函数的单调性,解法3巧妙地利用了反证法的技巧.2已知a >0,b >0,log9a =log 12b =log 16(a +b ),求ba的值.【解法1】设log 9a =log 12b =log 16(a +b )=k ,则a =9k ,b =12k ,a +b =16k .由于9k ×16k =12k 2故(a +b )a =b 2,解得:b a =1+52(负根舍去).【解法2】设log 9a =log 12b =log 16(a +b )=k ,则a =9k ,b =12k ,a +b =16k .b a =12k 9k =43 k ,而9k +12k =16k,故1+12k 9k =16k 9k ,即43 k 2-43 k -1=0,故b a =43 k =1+52(负根舍去).【评注】对数运算和指数运算互为逆运算,有关对数的运算和处理,往往可以转化为指数的运算和处理.3已知函数f (x )=1x +1+log 13x 2-x,试解不等式f x x -12 >12.【分析】本题为分式不等式与对数不等式混合.初看不易解决,但可以发现该函数在其定义域内单调递减,这是本题的解题关键.【解】易证函数y =f (x )在其定义域(0,2)内是单调减函数.并且f (1)=12,所以原不等式即为f x x -12 >f (1)等价于x x -12 <10<x x -12 <2⇒ x 12<x <1+174或1-174<x <0 .【评注】利用函数单调性解决不易入手的不等式是一种常用方法.4设方程lg (kx )=2lg (x +1)仅有一个实根,求k 的取值范围.【分析】本题要注意函数的定义域.【解法1】当且仅当kx >0①x +1>0②x 2+(2-k )x +1=0③时原方程仅有一个实根,对方程③使用求根公式,得x 1,x 2=12k -2±k 2-4k ④Δ=k 2-4k ≥0⇒k <0或k ≥4.当k <0时,由方程③,得x 1+x 2=k -2<0,x 1x 2=1>0,所以x 1,x 2同为负根.又由方程程④知x 1+1>0,x 2+1<0,所以原方程有一个解x 1.当k =4时,原方程有一个解x =k2-1=1.当k >4时,由方程③,得x 1+x 2=k -2>0,x 1x 2=1>0. 所以x 1,x 2同为正根,且x 1≠x 2,不合题意,舍去.综上所述可得k <0或k =4为所求.【解法2】由题意,方程kx =(x +1)2,也即方程k =x +1x+2在满足关于x 的不等式kx >0x +1>0 的范围内有唯一实数根,以下分两种情况讨论:(1)当k >0时,k =x +1x +2在x >0范围内有唯一实数根,则有k =4;(2)当k <0时,k =x +1x+2在-1<x <0范围内有唯一实数根,则有k <0.综上可得k <0或k =4为所求.【评注】本题实质上是一道一元二次方程问题.5解不等式:log 12(x +3x )>log 64x .【分析】若考虑到去根号,可设x =y 6(y >0),原不等式变为log 12y 3+ y 2 >log 6446=log 2y ,即2log 12y +log 2(y +1)>log 2y ,陷入困境.原不等式即6log 12(x +3x )>log 2x ⇒2log 12x +log 121+x166>log 2x ,设t =log 2x ,则log 12x =1log x12=12log x 2+log x 3,同样陷入困境.下面用整体代换y =log 64x .【解】设y =log 64x ,则x =64y,代人原不等式,有log 128y +4y >y ,8y +4y >12y,23 y +13 y >1,由指数函数的单调性知y =log 64x <1,则0<x <64.故原不等式的解集为(0,64).6已知1<a ≤b ≤c 证明:log a b +log b c +log c a ≤log b a +log c b +log a c .【证法1】注意到log a b +log b c +log c a -log b a +log c b +log a c=ln b ln a +ln c ln b +ln a ln c -ln a ln b+ln b ln c +ln c ln a =ln 2b ln c +ln 2c ln a +ln 2a ln b -ln 2b ln a +ln 2c ln b +ln 2a ln c ln a lnb ln c=-(ln a -ln b )(ln b -ln c )(ln c -ln a )ln a ln b ln c.【证法2】设log b a =x ,log c b =y ,则log a c =1xy ,于是原不等式等价于x +y +1xy ≤1x +1y+xy ,即x 2y +xy 2+1≤y +x +x 2y 2,即xy (x +y )-(x +y )+1-x 2y 2 ≤0,也即(x +y -1-xy )(xy -1)≤0也即(x -1)(y -1)(xy -1)≥0,由1<a ≤b ≤c 知x ≥1,y ≥1,所以(x -1)(y -1)(xy -1)≥0,得证.因为1<a ≤b ≤c ,所以ln a ln b ln c >0,(ln a -ln b )(ln b -ln c )(ln c -ln a )≥0所以log a b +log b c +log c a -log b a +log c b +log a c ≤0即log a b +log b c +log c a ≤log b a +log c b +log a c °【评注】若令x =ln a ,y =ln b ,z =ln c 则原不等式等价于:设0<x ≤y ≤z ,求证:x 2y +y 2z +z 2x ≤xy 2+yz 2+zx 2.7设函数f (x )=|lg (x +1)|,实数a ,b (a <b )满足f (a )=f -b +1b +2,f (10a +6b +21)=4lg2,求a 、b 的值.【分析】利用已知条件构建关于a 、b 的二元方程组进行求解.【解】因为f (a )=f -b +1b +2 ,所以|lg (a +1)|=lg -b +1b +2+1 =lg 1b +2=|lg (b +2)|所以,a +1=b +2或(a +1)(b +2)=1,又因为a <b ,所以a +1≠b +2,所以(a +1)(b +2)=1又由于0<a +1<b +1<b +2,于是0<a +1<1<b +2,所以(10a +6b +21)+1=10(a +1)+6(b +2)=6(b +2)+10b +2>1,从而f (10a +6b +21)=lg 6(b +2)+10b +2=lg 6(b +2)+10b +2,又f (10a +6b +21)=4lg2,所以lg 6(b +2)+10b +2 =4lg2,故6(b +2)+10b +2=16.解得b =-13或b =-1(舍去).把b =-13代故(a +1)(b +2)=1,解得a =-25.所以,a =-25,b =-13.同步训练一、选择题1已知a 、b 是方程log 3x 3+log 27(3x )=-43的两个根,则a +b =().A.1027B.481C.1081D.2881【答案】C .【解析】原方程变形为log 33log 3(3x )+log 3(3x )log 327=-43,即11+log 3x +1+log 3x 3=-43.令1+log 3x =t ,则1t +t 3=-43,解得t 1=-1,t 2=-3.所以1+log 3x =-1或1+log 3x =-3,方程的两根分别为19和181,所以a +b =1081.故选C .2已知函数f (x )=1a x -1+12x 2+bx +6(a ,b 为常数,a >1),且f lglog 81000 =8,则f (lglg2)的值是().A.8 B.4 C.-4 D.-8【答案】B .【解析】由已知可得f lglog 81000 =f lg33lg2=f (-lglg2)=8,又1a -x -1+12=a x 1-a x +12=-1+11-a x +12=-1a x -1-12,令F (x )=f (x )-6,则有F (-x )=-F (x ).从而有f (-lglg2)=F (-lglg2)+6=-F (lglg2)+6=8,即知F (lglg2)=-2,f (lglg2)=F (lglg2)+6=4.3如果f (x )=1-log x 2+log x 29-log x 364,则使f (x )<0的x 的取值范围为().A.0<x <1 B.1<x <83C.x >1D.x >83【答案】B .【解析】显然x >0,且x ≠1.f (x )=1-log x 2+log x 29-log x 364=1-log x 2+log x 3-log x 4=log x 38x .要使f (x )<0.当x >1时,38x <1,即1<x <83;当0<x <1时,38x >1,此时无解.由此可得,使得f (x )<0的x 的取值范围为1<x <83.应选B .4若f (x )=lg x 2-2ax +a 的值域为R ,则a 的取值范围是().A.0<a <1 B.0≤a ≤1 C.a <0或a >1 D.a ≤0或a ≥1【答案】D .【解析】由题目条件可知,(0,+∞)⊆y |y =x 2-2ax +a ,故Δ=(-2a )2-4a ≥0,解得a ≤0或a ≥1.选D .二、填空题5设f (x )=log 3x -4-x ,则满足f (x )≥0的x 的取值范围是.【答案】[3,4].【解析】定义域(0,4].在定义域内f (x )单调递增,且f (3)=0.故f (x )≥0的x 的取值范围为[3,4].6设0<a <1,0<θ<π4,x =(sin θ)log asin θ,y =(cos θ)log atan θ,则x 与y 的大小关系为.【答案】x <y .【解析】根据条件知,0<sin θ<cos θ<1,0<sin θ<tan θ<1,因为0<a <1,所以f (x )=log a x 为减函数,所以log a sin θ>log a tan θ>0,于是x =(sin θ)log a sin θ<(sin θ)log a tan θ<(cos θ)log a tan θ=y .7设f (x )=12x +5+lg 1-x 1+x ,则不等式f x x -12<15的解集为.【答案】1-174,0 ∪12,1+174.【解析】原不等式即为f x x -12<f (0).因为f (x )的定义域为(-1,1),且f (x )为减函数.所以-1<x x -12 <1x x -12 >0.解得x ∈1-174,0∪12,1+174.8设f (x )=11+2lg x +11+4lg x +11+8lg x ,则f (x )+f 1x =.【答案】3.【解析】f (x )+f 1x =11+2lg x +11+4lg x +11+8lg x +11+2-lg x +11+4-lg x +11+8-lg x =3.三、解答题9已知函数f (x )=a x +3a (a >0,a ≠1)的反函数是y =f -1(x ),而且函数y =g (x )的图像与函数y =f -1(x )的图像关于点(a ,0)对称.(1)求函数y =g (x )的解析式;(2)若函数F (x )=f -1(x )-g (-x )在x ∈[a +2,a +3]上有意义,求a 的取值范围.【解析】(1)由f (x )=a x +3a (a >0,a ≠1),得f -1(x )=log a (x -3a ).又函数y =g (x )的图像与函数y =f -1(x )的图像关于点(a ,0)对称,则g (a +x )=-f -1(a -x ),于是,g (x )=-f -1(2a -x )=-log a (-x -a ),(x <-a ).(2)由(1)的结论,有F (x )=f -1(x )-g (-x )=log a (x -3a )+log a (x -a ).要使F (x )有意义,必须满足x -3a >0,x -a >0. 又a >0,故x >3a .由题设F (x )在x ∈[a +2,a +3]上有意义,所以a +2>3a ,即a <1.于是,0<a <1.10设f (x )=log a (x -2a )+log a (x -3a ),其中a >0且a ≠1.若在区间[a +3,a +4]上f (x )≤1恒成立,求a 的取值范围.【解析】f (x )=log a x 2-5ax +6a 2=log a x -5a 2 2-a 24.由x -2a >0x -3a >0, 得x >3a ,由题意知a +3>3a ,故a <32,从而(a +3)-5a 2=-32(2-a )>0,故函数g (x )=x -5a 2 2-a 24在区间[a +3,a +4]上单调递增.若0<a <1,则f (x )在区间[a +3,a +4]上单调递减,所以f (x )在区间[a +3,a +4]上的最大值为f (a +3)=log a 2a 2-9a +9 .在区间[a +3,a +4]上不等式f (x )≤1恒成立,等价于不等式loglog a 2a 2-9a +9 ≤1恒成立,从而2a 2-9a +9≥a ,解得a ≥5+72或a ≤5-72.结合0<a <1,得0<a <1.若1<a <32,则f (x )在区间[a +3,a +4]上单调递增,所以f (x )在区间[a +3,a +4],上的最大值为f (a +4)=log a 2a 2-12a +16 .在区间[a +3,a +4]上不等式f (x )≤1恒成立,等价于不等式log a 2a 2-12a +16 ≤1恒成立,从而2a 2-12a +16≤a ,即2a 2-13a +16≤0,解得13-414≤a ≤13+414.易知13-414>32,所以不符合.综上所述,a 的取值范围为(0,1).11解方程组x x +y=y 12y x +y =x 3,(其中x ,y ∈R * .【解析】两边取对数,则原方程组可化为(x +y )lg x =12lg y ①(x +y )lg y =3lg x ②把式①代入式②,得(x +y )2lg x =36lg x ,所以(x +y )2-36 lg x =0.由lg x =0,得x =1;代入式①,得y =1.由(x +y )2-36=0x ,y ∈R * 得x +y =6.代入式①得lg x =2lg y ,即x =y 2,所以y 2+y -6=0.又y >0,所以y =2,x =4.所以方程组的解为x 1=1y 1=1 ,x 2=4y 2=2 .12已知f (x )=lg (x +1)-12log 3x .(1)解方程f (x )=0;(2)求集合M =n f n 2-214n -1998 ≥0,n ∈Z 的子集个数.【解析】(1)任取0<x 1<x 2,则f x 1 -f x 2 =lg x 1+1 -lg x 2+1 -12log 3x 1-log 3x 2=lgx 1+1x 2+1-12log 3x 1x 2=lg x 1+1x 2+1-log 9x 1x 2,因为x 1+1x 2+1>x 1x 2,所以lg x 1+1x 2+1>lg x 1x 2.故f x 1 -f x 2 =lg x 1+1x 2+1-log 9x 1x 2>lg x 1x 2-lg x1x 2lg9,因为0<lg9<1,lg x 1x 2<0,所以f x 1 -f x 2 >lg x 1x 2-lg x1x 2=0,f (x )为(0,+∞)上的减函数,注意到f (9)=0,当x >9时,f (x )<f (9)=0;当<x <9时,f (x )>f (9)=0,所以f (x )=0有且仅有一个根x =9.(2)由f n 2-214n -1998 ≥0⇒f n 2-214n -1998 ≥f (9)所以n 2-214n -1998≤9n 2-214n -1998>0 ⇔n 2-214n -2007≤0n 2-214n -1998>0⇔(n -223)(n +9)≤0(n -107)2>1998+1072=13447>1152⇔-9≤n ≤223n >222或n <-8 ⇔⇔-9≤n ≤223n ≥223或n ≤-9 ,所以n =223或n =-9,M ={-9,223},M 的子集的个数是4.13已知a >0,a ≠1,试求使得方程log a (x -ak )=log a x 2-a 2 有解的k 的取值范围.【解析】由对数性质知,原方程的解x 应满足(x -ak )2=x 2-a 2x -ak >0x 2-a 2>0(1)(2)(3)若式(1)、式(2)同时成立,则式(3)必成立,故只需要解(x -ak )2=x 2-a 2x -ak >0.由式(1)可得2kx =a 1+k 2(4)当k =0时,式(4)无解;当k ≠0时,式(4)的解是x =a 1+k 2 2k ,代人式(2),得1+k 22k>k .若k <0,则k 2>1,所以k <-1;若k >0,则k 2<1,所以0<k <1.综上所述,当k ∈(-∞,-1)∪(0,1)时,原方程有解.14已知0.301029<lg2<0.301030,0.477120<lg3<0.477121,求20001979的首位数字.【解析】lg20001979=1979lg2000=1979(3+lg2).所以6532.736391<lg20001979<6532.73837.故20001979为6533位数,由lg5=1-lg2,lg6=lg2+lg3,得0.698970<lg5<0.6989710.778149<lg6<0.778151⇒lg5<0.736391<0.73837<lg6,说明20001979的首位数字是5.15已知3a +13b =17a ,5a +7b =11b ,试判断实数a 与b 的大小关系,并证明之.【解析】令a =1,则13b =14,5+7b =11b ,可见b >1.猜想a <b .下面用反证法证明:若a ≥b ,则13a ≥13b ,5a ≥5b ,所以17a =3a +13b ≤3a +13a ,11b =5a +7b ≥5b +7b ,即317 a +1317 a ≥1,511 b +711 b ≤1,而函数f (x )=317 x +1317 x和g (x )=511 x +711 x在R 上均为减函数,且f (1)=317+1317=1617<1≤f (a ),g (1)=511+711=1211>1≥g (b ).所以a <1,b >1.这与a ≥b 矛盾,故a <b .16解不等式log 2x 12+3x 10+5x 8+3x 6+1 <1+log 2x 4+1 .【解析】原不等式等价于log 2x 12+3x 10+5x 8+3x 6+1 <log 22x 4+2 .由于y =log 2x 为单调递增函数,于是x 12+3x 10+5x 8+3x 6+1<2x 4+2,两端同时除以x 6,并整理得2x2+1x 6>x 6+3x 4+3x 2+1+2x 4+2=x 2+1 3+2x 2+1 构造函数g (t )=t 3+2t ,则上述不等式转化为g1x2>g x 2+1 .显然g (t )=t 3+2t 在R 上为增函数.于是以上不等式等价于1x2>x 2+1,即x 2 2+x 2-1<0,解得x 2<5-12.故原不等式的解集为-5-12,5-12.。
指数函数、对数函数、幂函数图像与性质

指数函数、对数函数、幂函数的图像与性质(一)指数与指数函数1.根式(1)根式的观点(2).两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a aa nn ;②a a n n =)((注意a 一定使n a 存心义)。
2.有理数指数幂 (1)幂的相关观点 ①正数的正分数指数幂:0,,1)m na a m n N n *=>∈>、且; ②正数的负分数指数幂: 10,,1)mnm naa m n N n a-*==>∈>、且③0的正分数指数幂等于0,0的负分数指数幂没存心义.注:分数指数幂与根式能够互化,往常利用分数指数幂进行根式的运算。
(2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q ); ②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );.n 为奇数 n 为偶数3.指数函数的图象与性质 y=a x a>10<a<1图象定义域 R值域 (0,+∞)性质(1)过定点(0,1) (2)当x>0时,y>1; x<0时,0<y<1(2) 当x>0时,0<y<1; x<0时, y>1(3)在(-∞,+∞)上是增函数 (3)在(-∞,+∞)上是减函数注:如下图,是指数函数(1)y=a x ,(2)y=b x,(3),y=c x (4),y=d x 的图象,怎样确立底数a,b,c,d 与1之间的大小关系?提示:在图中作直线x=1,与它们图象交点的纵坐标即为它们各自底数的值,即c 1>d 1>1>a 1>b 1,∴c>d>1>a>b 。
即不论在轴的左边仍是右边,底数按逆时针方向变大。
(二)对数与对数函数 1、对数的观点 (1)对数的定义假如(01)x a N a a =>≠且,那么数x 叫做认为a 底,N 的对数,记作log N a x =,此中a 叫做对数的底数,N 叫做真数。
六大基本初等函数图像及其性质
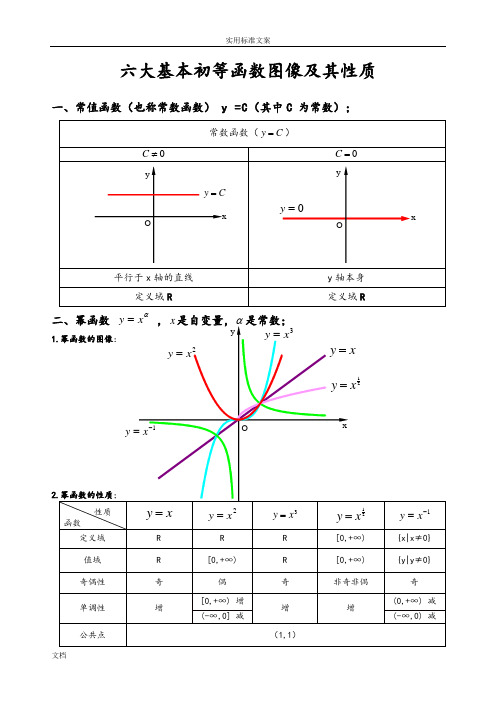
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
指数函数、对数函数、幂函数的图像和性质知识点总结.docx

(一)指数与指数函数1.根式(1)根式的概念根式的It念3符号表示a备注3如果x n=a,那么x叫做a的〃次方根a n > lfin e AT P 当«为奇数时,正数的«次方根是一个正数,负数的川次方根是一个负数3零的兀次方根是零3当n为偶数时,正数的n次方根有两个,它们互为相反数"土嚅(° >0)3负数没有偶次方根卩(2).两个重要公式*a①> 0)\a\=<[-a{ci < 0)②=a (注意a必须使砺有意义)。
2.有理数指数幕(1)幕的有关概念①正数的正分数指数幕:a"= 奸(d > (),m. n w AT,且〃〉1);豐 1 1②正数的负分数指数幕:a n = —=-=(^7>0,/?K /?G N\JBL H>1)a n③0的正分数指数幕等于0,0的负分数指数幕没有意义.注:分数指数幕与根式可以互化,通常利用分数指数幕进行根式的运算。
(2)有理数指数幕的性质①a I a'=a H'"(a>0,r、s G Q);②(a r)s=a re(a>0,r> sEQ);③(ab)'=a r b s(a>0,b>0,r E Q);.3.指数函数的图象与性质y=a x a>l 0<a<l图象~d 1 *定义域 R 值域 (0, +oo) 性质(1)过定点(0, 1)(2)当 x>0 时,y>l; x<0 时,0<y<l(2)当 x>0 时,0<y<l; x<0 时,y>l(3)在(-oo, +oo)上是增函数(3)在 (-00 , 4-00 )上是减函数注:如图所示,是指数函数(1) y=a x , (2) y=b x ' (3) ,y=c x (4) ,y=d x 的图象,如何确 定底数a,b,c,d 与1之间的大小关系?提示:在图屮作直线x=l,与它们图象交点的纵坐标即为它们各自底数的值,即 ci>』>l>ai>bi,・・・c>d>l>a>b 。
幂函数指数函数与对数函数的性质与计算

幂函数指数函数与对数函数的性质与计算幂函数、指数函数与对数函数是数学中常见的函数类型,它们具有一些独特的性质以及特定的计算方式。
在本文中,我们将探讨这些函数的基本概念、性质以及如何进行计算。
一、幂函数的性质与计算幂函数是形如y=x^n的函数,其中n为实数。
幂函数的性质如下:1. 幂函数的定义域为实数集R,值域则取决于n的值。
- 当n为正奇数时,f(x)为增函数,值域为R+(正实数集);- 当n为正偶数时,f(x)为非负且有最小值0,值域为[0, +∞);- 当n为负数时,f(x)有正负之分,值域为R+和R-(负实数集),且在不同的定义域上具有不同的增减性;- 当n为0时,0的0次方没有定义。
2. 幂函数的图像特点:- 当n为正数时,随着x的增大,函数值也随之增大,图像呈现递增趋势;- 当n为负数时,随着x的增大,函数值递减,图像呈现递减趋势。
3. 幂函数的计算方法:- 幂函数的运算法则遵循指数运算法则,如x^m * x^n = x^(m+n),x^m / x^n = x^(m-n),(x^m)^n = x^(m*n)等。
二、指数函数的性质与计算指数函数是形如y=a^x的函数,其中a为常数且a>0且a≠1。
指数函数的性质如下:1. 指数函数的定义域为实数集R,值域为正实数集R+。
2. 指数函数以a为底,随着自变量x的增大,函数值呈现指数增长的特征。
3. 指数函数的计算方法:- 当a为正数时,指数函数的运算法则与幂函数相似,如a^m *a^n = a^(m+n),a^m / a^n = a^(m-n)等。
- 当a为负数时,指数函数的运算方法可以通过转化为幂函数的形式进行计算。
三、对数函数的性质与计算对数函数是指数函数的逆运算,以b为底,记作y=logₐx。
对数函数的性质如下:1. 对数函数的定义域为正实数集R+,值域为实数集R。
2. 对数函数以b为底,将正实数x映射到实数y,即b^y=x。
3. 对数函数的计算方法主要包括:- 同底数的对数乘法法则:logₐ(x * y) = logₐx + logₐy;- 同底数的对数除法法则:logₐ(x / y) = logₐx - logₐy;- 对数的换底公式:logₐx = log_bx / log_ba,其中a、b为正实数且a≠1,b≠1。
指数函数、对数函数、幂函数的图像与性质的讲义

指数函数、对数函数、幂函数的图像与性质理解有理数指数幂的含义,掌握幂的运算;理解指数函数的概念,理解指数函数的单调性,掌握指数函数图象通过的特殊点。
理解对数的概念及其运算性质。
理解对数函数的概念,理解对数函数的单调性,掌握对数函数图象通过的特殊点。
了解指数函数y=a x与对数函数y log a x互为反函数(a 0,且a 1)。
了解幂函数的概念。
结合函数y=x,y=x2,y=x3,112y ,y x2的图象,了解它们的变化情况。
指数函数、对数函数在高中数学中占有十x分重要的地位,是高考重点考查的对象,热点是指数函数、对数函数的图象与性质的综合应用.同时考查分类讨论思想和数形结合思想;多以选择、填空题的形式出现,有时会与其他知识结合在知识交汇点处命题。
一)指数与指数函数1.根式(1)根式的概念2).两个重要公式② (n a ) n a (注意 a 必须使na 有意义)。
2.有理数指数幂(1)幂的有关概念注: 分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。
(2)有理数指数幂的性质 ①a r a s=a r+s(a>0,r 、s ∈Q); ②(a r )s=a rs(a>0,r 、s ∈ Q); ③(ab)r=a r b s(a>0,b>0,r ∈ Q);.3.指数函数的图象与性质①正数的正分数指数幂m :an n a m(a 0,m 、n N ,且n 1);②正数的负分数指数幂m1 1 : a n 1m n 1m (a 0,m 、 n N , 且n 1) a n n a m③0 的正分数指数幂等于0,0 的负分数指数幂没有意义①n a nan 为奇数a(a 0)|a|n 为偶数a(a 0)注: 如图所示,是指数函数( 1) y=a x,(2) y=b x,( 3) ,y=c x( 4) ,y=d x的图象,如何确 定底数 a,b,c,d 与 1 之间的大小关系?提示:在图中作直线x=1 ,与它们图象交点的纵坐标即为它们各自底数的值,即c 1>d 1>1>a 1>b 1,∴c>d>1>a>b 。
指数函数对数函数与幂函数指数函数的性质与图像

指数函数对数函数与幂函数指数函数的性质与图像xx年xx月xx日CATALOGUE 目录•指数函数的定义与性质•对数函数的定义与性质•幂函数的定义与性质•指数函数、对数函数与幂函数的比较•指数函数、对数函数与幂函数的应用案例•总结与展望01指数函数的定义与性质指数函数的定义02指数函数:y=f(x)=a^x03a>0时,函数图像过一三象限;a<0时,函数图像过二四象限。
指数函数的性质函数图像恒过(0,1)点值域:R a>1时,函数为单调递增函数;0<a<1时,函数为单调递减函数奇偶性:当a>0时,为奇函数;当a=0时,既不是奇函数也不是偶函数;当a<0时,为偶函数指数函数的图像图像恒过(0,1)点当a>1时,函数的增长速度随着x的增大而逐渐加快;当0<a<1时,函数的增长速度随着x的增大而逐渐减慢。
a>1时,函数为单调递增函数,图像位于一三象限;0<a<1时,函数为单调递减函数,图像位于二四象限。
当a>1时,函数的最大值无限趋近于正无穷大;当0<a<1时,函数的最小值无限趋近于0。
02对数函数的定义与性质1 2 3自然对数:以数学常数e为底数的对数,记作ln(x)。
常用对数:以10为底数的对数,记作lg(x)。
底数为任意正数的对数,记作log(x)。
对数的运算性质log(a*b)=log(a)+log(b);log(a/b)=log(a)-log(b);log(a^n)=nlog(a)。
对数恒等式log(a/b)=log(a)-log(b);log(a^n)=nlog(a)。
对数的运算律如果a>0且a不等于1,M>0,N>0,那么log(a)(MN)=log(a)M +log(a)N;log(a)(M/N)=log(a)M -log(a)N;log(a)M^n=nlog(a)M。
•对数函数的图像与性质:图像与x轴交点为1,当x>1时,函数值大于0;当0<x<1时,函数值小于0。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质六大基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数。
1. 常数函数:y = c,其中c是一个常数。
常数函数的图像是一条平行于x轴的直线,与y轴相距c个单位。
它没有自变量的限制,函数值始终为常数。
2. 幂函数:y = x^n,其中n是任意实数。
幂函数的图像依赖于指数n的符号及大小。
当n为正数时,随着x的增大,函数值也增大;当n为负数时,随着x的增大,函数值减小。
若n为奇数,图像穿过原点;若n为偶数,图像在原点有一个极小值或极大值。
3. 指数函数:y = a^x,其中a是一个正数且不等于1。
指数函数的图像是递增或递减的曲线。
如果a大于1,函数图像是递增的,如果a在0和1之间,函数图像是递减的。
指数函数没有定义域的限制,但其值范围从0到正无穷大。
4. 对数函数:y = log_a(x),其中a是一个正数且不等于1。
对数函数的图像与指数函数的图像是关于直线y = x对称的。
当x在0到正无穷大之间变化时,函数值从负无穷大逐渐增大到正无穷大。
对数函数的定义域为正实数,值域为负无穷大到正无穷大。
5. 三角函数:包括正弦函数y = sin(x),余弦函数y = cos(x),正切函数y = tan(x),割函数y = sec(x),余割函数y = csc(x),和余切函数y = cot(x)。
三角函数的图像是周期性的波形,沿x 轴变化。
例如,正弦函数和余弦函数的图像是在[-π, π]范围上的曲线。
正弦函数的值域在[-1, 1]之间,余弦函数的值域也在[-1, 1]之间。
6. 反三角函数:包括反正弦函数y = arcsin(x),反余弦函数y = arccos(x),反正切函数y = arctan(x),反割函数y = arcsec(x),反余割函数y = arccsc(x),和反余切函数y = arccot(x)。
反三角函数的图像是由对应的三角函数的图像上截取而来的。
幂函数指数函数对数函数的图像和性质

幂函数指数函数对数函数的图像和性质在数学中,幂函数,指数函数和对数函数是一类十分重要的函数,它们在各种领域都有着重要的应用,它们之间也有着千丝万缕的联系,而本文的主要重点就是分析它们的关系,以及它们的图像和性质。
首先,对于幂函数而言,它的定义域为实数集,值域也为实数集,其函数多项式形式为$f(x)=a^x(a>0,aeq 1)$其中a为指数,当a>1时,函数图像呈现出递增趋势,而当a<1时,函数则呈现出递减趋势。
此外,还可以确定的是,幂函数是一种可导函数,其导函数的形式为$f(x)=ln(a)a^x$ 。
接下来,我们来看看指数函数及其图像和性质,它的定义域也为实数集,值域也为实数集,其函数多项式形式为$f(x)=a^x(a>0)$其中a为指数,当a>1时,函数图像呈现出递增趋势,而当a<1时,函数则呈现出递减趋势。
此外,还可以确定的是,指数函数也是一种可导函数,其导函数的形式为$f(x)=a^xln(a)$可以看出,指数函数也是一种以连续变量为参数的可导函数。
最后,我们再来看看对数函数及其图像和性质,它的定义域也为实数集,值域也为实数集,其函数多项式形式为$f(x)=ln x$,可以看出,对数函数的图像呈右斜线形,它是一个单调函数,且为可导函数,其导函数的形式为$f(x)=frac{1}{x}$ 。
接下来,我们来看看三种函数之间的关系,第一,它们之间有着联系,即可以从一种函数通过定义变换到另外一种函数,其具体形式为$f(x)=a^x=ln(y)$,即从一个函数求另一个函数,从而将三种函数联系在一起;第二,它们之间也存在着双射,可以实现函数的双向转换;第三,它们的应用场景类似,都是应用于数量的变化趋势分析中,以及特定概率的分析等领域。
以上,就是有关幂函数、指数函数和对数函数的图像和性质以及它们之间的联系的全部内容,它们在数学中都有着重要的应用,因此,理解它们的关系以及图像和性质也是十分重要的。
(完整版)指数函数、对数函数、幂函数的图像和性质知识点总结

(一)指数与指数函数1.根式(1)根式的概念(2).两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a aa nn ;②a a nn =)((注意a 必须使n a 有意义)。
2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1)mn m naa a m n N n *=>∈>、且;②正数的负分数指数幂: 10,,1)m nm nmnaa m n N n a a-*==>∈>、且③0的正分数指数幂等于0,0的负分数指数幂没有意义.注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。
(2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q ); ②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );. 3.指数函数的图象与性质 y=a xa>10<a<1n 为奇数 n 为偶数图象定义域R值域(0,+∞)性质(1)过定点(0,1)(2)当x>0时,y>1;x<0时,0<y<1(2) 当x>0时,0<y<1;x<0时, y>1(3)在(-∞,+∞)上是增函数(3)在(-∞,+∞)上是减函数注:如图所示,是指数函数(1)y=a x,(2)y=b x,(3),y=c x(4),y=d x的图象,如何确定底数a,b,c,d与1之间的大小关系?提示:在图中作直线x=1,与它们图象交点的纵坐标即为它们各自底数的值,即c1>d1>1>a1>b1,∴c>d>1>a>b。
即无论在轴的左侧还是右侧,底数按逆时针方向变大。
(二)对数与对数函数1、对数的概念(1)对数的定义如果(01)xa N a a=>≠且,那么数x叫做以a为底,N的对数,记作log Nax=,其中a 叫做对数的底数,N叫做真数。
(完整)六大基本初等函数图像及其性质
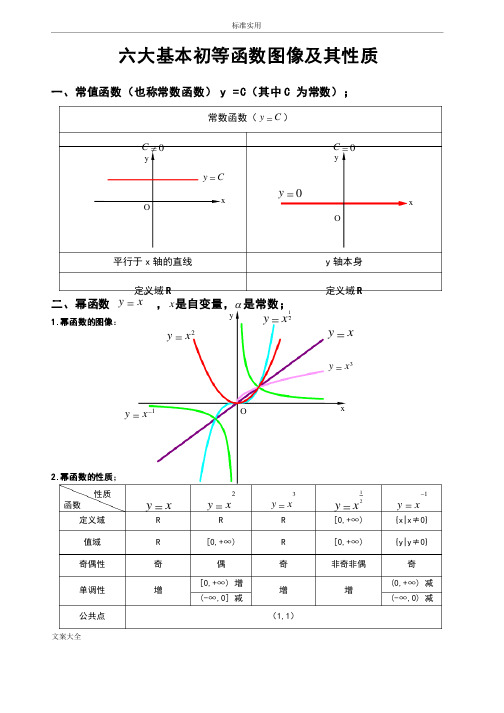
标准实用文案大全六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)≠C 0=C 平行于x 轴的直线y 轴本身定义域R 定义域R二、幂函数αx y=,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数xy =2xy =3xy =21x y =1-=xy 定义域R R R [0,+[0,+∞∞) {x|x {x|x≠≠0} 值域R [0,+[0,+∞∞) R [0,+[0,+∞∞) {y|y {y|y≠≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+[0,+∞∞) ) 增增增增(0,+(0,+∞∞) ) 减减(-(-∞∞,0] ,0] 减减(-(-∞∞,0) ,0) 减减公共点(1,11,1))xyOxy =2x y =3x y =1-=x y 21x y =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α,他们的图形都经过原点,并当α>1>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm 时,时,n n 为偶数时函数的定义域为(为偶数时函数的定义域为(0, +0, +0, +∞),∞),∞),n n 为奇数时函数的定义域为(为奇数时函数的定义域为(--∞,+,+∞),函数的图形均经过原点和(∞),函数的图形均经过原点和(∞),函数的图形均经过原点和(1 ,11 ,11 ,1););4)如果m>n 图形于x 轴相切,如果m<n,m<n,图形于图形于y 轴相切,且m 为偶数时,还跟y 轴对称;轴对称;m m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,)当α为负有理数时,n n 为偶数时,函数的定义域为大于零的一切实数;为偶数时,函数的定义域为大于零的一切实数;n n 为奇数时,定义域为去除x=0以外的一切实数。
指数函数、对数函数、幂函数的图像和性质知识点总结

(一)指数与指数函数1根式(1) 根式的概念(2).两个重要公式”n 为奇数a① 勺a =〈a(a 王0) n 为偶数\a\=: 、—a(a<0)② (n .a)n =a (注意a 必须使I a 有意义) 2. 有理数指数幂 (1)幂的有关概念m①正数的正分数指数幂:a n =n 孑(a 0,m> n N ,且n 1);注:分数指数幂与根式可以互化,通常利用分数指数幂进行 根式的运算。
(2) 有理数指数幂的性质 ① aras=ar+s(a>0,r 、s € Q);②正数的负分数指数幂1— ■ (a • 0, m 、n m 'n N ,且 n 1)③0的正分数指数幂等于 0,0的负分数指数幂没有意义② (ar)s=ars(a>O,r 、s€ Q);③ (ab)r=arbs(a>O,b>O,r € Q);.3. 指数函数的图象与性质注:如图所示,是指数函数(1)y=ax, (2)y=bx, (3),y=cx (4),y=dx的图象,如何确定底数a,b,c,d与1之间的大小关系?提示:在图中作直线x=1,与它们图象交点的纵坐标即为它们各自底数的值,即 c1>d1>1>a1>b1,二c>d>1>a>b 。
即无论在轴 的左侧还是右侧,底数按逆时针方向变大。
(二)对数与对数函数 1、对数的概念 (1) 对数的定义如果a * = N (a - 0且a "),那么数x 叫做以a 为底,N 的对数,记作 x=log a N ,其中a 叫做对数的底数,N 叫做真数。
(2) 几种常见对数2、对数的性质与运算法则(1)对数的性质(a -0,且 a=1):① log a^ 0,② log, =1,③ a 1* 二 N , ④ log a^ = N 。
(2)对数的重要公式:12叫(a,b 均为大于零且不等于1,N 0);log a(3)对数的运算法则:如果a 0,且a=1, M 0, N 0那么①换底公式: N log b② log a b1 iog b a①log a (MN ) = log a M log a N;②log a M-log a M-log a N;N③log a M n二n log a M (n・ R);④log m b n = —log a b。
六大基本初等函数图像及其性质
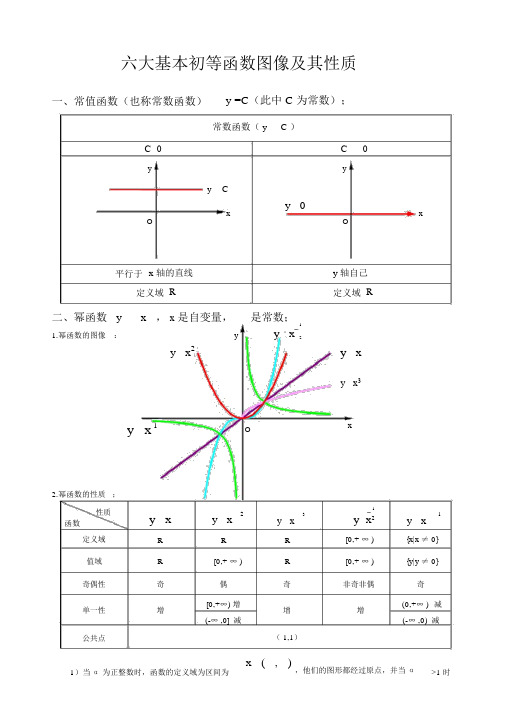
六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C(此中 C 为常数);常数函数( y C )C 0C0y yy Cx y 0xO O平行于x 轴的直线y 轴自己定义域R定义域R 二、幂函数 y x ,x是自变量,是常数;1y y x1.幂函数的图像:2y x2y xy x3y x1O x2.幂函数的性质;性质y x y x231y x1y x y x2函数定义域R R R[0,+ ∞ ){x|x ≠ 0}值域R[0,+ ∞ )R[0,+ ∞ ){y|y ≠ 0}奇偶性奇偶奇非奇非偶奇单一性增[0,+∞) 增增增(0,+∞ )减(-∞ ,0] 减(-∞ ,0)减公共点( 1,1)1)当α为正整数时,函数的定义域为区间为x ( , ),他们的图形都经过原点,并当α>1 时在原点处与x 轴相切。
且α为奇数时,图形对于原点对称;α为偶数时图形对于y 轴对称;2)当α为负整数时。
函数的定义域为除掉x=0 的全部实数;3)当α为正有理数m时,n为偶数时函数的定义域为(0, +∞),n为奇数时函数的定义域为(-n∞ ,+∞),函数的图形均经过原点和( 1 ,1);4)假如 m>n 图形于 x 轴相切,假如m<n,图形于 y 轴相切,且m 为偶数时,还跟y 轴对称; m, n均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一确实数;n 为奇数时,定义域为去除 x=0 之外的一确实数。
三、指数函数 y a x(x是自变量,a是常数且a0, a1),定义域是 R ;[ 无界函数 ]1.指数函数的图象:yy a x y a xy(a 1)(0a1)(0,1)y1(0,1)y1 O x O x2.指数函数的性质;性质y a x(a1)y a x(0 a 1)函数定义域R值域(0,+∞)奇偶性非奇非偶公共点过点 (0,1),即 x0 时,y 1单一性在(,)是增函数在(,)是减函数1 )当a 1时函数为单调增 , 当0a 1时函数为单调减;2 )不论x为何值 ,y 总是正的,图形在 x 轴上方;3 )当x 0时 , y 1, 所以它的图形通过 (0,1) 点。
指数函数、对数函数、幂函数的图像和性质知识点总结

当xo>l时,按交点的高低,从高到低依次为y=x3, y=x2, y=x ,y x2,y=x-1;
1
当0<xo<1时,按交点的高低,从高到低依次为y=x-1,y x2,y=x , y=x2, y=x3。
3、藉函数的性质
段X数
y=x
2y=x
3y=x
1
yx,
-1y=x
定义域
R
R
R
[0,)
x| x Rflx 0
值域
R
[0,)
R
[0,)
y | y Rfi y 0
奇偶性
奇
偶
奇
非奇非偶
奇
单调性
增
x € [0 ,)时,增;
xe(,0]时,减
增
增
x C (0,+)时,减;
x C (- ,0)时,减
定点
(1 , 1)
叫做对数的底数,N叫做真数。
(2)几种常见对数
对数形式
特点
记法
一般对数
底数为aa 0,且a 1
logaN
常用对数
底数为10
lg N
自然对数
底数为e
ln N
2、对数的性质与运算法则
(1)
(2)对数的重要公式:
lonN
-^b(a,b均为大丁零且不等丁1,N 0);loga
指数函数y=ax与对数函数y=logax互为反函数,它们的图象关于直线y=x对称。
(三)籍函数
1、藉函数的定义
形如y=x " (a£ R)的函数称为藉函数,其中x是自变量,a为常数
注:藉函数与指数函数有本质区别在于自变量的位置不同,备函数的自变量在底数位置,而
中考重点幂函数指数函数与对数函数的像与性质

中考重点幂函数指数函数与对数函数的像与性质中考重点幂函数、指数函数与对数函数的像与性质幂函数、指数函数与对数函数是数学中常见且重要的函数类型。
它们在中学数学教学中有深入的研究,对于中考也是必考知识点。
了解它们的像与性质对于学生理解数学概念、解题能力的提升至关重要。
本文将分别介绍幂函数、指数函数和对数函数的像与性质,帮助学生更好地掌握这些知识。
I. 幂函数的像与性质幂函数是指形如 $f(x)=ax^b$ 的函数,其中 $a$ 和 $b$ 是常数,$a\neq 0$。
幂函数的图像通常呈现出一条曲线,其性质主要有以下几点:1. 当 $a>0$ 且 $b>0$ 时,函数 $f(x)$ 的图像位于第一象限,并且随着 $x$ 的增大而增大。
2. 当 $a>0$ 且 $b<0$ 时,函数 $f(x)$ 的图像位于第一象限,并且随着 $x$ 的增大而趋近于零(但不会等于零)。
3. 当 $a<0$ 且 $b$ 为正偶数时,函数 $f(x)$ 的图像位于第二和第四象限,关于 $y$ 轴对称,并且随着 $x$ 的增大而增大。
4. 当 $a<0$ 且 $b$ 为正奇数时,函数 $f(x)$ 的图像位于第二和第四象限,关于原点对称,并且随着 $x$ 的增大而减小。
综上所述,幂函数的性质主要取决于 $a$ 和 $b$ 的值,不同的参数组合会导致不同的图像特点。
II. 指数函数的像与性质指数函数是指形如$f(x)=a^x$ 的函数,其中$a$ 是正数且不等于1。
指数函数的图像呈现出单调递增或单调递减的特点,其性质主要有以下几点:1. 当 $0<a<1$ 时,函数 $f(x)$ 的图像单调递减并且在 $+\infty$ 趋近于零。
2. 当 $a>1$ 时,函数 $f(x)$ 的图像单调递增并且在 $-\infty$ 趋近于零。
3. 当 $a>1$ 时,函数 $f(x)$ 的图像上任意两点 $(x_1, y_1)$ 和 $(x_2, y_2)$ 之间的斜率等于常数 $a^{x_1}$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数、对数函数、幂函数的图像与性质(一)指数与指数函数1.根式( 1)根式的概念根式的概念符号表示备注如果 x na ,那么 x 叫做 a 的 n 次方根n 1且 n N当 n 为奇数时 ,正数的 n 次方根是一个正数 ,负数的 n 次 na零的 n 次方根是零方根是一个负数当 n 为偶数时 ,正数的 n 次方根有两个 ,它们互为相反数na ( a 0) 负数没有偶次方根( 2).两个重要公式an 为奇数① n a na( a 0) ;| a |0)n 为偶数a(a② (n a ) n a (注意 a 必须使 n a 有意义)。
2.有理数指数幂 ( 1)幂的有关概念m①正数的正分数指数幂: a n n a m (a0, m 、 n N ,且n 1) ;m 11②正数的负分数指数幂: an0, m 、 nN , 且 n 1)m(aa nna m③0 的正分数指数幂等于 0,0 的负分数指数幂没有意义 .注: 分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。
( 2)有理数指数幂的性质① a r a s =a r+s (a>0,r 、 s ∈ Q);r srs② (a ) =a (a>0,r 、s ∈ Q); ③ (ab)r =a r b s (a>0,b>0,r ∈ Q);. 3.指数函数的图象与性质y=a x a>10<a<1图象定义域R值域(0,+ )性质( 1)过定点( 0, 1)( 2)当 x>0 时, y>1;(2) 当 x>0 时, 0<y<1;x<0 时 ,0<y<1x<0 时, y>1(3) 在( - ,+)上是增函数( 3)在( -, +)上是减函数注:如图所示,是指数函数(1) y=a x,(2) y=b x,( 3),y=c x( 4) ,y=d x的图象,如何确定底数 a,b,c,d 与 1 之间的大小关系?提示:在图中作直线x=1 ,与它们图象交点的纵坐标即为它们各自底数的值,即c1>d1>1>a1>b1,∴ c>d>1>a>b 。
即无论在轴的左侧还是右侧,底数按逆时针方向变大。
(二)对数与对数函数1、对数的概念(1)对数的定义如果 a x N ( a0且 a1) ,那么数 x 叫做以 a 为底,N的对数,记作 x log a N,其中 a叫做对数的底数,N 叫做真数。
(2)几种常见对数对数形式特点记法一般对数底数为 a a0,且a 1log a N常用对数底数为 10lg N自然对数底数为 e ln N2、对数的性质与运算法则(1)对数的性质(a0,且a110,② ogla gol):① log1,③ aaNa NN ,④ogl a N。
(2)对数的重要公式:①换底公式: log b N log a N(a,b均为大于零且不等于 1,N0) ;log a b②log ab1。
log b a(3)对数的运算法则:如果 a0,且a 1 ,M0, N0 那么① log a (MN )log a M log a N ;②log a Mlog a N ;log a MN③ log a M n n log a M ( n R) ;④ log m b n nlog a b 。
a m3、对数函数的图象与性质a 10 a 1图象性( 1)定义域:(0,+)质(2)值域: R(3)当 x=1 时, y=0 即过定点( 1,0)(4)当0x1时,y (,0) ;( 4)当x 1 时,y(,0) ;当x1时,y(0,)当0 x时,y(0,)1( 5)在( 0,+)上为增函数( 5)在(0,+)上为减函数注:确定图中各函数的底数a,b, c, d 与 1 的大小关系提示:作一直线y=1,该直线与四个函数图象交点的横坐标即为它们相应的底数。
∴0<c<d<1<a<b.4、反函数指数函数 y=a x 与对数函数 y=log a x 互为反函数,它们的图象关于直线y=x 对称。
(三)幂函数1、幂函数的定义形如 y=x α( a ∈R )的函数称为幂函数,其中 x 是自变量, α为常数注:幂函数与指数函数有本质区别在于自变量的位置不同,幂函数的自变量在底数位置,而指数函数的自变量在指数位置。
2、幂函数的图象1注:在上图第一象限中如何确定y=x 3, y=x 2,y=x , y x 2 , y=x -1 方法:可画出 x=x 0;1当 x 0>1 时,按交点的高低,从高到低依次为y=x 3, y=x 2, y=x , yx 2 , y=x -1 ;1当 0<x 0<1 时,按交点的高低,从高到低依次为 y=x -1, yx 2 ,y=x , y=x 2, y=x 3 。
3、幂函数的性质y=xy=x 2y=x 3 1y=x -1y x 2定义域RR R[0, )R 且 x 0x | x 值域R [0,)R [0,)R 且yy | y奇偶性 奇 偶奇非奇非偶 奇单调性增x ∈ [0, )时,增; 增增x ∈ (0,+ )时,减;x ∈ (,0] 时,减x ∈ (-,0) 时,减定点(1,1)三:例题诠释,举一反三知识点 1:指数幂的化简与求值例 1.(2007育才 A)[(33) 22113 (5 4)0.5(0.008) 3(0.02) 2 (0.32) 2 ] 0.06250.25(1)计算:89;412a38a 3b23ba 3a 2(a3)22a3(2)化简: 4b323aba35 aa变式:( 2007 执信 A )化简下列各式(其中各字母均为正数):2111(a 3 b 1 ) 2 a 2 b 3 ;(1)6 a b 5512112 3 1(2)6a 3b ( 3a 2b ) (4a 3 b )2.1( 7)021.5380.254 2( 323)6(2)3 (3)63知识点 2:指数函数的图象及应用例 2.(2009 广附 A) 已知实数 a 、 b 满足等式(1 ) a ( 1 )b,下列五个关系式:①0< b < a; ② a < b2 3< 0; ③ 0< a < b; ④b < a < 0; ⑤ a=b. 其中不可能成立的关系式有 ( )A.1 个B.2 个C.3 个D.4 个变式:( 2010 华附 A )若直线 y 2a 与函数 y | a x 1 | ( a 0 且 a1) 的图象有两个公共点,则 a 的取值范围是 _______.知识点 3:指数函数的性质例 3. ( 2010 省实 B )已知定义域为R 的函数 f (x)2x b2x 1是奇函数。
2(Ⅰ)求 b 的值;(Ⅱ)判断函数f x 的单调性 ;(Ⅲ)若对任意的t R ,不等式 f ( t 2 2t) f (2t 2 k ) 0 恒成立,求 k 的取值范围.变式:( 2010 东莞 B )设 a >0,f(x)=e xa 是 R 上的偶函数 .ae x( 1)求 a 的值;( 2)求证: f(x) 在( 0, +∞)上是增函数 . 知识点 4:对数式的化简与求值例 4. ( 2010 云浮 A )计算:( 1) log 2 3 (23)(2) 2(lg 2 ) 2+lg 2 · lg5+(lg2 ) 2lg 2 1 ;(3) 1 lg 32 -4lg 8 +lg 245 .2493变式:( 2010 惠州 A )化简求值 . (1) log 27 +log 212- 1log 242-1;482(2) (lg2) 2+lg2 · lg50+lg25;( 3) (log 32+log 92) · (log 43+log 83).知识点 5:对数函数的性质例 5. (2011 深圳 A )对于 0 a 1,给出下列四个不等式:① log a (1 a)log a (a1);② log a (1 a)log a (1 1) ;aa③ a 1 a a 1 1④ a 1 a 1 1a ;a a ; 其中成立的是( )(A )①与③( B )①与④( C )②与③( D )②与④变式:( 2011 韶关 A )已知 0< a < 1,b > 1,ab > 1,则 log a 1,log a b,log b1的大小关系是bb ( )A.log1 log a b log b 1 B. log a b log a 11ab log bbbb C. log a 1 log a 1 D. log b 1 1 log a bb log b bb log a b b例 6.( 2010 广州 B )已知函数 f(x)=log a x(a > 0,a ≠ 1) ,如果对于任意 x ∈[ 3,+∞)都有 |f(x)|≥ 1 成立,试求 a 的取值范围 .变式:( 2010 广雅 B )已知函数 f ( x )=log 2(x 2-ax-a) 在区间( - ∞ , 1-3]上是单调递减函数 . 求实数 a 的取值范围 .知识点 6:幂函数的图象及应用例 7.(2009佛山 B) 已知点 (2,2) 在幂函数 f (x) 的图象上,点1, ,在幂函数 g (x) 的图4象上.问当 x 为何值时有:(1) f (x) g ( x) ;(2) f (x) g (x) ;(3) f (x)g ( x) .变式:( 2009 揭阳 B )已知幂函数 f(x)=xm 22 m 3( m ∈ Z )为偶函数,且在区间( 0,+∞)上b是单调减函数 . ( 1)求函数 f(x);( 2)讨论 F ( x ) =af (x )的奇偶性 .xf (x )四:方向预测、胜利在望1.( A )函数 f ( x) lg1x 的定义域为( )x4A .(1, 4)B .[1,4)C . (-∞, 1)∪ (4,+∞ )D . (-∞, 1]∪ (4,+∞ )2.( A )以下四个数中的最大者是()2(B) ln(ln2)(C) ln2(D) ln2(A) (ln2)3( B )设 a>1,函数 f(x)=log a x 在区间[ a,2a ]上的最大值与最小值之差为1, 则 a=( )2(A) 2(B )2 (C ) 22(D )44.( A )已知 f (x) 是周期为 2 的奇函数,当x 1 时, f ( x) lg x. 设a63 5 )f ( ), bf ( ), cf ( ), 则(522( A ) a bc( B ) b a c( C ) c b a ( D ) c a b5.( B )设 f(x)=2e x 1 , x 2, 则不等式 f(x)>2 的解集为()log 3 (x21), x 2,(A) ( 1, 2) ( 3, +∞)(B) (10 , +∞)(C)( 1,2)(10 , +∞)(D) ( 1, 2)6.( A )设 P log 2 3 , Q log 3 2 , R log 2 (log 3 2) ,则( ) A.RQPB.PRQC.QRP D.RPQ7. (A) 已知 log 1b log 1 a log 1c ,则 ()222A . 2b 2a 2cB . 2a 2b2cC . 2c 2b 2aD . 2c 2 a2b8.( B )下列函数中既是奇函数,又是区间1,1 上单调递减的是( )( A ) f ( x) sin x(B)f ( x)x 1(C) f (x)1 (a x a x ) (D) f ( x) ln2 x 2 2 x9. ( A )函数 ylog 1 (3 x 2) 的定义域是: ( )2A [1,)B(32 ,)C[ 32 ,1]D( 32 ,1]10.(A) 已知函数 ylog 1 x 与y kx 的图象有公共点 A ,且点 A 的横坐标为 2,则 k ()4A .1B .1C .11442D .211.( B )若函数 f (x) a xb 1( a 0且 a 1)的图象经过第二、三、四象限,则一定有()A . 0 a 1且 b 0B . a 1且b 0C . 0 a 1且b 0D . a 1且b 0[a, 2a]. (B) 若函数 f (x)log a x(0 a 1) 在区间 上的最大值是最小值的3 倍,则 a=12( )A.2B.21142C.D.4213.(A) 已知 0<x < y < a <1,则有()( A ) log a ( xy) 0(B ) 0log a ( xy) 1(C )1log a (xy ) 2( D ) log a (xy ) 214. ( A )已知 f ( x 6 )log 2 x ,那么 f (8) 等于()4(B )8(C )181( A )( D )3215.( B )函数 y = lg|x| ( )A .是偶函数,在区间 (-∞,0) 上单调递增B .是偶函数,在区间 (- ∞,0)上单调递减C .是奇函数,在区间 (0,+ ∞)上单调递增D .是奇函数,在区间 (0,+ ∞)上单调递减16.( A )函数 ylg( 4 x )____________________________.x 3 的定义域是17.( B )函数 y a 1 x (a 0,a1) 的图象恒过定点 A ,若点 A 在直线 mx ny 1 0(mn1 1 .0) 上,则的最小值为m n18.( A )设 g( x)e x , x0.1lnx, x则 g( g ( )) __________0.219.( B )若函数 f(x) = 2x 22 ax a1的定义域为 R ,则 a 的取值范围为 ___________.20. (B)若函数 f (x)log a ( xx 2 2a 2 ) 是奇函数,则 a=.21.(B) 已知函数f ( x)1 1 x,求函数 f ( x) 的定义域,并讨论它的奇偶性和单调x log 2 1 x性.1136b3(a 3b 2 )7 1248422参考答案:三:例题诠释,举一反三例 1.解:( 1) 2,( 2) a 29135 ab .5a 2b 2 5 1(3)110变式:解:( 1) 1,(32)244 ab 4ab例 2. 解:B变式:解: (0, 1) ;2例 3. 解:(Ⅰ) b1 (Ⅱ)减函数。
