电大离散数学作业答案(图论部分)
离散数学测验题--图论部分(优选.)

离散数学图论单元测验题一、单项选择题(本大题共10小题,每小题2分,共20分)1、在图G =<V ,E >中,结点总度数与边数的关系是( )(A) deg(v i )=2∣E ∣ (B) deg(v i )=∣E ∣ (C)∑∈=V v E v 2)deg( (D) ∑∈=Vv E v )deg(2、设D 是n 个结点的无向简单完全图,则图D 的边数为( )(A) n (n -1) (B) n (n +1) (C) n (n -1)/2 (D) n (n +1)/23、 设G =<V ,E >为无向简单图,∣V ∣=n ,∆(G )为G 的最大度数,则有(A) ∆(G )<n (B)∆(G )≤n (C) ∆(G )>n (D) ∆(G )≥n4、图G 与G '的结点和边分别存在一一对应关系,是G ≌G '(同构)的( )(A) 充分条件 (B) 必要条件 (C)充分必要条件 (D)既非充分也非必要条件5、设},,,{d c b a V =,则与V 能构成强连通图的边集合是( )(A) },,,,,,,,,{><><><><><=c d b c d b a b d a E(B) },,,,,,,,,{><><><><><=c d d b c b a b d a E(C) },,,,,,,,,{><><><><><=c d a d c b a b c a E6、有向图的邻接矩阵中,行元素之和是对应结点的( ),列元素之和是对应结点的() (A)度数 (B) 出度 (C)最大度数 (D) 入度7、设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100000100则G 的边数为( ).A .5B .6C .3D .48、设m E n V E V G ==>=<,,,为连通平面图且有r 个面,则r =( )(A) m -n +2 (B) n -m -2 (C) n +m -2 (D) m +n +29、在5个结点的二元完全树中,若有4条边,则有 ( )片树叶。
最新国家开放大学电大《离散数学》形考任务1试题及答案

最新国家开放大学电大《离散数学》形考任务1试题及答案最新国家开放大学电大《离散数学》形考任务1试题及答.形考任务1(集合论部分概念及性质)单项选择.题目.若集合A=.a, {a}, {1, 2}}, 则下列表述正确的是().选择一项:A.{a, {a}}.B..C.{1, 2..D.{a..题目.设函数f: N→N, f(n)=n+1, 下列表述正确的是.).选择一项: A.f是满射.B.f存在反函.C.f是单射函.D.f是双射.题目.设集合A={1, 2, 3, 4, 5}, 偏序关系是A上的整除关系, 则偏序集<A, >上的元素5是集合A的.).选择一项:A.极小.B.极大.C.最大.D.最小.题目.设A={a, b}, B={1, 2}, C={4, 5}, 从A到B的函数f={<a,1>.<b, 2>}, 从B到C的函数g={<1, 5>.<2, 4>}, 则下列表述正确的是.).选择一项:A.g..={<a, 5>.<b, 4>.B.g..={<5, .>.<4, .>.C.f°.={<5, .>.<4, .>.D.f°.={<a, 5>.<b, 4>.题目.集合A={1.2.3.4}上的关系R={<x, y>|x=y且x.yA}, 则R的性质为.).选择一项:A.传递.B.不是对称.C.反自.D.不是自反.题目.设集合..{1..}, 则P(A...).选择一项:A.{{1}.{a}.{1..}.B.{{1}.{a}.C.{,{1}.{a}.D.{,{1}.{a}.{1..}.题目.若集合A={1, 2}, B={1, 2, {1, 2}},则下列表述正确的是.).选择一项:A.AB, 且A.B.AB, 且A.C.BA, 且A.D.AB, 且A.题目.设集合A={1.2.3}, B={3.4.5}, C={5.6.7},则A∪B–.=.).选择一项:A.{1.2.3.4.B.{4.5.6.7.C.{2.3.4.5.D.{1.2.3.5.题目.设集合..{1.2.3.4.5}上的偏序关系的哈斯图如右图所示, 若A的子集..{3.4.5}, 则元素3为B的.).选择一项:A.最小上.B.下.C.最大下.D.最小.题目1.如果R1和R2是A上的自反关系, 则R1∪R2, R1∩R2, R1-R2中自反关系有.)个.选择一项:A..B..C..D..以下资料为赠送资料:《滴水之中见精神》主题班会教案活动目的: 教育学生懂得“水”这一宝贵资源对于我们来说是极为珍贵的, 每个人都要保护它, 做到节约每一滴水, 造福子孙万代。
(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案

(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案 100%通过考试说明:2020年秋期电大把该网络课纳入到“国开平台”进行考核,该课程共有5个形考任务,针对该门课程,本人汇总了该科所有的题,形成一个完整的标准题库,并且以后会不断更新,对考生的复习、作业和考试起着非常重要的作用,会给您节省大量的时间。
做考题时,利用本文档中的查找工具,把考题中的关键字输到查找工具的查找内容框内,就可迅速查找到该题答案。
本文库还有其他网核及教学考一体化答案,敬请查看。
课程总成绩 = 形成性考核×30% + 终结性考试×70% 形考任务1 单项选择题题目1 若集合A={ a,{a},{1,2}},则下列表述正确的是().选择一项:题目2 若集合A={2,a,{ a },4},则下列表述正确的是( ).选择一项:题目3 设集合A={1 , 2 , 3 , 4}上的二元关系R={<1, 1>,<2, 2>,<2, 3>,<4, 4>},S={<1, 1>,<2, 2>,<2, 3>,<3, 2>,<4, 4>},则S是R的()闭包.选择一项:B. 对称题目4 设集合A={1, 2, 3},B={3, 4, 5},C={5, 6, 7},则A∪B–C=( ).选择一项:D. {1, 2, 3, 4} 题目5 如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有()个.选择一项:C. 2 题目6 集合A={1, 2, 3, 4}上的关系R={<x,y>|x=y且x, y∈A},则R的性质为().选择一项:D. 传递的题目7 若集合A={1,2},B={1,2,{1,2}},则下列表述正确的是( ).选择一项:题目8 设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为().选择一项:C. 8 题目9 设A={1, 2, 3, 4, 5, 6, 7, 8},R是A上的整除关系,B={2, 4, 6},则集合B的最大元、最小元、上界、下界依次为 ( ).选择一项:B. 无、2、无、2 题目10 设集合A ={1 , 2, 3}上的函数分别为:f = {<1, 2>,<2, 1>,<3, 3>},g = {<1, 3>,<2, 2>,<3, 2>},h = {<1, 3>,<2,1>,<3, 1>},则h =().选择一项:D. f◦g 判断题题目11 设A={1, 2}上的二元关系为R={<x, y>|xA,yA, x+y =10},则R的自反闭包为{<1, 1>, <2, 2>}.()选择一项:对题目12 空集的幂集是空集.()选择一项:错题目13 设A={a, b},B={1, 2},C={a, b},从A到B的函数f={<a, 1>, <b, 2>},从B到C的函数g={<1, b>, <2, a >},则g° f ={<1,2 >, <2,1 >}.()选择一项:错题目14 设集合A={1, 2, 3, 4},B={2, 4, 6, 8},下列关系f = {<1, 8>, <2, 6>,<3, 4>, <4, 2,>}可以构成函数f:.()选择一项:对题目15 设集合A={1, 2, 3},B={2, 3, 4},C={3, 4, 5},则A∩(C-B )= {1, 2, 3, 5}.()选择一项:错题目16 如果R1和R2是A上的自反关系,则、R1∪R2、R1∩R2是自反的.()选择一项:对题目17 设集合A={a, b, c, d},A上的二元关系R={<a, b>, <b, a>, <b, c>, <c, d>},则R具有反自反性质.()选择一项:对题目18 设集合A={1, 2, 3},B={1, 2},则P(A)-P(B )={{3},{1,3},{2,3},{1,2,3}}.()选择一项:对题目19 若集合A = {1,2,3}上的二元关系R={<1, 1>,<1, 2>,<3, 3>},则R是对称的关系.()选择一项:错题目20 设集合A={1, 2, 3, 4 },B={6, 8, 12}, A到B的二元关系R=那么R-1={<6, 3>,<8,4>}.()选择一项:对形考任务2 单项选择题题目1 无向完全图K4是().选择一项:C. 汉密尔顿图题目2 已知一棵无向树T中有8个顶点,4度、3度、2度的分支点各一个,T的树叶数为( ).选择一项:D. 5 题目3 设无向图G的邻接矩阵为则G的边数为( ).选择一项:A. 7 题目4 如图一所示,以下说法正确的是 ( ) .选择一项:C. {(d, e)}是边割集题目5 以下结论正确的是( ).选择一项:C. 树的每条边都是割边题目6 若G是一个欧拉图,则G一定是( ).选择一项:B. 连通图题目7 设图G=<V, E>,v∈V,则下列结论成立的是 ( ) .选择一项:题目8 图G如图三所示,以下说法正确的是 ( ).选择一项:C. {b, c}是点割集题目9 设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).选择一项:A. (a)是强连通的题目10 设有向图(a)、(b)、(c)与(d)如图六所示,则下列结论成立的是( ).选择一项:D. (d)只是弱连通的判断题题目11 设图G是有6个结点的连通图,结点的总度数为18,则可从G中删去4条边后使之变成树.( ) 选择一项:对题目12 汉密尔顿图一定是欧拉图.( ) 选择一项:错题目13 设连通平面图G的结点数为5,边数为6,则面数为4.( ) 选择一项:错题目14 设G是一个有7个结点16条边的连通图,则G为平面图.( ) 选择一项:错题目15 如图八所示的图G存在一条欧拉回路.( ) 选择一项:错题目16 设图G如图七所示,则图G的点割集是{f}.( ) 选择一项:错题目17 设G是一个图,结点集合为V,边集合为E,则( ) 选择一项:对题目18 设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树.( ) 选择一项:错题目19 如图九所示的图G不是欧拉图而是汉密尔顿图.( ) 选择一项:对题目20 若图G=<V, E>,其中V={ a, b, c, d },E={ (a, b), (a, d),(b, c), (b, d)},则该图中的割边为(b, c).( ) 选择一项:对形考任务3 单项选择题题目1 命题公式的主合取范式是( ).选择一项:题目2 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).选择一项:题目3 命题公式的主析取范式是( ).选择一项:题目4 下列公式成立的为( ).选择一项:题目5 设A(x):x是书,B(x):x是数学书,则命题“不是所有书都是数学书”可符号化为().选择一项:题目6 前提条件的有效结论是( ).选择一项:B. ┐Q 题目7 命题公式(P∨Q)→R的析取范式是 ( ).选择一项:D. (┐P∧┐Q)∨R 题目8 下列等价公式成立的为( ).选择一项:题目9 下列等价公式成立的为( ).选择一项:题目10 下列公式中 ( )为永真式.选择一项:C. ┐A∧┐B ↔ ┐(A∨B) 判断题题目11 设个体域D={1, 2, 3},A(x)为“x小于3”,则谓词公式(∃x)A(x) 的真值为T.( ) 选择一项:对题目12 设P:小王来学校, Q:他会参加比赛.那么命题“如果小王来学校,则他会参加比赛”符号化的结果为P→Q.( ) 选择一项:对题目13 下面的推理是否正确.( ) (1) (∀x)A(x)→B(x) 前提引入(2) A(y)→B(y) US (1) 选择一项:错题目14 含有三个命题变项P,Q,R的命题公式P∧Q的主析取范式(P∧Q∧R)∨(P∧Q∧┐R).( ) 选择一项:对题目15 命题公式P→(Q∨P)的真值是T.( ) 选择一项:对题目16 命题公式┐P∧P的真值是T.( ) 选择一项:错题目17 谓词公式┐(∀x)P(x)(∃x)┐P(x)成立.( ) 选择一项:对题目18 命题公式┐(P→Q)的主析取范式是P∨┐Q.( ) 选择一项:错题目19 设个体域D={a, b},则谓词公式(∀x)(A(x)∧B(x))消去量词后的等值式为(A(a)∧B(a))∧(A(b)∧B(b)).( ) 选择一项:对题目20 设个体域D={a, b},那么谓词公式(∃x)A(x)∨(∀y)B(y)消去量词后的等值式为A(a)∨B(b).( ) 选择一项:错形考任务4 要求:学生提交作业有以下三种方式可供选择:1. 可将此次作业用A4纸打印出来,手工书写答题,字迹工整,解答题要有解答过程,完成作业后交给辅导教师批阅. 2. 在线提交word文档. 3. 自备答题纸张,将答题过程手工书写,并拍照上传形考任务 5 网上学习行为(学生无需提交作业,占形考总分的10%)附:元宇宙(新兴概念、新型虚实相融的互联网应用和社会形态)元宇宙(Metaverse)是整合了多种新技术而产生的新型虚实相融的互联网应用和社会形态,通过利用科技手段进行链接与创造的,与现实世界映射与交互的虚拟世界,具备新型社会体系的数字生活空间。
离散数学及其应用图论部分课后习题答案
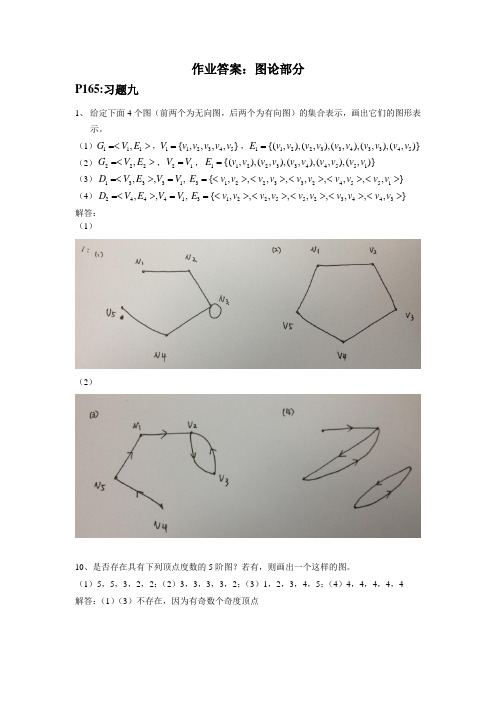
作业答案:图论部分P165:习题九1、 给定下面4个图(前两个为无向图,后两个为有向图)的集合表示,画出它们的图形表示。
(1)111,G V E =<>,112345{,,,,}V v v v v v =,11223343345{(,),(,),(,),(,),(,)}E v v v v v v v v v v = (2)222,G V E =<>,21V V =,11223344551{(,),(,),(,),(,),(,)}E v v v v v v v v v v = (3)13331,,,D V E V V =<>=31223324551{,,,,,,,,,}E v v v v v v v v v v =<><><><><> (4)24441,,,D V E V V =<>=31225523443{,,,,,,,,,}E v v v v v v v v v v =<><><><><> 解答: (1)(2)10、是否存在具有下列顶点度数的5阶图?若有,则画出一个这样的图。
(1)5,5,3,2,2;(2)3,3,3,3,2;(3)1,2,3,4,5;(4)4,4,4,4,4 解答:(1)(3)不存在,因为有奇数个奇度顶点。
14、设G 是(2)n n ≥阶无向简单图,G 是它的补图,已知12(),()G k G k δ∆==,求()G ∆,()G δ。
解答:2()1G n k ∆=--;1()1G n k δ=--。
15、图9.19中各对图是否同构?若同构,则给出它们顶点之间的双射函数。
解答:(c )不是同构,从点度既可以看出,一个点度序列为4,3,3,3,3而另外一个为4,4,3,3,1(d )同构,同构函数为12()345x a x bf x x c x d x e=⎧⎪=⎪⎪==⎨⎪=⎪=⎪⎩ 16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。
离散数学图论部分形成性考核书面作业4答案

离散数学作业4离散数学图论部分形成性考核书面作业本课程形成性考核书面作业共3次,内容主要分别是集合论部分、图论部分、数理逻辑部分的综合练习,基本上是按照考试的题型(除单项选择题外)安排练习题目,目的是通过综合性书面作业,使同学自己检验学习成果,找出掌握的薄弱知识点,重点复习,争取尽快掌握。
本次形考书面作业是第二次作业,大家要认真及时地完成图论部分的综合练习作业。
一、填空题1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是 15 .2.设给定图G (如右由图所示),则图G 的点割集是 {f} .3.设G 是一个图,结点集合为V ,边集合为E ,则 G 的结点 度数之和 等于边数的两倍.4.无向图G 存在欧拉回路,当且仅当G 连通且 等于出度 .5.设G=<V ,E >是具有n 个结点的简单图,若在G 中每一对结点度数之和大于等于 n-1 ,则在G 中存在一条汉密尔顿路.6.若图G=<V , E>中具有一条汉密尔顿回路,则对于结点集V 的每个非空子集S ,在G 中删除S 中的所有结点得到的连通分支数为W ,则S 中结点数|S|与W 满足的关系式为 W(G-V1) ≤∣V 1∣ .7.设完全图K n 有n 个结点(n ≥2),m 条边,当 n 为奇数 时,K n中存在欧拉回路.8.结点数v 与边数e 满足 e=v-1 关系的无向连通图就是树.9.设图G 是有6个结点的连通图,结点的总度数为18,则可从G 中删去 4 条边后使之变成树.10.设正则5叉树的树叶数为17,则分支数为i = 5 .二、判断说明题(判断下列各题,并说明理由.)1.如果图G 是无向图,且其结点度数均为偶数,则图G 存在一条欧拉回路..姓 名: 学 号: 得 分: 教师签名:(1) 不正确,缺了一个条件,图G应该是连通图,可以找出一个反例,比如图G是一个有孤立结点的图。
离散数学习题解答第6部分(图论)
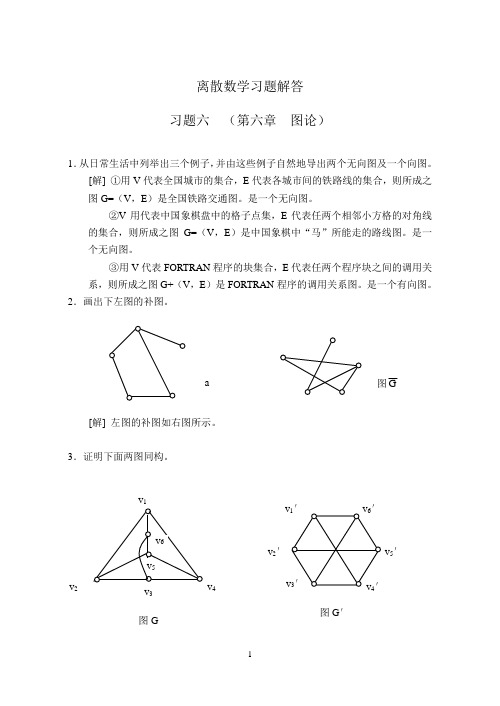
离散数学习题解答 习题六 (第六章 图论)1.从日常生活中列举出三个例子,并由这些例子自然地导出两个无向图及一个向图。
[解] ①用V 代表全国城市的集合,E 代表各城市间的铁路线的集合,则所成之图G=(V ,E )是全国铁路交通图。
是一个无向图。
②V 用代表中国象棋盘中的格子点集,E 代表任两个相邻小方格的对角线的集合,则所成之图G=(V ,E )是中国象棋中“马”所能走的路线图。
是一个无向图。
③用V 代表FORTRAN 程序的块集合,E 代表任两个程序块之间的调用关系,则所成之图G+(V ,E )是FORTRAN 程序的调用关系图。
是一个有向图。
2.画出下左图的补图。
[解] 左图的补图如右图所示。
3.证明下面两图同构。
a v 2 v 3 v 4图G图G ′[证] 存在双射函数ϕ:V →V ′及双射函数ψ : E →E ′ϕ (v 1)=v 1′ ϕ (v 1,v 2)=(v 1′,v 2′) ϕ (v 2)=v 2′ ϕ (v 2,v 3)=(v 2′,v 3′) ϕ (v 3)=v 3′ ϕ (v 3,v 4)=(v 3′,v 4′) ϕ (v 4)=v 4′ ϕ (v 4,v 5)=(v 4′,v 5) ϕ (v 5)=v 5′ ϕ (v 5,v 6)=(v 5′,v 6′) ϕ (v 6)=v 6′ϕ (v 6,v 1)=(v 6′,v 1′) ϕ (v 1,v 4)=(v 1′,v 4′) ϕ (v 2,v 5)=(v 2′,v 5′) ϕ (v 3,v 6)=(v 3′,v 6′)显然使下式成立:ψ (v i ,v j )=(v i ,v j ′)⇒ ϕ (v i )=v i ′∧ϕ (v j )=v j ′ (1≤i ·j ≤6) 于是图G 与图G ′同构。
4.证明(a ),(b )中的两个图都是不同构的。
图G 中有一个长度为4的圈v 1v 2v 6v 5v 1,其各顶点的度均为3点,而在图G ′中却没有这样的圈,因为它中的四个度为3的顶点v 1',v 5',v 7',v 3'不成长度的4的圈。
(图论)离散数学习题参考答案2
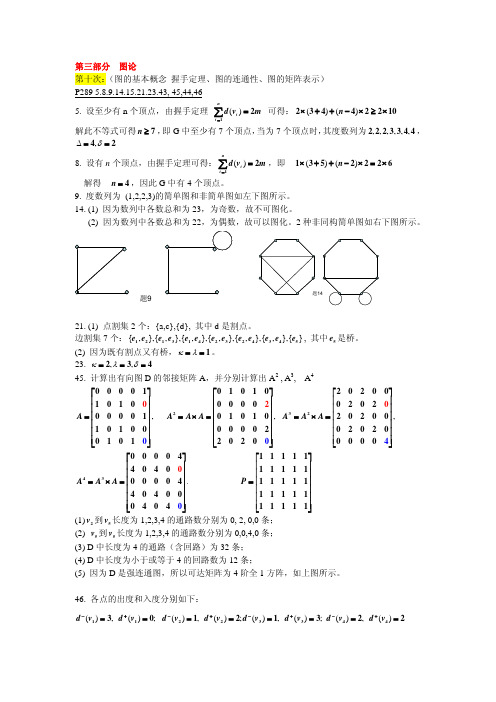
解此不等式可得 n ≥ 7 , 即 G 中至少有 7 个顶点, 当为 7 个顶点时, 其度数列为 2, 2, 2, 3, 3, 4, 4 , Δ = 4, δ = 2 8. 设有 n 个顶点,由握手定理可得: ∑ d (vi ) = 2m ,即
i =1 n
1 × (3 + 5) + (n − 2) × 2 = 2 × 6
d − (v1 ) = 3, d + (v1 ) = 0; d − (v2 ) = 1, d + (v2 ) = 2; d − (v3 ) = 1, d + (v3 ) = 3; d − (v4 ) = 2, d + (v4 ) = 2
第十一次: (欧拉图与哈密顿图)P305 1.2.11.21 (无向树及其性质)P318 2.24(a), 25(b) 1. (a),(c) 是欧拉图,因为它们均连通且都无奇度顶点; (b),(d)都不是欧拉图;因为(b) 不连通,(d) 既不连通又有奇度顶点;要使(b),(d)变为欧拉图 均至少加两条边,使其连通并且无奇度顶点。如下图所示。
(1) v2 到 v5 长度为 1,2,3,4 的通路数分别为 0, 2, 0,0 条; (2) v5 到 v5 长度为 1,2,3,4 的通路数分别为 0,0,4,0 条; (3) D 中长度为 4 的通路(含回路)为 32 条; (4) D 中长度为小于或等于 4 的回路数为 12 条; (5) 因为 D 是强连通图,所以可达矩阵为 4 阶全 1 方阵,如上图所示。 46. 各点的出度和入度分别如下:
(v2,12)** (v5, 7)*
根据上表的最后一行,从 v1 到其余各点的最短路径和距离如下: v1v2, d(v1,v2)=6 v1v2v6, d(v1,v6)=12 v1v3, d(v1,v3)=3 v1v3v4v5v7, d(v1,v7)=7 v1v3v4, d(v1,v4)=5 v1v3v4v5v7v8, d(v1,v8)=10 v1v3v4v5, d(v1,v5)=6
最新国家开放大学电大《离散数学(本)》期末题库及答案

最新国家开放大学电大《离散数学(本)》期末题库及答案考试说明:本人针对该科精心汇总了历年题库及答案,形成一个完整的题库,并且每年都在更新。
该题库对考生的复习、作业和考试起着非常重要的作用,会给您节省大量的时间。
做考题时,利用本文档中的查找工具,把考题中的关键字输到查找工具的查找内容框内,就可迅速查找到该题答案。
本文库还有其他网核及教学考一体化答案,敬请查看。
《离散数学》题库及答案一一、单项选择题(每小题3分,本题共15分)1.若集合A={a,b},B={ a,b,{ a,b }},则().A.A⊂B,且A∈B B.A∈B,但A⊄BC.A⊂B,但A∉B D.A⊄B,且A∉B2.集合A={1, 2, 3, 4, 5, 6, 7, 8}上的关系R={<x,y>|x+y=10且x, y∈A},则R的性质为().A.自反的B.对称的C.传递且对称的D.反自反且传递的3.如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有()个.A.0 B.2 C.1 D.34.如图一所示,以下说法正确的是( ) .A.{(a, e)}是割边B.{(a, e)}是边割集C.{(a, e) ,(b, c)}是边割集D.{(d, e)}是边割集图一5.设A(x):x是人,B(x):x是学生,则命题“不是所有人都是学生”可符号化为().A.(∀x)(A(x)∧B(x)) B.┐(∃x)(A(x)∧B(x))C.┐(∀x)(A(x) →B(x)) D.┐(∃x)(A(x)∧┐B(x))二、填空题(每小题3分,本题共15分)6.若集合A的元素个数为10,则其幂集的元素个数为.7.设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为.8.若A={1,2},R={<x, y>|x∈A, y∈A, x+y=10},则R的自反闭包为.9.结点数v与边数e满足关系的无向连通图就是树.10.设个体域D={a, b, c},则谓词公式(∀x)A(x)消去量词后的等值式为.三、逻辑公式翻译(每小题6分,本题共12分)11.将语句“尽管他接受了这个任务,但他没有完成好.”翻译成命题公式.12.将语句“今天没有下雨.”翻译成命题公式.四、判断说明题(每小题7分,本题共14分)判断下列各题正误,并说明理由.13.下面的推理是否正确,试予以说明.(1) (∀x)F(x)→G(x)前提引入(2) F(y)→G(y)US(1).14.若偏序集<A,R>的哈斯图如图二所示,则集合A的最大元为a,最小元不存在.图二五.计算题(每小题12分,本题共36分)15.求(P∨Q)→(R∨Q)的合取范式.16.设A={0,1,2,3,4},R={<x,y>|x∈A,y∈A且x+y<0},S={<x,y>|x∈A,y∈A且x+y≤3},试求R,S,R•S,R-1,S-1,r(R).17.画一棵带权为1, 2, 2, 3, 4的最优二叉树,计算它们的权.六、证明题(本题共8分)18.设G是一个n阶无向简单图,n是大于等于2的奇数.证明G与G中的奇数度顶点个数相等(G 是G的补图).试题解答一、单项选择题(每小题3分,本题共15分) 1.A 2.B 3.B 4.D 5.C 二、填空题(每小题3分,本题共15分) 6.1024 7.88.{<1,1>,<2,2>} 9.e=v -110.A (a ) ∧A (b )∧A (c )三、逻辑公式翻译(每小题6分,本题共12分)11.设P :他接受了这个任务,Q :他完成好了这个任务, (2分)P ∧⌝ Q . (6分)12.设P :今天下雨, (2分)⌝ P . (6分)四、判断说明题(每小题7分,本题共14分)13.错误. (3分) (2)应为F (y )→G (x ),换名时,约束变元与自由变元不能混淆. (7分) 14.错误. (3分) 集合A 的最大元不存在,a 是极大元. (7分) 五.计算题(每小题12分,本题共36分)15.(P ∨Q )→(R ∨Q )⇔⌝(P ∨Q )∨(R ∨Q ) (4分) ⇔(⌝P ∧⌝Q )∨(R ∨Q )⇔(⌝P ∨R ∨Q )∧(⌝Q ∨R ∨Q )⇔(⌝P ∨R ∨Q ) ∧R 合取范式 (12分) 16.R =∅, (2分) S ={<0,0>,<0,1>,<0,2>,<0,3>,<1,0>,<1,1>,<1,2>,<2,0>,<2,1>,<3,0>} (4分) R •S =∅, (6分)R -1=∅, (8分) S -1= S , (10分) r (R )=I A . (12分) 17.(10分)权为1⨯3+2⨯3+2⨯2+3⨯2+4⨯2=27 (12分)六、证明题(本题共8分)18.证明:因为n 是奇数,所以n 阶完全图每个顶点度数为偶数, (3分) 因此,若G 中顶点v 的度数为奇数,则在G 中v 的度数一定也是奇数, (6分)ο οο ο ο ο ο ο ο 1 2 23 34 75 12所以G 与G 中的奇数度顶点个数相等. (8分)《离散数学》题库及答案二一、单项选择题(每小题3分,本题共15分)1.若集合A ={1,{2},{1,2}},则下列表述正确的是( ). A .2⊂A B .{1}⊂AC .1∉AD .2 ∈ A2.已知一棵无向树T 中有8个顶点,4度、3度、2度的分支点各一个,T 的树叶数为( ). A .6 B .4 C .3 D .53.设无向图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101110011000011100111110 则G 的边数为( ). A .1 B .7 C .6 D .144.设集合A ={a },则A 的幂集为( ).A .{{a }}B .{a ,{a }}C .{∅,{a }}D .{∅,a }5.下列公式中 ( )为永真式.A .⌝A ∧⌝B ↔ ⌝A ∨⌝B B .⌝A ∧⌝B ↔ ⌝(A ∨B )C .⌝A ∧⌝B ↔ A ∨BD .⌝A ∧⌝B ↔ ⌝(A ∧B )二、填空题(每小题3分,本题共15分)6.命题公式P P ⌝∧的真值是 . 7.若无向树T 有5个结点,则T 的边数为 .8.设正则m 叉树的树叶数为t ,分支数为i ,则(m -1)i = .9.设集合A ={1,2}上的关系R ={<1, 1>,<1, 2>},则在R 中仅需加一个元素 ,就可使新得到的关系为对称的.10.(∀x )(A (x )→B (x ,z )∨C (y ))中的自由变元有 .三、逻辑公式翻译(每小题6分,本题共12分)11.将语句“今天上课.”翻译成命题公式.12.将语句“他去操场锻炼,仅当他有时间.”翻译成命题公式.四、判断说明题(每小题7分,本题共14分)判断下列各题正误,并说明理由.13.设集合A={1,2},B={3,4},从A到B的关系为f={<1, 3>},则f是A到B的函数.14.设G是一个有4个结点10条边的连通图,则G为平面图.五.计算题(每小题12分,本题共36分)15.试求出(P∨Q)→(R∨Q)的析取范式.16.设A={{1}, 1, 2},B={1, {2}},试计算(1)(A∩B)(2)(A∪B)(3)A (A∩B).17.图G=<V, E>,其中V={ a, b, c, d },E={ (a, b), (a, c) , (a, d), (b, c), (b, d), (c, d)},对应边的权值依次为1、2、3、1、4及5,试(1)画出G的图形;(2)写出G的邻接矩阵;(3)求出G权最小的生成树及其权值.六、证明题(本题共8分)18.试证明:若R与S是集合A上的自反关系,则R∩S也是集合A上的自反关系.试题解答一、单项选择题(每小题3分,本题共15分)1.B 2.D 3.B 4.C 5.B二、填空题(每小题3分,本题共15分)6.假(或F,或0)7.48.t-19.<2, 1>10.z,y三、逻辑公式翻译(每小题6分,本题共12分)11.设P :今天上课, (2分) 则命题公式为:P . (6分) 12.设 P :他去操场锻炼,Q :他有时间, (2分) 则命题公式为:P →Q . (6分) 四、判断说明题(每小题7分,本题共14分)13.错误. (3分) 因为A 中元素2没有B 中元素与之对应,故f 不是A 到B 的函数. (7分) 14.错误. (3分) 不满足“设G 是一个有v 个结点e 条边的连通简单平面图,若v ≥3,则e ≤3v -6.” (7分)五.计算题(每小题12分,本题共36分)15.(P ∨Q )→(R ∨Q )⇔ ┐(P ∨Q )∨(R ∨Q ) (4分)⇔ (┐P ∧┐Q )∨(R ∨Q ) (8分)⇔ (┐P ∧┐Q )∨R ∨Q (析取范式) (12分)16.(1)(A ∩B )={1} (4分)(2)(A ∪B )={1, 2, {1}, {2}} (8分) (3) A -(A ∩B )={{1}, 1, 2} (12分)17.(1)G 的图形表示如图一所示:(3分)(2)邻接矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0111101111011110 (6分) (3)最小的生成树如图二中的粗线所示:图一 ο ο ο ο a b c d1 124 53 图二ο ο ο ο a b cd1 1 2453(10分)权为:1+1+3=5 (12分)六、证明题(本题共8分)18.证明:设∀x∈A,因为R自反,所以x R x,即< x, x>∈R;又因为S自反,所以x R x,即< x, x >∈S.(4分)即< x, x>∈R∩S (6分)故R∩S自反.(8分)《离散数学》题库及答案三一、单项选择题(每小题3分,本题共15分)1.若集合A={ a,{a}},则下列表述正确的是( ).A.{a}⊆A B.{{{a}}}⊆AC.{a,{a}}∈A D.∅∈A2.命题公式(P∨Q)的合取范式是( )A.(P∧Q)B.(P∧Q)∨(P∨Q)C.(P∨Q)D.⌝(⌝P∧⌝Q)3.无向树T有8个结点,则T的边数为( ).A.6 B.7 C.8 D.9 4.图G如图一所示,以下说法正确的是( ).A.a是割点B.{b,c}是点割集C.{b, d}是点割集D.{c}是点割集图一5.下列公式成立的为( ).A.⌝P∧⌝Q ⇔P∨Q B.P→⌝Q⇔⌝P→QC.Q→P⇒ P D.⌝P∧(P∨Q)⇒Q二、填空题(每小题3分,本题共15分)6.设集合A ={2, 3, 4},B ={1, 2, 3, 4},R 是A 到B 的二元关系,},{y x B y A x y x R ≤∈∈><=且且则R 的有序对集合为 .7.如果R 是非空集合A 上的等价关系,a ∈A ,b ∈A ,则可推知R 中至少包含 等元素. 8.设G =<V , E >是有4个结点,8条边的无向连通图,则从G 中删去 条边,可以确定图G 的一棵生成树.9.设G 是具有n 个结点m 条边k 个面的连通平面图,则m 等于 10.设个体域D ={1, 2},A (x )为“x 大于1”,则谓词公式()()x A x ∃的真值为 三、逻辑公式翻译(每小题6分,本题共12分) 11.将语句“今天考试,明天放假.”翻译成命题公式. 12.将语句“我去旅游,仅当我有时间.”翻译成命题公式. 四、判断说明题(每小题7分,本题共14分)判断下列各题正误,并说明理由.13.如果图G 是无向图,且其结点度数均为偶数,则图G 是欧拉图.14.若偏序集<A ,R >的哈斯图如图二所示,则集合A 的最大元为a ,最小元是f .图二五.计算题(每小题12分,本题共36分)15.设谓词公式)),,()(),()((z x y B z y x A x ∀→∃,试(1)写出量词的辖域; (2)指出该公式的自由变元和约束变元. 16.设集合A ={{1},1,2},B ={1,{1,2}},试计算(1)(A -B ); (2)(A ∩B ); (3)A ×B .17.设G =<V ,E >,V ={ v 1,v 2,v 3,v 4 },E ={ (v 1,v 3),(v 2,v 3),(v 2,v 4),(v 3,v 4) },试 (1)给出G 的图形表示; (2)写出其邻接矩阵;(3)求出每个结点的度数; (4)画出其补图的图形. 六、证明题(本题共8分)18.设A ,B 是任意集合,试证明:若A ⨯A=B ⨯B ,则A=B .试题解答(供参考)一、单项选择题(每小题3分,本题共15分) 1.A 2.C 3.B 4.B 5.D 二、填空题(每小题3分,本题共15分)6.{<2, 2>,<2, 3>,<2, 4>,<3, 3>},<3, 4>,<4, 4>} 7.<a , a >,< b , b > 8.5 9.n +k -210.真(或T ,或1)三、逻辑公式翻译(每小题4分,本题共12分)11.设P :今天考试,Q :明天放假. (2分) 则命题公式为:P ∧Q . (6分)12.设P :我去旅游,Q :我有时间, (2分)则命题公式为:P →Q . (6分) 四、判断说明题(每小题7分,本题共14分)13.错误. (3分)当图G 不连通时图G 不为欧拉图. (7分) 14.错误. (3分) 集合A 的最大元与最小元不存在,a 是极大元,f 是极小元,. (7分) 五.计算题(每小题12分,本题共36分)15.(1)∃x 量词的辖域为)),,()(),((z x y B z y x A ∀→, (3分)∀z 量词的辖域为),,(z x y B , (6分) (2)自由变元为)),,()(),((z x y B z y x A ∀→中的y , (9分)约束变元为x 与z . (12分)16.(1)A -B ={{1},2} (4分)(2)A ∩B ={1} (8分) (3)A ×B={<{1},1>,<{1},{1,2}>,<1,1>,<1, {1,2}>,<2,1>,<2, {1,2}>} (12分) 17.(1)G 的图形表示为(如图三):(3分)图三 (2)邻接矩阵:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0110101111000100(6分) (3)v 1,v 2,v 3,v 4结点的度数依次为1,2,3,2 (9分) (4)补图如图四所示:(12分)图四六、证明题(本题共8分)18.证明:设x ∈A ,则<x ,x >∈A ⨯A , (1分) 因为A ⨯A=B ⨯B ,故<x ,x >∈B ⨯B ,则有x ∈B , (3分) 所以A ⊆B . (5分) 设x ∈B ,则<x ,x >∈B ⨯B , (6分) 因为A ⨯A=B ⨯B ,故<x ,x >∈A ⨯A ,则有x ∈A ,所以B ⊆A . (7分) 故得A=B . (8分)《离散数学》题库及答案四一、单项选择题(每小题3分,本题共15分)二、填空题(每小题3分,本题共15分)三、逻辑公式翻译(每小题6分,本题共12分)11.将语句“如果他掌握了计算机的用法,那么他就能完成这项工作.”翻译成命题公式.12.将语句“前天下雨,昨天还是下雨.”翻译成命题公式.四、判断说明题(判断各题正误,并说明理由.每小题7分,本题共14分)五、计算题(每小题12分,本题共36分)六、证明题(本题共8分)试题答案《离散数学》题库及答案五一、单项选择题(每小题3分,本题共15分)试题及答案《离散数学》题库及答案六一、单项选择题(每小题3分,本题共15分)二、填空题(每小题3分,本题共15分)三、逻辑公式翻译(每小题6分,本题共12分)11.将语句“昨天下雨”翻译成命题公式.12.将语句“小王今天上午或者去看电影或者去打球”翻译成命题公式.四、判断说明题(判断各题正误,并说明理由.每小题7分,本题共14分)五、计算题(每小题12分,本题共36分)六、证明题(本题共8分)试题答案及评分标准(供参考)。
电大 离散数学 形成性考核册 作业(三)答案

离散数学形成性考核作业〔三〕集合论与图论综合练习本课程形成性考核作业共4次,内容由中心电大确定、统一布置。
本次形考作业是第三次作业,大伙儿要认真及时地完成图论局部的形考作业,字迹工整,抄写题目,解答题有解答过程。
一、单项选择题1.假设集合A ={2,a ,{a },4},那么以下表述正确的选项是(B). A .{a ,{a }}∈A B .{a }⊆A C .{2}∈A D .∅∈A2.设B ={{2},3,4,2},那么以下命题中错误的选项是〔B 〕.A .{2}∈B B .{2,{2},3,4}⊂BC .{2}⊂BD .{2,{2}}⊂B3.假设集合A ={a ,b ,{1,2}},B ={1,2},那么〔B 〕. A .B ⊂A ,且B ∈A B .B ∈A ,但B ⊄A C .B ⊂A ,但B ∉A D .B ⊄A ,且B ∉A4.设集合A ={1,a },那么P (A )=(C). A .{{1},{a }}B .{∅,{1},{a }}C .{∅,{1},{a },{1,a }}D .{{1},{a },{1,a }}5.设集合A ={1,2,3,4,5,6}上的二元关系R ={<a ,b >⎢a ,b ∈A ,且a +b =8},那么R 具有的性质为〔B 〕. A .自反的B .对称的C .对称和传递的D .反自反和传递的6.设集合A ={1,2,3,4,5},B ={1,2,3},R 从A 到B 的二元关系,R ={<a ,b >⎢a ∈A ,b ∈B 且1=-b a } 那么R 具有的性质为〔〕.A .自反的B .对称的C .传递的D .反自反的[注重]:此题有误!自反性、反自反性、对称性、反对称性以及传递性指 某一个集合上的二元关系的性质。
7.设集合A ={1,2,3,4}上的二元关系R ={<1,1>,<2,2>,<2,3>,<4,4>},S ={<1,1>,<2,2>,<2,3>,<3,2>,<4,4>}, 那么S 是R 的〔C 〕闭包.A .自反B .传递C .对称D .以上都不对8.非空集合A 上的二元关系R ,满足(A),那么称R 是等价关系. A .自反性,对称性和传递性B .反自反性,对称性和传递性 C .反自反性,反对称性和传递性 D .自反性,反对称性和传递性9.设集合A ={a ,b },那么A 上的二元关系R={<a ,a >,<b ,b >}是A 上的(C)关系.A .是等价关系但不是偏序关系B .是偏序关系但不是等价关系C .既是等价关系又是偏序关系D .不是等价关系也不是偏序关系10.设集合A ={1,2,3,4,5}上的偏序关系的哈斯图如右图所示,假设A 的子集B ={3,4,5}, 那么元素3为B 的〔C 〕.A .下界B .最大下界C .最小上界D .以上答案都不对11.设函数f :R →R ,f (a )=2a +1;g :R →R ,g (a )=a 2.那么〔C 〕有反函数. A .g •f B .f •g C .f D .g12.设图G 的邻接矩阵为 那么G 的边数为(D). A .5B .6C .3D .413.以下数组中,能构成无向图的度数列的数组是(C). A .(1,1,2,3)B .(1,2,3,4,5)C .(2,2,2,2)D .(1,3,3) 14.设图G =<V ,E >,那么以下结论成立的是(C). A .deg(V )=2∣E ∣B .deg(V )=∣E ∣C .E v Vv 2)deg(=∑∈D .E v Vv =∑∈)deg(解;C 为握手定理。
离散数学及其应用图论部分课后习题答案
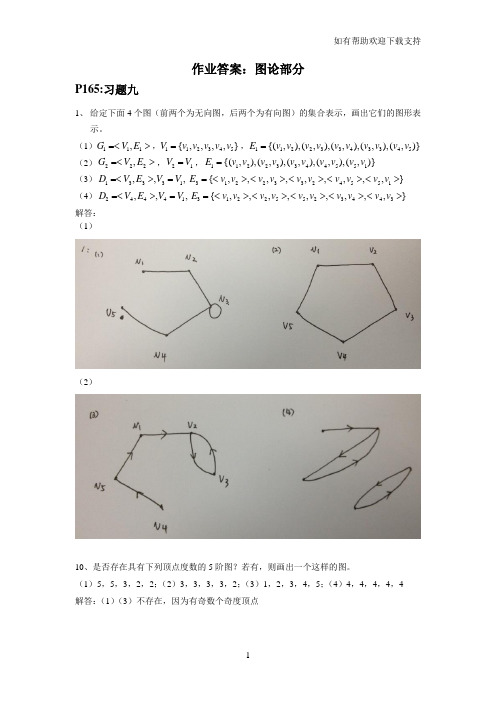
(2)构成了回路,但是不为简单回路和初级回路,因为有重复的边
(3)构成了初级通路,因为点不重复;
(4)不构成通路,因为边 不存在;
(5)构成通路,但是不为简单通路和初级通路,因为有重复的边
(6)构成了回路,但是不为简单回路和初级回路,因为有重复的边
(7)构成了初级通路;
(8)简单通路,但是不为初级通路,有重复边。
23、用Dijkstra标号法求图9.22中各图从顶点 到其余各点的最短路径和距离。
解答
步骤
1
2
3
4
5
6
7பைடு நூலகம்
到 最短路为 ,路长为6;
到 最短路为 ,路长为3;
到 最短路为 ,路长为5;
到 最短路为 ,路长为6;
到 最短路为 ,路长为12;
到 最短路为 ,路长为7;
那么对于n阶m条边的无向图G是 棵树组成的森林,在任意两棵树中分别找一点进行连一条边,那么得到的图则为n阶m+1条边的无向图G是 棵树组成的森林,
那么 ,所以 。
方法二:设 棵树中,分别有 个顶点和 条边, ,则有
, , ,即可得证。
19、求图10.17中两个带权图的最小生成树。
解答:
P204:习题十一
16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。
解答:
(1)三条边一共提供6度;所以点度序列可能是
①3,3,0,0,0,0;②3,2,1,0,0,0;③3,1,1,1,0,0;④2,2,2,0,0,0;⑤2,2,1,1,0,0;⑥2,1,1,1,1,0;⑦1,1,1,1,1,1;
由于是简单图,①②两种情形不可能
离散数学图论部分综合练习及答案

则对于结点集 V 的每个非空子集 S,在 G 中删除 S
中的所有结点得到的连通分支数为 W,则 S 中结点
数|S|与 W 满足的关系式为
.
4.无向图 G 存在欧拉回路,当且仅当 G 连通
且 每个节点的度数为偶数
.
fο
οc
eο οd
图四
5.设有向图 D 为欧拉图,则图 D 中每个结点的入度
.
应该填写:等于出度
3.解:图G是平面图. 因为只要把结点 v2 与 v6 的连线(v2, v6)拽 到结点 v1 的外面,把把结点 v3 与 v6 的连线 (v3, v6)拽到结点 v4, v5 的外面,就得到一个平 面图,如图九所示.
v1ο v6 ο
ο v5
οv2 ο v3
οv4
图九
4.解:错误. 不满足“设 G 是一个有 v 个结点 e 条边的连通简单平面图,若 v≥3,则 e ≤3v-6.”
方法(Huffman):从 2,3,5,7,11,13,17
,19,23,29,31 中选 2,3 为最低层结点,并
1ο60
从权数中删去,再添上他们的和数,即 5,5,7,11,13,17,19,23,29,31;
再从 5,5,7,11,13,17,19,23,29,31 中选 5,5 为倒数第 2 层结点,并从上述数列中 删去,再添上他们的和数,即 7,10,11,13, 17,19,23,29,31;
8.设完全图 K n 有 n 个结点(n≥2),m 条边,当( C )时,K n 中存在欧 拉回路.
A.m 为奇数
B.n 为偶数
C.n 为奇数
D.m 为偶数
9.设 G 是连通平面图,有 v 个结点,e 条边,r 个面,则 r= ( A ).
最新国开电大《离散数学》形考任务1-4作业及答案

形考任务一至四题目随机抽题,可用快捷方式Ctrl+F查询,查询技巧:以“中文字”作为关键字查询,不建议以“英文、公式、符号”为关键字查询。
复制(Ctrl+C)题目,粘贴(Ctrl+V)形考任务一若集合A={2,a,{ a },4},则下列表述正确的是( ).选择一项:A. {a,{ a }} AB. {2} AC. { a } AD. A反馈正确答案是:{ a } A若集合A的元素个数为10,则其幂集的元素个数为().A. 100B. 1C. 1024D. 10反馈正确答案是:1024设A={1, 2, 3, 4, 5, 6, 7, 8},R是A上的整除关系,B={2, 4, 6},则集合B的最大元、最小元、上界、下界依次为( ).选择一项:选择一项:A. 极大元B. 最小元C. 极小元D. 最大元反馈正确答案是:极大元设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为().选择一项:A. 3B. 6C. 8D. 2反馈正确答案是:8设集合A={1, 2, 3},B={3, 4, 5},C={5, 6, 7},则A∪B–C =( ).选择一项:A. {1, 2, 3, 5}B. {2, 3, 4, 5}C. {4, 5, 6, 7}D. {1, 2, 3, 4}反馈正确答案是:{1, 2, 3, 4}设集合A={2, 4, 6, 8},B={1, 3, 5, 7},A到B的关系R={<x, y>| y = x +1},则R= ( ).选择一项:正确答案是:对称的设集合A={1,2,3,4,5},偏序关系是A上的整除关系,则偏序集<A,>上的元素5是集合A的().选择一项:A. 极小元B. 极大元C. 最小元D. 最大元反馈正确答案是:极大元设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为().选择一项:A. 3B. 8C. 2D. 6反馈正确答案是:8若集合A的元素个数为10,则其幂集的元素个数为().选择一项:A. 1B. 100C. 10D. 1024反馈正确答案是:1024如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有()个.B. 1C. 3D. 2反馈正确答案是:2设集合A={1 , 2 , 3 , 4}上的二元关系R={<1, 1>,<2, 2>,<2, 3>,<4, 4>},S={<1, 1>,<2, 2>,<2, 3>,<3, 2>,<4, 4>},则S是R的()闭包.选择一项:A. 传递B. 对称C. 自反和传递D. 自反反馈正确答案是:对称设A={a,b},B={1,2},C={4,5},从A到B的函数f={<a,1>, <b,2>},从B到C的函数g={<1,5>, <2,4>},则下列表述正确的是().选择一项:A. f°g ={<5,a >, <4,b >}B. f°g ={<a,5>, <b,4>}C. g° f ={<a,5>, <b,4>}D. g° f ={<5,a >, <4,b >}反馈正确答案是:g° f ={<a,5>, <b,4>}设函数f:N→N,f(n)=n+1,下列表述正确的是().选择一项:A. f是双射的B. f是满射的C. f是单射函数D. f存在反函数反馈正确答案是:f是单射函数若集合A={ a,{a},{1,2}},则下列表述正确的是().B. {1,2} AC. {a,{a}} AD. {a} A反馈正确答案是:{a} A若集合A={2,a,{ a },4},则下列表述正确的是( ).选择一项:A. AB. {2} AC. {a,{ a }} AD. { a } A反馈正确答案是:{ a } A若集合A的元素个数为10,则其幂集的元素个数为().A. 1B. 10C. 1024D. 100反馈正确答案是:1024设A、B是两个任意集合,则A-B = ( ).选择一项:A. A BC. B =D. A B反馈正确答案是:A B设集合A={a},则A的幂集为( ).选择一项:C. {,a}正确答案是:{,{a}}设A、B是两个任意集合,则A-B = ( ).选择一项:A. A BC. B =D. A B反馈正确答案是:A B设集合A = {1, 2, 3, 4, 5}上的偏序关系的哈斯图如图所示,若A的子集B = {3, 4, 5},则元素3为B的().选择一项:A. 最小上界B. 下界C. 最小元D. 最大下界反馈正确答案是:最小上界设集合A = {1, a },则P(A) = ( ).选择一项:A. {,{1}, {a}, {1, a }}B. {,{1}, {a}}反馈正确答案是:{,{1}, {a}, {1, a }}设集合A={2, 4, 6, 8},B={1, 3, 5, 7},A到B的关系R={<x, y>| y = x +1},则R= ( ).正确答案是:{<2, 3>, <4, 5>, <6, 7>}集合A={1, 2, 3, 4}上的关系R={<x,y>|x=y且x, y A},则R的性质为().选择一项:A. 不是自反的B. 传递的C. 反自反D. 不是对称的反馈正确答案是:传递的设A={1, 2, 3, 4, 5, 6, 7, 8},R是A上的整除关系,B={2, 4, 6},则集合B的最大元、最小元、上界、下界依次为( ).选择一项:A. 8、2、8、2B. 无、2、无、2C. 6、2、6、2D. 8、1、6、1反馈正确答案是:无、2、无、2设集合A ={1 , 2, 3}上的函数分别为:f = {<1, 2>,<2, 1>,<3, 3>},g = {<1, 3>,<2, 2>,<3, 2>},h = {<1, 3>,<2, 1>,<3, 1>},则h =().选择一项:A. g◦gC. f◦gD. g◦f反馈正确答案是:f◦g若集合A={ a,{a},{1,2}},则下列表述正确的是().选择一项:A. {1,2} AB. {a,{a}} AC. AD. {a} A反馈正确答案是:{a} A若集合A={1,2},B={1,2,{1,2}},则下列表述正确的是( ).选择一项:A. A B,且A BB. A B,且A BC. A B,且A BD. B A,且A B反馈正确答案是:A B,且A B集合A={1, 2, 3, 4, 5, 6, 7, 8}上的关系R={<x,y>|x+y=10且x, y A},则R的性质为().选择一项:A. 传递且对称的B. 自反的C. 反自反且传递的D. 对称的反馈正确答案是:对称的设A={a,b},B={1,2},C={4,5},从A到B的函数f={<a,1>, <b,2>},从B到C的函数g={<1,5>, <2,4>},则下列表述正确的是().选择一项:A. f°g ={<5,a >, <4,b >}C. g° f ={<5,a >, <4,b >}D. g° f ={<a,5>, <b,4>}反馈正确答案是:g° f ={<a,5>, <b,4>}设函数f:N→N,f(n)=n+1,下列表述正确的是().选择一项:A. f是满射的B. f是双射的C. f存在反函数D. f是单射函数反馈正确答案是:f是单射函数设集合A={1, 2, 3},B={3, 4, 5},C={5, 6, 7},则A∪B–C =( ).选择一项:A. {4, 5, 6, 7}B. {1, 2, 3, 5}C. {1, 2, 3, 4}D. {2, 3, 4, 5}反馈正确答案是:{1, 2, 3, 4}设集合A={a},则A的幂集为( ).选择一项:B. {,a}D. {,{a}}反馈正确答案是:{,{a}}集合A={1, 2, 3, 4}上的关系R={<x,y>|x=y且x, y A},则R的性质为().选择一项:A. 传递的C. 不是自反的D. 反自反反馈正确答案是:传递的设A={1, 2, 3, 4, 5, 6, 7, 8},R是A上的整除关系,B={2, 4, 6},则集合B的最大元、最小元、上界、下界依次为( ).选择一项:正确答案是:无、2、无、2设集合A={1,2,3,4,5},偏序关系是A上的整除关系,则偏序集<A,>上的元素5是集合A的().选择一项:A. 最大元B. 极大元C. 最小元D. 极小元反馈正确答案是:极大元设集合A = {1, a },则P(A) = ( ).选择一项:A. {,{1}, {a}}B. {,{1}, {a}, {1, a }}正确答案是:{,{1}, {a}, {1, a }}如果R和R是A上的自反关系,则R∪R,R∩R,R-R中自反关系有()个.A. 3C. 2D. 1反馈正确答案是:2设集合A={1 , 2 , 3 , 4}上的二元关系R={<1, 1>,<2, 2>,<2, 3>,<4, 4>},S={<1, 1>,<2, 2>,<2, 3>,<3, 2>,<4, 4>},则S是R的()闭包.选择一项:A. 自反和传递B. 传递C. 对称D. 自反反馈正确答案是:对称设函数f:N→N,f(n)=n+1,下列表述正确的是().选择一项:A. f是双射的B. f是单射函数C. f存在反函数D. f是满射的反馈正确答案是:f是单射函数若集合A={1,2},B={1,2,{1,2}},则下列表述正确的是( ).选择一项:A. A B,且A BB. A B,且A BC. B A,且A BD. A B,且A B反馈正确答案是:A B,且A B若集合A={2,a,{ a },4},则下列表述正确的是( ).选择一项:A. {a,{ a }} AC. AD. {2} A反馈正确答案是:{ a } A设集合A={2, 4, 6, 8},B={1, 3, 5, 7},A到B的关系R={<x, y>| y = x +1},则R= ( ).A. {<2, 1>, <4, 3>, <6, 5>}B. {<2, 2>, <3, 3>, <4, 6>}C. {<2, 3>, <4, 5>, <6, 7>}D. {<2, 1>, <3, 2>, <4, 3>}反馈正确答案是:{<2, 3>, <4, 5>, <6, 7>}如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有()个.选择一项:A. 0B. 1C. 3D. 2反馈正确答案是:2设集合A ={1 , 2, 3}上的函数分别为:f = {<1, 2>,<2, 1>,<3, 3>},g = {<1, 3>,<2, 2>,<3, 2>},h = {<1, 3>,<2, 1>,<3, 1>},则h =().选择一项:A. g◦fB. f◦fC. g◦gD. f◦g反馈正确答案是:f◦g设集合A={1, 2, 3},B={2, 3, 4},C={3, 4, 5},则A∩(C-B )= {1, 2, 3, 5}.()选择一项:错反馈正确的答案是“错”。
《离散数学》图论部分习题

《离散数学》图论部分习题《离散数学》图论部分习题1.已知⽆向图G有12条边,6个3度顶点,其余顶点的度数均⼩于3,问G⾄少有⼏个顶点?并画出满⾜条件的⼀个图形. (24-3*6)/2 +6=92.是否存在7阶⽆向简单图G,其度序列为1、3、3、4、6、6、7.给出相应证明.不存在;7阶⽆向简单图G中最⼤度≤63.设d1、d2、…、d n为n个互不相同的正整数. 证明:不存在以d1、d2、…、d n为度序列的⽆向简单图.Max{d1,d2,…,dn}≥n,n阶⽆向简单图G中最⼤度≤n-14.求下图的补图.5.1)试画⼀个具有5个顶点的⾃补图2)是否存在具有6个顶点的⾃补图,试说明理由。
对于n阶图,原图与其补图同构,边数应相等,均为(n*(n-1)/2)/2,即n*(n-1)/4且为整数,n=4k或n=4k+1,不存在6阶⾃补图。
6.设图G为n(n>2且为奇数)阶⽆向简单图,证明:G与G的补图中奇度顶点个数相等.n(n>2且为奇数),奇度点成对出现7.⽆向图G中只有2个奇度顶点u和v,u与v是否⼀定连通.给出说明或证明。
只有2个奇度顶点u和v,如果不连通,在u和v在2个连通分⽀上,每个分⽀上仅有⼀个奇度顶点,与握⼿引理相⽭盾。
8.图G如下图所⽰:1)写出上图的⼀个⽣成⼦图.2)δ(G),κ(G),λ(G).δ(G)=2,κ(G)=1,λ(G)=2.说明:δ(G)=min{ d(v) | v V } ;κ(G)=min{ |V’| |V’是图G的点割集} ;λ(G)=min{ |E’| |E’是图G的边割集} 9.在什么条件下⽆向完全图K n为欧拉图?n为奇数时10.证明:有桥的图不是欧拉图.假设是欧拉图:桥的端点是u和v,并且图各顶点度均为偶数;桥为割边,删除桥,图不再连通,u和v应该在2各不同的连通分⽀上;且u和v度数变为奇数;由于其他顶点度数均为偶数,则u和v所在的连通分⽀上只有⼀个奇度顶点,与握⼿引理⽭盾。
离散数学习题集及答案第6-7章图论含答案

第6-7章一.选择/填空1、设图G 的邻接矩阵为0101010010000011100000100,则G 的边数为( D ). A .5 B .6 C .3 D .42、设有向图(a )、(b )、(c )与(d )如下图所示,则下列结论成立的是( A ).A .(a )是强连通的B .(b )是强连通的C .(c )是强连通的D .(d )是强连通的3、给定无向图G 如下图所示,下面给出的结点集子集中,不是点割集的为( B ).A .{b , d }B .{d }C .{a , c }D .{b , e }4、图G 如下图所示,以下说法正确的是 ( D ) .A .{(a , c )}是割边B .{(a , c )}是边割集C .{(b , c )}是边割集D .{(a, c ) ,(b, c )}是边割集5、无向图G 存在欧拉通路,当且仅当(D ).A .G 中所有结点的度数全为偶数B .G 中至多有两个奇数度结点C .G 连通且所有结点的度数全为偶数D .G 连通且至多有两个奇数度结点6、设G 是有n 个结点,m 条边的连通图,必须删去G 的( A )条边,才能确定G 的一棵生成树.A .1m n −+B .m n −C .1m n ++D .1n m −+7、已知一棵无向树T 中有8个结点,4度,3度,2度的分支点各一个,T 的树叶数为(B ).A .8B .5C .4D .38、已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是 15 . 9、连通无向图G 有6个顶点9条边,从G 中删去 4 条边才有可能得到G 的一棵生成树T .10、如右图 相对于完全图K 5的补图为(A )。
11、给定无向图,如下图所示,下面哪个边集不是其边割集( B )。
A 、;B 、{<v1,v4>,<v4,v6>};C 、;D 、。
12、设D 是有n 个结点的有向完全图,则图D 的边数为( A ) (A))1(−n n (B))1(+n n (C)2/)1(+n n (D)2/)1(−n n 13、无向图G 是欧拉图,当且仅当( C )(A) G 的所有结点的度数都是偶数 (B)G 的所有结点的度数都是奇数(C)G 连通且所有结点的度数都是偶数 (D) G 连通且G 的所有结点度数都是奇数。
离散数学作业答案

离散数学作业5离散数学图论部分形成性考核书面作业 本课程形成性考核书面作业共3次,内容主要分别是集合论部分、图论部分、数理逻辑部分的综合练习,基本上是按照考试的题型(除单项选择题外)安排练习题目,目的是通过综合性书面作业,使同学自己检验学习成果,找出掌握的薄弱知识点,重点复习,争取尽快掌握。
本次形考书面作业是第二次作业,大家要认真及时地完成图论部分的综合练习作业。
要求:将此作业用A4纸打印出来,手工书写答题,字迹工整,解答题要有解答过程,要求本学期第15周末前完成并上交任课教师(不收电子稿)。
并在05任务界面下方点击“保存”和“交卷”按钮,以便教师评分。
一、填空题1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是15. 2.设给定图G (如右由图所示),则图G 的点割集是{f}.3.设G 是一个图,结点集合为V ,边集合为E ,则G 的结点度数之和等于边数的两倍.4.无向图G 存在欧拉回路,当且仅当G 连通且等于出度.5.设G=<V ,E >是具有n 个结点的简单图,若在G 中每一对结点度数之和大于等于n-1,则在G 中存在一条汉密尔顿路.6.若图G=<V ,E>中具有一条汉密尔顿回路,则对于结点集V 的每个非空子集S ,在G 中删除S 中的所有结点得到的连通分支数为W ,则S 中结点数|S|与W 满足的关系式为W ?|S|.7.设完全图K n 有n 个结点(n ?2),m 条边,当n 为奇数时,K n 中存在欧拉回路.8.结点数v 与边数e 满足e=v -1关系的无向连通图就是树.9.设图G 是有6个结点的连通图,结点的总度数为18,则可从G 中删去 4条边后使之变成树.10.设正则5叉树的树叶数为17,则分支数为i =5.二、判断说明题(判断下列各题,并说明理由.)1.如果图G 是无向图,且其结点度数均为偶数,则图G 存在一条欧拉回路.. 错。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学作业5
离散数学图论部分形成性考核书面作业
本课程形成性考核书面作业共3次,内容主要分别是集合论部分、图论部分、数理逻辑部分的综合练习,基本上是按照考试的题型(除单项选择题外)安排练习题目,目的是通过综合性书面作业,使同学自己检验学习成果,找出掌握的薄弱知识点,重点复习,争取尽快掌握。
本次形考书面作业是第二次作业,大家要认真及时地完成图论部分的综合练习作业。
要求:将此作业用A4纸打印出来,手工书写答题,字迹工整,解答题要有解答过程,要求2018年12月5日前完成并上交任课教师(不收电子稿)。
并在05任务界面下方点击“保存”和“交卷”按钮,以便教师评分。
一、填空题
1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是15.
2.设给定图G (如右由图所示),则图G 的点割集是 {f}.
3.设G 是一个图,结点集合为V ,边集合为E ,则 G 的结点度数之和等于边数的两倍.
4.无向图G 存在欧拉回路,当且仅当G 连通且等于出度.
5.设G=<V ,E >是具有n 个结点的简单图,若在G 中每一对结点度数之和大于等于n-1,则在G 中存在一条汉密尔顿路.
6.若图G=<V ,E>中具有一条汉密尔顿回路,则对于结点集V 的每个非空子集S ,在G 中删除S 中的所有结点得到的连通分支数为W ,则S 中结点数|S|与W 满足的关系式为W(G-V1)≤∣V 1∣.
7.设完全图K n 有n 个结点(n ≥2),m 条边,当n 为奇数时,K n 中存在欧拉回路.
8.结点数v 与边数e 满足e=v-1关系的无向连通图就是树.
9.设图G 是有6个结点的连通图,结点的总度数为18,则可从G 中删去 4条边后使之变成树.
10.设正则5叉树的树叶数为17,则分支数为i =5.
二、判断说明题(判断下列各题,并说明理由.)
1.如果图G 是无向图,且其结点度数均为偶数,则图G
存在一条欧拉回
路..
(1) 不正确,缺了一个条件,图G应该是连通图,可以找出一个反例,比如图G是一个有孤立结点的图。
2.如下图所示的图G存在一条欧拉回路.
(2) 不正确,图中有奇数度结点,所以不存在是欧拉回路。
3.如下图所示的图G不是欧拉图而是汉密尔顿图.
G
解:正确
因为图中结点a,b,d,f的度数都为奇数,所以不是欧拉图。
如果我们沿着(a,d,g,f,e,b,c,a),这样除起点和终点是a外,我们经过每个点一次仅一次,所以存在一条汉密尔顿回路,是汉密尔顿图
4.设G是一个有7个结点16条边的连通图,则G为平面图.
解:(1) 错误
假设图G是连通的平面图,根据定理,结点数v,边数为e,应满足e小于等于3v-6,但现在16小于等于3*7-6,显示不成立。
所以假设错误。
5.设G是一个连通平面图,且有6个结点11条边,则G有7个面.
(2) 正确
根据欧拉定理,有v-e+r=2,边数v=11,结点数e=6,代入公式求出面数
r=7
三、计算题
1.设G=<V,E>,V={ v1,v2,v3,v4,v5},E={ (v1,v3),(v2,v3),(v2,v4),(v3,v4),(v3,v5),(v4,v5) },试
(1) 给出G的图形表示; (2) 写出其邻接矩阵;
(3) 求出每个结点的度数; (4) 画出其补图的图形.
解:(1)
(2) 邻接矩阵为
⎪⎪⎪
⎪⎪⎪
⎭
⎫
⎝
⎛0110010110110110110000100
(3) v 1结点度数为1,v 2结点度数为2,v 3结点度数为3,v 4结点度数为2,v 5结点度数为2
(4) 补图图形为
2.图G =<V , E >,其中V ={ a , b , c ,d ,e },E ={ (a , b ), (a , c ), (a , e ), (b , d ),(b , e ), (c , e ), (c , d ), (d , e ) },对应边的权值依次为2、1、2、3、6、1、4及5,试
(1)画出G 的图形; (2)写出G 的邻接矩阵; (3)求出G 权最小的生成树及其权值.
(1)G 的图形如下:
ο
ο ο ο v 1
ο v 5
v 2 v 3 v 4
ο
ο ο ο v 1 ο
v 5
v 2 v 3
v 4
(2)写出G的邻接矩阵
(3)G权最小的生成树及其权值
3.已知带权图G如右图所示.
(1) 求图G的最小生成树; (2)计算该生成树的权值.解:(1) 最小生成树为
(2) 该生成树的权值为(1+2+3+5+7)=18
4.设有一组权为2,3,5,7,17,31,试画出相应的最优二叉树,计算该最优二叉树的权.
3
5
2
5
1
7
17
31
1
3
61
2
3
5
7
权为 2*5+3*5+5*4+7*3+17*2+31=131
四、证明题
1.设G 是一个n 阶无向简单图,n 是大于等于3的奇数.证明图G 与它的补图G 中的奇数度顶点个数相等.
证明:设,G V E =<>,,G V E '=<>.则E '是由n 阶无向完全图n K 的边删去E 所得到的.所以对于任意结点u V ∈,u 在G 和G 中的度数之和等于u 在n K 中的度数.由于n 是大于等于3的奇数,从而n K 的每个结点都是偶数度的( 1 (2)n -≥度),于是若u V ∈在G 中是奇数度结点,则它在G 中也是奇数度结点.故图G 与它的补图G 中的奇数度结点个数相等.
2.设连通图G 有k 个奇数度的结点,证明在图G 中至少要添加2
k
条边才能使其成为欧拉图.
证明:由定理3.1.2,任何图中度数为奇数的结点必是偶数,可知k 是偶数.
又根据定理4.1.1的推论,图G 是欧拉图的充分必要条件是图G 不含奇数度结点.因此只要在每对奇数度结点之间各加一条边,使图G 的所有结点的度数变为偶数,成为欧拉图.
故最少要加2
k
条边到图G 才能使其成为欧拉图.。
