铁路公路坐标计算方法
中线逐桩坐标的计算

YO YZY R sin(ZY JD k 90)
注:曲线右偏时K值取“+1”;曲线左偏 时取“-”1;
3.计算全曲线上任意未知里程点 里程差: l DK P DK ZH
里程差所对应的圆心角 : l 180
R
计算
点坐标:
XP YP
X YO
O
y
m
(R
p
l3
0 240R
p)
2
R
c
osβ
p
l2 0
24R
的角度值等于角AOP的角度值
最终公式为:
P点坐标:
X P X ZH xP cos r kyP sin r
YP YZH xP sin r kyP cos r
已知直线A点坐标和直线方位角 以及直 线AB之间的距离 推算B点坐标:
XB X YB YA
A
d
d AB c AB sin
os AB
AB
二、 圆曲线逐桩坐标计算原理
1.ZY点与YZ点坐标计算
由已知条件和计算出的曲线要素 用极坐 标法求出ZY和YZ点坐标。
(1)ZY点坐标计算:
X ZY YZY
X JD YJD
T
T cos JDZY sin JDZY
(2) YZ点坐标计算:
X YZ X JD T cos JDYZ
YYZ YJD T sin JDYZ
2. 圆心O点坐标计算
XO X ZY R cos(ZY JD k 90)
铁路工程独立坐标系的选择与计算

铁路工程独立坐标系的选择与计算摘要:在铁路工程设计和建设阶段,各工程所处地理位置和环境不同,有的地形平坦,海拔较低,而中国西部大部分地形起伏较大,山脉纵横,为满足规范对于投影长度变形值的要求,必须针对施工地区地形条件和所处高斯投影带综合考虑,选择合适的投影面和中央子午线变得非常关键。
本文结合实例对独立坐标系建立方法进行了研究,供铁路施工技术人员参考。
关键词:铁路工程测量;独立坐标系;投影面;中央子午线一、引言铁路线路一般较长,经常会跨越不同的投影带,采用国家统一3°带高斯正形投影坐标系统时,投影带边缘的长度变形值不能满足铁路施工要求。
《铁路工程测量规范》等一系列规范都要求铁路在对应的线路轨面设计高程面上坐标系的投影长度变形值不宜大于25mm/km。
当测区位于地形起付较大的山区时,采用标准高斯正形投影坐标系不能满足规范要求,可采用投影于抵偿高程面上的高斯投影坐标系。
二、长度元素高程归化改正与高斯投影长度改化高斯投影为正形投影,椭球面上的角度在投影后不变,但长度产生了变形,长度变形来源于以下两个过程:1、实测边长化算到椭球面上时所产生的变形在导线测量中,实测边长D归化至参考椭球面上时,长度会缩短ΔD。
设归化高程为H,地球平均曲率半径为Rm,其近似关系为:2、椭球面上的长度投影到高斯平面时产生的变形归化至参考椭球面上的边长S,再投影到高斯平面时,其长度会被放大ΔS。
设该边两端的平均横坐标为ym,则有:4、地球平均曲率半径在实际计算时,应按照测区所处位置计算测区的地球平均曲率半径,地球平均曲率半径与所处位置的子午圈半径M和卯酉圈半径N有关,其关系式如下:式(4)三、独立坐标系的建立方法由上述可得出,对于一定的测区,Rm为定值,因此长度变形主要取决于测区横坐标值ym和归化高程Hm。
因此,在建立地方独立坐标系时,有以下常用的三种方法:1.高程面抵偿坐标系当线路基本南北走向,东西摆动在一定狭窄的范围内时,为保证投影长度变形值不超过该规定,可以采用抵偿高程面的高斯正形统一3°带平面直角坐标系,即抵偿坐标系。
铁路线形及其相关计算-精

铁路线形及其相关计算-精铁路线形及其相关计算1.线路线形的平⾯和竖⾯组成及其设计要素:直线、圆曲线和缓和曲线;坡段和竖曲线2. 线路平⾯和竖⾯的设计⽂件:3. 平⾯计算:任⼀⾥程处线路中线设计坐标的计算(缓和曲线和圆曲线上任意点的坐标⽅位⾓怎么算?)4. 竖⾯计算:任⼀⾥程处线路中线设计⾼程的计算(注意坡段上的点可能有平曲线,即可能有超⾼)5. 根据线路测点坐标计算测点⾥程2.4 设计线路中线上任意点平⾯坐标和⾼程计算⽅法线路测量,需在线路专业提供的设计线形的基础上,计算线路上⼀定间隔点(特征变化点)的平⾯坐标和⾼程,⽤于线路与线路测量的结果进⾏⽐较,以反映线路的品茶情况。
⾼速铁路中平曲线描述线路的平断⾯线形,由曲线和与之相切的直线组成,曲线分缓和曲线和圆曲线,在曲线上还需设置抵制离⼼⼒影响的超⾼值;竖曲线描述线路的纵断⾯线形,线路纵断⾯由竖曲线和与之相切的带坡度的直线组成,竖曲线采⽤圆曲线[13-14]。
2.4.1 线路任意点平⾯坐标计算⾼速铁路线路设计中,线路专业给出的线路平⾯设计⽂件主要有两类:⼀类是包括五⼤桩坐标以及圆曲线半径、缓和曲线长度与圆曲线处超⾼;另⼀类是包括交点坐标、圆曲线半径、缓和曲线长度、圆曲线处超⾼以及起点⾥程的设计⽂件,其中第⼆类设计⽂件更加简洁,如下表错误!⽂档中没有指定样式的⽂字。
-1所⽰,且第⼆类设计⽂件可通过计算曲线要素换算为第⼀类设计⽂件。
表错误!⽂档中没有指定样式的⽂字。
-1 某⾼速铁路平曲线部分第⼆类设计⽂件属性X(m) Y(m) 曲线半径(m)前缓长(m)后缓长(m)超⾼(mm)起始⾥程(m)QD 4414887.9736 469387.1201 2823.578 JD1 4415106.5310 470472.8130 3000 140 140 60JD2 4415240.7190 471594.4980 -2000 220 220 135JD3 4415091.0520 473528.4950 2500 350 350 150JD4 4410683.6980 478343.8110 -4500 600 600 160JD5 4411126.9070 483927.8110 -5500 700 700 165JD6 4407242.0780 488477.9600 8000 570 570 120由设计可知⾼速铁路平断⾯线形可分为直线段、缓和曲线段、圆曲线段等三种,平断⾯⽤图形可表⽰为如下图错误!⽂档中没有指定样式的⽂字。
铁路缓和曲线坐标计算方法 (0517)
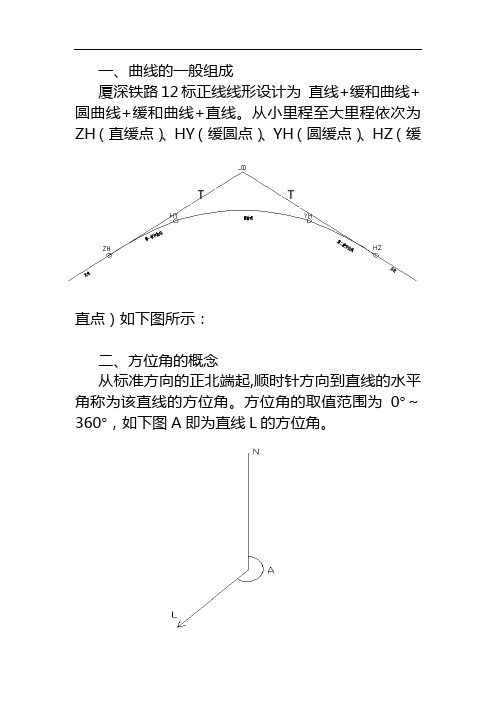
一、曲线的一般组成厦深铁路12标正线线形设计为 直线+缓和曲线+圆曲线+缓和曲线+直线。
从小里程至大里程依次为ZH (直缓点)、HY (缓圆点)、YH (圆缓点)、HZ (缓直点)如下图所示:二、方位角的概念从标准方向的正北端起,顺时针方向到直线的水平角称为该直线的方位角。
方位角的取值范围为0°~360°,如下图A 即为直线L 的方位角。
TT三、某点坐标的计算已知A 点坐标为(491548,2505452),B 点距离A 点L=125m ,直线AB 的方位角为235°,计算B 点坐标。
计算方法:Y=491548+125×SIN235=491445.606X=2505452+125×COS235=2505380.303四、曲线上任一点的坐标及切线方位角计算1 直线段上任一点的坐标及方位角直线上的坐标计算比较简单,只需要求出该点所在直线的方位角以及线路中的里程即可求得例1,求DK495+520处左中线的坐标及方位角由设计院所给的曲线要素表可知该点位于JD57 JD58的直线上,查曲线要素表JD57,JD58的坐标分别为(488809.902,2504127.029),(485660.627,2504491.226)。
通过坐标反算直线JD57 JD58的方位角:TTA=atg((485660.627-488809.902)/( 2504491.226-25 04127.029))=276.59665°注意:A的取值可根据下述条件确定ΔY>0,ΔX>0,第一象限0-90°ΔY>0,ΔX<0,第二象限90°-180°ΔY<0,ΔX<0,第三象限180°-270°ΔY<0,ΔX>0,第四象限270°-360°查曲线表,JD58切线长T= 690.303m,JD58坐标(Y58,X58)=(485660.627,2504491.226),ZH点里程为DK496+093.885。
铁路曲线桥坐标及相关参数计算

浅谈铁路曲线桥坐标及相关参数计算————————————————————————————————作者:————————————————————————————————日期:浅谈铁路曲线桥坐标及相关参数计算井昭义中交一公局张呼客专五标一分部【摘要】铁路曲线桥与直线桥相比桥墩、台坐标计算要复杂得多,涉及的内容也较多,本文结合张呼铁路工程实例,对铁路曲线桥坐标、参数计算提出了具体建议。
【关键词】铁路;曲线桥;坐标、参数计算;新建张家口至呼和浩特铁路站前工程ZHZQ-5合同段一分部管段DK167+550~DK179+950,起于集宁新区六间房村,而后经察哈尔右翼前旗止于卓资山县芦家卜子村,全长12.4km,特大桥2137.66m/2座、大桥706.44m/2座、中桥112.6m/1座,其中曲线桥3座,直线桥2座。
直线桥坐标计算较为简单,在此不进行详细说明,下面以西土外大桥为例进行曲线桥坐标、参数计算。
西土外大桥位于内蒙古乌兰察布市西土坑村西南,起止里程为DK178+163.13~DK178+373.97,桥中心里程为DK178+268.55,全长210.84m,孔跨类型为6-32.6m简支梁。
桥台采用双线矩形空心桥台,桥墩1~5号墩采用圆端形实体桥墩,桥墩台桩基础采用钻孔灌注桩,1~5墩范围简支梁固定支座设于每孔跨的小里程侧,横向活动支座均设置于线路右侧。
曲线布置采用平分中矢法,按左线中心线里程进行计算、绘图,左右线线间距4.6m,桥墩中心线与线路中心线之间的距离等于曲线偏距E。
相关设计数据如下图所示:设在曲线上的简支梁桥,每孔梁仍是直的,于是各孔梁中线的连接线为折线,以适应梁上曲线线路需要,而线路中线为曲线,两者并不重合,简支梁中心线总是偏在线路中线内侧,当列车通过时,桥梁必然承受偏心荷载。
为使桥梁承受较小的偏心荷载,桥梁设计中,每孔梁中心线的两个端点并不位于线路中心线上,而是将梁的中线向曲线外侧移动一段距离。
铁路工程曲线坐标计算步骤

第9讲教学目标:了解偏角法的概念,理解正拨、反拨的含义,掌握曲线偏角计算公式和方法。
重点难点:5—4 一. 偏角法原理正拨 反拨二. 偏角计算1.圆曲线偏角Rl j i j i 2,,=δ 2.缓和曲线偏角δi ,j=βi -αj ,ij i i tg l Rl =,221αβ、、661 03j j j j i i i i Rl l Rl y l x ≈≈)(6122,j j i i j i j i ij l l l l Rl x x y y ++=--≈α)2)((610,j i j i j i l l l l Rl +-=δ若j 点位于i 点与缓和曲线终点之间,则同样方法可得,)2)((610,j i i j j i l l l l Rl +-=δ故其一般表达式为)2(6||0,j i j i j i l l Rl l l +-=δ若1010610210j i l j l i Rl ===、、δ,即在缓和曲线上,曲线点号等于以10m 为单位曲线长,则式中,R 为圆曲线半径,l 0为缓和曲线长,δ10为缓和曲线基本角。
)2(||10,j i j i j i +-=δδ102,0δδj j =当i 点位于缓和曲线起点时,则上式可化简为三. 弦线长度计算向,2至i f Z5—5 曲线详细测设的直角坐标法一. 直角坐标法测设曲线原理X 轴上丈量x P ,得P'点;自P'点,沿与X 轴垂直且指向曲线内侧的方向丈量y P ,即得P 点。
直角坐标法中,坐标系X 轴均选主点的切线,故曲线点的y 坐标为相对于切线的支距。
因此,直角坐标法也称为切线支距法。
二. 曲线点坐标计算直角坐标法所选定的坐标系通常为缓和曲线坐标系,则在该坐标系下,缓和曲线段曲线点坐标的计算公式为缓和曲线方程,圆曲线段曲线点的坐标:⎭⎬⎫+-=+=p R y m R x t t t t )cos 1(sin αα式中0βα+-=RK K HYt t ,K t 为t 点的里程,K HY 为HY 里程。
铁路、公路线路测量公式

4)、圆曲线上任意点法线方向上任意点的大地坐标(X法,Y法),法线方位角α法,
如果转向角左偏取α法=α-3*β-3.1415/2,若α法<0,则计算结ห้องสมุดไป่ตู้加上2倍的圆周率即α法=α-3*β-l/R-3.1415/2+2*3.1415;
即α法=α-3(20Rls/(40R^2-ls^2)) -l/R-3.1415/2+2*3.1415
如果转向角右偏取
α法=α+3(20Rls/(40R^2-ls^2)) +l/R +3.1415/2;
若α法>360,
则α法=α+3(20Rls/(40R^2-ls^2)) +l/R +3.1415/2-2*3.1415;
如果转向角左偏取α法=α-3*β-3.1415/2,若α法<0,则计算结果加上2倍的圆周率即α法=α-3*β-3.1415/2+2*3.1415;
如果转向角右偏取α法=α+3*β+3.1415/2;若α法>360,则计算结果加上2倍的圆周率即α法=α+3*β+3.1415/2-2*3.1415;
法线上任意一点到切点的距离为D法,
X=l-l5/(40*R2*ls2)
Y= l3/(6*R*ls)
αi为直缓点到待求点直线的方位角(弧度);
如果转向角左偏取αi=(α-β)=(α-20R lsl2/3(40R2ls2- l4))
若(α-β)<0,则αi=(α-β)+2*3.1415,但在计算坐标中可不考虑;
如果转向角右偏取αi=(α+β)=(α+20R lsl2/3(40R2ls2- l4))
铁路桥梁坐标计算及桥墩结构绘图研究

铁路桥梁坐标计算及桥墩结构绘图研究发布时间:2023-02-24T00:55:15.658Z 来源:《工程建设标准化》2022年第10月19期作者:曲亮[导读] 结构物坐标计算及绘图是铁路桥梁工程测量的重要组成部分,而桥梁结构坐标计算及桥墩结构绘图过程相对复杂,出错概率较高曲亮身份证号:23030519940522****摘要:结构物坐标计算及绘图是铁路桥梁工程测量的重要组成部分,而桥梁结构坐标计算及桥墩结构绘图过程相对复杂,出错概率较高。
基于此,本文以天津至北京大兴国际机场三标段工程DK46+967.66~DK48+973.56胜芳左线特大单线桥为例,探讨铁路桥梁坐标计算及桥墩结构绘图方法,以供参考。
关键词:铁路桥梁;桥梁坐标;坐标计算;桥墩结构;绘图在铁路工程建设中,桥梁工程测量和定位非常重要,要求测量人员从现场实际情况出发,制订一套合理的测量方案,再精确计算桥梁各细部结构的坐标,并经过多次校验,确认无误后才能进行现场放样。
由于铁路桥梁工程施工环境复杂恶劣,测量作业受到施工干扰、通视性等条件的影响,测量难度较大,如测量方法不当,不但会增加测量工作量,而且易出现差错,造成巨大损失。
本文以天津至北京大兴国际机场三标段工程DK46+967.66~DK48+973.56胜芳左线特大单线桥为例,对铁路桥梁坐标计算及桥墩结构绘图进行分析和总结。
1直线桥坐标计算1.1直线桥墩与台的布置直线桥墩台布置与桥梁线路定位一致,即墩台的几何重心与线路中心完全一致。
在计算直线桥墩台坐标时,根据线路对应的墩台里程,分别求出桥墩、台对应的中桩坐标,即为桥墩、桥台的坐标。
1.2直线桥桥墩及以下结构物坐标计算在普通的铁路桥梁施工设计图纸上仅标明梁缝中心里程,据此可计算出桥中心里程。
若墩端架设的梁长相等,桥墩中心线与梁缝中心线重合,而桥墩中心里程即为梁缝中心里程;若墩端架设的梁长不相等,即不等跨,则要按图纸确定是否设置纵向预偏心。
铁路曲线要素的测设

铁路曲线要素的测设、计算与精度分析摘要铁路线路平面曲线分为两种类型:一种是圆曲线,主要用于专用线和行车速度不高的线路上,另一种是带有缓和曲线的圆曲线,铁路干线上均用此种曲线。
曲线的五大要素,ZH(直缓点)、HY(缓圆点)、QZ(曲中点)、YH(圆缓点)、HZ(缓直点),是曲线的重要线形特征铁路曲线测设一般分两步进行,先测设曲线主点,然后依据主点详细测设曲线上的任意点。
结合本人的工作经验,就铁路圆曲线和缓和曲线上任一点坐标的计算及法向方位角的计算进行实例解析。
绪论一、工程测量学概述工程测量学是研究各种工程在规划设计、施工建设和运营管理阶段进行的各种测量工作的学科。
工程测量的特点是应用基本的测量理论、方法、技术及仪器设备,结合具体的工程特点采川具有特殊性的施测工绘方法。
它是大地测量学、摄影测量学及普通测量学的理论与方法在程工中的具体应用。
工程建设一般可分为:勘测设计、建设施工、生产运营三个阶段。
勘测设计阶段的测量主要任务是测绘地形图。
测绘地形图是在建立测绘控制网的基础上进行大比例尺地面测图或航空摄影测量。
建设施工阶段的测量主要任务是按照设计要求,在实地准确地标定建筑物或构筑物各部分的平而位置和高程,作为施工安装的依据(简称为标定);是在建立仁程控制网的基础上,根据工程建设的要求进行的施工几测量。
生产运营阶段的测量主要任务是竣工验收测量和变形监测等测量工作。
工程测量按所服务的工程种类,可分为建筑工程测量、线路工程测量、桥梁与隧道工程测量、矿石工程测量、城市工程测量、水利工程测量等。
此外,还将用于大型设备的高精度定位和变形监测称为高精度工程测量;将摄影测量技术应用于工程建设称为工程摄影测量;而将自动化的全站仪或摄影仪在计算机控制下的测量系统称为三维工业测量。
测量学是研究地球的形状和大小以及确定地而(包含空中、地表、地下和海底)物体的空间位置,井将这些空间位置信息进行处理、存储、管理、应用的科学。
它是测绘学科重要的组成部分,其核心问题是研究如何测定点的空间位置。
铁路车站信号平面布置图设计—坐标计算

• 3.信号机坐
• (2)设在辙叉后所连接两线路外侧 的矮型信号机坐标
•
设在辙叉后警冲标内方3.5m~4m处。
• (3)设在辙叉后所连接两线路中间 的高柱信号机坐标
•
因为高柱信号机高出轨面大于1100mm,若设于警冲标内方3.5m
~4m处必然侵限,需要移设。
•
信号机的设置有多种情况,在此不一一列举,按表1-7a、b、c可查
(岔心)的距b,就可以把岔心坐标换算成岔尖坐标了。
2.计算方法 方法1:如果岔尖较岔心远离站中心,则将岔心坐标加上长度b,就是岔尖坐标。
例如:3号道岔辙叉号为12号钢轨类型为50 kg/m的道岔岔心距信号楼289 m。 (混凝土枕)
3
289 信号楼
查表1-1,可知该道岔岔心至岔尖距 离为14 m。
警冲标
警冲标示意图
2.警冲标坐标计算 如果车站缩尺平面图上没有标出警冲标位置,可以先从表1-4查出警冲标至
岔心的距离,再由岔心坐标计算出警冲标坐标。
1 730 5 694 3 645 7 606 9 593 19 592 13 552 11 506 15 463 17 442 16 379 12 460 14 462 8 504 10 549 6 592 4 642 2 722
二、坐标计算 3.信号机坐标 计算表明,矮型不带进路表示器信号机,在警冲标内方不少
于3.5m处,按安装标准安装,不会侵人限界。并且,车体轮对在信 号机前方,该车体还不会影响邻线车辆安全通过。当然,又不能离 警冲标太远,否则,会过多影响线路有效长。一般设在警冲标内方 3. 5-4 m的地方。在实际安装时,还需要考虑信号机处的钢轨绝缘应 与信号机处在同一坐标。而从道岔跟端算起到信号机处的距离往往 不是标准轨长12.5m的整数倍,要在信号机坐标处设置钢轨绝缘,就 要配置短轨。标准短轨的长度只有4.5 m、6. 25 m和8. 0 m三种。显 然,配置短轨后,设置钢轨绝缘的轨缝至道岔跟端的距离不得小于 道岔跟端至信号机的距离,应该是最接近值。此时,设置钢轨绝缘 轨缝的坐标,就是最后确定的信号机的坐标。为了设计方便,已经 将矮型一机构、二机构信号机至岔心距离编制成表,见表1-5、表1-6。
线路中线及相关点位坐标计算

线路中线及相关点位坐标计算的快捷方法及桥梁主要点的坐标计算1 前言在二十一世纪的今天,使用传统的铁路测量方法已越来越不适应发展趋势的需要,用坐标控制、全站仪测量已越来越适应今天的发展。
在渝怀线的施工控制测量中,在原有坐标公式的基础上把一些公式加以发展,使坐标计算更快、更方便,缩短了计算时间。
下面就铁路中线及与线路成任意夹角相关点位点的坐标计算及桥梁上的应用进行探讨,特别是对线路垂线及任意夹角的相关点的坐标计算进行着重探讨。
2 公式的分类铁路线路线型包括:直线、缓和曲线、圆曲线。
又因在坐标计算此两点距、方位角及已知一点坐标、方位角、距离计算另一点坐标两种情况。
所以把公式分为:(1)已知两点坐标求两点距及方位角。
(2)已知一点坐标、方位角、距离求另一点坐标。
(3)直线上中线及相关点坐标公式。
(4)缓和曲线上中线及相关点坐标公式。
(5)圆曲线上中线及相关点坐标计算。
3 坐标系的建立通常数学坐标系是以X 轴为横轴、Y 轴为纵轴(如图1)。
但为了满足坐标计算的需要,通常把Y 轴反向(如图2)。
再逆时针旋转90°即得以Y 轴为横轴、X 轴为纵轴的坐标和纱(如图3)。
以X 轴方向为线路走向方向,Y 轴为线路垂直方向,由(图3)可以看出线路左偏时Y 值逐渐减小,右偏时Y 值逐渐增大。
4 已知两点坐标计算两点距及方位于角(如图4) 4.1 公式在CASIO 计算器中的输入在CASIO 计算器中输入公式要进入编程状态需按MODE 再按EXP 即可,然后输入文件名再按EXE 进入编程行即可编程。
CASIO 计算器的功能控制键有SHIFT 、2DNF 、ALPHA 三种分别A ,按键ALPHA 再按(一)键即右输入。
4.1.1 第一步:输入LBI 0 4.1.2 第二步:输入变量(Y )4.1.3 第三步:输入Y ≥N=〉A=90-tan -1((X-M )/(Y-N )◢ L= √((X-M )2+(Y-N )2)◢ ≠)A=270-tan -1((X-M )/(Y-N )◢ L= √((X-M )2+(Y-N )2)◢4.2 说明:(1)M 、N 为置镜点坐标。
铁路、公路坐标计算(中桩、边桩)

第2排桩基坐标 桩基编号 0台-04# 0台-05# 0台-06# X(N) 3061754.0117 3061753.0165 3061752.0213 Y(E) 519734.5137 519730.7428 519726.9719
1 2 3
A
4 5 6
A
7 8 9
B B
梁缝桩号
台背桩号
3
A
6
第4排桩基坐标 X(N) 3061587.0001 3061586.1382 3061585.2763 Y(E) 519782.0167 519779.3527 519776.6886
计算
3.9m 2.8m 1.98m 两点间直 线距离 8.000
桩基编号
起点桥台桩基坐标
X(N) 3061756.6223 3061755.6271 3061754.6319 3061754.0117 3061753.0165 3061752.0213 3061751.4010 3061750.4059 3061749.4107 3061748.7904 3061747.7952 3061746.8000 Y(E) 519733.8247 519730.0538 519726.2829 519734.5137 519730.7428 519726.9719 519735.2027 519731.4318 519727.6609 519735.8916 519732.1208 519728.3499
台背桩号 K10+780.865 3061756.7571 519732.1809 梁缝桩号 K10+788.090 3061749.7609 519733.9849 7.225 注:如是斜交桥,斜交角与桥墩同步,斜交角在墩基计算中输入。 计算起点桩号选择 第1排桩基坐标 桩基编号 0台-01# 0台-02# 0台-03# X(N) 3061756.6223 3061755.6271 3061754.6319 Y(E) 519733.8247 519730.0538 519726.2829
铁路、公路坐标计算(中桩、边桩和桩

3061756.7571
519732.1809
梁缝桩号 K10+788.090 3061749.7609 519733.9849 7.225 注:如是斜交桥,斜交角与桥墩同步,斜交角在墩基计算中输入。 计算起点桩号选择 第1排桩基坐标 桩基编号 0台-01# 0台-02# 0台-03# X(N) 3061756.6223 3061755.6271 3061754.6319 Y(E) 519733.8247 519730.0538 519726.2829
N-00# N-00# N-00# N-00# N-00# N-00# N-00# N-00# N-00# N-00# N-00# N-00# N-00# N-00# N-00#
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
N-00# N-00# N-00# N-00# N-00# N-00#
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
公路、铁路高精度施工放样坐标简易计算法

局 部
X
/
1 0)
K 点的坐标 :
X =U+ f0 C S(x +B +C d K L O A 2 x )x
Y = + f L I( x +B + )x K V S NA 2 x C d O
( 11)
(1 ) 中 : 1 式
O~L 积分 区间,+ b K F) L A s( - DE , 为起 点F终点G . 的曲率, 左偏 一右偏 + . FG 、终 点 桩 号 。起 AB ( ,( 式 ,见 7) 8) 其 它符号 同上
【 关键词 】施工放样
坐标 计算法
现将定积 分计算 法介绍 如下
三 、K 的坐标 方位 角 k 其 坐标计 算公 式 点 及
令 ( 式 中 := ( 0E D /A s(G F ) 4) A 9 (- ) b (- )
( 7)
B 8 D/ 叮 =1 0 r
一
、
曲线上任 意 点K 坐标 的计 算公 式
( 2)
Y =+ f LI( + ) = + ( O(L C OC) / K V SNB Cd V C SB+ 卜C s O x x B
b= f iF i A d = A iF ii l A L 2) l K F i L L 2 L I 2f L Ld = 2( 1 k k L L
2 .当为园 曲线时。= . AO
(1 1)式积分计算
(3 1)
二 、 曲线 上 I点 坐标 方 位角a的计算 ( i j
从 图 中可 以 看 出 : = + i a C b i
d =dL R , bi i
X U f LO (x Cd = + ( l (L ) SN K + C SB + )x U 0 S NB +C一 IC) /B
铁路施工反向曲线桥位坐标测量计算

铁路反向曲线桥位坐标计算摘要:介绍运用运用计算机辅助设计软件——AUTOCAD,将复杂的反向曲线和桥位按设计参数绘制到坐标系统中,即可查询细部点坐标,用于施工放样.关键词:反向曲线坐标 AUTOCAD 命令1、工程概况包西铁路陈家坡无定河特大桥位于R=1600及R=2000的反向曲线上,为跨210国道、织女渠及无定河而设,中心里程DK301+622.桥跨布置41孔32m+2孔24m+2孔32m预应力混凝土梁.15#、16#、43#、44#墩按顺时针扭转45°设置,41#、43#墩为不等跨墩,纵向设有15cm预偏心.该桥桥位坐标计算有以下难点:1、桥梁位于复杂的反向曲线,计算的结构物坐标种类多、数量大,向下而上包括桩基、承台、桥墩合计两台44墩;2、为保证桥梁工作线与线路中线基本一致,缓和曲线、圆曲线的桥墩设1-3cm不等的横向偏心,不等跨桥墩设有15cm纵向偏心;3、跨越道路及渠道的桥墩,为避免侵线按斜角45°设置.面对此种桥位参数复杂多样的情况,传统的坐标计算方法——使用编辑计算器,不仅繁琐,而且容易出错,下面笔者介绍一种合适此类情况的解法.2、总体思路依据设计曲线要素,使用EXEL计算出圆曲线主点及加密点,缓和曲线坐标,将数据导入AUTOCAD 中生成线路图,按照设计图中墩位的里程尺寸、偏心、角度等参数,使用软件中的定距等分、偏移、拉长等命令,把桩基、承台、墩位绘制到线路图坐标系统中,即可查询任意部位、任意点坐标.3、方法与步骤3.1生成线路图陈家坡无定河特大桥起讫里程DK300+882.17——DK302+359.01,所在曲线交点为JD205、JD206,前后交点分别是JD204、JD207.曲线要素如表1 表1根据交点坐标、半径、缓和曲线长即可在EXEL中编写公式,计算出ZH、HY、YH、HZ点及缓和曲线加密点坐标。
该曲线半径大、缓和曲线加密点2米计算一个数据,即可满足精度需要,将数据导入AUTOCAD,使用多段线命令,线路图即可生成,如图1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
铁路公路曲线防样坐标计算方法一、
随着我国公路铁路的大力建设,对坐标放样的要求精度越来越高,以及通过一种快速的捷径来达到一次性对整个路基、桥梁的中线编辑公式,准确较快的计算出中心坐标,使得坐标放样在我们的施工中带来更大的方便。
1、首先熟悉测量知识圆曲线基本公式及概念。
偏角法测设圆曲线
1-1
知道了圆曲线的测设里程,即测设的曲线长Li ,即可进行计算,其计算公式如下:
π
α0180∙=R L i i
2
i
i
αδ=
i i R c δsin 2= (1-1)
式中,i δ,i c 为曲线测设曲线点i 的偏角与弦长。
切线支距法测设圆曲线
ZY
i i R x αsin ∙= )c o s 1(i i R y α-∙= π
180∙=R L a i i
(1-2)
1-2
式中i L 为曲线上点i 至ZY (或YZ )的曲线长。
2、缓和曲线的基本公式及概念。
缓和曲线是直线与圆曲线之间的一种过渡曲线,它与直线分界处半径为∞,与圆曲线相接处半径与圆曲线半径R 相等,缓和曲线上任一点的曲率半径ρ与该点到曲线起点的长度成反比。
如下图中,存在公式: ρ∝l
1 或C
l =ρ (2-1)
公式中C 是一个常数,称缓和曲线半径变更率。
当0l l =时,R =ρ 所以C l R =∙0,C l =ρ,是缓和曲线的必要条件,实用中能满足这一条件的曲线可称为缓和曲线,如辐射螺旋线、三次抛物线等,我国缓和曲线均采用辐射螺旋线。
1-3
3、缓和曲线方程式:
按照C l =ρ为必要条件导出的缓和曲线方程为:
∙∙∙∙++-=∙∙∙∙∙++-=5
11
3734
9
25422403366345640C
l C l C l y C
l C l l x (3-1) 根据测设精度的要求,实际应用中可将高次项舍去,并顾及到C Rl =0,则上式变为
3
2
025
640Rl l y l R l l x =
-=(3-2)
式中,x ,y 为缓和曲线上任一点的直角坐标,坐标原点为直缓点(ZH )或缓直(HZ ),通过该点的缓和曲线切线为x 轴。
1-4
l 为缓和曲线上任一点P 到ZH (或HZ )的曲线长。
0l 为缓和曲线的总长度。
当0l l =时,则0x x =,0y y =,代入上式得
R
l y R l l x 64020
0230
00=
-
= (3-3)
式中0x x =,0y y =为缓圆点(HY )或圆缓点(YH )的坐标。
4、缓和曲线常数的计算。
0β、0δ、m 、p 、0χ、0y 等称为缓和曲线的常数,其物理意义及
几何关系由下图可以推出:(3-4)
R l R
l R l p R l l m R l R l 242688242402180631180220
3
40202
3
00
0000
00≈-=-
=∙
==∙
=π
βδβ
)
1-5
下面我们来推证最常用的两个常数0β、0δ。
4.1求0β
设β为缓和曲线上任一点的切线角;ρ为该点的曲线曲率半径;
l 为该点至ZH 点的缓和曲线长。
π
ββββββρβ0
00
00
2
00
0018022/,/∙=====
=
∴
∙===⎰
⎰
R l l l Rl l Rl ld d Rl dl l d Rl pl dl d l
l l
则
时,当代入上式,则将
(4-1)
4.2求0δ
3
6/1512tan tan 0
0000
00000
0β
δβδδδδ==
∴
∙=∴
-=
==
R l Rl dl l d x y x y 次项)代入上式,并取至二将(很小,故由上图得知: (4-2) 5、缓和曲线连同圆曲线的测设计算公式:
L
T q R
p R E R l R l L p R m T -=-∙+=+
=-+
=∙++=22
s ec )(180180)
2(22tan )(00
00
00切曲差外矢距曲线长切线长α
α
πβαπα
7
二
1、坐标方位角
熟悉了以上基本公式及概念后,知道什么是坐标方位角。
坐标方位角是以正北方向为起点,按顺时针方向旋转,其角度为(0~3600),已知两点的坐标,就可以求出这两点的坐标方位角,已知一点的坐标及该点到另一点的长度及坐标方位角,就可以求出另一点的坐标方位角;在计算坐标方位角时候要注意坐标方位角大小的问题,当计算坐标方位角为负时,应加上360度。
下面是计算坐标方位角的示例。
B
A
根据一已知A 点坐标及该点到B 点的距离及A-B 的坐标方位角,求B 点坐标。
其计算过程如下:
)5706.6s in(076.28)5706.6cos (076.28∙+=∙+=B B A B Y Y X X
其余几点按照同样的方法计算。
根据一已知B 点坐标及该点到B 点的距离及B-A 的坐标方位角,求A 点坐标。
其计算过程如下:
)
5706.186s in(076.28)
5706.186cos (076.28∙+=∙+=B A B A
Y Y X X
其余几点按照同样的方法计算。
从以上例子当中我们可以看出,根据一已知点坐标及该点到另一点的距离及方位角,就可以计算未知点的坐标,这就刚好符合我们在施工中,设计院一般给我们提供交点坐标,或者直缓点坐标,以及整个曲线线路的基本情况,根据这些条件,就可以求出我们在施工中需要放样的线路中心坐标或者桥梁墩台中心坐标。
下面举一个例子来说明具体的计算方法。
由1-7图可以知道,根据坐标方位角的定义,α为ZH 点的坐标方位角,XOY 坐标系一般是我国的大地坐标系,我国修铁路就是建立在我国的大地坐标系的基础上的,X 1OY 1 为我们施工时,根据设计院提供的JD 坐标或者是ZH 点坐标,自己建立的坐标系,根据曲线内任意一点的坐标,换算成XOY 坐标,下面以缓和曲线和圆曲线任意一点,来讨论其计算过程。
1、设P 为缓和曲线上任意一点,根据P 点的里程及直缓点的里程可以知道,ZH 点到P 点的曲线长度l ,根据公式(3-2)我们可以知道ZH 点到P 点的弦线长度S
2032202522)6()40(Rl l l R l l y x S +-=+=
弦线01P 的方位角αp 为:
)arctan(0101
y y x x p p p ---=αα
所以根据ZH 点坐标, ZH 点到P 点距离及坐标方位角,可得P 点的坐标为:
)sin()
cos(0101p P p p S Y Y S X X αα∙+=∙+=
2、圆曲线上任意一点坐标的计算。
设J 为圆曲线任意一点的坐标,根据图1-7可知,HY 点的切线方位角为:
00βαβα-=-=zh hy a
可以知道ZH 点到HY 点的曲线长度为0l ,根据公式(3-3)可以求得ZH 点
到HY 点的弦线长0102
2202230212121)6()40(00R l R l l y x +-=+=
所以根据HY 点方位角,我们可以求HY 点坐标:
)sin(00)
cos(00210102210102hy hy Y Y X X αα∙+=∙+=
根据J 点的里程及HY 点的里程(HY 点里程为ZH 点里程加上缓和曲线长)可以知道HY 点到J 点的圆曲线长度L ,根据L 及圆曲线要素,可以求得弦线02P 的长度,及02P 的坐标方位角。
j hy j θαα-=20 πθ0
1802∙=R L j j
2
22))1cos(())2sin((0j j R R p θθ-∙+∙=
所以J 点的坐标为:
)sin(0)
cos(022********j j j j p Y Y p X X αα∙+=∙+=
值得注意一点就是,在YH 点以后的曲线,应以HZ 点为坐标原点,以HZ 点的切线为X 轴,建立坐标系,其余计算与上面方法一样。
注意:坐标方位角的计算,是以正北方向为起始边(方位角以0~3600表示),也就是平行于XOY 坐标系中的X 轴。
坐标方位角绕着某一点旋转一个角度的到另一点,以顺时针方向旋转为正,即加上一个旋转角度,以逆时针方向旋转为负,即减去一个旋转角度。
在设计时,设计院一般跟施
工单位提供JD的坐标及JD跟ZH方位角(或者ZH到JD的方位角),我们根据JD坐标及方位角可以反算ZH点坐标,又根据设计院提供的曲线要素就可以计算曲线每一点的。
