数学九年级上册同步分层练习2.2 第1课时圆的旋转不变性

合集下载

人教版九年级上册数学《图形的旋转》同步练习(含答案)

23.1.2 图形的旋转知识点1.图形旋转的性质是：(1)旋转前后的图形；(2)对应点到旋转中心的距离； (3)对应点与旋转中心所连线段的夹角等于2.简单的旋转作图---旋转作图的步骤（1）确定旋转；（2）找出图形的关键点；（3）将图形的关键点与旋转中心连接起来，然后按旋转方向分别将它们旋转一个角，得到此关键点的对应点；(4)按图形的顺序连接这些对应点，所得到的图形就是旋转后的图形。

一、选择题1．在图形旋转中，下列说法错误的是（） A ．在图形上的每一点到旋转中心的距离相等 B ．图形上每一点移动的角度相同 C ．图形上可能存在不动的点D ．图形上任意两点的连线与其对应两点的连线长度相等2．如图，下面的四个图案中，既包含图形的旋转，又包含图形的轴对称的是（）3.如图所示的图案绕旋转中心旋转后能够与自身重合，那么它的旋转角可能是（）。

A.60° B.90° C.72° D.120°4．如图，摆放有五杂梅花，下列说法错误的是（以中心梅花为初始位置）（• ） A ．左上角的梅花只需沿对角线平移即可B ．右上角的梅花需先沿对角线平移后，再顺时针旋转45°C ．右下角的梅花需先沿对角线平移后，再顺时针旋转180D ．左下角的梅花需先沿对角线平移后，再顺时针旋转90°5 △ABC 绕着A 点旋转后得到△AB ′C ′，若∠BAC ′=130°，∠BAC=80°，•则旋转角等于（）A ．50°B ．210°C ．50°或210°D ．130° 二、填空题6．图形的平移、旋转、轴对称中，其相同的性质是_________.7．如图，△ABC和△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，图中的△ABD 绕A旋转42°后得到的图形是________，它们之间的关系是______，•其中BD=_________．8、如图，将△OAB绕点0按逆时针方面旋转至△0A′B′，使点B恰好落在边A′B′上．已知AB=4cm，BB′=lcm，则A′B长是_______cm．9、如图，在平面直角坐标系中，点A的坐标为(1，4)，将线段O A绕点O顺时针旋转90°得到线段OA′，则点A′的坐标是___________.10．如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，•∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+•DF•与EF的关系是________．11.如图，在直角坐标系中，已知点)0,3A、)4,0(B，对△OAB连续作旋转变换，依次得(到三角形①、②、③、④…，则三角形⑩的直角顶点的坐标为__________．三、综合提高题12.观察下列图形，它可以看作是什么“基本图形”通过怎样的旋转而得到的？13.如图：若∠AOD=∠BOC=60°,A 、O 、C 三点在同一条线上，△AOB 与△COD 是能够重合的图形。

人教版九年级上册数学同步练习第1课时图形的旋转

第1课时图形的旋转第1课时1.填空：如图，钟表的时针在不停地旋转，从3时到5时，时针的旋转中心是点，旋转角等于 °，点B的对应点是点.2.填空：如图，杠杆绕支点转动撬起重物，杠杆的旋转中心是点，旋转角是∠ ，点A 的对应点是点 .3.如图，扎西坐在旋转的秋千上，请在图中画出点A ，B ，C 的对应点A ′，B ′，C ′.第2课时（一）基本训练，巩固旧知1.填空：把一个平面图形绕着平面内某一点O 转动一个角度，就叫做图形的旋转，点O 叫做旋转，转动的角叫做旋转 .如果图形上的点P 经过旋转变为点P ′，那么这两个点叫做旋转的 .2.填空：(1)如图，△ABC 绕点A 旋转得到△ADE ，旋转中心 EDA C B是点，点B 的对应点是点，点C 的对应点是点，∠ 等于于旋转角；(2)如图，△ABC 绕点O 旋转得到△DEF ，旋转中心是点，点A 的对应点是点，点B 的对应点是点，点C 的对应点是点，∠ 等于于旋转角.3.利用“对应点与旋转中心所连线段的夹角等于旋转角”，画出下图中的旋转角，并用量角器量出旋转角的度数.4.如图，四边形ABCD 是正方形，以点A 为中心，把△ADE 顺时针旋转90°，利用图形旋转的性质，画出旋转后的图形.（先让生做4题，然后师出示旋转后的图形，并利用性质解释点D 转到了点B ，点E 转到了点F ）O .F E D A B C E D CB A第3课时（一）基本训练，巩固旧知1.填空：图形旋转的性质是：(1)旋转前后的图形； (2)对应点到旋转中心的距离； (3)对应点与旋转中心所连线段的夹角等于 .2.如图，以点O 为中心，把点P 顺时针旋转45°.3.如图，以点O 为中心，把线段AB 逆时针旋转90°.4.如图，以点O 为中心，把△ABC 顺时针旋转120°.5.如图，以点B 为中心，把△ABC 旋转180°.B AC BA C.OA B O ..O P .。

2020-2021沪科版九年级数学24.2圆的基本性质-知识点+习题同步练习提升 (1)

圆的基本性质记忆导图 ()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧对称、旋转对称对称性：轴对称、中心角形顶点的距离相等定理：三角形外心到三、圆的内接三角形三角形的外接圆、外心圆的作法圆的确定几者之间的关系圆心角的概念距间的关系圆心角、弧、弦、弦心弦心距垂径定理的推论垂径定理垂径分弦点在圆外点在圆内点在圆上点与圆的位置关系半圆、等圆弓形特殊弦：直径普通弦：小于直径的弦弦等弧优弧劣弧或弧圆弧圆、圆心、半径圆的相关概念圆的基本性质考点1 圆的相关概念1、圆的定义（1）线段OA 绕着它的一个端点O 旋转一周，另一个端点A 所形成的封闭曲线，叫做圆。

（2）圆是到定点的距离等于定长的点的集合。

（3）固定的端点O 叫做圆心。

（4）线段OA 的长为r 叫做半径。

2、圆弧（1）圆上任意两点间的部分叫做圆弧，简称弧。

（2）大于半圆的弧叫做优弧，一般用三个字母表示。

（3）小于半圆的弧叫做劣弧。

（4）在同圆或等圆中，能够互相重合的弧叫做等弧。

3、弦（1）连接圆上任意两点的线段叫做弦。

（2）经过圆心的弦叫做直径。

4、弓形由弦及其所对的弧组成的图形叫做弓形。

5、半圆、等圆（1）圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。

（2）能够重合的两个圆叫做等圆，等圆的半径相等。

考点2 点与圆的位置关系平面上一点P 与⊙O （半径为r ）的位置关系有以下三种情况：（1）点P在⊙O上⇔OP=r；（2）点P在⊙O内⇔OP<r；（3）点P在⊙O外⇔OP>r。

考点3垂径分弦1、垂径定理：垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧。

2、推论：①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧。

②弦的垂直平分线过圆心，且平分弦对的两条弧。

③平分一条弦所对的两条弧的直线过圆心，且垂直平分此弦。

④平行弦夹的弧相等。

苏科版数学九年级上册第1课时圆的旋转不变性同步课件

( (
提示：连接CD,利用Rt△ABC求得∠BAC=62°.
B
在△ACD中求得∠ACD=56°，从而求得∠ECD=34°，
AD、DE的度数分别为56°，34°.
E D
A
C
课堂小结
圆的旋转不变性
圆是中心对称图形，圆心是它的对称中心．
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等.
发现：“车轮绕固定轴心旋转时是不变的”．
获取新知
圆绕着圆心旋
有
转任何角度后,都
何
能与自身重合.
发
现
摩天轮和车轮旋转，说明了圆具有旋转不变性;揭示了：圆是中心对称图形,圆心是它的对称中心.
圆心角、弧、弦之间的关系（1）相关概念圆心角：顶点在圆心的角圆心角所对的弧圆心角所对的弦
（2）在同圆或等圆中，圆心角、弧、弦之间的关系?
第2章对称图形——圆
2.2 第1课时圆的旋转不变性
知识回顾
1.下列说法正确的有（ B ）
(1)长度相等的弧是等弧; (2)等圆的半径相等;
(3)直径是弦;
(4)两个半圆是等弧.
A.1个 B.2个 C.3个 D.4个
2.长度等于半径的弦所对的圆心角的度数是 60° .
情景引入
你知道车轮为什么设计成圆形？设计成三角形、四边形又会怎样？从中你发现了什么？
证明：连接AO,BO,CO,DO.
∵A⌒D=⌒BC
AOD BOC. AOD+BOD=BOC+BOD. 即AOB COD， AB=CD.
C B
O.
D A
4.如图,在△ABC中, ∠C＝90°, ∠B＝28°,以点C为圆心,CA为半径的圆交AB于点D,交BC与点E．求AD、DE的度数.

新苏科版数学九年级上册同步练习2.2 第1课时圆的旋转不变性

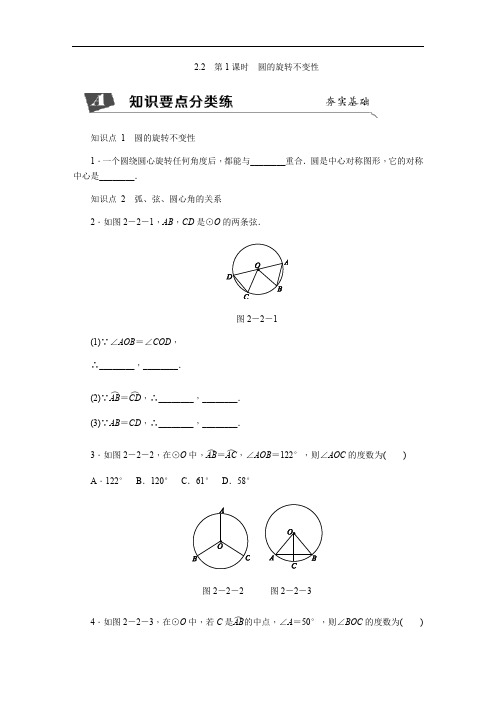
2.2 第1课时圆的旋转不变性知识点 1 圆的旋转不变性1．一个圆绕圆心旋转任何角度后，都能与________重合．圆是中心对称图形，它的对称中心是________．知识点 2 弧、弦、圆心角的关系2．如图2－2－1，AB ，CD 是⊙O 的两条弦．图2－2－1(1)∵∠AOB ＝∠COD ， ∴________，________．(2)∵AB ︵＝CD ︵，∴________，________． (3)∵AB ＝CD ，∴________，________．3．如图2－2－2，在⊙O 中，AB ︵＝AC ︵，∠AOB ＝122°，则∠AOC 的度数为( ) A ．122° B ．120° C ．61° D ．58°图2－2－2 图2－2－34．如图2－2－3，在⊙O 中，若C 是AB ︵的中点，∠A ＝50°，则∠BOC 的度数为( )A ．40°B ．45°C ．50°D ．60°5．如图2－2－4，已知BD 是⊙O 的直径，点A ，C 在⊙O 上，AB ︵＝BC ︵，∠AOB ＝60°，则∠COD 的度数是________．图2－2－46．[教材练习第1题变式]如图2－2－5，AB 是⊙O 的直径，BC ︵＝CD ︵＝DE ︵，∠BOC ＝40°，则∠AOE ＝________°.图2－2－57．在⊙O 中，若弦AB 的长恰好等于半径，则弦AB 所对的圆心角的度数为________． 8．[教材习题2.2第4题变式]如图2－2－6，在⊙O 中，AB ，CD 是两条直径，弦CE ∥AB ，EC ︵的度数是40°，求∠BOD 的度数．图2－2－69. 已知：如图2－2－7，点A ，B ，C ，D 在⊙O 上，AB ＝CD .求证：∠AOC ＝∠DOB .图2－2－710．[2018·沛县期中]如图2－2－8，点A ，B ，C 在⊙O 上，M ，N 分别是半径OA ，OB 的中点，且CM ＝CN .求证：AC ︵＝CB ︵.图2－2－811．下列结论中，正确的是( ) A ．同一条弦所对的两条弧一定是等弧 B ．等弧所对的圆心角相等 C ．相等的圆心角所对的弧相等 D ．长度相等的两条弧是等弧12．在同圆中，若AB ︵和CD ︵都是劣弧，且AB ︵＝2CD ︵，则弦AB 和弦CD 的大小关系是( ) A ．AB ＝2CD B ．AB ＞2CD C ．AB ＜2CDD ．无法比较它们的大小13．如图2－2－9，A ，B 是⊙O 上的两点，∠AOB ＝120°，C 是AB ︵的中点，则四边形AOBC 是( )图2－2－9A ．梯形B ．矩形C ．菱形D ．正方形14．如图2－2－10，在△ABO 中，∠A ＝∠B ，⊙O 与OA 交于点C ，与OB 交于点D ，与AB 交于点E ，F .(1)求证：CE ︵＝DF ︵；(2)写出图中所有相等的线段(不要求证明)．图2－2－1015．[2017·响水期末]如图2－2－11，AB 为⊙O 的直径，点C ，D 在⊙O 上，CE ⊥AB ，DF ⊥AB ，且AC ︵＝BD ︵.求证：AE ＝BF .图2－2－1116．如图2－2－12，P A ︵＝PB ︵，C ，D 分别是半径OA ，OB 的中点，连接PC ，PD 交弦AB 于E ，F 两点．求证：(1)PC ＝PD ； (2)PE ＝PF .图2－2－1217．如图2－2－13所示，在⊙O 中，AB ，CD 是两条弦，OE ⊥AB ，OF ⊥CD ，垂足分别为E ，F .(1)如果∠AOB ＝∠COD ，那么OE 与OF 的大小有什么关系？为什么？(2)如果OE ＝OF ，那么AB 与CD 的大小有什么关系？AB ︵与CD ︵的大小有什么关系？∠AOB 与∠COD 呢？为什么？图2－2－13教师详解详析1．自身圆心2．(1)AB ︵＝CD ︵AB ＝CD (2)∠AOB ＝∠COD AB ＝CD (3)∠AOB ＝∠COD AB ︵＝CD ︵3．A4．A [解析] ∵∠A ＝50°，OA ＝OB ，∴∠B ＝∠A ＝50°，∴∠AOB ＝180°－50°－50°＝80°.∵C 是AB ︵的中点， ∴∠BOC ＝12∠AOB ＝40°.故选A .5．120° [解析] ∵AB ︵＝BC ︵，∠AOB ＝60°，∴∠BOC ＝∠AOB ＝60°. ∵BD 是⊙O 的直径， ∴∠BOD ＝180°，∴∠COD ＝180°－∠BOC ＝120°.6．60 [解析] 由BC ︵＝CD ︵＝DE ︵，可得∠BOC ＝∠COD ＝∠DOE ＝40°，所以∠AOE ＝180°－3×40°＝60°.7．60°8．解：如图，连接OE.∵EC ︵的度数是40°，∴∠EOC ＝40°.∵OE ＝OC ，∴∠C ＝70°. ∵CE ∥AB ，∴∠BOC ＝∠C ＝70°， ∴∠BOD ＝110°.9．证明：∵AB ＝CD ，∴AB ︵＝CD ︵， ∴∠AOB ＝∠COD ，∴∠AOB －∠BOC ＝∠COD －∠BOC ，即∠AOC ＝∠DOB.10．证明： ∵OA ＝OB ，M ，N 分别是OA ，OB 的中点，∴OM ＝ON. 在△OCM 和△OCN 中，⎩⎨⎧OM ＝ON ，OC ＝OC ， CM ＝CN ，∴△OCM ≌△OCN ， ∴∠MOC ＝∠NOC. 故AC ︵＝CB ︵.11．B [解析] A ．同一条弦所对的两条弧不一定是等弧，有可能是一条优弧和一条劣弧，故本选项错误；B .正确；C .在两个同心圆中，同一个圆心角所对的弧不相等，故本选项错误；D .长度相等的两条弧，弯曲程度不同，就不能重合，就不是等弧，故本选项错误．故选B .12．C [解析] 如图，取AB ︵的中点E ，连接AE ，BE ，∴AB ︵＝2AE ︵＝2BE ︵， ∴AE ＝BE. ∵AB ︵＝2CD ︵， ∴AE ︵＝BE ︵＝CD ︵，则AE ＝BE ＝CD ， ∴AE ＋BE ＝2CD. ∵AE ＋BE ＞AB ， ∴2CD ＞AB. 故选C .13．C [解析] 如图，连接OC.∵C 是AB ︵的中点， ∠AOB ＝120°， ∴∠AOC ＝∠BOC ＝60°. 又∵OA ＝OC ＝OB ，∴△OAC 和△OBC 都是等边三角形． ∴AC ＝OA ＝BC ＝OB. 故四边形AOBC 是菱形．14．解：(1)证明：连接OE ，OF ，则OE ＝OF ，∴∠OEF ＝∠OFE. ∵∠A ＝∠B ， ∴∠AOE ＝∠BOF ， ∴CE ︵＝DF ︵.(2)OA ＝OB ，OC ＝OD ，AC ＝BD ，AE ＝BF ，AF ＝BE. 15．证明：如图，连接OC ，OD.∵AC ︵＝BD ︵， ∴∠COE ＝∠DOF. ∵CE ⊥AB ，DF ⊥AB ，∴∠CEO ＝∠DFO ＝90°. 在△OCE 和△ODF 中，⎩⎨⎧∠COE ＝∠DOF ，∠CEO ＝∠DFO ，OC ＝OD ，∴△OCE ≌△ODF ，∴OE ＝OF. 又∵OA ＝OB ，∴AE ＝BF. 16．证明：(1)连接PO. ∵PA ︵＝PB ︵，∴∠POC ＝∠POD. ∵C ，D 分别是半径OA ，OB 的中点， ∴OC ＝OD. 又∵PO ＝PO ， ∴△PCO ≌△PDO ， ∴PC ＝PD.(2)∵△PCO ≌△PDO ， ∴∠PCO ＝∠PDO.∵OA ＝OB ，∴∠A ＝∠B ， ∴∠AEC ＝∠BFD ，即∠PEF ＝∠PFE ， ∴PE ＝PF.17．[解析] 本题可利用圆的旋转不变性或者利用全等三角形的知识加以解决．解：(1)OE ＝OF.理由如下：∵OA ＝OC ，∠AOB ＝∠COD ，OB ＝OD ， ∴△AOB ≌△COD(SAS )． ∵OE ⊥AB ，OF ⊥CD ，∴OE ＝OF(全等三角形对应边上的高相等)．(2)AB ＝CD ，AB ︵＝CD ︵，∠AOB ＝∠COD.理由如下：∵OE ⊥AB ，OF ⊥CD ，∴∠AEO ＝∠CFO ＝90°.在Rt △AOE 和Rt △COF 中，∵OE ＝OF ，OA ＝OC ，∴Rt △AOE ≌Rt △COF(HL )，∴AE ＝CF.同理BE ＝DF ，∴AB ＝CD ，∴AB ︵＝CD ︵，∠AOB ＝∠COD.[点评] 圆心到弦的垂线段的长叫做这条弦的弦心距．通过本题可以发现：在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等．。

九年级(初三)《旋转》知识点及练习(带答案)

旋转一.知识框架二．知识概念1.旋转：在平面内，将一个图形绕一个图形按某个方向转动一个角度，这样的运动叫做图形的旋转。

这个定点叫做旋转中心，转动的角度叫做旋转角。

（图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。

）2.旋转对称中心：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角（旋转角小于0°，大于360°）。

3．中心对称图形与中心对称：中心对称图形：如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形。

中心对称：如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称。

4.中心对称的性质：关于中心对称的两个图形是全等形。

关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。

关于中心对称的两个图形，对应线段平行（或者在同一直线上）且相等。

一、精心选一选 (每小题3分，共30分)1．下面的图形中，是中心对称图形的是（）A．B．C．D．2．平面直角坐标系内一点P （－2,3）关于原点对称的点的坐标是（）A ．（3，－2）B ． (2,3）C ．（－2，－3）D ． (2，－3）3．3张扑克牌如图1所示放在桌子上，小敏把其中一张旋转180º后得到如图（2）所示，则她所旋转的牌从左数起是（）A ．第一张B ．第二张C ．第三张D ．第四张 4．在下图右侧的四个三角形中，不能由△ABC 经过旋转或平移得到的是（）5．如图3的方格纸中，左边图形到右边图形的变换是（） A ．向右平移7格B ．以AB 的垂直平分线为对称轴作轴对称，再以AB 为对称轴作轴对称C ．绕AB 的中点旋转1800，再以AB 为对称轴作轴对称D ．以AB 为对称轴作轴对称，再向右平移7格6．从数学上对称的角度看，下面几组大写英文字母中，不同于另外三组的一组是（）A ．A N E GB ．K B X NC ．X I H OD ．Z D W H7．如图4，C 是线段BD 上一点，分别以BC 、CD 为边在BD 同侧作等边△ABC 和等边△CDE,AD 交CE 于F ，BE 交AC 于G ，则图中可通过旋转而相互得到的三角形对数有( )． A ．1对B ．2对C ．3对D ．4对8．下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的角度是（）A ︒30B ︒45C ︒60D ︒909．如图5所示，图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是（） A ．l 个B ．2个C ．3个D ．4个ABCABCDCDE图4图5图图1210．如图6，ΔABC 和ΔADE 都是等腰直角三角形，∠C 和∠ADE 都是直角，点C 在AE 上，ΔABC 绕着A 点经过逆时针旋转后能够与ΔADE 重合得到图7，再将图23—A —4作为“基本图形”绕着A 点经过逆时针连续旋转得到图7.两次旋转的角度分别为（）A ．45°，90°B ．90°，45°C ．60°，30°D ．30°，60 二、耐心填一填（每小题3分，共24分）11．关于中心对称的两个图形，对称点所连线段都经过，而且被_____________平分.12．在平行四边形、矩形、菱形、正方形、等腰梯形这五种图形中，既是轴对称图形，又是中心对称图形的是_____________．13．时钟上的时针不停地旋转，从上午8时到上午11时，时针旋转的旋转角是_____________． 14．如图8，△ABC 以点A 为旋转中心，按逆时针方向旋转60°，得△AB ′C ′，则△ABB ′是三角形.15．已知ａ＜0，则点Ｐ（ａ2，－ａ＋3）关于原点的对称点Ｐ1在第＿＿＿象限16．如图9，△COD 是△AOB 绕点O 顺时针方向旋转40°后所得的图形，点C 恰好在AB 上，∠AOD ＝90°，则∠D 的度数是．17．如图10，在两个同心圆中，三条直径把大圆分成相等的六部分，若大圆的半径为2，则图中阴影部分的面积是＿＿＿.18．如图,四边形ABCD 中，∠BAD=∠C=90º，AB=AD ，AE ⊥BC 于E ，若线段AE=5，则S 四边形ABCD＝。

《圆的基本概念和性质—知识讲解》同步 2022人教九年级上册专练

圆的基本概念和性质—知识讲解（基础）【学习目标】1．知识目标：在探索过程中认识圆，理解圆的本质属性；2．能力目标：了解圆及其有关概念，理解弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念，理解概念之间的区别和联系；3．情感目标：通过圆的学习养成学生之间合作的习惯.【要点梳理】要点一、圆的定义及性质1.圆的定义(1)动态：如图，在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径. 以点O为圆心的圆，记作“⊙O”，读作“圆O”．要点诠释：①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可；②圆是一条封闭曲线.(2)静态：圆心为O，半径为r的圆是平面内到定点O的距离等于定长r的点的集合.要点诠释：①定点为圆心，定长为半径；②圆指的是圆周，而不是圆面；③强调“在一个平面内”是非常必要的，事实上，在空间中，到定点的距离等于定长的点的集合是球面，一个闭合的曲面.2.圆的性质①旋转不变性：圆是旋转对称图形，绕圆心旋转任一角度都和原来图形重合；圆是中心对称图形，对称中心是圆心；②圆是轴对称图形：任何一条直径所在直线都是它的对称轴.或者说，经过圆心的任何一条直线都是圆的对称轴.要点诠释：①圆有无数条对称轴；②因为直径是弦，弦又是线段，而对称轴是直线，所以不能说“圆的对称轴是直径”，而应该说“圆的对称轴是直径所在的直线”.3.两圆的性质两个圆组成的图形是一个轴对称图形，对称轴是两圆连心线（经过两圆圆心的直线叫做两圆连心线）.要点二、与圆有关的概念1.弦弦：连结圆上任意两点的线段叫做弦.直径：经过圆心的弦叫做直径.弦心距：圆心到弦的距离叫做弦心距.要点诠释：直径是圆中通过圆心的特殊弦，也是圆中最长的弦，即直径是弦，但弦不一定是直径.为什么直径是圆中最长的弦？如图，AB是⊙O的直径，CD是⊙O中任意一条弦，求证：AB≥CD.证明：连结OC、OD∵AB=AO+OB=CO+OD≥CD(当且仅当CD过圆心O时，取“=”号)∴直径AB是⊙O中最长的弦.2.弧弧：圆上任意两点间的部分叫做圆弧，简称弧.以A、B为端点的弧记作，读作“圆弧AB”或“弧AB”.半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆；优弧：大于半圆的弧叫做优弧；劣弧：小于半圆的弧叫做劣弧.要点诠释：①半圆是弧，而弧不一定是半圆；②无特殊说明时，弧指的是劣弧.3.同心圆与等圆圆心相同，半径不等的两个圆叫做同心圆.圆心不同，半径相等的两个圆叫做等圆.同圆或等圆的半径相等.4.等弧在同圆或等圆中，能够完全重合的弧叫做等弧.要点诠释：①等弧成立的前提条件是在同圆或等圆中，不能忽视；②圆中两平行弦所夹的弧相等.【典型例题】类型一、圆的定义1．（2020秋•邳州市校级月考）如图所示，BD，CE是△ABC的高，求证：E，B，C，D四点在同一个圆上．【思路点拨】要证几个点在同一个圆上，就是证明这几个点到同一点的距离都相等即可.【答案与解析】证明：如图所示，取BC的中点F，连接DF，EF．∵BD，CE是△ABC的高，∴△BCD和△BCE都是直角三角形．∴DF，EF分别为Rt△BCD和Rt△BCE斜边上的中线，∴DF=EF=BF=CF．∴E，B，C，D四点在以F点为圆心，BC为半径的圆上．【总结升华】要证几个点在同一个圆上，只能依据圆的定义，去说明这些点到平面内某一点的距离相等. 举一反三：【变式】下列命题中，正确的个数是（）⑴直径是弦，但弦不一定是直径；⑵半圆是弧，但弧不一定是半圆；⑶半径相等且圆心不同的两个圆是等圆；⑷一条弦把圆分成的两段弧中，至少有一段是优弧.A.1个B.2个C.3个D.4个【答案】⑴、⑵、⑶是正确的，⑷是不正确的.故选C.类型二、圆及有关概念2．判断题(对的打√，错的打×，并说明理由)①半圆是弧，但弧不一定是半圆；（）②弦是直径；（）③长度相等的两段弧是等弧；（）④直径是圆中最长的弦. （）【答案】①√②×③×④√.【解析】①因为半圆是弧的一种，弧可分为劣弧、半圆、优弧三种，故正确；②直径是弦，但弦不一定都是直径，只有过圆心的弦才是直径，故错；③只有在同圆或等圆中，长度相等的两段弧才是等弧，故错；④直径是圆中最长的弦，正确.【总结升华】理解弦与直径的关系，等弧的定义.举一反三：【变式】（2020•长宁区一模）下列说法中，结论错误的是（）A．直径相等的两个圆是等圆B．长度相等的两条弧是等弧C．圆中最长的弦是直径D．一条弦把圆分成两条弧，这两条弧可能是等弧【答案】B.提示：A、直径相等的两个圆是等圆，正确，不符合题意；B、长度相等的两条弧圆周角不一定相等，它们不一定是等弧，原题的说法是错误的，符合题意；C、圆中最长的弦是直径，正确，不符合题意；D、一条直径把圆分成两条弧，这两条弧是等弧，正确，不符合题意，故选：B．3．直角三角形的三个顶点在⊙O上，则圆心O在 .【答案】斜边的中点.【解析】根据圆的定义知圆心O到三角形的三个顶点距离相等，由三角形斜边的中线等于斜边的一半可知，斜边上的中点到各顶点的距离相等.【总结升华】圆心到圆上各点的距离相等.4．判断正误：有AB、CD，AB的长度为3cm, CD的长度为3cm，则AB与CD是等弧. 【答案】错误.【解析】“能够完全重合的弧叫等弧”.在半径不同的圆中也可以出现弧的长度相等，但它们不会完全重合，因此，只有在同圆或等圆中，长度相等的弧才是等弧.【总结升华】在同圆或等圆中，长度相等的弧才是等弧.举一反三：【变式】有的同学说：“从优弧和劣弧的定义看，大于半圆的弧叫优弧，小于半圆的弧叫劣弧，所以优弧一定比劣弧长.”试分析这个观点是否正确.甲同学：此观点正确，因为优弧大于半圆，劣弧小于半圆，所以优弧比劣弧长.乙同学：此观点不正确，如果两弧存在于半径不相等的两个圆中，如图，⊙O中的优弧AmB，中的劣弧CD，它们的长度大小关系是不确定的，因此不能说优弧一定比劣弧长.请你判断谁的说法正确？【答案】弧的大小的比较只能是在同圆或等圆中进行. 乙的观点正确.类型三、圆的对称性5．已知：如图，两个以O为圆心的同心圆中，大圆的弦AB交小圆于C，D．求证：AC=BD．【答案与解析】证明：过O点作OM⊥AB于M，交大圆与E、F两点.如图，则EF所在的直线是两圆的对称轴，所以AM=BM，CM=DM，故AC=BD.【总结升华】作出与AB垂直的圆的对称轴，由圆的对称性可证得结论.《圆》全章复习与巩固—巩固练习（提高）【巩固练习】一、选择题1．如图所示，AB、AC为⊙O的切线，B和C是切点，延长OB到D，使BD＝OB，连接AD．如果∠DAC＝78°，那么∠ADO等于( )．A．70° B．64° C．62° D．51°2．在半径为27m的圆形广场中心点O的上空安装了一个照明光源S，S射向地面的光束呈圆锥形，其轴截面SAB的顶角为120°(如图所示)，则光源离地面的垂直高度SO为( )．A．54m B．63m C．93m D．183m第1题图第2题图第3题图第4题图3．设计一个商标图案，如图所示，在矩形ABCD中，AB=2BC，且AB=8cm，以A为圆心、AD的长为半径作半圆，则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm2B.(4π+16)cm2C.(3π+8)cm2D.(3π+16)cm24．如图，的半径为5，弦的长为8，点在线段(包括端点)上移动，则的取值范围是( ).A. B. C. D.5.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何?”用数学语言可表示为：如图所示，CD为⊙O的直径，弦AB⊥CD于E，CE=1寸，AB=10寸，则直径CD的长为( )A．12.5寸 B．13寸 C．25寸D．26寸6．（2020•贵港）如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O的半径为2，OP=4，则线段OM的最小值是（）A．0 B．1 C．2 D．37．一条弦的两个端点把圆周分成4:5两部分，则该弦所对的圆周角为( )．A．80° B．100° C．80°或100° D．160°或200°8．如图所示，AB、AC与⊙O分别相切于B、C两点，∠A＝50°，点P是圆上异于B、C的一动点，则∠BPC的度数是( )．A．65° B．115° C．65°或115° D．130°或50°二、填空题9．如下左图，是的内接三角形，，点P在上移动(点P不与点A、C重合)，则的变化范围是__ ________.第9题图第10题图10．如图所示，EB、EC是⊙O是两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，那么∠A的度数是________________.11．已知⊙O 1与⊙O 2的半径1r 、2r 分别是方程2680x x -+= 的两实根，若⊙O 1与⊙O 2的圆心距d =5．则⊙O 1与⊙O 2的位置关系是 __ __ .12．（2020•巴彦淖尔）如图，AB 为⊙O 的直径，AB=AC ，BC 交⊙O 于点D ，AC 交⊙O 于点E ，∠BAC=45°，给出以下五个结论：①∠EBC=22.5°；②BD=DC ；③AE=2EC ；④劣弧是劣弧的2倍；⑤AE=BC ，其中正确的序号是．13.两个圆内切，其中一个圆的半径为5，两圆的圆心距为2，则另一个圆的半径是_______ ________. 14.已知正方形ABCD 外接圆的直径为2a ，截去四个角成一正八边形，则这个正八边形EFGHIJLK 的边长为____ ____，面积为_____ ___．15．如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n 边形，分别以它们的各顶点为圆心，以l 为半径画弧与两邻边相交，得到3条弧，4条弧，……(1)图(1)中3条弧的弧长的和为___ _____，图(2)中4条弧的弧长的和为_____ ___； (2)求图(m)中n 条弧的弧长的和为____ ____(用n 表示)．16．如图所示，蒙古包可以近似地看做由圆锥和圆柱组成，如果想用毛毡搭建20个底面积为9πm 2，高为3.5m ，外围高4 m 的蒙古包，至少要____ ____m 2的毛毡．三、解答题17. 如图，⊙O 是△ABC 的外接圆，FH 是⊙O 的切线，切点为F ，FH ∥BC ，连结AF 交BC 于E ，∠ABC 的平分线BD 交AF 于D ，连结BF ．（1）证明：AF 平分∠BAC ；（2）证明：BF ＝FD.18.（2020•南京）如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．（1）求证：∠A=∠AEB；（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．19．如图，相交两圆的公共弦长为120cm，它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景：课外学习小组在一次学习研讨中，得到了如下两个命题：①如图(1)，在正△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM＝CN；②如图(2)，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM＝CN．然后运用类似的思想提出了如下命题：③如图(3)，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM＝CN．任务要求：(1)请你从①②③三个命题中选择一个进行证明；(2)请你继续完成下面的探索；①在正n(n≥3)边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM＝CN成立(不要求证明)；②如图(4)，在正五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，∠BON＝108°时，试问结论BM＝CN是否成立．若成立，请给予证明；若不成立，请说明理由．【答案与解析】一、选择题1．【答案】B；【解析】由AB为⊙O的切线，则AB⊥OD．又BD＝OB，则AB垂直平分OD，AO＝AD，∠DAB＝∠BAO．由AB、AC为⊙O的切线，则∠CAO＝∠BAO＝∠DAB．所以，∠DAB＝∠DAC＝26°．∠ADO＝90°-26°＝64°．本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等．2．【答案】C；【解析】圆锥的高、底面半径与母线组成直角三角形．由题意，SO⊥AB于O，∴∠SOA＝∠SOB＝90°．又SA＝SB，∠ASB＝120°，∴∠SAB＝∠SBA＝180120302=°-?°，设SO＝x m，则AS＝2x m．∵ AO＝27，由勾股定理，得(2x)2-x2＝272，解得93x=(m)．3．【答案】A.；【解析】对图中阴影部分进行分析，可看做扇形、矩形、三角形的面积和差关系.∵矩形ABCD中，AB=2BC，AB=8cm，∴ AD=BC=4cm，∠DAF=90°，，，又AF=AD=4cm，∴ ，∴.4.【答案】A ；【解析】OM 最长是半径5；最短是OM ⊥AB 时，此时OM=3，故选A. 5．【答案】D ；【解析】因为直径CD 垂直于弦AB ，所以可通过连接OA(或OB)，求出半径即可. 根据“垂直于弦的直径平分弦，并且平分弦所对的两条弧”，知(寸)，在Rt △AOE 中，，即，解得OA=13，进而求得CD=26(寸).故选D. 6．【答案】B.【解析】设OP 与⊙O 交于点N ，连结MN ，OQ ，如图，∵OP=4，ON=2， ∴N 是OP 的中点， ∵M 为PQ 的中点，∴MN 为△POQ 的中位线，∴MN=OQ=×2=1，∴点M 在以N 为圆心，1为半径的圆上，当点M 在ON 上时，OM 最小，最小值为1， ∴线段OM 的最小值为1．故选B ． 7．【答案】C ；【解析】圆周角的顶点在劣弧上时，圆周角为5136010092⨯⨯=°°；圆周角的顶点在优弧上时，圆周角为413608092⨯⨯=°°．注意分情况讨论． 8．【答案】C ；【解析】连接OC 、OB ，则∠BOC ＝360°-90°-90°-50°＝130°．点P 在优弧上时，∠BPC ＝12∠BOC ＝65°；点P 在劣弧上时，∠BPC ＝180°-65°＝115°．主要应用了切线的性质定理、圆周角定理和多边形内角和定理．二、填空题 9．【答案】； 10．【答案】99°；【解析】由EB=EC ，∠E=46°知，∠ECB= 67°，从而∠BCD=180°-67°-32°=81°，在⊙O 中，∠BCD 与∠A 互补，所以∠A=180°-81°=99°. 11．【答案】相交；【解析】求出方程2680x x -+= 的两实根1r 、2r 分别是4、2，则1r -2r <d <1r +2r ,所以两圆相交.12.【答案】①②④；【解析】连接AD ，AB 是直径，则AD ⊥BC ，又∵△ABC 是等腰三角形，故点D 是BC 的中点，即BD=CD ，故②正确； ∵AD 是∠BAC 的平分线，由圆周角定理知，∠EBC=∠DAC=∠BAC=22.5°，故①正确；∵∠ABE=90°﹣∠EBC ﹣∠BAD=45°=2∠CAD ，故④正确； ∵∠EBC=22.5°，2EC ≠BE ，AE=BE ，∴AE ≠2CE ，③不正确； ∵AE=BE ，BE 是直角边，BC 是斜边，肯定不等，故⑤错误．综上所述，正确的结论是：①②④．13.【答案】7或3；【解析】两圆有三种位置关系：相交、相切(外切、内切)和相离(外离、内含).两圆内切时，圆心距，题中一圆半径为5，而d=2，所以有，解得r=7或r=3，即另一圆半径为7或3.14.【答案】(21)a -； 2(222)a -；【解析】正方形ABCD 外接圆的直径就是它的对角线，由此求得正方形边长为a ．如图所示，设正八边形的边长为x ．在Rt △AEL 中，LE ＝x ，AE ＝AL ＝22x ，∴ 222x x a ⨯+=，(21)x a =-，即正八边形的边长为(21)a -．222224[(21)](222)AEL S S S a x a a a =-=-=--=-△正方形正八边形．15.【答案】(1)π； 2π； (2)(n-2)π；【解析】∵ n 边形内角和为(n-2)180°，前n 条弧的弧长的和为(2)1801(2)3602n n -=-个以某定点为圆心，以1为半径的圆周长，∴ n 条弧的弧长的和为121(2)(2)2n n ππ⨯⨯-=-．本题还有其他解法，比如：设各个扇形的圆心角依次为1α，2α，…，n α，则12(2)180n n ααα+++=-…°， ∴ n 条弧长的和为1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-．16.【答案】720π；【解析】∵ S ＝πr 2，∴ 9π＝πr 2，∴ r ＝3．∴ h 1＝4，∴ 2215l h r =+=，∴ 223523 3.5152136S S S rl rh πππππππ=+=+=⨯⨯+⨯⨯=+=锥柱，2036720S ππ=⨯=总．所求面积包括圆锥的侧面积和圆柱的侧面积，不包括底面积．三、解答题17.【答案与解析】（1）连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵FH∥BC ，∴OF 垂直平分BC∴BF FC =∴AF 平分∠BAC .（2）由（1）及题设条件可知∠1=∠2，∠4=∠3，∠5=∠2 ∴∠1+∠4=∠2+∠3 ∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18．【答案与解析】证明：（1）∵四边形ABCD 是⊙O 的内接四边形， ∴∠A+∠BCD=180°， ∵∠DCE+∠BCD=180°， ∴∠A=∠DCE ， ∵DC=DE ，∴∠DCE=∠AEB ， ∴∠A=∠AEB ；（2）∵∠A=∠AEB ，A BCDEO 12345HA BCD EO 12∴△ABE 是等腰三角形， ∵EO ⊥CD ， ∴CF=DF ，∴EO 是CD 的垂直平分线， ∴ED=EC ， ∵DC=DE ， ∴DC=DE=EC ，∴△DCE 是等边三角形， ∴∠AEB=60°，∴△ABE 是等边三角形．19.【答案与解析】解：∵公共弦AB ＝120r R a 6624222212060603=-⎛⎝ ⎫⎭⎪=-=.20. 【答案与解析】 (1)如选命题①．证明：在图(1)中，∵ ∠BON ＝60°，∴ ∠1+∠2＝60°． ∵ ∠3+∠2＝60°，∴ ∠1＝∠3．又∵ BC ＝CA ，∠BCM ＝∠CAN ＝60°， ∴ △BCM ≌△CAN ，∴ BM ＝CM ．如选命题②．证明：在图(2)中，∵∠BON＝90°，∴∠1+∠2＝90°．∵∠3+∠2＝90°，∴∠1＝∠3．又∵ BC＝CD，∠BCM＝∠CDN＝90°，∴△BCM≌△CDN，∴ BM＝CN．如选命题③．证明：在图(3)中，∵∠BON＝108°，∴∠1+∠2＝108°．∵∠2+∠3＝108°，∴∠1＝∠3．又∵ BC＝CD，∠BCM＝∠CDN＝108°，∴△BCM≌△CDN，∴ BM＝CN．(2)①答：当∠BON＝(2)180nn°时结论BM＝CN成立．②答：当∠BON＝108°时．BM＝CN还成立．证明：如图(4)，连接BD、CE在△BCD和△CDE中，∵ BC＝CD，∠BCD＝∠CDE＝108°，CD＝DE，∴△BCD≌△CDE．∴ BD＝CE，∠BDC＝∠CED，∠DBC＝∠ECD．∵∠CDE＝∠DEN＝108°，∴∠BDM＝∠CEM．∵∠OBC+∠OCB＝108°，∠OCB+∠OCD＝108°．∴∠MBC＝∠NCD．又∵∠DBC＝∠ECD＝36°，∴∠DBM＝∠ECM．∴△BDM≌△CEN，∴ BM＝CN．。

九年级上册数学旋转几何综合同步单元检测(Word版含答案)

九年级上册数学旋转几何综合同步单元检测（Word版含答案）一、初三数学旋转易错题压轴题（难）1．如图，四边形ABCD为正方形，△AEF为等腰直角三角形，∠AEF＝90°，连接FC，G 为FC的中点，连接GD，ED．（1）如图①，E在AB上，直接写出ED，GD的数量关系．（2）将图①中的△AEF绕点A逆时针旋转，其它条件不变，如图②，（1）中的结论是否成立？说明理由．（3）若AB＝5，AE＝1，将图①中的△AEF绕点A逆时针旋转一周，当E，F，C三点共线时，直接写出ED的长．【答案】（1）DE＝2DG；（2）成立，理由见解析；（3）DE的长为42或32．【解析】【分析】（1）根据题意结论：DE=2DG，如图1中，连接EG，延长EG交BC的延长线于M，连接DM，证明△CMG≌△FEG（AAS），推出EF=CM，GM=GE，再证明△DCM≌△DAE （SAS）即可解决问题；（2）如图2中，结论成立．连接EG，延长EG到M，使得GM=GE，连接CM，DM，延长EF交CD于R，其证明方法类似；（3）由题意分两种情形：①如图3-1中，当E，F，C共线时．②如图3-3中，当E，F，C 共线时，分别求解即可．【详解】解：（1）结论：DE＝2DG．理由：如图1中，连接EG，延长EG交BC的延长线于M，连接DM．∵四边形ABCD是正方形，∴AD＝CD，∠B＝∠ADC＝∠DAE＝∠DCB＝∠DCM＝90°，∵∠AEF＝∠B＝90°，∴EF∥CM，∴∠CMG＝∠FEG，∵∠CGM＝∠EGF，GC＝GF，∴△CMG≌△FEG（AAS），∴EF＝CM，GM＝GE，∵AE＝EF，∴AE＝CM，∴△DCM≌△DAE（SAS），∴DE＝DM，∠ADE＝∠CDM，∴∠EDM＝∠ADC＝90°，∴DG⊥EM，DG＝GE＝GM，∴△EGD是等腰直角三角形，∴DE＝2DG．（2）如图2中，结论成立．理由：连接EG，延长EG到M，使得GM＝GE，连接CM，DM，延长EF交CD于R．∵EG＝GM，FG＝GC，∠EGF＝∠CGM，∴△CGM≌△FGE（SAS），∴CM＝EF，∠CMG＝∠GEF，∴CM∥ER，∴∠DCM＝∠ERC，∵∠AER+∠ADR＝180°，∴∠EAD+∠ERD＝180°，∵∠ERD+∠ERC＝180°，∴∠DCM＝∠EAD，∵AE＝EF，∴AE＝CM，∴△DAE≌△DCM（SAS），∴DE＝DM，∠ADE＝∠CDM，∴∠EDM＝∠ADC＝90°，∵EG＝GM，∴DG＝EG＝GM，∴△EDG是等腰直角三角形，∴DE ＝2DG ．（3）①如图3﹣1中，当E ，F ，C 共线时，在Rt △ADC 中，AC ＝22AD CD +＝2255+＝52，在Rt △AEC 中，EC ＝22A AE C -＝22(52)1-＝7，∴CF ＝CE ﹣EF ＝6，∴CG ＝12CF ＝3， ∵∠DGC ＝90°， ∴DG ＝22CD CG -＝2253-＝4，∴DE ＝2DG ＝42．②如图3﹣3中，当E ，F ，C 共线时，同法可得DE ＝32．综上所述，DE 的长为2或2．【点睛】本题属于四边形综合题，考查正方形的性质，全等三角形的判定和性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．2．小明研究了这样一道几何题：如图1，在△ABC 中，把AB 点A 顺时针旋转α (0°＜α＜180°)得到AB ′，把AC 绕点A 逆时针旋转β得到AC ′，连接B ′C ′．当α+β=180°时，请问△AB ′C ′边B ′C ′上的中线AD 与BC 的数量关系是什么？以下是他的研究过程：特例验证：(1)①如图2，当△ABC 为等边三角形时，AD 与BC 的数量关系为AD = BC ；②如图3，当∠BAC=90°，BC=8时，则AD长为．猜想论证：(2)在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．拓展应用(3)如图4，在四边形ABCD，∠C=90°，∠A+∠B=120°，BC=12，CD=6，DA=63，在四边形内部是否存在点P，使△PDC与△PAB之间满足小明探究的问题中的边角关系？若存在，请画出点P的位置(保留作图痕迹，不需要说明)并直接写出△PDC的边DC上的中线PQ的长度；若不存在，说明理由．【答案】(1)①12；②4(2) AD=12BC，理由见解析(3)存在，313【解析】【分析】(1)①由已知条件可得AD⊥B′C′，由α+β=180°可得∠BAC+∠B′AC′=180°，已知∠BAC=60°，可求得∠B′AC′=120°继而∠B′=∠C′=30°，可得AD=12AB′=12BC②当∠BAC=90°时，可得∠B′AC′=∠BAC=90°，△B′AC′是直角三角形，可证得△BAC≌△B′AC′，推出对应边相等，已知BC=8求出AD的长.（2）先做辅助线，延长AD到M，使得AD=DM，连接B′M、C′M，如图1所示：因为B′D=DC′，AD=DM，对角线相互平分，可得四边形AC′MB′是平行四边形，得出对应边相等，由∠BAB′+∠CAC′=180°推得∠BAC=∠AB′M，可证明△BAC≌△AB′M，所以BC=AM，AD=12 BC；(3)先做辅助线，作线段BC的垂直平分线交BE于P，即为点P的位置；延长AD交BC的延长线于M，线段BC的垂直平分线交BC于F，连接PA、PD、PC，作△PDC的中线PQ，连接DF交PC于O假设P点存在，再证明理由.根据已知角可得出△DCM是直角三角形，∠MDC=30°，可得出CMDM在；∵CD=6，∠DCM=90°，∠MDC=30°，∠M=90°﹣∠MDC=60°，可求得EM=12 BMDE=EM﹣DM﹣由已知DAAE=DE且BE⊥AD，可得PF是线段BC的垂直平分线，证得PA=PD因为PB=PC，PF∥CD，可求得CF=12BC，利用线段长度可求得∠CDF=60°利用全等三角形判定定理可证得△FCP≌△CFD(AAS)，进而证得四边形CDPF是矩形，得∠CDP=90°，∠ADP =60°，可得△ADP是等边三角形，求出DQ、DP，在Rt△PDQ中可求得PQ长度.【详解】(1)①∵△ABC是等边三角形∴AB=BC=AC=AB′=AC′，∠BAC=60°∵DB′=DC′∴AD⊥B′C′∵∠BAB′+∠CAC′=180°∴∠BAC+∠B′AC′=180°∴∠B′AC′=180°﹣∠BAC=180°﹣60°=120°∴∠B′=∠C′=30°∴AD=12AB′=12BC故答案：1 2②∵∠BAB′+∠CAC′=180°∴∠BAC+∠B′AC′=180°∵∠BAC=90°∴∠B′AC′=∠BAC=90°在△BAC和△B′AC′中，''"90"AB ABBAC B ACAC AC=⎧⎪∠=∠=︒⎨⎪=⎩∴△BAC≌△B′AC′(SAS)∴BC=B′C′∵B′D=DC′∴AD=12B′C′=12BC=4故答案：4(2)AD与BC的数量关系：AD=12BC；理由如下：延长AD到M，使得AD=DM，连接B′M、C′M，如图1所示：∵B′D=DC′，AD=DM，∴四边形AC′MB′是平行四边形，∴∠B′AC′+∠AB′M=180°，AC′=B′M=AC，∵∠BAB′+∠CAC′=180°，∴∠BAC+∠B′AC′=180°，∴∠BAC=∠AB′M，在△BAC和△AB′M中，'''AC B MBAC AB MAB AB=⎧⎪∠=∠⎨⎪=⎩，∴△BAC≌△AB′M(SAS)，∴BC=AM，∴AD=12 BC；(3)存在；作BE⊥AD于E，作线段BC的垂直平分线交BE于P，即为点P的位置；理由如下：延长AD交BC的延长线于M，线段BC的垂直平分线交BC于F，连接PA、PD、PC，作△PDC的中线PQ，连接DF交PC于O，如图4所示：∵∠A+∠B=120°，∴∠ADC=150°，∴∠MDC=30°，在Rt△DCM中，∵CD=6，∠DCM=90°，∠MDC=30°，∴CM3DM3，∠M=90°﹣∠MDC=60°，在Rt△BEM中，∵∠BEM=90°，BM=BC+CM333，∠MBE=90°﹣∠M=30°，∴EM=12BM3∴DE=EM﹣DM333∵DA∴AE=DE，∵BE⊥AD，∴PA=PD，∵PF是线段BC的垂直平分线，∴PB=PC，PF∥CD，在Rt△CDF中，∵CD=6，CF=12 BC∴tan∠CDF=CFCD=6，∴∠CDF=60°，∴∠MDF=∠MDC+∠CDF=30°+60°=90°，∴∠ADF=90°=∠AEB，∴∠CBE=∠CFD，∵∠CBE=∠PCF，∴∠CFD=∠PCF=30°，∵∠CFD+∠CDF=90°，∠PCF+∠CPF=90°，∴∠CPF=∠CDF=60°，在△FCP和△CFD中，CPF CDFPCF CFD CF CF∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△FCP≌△CFD(AAS)，∴CD=PF，∵CD∥PF，∴四边形CDPF是矩形，∴∠CDP=90°，∴∠ADP=∠ADC﹣∠CDP=60°，∴△ADP是等边三角形，∴∠APD=60°，∵∠BPF=∠CPF=90°﹣30°=60°，∴∠BPC=120°，∴∠APD+∠BPC=180°，∴△PDC与△PAB之间满足小明探究的问题中的边角关系；在Rt△PDQ中，∵∠PDQ=90°，PD=DADN=12CD=3，∴PQ．【点睛】本题考查了三角形的边旋转的问题，旋转前后边长不变，根据已知角度变化，求得线段之间关系.在证明某点知否存在时，先假设这点存在，能求出相关线段或坐标，即证实存在性.3．如图1，在正方形ABCD中，点E、F分别在边BC，CD上，且BE=DF，点P是AF的中点，点Q是直线AC与EF的交点，连接PQ，PD．（1）求证：AC垂直平分EF；（2）试判断△PDQ的形状，并加以证明；（3）如图2，若将△CEF绕着点C旋转180°，其余条件不变，则（2）中的结论还成立吗？若成立，请加以证明；若不成立，请说明理由．【答案】（1）证明见解析；（2）△PDQ是等腰直角三角形；理由见解析（3）成立；理由见解析.【解析】试题分析：（1）由正方形的性质得出AB=BC=CD=AD，∠B=∠ADF=90°，∠BCA=∠DCA=45°，由BE=DF，得出CE=CF，△CEF是等腰直角三角形，即可得出结论；（2）由直角三角形斜边上的中线的性质得出PD=AF，PQ=AF，得出PD=PQ，再证明∠DPQ=90°，即可得出结论；（3）由直角三角形斜边上的中线的性质得出PD=AF，PQ=AF，得出PD=PQ，再证明点A、F、Q、P四点共圆，由圆周角定理得出∠DPQ=2∠DAQ=90°，即可得出结论．试题解析：（1）证明：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠ADF=90°，∠BCA=∠DCA=45°，∵BE=DF，∴CE=CF，∴AC垂直平分EF；（2）解：△PDQ是等腰直角三角形；理由如下：∵点P是AF的中点，∠ADF=90°，∴PD=AF=PA，∴∠DAP=∠ADP，∵AC垂直平分EF，∴∠AQF=90°，∴PQ=AF=PA，∴∠PAQ=∠AQP，PD=PQ，∵∠DPF=∠PAD+∠ADP，∠QPF=∠PAQ+∠AQP，∴∠DPQ=2∠PAD+2∠PAQ=2（∠PAD+∠PAQ）=2×45°=90°，∴△PDQ是等腰直角三角形；（3）成立；理由如下：∵点P是AF的中点，∠ADF=90°，∴PD=AF=PA，∵BE=DF，BC=CD，∠FCQ=∠ACD=45°，∠ECQ=∠ACB=45°，∴CE=CF，∠FCQ=∠ECQ，∴CQ⊥EF，∠AQF=90°，∴PQ=AF=AP=PF，∴PD=PQ=AP=PF，∴点A、F、Q、P四点共圆，∴∠DPQ=2∠DAQ=90°，∴△PDQ是等腰直角三角形．考点：四边形综合题．4．某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：操作发现（1）某小组做了有一个角是120︒的等腰三角形DAC和等边三角形GEB纸片，=，让两个三角形如图①放置，点C和点G重合，点D，点E在AB的同侧，AC DA DC和GB在同一条直线上，点F为AB的中点，连接DF，EF，则DF和EF的数量关系与位置关系为：________；数学思考（2）在图①的基础上，将GEB绕着C点按顺时针方向旋转90︒，如图②，试判断DF和EF的数量关系和位置关系，并说明理由；类比探索（3）①将GEB绕着点C任意方向旋转，如图③或图④，请问DF和EF的数量关系和位置关系改变了吗？无论改变与否，选择图③或图④进行证明；②GEB绕着点C旋转的过程中，猜想DF与EF的数量关系和位置关系，用一句话表述：________.【答案】（1）3EF DF =，DFEF ；（2）3EF DF =，DFEF ,理由见解析; （3）①3EF DF =，DFEF ;②旋转过程中3EF DF =，DF EF 始终成立.【解析】【分析】（1）由题意过点D 作DM AB ⊥于点M ，过点E 作EN AB ⊥于点N ，利用等边三角形和中点性质设DM a =，2GB b =，结合相似三角形判定和性质进行综合分析求解；（2）根据题意要求判断DF 和EF 的数量关系和位置关系，连接CF ，OB 与AE 交于点M ，并综合利用垂直平分线定理以及矩形和等边三角形性质与三角函数进行综合分析；（3）①根据题意延长DF 并截取FN DF =，连接NE ，连接NB 并延长交CE 于点P ，交DC 的延长线于点O ，连接DE ，并利用全等三角形判定和性质以及三角函数进行分析证明；②由题意可知结合①猜想可知旋转过程中3EF DF =，DFEF 始终成立. 【详解】解：（1）3EF DF =，DF EF ；如解图，过点D 作DM AB ⊥于点M ，过点E 作EN AB ⊥于点N ，AD CD =，EGB 为等边三角形.AM MC ∴=，GN BN =.又点F 为AB 的中点，AF BF ∴=.()12MF CF NC NB AC AM CB MC NC +=++=+=+∴. MF NC NB ∴==，CF CN FN AM +==.设DM a =，2GB b =， 120ADC ∠=︒，DA DC =，3AM a ∴=，3FN a =，MF NC NB b ===.tan 33EGB NE GN GN b =⋅==∠.在DMF 和FNE 中，333DM FN a==， 333MF NE b==，又90DMF FNE ∠=∠=︒，DMF FNE ∴∽. MDF NFE ∴∠=∠，3DF DM FE FN ==，即3EF DF =. 90MDF DFM ∠+∠=︒，90DFM NFE ∴∠+∠=︒.90DFE ∴∠=︒.3EF DF ∴=且DFEF . （2）3EF DF =，DF EF . 理由如下：如解图，连接CF ，OB 与AE 交于点M ，当旋转角是90︒时，则90ACB ∠=︒，在Rt ACB △中，点F 是AB 的中点，CF BF ∴=.又CE EB =，EF ∴垂直平分BC.同理，DF 垂直平分AC ，∴四边形LCMF 为矩形，90DFE ∴∠=︒.DF EF ∴⊥，//AC EF .DA DC =，120ADC =∠︒，30DCA ∴∠=︒.GEB 为等边三角形，60ECB ∴∠=︒.∴∠DCA+∠ACB+∠ECB=180^∘∴D ，C ，E 三点共线.30DCA DEF ∴∠=∠=︒.∴在RtDEF △中，3tan 33DE DF F F E DF ===∠；（3）①3EF DF =，DFEF .选择题图进行证明：如解图，延长DF 并截取FN DF =，连接NE ，连接NB 并延长交CE 于点P ，交DC 的延长线于点O ，连接DE ，在ADF 和BNF 中，AF BF AFD BFN DF NF =⎧⎪∠=∠⎨⎪=⎩，()SAS ADF BNF ∴≅.AD NB ∴=，ADF BNF ∠=∠.//AD NB ∴.18060O ADC ∴∠=︒-∠=︒.又CPO BPE ∠=∠，60O CEB ∠=∠=︒，OCP OBE ∴∠=∠.DCE NBE ∴∠=∠.又GEB 是等边三角形，GE BE ∴=，又AD BN CD ==，()SAS DCE NBE ∴≅.DE NE ∴=，BEN CED ∠=∠.BEN BED CED BED ∴∠+∠=∠+∠，即60NED BEC ∠=∠=︒.DEN ∴是等边三角形.又DF FN =，DF EF ∴⊥，60FDE ∠=︒.tan 3E E F DF DF FD ∴∠=⋅=.或选择图进行证明，证明如下：如解图，延长DF 并延长到点N ，使得FN DF =，连接NB ，DE ，NE ，NB 与CD 交于点O ，EB 与CD 相交于点J ，在ADF 和BNF 中，AF BF AFD BFN DF NF =⎧⎪∠=∠⎨⎪=⎩，()SAS ADF BNF ∴≅.AD NB ∴=，ADF BNF ∠=∠.//AD NB ∴.120NOC ADC ∴∠=∠=︒.60BOJ ∴∠=︒，60JEC ∠=︒.又OJB EJC ∠=∠，OBE ECJ ∴∠=∠.AD CD =，AD NB =，CD NB ∴=. 又GEB 是等边三角形，CE BE ∴=.()SAS DCE NBE ∴≅.DE NE ∴=，BEN CED ∠=∠.BEN BED CED BED ∴∠-∠=∠-∠，即60NED BEC ∠=∠=︒. DEN ∴是等边三角形.又DF FN =，DF EF ∴⊥，60FDE ∠=︒.tan 3E E F DF DF FD ∴∠=⋅=.②旋转过程中3EF DF =，DFEF 始终成立.【点睛】本题考查几何图形的综合探究题，难度大，运用数形结合思维分析以及掌握并灵活利用全等三角形判定和性质以及三角函数、相似三角形判定和性质等是解题关键.错因分析：①未掌握旋转的性质，即旋转前后线段、角度均不变；②不能合理利用类比关系，由浅到深解决问题.5．在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°，得到△ABG(如图①)，求证：△AEG≌△AEF；(2)若直线EF与AB，AD的延长线分别交于点M，N(如图②)，求证：EF2=ME2+NF2；(3)将正方形改为长与宽不相等的矩形，若其余条件不变(如图③)，请你直接写出线段EF，BE，DF之间的数量关系.【答案】（1）证明见解析；（2）证明见解析；（3）EF2=2BE2+2DF2.【解析】试题分析：（1）根据旋转的性质可知AF=AG，∠EAF=∠GAE=45°，故可证△AEG≌△AEF；（2）将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．由（1）知△AEG≌△AEF，则EG=EF．再由△BME、△DNF、△CEF均为等腰直角三角形，得出CE=CF，BE=BM，NF=DF，然后证明∠GME=90°，MG=NF，利用勾股定理得出EG2=ME2+MG2，等量代换即可证明EF2=ME2+NF2；（3）将△ADF绕着点A顺时针旋转90°，得到△ABG，根据旋转的性质可以得到△ADF≌△ABG，则DF=BG，再证明△AEG≌△AEF，得出EG=EF，由EG=BG+BE，等量代换得到EF=BE+DF．试题解析：（1）∵△ADF绕着点A顺时针旋转90°，得到△ABG，∴AF=AG，∠FAG=90°，∵∠EAF=45°，∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）设正方形ABCD的边长为a．将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF，∴EG=EF．∵∠CEF=45°，∴△BME、△DNF、△CEF均为等腰直角三角形，∴CE=CF，BE=BM，NF=DF，∴a﹣BE=a﹣DF，∴BE=DF，∴BE=BM=DF=BG，∴∠BMG=45°，∴∠GME=45°+45°=90°，∴EG2=ME2+MG2，∵EG=EF，MG=BM=DF=NF，∴EF2=ME2+NF2；（3）EF2=2BE2+2DF2．如图所示，延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，则由勾股定理有（GH+BE）2+BG2=EH2，即（GH+BE）2+（BM﹣GM）2=EH2又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，即2（DF2+BE2）=EF2考点：四边形综合题6．请认真阅读下面的数学小探究系列，完成所提出的问题：()1探究1：如图1，在等腰直角三角形ABC 中，90ACB ∠=，BC a =，将边AB 绕点B 顺时针旋转90得到线段BD ，连接.CD 求证：BCD 的面积为21.(2a 提示：过点D 作BC 边上的高DE ，可证ABC ≌)BDE ()2探究2：如图2，在一般的Rt ABC 中，90ACB ∠=，BC a =，将边AB 绕点B 顺时针旋转90得到线段BD ，连接.CD 请用含a 的式子表示BCD 的面积，并说明理由． ()3探究3：如图3，在等腰三角形ABC 中，AB AC =，BC a =，将边AB 绕点B 顺时针旋转90得到线段BD ，连接.CD 试探究用含a 的式子表示BCD 的面积，要有探究过程．【答案】（1）详见解析；（2）BCD 的面积为212a ，理由详见解析；（3）BCD 的面积为214a ．【解析】【分析】 ()1如图1，过点D 作BC 的垂线，与BC 的延长线交于点E ，由垂直的性质就可以得出ABC ≌BDE ，就有DE BC a.==进而由三角形的面积公式得出结论；()2如图2，过点D 作BC 的垂线，与BC 的延长线交于点E ，由垂直的性质就可以得出ABC ≌BDE ，就有DE BC a.==进而由三角形的面积公式得出结论；()3如图3，过点A 作AF BC ⊥与F ，过点D 作DE BC ⊥的延长线于点E ，由等腰三角形的性质可以得出1BF BC 2=，由条件可以得出AFB ≌BED 就可以得出BF DE =，由三角形的面积公式就可以得出结论．【详解】()1如图1，过点D 作DE CB ⊥交CB 的延长线于E ，BED ACB90∠∠∴==，由旋转知，AB AD =，ABD 90∠=，ABC DBE 90∠∠∴+=，A ABC 90∠∠+=，A DBE ∠∠∴=，在ABC 和BDE 中，ACB BED A DBE AB BD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ABC ∴≌()BDE AASBC DE a ∴==，BCD 1S BC DE 2=⋅， 2BCD 1S a 2∴=； ()2BCD 的面积为21a 2，理由：如图2，过点D 作BC 的垂线，与BC 的延长线交于点E ，BED ACB 90∠∠∴==，线段AB 绕点B 顺时针旋转90得到线段BE ，AB BD ∴=，ABD 90∠=，ABC DBE 90∠∠∴+=，A ABC 90∠∠+=，A DBE ∠∠∴=，在ABC 和BDE 中，ACB BED A DBE AB BD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ABC ∴≌()BDE AAS ，BC DE a ∴==，BCD1S BC DE2=⋅，2BCD1S a2∴=；()3如图3，过点A作AF BC⊥与F，过点D作DE BC⊥的延长线于点E，AFB E90∠∠∴==，11BF BC a22==，FAB ABF90∠∠∴+=，ABD90∠=，ABF DBE90∠∠∴+=，FAB EBD∠∠∴=，线段BD是由线段AB旋转得到的，AB BD∴=，在AFB和BED中，AFB EFAB EBDAB BD∠=∠⎧⎪∠=∠⎨⎪=⎩，AFB∴≌()BED AAS，1BF DE a2∴==，2BCD1111S BC DE a a a2224=⋅=⋅⋅=，BCD∴的面积为21a4．【点睛】本题考查了旋转的性质、直角三角形的性质、等腰三角形的性质、全等三角形的判定与性质、三角形的面积等，综合性较强，有一定的难度，正确添加辅助线、熟练掌握和灵活运用相关的性质与定理是解题的关键.7．已知，如图：正方形ABCD，将Rt△EFG斜边EG的中点与点A重合，直角顶点F落在正方形的AB边上，Rt△EFG的两直角边分别交AB、AD边于P、Q两点，（点P与点F重合），如图1所示：（1）求证：EP2+GQ2=PQ2；（2）若将Rt△EFG绕着点A逆时针旋转α（0°＜α≤90°），两直角边分别交AB、AD边于P、Q两点，如图2所示：判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系？若存在，证明你的结论．若不存在，请说明理由；（3）若将Rt△EFG绕着点A逆时针旋转α（90°＜α＜180°），两直角边所在的直线分别交BA、AD两边延长线于P、Q两点，并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系？按题意完善图3，请直接写出你的结论（不用证明）．【答案】（1）见解析；（2）PF2+FQ2=EP2+GQ2；（3）四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2．【解析】【分析】（1）过点E作EH∥FG，由此可证△EAH≌△GAQ，然后根据全等三角形的性质得到EH=QG，又PQ=PH，在Rt△EPH中，EP2+EH2=PH2，由此可以得到EP2+GQ2=PQ2；（2）过点E作EH∥FG，交DA的延长线于点H，连接PQ、PH，由此可证△EAH≌△GAQ，然后根据全等三角形的性质得到EH=QG，又PH=PQ，在Rt△EPH中，EP2+EH2=PH2，即EP2+GQ2=PH2，在Rt△PFQ中，PF2+FQ2=PQ2，故PF2+FQ2=EP2+GQ2；（3）四条线段EP、PF、FQ、QG之间的关系为PE2+GQ2=PF2+FQ2，证明方法同上．【详解】（1）过点E作EH∥FG，连接AH、FH，如图所示：∵EA=AG，∠HEA=∠AGQ，∠HAE=∠GAD，∴△EAH≌△GAQ，∴EH=QG，HA=AQ，∵FA⊥AD，∴PQ=PH．在Rt△EPH中，∵EP2+EH2=PH2，∴EP2+GQ2=PQ2；（2）过点E作EH∥FG，交DA的延长线于点H，连接PQ、PH，∵EA=AG，∠HEA=∠AGQ，∠HAE=∠GAD，∴△EAH≌△GAQ，∴EH=QG，HA=AQ，∵PA⊥AD，∴PQ=PH．在Rt△EPH中，∵EP2+EH2=PH2，∴EP2+GQ2=PH2．在Rt△PFQ中，∵PF2+FQ2=PQ2，∴PF2+FQ2=EP2+GQ2．（3）四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2．【点睛】本题主要考查了旋转的性质，全等三角形的判定与性质，三线合一，勾股定理，正确作出辅助线是解答本题的关键.8．如图，已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE的中点，连接CF，DF．（1）如图1，当点D在AB上，点E在AC上时①证明：△BFC是等腰三角形；②请判断线段CF，DF的关系？并说明理由；（2）如图2，将图1中的△ADE绕点A旋转到图2位置时，请判断（1）中②的结论是否仍然成立？并证明你的判断．【答案】（1）①证明见解析；②结论：CF=DF且CF⊥DF．理由见解析；（2）（1）中的结论仍然成立．理由见解析.【解析】【详解】分析：(1)、根据“直角三角形斜边上的中线等于斜边的一半”可知CF=BF=EF，根据∠CFD=2∠ABC，∠ACB=90°，∠ABC=45°得出∠CFD=90°，从而得出答案；(2)、延长DF至G使FG=DF，连接BG，CG，DC，首先证明△BFG和△EFD全等，然后再证明△BCG和△ACD全等，从而得出GC=DC，∠BCG=∠ACD，∠DCG=∠ACB=90°，最后根据直角三角形斜中线的性质得出答案．详解：（1）①证明：∵∠BCE=90°．EF=FB，∴CF=BF=EF，∴△BFC是等腰三角形．②解：结论：CF=DF且CF⊥DF．理由如下：∵∠ADE=90°，∴∠BDE=90°，又∵∠BCE=90°，点F是BE的中点，∴CF=DF=12BE=BF，∴∠1=∠3，∠2=∠4，∴∠5=∠1+∠3=2∠1，∠6=∠2+∠4=2∠2，∴∠CFD=∠5+∠6=2（∠1+∠2）=2∠ABC，又∵△ABC是等腰直角三角形，且∠ACB=90°，∴∠ABC=45°，∴∠CFD=90°，∴CF=DF且CF⊥DF．（2）（1）中的结论仍然成立．理由如下：如图，延长DF至G使FG=DF，连接BG，CG，DC，∵F是BE的中点，∴BF=EF，又∵∠BFG=∠EFD，GF=DF，∴△BFG≌△EFD（SAS），∴∠FBG=∠FED，BG=ED，∴BG∥DE，∵△ADE和△ACB都是等腰直角三角形，∴DE=DA，∠DAE=∠DEA=45°，AC=BC，∠CAB=∠CBA=45°，又∵∠CBG=∠EBG﹣∠EBA﹣∠ABC=∠DEF﹣（180°﹣∠AEB﹣∠EAB）﹣45°=∠DEF﹣180°+∠AEB+∠EAB﹣45°=（∠DEF+∠AEB）+∠EAB﹣225°=360°﹣∠DEA+∠EAB﹣225°=360°﹣45°+∠EAB﹣225°=90°+∠EAB，而∠DAC=∠DAE+∠EAB+∠CAB=45°+∠EAB+45°=90°+∠EAB ，∴∠CBG=∠DAC ，又∵BG=ED ，DE=DA ，∴BG=AD ，又∵BC=AC ，∴△BCG ≌△ACD （SAS ），∴GC=DC ，∠BCG=∠ACD ，∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°，∴△DCG 是等腰直角三角形，又∵F 是DG 的中点，∴CF ⊥DF 且CF=DF ．点睛：主要考查了旋转的性质，等腰三角形和全等三角形的判定，及勾股定理的运用．要掌握等腰三角形和全等三角形的性质及其判定定理并会灵活应用是解题的关键． 9．在矩形ABCD 中，2AB =，1BC =，以点A 为旋转中心，逆时针旋转矩形ABCD ，旋转角为(0180)αα<<，得到矩形AEFG ，点B 、点C 、点D 的对应点分别为点E 、点F 、点G ． ()1如图①，当点E 落在DC 边上时，直写出线段EC 的长度为______；()2如图②，当点E 落在线段CF 上时，AE 与DC 相交于点H ，连接AC ，①求证：ACD ≌CAE ；②直接写出线段DH 的长度为______．()3如图③设点P 为边FG 的中点，连接PB ，PE ，在矩形ABCD 旋转过程中，BEP 的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由．【答案】（1）23；（2）①见解析；34②；（3）存在，PBE 的面积的最大值为21，理由见解析【解析】【分析】()1如图①中，在Rt ADE 中，利用勾股定理即可解决问题；()2①证明：如图②中，根据HL 即可证明ACD ≌CAE ；②如图②中，由ACD ≌CAE ，推出ACD CAE ∠∠=，推出AH HC =，设AH HC m ==，在Rt ADH 中，根据222AD DH AH +=，构建方程即可解决问题； ()3存在.如图③中，连接PA ，作BM PE ⊥交PE 的延长线于M.由题意：PF PC 1==，由AG EF 1==，G F 90∠∠==，推出PA PE ==PBE 1S PE BM 22=⋅⋅=，推出当BM 的值最大时，PBE 的面积最大，求出BM 的最大值即可解决问题；【详解】()1四边形ABCD 是矩形，AB CD 2∴==，BC AD 1==，D 90∠=，矩形AEFG 是由矩形ABCD 旋转得到，AE AB 2∴==，在Rt ADE 中，DE ==CE 2∴=，故答案为2．()2①当点E 落在线段CF 上，AEC ADC 90∠∠∴==，在Rt ADC 和Rt AEC 中，{AC CACD AE ==， Rt ACD ∴≌()Rt CAE HL ； ACD ②≌CAE ，ACD CAE ∠∠∴=，AH HC ∴=，设AH HC m ==，在Rt ADH 中，222AD DH AH +=，2221(2m)m ∴+-=，5m 4∴=， 53DH 244∴=-=，故答案为34；()3存在．理由如下：如图③中，连接PA，作BM PE⊥交PE的延长线于M，由题意：PF PC1==，AG EF1==，G F90∠∠==，PA PE2∴==，PBE 12S PE BM BM22∴=⋅⋅=，∴当BM的值最大时，PBE的面积最大，BM PB≤，PB AB PA≤+，PB22∴≤+，BM22∴≤+，BM∴的最大值为22+，PBE∴的面积的最大值为21+．【点睛】本题是四边形综合题，考查了矩形的性质，旋转变换，全等三角形的判定和性质，勾股定理，三角形的面积，三角形的三边关系等知识，解题的关键是正确寻找全等三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．10．已知ABC∆是边长为4的等边三角形，点D是射线BC上的动点，将AD绕点A逆时针方向旋转60得到AE，连接DE．(1).如图，猜想ADE∆是_______三角形；（直接写出结果）(2).如图，猜想线段CA、CE、CD之间的数量关系，并证明你的结论；(3).①当BD=___________时，30DEC∠=；（直接写出结果）②点D 在运动过程中，DEC ∆的周长是否存在最小值？若存在．请直接写出DEC ∆周长的最小值；若不存在，请说明理由．【答案】（1）等边三角形；（2）AC CD CE +=，证明见解析；（3）①BD 为2或8时，30DEC ∠=；②最小值为4+【解析】【分析】（1）根据旋转的性质得到,60AD AE DAE =∠=，根据等边三角形的判定定理解答；（2）证明ABD ACE ∆≅∆，根据全等三角形的性质得到BD CE =，结合图形计算即可；（3）①分点D 在线段BC 上和点D 在线段BC 的延长线上两种情况，根据直角三角形的性质解答；②根据ABD ACE ∆≅∆得到CE BD =，根据垂线段最短解答．【详解】解：（1）由旋转变换的性质可知，,60AD AE DAE =∠=，ADE ∴∆是等边三角形，故答案为等边三角形；（2）AC CD CE +=，证明：由旋转的性质可知，60,DAE AD AE ∠==，ABC ∆是等边三角形60AB AC BC BAC ∴∠︒＝＝，＝，60BAC DAE ∴∠∠︒＝＝，BAC DAC DAE DAC ∴∠+∠∠+∠＝，即BAD CAE ∠∠＝，在ABD ∆和ACE ∆中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ABD ACE SAS ∴∆∆≌（）BD CE ∴=，CE BD CB CD CA CD ∴++＝＝＝；（3）①BD 为2或8时，30DEC ∠=，当点D 在线段BC 上时，3060DEC AED ∠︒∠︒＝，＝，90AEC ∴∠︒＝，ABD ACE ∆∆≌，9060ADB AEC B ∴∠∠︒∠︒＝＝，又＝，30BAD ∴∠︒＝，122BD AB ∴＝＝，当点D 在线段BC 的延长线上时，3060DEC AED ∠︒∠︒＝，＝，30AEC ∴∠︒＝，ABD ACE ∆∆≌，3060ADB AEC B ∴∠∠︒∠︒＝＝，又＝，90BAD ∴∠︒＝，28BD AB ∴＝＝，BD ∴为2或8时，30DEC ∠︒＝；②点D 在运动过程中，DEC ∆的周长存在最小值，最小值为4+理由如下：ABD ACE ∆∆≌，CE BD ∴＝，则DEC ∆的周长DE CE DC BD CD DE BC DE +++++＝＝＝，当CE 最小时，DEC ∆的周长最小，ADE ∆为等边三角形，DE AD ∴=，AD 的最小值为DEC ∴∆的周长的最小值为4+【点睛】本题考查的是旋转变换的性质、全等三角形的判定和性质、直角三角形的性质，掌握全等三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键．。

九年级(上)《圆》-同步练习(A4有答案)

九年级《圆》1 圆的基本性质(1)学习要求：理解圆的定义，理解弦、直径、圆弧、半圆、优弧、劣弧等有关概念．做一做：填空题：1．确定一个圆的要素是______和______．2．平面上，与已知点P的距离为3cm的所有点组成的图形是______．3．A、B是⊙O上不同的两点，⊙O的半径为r，则弦AB长的取值范围是______选择题：4．如图，⊙O中的点A、O、D以及点B、O、C分别在不同的两直线上，图中弦的条数为( )(A)2 (B)3 (C)4 (D)55．下列说法中，正确的是( )(A)过圆心的线段是直径(B)小于半圆的弧是优弧(C)弦是直径(D)半圆是弧6．下列说法中：①直径相等的两个圆是等圆；②圆中最长的弦是直径；③一条弦把圆分成两条弧，一条是优弧，另一条是劣弧；④顶点在圆心的角是圆心角．其中正确的是( )(A)①②(B)①②④(C)①②(D)②③解答题：7．已知：如图，OA、OB为⊙O的半径，C、D分别为OA、OB上的点，且AC＝BD．求证：AD＝BC．8．如图，在△ABC中，∠ACB＝90°，AC＝12，BC＝5，分别以A为圆心，12为半径，以B为圆心，5为半径画弧，分别交斜边AB于M、N两点，求线段MN的长度．9．如图，在⊙O中，AB，CD为⊙O的两条直径，AE＝BF，求证四边形CEDF是平行四边形．10．已知：如图，矩形ABCD的对角线AC和BD相交于O点，E、F、C、H分别为OD、OA、OB、OC 的中点．试说明：E、F、G、H四个点在以点O为圆心、OE为半径的同一个圆上．问题探究：11．如图，点A、D、G、M在半圆O上，四边形ABOC、DEOF、HMNO均为矩形，设BC＝a，EF＝b，NH＝c，则下列各式中正确的是( )(A)a＞b＞c(B)a＝b＝c(C)c＞a＞b(D)b＞c＞a九年级《圆》2 圆的基本性质(2)学习要求：探索并认识圆的轴对称性、中心对称性及圆的旋转不变性．掌握圆心角、弧、弦和弦心距之间的关系以及垂径定理．做一做：填空题：1．如图1，在⊙O中，＝，若∠AOB＝40°，则∠COD＝______°．2．如图2，⊙O的半径为5，弦AB的长为6，OC⊥AB于C，则OC的长为______．3．如图3，四边形ABCD中，AB＝AC＝AD，若∠CAD＝82°，则∠CBD＝______度．图1 图2 图34．已知⊙O的半径为r，那么垂直平分半径的弦长为______．5．AB是⊙O的直径，弦CD⊥AB，E为垂足，若AB＝9，BE＝1，则CD＝______．6．⊙O的直径为10cm，弦AB为8cm，P是弦AB上一点，若OP的长为整数，则满足条件的点P有_个．选择题：7．在同圆或等圆中，若的长度＝的长度，则下列说法正确的个数是( )①的度数等于；②所对的圆心角等于所对的圆心角；③和是等弧；④弦AB所对的弦心距等于弦CD所对的弦心距．(A)1个(B)2个(C)3个(D)4个8．下面四个命题中正确的一个是( )(A)平分一条直径的弦必垂直于这条直径(B)平分一条弧的直线垂直于这条弧所对的弦(C)弦的垂线必过这条弦所在圆的圆心(D)在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心9．如图，AB是⊙O直径，CD是⊙O的弦，AB⊥CD于E，则图中不大于半圆的相等弧有( )(A)1对(B)2对(C)3对(D)4对10．过⊙O内一点M的最长弦为4cm，最短的弦长为2cm，则OM的长为( )(A)3m (B)2m (C)1cm (D)3cm11．如图，AB 是⊙O 的直径，弦CD ⊥AB 于P ，35=CD ，25=OP ，则弦AC 的长为( )(A)56(B)36(C)35(D)55解答题：12．⊙O 的半径为5，弦AB ∥CD ，CD ＝6，AB ＝8，求AB 和CD 之间的距离．13．如图，CE 为⊙O 的直径，AB 为⊙O 的弦，且AB ⊥CE ，垂足为点D ，设⊙O 的半径为r ，AB ＋CD ＝2r ，CD ＝1，求⊙O 的半径．14．如图，半径为5的⊙P 与轴交于点M (0，－4)，N (0，－10)，函数)0(<=x xky的图像过点P ，求k 的值．问题探究：15．如图，在⊙O 中，AB ＝2CD ．试判断与2是否相等，并说明理由．九年级《圆》3 圆的基本性质(3)学习要求：了解圆周角与圆心角的区别和联系，掌握圆周角的概念及性质，并学会应用圆周角的性质解决问题．做一做：填空题：1．如图1，已知圆心角∠AOB＝100°，则圆周角∠ACB的度数为______．2．如图2，在⊙O中，＝，若∠BOC＝70°，则∠ABC＝______°．3．如图3，AB为直径，∠BED＝40°，则∠ACD＝______度．图1 图2 图34．如图4，AB是⊙O的直径，点C在⊙O上，∠BAC＝30°，点P在线段OB上运动．设∠ACP＝x，则x的取值范围是____________．5．若一条弦把圆周分成2∶3的两段弧，则劣弧所对圆心角的度数是______度，弦所对的圆周角的度数是______．6．如图5，A、B、C、D是⊙O上四点，且点D是的中点，CD交OB于E，∠AOB＝100°，∠OBC ＝55°，则∠OEC＝______度．7．如图6，图中圆周角的个数是( )图4 图5 图6(A)9个(B)12个(C)8个(D)14个8．如图，C是以AB为直径的半圆弧上的一点，已知BC的弦心距与直径AB的比为3∶4，则所对的圆心角为( )(A)100°(B)90°(C)115°(D)120°9．下列命题中，正确的个数为( )(1)相等的圆周角所对的弧相等(2)同圆或等圆中，同弦或等弦所对的圆周角相等(3)一边上的中线等于这条边的一半的三角形是直角三角形(4)等弧所对的圆周角相等(A)1个(B)2个(C)3个(D)4个10．使用直角钢尺检查某一工件是否恰好是半圆形的凹面，成半圆形的为合格，如图所示的四种情况中的合格的是( )11．如图8，BD 为圆O 直径，弦AC 、BD 相交于点E ，下列结论一定成立的是( )(A)∠BAO ＝∠C (B)∠B ＝∠D (C)∠OAE ＝∠C (D)∠BAO ＝∠D 12．如图9，A 、B 、C 是⊙O 上的三点，∠α ＝140°，那么∠A 等于( )(A)70° (B)110° (C)140° (D)220° 13．如图10，A 点是半圆上一个三等分点，B 点是的中点，P 点是直径MN 上一动点，⊙O 的半径为1，则AP ＋BP 的最小值为( )图8 图9 图10(A)1 (B)22(C)2 (D)13-解答题：14．如图，△ABC 中，已知AB ＝AC ，∠BAC ＝50°，以AB 为直径的圆分别交BC 、AC 于D 、E ，求，，的度数．15．如图，射线AM 交一圆于点B 、C ，射线AN 交该圆于点D 、E ，且＝，求证：AC ＝AE ．问题探究： 16．如图，△ABC 是⊙O 的内接三角形，点C 是优弧AB 上一点(点C 不与A ，B 重合)，设∠OAB ＝α ，∠C ＝β ．(1)当α ＝35°时，求β 的度数；(2)猜想α 与β 之间的关系，并给予证明．九年级《圆》4 与圆有关的位置关系(1)学习要求：理解点和圆的位置关系，以及确定一个圆的条件，了解三角形的外接圆的概念．做一做：填空题：1．若⊙O的半径为r，点A到圆心O的距离为d，当点A在圆外时，d______r；当点A在圆上时，d______r；当点A在圆内时，d______r．5长为半径画圆，2．在△ABC中，∠C＝90°，AC＝2cm，BC＝4cm，CM是中线，以C为圆心，以cm 则A、B、C、M四点在圆外的有点______，在圆上的有点______，在圆内的有点______．3．已知⊙O的半径为1，点P与O的距离为d，且方程x2－2x＋d＝0有实数根，则P在⊙O的______．4．过一点A可作______个圆，过两点A、B可作______个圆，且圆心在线段AB的______上，过三点A、B、C，当这三点______时能且只能作一个圆，且圆心在______上．5．等边三角形的边长为6cm，则它的外接圆的面积为______．6．在Rt△ABC中，已知两直角边的长分别为6cm和8cm，那么Rt△ABC的外接圆的面积是7．锐角三角形的外心在______，直角三角形的外心在______，钝角三角形的外心在______．选择题：8．两个圆的圆心都是O，半径分别为r1和r2，且r1＜OA＜r2，那么点A在( )(A)⊙r1内(B)⊙r2外(C)⊙r1外，⊙r2内(D)⊙r1内，⊙r2外9．⊙O的半径r＝10cm，圆心到直线L的距离OM＝8cm，在直线L上有一点P，且PM＝6，则点P( )(A)在⊙O内(B)在⊙O上(C)在⊙O外(D)可能在⊙O内也可能在⊙O外10．⊙O的半径为5，圆心O的坐标为(0，0)，点P的坐标为(4，2)，则点P与⊙O的位置关系是( )(A)点P在⊙O内(B)点P在⊙O上(C)点P在⊙O外(B)点P在⊙O上或在⊙O外11．三角形的外心是( )(A)三条中线的交点(B)三条中垂线的交点(C)三条高的交点(D)三条角平分线的交点解答题：12．如图1，使用直尺和圆规确定如图所示的破残轮片的圆心位置．图113．点P到⊙O上的点的最大距离是6cm，最小距离是2cm，求⊙O的半径．14．某商场有三个销量较大的柜台，经理想修建一个收银台，使得三个柜台到收银台的距离相等．如果三个柜台的位置如图2所示，那么如何确定收银台的位置?图2问题探究：15．已知：如图3，三个边长为2a个单位长度的正方形如图所示方式摆放．图①图②图③图3∴______为所求作的圆．∴______为所求作的圆．(1)画出覆盖图①的最小圆；(2)将图①中上面的正方形向右平移a个单位长度，得到图②，请用尺规作出覆盖新图形的最小圆(不写作法，保留作图痕迹)；(3)可以利用图③，比较(1)和(2)中的两个圆的大小，通过计算简要说明理由．九年级《圆》5 与圆有关的位置关系(2)学习要求：探索与了解直线与圆的位置关系．掌握切线的识别方法，理解切线长定理和三角形的内切圆的概念．做一做：填空题：1．直线和圆的位置关系有：______、______、______．2．两个同心圆，大圆半径R＝3cm，小圆半径r＝2cm，d是圆心到直线l的距离，当d＝2cm，l与小圆的交点个数为______，l与大圆的交点个数为______，当d＝2.5cm，l与小圆的交点个数为______，l与大圆的交点个数为______．3．如图1，AB是⊙O的直径，点D在AB的延长线上，BD＝OB，CD与⊙O切于C，那么∠CAB＝______度．图14．两个同心圆的半径分别为3cm和5cm，大圆的弦AB与小圆相切，则AB＝______cm．5．如图2，AB是半圆直径，直线MN切半圆于C，AM⊥MN，BN⊥MN，如果半圆直径为m，则AM＋BN ＝______．图26．在△ABC中，若∠C＝90°，∠A＝30°，AC＝3，则内切圆的直径为______．选择题：7．下列说法正确的是( )(A)若直线与圆有一个交点则直线是圆的切线(B)经过半径的外端的直线是圆的切线(C)和半径垂直的直线是圆的切线(D)经过圆心且垂直于切线的直线，必经过切点8．若CD是⊙O的切线，要判定AB⊥CD，还需要添加的条件是( )(A)AB经过圆心O(B)AB是直径(C)AB是直径，B是切点(D)AB是直线，B是切点9．在△ABC中，∠C＝90°，AC＝12cm，BC＝5cm，若以C为圆心，5cm为半径作圆，则斜边AB与⊙O 的位置关系是( )(A)相离(B)相切(C)相交(D)不能确定10．如图，P A、PB分别与⊙O相切于A、B两点，C是⊙O上一点，且∠ACB＝55°，则∠P等于( )(A)70°(B)65°(C)110°(D)55°11．如图，AB是半⊙O直径、P点是AB延长线上一点，PC切半⊙O于C，若∠P＝32°，则∠A等于( )(A)30°(B)32°(C)29°(D)31°12．如图，⊙O的外切梯形ABCD中，若AD∥BC，那么∠DOC的度数为( )(A)70°(B)90°(C)60°(D)45°13．如图，以正方形ABCD的BC边为直径作半圆O，过点D作直线切半圆于点F，交AB边于E．则三角形ADE和直角梯形EBCD周长之比为( )(A)3∶4 (B)4∶5 (C)5∶6 (D)6∶714．如图，⊙O是△ABC的内切圆，D、E、F是切点，∠A＝50°，∠C＝60°，则∠DOE＝( )(A)70°(B)110°(C)120°(D)130°解答题：15．在△ABC 中，AB ＝4cm ，AC ＝,cm 22若以A 为圆心，2cm 为半径的圆与直线BC 相切，求∠BAC的度数．16．如图，AB 是⊙O 的直径，C 为⊙O 上一点，AD 和过C 点的切线互相垂直，垂足为D ．求证：AC 平分∠DAB ．17．(08福州)如图，AB 是⊙O 的直径，AD 是弦，∠DAB ＝22.5°，延长AB 到点C ，使∠ACD ＝45°(1)求证：CD 是⊙O 的切线； (2)若,22 AB 求BC 的长．问题探究：18．已知：如图，正方形ABCD 中，有一个直径为BC 的半圆，BC ＝2cm ，现有两点E 、F ，分别从点B 、点A 同时出发，点E 沿线段BA 以1cm/s 的速度向点A 运动，点F 沿折线A －D －C 以2cm/s 的速度向点C 运动，设点E 离开点B 的时间为t 秒． (1)当t 为何值时，线段EF 与BC 平行? (2)设1＜t ＜2，当t 为何值时，EF 与半圆相切?九年级《圆》6 与圆有关的位置关系(3)学习要求：探索并了解圆与圆的五种位置关系及数量关系，学会区别的方法．做一做：填空题：1．两个同心圆，大圆的半径为9，小圆的半径为5，如果⊙O与这两圆都相切，那么⊙O的半径等于______．2．相切两圆的圆心距为18cm，其中小圆半径为7cm，则大圆半径为______．3．两圆半径分别为5cm和x cm，圆心距离为7cm，若两圆相交时，则x的取值范围是4．已知两圆的半径分别为7cm和11cm，当圆心距为3cm时，两圆位置关系为______；当圆心距为12cm 时，两圆位置关系为______．5．如图1，在12×6的网格图中(每个小正方形的边长均为1个单位)，⊙A的半径为1，⊙B的半径为2，要使⊙A与静止的⊙B相切，那么⊙A由图示位置需向右平移______个单位．图16．如图2，图中各圆两两相切，⊙O的半径为6，⊙A和⊙B的半径相等，则⊙C的半径r＝______．图27．两圆半径的比为5∶3，当这两圆外切时，圆心距是24，若这两圆相交，则圆心距d的取值范围是______．8．已知两圆内切，一个圆的半径是3，圆心距是2，那么另一个圆的半径是______．选择题：9．半径分别为5.5cm和4.5cm的两个圆内切，这两圆的圆心距是( )(A)0.5cm (B)1cm (C)5cm (D)10cm10．设两圆半径分别为R和r(R＞r)，圆心距d，若这两圆内含，则下列不等式成立的是( )(A)R＋r＜d(B)R－r＞d(C)R－r＜d(D)R＋r＞d＞R－r11．两圆半径分别为3和5，圆心距d，若两圆相切，那么( )(A)d＝2 (B)d＝8(C)2＜d＜8 (D)d＝2或d＝8解答题：12．若两圆的圆心距d满足等式|d－4|＝3，且两圆半径是方程x2－7x＋12＝0的两个根，判断这两圆的位置关系．13．已知：如图3，⊙O1与⊙O2交于A，B两点，O1A切⊙O2于A，若O1A＝2cm，⊙O2半径为1cm，求AB的长．图3问题探究：14．在种植农作物时，一个很重要的问题就是“合理密植”．如图4是栽植一种蔬菜时的两种方法，A、B、C、D四株顺次连结成为一个菱形，且AB＝BD；A′、B′、C′、D′四株顺次连结成为一个正方形．这两种图形的面积为四株作物所占的面积，两行作物间的距离为行距；一行中相邻两株作物的距离为株距；设这两种作物充分生长后，每株在地面上的影子近似成一个圆面(相邻两圆如图相切)，其中阴影部分的面积表示生长后空隙地面积．在株距都为a，其他客观原因也相同的条件下，请从栽植的行距，蔬菜所占地面积，充分生长后空隙地面积三个方面比较两种栽植方法，哪种方法能更充分地利用土地．图4九年级《圆》7 正多边形与圆学习要求：理解正多边形的中心、半径、中心角、边心距等概念，学会用等分圆周的方法画正多边形．做一做：填空题：1．正六边形内接于⊙O，⊙O的半径为4cm，则这个正六边形的边长为______cm，面积为______cm2．2．等边三角形外接圆半径与内切圆半径之比为______．3．若等边三角形的边长为3，则它的外接圆的半径的长为______．4．一个正三角形与一个正六边形的周长相等，则它们的面积之比为______．解答题：5．已知正四边形的边心距为2，求它的外接圆的面积．6．如图1，圆内接正六边形ABCDEF中，对角线BD，EC相交于点G，求∠BGC的度数．图17．一个不等边三角形是不是一定有外接圆和内切圆?画图试一试．如果有，这两个圆是不是同心圆? 8．如图2，已知点A、B、C、D、E是⊙O的5等分点，画出⊙O的内接和外切正五边形．图29．要用圆形铁片截出边长为a的正方形铁片，选用的圆铁片的直径最小要多长?10．如图3，正六边形的螺帽的边长a ＝12mm ，这个搬手的开口b 最小应是多少?(结果精确到0.1mm)图311．试画出下列图形：问题探究：12．如图4，八边形A B C D E F G H 中，∠A ＝∠B ＝∠C ＝∠D ＝∠E ＝∠F ＝∠G ＝∠H ＝135°，AB ＝CD ＝EF ＝GH ＝1cm ，BC ＝DE ＝FG ＝HA ＝,cm 2则这个八边形的面积等于( )图4(A)7cm 2 (B)8cm 2(C)9cm 2(D)2cm 214九年级《圆》8 有关圆的计算学习要求：学会计算弧长及扇形的面积，学会计算圆锥的侧面积和全面积．做一做：填空题：1．若⊙O 的半径为4cm ，其中一条弧长为2πcm ，则这条弧所对的圆心角是______ 2．一个扇形的圆心角为60°，半径是10cm ，则这个扇形的弧长是______cm ．3．如图1，在正方形铁皮上剪下一个圆形和扇形，使之恰好围成一个圆锥模型，设圆的半径为r ，扇形半径为R ，则圆的半径与扇形半径之间的关系为______．4．如图2，矩形ABCD 的长为a ，宽为b ，以A ，B ，C ，D 为圆心的四个圆的半径都是r (a ＞b ＞2r )，则图中阴影部分的面积是______．5．圆锥可以看作是由______旋转而得的，圆锥的侧面展开图是______．6．一个圆锥的底面圆半径为4cm ，母线长为9cm ，则该圆锥的全面积为______．7．一个圆锥的侧面积是底面积的4倍，这个圆锥的侧面展开图圆心角的度数为______． 8．如图3是一人用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF 长为10cm ．母线OE (OF )长为10cm ．在母线OF 上的点A 处有一块爆米花残渣，且F A ＝2cm ，一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点．则此蚂蚁爬行的最短距离为______cm ．图1 图2 图3选择题： 9．如图4，以O 为圆心的两个同心圆中，两圆半径分别为2和1，∠AOB ＝120°，则阴影部分的面积为( ) (A)4π(B)2π(C)π34(D)π10．如图5，图中实线部分是半径为9cm 的两条等弧组成的游泳池．若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长为( ) (A)12πcm (B)18πcm (C)20πcm (D)24πcm11．如图6，在△ABC 中，BC ＝4，以点A 为圆心，2为半径的⊙A 与BC 相切于点D ，交AB 于E ，交AC于F ，点P 是⊙A 上的一点，且∠EPF ＝40°，则图中阴影部分的面积是( )(A)π944-(B)π984-(C)π948-(D)π988-图4 图5 图612．如图7，在下列边长相同的正方形中，阴影部分的面积相同的有( )图7(A)1个(B)2个(C)3个(D)4个13．如图8，有六个等圆按甲、乙、丙三种摆放，使相邻两圆互相外切，圆心连线分别构成正六边形、平行四边形、正三角形，圆心连线外侧的六个扇形(阴影部分)的面积之和依次记为S、P、Q，则( )图8(A)S＞P＞Q(B)S＞Q＞P(C)S＞P＝Q(D)S＝P＝Q14．如图，圆锥形烟囱帽的底面直径是40cm，母线长是25cm，则这个圆锥形零件的展开图面积是( )(A)200πcm2(B)300πcm2(C)50πcm2(D)500πcm215．一个扇形的半径为30cm，圆心角为150°，若用它做成一个圆锥的侧面，则这个圆锥的底面半径为( )(A)12.5cm (B)30cm (C)25cm (D)35cm解答题：16．如图10，有一个半径为12米的圆形花坛，现要用两个同心圆把花坛的面积三等分，以便种植三种不同颜色的花卉，求这两个同心圆的半径．图1017．如图11，AB为半圆O的直径，C、D是的三等分点，若⊙O的半径为1，E为直线AB上任意一点，求图中阴影部分的面积．图1118．如图12，扇形AOB 的圆心角为直角，正方形OCDE 内接于扇形，点C 、E 、D 分别在OA 、OB 、上，过A 作AF ⊥ED 交ED 的延长线于F ．如果正方形的边长为1，那么阴影部分的面积为多少?图1219．如图13，是一块从生日蛋糕中切下的楔型蛋糕．(1)计算扇形OAD 的面积；(2)计算楔型蛋糕的整个表面积．图1320．若△ABC 为等腰直角三角形，其中∠ABC ＝90°，,cm 22==BC AB ，求将等腰直角三角形绕其直线AC 旋转一周所得圆锥的表面积．问题探究：21．如图14所示的曲边三角形可按下述方法作出：分别以正三角形的一个顶点为圆心，边长为半径，画弧使其经过另外两个顶点，然后擦去正三角形，三段圆弧所围成的图形就是一个曲边三角形．如果一个曲边三角形的周长为π，求它的面积．图14圆 9 复习学习要求：通过复习，进一步理解圆中的概念、性质，掌握运用圆的有关知识解决问题的方法．做一做：选择题：1．如图1，在两半径不同的同心圆中，∠AOB ＝∠A ′OB ′＝60°，则( )图1 (A)＝ (B)＞ (C)的度数＝的度数 (D)的长度＝的长度 2．下列说法正确的是( ) (A)两个半圆是等弧 (B)同圆中优弧与半圆的差必为劣弧 (C)同圆中优弧与劣弧的差必为劣弧 (D)由弦和弧组成的图形叫弓形3．已知⊙O 的直径是6cm ，若P 是⊙O 内部的一点，则OP 的长度的取值范围是( ) (A)OP ＜6cm (B)OP ≤3cm (C)0≤OP ＜3cm (D)0＜OP ＜3cm4．如图2，已知O 为圆锥的顶点，M 为圆锥底面上一点，点P 在OM 上，一只蜗牛从P 点出发，绕圆锥侧面爬行，回到P 点时所爬过的最短路线的痕迹如右图所示．若沿OM 将圆锥侧面剪开并展开，所得侧面展开图是( )图25．已知⊙O 的半径为2cm ，弦AB 长cm 32，则这条弦的中点到弦所对劣弧的中点的距离为( ) (A)1cm(B)2cm(C)cm 2(D)cm 36．如图3，在以O 为圆心的两个同心圆中，大圆的弦AB 交小圆于C 、D 两点，AB ＝10cm ，CD ＝6cm ，则AC 的长为( )图3 (A)0.5cm(B)1cm(C)1.5cm(D)2cm7．在⊙O 中，圆心角∠AOB ＝90°，点O 到弦AB 的距离为4，则⊙O 的直径的长为( ) (A)24(B)28(C)24( D)168．⊙O 的弦AB 等于半径，那么弦AB 所对的圆周角一定是( ) (A)30° (B)150° (C)30°或150° (D)60°9．如图，有一圆心角为120°、半径长为6cm 的扇形，若将OA 、OB 重合后围成一圆锥侧面，那么圆锥的高是( )(A)cm 24(B)cm 35(C)cm 62(D)cm 32 10．如图，A 、B 、C 、D 是圆上四点，AB 、DC 延长线交于点E ，、分别为120°、40°，则∠E 等于( )(A)40° (B)35°(C)60°(D)30°11．如图，D 是的中点，与∠ABD 相等的角的个数是( )(A)7个 (B)3个 (C)2个 (D)1个12．如图，⊙O 与直线MN 相切于C 、AB 是⊙O 的直径，∠ABC ＝56°，则∠BCN 等于( )(A)34°(B)56° (C)24°(D)124°13．等边三角形的内切圆半径、外接圆半径和高的比为( )(A)321::(B)321::(C)231::(D)1∶2∶314．已知△ABC 的三边长分别为6，8，10，分别以A ，B ，C 三点为圆心，作两两相外切的三个圆，那么这三个圆的半径分别为( ) (A)3，4，5 (B)2，4，6 (C)6，8，10 (D)4，6，8填空题：15．一个圆的最大的弦长为10cm ，则此圆的半径为______． 16．已知：⊙O 的半径为4cm ，弦AB 所对的劣弧为圆的31，则弦AB 的长为______cm ，AB 的弦心距为______cm ．17．圆内接三角形三个内角所对的弧长之比为3∶4∶5，那么这个三角形内角的度数分别为 18．如图8，圆锥的底面半径为6cm ，高为8cm ，那么这个圆锥的侧面积是______cm 2．图819．如图9，小丽要制作一个圆锥模型，要求圆锥的母线长为9cm ，底面圆的直径为10cm ，那么小丽要制作的这个圆锥模型的侧面展开扇形的纸片的圆心角度数是______．图920．如图10，矩形ABDC 中，AC ＝2，DC ＝4，以 AB 为直径的半圆O 与DC 相切于点E ，则阴影部分的面积为______(结果保留 )图1021．如图11①，O 1，O 2，O 3，O 4为四个等圆的圆心，A ，B ，C ，D 为切点，请你在图中画出一条直线，将这四个圆分成面积相等的两部分，并说明这条直线经过的两个点是______；如图11②，O 1，O 2，O 3，O 4，O 5为五个等圆的圆心，A ，B ，C ，D ，E 为切点，请你在图中画出一条直线，将这五个圆．．．分成面积相等的两部分，并说明这条直线经过的两个点是______．图11解答题：22．已知：⊙O的半径OA＝1，弦AB、AC的长分别是2、3，求∠BAC的度数．23．如图12，在矩形ABCD中，AB＝24，AD＝7，以A为圆心作圆，如果B、C、D三点中，至少有一个点在圆内，且至少有一个点在圆外，求⊙A的半径R的取值范围．图1224．如图13，在平面直角坐标系中，点A的坐标是(10，0)，点B的坐标为(8，0)，点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形．求点C的坐标．图1325．如图14，BC为直径，G为半圆上任一点，A为中点，AP⊥BC于P．求证：AE＝BE＝EF．图1426．已知：如图15，AB是⊙O的直径，AC⊥l，BD⊥l，C、D是垂足，且AC＋BD＝AB．求证：DC是⊙O的切线．图1527．已知：如图16，A、C为⊙O上两点，AD为直径，∠1＝∠2(1)求证：AB是⊙O的切线；(2)若AC＝10cm，∠2＝30°，求图中阴影部分面积．图1628．在一次数学探究性学习活动中，某学习小组要制作一个圆锥体模型，操作规则是：在一块边长为16cm 的正方形纸片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面．他们首先设计了如图所示的方案一，发现这种方案不可行，于是他们调整了扇形和圆的半径，设计了如图17所示的方案二．(两个方案的图中，圆与正方形相邻两边及扇形的弧均相切．方案一中扇形的弧与正方形的两边相切)(1)请说明方案一不可行的理由；(2)判断方案二是否可行?若可行，请确定圆锥的母线长及其底面圆半径；若不可行，请说明理由．方案一方案二图17圆10 测试题选择题：(每题4分，共40分)1．如图，是一个由四个同心圆构成的靶子示意图，点O 为圆心，且OA ＝AB ＝BC ＝CD ＝1，则周长更接近于20的是( )(A)以OA 为半径的圆 (B)以OB 为半径的圆 (C)以OC 为半径的圆 (D)以OD 为半径的圆2．在同圆或等圆中，如果＝2，则AB 与CD 的关系是( )(A)AB ＞2CD (B)AB ＝2CD (C)AB ＜2CD (D)AB ＝CD3．在⊙O 中，两弦AB ＜CD ，OM ，ON 分别为这两条弦的弦心距，则OM ，ON 的关系是( ) (A)OM ＞ON (B)OM ＝ON (C)OM ＜ON (D)无法确定 4．一个点到一个圆的最短距离是3cm ，最长距离是6cm ，则这个圆的半径是( ) (A)4.5cm (B)1.5cm (C)4.5cm 或1.5cm (D)9cm 或3cm 5．在下列三角形中，外心在它一条边上的三角形是( ) (A)边长分别为2cm 、2cm 、3cm (B)三角形的边长都等于5cm(C)三角形的边长分别为5cm 、12cm 、13cm (D)三角形的边长为4cm 、6cm 、8cm 6．如图，AB 为⊙O 的一固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当点C 在上半圆(不包括A 、B 两点)上移动时，点P ( )(A)到CD 的距离保持不变 (B)位置不变 (C)等分 (D)随C 点的移动而移动7．圆的弦与直径相交成30°角，并且分直径为6cm 和4cm 两部分，则弦心距为( ) (A)33 (B)3(C)21 (D)23 8．△ABC 中，∠B ＝90°，以BC 为直径作圆交AC 于E ，若BC ＝12，312=AB 则的度数为( )(A)60° (B)80°(C)100°(D)120°9．如图，BC 为半圆O 直径，A 、D 为半圆O 上两点，3=AB ，BC ＝2，则∠D 的度数是( ) (A)60° (B)120° (C)135°(D)150°10．如图，P A 、PB 切⊙O 于点A 、B ，C 是优弧上的点，∠C ＝64°，那么∠P 等于( )(A)26° (B)62° (C)60° (D)52°填空题：(每题4分，共28分)11．如图5，在⊙O 的内接四边形ABCD 中，若∠BAD ＝110°，则∠BCD 等于______．12．如图6，一把宽为2cm 的刻度尺在⊙O 上移动，当刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数恰好为“2”和“8”(单位：cm)，则该圆的半径为______cm ．13．已知圆锥的侧面展开图是一个半圆，则这个圆锥的母线长与底面半径长的比是______．14．如图7，是一个水平放置的圆柱形水管的截面，已知水面高cm 22+=CD 水面宽AB ＝22cm ，那么水管截面圆的半径是______cm图5 图6 图715．如图8，∠ABC ＝90°，O 为射线BC 上一点，以点O 为圆心、BO 21长为半径作⊙O ，当射线BA 绕点B 按顺时针方向旋转______度时与⊙O 相切． 16．如图9，外接圆半径为r 的正六边形周长为______．17．如图10，AB 是半圆O 的直径，点C 、点D 是半圆O 的三等分点，若CD 为cm 3，则图中阴影部分的面积为______．图8 图9 图10解答题：(每题8分，共32分)18．已知：如图11，在Rt △ABC 中，∠C ＝90°，点O 在AB 上，以O 为圆心，OA 长为半径的圆与AC ，AB 分别交于点D ，E ，且∠CBD ＝∠A ．判断直线BD 与⊙O 的位置关系，并证明你的结论．图1119．如图12，AB 是⊙O 的直径，过圆上一点D 作⊙O 的切线DE ，与过点A 的直线垂直于E ，弦BD 的延长线与直线AE 交于C 点，若=21，⊙O 的半径为r ，求由线段DE 、AE 、和所围成的阴影部分的面积．图1220．如图13，已知△ABC 内接于⊙O ，AB 为⊙O 的直径，AB ＝8cm ，以OA 为直径的⊙D 与⊙O 的弦AC交于E 点，若CE ＝2cm ．求：(1)AC 的长；(2)所对的圆周角．图1321．如图14，六边形ABCDEF 内接于半径为r (常数)的⊙O ，其中AD 为直径，且AB ＝CD ＝DE ＝F A ． (1)当∠BAD ＝75°时，求的长；(2)求证：BC ∥AD ∥FE ．图14参考答案第二十四章圆九年级《圆》1 圆的基本性质(1)1．圆心，半径 2．以点P 为圆心，3cm 长为半径的圆 3．0＜AB ≤2r 4．B 5．D 6．B 7．提示：可证△AOD ≌△BOC 8．4 9．证OC ＝OD ，OE ＝OF 即可 10．提示：证明E 、F 、G 、H 四个点到点O 的距离相等 11．B九年级《圆》1 圆的基本性质(2)1．40 2．4 3．41 4．r 3 5．24 6．5 7．D 8．D9．C 10．A 11．C 12．AB 、CD 在圆心O 的同侧时，距离为1；AB 、CD 在圆心O 的异侧时，距离为7 13．25=r 14．28 15．提示：取的中点E ，则＝ ∴AE ＝EB ∵AE ＋EB ＞AB ＝2CD ∴2AE ＞2CD ∴AE ＞CD ，∴＞，∴2＞2∴＞2九年级《圆》1 圆的基本性质(3)1．50° 2．72.5 3．50 4．30°≤x ≤90° 5．144；72度或108度 6．80 7．B 8．D 9．B 10．C 11．A 12．B 13．C 14．连OD ，OE ．，，的度数分别是50°，50°，80° 15．连接C E ，利用“在同圆中等弧所对圆周角相等”，证出 ∠DEC ＝∠BCE ，∴AC ＝AE 16．(1)连接OB ，β ＝55° (2)α ＋β ＝90°九年级《圆》2 与圆有关的位置关系(1)1．＞，＝，＜ 2．B ，M ，A 、C 3．P 在⊙O 的内部或圆周上 4．无数个，无数个，垂直平分线，不在同一条直线上，其中任意两条线段的中垂线的交点 5．12πcm 2 6．25πcm 2 7．三角形内部，斜边中点上，三角形外部 8．C 9．B 10．A 11．B 12．提示：在圆弧上任取两条不平行的弦，分别作它们的垂直平分线，交点即为圆心 13．点P 在⊙O 外，21=r (PB －P A )＝2cm ；点P 在⊙O 内，21=r (PB ＋P A )＝4cm 14．提示：过不共线的三点作圆，找出圆心的位置 15．(1)∴⊙O 为所求作的圆(2)方法一：方法二：∴⊙O ＇为所求作的圆．(3)计算过程略，(1)中的圆比 (2)中的圆大．九年级《圆》2 与圆有关的位置关系(2)1．相交，相切，相离 2．一个，两个；没有，两个 3．30 4．8 5．m 6．33- 7．D 8．C 9．C 10．A 11．C 12．B 13．D 14．B 15．∠BAC ＝105°或∠BAC ＝15° 16．提示：连结OC 17．(1)连接OD ，∠ODC ＝90° (2)BC ＝OC －OB ＝22-18．(1)34(2)222+九年级《圆》2 与圆有关的位置关系(3)1．2或7 2．11cm 或25cm 3．2＜x ＜12 4．内含；相交 5．2、4、6、86．2 7．6＜d ＜24 8．5或1 9．B 10．B 11．D 12．d ＝1时，两圆内切，d ＝7时，两圆外切 13．cm 55414．种植方法 (1)比种植方法 (2)能更充分地利用土地九年级《圆》3 正多边形与圆1．4，324 2．2 3．1 4．2∶3 5．8π 6．60° 7．有，不是同心圆 8．图略 9．a 2 10．约为20．8mm 11．提示：先画圆的三等分点，再利用对称 12．A九年级《圆》4 有关圆的计算1．90 2．π3103．R ＝4r 4．ab －πr 2 5．一个直角三角形，扇形 6．52πcm 2 7．90° 8．412 9．B 10．D 11．A 12．D 13．D 14．D 15．A 16．34米和64米 12．43 18．提示：连结OD ，OD ＝OA ＝2，S阴影＝S矩形ACDF ＝(OA －OC )CD ＝(OD －OC )CD ＝12-19．(1)20πcm 2 (2)3220240(+π)cm 2 20．提示：作BD ⊥AC 于D ，2πcm 28=表S 21．232π-复习1．C 2．B 3．C 4．D 5．A 6．D 7．B 8．C9．A 10．A 11．B 12．A 13．D 14．B 15．5cm 16．2,3417．45°，60°，75° 18．60π 19．200° 20．π 21．O 1，O 3，如图①(答案不惟一，过O 1O 3与O 2O 4交点O 的任意直线都能将四个圆分成面积相等的两部分)；O 5，O ，如图②(答案不惟一，如AO 4，DO 3，EO 2，CO 1等均可)．图① 图②22．当AC 、AB 位于OA 同侧时，∠BAC ＝15°；当AC 、AB 位于OA 两侧时，∠BAC ＝75° 23．7＜R ＜25 24．(1，3)25．连AB ．证∠EAB ＝∠EBA ，∠EAF ＝∠EF A。

人教版九年级上册数学同步练习《图形的旋转》(习题+答案)

23.1图形的旋转内容提要1.在平面内，将一个图形绕一个定点沿某个方向（顺时针或逆时针）转动一个角度，这样的图形运动称为旋转.定点叫旋转中心，转动的角度叫做旋转角.2.旋转的三要素：旋转中心、旋转方向、旋转角.3.旋转的性质：（1）对应点到旋转中心的距离相等；（2）对应点与旋转中心所连线段的夹角等于旋转角；（3）旋转前、后的图形全等.4.旋转作图步骤：（1）首先确定旋转中心和图形中的关键点（如线段的端点、角的顶点等）；（2）将这些关键点沿指定的方向旋转指定的角度；（3）然后连接对应部分，形成相应的图形.23.1.1旋转的特征基础训练1．将如图的图案按逆时针方向旋转90︒后得到的是（）2．下列说法不正确的是（）A．旋转后的图形与原来图形面积相等B．旋转后的图形改变了图形的大小C．旋转不改变图形的大小D．旋转不改变图形的形状3．如图，将ABC∆绕点A旋转后得到ADE∆，则旋转方式是（）A．顺时针旋转90︒B．逆时针旋转90︒C．顺时针旋转45︒D．逆时针旋转45︒4．如图，ABC∆，图中旋转中心是，旋∆按顺时针方向转动一个角度后成为''A B C转了度.5.如图，Rt ABC ∆的斜边16AB =，Rt ABC ∆绕点O 顺时针旋转后得到'''Rt A B C ∆，则'''Rt A B C ∆的斜边''A B 上的中线'C D 的长度为.6.如图，将OAB ∆绕着点O 逆时针旋转两次得到OA B ''''∆，每次旋转的角度都是50︒，若120B OA ''∠=︒，则AOB ∠=.7.如图，在正方形ABCD 中，点E 在AB 边上，点F 在BC 边的延长线上，且AE CF =. （1）求证AED CFD ∆∆≌；（2）将AED ∆按逆时针方向至少旋转多少度才能与CFD ∆重合，旋转中心是什么？8.如图，ABC ∆中，1AB AC ==，45BAC ∠=︒，AEF ∆是由ABC ∆绕点A 按顺时针方向旋转得到的，连接BE ，CF 相交于点D .（1）求证BE CF =；（2）当四边形ACDE 为菱形时，求BD 的长.9.在ABC ∆中，AB BC =，120ABC ∠=︒，将ABC ∆绕点B 顺时针旋转角()090αα︒<<︒得11A BC ∆，1A B 交AC 于点E ，11A C 分别交AC ，BC 于D ，F 两点.（1）如图（1），观察并猜想，在旋转过程中，线段BE 与BF 有怎样的数量关系？并证明你的结论.（2）如图（2），当30α=︒时，试判断四边形1BC DA 的形状，并说明理由.10.如图，在直角坐标系中，Rt AOB ∆的两条直角边OA ，OB 分别在x 轴的负半轴，y 轴的负半轴上，且2OA =，1OB =.将Rt AOB ∆绕点O 按顺时针方向旋转90︒，再把所得的图象沿x 轴正方向平移1个单位，得CDO ∆.（1）写出点A ，C 的坐标；（2）求点A 和点C 之间的距离.23.1.2 简单的旋转作图及图案设计基础训练1．将如图所示的图案以圆心为中心，旋转180︒后得到的图案是（）2．……依次观察左边这三个图形，并判断照此规律从左到右第四个图形是（）3．如图，在44⨯的正方形网格中，MNP ∆绕某点旋转一定的角度，得到111M N P ∆，则其旋转中心一定是.4.如图，将图①绕某点经过几次旋转后得到图②，则每次旋转的最小角度是.5.如图，把五角星图案绕着它的中心点O至少旋转（角度）时，它与自身重合；把等边三角形绕着它的中心O至少旋转（角度）时，它与自身重合.6.如图所示的图案由三个叶片组成，绕点O旋转120︒后可以和自身重合，若每个叶片的面积为24cm，AOBcm.∠为120︒，则图中阴影部分的面积之和为27.在格纸上按以下要求作图，不用写作法：（1）作出“小旗子”向右平移6格后的图案；（2）作出“小旗子”绕O点按逆时针方向旋转90︒的图案.8.如图，在等腰直角ABC ∆中，90C ∠=︒，2BC cm =，如果以AC 的中点O 为旋转中心，将这个三角形旋转180︒，点B 落在点'B 处，求'BB 的长度.9.如图所示，画出ABC ∆绕点A 顺时针旋转90︒后的图形.10.如图，在平面直角坐标系中，有一Rt ABC ∆，且()1,3A -，()3,1B --，()3,3C -.已知11A AC ∆是由ABC ∆旋转得到的，（1）请写出旋转中心的坐标是，旋转角是度；（2）以（1）中的旋转中心为中心，分别画出11A AC ∆顺时针旋转90︒，180︒的三角形.能力提高1.如图，在方格纸中，ABC∆经过变换得到DEF∆，正确的变换是（）A．把ABC∆绕点C逆时针方向旋转90︒，再向下平移2格B．把ABC∆绕点C顺时针方向旋转90︒，再向下平移5格C．把ABC∆向下平移4格，再绕点C逆时针方向旋转180︒D．把ABC∆向下平移5格，再绕点C逆时针方向旋转180︒2．图ABC∆，且'C在BC上，则∆中，67AB C∆绕点A顺时针旋转后，得到''C∠=︒，将ABC∠的度数为（）''B C BA．56︒B．50︒C．46︒D．40︒3．下列图形中，旋转60︒后可以和原图形重合的是（）A．正六边形B．正五边形C．正方形D．正三角形4．如图，已知直线443y x =-+与x 轴、y 轴分别交于A ，B 两点，把AOB ∆绕点A 按顺时针方向旋转90︒后得到''AO B ∆，则点'B 的坐标是.5.如图，在等边ABC ∆中，6AB =，D 是BC 的中点，将ABD ∆绕点A 旋转后得到ACE ∆，那么线段DE 的长度为.6.如图，把ABC ∆绕着点C 顺时针旋转35︒，得到''A B C ∆，''A B AC ⊥于点D ，则A ∠的度数是.7.如图所示，在四边形ABCD 中，180B D ∠+∠=︒，AB AD =，1AC =，60ACD ∠=︒，求四边形ABCD 的面积.8.如图，在平面直角坐标系中，ABC ∆的三个顶点的坐标分别是()3,2A -，()1,4B -，()0,2C . （1）将ABC ∆以点C 为旋转中心旋转180︒，画出旋转后对应的11A B C ∆；（2）平移ABC ∆，若点A 的对应点2A 的坐标为()5,2--，画出平移后的222A B C ∆；（3）若将222A B C ∆绕某一点旋转可以得到11A B C ∆，请直接写出旋转中心的坐标.9.如图①，正方形ABCD是一个66⨯网格电子屏的示意图，其中每个小正方形的边长为1.位于AD中点处的光点P按图②的程序移动.（1）请在图①中画出光点P经过的路径；（2）求光点P经过的路径总长（结果保留π）.拓展探究1.如图，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，90∆绕点A旋转，AF，AG与边BC的∆固定不动，AFGBAC AGF∠=∠=︒，若ABC交点分别为D ，E （点D 不与点B 重合，点E 不与点C 重合），在旋转过程中，等量关系222BD CE DE +=是否成立？若成立，请证明；若不成立，请说明理由.2.在ABC ∆中，90BAC ∠=︒，AB AC =，P 是ABC ∆内一点，2PA =，1PB =，3PC =，求APB ∠的度数.3.在ABC ∆中，AB AC =，BAC α∠=（060α︒<<︒），将线段BC 绕点B 逆时针旋转60︒得到线段BD .（1）如图①，直接写出ABD ∠的大小（用含α的式子表示）；（2）如图②，150BCE ∠=︒，60ABE ∠=︒，判断ABE ∆的形状并加以证明；（3）在（2）的条件下，连接DE ，若45DEC ∠=︒，求α的值.23.1 参考答案：23.1.1 旋转的特征基础训练1．D 2．B 3．B 4．点C 40 5．8 6．20︒7．（1）证明：在正方形ABCD 中，90A BCD ∠=∠=︒，AD CD =，90FCD ∴∠=︒．90A FCD ∴∠=∠=︒．又AE CF =，(SAS)AED CFD ∴∆∆≌．（2）90ADC ∠=︒，∴将AED ∆按逆时针方向至少旋转90度才能与CFD ∆重合，旋转中心是点D ．8．（1）证明：由旋转可知EAF BAC ∠=∠，AF AC =，AE AB =．EAF BAF BAC BAF ∴∠=∠=∠+∠，即BAE CAF ∠=∠．又AB AC =，AE AF ∴=．ABE ACF ∴∆∆≌．BE CF ∴=．（2）四边形ACDE 是菱形，1AB AC ==，AC DE ∴∥，1DE AE AB ===．又45BAC ∠=︒，45AEB ABE BAC ∴∠=∠=∠=︒．180AEB BAE ABE ∠+∠+∠=︒，90BAE ∴=︒．2222112BE AB AE ∴=++=21BD BE DE ∴=-=．9．（1）AB BC =，A C ∴∠=∠．由旋转可知，1AB BC =，1A C ∠=∠，1ABE C BF ∠=∠，1ABE C BF ∴∆∆≌．BE BF ∴=．（2）四边形1BC DA 是菱形．证明：1130A ABA ∠=∠=︒，11AC AB ∴∥，同理1AC BC ∥．∴四边形1BC DA 是平行四边形．又1AB BC =，∴四边形1BC DA 是菱形．10．（1）点A 的坐标是(2,0)-，点C 的坐标是(1,2)；（2）连接AC ，在Rt ACD ∆中，3AD OA OD =+=，2CD =，222222313AC CD AD ∴=+=+=，13AC ∴=．23.1.2 简单的旋转作图及图案设计基础训练1．D 2．D 3．B 4．60︒ 5．72︒ 120︒ 6．4 7．如图 8．25 9．如图10．（1）(0,0) 90 （2）画出图形如图能力提高1．B 2．C 3．A 4．(7,3) 5．33 6．55︒ 7．3 8．（1）图略（2）图略（3）旋转中心的坐标为(1,0)-9．（1）如图；（2）因为12364ππ⨯⨯=，所以点P 经过的路径总长为6π．拓展探究1．如图，将ACE ∆绕点A 顺时针旋转90︒至ABH ∆的位置，则CE HB =，AE AH =，45ABH C ∠=∠=︒，旋转角90GAH ∠=︒．连接HD ，在EAD ∆和HAD ∆中，AE AH =，45HAD EAH FAG EAD ∠=∠-∠=︒=∠，AD AD =，EAD HAD ∴∆∆≌． DH DE ∴=．又90HBD ABH ABC ∠=∠+∠=︒，222BD HB DH ∴+=，即222BD CE DE +=．2．135︒3．（1）1302α︒-．（2）ABE ∆为等边三角形．证明：连接AD ，CD ，ED ．线段BC 绕点B 逆时针旋转60︒得到线段BD ，BC BD ∴=，60DBC ∠=︒．60ABE ∠=︒，160302ABD DBE EBC α∴∠=︒-∠=∠=︒-．又BD BC =，60DBC ∠=︒，BCD ∴∆为等边三角形，BD CD ∴=．又AB AC =，AD AD =，(SSS)ABD ACD ∴∆∆≌．1122BAD CAD BAC α∆∠=∠=∠=． 150BCE ∠=︒，11180(30)15022BEC αα∴∠=︒-︒--︒=．BAD BEC ∴∠=∠．在ABD ∆与EBC ∆中，,,,BEC BAD EBC ABD BC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)ABD EBC ∴∆∆≌．AB BE ∴=．又60ABE ∠=︒，ABE ∴∆为等边三角形．（3）60BCD ∠=︒，150BCE ∠=︒，1506090DCE ∴∠=︒-︒=︒． 45DEC ∠=︒，DCE ∴∆为等腰直角三角形．CD CE BC ∴==． 150BCE ∠=︒，(180150)152EBC ︒-︒∴∠==︒．又130152EBC α∠=︒-=︒，30α∴=︒．。

九年级数学上册第2章对称图形_圆2.2圆的对称性第1课时圆的旋转不变性作业新版苏科版

2.2圆的对称性[2.2第1圆的旋转不变性]一、选择题1．下列说法中，正确的是() (1)相等的弦所对的弧相等； (2)等弧所对的弦相等； (3)等弧所对的圆心角相等； (4)相等的圆心角所对的弧相等． A ．(1)和(2) B ．(1)和(3) C ．(2)和(3) D ．(3)和(4)2．如图15－K －1所示，AB 是⊙O 的直径，BC ︵＝CD ︵＝DE ︵，∠COD ＝34°，则∠AEO 的度数是()A ．51°B ．56°C ．68°D ．78°图15－K －1 图15－K －23．如图15－K －2所示，已知AB ，CD 是⊙O 的两条直径，∠ABC ＝28°，那么∠BAD 等于()A ．28°B ．42°C ．56°D ．84°4．如图15－K －3，在⊙O 中，若C 是AB ︵的中点，∠A ＝50°，则∠BOC 的度数是()图15－K －3A ．40°B ．45°C ．50°D ．60° 二、填空题5．如图15－K －4，在⊙O 中，CA ︵＝DB ︵，∠1＝30°，则∠2＝________图15－K －4 图15－K －56．如图15－K －5，AB 是⊙O 的直径，BC ，CD ，DA 是⊙O 的弦，且BC ＝CD ＝DA ＝2，则AB ＝________.7．如图15－K －6，在△ABC 中，∠C ＝90°，∠A ＝25°，以点C 为圆心，BC 长为半径的圆交AB 于点D ，交AC 于点E ，则BD ︵的度数为________°.图15－K －6 图15－K －78．2016·江宁区期中如图15－K －7，⊙O 经过五边形OABCD 的四个顶点．若∠AOD ＝150°，∠A ＝65°，∠D ＝60°，则BC ︵的度数为________°.三、解答题9．如图15－K －8，已知在⊙O 中，AB ＝CD ，连接AC ，BD .求证：AC ＝BD .图15－K －810．一条弦把圆周分成3∶7两部分，求这条弦所对的圆心角的度数．11．如图15－K －9所示，在⊙O 中，AC ︵＝BC ︵，M ，N 分别是OA ，OB 的中点，判断CM 与的数量关系，并说明理由．图15－K －912．如图15－K －10，在⊙O 中，AB ︵＝AC ︵，∠A ＝40°，求∠B 的度数．图15－K －1013．如图15－K －11所示，A ，B 是⊙O 上的两点，∠AOB ＝120°，C 是AB ︵的中点，试确定四边形OACB 的形状，并说明理由．图15－K －1114．如图15－K －12所示，已知AB 为⊙O 的直径，M ，N 是直径AB 上的两点，且AM ＝BN ，过点M ，N 分别作CM ⊥AB 于点M ，DN ⊥AB 于点N ，交⊙O 于点C ，D ，AC ︵与BD ︵相等吗？为什么？图15－K －12动点问题2017·南通一模改编如图15－K －13所示，A 是半圆上的一个三等分点，B 是AN ︵的中点，P 是直径MN 上的一动点．若⊙O 的直径为2，求AP ＋BP 的最小值．图15－K －13详解详析作业[课堂达标]1．[解析] C (1)在同圆或等圆中，相等的弦所对的弧相等，故本选项错误；(2)等弧所对的弦相等，故本选项正确；(3)等弧所对的圆心角相等，故本选项正确；(4)在同圆或等圆中，相等的圆心角所对的弧相等，故本选项错误．故选C .2．[解析] A ∵BC ︵＝CD ︵＝DE ︵，∠COD ＝34°，∴∠BOE ＝3×34°＝102°. 又∵OA＝OE ，∴∠AEO ＝∠EAO ＝12∠BOE＝51°.故选A .3．[解析] A 利用三角形全等找出对应关系． ∵AB ，CD 是⊙O 的两条直径， ∴OA ＝OB ，OD ＝OC.又∵∠AOD＝∠BOC，∴△AOD ≌△BOC ， ∴∠BAD ＝∠ABC＝28°.4．[解析] A ∵∠A＝50°，OA ＝OB ，∴∠OBA ＝∠A ＝50°，∴∠AOB ＝180°－50°－50°＝80°. ∵C 是AB ︵的中点， ∴∠BOC ＝12∠AOB＝40°.5．[答案] 30[解析] 根据同圆中圆心角与它所对弧之间的关系可得答案．∵CA ︵＝DB ︵，∴AB ︵＝CD ︵.∵AB ︵所对的圆心角是∠1，CD ︵所对的圆心角是∠2，∴∠2＝∠1＝30°. 6．[答案] 4[解析] 如图，连接OC ，OD.∵BC ＝CD ＝DA ， ∴BC ︵＝CD ︵＝DA ︵，∴弦BC ，CD ，DA 三等分半圆，∴弦BC ，CD ，DA 所对的圆心角均为60°，则△BOC，△COD ，△AOD 均为等边三角形， ∴AB ＝OA ＋OB ＝DA ＋BC ＝4.7．[答案] 50[解析] 如图，连接CD.因为∠ACB＝90°，∠A ＝25°，所以∠B＝65°.在△BCD 中，因为BC ＝CD ，所以∠BDC＝∠B＝65°，所以∠BCD＝50°，故答案为50°.8．[答案] 40[解析] 连接OB ，OC ，如图．∵OA ＝OB ，OC ＝OD ，∴∠OBA ＝∠A＝65°，∠OCD ＝∠D＝60°，∴∠AOB ＝180°－2×65°＝50°，∠COD ＝180°－2×60°＝60°， ∴∠BOC ＝∠AOD－∠AOB－∠COD＝150°－50°－60°＝40°， ∴BC ︵的度数为40°.9．证明：∵AB＝CD ，∴AB ︵＝CD ︵， ∴AB ︵＋AD ︵＝CD ︵＋AD ︵，即BD ︵＝AC ︵，∴AC ＝BD.10．[解析] 一条弦所对的圆心角实质上就是弦把圆分出的劣弧所对的圆心角．可以利用方程求出劣弧的度数，进而求出弦所对的圆心角的度数．解：设弦把圆周分成的两条弧的度数分别为(3x)°，(7x)°. 根据题意，得3x ＋7x ＝360，解这个方程，得x ＝36，∴(3x)°＝3×36°＝108°，∴这条弦所对的圆心角的度数为108°. 11．解：CM ＝.理由如下：∵M ，N 分别是OA ，OB 的中点，OA ＝OB ， ∴OM ＝ON.又∵AC ︵＝BC ︵，∴∠AOC ＝∠BOC. 又∵OC＝OC ，∴△MOC ≌△NOC ， ∴CM ＝.12．解：在⊙O 中，∵AB ︵＝AC ︵，∴AB ＝AC ， ∴∠B ＝∠C.∵∠A ＝40°，∠A ＋∠B＋∠C＝180°， ∴∠B ＝12(180°－∠A)＝70°.13．[解析] 连接OC.利用圆心角、弦、弧之间的关系可求出∠AOC，∠COB 的度数，找到OA ，OB ，BC ，AC 之间的数量关系，进而得出四边形OACB 的形状．解：四边形OACB 是菱形．理由：连接OC.∵C 是AB ︵的中点， ∴AC ︵＝BC ︵，∴∠AOC ＝∠COB. ∵∠AOB ＝120°，∴∠AOC ＝∠C OB ＝12∠AOB＝60°.又∵OA＝OC ，OC ＝OB ，∴△AOC 和△BOC 都是等边三角形， ∴OA ＝AC ＝OC ＝OB ＝BC ， ∴四边形OACB 是菱形．14． [解析] 要证明AC ︵＝BD ︵，只要证明它们所对的圆心角∠AOC＝∠BOD 即可，由Rt △≌Rt △DON ，可得∠AOC＝∠BOD.解：AC ︵＝BD ︵.理由如下：连接OC ，OD.∵AM ＝BN ，OA ＝OB ， ∴OM ＝ON.又∵OC＝OD ，∠CMO ＝∠DNO＝90°， ∴Rt △CMO ≌Rt △DNO ， ∴∠AOC ＝∠BOD， ∴AC ︵＝BD ︵.[素养提升]解：如图，作点B 关于MN 的对称点B′，连接AB′交MN 于点P ，连接BP ，此时AP ＋BP ＝AB′最小，连接OB′.∵点B 和点B′关于MN 对称， ∴PB ＝PB′.∵A 是半圆上的一个三等分点，B 是AN ︵的中点，∴∠AON ＝180°÷3＝60°，∠B ′ON ＝∠BON＝12∠AON＝30°，∴∠AOB ′＝∠AON＋∠B′ON＝90°. ∵OA ＝OB′＝1， ∴AB ′＝ 2.。

人教版-数学-九年级上册- 图形的旋转同步精品练习及解析(2个课时)

23.1图形的旋转第1课时旋转的概念及性质1．将图23－1－1按顺时针方向旋转90°后得到的是(A)图23－1－12．如图23－1－2，该图形围绕点O按下列角度旋转后，不能与其自身重合的是(B)图23－1－2A．72°B．108°C．144°D．216°图23－1－33．如图23－1－3，点A，B，C，D都在方格纸的格点上，若△AOB绕点O按逆时针方向旋转到△COD的位置，则旋转的角度为(C)A．30°B．45°C．90°D．135°4．如图23－1－4，将△ABC绕着点C顺时针旋转50°后得到△A′B′C，若∠A＝40°，∠B′＝110°，则∠BCA′的度数是(B)A．110°B．80°C．40°D．30°【解析】根据旋转的性质可得∠A′＝∠A，∠A′CB′＝∠ACB.∵∠A＝40°，∴∠A′＝40°.∵∠B′＝110°，∴∠A′CB′＝180°－110°－40°＝30°.∴∠ACB＝30°.∵将△ABC绕着点C顺时针旋转50°后得到△A′B′C，∴∠ACA′＝50°，∴∠BCA′＝30°＋50°＝80°.图23－1－4图23－1－55．如图23－1－5，在Rt△ABC中，∠BAC＝90°，∠B＝60°，△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点，点C′与点C是对应点)，连接C C′，则∠CC′B′ 的度数是(D) A．45°B．30°C．25°D．15°6．如图23－1－6，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α(0°＜α＜90°)．若∠1＝110°，则∠α＝__20°__．图23－1－6第6题答图【解析】如图，∵四边形ABCD为矩形，∴∠B＝∠D＝∠BAD＝90°，∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′，∴∠D′＝∠D＝90°，∠4＝α∵∠1＝∠2＝110°，∴∠3＝360°－90°－90°－110°＝70°，∴∠4＝90°－70°＝20°，∴∠α＝20°.23－1－77．如图23－1－7，将Rt△ABC绕点A逆时针旋转40°，得到Rt△AB′C′，点C′恰好落在斜边AB上，连接BB′，则∠BB′C′＝__20__度．8．同学们都玩过万花筒吧，它是由三块等宽等长的玻璃片围成的．如图23－1－8所示是可以看作万花筒的一个图案，图中所有小三角形是全等的等边三角形，其中菱形AEFG可以看成是把菱形ABCD以点A为中心按照什么方向旋转多少度得到的？图23－1－8【解析】将一个图形绕一个定点沿某个方向旋转一定的角度，意味着图形上每个点同时都旋转相同的角度，所以找一点观察即可．以点B为例，旋转后点B旋转到点E的位置，是以点A为中心，按逆时针方向旋转120°得到的，整个菱形亦然．解：菱形AEFG可以看成是把菱形ABCD以点A为中心，按逆时针方向旋转120°得到的．图23－1－99．如图23－1－9，将△ABC绕点A逆时针旋转一定角度，得到△ADE，若∠CAE＝65°，∠E＝70°，且AD⊥BC，则∠BAC的度数为(C)A．60°B．75°C．85°D．90°10．如图23－1－10，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2，将△ABC绕点C按顺时针方向旋转n度后，得到△EDC，此时，点D在AB边上，斜边DE交AC边于点F，则n的大小和图中阴影部分的面积分别为(C)A．30，2 B．60，2 C．60，32D．60， 3【解析】由旋转性质知△BCD是等边三角形，n＝60，DC＝BC＝2，∴∠DCF＝30°，△CDF是直角三角形，∴DF＝1，CF＝3，∴阴影部分的面积为12×1×3＝32，故选C.图23－1－10图23－1－11 11．如图23－1－11，在Rt △OAB 中，∠OAB ＝90°，OA ＝AB ＝6，将△OAB 绕点O 沿逆时针方向旋转90°得到△OA 1B 1.(1)线段OA 1的长是__6__，∠AOB 1的度数是__135°__；(2)连接AA 1，求证：四边形OAA 1B 1是平行四边形；(3)求四边形OAA 1B 1的面积．【解析】 (1)OA 1＝OA ＝6，∠AOB 1＝∠A 1OB 1＋∠A 1OA ＝45°＋90°＝135°；(2)证明OA 綊A 1B 1；(3)四边形OAA 1B 1的面积＝OA ·OA 1＝6×6＝36.解： (2)证明：∵∠AOA 1＝∠OA 1B 1＝90°，∴OA ∥A 1B 1.又OA ＝AB ＝A 1B 1，∴四边形OAA 1B 1是平行四边形；(3)四边形OAA 1B 1的面积＝OA ·OA 1＝6×6＝36.12．把正方形ABCD 绕着点A 按顺时针方向旋转得到正方形AEFG ，边FG 与BC 交于点H (如图23－1－12所示)．试问线段HG 与线段HB 相等吗？请先观察猜想，然后再证明你的猜想．图23－1－12第12题答图解：HG＝HB.证法1：如图(a)所示，连接AH.∵四边形ABCD，AEFG都是正方形，∴∠B＝∠G＝90°.由题意知AG＝AB，又AH＝AH，∴Rt△AGH≌Rt△ABH(HL)，∴HG＝HB.证法2：如图(b)所示，连接GB.∵四边形ABCD，AEFG都是正方形，∴∠ABC＝∠AGF＝90°.由题意知AB＝AG，∴∠AGB＝∠ABG，∴∠HGB＝∠HBG，∴HG＝HB.13．如图23－1－13所示，直角梯形ABCD中，AD∥BC，AB⊥BC，AD＝2，BC＝3，∠BCD＝45°，将腰CD以点D为中心逆时针旋转90°至ED，连接AE，CE，求△ADE的面积．图23－1－13第13题答图解：如图，过点D作DF⊥BC于点F，连接AC，易证四边形ABFD是矩形，所以BF＝AD＝2，所以FC＝BC－BF＝3－2＝1.因为∠BCD＝45°，DF⊥BC，所以△DFC是等腰直角三角形，所以DF＝FC＝1.因为CD以点D为中心逆时针旋转90°至ED，所以∠CDE＝90°，CD＝ED.因为∠ADC＝180°－∠BCD＝135°，所以∠ADE＝360°－∠ADC－∠CDE＝135°＝∠ADC，又因为AD＝AD，所以△ADE≌△ADC，所以S△ADE＝S△ADC.因为平行线间的距离处处相等，所以S△ADE＝S△ADC＝12AD·DF＝12×2×1＝1.图23－1－1414．一副三角板按图23－1－14所示叠放在一起，若固定△AOB，将△ACD绕着公共顶点A，按顺时针方向旋转α角(0°<α<180°)，当△ACD的一边与△AOB的某一边平行时，相应的旋转角α的值是__30°，45°，75°，135°，165°__．第2课时旋转作图1．△ABC在如图23－1－15所示的平面直角坐标系中，将△ABC向右平移3个单位长度后得到△A1B1C1，再将△A1B1C1绕点O旋转180°后得到△A2B2C2，则下列说法正确的是(D)A．A1的坐标为(3，1)B．S四边形ABB1A1＝3C．B2C＝2 2 D．∠AC2O＝45°【解析】因为A点坐标为(－2，3)，所以该点向右平移3个单位长度后得A1(1，3)；平移后四边形ABB1A1的面积为3×2＝6；同样可求出B2(0，－1)，C2(－2，－2)，所以B2C＝10，∠AC2O＝45°.图23－1－15图23－1－162．如图23－1－16，P是正△ABC内的一点，若将△PBC绕点B旋转到△P′BA，则∠PBP′的度数是(B) A．45°B．60°C．90°D．120°【解析】∵△PBC绕点B旋转到△P′BA，∴∠P′BA＝∠CBP，∴∠PBP′＝∠P′BA＋∠ABP＝∠ABP＋∠CBP ＝∠ABC＝60°，故选B.3．如图23－1－17所示，E是正方形ABCD内一点，∠AEB＝130°，BE＝3 cm，△ABE按顺时针方向旋转一个角度后成为△CBF，图中__B__是旋转中心，旋转__90__度，点A与点__C__是对应点，△BEF是__等腰直角__三角形，∠CBF＝__∠ABE__，∠BFC＝__130__度，BF＝__3__cm.4．图23－1－17图23－1－184．分别以正方形的各边为直径向其内部作半圆得到的图形如图23－1－18所示．将该图形绕其中心旋转一个合适的角度后会与原图形重合，则这个旋转角的最小度数是__90__度．【解析】题中图形可看作由一个基本图形每次旋转90°，旋转3次所组成，故最小旋转角为90°.5．如图23－1－19所示，五角星的顶点是一个正五边形的五个顶点．这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过__4__次旋转而得到，每一次旋转__72__度．【解析】由旋转特征作答．图23－1－19图23－1－206．如图23－1－20所示，△ABC的顶点坐标分别为A(3，6)，B(1，3)，C(4，2)．如果将△ABC绕点C顺时针旋转90°，得到△A′B′C，那么点A的对应点A′的坐标为__(8，3)__．【解析】作出△A′B′C，认真看图可得A′(8，3)．7．如图23－1－21，E，F分别是正方形ABCD的边BC，CD上的点，BE＝CF，连接AE，BF，将△ABE 绕正方形的中心按逆时针方向转到△BCF，旋转角为α(0°＜α＜180°)，则α＝__90°__．hslx3y3h图23－1－21图23－1－228．如图23－1－22所示，已知四边形ABCD绕点O顺时针旋转一定角度后，使得点A落在点A′处，试作出旋转后的图形．【解析】要作出旋转后的图形，关键是缺少“旋转的角度”，需要从图中找出来．解：图略．作法：(1)连接OA，OA′.(2)连接OB，OC，OD，分别以OB，OC，OD为始边，点O为顶点顺时针作∠BOB′，∠COC′，∠DOD′，并使得∠BOB′＝∠COC′＝∠DOD′＝∠AOA′，OB′＝OB，OC′＝OC，OD′＝OD.(3)顺次连接A′，B′，C′，D′四点．则四边形A′B′C′D′就是所要作的图形．9．如图23－1－23，在方格纸上，以格点连线为边的三角形叫做格点三角形，请按要求完成下列操作：先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1，再将△A1B1C1沿直线B1C1作轴对称得到△A2B2C2.图23－1－23解：如图所示：10．如图△ABC 是等腰直角三角形，BC 是斜边，P 为△ABC 内一点，将△ABP 绕点A 逆时针旋转后与△ACP ′重合，如果AP ＝3，那么线段PP ′的长等于__32__．【解析】由题意可知AP ＝AP ′＝3，∠PAP ′＝90°，所以PP ′＝3 2.图23－1－2411．如图23－1－24，Rt △ABC 中，已知∠C ＝90°，∠B ＝50°，点D 在边BC 上，BD ＝2CD .把△ABC 绕着点D 逆时针旋转m (0＜m ＜180)度后，如果点B 恰好落在初始Rt △ABC 的边上，那么m ＝__80或120__．12．12．如图23－1－25，在平面直角坐标系中，O 为坐标原点，四边形OABC 是矩形，点A ，B 的坐标分别为A (－4，0)，B (－4，2)．(1)现将矩形OABC 绕点O 顺时针方向旋转90°后得到矩形OA 1B 1C 1，请画出矩形OA 1B 1C 1；(2)画出直线BC 1，并求直线BC 1的函数解析式．图23－1－25第12题答图解：(1)矩形OA 1B 1C 1如图所示．(2)连接BC 1，矩形OA 1B 1C 1是由矩形OABC 绕O 点顺时针方向旋转90°得到的，所以OC ＝OC 1＝2，又因为点C 1在x 轴的正半轴上，所以点C 1的坐标为(2，0)．设直线BC 1的解析式为y ＝kx ＋b ，且经过(－4，2)和(2，0)两点，可列方程组为⎩⎪⎨⎪⎧－4k ＋b ＝2，2k ＋b ＝0，解得⎩⎨⎧k ＝－13，b ＝23，所以直线BC 1的函数解析式是y ＝－13x ＋23.初中-数学-打印版初中-数学-打印版图23－1－2613．如图23－1－26，B ，C ，E 是同一直线上的三个点，四边形ABCD 与四边形CEFG 都是正方形．连接BG ，DE .(1)观察猜想BG 与DE 之间的大小关系，并证明你的结论．(2)图中是否存在通过旋转能够互相重合的两个三角形？若存在，请指出，并说明旋转过程；若不存在，请说明理由．【解析】 (1)由已知可证明△BCG ≌△DCE ，得BG ＝DE ；(2)△BCG 绕点C 顺时针方向旋转90°后与△DCE 重合．解：(1)BG ＝DE .证明如下：∵四边形ABCD 和四边形CEFG 都是正方形，∴CG ＝CE ，BC ＝DC ，∠BCG ＝∠DCE ＝90°，∴△BCG ≌△DCE ，∴BG ＝DE .(2)存在．△BCG 和△DCE .△BCG 绕点C 顺时针方向旋转90°后与△DCE 重合．(△DCE 绕点C 逆时针方向旋转90°后与△BCG 重合)．。

23.1 第1课时旋转的概念与性质人教版九年级数学上册练习(含答案)

定义进行判断即可得到答案.
【详解】
A. 火箭升空的运动是平移，故不符合题意；
B. 足球在草地上滚动时绕着旋转的点不是同一个点，故不符合题意；
C. 大风车运动的过程是旋转，符合题意； D. 传输带运输的东西是平移，不符合题意；故选：C. 【点拨】此题考查旋转的定义，熟记定义掌握旋转的特点是解题的关键. 4．C 【分析】根据旋转的性质：对应点到旋转中心的距离相等，可知旋转中心一定在任何一对对应点所连线段的垂直平分线上，找出两组对应点 M 和«Skip Record If...»，N 和«Skip Record If...»，连接«Skip Record If...»，作出线段«Skip Record If...»与«Skip Record If...»的垂直平分线，交点即为所求旋转中心．【详解】解：如图，找出两组对应点，«Skip Record If...»和«Skip Record If...»，连接«Skip Record If...»，分别作出«Skip Record If...»的垂直平分线，交点即为旋转中心，故旋转中心为点 C，故选：C．
10．如图，Rt△OCB 的斜边在 y 轴上，OC＝«Skip Record If...»，直角顶点 C 在第二象限，将 Rt△OCB 绕原点顺时针旋转 120°后得到△OC′B′，则«Skip Record If...»坐标是___．
11．在△ABC 中，∠B+∠ACB＝30°，AB＝4，△ABC 逆时针旋转一定角度后与△ADE 重合，且点 C 恰好成为 AD 中点，如图．
1．A
参考答案
【分析】
根据平移或者旋转的性质逐一分析即可．
【详解】
A.经过平移和轴对称可得，符合题意；

人教版九年级数学上册《23-1 第1课时图形的旋转》作业同步练习题及参考答案

23.1 图形的旋转第 1 课时图形的旋转1.将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )A.96B.69C.66D.992.如图,已知△OAB 是正三角形,OC⊥OB,OC=OB,将△OAB 绕点O 按逆时针方向旋转,使得OA 与OC 重合,得到△OCD,则旋转的角度是( )A.150°B.120°C.90°D.60°3.如图,在△ABC 中,∠C=90°,AC=4,BC=3,将△ABC 绕点A 逆时针旋转,使点C 落在线段AB 上的点E 处,点B 落在点D 处,则B,D 两点间的距离为( )A. 10B.2 2C.3D.2 54.如图,将△ABC 绕点C 顺时针旋转,使点B 落在AB 边上点B'处,此时,点A 的对应点A'恰好落在BC 边的延长线上,下列结论错误的是( )A.∠BCB'=∠ACA'B.∠ACB=2∠BC.∠B'CA=∠B'ACD.B'C 平分∠BB'A'5.如图所示,在△ABC 中,∠BAC=33°,将△ABC 绕点A 按顺时针方向旋转50°,对应得到△AB'C',则∠B'AC 的度数为.6.如图,有五个图形,其中四个是相同图形的不同摆法,另一个与众不同,与众不同的是.7.如图,把矩形OABC 放在平面直角坐标系中,OC 在x 轴上,OA 在y 轴上,且OC=2,OA=4,把矩形OABC 绕着原点顺时针旋转90°得到矩形OA'B'C',则点B'的坐标为.8.已知点P 的坐标为(1,1),若将点P 绕原点顺时针旋转45°,得到点P',则点P'的坐标为.9.如图,B,C,E 是同一直线上的三个点,四边形ABCD 与四边形CEFG 都是正方形.连接BG,DE.图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说明理由,并指出旋转过程.10.观察图①和图②,回答下列问题:(1)请简述由图①变换为图②的形成过程;(2)若AD=3,DB=4,求△ADE 与△BDF 的面积和.11.如图,将△ABC 绕点B 顺时针旋转60°得到△DBE,点C 的对应点E 恰好落在AB 的延长线上,连接AD.下列结论一定正确的是( )A.∠ABD=∠EB.∠CBE=∠CC.AD∥BCD.AD=BC12.如图,网格纸上正方形小格的边长为1,图中线段AB 和点P 绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )区 B.2 区 C.3 区 D.4 区13.如图,在Rt△ABC 中,∠ACB=90°,∠BAC=60°,AB=6.Rt△AB'C'可以看成是由Rt△ABC 绕点A 按逆时针方向旋转60°得到的,则线段B'C 的长为.14.如图,△ABC≌△DEF.△DEF 能否由△ABC 通过一次旋转得到?若能,请用直尺和圆规画出旋转中心; 若不能,试简要说明理由.★15.如图.(1)△ABC 按照逆时针方向转动一个角度后成为△AB'C',∠CAC'=90°,图中哪一点是旋转中心?旋转了多少度?(2)以点C'为旋转中心,顺时针旋转(1)问中相同的角度,那么线段AC 与A″C',BC 与B″C',AB 与A″B″有怎样的关系?B'C'与B″C'的位置关系呢?★16.如图,方格中每个小正方形的边长都是单位1,△ABC 在平面直角坐标系中的位置如图.(1)画出将△ABC 向右平移2 个单位得到的△A1B1C1;(2)画出将△ABC 绕点O 顺时针方向旋转90°得到的△A2B2C2.参考答案夯基达标1.B2.A3.A 由题意可知在△ABC 中AB 为斜边,易得AB=5,由图形的旋转可知△ABC≌△ADE,所以AC=AE=4,DE=BC=3.而AB=5,所以EB=AB-AE=5-4=1.连接DB,易得△DEB 为直角三角形,所以BD= ��2 + ��2 = 12 + 32 = 10. 故选A.4.C 根据旋转的性质得,∠BCB'和∠ACA'都是旋转角,则∠BCB'=∠ACA',故A 正确;∵CB=CB',∴∠B=∠BB'C.又∠A'CB'=∠B+∠BB'C,∴∠A'CB'=2∠B.又∠ACB=∠A'CB',∴∠ACB=2∠B,故 B 正确;∵∠A'B'C=∠B,∴∠A'B'C=∠BB'C ,∴B'C 平分∠BB'A',故 D 正确;故选 C .5.17° 由题意易知∠B'AB 为旋转角,∠B'AB=50°,∵∠BAC=33°,∴∠B'AC=50°-33°=17°.故答案为 17°.6.② 将图②③④⑤均绕各自对角线的交点旋转,使其含有黑点的三角形向上,此时图③④⑤与图① 完全相同,只有图②的阴影在含黑点的三角形的右侧.7.(4,2)8.( 2,0)9. 解存在,△BCG 和△DCE.理由:因为四边形 ABCD 和四边形 CEFG 都是正方形,所以 GC=CE ,BC=CD ,∠BCG=∠DCE=90°.所以△BCG ≌△DCE.所以△BCG 绕点 C 顺时针方向旋转 90°后能与△DCE 重合.10. 解 (1)把△ADE 绕点 D 逆时针旋转 90°得到△DA 1F ,即由图①变换为图②.(2)由题意,得∠A 1DB=90°,A 1D=AD=3,DB=4,所以�△+ �△= �△� ��= 1×3×4=6. ��12培优促能11.C ∵△ABC 绕点 B 顺时针旋转 60°得△DBE ,∴∠ABD=∠CBE=60°,AB=BD ,∴△ABD 是等边三角形,∴∠DAB=60°,∴∠DAB=∠CBE ,∴AD ∥BC ,故选 C .12.D 如图,连接 AA',BB',分别作 AA',BB'的中垂线,两直线的交点即为旋转中心,2由图可知,线段 AB 和点 P 绕着同一个点逆时针旋转 90°,点 P 逆时针旋转 90°后所得对应点 P'落在 4区,故选 D .13.3 7 如图,连接 BB'.在 Rt △ABC 中,∠ABC=90°-60°=30°,所以 AC=1AB=3.根据勾股定理,得BC= ��2-��2=3 3.根据旋转的性质知,B'C'=BC=3 3,AC'=AC=3,∠B'C'B=90°.所以 BC'=AB-AC'=3.在 Rt △B'C'B 中,BB'= �'�'2 + ��'2=6.由题易知∠B'BC 是直角,所以在 Rt △B'BC 中,B'C= ��'2 + ��2=3 7.14. 解能.如图,点 O 就是所求作的旋转中心.15. 解 (1)点 A 是旋转中心,旋转了 90°.(2)AC ∥A″C',且 AC=A″C';BC ∥B″C',且 BC=B″C';AB ∥A″B″,且 AB=A″B″.B'C'⊥B″C'.创新应用16.解(1)如图所示.(2)如图所示.。

数学圆的旋转不变性

对“等对等”定理的理解弧、弦、圆心角之间的关系:在同圆或等圆中，如果两条劣弧（优弧）、两条两个圆心角中有一组量对应相等，那么它们所对应的其余各组量也分别对应相等.判断题1．在同圆中, 如果两条弦相等, 则它们所对的弧也相等．（）2．顶点在圆心的角叫圆心角．（）3．在圆上取一A引两弦AB、AC，若AB=2AC，则=2．（）4．圆内弦的长, 与弦的弦心距的长成正比．（）5．圆心角相等,则它们所对的弧不一定相等．（）6．在同圆或等圆中, 不等的弦, 它的弦心距也不等, 较大的弦, 它的弦心距也较大．（）在下列命题中, 正确的是_________．[ ] A．在同圆中, 大弧对大弦B．在同圆中, 大弦对大弧C．在同圆中, 等弧对等弦D．在同圆中, 等弦对等弧如果两条弦相等，那么[ ] A．这两条弦所对的弧相等；B．这两条弦所对的圆心角相等；C．这两条弦的弦心距相等；D．以上都不对．命题“在两个圆中，如果两个圆心角相等，那么它们所对的弦相等，它们所对的弧相等”是真命题吗？为什么？如图，⊙O和⊙O'是等圆，AD∥OO'，下面答案中正确的是[ ]D．以上答案都不对．定理应用：如图，在⊙O中，，，△ACE与△BDF全等吗？为什么？如果A，B，C是⊙O上的三点，，那么AC与2AB有什么大小关系？为什么？如图，在⊙O中，弦AB＝CD，AB的延长线与CD的延长线相交于点P，直线OP交⊙O于点E，F，你认为∠APE与∠CPE有什么大小关系？为什么？已知：如图，M为⊙O外一点，MA和MC分别和⊙已知：如图，E是⊙O外一点，EB，ED分别交⊙O于A，C，且AB=C D．求证：EA=E C．如图，在⊙O中，弦AB＝CD，AB与CD相交于点P，直线OP交⊙O于点E，F．你认为∠BPE与∠DPE有什么大小关系？为什么？如图，在⊙O中，弦AB＝CD，AB与CD相交于点P．你认为PA与PC有什么大小关系？为什么？如图，在⊙O中，直径AB与弦CD相交于点E，且AE∶EB＝1∶5，如果AB＝12 cm，∠CEA＝30°，那么CD的长是多少？已知：如图，MN是⊙O的直径，P是MN上一点，弦AC，BD过P点，且∠1=∠2．求证：PA=P B．已知：如图，在⊙O中，弦AB，CD相交于P，且AB=C D．求证：OP平分∠DP B．如图，在⊙O中，=，那么[ ] A．AB=AC；B．AB=2AC；C．AB＜2AC；D．AB＞2A C．已知：如图，，OE⊥AB，OF⊥CD，∠OEF=25°．求∠OFE的度数．已知：如图，在⊙O中，弦AB=CD，且AB⊥CD于E，BE=7cm，AE=3cm，O G为弦AB的弦心距．求：O G及⊙O的半径长已知：如图，在⊙O中，，D，E分别是半径OA，OB的中点．求证：CD=CE．已知：如图7－33，AB，CD是⊙O的两条直径，AE是⊙已知：AB是⊙O的直径，AC，AD是弦，且AB平分∠CA D．求证：AC=A D．已知：如图，AB是⊙O的弦，且AC=BD，半径OE，已知：如图7－36，在⊙O中，弦AB和CD相交于P，且AB=C D．求证：PA=PC，PD=P B．已知：如图，过⊙O上一点A作弦AB，AC，且AB=AC，M，N分别是AB，AC的中点，弦PQ过M，N两点．求证：PM=NQ．中考链接（08广州）如图，射线AM 交一圆于点B 、C ，射线AN 交该圆于点D 、E ，且BC ⌒ =DE ⌒ ．（1）求证：AC = AE ；（2）利用尺规作图，分别作线段CE 的垂直平分线与∠MCE 的平分线，两线交于点F （保留作图痕迹，不写作法），求证：EF 平分∠CEN ．（08呼伦贝尔）如图：AC ⌒ =CB⌒ ，D E ，分别是半径OA 和OB 的中点，CD 与CE 的大小有什么关系？为什么？文 - 汉语汉字编辑词条文，wen ，从玄从爻。

数学：《旋转》同步练习2(人教版九年级上)

数学：《旋转》同步练习2（人教版九年级上）1．如果两个图形可通过旋转而相互得到，则下列说法中正确的有( )． ①对应点连线的中垂线必经过旋转中心． ②这两个图形大小、形状不变． ③对应线段一定相等且平行．④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合． A ．1个 B ．2个 C ．3个 D ．4个2．如图，同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的，其中菱形AEFG 可以看成是把菱形ABCD 以A 为中心( )． A ．顺时针旋转60°得到 B ．顺时针旋转120°得到 C ．逆时针旋转60°得到 D ．逆时针旋转120°得到3．如图，C 是线段BD 上一点，分别以BC 、CD 为边在BD 同侧作等边△ABC 和等边△CDE,AD 交CE 于F ，BE 交AC 于G ，则图中可通过旋转而相互得到的三角形对数有( )． A ．1对 B ．2对 C ．3对 D ．4对4．如图，△ABC 中，AD 是∠BAC 内的一条射线，BE ⊥AD ，且△CHM 可由△BEM 旋转而得，则下列结论中错误的是( )． A ．M 是BC 的中点 B ．EH 21FMC ．CF ⊥AD D ．FM ⊥BC5．如图，O 是锐角三角形ABC 内一点，∠AOB ＝∠BOC ＝∠COA ＝120°，P 是△ABC 内不同于O 的另一点；△A′BO′、△A′BP′分别由△AOB、△APB旋转而得，旋转角都为60°，则下列结论中正确的有( )．①△O′BO为等边三角形，且A′、O′、O、C在一条直线上．②A′O′＋O′O＝AO＋BO．③A′P′＋P′P＝PA＋PB．④PA＋PB＋PC>AO＋BO＋CO．A．1个 B．2个 C．3个 D．4个6．如图，有四个图案，它们绕中心旋转一定的角度后，都能和原来的图案相互重合，其中有一个图案与其余三个图案旋转的角度不同，它是( )．7．把26个英文字母按规律分成5组，现在还有5个字母D、M、Q、X、Z，请你按原规律补上，其顺序依次为（）① F R P J L G （）② H I O （）③ N S （）④ B C K E （）⑤ V A T Y W U （）A．Q X Z M D B．D M Q Z XC．Z X M D Q D．Q X Z D M8．4张扑克牌如图（1）所示放在桌子上，小敏把其中一张旋转180°后得到如图（2）所示，那么她所旋转的牌从左起是（）A．第一张、第二张 B．第二张、第三张C．第三张、第四张 D．第四张、第一张（1）（2）9．下列图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们的共性是都可以由一个“基本图案”通过连续旋转得来，旋转的角度是（）.（A）︒9060（D）︒45（C）︒30（B）︒10．下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的角度是（）（A）︒60（D）︒9045（C）︒30（B）︒11．如图所示，P是等边△ABC内一点，△BMC是由△BPA旋转所得，则∠PBM＝_____________．12．如图，设P是等边三角形ABC内任意一点，△ACP′是由△ABP旋转得到的，则PA_______PB＋PC(填“>”、“<”或“＝”)．13．如图，E、F分别是正方形ABCD的边BC、CD上一点，且BE＋DF＝EF，则∠EAF＝_____________．14．如图，O是等边△ABC内一点，将△AOB绕B点逆时针旋转，使得B、O两点的对应点分别为C、D，则旋转角为_____________，图中除△ABC外，还有等边三形是_____________．15．如图，Rt△ABC中，P是斜边BC上一点，以P为中心，把这个三角形按逆时针方向旋转90°得到△DEF，图中通过旋转得到的三角形还有_____________．16．如图，将图形绕O点按顺时针方向旋转45°，作出旋转后的图形．17．如图，△ABC、△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，图中的哪两个三角形可以通过怎样的旋转而相互得到？AB CD EM18．如图，△ABC 是等腰三角形，∠BAC=36°，D 是BC 上一点， △ABD 经过旋转后到达△ACE 的位置， ⑴旋转中心是哪一点？ ⑵旋转了多少度？⑶如果M 是AB 的中点，那么经过上述旋转后，点M 转到了什么位置？19．如图所示，△ABP 是由△ACE 绕A 点旋转得到的，那么△ABP 与△ACE 是什么关系？若∠BAP ＝40°，∠B ＝30°，∠PAC ＝20°，求旋转角及∠CAE 、∠E 、∠BAE 的度数。

人教版九年级上册数学：《旋转》分层作业(含答案)

第二十三章旋转图形的旋转第1课时旋转的概念及性质1．下列四个图形中，图中的一个矩形是由另一个矩形按顺时针方向旋转90°后所形成的是( )图2317A．①②B．②③C．①④D．②④2．如图2318，在Rt△ABC中，∠BAC＝90°，将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，点A在边B′C上，则∠B′的大小为( )图2318A．42° B．48°C．52° D．58°3．如图2319，将Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C，连接AA′，若∠1＝25°，则∠BAA′的度数是( )图2319A．55° B．60°C．65° D．70°4．如图23110，将△ABC绕点C顺时针旋转，使点B落在AB边上点B′处，此时，点A的对应点A′恰好落在BC的延长线上，下列结论错误的是( )图23110A．∠BCB′＝∠ACA′B．∠ACB＝2∠BC．∠B′CA＝∠B′ACD．B′C平分∠BB′A′5．如图23111，将△ABC绕点C按顺时针方向旋转至△A′B′C，使点A′落在BC的延长线上．已知∠A＝27°，∠B＝40°，则∠ACB′＝____.图231116．如图23112，△ACD，△AEB都是等腰直角三角形，∠CAD＝∠EAB＝90°，∠BAC ＝30°，若△EAC绕某点逆时针旋转后能与△BAD重合，请完成下列问题：(1)指出旋转中心；(2)指出逆时针旋转的角度；(3)若EC＝10 cm，求BD的长度.图231127．如图23113，在四边形ABCD中，∠DAB＝60°，AB＝AD，线段BC绕点B顺时针旋转60°得到线段BE，连接AC，ED.(1)求证：AC＝DE；(2)若DC＝4，BC＝6，∠DCB＝30°，求AC的长．参考答案【分层作业】1．D 2.A 3.C 4.C 5.46°6．(1)旋转中心是点A.(2)旋转的角度为90°.(3)BD＝EC＝10 cm.7.(1)略(2)AC＝213.第2课时旋转作图1．如图23119，E，F分别是正方形ABCD的边AB，BC上的点，且BE＝CF，连接CE，DF，将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置，则旋转角为( )图23119A．30° B．45°C．60° D．90°2．如图23120，A点的坐标为(－1,5)，B点的坐标为(3,3)，C点的坐标为(5,3)，D 点的坐标为(3，－1)．小明发现线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，你认为这个旋转中心的坐标是___ _．图231203．如图23121，在平面直角坐标系中，△ABC三个顶点的坐标分别为A(2,3)，B(1,1)，C(5,1)．(1)△ABC平移后，其中点A移到点A1(4,5)，画出平移后得到的△A1B1C1；(2)把△A1B1C1绕点A1按逆时针方向旋转90°，画出旋转后的△A2B2C2.4．在4×4的方格纸中，△ABC的三个顶点都在格点上．(1)在图23122中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可)；(2)将图23123中的△ABC绕着点C按顺时针方向旋转90°，画出经旋转后的三角形．5．如图23124所示，在平面直角坐标系中，有Rt△ABC，且A(－1，3)，B(－3，－1)，C(－3，3)，已知△A1AC1是由△ABC旋转变换得到的．(1)旋转中心的坐标是____，旋转角是____；(2)以(1)中的旋转中心为中心，分别画出△A1AC1顺时针旋转90°，180°后的三角形；(3)设Rt△ABC的两直角边BC＝a，AC＝b，斜边AB＝c，利用变换前后所形成的图案证明勾股定理．图23124参考答案【分层作业】1．D 2.(1,1)或(4,4) 3.略4.略5.(1)(0,0) 90°(2)略(3)略。

人教版-数学-九年级上册- 旋转同步练习2

《旋转》同步练习2一、填空题1、下列三个图形，各绕自己的中心最少旋转多少度可与自身重合？（1）（2）（3）2、点(2,3)关于原点对称的点的坐标是_________.3、请列出四个常见的中心对称图形:______、______、______4、请你写出四个成中心对称的汉字5、直线y=x＋3上有一点P(m-5,2m),则P点关于原点的对称点P′为______.6、如图，将矩形ABCD绕点A顺时针旋转90°后，得到矩形AB′C ′D′，如果CD＝2DA＝2，那么CC′=_________．7、如图，△COD是△AOB绕点O顺时针方向旋转40°后所得的图形，点C恰好在AB上，∠AOD＝90°，则∠D的度数是．8、点A的坐标为（2，0），把点A绕着坐标原点顺时针旋转135º到点B，那么点B的坐标是 _________ ．二、选择题9. 下列图形中，既是轴对称图形，又是中心对称图形的是（）A B C D10. 若点P（m，2）与点Q（3，n）关于原点对称，则m，n的值分别是（）A、-3，2B、3，-2C、-3，-2D、3，2B'D'C'DC BAO DCBA(第6题)(第7题)11. 如图，紫荆花图案旋转一定角度后能与自身重合，则旋转的角度可能是( )A．30° B．60° C．72°D．90°12．如图，在平面直角坐标系中，点A、B的坐标分别为（﹣2，0）和（2，0）.月牙①绕点B顺时针旋转900得到月牙②，则点A的对应点A’的坐标为（）A.（2，2）B.（2，4）C.（4，2）D.（1，2）13. 如图,四边形ABCD是正方形,ΔADE绕着点A旋转90°后到达ΔABF的位置，连接EF，则ΔAEF的形状是（）A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等边三角形（11题）（12题）（13题）14. 如图,将正方形图案绕中心O旋转180°后,得到的图案是( )15. 下列命题中的真命题是( )A．全等的两个图形是中心对称图形 B．关于中心对称的两个图形全等C．中心对称图形都是轴对称图形 D．轴对称图形都是中心对称图形三、解答题16. 如图所示，把一个直角三角尺ACB绕着30角的顶点B顺时针旋转，使得点A与CB的延长线上的点E重合。

数学九年级上册同步分层练习2.2 第1课时 圆的旋转不变性

人教版九年级上册数学《图形的旋转》同步练习(含答案)

人教版九年级上册数学同步练习 第1课时 图形的旋转

2020-2021沪科版九年级数学24.2圆的基本性质-知识点+习题同步练习提升 (1)

苏科版数学九年级上册第1课时圆的旋转不变性同步课件

新苏科版数学九年级上册同步练习2.2 第1课时 圆的旋转不变性

九年级(初三)《旋转》知识点及练习(带答案)

《圆的基本概念和性质—知识讲解 》同步 2022人教九年级上册专练

九年级上册数学 旋转几何综合同步单元检测(Word版 含答案)