南京工业大学浦江学院08-09第一学期高等数学期末考试试卷答案
高数上册期末考试试题及答案

《高等数学2-1》模拟试题二一.填空题(本题共4小题,每小题5分,满分20)1 当x x →0时,)(x f 是比)(x g 高阶的无穷小,则当x x →0时, 无穷小)()(x g x f +f(x)+g(x) 与无穷小)(x g 的关系是___________________.2. 若)(x f 为可导的奇函数,且()f x '05=,则()=-0 'x f __________.3. ().1,0._______________41lim 20≠>=-→a a x a x x4. ()⎰=-dx x x x tan sec sec ____________________.二.选择题(本题共4小题,每小题5分,满分20分。
每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内) 1. 极限.cos 22limx xx -→的结果是(A)1, (B)2, (C)2, (D)极限不存在. 答: () 2. 已知a 是大于零的常数()f x a x()ln =+-12,,则f (')0的值应是:()ln ()ln ()ln ()A aB aC aD -1212答: ()3. 设)(''u f 连续,已知n xf x dx tf t dt''()''()2012⎰⎰=则n 应是(A)2, (B)1, (C)4, (D)41答: ()4. 曲线x y sin =在[,]-ππ上与x 轴所围成的图形的面积为(A)2, (B)0, (C)4, (D)6.三.计算题(本题共7小题,每小题7分,满分49分。
)1. 设(),2ln 1)(22x x x x x f -+-=求)(x f 的定义域2.设函数)(x f 具有二阶导数,且2)0( '' ,1)0(' ,0)0(===f f f 求.)(lim20x xx f x -→3.求()⎰+dx x x 2cot 3tan 24.求⎰. arctan xdx5.求.sin1cossin24dxxxx⎰+π6. 设()⎩⎨⎧==2)( t f y t f x 其中)(t f 三阶可导且,0)( ≠t f 求.22dx y d7.设)(x y y =由方程3=+x y y x 所确定求)1( 'y四、证明题:(本题11分)证明当0≥x 时有不等式().1ln x xex+≤-《高等数学》一、1.等价无穷小. 2.f x '()-=05. 3.12ln .a 4. tanx-secx+c .二、1。
(完整版)高等数学期末考试试题及答案(大一考试),推荐文档

x1 x 1
(A) 1; (B) 0;
(C) 2;
1
(D)
2
2.若 f (x) 的一个原函数为 F (x) ,则 ex f (ex )dx 为(
)
(A) F (e x ) c ;
(B) F (ex ) c ;
(C) F (ex ) c ;
(D ) F (ex ) c x
3.下列广义积分中 ( )是收敛的.
.
2
4. 设 f (x) 在 x 2 处连续,且 lim f (x) 2 ,则 f (2) _____ x2 x 2
5.由实验知道,弹簧在拉伸过程中需要的力 F (牛顿)与伸长量 s 成正比,即 F ks (
k 为比例系数),当把弹簧由原长拉伸 6 cm 时,所作的功为 _________ 焦耳。
6.曲线
y
2
3
x2
上相应于
x
从
3
到
8
的一段弧长为
.
3
得分 评阅教师
三、设 x 0 时, e x2 (ax 2 bx c) 是比 x 2 高阶的无穷小,求常数 a, b , c 的值(6 分)
2
线
姓名
得分 评阅教师
四、 已知函数 y arcsin x ex cos(3 2x) ,求 dy .(6 分)
f (x) ce3x 1 (c 为任意常数)…………6 分
x 0, f (0) 3
f (x) 2e3x 1………..8 分
七、解:(1) (1 sin 3 )d . d (1 cos2 )d cos ……..3 分
7
cos 1 cos3 c …………………….6 分 3
(2) x arctan xdx 1 x2 arctan x 1
南京工业大学浦江学院 线性代数 试题(B)卷

3 1
x1 9x2 3x3 7x4 7
南京工业大学浦江学院
第3页共6页
七、(16 分)已知二次型 f (x1, x2 , x3 ) 2x12 4x22 5x32 4x1x3 ,试回答下列问题 1) 写出此二次型的矩阵 A ; 2) 利用正交变换 X QY 该二次型化为标准型,并给出所使用的正交变换和标准型;
五、(12 分)求下列向量组的秩及其一个极大线性无关组,并将其余向量用这个极大线性无关组
线性表示. 1 (1,1,1, 1),2 (1,1, 1, 1),3 (1, 1, 1,1),4 (1, 1, 1,1).
六、(13分)求线性非齐次方程组的通解.
x1 5x2 x3 x4 1
3x1x128xx2 2xx3 33xx44
0 0
= (1)n1 (n 1)! ――――――12 分 2
0
0 0 n 1 (n 1)
四(12 分)解:由 AB=A+2B,可见(A-2E)B=A,因此 B=(A-2E)-1A ―――――――4 分
2 2 3
1 4 3
又
(
A
2E)
1
1
0
,其逆矩阵
(A
2 E ) 1
1
5 3 ―
――――――16 分
3 5
南京工业大学浦江学院
第6页共6页
( A) R( A) 5 (B) R( A) 4 (C) R( A) 3 (D) R( A) 2
5.若矩阵 A 的秩为 r,则(
)。
(A)A 中至少存在一个 r 阶子式不为零
(C)A 中所有 r-1 阶子式均不为零
(B)A 中存在一个 r+1 阶子式不等于零 (D)A 中只有一个 r 阶子式不为零
高等数学上学期期末考试试卷及答案四份

高等数学试卷(B 卷)答案及评分标准2004-2005年度第一学期科目: 高等数学I 班级: 姓名: 学号: 成绩:一、填空题(5153'=⨯')1、()3)2ln(--=x x x f 的定义域是_2、 2 )1sin 2sin (lim 0x =⋅+→xx x x 3、 e )31(lim 3=+∞→xx x e )31(lim 3=+∞→x x x4、如果函数x x a x f 3sin 31sin )(+=,在3π=x 处有极值,则2=a5、34d )1(sin cos 223=+⋅⎰-x x x ππ二、单项选择题(5153'=⨯')1、当0→x 时,下列变量中与2x 等价的无穷小量是( )A . x cos 1-B .2x x + C . 1-x e D . x x sin )ln(1+2、)A ()(' ,)(的是则下列极限中等于处可导在设a f a x x f =。
A .h h a f a f h )()(lim0--→ B .hh a f h a f h )()(lim 0--+→C .h a f h a f h )()2(lim 0-+→ D . hh a f h a f h 3)()2(lim 0--+→3、设在[]b a ,上函数)(x f 满足条件()0)(,0<''>'x f x f 则曲线()x f y =在该区间上( ) A. 上升且凹的 B. 上升且凸的 C. 下降且凹的 D. 下降且凸的4、设函数()x f 具有连续的导数,则以下等式中错误的是( )A.)(d )(d d x f x x f xb a =⎪⎭⎫ ⎝⎛⎰ B. x x f t t f x a d )(d )(d =⎪⎭⎫ ⎝⎛⎰ C. ()x x f x x f d )(d )(d=⎰ D. C t f t t f +='⎰)(d )(5、反常积分⎰∞+- 0d 2x xex ( )A. 发散B. 收敛于1C. 收敛于21D. 收敛于21-三、算题('488'6=⨯)1、求极限xxx x 30sin sin tan lim -→2、求22)2()ln(sin lim x x x -→ππ3、求曲线⎩⎨⎧==ty tx 2cos sin 在当4π=t 处的切线方程和法线方程4、已知函数0,sin >=x x y x ,计算xy d d5、求积分⎰x e x d6、求积分x x e ed ln 1⎰7、计算曲线π≤≤=x x y 0,sin 与x 轴围成的图形面积,并求该图形绕y 轴所产生的旋转体体积。
南京工业大学线性代数江浦A答案
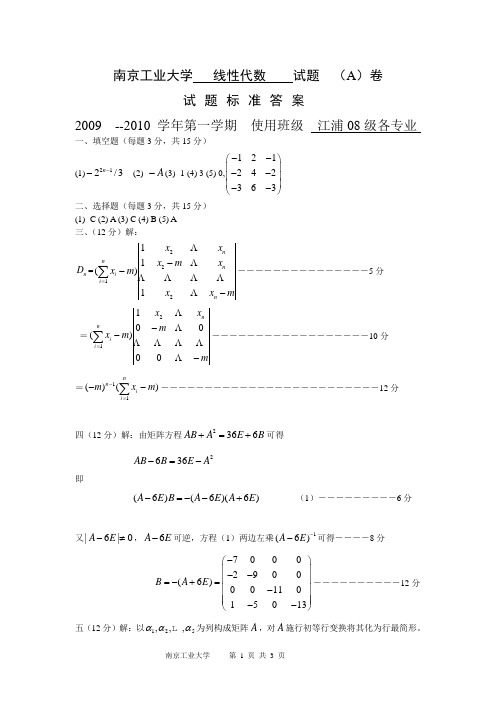
南京工业大学 线性代数 试题 (A )卷试题标准答案2009 --2010 学年第一学期 使用班级 江浦08级各专业一、填空题(每题3分,共15分)(1)3/212--n (2) A -(3) -1 (4) 3 (5) 0,121242363--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭二、选择题(每题3分,共15分)(1) C (2) A (3) C (4) B (5) A 三、(12分)解:n D =mx x x m x x x m x n n n ni i ---∑=2221111)(―――――――――――――――5分=mm x x m x nn i i ---∑= 00001)(21――――――――――――――――――10分=)()(11m x m ni i n --∑=-―――――――――――――――――――――――――12分四(12分)解:由矩阵方程2366AB A E B +=+可得 2636AB B E A -=- 即(6)(6)(6)A E B A E A E -=--+ (1)―――――――――6分又|6|0A E -≠,6A E -可逆,方程(1)两边左乘1(6)A E --可得――――8分70002900(6)0011015013B A E -⎛⎫ ⎪--⎪=-+= ⎪- ⎪ ⎪--⎝⎭――――――――――12分 五(12分)解:以125,,,ααα 为列构成矩阵A ,对A 施行初等行变换将其化为行最简形。
A =103211301121752421460⎛⎫ ⎪--⎪⎪⎪⎝⎭21314124r r r r r r +--10321033300111002224⎛⎫ ⎪ ⎪ ⎪ ⎪--⎝⎭ 234332r r r r --1032100000011100044⎛⎫⎪ ⎪⎪ ⎪--⎝⎭233413r r r r r ↔↔-1032101110000110000⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭23132r r r r -- 10301011010001100-⎛⎫ ⎪- ⎪ ⎪ ⎪⎝⎭――――――――――――――――――――――――――――――――――――6分 故15(,,)3,R αα= ―――――――――――――――――――――――――――8分 其一个极大线性无关组为124,,ααα且31254123,ααααααα=+=--――――――12分六、(13分)解:系数行列式)4)(1(2111111k k k k-+=--由克莱姆法则得,当,1-≠k 且4≠k 时,方程组有唯一解。
高等数学上学期期末考试试题和答案解析四份

高等数学试卷(B 卷)答案及评分标准2004-2005年度第一学期科目: 高等数学I 班级: 姓名: 学号: 成绩:一、填空题(5153'=⨯') 1、()3)2ln(--=x x x f 的定义域是_ 2、 2 )1sin 2sin (lim 0x =⋅+→xx x x 3、 e )31(lim 3=+∞→xx x e )31(lim 3=+∞→x x x4、如果函数x x a x f 3sin 31sin )(+=,在3π=x 处有极值,则2=a5、34d )1(sin cos223=+⋅⎰-x x x ππ二、单项选择题(5153'=⨯')1、当0→x 时,下列变量中与2x 等价的无穷小量是( )A . x cos 1-B . 2x x +C . 1-x eD . x x sin )ln(1+ 2、)A ()(' ,)(的是则下列极限中等于处可导在设a f a x x f =。
A .h h a f a f h )()(lim0--→ B .hh a f h a f h )()(lim 0--+→C .h a f h a f h )()2(lim 0-+→ D . hh a f h a f h 3)()2(lim 0--+→3、设在[]b a ,上函数)(x f 满足条件()0)(,0<''>'x f x f 则曲线()x f y =在该区间上( ) A. 上升且凹的 B. 上升且凸的 C. 下降且凹的 D. 下降且凸的4、设函数()x f 具有连续的导数,则以下等式中错误的是( )A. )(d )(d d x f x x f x b a=⎪⎭⎫ ⎝⎛⎰ B. x x f t t f x a d )(d )(d =⎪⎭⎫ ⎝⎛⎰ C. ()x x f x x f d )(d )(d=⎰ D. C t f t t f +='⎰)(d )(5、反常积分⎰∞+- 0d 2x xex ( )A. 发散B. 收敛于1C. 收敛于21D. 收敛于21-三、算题('488'6=⨯) 1、求极限xxx x 3sin sin tan lim -→ 2、求22)2()ln(sin lim x x x -→ππ3、求曲线⎩⎨⎧==ty tx 2cos sin 在当4π=t 处的切线方程和法线方程4、已知函数0,sin >=x x y x,计算xy d d 5、求积分⎰x e x d6、求积分x x e ed ln 1⎰7、计算曲线π≤≤=x x y 0,sin 与x 轴围成的图形面积,并求该图形绕y 轴所产生的旋转体体积。
南京工业大学近几年线性代数考试试卷及答案

南京工业大学近些年线代期末考试卷及答案包括以下六份试卷1南京工业大学线性代数课程考试试卷(A)(江浦、浦江2005-2006学年第1学期)2南京工业大学线性代数课程考试试卷(B)(江浦、浦江2005-2006学年第1学期)3南京工业大学线性代数试题(B)卷(闭)2007--2008学年第一学期使用班级江浦各专业本科生4南京工业大学线性代数试题(A)卷(闭)2008--2009学年第一学期使用班级江浦各专业本科生5南京工业大学线性代数试题(B)卷(闭)2008--2009学年第一学期使用班级江浦各专业本科生6南京工业大学线性代数试题(A)卷(闭)2008--2009学年第二学期使用班级计软0801-3南京工业大学 线性代数 课程考试试卷(A )(江浦、浦江2005-2006学年第1学期)所在系(院) 班 级 学号 姓名一. ___ 填空题(每空3分,共15分)1、 若n 阶方阵A 满足02=+-E A A (E 为单位阵),则A 的逆矩阵=-1A ____________.2、设矩阵B 是由矩阵A 划去某一列所得, 则秩(B )________秩(A ).3、若1111320=z y x, 则=---222431111z y x ________..4、若向量⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=0112k α 与⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=110k β 正交,则=k ________.5、已知三阶矩阵A 的特征值为,2,1,1-设,223A AB -=则B 的三个特征值为 ________.二. 单项选择题(每题3分,共15分)1、齐次线性方程组0=x A 的一个基础解系为123212131,,100010001ααα--⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则A 的秩为 ( )5)()(=A R A 4)()(=A R B 3)()(=A R C 2)()(=A R D 2、设有m 个n 维向量)(n m >,则 ( ))(A 必线性相关 )(B 必线性无关 )(C 不一定 )(D 无法确定3、设A 为n 阶方阵,则下列方阵中为对称矩阵的是 ( )()A A A '- ()B CAC ' (C 为任意n 阶方阵) ()C AA ' ()()D AA B ' (B 为任意n 阶方阵)4、设A 与B 均为n 阶方阵,若A 与B 相似,则下面论断错误的是 ( ))(A 存在M ,且0M ≠,并有AM MB = )(B A 与B 有相同的特征值B E A EC -=-λλ)( )(D A 与B 均可对角化5、若向量组321,,ααα 线性无关,向量组421,,ααα线性相关, 则 ( ))(A 4α 必不可由321,,ααα 线性表示 )(B 4α必可由321,,ααα 线性表示 )(C 2α 必不可由431,,ααα 线性表示 )(D 2α必可由431,,ααα 线性表示三. (12分) 求n 阶行列式:)1(10000022000111321------n n n n 。
高等数学期末考试试题及答案(大一考试)
(2010至2011学年第一学期)课程名称: 高等数学(上)(A 卷)考试(考查): 考试 2008年 1 月 10日 共 6 页 注意事项:1、 满分100分。
要求卷面整洁、字迹工整、无错别字。
2、 考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方,否则视为废卷。
3、 考生必须在签到单上签到,若出现遗漏,后果自负。
4、 如有答题纸,答案请全部写在答题纸上,否则不给分;考完请将试卷和答题卷分别一同交回,否则不给分。
试 题一、单选题(请将正确的答案填在对应括号内,每题3分,共15分)1. =--→1)1sin(lim21x x x ( ) (A) 1; (B) 0; (C) 2; (D)212.若)(x f 的一个原函数为)(x F ,则dx e f e xx )(⎰--为( )(A) c e F x +)(; (B) c eF x+--)(;(C) c e F x+-)(; (D )c xe F x +-)( 3.下列广义积分中 ( )是收敛的. (A)⎰+∞∞-xdx sin ; (B)dx x⎰-111; (C) dx x x ⎰+∞∞-+21; (D)⎰∞-0dx e x。
4. )(x f 为定义在[]b a ,上的函数,则下列结论错误的是( )(A) )(x f 可导,则)(x f 一定连续; (B) )(x f 可微,则)(x f 不一定可导;(C) )(x f 可积(常义),则)(x f 一定有界; (D) 函数)(x f 连续,则⎰xadt t f )(在[]b a ,上一定可导。
5. 设函数=)(x f nn x x211lim++∞→ ,则下列结论正确的为( )(A) 不存在间断点; (B) 存在间断点1=x ; (C) 存在间断点0=x ; (D) 存在间断点1-=x二、填空题(请将正确的结果填在横线上.每题3分,共18分)1. 极限=-+→xx x 11lim 20 _____.2. 曲线⎩⎨⎧=+=321ty t x 在2=t 处的切线方程为______. 3. 已知方程xxe y y y 265=+'-''的一个特解为x e x x 22)2(21+-,则该方程的通解为 .4. 设)(x f 在2=x 处连续,且22)(lim2=-→x x f x ,则_____)2(='f5.由实验知道,弹簧在拉伸过程中需要的力F (牛顿)与伸长量s 成正比,即ks F =(k 为比例系数),当把弹簧由原长拉伸6cm 时,所作的功为_________焦耳。
南京工业大学近几年线性代数考试试卷及答案解析

南京工业大学近些年线代期末考试卷及答案包括以下六份试卷1南京工业大学线性代数课程考试试卷(A)(江浦、浦江2005-2006学年第1学期)2南京工业大学线性代数课程考试试卷(B)(江浦、浦江2005-2006学年第1学期)3南京工业大学线性代数试题(B)卷(闭)2007--2008学年第一学期使用班级江浦各专业本科生4南京工业大学线性代数试题(A)卷(闭)2008--2009学年第一学期使用班级江浦各专业本科生5南京工业大学线性代数试题(B)卷(闭)2008--2009学年第一学期使用班级江浦各专业本科生6南京工业大学线性代数试题(A)卷(闭)2008--2009学年第二学期使用班级计软0801-3南京工业大学线性代数课程考试试卷(A)(江浦、浦江2005-2006学年第1学期)所在系(院) 班级学号姓名一. 填空题(每空3分,共15分)1、 若n 阶方阵A 满足02=+-E A A (E 为单位阵),则A 的逆矩阵=-1A ____________.2、设矩阵B 是由矩阵A 划去某一列所得, 则秩(B )________秩(A ).3、若1111320=z y x, 则=---222431111z y x ________..4、若向量⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=0112k α 与⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=110k β 正交,则=k ________.5、已知三阶矩阵A 的特征值为,2,1,1-设,223A AB -=则B 的三个特征值为________.二. 单项选择题(每题3分,共15分)1、齐次线性方程组0=x A 的一个基础解系为123212131,,100010001ααα--⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则A 的秩为 ( )5)()(=A R A 4)()(=A R B 3)()(=A R C 2)()(=A R D 2、设有m 个n 维向量)(n m >,则 ( ))(A 必线性相关 )(B 必线性无关 )(C 不一定 )(D 无法确定3、设A 为n 阶方阵,则下列方阵中为对称矩阵的是 ( )()A A A '- ()B CAC ' (C 为任意n 阶方阵) ()C AA ' ()()D AA B ' (B 为任意n 阶方阵)4、设A 与B 均为n 阶方阵,若A 与B 相似,则下面论断错误的是 ( ))(A 存在M ,且0M ≠,并有AM MB = )(B A 与B 有相同的特征值B E A EC -=-λλ)( )(D A 与B 均可对角化5、若向量组321,,ααα 线性无关,向量组421,,ααα线性相关, 则 ( ))(A 4α 必不可由321,,ααα 线性表示 )(B 4α必可由321,,ααα 线性表示 )(C 2α 必不可由431,,ααα 线性表示 )(D 2α必可由431,,ααα 线性表示三. (12分) 求n 阶行列式:)1(10000220000111321------n n n n。
2008-2009(1)高等数学试题(B卷)(90)答案

广州大学2008-2009学年第一学期考试卷参考答案课 程:高等数学(B 卷)(90学时) 考 试 形 式: 闭卷 考试一.填空题(每空2分,本大题满分16分)1.设⎩⎨⎧≤>=002x x x x x f ,,)(,则=-))2((f f 4 .2. 若函数 ⎩⎨⎧>+≤=112x b ax x x x f ,,)( 在1=x 处可导,则=a 2 ,=b -1 .3.0=x 是x xy sin =的第 一 类间断点,是xy 1si n =的第 二 类间断点。
4.已知10=')(x f ,则=--+→hh x f h x f h )()(lim0002 .5.设)(),(x G x F 是)(x f 的两个原函数,则='=')()(x G x F )(x f ,='-])()([x G x F ___0___.二.选择题 (每小题3分, 本大题满分15分)学院专业班 级 姓 名1. 当0→x 时, 12-x e是2x 的( C )无穷小.(A) 高阶 (B) 低阶 (C) 同阶 (D) 等价 2. 函数3x y =在点(1,1)处的切线方程为 ( B ).(A) 23--=x y (B) 23-=x y (C) 23+=x y (D) 13+-=x y 3.设)(x f 的一个原函数是x cos ,则='⎰dx x f x )( ( A ). (A) C x x x +--cos sin (B) C x x x +-cos sin (C) C x x x +-sin cos (D) C x x x ++-sin cos .4. 若函数)(x f 在点0x x =可导是)(x f 在点0x x =连续的( A )。
(A) 充分条件 (B) 必要条件 (C) 充要条件 (D) 无关条件.5.设)(x f 在区间I 内具有二阶导数,且在I 内0>'')(x f ,则)(x f 在I 内是( B ).(A) 凸函数 (B) 凹函数 (C) 周期函数 (D )单减函数三.解答下列各题(每小题6分,本大题满分30分)1.2211xx y +-=ln ,求dy . 解:)ln()ln(2211x x y +--=221212x xx x y +--=' 144-=x x………………………………………………………………..4分 dx x xdx y dy 144-='=∴……………………………………………….6分2.=y x e 2,求n 阶导数).()(0n y .解:,xe y 22=',x e y 222='',x e y 232=''',)()(x n n e x y 22=∴……………………………………………………………4分 .)()(n n y 20=∴………………………………………………………………..6分3.设曲线参数方程为)(sin cos 0>>⎩⎨⎧==b a tb y ta x ,求dxdy . 解:dt dxdt dy dx dy =………………………………………………………………….3分 t ab t a t b cot sin cos -=-=……………………………………………….6分4.求321x x x )sin (lim +→.解:22223123211x x xx x x x x sin sin)sin (lim )sin (lim ⋅→→+=+2231201⎪⎭⎫⎝⎛→⎪⎪⎭⎫⎝⎛+=x x x x x sin sin )sin (lim …………………………………………….3分3e =…………………………………………………...……………………….6分5.求⎪⎭⎫⎝⎛--→x x x ln lim 1111.解:=⎪⎭⎫⎝⎛--→x x x ln lim 1111⎪⎪⎭⎫⎝⎛--+→x x x x x ln )(ln lim 111……………………………….2分 ⎪⎪⎪⎪⎭⎫⎝⎛-+-+=→x x x x x 1111ln lim⎪⎭⎫⎝⎛+--+=→111x x x x x ln lim ………………………………………………………4分 ∞= …………………………………………………………..…..6分四.计算下列积分(每小题6分,本大题满分18分)1.xdx x 22⎰cos . 解:x d x xdx x 221222sin cos ⎰⎰=()dx x x x x ⎰⋅-=222212sin sin ……………………………………………..2分 ()x d x x x 22212cos sin ⎰+= ()xdx x x x x 222212cos cos sin ⎰-+=……………………………………4分 C x x x x x +⎪⎭⎫⎝⎛-+=22122212sin cos sin ………………………….…..…..6分 2.⎜⎠⎛-220221dx xx .解:令t x sin =,则tdt dx cos =⎜⎠⎛-=⎜⎠⎛-40222202211πtdt t t dx x xcos sin sin ……………………..………....2分 dt t ⎰=402πsin ……………………..…………………………………………..3分dt t ⎰-=4221πcos 40422π⎪⎭⎫ ⎝⎛-=t t sin ………………………………………………………….….5分.418-=π……………………..……………………………………………….6分3.⎰∞++12211dx x x )(.解:⎰∞++12211dx x x )( ⎰∞+⎪⎭⎫ ⎝⎛+-=122111dx x x…………………………………………………...….2分 +∞⎪⎭⎫⎝⎛--=11x x arctan ……………………..………………………………....4分 .41π-=………………………………………………………………………..6分六.(本题满分6分)计算由抛物线2x y =与x y =所围图形绕x 轴旋转一周所得立体的体积. 解:根据旋转体体积公式知dx x x V ⎰-=142)(π……………………..…………………………………3分105353⎪⎪⎭⎫⎝⎛-=x x π π152=………..………………………………………………………………6分七.(本题满分7分)1. 证明当0>x 时,有x x x >++212)ln(. 证明:令x x x x f -++=212)ln()(,………………………………...2分 则当0>x 时,011112>+=-++='xx x x x f )(,……………………….4分x x x x f -++=212)ln()(在),(+∞0上严格单调递增。
大一上半学期高数期末考试试题答案一

一、填空题(每题2分,共20分)1.}3231{≠>x x x 且;2.e 1; 3.0; 4. 4; 5. 21,1; 6. )10(, ; 7. x e 22--; 8.6; 9. c x y y +=+-2)1ln(; 10. 0.二、单项选择题1. D2. C3. B4. D5. C三、计算题1. 解:原式)332)(3(6-2lim0++-=→x x x x 31= .2. 解:原式xxx x x sin 2210])21[(lim +=→ 2e = .3. 解:原式2254-3132lim xx x x x +++=+∞→ 32= .4. 解:x v v u u y 2,cos ,ln ===dx dv dv du du dy dx dy y ⋅⋅=='x v u 21)sin (1-=x xx x x 22tan 212cos 2sin -=⋅-= .5. 解:式子左右两边同时求导,得y xe e y y y '⋅+=',移项,得 y y xe e y dx dy -='=1 . ='=dx y dy dx xee y y-1 . 6. 解:.221112)()(t t t t x t y dx dy ++=''= t 2= .7. 解:])cos ([])sin ([22'+'='x f x f y)sin (2cos )cos (cos 2sin )sin (22x x x f x x x f -⋅'+⋅'= )]cos ()sin ([2sin 22x f x f x '-'= .8. 解:原式⎰---=2232)32(61x x d C x +--=23231. 9. 解:令u x =-1,则12+=u x . 于是原式du u u ⎰⋅+=2u 12C u u++=2323C x x +-+-=2123)1(23)1(2.10. 解: 令x v x u ==',arctan ,则 原式=dx x x x x ⎰+-)1(2arctan 2222C )arctan -(21arctan 22+-=x x x x C 21arctan 212+-+=x x x . 11. 解:令t x =-1-1,2)1(1+-=t x , 原式=dt t t ⎰+-121-)1(2-[]121ln -2--+=t t =2ln 2-1 12. 解:令t x =,则2t x =,2t x =,tdt dx 2=.且当0=x 时,0=t ;当42π=x 时,2π=t .于是=⎰dx x 402sin πdt t t ⎰20sin 2π=-=⎰)(cos 220t d t π⎭⎬⎫⎩⎨⎧--⎰2020cos ]cos [2ππtdt t t 2][sin 220==πt .13. 解: 原式等价于⎰⎰=+x dxdy y y 21, 即C x y +=+ln )1ln(212, 因此 221Cx y =+. 将10x y == 代入,得 1c =,故特解为 221y x +=.14.解 特征方程为0652=-+r r , 解得-6,121==r r , 则通解为 x x e c e c y -621+=.四、应用1. 解 ①函数的定义域为),(+∞-∞②231212x x y -=',x x y 24362-='', 令,0=''y 得32,021==x x , ③④故下凸区间为)0,(-∞和),3(+∞,上凸区间为)3,0(.2. 设长、宽、高分别为y x x ,,2, 且7222=y x 即236xy =,设表面积为S ,则 xy xy x 4222S 2++⨯=2223643624x x x x x ++=x x x 1447242++= , 得到 22144728S xx x --=' , 令 ,0='S 得 3=x ,4=y . 则各边长为cm cm cm 4,3,6时,表面积最小.3. 解 交点坐标)8,2(,(1)44122043===⎰xdx x A ,(2)dx x V ⎰=206πππ7128727==x .。
高等数学期末考试试题与答案(大一考试)

( 2010 至 2011 学年第一学期)课程名称: 高等数学 ( 上 )(A 卷)考试 (考查 ): 考试2008年 1 月 10 日共 6页题 二三四五六七 八九十十一评阅 (统分 )一总分师号 教得线分注意事项:1、 满分 100 分。
要求卷面整洁、字迹工整、无错别字。
名2、 考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方,否姓则视为废卷。
3、 考生必须在签到单上签到,若出现遗漏,后果自负。
题4、 如有答题纸,答案请全部写在答题纸上,否则不给分;考完请将试卷和答题卷分别一同交回,否则不给分。
答号试题学要得分评阅教师封不班一、单选题(请将正确的答案填在对应括号内,每题3 分,共 15 分)内级 线1.lim sin( x 21)()x 1x 1封1; (B)0; (C)2;1(A)(D)2业 密F ( x) ,则 exf (e x)dx 为 ()专2.若 f ( x) 的一个原函数为(A) F (e x) c ;(B)F (e x) c ;密F (e x)(C)F (e x) c ;(D ) cx3.下列广义积分中 () 是收敛的 .(A)sin xdx ;(B)1 1(C)xdx ;0 x dx。
系dx ;(D) e1x1 x 24. f (x) 为定义在 a, b 上的函数,则下列结论错误的是 ()(A) f (x) 可导,则 f ( x) 一定连续;(B)f (x) 可微,则 f ( x) 不一定可导;(C) f ( x) 可积(常义),则 f (x) 一定有界;(D) 函数f ( x)连续,则xf (t )dt 在 a, b 上一定可导。
a5. 设函数f ( x)1x() lim2n ,则下列结论正确的为n1x(A) 不存在间断点;(B)存在间断点 x1;(C) 存在间断点x0 ;(D)存在间断点 x1得分评阅教师二、填空题(请将正确的结果填在横线上.每题 3 分,共 18 分)1.极限 lim x 2 1 1_____.xx 02.x1t22 处的切线方程为______.曲线t3在 ty3.已知方程 y 5 y 6y xe2 x的一个特解为 1 ( x22x)e2x,则该方程的通解2为.4. 设f ( x)在x 2 处连续,且 lim f ( x) 2 ,则 f (2)_____x 2x2F (牛顿)与伸长量s 成正比,即F ks ( k 5.由实验知道,弹簧在拉伸过程中需要的力为比例系数),当把弹簧由原长拉伸6cm 时,所作的功为_________ 焦耳。
南京工业大学浦江学院08-09第一学期高等数学期末考试试卷

南京工业大学浦江学院高等数学(A )课程考试试题(B 卷)(2008/2009学年第一学期) (闭卷)院系 姓名 学号一、单项选择题(本题共5小题,每小题2分,满分10分) 1.设函数x x x f -=-2)1(,则=)(x f ( )(A))1(-x x ; (B))1(+x x ; (C))1()1(2---x x ; (D))2)(1(-+x x ; 2.设4ln )(=x f ,则=∆-∆+→∆xx f x x f x )()(lim 0( )(A)4; (B)41; (C)0; (D)∞; 3.设13)(315+-+=x x x x f ,则=)1()16(f ( )(A)!16; (B)!15; (C)!14; (D)0; 4.=+⎰dx x 100)12( ( ) (A)C x ++101)12(1011; (B)C x ++101)12(2021; (C)C x ++99)12(100; (D)C x ++99)12(200; 5.设)(x f 是连续函数,且⎰=xx x dt t f 0cos )(,则=)(x f ( )(A)x x x sin cos -; (B)x x x sin cos +; (C)x x x cos sin -; (D)x x x cos sin +; 二、填空题(本题共5小题,每小题2分,满分10分) 1.)(x f 可导,且21)0()2(lim=-→x f x f x ,则=')0(f2.设⎪⎩⎪⎨⎧≤+>=00sin )(x ae x xxx f x ,当=a 时,)(x f 在0=x 连续。
3.设1)(-=x x x f ,则='+)1(f ,='-)1(f4.已知)4)(3)(2)(1()(----=x x x x x f ,则0)(='x f 在区间)4,1(内有 个根。
5.设x x f -='1)(ln ,则=)(x f三、计算题(本题共3小题,每小题5分,满分15分)1. 3)21(lim +∞→+x x x2. )arctan 2(lim x x x -+∞→π3.设212)1(lim 2334=-++++∞→x x bx x a x ,求常数 b a ,。
08-09A答案

南京工业大学 线 性 代 数 试题 (A )卷试题标准答案2008--2009学年第一学期 使用班级 江浦各专业本科生一、填空题(每题3分,共15分)(1) 0 (2.) -432 (3) (1,1,,1),T k k 为任意常数.(4) 1或-1 (5)1/2()A E -. 二、选择题(每题3分,共15分) (1) D (2) C (3) B (4) A (5) C 三、(10分)解:231123231123123231123231nin i n nin i n nn in i nnini x a a a a x a a a a x a x a a a a x a a a D a a x a a x a a x a a a a a x a x a a a x a ====+++++=+=+++++∑∑∑∑(从第二列至第n 列加到第1列)――――――――――――――――――――5分23232312311()11n n ni n i na a a x a a a x a a x a a a a x a =+=+++∑(提取公因子)=11000100()10100n i i xx a xx=+∑(1(2)i i c a c i -≥)――――――――――8分=11()nn i i xx a -=+∑―――――――――――――――――――――――10分四、(10分)解:由239AX A X E +=+得(3)(3)(3)A E X A E A E -=--+―――――――6分又30A E -≠,故3A E -可逆,上式两边同时左乘1(3)A E --得500(3)480127X A E -⎛⎫ ⎪=-+=-- ⎪ ⎪--⎝⎭。
――――――――10分五、(14分)解:以122,,,T T T ααα 为列生成矩阵A ,并对A 施行初等行变换将其化为行最简形.31710231171113434223A -⎛⎫⎪- ⎪= ⎪--- ⎪--⎝⎭13r r ↔ 11134231173171034223---⎛⎫⎪- ⎪ ⎪-⎪--⎝⎭213141233r r r r r r --- 1113401170448011715---⎛⎫--⎪--⎝⎭42111340117150112300000---⎛⎫ ⎪-- ⎪ ⎪ ⎪⎝⎭ 32r r +1113401171500091800000---⎛⎫ ⎪-- ⎪ ⎪ ⎪⎝⎭ 231/9r r - 111340117150001200000---⎛⎫⎪-- ⎪ ⎪⎪⎝⎭―6分231373r r r r ++1110201101000120000-⎛⎫⎪- ⎪⎪⎪⎝⎭12r r +10201011010001200⎛⎫ ⎪- ⎪ ⎪ ⎪⎝⎭―――8分 所以15(,,)3R αα= ,一个极大无关组为124,,ααα,―――――――(12分) 且31251242,2.ααααααα=+=-+―――――――――――――――(14分) 六、(13分)对方程组的增广矩阵进行初等行变换1111012331(|)01323211A b a b a ⎛⎫⎪⎪= ⎪--- ⎪-⎝⎭ 21313r r r r -- 1111001221013201231a b a ⎛⎫⎪ ⎪ ⎪--- ⎪----⎝⎭ 3242r r r r ++ 11110012210010100010B a b a ⎛⎫⎪⎪= ⎪-+ ⎪-⎝⎭------------------------5分显然可见: 当1,1a b =≠-时方程组无解,当1a ≠时方程组有唯一解,当1,1a b ==-时方程组有无穷多组解.――――――――――――――――――――――――8分 当1,1a b ==-时继续将矩阵B 化为行最简形得B =11110012210000000000⎛⎫ ⎪⎪⎪ ⎪⎝⎭12r r - 10111012210000000000---⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭与原方程组等价的方程组为1342341122x x x x x x =-++⎧⎨=--⎩令3400x x ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,得原方程组的一个特解为1100η-⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭。
高数(大一上)期末试题及答案

第一学期期末考试试卷(1)课程名称: 高等数学(上) 考试方式: 闭卷 完成时限:120分钟班级: 学号: 姓名: 得分: . 一、填空(每小题3分,满分15分)1、xx x x 2sin 3553lim 2++∞→ 2、设A f =-'')1(,则=--'--'→hh f f h )12()1(lim 0 3、曲线⎩⎨⎧==-t tey e x 2在0=t 处切线方程的斜率为4、已知)(x f 连续可导,且2)2(,)1(,1)0(,0)(e f e f f x f ===>,='⎰10)2()2(dx x f x f5、已知21)(xe xf x+=,则='')0(f 二、单项选择(每小题3分,满分15分)1、函数x x x f sin )(=,则 ( )A 、当∞→x 时为无穷大B 、当∞→x 时有极限C 、在),(+∞-∞内无界D 、在),(+∞-∞内有界2、已知⎩⎨⎧≥<=1,ln 1,)(x x x e x f x ,则)(x f 在1=x 处的导数( )A 、等于0B 、等于1C 、等于eD 、不存在3、曲线xxe y -=的拐点是( )A 、1=xB 、2=xC 、),1(1-eD 、)2,2(2-e 4、下列广义积分中发散的是( )A 、⎰10sin x dxB 、⎰-101xdx C 、⎰+∞+02/31x dx D 、⎰+∞22ln xx dx5、若)(x f 与)(x g 在),(+∞-∞内可导,)()(x g x f <,则必有( ) A 、)()(x g x f -<- B 、)()(x g x f '<'C 、)(lim )(lim 0x g x f xx xx →→< D 、⎰⎰<0000)()(x x dx x g dx x f三、计算题(每小题7分,共56分)答题要求:写出详细计算过程1、求xx e e x x x x sin )cos 1()(lim 220---→2、求)arcsin(lim 2x x x x -++∞→3、设)(x y y =由03=-+xyy x 确定,求0|=x dy 。
大一(第一学期)高数期末考试题及答案(完整版).doc

大一上学期高数期末考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分) 1. )(0),sin (cos )( 处有则在设=+=x x x x x f .(A )(0)2f '= (B )(0)1f '=(C )(0)0f '= (D )()f x 不可导.2. )时( ,则当,设133)(11)(3→-=+-=x x x x xx βα.(A )()()x x αβ与是同阶无穷小,但不是等价无穷小; (B )()()x x αβ与是等价无穷小;(C )()x α是比()x β高阶的无穷小; (D )()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰,其中()f x 在区间上(1,1)-二阶可导且'>()0f x ,则( ).(A )函数()F x 必在0x =处取得极大值; (B )函数()F x 必在0x =处取得极小值;(C )函数()F x 在0x =处没有极值,但点(0,(0))F 为曲线()y F x =的拐点; (D )函数()F x 在0x =处没有极值,点(0,(0))F 也不是曲线()y F x =的拐点。
4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数,且设(A )22x (B )222x+(C )1x - (D )2x +.二、填空题(本大题有4小题,每小题4分,共16分) 5. =+→xx x sin 2)31(lim .6. ,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则.7.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ .8. =-+⎰21212211arcsin -dx xx x .三、解答题(本大题有5小题,每小题8分,共40分)9. 设函数=()y y x 由方程sin()1x ye xy ++=确定,求'()y x 以及'(0)y . 10. .d )1(177x x x x ⎰+-求11. . 求,, 设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12. 设函数)(x f 连续,=⎰10()()g x f xt dt,且→=0()limx f x A x ,A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题(本大题10分)14. 已知上半平面内一曲线)0()(≥=x x y y ,过点(,)01,且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和,求此曲线方程. 五、解答题(本大题10分)15. 过坐标原点作曲线x y ln =的切线,该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ;(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V .六、证明题(本大题有2小题,每小题4分,共8分)16. 设函数)(x f 在[]0,1上连续且单调递减,证明对任意的[,]∈01q ,1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续,且0)(0=⎰πx d x f ,0cos )(0=⎰πdx x x f .证明:在()π,0内至少存在两个不同的点21,ξξ,使.0)()(21==ξξf f (提示:设⎰=xdxx f x F 0)()()解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题(本大题有4小题,每小题4分,共16分)5. 6e . 6.c x x +2)cos (21 .7. 2π. 8.3π.三、解答题(本大题有5小题,每小题8分,共40分) 9. 解:方程两边求导(1)cos()()0x y e y xy xy y +''+++= cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==,(0)1y '=-10. 解:767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式 1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11. 解:1033()x f x dx xe dx ---=+⎰⎰⎰03()x xd e --=-+⎰⎰0232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰ 令3214e π=--12. 解:由(0)0f =,知(0)0g =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京工业大学浦江学院高等数学(A )课程考试试题(B 卷)
(2008/2009学年第一学期) (解答)
一、单项选择题(本题共5小题,每小题2分,满分10分)
1.B
2.C
3.D
4.B
5.A
二、填空题(本题共5小题,每小题2分,满分10分)
1.4
1 2.0 3.-1 4.3 5.C e x x +- 三、计算题(本题共3小题,每小题5分,满分15分)
1. 解:原式=x x x )21(lim +∞→=22])21[(lim x
x x +∞→=2e 2. 解:原式=22111
lim x
x x -+-
+∞→=1
3.解:因为极限存在为常数,从而分子分母都应当为三阶无穷大 从而 01=+a ,可得1-=a 原极限变为21112lim 12lim 33233==-++=-++∞→∞→b x
x x b x x bx x x
四、计算题(本题共5小题,每小题5分,满分25分)
1. 解:221)(1arcsin x x x x
x y --+-+='x arcsin =
2. 解:两边取对数可得]arccos ln )1[ln(2
1ln x x x y -+-= 两边关于x 求导可得]1arccos 1111[212x
x x y y +-+-=' 解得]1arccos 11[22x x x x y y +--=
' 3. 解:方程两边关于x 求导可得 012='+
'--y y
y x y x 解得122--='xy y xy y 从而=dy dx xy y xy 122
--
4.解:t
t t dt dx dt dy dx dy 3cos sin //== 5.解:因为04)(24=='-x xe
x I ,解得驻点0=x 又04324)0(042422>=-=''=--x x
x e x e I
所以,在0=x ,函数)(x I 有极小值0)0(=I
五、计算题(本题共4小题,每小题5分,满分20分)
1. 解:⎰=x d e I x 2C e x +=2
2. 解:dx x x I )1
11(+-=⎰C x x ++-=)1ln(ln 3. 解:127232arctan sin 1101203012πππ
=+=++=--⎰⎰x xdx dx x I 4. 解:)1(4
1121ln 21)21(ln 2121221+=-==⎰⎰e dx x x x x x xd I e e e 六、计算题(本题共3小题,满分16分)
1.(1)解:3
1102==⎰dx x S (2)解:⎰==10225)(ππdx x V
2. 解:分离变量dx y
dy =+1, 两边积分可得1)1ln(C x y +=+ 解得1-=-x Ce y
3. (5分)解:特征方程0322=--r r ,特征根为3,121=-=r r 原方程对应齐次方程的通解为x x e C e C y 321+=-
设方程的特解为x Ae y =,代入方程解得4
1-=A 原方程的通解为x x x e e C e C y 4
1321-+=- 七.(4分)证:由于⎰⎰=<+<10103
1110dt dt t 1)0(-=f 2113)1(103>+-=⎰dt t f 由零点定理可知至少存在一点)1,0(∈ξ,使得0)(=ξf 又03114)(3
>>+-
='x x f 所以)(x f 在)1,0(内单调递增。
所以方程只有唯一解。
