株洲市2011年初中毕业学业考试试卷数学参考答案及评分标准

合集下载

湖南省长沙2011年初中毕业学业水平考试数学试卷及答案(word版)[1].doc

2011年长沙市初中毕业学业水平考试试卷数学注意事项：1、答题前，请考生先将自己的姓名、准考证号填写清楚，并认真核对条形码上的姓名、准考证号、考室和座位号；2、必须在答题卡上答题，在草稿纸、试题卷上答题无效；3、答题时，请考生注意各大题题号后面的答题提示；4、请勿折叠答题卡，保持字体工整、笔迹清晰、卡面清洁；5、答题卡上不得使用涂改液、涂改胶和贴纸；6、本学科试卷共26个小题，考试时量l20分钟，满分I20分。

一、选择题(在下列各题的四个选项中，只有一项是符合题意的。

请在答题卡中填涂符合题意的选项。

本题共l0个小题，每小题3分，共30分) 1．2-等于A ．2B ．2-C ．12 D ．12- 2．下列长度的三条线段，能组成三角形的是A ．1、l 、2B ．3、4、5C ．1、4、6D ．2、3、73．下列计算正确的是 A ．133-=-B ．236a a a ⋅=C ．22(1)1x x +=+ D ．32222-=4．如图，在平面直角坐标系中，点P(-1，2)向右平移3个单位长度后的坐标是 A ．（2,2） B ．（42-，） C ．（15-，） D ．（11--，）5．一个多边形的内角和是900°，则这个多边形的边数为 A ．6 B ．7 C ．8 D ．9 6．若12x y =⎧⎨=⎩是关于工x y 、的二元一次方程31ax y -=的解，则a 的值为A ．5-B ．1-C ．2D ．77．如图，关于抛物线2(1)2y x =--，下列说法错误的是A ．顶点坐标为(1，2-)B ．对称轴是直线x=lC ．开口方向向上D ．当x>1时，Y 随X 的增大而减小8．如图是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体的表面上，与汉字“美"相对的面上的汉字是A ．我B ．爱C ．长D ．沙9．谢老师对班上某次数学模拟考试成绩进行统计，绘制了如图所示的统计图，根据图中给出的信息，这次考试成绩达到A 等级的人数占总人数的 A ．6％ B ．10％ C ．20％ D ．25％10．如图，等腰梯形ABCD 中，AD ∥BC，∠B=45°， AD=2，BC=4，则梯形的面积为 A ．3 B ．4 C ．6 D ．8二、填空题(本题共8个小题，每小题3分，共24分) 11．分解因式：22a b -=____________。

2011年初中数学竞赛市区获奖学生通报

株洲市2011年初中数学竞赛市区获奖名单(市区部分)市一等奖初三年级组：景炎学校：谭鹏程寅翥刘熠曹晶殷骁肖圣圣尹昊黄鹏唐帅杰付哲睿王炜轩崔明轩綦麟刘涵唐其昌李彦茹曾成昕颜畅易玮秀付文凯孟凯威李楚楠景弘中学：刘佳轩袁志立罗蓓吴雨晗唐杰张智昊言评洪泽宇刘华雄叶坚肖敖夏刘凌志沈庆辉补天天李轩陈思凯戴佳成北师大株洲附校：张鹏尹龙涵肖士钧刘倩妤外国语学校：萧子洲谭伟伟段振文邓旻玥市五中：蒋新市十九中：杨霖琳初二年级组：景炎学校：郭若木方子为周文杰米泓博叶紫薇石镇洪肖懿嘉李常阳安平谢天玙袁中锦唐腾越熊艺航戴承志郭永康曹鸿皓彭至为杨崴华熊可欣汪啸峰陈艺贤丁泽华宾胜杰成爵良景弘中学：李玲轶陈唯戴宁陈奕泽佘崧林谭博雅北师大株洲附校：刘迪嘉傅益斌外国语学校：刘欣玥王姝上智李畅林刘孜博刘依依梁瑞青漆凤辉陆天翌市十五中：袁晟欧阳瑞斌市十六中：刘敏市二等奖初三年级组：景炎学校：彭理文夏虓林易国文张普李威炀唐博蒋钰昕杨涛杨召豪刘素琪肖添铭唐甜陈景翼李俊霖苏永萍廖泽文邓亦琪庄鑫杰邓凯键滕菲易珺陈思新林远志钱旺唐紫琦易阳俊曾思佳吴奕楠邹泽敏黄佳琳刘湛黎峰王依琛彭子灿曾轲周煜景弘中学：刘培松王林峰袁盛强何迎港刘智琦郭圣郁李宾张颖霖陈晓婧蒋嘉怡刘颖郭阳郭胜齐希斯戴羽李维政唐婉荧凌向荣唐俊玮北师大株洲附校：寻德昕刘志成王曦李锦鑫刘周石伟鹏外国语学校：徐丹妮袁正午谭佳菲张行健周泽霖龙昊旻李清扬毛晟轩顾玮琛贺子琼杨凌波吴梦萍市十六中：桂烨市十九中：杨莅徐志良邓淇匀刘佳斌阳鹏飞田心中学：邱艺铭初二年级组：景弘中学：潘康周睿戴璇鲁添郭文静易星汉龚睿谢庆忠谭宇豪廖聪张聪周煜昊尹可人景炎学校：刘华光谭畅黎倩瑶任星华胡杨孙赫张航程修欧阳毅铮罗瑞华孟李清旷嘉奇蒋佳洲梁步云张菁徐颖华舒子瑞符恒迈曹勋平龚雅婷李赫何杼鑫洪采菲段子韬刘扬帆罗煊昭廖天怡王昀昊刘珊张熙谢柯毅黄志轩邹孟志任鸿翔刘佳昊颜竞人罗钰婷谭钰峰张有驰外国语学校：胡智怿童旻敏余嘉文曹龙佳石超唐珑涛曹远志刘鑫淼戴如彦曹向琳方舟唐依婷梁杰俊周鑫漆嘉威王锦涛王瑀李慧敏汪圣焘黎晓玮叶晓卉娄懿邹伊涵刘溈厉建树蒋柠鸿李薇北师大株洲附校：周楠龙霖萱甘成昱黄燊诚蔡博诚唐硕游紫荆市五中：郑鑫市十五中：李河舟市十六中：符钰婷林文志市十九中：付亮亮师专附中：聂之翔枫叶中学：宋博贺家土中学：王州市三等奖初三年级组：景炎学校：谭伏宁杨冬辰吴鸿玉李娜罗豪郭亚琪刘云鹤吴雪婧谭齐家董雅蓉李子彦宾汝聪黄翔蔡灏禹钱书宁张文璐罗杰中孟柯成谭伊航严伊峻罗晓琴李爽许原源吴沁雯谭元珍廖彧易子钧贾慧萱向维哲肖悦成施筱琪陈志方程志豪谭子杰夏慧雯郭一廷黄牧晨林鹤洲彭思璇范知名李炜涛刘立柱龙姝羽李东骏李昱璇李敏琦陈柱彬张万千刘文俊宾雨儿盛云祥肖智乙邹妤婷龙铭翁浩谱宋颖邓文陈杰斌王泽远何锦涛黄放周裴珂李梦嘉刘佳欣文佳程熊宇蒋荣卿黄睿邦伍龙姝王非凡刘云松徐凯澜文婕景弘中学：虞资兴李云啸黄魁颜赠钰尹恩民文川苇袁隆瑞陈易帜肖一男邓超陈伯钧王淑臻申桢陈送福刘剀强刘宇练易凌邓远宏吴斐毓冯文龙张鸿远刘鹏程龙赛楠刘思为臧诗槐朱旦言韬胤杨子欣北师大株洲附校：喻姝研刘佳豪范崇星房靖雅彭之臻谭心睿虞志辉高楠彭清扬刑方圆易大鹏蒋佳伟邹欣哲外国语学校：邹疏雨董骏灿李依竹刘康妮谢一鸣周杨平冯金铭周芊骞周柽朱浩骅俞一波兰天陶熙家彭澍杨孟宸李依松傅宇喧唐宇杰高婧雯贺源易昊杰陈思瑶焦文彬杨柳青市五中：曹逸飞唐格西石冲曾艳姣周红利市七中：陈成市十二中：肖宇恒市十五中：唐西昊市十六中：万磊市十九中：李中玉卢先尚吴陈朱家豪汤佳蒙师专附中：谭修远易凡易可彬田洪奔胡翔宇贺家土中学：易泽恩枫叶中学：左荻殷登峰曾江袁海鹏芦鑫宏谢明田心中学：莫婷婷徐诗睿体育路中学：曹雨晴泰山学校：汤洪马文韬李海生淞欣学校：黄艺鸿淞南中学：刘瑞琪雷打石中学：张辉鸿初二年级组：景弘中学：喻江波范志军张逸豪沈彦岐赵益明熊立彬李钰瑶杨鸿雁郭柏平苏嵘楷唐凯鑫黄威彭杰赵承凯桂望哲宾绮昱周宇航宋尹嘉周俊智程斌景炎学校：黄敏萱周宇刘迪威梁彦超万诗雨张若晨周欣艺聂俊韬黄永刚申美晴陈丽芳谢瑜璋雷云霖肖悦心郭璠颖王祎琳石宇杰曾郁文王泓涛谭歆仪李文韬刘钰江熊紫珂刘鑫正黄易奇王艺璇罗晶邓卓文何祎纯彭彦卿罗涵宇姜文琪易振宇刘惟瑾刘冰莹孙原谭力铭刘紫乐王柯张一弛凌俣茜盛雅琪粟惠民刘燕玲毛喆远杨熙婷沈紫薇资丰源周文妍宋文君彭旖婧杨小萌牛子昂言佳欧阳羽刘威胡震宇丁沁王磊刘鑫浩吴铮童鑫牛麒麟李慧敏外国语学校：颜金波唐梓杰王诗洋唐鑫铸徐铬秦柯卓谢亚奇肖开阳彭佳琪黄颖烜刘健宇余可人曾卓邓湘李棹安彭雨阳倪思敏唐健杨磊黄标成金石梦刘新康宋超然黄亦晨颜文吉易鑫张俊涂冰婧吕文超杨展俏田小溪龚梓钰邱卓刘迅陈家立刘颖逸刘博张凌雁冯钜石北师大株洲附校：肖湘钰曹嘉珊谢鑫和杨帆邓轩肖勇张杰铭章荣康吴广涵郭雅婷周仕杰彭小洛市十五中：易钰陈锾焕凌志威市十六中：文静市十九中：潘鑫府范爱军袁琼泰山学校：贺东陈恩祺师专附中：曹茳林周佳旺体育路中学：黄旭张浩高添雄杨洁林咏琴苏志成田心中学：王程红董雅静刘鑫洋常若婕枫叶中学：龚迪琳白关中学：罗奕龙头铺中学：丁皓宇株洲市教育科学研究院株洲市中学数学教学专业委员会2011年12月。

份全国中考数学真题汇编第15章数据的集中趋势与离散程度

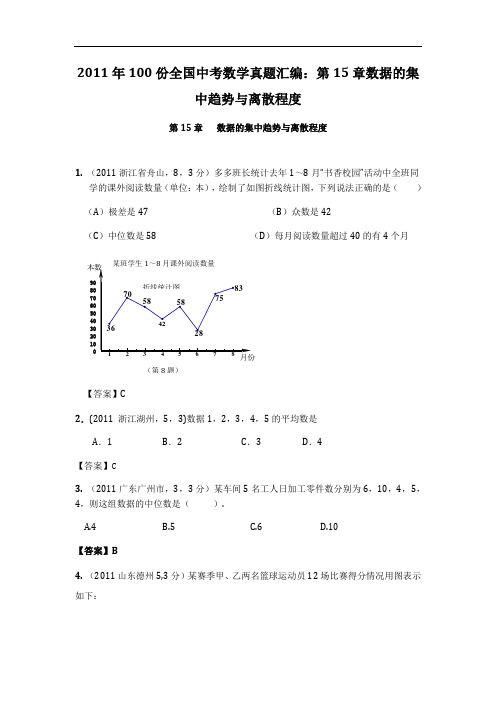
2011年100份全国中考数学真题汇编：第15章数据的集中趋势与离散程度第15章数据的集中趋势与离散程度1. （2011浙江省舟山，8，3分）多多班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，下列说法正确的是（）（A）极差是47 （B）众数是42（C）中位数是58 （D）每月阅读数量超过40的有4个月【答案】C2．(2011 浙江湖州，5，3)数据1，2，3，4，5的平均数是A．1 B．2 C．3 D．4【答案】C3. （2011广东广州市，3，3分）某车间5名工人日加工零件数分别为6，10，4，5，4，则这组数据的中位数是（）.A.4B.5C.6D.10【答案】B4. （2011山东德州5,3分）某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下：对这两名运动员的成绩进行比较，下列四个结论中，不正确．．．的是（A）甲运动员得分的极差大于乙运动员得分的极差（B）甲运动员得分的的中位数大于乙运动员得分的的中位数（C）甲运动员的得分平均数大于乙运动员的得分平均数（D）甲运动员的成绩比乙运动员的成绩稳定【答案】D5. （2011山东泰安，9 ，3分）某校篮球班21名同学的身高如下表：身高180 186 188 192 208（cm）人数（个） 4 6 5 4 2 则该校篮球班21名同学身高的众数和中位数分别是（单位：cm）（）A.186,186B.186,187C.186,188D.208,188【答案】C6. （2011山东威海，2，3分）今年体育学业考试增加了跳绳测试项目，下面是测试时记录员记录的一组（10名）同学的测试成绩（单位：个/分钟）．176 180 184 180 170 176 172 164 186 180该组数据的众数、中位数、平均数分别为（）A．180，180，178 B．180，178，178C．180，178，176.8 D．178，180，176.8【答案】C7. （2011山东烟台，8,4分）体育课上测量立定跳远，其中一组六个人的成绩（单位：米）分别是：1.0,1.3,2.2,2.0,1.8,1.6 ,则这组数据的中位数和极差分别是（）A.2.1,0.6B. 1.6,1.2C.1.8,1.2D.1.7,1.2 【答案】D8. （2011四川南充市，2，3分）学校商店在一段时间内销售了四种饮料共100瓶，各种饮料的销售量如下表：品牌甲乙丙丁销售量（瓶）12321343建议学校商店进货数量最多的品牌是（）（A ）甲品牌（B ）乙品牌（C ）丙品牌（D ）丁品牌【答案】D9. （2011广东湛江9,3分）甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数都是8.9环，方差分别是20.65S =甲，20.55S =乙，20.50S =丙20.45S =丁，则射箭成绩最稳定的是A 甲B 乙C 丙D 丁【答案】D10. （2011贵州安顺，4，3分）我市某一周的最高气温统计如下表：最高气温（℃）25 26 27 28 天数1123则这组数据的中位数与众数分别是（） A ．27，28 B ．27.5，28C ．28，27D ．26.5，27【答案】A11.（2011浙江衢州，1,3分）在九年级体育中考中，某校某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）：44,45,42,48,46,47,45.则这组数据的极差为（）A.2B.4C.6D.8【答案】C12. （2011浙江省，4，3分）某校七年级有13名同学参加百米竞赛，预赛成绩各不相同，要取前6名参加决赛，小梅已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这13名同学成绩的（）A.中位数B.众数C.平均数D. 极差【答案】A13. （2011浙江台州，3,4分）要反映台州某一周每天的最高气温的变化趋势，宜采用（）A.条形统计图B.扇形统计图C.折线统计图D.频数分布直方图【答案】C14. （2011浙江温州，2，4分）某校开展形式多样的“阳光体育”活动，七(3)班同学积极响应，全班参与，晶晶绘制了该班同学参加体育项目情况的扇形统计图（如图所示），由图可知参加人数最多的体育项目是( )A．排球B．乒乓球C．篮球D．跳绳【答案】C16. （2011浙江省嘉兴，8，4分）多多班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，下列说法正确的是（）（A ）极差是47 （B ）众数是42（C ）中位数是58（D ）每月阅读数量超过40的有4个月【答案】C18. （2011台湾台北，14）图(四)为某班甲、乙两组模拟考成绩的盒状图。

湖南省株洲市2009年初中毕业学业考试数学试题(含答案)

2009年湖南省株洲市初中毕业学业考试数学试题卷时量：120分钟满分：120分注意事项：1．答题前，请按要求在答题卡上填写好自己的姓名、就读学校和准考证号。

2．答题时，切记答案要填在答题卡上，答在试题卷上的答案无效。

3．考试结束后，请将试题卷和答题卡都交给监考老师。

一、一、选择题选择题（每小题有且只有一个正确答案，本题共8小题，每小题3分，共24分）1．2−的相反数是A ．0B ．2C ．12−D ．122．若使二次根式...，则x 的取值范围是A ．2x ≥B ．2x >C ．2x <D ．2x ≤3．下列四个图形中，不是..轴对称图形的是A ．B ．C ．D ．4．一次函数2y x =+的图象不.经过A ．第一象限B ．第二象限C ．第三象限D ．第四象限5．估计A ．1到2之间B ．2到3之间C ．3到4之间D ．4到5之间6．从分别写有数字4−、3−、2−、1−、0、1、2、3、4的九张一样的卡片中，任意抽取一张卡片，则所抽卡片上数字的绝对值小于2的概率是A ．19B ．13C ．12D ．237．如图是“北大西洋公约组织”标志的主体部分（平面图），它是由四个完全相同的四边形OABC 拼成的．测得AB BC =，OA OC =，OA OC ⊥，36ABC ∠=°，则OAB ∠的度数是A ．116°B ．117°C ．118°D ．119°8．定义：如果一元二次方程20(0)ax bx c a ++=≠满足0a b c ++=，那么我们称这个方程为“凤凰”方程.已知20(0)ax bx c a ++=≠是“凤凰”方程，且有两个相等的实数根，则下列结论正确的是A ．a c=B ．a b=C ．b c=D ．a b c==二、填空题（本题共8小题，每小题3分，共24分）9．分解因式：3+2x x=.10．孔明同学买铅笔m 支，每支0.4元，买练习本n 本，每本2元．那么他买铅笔和练习本一共花了元.11．如图，AB//CD ，AD AC ⊥，32ADC ∠=°，则CAB ∠的度数是.12．反比例函数图象如图所示，则这个反比例函数的解析式是y =.第12题图第7题图第11题图DCBA13．在一次体检中，测得某小组5名同学的身高分别是170、162、155、160、168（单位：厘米），则这组数据的极差是厘米．14．如图，已知AC BD ⊥于点P ，AP CP =，请增加一个..条件，使ABP ∆≌CDP ∆(不能添加辅助线)，你增加的条件是.15．如图，AC 是O ⊙的直径，CB 与O ⊙相切于点C ，AB 交O ⊙于点D ．已知51B ∠=°，则DOC ∠等于度．16．孔明同学在解方程组2y kx by x=+⎧⎨=−⎩的过程中，错把b 看成了6，他其余的解题过程没有出错，解得此方程组的解为12=−⎧⎨=⎩x y ，又已知直线=+y kx b 过点（3，1），则b 的正确值应该是．三、解答题（本大题共7小题，共72分）17．（本题满分10分，每小题5分）（1）计算：1021)sin 30−++°（2）先化简，再求值：23393x x x ++−−，其中1x =−．第14题图PDCBA第15题图CA小学生20％大学生10％初中生？高中生30％B18．（本题满分10分）如图，在Rt OAB ∆中，90OAB ∠=°，6OA AB ==，将OAB ∆绕点O 沿逆时针方向旋转90°得到11OA B ∆．（1）线段1OA 的长是，1AOB ∠的度数是；（2）连结1AA ，求证：四边形11OAA B 是平行四边形；（3）求四边形11OAA B 的面积．19．（本题满分10分）某次学生夏令营活动，有小学生、初中生、高中生和大学生参加，共200人，各类学生人数比例见扇形统计图．（1）参加这次夏令营活动的初中生...共有多少人？（2）活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款5元，初中生每人捐款10元，高中生每人捐款15元，大学生每人捐款20元，问平均每人捐款是多少元？（3）在（2）的条件下，把每个学生的捐款数额（以元为单位）一一记录下来，则在这组数据中，众数是多少？20．（本题满分10分）初中毕业了，孔明同学准备利用暑假卖报纸赚取140～200元钱，买一份礼物送给父母．已知：在暑假期间，如果卖出的报纸不超过1000份，则每卖出一份报纸可得0.1元；如果卖出的报纸超过1000份，则超过部分....每份可得0.2元．（1）请说明：孔明同学要达到目的，卖出报纸的份数必须超过1000份．（2）孔明同学要通过卖报纸赚取140～200元，请计算他卖出报纸的份数在哪个范围内．A21．（本题满分10分）如图，点A 、B 、C 是O ⊙上的三点，//AB OC .（1）求证：AC 平分OAB ∠.（2）过点O 作OE AB ⊥于点E ，交AC 于点P .若2AB =，30AOE ∠=°，求PE 的长．22．（本题满分10分）如图1，Rt ABC ∆中，90A ∠=°，3tan 4B =，点P 在线段AB 上运动，点Q 、R 分别在线段BC 、AC 上，且使得四边形APQR 是矩形．设AP 的长为x ，矩形APQR 的面积为y ，已知y 是x 的函数，其图象是过点（12，36）的抛物线的一部分（如图2所示）．（1）求AB 的长；（2）当AP 为何值时，矩形APQR 的面积最大，并求出最大值．为了解决这个问题，孔明和研究性学习小组的同学作了如下讨论：张明：图2中的抛物线过点（12，36）在图1中表示什么呢？李明：因为抛物线上的点(,)x y 是表示图1中AP 的长与矩形APQR 面积的对应关系，那么，（12，36）表示当12AP =时，AP 的长与矩形APQR 面积的对应关系.赵明：对，我知道纵坐标36是什么意思了！孔明：哦，这样就可以算出AB ，这个问题就可以解决了.请根据上述对话，帮他们解答这个问题.图1R Q PCBA23．（本题满分12分）如图，已知ABC ∆为直角三角形，90ACB ∠=°，AC BC =,点A 、C 在x 轴上，点B 坐标为（3，m ）（0m >），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B 、D ．（1）求点A 的坐标（用m 表示）；（2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点B 之间的一动点，连结PQ 并延长交BC 于点E ，连结BQ 并延长交AC 于点F ，试证明：(FC 再次提醒：所有的答案都填（涂）到答题卡上，答在本卷上的答案无效。

2011年湖南省株洲市中考数学试题(word版含答案)

姓名准考证号绝密★启用前株洲市2011年初中毕业学业考试数学试题卷时量：120分钟满分：100分注意事项：1．答题前，请按要求在答题卡上填写好自己的姓名和准考证号。

2．答题时，切记答案要填在答题卡上，答在试题卷上的答案无效。

3．考试结束后，请将试题卷和答题卡都交给监考老师。

一、选择题（每小题有且只有一个正确答案，本题共8小题，每小题3分，共24分） 1．8的立方根是A ．2B ．2-C ．3D ． 42．计算234x x ⋅的结果是A ．34xB ．44xC ．54xD ． 64x3．孔明同学在庆祝建党90周年的演讲比赛中，6位评委给他的打分如下表：评委代号 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ 评分859080959090则孔明得分的众数为A ．95B ．90C ．85D ．804．株洲市关心下一代工作委员会为了了解全市初三学生的视力状况，从全市30000名初三学生中随机抽取了500人进行视力测试，发现其中视力不良的学生有100人，则可估计全市30000名初三学生中视力不良的约有 A ．100人B ．500人C ．6000人D ．15000 人5．某商品的商标可以抽象为如图所示的三条线段，其中AB ∥CD ，45EAB ∠=︒，则FDC ∠的度数是A ．30︒B ．45︒C ．60︒D ．75︒6．右图是一个由7个同样的立方体叠成的几何体.请问下列选项中，既是中心对称图形，又是这个几何体的三视图之一的是 EFA BCD7．根据生物学研究结果，青春期男女生身高增长速度呈现如下图规律，由图可以判断，下列说法错误的是： A ．男生在13岁时身高增长速度最快B ．女生在10岁以后身高增长速度放慢C ．11岁时男女生身高增长速度基本相同D ．女生身高增长的速度总比男生慢8．某广场有一喷水池，水从地面喷出，如图，以水平地面为x 轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线24y x x =-+（单位：米）的一部分，则水喷出的最大高度是 A ．4米 B ．3米 C ．2米 D ．1米二、填空题（本题共8小题，每小题3分，共24分） 9．不等式10x ->的解集是．10．当10x =，9y =时，代数式22x y -的值是．11．如图，孔明同学背着一桶水，从山脚A 出发，沿与地面成30︒角的山坡向上走，送水到山上因今年春季受旱缺水的王奶奶家（B 处），80AB =米，则孔明从A 到B 上升的高度BC 是米．12．为建设绿色株洲，某校初三0801、0802、0803、0804四个班同学参加了植树造林，每班植树株数如下表，则这四个班平均每班植树株．班次植树株数 0801 22 0802 25 080335第7题图年龄/岁7 8 910 11 12 13 14 15 16 17 188 7 6 5 4 3 2 1增长速度(厘米/年)男女女男第8题图x (米)y (米)OAB- 1 1xyO第14题图13．孔明同学在解一元二次方程230x x c -+=时，正确解得11x =，22x =，则c 的值为．14．如图，直线l 过A 、B 两点，A （0，1-），B （1，0），则直线l 的解析式为． 15．按下面摆好的方式，并使用同一种图形，只通过平移方式就能进行平面镶嵌(即平面密铺)的有（写出所有正确答案的序号）.16．如图，第（1）个图有1个黑球；第（2）个图为3个同样大小球叠成的图形，最下一层的2个球为黑色，其余为白色；第（3）个图为6个同样大小球叠成的图形，最下一层的3个球为黑色，其余为白色；；则从第（n ）个图中随机取出一个球，是黑球的概率是 .三、解答题（本大题共8小题，共52分）17．（本题满分4分）计算：02011|2|(3)(1)--+-18．（本题满分4分）当2x =-时，求22111x x x x ++++的值． 0804 18（1）（2）（3）（4）· · ·第11题图第12题表30︒BAC正三角形①正方形 ②矩形③正五边形 ④AB19．（本题满分6分）食品安全是老百姓关注的话题，在食品中添加过量的添加剂对人体有害，但适量的添加剂对人体无害且有利于食品的储存和运输．某饮料加工厂生产的A B 、两种饮料均需加入同种添加剂，A 饮料每瓶需加该添加剂2克，B 饮料每瓶需加该添加剂3克，已知270克该添加剂恰好生产了A B 、两种饮料共100瓶，问A B 、两种饮料各生产了多少瓶？20．（本题满分6分）如图， ABC ∆中，AB AC =，36A ∠=︒，AC 的垂直平分线交AB 于E ，D 为垂足，连结EC ．（1）求ECD ∠的度数；（2）若5CE =，求BC 长．EDCBA21．（本题满分6分）我国网球名将李娜在今年法国网球公开赛上的出色表现，大大激发了国人对网球的热情．在一项“你最喜欢的球类运动”的调查中，共有50名同学参与调查，每人必选且只选一项，将调查结果绘制成频数分布直方图如下，根据图中信息回答：（1）被调查的同学中选择喜欢网球的有____________________人；（2）孔明同学在被调查中选择的是羽毛球，现要在参与调查选择喜欢羽毛球的同学中随机抽取2人参加一项比赛，求孔明被选中的概率.22．（本题满分8分）如图，AB 为O 的直径，BC 为O 的切线，AC 交O 于点E ，D 为AC 上一点，AOD C ∠=∠．（1）求证：OD AC ⊥；（2）若8AE =，3tan 4A =，求OD 的长．23．（本题满分8分）如图，矩形ABCD 中，点P 是线段AD 上一动点，O 为BD 的中点，PO 的延长线交BC 于Q .（1）求证：OP OQ =；（2）若8AD =厘米，6AB =厘米，P 从点A 出发，以1厘米/秒的速度向D 运动（不与D 重合）. 设点P 运动时间为t 秒，请用t 表示PD 的长；并求t 为何值时，四边形PBQD 是菱形．24．（本题满分10分）孔明是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线2(0)y ax a =<的性质时，将一把直角三角板的直角顶点置于平面直角坐标系的原点O ，两直角边与该抛物线交于A 、B 两点，请解答以下问题：（1）若测得22OA OB ==（如图1），求a 的值； Q P ODCBA羽毛球排球网球足球篮球项目人数(人)58 10 12 OE D CBA（2）对同一条抛物线，孔明将三角板绕点O 旋转到如图2所示位置时，过B 作BF x⊥轴于点F ，测得1OF =，写出此时点B 的坐标，并求点A 的横坐标．．．；（3）对该抛物线，孔明将三角板绕点O 旋转任意角度时惊奇地发现，交点A 、B 的连线段总经过一个固定的点，试说明理由并求出该点的坐标．再次提醒：所有的答案都填（涂）到答题卡上，答在本卷上的答案无效。

2011年中考数学模拟试卷及参考答案(含答题卷)

2009年上学期株洲市景弘中学初三年级数学学科月考试卷时量：120分钟满分：120分注意：本卷分为问卷和答卷，只交答卷。

请考生务必．．将选择题、填空题、解答题（包括作图）的全部答案填入答卷的相应位置．．．．，答案未填入答卷的该题不予记分．．．．。

一、填空题（本题共8小题，每题3分，共24分） 1、－3的相反数是____________. 2、因式分解：21x -=______________.3、如右图，已知ABE =∠142°，C =∠72°，则A =∠ .4、正六边形的一个内角为度.5、掷两枚质地均匀的硬币，则两枚硬币全部正面朝上的概率为 .6、如图，在菱形ABCD 中，对角线AC BD ，相交于点O E ，为AB 的中点，且1OE =，则菱形ABCD 的周长为 .7、下列是三种化合物的结构式及分子式，请按其规律，写出后一种化合物的分子式．．．为___________.8、如图，已知矩形OABC 的面积为1003，它的对角线OB 与双曲线x k y =相交于点D ，且OD ∶OB ＝3∶5，则k ＝____________.二、选择题（每小题有且只有一个正确答案，本题共8小题，每题3分，共24分） 9）A. 点AB. 点BC. 点CD. 点D 10、下列运算中，正确的是（）A. 236a a a ⋅= B. 4222a a a =+C.2=± D. 228=-11、如图（1）所示的物体是一个几何体，其主视图是（）12元）：50，20，50，30，50，25，135；这组数据的众数和中位数分别是（） A. 50，50 B. 50，30 C. 50，20 D. 135，50H HHCCC HH HH CC HHHH CH C 2H 6 C 3H 8CH 4第7题图第9题图ABCE14272第3题图第6题图座位号13、已知圆锥的母线长为5cm ，底面半径为3cm ，则圆锥的全面积为（）A. 15πcm 2B. 24πcm 2C. 30πcm 2D. 39πcm 2 14、下列命题中正确的是（）A. 两条对角线互相平分的四边形是平行四边形B. 两条对角线相等的四边形是矩形C. 两条对角线互相垂直的四边形是菱形D. 两条对角线互相垂直且平分的四边形是正方形 15、如图甲，小亮在操场上玩，一段时间内从操场中心沿M →A →B →M 的路径匀速散步，能近似刻画小亮到出发点M 的距离．．y 与时间x 之间关系的函数图象是（）16、如图甲是一种带有黑白双色、边长是20cm 的正方形装饰瓷砖，用这样的四块瓷砖可以拼成如图乙的图案。

2011年湖南省株洲市中考数学试卷

2011年湖南省株洲市中考数学试卷一、选择题（每小题有且只有一个正确答案，本题共8小题，每小题3分，共24分）1．（3分）8的立方根是（）A．2 B．﹣2 C．3 D．42．（3分）计算x2•4x3的结果是（）A．4x3B．4x4C．4x5D．4x63．（3分）孔明同学在庆祝建党90周年的演讲比赛中，6位评委给他的打分如下表：评委代号ⅠⅡⅢⅣⅤⅥ评分859080959090则孔明得分的众数为（）A．95 B．90 C．85 D．804．（3分）株洲市关心下一代工作委员会为了了解全市初三学生的视力状况，从全市30000名初三学生中随机抽取了500人进行视力测试，发现其中视力不良的学生有100人，则可估计全市30000名初三学生中视力不良的约有（）A．100人B．500人C．6000人D．15000人5．（3分）某商品的商标可以抽象为如图所示的三条线段，其中AB∥CD，∠EAB=45°，则∠FDC的度数是（）A．30°B．45°C．60°D．75°6．（3分）如图是一个由7个同样的立方体叠成的几何体．请问下列选项中，既是中心对称图形，又是这个几何体的三视图之一的是（）A．B．C．D．7．（3分）根据生物学研究结果，青春期男女生身高增长速度呈现如下图规律，由图可以判断，下列说法错误的是（）A．男生在13岁时身高增长速度最快B．女生在10岁以后身高增长速度放慢C．11岁时男女生身高增长速度基本相同D．女生身高增长的速度总比男生慢8．（3分）某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y=﹣x2+4x（单位：米）的一部分，则水喷出的最大高度是（）A．4米 B．3米 C．2米 D．1米二、填空题（本题共8小题，每小题3分，共24分）9．（3分）不等式x﹣1＞0的解集为．10．（3分）当x=10，y=9时，代数式x2﹣y2的值是．11．（3分）如图，孔明同学背着一桶水，从山脚A出发，沿与地面成30°角的山坡向上走，送水到山上因今年春季受旱缺水的王奶奶家（B处），AB=80米，则孔明从A到B上升的高度BC是米．12．（3分）为建设绿色株洲，某校初三0801、0802、0803、0804四个班同学参加了植树造林，每班植树株数如下表，则这四个班平均每班植树株．班次植树株数08012208022508033508041813．（3分）孔明同学在解一元二次方程x2﹣3x+c=0时，正确解得x1=1，x2=2，则c的值为．14．（3分）如图，直线l过A、B两点，A（0，﹣1），B（1，0），则直线l的解析式为．15．（3分）按下面摆好的方式，并使用同一种图形，只通过平移方式就能进行平面镶嵌（即平面密铺）的有（写出所有正确答案的序号）．16．（3分）如图，第（1）个图有1个黑球；第（2）个图为3个同样大小球叠成的图形，最下一层的2个球为黑色，其余为白色；第（3）个图为6个同样大小球叠成的图形，最下一层的3个球为黑色，其余为白色；…；则从第（n）个图中随机取出一个球，是黑球的概率是．三、解答题（本大题共8小题，共52分）17．（4分）计算：．18．（4分）当x=﹣2时，求的值．19．（6分）食品安全是老百姓关注的话题，在食品中添加过量的添加剂对人体有害，但适量的添加剂对人体无害且有利于食品的储存和运输．某饮料加工厂生产的A、B两种饮料均需加入同种添加剂，A饮料每瓶需加该添加剂2克，B饮料每瓶需加该添加剂3克，已知270克该添加剂恰好生产了A、B两种饮料共100瓶，问A、B两种饮料各生产了多少瓶？20．（6分）如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D 为垂足，连接EC．（1）求∠ECD的度数；（2）若CE=5，求BC长．21．（6分）我国网球名将李娜在今年法国网球公开赛上的出色表现，大大激发了国人对网球的热情．在一项“你最喜欢的球类运动”的调查中，共有50名同学参与调查，每人必选且只选一项，将调查结果绘制成频数分布直方图如下，根据图中信息回答：（1）被调查的同学中选择喜欢网球的有人；（2）孔明同学在被调查中选择的是羽毛球，现要在参与调查选择喜欢羽毛球的同学中随机抽取2人参加一项比赛，求孔明被选中的概率．22．（8分）如图，AB为⊙O的直径，BC为⊙O的切线，AC交⊙O于点E，D为AC上一点，∠AOD=∠C．（1）求证：OD⊥AC；（2）若AE=8，，求OD的长．23．（8分）如图，矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q．（1）求证：OP=OQ；（2）若AD=8厘米，AB=6厘米，P从点A出发，以1厘米/秒的速度向D运动（不与D重合）．设点P运动时间为t秒，请用t表示PD的长；并求t为何值时，四边形PBQD是菱形．24．（10分）孔明是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线y=ax2（a＜0）的性质时，将一把直角三角板的直角顶点置于平面直角坐标系的原点O，两直角边与该抛物线交于A、B两点，请解答以下问题：（1）若测得（如图1），求a的值；（2）对同一条抛物线，孔明将三角板绕点O旋转到如图2所示位置时，过B作BF⊥x轴于点F，测得OF=1，写出此时点B的坐标，并求点A的横坐标；（3）对该抛物线，孔明将三角板绕点O旋转任意角度时惊奇地发现，交点A、B 的连线段总经过一个固定的点，试说明理由并求出该点的坐标．2011年湖南省株洲市中考数学试卷参考答案与试题解析一、选择题（每小题有且只有一个正确答案，本题共8小题，每小题3分，共24分）1．（3分）（2011•株洲）8的立方根是（）A．2 B．﹣2 C．3 D．4【分析】根据立方根的定义进行解答即可．【解答】解：∵23=8，∴8的立方根是2．故选A．【点评】本题考查的是立方根的定义，即如果一个数的立方等于a，那么这个数叫做a的立方根或三次方根．2．（3分）（2011•株洲）计算x2•4x3的结果是（）A．4x3B．4x4C．4x5D．4x6【分析】本题根据单项式乘以单项式的法则进行计算，即可求出结果．【解答】解：x2•4x3=4x5故选C．【点评】本题主要考查了单项式乘以单项式，在解题时要注意灵活运用单项式乘以单项式的法则是本题的关键．3．（3分）（2011•株洲）孔明同学在庆祝建党90周年的演讲比赛中，6位评委给他的打分如下表：评委代号ⅠⅡⅢⅣⅤⅥ评分859080959090则孔明得分的众数为（）A．95 B．90 C．85 D．80【分析】根据众数的定义，从表中找出出现次数最多的数即为众数．【解答】解：孔明同学共有6个得分，其中90分出现3次，次数最多，故孔明得分的众数为90分．故选B．【点评】此题结合图表考查了众数的概念﹣﹣﹣一组数据中出现次数最多的数叫该组数据的众数．4．（3分）（2011•株洲）株洲市关心下一代工作委员会为了了解全市初三学生的视力状况，从全市30000名初三学生中随机抽取了500人进行视力测试，发现其中视力不良的学生有100人，则可估计全市30000名初三学生中视力不良的约有（）A．100人B．500人C．6000人D．15000人【分析】利用样本来估计总体，首先计算出样本中视力不良的学生所占的百分比，再用30000名初三学生×视力不良的学生所占的百分比即可得到答案．【解答】解：100÷500=20%，30000×20%=6000，故选：C．【点评】本题考查的是通过样本去估计总体，题目比较基础．5．（3分）（2011•株洲）某商品的商标可以抽象为如图所示的三条线段，其中AB∥CD，∠EAB=45°，则∠FDC的度数是（）A．30°B．45°C．60°D．75°【分析】由邻补角的定义即可求得∠BAD的度数，又由AB∥CD，即可求得∠ADC 的度数，则问题得解．【解答】解：∵∠EAB=45°，∴∠BAD=180°﹣∠EAB=180°﹣45°=135°，∵AB∥CD，∴∠ADC=∠BAD=135°，∴∠FDC=180°﹣∠ADC=45°．故选B．【点评】此题考查了平行线的性质．注意两直线平行，内错角相等．6．（3分）（2011•株洲）如图是一个由7个同样的立方体叠成的几何体．请问下列选项中，既是中心对称图形，又是这个几何体的三视图之一的是（）A．B．C．D．【分析】首先把此几何体的三视图画出来，然后找出是中心对称图形．【解答】解：A，这是主视图，它不是中心对称图形，故此选项错误；B，这是俯视图，它是中心对称图形，故此选项正确；C，这是左视图，它不是中心对称图形，故此选项错误；D，它不是由7个同样的立方体叠成的几何体的三视图，故此选项错误；故选：B．【点评】此题主要考查了三视图的几何知识，考查了学生的空间思维想象能力．7．（3分）（2011•株洲）根据生物学研究结果，青春期男女生身高增长速度呈现如下图规律，由图可以判断，下列说法错误的是（）A．男生在13岁时身高增长速度最快B．女生在10岁以后身高增长速度放慢C．11岁时男女生身高增长速度基本相同D．女生身高增长的速度总比男生慢【分析】根据图象即可确定男生在13岁时身高增长速度是否最快；女生在10岁以后身高增长速度是否放慢；11岁时男女生身高增长速度是否基本相同；女生身高增长的速度是否总比男生慢．【解答】解：A、依题意男生在13岁时身高增长速度最快，故选项正确；B、依题意女生在10岁以后身高增长速度放慢，故选项正确；C、依题意11岁时男女生身高增长速度基本相同，故选项正确；D、依题意女生身高增长的速度不是总比男生慢，有时快，故选项错误．故选D．【点评】本题考查利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．需注意计算单位的统一．8．（3分）（2011•株洲）某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y=﹣x2+4x（单位：米）的一部分，则水喷出的最大高度是（）A．4米 B．3米 C．2米 D．1米【分析】根据题意可以得到喷水的最大高度就是水在空中划出的抛物线y=﹣x2+4x的顶点坐标的纵坐标，利用配方法或公式法求得其顶点坐标的纵坐标即为本题的答案．【解答】解：∵水在空中划出的曲线是抛物线y=﹣x2+4x，∴喷水的最大高度就是水在空中划出的抛物线y=﹣x2+4x的顶点坐标的纵坐标，∴y=﹣x2+4x=﹣（x﹣2）2+4，∴顶点坐标为：（2，4），∴喷水的最大高度为4米，故选A．【点评】本题考查了二次函数的应用，解决此类问题的关键是从实际问题中整理出函数模型，利用函数的知识解决实际问题．二、填空题（本题共8小题，每小题3分，共24分）9．（3分）（2011•株洲）不等式x﹣1＞0的解集为x＞1．【分析】根据不等式的基本性质，左右两边同时加上1，就可求出x的取值范围．【解答】解：解不等式x﹣1＞0得，x＞1．【点评】解答此题的关键是要熟知不等式两边同时加上一个数，不等号的方向不变．10．（3分）（2011•株洲）当x=10，y=9时，代数式x2﹣y2的值是19．【分析】本题需先对要求的代数式进行变形，再把x=10，y=9代入即可求出结果．【解答】解：x2﹣y2=（x+y）（x﹣y）当x=10，y=9时原式=（10+9）×（10﹣9）=19故答案为19．【点评】本题主要考查了如何求代数式的值，在解题时要能对代数式进行变形是本题的关键．11．（3分）（2011•株洲）如图，孔明同学背着一桶水，从山脚A出发，沿与地面成30°角的山坡向上走，送水到山上因今年春季受旱缺水的王奶奶家（B处），AB=80米，则孔明从A到B上升的高度BC是40米．【分析】根据题意将实际问题转化为关于解直角三角形的问题解答，利用“直角三角形中30°的角所对的直角边是斜边的一半”即可解答．【解答】解：在Rt△ABC中，∠A=30°，AB=80米，则BC=80×=40 米．故答案为40米．【点评】此题考查了解直角三角形的应用﹣﹣﹣坡度坡角问题，将实际问题转化为解直角三角形的问题是解题的关键．12．（3分）（2011•株洲）为建设绿色株洲，某校初三0801、0802、0803、0804四个班同学参加了植树造林，每班植树株数如下表，则这四个班平均每班植树25株．班次植树株数080122080225080335080418【分析】本题需先利用算术平均数的计算方法列出式子，最后求出结果即可得出正确答案．【解答】解：∵这四个班平均每班植树=（22+25+35+18）÷4=25故答案为：25【点评】本题主要考查了算术平均数的计算方法，在解题时要能结合实际问题求出平均数是本题的关键．13．（3分）（2011•株洲）孔明同学在解一元二次方程x2﹣3x+c=0时，正确解得x1=1，x2=2，则c的值为2．【分析】根据两根x1=1，x2=2，得出两根之积求出c的值即可．【解答】解：解方程x2﹣3x+c=0得x1=1，x2=2，∴x1x2=c=1×2，∴c=2，故答案为：2．【点评】此题主要考查了根与系数的关系，将根与系数的关系利用两根之积得出c的值是解决问题的关键．14．（3分）（2011•株洲）如图，直线l过A、B两点，A（0，﹣1），B（1，0），则直线l的解析式为y=x﹣1．【分析】从图象上找到直线所过的两个点的坐标，利用待定系数法求解即可．【解答】解：设函数解析式为y=kx+b，将（1，0），（0，﹣1）分别代入解析式得，，解得，函数解析式为y=x﹣1．故答案为y=x﹣1．【点评】此题考查了待定系数法求函数解析式，从图象所在坐标系找出关键点是列方程组的必要步骤．15．（3分）（2011•株洲）按下面摆好的方式，并使用同一种图形，只通过平移方式就能进行平面镶嵌（即平面密铺）的有②③（写出所有正确答案的序号）．【分析】根据一种图形平面镶嵌的条件，即能整除360°的多边形，而且只通过平移就能进行平面镶嵌，得出每个内角必须是90°，分别分析即可．【解答】解：根据一种图形平面镶嵌的条件，即能整除360°的多边形，而且只通过平移就能进行平面镶嵌，∴①正三角形虽然能平面镶嵌但是需通过旋转得出，故此选项错误；②正方形，每个内角等于90°，通过平移就能进行平面镶嵌，故此选项正确；③矩形，每个内角等于90°，通过平移就能进行平面镶嵌，故此选项正确；④正五边形，每个内角等于108°，不能平面镶嵌，故此选项错误．故答案为：②③．【点评】此题主要考查了平面镶嵌的性质以及平移的性质，得出符合两个图形的条件是解决问题的关键．16．（3分）（2011•株洲）如图，第（1）个图有1个黑球；第（2）个图为3个同样大小球叠成的图形，最下一层的2个球为黑色，其余为白色；第（3）个图为6个同样大小球叠成的图形，最下一层的3个球为黑色，其余为白色；…；则从第（n）个图中随机取出一个球，是黑球的概率是．【分析】根据图示情况，得出黑球和白球出现的规律，求出第n个图中球的总数和黑球的个数，即可求出从第（n）个图中随机取出一个球，是黑球的概率．【解答】解：根据图示规律，第n个图中，黑球有n个，球的总数有1+2+3+4+5+…+n=，则从第（n）个图中随机取出一个球，是黑球的概率是=．故答案为：．【点评】此题将规律性问题与概率公式相结合，考查了同学们的综合运用能力，而计算出球的总数和归纳出黑球的个数是解题的关键．三、解答题（本大题共8小题，共52分）17．（4分）（2011•株洲）计算：．【分析】本题涉及零指数幂、乘方、绝对值的化简三个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．【解答】解：原式=2﹣1﹣1，=0．【点评】此题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握零指数幂、乘方、绝对值等考点的运算．18．（4分）（2011•株洲）当x=﹣2时，求的值．【分析】将两个分式直接通分，分子写成完全平方式，再与分母约分，代值计算．【解答】解：原式===x+1，（3分）当x=﹣2时，原式=x+1=﹣2+1=﹣1．（4分）【点评】本题考查了分式的化简求值．关键是利用分式的加减法则，将分式化简，代值计算．19．（6分）（2011•株洲）食品安全是老百姓关注的话题，在食品中添加过量的添加剂对人体有害，但适量的添加剂对人体无害且有利于食品的储存和运输．某饮料加工厂生产的A、B两种饮料均需加入同种添加剂，A饮料每瓶需加该添加剂2克，B饮料每瓶需加该添加剂3克，已知270克该添加剂恰好生产了A、B 两种饮料共100瓶，问A、B两种饮料各生产了多少瓶？【分析】本题需先根据题意设出未知数，再根据题目中的等量关系列出方程组，求出结果即可．【解答】解：设A饮料生产了x瓶，B饮料生产了y瓶，由题意得：，解得：，答：A饮料生产了30瓶，B饮料生产了70瓶．【点评】本题主要考查了二元一次方程组的应用，在解题时要能根据题意得出等量关系，列出方程组是本题的关键．20．（6分）（2011•株洲）如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC．（1）求∠ECD的度数；（2）若CE=5，求BC长．【分析】（1）ED是AC的垂直平分线，可得AE=EC；∠A=∠C；已知∠A=36，即可求得；（2）△ABC中，AB=AC，∠A=36°，可得∠B=72°又∠BEC=∠A+∠ECA=72°，所以，得BC=EC=5；【解答】解：（1）∵DE垂直平分AC，∴CE=AE，∴∠ECD=∠A=36°；（2）∵AB=AC，∠A=36°，∴∠B=∠ACB=72°，∴∠BEC=∠A+∠ECD=72°，∴∠BEC=∠B，∴BC=EC=5．答：（1）∠ECD的度数是36°；（2）BC长是5．【点评】本题考查了等腰三角形、线段垂直平分线的性质，应熟记其性质：线段的垂直平分线上的点到线段的两个端点的距离相等．21．（6分）（2011•株洲）我国网球名将李娜在今年法国网球公开赛上的出色表现，大大激发了国人对网球的热情．在一项“你最喜欢的球类运动”的调查中，共有50名同学参与调查，每人必选且只选一项，将调查结果绘制成频数分布直方图如下，根据图中信息回答：（1）被调查的同学中选择喜欢网球的有15人；（2）孔明同学在被调查中选择的是羽毛球，现要在参与调查选择喜欢羽毛球的同学中随机抽取2人参加一项比赛，求孔明被选中的概率．【分析】（1）根据频数分布直方图中每一组内的频数总和为50，计算出喜欢网球的人数；（2）列举出所有的结果，根据孔明被选中的有4种，除以总个数即可得出概率．【解答】解：（1）50﹣5﹣10﹣12﹣8=15；（2）记喜欢羽毛球的5个同学分别表示为1，2，3，4，5，其中1为孔明，从中随机抽取2人，方法有：（1，2）（1，3）（1，4）（1，5）（2，3）（2，4）（2，5）（3，4）（3，5）（4，5），共10种，其中孔明被选中的有4种，所以孔明被选中的概率是（或写成0.4），【点评】此题主要考查了条形图以及列举法求概率，根据已知得出符合要求的个数是求出概率的关键．22．（8分）（2011•株洲）如图，AB为⊙O的直径，BC为⊙O的切线，AC交⊙O 于点E，D为AC上一点，∠AOD=∠C．（1）求证：OD⊥AC；（2）若AE=8，，求OD的长．【分析】（1）根据切线的性质得出∠ABC=90°，进而得出∠A+∠C=90°，再由∠AOD=∠C，可得∠AOD+∠A=90°，即可证明；（2）由垂径定理可得，D为AE中点，根据已知可利用锐角三角函数求出．【解答】（1）证明：∵BC是⊙O的切线，AB为⊙O的直径∴∠ABC=90°，∴∠A+∠C=90°，又∵∠AOD=∠C，∴∠AOD+∠A=90°，∴∠ADO=90°，∴OD⊥AC；（2）解：∵OD⊥AE，O为圆心，∴D为AE中点，AE=8，∴，又，∴OD=3．【点评】此题主要考查了圆的切线性质，及解直角三角形的知识和垂径定理的应用等知识，利用OD⊥AE，O为圆心，得出D为AE中点，再利用解直角三角形知识是解决问题的关键．23．（8分）（2011•株洲）如图，矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q．（1）求证：OP=OQ；（2）若AD=8厘米，AB=6厘米，P从点A出发，以1厘米/秒的速度向D运动（不与D重合）．设点P运动时间为t秒，请用t表示PD的长；并求t为何值时，四边形PBQD是菱形．【分析】（1）本题需先根据四边形ABCD是矩形，得出AD∥BC，∠PDO=∠QBO，再根据O为BD的中点得出△POD≌△QOB，即可证出OP=OQ．（2）本题需先根据已知条件得出∠A的度数，再根据AD=8厘米，AB=6厘米，得出BD和OD的长，再根据四边形PBQD是菱形时，即可求出t的值，判断出四边形PBQD是菱形．【解答】（1）证明：∵四边形ABCD是矩形，∴AD∥BC，∴∠PDO=∠QBO，又∵O为BD的中点，∴OB=OD，在△POD与△QOB中，∵∴△POD≌△QOB（ASA），∴OP=OQ；（2）解：PD=8﹣t，∵四边形PBQD是菱形，∴PD=BP=8﹣t，∵四边形ABCD是矩形，∴∠A=90°，在Rt△ABP中，由勾股定理得：AB2+AP2=BP2，即62+t2=（8﹣t）2，解得：t=，即运动时间为秒时，四边形PBQD是菱形．【点评】本题主要考查了矩形的性质，在解题时要注意与全等三角形、矩形的知识点结合起来是解本题的关键．24．（10分）（2011•株洲）孔明是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线y=ax2（a＜0）的性质时，将一把直角三角板的直角顶点置于平面直角坐标系的原点O，两直角边与该抛物线交于A、B两点，请解答以下问题：（1）若测得（如图1），求a的值；（2）对同一条抛物线，孔明将三角板绕点O旋转到如图2所示位置时，过B作BF⊥x轴于点F，测得OF=1，写出此时点B的坐标，并求点A的横坐标﹣4；（3）对该抛物线，孔明将三角板绕点O旋转任意角度时惊奇地发现，交点A、B 的连线段总经过一个固定的点，试说明理由并求出该点的坐标．【分析】（1）先求出B点坐标，代入抛物线y=ax2（a＜0）得a的值；（2）过点A作AE⊥x轴于点E，可证△AEO∽△OFB，得出AE=2OE，可得方程点A的横坐标．（3）设A（﹣m，）（m＞0），B（n，）（n＞0），易知△AEO∽△OFB，根据相似三角形的性质可知交点A、B的连线段总经过一个固定的点（0，﹣2）．【解答】解：（1）设线段AB与y轴的交点为C，由抛物线的对称性可得C为AB 中点，∵，∠AOB=90°，∴AC=OC=BC=2，∴B（2，﹣2），将B（2，﹣2）代入抛物线y=ax2（a＜0）得，．（2）解法一：过点A作AE⊥x轴于点E，∵点B的横坐标为1，∴B（1，），∴．又∵∠AOB=90°，易知∠AOE=∠OBF，又∵∠AEO=∠OFB=90°，∴△AEO∽△OFB，∴，∴AE=2OE，设点A（﹣m，）（m＞0），则OE=m，，∴，∴m=4，即点A的横坐标为﹣4．解法二：过点A作AE⊥x轴于点E，∵点B的横坐标为1，∴B（1，），∴，∵∠AOB=90°，易知∠AOE=∠OBF，∴，∴AE=2OE，设点A（﹣m，）（m＞0），则OE=m，，∴，∴m=4，即点A的横坐标为﹣4．解法三：过点A作AE⊥x轴于点E，∵点B的横坐标为1，∴B（1，），设A（﹣m，）（m＞0），则，，，∵∠AOB=90°∴AB2=OA2+OB2，∴（1+m）2+（﹣+m2）2=+m2+m4，解得：m=4，即点A的横坐标为﹣4．（3）解法一：设A（﹣m，）（m＞0），B（n，）（n＞0），设直线AB的解析式为：y=kx+b，则，（1）×n+（2）×m得，，∴（8分）又易知△AEO∽△OFB，∴，∴，∴mn=4，∴．由此可知不论k 为何值，直线AB 恒过点（0，﹣2）．（说明：写出定点C 的坐标就给2分）解法二：∵点A 是抛物线y=﹣x 2上的点，∴设A （﹣m ，）（m ＞0），B （n ，）（n ＞0），直线AB 与y 轴的交点为C ，根据S △AOB =S 梯形ABFE ﹣S △AOE ﹣S △B0F =S △AOC +S △BOC ，可得，化简，得．又易知△AEO ∽△OFB ， ∴， ∴，∴mn=4，∴OC=2为固定值．故直线AB 恒过其与y 轴的交点C （0，﹣2），说明：mn 的值也可以通过以下方法求得．由前可知，，，，由OA 2+OB 2=AB 2，得：，化简，得mn=4．本答案仅供参考，若有其他解法，请参照本评分标准评分．【点评】本题着重考查了抛物线的对称性和相似三角形的判定和性质，第（3）问求出mn=4是解题的关键，综合性较强，有一定的难度．参与本试卷答题和审题的老师有：ZJX；lantin；CJX；sd2011；zcx；gbl210；Liuzhx；sjzx；cook2360；zhangCF；wangjc3；HJJ（排名不分先后）菁优网2017年4月23日。

湖南省株洲市中考数学试题解析

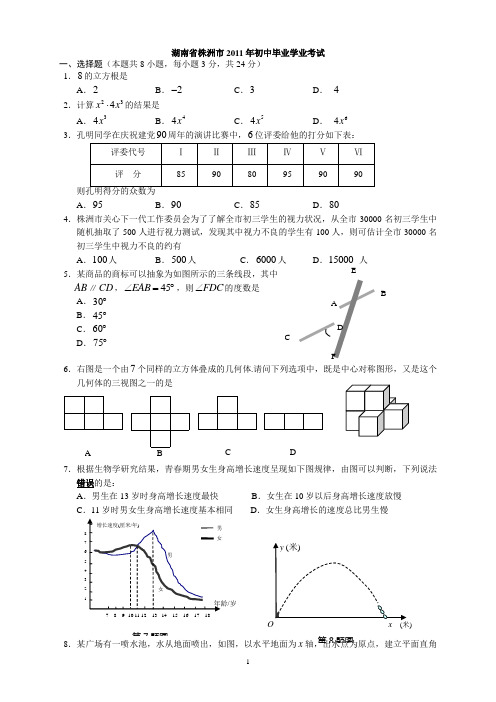
湖南省株洲市2011年初中毕业学业考试一、选择题（本题共8小题，每小题3分，共24分） 1．8的立方根是 A ．2B ．2-C ．3D ． 4 2．计算234x x ⋅的结果是A ．34xB ．44xC ．54x D ． 64x 3．孔明同学在庆祝建党90周年的演讲比赛中，6位评委给他的打分如下表：A ．95B ．90C ．85D ．804．株洲市关心下一代工作委员会为了了解全市初三学生的视力状况，从全市30000名初三学生中随机抽取了500人进行视力测试，发现其中视力不良的学生有100人，则可估计全市30000名初三学生中视力不良的约有 A ．100人B ．500人C ．6000人D ．15000 人5．某商品的商标可以抽象为如图所示的三条线段，其中 AB ∥CD ，45EAB ∠=︒，则FDC ∠的度数是 A ．30︒ B ．45︒C ．60︒D ．75︒6．右图是一个由7个同样的立方体叠成的几何体.请问下列选项中，既是中心对称图形，又是这个几何体的三视图之一的是7．根据生物学研究结果，青春期男女生身高增长速度呈现如下图规律，由图可以判断，下列说法错误的是：A ．男生在13岁时身高增长速度最快B ．女生在10岁以后身高增长速度放慢C ．11岁时男女生身高增长速度基本相同D ．女生身高增长的速度总比男生慢8．某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角A B D C EFA BCD第7题图 /岁)第8题图x第14题图坐标系，水在空中划出的曲线是抛物线24y x x =-+（单位：米）的一部分，则水喷出的最大高度是A ．4米B ．3米C ．2米D ．1米二、填空题（本题共8小题，每小题3分，共24分） 9．不等式10x ->的解集是．10．当10x =，9y =时，代数式22x y -的值是．11．如图，孔明同学背着一桶水，从山脚A 出发，沿与地面成30︒角的山坡向上走，送水到山上因今年春季受旱缺水的王奶奶家（B 处），80AB =米，则孔明从A 到B 上升的高度BC 是米． 12．为建设绿色株洲，某校初三0801、0802、0803、0804四个班同学参加了植树造林，每班植树株数如下表，则这四个班平均每班植树株．13．孔明同学在解一元二次方程230x x c -+=时，正确解得11x =，22x =，则c 的值为．14．如图，直线l 过A 、B 两点，A （0，1-），B （1，0），则直线l 的解析式为．15．按下面摆好的方式，并使用同一种图形，只通过平移方式就能进行平面镶嵌(即平面密铺)的有（写出所有正确答案的序号）.16．如图，第（1）个图有1个黑球；第（2）个图为3个同样大小球叠成的图形，最下一层的2个球为黑色，其余为白色；第（3）个图为6个同样大小球叠成的图形，最下一层的3个球为黑色，其余为白色；；则从第（n ）个图中随机取出一个球，是黑球的概率是 .三、解答题（本大题共8小题，共52分） 17．（本题满分4分）计算：02011|2|(1)--+-第11题图第12题表正三角形 ① 正方形 ② 矩形③正五边形 ④18．（本题满分4分）当2x =-时，求22111x x x x ++++的值． 19．（本题满分6分）食品安全是老百姓关注的话题，在食品中添加过量的添加剂对人体有害，但适量的添加剂对人体无害且有利于食品的储存和运输．某饮料加工厂生产的A B 、两种饮料均需加入同种添加剂，A 饮料每瓶需加该添加剂2克，B 饮料每瓶需加该添加剂3克，已知270克该添加剂恰好生产了A B 、两种饮料共100瓶，问A B 、两种饮料各生产了多少瓶？20．（本题满分6分）如图， ABC ∆中，AB AC =，36A ∠=︒，AC 的垂直平分线交AB 于E ，D 为垂足，连结EC ．（1）求ECD ∠的度数；（2）若5CE =，求BC 长．21．（本题满分6分）我国网球名将李娜在今年法国网球公开赛上的出色表现，大大激发了国人对网球的热情．在一项“你最喜欢的球类运动”的调查中，共有50名同学参与调查，每人必选且只选一项，将调查结果绘制成频数分布直方图如下，根据图中信息回答：（1）被调查的同学中选择喜欢网球的有____________________人；（2）孔明同学在被调查中选择的是羽毛球，现要在参与调查选择喜欢羽毛球的同学中随机抽取2人参加一项比赛，求孔明被选中的概率.22．（本题满分8分）如图，AB 为O 的直径，BC 为O 的切线，AC 交O 于点E ，D 为AC上一点，AOD C ∠=∠．（1）求证：OD AC ⊥；（2）若8AE =，3tan 4A =，求OD 的长．EDCBA羽毛球排球网球足球篮球项目OE D CBA23．（本题满分8分）如图，矩形ABCD 中，点P 是线段AD 上一动点，O 为BD 的中点， PO 的延长线交BC 于Q . （1）求证：OP OQ =；（2）若8AD =厘米，6AB =厘米，P 从点A 出发，以1厘米/秒的速度向D 运动（不与D 重合）. 设点P 运动时间为t 秒，请用t 表示PD 的长；并求t 为何值时，四边形PBQD 是菱形．24．（本题满分10分）孔明是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线2(0)y ax a =<的性质时，将一把直角三角板的直角顶点置于平面直角坐标系的原点O ，两直角边与该抛物线交于A 、B 两点，请解答以下问题：（1）若测得OA OB ==1），求a 的值；（2）对同一条抛物线，孔明将三角板绕点O 旋转到如图2所示位置时，过B 作BF x ⊥轴于点F ，测得1OF =，写出此时点B 的坐标，并求点A 的横坐标．．．；（3）对该抛物线，孔明将三角板绕点O 旋转任意角度时惊奇地发现，交点A 、B 的连线段总经过一个固定的点，试说明理由并求出该点的坐标．参考答案及评分标准Q P ODCBA一、选择题：29．1x > 10. 19 11. 40 12. 25 13．2 14．1y x =- 15． ②③ 16．21n + 三、解答题：17．解：原式=211-- ……3分0= ……4分18．解：原式=2221(1)111x x x x x x +++==+++ ……3分当2x =-时，原式1211x =+=-+=- ……4分（说明：直接代入求得正确结果的给满分）19.解法一：设A 饮料生产了x 瓶，则B 饮料生产了（100x -）瓶，依题意得： ……1分23(100)270x x +-= ……3分解得：30x = 10070x -= ……5分答：A 饮料生产了30瓶，B 饮料生产了70瓶 ……6分解法二：设A 饮料生产了x 瓶，B 饮料生产了y 瓶，依题意得： ……1分10023270x y x y +=⎧⎨+=⎩ ……3分解得：3070x y =⎧⎨=⎩……5分答：A 饮料生产了30瓶，B 饮料生产了70瓶 ……6分 20.（1）解法一：AC DE 垂直平分CE=AE ∴ E C D =A =36∴∠∠︒ …… 3分解法二：AC DE 垂直平分 A D =C D A D E =C D E=∴∠∠︒ 又DE=DE ADE ∴∆≌CDE ∆ECD=A=36∴∠∠︒ …… 3分（2）解法一：AB=AC,A=36∠︒B=ACB=72∴∠∠︒ …… 4分ECD=36∠︒BCE=ACB-ECD=36∴∠∠∠︒ …… 5分 BEC=72=B ∴∠︒∠BC=EC=5∴ ……6分解法二：AB=AC,A=36∠︒B=ACB=72∴∠∠︒ …… 4分BEC=A+ECD=72∴∠∠∠︒ …… 5分 BEC=B ∴∠∠BC=EC=5∴ ……6分21．（1）15 ……3分EDCBA（2）记喜欢羽毛球的5个同学分别表示为 1，2，3，4，5，其中1为孔明，从中随机抽取2人，方法有：（1,2）（1,3）（1,4）（1,5）（2,3）（2,4）（2,5）（3,4）（3,5）（4,5）共10种，其中孔明被选中的有4种，所以孔明被选中的概率是42105= (或写成0.4)……6分 (说明：第2问只写出正确结果的也给满分.)22．（1）证明：BC 是O 的切线，AB 为O 的直径ABC=90∴∠︒，A+C=90∴∠∠︒ …… 2分又AOD=C ∠∠AOD+A=90∴∠∠︒ …… 3分90ADO ∴∠=︒OD AC ∴⊥ …… 4分（2）解：OD AE ⊥ ，O 为圆心D ∴为AE 中点 …… 6分 1AD=AE=42∴ 又3tan 4A = OD=3∴ …… 8分23．（1）证明：四边形ABCD 是矩形，∴AD ∥BC …… 1分 ∴PDO QBO ∠=∠，又OB OD =，POD QOB ∠=∠∴△POD ≌△QOB …… 3分 ∴OP OQ = …… 4分（2）解法一： 8PD t =- …… 5分四边形ABCD 是矩形，∴90A ∠=︒，8AD cm =，6AB cm =，∴10BD cm =，∴5OD cm =. 当四边形PBQD 是菱形时， PQ ⊥BD ，∴POD A ∠=∠，又ODP ADB ∠=∠∴△ODP ∽△ADB ， …… 6分 ∴OD AD PD BD =，即58810t =-， …… 7分解得74t =,即运动时间为74秒时，四边形PBQD 是菱形. …… 8分解法二：8PD t =- …… 5分当四边形PBQD 是菱形时，(8)PB PD t cm ==- …… 6分四边形ABCD 是矩形，∴90A ∠=︒，在Rt △ABP 中，6AB cm =∴222AP AB BP +=， ∴2226(8)t t +=-， …… 7分解得74t =,即运动时间为74秒时，四边形PBQD 是菱形. …… 8分 24.解：（1）设线段AB 与y 轴的交点为C ，由抛物线的对称性可得C 为AB 中点，OA OB ==90AOB ∠=︒，Q PODCBAOE D CBA∴2AC OC BC ===，∴B (2，2-) ……… 2分将B (2，2-)代入抛物线2(0)y ax a =<得，12a =-. ……… 3分（2）解法一：过点A 作AE x ⊥轴于点E ，点B 的横坐标为1，∴B (1，12-)， ……… 4分∴12BF =. 又 90AOB ∠=︒，易知AOE OBF ∠=∠，又90AEO OFB ∠=∠=︒，∴△AEO ∽△OFB ，∴1212AE OF OE BF === ∴2AE OE = ……… 5分设点A （m -，212m -）（0m >），则OE m =，212AE m =，∴212m m =∴4m =，即点A 的横坐标为4-. ……… 6分解法二：过点A 作AE x ⊥轴于点E ，点B 的横坐标为1，∴B (1，12-)， ……… 4分∴1tan 212OF OBF BF ∠=== 90AOB ∠=︒，易知AOE OBF ∠=∠， ∴tan tan 2AEAOE OBF OE=∠=∠=，∴2AE OE = 设点A （-m ，212m -）（0m >），则OE m =，212AE m =，∴4m =，即点A 的横坐标为4-. ……… 6分解法三：过点A 作AE x ⊥轴于点E ，点B 的横坐标为1，∴B (1，12-)， ……… 4分设A （-m ，212m -）（0m >），则222151()24OB =+=，22414OA m m =+，222211(1)()22AB m m =++-+，90AOB ∠=︒∴222AB OA OB =+， ∴2222221111(1)()(1)()2222m m m m ++-+=++-+，解得：4m =，即点A 的横坐标为4-. ……… 6分（3）解法一：设A （m -，212m -）（0m >），B （n ，212n -）（0n >），设直线AB 的解析式为：y kx b =+，则221 (1) 21 (2) 2mk b m nk b n ⎧-+=-⎪⎪⎨⎪+=-⎪⎩，……… 7分 (1)(2)n m ⨯+⨯得，2211()()()22m n b m n mn mn m n +=-+=-+∴12b mn =- ……… 8分又易知△AEO ∽△OFB ，∴AE OEOF BF=，∴220.50.5m m n n =，∴4mn =……… 9分 ∴1422b =-⨯=-.由此可知不论k 为何值，直线AB 恒过点（0，2-）………10分（说明：写出定点C 的坐标就给2分）解法二：设A （m -，212m -）（0m >），B （n ，212n -）（0n >），直线AB 与y 轴的交点为C ，根据0AOB AOE B F AOC BOC ABFE S S S S S S ∆∆∆∆∆=--=+梯形，可得2222111111111()()222222222n m m n m m n n OC m OC n ⋅++-⋅⋅-⋅⋅=⋅⋅+⋅⋅，化简，得12OC mn =. ……… 8分又易知△AEO ∽△OFB ，∴AE OEOF BF=，∴220.50.5m m n n =，∴4mn =……… 9分∴2OC =为固定值.故直线AB 恒过其与y 轴的交点C （0,2-）……… 10分说明：mn 的值也可以通过以下方法求得.由前可知，22414OA m m =+，22414OB n n =+，2222211()()22AB m n m n =++-+，由222OA OB AB +=，得：242422221111()()()()4422m m n n m n m n +++=++-+，化简，得4mn =.。

2011年中考数学考试试题答案

1 / 12高中阶段教育学校招生统一考试数学全卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页．全卷满分120分，考试时间共120分钟．答题前，请考生务必在答题卡上正确填涂自己的姓名、考号和考试科目，并将试卷密封线内的项目填写清楚；考试结束，将试卷和答题卡一并交回．第Ⅰ卷(选择题共30分)注意事项：每小题选出的答案不能答在试卷上，须用2B 铅笔在答题卡上把对应题目．．．．的答案标号涂黑．如需改动，用橡皮擦擦净后，再选涂其它答案．一、选择题：(本大题共10个小题，每小题3分，共30分)在每小题给出的四个选项中，只有一个选项符合题意．1. -3的绝对值是( )A. 3B. -3C.13 D. 13- 2. “中国国家馆”作为2010年上海世博会的主题场馆，充分体现了中国文化的精神与气质. 资料表明，在建设过程中使用的一种工艺，需要对中国馆的大台阶进行约5.4×107次加工. 其中5.4×107表示的数为( )A. 5 400 000B. 54 000 000C. 540 000 000D. 5 400 000 000 3. 小明调查了本班同学最喜欢的课外活动项目，并作出如图1所示的扇形统计图，则从图中可以直接看出的信息是( )A. 全班总人数B. 喜欢篮球活动的人数最多C. 喜欢各种课外活动的具体人数D. 喜欢各种课外活动的人数占本班总人数的百分比4. 顺次连接边长为2的等边三角形三边中点所得的三角形的周长为( )A. 1B. 2C. 3D. 45. 用一个平面截一个几何体，得到的截面是四边形，则这个几何体可能是( ) A. 球体 B. 圆柱 C. 圆锥 D. 三棱锥6. 若实数a 、b 满足5a b +=，2210a b ab +=-，则ab 的值是( ) A. -2B. 2图1图22 / 12C. -50D. 507. 如图2，A 为⊙O 上一点，从A 处射出的光线经圆周4次反射后到达F 处. 如果反射前后光线与半径的夹角均为50°，那么∠AOE 的度数是( )A. 30°B. 40°C. 50°D. 80°8. 为缓解考试前的紧张情绪，某校九年级举行了“猪八戒背媳妇”的趣味接力比赛. 比赛要求每位选手在50米跑道上进行折返跑，其中有50米必须“背媳妇”. 假设某同学先跑步后“背媳妇”，且该同学跑步、“背媳妇”均匀速前进，他与起点的距离为s ，所用时间为t ，则s 与t 的函数关系用图象可表示为()A. B. C. D.9. 在同一平面内，如果两个多边形(含内部)有除边界以外的公共点，则称两多边形有“公共部分”.如图3，若正方形ABCD 由9个边长为1的小正方形镶嵌而成，另有一个边长为1的正方形与这9个小正方形中的n 个有“公共部分”，则n 的最大值为( ) A. 4 B. 5 C. 6 D. 710. 如图4，已知点A 1，A 2，…，A 2011在函数2y x =位于第二象限的图象上，点B 1，B 2，…，B 2011在函数2y x =位于第一象限的图象上，点C 1，C 2，…，C 2011在y 轴的正半轴上，若四边形111OA C B 、1222C A C B ，…，2010201120112011C A C B 都是正方形，则正方形2010201120112011C A C B 的边长为( )A. 2010B. 2011C. 20102D. 20112图3图43 / 12高中阶段教育学校招生统一考试数学第Ⅱ卷(非选择题共90分)题号二三总分总分人171819202122232425得分注意事项：本卷共6页，用黑色或蓝色钢笔或圆珠笔直接答在试卷上．请注意准确理解题意、明确题目要求，规范地表达、工整地书写解题过程或结果．二、填空题：(本大题共6个小题，每小题3分，共18分)把答案直接填在题中横线上．11. 9的平方根为____________.12. 第16届亚运会将于2010年11月12日至27日在中国广州进行，各类门票现已开始销售. 若部分项目门票的最低价和最高价如图5所示，则这六个项目门票最高价的中位数是____________ .13. 若菱形一边的垂直平分线经过这个菱形的一个顶点，则此菱形较大内角的度数为_______.14. 若关于x 的方程2220x m x m m -+-=无实数根，则实数m 的取值范围是____________.15. 如图6，已知△ABC是等腰直角三角形，CD 是斜边AB 的中线，△ADC 绕点D 旋转一定角度得到△A DC ''，A D '交AC 于点E ，DC '交BC 于点F ，连接EF ，若25A E ED '=，则EF A C ''=_________ . 16. 给出下列命题：① 若方程2560x x +-=的两根分别为1x ，2x ，则121156x x +=；② 对于任意实数x 、y ，都有2233()()x y x xy y x y -++=-；③ 如果一列数3，7，11，…满足条件：“以3为第一个数，从第二个数开始每一个数与它前面相邻的数的差为4”，那么99不是这列数中的一个数；④若※表示一种运算，且1※2=1，3※2=7，4※4=8，…，按此规律，则可能有a ※b =3a -b . 其中所有正确命题的序号是__________________ .图6图54 / 12三、解答题：(本大题共9个小题，共72分)解答应写出必要的文字说明、证明过程或演算步骤．17．(本小题满分7分)化简：2162393m m m -÷+--.18．(本小题满分7分)在为迎接“世界环境日”举办的“保护环境、珍爱地球”晚会上，主持人与观众玩一个游戏：取三张完全相同、没有任何标记的卡片，分别写上“物种”、“星球”和“未来”，并将写有文字的一面朝下，随机放置在桌面上，然后依次翻开三张卡片.(1) 用列表法(或树状图)求翻开卡片后第一张是“物种”且第二张是“星球”的概率； (2) 主持人规定：若翻开的第一张卡片是“未来”，观众获胜，否则主持人获胜. 这个规定公平吗？为什么？19．(本小题满分8分)如图7，已知A 、B 、C 是数轴上异于原点O 的三个点，且O 为AB 的中点，B为AC 的中点. 若点B 对应的数是x ，点C 对应的数是2x -3x ，求x 的值.图75 / 1220．(本小题满分8分)已知关于x 的不等式组4(1)23,617x x x ax -+>⎧⎪+⎨-<⎪⎩有且只有三个整数解，求a 的取值范围.21．(本小题满分8分)如图8，已知直线l ：y =kx +b 与双曲线C ：my x=相交于点A (1，3)、B (32-，-2)，点A 关于原点的对称点为P .(1) 求直线l 和双曲线C 对应的函数关系式； (2) 求证：点P 在双曲线C 上；(3) 找一条直线l 1，使△ABP 沿l 1翻折后，点P 能落在双曲线C 上. (指出符合要求的l 1的一个解析式即可，不需说明理由)图86 / 1222．(本小题满分8分)在军事上，常用时钟表示方位角(读数对应的时针方向)，如正北为12点方向，北偏西30°为11点方向. 在一次反恐演习中，甲队员在A 处掩护，乙队员从A 处沿12点方向以40米/分的速度前进，2分钟后到达B 处. 这时，甲队员发现在自己的1点方向的C 处有恐怖分子，乙队员发现C 处位于自己的2点方向(如图9). 假设距恐怖分子100米以外为安全位置.(1) 乙队员是否处于安全位置？为什么？(2) 因情况不明，甲队员立即发出指令，要求乙队员沿原路后撤，务必于15秒内到达安全位置. 为此，乙队员至少．．应用多快的速度撤离？(结果精确到个位. 参考数据：13 3.6≈0，14 3.74≈.)23．(本小题满分8分)如图10-1，已知AB 是⊙O 的直径，直线l 与⊙O 相切于点B ，直线m 垂直AB 于点C ，交⊙O 于P 、Q 两点. 连结AP ，过O 作OD ∥AP 交l 于点D ，连接AD 与m 交于点M .(1) 如图10-2，当直线m 过点O 时，求证：M 是PO 的中点；(2) 如图10-1，当直线m 不过点O 时，M 是否仍为PC 的中点？证明你的结论.图9图10-1 图10-27 / 1224．(本小题满分9分)如图11，在直角梯形ABCD 中，已知AD ∥BC ，AB =3，AD =1，BC =6，∠A =∠B =90°.设动点P 、Q 、R 在梯形的边上，始终构成以P 为直角顶点的等腰直角三角形，且△PQR 的一边与梯形ABCD 的两底边平行.(1) 当点P 在AB 边上时，在图中画出一个符合条件的△PQR (不必说明画法)； (2) 当点P 在BC 边或CD 边上时，求BP 的长.图118 / 1225．(本小题满分9分)如图12，已知直线22y x =+交y 轴于点A ，交x 轴于点B ，直线l ：39y x =-+交x 轴于点C .(1) 求经过A 、B 、C 三点的抛物线的函数关系式，并指出此函数的函数值随x 的增大而增大时，x 的取值范围；(2) 若点E 在(1)中的抛物线上，且四边形ABCE 是以BC 为底的梯形，求梯形ABCE 的面积； (3) 在(1)、(2)的条件下，过E 作直线EF ⊥x 轴，垂足为G ，交直线l 于F . 在抛物线上是否存在点H ，使直线l 、直线FH 和x 轴所围成的三角形的面积恰好是梯形ABCE 面积的12？若存在，求点H 的横坐标；若不存在，请说明理由.图12高中阶段教育学校招生统一考试数学试题参考答案及评分意见说明：1. 解答题中各步骤所标记分数为考生解答到这一步应得的累计分数．2. 参考答案一般只给出该题的一种解法，如果考生的解法和参考答案所给解法不同，请参照本答案及评分意见给分．3. 考生的解答可以根据具体问题合理省略非关键步骤．4. 评卷时要坚持每题评阅到底，当考生的解答在某一步出现错误、影响了后继部分时，如果该步以后的解答未改变问题的内容和难度，可视影响程度决定后面部分的给分，但不得超过后继部分应给分数的一半；如果这一步后面的解答有较严重的错误，就不给分；若是几个相对独立的得分点，其中一处错误不影响其他得分点的得分．5. 给分和扣分都以1分为基本单位．6. 正式阅卷前应进行试评，在试评中须认真研究参考答案和评分意见，不能随意拔高或降低给分标准，统一标准后须对全部试评的试卷予以复查，以免阅卷前后期评分标准宽严不同．一、选择题(每小题3分，共10个小题，满分30分)：1-5. ABDCB；6-10. ABCCD．二、填空题(每小题3分，共6个小题，满分18分)：11．±3；12．800元；13. 120°；14．m<0；15．57；16．①②④．(注：12、13题有无单位“元”或“°”均不扣分. ) 三、解答题(共9个小题，满分72分)：17．解：原式=1633(3)(3)2mm m m-+++-····················································3分=1333m m+++···················································································5分=43m+. ··························································································7分18．(1) 解一：列表如下： ············································································································3分∴第一张是“物种”且第二张是“星球”的概率是16. ······························4分解二：树状图如下：9 / 1210 / 12···························· 3分∴ 第一张是“物种”且第二张是“星球”的概率是16. ············································(2) 这个规定不公平. ··········································································5分因为观众获胜的概率是13，主持人获胜的概率是23. ·································7分19．解：由已知，点O 是AB 的中点，点B 对应的数是x ，∴ 点A 对应的实数为-x . ····································································1分 ∵ 点B 是AC 的中点，点C 对应的数是2x -3x ， ∴ (2x -3x )-x =x -(-x ). ··········································································4分整理，得2x -6x =0，解之得 x =0，或x =6. ···············································6分 ∵ 点B 异于原点，故x =0应舍去. ∴ x 的值为6. ·····································7分 20．解：由4(1)23x x -+>得，x >2； ···························································2分由617x ax +-<得，x <a +7. ··································································5分依题意得，不等式组的解集为2<x <a +7. ··················································6分又 ∵ 此不等式组有且只有三个整数解，故整数解只能是x =3，4，5， ∴ 5<a +7≤6，则-2<a ≤-1. ·································································8分 (注：未取等号扣1分)21. 解：(1) 将点A 、B 的坐标代入y =kx +b ，有31,32().2k b k b =⨯+⎧⎪⎨-=⨯-+⎪⎩ ·············································································2分解得，2k =，b =1，即直线l 对应的函数关系为y =2x +1. ·····························3分将点A (1，3)(或B )的坐标代入my x =，得m =3，∴ 双曲线C 对应的函数关系为y =3x. ·····················································4分(2) ∵ P 为点A 关于原点的对称点，∴ 点P 的坐标为(-1，-3)，符合双曲线C 的函数关系，故点P 在双曲线C 上. ·················································································6分(3) l 1的解析式为y =x ，或y =-x . ·····························································8分 (注：写出一个解析式即得2分.) 22．解：(1) 乙队员不安全. ······················································· 1分易求AB =80米. ∵ ∠BAC =∠C =30°，∴ BC =AB =80米<100米. ·························· 3分 ∴ 乙队员不安全.(2) 过C 点作CD ⊥AB ，垂足为D ，在AB 边上取一点B 1，使CB 1=100. ······················································································ 4分在Rt △CBD 中，∠CBD =60°，BC =80，则BD =40，CD =403. ···· 5分在Rt △1CDB 中，由勾股定理知22112013B D B C CD =-=， ·····················6分11 / 12而20134015-≈2.13米/秒， ·······························································7分依题意，乙队员至少应以3米/秒的速度撤离. ··········································8分 (注：结果为2米/秒，本步不给分.)23．(1) 证明：连接PD ，∵ 直线m 垂直AB 于点C ，直线l 与⊙O 相切于点B ，AB 为直径，∴ ∠POA =∠DBA =90°.又∵ AP ∥OD ，∴ ∠P AO =∠DOB . ························································1分又∵ AO =BO ，∴ △APO ≌△ODB . ·······················································2分 ∴ AP =OD ，∴ 四边形APDO 是平行四边形， ·········································3分 ∴ M 是PO 的中点. ···········································································4分(其他解法：证△APO ≌△ODB 后，据中位线定理证12OM BD =；或证△DPO ≌△DBO ，得∠DPO =∠DBO =90°，从而证四边形APDO 是平行四边形等.)(2) M 是PC 的中点. 证明如下：∵AP ∥OD ，∴ ∠P AO =∠DOB ，又 ∠PCA =∠DBO =90°，∴ △APC ∽△ODB ，∴ PC AC BD BO=.①·····················································5分又易证△ACM ∽△ABD ，∴ AC MC AB BD=. ·················································6分又∵ AB =2OB ，∴ 2AC MC OB BD =，∴2AC MC OB BD=.② ····································7分由①②得，2PC MC BD BD=，∴ PC =2MC ，即M 是PC 的中点. ·························8分 24．(1) 如图.(注：答案不唯一，在图中画出符合条件的图形即可) ······················2分(2) ① 当P 在CD 边上时，由题意，PR ∥BC ，设PR =x .可证四边形PRBQ 是正方形，∴ PR =PQ =BQ =x .过D 点作DE ∥AB ，交BC 于E ，易证四边形ABED 是矩形.∴ AD =BE =1，AB =DE =3. ··········································· 3分又 PQ ∥DE ，∴△CPQ ∽△CDE ，PQ CQ DE CE=. ∴ 635x x -=， ························································ 4分 ∴ x =94，即BP =942. ············································ 5分 (注：此时，由于∠C ≠45°，因此斜边RQ 不可能平行于BC . 在答题中未考虑此问题者不扣分.) ② 当P 在BC 边上，依题意可知RQ ∥BC .过Q 作QF ⊥BC ，易证△BRP ≌△FQP ，则PB =PF . ········· 6分易证四边形BFQR 是矩形，设BP =x ，则BP =BR =QF =PF =x ，BF =RQ =2x . ·················· 7分∵ QF ∥DE ，∴ △CQF ∽△CDE ，∴ QF CF DE CE =. ······································8分12 / 12 ∴6235x x -=，∴ x =1811. ···································································9分 (注：此时，直角边不可能与两底平行. 在答题中未考虑此问题者不扣分.)25．(1) ∵ 直线AB 的解析式为22y x =+，∴ 点A 、B 的坐标分别为A (0，2)，B (-1，0).又直线l 的解析式为39y x =-+，∴ 点C 的坐标为(3，0). ··························1分由上，可设经过A 、B 、C 三点的抛物线的解析式为y =a (x +1)(x -3)，将点A 的坐标代入，得 a =23-，∴ 抛物线的解析式为224233y x x =-++. ·····2分 ∴ 抛物线的对称轴为x =1.由此可知，函数值随x 的增大而增大时，x 的取值范围是x ≤1. ···················3分 (注：本步结果无等号不扣分.)(2) 过A 作AE ∥BC ，交抛物线于点E . 显然，点A 、E 关于直线x =1对称，∴ 点E 的坐标为E (2，2). ····································································4分故梯形ABCE 的面积为 S =12(2+4)×2=6. ··················································5分 (3) 假设存在符合条件的点H ，作直线FH 交x 轴于M ，由题意知，3CFM S =. 设F (m ，n )，易知m =2，将F (2，n )的坐标代入y =-3x +9中，可求出n =3，则FG =3. ························6分∴ 132CFM S FG CM ==，∴ CM =2. 由C (3，0)知，1M (5,0)，2M (1,0)， ·······················································7分设FM 的解析式为y =kx +b ,由1M (5,0)，F (2，3)得，F 1M 的解析式为y =-x +5，则F 1M 与抛物线的交点H 满足： 25,24 2.33y x y x x =-+⎧⎪⎨=-++⎪⎩整理得，22790x x -+=， ∵ △<0，∴ 不符合题意，舍去. ······················· 8分由2M (1,0)，F (2，3)得，F 2M 的解析式为y =3x -3，则F 2M 与抛物线的交点H 满足：233,24 2.33y x y x x =-⎧⎪⎨=-++⎪⎩整理得，225150x x +-=， ∴ 51454x -±=. ··············································································9分即：H点的横坐标为51454-±.。

湖南省株洲市初中毕业学业考试数学试题(含答案)

株洲市初中毕业学为考试数学试题卷一、选择题(每小题只有一个正确答案，本题共10小题，共30分) 1、下列数中，-3的倒数是(A)A 、13-B 、13C 、－3D 、3 2、下列等式错误的是(D) A 、222(2)4mn m n =B 、222(2)4mn m n -=C 、22366(2)8m n m n =D 、22355(2)8m n m n -=-3、甲、乙、丙、丁四名射击队员考核赛的平均成绩（环）及方差统计如下表，现要根据这些数据，从中选出一人参加比赛，如果你是教练员，你的选择是C A 、甲 B 、乙 C 、丙 D 、丁4、如图，在三角形ABC中，∠ACB ＝90°，，∠B ＝50°，将此三角形绕点C 沿顺时针方向旋转后得到三角形``A B C ，若点`B 恰好落在线段AB 上，AC 、``A B 交于点O ，则∠CO `A 的度数是(B)A 、50°B 、60°C 、70°D 、80°第4小题图C'B第3小题5、不等式21120x x -≥⎧⎨-<⎩的解集在数轴上表示为CAB 、C 、D 6在解方程13132x x x -++=时，方程两边同时乘以6，去分母后，正确的是B A 、2163(31)x x x -+=+ B 、2(1)63(31)x x x-+=+ C 、2(1)3(31)x x x -+=+D 、(1)3(1)x x x -+=+7、已知四边形ABCD 是平行四边形，对角线AC 、BD 交于点O ，E 是BC的中点，以下说法错误的是DA 、OE ＝12DC B 、OA=OCC 、∠BOE ＝∠OBAD 、∠OBE ＝∠OCE8、如图，以直角三角形a 、b 、c 为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四各情况的面积关系满足123S S S +=B 、2D 、4有两种理解方式：一、利用面积的计算方法来算出来第一个图：222123,,444S a S b S === 其他的依此类推二、利用相似，依题意所作出的三个图形都是相似形，故：222123::::S S S a b c =从而得出结论第7题图B9、已知，如图一次函数1y ax b =+与反比例函数2ky x=的图象如图示，当12y y <时，x 的取值范围是DA 、2x <B 、5x >C 、25x <<D 、02x <<或5x >【解析】由图直接读出答案为D10、已知二次函数2(0)y ax bx c a =++>2，5）顶点坐标为(,)m n ，则下说法错误的是(B)A 、3c <B 、12m ≤ C 、2n ≤ D 、1b <【解析】由已知可知：2425a b c a b c -+=⎧⎨++=⎩消去b 得：323ca =-<消去c 得：11b a =-<对称轴：111122222b a x a a a -=-=-=-< 故B 错。

株洲中考数学试题及解答分析

绝密★启用前数学试题及解答时量：120分钟满分：100分注意事项:1、答题前，请按要求在答题卡上填写自己的姓名和准考证号.2、答题时，切记答案要填写在答题卡上，答在试题卷上的答案无效。

3、考试结束后，请将试题卷和答题卡都交给监考老师。

选择题：答案为A D D B C C B C一、选择题（每小题有且只有一个正确答案,本题共8小题，每小题3分，共24分）1、下列各数中，绝对值最大的数是A、－3B、－2C、0D、12、取下列各数中的哪个数时，二次根式有意义A、－2B、0C、2D、4解：本题变相考二次根式有意义的条件3、下列说法错误的是A、必然事件的概率为1B、数据1、2、2、3的平均数是2C、数据5、2、－3、0的极差是8D、如果某种游戏活动的中奖率为40%,那么参加这种活动10次必有4次中奖4、已知反比例函数的图象经过点(2,3)，那么下列四个点中，也在这个函数图象上的是A、(－6,1)B、（1，6）C、（2，－3)D、（3，－2）解：本题主要考查反比例函数三种表达中的5、下列几何何中,有一个几何体的主视图与俯视图形状不一样，这个几何体是6、一元一次不等式组的解集中，整数解的个数是A、4B、5C、6D、7解：分析本题主要考查学生解一元一次不等式的能力及找特解的能力.7、已知四边形ABCD是平行四边形，再从①AB＝BC，②∠ABC＝90°,③AC＝BD，④AC ⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是A、选①②B、选②③C、选①③D、选②④解：分析本题主要考查学生由平行四边形判定要正方形的判定方法答案：选B8、在平面直角坐标系中，孔明做走棋游戏，其走法是：棋子从原点和，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步走1个单位……依此类推，第步的是：当能被3整除时，则向上走1个单位;当被3除,余数是1时，则向右走1个单位，当被3除，余数为2时，则向右走2个单位，当他走完第100步时，棋子所处位置的坐标是: A、（66，34）B、（67,33）C、(100，33)D、（99,34)解:本题主要考查学生对信息的分类在1至100这100个数中:（1）能被3整除的为33个，故向上走了33个单位（2)被3除,余数为1的数有34个,故向右走了34个单位（3）被3除，余数为2的数有33个，故向右走了66个单位故总共向右走了34＋66＝100个单位，向上走了33个单位。

2011年株洲市初中毕业会考数学.doc

2011年株洲市初中毕业会考数学模拟一、选择题（本大题满分24分，每小题3分） 1. 在0，-3，1，41这四个数中，最小的数是（） A. 0 B. -3 C. 1 D.41 2. 数据0.00000026用科学记数法表示为2.6×10n，则n 的值是（）A. -7B. -6C. 6D. 7 3. 若点P （a -2，3+-a ）是第二象限的点，则a 必须满足（）A 、a ＜3B 、a ＞2C 、a ＜2D 、2＜a ＜34. 某班抽取5名同学参加体能测试，成绩如下:80，90，75，75，80.下列表述错误．．的是（）Ａ．众数是80 Ｂ．中位数是75 Ｃ．平均数是80 Ｄ．极差是15 5. 如果点11()A x y ，和点22()B x y ，是直线y kx b =-上的两点，且当12x x <时，12y y <，那么函数ky=的图象大致是（）6、设x1，x 2是方程2x 2－6x ＋3＝0的两根，则x12＋x 22的值是（） A 、15 B 、12 C 、6 D 、37.方程01122=--+x x x 的解是（） A. x =-1 B. x =2 C. x =-1或x =2 D. 无解8. 如图，P 为⊙O 外一点，PA 切⊙O 于点A ，且OP=5，PA=4，则sin ∠APO 等于（）A 、54B 、53C 、34D 、43二、填空题（本大题满分24分，每小题3分） 9.计算：)52)(52(+-x x = .10.方程0322=--x x 的解是 . （第8题）11.反比例函数ky x =的图象经过点(-3,1)，则k 的值为 .12. 将抛物线22y x =-向上平移1个单位后，再向左平移2个单位，得一新的抛物线，那么新的抛物线的表达式是．13.学校篮球队五名队员的年龄分别为17、15、17、16、15（单位：岁），其方差为0.8，则一年前，这五名队员年龄的方差是．POA · xxxxD ．14. 如图，在Rt △ABC 中，∠C=90︒，AB=5cm ，D 为AB 的中点，则CD= cm .（第14题）（第15题）15. 如图8, AB 是⊙O 的直径，点C 在⊙O 上，∠BAC =30°，点P 在线段OB 上运动.设∠ACP =x ，则x 的取值范围是 .16.观察下列各式：1×3+1=4=22；2×4+1=9=32；3×5+1=16=42；4×6+1=25=52；……，请写出第n 个式子 . 三、解答题（本大题满分52分）17. （本题41012sin 45(2)3-⎛⎫+-π- ⎪⎝⎭18.（本题4分）先化简，后求值：()2111211x x x ⎛⎫+÷-- ⎪--⎝⎭，其中x =19. （本题6分）某商店用3000元购进一批学习用品，后发现供不应求，商店又购进第二批同样的学习用品，数量是第一批购进数量的3倍，单价贵了4元，结果第二批用了9720元。

完整word版,2011年湖南普通高中学业水平考试数学试卷真题+答案[1]

湖南普通高中学业水平考试数学试卷时量120分钟满分100分班次：________学号：______ 姓名：___________得分：_________一、选择题：(本大题共10小题，每小题4分，满分40分)1．已知集合{1,2,3,4,5}=A ，{2,5,7,9}=B ，则A B 等于（） A ．{1,2,3,4,5} B ．{2,5,7,9}C ．{2,5}D ．{1,2,3,4,5,7,9}2．若函数()3=+f x x ，则(6)f 等于（）A ．3B ．6C ．9D ．63．直线1:2100--=l x y 与直线2:3440+-=l x y 的交点坐标为（）A ．(4,2)-B ．(4,2)-C ．(2,4)-D ．(2,4)-4．两个球的体积之比为8：27，那么这两个球的表面积之比为（） A ．2:3B ．4:9C ．2:3D ．22:335．已知函数()sin cos =f x x x ，则()f x 是（） A ．奇函数B ．偶函数C ．非奇非偶函数D ．既是奇函数又是偶函数6．向量(1,2)=-a ，(2,1)=b ，则（） A ．//a bB ．⊥a bC ．a 与b 的夹角为60D ．a 与b 的夹角为307．等差数列{}n a 中，7916+=a a ，41=a ，则12a 的值是（） A ．15B ．30C ．31D ．648．阅读右边的流程图，若输入的a ，b ，c 分别是6，2，5。

则输出的a ，b ，c 分别是（） A ．6，5，2 B ．5，2，6C ．2，5，6D ．6，2，59．已知函数2()2=-+f x x x b 在区间（2，4）内有唯一零点，则b 的取值范围是（） A ．R B ．(,0)-∞ C ．(8,)-+∞D ．(8,0)-10．在ABC ∆中，已知120=A ，1=b ，2=c ，则a 等于（） A ．3B ．523+C ．7D ．523-二、填空题：(本大题共5小题，每小题4分，满分20分．)11．某校有高级教师20人，中级教师30人，其他教师若干人，为了了解该校教师的工资收入情况，拟按分层抽样的方法从该校所有的教师中抽取20人进行调查.已知从其他教师中共抽取了10人，则该校共有教师人．12．3log 4(3)的值是．13．已知0m >，0n >，且4m n +=，则mn 的最大值是． 14．若幂函数()y f x =的图像经过点1(9,)3，则(25)f = ．15．已知()f x 是定义在[)(]2,00,2-上的奇函数，当0x >时，()f x 的图像如图所示，那么()f x 的值域是．一、选择题: 本大题共10小题，每小题4分，满分40分题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题: 本大题共5小题，每小题4分，满分20分．9、； 10、； 11、； 12、； 13、； 14、；15、三、解答题：本大题共5小题，满分40分． 16．（本小题满分6分）一个均匀的正方体玩具，各个面上分别写有1，2，3，4，5，6，将这个玩具先后抛掷2次，求：（1）朝上的一面数相等的概率；（2）朝上的一面数之和小于5的概率．23y 2xO17．（本小题满分8分）如图，圆心C 的坐标为（1，1），圆C 与x 轴和y 轴都相切. （1）求圆C 的方程；（2）求与圆C 相切，且在x 轴和y 轴上的截距相等的直线方程．18．（本小题满分8分）如图，在三棱锥P ABC -，PC ⊥底面ABC ，AB BC ⊥，D 、E 分别是AB 、PB 的中点．（1）求证：//DE 平面PAC ；（2）求证：AB PB ⊥．11 0 x y19．（本小题满分8分）已知数列{}n a 的前n 项和为2n S n n =+．（1）求数列{}n a 的通项公式；（2）若()12na nb =，求数列{}n b 的前n 项和为n T ．20．（本小题满分10分）设函数()f x a b =⋅，其中向量(cos 21,1)a x =+，(1,3sin 2)b x m =+．（1）求()f x 的最小正周期；（2）当0,6x π⎡⎤∈⎢⎥⎣⎦时，4()4f x -<<恒成立，求实数m 的取值范围．湖南普通高中学业水平考试数学答卷一．选择题：1, C 2,A 3,B 4,B 5,A 6,B 7,A 8,C 9,C 10，C 二．填空题11, 100 12, 2 13, 4 14,)2.0(51或 15，]3,2()2,3[⋃--三．解答题： 16．（本小题满分6分）一个均匀的正方体玩具，各个面上分别写有1，2，3，4，5，6，将这个玩具先后抛掷2次，求：（1）朝上的一面数相等的概率；（2）朝上的一面数之和小于5的概率．解：由题意可把所有可能性列表如下： 1 2 3 4 5 6 1 （1,1）（1,2）（1,3）（1,4）（1,5）（1,6） 2 （2,1）（2,2）（2,3）（2,4）（2,5）（2,6） 3 （3,1）（3,2）（3,3）（3,4）（3,5）（3,6） 4 （4,1）（4,2）（4,3）（4,4）（4,5）（4,6） 5 （5,1）（5,2）（5,3）（5,4）（5,5）（5,6） 6 （6,1）（6,2）（6,3）（6,4）（6,5）（6,6）（1）朝上一面数相等的次数出现6种，故发生的概率为61666=⨯；（2）朝上朝上的一面数之和小于5的的情况共有6种，故发生的概率为61666=⨯。

株洲中考数学试题及解答分析

绝密★启用前数学试题及解答时量：120分钟满分：100分注意事项:1、答题前，请按要求在答题卡上填写自己的姓名和准考证号。

2、答题时,切记答案要填写在答题卡上，答在试题卷上的答案无效。

3、考试结束后，请将试题卷和答题卡都交给监考老师。

选择题：答案为A D D B C C B C一、选择题(每小题有且只有一个正确答案，本题共8小题，每小题3分，共24分）1、下列各数中，绝对值最大的数是A、－3B、－2C、0D、12、取下列各数中的哪个数时，二次根式有意义A、－2B、0C、2D、4解：本题变相考二次根式有意义的条件3、下列说法错误的是A、必然事件的概率为1B、数据1、2、2、3的平均数是2C、数据5、2、－3、0的极差是8D、如果某种游戏活动的中奖率为40％，那么参加这种活动10次必有4次中奖4、已知反比例函数的图象经过点（2，3)，那么下列四个点中，也在这个函数图象上的是A、（－6，1）B、（1,6）C、(2，－3）D、(3，－2）解：本题主要考查反比例函数三种表达中的5、下列几何何中，有一个几何体的主视图与俯视图形状不一样，这个几何体是6、一元一次不等式组的解集中，整数解的个数是A、4B、5C、6D、7解：分析本题主要考查学生解一元一次不等式的能力及找特解的能力。

7、已知四边形ABCD是平行四边形，再从①AB＝BC，②∠ABC＝90°，③AC＝BD，④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形，现有下列四种选法，其中错误的是A、选①②B、选②③C、选①③D、选②④解：分析本题主要考查学生由平行四边形判定要正方形的判定方法答案:选B8、在平面直角坐标系中，孔明做走棋游戏，其走法是：棋子从原点和，第1步向右走1个单位,第2步向右走2个单位，第3步向上走1个单位，第4步走1个单位……依此类推，第步的是：当能被3整除时,则向上走1个单位；当被3除，余数是1时，则向右走1个单位，当被3除，余数为2时，则向右走2个单位，当他走完第100步时，棋子所处位置的坐标是:A、(66,34)B、（67，33）C、（100，33)D、（99，34）解：本题主要考查学生对信息的分类在1至100这100个数中：（1）能被3整除的为33个，故向上走了33个单位（2)被3除，余数为1的数有34个,故向右走了34个单位（3)被3除,余数为2的数有33个，故向右走了66个单位故总共向右走了34＋66＝100个单位，向上走了33个单位。

株洲中考数学试题及解答分析

绝密★启用前数学试题及解答时量：120分钟满分:100分注意事项：1、答题前，请按要求在答题卡上填写自己的姓名和准考证号。

2、答题时，切记答案要填写在答题卡上，答在试题卷上的答案无效.3、考试结束后,请将试题卷和答题卡都交给监考老师。

选择题:答案为A D D B C C B C一、选择题(每小题有且只有一个正确答案，本题共8小题，每小题3分,共24分）1、下列各数中，绝对值最大的数是A、－3B、－2C、0D、12、取下列各数中的哪个数时，二次根式有意义A、－2B、0C、2D、4解：本题变相考二次根式有意义的条件3、下列说法错误的是A、必然事件的概率为1B、数据1、2、2、3的平均数是2C、数据5、2、－3、0的极差是8D、如果某种游戏活动的中奖率为40%,那么参加这种活动10次必有4次中奖4、已知反比例函数的图象经过点（2,3），那么下列四个点中，也在这个函数图象上的是A、（－6,1）B、(1,6）C、（2，－3)D、（3,－2）解：本题主要考查反比例函数三种表达中的5、下列几何何中，有一个几何体的主视图与俯视图形状不一样,这个几何体是6、一元一次不等式组的解集中，整数解的个数是A、4B、5C、6D、7解:分析本题主要考查学生解一元一次不等式的能力及找特解的能力。

7、已知四边形ABCD是平行四边形，再从①AB＝BC，②∠ABC＝90°,③AC＝BD，④AC ⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是A、选①②B、选②③C、选①③D、选②④解：分析本题主要考查学生由平行四边形判定要正方形的判定方法答案：选B8、在平面直角坐标系中，孔明做走棋游戏，其走法是：棋子从原点和，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位,第4步走1个单位……依此类推,第步的是：当能被3整除时，则向上走1个单位；当被3除，余数是1时，则向右走1个单位，当被3除，余数为2时，则向右走2个单位，当他走完第100步时,棋子所处位置的坐标是：A、（66,34）B、（67,33）C、(100,33）D、（99,34）解:本题主要考查学生对信息的分类在1至100这100个数中:（1）能被3整除的为33个，故向上走了33个单位（2）被3除，余数为1的数有34个，故向右走了34个单位（3）被3除，余数为2的数有33个，故向右走了66个单位故总共向右走了34＋66＝100个单位，向上走了33个单位。

株洲市中考数学试题及答案

姓名准考证号绝密★启用前株洲市2012年初中毕业学业考试数学试题卷时量：120分钟满分：100分注意事项：1．答题前，请按要求在答题卡上填写好自己的姓名和准考证号。

2．答题时，切记答案要填在答题卡上，答在试题卷上的答案无效。

3．考试结束后，请将试题卷和答题卡都交给监考老师。

一、选择题（每小题有且只有一个正确答案，本题共8小题，每小题3分，共24分）1．9-的相反数是A．9 B．-9 C．19D．19-2．在体育达标测试中，某校初三5班第一小组六名同学一分钟跳绳成绩如下：93，138，98，152，138，183；则这组数据的极差是A．138 B．183 C．90 D．933．下列图形中，既是轴对称图形又是中心对称图形的是A B C D4．如图，已知直线a∥b,直线c与a、b分别交于A、B；且1120,∠=o则2∠= A．60o B．120oC．30o D．150o5．要使二次根式24x-有意义，那么x的取值范围是A．2x>B．2x<C.2x≥D．2x≤6．如图，已知抛物线与x轴的一个交点A（1，0），对称轴是1x=-，则该抛物线与x 轴的另一交点坐标是A．(3,0)-B．(2,0)-C．3x=-D．2x=-7．已知关于x的一元二次方程20x bx c-+=的两根分别为121,2x x==-，则b与c 的值分别为 A ．1,2b c =-= B ．1,2==-b cC ．1,2==b cD ．1,2b c =-=-8．如图，直线(0)x t t =>与反比例函数21,y y x x -==的图象分别交于B 、C 两点，A 为y 轴上的任意一点，则∆ABC 的面积为A ．3B ．32t C ．32 D ．不能确定二、填空题（本题共8小题，每小题3分，共24分）9．因式分解：22a a -= .10．已知：如图，在⊙O 中，C 在圆周上，∠ACB=45°,则∠AOB= .11．依法纳税是中华人民共和国公民应尽的义务。